基于LQR的一级倒立摆仿真研究

直线一级倒立摆的PID和LQR控制及其仿真

KEY WORDS： Linear inverted pendulum, Control, PID, LQR, simulation
BY NB GONG
II
华北电力大学毕业设计（论文）
目
录
摘要 ........................................................................................................................................... I ABSTRACT ..................................................................................................................................... II 第 1 章：绪论 .................................................................................................................................. 1 1.1 倒立摆简介......................................................................................................................... 1 1.1.1 倒立摆分类.............................................................................................................. 2 1.1.2 倒立摆的特性......................................................................................................... 2 1.1.3 倒立摆的控制目标................................................................................................. 3 1.1.4 倒立摆的控制方式................................................................................................. 3 1.2 倒立摆控制研究的发展及其现状.................................................................................... 4 1.3 本文的主要内容................................................................................................................ 7 第 2 章：直线一级倒立摆系统数学模型....................................................................................... 8 2.1 直线一级倒立摆系统的物理模型.................................................................................... 8 2.2 直线一级倒立摆系统的数学模型.................................................................................... 9 2.3 直线一级倒立摆系统的系统分析.................................................................................. 12 2.3.1 直线一级倒立摆系统的系统稳定性分析 ........................................................... 12 2.3.2 直线一级倒立摆系统的系统能控性、能观性分析 ........................................... 14 第 3 章：直线一级倒立摆系统的 PID 控制及仿真..................................................................... 16 3.1 PID 控制概述 .................................................................................................................... 16 3.2 PID 的控制规律、原理 .................................................................................................... 17 3.3 PID 参数整定 .................................................................................................................... 17 3.4 直线一级倒立摆双闭环 PID 控制算法 ........................................................................... 18 第 4 章：直线一级倒立摆系统的线性二次最优控制及仿真..................................................... 24 4.1 线性二次最优控制简介.................................................................................................. 24 4.2 直线一级倒立摆 LQR 控制算法及仿真 ......................................................................... 26 结论 ........................................................................................................................................ 35 参考文献 .......................................................... 36 致谢 ........................................................................................................................................ 38

直线一级摆LQR控制设计与仿真

内蒙古科技大学控制系统仿真课程设计题目：直线一级摆LQR控制设计与仿真学生姓名：薛敏杰学号：0967112205专业：测控技术与仪器班级：2009-2指导教师：张勇摘要倒立摆是一个典型的快速、多变量、非线性、强耦合的自然不稳定系统,是自动控制理论中的典型试验设备,也是教学和科研中不可多得的典型物理模型[1]。

通过对倒立摆系统的研究,不仅可以解决控制中的理论问题,还能将控制理论所涉及的力学、数学和电学等多个基础学科有机地结合起来,其控制方法和思路对处理一般工业过程具有广泛的用途。

因此对倒立摆系统的研究具有重要的理论和应用价值,相关的科研成果已经应用到航天科技和机器人学等诸多领域。

1系统概述一级倒立摆系统由沿着光滑导轨自由运动的小车以及通过转轴与小车连接的摆杆组成。

在轨道一端安装位移传感器,用来测量小车的位移。

在连接处安装角度传感器,用来测量摆杆与竖直方向的角度,电机通过传送带控制小车沿导轨滑动,使倒立摆稳定在竖直位置。

控制目的是:小车和摆组成的系统在受到干扰后,小车处于轨道的中心位置,摆杆保持垂直位置。

倒立摆主要有两个方面的用途。

第一，作为一个非线性自然不稳定系统，倒立摆系统是进行控制理论教学及开展各种控制实验的理想实验平台。

对倒立摆系统的研究能有效直观地反映控制中的许多典型问题:如非线性问题、鲁棒性问题、镇定问题、随动问题以及跟踪问题等。

第二，由于倒立摆系统具有高阶次、不稳定、多变量、非线性和强耦合等特性，其作为控制理论研究中的一个严格的控制对象，通过对倒立摆的控制，用来检验新的控制方法是否有较强的处理非线性和不稳定性问题的能力。

对倒立摆的控制涉及到控制科学中处理非线性、高阶次、强耦合对象的关键技术，许多现代控制理论的研究人员一直将它视为研究对象。

因而倒立摆被誉为“控制领域中的一颗明珠”。

通过对倒立摆的研究不仅可以解决控制中的理论问题，还能将控制理论涉及的三个主要基础学科—力学、数学和电学进行有机合应用。

基于MATLAB的单级倒立摆的LQR控制研究_马扬龙

大，那么这种线性二次型问题称为稳态问题［1］。直线一级倒立摆系统的控制问题就可以理解为稳态时连续系统的状态调节器问题。那么该系统的状态方程为（1 ）式，系统的性能指标是：
J＝ 1 2
控制系统结构如图 2 ，图中 R 是施加在小车上的阶跃输入。设计控制器使得当给系统施加一个阶跃输入时，摆杆会摆动，然后仍然回到垂直位置，小车可以到达新的指定位置。假设全状态反馈可以实现（四个状态量都可测），R＝1 ，Q＝
98
基于 MATLAB 的单级倒立摆的 LQR 控制研究
基于 MATLAB 的单级倒立摆的 LQR 控制研究
Study of LQR Control Single Inverted Pendulum Based on MATLAB
马扬龙陈琼宁玉玲（南昌航空大学信息工程学院，江西南昌 330063）
表1 实际系统参数表
－1
T
量，F 为加在小车上的力，x 为小车位置，φ 为摆杆与垂直向上方向的夹角，θ 为摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下），因此系统状态空间方程为：
0 1 0 0 觶觶 x m gl 觶觶0 －（I＋ml ）b ¨ 0 x 觶 I （M＋m ）＋Mml I （M＋m ）＋Mml ＝觶觶觶觶觶 0 0 0 0 觶 0 －mlb mgl （M＋m ） ¨ 觶0 觶觶 I（M＋m ）＋Mml I（M＋m ）＋Mml 0 x 0 觶 x ＝ 1 0 0 0 x 0 y＝觶觶＋ 0觶 u 觶觶 0 0 0 1 0 觶 0 觶 0
图3
系统阶跃响应（Q＝diag （1 ，0 ，1 ，0 ））

基于LQR控制的一级倒立摆MATLAB仿真研究

基于LQR控制的一级倒立摆MATLAB仿真研究龙源期刊网 /doc/cb13039548.html,基于LQR控制的一级倒立摆MATLAB仿真研究作者：潘俊朋桑运晓吕国娜任保飞刘树骏来源：《科学与财富》2017年第25期摘要：：本文首先通过分析单级倒立摆系统建立相应的状态空间数学模型，然后对倒立摆系统进行LQR 控制器设计，最后使用Matlab 进行仿真，结果表明在本文加权矩阵Q、R 的取值下，LQR 控制器可使系统达到有效的控制，小车位置跟着摆杆的角度动作，系统具有较短的调整时间、较小的超调量和较好的动静态性能。

关键词：倒立摆 Matlab LQR 控制一、前言单级倒立摆系统是一种不稳定、多变量且具有强耦合的非线性系统。

如果把它当做一个单输出系统来处理将无法到达控制要求，所以对于这样的多输出系统，我们需要用到状态空间数学模型来对其进行分析。

二、建立系统的状态空间数学模型为了方便而又不失精确的对单级倒立摆系统建立数学模型，实际中忽略一些次要的因素后的一级倒立摆系统简图如图1所示，系统受力分析如图2所示。

定义各参数：作用在小车的外力用F表示；摆杆与垂直向上方向的夹角用φ表示；摆杆与垂直向下方向的夹角用θ表示；采样时间为T=0.005s；摆杆的质量为m=0.2kg；摆杆的惯量为I=0.006kg*m*m；摆杆转动轴心到摆杆质心的距离为l=0.3m；小车的摩擦系数为b=0.1N/m/sec；小车的质量为M=0.5kg；小车的位置用x表示。

应用Newton方法来建立系统的动力学方程并经过整理后得到系统状态空间方程：三、LQR控制器设计及其Matlab仿真为了同时对小车的位置和摆杆的角度都进行有效控制，我们使用线性二次性最优控制算法（LQR）。

这种控制算法在现代控制理论中占有举足轻重的地位，通过多年的研究，使最优控制算法得到越来越广泛的工程应用。

LQR控制系统框图如图3所示。

其中R是作用于小车的阶跃信号，四个状态量和分别代表小车的位移和速度、摆杆的位置和角速度。

直线倒立摆系统的LQR控制器设计及仿真设计

直线倒立摆系统的LQR控制器设计及仿真摘要倒立摆系统是非线形、强耦合、多变量和自然不稳定的系统。

在控制过程中能反映控制理论中的许多关键问题，如镇定问题、非线性问题、鲁棒性问题以及跟踪问题等。

不仅是验证现代控制理论方法的典型实验装置，而且其控制方法和思路对处理一般工业过程亦有广泛的用途，因此对倒立摆系统的研究具有重要的理论研究和实际应用价值。

本文以固高公司直线倒立摆为研究对象，利用Newton法建立直线一级倒立摆的动力学模型。

先对系统状态方程进行能控性和能观性分析，之后借助固高科技Matlab实时控制软件实验平台，设计LQR控制器，并利用LQR控制方法对直线一级倒立摆系统进行了Simulink在线实时仿真实验，并对实验结果分析，调节LQR参数，使之达到最佳稳定调节状态，通过在线对系统施加一定的扰动，系统均能在很短的时间里恢复平衡，取得了较好的实时控制效果。

关键词：直线倒立摆；建模；稳定性；LQR；仿真ABSTRACTInverted pendulum system is non-linear, strongly coupled, multivariable and naturally instable. In the control process this system can reflect some key problems of control theory, such as stabilization problem, nonlinear problems, robustness, and tracking problem. It’s a typically experimental facility which can verify the methods of modern control theory, moreover the control methods and thoughts play an important role in dealing with the general industrial process. So the studies of inverted pendulum system are theoretically and practically valued. Googol company linear inverted pendulum, Newton's method to create a straight line an inverted pendulum dynamic model using the Lagrange equation deduced straight line double inverted pendulum mathematical model of analytical mechanics methods. This thesis adopts Googol company linear inverted pendulum as the study object,. First controllability and observability analysis of system state equation should be analyzed, afterwards, with the Googol high-tech Matlab real-time control software experimental platform, LQR controller can be designed and LQR control method can conduct online real-time simulation experiment on straight line, double inverted pendulum Simulink, analyze results of experiment and adjust LQR parameters so as to achieve the best stability and regulation state. Some certain disturbance online imposed on the system enables it to restore the balance in a very short time, and achievevery good real-time control effects.Keywords：linear inverted pendulum; modeling；stability；LQR；Simulation目录第一章绪论 (1)1.1 倒立摆系统概述 (1)1.2 倒立摆系统发展及研究现状 (6)1.3 本文的主要研究内容与章节安排 (10)第二章直线倒立摆系统数学模型建立 (12)2.1 直线一级倒立摆系统数学模型 (12)2.2 直线一级倒立摆系统能控性与能观性分析 (19)2.3 本章小结 (227)第三章直线倒立摆系统LQR控制器设计与仿真 (238)3.1 线性二次最优控制LQR基本原理及分析 (238)3.2 直线一级倒立摆系统LQR控制器设计与仿真 (249)3.3 本章小结 (29)第四章直线倒立摆的实物稳定控制 (31)4.1 直线一级倒立摆LQR实物稳定控制 (31)4.2 本章小结 (379)结论与展望 (380)附录 (391)参考文献 (342)致谢 (345)第一章绪论1.1 倒立摆系统概述倒立摆控制系统是一个复杂的、高阶次、多变量、不稳定的、非线性并强耦合系统。

基于最优控制LQR的单级倒立摆系统仿真研究_么洪飞

− P(t ) A − AT P(t ) + P(t ) BR −1 B T P(t ) − Q = 0
对于最优反馈系数矩阵 K = R −1 B T P(t ) 。 Matlab 仿真软件控制系统工具箱中提供了解决线性二次型最优控制问题的函数，可使用 lqr ( A, B, Q, R) 命令来求取 K 。由于输入变量 u 为一维向量，所以 R 为 1 × 1 维矩阵，可取 R = 1 ；这里关键是选择加权矩阵
(t ) = − θ 6 6 g (m + M ) θ (t ) F (t ) + l (m + 4M ) l (m + 4M )
= Ax + Bu ，x，x )T ，u = F (t ) ，则系统状态空间表达式为 x 即系统的状态变量为 X = (θ，θ ，代入仿真数据 y = Cx
第 27 卷第 4 期 2011 年 7 月
齐齐哈尔大学学报 Journal of Qiqihar University
Vol.27,No.4 July,2011
基于最优控制 LQR 的单级倒立摆系统仿真研究
么洪飞，陆仲达，徐凤霞
（齐齐哈尔大学计算机与控制工程学院，黑龙江齐齐哈尔 161006）摘要：单级倒立摆控制是一个即复杂而又对准确性、快速性要求很高的非线性不稳定系统控制问题。在倒立摆系统数学模型的基础上，对系统进行了性能分析。应用现代控制理论最优控制LQR方法对单级倒立摆系统进行仿真控制研究，仿真结果说明反馈控制理论对倒立摆系统的控制是有效的，无论是系统的输出还是各个状态变量都具有较好稳定性和一定的鲁棒性。关键词：单级倒立摆；LQR；系统建模与仿真中图分类号：TP273 文献标识码：A 文章编号：1007-984X(2011)04-0034-04

基于卡尔曼滤波的一级倒立摆LQR控制研究

0/ 一级倒立摆系统的数学模型
在忽略了空气阻力和各种摩擦之后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如图 ! 所示。假设直线一级倒立摆各项参数的符号、意义与数据如表 ! 所示，分析小车水平方向、摆杆垂直方向上所受的合力，建立力和力矩的平衡方程。
万方数据验师 $
0<
实2 验2 技2 术2 与2 管2 理
3 # 。用 ) 来表示被控对象的输入力 & ，线性化后两个运） ! + ",$! - "$’ ; . * #’ / + "$! . - ) （ ! * "） ’
. :
:
（.）
3 6!
在经过一定步骤的运算后，增益矩阵和滤波误差方差阵均收敛。所以对系统的滤波误差方差阵初始值 A # B # 确定，初始可取为较大值的对角阵，经过仿真选取收敛矩阵为 A # B # ，再次仿真选取收敛矩阵为 A # B # ，并对比增益矩阵的变化，直至 A # B # 阵的选择对增益矩阵收敛已无影响，即选择该阵为 A# B # 。由滤波误差方差阵上界定理：如果离散系统如式（ / ）所示，是一致完全可控和一致完全可观测的，即存在 ’! C # ， ’. C # ， (! C # ， (. C # 和正整数 B，假定 A# B # &# ，使得对所有 @ &B，有 A 3? 3 * ! * C. ( ! ( . % ; ’! （ !! ）
. ，! 解代数方程，代入实际数据，可得到 2 2 对’ 系统的状态方程为 / !0 ### # ’ # . ’ # + #0 #<<0 #0 %.$0 ・ - # # # ! # + #0 .0/= .=0 <.</ : ! # ’ / # ’ * ! ! ・ # ! # #0 <<0. ) ， # .0 0/%% （0） ’ # / # ’ ! # # # ’ 1 * ) ; （1） # # ! # ! # ! ・ ! # 2 2 直线一级倒立摆是一个单输入二输出的 1 阶系

直线倒立摆系统的LQR控制器设计及仿真_毕业设计精品

直线倒立摆系统的LQR控制器设计及仿真_毕业设计精品1.引言直线倒立摆系统主要由一个质量块和一个固定的轨道组成，质量块可以在轨道上自由运动。

该系统的目标是在面对各种扰动时保持质量块的平衡。

LQR控制器是一种优化控制方法，可以通过调整控制器的参数来实现系统动态响应的优化。

2.直线倒立摆系统建模m*x''+b*v+m*g=f-u在LQR控制器设计过程中，需要将系统的动力学方程转化为状态空间模型。

定义状态变量为x1=x，x2=x'，那么系统的状态空间模型可以表示为：x1'=x2x2'=(1/m)*(f-u-b*x2-m*g)3.LQR控制器设计LQR控制器设计的目标是通过调整控制器的参数来最小化系统的性能指标J。

在直线倒立摆系统中，我们可以选择以能耗作为性能指标，即J = ∫(u(t)^2)dt。

那么LQR控制器设计的目标是最小化能耗。

LQR控制器设计方法的关键是设计系统的状态反馈增益矩阵K。

具体的设计步骤如下：1)将系统的状态空间模型表示为矩阵形式：x'=Ax+Buy=Cx+Du其中，A为状态转移矩阵，B为输入矩阵，C是输出矩阵，D为直接递增矩阵。

2) 根据系统的状态空间模型计算系统的LQR控制器增益矩阵K。

增益矩阵K可以通过解代数矩阵Riccati方程得到：K=(R+B'*S*B)^(-1)*B'*S*A其中，S为Riccati方程的解。

3) 计算系统的控制器增益矩阵L。

增益矩阵L可以通过解代数矩阵Riccati方程得到：L=(R+B'*S*B)^(-1)*B'*S*C4.LQR控制器仿真在设计完成LQR控制器之后，可以进行仿真实验来验证控制器的效果。

可以使用MATLAB或Simulink来进行仿真。

在仿真实验中，需要设置各个参数的初始值，并且加入一些扰动以测试控制器的稳定性。

通过观察系统的状态变量和控制力的响应曲线，可以评估控制器的性能。

一级直线倒立摆的控制策略与仿真分析

一级直线倒立摆的控制策略与仿真分析一、引言倒立摆系统是研究控制理论的一种典型的实验装置，具有成本低廉，结构简单，参数和结构易于调整的优点。

然而倒立摆系统具有高阶次、不稳定、多变量、非线性和强耦合特性，是一个绝对不稳定系统。

倒立摆实物仿真实验是控制领域中用来检验某种控制理论或方法的典型方案，它对一类不稳定系统的控制以及对深入理解反馈控制理论具有重要意义。

倒立摆系统在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义，相关的科研成果已经应用到航天科技和机器人学等诸多领域。

二、一级直线倒立摆模型的建立图1 一级直线倒立摆物理模型图2 小车和摆杆的受力分析图2.1 传递函数模型图1、2是系统中小车和摆杆的受力分析图。

设小车质量为M，摆杆质量为m，小车摩擦系数为b，摆杆转动轴心到杆质心的长度为l，摆杆的转动惯量为I，根据牛顿第二定律，可以得到系统的两个运动方程：F ml ml x b x m M =-+++∙∙∙∙∙∙θθθθsin cos )(2（1）θθθcos sin )(2∙∙∙∙-=++x m l m gl m l I （2）设φπθ+=, 假设φ与1（单位是弧度）相比很小，即c <<1，则可以进行近似处理：1cos -=θ,φθ-=sin ，0)(2=dtd θ。

用u 来代表被控对象的输入力F ，线性化后两个运动方程如下：2()()I ml mgl ml x M m x b x ml uϕϕϕ∙∙∙∙∙∙∙∙∙+-=++-= （3）假设初始条件为0，对式(3)进行拉普拉斯变换得到：22222()()()()()()()()()I ml s s mgl s mlX s s M m X s s bX s s ml s s U s +Φ-Φ=++-Φ=（4）由于输出为角度φ，求解方程组的第一个方程，可以得到：mgl s ml I mls s X s -+=Φ222)()()(（5）令∙∙=x v ，则有：mgls ml I mls V s -+=Φ22)()()(（6）把上式代入方程组的第二个方程，得到：)()()(])([)(])()[(222222s U s s ml s s sg ml ml I b s s s g ml ml I m M =Φ-Φ+++Φ-++（7）整理后得到传递函数：232()()()()mlss qb I ml M m mgl bmgl U s s s s q q qΦ=+++--（8）其中])())([(22ml ml I m M q -++=。

基于LQR理论的直线单级倒立摆PID控制仿真

计算方法和控制系统仿真课程设计报告题目基于LQR理论的直线单级倒立摆PID控制仿真项目成员蒋嘉楠、钱品武、刘元晟专业班级自动化091指导教师裘君分院信息分院完成日期 12年5月目录*项目组成员 (2)1课程设计目的 (2)2课程设计题目描述和要求 (2)3课程设计报告内容 (2)3.1、线性二次最优控制LQR基本理论 (2)3.2、系统状态方程 (3)3.3、程序代码 (4)3.4、系统调试和结果分析 (5)4.总结 (7)5.参考书目 (7)项目组成员基于LQR 理论的直线单级倒立摆控制仿真1.课程设计目的设计倒立摆二次型最优控制器，通过MATLAB 仿真和实际系统实验，实现对倒立摆的稳定控制。

建立模型，确定参数，进行控制算法设计、系统调试和分析等步骤实现。

2.课程设计题目描述和要求仿真要求：对论文中的LQR 理论进行验证，同时通过控制变量对离散系统进行优化。

3.课程设计报告内容3.1、线性二次最优控制LQR 基本理论LQR 控制器是应用线性二次型最优控制原理设计的控制器。

它的任务在于，当系统状态由于任何原因偏离了平衡状态时，能在不消耗过多能量的情况下，保持系统状态各分量仍接近于平衡状态。

线性二次型最优控制研究的系统是线性的或可线性化的，并且性能指标是状态变量和控制变量的二次型函数的积分。

线性二次最优控制LQR 基本原理为，由系统方程：Bu AX X +=•确定下列最佳控制向量的矩阵K ：)(*)(t X K t u -=使得性能指标达到最小值：dt Ru u QX X J T T ⎰∞+=0)(式中：Q---正定（或正半定）厄米特或实对称阵；R---为正定厄米特或实对称阵。

下面是最优控制LQR 控制原理图：图1 最优控制LQR 控制原理图方程右端第二项是是考虑到控制能量的损耗而引进的，矩阵Q 和R 确定了误差和能量损耗的相对重要性。

并且假设控制向量u(t)是无约束的。

对线性系统： ⎪⎩⎪⎨⎧=+=•CXY BuAX X根据期望性能指标选取Q 和R ，利用MATLAB 命令lqr 就可以得到反馈矩阵K 的值： ),,,(R Q B A lqr K =改变矩阵Q 的值，可以得到不同的响应效果，Q 值越大（在一定范围之内），系统抵抗干扰的的能力越强，调整时间越短。

基于LQR控制的单级倒立摆系统的研究

智能控制技术研究报告题目：基于LQR控制的单级倒立摆系统的研究学院：电气工程学院年级专业：仪器仪表工程学号：学生姓名：日期：2014.1.5第一章绪论1.1 课题的研究背景和意义倒立摆是日常生活中许多重心在上、支点在下的控制问题的抽象模型，本身是一种自然不稳定体，它在控制过程中能有效地反映控制中许多抽象而关键的问题，如系统的非线性、可控性、鲁棒性等问题。

对倒立摆系统的控制就是使小车以及摆杆尽快地达到预期的平衡位置，而且还要使它们不会有太强的振荡幅度、速度以及角速度，当倒立摆系统达到期望位置后，系统能克服一定范围的扰动而保持平衡。

作为一种控制装置，它具有形象直观、结构简单、便于模拟实现多种不同控制方法的特点，作为一个被控对象它是一个高阶次、非线性、多变量、强耦合、不稳定的快速系统。

由于倒立摆系统的特殊性，许多不同领域的专家学者在检验新提出理论的正确性和实际可行性时，都将倒立摆系统作为实验测试平台。

再将经过测试后的控制理论和控制方法应用到更为广泛的领域中去。

现代控制理论已经在工业生产过程、军事科学、航空航天等许多方面都取得了成功的应用。

例如极小值原理可以用来解决某些最优控制问题；利用卡尔曼滤波器可以对具有有色噪声的系统进行状态估计；预测控制理论可以对大滞后过程进行有效的控制。

但是它们都有一个基本的要求：需要建立被控对象的精确数学模型。

随着科学技术的迅猛发展，各个领域对自动控制控制精度、响应速度、系统稳定性与适应能力的要求越来越高，所研究的系统也日益复杂多变。

然而由于一系列的原因，诸如被控对象或过程的非线性、时变性、多参数间的强烈耦合、较大的随机干扰、过程机理错综复杂、各种不确定性以及现场测量手段不完善等，难以建立被控对象的精确模型。

虽然常规自适应控制技术可以解决一些问题，但范围是有限的。

对于像二级倒立摆这样的非线性、多参数、强耦合的被控对象，使用传统控制理论难以达到良好的控制性能。

而模糊控制理论能够克服这些困难，达到实际设计要求。

基于LQR的一阶倒立摆最优控制系统研究

基于LQR的一阶倒立摆最优控制系统研究“最优控制”大作业【摘要】介绍了最优竝制杲本旣念和原理，分析了最优控制国内外现状•针对饯性二次型最优崔制问題，以一阶倒立摆为对象•详细设计了LQR杲优控制器。

仿真表明•该控制器具有方法商单、便于实现的优点，在响应速度和控制效果方面优于传统的PID控制。

【矢楝河】最优竝制，倒立摆.LQR.PIDH制1最优控制基本概念与原理1.1最优控制简介最优控制理论是现代控制理论的核心。

近50年来,科学技术的迅速发展，对许多被控对象，如宇宙飞船、导弹、卫星和现代工业设备的生产过程等的性能提出了更高的要求，在许多情况卜要求系统的某种性能指标为最优⑴。

这就要求人们对控制问题都必须从最优控制的角度去进行研究分析和设计。

绘优控制问题就其本质来说，乃是一变分问题，而经典变分理论只能解决一类简单的址优控制问题。

为了满足工程实践的需要，20世纪50年代中期，出现了现代变分理论，其中最常用的方法是极人值原理和动态规划，这两种方法成为了目前最优控制理论的两个柱石入习。

最优控制在被控对象参数己知的情况下，己经成为设计复杂系统的有效方法之一。

1・2最优控制问题求解方法绘优控制可分为静态最优和动态最优两类⑶。

(1)静态放优是指在稳定工况I、•实现最优，它反映系统达到稳定后的静态尖系。

系统中各变量不随时间变化，而只表示对彖在稳定工况卜令参数之间的尖系，其特性用代数方程來描述。

大多数的生产过程受控对象町以用静态最优控制來处理，并且貝有足够的精度。

静态最优控制一般可用一个目标函数J=fvx)和若干个等式约束条件或不等式约束条件来描述，要求在满足约束条件卜•使目标函数J为最人或最小。

静态瑕优问题的目标函数是一个多尤普通函数，求解静态/优控制问题经常采用经典微分法、线性规划、分割法(优选法)和插値法等。

(2)动态最优是指系统从一个工况变化到另一个工况的变化过程中，应满足最优要求o在动态系统中，所有的参数都是时间的函数，其特性町用微分方程或差分方程来描述。

基于LQR控制的一级倒立摆MATLAB仿真研究

基于LQR控制的一级倒立摆MATLAB仿真研究作者：潘俊朋桑运晓吕国娜任保飞刘树骏来源：《科学与财富》2017年第25期摘要：：本文首先通过分析单级倒立摆系统建立相应的状态空间数学模型，然后对倒立摆系统进行LQR 控制器设计，最后使用Matlab 进行仿真，结果表明在本文加权矩阵Q、R 的取值下，LQR 控制器可使系统达到有效的控制，小车位置跟着摆杆的角度动作，系统具有较短的调整时间、较小的超调量和较好的动静态性能。

关键词：倒立摆 Matlab LQR 控制一、前言单级倒立摆系统是一种不稳定、多变量且具有强耦合的非线性系统。

如果把它当做一个单输出系统来处理将无法到达控制要求，所以对于这样的多输出系统，我们需要用到状态空间数学模型来对其进行分析。

二、建立系统的状态空间数学模型为了方便而又不失精确的对单级倒立摆系统建立数学模型，实际中忽略一些次要的因素后的一级倒立摆系统简图如图1所示，系统受力分析如图2所示。

定义各参数：作用在小车的外力用F表示；摆杆与垂直向上方向的夹角用φ表示；摆杆与垂直向下方向的夹角用θ表示；采样时间为T=0.005s；摆杆的质量为m=0.2kg；摆杆的惯量为I=0.006kg*m*m；摆杆转动轴心到摆杆质心的距离为l=0.3m；小车的摩擦系数为b=0.1N/m/sec；小车的质量为M=0.5kg；小车的位置用x表示。

应用Newton方法来建立系统的动力学方程并经过整理后得到系统状态空间方程：三、LQR控制器设计及其Matlab仿真为了同时对小车的位置和摆杆的角度都进行有效控制，我们使用线性二次性最优控制算法（LQR）。

这种控制算法在现代控制理论中占有举足轻重的地位，通过多年的研究，使最优控制算法得到越来越广泛的工程应用。

LQR控制系统框图如图3所示。

其中R是作用于小车的阶跃信号，四个状态量和分别代表小车的位移和速度、摆杆的位置和角速度。

设计这个控制器的目的就是要达到以下效果：当给系统作用一个阶跃信号输入时，摆杆晃动后会重新回到垂直位置，小车会重新处于一个命令位置。

毕业论文（设计）单级倒立摆lqr控制器的设计及仿真

毕业设计（论文）任务书I、毕业设计(论文)题目：单级倒立摆LQR控制器的设计及仿真II、毕业设计(论文)使用的原始资料(数据)及设计技术要求：1、在深入了解倒立摆的基础上，熟悉单级倒立摆控制的基本原理2、了解单级倒立摆控制的发展趋势。

3、熟悉线性系统的基本理论和非线性系统线性化的基本方法。

4、建立单级倒立摆的数学模型，并编写MATLAB程序，完成倒立摆的仿真。

I I I、毕业设计(论文)工作内容及完成时间：工作安排如下：1、查阅文献，翻译英文资料，书写开题报告第1---4周2、相关资料的获取和必要知识的学习第5---9周3、设计系统的硬件和软件模块并调试第10--14周4、撰写论文第15--17周5、总结，准备答辩第18周Ⅳ、主要参考资料：1．阳武娇.基于MATLAB的一阶倒立摆控制系统的建模与仿真[J].电子元器件应用.2007，9(1):29-312 .杨世勇，徐莉苹，王培进.单级倒立摆的PID控制研究[J].控制工程.2007,14:23-53.3．黄忠霖.控制系统MATLAB计算及仿真[M].北京：国防工业出版社，2006．4．薛安客，王俊宏．倒立摆控制仿真与实验研究现状[J].杭州电子工业学院学报.2002，21(6):25-27.5 .徐征.基于遗传算法的PID控制器参数寻优方法的研究[D].武汉：武汉大学，2004．6．Takahas M，Narukawa T，Y oshida K．Intelligent transfer andstabilization control to unstable equilibrium point of double inverted pendulum．Int SICE 2003 Annual Co nfeFence，2003，2：1451-145.信息工程系自动化专业类1082022班学生（签名）：填写日期： 2014 年 1 月 10 日指导教师（签名）：助理指导教师(并指出所负责的部分)：信息工程系主任（签名）：单级倒立摆LQR控制器的设计及仿真摘要：单级倒立摆系统是一个典型多变量、不稳定和强耦合的非线性系统。

基于LQR的一阶倒立摆控制

目录0. 前言 (1)1. LQR控制器基本理论 (2)2.方案设计 (4)3.软件编程 (5)3.1 GUI用户界面的设定 (5)3.2 数据从界面输入并被读取以 (6)3.3 编写开关控件响应下的程序 (6)4.系统调试和结果分析 (6)5. 结论及进一步设想 (8)参考文献 (8)课设体会 (9)附录1：keshe.m (10)附录2：keshezi.m (17)基于LQR的一阶倒立摆控制摘要：本次设计的目的在于采用MATLAB语言编写LQR算法，用于一阶倒立摆的控制。

在编写LQR算法程序的同时，引入MATLAB GUI编程设计用户界面，实现倒立摆的参数、极点位置和控制器参数由用户界面直接输入。

所设计完成的系统可以同时控制一阶倒立摆的小车的位置与摆杆的角度，使在尽可能短的时间内使细长杆与小车构成的随动系统能够保持相对稳定。

关键词：一阶倒立摆、控制、LQR算法、MATLAB、GUI用户界面0. 前言小时候我们常玩这样的一个游戏，把一根细长的木棍或竹竿放在伸展开的手心里，通过手位置的移动来使竹竿直立而不倒下。

其实，这就是本次实验最初的原型，竹竿和手就构成了一个倒立摆的模型，人的大脑则是这个模型的控制系统。

在自动控制系统中，倒立摆一直是人们十分感兴趣的被控对象。

这是因为，倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定的系统，它可以直观地表现出控制系统的许多抽象概念。

能够对倒立摆系统进行控制的方法很多，如PID算法、最优控制算法等都取得了一定的控制效果。

在最优控制算法中，基于最小值原理的线性二次型最优控制算法(LQR)，是线性系统综合中常用的方法之一。

由线性二次型问题解出的控制规律是状态变量的线性函数，通过状态反馈便可实现闭环系统的最优控制。

因而，LQR 算法具有控制算法简便快捷、较易实现和控制效果较好等优点，在工程实践上具有重要意义。

在研究双足机器人直立行走、火箭发射过程的姿态调整和直升机飞行控制领域中有重要的现实意义，相关的科研成果己经应用到航天科技和机器人学等诸多领域。

基于LQR的直线一级倒立摆最优控制系统研究

・4・
工业仪表与自动化装置 2007 年第 6 期
・杆的角度 ;φ 为摆杆的角速度 ; u 为输入 (采用小车加速度作为系统中的输入 ) ; y 为输出。 [3 ] 1. 2 系统能控性分析系统的能控性是控制器设计的前提 , 故在设计 2 前进行能控性分析。由能控性矩阵 M = [ B AB A B 3 A B ] , 在 MATLAB 中利用可控性矩阵的 ctrb 命令来计算 ,可以得出 R ank (M ) = 4, 可知系统可控 , 因此可以对系统进行控制器的设计 , 使系统稳定。
为摆杆惯量 , F 为加在小车上的力 , X 为小车位置 , Φ 为摆杆与垂直向上方向的夹角 , θ为摆杆与垂直向下方向的夹角 (考虑到摆杆初始位置为竖直向下 ) 。 [2 ] 应用牛顿 — 欧拉方法 , 可得到系统状态空间方程为 : 1 0 0
m gl 2 I (M + m ) +Mm l
3 直线一级倒立摆 L QR 实时控制
利用固高倒立摆系统 MATLAB 实时控制软件建立的系统模型如图 5 所示。利用 LQR 设计的控制器对倒立摆进行在线控制 ,可以使倒立摆达到稳定 ,在倒立摆系统稳定的情况下 ,对系统施加干扰 (可用手轻触摆杆使摆杆偏离竖直位置一个小角度 ) ,小车能迅速调整 , 使整个系统在很短的时间内恢复平衡 , 并得到小车位置和摆杆角度响应曲线如图 6 所示。
图 4 最佳加权阶跃响应曲线
达到消除稳态误差。如果再增大 Q 1, 1和 Q 3, 3 , 系统
图 5 直线一级 LQR 倒立摆系统仿真框图
4 结论
该文应用牛顿 — 欧拉方法建立了直线一级倒立摆的数学模型 ,并设计了 LQR 控制器。用 MATLAB 语言实现了控制系统的仿真 , 得到了直线一级倒立摆各状态变量及控制量的响应曲线 ,通过仿真 ,说明所设计控制器的有效性 ; 利用固高倒立摆系统和计算机实现了直线一级倒立摆的实物系统的控制 , 给出了直线一级倒立摆稳定时和受干扰时各状态变量的响应曲线和控制量曲线 ,在系统受到干扰时 ,小车能迅速调整 ,使整个系统在很短的时间内恢复平衡 , 表明设计的 LQR 控制器能够对直线一级倒立摆系统进行有效的实时控制。

单级倒立摆稳定控制实验

单级倒立摆稳定控制实验一．实验目的1.了解单级倒立摆的原理与数学模型的建立；2.掌握LQR控制器的设计方法；3.掌握基于LQR控制器的单级倒立摆稳定控制系统的仿真方法。

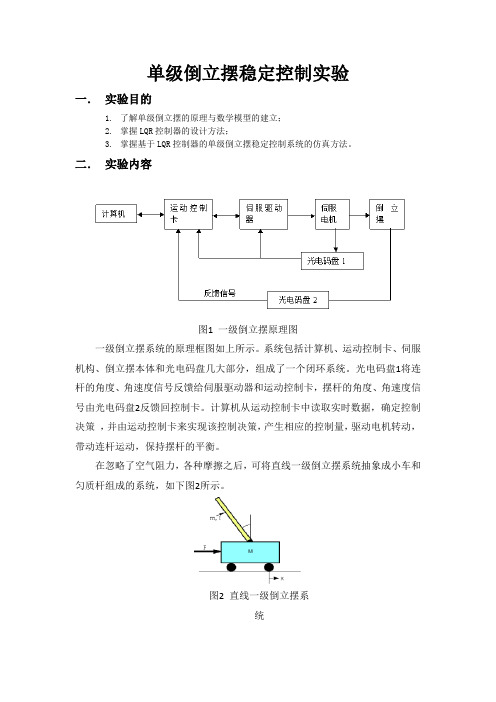
二．实验内容图1 一级倒立摆原理图一级倒立摆系统的原理框图如上所示。

系统包括计算机、运动控制卡、伺服机构、倒立摆本体和光电码盘几大部分，组成了一个闭环系统。

光电码盘1将连杆的角度、角速度信号反馈给伺服驱动器和运动控制卡，摆杆的角度、角速度信号由光电码盘2反馈回控制卡。

计算机从运动控制卡中读取实时数据，确定控制决策，并由运动控制卡来实现该控制决策，产生相应的控制量，驱动电机转动，带动连杆运动，保持摆杆的平衡。

在忽略了空气阻力，各种摩擦之后，可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统，如下图2所示。

图2直线一级倒立摆系统其中：M 小车质量 m 摆杆质量 b 小车摩擦系数l 摆杆转动轴心到杆质心的长度 I 摆杆惯量 F 加在小车上的力 x 小车位置φ摆杆与垂直向上方向的夹角θ摆杆与垂直向下方向的夹角（考虑到摆杆初始位置为竖直向下）下图是系统中小车和摆杆的受力分析图。

其中，N 和P 为小车与摆杆相互作用力的水平和垂直方向的分量。

注意：在实际倒立摆系统中检测和执行装置的正负方向已经完全确定，因而矢量方向定义如图所示，图示方向为矢量正方向。

图3 （a ）小车隔离受力图；（b ）摆杆隔离受力图分析小车水平方向所受的合力，可以得到以下方程：MxF bx N =-- (1) 由摆杆水平方向的受力进行分析可以得到下面等式：()22sin d N m x l dtθ=+ (2)即：2cos sin N mxml ml θθθθ=+- 为了推出系统的第二个运动方程，我们对摆杆垂直方向上的合力进行分析，可以得到下面方程：()22cos d P mg m l dtθ-= (3)即：2sin cos P mg ml ml θθθθ-=-- 力矩平衡方程如下：sin cos Pl Nl I θθθ--= (4) 注意：此方程中力矩的方向，由于θπφ=+，cos cos φθ=-，sin sin φθ=-故等式前面有负号。

倒立摆的LQR控制器算法的设计与仿真

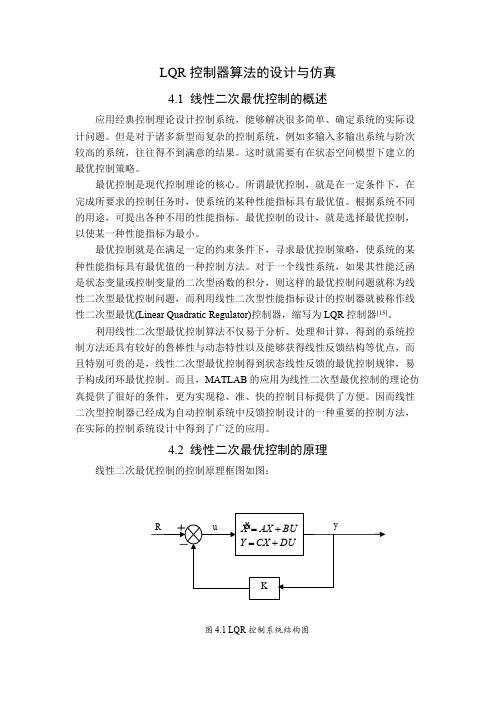
Fig 4.1 Conventional LQR control system structure对于状态方程式所表示的连续时间的线性被控对象有：(4-1)0)0(),()()(x x t Bu t Ax t x =+=上式中，x(t)为n 维状态向量；u(t)为m 维控制向量；A ，B 分别为n×n 及n×m 阶的常数矩阵。

在进行线性二次最优控制系统设计时，比较令人感兴趣的是如何选择控制向量u(t)，使得给定的性能指标达到最小，线性二次最优调节器( LQR) 是针对系统状态方程，寻找最优控制，使得控制性能指标 J 达到最小，其中 Q 、R 分别表示了对状态变量和输入变量的加权值。

二次型性能指标函数：(4-2)dt RU U QX X J T T )(+=⎰+∞∞-则有如下状态反馈控制律：(4-3))()(t Kx t U -=式中，K 为最优反馈矩阵：(4-4)P B R K T 1-=在式(4-4)中，P 为Riccati 方程非负定对称解。

而Riccati 方程为：(4-5)01=+-+-Q P B PBR P A PA T T 如此，可得到状态反馈增益向量K ：(4-6)P B R K T 1-= 由此可见最优控制器的设计的关键是选择合适的加权矩阵Q 和R ，并根据式(4-6)可以算出P ，这样就能求出反馈增益K 了。

而加权矩阵Q 和R 的具体作用为：Q 中某元素相对增加时，其对应的状态变量的响应速度增加，其他状态变量的响应速度相对减慢；R 增加时，控制力减小，角度变化变小，跟随速度变慢。

改变矩阵Q 的值，可以得到不同的响应效果，Q 主对角线元素的值在一定范围之内越大，系统调整时间越短，而且抵抗干扰的能力越强，但是Q 不能过大，不然将对实验结果有一定的影响[16]。

上述推导过程即为线性二次最优控制的控制原理。

而当今现在，随着计算机技术的飞速发展，已经可以不使用上述公式进行繁琐的计算，而利用 MATLAB 的lqr 命令轻松的得到反馈矩阵K 的值：(,,,)K lqr A B Q R = 4.3 二次最优控制器的参数调整二次最优控制器的参数调整关键在于选择好合适的加权矩阵Q 和R ，这样就能得出反馈增益K [17]。