线性反馈移位寄存器(LFSR)
zuc算法比特重组br层从上层lfsr寄存器单元

zuc算法比特重组br层从上层lfsr寄存器单元
ZUC算法是中国自主设计的一种流密码算法,主要用于无线通信或数
据传输的加密保护。
在ZUC算法中,比特重组(Bit Reorganization,BR)层负责从上层LFSR(线性反馈移位寄存器)寄存器单元中获取输入,进
行比特重组,然后输出给下一层。
比特重组层的作用是对输入比特流进行重组,改变其顺序和位置,从
而增强算法的安全性和抗攻击能力。
具体来说,BR层会将多个输入比特
合并成一个更长的比特串,并根据一定规则重组比特的位置,形成新的比
特串。
这个新的比特串会作为下一层LFSR的输入,继续流加密过程。
BR层的设计很重要,因为它直接影响到算法的安全性。
在ZUC算法中,BR层采用了一个巧妙的设计,通过增加输入比特的多样性,提高了
算法的随机性和强度。
具体来说,BR层会在输入比特之间插入特定的冗
余比特,增加不确定性,使得攻击者难以猜测和预测输入比特的分布情况。
这种设计能够有效抵御统计分析和差分攻击等常见攻击手段。
此外,BR层还对输出比特进行重组,以保证输出比特的随机性和均
匀性。
通过对输入和输出比特的巧妙重组,ZUC算法能够提供高强度的密
钥流,从而保证了加密过程的安全性和可靠性。
综上所述,比特重组(BR)层在ZUC算法中扮演着非常重要的角色,
它通过改变输入比特的顺序和位置,增加输入比特的多样性,提高算法的
随机性和强度,从而增强了算法的安全性和抗攻击能力。
BR层的设计需
要兼顾安全性和性能,以保证加密过程的有效性和可靠性。
线性反馈移位寄存器(LFSR)
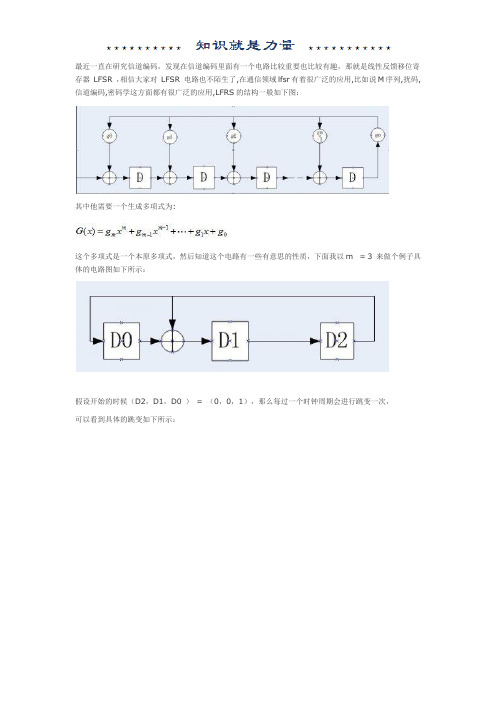
最近一直在研究信道编码,发现在信道编码里面有一个电路比较重要也比较有趣,那就是线性反馈移位寄存器LFSR ,相信大家对LFSR 电路也不陌生了,在通信领域lfsr有着很广泛的应用,比如说M序列,扰码,信道编码,密码学这方面都有很广泛的应用,LFRS的结构一般如下图:其中他需要一个生成多项式为:这个多项式是一个本原多项式,然后知道这个电路有一些有意思的性质,下面我以m = 3 来做个例子具体的电路图如下所示:假设开始的时候(D2,D1,D0 )= (0,0,1),那么每过一个时钟周期会进行跳变一次,可以看到具体的跳变如下所示:然后我们可以看到这个计数器循环起来了,很好玩吧,无论进入那样一个状态除了0之外,都可以循环着回来,其实这里就相当于了一个3bit的伪随机数,很有意思,不是所有的多项式都有这个特性,我们现在在从数学上面来看看这个问题,其实最上面的电路是可以看成是一个除法电路,在Galois域的一个除法电路。
现在假设的是R(x)是寄存器中剩余的数据,M(x)是输入的码字多项式,然后数学公式可以表示成:然后我分别计算出了M(x)的各种情况,然后我们单独进行一下7次方的运算发现7次方的运算和0次的时候的余数是一样的然后我们发现其实在上面的电路中对多项式的除法也是可以循环起来的,可以验证的是把这个记成上面的式子是可以循环的,然后我又想到了CRC的计算,CRC的计算也可以通过一个除法电路来实现, 假设码子多项式为生成多项式为那么CRC的码字为这样我们同样可以用LFSR电路来进行实现首先对M(x)乘以一个x的r次方,然后去去除G(x),在电路上的表现就是所以在输入码字以后还需要多输入r拍的0这样才能使最后的CRC码字数据.同理这个电路也可以进行CRC校验,把生成的数据全部都依次输入进这个Love is not a maybe thing. You know when you love someone.。
zuc算法的lfsr部分中移位寄存器总长度

zuc算法的lfsr部分中移位寄存器总长度ZUC算法中的LFSR(线性反馈移位寄存器)部分是该算法的关键组成部分之一,它的长度对于算法的安全性和性能起着重要的作用。
在这篇文章中,我们将全面介绍ZUC算法中LFSR部分的总长度,并解释它对于算法的性能和安全性的影响,以及如何选择合适的长度。
LFSR是一种基于位运算的寄存器,它能够生成伪随机序列。
在ZUC算法中,LFSR被用于生成密钥流,这是一种用于加密和解密数据的关键序列。
因此,LFSR的总长度直接影响了ZUC算法的安全性。
对于ZUC算法,LFSR的总长度是160位。
这个长度是经过密钥扩展算法计算出来的,并且是为了实现算法的安全性而选择的最优长度。
通过使用160位的LFSR,ZUC算法可以生成足够长的密钥流,以确保抵抗各种攻击,包括线性和差分攻击。
但是,LFSR的总长度也会对算法的性能产生一定的影响。
较长的LFSR可能会增加算法的计算复杂性和运算时间。
因此,在设计ZUC算法时,需要平衡安全性和性能。
选择160位的LFSR长度是基于可行性和效率方面的考虑,它既能够提供足够的安全性,又能够保持较高的算法性能。
另外,LFSR的总长度也是一种指导,以帮助开发者进行合理的密码学设计。
在实际应用中,除了选择合适的LFSR长度外,还应该注意密钥的选择和保护、算法的使用方式等其他因素。
只有将这些因素合理结合,才能够确保算法的安全性和性能。
总之,ZUC算法中LFSR部分的总长度为160位。
这个长度既能够满足算法的安全性要求,又能够保持较高的性能。
在实际应用中,开发者应该综合考虑安全性、性能和可行性等因素,选择适当的LFSR长度,并注意其他相关因素的影响,以确保算法的安全性和可靠性。
zuc算法比特重组br层从上层lfsr寄存器单元

zuc算法比特重组br层从上层lfsr寄存器单元ZUC(ZUC算法)是一种32位的流密码算法,被广泛应用于4G与5G移动通信网络中的安全性提升。
ZUC算法中包含了两个部分:比特重组(BR)层和线性反馈移位寄存器(LFSR)层。
比特重组层(BR层)是ZUC算法中的第一层,其作用是将输入的64位密钥和128位IV(初始向量)进行混合生成一个256位的密钥流。
具体的比特重组过程如下:1.将输入的64位密钥(K0-K63)和128位初始向量(IV0-IV127)进行扩展得到一个完整的512位密钥(W0-W511)。
2.对扩展密钥进行置换,通过一系列的操作,将拓展密钥乱序排列,增加其随机性,生成置换后的512位密钥(X0-X511)。
3.置换后的密钥(X0-X511)被分成4个128位的块(X0-X127,X128-X255,X256-X383,X384-X511)。
4.将置换后的密钥块依次与初始向量块(IV0-IV127)进行异或操作,生成4个异或结果块(Y0-Y127,Y128-Y255,Y256-Y383,Y384-Y511)。
5.将异或结果块通过一系列的移位和异或操作,进行进一步的混乱,生成4个混乱结果块(Z0-Z127,Z128-Z255,Z256-Z383,Z384-Z511)。
6.将混乱结果块拼接在一起,得到一个256位的密钥流(K0-K255)。
LFSR寄存器单元是ZUC算法中的第二层。
其作用是将BR层生成的256位密钥流进行进一步的置换和移位操作,生成一个具有高度非线性的伪随机序列。
LFSR寄存器单元由16个LFSR寄存器组成,每个寄存器的位数为31位。
具体的LFSR过程如下:1.初始化LFSR寄存器的初始值,具体的初始化值由BR层生成。
2.对每个LFSR寄存器进行移位操作,移位规则为使用寄存器中的最高位与第3位、第25位、第30位进行异或操作,并将异或结果作为移位后的最低位。
同时,将当前LFSR寄存器的值与第15个LFSR寄存器的值进行异或操作作为一个反馈位,并将反馈位作为最高位。
lfsr多项式系数选择表

LFSR(线性反馈移位寄存器)是一种广泛应用于数字通信和数据存储的设备。
它通过一个反馈多项式来产生序列,这个多项式决定了序列的特性。
多项式的选择对于LFSR的性能至关重要,因为它决定了序列的周期、噪声容限以及可能的冲突序列的数量。
在LFSR中,多项式的选择是通过一个系数选择表来实现的。
这个表是一个包含一系列可能的多项式的列表,每个多项式由一组系数表示。
选择哪一个多项式作为反馈多项式的过程通常取决于应用的需求和特定的硬件限制。
系数选择表的使用有几个优点。
首先,它允许开发者根据特定的应用需求来定制LFSR的行为。
例如,某些多项式可能更适合于高速数据传输,而其他多项式可能更适合于具有高噪声容限的应用。
其次,系数选择表还允许使用可编程硬件来实现LFSR,这意味着开发者可以根据需要进行调整和优化。
使用系数选择表还为LFSR提供了更好的可扩展性。
通过选择不同的多项式,开发者可以构建具有不同特性的序列生成器,从而适应不断变化的应用需求。
此外,系数选择表还提供了一种灵活的方法来处理硬件限制和错误。
如果硬件出现故障或出现错误,开发者可以通过更改多项式来恢复性能或减少错误的影响。
然而,系数选择表也带来了一些挑战。
首先,选择正确的多项式是一项具有挑战性的任务,因为它需要对应用的需求和硬件性能有深入的了解。
其次,系数选择表的实现可能需要更多的存储空间和计算资源,这可能会影响系统的性能和效率。
最后,随着硬件技术的不断发展,可能需要不断更新和优化系数选择表以适应新的硬件平台和需求。
总之,LFSR的多项式系数选择表是一种用于选择适合特定应用需求和硬件性能的多项式的有效方法。
它提供了一种灵活和可扩展的方法来构建高性能的序列生成器,并处理各种应用中的挑战。
然而,正确的多项式选择需要深入了解应用需求和硬件性能,以及适当的存储和计算资源。
因此,在实践中,正确使用系数选择表需要开发者具备丰富的数字设计和系统设计经验。
线性反馈移位寄存器LFSRverilog实现

线性反馈移位寄存器LFSRverilog实现⼀、什么是LFSR?线性反馈移位寄存器(linear feedback shift register, LFSR)是指,给定前⼀状态的输出,将该输出的线性函数再⽤作输⼊的移位寄存器。
异或运算是最常见的单⽐特线性函数:对寄存器的某些位进⾏异或操作后作为输⼊,再对寄存器中的各⽐特进⾏整体移位(百度百科定义)。
线性反馈移位寄存器反馈分为两种,⼀种是IE型的LFSR,即异或门内接的线性反馈移位寄存器:另⼀种是异或门外接的线性反馈移位寄存器,简称EE型LFSR:gi表⽰接不接⼊反馈,只能为0或1,为1即为接⼊,为0不接⼊。
关于线性反馈移位寄存器(LFSR)数学原理更加详细的介绍,可以参考下⾯这篇⽂章。
本⽂主要是介绍如果使⽤verilog来实现LFSR电路的编写。
需要注意的是,LFSR是伪随机的,这意味着它只是接近随机,并不是完全随机的。
这是因为其实从LFSR的任何状态,你都可以预测下⼀个状态。
有⼀些重要的移位寄存器属性需要注意:LFSR是伪随机的,从LFSR的任何状态,都可以预测下⼀个状态。
影响下⼀个状态的⽐特位叫做抽头。
当抽头使⽤XOR门时,全0状态不会出现,这是因为0与0异或将始终产⽣0,此时LFSR将停⽌运⾏。
当抽头使⽤XNOR门时,全1状态不会出现,这是因为1与1同或(异或⾮)将始终产⽣1,此时LFSR将停⽌运⾏。
任何LFSR的最⼤可能迭代次数 = 2^N-1,N为级数,也就是寄存器bit位的个数。
那么怎样的LFSR才能遍历2^N-1个状态,产⽣最⼤的迭代次数呢?也就是到底寄存器的哪些位去组合然后反馈到输⼊端,才能使该LFSR的所有2^N-1个状态都出现呢?这⾥官⽅给了⼀个表,我们可以根据这个表来确定LFSR的结构:需要注意的是LFSR的每⼀位的索引是从1开始,然后到N,⼀共2^N-1个状态(因为使⽤异或反馈时要除去全0状态,使⽤异或⾮反馈时要除去全1状态)。
《密码学》线性反馈移位寄存器

主要内容
• 移位寄存器 • 线性移位寄存器的综合 • 线性等价量的概念
移位寄存器-1
• 传统的,流密码基于移位寄存器,如今也有更广泛的各 类设计方法
• 移位寄存器包括
• 级,每级有1个比特 • 反馈函数
• 线性反馈移位寄存器(LFSR)的反馈பைடு நூலகம்数是线性的
实例-1
实例-2
是 fn+1(x)=1+xn+1 ln+1=n+1
fn+1(x)=fn(x)+xn-mfm(x) ln+1=max{ln,n+1-ln}
n<N-1?
是
否
输出
算法流程
梅森算法举例
• N=7,
• 定义:能产生该序列的线序性列移位的寄存线器性的最等小价长度量
• 多项式及其解空间的关系 • 极小特征多项式的唯一性 • 极小特征多项式的次数称为其线性等价量或递归长度 • 线性等价量相同的序列,周期为多少?
移位寄存器-2
• 举例 • (非线性) 反馈函数
f(xi, xi+1, xi+2) = 1 xi xi+2 xi+1xi+2
• (非线性) 移位寄存器
• 前3 bits是初态: (x0, x1, x2)
• 举例 • LFSR
移位寄存器-3
• 则对于所有的i,xi+4 = xi xi+2 • 若初态 (x0,x1,x2,x3,x4) = 01110
• 问题提出:对于长度为N的二元序L列F,S求R 出的产综生这合一序列的技术最小的LFSR ,即最短的
线性移位寄存器的特征多项式
• 思路:BCH码的译码中,从校验子求找错位多项式的迭代算法。运用归纳法求出一系列 线性移位寄存器,使每一个线性移位寄存器都产生该序列的前n项,从而使最后得到的 线性移位寄存器是产生所给N长的二元序列的最短线性移位寄存器
lfsr离散数学

lfsr离散数学
LFSR,即线性反馈移位寄存器,是离散数学和密码学中的一个重要概念。
LFSR是一种数字线性系统,它能够产生一个伪随机数序列。
这种寄存器通过将寄存器中的某些位进行异或操作(这是一种二进制运算),并将结果反馈到寄存器的最左端来生成序列。
参与异或的位称为抽头。
LFSR的输出状态值会呈现规律循环,且这个循环可以通过本原多项式来定义。
本原多项式是一种特殊的多项式,它的项数最少且每项系数为1,基于本原多项式所实现的电路最简单。
本原多项式具有这样的特性:本原多项式的反也是本原多项式,根据本原多项式的反也可以生成最大序列。
在实际应用中,LFSR因其简单的结构和良好的统计特性而被广泛应用于加密、通信和计算机科学等领域。
例如,它可以用于生成密钥流、伪随机数生成器和编码理论中的一些算法。
由于其与密码学的紧密联系,LFSR也在CTF(Capture The Flag)竞赛中成为常见的考点之一。
【常用电路】线性反馈移位寄存器(LFSR)

【常⽤电路】线性反馈移位寄存器(LFSR)读华为技术⽂档《FIFO经验谈》看到的这个电路: FIFO的读写地址产⽣⽐较简单,当读使能有效时,在时钟作⽤下,读地址加1;当写使能有效时,写地址加1。
当FIFO深度较⼤时,同时FIFO的速度要求较⾼时,可以采⽤线性反馈移位计数器(LFSR)。
它的速度⾮常快,但是要牺牲⼀个地址。
针对同步的⼤FIFO,它们的读写地址完全可以使⽤线性反馈移位寄存器 LFSR 产⽣,⽽不是简单的加1操作,极⼤的提⾼了速度,如果对FIFO的利⽤率没有很⾼要求的时候,推荐使⽤该⽅法。
使⽤LFSR的优点是在XILINX的FPGA中布线,可以使⽤LUT直接完成。
1/************************************************************\2* *3* Generation of Read and Write address pointers. They use *4* LFSR counters, which are very fast. Because of the *5* nature of LFSR, one address is sacrificed. *6* *7\************************************************************/8wire read_linearfeedback, write_linearfeedback;910assign read_linearfeedback = ! (read_addr[8] ^ read_addr[4]);11assign write_linearfeedback = ! (write_addr[8] ^ write_addr[4]);1213always @(posedge clock or posedge fifo_gsr)14if (fifo_gsr) read_addr <= 9'h0;15else if (read_allow)16 read_addr <= { read_addr[7], read_addr[6], read_addr[5],17 read_addr[4], read_addr[3], read_addr[2],18 read_addr[1], read_addr[0], read_linearfeedback };1920always @(posedge clock or posedge fifo_gsr)21if (fifo_gsr) write_addr <= 9'h022else if (write_allow)23 write_addr <= { write_addr[7], write_addr[6], write_addr[5],24 write_addr[4], write_addr[3], write_addr[2],25 write_addr[1], write_addr[0], write_linearfeedback };。
线性反馈移位寄存器的设计与仿真

原多项式设计的线性反馈移位寄存器的序列周期数<2" - 1,为非M序列。通过使用ModelSim仿真器进行仿真,仿
真结果验证了本课题设计的正确性和有效性。
关键词:可测性设计;BIST测试;伪随机序列;反馈移位寄存器;M序列
中图分类号:TP309
文献标识码:A
文章编号:1674-6341 (2021 )04-0050-04
VLSI测试是确保由合成设计制造的物理设备没有制造 缺陷的一个步骤。要保证产品无缺陷,不仅仅是看测试技术 是否成熟、测试装置是否有效,而且还涉及到电路和系统的 设计、模拟和验证、制造等诸多过程,只有将集成电路的所有 步骤中的问题都变小并解决才能保证产品的质量⑷。所以 即便集成电路测试技术在集成电路的生产制造过程中有着 重要且不可忽视的地位,但其他步骤也尤为关键,相比之下 测试问题还是重中之重。测试集成电路不仅要测试电路的
Design and Simulation of Linear Feedback Shift Register
ZHANG Zhou
(Heilongjiang Vocational Institute of Ecological Engineering, Harbin 150025 , China)
Abstract: In this paper, the linear feedback shift register structure based on primitive polynomial is used to verify
又具有某种随机序列的随机特性,我们便称这种序列为伪随 机序列。 3.2.1同余伪随机序列
生成伪随机序列通常采用两种方法,第一种方法采用复 现关系:
兀=AXk_. +B (模为 M) (k = 1,2,3…)
20级m序列反馈系数表

在通信系统和密码学中,m序列(maximal length sequence)是由线性反馈移位寄存器(LFSR)生成的伪随机序列。
对于一个给定长度n的移位寄存器,其能够产生的最长m序列对应的周期是。
通常情况下,一个n级的移位寄存器要产生m序列,其反馈系数可以通过多项式生成函数来确定,并且该多项式的最高次幂必须为n-1,并且是一个本原多项式,即它除了最高次项外的所有系数均为0或1,且它的根不在有限域GF(2)上。
对于更长的序列如20级m序列,其反馈系数会是一个包含20个元素的向量,并且每个元素都是0或1。
由于具体的20级m序列有很多种可能,这里无法列出所有可能的反馈系数表,但您可以使用已知的本原多项式生成算法或者查阅相关文献获取这些系数。
lfft算法原理 -回复

lfft算法原理-回复LFFT算法原理中括号内的内容为主题,是LFFT(Linear Feedback Shift Register Feedback)算法原理。
对于此主题,本文将分为以下几个部分来一步一步地解释:1. 引言2. LFSR的基本原理与应用3. LFFT的概述4. LFFT算法详解5. LFFT算法的优势与应用6. 总结1. 引言在现代的信息安全领域,加密算法起着至关重要的作用,而其中的众多算法中,LFSR算法也是被广泛使用的一种。
LFSR算法是一种基于寄存器的线性反馈移位寄存器算法,其在伪随机序列生成、扩散码生成等领域有着重要的应用。
而LFFT算法则是在LFSR算法的基础上进行了改进和优化的一种算法,能够更有效地生成伪随机序列。
2. LFSR的基本原理与应用LFSR(Linear Feedback Shift Register)是一种串行寄存器,它由若干个存储单元组成,并通过一个线性反馈函数来控制数据的移位和反馈。
LFSR的基本原理是通过多个存储单元(比特)之间的移位和异或运算来生成伪随机序列。
LFSR的移位寄存器有两个输入信号:数据输入和移位控制信号,通过控制移位寄存器的移位速度,可以控制伪随机序列的产生速度。
LFSR算法在信息安全中有着广泛的应用,其中最常见的应用是在序列密码、流密码和扩频通信中。
在序列密码中,LFSR算法通过产生伪随机序列来进行加密和解密操作;在流密码中,LFSR算法作为密钥流生成器,将伪随机序列和明文进行异或运算来实现加密和解密;在扩频通信中,由于LFSR算法能够生成高质量的伪随机序列,因此可以用作扩频码的生成和伪噪声信号的生成。
3. LFFT的概述尽管LFSR算法在伪随机序列的生成方面具有很好的性能,但是在大规模应用中可能会存在一些局限性。
例如,当需要生成大量的伪随机序列时,采用传统的LFSR算法可能会需要很长的寄存器长度,这会带来硬件和计算复杂度的问题。
a5-1序列密码算法__概述及解释说明

a5-1序列密码算法概述及解释说明1. 引言1.1 概述A5/1序列密码算法是一种用于加密通信数据的流密码算法。
它由三个线性反馈移位寄存器(LFSR)组成,分别命名为X、Y和Z,并且这些寄存器都有自己的特定移位规则。
这个算法以其高效性、可靠性和广泛应用性而闻名,尤其在无线通信领域和移动电话领域得到了广泛的应用。
1.2 文章结构本文主要围绕A5/1序列密码算法展开详细的解释和说明。
首先,将对该算法进行概述,包括其基本原理和组成部分;然后,将深入分析A5/1序列密码算法在安全性方面的评估;接下来,将探讨该算法在不同应用领域中的实际运用情况;最后,将对A5/1序列密码算法的优缺点进行分析,并提出改进方向与展望。
1.3 目的本文旨在全面了解A5/1序列密码算法,并通过对其原理、应用和评估进行详细研究,帮助读者深入了解该算法在加密通信中的重要作用。
同时,通过对该算法的优缺点分析,进一步探讨如何改进和提升其安全性和性能。
通过本文的阅读,读者将能够更好地理解和应用A5/1序列密码算法。
2. A5/1序列密码算法2.1 简介A5/1序列密码算法是一种对称密钥流密码算法,广泛应用于无线通信、移动电话和数据加密领域。
该算法由三个独立的线性反馈移位寄存器(LFSR)组成,分别被称为X寄存器、Y寄存器和Z寄存器。
这三个寄存器的长度相互不同,为19位、22位和23位。
2.2 原理解析A5/1序列密码算法根据输入密钥和初始化向量(IV),通过连续的循环移位操作生成密钥流。
先将输入密钥和IV加载到相应的寄存器中,并通过多次时钟周期执行循环移位操作来产生密钥流。
具体而言,每经过一个时钟周期,X、Y和Z寄存器中的比特会按照特定规则进行异或运算,并输出最左侧的比特作为密钥流输出。
其中,X、Y和Z寄存器中的比特用于决定下一个时钟周期是否要执行循环移位操作。
2.3 安全性评估尽管A5/1序列密码算法在早期被用于保护无线通信系统以及其他应用领域的安全性,在后来的研究中发现了一些潜在的安全漏洞。
lfsr流密码加密原理

lfsr流密码加密原理
LSFR流密码加密原理是一种基于线性反馈移位寄存器的加密算法。
LSFR即LinearFeedbackShiftRegister,是一种能够产生伪随机序列的寄存器。
在LSFR流密码加密中,数据会被分成一定长度的块,每个块会被加密成一个伪随机序列。
这个伪随机序列的产生过程就是通过LSFR 寄存器不断地进行异或运算,从而得到新的输出。
LSFR寄存器的输入由当前状态和一些固定的参数决定,每次输入产生一个位的输出。
这个输出位就是用来加密数据的一部分。
在加密数据时,每个块都会先与一个密钥进行异或运算,然后再与LSFR产生的伪随机序列进行异或运算。
这样,每个块都会根据不同的密钥产生不同的伪随机序列,从而增加了加密的安全性。
在解密时,只需要知道使用的密钥和LSFR寄存器的初始状态,就可以根据相同的算法得到和加密时相同的伪随机序列,从而还原出原始的数据。
LSFR流密码加密算法的优点是简单易实现,加密速度较快。
但是由于其产生的伪随机序列是固定的,因此需要注意密钥的安全性,以免被攻击者破解。
- 1 -。
密码学 线性反馈

如果对连续多个行列式都是0,就停下来。最后一 个非零行列式对应的n就是LFSR的单元数。
Note:假设l为单元数,则只需2l长度的密钥流,就可求出递推关系。
反馈函数
bm
b m f ( b 0 , b1 , , b m 1 )
输 出
i
反馈
b0
b1
k
b2
b m 1
线性反馈移位寄存器
在一个线性反馈移位寄存器(LFSR)中,bm是 b0,b1,bm-1的线性函数。
b m c 0 b 0 c1 b1 c m 1 b m 1, 其中 c 0 1, c i 非 1即 0。
b0
b2
b3
生成的密钥流: 1000100 1101011110001001101011110001001 101011110001… Note:此密钥流的周期为15位
一个LFSR的最大周期是 2
m
1
LFSR生成密钥流 的优点
适于硬件的实现,即LFSR生成的密钥流速度很快。 用较少比特位可以产生周期大的序列。也就说,大 周期的密钥流可用相当少的信息来生成。
例2 设周期为15的密钥流(LFSR产生)为
011010111100011010111100 …。
求线性反馈函数?
解:设LFSR的单元数为m. 假设m=1。则线性反馈函数只能为 b1 b 0 ,此时产生的 密钥流为常数流000000000 …。矛盾 有 假设m=2。设线性反馈函数为 b 2 c 0 b 0 c1b1 ,
LFSR可以生成的一些统计性质良好的密钥流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
