2018年高考数学二轮复习专题5 第3讲用空间向量的方法解立体几何问题(理)

合集下载

高考数学大二轮复习第1部分专题5立体几何第3讲用空间向量的方法解立体几何问题课件201811225190

利用空间向量求线线角、线面角、面面角
以具体几何体为命题背景，直接求角或已知角求相关量
利用空间向量解决探索性问题或其他问题
1.常借助空间直角坐标系，设点的坐标探求点的存在问题 2．常利用空间向量的关系，设某一个参数，利用向量运算探究平行、垂直问题
• 备考策略 • 本部分内容在备考时应注意以下几个方面： • (1)加强对空间向量概念及空间向量运算律的理解，掌握空
又PF＝1，EF＝2，故PE⊥PF.
可得PH＝ 23，EH＝32.
则H(0,0,0)，P
0，0，
3 2
，D
－1，－32，0
，
―→ DP
＝
1，32，
3 2
，
―→ HP
＝
0，0， 23为平面ABFD的一个法向量．
设DP与平面ABFD所成角为θ，则sinθ＝所以BF⊥平 NhomakorabeaPEF.
又BF⊂平面ABFD，所以平面PEF⊥平面ABFD．
(2)方法一：作PH⊥EF，垂足为H.
由(1)得，PH⊥平面ABFD．
以H为坐标原点，
―→ HF
的方向为y轴正方向，设正方形ABCD的边长为2，建立
如图所示的空间直角坐标系H-xyz.
由(1)可得，DE⊥PE.
又DP＝2，DE＝1，所以PE＝ 3.
1．(2018·全国卷Ⅰ，18)如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF.
(1)证明：平面PEF⊥平面ABFD．
(2)求DP与平面ABFD所成角的正弦值．
[解析] (1)由已知可得，BF⊥PF，BF⊥EF，PF∩EF＝F，
3．模、夹角和距离公式 (1)设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则 |cao|＝s〈aa，·a＝b〉__＝___a__21＋____a__22__＋__|aa__a|·|__bb32__|＝________a，_21＋_a_1ba_122_＋＋__aa_223_b_2b＋_21_＋a_3_bb_223_＋__b_32 . (2)距离公式设A(x1，y1，z1)，B(x2，y2，z2)，则 |A→B|＝ x1－x22＋y1－y22＋z1－z22.

2018年高考数学二轮复习考前专题五立体几何与空间向量第3讲立体几何中的向量方法讲学案理

第3讲立体几何中的向量方法以空间几何体为载体考查空间角是高考命题的重点，常与空间线面关系的证明相结合，热点为二面角的求解，均以解答题的形式进行考查，难度主要体现在建立空间直角坐标系和准确计算上.热点一利用向量证明平行与垂直设直线l 的方向向量为a ＝(a 1，b 1，c 1)，平面α，β的法向量分别为μ＝(a 2，b 2，c 2)，v ＝(a 3，b 3，c 3)，则有： (1)线面平行l ∥α⇔a ⊥μ⇔a ·μ＝0⇔a 1a 2＋b 1b 2＋c 1c 2＝0.(2)线面垂直l ⊥α⇔a ∥μ⇔a ＝k μ⇔a 1＝ka 2，b 1＝kb 2，c 1＝kc 2.(3)面面平行α∥β⇔μ∥v ⇔μ＝λv ⇔a 2＝λa 3，b 2＝λb 3，c 2＝λc 3. (4)面面垂直α⊥β⇔μ⊥v ⇔μ·v ＝0⇔a 2a 3＋b 2b 3＋c 2c 3＝0.例1 如图，在直三棱柱ADE —BCF 中，面ABFE 和面ABCD 都是正方形且互相垂直，点M 为AB 的中点，点O 为DF 的中点．运用向量方法证明：(1)OM ∥平面BCF ； (2)平面MDF ⊥平面EFCD .证明方法一 (1)由题意，得AB ，AD ，AE 两两垂直，以点A 为原点建立如图所示的空间直角坐标系．设正方形边长为1，则A (0,0,0)，B (1，0,0)，C (1,1,0)，D (0,1,0)，F (1,0,1)，M ⎝⎛⎭⎪⎫12，0，0，O ⎝⎛⎭⎪⎫12，12，12.OM →＝⎝⎛⎭⎪⎫0，－12，－12，BA →＝(－1,0,0)，∴OM →·BA →＝0, ∴OM →⊥BA →. ∵棱柱ADE —BCF 是直三棱柱，∴AB ⊥平面BCF ，∴BA →是平面BCF 的一个法向量，且OM ⊄平面BCF ，∴OM ∥平面BCF .(2)设平面MDF 与平面EFCD 的一个法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)．∵DF →＝(1，－1,1)，DM →＝⎝ ⎛⎭⎪⎫12，－1，0，DC →＝(1,0,0)，CF →＝(0，－1,1)，由⎩⎪⎨⎪⎧n 1·DF →＝0，n 1·DM →＝0，得⎩⎪⎨⎪⎧x 1－y 1＋z 1＝0，12x 1－y 1＝0，令x 1＝1，则n 1＝⎝ ⎛⎭⎪⎫1，12，－12.同理可得n 2＝(0,1,1)．∵n 1·n 2＝0，∴平面MDF ⊥平面EFCD . 方法二 (1)OM →＝OF →＋FB →＋BM →＝12DF →－BF →＋12BA →＝12(DB →＋BF →)－BF →＋12BA →＝－12BD →－12BF →＋12BA → ＝－12(BC →＋BA →)－12BF →＋12BA →＝－12BC →－12BF →.∴向量OM →与向量BF →，BC →共面，又OM ⊄平面BCF ，∴OM ∥平面BCF . (2)由题意知，BF ，BC ，BA 两两垂直， ∵CD →＝BA →，FC →＝BC →－BF →，∴OM →·CD →＝⎝ ⎛⎭⎪⎫－12BC →－12BF →·BA →＝0，OM →·FC →＝⎝ ⎛⎭⎪⎫－12BC →－12BF →·(BC →－BF →)＝－12BC →2＋12BF →2＝0.∴OM ⊥CD ，OM ⊥FC ，又CD ∩FC ＝C ，CD ，FC ⊂平面EFCD ， ∴OM ⊥平面EFCD .又OM⊂平面MDF，∴平面MDF⊥平面EFCD.思维升华用向量知识证明立体几何问题，仍然离不开立体几何中的定理．如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a ∥b ，只需证明向量a ＝λb (λ∈R )即可．若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外．跟踪演练1 如图，在底面是矩形的四棱锥P —ABCD 中，PA ⊥底面ABCD ，点E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2. (1)求证：EF ∥平面PAB ； (2)求证：平面PAD ⊥平面PDC .证明 (1)以点A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴，AP 所在直线为z 轴，建立如图所示的空间直角坐标系，则A (0,0,0)，B (1,0,0)，C (1,2,0)，D (0,2,0)，P (0,0,1)．∵点E ，F 分别是PC ，PD 的中点， ∴E ⎝ ⎛⎭⎪⎫12，1，12，F ⎝ ⎛⎭⎪⎫0，1，12，EF →＝⎝ ⎛⎭⎪⎫－12，0，0，AB →＝(1,0,0)．∵EF →＝－12AB →，∴EF →∥AB →，即EF ∥AB ，又AB ⊂平面PAB ，EF ⊄平面PAB ， ∴EF ∥平面PAB .(2)由(1)可知，PB →＝(1,0，－1)，PD →＝(0,2，－1)，AP →＝(0,0,1)，AD →＝(0,2,0)，DC →＝(1,0,0)，∵AP →·DC →＝(0,0,1)·(1,0,0)＝0，AD →·DC →＝(0,2,0)·(1,0,0)＝0， ∴AP →⊥DC →，AD →⊥DC →，即AP ⊥DC ，AD ⊥DC . 又AP ∩AD ＝A ，AP ，AD ⊂平面PAD ， ∴DC ⊥平面PAD . ∵DC ⊂平面PDC ，∴平面PAD ⊥平面PDC . 热点二利用空间向量求空间角设直线l ，m 的方向向量分别为a ＝(a 1，b 1，c 1)，b ＝(a 2，b 2，c 2)．平面α，β的法向量分别为μ＝(a 3，b 3，c 3)，v ＝(a 4，b 4，c 4)(以下相同)． (1)线线夹角设l ，m 的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2，则cos θ＝|a ·b ||a ||b |＝(2)线面夹角设直线l 与平面α的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2，则sin θ＝|a ·μ||a ||μ|＝|cos 〈a ，μ〉|.(3)二面角设α—a —β的平面角为θ(0≤θ≤π)，则|cos θ|＝|μ·v ||μ||v |＝|cos 〈μ，v 〉|.例2 在三棱柱ABC －A 1B 1C 1中，AB ⊥平面BCC 1B 1, ∠BCC 1＝π3，AB ＝BC ＝2, BB 1＝4，点D 在棱CC 1上，且CD ＝λCC 1(0<λ≤1)．建立如图所示的空间直角坐标系．(1)当λ＝12时，求异面直线AB 1与A 1D 的夹角的余弦值；(2)若二面角A －B 1D －A 1的平面角为π3，求λ的值．解 (1)易知A ()0，0，2，B 1()0，4，0，A 1()0，4，2. 当λ＝12时，因为BC ＝CD ＝2, ∠BCC 1＝π3，所以C ()3，－1，0，D ()3，1，0.所以AB 1→＝()0，4，－2，A 1D →＝()3，－3，－2.所以cos 〈AB 1→，A 1D →〉＝AB 1→·A 1D→||AB 1→||A 1D →，＝0×3＋4×()－3＋()－2×()－242＋()－22·()32＋()－32＋()－22＝－55. 故异面直线AB 1与A 1D 的夹角的余弦值为55. (2)由CD ＝λCC 1可知，D ()3，4λ－1，0，所以DB 1→＝()－3，5－4λ，0，由(1)知，AB 1→＝()0，4，－2.设平面AB 1D 的法向量为m ＝()x ，y ，z ，则⎩⎪⎨⎪⎧AB 1→·m ＝0，DB 1→·m ＝0，即⎩⎨⎧4y －2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3，z ＝2，所以平面AB 1D 的一个法向量为m ＝⎝ ⎛⎭⎪⎫5－4λ3，1，2.设平面A 1B 1D 的法向量为n ＝()x ，y ，z ，则⎩⎪⎨⎪⎧B 1A 1→·n ＝0，DB 1→·n ＝0，即⎩⎨⎧2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3，z ＝0，所以平面A 1B 1D 的一个法向量为n ＝⎝ ⎛⎭⎪⎫5－4λ3，1，0.因为二面角A －B 1D －A 1的平面角为π3，所以||cos 〈m ，n 〉＝|m·n |||m ||n＝⎪⎪⎪⎪⎪⎪5－4λ3×5－4λ3＋1×1＋2×0⎝ ⎛⎭⎪⎫5－4λ32＋12＋22·⎝ ⎛⎭⎪⎫5－4λ32＋12＝12，即()5－4λ2＝1，解得λ＝32(舍)或λ＝1，故λ的值为1.思维升华 (1)运用空间向量坐标运算求空间角的一般步骤：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论． (2)求空间角注意：①两条异面直线所成的角α不一定是直线的方向向量的夹角β，即cos α＝|cos β|；②两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角；③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，注意函数名称的变化．跟踪演练2 如图，在四棱锥S －ABCD 中，SD ⊥平面ABCD ，四边形ABCD 是直角梯形，∠ADC ＝∠DAB ＝90°，SD ＝AD ＝AB ＝2，DC ＝1. (1)求二面角S －BC －A 的余弦值；(2)设P 是棱BC 上一点，E 是SA 的中点，若PE 与平面SAD 所成角的正弦值为22613，求线段CP 的长．解 (1)以D 为坐标原点，建立如图所示空间直角坐标系Dxyz ，则D (0,0,0)，B (2,2,0)，C (0,1,0)，S (0,0,2)，所以SB →＝(2,2，－2)，SC →＝(0,1，－2)，DS →＝(0,0,2)．设平面SBC 的法向量为n 1＝(x ，y ，z )，由n 1·SB →＝0，n 1·SC →＝0，得2x ＋2y －2z ＝0且y －2z ＝0. 取z ＝1，得x ＝－1，y ＝2，所以n 1＝(－1,2,1)是平面SBC 的一个法向量．因为SD ⊥平面ABC ，取平面ABC 的一个法向量n 2＝(0,0,1)．设二面角S －BC －A 的大小为θ，所以|cos θ|＝|n 1·n 2||n 1||n 2|＝|1|6＝66，由图可知二面角S －BC －A 为锐二面角，所以二面角S －BC －A 的余弦值为66.(2)由(1)知，E (1,0,1)，则CB →＝(2,1,0)，CE →＝(1，－1,1)．设CP →＝λCB →(0≤λ≤1)，则CP →＝λ(2,1,0)＝(2λ，λ，0)，所以PE →＝CE →－CP →＝(1－2λ，－1－λ，1)．易知CD ⊥平面SAD ，所以CD →＝(0，－1,0)是平面SAD 的一个法向量．设PE 与平面SAD 所成的角为α，所以sin α＝|cos 〈PE →，CD →〉| ＝|PE →·CD →||PE →||CD →|＝λ＋15λ2－2λ＋3，即λ＋15λ2－2λ＋3＝22613，得λ＝13或λ＝119(舍)．所以CP →＝⎝ ⎛⎭⎪⎫23，13，0，|CP →|＝53，所以线段CP 的长为53. 热点三利用空间向量求解探索性问题存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对象(数值、图形、函数等)是否存在或某一结论是否成立．解决这类问题的基本策略是先假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论，然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论．例3 如图，在四棱锥E －ABCD 中，平面ABE ⊥底面ABCD ，侧面AEB 为等腰直角三角形，∠AEB ＝π2，底面ABCD 为直角梯形，AB ∥CD ，AB ⊥BC ，AB ＝2CD ＝2BC .(1)求直线EC 与平面ABE 所成角的正弦值；(2)线段EA 上是否存在点F ，使EC ∥平面FBD ？若存在，求出EFEA；若不存在，说明理由．解 (1)因为平面ABE ⊥平面ABCD ，且AB ⊥BC ，平面ABE ∩平面ABCD ＝AB ，BC ⊂平面ABCD ，所以BC ⊥平面ABE, 则∠CEB 即为直线EC 与平面ABE 所成的角，设BC ＝a ，则AB ＝2a ，BE ＝2a ，所以CE ＝3a ，则在Rt △CBE 中， sin ∠CEB ＝CB CE＝13＝33，即直线EC 与平面ABE 所成角的正弦值为33. (2)存在点F ，且EF EA ＝13时，有EC ∥平面FBD ，证明如下：取AB 中点O 为坐标原点，OB ，OD ，OE 分别为x ，y ，z 轴建立空间直角坐标系，如图所示，设CD ＝1，则E (0,0,1)，A (－1,0,0)，B (1,0,0)，C (1,1,0)，D (0,1,0)，所以EA →＝(－1,0，－1)，BD →＝(－1,1,0)，EC →＝(1,1，－1)．由EF →＝13EA →＝⎝ ⎛⎭⎪⎫－13，0，－13，得F ⎝ ⎛⎭⎪⎫－13，0，23，所以FB →＝⎝ ⎛⎭⎪⎫43，0，－23.设平面FBD 的法向量为v ＝()a ，b ，c ，则⎩⎪⎨⎪⎧v ·BD →＝0，v ·FB →＝0，所以⎩⎪⎨⎪⎧－a ＋b ＝0，43a －23c ＝0，取a ＝1，得v ＝()1，1，2，因为EC →·v ＝()1，1，－1·()1，1，2＝0，且EC ⊄平面FBD ，所以EC ∥平面FBD ，即当点F 满足EF EA ＝13时，有EC ∥平面FBD .思维升华空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断．解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法．跟踪演练3 如图所示的空间几何体中，底面四边形ABCD 为正方形，AF ⊥AB ，AF ∥BE ，平面ABEF ⊥平面ABCD ，DF ＝5，CE ＝22，BC＝2.(1)求二面角F －DE －C 的大小；(2)若在平面DEF 上存在点P ，使得BP ⊥平面DEF ，试通过计算说明点P 的位置．解 (1)因为AF ⊥AB ，平面ABCD ⊥平面ABEF ，平面ABEF ∩平面ABCD ＝AB ，所以AF ⊥平面ABCD ，所以AF ⊥AD .因为四边形ABCD 为正方形，所以AB ⊥AD ，所以AD ，AB ，AF 两两垂直，以A 为原点，AD ，AB ，AF 分别为x ，y ，z 轴建立空间直角坐标系(如图)．由勾股定理可知，AF ＝1，BE ＝2，所以A (0,0,0)，B (0,2,0)，C (2,2,0)，D (2,0,0)，E (0,2,2)，F (0,0,1)，所以AC →＝(2,2,0)，CD →＝(0，－2,0)， CE →＝(－2,0,2)．设平面CDE 的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·CD →＝0，n ·CE →＝0，得⎩⎪⎨⎪⎧－2y ＝0，－2x ＋2z ＝0，即⎩⎪⎨⎪⎧y ＝0，x －z ＝0，取x ＝1，得n ＝(1,0,1)．同理可得平面DEF 的一个法向量m ＝(1，－1,2)，故cos 〈m ，n 〉＝m·n |m||n|＝32，因为二面角F －DE －C 为钝角，故二面角F －DE －C 的大小为5π6. (2)设DP →＝λDE →＋μDF →，因为DE →＝(－2,2,2)，DF →＝(－2,0,1)，又BD →＝(2，－2,0)，DP →＝λDE →＋μDF →＝(－2λ，2λ，2λ)＋(－2μ，0，μ)＝(－2λ－2μ，2λ，2λ＋μ)，所以BP →＝BD →＋DP →＝(2－2λ－2μ，2λ－2,2λ＋μ)，因为⎩⎪⎨⎪⎧BP →·DF →＝0，BP →·DE →＝0，所以⎩⎪⎨⎪⎧－2(2－2λ－2μ)＋2λ＋μ＝0，－2(2－2λ－2μ)＋2(2λ－2)＋2(2λ＋μ)＝0，解得⎩⎪⎨⎪⎧μ＝0，λ＝23，即DP →＝23DE →.所以P 是线段DE 上靠近E 的三等分点．真题体验1．(2017·浙江改编)如图，已知正四面体D —ABC (所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP ＝PB ，BQ QC ＝CRRA＝2，分别记二面角D —PR —Q ，D —PQ —R ，D —QR —P 的平面角为α，β，γ，则α，β，γ的大小关系为________．答案 α＜γ＜β解析如图①，作出点D 在底面ABC 上的射影O ，过点O 分别作PR ，PQ ，QR 的垂线OE ，OF ，OG ，连接DE ，DF ，DG ，则α＝∠DEO ，β＝∠DFO ，γ＝∠DGO .由图可知，它们的对边都是DO ， ∴只需比较EO ，FO ，GO 的大小即可．如图②，在AB 边上取点P ′，使AP ′＝2P ′B ，连接OQ ，OR ，则O 为△QRP ′的中心．设点O 到△QRP ′三边的距离为a ，则OG ＝a ，OF ＝OQ ·sin∠OQF ＜OQ ·sin∠OQP ′＝a ， OE ＝OR ·sin∠ORE ＞OR ·sin∠ORP ′＝a ，∴OF ＜OG ＜OE ， ∴ODtan β＜ODtan γ＜ODtan α，∴α＜γ＜β.2．(2017·北京)如图，在四棱锥P —ABCD 中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，PD ∥平面MAC ，PA ＝PD ＝6，AB ＝4.(1)求证：M 为PB 的中点；(2)求二面角B —PD —A 的大小；(3)求直线MC 与平面BDP 所成角的正弦值． (1)证明设AC ，BD 交于点E ，连接ME ，如图所示．因为PD ∥平面MAC ，平面MAC ∩平面PDB ＝ME ，所以PD ∥ME .因为四边形ABCD 是正方形，所以E 为BD 的中点，所以M 为PB 的中点．(2)解取AD 的中点O ，连接OP ，OE . 因为PA ＝PD ，所以OP ⊥AD ，又因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，且OP ⊂平面PAD ，所以OP ⊥平面ABCD .因为OE ⊂平面ABCD ，所以OP ⊥OE . 因为四边形ABCD 是正方形，所以OE ⊥AD ，如图，建立空间直角坐标系Oxyz ，则P (0,0，2)，D (2,0,0)，B (－2,4,0)，BD →＝(4，－4,0)，PD →＝(2,0，－2)．设平面BDP 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·BD →＝0，n ·PD →＝0，即⎩⎨⎧4x －4y ＝0，2x －2z ＝0.令x ＝1，则y ＝1，z ＝ 2.于是n ＝(1,1，2)．平面PAD 的法向量为p ＝(0,1,0)，所以cos 〈n ，p 〉＝n ·p |n ||p |＝12.由题意知，二面角B －PD －A 为锐角，所以它的大小为π3.(3)解由题意知M ⎝ ⎛⎭⎪⎫－1，2，22，C (2,4,0)， MC →＝⎝ ⎛⎭⎪⎫3，2，－22. 设直线MC 与平面BDP 所成的角为α，则 sin α＝|cos 〈n ，MC →〉|＝|n ·MC →||n ||MC →|＝269.所以直线MC 与平面BDP 所成角的正弦值为269.押题预测(2017届太原模拟)如图，在几何体ABCDEF 中，四边形ABCD 是菱形，BE ⊥平面ABCD, DF ∥BE, DF ＝2BE ＝2，EF ＝3. (1)证明：平面ACF ⊥平面BEFD ；(2)若二面角A －EF －C 是直二面角，求AE 与平面ABCD 所成角的正切值．押题依据利用空间向量求二面角全面考查了空间向量的建系、求法向量、求角等知识，是高考的重点和热点． (1)证明 ∵四边形ABCD 是菱形，∴AC ⊥BD . ∵BE ⊥平面ABCD ，∴BE ⊥AC ，又BE ∩BD ＝B ，BE ，BD ⊂平面BEFD ， ∴AC ⊥平面BEFD . ∵AC ⊂平面ACF ， ∴平面ACF ⊥平面BEFD . (2)解方法一 (向量法)设AC 与BD 交于点O ，以点O 为原点，OA 方向为x 轴，OB 方向为y 轴，BE 方向为z 轴建立空间直角坐标系，如图．取DF 的中点H ，连接EH . ∵BE 綊DH, DH ＝1，∴四边形BEHD 为平行四边形， ∵在Rt △EHF 中，FH ＝1，EF ＝3， ∴EH ＝22，∴BD ＝2 2.设AB 的长为a ，则各点坐标为A ()a 2－2，0，0，E ()0，2，1，F ()0，－2，2，C ()－a 2－2，0，0，∴AE →＝()－a 2－2，2，1，EF →＝()0，－22，1， CE →＝()a 2－2，2，1.设n 1＝()x 1，y 1，z 1为平面AEF 的法向量，n 2＝()x 2，y 2，z 2为平面CEF 的法向量．由n 1·AE →＝0，n 1·EF →＝0，得z 1＝22y 1，x 1＝32a 2－2y 1.令y 1＝a 2－2，得n 1＝()32，a 2－2，22a 2－4，同理得n 2＝()－32，a 2－2，22a 2－4. ∵二面角A －EF －C 是直二面角， ∴n 1·n 2＝0，得a ＝2，由题可得∠EAB 为AE 与平面ABCD 的夹角， ∵AB ＝2，BE ＝1，∴tan ∠EAB ＝BE AB ＝12.方法二 (几何法) 设AC 与BD 交于点O . ∵四边形ABCD 是菱形，∴△ADF ≌△CDF ，△ABE ≌△CBE ， ∴AF ＝CF ，AE ＝CE ，∴△AEF ≌△CEF . 过A 作AM ⊥EF ，连接CM ，则CM ⊥EF ，则∠AMC 为二面角A －EF －C 的平面角．设菱形的边长为a ，∵BE ＝1，DF ＝2，EF ＝3, DF ⊥BD ，∴BD ＝2 2. 在△AOB 中，AO ＝a 2－2，∴AC ＝2a 2－2，∵A －EF －C 的二面角为直角，∴∠AMC 为直角， ∴AM ＝2a 2－4，在△AEF 中，AM ⊥EF ，设ME ＝x ，则MF ＝3－x ，AF ＝a 2＋4，AE ＝a 2＋1，()a 2＋42－()3－x 2＝()a 2＋12－x 2，∴a ＝2.AE 与平面ABCD 所成角为∠EAB ，∴tan ∠EAB ＝12.A 组专题通关1．已知平面ABC ，点M 是空间任意一点，点M 满足条件OM →＝34OA →＋18OB →＋18OC →，则直线AM ( )A ．与平面ABC 平行B ．是平面ABC 的斜线 C ．是平面ABC 的垂线D ．在平面ABC 内答案 D解析由已知得M ，A ，B ，C 四点共面，所以AM 在平面ABC 内，故选D.2.(2017·湖南省衡阳市联考)如图所示，在正方体AC 1中，AB ＝2, A 1C 1∩B 1D 1＝E ，直线AC 与直线DE 所成的角为α，直线DE 与平面BCC 1B 1所成的角为β，则cos ()α－β等于()A.66B.33C.306 D.63答案 A解析由题意可知，α＝π2，则cos ()α－β＝sin β，以点D 为坐标原点，DA ，DC ，DD 1方向为x ，y ，z 轴正方向建立空间直角坐标系，则D ()0，0，0，E ()1，1，2，DE →＝()1，1，2，平面BCC 1B 1的法向量DC →＝()0，2，0，由此可得cos ()α－β＝sin β＝DE →·DC→|DE →||DC →|＝66.故选A.3．正方体ABCD －A 1B 1C 1D 1中，点P 在A 1C 上运动(包括端点)，则BP 与AD 1所成角的取值范围是( ) A.⎣⎢⎡⎦⎥⎤π4，π3 B.⎣⎢⎡⎦⎥⎤π4，π2C.⎣⎢⎡⎦⎥⎤π6，π2 D.⎣⎢⎡⎦⎥⎤π6，π3答案 D解析以点D 为原点，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系，设正方体棱长为1，设点P 坐标为()x ，1－x ，x (0≤x ≤1)，则BP →＝()x －1，－x ，x ，BC 1→＝()－1，0，1，设BP →，BC 1→的夹角为α，所以cos α＝BP →·BC 1→||BP →||BC 1→＝1()x －12＋2x 2×2＝13⎝ ⎛⎭⎪⎫x －132＋23·2，所以当x ＝13时，cos α取得最大值32，α＝π6.当x ＝1时， cos α取得最小值12，α＝π3. 因为BC 1∥AD 1.故选D.4．(2017·全国Ⅱ)已知直三棱柱ABC —A 1B 1C 1中，∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，则异面直线AB 1与BC 1所成角的余弦值为( ) A.32B.155 C.105 D.33答案 C解析方法一将直三棱柱ABC －A 1B 1C 1补形为直四棱柱ABCD －A 1B 1C 1D 1，如图所示，连接AD 1，B 1D 1，BD .由题意知∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，所以AD 1＝BC 1＝2，AB 1＝5，∠DAB ＝60°.在△ABD 中，由余弦定理知，BD 2＝22＋12－2×2×1×cos 60°＝3，所以BD ＝3，所以B 1D 1＝ 3.又AB 1与AD 1所成的角即为AB 1与BC 1所成的角θ，所以cos θ＝AB 21＋AD 21－B 1D 212×AB 1×AD 1＝5＋2－32×5×2＝105.故选C.方法二以B 1为坐标原点，B 1C 1所在的直线为x 轴，垂直于B 1C 1的直线为y 轴，BB 1所在的直线为z 轴建立空间直角坐标系，如图所示．由已知条件知B 1(0,0,0)，B (0,0,1)，C 1(1,0,0)，A (－1，3，1)，则BC 1→＝(1,0，－1)，AB 1→＝(1，－3，－1)．所以cos 〈AB 1→，BC 1→〉＝AB 1→·BC 1→|AB 1→||BC 1→|＝25×2＝105.所以异面直线AB 1与BC 1所成角的余弦值为105. 故选C.5．(2017·全国Ⅲ)a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论： ①当直线AB 与a 成60°角时，AB 与b 成30°角； ②当直线AB 与a 成60°角时，AB 与b 成60°角； ③直线AB 与a 所成角的最小值为45°； ④直线AB 与a 所成角的最大值为60°.其中正确的是________．(填写所有正确结论的编号) 答案 ②③解析依题意建立如图所示的空间直角坐标系，设等腰直角三角形ABC 的直角边长为1.由题意知，点B 在平面xOy 中形成的轨迹是以C 为圆心，1为半径的圆．设直线a 的方向向量为a ＝(0,1,0)，直线b 的方向向量为b ＝(1,0,0)，CB →以Ox 轴为始边沿逆时针方向旋转的旋转角为θ，θ∈[)0，2π，则B (cos θ，sin θ，0)，∴AB →＝(cos θ，sin θ，－1)，|AB →|＝ 2. 设直线AB 与直线a 所成的夹角为α，则cos α＝|AB →·a ||a ||AB →|＝22|sin θ|∈⎣⎢⎡⎦⎥⎤0，22，∴45°≤α≤90°，∴③正确，④错误；设直线AB 与直线b 所成的夹角为β，则cos β＝|AB →·b ||b ||AB →|＝22|cos θ|.当直线AB 与直线a 的夹角为60°，即α＝60°时，则|sin θ|＝2cos α＝2cos 60°＝22， ∴|cos θ|＝22，∴cos β＝22|cos θ|＝12. ∵45°≤β≤90°，∴β＝60°，即直线AB 与b 的夹角为60°. ∴②正确，①错误．6.如图，在直四棱柱ABCD －A 1B 1C 1D 1中，底面四边形ABCD 为菱形，A 1A ＝AB ＝2，∠ABC ＝π3，E ，F 分别是BC ，A 1C 的中点．(1)求异面直线EF ，AD 所成角的余弦值； (2)点M 在线段A 1D 上，A 1MA 1D＝λ .若CM ∥平面AEF ，求实数λ的值．解因为四棱柱ABCD －A 1B 1C 1D 1为直四棱柱，所以A 1A ⊥平面ABCD .又AE ⊂平面ABCD ，AD ⊂平面ABCD ，所以A 1A ⊥AE ，A 1A ⊥AD .在菱形ABCD 中，∠ABC ＝π3，则△ABC 是等边三角形．因为E 是BC 中点，所以BC ⊥AE . 因为BC ∥AD ，所以AE ⊥AD .以{AE →，AD →，AA 1→}为正交基底建立空间直角坐标系．则A (0,0,0)，C (3，1,0)，D (0,2,0)，A 1(0,0,2)，E (3，0,0)，F ⎝⎛⎭⎪⎫32，12，1. (1)AD →＝(0,2,0)，EF →＝⎝ ⎛⎭⎪⎫－32，12，1，从而cos 〈AD →，EF →〉＝AD →·EF →|AD →||EF →|＝24.故异面直线EF ，AD 所成角的余弦值为24. (2)设M (x ，y ，z )，由于点M 在线段A 1D 上，且A 1MA 1D＝λ，则A 1M →＝λA 1D →，即(x ，y ，z －2)＝λ(0,2，－2)．则M (0,2λ，2－2λ)，CM →＝(－3，2λ－1,2－2λ)．设平面AEF 的法向量为n ＝(x 0，y 0，z 0)．因为AE →＝(3，0,0)，AF →＝⎝ ⎛⎭⎪⎫32，12，1，由n ·AE →＝0，n ·AF →＝0，得x 0＝0，12y 0＋z 0＝0.取y 0＝2，则z 0＝－1，则平面AEF 的一个法向量为n ＝(0,2，－1)．由于CM ∥平面AEF ，则n ·CM →＝0，即2(2λ－1)－(2－2λ)＝0，解得λ＝23.7．(2017·全国Ⅲ)如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD ＝∠CBD ，AB ＝BD .(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D —AE —C 的余弦值．(1)证明由题设可得 △ABD ≌△CBD . 从而AD ＝CD ，又△ACD 为直角三角形，所以∠ADC ＝90°，取AC 的中点O ，连接DO ，BO ，则DO ⊥AC ，DO ＝AO .又因为△ABC 是正三角形，故BO ⊥AC ，所以∠DOB 为二面角D —AC —B 的平面角，在Rt △AOB 中，BO 2＋OA 2＝AB 2，又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°，所以平面ACD ⊥平面ABC .(2)解由题设及(1)知，OA ，OB ，OD 两两垂直，以O 为坐标原点， OA →为x 轴正方向，OB →为y 轴正方向，OD →为z 轴正方向，|OA →|为单位长度，建立如图所示的空间直角坐标系Oxyz ，则O (0,0,0)，A ()1，0，0，D ()0，0，1，B ()0， 3，0，C (－1，0,0)，由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E ⎝ ⎛⎭⎪⎫0，32，12，故AE →＝⎝⎛⎭⎪⎫－1，32，12，AD →＝()－1，0，1，OA →＝()1，0，0.设平面AED 的法向量为n 1＝(x 1，y 1，z 1)，平面AEC 的法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧AE →·n 1＝0，AD →·n 1＝0，即⎩⎪⎨⎪⎧－x 1＋32y 1＋12z 1＝0，－x 1＋z 1＝0，令x 1＝1，则n 1＝⎝⎛⎭⎪⎫1，33，1. ⎩⎪⎨⎪⎧AE →·n 2＝0，OA →·n 2＝0，即⎩⎪⎨⎪⎧－x 2＋32y 2＋12z 2＝0，x 2＝0，令y 2＝－1，则n 2＝(0，－1，3)，设二面角D —AE —C 的平面角为θ，易知θ为锐角，则cos θ＝|n 1·n 2||n 1||n 2|＝77.8．(2016·浙江)如图，在三棱台ABC —DEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3. (1)求证：BF ⊥平面ACFD ；(2)求二面角B —AD —F 的平面角的余弦值．(1)证明延长AD ，BE ，CF 相交于一点K ，如图所示．因为平面BCFE ⊥平面ABC ，且AC ⊥BC ，所以AC ⊥平面BCFE ，因此BF ⊥AC .又因为EF ∥BC ，BE ＝EF ＝FC ＝1，BC ＝2，所以△BCK 为等边三角形，且F 为CK 的中点，则BF ⊥CK ，且CK ∩AC ＝C ，所以BF ⊥平面ACFD .(2)解方法一过点F 作FQ ⊥AK 于点Q ，连接BQ . 因为BF ⊥平面ACFD ，所以BF ⊥AK ，则AK ⊥平面BQF ，所以BQ ⊥AK .所以∠BQF 是二面角B —AD —F 的平面角．在Rt △ACK 中，AC ＝3，CK ＝2，得FQ ＝31313.在Rt △BQF 中，FQ ＝31313，BF ＝3，得cos ∠BQF ＝34. 所以二面角B —AD —F 的平面角的余弦值为34.方法二如图，延长AD ，BE ，CF 相交于一点K ，则△BCK 为等边三角形．取BC 的中点O ，连接KO ，则KO ⊥BC ，又平面BCFE ⊥平面ABC ，所以KO ⊥平面ABC .以点O 为原点，分别以射线OB ，OK 的方向为x 轴，z 轴的正方向，建立空间直角坐标系Oxyz .由题意得B (1,0,0)，C (－1,0,0)，K (0,0，3)，A (－1，－3，0)，E ⎝ ⎛⎭⎪⎫12，0，32，F ⎝ ⎛⎭⎪⎫－12，0，32.因此，AC →＝(0,3,0)，AK →＝(1,3，3)，AB →＝(2,3,0)．设平面ACK 的法向量为m ＝(x 1，y 1，z 1)，平面ABK 的法向量为n ＝(x 2，y 2，z 2)．由⎩⎪⎨⎪⎧AC →·m ＝0，AK →·m ＝0，得⎩⎨⎧3y 1＝0，x 1＋3y 1＋3z 1＝0，取m ＝(3，0，－1)；由⎩⎪⎨⎪⎧AB →·n ＝0，AK →·n ＝0，得⎩⎨⎧2x 2＋3y 2＝0，x 2＋3y 2＋3z 2＝0，取n ＝(3，－2，3)．于是，cos 〈m ，n 〉＝m ·n |m ||n |＝34.所以二面角B —AD —F 的平面角的余弦值为34. B 组能力提高9．已知空间四边形ABCD ，满足||AB →＝3, ||BC →＝7, ||CD →＝11, ||DA →＝9，则AC →·BD →的值为( ) A ．－1 B ．0C.212 D.332答案 B解析如图，构造符合题设的空间四边形ABCD ，不妨设AB ⊥BD ，则BD ＝81－9＝72，因为BC 2＋BD 2＝CD 2，则CB ⊥BD ，故由线面垂直的判定定理可得BD ⊥平面ABC ，AC ⊂平面ABC ，所以AC ⊥BD ，即AC →·BD →＝0，故选B.10.(2017届上饶模拟)如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝3AD ＝3AA 1＝3，点P 为线段A 1C 上的动点(包含线段端点)，则下列结论正确的是________．①当A 1C →＝3A 1P →时，D 1P ∥平面BDC 1； ②当A 1C →＝5A 1P →时，A 1C ⊥平面D 1AP ； ③∠APD 1的最大值为90°； ④AP ＋PD 1的最小值为 5. 答案 ①②解析以D 为坐标原点建立空间直角坐标系，则A (1,0,0)，A 1(1,0,1)，C (0，3，0)，D 1(0,0,1)，C 1(0，3，1)，B (1，3，0)，则A 1C →＝(－1，3，－1)，设P (x ，y ，z )，A 1P →＝(x －1，y ，z －1)．对于①，当A 1C →＝3A 1P →时，(－1，3，－1)＝3(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫23，33，23，D 1P →＝⎝ ⎛⎭⎪⎫23，33，－13，设平面BDC 1的法向量为n 1＝(x 1，y 1，z 1)，则由⎩⎪⎨⎪⎧n 1·DB →＝0，n 1·DC 1→＝0，解得n 1＝(－3，1，－3)，由于D 1P →·n 1＝0，所以D 1P ∥平面BDC 1成立；对于②，当A 1C →＝5A 1P →时，(－1，3，－1)＝5(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫45，35，45，由⎩⎪⎨⎪⎧A 1C →·D 1A →＝0，A 1C →·D 1P →＝0，可知A 1C ⊥平面D 1AP 成立；对于③，设A 1C →＝λA 1P →，即(－1，3，－1)＝λ(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫1－1λ，3λ，1－1λ，由cos 〈PA →，PD 1→〉＝⎝ ⎛⎭⎪⎫1λ，－3λ，1λ－1⎝ ⎛⎭⎪⎫1λ－1，－3λ，1λ⎝ ⎛⎭⎪⎫1λ2＋⎝ ⎛⎭⎪⎫－3λ2＋⎝ ⎛⎭⎪⎫1λ－12，其分子化简得5－2λλ2，当λ>52时，cos 〈PA →，PD 1→〉<0，故∠APD 1的最大值可以为钝角，③错误．对于④，根据③计算的数据， PA →＝⎝ ⎛⎭⎪⎫1λ，－3λ，1λ－1，PD 1→＝⎝ ⎛⎭⎪⎫1λ－1，－3λ，1λ， |PA →|＋|PD 1→|＝2⎝ ⎛⎭⎪⎫1λ2＋⎝ ⎛⎭⎪⎫－3λ2＋⎝ ⎛⎭⎪⎫1λ－12 ＝25·1λ2－2·1λ＋1，在对称轴1λ＝15，即λ＝5时取得最小值245＝455，故④错误．11.如图，已知圆锥OO 1和圆柱O 1O 2的组合体(它们的底面重合)，圆锥的底面圆O 1半径为r ＝5, OA 为圆锥的母线，AB 为圆柱O 1O 2的母线，D ，E 为下底面圆O 2上的两点，且DE ＝6，AB ＝6.4，AO ＝52，AO ⊥AD . (1)求证：平面ABD ⊥平面ODE; (2)求二面角B —AD —O 的正弦值．(1)证明依题易知，圆锥的高为h ＝(52)2－52＝5，又圆柱的高为AB ＝6.4，AO ⊥AD ，所以OD 2＝OA 2＋AD 2，因为AB ⊥BD ，所以AD 2＝AB 2＋BD 2，连接OO 1，O 1O 2，DO 2，易知O ，O 1，O 2三点共线，OO 2⊥DO 2，所以OD 2＝OO 22＋O 2D 2，所以BD 2＝OO 22＋O 2D 2－AO 2－AB 2＝(6.4＋5)2＋52－(52)2－6.42＝64，解得BD ＝8，又因为DE ＝6，圆O 2的直径为10，圆心O 2在∠BDE 内，所以∠BDE ＝90°，所以DE ⊥BD . 因为AB ⊥平面BDE ，所以DE ⊥AB ，因为AB ∩BD ＝B ，AB ，BD ⊂平面ABD ，所以DE ⊥平面ABD . 又因为DE ⊂平面ODE ，所以平面ABD ⊥平面ODE .(2)解如图，以D 为原点，DB ，DE 所在的直线为x ，y 轴，建立空间直角坐标系．则D (0,0,0)，A (8,0,6.4)，B (8,0,0)，O (4,3,11.4)．所以DA →＝(8,0,6.4)，DB →＝(8,0,0)，DO →＝(4,3,11.4)，设平面DAO 的法向量为u ＝(x ，y ，z )，所以DA →·u ＝8x ＋6.4z ＝0， DO →·u ＝4x ＋3y ＋11.4z ＝0，令x ＝12，则u ＝(12,41，－15)．可取平面BDA 的一个法向量为v ＝(0,1,0)，所以cos 〈u ，v 〉＝u·v |u||v |＝41582＝8210，所以二面角B —AD —O 的正弦值为3210.12．(2017届北京市丰台区综合练习)如图所示的几何体中，四边形ABCD 为等腰梯形，AB ∥CD, AB ＝2AD ＝2, ∠DAB ＝60°，四边形CDEF 为正方形，平面CDEF ⊥平面ABCD .(1)若点G 是棱AB 的中点，求证：EG ∥平面BDF ； (2)求直线AE 与平面BDF 所成角的正弦值；(3)在线段FC 上是否存在点H ，使平面BDF ⊥平面HAD ？若存在，求FH HC的值；若不存在，说明理由．(1)证明由已知得EF ∥CD ，且EF ＝CD . 因为四边形ABCD 为等腰梯形，所以BG ∥CD . 因为G 是棱AB 的中点，所以BG ＝CD . 所以EF ∥BG ，且EF ＝BG ，故四边形EFBG 为平行四边形，所以EG ∥FB .因为FB ⊂平面BDF, EG ⊄平面BDF ，所以EG ∥平面BDF .(2)解因为四边形CDEF 为正方形，所以ED ⊥DC .因为平面CDEF ⊥平面ABCD ，平面CDEF ∩平面ABCD ＝DC ，DE ⊂平面CDEF ，所以ED ⊥平面ABCD .在△ABD 中，因为∠DAB ＝60°，AB ＝2AD ＝2，所以由余弦定理，得BD ＝3，所以AD ⊥BD .在等腰梯形ABCD 中，可得DC ＝CB ＝1.如图，以D 为原点，以DA ，DB ，DE 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，则D ()0，0，0，A ()1，0，0，E ()0，0，1，B ()0，3，0，F ⎝ ⎛⎭⎪⎫－12，32，1，所以AE →＝()－1，0，1，DF →＝⎝ ⎛⎭⎪⎫－12，32，1，DB →＝()0，3，0.设平面BDF 的法向量为n ＝()x ，y ，z ，因为⎩⎪⎨⎪⎧n ·DB →＝0，n ·DF →＝0，所以⎩⎪⎨⎪⎧3y ＝0，－12x ＋32y ＋z ＝0.取z ＝1，则x ＝2，y ＝0，则n ＝()2，0，1. 设直线AE 与平面BDF 所成的角为θ，则sin θ＝||cos 〈AE →，n 〉＝||AE →·n ||AE →||n ＝1010，所以AE 与平面BDF 所成角的正弦值为1010. (3)解线段FC 上不存在点H ，使平面BDF ⊥平面HAD .证明如下：假设线段FC 上存在点H ，设H ⎝ ⎛⎭⎪⎫－12，32，t ()0≤t ≤1，则DH →＝⎝ ⎛⎭⎪⎫－12，32，t .设平面HAD 的法向量为m ＝()a ，b ，c ，因为⎩⎪⎨⎪⎧m ·DA →＝0，m ·DH →＝0，所以⎩⎪⎨⎪⎧a ＝0，－12a ＋32b ＋tc ＝0.取c ＝1，则a ＝0，b ＝－23t ，得m ＝⎝ ⎛⎭⎪⎫0，－23 t ，1.要使平面BDF ⊥平面HAD ，只需m·n ＝0，即2×0－23t ×0＋1×1＝0, 此方程无解．所以线段FC 上不存在点H ，使平面BDF ⊥平面HAD .。

2018届高考数学二轮复习专题五立体几何 5.3 空间向量与立体几何讲义理

[技法领悟] 利用空间向量证明平行与垂直的步骤 (1)建立空间直角坐标系，建系时，要尽可能地利用载体中的垂直关系； (2)建立空间图形与空间向量之间的关系，用空间向量表示出问题中所涉及的点、直线、平面的要素； (3)通过空间向量的运算研究平行、垂直关系； (4)根据运算结果解释相关问题．
1．(2017·甘肃兰州质检)
3．向量法求二面角求出二面角 α-l-β 的两个半平面 α 与 β 的法向量 n1，n2，若二面角 α-l-β 所成的角 θ 为锐角，则 cosθ＝|cos〈n1，n2〉|＝||nn11|·|nn22||；若二面角 α-l-β 所成的角 θ 为钝角，则 cosθ＝－|cos〈n1，n2〉|＝－ ||nn11|·|nn22||.
所以|cos〈B→M，n〉|＝sin 45°， x－1|2z＋| y2＋z2＝ 22，即(x－1)2＋y2－z2＝0.① 又 M 在棱 PC 上，设P→M＝λP→C，则 x＝λ，y＝1，z＝ 3－ 3λ.②
例 1如图所示，在底面是矩形的四棱锥 P－ABCD 中，PA⊥底面 ABCD，E，F 分别是 PC，PD 的中点，PA＝AB＝1，BC＝2.
(1)求证：EF∥平面 PAB； (2)求证：平面 PAD⊥平面 PDC.
【证明】以 A 为原点，AB，AD，AP 所在直线分别为 x 轴， y 轴，z 轴，建立空间直角坐标系 A－xyz 如图所示，则 A(0,0,0)， B(1,0,0)，C(1,2,0)，D(0,2,0)，P(0,0,1)，
所以 E12，1，12，F0，1，12， E→F＝－12，0，0，A→P＝(0,0,1)，A→D＝(0,2,0)，D→C＝(1,0,0)，A→B ＝(1,0,0)．
(1)因为E→F＝－12A→B，所以E→F∥A→B，即 EF∥AB. 又 AB⊂平面 PAB，EF⊄平面 PAB，所以 EF∥平面 PAB. (2)因为A→P·→C＝(0,0,1)·(1,0,0)＝0， A→D·D→C＝(0,2,0)·(1,0,0)＝0，所以A→P⊥D→C，A→D⊥D→C，即 AP⊥DC，AD⊥DC. 又因为 AP∩AD＝A，AP⊂平面 PAD，AD⊂平面 PAD，所以 DC⊥平面 PAD.因为 DC⊂平面 PDC，所以平面 PAD⊥平面 PDC.

用空间向量法求解立体几何问题典例及解析

用空间向量法求解立体几何问题典例及解析以多面体为载体，以空间向量为工具，来论证和求解空间角、距离、线线关系以及线面关系相关问题，是近年来高考数学的重点和热点，用空间向量解立体几何问题，极大地降低了求解立几的难度，很大程度上呈现出程序化思想。

更易于学生们所接受，故而执教者应高度重视空间向量的工具性。

首先，梳理一下利用空间向量解决立体几何的知识和基本求解方法一：利用空间向量求空间角 (1)两条异面直线所成的夹角范围：两条异面直线所成的夹角的取值范围是。

向量求法：设直线,a b 的方向向量为a,b ，其夹角为θ，则有cos ___________.θ= (2)直线与平面所成的角定义：直线与平面所成的角是指直线与它在这个平面内的射影所成的角。

范围：直线和平面所夹角的取值范围是。

向量求法：设直线l 的方向向量为a ，平面的法向量为n ，直线与法向量所成角的余弦值为|cos |___________.θ=直线与平面所成的角为ϕ，则有sin ___________.ϕ=或在平面内任取一个向量m ，则|cos |___________.θ=.(3)二面角二面角的取值范围是 . 二面角的向量求法：方法一：在两个半平面内任取两个与棱垂直的向量，则这两个向量所成的即为所求的二面角的大小；方法二：设1n ，2n 分别是两个面的，则向量1n 与2n 的夹角(或其补角)即为所求二面角的平面角的大小。

二：利用空间向量求空间距离（1）点面距离的向量公式平面α的法向量为n ，点P 是平面α外一点，点M 为平面α内任意一点，则点P 到平面α的距离d 就是，即d =||||MP ⋅n n . （2）线面、面面距离的向量公式平面α∥直线l ，平面α的法向量为n ，点M ∈α、P ∈l ，平面α与直线l 间的距离d 就是MP 在向量n 方向射影的绝对值，即d = .平面α∥β，平面α的法向量为n ，点M ∈α、P ∈β，平面α与平面β的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n . （3）异面直线的距离的向量公式设向量n 与两异面直线a 、b 都垂直，M ∈a 、P ∈b ，则两异面直线a 、b 间的距离d 就是MP 在向量n 方向射影的绝对值，即d =||||MP ⋅n n .三：利用空间向量解证平行、垂直关系1：①所谓直线的方向向量，就是指的向量，一条直线的方向向量有个。

高考数学(理)二轮专题复习用空间向量的方法解立体几何问题Word版含解析

课时巩固过关练(十四)用空间向量的方法解立体几何问题
一、选择题
1．已知向量a＝(1,1,0)，b＝(－1,0,2)，且ka＋b与2a－b互相垂直，则k的值为()
A．1 B.
C. D.
解析：由题意知，ka＋b＝(k－1，k,2)，2a－b＝(3,2，－2)，∵ka＋b与2a－b垂直，∴3(k－1)＋2k－4＝0，解得k＝ .
解析：取CC1的中点E，连接AC，AE.因为正方体ABCD－A′B′C′D′的棱长为1，设＝a，＝b，＝c，则a＋b＋ c＝＋＋＝.所以＝||＝＝＝ .
答案：
三、解答题
9．如图所示的多面体中，AD⊥平面PDC，ABCD为平行四边形，E为AD的中点，F为线段BP上一点，∠CDP＝120°，AD＝3，AP＝5，PC＝2 .
A．EF至多与A1D，AC之一垂直
B．EF⊥A1D，EF⊥AC
C．EF与BD1相交
D．EF与BD1异面
解析：以D点为坐标原点，以DA，DC，DD1所在直线分别为x，y，z轴建立空间直角坐标系，设正方体的棱长为1，则A1(1,0,1)，D(0,0,0)，A(1,0,0)，C(0,1,0)，E ，F ，B(1,1,0)，D1(0,0,1)，＝(－1,0，－1)，＝(－1,1,0)，＝，＝(－1，－1,1)，＝－，·＝·＝0，从而EF∥BD1，EF⊥A1D，EF⊥AC.故选B.
∴a＝2 ，△ABC的外接圆半径为 AB＝1，三棱柱的外接球的球心为上、下底面直角三角形斜边中点连线的中点O，∴外接球的半径R＝＝2，∴外接球的表面积S＝4π×22＝16π.故选A.
答案：A
二、填空题
8．(2016·河北衡水武邑中学期中)已知正方体ABCD－A′B′C′D′的棱长为1，设＝a，＝b，＝c，则＝__________.

高考数学二轮：5.3《立体几何中的向量方法》试题(含答案)

第 3 讲立体几何中的向量方法1． (2014课·标全国Ⅱ )直三棱柱 ABC－ A1B1C1中，∠ BCA＝ 90°，M ，N 分别是 A1B1， A1C1的中点， BC＝ CA＝ CC1，则 BM 与 AN 所成角的余弦值为 ()12302A. 10B.5C. 10D. 22． (2015安·徽 ) 如图所示，在多面体A1B1D1DCBA 中，四边形AA1B1B，ADD 1A1， ABCD 均为正方形， E 为 B1D 1的中点，过A1，D ，E 的平面交CD1于 F.(1)证明： EF∥ B1C；(2)求二面角E-A1D- B1的余弦值．以空间几何体为载体考查空间角是高考命题的重点，与空间线面关系的证明相结合，热点为二面角的求解，均以解答的形式进行考查，难度主要体现在建立空间直角坐标系和准确计算上 .热点一利用向量证明平行与垂直设直线 l 的方向向量为a＝(a1，b1，c1)，平面α、β的法向量分别为μ＝( a2，b2，c2)，v＝(a3，b3， c3)则有：(1)线面平行l∥ α? a⊥ μ? a·μ＝ 0? a1a2＋ b1b2＋ c1c2＝ 0.(2)线面垂直l⊥ α? a∥ μ? a＝ kμ? a1＝ka2， b1＝ kb2， c1＝ kc2.(3)面面平行α∥ β? μ∥v? μ＝λv? a2＝λa， b ＝λb， c ＝λc32323.(4)面面垂直α⊥ β? μ⊥v? μ·v＝ 0? a2a3＋ b2b3＋c2c3＝ 0.例 1 如图，在直三棱柱 ADE— BCF 中，面 ABFE 和面 ABCD 都是正方形且互相垂直， M 为 AB 的中点， O 为 DF 的中点．运用向量方法证明：(1)OM ∥平面 BCF ；(2)平面 MDF ⊥平面 EFCD .思维升华用向量知识证明立体几何问题，仍然离不开立体几何中的定理．如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a∥ b，只需证明向量a＝λb(λ∈ R)即可．若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外．跟踪演练1如图所示，已知直三棱柱ABC— A1B1C1中，△ ABC 为等腰直角三角形，∠BAC＝ 90°，且 AB＝ AA1， D、 E、 F 分别为 B1A、 C1C、BC 的中点．求证：(1)DE ∥平面 ABC；(2)B1F ⊥平面 AEF .热点二利用空间向量求空间角设直线 l ，m 的方向向量分别为a＝( a1，b1，c1)，b＝(a2，b2，c2)．平面α，β的法向量分别为μ＝ (a3， b3， c3)，v＝ (a4， b4， c4)(以下相同 ) ．(1)线线夹角π设 l ， m 的夹角为θ(0≤θ≤2)，则|a·b|＝|a1a2＋ b1b2＋ c1c2 |cosθ＝|a||b|a12＋ b12＋ c12a22＋ b22＋ c22.(2)线面夹角π设直线 l 与平面α的夹角为θ(0≤θ≤2)，则 sin θ＝|a·μ|＝|cos〈a，μ〉 |. |a||μ|(3)面面夹角设平面α、β的夹角为θ(0≤θ<π)，则 |cos θ|＝|μ·v|＝ |cos〈μ，v〉 |. |μ||v|例 2 (2015 ·江苏 )如图，在四棱锥P－ABCD 中，已知PA⊥平面 ABCD ，πABCD 为直角梯形，∠ ABC＝∠ BAD＝， PA＝ AD ＝ 2， AB＝ BC2＝1.(1)求平面 PAB 与平面 PCD 所成二面角的余弦值；(2)点 Q 是线段 BP 上的动点，当直线CQ 与 DP 所成的角最小时，求线段BQ 的长．思维升华(1)运用空间向量坐标运算求空间角的一般步骤：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论．(2)求空间角注意：①两条异面直线所成的角α不一定是直线的方向向量的夹角β，即cosα＝|cos β|.②两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角．③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，即注意函数名称的变化．跟踪演练 2 (2014 ·福建 )在平面四边形ABCD中， AB＝BD＝CD＝1，AB⊥ BD，CD ⊥BD.将△ABD沿BD折起，使得平面ABD ⊥平面BCD ，如图所示．(1)求证： AB⊥ CD ；(2)若 M 为 AD 中点，求直线AD 与平面 MBC 所成角的正弦值．热点三利用空间向量求解探索性问题存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对象(数值、图形、函数等 )是否存在或某一结论是否成立．解决这类问题的基本策略是先假设题中的数学对象存在(或结论成立 )或暂且认可其中的一部分结论，然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论．例 3 如图，在直三棱柱 ABC－ A1B1C1中，AB＝ BC＝ 2AA1，∠ ABC＝90°，D 是 BC 的中点．(1)求证： A1 B∥平面 ADC 1；(2)求二面角C1－ AD－ C 的余弦值；(3)试问线段A1B1上是否存在点E，使 AE 与 DC 1成 60°角？若存在，确定 E 点位置；若不存在，说明理由．思维升华空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断．解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法．跟踪演练3如图所示，四边形ABCD 是边长为 1 的正方形， MD ⊥平面 ABCD ，NB⊥平面 ABCD ，且 MD ＝NB ＝1， E 为 BC 的中点．(1)求异面直线NE 与 AM 所成角的余弦值；(2)在线段 AN 上是否存在点 S，使得 ES⊥平面 AMN ？若存在，求线段AS 的长；若不存在，请说明理由．如图，五面体中，四边形ABCD 是矩形， AB∥EF ， AD⊥平面 ABEF ，1且 AD ＝1， AB＝2EF＝ 22， AF＝ BE＝ 2，P、 Q 分别为 AE 、BD 的中点．(1)求证： PQ∥平面 BCE；(2)求二面角A－ DF －E 的余弦值．提醒：完成作业专题五第3讲二轮专题强化练专题五第 3 讲立体几何中的向量方法A 组专题通关1．已知平面 ABC，点 M 是空间任意一点，点→3→1→1→M 满足条件 OM＝ OA＋OB＋ OC，则直线488AM()A ．与平面ABC 平行B ．是平面ABC 的斜线C．是平面ABC 的垂线D．在平面ABC 内2.如图，点P 是单位正方体ABCD － A1B1C1D1中异于 A 的一个顶点，→ →则 AP·AB的值为 ()A ． 0B．1C．0或1D．任意实数3.如图所示，正方体ABCD －A1B1C1D1的棱长为a， M、 N 分别为A1B和 AC 上的点， A1M＝ AN＝23a，则 MN 与平面 BB1C1C 的位置关系是()A ．相交B．平行C．垂直D．不能确定4．如图，三棱锥 A－ BCD 的棱长全相等， E 为 AD 的中点，则直线 CE 与 BD 所成角的余弦值为 ()33A.6B. 2331C.6D. 25．已知正三棱柱 ABC－A1B1C1的侧棱长与底面边长相等，则 AB1与侧面 ACC 1A1所成角的正弦值等于 ()610A.4B. 423C. 2D. 26．在棱长为 1 的正方体ABCD － A1B1C1D1中，M，N 分别为 A1B1，BB1的中点，那么直线 AM 与 CN 所成角的余弦值为 ________．7．在一直角坐标系中，已知A(－1,6)， B(3，－ 8)，现沿 x 轴将坐标平面折成60°的二面角，则折叠后 A、B 两点间的距离为 ________．→→→ 2→ 2→→→8．已知 ABCD －A1B1C1D1为正方体，① (A1A＋ A1D 1＋ A1B1) ＝3A1B1；②A1C·(A1B1－ A1 A)＝ 0；→→→ → →③向量 AD 1与向量 A1B的夹角是 60°；④正方体ABCD － A1B1C1D 1的体积为 |AB ·AA 1·AD |.其中正确命题的序号是________．9.如图，在底面是矩形的四棱锥P— ABCD 中， PA⊥底面 ABCD，E，F 分别是 PC， PD 的中点， PA＝ AB＝ 1， BC＝ 2.(1)求证： EF∥平面 PAB；(2)求证：平面PAD ⊥平面 PDC .10．(2015 ·庆重 )如图，三棱锥 P-ABC 中，PC⊥平面 ABC，PC＝ 3，∠ ACB π＝2.D， E 分别为线段AB， BC 上的点，且CD＝DE ＝2， CE＝ 2EB＝2.(1)证明： DE⊥平面 PCD；(2)求二面角APDC 的余弦值．B 组能力提高11． (2014 ·川四 )如图，在正方体 ABCD －A 1B 1C 1D 1 中，点 O 为线段 BD 的中点．设点 P 在线段 CC 1 上，直线 OP 与平面 A 1BD 所成的角为 α，则 sin α的取值范围是 ()3，1]B ． [6， 1]A ．[ 33 62 2 2 2， 1]C ．[3，3]D ．[ 312．如图，在正方体 ABCD － A 1B 1C 1D 1 中，点 P 在直线 BC 1 上运动时，有下列三个命题：①三棱锥 A － D 1PC 的体积不变；②直线 AP 与平面ACD 1 所成角的大小不变；③二面角 P － AD 1－ C 的大小不变．其中真命题的序号是 ________．13．已知正方体 ABCD － A 1 B 1 C 1D 1 的棱长为 1， E 、 F 分别为 BB 1、 CD 的中点，则点 F 到平面 A 1D 1E 的距离为 ______________．14.如图，在三棱锥 P —ABC 中， AC ＝ BC ＝2，∠ ACB ＝90°，AP ＝ BP ＝AB ，PC ⊥ AC ，点 D 为 BC 的中点．(1)求二面角A— PD —B 的余弦值；1(2)在直线 AB 上是否存在点M，使得 PM 与平面 PAD 所成角的正弦值为6，若存在，求出点M的位置；若不存在，说明理由．学生用书答案精析第 3 讲立体几何中的向量方法高考真题体验1． C [方法一补成正方体，利用向量的方法求异面直线所成的角．由于∠ BCA ＝ 90°，三棱柱为直三棱柱，且 BC ＝ CA ＝ CC 1，可将三棱柱补成正方体．建立如图 (1)所示空间直角坐标系．设正方体棱长为 2，则可得 A(0,0,0) ，B(2,2,0) ， M(1,1,2) ， N(0,1,2) ，→∴ BM ＝ (－1，－ 1,2)，→．AN ＝ (0,1,2)→ → → →BM ·AN∴ cos 〈BM ， AN 〉＝ → →|BM||AN|－ 1＋ 4＝－2＋－ 2＋ 22× 02＋ 12＋ 22330＝6×5＝10.方法二通过平行关系找出两异面直线的夹角，再根据余弦定理求解．如图 (2) ，取 BC 的中点 D ，连接 MN ，ND ，AD ，由于 MN 綊1 B 1C 1 綊 BD ，因此有 ND 綊 BM ，2则 ND 与 NA 所成的角即为异面直线BM 与 AN 所成的角．设 BC ＝ 2，则 BM ＝ ND ＝ 6， AN＝ 5， AD ＝ 5，因此 cos ∠ AND ＝ ND 2＋ NA 2－ AD 230 2ND ·NA＝10.]2． (1)证明由正方形的性质可知A 1B 1∥ AB ∥ DC ，且 A 1B 1＝ AB ＝ DC ，所以四边形A 1B 1CD为平行四边形，从而 B 1 C ∥ A 1D ，又 A 1D ? 面 A 1DE ， B 1 C?面 A 1DE ，于是 B 1C ∥面 A 1DE.又B 1C? 面 B 1 CD 1.面 A 1DE ∩面 B 1CD 1＝ EF ，所以 EF ∥ B 1C.(2)解因为四边形 AA 1B 1B ，ADD 1A 1， ABCD 均为正方形，所以 AA 1⊥ AB ， AA 1⊥AD ， AB ⊥ AD 且AA 1 ＝AB ＝AD .以 A 为原点，分别以 → → →AB ， AD ，AA 1为 x 轴， y 轴和 z 轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A(0,0,0) ，B(1,0,0) ，D(0,1,0) ，A 1(0,0,1) ， B 1(1,0,1) ，D 1 (0,1,1) ，而 E 点为 B 1D 1 的11中点，所以 E 点的坐标为，， 1 .设面 A 1DE 的法向量n 1＝ (r 1， s 1， t 1)，而该面上向量→1 1 →A 1E ＝，， 0， A 1D ＝ (0,1，－ 1)，由2 2→n 1⊥A 1E ，→11r 1＋ s 1＝ 0，n 1⊥ A 1D 得 r 1， s 1， t 1 应满足的方程组2 2s 1－ t 1＝ 0，(－ 1,1,1)为其一组解，所以可取 n 1＝ (－ 1,1,1)．设面 A 1B 1CD 的法向量 n 2＝ (r 2，s 2，t 2)，而该面上向量 →→A 1B 1＝ (1,0,0) ，A 1 D ＝ (0,1，－ 1)，由此同理可得 n 2＝ (0,1,1) ．所以结合图形知二面角E-A 1D -B 1 的余弦值为 |n 1·n 2| ＝ 2 ＝ 6.|n 1| ·|n 2| 3× 2 3热点分类突破例1 证明方法一由题意，得 AB ， AD ，AE 两两垂直，以 A 为原点建立如图所示的空间直角坐标系．设正方形边长为 1，则 A(0,0,0) ， B(1，0,0)， C(1,1,0) ，D (0,1,0) ，11 1 1 F(1,0,1)，M 2， 0， 0 ， O 2， 2，2 .→ 1 1 →1,0,0) ， (1)OM ＝ 0，－，－， BA ＝ (－ 2 2→ → → →∴OM ·BA ＝0, ∴OM ⊥BA.∵棱柱 ADE —BCF 是直三棱柱，→∴ AB ⊥平面 BCF ，∴ BA 是平面且 OM?平面 BCF ，∴ OM ∥平面BCF 的一个法向量，BCF .(2)设平面 MDF 与平面 EFCD 的一个法向量分别为n 1＝ (x 1， y 1， z 1 )，n 2＝ ( x 2， y 2 ， z 2)．→→∵ DF ＝ (1，－ 1,1)， DM ＝n 1 ·DF →＝ 0，由→n 1 ·DM ＝ 0.x 1－ y 1＋ z 1＝ 0，得 1解得x 1－ y 1＝ 0，21→→，，－ 1，0 ， DC ＝(1,0,0)， CF ＝ (0，－ 1,1)21y 1＝2x 1，1z 1 ＝－ x 1，1 1 令 x 1＝ 1，则 n 1＝ 1，2，－2 . 同理可得 n 2＝ (0,1,1) ．∵ n 1·n 2＝ 0，∴平面MDF ⊥平面 EFCD .方法二→ → → →1 →→ ＋ 1 →(1)OM ＝ OF ＋ FB ＋BM＝ DF －BF BA2 21 →→→1→1 → 1 → 1 →＝(DB ＋ BF)－ BF ＋ BA ＝－BD － BF ＋BA2 2222＝－ 1 → →1 → 1 →2 (BC ＋ BA)－ BF ＋2BA2＝－ 1 → 1 →2 BC － BF .2→ → →∴向量 OM 与向量 BF ， BC 共面，又 OM?平面 BCF ，∴ OM ∥平面 BCF .(2)由题意知， BF ， BC ， BA 两两垂直，∵→ ＝→，→＝→－→， CD BA FC BC BF→ →1 → 1 → → ＝ 0， ∴ OM·CD ＝－BC －BF2 2·BA→ → 1 → 1 →→ → OM ·FC ＝－ BC － BF ·(BC －BF )22＝－ 1BC →2＋ 1BF → 2＝ 0.2 2∴ OM ⊥ CD ， OM ⊥ FC ，又 CD ∩FC ＝ C ，∴ OM ⊥平面 EFCD .又 OM? 平面 MDF ，∴平面 MDF ⊥平面 EFCD .跟踪演练 1证明 (1)如图建立空间直角坐标系 A － xyz ，令 AB ＝ AA 1＝ 4，则 A(0,0,0) ， E(0,4,2) ，F(2,2,0) ， B(4,0,0) ， B 1(4,0,4) ．取 AB 中点为 N ，连接 CN ，则 N(2,0,0) ， C(0,4,0) ，D (2,0,2) ，→∴ DE ＝ (－ 2,4,0)，→NC ＝ (－ 2,4,0) ，→ →∴ DE ＝NC ，∴ DE ∥ NC ，又∵ NC? 平面 ABC ， DE?平面 ABC.故 DE ∥平面 ABC.→(2)B 1F ＝ (－ 2,2，－ 4)，→ →．EF ＝ (2，－ 2，－ 2)， AF ＝ (2,2,0)→ →B 1F ·EF ＝ (－ 2) ×2＋ 2×(－2)＋ (－ 4) ×(－ 2)＝ 0，→ →B 1F ·AF ＝ (－ 2) ×2＋ 2×2＋ (－ 4) ×0＝0.∴→⊥→，→⊥→，即B 1F EF B 1F AF B 1F ⊥ EF ， B 1F ⊥AF ，又∵ AF ∩FE ＝ F ，∴ B 1F ⊥平面 AEF.例 2解→ → →以 { AB ，AD ，AP } 为正交基底建立如图所示的空间直角坐标系 Axyz ，则各点的坐标为B(1,0,0) ，C(1,1,0) ， D(0,2,0) ， P(0,0,2)．(1)因为 AD ⊥平面→ →．PAB ，所以 AD 是平面 PAB 的一个法向量， AD ＝ (0,2,0) → ，－ →＝ (0,2，－ 2)．因为 PC ＝(1,1 2)， PD设平面 PCD 的法向量为 m ＝( x ， y ， z)，→ →则 m ·PC ＝ 0， m ·PD ＝ 0，x ＋ y － 2z ＝ 0，令 y ＝1，解得 z ＝1， x ＝ 1.即2y － 2z ＝ 0.所以 m ＝(1,1,1) 是平面 PCD 的一个法向量．→ →3AD ·m从而 cos 〈 AD ， m 〉＝ → ＝ 3 ，|AD ||m |所以平面 PAB 与平面 PCD 所成二面角的余弦值为33 .→ → →≤λ≤1)，(2)因为 BP ＝ (－ 1,0,2)，设 BQ ＝ λBP ＝ (－ λ， 0,2λ)(0 → → → →又 CB ＝ (0，－ 1,0) ，则 CQ ＝CB ＋BQ ＝ (－ λ，－ 1,2λ)， →，又 DP ＝ (0，－ 2,2)→ → → →1＋ 2λCQ ·DP＝ .从而 cos 〈 CQ ， DP 〉＝ → → 2|CQ||DP | 10λ＋ 2设 1＋2λ＝ t ， t ∈ [1,3] ，2→→2t 2＝2 9则 cos 〈 CQ ，DP 〉＝21 5≤ .5t － 10t ＋ 92 20 109 t －9 ＋ 99 2→ →3 10 当且仅当 t ＝，即 λ＝时， |cos 〈CQ ， DP 〉 |的最大值为10.55π因为 y ＝ cos x 在 0，2 上是减函数，此时直线CQ 与 DP 所成角取得最小值．又因为 BP ＝ 12＋ 22＝ 5，所以 BQ ＝ 2BP ＝2 5.55跟踪演练 2 (1)证明 ∵平面 ABD ⊥平面 BCD ，平面 ABD ∩平面 BCD ＝ BD ，AB? 平面 ABD ，AB ⊥ BD ，∴ AB ⊥平面 BCD .又 CD ? 平面 BCD ，∴ AB ⊥ CD .(2)解过点 B 在平面 BCD 内作 BE ⊥ BD ，如图．由 (1) 知 AB ⊥平面 BCD ， BE? 平面 BCD ， BD ? 平面 BCD ， ∴ AB ⊥ BE ， AB ⊥ BD.以 B 为坐标原点，分别以→ → →BE ， BD ， BA 的方向为 x 轴， y 轴， z 轴的正方向建立空间直角坐标系．依题意，得 B(0,0,0) ， C(1,1,0) ，D (0,1,0) ，A(0,0,1) 11，M (0，， )，2 2→→1 1 →，－ 1)．则 BC ＝(1,1,0) ，BM ＝ (0，， )， AD ＝ (0,122设平面 MBC 的法向量 n ＝ (x 0， y 0， z 0)，n ·BC →＝0，x 0＋ y 0＝ 0，则即 1＋ 1＝ 0，→2y 0 n ·BM ＝ 0，2z 0取 z 0＝ 1，得平面 MBC 的一个法向量 n ＝ (1，－ 1,1)．设直线 AD 与平面 MBC 所成角为 θ，→ →6|n ·AD |则 sin θ＝ |cos 〈n ， AD 〉 |＝ → ＝ 3 ，|n | ·|AD |即直线 AD 与平面 MBC 所成角的正弦值为63.例 3 (1) 证明连接 A 1C ，交 AC 1 于点 O ，连接 OD . 由 ABC －A 1B 1C 1 是直三棱柱，得四边形ACC 1A 1 为矩形， O 为 A 1C的中点．又D 为BC 的中点，所以 OD 为 △ A 1BC 的中位线，所以 A 1B ∥ OD.因为 OD? 平面 ADC 1， A 1B?平面 ADC 1，所以 A 1B ∥平面 ADC 1.(2)解由 ABC － A 1B 1C 1 是直三棱柱，且∠ A BC ＝ 90°，得 BA ， BC ， BB 1 两两垂直．以 BC ， BA ， BB 1 所在直线分别为 x ， y ， z 轴，建立如图所示的空间直角坐标系B － xyz.设 BA ＝ 2，则 B(0,0,0) ，C(2,0,0) ， A(0,2,0) ， C 1(2,0,1) ， D(1,0,0) ，→ →所以 AD ＝ (1，－ 2,0) ， AC 1＝ (2，－ 2,1)．设平面 ADC 1 的法向量为 n ＝ (x ， y ， z)， →n ·AD ＝ 0，则有→n ·AC 1＝ 0.x － 2y ＝ 0，取 y ＝1，得 n ＝ (2,1，－ 2)．所以 2x － 2y ＋ z ＝ 0.易知平面 ADC 的一个法向量为 v ＝(0,0,1) ．所以 cos 〈 n ， v 〉＝ n ·v2＝－ .|n | |·v | 3因为二面角 C 1－ AD － C 是锐二面角，所以二面角 C 1－ AD － C 的余弦值为2 .3(3)解假设存在满足条件的点 E.因为点 E 在线段 A 1B 1 上， A 1(0,2,1) ， B 1(0,0,1) ，故可设 E(0， λ，1)，其中 0≤λ≤2.→→．所以 AE ＝ (0， λ－ 2,1)， DC 1＝ (1,0,1) 因为 AE 与 DC 1 成 60°角，→→→ →1|AE ·DC 1|所以 |cos 〈AE ，DC 1〉 |＝ → →＝2，|AE| |DC ·1 |即12＋1· 2＝1，解得 λ＝ 1 或 λ＝ 3(舍去 )．λ－2所以当点 E 为线段 A 1 B 1 的中点时， AE 与 DC 1 成 60°角．跟踪演练 3解 (1) 如图，以 D 为坐标原点， DA ， DC ， DM 所在直线分别为 x 轴，y 轴，z 轴，建立空间直角坐标系，则 D(0,0,0) ，A(1,0,0)，M(0,0,1) ， C(0,1,0) ， B(1,1,0) ，1 →1 ， 0，－ 1)， N(1,1,1)， E(， 1,0)，所以 NE ＝ (－22→AM ＝(－ 1,0,1)．→ →1→ →2 10|NE ·AM |因为 |cos 〈NE ，AM 〉 |＝ → → ＝5＝10 ，|NE| ×|AM| 2 × 2所以异面直线 NE 与 AM 所成角的余弦值为1010.(2)假设在线段 AN 上存在点 S ，使得 ES ⊥平面 AMN . →＝(0,1,1) ，因为 AN→ → ＝(0 ，λ， λ)(0 ≤λ≤1)，可设 AS ＝ λAN→1 又 EA ＝ (2，－ 1,0)，→→→1所以 ES ＝ EA ＋ AS ＝ ( ， λ－1， λ)．2由 ES ⊥平面 AMN ，→→ES ·AM ＝ 0，得→ →ES ·AN ＝ 0，－ 1＋ λ＝ 0，即 2λ－＋ λ＝ 0，1 → 1 1 →2 . 故 λ＝，此时 AS ＝ (0，， )， |AS|＝222 2经检验，当 AS ＝2时， ES ⊥平面 AMN .2故线段 AN 上存在点 S ，使得 ES ⊥平面 AMN ，此时 AS ＝ 2.2高考押题精练(1)证明连接 AC ，∵四边形 ABCD 是矩形，且 Q 为 BD 的中点，∴Q 为 AC 的中点，又在 △AEC 中， P 为 AE 的中点，∴ PQ ∥EC ，∵ EC? 面 BCE ， PQ?面 BCE ，∴ PQ ∥平面 BCE.(2)解如图，取 EF 的中点 M ，则 AF ⊥ AM ，以 A 为坐标原点，以 AM ，AF ，AD 所在直线分别为 x ，y ，z 轴建立空间直角坐标系．则 A(0,0,0) ， D (0,0,1) ，M (2,0,0)， F(0,2,0) ．→ → →可得 AM ＝ (2,0,0) ， MF ＝ (－ 2,2,0)， DF ＝ (0,2，－ 1)．→n ·MF ＝ 0，设平面 DEF 的法向量为n ＝ (x ， y ， z)，则→n ·DF ＝ 0.－ 2x ＋ 2y ＝0，x － y ＝ 0，故 2y －z ＝0，即2y － z ＝ 0.令 x ＝1，则 y ＝1， z ＝ 2，故 n ＝(1,1,2) 是平面 DEF 的一个法向量．→∵ AM ⊥面 ADF ，∴ AM 为平面 ADF 的一个法向量．→→2×1＋ 0×1＋ 0×26n ·AM∴ cos 〈n ， AM 〉＝→ ＝ 6×2＝ 6.|n | ·|AM|由图可知所求二面角为锐角，6∴二面角A－DF － E 的余弦值为 6 .二轮专题强化练答案精析第 3 讲立体几何中的向量方法1． D [由已知得 M 、 A 、 B 、C 四点共面．所以 AM 在平面 ABC 内，选 D.]→→ → → → → →→ 1，其中一个与 →2． C [AP 可为下列 7 个向量： AB ， AC ， AD ， AA 1， AB 1，AC 1， AD AB 重合，→→→2→→→→→ → → →→AP ·AB ＝ |AB| ＝ 1； AD ，AD 1， AA 1 与AB 垂直，这时 AP ·AB ＝ 0； AC ， AB 1 与 AB 的夹角为45°，→ → π → → 3×1×cos ∠ BAC 1＝ 3× 1＝ 1，故选 C.] 这时 AP ·AB ＝ 2×1×cos ＝ 1，最后 AC 1·AB ＝3 4 3． B [分别以 C 1B 1、 C 1D 1、 C 1C 所在直线为 x ， y ， z 轴，建立空间直角坐标系，如图所示．∵ A 1M ＝ AN ＝ 23 a ，∴ M a ， 2 a ，N 2 23a ， 3 3a ，3a ， a ，→ a 2 a .∴MN ＝－，0， 33→又 C 1 (0,0,0) ，D 1(0， a,0)，∴ C 1D 1＝ (0， a,0)，∴→ →＝，∴→⊥→MN ·C 1D 1 0 MN C 1D 1.→MN?平面 BB 1C 1C ，∴ MN ∥平面 BB 1C 1C.]∵ C 1D 1是平面 BB 1C 1C 的法向量，且 4． A [设 AB ＝ 1，→ → → → → → 则 CE ·BD ＝ (AE － AC) ·(AD － AB)＝ 1 → 2 1 → →→ → → →2 AD － AD ·AB － AC ·AD ＋ AC ·AB2＝ 1 112 － cos 60 －°cos 60 ＋°cos 60 ＝° .24→ →1→ →43CE ·BD∴ cos 〈CE ，BD 〉＝ → → ＝ 3＝6 .选 A.]|CE||BD | 25． A [如图所示建立空间直角坐标系，设正三棱柱的棱长为2， O(0,0,0)，B(3， 0,0)， A(0，－ 1,0)， B 1(→ 3， →3， 0,2)，则 AB 1＝ ( 1,2)，则 BO ＝ (－ 3，→ →0,0)为侧面ACC 1A 1的法向量，由 sin θ＝ |AB 1·BO|＝ 6.] → →4|AB 1||BO|2 6.5解析以 D 点为坐标原点，分别以DA ， DC ，DD 1 所在直线为 x 轴， y轴， z 轴建立如图所示的空间直角坐标系，则A(1,0,0) ， M(1， 1， 1)，21C(0,1,0)， N(1,1， 2) ．→ 1 →1所以 AM ＝ (0，， 1)，CN＝ (1,0， )．22 → →111故 AM ·CN ＝ 0×1＋ ×0＋1× ＝，2 2 2→2 1 2 ＋ 1 25|AM |＝0 ＋ 2 ＝，2→2 21 2 ＝5|CN|＝ 1＋0＋ 2 ，2→ →1→→2 2AM ·CN＝所以 cos 〈 AM ， CN 〉＝→ → 5 5＝ .5|AM ||CN|2 ×27．2 17解析如图为折叠后的图形，其中作 AC ⊥ CD ， BD ⊥ CD ，则 AC ＝ 6， BD ＝ 8， CD ＝ 4，两异面直线 AC 、 BD 所成的角为 60°，故由→＝→＋→＋→，AB AC CD DB→ 2 →→→2，得 |AB| ＝ |AC ＋CD ＋ DB | ＝ 68→∴|AB|＝ 2 17.8．①②→→→2→ 2→ 2 → 解析设正方体的棱长为 1，①中 (A 1A ＋ A 1D 1＋A 1B 1) ＝A 1C ＝ 3A 1B 1 ＝3，故①正确； ②中 A 1B 1→ →→－ A 1A ＝ AB 1，由于 AB 1⊥ A 1C ，故②正确； ③中 A 1B 与 AD 1 两异面直线所成的角为 60°，但 AD 1→→ → →与 A 1B 的夹角为 120°，故③不正确；④中 |AB ·AA 1·AD |＝ 0.故④也不正确．9．证明(1) 以 A 为原点， AB 所在直线为 x 轴， AD 所在直线为 y 轴， AP 所在直线为 z 轴，建立如图所示的空间直角坐标系，则 A(0,0,0) ， B(1,0,0) ，C(1,2,0) ， D(0,2,0) ， P(0,0,1) ，∵ E， F 分别是 PC， PD 的中点，∴ E 1， 1，1，F 0，1，1，222→1，0， 0→．EF＝－，AB＝ (1,0,0)2→ 1 →→ →∵EF＝－AB ，∴ EF ∥ AB，2即 EF∥AB，又 AB? 平面 PAB， EF?平面 PAB，∴ EF ∥平面 PAB.→，－ 1)→→→→，(2)由 (1)可知 PB＝ (1,0，PD ＝ (0,2，－ 1)，AP＝ (0,0,1)， AD＝ (0,2,0)， DC ＝ (1,0,0)→→∵ AP·DC ＝ (0,0,1) (1,0,0)·＝ 0，→→AD ·DC ＝ (0,2,0) (1,0,0)·＝ 0，→→→→∴ AP⊥ DC，AD ⊥DC ，即 AP⊥ DC ，AD⊥ DC .又 AP∩AD＝ A，∴ DC ⊥平面 PAD .∵DC ? 平面 PDC，∴平面 PAD ⊥平面 PDC .10． (1)证明由PC⊥平面ABC，DE ?平面ABC，故PC⊥ DE.由 CE＝ 2， CD＝ DE＝ 2得△CDE 为等腰直角三角形，故 CD ⊥ DE .由 PC∩CD＝ C， DE 垂直于平面 PCD 内两条相交直线，故 DE ⊥平面 PCD .π(2)解由(1)知，△ CDE为等腰直角三角形，∠DCE ＝，如图，过 D 作4DF 垂直 CE 于 F，易知 DF ＝ FC＝ FE＝ 1，又已知EB＝ 1，故 FB＝ 2.πDF＝FB233.由∠ ACB＝得 DF ∥AC ，AC BC ＝，故 AC＝DF ＝2322以 C 为坐标原点，分别以→ →→轴， y 轴， z 轴的正方向建立空间直角坐标CA，CB，CP的方向为 x系，则 C(0,0,0) ，P(0,0,3) ，A 3，0， 0→→，2，E(0,2,0) ，D (1,1,0)，ED＝(1，－ 1,0)，DP＝ (－ 1，－ 1,3)→1，－ 1，0 . DA ＝2→→－ x1－y1＋3z1＝0，设平面 PAD 的法向量为n1＝(x1，y1，z1)，由 n1·DP＝0，n1·DA＝0，得1x1－ y1＝0，2故可取 n1＝(2,1,1)．→由 (1) 可知 DE ⊥平面 PCD ，故平面PCD 的法向量n2可取为ED，即 n2＝(1，－1,0)．从而法向量n1，n2的夹角的余弦值为cos 〈n1，n2〉＝n1·n2＝3，|n1| |·n2 |6故所求二面角 APDC 的余弦值为3 6 .11． B [ 根据题意可知平面A1BD ⊥平面 A1ACC 1且两平面的交线是A1O，所以过点P 作交线 A1O 的垂线 PE，则 PE⊥平面 A1BD，所以∠ A1OP 或其补角就是直线OP 与平面 A1BD 所成的角α.设正方体的边长为2，则根据图形可知直线OP 与平面 A1BD 可以垂直．当点 P 与点 C1重合时可得 A1O＝OP＝6，A1C1＝2 2，所以1× 6× 6×sin α＝1×22×2，22所以 sin α＝2 2；3当点 P 与点 C 重合时，可得sin α＝2＝6 6 3.根据选项可知 B 正确． ]12．①③解析①中，∵ BC1∥平面 AD1C，∴ BC1上任意一点到平面 AD 1C 的距离相等，所以体积不变，正确；②中，P 在直线 BC1上运动时，直线 AB 与平面 ACD 1所成角和直线 AC1与平面ACD 1 所成角不相等，所以不正确；③中，P 在直线 BC 1 上运动时，点 P 在平面 AD 1 C 1B 中，既二面角 P —AD 1－C 的大小不受影响，所以正确．3 513. 10解析以 A 为坐标原点， AB 、 AD 、AA 1 所在直线分别为 x 轴、 y 轴、 z 轴建立空间直角坐标系，如图所示，11则 A 1 (0,0,1) ，E(1,0，2)， F(2， 1,0)， D 1 (0,1,1) ．→1 →．∴ A 1E ＝ (1,0，－)，A 1D 1＝ (0,1,0)2设平面 A 1D 1E 的一个法向量为 n ＝ (x ， y ， z)，→＝0，1n ·A 1E即x － z ＝ 0，则2→ y ＝ 0.n ·A 1D 1＝ 0，令 z ＝ 2，则 x ＝ 1.∴ n ＝ (1,0,2) ．→1又 A 1F ＝ (2， 1，－ 1)，∴点 F 到平面 A 1D 1 E 的距离为→1－ 2|||A 1F ·n |＝2＝ 3 5d ＝ |n |510.14．解 (1)∵ AC ＝ BC ， PA ＝ PB ， PC ＝ PC ，∴△ PCA ≌△ PCB ，∴∠ PCA ＝∠ PCB ，∵ PC ⊥ AC ，∴ PC ⊥ CB ，又 AC ∩CB ＝ C ，∴ PC ⊥平面 ACB ，且 PC ， CA ， CB 两两垂直，故以 C 为坐标原点，分别以CB ， CA ， CP 所在直线为 x ，y ， z 轴建立空间直角坐标系，则C(0,0,0)， A(0,2,0) ， D(1,0,0) ， P(0,0,2)，→ →∴ AD ＝ (1，－ 2,0)， PD ＝ (1,0，－ 2)，设平面 PAD 的一个法向量为n ＝ (x ， y ， z) ，→n ·AD ＝0∴，∴取 n ＝ (2,1,1) ，→n ·PD ＝0→平面 PDB 的一个法向量为CA ＝ (0,2,0) ，→6∴ cos 〈n ， CA 〉＝ 6 ，设二面角 A —PD — B 的平面角为 θ，且 θ为钝角，6 6 ∴ cos θ＝－ 6 ，∴二面角 A — PD — B 的余弦值为－6.(2)方法一存在， M 是 AB 的中点或 A 是 MB 的中点．设 M(x,2－ x,0) (x ∈ R )，→∴ PM ＝ (x,2－ x ，－ 2)，∴ →|cos 〈 PM ， n 〉 ||x|1 ＝ x 2＋－ x2＋4· 6 ＝ 6，解得 x ＝ 1 或 x ＝－ 2，∴ M(1,1,0) 或 M(－ 2,4,0)，∴在直线 AB 上存在点 M ，且当 M 是 AB 的中点或 A 是 MB 的中点时，使得 PM 与平面 PAD所成角的正弦值为 16.方法二存在， M 是 AB 的中点或 A 是 MB 的中点． → →设 AM ＝ λAB ，→＝(2 λ，－ 2λ， 0) (λ∈ R )，则 AM ＝ λ(2，－ 2,0) → → →∴ PM ＝ PA ＋ AM ＝ (2λ，2－ 2λ，－ 2)，→|2λ|∴ |cos 〈 PM ， n 〉 |＝2＋－ 2λ 2＋ 4· 6 λ 1解得 λ＝或 λ＝－ 1.∴M 是 AB 的中点或 A 是 MB 的中点．∴在直线 AB 上存在点 M ，且当 M 是 AB 的中点或1＝6.A 是 MB 的中点时，使得 PM 与平面 PAD1所成角的正弦值为 .。

安徽省高考数学第二轮复习专题五立体几何第3讲用空间向量的方法解立体几何问题理

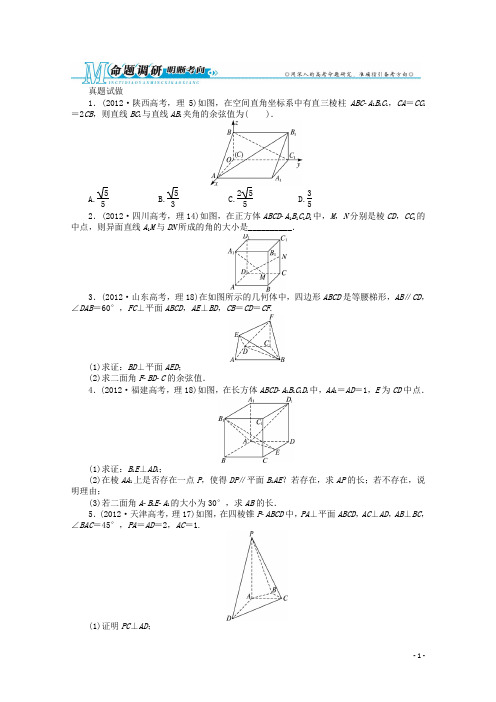
真题试做1．(2012·陕西高考，理5)如图，在空间直角坐标系中有直三棱柱ABC A 1B 1C 1，CA ＝CC 1＝2CB ，则直线BC 1与直线AB 1夹角的余弦值为( )．A.55B.53C.255D.352．(2012·四川高考，理14)如图，在正方体ABCD A 1B 1C 1D 1中，M ，N 分别是棱CD ，CC 1的中点，则异面直线A 1M 与DN 所成的角的大小是__________．3．(2012·山东高考，理18)在如图所示的几何体中，四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，FC ⊥平面ABCD ，AE ⊥BD ，CB ＝CD ＝CF .(1)求证：BD ⊥平面AED ；(2)求二面角F BD C 的余弦值．4．(2012·福建高考，理18)如图，在长方体ABCD A 1B 1C 1D 1中，AA 1＝AD ＝1，E 为CD 中点．(1)求证：B 1E ⊥AD 1；(2)在棱AA 1上是否存在一点P ，使得DP ∥平面B 1AE ？若存在，求AP 的长；若不存在，说明理由；(3)若二面角A B 1E A 1的大小为30°，求AB 的长． 5．(2012·天津高考，理17)如图，在四棱锥P ABCD 中，PA ⊥平面ABCD ，AC ⊥AD ，AB ⊥BC ，∠BAC ＝45°，PA ＝AD ＝2，AC ＝1.(1)证明PC ⊥AD ；(2)求二面角APCD的正弦值；(3)设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长．考向分析从近几年的高考试题来看，高考对本专题的考查主要有以下几个方面：一是证明空间平行关系，如(2012福建高考，理18)的第(2)问；二是利用空间向量证明垂直关系，如(2012山东高考，理18)的第(1)问和(2012福建高考，理18)的第(1)问；三是利用空间向量求角，如(2012山东高考，理18)的第(2)问；(2012天津高考，理17)的第(2)问和(2012四川高考，理14)，此类问题多以多面体为载体，常以解答题的形式出现，重在考查学生的空间想象能力．本专题是高考的必考内容之一，通常为一道综合题，常出现在几个解答题的中间位置，难度不是很大．在多数情况下传统法、向量法都可以解决，但首先应考虑向量法，这样可以降低难度．预测在今后高考中，本部分内容仍旧主要以解答题的形式出现，难度为中档．考查内容仍旧是利用空间向量的数量积及坐标运算来解决立体几何问题，其中利用空间向量求空间角仍然是重点．热点例析热点一利用空间向量证明平行问题【例1】如图所示，在平行六面体ABCDA1B1C1D1中，O是B1D1的中点．求证：B1C∥平面ODC1.规律方法利用空间向量证明平行问题的方法归纳．下面用数学语言描述为：(1)线线平行：直线与直线平行，只需证明它们的方向向量平行．(2)线面平行：利用线面平行的判定定理，证明直线的方向向量与平面内一条直线的方向向量平行；利用共面向量定理，证明平面外直线的方向向量与平面内两相交直线的方向向量共面；证明直线的方向向量与平面的法向量垂直．(3)面面平行：平面与平面的平行，除了利用面面平行的判定定理转化为线面平行外，只要证明两平面的法向量平行即可．下面用符号语言表述为：设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)，平面α，β的法向量分别为u＝(a3，b3，c3)，v＝(a4，b4，c4)．(1)线线平行：l∥m a∥b a＝k b a 1＝ka2，b1＝kb2，c1＝kc2.(2)线面平行：l∥αa⊥u a·u＝0a 1a3＋b1b3＋c1c3＝0.(3)面面平行：α∥βu∥v u＝k v a 3＝ka4，b3＝kb4，c3＝kc4.变式训练1(2012·安徽江南十校联考，理19)如图，在多面体ABCDEFG中，四边形ABCD 是边长为2的正方形，平面ABG、平面ADF、平面CDE都与平面ABCD垂直，且△ABG，△ADF，△CDE都是正三角形．(1)求证：AC∥EF；(2)求多面体ABCDEFG的体积．热点二利用空间向量证明垂直问题【例2】如图，在四棱锥PABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点，作EF⊥PB于点F，求证：(1)PA∥平面EDB；(2)PB⊥平面EFD.规律方法利用空间向量证明垂直问题的方法归纳．下面用数学语言描述为：(1)线线垂直：直线与直线的垂直，只要证明两直线的方向向量垂直．(2)线面垂直：利用线面垂直的定义，证明直线的方向向量与平面内的任意一条直线的方向向量垂直；利用线面垂直的判定定理，证明直线的方向向量与平面内的两条相交直线的方向向量垂直；证明直线的方向向量与平面的法向量平行．(3)面面垂直：平面与平面的垂直，除了用面面垂直的判定定理转化为线面垂直外，只要证明两平面的法向量垂直即可．下面用符号语言表述为：设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2)．平面α，β的法向量分别为u＝(a3，b3，c3)，v＝(a4，b4，c4)．(1)线线垂直：l⊥m a⊥b a·b＝0a 1a2＋b1b2＋c1c2＝0.(2)线面垂直：l⊥αa∥u a＝k u a 1＝ka3，b1＝kb3，c1＝kc3.(3)面面垂直：α⊥βu⊥v u·v＝0a 3a4＋b3b4＋c3c4＝0.变式训练2如图，在四棱锥PABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB＝2，∠BAD＝60°.(1)求证：BD⊥平面PAC；(2)若PA＝AB，求PB与AC所成角的余弦值；(3)当平面PBC与平面PDC垂直时，求PA的长．热点三利用空间向量求角和距离【例3】如图所示，在三棱柱ABCA1B1C1中，H是正方形AA1B1B的中心，AA1＝22，C1H⊥平面AA1B1B，且C1H＝ 5.(1)求异面直线AC 与A 1B 1所成角的余弦值； (2)求二面角A A 1C 1B 1的正弦值；(3)设N 为棱B 1C 1的中点，点M 在平面AA 1B 1B 内，且MN ⊥平面A 1B 1C 1，求线段BM 的长．规律方法(1)夹角计算公式 ①两异面直线的夹角若两条异面直线a 和b 的方向向量分别为n 1，n 2，两条异面直线a 和b 所成的角为θ，则cos θ＝|cos 〈n 1，n 2〉|＝⎪⎪⎪⎪⎪⎪n 1·n 2|n 1||n 2|.②直线与平面所成的角若直线a 的方向向量为a ，平面α的法向量为n ，直线a 与平面α所成的角为θ，则sin θ＝|cos 〈a ，n 〉|＝⎪⎪⎪⎪⎪⎪a ·n |a ||n |.③二面角设n 1，n 2分别为二面角的两个半平面的法向量，其二面角为θ，则θ＝〈n 1，n 2〉或θ＝π－〈n 1，n 2〉，其中cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|.(2)距离公式①点点距：点与点的距离，是以这两点为起点和终点的向量的模；②点线距：点M 到直线a 的距离，设直线的方向向量为a ，直线上任一点为N ，则点M 到直线a 的距离d ＝|MN |sin 〈MN ，a 〉；③线线距：两平行线间的距离，转化为点线距离；两异面直线间的距离，转化为点面距离或者直接求公垂线段的长度；④点面距：点M 到平面α的距离，如平面α的法向量为n ，平面α内任一点为N ，则点M 到平面α的距离d ＝|MN ||cos 〈MN ，n 〉|＝MN n n⋅；⑤线面距：直线和与它平行的平面间的距离，转化为点面距离； ⑥面面距：两平行平面间的距离，转化为点面距离．变式训练3已知ABCD A 1B 1C 1D 1是底面边长为1的正四棱柱，O 1为A 1C 1与B 1D 1的交点．(1)设AB 1与底面A 1B 1C 1D 1所成角的大小为α，二面角A B 1D 1A 1的大小为β.求证：tan βtan α；(2)若点C 到平面AB 1D 1的距离为43，求正四棱柱ABCD A 1B 1C 1D 1的高．热点四用向量法解决探索性问题【例4】如图，四棱锥S ABCD 的底面是正方形，每条侧棱的长都是底面边长的2倍，P 为侧棱SD 上的点．(1)求证：AC ⊥SD ；(2)若SD ⊥平面PAC ，求二面角P AC D 的大小；(3)在(2)的条件下，侧棱SC 上是否存在一点E ，使得BE ∥平面PAC ？若存在，求SE ∶EC 的值；若不存在，请说明理由．规律方法(1)用空间向量解决立体几何问题的步骤及注意事项： ①建系，要写理由，坐标轴两两垂直要证明；②准确求出相关点的坐标(特别是底面各点的坐标，若底面不够规则，则应将底面单独抽出来分析)，坐标求错将前功尽弃；③求平面法向量；④根据向量运算法则，求出三角函数值或距离； ⑤给出问题的结论．(2)利用空间向量巧解探索性问题：空间向量最适合于解决这类立体几何中的探索性问题，它无需进行繁杂的作图、论证、推理，只需通过坐标运算进行判断．在解题过程中，往往把“是否存在”问题，转化为“点的坐标是否有解，是否有规定范围的解”等，所以使问题的解决更简单、有效，应善于运用这一方法解题．变式训练4如图，平面PAD ⊥平面ABCD ，ABCD 为正方形，∠PAD ＝90°，且PA ＝AD ＝2；E ，F ，G 分别是线段PA ，PD ，CD 的中点．(1)求证：PB ∥平面EFG ；(2)求异面直线EG 与BD 所成的角的余弦值；(3)在线段CD 上是否存在一点Q ，使得A 到平面EFQ 的距离为45？若存在，求出CQ 的值；若不存在，请说明理由．思想渗透转化与化归思想——利用向量解决空间位置关系及求角问题主要问题类型：(1)空间线面关系的证明； (2)空间角的求法；(3)存在性问题的处理方法．求解时应注意的问题：(1)利用空间向量求异面直线所成的角时，应注意角的取值范围；(2)利用空间向量求二面角的平面角时，应注意观察二面角是钝角还是锐角．(2012·北京高考，理16)如图1，在Rt△ABC 中，∠C ＝90°，BC ＝3，AC ＝6.D ，E 分别是AC ，AB 上的点，且DE ∥BC ，DE ＝2，将△ADE 沿DE 折起到△A 1DE 的位置，使A 1C ⊥CD ，如图2.图1 图2(1)求证：A 1C ⊥平面BCDE ；(2)若M 是A 1D 的中点，求CM 与平面A 1BE 所成角的大小；(3)线段BC 上是否存在点P ，使平面A 1DP 与平面A 1BE 垂直？说明理由．解：(1)因为AC ⊥BC ，DE ∥BC ，所以DE ⊥AC .所以DE ⊥A 1D ，DE ⊥CD . 所以DE ⊥平面A 1DC .所以DE ⊥A 1C . 又因为A 1C ⊥CD ，所以A 1C ⊥平面BCDE .(2)如图，以C 为坐标原点，建立空间直角坐标系Cxyz，则A 1(0,0,23)，D(0,2,0)，M(0,1，3)，B(3,0,0)，E(2,2,0)．设平面A 1BE 的法向量为n=(x ，y ，z)，则n ·1A B =0，n ·BE =0. 又1A B =(3,0，-23)，BE =(-1,2,0)，所以3230,20.x z x y ⎧-=⎪⎨-+=⎪⎩令y=1，则x=2，z=3.所以n=(2,1，3)．设CM 与平面A 1BE 所成的角为θ. 因为CM =(0,1，3)，所以sin θ＝|cos 〈n ，CM 〉|＝n CM n CM⋅＝48×4＝22，所以CM 与平面A 1BE 所成角的大小为π4.(3)线段BC 上不存在点P ，使平面A 1DP 与平面A 1BE 垂直．理由如下：假设这样的点P 存在，设其坐标为(p,0,0)，其中p [0,3]．设平面A 1DP 的法向量为m ＝(x ，y ，z )，则m ·1A D ＝0，m ·DP ＝0.又1A D ＝(0,2，－23)，DP ＝(p ，－2,0)，所以⎩⎨⎧2y －23z ＝0，px －2y ＝0.令x ＝2，则y ＝p ，z ＝p3.所以m ＝⎝ ⎛⎭⎪⎫2，p ，p 3.平面A 1DP ⊥平面A 1BE ，当且仅当m·n ＝0，即4＋p ＋p ＝0.解得p ＝－2，与p [0,3]矛盾．所以线段BC 上不存在点P ，使平面A 1DP 与平面A 1BE 垂直．1．已知AB ＝(1,5，－2)，BC ＝(3,1，z )，若AB ⊥BC ，BP ＝(x －1，y ，－3)，且BP ⊥平面ABC ，则实数x ，y ，z 的值分别为( )．A.337，－157， 4B.407，－157，4C.407，－2,4 D ．4，407，－15 2．已知平面α内有一个点M (1，－1,2)，平面α的一个法向量是n ＝(6，－3,6)，则下列点P 在平面α内的是( )．A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－3,4)3．(2012·湖北武昌调研，7)已知E ，F 分别是正方体ABCD A 1B 1C 1D 1棱BB 1，AD 的中点，则直线EF 和平面BDD 1B 1所成的角的正弦值是( )．A.26 B.36 C.13 D.664．在四面体PABC 中，PA ，PB ，PC 两两垂直，设PA ＝PB ＝PC ＝a ，则点P 到平面ABC 的距离为__________．5．如图，在直三棱柱ABC A 1B 1C 1中，∠ACB ＝90°，AA 1＝2，AC ＝BC ＝1，则异面直线A 1B 与AC 所成角的余弦值是__________．6．已知在长方体ABCD A 1B 1C 1D 1中，AB ＝2，BC ＝4，AA 1＝4，点M 是棱D 1C 1的中点．求直线AB 1与平面DA 1M 所成角的正弦值．7．(2012·安徽合肥第一次质检，理18)如图，在多面体ABC A 1B 1C 1中，AA 1⊥平面ABC ，AA 1綉BB 1，AB ＝AC ＝AA 1＝22BC ，B 1C 1綉12BC .(1)求证：A 1B 1⊥平面AA 1C ；(2)求证：AB 1∥平面A 1C 1C ；(3)求二面角C 1A 1C A 的余弦值．参考答案命题调研·明晰考向真题试做1．A 解析：不妨设CB ＝1，则CA ＝CC 1＝2.由题图知，A 点的坐标为(2,0,0)，B 点的坐标为(0,0,1)，B 1点的坐标为(0,2,1)，C 1点的坐标为(0,2,0)．所以1BC ＝(0,2，－1)，1AB ＝(－2,2,1)．所以cos 〈1BC ，1AB 〉＝0×(－2)＋2×2＋(－1)×135＝55.2．90° 解析：如图，以点D 为原点，以DA ，DC ，DD 1为x 轴、y 轴、z 轴建立坐标系D xyz .设正方体的棱长为2，则1MA ＝(2，－1，2)，DN ＝(0,2,1)，1AB ·DN ＝0，故异面直线A 1M 与ND 所成角为90°.3．(1)证明：因为四边形ABCD 是等腰梯形，AB ∥CD ，∠DAB ＝60°，所以∠ADC ＝∠BCD ＝120°. 又CB ＝CD ，所以∠CDB ＝30°. 因此∠ADB ＝90°，AD ⊥BD .又AE ⊥BD ，且AE ∩AD ＝A ，AE ，AD ⊂平面AED ，所以BD ⊥平面AED . (2)解法一：由(1)知AD ⊥BD ，所以AC ⊥BC .又FC ⊥平面ABCD ，因此CA ，CB ，CF 两两垂直，以C 为坐标原点，分别以CA ，CB ，CF 所在的直线为x 轴，y 轴，z 轴，建立如图所示的空间直角坐标系，不妨设CB ＝1，则C (0,0,0)，B (0,1,0)，D ⎝ ⎛⎭⎪⎫32，－12，0，F (0,0,1)，因此BD ＝⎝⎛⎭⎪⎫32，－32，0，BF ＝(0，－1,1)．设平面BDF 的一个法向量为m ＝(x ，y ，z )，则m ·BD ＝0，m ·BF ＝0，所以x ＝3y ＝3z ，取z ＝1，则m ＝(3，1,1)．由于CF ＝(0,0,1)是平面BDC 的一个法向量，则cos 〈m ，CF 〉＝m CF m CF⋅＝15＝55，所以二面角F BD C 的余弦值为55.解法二：取BD 的中点G ，连接CG ，FG ，由于CB=CD ，因此CG ⊥BD.又FC ⊥平面ABCD ，BD ⊂平面ABCD ，所以FC ⊥BD .由于FC ∩CG ＝C ，FC ，CG ⊂平面FCG ，所以BD ⊥平面FCG .故BD ⊥FG .所以∠FGC 为二面角F BD C 的平面角．在等腰三角形BCD 中，由于∠BCD ＝120°，因此CG ＝12CB .又CB ＝CF ，所以GF ＝CG 2＋CF 2＝5CG ，故cos∠FGC ＝55，因此二面角F BD C 的余弦值为55. 4．解：(1)以A 为原点，1,,AB CF AA 的方向分别为x 轴，y 轴，z 轴的正方向建立空间直角坐标系(如图)．设AB ＝a ，则A (0,0,0)，D (0,1,0)，D 1(0,1,1)，E ⎝ ⎛⎭⎪⎫a2，1，0，B 1(a,0,1)，故1AD ＝(0,1,1)，1B E ＝⎝ ⎛⎭⎪⎫－a 2，1，－1，1AB ＝(a,0,1)，AE ＝⎝ ⎛⎭⎪⎫a2，1，0.∵1AD ·1B E ＝－a2×0＋1×1＋(－1)×1＝0，∴B 1E ⊥AD 1.(2)假设在棱AA 1上存在一点P (0,0，z 0)，使得DP ∥平面B 1AE . 此时DP ＝(0，－1，z 0)．又设平面B 1AE 的法向量n ＝(x ，y ，z )． ∵n ⊥平面B 1AE ，∴n ⊥1AB ，n ⊥AE ，得⎩⎪⎨⎪⎧ax ＋z ＝0，ax2＋y ＝0.取x ＝1，得平面B 1AE 的一个法向量n ＝⎝ ⎛⎭⎪⎫1，－a2，－a .要使DP ∥平面B 1AE ，只要n ⊥DP ，有a 2－az 0＝0，解得z 0＝12.又DP 平面B 1AE ，∴存在点P ，满足DP ∥平面B 1AE ，此时AP ＝12.(3)连接A 1D ，B 1C ，由长方体ABCD A 1B 1C 1D 1及AA 1＝AD ＝1，得AD 1⊥A 1D . ∵B 1C ∥A 1D ，∴AD 1⊥B 1C .又由(1)知B 1E ⊥AD 1，且B 1C ∩B 1E ＝B 1，∴AD 1⊥平面DCB 1A 1.∴1AD 是平面A 1B 1E 的一个法向量，此时1AD ＝(0,1,1)．设1AD 与n 所成的角为θ，则cos θ＝11n AD n AD ⋅＝－a2－a 21＋a 24＋a2.∵二面角A B 1E A 1的大小为30°，∴|cos θ|＝cos 30°，即3a 221＋5a24＝32，解得a ＝2，即AB 的长为2.5．解法一：如图，以点A 为原点建立空间直角坐标系，依题意得A (0,0,0)，D (2,0,0)，C (0,1,0)，B ⎝ ⎛⎭⎪⎫－12，12，0，P (0,0,2)． (1)证明：易得PC ＝(0,1，－2)，AD ＝(2,0,0)，于是PC ·AD ＝0，所以PC ⊥AD .(2) PC ＝(0,1，－2)，CD ＝(2，－1,0)．设平面PCD 的法向量n ＝(x ，y ，z )，则0,0,n PC n CD ⎧⋅=⎪⎨⋅=⎪⎩即⎩⎪⎨⎪⎧y －2z ＝0，2x －y ＝0.不妨令z ＝1，可得n ＝(1,2,1)．可取平面PAC 的法向量m ＝(1,0,0)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝16＝66，从而sin 〈m ，n 〉＝306. 所以二面角A PC D 的正弦值为306. (3)设点E 的坐标为(0,0，h )，其中h ∈[0,2]，由此得BE ＝⎝ ⎛⎭⎪⎫12，－12，h .由CD ＝(2，－1,0)，故 cos 〈BE ，CD 〉＝BE CD BE CD⋅＝3212＋h 2×5＝310＋20h 2，所以，310＋20h2＝cos 30°＝32，解得h ＝1010，即AE ＝1010. 解法二：(1)证明：由PA ⊥平面ABCD ，可得PA ⊥AD ，又由AD ⊥AC ，PA ∩AC ＝A，故AD ⊥平面PAC .又PC ⊂平面PAC ，所以PC ⊥AD .(2)如图，作AH ⊥PC 于点H ，连接DH .由PC ⊥AD ，PC ⊥AH ，可得PC ⊥平面ADH .因此DH ⊥PC ，从而∠AHD 为二面角A PC D 的平面角．在Rt△PAC 中，PA ＝2，AC ＝1，由此得AH ＝25.由(1)知AD ⊥AH ，故在Rt△DAH 中，DH ＝AD 2＋AH 2＝2305.因此sin∠AHD ＝AD DH＝306.所以二面角A PC D 的正弦值为306. (3)如图，因为∠ADC<45°，故过点B 作CD 的平行线必与线段AD 相交，设交点为F ，连接BE ，EF.故∠EBF或其补角为异面直线BE 与CD 所成的角．由于BF ∥CD ，故∠AFB=∠ADC. 在Rt △DAC 中，，sin ∠ADC=15，故sin∠AFB ＝15.在△AFB 中，由BF sin∠FAB ＝AB sin∠AFB ，AB ＝12，sin∠FAB ＝sin 135°＝22，可得BF ＝52.由余弦定理，BF 2＝AB 2＋AF 2－2AB ·AF ·cos∠FAB ，可得AF ＝12.设AE ＝h .在Rt△EAF 中，EF ＝AE 2＋AF 2＝h 2＋14.在Rt△BAE 中，BE ＝AE 2＋AB 2＝h 2＋12.在△EBF 中，因为EF <BE ，从而∠EBF ＝30°，由余弦定理得cos 30°＝BE 2＋BF 2－EF 22BE ·BF .可解得h ＝1010.所以AE ＝1010.精要例析·聚焦热点热点例析【例1】证明：设11C B ＝a ，11C D ＝b ，1C C ＝c ，因为B 1BCC 1为平行四边形，所以1B C ＝c －a .又O 是B 1D 1的中点，所以 1C O ＝12(a ＋b )，1OD ＝11C D －1C O ＝b －12(a ＋b )＝12(b －a )．因为D 1D 綉C 1C ，所以1D D ＝c ，所以OD ＝1OD ＋1D D ＝12(b －a )＋c .若存在实数x ，y ，使1B C ＝x OD ＋y 1OC (x ，y ∈R )成立，则c －a ＝x ⎣⎢⎡⎦⎥⎤12(b －a )＋c ＋y ⎣⎢⎡⎦⎥⎤－12(a ＋b )＝－12(x ＋y )a ＋12(x －y )b ＋x c .因为a ，b ，c 不共线，所以⎩⎪⎨⎪⎧12(x ＋y )＝1，12(x －y )＝0，x ＝1，所以⎩⎪⎨⎪⎧x ＝1，y ＝1，所以11B C OD OC =+，所以1B C ，OD ，1OC 是共面向量．因为1B C 不在OD ，1OC 所确定的平面ODC 1内，所以1B C ∥平面ODC 1，即B 1C ∥平面ODC 1. 【变式训练1】解：(1)证明：方法一：如图，分别取AD ，CD 的中点P，Q ，连接FP ，EQ .∵△ADF 和△CDE 是边长为2的正三角形，∴FP ⊥AD ，EQ ⊥CD ，且FP ＝EQ ＝ 3.又∵平面ADF 、平面CDE 都与平面ABCD 垂直， ∴FP ⊥平面ABCD ，EQ ⊥平面ABCD ， ∴FP ∥QE 且FP ＝EQ ，∴四边形EQPF 是平行四边形， ∴EF ∥PQ .∵PQ 是△ACD 的中位线， ∴PQ ∥AC ，∴EF ∥AC .方法二：以A 点作为坐标原点，以AB 所在直线为x 轴，以AD 所在直线为y 轴，过点A 垂直于xOy 平面的直线为z 轴，建立空间直角坐标系，如图所示．根据题意可得，A (0,0,0)，B (2,0,0)，C (2,2,0)，D (0,2,0)，E (1,2，3)，F (0,1，3)，G (1,0，3)．∴AC ＝(2,2,0)，FE ＝(1,1,0)，则2AC FE =，∴AC ∥FE ，即有AC ∥FE .(2)V 多面体ABCDEFG ＝V 三棱柱ABG CDE ＋V 四棱锥F ADEG ＝23＋233＝833.【例2】证明：如图所示建立空间直角坐标系，D 为坐标原点，设DC ＝a .(1)连接AC 交BD 于G ，连接EG .依题意得A (a,0,0)，P (0,0，a )，E ⎝ ⎛⎭⎪⎫0，a 2，a 2.∵底面ABCD 是正方形，∴G 是此正方形的中心，故点G 的坐标为⎝ ⎛⎭⎪⎫a 2，a 2，0，PA ＝(a,0，－a )，EG ＝⎝ ⎛⎭⎪⎫a 2，0，－a2，∴PA ＝2EG ，则PA ∥EG .而EG ⊂平面EDB 且PA 平面EDB ， ∴PA ∥平面EDB .(2)依题意得B (a ，a,0)，PB ＝(a ，a ，－a )．又DE ＝⎝ ⎛⎭⎪⎫0，a 2，a 2，故PB ·DE ＝0＋a 22－a 22＝0，∴PB ⊥DE .由已知EF ⊥PB ，且EF ∩DE ＝E ，∴PB ⊥平面EFD . 【变式训练2】解：(1)证明：因为四边形ABCD 是菱形，所以AC ⊥BD .又因为PA ⊥平面ABCD ，所以PA ⊥BD . 又PA ∩AC ＝A ，所以BD ⊥平面PAC . (2)设AC ∩BD ＝O .因为∠BAD ＝60°，PA ＝AB ＝2，所以BO ＝1，AO ＝CO ＝ 3.如图，以O 为坐标原点，建立空间直角坐标系O xyz ，则P (0，－3，2)，A (0，－3，0)，B (1,0,0)，C (0，3，0)，所以PB ＝(1，3，－2)，AC ＝(0,23，0)．设PB 与AC 所成角为θ，则cos θ＝PB ACPB AC ⋅＝622×23＝64.(3)由(2)知BC ＝(－1，3，0)．设P (0，－3，t )(t >0)，则BP ＝(－1，－3，t )．设平面PBC 的法向量m ＝(x ，y ，z )，则BC ·m ＝0，BP ·m ＝0.所以⎩⎨⎧－x ＋3y ＝0，－x －3y ＋tz ＝0.令y ＝3，则x ＝3，z ＝6t.所以m ＝⎝ ⎛⎭⎪⎫3，3，6t .同理，平面PDC 的法向量 n ＝⎝ ⎛⎭⎪⎫－3，3，6t .因为平面PBC ⊥平面PDC ，所以m ·n ＝0，即－6＋36t2＝0，解得t ＝6，所以PA ＝ 6.【例3】解：如图所示，建立空间直角坐标系，点B 为坐标原点．依题意得A (22，0,0)，B (0,0,0)，C (2，－2，5)，A 1(22，22，0)，B 1(0，22，0)，C 1(2，2，5)．(1)易得AC ＝(－2，－2，5)，11A B ＝(－22，0,0)，于是cos 〈AC ，11A B 〉＝1111AC A B AC A B ⋅＝43×22＝23. 所以异面直线AC 与A 1B 1所成角的余弦值为23. (2)易知1AA ＝(0,22，0)，11AC ＝(－2，－2，5)．设平面AA 1C 1的法向量m ＝(x ，y ，z )，则1110,0.m AC m AA ⎧⋅=⎪⎨⋅=⎪⎩ 即⎩⎨⎧ －2x －2y ＋5z ＝0，22y ＝0.不妨令x ＝5，可得m ＝(5，0，2)．同样地，设平面A 1B 1C 1的法向量n ＝(r ，p ，q )，则11110,0.n AC n A B ⎧⋅=⎪⎨⋅=⎪⎩ 即⎩⎨⎧－2r －2p ＋5q ＝0，－22r ＝0.不妨令p ＝5，可得n ＝(0，5，2)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝27×7＝27，从而sin 〈m ，n 〉＝357.所以二面角A A 1C 1B 1的正弦值为357.(3)由N 为棱B 1C 1的中点，得N ⎝ ⎛⎭⎪⎫22，322，52.设M (a ，b,0)，则MN ＝⎝ ⎛⎭⎪⎫22－a ，322－b ，52.由MN ⊥平面A 1B 1C 1，得11110,0.MN A B MN AC ⎧⋅=⎪⎨⋅=⎪⎩即 ⎩⎪⎨⎪⎧⎝ ⎛⎭⎪⎫22－a ·(－22)＝0，⎝ ⎛⎭⎪⎫22－a ·(－2)＋⎝ ⎛⎭⎪⎫322－b ·(－2)＋52·5＝0.解得⎩⎪⎨⎪⎧a ＝22，b ＝24，故M ⎝⎛⎭⎪⎫22，24，0，因此BM ＝⎝⎛⎭⎪⎫22，24，0. 所以线段BM 的长|BM |＝104. 【变式训练3】解：设正四棱柱的高为h . (1)连接AO 1，AA 1⊥底面A 1B 1C 1D 1于A 1，∴AB 1与底面A 1B 1C 1D 1所成的角为∠AB 1A 1，即∠AB 1A 1＝α. ∵AB 1＝AD 1，O 1为B 1D 1中点， ∴AO 1⊥B 1D 1.又A 1O 1⊥B 1D 1，四边形A 1B 1C 1D 1是正方形．∴∠AO 1A 1是二面角A B 1D 1A 1的平面角，即∠AO 1A 1＝β.∴tan α＝AA 1A 1B 1＝h ，tan β＝AA 1A 1O 1＝2h . ∴tan β＝2tan α.(2)建立如图空间直角坐标系，有A (0,0，h )，B 1(1,0,0)，D 1(0,1,0)，C (1,1，h )，1AB ＝(1,0，－h )，1AD ＝(0,1，－h )，AC ＝(1,1,0)．设平面AB 1D 1的一个法向量为n ＝(x ，y ，z )．∵11,n AB n AD ⎧⊥⎪⎨⊥⎪⎩110,0.n AB n AD ⎧⋅=⎪⎨⋅=⎪⎩ 取z ＝1得n ＝(h ，h,1)， ∴点C 到平面AB 1D 1的距离为d ＝n AC n⋅＝|h ＋h ＋0|h 2＋h 2＋1＝43，则h ＝2. 【例4】 (1)证明：连接BD ，设AC 交BD 于点O ，连接SO .由题意知SO ⊥平面ABCD .以O 为坐标原点，OB ，OC ，OS 所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系O xyz ，设底面边长为2，则高SO ＝6，∴S (0,0，6)，D (－2，0,0)，C (0，2，0)． ∴OC ＝(0，2，0)，SD ＝(－2，0，－6)． ∴OC SD ⋅＝0，故OC ⊥SD ，即AC ⊥SD .(2)解：由题意知，平面PAC 的一个法向量DS ＝(2，0，6)，平面DAC 的一个法向量为OS ＝(0,0，6)，设所求的二面角为θ，则cos θ＝OS DS OS DS⋅＝32. 故所求二面角的大小为30°.(3)解：在侧棱SC 上存在一点E ，使BE ∥平面PAC .由(2)知DS 是平面PAC 的一个法向量，且DS ＝(2，0，6)，CS ＝(0，－2，6)．设CE tCS =，则BE BC CE =+＝(－2，2(1－t )，6t )，而BE DS ⋅＝0t ＝13，从而当SE ∶EC ＝2∶1时，BE DS ⊥，又BE 不在平面PAC 内，故BE ∥平面PAC . 【变式训练4】解：∵平面PAD ⊥平面ABCD ，而∠PAD ＝90°， ∴PA ⊥平面ABCD .而ABCD 是正方形，即AB ⊥AD ，故可建立如图所示的空间直角坐标系，则A (0,0,0)，B (2,0,0)，C (2,2,0)，D (0,2,0)，P (0,0,2)，E (0,0,1)，F (0,1,1)，G (1,2,0)． (1)证明：∵PB ＝(2,0，－2)，FE ＝(0，－1,0)，FG ＝(1,1，－1)，设平面EFG 的法向量为n 0＝(x 0，y 0，z 0)．则000,0,n FE n FG ⎧⋅=⎪⎨⋅=⎪⎩∴⎩⎪⎨⎪⎧－y 0＝0，x 0＋y 0－z 0＝0.令x 0＝1，则⎩⎪⎨⎪⎧x 0＝1，y 0＝0，z 0＝1，∴n 0＝(1,0,1)．又∵PB ·n 0＝2×1＋0＋(－2)×1＝0， ∴PB ⊥n 0.又∵PB 平面EFG ，∴PB ∥平面EFG .(2)∵EG ＝(1,2，－1)，BD ＝(－2,2,0)， ∴cos 〈EG ，BD 〉＝EG BD EG BD⋅＝36，故异面直线EG 与BD 所成的角的余弦值为36. (3)假设在线段CD 上存在一点Q 满足题设条件，令CQ ＝m (0≤m ≤2)，则DQ ＝2－m ， ∴点Q 的坐标为(2－m,2,0)，∴EQ ＝(2－m,2，－1)．而EF ＝(0,1,0)，设平面EFQ 的法向量为n ＝(x ，y ，z )，则()()()(),,0,1,00,,,2,2,10n EF x y z n EQ x y z m ⎧⋅=⋅=⎪⎨⋅=⋅--=⎪⎩∴⎩⎪⎨⎪⎧y ＝0，(2－m )x ＋2y －z ＝0.令x ＝1，则n ＝(1,0,2－m )， ∴点A 到平面EFQ 的距离d ＝AE n n⋅＝|2－m |1＋(2－m )2＝45，即(2－m )2＝169， ∴m ＝23或m ＝103>2不合题意，舍去，故存在点Q ，当CQ ＝23时，点A 到平面EFQ 的距离为45.创新模拟·预测演练1．B 解析：∵AB BC ⊥，∴AB BC ⋅＝0，即3＋5－2z ＝0，得z ＝4.又BP ⊥平面ABC ，∴BP ⊥AB ，BP ⊥BC ，BC ＝(3,1,4)，则⎩⎪⎨⎪⎧(x －1)＋5y ＋6＝0，3(x －1)＋y －12＝0，解得⎩⎪⎨⎪⎧x ＝407，y ＝－157.2．A3．B 解析：建立如图所示空间直角坐标系，D 1(0,0,0)，F (1,0,2)，E (2,2,1)，则EF ＝(－1，－2,1)．设平面BDD 1B 1的法向量为n ，则n ＝(1，－1,0)． sin θ＝|cos 〈EF ，n 〉|＝EF n EF n⋅＝123＝36.故选B. 4.33a 解析：根据题意，可建立如图所示的空间直角坐标系P xyz ，则P (0,0,0)，A (a,0,0)，B (0，a,0)，C (0,0，a )．过点P 作PH ⊥平面ABC ，交平面ABC 于点H ，则PH 的长即为点P 到平面ABC 的距离． ∵PA ＝PB ＝PC ，∴H 为△ABC 的外心．又∵△ABC 为正三角形，∴H 为△ABC 的重心，可得H 点的坐标为⎝ ⎛⎭⎪⎫a 3，a 3，a3. ∴PH ＝⎝ ⎛⎭⎪⎫0－a 32＋⎝ ⎛⎭⎪⎫0－a 32＋⎝ ⎛⎭⎪⎫0－a 32 ＝33a .5.66解析：以C 为坐标原点，CA ，CB ，CC 1所在直线分别为x ，y ，z 轴建立空间直角坐标系，A 1(1,0,2)，B (0,1,0)，A (1,0,0)，C (0,0,0)，则1A B ＝(－1,1，－2)，AC ＝(－1,0,0)． cos 〈1A B ，AC 〉＝11A B AC A B AC⋅＝11＋1＋4＝66.6．解：建立如图所示的空间直角坐标系，可得有关点的坐标为D (0,0,0)，A (4,0,0)，B (4,2,0)，C (0,2,0)，A 1(4,0,4)，B 1(4,2,4)，C 1(0,2,4)，D 1(0,0,4)，∴M (0,1,4)．∴DM ＝(0,1,4)，1DA ＝(4,0,4)，1A B ＝(0,2,4)．设平面DA 1M 的法向量为n ＝(x ，y ，z )，则10,0,n DM n DA ⎧⋅=⎪⎨⋅=⎪⎩即⎩⎪⎨⎪⎧y ＋4z ＝0，4x ＋4z ＝0.取z ＝－1，得x ＝1，y ＝4.所以平面DA 1M 的一个法向量为n ＝(1,4，－1)．设直线AB 1与平面DA 1M 所成角为θ，则sin θ＝11n A B n AB ⋅＝1015，所以直线AB 1与平面DA 1M 所成角的正弦值为1015. 7．证明：(1)∵AB ＝AC ＝22BC ， ∴AB 2＋AC 2＝BC 2，∴AB ⊥AC . 又AA 1⊥平面ABC ，∴AA 1⊥AB .又AA 1∩AC ＝A ，∴AB ⊥平面AA 1C . ∵AA 1綉BB 1，∴四边形ABB 1A 1为平行四边形． ∴A 1B 1∥AB ，∴A 1B 1⊥平面AA 1C .(2)取BC 的中点D ，连接AD ，DC 1，B 1D .由条件知CD 綉B 1C 1，BD 綉B 1C 1，∴四边形B 1DCC 1和BDC 1B 1为平行四边形，∴B 1D 綉CC 1，C 1D 綉B 1B . 由(1)B 1B 綉AA 1，∴C 1D 綉A 1A ， ∴四边形AA 1C 1D 为平行四边形， ∴AD ∥A 1C 1.∵B 1D ∩AD ＝D ，B 1D ，AD ⊂平面AB 1D ， ∴平面AB 1D ∥平面A 1C 1C . 又∵AB 1⊂平面AB 1D ， ∴AB 1∥平面A 1C 1C .(3)由(1)知AA 1，AB ，AC 两两垂直，建立如图所示的空间直角坐标系．设BC ＝2，则A (0,0,0)，A 1(0,0，2)，C (0，－2，0)，C 1⎝ ⎛⎭⎪⎫－22，－22，2， ∴11AC ＝⎝ ⎛⎭⎪⎫－22，－22，0， 1AC ＝(0，－2，－2)．设平面A 1C 1C 的法向量为m ＝(x ，y ，z )，则由m ·11AC ＝0，,m ·1AC ＝0，得－22x －22y ＝0，,－2y －2z ＝0. 取x ＝1，则y ＝－1，z ＝1，故m ＝(1，－1,1)．而平面A 1AC 的法向量为n ＝(1,0,0)，cos 〈m ，n 〉＝m ·n |m ||n |＝13.易知二面角C 1A 1C A 为钝二面角，故二面角C 1A 1C A 的余弦值为－33.。

高考数学二轮复习第一篇专题五立体几何第3讲立体几何中的向量方法课件理0226396

热点训练 1:(2018·太原市一模)在四棱锥 P-ABCD 中,底面 ABCD 是边长为 2 的正方形,PA⊥BD. (1)求证:PB=PD;
(1)证明:如图,连接AC,交BD于点O,连接PO, 因为四边形ABCD是正方形,所以AC⊥BD,OB=OD, 又PA⊥BD,PA⊂平面PAC,AC⊂平面PAC,PA∩AC=A, 所以BD⊥平面PAC, 又PO⊂平面PAC,所以BD⊥PO, 又OB=OD,所以PB=PD.
AB1 =(0,1,-1), B1C =(0,-2,0), A1B1 = AB =( 3 ,0,-1).
设 n=(x,y,z)是平面 A1B1C 的法向量,
则
n

A1B1

0,
即

3x 0 y z 0,
n B1C 0, 0 x 2 y 0 z 0.
(1)证明:由已知可得,BF⊥PF,BF⊥EF, 又PF∩EF=E,所以BF⊥平面PEF. 又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.
(2)求DP与平面ABFD所成角的正弦值.
(2)解:如图,作 PH⊥EF,垂足为 H. 由(1)得,PH⊥平面 ABFD. 以 H 为坐标原点, HF 的方向为 y 轴正方向,| BF |为单位长度,建立如图所示的空间直角坐标系 H xyz. 由(1)可得,DE⊥PE. 又 DP=2,DE=1,所以 PE= 3 . 又 PF=1,EF=2,故 PE⊥PF.
可得 PH= 3 ,EH= 3 .
2
2
则 H(0,0,0),P(0,0, 3 ),D(-1,- 3 , 3 ), HP =(0,0, 3 ).
22
2
又 HP 为平面 ABFD 的法向量. 设 DP 与平面 ABFD 所成角为θ,

2018年高考数学二轮复习考前专题五立体几何与空间向量第3讲立体几何中的向量方法讲学案理

第3讲立体几何中的向量方法L考情考向分析------------------------------------以空间几何体为载体考查空间角是高考命题的重点，常与空间线面关系的证明相结合，热点为二面角的求解，均以解答题的形式进行考查，难度主要体现在建立空间直角坐标系和准确计算上•n热点分类突破热占~一八、、八\、利用向量证明平行与垂直设直线l的方向向量为a= (a1 , b1 , C1),平面a , 3的法向量分别为= (a2,b2 , C2), V =(a3, b3, C3)，则有:(1)线面平行l // a ?a丄口? a •= 0? a1a2+ bb + C1 C2= 0.(2)线面垂直l 丄a ? a /? a= k? a1= ka2 , b= kb2 , C1= kC2(3)面面平行\ *a / 3 ? v? 卩=入v? a2=入a3 , b2=入b3 , C2= 入C3.(4)面面垂直b2b3 + C2C3= 0.a丄3 ?卩丄V?卩• V = 0?例1如图，在直三棱柱ADE- BCF中，面ABFE和面ABCD都是正方形且互相垂直，点M为AB 的中点，点O为DF的中点. 运用向量方法证明:(1) 0M 平面BCF⑵平面MDIF平面EFCD证明方法一(1)由题意，得AB AD, AE两两垂直，以点A为原点建立如图所示的空间直角坐标系.设正方形边长为1,则A(0,0,0),B(i, 0,0) , qi,i,o), qo,i,o),F(1,0,1) , M1, 0 , 0 ,。

2 , T, , .0M= 0, - 2 , 1, BA= ( - 1,0,0),••• Ol M- BA\= 0, ••• SlVL匪•••棱柱 AD — BCF 是直三棱柱,• AB 丄平面BCF •- BA 是平面BCF 的一个法向量, 且OIM 平面BCF • OM 平面BCF(2)设平面 MDF 与平面EFCD 勺一个法向量分别为•••OML CD OML FC, 又 Cm FC = C, CD FC ?平面 EFCD •••OM L 平面 EFCDn i = (x i ，y i ，z i ),n 2=(X 2, y 2, Z 2).T DF = (1 , - 1,1) , DM= 2，- 1，0 , DC= (1,0,0) , CF = (0 ,—1,1),n i - DF = 0,由 Tm • DM=*1— y 1 + 乙=0,得』12X 1 — y 1= 0,令 X 1 = 1,贝U n 1 = 1, 2，n 1 - n 2= 0，•平面 MD 丄平面EFCD—T —T —T —T 1—T —T 1 —T万法二 (1) OIM= OR FB+ BM = ?DF — BF + 二 BA=2(瞄函—B F + ^B A ^ — 2BD-2T + —2(BC > BA — 1B F + 2§A1 T2BF•••向量6M 与向量B F ,目共|面又OM 平面BCF •- OM 平面BCFi -、］⑵由题意知，BF, BC BA 两两垂直,OM FC= —^B C +• O lM-C D=-BA = 0,又0M平面MDF：平面MDB_平面EFCDJyL *又AB ?平面PAB EF ?平面PAB • EF//平面 PAB⑵ 由(1)可知，P B = (1,0 , - 1) , PD= (0,2 , - 1),辰(0,0,1) , AD= (0,2,0) , DC= (1,0,0),•/AiP- 6C= (0,0,1)• (1,0,0) = 0 ,A D- DC= (0,2,0) • (1,0,0) = 0 ,• AP I DC XDh DC ,即 API DC ADL DC 又 APA AD= A , AP, AC ?平面 PAD • DC!平面 PAD•/ DC ?平面 PDC思维升华用向量知识证明立体几何问题，仍然离不开立体几何中的定理. 如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行，用向量方法证明直线 a // b ,只需证明向量b （入€ R ）即可.若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外. 跟踪演练1如图，在底面是矩形的四棱锥面ABCD 点E, F 分别是PC PD 的中点, （1）求证：EF//平面PAB⑵求证：平面PADL 平面PDC••• EF =- 2A B ••• EF// AB >即 EF// ABPA= AB= 1, BC= 2.i ABCDh PA !底 ,D (0,2,0) , R0,0,1).证明（1）以点A 为原点，AB 所在直线为0,EF =x 轴，AD 所在直线为0 , A B= (1,0,0).•••平面PAD 平面PDC 热点二利用空间向量求空间角设直线I , m 的方向向量分别为 a = (a i , b i , c i ), b = (a 2, b 2, C 2).平面a , 3的法向量分别为卩=(a 3, b 3, C 3), v = (a 4, b 4, C 4)(以下相同). (1)线线夹角设I , m 的夹角为9 0< 0,a i a 2b i b 2 C 1C 2a fb ； C 2」■a ； bfC| (2)线面夹角设直线I 与平面a 的夹角为0 O W 0 W —,nrI a • a I则 sin 0 = = |COS 〈a , a 〉|.1 a |1a 1(3)二面角设a — a — 3的平面角为 0 (0 W 0 W -),—例 2 在三棱柱 ABC- ABC 中，AB 丄平面 BCCB , / BCO*, AB= BC= 2, BB = 4，点 D 在3棱CC 上，且CD=入CC (0<入W 1).建立如图所示的空间直角坐标系. (1)当入=*时，求异面直线 AB 与AD 的夹角的余弦值; —⑵若二面角A- BD- A 的平面角为 §，求入的值. 解(1)易知 A (0, 0, 2) , B (0, 4, 0) , A (0, 4, 2). 1 —当入=2时，因为 BC= CD= 2, / BCC =3, 所以 C ( 3, - i , 0), D ( 3, 1, 0).所以 AB = (0, 4,- 2), A T D = ( 3, - 3,- 2).则cosI a • b | = I a || b | =则 |cos| a • v | _ | a || v |所以 cos 〈AB , AD 〉= | A B | 丨初, 0X ,3+ 4X (— 3)+ (— 2)X (— 2)J ________________________ 更 42+ (— 2)2・，(⑶2+ (— 3)2+ ( — 2)2 5故异面直线AB 与AD 的夹角的余弦值为甞.⑵由CD=入CG 可知，D ( 3, 4入一1 , 0), 所以 DB = (— 3, 5— 4 入，0), 由(1)知,AB =(0, 4,— 2). 设平面ABD 的法向量为m= (x , y , z ), 则;尬作0, D B • m = 0,令y = 1，解得所以平面ABD 的一个法向量为作 C , 1, 3A I设平面ABD 的法向量为n = (x , y , z ), '4y — 2z = 0, (5 — 4 入)y —羽x = 0, 5— 4入X =—3一，Z = 2, BA 1 • n = 0,则〜DB • n = 0,2z = 0, 即/ \ • (5 — 4 入)y — . 3x = 0,5— 4入令y = 1，解得x =活亠,z = 0, *3 所以平面 ABD 的一个法向量为 n = ,1, 0 ZyTX> 因为二面角A —BD- A 的平面角为n^, 所以 |cos 〈 m , n >| =丨m ・n 1 =i m i n|5 — 4入 5 — 4入 —:—X+1 X 1 + 2X 0■ .'3- . 35— 4 入 2 22帀广1+ L故入的值为1.思维升华(1)运用空间向量坐标运算求空间角的一般步骤：①建立恰当的空间直角坐标系;②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论.(2)求空间角注意：①两条异面直线所成的角a不一定是直线的方向向量的夹角 3 ,即COSa = |COS 3 | ；②两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角；③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，注意函数名称的变化.跟踪演练2 如图，在四棱锥S— ABCDh SD丄平面ABCD四边形ABCD 是直角梯形，/ ADC=/ DAB= 90°, SD= AD= AB= 2, DC= 1.(1) 求二面角S- BC—A的余弦值；⑵设P是棱BC上一点，E是SA的中点，若PE与平面SAD所成角的正弦值为I6,求线段CP的长.解⑴以D为坐标原点，建立如图所示空间直角坐标系Dxyz，贝U D(0,0,0) , B(2,2,0), qo,1,o), S(0,0,2),所以S B= (2,2 , - 2) , S C= (0,1，- 2) , D S= (0,0,2)设平面SBC的法向量为n1= (x, y, z),由n• SB= 0, n• SC= 0 ,得2x + 2y- 2z= 0 且y—2z = 0.取z= 1,得x=- 1 , y = 2 ,所以n1 = ( - 1,2,1)是平面SBC勺一个法向量.因为SDL平面ABC取平面ABC的一个法向量压=(0,0,1) 设二面角S- BC- A的大小为0 ,所以|cos| n 1・n| =吐卫0 |= |门帅2|=一6 = 6 ,由图可知二面角S- BC- A为锐二面角,所以二面角S- BC- A的余弦值为6.6⑵由(1)知，E(1,0,1),则C B= (2,1,0) , C E= (1 , - 1,1). 设CP=入CB0 < 入W 1),则CP=入(2,1,0)= (2 入，入，0),~所以PE= CE- CP= (1 - 2 入，一1—入，1).易知CDL平面SAD所以CD= (0, - 1,0)是平面SAD勺一个法向量.3设PE 与平面SAD 所成的角为a , 所以 sin a = |cos 〈 PE S b | i P E- S b _ 入 +1 i P E I S D5入 $-2 入 + 3’等，得入=3或入=#舍）-所以 SP = 3,3，0，I SP ，所以线段CP 的长为身.3热点三利用空间向量求解探索性问题存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对象（数值、图形、函数等）是否存在或某一结论是否成立•解决这类问题的基本策略是先假设题中的数学对象存在（或结论成立）或暂且认可其中的一部分结论，然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论.例3如图，在四棱锥 E - ABC ［中，平面ABEL 底面ABCb 侧面AEB 为等腰直角三角形，/nAEB= y ，底面 ABC ［为直角梯形，AB// CD AB L BC AB= 2Cb= 2BCEF（2）线段EA 上是否存在点F ,使EC//平面FBb 若存在，求出云；若不存在，说明理由.EA解 ⑴因为平面 ABEL 平面 ABCD 且 AB 丄BQ 平面 ABE^平面 ABC 仔AB BC ?平面ABCD 所以BC L 平面ABE,则/ CEB 即为直线EC 与平面ABE 所成的角，设 BC= a ,则 AB= 2a , BE= 2a ，所以 CE= 3a , 即直线EC 与平面ABE 所成角的正弦值为则在 Rt △ CBE 中, sin CB 1 /CEB = C B =汀（1）求直线EC 与平面ABE 所成角的正弦值；⑵存在点F,且手1时，有EC//平面FBb3证明如下：取 AB 中点O 为坐标原点，OB OD OE 分别为x , y , z 轴建立空间直角坐标系, 如图所示，设CD= 1,则曰0,0,1) , A —1,0,0)所以设平面FBD 勺法向量为v = (a , b , c ),—a + b = 0,所以423a — 3c =0 ,取 a = 1,得 v = (1, 1 , 2),因为 E C- v = (1, 1, — 1) • (1, 1 , 2) = 0 , 且EC?平面FBD 所以EC//平面FBDEF 1即当点F 满足EA = 3时，有EC/平面FBD思维升华空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断•解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法.跟踪演练3如图所示的空间几何体中，底面四边形ABCD^正方形，AF! AB AF// BE 平面 ABEFL 平面 ABCD DF = 5 , CE= 2 2 , BC =2.(1) 求二面角F — DE- C 的大小；(2) 若在平面DEF 上存在点P,使得BP!平面DEF 试通过计算说明点P 的位置.解 ⑴因为 AFL AB 平面 ABC !平面 ABEF 平面 ABE A 平面 ABC = AB 所以 AFL 平面ABCD 所以AF L AD 因为四边形 ABCD 为正方形，所以 AE L AD 所以AD, AB AF 两两垂直,由E F = 1E A= — 3, 0, v • FB=0 ,所以 EA= ( — 1,0，— 1),,B (1,0,0), C (1,1,0) , Q0,1,0),—3 '得 F - 3 , 0 ,1 2 3 …,3 ,E所以A(0,0,0) , B(0,2,0) , C(2,2,0) , Q2,0,0) , E(0,2,2) ,F(0,0,1)，所以AC= (2,2,0),11 C D= (0，—2,0),CE= ( —2,0,2).设平面CDE勺一个法向量为n = （x, y, z）,n • 6b= 0, 由Tn • CE= 0, 得厂I—2x+ 2z= 0,y = 0,x —Z= 0, 取x = 1, 得n= (1,0,1).同理可得平面DEF的一个法向量m^ (1 , —1,2),故cos〈m, n〉m-n 3mn厂=步因为二面角F-DE-C为钝角，故二面角F-DE-C的大小(2)设DP=入DE^ DF,因为DE= ( —2,2,2) , DF= ( —2,0,1),又BD= (2 , 2入，2入+卩),2,0) , Dfe 入阳卩6F= ( —2 入，2 入，2 入)+ ( —2卩，0,卩)=(—2入—2 卩，所以直E3D+ D F^ （2 —2入一2卩，2入一2,2入+卩）,BP- DF= 0, 因为BP- 0E= 0,所以—2(2 — 2 入—2 卩J+ 2 入 + 卩=0,—2(2 —2 入一2口 + 2(2 入一2 + 2(2 入 + 卩=0,以A为原点，AD AB AF分别为x, y, z轴建立空间直角坐标系（如图）.如图②，在 AB 边上取点 P',使 AP = 2P' B,连接 OQ OR 贝U 0为厶QRP 的中心. 设点O 到厶QRP 三边的距离为a ,则OG= a , OF= OQ sin / OQ V OQ sin / OQP = a , OE= OR- sin / ORE> OR- sin / ORP = a , •••OF V OGc OEOD OD OD •• V V -------tan 3 tan 丫 tan a• a V 丫 <3 .2. （2017 •北京）如图，在四棱锥 P-ABC ［中 ,底面ABC ［为正方形，平面 PAD L 平面 ABCD 点 M 在线段 PB 上 , PD/平面 MACPA = PD = 6 ,乙=0, _2 _ 解得$2 即DP = 2DE1入=3， 3k所以P 是线段DE 上靠近E 的三等分点.真题押题精真题体验1. （2017 •浙江改编）如图，已知正四面体 D — ABC 所有棱长均相等的BQ CR三棱锥），P, Q R 分别为AB BC CA 上的点，AP = PB, Q = R = 2,分别记二面角 D-PF — Q D — PQ-R, D — QF — P 的平面角为 a , 3 ,Y ,则a , 3 , Y 的大小关系为 ____________ .答案 a V 丫 V 3解析如图①，作出点 D 在底面ABC h 的射影0,过点O 分别作PR PQ QR 勺垂线OE OF0G 连接 DE DF, DG 贝卩 a=Z DEO 3 =/ DFO Y =/ DGOAB= 4.（1）求证：M为PB的中点;(2) 求二面角B- PD — A 的大小；(3) 求直线MC 与平面BDP 所成角的正弦值. (1)证明设AC , BD 交于点E ,连接ME 如图所示.因为PD//平面 MAC 平面MA ©平面PDB= ME 所以PD// ME 因为四边形ABCD 是正方形，所以E 为BD 的中点，所以M 为PB 的中点.⑵解取AD 的中点O 连接OP 0E因为PA= PD 所以OPL AD,又因为平面 PAD L 平面 ABCD 平面PA 助平面 ABC 』AD 且OF ?平面PAD 所以OPL 平面ABCD因为OE ＞平面ABCD 所以OPL OE 因为四边形ABCD 是正方形，所以OEL ADI、如图，建立空间直角坐标系 Oxyz,n • B D= 0 , n • PD=0 ,令 x = 1,则 y = 1, z = .2.于是 n = (1,1 , .2).平面PAD 的法向量为p = (0,1,0),所以它的大小由题意知，二sin a 十s 〈n ,朮U 血=鬱.I n || M C 9押题预测(2017届太原模拟)如图，在几何体 ABCDE 中，四边形 ABCD 是菱形，BE!平面 ABCD, DF/ BE, DF = 2BE= 2, EF = 3.(1) 证明：平面AC !平面BEFD(2) 若二面角A- EF- C 是直二面角，求AE 与平面ABCC 所成角的正切值. 押题依据利用空间向量求二面角全面考查了空间向量的建系、求法向量、求角等知识，是高考的重点和热点.(1)证明•••四边形ABCD1菱形，••• ACLBD •/ BE L 平面 ABCD ： BE! AC 又 BE n BD= B, BE BD ?平面 BEFD • AC L 平面 BEFD •/ AC ?平面 ACF •平面ACFL 平面BEFD ⑵解方法一(向量法)设AC 与 BD 交于点Q 以点O 为原点，OA 方向为x 轴，OB 方向为y 轴，BE 方向为z 轴建立空间直角坐标系，如图.取 DF 的中点H 连接EH•/ BE 綊 DH, DH= 1,•四边形BEHD^平行四边形， •/在 Rt △ EHF 中, FH= 1, EF = 3, • EH= 2 2, • BD= 2 ,2.所以直线MC 与平面BDP 所成角的正弦值为 2.69设直线MC 与平面BDP 所成的角为a ，则E (0 , 2 , 1),F (0 , — 2 , 2), C —a 2— 2 , 0 , 0),--AE = ( — ：；a — 2 , ■■■..；'2 , 1) , EF = ( 0 , — 2 2 , 1),设n i = (x i , y i , z i )为平面AEF 的法向量, n 2= (x 2 , y 2 , Z 2)为平面CEF 的法向量. •••二面角 A- EF — C 是直二面角，/曰AT• n i • n 2= 0，得 a = 2 ,由题可得/ EAB 为AE 与平面ABC 啲夹角，<r{ //••• AB= 2 , BE= i ,BE 1•tan / EA B AB = 2*方法二（几何法）设AC 与BD 交于点O •••四边形ABCD^菱形,•••△ ADF^A CDF △ ABE ^A CBE••• AF = CF , AE= CEAEF^A CEF过 A 作 AM L EF,连接 CM 贝U CM L EF,设AB 的长为矗( a 2— 2, 2, 1).得 z i = 2 ：?2y i , x i =由 n i • Afe= 0 , n i • E F = 0 , 令 y i = :a — 2，得 n i = (3 12 , a 2— 2 , 2 2a 2 — 4), 同理得 n 2= ( — 3 2 , ya 2 — 2 , 2 2a 2— 4).则/ AMC为二面角A- EF—C的平面角. 设菱形的边长为a ,30 ••• BE = 1, DP 2, EP 3, DF l BDBD= 2富.•/ A — EF — C 的二面角为直角，•/ AM （为直角,• AM= 2a 2— 4,在厶 AEF 中，AML EF 设 ME= x ，贝U MF= 3— x ,AF = ,a 2+ 4, AE= a 2+ 1,(a 2+ 4)2 —(3― x )2= ( a 2+ 1)2 — x 2, • a = 2.AE 与平面ABC 靳成角为/ EAB••• tan / EAB= 1.专题强化练A 组专题通关3ii1.已知平面ABC 点M 是空间任意一点，点M 满足条件O M = OAF;O 內；O C 则直线AM ）4 8 8A.与平面 ABC 平行B.是平面 ABC 勺斜线C.是平面 ABC 勺垂线D .在平面 ABC 内答案 D解析由已知得M 代B, C 四点共面，所以 AM 在平面ABC 内，故选D. 2.（2017 •湖南省衡阳市联考）如图所示，在正方体 AC 中，AB= 2, AC n BD =E ,直线AC 与直线DE 所成的角为 a ，直线DE 与平面BCC 所成的角为3，贝U cos （ a — 3 ）等于（）A ，B.仝63在厶 AOB 中 AO= a 2— 2, ••• AC 2 a 2 —2,cC.D.答案A解析由题意可知，a = n^，贝U cos( a —3 ) = sin 3 ,以点D 为坐标原点，DA DC DD 方向为x,y ,z 轴正方向建立空间直角坐标系，则D（ 0, 0, 0）,E (1, 1 , 2),DE= (1, 1, 2)，平面 BCC 1 的法向量 DC= (0, 2, 0),由此可得cos ( a — 3 ) = sinPfe. 5C —述IDffl DC6故选A.3.正方体 ABC — ABCD 中，点 P 在AC 上运动（包括端点），则BP 与AD 所成角的取值范围i n n -— B. ]4 3Ji n n 1D . 答案解析以点D 为原点，DA DC设点P 坐标为（X , 1 — X , DD 分别为x , y , z 轴建立空间直角坐标系，设正方体棱长x ）（0 < x < 1）,则 B P= （ x — 1, — x , x ）,BC // AD .故选 D.4. (2017 •全国 n )已知直三棱柱 ABC-ABC 中，/ ABC= 120° , AB= 2 , BC= CC = 1,则异 vj/y / 面直线AB 与BC 所成角的余弦值为( )■牛C.严D.手553因为 A. 答案 C解析方法一将直三棱柱 ABC-ABC 补形为直四棱柱 ABC — ABCD ,如图所示,连接AD , BD , BD由题意知/ ABC= 120° , AB= 2 , BC= CC = 1 , 所以 AD = BC = 2 , AB = ,5 , / DAB= 60°.在厶 ABD 中 ,由余弦定理知， BD = 22+ 12— 2X 2 x 1 x cos 60°= 3,所以 BD= , 3 ,所以 BD =\ 3.)A. C. D 所以cosX =1 时,BC = ( — 1, 0, 1)，设 BP , BC 的夹角为 a ,4 ____ P又AB 与AD 所成的角即为 AB 与BG 所成的角0 ,故选G.5. (2017 •全国川)a , b 为空间中两条互相垂直的直线，等腰直角三角形 ABG 的直角边 AG所在直线与a , b 都垂直，斜边 AB 以直线AC 为旋转轴旋转，有下列结论： ① 当直线 AB 与a 成60°角时，AB 与b 成30°角； ② 当直线 AB 与a 成60°角时，AB 与b 成60°角； ③ 直线AB 与 a 所成角的最小值为45°; ④ 直线AB 与 a 所成角的最大值为60°.其中正确的是 ________ .(填写所有正确结论的编号)答案②③ 解析依题意建立如图所示的空间直角坐标系，设等腰直角三角形 ABC 的直角边长为1.由题意知，点B 在平面xOy 中形成的轨迹是以 C 为圆心，1为半径的圆. 设直线a 的方向向量为a = (0,1,0)，直线b 的方向向量为b = (1,0,0),CE 以 Ox 轴为始边沿逆时针方向旋转的旋转角为 0, [ 0, 2 n )，贝UB (cos 0 , sin 0 ,0), ••• ABs= (cos 0 , sin 0，— 1) , | AB| = , 2.设直线AB 与直线a 所成的夹角为a ,• 45°w a < 90°,.・.③正确，④错误;所以cosAB 2+ AD — BD f 2 x AB X AD5+ 2— 3 何2「'5X .,2— 5故选C. 方法二以B i 为坐标原点，BG 所在的直线为x 轴，垂直于 BG 的直线为y 轴，BB 所在的直线为z 轴建立空间直角坐标系，如图所示.由已知条件知 B i (0,0,0)，氏0,0,1) , G (1,0,0), A ( — 1, 3, 1)，则BG=(1,0 , — 1),AB = (1，— . 3, — 1).所以 cos 〈AB , BG 〉 AB • BG _2^10|AB || BG |5 x；25所以异面直线 AB 与BG 所成角的余弦值为10~5~则 cos a吟冷sinI a || AB0 1€ 0, -2 ,/ *设直线AB 与直线b 所成的夹角为3 ,e | = J2cos a = ■ 2cos 60 ° = e | 冷，-cos 3 冷|cos e | = 2.值.又AE?平面ABCD AD ?平面ABCDJF «所以 AA L AE AA L ADn在菱形ABCDK / ABC= y ，则△ ABC 是等边三角形. 因为E 是BC 中点，所以BCLAE 因为BC// AD 所以AEL AD以｛AE AD AA ｝为正交基底建立空间直角坐标系.则 A (0,0,0) , C ( .3 , 1,0) , Q0,2,0),则cos 3=迪字十eI b || AB 2|.当直线 AB 与直线a 的夹角为60° ，即 a = 60° 时,•/45°W 3 W 90°, ••• 3 = 60°,即直线 AB 与b 的夹角为60°.•••②正确，①错误. 6.如图，在直四棱柱 ABC D ABCD 中，底面四边形 ABC ［为菱形,n AA = AB= 2，/ ABC= 3, E , F 分别是 BC AC 的中点. (1)求异面直线EF, AD 所成角的余弦值; ⑵点M 在线段AD 上, AD =入严、彳.若CM/平面AEF 求实数入口、、M的贝 U |sin |cos解因为四棱柱ABC B ABCD 为直四棱柱，所以AA 丄平面ABCDA (0,0,2) ,曰.3 , 0,0) , F# , 2 , 1 .(1) AD= (020) , E F = ^23, 1, i ,故异面直线EF, AD 所成角的余弦值为盲2.则AM=入 AD, 即 (x , y , z — 2)=入(0,2 , - 2).则 M 0,2 入，2— 2 入),CM= ( — 3, 2 入-1,2 — 2 入). 设平面 AEF 的法向量为 n = (X 0, y 。

空间向量法解决立体几何问题全面总结

由OA1 =（-1，-1，2），OD1 =（-1，1，2）
得:
x x

y y

2z 2z

0 0
解得:xy20z
取z =1
得平面OA1D1的法向量的坐标n=(2,0,1).
(2)求平面的法向量的坐标的特殊方法:
• 第一步:写出平面内两个不平行的向量 • a = (x1,y1,z1), b = (x2,y2,z2), • 第二步:那么平面法向量为
z
C1
A1
A x
B1
C O
B y
• 解:建立如图示的直角坐标系,则
•
A(
a 2
,0,0),B(0,
3 2
a
,0)
A1(
a 2
,0,).
C(-
a 2
,0,
2a)
• 设面ABB1A1的法向量为n=(x,y,z)
•得 a 3
AB ( , 2
2
a,0), AA1 (0,0,
2a)
• •

a
一.引入两个重要的空间向量
1.直线的方向向量
把直线上任意两点的向量或与它平行的向
量都称为直线的方向向量.如图,在空间直角
坐标系中,由A(x1,y1,z1)与B(x2,y2,z2)确定的直线AB的方向向量是
z
AB (x2 x1, y2 y1, z2 z1)
B
A
y
x
2.平面的法向量 • 如果表示向量n的有向线段所在的直线垂直
n
a
b
α
(1)求平面的法向量的坐标的一般步骤:
• 第一步(设):设出平面法向量的坐标为n=(x,y,z).

2018年高考数学二轮复习课件专题5 第3讲用空间向量的方法解立体几何问题(理)(74张)

如图，建立空间直角坐标系 O－xyz，则 P(0,0， 2)，D(2,0,0)，B(－2,4,0)， → → BD＝(4，－4,0)，PD＝(2,0，－ 2)．设平面 BDP 的法向量为 n＝(x，y，z)， → n· BD＝0，则 → n · PD ＝0，
4x－4y＝0，即 2x－ 2z＝0.
(4)点到平面的距离的向量求法
如图，设 AB 为平面 α 的一条斜线段，n 为平面 α 的法向量，则点 B 到平面 → |AB· n| α 的距离 d＝ |n| ．
• 2．利用向量方法证明平行与垂直 • 设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2， c2)．平面α，β的法向量分别为μ＝(a3，b3，c3)，v＝(a4， b4，c4)． a1＝ka2，b1＝kb2，c1＝kc2 • (1)线线平行 • l∥m⇔a∥b⇔a＝0 kb⇔_________________________ ． a1a2＋b1b2＋c1c2＝0 • (2)线线垂直 • l⊥m⇔a⊥b⇔a·b＝ _______⇔________________________．
核心知识整合
1．向量法求空间角 (1)异面直线所成的角：设 a，b 分别为异面直线 a，b 的方向向量，则两异面
|a· b| |a||b| 直线所成的角满足 cos θ＝__________ ．
(2)线面角设 l 是斜线 l 的方向向量，n 是平面 α 的法向量，则斜线 l 与平面 α 所成的角
(2)距离公式设 A(x1，y1，z1)，B(x2，y2，z2)，则 → |AB|＝ x1－x22＋y1－y22＋z1－z22．
• 1．在建立空间直角坐标系时，易忽略说明或证明建系的条件． • 2．忽略异面直线的夹角与方向向量夹角的区别：两条异面直线所成的角是锐角或直角，与它们的方向向量的夹角不一定相等． • 3．不能区分二面角与两法向量的夹角：求二面角时，两法向量的夹角有可能是二面角的补角，要注意从图中分析．

2018届高考数学(理)二轮复习命题热点课件专题 5.3 立体几何中的向量方法

高频考点命题热点一命题热点二命题热点三
-3-
用空间向量证明空间的平行与垂直【思考】如何用空间向量证明空间的平行与垂直? 例1已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
(1)求证:BC1⊥AB1; (2)求证:BC1∥平面CA1D.
高频考点命题热点一命题热点二命题热点三
题命题规律型求解立体几何问题是高考的必考内容,每套试卷必有立体选几何解答题,一择般设 2 至 3 问,2 题问的较多,前一解问较简单,最后答一问难度较大, 题而选用向量法可以降低解题难度,但增加了计算量.
复习策略抓住考查的主要题目类型进行训练, 重点是利用向量知识证明空间的平行与垂直;利用向量知识求线线角、线面角、二面角的大小;利用向量知识求空间中的距离以及利用向量知识解决立体几何中的探索性问题.
高频考点命题热点一命题热点二命题热点三
-8-
(2)由(1)知,E(0,0,3), G 则�� =
�� 2
�� 2
ห้องสมุดไป่ตู้
,1,4 ,F(0,1,4),
,1,1 , �� =(0,1,1), ��1 �� ·�� =0+2-2
��· ��1 = 0, ��· �� = 0,
高频考点命题热点一命题热点二命题热点三
-6-
题后反思用向量方法证明空间线面位置关系的方法:设直线l1,l2 的方向向量分别为a,b,平面α,β的法向量分别为e1,e2,A,B,C分别为平面α内的相异且不共线的三点(其中l1与l2不重合,α与β不重合),则 (1)l1∥l2⇔a∥b⇔存在实数λ,使b=λa(a≠0);l1⊥l2⇔a⊥b⇔a· b=0. (2)l1⊥α⇔a∥e1⇔存在实数λ,使e1=λa(a≠0);l1∥α⇔a· e1=0⇔存在非零实数λ1,λ2,使a=λ1 ��+λ2�� . (3)α∥β⇔e1∥e2⇔存在实数λ,使 e2=λe1(e1≠0);α⊥β⇔e1⊥e2⇔e1· e2=0.

高三数学二轮复习第一篇专题通关攻略专题五立体几

所以cos〈BM，AN〉 BM AN 30 ，
| BM || AN | 10
所以BM与AN所成角的余弦值为 30 .
10
2.(2016·北京高考)如图，在四棱锥P-ABCD中，平面 PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1， AD=2，AC=CD= 5 .
(1)求证：PD⊥平面PAB.
A. 1
B. 2
C. 30
D. 2
10
5
10
2
【解析】选C.由题意，以C为坐标原点，建立如图所示的空间直角坐标系.
令BC=CA=CC1=2，则C(0，0，0)，A(0，2，0)， B(2，0，0)，A1(0，2，2)，B1(2，0，2)， C1(0，0，2). 因为M，N分别为A1B1，A1C1的中点，所以M(1，1，2)，N(0，1，2)，这时 BM (1，1，2)，AN (0，1，2)，
｜a b｜
直线所成的角θ 满足cosθ =_｜__a_｜_｜__b_｜__.
(2)设l是斜线l的方向向线l与平面α 所成的角θ 满足sinθ =_｜_｜l__｜__n_｜_.
(3)二面角 ①如图(Ⅰ)，AB，CD是二面角α -l-β的两个半平面内与棱l垂直的直线，则二面角的大小θ =_〈_A_B_，_C_D_〉_;
公式致误：空间向量求直线与平面所成的角公式是
sinθ = ｜l n｜，而非cosθ = ｜l n｜ .
｜｜l ｜n｜
｜｜l ｜n｜
【考题回访】
1.(2014·全国卷Ⅱ)直三棱柱ABC-A1B1C1中，∠BCA= 90°，M，N分别为A1B1，A1C1的中点.BC=CA=CC1，则BM 与AN所成角的余弦值为( )

2018年高考数学(理) 讲学案：考前专题五立体几何与空间向量第3讲立体几何中的向量方法(含答案解析)

第3讲立体几何中的向量方法以空间几何体为载体考查空间角是高考命题的重点，常与空间线面关系的证明相结合，热点为二面角的求解，均以解答题的形式进行考查，难度主要体现在建立空间直角坐标系和准确计算上.热点一利用向量证明平行与垂直设直线l 的方向向量为a ＝(a 1，b 1，c 1)，平面α，β的法向量分别为μ＝(a 2，b 2，c 2)，v ＝(a 3，b 3，c 3)，则有： (1)线面平行l ∥α⇔a ⊥μ⇔a ·μ＝0⇔a 1a 2＋b 1b 2＋c 1c 2＝0.(2)线面垂直l ⊥α⇔a ∥μ⇔a ＝k μ⇔a 1＝ka 2，b 1＝kb 2，c 1＝kc 2.(3)面面平行α∥β⇔μ∥v ⇔μ＝λv ⇔a 2＝λa 3，b 2＝λb 3，c 2＝λc 3.(4)面面垂直α⊥β⇔μ⊥v ⇔μ·v ＝0⇔a 2a 3＋b 2b 3＋c 2c 3＝0.例1 如图，在直三棱柱ADE —BCF 中，面ABFE 和面ABCD 都是正方形且互相垂直，点M 为AB 的中点，点O 为DF 的中点．运用向量方法证明：(1)OM ∥平面BCF ； (2)平面MDF ⊥平面EFCD .证明方法一 (1)由题意，得AB ，AD ，AE 两两垂直，以点A 为原点建立如图所示的空间直角坐标系．设正方形边长为1，则A (0,0,0)，B (1，0,0)，C (1,1,0)，D (0,1,0)，F (1,0,1)，M ⎝ ⎛⎭⎪⎫12，0，0，O ⎝ ⎛⎭⎪⎫12，12，12. OM →＝⎝⎛⎭⎪⎫0，－12，－12，BA →＝(－1,0,0)，∴OM →·BA →＝0, ∴OM →⊥BA →. ∵棱柱ADE —BCF 是直三棱柱，∴AB ⊥平面BCF ，∴BA →是平面BCF 的一个法向量，且OM ⊄平面BCF ，∴OM ∥平面BCF .(2)设平面MDF 与平面EFCD 的一个法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)．∵DF →＝(1，－1,1)，DM →＝⎝ ⎛⎭⎪⎫12，－1，0，DC →＝(1,0,0)，CF →＝(0，－1,1)，由⎩⎪⎨⎪⎧n 1·DF →＝0，n 1·DM →＝0，得⎩⎪⎨⎪⎧x 1－y 1＋z 1＝0，12x 1－y 1＝0，令x 1＝1，则n 1＝⎝ ⎛⎭⎪⎫1，12，－12.同理可得n 2＝(0,1,1)．∵n 1·n 2＝0，∴平面MDF ⊥平面EFCD . 方法二 (1)OM →＝OF →＋FB →＋BM →＝12DF →－BF →＋12BA →＝12(DB →＋BF →)－BF →＋12BA →＝－12BD →－12BF →＋12BA →＝－12(BC →＋BA →)－12BF →＋12BA →＝－12BC →－12BF →.∴向量OM →与向量BF →，BC →共面，又OM ⊄平面BCF ，∴OM ∥平面BCF . (2)由题意知，BF ，BC ，BA 两两垂直， ∵CD →＝BA →，FC →＝BC →－BF →，∴OM →·CD →＝⎝ ⎛⎭⎪⎫－12BC →－12BF →·BA →＝0，OM →·FC →＝⎝ ⎛⎭⎪⎫－12BC →－12BF →·(BC →－BF →) ＝－12BC →2＋12BF →2＝0.∴OM ⊥CD ，OM ⊥FC ，又CD ∩FC ＝C ，CD ，FC ⊂平面EFCD ， ∴OM ⊥平面EFCD .又OM ⊂平面MDF ，∴平面MDF ⊥平面EFCD .思维升华用向量知识证明立体几何问题，仍然离不开立体几何中的定理．如要证明线面平行，只需要证明平面外的一条直线和平面内的一条直线平行，即化归为证明线线平行，用向量方法证明直线a ∥b ，只需证明向量a ＝λb (λ∈R )即可．若用直线的方向向量与平面的法向量垂直来证明线面平行，仍需强调直线在平面外．跟踪演练1 如图，在底面是矩形的四棱锥P —ABCD 中，PA ⊥底面ABCD ，点E ，F 分别是PC ，PD 的中点，PA ＝AB ＝1，BC ＝2. (1)求证：EF ∥平面PAB ； (2)求证：平面PAD ⊥平面PDC .证明 (1)以点A 为原点，AB 所在直线为x 轴，AD 所在直线为y 轴，AP 所在直线为z 轴，建立如图所示的空间直角坐标系，则A (0,0,0)，B (1,0,0)，C (1,2,0)，D (0,2,0)，P (0,0,1)．∵点E ，F 分别是PC ，PD 的中点， ∴E ⎝ ⎛⎭⎪⎫12，1，12，F ⎝ ⎛⎭⎪⎫0，1，12， EF →＝⎝ ⎛⎭⎪⎫－12，0，0，AB →＝(1,0,0)．∵EF →＝－12AB →，∴EF →∥AB →，即EF ∥AB ，又AB ⊂平面PAB ，EF ⊄平面PAB ， ∴EF ∥平面PAB .(2)由(1)可知，PB →＝(1,0，－1)，PD →＝(0,2，－1)，AP →＝(0,0,1)，AD →＝(0,2,0)，DC →＝(1,0,0)，∵AP →·DC →＝(0,0,1)·(1,0,0)＝0，AD →·DC →＝(0,2,0)·(1,0,0)＝0，∴AP →⊥DC →，AD →⊥DC →，即AP ⊥DC ，AD ⊥DC . 又AP ∩AD ＝A ，AP ，AD ⊂平面PAD ， ∴DC ⊥平面PAD . ∵DC ⊂平面PDC ， ∴平面PAD ⊥平面PDC . 热点二利用空间向量求空间角设直线l ，m 的方向向量分别为a ＝(a 1，b 1，c 1)，b ＝(a 2，b 2，c 2)．平面α，β的法向量分别为μ＝(a 3，b 3，c 3)，v ＝(a 4，b 4，c 4)(以下相同)．(1)线线夹角设l ，m 的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2，则cos θ＝|a ·b ||a ||b |＝.(2)线面夹角设直线l 与平面α的夹角为θ⎝ ⎛⎭⎪⎫0≤θ≤π2，则sin θ＝|a ·μ||a ||μ|＝|cos 〈a ，μ〉|.(3)二面角设α—a —β的平面角为θ(0≤θ≤π)，则|cos θ|＝|μ·v ||μ||v |＝|cos 〈μ，v 〉|.例 2 在三棱柱ABC －A 1B 1C 1中， AB ⊥平面BCC 1B 1, ∠BCC 1＝π3， AB ＝BC ＝2, BB 1＝4，点D 在棱CC 1上，且CD ＝λCC 1(0<λ≤1)．建立如图所示的空间直角坐标系．(1)当λ＝12时，求异面直线AB 1与A 1D 的夹角的余弦值；(2)若二面角A －B 1D －A 1的平面角为π3，求λ的值．解 (1)易知A ()0，0，2， B 1()0，4，0， A 1()0，4，2. 当λ＝12时，因为BC ＝CD ＝2, ∠BCC 1＝π3，所以C ()3，－1，0，D ()3，1，0.所以AB 1→＝()0，4，－2， A 1D →＝()3，－3，－2. 所以cos 〈AB 1→，A 1D →〉＝AB 1→·A 1D→||AB 1→||A 1D →，＝0×3＋4×()－3＋()－2×()－242＋()－22·()32＋()－32＋()－22＝－55. 故异面直线AB 1与A 1D 的夹角的余弦值为55.(2)由CD ＝λCC 1可知， D ()3，4λ－1，0，所以DB 1→＝()－3，5－4λ，0，由(1)知， AB 1→＝()0，4，－2.设平面AB 1D 的法向量为m ＝()x ，y ，z ，则⎩⎪⎨⎪⎧AB 1→·m ＝0，DB 1→·m ＝0，即⎩⎨⎧4y －2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3， z ＝2，所以平面AB 1D 的一个法向量为m ＝⎝⎛⎭⎪⎫5－4λ3，1，2.设平面A 1B 1D 的法向量为n ＝()x ，y ，z ，则⎩⎪⎨⎪⎧B 1A 1→·n ＝0，DB 1→·n ＝0，即⎩⎨⎧2z ＝0，()5－4λy －3x ＝0，令y ＝1，解得x ＝5－4λ3， z ＝0，所以平面A 1B 1D 的一个法向量为n ＝⎝ ⎛⎭⎪⎫5－4λ3，1，0.因为二面角A －B 1D －A 1的平面角为π3，所以||cos 〈m ，n 〉＝|m·n |||m ||n＝⎪⎪⎪⎪⎪⎪5－4λ3×5－4λ3＋1×1＋2×0⎝ ⎛⎭⎪⎫5－4λ32＋12＋22·⎝ ⎛⎭⎪⎫5－4λ32＋12＝12，即()5－4λ2＝1，解得λ＝32(舍)或λ＝1，故λ的值为1.思维升华 (1)运用空间向量坐标运算求空间角的一般步骤：①建立恰当的空间直角坐标系；②求出相关点的坐标；③写出向量坐标；④结合公式进行论证、计算；⑤转化为几何结论．(2)求空间角注意：①两条异面直线所成的角α不一定是直线的方向向量的夹角β，即cos α＝|cos β|；②两平面的法向量的夹角不一定是所求的二面角，有可能为两法向量夹角的补角；③直线和平面所成的角的正弦值等于平面法向量与直线方向向量夹角的余弦值的绝对值，注意函数名称的变化．跟踪演练2 如图，在四棱锥S －ABCD 中，SD ⊥平面ABCD ，四边形ABCD 是直角梯形，∠ADC ＝∠DAB ＝90°，SD ＝AD ＝AB ＝2，DC ＝1.(1)求二面角S －BC －A 的余弦值；(2)设P 是棱BC 上一点，E 是SA 的中点，若PE 与平面SAD 所成角的正弦值为22613，求线段CP 的长．解 (1)以D 为坐标原点，建立如图所示空间直角坐标系Dxyz ，则D (0,0,0)，B (2,2,0)，C (0,1,0)，S (0,0,2)，所以SB →＝(2,2，－2)，SC →＝(0,1，－2)，DS →＝(0,0,2)．设平面SBC 的法向量为n 1＝(x ，y ，z )，由n 1·SB →＝0，n 1·SC →＝0，得2x ＋2y －2z ＝0且y －2z ＝0. 取z ＝1，得x ＝－1，y ＝2，所以n 1＝(－1,2,1)是平面SBC 的一个法向量．因为SD ⊥平面ABC ，取平面ABC 的一个法向量n 2＝(0,0,1)．设二面角S －BC －A 的大小为θ，所以|cos θ|＝|n 1·n 2||n 1||n 2|＝|1|6＝66，由图可知二面角S －BC －A 为锐二面角，所以二面角S －BC －A 的余弦值为66.(2)由(1)知，E (1,0,1)，则CB →＝(2,1,0)，CE →＝(1，－1,1)．设CP →＝λCB →(0≤λ≤1)，则CP →＝λ(2,1,0)＝(2λ，λ，0)，所以PE →＝CE →－CP →＝(1－2λ，－1－λ，1)．易知CD ⊥平面SAD ，所以CD →＝(0，－1,0)是平面SAD 的一个法向量．设PE 与平面SAD 所成的角为α，所以sin α＝|cos 〈PE →，CD →〉| ＝|PE →·CD →||PE →||CD →|＝λ＋15λ2－2λ＋3，即λ＋15λ2－2λ＋3＝22613，得λ＝13或λ＝119(舍)．所以CP →＝⎝ ⎛⎭⎪⎫23，13，0，|CP →|＝53，所以线段CP 的长为53. 热点三利用空间向量求解探索性问题存在探索性问题的基本特征是要判断在某些确定条件下的某一数学对象(数值、图形、函数等)是否存在或某一结论是否成立．解决这类问题的基本策略是先假设题中的数学对象存在(或结论成立)或暂且认可其中的一部分结论，然后在这个前提下进行逻辑推理，若由此导出矛盾，则否定假设；否则，给出肯定结论．例3 如图，在四棱锥E －ABCD 中，平面ABE ⊥底面ABCD ，侧面AEB 为等腰直角三角形， ∠AEB ＝π2，底面ABCD 为直角梯形， AB ∥CD ，AB ⊥BC ，AB ＝2CD ＝2BC .(1)求直线EC 与平面ABE 所成角的正弦值；(2)线段EA 上是否存在点F ，使EC ∥平面FBD ？若存在，求出EF EA；若不存在，说明理由．解 (1)因为平面ABE ⊥平面ABCD ，且AB ⊥BC ，平面ABE ∩平面ABCD ＝AB ，BC ⊂平面ABCD ，所以BC ⊥平面ABE, 则∠CEB 即为直线EC 与平面ABE 所成的角，设BC ＝a ，则AB ＝2a ，BE ＝2a ，所以CE ＝3a ，则在Rt△CBE 中， sin∠CEB ＝CB CE＝13＝33，即直线EC 与平面ABE 所成角的正弦值为33. (2)存在点F ，且EF EA ＝13时，有EC ∥平面FBD ，证明如下：取AB 中点O 为坐标原点，OB ，OD ，OE 分别为x ，y ，z 轴建立空间直角坐标系，如图所示，设CD ＝1，则E (0,0,1)，A (－1,0,0)，B (1,0,0)，C (1,1,0)，D (0,1,0)，所以EA →＝(－1,0，－1)，BD →＝(－1,1,0)，EC →＝(1,1，－1)．由EF →＝13EA →＝⎝ ⎛⎭⎪⎫－13，0，－13，得F ⎝ ⎛⎭⎪⎫－13，0，23，所以FB →＝⎝ ⎛⎭⎪⎫43，0，－23.设平面FBD 的法向量为v ＝()a ，b ，c ，则⎩⎪⎨⎪⎧v ·BD →＝0，v ·FB →＝0，所以⎩⎪⎨⎪⎧－a ＋b ＝0，43a －23c ＝0，取a ＝1，得v ＝()1，1，2，因为EC →·v ＝()1，1，－1·()1，1，2＝0，且EC ⊄平面FBD ，所以EC ∥平面FBD ，即当点F 满足EF EA ＝13时，有EC ∥平面FBD .思维升华空间向量最适合于解决这类立体几何中的探索性问题，它无需进行复杂的作图、论证、推理，只需通过坐标运算进行判断．解题时，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等，所以为使问题的解决更简单、有效，应善于运用这一方法．跟踪演练3 如图所示的空间几何体中，底面四边形ABCD 为正方形，AF ⊥AB ，AF ∥BE ，平面ABEF ⊥平面ABCD ，DF ＝5，CE ＝22，BC ＝2.(1)求二面角F －DE －C 的大小；(2)若在平面DEF 上存在点P ，使得BP ⊥平面DEF ，试通过计算说明点P 的位置．解 (1)因为AF ⊥AB ，平面ABCD ⊥平面ABEF ，平面ABEF ∩平面ABCD ＝AB ，所以AF ⊥平面ABCD ，所以AF ⊥AD .因为四边形ABCD 为正方形，所以AB ⊥AD ，所以AD ，AB ，AF 两两垂直，以A 为原点，AD ，AB ，AF 分别为x ，y ，z 轴建立空间直角坐标系(如图)．由勾股定理可知，AF ＝1，BE ＝2，所以A (0,0,0)，B (0,2,0)，C (2,2,0)，D (2,0,0)，E (0,2,2)，F (0,0,1)，所以AC →＝(2,2,0)，CD →＝(0，－2,0)， CE →＝(－2,0,2)．设平面CDE 的一个法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧n ·CD →＝0，n ·CE →＝0，得⎩⎪⎨⎪⎧－2y ＝0，－2x ＋2z ＝0，即⎩⎪⎨⎪⎧y ＝0，x －z ＝0，取x ＝1，得n ＝(1,0,1)．同理可得平面DEF 的一个法向量m ＝(1，－1,2)，故cos 〈m ，n 〉＝m·n |m||n|＝32，因为二面角F －DE －C 为钝角，故二面角F －DE －C 的大小为5π6.(2)设DP →＝λDE →＋μDF →，因为DE →＝(－2,2,2)，DF →＝(－2,0,1)，又BD →＝(2，－2,0)，DP →＝λDE →＋μDF →＝(－2λ，2λ，2λ)＋(－2μ，0，μ)＝(－2λ－2μ，2λ，2λ＋μ)，所以BP →＝BD →＋DP →＝(2－2λ－2μ，2λ－2,2λ＋μ)，因为⎩⎪⎨⎪⎧BP →·DF →＝0，BP →·DE →＝0，所以⎩⎪⎨⎪⎧－2(2－2λ－2μ)＋2λ＋μ＝0，－2(2－2λ－2μ)＋2(2λ－2)＋2(2λ＋μ)＝0，解得⎩⎪⎨⎪⎧μ＝0，λ＝23，即DP →＝23DE →.所以P 是线段DE 上靠近E 的三等分点．真题体验1．(2017·浙江改编)如图，已知正四面体D —ABC (所有棱长均相等的三棱锥)，P ，Q ，R 分别为AB ，BC ，CA 上的点，AP ＝PB ，BQ QC ＝CRRA＝2，分别记二面角D —PR —Q ，D —PQ —R ，D —QR —P 的平面角为α，β，γ，则α，β，γ的大小关系为________．答案 α＜γ＜β解析如图①，作出点D 在底面ABC 上的射影O ，过点O 分别作PR ，PQ ，QR 的垂线OE ，OF ，OG ，连接DE ，DF ，DG ，则α＝∠DEO ，β＝∠DFO ，γ＝∠DGO . 由图可知，它们的对边都是DO ， ∴只需比较EO ，FO ，GO 的大小即可．如图②，在AB 边上取点P ′，使AP ′＝2P ′B ，连接OQ ，OR ，则O 为△QRP ′的中心．设点O 到△QRP ′三边的距离为a ，则OG ＝a ，OF ＝OQ ·sin∠OQF ＜OQ ·sin∠OQP ′＝a ， OE ＝OR ·sin∠ORE ＞OR ·sin∠ORP ′＝a ，∴OF ＜OG ＜OE ， ∴ODtan β＜ODtan γ＜ODtan α，∴α＜γ＜β.2．(2017·北京)如图，在四棱锥P —ABCD 中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，PD ∥平面MAC ，PA ＝PD ＝6，AB ＝4. (1)求证：M 为PB 的中点； (2)求二面角B —PD —A 的大小；(3)求直线MC 与平面BDP 所成角的正弦值． (1)证明设AC ，BD 交于点E ，连接ME ，如图所示．因为PD ∥平面MAC ，平面MAC ∩平面PDB ＝ME ，所以PD ∥ME .因为四边形ABCD 是正方形，所以E 为BD 的中点，所以M 为PB 的中点．(2)解取AD 的中点O ，连接OP ，OE . 因为PA ＝PD ，所以OP ⊥AD ，又因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，且OP ⊂平面PAD ，所以OP ⊥平面ABCD .因为OE ⊂平面ABCD ，所以OP ⊥OE . 因为四边形ABCD 是正方形，所以OE ⊥AD ，如图，建立空间直角坐标系Oxyz ，则P (0,0，2)，D (2,0,0)，B (－2,4,0)，BD →＝(4，－4,0)，PD →＝(2,0，－2)．设平面BDP 的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·BD →＝0，n ·PD →＝0，即⎩⎨⎧4x －4y ＝0，2x －2z ＝0.令x ＝1，则y ＝1，z ＝ 2.于是n ＝(1,1，2)．平面PAD 的法向量为p ＝(0,1,0)，所以cos 〈n ，p 〉＝n ·p |n ||p |＝12. 由题意知，二面角B －PD －A 为锐角，所以它的大小为π3. (3)解由题意知M ⎝ ⎛⎭⎪⎫－1，2，22，C (2,4,0)， MC →＝⎝ ⎛⎭⎪⎫3，2，－22. 设直线MC 与平面BDP 所成的角为α，则sin α＝|cos 〈n ，MC →〉|＝|n ·MC →||n ||MC →|＝269. 所以直线MC 与平面BDP 所成角的正弦值为269. 押题预测(2017届太原模拟)如图，在几何体ABCDEF 中，四边形ABCD 是菱形，BE ⊥平面ABCD, DF ∥BE,DF ＝2BE ＝2，EF ＝3.(1)证明：平面ACF ⊥平面BEFD ；(2)若二面角A －EF －C 是直二面角，求AE 与平面ABCD 所成角的正切值．押题依据利用空间向量求二面角全面考查了空间向量的建系、求法向量、求角等知识，是高考的重点和热点．(1)证明 ∵四边形ABCD 是菱形，∴AC ⊥BD .∵BE ⊥平面ABCD ，∴BE ⊥AC ，又BE ∩BD ＝B ，BE ，BD ⊂平面BEFD ，∴AC ⊥平面BEFD .∵AC ⊂平面ACF ，∴平面ACF ⊥平面BEFD .(2)解方法一 (向量法)设AC 与BD 交于点O ，以点O 为原点， OA 方向为x 轴， OB 方向为y 轴， BE 方向为z 轴建立空间直角坐标系，如图．取DF 的中点H ，连接EH .∵BE 綊DH, DH ＝1，∴四边形BEHD 为平行四边形，∵在Rt△EHF 中， FH ＝1，EF ＝3， ∴EH ＝22，∴BD ＝2 2.设AB 的长为a ，则各点坐标为A ()a 2－2，0，0，E ()0，2，1，F ()0，－2，2，C ()－a 2－2，0，0，∴AE →＝()－a 2－2，2，1，EF →＝()0，－22，1，CE →＝()a 2－2，2，1.设n 1＝()x 1，y 1，z 1为平面AEF 的法向量，n 2＝()x 2，y 2，z 2为平面CEF 的法向量．由n 1·AE →＝0，n 1·EF →＝0，得z 1＝22y 1，x 1＝32a 2－2y 1.令y 1＝a 2－2，得n 1＝()32，a 2－2，22a 2－4，同理得n 2＝()－32，a 2－2，22a 2－4.∵二面角A －EF －C 是直二面角，∴n 1·n 2＝0，得a ＝2，由题可得∠EAB 为AE 与平面ABCD 的夹角，∵AB ＝2，BE ＝1，∴tan∠EAB ＝BEAB ＝12.方法二 (几何法)设AC 与BD 交于点O .∵四边形ABCD 是菱形，∴△ADF ≌△CDF ，△ABE ≌△CBE ，∴AF ＝CF ，AE ＝CE ，∴△AEF ≌△CEF .过A 作AM ⊥EF ，连接CM ，则CM ⊥EF ，则∠AMC 为二面角A －EF －C 的平面角．设菱形的边长为a ，∵BE ＝1，DF ＝2，EF ＝3, DF ⊥BD ，∴BD ＝2 2.在△AOB 中， AO ＝a 2－2，∴AC ＝2a 2－2，∵A －EF －C 的二面角为直角，∴∠AMC 为直角，∴AM ＝2a 2－4，在△AEF 中， AM ⊥EF ，设ME ＝x ，则MF ＝3－x ， AF ＝a 2＋4，AE ＝a 2＋1， ()a 2＋42－()3－x 2＝()a 2＋12－x 2，∴a ＝2. AE 与平面ABCD 所成角为∠EAB ，∴tan∠EAB ＝12.A 组专题通关1．已知平面ABC ，点M 是空间任意一点，点M 满足条件OM →＝34OA →＋18OB →＋18OC →，则直线AM ( ) A ．与平面ABC 平行B ．是平面ABC 的斜线 C ．是平面ABC 的垂线D ．在平面ABC 内答案 D解析由已知得M ，A ，B ，C 四点共面，所以AM 在平面ABC 内，故选D.2.(2017·湖南省衡阳市联考)如图所示，在正方体AC 1中， AB ＝2, A 1C 1∩B 1D 1＝E ，直线AC 与直线DE 所成的角为α，直线DE 与平面BCC 1B 1所成的角为β，则cos ()α－β等于( ) A.66B.33C.306D.63 答案 A解析由题意可知，α＝π2，则cos ()α－β＝sin β，以点D 为坐标原点，DA ，DC ，DD 1方向为x ，y ，z 轴正方向建立空间直角坐标系，则D ()0，0，0，E ()1，1，2， DE →＝()1，1，2，平面BCC 1B 1的法向量DC →＝()0，2，0，由此可得cos ()α－β＝sin β＝DE →·DC →|DE →||DC →|＝66. 故选A. 3．正方体ABCD －A 1B 1C 1D 1中，点P 在A 1C 上运动(包括端点)，则BP 与AD 1所成角的取值范围是( )A.⎣⎢⎡⎦⎥⎤π4，π3 B.⎣⎢⎡⎦⎥⎤π4，π2 C.⎣⎢⎡⎦⎥⎤π6，π2 D.⎣⎢⎡⎦⎥⎤π6，π3 答案 D 解析以点D 为原点，DA ，DC ，DD 1分别为x ，y ，z 轴建立空间直角坐标系，设正方体棱长为1，设点P 坐标为()x ，1－x ，x (0≤x ≤1)，则BP →＝()x －1，－x ，x ，BC 1→＝()－1，0，1，设BP →，BC 1→的夹角为α，所以cos α＝BP →·BC 1→||BP →||BC 1→＝1()x －12＋2x 2×2＝13⎝ ⎛⎭⎪⎫x －132＋23·2，所以当x ＝13时，cos α取得最大值32，α＝π6.当x ＝1时， cos α取得最小值12，α＝π3.因为BC 1∥AD 1.故选D.4．(2017·全国Ⅱ)已知直三棱柱ABC —A 1B 1C 1中，∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，则异面直线AB 1与BC 1所成角的余弦值为( )A.32B.155C.105D.33 答案 C解析方法一将直三棱柱ABC －A 1B 1C 1补形为直四棱柱ABCD －A 1B 1C 1D 1，如图所示，连接AD 1，B 1D 1，BD .由题意知∠ABC ＝120°，AB ＝2，BC ＝CC 1＝1，所以AD 1＝BC 1＝2，AB 1＝5，∠DAB ＝60°.在△ABD 中，由余弦定理知，BD 2＝22＋12－2×2×1×cos 60°＝3，所以BD ＝3，所以B 1D 1＝ 3.又AB 1与AD 1所成的角即为AB 1与BC 1所成的角θ，所以cos θ＝AB 21＋AD 21－B 1D 212×AB 1×AD 1＝5＋2－32×5×2＝105. 故选C.方法二以B 1为坐标原点，B 1C 1所在的直线为x 轴，垂直于B 1C 1的直线为y 轴，BB 1所在的直线为z 轴建立空间直角坐标系，如图所示．由已知条件知B 1(0,0,0)，B (0,0,1)，C 1(1,0,0)，A (－1，3，1)，则BC 1→＝(1,0，－1)，AB 1→＝(1，－3，－1)．所以cos 〈AB 1→，BC 1→〉＝AB 1→·BC 1→|AB 1→||BC 1→|＝25×2＝105. 所以异面直线AB 1与BC 1所成角的余弦值为105. 故选C. 5．(2017·全国Ⅲ)a ，b 为空间中两条互相垂直的直线，等腰直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以直线AC 为旋转轴旋转，有下列结论：①当直线AB 与a 成60°角时，AB 与b 成30°角；②当直线AB 与a 成60°角时，AB 与b 成60°角；③直线AB 与a 所成角的最小值为45°；④直线AB 与a 所成角的最大值为60°.其中正确的是________．(填写所有正确结论的编号)答案 ②③解析依题意建立如图所示的空间直角坐标系，设等腰直角三角形ABC 的直角边长为1.由题意知，点B 在平面xOy 中形成的轨迹是以C 为圆心，1为半径的圆．设直线a 的方向向量为a ＝(0,1,0)，直线b 的方向向量为b ＝(1,0,0)，CB →以Ox 轴为始边沿逆时针方向旋转的旋转角为θ，θ∈[)0，2π，则B (cos θ，sin θ，0)，∴AB →＝(cos θ，sin θ，－1)，|AB →|＝ 2.设直线AB 与直线a 所成的夹角为α，则cos α＝|AB →·a ||a ||AB →|＝22|sin θ|∈⎣⎢⎡⎦⎥⎤0，22， ∴45°≤α≤90°，∴③正确，④错误；设直线AB 与直线b 所成的夹角为β，则cos β＝|AB →·b ||b ||AB →|＝22|cos θ|. 当直线AB 与直线a 的夹角为60°，即α＝60°时，则|sin θ|＝2cos α＝2cos 60°＝22， ∴|cos θ|＝22，∴cos β＝22|cos θ|＝12. ∵45°≤β≤90°，∴β＝60°，即直线AB 与b 的夹角为60°.∴②正确，①错误．6.如图，在直四棱柱ABCD －A 1B 1C 1D 1中，底面四边形ABCD 为菱形，A 1A ＝AB ＝2，∠ABC ＝π3，E ，F 分别是BC ，A 1C 的中点．(1)求异面直线EF ，AD 所成角的余弦值；(2)点M 在线段A 1D 上，A 1MA 1D ＝λ .若CM ∥平面AEF ，求实数λ的值．解因为四棱柱ABCD －A 1B 1C 1D 1为直四棱柱，所以A 1A ⊥平面ABCD .又AE ⊂平面ABCD ，AD ⊂平面ABCD ，所以A 1A ⊥AE ，A 1A ⊥AD .在菱形ABCD 中，∠ABC ＝π3，则△ABC 是等边三角形．因为E 是BC 中点，所以BC ⊥AE .因为BC ∥AD ，所以AE ⊥AD .以{AE →，AD →，AA 1→}为正交基底建立空间直角坐标系．则A (0,0,0)，C (3，1,0)，D (0,2,0)，A 1(0,0,2)，E (3，0,0)，F ⎝ ⎛⎭⎪⎫32，12，1.(1)AD →＝(0,2,0)，EF →＝⎝ ⎛⎭⎪⎫－32，12，1，从而cos 〈AD →，EF →〉＝AD →·EF →|AD →||EF →|＝24.故异面直线EF ，AD 所成角的余弦值为24.(2)设M (x ，y ，z )，由于点M 在线段A 1D 上，且A 1MA 1D ＝λ，则A 1M →＝λA 1D →，即(x ，y ，z －2)＝λ(0,2，－2)．则M (0,2λ，2－2λ)，CM →＝(－3，2λ－1,2－2λ)．设平面AEF 的法向量为n ＝(x 0，y 0，z 0)．因为AE →＝(3，0,0)，AF →＝⎝ ⎛⎭⎪⎫32，12，1，由n ·AE →＝0，n ·AF →＝0，得x 0＝0，12y 0＋z 0＝0. 取y 0＝2，则z 0＝－1，则平面AEF 的一个法向量为n ＝(0,2，－1)．由于CM ∥平面AEF ，则n ·CM →＝0，即2(2λ－1)－(2－2λ)＝0，解得λ＝23.7．(2017·全国Ⅲ)如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD＝∠CBD ，AB ＝BD .(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D —AE —C 的余弦值．(1)证明由题设可得△ABD ≌△CBD .从而AD ＝CD ，又△ACD 为直角三角形，所以∠ADC ＝90°，取AC 的中点O ，连接DO ，BO ，则DO ⊥AC ，DO ＝AO .又因为△ABC 是正三角形，故BO ⊥AC ，所以∠DOB 为二面角D —AC —B 的平面角，在Rt△AOB 中，BO 2＋OA 2＝AB 2，又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°，所以平面ACD ⊥平面ABC .(2)解由题设及(1)知，OA ，OB ，OD 两两垂直，以O 为坐标原点， OA →为x 轴正方向，OB →为y 轴正方向，OD →为z 轴正方向，|OA →|为单位长度，建立如图所示的空间直角坐标系Oxyz ，则O (0,0,0)，A ()1，0，0，D ()0，0，1，B ()0， 3，0，C (－1，0,0)，由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E ⎝ ⎛⎭⎪⎫0，32，12，故AE →＝⎝⎛⎭⎪⎫－1，32，12，AD →＝()－1，0，1，OA →＝()1，0，0.设平面AED 的法向量为n 1＝(x 1，y 1，z 1)，平面AEC 的法向量为n 2＝(x 2，y 2，z 2)，则⎩⎪⎨⎪⎧AE →·n 1＝0，AD →·n 1＝0，即⎩⎪⎨⎪⎧－x 1＋32y 1＋12z 1＝0，－x 1＋z 1＝0，令x 1＝1，则n 1＝⎝ ⎛⎭⎪⎫1，33，1. ⎩⎪⎨⎪⎧ AE →·n 2＝0，OA →·n 2＝0，即⎩⎪⎨⎪⎧－x 2＋32y 2＋12z 2＝0，x 2＝0，令y 2＝－1，则n 2＝(0，－1，3)，设二面角D —AE —C 的平面角为θ，易知θ为锐角，则cos θ＝|n 1·n 2||n 1||n 2|＝77.8．(2016·浙江)如图，在三棱台ABC —DEF 中，平面BCFE ⊥平面ABC ，∠ACB ＝90°，BE ＝EF ＝FC ＝1，BC ＝2，AC ＝3.(1)求证：BF ⊥平面ACFD ；(2)求二面角B —AD —F 的平面角的余弦值．(1)证明延长AD ，BE ，CF 相交于一点K ，如图所示．因为平面BCFE ⊥平面ABC ，且AC ⊥BC ，所以AC ⊥平面BCFE ，因此BF ⊥AC .又因为EF ∥BC ，BE ＝EF ＝FC ＝1，BC ＝2，所以△BCK 为等边三角形，且F 为CK 的中点，则BF ⊥CK ，且CK ∩AC ＝C ，所以BF ⊥平面ACFD .(2)解方法一过点F 作FQ ⊥AK 于点Q ，连接BQ .因为BF ⊥平面ACFD ，所以BF ⊥AK ，则AK ⊥平面BQF ，所以BQ ⊥AK .所以∠BQF 是二面角B —AD —F 的平面角．在Rt△ACK 中，AC ＝3，CK ＝2，得FQ ＝31313. 在Rt△BQF 中，FQ ＝31313，BF ＝3，得cos∠BQF ＝34. 所以二面角B —AD —F 的平面角的余弦值为34.方法二如图，延长AD ，BE ，CF 相交于一点K ，则△BCK 为等边三角形．取BC 的中点O ，连接KO ，则KO ⊥BC ，又平面BCFE ⊥平面ABC ，所以KO ⊥平面ABC .以点O 为原点，分别以射线OB ，OK 的方向为x 轴，z 轴的正方向，建立空间直角坐标系Oxyz .由题意得B (1,0,0)，C (－1,0,0)，K (0,0，3)，A (－1，－3，0)，E ⎝ ⎛⎭⎪⎫12，0，32，F ⎝ ⎛⎭⎪⎫－12，0，32. 因此，AC →＝(0,3,0)，AK →＝(1,3，3)，AB →＝(2,3,0)．设平面ACK 的法向量为m ＝(x 1，y 1，z 1)，平面ABK 的法向量为n ＝(x 2，y 2，z 2)．由⎩⎪⎨⎪⎧AC →·m ＝0，AK →·m ＝0，得⎩⎨⎧ 3y 1＝0，x 1＋3y 1＋3z 1＝0，取m ＝(3，0，－1)；由⎩⎪⎨⎪⎧ AB →·n ＝0，AK →·n ＝0，得⎩⎨⎧ 2x 2＋3y 2＝0，x 2＋3y 2＋3z 2＝0，取n ＝(3，－2，3)．于是，cos 〈m ，n 〉＝m ·n |m ||n |＝34. 所以二面角B —AD —F 的平面角的余弦值为34. B 组能力提高9．已知空间四边形ABCD ，满足||AB →＝3, ||BC →＝7, ||CD →＝11, ||DA→＝9，则AC →·BD →的值为( ) A ．－1B ．0 C.212D.332答案 B解析如图，构造符合题设的空间四边形ABCD ，不妨设AB ⊥BD ，则BD ＝81－9＝72，因为BC 2＋BD 2＝CD 2，则CB ⊥BD ，故由线面垂直的判定定理可得BD ⊥平面ABC ，AC ⊂平面ABC ，所以AC ⊥BD ，即AC →·BD →＝0，故选B.10.(2017届上饶模拟)如图，在长方体ABCD —A 1B 1C 1D 1中，AB ＝3AD ＝3AA 1＝3，点P 为线段A 1C 上的动点(包含线段端点)，则下列结论正确的是________．①当A 1C →＝3A 1P →时，D 1P ∥平面BDC 1；②当A 1C →＝5A 1P →时，A 1C ⊥平面D 1AP ；③∠APD 1的最大值为90°；④AP ＋PD 1的最小值为 5.答案 ①②解析以D 为坐标原点建立空间直角坐标系，则A (1,0,0)，A 1(1,0,1)，C (0，3，0)，D 1(0,0,1)，C 1(0，3，1)，B (1，3，0)，则A 1C →＝(－1，3，－1)，设P (x ，y ，z )，A 1P →＝(x －1，y ，z －1)．对于①，当A 1C →＝3A 1P →时，(－1，3，－1)＝3(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫23，33，23， D 1P →＝⎝ ⎛⎭⎪⎫23，33，－13，设平面BDC 1的法向量为n 1＝(x 1，y 1，z 1)，则由⎩⎪⎨⎪⎧n 1·DB →＝0，n 1·DC 1→＝0，解得n 1＝(－3，1，－3)，由于D 1P →·n 1＝0，所以D 1P ∥平面BDC 1成立；对于②，当A 1C →＝5A 1P →时，(－1，3，－1)＝5(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫45，35，45，由⎩⎪⎨⎪⎧ A 1C →·D 1A →＝0，A 1C →·D 1P →＝0，可知A 1C ⊥平面D 1AP 成立；对于③，设A 1C →＝λA 1P →，即(－1，3，－1)＝λ(x －1，y ，z －1)，解得P ⎝ ⎛⎭⎪⎫1－1λ，3λ，1－1λ，由cos 〈PA →，PD 1→〉＝⎝ ⎛⎭⎪⎫1λ，－3λ，1λ－1⎝ ⎛⎭⎪⎫1λ－1，－3λ，1λ⎝ ⎛⎭⎪⎫1λ2＋⎝ ⎛⎭⎪⎫－3λ2＋⎝ ⎛⎭⎪⎫1λ－12，其分子化简得5－2λλ2，当λ>52时，cos 〈PA →，PD 1→〉<0，故∠APD 1的最大值可以为钝角，③错误．对于④，根据③计算的数据，PA →＝⎝ ⎛⎭⎪⎫1λ，－3λ，1λ－1，PD 1→＝⎝ ⎛⎭⎪⎫1λ－1，－3λ，1λ，|PA →|＋|PD 1→|＝2⎝ ⎛⎭⎪⎫1λ2＋⎝ ⎛⎭⎪⎫－3λ2＋⎝ ⎛⎭⎪⎫1λ－12＝25·1λ2－2·1λ＋1，在对称轴1λ＝15，即λ＝5时取得最小值245＝455，故④错误．11.如图，已知圆锥OO 1和圆柱O 1O 2的组合体(它们的底面重合)，圆锥的底面圆O 1半径为r ＝5, OA为圆锥的母线，AB 为圆柱O 1O 2的母线，D ，E 为下底面圆O 2上的两点，且DE ＝6，AB ＝6.4，AO ＝52，AO ⊥AD .(1)求证：平面ABD ⊥平面ODE;(2)求二面角B —AD —O 的正弦值．(1)证明依题易知，圆锥的高为h ＝(52)2－52＝5，又圆柱的高为AB ＝6.4，AO ⊥AD ，所以OD 2＝OA 2＋AD 2，因为AB ⊥BD ，所以AD 2＝AB 2＋BD 2，连接OO 1，O 1O 2，DO 2，易知O ，O 1，O 2三点共线，OO 2⊥DO 2，所以OD 2＝OO 22＋O 2D 2，所以BD 2＝OO 22＋O 2D 2－AO 2－AB 2＝(6.4＋5)2＋52－(52)2－6.42＝64，解得BD ＝8，又因为DE ＝6，圆O 2的直径为10，圆心O 2在∠BDE 内，所以∠BDE ＝90°，所以DE ⊥BD .因为AB ⊥平面BDE ，所以DE ⊥AB ，因为AB ∩BD ＝B ，AB ，BD ⊂平面ABD ，所以DE ⊥平面ABD .又因为DE ⊂平面ODE ，所以平面ABD ⊥平面ODE .(2)解如图，以D 为原点， DB ，DE 所在的直线为x ，y 轴，建立空间直角坐标系．则D (0,0,0)，A (8,0,6.4)，B (8,0,0)，O (4,3,11.4)．所以DA →＝(8,0,6.4)，DB →＝(8,0,0)，DO →＝(4,3,11.4)，设平面DAO 的法向量为u ＝(x ，y ，z )，所以DA →·u ＝8x ＋6.4z ＝0，DO →·u ＝4x ＋3y ＋11.4z ＝0，令x ＝12，则u ＝(12,41，－15)．可取平面BDA 的一个法向量为v ＝(0,1,0)，所以cos 〈u ，v 〉＝u·v |u||v |＝41582＝8210，所以二面角B —AD —O 的正弦值为3210. 12．(2017届北京市丰台区综合练习)如图所示的几何体中，四边形ABCD 为等腰梯形， AB ∥CD, AB ＝2AD ＝2, ∠DAB ＝60°，四边形CDEF 为正方形，平面CDEF ⊥平面ABCD .(1)若点G 是棱AB 的中点，求证： EG ∥平面BDF ；(2)求直线AE 与平面BDF 所成角的正弦值；(3)在线段FC 上是否存在点H ，使平面BDF ⊥平面HAD ？若存在，求FH HC的值；若不存在，说明理由．(1)证明由已知得EF ∥ CD ，且EF ＝CD .因为四边形ABCD 为等腰梯形，所以BG ∥CD .因为G 是棱AB 的中点，所以BG ＝CD .所以EF ∥BG ，且EF ＝BG ，故四边形EFBG 为平行四边形，所以EG ∥FB .因为FB ⊂平面BDF, EG ⊄平面BDF ，所以EG ∥平面BDF .(2)解因为四边形CDEF 为正方形，所以ED ⊥DC .因为平面CDEF ⊥平面ABCD ，平面CDEF ∩平面ABCD ＝DC ，DE ⊂平面CDEF ，所以ED ⊥平面ABCD .在△ABD 中，因为∠DAB ＝60°， AB ＝2AD ＝2，所以由余弦定理，得BD ＝3，所以AD ⊥BD .在等腰梯形ABCD 中，可得DC ＝CB ＝1.如图，以D 为原点，以DA ，DB ，DE 所在直线分别为x ，y ，z 轴，建立空间直角坐标系，则D ()0，0，0，A ()1，0，0， E ()0，0，1， B ()0，3，0，F ⎝ ⎛⎭⎪⎫－12，32，1，所以AE →＝()－1，0，1， DF →＝⎝ ⎛⎭⎪⎫－12，32，1， DB →＝()0，3，0.设平面BDF 的法向量为n ＝()x ，y ，z ，因为⎩⎪⎨⎪⎧ n ·DB →＝0，n ·DF →＝0，所以⎩⎪⎨⎪⎧ 3y ＝0，－12x ＋32y ＋z ＝0.取z ＝1，则x ＝2，y ＝0，则n ＝()2，0，1.设直线AE 与平面BDF 所成的角为θ，则sin θ＝||cos 〈AE →，n 〉＝||AE →·n ||AE →||n ＝1010，所以AE 与平面BDF 所成角的正弦值为1010.(3)解线段FC 上不存在点H ，使平面BDF ⊥平面HAD .证明如下：假设线段FC 上存在点H ，设H ⎝ ⎛⎭⎪⎫－12，32，t ()0≤t ≤1，则DH →＝⎝ ⎛⎭⎪⎫－12，32，t .设平面HAD 的法向量为m ＝()a ，b ，c ，因为⎩⎪⎨⎪⎧ m ·DA →＝0，m ·DH →＝0，所以⎩⎪⎨⎪⎧ a ＝0，－12a ＋32b ＋tc ＝0.取c ＝1，则a ＝0，b ＝－23t ，得m ＝⎝ ⎛⎭⎪⎫0，－23 t ，1.要使平面BDF ⊥平面HAD ，只需m·n ＝0，即2×0－23t×0＋1×1＝0, 此方程无解．所以线段FC上不存在点H，使平面BDF⊥平面HAD.。

2018版高考数学考点34利用空间向量法解决立体几何的综合问题试题解读与变式

考点34：利用空间向量法解决立体几何的综合问题【考纲要求】1.能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题.2.了解向量方法在研究立体几何问题中的应用. 【命题规律】利用空间向量法解决立体几何的综合问题是高考热点问题，解答题考查的比较多.预计2018年的高考对本知识的考查空间向量的应用，仍然是以简单几何体为载体．【典型高考试题变式】（一）利用向量证明直线和平面的位置关系及其空间角例1.【2016全国1卷（理）】如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF 为正方形，AF=2FD ，90AFD ∠=，且二面角D AF E 与二面角C BEF 都是60．（Ⅰ）证明：平面ABEF ⊥平面EFDC ；（Ⅱ）求二面角E BC A 的余弦值．【解析】（Ⅱ）过D 作DG ΕF ⊥，垂足为G ，由（Ⅰ）知DG ⊥平面ΑΒΕF ．以G 为坐标原点，GF 的方向为x 轴正方向，GF 为单位长，建立如图所示的空间直角坐标系G xyz -．由（Ⅰ）知DFE ∠为二面角D AF E --的平面角，故60DFE ∠=，则2DF =，3DG =，可得()1,4,0A ，()3,4,0B -，()3,0,0E -，(3D ．由已知，//AB EF ，所以//AB 平面EFDC ．又平面ABCD平面EFDC DC =，故//AB CD ，//CD EF ．由//BE AF ，可得BE ⊥平面EFDC ，所以C ΕF ∠为二面角C BE F --的平面角，60C ΕF ∠=．从而可得()2,0,3C -．所以()1,0,3ΕC =，()0,4,0ΕΒ=，()3,4,3ΑC =--，()4,0,0ΑΒ=-．设(),,x y z =n 是平面ΒC Ε的法向量，则00ΕC ΕΒ⎧⋅=⎪⎨⋅=⎪⎩n n ，即3040x z y ⎧+=⎪⎨=⎪⎩，所以可取()3,0,3=-n ．设m 是平面ΑΒCD 的法向量，则0ΑC ΑΒ⎧⋅=⎪⎨⋅=⎪⎩m m ，同理可取()0,3,4=m ．则219cos ,19⋅==-n m n m n m ．故二面角E BC A 的余弦值为21919-．【方法技巧归纳】立体几何解答题第一问通常考查线面位置关系的证明,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,注意防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.第二问一般考查角度问题,多用空间向量法解决.【变式1】【改编例题条件】【2016全国2卷（理）】如图,菱形ABCD 的对角线AC 与BD 交于点O,AB=5,AC=6,点E,F 分别在AD,CD 上,AE=CF=,EF 交BD 于点H.将△DEF 沿EF 折到△D'EF 的位置,OD'=.（Ⅰ）证明:D'H⊥平面ABCD. （Ⅱ）求二面角B-D'A-C 的正弦值.【解析】试题分析：（Ⅰ）证，再证，最后证；（Ⅱ）用向量法求解.试题解析：（Ⅰ）由已知得，，又由得，故.因此，从而.由,得.由得.所以，.于是，故.又，而，所以.（Ⅱ）如图，以为坐标原点，的方向为轴正方向，建立空间直角坐标系，则，，，，，，，.设是平面的法向量，则，即，所以可取.设是平面的法向量，则，即，所以可取.于是，.因此二面角的正弦值是.【变式2】【改编例题条件，利用导数运算法则构造函数求解不等式】【2016全国3卷（理）】如图，四棱锥P −ABC 中，PA⊥底面ABCD ，AD∥BC，AB=AD=AC=3，PA=BC=4，M 为线段AD 上一点，AM=2MD ，N 为PC 的中点.（Ⅰ）证明MN∥平面PAB;（Ⅱ）求直线AN 与平面PMN 所成角的正弦值. 【解析】试题分析：（Ⅰ）取BP 的中点T ，然后结合条件中的数据证明四边形AMNT 为平行四边形，从而得到MNAT ，由此结合线面平行的判定定理可证；（Ⅱ）以A 为坐标原点，AE 的方向为x 轴正方向,建立空间直角坐标系，然后通过求直线AN 的方向向量与平面PMN 的法向量的夹角的余弦值来求解AN 与平面PMN 所成角的正弦值．（Ⅱ）取BC 的中点E ，连结AE .由AC AB =得BC AE ⊥，从而AD AE ⊥，且5)2(2222=-=-=BC AB BE AB AE . 以A 为坐标原点，AE 的方向为x 轴正方向，建立如图所示的空间直角坐标系xyz A -.由题意知，)4,0,0(P ，)0,2,0(M ，)0,2,5(C ，)2,1,25(N ， (0,2,4)PM =-，5(,1,2)2PN =-，5(,1,2)2AN =. 设(,,)x y z =n 为平面PMN 的一个法向量，则0,0,PM PN ⎧⋅=⎪⎨⋅=⎪⎩n n 即240,520,2y z x y z -=⎧⎪⎨+-=⎪⎩ 可取(0,2,1)=n .于是||85|cos ,|25||||AN AN AN ⋅==n n n .（二）利用向量解决立体几何中的探索问题例2.【2016北京卷】如图，在四棱锥P ABCD -中，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，AB AD ⊥，1AB =，2AD =，5AC CD ==（Ⅰ）求证：PD ⊥平面PAB ；（Ⅱ）求直线PB 与平面PCD 所成角的正弦值；（Ⅲ）在棱PA 上是否存在点M ，使得BM∥平面PCD?若存在，求AMAP的值；若不存在，说明理由. 【解析】试题解析：（Ⅰ）因为平面⊥PAD 平面ABCD ，AD AB ⊥，所以⊥AB 平面PAD . 所以PD AB ⊥. 又因为PD PA ⊥，所以⊥PD 平面PAB .（Ⅱ）取AD 的中点O ，连结CO PO ,. 因为PD PA =，所以AD PO ⊥.又因为⊂PO 平面PAD ，平面⊥PAD 平面ABCD ，所以⊥PO 平面ABCD .因为⊂CO 平面ABCD ，所以⊥PO CO . 因为CD AC =，所以AD CO ⊥.如图建立空间直角坐标系xyz O -.由题意得，)1,0,0(),0,1,0(),0,0,2(),0,1,1(),0,1,0(P D C B A -.设平面PCD 的法向量为(,,)x y z =n ，则0,0,PD PC ⎧⋅=⎪⎨⋅=⎪⎩n n 即⎩⎨⎧=-=--,02,0z x z y 令2=z ，则2,1-==y x . 所以(1,2,2)=-n .又)1,1,1(-=PB ，所以3cos ,3PB PB PB⋅==-n n n . 所以直线PB 与平面PCD 所成角的正弦值为33.（Ⅲ）设M 是棱PA 上一点，则存在]1,0[∈λ使得AP AM λ=. 因此点),,1(),,1,0(λλλλ--=-BM M .因为⊄BM 平面PCD ，所以∥BM 平面PCD 当且仅当0BM ⋅=n ，即0)2,2,1(),,1(=-⋅--λλ，解得41=λ. 所以在棱PA 上存在点M 使得∥BM 平面PCD ，此时41=AP AM .【方法技巧归纳】平面与平面垂直的性质定理的应用：当两个平面垂直时，常作的辅助线是在其中一个平面内作交线的垂线，把面面垂直转化为线面垂直，进而可以证明线线垂直(必要时可以通过平面几何的知识证明垂直关系)，构造(寻找)二面角的平面角或得到点到面的距离等.【变式1】【改编例题的条件】【2015湖北卷（理）】《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的四面体称之为鳖臑．如图，在阳马P ABCD -中，侧棱PD ⊥底面ABCD ，且PD CD =，过棱PC 的中点E ，作EF PB ⊥交PB 于点F ，连接,,,.DE DF BD BE（Ⅰ）证明：PB DEF ⊥平面．试判断四面体DBEF 是否为鳖臑，若是，写出其每个面的直角（只需写出结论）；若不是，说明理由；（Ⅱ）若面DEF 与面ABCD 所成二面角的大小为π3，求DCBC的值．【解析】（解法1）（Ⅰ）因为PD ⊥底面ABCD ，所以PD BC ⊥，由底面ABCD 为长方形，有BC CD ⊥，而PDCD D =，所以BC PCD ⊥平面．而DE PCD ⊂平面，所以BC DE ⊥．又因为PD CD =，点E 是PC 的中点，所以DE PC ⊥．而PCBC C =，所以DE ⊥平面PBC ．而PB PBC ⊂平面，所以PB DE ⊥．又PB EF ⊥，DEEF E =，所以PB ⊥平面DEF ．由DE ⊥平面PBC ，PB ⊥平面DEF ，可知四面体BDEF 的四个面都是直角三角形，即四面体BDEF 是一个鳖臑，其四个面的直角分别为DEB DEF ∠∠，，EFB D FB ∠∠，．（Ⅱ）如图1，在面PBC 内，延长BC 与FE 交于点G ，则DG 是平面DEF 与平面ABCD的交线．由（Ⅰ）知，PB DEF ⊥平面，所以PB DG ⊥．又因为PD ⊥底面ABCD ，所以PD DG ⊥．而PDPB P =，所以DG PBD ⊥平面．故BDF ∠是面DEF 与面ABCD 所成二面角的平面角，设1PD D C ==，BC λ=，有21BD λ=+，在Rt△PDB 中, 由DF PB ⊥, 得π3DPF FDB ∠=∠=, 则 2πtan tan 133BD DPF PDλ=∠==+=, 解得2λ=．所以12.2DC BC λ== 故当面DEF 与面ABCD 所成二面角的大小为π3时，22DC BC =．因(0,1,1)PC =-, 0DE PC ⋅=, 则DE PC ⊥, 所以DE PBC ⊥平面．由DE ⊥平面PBC ，PB ⊥平面DEF ，可知四面体BDEF 的四个面都是直角三角形，即四面体BDEF 是一个鳖臑，其四个面的直角分别为DEB DEF ∠∠，，EFB D FB ∠∠，．（Ⅱ）由PD ABCD ⊥平面，所以(0,0,1)DP =是平面ABCD 的一个法向量；由（Ⅰ）知，PB DEF ⊥平面，所以(,1,1)BP λ=--是平面DEF 的一个法向量．若面DEF 与面ABCD 所成二面角的大小为π3，则2π11cos32||||2BP DP BP DP λ⋅===⋅+，解得2λ=．所以12.2DC BC λ==故当面DEF 与面ABCD 所成二面角的大小为π3时，22DC BC =．【变式2】【改编例题的条件和问法】【2014湖北卷】如图，在棱长为2的正方体1111D C B A ABCD -中，N M F E ,,,分别是棱1111,,,D A B A AD AB 的中点，点Q P ,分别在棱1DD ,1BB 上移动，且()20<<==λλBQ DP .（1）当1=λ时，证明：直线//1BC 平面EFPQ ；（2）是否存在λ，使平面EFPQ 与面PQMN 所成的二面角为直二面角？若存在，求出λ的值；若不存在，说明理由.【解析】试题分析：（1）由正方体1111D C B A ABCD -的性质得11//AD BC ，当1=λ时，证明1//AD FP ，由平行于同一条直线的两条直线平行得FP BC //1，根据线面平行的判定定理证明//1BC 平面EFPQ ；（2）解法1，如图2，连结BD ，证明四边形EFPQ 与四边形PQMN 是等腰梯形，分别取EF 、PQ 、MN 的中点为H 、O 、G ，连结OH 、OG ，证明GOH ∠是平面EFPQ 与平面PQMN 所成的二面角的平面角，设存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角，求出λ的值；解法2，以D 为原点，射线1,,DD DC DA 分别为z y x ,,轴的正半轴建立如图3的空间直角坐标系xyz D -，用向量法求解. 几何法：（1）证明：如图1，连结1AD ，由1111D C B A ABCD -是正方体，知11//AD BC ，当1=λ时，P 是1DD 的中点，又F 是AD 的中点，所以1//AD FP ，所以FP BC //1，而⊂FP 平面EFPQ ，且⊄1BC 平面EFPQ ，故//1BC 平面EFPQ .于是，21λ+==FP EQ ，所以四边形EFPQ 是等腰梯形，同理可证四边形PQMN 是等腰梯形，分别取EF 、PQ 、MN 的中点为H 、O 、G ，连结OH 、OG ，则PQ GO ⊥，PQ HO ⊥，而O HO GO = ，故GOH ∠是平面EFPQ 与平面PQMN 所成的二面角的平面角，若存在λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角，则90=∠GOH ，连结EM 、FN ，则由MN EF //，且MN EF =，知四边形EFNM 是平行四边形，连结GH ，因为H 、G 是EF 、MN 的中点，所以2==ME GH ，在GOH ∆中，42=GH ，21)22(12222+=-+=λλOH ， 21)2()22()2(12222+-=--+=λλOG ，由222GH OH OG =+得42121)2(22=+++-λλ，解得221±=λ，故存在221±=λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角. 向量法：以D 为原点，射线1,,DD DC DA 分别为z y x ,,轴的正半轴建立如图3的空间直角坐标系xyz D -，由已知得),0,0(),0,0,1(),2,2,0(),0,2,2(1λP F C B ，所以)2,0,2(1-=BC ，),0,1(λ-=FP ，)0,1,1(=FE ，（1）证明：当1=λ时，)1,0,1(-=FP ，因为)2,0,2(1-=BC ，所以FP BC 21=，即FP BC //1，而⊂FP 平面EFPQ ，且⊄1BC 平面EFPQ ，故直线//1BC 平面EFPQ .故存在221±=λ，使平面EFPQ 与平面PQMN 所成的二面角为直二面角. 【方法总结】立体几何中的探索性问题立意新颖，形式多样，近年来在高考中频频出现，而空间向量在解决立体几何的探索性问题中扮演着举足轻重的角色，它是研究立体几何中的探索性问题的一个有力工具，应用空间向量这一工具，为分析和解决立体几何中的探索性问题提供了新的视角、新的方法．下面借“题”发挥，透视有关立体几何中的探索性问题的常见类型及其求解策略． 1．条件追溯型解决立体几何中的条件追溯型问题的基本策略是执果索因．其结论明确，需要求出使结论成立的充分条件，可将题设和结论都视为已知条件，即可迅速找到切入点．这类题目要求考生变换思维方向，有利于培养考生的逆向思维能力． 2．存在判断型以“平行、垂直、距离和角”为背景的存在判断型问题是近年来高考数学中创新型命题的一个重要类型，它以较高的新颖性、开放性、探索性和创造性深受命题者的青睐，此类问题的基本特征是：要判断在某些确定条件下的某一数学对象(数值、图形等)是否存在或某一结论是否成立．“是否存在”的问题的命题形式有两种情况：如果存在，找出一个来；如果不存在，需要说明理由．这类问题常用“肯定顺推”的方法．求解此类问题的难点在于涉及的点具有运动性和不确定性，所以用传统的方法解决起来难度较大，若用空间向量方法来处理，通过待定系数法求解其存在性问题，则思路简单、解法固定、操作方便． 3．结论探索型立体几何中的结论探索型问题的基本特征是：给出一定的条件与设计方案，判断设计的方案是否符合条件要求．此类问题的难点是“阅读理解”和“整体设计”两个环节，因此，应做到审得仔细、找得有法、推得有理、证得有力，整合过程无可辩驳．【空间角的范围处理错误注意点】解决此类问题，要注意各种空间角的给定范围，容易在范围上出现问题. 【典例试题演练】1．【2016黔东南州高考第一次模拟】在平行四边形中，,,若将其沿折成直二面角,则与所成的角的余弦值为（）A. B. C.D.【答案】B 【解析】∵，，如图∴，∴，过点A 作，在和，，则，，在空间四边形中，直二面角，∵，，∴平面，以点为原点，以为轴，为轴，过点与平行的直线为轴，建立空间直角坐标系，∴，，，，∴，，∴，，，设与所成的角为，则，故选B.2．【2017届湖南省衡阳市高三下学期第三次联考】如图所示，在正方体1AC 中， 2AB =，1111AC B D E ⋂=，直线AC 与直线DE 所成的角为α，直线DE 与平面11BCC B 所成的角为β，则()cos αβ-=（）A.66 B. 33 C. 306 D. 63【答案】A【解析】由题意可知2πα=，则()cos sin αββ-=，以点D 为坐标原点，DA,DB,DD 1方向为,,x y z 轴正方向建立空间直角坐标系可知：()()()0,0,0,1,1,2,1,1,2D E DE ⇒=，平面11BCC B 的法向量()0,2,0DC =，据此可得： ()6cos sin 6DE DC DE DCαββ⋅-===⨯. 本题选择A 选项.3．【2017届安徽省江淮十校高三下学期第三次联考】如图，正四面体ABCD 中， E 、F 分别是棱BC 和AD 的中点，则直线AE 和CF 所成的角的余弦值为（）A.13 B. 23 C. 14 D. 34【答案】B【解析】解：如图所示，作AO⊥底面BCD ，垂足为O ，O 为底面等边△BCD 的中心，建立空间直角坐标系．不妨取CD=2．则：332313,,0,,,2C D B E ⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，设点M 是线段CD 的中点，则：22133,,,3326,3261330,0,,,,,32661326336,,,,,.263263AM OM BM AO AM OM A F AE CF ===∴=-=⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎛⎫⎛⎫∴=--=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭利用空间向量求解余弦值有：2cos ,3AE CF AE CF AE CF⋅〈〉==-⨯ . ∴异面直线AE 与CF 所成角的余弦值为23.4．【2017届河北省衡水中学押题卷】如图所示，在棱长为2的正方体1111ABCD A BC D -中，E ，F 分别是1CC ， AD 的中点，那么异面直线1D E 和1A F 所成角的余弦值等于__________．【答案】25【解析】以AD,DC,DD1建立空间直角坐标系，则：()()()()()()11112,0,2,1,0,0,0,0,2,0,2,11,0,2,0,2,1A F D E A F D E =--=-得直线1D E和1A F 所成角的余弦值等于11112cos 5A F D E A F D Eθ⋅==⋅ 5．【2017届河北省武邑中学高三下学期一模】高为的四棱锥的底面是边长为1的正方形，点、、、、均同一球面上，底面的中心为，球心到底面的距离为，则异面直线与所成角的余弦值的范围为__________．【答案】【解析】建立如图所示的空间直角坐标系，设由题设外接球的半径，则，即。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第一部分专题五第三讲A 组1．已知AB →＝(1,5，－2)，BC →＝(3,1，z )，若AB →⊥BC →，BP →＝(x －1，y ，－3)，且BP ⊥平面ABC ，则实数x ，y ，z 分别为导学号 52134638( B )A ．337，－157，4B ．407，－157，4C ．407，－2,4D ．4，407，－15[解析] AB →⊥BC →⇒AB →·BC →＝3＋5－2z ＝0，所以z ＝4，又BP ⊥平面ABC ，所以BP →·AB →＝x －1＋5y ＋6＝0，① BP →·BC →＝3x －3＋y －3z ＝0，② 由①②得x ＝407，y ＝－157．2．已知在正四棱锥ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，点E 是AA 1的中点，则异面直线DC 1与BE 所成角的余弦值为导学号 52134639( B )A ．15B ．1010C ．31010D ．35[解析] 建立如图所示空间直角坐标系，设AB ＝1，则AA 1＝2，所以B (1,0,0)，E (0,0,1)，D (0,1,0)，C 1(1,1,2)，则DC 1→＝(1,0,2)，BE →＝(－1,0,1)，设异面直线DC 1与BE 所成的角为θ，则cos θ＝|DC 1→·BE →||DC 1→||BE →|＝|1×(－1)＋0＋2×1|5·2＝1010． 3．已知正三棱柱ABC －A 1B 1C 1的侧棱长与底面边长相等，则直线AB 1与侧面ACC 1A 1所成角的正弦值等于导学号 52134640( A )A ．64 B ．104 C ．22D ．32[解析] 设直线AB 1与侧面ACC 1A 1所成角为θ，建立如图所示空间直角坐标系，设正三棱柱的棱长为2，则A (0，－1,0)，B 1(3，0,2)，AB 1→＝(3，1,2)，O (0,0,0)，B (3，0,0)，所以BO →＝(－3，0,0)为侧面ACC 1A 1的法向量，所以sin θ＝|AB 1→·BO →||AB 1→||BO →|＝64．4．已知正方体ABCD －A 1B 1C 1D 1，下列命题：①(A 1A →＋A 1D 1→＋A 1B 1→)2＝3A 1B 1→2，②A 1C →·(A 1B 1→－A 1A →)＝0，③向量AD 1→与向量A 1B →的夹角为60°，④正方体ABCD －A 1B 1C 1D 1的体积为|AB →·A 1A →·AD →|，其中正确命题的序号是导学号 52134641( B )A ．①③B ．①②C ．①④D ．①②④[解析] 如图所示：以点D 为坐标原点，以向量DA →，DC →，DD 1→所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系，设棱长为1，则D (0,0,0)，A (1,0,0)，B (1,1,0)，C (0,1,0)，A 1(1,0,1)，B 1(1,1,1)，C 1(0,1,1)，D 1(0,0,1)，对于①：A 1A →＝(0,0，－1)，A 1D 1→＝(－1,0,0)， A 1B 1→＝(0,1,0)，所以A 1A →＋A 1D 1→＋A 1B 1→＝(－1,1，－1)，(A 1A →＋A 1D 1→＋A 1B 1→)2＝3，而A 1B 1→2＝1，所以(A 1A →＋A 1D 1→＋A 1B 1→)2＝3A 1B 1→2.所以①正确；对于②：A 1C →＝(－1,1，－1)，A 1A →＝(0,0，－1)，A 1B 1→＝(0,1,0)，所以A 1C →·(A 1B 1→－A 1A →)＝0.所以②正确；对于③：AD 1→＝(－1,0,1)，A 1B →＝(0,1，－1)，AD 1→·A 1B →＝－1，cos 〈AD 1→，A 1B →〉＝AD 1→·A 1B →|AD 1→||A 1B →|＝－12×2＝－12，所以AD 1→与A 1B →的夹角为120°，所以③不正确；对于④：因为AB →·A 1A →＝0，所以④错误．故选B ．5．在底面是直角梯形的四棱锥S －ABCD 中，∠ABC ＝90°，AD ∥BC ，SA ⊥平面ABCD ，SA ＝AB ＝BC ＝1，AD ＝12，则平面SCD 与平面SAB 所成锐二面角的余弦值是3__.导学号 52134642[解析] 如图所示建立空间直角坐标系，则依题意可知D (12，0,0)，C (1,1,0)，S (0,0,1)，可知AD →＝(12，0,0)是平面SAB 的一个法向量．设平面SCD 的法向理n ＝(x ，y ，z )，因为SD →＝(12，0，－1)，DC →＝(12，1,0)，所以n ·SD →＝0，n ·DC →＝0，可推出x 2－z ＝0，x 2＋y ＝0，令x ＝2，则有y ＝－1，z ＝1，所以n ＝(2，－1,1)．设平面SCD 与平面SAB 所成的锐二面角为θ，则cos θ＝|AD →·n ||AD →||n |＝12×2＋0×(－1)＋0×1(12)2·22＋(－1)2＋12＝63．6．已知正三棱柱ABC －A 1B 1C 1的各条棱长都相等，M 是侧棱CC 1的中点，则异面直线AB 1和BM 所成的角的大小是__90°__.导学号 52134643[解析] 延长A 1B 1至D ，使A 1B 1＝B 1D ，连接BD ，C 1D ，DM ，则AB 1∥BD ，∠MBD 就是直线AB 1和BM 所成的角．设三棱柱的各条棱长为2，则BM ＝5，BD ＝22，C 1D 2＝A 1D 2＋A 1C 21－2A 1D ·A 1C 1cos 60°＝16＋4－2×4＝12.DM 2＝C 1D 2＋C 1M 2＝13，所以cos ∠DBM ＝BM 2＋BD 2－DM 22·BM ·BD＝0，所以∠DBM ＝90°．7．如图，正方形ABCD 和四边形ACEF 所在平面互相垂直，CE ⊥AC ，EF ∥AC ，AB ＝2，CE ＝EF ＝1.导学号 52135099(1)求证：AF ∥平面BDE ； (2)求证：CF ⊥平面BDE ； (3)求二面角A －BE －D 的大小．[解析] (1)设AC 与BD 交于点G ，因为EF ∥AG ，且EF ＝1，AG ＝12AC ＝1，所以四边形AGEF 为平行四边形．所以AF ∥EG .因为EG ⊂平面BDE ，AF ⊄平面BDE ，所以AF ∥平面BDE ．(2)因为正方形ABCD 和四边形ACEF 所在的平面互相垂直，且CE ⊥AC ，所以CE ⊥平面ABCD .如图以C 为原点，建立空间直角坐标系C －xyz .则C (0,0,0)，A (2，2，0)，D (2，0,0)，E (0,0,1)，B (0，2，0)，F (22，22，1)．所以CF →＝(22，22，1)，BE →＝(0，－2，1)，DE →＝(－2，0,1)．所以CF →·BE →＝0－1＋1＝0，CF →·DE →＝－1＋0＋1＝0.所以CF ⊥BE ，CF ⊥DE ，所以CF ⊥平面BDE ．又∵BE ∩DE ＝E ，BE 、DE ⊂平面BDE ．(3)由(2)知，CF →＝(22，22，1)是平面BDE 的一个法向量，设平面ABE 的法向量n ＝(x ，y ，z )，则n ·BA →＝0，n ·BE →＝0．即⎩⎨⎧(x ，y ，z )·(2，0，0)＝0(x ，y ，z )·(0，－2，1)＝0所以x ＝0，z ＝2y .令y ＝1，则z ＝2．所以n ＝(0,1，2)，从而cos 〈n ，CF →〉＝n ·CF →|n ||CF →|＝32因为二面角A －BE －D 为锐角，所以二面角A －BE －D 为π6．B 组1．(2017·全国卷Ⅲ，19)如图，四面体ABCD 中，△ABC 是正三角形，△ACD 是直角三角形，∠ABD ＝∠CBD ，AB ＝BD ．导学号 52134644(1)证明：平面ACD ⊥平面ABC ；(2)过AC 的平面交BD 于点E ，若平面AEC 把四面体ABCD 分成体积相等的两部分，求二面角D －AE －C 的余弦值．[解析] (1)证明：由题设可得△ABD ≌△CBD ，从而AD ＝CD ．又△ACD 是直角三角形，所以∠ADC ＝90°．取AC 的中点O ，连接DO ，BO ，则DO ⊥AC ，DO ＝AO ．又因为△ABC 是正三角形，故BO ⊥AC ，所以∠DOB 为二面角D －AC －B 的平面角．在Rt △AOB 中，BO 2＋AO 2＝AB 2，又AB ＝BD ，所以BO 2＋DO 2＝BO 2＋AO 2＝AB 2＝BD 2，故∠DOB ＝90°．所以平面ACD ⊥平面ABC ．(2)由题设及(1)知，OA ，OB ，OD 两两垂直，以O 为坐标原点，OA →的方向为x 轴正方向，|OA →|为单位长度．建立如图所示的空间直角坐标系O －xyz ，则A (1,0,0)，B (0，3，0)，C (－1,0,0)，D (0,0,1)．由题设知，四面体ABCE 的体积为四面体ABCD 的体积的12，从而E 到平面ABC 的距离为D 到平面ABC 的距离的12，即E 为DB 的中点，得E (0，32，12)，故AD →＝(－1,0,1)，AC →＝(－2,0,0)，AE →＝(－1，32，12)．设n ＝(x ，y ，z )是平面DAE 的法向量，则⎩⎪⎨⎪⎧ n ·AD →＝0，n ·AE →＝0，即⎩⎪⎨⎪⎧－x ＋z ＝0，－x ＋32y ＋12z ＝0，可取n ＝(1，33，1)．设m 是平面AEC 的法向量，则⎩⎪⎨⎪⎧m ·AC →＝0，m ·AE →＝0，同理可取m ＝(0，－1，3)，则cos 〈n ，m 〉＝n ·m |n ||m |＝77．所以二面角D －AE －C 的余弦值为77． 2．(2017·天津卷，17)如图，在三棱锥P －ABC 中，P A ⊥底面ABC ，∠BAC ＝90°.点D ，E ，N 分别为棱P A ，PC ，BC 的中点，M 是线段AD 的中点，P A ＝AC ＝4，AB ＝2．导学号 52134645(1)求证：MN ∥平面BDE ； (2)求二面角C －EM －N 的正弦值；(3)已知点H 在棱P A 上，且直线NH 与直线BE 所成角的余弦值为721，求线段AH 的长． [解析] 如图，以A 为原点，分别以AB →，AC →，AP →的方向为x 轴、y 轴、z 轴的正方向建立空间直角坐标系，依题意可得A (0,0,0)，B (2,0,0)，C (0,4,0)，P (0,0,4)，D (0,0,2)，E (0,2,2)，M (0,0,1)，N (1,2,0)．(1)证明：DE →＝(0,2,0)，DB →＝(2,0，－2)．设n ＝(x ，y ，z )为平面BDE 的一个法向量，则⎩⎪⎨⎪⎧n ·DE →＝0，n ·DB →＝0，即⎩⎪⎨⎪⎧2y ＝0，2x －2z ＝0.不妨设z ＝1，可得n ＝(1,0,1)，又MN →＝(1,2，－1)，可得MN →·n ＝0．因为MN ⊄平面BDE ，所以MN ∥平面BDE ． (2)易知n 1＝(1,0,0)为平面CEM 的一个法向量．设n 2＝(x 1，y 1，z 1)为平面EMN 的一个法向量，则⎩⎪⎨⎪⎧n 2·EM →＝0，n 2·MN →＝0.因为EM →＝(0，－2，－1)，MN →＝(1,2，－1)，所以⎩⎪⎨⎪⎧－2y 1－z 1＝0，x 1＋2y 1－z 1＝0.不妨设y 1＝1，可得n 2＝(－4,1，－2)．因此有cos 〈n 1，n 2〉＝n 1·n 2|n 1||n 2|＝－421，于是sin 〈n 1，n 2〉＝10521．所以二面角C －EM －N 的正弦值为10521． (3)依题意，设AH ＝(0≤h ≤4)，则H (0,0，h )，进而可得NH →＝(－1，－2，h )，BE →＝(－2,2,2)．由已知得|cos 〈NH →，BE →〉|＝|NH →·BE →||NH →||BE →|＝|2h －2|h 2＋5×23＝721，整理得10h 2－21h ＋8＝0，解得h ＝85或h ＝12.所以线段AH 的长为85或12．。

2018年高考数学二轮复习专题5 第3讲用空间向量的方法解立体几何问题(理)

高考数学大二轮复习第1部分专题5立体几何第3讲用空间向量的方法解立体几何问题课件201811225190

2018年高考数学二轮复习考前专题五立体几何与空间向量第3讲立体几何中的向量方法讲学案理

2018届高考数学二轮复习 专题五 立体几何 5.3 空间向量与立体几何讲义 理

用空间向量法求解立体几何问题典例及解析

高考数学(理)二轮专题复习用空间向量的方法解立体几何问题Word版含解析

高考数学二轮：5.3《立体几何中的向量方法》试题(含答案)

安徽省高考数学第二轮复习 专题五立体几何第3讲 用空间向量的方法解立体几何问题 理

高考数学二轮复习第一篇专题五立体几何第3讲立体几何中的向量方法课件理0226396

2018年高考数学二轮复习考前专题五立体几何与空间向量第3讲立体几何中的向量方法讲学案理

空间向量法解决立体几何问题全面总结

2018年高考数学二轮复习课件 专题5 第3讲用空间向量的方法解立体几何问题(理)(74张)

最新-2018届高考数学二轮复习 第3讲 空间向量与立体几何考点突破课件 新 精品

2018届高考数学(理)二轮复习命题热点课件 专题 5.3 立体几何中的向量方法

高三数学二轮复习 第一篇 专题通关攻略 专题五 立体几

2018年高考数学(理) 讲学案：考前专题五 立体几何与空间向量 第3讲 立体几何中的向量方法(含答案解析)

2018版高考数学考点34利用空间向量法解决立体几何的综合问题试题解读与变式

2018届高考数学二轮复习专题五立体几何 5.3 空间向量与立体几何讲义理

安徽省高考数学第二轮复习专题五立体几何第3讲用空间向量的方法解立体几何问题理

2018年高考数学二轮复习课件专题5 第3讲用空间向量的方法解立体几何问题(理)(74张)

最新-2018届高考数学二轮复习第3讲空间向量与立体几何考点突破课件新精品

2018届高考数学(理)二轮复习命题热点课件专题 5.3 立体几何中的向量方法

高三数学二轮复习第一篇专题通关攻略专题五立体几

2018年高考数学(理) 讲学案：考前专题五立体几何与空间向量第3讲立体几何中的向量方法(含答案解析)