Matlab 6.5 中使用LindoAPI 2.0(简介)
MATLAB-LINGO使用基础

§5. 程序设计----------------------------------------------------------------------21
一、 二、 三、 四、 五、 六、 关系运算和逻辑运算--------------------------------------------------21 M-文件的结构--------------------------------------------------------- 23 M-文件的建立、编辑与调用--------------------------------------- 24 MATLAB 的控制流语句----------------------------------------------- 24 参数传递的可调性与数据文件的读写-------------------------- 29 子函数-----------------------------------------------------------------作环境
3.MATLAB 的退出 方法 1:单击菜单“File\Exit MATLAB” ; 方法 2:单击 MATLAB 命令窗口右上角关闭钮 X 方法 3:在命令窗口中键入命令: quit 或 exit. (注意小写)
二、MATLAB 的窗口构成
1.标题栏、菜单栏、工具栏 2.命令窗口(右边) 这是用户的主工作窗口。命令窗口下提符为“>>”,表示可以接受用户在此输入的行 命令,输入的关键词、字符串、注释、普通指令表达式等会用不同的颜色表示。命令或 程序执行的结果也显示在此窗口中。 3.工作区/当前目录窗口(左上) 工作区窗口也称内存浏览器,用于显示当前已定义的内存变量信息;当前目录窗口 用于显示当前工作目录所包含的文件夹和文件。
《MATLAB辅助分析与设计软件2.0》使用说明

的《自动控制原理(第五版)》、《自动控制原理简明教程(第二版)》和《自动控制原理题海大全》
的配套学习工具,不但便于读者使用,而且给任课老师提供了生成数量不限的题库的功能,便于因人施教。
本光盘内的全部程序是在MATLAB6.5的环境下编写的,已全部调用验证,且能修改,便于读者
的分与设计。
需进一步说明的是,MATLAB6.5的M文件程序部分在MATLAB7.0以上的版本内完全兼容,使用正常。
但Simulink程序部分在MATLAB7.0以上的版本内可能无法运行。这是由MATLAB软件自身所引起的问题。
MATLABAPI详解

MATLAB、API详解【例12.1.4-1】有一个绘圆的M脚本文件circle.m如下。
希望获得一个MEX绘圆程序。
(1)原始的绘圆脚本文件[circle.m]clf;r=2;t=0:pi/100:2*pi;x=r*exp(i*t);plot(x,'r*');axis('square')(2)对这脚本文件直接编译将因错误而失败mcc -x circle??? Error: File "circle" is a Script M-file and cannot be compiled with the current Compiler.Error in ==> H:\MATLAB53\toolbox\compiler\mcc.dll(3)把脚本文件改写成函数文件。
[circle_f.m]:function circle_f(r)clf;t=0:pi/100:2*pi;x=r*exp(i*t);plot(x,'r*');axis('square')(4)再对circle_f.m进行编译,将顺利通过。
mcc -x circle_f %mcc是编译指令,详见12.4节。
(5)运行生成的MEX文件circle_f.dllcircle_f(0.5) %调用circle_f绘制一半径为0.5的圆which circle_f %查询所调用的circle_f的路径全称。
图 12.2.1-1 【Select MATLAB Componets】对话窗的选项局部图图 12.2.2.1-1 为产生MEX文件所产生的配置屏1图 12.2.2.1-2 为产生MEX文件所产生的配置屏212.1.1.1配置正确性的验证(1)mex应用程序的验证cd d:\mywork %把用户目录指定为当前目录mex my_yprime.c %由my_yprime.c文件生成my_yprime.dll文件my_yprime(1,1:4) %运行my_yprime.dll文件which my_yprime %获得my_yprime.dll文件的位置信息ans =2.0000 8.9685 4.0000 -1.0947d:\mywork\my_yprime.dll(2)在MATLAB命令窗中验证mcc应用程序mcc -x my_yprime_m%<1> my_yprime_m(1,1:4)which my_yprime_mans =2.00008.96854.0000-1.0947d:\mywork\my_yprime_m.dll(3)在 DOS提示符后验证mex、mcc应用程序图 12.2.2.2-1 在DOS状态下验证编译指令12.1.2为产生独立外部应用程序进行预配置12.1.2.1对MATLAB编译器mbuild应用程序的设置(2.0版)图 12.2.3.1-1 为产生独立外部应用程序所产生的配置屏1图 12.2.3.1-2 为产生独立外部应用程序所产生的配置屏212.1.2.2对MATLAB编译器mbuild应用程序的设置(1.2版)12.1.2.3配置正确性的验证(1)mbuild应用程序的验证cd d:\mywork %把用户目录指定为当前目录mbuild my_ex1.c %在d:\mywork下生成my_ex1.exe文件图 12.2.3.2-1 在DOS窗口运行验证程序my_ex1.exe所得的结果(2)mcc应用程序的验证mcc -p my_hello.m %<1>图12.2.3.2-2 在DOS窗口运行验证程序my_hello.exe所得的结果(3)在DOS状态下验证mbuild、mcc工作正确性图 12.2.3.2-3 在DOS状态验证编译指令12.2M ATLAB编译器使用入门12.2.1由M文件创建C MEX文件的入门算例【例12.3.1-1】先编写M文件,然后生成相应的MEX文件。
数学建模讲座之三--用MATLAB求解线性规划linprog函数

n
(r p ) x
i i i 0
i i
n
i
MINmax{ q ix i} 约束条件
(1 p ) x =M
i0
xi≥0
2019/2/13
i=0,1,…n
数学建模
4. 模型简化:
a. 在实际投资中,投资者承受风险的程度不一样,若给定 风险一个界限 a,使最大的一个风险 qixi/M≤a,可找到相 应的投资方案。 这样把多目标规划变成一个目标的线性规 划。 模型 1 固定风险水平,优化收益 Q=MAX ( ri pi ) xi
2019/2/13
数学建模
0
2019/2/13
数学建模
三、模型的建立与分析 1.总体风险用所投资的Si中最大的一个风险来衡量,即max{ qixi|i=1,2,…n}
2.购买 Si 所付交易费是一个分段函数,即 pixi xi>ui 交易费 = piui xi≤ui 而题目所给定的定值 u i(单位 :元)相对总投资 M 很小, piu i 更小, 可以忽略不计,这样购买 Si 的净收益为(ri-p i)x i
计算结果:
a = 0.0030 a = 0.0060 a = 0.0080 a = 0.0100 a = 0.0200 a = 0.0400 x = 0.4949 0.1200 0.2000 x=0 0.2400 0.4000 x = 0.0000 0.3200 0.5333 x=0 0.4000 0.5843 x=0 0.8000 0.1882 x = 0.0000 0.9901 0.0000 0.0545 0.1154 0.1091 0.2212 0.1271 0.0000 0 0 0 0 0 0 Q = 0.1266 Q = 0.2019 Q = 0.2112 Q =0.2190 Q =0.2518 Q =0.2673
用Matlab与Lindo求解线性规划_田维

作者简介: 田维 ( 1978) ) , 男, 云南宣威人, 德宏师范高 等专科学校数学系助教。 * 本文为德宏教育学院 2004~ 2005 年二级科研课题成果之一。课题批准号: 德教院字 2005 [ 26] 号。
1 08
田维: 用 Matlab 与 Lindo 求解线性规划
2006 年
果用单纯形法的软件, 在电子计算机上计算, 只 需要几秒钟便可得出结果。0[ 4] 由此可见数学软件 和计算 机在求解 大规模线 性规划问 题上的重 要 性。在 1951 年, 国际水平只 能求解约束条 件为 10 个方程的线性规划问题, 到了 1963 年, 就能 求解 1000~ 10000 个方程的线性规划问 题; 1956 年, 解一个 67 个方程的线性规划问题要 1 小时, 而到 1963 年只需要 28 秒。之后, 在 1984 年, 美 国贝尔实验室的数学家卡玛卡把射影几何原理用 于大规模线性规划问题的求解, 取得重大 突破, 成功地用于美国电话电报公司改建太平洋沿岸 20 个国家的庞大电话网计划, 求出了涉及 412 万个 因素设计的最小投资数, 曾 引起轰动。[ 4] 而且由 于电子计算机的普及, 求解线性规划以及许许多 多运 筹学问题 的软件包 也应 运而生, 并走向 市 场, 成为大型科研机构、厂矿企业、学校和普通 用户都不可缺 少的一种工具, Matlab 和 Lindo 就 是其中比较常用的两个软件包。Matlab 是一个通 用数学软件包, 除了可以用其中的优化工具箱来 求解线性规划外, 还有许多其他的强大功能; 而 Lindo 是一个求解运筹学问题的专用数学软件包, 特别是为规划问题量身定做的一个软件包。下面 我们就分别讨论一下运用这两个数学软件包来求 解线性规划问题的方法及步骤。 2 用 Matlab 求解线性规划 211 Matlab 简介
数学建模软件LinDoLinGo的简介(修改版)

优化模型的基本类型
若x的一个或多个分量只取离散数值,则优 化模型称为离散优化,或称为组合优化。 如果x的一个或多个分量只取整数数值,称 为整数规划,并可以进一步明确地分为纯 整数规划(x的所有分量只取整数数值)和 混合整数规划(x的部分分量只取整数数 值)。特别地,若x的分量中取整数数值的 范围还限定为只取0或1,则称0-1规划。 此外,整数规划也可以分成整数线性规划 和整数非线性规划。
LINDO/LINGO软件 使用简介
LinDo/LinGo简介
LINDO(Linear Interactive and Discrete Optimizer),即“交互式的线性和离散优化求解 器”,可以用来求解线性规划(LP)和二次规划 (QP);
LINGO(Linear Interactive and General Optimizer),即“交互式的线性和通用优化求解 器”,除了用来求解线性规划(LP)、二次规划 (QP)和非线性规划,还可用于线性和非线性方程 组的求解。
最大的特色:允许决策变量是整数(即整数规划,包 括0-1规划)。
优化建模的一般形式
优化模型是一种特殊的数学模型,优化建 模方法是一种特殊的数学建模方法。
优化模型一般有以下三个要素: 1)决策变量 2)目标函数 3)约束条件
优化建模的一般形式
优化模型从数学上可表述成如下一般形式:
opt z f (x)
连续优化
优化
整数规划
线性规划
二次规划
非线性规划
问题求解的难度增加
优化模型的简单分类和求解难度
简单例子
max
z 2x 3y;
s.t.
4x 3y 10; 3x 5y 12; x, y 0.
关于LINDO&lingo学习心得

网上关于LINDO/LINGO的学习心得材料1、LINDO这个就是一开始的那个软件,主要求解线性规划、整数规划、二次规划问题。
现在版本好像是6.1。
2、GINO一开始的时候这也是一个求非线性规划的工具,甚至她还用来求解一些非线性的方程根。
它的特点是:包含了丰富的数学函数,尤其是概率函数!但是随着像Mathematica/Matlab的迅速发展,他逐渐的消亡,并演化为现在的函数引擎LINDO API,呵呵,现在版本2.0。
3、LINGO/LINGO NL大家现在看到的LINGO8.0在一开始也是两部分:LINGO and LINGO NL,他们分别用于求解线性、整数规划以及非线性、线性、整数规划问题。
可见这很混乱,所以现在就统一成为了LINGO,它与LINDO的主要主要区别在于:她内建了建模语言,可以简约的得描述大规模的优化问题。
现在版本是8.0。
4、What's the best这是一个组件,主要处理由Excell/Access生成数据文件的规划问题,安装之后会在你的Office中添加一个名为What's the best的宏,启用后会在Excell中生成一个工具条,就像Adobe的pdf插件一样。
现在版本是7.0。
注解:上面这些旨在说明这些软件名字是有各自的含义的,首先要明确他们各自的长处是什么,才能有的放矢!至于学习方法,很简单,阅读、运行程序自带实例。
呵呵,打算每天一个例子吧:)一些他们的区别在具体例子中会比较说明!说一下这里的lindo和lingo程序结构的差异:1、基本程序架构(1)lindo是这样的:MAX 目标函数表达ST变量约束1变量约束2变量约束3END(2)lingo是这样的:MAX=目标函数表达;变量约束1;变量约束2;变量约束3;注意:可见它们的基本frame不同,在lingo80中每个语句后面必须以分号结束,包括以开头的注释语句。
2、简单的示例假设现在一个计算机厂商要生产两种型号的PC:标准型(standard)和增强型(turbo),由于生产线和劳动力工作时间的约束,使得标准型PC最多生产100台。
Matlab使用方法详解

Matlab使用方法详解Matlab是一种广泛应用于科学计算、工程设计以及数据分析的高级编程语言和环境。
它的强大功能和易于使用性使其成为许多研究人员和工程师的首选软件之一。
本文将详细介绍Matlab常用的功能和使用方法,帮助读者快速入门和提高使用效率。
一、Matlab基本介绍Matlab是由MathWorks公司开发的一种计算机编程语言和环境。
它具有强大的数值计算和图形处理能力,能够有效地进行数据处理、模拟仿真、图像处理、符号计算等各种科学计算任务。
Matlab通过命令窗口、脚本和函数等方式进行交互式编程,具有简洁的语法和丰富的函数库,支持多种数据结构和矩阵运算。
二、Matlab环境设置在正式使用Matlab之前,我们需要进行一些基本的环境设置。
首先,安装Matlab软件,并确保系统具备所需的硬件要求。
然后,打开Matlab软件,在主界面的左上角可以看到一个命令窗口,这是我们与Matlab交互的主要窗口。
在命令窗口中,我们可以直接输入Matlab命令并执行,也可以编写脚本文件或者函数进行程序开发。
此外,Matlab还提供了丰富的图形用户界面工具箱,可以帮助开发者进行图形界面设计和数据可视化。
三、Matlab基本操作1. 变量和赋值在Matlab中,我们可以使用变量来存储数据并进行计算。
变量的命名规则与其他编程语言相似,需要遵循大小写敏感和命名规范。
例如,我们可以使用以下命令定义一个变量a,并给其赋值:a = 10;在这个例子中,我们将变量a赋值为10。
在Matlab中,变量的赋值是通过等号(=)来实现的。
2. 数组和矩阵运算Matlab是一种基于矩阵运算的语言,对于数组和矩阵的操作非常方便。
我们可以使用以下命令创建一个数组:b = [1, 2, 3, 4, 5];在这个例子中,我们创建了一个包含5个元素的数组b。
我们还可以使用以下命令创建一个矩阵:A = [1, 2, 3; 4, 5, 6; 7, 8, 9];在这个例子中,我们创建了一个包含3行3列的矩阵A。
Lingo教程(一)
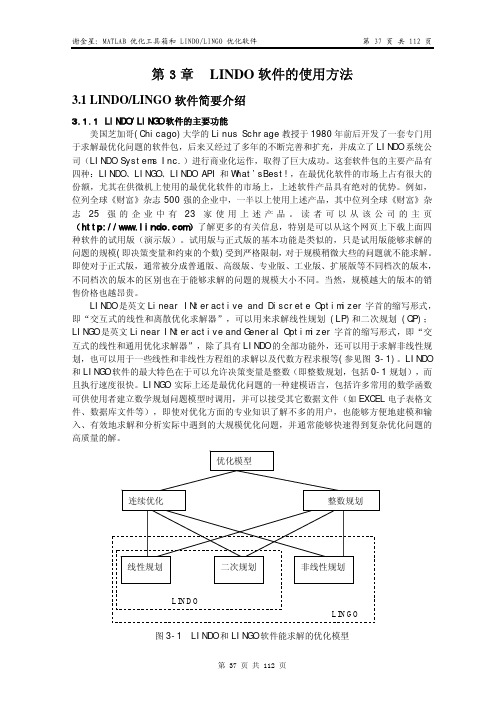
本章和下一章扼要介绍在 Microsoft Windows 环境下运行的 LINDO 6.1,LINGO 8.0 最新版本的使用方法,并包括社会、经济、工程等方面的一些实际应用问题的数学建模和求 解实例。
xyz=30
x+y=8
y=5 则 LINDO/LINGO 软件能直接确定出 y=5, 然后确定出 x=3,最后确定出 z=2, 这三个变量就是 常量了。经过这样的处理,将尽量减小模型中实际需要求解的决策变量的个数,使问题的规 模有所下降,从而使求解更有效。
LINDO/LINGO 预处理程序
LP QP
5、模型中使用的单位的数量级要适当 如果同一模型甚至同一约束中有的数很小而有的数很大, 如 0.01 和 10000000000, 则这两 个数的数量级相差太大了,不利于优化模型求解,因为大的数与小的数运算时误差会很大, 运算精度降低。LINDO/LINGO 通常希望模型中数据之间的数量级不要相差超过 103,否则会 给出警告提示信息,这时你应该尽量选择适当的单位,使数据之间的数量级相差减小。
优化模型
连续优化
整数规划
线性规划
二次规划
非线性规划
LINDO
LINGO
图 3-1 LINDO 和 LINGO 软件能求解的优化模型
第 37 页 共 112 页
谢金星:MATLAB 优化工具箱和 LINDO/LINGO 优化软件
第 38 页 共 112 页
优化建模与LINDO,LINGO优化软件
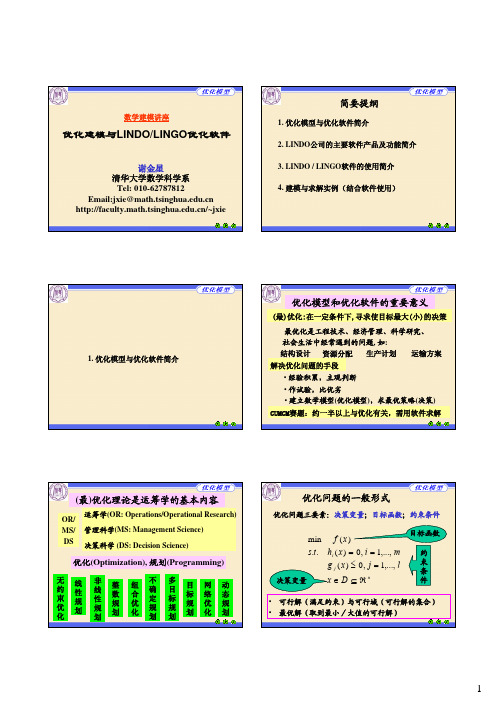
ROW SLACK OR SURPLUS DUAL PRICES
三
原料无剩余
2)
0.000000
种
时间无剩余
3)
0.000000
资 源
加工能力剩余40
4)
40.000000
48.000000 2.000000 0.000000
“资源” 剩余为零的约束为紧约束(有效约束)
结果解释
OBJECTIVE FUNCTION VALUE
1. 优化模型与优化软件简介
优化模型和优化软件的重要意义
(最)优化:在一定条件下,寻求使目标最大(小)的决策
最优化是工程技术、经济管理、科学研究、 社会生活中经常遇到的问题, 如: 结构设计 资源分配 生产计划 运输方案 解决优化问题的手段 • 经验积累,主观判断 • 作试验,比优劣 • 建立数学模型(优化模型),求最优策略(决策) CUMCM赛题:约一半以上与优化有关,需用软件求解
2)
0.000000
48.000000
3)
0.000000
2.000000
4) 40.000000
0.000000
NO. ITERATIONS= 2
reduced cost值表 示当该非基变量 增加一个单位时 (其他非基变量 保持不变)目标 函数减少的量(对 max型问题)
也可理解为:
为了使该非基变 量变成基变量, 目标函数中对应 系数应增加的量
2
50.000000 10.000000
6.666667 90,在允许范
3 480.000000 53.333332
80.000000 围内
4 100.000000 INFINITY 40.000000
Lingo教程(一)

NLP
IP
分枝定界管理程序
ILPBiblioteka INLPIQP线性优化求解程序
非线性优化求解程序
图 3-2 LINDO/LINGO 软件的求解过程
第 38 页 共 112 页
谢金星:MATLAB 优化工具箱和 LINDO/LINGO 优化软件
第 39 页 共 112 页
2、识别优化模型的类型:对等式约束的预处理完成后,预处理程序能自动识别优化模型 的类型,从而决定下一步采用什么求解程序。如果模型是连续线性规划,下一步直接调用线 性优化求解程序;如果模型是连续非线性规划,下一步直接调用非线性优化求解程序;如果 模型是整数规划,则下一步直接调用分枝定界管理程序。
优化模型
连续优化
整数规划
线性规划
二次规划
非线性规划
LINDO
LINGO
图 3-1 LINDO 和 LINGO 软件能求解的优化模型
第 37 页 共 112 页
谢金星:MATLAB 优化工具箱和 LINDO/LINGO 优化软件
第 38 页 共 112 页
此外,LINDO 系统公司还提供了 LINDO/LINGO 软件与其它开发工具(如 C++和 Java 等语言)的接口软件 LINDO API(Application Program Interface),因此使 LINDO 和 LINGO 软件还能方便地融入到用户应用软件的开发中去。
线性优化求解程序通常使用单纯形算法,对高级版本的 LINDO/LINGO 软件,为了能解 大规模问题,也可以使用内点算法。非线性优化求解程序采用的是顺序线性规划法(Sequential Linear Programming, 简称 SLP),即通过迭代求解一系列线性规划来达到求解非线性规划的 目的。非线性优化求解程序也可以使用其他算法,如广义既约梯度法(Generalized Reduced Gradient, 简称 GRG),并可以自动选用多个初始点开始进行迭代,以便增加找到全局最优解 的可能性。分枝定界管理程序用于管理整数规划问题的分枝定界算法,在运行中还要不断调 用线性优化求解程序和非线性优化求解程序进行定界处理。
Matlab的使用方法及步骤详解

Matlab的使用方法及步骤详解一、Matlab简介Matlab是一种非常流行的科学计算软件,其全称为Matrix Laboratory(矩阵实验室)。
Matlab具有强大的数学计算和数据分析能力,广泛应用于工程、科学、经济等领域。
本文将详细介绍Matlab的使用方法及步骤。
二、安装与启动Matlab1. 下载与安装首先,访问MathWorks官方网站,找到适用于您操作系统的Matlab版本,并下载安装程序。
安装程序将引导您进行安装,按照提示完成即可。
2. 启动Matlab安装完成后,您可以在开始菜单或桌面上找到Matlab的启动图标。
点击启动图标,Matlab将打开并显示初始界面。
三、Matlab基本操作1. 工作区与编辑器Matlab的界面主要由工作区和编辑器组成。
工作区显示变量及其值,可用于查看和操作数据。
编辑器则用于编写和编辑Matlab脚本、函数等。
2. 脚本与命令窗口Matlab提供了两种主要的运行方式:脚本和命令窗口。
脚本是一系列命令的集合,可以一次性执行,适用于较复杂的计算任务。
命令窗口则可逐行输入命令并立即执行,用于快速测试和调试。
3. 基本算术和数学运算Matlab支持各种基本算术和数学运算,如加减乘除、幂运算、三角函数等。
可以直接在命令窗口输入表达式并执行。
四、数据操作与处理1. 数组的创建与操作在Matlab中,数组是最基本的数据结构之一。
可以使用多种方法创建数组,例如手动输入、加载外部文件、使用特定函数等。
一旦创建,可以对数组进行各种操作,如索引、切片、拼接等。
2. 矩阵运算Matlab对矩阵运算提供了强大的支持。
可以进行矩阵加减乘除、转置、求逆等运算。
矩阵运算在解决线性方程组、最小二乘拟合等问题时非常有用。
3. 数据可视化Matlab提供了丰富而强大的数据可视化功能。
使用plot、scatter、histogram等函数可以绘制各种类型的图表。
还可以对图表进行格式设置、添加标签、调整坐标轴等。
数学建模讲座之三-用MATLAB求解线性规划linprog函数

线性规划的求解方法
01
线性规划的求解方法有 多种,包括图解法、单 纯形法、对偶法等。
02
运输问题
总结词
运输问题是一个经典的线性规划应用案例,旨在通过合理安排运输路线和车辆配 置,降低运输成本并提高运输效率。
详细描述
在运输问题中,企业需要考虑货物的运输路线、车辆配置、运输时间等多个因素 ,以最小化运输成本并最大化运输效率。通过建立线性规划模型,可以找到最优 的运输方案,使得企业在满足客户需求的同时获得最大的利润。
02
fval
目标函数的最小值
03
04
exitflag
退出标志,表示求解是否成功 ,0表示成功,其他值表示失
败
output
输出信息,包括迭代次数、最 优解等信息
03
使用linprog函数求解线 性规划问题
建立线性规划问题
确定决策变量
首先需要确定问题的决策 变量,即需要优化的变量。
确定目标函数
根据问题需求,确定目标 函数,即需要最大化或最 小化的函数。
05
总结与展望
线性规划的重要性和应用领域
线性规划是一种优化技术,通 过合理分配有限资源达到最优 目标。它在生产计划、物流管 理、金融投资等领域有广泛应
用。
在生产计划中,线性规划可用 于确定最优的生产组合,以最
小化成本或最大化利润。
在物流管理中,线性规划可用 于货物运输和配送路线优化, 降低运输成本和提高效率。
Lingo软件简介

Lingo软件简介Lindo/Lingo 运筹学软件LINDO和LINGO是美国LINDO系统公司开发的一套专门用于求解最优化问题的软件包。
LINDO用于求解线性规划和二次规划,LINGO除了具有LINDO的全部功能外,还可以用于求解非线性规划,也可以用于一些线性和非线性方程组的求解以及代数方程求根等。
LINDO和LINGO软件的最大特色在于可以允许优化模型中的决策变量是整数(即整数规划),而且执行速度很快。
LINGO实际上还是最优化问题的一种建模语言,包括许多常用的函数可供使用者建立优化模型时调用,并提供与其它数据文件(如文本文件、EXCEL 电子表格文件、数据库文件等)的接口,易于方便地输入、求解和分析大规模最优化问题。
由于这些特点,LINDO和LINGO软件在教学、科研和工业、商业、服务等领域得到广泛应用。
LINDO系统公司的产品主要有以下几种:What'sBest!What'sBest! 是附加在Excel电子表格中用于建立大规模最优化模型的软件。
What's Best! 将强大的线性规划、非线性规划、整数最优化求解功能同当今经济建模中最流行、最具灵活性的Microsoft Excel结合起来共同求解问题。
What'sBest! 的主要优势:●世界上最强大的Microsoft Excel 求解软件●建模方便快捷●可以为客户和同行建立简单易懂的模型●提供大量的文档和帮助信息LINGOLINGO是快速、便捷、高效地建立模型并求解线性规划、非线性规划和整数最优化问题的工具。
LINGO提供一个综合的软件包,其中包括强大的最优化模型建模语言、建模和求解问题的特征环境以及一套内置的解算机。
LINGO 的主要优势●简单的建模语言●方便数据选择●强大的解算机●交互式模型●提供大量的文档和帮助信息LINDO API通过LINDO API你可以轻松创建自己的最优化模型。
它允许将LINDO解算机加载到自己编写的特定应用程序中。
MATLAB的基本使用教程详解

MATLAB的基本使用教程详解MATLAB(Matrix Laboratory,矩阵实验室)是一种用于数值计算和可视化的编程环境。
它提供了强大的数值计算功能、丰富的数学函数库、快捷的可视化工具和易于使用的编程语言。
以下是关于MATLAB基本使用的一些教程:1. 安装和启动MATLAB:- 访问MATLAB官方网站下载并安装MATLAB。
- 安装完成后,在桌面上找到MATLAB图标并点击启动。
2. 创建一个新的MATLAB文件:- 在MATLAB界面,点击“新建”按钮,选择“新建图形”,或者使用快捷键Ctrl+N。
3. 基本的MATLAB命令:- 在命令窗口中输入命令并按Enter键执行。
例如,输入`1+2`并按Enter 键,将显示结果`3`。
- 可以使用括号对表达式进行组包。
例如,输入`(1+2)*3`并按Enter键,将显示结果`9`。
- 在MATLAB中,可以使用逗号将多个命令分开执行。
例如,输入`a = 1,b = 2,c = a+b`,将依次执行这三个命令并显示结果。
4. 变量和数组:- 在MATLAB中,可以使用`a = 1`的形式创建一个变量a并将其值设为1。
- 数组是一种可以存储多个相同类型数据的数据结构。
例如,可以使用`A = [1,2,3;4,5,6]`创建一个包含两行三列的数组。
5. 数学函数:- MATLAB提供了丰富的数学函数库,例如可以使用`sin(pi/2)`计算sin(π/2)的值。
- 可以同时使用多个函数对同一组输入参数进行操作。
例如,可以使用`c = a*b; d = log(a/b); e = sin(a)+cos(b)`同时对变量a、b进行多种操作。
6. 控制结构:- 可以使用`if`、`else`和`end`关键字创建条件语句。
例如,输入`if a > b, a = b; end`将使a的值等于b的值(如果a大于b)。
- 可以使用`for`循环遍历数组或向量。
Matlab 6.5 中使用LindoAPI 2.0(简介)

Matlab 6.5 中使用LindoAPI 2.0(简介)(2003.04.02)1. 安装LindoAPI2.0(1)下载LINDO API 2.0安装程序lindoDLL.exe, 直接运行进行安装(以下假设LINDO API 2.0安装目录为'C:\LINDOAPI')。
(2)建立MA TLAB与LINDO API 2.0之间的接口(以下假设MATLAB 6.5安装目录为'C:\ MATLAB6P5')。
请按照以下步骤进行:(2A)用任何文本编辑器直接编辑C:\MATLAB6P5\TOOLBOX\LOCAL\STARTUP.M 文件(通常直接打开MA TLAB,用MATLAB本身的程序编辑器编辑该文件)。
如果该目录下没有该文件,则将该目录下的STARTUPSA V.M改名为STARTUP.M,然后进行编辑;并且,如果STARTUPSA V.M 或STARTUP.M中有"load matlab.mat"语句,则将该语句直接删除.(2B)在STARTUP.M中增加以下程序行,然后保存文件,退出编辑器:global MY_LICENSE_FILEMY_LICENSE_FILE = 'C:\LINDOAPI\LICENSE\LICENSE.H';path(path,'C:\LINDOAPI\BIN')path(path,'C:\LINDOAPI\INCLUDE')path(path,'C:\LINDOAPI\MA TLAB');(2C)启动MA TLAB,在命令提示符下键入'mxLINDO',屏幕上将显示以下信息:mxLINDO (R) Matlab Interface Version 2.x.xfor LINDO API (R) Version 2.x.xCopyright (c) 2001-200x by LINDO Systems, Inc.All rights reserved.Usage: [z1,z2,..,zk] = mxLINDO('LSfuncName',a1,a2,...,an)这就表示已经成功建立了MATLAB与LINDO API 2.0之间的接口。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Matlab 6.5 中使用LindoAPI 2.0(简介)(2003.04.02)1. 安装LindoAPI2.0(1)下载LINDO API 2.0安装程序lindoDLL.exe, 直接运行进行安装(以下假设LINDO API 2.0安装目录为'C:\LINDOAPI')。
(2)建立MA TLAB与LINDO API 2.0之间的接口(以下假设MATLAB 6.5安装目录为'C:\ MATLAB6P5')。
请按照以下步骤进行:(2A)用任何文本编辑器直接编辑C:\MATLAB6P5\TOOLBOX\LOCAL\STARTUP.M 文件(通常直接打开MA TLAB,用MATLAB本身的程序编辑器编辑该文件)。
如果该目录下没有该文件,则将该目录下的STARTUPSA V.M改名为STARTUP.M,然后进行编辑;并且,如果STARTUPSA V.M 或STARTUP.M中有"load matlab.mat"语句,则将该语句直接删除.(2B)在STARTUP.M中增加以下程序行,然后保存文件,退出编辑器:global MY_LICENSE_FILEMY_LICENSE_FILE = 'C:\LINDOAPI\LICENSE\LICENSE.H';path(path,'C:\LINDOAPI\BIN')path(path,'C:\LINDOAPI\INCLUDE')path(path,'C:\LINDOAPI\MA TLAB');(2C)启动MA TLAB,在命令提示符下键入'mxLINDO',屏幕上将显示以下信息:mxLINDO (R) Matlab Interface Version 2.x.xfor LINDO API (R) Version 2.x.xCopyright (c) 2001-200x by LINDO Systems, Inc.All rights reserved.Usage: [z1,z2,..,zk] = mxLINDO('LSfuncName',a1,a2,...,an)这就表示已经成功建立了MATLAB与LINDO API 2.0之间的接口。
2. 运行LINDOAPI2.0提供的优化问题实例LINDOAPI2.0提供的优化问题的例子放在'C:\LINDOAPI\MA TLAB'目录下。
启动MA TLAB,可以打开该目录下的‘.M’文件进行查看、编辑或运行(有些程序可以不需要输入参数直接运行,有些则只是子程序)。
对于可以直接运行的程序,可以在命令提示符下键入这些文件的名称运行。
如‘LMTESTLP ’(线性规划)、“MLTESTNLP1”(非线性规划)、‘LMTESTQP ’(二次规划)、“MLTESTMINLP1”(非线性混合整数规划)等。
一般来说,文件名中带有“TEST ”的程序是可以直接运行的实际例子,其他程序一般只是子程序。
3. ‘l msolvem’程序的使用 3.1 一般使用方法该程序的“.M ”源文件放在'C:\LINDOAPI\MA TLAB'目录下,可用于求解目标函数和约束函数均为二次函数(包括线性函数)的数学规划(包括整数规划),例如:线性规划(LP )、二次规划(QP )、混合整数线性规划(MIP )、混合整数二次规划(MIQP ),等等。
优化问题的一般模型为:},...,n-,{J j x ux l m i b x Q x x a t s x Q x cx Max Min j i i i c121,0 , 1,...,1,0,?'..')(2121⊆∈≤≤-=++是整数其中Q c ,Q i 为n 阶对称方阵,c 、a i 为n 维(行)向量,l 、u 为n 维(列)向量,决策变量为x (n 维列向量)。
“?”表示任意一种比较符号(等于、大于等于、小于等于之一),J 为整数变量的下标集合。
最复杂的调用语法为:[x,y,s,dj,pobj,solstat] = LMsolvem(A,b,c,csense,l,u,vtype, QCrows,QCvar1,QCvar2,QCcoef, objsen,solver,verbose)输出参数最多为6个, 含义是:x: 最优解;y: 对偶最优解(影子价格);s: 原问题的松弛变量;dj: 对偶问题的松弛变量;pobj: 最优目标值;solstat: 程序求解结束状态.3.2例1:线性规划对于如下问题:MIN {cx: Ax >=b}其中A = [1 1 1 1;0.2 0.1 0.4 0.9;0.15 0.10 0.10 0.80;-30 -40 -60 -100 ]b = [ 4000 3000 2000 -350000]'c = [ 65 42 64 110]编写MATLAB程序如下:A = [1.0000 1.0000 1.0000 1.0000;0.2000 0.1000 0.4000 0.9000;0.1500 0.1000 0.1000 0.8000;-30.0000 -40.0000 -60.0000 -100.0000 ];b = [ 4000 3000 2000 -350000]';c = [ 65 42 64 110];csense = 'GGGG';l=[-Inf,-Inf,-Inf,-Inf];[x,y,s,dj,obj,solstat] = LMsolvem(A, b, c, csense, l)运行结果为:x =1.0e+003 *-0.08333333333333-0.791666666666672.583333333333342.29166666666667y =1.0e+002 *0.616666666666671.316666666666670.216666666666670.00875000000000s =dj =1.0e-013 *0.03552713678801-0.14210854715202obj =378750solstat =2这表明:最优值z =378750(最优解x, 对偶最优解y等也能得到).这一结果与MATLAB优化工具箱的计算结果是否一样?为此,我们可以将下面的语句加入以上程序的最后,进行比较和检验:[xx,ff]=linprog(c,-A,-b)运行结果为:xx =1.0e+003 *-0.08333333333324-0.791666666666742.583333333333322.29166666666666ff =3.787500000000018e+005这表明,MATLAB优化工具箱的运行结果与LINDO API的运行结果是一样的。
3.3例2:线性整数规划生产中常会遇到通过切割、剪裁、冲压等手段,将原材料加工成所需大小这种工艺过程,称为原料下料问题(cutting stock problem)。
按照进一步的工艺要求,确定下料方案,使用料最省,或利润最大,是典型的优化问题。
本节通过两个实例讨论用数学规划模型解决这类问题的方法。
考虑如下钢管下料问题: 某钢管零售商从钢管厂进货,将钢管按照顾客的要求切割后售出。
从钢管厂进货时得到的原料钢管都是19米长。
现有一客户需要50根4米长、20根6米长和15根8米长的钢管。
应如何下料最节省?问题分析首先,应当确定哪些切割模式是可行的。
所谓一个切割模式,是指按照客户需要在原料钢管上安排切割的一种组合。
例如,我们可以将19米长的钢管切割成3根4米长的钢管,余料为7米;或者将19米长的钢管切割成4米、6米和8米长的钢管各1根,余料为1米。
显然,可行的切割模式是很多的。
其次,应当确定哪些切割模式是合理的。
通常假设一个合理的切割模式的余料不应该大于或等于客户需要的钢管的最小尺寸。
例如,将19米长的钢管切割成3根4米的钢管是可行的,但余料为7米,可以进一步将7米的余料切割成4米钢管(余料为3米),或者将7米的余料切割成6米钢管(余料为1米)。
在这种合理性假设下,切割模式一共有7种,如表1所示。
问题化为在满足客户需要的条件下,按照哪些种合理的模式,切割多少根原料钢管,最为节省。
而所谓节省,可以有两种标准,一是切割后剩余的总余料量最小,二是切割原料钢管的总根数最少。
下面将对切割后剩余的总余料量最小这个目标讨论。
模型建立决策变量 用x i 表示按照第i 种模式(i =1, 2, …, 7)切割的原料钢管的根数,显然它们应当是非负整数。
决策目标 以切割后剩余的总余料量最小为目标,则由表1可得765432113333x x x x x x x Z Min ++++++= (1)约束条件 为满足客户的需求,按照表1应有5023454321≥++++x x x x x (2) 20326542≥+++x x x x (3) 152753≥++x x x (4) x 为整数 (5) 模型求解编写MATLAB 程序如下:A= [ 4 3 2 1 1 0 0 0 1 0 2 1 3 00 0 1 0 1 0 1];b=[50 20 15];c=[3 1 3 3 1 1 3]; csense = 'GGG'; vtype = 'IIIIIII';[x,y,s,dj,obj,solstat] = LMsolvem(A, b, c, csense, [], [], vtype); x运行结果: x = 0 12 0 0 15 0 0 这就是最优解(即12次采用模式2,15次采用模式5).3.4例3:二次规划考虑投资组合的最优选择问题: 某投资公司经理正在考虑将一定数量的基金用于股票投资。
经过慎重考虑,他从所有上市交易的股票中选择了4种股票作为侯选投资对象。
经过分析,该经理认为每单位投资(如1元)股票1、2、3、4的期望收益分别为0.3、0.2、-0.4、0.2(元),标准差均为1(元)。
此外,股票1、2收益的相关系数为0.64,股票1、3收益的相关系数为 0.27,股票1、4收益的相关系数为 0; 股票2、3收益的相关系数为0.13,股票2、4收益的相关系数为 0;股票3、4收益的相关系数为 0。
该公司经理应如何投资? 记r 为收益向量,Q 为相关系数矩阵:Q =设投资向量为w ,即投资于股票1、2、3、4的比例分别为w(1), w(2), w(3), w(4). 则(单位投资)期望收益为r(1)w(1)+r(2)w(2)+r(3)w(3)+r(4)w(4) 此外,需要考虑投资风险。
