随机森林算法介绍及R语言实现

r语言随机森林模型怎么求出回归方程

r语言随机森林模型怎么求出回归方程全文共四篇示例，供读者参考第一篇示例：随机森林是一种强大的机器学习算法，它结合了决策树和集成学习的优势，在回归问题中也有很好的表现。

在R语言中，使用随机森林模型可以很容易地求出回归方程，下面我们就来详细介绍一下如何在R语言中求出随机森林回归方程。

1. 数据准备我们需要准备好用于建模的数据集。

数据集应该包含输入变量和目标变量，输入变量用于建立回归模型，目标变量是我们要预测的值。

在R语言中可以使用data.frame()函数将数据加载进来，确保数据集中不含有缺失值。

2. 导入随机森林库在R语言中，可以使用randomForest包来构建随机森林模型。

首先需要安装包并导入到R中，可以使用以下代码完成这一步：```install.packages("randomForest")library(randomForest)```3. 构建随机森林模型接下来，我们使用randomForest()函数来构建随机森林模型。

在函数中需要指定输入变量和目标变量，以及其他一些参数，如树的数量、节点最小样本数等。

以下是一段示例代码：这里的"data"是我们准备好的数据集，"Target"是目标变量的列名，"~ ."表示使用所有其他变量作为输入变量，"ntree"表示森林中树的数量，"mtry"表示每个节点中考虑的变量数量。

根据具体情况可以调整这些参数来优化模型。

4. 提取回归方程随机森林模型是由多个决策树组成的集合模型，因此没有明确的回归方程。

但是可以通过查看变量的重要性来理解模型的影响因素。

可以使用以下代码来查看变量的重要性：```varImpPlot(rf_model)```这个函数会返回一个图表，显示每个变量的重要性以及它们对模型的贡献程度。

可以根据这个图表来了解模型中哪些变量对预测结果具有更大的影响。

r语言随机森林回归最优参数

系好安全带，伙计们！我们正在潜入令人兴奋的机器学习的世界与永远流行的随机森林回归算法。

这个坏孩子不仅能把事物分类，而且能预测数值。

准备好卷起你的袖子，加入我，当我们利用R语言的力量创建我们自己的随机森林回归模型。

嘿，我们不会停下来的——我们正在寻找最终的参数，让这个模型歌舞。

让我们在这个算法上撒点魔法释放出它的全部潜力！
让我们给R环境注入一些魔法通过召唤必要的R包随机森林回归。

我们将利用“install。

packages（）”咒语来构思“随机森林”软件包，它将赋予我们构建神秘的随机森林模型所需的魔法功能。

一旦套件安全了，我们可以挥动我们的魔杖，用“ library（）” 咒语在我们的 R 会话中恢复它。

现在，我们到森林的旅程随机的可能性是真正开始的！
"好，系好安全带，准备潜入随机森林的世界！一旦我们得到了随机森林包的火力，它去时间开始设计我们可怕的回归模型。

我们需要准备我们的数据集，把它分成一个训练集和一个测试集。

我们释放出“兰多姆森林（）”功能的魔法，用训练数据来训练我们的模型，并通过在测试数据上作出预测来观察它的工作。

等等，还有更多！我们可以通过使用诸如交叉验证等很酷的技术来寻找我们随机森林回归模型的完美参数这就像找到宝藏图回归成功！让我们一起征服这个随机的森林！"。

R随机森林算法

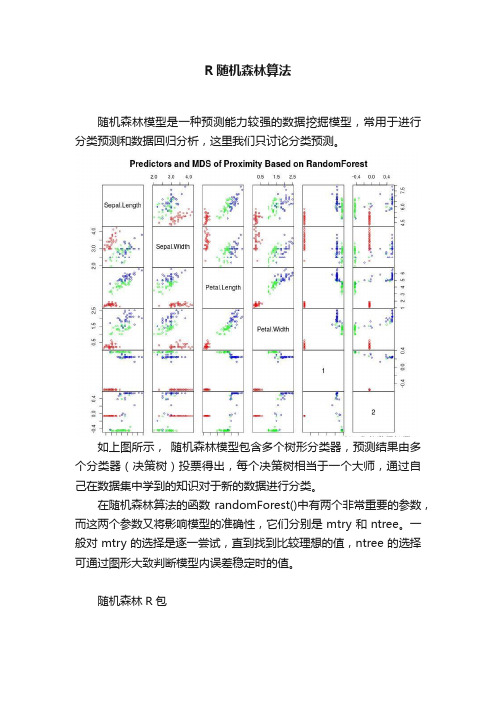
R随机森林算法随机森林模型是一种预测能力较强的数据挖掘模型，常用于进行分类预测和数据回归分析，这里我们只讨论分类预测。

如上图所示，随机森林模型包含多个树形分类器，预测结果由多个分类器（决策树）投票得出，每个决策树相当于一个大师，通过自己在数据集中学到的知识对于新的数据进行分类。

在随机森林算法的函数randomForest()中有两个非常重要的参数，而这两个参数又将影响模型的准确性，它们分别是mtry和ntree。

一般对mtry的选择是逐一尝试，直到找到比较理想的值，ntree的选择可通过图形大致判断模型内误差稳定时的值。

随机森林R包randomForest::randomForest 该包中主要涉及5个重要函数，关于这5个函数的语法和参数请见下方：randomForest()：此函数用于构建随机森林模型randomForest(formula, data=NULL, ..., subset, na.action=na.fail)1. formula：指定模型的公式形式，类似于y~x1+x2+x3...;2. data：指定分析的数据集；3.ntree：指定随机森林所包含的决策树数目，默认为500；4. mtry：指定节点中用于二叉树的变量个数，默认情况下数据集变量个数的二次方根（分类模型）或三分之一（预测模型）。

一般是需要进行人为的逐次挑选，确定最佳的m值；估值过程指定m值，即随机产生m个变量用于节点上的二叉树，m的选择原则是使错误率最低。

应用bootstrap自助法在原数据集中又放回地抽取k个样本集，组成k棵决策树，每个决策树输出一个结果。

对k个决策树组成的随机森林对样本进行分类或预测：分类原则：少数服从多数；预测原则：简单平均。

oob error如何选择最优的特征个数m，要解决这个问题，我们主要依据计算得到的袋外错误率.在构建每棵树时，对训练集使用了不同的bootstrap sample（随机且有放回地抽取）。

用R实现随机森林的分类与回归

用R实现随机森林的分类与回归第五届中国R语言会议北京2012 李欣海用R实现随机森林的分类与回归Applications of Random Forest using RClassification and Regression李欣海中科院动物所邮件:lixh@//0>.主页:////.博客:////.微博:////. 第五届中国R语言会议北京2012 李欣海随机森林简介Random Forest////.an-introduction-to-data-mining-for-marketing-and-business-intelli gence/Random Forest is an ensemble classifier thatconsists of many decision trees It outputs the class that is the mode of the class'soutput by individual trees Breiman 2001 It deals with “small n large p”-problems, high-orderinteractions, correlated predictor variables.Breiman, L. 2001. Random forests. Machine Learning 45:5-32. Being cited 6500 times until 20123/25 第五届中国R语言会议北京2012 李欣海随机森林简介History////.an-introduction-to-data-mining-for-marketing-and-business-intelli gence/The algorithm for inducing a random forest was developed byLeo Breiman 2001 and Adele Cutler, and "Random Forests" istheir trademarkThe term came from random decision forests that was firstproposed by Tin Kam Ho of Bell Labs in 1995The method combines Breiman's "bagging" idea and therandom selection of features, introduced independently by Ho1995 and Amit and Geman 1997 in order to construct acollection of decision trees with controlled variation.4/25 第五届中国R语言会议北京2012 李欣海随机森林简介Tree modelsy β + β x + β x + β x + εi 0 1 1i 2 2 i 3 3i iClassification treeRegression treeCrawley 2007 The R Book p691 Crawley 2007 The R Book p6945/25 第五届中国R语言会议北京2012 李欣海随机森林简介The statistical community uses irrelevant theory,questionable conclusions?David R. Cox Emanuel Parzen Bruce HoadleyBrad EfronNO YES6/25 第五届中国R语言会议北京2012 李欣海随机森林简介Ensemble classifiers////.Tree models are simple, often produce noisy bushy or weakstunted classifiers Bagging Breiman, 1996: Fit many large trees to bootstrap-resampled versions of the training data, and classify by majority vote Boosting Freund & Shapire, 1996: Fit many large or small trees to reweighted versions of the training data. Classify by weighted majority vote Random Forests Breiman 1999: Fancier version of bagging.In general Boosting Random Forests Bagging Single TreeTrevor Hastie.7/25 第五届中国R语言会议北京2012 李欣海随机森林简介How Random Forest Works////.At each tree split, a random sample of m features is drawn, and only those m features are considered for splittingTypically m sqrtp or logp, where p is the number offeatures For each tree grown on a bootstrap sample, the error rate for observations left out of the bootstrap sample ismonitored. This is called the out-of-bag OOB error rate Random forests tries to improve on bagging by “de-correlating” the trees. Each tree has the same expectation.Trevor Hastie, p21 in Trees, Bagging, Random Forests and Boosting8/25 第五届中国R语言会议北京2012 李欣海随机森林简介R PackagesrandomForest randomForestTitle: Breiman and Cutler’s random forests for classification and regressionVersion: 4.6-6Date: 2012-01-06Author:Fortran original by Leo Breiman and Adele Cutler, R port by Andy Liawand Matthew Wiener.Implementation based on CART trees for variables of different types.Biased in favor of continuous variables and variables with many categories.partycforestBased on unbiased conditional inference trees.For variables of different types: unbiased when subsampling.黄河渭河9/25 第五届中国R语言会议北京2012 李欣海随机森林:分类# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #宁夏# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #青海# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #朱?的分布# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #山西# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #甘肃# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # #陕西 ## ## ## # # # # # # # # # # ## ## ## # # ## ##### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### #河南## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ############ # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # #### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ######### ## ######## ######## ### #### ### ## ######## ## ############################ ####### ########## ## #### #### #### ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # ### ## ################## ## #### ######## ## ######### ###### ####### ## # ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## # ## #### ## ## #### ### ## #### ## # # ## # ##### ## ## ########### #### ##### ## ## ############ ######## ### ## ##### ###### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # ##### #### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ###### #### ## ## ##### ##### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # ######### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ######## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### ###### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # #四川 # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #湖北# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #重庆# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # ## ## ## ## ## ## ## ## # # # # # # # # ## ## ## ## ## ## # # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # ### #湖南湖南黄河汉江岷江嘉陵江10/25 第五届中国R语言会议北京2012 李欣海随机森林:分类DataLand Foot prec_ prec_ prec_ Nestuse x y Elev Aspect Slope Pop GDP t_ann t_jan t_july yearcover print ann jan july site1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1981 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1981 姚家沟1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1982 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1982 姚家沟1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1983 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1983 姚家沟1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1984 姚家沟1 107.405 33.406 1056 0.54 11.4 21 0.0 20 0.98 892 7 161 11.4 -0.5 22.9 1984 三岔河1 107.405 33.406 1056 0.54 11.4 21 0.0 20 0.98 892 7 161 11.4 -0.5 22.9 1985 三岔河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1985 姚家沟0 107.400 32.780 980 0.46 42.1 11 45.8 14 1.78 927 6 170 13.0 1.3 24.0 0 3030 107.430 32.780 1553 0.97 29.6 14 171.8 32 4.76 887 5 162 13.0 1.3 24.0 0 3040 107.460 32.780 1534 0.51 25.7 14 12.7 14 1.78 886 5 162 14.0 2.15 25.2 0 3050 107.490 32.780 996 0.72 29.4 14 76.1 20 2.97 886 5 162 12.4 0.8 23.4 0 3060 107.520 32.780 1144 0.16 9.3 14 29.3 20 1.78 956 6 175 12.4 0.8 23.4 0 3070 107.550 32.780 915 0.91 20.7 11 214.7 20 5.95 956 6 175 11.6 0.15 22.5 0 3080 107.580 32.780 930 0.13 35.7 22 153.2 29 4.76 993 7 181 11.6 0.15 22.5 0 3090 107.610 32.780 873 0.40 31.9 11 66.4 29 2.97 931 6 171 12.7 1.1 23.8 0 3100 107.640 32.780 1147 0.50 35.5 11 46.8 20 2.38 1041 7 189 12.7 1.1 23.8 0 3110 107.670 32.780 1699 0.89 21.1 14 20.5 20 1.78 1060 8 192 10.4 -0.8 21.2 0 312tableibis$use ibis$use - as.factoribis$useibis$landcover - as.factoribis$landcover0 12538 560 11/25 第五届中国R 语言会议北京2012 李欣海随机森林:分类Multicollinearity is a painVariables in the two-principal-component space-50 0 50306530643018biplotprincompibis[,2:16], corT3017 2971 306330623060 2970306130582923 2969 2924 3016 y 3057 3059 3015 3056 30143013305530123010 30112968296329662967 30093005 2877 2922 2965 30542830 2964 3008 3006 3007292129622914 30192829 2876 30522919 2920 30533048 2960 3003 2961 3050 30013021 304929983000 3002 29593022 29173004 3051278329553020 2958 2957 2875282830472913291829993023290626892641 28272737 29732836 2784 2826 3046 2956 2874 2986 3033 2735 30442867 2690 2688 2915 30452975 2974 29163024 2789 2739 2788 2740 2642 2925 2972 3041 2869 28682927 2839 27362977 2793 2741 3037 29533025 2928 2820 2791 29103030 2832 2592 2995 2640 2994 2952 28592978 2881 2930 2879 3042 2863 3039 2909 29072983 3029 2880 2990 2992 2989 3036 3043 29542931 2834 2991 2884 2996 28622982 2981 3028 2985 2833 2993 3040 28722940 3032 2878 2883 2835 2882 2786 2787 2831 2873 26442976 2886 3035 2837 2785 2790 2951 2911 28252929 2870 26932926 2866 3034 2988 2864 2848 2782 2646 2871 2692 2745 29083027 2980 2943 2987 2847 2849 2912 2824 2742 2905 2823 29972942 2895 2865 2738 28613031 2984 2979 2941 2733 2840 2841 2643 2781 2744 2858 2645 2691 2896 2838 2647 2855 27432935 3026 2933 2893 2890 2892 2891 2894 2845 2794 2796 2792 2846 2746 2748 2695 2904 2747 2694 2545 3038 27002850 2851 2749 2795 2648 2696 2699 25962897 2842 2843 2798 2885 2556 25972934 293727012844 2797 2652 2697 28572887 2932 2800 2854 2598 2856 2650 2651 26982702 2550 2750 26492888 2947 2802 2751 2852 2654 2811 2853 2653 25902939 2945 2949 2753 27042711 2938 2946 2944 2706 2948 2779 2600 2780 2364 2602 2603 2317 2639 2898 2505 2601 2764 24662936 2552 2902 2551 2717 25082755 2503 2561 2549 2502 2734 25552761 2899 2900 2822 2606 2655 2703 2605 2752 2686 2608 2513 2821 2599 2801 2507 2414 2544 28602504 2950 25542889 2901 2803 2656 2799 2778 2687 2560 2510 260723712709 2558 2456 2609 2。

机器学习-R语言-随机森林-分类、回归、预测、筛选变量有史以来超详细解析（干货满满）

机器学习-R语⾔-随机森林-分类、回归、预测、筛选变量有史以来超详细解析（⼲货满满）R语⾔随机森林详细解析（基于randomforest包和varSelRF包）研究如何⽤R去实现随机森林也有三个⽉的时间了，从⼀开始的完全不理解，到现在的游刃有余，我似乎花了过多的时间，毕竟是初学者嘛。

不知各位有没有发现，CSDN上随机森林的教程都说的有些模糊，好像在刻意回避着什么，⽽且很少有⼈说变量筛选的问题。

所以，今⽇，我觉得有必要记录⼀下了。

随机森林基于R你即将从这⾥看到1.如何使⽤随机森林做回归、分类、预测、交叉验证2.如何评价模型效能（ROC、AUC）3.如何筛选变量在这⾥你不会看到1.长篇⼤段没有注释的代码2.故弄⽞虚，简单问题复杂化3.重复造轮⼦（本⽂以解决实际问题为主）分类与回归数据科学最基础的问题，分类与回归。

⽽随机森林做分类还是回归是取决于label是factor类型的还是numerical类型的1.导包⼀般需要四个包，如下，第⼀个是导⼊数据⽤的，第⼆个是随机森林包，第三个是筛选变量⽤的，第四个是绘制ROC曲线、计算AUC得分的包library(xlsx)library(randomForest)library(varSelRF)library(pROC)2.数据读取、缺失值处理读取数据，此数据是我做社会调查⾃⼰收集来的数据，各位可替换成鸢尾花数据集d<-read.xlsx('socialrecode2.xlsx',1)#这种直接引⽤⽂件名的写法请确保⽂件在⼯作空间内#参数1代表使⽤第⼀⾏作为列名d1<-na.omit(d) #删去缺失值，随机森林分类器内不能传⼊缺失值#如果⼿头没有待处理的数据，请使⽤鸢尾花数据集d1<-data(iris) #鸢尾花数据集是⽆缺失值的，故不需删去缺失值如果你的数据量不够多，但是⼜含有许多缺失值，建议使⽤randomforest包⾃带的缺失值填充函数：na.roughfix(object, …)按中位数或者模型进⾏填充3.训练模型在直觉上，似乎⼀⽚森林中决策树越多越好，但真的是这样吗？（此处有疑问不要紧，可参考⽂末原理部分）为了测试出多少棵树时模型是最优的，我们先试探性的⽤800棵树试⼀下，即第⼆部分的代码。

利用随机森林构建分类模型,并用十折交叉验证。r语言教程

利用随机森林构建分类模型,并用十折交叉验证。

r语言教程在R语言中，我们可以使用`caret`包中的`train`函数进行模型的训练，并使用`caret`包的`createDataPartition`函数进行十折交叉验证。

以下是使用随机森林构建分类模型的示例代码：首先，确保你已经安装了必要的包。

如果没有，你可以使用以下命令进行安装：```r("caret")("randomForest")```然后，加载这些包：```rlibrary(caret)library(randomForest)接下来，我们需要加载数据。

假设我们有一个名为`data`的数据框，其中包含我们的特征和目标变量：```rdata <- ("your_") 请将"your_"替换为你的数据文件路径```然后，我们将使用`createDataPartition`函数进行十折交叉验证的数据分割：```r(123) 为了结果的可重复性control <- rbind(trainControl(method = "cv", number = 10), 10折交叉验证trainControl(method = "oob") 用于随机森林的外部验证)```接着，我们将使用`train`函数训练我们的模型：(123) 为了结果的可重复性rf_model <- train(target ~ ., data = data, trControl = control, method = "rf") 使用随机森林方法训练模型```最后，我们可以输出模型的详细信息：```rprint(rf_model)```以上代码演示了如何使用随机森林和十折交叉验证在R语言中构建分类模型。

请注意，你可能需要根据自己的数据和需求对代码进行一些调整。

随机森林算法介绍及R语言实现

随机森林算法介绍及R语言实现随机森林算法介绍算法介绍：简单的说，随机森林就是用随机的方式建立一个森林，森林里面有很多的决策树，并且每棵树之间是没有关联的。

得到一个森林后，当有一个新的样本输入，森林中的每一棵决策树会分别进行一下判断，进行类别归类（针对分类算法），最后比较一下被判定哪一类最多，就预测该样本为哪一类。

随机森林算法有两个主要环节：决策树的生长和投票过程。

决策树生长步骤：1.从容量为N的原始训练样本数据中采取放回抽样方式(即bootstrap取样)随机抽取自助样本集，重复k（树的数目为k）次形成一个新的训练集N，以此生成一棵分类树；2.每个自助样本集生长为单棵分类树，该自助样本集是单棵分类树的全部训练数据。

设有M个输入特征，则在树的每个节点处从M个特征中随机挑选m(m < M)个特征，按照节点不纯度最小的原则从这m个特征中选出一个特征进行分枝生长，然后再分别递归调用上述过程构造各个分枝，直到这棵树能准确地分类训练集或所有属性都已被使用过。

在整个森林的生长过程中m将保持恒定；3.分类树为了达到低偏差和高差异而要充分生长，使每个节点的不纯度达到最小，不进行通常的剪枝操作。

投票过程：随机森林采用Bagging方法生成多个决策树分类器。

基本思想：1.给定一个弱学习算法和一个训练集，单个弱学习算法准确率不高，可以视为一个窄领域专家；2.将该学习算法使用多次，得出预测函数序列，进行投票，将多个窄领域专家评估结果汇总，最后结果准确率将大幅提升。

随机森林的优点：∙可以处理大量的输入变量;∙对于很多种资料，可以产生高准确度的分类器;∙可以在决定类别时，评估变量的重要性;∙在建造森林时，可以在内部对于一般化后的误差产生不偏差的估计;∙包含一个好方法可以估计遗失的资料，并且，如果有很大一部分的资料遗失，仍可以维持准确度;∙提供一个实验方法，可以去侦测 variable interactions;∙对于不平衡的分类资料集来说，可以平衡误差;∙计算各例中的亲近度，对于数据挖掘、侦测偏离者（outlier）和将资料视觉化非常有用;∙使用上述。

用R实现随机森林的分类与回归

用R实现随机森林的分类与回归第五届中国R语言会议北京2012 李欣海用R实现随机森林的分类与回归Applications of Random Forest using RClassification and Regression李欣海中科院动物所邮件:lixh@//0>.主页:////.博客:////.微博:////. 第五届中国R语言会议北京2012 李欣海随机森林简介Random Forest////.an-introduction-to-data-mining-for-marketing-and-business-intelli gence/Random Forest is an ensemble classifier thatconsists of many decision trees It outputs the class that is the mode of the class'soutput by individual trees Breiman 2001 It deals with “small n large p”-problems, high-orderinteractions, correlated predictor variables.Breiman, L. 2001. Random forests. Machine Learning 45:5-32. Being cited 6500 times until 20123/25 第五届中国R语言会议北京2012 李欣海随机森林简介History////.an-introduction-to-data-mining-for-marketing-and-business-intelli gence/The algorithm for inducing a random forest was developed byLeo Breiman 2001 and Adele Cutler, and "Random Forests" istheir trademarkThe term came from random decision forests that was firstproposed by Tin Kam Ho of Bell Labs in 1995The method combines Breiman's "bagging" idea and therandom selection of features, introduced independently by Ho1995 and Amit and Geman 1997 in order to construct acollection of decision trees with controlled variation.4/25 第五届中国R语言会议北京2012 李欣海随机森林简介Tree modelsy β + β x + β x + β x + εi 0 1 1i 2 2 i 3 3i iClassification treeRegression treeCrawley 2007 The R Book p691 Crawley 2007 The R Book p6945/25 第五届中国R语言会议北京2012 李欣海随机森林简介The statistical community uses irrelevant theory,questionable conclusions?David R. Cox Emanuel Parzen Bruce HoadleyBrad EfronNO YES6/25 第五届中国R语言会议北京2012 李欣海随机森林简介Ensemble classifiers////.Tree models are simple, often produce noisy bushy or weakstunted classifiers Bagging Breiman, 1996: Fit many large trees to bootstrap-resampled versions of the training data, and classify by majority vote Boosting Freund & Shapire, 1996: Fit many large or small trees to reweighted versions of the training data. Classify by weighted majority vote Random Forests Breiman 1999: Fancier version of bagging.In general Boosting Random Forests Bagging Single TreeTrevor Hastie.7/25 第五届中国R语言会议北京2012 李欣海随机森林简介How Random Forest Works////.At each tree split, a random sample of m features is drawn, and only those m features are considered for splittingTypically m sqrtp or logp, where p is the number offeatures For each tree grown on a bootstrap sample, the error rate for observations left out of the bootstrap sample ismonitored. This is called the out-of-bag OOB error rate Random forests tries to improve on bagging by “de-correlating” the trees. Each tree has the same expectation.Trevor Hastie, p21 in Trees, Bagging, Random Forests and Boosting8/25 第五届中国R语言会议北京2012 李欣海随机森林简介R PackagesrandomForest randomForestTitle: Breiman and Cutler’s random forests for classification and regressionVersion: 4.6-6Date: 2012-01-06Author:Fortran original by Leo Breiman and Adele Cutler, R port by Andy Liawand Matthew Wiener.Implementation based on CART trees for variables of different types.Biased in favor of continuous variables and variables with many categories.partycforestBased on unbiased conditional inference trees.For variables of different types: unbiased when subsampling.黄河渭河9/25 第五届中国R语言会议北京2012 李欣海随机森林:分类# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #宁夏# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #青海# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #朱?的分布# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #山西# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #甘肃# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # #陕西 ## ## ## # # # # # # # # # # ## ## ## # # ## ##### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### #河南## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ############ # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # #### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ######### ## ######## ######## ### #### ### ## ######## ## ############################ ####### ########## ## #### #### #### ## ### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # ### ## ################## ## #### ######## ## ######### ###### ####### ## # ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## # ## #### ## ## #### ### ## #### ## # # ## # ##### ## ## ########### #### ##### ## ## ############ ######## ### ## ##### ###### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # ##### #### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ###### #### ## ## ##### ##### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # ######### ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ######## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ### ###### # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # #四川 # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #湖北# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # ### ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## #重庆# # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # ## ## ## ## ## ## ## ## # # # # # # # # ## ## ## ## ## ## # # # # ## ## ## ## # # # # # # # # # # # # # ### # # ## ## ## # # # # # # # # # # ## ## ## # # ## ## ## # # # # # # # # # # ## ## ## # ### #湖南湖南黄河汉江岷江嘉陵江10/25 第五届中国R语言会议北京2012 李欣海随机森林:分类DataLand Foot prec_ prec_ prec_ Nestuse x y Elev Aspect Slope Pop GDP t_ann t_jan t_july yearcover print ann jan july site1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1981 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1981 姚家沟1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1982 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1982 姚家沟1 107.505 33.392 984 0.67 29.6 21 42.0 20 2.95 845 6 153 12.4 0.3 24.0 1983 金家河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1983 姚家沟1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1984 姚家沟1 107.405 33.406 1056 0.54 11.4 21 0.0 20 0.98 892 7 161 11.4 -0.5 22.9 1984 三岔河1 107.405 33.406 1056 0.54 11.4 21 0.0 20 0.98 892 7 161 11.4 -0.5 22.9 1985 三岔河1 107.548 33.409 1315 0.90 19.0 14 22.5 26 1.97 869 6 157 11.3 -0.6 22.7 1985 姚家沟0 107.400 32.780 980 0.46 42.1 11 45.8 14 1.78 927 6 170 13.0 1.3 24.0 0 3030 107.430 32.780 1553 0.97 29.6 14 171.8 32 4.76 887 5 162 13.0 1.3 24.0 0 3040 107.460 32.780 1534 0.51 25.7 14 12.7 14 1.78 886 5 162 14.0 2.15 25.2 0 3050 107.490 32.780 996 0.72 29.4 14 76.1 20 2.97 886 5 162 12.4 0.8 23.4 0 3060 107.520 32.780 1144 0.16 9.3 14 29.3 20 1.78 956 6 175 12.4 0.8 23.4 0 3070 107.550 32.780 915 0.91 20.7 11 214.7 20 5.95 956 6 175 11.6 0.15 22.5 0 3080 107.580 32.780 930 0.13 35.7 22 153.2 29 4.76 993 7 181 11.6 0.15 22.5 0 3090 107.610 32.780 873 0.40 31.9 11 66.4 29 2.97 931 6 171 12.7 1.1 23.8 0 3100 107.640 32.780 1147 0.50 35.5 11 46.8 20 2.38 1041 7 189 12.7 1.1 23.8 0 3110 107.670 32.780 1699 0.89 21.1 14 20.5 20 1.78 1060 8 192 10.4 -0.8 21.2 0 312tableibis$use ibis$use - as.factoribis$useibis$landcover - as.factoribis$landcover0 12538 560 11/25 第五届中国R 语言会议北京2012 李欣海随机森林:分类Multicollinearity is a painVariables in the two-principal-component space-50 0 50306530643018biplotprincompibis[,2:16], corT3017 2971 306330623060 2970306130582923 2969 2924 3016 y 3057 3059 3015 3056 30143013305530123010 30112968296329662967 30093005 2877 2922 2965 30542830 2964 3008 3006 3007292129622914 30192829 2876 30522919 2920 30533048 2960 3003 2961 3050 30013021 304929983000 3002 29593022 29173004 3051278329553020 2958 2957 2875282830472913291829993023290626892641 28272737 29732836 2784 2826 3046 2956 2874 2986 3033 2735 30442867 2690 2688 2915 30452975 2974 29163024 2789 2739 2788 2740 2642 2925 2972 3041 2869 28682927 2839 27362977 2793 2741 3037 29533025 2928 2820 2791 29103030 2832 2592 2995 2640 2994 2952 28592978 2881 2930 2879 3042 2863 3039 2909 29072983 3029 2880 2990 2992 2989 3036 3043 29542931 2834 2991 2884 2996 28622982 2981 3028 2985 2833 2993 3040 28722940 3032 2878 2883 2835 2882 2786 2787 2831 2873 26442976 2886 3035 2837 2785 2790 2951 2911 28252929 2870 26932926 2866 3034 2988 2864 2848 2782 2646 2871 2692 2745 29083027 2980 2943 2987 2847 2849 2912 2824 2742 2905 2823 29972942 2895 2865 2738 28613031 2984 2979 2941 2733 2840 2841 2643 2781 2744 2858 2645 2691 2896 2838 2647 2855 27432935 3026 2933 2893 2890 2892 2891 2894 2845 2794 2796 2792 2846 2746 2748 2695 2904 2747 2694 2545 3038 27002850 2851 2749 2795 2648 2696 2699 25962897 2842 2843 2798 2885 2556 25972934 293727012844 2797 2652 2697 28572887 2932 2800 2854 2598 2856 2650 2651 26982702 2550 2750 26492888 2947 2802 2751 2852 2654 2811 2853 2653 25902939 2945 2949 2753 27042711 2938 2946 2944 2706 2948 2779 2600 2780 2364 2602 2603 2317 2639 2898 2505 2601 2764 24662936 2552 2902 2551 2717 25082755 2503 2561 2549 2502 2734 25552761 2899 2900 2822 2606 2655 2703 2605 2752 2686 2608 2513 2821 2599 2801 2507 2414 2544 28602504 2950 25542889 2901 2803 2656 2799 2778 2687 2560 2510 260723712709 2558 2456 2609 2。

r语言随机森林结果解读

r语言随机森林结果解读
在R语言中，使用随机森林模型进行数据分析后，可以使用各种方法和技巧来解读模型结果。

以下是一些常用的方法和步骤：
1.查看模型摘要：使用summary()函数可以查看随机森林模型的摘
要，其中包括模型的各项指标和参数。

2.查看变量重要性：使用importance()函数可以查看每个变量在模型
中的重要性，通常用“MeanDecreaseAccuracy”和“MeanDecreaseGini”两个指标来衡量。

3.查看模型系数：使用coef()函数可以查看模型中的系数，即各个特
征对最终预测结果的影响程度。

4.查看特征重要性：可以通过特征重要性图（feature importance plot）
来查看各个特征对模型预测结果的影响程度。

使用plot(model$importance)可以生成特征重要性图。

5.查看模型预测结果：使用predict()函数可以对新的数据进行预测，
并将预测结果与实际值进行比较，以评估模型的准确性。

6.查看模型评估指标：可以使用各种评估指标来衡量模型的性能，
如准确率、精确率、召回率、F1得分等。

可以使用confusionMatrix()函数来计算混淆矩阵，从而得到各种评估指标。

7.查看模型交互式可视化：使用R中的交互式可视化工具，如shiny
包或plotly包等，可以更直观地查看模型结果，包括特征重要性图、混淆矩阵、ROC曲线等。

总之，在R语言中解读随机森林模型结果需要结合实际问题和数据集来进行深入分析和理解。

R语言实现随机森林

R语⾔实现随机森林R语⾔实现随机森林install.packages("pacman")install.packages("caret")install.packages("pROC")install.packages()install.packages("randomForest")library(randomForest)library(ggplot2)library(lattice)library(pacman)library(caret)library(pROC)library(rpart)data(iris)dim(iris)trainlist<-createDataPartition(iris$Species,p=0.7,list=FALSE)#取出百分之七⼗的iris数据trainset<-iris[trainlist,]testset<-iris[-trainlist,]#⼀部分分成训练集，另⼀部分则为测试集set.seed(2000)#⽣成2000个随机数rf.train<-randomForest(as.factor(Species)~.,data=trainset,importance=TRUE,na.action = na.pass)#因变量是Species，.表⽰其他都为⾃变量，数据来⾃trainset#importance表⽰随机森林需要给出每⼀个变量重要性的排序#na.action表⽰如何处理缺失值plot(rf.train,main = "randomforest")#画图，main表⽰设置标题#三种颜⾊代表三种鸢尾花，⿊⾊代表三种鸢尾花平均值#横轴是决策树的数⽬，纵轴是误差数rf.test<-predict(rf.train,newdata = testset,type = "class")rf.testrf.cf<-caret::confusionMatrix(as.factor(rf.test),as.factor(testset$Species))rf.test2<-predict(rf.train,newdata = testset,type="prob")roc.rf<-multiclass.roc(testset$Species,rf.test2)fit1=rpart(Species~.,data=trainset)pre2=predict(fit1,testset,type="prob")roc1<-multiclass.roc(testset$Species,pre2[,1])plot(roc1$rocs[[1]],col="red")plot(roc1$rocs[[3]],add=TRUE,col="green")#画出roc曲线，显⽰预测效果。

随机森林.ppt

可以得到变量重要性排序（两种：基于OOB误分率的增加量和基于分裂时的分类节点纯度下降量）
两个重要的代码
randomForest
主要参数是ntree，mtry
Predict
第一步，随机森林的安装
随机森林是基于R语言运行，安装过程分两步： 1.ubuntu系统下首先安装R语言包。
用一行代码。 sudo apt-get install R 然后ubuntu系统就自动的帮你安装完R。 2.安装random forest 意想不到的简单。打开终端，输入R，就算进入到了R语言的编码界面。在大于号后面入
决策树的定义
Hale Waihona Puke 决策树是这样的一颗树:每个内部节点上选用一个属性进行分割每个分叉对应一个属性值每个叶子结点代表一个分类
A1
a11 A2
a12 c1
a21
a22
c1
c2
a13
A3
a31
a32
c2
c1
决策树框架
决策树生成算法分成两个步骤
树的生成
开始，数据都在根节点递归的进行数据分片
0,mtry=3,proximity=TRUE,importance=TRUE) print(iris.rf) iris.pred<-predict( iris.rf,iris[ind==2,] ) table(observed=iris[ind==2,"Species"],predicted=iris.pred )
随机森林的特点
两个随机性的引入，使得随机森林不容易陷入过拟合
两个随机性的引入，使得随机森林具有很好的抗噪声能力
对数据集的适应能力强：既能处理离散型数据，也能处理连续型数据，数据集无需规范化。

随机森林特征重要性计算_R语言随机森林模型中具有相关特征的变量重要性

随机森林特征重要性计算_R语言随机森林模型中具有相关特征的变量重要性随机森林（Random Forest）是一种常用的机器学习方法，可以用于特征选择和变量重要性评估。

在R语言中，可以使用randomForest包来构建随机森林模型，并计算变量的重要性。

在随机森林算法中，变量的重要性可以通过两种方式来评估：基于节点的重要性（Node Importance）和基于变量的重要性（Variable Importance）。

基于节点的重要性是通过计算每个节点在模型中的准确率改变来评估，它只对拆分节点的变量感兴趣。

可以使用varImp函数计算每个节点的重要性。

```R# 导入randomForest包library(randomForest)#构建随机森林模型model <- randomForest(Species ~ ., data = iris)#计算节点的重要性node_importance <- varImp(model)print(node_importance)```上面的代码将计算随机森林模型中每个节点的重要性，并打印结果。

基于变量的重要性是通过计算每个变量的平均节点准确率改变来评估。

可以使用importance函数计算变量的重要性。

```R#计算变量的重要性variable_importance <- importance(model)print(variable_importance)```上面的代码将计算随机森林模型中每个变量的重要性，并打印结果。

基于变量的重要性是基于基于节点的重要性的总和来计算的，通常更为常用。

例如，可以使用以下代码将变量按重要性进行排序并绘制柱状图：```R#按重要性对变量进行排序sorted_importance <- sort(variable_importance, decreasing = TRUE)#绘制柱状图barplot(sorted_importance, main = "Variable Importance",xlab = "Variables", ylab = "Importance")```上面的代码将变量按重要性进行排序，并绘制了一个柱状图来展示变量的重要性。

随机森林算法案例

随机森林算法案例随机森林算法是一种用于分类和回归的集成学习方法。

它通过构建多个决策树，并将它们的结果进行组合来提高整体预测准确率。

随机森林算法采用了随机特征选择和随机样本选择的策略，以增加模型的多样性，从而降低过拟合的风险。

在本文中，我们将介绍随机森林算法的原理和应用，并通过一个实际案例来展示其效果。

1.随机森林算法原理随机森林算法是由Leo Breiman在2001年提出的，它是一种集成学习方法，通过结合多个弱学习算法来构建一个强学习算法。

随机森林算法的基本原理是通过构建多个决策树，并将它们的结果进行组合来进行分类或回归。

在构建决策树时，随机森林算法采用了以下两种随机性策略：1）随机特征选择：在每个节点分裂时，随机森林算法从所有特征中随机选择一定数量的特征，然后从中选择最佳的特征进行分裂，这可以增加模型的多样性，从而提高整体预测准确率。

2）随机样本选择：在构建每棵决策树时，随机森林算法通过随机选择训练样本来构建不同的决策树，这样可以使每棵树都有不同的训练数据，从而减少过拟合的风险。

通过这两种随机性策略，随机森林算法可以有效地提高模型的泛化能力，从而得到更好的预测结果。

2.随机森林算法应用随机森林算法在分类和回归问题上都有很好的应用效果，尤其是在处理大规模数据集和高维特征空间时效果显著。

随机森林算法的优势在于它可以处理大量的特征和样本数据，同时对参数的选择相对较少，模型的训练和预测都比较快速。

随机森林算法在多个领域都得到了广泛应用，如金融、医疗、生物科学等。

在金融领域，随机森林算法可以用来进行风险评估、信用评分、股价预测等。

在医疗领域，随机森林算法可以用来进行疾病诊断、药物治疗效果评估等。

在生物科学领域，随机森林算法可以用来分析基因数据，预测蛋白质结构等。

3.随机森林算法案例接下来，我们将通过一个实际案例来展示随机森林算法的应用效果。

假设我们有一个数据集，包括了一些关于鸢尾花的特征数据，如花萼长度、花萼宽度、花瓣长度、花瓣宽度等。

实验报告及分析_R中bagging回归与随机森林以及boosting回归

一、R中boosting回归这个主要用R中的mboost包中的mboost函数来实现。

但是作为铺助，还要加载party包。

函数如下mboost(formula, data = list(),baselearner = c("bbs", "bols", "btree", "bss", "bns"), ...)其中的参数需要注意formula的输入格式。

至于data也可以是数据框。

我们用决策树的boosting方法。

要注意查看formula的输入格式，参见下面的具体例子。

一个具体的例子我们使用我的电脑上自带的数据，即E:\Documents\R中的mg文本文件中的数据。

该数据无任何说明，知道它是由6个自变量和一个因变量构成。

试验如下。

> library(party)> library(mboost)> w<-read.table('mg.txt',header=T)>B1<-mboost(y~btree(x1)+btree(x2)+btree(x3)+btree(x4)+btree(x5)+btre e(x6),data=w[-1,]) #构建分类器，用除掉第一个样本的数据做训练数据。

>y0<-predict(B1,w[1,]) #用第一个样本作测试。

二、bagging回归与boosting回归想法类似，bagging回归的做法就是不断放回地对训练样本进行再抽样，对每个自助样本都建立一棵回归树，对于每一个观测，每棵树给一个预测，最后将其平均。

使用到的函数包为ipred，使用函数为bagging（），用法如下：bagging(formula, data, subset, na.action=na.rpart, ...)主要参数介绍：formula：回归方程形式data：数据集（数据框）control：对树枝的控制，使用函数rpart.control（），可以控制诸如cp值，xval等参量。

随机森林算法构建模型 roc r语言

随机森林算法构建模型 roc r语言随机森林算法是一种常用的机器学习算法，可以用于分类和回归问题。

本文将介绍随机森林算法的原理和在R语言中的实现，并讨论其在模型评估中的重要指标——ROC曲线。

一、随机森林算法原理随机森林算法是基于决策树的集成学习算法。

它通过构建多个决策树，然后将它们的结果进行集成，以提高预测的准确性和鲁棒性。

具体来说，随机森林算法通过自助采样（bootstrap sampling）从原始训练集中随机选择一部分样本，用于构建每个决策树。

在构建每个决策树时，随机森林还会随机选择一部分特征，以增加模型的多样性。

这样可以减少过拟合的风险，并且使得模型更具有泛化能力。

在进行预测时，随机森林算法将所有决策树的预测结果进行投票或平均，得到最终的预测结果。

二、在R语言中实现随机森林算法在R语言中，我们可以使用randomForest包来实现随机森林算法。

下面是一个简单的示例代码：```R# 导入randomForest包library(randomForest)# 读取数据data <- read.csv("data.csv")# 划分训练集和测试集train <- data[1:500, ]test <- data[501:1000, ]# 构建随机森林模型model <- randomForest(target ~ ., data = train, ntree = 100)# 预测predictions <- predict(model, newdata = test)# 模型评估confusionMatrix(predictions, test$target)```在上述代码中，我们首先导入randomForest包，并读取了一个名为data.csv的数据集。

然后，我们将数据集划分为训练集和测试集。

接下来，使用randomForest函数构建随机森林模型，其中`target ~ .`表示使用所有特征来预测目标变量。

ML之RF：随机森林RF算法简介、应用、经典案例之详细攻略

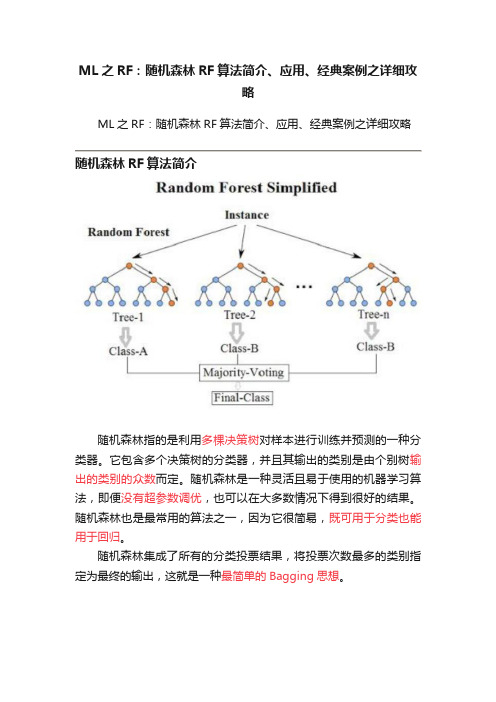
ML之RF：随机森林RF算法简介、应用、经典案例之详细攻略ML之RF：随机森林RF算法简介、应用、经典案例之详细攻略随机森林RF算法简介随机森林指的是利用多棵决策树对样本进行训练并预测的一种分类器。

它包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

随机森林是一种灵活且易于使用的机器学习算法，即便没有超参数调优，也可以在大多数情况下得到很好的结果。

随机森林也是最常用的算法之一，因为它很简易，既可用于分类也能用于回归。

随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的Bagging思想。

1、RF基本的构建算法过程•1. 用N来表示训练用例（样本）的个数，M表示特征数目。

•2. 输入特征数目m，用于确定决策树上一个节点的决策结果；其中m应远小于M。

•3. 从N个训练用例（样本）中以有放回抽样的方式，取样N次，形成一个训练集（即bootstrap取样），并用未抽到的用例（样本）作预测，评估其误差。

•4. 对于每一个节点，随机选择m个特征，决策树上每个节点的决定都是基于这些特征确定的。

根据这m个特征，计算其最佳的分裂方式。

•5. 每棵树都会完整成长而不会剪枝，这有可能在建完一棵正常树状分类器后被采用）。

2、RF算法相关文献、论文1. Panda Biswanath , Joshua S. Herbach , Sugato Basu , and Roberto J. Bayardo .( 2009 ).PLANET: Massively Parallel Learning of Tree Ensembles with MapReduce. Proceedings of the 35th International Conference on Very Large Data Bases. Retrieved from /pubs/pub36296.html .2. Leo Breiman . (September, 1994 ). Bagging Predictors. Technical Report No. 421.Department of Statistics, UC Berkeley. Retrieved from http:// /sites/default/files/tech-reports/421.pdf .3. Leo Breiman . (2001). Random forests . Machine Learningg , 45 : 5 –32 . Retrieved from/~breiman/randomforest2001.pdf .4. J.H. Friedman . (2001). Greedy Function Approximation: A Gradient Boosting Machine .Annals of Statistics,29(5): 1189–1232.Retrieved from http://statweb. /~jhf/ftp/trebst.pdf.5. J.H. Friedman . (2002). Stochastic Gradient Boosting . Computational Statistics and Data Analysis , 38 (4): 367– 378 . Retrieved from /~jhf/ftp/stobst.pdf . 随机森林RF算法的应用1、RF用于回归klearn.ensemble.RandomForestRegressor的类构造函数函数API官方解释：https:///stable/modules/generated/sklearn.ensemble.Random ForestRegressor.html#sklearn.ensemble.RandomForestRegressor(1)、重点参数解释n_estimators：整型，可选（缺省值为10）。

boruta算法r语言

boruta算法r语言
Boruta算法是一种基于随机森林的特征选择算法，它可以帮助我们在大量特征中快速筛选出最重要的特征，从而提高模型的性能和解释能力。

在R语言中，Boruta算法可以通过“Boruta”包来实现。

首先，我们需要使用随机森林对原始数据集进行训练，并获取每个特征的重要性指标。

然后，使用Boruta算法进行特征选择，它会根据每个特征的重要性指标和随机性生成一组假特征，与原始特征进行比较，以确定每个特征的重要性。

在使用Boruta算法时，我们需要设置一些参数，如随机森林的数量、最大深度、控制假特征数量的阈值等。

此外，还可以根据需要进行交叉验证等操作，以提高模型的泛化能力和稳定性。

总之，Boruta算法是一种非常实用的特征选择技术，在处理大规模数据时尤为重要。

只要掌握了基本的R语言编程技巧和Boruta 算法的原理，我们就可以快速地进行特征选择，并构建出高效、可解释性强的预测模型。

- 1 -。

r语言之randomforest随机森林

R语言之Random Forest随机森林什么是随机森林？随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习（Ensemble Learning）方法。

随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。

“森林”我们很好理解，一棵叫做树，那么成百上千棵就可以叫做森林了，这样的比喻还是很贴切的，其实这也是随机森林的主要思想--集成思想的体现。

随机森林算法的实质是基于决策树的分类器集成算法，其中每一棵树都依赖于一个随机向量，随机森林的所有向量都是独立同分布的。

随机森林就是对数据集的列变量和行观测进行随机化，生成多个分类数，最终将分类树结果进行汇总。

随机森林相比于神经网络，降低了运算量的同时也提高了预测精度，而且该算法对多元共线性不敏感以及对缺失数据和非平衡数据比较稳健，可以很好地适应多达几千个解释变量数据集。

随机森林的组成随机森林是由多个CART分类决策树构成，在构建决策树过程中，不进行任何剪枝动作，通过随机挑选观测（行）和变量（列）形成每一棵树。

对于分类模型，随机森林将根据投票法为待分类样本进行分类；对于预测模型，随机森林将使用单棵树的简单平均值来预测样本的Y值。

随机森林的估计过程1）指定m值，即随机产生m个变量用于节点上的二叉树，二叉树变量的选择仍然满足节点不纯度最小原则；2）应用Bootstrap自助法在原数据集中有放回地随机抽取k 个样本集，组成k棵决策树，而对于未被抽取的样本用于单棵决策树的预测；3）根据k个决策树组成的随机森林对待分类样本进行分类或预测，分类的原则是投票法，预测的原则是简单平均。

随机森林的两个重要参数：1.树节点预选的变量个数：单棵决策树决策树的情况。

2.随机森林中树的个数：随机森林的总体规模。

随机森林模型评价因素1）每棵树生长越茂盛，组成森林的分类性能越好；2）每棵树之间的相关性越差，或树之间是独立的，则森林的分类性能越好。

矿产

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

随机森林算法介绍及R语言实现

r语言随机森林模型怎么求出回归方程

r语言 随机森林 回归 最优参数

R随机森林算法

用R实现随机森林的分类与回归

机器学习-R语言-随机森林-分类、回归、预测、筛选变量有史以来超详细解析（干货满满）

利用随机森林构建分类模型,并用十折交叉验证。r语言教程

随机森林算法介绍及R语言实现

用R实现随机森林的分类与回归

r语言随机森林结果解读

R语言实现随机森林

随机森林.ppt

随机森林特征重要性计算_R语言随机森林模型中具有相关特征的变量重要性

随机森林算法案例

实验报告及分析_R中bagging回归与随机森林以及boosting回归

随机森林算法构建模型 roc r语言

ML之RF：随机森林RF算法简介、应用、经典案例之详细攻略

boruta算法r语言

r语言之randomforest随机森林

矿产

r语言随机森林回归最优参数