大学物理第节狭义相对论基本原理相对时空观-讲义
大学物理2相对论基础_01_狭义相对论的时空观6.2 4.2爱因斯坦相对性原理

2
22
t t 1 u2 / c2
—— 时间变长了!运动的时钟走慢了!
第一讲 狭义相对论的时空观_20150909 XCH
20 / 38
惯性系S’ —— 同地不同时
x 0
t
2d c
相对论基础-大学物理
第一讲 狭义相对论的时空观_20150909 XCH
惯性系S —— 不同地不同时
0 2.6 108 s —— 本征时间
实验室
0
4.33108 s
1 u2 / c2
2) 在实验室中通过的平均距离 l u 10.4m
第一讲 狭义相对论的时空观_20150909 XCH
相对论基础-大学物理
05 同时性的相对性 —— 长度收缩(动尺变短)
—— 惯性参考系S’以速度相对于惯性参考系S运动 —— S’中的棒AB静止(固定在S’的x轴上)
t1)
l
v2 c2
干涉仪转动900,移过的条纹数
N
2
2l
v2 c2
0.04
???
第一讲 狭义相对论的时空观_20150909 XCH
狭义相对论的基本原理
相对论基础-大学物理
1905年爱因斯坦 —— 提出两个基本假设
假设 I 物理学定律在所有惯性参考系都是等价的 —— 爱因斯坦相对性原理
—— 两种方法测得AB的长度一样
第一讲 狭义相对论的时空观_20150909 XCH
S系中 —— AB长度的测量
相对论基础-大学物理
1) 同时测量AB两点的坐标
t
t2
t1
0
xA and xB
大学物理课件—狭义相对论(免费版)

狭义相对论基础
实验学院数理教研室
Albert Einstein ( 1879 – 1955 ) 20世纪最伟大的物理学家, 于 1905年和1915年先后创立了狭义相 对论和广义相对论, 他于1905年提 出了光量子假设, 为此他于1922年 获得诺贝尔物理学奖, 他还在量子 理论方面具有很多的重要的贡献 .
-
第四章
狭义相对论基础
实验学院数理教研室
例2 静止时边长为50cm的立方体,沿着某棱边方向相对 于地面运动,v=2.4108 ms-1,则在地面上测得其体积 是 . 解:
v
在运动方向上,边长:
l l0 1
2
2
在与此垂直的方向上,边长不变! 体积:
V l l l
2 0
3 0
二 . 伽利略变换 当
t t' 0
时
s y
y
ut
o
s'
y'
u
*
o与
o'重合
y'
P ( x, y , z ) ( x' , y ' , z ' )
位置坐标变换公式
z' z
t' t
x' x ut y' y
x'
x
z z
o' z' z'
x' x
v ' v u a' a
z
y
y'
u
l0 x '2 x '1 l '
o
x '1
o' x1
l0
4.3 狭义相对论基本原理 相对时空观

Guangxi university
S
y S' O
u y' O' c c c x' c x
在S系中, 若按伽利略变换: 往左:v=c-u 往右:v=c+u
Guangxi university
讨论:
1 Einstein 的相对性理论 是 Newton理论的发展 一切物理规律 力学规律
解1:以地面为参照系 介子寿命延长。 用经典时空观 介子所走路程
y 0.998c 0 8 6 y 0.998 3 10 2.15 10 644(m )
还没到达地面,就已经衰变了。但实际探测 仪器不仅在地面,甚至在地下 3km 深的矿井 中也测到了 介子。
Guangxi university
S
S
u
弟 a. e f 弟 0 .
x
x
x
) 花开事件:( x, t1 S 系x处发生两个事件 ) ( x, t 2 花谢事件:
t1 (寿命) t t2
在S系中观察者测量花的寿命是多少?
Guangxi university
S
第三节
狭义相对论基本原理 相对时空观
Guangxi university
返回
一、 狭义相对论的两条基本原理
爱因斯坦在1905年发表的《论动体的电动力学》 论文中提出了狭义相对论两条基本原理 1.相对性原理
所有物理规律在一切惯性系中都具有相同形式。 (所有惯性系都是平权的,在它们之中所有物理规 律都一样) 2.光速不变原理
2 光速不变与伽利略变换 与伽利略的速度相加原理不相容
大学物理2 -5-第1章-狭义相对论时空观

第 1 章 狭义相对论时空观
本章主要讲解四个方面问题:
1)伽利略坐标变换、力学相对性原理及牛顿力 学的时空观 。 2)狭义相对论基本原理。 3)洛仑兹坐标变换和速度变换。 4)狭义相对论时空观。 第 1 章 狭义相对论时空观
狭义相对论时空观 (相对论运动学)
t 与运动状态无关, 时空独立。 牛顿时空观: r 、 空 间 r、 时 间t 相对论时空观 : r 、 t 与运动状态有关, 时空统一。
2、长度收缩(长度的相对性,运动尺度缩短)
Y
O
O Y
u
x 2 t
X
t x1
x1
x2
X
棒的长度: 测量两端坐标来确定
(i ) 棒相对于 K 参考系静止 K系测量: 无论同时或不同时l0 x2 x1 本征长度( 静长 ) (ii) 棒相对于 K 参考系运动 t1 t ) K系测量: 必须同时测量两端坐标 ( t2
空间间隔测量的相对性的反映。
③ 在与相对运动垂直的方向上,无相对运动,故不发
生长度收缩。
第 1 章 狭义相对论时空观
l l0
u 1 c
2
【例题】 马路边竖立着一块正方形广告牌,其面积为 100 m2,以 0.80C 的速度行驶的“爱因斯坦”牌摩托
车的驾驶员测得该广告牌的面积为多少?
dx
dx udt
2
vx u
2
dt
第 1 章 狭义相对论时空观
所以得:
vx u v x uv x 1 2 c 2 u vy 1 c v y uv x 1 2 c 2 u vz 1 c v z uv x 1 c2
狭义相对论讲义课件

04
狭义相对论的时空观
同时性的相对性
01
同时性的相对性是狭义相对论 中的一个基本概念,指的是观 察者在不同参考系中观察到的 事件发生顺序可能会不同。
02
在相对论中,两个事件在不同 的参考系中同时发生,并不意 味着它们在所有参考系中都是 同时发生的。
狭义相对论的基本原理
相对性原理
物理规律在所有惯性参考系中形 式都保持不变。
光速不变原理
光在真空中的速度在所有惯性参 考系中都是相同的,约为每秒 299,792,458米。
02
洛伦兹变换
洛伦兹变换的定义
洛伦兹变换是用来描述不同惯性参考系之间坐 标和时间的变换。
在狭义相对论中,所有惯性参考系都是等价的 ,因此可以通过洛伦兹变换将一个惯性参考系 中的事件变换到另一个惯性参考系中。
3
通过洛伦兹变换,我们可以更好地理解狭义相对 论中的基本原理和概念,从而更深入地了解这个 理论。
03
光速不变原理
光速不变原理的表述
光速不变原理是狭义相对论的基本假设之一,它指出在任何惯性参考系中,真空 中光的传播速度都是恒定不变的,约为每秒299,792,458米。
光速不变原理可以表述为:无论观察者的运动状态如何,光的速度在真空中总是 相同的。
狭义相对论的质量和能量 质量与能量的关系
质量和能量是等价的:在狭义相对论中,质量和能量被视 为同一事物的两个方面,它们之间可以相互转换。
核能释放:核反应过程中,原子核中的质量会转化为能量 释放出来。
质能方程E=mc²:该方程表达了质量和能量之间的关系 ,其中E代表能量,m代表质量,c代表光速。
大学物理课件-狭义相对论的时空观

s s'
y y' u
d
12
s'系同一地点 B 发生两事件
9 6 3
o o'
B
12
x' x
( x ' , t '1 ) 接受一光信号 ( x ' , t '2 )
发射一光信号 时间间隔 t ' t '2 t '1 2d c 在 S 系中观测这两事件:
s
y
9
3 6
o
9
x1
12
d
3
( x1 , t1 ), ( x2 , t 2 )
9 6
x' 3 x
在 S 系中这两个事件是同时发生的。 注意 此结果反之亦然。
结论:
沿两个惯性系运动方向,不同地点发生的两个 事件,在其中一个惯性系中是同时的,在另一惯性 系中观察则不同时,所以同时具有相对意义。 只有在同一地点,同一时刻发生的两个事件, 在其他惯性系中观察也是同时的。 说明: 1)同时性是相对的。 2)同时的相对性是光速不变原理的直接结果。 3)同时的相对性否定了各个惯性系具有统一 时间的可能性,否定了牛顿的绝对时空观。
强调:要在某一参照系中测棒的长度,就要测 量它的两端在同一时刻的位置间隔,尤其在相 对被测物体运动的参照系中。
长度的测量是和同时性概念密切相关的。 根据爱因斯坦的观点,既然同时是相对的, 那么长度的测量也必定是相对的。
二、长度的收缩
设有一刚性棒,相对于S 系静止,沿 x 轴方向放置。
在S´系测量,长度为:
事实应当如何呢 ? 这就是著名的双生子佯谬。
如果以地球为一个惯性系,飞船相对地球作匀 速直线运动,为另一个惯性系,两个惯性系是对称 的。兄弟俩都以自己参考系内异地同步的钟与对方 参考系内同一个钟进行比较,各自认为对方的钟变 慢,是没有矛盾的。 但如果两参考系真是对称的,则兄弟分开后就 再也不会相遇,也就无法比较谁更年轻了。 问题的关键在于长兄要返回,他必须作变速运 动,飞船至少不可能永远是惯性系,因此两参考系 就不再对称了。 事实上,若不考虑飞船变速运动引起的时间修 正,设兄弟于20岁分开,取γ =5 ,哥哥航行了10 年,返回时是30岁,而弟弟 t 20 10 70 70岁了!
大学物理上册课件:第6章 狭义相对论

例题6-8 带电π介子静止时的平均寿命为2.6×10 – 8 s,某加 速器射出的带电π介子的速率为2.4×10 8 m/s,试求1)在实验室 中测得这种粒子的平均寿命;2)这种π介子衰变前飞行的平均 距离。
解 1) 由于u = 2.4×10 8m/s=0.8c,故在实验室中测得
这种π介子的平均寿命为:
1 2
Δx Δx uΔt
1 2
Δt uΔx / c 2 Δt
1 2
1、不同地事件的同时性是相对的。
Δx Δx uΔt
1 2
Δt Δt uΔx / c2
1 2
Δx uΔt Δx
1 2
Δt uΔx / c2 Δt
1 2
即x 0, t 0时 ,t ux / c2
二、洛仑兹变换
惯性系S、S ′,在 t = t ′= 0时,原点重合,S ′以u 相对 S 系沿
x 轴正向匀速运动。某事件P,在 S 和S ′系中的时空坐标分别为:
y
y
S : P(x , y , z ,t ) S : P( x', y', z', t' )
S
S
u •P(x, y, z, t)
(x, y, z, t)
解 取速度为- 0.9c 的飞船
为S 系,地面为S ′系。
u = 0.9 c v′ x = 0.9 c
y S
y 0.9c
Sx
O
0.9c x
vx
vx u 1 uvx / c2
0.9c 0.9c 1 0.9 0.9
0.994c
说明 洛仑兹变换中 vx 0.994c,这和伽利略变换的结果
vx v'x u是不1同.8的c 。
大学物理-第七讲-狭义相对论基本原理-相对论的时空观PPT课件

在地面参考系S上看,
-的寿命是两地时,记作△t
Δ t Δ t 2 106
x
1
u2 c2
1 0.9982
x
3.16 105 s
它比原时 2×10-6 s 约长16倍!
按此寿命计算,它在这段时间里,在地面系走的距离 为 u△t =2.994×108×3.16×10-5 = 9461 m
(所以能到地面,与实验一致)
我们记 (原时) △t ’= 2×10-6s
若没有时间延缓效应,它们从产生到衰变掉 的时间里,是根本不可能到达地面的实验室的:
因为,它走过的距离只有
u△t’=2.99×108×2×10-6 = 600 m!
但事实是, 介子到达了地面实验室!
这可用时间延缓效应来解释:
将运动参考系S’建立在 -上,
y y
z z
t t
v v - u a a
— 伽利略变换
牛不顿同力惯学 性中 系力 中和F质 量m都a 与的参形考式系不变的。选择无关,所以在
这表明伽利略变换和力学相对性原理是一致的 。 力学实验无法判定一个惯性系的运动状态
二、经典理论遇到的困难
19世纪下半叶,得到了电磁学的基本规律即麦克斯韦 电磁场方程组,不具有伽利略变换下形式不变的特点。
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
演讲人:XXXXXX 时 间:XX年XX月XX日
于是测得动长 l = x4 - x3 = u△t
△t = ?
△t = l /u
△t = l /u ----(1)
在S’系: 设这两个事件的时间间隔为 △t’。
大学物理学习课件-§18.3 狭义相对论的时空观

x ( x v t) t (t v x / c2 )
2.时间膨胀 在不同的惯性参照系中,同时是相对的,两事件发 生的时间间隔同样也与参照系有关。
实验:固定在小车上的光脉
s
平面镜
s
冲装置发射和接受光 脉冲的时间间隔的测 量。
o
o
x
x
S系中观测者测得光脉冲的发射与接收时间
间隔:
t 2d c
异地同时:x 0, t 0 t 0
若在 S系
即在S系不同时。
同地同时: x 0, t 0 t 0
即在S系亦同时。
结论:“异地”同时性与具体参照系有关,
即具有相对意义。
同样可证明:“同地”同时性与参照系的选择 无关,具有绝对意义。
常用的空间间隔、时间间隔的变换:
x ( x v t) t (t v x / c2)
试用洛沦兹变换证明该结论。
证明: 设两事件的坐标分别为
A
:
S S
: :
( (
x1 x1
, ,
t1 ) t1 )
B
:
S S
: :
( (
x2 x2
, ,
t2 ) 则:
t2 )
t1 (t1 vx1 / c2 ) t2 (t2 vx2 / c2 )
t t2 t1 [(t2 t1 ) v( x2 x1 ) / c2 ] (t vx / c2 )
s sv
当两坐标系原点重合时,S′系中的观 测者将S′系中所有步钟调零。
oo
x x
S系:A、B两步钟同时调到零,即Δt = tA-tB=0。
S′系:A、B两步钟调到零的时间间隔为
Δt tB tA (t vx / c2 ) vx / c2 而 Δx xB xA 0
大学物理教程讲义狭义相对论基础优秀课件

15
10.3 爱因斯坦的时空观
10.3.1
1.时间的概念
首先,我们必须明确“时间”的概念。我们所考虑到的时间总是关 于同时事件的判断。例如,当我们说“火车七点钟到站”时,意思是“我 的表指针指向7与火车到站是同时的事件”。表面上看似乎可以通过用“ 表的指针位置”代替“时间”来克服一切伴随着“时间”这个定义带来的 困难,实际上只有时钟的位置和事件发生位置相同时这种定义才适合;而 当我们需要把发生在不同地点的一系列事件用时间联系起来时,由于信号 传递速度的有限性,这种定义方法就不再适用了。
13
10.2 爱因斯坦的两个基本假设 洛伦兹变换
10.2.3
1.洛伦兹坐标变换
洛伦兹变换是荷兰物理学家洛伦兹为了解释迈克尔 。他认为刚体长
度在沿运动的方向会有一定的收缩,称为洛伦兹收缩. 洛伦兹变换的定义如下。若存在两个惯性参考系S、S′ 以及固定在两个参考系上的时钟t、t′。
14
10.2 爱因斯坦的两个基本假设 洛伦兹变换
下面讨论在不同的惯性参考 系中长度的测量是否相同。如图 10.7所示,设在S′参考系中沿x′ 轴静止放置一刚性杆,杆两端的坐 标分别是x′1和x′2,测得杆长为 l0=x′2-x′1。这就是通常所讲的杆 的长度,称为杆的“静长”或“原 长”。
19
图10.7 动杆的收缩
10.4 狭义相对论动力学基础
10.4.1 动量守恒定律的洛伦兹变换
动量守恒定律是力学中最重要的定律之一,其内容为: 当系统所受到的合外力为零时,系统动量守恒。下面我们考 虑一种特例。如图10.8所示。以地面为参考系S,在光滑平面 上有两个完全相同的小球A和B,小球A以速度v与静止在平面 上的小球B发生碰撞后,粘在一起并以速度u运动。
《狭义相对论的基本原理》 讲义

《狭义相对论的基本原理》讲义在物理学的发展历程中,爱因斯坦的狭义相对论无疑是一颗璀璨的明珠。
它彻底改变了我们对时间和空间的理解,为现代物理学的发展奠定了坚实的基础。
接下来,让我们一同深入探索狭义相对论的基本原理。
一、相对性原理相对性原理是狭义相对论的首要基本原理。
它指出,物理规律在所有惯性参考系中都是相同的。
这意味着,无论我们处于何种匀速直线运动的惯性参考系中,通过实验所观察到的物理现象和所总结出的物理规律都应该是一致的。
为了更好地理解这一原理,我们可以想象这样一个场景:在一辆平稳行驶的火车上,有一个人正在做一个物理实验,比如测量小球下落的时间和轨迹。
同时,在地面上也有一个人在做完全相同的实验。
按照相对性原理,只要火车是匀速直线运动的,那么这两个人所得到的实验结果应该是相同的。
相对性原理打破了传统的绝对时空观。
在牛顿力学中,存在一个绝对静止的参考系,而相对性原理则否定了这种绝对静止的存在,强调了物理规律的相对性和普适性。
二、光速不变原理光速不变原理是狭义相对论的另一个重要基石。
它表明,真空中的光速在任何惯性参考系中都是恒定不变的,其大小约为 299792458 米/秒。
这一原理与我们日常生活中的经验似乎相违背。
因为在我们的直观感受中,如果一个人拿着手电筒在奔跑,那么相对于静止的观察者,手电筒发出的光的速度应该是光本身的速度加上人的奔跑速度。
但光速不变原理告诉我们,这种想法是错误的。
无论光源是静止的还是运动的,光在真空中的传播速度始终保持不变。
这意味着,光速是一个绝对的常数,不依赖于观察者的运动状态。
为了验证光速不变原理,科学家们进行了一系列的实验。
其中,最著名的是迈克尔逊莫雷实验。
这个实验试图测量地球在以太中运动时,不同方向上的光速差异。
但实验结果却表明,无论在哪个方向上,光速都是相同的,这有力地支持了光速不变原理。
三、时间膨胀基于相对性原理和光速不变原理,狭义相对论引出了时间膨胀的概念。
当一个物体以接近光速的速度运动时,相对于静止的观察者,运动物体上的时间流逝会变慢。
大学物理A1 课件 第4章 狭义相对论

x = ax + bt + e t = ct + dx + f
v
o
P x , y , z , t
x x
S系看 x =0点,
设 t = t =0 时,在o=o点 发出一光信号, 在两个参考 代入以上方程组可得 系中测得的光到达某时空 x = a(x vt)(1)点的事件为p和p '
(2) 长度收缩是“测量”结果,不是“视觉”效 应。
例4-2. 静系中子的平均寿命为2.210-6s。 据报导,在一组高能物理实验中,当它 的速度为u=0.9966c时通过的平均距离为 8km。试说明这一现象:(1) 用经典力学 计算与上述结果是否一致;(2) 用时间膨 胀说明;(3) 用尺缩效应说明。
1 v2 c 2
l l0 1 v c
2
2
原长:在相对于观察者静止 l 的参考系中测得的物体长度。 0
长度收缩:运动物体的长度小于原长, l
当
l0
v c l l0
注意:长度收缩只发生在运动的方向上。
结论:
(1) 相对于观察者运动物体沿运动方向长度缩短了— — 长度收缩 (动尺缩短)
事件 1 A M 发生
B
k
事件 2 发生
K’系:1、2 两事件同时发生
K 系1事件先于2 事件发生
结论:“同时性”具有相对性 ——光速不变原理的直接结果
4.2.2 时间延缓
火车系:
S 系
理想实验:爱因斯坦火车 M y
d
o
A'
, t1 ) I(x1
x1
x
, t2 ) II(x1
0
1 2
《狭义相对论的基本原理》 讲义

《狭义相对论的基本原理》讲义在探索物理学的奇妙世界时,狭义相对论无疑是一座令人瞩目的高峰。
它彻底改变了我们对时间和空间的理解,为现代物理学的发展奠定了坚实的基础。
接下来,让我们一同深入了解狭义相对论的基本原理。
狭义相对论建立在两条基本原理之上。
第一个基本原理是相对性原理。
相对性原理指出,物理规律在所有惯性参考系中都是相同的。
这意味着,无论你是在一个静止的实验室中,还是在一艘以匀速直线运动的飞船里,只要是惯性参考系,你进行的物理实验都会得到相同的结果。
为了更好地理解这个原理,让我们想象一个简单的实验。
假设你在一个封闭的车厢里,无法看到外面的景象。
你手里拿着一个小球,松手让它自由下落。
在这个车厢里,小球会垂直下落。
现在,假设这个车厢正在以匀速直线运动前进,从外面静止的观察者来看,小球的运动轨迹是一条抛物线。
但对于身处车厢内的你来说,小球依然是垂直下落的。
这就是相对性原理的一个直观体现:在不同的惯性参考系中,物理现象的表现形式可能不同,但背后的物理规律是一致的。
第二个基本原理是光速不变原理。
这一原理表明,真空中的光速在任何惯性参考系中都是恒定不变的,与光源和观察者的相对运动状态无关。
想象一下这样的场景:有一束光从一个静止的光源发出。
当你以一定的速度朝着光源运动时,按照我们的日常经验,你会觉得光相对于你的速度变快了。
但在狭义相对论中,不是这样的!无论你是朝着光源运动,还是背向光源运动,光相对于你的速度始终是恒定的,约为299792458 米/秒。
这个原理初看起来似乎与我们的直觉相悖,但它却有着深刻的实验基础和逻辑必然性。
那么,基于这两个基本原理,狭义相对论带来了哪些令人惊叹的结论呢?首先是时间膨胀。
简单来说,运动中的时钟会比静止的时钟走得慢。
这可不是说时钟出了故障,而是时间本身的流逝发生了变化。
假如有一对双胞胎,其中一个留在地球上,另一个乘坐高速飞船去太空旅行。
当旅行者回来时,他会发现留在地球上的兄弟比自己老了很多。
《狭义相对论的基本原理》 讲义

《狭义相对论的基本原理》讲义在物理学的发展历程中,爱因斯坦的狭义相对论无疑是一座具有里程碑意义的理论大厦。
它以其独特的视角和深刻的洞察,彻底改变了我们对时间和空间的理解。
接下来,让我们一同走进狭义相对论的世界,深入探讨其基本原理。
一、相对性原理相对性原理是狭义相对论的核心支柱之一。
它指出,物理规律在所有惯性参考系中都是相同的。
这意味着,无论我们是处于静止状态还是以匀速直线运动的状态观察物理现象,所遵循的物理定律都应该是一致的。
想象一下,你坐在一辆匀速行驶的火车上,车内有一个小球自由下落。
对于车内的你来说,小球是垂直下落的。
而对于站在地面上的观察者,由于火车的运动,小球的下落轨迹看起来是一条斜线。
但神奇的是,通过运用相同的物理定律,无论是你还是地面上的观察者,都能准确地描述和预测小球的运动。
相对性原理打破了传统的绝对时空观。
在牛顿力学中,存在一个绝对静止的空间和绝对均匀流逝的时间。
而狭义相对论告诉我们,不存在这样的绝对参考系,所有的惯性参考系都是平等的。
二、光速不变原理光速不变原理是狭义相对论中另一个令人惊叹的基本原理。
它表明,真空中的光速在任何惯性参考系中都是恒定不变的,其大小约为299792458 米/秒。
这与我们日常生活中的经验似乎有些相悖。
比如,当我们坐在一辆飞驰的汽车上向前扔出一个球,球的速度会是汽车的速度加上我们扔球的速度。
但对于光来说,无论光源是静止的还是运动的,光的速度始终保持不变。
假设一艘宇宙飞船以接近光速的速度飞行,当飞船上的人打开一盏灯时,这束光对于飞船内的人和地球上的观察者来说,速度都是一样的。
光速不变原理是狭义相对论中许多奇妙结论的根源。
它使得时间和空间不再是绝对的,而是相对的,取决于观察者的运动状态。
三、时间膨胀由于光速不变原理,导致了一个奇特的现象——时间膨胀。
简单来说,运动的时钟会比静止的时钟走得慢。
为了更好地理解这一点,我们可以想象一个思想实验。
有一对双胞胎,其中一个留在地球上,另一个乘坐高速飞船去太空旅行。
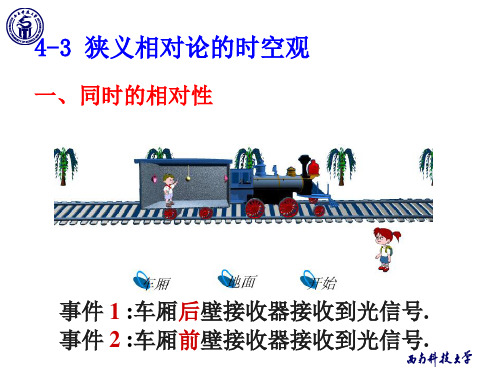
《物理学教学课件》4-3 狭义相对论的时空观
s s' x'1
x'2
x'
o o' z z' x1 10米 x2
x
t1 t2
在火车上看:火车车厢上的两道痕迹的距离 x
是原长, 故地面上看这两道痕迹的距离 x 将
收缩。
按 l 1 v2 c2 l0 得
地面上测量车厢上两道痕迹的距离收缩为:
x 1 v2 c2 x 10 (米)
则火车车厢上的两道痕迹的距离
2 长度具有相对意义
将直尺固定在火车系上,在火车上观察,直 尺的长度是原长,而在地面系上观察,长度将收 缩,即在地面上观察火车上的直尺变短了;同样, 如果将直尺固定于地面上,则在地面系上观察, 直尺的长度是原长,而在火车系上观察,长度将 收缩,即在火车上观察地面的直尺变短了,
S
S
在S中的
观察者
o
l0
为l 。
固有长度:物体相对静止时所测得的长 度 .(最长)
s
y
s'
y' v
l0
o o'
z z'
这里,在 S 系
中测得棒的长
x'
x
度为固有长度
l l0
若直尺的前端和后端相继通过地面某一标 记点的时间差为 t ,则在地面系中测得直尺 的长度应为
l ut
在火车系上观察, 地面上的标记点向左 运动,相继通过直尺 的前端 和后端 时间 差为 t, 则在车系中 测得直尺的长度应为
u
ua
火车
a
火车
A
隧道
B
地系 t l0 / u
火车参照系中测量到的时间是固有时间 t t0
按时间膨胀有 即
