土体应力计算
第三章 土体中的应力计算(1-3节)

3.均质、等向问题 理想弹性体是均质且各向同性的。天然
地基是各向异性的。但当土层性质变化 不大时,这样假定对竖直应力分布引起 的误差通常在容许范围之内。
5
二、地基中的几种应力状态
1.三维应力状态(空间应力状态)
局部荷载作用下,地基中的应力状态属 三维应力状态。每一点的应力可写成矩 阵形式
24
25
在空间将z相同的点连 接成曲面即形成应力泡。
当地基表面作用有几个集中力时,根据弹 性体应力叠加原理求出附加应力的总和
26
(二)水平集中力作用-西罗提解
z
3Ph
2
xz 2 R5
(3- 9)
27
28
二、矩形面积上各种分布荷载作用下的附 加应力计算
(一)矩形面积竖直均布荷载 1.角点下的应力
x
K
s x
p
τ
xz
K
s xz
p
(3- 25) (3- 26)
剪Kx应s和力K分xzs布分系别数为(水表平3向-5应)力,m分布x ,系n 数z和。
BB
55
P
56
57
(三)条形面积竖直三角形分布荷载 条形面积上竖直三角形分布荷载在地基
内引起的应力也可利用应力叠加原理, 通过积分求得。
zM ' (KsI KsII KsIII KsIV ) p
(3 -13a)
37
第二种情况:计算矩形面积外任一点M’ 下深度为z的附加应力(图3-17b)。设法使 M’点为几个小矩形的公共角点,然后将 其应力进行代数迭加。
zM ' (KsI KsII KsIII KsIV ) p
29
土中自重应力计算

确定土体初始 应力状态
土体在自重作用下,在漫长的地质历史时期,已经 压缩稳定,因此,土的自重应力不再引起土的变形。 但对于新沉积土层或近期人工充填土应考虑自重应力 引起的变形。
一、竖向自重应力
土体中任意深度处的竖向自重应力等于单位面积上土柱 的有效重量
天然地面
103.1kPa 150.1kPa
n
cz 1h1 2h2 nhn ihi i 1
194.1kPa
本节演示结束 谢谢观看!
地下水位以上土层采用天然重度地下水位以下土层采用浮重度力沿深度呈折线分布天然地面三水平向自重应力czcycx静止侧压力系数例一地基由多层土组成地质剖面如下图所示试计算并绘制自重应力cz沿深度的分布图570kpa801kpa1031kpa1501kpa1941kpa本节演示结束谢谢观看
土中自重应力计算
cz
z
cy
cz cxຫໍສະໝຸດ cz z1 1z
σcz= z
二、成层土的自重应力计算
n
cz 1h1 2h2 nhn ihi i 1
天然地面
说明:
h1 1
1 h1
1.地下水位以上土层 采用天然重度,地下
h2 2 水位面
1 h1 + 2h2
水位以下土层采用浮 重度
2.非均质土中自重应
h3 3
力沿深度呈折线分布
1 h1 + 2h2 + 3h3
三、水平向自重应力
天然地面
z
cy
cz cx
cz z
cx cy K0 cz
静止侧压 力系数
四、例题分析 【例】一地基由多层土组成,地质剖面如下图所示,试 计算并绘制自重应力σcz沿深度的分布图
土体中的应力计算

x 0xy 0 xz x 0yx y 0 yz y ij = 0zy z 0zx
理论研究和工程实践中广泛应用
三、土的应力-应变关系的假定
1、室内测定方法及一般规律
轴对称问题 常规三轴试验 侧限压缩试验
特殊应力状态
一维问题
2、应力计算时的基本假定 1)连续性假定 2)均质、各向同性假定 3)线性变形体假定 4)半无限体假定
x y ; z xy , yz , zx 0
x y ; z xy , yz , zx 0
x y , z ; x y , z
二、地基中常见的应力状态----三维问题图解
z
zx
xy
x
o x z
y yz
y
x xy xz ij = yx y yz zx zy z
本章重点
1、应力状态及应力应变关系
地基中的应力状态 土力学中应力符号的规定 应力应变关系 强度问题 变形问题
2、自重应力
建筑物修建以前,地基中由土体 本身的有效重量所产生的应力。 建筑物修建以后,建筑物重 量等外荷载在地基中引起的 应力,所谓的“附加”是指 在原来自重应力基础上增加 的压力。
3、附加应力
碎散体 非线性 弹塑性 成层土 各向异性
① 连续介质(宏观平均) ② 线弹性体(应力较小时)
线弹性体
③ 均匀一致各向同性体 (土层性质变化不大时)
Δσ
加 载
卸 载
E、
与(x, y, z)无关 与方向无关
εp
εe
ε
§3.2 土体自重应力的计算
一、水平地基中的自重应力
定义:在修建建筑物以前,地基中由土体本身的有效重量而 产生的应力。
土的剪应力计算公式

土的剪应力计算公式
土的剪应力计算公式是土力学中的一个重要公式,用于计算土壤在剪切过程中的应力情况。
根据莫尔-库伦准则,土的强度是由有效应力和内聚力共同决定的,因此土的剪应力计算公式也涉及有效应力和内聚力的计算。
常用的土的剪应力计算公式有:
1. 黏聚土的剪应力计算公式:
τ = c + σn*tan(φ)
其中,τ为土的剪应力,c为内聚力,σn为垂直于剪切面的有效应力,φ为摩擦角。
2. 砂性土的剪应力计算公式:
τ = σn*tan(φ)
其中,τ为土的剪应力,σn为垂直于剪切面的有效应力,φ为摩擦角。
通过使用土的剪应力计算公式,可以有效地分析土的力学性质,为土工建筑的设计和施工提供重要的理论依据。
- 1 -。
地应力计算公式

地应力计算公式地应力是指地壳内存在的地质应力,是岩石或土体受到的压力和剪切力的结果。
地应力的大小和方向会影响地下工程的稳定性和可靠性,因此准确计算地应力十分重要。
地应力的计算公式主要有以下几种:1.水平地应力计算公式:水平地应力主要指x、y方向上的应力。
根据公式σh = ρgz,可以计算得出。
其中,σh为水平地应力,ρ为岩石密度,g为重力加速度,z为地下深度。
2.垂直地应力计算公式:垂直地应力主要指z方向上的应力。
根据公式σv = ρgz,可以计算得出。
其中,σv为垂直地应力,ρ为岩石密度,g为重力加速度,z 为地下深度。
3.科尔洛格尔-穆勒公式:科尔洛格尔-穆勒公式是用于计算地应力的常用公式之一、根据该公式,地应力可以表示为σ=(1-ζ)σh+ζσv,其中σ为地应力,σh为水平地应力,σv为垂直地应力,ζ为系数,代表了地层的应力状态。
4.微扰法:微扰法是一种计算地应力的数值方法。
通过在其中一点施加微小的扰动,测量变形或应力的响应,可以推断出该点的地应力。
常用的微扰法包括洛根-纳福尔斯基法、拟合椭球法等。
5.考虑地应力梯度的计算方法:地应力通常会随着地下深度变化而发生变化。
因此,在计算地应力时需要考虑地应力梯度的影响。
常用的方法有拉克鲁瓦法、密集级差法等。
此外,地应力的计算还需要考虑地质条件、岩石的物理力学参数等。
这些参数包括岩石的弹性模量、泊松比、内摩擦角等,常用的地应力计算方法还包括岩石力学模型、有限元法等。
总之,地应力的计算公式包括水平地应力、垂直地应力的简单计算公式,还可以通过科尔洛格尔-穆勒公式、微扰法、考虑地应力梯度的计算方法等进行计算。
在实际应用中,需要结合具体地质条件和岩石性质来选择适合的计算方法,以获得准确的地应力数据。
土力学与地基基础(土中的应力计算)

矩形基础:A=b× 矩形基础:A=b×L
d1 + d2 Gk =A
Gk = γ G Ad
γG=20kN/m3
2、偏心荷载下的基底压力 单向偏心荷载下的矩形基础如图。 单向偏心荷载下的矩形基础如图。 设计时, 设计时,通常基底长边方向取与偏心 方向一致, 方向一致,最大压力值与最小压力值 按材料力学短柱偏心受压公式计算: 按材料力学短柱偏心受压公式计算:
p0 = pk − σ c
四、地基附加应力
地基附加应力是指建筑物荷载在土体中引起的附加于原有应力之上的应力。 地基附加应力是指建筑物荷载在土体中引起的附加于原有应力之上的应力。
(一)竖向集中应力作用下的地基附加应力
1、布辛奈斯克解 、
3p z3 3 1 p σz = = 2π ( r 2 + z 2 )5 / 2 2π ( r / z )2 + 1 5 / 2 z 2
第三章 地基土中的应力计算
一、概述 地基土中的应力: 地基土中的应力: 1、自重应力 2、附加应力
建筑物修建以前, 建筑物修建以前,地基中由于土 体本身的有效重量所产生的应力。 体本身的有效重量所产生的应力。 建筑物修建以后,建筑物重量等 建筑物修建以后, 外荷载在地基中引起的应力, 外荷载在地基中引起的应力,所 谓的“附加” 谓的“附加”是指在原来自重应 力基础上增加的压力。 力基础上增加的压力。
γ
γ′
均质地 基
γ1(γ
1
< γ2 )
γ2 γ′ 2
成层地基
(二)水平向自重应力
σ cx = σ cy = K 0σ cz
式中: 土的侧压力系数或静止土压力系数, 式中:K0——土的侧压力系数或静止土压力系数,经验值可查课本 土的侧压力系数或静止土压力系数 表3.1
第二章 土中的应力计算

2.0m
3.0m
③ γ3=19.5
③ γ3sat=21.0
z
④ γ4=19.8
2.2 基底压力(接触应力) • 实测基底压力
室内地平 ±0.00 d p 基底压力的 大小、形状与 荷载大小及形状、基础刚度、 土性及状态、地基均匀性等 土压力 盒测试
• 基底压力简化计算
F
F
室外地平 -0.65
pdy
0 x r -∞ θ zR p
+∞ y y σz τzx M
x
M
τxz σx
z
• σz=∫+ ∞ -∞ 3/ [2π(x2+y2+z2)5/2] *dy= 2pz3/ π(x2+z)2 3pz
= 2p/ πz*cos4θ=αz p0
• σx= 2p/ πz* cos2θsin2θ=αx p0 • τxz= τzx= 2p/ πz* cos3θsinθ=αzx p0
• 由以上公式可知,附加应力与y轴无关。
2.4.5 非均质和各项异性地基中的附加应力 在以前介绍的均假定土体为均质、各项同性、半 无限的直线变形体。一般来说,只有当地基在很大 深度内是均质和各项同性时才适用。
硬土层
软土层
• 应力集中现象 当在基底以下不深处存在硬土 层时,则在土层界面以上基础轴线附近的σz比均 质时增大,边缘处应力减小的现象。 • 应力扩散现象 当存在软土层时,产生了与应 力集中相反的现象。
σcz=γz
σcx= σcy =K0σcz
τyz
A
σcx
τxy= τzx= τyz=0
K0-侧压力系数
τyx
静止土压力系数
•土颗粒之间的应力称为有效应力。一般不再说明 的话,自重应力是指其有效应力。
土体中的应力计算

4、 基础底面附加压力 0 、 基础底面附加压力p
• 1.定义:单纯由建筑物荷载引起的基础底面每平米 定义: 定义 上的压力, 表示, 上的压力,用p0 表示,kpa . • 2.计算方法: 计算方法: 计算方法 • p0= p - γ*d • p0: kpa • p: 同前,kpa 同前, • d: 同前,kpa 同前, • γ:基础底面以上土的天然重度,KN/m3 基础底面以上土的天然重度, 基础底面以上土的天然重度 • 释义:在基底接触压力中相当于土的自重应力部分 释义: 不会产生沉降,剩余部分是使地基产生沉降的原因。 不会产生沉降,剩余部分是使地基产生沉降的原因。 • 剩余部分即基础底面附加压力 0。 剩余部分即基础底面附加压力 。 基础底面附加压力p
a:求矩形受荷面积边缘上任意点 下的附加应力 求矩形受荷面积边缘上任意点m’下的附加应力 求矩形受荷面积边缘上任意点 (σz)m’=(αcI+ αCII )p α b: 求矩形受荷面积内部任意点 下的附加应力 求矩形受荷面积内部任意点m’下的附加应力 (σz ) m’ = (αcI+ αCII + αCIII + αCIV )p α c:求矩形受荷面积外任意点 下的附加应 求矩形受荷面积外任意点m’下的附加应 求矩形受荷面积外任意点 由于地基应力具有扩散作用, 由于地基应力具有扩散作用,所以并非只有荷载作用的垂直 范围内才有附加应力。 范围内才有附加应力。 (σz ) m’ =[(αcI -αCIII )+( αCII- αCIV )]p α α
第四章 土体中的应力计算
•基本内容: 应力状态 基本内容: 基本内容 土中应力计算 自重应力 附加应力 接触应力 有效应力原理 集中荷载作用、 地基中的应力计算 ( 集中荷载作用、分 布荷载) 布荷载) •重点内容: 有效应力原理 各种应力计算 重点内容:
第2章 土体中的应力计算

x y;
z , z F(z )
z K 0 z ; 1
K0:侧压力系数
x 0xy 0 0xz y 0yx 0 0yz ij = zy z 0zx 0
x 0xy 0 xz x 0yx y 0 yz y ij = 0zy z 0zx
P
e
P
Ph
Pv
B
P Mx p( x) B I
分解为竖直向和水平向荷 载,水平荷载引起的基底 水平应力视为均匀分布。
P 6e pmax 1 B B min
§2 土体中的应力计算
三. 实用简化计算
§2.2基底压力计算
基础形状与荷载条件的组合
荷载条件
竖直中心 P 矩 形 基 础 形 状 B
Valentin Joseph Boussinesq (1842-1929) 法国著名物理家和数学家,对数学物理、流体力 学和固体力学都有贡献。
§2 土体中的应力计算
3P z 3 z 2 R 5
§2.3地基中附加应力的计算
一. 竖直集中力作用下的附加应力计算-布辛涅斯克课题
R 2 r 2 z 2 x2 y 2 z 2
K
0.3
0.2 0.1 0
0.5 1.0
1.5
2.0
2.5
3.0
r/z
§2 土体中的应力计算
P z K 2 z
特点
§2.3地基中附加应力的计算
一. 竖直集中力作用下的附加应力计算-布辛内斯克课题
3 1 K 2 [1 (r / z )2 ]5 / 2
3P z 3 3 1 P z 5 2 R 2 [1 (r / z )2 ]5 / 2 z 2
土体中的应力计算

P 6e 1 A b
pmin
P 6e 1 A b
12
pmax
min
P 6e 1 A b
矩形面积单向偏心荷载
土不能承 受拉应力
P b e x y
p max
P b e
P b
压力调整
K e
L
x y
L
x
L
K=b/2-e
3K y pmin 0
L
y o b
L
b
L
pP A
P—集中力
P M y M yx p ( x, y ) x A Ix Iy
P’
P Pv Ph
P’
条 形
P’
b
b
b
p P b
P’—单位长 度上的荷载
P Mx p ( x) b I
P Pv Ph
14
§4.4竖直集中力作用下的附加应力计算
3
§4.2 地基中自重应力的计算
水平地基中的自重应力
定义:在修建建筑物以前,地基中由土体本身的有效重量而产生的应力。
目的:确定土体的初始应力状态 假定:水平地基半无限空间体半无限弹性体 侧限应变条件一维问题 计算:地下水位以上用天然容重,地下水位以下用浮容重
4
1.计算公式
均质地基
竖直向:
角点法
叠加原理
角点下垂直附加 应力的计算公式
地基中任意点的附加应 力
23
角点法计算地基附加应力
a.矩形面积内
C z ( aA aB a aD ) p
B
A
C
h
b.矩形面积外
土力学第四章 土中应力计算

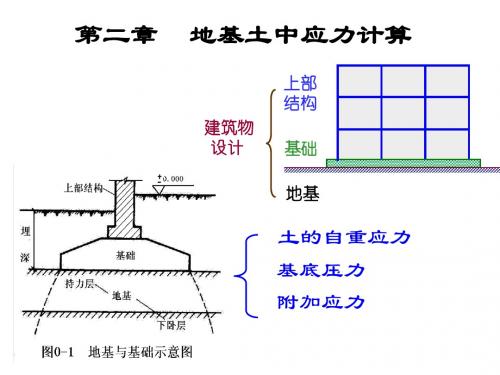
建 筑
上部结构 (a)理想柔性基础; (b)路堤下的基底压力
物
设
基础
计
地基
(2)刚性基础。基底压力大小、分布状况与上部荷载的大小、分布状况 不相同。
例如:砂土地基 黏性土地基
— 荷载较小 — 荷载较大
砂性土地基
— 接近弹性解 — 马鞍型 — 抛物线型 — 倒钟型
粘性土地基
三、基底压力的简化计算
1、中心荷载下的基底压力
1H1
sz
2H2
2H3
sy
sx
z
说明:
1.地下水位以上土层采用天然重度,地下水位以下土层采用浮重度 2.非均质土中自重应力沿深度呈折线分布
均质地基
1 (1 2)
2
2
成层地基
例题分析
【例4.1】某地基土层情况及其物理性质指标如下图所示,试计算 a、b、c三个点 处的自重应力,并画出应力分布图。 【解】 首先确定各层土的重度。 粗砂:在水下且透水,采用浮重度,有
2)基础的刚度、平面形状、尺寸大小、埋置深度有关;
3)作用在基础上的荷载性质、大小和分布情况有关;
4)地基土的性质有关。
二、基底压力的分布规律
基础按刚度分为:(1)柔性基础(抗弯曲变形能力为0) (2)刚性基础(抗弯曲变形能力为∞) (3)有限刚性基础(弹性地基上梁板分析方法)
土力学与基础工程地基土中的应力计算
标高处原有的自重应力后,新
增加于基底的压力。
m 1h1 2h2 nhn / d
注意:
p0 p cz p m d
基底附加压力 的计算
地下水位以下的重度取有效重度
基底附加压力
基础标高以上土的加 权平均容重
自重应力
p
0
p
0
d
p0 max pmax 基底压力呈梯形分布时, 0d p0 min pmin 基底附加压力
【例题分析】 • 【例】某条形地基,如下图所示。基础上作用荷载
F=400kN/m,M=20kN•m,试求基础中点下的附加压 力。
FK 0.1m MK
1.5m 0 =18.5kN/m3 2m
分析步骤I:
FK=400kN/m 0.1m MK=20kN •m
1.5m 2m
0 =18.5kN/m3
荷载偏心距 e=M/(F+G)
基础及上覆 土重G= GAd 140.3kPa
319.7kPa
pmax pmin
1.基底压力计算
条形基础取单 位长度计算
F G 6e 1 bl l
讨论:基底压力分布?
pmax pmin
F G 6e 1 bl l
当e<l/6时,pmax,pmin>0,基底压力呈梯形分布 当e=l/6时,pmax>0,pmin=0,基底压力呈三角形分布 当e>l/6时,pmax>0,pmin<0,基底出现拉应力
pmax
pmin e<l/6
cz2 cz1 2h2 7.85 17.8 2 43.45kN m 2
2 土体应力计算

2-2 地基中的自重应力
分布规律 自重应力在等容重地基中随深度呈直线分布; 自重应力在等容重地基中随深度呈直线分布; 自重应力在成层地基中呈折线分布; 自重应力在成层地基中呈折线分布; 在土层分界面处和地下水位处发生转折。 在土层分界面处和地下水位处发生转折。
γ
γ′
均质地基
γ1 (γ
1
< γ2 )
P αr x
R M’
y βz
M
x
P σ z = ap ⋅ 2 z
y z
2-4 地基中的附加应力计算
P σ z = ap ⋅ 2 z 式中: 式中:
3 1 y ap = 2 5/ 2 2π [1+ (r / z) ] 称为竖向集中力作用竖向附加应力系数 称为竖向集中力作用竖向附加应力系数
0.5 0.4 查表2查表 3
实际 碎散体 非线性 弹塑性 成层土 各向异性 假定 ①连续介质 宏观平均) (宏观平均) ②线弹性体 应力较小时) (应力较小时) ③均匀一致各向同性体 土层性质变化不大时) (土层性质变化不大时) 卸载
∆σ
加载
εp
ε
e
ε
土的非线性弹塑性应力应变曲线
2-2 地基中的自重应力
竖向应力
σ cz = γz
p
d
rd
2-4 地基中的附加应力计算
计算假定:半空间无限体假定;连续、 计算假定:半空间无限体假定;连续、均质各向同性的线弹 性体假定。 性体假定。 应力计算可分为空间问题 平面问题。 空间问题和 应力计算可分为空间问题和平面问题。 一、附加应力基本解答 (一)竖向集中力作用下地基附加应力 o
由布辛内斯克Boussinesq·J(1885)解答 解答 由布辛内斯克 得 σ z 的表达式
土体中的应力计算—附加应力的计算(土力学课件)

z 2 p
x
p x
z z
x z
二、条形面积受均布荷载土中附加应力
2.条形面积受三角形荷载作用下的附加应力
土中任意点所受的附加应力
z 3 p
-x 0
z x
p x
z
注意坐标系的建立,以荷载0为坐标原点,向荷 载增大的方向为正方向。
二、条形面积受均布荷载土中附加应力
3.圆形面积均布荷载作用下的竖向附加应力
(1)距离地面越深, 附加应力的分布范围 越广,r/z=2.5范围内。
(2)在距地面为z的平 面上,集中力作用线 下的附加应力最大, 向两侧逐渐减小。
集中力作用下附加应力分布图
一、竖直集中荷载作用下的地基附加应力计算
1、附加应力分布规律
(3)距P作用线为r竖直 线上的附加应力随深 度先增加再减小。
171
332 kPa
134
条形荷载作用下土中附加应力
(1)p1=134kPa
+x
+x
+(x 2)p2=198kPa
-x
z x1 x/b z/b
x2 x/b z/b
00 0 0 1
134 1 0.5 0 0.500 99 233
1 0 0 0.5 0.820 110 1 0.5 0.5 0.410 81 191
条形荷载作用下 土中附加应力
条形荷载作用下土中附加应力
条形荷载作用下土中附加应力
1.条形面积受均布荷载作用下的土中竖向附加应力
土中任意点所受的附加应力 x
z 2 p
2 ——条形均布荷载作用
下的竖向附加应力系数
2 (x / b, z / b)
土的自重应力

土的自重应力土是地球表面最常见的材料之一,它是由矿物质、有机物和水分组成的。
土的自重应力是指土体自身重力所产生的应力。
在土工工程中,土的自重应力是一个非常重要的参数,它对土体的稳定性和承载力有着重要的影响。
土的自重应力是由土体的密度和重力加速度决定的。
在地球表面,重力加速度的大小约为9.8米/秒²。
因此,土的自重应力可以通过以下公式计算:σ = γ × h其中,σ是土的自重应力,γ是土的单位重量,h是土体的深度。
单位重量是指单位体积土的重量,通常用千克/立方米或克/立方厘米表示。
土的密度是由土壤颗粒的种类、大小和排列方式决定的。
不同种类的土壤具有不同的密度。
例如,砂土的密度通常在1.5-1.7克/立方厘米之间,而黏土的密度通常在1.2-1.5克/立方厘米之间。
因此,不同种类的土壤在相同深度下的自重应力也会有所不同。
土的自重应力对土体的稳定性和承载力有着重要的影响。
在土工工程中,土的自重应力是计算土体承载力和稳定性的重要参数。
例如,在计算土体的承载力时,需要考虑土的自重应力对土体的压缩和变形的影响。
在计算土体的稳定性时,需要考虑土的自重应力对土体的抗剪强度和抗压强度的影响。
土的自重应力还对土体的水分运移和土壤侵蚀有着重要的影响。
在土壤侵蚀过程中,土的自重应力会影响土壤颗粒的运动和沉积,从而影响土壤侵蚀的速度和规模。
在土壤水分运移过程中,土的自重应力会影响土壤孔隙水的压力和流动速度,从而影响土壤水分的分布和运移。
土的自重应力是土工工程中一个非常重要的参数,它对土体的稳定性、承载力、水分运移和土壤侵蚀等方面都有着重要的影响。
在土工工程中,需要对土的自重应力进行准确的计算和分析,以保证工程的安全和可靠性。
