第三章双液系相图
双液系的气—液平衡相图

实验五双液系的气—液平衡相图一、实验目的1、绘制在标准压力下乙醇-正丙醇体系的沸点组成图,并确定其恒沸点及恒沸组成;2、熟练掌握测定双组分液体沸点的方法及用折光率确定二组分物系组成的方法;3、掌握超级恒温槽、阿贝折射仪、气压计等仪器的使用方法。
二、实验原理1、相图任意两个在常温时为液态的物质混合起来组成的体系称为双液系。
两种溶液若能按任意比例进行溶解,称为完全互溶双液系,如环已烷-乙醇、正丙醇-乙醇体系都是完全互溶体系。
若只能在一定比例范围内溶解,称为部分互溶双液系,例苯-水体系。
在完全互溶双液系中,有一部分能形成理想液态混合物,如苯-甲苯系统,二者的行为均符合拉乌尔定律,但大部分双液系是非理想液态混合物,其行为与拉乌尔定律有偏差。
液体的沸点是指液体的蒸气压与外界压力相等时的温度。
在一定外压下,纯液体的沸点有其确定值,但双液系的沸点不仅与外压有关,而且还与两种液体的相对含量有关。
双液系两相平衡时的气相组成和液相组成并不相同。
通常用几何作图的方法将双液系的沸点对其气相和液相的组成作图,所得图形叫双液系的沸点T(或t)-组成(x)图,即T(或t)—x图。
它表明了沸点与液相组成和与之平衡的气相组成之间的关系。
在恒定压力下,二组分系统气液达到平衡时,其沸点-组成(t-x)图分三类:(1)混合液的沸点介于A、B二纯组分沸点之间。
这类双液系可用分馏法从溶液中分离出两个纯组分。
如苯-甲苯系统,此时混合物的行为符合拉乌尔定律或对拉乌尔定律的偏差不大。
如图5-1(a)所示。
(2)有最低恒沸点体系,如环已烷-乙醇体系,t—x图上有一个最低点,此点称最低恒沸点,在此点相互平衡的液相和气相具有相同的组成,此时混合物的行为对拉乌尔定律产生最大正偏差,如图5-1(b)所示。
对于这类的双液系,用分馏法不能从溶液中同时分离出两个纯组分。
(3)有最高恒沸点体系,如氯仿-丙酮体系,t—x图上有一个最高点,此点称最高恒沸点,在此点相互平衡的液相和气相具有相同的组成,此时混合物的行为对拉乌尔定律产生最大负偏差,如图5-1(c)所示。
部分互溶双液体系的温度-组成图(液-液相图)

t
A(l)+g
gg
B(l)+g
A(l)+B(l)
19
三、蒸汽蒸馏
我们知道,有不少有机化合物在其沸 点以前就分解了;或者由于沸点较高, 不能或不易用通常的蒸馏方法来提纯。
根据上述不互溶双液体系的性质,可 采用水蒸汽蒸馏方法来提纯它们。
20
水蒸汽以鼓泡形式通过有机液体,
搅拌作用
产物易于分离
21
17
二、不互溶体系的蒸气压和沸点
在不互溶体系中,PA=PA* 其大小与另一种液体的存在与否及其数量均无 关;
所以这种体系的蒸气压应当是互不相溶的两 种液体在该温度下纯态的蒸气压之和,即:
18
P = PA* + PB* 因此,不相溶的两种液体的混合物的沸点应
当低于任何一纯组分的沸点;
由于总蒸气压与两种液体的相对数量无关, 故混合物在沸腾蒸馏时的温度亦保持不变。
f* = C + 1 = 22 + 1 = 1
共轭溶液的组成将随温度的不同而改变
3
水-酚体系在恒压下的温度-组成图
图中ACB曲线以外 的区域是单相区, 只有一个液相,自 由度:
f * = C +1 = 2 1 + 1 = 2
(黄色阴影面)
4
• 在ACB曲线以内的区 域是两相区,在此区 域内有两个相互平衡 的液相存在;
双液相图
t
A(l)+g
பைடு நூலகம்
gg
B(l)+g
A(l)+B(l)
两相平衡区的分析 结线,杠杆规则
22
§4.4.5 简单低共熔混合物体系
一、固-液凝聚体系
理论上,应考虑固-液-气三相(平衡蒸汽压) 在研究固体-液体平衡时,如果外压大于平衡蒸气
《物理化学实验报告》双液系的气液平衡相图

双液系的气液平衡相图2011年9月5日实验,2011年9月12日提交报告助教:柳清1 引言相图(phase diagram)是用图形表示多相系统的物理化学状态随温度、压力、组分含量等的变化的图1。
对于多相平衡系统,相律(phase rule)是其热力学基础。
本实验研究的是环己烷-乙醇(C6H12-C2H5OH)双液系的气液平衡状态。
根据相律,f+Φ = C+2其中相数Φ为2,独立自由组分数C为1,则系统自由度数f为1。
如果固定外压p不变,条件自由度数f′为0。
因此,在外压p不变时,温度T和组分含量x唯一确定了双液系气液平衡系统的状态。
用气液平衡时的温度T和组分含量x分别作为纵横坐标,同时测定气相和液相的组成,可以绘制双液系的气液平衡T-x相图。
不同组成的双液系具有不同形式的气液平衡T-x相图。
理想液体混合物或者接近理想液体混合物的双液系,混合物的沸点介于两纯物质沸点之间,如图1(a)。
各组分蒸气压对拉乌尔定律产生很大的正偏差时,混合溶液体系会具有最低恒沸点,如图1(b)。
反之,混合溶液体系会具有最高恒沸点,如图1(c)。
(a) (b) (c)图1 不同双液系的气液平衡T-x相图形式本实验选用具有最低恒沸点的环己烷-乙醇(C6H12-C2H5OH)双液系。
用沸点仪可以测定不同组成的双液系的恒压沸点T。
沸点仪是测定常量溶液沸点的工具。
沸腾时的溶液从喷嘴喷出,温度计测定的恰是该处蒸气和液相平衡的温度。
气相部分经过冷凝器冷凝后储存在小泡中,以备取样。
考虑到温度计的精度,需要对1/10℃温度计进行露茎校正。
由于温度计暴露于体系之外的部分所处温度与实测区域不同,二者膨胀系数略有差别。
为了补偿这部分损失,通过辅助温度计读出环境温度后,按下式校正:t = t0+1.57×10-4×n×(t0-t s)式中t0为温度计读数,n为温度计露茎在体系外的刻度数目,t s为辅助温度计读数。
t 为校正后的温度。
双液系气液平衡相图-物理化学实验
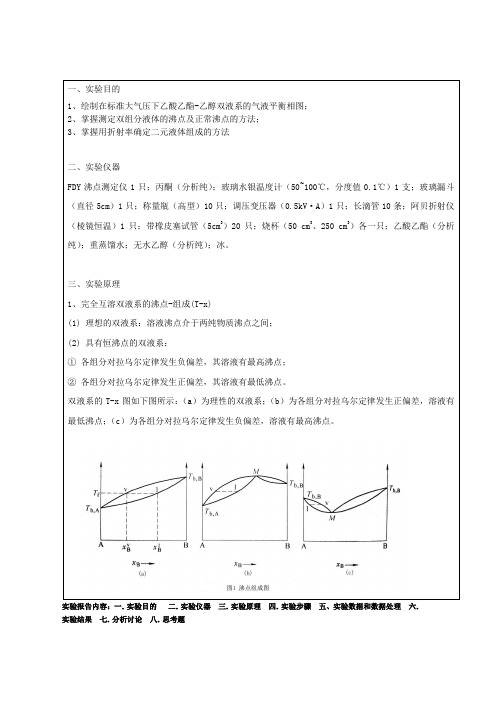
一、实验目的1、绘制在标准大气压下乙酸乙酯-乙醇双液系的气液平衡相图;2、掌握测定双组分液体的沸点及正常沸点的方法;3、掌握用折射率确定二元液体组成的方法二、实验仪器FDY沸点测定仪1只;丙酮(分析纯);玻璃水银温度计(50~100℃,分度值0.1℃)1支;玻璃漏斗(直径5cm)1只;称量瓶(高型)10只;调压变压器(0.5kV·A)1只;长滴管10条;阿贝折射仪(棱镜恒温)1只;带橡皮塞试管(5cm3)20只;烧杯(50 cm3、250 cm3)各一只;乙酸乙酯(分析纯);重蒸馏水;无水乙醇(分析纯);冰。
三、实验原理1、完全互溶双液系的沸点-组成(T-x)(1) 理想的双液系:溶液沸点介于两纯物质沸点之间;(2) 具有恒沸点的双液系:①各组分对拉乌尔定律发生负偏差,其溶液有最高沸点;②各组分对拉乌尔定律发生正偏差,其溶液有最低沸点。
双液系的T-x图如下图所示:(a)为理性的双液系;(b)为各组分对拉乌尔定律发生正偏差,溶液有最低沸点;(c)为各组分对拉乌尔定律发生负偏差,溶液有最高沸点。
实验报告内容:一实验目的二实验仪器三实验原理四实验步骤五、实验数据和数据处理六实验结果七.分析讨论八.思考题2、沸点测定仪本实验所用沸点仪是一只带回流冷凝管的长颈圆底烧。
冷凝管底部有一半球形小室,用以收集冷凝下来的气相样品。
电热丝直接加热液体以减少溶液沸腾时的过热现象及防止瓶暴沸。
小玻璃管有利于降低周围环境对温度计读数可能造成的波动。
3.组成分析本实验选用的乙酸乙酯和乙醇两者折射率相差颇大,而折射率测定又只需要少量样品,所以可用折射率-组成工作曲线来测得平衡体系的两相组成。
4、相图的绘制为了绘制二元双液系的T-x图,需在气液相达平衡后,同时测定气相组成、液相组成和溶液沸点。
实验装置图如图所示:四、实验步骤(1) 安装沸点仪并接通冷凝水;(2) 将乙醇加入沸点仪内,加热至缓慢沸腾(3) 记录乙醇的沸点(4) 测定乙醇的折射率(5) 加入不同摩尔分数的乙酸乙酯-乙醇溶液(6) 记录沸点(7) 吸取气相冷凝液、液相冷凝液测定折射率(8) 将溶液倒入回收瓶(9) 绘制曲线五、实验数据和数据处理室温:25℃大气压:100kPa M无水乙醇=46.07g/mol、M乙酸乙酯=88.11g/mol ρ无水乙醇=0.79g·mol-1ρ乙酸乙酯=0.902g·mol-1无水乙醇体积(ml) 乙酸乙酯体积(ml) 乙酸乙酯浓度(mol%)折射率n90 10 0.063 1.36380 20 0.131 1.36470 30 0.206 1.36560 40 0.287 1.36650 50 0.377 1.36740 60 0.476 1.36830 70 0.585 1.36920 80 0.707 1.37010 90 0.845 1.371 根据乙酸乙酯浓度与折射率,作图如下:添加直线拟合线及拟合方程,由拟合方程式可知:x=(y-1.3626)/0.0104室温:25℃大气压:100kPa混合体系沸点气相冷凝液折射率n 液相冷凝液折射率n 气相组成液相组成78 -- --0 076.8 1.3635 1.3626 0.0865 0.000076.2 1.3642 1.3629 0.1538 0.028875.5 1.3648 1.3632 0.2115 0.057774.7 1.3655 1.3635 0.2788 0.086574 1.3663 1.3642 0.3558 0.153873.3 1.3668 1.3651 0.4038 0.240472.6 1.3673 1.3659 0.4519 0.317372 1.368 1.3672 0.5192 0.442372.7 1.3695 1.3701 0.6635 0.721273.4 1.3697 1.3703 0.6827 0.740474.8 1.3703 1.3709 0.7404 0.798175.5 1.3708 1.3712 0.7885 0.826976.2 1.3713 1.3715 0.8365 0.855876.7 1.3716 1.3717 0.8654 0.875077 -- -- 1 1 查询数据可知:无水乙醇沸点:78℃乙酸乙酯沸点:77℃;由图可知在液相组成时,混合体系沸点76.8℃对应的值为0.0000;此数值属于误差,应当剔除。
双液系相图

3.1使用阿贝折射仪时要注意什么问题?如何使用才能测准数据?
应注意的问题:
1.阿贝折射仪应在通风、无光线直射的桌上使用。
2.棱镜不能触及硬物;棱镜上加入被测溶液后立即关闭镜头,且测量时间不宜过长,防止溶液迅速挥发。
3.测定折光率时需要恒温操作,因此应当在实验前通入恒温水,并记录温度。
4.使用之前先校正仪器,旋转色散调节手轮使色彩消失;调节黑色线的清晰度,使得黑色边界分明。
气相环己烷百分数
5.99%
42.44%
45.83%
71.41%
74.89%
85.94%
101.79%
利用origin作图如下:
2.3.2实验结果
从图二中可以读出恒沸点的恒沸温度为64.78℃,恒沸物中环己烷的质量分数为73.0%。
查阅得到的文献值为在101.3kPa下环己烷-乙醇体系的恒沸温度为64.80℃,恒沸物中环己烷的质量分数为70.8%。故恒沸温度测量值偏小,质量分数的测量值偏大。但是测量值与实验值差异较小,说明本次实验的测量是较为准确的。
1.4273
80.70
利用之前得到的工作曲线,计算得到沸点下对应的气相和液相的成分组成如下表所示:
表三不同沸点下的液相和气相组成
沸点t/℃
78.22
72.29
70.66
64.67
64.77
71.48
80.70
液相环己烷百分数
5.06%
11.16%
14.80%
64.37%
80.71%
100.77%
101.11%
4.6165
1.4165
83.654%
7
-
-
1.4260
部分互溶双液体系的温度-组成图(液-液相图)

4)某些盐和水的最低共熔点和组成表
盐 最低共熔点 (C) NaCl 21.1 NaBr 28.0 NaI 31.5 KCl 10.7 KBr 12.6 KI 23.0 KNO3 3.0 (NH4)2SO4 18.3 Na2SO4 1.1 MgSO4 3.9 CaCl2 55.0 FeCl2 55.0
23
由相律:
f* = C + 1 = 2 + 1 = 3
最多三相共存
关于二组分固-液体系的相图类型很多,但
不论相图如何复杂,都是由若干基本类型
的相图构成。
只要掌握基本类型的相图知识,就能看懂
复杂相图的含义。
24
二、简单低共熔混合物体系相图
1. 冰点降低及溶液的饱和浓度
构成的混合物,它并非固体溶液,所以不
是单相,而是两相。
42
3. 合金体系和化合物体系
在合金体系(如 Bi-Cd,Pb-Sb)和化合 中也有类似的相图。
物 体 系 ( 如 : KCl-AgCl,C6H6-CH3Cl)
以 Bi-Cd 体系为例,其相图如图:
43
B A
相区分析
D
C
• 使用此相图的方法与水-盐体系相同,由图
水的冰点随 (NH4)2SO4 浓 度的增加而下降
EM曲线是固体 (NH4)2SO4 与溶液成平衡的曲线,一 般称为 (NH4)2SO4 在水中的溶解度曲线, 溶解度随温
度的升高而增大。
26
一般说来,盐的熔点很高,超过了饱和溶
液 的 沸 点 , 所 以 EM 曲 线 不 会 沿 长 到
(NH4)2SO4 的熔点,高于M点,溶液气化。
实验三完全互溶双液系的平衡相图

实验三完全互溶双液系的平衡相图一、实验目的1.绘制常压下环己烷-异丙醇双液系的T— X 图,并找出恒沸点混合物的组成和最低恒沸点。
2.学会阿贝折射仪的使用。
二、预习要求1.了解绘制双液系相图的基本原理和方法。
2.了解本实验中有哪些注意事项。
3.熟悉阿贝折射仪的使用。
三、实验原理在常温下,任意两种液体混合组成的体系称为双液体系。
若两液体能按任意比例相互溶解,则称完全互溶双液体系 ;若只能部分互溶,则称部分互溶双液体系。
液体的沸点是指液体的蒸气压与外界大气压相等时的温度。
在一定的外压下,纯液体有确定的沸点。
而双液体系的沸点不仅与外压有关,还与双液体系的组成有关。
图Ⅲ -4-1是一种最简单的完全互溶双液系的T—X 图。
图中纵轴是温度(沸点 )T ,横轴是液体 B 的摩尔分数X B(或质量百分组成),上面一条是气相线,下面一条是液相线,对应于同一沸点温度的二曲线上的两个点,就是互相成平衡的气相点和液相点,其相应的组成可从横轴上获得。
因此如果在恒压下将溶液蒸馏,测定气相馏出液和液相蒸馏液的组成就能绘出 T—X 图。
如果液体与拉乌尔定律的偏差不大,在 T—X 图上溶液的沸点介于 A、 B 二纯液体的沸点之间(见图Ⅲ -4-1) ,实际溶液由于 A 、B 二组分的相互影响,常与拉乌尔定律有较大偏差,在 T—X 图上会有最高或最低点出现,如图Ⅲ-4-2 所示,这些点称为恒沸点,其相应的溶液称为恒沸点混合物。
恒沸点混合物蒸馏时,所得的气相与液相组成相同,靠蒸馏无法改变其组成。
如 HCl 与水的体系具有最高恒沸点,苯与乙醇的体系则具有最低恒沸点。
图Ⅲ -4-1完全互溶双液系的图III-4-2完全互溶双液系的另一种类型相图一种蒸馏相图本实验是用回流冷凝法测定环已烷—异丙醇体系的沸点—组成图。
其方法是用阿贝折射仪测定不同组成的体系,在沸点温度时气、液相的折射率,再从折射率—组成工作曲线上查得相应的组成,然后绘制沸点—组成图。
物化实验报告-双液系气液平衡相图的绘制

双液系气液平衡相图的绘制(物化实验得认真做)一、实验目的1. 用回流冷凝法测定沸点是气相和液相的组成,绘制双液系相图。
2 找出恒沸点混合物的组成和恒沸点的温度。
掌握测定双组分液体的沸点及正常沸点的测定方法。
3 了解阿贝折射计的构造原理,熟悉掌握阿贝折射计的使用方法。
二、实验原理1 液体的沸点是液体饱和蒸汽压和外压相等时的温度,在外压一定时,纯液体的沸点有一个确定值。
但双液系的沸点不仅与外压有关,而且还与两种液体的相对含量有关。
2 大多数情况下,T-x 曲线将出现或正或负的偏差,当这个偏差足够大的时候,在曲线上将出现极大点或极小点。
这种极大点或者极小点就称为恒沸点。
3 考虑综合因素,实验选择具有最低恒沸点的乙醇- 乙酸乙酯双液系。
4 根据相平衡原理,对两组分体系,当压力恒定时,在气液平衡两相去,体系的自由度为1. 若温度一定时,则气液两相的组成也随之而定。
当原溶液的组成一定时,根据杠杆原理,两相的相对量一定。
反之,实验中利用回流的方法保持气液两相相对量一定,测量体系温度不发生改变时,即两相平衡后,取出两相的样品,用阿贝折射计测定气相、液相的折射率,再通过预先测定的折射率- 组成工作曲线来确定平衡时气相、液相的组成(即该温度下气液两相平衡成分的坐标点)。
改变体系的总成分,再如上法找出另一对坐标点。
这样得若干对坐标点分别按气相点和液相点连成气相线和液相线,即得T-x 平衡图。
三、实验仪器和试剂1、实验仪器沸点仪、阿贝折射仪、调压变压器、温度计两只、干燥小烧杯3只,干燥5ml小试管16只,软木塞若干,擦镜纸2、实验试剂无水乙醇(AR乙酸乙酯(AR丙酮(C.P)乙醇体积分数为5% 10% 15% 22% 38% 50% 70% 90%组成的乙醇- 乙酸乙酯溶液。
四实验过程1、将干燥的沸点仪安装好。
从侧管加入约20mL5混合液于蒸馏瓶内,并使温度计浸入液体内。
冷凝管接通冷凝水。
将稳流电源电压调至13V左右,使加热丝将液体加热至缓慢沸腾。
双液系相图数据处理

双液系的气——液平衡相图数据处理一、蒸馏水、乙酸乙酯和无水乙醇的折光率值室温:295K 大气压:101.325KPa 样品 n 1 n 2 n 3 n 平均 n 理论 △n n 校正 H 2O 1.33280 1.33290 1.33280 1.33283 1.33281 0.00002 —— 乙酸乙酯 1.37120 1.37130 1.37130 1.37137 —— —— 1.37135 无水乙醇 1.360701.360901.360801.36090————1.36088无水乙醇方程:y=-9551.1x+13098; 乙酸乙酯方程:y= 9551.1x-12998。
根据所测得实验过程中的折光率,查上图的工作曲线,可得下表2。
二、未知液的组成溶液沸点/℃ 液相气相 n 1 n 2 n 3 n 平均校正 x 乙酸乙酯 n 1 n 2 n 3 n 平均校正 y 乙酸乙酯 0.05 77.431.36111.3611 1.3612 1.361213 0.022286 1.3628 1.3624 1.3624 1.362113 0.156001 0.20 75.05 1.362 1.3619 1.3621 1.36208 0.105062 1.3634 1.3634 1.3636 1.363647 0.245145 0.30 73.99 1.3626 1.3626 1.3624 1.362947 0.156001 1.3647 1.3649 1.3647 1.36518 0.369309 0.40 73.06 1.3633 1.3632 1.3634 1.363813 0.229226 1.3653 1.3652 1.3653 1.366713 0.417065 0.50 72.46 1.3646 1.3645 1.3647 1.36468 0.353391 1.3659 1.3657 1.3657 1.368247 0.46482 0.6072.121.36591.36581.3661.3655470.4775551.3661.36621.36621.369780.4998410.70 71.97 1.36731.36721.3671.3664130.5985361.36691.36681.36681.3713130.5666990.95 74.4 1.369 1.369 1.36941.367280.7863741.36891.36891.3691.3728470.767272用上表所得的数据绘制作图如下:由上图中读出其最低恒沸点为71.97℃,乙酸乙酯摩尔分数为0.5285。
双液系的气-液平衡相图ppt课件

三.仪器与试剂 [注意按实际使用的记录]
四.试验步骤
1.工作曲线绘制
(1)调节超级恒温水浴温度在室温5℃以上,以适应季 节的变化,但所选温度应易于获得试样的密度数据。 环己烷和乙醇分别恒温10min,根据配制混合物所需 的体积,用移液管精确量取,配制环己烷摩尔分数为 0.10,0.20,0.30,0.40,0.50,0.60,0.70, 0.80,0.90 的环己烷-乙醇溶液各10ml。为避免样 品的挥发带来的误差,配制应尽可能迅速。 (2)用尽可能短的软管将阿贝折光仪连接在前述调好 的恒温水浴上,以保持折光仪棱镜处于恒定温度。测 量上述9个溶液以及无水乙醇和纯环己烷的折光率。
按上述相同的步骤,用第二套沸点仪测定环己 烷摩尔分数为0.90 的环己烷-乙醇溶液的沸 点以及气相和液相的折射率测定。
6.系列环己烷-乙醇溶液以及环己烷的测定 按上述第5步所述步骤,分别用第一套沸点仪从
低组成向高组成逐一测定各溶液的沸点、大气压 及两相样品的折光率,而用第二套沸点仪从高组成 向低组成逐一测定各溶液的沸点、大气压及两相 样品的折光率。直至完成所有溶液的测定。 系列溶液可回收供其它同学使用;每个试样测定 后,将沸点仪尽量倒干净即可,不必干燥。记录温度 数据时千万不要忘记注明所用温度计的编号或代 码!
2.精密数字温度温差仪温度的校正
将两套精密数字温度温差仪的探头同时放入 恒温水浴中,测定温度的差值,以其中一套的 读数为基准,对另一套精密数字温度温差仪读 数进行校正。并作燥的沸点仪安装好。检查 带有温度计的软木塞是否塞紧,电热丝要靠 近烧瓶底部的中心。温度计探头的位置应 处在支管之下,但至少要高于电热丝1 cm。 温度计套管中应加入适量的硅油或液体石 蜡,以完全浸没测温探头敏感部分(约2.5~ 3cm),便于传热。
双液系的气—液平衡相图

双液系的气—液平衡相图一、实验目的1.绘制在Pθ环已烷—乙醇的气液平衡相图,了解相图和相律基本概念;2.掌握测定双组分液体的沸点及正常沸点的方法;3.掌握用折光率确定二元液体的组成方法。
二、实验原理液体的沸点是指液体的蒸气压和外压相等时的温度,在一定的外压下,纯液体的沸点有确定值。
但双液系的沸点不仅与外压有关,而且还与两种液体的相对含量有关。
根据相律:自由度=组分数-相数+2因此,一个气—液共存的二组分体系,其自由度为2。
只要任意再确定一个变量,整个体系的存在状态就可以用二维图形来描述。
两种挥发性液体混合,假设该二组分的蒸气压不同,则溶液的组成与其平衡气相的组成不同。
在压力保持一定,二组分系统气液到达平衡时,表示液态混合物的沸点与平衡时组成关系的相图,称为沸点和组成〔T-x〕图。
沸点和组成〔T-x〕的关系有以下三种:〔1〕理想液体混合物或接近理想液体混合物的双液系,其液体混合物的沸点介于两纯物质沸点之间见图1(a);〔2〕各组分蒸气压对拉乌尔定律产生很大的负偏差,其溶液有最高恒沸点见图1(b);〔3〕各组分蒸气压对拉乌尔定律产生很大的正偏差,其溶液有最低恒沸点见图1(c)。
第〔2〕、〔3〕两类溶液在最高或最低恒沸点时的气液两相组成相同,加热蒸发的结果只使气相总量增加,气液相组成及溶液沸点保持不变,这时的温度称恒沸点,相应的组成称恒沸组成。
图1. 沸点和组成〔T-x〕图本实验是测定具有最低恒沸点的环己烷—乙醇双液系的T-x图。
方法是用沸点仪〔如图2所示〕直接测定一系列不同组成之溶液的气液平衡温度〔即沸点),并收集少量馏出液〔即气相冷凝液〕及吸取少量溶液〔即液相〕,分别用阿贝折光仪测定其折光率。
根据已知组成的溶液折光率,作出一定温度下〔25℃〕该溶液的折光率—组成工作曲线,然后根据测得的样品溶液的气液两相的折光率,在此曲线上即可按内描法得到待测未知样品溶液的组成。
图2. 沸点测定仪示意图三、仪器与药品沸点测定仪1只丙酮〔分析纯〕水银温度计〔50~100℃,分度值0.1℃〕1支超级恒温水浴1台玻璃温度计〔0~100℃,分度值1℃〕1支称量瓶〔高型〕10只调压变压器〔0.5kVA〕1只25mL移液管数字式Abbbe折光仪〔棱镜恒温〕1台长滴管10支带玻璃磨口塞试管〔5mL〕4支无水乙醇〔分析纯〕烧杯〔50ml,250ml〕各1支环己烷〔分析纯〕玻璃漏斗〔直径5cm〕1只重蒸馏水,冰四、实验步骤1.调节超级恒温水浴温度,使阿贝折光仪上的温度计读数保持在25℃。
双液系的气液平衡相图-物化实验报告
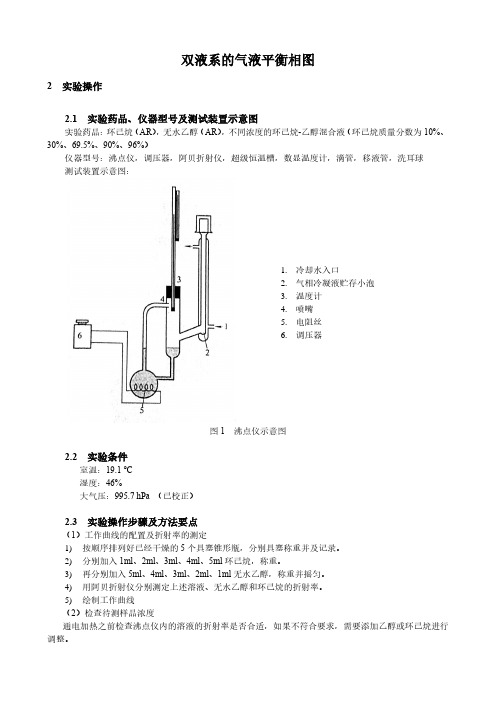
双液系的气液平衡相图2 实验操作2.1 实验药品、仪器型号及测试装置示意图实验药品:环己烷(AR),无水乙醇(AR),不同浓度的环己烷-乙醇混合液(环己烷质量分数为10%、30%、69.5%、90%、96%)仪器型号:沸点仪,调压器,阿贝折射仪,超级恒温槽,数显温度计,滴管,移液管,洗耳球测试装置示意图:1.冷却水入口2.气相冷凝液贮存小泡3.温度计4.喷嘴5.电阻丝6.调压器图1 沸点仪示意图2.2 实验条件室温:19.1 ℃湿度:46%大气压:995.7 hPa (已校正)2.3 实验操作步骤及方法要点(1)工作曲线的配置及折射率的测定1)按顺序排列好已经干燥的5个具塞锥形瓶,分别具塞称重并及记录。
2)分别加入1ml、2ml、3ml、4ml、5ml环己烷,称重。
3)再分别加入5ml、4ml、3ml、2ml、1ml无水乙醇,称重并摇匀。
4)用阿贝折射仪分别测定上述溶液、无水乙醇和环己烷的折射率。
5)绘制工作曲线(2)检查待测样品浓度通电加热之前检查沸点仪内的溶液的折射率是否合适,如果不符合要求,需要添加乙醇或环己烷进行调整。
(3)测定各溶液达到汽液平衡时的气相和液相组成打开冷却水,接通电源,慢慢调节调压器电压进行加热,直到溶液沸腾或者出现小气泡,再将电压调到33V。
待温度恒定后,记下该温度值,关电压,停止加热,同时用长滴管从冷凝管上口在小泡中取气相冷凝液,迅速测定折射率,液相溶液稍冷后,从温度计口取液相溶液测定折射率(沸腾过程已经使液相混合比较均匀了,类似“鼓泡法”;而且实际上也没有地方伸入滴管进行搅拌)。
如果沸点仪圆底烧瓶内液体快要蒸干了、电阻丝没有浸泡在液体中,就要及时补充溶液,否则体系内温度会急剧上升。
如果液面低于烧瓶侧面支管口,应及时补充液体,否则无法取液相溶液。
补充溶液时,要等到体系冷却下来。
3 结果与讨论3.1 原始实验数据表1 环己烷-乙醇混合液(标准液)的折射率序号空瓶质量/g瓶+乙醇质量/g瓶+混合液质量/g折射率129.932130.624634.4739 1.3701231.016832.487935.5774 1.3810331.169233.423335.6596 1.3926427.875530.927732.4152 1.4040528.387232.241132.9446 1.41696无水乙醇 1.36387纯环己烷 1.4284表2 环己烷-乙醇混合液(待测液)沸点及气相、液相的折射率序号环己烷质量分数温度/℃气相冷凝液折射率液相折射率1077.56 1.3638 1.3634210%75.63 1.3704 1.3654330%73.16 1.3825 1.3668469.50%64.42 1.3978 1.3817590%64.65 1.4072 1.4162696%67.26 1.4108 1.42417100%80.13 1.4278 1.4272 3.2计算的数据、结果(1)绘制折射率-组成工作曲线根据表1数据计算出各个标准溶液对应的环己烷质量分数,如表3。
物理化学中国药科大学相平衡第三章24节

2.4
179
49.3
二、 克劳修斯-克拉珀龙方程
T, p T+dT,p+dp
相 G=0 相
dG()
dG()
相 G=0 相
显然 dG()=dG() dG=-SdT+Vdp
-S()dT+V()dp=-S()dT+V()dp
[V()- V()] dp =[S() -S()]dT
dp S (β )S (α ) Sm dT V (β )V (α ) Vm
n总 nA nB nl ng
n总xA
nl x1
ng x2
物系点中 分配在液相 分配在气相
A的总量 A的量 A的量
(nl ng)xA nl x1 ng x2
n(l
xA
x1)
n(g x2
x
)
A
nl CD ng CE
此等式称杠杆规则
推广到任意相图的两相平衡区(液-气、 液-固、固-固平衡),杠杆规则都适用。 如横坐标为重量百分数,ng、nl改为wg、 wl(摩尔改为重量)。
(3)继续降压,离开P点时,最后液滴消失,成单 一气相,f = 2。通常只考虑(2)的情况。
三相点与冰点的区别
三相点是物质自身的特性,不能加以改变, 如H2O的三相点 T 273.16 K , p 610.62 Pa .
冰点是在大气压力下,水、冰、气三相共存。当大
气压力为105 Pa时,冰点温度为273.15 K,改变外压, 冰点也随之改变。
(1)95oC时的p*水=? (2)p=1.10105Pa时水的沸点
• 解:
(1) ln p2 VapH m (T2 T1)
p1
R T1T2
双液系的气-液平衡相图

双液系的气—液平衡相目的要求(1) 绘制在pΘ下环己烷-乙醇双液系的气-液平衡相图,了解相图和相律的基本概念。
(2) 掌握测定双组分液体沸点及正常沸点的方法。
(3) 掌握用折光率确定二元液体组成的方法。
基本原理一、气-液相图两种液态物质混合而成的二组分体系称为双液系。
两种组分若能按任意比例互相溶解,称为完全互溶双液系。
液体的沸点是指液体的蒸气压与外界压力相等时的温度。
在一定的外压力下,纯液体的沸点有其确定的值。
但双液系的沸点不仅与外压有关,而且还与两种液体的相对含量有关。
根据相律,自由度=组分数-相数+2因此,一个气-液共存的二组分体系,其自由度为2.只要任意再确定一个变量,整个体系的存在状态就可以用二维图形来描述。
例如,在一定温度下,可以画出体系的压力p和组分x的关系图,如体系的压力确定,则可作温度T对x的关系图。
这就是相图。
在T-x相图上,还有温度,液相组成和气相组成三个变量,但只有一个自由度。
一旦设定某个变量,则其他两个变量必有相应的确定值。
图Ⅱ-5-1以苯-甲苯为例表明,温度T这一水平线指出了在此温度时处于平衡的液相组分x和气相组分y的相应值。
苯与甲苯这一双液系基本上接近理想溶液,然而绝大多数实际体系与拉乌尔定律有一定偏差。
偏差不大时,温度-组分相图与图Ⅱ-5-1相似,溶液的沸点仍介于两纯物质的沸点之间。
但是,有些体系的偏差很大,以至其相图将出现极值。
正偏差很大的体系在T-x图上呈现极小值,负偏差很大时则会有极大值。
这样的极值称为恒沸点,其气,液两相的组成相同。
例如,H2O-HCl体系的最高恒沸点在P0时为108.5,恒沸物的组成含HCl20.242%。
通常,测定一系列不同配比溶液的沸点及气、液两相组成,就可绘制气-液体系的相图。
压力不同时,双液系相图将略有差异。
本实验要求将外压校正到1个大气压力。
二、沸点测定仪各种沸点仪的具体构造虽各有特点,但其设计思想则都集中于如何正确测定沸点、便于取样分析、防止过热及避免分馏等方面。
第三章双液系相图

双液系相图
两组分相图
• 两组分体系的相律可表达为:
• • • f=0, K=2; =2
f=4-
一. phase diagram of ideal solution: • 理想溶液各组分在全部浓度范围内均遵守拉 乌尔定律,只要掌握了A,B的饱和蒸汽压数据, 其相图可以计算出来.
• p-x图:
• • • • pA= pA*xA pB= pB*xB= pB*(1-xA) p = pA+ pB = pA*xA + pB*(1-xA)
pB
*
pA*
L
H
G
l+g,
0
xAl
xA xAg
x
杠杆规则 (lever rule):
p
HL和HG分别为 体系点 H到液 相 线和气相线的距 离. 因为此规则 与物理学中的杠 杆定律相似,故称 为 杠 杆 规 则 .
pA*
L l+g, pB
*
H
G
0
xAl
xA xAg
x
p
杠杆规则:
pA*
nlHL=ngHG
• 体系的总压为:
•
p = pB*+(pA*-pB*)xA
(2)
双液系的p-x相图的绘制
将组成为xA,xB的A,B理想溶液置于 一带活塞的气缸中, 保持恒温,并施 加足够大的压力,使体系呈溶液单相 状态.如图所示. 逐步降低环境压力,当 压力降到等于 此溶液的饱和蒸汽压时,开始出现气相. 当体系压力降到某一定值时,体系主 要以气相形式存在,液相几乎消失,但 仍然保持两相 平衡. 若进一步降低体系的压力,体系中的 液相将完全消失,体系为气态单相.
环己烷-异丙醇双液系相图

2.6 环己烷-异丙醇双液系相图2.6.1 实验目的1.了解物理化学实验手段中常用的物理方法—光学方法的基本原理。
2.绘制环己烷-异丙醇双液系的沸点~组成图,并找出恒沸点及恒沸点混合物的组成。
3.进一步理解分馏原理。
4.掌握阿贝折射仪的原理及使用方法。
2.6.2 实验原理单组分液体在一定的外压下沸点为一定值。
把两种完全互溶的挥发性液体(组分A和B)混合后,在一定的温度下,平衡共存的气液两相组成通常并不相同。
因此在恒压下将溶液蒸馏,测定馏出物(气相)和蒸馏液(液相)的组成,就能找到平衡时气、液两相的成分并绘出T—x图,即所谓的相图。
完全互溶双液系在恒定压力下的沸点~组成图可分为三类:(1)液体与拉乌尔定律的偏差不大,沸点介于A、B两纯组分沸点之间(图6一1),如苯~甲苯体系。
(2) A、B两纯组分混合后与拉乌尔定律有较大的正偏差,溶液存在最低沸点(图6一2),如水~乙醇;苯~乙醇等体系。
(3)实际溶液由于A、B两纯组分相互影响,常与拉乌尔定律有较大负偏差,溶液存在最高沸点(图6一3),如盐酸~水体系;丙酮~氯仿体系。
图6—1 偏差不大的体系图6—2 正偏差很大的体系图6—3 负偏差很大的体系对(2)、(3)类体系有时被称为具有恒沸点的双液系。
它与(1)类的根本区别在于,体系处于恒沸点时气、液两相的组成相同。
因而也就不能象(1)类那样通过反复蒸馏而使双液系的两个组分完全分离。
对(2)、(3)类的溶液进行简单的反复蒸馏只能获得某一纯组分和组成为恒沸点的相应组成的混合物。
如要获得两纯组分,需采取其他方法。
体系的最低或最高恒沸点即为恒沸温度,恒沸温度对应的组成为恒沸组成。
环己烷-异丙醇双液系属于具有最低恒沸点一类。
为了绘制沸点~组成图,可采取不同的方法。
比如取该体系不同组成的溶液,用化学分析方法分析沸腾时该组成的气、液组成,从而绘制出完整的相图。
可以想象,对于不同的体系要用不同的化学分析方法来确定其组成,这种方法是很繁杂的。
双液相图 (2)PPT课件

取20mL环己烷加入沸点仪中,然后依次加入无水乙醇0.5mL、 0.5mL、1.0mL、2.0mL、5.0mL,用前述方法分别测定溶液沸 点液及倒气入相回组收分瓶折中射。率ng、液相组分折射率nl。实验完毕,将溶
第十三页,编辑于星期五:十二点 三十四分。
四、实验步骤(6)
► 精馏是最常用内—种分离方法。对一个混合物系统设计精馏装置,要求 算精馏塔所需的理论塔板数,系统的气、液平衡数据是必不可少的。工 业生产中遇到的系统,其气、液平衡 数据往往很难由理论计算,可以由本实验装置直接测定。
第十八页,编辑于星期五:十二点 三十四分。
附2:阿贝折射仪的使用:
◦ 1、将折射仪与超级恒温器相连接,并调节好水温进行恒温并通入 恒温水。
用阿贝折射仪测定每份溶液的折射率及纯环己烷和纯无水乙醇的折射率。 以折射率对浓度作图(按纯样品的密度,换算成质量百分浓度),即得工作曲线。
第十一页,编辑于星期五:十二点 三十四分。
四、实验步骤(4)
3. 测定乙醇和环己烷的沸点
▪ 将干燥的沸点仪安装好,检查带有电极的木塞是否塞紧,加热用 的电热丝要靠近容器底部的中心点离温度计2-3厘米,温度计
第九页,编辑于星期五:十二点 三十四分。
附:标准溶液的配制
► 将11个小滴瓶编号,依次移0mL、1.00 mL、 2.00 mL、…、9.00 mL、10 mL的环己烷、, 然后依次移入10 mL、 9.00 mL、8.00 mL、…、1.00 mL、0 mL的无水乙醇,摇匀, 配成11份已知浓度的溶液(公用)。
小玻管和 电 热丝的位置
作用?
第六页,编辑于星期五:十二点 三十四分。
三、仪器与药品
沸点仪;阿贝折射仪;超级恒温槽;调压变
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气相,f=2
D
气-液平衡,f=1
Tmix
E
液相,f=2
B
• 2. 部分互溶双液系:
• 当A,B的极性相差较大时,相互溶解度较小,在一 定浓度范围, 可能出现A,B不完全互溶的现象. • 不完全互溶的双液系表观上为两液层. • 部分互溶的双液系可分为三种类型: • (1) 温度较低时出现分层现象,温度较高时可以 无限互溶; • (2) 温度较高时出现分层现象,温度较低时可以 无限互溶; • (3) 温度较低和温度较高时均可以完全互溶,体 系只是在某一温度段出现部分互溶的现象.
有恒沸物双液系的精馏
E: 最低恒沸点 组成:xE, 沸点: Tmin. 体系组成为x, 精馏,低沸 点端得到恒沸物G,高沸点 端得到纯A. 有恒沸物生成的双液系, 精馏不可能同时得到纯A 和纯B,只能得到恒沸物和 某一个纯组分. 恒沸物仍是混合物,其组成 随着体系压力的改变而有 所改变.
A x xE C T
完全互溶双液系的p-x图
虚线:理想溶液 红色: A的蒸汽压曲线; 蓝色: B的蒸汽压曲线; 紫色: 实际溶液的总压 此类非理想溶液相图与 理想溶液的相图有偏差. 但其偏离的程度不至于 使体系的相图发生明显 的变化.
pA* p
(偏离理想溶液程度不大)
pB
*
p
pB
pA
A
B
有较大正偏差的实际溶液相图
当实际溶液的行为偏离 理想溶液较大(如正偏 差)时,其p-x图中会出现 总压的极大值,如图中G 点所示. 图中,B的挥发性较大,但 G点的压力比纯B的蒸汽 压 更 大 . 这 是 因 为 A,B 均 对拉乌尔定律有较大正 偏差的缘故.
pB*
A
p C
p
pA*
单相区,液 相, f=2
B
L
H G
l+g,f=1
单相区,气 相, f=2 0
x’’
xA
x’
xA
理想溶液的p-x相图
p
组成为xA的体系点C位 于单相区, 为液相溶液. D点:开始出现气相,气 相点为K,达两相平衡. H点: 气相组成为x’,液 相组成为x’’.
C 单相区,液相 pA*
nl/ng=HG/HL = (xAg-xA)/(xA-xAl)
pB
*
L
H
G
l+g,f= 1
0
xAl
xA xAg
x
A
液相质量 气相点与体系点的距离 = 气相质量 液相点与体系点的距离
理想溶液的T-x相图
体系点为H点, 落在两相区内, 体系两相共存. E: 液相点, A的浓度为xAl. F: 气相点, A的浓度为xAg.
气相
y2 x3 x4 x5 y3 y4
T4
y5
液相
A
x
B
精馏塔示意图
原料进口 低沸点产品
高沸点产品
电加热器
理想溶液的T-p-x图
把p-x图和T-x图合在一起,就得到T-p-x三维图。 三个坐标分别代表p,T,和x; 在右边的垂直面xA=1, xB=0,则压力和温度坐 标分别代表纯A组分的饱 和蒸气压pA*和沸点TA*. 同理左边垂直面上是pB* 和TB*。连线pA*-TA* 和 pA*-TA*分别代表了纯A 和纯B的蒸气压随温度的 变化曲线。
pB
*
pA*
L
H
G
l+g,
0
xAl
xA xAg
x
杠杆规则 (lever rule):
p
HL和HG分别为 体系点 H到液 相 线和气相线的距 离. 因为此规则 与物理学中的杠 杆定律相似,故称 为 杠 杆 规 则 .
pA*
L l+g, pB
*
H
G
0
xAl
xA xAg
x
p
杠杆规则:
pA*
nlHL=ngHG
*
H
G
0
xAl
xA xAg
x
杠杆规则 (lever rule):
p
(1)式与(2)式相等: nlxA+ngxA = nlxAl + ngxAg
p A*
nl( xA-xAl) = ng( xAg-xA) (3)
pB
*
L l+g,
H
G
0
xAl
xA xAg
x
杠杆规则 (lever rule):
p
从相图可以求出: ( xA-xAl)=HL ( xAg-xA)=HG 有: nlHL=ngHG (4) (4)式即为杠杆规则 的数学表达式.
p x1 x2 x3 x4 381K 373K 365K 357K p0
0
0.2
0.4
0.6
0.8
1.0 xA
T/K
383
381K 373K 365K 357K
373
363
353
0
0.2
0.4
0.6
0.8
1.0 xA
精 馏 原 理
B的沸点低,挥发性较强, B在 气相中的浓度较液相高,将组 成为y1的气相收集起来,并将 其冷却至温度T1,其中将有部 分冷凝为液体,液相的组成为 x2, 与之达平衡的气相组成为 y2,由相图可见y2>y1.重复以上 过程,气相中B的浓度愈来愈 高,最后可以获得纯的B。 而由液相可以获得纯的A。
液 pB* TB* pA*
气
T
TA* 液
B
xA
A
气-液两相共存的 * * 梭形面沿 pA TA * p B TB* 两线 和 移动,形成扁圆 柱状气-液两相共 存区。
在共存区的上前 方是高温、低压 区,所以是气相 区;在共存区的 后下方,是低温、 高压区,所以是 液相区。
液 pB* TB* 气
一. phase diagram of ideal solution: • 理想溶液各组分在全部浓度范围内均遵守拉 乌尔定律,只要掌握了A,B的饱和蒸汽压数据, 其相图可以计算出来.
• p-x图:
• • • • pA= pA*xA pB= pB*xB= pB*(1-xA) p = pA+ pB = pA*xA + pB*(1-xA)
A
x
pmax p
G D
C
pB
pA
B
有较大正偏差的实际溶液p-x图
pma
x
G
pma
G p D
p
D
x
C
C
A
x
B
A
x
B
若双液系压力有极大值,液相线有极点G, 气相线的形状 若如图中蓝线,则G点无对应的气相点的现象. 实际相图如右图所示.液相线与气相线将交会于G点,体 系在G点达气-液两相平衡,两相组成相同.
• 体系的总压为:
•
p = pB*+(pA*-pB*)xA
(2)
双液系的p-x相图的绘制
将组成为xA,xB的A,B理想溶液置于 一带活塞的气缸中, 保持恒温,并施 加足够大的压力,使体系呈溶液单相 状态.如图所示. 逐步降低环境压力,当 压力降到等于 此溶液的饱和蒸汽压时,开始出现气相. 当体系压力降到某一定值时,体系主 要以气相形式存在,液相几乎消失,但 仍然保持两相 平衡. 若进一步降低体系的压力,体系中的 液相将完全消失,体系为气态单相.
T
气相
y1
y2 液相 y3
A
xB
x2
x3
B
精 馏 原 理
T
实际的工业精馏 工段,为连续操 作,各层的操作 温度相对稳定, 溶液的组成也稳 定,在精馏塔的 低温段一般可以 获得纯净的B, 在高温段, 可获 得 纯 净 的 A .
T7 T6 T5 T T1 T2 T3
y8
x8
x7 x6 x1 x2
y7 y6 O y1
p
C
pA*
D G
L
F
l+g pB*
0
xAl
xA
xAg
xA
杠杆规则 (lever rule):
p
H:体系点,组成为xA L: 液相点 G: 气相点 A的总量: nA=nxA n=nl+ng nA= nlxA+ngxA (1) 又: nA=nAl +nAg nA=nlxAl+ngxAg (2)
pA*
L l+g, pB
pA*
T
TA* 液
B
xA
A
• 二.
phase diagram of real solution
• 严格意义上的理想溶液只是一种理想模型, 实际上的溶液体系 多为非理想溶液, 非理想溶液存在多种类型.
• 1. 完全互溶的双液系:
• 如果实际溶液的性质偏离理想溶液的程度不大,则其相 图与理想溶液的相图相类似. • 实际溶液若相对理想溶液有很大偏差,则可能出现最大 饱和蒸汽压(定温下)的极点,或最小蒸汽压的极点;若在 等压条件下,这类非理想溶液将出现最低恒沸物或最高 恒沸物.此类非理想溶液的相图将会出现比较大的变化. • 固体物质间达分子水平的混合,这类体系称为固溶体, 即固态溶液.完全互溶固溶体的相图类似于双液系相图.
开始出现气相, 体系达气液两相 平衡.
A+B, 气相, T
A+B, 气 A+B, T 相, 气相, T A+B, 气相, T
A+B, 溶液, T A+B, 溶液, T A+B, 溶液, T A+B, 溶液, T
理想溶液的p-x相图
C点: 组成xA, 单相溶液. D点:开始出现气相, 液 相与总组成仍相同.
D pB
*
0
