横向分布影响线数据
桥梁工程荷载横向分布计算简介

•由于跨中截面车轮加载值占总荷载的绝大多 数, 近似认为其它截面的横向分布系数与跨中 相同 •对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
计算剪力时横向分布沿桥纵向的变化
与铰接板、梁的区别: 未知数增加一倍, 力法方程数增加一倍
5 .铰接板桥计算m举例:
如图所示,l=12.60m的铰接空心板桥横截面布置。 桥面净空为净-7+2x0.75m人行道。全桥由9块预应力混凝 土空心板组成,欲求1、3.5号板的公路-I级和人群荷载作用 的跨中横向分布系数?
分析: 荷载横向分布影响线竖标值与刚度参数γ ,板 块数n以及荷载作用位置有关。 5.8 I (b)2
4.目前常用的荷载横向分布计算方法: (1)梁格系模型
①杠杆原理法
②偏心压力法
③横向铰接梁(板)法
④ 横向刚接梁法 (2)平板模型——比拟正交异性板法(简称G—M法) 各计算方法的共同点: (1)横向分布计算得m (2)按单梁求主梁活载内力值
二、杠杆原理法 (一)计算原理 1.基本假定:
忽略主梁间横向结构的联系作用,假设桥面 板在主梁上断开,当作沿横向支承在主梁上的简 支梁或悬臂梁来考虑。
荷载横向分布计算
一、概述
荷载: 恒载: 均布荷载(比重×截面积)
活载: 荷载横向分布
1.活载作用下,梁式桥内力计算特点:
(1)单梁 (平面问题)
P
S=P·η1(x)
x
L/4
1
(2)梁式板桥或由多片主梁组成的梁桥(空间问题): S=P·η(x,y) 实际中广泛使用方法: 将空间问题转化成平面问题
S P (x, y) P 2 (y) 1(x)
为求1号梁的荷载 假设: a、P=1作用于1号梁梁轴, 跨中,偏心距为e; b、 各主梁惯性矩Ii不相等; c、横隔梁刚度无穷大。 则由刚体力学: 偏心力P=1 <====> 中心荷载 P=1+偏心力矩M=1·e
横向分布影响线的变化规律研究

O
8
0
6
O
4
0
2
由表3 和表4 求得不同横梁刚度时 , , 相应的 和
关 系见 表 5 。
表5 与 函数关系
图6 影响线斜 率修正 系数
5 结束 语
根据以上算例分析, 得出以下结论:
( )根据判别式能够明确横向分布影响线形 1 状, 当 > . 横向影响线为曲线 , 0 时, 3 此时可以选用
刚接梁法 ; < . , 向影响线为直线, 当 03 横 时 此时可 以选用刚性横梁法。 ( ) 正确计算横梁刚度和支承刚度对结果至 2
关重要 。横梁刚度影响横 向影响线的曲率和斜率 ,
支承刚度影响横 向影响线的曲率。随着横梁刚度的 增加 , 向影响线 曲率逐渐减小 、 横 斜率逐渐减小 , 随 着支承刚度的增加 , 向影响线 曲率逐渐增大。 横 ( ) 刚性横梁法修正系数的引入对原方法是 3
式 中B 为桥宽 ,为跨径 , 为纵 向单宽抗弯 刚 L J x 度 , 为横向单宽抗弯刚度。 J y 当 >. 03 时是宽桥 , 横向影 响线为曲线。 当0 ≤0 时是窄桥 , 向影响线为直线 。 < . 3 横 因此上式是影响线形状的判别式。 由于桥梁为空间结构,主梁与横梁为互 为支承 关系, 主梁的挠曲刚度即为横梁的支承刚度 , 横梁即
吉林 交通 科技
S I N E A D T C NO O Y O II O CE C N E H L G FJLN C MMU I A I N N C TO S
2 年 第 3期 0 1 1
横 向分布 影响线的变化规律研究
王柏璎 马 壮 陈 恒 君
100 ) 30 0
41
横向分布系数和偏载系数

一、 横向分布如图3—2—1a所示,梁桥的上部结构由承重结构(①~④号主梁)及传力结构(横隔梁、行车道板)两大部分组成,各片主梁靠横隔梁和行车道板连成空间整体结构,当桥上作用荷载(桥面板上作用2个车轴,前轴轴重为P1,后轴轴重为P2)时,各片主梁共同参与工作,形成了各片主梁之间的内力分布。
在计算恒载时,除主梁的自重外,一般将桥面铺装、人行道、栏杆等的重量近似平均分配给各片主梁,即计算出桥面铺装、人行道、栏杆等的总重量除以梁的片数(本例4片梁),得到每片主梁承担的桥面铺装、人行道、栏杆的重量。
由于人行道、栏杆等构件一般位于边梁上(①、④号主梁),精确计算时,也可考虑它们的重量在各梁间的分布,即中梁(②、③号主梁)也分担一部分人行道、栏杆的重量。
在计算活载时,需要考虑活载在各片主梁间的分布。
《标准》规定,车道荷载的横向分布系数应按设计车道数布置车辆荷载进行计算。
车辆荷载的横向布置如图3—2—1c所示。
对于车道荷载,最外车轮距人行道缘石之距不得小于0.5m,车道荷载的横向轮距为1.8m,两列车道荷载车轮的横向间距不得小于1.3m。
如图3—2—1b所示,在车道荷载的作用下,①号边梁所分担的荷载,也就是说,①号边梁所分担的荷载R1为轴重P1的。
若将第i号梁所承担的力R i表示为系数m i与轴重P的乘积(R i=m i×P),则m i称为第i号梁的荷载横向分布系数。
由此,1号梁的横向分布系数。
荷载所引起的各片主梁的内力大小(横向分布)与桥梁的构造特点、荷载的作用位置有关,因此求解荷载作用下各主梁的内力是一个空间问题,目前广泛采用的方法是将复杂的空间问题转化为平面问题。
本节将着重介绍几种横向分布系数的计算方法。
二、杠杆法基本原理:杠杆法忽略了主梁之间横向结构的联系作用,即假设桥面板在主梁上断开,把桥面板看作沿横向支承在主梁上的简支梁或悬臂梁。
如图3—2—1b所示,由于杠杆法忽略了主梁之间横向结构的联系作用,当桥上作用车道荷载时,左边的轮重P1/2仅传递给1号和2号梁,右边的轮重P1/2传递给2号梁和3号梁。
横向分布系数和偏载系数

一、 横向分布如图3—2—1a所示,梁桥的上部结构由承重结构(①~④号主梁)及传力结构(横隔梁、行车道板)两大部分组成,各片主梁靠横隔梁和行车道板连成空间整体结构,当桥上作用荷载(桥面板上作用2个车轴,前轴轴重为P1,后轴轴重为P2)时,各片主梁共同参与工作,形成了各片主梁之间的内力分布。
在计算恒载时,除主梁的自重外,一般将桥面铺装、人行道、栏杆等的重量近似平均分配给各片主梁,即计算出桥面铺装、人行道、栏杆等的总重量除以梁的片数(本例4片梁),得到每片主梁承担的桥面铺装、人行道、栏杆的重量。
由于人行道、栏杆等构件一般位于边梁上(①、④号主梁),精确计算时,也可考虑它们的重量在各梁间的分布,即中梁(②、③号主梁)也分担一部分人行道、栏杆的重量。
在计算活载时,需要考虑活载在各片主梁间的分布。
《标准》规定,车道荷载的横向分布系数应按设计车道数布置车辆荷载进行计算。
车辆荷载的横向布置如图3—2—1c所示。
对于车道荷载,最外车轮距人行道缘石之距不得小于0.5m,车道荷载的横向轮距为1.8m,两列车道荷载车轮的横向间距不得小于1.3m。
如图3—2—1b所示,在车道荷载的作用下,①号边梁所分担的荷载,也就是说,①号边梁所分担的荷载R1为轴重P1的。
若将第i号梁所承担的力R i表示为系数m i与轴重P的乘积(R i=m i×P),则m i称为第i号梁的荷载横向分布系数。
由此,1号梁的横向分布系数。
荷载所引起的各片主梁的内力大小(横向分布)与桥梁的构造特点、荷载的作用位置有关,因此求解荷载作用下各主梁的内力是一个空间问题,目前广泛采用的方法是将复杂的空间问题转化为平面问题。
本节将着重介绍几种横向分布系数的计算方法。
二、杠杆法基本原理:杠杆法忽略了主梁之间横向结构的联系作用,即假设桥面板在主梁上断开,把桥面板看作沿横向支承在主梁上的简支梁或悬臂梁。
如图3—2—1b所示,由于杠杆法忽略了主梁之间横向结构的联系作用,当桥上作用车道荷载时,左边的轮重P1/2仅传递给1号和2号梁,右边的轮重P1/2传递给2号梁和3号梁。
荷载横向分布影响线

荷载横向分布影响线1. 介绍荷载横向分布影响线是一种用于结构工程设计的分析方法,用于确定在结构上任意点的荷载影响分布。
该方法可以提供结构在承受荷载时的变形、应力和稳定性信息,对于结构的设计和评估至关重要。
本篇文章将对荷载横向分布影响线进行全面、详细、完整和深入的探讨。
2. 荷载横向分布影响线的基本原理荷载横向分布影响线的计算基于结构受到的集中荷载在结构上的传递规律。
该方法利用力学平衡和材料力学的基本原理,通过建立合适的数学模型来求解结构各部位的荷载作用。
3. 荷载横向分布影响线的计算步骤荷载横向分布影响线的计算步骤主要包括以下几个方面:3.1 初始条件的确定在进行荷载横向分布影响线的计算之前,需要确定结构的初始条件,包括结构的几何形状、材料特性、边界条件等。
这些初始条件将影响到计算结果的准确性和可靠性。
3.2 荷载传递方程的建立根据结构的几何形状、材料特性和边界条件,可以建立结构中各个部位的荷载传递方程。
这些方程可以描述结构在受到荷载作用时的变形和应力分布情况。
3.3 荷载横向分布影响线的计算根据荷载传递方程,可以求解结构上各点的荷载横向分布影响线。
这些影响线可以反映出结构在不同荷载作用下的荷载分布情况,从而为结构的设计和评估提供重要的依据。
3.4 结果的分析和评估根据计算得到的荷载横向分布影响线,可以对结构的变形、应力和稳定性进行分析和评估。
这些分析和评估结果可以用于指导结构的设计和优化,确保结构的安全性和可靠性。
4. 荷载横向分布影响线的应用领域荷载横向分布影响线的方法在各个结构工程领域有广泛的应用。
以下是一些常见的应用领域:4.1 桥梁设计荷载横向分布影响线可以用于桥梁结构的设计和评估。
通过分析桥梁在不同荷载作用下的荷载分布情况,可以确定合理的结构尺寸和截面形状,以满足设计要求。
4.2 建筑结构设计荷载横向分布影响线也可以应用于建筑结构的设计。
通过分析建筑结构在不同荷载作用下的荷载分布情况,可以确定合理的结构尺寸和材料使用,以确保建筑的稳定性和安全性。
荷载横向分布影响线

荷载横向分布影响线荷载横向分布影响线是指在桥梁设计中,考虑横向分布荷载对桥梁结构产生的影响时所绘制的一种图形。
该图形可以用于评估桥梁的承载能力,以及确定桥墩和支撑结构的位置和尺寸等重要参数。
一、荷载横向分布影响线的定义和作用1.1 定义荷载横向分布影响线是指在考虑桥梁承受横向分布荷载时,绘制出来的一种图形。
该图形可以显示出不同位置处的最大弯矩、最大剪力、最大轴力等参数,从而帮助工程师评估桥梁结构的承载能力。
1.2 作用荷载横向分布影响线可以帮助工程师确定桥墩和支撑结构的位置和尺寸等重要参数。
通过对不同位置处的最大弯矩、最大剪力、最大轴力等参数进行分析,可以确定合适的支撑结构类型和数量,并计算出所需材料的数量和尺寸。
二、荷载横向分布影响线的绘制方法2.1 横向分布荷载的计算在绘制荷载横向分布影响线之前,需要先计算出桥梁所承受的横向分布荷载。
这可以通过使用桥梁设计规范中提供的公式来完成。
一般来说,横向分布荷载是由车辆荷载和风荷载等因素共同作用产生的。
2.2 荷载影响线的绘制绘制荷载横向分布影响线时,需要先确定一条基准线,并在该基准线上标出桥墩和支撑结构的位置。
根据不同位置处的最大弯矩、最大剪力、最大轴力等参数,在基准线上画出对应的影响线。
在绘制影响线时,需要注意以下几点:(1)弯矩和剪力应该按照正负号进行区分,并在图中标明。
(2)轴力一般只在两端点处存在,因此只需在两端点处画出对应的影响线即可。
(3)为了使影响线更加清晰易读,可以使用不同颜色或不同类型的曲线进行标识。
三、荷载横向分布影响线的应用实例为了更好地理解荷载横向分布影响线的应用,下面以一座简单的跨径为10米的桥梁为例进行说明。
3.1 计算横向分布荷载假设该桥梁承受的车辆荷载为20吨,风荷载为5吨,则该桥梁所承受的总横向分布荷载为25吨。
3.2 绘制荷载影响线在基准线上标出两个桥墩和两个支撑结构的位置,然后根据不同位置处的最大弯矩、最大剪力、最大轴力等参数,在基准线上画出对应的影响线。
桥博中横向分布系数取值详细介绍

桥博中横向分布系数取值详细介绍关于横向分布调整系数:一、对于桥梁的纵向计算:a)汽车荷载1.整体结构,如整体箱梁和整体板梁其分布调整系数就是其所承受的汽车总列数,考虑纵横向折减、偏载后的修正值。
例如,对于一个跨度为230米的桥面4车道的整体箱梁验算时,其横向分布系数应为4x0.67(四车道的横向折减系数)x1.15(经计算而得的偏载系数)x0.97(大跨径的纵向折减系数)=2.990。
汽车的横向分布系数已经包含了汽车车道数的影响。
2.当选择一根梁计算多根梁时按桥工书中的几种算法计算即可,也可用程序自带的横向分布计算工具来算。
计算时中梁边梁分别建模计算,中梁取横向分布系数最大的那片中梁来建模计算。
b)人群荷载1.整体结构,如整体箱梁和整体板梁人群集度,人行道宽度,公路荷载填所建模型的人行道总宽度,横向分布系数填1即可。
因为在桥博中人群效应=人群集度x人行道宽度x人群横向分布调整系数。
城市荷载填所建模型的单侧人行道宽度,若为双侧人行道且宽度相等,横向分布系数填2,因为城市荷载的人群集度要根据人行道宽度计算。
2多片梁取一片梁计算时人群集度按实际的填写,横向分布调整系数按求得的横向分布系数填写,一般算横向分布时,人行道宽度已经考虑了,所以人行道宽度填1。
c)满人荷载1.整体结构,如整体箱梁和整体板梁满人宽度填所建模型扣除所有护栏的宽度,横向分布调整系数填1。
与人群荷载不同,城市荷载不对满人的人群集度折减。
2多片梁取一片梁计算时全宽填入1,水平分布调整系数填入。
注:1、由于最终效应:人群效应=人群集中度x人行道宽度x人群水平分布调整系数。
全人口效应=人口集中度x全人口总宽度x全人口水平分布调整系数。
所以,关于两项的一些参数,也并非一定按上述要求填写,只要保证几项参数乘积不变,也可按其他方式填写。
2.无特殊规范和新要求。
因此,该程序不对满载条件进行任何设计校核计算。
如果用户需要检查满载,他们可以自定义组合。
桥梁工程荷载横向分布计算简介

2、横向分布系数(m)的概念:
• 多片式梁桥,在横向分布影响线上用规范规定的车轮 横向间距按最不利位置加载
说明:1)近似计算方法,但对直线梁桥,误差不大
2)不同梁,不同荷载类型,不同荷载纵向位置, 不同横向连接刚度,m不同。
3、横向连结刚度对荷载横向分布的影响
结论:横向分布的规律与结构横向连结刚度关系密切,
根据表中的横向影响线坐 标值绘制影响线图
公路-I级
七、横向分布系数沿桥纵向的变化
•对于弯矩
由于跨中截面车轮加载值占总荷载的绝大多数,近 似认为其它截面的横向分布系数与跨中相同
•对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
计算剪力时横向分布沿桥纵向的变化
横向分布系数
横向分布系数 :在横向分布影响线上加载
3. 铰接梁法
假定各主梁除刚体 位移外,还存在截 面本身的变形
与铰接板法的区别:变位系数中增加桥面板变形项
4.刚接梁法
假定各主梁间除传递剪力外,还传递弯矩
与铰接板、梁的区别: 未知数增加一倍,力法方程数增加一倍
5 .铰接板桥计算m举例:
如图所示,l=12.60m的铰接空心板桥横截面布置。 桥面净空为净-7+2x0.75m人行道。全桥由9块预应力混凝 土空心板组成,欲求1、3、5号板的公路-I级和人群荷载作用 的跨中横向分布系数?
值(ki)
1 ai ak 若各梁截面尺寸相同: ki Rki Rik n n 2 ai
i 1
(三) 计算举例
例2-5-3: 已知:l=19.50m,荷载位于跨中 试求:1#边梁,2#中梁的mcq,mcr
作业
已知:l=29.16m, 38.88m,荷载位于跨中时 试求:2#中梁的mcq,mcr
荷载横向分布系数的计算

适用情况 ①只有邻近两根主梁参与受力 ②虽为多主梁,但计算梁端支承处荷载 ③无中间横隔梁
2、荷载横向分布系数的计算方法
(1)杠杆分配法
作业1:画 及出单3车、辆4荷号载梁作的用荷下载3横、向4分号布梁影荷响载线横,向
0.75m
分布系数 7m
0.75m
1
2 2m
3
4
(2)刚性横梁法(偏心受压法) 假定 ①横梁是刚性的:宽跨比B/l≤0.5 ②忽略主梁抗扭刚度
▪ 该方法视梁系为超静定结构,用力法求解, 适用于翼缘板之间是刚性连接的肋梁桥。
④ 比拟正交异性板法(G-M法)
▪ 适用情况:对于由主梁、连续桥面板及多根横隔板 组成的钢筋混凝土桥中,当其宽跨比>1/2。
▪ 每根主梁的截面抗弯惯矩和抗扭惯矩分别为Ix、ITx, 横隔梁的截面抗弯惯矩和抗扭惯矩分别为Iy、ITy。
▪ 三、荷载横向分布的计算
5、荷载在顺桥跨不同位置时主梁荷载横向分布系数 的取值
荷载在桥跨纵向作用位置不同,对某一主梁产生 的横向分布系数也不同。
处理方法:通常用杠杆原理法确定支点处的横向 分布系数m0,用其他各方法计算荷载位于跨中的横 向分布系数mc。
▪ 三、荷载横向分布的计算
5、荷载在顺桥跨不同位置时主梁荷载横向分布系数 的取值
荷载横向分布系数:
ηki
Ik
n
β ak Ike n
Ii
ai2 Ii
i 1
i 1
修正系数:
β
1
1 Gl2
12E
1 ITi ai2 I i
竖向反力与扭矩的关系
转动时的扭矩平衡
e、ai
同侧取正号, 异侧取负号
C4桥梁荷载横向分布影响线计算

1154 梁桥荷载横向分布影响线计算梁桥荷载横向分布计算的方法,有杠杆法、偏心压力法、铰接板(梁)法、刚接板(梁)法、比拟正交异性板法等。
其中杠杆法和偏心压力法公式简单,便于手算,而后几种方法则复杂些。
一般采用查图、表的方法。
由于计算机的发展带来设计手段的更新,这些图、表完全可以用电算来替换。
本章介绍常用的铰接板(梁)法和比拟正交异性板法(G-M 法)的电算方法。
4.1 铰接板(梁)法4.1.1 计算公式该方法适用于铰接板桥、不设中间横隔梁的T 梁桥。
基本假定:假定荷载沿纵向按半波正弦分布,则各根主梁的挠曲线也将是半波正弦曲线,它们所分配到的荷载也是具有不同峰值的半波正弦荷载,因此,我们可以在跨中取出一单位长,•并以半波正弦的峰值代表整个荷载或内力来分析横向分布问题(图4-1)。
在《桥梁工程》中推导了各片梁(板)刚度相同时求解铰缝处内力的正则方程,•下面对各梁(板)刚度不相同的更一般情况作正则方程的推导。
先推导铰接梁桥的正则方程。
取荷载峰值1=P ,铰缝(图4-1的结点)处只有剪力i g ,于是考虑i 号结点的变形协调条件,得:011,,11,=∆+⋅+⋅+⋅++--i i i i i i i i i i g g g δδδ(4-1)当1=i 时,无11,--⋅i i i g δ项; 当1-=m i 时,无11,++⋅i i i g δ项。
上式中1,-i i δ、i i ,δ、1,+i i δ为柔度系数,它们分别表示1-i g 、i g 、1+i g 等于1时在i 结点处引起的位移;i ∆为单位力1=P 在i 结点引起的位移。
在计算柔度系数时,用到如表4-1中的各个变形量。
116 表中:i EI 为(i 号梁的)抗弯刚度;Ti GI 为抗扭刚度;i i i di d h h I ,;123=见图4-2。
根据图4-1和表4-1,可写出各柔度系数为:1~12,22212111,112121,21,-⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=⋅⎪⎭⎫⎝⎛+-=++⋅⎪⎭⎫⎝⎛+⋅⎪⎭⎫ ⎝⎛++=⋅⎪⎭⎫ ⎝⎛+-=++++++++-m i b w f f b b w w b w i i i i i i i i i i i i i i i ii i i i φδφφδφδ(4-2)对每一结点按式(4-1)列出方程,得力法的正则方程式:[]{}{}0=∆+g A (4-3)令{}{}∆-=B ,得:[]{}{}B g A = (4-4)式中:[]A 为柔度矩阵,它是一对称的带状矩阵;{}B 为与荷载作用位置有关的变位项。
荷载横向分布系数的计算

2、荷载横向分布系数的计算方法 ▪ 荷载横向分布影响线:P=1在梁上横向移动时,
某主梁所相应分配到的不同的荷载作用力。 ▪ 对荷载横向分布影响线进行最不利加载Pi,
可求得某主梁可行最大荷载力
▪ 荷载横向分布系数:将Pi除以车辆轴重。
2、荷载横向分布系数的计算方法 (1)杠杆分配法
基本假定:忽略主梁之间横向结构的联系,假设桥面 板在主梁上断开并与主梁铰接,把桥面板视作横向支 承在主梁上的简支板或带悬臂的简支板
'' i
ai
tan
由 Ri '' Iii ''
Ri '' tanai Ii ai Ii
n
有
Ri ''ai ai2Ii 1 e
i 1
Ri ''
ai Iie
n
ai2Ii
i 1
(2)刚性横梁法
则偏心力P作用下,每片主梁分配的荷载为:
Ri Ri' Ri''
Ii
n
Ii
i 1
▪ 计算假设: ①铰式键只传递竖
荷载横向分布影响线为三角形
适用情况 ①只有邻近两根主梁参与受力 ②虽为多主梁,但计算梁端支承处荷载 ③无中间横隔梁
2、荷载横向分布系数的计算方法
(1)杠杆分配法
作业1:画 及出单3车、辆4荷号载梁作的用荷下载3横、向4分号布梁影荷响载线横,向
0.75m
分布系数 7m
0.75m
1
2 2m
3
4
(2)刚性横梁法(偏心受压法) 假定 ①横梁是刚性的:宽跨比B/l≤0.5 ②忽略主梁抗扭刚度
P/2
P/2 P/2
横向分布系数计算(多种方法计算)

2
150 (14 8) 18 130
38.2
2
y2 y y1 130 38.2 91.8
抗弯惯矩 I 为:
I
1
cy
3 2
by
3 1
(b
c)( y1
d )3
1 18 91.8 3 150 38.2 3 (150 18)( 38.2 11) 3
3
3
主梁的比拟单宽抗弯惯矩
J x I x 6543 103 43620cm4 / cm
P227 附录Ⅱ的精度也达不到小数点后两
位,所以仍用 θ =0.324 的 K1 和 K 0 计算:(见下表)
0.425E 275 103
2
19.5
1 1.042 E 6543 103 1.5 5
0.875
3 计算荷载横向影响线a12 ai2
0.55
1
15
n
a12 ai2
0.15
由 11 和 15 绘制荷载作用在 1 号梁上的影响线如上图所示,图中根据《公路桥涵设计
通用规范》 ( JTG D60-2004 )规定,在横向影响线上确定荷载沿横向最不利布置位置。
I y 3320 103
JY
a
485
( 3 )主梁和横隔梁的抗扭惯矩
6640cm4 / cm
对于 T 型翼板刚性连接的情况,应由式
2-5-74 来确定。
对于主梁梁肋:
主梁翼板的平均厚度:
h1 14 8 11cm 2
tb
18
0.151 ,由表 2-5-2 查得 c=0.300
130 11
t/b
1
0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
钢筋混凝土梁式桥的荷载横向分布影响线及横向分布系数.

荷载横向分布影响线及横向分布系数假设各构件处于弹性工作阶段,上部结构由若干个等截面构件组成,铰仅承受竖向剪力(图1)。
图1铰接板受力分析当单位荷载p=1作用在构件i 时,各构件(n i i i ,1,,,2,1+=')均受力,各构件实际受到的作用力称为单位荷载横向分布值。
如p=1作用在构件1时,构件1受到的作用力为,1111Q -=η,由静力平衡可知:5451434132312121Q Q Q Q Q Q Q Q -=-=-=-=ηηηη (1)式中 ηij —单位荷载作用于构件j 时,i 构件的单位荷载横向分布值; i —构件序号; j —荷载所在构件序号;Qi —构件i 与构件i+1间铰接处剪力;由于弹性变位与荷载大小成正比,按照弹性变位互等定理有:,2112ηη= ,3113ηη= 4114ηη=,5115ηη=,则上式又可写成:1111Q -=ηQ Q -=112η3213Q Q -=η (2)4314Q Q -=η 5415Q Q -=η式中的η11、η12、η13、η14、η15 即单位荷载作用于1、2、3、4、5构件时,1号构件在横向分配到的荷载。
如将η11、η12。
按比例画在各构件的基线中心,将各点连成直线,即为构件1的荷载横向分布影响线,如图2。
图2铰接板桥的荷载分布影响线欲求ηij 值需先求出铰接处的剪力Qi 。
Qi 与构件的抗弯刚度和抗扭刚度的比值γ有关。
比值 γ 可用下式表示:21)(8.5l b I I n =γ ( 3)式中 I ——构件截面抗弯惯性矩 In ――构件截面抗扭惯性矩 b1――构件的宽度 l ——构件的计算跨度 对于矩形截面实心板,γ值按下式计:22107.2l b βγ=(4)式中 β――与截面形状有关的系数,可查表8-5。
表8-5 β系数表b /h 1.0 1.2 1.5 1.75 2.0 2.5 3.0 4.0 6.0 8.0 10.0 ≥10 β0.1410.1660.1960.2140.2290.2490.2630.2810.2990.3070.3120.333对于矩形截面空心板,常用的有箱形和开洞矩形截面(图3)。
桥梁工程课程设计--荷载横向分布系数计算
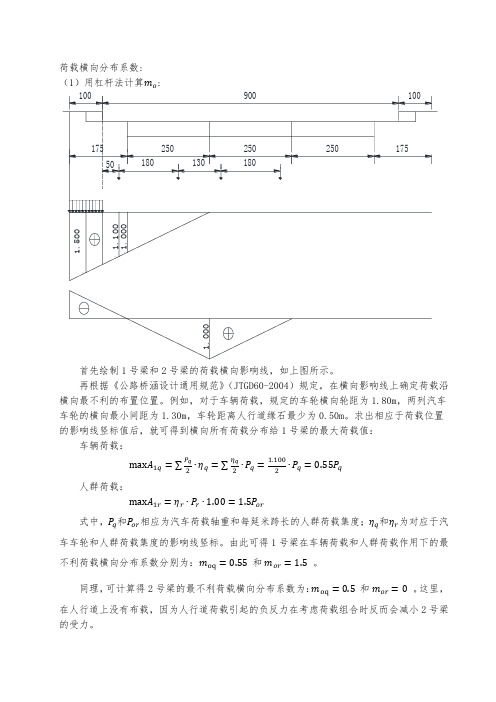
解得:
零点位置已知后,就可求出各类荷载相应于各个荷载位置的横向影响线竖标值 和 。
设行人道缘石至1号梁轴线的距离为 ,则:
于是,1号梁的荷载横向分布系数可以计算如下(以 分别表示影响线零点至汽车车轮和人群荷载集度的横坐标距离):
车辆荷载:
人群荷载值为:
由 和 绘制1号梁横向影响线,如下图所示,图中按《公路桥涵设计通用规范》(JTG D60-2004)规定确定了汽车荷载的最不利荷载位置。
进而由 和 计算横向影响线的零点位置,在本梁中,零点至2号梁的距离
零点位置已知后,就可求出各类荷载相应于各个荷载位置的横向影响线竖标值 和 。
2
跨中
0.900
0.520
支点
0.500
0
3
跨中
0.900
0.520
支点
0.500
0
4
跨中
0.749
0.783
支点
0.550
1.500
荷载横向分布系数:
(1)用杠杆法计算 :
首先绘制1号梁和2号梁的荷载横向影响线,如上图所示。
再根据《公路桥涵设计通用规范》(JTGD60-2004)规定,在横向影响线上确定荷载沿横向最不利的布置位置。例如,对于车辆荷载,规定的车轮横向轮距为1.80m,两列汽车车轮的横向最小间距为1.30m,车轮距离人行道缘石最少为0.50m。求出相应于荷载位置的影响线竖标值后,就可得到横向所有荷载分布给1号梁的最大荷载值:
车辆荷载:
人群荷载:
式中, 相应为汽车荷载轴重和每延米跨长的人群荷载集度; 为对应于汽车车轮和人群荷载集度的影响线竖标。由此可得1号梁在车辆荷载和人群荷载作用下的最不利荷载横向分布系数分别为: 。
横向影响线竖坐标表(精品)

附录 铰接板荷载横向分布影响线竖坐标表说明:1. 本表适用于横向铰接的梁或板,各片梁或板的截面是相同的;2. 表头的两个数字表示所要查的梁或板号,其中第一个数目表示该梁或板是属于几片梁或板铰接而成的体系,第二个数目表示该片梁或板在这个体系中自左而右的序号;3. 横向分布影响线竖坐标以ηij 表示,第一个脚标i 表示所要求的梁或板号,第二个脚标j表示受单位荷载作用的那片梁或板号,表中ηij 下的数字前者表示i ,后者表示j ,ηij 的竖坐标应绘在梁或板的中轴线处;4. 表中的ηij 值为小数点后的三位数字,例如278即为0.278,006即为0.006; 5. 表值按弯扭参数γ给出2)(8.5lb I I T =γ 式中: l ——计算跨径; b ——一片梁或板的宽度; I ——梁或板的抗弯惯矩; I T ——梁或板的抗扭惯矩。
铰接板 3-1ηij ηij ηij γ111213γ11 12 13 γ111213 0.00 333 333 333 0.084343252410.40626 294 080 0.01 348 332 319 0.104543232230.60683 278 040 0.02 363 331 306 0.15496317186 1.00750 2500000.04 389 329 282 0.20531313156 2.00829 200 -029 0.06 413 327 260 0.30585303112铰接板 3-2ηij ηij ηij γ212223γ2122 23 γ2122230.00 333 333 333 0.0832********.40294 412 294 0.01 332 336 332 0.103233553230.60278 444 278 0.02 331 338 331 0.153******** 1.00250 500 250 0.04 329 342 329 0.20313375313 2.00200 600 200 0.06327 346 3270.30303394303铰接板 4-1ηijηijγ1112 13 14 γ111213 14 0.00 250250 250 250 0.15484295139 082 0.01 276257 238 229 0.20524298119 060 0.02 300263 227 210 0.30583296089 033 0.04 341273 208 178 0.40625291066 018 0.06 375280 192 153 0.60682277035 005 0.08 405285 178 132 1.00750250000 000 0.10 4312891651142.00828201-034005铰接板 4-2ηij ηijγ212223 24 γ212223 24 0.00 250 250 250 250 0.152******** 139 0.01 257 257 248 238 0.20298345238 119 0.02 263 264 246 227 0.30296375240 089 0.04 273 276 243 208 0.40291400243 066 0.06 280 287 241 192 0.60277441247 035 0.08 285 298 239 178 1.00250500250 000 0.10 289 3072391652.00201593240-034铰接板 5-1ηij ηijγ11121314 15γ111213 14 15 0.00 200 200 200 200 2000.15481291130 061 036 0.01 237 216 194 180 1730.20523295114 045 023 0.02 269 229 188 163 1510.30583296087 026 010 0.04 321 249 178 136 1160.40625291066 015 004 0.06 362 263 168 115 0920.60682277035 004 001 0.08 396 273 158 099 073 1.00750250000 000 000 0.10 425 281 1500850592.00828201-034006-001ηij ηijγ21222324 25γ212223 24 25 0.00 200 200 200 200 2000.15291320222105 061 0.01 216 215 202 187 1800.20295341227091 045 0.02 229 228 204 176 1630.30296374235070 026 0.04 249 249 207 158 1360.40291399240055 015 0.06 263 267 211 144 1150.60277440246031 004 0.08 273 281 214 133 099 1.00250500250000 000 0.10 281 294 2161230852.00201593241-041006铰接板 5-3ηij ηijγ31323334 35γ313233 34 35 0.00 200 200 200 200 2000.15130222295222 130 0.01 194 202 208 202 1940.20114227318227 114 0.02 188 204 215 204 1880.30087235357235 087 0.04 178 207 230 207 1780.40066240389240 066 0.06 168 211 243 211 1680.60035246437246 035 0.08 158 214 256 214 158 1.00000250500250 000 0.10 150 216 2682161502.00-034241586241-034铰接板 6-1ηij ηijγ111213141516γ111213 1415160.00 167 167167 167 1671670.15481290129058 027 0160.01 214 192168 151 1401350.20523295113043 010 0090.02 252 212168 138 1191100.30583295086025 008 0030.04 312 239165 117 0900770.40625291065015 003 0010.06 358 257159 101 0690550.60682277035004 001 0000.08 394 270152 088 055041 1.00750250000000 000 0000.10 423 278146 078 0440312.00828201-034006 -001 009ηijηijγ21222324 25 26 γ2122 23 24 25 26 0.00 167 167 167 167 1671670.15290319219098 046 027 0.01 192 190 175 157 1461400.20295340226087 035 017 0.02 212 209 182 149 1291190.30295373234069 021 008 0.04 239 238 192 137 1050900.40291399240054 012 003 0.06 257 259 200 127 0870690.60277440246031 004 001 0.08 270 276 206119074055 1.002505002500000000000.10 278 291 210 112 0640442.00201593241-041 007 -001铰接板 6-3ηijηijγ31323334 35 36 γ3132 33 34 35 36 0.00 167 167 167 167 1671670.15129219288208 098 0580.01 168 175 179 170 1571510.20113226314217 087 0430.02 168 182 190 173 1491380.30086234356230 069 0250.04 165 192 210 179 1371170.40065240388238 054 0150.06 159 200 227 186 1271010.60035246437246 031 0040.08 152 206 243 191 119088 1.000002505002500000000.10 146 210 2571971120782.00-034241586243 -041 006铰接板 7-1ηij ηijγ11121314151617γ111213 141516170.00 143 143 143143 143 1431430.15480290128057 025 *******.01 200 177 152133 120 1111070.20523295113043 017 0070030.02 244 202 157125 102 0880820.30583295086025 007 0020010.04 309 235 159109 078 0590510.40625291065015 003 0010000.06 356 255 156096 061 0420340.60628277035004 001 0000000.08 293 268 151085 049 031023 1.00750250000000 000 0000000.10 423 278 144076 040 0230162.00828201-034006 -001 000000ηij ηijγ21222324252627γ212223242526270.00 143 143 143143 143 1431430.15290318219097 043 020 0120.01 177 175 158139 125 1151110.20295340225086 033 013 0070.02 202 198 170135 111 0960880.30295373234068 020 006 0020.04 235 232 185127 091 0690590.40291399240054 012 003 0010.06 255 256 196121 077 0530420.60277440246031 004 001 0000.08 268 275 203115 067 041031 1.00250500250000 000 000 0000.10 278 290 209109 058 0330232.00201593241-041 007 -001000铰接板 7-3ηij ηijγ31323334353637γ313233343536370.00 143 143 143143 143 1431430.15128219287205 092 043 0250.01 152 158 161150 134 1251200.20113225314216 083 033 0170.02 157 170 176156 128 1111020.30086234356229 067 020 0070.04 159 185 201167 119 0910780.40065240388237 053 012 0030.06 156 196 222176 112 0770610.60035246437246 031 004 0010.08 151 203 239184 107 067049 1.00000250500250 000 000 0000.10 144 209 255191 102 0580402.00-034241586243 -042 007 -001铰接板 7-4ηij ηijγ41424344454647γ4142 43444546470.00 143 143 143143 143 1431430.15057097205282 205 097 0570.01 133 139 150157 150 1391330.20043086216310 216 086 0430.02 125 135 156169 156 1351250.30025068229354 229 068 0250.04 109 127 167193 167 1271090.40015054237387 237 054 0150.06 096 121 176213 176 1210960.60004031246436 246 031 0040.08 085 115 184231 184 115085 1.00000000250500 250 000 0000.10 076 109 191248 191 1090762.00006-041243586 243 -041006ηijγ11 12 13 14 15 16 17 18 0.00 125 125 125 125 125 125 125 125 0.01 191 168 142 122 107 096 089 085 0.02 239 197 151 117 093 076 066 061 0.04 307 233 156 106 073 052 040 034 0.06 355 254 155 094 058 037 025 020 0.08 392 268 150 084 048 028 017 013 0.10 423 277 144 075 039 021 012 008 0.15 480 290 128 057 025 011 005 003 0.20 523 295 113 043 016 006 003 001 0.30 583 295 086 025 007 002 001 000 0.40 625 291 065 015 003 001 000 0000.60 682 277 035 004 001 000 000 0001.00 750 250 000 000 000 000 000 0002.00 828 201 -034 006 -001 000 000 000铰接板8-2ηijγ21 22 23 24 25 26 27 28 0.00 125 125 125 125 125 125 125 125 0.01 168 165 148 127 111 100 092 089 0.02 197 193 163 127 101 083 071 066 0.04 233 230 182 123 085 060 046 040 0.06 254 255 194 119 073 047 032 025 0.08 268 274 202 113 064 037 023 017 0.10 277 290 208 108 057 030 017 012 0.15 290 318 219 097 043 019 009 005 0.20 295 340 225 086 033 013 005 003 0.30 295 373 234 068 020 006 002 001 0.40 291 399 240 054 012 003 001 0000.60 277 440 246 031 004 001 000 0001.00 250 500 250 000 000 000 000 0002.00 201 593 241 -041 007 -001 000 000铰接板8-3γηij31 32 33 34 35 36 37 38 0.00 125 125 125 125 125 125 125 125 0.01 142 148 150 137 120 108 100 096 0.02 151 163 168 147 116 096 083 076 0.04 156 182 197 162 111 079 060 052 0.06 155 194 219 173 107 068 047 037 0.08 150 202 238 182 103 060 037 028 0.10 144 208 254 190 099 053 030 021 0.15 128 219 287 205 091 041 019 011 0.20 113 225 314 215 082 032 013 006 0.30 086 234 356 229 067 020 006 002 0.40 065 240 388 237 053 012 003 0010.60 035 246 437 246 031 004 001 0001.00 000 250 500 250 000 000 000 0002.00 -034 241 586 243 -042 007 -001 000铰接板8-4γηij41 42 43 44 45 46 47 48 0.00 125 125 125 125 125 125 125 125 0.01 122 127 137 143 134 120 111 107 0.02 117 127 147 158 142 116 101 093 0.04 106 123 162 185 156 111 085 073 0.06 094 119 173 208 168 107 073 058 0.08 084 113 182 227 178 103 064 048 0.10 075 108 190 245 186 099 057 039 0.15 057 097 205 281 203 091 043 025 0.20 043 086 215 310 214 082 033 016 0.30 025 068 229 354 229 067 020 007 0.40 015 054 237 387 237 053 012 0030.60 004 031 246 436 246 031 004 0011.00 000 000 250 500 250 000 000 0002.00 006 -041 243 586 243 -042 007 -00铰接板9-1γηij11 12 13 14 15 16 17 18 19 0.00 111 111 111 111 111 111 111 111 111 0.01 185 162 136 115 098 086 077 072 069 0.02 236 194 147 113 088 070 057 049 046 0.04 306 232 155 104 070 048 035 026 023 0.06 355 254 154 094 057 035 023 015 012 0.08 392 268 150 084 047 027 015 010 007 0.10 423 277 144 075 039 020 011 006 004 0.15 480 290 128 057 025 011 005 002 001 0.20 523 295 113 043 016 006 002 001 000 0.30 583 295 086 025 007 002 001 000 000 0.40 625 291 065 015 003 001 000 000 0000.60 682 277 035 004 001 000 000 000 0001.00 750 250 000 000 000 000 000 000 0002.00 828 201 -034 006 -001 000 000 000 000铰接板9-2γηij21 22 23 24 25 26 27 28 29 0.00 111 111 111 111 111 111 111 111 111 0.01 162 158 141 119 102 090 081 075 072 0.02 194 189 160 122 095 075 062 053 049 0.04 232 229 181 121 082 057 040 031 026 0.06 254 255 194 118 072 044 028 019 015 0.08 268 274 202 113 063 036 021 013 010 0.10 277 290 208 108 056 029 016 009 006 0.15 290 318 219 097 043 019 008 004 002 0.20 295 340 225 086 033 013 005 002 001 0.30 295 373 234 068 020 006 002 001 000 0.40 291 399 240 054 012 003 001 000 0000.60 277 440 246 031 004 001 000 000 0001.00 250 500 250 000 000 000 000 000 0002.00 201 593 241 -041 007 -001 000 000 000铰接板9-3γηij31 32 33 34 35 36 37 38 39 0.00 111 111 111 111 111 111 111 111 111 0.01 136 141 142 129 111 097 087 081 077 0.02 147 160 164 141 110 087 072 062 057 0.04 155 181 195 159 108 074 053 040 035 0.06 154 194 219 172 105 065 041 028 023 0.08 150 202 237 182 102 058 033 021 015 0.10 144 208 254 190 099 052 028 016 011 0.15 128 219 287 205 090 040 018 008 005 0.20 113 225 314 215 082 031 012 005 002 0.30 086 234 356 229 067 020 006 002 001 0.40 065 240 388 237 053 012 003 001 0000.60 035 246 431 246 031 004 001 000 0001.00 000 250 500 250 000 000 000 000 0002.00 -034 240 586 243 -042 007 -001 000 000铰接板9-4γηij41 42 43 44 45 46 47 48 49 0.00 111 111 111 111 111 111 111 111 111 0.01 115 119 129 133 123 108 097 090 086 0.02 113 122 141 152 134 106 087 075 070 0.04 104 121 159 182 151 104 074 057 048 0.06 094 118 172 206 165 102 065 044 035 0.08 084 113 182 226 176 099 058 036 027 0.10 075 108 190 244 185 097 052 029 020 0.15 057 097 205 281 202 089 040 019 011 0.20 043 086 215 310 214 082 031 013 006 0.30 025 068 229 354 229 067 020 006 002 0.40 015 054 237 387 237 053 012 003 0010.60 004 031 246 436 246 031 004 001 0001.00 000 000 250 500 250 000 000 000 0002.00 006 -041 243 586 243 -042 007 -001 000铰接板9-5γηij51 52 53 54 55 56 57 58 59 0.00 111 111 111 111 111 111 111 111 111 0.01 098 102 111 123 131 123 111 102 098 0.02 088 095 110 134 148 134 110 095 088 0.04 070 082 108 151 178 151 108 082 070 0.06 057 072 105 165 203 165 105 072 057 0.08 047 063 102 176 224 176 102 063 047 0.10 039 056 099 185 242 185 099 056 039 0.15 025 043 090 202 280 202 090 043 025 0.20 016 033 082 214 309 214 082 033 016 0.30 007 020 067 229 354 229 067 020 007 0.40 003 012 053 237 387 237 053 012 0030.60 001 004 031 246 436 246 031 004 0011.00 000 000 000 250 500 250 000 000 0002.00 -001 007 -042 243 586 243 -042 007 -001铰接板10-1γηij11 12 13 14 15 16 17 18 19 1,10 0.00 100 100 100 100 100 100 100 100 100 100 0.01 181 158 131 110 093 080 070 063 058 056 0.02 234 192 146 111 085 066 052 043 037 034 0.04 306 232 155 103 069 047 032 023 018 015 0.06 355 254 154 094 057 035 021 014 009 007 0.08 392 268 150 084 047 026 015 009 005 002 0.10 423 277 144 075 039 020 011 006 003 001 0.15 480 290 128 057 025 011 005 002 001 000 0.20 523 295 113 043 016 006 002 001 000 000 0.30 583 295 086 025 007 002 001 000 000 000 0.40 625 291 065 015 003 001 000 000 000 0000.60 682 277 035 004 001 000 000 000 000 0001.00 750 250 000 000 000 000 000 000 000 0002.00 828 201 -034 006 -001 000 000 000 000 000铰接板10-2γηij21 22 23 24 25 26 27 28 29 2,10 0.00 100 100 100 100 100 100 100 100 100 100 0.01 158 154 137 114 097 083 073 065 060 058 0.02 192 188 157 120 092 071 056 046 040 037 0.04 232 229 181 121 081 055 038 027 020 018 0.06 254 255 193 117 071 044 027 017 012 009 0.08 268 274 202 113 063 035 020 012 007 005 0.10 277 290 208 108 056 029 015 008 005 003 0.15 290 318 219 097 043 019 008 004 002 001 0.20 295 340 225 086 033 013 005 002 001 000 0.30 295 373 234 068 020 006 002 001 000 000 0.40 291 399 240 054 012 003 001 000 000 0000.60 277 440 246 031 004 001 000 000 000 0001.00 250 200 250 000 000 000 000 000 000 0002.00 201 293 241 -041 007 -001 000 000 000 000铰接板10-3γηij31 32 33 34 35 36 37 38 39 3,10 0.00 100 100 100 100 100 100 100 100 100 100 0.01 131 137 137 123 104 090 078 070 065 063 0.02 146 157 162 138 106 082 065 054 046 043 0.04 155 181 195 158 106 072 049 035 027 023 0.06 154 193 218 171 104 064 039 025 017 014 0.08 150 202 237 181 101 057 032 019 012 009 0.10 144 208 254 189 098 051 027 014 008 006 0.15 128 219 287 205 090 040 018 008 004 002 0.20 113 225 314 215 082 031 012 005 002 001 0.30 086 234 356 229 067 020 006 002 001 000 0.40 065 240 388 237 053 012 003 001 000 0000.60 035 246 437 246 031 004 001 000 000 0001.00 000 250 500 250 000 000 000 000 000 0002.00 -034 241 586 243 -042 007 -001 000 000 000铰接板10-4γηij41 42 43 44 45 46 47 48 49 4,10 0.00 100 100 100 100 100 100 100 100 100 100 0.01 110 114 123 127 116 100 087 078 073 070 0.02 111 120 138 148 129 100 080 065 056 052 0.04 103 121 158 180 149 101 069 049 038 032 0.06 094 117 171 205 163 100 062 039 027 021 0.08 084 113 181 226 175 098 056 032 020 015 0.10 075 108 189 244 185 096 050 027 015 011 0.15 057 097 205 281 202 089 040 018 008 005 0.20 043 086 215 310 214 082 031 012 005 002 0.30 025 068 229 354 229 067 020 006 002 001 0.40 015 054 237 387 237 053 012 003 001 0000.60 004 031 246 436 246 031 004 001 000 0001.00 000 000 250 500 250 000 000 000 000 0002.00 006 -041 243 586 243 -042 007 -001 000 000铰接板10-5γηij51 52 53 54 55 56 57 58 59 5,10 0.00 100 100 100 100 100 100 100 100 100 100 0.01 093 097 104 116 123 114 100 090 083 080 0.02 085 092 106 129 142 126 100 082 071 066 0.04 069 081 106 149 175 146 101 072 055 047 0.06 057 071 104 163 201 162 100 064 044 035 0.08 047 063 101 175 223 174 098 057 035 026 0.10 039 056 098 185 241 184 096 051 029 020 0.15 025 043 090 202 280 201 089 040 019 011 0.20 016 033 082 214 309 214 082 031 013 006 0.30 007 020 067 229 354 229 067 020 006 002 0.40 003 012 053 237 387 237 053 012 003 0010.60 001 004 031 246 436 246 031 004 001 0001.00 000 000 000 250 500 250 000 000 000 0002.00 -001 007 -042 243 586 243 -042 007 -001 000。
刚性横梁法计算桥梁荷载横向分布系数

可以结合实际工程情况,对刚性横梁法进行改进和调整,以更好地满 足实际需求。
此外,还可以将刚性横梁法与其他数值分析方法进行比较和结合,以 实现优势互补,提高整体计算效果。
感谢观看
THANKS
优点
计算简单
刚性横梁法是一种简化的计算方 法,其计算过程相对简单,易于 理解和实现。
适用性强
该方法适用于多种类型的桥梁, 特别是主梁间距较小、横截面形 式一致的桥梁。
精度满足要求
对于许多实际工程,刚性横梁法 的计算精度已经足够满足需求, 能够提供较为准确的横向分布系 数。
缺点
1 2
假设限制
刚性横梁法基于一系列假设,如横梁的刚性、横 梁之间的无转角等,这些假设可能与实际情况存 在偏差。
刚度计算
根据桥梁的结构形式和材 料特性,通过计算或试验 确定横梁的弹性模量和截 面惯性矩。
刚度分类
根据刚度大小,可分为刚 性横梁和柔性横梁,刚性 横梁在受力时变形较小, 而柔性横梁则变形较大。
计算横向分布影响线
影响线定义
横向分布影响线是指在桥 梁上施加单位力时,各横 梁上反力分布的图形。
影响线计算
桥梁荷载横向分布系数的定义
01
桥梁荷载横向分布系数是指桥梁 承受的荷载在各横向分布位置的 分布情况,是衡量桥梁承载能力 和稳定性的重要指标。
02
横向分布系数的计算方法有多种 ,其中刚性横梁法是一种常用的 方法,适用于等跨径的桥梁。
02
刚性横梁法的基本原理
刚性横梁法的概念
刚性横梁法是一种计算桥梁荷载横向 分布系数的简化方法,基于刚性横梁 的假设,将多跨连续梁等效为一系列 独立的简支梁或固支梁。
荷载横向分布计算
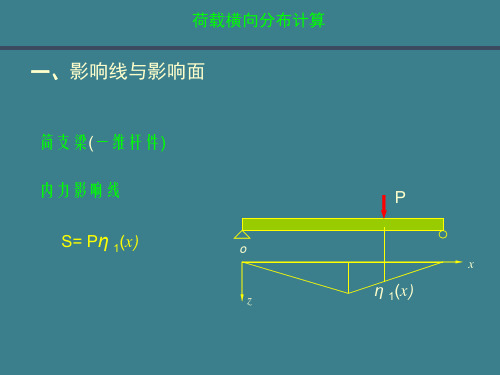
Ri'' I i wi''
Ri'' Ii wi'' Ii aitg ai Ii
弯矩静力平衡: M=Pe=e
'' 2 R a a i i i I i 1 e i 1 i 1
5
5
ai wi’’
R4’’
R5’’
φ
R1’’ R2’’
e
a
i 1
5
' i
w I i 1
' i i 1
5
w
' i
1
R1’
R2’
R3’
R4’
R5’
I
i 1
5
i
R
' i
Ii
Ii
i 1
5
……(1)
(2)偏心力矩作用M=Pe=e
各梁竖向挠度: M=Pe=e
w aitg
'' i
ai wi’’
R4’’
R5’’
根据位移与荷载的关系,
φ
R1’’ R2’’
2 a i Ii i 1 5
4、关于β 值
Gl I Ti 1 12 E ai2 I i
2
1
当各主梁截面相同时:
ξ
2
主梁根数
4 5 6 7
1 GITi 1 EI l B
1.067 1.042 1.028 1.021
5、关于IT 值
t1
b1
IT ci bi t 3 i
可以看出系数η 2(y) 的作用相当于将荷载P 沿横向分配给指定的梁,使该梁承受P ’的 荷载。这样一来, 可以将二维问题转化为 一维问题处理。
