1-121数字平方根表及11-100的平方数表
1--100平方立方表

72
73
74
75
76
77
78
79
80
原数
平方
5041
5184
5329
5476 |
5625
5776
5929
6084
6241
6400
平方
1、、・ 立方
35791
1
3
37324(
8
389017
405224
421875
4
38976
45653
3
4'
74552
1493039
5
12000
立方
原数
81
82
83
84
学习资料收集于网络,仅供参考
1的平方=1
13=1
2的平方=4
23=8
3的平方=9
33=27
4的平方=16
43=64
5的平方=25
53=125
6的平方=36
63=216
7的平方=49
73=343
8的平方=64
83=512
9的平方=81
93=729
10的平方=100
103=1000
11的平方=121
113=1331
12的平方=144
123=1728
13的平方=169
133=2197
14的平方=196
143=2744
15的平方=225
153=3375
16的平方=256
163=4096
17的平方=289
173=4913
18的平方=324
183=5832
19的平方=361
20的平方=400
1--100平方立方表

256
289
324
361
400
平方
立方
1331
1728
2197
2744
3375
4096
4913
5832
6859
8000
立方
原数
21
22
23
24
25
26
27
28
29
30
原数
平方
441
484
529
576
625
676
729
784
841
900
平方
立方
9261
10648
12167
13824
15625
17576
4624
4761
4900
平方
立方
226981
238328
250047
262144
274625
287496
300763
314432
328509
343000
立方
原数
71
72
73
74
75
76
77
78
79
80
原数
平方
5041
5184
5329
5476
5625
5776
5929
6084
6241
6400
平方
立方
357911
19683
21952
24389
27000
立方
原数
31
32
33
34
35
36
37
38
39
40
原数
以内平方表正式版

以内平方表正式版规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2+2ab(a-b)2=a2+b2 -2ab|| | || |a×ab×b2×a×ba×ab×b2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了.例如,判定2431是否为质数,因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
平方数的规律及100以内的平方表(最新编写)
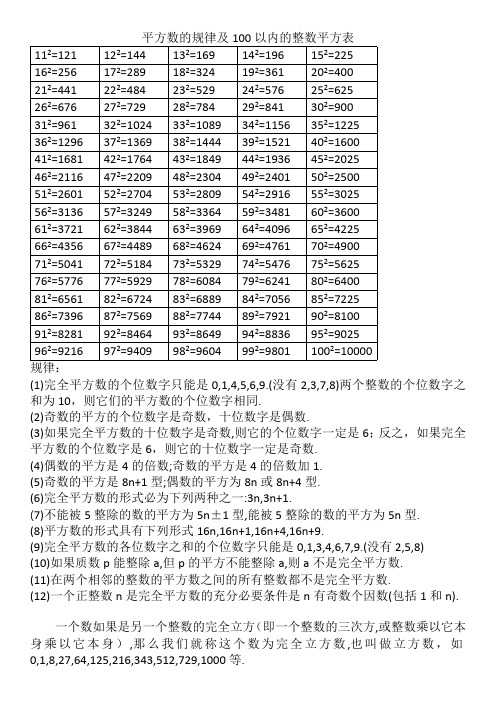
平方数的规律及100以内的整数平方表112=121122=144132=169142=196152=225162=256172=289182=324192=361202=400212=441222=484232=529242=576252=625262=676272=729282=784292=841302=900312=961322=1024332=1089342=1156352=1225362=1296372=1369382=1444392=1521402=1600412=1681422=1764432=1849442=1936452=2025462=2116472=2209482=2304492=2401502=2500512=2601522=2704532=2809542=2916552=3025562=3136572=3249582=3364592=3481602=3600612=3721622=3844632=3969642=4096652=4225662=4356672=4489682=4624692=4761702=4900712=5041722=5184732=5329742=5476752=5625762=5776772=5929782=6084792=6241802=6400812=6561822=6724832=6889842=7056852=7225862=7396872=7569882=7744892=7921902=8100912=8281922=8464932=8649942=8836952=9025962=9216972=9409982=9604992=98011002=10000规律:(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10,则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数,十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6;反之,如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方(即一个整数的三次方,或整数乘以它本身乘以它本身),那么我们就称这个数为完全立方数,也叫做立方数,如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数,不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25;25+144=169;49+576=625;64+225=289;400+441=841记忆技巧:(a+b)2= a2 + b2 + 2ab (a-b)2=a2 + b2 -2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22-2×90×2=8100+4-360=7744用处:①训练计算能力,使计算更快更准确;②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,n超过的都不必检查了.例如,判定2431是否为质数,因为n2431492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可,而53,59,61,67……等更大的质数都不用检查了,实际上2431=1117.×13×③增加对数字的熟悉程度,比如162=256=28,322=1024=210,642=4096=212 ,另外一些特殊结构的数字应该牢记,如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).。
1到30的算术平方根表格

1到30的算术平方根表格1的平方是1
2的平方是4
3的平方是9
4的平方是16
5的平方是25
6的平方是36
7的平方是49
8的平方是64
9的平方是81
10的平方是100
11的平方是121
12的平方是144
13的平方是169
14的平方是196
15的平方是225
16的平方是256
17的平方是289
18的平方是324
19的平方是361
20的平方是400
21的平方是441
22的平方是484
23的平方是529
24的平方是576
25的平方是625
26的平方是676
27的平方是729
28的平方是784
29的平方是841
30的平方是900
立方根的概念:
如果一个数的立方等于a,那么这个数叫a的立方根,也称为三次方根,也就是说,如果x³=a,那么x叫做a的立方根。
平方根的概念:
平方根,又叫二次方根,表示为〔±√ ̄〕,其中属于非负数的平方根称之为算术平方根(arithmetic square root)。
一个正数有两个实平方根,它们互为相反数;0只有一个平方根,就是0本身;负数有两个共轭的纯虚平方根。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11-100的平方数表
速求一个数平方的方法
1、求任意一个两位数的平方
方法:先把这个数看成 5 的倍数与一个小于5 的数的和(或差)的形式,再用这两个数的平方和加上(或减去)这两个数的积的 2 倍。
2、求任意一个两位数的平方
方法:用这个数加上它的个位数的补数的和乘以它们的差,再用这个积加上这个补数的平方。
3、求一千零几的平方
方法:先写上这个数加上个位数的 2 倍的和,再写上一个0,最后写上个位数的平方(个位数的平方小于10,就在它前面补一个0)。
