一种自适应LMS滤波的改进算法
一种改进的变步长LMS自适应滤波算法及性能分析
法均引入多个调整参数 ， 因此 步长 因子 不易设计 和控制 ； 文献
０ 引言
自适 应 滤 波 广 泛 应 用 于 自适 应 控 制 、 声 消 除 、 噪 系统 辨识 、
［ ］ 文 献 ［ ］ 基 础 上 引 人 了 测 量 噪 声 Ｖ的 方 差 ， 得 步 长 ８在 ６的 使 能 够 跟 随 测 量 噪 声 及 时 变 化 。文 献 ［ ］ 入 记 忆 因 子 ， 步 长 ９引 使
第２ ８卷 第 ３期
２１ ０ １年 ３月
计 算 机 应 用 研 究
Ａｐ ｌ ａ ｉｎ Ｒｅ ｅ ｒ ｈ ｏ。 ｏ ｕ ｅ ｓ ｐ ｉ ｔ ｓ ａ ｃ ｔＣ ｍｐ ｔ ｒ ｃ ｏ
Ｖｏ ． ８ Ｎｏ ３ １２ ．
Ｍａ． ２ １ ｒ ０１
一
种 改 进 的 变 步 长 Ｌ 自适 应 滤 波 ＭＳ 算 法及 性 能分 析
ａ ｄ ｃ ｎｒｌｆｎ ｔ ｎ ａｕ ｓｏ ｅｐ ｒｍｅｅｓ３（ ，ｓ ａ ｈ ｕ ｒｎ ｅａｉｎｓｅ ｒ ｅａｅ ｏｔｅｐｅ ｉｕ ｔｐａ ｄｔｅ ｎ ｏ ｔ ｕ ｃｉ ｓｖｌｅ ｆ ｈ ａａ ｔｒ ／ ｎ） ｏｔ ｔ ｅｃ ｒｅ ｔｔｒｔ ｔｐｗｅｅｒｌｔｄｔ ｈ ｒｖｏ ｓｓｅ ｎ ｏ ｏ ｔ ｈ ｔ ｉ ｏ ｈ
ｃ ｎｒ ｉ ｉ ｓ ｙｂ ｉ ｉｇ ｏ ｌ ｅ ｒ ｕ ｃ ｏ ａ ｒｌ ｉ ｓｉ ｂ ｔ ｅｎ （ ）ａ ｄｅ ｎ ， ｈｓ ａ ｅ ｒ ｏｅ ｎｉ ｐ ｏｅ ａｉ ｏ ｔ ｄｃ ｏ ．Ｂ ｕ ｄ ｎ ｎｉ ａ ｎ ｔ ｎ ｌ ｅ ｔ ｎ ｈｐ ｅ ｅ ｎ ｎ （ ） ｔｉ ｐ ｐ ｒ ｏ ｓｄａ ｒ ｄｖ ｒ ａ ｔｎ ｌｎ ａ ｎ ｆ ｉ ａｏ ｗ ｐ ｐ ｍ ｖ
任 自钊 ， 建 城 ，闫永 鹏 徐
lms算法基本思想及原理
lms算法基本思想及原理
LMS（Least Mean Squares）算法是一种常用的自适应滤波算法，也是一种在线学习算法。
它的基本思想是通过不断地调整滤波器的权值来最小化估计信号与实际信号之间的均方误差。
LMS算法的原理是基于梯度下降方法进行权值更新。
首先，LMS算法利用输入信号和期望信号之间的差异计算出误差信号。
然后，根据误差信号和输入信号的乘积以及一个适当的步长因子，调整滤波器的权值。
通过连续调整权值，LMS算法
能够逐渐逼近期望信号，从而实现滤波器的自适应。
具体而言，LMS算法的权值更新公式为：
w(n+1) = w(n) + μ * e(n) * x(n)
其中，w(n+1)表示更新后的权值，w(n)表示当前的权值，μ表
示步长因子，e(n)表示当前时刻的误差信号，x(n)表示当前时
刻的输入信号。
LMS算法的核心思想是利用实时数据对滤波器进行不断调整，使得滤波器能够在未知环境中适应信号特性的变化。
通过持续的学习和更新，LMS算法能够实现自适应滤波，从而提高信
号的处理性能和鲁棒性。
需要注意的是，LMS算法对于系统的遗忘因子和初始权值设
置较为敏感，这些参数的选择需要根据具体的应用场景来进行调整。
此外，LMS算法的收敛性和稳定性也是需要考虑的重
要因素。
一种新的LMS自适应滤波算法分析仿真研究
ｖ ｌ ｅ ｏ ｅ ｐ ｏ ｕ ｔ ｆ ｈ ｕ ｒ ｎ ｎ ｏ ｍｅ ｒｏｓ Ｔ ｅａ ｇ ｒｔ ｍ ｌｏ ｉｔｏ ｕ ｅ ｈ ｉｔ ｒ ａ ｃ ｆｔ ｅ ａ ｓ ｌ ｔ ａｕ ｆ ｈ ｒ ｄ ｃ ｅ ｃ ｒｅ ｔａ ｄ ｆ ｒ ｒｅ ｒ ． ｈ ｌ ｏ ｈ ａｓ ｎ ｒｄ ｃ ｓｔ ｅ ｄ ｓ ｂ ｎ ｅ ｏ ｂ ｏｕ ｅ ｔ ｏｔ ｉ ｕ ｈ
NLMSLMS算法介绍参考
NLMSLMS算法介绍参考NLMS（Normalized Least Mean Squares）算法是一种自适应滤波算法，是LMS（Least Mean Squares）算法的一种改进版本。
可以应用于许多信号处理应用领域，例如声音增强、自适应滤波、自适应降噪等。
LMS算法是一种采用最小均方误差准则的自适应滤波算法。
它通过最小化输入信号与期望输出信号之间的均方误差来调整滤波器的系数，实现自适应滤波。
然而，LMS算法存在一个缺陷，就是它对输入信号的动态范围非常敏感，需要较小的步长参数才能保证算法的收敛性。
为了解决LMS算法的不足，NLMS算法在每次迭代中对步长参数进行了归一化处理。
具体来说，在更新滤波器系数时，NLMS算法除以输入信号的功率来归一化步长。
这样可以有效地改善算法的收敛速度和稳定性，提高算法的适应性。
NLMS算法的更新公式如下：w(k+1)=w(k)+μ/(α+x(k)*x(k)')*e(k)*x(k)其中，w(k)表示第k个迭代步骤时的滤波器系数向量，μ是步长参数，α是一个小的正常数，x(k)表示第k个迭代步骤时的输入信号向量，e(k)表示第k个迭代步骤时的误差信号。
NLMS算法的优点是可以自动调节步长参数，能够快速适应信号的变化。
此外，由于步长参数的归一化处理，算法对输入信号的幅度变化不敏感，能够更好地处理动态范围大的信号。
然而，NLMS算法也存在一些问题。
首先，算法的收敛速度可能会受到输入信号的动态范围变化的影响。
当信号的动态范围较大时，步长参数的归一化处理会导致算法的收敛速度变慢，甚至可能导致算法无法收敛。
其次，算法对输入信号的变化有一定的延迟响应，可能导致一些误差信号被忽略。
总而言之，NLMS算法是一种改进的自适应滤波算法，通过归一化步长参数来提高算法的收敛速度和稳定性。
它在许多信号处理应用领域都有广泛应用，同时也存在一些局限性。
一种基于改进LMS算法的自适应消噪滤波器
这个解称为维纳解 ， 即最佳滤波 系数值 。 自适应调整过程是沿着梯度 向量的负方 向校正滤波系数 ，即在误 差性 能曲面 的最陡下降法方 向移动和逐步调整滤波系数 ，最终到达均 方误差为最小的状态 ， 获得最佳或准最优滤波器。即滤波器 系数调整方
程为：
＝
（ ２ １）
ｗｎ＝ （一 ） １ （） Ｊｎ １ （）ｗｎ １＋ ｎ （－ ） ＝ （一 ） （）（）（） ｗｎ １ ｎｅｎｕｎ ＋ ‘ （ ３ １） （） ｎ是第 ｎ次 自适应迭代的步长 ， 来控制稳定性和收敛速 率。由于 瞬时梯度的期望值等 于最 陡下降法中的真实梯 度向量 ，因此 瞬时梯度 的是真实梯度的无偏估计 ，自 适应 滤波器 系数 也是维 纳滤波器系数 的 无偏估计。 在本文 的 自 适应 干扰对消应用 中 ， 参考噪声 信号 ｖｎ 为滤波 器 ’） （作 输入 ， 混有噪声 的接收信号 ｘ ） （ 作为滤波器期望 响应 ， ｎ 当调整 自 适应滤 波器系数使 自适应滤波器输 出 （） ｎ与 ｎ的均方误差最小 时， ） 干扰对 消 器的输出 ｅｎ就和原始无噪声信号 ｓ ） （） （ 的均方误差最小 ， ｎ 即是所期望 的 输出结果。因此 自适应滤波算法步骤总结 如下 ： 步骤 １ 初始化 ： （）０ ｗ０＝ 步 骤 ２更 新 ：＝ ’， ｎ ｌ … ２ ｅ ）ｄ ） ． 一 ） ｎ （ ＝（一 Ｉ １ ’） ｎ ｎ ｗ（ ｖ ｎ ｗｎ＝ （一 ） ｎ 。）’ ） （）ｗｎ １＋ ）（ ｅｎ （ ｖ ｎ （ 其 中步长 因子 （） ｎ的选择关系到 自适应滤波器的收敛速度和稳态 性能 ， 其值应满足
ｗｎ＝ （— ） ￣ｎＶｄ（－ ） （）ｗｎ １ １ ｚ ） ＋ （ ｎ１
（ １ １）
Hale Waihona Puke 由于最 陡下 降算法需要求得 的误 差的梯度 Ｊ（） ｎ向量在实际工程 中很难实现 ， 因此用瞬时梯度 Ｖ （）一 【（ｄ（】２ｕＩｕ（） （） Ｊ ＝ ２ｕｎ ．） 【（ Ｉｗｎ ｎ ） ｎ ＋ Ｏ ｒ】 ２ （ 【 （ 一 ｝ ）（ 】 ｕｎ ｄ ｎ ｕ（ ｗｎ ） ） ｌ ｎ ） 作为梯度向量 的估计值带入 （ １式便得到 Ｌ Ｓ 】） Ｍ 算法。
改进的自适应LMS算法
Ｋｅ ｒ ｓ ａｉ ｌ ｓ ｐｓ ｅ Ｌ ａｔＭｅｎ Ｓ ｕ ｒ（ Ｍ Ｓ ｌｏｉ ｍ；ｏ ｖ ｒｅｃ ａ ；ｔａｙｓ ｔ ｅｒｒ ｙ ｗｏｄ ：ｖ ｒ ｂｅ ｔ —ｉ ；ｅｓ ａ ｅ ｚ ａ ｑ ａｅＬ ）ａｇ ｒｈ ｃｎ ｅｇｎｅ ｒｔ ｓ ｄ —ａｅ ｒ ｔ ｅ ｅ ｔ ｏ
４ （３ ：３ ．３ ． ７ １ ）１ ４１５
Ａｂ ｔ ａ ｔ Ｌ ｓｒ ｃ ： ＭＳ（ ｅ ｓ Ｍｅ ｎ ｑ ａｅ ｌｏ ｉ ｍ ｓ ｗｉｅｙ ｕ ｅ ｕ ｏ ｔ ｉ ｌ ａ ｄ ｔｂｅ ｐ ｒｏ ｍａ ｃ ． ｔ ｔｅｅ ｓ ａ ｉ— Ｌ ａｔ ａ Ｓ ｕ ｒ ）ａｇ ｒ ｈ ｉ ｄ ｌ ｓｄ ｄ ｅ ｔ ｉ ｓｍｐｅ ｎ ｓ ｌ ｅｆｒ ｎ ｅＢｕ ｈ ｒ ｉ ｎ ｎ ｔ ｓ ａ
关键词 ： 变步长； 最小均方误差（ ＭＳ 算法； Ｌ ） 收敛速 率； 稳态误差 ＤＯＩ１．７ ８ ．ｓ． ０ —３ １ ０ １１．３ 文章编号 ：０２８ ３ （０ １ １．１４０ 文献 标识码 ： 中图分类号 ： Ｎ ｌ． ：０ ７ ／ｉ ｎ１ ２８ ３ ． １． ０ ８ ３ ｊｓ ０ ２ ３ １０ —３ １２ １） ３０ ３ ．２ Ａ Ｔ ９ １ ７
摘
要 ： ＭＳ Ｌ ａｔＭｅｎ Ｓ ｕ ｒ） Ｌ （ ｅｓ ａ ｑ ａｅ 算法 因其结构 简单 、 定性好 等优 点， 稳 得到 了广 泛的应 用， 但在收敛速度 和稳态失调之 间存在
着 固有 矛盾 ， 通过对步长 因子 的调整 可以克服 这一矛盾。分析研究 了已有的变步长 Ｌ ＭＳ算法， 在此基础上提 出了一种 改进 的变 步长 Ｌ 算法。理论 分析和计 算机仿真表 明该 算法 不但具有较快的收敛速 率， ＭＳ 并且具有 更小的稳 态误 差。
基于LMS自适应的改进端点检测算法
基于LMS 自适应的改进端点检测算法刁鸿鹄，毛强，章小兵（安徽工业大学电气与信息工程学院，安徽 马鞍山 243032)摘要：语音识别技术早已不再局限于实验室中，但部分关键技术仍需进一步优化与改进，以适应社会和用户不断增加的需求。
从语音识别的技术理论入手，着重研究端点检测技术，拟在此基础上针对现有算法进行改进，提升其在低信噪比环境下的识别准确率。
提出了一种在对语音进行LMS 自适应降噪后,采用倒谱距离熵比的新型端点检测算法,并在MATLAB 平台上进行相应测试。
结果表明该算法相比于传统方法,检测正确率确有提升。
关键词：语音识别；自适应滤噪；倒谱距离；能熵比中图分类号：TN912.3 文献标志码：A 文章编号：1671-0436（2021）01-0031-10收稿日期：2020-09-28作者简介：刁鸿鹄（1996— ），男，安徽马鞍山人，硕士研究生，*****************，主要研究方向为语音识别与测控技术。
第 34 卷第 1 期2021 年 2 月常州工学院学报Journal of Changzhou Institute of TechnologyV ol. 34 No. 1Feb.2021doi:10.3969/j.issn.1671-0436.2021.01.0080 引言语音端点检测技术是对输入语音进行有话段起止端点的标记。
它是语音识别系统中一个关键环节。
端点检测的成功与否直接影响了语音识别系统的准确率。
现实生活中，因无法保证采集环境处于安静状态，故语音输入信号不可避免地带有各种噪声。
因此，研究在低信噪比环境下具有良好识别率的语音端点检测技术有实际意义，对提升系统在恶劣环境下的工作稳定性大有益处。
Improved Endpoint Detection Algorithm Based on LMS AdaptiveDIAO Honghu ，MAO Qiang ，ZHANG Xiaobing(School of Electrical and Information Engineering, Anhui University of Technology, Maanshan 243032)Abstract: Speech recognition technology is no longer limited to the laboratory. However, some key technologies still need to be further optimized and improved to adapt to the increasing demands of society and users. Starting from the technical theory of speech recognition and focusing on the endpoint detection technology, based on which, it is planned to improve the existing algorithm and enhance its recognition accuracy in a low signal-to-noise ratio environment. A new endpoint detection algorithm using cepstral distance-entropy ratio after LMS adaptive noise reduction is proposed, and the corresponding test is performed on the MATLAB platform. The results show that compared with traditional methods, the detection accuracy of this algorithm is indeed improved.Key words: speech recognition ；adaptive noise filtering ；cepstrum distance ；energy-entropy ratio322021年常州工学院学报1 自适应滤波减噪自适应信号的主要特征是在无预设值的条件下，实时调用运行数据，根据算法不断递归，更新参数，逐步逼近最优结果[1]。
一种改进的变步长的LMS自适应滤波算法及其仿真
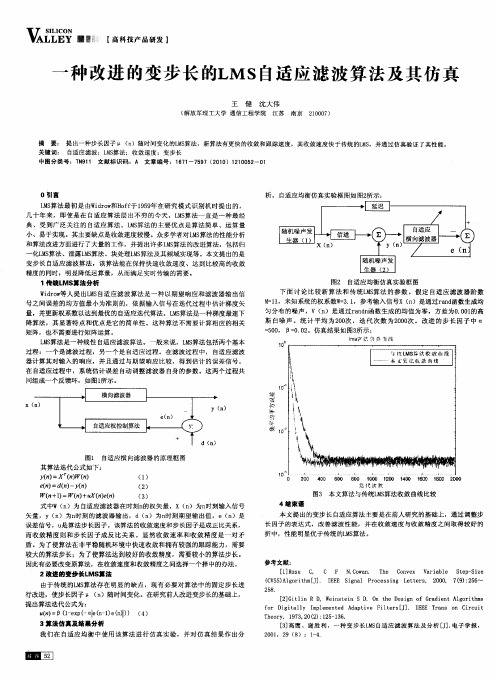
误 差信 号 ，ｕ 是算法 步长 因子 。该 算法 的收 敛速度 和 步长 因子 是成正 比关 系 ，
本文 提 出的变 步长 自适应 算法 主 要是在 前 人研 究 的基础 上 ，通过 调整 步
长 因子 的表 达式 ，改善 滤波 性 能 ，并在 收 敛速 度 与收 敛精 度之 间 取得较 好 的
１传统 Ｌ 算法 分析 ＭＳ Ｗ ｄｏ 等 人提 出ＬＳ ｉｒｗ Ｍ 自适应 滤 波 算法 是 一种 以期 望 响应 和滤 波 器 输 出信 号之 间误 差 的均 方值 最 小为 准则 的，依 据 输入 信 号在迭 代 过程 中估计 梯度 矢 量， 弗更新 权系 数 以达到 最优 的 自适应迭 代 算法 。Ｌ Ｓ Ｍ 算法 是一种 梯度 最速 下
逃 １ 淡 数
图３ 本 文算法 与传 统Ｌ Ｓ 法 收敛 曲线 比较 Ｍ算
４结束 语
式 中Ｗ （ ）为 自适 应滤 波器 在 时刻ｎ ｎ 的权 矢量 ，Ｘ （ ）为ｎ 刻输 入信 号 ｎ 时 矢 量 ，Ｙ （ ）为ｎ ｎ 时刻 的滤 波器 输 出 ，ｄ（ ）为ｎ 刻期 望 输 出值 ，ｅ （ ）是 ｎ 时 １ １
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第14卷第5期2000年10月 华 东 船 舶 工 业 学 院 学 报Journal of East China Shipbuilding Institute Vol 114No 15Oct.2000文章编号:1006-1088(2000)05-0018-04一种自适应LM S 滤波的改进算法刘怀国, 吴 越, 张尤赛(华东船舶工业学院电子与信息系,江苏 镇江 212003)摘 要:在传统的LM S(L east M ean Square)算法中,固定步长选取影响收敛速度与稳态误差,而且两者不可兼得。
为此,本文提出了一种改进的LM S 算法。
在计算机仿真自适应信道均衡中,该算法的性能明显优于传统的L M S 算法,而计算量增加甚少。
理论分析与计算机模拟证实了该算法的优越性。
关键词:自适应滤波;L M S 算法;信道均衡中图分类号:T N92915 文献标识码:A0 引 言自B.Widrow 等人1967年提出自适应滤波以来,因其计算量小,易于实现等优点,这30多年来发展极为迅速。
目前,已广泛地应用于通信、系统辩识、信号处理和自适应控制等领域。
具体的例子包括神经网络的学习过程、噪声背景下的信号检测、天线旁瓣干扰的自适应对消、电话线路中的回波消除、通信系统中的信道均衡、雷达和声纳的波束形成等。
在各种自适应滤波中,其中Widrow -Hoff 的LMS (Least M ean Square)算法以其计算量小,稳定性好且易于实现而得到广泛应用。
但这种算法中的固定步长因子L 对算法的性能有决定性的影响。
L 太小,算法收敛慢,为得到满意的结果所需要的采样数据很多,但稳态失调误差较小。
L 太大(在保证收敛的情况下),该算法收敛速度快,但稳态失调误差变大。
收敛速度与稳态失调噪声是不可兼得的两个指标。
为此本文提出了一种改进算法,使其在收敛速度与稳态失调误差之间作出折衷的处理。
1 传统的LMS 自适应滤波算法介绍如图1,传统的LM S 滤波算法[1,2]为:图1 自适应滤波器原理图Fig 11 T he principle diagr am of adaptive filtery (n )=6N-1i=0X i (n)x (n -i)e(n)=d (n )-y (n)X i (n +1)=X i (n )+2L e(n)x (n -i)(i =0,1,,,N -1)写成矩阵的形式为:y (n )=W (n)T X (n)e(n)=d (n )-y (n)W (n +1)=W (n )+2L e(n)X (n)收稿日期:1999-12-28基金项目:院青年基金课题(院编99305)作者简介:刘怀国(1976-),男,江苏海安人,华东船舶工业学院硕士研究生。
式中,W(n)为n 时刻自适应滤波器的权矢量;W(n)=[w 0(n),w 1(n),,,w N-1(n )]T ,N 为自适应滤波器的阶数;X (n)为n 时刻自适应滤波器的参考输入矢量,由最近N 个信号采样值构成,X (n)=[n(n),x (n -1),,,x (n -N +1)]T ;d (n )是期望的输出值;e(n)为自适应滤波器的输出误差调节信号(简称失调信号);L 是控制自适应速度与稳定性的增益常数,又叫收敛因子或步长因子。
该算法中步长因子L 对算法的性能有决定性的影响。
L 较小时,算法收敛慢,但稳态失调误差小。
L (假设其取值在收敛范围之内)较大时,算法收敛速度快,但稳态失调误差大。
可见,该算法在收敛速度与稳态失调误差之间存在着矛盾,因此,需要改进L 。
2 改进的LMS 算法改进的LM S 自适应滤波算法的权矢量按下式调整:y (n)=W (n)T X (n)(1)e(n)=d (n)-y (n)(2)W c (n)=W (n)+2L e(n )X (n )(3)y c (n)=W c (n )T X (n )(4)e c (n)=d (n)-y c (n )(5)W (n +1)=W c (n )+2L e c (n )X (n )(6)由式(1)~(6)可见,改进算法中的W c (n )、W c (n +1)分别相当于传统的LM S 算法中的W (n +1)、W (n +2),即改进的LMS 算法加快了自适应滤波算法权矢量的变化速率。
将(2)、(3)、(4)、(5)代入(6)式得:W (n +1)=W (n)+2L e(n )X (n )+2L {d (n)-[W (n )+2L e(n)X(n)]T X (n )}X (n )=W (n)+2L e(n )X (n )-2L {d (n)-y (n)-2L e(n )+X (n)+2}X (n )=W (n)+4L [1-L +X (n)+2]e(n )X (n )所以改进的算法可表示为:y (n)=W (n)T X (n)e(n)=d (n)-y (n)W (n +1)=W (n)+4L [1-L +X (n )+2]e(n)X(n)图2 L 与L e 的关系图F ig .2 T he relat ionship between L and L e此方案相当于将传统的LMS 算法中的L 变为2L [1-L +X (n)+2]。
记等效步长L e =2L [1-L +X (n )+2],L 与L e的关系如由图2所示(直线表示L e =L ),当L 较小时L e >L ,使得收敛速度变快,但稳态失调信号变大;当L 较大时L e <L ,使得收敛速度变慢,稳态失调信号变小。
又由图可以看出,随着L的增大等效步长L e 先增大后减小,所以L e 必可取一个最大值,在收敛速度和稳态失调信号之间作出折衷,即兼顾这两个指标。
又L e =2L [1-L +X (n )+2]=-2+X (n)+2(L 2-1+X (n)+2L )=-2+X (n)+2(L -12+X (n )+2)2+12+X (n )+2显然,L e 的最大值为12+X (n )+2,此时,L =12+X (n)+2=L e ,可见若兼顾收敛速度和稳态失调信号,在它们之间作出折衷,应取L =12+X(n)+。
所以,改进的算法可进一步写为:y (n)=W (n)T X (n)19第5期 刘怀国等:一种自适应LM S 滤波的改进算法e(n)=d (n)-y (n)W (n +1)=W (n )+1+X (n )+2e(n)X (n)3 自适应信道均衡计算机仿真图3 自适应信道均衡原理图F ig 13 T he principle diag ram of adapt ive channel equalizer 现在通过一个模拟实验来说明改进的LMS 算法的性能。
图3为一个自适应均衡系统[3,4],随机序列1产生的是x n =?1的贝努利(Bernoulli )随机序列,随机变量x n 的均值为0,方差为1。
信道的脉冲响应为升余弦,取h n =12[1+cos (2P W (n -2)] n =1,2,30其它,式中,W =3.5,随机序列2为零均值、方差为0.001的高斯白噪声随机序列发生器,随机序列1和随机序列2相互独立。
自适应横向滤波器的权数为11,延时的长度取为7。
图4 仿真图形Fig 14 T he w aveform of simulation然后再分别取L =0.075,L =0.0075,L=12+X (n)+,仿真100次后取平均值得到均方误差随迭代次数变化的曲线如图4所示。
图中曲线1为L =0.0075的情况,因L 较小,故收敛速度很慢,迭代1500次后失调信号仍比较大。
曲线2为L =0.075的情况,此时L 较大(仍在收敛范围之内),故收敛速度很快,但失调信号波动较大。
曲线3为L =12+X (n )+2的情况,此时随着迭代次数的增加迅速收敛,而且使失调信号也比较小。
4 结束语收敛速度、稳态误差和计算量是衡量一个自适应滤波算法性能优劣的三个主要参数。
LMS 算法以其计算简单,易于工程实现而深受人们的关注。
但为了满足算法收敛和稳态误差的要求值不能取得太大,这就决定了收敛速度不快。
本文提出的算法在计算量增加不是太大的情况下,通过建立步长因子与输入信号之间的关系L =12+X (n)+得到了一种变步长的LM S 算法,该算法具有在初始阶段步长自动增加,而稳态时步长很小的特点。
与传统的LMS 算法相比,该算法具有更快的收敛速度和较小的稳态误差,而且无须去关心步长因子的大小。
自适应信道均衡的例子验证了该算法的正确性。
理论分析和实验结果表明该算法是明显优于传统的LM S 算法的。
20 华 东 船 舶 工 业 学 院 学 报2000年参考文献:[1] 吴兆熊1数字信号处理(下册)[M ]1北京:国防工业出版社,1985.[2] 王宏禹1随机信号数字处理[M ]1北京:科学出版社,1988.[3] HA YK IN S.A daptive F ilter T heo ry (T hir d Editio n)[M ].U SA :Prentic -Hall Inc.,1996.[4] WI DROW B,ST EA RN S D.A daptiv e Signal Processing[M ].USA:Prentic -Hall Inc.,1985.An Improved Algorithm of LMS Adaptive FilteringLI U H uai -guo , W U Yue, ZHAN G You -sai(Dept.of Electronics and Informati on,East China Shipbuildi ng Institute,Zhenjiang Jiangsu 212003,China)Abstract:The convergent speed and steady -state error are affected by the fixed stepsize and can not be im -proved simultaneously in classical LMS algorithm.Presents an improved alg orithm of LM S.The new algo -rithm is better than classical LMS that is verified by computer simulation of adaptive channel equalizer,w hile the com putional amount is only increased slig htly.Theoretical analysis and computer simulations con -firm the ex cellent properties of this algorithm.Key words:adaptive filtering ;least -mean -square algorithm;channel equalizer(责任编辑:陈 辉)我深海探测技术获突破我国前不久利用自行研制的海底大地电磁探测仪成功地在台湾海峡采集到了海底自然电场数据,填补了我国地球物理在这一研究领域的空白。