云南师大附中2015届高考适应性月考卷(五)理科数学
云南师大附中2015届高三上学期第一次月考数学(理)试卷

2014-2015学年云南师大附中高三〔上〕第一次月考数学试卷〔理科〕一、选择题〔本大题共12小题,每题5分,共60分,在每题给出的四个选项中,只有一项是符合题目要求的〕1.已知全集U和集合A,B如下图,则〔∁U A〕∩B=( )A.{5,6} B.{3,5,6} C.{3} D.{0,4,5,6,7,8}2.设复数z1,z2在复平面内对应的点关于原点对称,z1=1+i,则z1z2=( )A.﹣2i B.2i C.﹣2 D.23.已知向量,满足|﹣|=,•=1,则|+|=( )A.B.2C. D.104.曲线y=e ax+在点〔0,2〕处的切线与直线y=x+3平行,则a=( )A.1 B.2 C.3 D.45.在△ABC中,已知sinC=2sinAcosB,那么△ABC一定是( )A.等腰直角三角形B.等腰三角形C.直角三角形D.等边三角形6.函数在区间上的最大值是( )A.1 B.C.D.1+7.已知实数x,y满足约束条件,则z=x+3y的取值范围是( ) A.[1,9]B.[2,9]C.[3,7]D.[3,9]8.如图,网格纸上小方格的边长为1〔表示1cm〕,图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯外表积与切削得的零件外表积的比值为( )A.B.C.D.9.假设任取x,y∈[0,1],则点P〔x,y〕满足y>x2的概率为( )A.B.C.D.10.已知椭圆+=1〔a>b>0〕的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x 轴,直线AB交y轴于点P.假设=2,则椭圆的离心率是( )A.B.C.D.11.把边长为2的正三角形ABC沿BC边上的高AD折成直二面角,设折叠后BC中点为M,则AC与DM所成角的余弦值为( )A.B.C.D.12.函数f〔x〕=x+x3〔x∈R〕当0<θ<时,f〔asinθ〕+f〔1﹣a〕>0恒成立,则实数a的取值范围是( )A.〔﹣∞,1]B.〔﹣∞,1〕C.〔1,+∞〕D.〔1,+∞〕二、填空题〔本大题共4小题,每题5分,共20分〕13.定义一种新运算“⊗”:S=a⊗b,其运算原理如图3的程序框图所示,则3⊗6﹣5⊗4=__________.14.等比数列{a n}的前n项和为S n,且4a1,2a2,a3成等差数列.假设a1=1,则S4=__________.15.关于sinx的二项式〔1+sinx〕n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为,当x∈[0,π]时,x=__________.16.已知三次函数f〔x〕=x3+x2+cx+d〔a<b〕在R上单调递增,则的最小值为__________.三、解答题〔共70分,解答应写出文字说明,证明过程或演算步骤〕17.一个口袋内有5个大小相同的球,其中有3个红球和2个白球.〔1〕假设有放回的从口袋中连续的取3次球〔每次只取一个球〕,求在3次摸球中恰好取到两次红球的概率;〔2〕假设不放回地从口袋中随机取出3个球,求取到白球的个数ξ的分布列和数学期望E 〔ξ〕.18.如图,在斜三棱柱ABC﹣A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.〔1〕求证:AB1⊥A l C;〔2〕求A1C1与平面AA1B1所成角的正弦值.19.设数列{a n}满足a1=0且a n+1=.n∈N*.〔1〕求证数列{}是等差数列,并求数列{a n}的通项公式;〔2〕设b n=,S n为数列{b n}的前n项和,证明:S n<1.20.已知函数f〔x〕=ax﹣1﹣lnx〔a∈R〕.〔Ⅰ〕讨论函数f〔x〕在定义域内的极值点的个数;〔Ⅱ〕已知函数f〔x〕在x=1处取得极值,且对∀x∈〔0,+∞〕,f〔x〕≥bx﹣2恒成立,求实数b的取值范围.21.如图,已知抛物线C:y2=2px〔p>0〕和圆M:〔x﹣4〕2+y2=1,过抛物线C上一点H 〔x0,y0〕〔y0≥1〕作两条直线与圆M相切于A,B两点,圆心M到抛物线准线的距离为.〔1〕求抛物线C的方程;〔2〕假设直线AB在y轴上的截距为t,求t的最小值.【[选修4-1:几何证明选讲】〔共1小题,总分值10分〕22.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.〔1〕求证:直线AB是⊙O的切线;〔2〕假设tan∠CED=,⊙O的半径为3,求OA的长.【选修4-4:坐标系与参数方程】〔共1小题,总分值0分〕23.在直角坐标系xOy中,直线l的参数方程为〔t为参数〕,在极坐标系〔与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴〕中,圆C 的方程为.〔Ⅰ〕求圆C的圆心到直线l的距离;〔Ⅱ〕设圆C与直线l交于点A、B.假设点P的坐标为〔3,〕,求|PA|+|PB|.【选修4-5:不等式选讲】〔共1小题,总分值0分〕24.已知一次函数f〔x〕=ax﹣2.〔1〕解关于x的不等式|f〔x〕|<4;〔2〕假设不等式|f〔x〕|≤3对任意的x∈[0,1]恒成立,求实数a的范围.2014-2015学年云南师大附中高三〔上〕第一次月考数学试卷〔理科〕一、选择题〔本大题共12小题,每题5分,共60分,在每题给出的四个选项中,只有一项是符合题目要求的〕1.已知全集U和集合A,B如下图,则〔∁U A〕∩B=( )A.{5,6} B.{3,5,6} C.{3} D.{0,4,5,6,7,8}【考点】交、并、补集的混合运算.【专题】计算题.【分析】先由文氏图求出集合U,A,B,再由集合的运算法则求出〔C U A〕∩B.【解答】解:由图可知,U={0,1,2,3,4,5,6,7,8},A={1,2,3},B={3,5,6},∴〔C U A〕∩B={0,4,5,6,7,8}∩{3,5,6}={5,6}.故选A.【点评】此题考查集合的运算和应用,解题时要认真审题,仔细解答,注意文氏图的合理运用.2.设复数z1,z2在复平面内对应的点关于原点对称,z1=1+i,则z1z2=( )A.﹣2i B.2i C.﹣2 D.2【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】通过复数的几何意义先得出z2,再利用复数的代数运算法则进行计算.【解答】解:z1=1+i在复平面内的对应点为〔1,1〕,它关于原点对称的点为〔﹣1,﹣1〕,故z2=﹣1﹣i,∴.故选:A.【点评】此题复数的运算法则、几何意义,属于基础题.3.已知向量,满足|﹣|=,•=1,则|+|=( )A.B.2C. D.10【考点】平面向量数量积的运算.【专题】计算题;平面向量及应用.【分析】运用向量数量积的性质:向量的平方即为模的平方和完全平方公式,计算即可得到.【解答】解:由已知得|﹣|2=〔﹣〕2=2+2﹣2•=2+2﹣2=6,即2+2=8,即有|+|2=〔+〕2=2+2+2•=8+2=10,即.故选C.【点评】此题考查向量的数量积的性质,主要考查向量的平方即为模的平方,考查运算能力,属于基础题.4.曲线y=e ax+在点〔0,2〕处的切线与直线y=x+3平行,则a=( )A.1 B.2 C.3 D.4【考点】利用导数研究曲线上某点切线方程.【专题】导数的概念及应用.【分析】求出原函数的导函数,由曲线y=e ax+在点〔0,2〕处的切线与直线y=x+3平行可得y'|x=0=a﹣1=1,由此求得a的值.【解答】解:由y=e ax+,得,∵曲线y=e ax+在点〔0,2〕处的切线与直线y=x+3平行,∴y'|x=0=a﹣1=1,∴a=2.故选:B.【点评】此题考查了利用导数研究过曲线上某点的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是基础题.5.在△ABC中,已知sinC=2sinAcosB,那么△ABC一定是( )A.等腰直角三角形B.等腰三角形C.直角三角形D.等边三角形【考点】三角形的形状判断.【专题】计算题;解三角形.【分析】三角形的内角和为π,利用诱导公式可知sinC=sin〔A+B〕,与已知联立,利用两角和与差的正弦即可判断△ABC的形状;【解答】解:∵在△ABC中,sinC=sin[π﹣〔A+B〕]=sin〔A+B〕,∴sinC=2sinAcosB⇔sin〔A+B〕=2sinAcosB,即sinAcosB+cosAsinB=2sinAcosB,∴sinAcosB﹣cosAsinB=0,∴sin〔A﹣B〕=0,∴A=B.∴△ABC一定是等腰三角形.故选B.【点评】此题考查三角形的形状判断,考查两角和与差的正弦,利用sinC=sin〔A+B〕是关键,属于中档题.6.函数在区间上的最大值是( )A.1 B.C.D.1+【考点】三角函数中的恒等变换应用;函数y=Asin〔ωx+φ〕的图象变换.【分析】先将函数用二倍角公式进行降幂运算,得到f〔x〕=,然后再求其在区间上的最大值.【解答】解:由,∵,∴.故选C.【点评】此题主要考查二倍角公式的应用和三角函数的最值问题.二倍角公式一般都是反向考查,一定要会灵活运用.7.已知实数x,y满足约束条件,则z=x+3y的取值范围是( )A.[1,9]B.[2,9]C.[3,7]D.[3,9]【考点】简单线性规划.【专题】不等式的解法及应用.【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,结合数形结合即可得到结论.【解答】解:根据线性约束条件作出可行域,如图1所示阴影部分.作出直线l:x+3y=0,将直线l向上平移至过点M〔0,3〕和N〔2,0〕位置时,z max=0+3×3=9,z min=2+3×0=2.故选:B【点评】此题主要考查线性规划的应用.此题先正确的作出不等式组表示的平面区域,再结合目标函数的几何意义进行解答是解决此题的关键.8.如图,网格纸上小方格的边长为1〔表示1cm〕,图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm,高为3cm的圆锥毛坯切割得到,则毛坯外表积与切削得的零件外表积的比值为( )A.B.C.D.【考点】由三视图求面积、体积.【专题】计算题;空间位置关系与距离.【分析】求出圆锥毛坯的外表积,切削得的零件外表积,即可求出毛坯外表积与切削得的零件外表积的比值.【解答】解:圆锥毛坯的底面半径为r=4cm,高为h=3cm,则母线长l=5cm,所以圆锥毛坯的外表积S圆表=πrl+πr2=π×4×5+π×42=36π,切削得的零件外表积S零件表=S圆表+2π×2×1=40π,所以所求比值为=.故选D.【点评】由三视图求几何体的外表积,关键是正确的分析原几何体的特征.9.假设任取x,y∈[0,1],则点P〔x,y〕满足y>x2的概率为( ) A.B.C.D.【考点】几何概型.【专题】概率与统计.【分析】当总体个数有无限多时的概率问题为几何概型,假设事件与两个变量有关时,可归结为面积问题进行解答.【解答】解:该题属几何概型,由积分知识易得点P〔x,y〕满足y>x2的面积为,所以所求的概率为.故选A.【点评】此题考查了几何概型公式的运用以及利用定积分求曲边梯形的面积;当总体个数有无限多时的概率问题为几何概型,假设事件与两个变量有关时,可归结为面积问题进行解答.10.已知椭圆+=1〔a>b>0〕的左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x 轴,直线AB交y轴于点P.假设=2,则椭圆的离心率是( )A.B.C.D.【考点】椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】先求出点B的坐标,设出点P的坐标,利用=2,得到a与c的关系,从而求出离心率.【解答】解:如图,由于BF⊥x轴,故x B=﹣c,y B =,设P〔0,t〕,∵=2,∴〔﹣a,t〕=2〔﹣c,﹣t〕.∴a=2c,∴e==,故选D.【点评】此题考查椭圆的简单性质以及向量坐标形式的运算法则的应用,表达了数形结合的数学思想.11.把边长为2的正三角形ABC沿BC边上的高AD折成直二面角,设折叠后BC中点为M,则AC与DM所成角的余弦值为( )A.B.C.D.【考点】异面直线及其所成的角.【专题】空间角.【分析】以D为原点,DB为x轴,DC为y轴,DA为z轴,建立空间直角坐标系D﹣xyz,利用向量法能求出AC与DM所成角的余弦值.【解答】解:以D为原点,DB为x轴,DC为y轴,DA为z轴,建立如下图的空间直角坐标系D﹣xyz,则M〔,,0〕,D〔0,0,0〕,∴=〔0,1,﹣〕,=〔〕,设AC与DM所成角为θ,则cosθ=|cos<>|==.∴AC与DM所成角的余弦值为.故选:B.【点评】此题考查异面直线所成角的大小的求法,是基础题,解题时要认真审题,注意向量法的合理运用.12.函数f〔x〕=x+x3〔x∈R〕当0<θ<时,f〔asinθ〕+f〔1﹣a〕>0恒成立,则实数a的取值范围是( )A.〔﹣∞,1]B.〔﹣∞,1〕C.〔1,+∞〕D.〔1,+∞〕【考点】函数奇偶性的性质;函数恒成立问题.【专题】函数的性质及应用.【分析】先判断函数的奇偶性,然后再结合单调性将给的不等式化归为两个函数值的大小比较问题,从而构造出关于θ的不等式恒成立,然后别离参数求a的取值范围.【解答】解:因为f'〔x〕=1+3x2>0,故f〔x〕=x+x3〔x∈R〕在R上单调递增,且为奇函数,所以由f〔asinθ〕+f〔1﹣a〕>0得f〔asinθ〕>f〔a﹣1〕,从而asinθ>a﹣1,即当时,恒成立,所以a≤1.故选:A.【点评】此题可先利用奇函数及函数的单调性进行转化,再把不等式恒成立问题转化为函数的最值问题进行解答.二、填空题〔本大题共4小题,每题5分,共20分〕13.定义一种新运算“⊗”:S=a⊗b,其运算原理如图3的程序框图所示,则3⊗6﹣5⊗4=﹣3.【考点】程序框图.【专题】算法和程序框图.【分析】由框图可知算法的功能是求从而由新定义可得3⊗6﹣5⊗4的值.【解答】解:由框图可知,从而得:3⊗6﹣5⊗4=6〔3﹣1〕﹣5〔4﹣1〕=﹣3.故答案为:﹣3.【点评】此题主要考查了程序框图和算法,读懂程序框图,理解所定义的新运算,即可解答,属于基本知识的考查.14.等比数列{a n}的前n项和为S n,且4a1,2a2,a3成等差数列.假设a1=1,则S4=15.【考点】等差数列的性质;等比数列的前n项和.【专题】计算题.【分析】由题意知2a2﹣4a1=a3﹣2a2,即2q﹣4=q2﹣2q,由此可知q=2,a1=1,a2=2,a3=4,a4=8,于是得到S41+2+4+8=15.【解答】解:∵2a2﹣4a1=a3﹣2a2,∴2q﹣4=q2﹣2q,q2﹣4q+4=0,q=2,∴a1=1,a2=2,a3=4,a4=8,∴S4=1+2+4+8=15.答案:15【点评】此题考查数列的应用,解题时要注意公式的灵活运用.15.关于sinx的二项式〔1+sinx〕n的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为,当x∈[0,π]时,x=或.【考点】二项式系数的性质.【专题】二项式定理.【分析】由题意可得,求得n=6,可得,求得.结合x∈[0,π],可得x的值.【解答】解:由题意可得,故n=6,所以第4项的系数最大,于是,所以,,即.又x∈[0,π],所以或.故答案为:或【点评】此题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式.一般遇到二项展开式某项或某项的系数问题,通常结合展开式的通项公式进行解答属于基础题.16.已知三次函数f〔x〕=x3+x2+cx+d〔a<b〕在R上单调递增,则的最小值为3.【考点】函数的单调性与导数的关系.【专题】导数的综合应用.【分析】由题意得f'〔x〕=ax2+bx+c在R上恒大于或等于0,得a>0,△=b2﹣4ac≤0,将此代入,将式子进行放缩,以为单位建立函数关系式,最后构造出运用基本不等式的模型使问题得到解决.【解答】解:由题意f'〔x〕=ax2+bx+c≥0在R上恒成立,则a>0,△=b2﹣4ac≤0.∴≥令,≥≥3.〔当且仅当t=4,即b=c=4a时取“=”〕故答案为:3【点评】此题考查了利用导数工具研究三次函数的单调性以及函数与方程的综合应用问题,属于中档题.三、解答题〔共70分,解答应写出文字说明,证明过程或演算步骤〕17.一个口袋内有5个大小相同的球,其中有3个红球和2个白球.〔1〕假设有放回的从口袋中连续的取3次球〔每次只取一个球〕,求在3次摸球中恰好取到两次红球的概率;〔2〕假设不放回地从口袋中随机取出3个球,求取到白球的个数ξ的分布列和数学期望E 〔ξ〕.【考点】离散型随机变量的期望与方差;列举法计算基本领件数及事件发生的概率;离散型随机变量及其分布列.【专题】概率与统计.【分析】〔1〕利用n次独立重复试验中事件A恰好发生k次的概率计算公式能求出在3次有放回的摸球中恰好取到两次红球的概率.〔2〕白球的个数ξ可取0,1,2,分别求出相应的概率,由此能求出取到白球的个数ξ的分布列和数学期望E〔ξ〕.【解答】解:〔1〕设在3次有放回的摸球中恰好取到两次红球的概率为P,由题设知,.〔2〕白球的个数ξ可取0,1,2,.所以ξ的分布列如下表:ξ0 1 2P.【点评】此题考查相互独立事件、互斥事件、随机变量的分布列、数学期望等概念及相关计算,考查运用概率知识与方法解决实际问题的能力.求离散随机变量的分布列一般先确定随机变量的所有取值,再计算各个取值的概率,最后得分布列并计算期望.18.如图,在斜三棱柱ABC﹣A1B1C1中,点O是A1C1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.〔1〕求证:AB1⊥A l C;〔2〕求A1C1与平面AA1B1所成角的正弦值.【考点】直线与平面所成的角;空间中直线与直线之间的位置关系.【专题】空间角.【分析】〔1〕由已知条件推导出四边形A1C1CA为菱形,从而得到A1C⊥平面AB1C1,由此能够证明AB1⊥A1C.〔Ⅱ〕设点C1到平面AA1B1的距离为d,利用等积法求出d=,由此能求出A1C1与平面AA1B1所成角的正弦值.【解答】〔1〕证明:∵AO⊥平面A1B1C1,∴AO⊥B1C1,又∵A1C1⊥B1C1,且A1C1∩AO=O,∴B1C1⊥平面A1C1CA,∴A1C⊥B1C1,又∵AA1=AC,∴四边形A1C1CA为菱形,∴A1C⊥AC1,且B1C1∩AC1=C1,∴A1C⊥平面AB1C1,∴AB1⊥A1C.〔Ⅱ〕解:设点C1到平面AA1B1的距离为d,∵=,∴=,又∵在△AA1B1中,,,∴d=,∴A1C1与平面AA1B1所成角的正弦值为.【点评】此题考查异面直线垂直的证明,考查直线与平面所成角的正弦值,解题时要认真审题,注意空间思维能力的培养.19.设数列{a n}满足a1=0且a n+1=.n∈N*.〔1〕求证数列{}是等差数列,并求数列{a n}的通项公式;〔2〕设b n=,S n为数列{b n}的前n项和,证明:S n<1.【考点】数列的求和;数列递推式.【专题】等差数列与等比数列.【分析】〔1〕把代入,能推导出,由此能证明数列是公差为1的等差数列,从而能求出.〔2〕由,利用裂项求和法能证明S n<1.【解答】〔1〕解:∵,∴===1,∴,∴数列是公差为1的等差数列.又,所以.〔2〕证明:由〔1〕得,.∴S n<1.【点评】此题主要考查数列的通项公式、前n项和公式的求法,考查等差数列、等比数列等基础知识,考查等差数列的证明,证明数列为等差数列通常利用等差数列的定义证明,遇到与数列的和有关的不等式可先考虑能否求和再证明.20.已知函数f〔x〕=ax﹣1﹣lnx〔a∈R〕.〔Ⅰ〕讨论函数f〔x〕在定义域内的极值点的个数;〔Ⅱ〕已知函数f〔x〕在x=1处取得极值,且对∀x∈〔0,+∞〕,f〔x〕≥bx﹣2恒成立,求实数b的取值范围.【考点】利用导数研究函数的极值;函数恒成立问题;函数在某点取得极值的条件.【专题】计算题;综合题.【分析】〔Ⅰ〕由f〔x〕=ax﹣1﹣lnx可求得f′〔x〕=,对a分a≤0与a>0讨论f′〔x〕的符号,从而确定f〔x〕在其定义域〔0,+∞〕单调性与极值,可得答案;〔Ⅱ〕函数f〔x〕在x=1处取得极值,可求得a=1,于是有f〔x〕≥bx﹣2⇔1+﹣≥b,构造函数g〔x〕=1+﹣,g〔x〕min即为所求的b的值.【解答】解:〔Ⅰ〕∵f〔x〕=ax﹣1﹣lnx,∴f′〔x〕=a﹣=,当a≤0时,f'〔x〕≤0在〔0,+∞〕上恒成立,函数f〔x〕在〔0,+∞〕单调递减,∴f〔x〕在〔0,+∞〕上没有极值点;当a>0时,f'〔x〕≤0得0<x≤,f'〔x〕≥0得,∴f〔x〕在〔0,]上递减,在[,+∞〕上递增,即f〔x〕在处有极小值.∴当a≤0时f〔x〕在〔0,+∞〕上没有极值点,当a>0时,f〔x〕在〔0,+∞〕上有一个极值点.〔Ⅱ〕∵函数f〔x〕在x=1处取得极值,∴a=1,∴f〔x〕≥bx﹣2⇔1+﹣≥b,令g〔x〕=1+﹣,则g′〔x〕=﹣﹣=﹣〔2﹣lnx〕,由g′〔x〕≥0得,x≥e2,由g′〔x〕≤0得,0<x≤e2,∴g〔x〕在〔0,e2]上递减,在[e2,+∞〕上递增,∴,即b≤1﹣.【点评】此题考查利用导数研究函数的极值,考查恒成立问题,着重考查分类讨论思想与构造函数思想的应用,表达综合分析问题与解决问题能力,属于难题.21.如图,已知抛物线C:y2=2px〔p>0〕和圆M:〔x﹣4〕2+y2=1,过抛物线C上一点H 〔x0,y0〕〔y0≥1〕作两条直线与圆M相切于A,B两点,圆心M到抛物线准线的距离为.〔1〕求抛物线C的方程;〔2〕假设直线AB在y轴上的截距为t,求t的最小值.【考点】抛物线的简单性质.【专题】圆锥曲线的定义、性质与方程.【分析】〔1〕由圆心M〔4,0〕到抛物线准线的距离为=,解出即可得出.〔2〕设A〔x1,y1〕,B〔x2,y2〕,由,可得,直线HA的方程为〔4﹣x1〕x﹣y1y+4x1﹣15=0,同理可得:直线HB的方程为〔4﹣x2〕x﹣y2y+4x2﹣15=0,把H〔x0,y0〕〔y0≥1〕代入可得:直线AB的方程为,令x=0,可得,利用其单调性即可得出.【解答】解:〔1〕∵点M〔4,0〕到抛物线准线的距离为=,∴,∴抛物线C的方程为y2=x.〔2〕设A〔x1,y1〕,B〔x2,y2〕,∵,∴,可得,直线HA的方程为〔4﹣x1〕x﹣y1y+4x1﹣15=0,同理可得:直线HB的方程为〔4﹣x2〕x﹣y2y+4x2﹣15=0,∴,,∴直线AB的方程为,令x=0,可得,∵t关于y0的函数在[1,+∞〕上单调递增,∴t min=﹣11.【点评】此题考查了抛物线与圆的定义标准方程及其性质、直线与圆相切问题、切线的性质、相互垂直的直线斜率之间的关系、函数的单调性,考查了推理能力与计算能力,属于中档题.【[选修4-1:几何证明选讲】〔共1小题,总分值10分〕22.如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD.〔1〕求证:直线AB是⊙O的切线;〔2〕假设tan∠CED=,⊙O的半径为3,求OA的长.【考点】圆的切线的性质定理的证明;直线与圆的位置关系;矩阵与矩阵的乘法的意义;简单曲线的极坐标方程;直线的参数方程.【专题】计算题;证明题.【分析】〔1〕要想证AB是⊙O的切线,只要连接OC,求证∠ACO=90°即可;〔2〕先由三角形判定定理可知,△BCD∽△BEC,得BD与BC的比例关系,最后由切割线定理列出方程求出OA的长.【解答】解:〔1〕如图,连接OC,∵OA=OB,CA=CB,∴OC⊥AB.∴AB是⊙O的切线;〔2〕∵BC是圆O切线,且BE是圆O割线,∴BC2=BD•BE,∵tan∠CED=,∴.∵△BCD∽△BEC,∴,设BD=x,BC=2x.又BC2=BD•BE,∴〔2x〕2=x•〔x+6〕,解得x1=0,x2=2,∵BD=x>0,∴BD=2,∴OA=OB=BD+OD=3+2=5..【点评】此题考查的是切线的判定、相似三角形的判定和性质,以及切割线定理的综合运用,属于基础题.【选修4-4:坐标系与参数方程】〔共1小题,总分值0分〕23.在直角坐标系xOy中,直线l的参数方程为〔t为参数〕,在极坐标系〔与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴〕中,圆C 的方程为.〔Ⅰ〕求圆C的圆心到直线l的距离;〔Ⅱ〕设圆C与直线l交于点A、B.假设点P的坐标为〔3,〕,求|PA|+|PB|.【考点】直线的参数方程;简单曲线的极坐标方程.【专题】直线与圆.【分析】〔I〕圆C的极坐标方程两边同乘ρ,根据极坐标公式进行化简就可求出直角坐标方程,最后再利用三角函数公式化成参数方程;〔Ⅱ〕将直线l的参数方程代入圆C的直角坐标方程,得即,根据两交点A,B所对应的参数分别为t1,t2,利用根与系数的关系结合参数的几何意义即得.【解答】解:〔Ⅰ〕由,可得,即圆C的方程为.由可得直线l的方程为.所以,圆C的圆心到直线l的距离为.…〔Ⅱ〕将l的参数方程代入圆C的直角坐标方程,得,即.由于△=.故可设t1、t2是上述方程的两个实根,所以,又直线l过点,故由上式及t的几何意义得.…【点评】此题考查学生会将极坐标方程和参数方程分别化为直角坐标方程和普通方程,掌握直线参数方程中参数的几何意义,是一道中档题.【选修4-5:不等式选讲】〔共1小题,总分值0分〕24.已知一次函数f〔x〕=ax﹣2.〔1〕解关于x的不等式|f〔x〕|<4;〔2〕假设不等式|f〔x〕|≤3对任意的x∈[0,1]恒成立,求实数a的范围.【考点】绝对值不等式的解法;函数恒成立问题.【专题】计算题;函数的性质及应用;不等式的解法及应用.【分析】〔1〕解绝对值不等式的关键是去绝对值,可利用绝对值不等式的解集,对a讨论,分a>0,a<0,即可得到解集;〔2〕对于不等式恒成立求参数范围问题,通常别离参数转化为函数的最值问题进行解答.【解答】解:〔1〕|f〔x〕|<4即为|ax﹣2|<4,即﹣2<ax<6,则当a>0时,不等式的解集为;当a<0时,不等式的解集为.〔2〕|f〔x〕|≤3⇔|ax﹣2|≤3⇔﹣3≤ax﹣2≤3⇔﹣1≤ax≤5⇔,∵x∈[0,1],∴当x=0时,不等式组恒成立;当x≠0时,不等式组转化为又∵,∴﹣1≤a≤5且a≠0【点评】此题考查绝对值不等式的解法,考查不等式的恒成立问题转化为求最值,运用参数别离和分类讨论是解题的关键.。
2015届云南省昆明市高三5月适应性模拟检测数学理试题-word版

2015届云南省昆明市高三5月适应性模拟检测数学理试题第I 卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合}0)1lg(|{≤-=x x A ,}31|{≤≤-=x x B ,则B A = A .]3,1[-B .]2,1[-C .)3,1[D .]2,1(2.设复数Z 满足i z i -=+3)1(,则=zA .i -1B .i +1C .-1D .i +-13.已知圆○:222=+y x 经过双曲线C :y x -22C 的实轴长为A .1B .2C .2D .4.如图,网格纸上小正方形的边长为1CM面积等于A .217cm πB .220cm πC .221cm πD .222cm π5.已知n S 是公差不为0的等差数列}{n a 的前项n 和,且421,,S S S 则48S S 等于 A .16 B .8 C .4 D .26.某批产品共100件,其中70件为一等品,20件为二等品,其余为三等品,规定一、二等品为合格品,现从该批产品中任取一件,已知取到的产品为合格品,则该产品为一等品的概率为A .97 B .92 C .109 D .107 7.若,x y 满足约束条件⎪⎩⎪⎨⎧≥≥≤+≥+2,210282y x y x y x ,则目标函数y x z 34+=的最小值为A .14B .17C .22D . 26 8.记数列1,1,2,3,5,8, ……为}{n a ,执行如图所示的程序框图, 则输出的结果为 A .21 B .61 C .21- D .61- y 的关系表,(记该港口 24:00 则)(t f y =的表达式为A .)43sin(8.1ππ+=t y B .)46sin(8.1ππ-=t yC .)23sin(8.1ππ+=t y D .)26sin(8.1ππ+=t y10.已知三棱锥D-ABC 四个顶点均在半径为R 的球面上,且AB=BC=3,AC=3,若该三棱锥体积的最大值为433,则R= 否是结束输出A -Mk=k+1k=1开始M =M +ak2S=S+a k输入a kA =Skk ≥4S=a 1,M =a 1输入a 1A .1B .2C .3D .32 )()2()(,)(x mf x f x g e e x f x x +=+=-,对任意0)(,>∈x g R x ,则m 的取值范围是 A .),4[+∞- B .),1[+∞- C .),0[+∞ D .),2[+∞12.已知椭圆C :)0(12222>>=+b a bx a y 的两个焦点分别为21,F F ,M 为C 上位于第一象限的点,且y MF ⊥1轴,2MF 与椭圆C 交于一点N,若N F MF 222=,则直线MN 的斜率为A .25 B .552 C .25- D .5 第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分,共20分.}{n a中,1,111+=-=+n a a a a nn n,则7a =_________33,1(=a ,则b 在a 方向上的投影为_______15.5名同学分配到3个不同宣传站做宣传活动,每站至少一人,其中甲、乙两名同学必须在同一个宣传站,则不同的分配方法的种数是_________(用数字作答)x ax x x x f +-=2ln )(在定义域内存在两个极点21,x x ,则实数a 的取值范围为____________三、解答题: 解答应写出文字说明,证明过程或演算步骤.17. (本小题满分12分)如图,四边形ABCD 中,AB=3,BC=22,AC=5,∠ADC=3∠ABC 。
云南省师范大学附属中学届高三高考适应性月考五数学理试题含答案

云南省师范大学附属中学2017届高三高考适应性月考五理科数学试卷第Ⅰ卷共60分一、选择题:本大题共12个小题;每小题5分;共60分.在每小题给出的四个选项中;只有一项是符合题目要求的.1.集合2{|0}{|2}A x x a B x x =-≤=<,;若A B ⊆;则实数a 的取值范围是 A .(,4]-∞ B .(,4)-∞ C .[0,4] D .(0,4)2.复数31i z i =-;则其共轭复数z 在复平面内对应的点位于A .第一象限B .第二象限C .第三象限D .第四象限 3. 下列说法正确的是A .“1x <”是“2log (1)1x +<”的充分不必要条件B .命题“0x ∀>;21x>”的否定是“00021xx ∃≤≤,” C.命题“若a b ≤;则22ac bc ≤”的逆命题为真命题 D .命题“若5a b +≠;则2a ≠或3b ≠”为真命题 4.已知函数()|sin |cos f x x x =•;则下列说法正确的是 A .()f x 的图象关于直线2x π=对称B .()f x 的周期为πC.若12|()||()|f x f x =;则122()x x k k Z π=+∈ D .()f x 在区间3[,]44ππ上单调递减5. 秦九韶算法是南宋时期数学家秦九韶提出的一种多项式简化算法;即使在现代;它依然是利用计算机解决多项式问题的最优算法;即使在现代;它依然是利用计算机解决多项式问题的最优算法;其算法的程序框图如图所示;若输入的012,,,,n a a a a 分别为0,1,2,,n ;若5n =;根据该算法计算当2x =时多项式的值;则输出的结果为A .248B .258 C.268 D .2786. 在棱长为2的正方体1111ABCD A B C D -中任取一点M ;则满足90AMB ∠>°的概率为 A .24πB .12πC.8πD .6π7. 某几何体的三视图如图所示;则该几何体的体积为A .8B . C. D .48. 已知实数,x y 满足2244x y +≤;则|24||3|x y x y +-+--的最大值为 A .6 B .12 C. 13 D .149.三棱锥A BCD -O 中;4AB CD ==;则三棱锥A BCD -的体积的最大值为 A.43 B.83 C.163 D.32310.已知抛物线24x y =的焦点为F ;准线为l ;抛物线的对称轴与准线交于点Q ;P 为抛物线上的动点;||||PF m PQ =;当m 最小时;点P 恰好在以,F Q 为焦点的椭圆上;则椭圆的离心率为A .3-B . 2-- D 1- 11.函数3|log |y x =的图象与直线1:l y m =从左至右分别交于点,A B ;与直线28:(0)21l y m m =>+从左至右分别交于点,C D .记线段AC 和BD 在x 轴上的投影长度分别为,a b ;则ba 的最小值为A .B ..12.若函数()ln f x x =与函数2()2(0)g x x x a x =++<有公切线;则实数a 的取值范围是 A . 1(ln,)2e+∞ B .(1,)-+∞ C.(1,)+∞ D .(ln 2,)-+∞ 第Ⅱ卷共90分二、填空题每题5分;满分20分;将答案填在答题纸上13.已知函数3()xf x e x =+;若2()(32)f x f x <-;则实数x 的取值范围是 . 14.点P 是圆22(3)(1)2x y ++-=上的动点;点(2,2)Q ;O 为坐标原点;则OPQ ∆面积的最小值是 .15.已知平面向量,,a b c 满足||112a a b b c a c ====,,•••;则||a b c ++的最小值是 .16.已知数列{}n a 满足12a =;且*112(2)1n n n na a n n N a n --=≥∈+-,;则n a = .三、解答题 本大题共6小题;共70分.解答应写出文字说明、证明过程或演算步骤.17. 本小题满分12分在ABC ∆中;角A ;B ;C 的对边分别为a ;b ;c ;已知223cos cos 2222B A a b c a b +==,.1证明:ABC ∆为钝角三角形; 2若ABC ∆的面积为;求b 的值. 18. 本小题满分12分某公司即将推车一款新型智能手机;为了更好地对产品进行宣传;需预估市民购买该款手机是否与年龄有关;现随机抽取了50名市民进行购买意愿的问卷调查;若得分低于60分;说明购买意愿弱;若得分不低于60分;说明购买意愿强;调查结果用茎叶图表示如图所示. 1根据茎叶图中的数据完成22⨯列联表;并判断是否有95%的把握认为市民是否购买该款手机与年龄有关2从购买意愿弱的市民中按年龄进行分层抽样;共抽取5人;从这5人中随机抽取2人进行采访;记抽到的2人中年龄大于40岁的市民人数为X ;求X 的分布列和数学期望.附:22()()()()()n ad bc k a b c d a c b d -=++++.19. 本小题满分12分如图;三棱锥P ABC -中;PA ⊥平面ABC ;90ABC ∠=°;2PA AC ==;D 是PA 的中点;E 是CD 的中点;点F 在PB 上;3PF FB =. 1证明://EF 平面ABC ;2若60BAC ∠=°;求二面角B CD A --的余弦值. 20. 本小题满分12分已知抛物线2:8E y x =;圆22:(2)4M x y -+=;点N 为抛物线E 上的动点;O 为坐标原点;线段ON 的中点P 的轨迹为曲线C .1求抛物线C 的方程;2点000(,)(5)Q x y x ≥是曲线C 上的点;过点Q 作圆M 的两条切线;分别与x 轴交于,A B 两点.求QAB ∆面积的最小值. 21. 本小题满分12分 已知函数2()xf x e x ax =--.1若曲线()y f x =在点0x =处的切线斜率为1;求函数()f x 在[0,1]上的最值; 2令221()()()2g x f x x a =+-;若0x ≥时;()0g x ≥恒成立;求实数a 的取值范围; 3当0a =且0x >时;证明2()ln 1f x ex x x x x -≥--+.请考生在22、23两题中任选一题作答;如果多做;则按所做的第一题记分.22. 本小题满分10分选修4-4:坐标系与参数方程在直角坐标系xOy 中;将曲线1cos :1sin 2x t C y t =+⎧⎪⎨=⎪⎩t 为参数上每一点的横坐标保持不变;纵坐标变为原来的2倍;得到曲线1C ;以坐标原点O 为极点;以x 轴的正半轴为极轴建立极坐标系;曲线2C的极坐标方程为2cos()6πρθ-=1求曲线1C 的极坐标方程;2已知点(1,0)M ;直线l 的极坐标方程为3πθ=;它与曲线1C 的交点为O ;P ;与曲线2C 的交点为Q ;求MPQ ∆的面积.23. 本小题满分10分选修4-5:不等式选讲 已知函数()|1|2|1|f x x x =+--.1求()f x 的图象与x 轴围成的三角形面积;2设24()x ax g x x-+=;若对(0,)s t ∀∈+∞,恒有()()g s f t ≥成立;求实数a 的取值范围.云南师大附中2017届高考适应性月考卷五理科数学参考答案第Ⅰ卷选择题;共60分一、选择题本大题共12小题;每小题5分;共60分1.当0a <时;集合A =∅;满足题意;当0a ≥时;[A =;若A B ⊆;则2<;∴0<4a ≤;所以(4)a ∈-∞,;故选B .2.∵i 1i i 12z --+==-;其共轭复数为1i 2z --=;对应点为1122⎛⎫-- ⎪⎝⎭,在第三象限;故选C .3.选项A :2log (1)101211x x x +<⇔<+<⇔-<<;所以“1x <”是其必要不充分条件;选项B :命题“021x x ∀>>,”的否定是“00021x x ∃>,≤”;选项C :命题“若a b ≤;则22ac bc ≤”的逆命题是“若22ac bc ≤;则a b ≤”;当c=0时;不成立;选项D :其逆否命题为“若2a =且3b =;则5a b +=”为真命题;故原命题为真;故选D .4.函数()f x 在区间[02π],上的解+析式为1sin 20π2()1sin 2π2π2x x f x x x ⎧⎪⎪=⎨⎪-<⎪⎩,,,,≤≤≤且()f x 是偶函数;画出图象可知;故选D .5.该程序框图是计算多项式5432()5432f x x x x x x =++++当x=2时的值;故选B . 6.以AB 为直径作球;球在正方体内部的区域体积为14ππ433V =⨯=;正方体的体积为8;所以π24P =;故选A . 7.由三视图还原出该几何体为长方体切去一部分;如图所示;所以剩余部分体积为222383V =⨯⨯⨯=;故选A . 8.实数x;y 满足的区域为椭圆2214x y +=及其内部;椭圆的参数方程为2cos sin x y θθ=⎧⎨=⎩,,θ为参数;记目标函数|24||3|z x y x y =+-+--;易知240x y +-≤,30x y --≥;故423723z x y x y x y =--+--=--.设椭圆上的点(2cos sin )P θθ,;则74cos 3sin 75sin()z θθθϕ=--=-+;其中4tan 3ϕ=;所以z 的最大值为12;故选B . 图19.如图;过CD 作平面ECD;使AB ⊥平面ECD;交AB 于点E;设点E 到CD 的距离为EF;当球心在EF 上时;EF 最大;此时E;F 分别为AB;CD 的中点;且球心O 为EF 的中点;所以EF=2;所以max 1116424323V =⨯⨯⨯⨯=;故选C .10.由已知;(01)(01)F Q -,,,;过点P 作PM 垂直于准线;则PM=PF .记PQM α∠=;则||||sin ||||PF PM m PQ PQ α===;当α最小时;m 有最小值;此时直线PQ 与抛物线相切于点P .设204x P x ⎛⎫ ⎪⎝⎭,;可得(21)P ±,;所以||||2PQ PF ==;则||||2PF PQ a +=;∴1a =+;1c =;∴1ce a==;故选D . 11.在同一坐标系中作出y m =;8(0)21y m m =>+;3|log |y x =的图象;如图;设11()A x y ,;22()B x y ,;33()C x y ,;44()D x y ,;由3|log |x m =;得13m x -=;23m x =;由3|log |x =821m +;得82133m x -+=;82143m x +=.依照题意得821|33|m ma -+-=-,821|33|m mb +=-,821821|33||33|m m mmb a +-+--=- 882121333m mm m +++==;∴minb a ⎛⎫= ⎪⎝⎭故选B .12.设公切线与函数()ln f x x =切于点111(ln )(0)A x x x >,;则切线方程为1111ln ()y x x x x -=-;设公切线与函数2()2g x x x a =++切于点22222(2)(0)B x x x a x ++<,;则切线方程为22222(2)2(1)()y x x a x x x -++=+-;所以有2121212(1)ln 1x x x x a ⎧=+⎪⎨⎪-=-+⎩,.∵210x x <<;∴1102x <<.又2211111111ln 11ln 2124a x x x x ⎛⎫⎛⎫=+--=-+-- ⎪ ⎪⎝⎭⎝⎭;令11t x =;∴2102ln 4t a t t t <<=--,.设21()ln (02)4h t t t t t =--<<;则211(1)3()1022t h t t t t--'=--=<;∴()h t 在0;2上为减函数;则1()(2)ln 21ln2e h t h >=--=;∴1ln 2e a ⎛⎫∈+∞ ⎪⎝⎭,;故选A . 第Ⅱ卷非选择题;共90分二、填空题本大题共4小题;每小题5分;共20分13.因为2()e 30x f x x '=+>;所以函数fx 为增函数;所以不等式2()(32)f x f x <-等价于232xx <-;即232012x x x -+<⇔<<;故(12)x ∈,.14.因为||OQ =;直线OQ 的方程为y=x;圆心(31)-,到直线OQ 的距离为d ==所以圆上的动点P 到直线OQ 的距离的最小值为-=;所以OPQ △面积的最小值为122⨯=.15.不妨设(10)()()a b m n c p q ===,,,,,,则m=1;p=2;211b c nq nq =+=⇒=-, 1n q =-;∴11(2)b c q q ⎛⎫=-= ⎪⎝⎭,,,;2222||222a b c a b c ab bc ac ++=+++++2222111142241414216q q q q=+++++++=+++=≥;∴||4a b c ++≥;当且仅当21q =;即1q =±时“=”成立. 16.由1121n n n na a a n --=+-;得11122n n n n a a --=+;于是111112n n n n a a -⎛⎫--=- ⎪⎝⎭(2)n n *∈N ≥,.又11112a -=-;∴数列1n n a ⎧⎫-⎨⎬⎩⎭是以12-为首项;12为公比的等比数列;故112n n n a -=-;∴221nn n n a =-()n *∈N .三、解答题共70分.解答应写出文字说明;证明过程或演算步骤17.本小题满分12分 解:Ⅰ由正弦定理:1cos 1cos 3sin sin sin 222B A AB C +++=; ∴sin sin cos sin sin cos 3sin A A B B B A C +++=; ∴sin sin sin()3sin A B A B C +++=.又∵sin()sin A B C +=;∴sin sin 2sin A B C +=;即a+b=2c;a=2b;所以32c b =;所以2222229414cos 032422b b b bc a A bc b b +-+-===-<; 所以A 为钝角;故ABC △为钝角三角形. ………………6分Ⅱ因为1cos 4A =-,∴15sin 4A =.又1sin 2S bc A =;∴11531524bc =;∴24bc =.又32c b =;所以23242b =;∴4b =.………………………………………12分18.本小题满分12分 解:Ⅰ由茎叶图可得:购买意愿强 购买意愿弱 合计 20~40岁 20 8 28 大于40岁 10 12 22 合计302050由列联表可得:2250(2012108)=3.46 3.84130202822K ⨯-⨯≈<⨯⨯⨯; 所以;没有95%的把握认为市民是否购买该款手机与年龄有关. ……………6分 Ⅱ购买意愿弱的市民共有20人;抽样比例为51204=; 所以年龄在20~40岁的抽取了2人;年龄大于40岁的抽取了3人; 则X 的可能取值为0;1;2;11222332222555C C C C 1633(0)(1)(2)C 10C 105C 10P X P X P X ==========,,;所以分布列为X 0 1 2 P数学期望为1336()012105105E X =⨯+⨯+⨯=. …………………………12分 19.本小题满分12分Ⅰ证明:法一:如图;过点F 作FM //PA 交AB 于点M; 取AC 的中点N;连接MN;EN . ∵点E 为CD 的中点;∴EN //12AD . 又3PF FB =,∴MF12AD ;∴FM EN ; 所以四边形MFEN 为平行四边形;∴//EF MN ;∵EF ⊄平面ABC;MN ⊂平面ABC;图4∴//EF 平面ABC . ………………6分 法二:如图;取AD 中点G;连接GE;GF; 则GE//AC;GF//AB;因为GE ∩GF=G;AC ∩AB=A;所以平面GEF//平面ABC; 所以EF//平面ABC .………………6分 Ⅱ解:作BO ⊥AC 于点O;过点O 作OH//PA;以O 为坐标原点;OB;OC;OH 所在直线为x 轴、y 轴、z 轴建立如图6所示的空间直角坐标系;则3100000122C B D ⎫⎛⎫⎛⎫-⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎭,,,,,,,, ∴33(021)022CD CB ⎛⎫=-=- ⎪ ⎪⎭,,,,,; 则平面CDA 的一个法向量为(100)m =,,. 设平面CDB 的一个法向量为()n x y z =,,,则2003002y z n CD y n CB -+=⎧⎧=⎪⇒⎨-==⎪⎩,,, 可取(312)n =,,;所以6cos 4||||m n m n m n 〈〉==,; 所以二面角B CD A …………………………12分 20.本小题满分12分解:Ⅰ设()P x y ,;则点(22)N x y ,在抛物线28y x =上; 所以2416y x =;即24y x =;所以曲线C 的方程为:24y x =. ……………4分Ⅱ设切线方程为:00()y y k x x -=-;令y=0;解得00y x x k=-; 所以切线与x 轴的交点为000y x k ⎛⎫- ⎪⎝⎭,;圆心2;0到切线的距离为2d ==; ∴2200(2)4(1)k y kx k +-=+;整理得:22200000(4)(42)40x x k y x y k y -+-+-=; 设两条切线的斜率分别为12k k ,;则20000121222000024444x y y y k k k k x x x x --+==--,; ∴2200012000012120112221QABy y x k k S x x y y k k k k x ⎛⎫⎛⎫-=---== ⎪ ⎪-⎝⎭⎝⎭△记01[4)t x =-∈+∞,;则1()2f t t t=++;∵22211()10t f t t t-'=-=>;∴()f t 在[4)+∞,上单增;∴125()4244f t ++=≥;∴2525242S ⨯=≥; ∴QAB △面积的最小值为252. ………………………………12分21.本小题满分12分解:Ⅰ∵()e 2x f x x a '=--;∴(0)11f a '=-=;∴0a =;∴()e 2x f x x '=-;记()e 2x h x x =-;∴()e 2x h x '=-;令()0h x '=得ln 2x =. 当(0ln 2)x ∈,时;()0()h x h x '<,单减;当(ln 21)x ∈,时;()0()h x h x '>,单增; ∴min ()(ln 2)22ln 20h x h ==->;故()0f x '>恒成立;所以()f x 在[01],上单调递增; ∴min max ()(0)1()(1)e 1f x f f x f ====-,. ……………………3分 Ⅱ∵21()e ()2x g x x a =-+;∴()e x g x x a '=--.令()e x m x x a =--;∴()e 1x m x '=-;当0x ≥时;()0m x '≥;∴()m x 在[0)+∞,上单增;∴min ()(0)1m x ma ==-. i 当10a -≥即1a ≤时;()0m x ≥恒成立;即()0g x '≥;∴()g x 在[0)+∞,上单增; ∴2min()(0)102a g x g a ==-⇒≥所以1a ≤.ii 当10a -<即1a >时;∵()m x 在[0)+∞,上单增;且(0)10m a =-<; 当21e 2a <<-时;(ln(2))2ln(2)0m a a +=-+>; ∴0(0ln(2))x a ∃∈+,;使0()0m x =;即00e x x a =+. 当0(0)x x ∈,时;()0m x <;即()0()g x g x '<,单减; 当0(ln(2))x x a ∈+,时;()0m x >;即()0()g x g x '>,单增.∴00022min 0011()()e ()e e 22x x x g x g x x a ==-+=-001e 1e 02x x ⎛⎫=- ⎪⎝⎭≥; ∴00e 20ln 2x x ⇒<≤≤;由00e x x a =+;∴00e x a x =-;记()e (0ln 2]x t x x x =-∈,,; ∴()e 10x t x '=->;∴()t x 在(0ln 2],上单调递增;∴()(ln 2)2ln 2t x t =-≤;∴12ln 2a <-≤;综上;[2ln 2]a ∈-. ………………………………8分Ⅲ2()e ln 1f x x x x x x ---+≥等价于22e e ln 1x x x x x x x ----+≥;即e e ln 1x x x x x --+≥.∵0x >;∴等价于e 1ln e 10x x x x---+≥. 令e 1()ln e 1x h x x x x=---+; 则2(1)(e 1)()x x h x x --'=. ∵0x >;∴e 10x ->.当01x <<时;()0h x '<;()h x 单减;当1x >时;()0h x '>;()h x 单增.∴()h x 在1x =处有极小值;即最小值;∴()(1)e 1e 10h x h =--+=≥;∴0a =且0x >时;不等式2()e ln 1f x x x x x x ---+≥成立. ………………12分22.本小题满分10分选修4 4:坐标系与参数方程解:Ⅰ由题意知;曲线1C 的参数方程为1cos sin x t y t ⎨=+=⎧⎩,,t 为参数; ∴曲线1C 的普通方程为22(1)1x y -+=;∴曲线1C 的极坐标方程为=2cos ρθ. ……………………………4分 Ⅱ设点P ;Q 的极坐标分别为11()ρθ,;22()ρθ,; 则由111π=3=2cos θρθ⎧⎪⎨⎪⎩,,可得P 的极坐标为π13⎛⎫ ⎪⎝⎭,;由222π=3π2cos 6θρθ⎧⎪⎪⎨⎛⎫⎪- ⎪⎪⎝⎭⎩,可得Q 的极坐标为π33⎛⎫ ⎪⎝⎭,. ∵12θθ=;∴12||||2PQ ρρ=-=;又M 到直线l;∴1=2MPQ S △. ……………………………10分 23.本小题满分10分选修4 5:不等式选讲解:Ⅰ∵()|1|2|1|f x x x =+--;∴31()311131x x f x x x x x -<-⎧⎪=--⎨⎪-+>⎩,,,,,,≤≤ ∴()f x 的图象与x 轴围成的三角形的三个顶点分别为103A ⎛⎫ ⎪⎝⎭,;(30)B ,;(12)C ,; ∴1882=233ABC S =⨯⨯△; ∴()f x 的图象与x 轴围成的三角形面积是83.……………………………5分 Ⅱ∵(0)s ∀∈+∞,;244()4s as g s s a a a s s -+==+--=-≥; ∴当且仅当2s =时;()g s 有最小值4a -.又由Ⅰ可知;对(0)t ∀∈+∞,;()(1)=2f t f ≤.(0)s t ∀∈+∞,,恒有()()g s f t ≥成立;等价于(0)s t ∀∈+∞,,;min max ()()g s f t ≥;等价于42a -≥;即2a ≤;∴实数a 的取值范围是(2]-∞,.……………………………10分。
师范大学附属中学高三高考适应性月考卷数学(理)试题

云南师大附中2015届高考适应性月考卷(三)理科数学参考答案第Ⅰ卷(选择题,共60分)【解析】1.分别取1212x y ==,,,,计算可得{101}Q =-,,,故选B.2.123i 32(6)i 12i 55z b b b z -+-==+-,当605b -=时,12z z 是实数,6b ∴=,故选A. 3.A 中否命题应为“若21x ≠,则1x ≠”;B 中否定应为“210x x x ∀∈+-,≥R ”;C 中原命题为真命题,故其逆否命题为真命题;易知D 正确,故选D .4.(10)(12)(12)(34)b a c +=+=+=,,,,,λλλλ,又()b a c +⊥λ,()0b a c ∴+⋅=λ,即(12)+⋅,λλ(34)3380=++=,λλ,解得311=-λ,故选C. 5.由题意可知输出结果为1234105S =-+-+-⋅⋅⋅+=,故选C.6.3πsin cos cos 26y x x x x ⎛⎫=+=- ⎪⎝⎭,故其对称轴为π2π6x k k -=∈,Z ,ππ212k x ∴=+, k ∈Z ,当0k =时,π12x =,故选A. 7.对于①,已知其正确;由正态分布的概念的对称性可得(10)(01)P P -<<=<<=ξξ 11(1)22P m ->=-ξ,故②正确;随机变量2K 的观测值k 越大,判断“X 与Y 有关系”的把握越大,故③错误,所以正确的有①②两个,故选C. 8.该几何体下方是一个长方体,上方是一个圆柱被切掉一部分,体积为442π3V =⨯⨯+⨯ 1π2324π2+⨯⨯=+,故选D. 9. 123221213112132a a a ==-=-=-=--+,,,452121*********a a =-==-=+-,, 推理得{}n a 是周期为4的数列,所以3201512a a ==-,故选B .10.1122()2cos ()()2()2f x x g x x x f x g x -''''==+,,≤,≥,故函数()2sin f x x =([0π])x ∈,上点P 的坐标必为(00),,函数()13x g x ⎛⎫=+ ⎪⎝⎭上点Q 的坐标必为813⎛⎫ ⎪⎝⎭,,故直线PQ 的斜率为83,故选C . 11.由题意可知22222m c m n a ⎧=⎪⎨-=⎪⎩,,则22n b =,椭圆的方程可化为22221x y c b +=.由0AP PQ ⋅=知AP 与渐近线垂直.不妨设P 在第一象限,则直线AP 的方程为()a y x c b=--,与渐近线b y x a =联立可解得P 的坐标为2a ab c c ⎛⎫ ⎪⎝⎭,.又点P 在椭圆上,代入椭圆方程可得42421a a c c +=,即42111e e +=,整理得4210e e --=,所以2e ,故选D . 12.1121212212()(()()),()()()()()()(()())22f x f x f x f x f x f x f x g x f x f x f x -⎧+=+=⎨<⎩≥1113e ((,0][3,)),e ((0,3)),x x x x -+⎧∈-∞+∞⎪=⎨⎪∈⎩又当[]x a b ∈,时,1212()()0g x g x x x ->-恒成立,故()g x 在[]x a b ∈,时是增函数,结合图象可知()g x 在[0)x ∈+∞,时是增函数,又[15]a b ∈-,,,故b a -的最大值在05a b ==,时取得,故选D .第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.由4652a a a ⋅=,得2552a a =,即52a =,所以54b=,19959()9362b b S b +===. 14.ππ00sin d (cos )cos πcos02a x x x ==-=-+=⎰,二项式6⎛ ⎝展开式的通项公式为663166C (1)2C rr r r r r r r T x ---+⎛=⋅=- ⎝.令30r -=,得3r =,此时展开式中常数项为363346(1)2C 160T -=-⨯=-.15.函数(1)y f x =+的图象关于点(10)-,成中心对称,∴函数()y f x =的图象关于点(00),成中心对称,即()y f x =为奇函数.不等式22(2)(2)0f x x f y y -+-≤,可化为222(2)(2)(2)f x x f y y f y y ---=-≤,又定义在R 上的函数()y f x =是减函数,2222x x y y ∴--≥,由14x ≤≤得22(22)014x y x y x ⎧---⎨⎩≥,≤≤,故()(2)014x y x y x -+-⎧⎨⎩≥,≤≤,即02014x y x y x -⎧⎪+-⎨⎪⎩≥,≥,≤≤或02014x y x y x -⎧⎪+-⎨⎪⎩≤,≤,≤≤,作出可行域,又(12)()M N x y ,,,,故2OM ON x y ⋅=+,利用线性规划知识可求得OM ON ⋅的取值范围为[012],.16.如图1,设P ABCD -的外接球的球心为G ,A B C D ,,,在球面上,∴球心在正方体1111ABCD A B C D -上下底面中心连线1O O上,点P 也在球上,GP GA R ∴==,棱长为1,22OA ∴=,设11O P x O G y ==,,则1OG y =-,在1Rt GO P △中,有222R x y =+①,在Rt GOA △中,三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)【注:本题题干第一行中“且sin 2m n C ⋅=-”改为“且sin 2m n C ⋅=”,改后答案如下:】解:(Ⅰ)sin()2cos sin sin cos cos sin sin()m n A B A B A B A B A B ⋅=-+=+=+,…………………………………………………………………………………(2分)在ABC △中,π0πA B C C +=-<<,,所以sin()sin A B C +=,……………………(4分)又sin 2m n C ⋅=,所以sin sin 22sin cos C C C C ==,所以1cos 2C =,即π3C =. ……………………………………………………………………………………(6分)(Ⅱ)sin sin 2sin A B C +=,由正弦定理得2c a b =+,………………………………(7分)1sin 2ABC S ab C =△,得4ab =,……………………………………………(9分)由余弦定理得22222222cos ()3412c a b ab C a b ab a b ab c =+-=+-=+-=-, 得2c =.………………………………………………………………………………(12分)18.(本小题满分12分)解:(Ⅰ)芯片甲为合格品的概率为4032841005++=, 芯片乙为合格品的概率为4029631004++=,…………………………………………(3分) 随机变量X 的所有可能取值为90453015-,,,.433(90)545P X ==⨯=;133(45)5420P X ==⨯=; 411(30)545P X ==⨯=;111(15)5420P X =-=⨯=, 所以随机变量X 的分布列为………………………………………………………………………………………(7分)则X 的数学期望3311()904530(15)66520520E X =⨯+⨯+⨯+-⨯=.…………………(8分)(Ⅱ)设生产的5件芯片乙中合格品有n 件,则次品有5n -件. 依题意,得5010(5)140n n --≥, 解得196n ≥,所以4n =或5n =.……………………………………………………(10分)设“生产5件芯片乙所获得的利润不少于140元”为事件A , 则454531381()C 444128P A ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭.……………………………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:如图2,取AB 的中点H ,连接PH HC ,. PAB △是正三角形,且H 为AB 的中点,2AB =,PH AB ∴⊥,且3PH =…………………………………………………(2分) 底面ABCD 是矩形,22AB BC ==,123HC ∴=+. 又6PC =222PC PH CH ∴=+,PH HC ∴⊥.………………………………………………………(4分)AB HC H =,PH ∴⊥平面ABCD .PH ⊂平面PAB ,∴平面PAB ⊥平面ABCD .………………………………………(6分)(Ⅱ)解:如图2所示,以H 为原点建立空间直角坐标系H xyz -, 则(100)(100)A B -,,,,,,(003)P ,,,(120)D ,,.……………………………(7分)设(01)AE AP =<<λλ,则(203)BE BA AE =+=-,,λλ,(220)BD =,,, 设()n x y z =,,为平面EBD 的法向量, 由0,()(220)=0,0,()(203)=0,n BD x y z n BE x y z ⎧⎧⋅=⎪⎪∴⎨⎨⋅=-⎪⎪⎩⎩,,,,,,,,λλ 220,(2)30,x x z ⎧=⎪∴⎨-=⎪⎩λλ令2z =-λ,得(362)n =--,,λλλ.易知(003)HP =,,为平面ABD 的一个法向量.………………………………………(9分)二面角E BD A --的大小为45︒, 22332cos45cos 210443n HP n HP n HP -⋅∴︒=〈〉===⋅-+⨯,λλλ. ………………………(10分)又由01<<λ,得12=λ,1AE EP ∴=∶.……………………………………………(12分) 由221(4),44,y x x y m ⎧=+⎪⎨⎪-=⎩得2381640x x m ---=, 则816433A B A B m x x x x ++==-,.(*) ……………………………………………………(3分)因为2PA PB PC ⋅=,P A B C ,,,共线且P 在线段AB 上, 所以2()()()P A B P P C x x x x x x --=-, 整理得:4()320A B A B x x x x +++=, 将(*)代入上式可解得:28m =. 所以双曲线G 的方程为221287x y -=.……………………………………………………(6分)(Ⅱ)由题意可设椭圆S 的方程为:2221(7)28x y a a +=>,弦的两个端点分别为11()M x y ,,22()N x y ,,MN 的中点为00()Q x y ,, 由22112222221,281,28x y a x y a ⎧+=⎪⎪⎨⎪+=⎪⎩得121212122()()()()028x x x x y y y y a -+-++=,……………………………(8分) 因为1212012012422y y x x x y y y x x -=-+=+=-,,,所以0024028x y a-=,…………………(9分)所以S 中垂直于l 的平行弦的中点的轨迹为直线24028x y a -=截在椭圆S 内的部分. 又这个轨迹恰好是G 的渐近线截在S 内的部分,所以211122a =,所以256a =, 椭圆S 的方程为2212856x y +=.…………………………………………………………(12分)21.(本小题满分12分)(Ⅰ)解:()[(1)]()f x g x a g x '''=+--λλλλ,………………………………………(1分)令()0f x '>,得[(1)]()g x a g x ''+->λλ,(1)x a x ∴+->λλ,即(1)()0x a --<λ,解得x a <, ………………………………………………………(3分)故当x a <时,()0f x '>;当x a >时,()0f x '<,……………………………………(4分)∴当x a =时,()f x 取极大值,但()f x 没有极小值. ()f x 的极大值为()[(1)]()()()(1)e a f a g a a g a g a g a =+--=-=-⋅λλλλλ.………(6分)(Ⅱ)证明:e 1e 11x x x x x----=,又当0x >时,令()e 1x t x x =--,则()e 10x t x '=->, 故()(0)0t x t >=,因此原不等式化为e 1x x a x--<,即e (1)10x a x -+-<,…………(8分)令()e (1)1x h x a x =-+-,则()e (1)x h x a '=-+,由()0h x '=,得e 1x a =+,解得ln(1)x a =+,当0ln(1)x a <<+时,()0h x '<;当ln(1)x a >+时,()0h x '>,故当ln(1)x a =+时,()h x 取得最小值[ln(1)](1)ln(1)h a a a a +=-++,……………(10分) 令()ln(1)01a s a a a a=-+>+,, 则2211()0(1)1(1)a s a a a a '=-=-<+++. 故()(0)0s a s <=,即[ln(1)](1)ln(1)0h a a a a +=-++<.因此,存在正数ln(1)x a =+,使原不等式成立. ……………………………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】(Ⅰ)证明:PA 为圆O 的切线,PAB ACP ∴∠=∠,又P ∠为公共角,PAB PCA ∴△∽△,AB PA AC PC∴=, 所以,AB PC AC PA ⋅=⋅. ………………………………………………………………(4分)(Ⅱ)解:PA 为圆O 的切线,BC 是过点O 的割线,2PA PB PC ∴=⋅,4540PC BC ∴==,,又222901600CAB AC AB BC ∠=︒∴+==,, 又由(Ⅰ)知13AB PA AC PC ==,AC AB ∴==,连接EC ,CAE EAB ∠=∠,ACE ADB △∽△, AB AD AE AC∴=,480.AD AE AB AC ∴⋅=⋅==……………………………………………(10分)变形得213sin =+ρθ.由OA OB ⊥可设12π()2A B ⎛⎫+ ⎪⎝⎭,,,ρθρθ, 所以2211OA OB +222212π13sin 1113sin 244⎛⎫++ ⎪+⎝⎭=+=+θθρρ 2223sin 3cos 544++==θθ(定值). ……………………………………………………(7分)1222222129(13sin )(13cos )139sin cos 4sin 24AOB S ===+++++△ρρθθθθθ, 易知当sin 20=θ时,max ()1AOB S =△.……………………………………………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)因为4(4)()4x x a x x a a -+----=-≥,因为4a <,所以当且仅当4a x ≤≤时等号成立, 故431a a -=∴=,.……………………………………………………………………(5分)(Ⅱ)当1a =时,若1()()g x f x m=+的定义域为R ,则()0f x m +≠恒成立,即()0f x m +=在R 上无解, 又()441(4)(1)3f x x x a x x x x =-+-=-+----=≥,当且仅当14x ≤≤时取等号,3m ∴>-.………………………………………………………………………………(10分)。
云南师大附中2015届高考适应性月考卷(二)理科数学-答案

理科数学参考答案·第1页(共8页)云南师大附中2015届高考适应性月考卷(二)理科数学参考答案第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.由{0,2}A =,{0,1,2}B =,所以{0,2}AB =,故选C.2.由42015i i 1i z =+=-,则1i z =+,其对应点为(1,1),在第一象限,故选A. 3.由{}n a 为等差数列,故而39662a a a +==,又1161166S a ==,故选D. 4.框图的运行如下:第一步1,πcos ;6k S =⎧⎪⎨=⎪⎩第二步3,ππcos cos ;63k S =⎧⎪⎨=⎪⎩第三步5,ππ2πcos cos cos .633k S =⎧⎪⎨=⎪⎩第三步结束跳出循环,即最后输出的ππ2πcos cos cos 633S =,又由ππ2πc o sc o s c 6338S ==,故选D. 5.①错,因为分别与两平行平面平行的两直线可以是平行、相交或异面; ②错,因为两直线的位置关系可以是平行、相交或异面; ③错,因为两直线的位置关系可以是平行、相交或异面;④对,直线m 、n 的方向向量分别是两互相垂直平面α、β的法向量,故而m n ⊥,所以有3个命题是假命题,故选C .6.如图1所示,由椭圆的第一定义知,1214PF PF +=, 又有122PF PF -=,故而18PF =,26PF =,而1210F F =,所以2221212PF PF F F +=, 故12PF F △为Rt △,则12121242PF F S PF PF =⋅=△,故选B.7.由于1A 、2A 串联,故其能通过电流的概率为0.81, 则1A 、2A 不能通过电流的概率为10.810.19-=,图2图1理科数学参考答案·第2页(共8页)由1A 、2A 串联后与3A 并联,如图2,故,A B 之间能通过电流的概率为1(10.81)(10.9)0.981---=,又由于电路再与4A 串联,故而电流能在,M N 之间通过的概率是0.9810.90.8829⨯=,故选B.8.由双曲线22221(0,0)x y a b a b-=>>的一个焦点与抛物线220y x =的焦点重合,则5c =,由点到线的距离公式可知焦点(,0)c 到双曲线渐近线by x a=±的距离d b =,所以4b =,故而3a ==,故其离心率53e =,故选C.9.由题意知,2n B =,令1x =,则4n A =,故而4272n n A B +=+=, 解之得:3n =,故选A.10.由题意可知该三棱锥为如图3所示的边长为1的正方体中以,,,A B C D为顶点的正四面体,故而其体积313V ==,故选C. 11.由(())()()0xf x xf x f x ''=+>,则函数()xf x 为R 上的增函数. 由于01a b <<<,则01b a a <=,01a b b <=,log log 1a a b a <=,而lo g l o g 1b ba b >=,则log (log )b b a f a ⋅最大,故选D.12.必要条件,若ABC △是锐角三角形,则π,,0,2A B C ⎛⎫∈ ⎪⎝⎭,tan 0,tan 0,tan 0A B C >>>,所以tan tan tan 0A B C ++>,必要性成立;充分条件,由tan tan tan 0A B C ++>,即tan ,tan ,tan A B C 有意义,ABC △不是直角三角形. 又在ABC △中,由πA B C ++=,得:πA B C +=-,所以tan()tan(π)A B C +=-⇒tan tan tan 1tan tan A BC A B+=--tan tan tan tan tan tan A B C A B C ⇒++=,由tan tan tan 0A B C ++>, 则tan tan tan 0A B C >,所以ABC △是锐角三角形,故选B.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)图3理科数学参考答案·第3页(共8页)13.由223a b +=,得2(2)12a b +=,即224()4()12a a b b +⋅+=,所以21441122b b +⨯⨯⨯+=,解得2b =.14.,x y 满足的线性区域如图4阴影部分所示,222x y +=,由两点间距离公式知,22x y+的最小值的几何意义是点 (0,0)到阴影区域中点的最小距离的平方,如图可知点(0,0)到阴影区域 的最小距离为点(0,0)到直线220x y+-=的距离d , 故d ==222min4()5x y +==.15.经观察可知,由两位的“和谐数”有9个,而三位的“和谐数”相当于在两位数的中间增加0至9中任意一个数,故而三位的“和谐数”有91090⨯=个,而四位的“和谐数”相当于三位的“和谐数”中间的数字重复出现一次,则四位的“和谐数”有90个;同理,五位的“和谐数”有9010900⨯=个,六位的“和谐数”有900个,七位的“和谐数”有900109000⨯=个,八位的“和谐数”有9000个.16.记三个球心分别是1O ,2O ,3O ,球I 与桌面的切点为O ,反过来看图,由题意可知:三棱锥123IO O O 是以I 为顶点 123O O O 为底面的正三棱锥,三棱锥123OO O O 是以O 为顶点 123O O O 为底面的正三棱锥. 如图5所示,记A 为底面123O O O的中心,则OIA 三点共线且OA 垂直底面123O O O ,由题意知126O O =, 3OA =,1O A =,设球I 的半径为r ,则3AI r =-,13IO r =+,有22211()()()AO AI IO +=,即22(3)(3)12r r +=-+,解得1r =,所以球I 的半径为1.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)图4图5理科数学参考答案·第4页(共8页)证明:(Ⅰ)由121(2)n n a a n -=+≥,知112(1)(2)n n a a n -+=+≥, 所以{1}n a +是以11a +为首项,2为公比的等比数列,故而111(1)2n n a a -+=+⋅,即12n n a +=,所以21n n a =-. ……………………(6分) (Ⅱ)由(Ⅰ)知221log (1)21n n b a n +=+=+, 21111114(1)41n n c b n n n n ⎛⎫===- ⎪-++⎝⎭, 所以1111111111142231414n S n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-< ⎪ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. ……………(12分)18.(本小题满分12分)(Ⅰ)证明:如图6,取BC 的中点O , 因为PBC △为等边三角形,所以PO BC ⊥,又因为侧面PBC ⊥底面ABCD ,所以PO ⊥平面ABCD , 如图6,以O 为坐标原点,BC 所在直线为x 轴,过点O 与AB 平行的直线为y 轴,直线OP 为z 轴,建立空间直角坐标系, 则(1,2,0)A -,(1,0,0)B ,(1,1,0)D --,(0,0,P ,所以(2,1,0)BD=--,(1,2,PA =-,0BD PA ⋅=, 则BD PA ⊥,即B D P A⊥.………………………………………………………(6分)(Ⅱ)解:因为PFPA λ=,(1,2,PA =-,所以(,2,)PF λλ=-, 又(1,1,DP =,所以(1,12,))DF DP PF λλλ=+=+--,又平面ABCD 的一个法向量(0,0,1)n =,直线DF 与平面ABCD 所成角为30︒.sin 30DF n DF n⋅︒=,所以12=, 所以241670λλ-+=,则12λ=或72λ=(舍). 当12λ=时,直线DF 与平面ABCD 所成角为30︒. …………………………(12分) 19.(本小题满分12分)解:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为18的等差数列,图6理科数学参考答案·第5页(共8页)又甲同学第一次参加测试就合格的概率为P ,故而甲同学参加第二、三次测试合格的概率分别是18P +、14P +,由题意知,19(1)832P P ⎛⎫-+= ⎪⎝⎭,解得14P =或58P =(舍),所以甲同学第一次参加测试就合格的概率为14. ………………………………(4分) (Ⅱ)由(Ⅰ)知甲同学参加第二、三次测试合格的概率分别是38、12,由题意知,ξ的可能取值为2,3,4,5,6,由题意可知121(2)(1,1)436P P m n ξ=====⨯=,11233235(3)(1,2)(2,1)433483144P P m n P m n ξ⎛⎫⎛⎫====+===⨯⨯+⨯⨯= ⎪ ⎪⎝⎭⎝⎭, (4)(1,3)(2,2)(3,1)P P m n P m n P m n ξ====+==+==1113312352584334833483144⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯⨯+⨯⨯=⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,(5)(2,3)(3,2)P P m n P m n ξ====+==33113512134833483396⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,35115(6)(3,3)483396P P m n ξ⎛⎫⎛⎫=====⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,所以ξ的分布列为:……………………………………………………………………(12分) 20.(本小题满分12分)解:(Ⅰ)由抛物线方程,得焦点20)F ,故可设椭圆的方程为222213x y b b +=+,解方程组2,y x ⎧=⎪⎨=⎪⎩解得C,D -,理科数学参考答案·第6页(共8页)由抛物线与椭圆的对称性,可得:22F C CD F SST==,所以212F S =,所以12S ⎫⎪⎭.因此2213413b b+=+,解得21b =,故而24a =, 所以椭圆E 的方程为2214x y +=. ……………………………………………………(4分)(Ⅱ)由题意知直线l 的斜率存在,设其为k . ①当0k =时,0OA OB tOP +==,所以0t =; ②当0k ≠时,则直线l 的方程为(3)y k x =-,联立221,4(3),x y y k x ⎧+=⎪⎨⎪=-⎩消去y 并整理得:2222(14)243640k x k x k +-+-=,由Δ2222(24)4(14)(364)0k k k =-+->,得2105k <<,设11(,)A x y ,22(,)B x y ,00(,)P x y ,则2212122224364,1414k k x x x x k k -+==++. 因为OA OB tOP +=,所以121200(,)(,)x x y y t x y ++=, 所以20122124()(14)k x x x t t k =+=+,012122116()[()6](14)ky y y k x x k t t t k -=+=+-=+.因为点P 在椭圆上,所以2222224644(14)(14)k k t k t k ⎡⎤⎡⎤-+=⎢⎥⎢⎥++⎣⎦⎣⎦, 解得222236991414k t k k ==-++, 由于2105k <<,故而204t <<,所以(2,0)(0,2)t ∈-,综合①②可知,(2,2)t ∈-. ……………………………………………………(12分) 21.(本小题满分12分)(Ⅰ)解:由题意知,()ln 2(0)f x x x '=+>,所以2()ln 2(0)F x ax x x =++>,2121()2(0)ax F x ax x x x+'∴=+=>.理科数学参考答案·第7页(共8页)①当0a ≥时,恒有()0F x '>,故()F x 在(0,)+∞上是增函数; ②当0a <时,令()0F x '>,得2210ax +>,解得0x << 令()0F x '<,得2210ax +<,解得x 综上所述,当0a ≥时,()F x 在(0,)+∞上单调递增;当0a <时,()F x在0,⎛⎝上单调递增;在⎫+∞⎪⎪⎭上单调递减. ………………………………………………………………………(5分)(Ⅱ)证明:由题意知,21212121()()ln ln f x f x x x k x x x x ''--==--,要证121x x k <<,即要证22112122211111ln ln ln x x x x x x x x x x x x --<<⇔<<-, 令211x t x =>,则只需要证明11ln t t t-<<,由l n 0t >,即等价证明:ln 1ln (1)t t t t t <-<>. ①设()1ln (1)g t t t t =--≥,则1()10(1)g t t t '=-≥≥,故而()g t 在[1,)+∞上单调递增,而当1t >时,()1ln (1)0g t t t g =-->=,即ln 1(1)t t t <->;②设()ln (1)(1)h t t t t t =--≥,则()ln 0(1)h t t t '=≥≥,故而()h t 在[1,)+∞上单调递增, 而当1t >时,()ln (1)(1)0(1)h t t t t h t =-->=>,即1ln (1)t t t t -<>. 综上①②知,ln 1ln (1)t t t t t <-<>成立,即121x x k<<. …………………(12分) 22.(本小题满分10分)【选修4−1:几何证明选讲】证明:(Ⅰ)如图7,连接DG ,AB , ∵AD 为⊙M 的直径, ∴90ABD AGD ∠=∠=︒,在⊙O 中,90ABC AEC ABD ∠=∠=∠=︒,∴AC 为⊙O 的直径. …………………………………………………………(5分) (Ⅱ)∵90AEC ∠=︒,∴90CEF ∠=︒,∵点G 为弧BD 的中点,∴BAG GAD ∠=∠,图7理科数学参考答案·第8页(共8页)在⊙O 中,BAE ECB ∠=∠,∴AGD CEF △∽△,∴AG EF CE GD ⋅=⋅. …………………………………………………………(10分) 23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)由cos ,sin ,x y ρθρθ=⎧⎨=⎩故而C 的直角坐标方程为22.y ax =消去t 得直线l 的普通方程为2y x =-. ……………………………………………(4分)(Ⅱ)由题意可知直线l的标准参数方程为2,4,x y ⎧=-⎪⎪⎨⎪=-⎪⎩(t 为参数), 代入22y ax =得到2)8(4)0t a t a -+++=,则有1212),8(4)t t a t t a +=+⋅=+,由28(4)48(4)0a a ∆=+-⨯+>,即0a >或4a <-.因为2||||||MN PM PN =⋅,所以2212121212()()4t t t t t t t t -=+-⋅=⋅, 解得1a =或4a =-(舍),所以1a =. ………………………………………………………………(10分) 24.(本小题满分10分)【选修4−5:不等式选讲】证明:(Ⅰ)因为0,0m n >>, 则2422m n mn +≥,4222m n m n +≥, 所以244233()()4m n m n m n ++≥,当且仅当1m n ==时,取等号. …………………………………………(5分) (Ⅱ)由柯西不等式知:22222()()()a b m n am bn +++≥, 即2225()(5)m n +≥,所以225m n +≥, 当且仅当a bm n=时取等号. …………………………………………(10分)。
云南省师大附中高三数学上学期第二次月考试卷理(含解析)

云南师大附中2015届高三上学期第二次月考数学试卷(理科)一、选择题(本大题12小题,每题5分,共60分)1.(5分)已知集合A={x|x2﹣2x=0},B={0,1,2},则A∩B=()A.{0} B.{0,1} C.{0,2} D.{0,1,2}2.(5分)在复平面内,复数z=i4+i2015的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)在等差数列{a n}中,a3+a9=12,则数列{a n}的前11项和S11等于()A.33 B.44 C.55 D.664.(5分)执行如图所示框图,则输出S的值为()A.B.﹣C.D.﹣5.(5分)关于两条不同的直线m、n与两个不同的平面α、β,有下列四个命题:①若m∥α,n∥β且α∥β,则m∥n;②若m∥α,n⊥β且α⊥β,则m∥n;③若m⊂α,n⊂β且α⊥β,则m⊥n;④若m⊥α,n⊥β且α⊥β,则m⊥n.其中假命题有()A.1个B.2个C.3个D.4个6.(5分)F1、F2分别是椭圆=1的左、右焦点,点P在椭圆上,且|PF1|﹣|PF2|=2,则△PF1F2的面积为()A.24B.24 C.48D.487.(5分)如图,元件A i(i=1,2,3,4)通过电流的概率均为0.9,且各元件是否通过电流相互独立,则电流能在M,N之间通过的概率是()A.0.729 B.0.8829 C.0.864 D.0.98918.(5分)双曲线=1(a>0,b>0)的一个焦点与抛物线y2=20x的焦点重合,且抛物线的焦点到双曲线渐近线的距离为4,则双曲线的离心率为()A.B.C.D.9.(5分)若在的展开式中,各系数之和为A,各二项式系数之和为B,且A+B=72,则n的值为()A.3 B.4 C.5 D.610.(5分)如图所示,某三棱锥的三视图均为边长为1的正方形,则该三棱锥的体积是()A.B.C.D.11.(5分)已知定义在R上的函数f(x)满足xf′(x)+f(x)>0,当0<a<b<1时,下面选项中最大的一项是()A.a b f(a b)B.b a f(b a)C.log a b•f(log a b)D.log b a•f(log b a)12.(5分)在△ABC中,tanA+tanB+tanC>0是△ABC是锐角三角形的()A.既不充分也不必要条件B.充分必要条件C.必要不充分条件D.充分不必要条件二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知向量,夹角为60°,且||=1,|2﹣|=2,则||=.14.(5分)已知,则x2+y2的最小值是.15.(5分)无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“和谐数”,如88,545,7337,43534等都是“和谐数”.两位的“和谐数”有11,22,33,44,55,66,77,88,99,共9个;三位的“和谐数”有101,111,121,131,…,969,979,989,999,共90个;四位的“和谐数”有1001,1111,1221,…,9669,9779,988,9999,共90个;由此推测:八位的“和谐数”总共有个.16.(5分)三个半径均为3且两两外切的球O1、O2、O3放在水平桌面上,现有球I放在桌面上与球O1、O2、O3都外切,则球I的半径是.三、解答题17.(12分)已知数列{a n}满足a n=2a n﹣1+1(n≥2)且a1=1,b n=log2(a2n+1+1),.求证:(Ⅰ)数列{a n+1}为等比数列,并求数列{a n}的通项公式;(Ⅱ)数列{c n}的前n项和.18.(12分)如图所示,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足.(1)证明:PA⊥BD;(2)当λ取何值时,直线DF与平面ABCD所成角为30°?19.(12分)甲乙两位同学参加学校安排的3次体能测试,规定按顺序测试,一旦测试合格就不必参加以后的测试,否则3次测试都要参加.甲同学3次测试每次合格的概率组成一个公差为的等差数列,他第一次测试合格的概率不超过,且他直到第二次测试才合格的概率为,乙同学3次测试每次测试合格的概率均为,每位同学参加的每次测试是否合格相互独立.(Ⅰ)求甲同学第一次参加测试就合格的概率P;(Ⅱ)设甲同学参加测试的次数为m,乙同学参加测试的次数为n,求ξ=m+n的分布列.20.(12分)如图,椭圆E:=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线与椭圆交于S、T两点,与抛物线交于C、D两点,且.(Ⅰ)求椭圆E的方程;(Ⅱ)若过点M(3,0)的直线l与椭圆E交于两点A、B,设P为椭圆上一点,且满足+=t (O为坐标原点),求实数t的取值范围.21.(12分)已知函数f(x)=x(lnx+1)(x>0).(Ⅰ)设F(x)=ax2+f'(x)(a∈R),讨论函数F(x)的单调性;(Ⅱ)若斜率为k的直线与曲线y=f′(x)交于A(x1,y1)、B(x2,y2)(x1<x2)两点,求证:x1<<x2.选修4-1:几何证明选讲22.(10分)如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD的中点,连接AG分别交⊙O、BD于点E、F,连接CE.(Ⅰ)求证:AC为⊙O的直径.(Ⅱ)求证:AG•EF=CE•GD.选修4-4:坐标系与参数方程23.(10分)在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),已知过点P(﹣2,﹣4)的直线l的参数方程为,直线l与曲线C分别交于M,N.(1)写出曲线C和直线l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.选修4-5:不等式选讲24.(10分)设a>0,b>0,m>0,n>0.(Ⅰ)证明:(m2+n4)(m4+n2)≥4m3n3;(Ⅱ)a2+b2=5,ma+nb=5,求证:m2+n2≥5.云南师大附中2015届高三上学期第二次月考数学试卷(理科)参考答案与试题解析一、选择题(本大题12小题,每题5分,共60分)1.(5分)已知集合A={x|x2﹣2x=0},B={0,1,2},则A∩B=()A.{0} B.{0,1} C.{0,2} D.{0,1,2}考点:交集及其运算.专题:集合.分析:解出集合A,再由交的定义求出两集合的交集.解答:解:∵A={x|x2﹣2x=0}={0,2},B={0,1,2},∴A∩B={0,2}故选C点评:本题考查交的运算,理解好交的定义是解答的关键.2.(5分)在复平面内,复数z=i4+i2015的共轭复数对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限考点:复数的代数表示法及其几何意义.专题:数系的扩充和复数.分析:直接利用复数的单位i的指数运算,化简复数为a+bi的形式,即可得到复数的共轭复数的形式,判断选项即可.解答:解:复数z=i4+i2015=1+i2012+3=1﹣i,复数的共轭复数我1+i,对应的点(1,1)在第一象限.故选:A.点评:本题考查复数的基本运算,复数的几何意义,基本知识的考查.3.(5分)在等差数列{a n}中,a3+a9=12,则数列{a n}的前11项和S11等于()A.33 B.44 C.55 D.66考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由已知得S11==,由此能求出结果.解答:解:∵在等差数列{a n}中,a3+a9=12,∴数列{a n}的前11项和:S11====66.故选:D.点评:本题考查等差数列的前11项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.4.(5分)执行如图所示框图,则输出S的值为()A.B.﹣C.D.﹣考点:程序框图.专题:算法和程序框图.分析:执行程序框图,写出每次循环得到的S,α的值,当k=5时,满足条件k>4,输出S的值为﹣.解答:解:执行程序框图,有k=1,S=1,α=S=,α=不满足条件k>4,k=3S=,α=不满足条件k>4,k=5S=﹣,α=满足条件k>4,输出S的值为﹣.故选:D.点评:本题主要考察了程序框图和算法,属于基础题.5.(5分)关于两条不同的直线m、n与两个不同的平面α、β,有下列四个命题:①若m∥α,n∥β且α∥β,则m∥n;②若m∥α,n⊥β且α⊥β,则m∥n;③若m⊂α,n⊂β且α⊥β,则m⊥n;④若m⊥α,n⊥β且α⊥β,则m⊥n.其中假命题有()A.1个B.2个C.3个D.4个考点:空间中直线与直线之间的位置关系.专题:计算题;空间位置关系与距离.分析:对四个命题,利用空间中线线、线面、面面间的位置关系,分别判断能求出结果.解答:解:对于①,在正方体ABCD﹣A1B1C1D1中,平面ABCD∥平面A1B1C1D1,A1D1∥平面ABCD,AD∥平面A1B1C1D1,A1D1∥AD;E P∥平面ABCD,PQ∥平面A1B1C1D1,EP∩PQ=P;A1D1∥平面ABCD,PQ∥平面A1B1C1D1,A1D1与PQ异面.综上,直线m,n与平面α,β,m∥α,n∥β且α∥β,则直线m,n的位置关系为平行或相交或异面.故①为假命题;当m⊂β时,则m⊥n,故②为假命题;∵m⊂α,n⊂β,且α⊥β,∴根据当m⊥β,可以推出直线m垂直于β内的所有条件,可以得到垂直与直线n,故③为假命题;由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m与n相交,且设m与n确定的平面为γ,则γ与α和β的交线所成的角即为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,故④正确故选:C.点评:本题考查两直线位置关系的判断,是中档题,解题时要注意空间思维能力的培养.6.(5分)F1、F2分别是椭圆=1的左、右焦点,点P在椭圆上,且|PF1|﹣|PF2|=2,则△PF1F2的面积为()A.24B.24 C.48D.48考点:椭圆的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:利用椭圆的定义,结合|PF1|﹣|PF2|=2,可得|PF1|=8,|PF2|=6,进而PF1⊥PF2,则△PF1F2的面积可求.解答:解:由题意,|PF1|+|PF2|=14,∵|PF1|﹣|PF2|=2,∴|PF1|=8,|PF2|=6,∵|F1F2|=10,∴PF1⊥PF2,∴△PF1F2的面积为=24,故选:B.点评:本题考查了椭圆的标准方程、椭圆的简单性质以及根据一些性质求面积,确定PF1⊥PF2是关键.7.(5分)如图,元件A i(i=1,2,3,4)通过电流的概率均为0.9,且各元件是否通过电流相互独立,则电流能在M,N之间通过的概率是()A.0.729 B.0.8829 C.0.864 D.0.9891考点:相互独立事件的概率乘法公式.专题:概率与统计.分析:求出电流不能通过A1 、A2 ,且也不能通过A3的概率,用1减去此概率,即得电流能通过系统A1 、A2 、A3的概率.再根据电流能通过A4的概率为0.9,利用相互独立事件的概率乘法公式求得电流能在M,N之间通过的概率.解答:解:电流能通过A1 、A2 ,的概率为0.9×0.9=0.81,电流能通过A3的概率为0.9,故电流不能通过A1 、A2 ,且也不能通过A3的概率为(1﹣0.81)(1﹣0.9)=0.019,故电流能通过系统A1 、A2 、A3的概率为 1﹣0.019=0.981,而电流能通过A4的概率为0.9,故电流能在M,N之间通过的概率是(1﹣0.019)×0.9=0.8829,故选:B.点评:本题主要考查相互独立事件的概率乘法公式,所求的事件的概率与它的对立事件的概率之间的关系,体现了转化的数学思想,属于基础题.8.(5分)双曲线=1(a>0,b>0)的一个焦点与抛物线y2=20x的焦点重合,且抛物线的焦点到双曲线渐近线的距离为4,则双曲线的离心率为()A.B.C.D.考点:双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:确定抛物线y2=20x的焦点坐标、双曲线=1(a>0,b>0)的一条渐近线的方程,利用抛物线的焦点到双曲线渐近线的距离为4,求出b,a,即可求出双曲线的离心率.解答:解:抛物线y2=20x的焦点坐标为(5,0),双曲线=1(a>0,b>0)的一条渐近线的方程为bx+ay=0,∵抛物线的焦点到双曲线渐近线的距离为4,∴=4,即b=4,∵c=5,∴a=3,∴双曲线的离心率为e==,故选:C.点评:本题考查双曲线的离心率,考查抛物线的性质,考查学生的计算能力,比较基础.9.(5分)若在的展开式中,各系数之和为A,各二项式系数之和为B,且A+B=72,则n的值为()A.3 B.4 C.5 D.6考点:二项式系数的性质.专题:二项式定理.分析:由题意可得A==4n,B=2n,再由A+B=4n+2n=72,求得2n的值,可得n的值.解答:解:由题意可得A==4n,B=2n,再由A+B=4n+2n=72,可得(2n﹣8)(2n+9)=0,∴2n=8,n=3,故选:A.点评:本题主要考查二项式定理的应用,注意各系数之和,与各二项式系数之和的区别,属于基础题.10.(5分)如图所示,某三棱锥的三视图均为边长为1的正方形,则该三棱锥的体积是()A.B.C.D.考点:由三视图求面积、体积.专题:计算题;空间位置关系与距离.分析:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,该几何体可看成边长为什么的正方体内截出的正四面体.解答:解:该几何体可看成边长为什么的正方体内截出的正四面体,则其体积V=1﹣4××(×1×1)×1=,故选C.点评:三视图中长对正,高对齐,宽相等;由三视图想象出直观图,一般需从俯视图构建直观图,本题考查了学生的空间想象力,识图能力及计算能力.11.(5分)已知定义在R上的函数f(x)满足xf′(x)+f(x)>0,当0<a<b<1时,下面选项中最大的一项是()A.a b f(a b)B.b a f(b a)C.log a b•f(log a b)D.log b a•f(log b a)考点:利用导数研究函数的单调性.专题:导数的综合应用.分析:通过构造新函数构造函数F(x)=xf(x)得出F(x)在R上是增函数,在a b,b a,loga(b),logb(a)中logb(a)最大,从而得出答案.解答:解:构造函数F(x)=xf(x)则F'(x)=xf'(x)+f(x)>0即F(x)在R上是增函数,又由0<a<b<1知a b,b a<1而loga(b)<loga(a)=1logb(a)>logb(b)=1故在a b,b a,loga(b),logb(a)中logb(a)最大故F(logb(a))=logb a•f(logb a)最大故选D.点评:本题考查了函数的单调性问题,考查了转化思想,是一道中档题.12.(5分)在△ABC中,tanA+tanB+tanC>0是△ABC是锐角三角形的()A.既不充分也不必要条件B.充分必要条件C.必要不充分条件D.充分不必要条件考点:必要条件、充分条件与充要条件的判断.专题:简易逻辑.分析:根据充分必要条件的定义,分别证明充分性和必要性,从而得出答案.解答:解:先证充分性:∵tan(A+B)=,∴tan(A+B)=tan(180°﹣C)=﹣tanC,∴tanA+tanB=﹣tanC+tanAtanBtanC,∴tanA+tanB+tanC=tanA•tanB•tanC,若三角形有一个钝角,必有一个值为负值,tanA•tanB•tanC<0,若三角形有一个为直角,则tanA•tanB•tanC无意义,∴当tanA•tanB•tanC>0时三个角为锐角,故tanA+tanB+tanC>0时,△ABC是锐角三角形;再证必要性:∵△ABC是锐角三角形;∴tanA•tanB•tanC>0,又tan(A+B)=,∴tan(A+B)=tan(180°﹣C)=﹣tanC,∴tanA+tanB=﹣tanC+tanAtanBtanC,∴tanA+tanB+tanC=tanA•tanB•tanC>0,∴△ABC是锐角三角形时,tanA+tanB+tanC>0.故选:B.点评:本题考查了充分必要条件,考查了三角恒等变换,是一道中档题.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)已知向量,夹角为60°,且||=1,|2﹣|=2,则||=4.考点:数量积表示两个向量的夹角;向量的模;平面向量数量积的运算.专题:平面向量及应用.分析:利用数量积运算和性质即可得出.解答:解:∵|2﹣|=2,∴=12,∴,化为,解得=4.故答案为:4.点评:本题考查了数量积运算和性质,属于基础题.14.(5分)已知,则x2+y2的最小值是.考点:简单线性规划的应用.专题:数形结合.分析:本题属于线性规划中的延伸题,对于可行域不要求线性目标函数的最值,而是求可行域内的点与原点(0,0)构成的线段的长度问题.解答:解:先根据约束条件画出可行域,z=x2+y2,表示可行域内点到原点距离OP的平方,当O点到直线2x+y﹣2=0的距离平方时,z最小,最小值为=,故答案为:.点评:本题利用直线斜率的几何意义,求可行域中的点与原点的斜率.本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.15.(5分)无论从左往右读,还是从右往左读,都是同一个数,称这样的数为“和谐数”,如88,545,7337,43534等都是“和谐数”.两位的“和谐数”有11,22,33,44,55,66,77,88,99,共9个;三位的“和谐数”有101,111,121,131,…,969,979,989,999,共90个;四位的“和谐数”有1001,1111,1221,…,9669,9779,988,9999,共90个;由此推测:八位的“和谐数”总共有9000个.考点:进行简单的合情推理.专题:探究型;推理和证明.分析:根据“和谐数”的定义和特点,一位的“和谐数”有10个,二位的“和谐数”有9个,三位的“和谐数”有9×10个,四位的“和谐数”有9×10个,五位和六位的“和谐数”总共有9×10×10 个,位和八位的“和谐数”总共有9×10×10×10=9000 个,从而得出结论.解答:解:根据“和谐数”的定义,“和谐数”的首位和末尾是相同的,故两位或两位以上的“和谐数”的末尾不能为0,故末尾和首位有9种选择,其余的有10种选择.对于位数是偶数的“和谐数”,其中有一半位数确定了,这个数就确定了.对于位数是奇数的“和谐数”,最中间的那位数字可任意取,有10种方法.故一位的“和谐数”有0,1,2,3,4,5,6,7,8,9,共10个;二位的“和谐数”有11,22,33,44,55,66,77,88,99,共9个;三位的“和谐数”有101,111,121,131,…,969,979,989,999,共9×10=90个;四位的“和谐数”有1001,1111,1221,…,9669,9779,9889,9999,共9×10=90个;故五位和六位的“和谐数”总共有9×10×10=900 个,七位和八位的“和谐数”总共有9×10×10×10=9000 个,故答案为:9000.点评:本题主要考查排列、组合以及两个基本原理的应用,注意理解“和谐数”的定义和特点,属于中档题.16.(5分)三个半径均为3且两两外切的球O1、O2、O3放在水平桌面上,现有球I放在桌面上与球O1、O2、O3都外切,则球I的半径是1.考点:球内接多面体.专题:计算题;空间位置关系与距离.分析:由题意,球心I到平面O1O2O3的距离为3﹣r,|O1I|=3+r,由勾股定理可得方程,解方程即可得出结论.解答:解:设球I的半径是r,则|O1I|=3+r,由题意,球I放在桌面上与球O1、O2、O3都外切,∴球心I到桌面的距离为r,球心O1到桌面的距离为3,∴球心I到平面O1O2O3的距离为3﹣r,则由勾股定理可得(3+r)2=(3﹣r)2+(2)2,∴r=1,故答案为:1.点评:本题考查球与球的位置关系,考查学生的计算能力,比较基础.三、解答题17.(12分)已知数列{a n}满足a n=2a n﹣1+1(n≥2)且a1=1,b n=log2(a2n+1+1),.求证:(Ⅰ)数列{a n+1}为等比数列,并求数列{a n}的通项公式;(Ⅱ)数列{c n}的前n项和.考点:数列递推式;数列的求和.专题:综合题;等差数列与等比数列.分析:(Ⅰ)把已知的等式a n=2a n﹣1+1变形,得到a n+1=2(a n﹣1+1),同时求出当n=2时得到a2+1=2(a1+1),将a1的值代入求出a2+1的值,确定出数列{a n+1}以2为首项,2为公比的等比数列,表示出等比数列的通项公式,可得出a n的通项公式;(Ⅱ)确定数列{c n}的通项,利用裂项法求和,即可得出结论.解答:证明:(Ⅰ)∵a n=2a n﹣1+1,∴a n+1=2(a n﹣1+1),令n=2得:a2+1=2(a1+1),又a1=1,∴a2+1=4,a1+1=2,∴数列{a n+1}以2为首项,2为公比的等比数列,则通项公式为a n+1=2n,即a n=2n﹣1,…(6分)(Ⅱ)由(Ⅰ)知b n=log2(a2n+1+1)=2n+1,=(﹣),所以S n=[(1﹣)+(﹣)+…+(﹣)]=(1﹣)<.…(12分)点评:此题考查了等比数列的性质,等比数列的通项公式,以及等比数列的确定,考查裂项法求和,熟练掌握等比数列的性质是解本题的关键.18.(12分)如图所示,已知四棱锥P﹣ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=PB=PC=2,CD=1,侧面PBC⊥底面ABCD,点F在线段AP上,且满足.(1)证明:PA⊥BD;(2)当λ取何值时,直线DF与平面ABCD所成角为30°?考点:用空间向量求直线与平面的夹角;向量语言表述线线的垂直、平行关系.专题:综合题;空间位置关系与距离.分析:(1)先证明PO⊥平面ABCD,再建立空间直角坐标系,利用向量的数量积为0,可证得PA⊥BD;(2)利用平面ABCD的一个法向量=(0,0,1),直线DF与平面ABCD所成角为30°,根据向量的夹角公式,即可求得结论.解答:(1)证明:如图,∵△PBC是等边三角形,O是BC中点,∴PO⊥BC.由侧面PBC⊥底面ABCD,得PO⊥平面ABCD,以BC中点O为原点,以BC所在直线为x轴,过点O与AB平行的直线为y轴,建立如图所示的空间直角坐标系O﹣xyz.∵AB=BC=PB=PC=2CD=2,∴A(1,﹣2,0),B(1,0,0),D(﹣1,﹣1,0),P(0,0,)∴∴∴∴PA⊥BD;(2)解:∵,∴∵∴=∵平面ABCD的一个法向量=(0,0,1),直线DF与平面ABCD所成角为30°∴sin30°=||∴4λ2﹣16λ+7=0∴,(舍去)∴λ=时,直线DF与平面ABCD所成角为30°.点评:本题考查线线垂直,考查线面角,考查李建勇空间向量解决立体几何问题,属于中档题.19.(12分)甲乙两位同学参加学校安排的3次体能测试,规定按顺序测试,一旦测试合格就不必参加以后的测试,否则3次测试都要参加.甲同学3次测试每次合格的概率组成一个公差为的等差数列,他第一次测试合格的概率不超过,且他直到第二次测试才合格的概率为,乙同学3次测试每次测试合格的概率均为,每位同学参加的每次测试是否合格相互独立.(Ⅰ)求甲同学第一次参加测试就合格的概率P;(Ⅱ)设甲同学参加测试的次数为m,乙同学参加测试的次数为n,求ξ=m+n的分布列.考点:离散型随机变量及其分布列.专题:概率与统计.分析:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为的等差数列,又甲同学第一次参加测试就合格的概率为P,故而甲同学参加第二、三次测试合格的概率分别是p+、p+,由题意知,(1﹣p)(p+)=,由此能求出甲同学第一次参加测试就合格的概率.(Ⅱ)甲同学参加第二、三次测试合格的概率分别是、,由题意知,ξ的可能取值为2,3,4,5,6,分别求出相应的概率,由此能求出ξ=m+n的分布列.解答:解:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为的等差数列,又甲同学第一次参加测试就合格的概率为P,故而甲同学参加第二、三次测试合格的概率分别是p+、p+,由题意知,(1﹣p)(p+)=,解得p=或p=(舍),所以甲同学第一次参加测试就合格的概率为.…(4分)(Ⅱ)由(Ⅰ)知甲同学参加第二、三次测试合格的概率分别是、,由题意知,ξ的可能取值为2,3,4,5,6,由题意可知P(ξ=2)==,P(ξ=3)==,P(ξ=4)==,P(ξ=5)=()×()+()×()=,P(ξ=6)==,所以ξ的分布列为:ξ 2 3 4 5 6P…(12分)点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题,在历年2015届高考中都是必考题型.20.(12分)如图,椭圆E:=1(a>b>0)的右焦点F2与抛物线y2=4x的焦点重合,过F2作与x轴垂直的直线与椭圆交于S、T两点,与抛物线交于C、D两点,且.(Ⅰ)求椭圆E的方程;(Ⅱ)若过点M(3,0)的直线l与椭圆E交于两点A、B,设P为椭圆上一点,且满足+=t (O为坐标原点),求实数t的取值范围.考点:直线与圆锥曲线的关系;椭圆的标准方程.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)由焦点F2(,0),故可设椭圆的方程为,求出C,D的坐标,由抛物线与椭圆的对称性,可得S(,),代入椭圆方程,即可求椭圆E的方程;(Ⅱ)分类讨论,设出直线的方程,代入椭圆方程,利用韦达定理,结合+=t,求出P的坐标,代入椭圆方程,求出实数t的取值范围.解答:解:(Ⅰ)由抛物线方程,得焦点F2(,0),故可设椭圆的方程为,解方程组解得C(,2),D(,﹣2),由抛物线与椭圆的对称性,可得:=,所以|F2S|=,所以S(,).因此,解得b=1,故而a=2,所以椭圆E的方程为.(Ⅱ)由题意知直线l的斜率存在,设其为k.①当k=0时,所以t=0;②当k≠0时,则直线l的方程为y=k(x﹣3),代入椭圆方程,消去y并整理得:(1+4k2)x2﹣24k2x+36k2﹣4=0,由△>0,得0<k2<,设A(x1,y1),B(x2,y2),P(x0,y0),则x1+x2=,x1x2=.因为+=t,所以(x1+x2,y1+y2)=t(x0,y0),所以x0=(x1+x2)=,y0=.因为点P在椭圆上,所以[]2+[]2=4,解得t2=9﹣,由于0<k2<,故而0<t2<4,所以t∈(﹣2,0)∪(0,2),综合①②可知,t∈(﹣2,2).点评:本题重点考查圆锥曲线的方程,考查直线与圆锥曲线的位置关系,解题的关键是利用待定系数法求圆锥曲线的方程.21.(12分)已知函数f(x)=x(lnx+1)(x>0).(Ⅰ)设F(x)=ax2+f'(x)(a∈R),讨论函数F(x)的单调性;(Ⅱ)若斜率为k的直线与曲线y=f′(x)交于A(x1,y1)、B(x2,y2)(x1<x2)两点,求证:x1<<x2.考点:利用导数研究函数的单调性;不等式的证明.专题:导数的综合应用.分析:(Ⅰ)求出函数f(x)的导函数,代入函数F(x)=ax2+f'(x)(a∈R),进一步求出函数F(x)的导函数,然后分a≥0和a<0分析导函数在不同区间内的符号,从而得到函数F(x)的单调性;(Ⅱ)由两点式求出,利用分析法得到证,转化为证,换元后构造函数,利用导函数得到单调性,从而得到要证的结论.解答:解:(Ⅰ)由f(x)=x(lnx+1)(x>0),得f′(x)=lnx+2(x>0),F(x)=ax2+lnx+2(x>0),∴(x>0).①当a≥0时,恒有F′(x)>0,故F(x)在(0,+∞)上是增函数;②当a<0时,令F′(x)>0,得2ax2+1>0,解得;令F′(x)<0,得2ax2+1<0,解得;综上,当a≥0时,F(x)在(0,+∞)上是增函数;当a<0时,F(x)在()上单调递增,在()上单调递减;(Ⅱ).要证,即证,等价于证,令,则只要证1<,由t>1,知lnt>0,故等价于lnt<t﹣1<tlnt(t>0)(*)①设g(t)=t﹣1﹣lnt(t≥1),则(t≥1),故g(t)在[1,+∞)上是增函数,∴当t>1时,g(t)=t﹣1﹣lnt>g(1)=0,即t﹣1>lnt,②设h(t)=tlnt﹣(t﹣1)(t≥1),则h′(t)=lnt≥0(t≥1),故h(t)在[1,+∞)上是增函数.∴当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1(t>1).由①②知(*)成立,故.点评:本题考查了利用导数研究函数的单调性,考查了不等式的证明,考查了分类讨论的数学思想方法和数学转化思想方法,训练了函数构造法,解答的关键在于正确分类,是有一定难度题目.选修4-1:几何证明选讲22.(10分)如图,已知⊙O和⊙M相交于A、B两点,AD为⊙M的直径,直线BD交⊙O于点C,点G为弧BD的中点,连接AG分别交⊙O、BD于点E、F,连接CE.(Ⅰ)求证:AC为⊙O的直径.(Ⅱ)求证:AG•EF=CE•GD.考点:圆周角定理;相似三角形的判定;相似三角形的性质.专题:证明题.分析:( I)要证AC为⊙O的直径,只需证出=90°即可.∠ABC连接DG,AB,根据圆周角定理得出∠ABD=∠AGD=90°后,则可得到证明.(Ⅱ)要证AG•EF=CE•GD,可考虑证明△AGD∽△ECF.两三角形均为直角三角形,再通过∠GAD=∠GAB=∠BCE,则可证出△AGD∽△ECF.解答:证明:( I)连接DG,AB∵AD为⊙M的直径∴∠ABD=∠AGD=90°在⊙O中,∠ABC=∠AEC=∠ABD=90°∴AC为⊙O的直径.…(4分)( II)∵∠AEC=90°∴∠CEF=90°∵点G为弧BD的中点∴∠GAD=∠GAB,在⊙O中,∠BCE=∠GAB∴△AGD∽△E CF∴AG•EF=CE•GD…(10分)点评:本题考查相似三角形的判定和性质、圆周角定理.在以圆为背景的条件下,要充分利用圆的几何性质、圆周角定理,弦切角定理等,寻求相等角实现转化与代换.选修4-4:坐标系与参数方程23.(10分)在直角坐标系中,以原点为极点,x轴的正半轴为极轴建坐标系,已知曲线C:ρsin2θ=2acosθ(a>0),已知过点P(﹣2,﹣4)的直线l的参数方程为,直线l与曲线C分别交于M,N.(1)写出曲线C和直线l的普通方程;(2)若|PM|,|MN|,|PN|成等比数列,求a的值.考点:直线的参数方程.专题:坐标系和参数方程.分析:(1)利用极坐标化为直角坐标方程的公式x=ρcosθ,y=ρsinθ可得曲线C的方程;消去参数t即可得到直线l的方程;(2)把直线的方程代入抛物线的方程得到根与系数的关系,利用两点间的距离公式和等比数列的定义即可得出.解答:解:(1)由曲线C:ρsin2θ=2acosθ(a>0),可得ρ2sin2θ=2aρcosθ,化为y2=2ax.由直线l的参数方程为,消去参数t可得直线l:y=x﹣2.(2)联立,化为x2﹣(4+2a)x+4=0,∵直线l与抛物线相交于两点,∴△=(4+2a)2﹣16>0,解得a>0或a<﹣4.(*)∴x1+x2=4+2a,x1x2=4.∴|MN|===.=,|PN|=.∴|PM||PN|=2|(x1+2)(x2+2)|=2|x1x2+2(x1+x2)+4|=2|16+4a|∵|PM|,|MN|,|PN|成等比数列,∴|MN|2=|PM||PN|,∴=2|16+4a|,化为a(4+a)=|4+a|,∵a>0或a<﹣4.解得a=1.∴a=1.点评:本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与抛物线相交问题转化为把直线的方程与抛物线的方程联立得到根与系数的关系、两点间的距离公式和等比数列的定义等基础知识与基本技能方法,属于难题.选修4-5:不等式选讲24.(10分)设a>0,b>0,m>0,n>0.(Ⅰ)证明:(m2+n4)(m4+n2)≥4m3n3;(Ⅱ)a2+b2=5,ma+nb=5,求证:m2+n2≥5.考点:不等式的证明.专题:综合题;不等式.分析:(Ⅰ)利用基本不等式,即可得出结论;(Ⅱ)利用柯西不等式即可得出.解答:证明:(Ⅰ)因为m>0,n>0,则m2+n4≥2mn2,m4+n2≥2m2n,所以(m2+n4)(m4+n2)≥4m3n3,当且仅当m=n=1时,取等号.…(5分)(Ⅱ)由柯西不等式可得:(m2+n2)(a2+b2)≥(ma+nb)2,∵a2+b2=5,ma+nb=5,∴5(m2+n2)≥25,∴m2+n2≥5,当且仅当na=mb时取等号.…(10分)点评:本题考查了基本不等式、柯西不等式的应用,属于基础题.。
云南省师大附中高考数学适应性月考卷 理(扫描版)

云南省师大附中2015届高考数学适应性月考卷理(扫描版)理科数学参考答案一、选择题(本大题共12小题,每小题5分,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CDDCCBAABBAD【解析】1.易得{|41}M x x =-<<,{210}M N =--I ,,,故选C .2.221i 1iz =-+=-+-,故选D .3.(1)(24)x =-∵,,,,且,a =b a b P 420x --=∴,2x =-,(12)10-⋅∴,,a =a b =,故选D . 4.437C 2802a a ==由,得,故选C . 5.因为2311a a a ,,成等差数列,所以1233122a a a a +=⨯=,即2111a a q a q +=,所以210q q --=,解得15q +=或150q -=<(舍去),所以2256343434()a a a a q q a a a a ++==++ 35+=,故选C . 6.150=0+2=2=21+2=4i S i =>⨯不成立,,;45022424412i S i =>=+==⨯+=不成立,,;1250426212630i S i =>=+==⨯+=不成立,,; 3050628230868i S i =>=+==⨯+=不成立,,;68508i S =>=成立,,故选B .7.01ln ln (01)ln 102x x y a a y a x a y a =''==-+==,,切点为,,切线方程为,∴,故选A . 8.由三视图还原出几何图形如图1,其中正视图由SBC 面看入,SD ABCD AB ⊥平面,与DC 平行,2433AB DC AD SD ====,,,,11(24)33932V =⨯⨯+⨯⨯=,故选A .9.作出不等式组表示的区域如图2阴影部分所示,由图可知,(00)z ax by a b =+>>,过点(1,1)A 时取最大值, 所以4a b +=,242a b ab +⎛⎫= ⎪⎝⎭≤,00(04]a b ab >>∈∵,,∴,,故选B .10.由于P 为抛物线26y x =-上一个动点,Q 为圆221(6)4x y +-=上一个动点,那么点P 到点Q 的距离与点P 到y 轴距离之和的最小值可结合抛物线的定义,P 到y 轴距离为P 到焦点距离减去32,则最小值为抛物线的焦点到圆心的距离减去半径和323174-,故选B .11.取ABC △外接圆圆心F ,连接AD 的中点即球心O 与F ,由球的性质可知OF 与平面ABC 垂直,2AB BD =在Rt AOF △中,1AO =,6AF =,故26313OF ⎛⎫=- ⎪ ⎪⎝⎭,又2AD OA =,故D 到平面ABC 的距离232h OF ==,因此133A BCD D ABC V V --==2231(2)3=,故选A .12.()2e sin (222)()0()(222x f x x x k k f x f x x k k ''=∈π+ππ+π<∈π+ππ∵,∴,时,,递减,, 3)+π时,()0()f x f x '>,递增,故当22x k =π+π时,()f x 取极小值,其极小值为22(22)e k f k π+ππ+π=-,02015x π又≤≤,所以()f x 的各极小值之和242014e e eS πππ=----=L 2π2014π2πe (1e )1e ---,故选D . 二、填空题(本大题共4小题,每小题5分,共20分)图1图2题号 13 14 15 16 答案19- 15(31)-,(1e),【解析】13.2sin23α=∵,21cos(π)cos 12sin 29ααα⎛⎫-=-=--=- ⎪⎝⎭∴.14.23223255A A A 1A 5P ⋅⋅==. 15.()f x ∵是R 上的奇函数,()2cos 0f x x '=+>,则()f x 在定义域内为增函数,(3)()0f mx f x -+<∴可变形为(3)()f mx f x -<-,3mx x -<-∴,将其看作关于m 的一次函数()3[2,2]g m x m x m =⋅-+∈-,,可得当[2,2]m ∈-时,()0g m <恒成立,若0x ≥,(2)0g <,若0x <,(2)0g -<,解得31x -<<. 16.令1e 1b a =>,则ex x y a b ==,1eelog log log a b a y x x x ===,即这两个函数互为反函数且为增函数,故其有两个交点等价于log b y x =与y x =有两个交点,即函数()log b f x x x =-有两个零点.由max 1()(log e )()(log e)b b f x x f x f x'=-⇒=(log e)01e b f a ⇒>⇒<<.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分) 解:(Ⅰ)由正弦定理,得sin sin 3sin cos C A A C =,因为sin 0A ≠,解得tan 3(0),3C C C π∈π=,又,∴. ……………………(4分)(Ⅱ)由sin sin()3sin 2C B A A +-=,得sin()sin()3sin 2B A B A A ++-=,整理,得sin cos 3sin cos B A A A =. ……………………………………………(6分)若cos 0A =,则2A π=,21tan 3cb bπ==,,1732ABC S bc ==△; ………(7分)若cos 0A ≠,则sin 3sin B A =,3b a =.由余弦定理,得2222cos c a b ab C =+-,解得13a b ==,. …………………(9分)133sin 2ABC S ab C ==△ ……………………………………………(11分) 综上,ABC △7333. ……………………………………………(12分)18.(本小题满分12分)(Ⅰ)证明:由题条件知,PQ AD BQ AD ⊥⊥,, PQ BQ Q =I ,所以AD PQB ⊥平面,AD PAD ⊂∵平面,PQB PAD ⊥∴平面平面. …………………………………(4分) (Ⅱ)解:PA PD Q AD PQ AD =⊥∵,为中点,∴.PAD ABCD PAD ABCD AD PQ ABCD ⊥=⊥I ∵平面平面,平面平面,∴平面. 如图3所示,以Q 为坐标原点,分别以QA QB QP 、、为x y z 、、轴建立空间直角坐标系,…………………………………………………(5分)则(000)(100)(003)Q A P ,,,,,,,,, (030)(230)B C -,,,,,,(030)QB =u u u r,,, 设(01)PM PC λλ=u u u u r u u u r ≤≤,(233(1))QM QP PM QP PC λλλλ=+=+=--u u u u r u u u r u u u u r u u u r u u u r,,,……………………………………………………………………………………(6分) 设()n x y z =r,,是平面MBQ 的一个法向量,则00QM n QB n ⎧⋅=⎪⎨⋅=⎪⎩u u u u r r u u u r r ,,即3(1)0z x y λ⎧-⋅=⎪⎨⎪=⎩, 图3令1z =,得01n ⎫=⎪⎪⎝⎭r ,, ………………………………………(7分) 又(001)m =u r,,是平面BQC 的一个法向量,1cos 2m n m n m n ⋅〈〉===⋅u r ru r r u r r ∴,, 1013λλ=∵≤≤,∴,13PM PC =∴, …………………………………………(9分)PQ =∵∴M 到平面ABCD122BQC S =⨯=△1233M BCQ V -==. …………………………(12分) 19.(本小题满分12分)解:(Ⅰ)依题意,每场比赛获得的门票收入组成首项为40,公差为10的等差数列.设此数列为{}n a ,则易知1(1070)4010302202n n n n a a n S +==+==,,∴,解得11()n =-舍去或4n =,所以此决赛共比赛了4场.则前3场的比分必为1∶2,且第4场比赛为领先的球队获胜,其概率为31313C 28⎛⎫= ⎪⎝⎭. ……………………………………………………………(6分)(Ⅱ)随机变量X 可取的值为345S S S ,,,即150,220,300.又311(150)224P X ⎛⎫==⋅= ⎪⎝⎭,31313(220)C 28P X ⎛⎫==⋅= ⎪⎝⎭,42413(300)C 28P X ⎛⎫==⋅= ⎪⎝⎭.…………………………………………………………………………(9分)………………………………………………………………………(10分)所以X 的数学期望为133()=150+220+300232.5488E X ⨯⨯⨯=万元. ……………(12分)20.(本小题满分12分)解:(Ⅰ)设椭圆的焦距为2c ,234c a ⎛⎫= ⎪⎝⎭∴,所以2234a c =,又点0)是抛物线的焦点,23c =∴.所以椭圆C 的方程为2214x y +=. ……………………………………………(4分)(Ⅱ)因为ON OA OB =+u u u r u u u r u u u r,所以四边形OANB 为平行四边形, 当直线l 的斜率不存在时,显然不符合题意;当直线l 的斜率存在时,设直线l 的方程为3y kx =+,l 与椭圆交于11()A x y ,,22()B x y ,两点,由22223(14)2432014y kx k x kx x y =+⎧⎪⇒+++=⎨+=⎪⎩,. 由222(24)128(14)02k k k ∆=-+>⇒>. …………………………………………(6分)12122224321414k x x x x k k +=-=++,. …………………………………………(7分)12121322OAB S OD x x x x =-=-△∵,1223||OANB OABS S x x ==-=Y △∴== …………………………………………(9分)令22k t -=,则22k t =+(0)t >由上式知,2OANB S ===Y ∴,当且仅当9t =,即2174k =时取等号,k =∴当时,平行四边形OANB 的面积最大值为2. 此时直线l 的方程为3y =+. ……………………………………………(12分)21.(本小题满分12分)解:(Ⅰ)()ln 1f x x px =-+的定义域为(0)+∞,,1()pxf x x-'=,00p x >>∵,,10x p ⎛⎫∈ ⎪⎝⎭∴,时,()0()f x f x '>,单调递增,1x p ⎛⎫∈+∞ ⎪⎝⎭,时,()0()f x f x '<,单调递减, ()f x ∴在1x p=处取得极大值11ln f p p ⎛⎫= ⎪⎝⎭,此极大值也是最大值,所以要使()0f x ≤恒成立,只需11ln 0f p p ⎛⎫= ⎪⎝⎭≤,1p ∴≥,∴p 的取值范围为[1)+∞,. ………………………………………………………(5分) (Ⅱ)令1p =,由(Ⅰ)知,ln 10x x -+≤,ln 1x x -∴≤,()31ln (31)3(1)ln g x ax x a a x x '=----=--, ……………………………………(6分) 则()3(1)(1)(31)(1)g x a x x a x '---=--≥,当310a -≥即13a ≥时,由[1)x ∈+∞,得()0g x '≥恒成立,()g x 在[1)+∞,上单调递增,()(1)0g x g =≥符合题意,所以13a ≥;……………(7分)当0a ≤时,由[1)x ∈+∞,得()0g x '≤恒成立,()g x 在[1)+∞,上单调递减,()(1)0g x g =≤,显然不成立,0a ≤舍去; ……………………………………(8分)当103a <<时,由ln 1x x -≤,得11ln 1x x -≤,即1ln 1x x-≥,则11()3(1)1(31)x g x a x ax x x -⎛⎫⎛⎫'---=- ⎪ ⎪⎝⎭⎝⎭≤,因为103a <<,所以113a>. ……………………………………………(10分)113x a ⎡⎫∈⎪⎢⎣⎭,时,()0g x '≤恒成立, ()g x 在113a ⎡⎫⎪⎢⎣⎭,上单调递减,()(1)0g x g =≤,显然不成立,103a <<舍去.综上可得:13a ⎡⎫∈+∞⎪⎢⎣⎭,. ………………………………………………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】 证明:(Ⅰ)如图4,连接BE ,则BE EC ⊥,又D 是BC 的中点,所以DE BD =.又OE OB OD OD ==,,所以ODE ODB △≌△, 所以90OBD OED ∠=∠=︒.故D E O B ,,,四点共圆. …………………………………………………………(5分)(Ⅱ)如图4,延长DO 交圆于点H ,2()DE DM DH DM DO OH DM DO =⋅=⋅+=⋅+∵DM OH ⋅, 21122DE DM AC DM AB ⎛⎫⎛⎫=⋅+⋅ ⎪ ⎪⎝⎭⎝⎭∴,即22DE DM AC DM AB =⋅+⋅,,2BCDE DC ==∵ ∴22DC DM AC DM AB =⋅+⋅. ……………………………(10分)23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)半圆C 的普通方程为22(1)1x y -+=(01)y ≤≤,又cos sin x y ρθρθ==,,所以半圆C 的极坐标方程是2cos 02ρθθπ⎡⎤=∈⎢⎥⎣⎦,,. …………………………(5分)(Ⅱ)设11()ρθ,为点P 的极坐标,则有1112cos ,,3ρθθ=⎧⎪⎨π=⎪⎩ 解得111,,3ρθ=⎧⎪π⎨=⎪⎩ 设22()ρθ,为点Q 的极坐标,则有2222(sin 3)53,,3ρθθθ⎧+=⎪⎨π=⎪⎩解得225,,3ρθ=⎧⎪π⎨=⎪⎩ 由于12θθ=,所以124PQ ρρ=-=,所以PQ 的长为4. …………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】证明:(Ⅰ)因为a b c ,,为正实数,由均值不等式可得33333331111113a b c a b c ++⋅⋅≥3331113a b c abc++≥,所以3331113abc abc a b ++++≥,而33223abc abc abc abc +⋅≥,所以33311123abc a b c+++≥ 当且仅当63a b c ===时,取等号. ……………………………………………(5分) (Ⅱ)3311113A B C ABCABC++≥39π3A B C =++≥,πππ9A B C++∴≥, 当且仅当π3A B C ===时,取等号. ……………………………………………(10分)图4。
高三数学月考试题及答案-师大附中2015届高考适应性月考卷(六)(理)

云南师大附中2015届高考适应性月考卷(六)理科数学一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、已知集合{}U 1,3,5,7,9=,{}1,5,7A =,则U A =ð( )A .{}1,3B .{}3,7,9C .{}3,5,9D .{}3,9 2、复数3223ii+=-( ) A .i B .i - C .1213i - D .1213i +3、函数sin 22y x π⎛⎫=- ⎪⎝⎭是( )A .周期为π的奇函数B .周期为π的偶函数C .周期为2π的奇函数D .周期为2π的偶函数4、给定下列两个命题:①“p q ∨”为真是“p ⌝”为假的必要不充分条件②“0R x ∃∈,使0s i n 0x >”的否定是“R x ∀∈,使s i n 0x ≤” 其中说法正确的是( )A .①真②假B .①假②真C .①和②都为假D .①和②都为真 5、在图1所示的程序中,若5N =时,则输出的S 等于( ) A .54B .45C .65D .566、已知数列{}n a 满足130n n a a ++=,243a =-,则{}n a 的前10项和等于( )A .()10613--- B .()101139-- C .()10313-- D .()10313-+ 7、若已知向量()cos 25,sin 25a =,()sin 20,cos 20b =,u a tb =+,R t ∈,则u 的最小值是( )A B .2C .1D .128、如图2所示,一个几何体的三视图中四边形均为边长为4的正方形,则这个几何体的表面积为( )A .64+B .()968π+C .64+D .()968π+9、过点)引直线l 与曲线y =A ,B 两点,O 为坐标原点,当∆AOB 的面积取最大值时,直线l 的斜率等于( )A B .C .3±D .10、已知双曲线22221x y a b-=(0a >,0b >),若过右焦点F 且倾斜角为30的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是( )A .()1,2B .⎛ ⎝⎭C .[)2,+∞D .⎫+∞⎪⎪⎣⎭11、已知三棱锥C S -AB 的所有顶点都在球O 的球面上,C ∆AB 是边长为2的正三角形,C S 为球O 的直径,且C 4S =,则此棱锥的体积为( )A B C D .12、()()2222f x x a x a =-++,()()22228g x x a x a =-+--+.设()(){}1m a x ,f x g x H =,()()(){}2min ,x f x g x H =({}max ,p q 表示p ,q 中的较大值,{}min ,p q 表示p ,q 中的较小值).记()1x H 的最小值为A ,()2x H 的最大值为B ,则A -B =( )A .16B .16-C .2216a a --D .2216a a +-二、填空题(本大题共4小题,每小题5分,共20分.) 13、()5234501234512x a a x a x a x a x a x -=+++++,则3a = .14、已知等比数列{}n a 是递增数列,n S 是{}n a 的前n 项和.若1a ,3a 是方程2540x x -+=的两个根,则6S = . 15、若x ,y 满足1x y +≤,则3yz x =-的取值范围是 . 16、设x ,R y ∈,且满足()()()()2015201512013sin 1201412013sin 12012x x x y y y ⎧-++-=⎪⎨-++-=⎪⎩,则x y += .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17、(本小题满分12分)已知向量()sin ,1m x =,13cos ,2n x ⎛⎫= ⎪⎭,函数()()f x m n m=+⋅. ()I 求函数()f x 的最小正周期;()II若a ,b ,c 分别是C ∆AB的三边,a =,c =且()f A 是函数()f x 在0,2π⎛⎤⎥⎝⎦上的最大值,求角A 、角C .18、(本小题满分12分)为了解我市大学生的体质状况,对昆明地区部分大学的学生进行了身高、体重和肺活量的抽样调查.现随机抽取100名学生,测得其身高情况如下表所示.()I 求出频率分布表中①、②、③位置上相应的数据,并补全图3所示频率分布直方图,再根据频率分布直方图估计众数的值;()II 若按身高分层抽样,抽取20人参加2015年庆元旦全民健身运动,其中有3名学生参加越野比赛,记这3名学生中“身高低于170cm ”的人数为ξ,求ξ的分布列及数学期望.19、(本小题满分12分)如图4,已知菱形C S A B 中,60S ∠AB =.沿着对角线S A 将菱形C S A B 折成三棱锥C S -AB ,且在三棱锥C S -AB 中,C 90∠BA =,O为C B 中点.()I 求证:S O ⊥平面C AB ;()II 求平面C S A 与平面C S B 夹角的余弦值.20、(本小题满分12分)已知椭圆:E 22221x y a b+=(0a b >>)的焦距为2,且椭圆短轴的两个三等分点与一个焦点构成正三角形.()I 求椭圆的方程;()II 若以k (0k ≠)为斜率的直线l 与椭圆E 相交于两个不同的点A ,B ,且线段AB 的垂直平分线与两坐标轴围成的三角形的面积为116,求k 的取值范围. 21、(本小题满分12分)已知函数()()1ln 1a x f x x x -=-+. ()I 若函数()f x 在()0,+∞上为单调增函数,求a 的取值范围; ()II 设0m n >>,求证:ln ln 2m n m nm n -+<-.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.22、(本小题满分10分)选修4-1:几何证明选讲如图5,圆O 的直径10AB =,弦D E ⊥AB 于点H ,2BH =.()I 求D E 的长;()II 延长D E 到P ,过P 作圆O 的切线,切点为C,若C P =D P 的长.23、(本小题满分10分)选修4-4:坐标系与参数方程已知圆1O 和圆2O 的极坐标方程分别为2ρ=,2cos 24πρθ⎛⎫--= ⎪⎝⎭.()I 把圆1O 和圆2O 的极坐标方程化为直角坐标方程; ()II 求经过两圆交点的直线的极坐标方程.24、(本小题满分10分)选修4-5:不等式选讲 已知函数()2f x x =-,()3g x x m =-++. ()I 解关于x 的不等式()10f x a +->(R a ∈); ()II 若函数()f x 的图象恒在函数()g x 图象的上方,求m 的取值范围.学参考答案一、选择题(本小题共12小题,每小题5分,共60分)1、D2、A3、B4、D5、D6、C7、B8、D9、B 10、B 11、A 12、B 【解析】1.由{13579}U =,,,,,{157}A =,,,则{39}U A =,ð,故选D . 2.由32i (32i)(23i)i 23i (23i)(23i)+++==--+,故选A . 3.由πsin 2cos 22y x x ⎛⎫=-= ⎪⎝⎭,则函数为周期为π的偶函数,故选B .4.(1)当“p q ∨”为真时,可以是p 假q 真,故而p ⌝为假不成立;当p ⌝为假时,p 为真,则“p q ∨”为真,故①正确;(2)由特称命题的否定为全称命题,故②正确,综上所述,①②均正确,故选D . 5.由程序框图可知,输出的1111111111511223344556223566S ⎛⎫⎛⎫⎛⎫=++++=-+-++-= ⎪ ⎪ ⎪⨯⨯⨯⨯⨯⎝⎭⎝⎭⎝⎭…,故选D . 6.因为124303n n a a a ++==-,,所以11143n n a a a +=-=,,所以数列{}n a 是公比为13-的等比数列,所以{}n a 的前10项和等于103(13)--,故选C . 7.由题意(cos 25sin 20sin 25cos 20)u a tb t t =+=︒+︒︒+︒,,则2||1u t =+,当t = 时,min 2||u =,故选B . 8.由题意可知:该几何体为边长为4的正方体上下各挖去底面半径为2,高为2的圆锥,故而其表面积是1642(164π)24π968)π2+-+⨯⨯=+-,故选D .9.由于y =221(0)x y y +=≥,直线l 与221(0)x y y +=≥交于A ,B 两点, 如图1所示,11sin 22AOB S AOB =∠△≤, 且当90AOB ∠=︒时,AOB S △取得最大值,此时 AB=O 到直线l ,则30OCB ∠=︒,所以直线l 的倾斜角为150°,则斜率为,故选B . 图111.ABC △外接圆的半径r =,点O 到平面ABC的距离d ==SC 为球O 的直径⇒点S 到平面ABC 的距离为2d =,此棱锥的体积为123ABC V S d =⨯△13==A . 12.由()()f x g x =,得2()4x a -=,所以当2x a =-和2x a =+时,两函数值相等,()f x 图象为开口向上的抛物线,()g x 图象为开口向下的抛物线,两图象在2x a =-和2x a =+处相交,则1()(2)()()(22)()(2)f x x a H x g x a x a f x x a -⎧⎪=-<<+⎨⎪+⎩≤,,≥,2()(2)()()(22)()(2)g x x a H x f x a x a g x x a -⎧⎪=-<<+⎨⎪+⎩≤,,≥,所以1min ()A H x = (2)44f a a =+=--,2max ()(2)412B H x g a a ==-=-+,故选B .二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.由题意知,3334315C (2)80T T x x +==-=-,故而380a =-. 14.因为13a a ,是方程2540x x -+=的两个根,且数列{}n a 是递增的等比数列,所以13142a a q ===,,,所以66126312S -==-. 15.如图2,由033y y z x x -==--,由斜率公式可知,其几 何意义是点()x y ,与点(30),所在直线的斜率,故而 由图可知,min 13AI z k ==-,max 13BI z k ==,故而z 的取值范围是1133⎡⎤-⎢⎥⎣⎦,.16.令2015()2013sin f t t t t =++,则函数()f t 为单调递增的奇函数,由题意知:(1)f x -=2015(1)2013(1)sin(1)1x x x -+-+-=,2015(1)(1)2013(1)sin(1)1f y y y y -=-+-+-=-,图2故而(1)(1)0x y -+-=,所以2x y +=.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)解:(Ⅰ)3sin 2m n x x ⎛⎫+=+ ⎪⎝⎭,,233()(sin )sin sin sin 22f x x x x x x x =++=++1cos 23122cos 22222x x x x -=+=-+, π()sin 226f x x ⎛⎫=-+ ⎪⎝⎭,∴函数()f x 的最小正周期πT =. ………………………………………………(6分)(Ⅱ)πππ5π022666x x <-<-∵≤,∴≤,∴当ππ262x -=,即π3x =时,max ()3f x =, π3A =∴,由正弦定理sin sin a c A C=, 得sin C =π4C =∴. ……………………………………………………(12分)18.(本小题满分12分)解:(Ⅰ)①、②、③处分别填5、35、0.350,众数是172.5cm , 补全频率分布直方图如图3所示.…………………………………………………………………………(4分) (Ⅱ)用分层抽样的方法,从中选取20人,则“身高低于170cm ”的有5人, 所以ξ可能的取值为0,1,2,3,则315320C 91(0)C 228P ξ===;21155320C C 35(1)C 76P ξ===; 12155320C C 5(2)C 38P ξ===;35320C 1(3)C 114P ξ===, 图3则ξ的分布列如下:3()4E ξ=∴. ……………………………………………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:由题设AB AC SB SC SA ====, 如图4,连接OA ,因为ABC △为等腰直角三角形, 所以OA OB OC ==,且AO BC ⊥, 又SBC △为等腰三角形, 故SO BC ⊥,且SO =, 从而222OA SO SA +=,所以SOA △为直角三角形,SO AO ⊥, 又AOBC O =,所以SO ⊥平面ABC . ………………………………………(6分)(Ⅱ)解:以O 为坐标原点,射线OB ,OA ,OS 分别为x 轴,y 轴,z 轴的正半轴,建立如图5所示的空间直角坐标系O xyz -.设(100)B ,,,则(100)C -,,,(010)A ,,,(001)S ,,, (011)SA =-,,,(101)SC =--,,.设平面SAC 的法向量1()x y z =,,n , 由1100SA y z y x z x SC x z ⎧=-==-⎧⎪⇒⎨⎨=-=--=⎩⎪⎩,,,n n 令1x =,得1(111)=--,,n .由(Ⅰ)可知AO ⊥平面SCB ,因此取平面SCB 的法向量2(010)OA ==,,n .………………………………………………………………………………(10分)设平面ASC 与平面SCB 的夹角为θ,则1212||3cos ||||θ==n n n n…………………………………………………………………………………(12分)20.(本小题满分12分)图5图4解:(Ⅰ)1c =,设M N ,为短轴的两个三等分点,F 为焦点, 因为MNF △为正三角形,所以||||OF MN =,即213b=,解得b =,2214a b =+=,因此,椭圆方程为22143x y +=.………………………………………………(4分)(Ⅱ)设直线的方程为(0)y kx m k =+≠.点1122()()A x y B x y ,,,的坐标满足方程组22143y kx m x y =+⎧⎪⎨+=⎪⎩,①,②将①式代入②式,得2234()12x kx m ++=, 整理得222(43)84120k x kmx m +++-=,此方程有两个不等实根,于是222(8)4(43)(412)0km k m ∆=-+->, 整理得22430k m -+>,③ 由根与系数的关系,可知线段AB 的中点坐标00()x y ,满足12024243x x km x k +-==+,002343my kx m k =+=+, 从而线段AB 的垂直平分线方程为223144343m km y x k k k ⎛⎫-=-+ ⎪++⎝⎭, 此直线与x 轴,y 轴的交点坐标分别为22004343km m k k --⎛⎫⎛⎫ ⎪ ⎪++⎝⎭⎝⎭,,,.由题设可得22112434316km m k k --=++, 整理得222(43)08||k m k k +=≠,,将上式代入③式得222(43)4308||k k k +-+>,整理得22(43)(48||3)00k k k k +-+<≠,, 解得13||22k <<,所以k 的取值范围是31132222⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭,,. ………………(12分)21.(本小题满分12分)(Ⅰ)解:222221(1)(1)(1)2(22)1()(1)(1)(1)a x a x x ax x a x f x x x x x x x +--+-+-+'=-==+++, 因为()(0)f x +∞在,上为单调增函数,所以()0f x '≥在(0)+∞,上恒成立,即2(22)10x a x +-+≥在(0)+∞,上恒成立.当(0)x ∈+∞,时,由2(22)10x a x +-+≥, 得122a x x-+≤. 设1()(0)g x x x x=+∈+∞,,,1()2g x x x x x =+=≥, 所以当且仅当1x x=,即1x =时,()g x 有最小值2, 所以222a -≤,所以2a ≤, 所以a 的取值范围是(2]-∞,.………………………………………………(5分) (Ⅱ)证明:要证ln ln 2m n m n m n -+<-, 0m n >>∵,ln 0m n >∴,只需证112ln m m n n m n-+<, 即证21ln 1m m n m n n ⎛⎫- ⎪⎝⎭>+,只需证21ln 01m m n m n n⎛⎫- ⎪⎝⎭->+. 设2(1)()ln 1x h x x x -=-+, 由(Ⅰ)知()h x 在(1)+∞,上是单调增函数,又1m n >, 所以(1)0m h h n ⎛⎫>= ⎪⎝⎭,即21ln 01m m n m n n ⎛⎫- ⎪⎝⎭->+成立, 所以ln ln 2m n m n m n -+<-. ……………………………………………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】解:(Ⅰ)AB ∵为圆O 的直径,AB DE ⊥,DH HE =,22(102)16DH AH BH ==-=∴,48DH DE ==∴,. ………………………………………………………………(5分) (Ⅱ)PC ∵切圆O 于点C ,2PC PD PE =∴,2(8)2PD PD PD =+=∴,∴. …………………………………………(10分)23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)由cos sin x y ρθρθ=⎧⎨=⎩,, 则圆1O 的直角坐标方程为224x y +=,圆2O 的直角坐标方程为22(1)(1)4x y -+-=. …………………………………(5分)(Ⅱ)由(Ⅰ)知,圆1O 与圆2O 的交点所在的直线方程为1x y +=,其极坐标方程为(sin cos )1ρθθ+=. …………………………………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)不等式()10f x a +->,即|2|10x a -+->.当1a =时,不等式的解集是(2)(2)-∞+∞,,; 当1a >时,不等式的解集为R ;当1a <时,即|2|1x a ->-,即21x a -<-或21x a ->-,即1x a <+或3x a >-, 不等式解集为(1)(3)a a -∞+-+∞,,. ………………………………………(5分) (Ⅱ)函数()f x 的图象恒在函数()g x 图象的上方,即|2||3|x x m ->-++对任意实数x 恒成立,即|2||3|x x m -++>对任意实数x 恒成立.由于|2||3||(2)(3)|5x x x x -++--+=≥,当且仅当32x -≤≤时取等,故只要5m <, 所以m 的取值范围是(5)-∞,.………………………………………………(10分)。
云南师大附中2015届高考适应性月考卷(二)理科数学试卷及参考答案

云南师大附中2015届高考适应性月考卷(二)双向细目表理科数学第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.由{0,2}A =,{0,1,2}B =,所以{0,2}AB =,故选C.2.由42015i i 1i z =+=-,则1i z=+,其对应点为(1,1),在第一象限,故选A. 3.由{}n a 为等差数列,故而39662a a a +==,又1161166S a ==,故选D. 4.框图的运行如下:第一步1,πcos ;6k S =⎧⎪⎨=⎪⎩第二步3,ππcos cos ;63k S =⎧⎪⎨=⎪⎩第三步5,ππ2πcos cos cos .633k S =⎧⎪⎨=⎪⎩ 第三步结束跳出循环,即最后输出的ππ2πcos cos cos 633S =,又由ππ2πcos cos cos 633S ==,故选D.5.①错,因为分别与两平行平面平行的两直线可以是平行、相交或异面; ②错,因为两直线的位置关系可以是平行、相交或异面; ③错,因为两直线的位置关系可以是平行、相交或异面;④对,直线m 、n 的方向向量分别是两互相垂直平面α、β的法向量,故而m n ⊥,所以有3个命题是假命题,故选C .6.如图1所示,由椭圆的第一定义知,1214PF PF +=, 又有122PF PF -=,故而18PF =,26PF =,而1210F F ==,所以2221212PF PF F F +=, 故12PF F △为Rt △,则12121242PF F S PF PF =⋅=△,故选B.7.由于1A 、2A 串联,故其能通过电流的概率为0.81, 则1A 、2A 不能通过电流的概率为10.810.19-=, 由1A 、2A 串联后与3A 并联,如图2,故,A B 之间能通过电流的概率为1(10.81)(10.9)0.981---=,又由于电路再与4A 串联,故而电流能在,M N 之间通过的概率是0.9810.90.8829⨯=,故选B.8.由双曲线22221(0,0)x y a b a b-=>>的一个焦点与抛物线220y x =的焦点重合,则5c =,由点到线的距离公式可知焦点(,0)c 到双曲线渐近线by x a=±的距离d b =,所以4b =,故而3a ==,故其离心率53e =,故选C.9.由题意知,2n B =,令1x =,则4n A =,故而4272n n A B +=+=, 解之得:3n =,故选A.10.由题意可知该三棱锥为如图3所示的边长为1的正方体中以,,,A B C D为顶点的正四面体,故而其体积313V ==,故选C. 11.由(())()()0xf x xf x f x ''=+>,则函数()xf x 为R 上的增函数. 由于01a b <<<,则01b a a <=,01a b b <=,log log 1a a b a <=,而log log 1b b a b >=,则log (log)b ba f a ⋅最大,故选D.12.必要条件,若ABC △是锐角三角形,则π,,0,2A B C ⎛⎫∈ ⎪⎝⎭,tan 0,tan 0,tan 0A B C >>>,所以tan tan tan 0A B C ++>,必要性成立;充分条件,由tan tan tan 0A B C ++>,即tan ,tan ,tan A B C 有意义,ABC △不是直角三角形. 又在ABC △中,由πA B C ++=,得:πA B C +=-,所以tan()tan(π)A B C +=-⇒tan tan tan 1tan tan A BCA B+=--tan tan tan tan tan tan A B C A B C ⇒++=,由图3图2tan tan tan 0A B C ++>,则tan tan tan 0A B C >,所以ABC △是锐角三角形,故选B.第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.由223a b +=,得2(2)12a b +=,即224()4()12a a b b +⋅+=,所以21441122b b +⨯⨯⨯+=,解得2b =.14.,x y 满足的线性区域如图4阴影部分所示,222x y +=,由两点间距离公式知, 22x y +的最小值的几何意义是点 (0,0)到阴影区域中点的最小距离的平方,如图可知点(0,0)到阴影区域 的最小距离为点(0,0)到直线220x y +-=的距离d ,故d =,所以222min4()5x y +==.15.经观察可知,由两位的“和谐数”有9个,而三位的“和谐数”相当于在两位数的中间增加0至9中任意一个数,故而三位的“和谐数”有91090⨯=个,而四位的“和谐数”相当于三位的“和谐数”中间的数字重复出现一次,则四位的“和谐数”有90个;同理,五位的“和谐数”有9010900⨯=个,六位的“和谐数”有900个,七位的“和谐数”有900109000⨯=个,八位的“和谐数”有9000个. 16.记三个球心分别是1O ,2O ,3O ,球I 与桌面的切点为O ,反过来看图,由题意可知:三棱锥123IO O O 是以I 为顶点 123O O O 为底面的正三棱锥,三棱锥123OO O O 是以O 为顶点图4图5123O O O 为底面的正三棱锥. 如图5所示,记A 为底面123O O O的中心,则OIA 三点共线且OA 垂直底面123O O O ,由题意知126O O =, 3OA =,1O A =I 的半径为r ,则3AI r =-,13IO r =+,有22211()()()AO AI IO +=,即22(3)(3)12r r +=-+,解得1r =,所以球I 的半径为1.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)证明:(Ⅰ)由121(2)n n a a n -=+≥,知112(1)(2)n n a a n -+=+≥, 所以{1}n a +是以11a +为首项,2为公比的等比数列,故而111(1)2n n a a -+=+⋅,即12n n a +=,所以21n n a =-. ……………………(6分)(Ⅱ)由(Ⅰ)知221log (1)21n n b a n +=+=+, 21111114(1)41n n c b n n n n ⎛⎫===- ⎪-++⎝⎭, 所以1111111111142231414n S n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-=-< ⎪ ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭. ……………(12分)18.(本小题满分12分)(Ⅰ)证明:如图6,取BC 的中点O , 因为PBC △为等边三角形,所以PO BC ⊥,又因为侧面PBC ⊥底面ABCD ,所以PO ⊥平面ABCD , 如图6,以O为坐标原点,BC 所在直线为x 轴,过点O 与AB平行的直线为y 轴,直线OP 为z 轴,建立空间直角坐标系, 则(1,2,0)A-,(1,0,0)B ,(1,1,0)D --,(0,0,P ,所以(2,1,0)BD =--,(1,2,PA =-,0BD PA ⋅=,图6则BD PA ⊥,即BD PA ⊥. ………………………………………………………(6分)(Ⅱ)解:因为PF PA λ=,(1,2,PA =-,所以(,2,)PF λλ=-,又(1,1,DP =,所以(1,12,))DF DP PF λλλ=+=+--,又平面ABCD 的一个法向量(0,0,1)n =,直线DF 与平面ABCD 所成角为30︒.sin 30DF n DF n⋅︒=,所以12=, 所以241670λλ-+=,则12λ=或72λ=(舍). 当12λ=时,直线DF 与平面ABCD 所成角为30︒. …………………………(12分)19.(本小题满分12分)解:(Ⅰ)由甲同学3次测试每次合格的概率组成一个公差为18的等差数列,又甲同学第一次参加测试就合格的概率为P ,故而甲同学参加第二、三次测试合格的概率分别是18P +、14P +,由题意知,19(1)832P P ⎛⎫-+= ⎪⎝⎭,解得14P =或58P =(舍),所以甲同学第一次参加测试就合格的概率为14. ………………………………(4分)(Ⅱ)由(Ⅰ)知甲同学参加第二、三次测试合格的概率分别是38、12,由题意知,ξ的可能取值为2,3,4,5,6,由题意可知121(2)(1,1)436P P m n ξ=====⨯=,11233235(3)(1,2)(2,1)433483144P P m n P m n ξ⎛⎫⎛⎫====+===⨯⨯+⨯⨯= ⎪ ⎪⎝⎭⎝⎭, (4)(1,3)(2,2)(3,1)P P m n P m n P m n ξ====+==+==1113312352584334833483144⎛⎫⎛⎫⎛⎫⎛⎫=⨯+⨯⨯+⨯⨯=⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,(5)(2,3)(3,2)P P m n P m n ξ====+==33113512134833483396⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯⨯+⨯⨯⨯= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,35115(6)(3,3)483396P P m n ξ⎛⎫⎛⎫=====⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,所以ξ的分布列为:……………………………………………………………………(12分) 20.(本小题满分12分)解:(Ⅰ)由抛物线方程,得焦点20)F ,故可设椭圆的方程为222213x y b b +=+,解方程组2,y x ⎧=⎪⎨⎪⎩解得C,D -,由抛物线与椭圆的对称性,可得:22F C CD F SST==212F S =,所以12S ⎫⎪⎭.因此2213413b b+=+,解得21b =,故而24a =, 所以椭圆E 的方程为2214x y +=. ……………………………………………………(4分)(Ⅱ)由题意知直线l 的斜率存在,设其为k . ①当0k =时,0OA OB tOP +==,所以0t =; ②当0k ≠时,则直线l 的方程为(3)y k x =-,联立221,4(3),x y y k x ⎧+=⎪⎨⎪=-⎩消去y 并整理得:2222(14)243640k x k x k +-+-=,由Δ2222(24)4(14)(364)0k k k =-+->,得2105k <<,设11(,)A x y ,22(,)B x y ,00(,)P x y ,则2212122224364,1414k k x x x x k k-+==++. 因为OA OB tOP +=,所以121200(,)(,)x x y y t x y ++=,所以20122124()(14)k x x x t t k =+=+,012122116()[()6](14)ky y y k x x k t t t k -=+=+-=+.因为点P 在椭圆上,所以2222224644(14)(14)k k t k t k ⎡⎤⎡⎤-+=⎢⎥⎢⎥++⎣⎦⎣⎦, 解得222236991414k t k k ==-++, 由于2105k <<,故而204t <<,所以(2,0)(0,2)t ∈-,综合①②可知,(2,2)t ∈-. ……………………………………………………(12分) 21.(本小题满分12分)(Ⅰ)解:由题意知,()ln 2(0)f x x x '=+>,所以2()ln 2(0)F x ax x x =++>,2121()2(0)ax F x ax x x x+'∴=+=>.①当0a ≥时,恒有()0F x '>,故()F x 在(0,)+∞上是增函数; ②当0a <时,令()0F x '>,得2210ax +>,解得0x << 令()0F x '<,得2210ax +<,解得x > 综上所述,当0a ≥时,()F x 在(0,)+∞上单调递增; 当0a <时,()F x在0,⎛⎝上单调递增;在⎫+∞⎪⎪⎭上单调递减. ………………………………………………………………………(5分)(Ⅱ)证明:由题意知,21212121()()ln ln f x f x x x k x x x x ''--==--,要证121x x k <<,即要证22112122211111ln ln ln x x x x x x x x x x x x --<<⇔<<-, 令211x t x =>,则只需要证明11ln t t t-<<,由l n 0t >,即等价证明:ln 1ln (1)t t t t t <-<>. ①设()1ln (1)g t t t t =--≥,则1()10(1)g t t t '=-≥≥,故而()g t 在[1,)+∞上单调递增,而当1t >时,()1ln (1)0g t t t g =-->=,即ln 1(1)t t t <->;②设()ln (1)(1)h t t t t t =--≥,则()l n 0(1)h t t t '=≥≥,故而()h t 在[1,)+∞上单调递增,而当1t >时,()ln (1)(1)0(1)h t t t t h t =-->=>,即1ln (1)t t t t -<>. 综上①②知,ln 1ln (1)t t t t t <-<>成立,即121x x k<<. …………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】证明:(Ⅰ)如图7,连接DG ,AB , ∵AD 为⊙M 的直径,∴90ABD AGD ∠=∠=︒,在⊙O 中,90ABC AEC ABD ∠=∠=∠=︒,∴AC 为⊙O 的直径. …………………………………………………………(5分)(Ⅱ)∵90AEC ∠=︒,∴90CEF ∠=︒,∵点G 为弧BD 的中点,∴BAG GAD ∠=∠, 在⊙O 中,BAE ECB ∠=∠,∴AGD CEF △∽△,∴AG EF CE GD ⋅=⋅. …………………………………………………………(10分)23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)由cos ,sin ,x y ρθρθ=⎧⎨=⎩故而C 的直角坐标方程为22.y ax =消去t 得直线l 的普通方程为2y x =-. ……………………………………………(4分)(Ⅱ)由题意可知直线l的标准参数方程为2,4,x y ⎧=-+⎪⎪⎨⎪=-+⎪⎩(t 为参数), 代入22y ax =得到2)8(4)0t a t a -+++=,则有1212),8(4)t t a t t a +=+⋅=+,由28(4)48(4)0a a ∆=+-⨯+>,即0a >或4a <-.图7因为2||||||MN PM PN =⋅,所以2212121212()()4t t t t t t t t -=+-⋅=⋅, 解得1a =或4a =-(舍),所以1a =. ………………………………………………………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】证明:(Ⅰ)因为0,0m n >>, 则2422m n mn +≥,4222m n m n +≥, 所以244233()()4m n m n m n ++≥,当且仅当1m n ==时,取等号. …………………………………………(5分)(Ⅱ)由柯西不等式知:22222()()()a b m n am bn +++≥, 即2225()(5)m n +≥,所以225m n +≥, 当且仅当a bm n=时取等号. …………………………………………(10分)。
云南省师大附中高考理综适应性月考(五)试题(扫描版,含解析)

云南省师大附中2015届高考理综适应性月考(五)试题(扫描版,含解析)附答案解析云南师大附中2015届高考适应性月考卷(五)理科综合参考答案生物部分第Ⅰ卷(选择题,共36分)选择题(本题共6小题,每小题6分,共36分)【解析】1.有氧呼吸第三阶段需要酶催化反应,但ATP 是反应的产物,不参与反应。
2.赤霉素能使水稻幼苗疯长,患恶苗病,A 项正确。
在高于和低于最适浓度时,可获得两个促进生长效果相同的生长素浓度,B 项正确。
乙烯能促进果实成熟,不能促进果实发育,C 项错误。
脱落酸促进叶片和果实的脱落,D 项正确。
3.胰高血糖素不能促进肌糖原分解为葡萄糖,B 项错误。
4.种群“S”型增长达到K 值时,数量趋于稳定,此时种群的数量才处于动态平衡中,此前种群数量一直在增长,C 项错误。
5.根据题意,显性基因个数越多,合成的色素越多,即AABBCC 体色最深,aabbcc 体色最浅,与AaBbCC 个体表现型相同,需要具有4个显性基因,则后代的基因型为AABbCc111428⎛⎫⨯= ⎪⎝⎭或AaBBCc 111248⎛⎫⨯= ⎪⎝⎭,共1/4,C 项正确。
AaBbCc 的蝴蝶相互交配,后代有7种表现型,3×3×3=27种基因型,D 项错误。
6.前4年λ=1,种群数量不变,年龄组成为稳定型,第4年到第10年间,λ<1,种群数量一直下降,直到第10年后开始上升,B 项正确。
16~20年之间,λ大于2,雪兔的种群数量仍在增长未达到K 值,C 项错误。
第Ⅱ卷(非选择题,共54分)(一)必考题(共4题,共39分) 29.(每空1分,共7分)(1)ATP 、[H] 减少 C 3 减少 (2)乙(3)遮光 装置甲有色液滴向左移动的距离小于装置乙 30.(除特殊标注外,每空2分,共11分) (1)Z bW×Z B Z b(1分)(2)①黄色雄蛾︰白色雌蛾=1︰1 Z b Z b②黄色雄蛾︰白色雌蛾=2︰1③雌雄个体均有黄色和白色 Z b Z b W31.(除特殊标注外,每空1分,共10分)(1)反射神经递质流动性需要 T 体液免疫和细胞免疫(2分)(2)靶细胞进行细胞间信息的交流(3)神经—体液—免疫调节网络32.(每空1分,共11分)(1)样方偏小(2)竞争腐生菌(3)水平光照(4)初生森林(5)植物(生产者)固定的太阳能生物多样性抵抗力(二)选考题(共2小题,共15分)39.(除特殊标注外,每空2分,共15分)(1)附着在葡萄皮上的野生型酵母重铬酸钾(2)选择(1分)(3)3(4)无菌空气 30~35℃ C2H5OH+O2――→CH3COOH+H2O 醋酸菌40.(除特殊标注外,每空2分,共15分)(1)DNA连接酶(1分)识别特定的碱基序列并加以切割(2)Bam H I Sma I 和Msp I Mbo I(3)1327bp(4)抗生素B 抗生素A化学部分第Ⅰ卷(选择题,共42分)选择题(本题共7小题,每小题6分,共42分)【解析】7.A为氯离子的离子结构示意图,A项错;原子序数为114的元素位于第七周期第ⅣA族,与Pb处于同一主族,最外层电子数与Pb相等,B项正确;C项没有条件,3.5g的35Cl2气体在标况下的体积约为1.12L,C项错误;H3O+的质子数和电子数分别为11、10,OH-的质子数和电子数分别为9、10,D项错误,故选B。
云南师大附中2015届高考适应性月考卷(五)理科数学-答案

理科数学参考答案·第1页(共11页)云南师大附中2015届高考适应性月考卷(五)理科数学参考答案第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)【解析】1.{23568}(){368}U U A A B ==∵,,,,,∴,,痧,故选B .2.5i (5i)(1i)23i 1i (1i)(1i)z +++===+--+,在复平面内对应的点的坐标为(23),,故选A . 3.1248161024⨯⨯⨯⨯=,结束循环时32i =,故条件可为32i ≥,故选A . 4.如图1所示,x y ,所满足的可行域为图中阴影部分区域,对于直线33x zy =-+,显然经过P 点时截距取得最小值,即z 取得最小值,此时3303z =+⨯=,故选B . 5.易知,A 、B 、D 选项分别对应的是俯视、正视、侧视时 的投影,故选C .6.3711343(2)4(6)a a a d a d =+=+∵,∴,得1180a d +=,即190a =,1819S S =.而100d a ><,,故n S 的最小值在18n =或19n =处取得,故选C .7.在ABC △中,b a c b a -<<+,故13c <<.又ABC △为钝角三角形,显然钝角不为A ,cos 0B <∴或cos 0C <,即22202a c b ac +-<或22202a b c ab+-<,将12a b ==,代入,最终解得1c <3c <<,故选C .8.假如A 书给谁没有规定,一共有2343C A ⋅种分法,本来A 书给哪个同学都是等可能的,现在图1理科数学参考答案·第2页(共11页)规定A 书只能给甲同学,所以一共有2343C A 123⋅=种分法,故选B . 9.||=1OB OC -,即||=1CB ,则C 点在以B 为圆心,1为半径的 圆上运动,如图2所示,连接AB ,与此圆相交于点12C C ,,显 然12||||||AC AC AC ≤≤,由余弦定理可知,22π||||||2||||cosAB OB OA OB OA =+-⋅⋅ 1||71AC ≤≤,故选D .10.如图3,M N AB AP MN PB ∵、分别为和的中点,∴∥, MN CN PB CN ⊥⊥∵,∴,又P ABC -为正三棱锥, PB AC ⊥∴,ACCN C =,PB PAC ⊥∴平面,PB PA PB PC ⊥⊥∴,,同理可得PA PC ⊥,所以PA PB PC ,,两两垂直,且1PA PB PC ===,所以外接球半径为3π,故选C . 11.()0f x kx k --=,即方程()(1)f x k x =+有四个实数根,即函数()y f x =和函数(1)y k x =+的图象有四个交点,分析得,ln(1)1x y x +=+的图象先增后减,在 e 1x =-处取得最大值,如图4所示,设直线与ln(1)(0)1x y x x +=+≥的图象相切时斜率为0k ,则00k k <<即可.设切点为000ln(1)1x x x ⎛⎫+ ⎪+⎝⎭,,则00201ln(1)(1)x k x -+=+,则切线方程为000200ln(1)1ln(1)()1(1)x x y x x x x +-+-=-++,又切线经过点图2图3图4理科数学参考答案·第3页(共11页)(10)-,,代入解得01x ,故012ek =,故概率为14e P =,故选D .12.如图5所示,设右焦点为2F ,连接2PF ,12F F 为圆的直径,12PF PF ⊥,112F MA F PF ∴△∽△,13F M MP =,∴A .第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】时,5240T =.15.当2015x ≤时,()(3)[(6)](6)f x f x f x f x =-+=--+=+,此时()f x 为周期为6的周期函数,201563355=⨯+,(1)(2011)(2014)(2017)2017f f f f ==-==∴.图5理科数学参考答案·第4页(共11页)称的点为π24P x y ⎛⎫'--⎪⎝⎭,,而P '在函数π()2sin 34f x x ⎛⎫=- ⎪⎝⎭图象上,故ππ22sin 344y x ⎡⎤⎛⎫-=-- ⎪⎢⎥⎝⎭⎣⎦ π2sin 32x ⎛⎫=- ⎪⎝⎭2cos3x =,22cos3y x =-∴,故③正确.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)理科数学参考答案·第5页(共11页)18.(本小题满分12分)(Ⅰ)证明:如图6所示,连接BD ,交AE 于点F ,因为E 为CD 中点,故1DE =,AD ABDE AD=,又90BAD ADE ∠=∠=︒, BAD ADE ∴△∽△,ABD D AE ∠=∠∴,90DAE ADB ABD ADB ∠+∠=∠+∠=︒∴, 90AFD ∠=︒∴,即AE BD ⊥.因为是沿着AE 折叠的,故不改变1D F AE BF AE ⊥⊥,,又1D FBF F =,AE ⊥∴平面1BD F ,而1BD ⊂平面1BD F ,1AE BD ⊥∴. ……………………………………(6分)(Ⅱ)解:(法一)如图7所示,1D F AE ⊥∵,且1D AE B --为直二面角, 1D F ⊥∴平面ABCE ,1D F BC ⊥∴, 过F 作FGEC ∥,FG BC ⊥∴, 1FGD F F =,BC⊥平面1D GF ,1BC D G ⊥∴,1D GF ∠∴为二面角1D BC A --的一个平面角,易求得1D F ,43FG =,1D G ==∴, 114cos GF D GF GD ∠==,(法二)已知1DF AE BF AE ⊥⊥,,且1D AE B --为直二面角,故知1FD FE FB 、、两两垂直,故可建立如图8所示的空间直角坐标系,00B ⎫⎪⎪⎝⎭,,0C ⎫⎪⎪⎝⎭, 图6图7理科数学参考答案·第6页(共11页)100D ⎛ ⎝⎭,,16D C ⎛=⎝⎭∴, 0BC ⎛⎫=- ⎪ ⎪⎝⎭, 由(Ⅰ)知100FD ⎛= ⎝⎭,为平面ABC 的一个法向量, 设平面1D BC 的一个法向量为222()n x y z =,,,则1n D C n BC ⎧⊥⎪⎨⊥⎪⎩,, 即100n D C n BC⎧⋅=⎪⎨⋅=⎪⎩,,有222222()0()00x y z x y z ⎧⋅-=⎪⎪⎝⎭⎨⎛⎫⎪⋅= ⎪⎪ ⎪⎝⎭⎩,,,,,,从而2222200x y y =⎨⎪+=⎪⎩,,取21y =,则22x z =,所以(21n =,,.设二面角1D BC A --的大小为θ,113cos ||||6FD nFD n θ⋅===⋅∴,19.(本小题满分12分)解:(Ⅰ)设甲球员罚球命中数为x ,乙球员罚球命中数为y ,则应有2x y +=, 22139(02)55625P x y ⎛⎫⎛⎫===⋅= ⎪⎪⎝⎭⎝⎭,, 1122413296(11)C C 5555625P x y ===⋅⋅⋅⋅⋅=,, 图8理科数学参考答案·第7页(共11页)224264(20)55625P x y ⎛⎫⎛⎫===⋅= ⎪⎪⎝⎭⎝⎭,,若犯规,则甲球员得分2X 可以的取值为0123,,,, 24114(0)555125P X ==⋅⋅=,12244132(1)C 555125P X ==⋅⋅=, 22441169(2)5555125P X ⎛⎫==⋅+⋅= ⎪⎝⎭,2144(3)5525P X ==⋅=,2432694()0123 1.8412512512525E X =⨯+⨯+⨯+⨯=∴, 12()()E X E X >,所以应该犯规.…………………………(12分)20.(本小题满分12分)解:(Ⅰ)12ce a ===,又菱形面积2S ab ==2a b ==,(Ⅱ)设点1122()()M x y N x y ,,,,当切线与x 轴不垂直时,设切线方程为y kx m =+, 联立22143x y y kx m ⎧+=⎪⎨⎪=+⎩,,得222(43)84120k x kmx m +++-=, 212122284124343km m x x x xk k --+==++,, MN ==∴理科数学参考答案·第8页(共11页)化简得:MN ,①因为直线y kx m =+与圆2253x y +==即225(1)3m k =+,将其代入①式得:MN =2(0)t k t =≥,则4MN44=44==, 当且仅当25181812t t t +==+,即时等号成立,此时k =. 当斜率不存在时,253x =,代入算得MN =故当k =||MN,又1||2OMN S MN r =⋅⋅△,r,21.(本小题满分12分)解:(Ⅰ)若1a =-,2e ()23xf x x x x=+--,则222e e (e 2)(1)()22x x x x x x f x x x x⋅-+-'=+-=,2e 20x x +>恒成立, 故知()f x 的单调递增区间为(1)+∞,,单调递减区间为(0)-∞,和(01),.理科数学参考答案·第9页(共11页)………………………………………………………………(4分)(Ⅱ)对任意的(04]x ∈,,2e ()(23)0xf x a x x x=---≥恒成立,由于223(1)(3)x x x x --=+-,3x =时,任意a 都成立.当(03)x ∈,时,2230x x --<,故等价于2e (23)xa x x x --≥恒成立,令2e ()(03)(23)xg x x x x x =∈--,,,故等价于max ()a g x ≥, 322322222222e (23)(343)e e (53)e (1)(43)()[(23)][(23)][(23)]x x x x x x x x x x x x x x x g x x x x x x x x x x ------++---'===------∴,当(03)x ∈,时,知2430x x --<,故易得当(01)x ∈,时,()0g x '>,()g x 单调递增; 当(13)x ∈,时,()0g x '<,()g x 单调递减, max e ()(1)4g x g ==-∴,e4a -∴≥;当(34]x ∈,时,2230x x -->,故等价于2e (23)xa x x x --≤恒成立,令2e ()(34](23)xh x x x x x =∈--,,,故等价于min ()a h x ≤, 同理可得222e (1)(43)()[(23)]x x x x h x x x x ---'=--,当(34]x ∈,时,知10x ->,2430x x --<, 故()0h x '<,故()h x 单调递减,故4mine ()(4)20h x h ==,4e 20a ∴≤.22.(本小题满分10分)【选修4−1:几何证明选讲】 (Ⅰ)证明:如图9,∵PA 是切线,AB 是弦, ∴BAP C ∠=∠. 又∵APD CPE ∠=∠,图9理科数学参考答案·第10页(共11页)∴BAP APD C CPE ∠+∠=∠+∠.AD E BAP APD ∠=∠+∠,AED C CPE ∠=∠+∠,∴ADE AED ∠=∠. …………………………………………………………………(5分) (Ⅱ)解:由(Ⅰ)知BAP C ∠=∠,又∵APC BPA ∠=∠, ∴APC △∽BPA △,∴PC CAPA AB=. ∵AC AP =,∴APC C ∠=∠,∴APC C BAP ∠=∠=∠. 由三角形内角和定理可知,180APC C CAP ∠+∠+∠=︒.∵BC 是圆O 的直径,∴90BAC ∠=︒,∴1809090APC C BAP ∠+∠+∠=︒-︒=︒,∴190303C APC BAP ∠=∠=∠=⨯︒=︒.在Rt ABC △中,1tan CA C AB =,即1tan30CAAB=︒,∴CA AB =∴PC CA PA AB== ……………………………………………(10分) 23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)圆的直角坐标方程为:222x y r ⎛⎛+= ⎝⎭⎝⎭,圆心坐标为C ⎛ ⎝⎭,ρ1, 圆心C 在第二象限,3π4θ=,圆心极坐标为3π14⎛⎫⎪⎝⎭,. …………………………(5分)(Ⅱ)圆C 上的点到直线l 的最大距离等于圆心C 到直线l 的距离和半径之和,l 的直角坐标方程为10x y +-=,r +=r =. ……………………………………………(10分) 24.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)31(1)()3(11)31(1)x x f x x x x x +>⎧⎪=+-⎨⎪--<-⎩,≤≤,,理科数学参考答案·第11页(共11页) ()5f x >∴的解集为4 2 3x x x ⎧⎫><-⎨⎬⎩⎭或. ……………………………………(5分) (Ⅱ)()[2)f x ∈+∞,,()()f x a a <∈R 的解集为空集,则(2]a ∈-∞,. …………(10分)。
云南师大附中高考适应性月考卷(五)——理科数学.docx

云南师大附中2016届高考适应性月考卷(五)——理科数学云南师大附中2016届高考适应性月考卷(五)理科数学参考答案第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 ACDBDCBBCAAB【解析】1.当{0123}M =,,,时,M 的子集最多有4216=个,故选A .2.22(1i)2i (1i)(1i)2i(1i)(1i )2(i i )22(1i)z z z z +=+-=--=-=+∵,∴,,,1i z =+∴,故选C . 3.当0x >时,()ln f x x =在(0)+∞,上单调递增,又函数()f x 为偶函数,所以(π)(π)M f f =-=,而πe 5>>,所以M N K >>,故选D .4.2sin cos 3A A +=∵,22(sin cos )9A A +=∴,72sin cos 09A A =-<,则A 为钝角,故选B . 5.由ξ服从正态分布(4,1)N ,得4μ=,1σ=.(35)(4141)0.6826P P ξξ<=-<+=∵≤≤, 1(5)[1(35)]0.15872P P ξξ>=⨯-<=∴≤,故选D .6.由线面关系易知,①②③均正确,在④中如图1所示,平面α,β,γ两两垂直,m αβ=I ,且n γ⊂,n α⊥,过直线n 作平面ϕ,此时βγ⊥,αϕ⊥,二面角m αβ--为90︒,而满 足条件的平面ϕ有无穷多个,所以其二面角n γϕ--无法确定, 故④错,故选C .7.依据程序框图,可知,m 表示数学成绩90i a <的学生人数,则18m =;n 表示数学成绩90120i a ≤≤的学生人数,则33n =;k 表示数学成绩120i a >的学生人数,则9k =,故选B .8.如图2,几何体的直观图为三棱柱和三棱锥的组合体,其体积为 11133331315232V =⨯⨯⨯+⨯⨯⨯⨯=,故选B .9.由等比数列{}n a 的性质, 得313538a a a a ==,32a =∴,又∵当1n =时,212212S a a a =+=, 1122a q ==-∴,,781(2)642a =⨯-=-∴,故选C .10.∵函数3211()232f x x ax bx c =+++的两个极值点分别位于区间(10)-,与(01),内,图2图12()2f x x ax b '=++∴的两个零点分别位于区间(10)-,与(01),内,(1)0(0)0(1)0f f f '->⎧⎪'<⇒⎨⎪'>⎩,∴,2100210a b b a b -++>⎧⎪<⎨⎪++>⎩,,,设点()P a b ,,112A ⎛⎫⎪⎝⎭,, 则1111121222PA b b k a a --==--g (PA k 为直线PA 的斜率), 如图3所示,由线性规划知,2(2)3PA k ⎛⎫∈-∞-+∞ ⎪⎝⎭U ,,,11(,1),23PA k ⎛⎫∈-∞-+∞ ⎪⎝⎭U ∴,故选A . 11.对于圆O :221x y +=外的点P 和圆上点Q ,当90OQP ∠=︒时,OPQ ∠最大,此时,由30OPQ ∠=︒,得||2OP =,当||2OP >时,30OPQ ∠<︒,2200||2OP x y =+∴≤,即22004x y +≤,又0020x y -+=,即002y x =+,22220000(2)4x y x x +=++∴≤,解得020x -≤≤,故选A .12.由“域倍函数”定义知()2,()2,f m m f n n =⎧⎨=⎩即方程()2f x x =有两个不同实根,即方程2e 6e x x x t ++=有两个不同实根.设函数2()e e 6x x g x x t =---()x ∈R ,2()2e e 6(2e 3)(e 2)x x x x g x '=--=+-∴.令()0g x '=,解得ln2x =.当ln2x <时,()0g x '<,所以()g x 在(,ln 2)-∞上是减函数;当ln2x >时,()0g x '>,所以()g x 在(ln 2,)+∞上是增函数.∴当ln2x =时,min ()426ln 2g x t =---,x ∈R ∴,()[26ln 2,)g x t ∈--+∞,∴方程()0g x =有两个不同实根的充要条件为26ln20t --<,所以26ln2t >-,故选B .第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)题号 13 14 15 16 答案152π46720图3【解析】13.621x x ⎛⎫- ⎪⎝⎭∵的展开式的通项为26161C ()rrr r T x x -+⎛⎫=- ⎪⎝⎭1236C (1)r r r x -=-(0,1,2,,6)r =…,∴当4r =时,4456C (1)15T =-=,故621x x ⎛⎫- ⎪⎝⎭的展开式中常数项为15.14.由题意,得2222|2|(2)44449404a b a b a a b b a b -=-=-+=-=+⨯r r r r r r r r r r g g ,0a b =r rg ∴,a b r r ∴⊥,设a r 与b r 的夹角为θ,[0,]θ∈π,2θπ=∴.15.满足1212()()()n nf x f x f x x x x ===…的x 的个数n 即为 函数()sin 2f x x =与y kx =的图象的交点个数,但 不含原点,如图4所示,存在(,0)k ∈-∞,使得n取到最大值4.16.(ⅰ)当1a 为奇数时,1212a a +=,此时若2a 为奇数,则121311132224a a a a ++++===, 11131137510244a a a S a +++=++==∴,解得15a =,此时的数列{}n a 为5,3,2,5,3,2,…;(ⅱ)当1a 为奇数时,1212a a +=,此时若2a 为偶数,则11323(1)3131122a a a a ++=-=-=,11311131311022a a S a a ++=++=+=∴,解得13a =,此时的数列{}n a 为3,2,5,3,2,5,…;(ⅲ)当1a 为偶数时,2131a a =-,此时2a 为奇数,则21131(31)13222a a a a +-+===,131113113111022a S a a a =+-+=-=∴,解得12a =,此时的数列{}n a 为2,5,3,2,5,3,….上述三种情况数列{}n a 均为周期数列,又67232016⨯=,所以20166720S =.三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)解:(Ⅰ)422()2cos 2sin cos 23sin cos 1f x x x x x x =++-g g 2222cos (cos sin )23sin cos 1x x x x x =++-g 22cos 123sin cos x x x =-+g图43sin 2cos2x x =+π2sin 2,6x x ⎛⎫=+∈ ⎪⎝⎭R ,…………………………………………………………(4分) ∴函数()f x 的最小正周期2ππ2T ==. ………………………………………(6分)(Ⅱ)π12A f ⎛⎫-=- ⎪⎝⎭∵,ππ2sin 2π2sin 2π1266A A ⎡⎤⎛⎫⎛⎫-+=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∴,π1sin 62A ⎛⎫-= ⎪⎝⎭∴,ππ5π(0π)666A A ⎛⎫∈-∈- ⎪⎝⎭∵,,,,ππ66A -=∴,即π3A =. 设ABC △的边BC 上的高为h ,又2a =,则1113||sin 2224ABC S BC h ah h bc A bc =====△. 由余弦定理知,22222π42cos 23a b c bc b c bc bc bc bc ==+-=+--=≥(当且仅当2b c ==时取“=”),334344h bc =⨯=∴≤(当且仅当2b c ==时取“=”), 即BC 边上的高的最大值为3. ………………………………………………(12分)18.(本小题满分12分)解:(Ⅰ)设事件A =“抽出的2组数据恰好是相邻两个月的数据”,所有的基本事件(,)m n (其中m ,n 为月份)有:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共25C =10种, 其中事件A 包含的基本事件有:(1,2),(2,3),(3,4),(4,5),共4种, 42()105P A ==∴. …………………………………………………………………(6分)(Ⅱ)11(12345)3(44566)555x y =++++==++++=,,51142435465681i ii x y==⨯+⨯+⨯+⨯+⨯=∑,522222211234555i i x ==++++=∑,515221581535ˆ0.655595i ii ii x yxybxx ==--⨯⨯===-⨯-∑∑∴,ˆˆ50.63 3.2ay bx =-=-⨯=,ˆ0.6 3.2y x =+∴, 当6x =时, 6.8y =.故今年6月份该种产品的产量大约为6.8万件. ……………………………(12分)19.(本小题满分12分)(Ⅰ)证明:AEF ∵△为等边三角形,O 为EF 的中点,AO EF ⊥∴.AEF EFCB ⊥∵平面平面,AEF EFCB EF =I 平面平面,AO AEF ⊂平面, AO EFCB ⊥∴平面, 又BE EFCB ⊂平面,AO BE ⊥∴.……………………………………………………………………(4分)(Ⅱ)解:如图5,取CB 的中点D ,连接OD , 以O 为原点,分别以OE ,OD ,OA 为x ,y ,z 轴建立空间直角坐标系, 则(0,0,3),(,0,0),(2,233,0)A a E a B a -,(,0,3),(2,233,0)AE a a EB a a =-=--u u u r u u u r∴. 设平面AEB 的法向量为1(,,)n x y z =u u r,则1130,(2)(233)0,n AE ax az n EB a x a y ⎧=-=⎪⎨=-+-=⎪⎩r u u u r g r u u ur g 令3z =,则3,3x y ==-,1(3,3,3)n =-u u r,易知平面AEF 的法向量为2(0,1,0)n =u u r,12121235cos ,5||||15n n n n n n -〈〉===-u u r u u ru u r u u r g u u r u u r ∴,∴二面角F AE B --的正弦值为255. ………………………………………(12分) 20.(本小题满分12分)图5解:(Ⅰ)设点11(,)A x y ,22(,)B x y ,则有2112222,2,x py x py ⎧=⎪⎨=⎪⎩2AM MB =u u u u r u u u r ∵,11(,1)AM x y =--u u u ur ,22(,1)MB x y =-u u u r ,12122,12(1),x x y y -=⎧⎨-=-⎩∴即12122,32,x x y y -=⎧⎨=-⎩ 代入抛物线方程得22222242(32),2,x p y x py ⎧=-⎪⎨=⎪⎩22,12x p y ⎧=⎪⎨=⎪⎩∴或22,1,2x p y ⎧=-⎪⎨=⎪⎩ ∵直线l 的倾斜角为4π,即2122212233113AB y y y y k x x x x ---====-,1121p -=∴(舍去)或1121p -=-, 14p =∴,∴抛物线C :212x y =. ………………………………………………(6分)另解:由题意,得直线l 的方程为1y x =+,直线l 与C 相交于A ,B 两点, 设点11(,)A x y ,22(,)B x y , 22,1,x py y x ⎧=⎨=+⎩∵2220x px p --=∴, 12122,2,x x p x x p +=⎧⎨=-⎩g ∴又2AM MB =u u u u r u u u r ∵,11(,1)AM x y =--u u u ur ,22(,1)MB x y =-u u u r ,122x x -=∴,即1212122,2,2,x x p x x p x x +=⎧⎪=-⎨⎪-=⎩g解方程得121,1,21,4x x p ⎧⎪=⎪⎪=-⎨⎪⎪=⎪⎩∴抛物线C :212x y =. …………………………………………………………(6分)(Ⅱ)212x y =∵,即22y x =, 4y x '=∴. 设抛物线C 上任意一点200(,2)N x x ,004x x y x ='=,则在点200(,2)N x x 处的切线l '的方程为200024()y x x x x -=-, 即l ':200420x x y x --=, ∴点(0,1)M 到直线l '的距离为22000220|12|12()116116x x d x xx--+==∈++R .令201161t x =+≥,则220116t x -=, 27177884t d t t t +⎛⎫==+ ⎪⎝⎭∴≥(当且仅当7t =时取等号),∴当064x =±时,min 74d =. ∴点M 到直线l '的距离的最小值为74. ……………………………………(12分)21.(本小题满分12分)解:(Ⅰ)函数()f x 的定义域为(0,)+∞,2221122()22a x x af x x x x -+-'=--=. 令()0f x '=,则222048x x a a -+-=∆=-,, ①当12a ≥时,0∆≤,()0f x '≤,()f x ∴在(0,)+∞上为减函数;②当12a <时,0∆>,2220x x a -+-=有两不等根, 1112x a =--,2112x a =+-.i)当102a <<时,120x x <<, 令()0f x '>得12x x x <<,则()f x 在12(,)x x 上单调递增;令()0f x '<得120x x x x <<>或,则()f x 在1(0,)x ,2(,)x +∞上单调递减.ii)当0a ≤时,120x x <≤,令()0f x '>得20x x <<,则()f x 在2(0,)x 上单调递增; 令()0f x '<得2x x >,则()f x 在2(,)x +∞上单调递减. 综合①、②得,当12a ≥时,()f x 在(0,)+∞上是减函数;当102a <<时,()f x 在(0,112)a --,(112,)a +-+∞上是减函数, 在(112,112)a a --+-上是增函数;当0a ≤时,()f x 在(0,112)a +-上是增函数,在(112,)a +-+∞上是减函数.………………………………………………………………………………(6分)(Ⅱ)对于任意的12,[1,2]x x ∈,都有12()()1f x g x -≤恒成立, 等价于[1,2]x ∀∈,max min ()1()f x g x +≤, 由(Ⅰ)知,当12a >时,()f x 在[1,2]上为减函数, max 1()(1)2f x f a ==-+∴.下面求当[1,2]x ∈时()g x 的最小值,22ln(1)(1)ln(1)1()(1)xx x x x x g x x x x -+-+++'==+,[1,2]x ∈, 令()(1)ln(1)h x x x x =-++,则()1[ln(1)1]ln(1)h x x x '=-++=-+, [1,2]x ∈∵,()0h x '<∴,()h x ∴在[1,2]上为减函数,∴当[1,2]x ∈时,()(1)12ln 21ln 40h x h =-=-<≤, ∴当[1,2]x ∈时,()0g x '<,()g x ∴在[1,2]上为减函数, ∴当[1,2]x ∈时,min ln3()(2)2g x g ==, 1ln3122a -++∴≤,ln332a +∴≤,又12a >, 故1ln3322a +<≤时,对于任意的12,[1,2]x x ∈,都有12()()1f x g x -≤恒成立.…………………………………………………………………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】证明:(Ⅰ)如图6,连接MN ,BN , ∵NA 为⊙O 2的直径,90AMN ∠=︒∴,90BMN ∠=︒∴,∴BN 为⊙O 1的直径,90BEN ∠=︒∴,90BEC ∠=︒∴,又∵NA 为⊙O 2的直径,90ACN ∠=︒, BEC ACN ∠=∠∴, AC BE ∴∥.……………………………………………………………………(5分)(Ⅱ)AC BE ∵∥, ACD BED ∴△∽△,AC CDBE DE=∴; ∵点C 为¼AM 的中点,ANC CAM ∠=∠∴, 又ACN DCA ∠=∠∵,ACN DCA ∴△∽△, AC CNCD AC=∴, 2AC CD CN =g ∴.又2222AC CD BE DE =∵,222CD CN CD BE DE =g ∴, 22CD BE CN DE =g g ∴. …………………………………………………………(10分) 23.(本小题满分10分)【选修4−4:坐标系与参数方程】解:(Ⅰ)cos ,sin ,x y ρθρθ=⎧⎨=⎩∵且曲线C :2cos ρθ=,∴曲线C 的直角坐标方程为222x y x +=,即22(1)1x y -+=, 曲线C 是圆心为(1,0),半径为1r =的圆.图6∵直线l 的参数方程为221,31,3x t y t ⎧=--⎪⎪⎨⎪=⎪⎩(t 为参数), ∴直线l 的普通方程为2210x y ++=, ∴圆心C 到直线l 的距离为|11|2318d +==+, 222225||22133AB r d ⎛⎫=-=⨯-= ⎪⎝⎭∴. ………………………………………(5分)(Ⅱ)由题,可得圆C 的参数方程为1cos ,sin ,x y ϕϕ=+⎧⎨=⎩(其中ϕ为参数,[0,2)ϕ∈π),设圆C 上的任意一点(1cos ,sin )Q ϕϕ+,则线段PQ 的中点R 11cos ,sin 22ϕϕ⎛⎫⎪⎝⎭,RH x ⊥∵轴, 1cos ,02H ϕ⎛⎫⎪⎝⎭∴,∵点G 在射线HR 上,且满足||3||HG HR =, 1cos ,233sin ,2G R G R x x y y ϕϕ⎧==⎪⎪⎨⎪==⎪⎩∴∴点G 的轨迹C '的参数方程为1cos ,23sin ,2x y ϕϕ⎧=⎪⎪⎨⎪=⎪⎩(其中ϕ为参数,[0,2)ϕ∈π),轨迹C '是焦点在y 轴,长轴长为3,短轴长为1的椭圆. ……………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】(Ⅰ)解:由绝对值三角不等式,得()|2||5||(2)(5)||52|f x x a x x a x a =------=-≤, ∵对于任意x ∈R 都有()1f x ≤恒成立, |52|1a -∴≤,1521a --∴≤≤,即426a ≤≤, 23a ∴≤≤.………………………………………………………………………(5分)(Ⅱ)证明:∵01b <<, 011b <-<∴,112b <+<. 23a ∵≤≤,∴由对数函数的性质,可得log (1)0a b -<,log (1)0a b +>,|log (1)||log (1)|log (1)log (1)log [(1)(1)]a a a a a b b b b b b --+=---+=--+g ∴2log (1)a b =--.∵01b <<,2011b <-<∴,2log (1)0a b -<∴,2|log (1)||log (1)|log (1)0a a a b b b --+=-->∴, 即|log (1)||log (1)|a a b b ->+.……………………………………………………(10分)。
【数学】云南师大附中2015届高考适应性月考卷(六)(理)

【数学】云南师大附中2015届高考适应性月考卷(六)(理)一、选择题(本大题共12小题,每小题5分,共60分)1. 设集合A={x|0≤x≤2},集合B={x|x²3x+2=0},则A∩B=()A. {1, 2}B. {1}C. {2}D. φ2. 已知复数z满足|z|=1,则|z1|的最小值为()A. 0B. 1C. √2D. 23. 设函数f(x)=x²+2ax+a²1(a为常数),若f(x)在区间(1,1)上单调递增,则a的取值范围是()A. a≥1B. a≤1C. a≥0D. a≤04. 在三角形ABC中,角A、B、C的对边分别为a、b、c,若sinA+sinB=sinC,则三角形ABC的形状是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能确定5. 已知等差数列{an}的前n项和为Sn,若S3=9,S6=36,则a4+a5+a6=()A. 27B. 18C. 9D. 36. 设函数f(x)=x²+bx+c(b、c为常数),若f(x)在x=1处取得极小值,则b和c的关系为()A. b²4c>0B. b²4c=0C. b²4c<0D. 不能确定7. 已知数列{an}的通项公式为an=2n+1,则数列{an}的前10项和为()A. 110B. 220C. 330D. 4408. 在平面直角坐标系中,点A(2,3)关于原点的对称点坐标为()A. (2,3)B. (2,3)C. (2,3)D. (3,2)9. 若直线y=kx+b与圆(x1)²+(y2)²=4相切,则k和b的关系为()A. k²+b²=4B. k²+b²=3C. k²+b²=2D. k²+b²=110. 已知函数f(x)=x³3x,则f'(x)的零点个数为()A. 0B. 1C. 2D. 311. 在等比数列{an}中,若a1=2,公比为q,且a1+a2+a3+a4=15,则q的值为()A. 2B. 1C. 1/2D. 1/212. 设函数f(x)=x²2x+3,则f(x)在区间(1,3)上的最小值为()A. 2B. 3C. 4D. 5二、填空题(本大题共4小题,每小题5分,共20分)13. 若向量a=(2,1),向量b=(1,2),则2a3b=______。
云南师大附中2015届高三高考适应性月考(一)数学(理)试题 Word版含解析

云南师大附中2015届高考适应性月考卷(一)理科数学【试卷综析】本试卷是高三理科试卷,以基础知识和基本技能为载体,以能力测试为主导,在注重考查学科核心知识的同时,突出考查考纲要求的基本能力,重视学生科学素养的考查.知识考查注重基础、注重常规、注重主干知识,兼顾覆盖面.试题重点考查:不等式、复数、向量、三视图、导数、简单的线性规划、直线与圆、圆锥曲线、立体几何、数列、函数的性质及图象、三角函数的性质、三角恒等变换与解三角形、命题、程序框图、排列组合、概率与随机变量分布列与期望、不等式选讲、几何证明选讲、参数方程极坐标等;考查学生解决实际问题的综合能力,是份较好的试卷.一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 【题文】1、已知全集U 和集合A 如图1所示,则()U C A B ⋂= A.{3} B.{5,6} C.{3,5,6} D.{0,4,5,6,7,8}【知识点】集合及其运算A1 【答案解析】B 解析:由图易知()U A B =ð{5,6}.则选B.【思路点拨】本题主要考查的是利用韦恩图表示集合之间的关系,理解集合的补集与交集的含义是解题的关键.【题文】2、设复数12,z z 在复平面内对应的点关于原点对称,11z i =+,则12z z = A .-2i B.2i C .-2 D.2 【知识点】复数的概念与运算L4【答案解析】A 解析:11i z =+在复平面内的对应点为(1,1),它关于原点对称的点为(1,1)--,故21i z =--,所以212(1i)2i.z z =-+=-则选A.【思路点拨】通过复数的几何意义先得出2z ,再利用复数的代数运算法则进行计算. 【题文】3、已知向量,a b 满足6a b -=,1a b ∙=,则a b += A .6 B.22 C .10 D.10 【知识点】向量的数量积及其应用F3【答案解析】C 解析:由已知得222222()226-=-=+-⋅=+-=a b a b a b a b a b ,即228+=a b ,所以2+=a b 222()210+=++⋅=a b a b a b ,即10.+=a b 则选C.【思路点拨】遇到求向量的模时,一般利用向量的模的平方等于向量的平方转化求解. 【题文】4、曲线11axy e x =++在点(0,2)处的切线与直线y=x+3平行,则a= A .1 B.2 C .3 D.4 【知识点】导数的应用B12 【答案解析】B 解析:21e (1)ax y a x '=-+,由题意得011x y a ='=-=,所以 2.a =则选B.【思路点拨】理解导数与其切线的关系是解题的关键.【题文】5、在△ABC 中,若sinC=2sinAcosB,则此三角形一定是A .等腰直角三角形 B.直角三角形 C .等腰三角形 D.等边三角形 【知识点】解三角形C8【答案解析】C 解析:由已知及正、余弦定理得,22222a c b c a ac+-=,所以22a b =,即a b =.则选C.【思路点拨】判断三角形形状,可以用正弦定理及余弦定理把角的关系转化为边的关系,也可利用三角形内角和的关系进行转化求解.【题文】6、函数()2sin 3sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是 A .1 B.132+ C .32 D.13+【知识点】函数sin()y A x ωϕ=+的图象与性质C4【答案解析】C 解析:函21cos 231π()sin 3sin cos sin 2sin 22226x f x x x x x x -⎛⎫=+=+=+- ⎪⎝⎭, ππππ5π,,2,42636x x ⎡⎤⎡⎤∈-∈⎢⎥⎢⎥⎣⎦⎣⎦∵∴, ()f x 的最大值是32.则选C.【思路点拨】一般研究三角函数的性质,通常先化成一个角的三角函数再进行解答.【题文】7、已知实数x,y 满足约束条件0024030220x y x y x y x y ≥⎧⎪≥⎪⎪+-≤⎨⎪+-≤⎪⎪+-≥⎩,则z=x+3y 的取值范围是A .[1,9] B.[2,9] C .[3,7] D.[3,9]【知识点】简单的线性规划问题E5【答案解析】B 解析:根据线性约束条件作出可行域, 如图1所示阴影部分.作出直线l :30x y +=,将直线l 向上平移至过点 (0,3)M 和(2,0)N 位置时,max 0339z =+⨯=,min 230 2.z =+⨯=则选B.【思路点拨】本题先正确的作出不等式组表示的平面区域,再结合目标函数的几何意义进行解答.【题文】8、如图,网格纸上小方格的边长为1(表示1cm),图中粗线和虚线是某零件的三视图,该零件是由一个底面半径为4cm ,高为3cm 的圆锥毛坯切割得到,则毛坯表面积与切削得的零件表面积的比值为 A .310 B.510 C .710 D.910【知识点】三视图G2【答案解析】D 解析:圆锥毛坯的底面半径为4cm r =,高为3cm h =,则母线长5cm l =,所以圆锥毛坯的表面积2ππ36πS rl r =+=原表,切削得的零件表面积2π2140πS S =+⨯⨯=零件表原表,所以所求比值为910.则选D. 【思路点拨】由三视图求几何体的表面积,关键是正确的分析原几何体的特征.【题文】9、若任取x,y ∈[0,1],则点P(x,y)满足2y x >的概率为 A .23 B.13 C .12 D.34【知识点】定积分 几何概型K3 B13【答案解析】A 解析:该题属几何概型,由积分知识易得点(,)P x y 满足2y x >的面积为12310012(1)33x dx x x ⎛⎫-=-= ⎪⎝⎭⎰,所以所求的概率为23.则选A. 【思路点拨】当总体个数有无限多时的概率问题为几何概型,若事件与两个变量有关时,可归结为面积问题进行解答.【题文】10、已知椭圆()222210x y a b a b+=>>的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P ,若2AP PB =,则椭圆的离心率是A .32 B.22C .13 D.12【知识点】椭圆的几何性质H5【答案解析】D 解析:因为2AP PB =,则12,2,2OA OF a c e ===∴∴.则选D.【思路点拨】求椭圆的离心率一般先结合条件寻求a,b,c 关系,再结合离心率的定义解答即可.【题文】11、把边长为2的正三角形ABC 沿BC 边上的高AD 折成直二面角,设折叠后BC 中点为M ,则AC 与DM 所成角的余弦值为 A .23 B.24 C .32 D.33【知识点】异面直线所成的角G11【答案解析】B 解析:建立如图2所示的空间直角坐标系D xyz -,则(0,0,3),(1,0,0),(0,1,0),A B C11,,0,(0,0,0),2211(0,1,3),,,0,222cos ,,4M D AC DM AC DM AC DM AC DM⎛⎫⎪⎝⎭⎛⎫=-= ⎪⎝⎭⋅〈〉==∴∴则AC 与DM 所成角的余弦值为24.所以选C. 本题也可用几何法:在△ABC 中过点M 作AC 的平行线,再解三角形即得.【思路点拨】求异面直线所成角时,可先考虑用定义法作出其平面角,再利用三角形解答,若作其平面角不方便时,可采取向量法求解. 【题文】12、函数()()3f x x xx R =+∈当02πθ<<时,()()sin 10f a f a θ+->恒成立,则实数a 的取值范围是A .(﹣∞,1] B.(﹣∞,1) C .(1, +∞) D.(1, +∞) 【知识点】奇函数 函数的单调性B3 B4【答案解析】A 解析:2()130f x x '=+>,故3()()f x x x x =+∈R 在R 上单调递增,且为奇函数,所以由(sin )(1)0f a f a θ+->得(sin )(1)f a f a θ>-,从而sin 1a a θ>-,即当π02θ<<时,1sin 1a θ<--恒成立,所以1a ≤.则选A.【思路点拨】本题可先利用奇函数及函数的单调性进行转化,再把不等式恒成立问题转化为函数的最值问题进行解答.二、填空题(本大题共4小题,每小题5分,共20分)【题文】13、定义一种新运算“⊗”:S a b =⊗,其运算原理如图3的程序框图所示,则3654⊗-⊗=_______.【知识点】程序框图L1【答案解析】﹣3解析:由框图可知(1),,(1),.a b a b S b a a b ->⎧=⎨-⎩≤ 从而得36546(31)5(41)3⊗-⊗=---=-.【思路点拨】读懂程序框图,理解所定义的新运算,即可解答.【题文】14、等比数列{}n a 的前n 项和为n S ,且1234,2,a a a 成等差数列,若11a =,则4S =_____.【知识点】等比数列与等差数列D2 D3【答案解析】15解析:1234,2,a a a ∵成等差数列,2213211144,44,440,a a a a a q a q q q +=+=-+=∴即∴42,15q S ==∴.【思路点拨】遇到等差数列与等比数列,若无性质特征,则用其公式转化为首项与公比关系进行解答.【题文】15、关于sinx 的二项式()1sin nx +的展开式中,末尾两项的系数之和为7,且系数最大的一项的值为52,当x ∈[0, π]时,x=___________. 【知识点】二项式定理J3 【答案解析】π6或5π6. 解析:1C C 17n n n n n -+=+=,故6n =,所以第4项的系数最大,于是3365C sin 2x =,所以,31sin 8x =,即1sin 2x =,又[0,π]x ∈,所以π6x =或5π6. 【思路点拨】一般遇到二项展开式某项或某项的系数问题,通常结合展开式的通项公式进行解答.【题文】16、已知函数()3232a b f x x x cx d =+++(a <b)在R 上单调递增,则a b c b a++-的最小值为______.【知识点】导数的应用 基本不等式B12 E6【答案解析】3解析:由题意2()0f x ax bx c '=++≥在R 上恒成立,故0b a >>,24b c a≥,于是a b c b a ++-≥2211441b b b a b a a a b b a a ⎛⎫++++ ⎪⎝⎭=--,设b t a =(1)t >,则问题等价于求函数244()4(1)t t g t t ++=-(1)t >的最小值,又()()244191()166634(1)414t t g t t t t ++⎡⎤==-++≥+=⎢⎥--⎣⎦,由此可得min ()(4)3g t g ==.【思路点拨】先由函数的单调性结合导数得到abc 的关系,再通过换元法转化为熟悉函数的最小值问题.三、解答题(共70分,解答应写出文字说明,证明过程或演算步骤) 【题文】17、(本小题满分12分)一个口袋内有5个大小相同的球,其中有3个红球和2个白球. (1)若有放回的从口袋中连续的取3次球(每次只取一个球),求在3次摸球中恰好取到两次红球的概率;(2)若不放回地从口袋中随机取出3个球,求取到白球的个数ξ的分布列和数学期望E(ξ). 【知识点】概率 离散随机变量的分布列和数学期望K6 K7【答案解析】(1)54125(2)6()5E ξ=解析:(1)设在3次有放回的摸球中恰好取到两次红球的概率为P ,由题设知, 21233354C 155125P ⎛⎫⎛⎫=-=⎪⎪⎝⎭⎝⎭. (2)白球的个数ξ可取0,1,2,3211233232333555C C C C C 133(0),(1),(2)C 10C 5C 10P P P ξξξ=========.所以ξ的分布列如下表:ξ0 1 2P110 35 3101336()012105105E ξ=⨯+⨯+⨯=.【思路点拨】求离散随机变量的分布列一般先确定随机变量的所有取值,再计算各个取值的概率,最后得分布列并计算期望. 【题文】18、(本小题满分12分)如图4,在斜三棱柱111ABC A B C -中,点O 、E 分别是111,AC AA 的中点,111AO A B C ⊥平面,已知∠BCA=90°,12AA AC BC ===. (1)证明:OE ∥平面11AB C ;(2)求直线11AC 与平面11AA B 所成角的正弦值.【知识点】直线与平面平行,线面所成的角G4 G11【答案解析】(1) 略(2) 217解析:方法一:(1)证明:∵点O 、E 分别是11AC 、1AA 的中点,∴1OE AC ∥,又∵OE ⊄平面11AB C ,1AC ⊂平面11AB C , ∴OE ∥平面11AB C .(2)解:设点1C 到平面11AA B 的距离为d ,∵111111A A B C C AA B V V --=, 即1111111323AC B C AO ⋅⋅⋅⋅=⋅11AA B S d ⋅△.又∵在11AA B △中,11122A B AB ==, ∴11AA B S △7=.∴2217d =,∴11AC 与平面11AA B 所成角的正弦值为217. 方法二:建立如图3所示的空间直角坐标系O xyz -, 则(0,0,3)A ,113(0,1,0),0,,22A E ⎛⎫-- ⎪ ⎪⎝⎭, 1(0,1,0)C ,1(2,1,0)B ,(0,2,3)C .(1)证明:∵OE =130,,22⎛⎫- ⎪ ⎪⎝⎭, 1(0,1,3)AC =-,∴112OE AC =-,∴1OE AC ∥,又∵OE ⊄平面11AB C ,1AC ⊂平面11AB C ,∴OE ∥平面11AB C .(2)解:设11AC 与平面11AA B 所成角为θ,∵11(0,2,0)AC =,11(2,2,0)A B =,1(0,1,3)A A =.设平面11AA B 的一个法向量为(,,)n x y z =,111220,0,30,0,x y A B n y z A A n ⎧+=⎧⋅=⎪⎪⎨⎨+=⎪⋅=⎪⎩⎩则即 不妨令1x =,可得31,1,3n ⎛⎫=- ⎪ ⎪⎝⎭, ∴11221sin cos ,7723AC n θ=〈〉==⋅, ∴11AC 与平面11AA B 所成角的正弦值为217. 【思路点拨】证明直线与平面平行通常利用线面平行的判定定理,求线面所成角可以先作出其平面角,再利用三角形求解,若直接作角不方便时可考虑用向量的方法求解. 【题文】19、设数列{}n a 满足10a =且*11.2n na n N a +=∈-. (1)求证数列11n a ⎧⎫⎨⎬-⎩⎭是等差数列,并求数列{}n a 的通项公式; (2)设11,n n n a b S n+-=为数列{}n b 的前n 项和,证明:n S <1.【知识点】等差数列 数列求和D2 D4【答案解析】(1) 11n a n =-. (2)略解析:(1)解:将112n n a a +=-代入11111n n a a +---可得111111n n a a +-=--,即数列11n a ⎧⎫⎨⎬-⎩⎭是公差为1的等差数列.又1111,,11nn a a ==--故 所以11n a n=-.(2)证明:由(Ⅰ)得11111,11n n a n n b nn nnn +-+-===-+⋅+111111111nnn k k k S b k k n ==⎛⎫==-=-< ⎪++⎝⎭∑∑.【思路点拨】证明数列为等差数列通常利用等差数列的定义证明,遇到与数列的和有关的不等式可先考虑能否求和再证明. 【题文】20、已知函数()()1ln f x ax x a R =--∈. (1)讨论函数f(x)在定义域内的极值点的个数;(2)若函数f(x)在x=1处取得极值,对()()0,,2x f x bx ∀∈+∞≥-恒成立,求实数b 的取值范围.【知识点】导数的应用B12【答案解析】(1) 当0a ≤时,没有极值点;当0a >时,有一个极值点. (2) 211e b -≤ 解析:(1)11()ax f x a x x-'=-=, 当0a ≤时,()0f x '<在(0,)+∞上恒成立,函数()f x 在(0,)+∞上单调递减, ∴()f x 在(0,)+∞上没有极值点;当0a >时,由()0f x '<得10x a <<,由()0f x '>得1x a>, ∴()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递减,在1,a ⎛+∞⎫⎪⎝⎭上单调递增,即()f x 在1x a =处有极小值.∴当0a ≤时,()f x 在(0,)+∞上没有极值点;当0a >时,()f x 在(0,)+∞上有一个极值点.(2)∵函数()f x 在1x =处取得极值,∴1a =, ∴1ln ()21x f x bx b x x -⇔+-≥≥,令1ln ()1xg x x x=+-,可得()g x 在2(0,e ]上递减,在2[e ,)+∞上递增,∴2min 21()(e )1e g x g ==-,即211e b -≤. 【思路点拨】一般遇到不等式恒成立求参数范围问题,通常分离参数转化为函数的最值问题进行解答.【题文】21、如图5,已知抛物线C:()220y px p =>和圆M :()2241x y -+=,过抛物线C 上一点H ()00,x y ()01y ≥作两条直线与圆M 相切于A,B 两点,圆心M 到抛物线准线的距离为174. (1)求抛物线C 的方程;(2)若直线AB 在y 轴上的截距为t ,求t 的最小值.【知识点】抛物线 直线与圆锥曲线H8 H7【答案解析】(1) 2y x = (2) min 11t =- 解析:(1)∵点M 到抛物线准线的距离为42p +=174,∴12p =,即抛物线C 的方程为2y x =.(2)方法一:设1122(,),(,)A x y B x y ,∵114MA y k x =-,∴114HA x k y -=, 可得,直线HA 的方程为111(4)4150x x y y x --+-=,同理,直线HB 的方程为222(4)4150x x y y x --+-=,∴210101(4)4150x y y y x --+-=,220202(4)4150x y y y x --+-=,∴直线AB 的方程为22000(4)4150y x y y y --+-=,令0x =,可得000154(1)t y y y =-≥,∵t 关于0y 的函数在[1,)+∞上单调递增, ∴min 11t =-.方法二:设点2(,)(1)H m m m ≥,242716HM m m =-+,242715HA m m =-+. 以H 为圆心,HA 为半径的圆方程为22242()()715x m y m m m -+-=-+,① ⊙M 方程为22(4)1x y -+=.②①-②整理得直线AB 的方程为:2242(24)(4)(2)714x m m y m m m m -----=-+. 当0x =时,直线AB 在y 轴上的截距154t m m=-(1)m ≥, ∵t 关于m 的函数在[1,)+∞上单调递增, ∴min 11t =-.【思路点拨】求抛物线的方程关键是利用圆心到其准线的距离求p ,求两切点所在直线方程,可利用两圆的公共弦所在直线方程的方法进行解答.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号.【题文】22、(本小题10分)[选修4-1:几何证明选讲]如图6,直线AB 经过圆O 上一点C ,且OA=OB,CA=CB,圆O 交直线OB 于E,D. (1)求证:直线AB 是圆O 的切线; (2)若1tan 2CED ∠=,圆O 的半径为3,求OA 的长.【知识点】几何证明选讲N1 【答案解析】(1)略; (2)5解析:(1)证明:如图4,连接OC ,∵,,OA OB CA CB == ∴OC AB ⊥,∴AB 是⊙O 的切线. (2)解:∵ED 是直径,∴90ECD ∠=︒, 在Rt △ECD 中,∵1tan 2CED ∠=, ∴12CD EC =. ∵AB 是⊙O 的切线, ∴BCD E ∠=∠, 又∵CBD EBC ∠=∠,∴ △BCD ∽△BEC , ∴BD BC =CD EC =12,设,BD x =则2BC x =, 又2BC BD BE =⋅,∴2(2)(6)x x x =⋅+,解得:120,2x x ==, ∵0BD x =>, ∴2BD =, ∴235OA OB BD OD ==+=+=.【思路点拨】证明直线是圆的切线,只需证明圆心到直线的距离等于圆的半径,若直线与圆有公共点,则公共点为切点;第二问利用三角形相似解答即可. 【题文】23、(本小题10分)[选修4-4:坐标系与参数方程]在直角坐标系xOy 中,直线l 的参数方程为232252x t y t ⎧=-⎪⎪⎨⎪=+⎪⎩ (t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为25sin ρθ=.(1)求圆C 的圆心到直线l 的距离;(2)设圆C 与直线l 交于点A,B ,若点P 的坐标为()3,5,求PA PB +. 【知识点】坐标系与参数方程N3【答案解析】(1)322(2)32 解析:(1)由25sin ρθ=,可得22250x y y +-=, 即圆C 的方程为22(5)5x y +-=.由23,225,2x t y t ⎧=-⎪⎪⎨⎪=+⎪⎩ (t 为参数)可得直线l 的方程为530x y +--=.所以,圆C 的圆心到直线l 的距离为05533222+--=. (2)将l 的参数方程代入圆C 的直角坐标方程,得22223522t t ⎛⎫⎛⎫-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭, 即23240t t -+=.由于2(32)4420∆=-⨯=>.故可设12t t 、是上述方程的两个实根, 所以1212324t t t t ⎧+=⎪⎨⋅=⎪⎩,.又直线l 过点(35)P ,,故由上式及t 的几何意义得1212||||||||32PA PB t t t t +=+=+=.【思路点拨】一般由参数方程或极坐标方程研究曲线之间的位置关系不方便时,可转化为直角坐标方程进行解答;第二问可利用直线参数的几何意义进行解答. 【题文】24、(本小题10分)[选修4-5:不等式选讲] 已知一次函数f(x)=ax -2.(1)解关于x 的不等式()4f x <;(2)若不等式()3f x ≤对任意的x ∈[0,1]恒成立,求实数a 的范围. 【知识点】不等式选讲N4【答案解析】(1) 当0a >时,不等式的解集为26x x a a ⎧⎫-<<⎨⎬⎩⎭;当0a <时,不等式的解集为62x x aa ⎧⎫<<-⎨⎬⎩⎭.(2) 15a-≤≤且a≠0.解析:(1)()4f x<⇔24ax-<⇔424ax-<-<⇔26ax-<<,当0a>时,不等式的解集为26x xa a⎧⎫-<<⎨⎬⎩⎭;当0a<时,不等式的解集为62x xa a⎧⎫<<-⎨⎬⎩⎭.(2)()3f x≤⇔23ax-≤⇔323ax--≤≤⇔15ax-≤≤⇔5,1, axax⎧⎨-⎩≤≥∵[0,1]x∈,∴当x=0时,不等式组恒成立;当x≠0时,不等式组转化为5,1, axax ⎧⎪⎪⎨⎪-⎪⎩≤≥又∵515,1x x--≥≤,所以15a-≤≤且a≠0.【思路点拨】解绝对值不等式的关键是去绝对值,可利用性质、分段讨论等方法,对于不等式恒成立求参数范围问题,通常分离参数转化为函数的最值问题进行解答.。
云南省师范大学附属中学2015届高三高考适应性月考卷(三)数学(理)试题扫描版含答案

云南师大附中2015届高考适应性月考卷(三)理科数学参考答案第Ⅰ卷(选择题,共60分)【解析】1.分别取1212x y ==,,,,计算可得{101}Q =-,,,故选B. 2.123i 32(6)i 12i 55z b b b z -+-==+-,当605b-=时,12z z 是实数,6b ∴=,故选A. 3.A 中否命题应为“若21x ≠,则1x ≠”;B 中否定应为“210x x x ∀∈+-,≥R ”;C 中原命题为真命题,故其逆否命题为真命题;易知D 正确,故选D .4.(10)(12)(12)(34)b a c +=+=+=,,,,,λλλλ,又()b a c +⊥λ,()0b a c ∴+⋅=λ,即(12)+⋅,λλ(34)338=++=,λλ,解得311=-λ,故选C. 5.由题意可知输出结果为1234105S =-+-+-⋅⋅⋅+=,故选C. 6.πsin cos cos 26y x x x x ⎛⎫==- ⎪⎝⎭,故其对称轴为π2π6x k k -=∈,Z ,ππ212k x ∴=+, k ∈Z ,当0k =时,π12x =,故选A. 7.对于①,已知其正确;由正态分布的概念的对称性可得(10)(01)P P -<<=<<=ξξ11(1)22P m ->=-ξ,故②正确;随机变量2K 的观测值k 越大,判断“X 与Y 有关系”的把握越大,故③错误,所以正确的有①②两个,故选C.8.该几何体下方是一个长方体,上方是一个圆柱被切掉一部分,体积为442π3V =⨯⨯+⨯1π2324π2+⨯⨯=+,故选D.9. 123221213112132a a a ==-=-=-=--+,,,452121*********a a =-==-=+-,, 推理得{}n a 是周期为4的数列,所以3201512a a ==-,故选B .10.1122()2cos ()()2()2f x x g x x x f x g x -''''==+,≤,≥,故函数()2sin f x x =([0π])x ∈,上点P的坐标必为(00),,函数()13x g x ⎛⎫=+ ⎪⎝⎭上点Q 的坐标必为813⎛⎫⎪⎝⎭,,故直线PQ 的斜率为83,故选C . 11.由题意可知22222m c m n a ⎧=⎪⎨-=⎪⎩,,则22n b =,椭圆的方程可化为22221x y c b +=.由0AP PQ ⋅=知AP 与渐近线垂直.不妨设P 在第一象限,则直线AP 的方程为()a y x c b =--,与渐近线by xa =联立可解得P 的坐标为2a abc c ⎛⎫ ⎪⎝⎭,.又点P 在椭圆上,代入椭圆方程可得42421a a c c +=,即42111e e +=,整理得4210e e --=,所以2e ,故选D . 12.1121212212()(()()),()()()()()()(()())22f x f x f x f x f x f x f x g x f x f x f x -⎧+=+=⎨<⎩≥1113e ((,0][3,)),e ((0,3)),x x x x -+⎧∈-∞+∞⎪=⎨⎪∈⎩又当[]x a b ∈,时,1212()()0g x g x x x ->-恒成立,故()g x 在[]x a b ∈,时是增函数,结合图象可知()g x 在[0)x ∈+∞,时是增函数,又[15]a b ∈-,,,故b a -的最大值在05a b ==,时取得,故选D .第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分)【解析】13.由4652a a a ⋅=,得2552a a =,即52a=,所以54b =,19959()9362b b S b +===. 14.ππsin d (cos )cos πcos02a x x x ==-=-+=⎰,二项式6⎛⎝展开式的通项公式为663166C (1)2C rr rr r r r r T x ---+⎛=⋅=- ⎝.令30r -=,得3r =,此时展开式中常数项为363346(1)2C 160T -=-⨯=-.15.函数(1)y f x =+的图象关于点(10)-,成中心对称,∴函数()y f x =的图象关于点(00),成中心对称,即()y f x =为奇函数.不等式22(2)(2)0f x x f y y -+-≤,可化为222(2)(2)(2)f x x f y y f y y ---=-≤,又定义在R 上的函数()y f x =是减函数,2222x x y y ∴--≥,由14x ≤≤得22(22)014x y x y x ⎧---⎨⎩≥,≤≤,故()(2)014x y x y x -+-⎧⎨⎩≥,≤≤,即02014x y x y x -⎧⎪+-⎨⎪⎩≥,≥,≤≤或02014x y x y x -⎧⎪+-⎨⎪⎩≤,≤,≤≤,作出可行域,又(12)()M N x y ,,,,故2OM ON x y ⋅=+,利用线性规划知识可求得OM ON ⋅的取值范围为[012],. 16.如图1,设P ABCD -的外接球的球心为G ,A B C D ,,,在球面上,∴球心在正方体1111ABCD A B C D -上下底面中心连线1O O 上,点P 也在球上,GP GA R ∴==,棱长为1,OA ∴=,设11O P x O G y ==,,则1O G y =-,在1Rt GO P △中,有222R x y =+①,在Rt GOA △中,三、解答题(共70分.解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分12分)【注:本题题干第一行中“且sin 2m n C ⋅=-”改为“且sin 2m n C ⋅=”,改后答案如下:】解:(Ⅰ)sin()2cos sin sin cos cos sin sin()m n A B A B A B A B A B ⋅=-+=+=+,…………………………………………………………………………………(2分) 在ABC △中,π0πA B C C +=-<<,,所以sin()sin A B C +=,……………………(4分)又sin 2m n C ⋅=,所以sin sin 22sin cos C C C C ==,所以1cos 2C =,即π3C =. ……………………………………………………………………………………(6分) (Ⅱ)sin sin 2sin A B C +=,由正弦定理得2c a b =+,………………………………(7分)1sin 2ABC S ab C ==△得4a b =,……………………………………………(9分)由余弦定理得22222222cos ()3412c a b ab C a b ab a b ab c =+-=+-=+-=-,得2c =.………………………………………………………………………………(12分) 18.(本小题满分12分)解:(Ⅰ)芯片甲为合格品的概率为4032841005++=,芯片乙为合格品的概率为4029631004++=,…………………………………………(3分)随机变量X 的所有可能取值为90453015-,,,. 433(90)545P X ==⨯=;133(45)5420P X ==⨯=; 411(30)545P X ==⨯=;111(15)5420P X =-=⨯=, 所以随机变量X 的分布列为………………………………………………………………………………………(7分)则X 的数学期望3311()904530(15)66520520E X =⨯+⨯+⨯+-⨯=.…………………(8分)(Ⅱ)设生产的5件芯片乙中合格品有n 件,则次品有5n -件. 依题意,得5010(5)140n n --≥, 解得196n ≥,所以4n =或5n =.……………………………………………………(10分) 设“生产5件芯片乙所获得的利润不少于140元”为事件A ,则454531381()C 444128P A ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭.……………………………………………………(12分)19.(本小题满分12分)(Ⅰ)证明:如图2,取AB 的中点H ,连接PH HC ,. PAB △是正三角形,且H 为AB 的中点,2AB =,PH AB ∴⊥,且PH …………………………………………………(2分) 底面ABCD是矩形,2AB BC =,HC ∴又PC 222PC PH CH ∴=+,PH HC ∴⊥.………………………………………………………(4分) ABHC H =,PH ∴⊥平面ABCD .PH ⊂平面PAB ,∴平面PAB ⊥平面ABCD .………………………………………(6分) (Ⅱ)解:如图2所示,以H 为原点建立空间直角坐标系H xyz -,则(100)(100)A B -,,,,,,(00P,(10)D .……………………………(7分)设(01)AE AP =<<λλ,则(20)BE BA AE =+=-λ,(20)BD =, 设()n x y z =,,为平面EBD 的法向量,由0,()(20)=0,0,()(20)=0,n BD x y z n BE x y z ⎧⎧⋅=⎪⎪∴⎨⎨⋅=-⎪⎪⎩⎩,,,,,λ20,(2)0,x x z ⎧=⎪∴⎨-=⎪⎩λ令2z =-λ,得(32)n =--,λλ. 易知(00HP =为平面ABD 的一个法向量.………………………………………(9分) 二面角E BD A --的大小为45︒,cos45cos 10n HP n HP n HP⋅∴︒=〈〉==⋅,. ………………………(10分)又由01<<λ,得12=λ,1AE EP ∴=∶.……………………………………………(12分)由221(4),44,y x x y m ⎧=+⎪⎨⎪-=⎩得2381640x x m ---=, 则816433A B A B mx x x x ++==-,.(*) ……………………………………………………(3分)因为2PA PB PC ⋅=,P A B C ,,,共线且P 在线段AB 上, 所以2()()()P A B P P C x x x x x x --=-, 整理得:4()320A B A B x x x x +++=, 将(*)代入上式可解得:28m =.所以双曲线G 的方程为221287x y -=.……………………………………………………(6分) (Ⅱ)由题意可设椭圆S的方程为:2221(28x y a a+=>,弦的两个端点分别为11()M x y ,,22()N x y ,,MN 的中点为00()Q x y ,,由22112222221,281,28x y a x y a ⎧+=⎪⎪⎨⎪+=⎪⎩得121212122()()()()028x x x x y y y y a -+-++=,……………………………(8分) 因为1212012012422y y x x x y y y x x -=-+=+=-,,,所以0024028x ya-=,…………………(9分)所以S 中垂直于l 的平行弦的中点的轨迹为直线24028x ya -=截在椭圆S 内的部分. 又这个轨迹恰好是G 的渐近线截在S 内的部分,所以211122a =,所以256a =,椭圆S 的方程为2212856x y +=.…………………………………………………………(12分)21.(本小题满分12分) (Ⅰ)解:()[(1)]()f x g x a g x '''=+--λλλλ,………………………………………(1分)令()0f x '>,得[(1)]()g x a g x ''+->λλ,(1)x a x ∴+->λλ, 即(1)()0x a --<λ,解得x a <, ………………………………………………………(3分) 故当x a <时,()0f x '>;当x a >时,()0f x '<,……………………………………(4分) ∴当x a =时,()f x 取极大值,但()f x 没有极小值.()f x 的极大值为()[(1)]()()()(1)e a f a g a a g a g a g a =+--=-=-⋅λλλλλ.………(6分)(Ⅱ)证明:e 1e 11x x x x x----=,又当0x >时,令()e 1x t x x =--,则()e 10x t x '=->, 故()(0)0t x t >=,因此原不等式化为e 1x x a x--<,即e (1)10x a x -+-<,…………(8分) 令()e (1)1x h x a x =-+-,则()e (1)x h x a '=-+,由()0h x '=,得e 1x a =+,解得ln(1)x a =+,当0ln(1)x a <<+时,()0h x '<;当ln(1)x a >+时,()0h x '>, 故当ln(1)x a =+时,()h x 取得最小值[ln(1)](1)ln(1)h a a a a +=-++,……………(10分)令()ln(1)01a s a a a a=-+>+,, 则2211()0(1)1(1)a s a a a a '=-=-<+++. 故()(0)0s a s <=,即[ln(1)](1)ln(1)0h a a a a +=-++<. 因此,存在正数ln(1)x a =+,使原不等式成立. ……………………………………(12分)22.(本小题满分10分)【选修4−1:几何证明选讲】(Ⅰ)证明:PA 为圆O 的切线,PAB ACP ∴∠=∠, 又P ∠为公共角,PAB PCA ∴△∽△,AB PA AC PC∴=, 所以,AB PC AC PA ⋅=⋅. ………………………………………………………………(4分) (Ⅱ)解:PA 为圆O 的切线,BC 是过点O 的割线, 2PA PB PC ∴=⋅,4540PC BC ∴==,,又222901600CAB AC AB BC ∠=︒∴+==,, 又由(Ⅰ)知13AB PA AC PC ==,AC AB ∴==连接EC ,CAE EAB ∠=∠,ACE ADB △∽△, AB AD AE AC ∴=,480.AD AE AB AC ∴⋅=⋅=……………………………………………(10分)变形得ρ.由OA OB ⊥可设12π()2A B ⎛⎫+ ⎪⎝⎭,,,ρθρθ, 所以2211OA OB +222212π13sin 1113sin 244⎛⎫++ ⎪+⎝⎭=+=+θθρρ 2223sin 3cos 544++==θθ(定值). ……………………………………………………(7分)1212AOB S =△ρρ, 易知当sin 20=θ时,max ()1AOB S =△.……………………………………………………(10分)24.(本小题满分10分)【选修4−5:不等式选讲】解:(Ⅰ)因为4(4)()4x x a x x a a -+----=-≥, 因为4a <,所以当且仅当4a x ≤≤时等号成立, 故431a a -=∴=,.……………………………………………………………………(5分) (Ⅱ)当1a =时,若1()()g x f x m=+的定义域为R , 则()0f x m +≠恒成立,即()0f x m +=在R 上无解, 又()441(4)(1)3f x x x a x x x x =-+-=-+----=≥,当且仅当14x ≤≤时取等号,∴>-.………………………………………………………………………………(10分)m3。
云南师大附中高考数学适应性月考卷(五)理(含解析)新人教A版

2012-2013学年云南师大附中高考适应性月考数学试卷5(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)已知集合A={x|ax﹣1=0},b={3,4},且A∩B=A,则a的所有可能值组成的集合,,{,,时,,2.(5分)设复数Z=1﹣(其中i为虚数单位),则Z2﹣3Z为()=1+2i3.(5分)设向量=(sinα,)的模为,则cos2α=()===4.(5分)(2011•江西模拟)如图,设D是图中所示的矩形区域,E是D内函数y=cosx图象上方的点构成的区域,向D中随机投一点,则该点落入E(阴影部分)中的概率为()的面积为=2=5.(5分)(2013•日照二模)在同一个坐标系中画出函数y=a x,y=sinax的部分图象,其中..C..T=(5分)一个几何体的三视图如图2所示,其中俯视图是菱形,则该几何体的侧面积为()6.,∴AE=,,,S=2×()+2×(+7.(5分)(2013•东莞一模)图是某算法的程序框图,则程序运行后输出的T是()8.(5分)函数y=sin(ωx+φ)在区间上单调递减,,]=﹣,,(2×++,<.)y=sin.轴交点的纵坐标为9.(5分)(2012•深圳二模)设a,b,c,d∈R,若a,1,b成等比数列,且c,1,d 成等|a+b|=|a|+|b|,,|a+b|=|a|+|b|10.(5分)P是双曲线﹣=1(a>0,b>0)上的点,F1、F2是其焦点,且=0,若△F1PF2的面积是9,a+b=7,则双曲线的离心率为()|=m|=n||mn=9c==5e=11.(5分)如图,已知O、A、B是平面上三点,向量=,=.在平面AOB上,P是线段AB垂直平分线上任意一点,向量=,且||=3,||=2,则•()的值是()=与向量垂直,得•(•表示成的和,从而•()==(,代入题中的数据即可得到•(,根据题意得=•(()•((•(,⊥,得•(=••(==(﹣=12.(5分)已知a>0且a≠1,f(x)=x2﹣a x,当x∈(﹣1,1)时均有f(x)<,则实∪[2,∪(1,∪(1,∪[4,=,即,可得≤a<二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.13.(5分)在△ABC中,角A、B、C所对的边分别为a、b、c,且cosA=,则sin(A﹣)的值为﹣.cosA=,∴sinA==)=sinA﹣cosA=﹣=.14.(5分)若数列{a n}满足a1=,a1+a2+…+a n=n2a n,则数列{a n}的前60项和为.,得到.用累,且,故,=××…×××…××====﹣,﹣﹣)﹣)+…+(﹣)=.项和为故答案为:15.(5分)若不等式组所表示的平面区域被直线分为面积相等的两部分,则k的值是.先由不等式组画出可行域,再根据直线,过点,)k=故答案为16.(5分)如图,已知球O是棱长为1的正方体ABCD﹣A1B1C1D1的内切球,则以球心O为顶点,以球O被平面ACD1所截得的圆为底面的圆锥的体积为π.D,球的半径,=,V=h=故答案为:π三、解答题:本大题共5小题,共70分,解答应写出文字说明,证明过程或演算步骤.17.(12分)已知等比数列{a n}满足a2=2,且2a3+a4=a5,a n>0.(1)求数列{a n}的通项公式;(2)设b n=(﹣1)n3a n+2n+1,数列{b n}的前项和为T n,求T n.,则,则.…(=18.(12分)在一次抢险救灾中,某救援队的50名队员被分别分派到四个不同的区域参加2人去完成一项特殊任务.(2)若这2人来自区域A,D,并记来自区域A队员中的人数为ξ,求随机变量ξ的分布列及数学期望.==.=,==0 1 2+1×+2×=19.(12分)在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD为平行四边形,∠ACB=90°,EF∥BC,AC=BC=2EF,.(1)求证:AE⊥平面BCEF;(2)求二面角A﹣BF﹣C的大小.,则=,,,,,中,,中,20.(12分)已知函数f(x)=﹣lnx,x∈[1,3],(1)求f(x)的最大值与最小值;(2)若f(x)<4﹣at于任意的x∈[1,3],t∈[0,2]恒成立,求实数a的取值范围.对任意通过,∵ln3>1∴)的最大值为﹣对任意恒成立)21.(12分)(2011•江西模拟)已知椭圆C:+=1(a>b>0)的离心率为,以原点为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+=0相切.(Ⅰ)求椭圆C的方程;(Ⅱ)若过点M(2,0)的直线与椭圆C相交于A,B两点,设P为椭圆上一点,且满足(O为坐标原点),当|﹣|<时,求实数t取值范围.,所以得((Ⅰ)由题意知,所以.,的方程为.∴(,∴<,∴,∴四、请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.作答时请写清题号.(本小题满分10分)【选修4-1:几何选讲】22.(10分)选修4﹣1:几何证明选讲如图所示,PA为⊙O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和⊙O分别交于点D和E.( I)求证:;( II)求AD•AE的值.)知,,五、(本小题满分0分)【选修4-4:坐标系与参数方程】23.(2010•沈阳模拟)已知曲线C的极坐标方程是ρ=1,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l的参数方程为为参数).(1)写出直线l与曲线C的直角坐标方程;(2)设曲线C经过伸缩变换得到曲线C′,设曲线C′上任一点为M(x,y),求的最小值.的参数方程为)代入下式得)∵(设椭圆的参数方程六、(本小题满分0分)【选修4-5:不等式选讲】24.(2009•辽宁)设函数f(x)=|x﹣1|+|x﹣a|,(1)若a=﹣1,解不等式f(x)≥3;(2)如果x∈R,f(x)≥2,求a的取值范围.用数轴上表示实数﹣左侧的点与表示实数左侧的点与数]∪[。
云南师大附中2015届高考适应性月考卷(五)理科综合-双向细目表
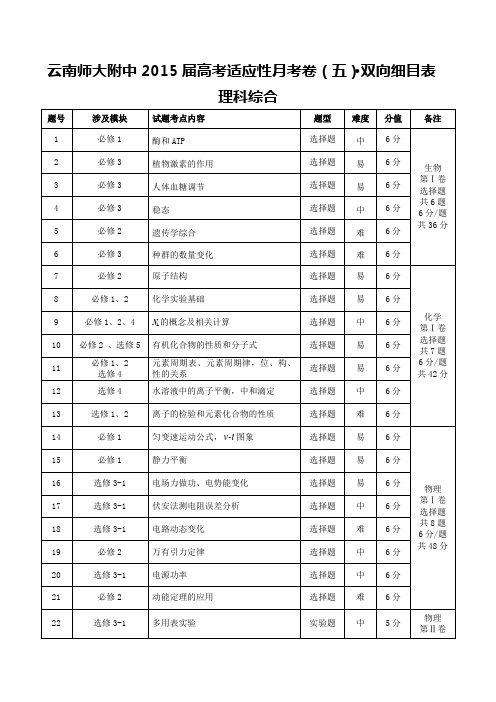
元素周期表、元素周期律,位、构、 性的关系
选择题
易
6分
6 分/题 共 42 分
12
选修 4
水溶液中的离子平衡,中和滴定
选择题 中 6 分
13
选修 1、2
离子的检验和元素化合物的性质
选择题 难 6 分
14
必修 1
匀变速运动公式, v-t 图象
选择题 易 6 分
15
必修 1
静力平衡
选择题 易 6 分
16
选修 3-1
多用表实验
选择题 难 6 分
实验题
中
5分
物理 第Ⅱ卷
23
选修 3-1
电阻伏安特性曲线实验
实验题
22、23、 中 10 分 24、25 为
必答题,
24
必修 2
传送带问题
计算题
中 13 分 33、34、 35 为选
25
选修 3-1
电路分析、动能定理
计算题
中偏 难
19 分
答题(3 选 1) 共 62 分
易 1分
中 2分
化学
第Ⅱ卷
中 2 分 26、27、
学平衡平衡常数 ③改变外界条件使化学平衡的移动
27
及化学平衡的移 动、难溶物质的溶 ④外界因素对转化率的影响
填空题
中
2分
28 为必 答题,36、
中 2 分 37、38 为
解平衡计算和外 界因素对溶解以
选答题
易
2 分 (三选
及溶解平衡的影 响(16 分) (2)难溶物质的溶解平衡的计算
(1)根据转化关系和题目所给信息推
必修 1
断元素,写出氢硫酸与 NaOH 反应的离
