A-D-E Polynomial and Rogers--Ramanujan Identities
CFD的基本原理

Nanjing University of Technology
38
Nanjing University of Technology
39
Nanjing University of Technology
40
Nanjing University of Technology
41
Nanjing University of Technology
77
Nanjing University of Technology
78
Nanjing University of Technology
79
Nanjing University of Technology
80
Nanjing University of Technology
81
Nanjing University of Technology
27
Nanjing University of Technology
28
Nanjing University of Technology
29
Nanjing University of Technology
30
Nanjing University of Technology
31
Nanjing University of Technology
Important Journals
Transactions of ASME ✓ Journal of Fluids Engineering ✓ Journal of Engineering for Gas Turbines ✓ Journal of Heat Transfer
AIAA Journal Journal of Fluids Mechanics Proceeding of the IMechE
有限域上的置换多项式

dd#0,_是為/2中的元素,。2 +_2 = 0.我们可得(1)有唯一的解/(x)是鱼上的一个置换多项式.
定理2 设5eF2m且Tr(5)=1,其中肌三0(mod4),那么满足(2m/2 —2)力三2^/2 — 1(mod 2m — 1)的正整 数%,/(x)= (x2 +x+5)k +x是 唇上的一个置换多项式.
1 /( ax^+ax+5) Et - (_+d)旳1.
唯一的解.由于Tr(5)=1,对于所有的x e F2m,因此ax^+ax+5^0.方程f(_)= d等价于
进一步等价于
(ax" +a_+5)k - x+d.
ax^+ax+5二(x+d)旳1.
即
_2k+1 +( d+a)_2k + ( d2k +a)x+d2©1 +5- 0. 因为 a e F?k,所以我们有 a2k - a ,即 _2k+1 +( d+a) _2k + ( d+a) "x+d2®1 +5 = 0.公式等价于
—x2+ax +5+1 -
ax =
_ +5+d.
(5)
x2+d
比较(3)(5)我们有
_2(d(x2+d) +1 ] (x2+ax +5+1)+(x2+d) (5+d) 2
a [ z-0 =
],
因此
简化可得
[d(x2+d) +1] (x2+d) = [ (x2+x +5+1) +(x2+d) (5+d) ] 2.
美国哈佛大学 数学系使用教材

Intersection William theory Fulton James R. Munkres
Topology
Prentice Hall Princeton University Press AddisonWesley
2000
John W. Characterist Milnor and ic classes James D. Stasheff Probability and statistics Morris H. DeGroot
Springer
1991
O211.61 /B864(2)(HF )
Springer
2000
O211.63 /O41(5)(HF)
Springer
1998
O211.67 /L523(2)(HF )
Herman Elementary Chernoff, decision Lincoln E. theory Moses Theoretical statistics D. R. Cox, D. V. Hinkley
2000
O151.2 /A634(8)(HF )
1984
O151.2 /C978(HF)
1977
O152.1 /S488(HF)
1969
O153 /A872(HF) O157 /T891(4)(HF ) O158 /B592(r)(HF) O17 /R916(3)(HF )
2002
1989
McGraw-Hillຫໍສະໝຸດ 19761995American Mathematic 1999 al Society
O413.3 /Q1q2(HF)
Duxbury
2000
Q-332 /R822(5)(HF )
NUMB3RS数学破案说明书

380 N otices of the AMsV oluMe 56, N uMber 3Book ReviewThe Numbers Behind NUMB3RS : Solving Crime with MathematicsReviewed by Brent DeschampThe Numbers Behind NUMB3RS : Solving Crimewith MathematicsKeith Devlin and Gary LordenPlume, 2007US$15.00, 256 pagesISBN-13: 978-0-452-28857-7Since reading The Numbers Behind NUMB3RS : Solv-ing Crime with Mathematics , I’ve started watchingthe television show NUMB3RS again. I’ve alwaysfound crime dramas predictable and repetitive,and nothing much has changed. Still, I’ve tunedin a few times out of a morbid curiosity spawnedfrom this book.As many readers know, NUMB3RS focuses onFBI agent Don Eppes, who solves crime with thehelp of his younger brother Charlie, a mathemati-cian.The question I’ve been asking myself since Ifinished the book is: why was this book written?The authors, Keith Devlin and Gary Lorden, offera reason in the opening line of the appendix. Theywrite, “‘Is the math in NUMB3RS real?’ Both of usare asked this question a lot.” The two are cer-tainly qualified to answer. Both hold doctorates inmathematics, Devlin works at Stanford, and Lordenworks at Caltech. Both are also reasonable peopleto ask. Devlin is known for his work promotingmathematics on National Public Radio, and Lordenis the mathematical consultant to NUMB3RS .From this question one infers the book was writ-ten to show how the math in NUMB3RS is real, butI’m not entirely comfortable with that response.This is not really a book about mathematics;deals too much the television to merit that Thus, I keep ask-is this book math, or is To be sure, this authors cover profil-statistics, data mining, link analysis, geometric clustering, ma-chine learning, neural networks, facial recognition software, change-point detection, Bayesian infer-ence, DNA profiling, cryptography, fingerprints, networks, risk analysis, and math in casinos. It’s interesting, and for the most part it’s well written.But then the book ends with an appendix pro-viding an episode guide for the first three seasons of the television show. Why is that important, and what does it have to do with the math involved in crime solving? Most of the entries read like a slightly more intelligent version of the kind of entries logged on a fan’s website. Yes, vague de-scriptions of the math used in each episode are mentioned, but they are just that: vague.If this 256-page book is meant to explore the use of math in crime solving, then why is nearly fifteen percent of the book solely devoted to the television show?Brent Deschamp is professor of mathematics at CaliforniaState Polytechnic University, Pomona. His email addressis ************************.Based on what has been written thus far, it may seem as if my opinion of this book is rather poor. Certainly, parts of the book are rather disappoint-ing, but other parts are fascinating. I learned a lot from this book. I’ll focus on the two chapters I found most intriguing.The chapter on DNA profiling was an eye-opener for me. Like most people I have a rough under-standing of how DNA matches are done, but until reading this book I had little idea of what truly goes into performing a DNA comparison. Only certain loci on the DNA strand are used in the comparison, thirteen locations in all, and even then the exact sequence is not recorded, but in-stead a count of the various basepairs is recorded. A DNA profile,to me, now feels more like a hashfunction.What was more surprising,though, was the authors’ discus-sion of the FBI CODIS system thathouses DNA profiles. If evidencepoints to a suspect, then obtain-ing a DNA sample and comparingit to DNA evidence found at thescene has a very low probabilityof showing an incorrect match.If instead the authorities run asearch of CODIS looking for a DNAmatch, a “cold hit”, then the oddsof finding an incorrect match rise dramatically. The authors end thechapter with calculations based on the Arizona state database. With 65,000 entries they show the probability of finding two matches that agree on nine of thirteen loci during a search for cold hits is about five percent.These sorts of discussions are fascinating for two reasons. First, it’s nice to see math in action. The science is well presented, and the book dis-cusses the differences inherent in the two view-points of having a suspect and searching for a suspect. By the end of the chapter an argument has been made that is based on sound mathematical principles and shown in direct calculation.Second, it points out a common misconception. I’ve seen my fair share of crime dramas, and I can recall many instances where a DNA sample was run through the system and a cold hit was found. Inevitably, the name on the screen turned out to be the killer. On television, DNA enjoys an aura of infallibility, and discussions like these point out that methodology is just as important as facts.The discussion is also paired with an actual court case and reports from the forensic com-munity about DNA profiling. In this way the facts become more than an academic enterprise. The chapter has a reality to it that sells the material.Another chapter that revolves around an actual court case is the discussion of image enhancement. The case involves the beating of Reginald Denny in 1992 during the Los Angeles riots following the Rodney King trial. Damian Williams stood trial for his participation in the beating, and the defense used image enhancement of news footage to show the attacker in the film had the same rose tattoo as Williams.Since the book is aimed at a general audience, the process of image enhancement is not described in detail. An additional section offers a brief glimpse of deeper math using functions and derivatives, and the readers are told they can skip this section if they don’t have the requisite background. It is anice inclusion, but at a singlepage it could have been moredetailed. Still, the discussionis clear and informative, andreaders should have a betterunderstanding of how imageenhancement works.In terms of detail this bookis rather light. The chapteron geographic profiling has awonderful discussion of howeach piece of a given equationrelates to the rationale usedin geographic profiling. Thediscussion of DNA profiling isjust as detailed. The chapterson change-point detection andgraph theory both have ad-equate discussions, but some chapters are woefully vague.For example, in the chapter on data mining, many forms of data mining are discussed, but none is explained in any depth. This is an area I know nothing about, and so I had hoped I would walk away with a better understanding of neural networks and other forms of data mining. Instead I learned just enough to realize that I still knew nothing. Why not devote a few pages to providing some additional detail, as in the chapter on image enhancement? If twenty-five pages can be used to provide episode summaries, why can’t a few pages be used to better explain data mining?My frustration with this book is that when it succeeds, it provides great insight, but most of the time it falls short.My other frustration has to do with the contin-ual inclusion of material from the television show. Only four out of thirteen chapters are motivated by real-world cases in which mathematics played a vital role. The remaining chapters begin with a plot synopsis of some episode as motivation for the discussion. The topic is explored, but eventually we find ourselves once again reading about how Don and Charlie get the bad guys using math.Why?Is this book a product tie-in for the show, a mar-keting ploy, or is this a book about mathematics?Is this booka product tie-infor the show,…or is it abook aboutmathematics?M Arch 2009 N otices of the AMs 381I get the impression the authors can’t decide. If mathematics is as useful as this book claims, then shouldn’t there be plenty of actual cases where math played a role? Why should the authors have to resort to using television fiction to make their case? In fact, they answer this question by present-ing numerous cases where math played a role. So, the fiction isn’t needed, but it overwhelmingly overshadows the real world in this book. Couple that with the episode guide in the appendix, and the entire book feels less like a book about math and more like something concocted in a market-ing meeting.Some people will argue that Charlie Eppes and NUMB3RS provide a way to reach people about the power of math. I cannot argue that point. It is nice having a figure in popular entertainment who puts an accessible and interesting face on a subject that is often disliked. Those same people could also argue that using Charlie in a book like this does much the same thing. People who would not ordinarily read a book about math might just pick this one up because the presentation is accessible: Charlie, a fictional character, provides the link to the applications of math.But I disagree. The discussion of real-world cases riveted me. The chapter on statistics involved a discussion of a nurse nicknamed the “Angel of Death”. Statistics led to her indictment but wasn’t used in her trial. The chapter provided a wonder-ful look at the power and limitations of math in crime solving. If instead a fictional television epi-sode were used as the basis for that discussion, then such an approach merely brings us back to the first line of the appendix: Is any of this real? Does it take a team of writers and mathematical consultants to come up with bizarre scenarios where math might actually be of use? When every chapter relies on fiction, then yes, it begins to feel that way. On the other hand, point to enough real cases and suddenly math is being used every day in a tangible way.This leads to the efficacy of having a character like Charlie. NUMB3RS is entering its fifth season, but does public perception about math remain the same? Does having a mathematician on television increase the number of math majors? Has Charlie helped in any way?The problem is that NUMB3RS is ultimately a crime drama, and Charlie is its gimmick. Most crime dramas have a gimmick. CSI has its forensic technicians, Bones has its anthropologist, Criminal Minds has its profilers, and the new drama The Mentalist proudly displays its gimmick in the title. NUMB3RS isn’t really about mathematics; it’s about selling a crime drama in a market crowded with similar shows. The math is used as a gimmick, so the mathematics will always be secondary. A similar approach is taken in The Numbers Behind NUMB3RS, so the mathematics in the book suffers a similar fate.Strangely, if someone came to me wanting to know if math was ever really used in the real world, I would probably point them to this book. It’s inoffensive, accessible, and filled with enough information that they would probably finish the book with the sense that math is out there being used. Devlin and Lorden have brought together in-teresting and insightful information about certain areas of math and crime solving, and I appreciate their effort.But, and I want to emphasize the following caveat, I am disappointed with this book. Yes, the book is interesting, but only when the authors take the time to delve into the subject matter. Too much of this book feels like the commercials that punctuate the television show—short snippets of vague descriptions designed to titillate but not educate. My feeling is this approach will do noth-ing to help the public perception of math, will gain few converts, and will ultimately be forgotten like so many thirty-second ads.Finally, we should have enough confidence in our chosen field to feel comfortable writing a book about mathematics that does not need gim-micks. The Numbers Behind NUMB3RS shows us a glimmer of how this could be done. I just wish the authors had chosen to put their faith in the power of math to make its own case instead of giving in to what seems like marketing pressure.That said, I also cannot deny the results of clever marketing—it got me watching again.382 N otices of the AMs V oluMe 56, N uMber 3。
拉马努金恒等式的证明

∞ k=−∞
(q/a, q/b, q/c, q/d, q/e)k (aq, bq, cq, dq, eq)k
(abcdeq−1)k
=
(q, ab, bc, ac)∞ (aq, bq, cq, abc/q)∞
∞ k=0
(q/a, (q, q2
q/b, q/c, /abc, dq,
de)k eq)k
qk
jouhet@math.univ-lyon1.fr, http://math.univ-lyon1.fr/~jouhet
3Universit´e de Lyon, Universit´e Lyon 1, UMR 5208 du CNRS, Institut Camille Jordan, F-69622, Villeurbanne Cedex, France
∞ k=−∞
(q/a)k (a)k
ak
qk2
−k
=
(q)∞ (a)∞
,
while the right-hand side of (1.7) is equal to 0 (since ab/q = 1). Similarly, if bc = 1, the left-hand side of (1.8) becomes
=
(q, ab/q, bc/q, ac/q)∞ (a, b, c, abc/q2)∞
∞ k=0
(q/a, q/b, q/c)k (q, q3/abc)k
qk
,
∞ k=−∞
(q/a, q/b, q/c)k (aq, bq, cq)k
(abc)k
q
k2
=
(q, ab, bc, ac)∞ (aq, bq, cq, abc/q)∞
普林斯顿高等研究院

现任研究人员
数学学院 自然科学学院
历史研究学院 社会科学学院
恩里科·蓬皮埃利(菲尔兹奖得主) 辛康·布尔甘(菲尔兹奖得主) 皮埃尔·德利涅(菲尔兹奖得主) 菲利普·格里菲斯 罗伯特·郎兰兹(沃尔夫奖得主) Robert MacPherson Atel Selberg(菲尔兹奖和沃尔夫奖得主) Thomas Spencer Vladimir Voevodsky(菲尔兹奖得主) Avi Wigderson(奈望林纳奖得主)
研究院虽然和大学没有互属关系,但是有很深的渊源。研究院最早是借用普林斯顿数学系的办公室,主要人 员如约翰·冯·诺依曼、范布伦也来自数学系。研究院的许多教授也同时兼职普林斯顿教授。
数学家丘成桐是第一位受聘为美国高等研究院终身教授的华人学者。杨振宁教授也曾在高等研究院度过十几 年学术生涯的黄金岁月。
罗伯特·奥本海默在二战后曾长期任研究院的院长。
普林斯顿高等研究院
世界著名理论研究机构
01 历史发展
03 组织结构 05 研究成果
目录
02 现任院长 04 itute for Advanced Study),简称IAS,1930年成立于美国新泽西州普林斯 顿市,是世界著名理论研究机构,但并不是普林斯顿大学的一部分。
2022年9月23日,普林斯顿高等研究院詹姆斯·梅纳德(James Maynard)对解析数论的多项贡献,特别是 对素数分布的贡献,荣获“ 2023年数学新视野奖”。
历史名人
阿尔伯特·爱因斯坦 冯·诺依曼 哥德尔 奥本海默 阿蒂亚 外尔 陈省身 杨振宁 李政道 华罗庚
感谢观看
普林斯顿高等研究院是各个领域的最一流学者做最纯粹的尖端研究,而不受任何教学任务、科研资金或者赞 助商压力的研究机构。二十世纪上半叶,阿尔伯特·爱因斯坦、约翰·冯·诺依曼、库尔特·哥德尔、罗伯 特·奥本海默等学者迁往普林斯顿高等研究院之后,使之成为世界著名的学术圣地,不少著名学者在这里做出了 一生中最重要的成果。在其它地方也有效仿普林斯顿高等研究院而建立的高等研究院,例如清华大学设立的高等 研究院或香港科技大学的高等研究院。
与RAMANUJAN的1ψ1-级数恒等式相关的双边级数求和公式

参 考文 献
[】 . . n rw , . s e, . o ,S e i u ci s a big nvri 1 G E A d e s R A k y R R y p ca F n t n ,C m r eU i s y l o d e t
(;) cg 2 2(;) ( / g (;)(/ zg cg。g ;) zg c a;) 。
.
定理1 :设 m 是一个正整数。对满足条件 0 t <m的整数 t ,有
巫 … :
(g c) ;…
其中,
l ,f ≤ 卅
n ( 一 )
( gt c )+ ; 21
南
,
公式 。
关键 词 Rmaua — 数恒等式 ;双边级数求 和公式 ;本 原单位根 a nj n的1 级
中 图分 类号 O 5. 171 文献 标识 码 A 文章 编 号 17—6 1( 1)1—0 50 63 97一2 0 2 06— 1 0 0
~ 设a g 和 是两个复数并且满足 <1 。定义升阶乘为
(a;)(q a; 1 -zq 一 /zq ) (zg (c a;) 一 ;) 一 /z 』 q 2 c )(/;)l z )(/z ) ( g g 口 ( g c a; ; g ; q
(a ;)(q a;) 一 zq 一 /zq 1 (z9 一 /zq J 一;)(C a;)
宰 霸
教 育 科 学
6 5
与RAMANU AN 的 一 J 级数恒等 式相关 的
双边 级数 求和公式
杨 芳
( 海南 医学 院信息技 术部 ,海南海 口 5 10 ) 7 11
Numerical Recipes in C the art of scientific computing 2nd ed

(1.5) U0(x; a; b) = 1; U1(x; a; b) = x(1 + a); (1.6) Un+1(x; a; b) = x(1 + aqn)Un(x; a; b) ? bqn?1Un?1(x; a; b); n 1:
To indicate the dependence of Un(x; a; b) on q, when necessary we will use the notation Un(x; a; bjq). In accordance with the theory of orthogonal polynomials 4], the numerator polynomials fUn(x; a; b)g satisfy the recursion in (1.6) and the initial conditions (1.7) U0 (x; a; b) = 0; U1 (x; a; b) = 1 + a: Therefore (1.8) Un(x; a; b) = (1 + a)Un?1(x; qa; qb): Schur 8] actually considered the polynomials Un(1; 0; ?q) and Un(1; 0; ?q). In the notation of (1.2) and (1.3) we have (1.9) Dn = Un+1(1; 0; ?q); En = Un+1(1; 0; ?q) = Un(1; 0; ?q2):
(2.2) Schurn = Dn+m + En+m:
We can determine the parameters and using the initial conditions Schur0 = 1, Schur1 = 1 + q1+m, which leads to the evaluations
安托因方程引用文献

安托因方程引用文献安托因方程是描述一维无界介质中弦振动的方程。
它以法国物理学家安托因(Jean-Baptiste Joseph Fourier)的名字命名,是控制许多物理现象的重要方程之一。
这篇文章将介绍一些经典的文献,这些文献对安托因方程的理解和应用做出了重要贡献。
1. Fourier, Jean-Baptiste Joseph (1822). "Théorie analytique de la chaleur"(《热的解析理论》)。
这是安托因本人的经典著作,他在这本书中首次提出了安托因方程。
书中详细讨论了温度分布在不同时间和空间上的变化,并解释了热传导过程中的数学原理。
这本书被认为是热传导领域的重要里程碑,对后来的热方程研究起了巨大的影响。
2. Carslaw, H.S., Jaeger, J.C. (1959). "Conduction of Heat in Solids"(《固体传热导论》)。
这本经典的教材详细介绍了固体热传导的数学和物理原理,包括安托因方程的推导和求解方法。
书中使用了大量的实际例子和计算示例,使读者更容易理解和应用安托因方程。
3. Ingersoll, R.V. (2005). "Teaching Differential Equations with AnticipatorySoftware".这篇论文针对安托因方程的教学方法进行了探讨,提出了一种基于预测软件的教学方法。
这种方法通过图形和数值结果,引导学生深入理解安托因方程的解析和数值解。
这篇论文为安托因方程的教学提供了一种新的方法,帮助学生更好地理解和应用这个重要的方程。
4. Brown, R.A. (1983). "The Method of Layer Potentials and Boundary IntegralEquations for the Heat Equation". 这篇论文介绍了使用“层势方法”和“边界积分方程”来解决安托因方程的新方法。
新闻哥大教授约阿希姆·弗兰克获得2017年诺贝尔化学奖

新闻哥大教授约阿希姆·弗兰克获得2017年诺贝尔化学奖2017 Nobel Prize in Chemistry Awarded to Prof. Joachim Frank哥伦比亚大学举办约阿希姆·弗兰克教授诺奖获奖座谈,哥大校长李·C·布林格博士与哥大医学中心执行长李·戈德曼博士致贺词2017年10月4日,瑞典皇家科学院公布,2017年诺贝尔化学奖由哥伦比亚大学教授约阿希姆·弗兰克博士,瑞士洛桑大学教授雅克·杜博谢博士,以及英国剑桥大学分子生物学实验室科学家理查德·亨德森博士共同获得。
截至2017年,哥伦比亚大学的校友、教授、教员、研究员、助教与管理者中共产生了83位诺贝尔奖获得者。
具体名单请访问:/content/nobel-laureates.html哥伦比亚大学祝贺生化与分子生物物理学及生命科学教授约阿希姆·弗兰克(Joachim Frank)博士,因“开发用于对溶液中的生物分子进行高分辨率结构测定的冷冻电镜技术”,与理查德·亨德森(Richard Henderson)和雅克·杜伯谢(Jacques Dubochet)共同获得2017年诺贝尔化学奖。
Columbia University congratulatesJoachim Frank, PhD, professor ofbiochemistry and molecular biophysicsand of biological sciences, a winner of theNobel Prize in Chemistry 2017, sharedwith Richard Henderson and JacquesDubochet 'for developing cryo-electronmicroscopy for the high-resolutionstructure determination of biomoleculesin solution.'约阿希姆·弗兰克(Joachim Frank)博士,哥伦比亚大学医学中心(CUMC)生物化学与分子生物物理学教授,哥伦比亚大学生命科学教授。
From Data Mining to Knowledge Discovery in Databases

s Data mining and knowledge discovery in databases have been attracting a significant amount of research, industry, and media atten-tion of late. What is all the excitement about?This article provides an overview of this emerging field, clarifying how data mining and knowledge discovery in databases are related both to each other and to related fields, such as machine learning, statistics, and databases. The article mentions particular real-world applications, specific data-mining techniques, challenges in-volved in real-world applications of knowledge discovery, and current and future research direc-tions in the field.A cross a wide variety of fields, data arebeing collected and accumulated at adramatic pace. There is an urgent need for a new generation of computational theo-ries and tools to assist humans in extracting useful information (knowledge) from the rapidly growing volumes of digital data. These theories and tools are the subject of the emerging field of knowledge discovery in databases (KDD).At an abstract level, the KDD field is con-cerned with the development of methods and techniques for making sense of data. The basic problem addressed by the KDD process is one of mapping low-level data (which are typically too voluminous to understand and digest easi-ly) into other forms that might be more com-pact (for example, a short report), more ab-stract (for example, a descriptive approximation or model of the process that generated the data), or more useful (for exam-ple, a predictive model for estimating the val-ue of future cases). At the core of the process is the application of specific data-mining meth-ods for pattern discovery and extraction.1This article begins by discussing the histori-cal context of KDD and data mining and theirintersection with other related fields. A briefsummary of recent KDD real-world applica-tions is provided. Definitions of KDD and da-ta mining are provided, and the general mul-tistep KDD process is outlined. This multistepprocess has the application of data-mining al-gorithms as one particular step in the process.The data-mining step is discussed in more de-tail in the context of specific data-mining al-gorithms and their application. Real-worldpractical application issues are also outlined.Finally, the article enumerates challenges forfuture research and development and in par-ticular discusses potential opportunities for AItechnology in KDD systems.Why Do We Need KDD?The traditional method of turning data intoknowledge relies on manual analysis and in-terpretation. For example, in the health-careindustry, it is common for specialists to peri-odically analyze current trends and changesin health-care data, say, on a quarterly basis.The specialists then provide a report detailingthe analysis to the sponsoring health-care or-ganization; this report becomes the basis forfuture decision making and planning forhealth-care management. In a totally differ-ent type of application, planetary geologistssift through remotely sensed images of plan-ets and asteroids, carefully locating and cata-loging such geologic objects of interest as im-pact craters. Be it science, marketing, finance,health care, retail, or any other field, the clas-sical approach to data analysis relies funda-mentally on one or more analysts becomingArticlesFALL 1996 37From Data Mining to Knowledge Discovery inDatabasesUsama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth Copyright © 1996, American Association for Artificial Intelligence. All rights reserved. 0738-4602-1996 / $2.00areas is astronomy. Here, a notable success was achieved by SKICAT ,a system used by as-tronomers to perform image analysis,classification, and cataloging of sky objects from sky-survey images (Fayyad, Djorgovski,and Weir 1996). In its first application, the system was used to process the 3 terabytes (1012bytes) of image data resulting from the Second Palomar Observatory Sky Survey,where it is estimated that on the order of 109sky objects are detectable. SKICAT can outper-form humans and traditional computational techniques in classifying faint sky objects. See Fayyad, Haussler, and Stolorz (1996) for a sur-vey of scientific applications.In business, main KDD application areas includes marketing, finance (especially in-vestment), fraud detection, manufacturing,telecommunications, and Internet agents.Marketing:In marketing, the primary ap-plication is database marketing systems,which analyze customer databases to identify different customer groups and forecast their behavior. Business Week (Berry 1994) estimat-ed that over half of all retailers are using or planning to use database marketing, and those who do use it have good results; for ex-ample, American Express reports a 10- to 15-percent increase in credit-card use. Another notable marketing application is market-bas-ket analysis (Agrawal et al. 1996) systems,which find patterns such as, “If customer bought X, he/she is also likely to buy Y and Z.” Such patterns are valuable to retailers.Investment: Numerous companies use da-ta mining for investment, but most do not describe their systems. One exception is LBS Capital Management. Its system uses expert systems, neural nets, and genetic algorithms to manage portfolios totaling $600 million;since its start in 1993, the system has outper-formed the broad stock market (Hall, Mani,and Barr 1996).Fraud detection: HNC Falcon and Nestor PRISM systems are used for monitoring credit-card fraud, watching over millions of ac-counts. The FAIS system (Senator et al. 1995),from the U.S. Treasury Financial Crimes En-forcement Network, is used to identify finan-cial transactions that might indicate money-laundering activity.Manufacturing: The CASSIOPEE trou-bleshooting system, developed as part of a joint venture between General Electric and SNECMA, was applied by three major Euro-pean airlines to diagnose and predict prob-lems for the Boeing 737. To derive families of faults, clustering methods are used. CASSIOPEE received the European first prize for innova-intimately familiar with the data and serving as an interface between the data and the users and products.For these (and many other) applications,this form of manual probing of a data set is slow, expensive, and highly subjective. In fact, as data volumes grow dramatically, this type of manual data analysis is becoming completely impractical in many domains.Databases are increasing in size in two ways:(1) the number N of records or objects in the database and (2) the number d of fields or at-tributes to an object. Databases containing on the order of N = 109objects are becoming in-creasingly common, for example, in the as-tronomical sciences. Similarly, the number of fields d can easily be on the order of 102or even 103, for example, in medical diagnostic applications. Who could be expected to di-gest millions of records, each having tens or hundreds of fields? We believe that this job is certainly not one for humans; hence, analysis work needs to be automated, at least partially.The need to scale up human analysis capa-bilities to handling the large number of bytes that we can collect is both economic and sci-entific. Businesses use data to gain competi-tive advantage, increase efficiency, and pro-vide more valuable services to customers.Data we capture about our environment are the basic evidence we use to build theories and models of the universe we live in. Be-cause computers have enabled humans to gather more data than we can digest, it is on-ly natural to turn to computational tech-niques to help us unearth meaningful pat-terns and structures from the massive volumes of data. Hence, KDD is an attempt to address a problem that the digital informa-tion era made a fact of life for all of us: data overload.Data Mining and Knowledge Discovery in the Real WorldA large degree of the current interest in KDD is the result of the media interest surrounding successful KDD applications, for example, the focus articles within the last two years in Business Week , Newsweek , Byte , PC Week , and other large-circulation periodicals. Unfortu-nately, it is not always easy to separate fact from media hype. Nonetheless, several well-documented examples of successful systems can rightly be referred to as KDD applications and have been deployed in operational use on large-scale real-world problems in science and in business.In science, one of the primary applicationThere is an urgent need for a new generation of computation-al theories and tools toassist humans in extractinguseful information (knowledge)from the rapidly growing volumes ofdigital data.Articles38AI MAGAZINEtive applications (Manago and Auriol 1996).Telecommunications: The telecommuni-cations alarm-sequence analyzer (TASA) wasbuilt in cooperation with a manufacturer oftelecommunications equipment and threetelephone networks (Mannila, Toivonen, andVerkamo 1995). The system uses a novelframework for locating frequently occurringalarm episodes from the alarm stream andpresenting them as rules. Large sets of discov-ered rules can be explored with flexible infor-mation-retrieval tools supporting interactivityand iteration. In this way, TASA offers pruning,grouping, and ordering tools to refine the re-sults of a basic brute-force search for rules.Data cleaning: The MERGE-PURGE systemwas applied to the identification of duplicatewelfare claims (Hernandez and Stolfo 1995).It was used successfully on data from the Wel-fare Department of the State of Washington.In other areas, a well-publicized system isIBM’s ADVANCED SCOUT,a specialized data-min-ing system that helps National Basketball As-sociation (NBA) coaches organize and inter-pret data from NBA games (U.S. News 1995). ADVANCED SCOUT was used by several of the NBA teams in 1996, including the Seattle Su-personics, which reached the NBA finals.Finally, a novel and increasingly importanttype of discovery is one based on the use of in-telligent agents to navigate through an infor-mation-rich environment. Although the ideaof active triggers has long been analyzed in thedatabase field, really successful applications ofthis idea appeared only with the advent of theInternet. These systems ask the user to specifya profile of interest and search for related in-formation among a wide variety of public-do-main and proprietary sources. For example, FIREFLY is a personal music-recommendation agent: It asks a user his/her opinion of several music pieces and then suggests other music that the user might like (<http:// www.ffl/>). CRAYON(/>) allows users to create their own free newspaper (supported by ads); NEWSHOUND(<http://www. /hound/>) from the San Jose Mercury News and FARCAST(</> automatically search information from a wide variety of sources, including newspapers and wire services, and e-mail rele-vant documents directly to the user.These are just a few of the numerous suchsystems that use KDD techniques to automat-ically produce useful information from largemasses of raw data. See Piatetsky-Shapiro etal. (1996) for an overview of issues in devel-oping industrial KDD applications.Data Mining and KDDHistorically, the notion of finding useful pat-terns in data has been given a variety ofnames, including data mining, knowledge ex-traction, information discovery, informationharvesting, data archaeology, and data patternprocessing. The term data mining has mostlybeen used by statisticians, data analysts, andthe management information systems (MIS)communities. It has also gained popularity inthe database field. The phrase knowledge dis-covery in databases was coined at the first KDDworkshop in 1989 (Piatetsky-Shapiro 1991) toemphasize that knowledge is the end productof a data-driven discovery. It has been popular-ized in the AI and machine-learning fields.In our view, KDD refers to the overall pro-cess of discovering useful knowledge from da-ta, and data mining refers to a particular stepin this process. Data mining is the applicationof specific algorithms for extracting patternsfrom data. The distinction between the KDDprocess and the data-mining step (within theprocess) is a central point of this article. Theadditional steps in the KDD process, such asdata preparation, data selection, data cleaning,incorporation of appropriate prior knowledge,and proper interpretation of the results ofmining, are essential to ensure that usefulknowledge is derived from the data. Blind ap-plication of data-mining methods (rightly crit-icized as data dredging in the statistical litera-ture) can be a dangerous activity, easilyleading to the discovery of meaningless andinvalid patterns.The Interdisciplinary Nature of KDDKDD has evolved, and continues to evolve,from the intersection of research fields such asmachine learning, pattern recognition,databases, statistics, AI, knowledge acquisitionfor expert systems, data visualization, andhigh-performance computing. The unifyinggoal is extracting high-level knowledge fromlow-level data in the context of large data sets.The data-mining component of KDD cur-rently relies heavily on known techniquesfrom machine learning, pattern recognition,and statistics to find patterns from data in thedata-mining step of the KDD process. A natu-ral question is, How is KDD different from pat-tern recognition or machine learning (and re-lated fields)? The answer is that these fieldsprovide some of the data-mining methodsthat are used in the data-mining step of theKDD process. KDD focuses on the overall pro-cess of knowledge discovery from data, includ-ing how the data are stored and accessed, howalgorithms can be scaled to massive data setsThe basicproblemaddressed bythe KDDprocess isone ofmappinglow-leveldata intoother formsthat might bemorecompact,moreabstract,or moreuseful.ArticlesFALL 1996 39A driving force behind KDD is the database field (the second D in KDD). Indeed, the problem of effective data manipulation when data cannot fit in the main memory is of fun-damental importance to KDD. Database tech-niques for gaining efficient data access,grouping and ordering operations when ac-cessing data, and optimizing queries consti-tute the basics for scaling algorithms to larger data sets. Most data-mining algorithms from statistics, pattern recognition, and machine learning assume data are in the main memo-ry and pay no attention to how the algorithm breaks down if only limited views of the data are possible.A related field evolving from databases is data warehousing,which refers to the popular business trend of collecting and cleaning transactional data to make them available for online analysis and decision support. Data warehousing helps set the stage for KDD in two important ways: (1) data cleaning and (2)data access.Data cleaning: As organizations are forced to think about a unified logical view of the wide variety of data and databases they pos-sess, they have to address the issues of map-ping data to a single naming convention,uniformly representing and handling missing data, and handling noise and errors when possible.Data access: Uniform and well-defined methods must be created for accessing the da-ta and providing access paths to data that were historically difficult to get to (for exam-ple, stored offline).Once organizations and individuals have solved the problem of how to store and ac-cess their data, the natural next step is the question, What else do we do with all the da-ta? This is where opportunities for KDD natu-rally arise.A popular approach for analysis of data warehouses is called online analytical processing (OLAP), named for a set of principles pro-posed by Codd (1993). OLAP tools focus on providing multidimensional data analysis,which is superior to SQL in computing sum-maries and breakdowns along many dimen-sions. OLAP tools are targeted toward simpli-fying and supporting interactive data analysis,but the goal of KDD tools is to automate as much of the process as possible. Thus, KDD is a step beyond what is currently supported by most standard database systems.Basic DefinitionsKDD is the nontrivial process of identifying valid, novel, potentially useful, and ultimate-and still run efficiently, how results can be in-terpreted and visualized, and how the overall man-machine interaction can usefully be modeled and supported. The KDD process can be viewed as a multidisciplinary activity that encompasses techniques beyond the scope of any one particular discipline such as machine learning. In this context, there are clear opportunities for other fields of AI (be-sides machine learning) to contribute to KDD. KDD places a special emphasis on find-ing understandable patterns that can be inter-preted as useful or interesting knowledge.Thus, for example, neural networks, although a powerful modeling tool, are relatively difficult to understand compared to decision trees. KDD also emphasizes scaling and ro-bustness properties of modeling algorithms for large noisy data sets.Related AI research fields include machine discovery, which targets the discovery of em-pirical laws from observation and experimen-tation (Shrager and Langley 1990) (see Kloes-gen and Zytkow [1996] for a glossary of terms common to KDD and machine discovery),and causal modeling for the inference of causal models from data (Spirtes, Glymour,and Scheines 1993). Statistics in particular has much in common with KDD (see Elder and Pregibon [1996] and Glymour et al.[1996] for a more detailed discussion of this synergy). Knowledge discovery from data is fundamentally a statistical endeavor. Statistics provides a language and framework for quan-tifying the uncertainty that results when one tries to infer general patterns from a particu-lar sample of an overall population. As men-tioned earlier, the term data mining has had negative connotations in statistics since the 1960s when computer-based data analysis techniques were first introduced. The concern arose because if one searches long enough in any data set (even randomly generated data),one can find patterns that appear to be statis-tically significant but, in fact, are not. Clearly,this issue is of fundamental importance to KDD. Substantial progress has been made in recent years in understanding such issues in statistics. Much of this work is of direct rele-vance to KDD. Thus, data mining is a legiti-mate activity as long as one understands how to do it correctly; data mining carried out poorly (without regard to the statistical as-pects of the problem) is to be avoided. KDD can also be viewed as encompassing a broader view of modeling than statistics. KDD aims to provide tools to automate (to the degree pos-sible) the entire process of data analysis and the statistician’s “art” of hypothesis selection.Data mining is a step in the KDD process that consists of ap-plying data analysis and discovery al-gorithms that produce a par-ticular enu-meration ofpatterns (or models)over the data.Articles40AI MAGAZINEly understandable patterns in data (Fayyad, Piatetsky-Shapiro, and Smyth 1996).Here, data are a set of facts (for example, cases in a database), and pattern is an expres-sion in some language describing a subset of the data or a model applicable to the subset. Hence, in our usage here, extracting a pattern also designates fitting a model to data; find-ing structure from data; or, in general, mak-ing any high-level description of a set of data. The term process implies that KDD comprises many steps, which involve data preparation, search for patterns, knowledge evaluation, and refinement, all repeated in multiple itera-tions. By nontrivial, we mean that some search or inference is involved; that is, it is not a straightforward computation of predefined quantities like computing the av-erage value of a set of numbers.The discovered patterns should be valid on new data with some degree of certainty. We also want patterns to be novel (at least to the system and preferably to the user) and poten-tially useful, that is, lead to some benefit to the user or task. Finally, the patterns should be understandable, if not immediately then after some postprocessing.The previous discussion implies that we can define quantitative measures for evaluating extracted patterns. In many cases, it is possi-ble to define measures of certainty (for exam-ple, estimated prediction accuracy on new data) or utility (for example, gain, perhaps indollars saved because of better predictions orspeedup in response time of a system). No-tions such as novelty and understandabilityare much more subjective. In certain contexts,understandability can be estimated by sim-plicity (for example, the number of bits to de-scribe a pattern). An important notion, calledinterestingness(for example, see Silberschatzand Tuzhilin [1995] and Piatetsky-Shapiro andMatheus [1994]), is usually taken as an overallmeasure of pattern value, combining validity,novelty, usefulness, and simplicity. Interest-ingness functions can be defined explicitly orcan be manifested implicitly through an or-dering placed by the KDD system on the dis-covered patterns or models.Given these notions, we can consider apattern to be knowledge if it exceeds some in-terestingness threshold, which is by nomeans an attempt to define knowledge in thephilosophical or even the popular view. As amatter of fact, knowledge in this definition ispurely user oriented and domain specific andis determined by whatever functions andthresholds the user chooses.Data mining is a step in the KDD processthat consists of applying data analysis anddiscovery algorithms that, under acceptablecomputational efficiency limitations, pro-duce a particular enumeration of patterns (ormodels) over the data. Note that the space ofArticlesFALL 1996 41Figure 1. An Overview of the Steps That Compose the KDD Process.methods, the effective number of variables under consideration can be reduced, or in-variant representations for the data can be found.Fifth is matching the goals of the KDD pro-cess (step 1) to a particular data-mining method. For example, summarization, clas-sification, regression, clustering, and so on,are described later as well as in Fayyad, Piatet-sky-Shapiro, and Smyth (1996).Sixth is exploratory analysis and model and hypothesis selection: choosing the data-mining algorithm(s) and selecting method(s)to be used for searching for data patterns.This process includes deciding which models and parameters might be appropriate (for ex-ample, models of categorical data are differ-ent than models of vectors over the reals) and matching a particular data-mining method with the overall criteria of the KDD process (for example, the end user might be more in-terested in understanding the model than its predictive capabilities).Seventh is data mining: searching for pat-terns of interest in a particular representa-tional form or a set of such representations,including classification rules or trees, regres-sion, and clustering. The user can significant-ly aid the data-mining method by correctly performing the preceding steps.Eighth is interpreting mined patterns, pos-sibly returning to any of steps 1 through 7 for further iteration. This step can also involve visualization of the extracted patterns and models or visualization of the data given the extracted models.Ninth is acting on the discovered knowl-edge: using the knowledge directly, incorpo-rating the knowledge into another system for further action, or simply documenting it and reporting it to interested parties. This process also includes checking for and resolving po-tential conflicts with previously believed (or extracted) knowledge.The KDD process can involve significant iteration and can contain loops between any two steps. The basic flow of steps (al-though not the potential multitude of itera-tions and loops) is illustrated in figure 1.Most previous work on KDD has focused on step 7, the data mining. However, the other steps are as important (and probably more so) for the successful application of KDD in practice. Having defined the basic notions and introduced the KDD process, we now focus on the data-mining component,which has, by far, received the most atten-tion in the literature.patterns is often infinite, and the enumera-tion of patterns involves some form of search in this space. Practical computational constraints place severe limits on the sub-space that can be explored by a data-mining algorithm.The KDD process involves using the database along with any required selection,preprocessing, subsampling, and transforma-tions of it; applying data-mining methods (algorithms) to enumerate patterns from it;and evaluating the products of data mining to identify the subset of the enumerated pat-terns deemed knowledge. The data-mining component of the KDD process is concerned with the algorithmic means by which pat-terns are extracted and enumerated from da-ta. The overall KDD process (figure 1) in-cludes the evaluation and possible interpretation of the mined patterns to de-termine which patterns can be considered new knowledge. The KDD process also in-cludes all the additional steps described in the next section.The notion of an overall user-driven pro-cess is not unique to KDD: analogous propos-als have been put forward both in statistics (Hand 1994) and in machine learning (Brod-ley and Smyth 1996).The KDD ProcessThe KDD process is interactive and iterative,involving numerous steps with many deci-sions made by the user. Brachman and Anand (1996) give a practical view of the KDD pro-cess, emphasizing the interactive nature of the process. Here, we broadly outline some of its basic steps:First is developing an understanding of the application domain and the relevant prior knowledge and identifying the goal of the KDD process from the customer’s viewpoint.Second is creating a target data set: select-ing a data set, or focusing on a subset of vari-ables or data samples, on which discovery is to be performed.Third is data cleaning and preprocessing.Basic operations include removing noise if appropriate, collecting the necessary informa-tion to model or account for noise, deciding on strategies for handling missing data fields,and accounting for time-sequence informa-tion and known changes.Fourth is data reduction and projection:finding useful features to represent the data depending on the goal of the task. With di-mensionality reduction or transformationArticles42AI MAGAZINEThe Data-Mining Stepof the KDD ProcessThe data-mining component of the KDD pro-cess often involves repeated iterative applica-tion of particular data-mining methods. This section presents an overview of the primary goals of data mining, a description of the methods used to address these goals, and a brief description of the data-mining algo-rithms that incorporate these methods.The knowledge discovery goals are defined by the intended use of the system. We can distinguish two types of goals: (1) verification and (2) discovery. With verification,the sys-tem is limited to verifying the user’s hypothe-sis. With discovery,the system autonomously finds new patterns. We further subdivide the discovery goal into prediction,where the sys-tem finds patterns for predicting the future behavior of some entities, and description, where the system finds patterns for presenta-tion to a user in a human-understandableform. In this article, we are primarily con-cerned with discovery-oriented data mining.Data mining involves fitting models to, or determining patterns from, observed data. The fitted models play the role of inferred knowledge: Whether the models reflect useful or interesting knowledge is part of the over-all, interactive KDD process where subjective human judgment is typically required. Two primary mathematical formalisms are used in model fitting: (1) statistical and (2) logical. The statistical approach allows for nondeter-ministic effects in the model, whereas a logi-cal model is purely deterministic. We focus primarily on the statistical approach to data mining, which tends to be the most widely used basis for practical data-mining applica-tions given the typical presence of uncertain-ty in real-world data-generating processes.Most data-mining methods are based on tried and tested techniques from machine learning, pattern recognition, and statistics: classification, clustering, regression, and so on. The array of different algorithms under each of these headings can often be bewilder-ing to both the novice and the experienced data analyst. It should be emphasized that of the many data-mining methods advertised in the literature, there are really only a few fun-damental techniques. The actual underlying model representation being used by a particu-lar method typically comes from a composi-tion of a small number of well-known op-tions: polynomials, splines, kernel and basis functions, threshold-Boolean functions, and so on. Thus, algorithms tend to differ primar-ily in the goodness-of-fit criterion used toevaluate model fit or in the search methodused to find a good fit.In our brief overview of data-mining meth-ods, we try in particular to convey the notionthat most (if not all) methods can be viewedas extensions or hybrids of a few basic tech-niques and principles. We first discuss the pri-mary methods of data mining and then showthat the data- mining methods can be viewedas consisting of three primary algorithmiccomponents: (1) model representation, (2)model evaluation, and (3) search. In the dis-cussion of KDD and data-mining methods,we use a simple example to make some of thenotions more concrete. Figure 2 shows a sim-ple two-dimensional artificial data set consist-ing of 23 cases. Each point on the graph rep-resents a person who has been given a loanby a particular bank at some time in the past.The horizontal axis represents the income ofthe person; the vertical axis represents the to-tal personal debt of the person (mortgage, carpayments, and so on). The data have beenclassified into two classes: (1) the x’s repre-sent persons who have defaulted on theirloans and (2) the o’s represent persons whoseloans are in good status with the bank. Thus,this simple artificial data set could represent ahistorical data set that can contain usefulknowledge from the point of view of thebank making the loans. Note that in actualKDD applications, there are typically manymore dimensions (as many as several hun-dreds) and many more data points (manythousands or even millions).ArticlesFALL 1996 43Figure 2. A Simple Data Set with Two Classes Used for Illustrative Purposes.。
affect in language learning

Approaches and Methods in Language Teaching by Jack C. Richards and Theodore S. Rodgers
Appropriate Methodology and Social Context by Adrian Holliday Beyond Training by Jack C. Richards Collaborative Language Learning and Teaching edited by David Nunan Communicative Language Teaching by William Littlewood Communicative Methodology in Language Teaching by Christopher Brum®t Course Design by Fraida Dubin and Elite Olshtain Culture Bound edited by Joyce Merrill Valdes Designing tasks for the Communicative Classroom by David Nunan Developing Reading Skills by FrancËoise Grellet Developments in ESP by Tony Dudley-Evans and Maggie Jo St John Discourse Analysis for Language Teachers by Michael McCarthy Discourse and Language Education by Evelyn Hatch English for Academic Purposes by R.R. Jordan English for Speci®c Purposes by Tom Hutchinson and Alan Waters Focus on the Language Classroom by Dick Allwright and Kathleen M. Bailey Foreign and Second Language Learning by William Littlewood Language Learning in Intercultural Perspective edited by Michael Byram and
INSEARCHOFEXCELLENCE

IN SEARCH OF EXCELLENCEExcellence is a journey and not a destination. In science itimplies perpetual efforts to advance the frontiers of knowledge.This often leads to progressively increasing specialization andemergence of newer disciplines. A brief summary of salientcontributions of Indian scientists in various disciplines isintroduced in this section.92P U R S U I T A N D P R O M O T I O N O F S C I E N C EThe modern period of mathematics research in India started with Srinivasa Ramanujan whose work on analytic number theory and modular forms ishighly relevant even today. In the pre-Independence period mathematicians like S.S. Pillai,Vaidyanathaswamy, Ananda Rau and others contributed a lot.Particular mention should be made of universities in Allahabad, Varanasi, Kolkata,Chennai and Waltair and later at Chandigarh,Hyderabad, Bangalore and Delhi (JNU). The Department of Atomic Energy came in a big way to boost mathematical research by starting and nurturing the Tata Institute of Fundamental Research (TIFR), which, under the leadership of Chandrasekharan, blossomed into a great school of learning of international standard. The Indian Statistical Institute, started by P.C. Mahalanobis,made its mark in an international scene and continues to flourish. Applied mathematics community owes a great deal to the services of three giants Ñ N.R. Sen, B.R. Seth and P .L. Khastgir. Some of the areas in which significant contributions have been made are briefly described here.A LGEBRAOne might say that the work on modern algebra in India started with the beautiful piece of work in 1958 on the proof of SerreÕs conjecture for n =2. A particular case of the conjecture is to imply that a unimodular vector with polynomial entries in n vari-ables can be completed to a matrix of determinantone. Another important school from India was start-ed in Panjab University whose work centres around Zassanhaus conjecture on groupings.A LGEBRAIC G EOMETRYThe study of algebraic geometry began with a seminal paper in 1964 on vector bundles. With further study on vector bundles that led to the mod-uli of parabolic bundles, principle bundles, algebraic differential equations (and more recently the rela-tionship with string theory and physics), TIFR has become a leading school in algebraic geometry. Of the later generation, two pieces of work need special mention: the work on characterization of affine plane purely topologically as a smooth affine surface, sim-ply connected at infinity and the work on Kodaira vanishing. There is also some work giving purely algebraic geometry description of the topologically invariants of algebraic varieties. In particular this can be used to study the Galois Module Structure of these invariants.L IE T HEORYThe inspiration of a work in Lie theory in India came from the monumental work on infinite dimensional representation theory by Harish Chandra, who has, in some sense, brought the sub-ject from the periphery of mathematics to centre stage. In India, the initial study was on the discrete subgroups of Lie groups from number theoretic angle. The subject received an impetus after an inter-national conference in 1960 in TIFR, where the lead-ing lights on the subject, including A. Selberg partic-M ATHEMATICAL S CIENCESC H A P T E R V I Iipated. Then work on rigidity questions was initiat-ed. The question is whether the lattices in arithmetic groups can have interesting deformations except for the well-known classical cases. Many important cases in this question were settled.D IFFERENTIALE QUATIONA fter the study of L-functions were found to beuseful in number theory and arithmetic geome-try, it became natural to study the L-functions arising out of the eigenvalues of discrete spectrum of the dif-ferential equations. MinakshisundaramÕs result on the corresponding result for the differential equation leading to the Epstein Zeta function and his paper with A. Pleijel on the same for the connected com-pact Riemanian manifold are works of great impor-tance. The idea of the paper (namely using the heat equation) lead to further improvement in the hands of Patodi. The results on regularity of weak solution is an important piece of work. In the later 1970s a good school on non-linear partial differential equa-tions that was set up as a joint venture between TIFR and IISc, has come up very well and an impressive lists of results to its credit.For differential equations in applied mathematics, the result of P.L. Bhatnagar, BGK model (by Bhatnagar, Gross, Krook) in collision process in gas and an explanation of Ramdas Paradox (that the temperature minimum happens about 30 cm above the surface) will stand out as good mathematical models. Further significant contributions have been made to the area of group theoretic methods for the exact solutions of non-liner partial differential equations of physical and engineering systems.E RGODIC T HEORYE arliest important contribution to the Ergodic the-ory in India came from the Indian Statistical Institute. Around 1970, there was work on spectra of unitary operators associated to non-singular trans-formation of flows and their twisted version, involv-ing a cocycle.Two results in the subjects from 1980s and 1990s are quoted. If G is lattice in SL(2,R) and {uÐt} a unipotent one parameter subgroup of G, then all non-periodic orbits of {uÐt} on GÐ1 are uniformly distributed. If Q is non-generate in definite quadratic form in n=variables, which is not a multiple of rational form, then the number of lattice points xÐwith a< ½Q(x)½< b, ½½x½½< r, is at least comparable to the volume of the corresponding region.N UMBER T HEORYT he tradition on number theory started with Ramanujan. His work on the cusp form for the full modular group was a breakthrough in the study of modular form. His conjectures on the coefficient of this cusp form (called RamanujanÕs tau function) and the connection of these conjectures with conjectures of A. Weil in algebraic geometry opened new research areas in mathematics. RamanujanÕs work (with Hardy) on an asymptotic formula for the parti-tion of n, led a new approach (in the hands of Hardy-Littlewood) to attack such problems called circle method. This idea was further refined and S.S. Pillai settled WaringÕs Conjecture for the 6th power by this method. Later the only remaining case namely 4th powers was settled in mid-1980s. After Independence, the major work in number theory was in analytic number theory, by the school in TIFR and in geometry of numbers by the school in Panjab University. The work on elliptic units and the con-struction of ray class fields over imaginary quadratic fields of elliptic units are some of the important achievements of Indian number theory school. Pioneering work in BakerÕs Theory of linear forms in logarithms and work on geometry of numbers and in particular the MinkowskiÕs theorem for n = 5 are worth mentioning.P ROBABILITY T HEORYS ome of the landmarks in research in probability theory at the Indian Statistical Institute are the following:93 P U R S U I T A N D P R O M O T I O N O F S C I E N C Eq A comprehensive study of the topology of weak convergence in the space of probability measures on topological spaces, particularly, metric spaces. This includes central limit theorems in locally compact abelian groups and Milhert spaces, arithmetic of probability distributions under convolution in topological groups, Levy-khichini representations for characteristic functions of probability distributions on group and vector spaces.q Characterization problems of mathematical statistics with emphasis on the derivation of probability laws under natural constraints on statistics evaluated from independent observations.q Development of quantum stochastic calculus based on a quantum version of ItoÕs formula for non-commutative stochastic processes in Fock spaces. This includes the study of quantum stochastic integrals and differential equations leading to the construction of operator Markov processes describing the evolution of irreversible quantum processes.q Martingale methods in the study of diffusion processes in infinite dimensional spaces.q Stochastic processes in financial mathematics.C OMBINATORICST hough the work in combinatorics had been ini-tiated in India purely through the efforts of R.C.Bose at the Indian Statistical Institute in late thirties, it reached its peak in late fifties at the University of North Carolina, USA, where he was joined by his former student S.S.Shrikhande. They provided the first counter-example to the celebrat-ed conjecture of Euler (1782) and jointly with Parker further improved it. The last result is regarded a classic.In the absence of these giants there was practically no research activity in this area in India. However, with the return of Shrikhande to India in 1960 activities in the area flourished and many notable results in the areas of embedding of residual designs in symmetric designs, A-design conjecture and t-designs and codes were reported.T HEORY OF R ELATIVITYI n a strict sense the subject falls well within the purview of physics but due to the overwhelming response by workers with strong foundation in applied mathematics the activity could blossom in some of the departments of mathematics of certain universities/institutes. Groups in BHU, Gujarat University, Ahmedabad, Calcutta University, and IIT, Kharagpur, have contributed generously to the area of exact solutions of Einstein equations of gen-eral relativity, unified field theory and others. However, one exact solution which has come to be known as Vaidya metric and seems to have wide application in high-energy astrophysics deserves a special mention.N UMERICAL A NALYSIST he work in this area commenced with an attempt to solve non-linear partial differential equations governing many a physical and engineering system with special reference to the study of Navier-Stabes equations and cross-viscous forces in non-Newtonian fluids. The work on N-S equation has turned out to be a basic paper in the sense that it reappeared in the volume, Selected Papers on Numerical Solution of Equations of Fluid Dynamics, Applied Mathematics, through the Physical Society of Japan. The work on non-Newtonian fluid has found a place in the most prestigious volume on Principles of Classical Mechanics & Field Theory by Truesdell and Toupin. The other works which deserve mention are the development of extremal point collocation method and stiffy stable method.A PPLIED M ATHEMATICST ill 1950, except for a group of research enthusi-asts working under the guidance of N.R.Sen at Calcutta University there was practically no output in applied mathematics. However, with directives from the centre to emphasize on research in basic94P U R S U I T A N D P R O M O T I O N O F S C I E N C Eand applied sciences and liberal central fundings through central and state sponsored laboratories, the activity did receive an impetus. The department of mathematics at IIT, Kharagpur, established at the very inception of the institute of national importance in 1951, under the dynamic leadership of B.R.Seth took the lead role in developing a group of excellence in certain areas of mathematical sciences. In fact, the research carried out there in various disciplines of applied mathematics such as elasticity-plasticity, non-linear mechanics, rheological fluid mechanics, hydroelasticity, thermoelasticity, numerical analysis, theory of relativity, cosmology, magneto hydrody-namics and high-temperature gasdynamics turned out to be a trend setting one for other IITs, RECs, other Technical Institutes and Universities that were in the formative stages. B.R. SethÕs own researches on the study of Saint-VenamtÕs problem and transi-tion theory to unify elastic-plastic behaviour of mate-rials earned him the prestigious EulerÕs bronze medal of the Soviet Academy of Sciences in 1957. The other areas in which applied mathematicians con-tributed generously are biomechanics, CFD, chaotic dynamics, theory of turbulence, bifurcation analysis, porous media, magnetics fluids and mathematicalphysiology.95 P U R S U I T A N D P R O M O T I O N O F S C I E N C E。
depthmap使用手册

31.131Abstract Here we present Depthmap, a program designed to perform visibility graph analysis of spatial environments. The program allows a user to import a 2D layout in drawing exchange format (DXF), and to fill the open spaces of this layout with a grid of points. The user may then use the program to make a visibility graph representing the visible connections between those point locations. Once the graph has been constructed the user may perform various analyses of the graph, concentrating on those which have previously been found to be useful for spatial description and movement forecasting within the Space Syntax literature. Some measures which have not received so much mainstream attention have also been imple-mented. In addition to graph analysis, a few sundry tools are also enabled so that the user may make minor adjustments to the graph. Depthmap has been implemented for the Windows 95/98/NT and 2000 platforms.1 IntroductionThe application of visibility graph analysis (VGA) to building environments was first intro-duced by Braaksma and Cook (1980). Braaksma and Cook calculate the co-visibility of vari-ous units within an airport layout, and produce an adjaceny matrix to represent these relation-ships, placing a 1 in the matrix where two locations are mutually visible, and a 0 where they are not. From this matrix they propose a metric to compare the number of existing visibility relationships with the number which could possibly exist, in order to quantify how usefully a plan of an airport satisfies a goal of total mutual visibility of locations. This type of analysis was recently rediscovered by Turner et al. (Turner and Penn, 1999; Turner et al., 2001), through considering recent developments in Space Syntax of various isovist approaches (see Hanson,1998, for further background). They recast the adjaceny matrix as a visibility graph of loca-tions, where a graph edge connects vertices representing mutually visible locations. Turner et al. then use several graph metrics as a few representative measures which could be performed on such graphs. The metrics they apply are taken from a combination of techniques used in Space Syntax and those employed in the analysis of small-worlds networks by Watts and Strogatz (1998).Here we present a tool which enables a user to perform VGA on both building and urban environments, allowing the user to perform the kind of analysis proposed by Turner et al..We call this tool Depthmap . Depthmap first allows the user to import layouts in 2D DXF format and to fill the layout with a rectilinear grid of points. These points may then be used to construct a visibility graph, and we describe this procedure in section 2. After the graph hasDepthmap A program to perform visibility graph analysisAlasdair Turner University College London, UK Keywords:visibility graph,spatial analysis,software develop-ment Alasdair Turner Center for Advanced Spatial Analysis,Torrington Place Site, University College London,Gower Street,London WC1E 6BT ,UK alasdair .turner@31.2been constructed, Depthmap gives the user several options to perform analysis on the graph,which we describe in detail in section 3. The methods include those employed by Turner et al.,but also some, such as control (Hillier and Hanson, 1984) or point depth entropy (following a formula proposed by Hiller et al., 1987), which have not been previously applied to visibility graph analysis. We supply algorithmic and mathematical details of each measure, as well as samples of results, and short explanations of why we believe these may be of interest to other researchers. In section 4 we include a brief description of extra facilities included in Depthmap to adjust the edge connections in the visibility graph, and give guidance for their use in spatial analysis. Finally, we present a summary in section 5.2 Making a visibility graph from a DXF fileIn this section we describe how the user may get from a layout to a visibility graph using Depthmap. When the user first enters Depthmap, she or he may create a new graph file from the File menu. This graph file initially appears blank, and the first thing the user must do is to import a layout to be analysed. The import format used is AutoDesk s drawing exchangeformat (DXF), and only two dimensional layouts maybe imported. Once loaded, the user is shown the lay-out on the screen, and she or he may move it andzoom in and out as desired. Figure 1 shows the pro-gram at this stage. After the DXF file has been im-ported, the user is ready to add a set of locations to beused as a basis for the visibility graph.2.1 Making a grid of locations To make a set of locations, the user selects the Fill tool from the toolbar, and then clicks on a seed point in open space to make a grid of points, as shown in figure 2. When the user clicks for the first time, she or he is given the option of choosing a grid spacing,based on the units used in the original DXF, and may use for example, a 1m grid. The grid is filled from the seed point using a simple flood fill algorithm. Points may be deleted by selecting either individual points or ranges of points. Once the user is happy with the grid,she or he may then go on to make the visibility graph.The user is restricted to a rectilinear grid of points at present. We realise that this is a problem for anyone attempting a methodological investigation of VGA,rather than simply using it to analyse environments.This is due to using a grid assumption when we calculate point intervisibility, and unfortu-nately a constraint. However, various themes on the basic grid are still available, for example by using different resolutions or by rotating the DXF prior to import, or by only partiallyfilling grids.Figure 1: Theapplication as itappears after the DXFfile has beenimportedFigure 2: The userfills a section of openspace using the filltool31.32.2 Making the graphThe graph is made by Depthmap by selecting the Make Graph option from the Tools menu. The program attempts to find all the visible locations from each grid location in the layout one by one, and uses a simple point visibility test radiating from the current location to achieve this. As each location is considered, a vertex is added to the graph for this point,and the set of visible vertices is stored. Note that this is only one way that the visibility graph could be stored. It is actually more space efficient only to store the edges, but this would lead to slower algorithms later when analysing the graph. We can write a simplified form of the algorithm in pseudocode as follows. In the algorithm we use graph set notation: V(G) is the set of all locations or vertices that exist, and v i an individual location or vertex in the graph we are making. Each vertex v i will have a set of vertices connected to it, which will labelled the set V (G i ), otherwise known as the vertex s neighbourhood.The number of vertices in the neighbourhood is obviouslyeasily calculable, and Depthmap records these neighbourhoodsizes as it makes the graph. In graph theory, the neighbourhoodsize for a vertex is commonly written ki, and may be expressed as in equation 1..(1)where E(G) is the set of all edges (i.e., visibility connections) inthe graph. Note that the set E(G) is not actually stored byDepthmap, and so k i is actually calculated using the first formof this equation. Figure 3 shows a simple layout after the vis-ibility graph has been made using Depthmap. As the actual number of connections is huge for each vertex, only k i values are shown for each location rather than the mess of actual connections. Depthmap colours k i values using a spectral range from indigo for low values through blue, cyan, green, yellow, orange, red to magenta for high values. The user may change the bounds for this range, or choose to use a greyscale instead, using a menu option from the View menu. Since this paper is reproduced in greyscale, all the figures shown have used the greyscale option, where black represents low values and white represents high values.Once the graph has been constructed, the user has various options, including graph analysis,which we describe in the next section, and modification of the graph, which we describe insection 4.Figure 3:Neighbourhood size calculated for a sample layout31.4 3 Measurement of the graph In this section we describe the graph measures available to a user of Depthmap. Analysis of the graph is split into two types: global measures (which are constructed using information from all the vertices in the graph) and local measures (which are constructed using informa-tion from the immediate neighbourhood of each vertex in the graph). The user may elect to perform either or both of these types of measure by selecting from the Tools menu. She or he is presented with a dialog box, as shown in figure 4. The radius box allows the user to restrict global measures to only include vertices up to n-edge steps from each vertex. When the user clicks OK, the program calculates the measures for the whole system. The key global measures are mean depth and point depth entropy, while the key local measures are clustering coefficient and control. Once the measures have been calculated, these and derived measures are given as options on the View menu, and may be exported as plain text for use in GIS and statistical packages from File menu. We now turn to a discussion of the algorithmic imple-mentation of each measure, and explore possibilities for their use within Space Syntax re-search.3.1 Clustering Coefficient Clustering coefficient, g i , is described in detail by Watts (1999) and has its origin in theanalysis of small-world networks. Turner et al. found it useful for the detection of junction points in environments. Clustering coefficient is defined as the proportion of vertices which are actually connected within the neighbourhood of the current vertex, compared to thenumber that could possibly be connected, as shown in equation 2.(2)where E(G i ) is the set of edges in the neighbourhood of v i and k i is the as previously calculated. This is implemented in Depthmap by the following algorithm for each vertex inthe graph*Figure 4: The optionsdialog box for graphanalysis * Again note that as the set of edges E(G i ) is not recorded, the information must be recovered from the vertices in the neighbourhood, V(G i )31.5Figure 5 shows the clustering coefficient calculated for a sample spatial configuration. As noted by Turner et al. junctions in the configuration are picked out. However, as they suggest,and looking at the figure, it actually seems to pick out better the changes in visual information as the system is navigated, so low clustering coefficients occur where a new area of the system may be discovered. Examining g i , seems a promising line of investigation when looking at how visual information varies within an environment - for example, as suggested by Conroy (2000) for finding pause points on journeys.3.2 ControlControl for a location, which we will labelci, is defined by Hillier and Hanson (1984), andis calculated by summing the reciprocals of theneighbourhood sizes adjoining the vertex, asshown in equation 3.(3)A simple algorithm can be used to calculate thisvalue as follows:It should be noted that in VGA many of theimmediately adjoining neighbourhoods willoverlap, so that perhaps a better definition ofVGA control would be the area of the currentneighbourhood with respect to the total areaof the immediately adjoining neighbourhood- that is, rather than use the sum the size of allthe adjoining neighbourhoods, use the size ofthe union of those adjoining neighbourhoodsas shown in equation 4. The results of applyingthis method are shown in figure 6, althoughDepthmap is also capable of calculating controlas defined by Hillier and Hanson.(4)Figure 5: Clusteringcoefficient calculatedfor a sample layoutFigure 6: Controlcalculated for asample layout31.63.3 Mean DepthThe mean path length L i from a vertex is the average number of edge steps to reach any other vertex in the graph using the shortest number of steps possible in each case. This sort of graph measure has a long history stretching back as far as Wiener (1947), and is pertinent to visibility graph analysis due to the parallels with the use of integration in space syntax theory (Hillier et al., 1993), showing how visually connected a vertex is to all other vertices in the system. We calculate L i by constructing the set of point depths, as follows. The algorithm we use is not the most time efficient, as shortest paths are recalculated for each vertex, rather than being stored in a cache. However, the memory constraints on current personal computers mean that storing all the shortest paths in the system would rapidly use up the available memory. Hence, the algorithm that follows works in O(n 2) time. It obtains point depths for all the vertices in the system from the current vertex, by adding ordered pairs of vertices and depths to the set P.An asterisk, such as in the set pair {v 1, *}, represents a wild card matching operation. For example, {v 1, *} matches any of {v 1,1}, {v 1, 2} or {v 1, 4}.Once the point depth set has been constructed, it is facile to calculate measures such as mean depth and integration. Figure 7 shows mean depth for our sample system. As has been shown, this measure would seem to be useful understanding movement of people within building environments, where it isdifficult to apply traditional Space Syntax methods such as axial analyses at high resolutions.However, in urban environments, since we are measuring numbers of turns from location to location, VGA integration quickly approximates to axial integration (albeit with each line weighted by the street area), and due to speed considerations, it may not be as beneficial to useVGA integration in these situations.Figure 7: Mean depthcalculated for asample layout31.73.4 Point Depth EntropyIn addition to calculating measures such as mean depth, the point depth set P i allows us to explore measures based on the frequency distribution of the depths. One such measure is the point depth entropy of a location, s i , which we can express using Shannon s formula of uncertainty, as shown in equation 5. Entropy occurs in many fields, including informatics,and is proposed for use in Space Syntax by Hiller et al. (1987).(5)where d max is the maximum depth from vertex v i and p d is the frequency of point depth *d*from the vertex. This is implemented algorithmically in Depthmap as follows:.Calculating point depth entropy can give an insight into how ordered the system is from a location. For example, if a doorway is connected to a main street then there is a marked disorder in the point depths from the point of view of the doorway: at depth 1 there are only a few locations visible from the doorway, then at depth 2 there are many locations from the street, and then order contained within further depths will depend on how the street is integrated within its environment. Figure 8 shows the point depth entropy as calculated by Depthmap. Other entropy-like measures are also calculated. The information from a point is calculated using the frequency with respect to the expected frequency of locations at each depth, as shown in equation 6. Obviously, what is meant by expected is debatable, but as the frequency is based on the probability of events occurring (that is, of the j graph splitting), it seems appropriate to use a Poisson distribution (see Turner, 2001, for a more detailed discussion), which has the advantage of depending only on a single variable, the mean depth of the j graph. The resulting formula is shown in equation 6 and is similar to that used by Hiller et al. for relativised entropy. So, why calculate the entropy or information from a point?The answer is threefold: firstly, it was found to be useful by Hiller et al.; secondly, it appeals intuitively to a tentative model of people occupation of a system, in that the entropy corre-sponds to how easy it is to traverse to a certain depth within the system (low disorder is easy,31.8high disorder is hard); and thirdly, it remedies the problem that VGA integration is heavily biased towards large open areas. In axial integration, because the system is dimensionless,large open areas do not unduly weight the values of the lines; that is, the large areas only weight the values by their increased connections, not through their area. By contrast, in VGA integration the measure approximates a mean of distance times area, as discussed in the previous section. Hence, by using a topological measure such as point depth entropy we eliminate the area dependence of the measure, and instead concentrate on the visual accessi-bility of a point from all other points.(6)4 Further tools available in Depthmap As well as allowing the user to make and analyse graphs, Depthmap includes the facility to modify the graph connections. We believe this will be useful when the user wishes to model something other than a two dimensional plan - for example, when modelling a building with more than one storey, or trying to include one way entrances or exit, escalators and so on. The method to modify connections in Depthmap is as follows. Once the graph has been made, the user first selects an area by dragging a select box across the desired portion of the graph, as she or he would in many computer applications. She or he may also select other areas by holding down the Shift key and then selecting again. The user then pins this selection, using a toolbar button. Now the user may select another area in the same way.Once these two areas have been selected, the user can alter the connections between them by selecting the Edit Connections dia-log box from the Edit menu. An example is shown in figure 9.The dialog box gives several options but essentially these reduce to set operations on the neighbourhoods of the selected points. The Add option simply adds the selected points in the other set to the neighbourhood, and is useful for turning points, for example a stairwell landing. The Merge option allows the user to union the neighbourhoods of the two selected sets, and is usefulfor adding seamless merges, for example, descending an incline. Finally the Remove option can be used to take away any connections from the selected set, and for example, might be useful to convert a two way entrance to a one way entrance.5 ConclusionIn this paper, we have presented a description of the Depthmap program, designed to perform visibility graph analysis (VGA). Depthmap can be used to analyse a layout to obtain various graph measures, including integration, which has been shown to correlate well with observed movement patterns when used with axial maps (see Hillier et al., 1993, for ex-ample), and also shown to correlate with movement patterns when used with VGA (see Turner and Penn, 1999). Although we have talked only about the overall application ofDepthmap to a system to make and analyse graphs, Depthmap also has many other features Figure 8: Point depthcalculated for asample layout31.9which a user would expect from a program, such as printing, summarising graph data and so on, which we have restricted to a user manual. What we do hope to have given here is a flavour of what is achievable with the program, an insight into how the graph is analysed,and our reasons for choosing the graph measures we have included.Finally, it is worth noting that Depthmap is designed to be a tool for Space Syntax researchers. This means that we have chosen DXF as the input medium, and that the pro-gram runs interactively, allowing the graph to be modified and the analysis to be reapplied. It also means that sometimes we have not used the fastest algorithm to achieve a task, but have instead designed the program to work with the memory available on most personal comput-ers today. On a 333 MHz machine running Windows 98, Depthmap takes around an hour to process a graph with 10 000 point locations, from start to finish, and the program has been tested on graphs with up to 30 000 point locations. We hope that the Space Syntax commu-nity will enjoy using our tool and we look forward to improving it with the input and insight of future researchers.References Braaksma, J P and Cook, W J, 1980, Human orientation in transportation terminals Transportation Engineering Journal 106(TE2) 189-203Conroy, R, 2000 Spatial Navigation in Immersive Vir-tual Environments PhD thesis, Bartlett School of Graduate Studies, UCL Hanson, J, 1998 Decoding Houses and Homes (Cam-bridge University Press, Cambridge, UK)Hiller, B, Hanson, J and Peponis, J, 1987, The syntactic analysis of settlements Architecture and Behaviour 3(3) 217-231Hillier, B and Hanson, J, 1984 The Social Logic of Space (Cambridge University Press, Cambridge,UK)Hillier, B, Penn, A, Hanson, J, Grajewski, T and Xu, J, 1993, Natural movement: or configura-tion and attraction in urban pedestrian move-ment Environment and Planning B: Planning and Design 20 29-66Turner, A, 2001, Angular analysis Proceedings of the 3rd International Symposium on Space Syntax Georgia Institute of Technology, Atlanta, Geor-gia.Turner, A, Doxa, M, O Sullivan, D and Penn, A,2001, From isovists to visibility graphs: a methodology for the analysis of architectural space Environment and Planning B: Planning and Design 28(1) Forthcoming Turner, A and Penn, A, 1999, Making isovists syntatic: Isovist integration analysis Proceedings of the 2nd International Symposium on Space Syntax Vol. 3, Universidad de Brasil, Brasilia, Brazil Watts, D J, 1999 Small Worlds (Princeton University Press, Princeton, NJ)Watts, D J and Strogatz, S H, 1998, Collective dynamics of small-world networks Nature 393440-442Wiener, H, 1947, Structural determination of paraffin boiling points Journal of the American Chemistry Society 6917-20Figure 9: Editing connections。
【材料】美国西北太平洋国家实验室陈春龙:可编程二维纳米晶体用于高效的人工光收集系统
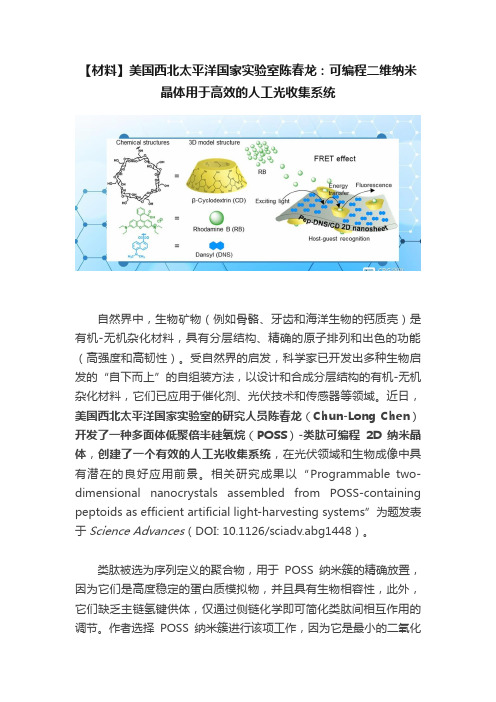
【材料】美国西北太平洋国家实验室陈春龙:可编程二维纳米晶体用于高效的人工光收集系统自然界中,生物矿物(例如骨骼、牙齿和海洋生物的钙质壳)是有机-无机杂化材料,具有分层结构、精确的原子排列和出色的功能(高强度和高韧性)。
受自然界的启发,科学家已开发出多种生物启发的“自下而上”的自组装方法,以设计和合成分层结构的有机-无机杂化材料,它们已应用于催化剂、光伏技术和传感器等领域。
近日,美国西北太平洋国家实验室的研究人员陈春龙(Chun-Long Chen)开发了一种多面体低聚倍半硅氧烷(POSS)-类肽可编程2D纳米晶体,创建了一个有效的人工光收集系统,在光伏领域和生物成像中具有潜在的良好应用前景。
相关研究成果以“Programmable two-dimensional nanocrystals assembled from POSS-containing peptoids as efficient artificial light-harvesting systems”为题发表于Science Advances(DOI: 10.1126/sciadv.abg1448)。
类肽被选为序列定义的聚合物,用于POSS纳米簇的精确放置,因为它们是高度稳定的蛋白质模拟物,并且具有生物相容性,此外,它们缺乏主链氢键供体,仅通过侧链化学即可简化类肽间相互作用的调节。
作者选择POSS纳米簇进行该项工作,因为它是最小的二氧化硅纳米颗粒,并且具有精确的原子笼状构象。
此外,POSS纳米簇的高稳定性和强疏水性使其成为极具吸引力的构建基块,可以与自组装分子共价结合以获得具有独特性能的复合材料。
图1.类肽Pep-1至Pep-16的各种骨架位置上精确放置POSS纳米簇(来源:Science Advances)首先,作者开发了一种改变的蛋白质样结构,称为类肽,在“亚单体”固相合成方法的置换步骤中,使用溶于CH2Cl2的多面体低聚倍半硅氧烷合成了这些杂合类肽,即在类肽的一端连接一种精确的POSS 作为侧链。
海特勒

Walter Heitler Der Mensch und die naturwissenschaftliche Erkenntnis(Vieweg Friedr. & Sohn Ver, 1961, 1962, 1964, 1966, 1984)
Walter Heitler Man and Science(Oliver and Boyd, 1963) Walter Heitler Die Frage nach dem Sinn der Evolution(Herder, 1969) Walter Heitler Naturphilosophische Streifzüge(Vieweg Friedr. & Sohn Ver, 1970, 1984) W. Heitler Naturwissenschaft ist Geisteswissenschaft(Zürich : Verl. die Waage, 1972) K. Rahner, ette, B. Welte, R. Affemann, D. Savramis, W. Heitler Gott in dieser Zeit(, 1972) Walter Heitler Die Natur und das Göttliche(Klett & Balmer; 1.
出版作品
物理学
科学与宗教论 述
Walter Heitler Elementary Wave Mechanics: Introductory Course of LecturesNotes taken and prepared by W.son (Oxford, 1943年)
Walter Heitler Elementary Wave Mechanics(Oxford, 1945, 1946, 1948, 1950) Walter Heitler The Quantum Theory of Radiation(Clarendon Press, 1936, 1944, 1947, 1949, 1950, 1953, 1954, 1957, 1960, 1966, 1970) Walter Heitler The Quantum Theory of Radiation(Dover, 1984) Walter Heinrich Heitler 14 Offprints: 1928-1947(1947) Walter Heitler Eléments de Mécanique Ondulatoire(Presses Universitaires de France, PUF, Paris, 1949, 1964) Walter Heitler Elementi di Meccanica Ondulatoriacon presentazione di R.
4. Polynomial Functions

(coefficient of x2) (coefficient of x) (coefficient of x0, the constant term of the polynomial)
ISBN 978-1-107-67685-5
© Michael Evans et al. 2011
Photocopying is restricted under law and this material must not be transferred to another party.
Cambridge University Press
If x3 + 3x2 + 3x + 8 = ax3 + 3ax2 + 3ax + a + b for all x ∈ R, equating coefficients gives:
(coefficient of x3) (coefficient of x2) (coefficient of x) (coefficient of x0, the constant term of the polynomial)
a, b and c.
Solution a The expansion of the right-hand side of the equation gives:
a(x + 1)3 + b = a(x3 + 3x2 + 3x + 1) + b = ax3 + 3ax2 + 3ax + a + b
神学视阈下的悖论_达_芬奇密码_的文化研究

神学视阈下的悖论———《达·芬奇密码》的文化研究朱长泉 钱志富内容提要:《达·芬奇密码》在世界范围内的畅销因素之一在于小说所引发的文化论战:丹·布朗在小说中对基督教基本教义的公开挑衅和基督教各教派对其论说的奋起批判。
本论文从神学的视角揭示所研究的文本与收集材料中存在的相互抵牾的典型悖论。
《达·芬奇密码》是部精彩的小说,但如果认同小说中对基督教早期历史改写的可行性,则是忽略了小说与基本史实的区别。
关键词:《达·芬奇密码》 悖论 文化研究作者简介:朱长泉,江西省万年中学英语教师,宁波大学外语学院硕士,研究方向为现当代英语文学;钱志富,文学博士,宁波大学外语学院副教授,研究方向为西方文论、诗歌研究。
T itle:Paradoxes in the Theol ogical Pers pective:Cultural Studies of The D a V inci CodeAbstract:One of the popular fact ors in the success of The D a V inci Code is the cultural contr ovacies it brings about,na mely Dan B r own’s defiance of the Canon of the B ible and accordingly the religi ous defenses fr o m the sects of Christianity.I n the theol ogical pers pective,this paper expounds the typ ical paradoxes a mong the novel and the related critical papers.W hilst The D a V inci Code is a successful st ory,its descri p ti ons of art w ork,docu ments,and religi ous rituals are paradoxical with the state ments of other scholars thus can not be taken for granted.Key words:The D a V inci Code paradoxes cultural studiesAuthors:Zhu Changquan,is a teacher atW annian Seni or H igh School in J iangxi Pr ovince(W annian335500,China).H is re2 search area is Contemporary B ritish and American literature.E mail:zhuchangquan405@.Q i a n Zh i fu,Ph.D.,is an ass ociate p r ofess or at N ingbo University(N ingbo315211,China).H is research areas are western critical studies and poe m stud2 ies.E mail:qianzhifu@一、《达·芬奇密码》中的文化悖论在研读《达·芬奇密码》和基督学者针对它的批判文章时,我们发现它们之间有不少相互抵牾之处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S. Ole Warnaar∗ and Paul A. Pearce† Mathematics Department University of Melbourne Parkville, Victoria 3052 Arify that both the left- and right-hand-sides of equation (1.2) satisfy the recurrence fL = fL−1 + q L−1 fL−2 . Given appropriate initial conditions, this recurrence has a unique solution hence establishing the polynomial identity and its limiting form (1.1). Identities of the Rogers–Ramanujan type occur in various branches of mathematics and physics. First, their connection with the theory of (affine) Lie algebras [5, 6] and with partition theory [4] has led to many generalizations of (1.1). To illustrate these connections, it is for example easily established that for σ = 1 the right-hand-side of (1.1) can be rewritten in a more algebraic fashion asa q c/24 η (q ) p′ ρ − p w (ρ) pp α − p p′ sgn(w ) q
a
functions of solvable RSOS models using CTMs along the lines of ref. [10] one is naturally led to the computation of so-called one-dimensional configuration sums. These configuration sums take forms very similar to the right-hand-side of (1.2). On the other hand, in performing Bethe Ansatz, and more particularly Thermodynamic Bethe Ansatz (TBA) computations, one is led to expressions of a similar nature to the left-hand-side of (1.2). Starting with the ABF models and pursuing the lines sketched above, Melzer conjectured [14] an infinite family of polynomial identities similar to those in (1.2). In the infinite limit these identities (p,p+1) again lead to Rogers–Ramanujan type identities, but now for Virasoro characters χr,s of unitary minimal models, i.e., for characters with the Rocha-Caridi right-hand-side form (in the sense of (1.1))
q m(m+σ)
m=0 ∞
L−m−σ m
q
=
j =−∞
∗ †
q 10j
2 +(1−4σ )j
⌊L ⌋ 2
L − 5j + σ
− q 10j
q
2 +(11−4σ )j +3−2σ
5 ⌋ ⌊ L− 2
e-mail: warnaar@mundoe.maths.mu.oz.au e-mail: pap@mundoe.maths.mu.oz.au
=
q
(q )N (q )m (q )N − m 0
0≤m≤N (1.3) otherwise.
N m q
Using the elementary formulae
=
N −1 m q
+ q N −m
N −1 m−1 q
and
N m q
=
N −1 m−1 q
+ qm
N −1 m q
1 2 ′ α∈Q w ∈W 2
p = 2 , p′ = 5 ,
(1.4)
with Q the root lattice, W the Weyl group and ρ the Weyl vector of the classical Lie algebra A1 , η (q ) = q 1/24 (q )∞ the Dedekind eta function and c=1− 6(p − p′ )2 . p p′ (1.5)
1
Introduction
1 q m(m+σ) = (q )∞ m=0 (q )m
∞ ∞
Without doubt, the Rogers–Ramanujan identities q 10j
j =−∞
2 +(1−4σ )j
− q 10j
2 +(11−4σ )j +3−2σ
σ = 0, 1 ,
(1.1)
arXiv:hep-th/9411009v1 2 Nov 1994
Abstract We conjecture polynomial identities which imply Rogers–Ramanujan type identities for branching functions associated with the cosets (G (1) )ℓ−1 ⊗ (G (1) )1 /(G (1) )ℓ , with G =An−1 (ℓ ≥ 2), Dn−1 (ℓ ≥ 2), E6,7,8 (ℓ = 2). In support of our conjectures we establish the correct behaviour under level-rank duality for G =An−1 and show that the A-D-E Rogers–Ramanujan identities have the expected q → 1− asymptotics in terms of dilogarithm identities. Possible generalizations to arbitrary cosets are also discussed briefly.
Similarly, if Qk,i(n) denotes the number of partitions of n with each successive rank in the interval [2 − i, 2k − i − 1], then by sieving methods the generating function of Qk,i can be seen to again yield the right-hand-side of (1.1) provided we choose k = 2 and i = 3 − 2σ [4]. Second, Rogers–Ramanujan identities also appear in various areas of physics. Most notable is perhaps the fact that (1.4) can be identified as the normalized Rocha-Caridi form [7] for the (p,p′ ) identity character χ1,1 of the Virasoro algebra. Indeed, each pair of positive integers p, p′ with p and p′ coprime, labels a minimal conformal field theory [8] of central charge c given by (1.5). Another branch of physics where Rogers–Ramanujan type identities have occurred is in the theory of solvable lattice models [9]. Among other works, in refs. [10, 11] Andrews, Baxter and Forrester (ABF) encountered generalized Rogers–Ramanujan identities in their corner transfer matrix (CTM) calculation of one-point functions of an infinite series of restricted solid-on-solid (RSOS) models. In addition, in refs. [12, 13] Kedem et al. conjectured many identities motivated by a Bethe Ansatz study of the row transfer matrix spectrum of the 3-state Potts model. Interestingly though, it is in fact the combination of the approaches of ref. [10] and ref. [12] to solvable models that leads to polynomial identities of the type (1.2). In computing one-point
