对分查找算法复习课件图文.ppt
VB大讲堂之对分查找(共14张PPT)

信息那些事儿
一 基本思想
猜数游戏
查找
一 基本思想
1. 对分查找有哪些要求? 被查找数据必须是有序 2. 对分查找的基本思想是什么?
首先将要查找的数据与待查找有序数组内处于中间位置的数据 进行比较,如中间位置上的数与目标数据不同,根据有序性, 就可确定应该继续在数组的前半部分还是后半部分查找。 在新确定的范围内,继续按上述方法进行查找,直到获得最终 结果。
查找
二 流程图
mid=(i+j)\2 ……
Y imid+1
ห้องสมุดไป่ตู้
开始
i1,j10
继续查找? Y
计算mid
d(mid)=key? N
d(mid)<key?
Do while i<=j
N
输出“未找到”
Y
输出找到的信息
N jmid-1
结束
查找
三 程序实现
年
请结合流程图写出对分查找核心伪代码? 已知:被查找数据已经存储在数组d中并是有序的
i
1
55
j
7
75
mid 4 a(mid) 44
65 66 55(找到了)
查找
一 基本思想
请写出在数组a(1)-a(7):1,22,33,44,55,66,77中查找目标key=11 过程中i,j,mid,a(mid)的变化过程
i
1
j
7
mid 4
a(mid) 44
1 12
3 11
何时停下查找?
2 1 (头>尾?)
Loop
Thanks
信息那些事儿
22 1
查找
对分查找

28
35
46
58
60
i
mid
j
Key>d(mid) i=mid+1
Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的 元素序列,查找键Key为12
1 2 3 4 5 6 7 8 9 10 11
6
12
15
18
22
25
28
35
46
58
60
j i
mid Key=d(mid) 输出:Mid=2 Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的 元素序列,查找键Key为12
1 2 3 4 5 6 7 8 9 10 11
6
12
15
18
22
25
28
35
46
58
60
i
mid Key<d(mid)
j
j=mid-1
Mid=(i+j)\2
若用一个数组d(1)到d(11)来存放升序的 元素序列,查找键Key为12
对分查找(有序数组)
• 对分查找的基本思想:首先将查找键与有序数 组内处于中间位置的元素进行比较,如果中间 位置上的元素数值与查找键相同,表示找到, 否则根据数组元素的有序性,就可确定应该在 数组的前半部分还是后半部分继续进行查找。 在新确定的范围内,继续按上述方法进行查找, 直到获得最终结果。
• 对分查找是一种效率很高的查找方法,但被查 找的数据必须是有序的。
若用一个数组d(1)到d(11)来存放升序的 元素序列,查找键Key为12
1 2 3 4 5 6 7 8 9 10
11
6
查找算法——顺序、对分查找
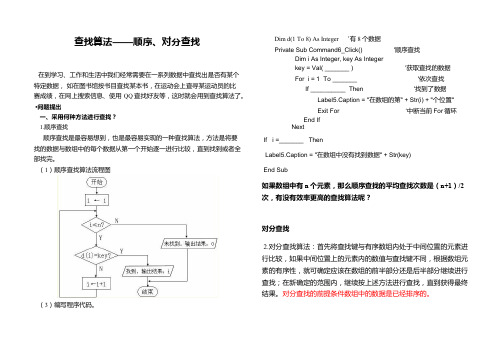
查找算法——顺序、对分查找在到学习、工作和生活中我们经常需要在一系列数据中查找出是否有某个特定数据,如在图书馆按书目查找某本书,在运动会上查寻某运动员的比赛成绩,在网上搜索信息、使用QQ查找好友等,这时就会用到查找算法了。
•问题提出一、采用何种方法进行查找?1.顺序查找顺序查找是最容易想到,也是最容易实现的一种查找算法,方法是将要找的数据与数组中的每个数据从第一个开始逐一进行比较,直到找到或者全部找完。
(1)顺序查找算法流程图(3)编写程序代码。
Dim d(1 To 8) As Integer ‘有8个数据Private Sub Command6_Click() '顺序查找Dim i As Integer, key As Integerkey = Val( _______ ) '获取查找的数据For i = 1 To _______ '依次查找If __________ Then '找到了数据Label5.Caption = "在数组的第" + Str(i) + "个位置"Exit For ‘中断当前For循环End IfNextIf i =_______ ThenLabel5.Caption = "在数组中没有找到数据" + Str(key)End Sub如果数组中有n个元素,那么顺序查找的平均查找次数是(n+1)/2次,有没有效率更高的查找算法呢?对分查找2.对分查找算法:首先将查找键与有序数组内处于中间位置的元素进行比较,如果中间位置上的元素内的数值与查找键不同,根据数组元素的有序性,就可确定应该在数组的前半部分还是后半部分继续进行查找;在新确定的范围内,继续按上述方法进行查找,直到获得最终结果。
对分查找的前提条件数组中的数据是已经排序的。
对分查找算法流程图(3)编写程序代码。
Private Sub Command4_Click() '对分查找Dim i As Integer, j As Integer, key As Integer, m As Integer Dim nc,flag As Integerflag=0 ‘flag 用于标志是否找到 key = Val(Text2.Text) '输入查找的数据 i = 1 j = 18nc = 0 '查找次数nc Do While i <= j '对分查找 nc =—————— '查找次数增加1m = __________ ‘求中间下标,若有小数,只保留整数 If __________Then ‘找到了 Label6.Caption = "在数组的第" + Str(m) + "个位置,共查找了" + Str(___) + "次"flag=_____Exit do ‘强制退出循环’End IfIf key < d(m) Then '未找到,继续查找 j=__________ Elsei = __________ End IfLoopIf flag==____ thenLabel6.Caption = "在数组中没有找到数据" + Str(key) + ",共查找了" + Str(nc) + "次"EndifEnd Sub使用对分查找,每次都把规模缩小一半,效率比顺序查找要高,但在进行对分查找前,需要将它排好序。
顺序查找和对分查找

(1)key<d(m),查找键小于中点d(m)处的数据。由数组d中数据的递增性可 以确定上:在(m,j)内不可能存在值为key的数据,必须在新的范围(I,m-1)中 继续查找。 (2)key=d(m),找到了需要的数据。 (3)key>d(m)与(1)相同的理由,必须在新的范围(m+1,j)中继续查找。 这样除了出现情况(2)在通过一次比较后新的查找范围不超过上一次查找范围的一半。
程序界面(可以在排序程序的基础上做)
command1
command2
text2
text3 text4
怎样自动生成数据呢? 怎样自动生成数据呢?
利用随机函数rnd():产生 产生[0,1)之间的随机数 利用随机函数 产生 之间的随机数 For I=1 to n randomize d(i)=fix(1000*rnd) Next i
需要
log2n
m = (i + j) \ 2或m=fix((I+j)/2)
i=m+1 j=m-1
End If Loop If pos = 0 Then Text3.Text = "找不到" + Str(Key) End If
顺序查找与对分查找比较
是否需要 事先排序 顺序查找 不需要 平均查找次数
(n+1)/2
对分查找
顺序查找分析
若一个数组有n个元素 找到第1个元素,查找1次 找到第2个元素,查找2次 …… 找到第n个元素,查找n次 平均查找次数(1+2+……+n)/n (n+1)/2
对分查找算法及程序实现27页PPT

36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
对分查找算法及程序实现
46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。——
第2轮复习对分查找算法

第2轮复习对分查找算法顺序查找次数在1和n之间对分查找成功,最少查找1;对分查找无论是否找的到,最多查找[log2n]+1对分查找不成功,则最少查找[log2n]次比如 1 2 3 4 5 key=0.5(1) i=1 j=5 循环比较(i<=j)m=3 if比较(key<d(3))i=1 j=2(2) i=1 j=2 循环比较(i<=j)m=1 if比较(key<d(1))i=1 j=0(3) i=1 j=0 循环比较(i<=j)不成立,直接退出所以总共查找了2次,即[log2n]次1 2 3 4 5 6 7对分查找次数 3 2 3 1 3 2 31 2 3 4 5 6 7 8对分查找次数 3 2 3 1 3 2 3 4 平均查找次数=19/81 2 3 4 5 6 7 8 9对分查找次数 3 2 3 4 1 3 2 3 4 平均查找次数=25/9'对分查找原数组递减(1)i = 1: j = 6: nc = 0Do While i <= jnc = nc + 1·m = Int((i + j) / 2)If a(m) = Key ThenExit DoEnd IfIf Key>a(m) Thenj = m - 1Elsei = m + 1End If等价于Find=falsei = 1: j = 6: nc = 0Do While i <= j and not findnc = nc + 1m = Int((i + j) / 2)If a(m) = Key ThenFind=trueEnd IfIf Key>a(m) Thenj = m - 1Elsei = m + 1End IfIf find=true then print原数组递减以下代码能找到If Key>a(m) Thenj = m – 1Elsei = m + 1End If相关参考题目名卷精编2018A版 P11-18 P13-11 P31-11 P17-11P加试题训练4-11 此题没有简便方法P加试题训练10-12 此题没有简便方法变式题目1:Private Sub Command1_Click()Dim a(1 To 10) As Integera(1) = 8: a(2) = 15: a(3) = 26: a(4) = 30: a(5) = 37: a(6) = 50: a(7) = 55: a(8) = 68: a(9) = 83: a(10) = 106i = 1: j = 10Key = 15Text1.Text = ""Do While i < jm = (i + j + 1) \ 2 '注意取中值范围If Key = a(m) Then Exit DoIf Key < a(m) Then j = m - 1 Else i = m + 1Text1.Text = Str(a(m)) + Text1.Text '注意输出顺序答案 26 50LoopEnd Sub'i=1 j=10 m=6 a(m)=50'i=1 j=5 m=3 a(m)=26'i=1 j=2 m=2 a(2)=key 这一步很关键变式题目2:对分查找的递归函数表示方法Dim a(1 To 100) As IntegerDim k As IntegerFunction search(key As Integer, left As Integer, right As Integer) As Integer middle = (left + right) \ 2If left > right Thensearch = -1ElseIf a(middle) > key Thenk = k + 1: search = search(key, left, middle - 1)ElseIf a(middle) < key Thenk = k + 1: search = search(key, middle + 1, right)ElseIf a(middle) = key Thenk = k + 1: search = middle: Exit FunctionEnd IfEnd IfEnd FunctionPrivate Sub Command1_Click()k = 0a(1) = 2: a(2) = 4: a(3) = 6: a(4) = 8: a(5) = 10: a(6) = 13: a(7) = 15Print Str(search(6, 1, 7))'【6】表示查找数组元素值是6,【1】数组的开始下标为1,【7】数组的结束下标为7 'search函数的返回值是值为6的数组元素的下标Print k'值为6的数组元素查找次数End Sub。
对分查找综合复习

f=false End If If Key > a(m) Then
i=m+1 Else
j=m-1 End If Loop
j
1、请分析两段程序不同之处?
2、易错点在何处?程序运行后,哪个变量值可能不一样?
三、二叉树在对分中的应用
二叉树常用于对分程序运行后,判读i、j、m、c等值
i i = 1: j = n Do While _i _<_=_j __ m = (i + j) \ 2 If Key = a(m) Then Exit Do End If
m If Key > a(m) Then _i _=_m__+_1
Else _j_=_m__- _1
End If Loop
i = 1: j = n:f=true D码:
四、对分算法综合实例
*
如何判断?
解题思路
阅读题目:探寻可能用到的算法 (高度枚举、木板起点枚举) 阅读程序:
1、确认程序目的 (寻找修补后最短木板高度) 2、初步理解各变量含义。 如ans 3、划分程序模块,按模块分析代码 (主程序,judge函数) 4、在代码中寻找算法 (对分算法) 5、文字描述与代码对应逐步分析。
If key > a(m) then
j=m-1:n=n+1
Else i=m+1:n=n-1
End if Loop Label1.caption=str(n)
1、当输入不同的key值,运行该程序,在 标签label1中的显示不同的结果共有 ______种。
2、若变量n的值最终为0,则文本框Text1 输入的数字可能是:______
对分查找算法

二分查找算法1. 算法简介二分查找算法,也称为折半查找算法,是一种在有序数组中查找特定元素的高效算法。
它通过将数组分成两部分,并重复比较目标值与数组中间元素的大小关系,从而缩小搜索范围,最终定位到目标元素的位置。
2. 算法原理二分查找算法的基本思想是不断将待搜索区间缩小一半,直到确定目标值的位置或者确定不存在目标值为止。
具体步骤如下:1.初始化待搜索区间的左边界left和右边界right,初始时left = 0,right = n-1。
2.计算待搜索区间的中间位置mid = (left + right) / 2。
3.比较目标值与中间元素的大小关系:–如果目标值等于中间元素,则返回中间元素的索引。
–如果目标值小于中间元素,则更新右边界为mid - 1,继续在左半部分进行查找。
–如果目标值大于中间元素,则更新左边界为mid + 1,继续在右半部分进行查找。
4.重复步骤2和步骤3,直到找到目标元素或者确定不存在目标元素。
3. 算法实现以下是二分查找算法的Python实现:def binary_search(nums, target):left = 0right = len(nums) - 1while left <= right:mid = (left + right) // 2if nums[mid] == target:return midelif nums[mid] < target:left = mid + 1else:right = mid - 1return -14. 算法分析时间复杂度二分查找算法的时间复杂度为 O(logn),其中 n 是数组的长度。
每次比较都将搜索范围缩小一半,因此最多需要进行 logn 次比较。
空间复杂度二分查找算法的空间复杂度为 O(1),因为只需要使用常数级别的额外空间。
算法特点•只适用于有序数组:由于二分查找算法依赖有序性,所以只能应用于有序数组。
对分课堂PPT课件

如何把握讲授深度?
关注反馈、提升自我能力
内容切割
45
教已不是那个教,学也不是那个学
第一次课
讲授 (Presentation)
重点和难点 利用式讲解
相隔一定时间(如一周)
课外
吸收 (Assimilation)
个性化学习投入 学习的负担合适
第二次课
讨论 (Discussion)
分组讨论
46
17
对比:翻转课堂从起步到流行10年历程
2000,美国 Lage等介绍在迈阿密大学教授“经济学入门”时采用
“颠倒教室”的模式以及取得的成绩
2000,Baker发表论文,正式提出翻转课堂的名称 2007, Bergmann等 在高中化学课堂中采用“翻转课堂式”教学
模式,但缺乏优质教学视频,未能在大范围推广
对分课堂
轻松高效、中国原创的高校教学新方法
1
提纲
发展过程 近期目标 操作方法 教学效果 教学难点 深层理念
2
最初想法
2006年开始在香港中文大学心理系教书 本科生《心理统计》、《生理心理学》等 学生为分数而学,不考就不学 满堂讲,讲完走人 自己觉得很不满意:教学不应该是这样的 产生了一个新想法
2008,加拿大学者提出MOOC 名称,首次开设了在线课程,包括25位本
地学生和2300网络学生。之后,各国很多教育工作者都采用了这种课程结 构开设了慕课
2011年,重要突破:16万人注册了斯坦福大学 《人工智能导论》课程,
Udacity, Coursera, edX 纷纷启动,慕课被誉为“印刷术发明以来教育最 大的革新”,呈现“未来教育”的曙光
普通教育学、 教育原理、教育学、教育学概论
排序算法--堆排序与对分查找课件-浙教版(2019)高中信息技术选修1

堆排序算法
排序算法
·图解堆排序算法(升序)
列表a: 40 38 65 97 76 13 27 49 10 索引: 0 1 2 3 4 5 6 7 8
i
40
7
38
65
9
97
76 13 27
49 10
7 40
列表a: 40 38 65 97 76 13 27 49 10 索引: 0 1 2 3 4 5 6 7 8
然后继续安排原先节点所在位置的前一个节点,重复比较+ 交换的过程,一直安排完所有元素。
注意: 构造堆结构时,真正构造堆结构会有元素移动的,一般是
从最后一个非叶子节点开始。
堆排序算法
·图解堆排序算法(升序)
列表a: 40 38 65 97 76 13 27 49 10 7 索引: 0 1 2 3 4 5 6 7 8 9
列表a: 40 38 65 97 76 13 27 49 10 7 索引: 0 1 2 3 4 5 6 7 8 9
堆排序算法
排序算法
·图解堆排序算法(升序)
②从最后一个元素开始,对列表进行构造堆结构。 规则: 当前元素节点和其左右孩子节点比较,若孩子节点比较大,
则把该节点和其孩子节点中最大的交换位置。若该节点交换后的 位置,还有孩子节点,则继续比较,直至完成堆结构。
①根节点元素与末尾元素进行交换
堆排序算法
排序算法
·图解堆排序算法(升序)
列表a: 7 索引: 0
76 65 49 40 13 27 38 10 97 123456789
7
76
65
49
40 13 27
38 10 97
②调整交换后的堆结构(调整根节点即可), 调整的元素个数减一。
对分法和一般迭代法43页PPT

71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
对分法和一般迭代法
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得此生。
•
49、勤学如春起之苗,不见其增,日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
谢谢你的阅读
高中信息技术对分查找

B
D
C
C
B
C
C
a> d(m)
j- result+ 1 4
第二单元 查找算法
课时34 二分查找
1、二分查找的概念 二分查找是一种高效的查找方法。 二分查找的前提是,被查找的数据序列是有序的(升序或降序)。 基本思想:在有序的数列中,首先将要查找的数据与有序数列内处
于中间位置的数据进行比较,如果两者相等,则查找成功;否则就根据 数据的有序性,再确定该数据的范围应该在数列的前半部分还是后半部 分;在新确定的缩小范围内,继续按上述方法进行查找,直到找到要查 找的数据,即查找成功,如果要查找的数据不存在,即查找不成功。
2、二分查找的过程
若key为查找键,数组d存放n个已按升序排序的数据。在使用二分查找 时,把查找范围[i,j]的中间位置上的数据d(m)与查找键key进行比较,结果必 然是如下三种情况之一:
(1)若key<d((m,j)内不可能存在值为key的数据,必须在新的范 围(i,m-1)中继续查找;
(2)key=d(m),找到了需要的数据; (3)key>d(m),由与(1)相同的理由,必须在新的范围(m+1,j)中 继续查找。
这样,除了出现情况(2),在通过一次比较后,新的查找范围将不超过 上次查找范围的一半。中间位置数据d(m)的下标m的计算方法:m=(i+j)\2或 m=fix((i+j)/2)
