第四章 正弦波振荡器
LC正弦波振荡器相关知识

一、石英晶体的压电效应及等效电路
石英晶体是硅石的一种。它的化学成分是二氧化硅(SiO2)。在石英晶体上按一定方位角切下的薄片,然后在晶片的两个对应表面上用喷涂金属的方法装上一对金属极板就构成石英晶体振荡元件,其结构示意如图4-21所示。
(4-1)
其中 ——总相移
——整数(包括0)
2.反馈信号必须足够大
如果从输出端送回到输入端的信号太弱,就不会产生振荡了,在图4-3电路中,可以调整 、 的数值以及放大量来实现这一要求。一般情况下,放大器的放大倍数 ,反馈电路的反馈系数 。为了使反馈信号足够大,放大器的增益必须补足反馈系数的衰减。例如,假定输入信号幅度为10mV, ,则输出信号幅度为1V。为使送回到输入端的电压仍可达到10mV,必须使 。因此,满足振荡的幅度平衡条件为:
由于它是利用电容 将谐振回路的一部分电压反馈到基极上,而且也是将LC谐振回路的三个端点分别与晶体管三个电极相连,所以这种电路又叫电容反馈三端式振荡器。
这种电路能否满足自激振荡的相位平衡条件呢?我们从放大器输入信号 开始,经过放大和反馈,看送回输入端的高频电压是否和起始电压相同。为了简化分析,假定振荡回路没有损耗,在这种情况下,如果反馈信号 和 反相,就不满足。
4.5振荡器的频率稳定问题
振荡器的频率稳定是一个十分重要的问题。例如,通讯系统的频率不稳,就会漏失信号而联系不上;测量仪器的频率不稳,就会引起较大的测量误差;在载波电话中,载波频率不稳,将会引起话音失真。
一、振荡器的频率稳定度
振荡器的频率稳定度指标是用频率稳定度来衡量的。频率稳定度有两种表示方法:
1.绝对频率稳定度。它是指在一定条件下实际振荡频率与标准频率的偏差
正弦波振荡器-PPT

2
2001年9月--12月
6
导致振荡频率不稳定得原因(续2)
2、 影响环路 Q 值得因素
o
Q1 Q2
2
Q2
Q1
f01 f02
f0
f
▪ 器件输入、输出阻抗中得有功 部分。
▪ 负载电阻得变化。
▪ 回路损耗电阻尤其就是电抗元 件 得高频损耗,环路元器件得高频 响应等。
2
2001年9月--12月
7
导致振荡频率不稳定得原因(续3)
• 泛音晶体振荡器:利用石英谐振器得泛音振动特性对频率 实行控制得振荡器称为泛音晶体振荡器。这种振荡器可以将 振荡频率扩展到甚高频以至超高频频段。
2001年9月--12月
19
1、 并联型晶体振荡电路
(1)皮尔斯(C-B)电路
RFC
Rb1
C
B
VCC
Rb 2
E
C1
Cb Re C2
JT
C
C1
E
C2
B
Lq
• 温度隔离法:将关键电抗元件置于特制得恒温槽内,使槽内得 温度基本上不随外界环境温度得变化。
▪ 利用石英谐振器等固体谐振系统代替由电感、电容构成得电 磁谐振系统,她就是高稳频率源得一个重要形式。 由于这种谐振系统构成得振荡器,不但频率稳定性、频率准确 度高,而且体积、耗电均很小,因此,在许多领域已被广泛地 采用。
0
2 L C
▪ 等号右边得负号表示频率变化得方向与电抗变化得方向刚好 相反。如电感量加大,振荡频率将降低。
2001年9月--12月
9
主要稳频措施(续1)
▪ 温度补偿法和温度隔离法:引起电抗元件电感量和电容量 变化最明显得环境因素就是温度得变化。
正弦波振荡器原理

正弦波振荡器原理
正弦波振荡器是一种产生正弦波信号的电路或设备,它的工作原理基于反馈回路和谐振现象。
首先,正弦波振荡器通常由放大器和反馈网络组成。
放大器负责提供信号的放大,而反馈网络则将一部分输出信号返回输入端,从而使电路产生振荡。
具体来说,当正弦波振荡器开始工作时,放大器会放大输入信号。
将一部分放大后的信号通过反馈网络返回到放大器的输入端,与输入信号相叠加。
这就形成了一个反馈回路。
在反馈回路中,存在向前传输的放大路径和反馈传输的路径。
放大路径将输入信号进行放大,而反馈路径则将一部分输出信号返回输入端。
在理想情况下,放大路径和反馈路径的增益相等,从而使得回路保持稳定。
当反馈回路的增益满足特定的条件时,回路会产生谐振现象。
也就是说,输入信号和反馈信号在回路中互相加强,形成一个持续不衰减的振荡。
为了保持回路稳定,正弦波振荡器会引入一些稳定元件,如电容和电感。
这些元件能够提供适当的频率选择和谐振调节,以确保输出信号的频率稳定和准确。
总之,正弦波振荡器通过反馈回路和谐振现象来产生稳定的正弦波信号。
合适的放大器、反馈网络和稳定元件的组合能够实
现不同频率范围内的正弦波振荡器。
这在电子通信、信号处理、声音合成等许多应用领域中都有着广泛的应用。
正弦波振荡器

设计实例分析
RC正弦波振荡器
适用于低频信号源,电路简单,但频率稳定性较差。
LC正弦波振荡器
适用于高频信号源,频率稳定性较高,但电路较为复 杂。
石英晶体振荡器
具有极高的频率稳定性和精度,广泛应用于各种高精 度测量和控制系统。
05
正弦波振荡器的调试与测试
调试步骤
01
检查电路连接
确保所有元件都正确连接,没有短 路或断路。
相位平衡条件
正弦波振荡器的相位平衡条件要求系统内部的相移与反馈路径上的相移之和为 整数倍的圆周,即相移之和必须等于2nπ(n为整数)。
幅度平衡条件
正弦波振荡器的幅度平衡条件要求系统内部的增益与反馈路径上的衰减之比等 于1,即系统内部的放大倍数与反馈路径上的衰减倍数相等。
04
正弦波振荡器的设计
设计流程
奈奎斯特判据
奈奎斯特判据通过分析系统的开环频率响应,判断闭环系统的稳定性。如果系统的开环频率响应在复平面的右半平面 没有极点,则闭环系统是稳定的。
伯德图判据
伯德图判据通过绘制系统开环频率响应的幅值和相位图,观察幅频特性和相频特性的变化趋势,判断系 统是否具有足够的相位裕量和幅值裕量以保证稳定性。
相位和幅度平衡条件
正弦波振荡器的应用
01
02
03
信号源
正弦波振荡器可作为各种 电子设备和系统的信号源, 提供稳定的正弦波信号。
通信
在无线通信领域,正弦波 振荡器用于生成载波信号, 实现信息的传输。
测量
正弦波振荡器产生的信号 可用于各种电学、磁学和 光学测量。
正弦波振荡器的分类
按照频率调节方式
01
分为固定频率和可调频率正弦波振荡器。
高频电子线路-第4章--习题答案
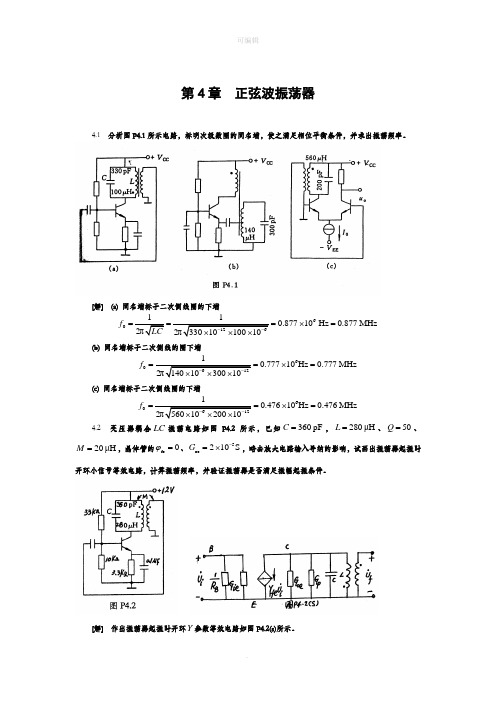
第4章 正弦波振荡器4.1 分析图P4.1所示电路,标明次级数圈的同名端,使之满足相位平衡条件,并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端601260.87710Hz 0.877MHz 2π2π3301010010f LC--===⨯=⨯⨯⨯(b) 同名端标于二次侧线的圈下端606120.77710Hz 0.777MHz 2π1401030010f --==⨯=⨯⨯⨯(c) 同名端标于二次侧线圈的下端606120.47610Hz 0.476MHz 2π5601020010f --==⨯=⨯⨯⨯4.2 变压器耦合LC 振荡电路如图P4.2所示,已知360pF C =,280μH L =、50Q =、20μH M =,晶体管的fe 0ϕ=、5oe 210S G -=⨯,略去放大电路输入导纳的影响,试画出振荡器起振时开环小信号等效电路,计算振荡频率,并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环Y 参数等效电路如图P4.2(s)所示。
略去晶体管的寄生电容,振荡频率等于0612Hz =0.5MHz 2π2π2801036010f LC--==⨯⨯⨯略去放大电路输入导纳的影响,谐振回路的等效电导为5661121042.7μS 502π0.51028010e oe oe o G G G G S S Q Lρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流EQ I 为12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以,三极管的正向传输导纳等于/0.6/260.023S fe m EQ T Y g I U mA mV ≈===因此,放大器的谐振电压增益为o muo eiU g A G U -==而反馈系数为f oU j M M F j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280meg M T A F G L -====⨯ 由于T >1,故该振荡电路满足振幅起振条件。
正弦波振荡器的组成

正弦波振荡器的组成
正弦波振荡器主要由四部分组成:放大电路、选频网络、反馈网络和稳幅电路。
其中,放大电路用于提供足够的增益,以补偿振荡过程中的能量损失;选频网络用于选择特定的振荡频率,使振荡器只在该频率下产生振荡;反馈网络则将输出信号的一部分反馈到输入端,与输入信号叠加,形成正反馈,从而维持振荡;稳幅电路则用于控制振荡幅度,使其保持稳定。
正弦波振荡器可以分为两大类:一类是利用反馈原理构成的反馈振荡器,它是应用最广的一类振荡器;另一类是负阻振荡器,它将负阻抗元件直接连接到谐振回路中,利用负阻器件的负阻抗效应去抵消回路中的损耗,从而产生出正弦波振荡。
此外,正弦波振荡器还可以根据使用的元件不同,分为LC振荡器、RC 振荡器和由这三种元件组成的复合振荡器。
其中,LC振荡器由电感(L)和电容(C)组成,可以产生高频振荡;RC振荡器由电阻(R)和电容(C)
组成,可以产生低频振荡;而复合振荡器则结合了LC和RC振荡器的特点,可以在一定范围内调节振荡频率。
总之,正弦波振荡器是一种能够产生稳定正弦波信号的电子电路,其组成包括放大电路、选频网络、反馈网络和稳幅电路等部分,可以根据不同的应用需求选择不同的元件类型和电路结构。
正弦波振荡器

要维持一定振幅的振荡,反馈系数F应设计得大 一些。一般取 1/ 2 ~ 1/8,这样就可以使得在 AoF 1 时 的情况下起振。
由上分析知,反馈型正弦波振荡器的起振条件是:
AoF 1
即
AAo
F1 F
2n
(n 1, 1, )
分别称为振幅起振条件和相位起振条件。
应用:无线电通讯、广播电视,工业上的高频感 应炉、超声波发生器、正弦波信号发生器、半导体 接近开关等。
正弦波振荡电路的组成
(1) 放大电路: 放大信号
(2) 反馈网络: 必须是正反馈,反馈信号即是 放大电路的输入信号
(3) 选频网络: 保证输出为单一频率的正弦波 即使电路只在某一特定频率下满足 自激振荡条件
17.3.2 正弦波振荡电路
正弦波振荡电路用来产生一定频率和幅值的正弦 交流信号。它的频率范围很广,可以从一赫以下到 几百兆以上;输出功率可以从几毫瓦到几十千瓦; 输出的交流电能是从电源的直流电能转换而来的。 常用的正弦波振荡器
LC振荡电路:输出功率大、频率高。 RC振荡电路:输出功率小、频率低。 石英晶体振荡电路:频率稳定度高。
在平衡条件下,反馈到放大管的输入信号正好等于放 大管维持及所需要的输入电压,从而保持反馈环路各点电 压的平衡,使振荡器得以维持。
4.1.2平衡条件
振荡器的平衡条件即为
T ( j) K( j)F( j) 1 也可以表示为 T ( j) KF 1
(4 ─ 9a)
T K F 2n
2) 相位平衡的稳定条件
相位稳定条件指相位平衡条件遭到破坏时,线路本 身能重新建立起相位平衡点的条件;若能建立则仍能保 持其稳定的振荡。
强调指出:相位稳定条件和频率稳定条件实质上是 一回事。因为振荡的角频率就是相位的变化率 d 。
正弦波振荡器的原理

正弦波振荡器的原理
正弦波振荡器是一种电路,用于产生稳定的正弦波信号。
它由几个基本组件构成,包括放大器、反馈电路和频率控制元件。
首先,放大器是振荡器的核心部分。
它负责放大输入信号的幅度,并提供足够的反馈信号以维持振荡器的振荡。
接下来是反馈电路。
它将一部分输出信号反馈到放大器的输入端,形成正反馈回路。
这样,输出信号经过放大后再次进入放大器,形成持续的振荡。
最后是频率控制元件,通常是由电容或电感构成的电路。
它的作用是控制振荡器的频率。
通过调整电容或电感的值,可以改变振荡器输出信号的频率。
当振荡器开始工作时,初始信号经过放大器放大后进入反馈电路。
由于正反馈的存在,输出信号不断增大,直到达到稳定的振荡状态。
振荡器的稳定性取决于正反馈回路的增益和频率控制元件的精确性。
需要注意的是,正弦波振荡器的工作受到许多因素的影响,例如温度、噪声和元件的非线性等。
因此,设计和优化正弦波振荡器需要考虑这些因素,并采取适当的措施来提高其性能和稳定性。
电工学-第四章 正弦波振荡电路

R
1 jL jC j(L 1
C
)
( R L)
.
I
L/C
R j(L 1 )
C
+ L
•
U
C
_
R
2020/4/18
24
LC并联谐振回路的选频特性
•
Z
U
•
I
L/C
R j(L
1)
C
.
I
+ L
•
U
C
_
R
•
当LC并联回路发生谐振时,端电压 U 与总电
流
•
I
同相,即阻抗Z表现为纯电阻性。
谐振频率
o
Uf
•
F
Uo
•
•
由以上知,放大电路产生自激振荡的条件是 U f U i
••
•
则
AuF
Uo
•
U
•
f
U
•
f
1
Ui Uo Ui
2020/4/18
7
自激振荡
总结出自激振荡的条件:
(1)相位平衡条件
反馈电压
•
U
f
与输入电压
•
U
i
同相位,形成正反馈
(2)幅值平衡条件
反馈电压与输入电压大小相等: U f U i
C2
uf
首先判断相位平衡条件,见瞬时极性
2020/4/18
35
RB1
RC
+
RB2
uf
+
ube
RE
UCC
+
C1
L
+
C2
CE
正弦波振荡器工作原理

正弦波振荡器工作原理
正弦波振荡器是一种能够产生连续的正弦波信号的电路或装置。
其工作原理主要涉及负反馈和多级放大。
首先,正弦波振荡器需要一个放大器来提供正反馈。
放大器输入一个小的信号,经过放大后得到一个较大的信号,然后再经过反馈回到放大器的输入端。
这个反馈信号会与输入信号相加,形成一个增强的信号。
其次,放大器需要一个频率选择网络。
频率选择网络可以选择特定频率范围内的信号进行放大,而抑制其他频率的信号。
这个频率选择网络由电容和电感组成,被称为谐振电路。
谐振电路能够产生一个特定的频率,使其成为正弦波振荡器的频率。
最后,通过不断调整放大器增益和频率选择网络的参数,正弦波振荡器能够在稳定的条件下产生连续的正弦波信号。
当输入的幅度大于输出信号的放大倍数时,放大器会把它抑制回到指定的幅度,使信号保持稳定。
总结起来,正弦波振荡器的工作原理是通过负反馈和多级放大实现连续的正弦波信号输出。
频率选择网络能够选择特定频率范围内的信号进行放大,而抑制其他频率的信号。
不断调整放大器增益和频率选择网络的参数,可以使正弦波振荡器产生稳定的正弦波信号。
高频电子线路作业及答案(胡宴如 狄苏燕版)四章
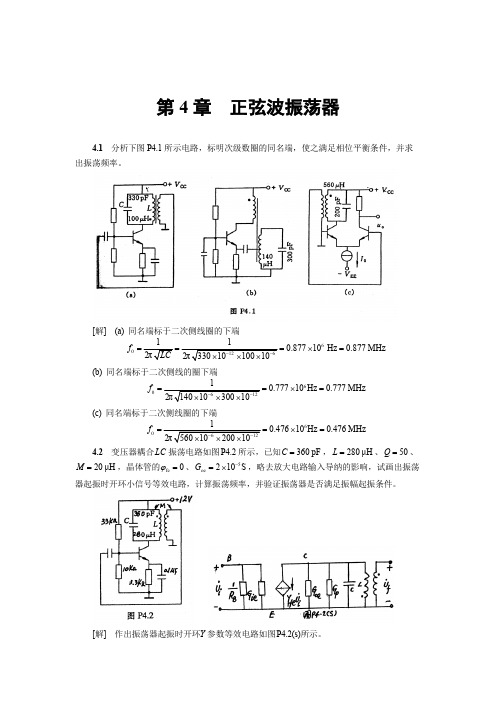
第4章 正弦波振荡器4.1 分析下图P4.1所示电路,标明次级数圈的同名端,使之满足相位平衡条件,并求出振荡频率。
[解] (a) 同名端标于二次侧线圈的下端600.87710Hz 0.877MHzf ===⨯=(b) 同名端标于二次侧线的圈下端600.77710Hz 0.777MHzf ==⨯=(c) 同名端标于二次侧线圈的下端600.47610Hz 0.476MHzf ==⨯=4.2 变压器耦合振荡电路如图P4.2所示,已知,、、LC 360pF C =280μH L =50Q =,晶体管的、,略去放大电路输入导纳的影响,试画出振荡20μH M =fe 0ϕ=5oe 210S G -=⨯器起振时开环小信号等效电路,计算振荡频率,并验证振荡器是否满足振幅起振条件。
[解] 作出振荡器起振时开环参数等效电路如图P4.2(s)所示。
Yhe b e12略去晶体管的寄生电容,振荡频率等于0Hz =0.5MHzf ==略去放大电路输入导纳的影响,谐振回路的等效电导为5661121042.7μS502π0.51028010e oe oe o G G G G S S Q L ρω--=+=+=⨯+=⨯⨯⨯⨯⨯由于三极管的静态工作点电流为EQ I 12100.712330.6mA 3.3k EQV I ⨯⎛⎫-⎪+⎝⎭==Ω所以,三极管的正向传输导纳等于/0.6/260.023Sfe m EQ T Y g I U mA mV ≈===因此,放大器的谐振电压增益为omuo eiU g A G U -==而反馈系数为f oU j M MF j L LU ωω-=≈=-这样可求得振荡电路环路增益值为60.023203842.710280m e g M T A F G L -====⨯???由于>1,故该振荡电路满足振幅起振条件。
T 4.3 试检查图P4.3所示振荡电路,指出图中错误,并加以改正。
[解] (a) 图中有如下错误:发射极直流被短路,变压器同各端标的不正确,构成负反f L 馈。
振荡器原理

分类:
– 并联谐振型晶体振荡器:等效为电感 – 串联谐振型晶体振荡器:等效为串联谐振回路
30
4.5.1 并联谐振型晶体振荡电路
C
C
C1
E
LJ T
C2
L1
E
C
JT
L2
B
B
C-b型电路(皮尔斯电路) b-e型电路(密勒电路)
VCC C
Cq C1
C1
E
Co Lq
JT C2
C2
rq
C L RL
3、起振条件
g n GT
4、平衡条件
g n GT
40
Vf 反馈网络F
振幅平衡条件: AF 1 相位平衡条件: A F 2n (n 0,1,2,3, )
7
二、 振荡器的起振条件
1、 平均放大倍数A
Vi
Vo
放大器A
2、 起振条件
Vf 反馈网络F
振幅起振条件: AF 1 相位起振条件: A F 2n (n 0,1,2,3, )
AF越大,起振越容易,通常取F =1/2~1/8
VC C
200pF 100pF C3 C4
0.01uF
C2 200pF
L 8uH
C5 5.1pF
C1 51pF
29
4.5 石英晶体振荡器
频率稳定度可达到10-6~10-11。 石英晶体振荡器的优点:
– 石英晶体的等效谐振回路有很高的标准性; – 石英晶体的Q值可高达数百万量级; – 在串并联谐振频率之间很窄的工作频带内,具有
1 L(C3 C4 )
❖可以通过调节C4来调节输出频率 ❖频率覆盖系数为1.6~1.8
27
例1:振荡电路如图示,它是什么类型振荡器?有何优 点?计算它的振荡频率。
高频电路课后答案
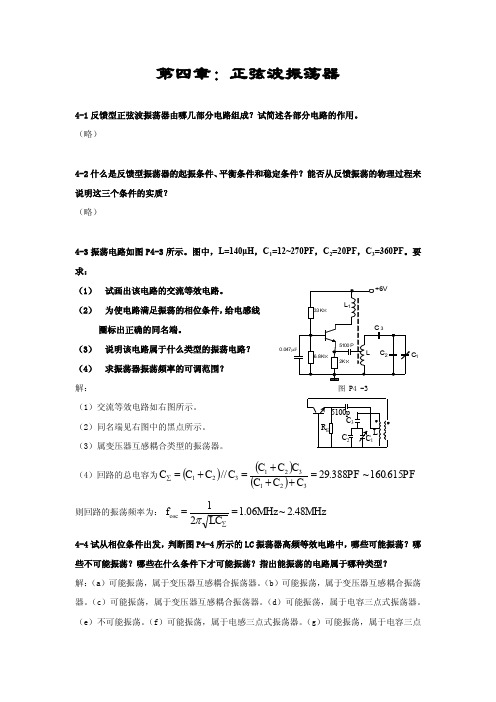
式振荡器(考虑晶体管内部的 BE 结电容) 。 (h)可能振荡,属于电感三点式振荡器,但要求 L1、C 等效为电容。(i)可能振荡,属于电容三点式振荡器,但要求 L2、C2 等效为电容,且 L1、C1 等效为电感。
C
L 1
L2 C L1 L2 L2 L1
(c)
C
(a )
(b)
C1 C1 C2
(d )
f1 f 0 f 2
4-12 10MHZ 晶体振荡器如图 P4-12 所示。图中,Ce、Cφ 视为对高频短路,LC 为高频扼流 圈。 (1) 画出交流等效电路。指出该晶振电路属于哪种类型? (2) 说明晶振器及 C、C3 在电路中的作用。 (3) 计算反馈系数 F=?求出电路能维持振荡的最小增益 AV 。
C1 // C2 C 90.71PF ~ 105.71PF
f osc
1 1.308MHz ~ 1.4123MHz 2 LC
反馈系数为: F
C1 100 0.17 。 C2 600
(3)为了保证电路起振,则要求 F A 1 即电路的增益至少为 A
1 6。 F
(3) 分析电路是否能满足振荡的相位条件。
LC
Rb1
Cb
C1
C2
Rb2
Ce LD C
Re C
L1 L2
C1 C 2 L1 L2
-1Байду номын сангаасV
图 P4 -8 题图 4. 8
解: (1)交流等效电路如右图所示。它属于电感三点式振荡器。 (2)振荡频率为:
f osc 2
1
L1 L2
f1
C1C2 C1 C2
C1 C2 L
正弦波振荡器

或者写成:
A F 1
A0F 1
A F 2n
课后思考题:在LC振荡器中,谐振回路是否等效成一个 电阻?振荡频率是否严格等于谐振回路的谐振频率?
三. 稳定条件
振荡器在工作过程中, 不可避免地要受到各种外界因素变化
的定影因响素,将如引电起源放电大压器波和动回、路温的度参变数化发、生变噪化声,干结扰果等使A。F这些变不化稳,
Uf
是反馈电压、 Ui 是输入电压、
A
是开环电压增益,
F 是反馈系数,
反馈型振荡器 正常工作的 三个条件:
一:起振条件
在接通电源瞬间, 电路中存在各种电扰动, 这些扰动均具
有很宽的频谱。 如果选频网络是由LC并联谐振回路组成,
则其中只有角频率为 谐振角频率ω0的分量才能通 过反馈产生
较大的 反馈电压 U f 。 如果在谐振频率处, U f 与原输入电
U f
j(
X
jX be be X
bc
)
U
c
X be X ce
U c
由电于路必中须U i满与足U正 c反反馈相:,所所以以UUi与f
U f
与
同相,而在共射 U c 反相
即:
X be 0 X ce
V
X1
X2
C2
C1
X3 L
(a)
V
L2
L1
X1
X2
X3 C
(b)
(a) 电容反馈振荡器; (b) 电感反馈振荡器
A 0
U c UC UCQ
Z
0
0
1)振幅平衡的稳定条件
2)相位平衡的稳定条件
第三节 反馈型LC振荡器
一 ,互感耦合振荡电路 二,电容反馈振荡电路 三,电感反馈振荡电路 电感三点式和电容三点式振荡电路的比较
第4章《高频电子线路》_(曾兴雯)_版高等教育出版社课后答案

第4章 正弦波振荡器
第一节
反馈振荡器的原理
一、反馈振荡器的原理分析
组成: (1)放大器
放大器通常是以某种选频网络(如振荡回路)作负载, 是调谐放大器。
(2)反馈网络 一般是由无源器件组成的线性网络。 正反馈: U’i(s)与Ui(s)相位相同。
5
第4章 正弦波振荡器
一、反馈振荡器的原理分析
Ui (s) Us (s) Ui(s)
若 Uo Uc
jL Uc ZL R L e 放大器的负载阻抗 所以 Ic T(j) Yf (j)ZLF(j) Yf ( j)ZL F( j) 1
9
U Uc Uo Ic c 又 K( j) Yf (j)ZL I Ui Ub c Ub 因为 jf Ic Yf ( j) Yf e 晶体管的正向转移导纳 Ub
振幅条件的图解表示
U0 U02 U01 Ub1 Ub2 Ub3 Ub
振荡开始时应为增幅振荡!
12
第4章 正弦波振荡器
四、稳定条件 1、振幅稳定条件
T U i
K U i
0
Ui UiA
0
U i U iA
U’i UiA U’’i
因此,振荡器由增幅振荡过渡到稳幅振荡,是由放
大器的非线性完成的。由于放大器的非线性,振幅稳定 条件很容易满足。
②相位平衡条件,即正反馈条件
U b jX 2 I
U c jX 1 I
X1、X2为同性质电抗元件
判断三端式振荡器能否振荡的原则:
“射同余异”
或 “源同余异”
18
第4章 正弦波振荡器
一、振荡器的组成原则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按选频回路元件性能分类
LC 振荡器 RC 振荡器 晶体振荡器等
ui uo u (s 能 产 生 自 激 振 荡 一 个f基)本 us 放大器 Σ T(s) = Ao (s)F(s) = A(s) () 其 中 : 必须 构成正反馈回路 , 的条件是 ui (s) 即反馈到输入端的信号和放 uf 称为反馈系统的环路增益。 大 器输入信号相位相同。 反馈网络 显然在某一个工作频率 ωo 时 , 如果设放大器的电压放大倍 F(s) () ) 如果 A( ωo, ( jωo ) = 1 ,即 ui (s) = uf (s 即 o( ) ,反馈网络的反馈系数 数为 A(js)F反馈网络的反馈系数) F( )( jω ) → ∞ 即表明在没有外加信号,也可以维持振荡输出 为 F(s)则有: ,即表明在没有外加信号 也可以维持振荡输出 则有 sA f 则有: 即表明在没有外加信号 也可以维持振荡输出, uo ( s) uo ( s) A f ( s) = 闭环增益 : 开环增益: A ( s) = u ( s) ω )F ( jω ) = 1 us ( 故自激振荡的条件为: 故自激振荡的条件为s) , A( j开环增益 : o i
实际上振荡器在开始建立振荡时 应 满 足 的 条 件 为 : A⋅ F > 1
Cb
主网络
ic ib
VT + Rb1 Rb2 - Re C
-
uo L1
+
反馈网络 M + Lf
uf
-
ui
Ce
EC
即有: 即有 A >
uf uo 1 .而 A = ,F = ∴有u f > ui F ui uo
∆u04
如右图:分别为基本放大器 A 和 反 馈 网 络 1/F 的 曲 线 , 如果设开启电源后产生扰动电压 {∆ u i 1 }, 则有 :
自动地重新建立起相位平衡点的条件。 自动地重新建立起相位平衡点的条件。 的符号应相反,以消弱或抵消由外因引起的变化, 因引起的相位变化 ∆ϕT 的符号应相反,以消弱或抵消由外因引起的变化,
dϕ dt
∆ω ∂ω 频率稳定的条件. 频率稳定的条件ϕ Z 其中 ϕ Y 为 放大器正 向传输 导纳 的相移 Q ϕ A = ϕY + . 如果设某种原因,相位平衡破坏,产生一个很小的相位增益量 ϕ Z 为 ,产生一个很小的相位增益量。 如果设某种原因,相位平衡破坏选频网络 负载阻 抗的 相移 。
Z
c1
或 ϕ Υ + ϕ Z + ϕ F = 2nπ
uf
反馈网络
ϕF
其中: 其中 ϕ Υ : 为集电极基波电流 i c1与基极谐振阻抗 的相角
A( jω )和F ( jω )的意义
& & & & 若: U 0 = U c 1 Ui = Ub & & & & U 0 U c1 I c1 U c1 A( jω ) = = = = −Y ( jω ) Z L & i U b U b I c1 & & & U & U c1 ZL = − = R L e jϕ 放大器的负载阻抗。 &c 1 I
T ( jω ) = −Y ( jω ) Z L F ( jω ) = Y ( jω ) Z L F ′( jω ) = 1 相位平衡条件: 振幅平衡条件:
ϕY + ϕ Z + ϕ F ′ = 2nπ
YRL F ′ = 1
(n = 0,1,2,.....)
2 振荡器平衡状态的稳定条件
为了维持振荡器稳定的工作, 为了维持振荡器稳定的工作,只满足平衡 条件和起振条件是不够的, 条件和起振条件是不够的,因为平衡条件只能 说明振荡可能平衡在某一状态, 说明振荡可能平衡在某一状态,而不能说明振 荡的平衡状态是否稳定. 荡的平衡状态是否稳定.
Z
ui
放大器
ϕY
ic1 ZL
LC选频 选频
ϕZ
uf
反馈网络
ϕF
uo
Y ( jω )为晶体管的正向转移导 纳 & I c1 Y ( jω ) = = Y e jϕ & Ub
Y
A ( jω ) F ( jω ) = 1
一般Y和 都是随信号大小而变化 F 一般 和A都是随信号大小而变化 。 ( jω) 一般情况下是线性电路的 F 电压比值。若考虑晶体管的输入电阻影响, 电压比值。若考虑晶体管的输入电阻影响,( jω ) 也会随信号大小 稍有变化,为了便于分析, 稍有变化,为了便于分析,引入一个与 F ( jω )反号的反馈系数 F ′( jω )
第四章 正弦波振荡器
概述 4.1 反馈振荡器原理 4.2 LC振荡电路 振荡电路 4.3振荡器的频率稳定性 4.3振荡器的频率稳定性 4.4 晶体振荡器 4.5 振荡器中的几种现象 RC振荡器 4.6 RC振荡器
第4章 正弦波振荡器 章
振荡器:在没有激励信号的情况下, 振荡器:在没有激励信号的情况下,能自动的将直流电源能量转 换为周期性交流信号输出的电子电路。 换为周期性交流信号输出的电子电路。
ϕYF ′ = −ϕ Z
ω0
Y F ′
外因作用 ϕ YF ′ ∆ ϕ
ω1 ω 2
∆ω
ϕ Y′ F
′
ω
1
→
ω
ϕY′F ′
ϕYF ′
ω
2
∆ϕ YF ′ − ∆ϕ Z
ω2 = ω1 + ∆ω
− ∆ϕ Z = ∆ϕYF ′
∑ϕ = 0
满足相位平衡
Q ∆ω = (ω2 − ω1 ) > 0
∆ϕ Z < 0
满足
uo (s) uo (s) ui (s) Ao (s) Ao (s) = = = ∴ Af (s) = u f (s) uo (s) u f (s) 1 − Ao (s)F(s) ui (s) − u f (s) 1− 1− ui (s) ui (s) uo (s)
4.1.2 振荡条件的分析
1、平衡条件: 、平衡条件:
∆ui 1 → ∆u01 → ∆u f 1 → ∆ui 2 = ∆u f 1 ∆ui 2 → ∆u02 → ∆u f 2 → ∆ui 3 = ∆u f 2 ∆ui 3 → ∆u03 → ∆u f 3 → ∆ui 4 = ∆u f 3
uo
∆u f 3 1/F
A
∆u03
∆u02
∆ u 01
∆u f 1
∆u f 2
若 令 s = jω 代 入 上 式 ,则 有 : 则 一o ( s反馈振荡器工作原理分析 A )F ( s ) = Ao ( jω )F ( jω )
4.1 反馈振荡器原理 .
反馈系数: 反馈系数 : F(s) = u (s)
o
uf (s)
又因为: 又因为: ui (s) =us (s) + uf (s)
A
. .
B
A
1) 振幅平衡的稳定条件
AF = 1 则A =
1 F
1 F
1 F
A曲线和 用A曲线和 讨论: 讨论:
相交图形研究。 相交图形研究。
•Q
O
UomQ
UOm
uom > uomQ
uom < uomQ
A<
1 F 1 A> F
即AF < 1
即AF > 1
软激励特性
表明:在平衡点附近,放大器增益随信号振幅的变化特性具有负斜率. 表明:在平衡点附近,放大器增益随信号振幅的变化特性具有负斜率.
A ( j ω ) = Ae 又由于 F ( j ω ) = Fe
jϕ A jϕ F
A ( jω ) F ( jω ) = 1
所以振荡平衡条件的约束方程可以分为两个方程: 所以振荡平衡条件的约束方程可以分为两个方程 ic1 ui LC ϕ 晶体管 AF = 1 ϕY 选频网络 12 ϕ A + ϕ F = 2nπ ( n = 0,,⋅ ⋅ ⋅ ⋅ ⋅ ⋅) u
外因去掉, 作用下, 外因去掉,在 − ∆ϕ Z 作用下, ∆ω ↓
∂ϕ Z <0 ∂ω
重新回到平衡态 ω1
.
振荡电路分析实例
如下图所示的电路为互感耦合正弦波振荡器.
自激振荡过程: 自激振荡过程
开启电源 → u i ↑→ i b ↑→ i c ↑→ i c 1 ↑ → u o ↑→ u f ↑= u i ↑
z
→ 信号周期缩短 ϕ → 信号频率 ↑→ ∂ (ϕ Y + ϕ Z + ↓ ) ∂ϕ Z F
∂ω
∂ω
∂ω
∆ω > 0 。
<<
∂ω
ωo
tω
ϕY + ϕ Z + ϕ F ′ = 2nπ
n=0 则 ϕ z = −(ϕ y + ϕ F ′ ) = −ϕYF ′
当ω = ω1 相位平衡
− ϕYF ′ ϕ Z
u
<< ,
即相位变化时, 0 或 ∂ ( ϕ A , 由于ω = :,∆ ( ϕ A + ϕ F ) < 频率也变化+ 故相位稳定条件也就是 即相位变化时,频率也变化, ϕ F ) < 0 即要求: 即要求
= 又因为一般 ϕ AF 和 ϕ f F 对频率变化的灵敏性远小于 ϕ Z , 即有 Y ui ∆ ϕ T > 0∂ ϕ Z 即设: 即设: Y 反馈信号 ϕ fF 超前原输入信号 ui 一个相角 ∂ u ∂ϕ Z ∂ϕ
