05电本信号与系统期末考试AB卷标准答案
信号与系统期末考试试题(有答案的)

信号与系统期末考试试题(有答案的)信号与系统期末考试试题一、选择题(共 10 题,每题 3 分,共 30 分,每题给出四个答案,其中只有一个正确的)1、卷积 f 1(k+5)*f 2(k-3) 等于。
(A ) f 1(k)*f 2(k) ( B ) f 1(k)*f 2(k-8) ( C )f 1(k)*f 2(k+8) ( D ) f 1(k+3)*f 2(k-3)2、积分(t 2) (1 2t )dt 等于。
(A ) 1.25( B ) 2.5( C ) 3(D ) 53、序列 f(k)=-u(-k) 的 z 变换等于。
(A )z( B ) -z(C )1( D )1z 1 z1 z 1z14、若 y(t)=f(t)*h(t), 则 f(2t)*h(2t) 等于。
(A )1y(2t ) ( B ) 1 y( 2t ) (C ) 1 y(4t) ( D ) 1 y( 4t ) 4 2 42 5、已知一个线性时不变系统的阶跃相应g(t)=2e-2tu(t)+ (t ) ,当输入 f(t)=3e—tu(t)时,系统的零状态响应y f (t)等于(A )(-9e -t+12e -2t)u(t)(B ) (3-9e -t +12e -2t)u(t)( C ) (t ) +(-6e -t +8e-2t)u(t)( D )3 (t ) +(-9e -t +12e-2t)u(t)6、连续周期信号的频谱具有(A )连续性、周期性(B )连续性、收敛性( C )离散性、周期性(D )离散性、收敛性7、周期序列 2 COS (1.5 k45 0) 的周期 N 等于(A ) 1( B ) 2( C )3( D ) 48、序列和kk 1 等于( A )1 (B) ∞ (C) u k1 (D) ku k 19、单边拉普拉斯变换F s2s1e 2 s的愿函数等于s 2A tu tB tu t 2C t 2 u tD t 2 u t 210、信号 f tte 3tu t 2 的单边拉氏变换 F s 等于A 2s 7 e s 32 s 3e 2s2B2s 3C se2 s 3D e 2s33 2s s3s二、填空题(共9 小题,每空 3 分,共 30 分)1、卷积和 [( 0.5)k+1u(k+1)]*(1 k) =________________________、单边z 变换F(z)=z的原序列 f(k)=______________________22z1,则函数 y(t)=3e -2t·f(3t) 的单、已知函数f(t)的单边拉普拉斯变换F(s)=s31s边拉普拉斯变换 Y(s)=_________________________4、频谱函数 F(j)=2u(1-)的傅里叶逆变换 f(t)=__________________5、单边拉普拉斯变换 F (s)s23s 1的原函数s2sf(t)=__________________________6、已知某离散系统的差分方程为2 y(k )y( k1) y(k2) f (k ) 2 f (k1),则系统的单位序列响应h(k)=_______________________t27、已知信号 f(t) 的单边拉氏变换是 F(s),则信号y(t) f (x)dx 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为y '' t 2 y ' t5y tf ' t f t该系统的冲激响应h(t)=、,22t k9 写出拉氏变换的结果66u t三、(8 分)四、( 10 分)如图所示信号 f t ,其傅里叶变换F jw F f t,求(1) F 0 (2) F jw dw六、( 10 分)某LTI 系统的系统函数H ss2,已知初始状态22ss1y 00, y 02, 激励 f t u t , 求该系统的完全响应。
信 与系统期末考试试卷有详细答案

《 信号与系统 》考试试卷(时间120分钟)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常 数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
《信号与系统》期末试卷A卷与答案.pptx

0
y(t)
1 t2 2
Tt
1 T2
1
2 t Tt
2
3T2
2
2
0
t 0 0t T
T t 2T 2T t 3T 3T t
3、(3×4 分=12 分)
j dX ( j / 2)
(1)
tx(2t) 2
d
(1t)x(1t) x(1t) tx(1t)
(2) X ( j)e j j d [X ( j)e j] jX ' ( j)e j d
(3)
t
dx(t) dt
X ( j)
dX ( j) d
第 页 4共 6 页
学海无 涯
4、(5 分)解 :
s2
1 2s 2
s2 2s 2
s2 2s 2
F (s) es 2(s 1) es (s 1)2 1
f (t) (t 1) 2e(t 1) cos(t 1)u(t 1)
学海无涯
《信号与系统》期末试卷 A 卷
班级:
学号:
姓名:
_ 成绩:
一. 选择题(共 10 题,20 分)
j( 2 )n
j( 4 )n
1、 x[n] e 3 e 3 ,该序列是
A.非周期序列 B.周期 N 3
D。
C.周期 N 3/ 8
CDCC
D. 周期 N 24
2、一连续时间系统y(t)= x(sint),该系统是
3
3
(b)若系统因果,则Re{s} 2,h(t) 1 e2tu(t)-1 et u(t) 4分
3
3
(c)若系统非稳定非因果,则Re{s} -1,h(t) 1 e2t u(t) 1 et u(t) 4分
信号及系统期末考试试题及答案

信号及系统期末考试试题及答案一、选择题(每题2分,共20分)1. 信号x(t)=3cos(2π(5t+π/4))是一个:A. 周期信号B. 非周期信号C. 随机信号D. 确定性信号2. 系统分析中,若系统对单位阶跃函数的响应为u(t)+2,则该系统为:A. 线性时不变系统B. 线性时变系统C. 非线性时不变系统D. 非线性时变系统3. 下列哪个是连续时间信号的傅里叶变换:A. X(k)B. X(n)C. X(f)D. X(z)4. 信号通过线性时不变系统后,其频谱:A. 仅发生相位变化B. 仅发生幅度变化C. 发生幅度和相位变化D. 不发生变化5. 单位脉冲函数δ(t)的拉普拉斯变换是:A. 1B. tC. e^(-st)D. 1/s二、简答题(每题5分,共10分)1. 解释什么是卷积,并给出卷积的数学表达式。
2. 说明傅里叶变换与拉普拉斯变换的区别。
三、计算题(每题15分,共30分)1. 给定连续时间信号x(t)=e^(-t)u(t),求其傅里叶变换X(f)。
2. 给定离散时间信号x[n]=u[n]-u[n-3],求其z变换X(z)。
四、分析题(每题15分,共30分)1. 分析信号x(t)=cos(ωt)+2cos(2ωt)通过理想低通滤波器后输出信号的表达式,其中滤波器的截止频率为ω/2。
2. 讨论线性时不变系统的稳定性,并给出判断系统稳定性的条件。
五、论述题(每题10分,共10分)1. 论述信号的采样定理及其在数字信号处理中的应用。
参考答案一、选择题1. A2. A3. C4. C5. A二、简答题1. 卷积是信号处理中的一种运算,它描述了信号x(t)通过系统h(t)时,输出信号y(t)的计算过程。
数学表达式为:y(t) = (x * h)(t) = ∫x(τ)h(t-τ)dτ。
2. 傅里叶变换用于连续时间信号的频域分析,而拉普拉斯变换则适用于连续时间信号,并且可以处理有初始条件的系统。
三、计算题1. X(f) = 3[δ(f-5) + δ(f+5)]。
信号与系统期末考试复习题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
信号与系统期末考试题及答案(第一套)

信号与系统期末考试题及答案(第⼀套)信号与系统期末考试题及答案(第⼀套)符号说明:为符号函数,为单位冲击信号,为单位脉冲序列,为单位阶跃信号,为单位阶跃序列。
⼀、填空(共30分,每⼩题3分)1. 已知某系统的输⼊输出关系为(其中X(0)为系统初始状态,为外部激励),试判断该系统是(线性、⾮线性)(时变、⾮时变)系统。
线性时变2. 。
03.4. 计算=。
5. 若信号通过某线性时不变系统的零状态响应为则该系统的频率特性=,单位冲激响应。
系统的频率特性,单位冲激响应。
6. 若的最⾼⾓频率为,则对信号进⾏时域取样,其频谱不混迭的最⼤取样间隔。
为7. 已知信号的拉式变换为,求该信号的傅⽴叶变换=。
不存在8. 已知⼀离散时间系统的系统函数,判断该系统是否稳定。
不稳定9.。
310. 已知⼀信号频谱可写为是⼀实偶函数,试问有何种对称性)sgn(t )(t δ)(k δ)(t ε)(k ε)0(2)()()(2X dt t df t f t t y +=)(t f ________________?∞-=-+32_________)221()32(dt t t t δ?∞∞-=--_________)24()22(dt t t εε??∞∞-==--1)24()22(21dt dt t t εε},3,5,2{)()},3()({2)(021=↓=--=K k f k k k f kεε)()(21k f k f *________}12,26,21,9,2{)()(21↓=*k f k f )(t f ),(),()(00为常数t K t t Kf t y f -=)(ωj H ________=)(t h ________0)(t j Ke j H ωω-=)()(0t t K t h -=δ)(t f )(Hz f m )2()()(t f t f t y ==max T ________m ax T )(6121max max s f f T m==)1)(1(1)(2-+=s s s F )(ωj F ______2121)(---+=z z z H ______=+-+?∞∞-dt t t t )1()2(2δ______)(,)()(3ωωωωA e A j F j -=)(t f。
精编《信号与系统》期末考试试卷a答案
西南交通大学2014-2015学年第(1)学期考试试卷阅卷教师签字: 一、选择题:(20分)本题共10个小题,每题回答正确得2分,否则得零分。
每小题所给答案中只有一个是正确的。
1.信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( B )A.2B.2)2(-t δC. 3)2(-t δD. 5)2(-t δ 2.已知)(t f ,为求)(0at t f - 则下列运算正确的是(其中a t ,0为正数)( B ) A .)(at f - 左移0t B . )(at f - 右移 at 0C . )(at f 左移 0tD . )(at f 右移at 03.某系统的输入-输出关系)1(t )(y 2-=t x t ,该系统是( C ) A .线性时不变系统 B .非线性时不变系统 C .线性时变系统 D .非线性时变系统4.一个因果稳定的LTI 系统的响应可分为自由响应与受迫响应两部分,其自由响应的形式完全取决于( A ) A.系统的特性 B.系统的激励 C.系统的初始状态D.以上三者的综合 5.信号)2()1(2)(-+--t r t r t r 的拉氏变换的收敛域为 ( C )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在 6.理想低通滤波器是( C )A .因果系统 B. 物理可实现系统C. 非因果系统D. 响应不超前于激励发生的系统 7.时域是实偶函数,其傅氏变换一定是( A )A .实偶函数 B.纯虚函数 C.任意复函数 D.任意实函数班 级 学 号 姓 名密封装订线 密封装订线 密封装订线8.信号)100()(t Sa t f =,其最低取样频率s f 为(A )A.π100B.π200C.100π D. 200π 9.已知信号)(t f 的傅氏变换为),(ωj F 则)3-2-(t f 的傅氏变换为( C ) A .ωω2)3(3j e j F - B.ωω2)3(3j e j F -- C .ωω6)3(3j e j F - D.ωω6)3(3j e j F -- 10.已知Z 变换Z 11[()]10.5x n z-=-,收敛域0.5z >,求逆变换得x (n )为( A ) A .0.5()n u n B. 0.5(1)n u n --- C. 0.5()n u n -- D. 0.5(1)n u n ---- 二、(14分)画图题1.已知)21(t f -波形如图所示,画出)(t f 的波形。
05电本信号与系统期末考试AB卷标准答案

05电本信号与系统期末考试AB卷标准答案一、选择题:(每小题2分,共40分,请把每道选择题唯一正确答1.积分dt t t e t )]()(['2δδ+?∞∞--等于:()(A )0 (B )1 (C )2 (D )3 2.序列和)2()4sin(-∑-∞=n n kn δπ等于:()(A )1 (B )u(k) (C )u(k-2) (D ))2(-k δ 3.序列卷积和)4()2()2()1(-*+--*+k k u k k u δδ等于:()(A ))(k δ (B ))1(-k δ (C ))1(-k u (D ))3(-k u 4.已知某系统的单位样值响应)(2)(n u n h n =,则该系统的因果性和稳定性:()(A )因果,稳定(B )因果,不稳定(C )非因果,稳定(D )非因果,不稳定5.已知某离散系统单位样值响应为:)1(2)()(-+=n n n h δδ,输入序列为:)2(3)1(2)(-+-=n n n x δδ,则该系统的零状态输出为:()(A ))3(6)2(7)1(2-+-+-n n n δδδ (B ))3()2()1(-+-+-n n n δδδ(C ))3(6)2(4)1(2-+-+-n n n δδδ (D ))3(6)2(7)1(-+-+-n n n δδδ 6.dt t f t t )()(0?∞∞--δ的结果为:()(A ))(t f (B ))(0t t f - (C ))(0t t f + (D ))(0t f 7.已知一因果序列)(n f 的Z 变换式为)2)(1(12)(+++=z z z z z F ,则)(n f 的初值为:()(A )0 (B )1 (C )0.5 (D )28.一LTI 无失真传输系统,它的幅度特性和相位特性要求为:()(A )幅度特性为常数,相位特性无要求(B )幅度特性和相位特性均无要求(C )幅度特性无要求,相位特性的斜率为-t 0 (D )幅度特性为常数,相位特性的斜率为-t 0 9.若一LTI 系统输入为)(1t e 时,输出为)(1t r ,输入为)(2t e 时,输出为)(2t r ,则输入为)]()([21t e t e a +,输出为:()(A ))()(21t r t r + (B ))()(21t r t ar + (C ))()(21t ar t ar + (D ))()(21t ar t r + 10.一理想低通滤波器的截止频率为c w ,下列信号经该滤波器滤波后信号不失真的是(cw w 2=):()(A ))2cos(wt (B ))2cos()cos(wt wt + (C ))cos(wt (D ))3cos(wt 11.请选出)2()1(2)()(-+--=t u t u t u t f 的波形图:()12.若)()]([s F t f L =,则])()([00at e t t u t t f L ---为:()(A )0)(st e a s F -+ (B )0)()(t a s e s F +- (C )0)()(t a s e a s F +-+ (D )0)(st e s F - 13.下列选项不.属于状态变量法分析系统的优点的是:()(A )便于研究系统内部物理量的变化(B )便于研究多输入多输出系统(C )可研究非线性系统或时变系统(D )便于研究系统的频率响应特性14.已知1)]([2-=z zn x Z ,(1>z ),则)](3[n x Z n 为:()(A )12-z z ,1>z (B )932-z z,1>z(C )12-z z ,3>z (D )932-z z,3>z15.求)()3/1()()5.0()(n u n u n y n n +=的Z 变换为:()0-11tf(t)(A)12021tf(t)(B)120-11tf(t)(C)120-11tf(t)(D)12(A )3121-+-z z z z ,21>z (B )3121-+-z z z z ,31>z (C )3121+++z z z z ,21>z (D )3121+++z z z z ,31>z 16.已知)]2(/[)12()]([++=s s s t f L ,则)(t f 的初值)0(+f 为:()(A )0.5 (B )2 (C )0 (D )3 17.若FE )()]([w F t f =,则FE ])()([0t jw e t f dtt df +为:()(A ))()(0w w F w jwF -+ (B ))()(0w w F w jwF ++ (C )jw w F w w F /)()(0+- (D )jw w F w w F /)()(0++ 18.一个频谱受限的信号)(t f ,如果频谱只占据m w -到m w +的范围,则信号)(t f 可以用等间隔的抽样值唯一表示。
信号与系统期末考试试题有标准答案的.doc

信 号与系统 期 末 考 试 试 题一、选择题(共10 题,每题 3 分 ,共30 分,每题给出四个答案,其中只有一个正确的)1、 卷积 f 1(k+5)*f2 (k-3)等于。
( A ) f 1 (k)*f 2(k)( B ) f 1(k)*f 2(k-8) ( C ) f 1(k)*f 2 (k+8) (D ) f 1(k+3)*f 2 (k-3)2、 积分(t 2) (1 2t )dt 等于。
( A )( B )( C ) 3( D ) 53、 序列 f(k)=-u(-k) 的 z 变换等于。
( A )z z ( B ) - z ( C ) 1 ( D ) 11 z 1 z 1z 14、 若 y(t)=f(t)*h(t), 则 f(2t)*h(2t) 等于。
( A )1y( 2t ) ( B ) 1 y(2t ) ( C ) 1 y( 4t ) ( D ) 1 y(4t)4 2 4 25、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+(t ) ,当输入 f(t)=3e — t u(t) 时,系统的零状态响应 y f (t) 等于(A ) (-9e -t +12e -2t )u(t)( B )(3-9e -t +12e -2t )u(t)(C ) (t) +(-6e -t +8e -2t )u(t)(D )3 (t )+(-9e -t +12e -2t)u(t) 6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 ( C )离散性、周期性(D )离散性、收敛性7、 周期序列 2COS (1.5 k 45 0 ) 的 周期 N 等于(A ) 1( B )2( C )3(D )48、序列和k 1 等于k( A ) 1 (B) ∞ (C)u k 1 (D) ku k19、单边拉普拉斯变换 F s2s 1e 2s 的愿函数等于s 210、信号 f tte 3t u t 2 的单边拉氏变换 F s 等于二、填空题(共 9 小题,每空 3 分,共 30 分)1、卷积和 [ ()k+1u(k+1)]* (1 k) =________________________、单边 z 变换 F(z)= z 的原序列 f(k)=______________________2 2z 1s、已知函数f(t) 的单边拉普拉斯变换F(s)=,则函数 y(t)=3e-2t ·f(3t)的单边拉普3s 1拉斯变换 Y(s)=_________________________4、频谱函数 F(j )=2u(1-)的傅里叶逆变换 f(t)=__________________5、单边拉普拉斯变换 F (s)s23s 1的原函数 f(t)=__________________________s 2s6、已知某离散系统的差分方程为 2y(k) y(k 1) y(k 2)f (k ) 2 f ( k 1) ,则系统的单位序列响应 h(k)=_______________________ 7、已知信号 f(t) 的单边拉氏变换是 F(s),则信号 y(t )t 2f ( x)dx 的单边拉氏变换Y(s)=______________________________8、描述某连续系统方程为该系统的冲激响应 h(t)=9、 写出拉氏变换的结果 66u t, 22t k三、 ( 8 分)四、( 10 分)如图所示信号f t,其傅里叶变换F jw F f t ,求( 1) F 0 ( 2)F jw dw六、( 10 分)某 LTI系统的系统函数H ss 2,已知初始状态y 00, y2, 激s 2 2s1励 f tu t , 求该系统的完全响应。
信号05年期末试题

(D)
je2 2 j
6、已知信号f(t)的奈奎斯特角频率为ω0,则信号f(t)cos(ω0t)的奈硅斯特角 频率为 (A) ω0 (B) 2ω0 (C) 3ω0 (D) 4ω0 7、信号 f(t) = (1-t)e-2t(t)的拉普拉斯变换F(s)等于 (A)
1 ( s 2) 2
(B)
d d d [ f1 (t ) f 2 (t )] [ f1 (t )] [ f 2 (t )] (D) f (t ) (t ) f (t ) (B) dt dt dt
3、用差分方程描述的系统为线性时变系统的是 (A) y (k ) 2 y (k 1) y (k 2) 2 f (k ) (B) y (k ) 2 y (k 1) y (k 2) 2 f (k )
F (s)
12、已知 f(t) 波形如题12图所示, 试画出f(2t-1)ε(t)的波形.
f(t)
1
f (2t-1)ε(t)
t
o
1 3
t
o
题 12 图
13、某因果信号的拉普拉斯变换为 F ( s)
2 ,则该信号的傅里叶变换为 s( s 2)
;
F ( j )
14、 已知 频谱函数F (j ) 4Sa( ) cos(2 ), 则原函数 f(t) =
2 | F ( j ) | d
1 2 1 2
2 F ( j )d
(B)
1 2
| F ( j ) | d
(D)
1 2
j 3 | F ( j ) | e d
Ⅱ、填空题(共5小题,每小题4分,共20分)
11、信号
f (t ) e2 t [ (t 1) (t 2)] 的单边拉普拉斯变换为
北京邮电大学信号与系统2005年(B)卷答案
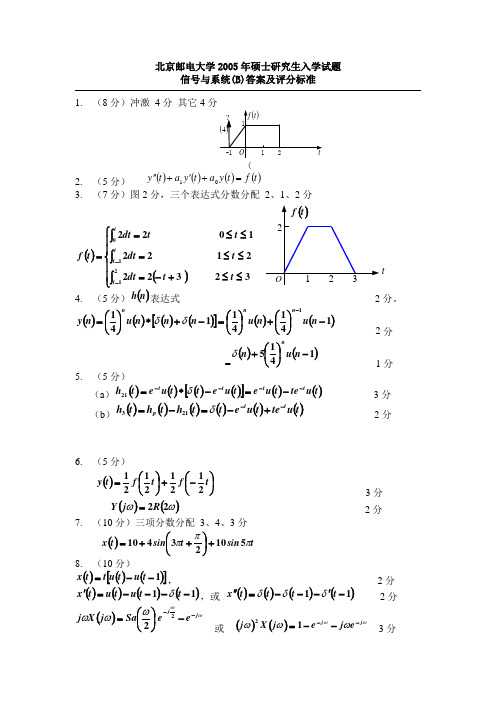
北京邮电大学2005年硕士研究生入学试题信号与系统(B)答案及评分标准1. (8分)冲激 4分 其它4分(2. (5分) ()()()()t f t y a t y a t y =+'+''013. (7分)图2分,三个表达式分数分配 2、1、2分()()⎪⎪⎩⎪⎪⎨⎧≤≤+-=≤≤=≤≤==⎰⎰⎰--21103232221221022t ttt t t dt t dt t t dt t f t4. (5分)()n h 表达式 2分。
()()()()[]()()141411411-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=-+*⎪⎭⎫ ⎝⎛=-n u n u n n n u n y n n n δδ 2分=()()1415-⎪⎭⎫⎝⎛+n u n nδ 1分 5. (5分)(a )()()()()[]()()t u te t u e t u e t t u e t h tt t t -----=-*=δ213分 (b )()()()()()()t u te t u e t t h t h t h t t p --+-=-=δ213 2分6. (5分)()⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛=t f t f t y 21212121 3分()()ωω22R j Y = 2分 7. (10分)三项分数分配 3、4、3分()tsin t sin t x πππ51023410+⎪⎭⎫ ⎝⎛++=8. (10分)()()()[]1--=t u t u t t x , 2分()()()()11----='t t u t u t x δ,或 ()()()()11-'---=''t t t t x δδδ 2分 ()ωωωωωj j e e Sa j X j ---⎪⎭⎫ ⎝⎛=22 或 ()()ωωωωωj j e j ej X j ----=12 3分⇒()⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛=--ωωωωωj j e e Sa j j X 221 或⇒()2211ωωωωωωωωω---=---=----j j j j e j e j e e j X 3分 9. (10分)()()()()()t x dt t dx t y dt t dy dtt y d 46522+=++ 3分 ()()()t u e e t h tt 322---= 3分()()()ωωωj j j Y ++=4212分()()t u e e t y t t ⎪⎭⎫⎝⎛-=--422121 2分10. (5分)(),:j X m πωω7500= 2分s .s T ,s s 317500115000 ===πω 2分因为 s T T < ()t x 能够从()t x p 中正确的恢复 1分 11. (5分)(B )不产生失真,幅度和相位特性都落在不失真区。
05级第二学期信号A类考题B卷

课程编号:XJ054015北京理工大学2006-2007学年第二学期2005级电子类信号与系统终考试卷(B 卷)姓名________ 学号________ 班级________ 成绩________1.求以下积分的值。
00()()t t u t t dt δ∞-∞+-=⎰(00t >)2.计算1()f t 与2()f t 的卷积积分()y t ,并画出()y t 的波形。
1t t 3、求信号()x t 的频谱密度函数()X ω4、设[]x n 如图示,不求出()j X e Ω而完成 下列运算 (1)()0j X e (2)()j X e d ππΩ-Ω⎰5.(8分)已知)()(3t u et x t-=-,求)2(t x 的拉氏变换及其收敛域。
6.(8分)已知离散时间系统的系统矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=51152031A ,求状态转移矩阵][n ϕ。
二、计算题(3小题,每题的分数写在题号上,总分为52分)1.(17分)已知系统的差分方程为51[][1][2][][2]66y n y n y n x n x n --+-=--要求: 用时域法求出系统的单位抽样响应h[n]。
2.(17分)图(a )为一单边带幅度调制系统,图(b )为其解调系统,()x t 的频谱()X ω如图(c )所示,()()sgn H j ωω=-,()1,0sgn 1,0ωωω>⎧=⎨-<⎩(1)分别画出()1y t 、()h x t 、()2y t 、()y t s 的频谱图;(2)确定 0,,c B ωω 的范围或大小,使()y t 的频谱与()x t 相同。
()x t )(S t y (a)3. (18分)已知一离散时间系统如图所示,(1)求因果系统的)(z H ,画出零极点图,并指出收敛域; (2)当k 为何值时,该系统稳定?(3)当k=1时,求输入为nn x ⎪⎭⎫⎝⎛=43][时的响应y[n]。
[VIP专享]信号与系统期末试卷-含答案全
![[VIP专享]信号与系统期末试卷-含答案全](https://img.taocdn.com/s3/m/059203627375a417866f8ff1.png)
e(t1) (t 1) (t) e (t2) (t 2) (1 t) .
y(t) et (t) (1 t) ;则 f (t) (t 1) (t 2) 时,输出 y f (t) =
某因果线性非时变(LTI)系统,输入 f (t) (t) 时,输出为:
7.
4 3m
max
Tmax
Tmax 为
根据时 2) 取样时,其频谱不混迭的最大抽样间隔
m
3 4
m 2
m 4
max
int level(BinTreeNodlesevt}r*Beutsl,icnBt(rtrTuiontrcaoTetgtert,_eyapNnpetg)oy;oeN_pddinoeeodtd;fde*esreafc*ttrphsB*au{l)ti;cilrn/duh/tT;ciB/lr/tdo1eiTt;u1ea//NcnrNgoto_loiu(fdn(dtnbe*oetpivdlt{(roe(e}TbidpEititrcfrl(ero!-pbmu>tintrTvritgaey-l(>hlpbulteeie,rtrf=xdt)e,=apr{xkextta,)rt;ru{;k,kr)sd+n;tra+;u1t;ac}0txyBpieTNxv},ooidi{ndet&m*lkac)hi}nil(de)}l;s/e/ js+tr}+uj;cBf+BtoB.+Bid.r.L(;+adikTe+taanN=;t[agojB]e[tdkh=l.se+L+eA1e*+]nr.i;dfc=g(d.-[d;{aiB]1a/it;f/a.;t(dkaA[}ia[]>.kBtdB<}=a];aii.T[BLjt+;aNke.+d[Loni;-]aed-g>t)netahg,B[jt*]+h.)wBd+]{avhi;T=otilareiAedi[n(Be.i{dtm;.<Laive=etAoarngi.0[dLgie],e;jt2Ch=n(o{Sg-0ut9q1h,n/kAL])/t)/iL/[;2s1/e1AtA…aABBmf"…,.S(h+Bq"mniLT6m+irsnet8]e&mhBTen),amidn+dtn&a2Ot*acx(7o10u)n+t)0x{11*ixf=0( nT+o1)d*{ex2i_1f c(+(o!uT2/xn/-*10>tx+l2+cxh=1il;+dnx)o&2/d/h&e=tt_(pn!c:To0o//-duw>1enrw*_c2t/wchx-oi0.1ldu;xon)/)1c*t;cinx6o42.1ucleonfmtt+d/+5ap;t-a5//r7iLg9Cihs4ot8lNuet5nmof9ttdreLp4iegme.=h*ap3tMfAmBol(a[aTrTlit]ex(-;(><i2)nAlccetl[ha0i]}ise=l=ds1,0}A…Tc;[yoine2pu<-nT6ein=-yH>12tp)(]Te;v;enn[Co1-A-ti1o3m1d[u]nA)pHin-[/;in(tv-kL21]ene;]1reyais=A+)nef=[+(t-nm(k1Ta])eAT-p){y>nyA;r-p%c2eh…1iAld3e[2,1]3c,2e1oi20Vn0(u3e=bt×n4i{)n3t1a5)B0);,5b20A}{7,B(2ce[2a150,(l0)ds0cn(a20e,a)]×ie[13j1)1cnr2,a17Af2e0A4,i58g2jtB]b1u(B03}(a5r4,21[En)]06a1B;=07A51([}{0]b937S<A/3)56/HaL([06C0c,sT1b3)]uo[A.>81A0c5u,493]cBn<B0.]=taC5H[L8(0,A1De(4g]k/,Aa5>2EBef0,[)Fy,<]*4C[G)G]b[=2B1,,DHk)g+[]e>,I1AEJy,/[<(,81%C1c]-[8,a5bD1)]C>3C]B,D1<[D1]2Bd62,GFc3E>=41A,V5</1I5EdH475,Gf1231>01+0*J5,91<420G4+0e*30G241,7W1d+*787>13P031,4*9<1L74=41f=0+,515a24953>**/546,17<5+15=0g37413,2*0c5572>/4+517,5<6451*g524,0d+3>956,*5<0315f9+2,3e5W12>14P,12*<3L157g+=56,52f13053>105*693}64*1,{73+80217+9596510*77046873+1*71249264+*9503182+79012*176208590=*2092+8123169831731237*793}W2+531P352L5*0313173+s3T3125158*,21T2052=5,2…915W063…303P5,LTS Tini k1i(2i={a1b,2c,d…e…fg}S0)1,1k10in1i011k11k10n+1kk1Pn21>r+0ikm…00…11+1k0s1=0n11+n21K…ru…snkas1l ns,s=nk,nk a11a121a02K1)aru2s2kaa=2l203*:9(a1i+03/1jA2-03aB(3a131+Aa12=3B+42[…0+]3A…+a3aij1+n3inn149-+iH10-41au+jnfi84+fnm4+16a5B8n+58F1544):52=5706305306.986,2T76:0150,D811:00148110683171,F10ST6:06D413S024H515,1H12:007412101402H*1291u60+22f{f7m4*63a2+n58307*71836+21102*72306+722774*0674128+493}*()4+86*312=513219 5:13/5671(130+7822+6261+p03a1+341352+401143,41)p0=83,21a.8425,913,,p66331:121,0A1a24B13G,,CP4pJ9AD3KG21EHD12AFDaJ3GBH,EPaDHKBApGIBM3J2HEKIF1AJMCKCAEFCMFIIM
05年信号与系统A卷及答案

2
共 4 页 第 2 页
π
∴ f (t ) =
1
π
Sa(t − 1) ……(2 分)
1 3.解: X ( z ) = 2 z − 3 z + 1 = − 5 +
z
z ( z + 1)( z − 5)
z
6 1 + 5 ……(2 分) z +1 z − 5
U 2 ( s ) 0.5s 10 = = 0.5 − ……(1 分) E ( s ) s + 20 s + 20
∴ 冲激响应为 h(t ) = 0.5δ (t ) − 10e−20t u (t )
(2) G ( s ) = U 2 ( s ) =
……(3 分)
0.5s 1 0.5 ⋅ = ……(3 分) s + 20 s s + 20
山东建筑大学试卷标准答案及评分标准
2006 至 2007 学年第 2 学期 课程名称 专业: 电子信息工程、通信工程 ; 120 分钟
四 50 总分 100
共 4 页 第 1 页
信号与系统
(本科) 试卷 A
考试性质:闭卷;
题号 分数 一 20 二 18
考试时间
三 12
一、填空题(共 20 分,每空 2 分) 1.周期 或 频率 4. 2πδ (t ) 2.叠加特性 或 叠加性 3.s 平面的左半平面 或 纵轴的左侧 6. 4 8. a
输出方程: r (t )
′ (2)通过以上方程化简得: λ1′′(t ) + 4λ1 (t ) + 3λ1 (t )
即: r ′′(t ) + 4r ′(t ) + 3r (t ) 系统函数:
《信号与系统》试卷A答案

第二学期《信号与系统》A 卷答案及评分标准一、选择题(每题4分,共20分)1.D 2.D 3.C 4.C 5.A二、填空题(每题4分,共24分)1.-12.u(t)+u(t-1)+u(t-2)3.稳定4.jdF(w)/dw-2F(w)5.线性,非线性6.0.5n u(n)三、计算题(共56分)1.f(t)=Ecos(πτt),22t ττ-≤≤ F(w)=22()jwt f t e dt ττ--⎰=22cos()jwt E t e dt ττπτ--⎰=202cos()cos E t tdt τπωτ⎰ =20[cos()cos()]E t t dt τππωωττ++-⎰ =2222cos 2E πτωτπτω- 共6分,写出表达式给2分,写对傅立叶变换公式给2分,积分过程及结果2分。
2.f(t)= f 1(t)*f 2(t)=sintu(t)*u(t-1)=sin ()(1)u u t d ττττ∞-∞--⎰ =10sin t d ττ-⎰=10cos |t τ--=1-cos(t-1),t>1 共8分,写对两个函数的表达式分别各给2分,带入卷积公式正确得2分,积分过程2分,结果表达正确2分。
3. 当输入为f(t)时, r(t)=(2e -t +cos2t)u(t)=r zs (t)+r zi (t)(2分)当输入为3f(t)时, r(t)=(e -t +cos2t)u(t)=3 r zs (t)+ r zi (t)(2分)联立上面两式得,r zs (t)= - 0.5e -t u(t)(1分) r zi (t)=(2.5 e -t +cos2t)u(t)(1分)当输入为5f(t)时,r(t)=5 r zs (t)+ r zi (t)(1分)=(-2.5 e -t +2.5 e -t +cos2t)=cos2t u(t)(1分)4.解:(1)冲激相应应满足方程h ’’(t)+4h ’(t)+3h(t)=δ’(t)+2δ(t)。
信号与系统考题本科期末考试 试卷 AB卷带答案 期末考试题 模拟卷 模拟试题 综合试卷自测试卷2套

试卷一一、填空题、选择题(选择题每题3分,填空题每空3分)共 36分1.系统函数22)()(c a s bs s H +-+=,a ,b ,c 为实常数,则该系统稳定的条件是( )。
(a )a <0 (b )a>0 (c )a=0 (d )c =02.离散系统的稳定条件_____ __。
3. 已知某系统的差分方程为)1()()2()1()(0101-+=-+-+n f b n f b n y a n y a n y ,则该系统的系统函数H (z )为( )。
(a ).201011)(z a z a z b b z H +++=(b ).211011)(1---+++=z a z a z b b z H(c ).102120)(a z a z zb z b z H +++=(d ).20111011)(---+++=z a z a z b b z H4. ()t δπ-= 。
(a )-π()t δ (b )π()t δ (c) 1()t δπ- (d)1()t δπ5.计算⎰∞∞-=-dt t t )6(sin 2πδ( )。
(a )1 (b )1/6 (c) 1/8 (d) 1/46. 若()(),f t F j ω↔则()F jt 的傅立叶变换为( )。
(a )()f ω (b) ()f ω- (c) 2()f πω (d) 2()f πω-7.某稳定系统的系统函数为:已知系统函数231)(2++=s s s H ,则h (t )= _____________。
8. 已知()(),f t F j ω←−→则(23)f t +的傅立叶变换为( )。
(a ) 32(2)j F j e ωω (b) 62(2)j F j eωω(c) 31()22j F j e ωω (d) 321()22j F j e ωω9.875(802)()t t t t δ--+= 。
10.已知信号)(t f 的波形如图所示,则)()1(t t f ε-的表达式为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题:(每小题2分,共40分,请把每道选择题唯一正确答1.积分dt t t e t )]()(['2δδ+⎰∞∞--等于:( )(A )0 (B )1 (C )2 (D )3 2.序列和)2()4sin(-∑-∞=n n kn δπ等于:( ) (A )1 (B )u(k) (C )u(k-2) (D ))2(-k δ 3.序列卷积和)4()2()2()1(-*+--*+k k u k k u δδ等于:( )(A ))(k δ (B ))1(-k δ (C ))1(-k u (D ))3(-k u 4.已知某系统的单位样值响应)(2)(n u n h n =,则该系统的因果性和稳定性:( )(A )因果,稳定 (B )因果,不稳定 (C )非因果,稳定 (D )非因果,不稳定5.已知某离散系统单位样值响应为:)1(2)()(-+=n n n h δδ,输入序列为:)2(3)1(2)(-+-=n n n x δδ,则该系统的零状态输出为:( )(A ))3(6)2(7)1(2-+-+-n n n δδδ (B ))3()2()1(-+-+-n n n δδδ(C ))3(6)2(4)1(2-+-+-n n n δδδ (D ))3(6)2(7)1(-+-+-n n n δδδ 6.dt t f t t )()(0⎰∞∞--δ的结果为:( )(A ))(t f (B ))(0t t f - (C ))(0t t f + (D ))(0t f 7.已知一因果序列)(n f 的Z 变换式为)2)(1(12)(+++=z z z z z F ,则)(n f 的初值为:( )(A )0 (B )1 (C )0.5 (D )28.一LTI 无失真传输系统,它的幅度特性和相位特性要求为:( )(A )幅度特性为常数,相位特性无要求 (B )幅度特性和相位特性均无要求(C )幅度特性无要求,相位特性的斜率为-t 0 (D )幅度特性为常数,相位特性的斜率为-t 0 9.若一LTI 系统输入为)(1t e 时,输出为)(1t r ,输入为)(2t e 时,输出为)(2t r ,则输入为)]()([21t e t e a +,输出为:( )(A ))()(21t r t r + (B ))()(21t r t ar + (C ))()(21t ar t ar + (D ))()(21t ar t r + 10.一理想低通滤波器的截止频率为c w ,下列信号经该滤波器滤波后信号不失真的是(cw w 2=):( ) (A ))2cos(wt (B ))2cos()cos(wt wt + (C ))cos(wt (D ))3cos(wt 11.请选出)2()1(2)()(-+--=t u t u t u t f 的波形图:( )12.若)()]([s F t f L =,则])()([00at e t t u t t f L ---为:( )(A )0)(st e a s F -+ (B )0)()(t a s e s F +- (C )0)()(t a s e a s F +-+ (D )0)(st e s F - 13.下列选项不.属于状态变量法分析系统的优点的是:( ) (A )便于研究系统内部物理量的变化 (B )便于研究多输入多输出系统(C )可研究非线性系统或时变系统 (D )便于研究系统的频率响应特性14.已知1)]([2-=z zn x Z ,(1>z ),则)](3[n x Z n 为:( )(A )12-z z ,1>z (B )932-z z,1>z(C )12-z z ,3>z (D )932-z z,3>z15.求)()3/1()()5.0()(n u n u n y n n +=的Z 变换为:( )0-11tf(t)(A)12021tf(t)(B)120-11tf(t)(C)120-11tf(t)(D)12(A )3121-+-z z z z ,21>z (B )3121-+-z z z z ,31>z (C )3121+++z z z z ,21>z (D )3121+++z z z z ,31>z 16.已知)]2(/[)12()]([++=s s s t f L ,则)(t f 的初值)0(+f 为:( ) (A )0.5 (B )2 (C )0 (D )3 17.若FE )()]([w F t f =,则FE ])()([0t jw e t f dtt df +为:( ) (A ))()(0w w F w jwF -+ (B ))()(0w w F w jwF ++ (C )jw w F w w F /)()(0+- (D )jw w F w w F /)()(0++18.一个频谱受限的信号)(t f ,如果频谱只占据m w -到m w +的范围,则信号)(t f 可以用等间隔的抽样值唯一表示。
该抽样频率的最低值为:( )(A )m f (B )2m f (C )3m f (D )4m f 19.已知1)]([2-=z zn x Z ,(1>z ),则)]([2n x n Z 为:( ) (A )2)1(2-z z (B )32)1(22-+z z z (C )32)1(-+z zz (D )12-z z20.已知23)]([1-+=z z n x Z ,(2>z ),)3)(1()]([2++=z z zn x Z ,(3>z ),则)]()([21n x n x Z *为:( ) (A ))2)(1(-+z z z ,6>z (B ))2)(1(-+z z z ,1>z(C ))2)(1(-+z z z ,2>z (D ))2)(1(-+z z z,3>z二.计算题(共14分)21.求)3()2(4)(2++=s s ss F 的拉普拉斯逆变换。
(6分) 22.用Z 变换法求解差分方程:1)1(),(2)(),()1(3)(=-==--y n u n x n x n y n y n 。
(8分)三.综合题(共46分)23.两个LTI 子系统的单位冲激响应分别是:)1()(1-=t u t h ,)2()(2+=-tu e t h t ;图1为由这两个子系统组成的复合系统。
试求该复合系统的单位冲激响应)(t h 。
(6分) 24.求图2所示电路的系统函数)(s H ,输入为电压)(t e ,输出为电压)(t r 。
其中Ω=1R ,H L R F C 5.0,2,5.00=Ω==。
(6分) 25.已知某LTI 系统输入为:)()(21t u e t f t -=,零状态响应为)()21()(21t u e e t y t t --+-=,试由S 域求系统在)()(2t u e t f t -=激励下产生的零状态响应)(2t y 。
(8分)26.某离散时间系统的输入输出差分方程为:)()2(2)1()(k f k y k y k y =----,设初始观察时刻为0=k ,已知75.0)2(,1)1(=--=-y y ,求输入)()(k u k f =时系统的零输入响应、零状态响应和完全响应。
(10分) 27.图3是某离散LTI 系统的仿真框图,试求: (1)该仿真框图的差分方程; (2)系统函数)(z H ,并确定其收敛域; (3)分析系统的稳定性;(4)若,25.0,1,110===b a a 大致画出)(z H 的幅度特性曲线。
(10分)f(t)h (t)h (t)y (t)12图 1图 2图 328.图4所示是某离散系统的仿真框图,,3/,2/mbma==问m为何值时可使系统稳定?(6分)x(n)y(n)图 4一.(每小题2分)1、DCBBA 6、DADCC 11、CCDDA 16、BABBC 二.21.(共6分)32)2()(2+++++=s Cs B s A s F (1分) 8)3()2()2(4222-=+++=-=s s s s s A (1分)12)3()2()2(4222=+++=-=s s s s s ds d B (1分)12)3()2()3(432-=+++=-=s s s s s C (1分)312212)2(8)(2+-++++-=s s s s F )()12128()(322t u e e te t f t t t ----+-= (2分) 22.(共8分))()]1()([3)(1z X zy z Y z z Y =-+-- (2分))2/(3)31)((1-=---z z z z Y (2分)3622)31)(2(63)(1-+--=---+=-z zz z z z z z z Y 3>z (2分) )(])3(6)2(2[)(n u n y n n +-= (2分)三.23.(共6分))()()(21t h t h t h *= (3分)ττττττd e e d t u eu t t t ⎰⎰+-∞∞---=+--=21)()2()1()1(][1221+-==-+-t u e e e e t t t τ(3分)24.(共6分))()()(s E s R s H =(2分)02000200R Ls LCs R LsR R R Ls LCs R LsR +++++= (2分)4322++=s s s(2分) 25.(共8分))2/(1)()]([11+==s s F t f L (1分))1/(1)()]([22+==s s F t f L (1分)21121)()]([11+++-==s s s s Y t y L (1分) )()()(11s F s Y S H =(1分) )1(2)21121)(2(+=+++-+=s s s s ss (1分) )()()(22s F s H s Y = (1分)])1(1111[2)1(1)1(22+-+-=++=s s s s s s (1分) )(])1(1[2)]([)(212t u e t s Y L t y t --+-== (1分)26.(共10分)特征值为:022=--αα1,221-==⇒αα (1分)故方程齐次解为:n n c c )1()2(21-+ (1分)(1)零输入响应为:⎩⎨⎧=-+-=-+----75.0)1(21)1(222211211c c c c (1分) ⎩⎨⎧=-=⇒6/53/121c c (1分) n nzi t y )1(65)2(31)(-+-= (1分)(2)零状态响应为:设特解为D ,则5.012-=⇒=--D D D D (1分)⎩⎨⎧==⇒⎩⎨⎧=--+=--+----6/13/405.0)1(205.0)1(22122211211c c c c c c (1分) 21)1(61)2(34)(--+=n n zs t y (1分) (3)完全响应为:21)1()2()()()(--+=+=nn zs zi t y t y t y (2分)27.(共10分)(1)差分方程为:)1()()2(2)1()(102-++-+-=n x a n x a n y b n by n y (2分)即:)1()()2(2)1()(102-+=----n x a n x a n y b n y b n y (2)系统函数为:)()()(2)()(110221z X z a z X a z Y z b z Y bz z Y ---+=-- (1分))()()(z X z Y z H =))(2(21120221110b z b z za z a zb bz z a a +-+=--+=--- (1分) 收敛域为:b z 2> (1分) (3)若5.0<b ,则系统稳定;若5.0>b ,则系统不稳定。
