2018年初中数学突破中考压轴题几何模型之旋转模型(5、26)

合集下载

中考数学旋转压轴题解题方法(详解答案)

中考数学旋转压轴题解题方法一、图形旋转知识与方法1、图形的变换是新课标中“空间与图形”领域的一个主要内容，体现运动变换的理念与思想，是教材中的一大亮点．初中数学所学的图形变换包括平移、轴对称、旋转、位似。

2、旋转，它是一种数学变换．生活中的旋转也是随处可见，汽车的轮子，钟表的指针，游乐园里的摩天轮，都是旋转现象．3、图形的旋转有三个要素：①旋转中心；②旋转方向；③旋转角度．三要素中只要任意改变一个，图形就会不一样．4、旋转具有以下性质：①对应点到旋转中心的距离相等，即边相等。

②对应点与旋转中心所连线段的夹角等于旋转角，即角相等③旋转前、后的图形全等。

5、旋转是近几年中考数学的热点题型，对旋转的特例“中心对称”的考查多以选择题或填空题的形式出现，题目比较简单，大多数属于送分题；利用旋转作图，是格点作图题中的重点。

利用旋转构造复杂几何图形，通常将旋转融合在综合题中，题目难度中等，在选择题、填空题、解答题中都有出现。

有旋转点的，有旋转线段的，更多的是旋转图形的。

旋转三角形，旋转平行四边形，旋转矩形，旋转正方形，其中，近两年的各地中考试题中，旋转矩形出现的最频繁，深受出题老师的青睐。

其实旋转的题目还有一个好听的名字就是“手拉手问题”，本文将对这一类问题分类汇总，以这三个性质为突破口，就能快速解决问题。

中考数学几何模型重点突破讲练：专题32 几何变换之旋转模型(教师版)

(2)正方形中的半角模型
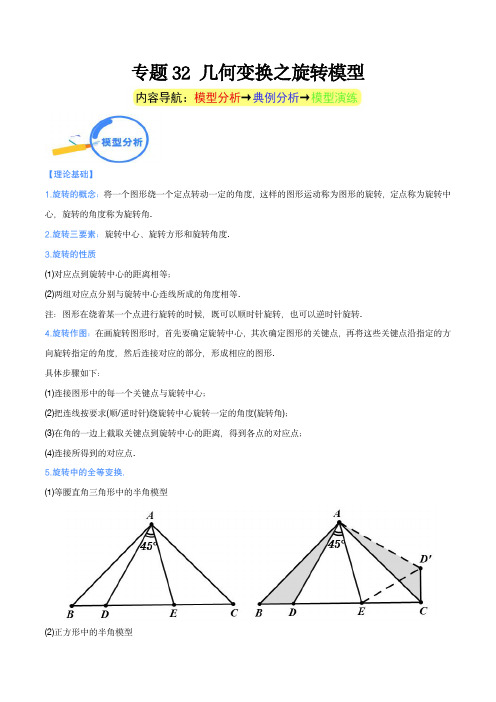
6.自旋转模型：有一组相邻的线段相等，可以通过构造旋转全等. (1)60º自旋转模型
(2)90º自旋转模型
(3)等腰旋转模型
(4)中点旋转模型(倍长中线模型)
7.共旋转模型 (1)等边三角形共顶点旋转模型
(2)正方形共顶点旋转模型
8.旋转相似
【例 1】如图，在 Rt△ABC 中，AB＝AC，D，E 是斜边 BC 上两点，且∠DAE＝45°，将△ADC 绕点 A 顺时针旋转 90°后，得到△AFB，连接 EF．下列结论：①△AED≌△AEF；②∠FAD＝90°，③BE+DC＝DE； ④∠ADC+∠AFE＝180°．其中结论正确的序号为（）
HPF =
DEP ，
EP PF
DH HF
，
∵ DPF = ADE+ DEP=45°+ DEP ，
DPF = ACE+ DAC=45°+ DAC ，
DEP= DAC ，
又∵ CDF = DAC ，
DEP= CDF ，
HPF = CDF ，
又∵ FD=FP ， F = F ，
ΔHPF≌ΔCDF （ASA），
A．①②③
B．②③④
C．①②④
D．①③④
【答案】C
【分析】根据旋转的性质可得，∠FAD＝90°，AF＝AD，BF＝DC，∠ABF＝∠C，从而证明△FAE≌△DAE，
∠FBE＝90°，进而可得 EF＝DE，然后在 Rt△BFE 中，利用勾股定理，进行计算即可判断①②④正确．
【解析】解：由旋转得：
∠FAD＝90°，AF＝AD，BF＝DC，∠ABF＝∠C，
的度数；
（2）①由旋转的性质得出 AC=AE ， CAE=90° ，证得 Fቤተ መጻሕፍቲ ባይዱD= FDP ，由三角形外角的性质可得出结论；

(完整版)中考数学旋转模型及例题

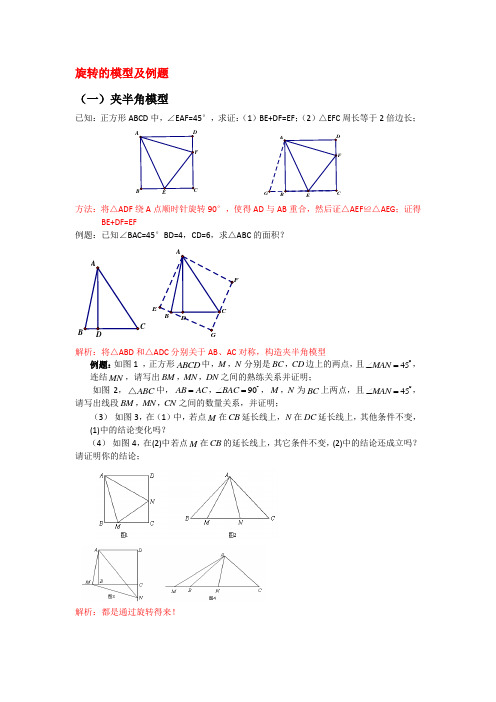
旋转的模型及例题（一）夹半角模型已知：正方形ABCD 中，∠EAF=45°，求证：（1）BE+DF=EF ；（2）△EFC 周长等于2倍边长；方法：将△ADF 绕A 点顺时针旋转90°，使得AD 与AB 重合，然后证△AEF ≌△AEG ；证得BE+DF=EF 例题：已知∠BAC=45°BD=4，CD=6，求△ABC 的面积？解析：将△ABD 和△ADC 分别关于AB 、AC 对称，构造夹半角模型例题：如图1 ，正方形ABCD 中，M N ，分别是BC CD ，边上的两点，且45MAN ∠=˚，连结MN ，请写出BM MN DN ，，之间的熟练关系并证明；如图2，ABC △中，90AB AC BAC =∠=，˚，M N ，为BC 上两点，且45MAN ∠=˚，请写出线段BM MN CN ，，之间的数量关系，并证明；（3）如图3，在（1）中，若点M 在CB 延长线上，N 在DC 延长线上，其他条件不变，(1)中的结论变化吗？（4）如图4，在(2)中若点M 在CB 的延长线上，其它条件不变，(2)中的结论还成立吗？请证明你的结论；解析：都是通过旋转得来！推广：一般的夹半角模型例题：边长为2m 的等边ABC △的两边AB AC 、上分别有两点M N 、，点D 为平面内一点，60MDN ∠=︒，120BDC BD CD ∠=︒=，．当点M 在线段AB 上运动时，探索AMN △的周长与ABC △边长的关系．⑴ 如图1，当点D 在ABC △外时，AMN △的周长是否发生变化？请证明你的结论． ⑵ 如图2，当点D 在ABC △内时，⑴中的结论是否成立？若成立，请求出此时AMN △的周长；若不成立，请说明理由．⑶ 如图3，ABC △是满足60BAC ∠=︒的任意三角形，其中BC a AC b AB c ===，，．D 是ABC ∠ 与ACB ∠平分线的交点，M N 、分别在AB AC 、上，且60MDN ∠=︒．当点M 在线段AB 上运动时，猜想AMN △的周长是否发生变化？若不变，请直接写出AMN △的周长（用a b c ，，表示，不需要化简）；若变化，请说明理由．（二）手拉手模型等边三角形B图3图2图1ABCDMNNMDCBANM BAB条件：AB=AD ，∠B+∠D=180°，2∠MAN=∠BAD结论：BM+DN=MN条件：△ABC 是等边三角形，BD=CD ，∠BDC=120°∠MDN=60°结论：BM+CN=MN △AMN 的周长=2倍边长结论：（1） △BCE ≌△ACD ，△BCM ≌△CAN ， △MCE ≌△NCD （2）AD=BE,∠AFB=60°（3）△MCN 为等边三角形（4）MN ∥BD(5)CF 为∠BFD 的角平分线（6）FC+FE=FD结论：（1） △BCE ≌△ACD （2） AD=BE,∠AFB=60°（3） CF 为∠BFD 的角平分线正方形中的旋转例题：如图，已知四边形ABCD 中，AD=CD ，∠ABC=75°，∠ADC=60°，AB=2，BC= 2（1）以线段BD 、AB 、BC 作为三角形的三边，○1则这个三角形为___________三角形，（锐角、直角、钝角） ○2求BD 边所对的角的度数。

中考数学旋转专题中的常见模型

旋转专题1、图形的旋转（1）在平面内，将一个图形绕一个定点沿某个方向旋转一个角度，这样的图形运动称为旋转，这个定点称为旋转中心，转动的角度称为旋转角．（2）性质：①在图形旋转过程中，图形上每一个点都绕旋转中心沿相同方向转动了相同角度；②注意每一对对应点与旋转中心的连线所成的角度都叫旋转角，旋转角都相等； ③对应点到旋转中心的距离相等．2、图形的中心对称（1）把一个图形绕着某一点旋转180°，如果它能够与另一个图形重合，那么这两个图形关于这个点对称或中心对称，该点叫做对称中心．（2）①关于中心对称的两个图形是全等形；②关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分； ③关于中心对称的两个图形,对应线段平行（或者在同一直线上）且相等.1、三垂直全等模型三垂直全等构造方法：从等腰直角三角形的两个锐角顶点出发向过直角顶点的直线作垂线。

CBE D CAB2、手拉手全等模型CCCABDEABBA方法技巧提炼高频核心考点EDCBAEDCBAEDCBAABCDEEDCBA3、等线段、共端点 (1) 中点旋转(旋转180°)(2) 等腰直角三角形(旋转90°)A'DCBAF'D'FEDCA(3) 等边三角形旋转(旋转60°)(4) 正方形旋转(旋转90°)②①FEDCBAPFEDCBAGFEDCBA例1、如图,设P 是等边△ABC 内的一点,PA=3,PB=4,PC=5,则∠APB 的度数是________。

类型一旋60°，造等边精题精讲精练例2、（1）如图，P是等边△ABC内一点，∠APB、∠BPC、∠CPA的大小之比为5:6:7，则以PA、PB、PC为边的三角形三内角大小之比（从小到大）是（）.A.2:3:4B.3:4:5C.4:5:6D.以上结果都不对（2）在等边△ABC中，P为BC边上一点,设以AP、BP、CP为边组成的新三角形的最大内角为θ，则（） A. θ≥90° B.θ≤120° C.θ=120° D.θ=135°例3、如图所示.△ABD是等边三角形，在△ABC中，BC=a,CA=b,问：当∠ACB为何值时，C,D 两点的距离最大？最大值是多少？例4、（1）如图，在四边形ABCD中，AB＝AD，∠BAD＝60°，∠BCD＝120°，证明：BC＋DC＝AC.（2）如图,四边形ABCD中,AB=BC,∠ABC=60°,P为四边形ABCD内一点,且∠APD＝120°.证明:PA+PD+PC≥BD.如图，P 为等边△ABC 内一点，∠APB ＝113°，∠APC ＝123°求证：以AP ，BP ，CP 为边可以构成一个三角形，并确定所构成的三角形的各内角的度数.如图,在四边形ABCD 中,∠ABC=30°,∠ADC ＝60°,AD=DC.证明:BD 2=AB 2+BC 2.例5、如图,以Rt △ABC 的斜边BC 为一边在△ABC 的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=62,那么AC 的长等于________。

初中数学旋转的六大模型,初中几何旋转经典例题

初中数学旋转的六大模型,初中几何旋转经典例题标题：初中数学旋转的六创作者，初中几何旋转经典例题在初中的数学学习中，旋转是一个重要的概念，它不仅在几何学中占据着核心地位，还在代数学、统计学等其他领域有着广泛的应用。

本文将详细介绍初中数学旋转的六创作者，并通过经典例题来深化理解。

旋转是指一个图形绕着某一点转动一定的角度。

在这个过程中，图形上任意一点所经过的路径形成一个圆，这个圆叫做旋转圆，点叫做旋转中心。

旋转的角度一般用角度或者弧度来表示。

中心对称旋转：图形以旋转中心为对称中心，旋转角度为偶数倍的180度。

绕固定点旋转：图形围绕一个固定点旋转，这个固定点称为旋转中心。

旋转对称图形：图形可以通过旋转得到，这种图形称为旋转对称图形。

旋转角相等：如果两个图形可以通过旋转互相得到，那么它们的旋转角必然相等。

旋转角互补：如果两个图形的一条边和另一条边的延长线组成一个平角，那么这两个图形的旋转角互补。

旋转改变形状：旋转可以改变图形的形状，但不会改变图形的面积。

例1：在正方形ABCD中，E是BC的中点，F是AC上一点，且CF=2AF。

求证：EF平分∠AEB。

证明：我们可以通过旋转证明。

把△ABE绕B点按逆时针方向旋转60°，得到△CBG，则BG//AE，所以∠FGB=∠FEA。

因为CF=2AF，所以FG=2FE。

所以可以得出∠FEB=∠FGB+∠GBF=∠FEA+∠AEB+∠ABE=∠FEA+∠AEB+∠EAB=180°即∠FEA+∠AEB=180°-∠EAB=∠BEF所以∠BEF = ∠FEA即 EF平分∠AEB。

例2：在Rt△ABC中，∠C=90°，D是AB的中点，E、F分别在AC和BC上，且DE⊥DF。

求证：EF^2=AE^2+BF^2。

证明：把Rt△ABC绕D点按顺时针方向旋转90°得到Rt△AB’C’，则可知：△ABC≌△AB’C’，所以可知DE=DF，因为DE⊥DF，所以可知四边形DECF’是正方形。

初中数学突破中考压轴题几何模型之旋转模型(、)

年初中数学突破中考压轴题几何模型之旋转模型(、)————————————————————————————————作者：————————————————————————————————日期：23 旋转提升专题知识点一旋转构造全等几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩（一）共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形4 以上给出了各种图形连续变化图形，图中出现的两个阴影部分的三角形是全等三角形，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二利用旋转思想构造辅助线（1）根据相等的边先找出被旋转的三角形（2）根据对应边找出旋转角度（3）根据旋转角度画出对应的旋转的三角形三旋转变换前后具有以下性质：（1）对应线段相等，对应角相等（2）对应点位置的排列次序相同（3）任意两条对应线段所在直线的夹角都等于旋转角θ．【例题精讲】例1.在四边形ABCD 中，∠ADC=∠ABC=90°，AD=CD ，DP ⊥AB 于P ，若S ABCD =25，求DP 的长。

例2.如图，四边形ABCD 是正方形，ABE ∆是等边三角形，M 为对角线BD 上任意一点，将BM 绕点B 逆时针旋转60︒得到BN ，连接AM 、CM 、EN ．⑴求证：AMB ENB ∆∆≌⑵①当M 点在何处时，AM CM +的值最小；②当M 点在何处时，AM BM CM ++的值最小，并说明理由；⑶当AM BM CM ++的最小值为31+时，求正方形的边长．ENMDCBA5 方法总结:1、共顶点的等线段中，最常用旋转思路，但也不可以思维定势，辅助线叙述中用一般语言2、旋转变换还用于处理：①几何最值问题：几何最值两个重要公理依据是：两点之间线段最短和垂线段最短； ②有关线段的不等关系； ③自己构造绕某点旋转某角度（特别是60度），把共顶点的几条线段变为首尾相接的几条线段，再变为共线取得最小值问题，计算中常用到等腰三角形或勾股定理等知识。

初中数学旋转的六大模型题

初中数学旋转的六大模型题旋转是数学中的一个重要概念，也是初中数学中经常会遇到的一个题型。

通过旋转，我们可以改变图形的朝向和位置，从而帮助我们更好地理解几何形状和解决问题。

下面是初中数学中常见的六大旋转模型题，帮助学生更好地理解旋转的概念和运用。

1. 点的旋转：题目给出一个点的坐标和旋转角度，要求求出旋转后的点的坐标。

这种题目可以帮助学生理解点的旋转规律和计算方法。

2. 图形的旋转：题目给出一个图形的坐标或者边长，要求将图形按照给定的角度进行旋转，然后求出旋转后的图形的坐标或者边长。

这种题目可以帮助学生理解图形的旋转规律和变化。

3. 对称图形的旋转：题目给出一个对称图形和旋转角度，要求求出旋转后的图形。

这种题目可以帮助学生理解对称图形的旋转规律和变化。

4. 旋转体的表面积和体积：题目给出一个旋转体的形状和旋转轴的位置，要求求出旋转体的表面积和体积。

这种题目可以帮助学生理解旋转体的形成过程和计算方法。

5. 旋转体的截面图形：题目给出一个旋转体的形状和旋转轴的位置，要求求出旋转体在某一截面上的图形。

这种题目可以帮助学生理解旋转体的截面变化和图形特征。

6. 旋转体的切面面积：题目给出一个旋转体的形状和旋转轴的位置，要求求出旋转体在某一位置上的切面面积。

这种题目可以帮助学生应用切线和面积计算，理解旋转体的切面特征。

通过这六大旋转模型题，学生可以更好地掌握旋转的概念和运用，提高解决数学问题的能力。

在解题过程中，学生需要善于利用旋转的几何性质和计算方法，灵活运用数学知识，加深对数学的理解和认识。

同时，这些题目也能够培养学生的逻辑思维能力和推理能力，提高解决问题的能力和思维水平。

中考数学里越来越重要的图形旋转,用5个模型就能搞定

中考数学里越来越重要的图形旋转，用5个模型就能搞定！旋转的定义常见的几种模型旋转类型题目举例1、正三角形类型在正ΔABC中，P为ΔABC内一点，将ΔABP绕A点按逆时针方向旋转60°，使得AB与AC重合。

经过这样旋转变化，将图（1-1-a）中的PA、PB、PC三条线段集中于图（1-1-b）中的一个ΔP'CP 中，此时ΔP'AP也为正三角形。

例1如图（1-1），设P是等边ΔABC内的一点，PA=3，PB=4，PC=5，∠APB的度数是________.2、正方形类型在正方形ABCD中，P为正方形ABCD内一点，将ΔABP绕B点按顺时针方向旋转90°，使得BA与BC重合。

经过旋转变化，将图（2-1-a）中的PA、PB、PC三条线段集中于图（2-1-b）中的ΔCPP'中，此时ΔBPP'为等腰直角三角形。

例2 如图（2-1），P是正方形ABCD内一点，点P到正方形的三个顶点A、B、C的距离分别为PA=1，PB=2，PC=3。

求正方形ABCD面积。

3、等腰直角三角形类型在等腰直角三角形ΔABC中，∠C=90°, P为ΔABC内一点，将ΔAPC绕C点按逆时针方向旋转90°，使得AC与BC重合。

经过这样旋转变化，在图（3-1-b）中的一个ΔP'CP为等腰直角三角形。

例3如图，在ΔABC中，∠ACB =90°，BC=AC，P为ΔABC内一点，且PA=3，PB=1，PC=2。

求∠BPC的度数。

总结：旋转是几何变换中的基本变换，它一般先对给定的图形或其中一部分，通过旋转，改变位置后得新组合，然后在新的图形中分析有关图形之间的关系，进而揭示条件与结论之间的内在联系，找出证题途径。

人教版初三数学压轴题解题模型之旋转模型(含解析)

【例题】如图（2-1）：是正方形内一点，点到正方形的三个顶点、、的距离分别为PA=1，PB=2，PC=3。求此正方形ABCD。
面.
（三）等腰直角三角形类型
在等腰直角三角形中，，为内一点，将绕点按逆时针方向旋转，使得与重合。经过这样旋转变化，在图（3-1-b）中的一个为等腰直角三角形。
（1）求∠1的度数；
（2）判断△GMH的形状。
【分析】：等边三角形是旋转对称图形，且每个角都是60°，∠1是△BCH的外角，可知∠1＝∠2＋∠3。
而∠2＝∠4
∴∠1＝∠4＋∠3＝60°，从而得证。
【解析】：（1）∵等边△ABC是旋转对称图形，且AE＝BF＝CD
所以，△ABC绕旋转中心旋转120°后，△AEC、△BFA、△CDB能够重合
（1）如图（1），两三角尺的重叠部分为，则重叠部分的面积为，周长为．
（2）将图（1）中的绕顶点逆时针旋转，得到图（2），此时重叠部分的面积为，周长为．
（3）如果将绕旋转到不同于图（1）和图（2）的图形，如图（3），请你猜想此时重叠部分的面积为．
3、如图，P是等边△ABC内一点，PA=2，，PC=4，求BC的长。
【例题】如图，在中，∠ACB =900，BC=AC，P为内一点，且PA=3，PB=1，PC=2。求的度数。
典型例题
利用旋转的特征，可巧妙解决很多数学问题，如
一.求线段长.
例1.如图，已知长方形ABCD的周长为20，AB=4，点E在BC上，且AE⊥EF，AE=EF，求CF的长。
【解析】：将△ABE以点E为旋转中心，顺时针旋转90°，此时点B旋转到点B'处，AE与EF重合，由旋转特征知：B'E⊥BC，

中考数学旋转压轴题解题方法(详解答案)

②对应点与旋转中心所连线段的夹角等于旋转角，即角相等③旋转前、后的图形全等。

利用旋转构造复杂几何图形，通常将旋转融合在综合题中，题目难度中等，在选择题、填空题、解答题中都有出现。

有旋转点的，有旋转线段的，更多的是旋转图形的。

旋转三角形，旋转平行四边形，旋转矩形，旋转正方形，其中，近两年的各地中考试题中，旋转矩形出现的最频繁，深受出题老师的青睐。

其实旋转的题目还有一个好听的名字就是“手拉手问题”，本文将对这一类问题分类汇总，以这三个性质为突破口，就能快速解决问题。

二、典例精讲典例．在△ABC中，AC＝BC，∠ACB＝α，点D为直线BC上一动点，过点D作DF∥AC 交直线AB于点F，将AD绕点D顺时针旋转α得到ED，ED交直线AB于点O，连接BE．（1）问题发现：如图1，α＝90°，点D在边BC上，猜想：①AF与BE的数量关系是；②∠ABE＝度．（2）拓展探究：如图2，0°＜α＜90°，点D在边BC上，请判断AF与BE的数量关系及∠ABE的度数，并给予证明．（3）解决问题如图3，90°＜α＜180°，点D在射线BC上，且BD＝3CD，若AB＝8，请直接写出BE 的长．思路点拨：（1）①由等腰直角三角形的判定和性质可得：∠ABC＝45°，由平行线的性质可得∠FDB＝∠C＝90°，进而可得由等角对等边可得DF＝DB，由旋转可得：∠ADF＝∠EDB，DA＝DE，继而可知△ADF≌△EDB，继而即可知AF＝BE；②由全等三角形的性质可知∠DAF＝∠E，继而由三角形内角和定理即可求解；（2）由平行线的性质可得∠ACB＝∠FDB＝α，∠CAB＝∠DFB，由等边对等角可得∠ABC＝∠CAB，进而根据等角对等边可得DB＝DF，再根据全等三角形的判定方法证得△ADF≌△EDB，进而可得求证AF＝BE，∠ABE＝∠FDB＝α；（3）分两种情况考虑：①如图（3）中，当点D在BC上时，②如图（4）中，当点D在BC的延长线上时，由平行线分线段成比例定理可得1==4AF CDAB CB、1==2AF CDAB CB，代入数据求解即可；满分解答：（1）问题发现：如图1中，设AB交DE于O．∵∠ACB＝90°，AC＝BC，∴∠ABC＝45°，∵DF∥AC，∴∠FDB＝∠C＝90°，∴∠DFB＝∠DBF＝45°，∴DF＝DB，∵∠ADE＝∠FDB＝90°，∴∠ADF＝∠EDB，∵DA＝DE，DF＝DB∴△ADF≌△EDB（SAS），∴AF＝BE，∠DAF＝∠E，∵∠AOD＝∠EOB，∴∠ABE＝∠ADO＝90°故答案为：①AF＝BE，②90°．（2）拓展探究：结论：AF＝BE，∠ABE＝α．理由如下：∵DF‖AC∴∠ACB＝∠FDB＝α，∠CAB＝∠DFB，∵AC＝BC，∴∠ABC＝∠CAB，∴∠ABC＝∠DFB，∴DB＝DF，∵∠ADF＝∠ADE﹣∠FDE，∠EDB＝∠FDB﹣∠FDE，∴∠ADF＝∠EDB，∵AD＝DE，DB＝DF∴△ADF≌△EDB（SAS），∴AF＝BE，∠AFD＝∠EBD∵∠AFD＝∠ABC+∠FDB，∠DBE＝∠ABD+∠ABE，∴∠ABE＝∠FDB＝α．（3）解决问题①如图（3）中，当点D在BC上时，由（2）可知：BE＝AF，∵DF∥AC，∴1==4 AF CDAB CB，∵AB＝8，∴AF＝2，∴BE＝AF＝2，②如图（4）中，当点D在BC的延长线上时，∵AC∥DF，∴1==2 AF CDAB CB，∵AB＝8，∴BE＝AF＝4，故BE的长为2或4．名师点评：（1）本题考查等腰直角三角形的判定和性质、平行线的性质、等边对等角的性质和等角对等边的性质、旋转的性质、相似三角形的判定及其性质、三角形内角和定理、平行线分线段成比例定理，涉及到的知识点较多，解题的关键是综合运用所学知识．（2）旋转问题三步走：第一步：我们要观察图形，看看这个图形的旋转中心，找到它的旋转方向，这是我们看到一个几何图形的第一印象．第二步：看看是什么旋转？因为旋转的种类有很多，你看它是点旋转还是线旋转或者是平面图形旋转·第三步：你再观察出有哪些三角形全等，从已知中找到两个三角形全等的条件（包括隐藏的对顶角、公共角、公共边等）．变式题．如图，在Rt△ABC中，∠ACB＝90°，∠BAC＝30°，点O是边AC的中点．（1）在图1中，将△ABC绕点O逆时针旋转n°得到△A1B1C1，使边A1B1经过点C．求n的值．（2）将图1向右平移到图2位置，在图2中，连结AA1、AC1、CC1．求证：四边形AA1CC1是矩形；（3）在图3中，将△ABC绕点O顺时针旋转m°得到△A2B2C2，使边A2B2经过点A，连结AC2、A2C、CC2．①请你直接写出m的值和四边形AA2CC2的形状；②若AB＝，请直接写出AA2的长．三、中考押题1．（1）问题感知如图1，在△ABC中，∠C＝90°，且AC＝BC，点P是边AC的中点，连接BP，将线段PB绕点P顺时针旋转90°到线段PD．连接AD．过点P作PE∥AB 交BC于点E，则图中与△BEP全等的三角形是，∠BAD＝°；（2）问题拓展如图2，在△ABC中，AC＝BC＝43AB，点P是CA延长线上一点，连接BP，将线段PB绕点P顺时针旋转到线段PD，使得∠BPD＝∠C，连接AD，则线段CP与AD之间存在的数量关系为CP＝43AD，请给予证明；（3）问题解决如图3，在△ABC中，AC＝BC＝AB＝2，点P在直线AC上，且∠APB ＝30°，将线段PB绕点P顺时针旋转60°到线段PD，连接AD，请直接写出△ADP 的周长．2．在ABC ∆，CA CB =，ACB α∠=．点P 是平面内不与点A ，C 重合的任意一点．连接AP ，将线段AP 绕点P 逆时针旋转α得到线段DP ，连接AD ，BD ，CP ．（1）观察猜想如图1，当60α︒=时，BDCP的值是，直线BD 与直线CP 相交所成的较小角的度数是．（2）类比探究如图2，当90α︒=时，请写出BDCP的值及直线BD 与直线CP 相交所成的小角的度数，并就图2的情形说明理由．（3）解决问题当90α︒=时，若点E ，F 分别是CA ，CB 的中点，点P 在直线EF 上，请直接写出点C ，P ，D 在同一直线上时ADCP的值．3．在正方形ABCD 中，AB ＝6，对角线AC 和BD 相交于点O ，E 是AB 所在直线上一点（不与点B 重合），将线段OE 绕点E 顺时针旋转90°得到EF ．（1）如图1，当点E 和点A 重合时，连接BF ，直接写出BF 的长为；（2）如图2，点E在线段AB上，且AE＝1，连接BF，求BF的长；（3）若DG：AG＝2：1，连接CF，H是CF的中点，是否存在点E使△GEH是以EG 为直角边的直角三角形？若存在，请直接写出EB的长；若不存在，试说明理由．4．观察猜想：（1）如图①，在Rt△ABC中，∠BAC＝90°，AB＝AC＝3，点D与点A重合，点E在边BC上，连接DE，将线段DE绕点D顺时针旋转90°得到线段DF，连接BF，BE与BF的位置关系是，BE+BF＝；探究证明：（2）在（1）中，如果将点D沿AB方向移动，使AD＝1，其余条件不变，如图②，判断BE与BF的位置关系，并求BE+BF的值，请写出你的理由或计算过程；拓展延伸：（3）如图③，在△ABC中，AB＝AC，∠BAC＝a，点D在边BA的延长线上，BD＝n，连接DE，将线段DE绕着点D顺时针旋转，旋转角∠EDF＝a，连接BF，则BE+BF的值是多少？请用含有n，a的式子直接写出结论．5．如图1，矩形DEFG中，DG＝2，DE＝3，Rt△ABC中，∠ACB＝90°，CA＝CB＝2，FG，BC的延长线相交于点O，且FG⊥BC，OG＝2，OC＝4．将△ABC绕点O逆时针旋转α（0°≤α＜180°）得到△A′B′C′．（1）当α＝30°时，求点C′到直线OF的距离．（2）在图1中，取A′B′的中点P，连结C′P，如图2．①当C′P与矩形DEFG的一条边平行时，求点C′到直线DE的距离．②当线段A′P与矩形DEFG的边有且只有一个交点时，求该交点到直线DG的距离的取值范围．6．在△ABC中，∠ACB=90°，BC=AC=2，将△ABC绕点A顺时针方向旋转α角(0°＜α＜180°)至△AB'C'的位置．问题探究：（1）如图1，当旋转角为60°时，连接C'C与AB交于点M，则C'C=，CM ．（2）如图2，在（1）条件下，连接BB'，延长CC'交BB'于点D，求CD的长．问题解决：（3）如图3，在旋转的过程中，连线CC'、BB'，CC'所在直线交BB'于点D，那么CD 的长有没有最大值？如果有，求出CD的最大值：如果没有，请说明理由．7．如图1，在正方形ABCD中，对角线AC、BD相交于点O，点E为线段BO上一点，连接CE，将CE绕点C顺时针旋转90°得到CF，连接EF交CD于点G．（1）若AB＝4，BE，求△CEF的面积．（2）如图2，线段FE的延长线交AB于点H，过点F作FM⊥CD于点M，求证：BH+MGBE；＝2（3）如图3，点E为射线OD上一点，线段FE的延长线交直线CD于点G，交直线AB 于点H，过点F作FM垂直直线CD于点M，请直接写出线段BH、MG、BE的数量关系．8．已知:如图①，将60∠=的菱形ABCD沿对角线AC剪开，将ADC沿射线DCDBCE点M为边BC上一点（点M不与点B、点C重合），将射线AM 方向平移，得到,绕点A逆时针旋转60，与EB的延长线交于点N，连接MN．()1①求证:ANB AMC∠=∠；②探究AMN的形状；()2如图②，若菱形ABCD变为正方形ABCD，将射线AM绕点A逆时针旋转45，原题其他条件不变，()1中的①和②两个结论是否仍然成立？若成立，请直接写出结论；若不成立，请写出变化后的结论并证明．9．已知点P 是线段AB 上与点,A B 不重合的一点，且,AP PB AP <绕点A 逆时针旋转角()090αα︒︒<≤得到1,AP BP 绕点B 顺时针旋转角α得到2BP ，连接12.PP PP 、（1）如图1，当90α︒=时，求12PPP ∠的度数；（2）如图2，当点2P 在1AP 的延长线上时，求证： 22122PP PP P A =⋅；（3）如图3，过BP 的中点E 作1l BP ⊥，过2BP 的中点F 作22l BP ⊥， 1l 与2l 交于点Q ，连接1,PQ PO ，若6,1BP AP QE ===，求1PQ 的长度.10．在锐角△ABC 中，AB=4，BC=5，∠ACB=45°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△ABA 1的面积为4，求△CBC 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转过程中，点P 的对应点是点P 1，求线段EP 1长度的最大值与最小值．11．有两张完全重合的矩形纸片，将其中一张绕点A 顺时针旋转90︒后得到矩形AMEF （如图1），连接BD ，MF ，若8BD cm =，30ADB ∠=︒．（1）试探究线段BD 与线段MF 的数量关系和位置关系，并说明理由；（2）把BCD ∆与MEF ∆剪去，将ABD ∆绕点A 顺时针旋转得11AB D ∆，边1AD 交FM 于点K （如图2），设旋转角为()090ββ︒<<︒，当AFK ∆为等腰三角形时，求β的度数；（3）若将AFM ∆沿AB 方向平移得到222A F M ∆（如图3），22F M 与AD 交于点P ，22A M 与BD 交于点N ，当//NP AB 时，求平移的距离．12．问题发现：（1）如图1，在Rt △ABC 中，∠BAC=30°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ， ∠BCD 的度数是；线段BD ，AC 之间的数量关系是．类比探究：（2）在Rt △ABC 中，∠BAC=45°，∠ABC ＝90°，将线段AC 绕点A 逆时针旋转，旋转角α=2∠BAC ，请问（1）中的结论还成立吗？；拓展延伸：（3）如图3，在Rt △ABC 中，AB ＝2，AC ＝4，∠BDC ＝90°，若点P 满足PB ＝PC ，∠BPC ＝90°，请直接写出线段AP 的长度．13．综合与实践问题情境数学活动课上，老师让同学们以“三角形的旋转”为主题开展数学活动，ABC 和DEC 是两个全等的直角三角形纸片，其中90ACB DCE ∠=∠=︒，30B E ∠=∠=︒，4AB DE ==．解决问题（1）如图①，智慧小组将DEC 绕点C 顺时针旋转，发现当点D 恰好落在AB 边上时，DE AC ，请你帮他们证明这个结论；（2）缜密小组在智慧小组的基础上继续探究，连接AE AD BD 、、，当DEC C 绕点C 继续旋转到如图②所示的位置时，他们提出BDCAECSS=，请你帮他们验证这一结论是否正确，并说明理由；探索发现（3）如图③，勤奋小组在前两个小组的启发下，继续旋转DEC ，当B A E 、、三点共线时，求BD 的长；（4）在图①的基础上，写出一个边长比为2的三角形（可添加字母）．14．探究：如图1和2,四边形ABCD 中,已知AB AD =，90BAD ∠=︒，点E ，F 分别在BC 、CD 上，45EAF ∠=︒．（1）①如图 1,若B 、ADC ∠都是直角，把ABE △绕点A 逆时针旋转90︒至ADG ，使AB 与AD 重合，则能证得EF BE DF =+，请写出推理过程；②如图 2，若B 、D ∠都不是直角，则当B 与D ∠满足数量关系_______时，仍有EF BE DF =+;（2）拓展：如图3,在ABC 中，90BAC ∠=︒,AB AC ==点D 、E 均在边BC 上,且45DAE ∠=︒．若1BD =，求DE 的长．15．操作与证明：如图1，把一个含45°角的直角三角板ECF 和一个正方形ABCD 摆放在一起，使三角板的直角顶点和正方形的顶点C 重合，点E 、F 分别在正方形的边CB 、CD 上，连接AF ．取AF 中点M ，EF 的中点N ，连接MD 、MN ．（1）连接AE ，求证：△AEF 是等腰三角形；猜想与发现：（2）在（1）的条件下，请判断MD 、MN 的数量关系和位置关系，得出结论．结论1：DM 、MN 的数量关系是；结论2：DM 、MN 的位置关系是；拓展与探究：（3）如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则（2）中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．16．已知，把45°的直三角板的直角顶点E放在边长为6的正方形ABCD的一边BC 上，直三角板的一条直角边经过点D，以DE为一边作矩形DEFG，且GF过点A，得到图1．（1）求矩形DEFG的面积；（2）若把正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC，把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC的直角顶点B重合，直三角板夹这个45°角的两边分别交CA和CA的延长线于点H、P，得到图2．猜想：CH、PA、HP之间的数量关系，并说明理由；（3）若把边长为6的正方形ABCD沿着对角线AC剪掉一半得到等腰直角三角形ABC，点M是Rt△ABC内一个动点，连接MA、MB、MC，设MA+MB+MC＝y，直接写出2y 的最小值．17．问题：如图(1)，点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．（发现证明）小聪把△ABE绕点A逆时针旋转90°至△ADG,从而发现EF=BE+FD,请你利用图（1）证明上述结论．（类比引申）如图(2)，四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足关系时，仍有EF=BE+FD．（探究应用）如图(3)，在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的=1.41=1.73）18．如图1，在矩形ABCD中，AB=6，BC=8，点E是对角线BD的中点，直角∠GEF 的两直角边EF、EG分别交CD、BC于点F、G．（1）若点F是边CD的中点，求EG的长．（2）当直角∠GEF绕直角顶点E旋转，旋转过程中与边CD、BC交于点F、G．∠EFG 的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠EFG的值．（3）当直角∠GEF绕顶点E旋转，旋转过程中与边CD、BC所在的直线交于点F、G．在图2中画出图形，并判断∠EFG的大小是否发生变化？如果变化，请说明理由；如果不变，请直接写出tan∠EFG的值．（4）如图3，连接CE交FG于点H，若13HFHG，请求出CF的长．参考答案变式题．思路点拨：（1）利用等腰三角形的性质求出∠COC1即可．（2）根据对角线相等的平行四边形是矩形证明即可．（3）①求出∠COC2即可，根据矩形的判定证明即可解决问题．②解直角三角形求出A2C2，再求出AA2即可．满分解答：（1）解：如图1中，由旋转可知：△A1B1C1≌△ABC，∴∠A1＝∠A＝30°，∵OC＝OA，OA1＝OA，∴OC＝OA1，∴∠OCA1＝∠A1＝30°，∴∠COC1＝∠A1+OCA1＝60°，∴n＝60°．（2）证明：如图2中，∵OC＝OA，OA1＝OC1，∴四边形AA1CC1是平行四边形，∵OA＝OA1，OC＝OC1，∴AC＝A1C1，∴四边形AA1CC1是矩形．（3）如图3中，①∵OA＝OA2，∴∠OAA2＝∠OA2A＝30°，∴∠COC2＝∠AOA2＝180°﹣30°﹣30°＝120°，∴m＝120°，∵OC＝OA，OA2＝OC2，∴四边形AA2CC2是平行四边形，∵OA＝OA2，OC＝OC2，∴AC＝A2C2，∴四边形AA2CC2是矩形．＝6，②∵AC＝A2C2＝AB•cos30°＝×2∴AA2＝A2C2•cos30°＝＝名师点评：本题属于四边形综合题，考查了旋转变换，平行四边形的判定和性质，矩形的判定和性质，解直角三角形等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．中考押题1．证明：（1）∵点P是边AC的中点，PE∥AB，∴点E是BC的中点，∴CE＝BE，∵AC＝BC，∴BE＝AP，∵将线段PB绕点P顺时针旋转90°到线段PD．∴PB＝PD，∵∠APD+∠BPC＝90°，∠EBP +∠BPC＝90°，∴∠EBP＝∠APD，又∵PB＝PD，∴△PAD≌△BEP（SAS），∴∠PAD＝∠BEP，∵∠C＝90°，AC＝BC，∴∠BAC＝∠ABC＝45°，∵PE∥AB，∴∠ABC＝∠PEC＝45°，∴∠BEP＝135°，∴∠BAD＝∠PAD﹣∠BAC＝135°﹣45°＝90°，故答案为：△PAD，90；（2）如图，过点P作PH∥AB，交CB的延长线于点H，∴∠CBA＝∠CHP，∠CAB＝∠CPH，∵CB＝CA，∴∠CBA＝∠CAB，∴∠CHP＝∠CPH，∴CH＝CP，∴BH＝AP，∵将线段PB绕点P顺时针旋转90°到线段PD．∴PB＝PD，∵∠BPD＝∠C，∴∠BPD+∠BPC ＝∠C+∠BPC ， ∴∠PBH ＝∠APD ， ∴△APD ≌△HBP （SAS ）， ∴PH ＝AD ， ∵PH ∥AB ， ∴△CAB ∽△CPH ，∴H AC PC ABP = ∴HAC AB CPP = ∵AC ＝BC ＝43AB ，∴43CP PH =， ∴CP ＝43PH ＝43AD ；（3）当点P 在CA 的延长线上时， ∵AC ＝BC ＝AB ＝2， ∴△ABC 是等边三角形， ∴∠ACB ＝60°，∵将线段PB 绕点P 顺时针旋转60°到线段PD ， ∴BP ＝PD ，∠BPD ＝60°＝∠ACB ，过点P 作PE ∥AB ，交CB 的延长线于点E ，∵∠ACB ＝∠APB+∠ABP ， ∴∠ABP ＝∠APB ＝30°， ∴AB ＝AP ＝2， ∴CP ＝4， ∵AB ∥PE ，∴PAB PE CAC = ∴CP ＝PE ＝4，由（2）得，PE ＝AD ＝4， ∵∠APD ＝∠APB+BPD ＝90°，∴DP =∴△ADP 的周长＝AD+AP+DP ＝，当点P 在AC 延长线上时，如图，同理可求△ADP 的周长＝6+综上所述：△ADP 的周长为6+2．解：（1）如图1中，延长CP 交BD 的延长线于E ，设AB 交EC 于点O ．60PAD CAB ︒∠=∠=，CAP BAD ∴∠=∠， CA BA =，PA DA =，()CAP BAD SAS ∴∆≅∆，PC BD ∴=，ACP ABD ∠=∠，AOC BOE ∠=∠，60BEO CAO ︒∴∠=∠=，1BDPC∴=，线BD 与直线CP 相交所成的较小角的度数是60︒，故答案为1，60︒．（2）如图2中，设BD 交AC 于点O ，BD 交PC 于点E ．45PAD CAB ︒∠=∠=，PAC DAB ∴∠=∠，AB ADAC AP== DAB PAC ∴∆∆，PCA DBA ∴∠=∠，BD ABPC AC==， EOC AOB ∠=∠，45CEO OAB ︒∴∠=∠=，∴直线BD 与直线CP 相交所成的小角的度数为45︒．（3）如图3﹣1中，当点D 在线段PC 上时，延长AD 交BC 的延长线于H ．CE EA =，CF FB =，EF AB∴∥，45EFC ABC︒∴∠=∠=，45PAO︒∠=，PAO OFH∴∠=∠，POA FOH∠=∠，H APO∴∠=∠，90APC︒∠=，EA EC=，PE EA EC∴==，EPA EAP BAH∴∠=∠=∠，H BAH∴∠=∠，BH BA∴=，45ADP BDC︒∠=∠=，90ADB︒∴∠=，BD AH∴⊥，22.5DBA DBC︒∴∠=∠=，90ADB ACB︒∠=∠=，∴A，D，C，B四点共圆，22.5DAC DBC︒∠=∠=，22.5DCA ABD︒∠=∠=，22.5DAC DCA︒∴∠=∠=，DA DC∴=，设=AD a，则DC AD a==，2PD a=，2ADCP∴==-c．如图3﹣2中，当点P在线段CD上时，同法可证：=DA DC，设=AD a，则CD AD a==，PD=，2PC a a ∴=-，22ADPC∴==+．3．解：（1）如图1，由旋转得：90OEF ∠=︒，OE EF =，四边形ABCD 是正方形，且边长为6， 62ACBD，45OAB ∠=︒，904545FEBOAB ，AB AB ，()AOBAFB SAS ，113222BFOBBDAC ，故答案为：（2）如图2，过O 作OG AB ⊥于G ，过F 作FHAB⊥于H ，四边形ABCD 是正方形，45OAB OBA ∴∠=∠=︒，90OGAOGB，AOG ∴∆和OGB 是等腰直角三角形，3AGBGOG，1AE =，2EG，90OEF ， 90OEG FEH，90FEHEFH，OEGEFH ，OE EF ，90OGEEHF，()OEG EFH AAS ，3OG EH，2EG FH ==，6132BHAB AE EH ，Rt FHB 中，由勾股定理得：22222222BFBH FH ；（3）存在GEH ∆是以EG 为直角边的直角三角形；6AD =，且:2:1DG AG ， 2AG ∴=，4DG =，分三种情况：①当90EGH ∠=︒时，E 在A 的左侧时，如图3，过F 作FM BC ⊥，交CB 的延长线于M ，过H 作HNFM 于N ，交AB 于P ，过H 作HQ AD ⊥于Q ，过O 作OKAB ⊥于K ，过F 作FL AB 于L ，设AE x =，同理得()OEK EFL AAS ，3OKEL，3EK FL x ，H 是CF 的中点，//HN CM ，113(63)222xFN MN BL x ，1639222x xHN CM ，93(3)22xxHPHNPN x ，Rt EGH 中，222EG GH EH ，∴22222233332(2)(6)(6)()2222x x x x x x，2720x x -+=，17412x ，27412x ，当17412x 时，7411941622BE （如图6所示），当27412x 时，7411941622BE；②当90GEH ∠=︒时，如图4，过F 作FM BC ⊥，交CB 的延长线于M ，过H 作HN FM于N ，交AB 于P ，过O 作OK AB ⊥于K ，过F 作FLAB 于L ，设BE x =，则6AE x ，同理得：3OK EL，3BLFMx ，3(6)3FL EKx x ，1322xHNCM ，3322x x EPBEPBx，39(3)22xxHP HN PNx，90GEH AEG PEH，90AEG AGE ∠+∠=︒，AGEPEH ，90EAG EPH ，GAE EPH ∽， ∴AG AEEPPH，即263922x x x ，250x x -=，解得：0x =（舍)或5，即5BE =；③如图5，当E 与B 重合时，90GEH∠=︒，此种情况不符合题意；综上，BE 的长是5． 4．【详解】（1）如图①中，∵∠EAF ＝∠BAC ＝90°， ∴∠BAF ＝∠CAE ， ∵AF ＝AE ，AB ＝AC ， ∴△BAF ≌△CAE ， ∴∠ABF ＝∠C，BF ＝CE ， ∵AB ＝AC ，∠BAC ＝90°，∴∠ABC＝∠C＝45°，∴∠FBE＝∠ABF+∠ABC＝90°，BC＝BE+EC＝BE+BF，故答案为BF⊥BE，BC；（2）如图②中，作DH∥AC交BC于H，∵DH∥AC，∴∠BDH＝∠A＝90°，△DBH是等腰直角三角形，由（1）可知，BF⊥BE，BF+BE＝BH，∵AB＝AC＝3，AD＝1，∴BD＝DH＝2，∴BH＝，∴BF+BE＝BH＝；（3）如图③中，作DH∥AC交BC的延长线于H，作DM⊥BC于M，∵AC∥DH，∴∠ACH＝∠H，∠BDH＝∠BAC＝α，∵AB＝AC，∴∠ABC＝∠ACB∴∠DBH＝∠H，∴DB＝DH，∵∠EDF＝∠BDH＝α，∴∠BDF＝∠HDE，∵DF ＝DE ，DB ＝DH ， ∴△BDF ≌△HDE ， ∴BF ＝EH ，∴BF +BE ＝EH +BE ＝BH ， ∵DB ＝DH ，DM ⊥BH ， ∴BM ＝MH ，∠BDM ＝∠HDM ， ∴BM ＝MH ＝BD •sin2α．∴BF +BE ＝BH ＝2n •sin 2α． 5．解：（1）如图，过点C′作C′H ⊥OF 于H ．∵△A′B′C′是由△ABC 绕点O 逆时针旋转得到， ∴C′O=CO=4，在Rt △HC′中， ∵∠HC′O ＝α＝30°，∴C′H ＝C′O•cos30°＝，∴点C′到直线OF 的距离为（2）①如图，当C′P ∥OF 时，过点C′作C′M ⊥OF 于M ．∵△A′B′C′为等腰直角三角形，P为A′B′的中点，∴∠A′C′P=45°，∵∠A′B′O=90°，∴∠OC′P=135°.∵C′P∥OF，∴∠O＝180°﹣∠OC′P＝45°，∴△OC′M是等腰直角三角形，∵OC′＝4，=∴C′M＝C′O•cos45°=4×2∴点C′到直线DE的距离为如图，当C′P∥DG时，过点C′作C′N⊥FG于N．同法可证△OC′N是等腰直角三角形，∴C′N＝∵GD=2，∴点C′到直线DE的距离为2．②设d为所求的距离．第一种情形：如图，当点A′落在DE上时，连接OA′，延长ED交OC于M．∵OC=4，AC=2，∠ACO=90°，=∴=OA=∵OM＝2，∠OMA′＝90°，∴A′M4，又∵OG=2，∴DM=2，∴A′D＝A′M-DM=4-2=2，即d＝2，如图，当点P落在DE上时，连接OP，过点P作PQ⊥C′B′于Q．∵P为A′B′的中点，∠A′C′B′=90°，∴PQ∥A′C′，∴12 B P CQ PQB A BC A C'=== ''''''∵B′C′=2∴PQ＝1，CQ=1，∴Q点为B′C′的中点，也是旋转前BC的中点，∴OQ=OC+CQ=5∴OP，∴PM=∴PD＝2PM DM-=-，∴d2，∴2．第二种情形：当A′P与FG相交，不与EF相交时，当点A′在FG上时，A′G＝2，即d＝2，如图，当点P落在EF上时，设OF交A′B′于Q，过点P作PT⊥B′C′于T，过点P作PR∥OQ 交OB′于R，连接OP．由上可知OP OF＝5，∴FP1，∵OF＝OT，PF＝PT，∠F＝∠PTO＝90°，∴Rt△OPF≌Rt△OPT（HL），∴∠FOP＝∠TOP，∵PQ∥OQ，∴∠OPR＝∠POF，∴∠OPR＝∠POR，∴OR＝PR，∵PT2+TR2＝PR2，22215PR PR∴+（﹣）＝∴PR＝2.6，RT＝2.4，∵△B′PR∽△B′QO，∴B ROB''＝PRQO，∴3.46＝2.6OQ，∴OQ＝78 17，∴QG＝OQ﹣OG＝4417，即d＝4417∴2≤d＜44 17，第三种情形：当A′P经过点F时，如图，此时FG=3，即d＝3．综上所述，﹣2或d ＝3．6．解：（1）如图1中，作MH AC ⊥于H ．当旋转角为60︒时，60CAC ，AC AC ='， ACC 是等边三角形，2CC AC ，60MCH ，设CH x =，则3MH AH x ，2x ∴=，1x ∴=，2232CM CH ．故答案为2，2．（2）如图2中，作BH CD ⊥于H ．AB AB ='，60BAB ，ABB 是等边三角形，60DBM ACM ， DMB AMC ，45BDC BAC ∴∠=∠=︒， 30BCH BCA ACC ，1BH DH BC，CH=12CD CH DH．13（3）CD的长有最大值．理由：如图3中，B AC BAC，45B ABC AC，='，AB AB'=，AC AC∴AB AB，AC AC∴△B AB∽△C AC，DBM ACM，DMB AMC，45BDM MAC，取AB的中点H，以H为圆心，HB为半径作H，连接CH．=，90CA CB∠=︒，ACB∴⊥，CH BH AH，CH ABBHC，901BDC BHC，2∴=时，CD的值最大，此时CD=．点D的运动轨迹是H，当CD AB7．【详解】（1）解：在正方形ABCD中，AB＝4，∴AO＝CO＝OB＝，∵BE ，∴OE ，∵AC ⊥BD ，∴∠COE ＝90°，∴CE ==,由旋转得：CE ＝CF ，∠ECF ＝90°，∴△CEF 的面积＝211522CE ==；（2）证明：如图2，过E 作EN ⊥AB 于N ，作EP ⊥BC 于P ，∵EP ⊥BC ，FM ⊥CD ，∴∠EPC ＝∠FMC ＝90°，∵∠BCD ＝∠ECF ＝90°，∴∠PCE ＝∠MCF ，∵CE ＝CF ，∴△CPE ≌△CMF （AAS ），∴EP ＝FM ，∵EP ⊥BC ，EN ⊥AB ，BE 平分∠ABC ，∴EP ＝EN ，∴EN ＝FM ，∵FM ⊥CD ，∴∠FMG ＝∠ENH ＝90°，∵AB ∥CD ，∴∠NHE ＝∠MGF ，∴△NHE ≌△MGF （AAS ），∴NH＝MG，∴BH+MG＝BH+NH＝BN，∵△BEN是等腰直角三角形，BE，∴BN＝2BE；∴BH+MG＝2BE，理由是：（3）解：BH﹣MG＝2如图3，过E作EN⊥AB于N，交CG于P，∵EP⊥BC，FM⊥CD，AB∥CD，∴EP⊥CD，∴∠EPC＝∠FMC＝90°，∵∠M＝∠ECF＝90°，∴∠ECP+∠FCM＝∠FCM+∠CFM＝90°，∴∠ECP＝∠CFM，∵CE＝CF，∴△CPE≌△FMC（AAS），∴PC＝FM，∵△DPE是等腰直角三角形，∴PE＝PD，∴EN＝BN＝PN+PE＝BC+PE＝CD+PD＝PC＝FM，∵AB ∥CD ，∴∠H ＝∠FGM ，∵∠ENH ＝∠M ＝90°，∴△HNE ≌△GMF （AAS ），∴NH ＝MG ，∴BH ﹣MG ＝BH ﹣NH ＝BN ，∵△BEN 是等腰直角三角形，∴BN ＝2BE ，∴BH ﹣MG ＝2BE ． 8．【详解】（1）如图1，①∵四边形ABCD 是菱形，∴AB BC CD AD ===，∵∠D =60°，∴△ADC 和△ABC 是等边三角形，∴AB AC =，∠BAC =60°，∵∠NAM =60°，∴∠NAB =∠CAM ，由△ADC 沿射线DC 方向平移得到△BCE ，可知∠CBE =60°， ∵∠ABC =60°，∴∠ABN =60°，∴∠ABN =∠ACB =60°∴△ANB ≌△AMC ，∴∠ANB =∠AMC ； ②如图1，△AMN 是等边三角形，理由是：由△ANB≌△AMC，∴AM=AN，∵∠NAM=60°，∴△AMN是等边三角形；（2）①如图2，∠ANB=∠AMC成立，理由是：在正方形ABCD中，∴∠BAC=∠DAC=∠BCA=45°，∵∠NAM=45°，∴∠ANB=∠AMC，由平移得：∠EBC=∠CAD=45°，∵∠ABC=90°，∴∠ABN=180°-90°−45°=45°，∴∠ABN=∠ACM=45°，∴△ANB∽△AMC，∴∠ANB=∠AMC；②如图2，不成立，△AMN是等腰直角三角形，理由是：∵△ANB∽△AMC，∴AN AB AM AC=，∴AN AM AB AC=，∵∠NAM=∠BAC=45°，∴△NAM∽△BAC，∴∠ANM =∠ABC =90°， ∴△AMN 是等腰直角三角形. 9．【详解】（1）解：由旋转的性质得：AP=AP 1，BP=BP 2． ∵α=90°，∴△PAP 1和△PBP 2均为等腰直角三角形， ∴∠APP 1=∠BPP 2=45°，∴∠P 1PP 2=180°-∠APP 1-∠BPP 2=90°；（2）证明：由旋转的性质可知△PAP 1和△PBP 2均为顶角为α的等腰三角形， ∴∠APP 1=∠BPP 2=90°2α-， ∴∠P 1PP 2=180°-（∠APP 1+∠BPP 2）=180°-2(90°2α-)=α，在△P 2P 1P 和△P 2PA 中，∠P 1PP 2=∠PAP 2=α，又∵∠PP 2P 1=∠AP 2P ，∴△P 2P 1P ∽△P 2PA ， ∴12222PP P P P P P A=， ∴22122PP PP P A =⋅；（3）证明：如图，连接QB ，并过A 作1AM PP ⊥，垂足为M ，则12PAM α∠=，112PM PP =， ∵l 1，l 2分别为PB ，P 2B 的中垂线，2BP BP =，∴QP=QB ，PE=BE=BF=12BP = 又∵BQ=BQ ，90QEB QFB ∠=∠=︒，∴()Rt QEB Rt QFB HL ∆∆≌， ∴21122QPE QBE QBF P BP α∠=∠=∠=∠=， ∴12111909090222APP QPE PAM P BP αα∠+∠=︒-∠+∠=︒-∠+∠=︒， ∴190PPQ ∠=︒， ∵12QPE PAM α∠=∠=∠，90AMP PEQ ∠=∠=︒， ∴AMP PEQ ∆∆， ∴AP PM PQ QE=，在Rt PEQ ∆中，4PQ ===，且AP=6，QE=1， ∴32AP QE AP QE PM PQ PQ ⋅⋅===，123PP PM ==， ∴1Rt PPQ ∆中，15PQ ===． 10．解：（1）∵由旋转的性质可得：∠A 1C 1B=∠ACB=45°，BC=BC 1，∴∠CC 1B=∠C 1CB=45°．∴∠CC 1A 1=∠CC 1B+∠A 1C 1B=45°+45°=90°．（2）∵由旋转的性质可得：△ABC ≌△A 1BC 1，∴BA=BA 1，BC=BC 1，∠ABC=∠A 1BC 1． ∴11BA BA BC BC =，∠ABC+∠ABC 1=∠A 1BC 1+∠ABC 1 ∴∠ABA 1=∠CBC 1．∴△ABA 1∽△CBC 1∴1122ABA CBC S AB 416S CB 525∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭． ∵S △ABA1=4，∴S △CBC1=254．（3）过点B 作BD ⊥AC ，D 为垂足，∵△ABC 为锐角三角形，∴点D 在线段AC 上．在Rt △BCD 中，BD=BC×sin45°①如图1，当P 在AC 上运动至垂足点D ，△ABC 绕点B 旋转，使点P 的对应点P 1在线段AB 上时，EP 1最小．最小值为：EP 1=BP 1﹣BE=BD ﹣2．②如图2，当P 在AC 上运动至点C ，△ABC 绕点B 旋转，使点P 的对应点P 1在线段AB 的延长线上时，EP 1最大．最大值为：EP 1=BC+BE=5+2=7．11．【详解】（1）解：BD MF =，BD MF ⊥．延长FM 交BD 于点N ，根据旋转的性质得：AB=AM ，AD=AF ，∠BAD=∠MAF=90°∴BAD MAF ∆∆≌．∴BD MF =，ADB AFM ∠=∠．又∵DMN AMF ∠=∠，∴90ADB DMN AFM AMF ∠+∠=∠+∠=︒，∴90DNM ∠=︒，∴BD MF ⊥（2）解：如图2，①当AK FK =时，30KAF F ∠=∠=︒，则111180*********BAB B AD KAF ︒︒︒︒︒∠=-∠-∠=--=，即60β=︒；②当AF FK =时，75FAK ∠=︒，∴19015BAB FAK ∠=︒-∠=︒，即15β=︒；∴β的度数为60︒或15︒（3）如图3，由题意得矩形2PNA A ．设2A A x =，则PN x =，在222Rt A M F ∆中，∵228F M FM ==，∴224A M =，22A F =∴2AF x =．∵290PAF ∠=︒，230PF A ∠=︒，∴2tan 3043AP AF x ︒=⋅=-．∴43PD AD AP x =-=+． ∵//NP AB ，∴DNP B ∠=∠．∵D D ∠=∠，∴DPN DAB ∆∆∽． ∴PN DP AB DA=．∴44x x =，解得6x =-26A A =-答：平移的距离是(6cm -．12．【详解】解：（1）如图3，过点D 作DE ⊥BC ，垂足为E ，设BC=m ．在Rt △ABC 中，∠BAC=30°，由BC=AB ·tan30°，BC=AC ·sin30°，得AC=2m ，， ∵AC=AD ，∠CAD=2×30°=60°，∴△ACD 为等边三角形，∴∠ACD=60°，CD=AC=2m ，∴∠BCD=60°×2=120°，在Rt △DEC 中，∠DCE=180°-120°=60°，DC=2m ，∴CE=CD·cos60°=m ，DE=CE ·tan60°，∴在Rt △BED 中，，∴BD AC ，故AC ．故答案为：120°；AC ．（2）不成立，理由如下：设BC=n ，在Rt △ABC 中，∠BAC=45°，∠ABC=90°，∴BC=AB=m ，n ，∵AC=AD ，∠CAD=90°，∴△CAD 为等腰直角三角形，∴∠ACD=45°，AC= 2n ，∴∠BCD=2×45°=90°，在Rt △BCD 中，，∴BD AC ，故AC ．答案为：90°；．故结论不成立．（3）AP 或；解答如下：∵PB=PC ，∴点P 在线段BC 的垂直平分线上，∵∠BAC=∠BCP=90°，故A 、B 、C 、P 四点共圆，以线段BC 的中点为圆心构造⊙O ，如图4，图5，分类讨论如下：①当点P 在直线BC 上方时，如图4，作PM ⊥AC ，垂足为M ，设PM=x ．∵PB=PC ，∠BPC=90°，∴△PBC 为等腰直角三角形，∴∠PBC=45°，∵∠PAC=∠PBC=45°，∴△AMP 为等腰直角三角形，∴AM=PM=x ，x ，在Rt △ABC 中，AB=2，AC=4，∴PC=BC·sin45°，在Rt △PMC 中，∵∠PMC=90°，PM=x ，PC=，CM=4-x ，∴()2224x x +-=，解得：11x =，23x =（舍），∴；②当点P 在直线BC 的下方时，如图5，作PN ⊥AB 的延长线，垂足为N ，设PN=y ．同上可得△PAN 为等腰三角形，∴AN=PN=y ，∴BN=y-2，在Rt △PNB 中，∵∠PNB=90°，PN=y ，BN=y-2，，∴()2222y y +-=，解得：13y =，21y =-（舍），∴=AP 或 13．【详解】（1）如图①中，∵△DEC 绕点C 旋转点D 恰好落在AB 边上，∴AC=CD ，∵∠BAC=90°-∠B=90°-30°=60°，∴△ACD 是等边三角形，∴∠ACD=60°，又∵∠CDE=∠BAC=60°，∴∠ACD=∠CDE ，∴DE ∥AC ；（2）如图②中，作DM ⊥BC 于M ，AN ⊥EC 交EC 的延长线于N ．∵△DEC 是由△ABC 绕点C 旋转得到∴BC=CE ，AC=CD ，∵∠ACN+∠BCN=90°，∠DCM+∠BCN=180°-90°=90°，∴∠ACN=∠DCM ，在△ACN 和△DCM 中，90ACN DCM CMD N AC CD ∠∠⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△ACN ≌△DCM （AAS ），∴AN=DM ，∴△BDC 的面积和△AEC 的面积相等（等底等高的三角形的面积相等），即S △BDC =S △AEC ．（3）如图③中，作CH ⊥AD 于H ．∵，∵B ，A ，E 共线，∴∠BAC+∠EAC=180°，∴∠EAC=120°，∵∠EDC=60°，∴∠EAC+∠EDC=180°，∴A ，E ，D ，C 四点共圆，∴∠CAD=∠CED=30°，∠BAD=90°，∵CA=CD ，CH ⊥AD ，AC=CD=12AB=2∴∴，∴BD ===（4）如图①中，设DE 交BC 于T ．因为含有30°的直角三角形的三边之比为12，由（1）可知△BDT ，△DCT ，△ECT 都是含有30°的直角三角形，∴△BDT ，△DCT ，△ECT 符合条件．14．【详解】（1）①如图1，∵把ABE △绕点A 逆时针旋转90︒至ADG ，使AB 与AD 重合，∴AE AG =，BAE DAG ∠=∠，BE DG =∵90BAD ∠=︒，45EAF ∠=︒，∴45BAE DAF ∠+∠=︒，∴45DAG DAF ∠+∠=︒，即45EAF GAF ∠=∠=︒，在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS ≌，∴EF GF =，∵BE DG =，∴EF GF BE DF ==+；②180B D ∠+∠=︒，理由是：把ABE △绕A 点旋转到ADG ，使AB 和AD 重合，则AE AG =，B ADG ∠=∠，BAE DAG ∠=∠，∵180B ADC ︒∠+∠=，∴180ADC ADG ∠+∠=︒，∴C ，D ，G 在一条直线上，和①知求法类似，45EAF GAF ∠=∠=︒，在EAF △和GAF 中AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩∴()EAF GAF SAS △≌△，∴EF GF =，∵BE DG =，∴EF GF BE DF ==+；故答案为：180B D ∠+∠=︒（2）∵ABC中，AB AC ==90BAC ∠=∴45ABC C ∠=∠=︒，由勾股定理得：4BC === ，把AEC 绕A 点旋转到AFB △,使AB 和AC 重合，连接DF ．则AF AE =，45FBA C ∠=∠=︒，BAF CAE ∠=∠，∵45DAE ∠=︒，∴904545FAD FAB BAD CAE BAD BAC DAE ∠=∠+∠=∠+∠=∠-∠=︒-︒=︒， ∴45FAD DAE ∠=∠=︒，在FAD △和EAD 中AD AD FAD EAD AF AE =⎧⎪∠=∠⎨⎪=⎩∴FAD EAD △≌△，∴DF DE =，设DE x =，则DF x =，∵1BC =，∴413BF CE x x ==--=-，∵45FBA ∠=︒，45ABC ∠=︒，∴90FBD ∠=︒，由勾股定理得：222DF BF BD =+，。

初中几何旋转模型(实例)

初中几何旋转模型(实例)
在初中几何学中，旋转模型是一个常见的概念。

旋转模型指的是一个二维图形沿着旋转轴进行旋转形成的立体图形。

本文将介绍一个关于旋转模型的实例。

实例
假设我们有一个矩形，长为10厘米，宽为5厘米。

我们想要通过将该矩形沿着一条边进行旋转，生成一个立体图形。

首先，我们选择将矩形沿着长的一边进行旋转。

这条边将成为旋转轴。

根据旋转模型的原理，我们可以将旋转后的立体图形看作是一系列平行的矩形组成的。

每一个平行矩形都是由原始矩形在旋转过程中的一个截面形成的。

在旋转的过程中，矩形的长度不变，而宽度则会发生变化。

旋转后，矩形的宽度将成为立体图形在旋转轴方向的高度。

以原始矩形的一个截面为例，当矩形的一个顶点位于旋转轴上时，该顶点对应的高度为0。

当矩形的另一个顶点位于旋转轴上时，该顶点对应的高度为5厘米，即矩形的宽度。

依次将原始矩形的每一个截面相连，我们可以得到旋转后的立
体图形，即一个圆柱体。

由于旋转过程中矩形的每一个截面都是平行的，所以它们的形
状是相同的，只是大小不同。

这就可以简化计算，只需要计算一个
截面的面积，然后乘以截面的数量，就可以得到整个旋转后立体图
形的表面积和体积。

这个实例展示了初中几何学中的旋转模型的基本原理和应用。

通过理解旋转模型，学生可以更好地理解立体图形的形成和性质，
有助于他们在几何学的研究中的深入理解和运用。

以上就是关于初中几何旋转模型的一个实例的介绍。

通过这个
实例，希望能够帮助学生更好地理解和应用旋转模型的概念。

2018初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型

一线三等角
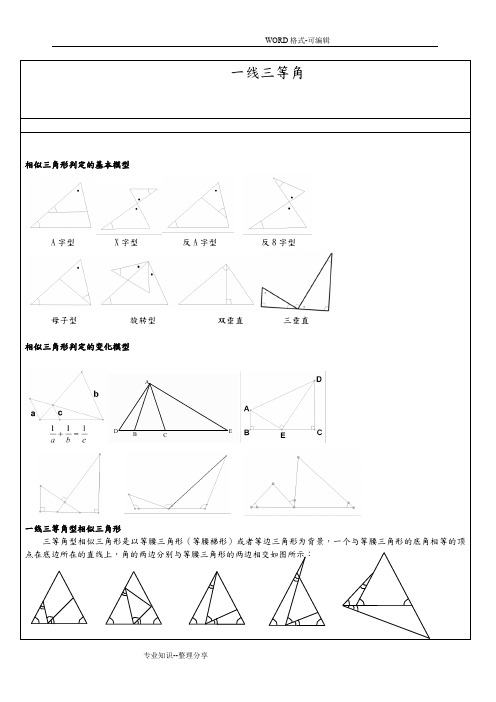
相似三角形判定的基本模型
A字型X字型反A字型反8字型
母子型旋转型双垂直三垂直
相似三角形判定的变化模型
一线三等角型相似三角形
三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景，一个与等腰三角形的底角相等的顶点在底边所在的直线上，角的两边分别与等腰三角形的两边相交如图所示：
等角的顶点在底边上的位置不同得到的相似三角形的结论也不同，当顶点移动到底边的延长线时，形成变式图形，图形虽然变化但是求证的方法不变。此规律需通过认真做题，细细体会。
定义域；
（2）正方形的边长为（如图12），点、分别在直线、上
（点不与点、点重合），且保持 .
当时，写出线段的长（不需要计算过程，请直接写出结果）.
点评：此题是典型的图形变式题，记住口诀：“图形改变，方法不变”。动点在线段上时，通过哪两个三角形相似求解，当动点在线段的延长线上时，还是找原来的两个三角形，多数情况下这两个三角形还是相似的，还是可以沿用原来的方法求解。
②当CE＝1时，写出AP的长（不必写出解题过程）
6. 已知在梯形ABCD中，AD∥BC，AD＜BC，且AD＝5，AB＝DC＝2．
（1）如图8，P为AD上的一点，满足∠BPC＝∠A．
①求证；△ABP∽△DPC
②求AP的长．
（2）如果点P在AD边上移动（点P与点A、D不重合），且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么
①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函数的定义域；
(1)求证：△FCE∽△EBD；
(2)当点D在线段AB上运动时，是否有可能使．
如果有可能，那么求出BD的长．如果不可能请说明理由．

(简略版)中考数学旋转模型及例题

(简略版)中考数学旋转模型及例题本文档旨在介绍中考数学中的旋转模型及相关例题。

以下是一些常见的旋转模型及其解题方法。

1. 点绕原点旋转当一个点绕原点进行旋转时，可以利用坐标系中点的坐标变化来解题。

假设有点P(x, y)绕原点逆时针旋转α角后得到的点为P'(x', y')，则有以下结论：- P'的横坐标x' = x * cosα - y * sinα- P'的纵坐标y' = x * sinα + y * cosα下面是一个例子：例题：点A(2, 3)绕原点逆时针旋转90°，求旋转后点的坐标。

解题思路：根据上述结论，带入坐标值可得：- A'的横坐标x' = 2 * cos90° - 3 * sin90° = -3- A'的纵坐标y' = 2 * sin90° + 3 * cos90° = 2因此，点A旋转90°后得到的点为A'(-3, 2)。

2. 图形绕原点旋转当一个图形绕原点进行旋转时，可以先找出图形中的点坐标，然后通过点的旋转来确定旋转后整个图形的形状和位置。

下面是一个例子：例题：如图所示的三角形ABC绕原点逆时针旋转60°，连接旋转后的点A', B', C'，求旋转后的三角形ABC'的面积。

解题思路：- 首先，可以求出点A(2, 3)、B(4, 5)、C(6, 1)绕原点逆时针旋转60°后的点坐标。

- 然后，连接旋转后的点A', B', C'得到旋转后的三角形。

- 最后，计算旋转后的三角形ABC'的面积。

通过上述步骤可以得到旋转后的三角形ABC'的面积。

以上是中考数学旋转模型的一些例题和解题思路。

旋转模型在中考数学中经常出现，掌握了旋转模型的解题方法，可以更好地应对考试中的相关问题。

2018年初中数学突破中考压轴题几何模型之旋转模型(5、26)

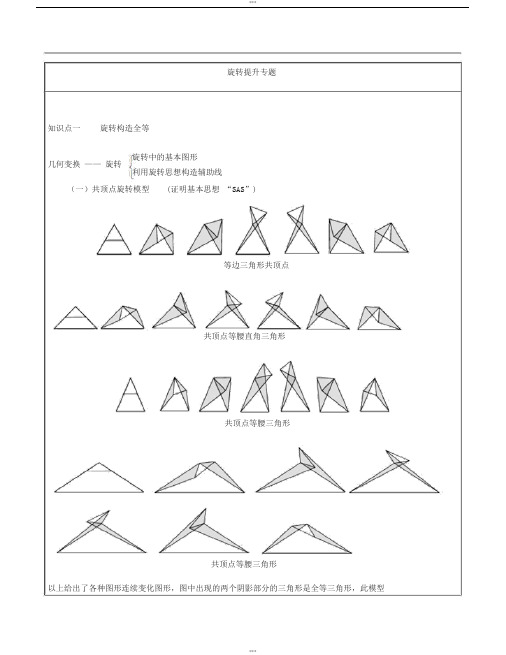
旋转提升专题知识点一旋转构造全等旋转中的基本图形几何变换——旋转利用旋转思想构造辅助线（一）共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形，图中出现的两个阴影部分的三角形是全等三角形，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二利用旋转思想构造辅助线（1）根据相等的边先找出被旋转的三角形（2）根据对应边找出旋转角度（3）根据旋转角度画出对应的旋转的三角形三旋转变换前后具有以下性质：（1）对应线段相等，对应角相等（2）对应点位置的排列次序相同（3）任意两条对应线段所在直线的夹角都等于旋转角．【例题精讲】例 1. 在四边形 ABCD 中，∠ADC= ∠ABC=90 °，AD=CD ，DP ⊥AB 于 P，若 SABCD =25 ，求DP 的长。

例 2. 如图，四边形 ABCD 是正方形，ABE 是等边三角形，M 为对角线 BD 上任意一点，将BM绕点 B 逆时针旋转60 得到 BN ，连接 AM 、CM 、EN ．⑴求证：AMB ≌ ENBE⑵①当 M 点在何处时， AM CM 的值最小；②当 M 点在何处时， AM BM CM 的值最小，并说明理由；⑶当 AM BM CM 的最小值为 3 1 时，求正方形的边长．A DNMB C方法总结 :1、共顶点的等线段中，最常用旋转思路，但也不可以思维定势，辅助线叙述中用一般语言2、旋转变换还用于处理：①几何最值问题：几何最值两个重要公理依据是：两点之间线段最短和垂线段最短；②有关线段的不等关系；③自己构造绕某点旋转某角度（特别是 60 度），把共顶点的几条线段变为首尾相接的几条线段，再变为共线取得最小值问题，计算中常用到等腰三角形或勾股定理等知识。

【课堂练习】1. 如图 1，已知边长为 a 的正方形 ABCD和边长为 b 的正方形 AEFG有一个公共点 A，（ a ≥ 2b）,且点 F 在 AD 上。

2018年初中数学突破中考压轴题几何模型之相似三角形中的一线三等角模型

（2）△PEF能为直角三角形吗?若能，求出CP的长，若不能，请说明理由。
5. 已知在等腰三角形中，，是的中点，是上的动点（不与、重合），连结，过点作射线，使，射线交射线于点，交射线于点 .
（1）求证： ∽ ；
（2）设 .
①用含的代数式表示；
②求关于的函数解析式，并写出的定义域.
②当CE＝1时，写出AP的长（不必写出解题过程）
【应用】
1.如图，在平面直角坐标中，四边形OABC是等腰梯形，CB∥OA，OA=7，BC=1，AB=5，点P为x轴上的一个动点，点P不与点0、点A重合．连接CP，过点P作PD交AB于点D．
（1）直接写出点B的坐标．
（2）当点P在线段OA上运动时，使得∠CPD=∠OAB，且BD: AD=3:2
，求点P的坐标．
(1)求证：△FCE∽△EBD；
(2)当点D在线段AB上运动时，是否有可能使．
如果有可能，那么求出BD的长．如果不可能请说明理由．
3.如图，在△ABC中，AB=AC=5，BC=6，P是BC上一点，且BP=2，将一个大小与∠B相等的角的顶点放在P点，然后将这个角绕P点转动，使角的两边始终分别与AB、AC相交，交点为D、E。
2、已知在梯形ABCD中，AD∥BC，AD＜BC，且BC=6，AB=DC=4，点E是AB的中点．
（1）如图，P为BC上的一点，且BP=2．求证：△BEP∽△CPD；
（2）如果点P在BC边上移动（点P与点B、C不重合），且满足∠EPF=∠C，PF交直线CD于点F，同时交直线AD于点M，那么
①当点F在线段CD的延长线上时，设BP= ，DF= ，求关于的函数解析式，并写出函数的定义域；②当时，求BP的长．

2018年中考数学专题：利用旋转巧解题

利用旋转巧解题在解几何问题时, 合理使用旋转法, 能把分散的线段或角相对集中在一个熟悉的基本图形中, 从而促使问题的解决.下面举例介绍利用旋转法解各类竞赛题, 供参考.一、三角形内的旋转例1 (全国初中数学竞赛题)如图1, 是等边三角形内部一点, , , 的大小之比是 , 则以为边的三角形的三个角的大小(从小到大)之比是( )(A) 2:3:4 (B) 3:4:5(C) 4:5:6 (D)不确定简析由于没有构成三角形, 则需作辅助线构造以它们为边的三角形, 可以将绕点顺时针转60º, 就是以为边的三角形.解 ∵ 是等边三角形, ∴将ABP ∆绕B 点顺时针转60º得CBD ∆.则是等边三角形, .而 ,∴PDC ∆就是以,,PA PB PC 为边的三角形.∵ , , 的大小之比是 [来源:1]∴,,PA PB PC 为边的三角形的三个角的大小之比是2:3:4.二、四边形内的旋转例2 (2019年全国初二年级数学竞赛题)如图2, 梯形中, , , 点在上.若 , , 则( ).(A)56 (B) 58 (C)60 (D) 62 简析由 , 可得四边形是正方形, 通过旋转得 .在中, 由勾股定理列出方程, 求得的长.解过点作交的延长线于点 , 将绕点逆时针方向旋转90º至 , 则由题意可得为正方形.[来源:学§科§网]由 , 得又由 ,设 ,则 ,在中 , 有 ,∴ , [来源:学_科_网]即58DE =.例3 (广东省竞赛题)如图3, 已知正方内一动点到、、三点的距离之和的最小值为 , 求此正方形的边长.简析本题的关键是确定最小值时点的位置, 通过旋转变换, 把集中起来, 可使问题得证.解将绕点逆时针旋转60º, 得 , 连 , 则为等边三角形, 即FC EA EB EC ≤++.为定长,当点和点落在上时,EA EB EC ++的最小值为FC ,即26FC =+. 作FH BC ⊥交CB 的延长线于H .设 ,在中,由2223(26)()()22xx x +=++, 得或 (舍去),即正方形的边长为2.三、五边形内的旋转例4 (北京市竞赛题)如图4, 已知五边形中, , 求证: .简析要证 , 可通过旋转得是等边三角形, 得 .证明将以为旋转中心顺时针旋转 , 使得与重合, 落在位置, 则由2ABC DBE ∠=∠,又,BF BE BD BD ==,FBD EBD ∴≅∆,FD ED ∴=.又CD BC CF ==,四、六边形内的旋转例5 (北京大学自主招生试题)如图5,已知六边形中, ,1111111111111,,BC BA CA CB B AC A BC ACB A B C ==∠+∠+∠=∠+∠+∠.求证: ABC ∆ 的面积是六边形111AC BACB 面积的一半.简析要得到的面积与六边形的关系, 可通过旋转将六边形化成两个和 . 证明旋转至 , 连 , 则 ,得。