数值实验一
MATLAB数值实验一(数据的插值运算及其应用完整版)

佛山科学技术学院实 验 报 告课程名称 数值分析 实验项目 插值法与数据拟合 专业班级 机械工程 姓 名 余红杰 学 号 10 指导教师 陈剑 成 绩 日 期 月 日一、实验目的1、学会Lagrange 插值、牛顿插值和三次样条插值等基本插值方法;2、讨论插值的Runge 现象3、学会Matlab 提供的插值函数的使用方法,会用这些函数解决实际问题。
二、实验原理1、拉格朗日插值多项式2、牛顿插值多项式3、三次样条插值 三、实验步骤1、用MATLAB 编写独立的拉格朗日插值多项式函数2、用MATLAB 编写独立的牛顿插值多项式函数3、用MATLAB 编写独立的三次样条函数(边界条件为第一、二种情形)4、已知函数在下列各点的值为:根据步骤1,2,3编好的程序,试分别用4次拉格朗日多项式4()L x 、牛顿插值多项式4()P x 以及三次样条函数()S x (自然边界条件)对数据进行插值,并用图给出 {(,),0.20.08,0,1,2,,10i i i x y x i i =+=},4()L x 、4()P x 和()S x 。
5、在区间[-1,1]上分别取10,20n =用两组等距节点对龙格函数21(),(11)125f x x x=-≤≤+作多项式插值,对不同n 值,分别画出插值函数及()f x 的图形。
6、下列数据点的插值可以得到平方根函数的近似,在区间[0,64]上作图。
(1)用这9个点作8次多项式插值8()L x 。
(2)用三次样条(第一边界条件)程序求()S x 。
7、对于给函数21()125f x x =+在区间[-1,1]上取10.2(0,1,,10)i x i i =-+=,试求3次曲线拟合,试画出拟合曲线并打印出方程,与第5题的结果比较。
四、实验过程与结果:1、Lagrange 插值多项式源代码:function ya=lag(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 ya=0; mu=1; %初始化%循环方式求L 系数,并求和: for i = 1:length(y) for j = 1:length(x) if i ~= jmu = mu * (xa - x(j) ) / ( x(i) - x(j) ); else continue end endya = ya + y(i) * mu ; mu = 1; end2、Newton 源代码:function ya = newton(x,y,xa) %x 所有已知插值点 %y 插值点对应函数值 %xa 所求点,自变量 %ya 所求点插值估计量 %建立系数零矩阵D 及初始化:D = zeros(length(x)-1);ya = y(1);xi = 1;%求出矩阵D,该矩阵第一行为牛顿插值多项式系数:for i=1:(length(x)-1)D(i,1) = (y(i+1) -y(i))/(x(i+1) -x(i));endfor j=2:(length(x)-1)for i=1:(length(x)-j)D(i,j) = (D(i+1,j-1) - D(i,j-1)) / (x(i+j) - x(i)); endend%xi为单个多项式(x-x(1))(x-x(2))...的值for i=1:(length(x)-1)for j=1:ixi = xi*(xa - x(j));endya = ya + D(1,i)*xi;xi = 1;end3、三次样条插值多项式(1)(第一边界条件)源代码:function y=yt1(x0,y0,f_0,f_n,x) _____________(1)%第一类边界条件下三次样条插值;%xi 所求点;%yi 所求点函数值;%x 已知插值点;%y 已知插值点函数值;%f_0左端点一次导数值;%f_n右端点一次导数值;n = length(x0);z = length(y0);h = zeros(n-1,1);k=zeros(n-2,1);l=zeros(n-2,1);S=2*eye(n);for i=1:n-1h(i)= x0(i+1)-x0(i);endfor i=1:n-2k(i)= h(i+1)/(h(i+1)+h(i));l(i)= 1-k(i);end%对于第一种边界条件:k = [1;k]; _______________________(2)l = [l;1]; _______________________(3)%构建系数矩阵S:for i = 1:n-1S(i,i+1) = k(i);S(i+1,i) = l(i);end%建立均差表:F=zeros(n-1,2);for i = 1:n-1F(i,1) = (y0(i+1)-y0(i))/(x0(i+1)-x0(i));endD = zeros(n-2,1);for i = 1:n-2F(i,2) = (F(i+1,1)-F(i,1))/(x0(i+2)-x0(i));D(i,1) = 6 * F(i,2);end%构建函数D:d0 = 6*(F(1,2)-f_0)/h(1); ___________(4)dn = 6*(f_n-F(n-1,2))/h(n-1); ___________(5)D = [d0;D;dn]; ______________(6)m= S\D;%寻找x所在位置,并求出对应插值:for i = 1:length(x)for j = 1:n-1if (x(i)<=x0(j+1))&(x(i)>=x0(j))y(i) =( m(j)*(x0(j+1)-x(i))^3)/(6*h(j))+...(m(j+1)*(x(i)-x0(j))^3)/(6*h(j))+...(y0(j)-(m(j)*h(j)^2)/6)*(x0(j+1)-x(i))/h(j)+... (y0(j+1)-(m(j+1)*h(j)^2)/6)*(x(i)-x0(j))/h(j) ; break;else continue;endendend(2)(自然边界条件)源代码:仅仅需要对上面部分标注的位置做如下修改:__(1):function y=yt2(x0,y0,x)__(2):k=[0;k]__(3):l=[l;0]__(4)+(5):删除—(6):D=[0:D:0]4、——————————————PS:另建了一个f方程文件,后面有一题也有用到。
数值分析实验报告1

实验一 误差分析实验(病态问题)实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。
对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。
通过本实验可获得一个初步体会。
数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。
病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。
问题提出:考虑一个高次的代数多项式)1.1()()20()2)(1()(201∏=-=---=k k x x x x x p显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。
现考虑该多项式的一个扰动)2.1(0)(19=+x x p ε其中ε是一个非常小的数。
这相当于是对()中19x 的系数作一个小的扰动。
我们希望比较()和()根的差别,从而分析方程()的解对扰动的敏感性。
实验内容:为了实现方便,我们先介绍两个Matlab 函数:“roots ”和“poly ”。
roots(a)u =其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。
设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程01121=+++++-n n n n a x a x a x a的全部根;而函数poly(v)b =的输出b 是一个n+1维变量,它是以n 维变量v 的各分量为根的多项式的系数。
可见“roots ”和“poly ”是两个互逆的运算函数。
;000000001.0=ess );21,1(zeros ve = ;)2(ess ve =))20:1((ve poly roots +上述简单的Matlab 程序便得到()的全部根,程序中的“ess ”即是()中的ε。
实验要求:(1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。
如果扰动项的系数ε很小,我们自然感觉()和()的解应当相差很小。
数值分析第一次实验报告

数值分析实验报告(一)2016级数学基地班尹烁翔320160928411一、问题重述:hamming级数求和二、问题分析级数为∑1k(k+x)∞k=1易知当X=1时,φ(1)=1我们可以考虑这个新级数:φ(x)−φ(1)用这个级数可以使精度更高,误差更小且迭代次数变少。
通分易得:φ(x)−φ(1)=1k(k+x)−1k(k+1)=1−xk(k+x)(k+1)我们还可以继续算得φ(2)及φ(x)−φ(2)这样精度会继续提高,且迭代次数也会减少。
下面考虑误差:由公式可得∑1−xk(k+x)(k+1)∞k=1<1k3<∫1k3∞n−1<10−10要把误差控制在范围内,需要k即迭代次数至少70001次。
三、算法实现:#include<iostream>#include<iomanip>>using namespace std;int main(){double sum;//sum为级数和double x;//x为代入的自变量int k=1;//k为迭代次数for (x=0; x<=10; x=x+0.1)//对0到10以内进行迭代运算,每次加0.1{sum=0;//每迭代完一个x,级数归零for (k=1; k<=70001; k++)//固定x并对k进行运算{sum=sum+1/(k*(k+x)*(k+1));}sum=(1-x)*sum+1.0;cout<<setiosflags(ios::fixed)<<" "<<setprecision(1)<<x;cout<<setiosflags(ios::fixed)<<" "<<setprecision(10)<<sum<<endl;}for (x=11; x<=290; x++)//对11到290以内进行迭代运算,每次加1{sum=0;for (k=1; k<=70001; k++)//固定x{sum=sum+1/(k*(k+x)*(k+1));}sum=(1-x)*sum+1.0;cout<<setiosflags(ios::fixed)<<" "<<setprecision(1)<<x;cout<<setiosflags(ios::fixed)<<" "<<setprecision(10)<<sum<<endl;}for (x=290; x<=300; x=x+0.1)//对290.1到300以内进行迭代运算,每次加0.1 {sum=0;for (k=1; k<=70001; k++)//固定x{sum=sum+1/(k*(k+x)*(k+1));}sum=(1-x)*sum+1.0;cout<<setiosflags(ios::fixed)<<" "<<setprecision(1)<<x;cout<<setiosflags(ios::fixed)<<" "<<setprecision(10)<<sum<<endl;}return 0;}四、数据结果:0.0 1.6449340667 0.1 1.5346072448 0.2 1.4408788415 0.3 1.3600825867 0.4 1.2895778007 0.5 1.2274112777 0.6 1.1721051961 0.7 1.1225193425 0.8 1.07775887270.9 1.03711091781.0 1.0000000000 1.1 0.9659560305 1.2 0.9345909181 1.3 0.9055811887 1.4 0.8786548819 1.5 0.853******* 1.6 0.8301644486 1.7 0.8082346082 1.8 0.78764591881.9 0.76827137672.0 0.7500000000 2.1 0.7327343381 2.2 0.7163884348 2.3 0.7008861540 2.4 0.6861597923 2.5 0.6721489224 2.6 0.6587994241 2.7 0.6460626684 2.8 0.63389482552.9 0.62225627673.0 0.6111111113 3.1 0.6004266954 3.2 0.5901732990 3.3 0.5803237751 3.4 0.5708532792 3.5 0.5617390263 3.6 0.5529600781 3.7 0.5444971556 3.8 0.53633247553.9 0.52844960504.0 0.5208333336 4.1 0.5134695598 4.2 0.5063451894 4.3 0.49944804604.4 0.49276679034.5 0.48629084784.6 0.48001034484.7 0.47391604974.8 0.46799932104.9 0.46225205975.0 0.45666666715.1 0.45123600545.2 0.44595336325.3 0.44081242345.4 0.43580723395.5 0.43093218145.6 0.42618196715.7 0.42155158445.8 0.41703629915.9 0.41263163046.0 0.40833333386.1 0.40413738606.2 0.40003996986.3 0.39603746096.4 0.39212641636.5 0.38830356206.6 0.38456578316.7 0.38091011406.8 0.37733372946.9 0.37383393577.0 0.37040816397.1 0.36705396157.2 0.36376898657.3 0.36055100097.4 0.35739786507.5 0.35430753177.6 0.35127804177.7 0.34830751887.8 0.34539416537.9 0.34253625788.0 0.33973214368.1 0.33698023688.2 0.33427901518.3 0.33162701648.4 0.32902283598.5 0.32646512338.6 0.32395258008.7 0.32148395698.8 0.31905805168.9 0.31667370669.0 0.31432980689.1 0.31202527809.2 0.30975908459.3 0.30753022799.4 0.30533774499.5 0.30318070609.6 0.30105821429.7 0.29896940319.8 0.29691343609.9 0.294889504210.0 0.292896826311.0 0.274534305112.0 0.258600891013.0 0.244625674714.0 0.232254453215.0 0.221215267616.0 0.211295563617.0 0.202326620618.0 0.194172672719.0 0.186723141720.0 0.179886984821.0 0.173588511822.0 0.167764240823.0 0.162360502724.0 0.157331593125.0 0.152638329626.0 0.148246914727.0 0.144128030628.0 0.140256111329.0 0.136608754530.0 0.133166240731.0 0.129911138432.0 0.126827978033.0 0.123902979834.0 0.121123826635.0 0.118479472636.0 0.115959981337.0 0.113556388138.0 0.111260583139.0 0.109065210040.0 0.106963580041.0 0.104949596342.0 0.103017690143.0 0.101162762944.0 0.099380138345.0 0.097665518246.0 0.096014944747.0 0.094424767348.0 0.092891612649.0 0.091412358750.0 0.089984111851.0 0.088604185152.0 0.087270081253.0 0.085979474654.0 0.084730197955.0 0.083520227556.0 0.082347672757.0 0.081210763958.0 0.080107843659.0 0.079037357560.0 0.077997846261.0 0.076987938262.0 0.076006343163.0 0.075051846164.0 0.074123301865.0 0.073219629966.0 0.072339810267.0 0.071482878568.0 0.070647922969.0 0.069834080070.0 0.069040532171.0 0.068266503872.0 0.067511259473.0 0.066774100374.0 0.066054362875.0 0.065351416076.0 0.064664659377.0 0.063993521278.0 0.063337457279.0 0.062695948280.0 0.062068499081.0 0.061454637382.0 0.0608539117 83.0 0.060265891284.0 0.059690163685.0 0.059126334986.0 0.058574027887.0 0.058032881288.0 0.057502549189.0 0.056982699990.0 0.056473015891.0 0.055973191792.0 0.055482935193.0 0.055001964994.0 0.054530011295.0 0.054066814696.0 0.053612125897.0 0.053165704998.0 0.052727321299.0 0.0522967526100.0 0.0518737853101.0 0.0514582132102.0 0.0510498380103.0 0.0506484683104.0 0.0502539197105.0 0.0498660140106.0 0.0494845798107.0 0.0491094512108.0 0.0487404681109.0 0.0483774760110.0 0.0480203256111.0 0.0476688725112.0 0.0473229772113.0 0.0469825047114.0 0.0466473244115.0 0.0463173100116.0 0.0459923394117.0 0.0456722940118.0 0.0453570593119.0 0.0450465242120.0 0.0447405812121.0 0.0444391259122.0 0.0441420572123.0 0.0438492771124.0 0.0435606905125.0 0.0432762052126.0 0.0429957316127.0 0.0427191829128.0 0.0424464746129.0 0.0421775249130.0 0.0419122542131.0 0.0416505852132.0 0.0413924428133.0 0.0411377539134.0 0.0408864476135.0 0.0406384549136.0 0.0403937087137.0 0.0401521437138.0 0.0399136963139.0 0.0396783048140.0 0.0394459089141.0 0.0392164502142.0 0.0389898715143.0 0.0387661174144.0 0.0385451338145.0 0.0383268679146.0 0.0381112684147.0 0.0378982853148.0 0.0376878698149.0 0.0374799743150.0 0.0372745524151.0 0.0370715590152.0 0.0368709499153.0 0.0366726822154.0 0.0364767137155.0 0.0362830036156.0 0.0360915118157.0 0.0359021994158.0 0.0357150281159.0 0.0355299609160.0 0.0353469614161.0 0.0351659940162.0 0.0349870241163.0 0.0348100178164.0 0.0346349421165.0 0.0344617645166.0 0.0342904534167.0 0.0341209780168.0 0.0339533080169.0 0.0337874138170.0 0.0336232666171.0 0.0334608381 172.0 0.0333001006 173.0 0.0331410270 174.0 0.0329835910 175.0 0.0328277666 176.0 0.0326735285 177.0 0.0325208518 178.0 0.0323697123 179.0 0.0322200861 180.0 0.0320719500 181.0 0.0319252812 182.0 0.0317800574 183.0 0.0316362566 184.0 0.0314938575 185.0 0.0313528391 186.0 0.0312131807 187.0 0.0310748622 188.0 0.0309378640 189.0 0.0308021665 190.0 0.0306677509 191.0 0.0305345985 192.0 0.0304026910 193.0 0.0302720107 194.0 0.0301425399 195.0 0.0300142615 196.0 0.029******* 197.0 0.029******* 198.0 0.029******* 199.0 0.029******* 200.0 0.029******* 201.0 0.029******* 202.0 0.029******* 203.0 0.029******* 204.0 0.028******* 205.0 0.028******* 206.0 0.028******* 207.0 0.028******* 208.0 0.028******* 209.0 0.028******* 210.0 0.028******* 211.0 0.028******* 212.0 0.028******* 213.0 0.027******* 214.0 0.027******* 215.0 0.027*******216.0 0.027*******217.0 0.027*******218.0 0.027*******219.0 0.027*******220.0 0.027*******221.0 0.027*******222.0 0.0269466153223.0 0.0268458877224.0 0.0267459700225.0 0.0266468523226.0 0.0265485248227.0 0.0264509777228.0 0.0263542015229.0 0.0262581869230.0 0.0261629247231.0 0.0260684057232.0 0.025*******233.0 0.025*******234.0 0.025*******235.0 0.025*******236.0 0.025*******237.0 0.025*******238.0 0.025*******239.0 0.025*******240.0 0.025*******241.0 0.025*******242.0 0.025*******243.0 0.024*******244.0 0.024*******245.0 0.024*******246.0 0.024*******247.0 0.024*******248.0 0.024*******249.0 0.024*******250.0 0.024*******251.0 0.024*******252.0 0.024*******253.0 0.024*******254.0 0.024*******255.0 0.024*******256.0 0.023*******257.0 0.023*******258.0 0.023*******259.0 0.023*******260.0 0.023*******261.0 0.023*******262.0 0.023*******263.0 0.023*******264.0 0.023*******265.0 0.023*******266.0 0.023*******267.0 0.023*******268.0 0.023*******269.0 0.022*******270.0 0.022*******271.0 0.022*******272.0 0.022*******273.0 0.022*******274.0 0.022*******275.0 0.022*******276.0 0.022*******277.0 0.022*******278.0 0.022*******279.0 0.022*******280.0 0.022*******281.0 0.022*******282.0 0.022*******283.0 0.021*******284.0 0.021*******285.0 0.021*******286.0 0.021*******287.0 0.021*******288.0 0.021*******289.0 0.021*******290.0 0.021*******290.1 0.021*******290.2 0.021*******290.3 0.021*******290.4 0.021*******290.5 0.021*******290.6 0.021*******290.7 0.021*******290.8 0.021*******290.9 0.021*******291.0 0.021*******291.1 0.021*******291.2 0.021*******291.3 0.021******* 291.4 0.021******* 291.5 0.021******* 291.6 0.021******* 291.7 0.021******* 291.8 0.021******* 291.9 0.021******* 292.0 0.021******* 292.1 0.021******* 292.2 0.021******* 292.3 0.021******* 292.4 0.021******* 292.5 0.021******* 292.6 0.021******* 292.7 0.021******* 292.8 0.021******* 292.9 0.021******* 293.0 0.021******* 293.1 0.021******* 293.2 0.021******* 293.3 0.021******* 293.4 0.021******* 293.5 0.021******* 293.6 0.021******* 293.7 0.021******* 293.8 0.021******* 293.9 0.021******* 294.0 0.021******* 294.1 0.021******* 294.2 0.021******* 294.3 0.021******* 294.4 0.021******* 294.5 0.021******* 294.6 0.021******* 294.7 0.021******* 294.8 0.021******* 294.9 0.021******* 295.0 0.021******* 295.1 0.021******* 295.2 0.021******* 295.3 0.021******* 295.4 0.021******* 295.5 0.021******* 295.6 0.021******* 295.7 0.021******* 295.8 0.021******* 295.9 0.021******* 296.0 0.021******* 296.1 0.021******* 296.2 0.021******* 296.3 0.021******* 296.4 0.021******* 296.5 0.021******* 296.6 0.021******* 296.7 0.021******* 296.8 0.021******* 296.9 0.021******* 297.0 0.021******* 297.1 0.021******* 297.2 0.021******* 297.3 0.021******* 297.4 0.021******* 297.5 0.021******* 297.6 0.021******* 297.7 0.021******* 297.8 0.021******* 297.9 0.021******* 298.0 0.021******* 298.1 0.021******* 298.2 0.021******* 298.3 0.021******* 298.4 0.021******* 298.5 0.021******* 298.6 0.021******* 298.7 0.021******* 298.8 0.021******* 298.9 0.021******* 299.0 0.021******* 299.1 0.020******* 299.2 0.020******* 299.3 0.020******* 299.4 0.020******* 299.5 0.020******* 299.6 0.020******* 299.7 0.020******* 299.8 0.020******* 299.9 0.020******* 300.0 0.020*******。
数值分析实验报告

数值分析实验报告篇一:数值分析实验报告(一)(完整)数值分析实验报告12345篇二:数值分析实验报告数值分析实验报告课题一:解线性方程组的直接方法1.实验目的:1、通过该课题的实验,体会模块化结构程序设计方法的优点;2、运用所学的计算方法,解决各类线性方程组的直接算法;3、提高分析和解决问题的能力,做到学以致用;4、通过三对角形线性方程组的解法,体会稀疏线性方程组解法的特点。
2.实验过程:实验代码:#include "stdio.h"#include "math.h"#includeiostreamusing namespace std;//Gauss法void lzy(double **a,double *b,int n) {int i,j,k;double l,x[10],temp;for(k=0;kn-1;k++){for(j=k,i=k;jn;j++){if(j==k)temp=fabs(a[j][k]);else if(tempfabs(a[j][k])){temp=fabs(a[j][k]);i=j;}}if(temp==0){cout"无解\n; return;}else{for(j=k;jn;j++){temp=a[k][j];a[k][j]=a[i][j];a[i][j]=temp;}temp=b[k];b[k]=b[i];b[i]=temp;}for(i=k+1;in;i++) {l=a[i][k]/a[k][k];for(j=k;jn;j++)a[i][j]=a[i][j]-l*a[k][j]; b[i]=b[i]-l*b[k];}if(a[n-1][n-1]==0){cout"无解\n;return;}x[n-1]=b[n-1]/a[n-1][n-1];for(i=n-2;i=0;i--){temp=0;for(j=i+1;jn;j++)temp=temp+a[i][j]*x[j];x[i]=(b[i]-temp)/a[i][i];}for(i=0;in;i++){printf("x%d=%lf\t",i+1,x[i]); printf("\n");}}//平方根法void pfg(double **a,double *b,int n)int i,k,m;double x[8],y[8],temp;for(k=0;kn;k++){temp=0;for(m=0;mk;m++)temp=temp+pow(a[k][m],2);if(a[k][k]temp)return;a[k][k]=pow((a[k][k]-temp),1.0/2.0);for(i=k+1;in;i++){temp=0;for(m=0;mk;m++)temp=temp+a[i][m]*a[k][m]; a[i][k]=(a[i][k]-temp)/a[k][k]; }temp=0;for(m=0;mk;m++)temp=temp+a[k][m]*y[m];y[k]=(b[k]-temp)/a[k][k];}x[n-1]=y[n-1]/a[n-1][n-1];for(k=n-2;k=0;k--){temp=0;for(m=k+1;mn;m++)temp=temp+a[m][k]*x[m];x[k]=(y[k]-temp)/a[k][k];}for(i=0;in;i++){printf("x%d=%lf\t",i+1,x[i]);printf("\n");}}//追赶法void zgf(double **a,double *b,int n){int i;double a0[10],c[10],d[10],a1[10],b1[10],x[10],y[10]; for(i=0;in;i++){a0[i]=a[i][i];if(in-1)c[i]=a[i][i+1];if(i0)d[i-1]=a[i][i-1];}a1[0]=a0[0];for(i=0;in-1;i++){b1[i]=c[i]/a1[i];a1[i+1]=a0[i+1]-d[i+1]*b1[i];}y[0]=b[0]/a1[0];for(i=1;in;i++)y[i]=(b[i]-d[i]*y[i-1])/a1[i];x[n-1]=y[n-1];for(i=n-2;i=0;i--)x[i]=y[i]-b1[i]*x[i+1];for(i=0;in;i++){printf("x%d=%lf\t",i+1,x[i]); printf("\n");}}int main(){int n,i,j;double **A,**B,**C,*B1,*B2,*B3;A=(double **)malloc(n*sizeof(double)); B=(double **)malloc(n*sizeof(double));C=(double **)malloc(n*sizeof(double));B1=(double *)malloc(n*sizeof(double));B2=(double *)malloc(n*sizeof(double));B3=(double *)malloc(n*sizeof(double));for(i=0;in;i++){A[i]=(double *)malloc((n)*sizeof(double));B[i]=(double*)malloc((n)*sizeof(double));C[i]=(double*)malloc((n)*sizeof(double)); }cout"第一题(Gauss列主元消去法):"endlendl; cout"请输入阶数n:"endl;cinn;cout"\n请输入系数矩阵:\n\n";for(i=0;in;i++)for(j=0;jn;j++){篇三:数值分析实验报告(包含源程序) 课程实验报告课程实验报告。
《数值分析实验》实验

数值分析实验实验1 方程求根一、实验目的:1.掌握常用的求非线性方程近似根的数值方法,用所学方法求非线性方程满足指定精度要求的数值解,比较各种方法的异同点并进行收敛性分析。
2.通过对二分法与牛顿迭代法作编程练习与上机运算,进一步体会二分法与牛顿迭代法的不同特点。
3.编写割线迭代法的程序,求非线性方程的解,并与牛顿迭代法作比较。
二、实验内容:1.用二分法求方程0104)(23=-+=x x x f 在1.5附近的根。
2.用牛顿迭代法求方程033)(23=--+=x x x x f 在1.5附近的根。
3.用简单迭代法求解非线性方程3sin )1(2=-+x x 的根。
取迭代函数)1sin 3(*5.0)(2x x x --+=ϕ,精度取2101-⨯4.(选做)用牛顿法求下列方程的根: (1)02=-x e x ; (2)01=-x xe ; (3)02lg =-+x x 。
5.(选做)编写一个弦截法程序,求解题目4中的方程。
6.(选做)Matlab 函数fzero 可用于求解非线性方程的根。
例如,fzero(@(x) x^3+4*x^2-10, 1.5)可以求解题目1。
尝试用此方法求解实验中的其他题三、实验要求:1.程序要添加适当的注释,程序的书写要采用缩进格式。
2.程序要具在一定的健壮性,即当输入数据非法时,程序也能适当地做出反应,如插入删除时指定的位置不对等等。
3.程序要做到界面友好,在程序运行时用户可以根据相应的提示信息进行操作。
四、实验步骤1.按照实验内容和实验要求编写代码 2.编译并运行代码 3.检查是否发生错误五、实验源代码与实验结果实验1源代码:运行结果:实验2源代码:运行结果:实验3源代码:运行结果:4(1)的源代码:运行结果:4(2)的源代码:运行结果:4(3)的源代码:运行结果:5(3)的源代码:运行结果:六、实验心得体会通过本次实验我加深了对二分法、简单迭代法、牛顿迭代法和弦截法算法思想的了解,并对各个不同方法的优劣有了更深的理解。
数值分析实验报告模板

数值分析实验报告模板篇一:数值分析实验报告(一)(完整)数值分析实验报告12345篇二:数值分析实验报告实验报告一题目:非线性方程求解摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。
本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。
利用二分法求解给定非线性方程的根,在给定的范围内,假设f(x,y)在[a,b]上连续,f(a)xf(b) 直接影响迭代的次数甚至迭代的收敛与发散。
即若x0 偏离所求根较远,Newton法可能发散的结论。
并且本实验中还利用利用改进的Newton法求解同样的方程,且将结果与Newton法的结果比较分析。
前言:(目的和意义)掌握二分法与Newton法的基本原理和应用。
掌握二分法的原理,验证二分法,在选对有根区间的前提下,必是收敛,但精度不够。
熟悉Matlab语言编程,学习编程要点。
体会Newton使用时的优点,和局部收敛性,而在初值选取不当时,会发散。
数学原理:对于一个非线性方程的数值解法很多。
在此介绍两种最常见的方法:二分法和Newton法。
对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b) Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式xk?1?xk?f(xk) f'(xk)产生逼近解x*的迭代数列{xk},这就是Newton法的思想。
当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。
另外,若将该迭代公式改进为xk?1?xk?rf(xk) 'f(xk)其中r为要求的方程的根的重数,这就是改进的Newton 法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。
程序设计:本实验采用Matlab的M文件编写。
其中待求解的方程写成function的方式,如下function y=f(x);y=-x*x-sin(x);写成如上形式即可,下面给出主程序。
数值分析实验报告1

p
得到m=(00)T
即M0=0 ;M1=;M2=;M3=;M4=0
则根据三次样条函数定义,可得:
S(x)=
接着,在Command Window里输入画图的程序代码,
下面是画牛顿插值以及三次样条插值图形的程序:
x=[ ];
y=[ ];
plot(x,y)
hold on
for i=1:1:5
y(i)= *(x(i)*(x(i)*(x(i)*(x(i)*(x(i)*(x(i)*(x(i)
Pn=f(x0)+f[x0,x1](x-x0)+ f[x0,x1,x2](x-x0) (x-x1)+···+ f[x0,x1,···xn](x-x0) ···(x-xn-1)
我们要知道牛顿插值多项式的系数,即均差表中得部分均差。
在MATLAB的Editor中输入程序代码,计算牛顿插值中多项式系数的程序如下:
【实验原理】
《数值分析》第二章“插值法”的相关内容,包括:牛顿多项式插值,三次样条插值,拉格朗日插值的相应算法和相关性质。
【实验环境】(使用的软硬件)
软件:
MATLAB 2012a
硬件:
电脑型号:联想 Lenovo 昭阳E46A笔记本电脑
操作系统:Windows 8 专业版
处理器:Intel(R)Core(TM)i3 CPU M 350 @
实验内容:
【实验方案设计】
第一步,将书上关于三种插值方法的内容转化成程序语言,用MATLAB实现;第二步,分别用牛顿多项式插值,三次样条插值,拉格朗日插值求解不同的问题。
【实验过程】(实验步骤、记录、数据、分析)
实验的主要步骤是:首先分析问题,根据分析设计MATLAB程序,利用程序算出问题答案,分析所得答案结果,再得出最后结论。
数值计算实验教案

2
教学
目的
要求
使学生加深对非线性方程牛顿法及加速迭代法等的理解,会用C及Excel软件求解一些简单的非线性方程。
教学
重点
难点
教学重点:各种算法的构造思路、算法的软件实现
教学难点:各种算法的收敛性及误差控制
实验软件
Excel、TURBOC2.0
教
学
内
容
提
纲
1.用Excel及C完成教材P23例4(牛顿法)和P25例5(弦割法)实验。
课外
学习
要求
实验报告,设计求收敛阶的实验。
教 学 后 记
学生基本能完成各实验,但对多种方法的比较不太清楚,这说明学生掌握了基本的计算方法,但对各种方法优缺点的理解不够深入,提醒任课教师在教学中注意多种计算方法的比较,一方面可以加深对每种算法的理解,另一方面还可提高学生综合分析问题的能力。
授课
内容
实验四:线性方程组直接法——高斯顺序消元法(LU分解法),列主元消去法
****学院
实 验教 案
开课单位:数学系
课程名称:数值计算方法
专业年级:2005级
任课教师:周均
教材名称:数值计算方法(李有法)
2007——2008学年第1学期
授课
内容
实验一、数值稳定性及算法设计原则
课时安排
2
教学
目的
要求
熟悉Excel及C语言程序的软件环境及基本操作,验证数值稳定性,体验数值计算与常见数学计算的异同,理解多项式的计算的两个算法的异同。
2.用Excel完成教材P28例7,注意埃特肯加速法的误差控制,并比较这些方法在相同精度情况下的迭代次数,从而粗略说明收阶。
3.用下列方法求方程 的近似根,要求误差不超过 ,并比较计算量。
数值计算方法实验1
学院(系)名称:)()()()(0101112x x x f x f x f x x ---=附录(源程序及运行结果):一.二分法#include<stdio.h>#include<math.h>double f(double x){return x*x-x-1;}void main(){float a=0,b=0,x=1,m,e;int k;while(f(a)*f(b)>0){printf("请输入区间a,b的值。
以及精度e\n");scanf("%f,%f,%f",&a,&b,&e);}k=0;if(f(a)*f(b)==0){if(f(a)==0)printf("使用二分法输出:a=%f,k=%d\n",a,k);elseprintf("使用二分法输出:b=%f,k=%d\n",b,k);}else{while(f(a)*f(b)!=0){m=(a+b)/2;if(fabs(a-b)/2<e){printf("使用二分法输出:m=%f,k=%d\n",m,k);break;}else {if(f(a)*f(m)>0)a=m;else b=m;k=k+1;}}}}运行结果:二.迭代法与牛顿迭代法#include<stdio.h>#include<math.h>double f(double x){return exp(-x);}double f1(double x){return (x*exp(x)-1);}double ff(double x){return (exp(x)+x*exp(x));}void diedaifa(double x0,double e,int N){double x1;int k=1;while(k!=N){x1=f(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用迭代法输出结果:%lf\n",x1);break;}}}void NDdiedaifa(double x0,double e,int N){int k=1;double x1;while(k!=N){if(ff(x0)==0)printf("公式f(x)奇异!\n");else{x1=x0-f1(x0)/ff(x0);if(fabs(x1-x0)>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;}else{printf("使用牛顿迭代法输出结果:%lf\n",x1);break;}}}}void main(){double x0,e;int N;printf("请输入初值:");scanf("%lf",&x0);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);diedaifa(x0,e,N);NDdiedaifa(x0,e,N);}运行结果:四.双点弦截法#include<stdio.h>#include<math.h>double f(double x){return (x*x*x+3*x*x-x-9);}void main(){double x0,x1,x2,e;int N;int k=1;printf("请输入初值x0和x1:");scanf("%lf,%lf",&x0,&x1);printf("精度:");scanf("%lf",&e);printf("以及判定迭代失败的最大次数N:");scanf("%d",&N);while(k!=N){x2=x1-f(x1)*(x1-x0)/(f(x1)-f(x0));if(fabs(f(x2))>=e){k++;if(k==N)printf("迭代失败!\n");x0=x1;x1=x2;}else{printf("使用双点弦截法输出结果:%lf\n",x2);break;}}}运行结果:。
数值计算方法实验报告

本科实验报告课程名称:计算机数值方法实验项目:计算机数值方法实验实验地点: 506 专业班级:学号:学生姓名:指导教师:2012 年 6 月 20 日太原理工大学学生实验报告b=c;printf("%f\n",b);}printf("X的值为:%f\n",c);}五、实验结果与分析二分法割线法分析:由程序知,使用二分法和割线法均能计算出方程的根,但利用割线法要比二分法计算的次数少,并且能够较早的达到精度要求。
相比之下,割线法程序代码量较少,精简明了。
六、讨论、心得本次数值计算方法程序设计实验从习题练习中跳脱出来,直接面对实用性较强的程序代码编写。
效果很好,不仅加深对二分法、割线法的理解,还加强了实际用运能力。
将理论知识成功地转化成实践结果。
实验地点北区多学科综合楼4506指导教师太原理工大学学生实验报告x[i] = y[i];for(j=i+1;j<=n;++j){x[i]-=u[i][j]*x[j];}x[i]/= u[i][i];}for(i=1;i<=n;++i){printf("%\n",x[i]);}return 0;}五、实验结果与分析完全主元素消元法:列主元素消元法:LU分解法:分析:对于两种高斯解方程,完全主元素跟列主元素都是先消元、再回代,由程序段可以发现,始终消去对角线下方的元素。
即,为了节约内存及时效,可以不必计算出主元素下方数据。
列主元素消元法的算法设计上优于完全主元素消元法,它只需依次按列选主元素然后换行使之变到主元素位置,再进行消元即可。
列主元素消元法的耗时比完全主元素法少很多,常采用之。
对于LU分解法,分解矩阵为单位下三角阵L与上三角阵U的乘积,然后解方程组Ly=b,回代,解方程组Ux=y。
其中的L为n阶单位下三角阵、U为上三角阵.六、讨论、心得本次试验中,感觉是最难的一次,完全主元素消元法程序编写过程相对来说花了好长时间。
数值分析实验 实验报告

数值分析实验实验报告数值分析实验实验报告引言在现代科学与工程领域,数值分析是一项重要的技术手段。
通过数值方法,我们可以利用计算机模拟和解决各种实际问题,如物理、化学、生物、经济等领域中的方程求解、优化问题、数据拟合等。
本实验旨在通过实际案例,探讨数值分析的应用和效果。
实验一:方程求解首先,我们考虑一个简单的方程求解问题。
假设我们需要求解方程f(x) = 0的根,其中f(x)是一个在给定区间[a, b]上连续且单调的函数。
为了实现这个目标,我们可以采用二分法、牛顿法、弦截法等数值方法。
在本实验中,我们选择使用二分法来求解方程f(x) = 0。
这种方法的基本思想是通过不断缩小区间[a, b]的范围,直到找到一个近似的根。
我们首先选取一个中间点c,计算f(c)的值,然后根据f(c)与0的关系,将区间[a, b]分成两部分。
重复这个过程,直到找到满足精度要求的根。
实验二:数据拟合接下来,我们考虑一个数据拟合的问题。
假设我们有一组离散的数据点,我们希望找到一个函数,使得该函数与这些数据点的拟合误差最小。
为了实现这个目标,我们可以采用最小二乘法等数值方法。
在本实验中,我们选择使用最小二乘法来进行数据拟合。
这种方法的基本思想是通过最小化数据点与拟合函数之间的误差平方和,来确定拟合函数的参数。
我们首先选择一个拟合函数的形式,如线性函数、多项式函数等。
然后,通过最小化误差平方和的方法,计算出拟合函数的参数。
实验三:优化问题最后,我们考虑一个优化问题。
假设我们需要在给定的约束条件下,找到一个使得目标函数取得最大或最小值的变量。
为了实现这个目标,我们可以采用梯度下降法、遗传算法等数值方法。
在本实验中,我们选择使用梯度下降法来解决优化问题。
这种方法的基本思想是通过迭代的方式,不断调整变量的取值,直到找到一个满足约束条件的最优解。
我们首先计算目标函数关于变量的梯度,然后根据梯度的方向和大小,更新变量的取值。
通过不断迭代,我们可以逐步接近最优解。
数值分析实验报告

《数值分析》实验报告学院:计算机科学与软件学院姓名:XXX班级:计算机XX班学号:XXXXXX实验一:舍入误差与数值稳定性实验目的:1、 通过上机编程,复习巩固以前所学程序设计语言;2、 通过上机计算,了解舍入误差所引起的数值不稳定性。
3、 通过上机计算,了解运算次序对计算结果的影响,从而尽量避免大数吃小数的现象。
实验内容:用两种不同的顺序计算644834.11000012≈∑=-n n ,分析其误差的变化。
实验流程图:实验源程序:#include <stdio.h>#include <math.h>void main(){ int i;float s1=0,s2=0,d1,d2;for (i=1;i<=10000;i++)s1=s1+1.0f/(i*i);for (i=10000;i>=1;i--)s2=s2+1.0f/(i*i);d1=(float)(fabs(1.644834-s1));d2=(float)(fabs(1.644834-s2));printf("正向求和结果为%f\n 误差为%f\n\n",s1,d1);printf("反向求和结果为%f\n 误差为%f\n\n",s2,d2);if(d1<d2)printf("正向求和误差小于负向求和误差\n");else if(d1==d2)printf("正向求和误差等于负向求和误差\n"); elseprintf("正向求和误差大于负向求和误差\n");}实验结果:实验分析:第一次做数值实验,又一次使用C语言编程,没有了刚学习C语言的艰难,能够将实验步骤转换成流程图并编写出完整的实验代码,在经过多次调试、改正后得到正确的程序和结果。
这个实验较简单,计算误差时如果输入数据有误差,而在计算过程中舍入误差不增长,则称此算法是稳定的,否则称此算法是数值不稳定的,减少运算次数可以减小舍入误差。
数值计算方法丁丽娟课后习题答案

数值计算方法丁丽娟课后习题答案【篇一:北京理工大学数值计算方法大作业数值实验1】)书p14/4分别将区间[?10,10]分为100,200,400等份,利用mesh或surf命令画出二元函数的三维图形。
z=|??|+ ??+?? +??++??【matlab求解】[x,y]=meshgrid(-10:0.1:10);a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);[x,y]=meshgrid(-10:0.05:10);a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);[x,y]=meshgrid(-10:0.025:10); a=exp(-abs(x));b=cos(x+y);c=1./(x.^2+y.^2+1);z=a+b+c;mesh(x,y,z);(二)书p7/1.3.2数值计算的稳定性(i)取= ??c语言程序—不稳定解 +=ln1.2,按公式=?? (n=1,2,…) #includestdio.h#includeconio.h#includemath.hvoid main(){float m=log(6.0)-log(5.0),n;int i;i=1;printf(y[0]=%-20f,m); while(i20){n=1/i-5*m;printf(y[%d]=%-20f,i,n);m=n;i++;if (i%3==0) printf(\n); }getch();}(ii) c语言程序—稳定解≈??[ ??+?? +?? ??+??按公式 =??(??)#includestdio.h#includeconio.h#includemath.hvoid main(){float m=(1/105.0+1/126.0)/2,n; k=n,n-1,n-2,…)(【篇二:北京理工大学数值计算方法大作业数值实验4】 p260/1考纽螺线的形状像钟表的发条,也称回旋曲线,它在直角坐标系中的参数方程为= ?????????????????? ?? ??????????= ?????????????? ??曲线关于原点对称,取a=1,参数s的变化范围[-5,5],容许误差限分别是,,和。
清华大学高等数值分析 第一次实验作业
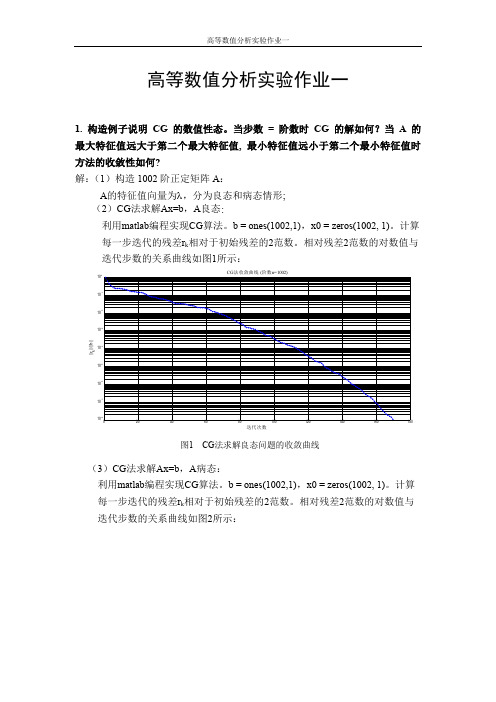
高等数值分析实验作业一
附件:主要算法代码
CG 法 CG.m function [x,Error,i,flag]=CG(A,b,x,ErrSet,uplimit) [m,n]=size(b); if m<n
b=b'; end [m,n]=size(x); if m<n
x=x'; end r=b-A*x; p=r; i=1; temp_rkrkplus=r'*r; Error=sqrt(temp_rkrkplus)/norm(b,2); while 1
Lanzcos算法的收敛曲线 (阶数n=1002)
100 m=10 m=50 m=100 m=400 m=800
10-5
||rk||/||b||
-10
10
-15
10 0
20
40
60
80
100
120
140
160
迭代次数
图5 对不同的m,Lanczos法求解Ax=b的收敛曲线
高等数值分析实验作业一
结论:如果 A 只有 m 个不同的特征值,则 Lanczos 方法至多 m 步就可以找到精 确解。实验中,在 m 较大的时候,算法收敛较快,迭代次数远小于 m。当 m 较 小时,可能需要接近于 m 步才能找到准确解。
2. 对于同样的例子,比较 CG 和 Lanczos 的计算结果。 解:(1)构造 1002 阶正定矩阵 A:
(2)Lanczos法求解Ax=b,A良态: 利用matlab编程实现CG算法。b = ones(1002,1),x0 = zeros(1002, 1)。计算 每一步迭代的残差rk相对于初始残差的2范数。相对残差2范数的对数值与 迭代步数的关系曲线如图3所示:
数值分析实验报告1

数值分析实验报告1数值分析上机实验报告(注:本实验报告中所有程序均为MATLAB语⾔程序)班级:姓名:学号:⼀章1、利⽤数值积分计算n I =21n x ex e -?dx (n=0,1,2,……). ⽬的:定积分数值求解原理:梯形公式法程序:clearformat long ;k=input('k=');m=input('m=');for n=1:kh=1/m;x=0:h:1;f=x.^n.*exp(x.^2);for i=1:ms(i)=(f(i)+f(i+1))*h/2;ends=sum(s);I(n)=exp(-1)*s;endI 运⾏结果:k=9m=1000I =Columns 1 through 60.3160604988 0.2309605799 0.1839401373 0.1535601302 0.1321211422 0.1161015912Columns 7 through 90.1036390735 0.0936475974 0.08544762262、利⽤秦九韶算法计算当0a =5,n a =21n a -+3;n=100,x=0.5;n=150,x=13多项式n p (x )=n a n x +…11n n a x --…1a x +0a 的值。
⽬的:通过调整程序以简化计算步骤,减少运算次数原理:秦久韶算法程序:n=input('n=');x=input('x=');a(1)=5;for k=1:n;a(k+1)=2.*a(k)+3;ends(n+1)=a(n+1);for i=n:-1:1s(i)=x.*s(i+1)+a(i);endPnx=s(1)运⾏结果:n=100x=0.5Pnx =802.0000000n=150x=13Pnx =1.4659714820e+2133、设0Y =28,按递推公式n Y = 1n Y -100Y ,500Y ≈27.982(五位有效数字),试问计算100Y 、500Y 将有多⼤的误差。
数值分析实验2014讲解

数值分析实验(2014,9,16~10,28)信计1201班,人数34人数学系机房数值分析计算实习报告册专业学号姓名2014~2015年第一学期实验一 数值计算的工具 Matlab1.解释下MATLAB 程序的输出结果 程序: t=0.1 n=1:10 e=n/10-n*te 的结果:0 0 -5.5511e-017 0 0 -1.1102e-016 -1.1102e-016 0 0 0 2.下面MATLAB 程序的的功能是什么? 程序:x=1;while 1+x>1,x=x/2,pause(0.02),end 用迭代法求出x=x/2,的最小值x=1;while x+x>x,x=2*x,pause(0.02),end 用迭代法求出x=2*x,的值,使得2x>X x=1;while x+x>x,x=x/2,pause(0.02),end 用迭代法求出x=x/2,的最小值,使得2x>X3.考虑下面二次代数方程的求解问题02=++c bx ax公式a acb b x 242-+-=是熟知的,与之等价地有ac b b c x 422-+-=,对于1,100000000,1===c b a ,应当如何选择算法。
应该用aacb b x 242-+-=计算,因为b做分母4.函数)sin(x 有幂级数展开...!7!5!3sin 753+-+-=x x x x x利用幂级数计算x sin 的MATLAB 程序为 function s=powersin(x) s=0; t=x; n=1;while s+t~=s; s=s+t ;t=-x^2/((n+1)*(n+2))*t ; n=n+2; end t1=cputime; pause(10); t2=cputime; t0=t2-t1(a)解释上述程序的终止准则。
当s+t=s ,终止循环。
(b)对于2/21,2/11,2/πππ=x 计算的进度是多少?分别计算多少项? X=pi/2时,s =1.0000 x=11pi/2时,s=-1.0000 x=21pi/2时,s =0.9999 Cputime 分别是0.1563 0.0469 0.01565.考虑调和级数∑∞=11n n,它是微积分中的发散级数,在计算机上计算该级数的部分和,会得到怎么样的结果,为什么?function s=fun(n) s=0; t=1/n;for i=1:n s=s+1/i; end当n=100时s =5.1874 当n=80时s =4.9655 当n=50时,s =4.4992 当n=10时,s =2.92906.指数函数的级数展开...!3!2132++++=x x x e x,如果对于0<x ,用上述的级数近似计算指数函数的值,这样的算法结果是否会好,为什么?function s=powerexp(x) s=1; n=1; t=1;while s+t~=s;t=(x^n)/factorial(n); s=s+t; n=n+1; end当x=-1时,s =0.3679 当x=-2时,s =0.1353 当x=-3时,s =0.04987.考虑数列n i x i ,...2,1,=,它的统计平均定义为∑==ni i x n x 11,标准差2121)(11⎥⎦⎤⎢⎣⎡--=∑=x x n n i i σ数学上等价于21221)(11⎥⎥⎦⎤⎢⎢⎣⎡--=∑=x n x n n i i σ作为标准差的两种算法,你将如何评价他们的得与失。
数值分析实验1

东北大学数学实验中心实验报告规范(暂行)一、每个学生每个实验项目一份实验报告。
二、实验报告内容一般包括以下几个内容:1.实验项目名称2.实验目的和要求3.实验原理4.实验内容及步骤5.实验数据记录和处理6.实验结果与分析(含以上1、2、3、4、5、6项,需经指导教师签字认可,附在实验报告后)注:各专业各课程的实验报告内容与格式可由指导教师根据实验具体情况做出要求。
三、实验报告第一页按学院统一的实验报告格式书写,附页用A4纸书写,字迹工整,曲线要画在座标纸上,线路图要整齐、清楚(不得徒手画)。
如打印也应采用统一的实验报告的版头(A4纸)。
四、每学期将拟存档的学生实验报告按课程、实验项目分类装订成册,即每个实验项目每门课程的所有实验报告装订成一本。
装订线在左侧,第一页加订实验报告封皮。
五、东北大学理学院数学实验报告模板范本,本实验报告双面打印(附后)。
理学院数学实验中心实验报告专业:软件工程姓名:黄蕾学号:成绩:实验地点:数学实验中心指导教师签名:。
在迭代过程中需要对最后一行进行直接计算,其公式为输出选取模尽可能小的非零元素为主元代码附件:实验一:列主元Gauss法:package Excise; public class Lie {static double a[][];static double b[];static double x[];static double l[][];static double h[];static int n = 3;static int count = 0;public static void main(String[] arg) { double max;int maxn;Scanner sc = new Scanner(System.in);int n = sc.nextInt();x = new double[n];l = new double[n][n];h = new double[n];a = new double[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (i == j) {a[i][j] = 6;if (j >= 1) {a[i][j - 1] = 8;}if (j < n - 1) {a[i][j + 1] = 1;}}if (i != j && j != (i + 1)) {a[i][j] = 0;}}}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {}}b = new double[n];b[0] = 7;b[n - 1] = 14;for (int i = 1; i < n - 1; i++) { b[i] = 15;}for (int i = 0; i < n; i++) {}for (int i = 0; i < n - 1; i++) { max = a[i][i];maxn = i;for (int j = i + 1; j < n; j++) {if (Math.abs(max) < Math.abs(a[j][i])) {max = a[i][j];maxn = j;}}if (max == 0) {}for (int p = 0; p < n; p++) {h[p] = a[maxn][p];a[maxn][p] = a[i][p];a[i][p] = h[p];}double jh;jh = b[maxn];b[maxn] = b[i];b[i] = jh;for (int k = i + 1; k < n; k++) {l[k][i] = a[k][i] / a[i][i];for (int m = i; m < n; m++) {a[k][m] = a[k][m] - l[k][i] * a[i][m];}b[k] = b[k] - l[k][i] * b[i];}}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {}}for (int i = 0; i < n; i++) {}x[n - 1] = b[n - 1] / a[n - 1][n - 1];for (int m = n - 2; m >= 0; m--) {double zj = b[m];for (int i = n - 1; i > m; i--) {zj = zj - a[m][i] * x[i];}x[m] = zj / a[m][m];}DecimalFormat df = new DecimalFormat("#,##0.000000");for (int i = 0; i < n; i++) {}}}顺序消去法(主要部分):for (int i = 0; i < n - 1; i++) {while (a[i][i] == 0) {count++;if (count == n - 1 - i) {}for (int j = 0; j < n; j++) {double temp[] = null;temp[j] = a[i][j];a[i][j] = a[i + count][j];a[i + count][j] = temp[j];}}for (int k = i + 1; k < n; k++) {l[k][i] = a[k][i] / a[i][i];for (int m = i; m < n; m++) {a[k][m] = a[k][m] - l[k][i] * a[i][m];}b[k] = b[k] - l[k][i] * b[i];} }。
数值计算方法实验指导(Matlab版)

《数值计算方法》实验指导(Matlab版)学院数学与统计学学院计算方法课程组《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则验证(之相近数相减、大数吃小数和简化计算步骤) 2. 实验题目(1) 取1610=z ,计算z z -+1和)1/(1z z ++,验证两个相近的数相减会造成有效数字的损失.(2) 按不同顺序求一个较大的数(123)与1000个较小的数(15310-⨯)的和,验证大数吃小数的现象.(3) 分别用直接法和九韶算法计算多项式n n n n a x a x a x a x P ++++=--1110)(在x =1.00037处的值.验证简化计算步骤能减少运算时间.对于第(3)题中的多项式P (x ),直接逐项计算需要2112)1(+=+++-+n n n 次乘法和n 次加法,使用九韶算法n n a x a x a x a x a x P ++++=-)))((()(1210则只需要n 次乘法和n 次加法. 3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应避免两个相近的数相减、防止大数吃小数、简化计算步骤减少运算次数以减少运算时间并降低舍入误差的积累.两相近的数相减会损失有效数字的个数,用一个大数依次加小数,小数会被大数吃掉,乘法运算次数太多会增加运算时间. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程(1) 直接计算并比较;(2) 法1:大数逐个加1000个小数,法2:先把1000个小数相加再与大数加; (3) 将由高次项到低次项的系数保存到数组A[n]中,其中n 为多项式次数.7. 结果与分析 (1) 计算的z z -+1= ,)1/(1z z ++.分析:(2) 123逐次加1000个6310-⨯的和是 ,先将1000个6310-⨯相加,再用这个和与123相加得.分析:(3) 计算次的多项式:直接计算的结果是,用时;用九韶算法计算的结果是,用时.分析:8. 附录:程序清单(1) 两个相近的数相减.%*************************************************************%* 程序名:ex1_1.m *%* 程序功能:验证两个相近的数相减会损失有效数字个数 *%*************************************************************z=1e16;x,y======================================================================(2) 大数吃小数%*************************************************************%* 程序名:ex1_2.m *%* 程序功能:验证大数吃小数的现象. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数z=123; % 大数t=3e-15; % 小数x=z; % 大数依次加小数% 重复1000次给x中加上ty=0; % 先累加小数% 重复1000次给y中加上ty=z + y; % 再加到大数x,y======================================================================(3) 九韶算法%*************************************************************%* 程序名:ex1_3.m *%* 程序功能:验证九韶算法可节省运行时间. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数A=[8,4,-1,-3,6,5,3,2,1,3,2,-1,4,3,1,-2,4,6,8,9,50,-80,12,35,7,-6,42,5,6,23,74,6 5,55,80,78,77,98,56];A(10001)=0; % 扩展到10001项,后面的都是分量0% A为多项式系数,从高次项到低次项x=1.00037;n=9000; % n为多项式次数% 直接计算begintime=clock; % 开始执行的时间 % 求x的i次幂% 累加多项式的i次项endtime=clock; % 完毕执行的时间time1=etime(endtime,begintime); % 运行时间disp('直接计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time1),'秒']);% 九韶算法计算begintime=clock; % 开始执行的时间% 累加九韶算法中的一项endtime=clock; % 完毕执行的时间time2=etime(endtime,begintime); % 运行时间disp(' ');disp('九韶算法计算');disp(['p(',num2str(x),')=',num2str(p)]);disp([' 运行时间: ',num2str(time2),'秒']);《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则验证(之数值稳定性) 2. 实验题目 计算定积分⎰==-1110,1,0,d n x e xI x nn ,分别用教材例1-7推导出的算法A 和B ,其中:算法A :⎩⎨⎧≈-=-6321.0101I nI I n n 算法B :⎪⎩⎪⎨⎧≈-=-0)1(1101I I nI n n 验证算法不稳定时误差会扩大.3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应采用数值稳定性好的算法.数值稳定的算法,误差不会放大,甚至会缩小;而数值不稳定的算法会放大误差. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程分别用数组IA[ ]和IB[ ]保存两种算法计算的结果. 7. 结果与分析 运行结果:(或拷屏)8. 附录:程序清单%*************************************************************%* 程序名:ex1_4.m *%* 程序功能:验证数值稳定性算法可控制误差. *%*************************************************************clc; % 清屏clear all; % 释放所有存变量format long; % 按双精度显示浮点数I=[0.856, 0.144, 0.712, 0.865, ...0.538, 0.308, 0.154, 0.938, ...0.492, 0.662, 0.843];% 保留14位小数的精确值, …是Matlab中的续行符% 算法AIA(1) = 0.6321; % Matlab下标从1开始,所以要用IA(n+1)表示原问题中的I(n)% 算法Bdisp('n 算法A 算法B 精确值');for n=1:11fprintf('%2d %14.6f %14.6f %14.6f\n',n-1,IA(n),IB(n),I(n));end% n显示为2位整数, 其它显示为14位其中小数点后显示6位的小数《数值计算方法》实验1报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验1 算法设计原则(除数绝对值不能太小) 2. 实验题目将线性方程组增广矩阵利用初等行变换可化为⎪⎪⎭⎫⎝⎛→-⎪⎪⎭⎫ ⎝⎛→-⎪⎪⎭⎫ ⎝⎛''0'0''02221112'12221121112222211121122121121b a b a r r b a b a a r r b a a b a a a a a a由此可解得'/',/'22221111a b x a b x ==.分别解增广矩阵为161011212-⎛⎫ ⎪⎝⎭和162121011-⎛⎫⎪⎝⎭的方程组,验证除数绝对值远小于被除数绝对值的除法会导致结果失真. 3. 实验目的验证数值算法需遵循的若干规则. 4. 基础理论设计数值算法时,应避免除数绝对值远小于被除数绝对值的除法,否则绝对误差会被放大,使结果失真. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab6. 实验过程用二维数组A 和B 存放方程组的增广矩阵,利用题目所给初等行变换求解方程组. 7. 结果与分析第1种顺序的方程组的解为x =,y =;第2种顺序的方程组的解为x =,y =. 分析:8. 附录:程序清单%************************************************************* %* 程 序 名:ex1_5.m * %* 程序功能:验证除数的绝对值太小可能会放大误差. * %*************************************************************clc;A=[1e-16, 1, 1; 2, 1, 2];B=[2, 1, 2; 1e-16, 1, 1]; % 增广矩阵% 方程组A% m = - a_{21}/a_{11} 是第2行加第1行的倍数% 消去a_{21}% m = - a_{12}/a_{22} 是第1行加第2行的倍数% 消去a_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组A的解: x1=',num2str(A(1,3)),', x2=',num2str(A(2,3))]); disp(' ');% 方程组B% m = - b_{21}/b_{11} 是第2行加第1行的倍数% 消去b_{21}% m = - b_{12}/b_{22} 是第1行加第2行的倍数% 消去b_{12}, 系数矩阵成对角线% 未知数x1的值% 未知数x2的值disp(['方程组B的解: x1=',num2str(B(1,3)),', x2=',num2str(B(2,3))]);《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之简单迭代法) 2. 实验题目用简单迭代法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的掌握非线性方程的简单迭代法. 4. 基础理论简单迭代法:将方程0)(=x f 改写成等价形式)(x x ϕ=,从初值0x 开始,使用迭代公式)(1k k x x ϕ=+可以得到一个数列,若该数列收敛,则其极限即为原方程的解.取数列中适当的项可作为近似解. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Newton 迭代法) 2. 实验题目用Newton 迭代法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的掌握求解非线性方程的Newton 迭代法. 4. 基础理论Newton 迭代法:解方程0)(=x f 的Newton 迭代公式为)(')(1k k k k x f x f x x -=+.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之对分区间法) 2. 实验题目用对分区间法求方程310x x --=在区间[1, 1.5]的一个实根,取绝对误差限为410-. 3. 实验目的掌握求解非线性方程的对分区间法. 4. 基础理论对分区间法:取[a ,b ]的中点p ,若f (p ) ≈ 0或b – a < ε,则p 为方程0)(=x f 的近似解;若f (a ) f (p ) < 0,则说明根在区间取[a ,p ]中;否则,根在区间取[p ,b ]中.将新的有根区间记为 [a 1,b 1],对该区间不断重复上述步骤,即可得到方程的近似根. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程用宏定义函数f (x );为了循环方便,得到的新的有根区间始终用[a ,b ]表示;由于新的有根区间可能仍以a 为左端点,这样会反复使用函数值f (a ),为减少运算次数,将这个函数值保存在一个变量fa 中;同样在判断新的有根区间时用到函数值f (p ),若新的有根区间以p 为左端点,则下一次用到的f (a )实际上就是现在的f (p ),为减少运算次数,将这个函数值保存在一个变量fp 中.算法的伪代码描述:Input :区间端点a ,b ;精度要求(即误差限)ε;函数f (x );最大对分次数N Output :近似解或失败信息7. 结果与分析8. 附录:程序清单说明: 源程序中带有数字的空行,对应着算法描述中的行号%**********************************************************%* 程序名:Bisection.m *%* 程序功能:使用二分法求解非线性方程. *%**********************************************************f=inline('x^3-x-1'); % 定义函数f(x)a=input('有根区间左端点: a=');b=input('右端点:b=');epsilon=input('误差限:epsilona=');N=input('最大对分次数: N=');1 % 对分次数计数器n置12 % 左端点的函数值给变量fafprintf('\n k p f(p) a(k) f(a(k))'); fprintf(' b(k) b-a\n');% 显示表头fprintf('%2d%36.6f%12.6f%12.6f%12.6f\n',0,a,fa,b,b-a);% 占2位其中0位小数显示步数0, 共12位其中小数6位显示各值3% while n≤ N 4 % 取区间中点p5% 求p 点函数值给变量fpfprintf('%2d%12.6f%12.6f',n,p,fp); % 输出迭代过程中的中点信息p 和f(p)6 % 如果f(p)=0或b-a 的一半小于误差限εfprintf('\n\n 近似解为:%f\n',p);% 则输出近似根p (7)return;% 并完毕程序 (7)89 % 计数器加110% 若f(a)与f(p)同号11% 则取右半区间为新的求根区间, 即a 取作p 12 % 保存新区间左端点的函数值 13% 否则14 % 左半区间为新的求根区间, 即b 取作p 15fprintf('%12.6f%12.6f%12.6f%12.6f\n',a,fa,b,b-a); %显示新区间端点与左端函数值、区间长度 16fprintf('\n\n 经过%d 次迭代后未达到精度要求.\n',N); % 输出错误信息(行17)《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Aitken-Steffensen 加速法) 2. 实验题目用Aitken-Steffensen 加速法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的熟悉求解非线性方程的Aitken-Steffensen 加速法. 4. 基础理论将方程0)(=x f 改写成等价形式)(x x ϕ=,得到从初值0x 开始的迭代公式)(1k k x x ϕ=+后,基于迭代公式)(1k k x x ϕ=+的Aitken-Steffensen 加速法是通过“迭代-再迭代-加速”完成迭代的,具体过程为kk k k k k k k k k k x y z z y x x y z x y +---===+2)(),(),(21ϕϕ. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程为了验证Aitken-Steffensen 加速法可以把一些不收敛的迭代加速成迭代收敛,我们使用将方程组变形为31021x x -=,取迭代函数31021)(x x -=ϕ,并利用宏定义出迭代函数.由于不用保存迭代过程,所以用x0表示初值同时也存放前一步迭代的值,y 和z 是迭代过程中产生的y k 和z k ,x 存放新迭代的结果.算法的伪代码描述:Input :初值x 0;精度要求(即误差限)ε;迭代函数φ(x );最大迭代次数N7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:Aitken_Steffensen.m * %* 程序功能:用Aitken-Steffensen 加速法求方程. * %************************************************************* clc;clear all;phi=inline('0.5 * sqrt( 10 - x^3)'); % 迭代函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon='); N=input('最大迭代次数: N=');disp(' n 迭代中间值y(n-1) 再迭代结构z(n-1) 加速后的近似值x(n)'); fprintf('%2d%54.6f\n',0,x0);% 占2位整数显示步数0, 为了对齐, 占54位小数6位显示x01 % n 是计数器2 % while n<=Ny= 3 ; % 迭代 z= 3 ; % 再迭代 x= 3 ; % 加速% x0初值与前一步的近似值, y 和z 是中间变量, x 是下一步的近似值fprintf('%2d%18.6f%18.6f%18.6f\n',n,y,z,x);%显示中间值和迭代近似值6 % 如果与上一步近似解差的绝对值不超过误差限 fprintf('\n\n 近似解 x≈x(%d)≈%f \n',n,x);% 则输出近似根 (7), 可简略为: fprintf('\n\n 近似解 x=%f',x); return; % 并完毕程序(7) 8 % 相当于endif9 % 计数器加110 % 新近似值x 作为下一次迭代的初值 11fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N); %输出错误信息(12)《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之Newton 下山法) 2. 实验题目用Newton 下山法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-.3. 实验目的熟悉非线性方程的Newton 下山法. 4. 基础理论Newton 下山法:Newton 下山法公式为)(')(1k k kk k x f x f x x λ-=+,使|)(||)(|1k k x f x f <+,其中10≤<k λ.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程定义函数f(x)和df(x),其中df(x)是f(x)的导函数.每步迭代时先取下山因子为1,尝试迭代,判断尝试结果是否满足下山因子,若满足则作为这步的迭代结果;否则将下山因子减半,然后再尝试.为防止当前的x k 是极小值点,附近不会有满足下述条件的其它点,使尝试陷入死循环,同时计算机中能表示出的浮点数也有下界,因此我们设置了最大尝试次数.当超过最大尝试次数时,不再进行下山尝试.由于反复尝试迭代且要判断下山条件,所以f (x 0)和f ‘(x 0)会反复使用,为避免重复计算浪费运行时间,将这两个值分别保存在变量fx0和dfx0.而尝试产生的节点,判断下山条件时要用到它的函数值,若尝试成功,这个点会作为下一步的初值再使用,所以把该点的函数值也保存在变量fx 中.算法的伪代码描述:Input :初值x 0;精度要求(即误差限)ε;函数与其导函数f (x )和f’(x);最大迭代次数N ;K 下山尝试最大次数Output :近似解或失败信息7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:NewtonDownhill.m *%* 程序功能:用Newton下山法求解非线性方程. *%*************************************************************clc;clear all;f=inline('x^3-x-1'); % 函数f(x)df=inline('3*x^2-1'); % 函数f(x)的导函数x0=input('初值: x0 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');K=input('最大下山尝试次数: K=');1 % 迭代次数计数器2 % 存x0点函数值fprintf('\n\n n x(n) f(x(n))\n'); % 显示表头fprintf('%2d%14.6f%14.6f\n',0,x0,fx0); % 2位整数显示0, 共14位小数6位显示x0和fx03 % while n≤ Ndisp(''); % 换行显示下山尝试过程的表头disp(' 下山因子尝试x(n) 对应f(x(n)) 满足下山条件');disp('');4 % 存x0点导数值, 每次下山尝试不用重新计算ifdfx0==0 % 导数为0不能迭代disp(‘无法进行Newton迭代’);return;endlambda=1.0; % 下山因子从1开始尝试k=1; % k下山尝试次数计数器while k<=K % 下山最多尝试K次% 下山公式fx=f(x); % 函数值fprintf('%22.6f%14.6f%14.6f',lambda,x,fx); % 显示尝试结果if (abs(fx)<abs(fx0)) % 判断是否满足下山条件fprintf(' 满足\n');break; % 是, 则退出下山尝试的循环elsefprintf(' 不满足\n');endlambda=lambda/2; % 不是, 则下山因子减半k=k+1; % 计数器加1endif k>Kfprintf('\n 下山条件无法满足, 迭代失败.\n\n');return;endfprintf('%2d%14.6f%14.6f\n',n,x,fx);% 2位整数显示步数n, 共14位小数6位显示下步迭代结果22 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n',x); % (23)return; % 达到, 则显示结果并完毕程序(23) end % (24)% 用x0,fx0存放前一步的近似值和它的函数值, 进行循环迭代25262728fprintf('\n 迭代%d次还不满足误差要求.\n\n',N);《数值计算方法》实验2报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验2 非线性方程的迭代解法(之弦截法) 2. 实验题目用弦截法求方程010423=-+x x 在区间[1,2]的一个实根,取绝对误差限为410-. 3. 实验目的熟悉非线性方程的弦截法. 4. 基础理论将Newton 迭代法中的导数用差商代替,得到弦截法(或叫正割法)公式)()()(111k k k k k k k x f x f x f x x x x --+---=.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程不保存迭代过程,所以始终以x 0和x 1分别存放x k -1和x k ,而x 存放新产生的迭代值x k +1,这样,下一次迭代时需要把上一步的x 1(即x k )赋值于x 0(做新的x k -1).这些点的函数值会重复用到,在迭代公式中也要用到,上一步的x 1作为下一步的x 0也会再一次用它的函数值,为减少重新计算该点函数值的运行时间,将x 1点的函数值保存在变量fx1中.算法的伪代码描述:Input :初值x 0,x 1;精度要求(即误差限)ε;函数f (x );最大迭代次数N7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:SecantMethod.m *%* 程序功能:用弦截法求解非线性方程. *%*************************************************************clc;clear all;f=inline('2*x^3-5*x-1'); % 函数f(x)x0=input('第一初值: x0 = ');x1=input('第二初值: x1 = ');epsilon=input('误差限: epsilon=');N=input('最大迭代次数: N=');fprintf('\n n x(n)\n'); % 显示表头fprintf('%2d%14.6f\n', 0, x0); % 占2位显示步数0, 共14位其中小数6位显示x0fprintf('%2d%14.6f\n', 1, x1); % 占2位显示步数1, 共14位其中小数6位显示x11 % 存x0点函数值2 % 存x1点函数值3 % 迭代计数器4 % while n≤ N% 弦截法公式fprintf('%2d%14.6f\n', n, x); %显示迭代过程6 % 达到精度要求否fprintf('\n\n 方程的近似解为: x≈%f\n\n', x);return; % 达到, 则显示结果并完毕程序89 % 原x1做x0为前两步的近似值10 % 现x做x1为一两步的近似值11 % x0点函数值12 % 计算x1点函数值, 为下一次循环13 % 计数器加1 14fprintf('\n 迭代%d 次还不满足误差要求.\n\n',N);《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Gauss 消去法) 2. 实验题目用Gauss 消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x . 3. 实验目的掌握解线性方程组的Gauss 消去法. 4. 基础理论Gauss 消去法是通过对增广矩阵的初等行变换,将方程组变成上三角方程组,然后通过回代,从后到前依次求出各未知数.Gauss 消去法的第k 步(1≤k≤n -1)消元:若0≠kk a ,则依次将增广矩阵第k 行的kk ik a a /-倍加到第i 行(k+1≤i≤n),将第k 列对角线下的元素都化成0.5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Gauss 列主元消去法) 2. 实验题目用Gauss 列主元消去法求解线性方程组⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛--000.3000.2000.1643.5072.1000.2623.4712.3000.1000.3000.2001.0321x x x . 3. 实验目的掌握解线性方程组的Gauss 列主元消去法. 4. 基础理论Gauss 列主元消去法也是通过对增广矩阵的初等行变换,将方程组变成上三角方程组,然后通过回代,从后到前依次求出各未知数.Gauss 列主元消去法的第k 步(1≤k≤n -1)消元:先在nk k k kk a a a ,,,,1 +中找绝对值最大的,将它所在的行与第k 行交换,然后将第k 行的kk ik a a /-倍加到第i 行(k+1≤i≤n),将第k 列对角线下的元素都化成0. 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之Doolittle 分解) 2. 实验题目对矩阵A 进行Doolittle 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A .3. 实验目的掌握矩阵的Doolittle 分解. 4. 基础理论矩阵的Doolittle 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵和一个上三角矩阵的乘积.若设⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=nn n n n n n n u u u u u u u u u u U l l ll l l L000000,1010010001333223221131211321323121则可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=+=-=∑∑-=-=1111,,2,1,/)(,,1,,k t kk tk it ik ik k r rj kr kj kj nk k i u u l a l nk k j u l a u其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程(1)按计算公式依次计算一行u 同时计算一列l ;(2)因为计算完u ij (或l ij )后,a ij 就不再使用,为节省存储空间,将计算的u ij (和l ij )仍存放在矩阵A 中的相应位置;(3)使用L 矩阵和U 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 对角线上的元素为1,上三角部分为0,下三角部分为A 中对应的元素;U 的下三角部分为0,上三角部分为A 中对应的元素.算法的伪代码描述: Input :阶数n ;矩阵A7. 结果与分析8. 附录:程序清单%****************************************************% 程序名: Doolittle.m *% 程序功能: 矩阵LU分解中的Doolittle分解. *%****************************************************clc;clear all;n=4; % 矩阵阶数A=[6 2 1 -1;2 4 1 0; 1 1 4 -1; -1 0 -1 3]disp('A=');disp(A);% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L 在A 下三角, U 在上三角(对角线为1) enddisp('分解结果:'); disp('L='); for i=1:n for j=1:nif i>j % 在下三角部分, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));elseif i==j % 在对角线上, 则显示1 fprintf(' %8d',1);else % 在上三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 enddisp('U='); for i=1:n for j=1:nif i<=j % 在上三角部分或对角线上, 则取A 对于的元素显示 fprintf(' %8.4f',A(i,j));else % 在下三角部分, 则显示0 fprintf(' %8d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之LU 分解法) 2. 实验题目用LU 分解(Doolittle 分解)法求解线性方程组⎪⎩⎪⎨⎧=++=++=++104615631552162321321321x x x x x x x x x 3. 实验目的熟悉解线性方程组LU 分解法.4. 基础理论若将矩阵A 进行了Doolittle 分解,A = LU ,则解方程组b x A=可以分解求解两个三角方程组b y L=和y x U =.它们都可直接代入求解,其中b y L=的代入公式为∑-==-=11,,2,1,k j j kj k k n k y l b y而y x U=的代入公式为∑+=-=-=nk j kk j kjk k n n k u x uy x 11,,1,,/)( .5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程(1)Doolittle 分解过程依次计算一行u 同时计算一列l 完成,并将计算的u ij (和l ij )仍存放在矩阵A 中的相应位置;(2)求解方程组的代入公式中用到的u ij 和l ij 都直接在A 的相应位置取值即可. 算法的伪代码描述:Input :阶数n ;矩阵A ;常数项向量b7. 结果与分析8. 附录:程序清单%**************************************************** % 程序名: LinearSystemByLU.m *% 程序功能: 利用LU分解(Doolittle分解)解方程组. *%****************************************************clc;clear all;n=3; % 矩阵阶数A=[1 2 6; 2 5 15; 6 15 46];b=[1;3;10];% LU分解(Doolittle分解)for k=1:n% 计算矩阵U的元素u_{kj}% (可参照下面l_{ik}的公式填写)% 计算矩阵L的元素l_{ik}% L在A下三角, U在上三角(对角线为1) endfor k=1:n % 用代入法求解下三角方程组Ly=by(k)=b(k);3 %∑-==-=11,,2,1,kjj kjk knkylby33enddisp('方程组Ly=b的解:y=');disp(y');for k=n:-1:1 % 回代求解上三角方程组Ux=y x(k)=y(k);6 %∑+=-=-=nkjj kjk knnkxuyx11,,1,,666 enddisp('原方程组的解:x='); disp(x');《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X成绩:1. 实验名称实验3 解线性方程组的直接法(之Cholesky 分解) 2. 实验题目对矩阵A 进行Cholesky 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A . 3. 实验目的理解矩阵的Cholesky 分解. 4. 基础理论矩阵的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个下三角矩阵L 和L 转置的乘积,即A =LL T,其中L 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t kktk it ik ik k r kr kk kk nk k i l l l a l l a l其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:VC++ 6. 实验过程(1)按计算公式依次先计算一列对角线上的元素l kk ,再计算这列其他元素l ik ,且对称位置的元素也取同一个值;(2)因为计算完l ij 后,a ij 就不再使用,为节省存储空间,将计算的l ij 仍存放在矩阵A 中的相应位置;(3)使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 上三角部分为0,对角线和下三角部分为A 中对应的元素.算法的伪代码描述:Input :阶数n ;矩阵AOutput :矩阵L (合并存储在数组A 中)行号 伪代码注释1 for k ← 1 to n2∑-=-=112k r krkk kk l a l3 for i ← k to n4 ∑-=-=11/)(k t kk tk it ik ik l l l a l计算结果存放在a ij5 endfor6 endfor7return L输出L7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:Cholesky.m * %* 程序功能:对称正定矩阵的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数 A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A ='); for i=1:n for j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n');% 一行完毕换行end% Cholesky 分解 for k=1:n % 计算对角线上的l _{kk}% 计算其他的l _{ik} % 和l _{ki}end % L 在A 下三角, L^T 在上三角disp('分解结果:'); disp('L='); for i=1:n for j=1:n if i>=j % 在下三角部分或对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 在上三角部分, 则显示0 fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X成绩:1. 实验名称实验3 解线性方程组的直接法(之改进的Cholesky 分解) 2. 实验题目对矩阵A 进行改进的Cholesky 分解,其中⎪⎪⎪⎪⎪⎭⎫⎝⎛----=3101141101421126A .3. 实验目的理解矩阵改进的Cholesky 分解. 4. 基础理论矩阵的改进的Cholesky 分解是指将矩阵n n ij a A ⨯=)(可以分解为一个单位下三角矩阵L 和对角矩阵D 与L 转置的乘积,即A =LDL T,其中L 和D 各元素可依如下顺序公式计算⎪⎪⎩⎪⎪⎨⎧++=-=-=∑∑-=-=11112,,2,1,/)(k t k kt it t ik ik k r kr r kk k nk k i d l l d a l l d a d其中k = 1,2,…,n .5. 实验环境操作系统:Windows xp ; 程序设计语言:VC++ 6. 实验过程(1)按计算公式依次先计算D 的一个元素d k ,再计算L 中这列的元素l ik ,且对称位置的元素也取同一个值;(2)因为计算完d k 和l ij 后,a kk 或a ij 就不再使用,为节省存储空间,将计算的a kk 或l ij 仍存放在矩阵A 中的相应位置;(3)使用L 矩阵时需要根据元素所在位置取固定值或A 中相应位置的值.L 对角线和上三角部分为0,下三角部分为A 中对应的元素;D 对角线为A 中对应的元素,其余都是0.算法的伪代码描述: Input :阶数n ;矩阵AOutput :矩阵L (合并存储在数组A 中)7. 结果与分析8. 附录:程序清单%************************************************************* %* 程 序 名:ImprovedCholesky.m * %* 程序功能:对称正定矩阵的改进的Cholesky 分解. * %*************************************************************n=4; % 矩阵阶数A=[6,2,1,-1; 2,4,1,0; 1,1,4,-1; -1,0,-1,3];disp('A =');for i=1:nfor j=1:nfprintf('%10.4f',A(i,j)); % 共占14位endfprintf('\n'); % 一行完毕换行end% Cholesky分解for k=1:n% 计算D对角线上的u_{kk}% 计算L的元素l_{ik}% 和L转置的元素l_{ki} end % L在A下三角, D在对角线disp('分解结果:');disp('L=');for i=1:nfor j=1:nif i>j % 在下三角部分, 则取A对于的元素显示fprintf('%10.4f',A(i,j));elseif i==j % 在对角线上, 则显示1fprintf('%10d',1);else % 在上三角部分, 则显示0fprintf('%10d',0);endendfprintf('\n'); % 换行enddisp('D='); for i=1:n for j=1:n if i==j % 在对角线上, 则取A 对于的元素显示fprintf('%10.4f',A(i,j));else % 其余显示0fprintf('%10d',0); end endfprintf('\n'); % 换行 end《数值计算方法》实验3报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验3 解线性方程组的直接法(之追赶法) 2. 实验题目用追赶法求解线性方程组⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-----101053001210023100124321x x x x 3. 实验目的熟悉解线性方程组的追赶法. 4. 基础理论对于系数矩阵为三对角矩阵的方程组,其Crout 分解可分解为⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=------11111211122111122211n n nn n n nn n n t t t s a s a s a s b a c b a c b a c b A这样,解方程组可以由如下2步完成:“追”:,,,3,2,/)(,,/,/,1111111111n i s y a f y t a b s s c t s f y b s i i i i i i i i i i i i =-=-====-----其中:Tn f f ),,(1 为方程组的常数项,n t 没用;“赶”:.1,,2,1,,1 --=-==+n n i x t y x y x i i i i n n5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程在“追”的过程中,向量s 和y 都有n 个元素,t 只有n -1个元素,又1s 和1y 的计算公式与其它i s 和i y 不同,所以先单独计算1s 和1y ,然后在一个n -1次循环中,求其它i s 和i y 以与i t .由于在“追”的过程中,i b ,i c 和i f 在分别计算完对应的i s ,i t 和i y 后就不再使用,所以借用数组b ,c 和f 存储向量s ,t 和y ;同样在“赶”的过程中,i y 在计算完对应的i x 后就不再使用,所以再一次借用数组f 存储向量x .追赶法算法的伪代码描述:Input :阶数n ;三对角矩阵的三条对角线向量a ,b ,c ,常数项向量f Output :方程组的解x改进的追赶法算法的伪代码描述:Input :阶数n ;三对角矩阵的三条对角线向量a ,b ,c ,常数项向量f Output :方程组的解x7. 结果与分析8. 附录:程序清单%*************************************************************%* 程序名:ChaseAfter.m *%* 程序功能:用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"s(1) = b(1);y(1) = f(1); % 先单独求s_1和y_1 for k = 1 : n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"x(n) = y(n); % 先单独求x_nfor k = n-1 : -1 : 1% 再求x_i(i=n-1,n-2, (1)endx=x' % 输出解向量-------------------------------------------------------------------------------------------------------------------改进的程序:%*************************************************************%* 程序名:ChaseAfter.m *%* 程序功能:用追赶法求解三对角线性方程组. *%*************************************************************clc;clear all;n=4;a=[0,-1,-1,-3];b=[2, 3, 2, 5];c=[-1, -2, -1, 0];f=[0, 1, 0, 1];% "追"% b(1)=b(1); % s_1仍在b_1中,不用重新计算y(1)=f(1)/b(1); % 先单独y_1for k=1:n-1% 再求t_i(i=1,2,…,n-1)% s_i(i=2,3,…,n)% y_i(i=2,3,…,n)end% "赶"% f(n)=f(n); % x_n等于y_n仍在f_n中for k=n-1:-1:1% 再求x_i(i=n-1,n-2, (1)endx=f' % 输出解向量《数值计算方法》实验4报告班级:20##级####x班学号:20##2409####:##X 成绩:1. 实验名称实验4 解线性方程组的迭代法(之Jacobi迭代)2. 实验题目用Jacobi迭代法求解线性方程组1231231232251223x x x x x x x x x +-=⎧⎪++=⎪⎨++=⎪⎪⎩任取3. 实验目的掌握解线性方程组的Jacobi 迭代法. 4. 基础理论将第i (n i ≤≤1)个方程i n in i i b x a x a x a =+++ 2211移项后得到等价方程ii n in i i i i i i i i i a x a x a x a x a b x /)(11,11,11------=++--便可构造出Jacobi 迭代公式,1,0,/)()()(11,)(11,)(11)1(=------=++--+k a x a x a x a x a b x ii k n in k i i i k i i i k i i k i . 5. 实验环境操作系统:Windows xp ; 程序设计语言:Matlab 6. 实验过程7. 结果与分析8. 附录:程序清单《数值计算方法》实验4报告班级: 20##级####x 班 学号: 20##2409#### : ##X 成绩:1. 实验名称实验4 解线性方程组的迭代法(之Gauss-Seidel 迭代) 2. 实验题目用Gauss-Seidel 迭代法求解线性方程组。
数值分析——实验1 秦九韶算法

实验1 秦九韶算法(贺俊杰 2020022060)一、实验目的人类的计算能力等于计算工具的效率与计算方法的效率的乘积,高效率计算方法大大减少了计算次数,从而也能较少舍入误差的传播和积累,构造高效率计算方法一直是科学计算的一个主要目的。
本次实验以完成秦九韶算法为契机,深入了解高效计算多项式结果的数值计算方法,同时加深对Matlab 环境的熟悉。
二、算法分析对于n 次多项式:1110()n n n n n P x a x a x a x a −−=+++ (1)可改写为嵌套形式:1210()((()))n n n n p x a x a x a x a x a −−=++++ (2)在(1)式中,n i n i a x −−需要计算n i −次乘法运算(其中0,1,1i n =−)和n 次加法运算,共需要进行(1)2n n+次乘法运算和n 次加法运算。
而在(2)式中,仅需要经过n 次乘法运算和n 次加法运算,能够极大地减少运算次数,提高运算效率。
根据程序设计地习惯,把公式(2)写成下来等价的地推形式:(1,2,)n n k y a y y x a k n −⇐⎧⎨⇐⋅+=⎩ (3)三、算法代码实现秦九韶算法Matlab 实现如下:Qinjiu.m 文件其中a 为多项式系数从高次向低次排列数组(缺项系数为0),n 为多项式多高次数,x 为变量。
四、实验结果1、 设543()851f x x x x =++−,计算()f x 在1,1.5,2.1,3x =上的值。
编写run_qinjiu.m 代码文件如下所示:run_qinjiu.m 文件取多项式系数a = [8, 5, 1, 0, 0, -1],运行结果如下图所示:图1 run_qinjiu.m 运行结果由图可知算法能正确运行。
2、 利用Matlab 库中的horner 命令,可直接把多项式变为如(2)式的嵌套形式。
编写run_horner.m 代码文件如下所示:程序运行结果如下图所示:从图中可看出,horner库函数可正确地将多项式转为嵌套形式。
《数值计算方法》实验 (1)

电子科技大学《数值计算方法》
实
验
报
告
输入6,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718263
输入10,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718282
输入100,1;0,1,21i i n a b i i n ===+=−" 结果得f=1.718282
从中计算结果看随n 增大迭代计算结果逐渐稳定,可认为出现此现象有两种情况一是对该输入序列a,b 用此迭代公式随序列増长会逐渐逼近一个稳定值,二是在迭代计算过程中产生大数“吃掉”小数现象且计算结果只取7为有效数字。
3. 实验结论
在计算机内做加法运算时,首先要对加数作对阶处理,加之计算机字长有限,因尽量避免出现大数吃小数现象,计算时要注意运算次序,否则会影响结果的可靠性。
报告评分:
指导教师签字:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称:计算机数值方法B
实验项目:方程求解
实验地点:致远楼B301
专业班级:软件工程1227学号:2012005757
学生姓名:韩龙
指导教师:程海青
2014年5月12日
学院
软件学院
专业
软件工程
日期
2014-05-12
学号
2012005757
姓名
韩龙
成绩
课题名称
实验题目
方程求解
一、实验目的和要求
{
floata;
cin>>a;
floatt, x;
x=a;
do{
x=sqrt((10-x*x*x)/4);
t=a;
a=x;
}while(fabs(a-t)>0.5*1e-5);
printf("x=%f",a);
}
割线法:
#include"stdio.h"
#include"math.h"
#include"iostream"
这样就可以不断接近零点。
通过每次把f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值
五、实验程序设计
迭代法:
#include"stdio.h"
#include"math.h"
#include"iostream"
usingnamespacestd;
floatmain()
迭代法:用迭代公式x=f(x)进行迭代计算,直到满足|x*-xn|<0.5×10-5为止。
割线法:x=x的导数,直到满足|x*-xn|<0.5×10-5为止。
三、主要仪器设备
笔记本电脑,VC++6.0
四、实验公式
设f(x)在区间(x,y)上连续先找到a、b属于区间(x,y),使f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求f[(a+b)/2],现在假设f(a)<0,f(b)>0,a<b
usingnamespacestd;
floatmain()
{
floatc,a=1.0,b=2.0;
//cin>>a>>b;
while(1)
{
c=b-(b*b*b+4*b*b-10)*(b-a)/(b*b*b+4*b*b-(a*a*a+4*a*a));
if(fabs(b-c)<0.5*0.000001)break;
b=c;
}
cout<<c;
}
六、实验结果与分析
使用不同的方法,方程解的精确度不同,且计算速度不同
(1)如果f[(a+b)/2]=0,该点就是零点,如果f[(a+b)/2]<0,则在区
((a+b)/2,b)内有零点,(a+b)/2=>a,从①开始继续使用中点函数值判断。
(2)如果f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2<=b,从(1)开始继续使用中点函数值判断。
1.熟练运用已学计算方法求解方程组
2.加深对计算方法技巧,选择正确的计算方法来求解各种方程组
3.培养使用电子计算机进行科学计算和解决问题的能力
4.熟练掌握二分法,迭代法,牛顿法,割线法对给定方程求解
5.加深对方程求根方法的认识,掌握算法
6.会进行误差分析,并能对不同方法进行比较
二、实验内容
方程求根
熟悉使用二分法、迭代法、牛顿法、割线法等方法对给定的方程进行根的求解。选择上述方法中的两种方法求方程:f(x)=x3+4x2-10=0在[1,2]内的一个实根,且要求满足精度|x*-xn|<0.5×10-5
