初一数学图形规律经典题
七年级数学规律题汇总(免费)

七年级数学规律题汇总(免费)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN【2012最新】七年级数学规律题汇总1. 把正方体摆放成如图所示的形状,若从上至下依次为第1层,第2层,第3层,……,则第n层有个正方体2.木材加工厂堆放木料的方式如图所示:依此规律可得出第6堆木料的根数是。
3. 如图:是用火柴棍摆出的一系列三角形图案,按这种方式摆下去,当每边上摆20(即n=20)根时,需要的火柴棍总数为根。
4. 用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律搭下去,搭n个三角形需要S支火柴棒,那么S关于n的函数关系式是 (n为正整数).5. 将一张长方形的纸对折,如图5所示可得到一条折痕(图中虚线).续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到条折痕.如果对折n次,可以得到条折痕.6.用黑白两种颜色的正六边形地面砖按如下所示的规律,拼成若干个图案:⑴第4个图案中有白色地面砖块;⑵第n个图案中有白色地面砖块。
7. 下图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,……,第n (n是正整数)个图案中由个基础图形组成.8. 为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示:按照上面的规律,摆n个“金鱼”需用火柴棒的根数____________9. 柜台上放着一堆罐头,它们摆放的形状见右图:第一层有2×3听罐头,第二层有3×4听罐头,第三层有4×5听罐头,……根据这堆罐头排列的规律,第n(n为正整数)层有听罐头(用含n的式子表示).(1) (2) (3)…………①②③第3个第2个第1个10. 下列图案由边长相等的黑、白两色正方形按一定规律拼接而成。
依次规律,第5个图案中白色正方形的个数为 ;第n 个图案中白色正方形的个数为 。
七年级数学探索规律——图形规律(人教版)(专题)(含答案)

试题难度:三颗星知识点:略
4.有一长条型链子,其外型由边长为1的正六边形排列而成.如图是此链子的任意一段示意图,其中每个黑色六边形与6个白色六边形相邻.若此链子上共有35个黑色六边形,则共有( )个白色六边形.
A.140 B.142
C.210 D.212
答案:B
解题思路:
分析:按照分类的思想来考虑,第1个黑色六边形周围的6个白色六边形可以分成两类,左边的2个白色六边形是一类,剩余的4个白色六边形是一类.黑色六边形每增加1个,白色六边形就增加4个.
第3个图中三角形个数为 ;
将上述规律标序号,如下:
① ;
② ;
③ ;
…
所以第 个图中三角形个数为 ;
当 时, ,
所以第20个图中三角形个数为77.
故选C.
试题难度:三颗星知识点:略
7.下列图形是由同样大小的五角星按一定的规律排列组成,其中第1个图形共有2个五角星,第2个图形共有8个五角星,第3个图形共有18个五角星,…,则第10个图形中五角星的个数为( )
当 时, ,
即此链子上共有35个黑色六边形时,共有142个白色六边形.
故选B.
试题难度:三颗星知识点:略
5.一块瓷砖的图案如图1所示,用这种瓷砖铺设地面,如果铺设成如图2的图案,其中完整的圆一共有5个,如果铺设成如图3的图案,其中完整的圆一共有13个,如果铺设成如图4的图案,其中完整的圆一共有25个,依此规律,第10个图中,完整的圆一共有( )
A.100个B.101个
C.181个D.221个
答案:C
解题思路:
分析:按照分类的思想来考虑,可以分为一块瓷砖自带的圆和多块瓷砖拼成的完整的圆;
第1个图案,自带的圆1个,拼成的圆0个,共 个;
(完整版)初中数学规律题解题基本方法------图形找规律

(完整版)初中数学规律题解题基本方法------图形找规律初中数学规律题解题基本方法------图形找规律1.探索常见图形的规律,用火柴棒按下图的方式搭三角形⑴填写下表:⑵照这样的规律搭建下去,搭n 个这样的三角形需要多少根火柴棒? 2.若按图2方式摆放桌子和椅子⑴一张桌子可坐6人,2张桌子可坐人。
⑵按照上图方式继续排列桌子,完成下表:3.如果按图3的方式将桌子拼在一起⑴2张桌子拼在一起可坐多少人?3张呢?n 张呢?⑵教室有40张这样的桌子,按上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐人。
⑶在⑵中,改成每8张桌子拼成1张大桌子,则共可坐人。
4.如图,把一个面积为1的正方形分等分成两个面积为21的矩形,接着把面积为21的矩形等分成两个面积为41的正方形,再把面积为41的矩形等分成两个面积为81的矩形,如此进行下去,试利用图形提示的规律计算:=+++++++256112816413211618141215.把棱长为a 的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这种规律摆放,第五层的正方体的个数是例8.观察下列图形并填表。
个数1 2 3 4 5 6 7…n32121 41 811611126.用黑白两颜色的正六边形地面砖按如图所示规律,拼成若干个图案:(1)第4个图案中有白色地面砖块;(2)第n 个图案中有白色地面砖块。
……7.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有)2(≥n n 个棋子,每个图案棋子总数为S ,按下图的排列规律推断,S 与n 之间的关系可以用式子来表示。
……8.观察与分析下面各列数的排列规律,然后填空。
①5,9,13,17,,。
②4,5,7,11,19,,。
③10,20,21,42,43,,,174,175。
④4,9,19,34,54,,,144。
⑤45,1,43,3,41,5,,,37,9。
⑥6,1,8,3,10,5,12,7,,。
初一找规律经典题型(含部分答案)

初一找规律经典题型(含部分答案)初一数学规律题应用知识汇总有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
因此,将变量和序列号放在一起比较,就更容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:一、基本方法——看增幅一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n个数可以表示为:a1+(n-1)b,其中a为数列的第一位数,b为增幅,(n-1)b为第一位数到第n位的总增幅。
然后再简化代数式a+(n-1)b。
例如,对于数列4、10、16、22、28……,求第n位数。
我们可以发现,从第二位数开始,每位数都比前一位数增加6,增幅都是6.因此,第n位数是4+(n-1)6=6n-2.二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
例如,古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,它们之间有一定的规律性。
要求第24个三角形数与第22个三角形数的差,我们可以通过求出第24个和第22个三角形数的值,再相减得到答案。
除了基本方法外,还可以用分析观察的方法求解。
例如,在一个面积为S的等边三角形中,我们将其各边n(n为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形。
当n=5时,共向外作出了4个小等边三角形;当n=k时,共向外作出了k-2个小等边三角形。
中考规律类试题在素材选取、文字表述、题型设计等方面都别具一格,旨在考察学生的创新意识与实践能力。
七年级找规律经典题汇总带答案

一、数字排列规律题1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( ) 二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是(填图形名称). 三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式:1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若 (21010)规律发现专题训练1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖块。
图形找规律专项练习60题(有标准答案解析)

图形找规律专项练习60 题(有答案)1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数;.2.观察表中三角形个数的变化规律:图形横截线012⋯n条数三角形6??⋯?个数若三角形的横截线有0 条,则三角形的个数是6;若三角形的横截线有n 条,则三角形的个数是(用含n 的代数式表示).3.如图,在线段AB 上,画 1 个点,可得 3 条线段;画 2 个不同点,可得 6 条线段;画 3 个不同点,可得10条线段;⋯照此规律,画10个不同点,可得线段条.4.如图是由数字组成的三角形,除最顶端的 1 以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x 的值是,y的值是.5.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有个单位正方形.6.如图,用相同的火柴棒拼三角形,依此拼图规律,第7 个图形中共有根火柴棒.7.图 1是一个正方形,分别连接这个正方形的对边中点,得到图 2 ;分别连接图 2 中右下角的小正方形对边中点,得到图 3;再分别连接图 3 中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n 个图的所有正方形个数是个.8.观察下列图案:它们是按照一定规律排列的,依照此规律,第 6 个图案中共有个三角形.9.如图,依次连接一个边长为 1 的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是;第六个正方形的面积是.10.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有 1 个小正方形,第 2 个图形有 3 个小正方形,第 3 个图形有 6 个小正方形,第 4 个图形有10个小正方形⋯,按照这样的规律,则第10 个图形有个小正方形.11.如图,用围棋子按下面的规律摆图形,则摆第n 个图形需要围棋子的枚数为.12.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n 条“金鱼”需用火柴棒的根数为.13.如图,两条直线相交只有 1 个交点,三条直线相交最多有 3 个交点,四条直线相交最多有相交最多有 10 个交点,六条直线相交最多有个交点,二十条直线相交最多有6 个交点,五条直线个交点.14.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号( 1)(2)(3)火柴根数从左到右依次为___________________________⋯.n15.图( 1)是一个黑色的正三角形,顺次连接三边中点,得到如图( 2)所示的第的正三角形);在图( 2 )的每个黑色的正三角形中分别重复上述的作法,得到如图(2 个图形(它的中间为一个白色3 )所示的第 3 个图形.如此继续作下去,则在得到的第 5 个图形中,白色的正三角形的个数是.16.如图,一块圆形烙饼切一刀可以切成 2 块,若切两刀最多可以切成 4 块,切三刀最多可以切成7 块⋯通过观察、计算填下表(其中S 表示切 n 刀最多可以切成的块数)后,可探究一圆形烙饼切n 刀最多能切成块(结果用 n 的代数式表示).n012345⋯nS124717.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为 3,周长为 7;第( 2 )个图案由 3 个等腰梯形拼成,其周长为13;⋯第( n )个图案由( 2n﹣ 1)个等腰梯形拼成,其周长为.(用正整数n 表示)18.下列各图均是用有一定规律的点组成的图案,用S 表示第 n 个图案中点的总数,则S=(用含n的式子表示).19.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n (n≥ 3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S 与 n( n ≥3 )的关系是.20.用火柴棍象如图这样搭图形,搭第n 个图形需要根火柴棍.21.现有黑色三角形“”和白色三角形“”共有2011个,按照一定的规律排列如下:则黑色三角形有个.22.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●⋯ 请问第 2011个棋子是黑的还是白的?答:.23.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:梯形的个数12345⋯图形的周长58111417⋯当梯形个数为2007 个时,这时图形的周长为_________24.如图,下面是一些小正方形组成的图案,第 4 个图案有个小正方形组成;第n 个图案有个小正方形组成.25.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7 个图形中火柴棒的根数是.26.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n ( n≥ 2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s 与 n 之间的关系可用式子表示.27.观察下列图形,它是按一定规律排列的,那么第个图形中,十字星与五角星的个数和为27个.28. 2 条直线最多只有 1 个交点; 3 条直线最多只有 3 个交点; 4 条直线最多只有 6 个交点; 2000 条直线最多只有个交点.29.以下各图分别由一些边长为1 的小正方形组成,请填写图2、图 3 中的周长,并以此推断出图10的周长为.30.如图所示,第 1 个图案是由黑白两种颜色的正六边形地面砖组成,第 2 个,第 3 个图案可以看作是第 1 个图案经过平移而得,那么设第n 个图案中有白色地面砖m 块,则 m 与 n 的函数关系式是.31.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第 6 、7 两个图形各有多少颗黑色棋子?(2)写出第 n 个图形黑色棋子的颗数?(3)是否存在某个图形有 2012 颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.32.如图,给出四个点阵,s 表示每个点阵中点的个数,按照图形中的点的个数变化规律,( 1)猜想第n 个点阵中的点的个数s=.( 2)若已知点阵中点的个数为37,问这个点阵是第几个?33.用棋子摆出下列一组图形:( 1)填写下表:图形编号123456图中棋子数5811141720( 2)照这样的方式摆下去,写出摆第n 个图形所需棋子的枚数;( 3)其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.34.观察图中四个顶点的数字规律:( 1)数字“ 30”在个正方形的;(2)请你用含有 n ( n ≥ 1 的整数)的式子表示正方形四个顶点的数字规律;(3)数字“ 2011”应标在什么位置.35.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n (n > 1)盆花,每个图案中花盆的总数为S.问:①当每条边有 2 盆花时,花盆的总数S 是多少?②当每条边有 3 盆花时,花盆的总数S 是多少?③当每条边有 4 盆花时,花盆的总数S 是多少?④当每条边有10盆花时,花盆的总数S 是多少?⑤按此规律推断,当每条边有n 盆花时,花盆的总数S 是多少?36.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:( 1)第④、第⑤个“上”字分别需用和枚棋子;( 2)第 n 个“上”字需用枚棋子;( 3)七( 3)班有 50 名同学,把每一位同学当做一枚棋子,能否让这字?若能,请计算最下一“横”的学生数;若不能,请说明理由.50 枚“棋子” 按照以上规律恰好站成一个“上”37.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计.线段上点的个数线段的总条数11+2=31+2+3=6⋯⋯( 1)请你完成探究,并把探究结果填在相应的表格里;( 2)若在同一线段上有10个点,则线段的总条数为;若在同一线段上有n 个点,则有(用含 n 的式子表示)( 3)若你所在的班级有60 名学生, 20 年后参加同学聚会,见面时每两个同学之间握一次手,共握手38.如图是用棋子摆成的“H ”字.( 1)摆成第一个“ H”字需要个棋子;摆第x个“H”字需要的棋子数可用含x 的代数式表示为( 2)问第几个“H”字棋子数量正好是2012 个棋子?条线段次.;39.我们知道,两条直线相交只有一个交点.请你探究:( 1)三条直线两两相交,最多有个交点;( 2)四条直线两两相交,最多有个交点;( 3) n 条直线两两相交,最多有个交点(n 为正整数,且n≥ 2 ).40.如图所示,小王玩游戏:一张纸片,第一次将其撕成四小片,手中共有 4 张纸片,以后每次都将其中一片撕成更小的四片.如此进行下去,当小王撕到第n 次时,手张共有S 张纸片.根据上述情况:(1)用含 n 的代数式表示 S;(2)当小王撕到第几次时,他手中共有70 张小纸片?41.如图①是一张长方形餐桌,四周可坐 6 人, 2 张这样的桌子按图②方式拼接,四周可坐10 人.现将若干张这样的餐桌按图③方式拼接起来:( 1)三张餐桌按题中的拼接方式,四周可坐人;( 2) n 张餐桌按上面的方式拼接,四周可坐人(用含n 的代数式表示).若用餐人数为26 人,则这样的餐桌需要张.42.用棋子摆出下列一组图形:( 1)填写下表:图形编号123456图形中的棋子(2)照这样的方式摆下去,写出摆第n 个图形棋子的枚数;(用含 n 的代数式表示)(3)如果某一图形共有 99 枚棋子,你知道它是第几个图形吗?43.如图①,图②,图③,图④,⋯,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,( 1)第 5 个“广”字中的棋子个数是.( 2)第 n 个“广”字需要多少枚棋子?44.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:( 1)在第 n 个图中共有块黑瓷砖,块白瓷砖;( 2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?45.用火柴棒按如图的方式搭三角形.照这样搭下去:( 1)搭 4 个这样的三角形要用( 2)搭 n 个这样的三角形要用根火柴棒; 13 根火柴棒可以搭根火柴棒(用含n 的代数式表示).个这样的三角形;46.观察图中的棋子:( 1)按照这样的规律摆下去,第 4 个图形中的棋子个数是多少?(2)用含 n 的代数式表示第 n 个图形的棋子个数;(3)求第 20 个图形需棋子多少个?47.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.( 1)填出下表中未填的两个空格:阶梯级数一级二级三级石墩块数39( 2)当垒到第n 级阶梯时,共用正方体石墩多少块(用含多少块?四级n 的代数式表示)?并求当n=100 时,共用正方体石墩48.有一张厚度为0.05 毫米的纸,将它对折1次后,厚度为2×0.05 毫米.(1)对折 3 次后,厚度为多少毫米?(2)对折 n 次后,厚度为多少毫米?(3)对折 n 次后,可以得到多少条折痕?49.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,第 n 个图形,每一横行有按此规律,铺设了一矩形地面,共用瓷砖块瓷砖,每一竖列有块瓷砖(用含 n 的代数式表示) 506 块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?50.找规律:观察下面的星阵图和相应的等式,探究其中的规律.( 1)在④、⑤和⑥后面的横线上分别写出相应的等式:①222 1=1② 1+3=2③ 1+3+5=3④;⑤;⑥;( 2)通过猜想,写出第n 个星阵图相对应的等式.51.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:( 1)完成下表:所剪次数 n12345正方形个数Sn4( 2)剪 n 次共有 S n个正方形,请用含n 的代数式表示S n=;( 3)若原正方形的边长为1,则第 n 次所剪得的正方形边长是(用含n的代数式表示).52.如图是用五角星摆成的三角形图案,每条边上有n(n> 1)个点(即五角星),每个图案的总点数(即五角星总数)用 S 表示.( 1)观察图案,当n=6 时, S=;( 2)分析上面的一些特例,你能得出怎样的规律?(用n 表示 S)(3)当 n=2008 时,求 S.53.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:( 1)由里向外第 1 个正方形(实线)四条边上的格点个数共有个;由里向外第 2 个正方形(实线)四条边上的格点个数共有个;由里向外第 3 个正方形(实线)四条边上的格点个数共有个;( 2)由里向外第10 个正方形(实线)四条边上的格点个数共有个;( 3)由里向外第n 个正方形(实线)四条边上的格点个数共有个.54.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n (n> 1)个花盆,每个图案花盆总数是S.( 1)按要求填表:n2345⋯S4812⋯( 2)写出当 n=10 时, S=.( 3)写出 S 与 n 的关系式: S=.( 4)用 42 个花盆能摆出类似的图案吗?55.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究并解答下列问题.( 1)在第 1 个图中,共有白色瓷砖块.( 2)在第 2 个图中,共有白色瓷砖块.( 3)在第 3 个图中,共有白色瓷砖块.( 4)在第 10 个图中,共有白色瓷砖块.( 5)在第 n 个图中,共有白色瓷砖块.56.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n ( n> 1)盆花,每个图案花盆的总数为S,当 n=2 时, S=3 ;n=3 时, S=6 ; n=4 时, S=10.( 1)当 n=6 时, S=( 2)你能得出怎样的规律?用;n=100 时, S=n 表示 S..57.下面是按照一定规律画出的一系列“树枝”经观察,图(图( 3)比图( 2 )多出 4 个“树枝”,图( 4)比图( 3)多出图( 5)比图( 4)多出个树枝;图( 6)比图( 5)多出个树枝;图( 8)比图( 7)多出个树枝;⋯图( n+1 )比图( n )多出个树枝.2 )比图( 1)多出 2 个“树枝”,8 个“树枝”,按此规律:58.如图是用棋子成的“要8 枚棋子,第三个“T ”字图案.从图案中可以出,第一个“T ”图案需要11枚棋子.T ”字图案需要 5 枚棋子,第二个“T ”字图案需(1)照此规律,摆成第八个图案需要几枚棋子?(2)摆成第 n 个图案需要几枚棋子?(3)摆成第 2010 个图案需要几枚棋子?59.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干图案:( 1)当黑砖 n=1 时,白砖有( 2)第 n 个图案中,白色地砖共块,当黑砖块.n=2时,白砖有块,当黑砖n=3时,白砖有块.60.下列图案是晋商大院窗格的一部分.其中,“ o”代表窗纸上所贴的剪纸.探索并回答下列问题:( 1)第 6 个图案中所贴剪纸“o”的个数是;( 2)第 n 个图案中所贴剪纸“o”的个数是;( 3)是否存在一个图案,其上所贴剪纸“o”的个数为2012 个?若存在,指出是第几个;若不存在,请说明理由.图形找规律 60 题参考答案:1.结合图形和表格,不难发现:1张桌子座 6 人,多一张桌子多 2 人. 4 张桌子可以座10+2=12.即 n 张桌子时,共座6+2 ( n﹣ 1)=2n+4 .2.当横截线有 n 条时,在 6 个的基础上多了 n 个 6,即三角形的个数共有 6+6n=6 ( n+1 )个.故应填 6(n+1)或 6n+63.∵画 1个点,可得 3 条线段, 2+1=3 ;画2 个点,可得 6 条线段, 3+2+1=6 ;画3 个点,可得 10条线段, 4+3+2+1=10 ;⋯;画n 个点,则可得( 1+2+3+ ⋯ +n+n+1 )=条线段.所以画 10个点,可得=66 条线段;4.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是 x,所以 x=61.另外,由图形可知, x 右边的数是 2×61=122, y 左边的数是 2 ×61+56=178 ,所以 y=178+46=2245.根据题意分析可得:第 1 个图案中正方形的个数2个,第 2 个图案中正方形的个数比第 1 个图案中正方形的个数多 4 个,第 3 个图案中正方形的个数比第 2 个图案中正方形的个数多 6 个⋯,依照图中规律,第六个图形中有 2+4+6+8+10+12=42 个单位正方形6.图形从上到下可以分成几行,第n行中,斜放的火柴有 2n 根,下面横放的有n 根,因而图形中有 n 排三角形时,火柴的根数是:斜放的是2+4+ ⋯ +2n=2 ( 1+2+ ⋯+n )横放的是:1+2+3+ ⋯+n ,则每排放 n 根时总计有火柴数是:3(1+2+ ⋯ +n ) = 3n(n1)把n=7代入就可以求2出.故第 7 个图形中共有=84 根火柴棒7.图 1中,是 1 个正方形;图2 中,是 1+4=5 个正方形;图3 中,是 1+4×2=9 个正方形;依此类推,第n 个图的所有正方形个数是1+4( n ﹣ 1)=4n ﹣ 3.8.∵第 1 个图案中有2×2+2 ×1=6 个三角形;第2 个图案中有 2×3+2 ×2=10 个三角形;第3 个图案中有 2×4+2 ×3=14 个三角形;⋯∴第 6 个图案中有2×7+2 ×6=26 个三角形.故答案为269.∵正方形的边长是1,所以它的斜边长是:= ,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第 n 个正方形的面积为()n﹣ 1,6﹣ 1所以第六个正方形的面积是()=;故答案为:,.10.∵第一个有 1 个小正方形,第二个有 1+2 个,第三个有1+2+3 个,第四个有 1+2+3+4 ,第五个有 1+2+3+4+5 ,∴则第 10个图形有 1+2+3+4+5+6+7+8+9+10=55 个.故答案为: 5511.依题意得:( 1)摆第 1 个“小屋子”需要 5 个点;摆第 2 个“小屋子”需要 11个点;摆第 3 个“小屋子”需要17个点.当n=n 时,需要的点数为( 6n﹣ 1)个.故答案为 6n﹣ 112.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8 ;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20 ;⋯;第 n 个金鱼需用火柴棒的根数为:2+n ×6=2+6n .故答案为 2+6n13.6 条直线两两相交,最多有n( n ﹣ 1)= ×6×5=15,20 条直线两两相交,最多有n( n ﹣ 1)=×20×19=190.故答案为: 15, 190.14.如表格所示:图形编( 1)(2)(3)⋯n号火柴根 71217⋯5n+2数15.设白三角形 x 个,黑三角形 y 个,故答案为:白则: n=1 时, x=0 , y=1;23.依题意可求出梯形个数与图形周长的关系为3n+2= n=2 时, x=0+1=1 , y=3 ;周长,n=3 时, x=3+1=4 ,y=9 ;当梯形个数为2007 个时,这时图形的周长为3×n=4 时, x=4+9=13 , y=27 ;2007+2=6023 .当 n=5 时, x=13+27=40 ,故答案为: 6023 .所以白的正三角形个数为:40,24.观察图形知:故答案为: 40第一个图形有2个小正方形;16. n=1 时, S=1+1=2 ,1=1n=2 时, S=1+1+2=4 ,第二个图形有1+3=4=22 个小正方形;n=3 时, S=1+1+2+3=7 ,n=4 时, S=1+1+2+3+4=11 ,第三个图形有1+3+5=9=3 2 个小正方形;⋯所以当切 n 刀时, S=1+1+2+3+4+ ⋯ +n=1+n(n+1 )⋯2第 n 个图形共有 1+2+3+ ⋯ +( 2n ﹣ 1)=n 2 个小正方形,n+1.= n +22n2 +n+1当 n=4 时,有 n =4 =16 个小正方形.故答案为17.根据题意得:故答案为: 16,n2第( 1)个图案只有 1 个等腰梯形,周长为3×1+4=7;25.根据已知图形可以发现:第( 2 )个图案由 3 个等腰梯形拼成,其周长为 3×3+4=13 ;第 2 个图形中,火柴棒的根数是7;第( 3)个图案由 5 个等腰梯形拼成,其周长为 3×5+4=19;第 3 个图形中,火柴棒的根数是10;⋯第 4 个图形中,火柴棒的根数是13;第( n)个图案由( 2n ﹣ 1)个等腰梯形拼成,其周长为∵每增加一个正方形火柴棒数增加3,3( 2n﹣ 1) +4=6n+1 ;∴第 n 个图形中应有的火柴棒数为: 4+3( n ﹣1)=3n+1 .故答案为: 6n+1当 n=7 时, 4+3 ( n ﹣ 1) =4+3 ×6=22 ,18.观察发现:故答案为: 22第 1 个图形有 S=9 ×1+1=10个点,26.观察图形发现:第 2 个图形有 S=9 ×2+1=19 个点,当 n=2 时, s=4 ,第 3 个图形有 S=9 ×3+1=28 个点,当 n=3 时, s=9 ,⋯当 n=4 时, s=16,第 n 个图形有 S=9n+1 个点.当 n=5 时, s=25 ,故答案为: 9n+1⋯19. n=3 时, S=6=3 ×3﹣ 3=3 ,当 n=n 时, s=n 2 ,n=4 时, S=12=4 ×4﹣ 4,n=5 时, S=20=5 ×5﹣ 5,故答案为: s=n2⋯,依此类推,边数为 n 数, S=n ?n﹣n=n ( n ﹣ 1).27.∵第 1 个图形中,十字星与五角星的个数和为3×故答案为: n ( n ﹣ 1).2=6 ,20.结合图形,发现:搭第n 个三角形,需要 3+2 ( n第 2 个图形中,十字星与五角星的个数和为3×3=9 ,﹣ 1) =2n+1 (根).第 3 个图形中,十字星与五角星的个数和为3×4=12,故答案为 2n+1⋯21.因为 2011÷6=335 ⋯ 1.余下的 1 个根据顺序应是黑而 27=3 ×9,色三角形,所以共有 1+335×3=1006.∴第 8 个图形中,十字星与五角星的个数和=3 ×9=27 .故答案为: 1006故答案为: 822 .从所给的图中可以看出,每六个棋子为一个循环,28. 2 条直线最多的交点个数为1,∵ 2011÷6=335 ⋯ 1, 3 条直线最多的交点个数为1+2=3 ,∴第 2011个棋子是白的. 4 条直线最多的交点个数为1+2+3=6 ,5 条直线最多的交点个数为1+2+3+4=10 ,33.( 1)观察图形,得出枚数分别是,5, 8, 11,⋯,⋯每个比前一个多 3 个,所以图形编号为5,6 的棋字子所以 2000条直线最多的交点个数为1+2+3+4+ ⋯数分别为 17, 20.+1999==1999000.故答案为: 17和 20.( 2 )由( 1)得,图中棋子数是首项为5,公差为 3 的故答案为 1999000等差数列,29.∵小正方形的边长是1,所以摆第 n 个图形所需棋子的枚数为:5+3 ( n﹣ 1)∴图 1 的周长是: 1×4=4 ,=3n+2 .图 2 的周长是:2×4=8 ,( 3)不可能图 3 的周长是 3×4=12,由 3n+2=2010 ,⋯解得: n=669,第 n 个图的周长是 4n,∴图 10的周长是10×4=40;∵ n 为整数,故答案为:8, 12, 40∴ n=669 不合题意30.首先发现:第一个图案中,有白色的是6 个,后边是依次多 4 个.故其中某一图形不可能共有2011 枚棋子所以第 n 个图案中,是6+4 ( n ﹣ 1) =4n+2 .34.( 1)由图可知,每个正方形标 4 个数字,∴ m 与 n 的函数关系式是m=4n+2 .∵ 30÷4=7 ⋯ 2,故答案为: 4n+2 .∴数字 30 在第 8 个正方形的第 2个位置,即右上角;31.第一个图需棋子 6,故答案为: 8,右上角;第二个图需棋子9,( 2 )左下角是 4 的倍数,按照逆时针顺序依次减1,第三个图需棋子12,即正方形左下角顶点数字:4n,第四个图需棋子15,正方形左上角顶点数字:4n﹣ 1,第五个图需棋子18,正方形右上角顶点数字:4n﹣ 2,⋯正方形右下角顶点数字:4n﹣ 3;第 n 个图需棋子3( n+1)枚.( 3) 2011÷4=502 ⋯3 ,( 1)当 n=6 时, 3×(6+1) =21 ;所以,数字“ 2011”应标第503 个正方形的左上角顶点当 n=7 时, 3 ×(7+1) =24 ;处( 2)第 n 个图需棋子3( n+1 )枚.35.依题意得:① n=2 , S=3=3 ×2﹣ 3.( 3)设第 n 个图形有2012 颗黑色棋子,② n=3 , S=6=3 ×3﹣ 3.根据( 1)得 3( n+1)=2012③ n=4 ,S=9=3 ×4﹣ 3解得 n=,④ n=10, S=27=3 ×10﹣3 .⋯所以不存在某个图形有2012 颗黑色棋子⑤按此规律推断,当每条边有n 盆花时, S=3n ﹣ 3 32.( 1)由点阵图形可得它们的点的个数分别为:1,5,36.( 1)第①个图形中有 6 个棋子;9,13,⋯,并得出以下规律:第②个图形中有6+4=10 个棋子;第一个点数: 1=1+4×(1﹣ 1)第③个图形中有6+2 ×4=14 个棋子;第二个点数: 5=1+4 ×(2 ﹣1)∴第⑤个图形中有 6+3 ×4=18 个棋子;第三个点数: 9=1+4 ×(3﹣ 1)第⑥个图形中有6+4 ×4=22 个棋子.第四个点数: 13=1+4×(4﹣ 1)故答案为 18、 22;(3 分)⋯( 2 )第 n 个图形中有 6+ ( n ﹣1)×4=4n+2 .因此可得:故答案为 4n+2 .(3 分)第 n 个点数: 1+4×(n ﹣ 1) =4n ﹣3 .( 3) 4n+2=50 ,故答案为: 4n﹣ 3;解得 n=12 .( 2)设这个点阵是 x 个,根据(1)得:最下一横人数为2n+1=25 .( 4 分)1+4×(x﹣ 1) =3737.( 1) 5 个点时,线段的条数:1+2+3+4=10 ,解得: x=10. 6 个点时,线段的条数:1+2+3+4+5=15 ;答:这个点阵是10个( 2 )10个点时,线段的条数: 1+2+3+4+5+6+7+8+9=45,n 个点时,线段的条数:1+2+3+ ⋯ + (n﹣ 1)图形 6912151821=;中的棋子(3)60人握手次数 ==1770.( 2 )依题意可得当摆到第n 个图形时棋子的枚数应为:6+3 ( n ﹣1) =6+3n ﹣ 3=3n+3 ;故答案为:( 2) 45,;( 3) 1770.( 3)由上题可知此时3n+3=99 ,∴ n=32 .38.( 1)摆成第一个“ H ”字需要7 个棋子,答:第 32 个图形共有99 枚棋子第二个“ H”字需要棋子12 个;13.由题目得:第 1 个“广”字中的棋子个数是7;第三个“ H”字需要棋子17个;第 2 个“广”字中的棋子个数是7+ (2 ﹣ 1)×2=9 ;⋯第 3 个“广”字中的棋子个数是7+ ( 3﹣ 1)×2=11;第 x 个图中,有7+5 ( x﹣ 1) =5x+2 (个).第 4 个“广”字中的棋子个数是7+ (4﹣ 1)×2=13;( 2)当 5x+2=2012时,解得: x=402 ,发现第 5 个“广”字中的棋子个数是 7+( 5﹣ 1)×2=15⋯故第 402 个“ H”字棋子数量正好是2012 个棋子进一步发现规律:第n 个“广”字中的棋子个数是7+ 39.(1)如图( 1),可得三条直线两两相交,最多有3( n ﹣ 1)×2=2n+5 .个交点;故答案为: 15( 2)如图( 2),可得三条直线两两相交,最多有 6 个44.( 1)在第 n 个图形中,需用黑瓷砖4n+6块,白瓷交点;砖 n(n+1 )块;( 3)由( 1)得,=3 ,( 2 )根据题意得n (n+1 ) =4n+6 ,n2﹣ 3n ﹣6=0 ,由( 2)得,=6 ;此时没有整数解,∴可得, n 条直线两两相交,最多有个交点所以不存在.故答案为: 4n+6 ; n(n+1 )( n 为正整数,且n≥ 2 ).45.(1)结合图形,发现:后边每多一个三角形,则需故答案为3;6;.要多 2 根火柴.则搭 4 个这样的三角形要用3+2 ×3=9 根火柴棒;13根火柴棒可以搭( 13﹣ 3)÷2+1=6 个这样的三角形;( 2 )根据( 1)中的规律,得搭 n 个这样的三角形要用3+2( n ﹣1)=2n+1根火柴棒.故答案为9; 6; 2n+140.( 1)由题目中的“每次都将其中﹣片撕成更小的四46.( 1)第 4 个图形中的棋子个数是13;片”,( 2 )第 n 个图形的棋子个数是3n+1 ;可知:小王每撕一次,比上一次多增加 3 张小纸片.( 3)当 n=20 时, 3n+1=3 ×20+1=61∴ s=4+3 (n ﹣ 1)=3n+1 ;∴第 20 个图形需棋子61 个( 2)当 s=70 时,有 3n+1=70 ,n=23 .即小王撕纸 2347.( 1)第一级台阶中正方体石墩的块数为:次=3 ;41.( 1)结合图形,发现:每个图中,两端都是坐 2 人,剩下的两边则是每一张桌子是 4 人.第一级台阶中正方体石墩的块数为:=9 ;则三张餐桌按题中的拼接方式,四周可坐3×4+2=14(人);第一级台阶中正方体石墩的块数为:;( 2) n 张餐桌按上面的方式拼接,四周可坐(4n+2 )人;⋯若用餐人数为 26人,则 4n+2=26 ,依此类推,可以发现:第几级台阶中正方体石墩的块数解得 n=6 .为: 3 与几的乘积乘以几加1,然后除以 2.故答案为: 14;( 4n+2 ),6阶梯级数一级二级三级四级42.( 1)如图所示:石墩块数391830图形 123456编号( 2)按照( 1)中总结的规律可得:当垒到第n 级阶梯时,共用正方体石墩块;当n=100 时,∴当 n=100 时,共用正方体石墩15150块.答:当垒到第n 级阶梯时,共用正方体石墩块;当 n=100 时,共用正方体石墩15150块48.由题意可知:第一次对折后,纸的厚度为 2×0.05;可以得到折痕为 1 条;第二次对折后,纸的厚度为2×2×0.05=2 2×0.05;可以得到折痕为 3=2 2﹣ 1 条;第三次对折后,纸的厚度为 2 ×2×2×0.05=2 3×0.05;可以3得到折痕为7=2 ﹣ 1 条;第 n 次对折后,纸的厚度为2×2×2 ×2 ×⋯×2×0.05=2 n×0.05.可以得到折痕为 2 n﹣ 1 条.故:(1)对折 3 次后,厚度为 0.4 毫米;(2)对折 n 次后,厚度为 2 n×0.05 毫米;(3)对折 n 次后,可以得到 2n﹣1 条折痕49.由图形我们不难看出横行砖数量为n+3 ,竖行砖数2量为 n+2 ,总数量为n +5n+6 ;若用瓷砖506 块,可以求n2 +5n+6=506 ;所以答案为:( 1)n+3 , n+2 ;( 2)每一行有23 块,每一列有22 块50.等号左边是从 1 开始,连续奇数相加,等号右边是奇数个数也就是 n 的平方.(1)① 1+3+5+7=4 2;2②1+3+5+7+9=5 ;③ 1+3+5+7+9+11=6 2.251.( 1)依题意得:所剪次数 n12345正方形个数 Sn 47101316(2 )可知剪 n 次时, S n=3n+1 .(3) n=1 时,边长 = ;n=2 时,边长 =;n=3 时,边长 =;⋯;剪 n 次时,边长 =.52.(1) S=15(2 )∵ n=2 时, S=3 ×(2﹣ 1)=3 ;n=3 时, S=3 ×(3﹣1) =6 ;n=4 时, S=3 ×(4﹣1) =9 ;⋯∴S=3 ×(n ﹣ 1) =3n ﹣ 3.(3)当 n=2008 时, S=3 ×2008 ﹣ 3=6021.53.第 1 个正方形四条边上的格点共有 4 个第 2 个正方形四条边上的格点个数共有(4+4×1)个第 3 个正方形四条边上的格点个数共有(4+4×2 )个⋯第 10个正方形四条边上的格点个数共有(4+4 ×9) =40个第 n 个正方形四条边上的格点个数共有[4+4 ×(n﹣1)]=4n 个54.由图可知,每个图形为边长是n 的正方形,因此四条边的花盆数为 4n ,再减去重复的四个角的花盆数,即S=4n ﹣ 4;( 1)将 n=5 代入 S=4n ﹣ 4,得 S=16;(2 )将 n=10 入 S=4n ﹣ 4,得 S=36 ;(3) S=4n ﹣ 4;(4)将 S=42 代入 S=4n ﹣ 4 得,4n﹣4=42解得 n=11.5所以用 42 个花盆不能摆出类似的图案55.( 1)在第 1 个图中,共有白色瓷砖1×(1+1)=2 块,( 2 )在第 2 个图中,共有白色瓷砖2×(2+1) =6 块,( 3)在第 3 个图中,共有白色瓷砖3×(3+1) =12 块,( 4)在第10个图中,共有白色瓷砖10×(10+1) =110块,( 5)在第 n 个图中,共有白色瓷砖n ( n+1 )块56.( 1)由分析得:当n=6 时, s=1+2+3+4+5+6=21;当n=100 时, s=1+2+3+ ⋯ +99+100=5050 ;( 2 )用 n 表示 S 得: S=。
七年级数学图形中的排列规律重难点题型总结(含解析版)
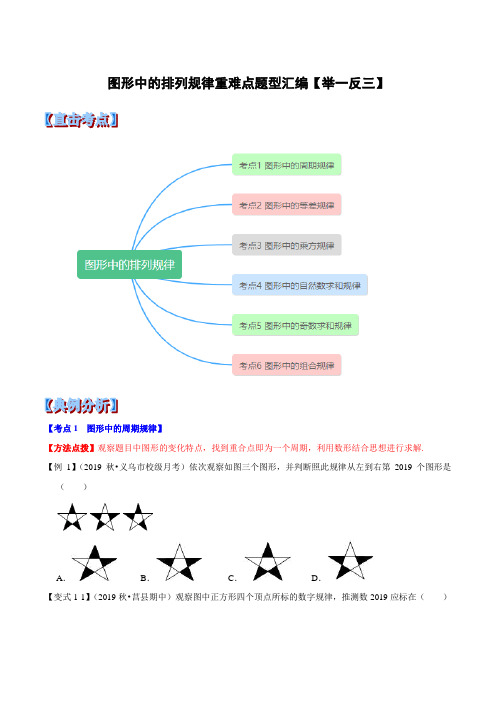
图形中的排列规律重难点题型汇编【举一反三】【考点1 图形中的周期规律】【方法点拨】观察题目中图形的变化特点,找到重合点即为一个周期,利用数形结合思想进行求解.【例1】(2019秋•义乌市校级月考)依次观察如图三个图形,并判断照此规律从左到右第2019个图形是()A.B.C.D.【变式1-1】(2019秋•莒县期中)观察图中正方形四个顶点所标的数字规律,推测数2019应标在()A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的右下角D.第505个正方形的左上角【变式1-2】(2019春•海安市校级月考)如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2018cm时停下,则它停的位置是()A.点F B.点E C.点A D.点C【变式1-3】(2019秋•工业园区期末)如图,物体从A点出发,按照A→B(第一步)→C(第二步)→D →A→E→F→G→A→B……的顺序循环运动,则第2018步到达()A.A点B.C点C.E点D.F点【考点2 图形中的等差规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,会发现后一项与前一项的差均相等,即为等差规律,应用公式:第n个图形的个数=第一个图形的个数+差数×(n-1). 【例2】(2019春•南岸区校级期中)用黑白两种颜色的正方形纸片,按白色纸片数逐渐加1并按下图的规律拼成一列图案,则第100个图案中黑色正方形纸片的张数是()A.300B.301C.302D.303【变式2-1】(2018秋•南山区校级期中)用棋子按下面的规律摆图形,则摆第2018个图形需要围棋子()枚.A.6053B.6054C.6056D.6060【变式2-2】(2018秋•宁都县期中)下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,…,按此规律排列下去第⑩个图中黑色正方形纸片的张数为()A.15B.17C.21D.27【变式2-3】(2018秋•万州区期中)如图,是用棋子摆成的“上”字:如果按照此规律继续摆下去,那么通过观察,可以发现:第10个“上”字需用多少枚棋子()A.36B.38C.42D.50【考点3 图形中的乘方规律】【方法点拨】观察题目中图形的特点,出现1,4,9,16,25.....正方形的图阵,即可联想到利用乘方来表示.【例3】(2019春•江岸区校级期中)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑥个图形中菱形的个数为()A.42B.43C.56D.57【变式3-1】(2019春•南岸区校级期中)如图是一组有规律的图案,第1个图案由5个基础图形组成,第2个图案由8个基础图形组成,……,如果按照以下规律继续下去,那么通过观察,可以发现:第20个图案需要()个基本图形.A.402B.404C.406D.408【变式3-2】(2018秋•亭湖区校级期中)下面是某同学在沙滩上用石子摆成的小房子观察图形的变化规律,则第10个小房子用了____颗石子.()A.119B.121C.140D.142【变式3-3】(2019秋•九龙坡区校级期中)如图,们一个图形都是由一些黑点按一定的规律排列组成的,其中第①个图形中共有6个小黑点,第②个图形中有10个黑点,第③个图形中一共有16个小黑点,…,按此规律,则第⑩个图形中小黑点的个数是()A.112B.114C.116D.118【考点4 图形中的自然数求和规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,利用1+2+3+4+...+n=n(n+1)/2求解即可,需注意若首项不为1,需将公式进行适当变形.【例4】(2019秋•青山区校级月考)如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……则下列说法:①10是三角点阵中前4行的点数和;②300是三角点阵中前24行的点数和;③前n个点数和为200的点,在这个三角点阵中位于第20行第10个点,其中正确的个数是()A.0个B.1个C.2个D.3个【变式4-1】(2019秋•沙坪坝区校级月考)如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(6)个图形中面积为1的正方形的个数为()A.14B.20C.24D.27【变式4-2】(2019春•北碚区校级期中)如图图形是用同样大小的铜币摆放的四个图案,根据摆放图案的规律,则第8个图案需要铜币的个数为()A.29B.36C.37D.46【变式4-3】(2018秋•市南区校级期中)下列是用火柴棒拼成的一组图形,第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第③个图形中有18根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是()A.63B.60C.56D.45【考点5 图形中的奇数求和规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,利用1+3+5+7+9+11+…+2n﹣1=(n+1)2求解即可,需注意若首项不为1,需将公式进行适当变形.【例5】(2018秋•九龙坡区校级期中)如图,将等边三角形按一定规律排列,第①个图形中有1个小等边三角形,第②个图形中有4个小等边三角形,按此规律,则第⑥个图形中有()个小等边三角形.A.36个B.49个C.35个D.48个【变式5-1】(2018秋•三台县期中)如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有()A.4n﹣1B.n2﹣1C.n2+2D.2n+1【变式5-2】(2019•云南模拟)如图用棋子摆成三角形的图案,第(1)个三角形中有4枚棋子,第(2)个三角形中有9枚棋子,第(3)个三形中有16枚棋了,…,按照这样的规律摆下去第()个三角形中有2025枚棋子.A.42B.43C.44D.45【变式5-3】(2019•沙坪坝区校级一模)观察下列图形,①中有1个圆,②中有5个圆,③中有13个圆……,若依此规律,则第⑥个图形中圆的个数为()A.25B.61C.41D.65【考点6 图形中的组合规律】【方法点拨】此类问题是将上述两种规律结合在一起,需将图形进行拆分,找出各个部分的规律进行组合即可.【例6】(2019•长寿区模拟)下列图形都是由●按照一定规律组成的,其中第①个图共有四个●,第②个图中共有8个●,第③个图中共有13个●,第④个图中共有19个●,…,照此规律排列下去,则第10 个图形中●的个数为()A.50B.53C.64D.76【变式6-1】(2018秋•九龙坡区校级期中)下列图形都是由同样大小的黑点按一定规律组成的,其中第①个图形中一共有3个黑点,第②个图形中一共有8个黑点,第③个图形中一共有14个黑点,……,则第⑧个图形中黑点的个数是()A.29B.38C.48D.59【变式6-2】(2018春•沙坪坝区校级期中)下列图形都是由同样大小的●和〇按照一定规律组成的,其中第①个图中共有6个●,第②个图中共有13个●,第③个图中共有25个●,第④个图中共有42个●,…,照此规律排列下去,则第⑦个图中●的个数为()A.91B.112C.123D.160【变式6-3】(2019春•北碚区校级月考)下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第①个图形中一共有6个黑色圆点第②个图形中一共有15个黑色圆点,第③个图形中一共有28个黑色圆点,…,按此规律排列下去,第⑦个图形中黑色圆点的个数为()A.66B.91C.120D.135图形中的排列规律重难点题型汇编【举一反三】【考点1 图形中的周期规律】【方法点拨】观察题目中图形的变化特点,找到重合点即为一个周期,利用数形结合思想进行求解.【例1】(2019秋•义乌市校级月考)依次观察如图三个图形,并判断照此规律从左到右第2019个图形是()A.B.C.D.【分析】根据题目中给出的图形,可知每五个一个循环,空白的大三角形按照顺时针旋转,从而可以得到从左到右第2019个图形是选项中的哪个图形,本题得以解决.【答案】解:由图可知,每连续的五个为一组,也就是五个一循环,2019÷5=403…4,故选:A.【点睛】本题考查图形的变化类,解答本题的关键是明确题意,发现题目中图形的变化特点,利用数形结合的思想解答.【变式1-1】(2019秋•莒县期中)观察图中正方形四个顶点所标的数字规律,推测数2019应标在()A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的右下角D.第505个正方形的左上角【分析】设第n个正方形中标记的最大的数为a n,观察给定图形,可找出规律“a n=4n”,依此规律即可得出结论.【答案】解:设第n个正方形中标记的最大的数为a n.观察给定正方形,可得出:每个正方形有4个数,即a n=4n.∵2019=504×4+3,∴数2019应标在第505个正方形左上角.故选:D.【点睛】本题考查了规律型中的图形的变化类,解题的关键是找出变换规律a n=4n.本题属于基础题,难度不大,需找出2019在第几个正方形上.【变式1-2】(2019春•海安市校级月考)如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2018cm时停下,则它停的位置是()A.点F B.点E C.点A D.点C【分析】观察图形不难发现,每移动8cm为一个循环组依次循环,用2018除以8,根据商和余数的情况确定最后停的位置所在的点即可.【答案】解:∵两个菱形的边长都为1cm,∴从A开始移动8cm后回到点A,∵2018÷8=252余2,∴移动2018cm为第253个循环组的第2cm,在点C处.故选:D.【点睛】本题是对图形变化规律的考查,观察图形得到每移动8cm为一个循环组依次循环是解题的关键.【变式1-3】(2019秋•工业园区期末)如图,物体从A点出发,按照A→B(第一步)→C(第二步)→D →A→E→F→G→A→B……的顺序循环运动,则第2018步到达()A.A点B.C点C.E点D.F点【分析】先求出由A点开始按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B→…的顺序循环运动走一圈所走的步数,在用2018除以此步数即可.【答案】解:∵如图物体从点A出发,按照A→B(第1步)→C(第2步)→D→A→E→F→G→A→B →…的顺序循环运动,此时一个循环为8步,∴2018÷8=252…2.∴当物体走到第252圈后再走2步正好到达C点.故选:B.【点睛】本题考查的是图形的变化类这一知识点,解答此题的关键是根据题意得出物体走一个循环的步数,找出规律即可轻松作答.【考点2 图形中的等差规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,会发现后一项与前一项的差均相等,即为等差规律,应用公式:第n个图形的个数=第一个图形的个数+差数×(n-1). 【例2】(2019春•南岸区校级期中)用黑白两种颜色的正方形纸片,按白色纸片数逐渐加1并按下图的规律拼成一列图案,则第100个图案中黑色正方形纸片的张数是()A.300B.301C.302D.303【分析】观察图形,发现:黑色纸片在4的基础上,依次多3个,根据其中的规律,计算出第100个图案的黑纸片个数即可.【答案】解:第1个图案中有黑色纸片3×1+1=4张,第2个图案中有黑色纸片3×2+1=7张,第3图案中有黑色纸片3×3+1=10张,…第n个图案中有黑色纸片:(3n+1)张,∴第100个图案中有黑纸片301张.故选:B.【点睛】本题主要考查学生对图形的变化类的知识点的理解和掌握,此题的关键是注意发现前后图形中的数量之间的关系,难度适中.【变式2-1】(2018秋•南山区校级期中)用棋子按下面的规律摆图形,则摆第2018个图形需要围棋子()枚.A.6053B.6054C.6056D.6060【分析】观察图形可知:第1个图形需要围棋子的枚数=5;第2个图形需要围棋子的枚数=5+3;第3个图形需要围棋子的枚数=5+3×2;第4个图形需要围棋子的枚数=5+3×3,…,则第n个图形需要围棋子的枚数=5+3(n﹣1),然后把n=2018代入计算即可.【答案】解:∵第1个图形需要围棋子的枚数=5,第2个图形需要围棋子的枚数=5+3,第3个图形需要围棋子的枚数=5+3×2,第4个图形需要围棋子的枚数=5+3×3,…,∴第n个图形需要围棋子的枚数=5+3(n﹣1)=3n+2,∴第2018个图形需要围棋子的枚数=3×2018+2=6056,故选:C.【点睛】此题考查图形的变化规律,找出图形之间的联系,得出一般的运算规律解决问题.【变式2-2】(2018秋•宁都县期中)下列图形都是由同样大小的黑色正方形纸片组成,其中第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片,…,按此规律排列下去第⑩个图中黑色正方形纸片的张数为()A.15B.17C.21D.27【分析】仔细观察图形知道第一个图形有3个正方形,第二个有5=3+2×1个,第三个图形有7=3+2×2个,由此得到规律求得第⑩个图形中正方形的个数即可.【答案】解:观察图形知:第一个图形有3个正方形,第二个有5=3+2×1个,第三个图形有7=3+2×2个,…故第⑩个图形有3+2×9=21(个),故选:C.【点睛】此题主要考查了图形的变化规律,是根据图形进行数字猜想的问题,关键是通过归纳与总结,得到其中的规律,然后利用规律解决一般问题.【变式2-3】(2018秋•万州区期中)如图,是用棋子摆成的“上”字:如果按照此规律继续摆下去,那么通过观察,可以发现:第10个“上”字需用多少枚棋子()A.36B.38C.42D.50【分析】由图可得,第1个“上”字中的棋子个数是6;第2个“上”字中的棋子个数是10;第3个“上”字中的棋子个数是14;…进一步发现规律:第n个“上”字中的棋子个数是(4n+2);由此求得问题答案.【答案】解:第1个“上”字中的棋子个数是6=4+2;第2个“上”字中的棋子个数是10=4×2+2;第3个“上”字中的棋子个数是14=4×3+2;…第n个“上”字中的棋子个数是(4n+2);所以第10个“上”字需用棋子的数量是4×10+2=42个.故选:C.【点睛】本题主要考查了图形的变化规律,对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后直接利用规律求解.【考点3 图形中的乘方规律】【方法点拨】观察题目中图形的特点,出现1,4,9,16,25.....正方形的图阵,即可联想到利用乘方来表示.【例3】(2019春•江岸区校级期中)如图图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有3个菱形,第②个图形中一共有7个菱形,第③个图形中一共有13个菱形,…,按此规律排列下去,第⑥个图形中菱形的个数为()A.42B.43C.56D.57【分析】设第n个图形中一共有a n个菱形(n为正整数),根据各图形中菱形个数的变化可得出变化规律“a n=n2+n+1(n为正整数)”,再代入n=6即可求出结论.【答案】解:设第n个图形中一共有a n个菱形(n为正整数),∵a1=12+2=3,a2=22+3=7,a3=32+4=13,a4=42+5=21,…,∴a n=n2+n+1(n为正整数),∴a6=62+7=43.故选:B.【点睛】本题考查了规律型:图形的变化类,根据各图形中菱形个数的变化,找出变化规律“a n=n2+n+1(n为正整数)”是解题的关键.【变式3-1】(2019春•南岸区校级期中)如图是一组有规律的图案,第1个图案由5个基础图形组成,第2个图案由8个基础图形组成,……,如果按照以下规律继续下去,那么通过观察,可以发现:第20个图案需要()个基本图形.A.402B.404C.406D.408【分析】仔细观察图形,找到图形变化的规律,利用规律求解即可.【答案】解:第1个图案由12+4=5个基础图形组成,第2个图案由22+4=8个基础图形组成,……,如果按照以下规律继续下去,可以发现:第20个图案需要202+4=404个基本图形.故选:B.【点睛】本题考查了图形的变化类问题,解题的关键是仔细观察图形并找到图形变化的规律,难度不大.【变式3-2】(2018秋•亭湖区校级期中)下面是某同学在沙滩上用石子摆成的小房子观察图形的变化规律,则第10个小房子用了____颗石子.()A.119B.121C.140D.142【分析】根据图示,可得:第1个小房子用的石子的数量是:1+22,第2个小房子用的石子的数量是:3+32,第3个小房子用的石子的数量是:5+42,…,据此求出第10个小房子用了多少颗石子即可.【答案】解:第1个小房子用的石子的数量是:1+22,第2个小房子用的石子的数量是:3+32,第3个小房子用的石子的数量是:5+42,…,∴第n个小房子用的石子的数量是:2n﹣1+(n+1)2,∴第10个小房子用的石子的数量是:19+112=19+121=140.故选:C.【点睛】此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.【变式3-3】(2019秋•九龙坡区校级期中)如图,们一个图形都是由一些黑点按一定的规律排列组成的,其中第①个图形中共有6个小黑点,第②个图形中有10个黑点,第③个图形中一共有16个小黑点,…,按此规律,则第⑩个图形中小黑点的个数是()A.112B.114C.116D.118【分析】第①个图形中有1×1+1+4=6个黑点;第②个图形中有2×2+2+4=10个黑点;第③个图形中有3×3+3+4=16个黑点,第④个图形中有4×4+4+4=24个黑点,那么可得第n个图形中有n•n+n+4个黑点.【答案】解:第①个图形中有1×1+1+4=6个黑点;第②个图形中有2×2+2+4=10个黑点;第③个图形中有3×3+3+4=16个黑点,第④个图形中有4×4+4+4=24个黑点,可得第n个图形中有n•n+n+4个黑点.把n=10代入可得:10×10+10+4=114,故选:B.【点睛】本题考查规律型:图形的变化类;根据图形的排列规律正确列式是解决本题的关键.【考点4 图形中的自然数求和规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,利用1+2+3+4+...+n=n(n+1)/2求解即可,需注意若首项不为1,需将公式进行适当变形.【例4】(2019秋•青山区校级月考)如图是一个三角点阵,从上向下数有无数多行,其中第一行有1个点,第二行有2个点……第n行有n个点……则下列说法:①10是三角点阵中前4行的点数和;②300是三角点阵中前24行的点数和;③前n个点数和为200的点,在这个三角点阵中位于第20行第10个点,其中正确的个数是()A.0个B.1个C.2个D.3个【分析】根据题意和题目中点的个数的变化,可以判断各个小题是否正确,从而可以解答本题.【答案】解:当n=4时,三角点阵中的点数之和是:1+2+3+4=10,故①正确,当1+2+…+n=300时,即,得n=24,故②正确,当n=19时,三角点阵中的点数之和为=190,∵190+10=200,∴前n个点数和为200的点,在这个三角点阵中位于第20行第10个点,故③正确;故选:D.【点睛】本题考查图形的变化类,解答本题的关键是明确题意,发现题目中点的个数的变化规律,利用数形结合的思想解答.【变式4-1】(2019秋•沙坪坝区校级月考)如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(6)个图形中面积为1的正方形的个数为()A.14B.20C.24D.27【分析】根据已知图形得出第n个图形中面积为1的正方形有2+3+4+…+n+1=,据此求解可得.【答案】解:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+(n+1)=个,则第(6)个图形中面积为1的正方形的个数为2+3+4+5+6+7=27个.故选:D.【点睛】此题考查图形的变化规律,找出图形与数字之间的运算规律,利用规律解决问题.【变式4-2】(2019春•北碚区校级期中)如图图形是用同样大小的铜币摆放的四个图案,根据摆放图案的规律,则第8个图案需要铜币的个数为()A.29B.36C.37D.46【分析】找出相邻两个图形铜币的数目的差,从而可发现其中的规律,于是可求得问题的答案.【答案】解:n=1时,铜币个数=1+1=2;当n=2时,铜币个数=1+1+2=4;当n=3时,铜币个数=1+1+2+3=7;当n=4时,铜币个数=1+1+2+3+4=11;…第n个图案,铜币个数=1+1+2+3+4+…+n=n(n+1)+1,当n=8时,×8×9+1=37,故选:C.【点睛】本题主要考查的是图形的变化规律,找出其中的规律是解题的关键.【变式4-3】(2018秋•市南区校级期中)下列是用火柴棒拼成的一组图形,第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第③个图形中有18根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是()A.63B.60C.56D.45【分析】由图可知:第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第②个图形中有18根火柴棒,…依此类推第n个有1+2+3+…+n个三角形,共有3×(1+2+3+…+n)=n(n+1)根火柴;由此代入求得答案即可.【答案】解:∵第①有1个三角形,共有3×1根火柴;第②个有1+2个三角形,共有3×(1+2)根火柴;第③个有1+2+3个三角形,共有3×(1+2+3)根火柴;…∴第n个有1+2+3+…+n个三角形,共有3×(1+2+3+…+n)=n(n+1)根火柴;∴第⑥个图形中火柴棒根数是3×(1+2+3+4+5+6)=63,故选:A.【点睛】此题考查了图形的变化规律,解题的关键是发现三角形个数的规律,从而得到火柴棒的根数.【考点5 图形中的奇数求和规律】【方法点拨】解此类问题的关键在于将图形的规律转化为数字规律,即将图形的个数转化为数字,利用1+3+5+7+9+11+…+2n﹣1=(n+1)2求解即可,需注意若首项不为1,需将公式进行适当变形.【例5】(2018秋•九龙坡区校级期中)如图,将等边三角形按一定规律排列,第①个图形中有1个小等边三角形,第②个图形中有4个小等边三角形,按此规律,则第⑥个图形中有()个小等边三角形.A.36个B.49个C.35个D.48个【分析】根据已知得出第n个图形有1+3+5+…+(2n﹣1)=n2个三角形,据此代入计算可得.【答案】解:第①个图有1=12个三角形,第②个图形有1+3=4=22个三角形,第③个图形有1+3+5=9=32个三角形,…第⑥个图形有62=36个三角形,故选:A.【点睛】本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.【变式5-1】(2018秋•三台县期中)如图是由一些黑点组成的图形,按此规律,在第n个图形中,黑点的个数有()A.4n﹣1B.n2﹣1C.n2+2D.2n+1【分析】分析数据可得:第①个图形中点的个数为3;第②个图形中点的个数为3+3;第③个图形中点的个数为3+3+5;第④个图形中点的个数为3+3+5+7;…则知第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1).据此可以求得答案.【答案】解:第①个图形中点的个数为3;第②个图形中点的个数为3+3;第③个图形中点的个数为3+3+5;第④个图形中点的个数为3+3+5+7;…第n个图形中小圆的个数为3+3+5+7+…+(2n﹣1)=n2+2.故选:C.【点睛】此题属于图形与数字结合规律的题目.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【变式5-2】(2019•云南模拟)如图用棋子摆成三角形的图案,第(1)个三角形中有4枚棋子,第(2)个三角形中有9枚棋子,第(3)个三形中有16枚棋了,…,按照这样的规律摆下去第()个三角形中有2025枚棋子.A.42B.43C.44D.45【分析】首先要从简单图形入手,抓住随着“编号”或“序号”增加时,后一个图形与前一个图形相比,在数量上增加(或倍数)情况的变化,找出数量上的变化规律,从而推出一般性的结论.【答案】解:第1个三角形图案:1+3=4=22,第2个三角形图案:1+3+5=9=32,第3个三角形图案:1+3+5+7=16=42,第4个三角形图案:1+3+5+7+9=16+9=25=52,第5个三角形图案:1+3+5+7+9+11=25+11=36,则第n个三角形图案:1+3+5+7+9+11+…+2n﹣1=(n+1)2,令(n+1)2=2025,解得:n=44或n=﹣46(舍去)故选:C.【点睛】本题是图形与数字类的变化规律的综合问题,首先要探寻规律,认真观察、仔细思考,善用联想来解决这类问题;本题不仅要从图形中看规律,还要从数字变化看规律,两方面结合得出结论.【变式5-3】(2019•沙坪坝区校级一模)观察下列图形,①中有1个圆,②中有5个圆,③中有13个圆……,若依此规律,则第⑥个图形中圆的个数为()A.25B.61C.41D.65【分析】仔细观察图形,找到图形的变化规律,利用规律解得即可.【答案】解:第一个图形有1个圆,第二个图形有1+3+1=5个圆,第三个图形有1+3+5+3+1=13个圆,第四个图形有1+3+5+7+5+3+1=25个圆,…第六个图形有1+3+5+7+9+11+9+7+5+3+1=61个圆,故选:B.【点睛】此题考查图形的变化规律,找出图形之间的运算规律,利用规律解决问题.【考点6 图形中的组合规律】【方法点拨】此类问题是将上述两种规律结合在一起,需将图形进行拆分,找出各个部分的规律进行组合即可.【例6】(2019•长寿区模拟)下列图形都是由●按照一定规律组成的,其中第①个图共有四个●,第②个图中共有8个●,第③个图中共有13个●,第④个图中共有19个●,…,照此规律排列下去,则第10 个图形中●的个数为()A.50B.53C.64D.76【分析】根据已知图形得出图n中点的个数为(n+1)2﹣(1+2+3+…+n﹣1),据此可得.【答案】解:因为图①中点的个数为4=22﹣0,图②中点的个数为8=32﹣1,图③中点的个数为13=42﹣(1+2),图④中点的个数为19=52﹣(1+2+3),……所以图⑨中点的个数为102﹣(1+2+3+…+8)=100﹣36=64,故选:C.【点睛】本题主要考查数字的变化规律,解题的关键是根据已知图形得出图n中点的个数为(n+1)2﹣(1+2+3+…+n﹣1).【变式6-1】(2018秋•九龙坡区校级期中)下列图形都是由同样大小的黑点按一定规律组成的,其中第①个图形中一共有3个黑点,第②个图形中一共有8个黑点,第③个图形中一共有14个黑点,……,则第⑧个图形中黑点的个数是()。
初一找规律经典题带答案

……一、数字排列1、观察下列各算式: 1+3=4=22,1+3+5=9=23,1+3+5+7=16=24… 按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值 ?(2)推广: 1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少 ?2、下面数列后两位应该填上什么数字呢? 2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 1 2 3 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第100个( )二、几何图形变化1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球 个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2008个图形是 (填图形名称).三、数、式计算 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ;由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,… 根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a aba b 则符合前面式子的规律,,若…21010 规律发现1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖 块。
2.我国著名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
找规律(图形类)七年级数学 原创

(1) (2) (3)
分析:
n=1, n=2, n=3, n=4, …… 第n个,
4 4+3 4+3+3 4+3+3+3
1×1+0×0 2×2+1×1 3×3+2×2 4×4+3×3 10×10+9×9
【例4】(2010柳州)2010年广州亚运会吉祥物取名“乐羊羊”.下面各图 是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,……, 1 则图⑩有 55 只羊, 第n个图形有 2 n(n+1) 只羊.
① 分析:
4+(n−1)×3=3n+1
【练1】(2010湖北荆州)用围棋子按下面的 规律摆图形,则摆第n个图形需要围棋 子的枚数是 3n+2 .
……
图1 分析: 图2 图3
n=1, n=2, n=3, ……
5 5+3 5+3+3
n, 5+(n−1)×3=3n+2
【练2】(2015· 湖南益阳)如图是用长度相等的小 棒按一定规律摆成的一组图案,第1个图案中 有6根小棒,第2个图案中有11根小棒,…, 则第n个图案中有 (5n+1) 根小棒.
图①
分析:
图②
图③
n=1, n=2, n=3, … n=6,
1 1+1×5 1+1×5+2×5 …… 76
【练15】 (2010江苏徐州)用棋子按下列方
初一数学:十个经典全等题目
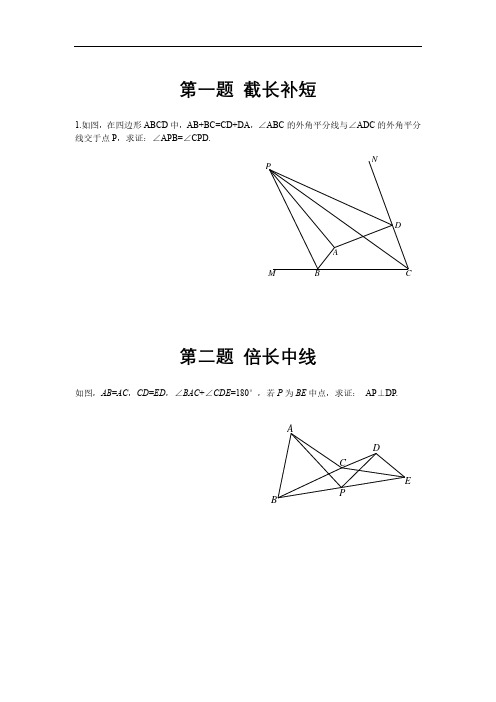
第一题 截长补短1.如图,在四边形ABCD 中,AB+BC=CD+DA ,∠ABC 的外角平分线与∠ADC 的外角平分线交于点P ,求证:∠APB=∠CPD.第二题 倍长中线如图,AB =AC ,CD =ED ,∠BAC +∠CDE =180°,若P 为BE 中点,求证: AP ⊥DP.ADMNPPABCDE第三题 中位线如图,AE ⊥AB ,BC ⊥CD ,且AE=AB ,BC=CD ,F 为DE 的中点,FM ⊥AC .证明:FM=12AC .第四题 三线合一如图,在四边形ABCD 中,AB=AD ,CA=CD ,∠CBD=30°,求证:∠CAD=2∠CBD.ABCDEF M DCBA第五题 一线三等角(穿越)如图,△ABC 为等腰直角三角形,D 为斜边AB 上一点,DE ⊥CD ,DE=CD ,连接AE ,求证:AE ∥BC.(同侧)如图,在△ABC 中,AB =AC ,点D 在BC 的延长线上,点E 在线段AD 上,点F 在DA 的延长线上,且∠AEC=∠BAC ,BF ∥CE ,求证:AE =BF .EBDCA ABCEF第六题 旋转变换1如图,OA=OB ,∠AOB=2∠ACB ,求证:OA=OC.第七题 旋转变换2如图,在△ABC 中,∠BAC=60°,∠ATB=∠BTC=∠CTA=120°,点M 是BC 的中点.求证:TA+TB+TC=2AM.ABCOMTCBA第七题 角格点如图,在等腰△ABC 中,AB=AC ,∠BAC=40°,D 、E 分别是AB 、AC 上的一点,且AD=CE ,CD=BC ,求∠EDC 的度数.第八题 分类讨论如图,在△ABC 中,D 是AB 的中点,∠DAC=2∠DCA ,∠BCD=30°,求∠ABC 的度数.EDCB AABD第九题 定值问题如图,在△ABC 中,∠ABC =90°,AB =BC ,P 是AC 边上一动点,D 是BC 边上一点,且PB =PD ,过D 作DE ⊥AC 于E .当点P 运动时,判断PE 的长度是否变化,并说明理由.第十题 强行构造如图,在Rt △ABC 中,∠BAC=90°,D 是BC 上一点,作BE ∥AC ,连接AE ,且∠EAD=∠C ,求证:ED ⊥AD.PED CBAED CB A。
初一找规律经典例题

奥数专题(三)找规律一、数字排列规律题1、观察下列各算式:1+3=4=22,1+3+5=9=23,1+3+5+7=16=24…猜想:1+3+5+7+…+2015+2017=推广:1+3+5+7+9+…+(2n-1)+(2n+1)=2、下面数列后两位应该填上什么数字呢?2 3 5 8 12 17 __ __3、请填出下面横线上的数字。
1 123 5 8 ____ 214、有一串数,它的排列规律是1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第2016个()5、有一串数字3 6 10 15 21 ___第6个是什么数?6、观察下列一组数的排列:1、2、3、4、3、2、1、2、3、4、3、2、1、…,那么第2016个数是().7、100个数排成一行,其中任意三个相邻数中,中间一个数都等于它前后两个数的和,如果这100个数的前两个数依次为1,0,那么这100个数中“0”的个数为_________个.二、几何图形变化规律题1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○○○○●……从第1个球起到第2004个球止,共有实心球个.2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若第一个图形是正方形,则第2016个图形是(填图形名称).三、数、式计算规律题 1、已知下列等式:① 13=12; ② 13+23=32; ③ 13+23+33=62; ④ 13+23+33+43=102 ; 由此规律知,第⑤个等式是 . 2、观察下面的几个算式: 1+2+1=4, 1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果: 1+2+3+…+99+100+99+…+3+2+1=____. 3、1+2+3+…+100= 经过研究,这个问题的一般性结论是 1+2+3+…+()121+=n n n ,其中n是正整数.现在我们来研究一个类似的问题: 1×2+2×3+…()1+n n = ? 观察下面三个特殊的等式()2103213121⨯⨯-⨯⨯=⨯ ()3214323132⨯⨯-⨯⨯=⨯ ()4325433143⨯⨯-⨯⨯=⨯ 将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯读完这段材料,请你思考后回答:⑴=⨯++⨯+⨯1011003221 ⑵()()=++++⨯⨯+⨯⨯21432321n n n ⑶()()=++++⨯⨯+⨯⨯21432321n n n11235...巩固练习:1.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…, 则100!98!的值为 2.有一列数:第一个数为x 1=1,第二个数为x 2=3,第三个数开始依次记为x 3,x 4,…,x n ; 从第二个数开始,每个数是它相邻两个数和的一半。
图形找规律(7年级)
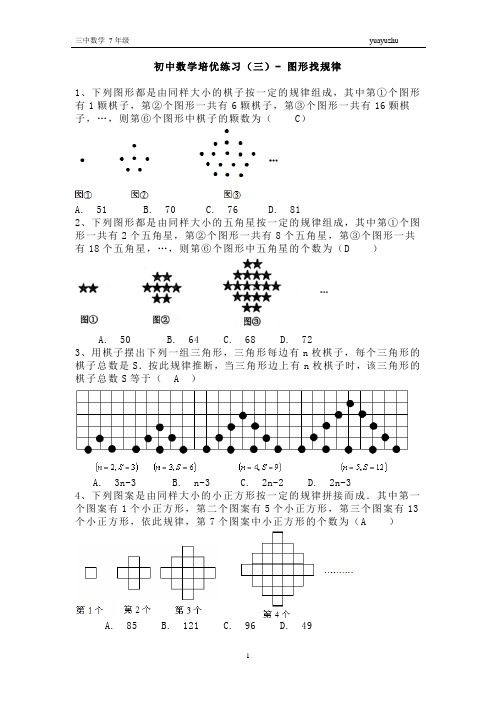
初中数学培优练习(三)- 图形找规律1、下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有1颗棋子,第②个图形一共有6颗棋子,第③个图形一共有16颗棋子,…,则第⑥个图形中棋子的颗数为(C)A. 51B. 70C. 76D. 812、下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为(D )A. 50B. 64C. 68D. 723、用棋子摆出下列一组三角形,三角形每边有n枚棋子,每个三角形的棋子总数是S.按此规律推断,当三角形边上有n枚棋子时,该三角形的棋子总数S等于( A )A. 3n-3B. n-3C. 2n-2D. 2n-34、下列图案是由同样大小的小正方形按一定的规律拼接而成.其中第一个图案有1个小正方形,第二个图案有5个小正方形,第三个图案有13个小正方形,依此规律,第7个图案中小正方形的个数为(A )A. 85B. 121C. 96D. 495、下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第8个图形中圆的个数为( A )A. 121B. 113C. 92D. 1916、下列图形都是由同样大小的矩形按一定的规律组成,其中第(1)个图形的面积为2cm2,第(2)个图形的面积为8cm2,第(3)个图形的面积为18c m2,…,则第(10)个图形的面积为(B )A. 196cm2B. 200cm2C. 216cm2D. 256cm27、观察下列图形及图形所对应的等式,探究其中的规律:1+8=32;1+8+16=52;1+8+16+24= ;(1)在横线上写出第3个图形所对应的算式的结果;(2)在横线上写出第4个图形所对应的等式;(3)根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为(用含n的代数式表示).8、将正方形图1作如下操作:第1次:分别连接各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形…,以此类推,根据以上操作,若要得到2013个正方形,则需要操作的次数是( B )A. 502B. 503C. 504D. 5059、如图,是一组按照某种规律摆放成的图案,则图5中三角形的个数是( C )A. 8B. 9C. 16D. 17【解:由图可知:第一个图案有三角形1个.第二图案有三角形1+3=4个.第三个图案有三角形1+3+4=8个,第四个图案有三角形1+3+4+4=12第五个图案有三角形1+3+4+4+4=16】10、有边长为1的等边三角形卡片若干张,使用这些三角形卡片拼出边长分别是2,3,4…的等边三角形(如图所示).根据图形推断每个等边三角形卡片总数S与边长n的关系式s=n2(n≥2).11、如图由小正方形依次排出以下图形.那么第9个图形中共有(C )个小正方形。
初一数学图形规律经典题
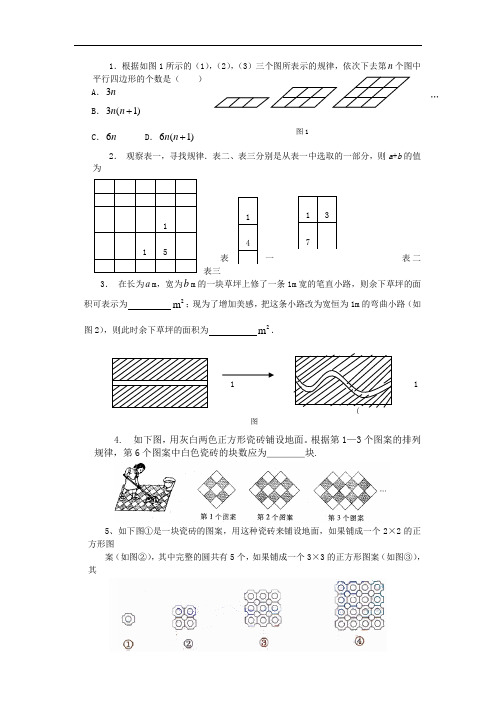
1.根据如图1所示的(1),(2),(3)三个图所表示的规律,依次下去第n 个图中平行四边形的个数是( ) A .3n B .3(1)n n + C .6n D .6(1)n n +2. 观察表一,寻找规律.表二、表三分别是从表一中选取的一部分,则a +b 的值为表一 表二 表三3. 在长为a m ,宽为b m 的一块草坪上修了一条1m 宽的笔直小路,则余下草坪的面积可表示为 2m ;现为了增加美感,把这条小路改为宽恒为1m 的弯曲小路(如图2),则此时余下草坪的面积为 2m .4. 如下图,用灰白两色正方形瓷砖铺设地面。
根据第1—3个图案的排列规律,第6个图案中白色瓷砖的块数应为____块.5、如下图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其0 1 2 3 …1 3 5 7 …2 5 8 11…371115 ………………1114a 1113 17 bba(1ba(1图图1…(((中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有个.6.观察下列图形:它们是按一定规律排列的,依照此规律,第20个图形共有个★.7.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:所剪次数1234…n正三角形个数47113…an则a n=(用含n的代数式表示).。
七年级数学规律分类专题(经典)

最新七年级数学规律分类专题(经典)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN4=1+3 9=3+6 16=6+10…规律问题【几何规律】1.如图5所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第n(n是大于0的整数)个图形需要黑色棋子的个数是.2.古希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:称图中的数1,5,12,22…为五边形数,则第6个五边形数是。
3.古希腊著名的毕达哥拉斯学派把1、3、6、10 …这样的数称为“三角形数”,而把1、4、9、16 …这样的数称为“正方形数”.从图7任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是()A.13 = 3+10 B.25 = 9+16 C.36 = 15+21 D.49 = 18+314. 将正方形图1作如下操作:第1次:分别连结各边中点如图2,得到5个正方形;第2次:将图2左上角正方形按上述方法再分割如图3,得到9个正方形……,以此类推,根据以上操作,若要得到2 013个正方形,则需要操作的次数是().(A)502 (B)503 (C)504 (D)5055.已知:如图,ΔABC 中,∠B 的平分线与∠ACB 的外角的平分线交于点D .求证:∠D =A ∠21.如图,∠ACD 是△ABC 的外角,ABC ∠的平分线与ACD ∠的平分线交于点1A ,1A BC ∠的平分线与1A CD ∠的平分线交于点2A ,…,1n A BC -∠的平分线与1n A CD -∠的平分线交于点An . 设∠A =θ.则(1)1A ∠= ; (2)n A ∠= .6.如图,按一定的规律用牙签搭图形:(1)按图示的规律填表:(2)搭第n 个图形需要________________________根牙签.7.如图,蜂巢的横截面由正六边形组成,且能无限无缝隙拼接.称横截面图形由全等正多边形组成,且能无限无缝隙拼接的多边形具有同形结构.若已知具有同形结构的正n 边形的每个风角度数为a ,满足:360=k a (k 为正整数),多这形外角和为360°,则k关于边数n 的函数是 (写出n 的取值范围即可).① ② 120°A 2A 1A【代数规律】1.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.根据如图1所示的(1),(2),(3)三个图所表示的规律,依次下去第n 个图中平行四边
形的个数是( ) A .3n
B .3(1)n n +
C .6n
D .6(1)n n +
2. 观察表一,寻找规律.表二、表三分别是从表一中选取的一部分,则a +b 的值为
表一 表二 表三
3. 在长为a m ,宽为b m 的一块草坪上修了一条1m 宽的笔直小路,则余下草坪的面积可表示为 2m ;现为了增加美感,把这条小路改为宽恒为1m 的弯曲小路(如图2),则此时余下草坪的面积为 2m .
4. 如下图,用灰白两色正方形瓷砖铺设地面。
根据第1—3个图案的排列规律,第
6个图案中白色瓷砖的块数应为____块.
5、如下图①是一块瓷砖的图案,用这种瓷砖来铺设地面,如果铺成一个2×2的正方形图 案(如图②),其中完整的圆共有5个,如果铺成一个3×3的正方形图案(如图③),其 中完整的圆共有13个,如果铺成一个4×4的正方形图案(如图④),其中完整的圆共有 25个,若这样铺成一个10×10的正方形图案,则其中完整的圆共有 个.
0 1 2 3 …
1 3 5 7 …
2 5 8 11 …
3 7 11 15 …
… … … … …
11 14 a 11 13 17 b b
a
(a
1m
b
a
(b )
1m
图2
图1
(1)
(2)
(3)
6.观察下列图形:
它们是按一定规律排列的,依照此规律,第20个图形共有个★.
7.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
所剪次数 1 2 3 4 …n
正三角形个数 4 7 10 13 …a n
则a n=(用含n的代数式表示).。
