初中平面几何相关公式
初中数学几何公式大全

初中数学几何公式大全几何是数学的一个分支,主要研究点、线、面以及它们之间的关系和性质。
在初中数学中,几何是一个重要的学习内容,涉及到很多基本概念和公式。
下面将详细介绍初中数学几何公式的大全。
一、平面几何公式1. 直角三角形的勾股定理:在一个直角三角形中,直角边的平方等于其他两边平方的和。
即a² + b² = c²,其中a和b为直角边,c为斜边。
2. 任意三角形的海伦公式:在任意三角形ABC中,设a、b、c为边长,p为半周长,则三角形的面积S可以通过海伦公式计算:S = √[p(p-a)(p-b)(p-c)]。
3. 任意三角形的正弦定理:在任意三角形ABC中,设a、b、c为边长,A、B、C为对应的角度,则正弦定理可以表达为a/sinA = b/sinB = c/sinC。
4. 任意三角形的余弦定理:在任意三角形ABC中,设a、b、c为边长,A、B、C为对应的角度,则余弦定理可以表达为c² = a² + b² - 2ab*cosC。
5. 任意三角形的面积公式:在任意三角形ABC中,设a、b、c为边长,h为对应高,则三角形的面积S可以通过公式S = 1/2 * b * h计算。
6. 等腰三角形的性质:在等腰三角形ABC中,两底边相等,顶角相等,底角相等。
7. 相似三角形的性质:如果三角形ABC和三角形DEF相似,那么它们的对应边长之比相等,即AB/DE = BC/EF = AC/DF。
8. 平行线的性质:平行线具有以下性质:互不相交;位于同一平面中;在同一平面内,与同一直线相交的两条平行线,与第三条直线所成的对应角相等;两个平行线被一条截线切割后,对应角相等。
二、立体几何公式1. 立方体的体积公式:立方体的体积V等于边长的立方,即V = a³,其中a为边长。
2. 正方体的面积公式:正方体的表面积S等于6倍边长的平方,即S = 6a²,其中a为边长。
几何公式知识点总结

几何公式知识点总结一、平面几何公式1. 长方形的面积公式:S = l * w,其中S表示面积,l表示长,w表示宽。
2. 正方形的面积公式:S = a * a,其中S表示面积,a表示边长。
3. 圆的面积公式:S = π * r^2,其中S表示面积,π是圆周率,r是半径。
4. 三角形的面积公式:S = 0.5 * b * h,其中S表示面积,b表示底边长,h表示高。
5. 梯形的面积公式:S = 0.5 * (a + b) * h,其中S表示面积,a、b表示上下底边长,h表示高。
6. 平行四边形的面积公式:S = b * h,其中S表示面积,b表示底边长,h表示高。
7. 等边三角形的面积公式:S = (a^2 * √3) /4,其中S表示面积,a表示边长。
8. 等腰三角形的面积公式:S = 0.5 * b * h,其中S表示面积,b表示底边长,h表示高。
9. 直角三角形的勾股定理公式:a^2 + b^2 = c^2,其中a、b、c分别表示直角三角形的两条直角边和斜边的长度。
10. 三角形的三边关系公式:a + b > c,a + c > b,b + c > a,其中a、b、c分别表示三角形的三条边长度。
11. 三角形的海伦公式:S = √[p * (p - a) * (p - b) * (p - c)],其中S表示面积,p表示半周长,a、b、c分别表示三角形的三条边长。
12. 圆的周长公式:C = 2 * π * r,其中C表示周长,π是圆周率,r是半径。
13. 圆环的面积公式:S = π * (R^2 - r^2),其中S表示面积,π是圆周率,R表示外圆半径,r表示内圆半径。
14. 扇形的面积公式:S = 0.5 * r^2 * θ,其中S表示面积,r表示半径,θ表示弧度。
15. 正多边形的内角和公式:内角和 = (n - 2) * 180°,其中n表示正多边形的边数。
二、立体几何公式1. 直方体的体积公式:V = l * w * h,其中V表示体积,l、w、h分别表示长、宽、高。
初中数学竞赛重要定理公式(平面几何篇)

初中数学竞赛重要定理公式(平面几何篇)初中数学竞赛中,平面几何是一个重要的考点。
以下是一些重要的定理、公式和结论。
三角形面积公式(包括海伦公式):三角形的面积S可以用以下公式计算:$S=\sqrt{p(p-a)(p-b)(p-c)}$,其中$p=\frac{1}{2}(a+b+c)$,$a$,$b$,$c$分别为三角形的三条边长。
另外,三角形的面积也可以用以下公式计算:$S=\frac{1}{2}ab\sin C$,其中$a$,$b$为两边,$C$为两边之间的夹角。
还有一个海伦公式:$S=\frac{1}{2}ah_a$,其中$h_a$为三角形顶点$A$到边$BC$的垂线长度,$a$为边$BC$的长度。
XXX定理:对于三角形$\triangle ABC$及其底边上的一点$D$,有$AB^2\cdot DC+AC^2\cdot BD-AD^2\cdotBC=BC\cdot DC\cdot BD$。
XXX定理:对于一个内接四边形,其对角线之积等于两组对边乘积之和,即$AC\cdot BD=AB\cdot CD+AD\cdot BC$。
逆命题也成立。
同时还有广义托勒密定理:$AB\cdotCD+AD\cdot BC\geq AC\cdot BD$。
蝴蝶定理:如果$AB$是圆$O$的弦,$M$是$AB$的中点,弦$CD$,$EF$经过点$M$,$CF$,$DE$交$AB$于$P$,$Q$,则$MP=QM$。
勾股定理(毕达哥拉斯定理):对于一个直角三角形,锐角对边的平方等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍;钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍。
同时还有广义勾股定理。
中线定理(巴布斯定理):对于一个三角形$\triangleABC$,如果$BC$的中点为$P$,则有$AB^2+AC^2=2(AP^2+BP^2)$。
同时,中线的长度可以用以下公式计算:$m_a=\frac{1}{2}\sqrt{2b^2+2c^2-a^2}$。
初中中平面几何重要定理汇总
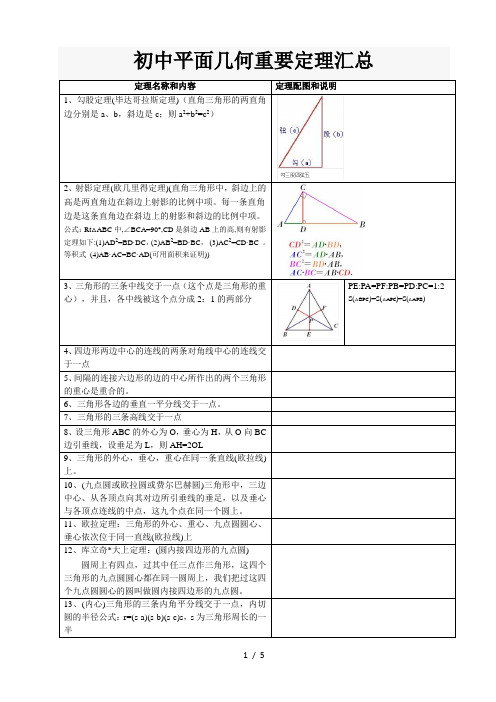
8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL
9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上。
29、塞瓦定理的逆定理:在△ABC的边BC,CA,AB上分别取点D,E,F,如果(AF:FB)(BD:DC)(CE:EA)=1那么直线AD,BE,CF相交于同一点。
30、塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点
31、塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点
15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)
16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC2
17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD
24、梅涅劳斯定理的逆定理:(略)
25、梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R三点共线。
26、梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接ቤተ መጻሕፍቲ ባይዱ的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线
初中几何公式大全

初中几何公式大全1.点与线-点:几何学中没有大小和形状的概念,只是一个位置。
-线:长度无穷,宽度为0,由无数个点组成。
2.线段-长度:AB的长度记作AB。
-中点:线段AB的中点为M,AM=MB。
-分点:P是线段AB上的一点,AP:PB=k:l,则P在线段AB上的坐标为(k/(k+l),l/(k+l))。
3.直线和射线-直线:长度无穷,无端点,可通过两点唯一确定。
-射线:起点至无限远的部分。
4.角度-角度:由两条线段的共同端点及其夹角所构成。
-顶点:角的公共端点。
-内角:映射到射线上的点在角内部。
-外角:映射到射线上的点在角外部。
-展角:角度为180度。
5.三角形-三角形:由3条线段组成的图形。
-内角和:三角形内角的和为180度。
-直角三角形:一角为90度的三角形。
6.平行四边形-平行四边形:具有4条边且两对边互相平行的四边形。
7.矩形和正方形-矩形:具有4个角均为直角的四边形。
-正方形:具有4个角均为直角且4条边相等的四边形。
8.梯形和同位角-梯形:具有一对平行边的四边形。
-同位角:两条直线被一条截线交叉形成的内角和外角互为补角。
9.圆-圆:由平面内与一个给定点的距离相等的所有点组成。
-圆心:圆心是到圆上任意一点距离都相等的点。
-直径:经过圆心的线段,两端点在圆上。
10.圆周率11.平面几何公式-面积公式:-正方形面积=边长²-矩形面积=长×宽-三角形面积=底边长×高/2-平行四边形面积=底边长×高-梯形面积=(上底+下底)×高/2-圆面积=π×半径²-周长公式:-正方形周长=4×边长-矩形周长=2×(长+宽)-三角形周长=边1+边2+边3-平行四边形周长=2×(边1+边2)-梯形周长=边1+边2+边3+边4-圆周长=2×π×半径-三角形的勾股定理:-a²=b²+c²,其中a、b、c分别为直角三角形的两条直角边与斜边。
初中数学知识归纳平面几何的基本定理和公式

初中数学知识归纳平面几何的基本定理和公式初中数学知识归纳:平面几何的基本定理和公式平面几何是数学中的一个重要分支,它研究的是平面上的点、线、面及其间的关系。
在初中数学学习中,学生将接触到许多关于平面几何的基本定理和公式,这些定理和公式在解题过程中起到了重要的作用。
本文将对初中数学中的平面几何的基本定理和公式进行归纳和总结,以帮助学生在学习和应用中理解和掌握这些知识点。
一、直线的基本概念及相交定理1. 直线:直线是由一条无穷延伸的点集合组成,可以用两个不同的点唯一确定一条直线。
2. 直线段:直线段是由直线两个特定的不同的端点所组成的线段。
3. 直线的相交类型:两条直线可以相交成三种类型,即相交、平行、重合。
二、角的基本概念及性质1. 角:角是由两条射线共享一个端点而形成的图形。
2. 角的三要素:角的三要素包括顶点、两边和夹角。
3. 角的分类:角可以分为锐角、直角、钝角和平角。
4. 角的性质:逆角、对顶角、同位角等性质在解题中有重要作用。
三、平行线与平行四边形的性质1. 平行线与转角:已知两条平行线和一条横切线,可以得出转角和对应角相等的结论。
2. 平行线的判定:平行线的判定包括一般判定、倒角判定和平行四边形特性判定。
3. 平行四边形的性质:平行四边形的特点包括对边平行、对角线等长和对角线平分。
四、三角形的性质及常用公式1. 三角形的分类:根据边长和角度等特点,三角形可分为等边三角形、等腰三角形和一般三角形。
2. 三角形的角性质:三角形的内角和为180度,外角等于其不相邻的内角之和。
3. 三角形的边关系:根据边长关系,三角形的边可分为等边、等腰和一般三角形。
4. 三角形的面积公式:利用底边和高、两边夹角的正弦定理和余弦定理等公式可以求解三角形的面积。
五、圆的基本概念及相关定理1. 圆:圆是平面上一组离一个固定点相等距离的点的集合。
2. 圆心角与弧度:通过圆心、圆周上的两点和圆周之间可以划分出的角称为圆心角。
初中平面几何知识的60个定理

初中平面几何知识的60个定理1、勾股定理、勾股定理((毕达哥拉斯定理毕达哥拉斯定理) )小学都应该掌握的重要定理小学都应该掌握的重要定理 2、射影定理、射影定理((欧几里得定理欧几里得定理) )重要重要3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分的两部分重要重要4、四边形两边中心的连线的两条对角线中心的连线交于一点、四边形两边中心的连线的两条对角线中心的连线交于一点学习中位线时的一个常见问题,中考不需要,初中竞赛需要学习中位线时的一个常见问题,中考不需要,初中竞赛需要5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
完全没有意义,学习解析几何后显然的结论,不用知道完全没有意义,学习解析几何后显然的结论,不用知道6、三角形各边的垂直一平分线交于一点。
、三角形各边的垂直一平分线交于一点。
重要重要7、从三角形的各顶点向其对边所作的三条垂线交于一点、从三角形的各顶点向其对边所作的三条垂线交于一点重要重要8、设三角形ABC 的外心为O ,垂心为H ,从O 向BC 边引垂线,设垂足不L ,则AH=2OL 中考不需要,竞赛中很显然的结论中考不需要,竞赛中很显然的结论9、三角形的外心,垂心,重心在同一条直线上。
、三角形的外心,垂心,重心在同一条直线上。
高中竞赛中非常重要的定理,称为欧拉线高中竞赛中非常重要的定理,称为欧拉线1010、、(九点圆或欧拉圆或费尔巴赫圆九点圆或欧拉圆或费尔巴赫圆))三角形中,三角形中,三边中心、三边中心、三边中心、从各顶点向其对边所引垂线的垂从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,高中竞赛中的常用定理高中竞赛中的常用定理1111、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线((欧拉线欧拉线))上 高中竞赛中会用,不常用高中竞赛中会用,不常用1212、库立奇、库立奇、库立奇**大上定理:大上定理:((圆内接四边形的九点圆圆内接四边形的九点圆) ) ) 圆周上有四点,过其中任三点作三角形,圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
初中数学平面几何基本定理

1. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=2. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例.如△ABC 中,AD 平分∠BAC ,则ACAB DC BD =;(外角平分线定理) 3. 正弦定理:R Cc B b A a 2sin sin sin ===,(其中R 为三角形外接圆半径) 4. 余弦定理:C ab b a c cos 2222-+=5. 布拉美古塔(Brahmagupta )定理: 在圆内接四边形ABCD 中,AC ⊥BD ,自对角线的交点P 向一边作垂线,其延长线必平分对边6. 托勒密(Ptolemy )定理:圆内接四边形对角线之积等于两组对边乘积之和,即AC ·BD =AB ·CD +AD ·BC ,(逆命题成立) .(广义托勒密定理)AB ·CD +AD ·BC ≥AC ·BD7. 蝴蝶定理:AB 是⊙O 的弦,M 是其中点,弦CD 、EF 经过点M ,CF 、DE 交AB 于P 、Q ,则有:MP =QM .8. 欧拉(Euler )公式:设三角形的外接圆半径为R ,内切圆半径为r ,外心与内心的距离为d ,则d 2=R 2-2Rr .重心性质:①设G 为△ABC 的重心,连结AG 并延长交BC 于D ,则D 为BC 的中点,则1:2:=GD AG ; ②设G 为△ABC 的重心,则ABC ACG BCG ABG S S S S ∆∆∆∆===31③设G 为△ABC 的重心,过G 作DE ∥BC 交AB 于D ,交AC 于E ,过G 作PF ∥AC 交AB 于P ,交BC 于F ,过G 作HK ∥AB 交AC 于K ,交BC 于H ,则2;32=++===ABKH CA FP BC DE AB KH CA FP BC DE ④到三角形三顶点距离的平方和最小的点是重心,即222GC GB GA ++最小;⑤三角形内到三边距离之积最大的点是重心;反之亦然(即满足上述条件之一,则G 为△ABC 的重心).11. 垂心性质:(1)三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍(2)垂心H 关于△ABC 的三边的对称点,均在△ABC 的外接圆上;(3)△ABC 的垂心为H ,则△ABC ,△ABH ,△BCH ,△ACH 的外接圆是等圆;(4)设O ,H 分别为△ABC 的外心和垂心, HCA BCO ABH CBO HAC BAO ∠=∠∠=∠∠=∠,,12. 内心:三角形的三条角分线的交点—内接圆圆心,即内心到三角形各边距离相等内心性质:(1)设I 为△ABC 的内心,则I 到△ABC 三边的距离相等,反之亦然(2)设I 为△ABC 的内心,则C AIB B AIC A BIC ∠+︒=∠∠+︒=∠∠+︒=∠2190,2190,219013. 外心:三角形的三条中垂线的交点——外接圆圆心,即外心到三角形各顶点距离相等;外心性质:(1)外心到三角形各顶点距离相等(2)设O 为△ABC 的外心,则A BOC ∠=∠2或A BOC ∠-︒=∠2360(3)∆=S abcR 4;(4)锐角三角形的外心到三边的距离之和等于其内切圆与外接圆半径之和14.其中a h 表示BC 边上的高,R 为外接圆半径,r 为内切圆半径,)(21c b a p ++= 1920·两条直线的平行和垂直(1)若111:l y k x b =+,222:l y k x b =+①121212||,l l k k b b ⇔=≠;②12121l l k k ⊥⇔=-.21·点到直线的距离d =(点00(,)P x y ,直线l :0Ax By C ++=).。
初中平面几何重要定理汇总

初中平面几何重要定理汇总1、勾股定理(毕达哥拉斯定理)(直角三角形的两直角边分别是a、b,斜边是c;则a*a+b*b=c*c)2、射影定理(欧几里得定理)(直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。
公式Rt△ABC 中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:(1)(AD)^2;=BD·DC,(2)(AB)^2;=BD·BC , (3)(AC)^2;=CD·BC 。
等积式(4)ABXAC=BCXAD(可用面积来证明))3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4、四边形两边中心的连线的两条对角线中心的连线交于一点5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6、三角形各边的垂直一平分线交于一点。
7、三角形的三条高线交于一点8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上12、库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,21、爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD、BE、CF的中心构成的三角形也是正三角形。
初中数学几何公式

初中数学几何公式数学几何是初中数学教学的重要内容之一,它主要研究空间中的点、线、面以及它们之间的位置关系和几何图形的性质等。
在初中数学中,几何公式是学生必须掌握的基础知识,接下来我将详细介绍一些常见的初中数学几何公式。
一、平面图形的面积公式1.矩形的面积公式:矩形的面积等于矩形的长乘以宽,即S=l*w。
2.正方形的面积公式:正方形的面积等于边长的平方,即S=a^23.三角形的面积公式:三角形的面积等于底边乘以高并除以2,即S=1/2*b*h。
4.梯形的面积公式:梯形的面积等于上底加下底乘以高再除以2,即S=1/2*(a+b)*h。
二、立体图形的表面积和体积公式1.正方体的表面积公式:正方体的表面积等于边长的平方乘以6,即S=6*a^22.正方体的体积公式:正方体的体积等于边长的立方,即V=a^33. 直方体的表面积公式:直方体的表面积等于底面积乘以2再加上侧面积,即S = 2lw + 2lh + 2wh。
4. 直方体的体积公式:直方体的体积等于底面积乘以高,即V = lwh。
5. 圆柱体的表面积公式:圆柱体的表面积等于底面积加上侧面积,即S = 2πr^2 + 2πrh。
6.圆柱体的体积公式:圆柱体的体积等于底面积乘以高,即V=πr^2h。
7.圆锥体的表面积公式:圆锥体的表面积等于底面积加上母线的周长乘以半个展开图的弧长,即S=πr^2+πr1+πr28.圆锥体的体积公式:圆锥体的体积等于底面积乘以高再除以3,即V=1/3*πr^2h。
三、平面几何常用的定理和公式1.同位角定理:同位角相等。
2.对顶角定理:对顶角相等。
3.垂直角定理:垂直角相等。
4.同位角、对顶角和垂直角之间的关系:同位角、对顶角和垂直角之间是互相等于180°的关系。
5.三角形内角和定理:三角形的三个内角之和等于180°。
6.三角形外角和定理:三角形的外角之和等于360°。
7.相似三角形的性质:相似三角形对应角相等,对应边成比例。
平面 解析几何公式

平面解析几何公式 1、 直线的斜率坐标公式:2121y y x x -- 2、直线方程点斜式:00(x x )y y k -=- 斜截式:y kx b =+ 两点式:112121y y x x y y x x --=-- (1212,x x y y ≠≠) 截距式:1x y ab+=一般式:0ax by c ++= (,a b 不同时为0) 3、两点之间的距离公式:A (11,x y )B (22,x y )两点的距离公式:4点到直线的距离公式:点P (00,x y )到直线0ax by c ++=的距离为:d =5、两平行直线的距离公式:直线1L :10Ax By C ++= 直线2L :20Ax By C ++=的距离公式为:d =6、圆的标准方程:222(x a)(y b)r -+-=圆心是:(a,b)o ,半径是:r 7圆的一般方程:220x y Dx Ey C ++++=圆心是:(,)22D E o --,半径是:r =8、椭圆的标准方程焦点在x 轴上的标准方程:22221x y a b+= (a b 0)>> 焦点坐标:12(a,0),(a,0)F F -准线方程:2a x c=±焦点在y 轴上的标准方程:22221y x a b+= (a b 0)>> 焦点坐标:12(0,b),(0,b)F F -准线方程:2a y c=±a,b,c 三者之间的关系:222a b c =+离心率:c e a=两准线之间的距离:22a d c =焦点到相应的准线的距离:2b d c=9、双曲线的标准方程:焦点在x 轴上的标准方程:22221x y a b-= (a 0,b 0)>>焦点坐标:12(a,0),(a,0)F F -准线方程:2a x c=±焦点在y 轴上的标准方程:22221y x a b-= (a 0,b 0)>>焦点坐标:12(0,b),(0,b)F F -准线方程:2a y c=±a,b,c 三者之间的关系:222c a b =+离心率:c e a=两准线之间的距离:22a d c =焦点到相应的准线的距离:2b d c=10、抛物线的标准方程:(1)焦点在x 轴的正半轴时:22y px = (0p >)焦点坐标:(,0)2p F 准线方程:x 2p=-(2)焦点在x 轴的负半轴时:22y px =- (0p >)焦点坐标:(,0)2p F -准线方程:x 2p=(3)焦点在y 轴的正半轴时:22x py = (0p >)焦点坐标:(0,)2p F 准线方程:2py =-(4)焦点在y 轴的负半轴时:22x py =- (0p >)焦点坐标:(0,)2p F -准线方程:2p y =。
数学平面解析几何公式

数学平面解析几何公式数学的世界中,平面解析几何占据着重要的地位。
它通过坐标系将几何问题转化为代数问题,使我们能够更直观地理解和解决几何问题。
本文将为您详细介绍平面解析几何中常用的公式。
一、直线方程1.一般式方程:Ax + By + C = 0其中,A、B、C为常数,且A和B不同时为0。
2.斜截式方程:y = kx + b其中,k为直线的斜率,b为直线在y轴上的截距。
3.点斜式方程:y - y1 = k(x - x1)其中,(x1, y1)为直线上的一个点,k为直线的斜率。
二、圆的方程圆的标准方程为:(x - a) + (y - b) = r其中,(a, b)为圆心坐标,r为圆的半径。
三、椭圆的方程椭圆的标准方程为:(x / a) + (y / b) = 1其中,a和b分别为椭圆的半长轴和半短轴。
四、双曲线的方程双曲线的标准方程为:(x / a) - (y / b) = 1其中,a和b分别为双曲线的实半轴和虚半轴。
五、抛物线的方程抛物线的标准方程为:y = 2px 或x = 2py其中,p为焦点到准线的距离。
六、坐标变换1.平移变换:(x", y") = (x + h, y + k)其中,(h, k)为平移向量。
2.比例变换:(x", y") = (kx, ly)其中,k和l为比例系数。
3.旋转变换:(x", y") = (x * cosθ - y * sinθ, x * sinθ + y * cosθ)其中,θ为旋转角度。
总结:平面解析几何公式为我们解决几何问题提供了强大的工具。
掌握这些公式,有助于我们更好地理解和运用几何知识。
初中几何公式汇总

初中几何公式汇总一、平面几何公式:1.常用线段的公式:-两点间距离公式:设点A(x1,y1)和点B(x2,y2),则AB的距离为√[(x2-x1)²+(y2-y1)²]。
-中点公式:设点A(x1,y1)和点B(x2,y2),则AB的中点坐标为((x2+x1)/2,(y2+y1)/2)。
- 分点公式:设点A(x1,y1)和点B(x2,y2)将线段AB分为m:n,则分点坐标为((mx2+nx1)/(m+n), (my2+ny1)/(m+n))。
2.常用角度的公式:-同位角定理:若两条直线被一条直线所截,即有一对同位角互为补角。
-锐角的余角和补角:设θ为锐角,则θ的余角为(90-θ),θ的补角为(90-θ)。
-相同弧对应的圆心角相等:如果两个圆上的弧AB和弧CD对应于同一个圆心角ACB和CAD,并且这两个弧互不相同,则ACB=CAD。
3.常用三角形公式:- 正弦定理:在三角形ABC中,边长为a,b,c,对应的内角为A,B,C,则有(a/sinA) = (b/sinB) = (c/sinC)。
- 余弦定理:在三角形ABC中,边长为a,b,c,对应的内角为A,B,C,则有c² = a² + b² - 2ab·cosC。
-长度平方和面积关系:在三角形ABC中,边长为a,b,c,对应的面积为S,则有4S²=2(a²b²+b²c²+c²a²)-(a⁴+b⁴+c⁴)。
-海伦公式:在已知三角形的三条边长分别为a,b,c的情况下,三角形的面积S可以由海伦公式计算,即S=√[s(s-a)(s-b)(s-c)],其中s=(a+b+c)/24.常用四边形公式:-矩形面积公式:设矩形的长为a,宽为b,则矩形的面积为S=a·b。
-平行四边形面积公式:设平行四边形的底边为a,高为h,则平行四边形的面积为S=a·h。
初中数学平面几何定理

初中数学平面几何定理初中数学平面几何定理大全平面几何,在初中数学中,是重点也是难点,如果同学们想要学好初中平面几何题的话,那么就要掌握好平面几何的定理,下面店铺就给大家介绍平面几何里面的定理有哪些?希望能够帮助到大家。
1.勾股定理(毕达哥拉斯定理)2.射影定理(欧几里得定理)3.三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分4.四边形两边中心的连线的两条对角线中心的连线交于一点5.间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。
6.三角形各边的垂直一平分线交于一点。
7.三角形的三条高线交于一点8.设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL9.三角形的外心,垂心,重心在同一条直线(欧拉线)上。
10.(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心.从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上,11.欧拉定理:三角形的外心.重心.九点圆圆心.垂心依次位于同一直线(欧拉线)上12.库立奇*大上定理:(圆内接四边形的九点圆)圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。
13.(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半14.(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点15.中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)16.斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC217.波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD18.阿波罗尼斯定理:到两定点A.B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上19.托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD20.以任意三角形ABC的边BC.CA.AB为底边,分别向外作底角都是30度的等腰△BDC.△CEA.△AFB,则△DEF是正三角形,21.爱尔可斯定理1:若△ABC和△DEF都是正三角形,则由线段AD.BE.CF的中心构成的三角形也是正三角形。
平面几何公式范文

平面几何公式范文平面几何是数学的一个分支,主要研究平面图形的性质和变换。
在平面几何中,许多图形都有一些特定的性质和规律,这些性质和规律被总结为一些公式,以方便我们进行计算和推导。
下面就给大家介绍一些常见的平面几何公式。
一、平面图形的周长和面积公式1.正方形正方形是一种四边相等、四个角相等的四边形,它的周长等于四个边长的和,面积等于边长的平方。
周长:P=4a面积:S=a^22.矩形矩形是一种有四个直角的四边形,它的周长等于两条长边长和两条短边长的和,面积等于长边长乘以短边长。
周长:P=2(a+b)面积:S = ab3.圆圆是一种由一条曲线所围成的图形,圆内任意两点之间的直线段都等于圆的半径,圆内任意两点所夹的弧长等于圆的半径乘以弧度。
周长:P=2πr或P=πd面积:S=πr^24.三角形三角形是由三条线段所围成的图形,它的周长等于三条边长的和,面积等于底边长乘以高再除以2周长:P=a+b+c面积:S = 1/2bh 或S = √(s(s-a)(s-b)(s-c))(海伦公式)二、平面图形的角度和线段公式1.垂直直角垂直直角是两条相交线段所形成的四个角中的其中一个,它的度数为90°。
2.三角形内角和三角形的内角和等于180°,即∠A+∠B+∠C=180°。
3.外角和一个三角形的外角和等于360°,即∠D+∠E+∠F=360°。
4.线段的中点线段的中点是指线段的中心位置,将线段分为两个相等的部分。
若线段AB的中点为M,则AM=MB。
5.平行线平行线是指在同一个平面内,永远不相交的两条直线。
若直线AB与直线CD平行,则有∠A=∠C、∠B=∠D。
6.同位角同位角是指两条平行线被一条横截线所交得的角,它们的度数相等。
若直线AB与直线CD平行,直线DE为横截线,则∠A=∠D、∠B=∠E。
三、平面图形的相似性公式1.两个三角形的相似性若两个三角形的对应角相等,则这两个三角形相似。
初中几何公式定理大全

.在平面直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一个点的位置都可以用一对有序实数 来表示。这样的有序实数对叫做这点的坐标。
.两条坐标轴将平面分成的4个区域称为象限,按逆时针顺序分别记为第一、二、三、四象限。
坐标轴上的点不属于任何象限。
第二象限 第一象限
■1
4
4
•
■4,
第三象限 第四象限
初中几何公式定理大全
初中几何 概念、定理 平面几何 .两点之间的所有连线中,线段最短。 .两点之间线段的长度叫做这两点之间的距寓。 .经过两点有一条直线,并且只有一条直线。 .将一个角分成相等的两部分的射线叫做这个角的角平分线。 .如果两个角的和是一个直角,这两个角叫做互为余角。简称互余,其中的一个角叫做另一个角的余角。 .如果两个角的和是一个平角,这两个角叫做互为补角。简称互补,其中的一个角叫做另一个角的补角。 .同角(或等角)的余角相等。 .同角(或等角)的补角相等。 .对顶角相等。 .在同一平面内,不相交的两条直线叫做平行线。 .经过直线外一点,有且只有一条直线与已知直线平行。
.图形由点、线、面组成。
.人们从不同的方向观察某个物体时,可以看到不同的图形。从正面看到的图形,称为主视图;从左面者到的图 形,称为左视图;
从上面看到的图形,称为俯视图。
三角函数
∠A的对边a与斜边c的比叫做NA的正弦,记作SinA,即
.梯形中,平行的一组对边称为底,不平行的一组对边称为腰。
.两腰相等的梯形叫做等腰梯形。
.等腰梯形是轴对称图形,过两底中点的直线是它的对称轴。
.等腰梯形在同一底上的两个角相等。
.直角三角形两直角边的平方和等于斜边的平方。
a2+b2=C2
.如果三角形的三边长a,b,c满足az-^b2=c29那么这个三角形是直角三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中平面几何相关公式1过两点有且只有一条直线 2 两点之间线段最短3 同角或等角的补角相等4 同角或等角的余角相等5 过一点有且只有一条直线和已知直线垂直6 直线外一点与直线上各点连接的所有线段中,垂线段最短7 平行公理经过直线外一点,有且只有一条直线与这条直线平行8 如果两条直线都和第三条直线平行,这两条直线也互相平行9 同位角相等,两直线平行 10 内错角相等,两直线平行11 同旁内角互补,两直线平行 12两直线平行,同位角相等13 两直线平行,内错角相等 14 两直线平行,同旁内角互补15 定理三角形两边的和大于第三边16 推论三角形两边的差小于第三边17 三角形内角和定理三角形三个内角的和等于180°18 推论1 直角三角形的两个锐角互余19 推论2 三角形的一个外角等于和它不相邻的两个内角的和20 推论3 三角形的一个外角大于任何一个和它不相邻的内角21 全等三角形的对应边、对应角相等22边角边公理有两边和它们的夹角对应相等的两个三角形全等23 角边角公理有两角和它们的夹边对应相等的两个三角形全等24 推论有两角和其中一角的对边对应相等的两个三角形全等25 边边边公理有三边对应相等的两个三角形全等26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27 定理1 在角的平分线上的点到这个角的两边的距离相等28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上29 角的平分线是到角的两边距离相等的所有点的集合30 等腰三角形的性质定理等腰三角形的两个底角相等31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边32 等腰三角形的顶角平分线、底边上的中线和高互相重合33 推论3 等边三角形的各角都相等,并且每一个角都等于60°34 等腰三角形的判定定理如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边)35 推论1 三个角都相等的三角形是等边三角形36 推论 2 有一个角等于60°的等腰三角形是等边三角形37 在直角三角形中,如果一个锐角等于30°那么它所对的直角边等于斜边的一半38 直角三角形斜边上的中线等于斜边上的一半39 定理线段垂直平分线上的点和这条线段两个端点的距离相等40 逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上41 线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42 定理1 关于某条直线对称的两个图形是全等形43 定理 2 如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线44定理3 两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上45逆定理如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方,即a+b=c 47勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c,那么这个三角形是直角三角形48定理四边形的内角和等于360°49四边形的外角和等于360°50多边形内角和定理 n边形的内角的和等于(n-2)×180°51推论任意多边的外角和等于360°52平行四边形性质定理1 平行四边形的对角相等53平行四边形性质定理2 平行四边形的对边相等54推论夹在两条平行线间的平行线段相等55平行四边形性质定理3 平行四边形的对角线互相平分56平行四边形判定定理1 两组对角分别相等的四边形是平行四边形57平行四边形判定定理2 两组对边分别相等的四边形是平行四边形58平行四边形判定定理3 对角线互相平分的四边形是平行四边形59平行四边形判定定理4 一组对边平行相等的四边形是平行四边形60矩形性质定理1 矩形的四个角都是直角61矩形性质定理2 矩形的对角线相等62矩形判定定理1 有三个角是直角的四边形是矩形63矩形判定定理2 对角线相等的平行四边形是矩形64菱形性质定理1 菱形的四条边都相等65菱形性质定理2 菱形的对角线互相垂直,并且每一条对角线平分一组对角66菱形面积=对角线乘积的一半,即S=(a×b)÷267菱形判定定理1 四边都相等的四边形是菱形68菱形判定定理2 对角线互相垂直的平行四边形是菱形69正方形性质定理1 正方形的四个角都是直角,四条边都相等70正方形性质定理2正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角71定理1 关于中心对称的两个图形是全等的72定理2 关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分73逆定理如果两个图形的对应点连线都经过某一点,并且被这一点平分,那么这两个图形关于这一点对称74等腰梯形性质定理等腰梯形在同一底上的两个角相等75等腰梯形的两条对角线相等76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77对角线相等的梯形是等腰梯形78平行线等分线段定理如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等79 推论1 经过梯形一腰的中点与底平行的直线,必平分另一腰80 推论2 经过三角形一边的中点与另一边平行的直线,必平分第三边81 三角形中位线定理三角形的中位线平行于第三边,并且等于它的一半82 梯形中位线定理梯形的中位线平行于两底,并且等于两底和的一半 L=(a+b)÷2 S=L×h83 (1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84 (2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85 (3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b86 平行线分线段成比例定理三条平行线截两条直线,所得的对应线段成比例87 推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例88 定理如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边89 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例90 定理平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似91 相似三角形判定定理1 两角对应相等,两三角形相似(ASA)92 直角三角形被斜边上的高分成的两个直角三角形和原三角形相似93 判定定理2 两边对应成比例且夹角相等,两三角形相似(SAS)94 判定定理3 三边对应成比例,两三角形相似(SSS)95 定理如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似96 性质定理1 相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比97 性质定理2 相似三角形周长的比等于相似比98 性质定理3 相似三角形面积的比等于相似比的平方99 任意锐角的正弦值等于它的余角的余弦值,任意锐角的余弦值等于它的余角的正弦值100任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值101圆是定点的距离等于定长的点的集合102圆的内部可以看作是圆心的距离小于半径的点的集合103圆的外部可以看作是圆心的距离大于半径的点的集合104同圆或等圆的半径相等105到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆106和已知线段两个端点的距离相等的点的轨迹,是着条线段的垂直平分线107到已知角的两边距离相等的点的轨迹,是这个角的平分线108到两条平行线距离相等的点的轨迹,是和这两条平行线平行且距离相等的一条直线109定理不在同一直线上的三个点确定一条直线110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧111推论1 ①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧②弦的垂直平分线经过圆心,并且平分弦所对的两条弧③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧112推论2 圆的两条平行弦所夹的弧相等113圆是以圆心为对称中心的中心对称图形114定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等115推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等116定理一条弧所对的圆周角等于它所对的圆心角的一半117推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等118推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径119推论3 如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形120定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角121①直线L和⊙O相交 d<r②直线L和⊙O相切d=r③直线L和⊙O相离 d>r122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线123切线的性质定理圆的切线垂直于经过切点的半径124推论1 经过圆心且垂直于切线的直线必经过切点125推论2 经过切点且垂直于切线的直线必经过圆心126切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角127圆的外切四边形的两组对边的和相等128弦切角定理弦切角等于它所夹的弧对的圆周角129推论如果两个弦切角所夹的弧相等,那么这两个弦切角也相等130相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等131推论如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项132切割线定理从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项133推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等134如果两个圆相切,那么切点一定在连心线上135①两圆外离 d>R+r ②两圆外切d=R+r③两圆相交 R-r<d<R+r(R>r)④两圆内切 d=R-r(R>r) ⑤两圆内含d<R-r(R>r)136定理相交两圆的连心线垂直平分两圆的公共弦137定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形138定理任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆139正n边形的每个内角都等于(n-2)×180°/n140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形141正n边形的面积Sn=pnrn/2 p表示正n边形的周长142正三角形面积√3a/4 a表示边长143如果在一个顶点周围有k个正n边形的角,由于这些角的和应为360°,因此k×(n-2)180°/n=360°化为(n-2)(k-2)=4144弧长计算公式:L=n∏R/180145扇形面积公式:S扇形=n∏R/360=LR/2146内公切线长= d-(R-r) 外公切线长= d-(R+r)。
