Applications of Game Theory and Information Economics in Capital Market Researches
40_game_theory_ch_2

Chapter2Nim and combinatorial games2.1Aims of the chapterThis chapter•introduces the basics of combinatorial games,and explains the central role of the game nim.A detailed summary of the chapter is given in section2.5.Furthermore,this chapter•demonstrates the use of abstract mathematics in game theory.This chapter is written more formally than the other chapters,in parts in thetraditional mathematical style of definitions,theorems and proofs.One reason fordoing this,and why we start with combinatorial games,is that this topic and styleserves as a warning shot to those who think that game theory,and this unit inparticular,is‘easy’.If we started with the well-known‘prisoner’s dilemma’(whichmakes its due appearance in Chapter3),the less formally inclined student might belulled into a false sense of familiarity and‘understanding’.We therefore startdeliberately with an unfamiliar topic.This is a mathematics unit,with great emphasis on rigour and clarity,and on usingmathematical notions precisely.As mathematical prerequisites,game theory requiresonly the very basics of linear algebra,calculus and probability theory.However,gametheory provides its own conceptual tools that are used to model and analyseinteractive situations.This unit emphasises the mathematical structure of theseconcepts,which belong to‘discrete mathematics’.Learning a number of newmathematical concepts is exemplified by combinatorial game theory,and it willcontinue in the study of classical game theory in the later chapters.2.2Learning objectivesAfter studying this chapter,you should be able to:•play nim optimally;•explain the concepts of game-sums,equivalent games,nim values and the mex rule;•apply these concepts to play other impartial games like those described in the exercises.40Game theory2.3Essential readingThis chapter of the guide.2.4Further readingVery few textbooks on game theory deal with combinatorial games.An exception ischapter1of the following book:•Mendelson,Elliot Introducing Game Theory and Its Applications.(Chapman& Hall/CRC,2004)[ISBN1584883006].The winning strategy for the game nim based on the binary system wasfirst describedin the following article,which is available electronically from the JSTOR archive:•Bouton,Charles‘Nim,a game with a complete mathematical theory.’The Annals of Mathematics,2nd Ser.,Vol.3,No.1/4(1902),pp.35–39.The definitive text on combinatorial game theory is the set of volumes‘WinningWays’by Berlekamp,Conway and Guy.The material of this chapter appears in thefirst volume:•Berlekamp,Elwyn R.,John H.Conway and Richard K.Guy Winning Ways for Your Mathematical Plays,Volume1,second edition.(A.K.Peters,2001)[ISBN1568811306].Some small pieces of that text have been copied here nearly verbatim,for example inSections2.7,2.9,and2.12below.The four volumes of‘Winning Ways’are beautiful books.However,they are notsuitable reading for a beginner,because the mathematics is hard,and the reader isconfronted with a wealth of material.The introduction to combinatorial game theorygiven here represents a very small fraction of that body of work,but may invite youto study it further.A very informative and entertaining mathematical tour of parlour games is•Bewersdorff,J¨o rg Logic,Luck and White Lies.(A.K.Peters,2005)[ISBN 1568812108].Combinatorial games are treated in part II of that book.2.5What is combinatorial game theory?This chapter is on the topic of combinatorial games.These are games with twoplayers,perfect information,and no chance moves,specified by certain rules.Familiargames of this sort are chess,go,checkers,tic-tac-toe,dots-and-boxes,and nim.Suchgames can be played perfectly in the sense that either one player can force a win orboth can force a draw.In reality,games like chess and go are too complex tofind anoptimal strategy,and they derive their attraction from the fact that(so far)it is notknown how to play them perfectly.We will,however,learn how to play nim perfectly.There is a‘classical’game theory with applications in economics which is verydifferent from combinatorial game theory.The games in classical game theory aretypically formal models of conflict and co-operation which cannot only be lost orWhat is combinatorial game theory? won,and in which there is often no perfect information about past and future moves.To the economist,combinatorial games are not very interesting.Chapters3–6of theunit are concerned with classical game theory.Why,then,study combinatorial games at all in a unit that is mostly about classicalgame theory,and which aims to provide an insight into the theory of games as usedin economics?The reason is that combinatorial games have a rich and interesting mathematical theory.We will explain the basics of that theory,in particular thecentral role of the game nim for impartial games.It is non-trivial mathematics,it isfun,and you,the student,will have learned something that you would most likelynot have learned otherwise.Thefirst‘trick’from combinatorial game theory is how to win in the game nim,using the binary system.Historically,that winning strategy was discoveredfirst(published by Charles Bouton in1902).Only later did the central importance of nim,in what is known as the Sprague–Grundy theory of impartial games,becomeapparent.It also revealed why the binary system is important(and not,say,theternary system,where numbers are written in base three),and learning that is more satisfying than just learning how to use it.In this chapter,wefirst define the game nim and more general classes of games withperfect information.These are games where every player knows exactly the state ofthe game.We then define and study the concepts listed in the learning outcomesabove,which are the concepts of game-sums,equivalent games,nim values and themex rule.It is best to learn these concepts by following the chapter in detail.Wegive a brief summary here,which will make more sense,and should be re-consulted,after afirst study of the chapter(so do not despair if you do not understand this summary).Mathematically,any game is defined by other‘games’that a player can reach in hisfirst move.These games are called the options of the game.This seemingly circulardefinition of a‘game’is sound because the options are simpler games,which needfewer moves in total until they end.The definition is therefore not circular,butrecursive,and the mathematical tool to argue about such games is that ofmathematical induction,which will be used extensively(it will also recur inchapter3as‘backward induction’for game trees).Here,it is very helpful to befamiliar with mathematical induction for proving statements about natural numbers.We focus here on impartial games,where the available moves are the same nomatter whether player I or player II is the player to make a move.Games are‘combined’by the simple rule that a player can make a move in exactly one of thegames,which defines a sum of these games.In a‘losing game’,thefirst player tomove loses(assuming,as always,that both players play as well as they can).Animpartial game added to itself is always losing,because any move can be copied inthe other game,so that the second player always has a move left.This is known asthe‘copycat’principle(lemma2.6).An important observation is that a losing gamecan be‘added’(via the game-sum operation)to any game without changing thewinning or losing properties of the original game.In section2.11,the central theorem2.10explains the winning strategy in nim.The importance of nim for impartial games is then developed in section2.12via thebeautiful mex rule.After the comparatively hard work of the earlier sections,wealmost instantly obtain that any impartial game is equivalent to a nim heap(corollary2.13).At the end of the chapter,the sizes of these equivalent nim heaps(called nim values)are computed for some examples of impartial games.Many other examples arestudied in the exercises.40Game theoryOur exposition is distinct from the classic text‘Winning Ways’in the followingrespects:First,we only consider impartial games,even though many aspects carryover to more general combinatorial games.Secondly,we use a precise definition ofequivalent games(see section2.10),because a game where you are bound to loseagainst a smart opponent is not the same as a game where you have already lost.Two such games are merely equivalent,and the notion of equivalent games is helpfulin understanding the theory.So this text is much more restricted,but to some extentmore precise than‘Winning Ways’,which should help make this topic accessible andenjoyable.2.6Nim–rulesThe game nim is played with heaps(or piles)of chips(or counters,beans,pebbles,matches).Players alternate in making a move,by removing some chips from one ofthe heaps(at least one chip,possibly the entire heap).Thefirst player who cannotmove any more loses the game.The players will be called,rather unimaginatively,player I and player II,with player Ito start the game.For example,consider three heaps of size1,1,2.What is a good move?Removingone of the chips from the heap with two chips will create the position1,1,1,thenplayer II must move to1,1,then player I to1,and then player II takes the last chipand wins.So this is not a good opening move.The winning move is to remove allchips from the heap of size2,to reach position1,1,and then player I will win.Hence we call1,1,2a winning position,and1,1a losing position.When moving in a winning position,the player to move can win by playing well,bymoving to a losing position of the other player.In a losing position,the player tomove will lose no matter what move she chooses,if her opponent plays well.Thismeans that all moves from a losing position lead to a winning position of theopponent.In contrast,one needs only one good move from a winning position thatgoes to a losing position of the next player.Another winning position consists of three nim heaps of sizes1,1,1.Here all movesresult in the same position and player I always wins.In general,a player in a winningposition must play well by picking the right move.We assume that players play well,forcing a win if they can.Suppose nim is played with only two heaps.If the two heaps have equal size,forexample in position4,4,then thefirst player to move loses(so this is a losingposition),because player II can always copy player I’s move by equalising the twoheaps.If the two heaps have different sizes,then player I can equalise them byremoving an appropriate number of chips from the larger heap,putting player II in alosing position.The rule for2-heap nim is therefore:Lemma2.1The nim position m,n is winning if and only if m=n,otherwise losing,for all m,n≥0.This lemma applies also when m=0or n=0,and thus includes the cases that oneor both heap sizes are zero(meaning only one heap or no heap at all).With three or more heaps,nim becomes more difficult.For example,it is notimmediately clear if,say,positions1,4,5or2,3,6are winning or losing positions.⇒At this point,you should try exercise2.1(a)on page28.Combinatorial games,in particular impartial games 2.7Combinatorial games,in particular impartial gamesThe games we study in this chapter have,like nim,the following properties:1.There are just two players.2.There are several,usuallyfinitely many,positions,and sometimes a particularstarting position.3.There are clearly defined rules that specify the moves that either player canmake from a given position to the possible new positions,which are called theoptions of that position.4.The two players move alternately,in the game as a whole.5.In the normal play convention a player unable to move loses.6.The rules are such that play will always come to an end because some player willbe unable to move.This is called the ending condition.So there can be nogames which are drawn by repetition of moves.7.Both players know what is going on,so there is perfect information.8.There are no chance moves such as rolling dice or shuffling cards.9.The game is impartial,that is,the possible moves of a player only depend onthe position but not on the player.As a negation of condition5,there is also the mis`e re play convention where a playerunable to move wins.In the surrealist(and unsettling)movie‘Last year atMarienbad’by Alain Resnais from1962,mis`e re nim is played,several times,withrows of matches of sizes1,3,5,7.If you have a chance,try to watch that movie andspot when the other player(not the guy who brought the matches)makes a mistake!Note that this is mis`e re nim,not nim,but you will be able tofind out how to play itonce you know how to play nim.(For games other than nim,normal play and mis`e reversions are typically not so similar.)In contrast to condition9,games where the available moves depend on the player(as in chess where one player can only move white pieces and the other only blackpieces)are called partisan games.Much of combinatorial game theory is aboutpartisan games,which we do not consider to keep matters simple.Chess,and the somewhat simpler tic-tac-toe,also fail condition6because they mayend in a tie or draw.The card game poker does not have perfect information(asrequired in7)and would lose all its interest if it had.The analysis of poker,althoughit is also a win-or-lose game,leads to the‘classical’theory of zero-sum games(withimperfect information)that we will consider later.The board game backgammon is agame with perfect information but with chance moves(violating condition8)because dice are rolled.We will be relatively informal in style,but our notions are precise.In condition3above,for example,the term option refers to a position that is reachable in onemove from the current position;do not use‘option’when you mean‘move’.Similarly,we will later use the term strategy to define a plan of moves,one for everyposition that can occur in the game.Do not use‘strategy’when you mean‘move’.However,we will take some liberty in identifying a game with its starting positionwhen the rules of the game are clear.40Game theory⇒Try now exercises2.2and2.3starting on page28.2.8Simpler games and notation for nim heapsA game,like nim,is defined by its rules,and a particular starting position.Let G besuch a particular instance of nim,say with the starting position1,1,2.Knowing therules,we can identify G with its starting position.Then the options of G are1,2,and1,1,1,and1,1.Here,position1,2is obtained by removing either thefirst or thesecond heap with one chip only,which gives the same result.Positions1,1,1and1,1are obtained by making a move in the heap of size two.It is useful to list the optionssystematically,considering one heap to move in at a time,so as not to overlook anyoption.Each of the options of G is the starting position of another instance of nim,definingone of the new games H,J,K,say.We can also say that G is defined by the movesto these games H,J,K,and we call these games also the options of G(byidentifying them with their starting positions;recall that the term‘option’has beendefined in point3of section2.7).That is,we can define a game as follows:Either the game has no move,and theplayer to move loses,or a game is given by one or several possible moves to newgames,in which the other player makes the initial move.In our example,G isdefined by the possible moves to H,J,or K.With this definition,the entire game iscompletely specified by listing the initial moves and what games they lead to,because all subsequent use of the rules is encoded in those games.This is a recursive definition because a‘game’is defined in terms of‘game’itself.We have to add the ending condition that states that every sequence of moves in agame must eventually end,to make sure that a game cannot go on indefinitely.This recursive condition is similar to defining the set of natural numbers as follows:(a)0is a natural number;(b)if n is a natural number,then so is n+1;and(c)allnatural numbers are obtained in this way,starting from0.Condition(c)can beformalised by the principle of induction that says:if a property P(n)is true for n=0,and if the property P(n)implies P(n+1),then it is true for all natural numbers.We use the following notation for nim heaps.If G is a single nim heap with nchips,n≥0,then we denote this game by∗n.This game is completely specified byits options,and they are:options of∗n:∗0,∗1,∗2,...,∗(n−1).(2.1) Note that∗0is the empty heap with no chips,which allows no moves.It is invisiblewhen playing nim,but it is useful to have a notation for it because it defines themost basic losing position.(In combinatorial game theory,the game with no moves,which is the empty nim heap∗0,is often simply denoted as0.)We could use(2.1)as the definition of∗n;for example,the game∗4is defined by itsoptions∗0,∗1,∗2,∗3.It is very important to include∗0in that list of options,because it means that∗4has a winning move.Condition(2.1)is a recursivedefinition of the game∗n,because its options are also defined by reference to suchgames∗k,for numbers k smaller than n.This game fulfils the ending conditionbecause the heap gets successively smaller in any sequence of moves.If G is a game and H is a game reachable by one or more successive moves from thestarting position of G,then the game H is called simpler than G.We will oftenprove a property of games inductively,using the assumption that the property appliesto all simpler games.An example is the–already stated and rather obvious–Sums of games property that one of the two players can force a win.(Note that this applies togames where winning or losing are the only two outcomes for a player,as implied bythe‘normal play’convention in5above.)Lemma2.2In any game G,either the starting player I can force a win,or player IIcan force a win.Proof.When the game has no moves,player I loses and player II wins.Now assumethat G does have options,which are simpler games.By inductive assumption,ineach of these games one of the two players can force a win.If,in all of them,thestarting player(which is player II in G)can force a win,then she will win in G byplaying accordingly.Otherwise,at least one of the starting moves in G leads to agame G where the second-moving player in G (which is player I in G)can force awin,and by making that move,player I will force a win in G.If in G,player I can force a win,its starting position is a winning position,and wecall G a winning game.If player II can force a win,G starts with a losing position,and we call G a losing game.2.9Sums of gamesWe continue our discussion of nim.Suppose the starting position has heap sizes1,5,5.Then the obvious good move is to option5,5,which is losing.What about nim with four heaps of sizes2,2,6,6?This is losing,because2,2and6,6independently are losing positions,and any move in a heap of size2can becopied in the other heap of size2,and similarly for the heaps of size6.There is asecond way of looking at this example,where it is not just two losing games puttogether:consider the game with heap sizes2,6.This is a winning game.However,two such winning games,put together to give the game2,6,2,6,result in a losinggame,because any move in one of the games2,6,for example to2,4,can be copiedin the other game,also to2,4,giving the new position2,4,2,4.So the secondplayer,who plays‘copycat’,always has a move left(the copying move)and hencecannot lose.Definition2.3The sum of two games G and H,written G+H,is defined asfollows:The player may move in either G or H as allowed in that game,leaving theposition in the other game unchanged.Note that G+H is a notation that applies here to games and not to numbers,evenif the games are in some way defined using numbers(for example as nim heaps).The result is a new game.More formally,assume that G and H are defined in terms of their options(via movesfrom the starting position)G1,G2,...,G k and H1,H2,...,H m,respectively.Then theoptions of G+H are given asoptions of G+H:G1+H,...,G k+H,G+H1,...,G+H m.(2.2) Thefirst list of options G1+H,G2+H,...,G k+H in(2.2)simply means that theplayer makes his move in G,the second list G+H1,G+H2,...,G+H m that hemakes his move in H.We can define the game nim as a sum of nim heaps,where any single nim heap isrecursively defined in terms of its options by(2.1).So the game nim with heaps ofsize1,4,6is written as∗1+∗4+∗6.40Game theoryThe‘addition’of games with the abstract+operation leads to an interestingconnection of combinatorial games with abstract algebra.If you are somewhatfamiliar with the concept of an abstract group,you will enjoy this connection;if not,you do not need to worry,because this connection it is not essential for ourdevelopment of the theory.A group is a set with a binary operation+that fulfils three properties:1.The operation+is associative,that is,G+(J+K)=(G+J)+K holds for allG,J,K.2.The operation+has a neutral element0,so that G+0=G and0+G=G forall G.3.Every element G has an inverse−G so that G+(−G)=0.Furthermore,4.The group is called commutative(or‘abelian’)if G+H=H+G holds for allG,H.Familiar groups in mathematics are,for example,the set of integers with addition,orthe set of positive real numbers with multiplication(where the multiplicationoperation is written as·,the neutral element is1,and the inverse of G is written asG−1).The games that we consider form a group as well.In the way the sum of two gamesG and H is defined,G+H and H+G define the same game,so+is commutative.Moreover,when one of these games is itself a sum of games,for example H=J+K,then G+H is G+(J+K)which means the player can make a move in exactly one ofthe games G,J,or K.This means obviously the same as the sum of games(G+J)+K,that is,+is associative.The sum G+(J+K),which is the same as(G+J)+K,can therefore be written unambiguously as G+J+K.An obvious neutral element is the empty nim heap∗0,because it is‘invisible’(itallows no moves),and adding it to any game G does not change the game.However,there is no direct way to get an inverse operation because for any game Gwhich has some options,if one adds any other game H to it(the intention beingthat H is the inverse−G),then G+H will have some options(namely at least theoptions of moving in G and leaving H unchanged),so that G+H is not equal to theempty nim heap.The way out of this is to identify games that are‘equivalent’in a certain sense.Wewill see shortly that if G+H is a losing game(where thefirst player to move cannotforce a win),then that losing game is‘equivalent’to∗0,so that H fulfils the role ofan inverse of G.2.10Equivalent gamesThere is a neutral element that can be added to any game G without changing it.By definition,because it allows no moves,it is the empty nim heap∗0:G+∗0=G.(2.3)However,other games can also serve as neutral elements for the addition of games.We will see that any losing game can serve that purpose,provided we considercertain games as equivalent according to the following definition.Equivalent games Definition2.4Two games G,H are called equivalent,written G≡H,if and only iffor any other game J,the sum G+J is losing if and only if H+J is losing.In definition2.4,we can also say that G≡H if for any other game J,the sum G+Jis winning if and only if H+J is winning.In other words,G is equivalent to H if,whenever G appears in a sum G+J of games,then G can be replaced by H without changing whether G+J is winning or losing.One can verify easily that≡is indeed an equivalence relation,meaning it is reflexive(G≡G),symmetric(G≡H implies H≡G),and transitive(G≡H and H≡K implyG≡K;all these conditions hold for all games G,H,K).Using J=∗0in definition2.4and(2.3),G≡H implies that G is losing if and only ifH is losing.The converse is not quite true:just because two games are winning doesnot mean they are equivalent,as we will see shortly.However,any two losing gamesare equivalent,because they are all equivalent to∗0:Lemma2.5If G is a losing game(the second player to move can force a win),thenG≡∗0.Proof.Let G be a losing game.We want to show G≡∗0By definition2.4,this istrue if and only if for any other game J,the game G+J is losing if and only if∗0+Jis losing.According to(2.3),this holds if and only if J is losing.So let J be any other game;we want to show that G+J is losing if and only if J islosing.Intuitively,adding the losing game G to J does not change which player in Jcan force a win,because any intermediate move in G by his opponent is simplycountered by the winning player,until the moves in G are exhausted.Formally,wefirst prove by induction the simpler claim that for all games J,if J islosing,then G+J is losing.(So wefirst ignore the‘only if’part.)Our inductive assumptions for this simpler claim are:for all losing games G that are simplerthan G,if J is losing,then G +J is losing;and for all games J that are simplerthan J,if J is losing,then G+J is losing.So suppose that J is losing.We want to show that G+J is losing.Any initial movein J leads to an option J which is winning,which means that there is acorresponding option J of J (by player II’s reply)where J is losing.Hence,whenplayer I makes the corresponding initial move from G+J to G+J ,player II cancounter by moving to G+J .By inductive assumption,this is losing because J islosing.Alternatively,player I may move from G+J to G +J.Because G is a losinggame,there is a move by player II from G to G where G is again a losing game,and hence G +J is also losing,by inductive assumption,because J is losing.Thiscompletes the induction and proves the claim.What is missing is to show that if G+J is losing,so is J.If J was winning,then therewould be a winning move to some option J of J where J is losing,but then,by ourclaim(the‘if’part that we just proved),G+J is losing,which would be a winningoption in G+J for player I.But this is a contradiction.This completes the proof.The preceding lemma says that any losing game Z,say,can be added to a game Gwithout changing whether G is winning or losing(in lemma2.5,Z is called G).Thatis,extending(2.3),Z losing=⇒G+Z≡G.(2.4)As an example,consider Z=∗1+∗2+∗3,which is nim with three heaps of sizes1,2,3.To see that Z is losing,we examine the options of Z and show that all ofthem are winning games.Removing an entire heap leaves two unequal heaps,whichis a winning position by lemma2.1.Any other move produces three heaps,two of40Game theorywhich have equal size.Because two equal heaps define a losing nim game Z,they can be ignored by(2.4),meaning that all these options are like single nim heaps and therefore winning positions,too.So Z=∗1+∗2+∗3is losing.The game G=∗4+∗5is clearly winning.By(2.4), the game G+Z is equivalent to G and is also winning.However,verifying directly that∗1+∗2+∗3+∗4+∗5is winning would not be easy to see without using(2.4). It is an easy exercise to show that in sums of games,games can be replaced by equivalent games,resulting in an equivalent sum.That is,for all games G,H,J,G≡H=⇒G+J≡H+J.(2.5)Note that(2.5)is not merely a re-statement of definition2.4,because equivalence of the games G+J and H+J means more than just that the games are either both winning or both losing(see the comments before lemma2.9below).Lemma2.6(The copycat principle)G+G≡∗0for any impartial game G. Proof.Given G,we assume by induction that the claim holds for all simpler games G .Any option of G+G is of the form G +G for an option G of G.This is winning by moving to the game G +G which is losing,by inductive assumption.So G+G is indeed a losing game,and therefore equivalent to∗0by lemma2.5.We now come back to the issue of inverse elements in abstract groups,mentioned at the end of section2.9.If we identify equivalent games,then the addition+of games defines indeed a group operation.The neutral element is∗0,or any equivalent game (that is,a losing game).The inverse of a game G,written as the negative−G,fulfilsG+(−G)≡∗0.(2.6) Lemma2.6shows that for an impartial game,−G is simply G itself.Side remark:For games that are not impartial,that is,partisan games,−G exists also.It is G but with the roles of the two players exchanged,so that whatever move was available to player I is now available to player II and vice versa.As an example, consider the game checkers(with the rule that whoever can no longer make a move loses),and let G be a certain configuration of pieces on the checkerboard.Then−G is the same configuration with the white and black pieces interchanged.Then in the game G+(−G),player II(who can move the black pieces,say),can also play‘copycat’.Namely,if player I makes a move in either G or−G with a white piece, then player II copies that move with a black piece on the other board(−G or G, respectively).Consequently,player II always has a move available and will win the game,so that G+(−G)is indeed a losing game for the starting player I,that is,G+(−G)≡∗0.However,we only consider impartial games,where−G=G.The following condition is very useful to prove that two games are equivalent. Lemma2.7Two impartial games G,H are equivalent if and only if G+H≡∗0.Proof.If G≡H,then by(2.5)and lemma2.6,G+H≡H+H≡∗0.Conversely,G+H≡∗0implies G≡G+H+H≡∗0+H≡H.Sometimes,we want to prove equivalence inductively,where the following observation is useful.Lemma2.8Two games G and H are equivalent if all their options are equivalent, that is,for every option of G there is an equivalent option of H and vice versa.。
Primary School English Game Teaching Methods

primary school students, encouraging them to participate more
actively in English learning.
02
Easy to understand and remember
Through games, dull knowledge points are made vivid and
The content of this research includes: the application of game teaching method in primary school English teaching, the classification and characteristics of game teaching method, the effect of game teaching method on students' English ability and interest, and the challenges and solutions of applying game teaching method in primary school English teaching
Research purpose and significance
This research aims to explore the application and effect of game teaching method in primary school English teaching
Through the research, we can provide a basis for teachers to select appropriate game teaching methods and improve the
英语第一章阅读 game theory 原文及翻译

In principle, any sequential game that ends after a finite sequence of moves can be “solved” completely. We determine each player’s best strategy by looking ahead to every possible outcome. Simple games, such as tic-tac-toe, can be solved in this way and are therefore not challenging. For many other games, such as chess, the calculations are too complex to perform in practice—even with computers. Therefore, the players look a few moves ahead and try to evaluate the resulting positions on the basis of experience.
原则上,在有限的一系列动作之后结束的任何连续游戏都可以完全“解决”。我们通过展望每一个可能的结果来 确定每个玩家的最佳策略。简单的游戏,如井字游戏,可以用这种方式解决,因此不具有挑战性。对于许多其 他游戏,如国际象棋,计算过于复杂,无法在实践中执行 - 即使使用计算机。因此,球员们会看到前进的几 步,并尝试根据经验评估所得到的位置。
管理经济学ppt课件

*
Schedule
Section I : Preliminaries & Demand Theory Section II : Production & Cost Of Production Section III: Theory Of Market Structure Section IV: Application Of Game Theory
X
Y
*
*
例
U(X,Y)=X2+2XY+Y2=(X+Y)2 则,MRS=MUX/MUY=1
*
*
二.消费者选择
预算线: 收入I,商品X与Y的价格为(PX,PY),则预算约束为:PX X+PY Y≤I
X
Y
斜率=-PX/PY
*
*
预算线的移动
收入变动 价格变动
PX下降
PX上升
*
*
消费者剩余
Customer Surplus
Q
P
10
9
8
1
2
3
◇消费者愿意为第一个产品 支付10元;为第二个产品 支付9元;为第三个产品支 付8元;… ◇现在按市场价格P=8购买 3个产品,实际支付24元, 所以,获得剩余为 (10-8)+(9-8)=3 ◇若连续变动,则剩余为 ∑(Pi-P*)=∫∞P*D(P)dP
产品消费者
土地所有者
管理人员
劳动力的 提供者
工程技术人员
体力劳动者
资本所有者
*
*
三.企业理论
企业的边界 企业本质上是将监督外部交易活动转化为内部控制 交易成本 Vs.代理成本 Coase定理(1937):
游戏理论概括英文作文

游戏理论概括英文作文英文:Game theory is a branch of applied mathematics and economics that studies strategic interactions between rational decision-makers. It provides a framework for analyzing and understanding how individuals, firms, and governments make decisions in competitive situations. The central concept of game theory is the "game," which is a formal model of a strategic interaction between two or more players. Each player in the game has a set of possible strategies, and the outcome of the game depends on the strategies chosen by all players.One of the most famous games in game theory is the prisoner's dilemma, which illustrates the concept of Nash equilibrium, named after the mathematician John Nash. In the prisoner's dilemma, two suspects are arrested and placed in separate cells. They are given the option to cooperate with each other by remaining silent, or to betrayeach other by confessing. The outcome of their decision depends on the choices made by both suspects. The Nash equilibrium in this game occurs when both suspects choose to betray each other, even though they would be better off if they both remained silent. This example demonstrates how rational individuals may not always make the best decisions when they are in a competitive situation.Another important concept in game theory is the notion of a dominant strategy, which is a strategy that always provides the best outcome for a player, regardless of the strategies chosen by other players. For example, in the game of rock-paper-scissors, if one player always chooses "rock" regardless of the other player's choice, they have a dominant strategy. Understanding dominant strategies can help players make optimal decisions in competitive games.Game theory has applications in various fields, including economics, political science, biology, and computer science. For example, it is used to analyze voting behavior in elections, to model the behavior of firms in oligopoly markets, and to study the evolution ofcooperation in biological systems. In computer science, game theory is used to design algorithms for multi-agent systems and to analyze the behavior of autonomous agents.In conclusion, game theory provides a powerful framework for analyzing strategic interactions and understanding the behavior of rational decision-makers in competitive situations. By studying game theory, we cangain insights into a wide range of phenomena in the social and natural sciences.中文:博弈论是应用数学和经济学的一个分支,研究理性决策者之间的战略互动。
game theory lecture7博弈论

behavioral strategy in Extensive-Form Games
a behavioral strategy is more in tune with the dynamic nature of the extensive-form game. When using such a strategy, a player mixes among his actions whenever he is called to play.
Normal-Form Representation of Extensive-Form Games
• Any extensive-form game can be transformed into a normal-form game by using the set of pure strategies of the extensive form (see definition 7.4) as the set of pure strategies in the normal form, and the set of payoff functions is derived from how combinations of pure strategies result in the selection of terminal nodes. • Therefore the normal-form representation of an extensive form will suffice to find all the Nash equilibria of the game.
博弈英语作文

博弈英语作文Game theory is a field of study that analyzes the strategic interactions between decision-makers with different, often conflicting, objectives. It provides a framework for understanding how individuals or entities make choices in situations where the outcome depends not only on their own actions but also on the actions of others. This discipline has applications in a wide range of fields, including economics, political science, computer science, biology, and even psychology.The foundations of game theory were laid in the 1940s by the mathematician John von Neumann and the economist Oskar Morgenstern, who published their seminal work "Theory of Games and Economic Behavior." In this book, they introduced the concept of the "game," which is a formal model of an interactive situation where players make decisions in order to achieve their desired outcomes.At the heart of game theory is the idea of the "rational player," an entity that seeks to maximize its own payoff or utility given theactions of the other players. The rational player is assumed to have complete information about the game, including the available strategies, the possible outcomes, and the payoffs associated with each outcome. The player is also assumed to be able to accurately assess the probabilities of different outcomes and to choose the strategy that will lead to the best possible outcome for themselves.One of the key concepts in game theory is the Nash equilibrium, named after the mathematician John Nash. A Nash equilibrium is a set of strategies, one for each player, where no player can improve their payoff by unilaterally changing their strategy. In other words, each player's strategy is the best response to the strategies of the other players. The existence of a Nash equilibrium is a fundamental result in game theory, and it has important implications for understanding the behavior of rational players in strategic situations.Another important concept in game theory is the idea of cooperation and competition. In some games, players may be able to achieve better outcomes by cooperating with each other, while in other games, the players' interests are inherently in conflict, and they must compete to achieve their desired outcomes. The study of these different types of games has led to the development of a range of solution concepts, such as the Pareto optimal solution and the minimax solution, which help to predict the outcomes of strategic interactions.Game theory has a wide range of applications in the real world. In economics, game theory is used to analyze market competition, bargaining, and the design of auctions and other market mechanisms. In political science, game theory is used to study the strategic behavior of political actors, such as voters, politicians, and interest groups. In computer science, game theory is used to design algorithms and protocols for distributed systems, such as the internet, where multiple agents must coordinate their actions to achieve a desired outcome.One of the most well-known applications of game theory is in the field of evolutionary biology, where it is used to understand the evolution of cooperation and competition among living organisms. The concept of the "evolutionary stable strategy" in game theory has been used to explain the emergence of complex social behaviors, such as altruism and reciprocity, in various species.Despite its many successes, game theory is not without its limitations. One of the key challenges in applying game theory is the difficulty of accurately modeling the behavior of real-world players, who may not always behave in a perfectly rational manner. Additionally, the complexity of many real-world situations can make it difficult to apply game-theoretic models in a straightforward way.Despite these challenges, game theory remains a powerful and influential field of study, with applications across a wide range of disciplines. As technology continues to advance and the world becomes increasingly interconnected, the need for a deeper understanding of strategic interactions and decision-making will only continue to grow. By providing a rigorous framework for analyzing these complex situations, game theory will likely play an increasingly important role in shaping our understanding of the world around us.。
game-theory1--博弈论-英文PPT课件

playersknowactionstakenotherplayersactionsknowngamesclassificationintroductioneconomicmodelsgametheorymodelsgamessummary38previewperfectinformationstaticgamesnashequilibriumdynamicgamesbackwardinduction倒推归imperfectinformationdynamicgamessubgame子博弈perfectneincompleteinformationstaticgamesauctions拍卖dynamicgamessignalinggamesclassificationintroductioneconomicmodelsgametheorymodelsgamessummaryeconomicmodelsgoodenoughapproximationrealworldmanyusefulpurposesgametheorymodelseconomicmodelssituationswheredecisionmakersinteractsummaryintroductioneconomicmodelsgametheorymodelsgamessummarystrategicgameconsistseachplayerseteachplayersetpreferencesoveractionprofilespreferencesrepresentedpayofffunctionsolvinggamesiterative重复的elimination消去strictlydominatedstrategiesnextlecturenashequilibriumnextlectureothermethodslatercoursesummaryiiintroductioneconomicmodelsgametheorymodelsgamessummary
game theory became a formal topic of study in the

game theory became a formal topic ofstudy in theGame theory, also known as the science of strategizing, has a rich and intriguing history that spans across multiple disciplines. However, it wasn't until the mid-20th century that game theory truly emerged as a formal topic of academic study.The foundations of game theory can be traced back to the early works of mathematicians such as Emile Borel and John von Neumann. Borel's concept of strategy in chess, published in 1921, introduced the idea of optimal play in games of perfect information. Von Neumann, on the other hand, is credited with developing the minimax theorem, a fundamental principle in game theory that deals with zero-sum games.It was the seminal work of John von Neumann and Oskar Morgenstern in 1944, titled "Theory of Games and Economic Behavior," that marked the official birth of game theory as a formal field of study. This book provided a rigorous mathematical framework for analyzing strategic interactions between rational players and established game theory as a branch of applied mathematics with widespread applications in economics, political science, and beyond.The subsequent decades saw significant contributions from other notable scholars like John Nash, who introduced the concept of the Nash equilibrium, a fundamental solution concept in non-cooperative games. This equilibrium, which describes a stable state where no player can improve their outcome by unilaterally changing their strategy, has become a cornerstone of modern game theory.Today, game theory is a thriving field of research with applications in various domains such as economics, finance, politics, sociology, and even biology. It provides a powerful toolbox for analyzing complex strategic interactions and understanding how rational individuals make decisions in competitive environments. The formalization of game theory has not only deepened our understanding of strategic behavior but has also opened up new avenues for exploring the intricacies of humandecision-making.。
有关博弈演讲稿英文版

有关博弈演讲稿英文版As we all know, game theory is a branch of mathematics that deals with the analysis of strategies for dealing with competitive situations where the outcome of a participant's choice of action depends critically on the actions of other participants. Today, I am going to talk about game theory and its applications in various fields.Game theory has been widely used in economics, political science, and biology, among other disciplines. It provides a framework for analyzing how individuals or groups make decisions in competitive situations. In economics, game theory has been used to study market competition, bargaining, and strategic pricing. In political science, it has been used to analyze voting behavior, coalition formation, and international relations. In biology, game theory has been used to study animal behavior, evolution, and the dynamics of ecological systems.One of the most famous concepts in game theory is the prisoner's dilemma, which illustrates the conflict between individual rationality and collective rationality. In this scenario, two individuals are arrested and charged with a crime. Each prisoner is given the opportunity to betray the other by confessing to the crime. If both prisoners confess, they will both receive a moderate sentence. If one prisoner confesses and the other remains silent, the one who confesses will be set free while the other will receive a heavy sentence. If both prisoners remain silent, they will both receive a light sentence. The dilemma arises from the fact that each prisoner's best option is to confess, but if they both confess, they will both be worse off than if they had remained silent.Another important concept in game theory is the Nash equilibrium, which is a solution concept that predicts the outcome of a game where each player's strategy is optimal given the strategies of the other players. The concept is named after John Nash, who introduced it in his doctoral dissertation in 1950. The Nash equilibrium has been used to analyze a wide range of competitive situations, from auctions and bargaining to military conflicts and environmental negotiations.In conclusion, game theory is a powerful tool for analyzing strategic interactions in a wide range of fields. It provides a formal framework for understanding how individuals or groups make decisions in competitive situations, and it has been used to study a wide range of phenomena, from market competition and political behavior to animal behavior and ecological dynamics. I hope that this brief introduction has given you a better understanding of the importance of game theory and its applications in various fields. Thank you for your attention.。
博弈论介绍PPT课件

2
Game of Chicken
driver who steers away looses What should drivers do?
Goal is to prescribe how conflicts can be resolved
Applications of Game Theory
But it can provide intuitions, suggestions and partial prescriptions
best mathematical tool we currently have
What is a Game?
A Game consists of
at least two players a set of strategies for each player a preference relation over possible outcomes
Normal form (strategic) game a finite set N of players
a set strategies A i for each player iN
payoff function u i ( s ) for each player iN • where sAjNAj is the set of strategies
Outline
Introduction to game theory Typical games in networking A sample game in Cognitive Radio Networks
What is Game Theory About?
Analysis of situations where conflict of interests are present
博弈论-Game Theory
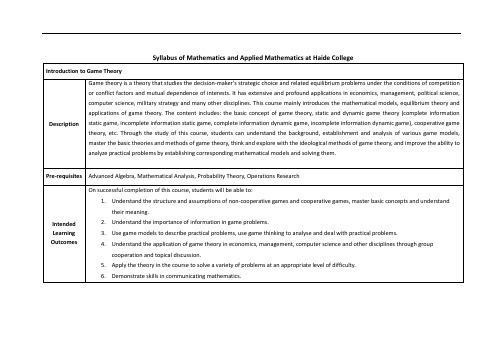
4.Understand the application of game theory in economics, management, computer science and other disciplines through group cooperation and topical discussion.
5.Apply the theory in the course to solve a variety of problems at an appropriate level of difficulty.
6.Demonstrate skills in communicating mathematics.
Pre-requisites
Advanced Algebra, Mathematical Analysis, Probability Theory, Operations Research
Intended Learning Outcomes
On successful completion of this course, students will be able to:
Syllabus ofMathematics and Applied Mathematicsat Haide College
Introduction to Game Theory
Description
Game theory is a theory that studies the decision-maker's strategic choice and related equilibrium problems under the conditions of competition or conflict factors and mutual dependence of interests. It has extensive and profound applications in economics, management, political science, computer science, military strategy and many other disciplines. This course mainly introduces the mathematical models, equilibrium theory and applications of game theory. The content includes: the basic concept of game theory, static and dynamic game theory (complete information static game, incomplete information static game, complete information dynamic game, incomplete information dynamic game), cooperative game theory, etc. Through the study of this course, students can understand the background, establishment and analysis of various game models, master the basic theories and methods of game theory, think and explore with the ideological methods of game theory, and improve the ability to analyze practical problems by establishing corresponding mathematical models and solving them.
1.Game Theory Introduction

Game theory is the formal study of conflict and cooperation. Game theoretic concepts apply whenever the actions of several agents are interdependent. These agents may be individuals, groups, firms, or any combination of these. The concepts of game theory provide a language to formulate, structure, analyze, and understand strategic scenarios.History of Game TheoryThe earliest example of a formal game-theoretic analysis is the study of a duopoly by Antoine Cournot in 1838. The mathematician Emile Borel suggested a formal theory of games in 1921, which was furthered by the mathematician John von Neumann in 1928 in a “theory of parlor games.” Game theory was established as a field in its own right after the 1944 publication of the monumental volume Theory of Games and Economic Behavior by von Neumann and the economist Oskar Morgenstern. This book provided much of the basic terminology and problem setup that is still in use today. In 1950, John Nash demonstrated that finite games have always have an equilibrium point, at which all players choose actions which are best for them given their opponents’ choices. This central concept of noncooperative game theory has been a focal point of analysis since then. In the 1950s and 1960s, game theory was broadened theoretically and applied to problems of war and politics. Since the 1970s, it has driven a revolution in economic theory. Additionally, it has found applications in sociology and psychology, and established links with evolution and biology. Game theory received special attention in 1994 with the awarding of the Nobel prize in economics to Nash, John Harsanyi, and Reinhard Selten. At the end of the 1990s, a high-profile application of game theory has been the design of auctions. Prominent game theorists have been involved in the design of auctions for allocating rights to the use of bands of the electromagnetic spectrum to the mobile telecommunications industry. Most of these auctions were designed with the goal of allocating these resources more efficiently than traditional governmental practices, and additionally raised billions of dollars in the United States and Europe.Backward inductionBackward induction is a technique to solve a game of perfect information. It first considers the moves that are the last in the game, and determines the best move for the player in each case. Then, taking these as given future actions, it proceeds backwards in time, again determining the best move for the respective player, until the beginning of the game is reached.Common knowledgeA fact is common knowledge if all players know it, and know that they all know it, and so on. The structure of the game is often assumed to be common knowledge among the players.Dominating strategyA strategy dominates another strategy of a player if it always gives a better payoff to that player, regardless of what the other players are doing. It weakly dominates the other strategy if it is always at least as good.Extensive gameAn extensive game (or extensive form game) describes with a tree how a game is played. It depicts the order in which players make moves, and the information each player has at each decision point.GameA game is a formal description of a strategic situation.Game theoryGame theory is the formal study of decision-making where several players must make choices that potentially affect the interests of the other players.Mixed strategyA mixed strategy is an active randomization, with given probabilities, which determines the player’s decision. As a special case, a mixed strategy can be the deterministic choice of one of the given pure strategies.Nash equilibriumA Nash equilibrium, also called strategic equilibrium, is a list of strategies, one for each player, which has the property that no player can unilaterally change his strategy and get a better payoff.PayoffA payoff is a number, also called utility, which reflects the desirability of an outcome to a player, for whatever reason. When the outcome is random, payoffs are usually weighted with their probabilities. The expected payoff incorporates the player’s attitude towards risk.Perfect informationA game has perfect information when at any point in time only one player makes a move, and knows all the actions that have been made until then.PlayerA player is an agent who makes decisions in a game.RationalityA player is said to be rational if he seeks to play in a manner which maximizes his own payoff. It is often assumed that the rationality of all players is common knowledge.Strategic formA game in strategic form, also called normal form, is a compact representation of a game in which players simultaneously choose their strategies. The resulting payoffs are presented in a table with a cell for each strategy combination.StrategyIn a game in strategic form, a strategy is one of the given possible actions of a player. In an extensive game, a strategy is a complete plan of choices, one for each decision point of the player.Zero-sum gameA game is said to be zero-sum if for any outcome, the sum of the payoffs to all players is zero. In a two-player zero-sum game, one player’s gain is the other player’s loss, so their interests are diametrically opposed.。
Game theory博弈论

that is:
* * i, xi Si : f i ( xi* , x ) f ( x , x i i i i )
To prove the existence of a Nash Equilibrium, we need using the Kakutani fixed point theorem, John Nash have proved it in 1951.
The end,thank you!
General and applied uses
As a method of applied mathematics, game theory has been used to study a wide variety of human and animal behaviors. It was developed in economics to understand a large collection of economic behaviors. Game theory in the social sciences has been applied to political, sociological, and psychological behaviors as well.
let xi be a strategy profile of player i and
x i be a strategy profile of player i , When each player i {1,, n},
xi resulting in strategy profile x ( x1 xn),
The games studied in game theory are welldefined mathematical objects. To be fully defined, a game must specify the following elements: the players of the game the information the actions available to each player at each decision point the payoffs for each outcome
喜欢数学的原因英语作文

喜欢数学的原因英语作文Mathematics is a field that has fascinated me since a young age. The elegance and precision of mathematical concepts, the challenge of solving complex problems, and the wide-ranging applications of mathematical principles have all contributed to my deep appreciation for this subject. In this essay, I will explore several key reasons why I have grown to love mathematics.Firstly, I am drawn to the inherent logic and structure of mathematics. The discipline is built upon a foundation of axioms, theorems, and proofs that form a cohesive and interconnected system. As I delve deeper into mathematical concepts, I am continually amazed by the way in which these building blocks can be combined to generate new insights and solve seemingly intractable problems. The process of working through a mathematical proof, step-by-step, to arrive at an undeniable conclusion is deeply satisfying and intellectually stimulating.Moreover, I find great joy in the process of problem-solving that is central to mathematics. Whether it is tackling a complex equation,devising a strategy for a geometric construction, or analyzing the behavior of a mathematical function, the challenge of arriving at a solution through careful reasoning and analysis is immensely rewarding. The thrill of the "aha" moment, when the pieces of a problem suddenly fall into place, is unparalleled. This sense of accomplishment and mastery fuels my passion for the subject and drives me to continually push the boundaries of my mathematical knowledge.Beyond the intrinsic appeal of the discipline itself, I am also captivated by the wide-ranging applications of mathematics in the real world. From the design of efficient transportation systems to the development of cutting-edge medical technologies, mathematical principles underpin countless aspects of modern society. This realization has broadened my perspective on the importance of mathematics and has inspired me to explore how this field can be used to address pressing global challenges.For example, in my study of statistics, I have gained a deeper understanding of how data can be leveraged to inform decision-making and drive positive change. The ability to analyze complex data sets, identify patterns and trends, and draw meaningful conclusions has proven invaluable in fields as diverse as public health, environmental policy, and business strategy. By mastering the tools of statistical analysis, I have developed a powerful set of skills thatcan be applied to a wide range of real-world problems.Similarly, my exploration of game theory has illuminated the ways in which mathematical models can be used to understand and predict human behavior in strategic interactions. From negotiating international treaties to designing effective incentive structures, the insights gained from game theory have far-reaching implications for fields such as economics, political science, and computer science. The opportunity to apply mathematical reasoning to the complexities of human interaction is both intellectually stimulating and socially impactful.Furthermore, I am captivated by the elegance and beauty inherent in mathematical concepts. The symmetry of geometric shapes, the harmonious patterns of fractals, and the graceful curves of calculus-based functions all evoke a sense of awe and wonder. This aesthetic dimension of mathematics, which is often overlooked, has had a profound impact on my appreciation for the subject. It is a testament to the inherent beauty of the discipline that some of the most profound mathematical discoveries have been driven by a pursuit of elegance and simplicity.Finally, I am drawn to the collaborative and interdisciplinary nature of mathematics. The field is characterized by a rich history of collaboration, with mathematicians from diverse backgrounds anderas building upon each other's work to push the boundaries of human knowledge. The opportunity to engage with a global community of scholars, to learn from their insights and perspectives, and to contribute to the collective understanding of mathematical principles is both humbling and exhilarating.Moreover, the versatility of mathematics allows it to intersect with a wide range of other disciplines, from physics and engineering to biology and economics. By bridging the gaps between these fields, mathematicians play a crucial role in driving interdisciplinary innovation and fostering a deeper understanding of the natural and social worlds. The chance to collaborate with experts from various domains and to apply mathematical reasoning to complex, real-world problems is a constant source of inspiration and intellectual growth.In conclusion, my love for mathematics stems from a deep appreciation for its inherent logic and structure, the joy of problem-solving, the wide-ranging applications of mathematical principles, the elegance and beauty of mathematical concepts, and the collaborative and interdisciplinary nature of the field. As I continue to explore the depths of this captivating discipline, I am confident that my passion for mathematics will only continue to grow, and that the insights and skills I gain will serve me well in my pursuit of knowledge and in my efforts to make a positive impact on the world.。
仿写学弈文言文英文作文

仿写学弈文言文英文作文全文共2篇示例,仅供读者参考仿写学弈文言文英文作文1:Certainly! Writing an essay in English that mimics the style of classical Chinese literature, particularly focusing on the concept of game theory, presents a unique and enriching challenge. Here's a structured outline to guide you through the process:Title: Exploring Game Theory Through Classical Chinese ProseI. Introduction- Setting the Context: Briefly introduce the concept of game theory and its significance in modern decision-making processes.- Objective: Explain the purpose of the essay, which is to emulate the style of classical Chinese prose while discussing game theory principles.II. The Essence of Game Theory in Classical ChinesePerspective- Understanding Conflict and Strategy: Discuss how classical Chinese philosophers like Sun Tzu and Confucius explored themes of conflict, strategy, and decision-making in their writings.- Analogies in Nature: Draw parallels between the strategies observed in nature and the principles of game theory, as observed by ancient Chinese scholars.III. Emulating Classical Chinese Prose- Language and Style: Analyze the distinctive features of classical Chinese prose, such as parallelism, symbolism, and aphoristic expressions.- Incorporating Proverbs and Allusions: Integrate traditional Chinese proverbs and allusions to enhance the authenticity and richness of the prose.IV. The Strategic Game of Life: A Parable- Narrative Structure: Craft a parable or allegory that illustrates the dynamics of strategic decision-making using characters and settings reminiscent of classical Chinese literature.- Symbolism and Allegory: Infuse the narrative with symbolic elements that represent different aspects of game theory, such as cooperation, competition, and negotiation.V. The Wisdom of the Ancients: Lessons for Modern Game Theorists- Interpreting the Parable: Analyze the moral or philosophical insights embedded within the parable, relating them to contemporary applications of game theory.- Relevance to Modern Society: Discuss how the principles elucidated in classical Chinese literature can inform and enrich the practice of game theory in diverse fields, including economics, politics, and psychology.VI. Conclusion- Summarizing Insights: Recap the key points discussed in the essay, emphasizing the synthesis of classical Chinese literary techniques and modern concepts of game theory.- Reflection and Implications: Reflect on the significance of bridging cultural traditions with contemporary theories, highlighting the enduring relevance of classical wisdom in an ever-evolving world.VII. References (Optional)- Cite Classical Chinese Texts: Provide citations for relevant classical Chinese texts and translations consulted during the writing process.- Additional Reading: Recommend further readings for readers interested in exploring the intersection of classical Chinese philosophy and game theory.By following this outline, you can craft a compelling and insightful essay that seamlessly blends the elegance of classical Chinese prose with the analytical rigor of game theory. Remember to immerse yourself in the nuances of both traditions to create a truly immersive and enlightening narrative.仿写学弈文言文英文作文2:Title: A Linguistic Experiment: Crafting a Classical Chinese-Inspired English EssayIn the vast expanse of literary exploration, there exists a realm where languages converge, where the ancient elegance of Classical Chinese meets the structured cadence of modernEnglish. This linguistic fusion invites us to embark on a journey of creative expression, transcending the barriers of time and culture. In this essay, we shall embark on a daring endeavor: to compose an English prose inspired by the nuanced style of Classical Chinese literature.In the realm of strategic contemplation, akin to the sage scholars of antiquity engaged in the art of strategy (弈), we shall navigate the intricate paths of language with careful deliberation. Let us first establish the foundational pillars of our composition, drawing inspiration from the timeless wisdom encapsulated within the pages of classical texts.In the grand tapestry of language, each word serves as a brushstroke, weaving a narrative that transcends mere communication. Thus, we shall adorn our prose with the ornamentation of imagery and metaphor, invoking the natural world and the celestial realm to imbue our words with depth and resonance.Behold the tranquil surface of a placid lake, mirroring the ethereal dance of the moon upon its waters. Here, amidst thestillness of the night, we find a reflection of the human soul, a repository of dreams and aspirations. Like the ripples that gently disturb the lake's surface, our words shall stir the hearts of readers, evoking emotions that resonate across the ages.In the realm of discourse, the art of rhetoric reigns supreme, guiding the flow of thought like a skilled navigator charting a course through treacherous waters. Let us harness the power of parallelism and antithesis, weaving a tapestry of contrasts that captivates the mind and stirs the spirit.Behold the juxtaposition of light and shadow, emblematic of the eternal struggle between opposing forces. In the arena of conflict, where adversaries clash like titans locked in mortal combat, we find the crucible of human endeavor. Through the interplay of opposing ideas and perspectives, we shall illuminate the path to enlightenment, guiding readers towards a deeper understanding of the human condition.In the realm of composition, the structure serves as the scaffold upon which our words are arrayed, guiding the reader's journey with clarity and purpose. Let us invoke thespirit of balance and harmony, crafting sentences that flow with the grace of a winding river, meandering through verdant valleys and towering peaks.Behold the symmetry of the classical form, a testament to the enduring beauty of proportion and balance. Here, amidst the intricate lattice of syntax and semantics, we find a refuge from the chaos of the world, a sanctuary where the mind may find solace and repose. Through the artful arrangement of words and phrases, we shall construct a narrative that resonates with clarity and conviction, guiding readers towards a deeper appreciation of the art of rhetoric.In the realm of conclusion, let us reflect upon the journey we have undertaken, weaving a tapestry of words that transcends the limitations of language and culture. Through the interplay of imagery and metaphor, rhetoric and structure, we have endeavored to capture the essence of the classical tradition, breathing new life into ancient wisdom for a modern audience.Behold the culmination of our efforts, a testament to theenduring power of language to inspire, to enlighten, and to elevate the human spirit. In the timeless dance of words and ideas, let us find solace and inspiration, forging a connection that transcends the boundaries of time and space. For in the symphony of language, we find a reflection of our shared humanity, a bond that unites us across the ages in a celebration of the human spirit.。
清华大学课程安排(所有学院所有课程超级全)

课程名
英文课程名
开课系所 学时 学分 教材
00510011
经济法
Economic Law
经管学院
32
《民商法原理 与实务》魏振 1 瀛著 北大出 版社
00510021
经济学基础
Introduction to Economics
经管学院
32
1
《经济学基础 》陈章武
00510031
企业管理基础
Foundation of Enterprise Management
经管学院
48
3
《国际经济学 》
00510281
日本经济专题讲座
Lectures on Japanese Economy 经管学院
16
1 自编讲义
00510291
现代金融研究方法
Methodology for modern finance study
经管学院
16
1
00510293
质量管理学
Quality Management
00510232
技术创新管理
Management of Technological 经管学院 Innovation
32
《技术创新管 理》吴贵生著 2 清华大学出版 社
00510241
商法原理与实务
The Theory and Practice of Business Law
经管学院
32
《经济法律原 理与实务》清 1 华大学出版社 吕春燕主编
经管学院
32
1
00510041
中国经济发展与改革 Topics on Chinese Economic 经管学院 专题 Development and Reformation
游戏基础培训的专业灾难管理执行人员的游戏玩法适应性设计:故事板设计说明书

Game-Based Training of Executive Staff of Professional Disaster Management: Storyboarding Adaptivity of Game Play Sebastian Arnold1, Jun Fujima1, Klaus P. Jantke1,Andreas Karsten2 & Harald Simeit21Fraunhofer IDM T, Children’s Media Department, Erfurt, Germany2German Federal Office of Civil Protection and Disaster AssistanceAbstractGame-Based Learning is a modern field of technology-enhanced learning cover-ing several sub-fields such as game-based training. Learning, in general, and train-ing, in particular, may be enormously more effective, if the process adapts to the particular needs of the human learner or trainee. The crux is that an e-learning system, in general, or a game deployed for learning resp. training, in particular, for being able to adapt needs to learn about the needs and desires of the human addressee. Essentially, adaptive systems are learning systems. Consequently, the design of any adaptive training systems requires an anticipation, first, of when and how to learn about the human trainee and, second, of when and how to adapt to the human trainee’s particular needs and desires hypothesized. When game-based learning and/or training goals and tasks are ambitious, related systems are easily becoming complex. Storyboarding is the methodology of the systematic reliable design of involved game-based training applications. The work reported has been developed for and is deployed by a gov-ernmental agency in charge of training executive staff in disaster management. Keywords: Game-Based Learning, Game-Based Training, Disaster Management, Adaptivity, Storyboarding. 1.IntroductionThere is surely no need to convince the scientific audience of a major conference on advanced information and communi-cation technologies for education of the relevance of adaptivity to successful learning and training. Cronbach [3] has made the issue clear and, beginning about 30 years ago, adaptivity concepts and technologies have been mushrooming. Nowadays, there is not much doubt that adaptivity is well-established, at least in the academia [2], [9].The aim of the present publication is to inform the audience about some rather interesting and practically relevant appli-cation. The interestingness and relevance lies in the peculiar application domain which is training of executive staff of professional disaster management.The authors’ implementation is some browser game running on the e-learning platform of the German Federal Office for Civil Protection and Disaster Assis-tance (German abbreviation: BBK). Besides informing the audience about this game-based training project, it is the authors’ intention to explicate the role of storyboarding for game design and, in particular, to demonstrate the role of the storyboard playing the game.This, apparently, requires to begin with some investigations into storyboarding.International Conference on Advanced Information and Communication Technology for Education (ICAICTE 2013)2.Storyboarding as a Methodology ofEducational Media DesignThe present paper uses storyboarding as a technology, but does not aim at anything such as an introductory course to story-boarding. The authors rely on the basics as introduced by [6] and confine them-selves to those notions and notations needed for the purpose of characterizing training games. Recent work on story-boarding digital games such as [1,7,8], e.g., is worth some comparison. Storyboards are hierarchically struc-tured graphs. The composite nodes are named episodes, whereas the atomic nodes are named scenes. Composite nodes may be subject to substitution by other graphs. In contrast, atomic nodes have some semantics in the underlying domain. They may represent documents such as videos, pictures, or text files in formats like pdf, e.g., but they may also represent some activities of human learn-ers, co-learners, teacher, tutors, or those actions performed by a digital systems. The usage of composite nodes in some storyboard graph allow for a remarkably declarative representation of anticipated experiences on different levels of granu-larity–cf. the idea of layered languages of ludology [12].Fig.1: Cutout of a Storyboard with 3 Episodes Just for illustration, the storyboard in the figure above shows two alternative substitutions for episode ‘Enter Room’. In general, storyboards contain parallel-isms and alternatives and, as shown, branches and loops.In contrast to the introductory examplePickupMessagePickupMessageSensitiveIntuitiveActive ReflectiveIntuitiveSensitiveFig. 2: Cutout of some Storyboard in Use for Game-Based Training of Disaster Management The usage of this storyboard in fig. 2 will be discussed in much detail below.3.Game-Based Training of Staff forProfessional Disaster Management Staff in professional disaster management has to be prepared for unforeseeable and usually rather severe events. The crux is to internalize principles of staff collabora-tion and patterns of behavior which are of a certain generality.Formally, many of those principles are represented in documents regulating the duties and responsibilities in much detail. However, it is almost impossible for a human learner to memorize the contents of those documents simply by reading, as the amount of information is much too large and descriptions are highly generic to fit larger numbers of varying cases. The right decision in the right moment and appropriate steps of the right process must be internalized by intensive training. Training, however, is a collaborative process depending on the behavior of the other trainees playing particular roles in a fictitious staff under fictitious conditions of an assumed disaster scenario. In other words, the training effectiveness of an individual trainee does not depend on this tra inee’s experience, engagement, and behavior, alone. It depends very much on the way in which the whole staff team works together.Imbalanced individual experience and prior knowledge is a severe obstacle to effective training.The authors provide a Web-based sys-tem for individual preparation of trainees. According to the needs of large-scale staff training for disaster management, there is the crucial requirement to make technology enhanced components highly adaptive to the varying needs, wishes and desires of individuals. The ultimate aim of this contribution is to explain the way in which the authors’ solution is made adaptive. The present approach is generic and may be adopted and adapted by other authors for largely varying purposes. 4.Adaptive Game Playing Behaviorfor Effective Learning and Training For teaching and training–whether it is technology-enhanced or not–intended to meet high expectations, adaptivity to the individ ual learner’s and/or trainee’s pec u-liarities is known to be essential [2,3,10]. Adaptivity depends on an assumption about how to model those peculiarities. There are models such as David Kolb’s Learning Style Inventory [11] focusing individual preferences of how to ap-proach learning situations and the Myers-Briggs Type Indicator [13] putting em-phasis on a human’s activity in team work. Within the training scenarios for preparedness in disaster management un-der consideration, both models–although widely differing from each other–seem to be appropriate, to some extent. Interest-ingly, the learner model by Felder and Silverman [5] looks a bit like compromis-ing the Kolb LSI and the MBTI. Accordingly, the authors decided to represent trainee profiles within a certain 4-dimensional space reflecting the four canonical dichotomies of the classical Felder/Silverman user modeling theory. These dichotomies are active – reflective, sensing –intuitive, visual –verbal and sequential – global ([5], see also [4]). For the purpose of trainee modeling, there is set up (nearly) a continuum between the endpoints of each of the dimensions.In dependence on the current state of trainee modeling, every trainee is guided through the game experience and is con-fronted to problems of the virtual disaster in an order and in a way which is likely to develop knowledge and preparedness in an optimal way.Within the highly complex process of game design, system development, and contents allocation, it is crucial to plan the multiple variants of potentially forth-coming experience. The technology of choice is storyboarding according to [6].5. Digital Game Playing Behavior as Dynamic Storyboard Interpretation Storyboards are digital documents designed to anticipate the trainee’s future exper ience in dependence on hypothesized needs [6]. The approach is known to work well on quite different levels of granularity [7,9].Fig. 3: Storyboard and Content Interpreted by the Game-Based Training System in OperationIt is basic that, in contrast to a majority of conventional approaches, the authors do not allow for handwritten storyboards which contain fancy sketches, artistic hand drawings, on the fly annotations, and the like, but that they insist in digital objects. As such, they may be either loaded into the resulting game system or may remain out-side the system in such a way that the sys-tem can access and interpret the content. Figure 3 is illustrating the storyboard of the authors’ application development with some relational database –visualized within some Excel file –containing content to bedisplayed during game play.Fig. 4: Zoom into Figure 3 Focusing Node 100The digital game system may be seen as an interpreter running on the storyboard.When it is reaching node 100 (the first read node in the right upper corner of figure 4 and, better to see, on top of figure 5 below), it is reading some text from the database (the highlighted cell of the Excel document) to display it on the screen. The text shown is announcing three alternatives to act. Those correspond to the three outgoingedges of node 100.Fig. 5: Anticipated Choices in Playing the GameThe situation at node 100 is made moreexplicit in figure 5 above.Fig. 6: The Trainee’s Choices when Interpre ting the Digital Storyboard has Reached Node 100The trainee (i) may take up some docu-ment sitting in the inbox on the table (left button) to fill in some particular command,(ii) may talk to some other staff member (central button) or (iii) may have a closer look at the situation map. In the storyboard (see figure 5), these choices are indicated by edges marked with related keywords such as ‘WriteCommand’, ‘TalkToS2’ and ‘LookAtMap’.As can be seen from figure 5, there are some more choices to come at node 102. The authors’ game system is understand-ing the trainee’s choice as some preference. Repeatedly observed preferences are taken as a basis for updating the internal trainee model.In dependence on the hypothesized char-acteristics of the human trainee in terms of the internal Felder-Silverman profile, the possible experiences of game playing arearranged differently.Fig. 7: Some Points of Adaptation to Train ee’s in Accordance to their Felder-Silverman ProfileFigure 7 shows some of several dozens of profile-depending branching points of the storyboard.The branching at node 50 distinguishes ‘JobYes’ and ‘JobNo’ meaning that the trainee has alrwady experience with staff training or not, respectively.The branching at node 53 offers totally different game playing experiences to those trainees who are global thinkers according to the Felder-Silverman model in contrastto those who are more locally oriented. The latter get offered more conversation and more detail to feel more secure in the cur-rent game state.The few illustrations and cases above are intended to exemplify what a storyboard is particularly seen from the viewpoint of adaptivity to trainees with largely varying preferences. In particular, emphasis was put on the need to have digital storyboards which may serve as components of the game system under consideration. In the authors’ approach, all the storyboards ar e XML files.When the storyboards may be used as system components, the usually quite error-prone process of implementing storyboards disappears from the development process. Didactic design by means of storyboard-ing means essentially two things: first, anticipating and specifying alternatives that are appropriate for drawing conclusions from a trainee’s choice useful for profiling, second anticipating and specifying different ways in which human trainees of different characteristics can be served best towards an optimal training outcome.The enormous advantage of storyboarding is that sophisticated decisions may be made in some highly declarative form. In this form, the decisions may be visualized as graphs that are understandable to domain experts without any particular preparation for technology enhanced learning/training. One can take a storyboard as a graph into a review meeting and debate branching points deployed for user modeling as well as those in which the system adapts to the hypothe-sized human needs. The intellectual power of the involved personal is released from pondering technicalities and may focus on the essential of the domain, on human needs, and on training effects.In dependence on the deployed system architecture, it is even possible to play, so to speak, with variants of storyboards for evaluating didactic concepts and for tuning the behavior of the system.6.AcknowledgementMembers of the three first authors’ d e-partment did enjoy the opportunity of participating in training courses at the BBK’s academy. In this way, the authors’ conceptual work as well as their practical implementations have been put on a firm basis.7.References[1]S. Arnold, J. Fujima and K. P. Jantke,“Storyboarding Serious Games forLarge-scale training Applications”, 5th International Conference onComputerSupported EducationCSEDU 2013, O. Fowley, M. T.Revisto, J. Uhomoibhi and M. Helfert(eds.), pp. 651-655, May 6-8, 2013,Aachen, Germany, SciTePress 2013.[2]P. Brusilovsky and M. T. Maybury,“From adaptive hypermedia to theadaptive Web”, Communications ofthe ACM 45(5):30-33, 2003.[3]L. J. Cronbach, “The two disciplinesof scientific psychology”, AmericanPsychologist, pp. 671-684, 12:1957. [4] S. Graf, S. R. Viola, T. Leo & Kin-shuk, “In-Depth Analysis of theFelder-Silverman Learning Style Di-men sions”, Journal of Research onTechnology in Education40(1): 79-93, 2007.[5] R. M. Felder and L. K. Silverman,“Learning and Teaching Styles inEngineering Education”, EngineeringEducation 78(7):674-681, 1988. [6] K. P. Jantke an d R. Knauf, “D idacticdesign through storyboarding: Stand-ard concepts for standard tools”, Proc.4th International Symposium on In-formation and Communication Tech-nologies, Cape Town, South Africa,2005, B.R. Baltes, L. Edwards, F.Galindo et al. (eds.), pp. 20-25, Dub-lin, Ireland: Computer Science Press,2005. [7] K. P. Jantke and R. Knauf, “Tax o-nomic concepts for storyboardingdigital games for learning in context”, 4th International Conference onComputer-Supported Education,CSEDU 2012, Porto, Portugal, M.Helfert, M.J. Martins, and J. Cordeiro(eds.), pp. 401-409, SciTePress, 2012.[8] K. P. Jantke and S. Spundflasch,…Understanding Pervasive Games forP urposes of Learning”, 5th Interna-tional Conference onComputerSupported EducationCSEDU 2013, O. Fowley, M. T.Revisto, J. Uhomoibhi and M. Helfert(eds.), pp. 696-701, May 6-8, 2013,Aachen, Germany, SciTePress 2013.[9] R. Knauf, Y. Sakurai, S. Tsuruta, andK. P. Jantke, “Modeling didacticknowledge by storyboarding”, J.Educational Computing Research42(4): 355-383, 2010.[10]A. Kobsa, “Generic User Mode lingSystems”, User Modeling and User-Adaptive Interaction11(1-2):49-63,2001.[11]D. A. Kolb, “Experiential Learning:Experience as the Source of Learningand Development”, NJ, USA: Pre n-tice-Hall.[12]C. Lenerz, “Layered Languages ofLudology –eine Fallstudie”, DigitaleSpiele –Herausforderungen undChance, A. Beyer und G.Kreuzberger (Hg.), Boizenburg,Germany: VWH, pp. 39-52, 2009. [13]I. Myers-Briggs, “The Myers-BriggsType Indicator Manual”, Pr inceton,NJ, USA: Educational Testing Ser-vice, 1962.[14]M. Prensky, “Digital Game-BasedLearning”, McGraw-Hill, 2001. [15]U. Ritterfeld, M. Cody, P. Vorderer,“Serious Games. Mechanisms and Ef-fects”, New York, NY, USA: Rout-ledge, 2009.。
Mathematical Models Game Theory 博弈论数学模型

Mathematical Models: Game TheoryMark FeyUniversity of RochesterThis course is designed to teach graduate students in political science the tools of game theory. The course will cover the standard group of essential concepts and some additional topics that are particularly important in formal theory. In addition, we will cover some specific applications of game theory in political science.Students should have, at a minimum, a mathematical background of algebra (solving equations, graphing functions, etc.) and a basic knowledge of probability. Development of the theory does not require calculus, although some applications will be presented that utilize basic calculus (i.e., derivatives). A very brief summary of the necessary mathematics is in Appendix One of Morrow.Game theory, as with most mathematical topics, is best learned by doing, rather than reading. Thus, an important part of the course will be the problem sets covering the lecture material and readings. These problem sets will count for 60% of the final grade, and a take-home exam at the end of the course will count for 40% of the final grade. Solutions to the problem sets will be covered in class. Auditors are welcome, and those who complete the problem sets and keep up with the lectures and reading will be entitled to seek help with problems and with the material. There are two required texts for the course:James Morrow, 1995. Game Theory for Political Scientists. Princeton University Press.Robert Gibbons, 1992. Game Theory for Applied Economists. Princeton University Press. Other readings will be made available to you for photocopying.ScheduleJune 27Introduction, Basic Assumptions of Rational ChoiceMorrow: Chs. 1-2June 28 Decision Theory, OptimizationJune 29 Representing Games, Strategic Form GamesMorrow: Chs. 3-4June 30 Strategic Form Games129July 3 & 4 No class, but lots of fireworks!July 5 Strategic Form Games, DominanceGibbons: Sec. 1.1July 6 Nash Equilibrium, Mixed StrategiesGibbons: Sec. 1.3July 7 Zero-sum Games, ApplicationsJuly 10 Extensive Form Games, Backwards Induction Morrow: Ch. 5July 11 Subgame Perfection, Forward InductionGibbons: Ch. 2July 12 Bayesian Games, Bayesian EquilibriumMorrow: Ch. 6July 13 Bayesian EquilibriumGibbons: Ch. 3July 14 Perfect Bayesian Equilibrium and Sequential Equilibrium Morrow: Ch. 7Gibbons: Sec. 4.1July 17 Sequential EquilibriumJuly 18 Signaling GamesMorrow: Ch. 8Gibbons: Sec. 4.2July 19 Cheap Talk GamesGibbons: Sec. 4.3July 20 Repeated GamesMorrow: Ch. 9July 21 Applications, Wrap-up130。
