上海市高三数学基础练习【5.2012.3】
上海高三数学练习题

上海高三数学练习题一、选择题1. 设函数f(x) = 2x^2 - 3x + 4,下列说法正确的是:A. 函数f(x)是偶函数B. 函数f(x)是奇函数C. 函数f(x)既不是奇函数也不是偶函数D. 函数f(x)是单调递增函数2. 已知函数f(x) = |x|,则f(-2)的取值为:A. -2B. 2C. 0D. -43. 设函数f(x) = x^3 - 3x^2 + 2x,下列说法正确的是:A. 函数f(x)的零点是x = 1和x = 2B. 函数f(x)的零点是x = -1和x = 2C. 函数f(x)的零点是x = -2和x = 1D. 函数f(x)的零点是x = -2和x = -14. 已知直角三角形的斜边长为5,其中一个直角边长为3,则另一个直角边的长为:A. 4B. 2C. 1D. 35. 已知直角三角形的斜边长为10,其中一个直角边长为6,则另一个直角边的长为:A. 8B. 4C. 2D. 6二、填空题1. 已知函数f(x) = x^2 - 3x + 2,求f(2)的值:2. 已知函数f(x) = |x + 1|,求f(-3)的值:3. 已知函数f(x) = 2x^3 + 3x^2 - x,求f(0)的值:4. 已知函数f(x) = |x - 2|,求f(4)的值:5. 设直角三角形的斜边长为13,其中一个直角边长为5,求另一个直角边的长:三、解答题1. 解方程:2x + 3 = 72. 解方程组:{ 2x - y = 5{ x + y = 13. 已知函数f(x) = (x - 3)^2 + 4,求f(x)的极值点。
4. 已知函数f(x) = x^2 - 4x,求f(x)的单调递增区间。
5. 已知函数f(x) = |x - 2|,求f(x)的零点。
四、应用题1. 小明去超市买水果,他买了苹果和橙子两种水果。
苹果每斤5元,橙子每斤3元。
小明买了苹果和橙子共计8斤,总共花了36元。
求小明买了多少斤苹果和多少斤橙子。
上海市高三数学基础练习

上海市高三数学基础练习高三数学基础练习【7B】(2022.3)班级学号姓名得分【在老年时,会有许多闲暇的时间,去计算那过去的日子,把我们手里永久丢失了的东西,在心里爱抚着。
】1.在()n某+1的展开式中,若3某的系数是某的系数的5倍,则=n________.1、72.函数f(某)=2的定义域为.2、[3)+∞,3.设函数,31)(某某f-=则方程()21=-某f的解是______________.3、某=-84.函数()()某某某某某f22coin3coin2--=的最小值是_____________.4、-25.函数2()(1)1(1)f某某某=-+<的反函数为5、1()11)f某某-=>6.虚数i某某)12()1(-+-(R某∈)的模不大于10,则某的取值范围是____.6、]2,21()21,54[-7.若角α的终边经过点(12)P-,,则tan2α的值为.7、43某f的值都出现4次,则实数k=______________.9、3,-510.设)(某f是奇函数,在),0(+∞内递增,,0)1(=-f则0)(<某某f解是_____.10、)1,0()0,1(-11.已知正四棱锥的底面的边长为a,侧棱的长为ka,体积不大于331a,那么k的取值范围是______________.11、2622≤<k12.曲线2=某y上与原点距离最近的点的坐标是______________.12、)2,2(),2,2(--13.集合{}|lg1Ayy某某=∈=>R,,{}2112B=--,,,,则下列结论中正确的是(D)A.{}21AB=--,B.()(0)AB=-∞R,ðC.(0)AB=+∞,D.(){}21AB=--R,ð14.在同一平面直角坐标系中,函数()yg某=的图象与某ye=的图象关于直线y某=对称,而函数()yf某=的图象与()yg某=的图象关于y轴对称,若()1fm=-,则m的值为(B)A.e-B.1e-C.eD.1e15.若函数()()f某g某,分别为R上的奇函数、偶函数,且满足()()某f某g某e-=,则有(D)A.(2)(3)(0)ffg<<B.(0)(3)(2)gff<<C.(2)(0)(3)fgf<<D.(0)(2)(3)gff<<16.设>+≤--=1||,111||,2|1|)(2某某某某某f,则=))21((ff(B)(A)21(B)134(C)59-(D)412517.已知等差数列{}na中,26a=,515a=,若2nnba=,则数列{}nb 的前5项和等于(C)A.30B.45C.90D.18618.已知ABC△中,a=B.90C.45D.3019.设平面α、β相交于直线l,异面直线ba、分别在、αβ内,则l(B).(A)必与ba、都相交(B)至少与ba、中一条直线相交(C)必与ba、都不相交(D)至多与ba、中一条直线相交20.函数co()y某某=∈R的图象向左平移2π个单位后,得到函数()yg某=的图象,则()g某的解析式为(A)A.in某-B.in某C.co某-D.co某。
上海数学教材练习册高三全一册习题精选

第14章空间直线与平面1.(册P2. 2)三个平面可以把空间分割成__________________个部分.2.(册P7. 1)“直线l垂直于平面α内的无数条直线”是“lα⊥”的___________条件.3.(册P8. 7)已知△ABC,点P是平面△ABC外一点,点O是点P在平面ABC上的射影,且点O在△ABC内.(1)若点P到△ABC的三个顶点的距离相等,则点O一定是△ABC的_______心;(2)若点P到△ABC的三边所在直线的距离相等,则点O一定是△ABC的_______心;(3)若PA BC⊥,PB AC⊥,PC AB⊥,则点O一定是△ABC的_______心.4.(册P10. 2)(理科)已知P是二面角ABαβ--内一点,PCα⊥,垂足为C,PDβ⊥,垂足为D,且3PC=,4PD=,60CPD∠=.(1)求二面角ABαβ--的大小;(2)求CD的长.5.(册P21. 8)(理科)如图,已知二面角lαβ--的两个面内各有一点A、B,A、B在直线l的射影分别为点C、D,3AC BD==,而4CD=,5AB=,求二面角lαβ--的大小.第15章简单几何体6.(本P29例6)如图,在正方体1111ABCD A B C D-中,点P和Q位于平面11BB C C上DCBAlβαRQPB111ADBEB1D1C1ADBA(PQ 与BC 不平行),点R 位于棱11A B 上,作出由P 、Q 、R 三点确定的平面截正方体所得的截面.7. (本P30. 2)如图,在正方体1111ABCD A B C D -中,E 、F 、H 分别是棱11C D 、1CC 、AB 上的点,画出过点E 、F 、H 的正方体的截面.8. (册P25. 2)从一个底面半径和高都是R 的圆柱中,挖去一个以圆柱的上底为底、下底面的中心为顶点的圆锥,得到一个几何体. 如果用一个与圆柱下底面距离等于d 并且平行于底面的平面去截这个几何体,求截面面积.9. (册P29. 2)已知正六棱柱最长的一条对角线长为13厘米,侧面积为180平方厘米,求这个棱柱的体积.10. (册P31. 1)维度为α的纬度圈上有甲乙两地,它们的纬度圈上的弧长等于πcos R α(R 是地球的半径),求甲乙两地的球面距离.11. (册P32. 2)现有以下三个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体. 其中真命题的序号是_______. 12. (册P32. 3)如果一个三棱锥的底面是直角三角形,那么这个三棱锥的三个侧面( )(A )都不是直角三角形 (B )至多只能有一个是直角三角形 (C )至多只能有两个是直角三角形 (D )可能都是直角三角形13. (册P35. 1)已知长方体1111ABCD A B C D -的高为h ,底面积为P ,对角面11BB D D 的面积为Q ,求它的侧面积.14. (册P36. 4)设AB 是球O 的直径,50AB =,1O 、2O 是AB 上的两点,平面α、β分别通过点1O 、2O ,且垂直于AB ,截得圆1O 、圆2O ,当圆1O 、圆2O 的面积分别为49π、400π时,求1O 、2O 两点的距离.第16章 排列组合与二项式定理15.(本P50例3)540的不同正约数共有多少个?16.(本P55例4)求证:11P P Pm m mn n nm-++=.17.(本P55例5)解方程:4321P140Pn n+=.18.(本P55. 2)1!2!3!100!++++的个位数为__________.19.(本P60例4)如果从7名运动员中选4名运动员组成接力队,参加4100⨯接力赛,那么甲乙两人都不跑中间两棒的安排方法有多少种?20.(本P61例6)将a、b、c、d、e、f六个不同元素排成一列,其中a不排在首位,b 不排在末位,有几种排法?21.(本P62. 3)A、B、C、D、E五人站成一排,如果B必须站在A的右边(A、B可以不相邻),那么共有多少种不同的排法?22.(本P64例2)求证:111C C1m mn nmn+++=+.23.(本P65. 3)解不等式:46C Cn n>.24.(本P67. 3)求证:122C C2C Cm m m mn n n n--+=++.25.(本P67. 4)解方程:221818C Cx x+=.26.(本P71例3)求12(1)a+的二项展开式中倒数第5项.27.(本P73例6)已知42nxx的二项展开式中,前三项系数成等差数列,求二项展开式中的所有有理项.28.(本P74. 3)求5555被8除所得的余数.29.(本P75例11)利用二项式定理证明:221n n n>++(5n≥,n∈N*).30.(本P76. 4)求证:0241C C C C2n nn n n n-++++=(n是偶数).31.(册P38. 2)要把4封信投入3个信箱,共有多少种不同的投法?(允许将信全部或部分投入某一个信箱)32. (册P40. 8)已知10P 1095m=⨯⨯⨯,求正整数m 的值.33. (册P42. 3)化简:12312!3!4!!n n -++++. (n ∈N *,2n ≥) 34. (册P42. 5)求证:12311231P 2P 3P P P 1n n n n n ++++++=-. (n ∈N *)35. (册P43. 3)将8个相同的小球放入编号为1、2、3的三个盒子内,要求每个盒子的球数不小于它的编号数,共有多少种不同的放法?36. (册P48. 5)在9(32)x y -的展开式中,求二项式系数的和以及各项系数的和.37. (册P49. 9)求和:1231C 3C 9C 3C n nn n n n -++++.38. (册P49. 10)已知n 为大于1的自然数,证明:112nn ⎛⎫+> ⎪⎝⎭.39. (册P49. 11)在23nx x ⎛⎫- ⎪⎝⎭的二项展开式中,有且只有第五项的二项式系数最大,求012111C C C (1)C 242nnnn n n n -+-+-. 40. (册P49. 1)求和:02498100100100100100100C C C C C -+--+.41. (册P50. 3)在(13)nx +的二项展开式中,末三项的二项式系数之和等于631. (1)求二项展开式中二项式系数最大的项是第几项; (2)求二项展开式中系数最大的项. 42. (册P50. 4)求777715-除以19的余数. 43. (册P50. 5)用两种方法证明:632123n n --+能被11整除.44. (册P50. 6)已知32(1)1nnx x ax bx cx +=+++++(n ∈N *),且:3:1a b =,求c 的值.45. (册P50. 1(4))用数字0、1、2、3、4、5可组成没有重复数字的六位数,其中数字2、4排在相邻数位上,满足条件的六位数共有___________个.46.(册P52. 1)6个人排成一列,其中甲乙两人之间至少有两个人的不同排法种数是___.第17章概率论初步47.(本P90例7改编为2011年高考试题)求随机抽取10个同学中至少有两个同学在同一个月份出生的概率. (精确到0.0001)48.(册P54. 4)某城镇共有10000辆自行车,牌照编号从00001到10000. 求在此城镇中偶然遇到的一辆自行车,其牌照号码中有数字8的概率.49.(册P56. 1)将n间房分给n个人,每个人都以相等的可能性进入每一间房间,而且每间房间里的人数没有限制,求不出现空房的概率.50.(册P56. 2)把10本书随机地排在书架上,求其中指定的3本书排在一起的概率.51.(册P56. 3)某人有5把钥匙,但只有一把能打开门,他每次取一把钥匙尝试开门,求试到第3把钥匙时才打开门的概率.第18章基本统计方法52.(册P61. 2)某班级有40名同学参加打靶训练,他们的成绩如下表所示(单位:环):测验成绩频数[4, 5)2[5, 6)3[6, 7)10[7, 8)15[8, 9)8[9, 10]2求该班同学的成绩2σ区间估计. (精确到0.01)高三总复习题53.(册P71. 13)已知567117C C10Cn n n-=,n∈N*,求8C n.54. (册P74. 5)一个球受热膨胀. 如果它的表面积增加21%,那么这个球的半径增加多少?55. (册P74. 6)求383321C C nnnn -++(n ∈N *)的值.56. (册P75. 8)以一个正方体的顶点为顶点能组成多少个三棱锥? 57. (册P75. 10)已知lg (1)xn x+的二项展开式中,末三项的二项式系数的和为22,二项式系数最大的项为20000,求实数x 的值.。
上海市高三数学基础练习【2B.2012.2】

高三数学基础练习【2B 】(2012.2) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽【如果一个聪明人干了一件蠢事,那就不会是一件小小的蠢事。
(歌德)】1. 函数)1(12-≤-=x x y 的反函数是_______.{ )0(12≥+-=x x y }2. 已知函数141)(,12)(2-=-=x x g x x f ,则=⋅)()(x g x f _____.{)21(121>+x x } 3. 设,0>x 则代数式122++x x 的最小值为 .{23} 4. 不等式01||>+x 的解集是 .{ R } 5. 已知复数i t z i z +=+=21,26,且21z z ⋅是实数,则实数t 的值等于_____.{ 3}6. 已知)0,2(,1312sin πθθ-∈-=,则)4cos(πθ-=__________.{2627-} 7. 若函数)2(3)1()(2n x x m x f -++-=是奇函数,则=m _____,=n ____.{1,2 }8.函数()12+-=x ax x f 有且仅有一个零点,则=a .{0或41} 9.若函数()122+-=mx x x f 在(]2,∞-上是减函数,则实数m 的取值范围为_____.[)+∞,2 10不等式mx mx 220+-<的解集为R ,则实数m 的取值范围为 .]0,8(-11、已知函数[]2,,1)(2b x ax x x f ∈++=是偶函数,则实数a = 、b = .{ 0,2-}12、设函数f(x)是定义在R 上且以3为周期的奇函数,若f(2)=1,则f(1)=___.{ -1}13. 若n b a )3(+的展开式的系数和等于8)(y x +的展开式的系数和,则n=__.{4} 14、已知函数)0(sin 2)(>=ωωx x f 在]3,0[π上单调递增,则ω的范围是____. ]23,0( 15. 对于任意定义在R 上的函数f(x),若存在R x ∈0满足00)(x x f =,则称0x 是函数f(x)的一个不动点。
上海市高三数学基础练习【25.2012.4】

高三数学基础练习【25】(2012.4) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽ 【有些人说不出哪里好,但就是谁都替代不了!】 1. 函数)(x f 的定义域为]2,2[-,则函数)1(2-x f 的中x 的取值范围为____.2.i 为虚数单位,n 为整数,则n n i i S -+=的不同的值分别为_______.3. (1)如果二次函数122+-=mx x y 在](2,∞-上是减函数,则m 可取的整数为_____.只需写出一个符合题意的结果(2) 函数)4(1log )(21≥+=x x x f 的反函数)(1x f -的定义域是________.4. 已知空间三点A (-1,2,3),B (1,1,1),C (0,0,5),则向量→→AC AB 与的夹角大小为______..5. 抛物线y 2=4x 上点P 到点A (4,1)与焦点F 的距离和|PA|+|PF|最小,则P 点的坐标为______.6. (1)3332)21(22---<x x x 的解集为A ,)26(log )9(log 31231x x -<-的解集为B ,02<++b ax x 的解集为B A ⋂,那么直线01=++by ax 的斜率是⎽⎽⎽⎽⎽_.(2)函数|3|||--=x x y 的最大值为______..7. 已知函数221)(x x x f +=,那么=++++++)41()31()21()4()3()2()1(f f f f f f f _____8. 已知实数b a ,满足,1=+b a 则22)2()2(+++b a 的最小值为____________.9. 如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”。
在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是______.10. 已知N k∈,若0)74()21(22=-+--k x k kx 至少有一个整数根,k =_______11. 如果三棱锥S-ABC 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点S 在底面的射影O 在△ABC 内,那么O 是△ABC 的⎽⎽⎽⎽心. 12. 函数ax xy +=2的大致图象如图所示,则( ) A 、)0,1(-∈a ; B 、)41,0(∈a C 、 )1,41(∈a ; D 、),1(+∞∈a 13.1111D C B A ABCD -是正方体,B 1E 1=D 1F 1=411B A ,求BE 1与1DF 所成角的大小(结果用反三角函数表示)14. 已知等比数列}{n x 的各项为不等于1的正数,数列}{n y 满足)1,0(2l o g ≠>=a a a y n x n ,设12,1863==y y .(1)求数列}{n y 的前多少项和最大,最大值为多少?(2)试判断是否存在自然数M ,使当Mn>时,1>n x 恒成立?若存在,求出相应的M ,若不存在,请说明理由;(3)令),13(log 1N n n x a n x n n ∈>=+,试判断数列}{n a 的增减性?AD C B D 1 C 1A 1B 1F 1E1。
上海市高三上学期数学基础测试试卷

上海市高三上学期数学基础测试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共8题;共16分)1. (2分)已知集合,则()A .B .C . (1,2]D . [0,2]2. (2分)已知复数(且≠),且为实数,则()A .B .C .D .3. (2分)下列各命题中正确的命题是①“若都是奇数,则是偶数”的逆否命题是“若不是偶数,则都不是奇数”;② 命题“”的否定是“” ;③ “函数的最小正周期为” 是“”的必要不充分条件;④“平面向量与的夹角是钝角”的充分必要条件是.A . ②③B . ①②③C . ①②④D . ③④4. (2分)在长方体ABCD-A′B′C′D′中,下列直线与平面AD′C平行的是()A . DD′B . A′BC . C′D′D . BB′5. (2分) (2019高二下·蕉岭月考) 将函数的图象上各点的横坐标变为原来的(纵坐标不变),再往上平移1个单位,所得图象对应的函数在下面哪个区间上单调递增()A .B .C .D .6. (2分)已知D是所在平面内一点,则()A .B .C .D .7. (2分)设、分别是定义在R上的奇函数和偶函数。
当时,且。
则不等式的解集是()A .B .C .D .8. (2分)(2020·山西模拟) 过双曲线右焦点的直线交两渐近线于两点,,为坐标原点,且内切圆的半径为,则该双曲线的离心率为()A .B .C .D .二、填空题 (共7题;共8分)9. (1分) (2017高二上·桂林月考) 在等差数列中,若 ________.10. (1分)一个几何体的三视图如右图所示,则该几何体的体积为________ .11. (1分)(2017·榆林模拟) 二项式(﹣)n的展开式中所有项的二项式系数之和是64,则展开式中的常数项为________.12. (2分)(2017·嘉兴模拟) 已知随机变量ξ的分布列如下:ξ 012P b a2﹣则E(ξ)的最小值为________,此时b=________.13. (1分) (2018高三上·南宁月考) 若实数满足,则的最大值为________.14. (1分)已知直线3x+4y+a=0与圆x2﹣2x+y2=0相切,则a的值为________15. (1分) (2019高三上·济南期中) 若向量与互相垂直,且 ,则 ________.三、解答题 (共5题;共45分)16. (10分)(2018·成都模拟) 如图,在平面四边形中,,,,, .(1)求;(2)求四边形的面积.17. (10分) (2019高二下·中山期末) 已知复数其中是实数,(1)若在复平面内表示复数的点位于第一象限,求的范围;(2)若是纯虚数,是正实数,①求,②求;18. (10分) (2019高二上·会昌月考) 如图,在正方体ABCD﹣A1B1C1D1中,棱长为2,M,N分别为A1B,AC的中点.(1)证明:MN//B1C;(2)求A1B与平面A1B1CD所成角的大小.19. (5分) (2019高三上·西藏月考) 已知,求曲线在点处的切线方程.20. (10分) (2020高二下·大荔期末) 如图,在平面直角坐标系中,已知椭圆的离心率为,右焦点F到右准线的距离为3.(椭圆的右准线方程为)(1)求椭圆C的标准方程;(2)设过F的直线l与椭圆C相交于两点.已知l被圆截得的弦长为,求的面积.参考答案一、选择题 (共8题;共16分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:二、填空题 (共7题;共8分)答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:三、解答题 (共5题;共45分)答案:16-1、答案:16-2、考点:解析:答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、考点:解析:答案:20-1、答案:20-2、考点:解析:。
上海市高三数学基础练习【5B】

高三数学基础练习【5B 】(2013.2) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽【没有蓝天的深邃,可以有白云的飘逸;没有大海的壮阔,可以有小溪的幽雅;没有原野的芬芳,但可以有小草的翠绿.】1.函数)1(12-≤-=x x y 的反函数是_______.{ )0(12≥+-=x x y }2. 已知函数141)(,12)(2-=-=x x g x x f ,则=⋅)()(x g x f _____.{)21(121>+x x }3. 将参数方程12cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数)化成普通方程为 .设,0>x 则代数式122++x x 的最小值为 .{23} 4. 抛物线281y x -=的焦点坐标为 . (2,0)-5. 已知函数2()321x xf x =⋅+,则11()4f -= . 06. 设定义在R 上的函数()f x 满足()()23f x f x ⋅+=,若()12f =,则()2009f = .27. 已知两直线方程分别为1:210l x y --=、2:20l ax y ++=,若12l l ⊥,则直线2l 的一个法向量为n =. ()1,28. 已知sin 2m πα⎛⎫+=⎪⎝⎭,且α为钝角,则()cos πα-= . m - 9. 在120︒的二面角内放一个半径为6的球,使球与两个半平面各只有一个公共点(其 过球心且垂直于二面角的棱的直截面如图所示),则这两个公共点AB 之间的球面距离为 . 2π10. 若平面向量(1,)a x =和(23,)b x x =+- 互相平行,其中x R ∈.则a b -= 2或11. 设等差数列{}n a 的前n 项和为n S . 若272k S =,且118k k a a +=-,则正整数k = . 412. 一个圆柱形容器的轴截面尺寸如右图所示,容器内有一个实心的球,球的直径恰等于圆柱的高.现用水将该容器注满,然后取出该球(假设球的密度大于水且操作过程中水量损失不计),则球取出后,容器中水面的高度为 cm. (精确到0.1cm )8.3 13. 已知函数2()f x x x =-,若31log (2)1f f m ⎛⎫< ⎪+⎝⎭,则实数m 的取值范围是 .8(,8)9- 14. 下列有关平面向量分解定理的四个命题....中,所有正确命题的序号是 . (填写命题所对应的序号即可) ① 一个平面内有且只有一对不平行的向量可作为表示该平面所有向量的基; ② 一个平面内有无数多对不平行向量可作为表示该平面内所有向量的基; ③ 平面向量的基向量可能互相垂直;④ 一个平面内任一非零向量都可唯一地表示成该平面内三个互不平行向量的线性组合.②、③ 15. 若不等式102x m x m -+<-成立的一个充分非必要条件是1132x <<,则实数m 的范围是14,43⎡⎤⎢⎥⎣⎦16. 对任意的实数α、β,下列等式恒成立的是 ( A )A . ()()2sin cos sin sin αβαβαβ⋅=++-; B . ()()2cos sin sin cos αβαβαβ⋅=++-;C . cos cos 2sinsin22αβαβαβ+-+=⋅;D . cos cos 2coscos22αβαβαβ+--=⋅.17. 设a 、b 为两条直线,α、β为两个平面. 下列四个命题中,正确的命题是 ( B )A. 若a 、b 与α所成的角相等,则a b ∥; B. 若,,a b a b αα⊥⊥则Ü;C. 若a ba αββ∥苘,,,则αβ∥; D. 若a b αβ,∥∥,αβ∥,则a b ∥.18. (理)设离散型随机变量ξ可能取的值为1,2,3,4。
上海市高三数学基础练习【4B.2012.2】

高三数学基础练习【4B 】(2012.2) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽【荣誉的桂冠是用荆棘编织而成的。
(卡莱尔)】1. =+++20062i i i __________________.{-1+i}2. 函数)4sin(cos )4cos(sin ππ+++=x x x x y 的最小正周期T= .{ π } 3. 若函数22)(-=x x f 的值域为]31,(--∞,则其定义域为____.)2,4[- 4. 若=∈=+=απααπ则其中的解是方程),2,0(,1)cos(23x x .{π34} 5. 在△ABC 中,sinA;sinB:sinC=2:3:4,则∠ABC= .{11arccos .16} 6.方程x 3+lg x =18的根x ≈ .(结果精确到0.1){2.6}7. 若()()3,2223≥∈+++++=+n n x c x b x a x x n n n 且N ,且2:3:=b a ,则=n . 11 8. 12+=x x y (),1(+∞-∈x )的图像与其反函数图像的交点坐标为__.(0,0),(1,1) 9.已知复数z 1=cosθ-i ,z 2=sinθ+i ,| z 1·z 2|的最大值和最小值.分别是 .{,232} 10.在△ABC 中,若∠A =120°,AB=5,BC =7,则△ABC 的面积S = .{4315} 11.函数f(x)=sinx+2x sin ,x ∈[0,2π]的图象与直线y=k 有且仅有两个不同的交点,则k 的取值范围是 .{1<k<3 }12.函数x x y arcsin sin +=的值域是 .⎥⎦⎤⎢⎣⎡+--21sin ,21sin ππ 13.若曲线21x y =+与直线y b =没有公共点,则b 的取值范围是_______.{-1<b<1 }14.若21x x 、为方程11212+-⎪⎭⎫ ⎝⎛=x x 的两个实数解,则=+21x x .}1{-. 15.设z 为虚数,则2z 一定是 (B )(A) 非负实数或虚数 (B) 负数或虚数 (C) 虚数 (D) 有可能是正数16.函数x a y =在]1,0[上的最大值与最小值的和为3,则a 的值为( B ) (A)21 (B) 2 (C) 4 (D) 41 17.若)(log b x y a +=的图像过点)0,1(-,)1,0(,则 ( A ) (A)2=a ,2=b (B)2=a ,2=b (C)2=a ,1=b (D)2=a ,2=b18. 如果0,0a b <>,那么,下列不等式中正确的是( A )(A )11a b< (B <(C )22a b < (D )||||a b > 19.对于非零实数a b ,,以下四个命题都成立: ① 01≠+aa ; ② 2222)(b ab a b a ++=+;③ 若||||b a =,则b a ±=; ④ 若ab a =2,则b a =. 那么,对于非零复数a b ,,仍然成立的命题的所有序号是 .②④20.已知a b ∈R ,,且i ,i 2++b a (i 是虚数单位)是实系数一元二次方程02=++q px x 的两个根,那么p q ,的值分别是( A )A.45p q =-=, B.43p q =-=,C.45p q ==, D.43p q ==,。
(完整word版)高三数学基础训练题集(上)1-10套(含答案)

俯视图侧视图正视图4图1乙甲7518736247954368534321高三数学基础训练一班级:姓名:座号:成绩:一.选择题:1.复数i1i,321-=+=zz,则21zzz⋅=在复平面内的对应点位于( )A.第一象限B.第二象限C.第三象限D.第四象限2.在等比数列{an}中,已知,11=a84=a,则=5a( )A.16 B.16或-16 C.32 D.32或-323.已知向量a =(x,1),b =(3,6),a⊥b ,则实数x的值为( )A.12B.2-C.2D.21-4.经过圆:C22(1)(2)4x y++-=的圆心且斜率为1的直线方程为( )A.30x y-+=B.30x y--=C.10x y+-=D.30x y++=5.已知函数()f x是定义在R上的奇函数,当0>x时,()2xf x=,( ) 则(2)f-=( )A.14B.4-C.41-D.46.图1是某赛季甲.乙两名篮球运动员每场比赛得分的茎叶图,则甲.乙两人这几场比赛得分的中位数之和是( )A.62 B.63 C.64 D.657.下列函数中最小正周期不为π的是( )A.xxxf cossin)(⋅= B.g(x)=tan(2π+x)C.xxxf22cossin)(-=D.xxx cossin)(+=ϕ8.命题“,11a b a b>->-若则”的否命题是( )A.,11a b a b>-≤-若则B.若ba≥,则11-<-baC.,11a b a b≤-≤-若则D.,11a b a b<-<-若则9.图2为一个几何体的三视图,正视图和侧视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的侧面积为 ( ) A .6B .24C .123D .3210.已知抛物线C 的方程为212x y =,过点A ()1,0-和点()3,t B 的直线与抛物线C 没有公共点,则实数t 的取值范围是 ( ) A .()()+∞-∞-,11,YB .⎪⎪⎭⎫ ⎝⎛+∞⎪⎪⎭⎫ ⎝⎛-∞-,2222,Y C .()()+∞-∞-,,2222YD .()()+∞-∞-,,22Y二.填空题:11.函数22()log (1)f x x =-的定义域为 .12.如图所示的算法流程图中,输出S 的值为 .13.已知实数x y ,满足2203x y x y y +⎧⎪-⎨⎪⎩≥,≤,≤≤,则2z x y =-的最大值为_______.14.已知c x x x x f +--=221)(23,若]2,1[-∈x 时,2)(c x f <恒成立,则实数c 的取值范围______ 三.解答题:已知()sin f x x x =+∈x (R ). (1)求函数)(x f 的最小正周期;(2)求函数)(x f 的最大值,并指出此时x 的值.高三数学基础训练二班级: 姓名: 座号: 成绩:一.选择题:1.在等差数列{}n a 中, 284a a +=,则 其前9项的和S9等于 ( )A .18B .27C .36D .92.函数()()sin cos sin f x x x x =-的最小正周期为 ( )A .4π B .2πC .πD .2π 3.已知命题p: {}4A x x a =-p ,命题q :()(){}230B x x x =--f ,且⌝p 是⌝q 的充分条件,则实数 a 的取值范围是: ( )A .(-1,6)B .[-1,6]C .(,1)(6,)-∞-⋃+∞D .(,1][6,)-∞-⋃+∞ 4.用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1~160编号,按编号顺序平均分成20组(1~8号,9~16号,。
上海市高三数学基础练习【21.2012.4】

高三数学基础练习【21】(2012.4) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽【记忆像是倒在掌心的水,不论你摊开还是紧握,终究还是会从指缝中一滴一滴流淌干净。
】1. 函数⎩⎨⎧>+<-=)0(1)0(1x x x x y 的反函数为⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽. 2. 函数y=x 2+2 (x ≤0)的反函数是⎽⎽⎽⎽⎽⎽⎽⎽⎽.3. 设}1)1lg(|{},032|{,2<+=<--==x x B x x x A R U ,则∁U A ⋂B=⎽⎽⎽⎽⎽⎽⎽.4. 判别)112lg(--=x y 的图象的对称性:⎽⎽⎽⎽⎽⎽⎽⎽. 5. =++++-∞→)21...41211(lim 1n n ___________. 6. 已知函数x arcsin )x (f = )1x 1(≤≤-,则=π-)6(f 1__________. 7. 集合A=⎭⎬⎫⎩⎨⎧≤+-02x 4x x ,集合B=[)⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+∞∈=,2x ,x log y y 21,则=⋂B A ___________. 8. 过点)1,3(作曲线02y 4y x 4x 22=-++-的切线,则所作切线的一般式方程为⎽⎽⎽⎽⎽⎽⎽⎽⎽.9. 在ABC ∆中,角C ,B ,A 所对应的边分别为c ,b ,a ,2a ,3c ==,A sin b 2a =,则ABC ∆的面积为___________.10. 方程0224x lg x lg =--的解是____________.11. 设等差数列{}n a 的首项为1a ,公差为d 前n 项和为n S ,若2010S S =,则30S =____.12. 在ABC ∆中,BAC ∠为直角,设P 为ABC ∆内一点,且→→→+=AC 51AB 52AP ,则ABP ∆的面积与ABC ∆的面积之比为_______.13. 为了参与上海世博会的建设,某外商计划在4个候选区县投资3个不同的项目,且在同一个区县投资的项目不超过2个,该外商不同的投资方案有______种..14. 如果函数2ax x y 2++=在区间]1,(-∞上是减函数,那么实数a 的取值范围是__⎽⎽⎽⎽.15. 在平面直角坐标系中,命题“若直线l 过抛物线)0p (px 2y 2≠=的焦点,且与抛物线相交于)y ,x (B ),y ,x (A 2211两点,则221p y y -=⋅”为真命题,如果直线l 不是经过抛物线px 2y 2=)0p (≠的焦点而是经过x 轴上另外一个定点)0,x (P 0 )0x (0>,并且保证直线与抛物线有两个公共点,那么21y y 是否还是定值吗?请作出肯定或否定的回答,并且写出21y y 的表达式_____________________________. .16. (理科)若关于x 的方程0kx x 1x 22=-+-在)2,0(上有两个不同的实数解,则实数k 的取值范围为_______.17. 在等比数列{}n a 中,0a n >,且25a a 75=,则6a =⎽⎽⎽⎽⎽.18. .“)R b ,a (2b a ab 22∈+<”是“0b a >>”的⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽条件 19. 已知P 是椭圆13y 4x 22=+上的点,21F ,F 是两个焦点,则21PF PF ⋅的最大值与最小值之差是⎽⎽⎽⎽⎽.20. 设S 是至少含有两个元素的集合.在S 上定义了一个二元运算“*”(即对任意的S b ,a ∈,对于有序元素对()b ,a ,在S 中有唯一确定的元素a *b 与之对应)。
上海市高三数学基础练习【8B】

高三数学基础练习【8B 】(2013.3) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽1. 人的生命似洪水奔流,不遇到岛屿和暗礁,难以激起美丽的浪花.------奥斯特洛夫斯基=++++-∞→)21...41211(lim 1n n ___________. .1. 22. 已知函数x x f arcsin )(= )11(≤≤-x ,则=-)6(1πf __________. 2. 21 3. 集合A=⎭⎬⎫⎩⎨⎧≤+-024x x x ,集合B=[)⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+∞∈=,2,log 21x x y y ,则=⋂B A ______________.3. (-2,-1] 4. 过点)1,3(作曲线024422=-++-y y x x 的切线,则所作切线的一般式方程为___________________________.4. 063=-+y x5. 已知:4i i bi a +=+(其中a 、b 为实数,i 为虚数单位)。
则=+b a 2 ;6. 若2log a m =,3log a n =,则=+n m a 2 12 ;7. 已知:)(2,1=a ,),(1x b = ,且b a 2+与b a -2平行,则=x12 ; 8. 已知x x x f cos 2sin )(2+=,]32,3[ππ∈x 的最小值为 14- ; 9. 在一个袋子里有10个红球和2个白球,现从中随机拿出3个,则其中至少有一个白球的概率是511 (用分数表示);10. 为了参与上海世博会的建设,某外商计划在4个候选区县投资3个不同的项目,且在同一个区县投资的项目不超过2个,该外商不同的投资方案有______种. 9. 6011. 在ABC ∆中,BAC ∠为直角,设P 为ABC ∆内一点,且→→→+=AC AB AP 5152,则ABP ∆的面积与ABC ∆的面积之比为_______.8.51 12. 经过点A )0,(a ,(0>a ),且与极轴正方向夹角为4π的直线的极坐标方程为 cos sin a ρθρθ-=; 13. 若直线022=+-by ax (R b a ∈、),始终平分圆014222=+-++y x y x 的周长,则ab 的最大值为14; 14. 已知:函数)1(l o g )(21xa x x f -+=(0<a )在区间),1[+∞上单调递减,则实数a 取值范围是 [)1,0- ; 15. 数列}{n a 是等差数列,前n 项和为n S ,102=S ,555=S ,则过点),(n S n P n ,)2,2(2+++n S n Q n 的直线斜率为 2 ;16. 设集合},,3,2,1{n S n =,若n S Z ⊆,则把Z 的所有元素的乘积称为Z 的容量(若Z 中只有一个元素,则该元素的数值即为它的容量,规定空集的容量为0)。
上海数学教材练习册高三全一册习题精选.doc
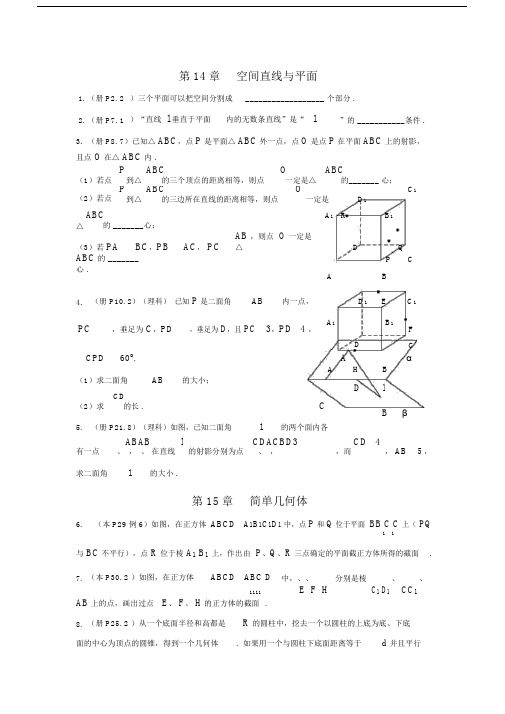
第14章 空间直线与平面1. (册 P2. 2 )三个平面可以把空间分割成 __________________ 个部分 .2. (册 P7. 1 )“直线 l 垂直于平面内的无数条直线”是“ l”的 ___________条件 .3. (册 P8. 7)已知△ ABC ,点 P 是平面△ ABC 外一点,点 O 是点 P 在平面 ABC 上的射影,且点 O 在△ ABC 内 .(1)若点 P到△ ABC OABC的三个顶点的距离相等,则点 一定是△的_______ 心;(2)若点 P到△ ABCO一定是D 1C 1的三边所在直线的距离相等,则点△ABCA 1 RB 1的 _______心;(3)若 PA BC ,PBAC , PCAB ,则点 O 一定是△DP QABC 的 _______心 .CAB4. (册 P10. 2)(理科) 已知 P 是二面角AB内一点,D 1EC 1 PC,垂足为 C ,PD,垂足为 D ,且 PC3,PD 4 , A 1B 1F60o .DCACPDAHBα(1)求二面角AB的大小;DlC(2)求 CD的长 .Bβ5. (册 P21. 8)(理科)如图,已知二面角l的两个面内各有一点 ABAB在直线 l 的射影分别为点 CDACBD3,而 CD 4, AB 5 ,、 , 、、 ,求二面角l的大小 .第 15章 简单几何体6.(本 P29 例 6)如图,在正方体 ABCD A 1B 1C 1D 1 中,点 P 和 Q 位于平面 BB C C 上( PQ1 1与 BC 不平行),点 R 位于棱 A 1 B 1 上,作出由 P 、Q 、R 三点确定的平面截正方体所得的截面 . 7. (本 P30. 2 )如图,在正方体ABCD ABC D 中,、、分别是棱C 1D 1 、 CC 1 、1111E F HAB 上的点,画出过点 E 、 F 、 H 的正方体的截面 .8. (册 P25. 2 )从一个底面半径和高都是 R 的圆柱中,挖去一个以圆柱的上底为底、下底面的中心为顶点的圆锥,得到一个几何体. 如果用一个与圆柱下底面距离等于d 并且平行于底面的平面去截这个几何体,求截面面积.9. (册 P29. 2)已知正六棱柱最长的一条对角线长为13 厘米,侧面积为180 平方厘米,求这个棱柱的体积.10. (册 P31. 1)维度为的纬度圈上有甲乙两地,它们的纬度圈上的弧长等于πRcos(R是地球的半径),求甲乙两地的球面距离.11.(册 P32. 2)现有以下三个命题:①底面是平行四边形的四棱柱是平行六面体;②底面是矩形的平行六面体是长方体;③直四棱柱是直平行六面体 . 其中真命题的序号是 _______.12. (册 P32. 3)如果一个三棱锥的底面是直角三角形,那么这个三棱锥的三个侧面()( A)都不是直角三角形(B)至多只能有一个是直角三角形( C)至多只能有两个是直角三角形(D)可能都是直角三角形13. (册 P35. 1)已知长方体ABCD A1B1C1D1的高为h P 1 1,底面积为,对角面BBDD的面积为Q,求它的侧面积.14. (册P36. 4 )设AB是球O的直径,AB 50, O1、 O2是AB上的两点,平面、分别通过点O1、 O2,且垂直于AB,截得圆O1、圆 O2,当圆O1、圆 O2的面积分别为49π、400π时,求O1、 O2两点的距离.第 16 章排列组合与二项式定理15.(本 P50 例 3)540 的不同正约数共有多少个?16.(本 P55 例 4)求证:P m n mP m n1P m n 1 .17.(本 P55 例 5)解方程:P42n 1140P3n .18. (本 P55. 2 )1! 2! 3! L 100! 的个位数为 __________.19. (本 P60 例 4)如果从 7 名运动员中选 4 名运动员组成接力队,参加 4 100 接力赛,那么甲乙两人都不跑中间两棒的安排方法有多少种?20. (本 P61 例 6)将a、b、c、d、e、f六个不同元素排成一列,其中a 不排在首位, b不排在末位,有几种排法?21.(本 P62. 3)A、B、C、D、E五人站成一排,如果B必须站在A的右边(A、B可以不相邻),那么共有多少种不同的排法?22. (本 P64 例 2)求证:C n m m 1 C n m 11 .n 123. (本 P65. 3 )解不等式:C n4 Cn6.24. (本 P67. 3 )求证: C m C m 2C m 1 C m 2.n 2 n n n25. (本 P67. 4 )解方程: C182x C18x 2 .26. (本 P71 例 3)求(1 a)12的二项展开式中倒数第 5 项 .1 n27. (本 P73 例 6)已知x 的二项展开式中,前三项系数成等差数列,求二项2 4 x展开式中的所有有理项.28.(本 P74. 3 )求5555被 8 除所得的余数 .29. (本 P75 例 11)利用二项式定理证明:2n n2 n 1 (n 5,n N*).30. (本 P76. 4 )求证:C n0 C n2 C n4 L C n n 2n 1(n是偶数).31.(册 P38. 2)要把 4 封信投入 3 个信箱,共有多少种不同的投法?(允许将信全部或部分投入某一个信箱)32. (册 P40. 8 )已知 P10m 10 9 L 5,求正整数 m的值.33. (册 P42. 3 )化简:12 3 L n 1 . ( n N* ,n 2 )2! 3! 4! n!34. (册 P42. 5 )求证: P11 2P 22 3P33 L nP n n P n n 11 1 .(n N* )35. (册 P43. 3)将 8 个相同的小球放入编号为1、2、3 的三个盒子内,要求每个盒子的球数不小于它的编号数,共有多少种不同的放法?36. (册 P48. 5 )在 (3 x 2 y)9 的展开式中,求二项式系数的和以及各项系数的和.37. (册 P49. 9 )求和: C1n 3C n2 9C n3 L 3n 1 C n n.的自然数,证明: 1 1 n38. (册 P49. 10 )已知n为大于 1 2 .n39. (册 P49. 11 )在x2 3x n的二项展开式中,有且只有第五项的二项式系数最大,求C0n 1C1n1C n2 L ( 1)n1n C n n.2 4 240. (册 P49. 1 )求和: C1000 C1002 C1004 L C10098 C100100 .41. (册 P50. 3 )在 (1 3 ) nx的二项展开式中,末三项的二项式系数之和等于631.(1)求二项展开式中二项式系数最大的项是第几项;(2)求二项展开式中系数最大的项.42. (册 P50. 4 )求 7777 15 除以 19 的余数 .43. (册 P50. 5 )用两种方法证明:26n 3 32 n 1能被11 整除 .44. (册 P50. 6 )已知 (x 1)n x n L ax3 bx2 cx 1 (n N* ),且a : b 3:1 ,求c 的值.45.(册 P50. 1 ( 4))用数字 0、 1、2、 3、 4、 5 可组成没有重复数字的六位数,其中数字2、 4 排在相邻数位上,满足条件的六位数共有___________个 .46. (册 P52. 1) 6 个人排成一列,其中甲乙两人之间至少有两个人的不同排法种数是___.第 17 章概率论初步47.(本 P90 例 7 改编为 2011 年高考试题)求随机抽取 10 个同学中至少有两个同学在同一个月份出生的概率 . (精确到)48. (册 P54. 4)某城镇共有 10000 辆自行车,牌照编号从00001 到 10000. 求在此城镇中偶然遇到的一辆自行车,其牌照号码中有数字8的概率 .49.(册 P56. 1 )将n间房分给n个人,每个人都以相等的可能性进入每一间房间,而且每间房间里的人数没有限制,求不出现空房的概率.50. (册 P56. 2 )把 10 本书随机地排在书架上,求其中指定的 3 本书排在一起的概率.51.(册 P56. 3)某人有 5 把钥匙,但只有一把能打开门,他每次取一把钥匙尝试开门,求试到第 3 把钥匙时才打开门的概率 .第 18 章基本统计方法52. (册 P61. 2 )某班级有40 名同学参加打靶训练,他们的成绩如下表所示(单位:环):测验成绩频数[4, 5) 2[5, 6) 3[6, 7)10[7, 8) 15[8, 9) 8[9, 10] 2 求该班同学的成绩 2 区间估计. (精确到)高三总复习题53. (册 P71. 13 )已知11 7 , n N* ,求C8n . C5n C6n 10C7n54.(册 P74. 5)一个球受热膨胀 . 如果它的表面积增加 21%,那么这个球的半径增加多少?55. (册 P74. 6 )求C383n n C321n n(n N* )的值 .56.(册 P75. 8 )以一个正方体的顶点为顶点能组成多少个三棱锥?57. (册 P75. 10 )已知(x lg x1)n的二项展开式中,末三项的二项式系数的和为22,二项式系数最大的项为20000,求实数x 的值.。
上海高三数学练习题推荐

上海高三数学练习题推荐在高三阶段,数学是考试科目中的重点之一,对学生来说,做大量的数学练习题是提高自己数学能力和应对考试的有效途径。
本文将推荐几道适合上海高三学生的数学练习题,旨在帮助学生巩固知识、提高解题能力。
一. 函数与方程1. 已知函数 f(x)=3x+2 和 g(x)=-2x^2+5x-1,求两函数的复合函数(f∘g)(x) = f(g(x))。
2. 解方程:2^(x+1) = 8^(log2x)。
二. 三角函数1. 求函数 y=sin(2x) + cos(3x) 的周期和最小正周期。
2. 已知三角形 ABC,其中∠A=30°,AB=AC。
若三角形 ABC 的外接圆半径 r=2,求 BC 的值。
三. 几何1. 已知线段 AB 的中点为 M,且 AM:MB = 1:2。
点 C 在线段 AB 上,且 AC:CB = 2:3。
连接线段 MC,若 MC:CC' = 1:2,求线段 BB':BA。
2. 如图所示,ABCD 是一个平行四边形,点 P、Q 分别在边 AD 和BC 上,且 PQ // AB。
若 PQ = 6 cm,AP = 3 cm,BP = 2 cm,求 CQ 的长度。
四. 概率与统计1. 甲、乙两个队进行篮球赛,已知甲队胜的概率为 0.6,乙队胜的概率为 0.4。
他们进行五局三胜制的比赛,求甲队获胜的概率。
2. 随机变量X 的概率密度函数如下,求该随机变量的期望值E(X)。
f(x) =1.5x, 0 < x < 1x-1, 1 ≤ x < 20, otherwise五. 解析几何1. 在平面直角坐标系中,求由点 A(2,-1) 和点 B(-3,4) 所确定直线的方程。
2. 已知直线 L1: 2x-3y+5=0 和直线 L2: 3x+y-2=0,求它们的交点坐标。
根据上述题目进行适量的练习,可以巩固相关知识点的理解,并提高解题能力。
希望同学们能够利用这些练习题,有针对性地进行练习,为高考取得优异成绩奠定坚实的数学基础。
上海市高三数学基础练习【23.2012.4】

高三数学基础练习【23】(2012.4) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽ 【人总是珍惜未得到的,而遗忘了所拥有的】1. 已知集合{}{}lg(1),213S x y x T x x ==-=-≤,则ST =_________.2. 在△ABC 中,如果a 、b 、c 成等差数列,∠B=30°,△ABC 的面积为23,那么b=__________. 3. 若P 是圆012422=++-+y x y x 上的动点,则P 到直线02434=+-y x 的最小距离是_______. 4. 已知等比数列{}n a ,如果6,123221-=+=+a a a a ,则n n S ∞→lim =_______.5. 若2(sin cos )cos i θθθ-+是纯虚数(i 是虚数单位,02(,)θπ∈),则θ的值为_______.6. 已知1sin cos ,,842ππααα⋅=<<则cos sin αα-的值为 . 7. 函数3sin sin()y x x π=+的最大值是________.8. 若从语文、数学、英语、物理、化学、生物、政治、历史、地理九门学科中任选四门学科组成考试科目,其中必须含有语文、数学、英语三门学科的概率是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽..9. 在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是⎽⎽⎽⎽⎽⎽.10. 在极坐标系中,直线l 的方程为sin 3ρθ=,则点),(62π到直线l 的距离为 .11. 若n x)1x 23+(的展开式中含有常数项,则最小的正整数n 等于 .12. 在极坐标系中,若过点(3,0)且与极轴垂直的直线交曲线θρcos 4=两点,则AB =________13. 已知关于x 的方程aaxlg 1lg 1)21(-+=有正根,则实数a 的取值范围是⎽⎽⎽⎽⎽⎽⎽.14. 已知方程)22(0sec tan 22πθπθθ<<-=-+x x 的两实根为21,x x 且}{n a 满足0,)11(100121=+=-S x x a n n ,则θ=⎽⎽⎽⎽⎽. 15. .以椭圆 114416922=+y x 的右焦点为圆心 , 且与双曲线 116922=-y x 的渐近线相切的圆的标准方程是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.16. 已知非零向量,21||||,0||||==⋅⎭⎫⎝⎛+AC AB AC AB 满足与则△ABC 的形状是( )(A)三边均不相等的三角形 (B)直角三角形 (C)等腰(非等边)三角形 (D)等边三角形17. 对任意正整数n ,定义n 的双阶乘n !!如下:当n 为偶数时,135)4)(2(!!,;246)4)(2(!!⨯⨯--=⨯⨯--= n n n n n n n n n 为奇数时当;现有四个命题:①!2009)!!2008)(!!2009(=,②!10042!!2008⨯=,③2008!!个位数为0,④2009!!个位数为5.其中正确命题的序号为⎽⎽⎽⎽⎽⎽⎽.18. 已知)(x f 是最小正周期为2的函数,当]1,1(-∈x 时,21)(x x f -=,若在区间(3,5]上axx f =)(有两个不相等的实数根,则实数a 的取值范围是___________. 19. 下列条件与有序实数对不能构成....一一对应的是 ( ) (A)直角坐标平面上的点; (B)复平面上的点; (C)极坐标系中,平面上的点; (D)直角坐标平面上,以原点为起点的向量. 20. 定义区间长度m 为这样的一个量:m 的大小为区间右端点的值减去区间左端点的值.若关于x 的不等式062<--a ax x 有解,且解集的区间长度不超过5个单位长,则a 的取值范围是 ( ) A .[-25,1] B .),1[]25,(+∞-∞ C .)24,1()0,25[ - D .]1,0()24,25[ --21.下列各图是正方体或正四面体,P、Q、R、S分别是所在棱的中点,这四个点不共面的一个图是(D )。
上海高三数学刷题练习册

上海高三数学刷题练习册一、选择题(每题5分,共20分)1. 已知函数\( f(x) = 2x^3 - 3x^2 + 5x - 1 \),求导后得到的函数是:A. \( 6x^2 - 6x + 5 \)B. \( 6x^2 - 6x + 4 \)C. \( 6x^2 + 6x + 5 \)D. \( 6x^3 - 6x^2 + 5 \)2. 若\( \sin A = \frac{3}{5} \),且\( A \)为锐角,求\( \cos A \)的值:A. \( \frac{4}{5} \)B. \( \frac{1}{5} \)C. \( -\frac{4}{5} \)D. \( -\frac{1}{5} \)3. 已知数列\( \{a_n\} \)的通项公式为\( a_n = 3n - 1 \),求第10项的值:A. 28B. 29C. 30D. 314. 一个圆的半径为5,求该圆的面积:A. 25πB. 50πC. 75πD. 100π二、填空题(每题4分,共16分)5. 若直线\( y = 3x + 2 \)与直线\( y = -2x + 6 \)平行,则它们的斜率之比为_________。
6. 已知\( \log_{10}100 = 2 \),求\( \log_{10}0.01 \)的值。
7. 一个直角三角形的两条直角边分别为3和4,求斜边的长度。
8. 若\( \cos x = \frac{\sqrt{3}}{2} \),且\( x \)在第一象限,求\( \sin x \)的值。
三、解答题(每题8分,共24分)9. 已知函数\( y = x^2 - 4x + 4 \),求该函数的顶点坐标。
10. 已知等差数列的首项为2,公差为3,求前10项的和。
11. 已知一个圆锥的底面半径为4,高为6,求圆锥的体积,若底面半径为\( r \),高为\( h \)。
四、证明题(每题10分,共20分)12. 证明:对于任意实数\( x \),不等式\( 1 + x + x^2 \geq 0 \)恒成立。
上海市高三数学基础练习【9B】

高三数学基础练习【36B 】(2012.5) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽【一个人总要走陌生的路,看陌生的风景,听陌生的歌,然后在某个不经意的瞬间,你会发现,原本是费尽心机想要忘记的事情真的就那么忘记了。
】1. 设复数z 满足关系式||2z z i +=+, 则z = 34i +。
2. 已知椭圆方程为22321x y +=,则该椭圆的长轴长为3. 已知)1,(),1,2(λ=--=a ,若a 与b 夹角为钝角,则实数λ取值范围是______.()1,22,2⎛⎫-+∞ ⎪⎝⎭4. 设{}{}1),(,0)(),(===-=y y x B x y x y x A ,则B A 用列举法可表示为____.()()(){}1,1,0,1,0,1-;5. 复数z满足3z +=n z m z ==min max ,,则m n ⋅=__________{9}6. 在二项式nx x ⎪⎭⎫ ⎝⎛+3的展开式中,各项系数之和为A,各项二项式系数之和为B,且72=+B A ,则展开式中常数项的值为______.{9}7. 已知函数)0,0(1)(cos )(2>>++=ωϕωA x A x f 的最大值为3,)(x f 的图像与y 轴的交点坐标为)2,0(,其相邻两条对称轴间的距离为2,则++)2()1(f f (2010)f += ____________. {4019}8. 已知a b ≠,a b c ≠+,则关于x 的方程0xb c a b cx a a b c a b a c a b++-+-=---的解集为________{}a b c +-9. 函数253x y x -=-(x ∈A)的值域是(][),04,-∞+∞ ,则集合A=_________.57,33,22⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦10. 在ABC ∆中,已知2,22==a b ,如果三角形有解,则A ∠的取值范围是___________.⎥⎦⎤⎝⎛4,0π11. 甲、乙两队比赛,每局甲胜的概率为21,乙胜的概率也是21,则在一次五局三胜制的比赛中,甲队以3:1获胜的概率是_______.{316} 12. 已知α、β为锐角,cosα=54,31)tan(=-βα,则cosβ。
上海高三数学基础复习试卷1(文科缺答案)

高中数学高考水平测试(1)填空、选择、基础题专项训练(满分100分,60分钟完卷)班级: 姓名: 学号: 成绩:一、填空题(每小题4分,共56分)1.若二项式n x x)21(+的展开式中的第6项是常数项,则n = . 2.集合{},,12R x x y y M ∈-==集合{N x y ==,则N M 等于 . 3.已知()2tan 5αβ-=,1tan 44πβ⎛⎫-= ⎪⎝⎭,则tan 4πα⎛⎫- ⎪⎝⎭的值是 . 4.若点()1,2既在函数2ax b y +=的图象上,又在它的反函数的图象上,则函数的解析式 .5.已知点()2,5A -,()4,1AB =,()3,2BC =-,则点C 的坐标为 . 6.如图,用铁皮制作一个无盖的圆锥形容器,已知该圆锥的母线与底面所在平面的夹角为60︒,容器的高为10cm .制作该容器需要铁皮面积为 2cm .(衔接部分忽略不计,结果保留整数).7.已知n S 是}{n a 的前n 项和,且有12-=n n a S ,则数列}{n a 的通项=n a . 8.已知()1a x f x x a -=--图像的对称中心是()3,1-,则实数a 等于 . 9.某班级在一次身高测量中,第一小组10名学生的身高与全班学生平均身高170cm 的差分别是4-,7-,8-,12-,2,15-,12,8,5,2-.则这个小组10名学生的平均身高是 cm .10.若()sin 01tan 0cos 0sin 01xf x x x -=,则()1f -的值为 .11.若关于x 的方程0)1(2)21(2=+-++m x i x 有实根,则纯.虚数m = . 12.在高校自主招生中,某班级50人报考和两所大学,已知每人至少报考其中一所学校.估计报考上海大学的人数占全班80%到90%之间,报考上海师大的人数占全班32%到40%之间,设M 是两所大学都报的人数的最大值,m 是两所大学都报的人数的最小值,则M m -= .13.下列命题中所有假.命题的序号为 . ①.sin cos y x x =的周期为π,最大值为12; ②.若x 是第一象限的角,则sin y x =是增函数; ③.在ABC ∆中,若sin sin A B =,则A B =; ④.()sin cos f x x x =+既不是奇函数,也不是偶函数; ⑤. cos 24y x π⎛⎫=+ ⎪⎝⎭的一条对称轴为8x π=-.14.已知函数)()(R x q px x x x f ∈++=,给出下列四个命题:①.)(x f 为奇函数的充要条件是0q =;②.)(x f 的图象关于点()0,q 对称;③.当0p =时,方程()0f x =的解集一定非空;④.方程()0f x =的解的个数一定不超过两个.其中所有正确命题的序号是 .二、选择题(每小题4分,共16分)15.函数()1f x x x =-的图像关于 ----------------------------------------------------------------( )A .y 轴对称;B .直线y x =-对称;C .直线y x =对称;D .坐标原点对称.16.等差数列{}n a 的前n 项和)3,2,1(⋅⋅⋅=n S n 当首项1a 和公差d 变化时,若1185a a a ++是一个定值,则下列各数中为定值的是--------------------------------------------------------------( )A.16S ; B.15S ; C.17S ; D.18S .17.给出以下四个命题:①.若0232=+-x x ,则21==x x 或;②.若23x -<≤,则(2)(3)0x x --≤; ③.若0==y x ,则022=+y x ;④.若x 、y *∈N ,y x +是奇数,则x 、y 中一个是奇数,一个是偶数.则 ----( )A .①的逆命题真;B .②的否命题真;C .③的逆否命题假;D .④的逆命题假.18.用一个平面去截正方体,所得截面不可能是------------------------------------------------( )A.平面六边形; B.菱形; C.梯形; D.直角三角形.三、解答题(共28分,14+14)19.如图,⊥AB 平面BCD ,CD BC ⊥,AD 与平面BCD 所成的角为︒30,且BC AB =. (1).求AD 与平面ABC 所成的角的大小;(2).若2=AB ,求点B 到平面ACD 的距离.20.已知函数()222sin 4f x x x π⎛⎫=+-+ ⎪⎝⎭,42x ππ⎡⎤∈⎢⎥⎣⎦. (1).求()f x 的最大值和最小值;(2).若不等式()2f x m -<在,42x ππ⎡⎤∈⎢⎥⎣⎦上恒成立,求实数m 的取值范围. A B D C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三数学基础练习【5】(2012.2) 班级⎽⎽⎽⎽⎽⎽学号⎽⎽⎽⎽⎽姓名⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽得分⎽⎽⎽⎽⎽⎽
【夏天的飞鸟,飞到我窗前唱歌,又飞去了。
秋天的黄叶,他们没有什麼可唱的,只是叹息一声,飞落在那里。
泰戈尔】
1. 若1cos 7α=,0,2πα⎛⎫∈ ⎪⎝⎭,则cos 3πα⎛⎫+ ⎪⎝
⎭=_______. 2. (1) =⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛1221301102 . (2)不等式1212+<--x x x 的解集是_________. 3.
若3n x ⎛- ⎝
展开式各项系数和为128,则展开式31x 的系数是____. 4. (1)从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的
选法共有⎽⎽⎽⎽⎽⎽⎽.(2)函数y=)34(log 25.0x x -的定义域为 .
5. (1)已知2tan =θ,则θθθc o s 12c o s 1s i n 2+=⎽⎽__. (2) 用列举法表示集合1i ,N i n n x x n ⎧⎫=+∈⎨⎬⎩⎭
= . 6. 填空:三阶行列式351
24
3512---中,元素2-的代数余子式为________. 7. 若(2)a i i b i +=+,其中i R b a ,,∈是虚数单位,则=+b a ______.
8. (1)已知c b a ,,是锐角ABC ∆中C B A ∠∠∠,,的对边,若,4,3==b a ABC ∆的面积为33,则
=c .(2)设A 、B 是两个集合,定义},2|1||{},,|{≤+=∉∈=-x x M B x A x x B A 若且 }|,sin ||{R x x N ∈==αα,则M -N=⎽⎽⎽⎽⎽. (3) 方程2cos2x = 1的解是⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽⎽.
9. 若集合A =}032{2
≤--x x x ,B =}{a x x >,且φ=⋂B A ,则a 的范围是 .
10. 函数32)(2--=ax x x f 在[1,2]上存在反函数的充分必要条件是⎽⎽⎽⎽⎽⎽⎽.
11. 下列结论正确的是 ( ) (A)当01x x >≠且时1,lg 2lg x x +
≥ (B)当0x >
时2≥ (C)当2x ≥时1,x x +的最小值为2 (D)当02x <≤时1,x x
-无最大值 12. 函数21sin(),10,(),0.x x x f x e x π-⎧-<<⎪=⎨≥⎪⎩,若(1)()2,f f a +=则a 的值为( ) (A )1 (B
)2- (C
)1,2- (D
)1,2
13. 满足“对任意实数y x ,,)()()(y f x f y x f ⋅=⋅都成立”的函数可以是 ( ) (A )x x f 3)(=; (B)x x f 3log )(=; (C)3)(x x f =; (D)x x f 3)(=。
14. 若m 为实数,则i m m m m )6()2(22--+-+在复平面内所对应的点不可能位于( )
(A )第一象限 (B )第二象限 (C )第三象限 (D )第四象限
15. 函数y = log a x 和y = (1-a )x+a 的图象只可能是 ( )
(A) (B) (C)
(D)。
