信息论基础-高等教育出版社-叶中行
《信息论基础》教学大纲

《信息论基础》教学大纲课程编码:1512105602课程名称:信息论基础学时/学分:36/2先修课程:《概率论与数理统计》、《随机过程》、《信息科学导论》适用专业:信息与计算科学开课教研室:信息与计算科学教研室一、课程性质与任务1.课程性质:本课程是信息与计算科学专业的一门专业选修课,是拟从事通信及相关行业工作的学生所必修,为本科三年级学生所选修。
2.课程任务:通过本课程的学习,学生应熟练掌握离散(连续)条件下的熵、条件熵、相对熵、互信息的概念,熟练掌握有(无)失真条件下的信源(信道)编码定理和一些常用编码并能熟练的应用它们,为今后的学习与科研打下坚实的基础。
二、课程教学基本要求掌握信息的基本理论,理解离散信源、连续信源的有关理论,熟练掌握信息、信息熵、条件熵、联合熵、互信息等的计算,了解通信系统的整个过程,熟练掌握基本的信源编码方法和信道编码方法,会判定信源码、信道码的优劣。
本课程主要以课堂讲授为主,在教学方法和手段上采用现代教育技术。
成绩考核形式:期终成绩(考查)(70%)+平时成绩(平时测验、作业、课堂提问、 课堂讨论等)(30%)。
成绩评定采用百分制,60分为及格。
三、课程教学内容第一章 随机变量的信息度量1.教学基本要求理解和掌握的定义和计算式,理解有关熵的一些基本性质,了解广义熵及相互间的关系。
2.要求学生掌握的基本概念、理论通过本章学习,使学生能准确理解并掌握信息、熵、联合熵、条件熵等有关信息量的定义及计算式,理解熵的基本性质,了解广义熵的多种形式并了解它们之间的关系。
3.教学重点和难点教学重点是要让学生掌握熵的概念和性质,熟练计算熵、联合熵、条件熵、相对熵和互信息,并会用熵求解一些实际问题。
4.教学内容第一节 自信息第二节 熵、联合熵、条件熵第三节 相对熵和互信息第四节 信息量的一些基本性质第五节 广义熵第二章 随机过程的信息度量和渐进等分性1.教学基本要求理解和掌握信源、随机过程的基本概念,掌握无记忆信源、马氏信源、平稳性、遍历性,理解AEP性质,理解AEP性质在数据压缩中的应用,了解香农-麦克米兰-布瑞曼定理。
《信息论基础》教学大纲

《信息论基础》教学大纲课程编号:CE6006课程名称:信息论基础英文名称:Foundation of Information Theory学分/学时:2/32 课程性质:选修课适用专业:信息安全,网络工程建议开设学期:6 先修课程:概率论与数理统计开课单位:网络与信息安全学院一、课程的教学目标与任务本课程是信息安全,网络工程专业选修的一门专业基础课。
通过课程学习,使学生能够较深刻地理解信息的表征、存储和传输的基本理论,初步掌握提高信息传输系统可靠性、有效性、保密性和认证性的一般方法,为后续专业课学习打下坚实的理论基础。
本课程的教学目标:本课程对学生达到如下毕业要求有贡献:1.能够将数学、自然科学、工程基础和专业知识用于解决复杂工程问题。
2.能够应用数学、自然科学和工程科学的基本原理,识别、表达,并通过文献研究分析复杂工程问题,以获得有效结论。
完成课程后,学生将具备以下能力:1.能够针对一个复杂系统或者过程选择一种数学模型,并达到适当的精度。
2.能够应用数学、自然科学和工程科学的基本原理分析、识别、表达、处理及扩展信息安全、网络工程专业的复杂问题。
本课程的性质:本课程是一门理论性较强的专业基础课程,在实施过程中以理论为主,共32学时。
二、课程具体内容及基本要求(一)绪论(2学时)1.基本要求(1)掌握消息、信息和信号;噪声和干扰的基本概念(2)掌握通信系统模型(3)明确Shannon信息论要解决的中心问题2.重点与难点(1)重点:掌握通信系统模型的构成及其相应功能(2)难点:理解Shannon信息论要解决的中心问题3.作业及课外学习要求(1)阅读IEEE IT 1998年信息论50年专刊(2)数字化革命进展-纪念shannon信息论诞生50周年http://202.117.112.49/xxl2/dzjiaoan/95shannon50y.ppt(3)信息论与通信、密码、信息隐藏(一)http://202.117.112.49/xxl2/dzjiaoan/信息论与通信、密码、信息隐藏(一).ppt (4)信息论与通信、密码、信息隐藏(二)http://202.117.112.49/xxl2/dzjiaoan/信息论与通信、密码、信息隐藏(二).ppt (5)清华大学朱雪龙“从通信与信号处理观点看信息论研究与应用中的若干问题”http://202.117.112.49/xxl2/dzjiaoan/sponit.mht(二)信息量和熵(8学时)1.基本要求(1)掌握离散随机变量的熵、平均互信息的基本概念及其性质(2)掌握平均互信息的凸性(3)理解信息处理定理2.重点与难点(1)重点:对信息量进行定量描述(2)难点:熵和平均互信息的物理含义及其性质,如何应用熵和平均互信息的基本概念解决实际问题3.作业及课外学习要求熵、平均互信息的计算、信息处理定理等应用(三)离散信源无失真编码(8学时)1.基本要求(1)掌握离散无记忆源等长编码、不等长编码基本概念(2)掌握离散无记忆信源无失真编码定理(3)掌握Huffman编码(4)理解算术编码和LZ编码基本原理2.重点与难点(1)重点:掌握离散无记忆信源无失真编码定理(2)难点:典型序列的概念及其性质、最佳不等长编码3.作业及课外学习要求离散无记忆信源无失真编码定理、无失真信源编码方法(四)信道容量(6学时)1.基本要求(1)掌握信道容量的基本概念(2)掌握离散无记忆信道、组合信道的信道容量计算2.重点与难点(1)重点:掌握信道容量的基本概念及一些特殊信道的容量计算(2)难点:信道的描述方法及信道容量的计算3.作业及课外学习要求信道容量的计算(五)离散信道编码定理(4学时)1.基本要求(1)掌握三种译码准则:最小错误概率译码、最大后验概率译码和最大似然译码(2)了解联合典型序列基本概念(3)理解离散信道编码定理2.重点与难点(1)重点:最大后验概率译码与最大似然译码和离散信道编码定理(2)难点:离散信道编码定理3.作业及课外学习要求译码准则的应用、离散信道编码定理的应用(六)信息论在信息安全中的应用(4学时)1.基本要求(1)了解保密系统模型(2)理解保密、认证的信息理论2.重点与难点(1)重点:完善保密性(2)难点:保密的信息理论3.作业及课外学习要求信息论在信息安全中的应用三、教学安排及方式四、本课程对培养学生能力和素质的贡献点信息论是一门运用概率论与数理统计的方法研究通信系统有效性、可靠性、保密性和认证性等问题的基础课程,也是信息与通信工程、计算机科学与技术、网络空间安全等学科的一门专业基础课程,对毕业要求各指标点的达成主要贡献如下:五、考核及成绩评定方式理论课最终成绩由平时成绩和期末考试成绩组成。
信息论发展

信息论发展现代信息论是从上世纪二十年代奈奎斯特和哈特莱的研究开始的,他们最早开始研究了通信系统传输信息的能力,并且试图度量系统的信道容量。
香农于1940年在普林斯顿高级研究所期间开始思考信息论与有效通信系统的问题。
经过8年的努力,1948年,来自贝尔研究所的ClaudeShannon(克劳德·香农)的《通信的数学理论》论文公诸于世,从此宣告了崭新的一门关于信息发面的学科──信息论的诞生。
1949年,香农又在该杂志上发表了另一著名论文《噪声下的通信》。
在这两篇论文中,香农阐明了通信的基本问题,给出了通信系统的模型,提出了信息量的数学表达式,并解决了信道容量、信源统计特性、信源编码、信道编码等一系列基本技术问题。
两篇论文成为了信息论的奠基性著作。
这两篇论文一起阐述了现代信息论的基础。
并且香农开始创造性的定义了“信息”。
信息论自从二十世纪四十年代中叶到二十一世纪初期,现已成为一门独立的理论科学,他给出一切传输、存储、处理信息系统的一般理论,并指出,实现有效、可靠地传输和存储信息的途径是走数字化的道路。
这是通信技术领域数字化革命的数学或理论基础。
1946年的计算机和1947年晶体管的诞生和相应技术的发展,是这一革命的物理或物质基础。
信息论是在长期的通信工程实践和理论研究的基础上发展起来的。
当物理学中的电磁理论以及后来的电子学理论一旦有某些进展,很快就会促进电信系统的创造发明或改进。
这是因为通信系统对人类社会的发展,其关系实在是太密切了。
日常生活、工农业生产、科学研究以及战争等等,一切都离不开消息传递和信息流动。
通信系统是人类社会的神经系统,即使在原始社会也存在着最简单的通信工具和通信系统,这方面的社会实践是悠久漫长的。
自从香农十九世纪四十年代末两篇论文发表后,前苏联和美国的科学家采取了不同的研究途径经一部发展了信息论。
柯尔莫哥洛夫、宾斯基和达布鲁新为首的一批著名数学家致力于信息论的公理化体系和更一般更抽象的数学模型,对信息论的基本定理给出了更为普遍的结果,为信息论发展成数学的一个分支作出了贡献。
信息与计算科学专业课程简介

信息与计算科学专业课程简介课程代码:3112001131.课程名称:解析几何 Analytic Geometry总学时: 64 周学时: 4学分: 3 开课学期:一修读对象:必修预修课程:无内容简介:《解析几何》是学科基础课程,是所有数学专业及应用数学专业的主要的基础课。
它是用代数的方法来研究几何图形性质的一门学科。
《解析几何》包括向量与坐标,轨迹与方程,平面与空间直线,柱面、锥面、旋转曲面与二次曲面,二次曲线的一般理论与二次曲面的一般理论等。
选用教材:吕林根,许子道,《解析几何》(第四版),高等教育出版社,2006年。
参考书目:周建伟,《解析几何》,高等教育出版社,2005年。
课程代码:311200214、311200314、311200616、3112007152.课程名称:数学分析Ⅰ-Ⅳ Mathematical AnalysisⅠ-Ⅳ总学时:334 周学时:4,4,6,5学分: 18 开课学期:一,二,三,四修读对象:必修预修课程:无内容简介:《数学分析》是学科基础课程,是所有数学专业及应用数学专业第一基础课。
它提供了利用函数性质分析和解决实际问题的方法, 培养学生严谨的抽象思维能力,为学习其他学科奠定基础。
主要内容有:实数、函数、极限论,函数的连续性。
一元函数微分学,微分学基本定理。
一元微分学应用,实数完备性基本定理,闭区间上连续函数性质的证明,不定积分,定积分及应用,非正常积分。
数项级数,函数列与函数项级数,幂级数,付里叶级数,多元函数的极限与连续,多元函数微分学。
隐函数定理及其应用,重积分,含参量非正常积分,曲线积分与曲面积分。
选用教材:华东师范大学数学系,《数学分析》(第三版)(上、下册),高等教育出版社,2001年。
参考书目:① 陈纪修,《数学分析》(第二版),高等教育出版社2004年。
② 刘玉琏,傅沛仁,《数学分析讲义》(第三版),高等教育出版社,1992年。
课程代码:311200416、3112005153.课程名称:高等代数Ⅰ-Ⅱ Advanced AlgebraⅠ-Ⅱ总学时:198 周学时:6,5学分: 11 开课学期:二,三修读对象:必修预修课程:无内容简介:《高等代数》是学科基础课程。
信息论PPt(叶中行)..

LZ算法
i
反之,对给定的满足上述不等式的一组 (l1,l2,...,lm ),必存在以它们为码字长的一个 即时码
例 设二进制码树中X (a1 , a2 , a3 , a4 ), l1 1, l2 2, l3 2, l4 3, 应用克莱夫特不等式判断是否为唯一 可译码
例 设离散信源 s6 S s1 s2 pi 1 p( s) p p p6 i 1 2 将此信源编码成r元唯一可译码,其对应的码长 为(l1 ,l2 , ,l6 )=(1,1,2,3,2,3),求r值的下限
第3章 数据压缩和信源编码
§3.1 等长码 §3.2 变长编码 §3.3 哈夫曼码 §3.4 香农码和费诺玛
§3.1 等长码
• 信源编码:以提高通信有效性为目的的编码。通常 通过压缩信源的冗余度来实现。采用的一般方法是 压缩每个信源符号的平均比特数或信源的码率。即 同样多的信息用较少的码率传送,使单位时间内传 送的平均信息量增加,从而提高通信的有效性。
*
3.5 通用信源编码
本节将主要介绍 • LZ算法, • 改进的LZ-Welcn 算法 • Kieffer-Yang算法, • LZ算法基于符号串匹配的算法,而LZWelcn 算法是基于字典的算法,它们都是 利用信源输出符号自身的信息来进行压缩 编码。Kieffer-Yang算法(简称YK算法)则 兼顾了字符串匹配和算术码结构的优点。
0 11 00 11
0 10 00 01
1 10 100 1000
1 01 001 0001
6 、同价码: 每个码字占相同的传输时间
7.码的N 次扩展: 若码C :{W1 , W2 ,..., Wq },B :{Bi (Wi1Wi 2 ...WiN )},则 码B称为码C的N 次扩展码
信息与计算科学专业培养计划

信息与计算科学专业培养计划一、培养目标本专业培养具有良好的数学基础与计算机基础,掌握信息与计算科学的基本理论、方法与技能,受到科学研究的初步训练,能解决信息处理和科学与工程计算中的实际问题,能在科技、教育、信息产业、经济金融等部门从事研究、教学、应用开发和管理工作的高级专门人才。
二、培养要求本专业学生主要学习基础数学、计算数学、计算机软件和信息处理等方面的基础理论、基本技能和主要方法;受到严格、系统的数学思维及计算机软件应用、设计与开发的训练,掌握一门外国语,能阅读本专业的外文文献,具有较强的自学能力和知识更新能力。
毕业生应获得以下几方面的知识和能力:1、具有良好的数学基础,掌握信息与计算科学的基础理论和基本方法;2、具备熟练应用计算机(包括常用语言、工具及专用软件)的基本技能,具有较强的算法分析、算法设计和编程能力;3、了解某个应用领域,能运用所学的理论、方法和技能解决科研、生产与管理中的某些实际课题;4、对信息与计算科学的理论、技术及应用的新发展有所了解,具有一定的科学研究和软件开发能力。
三、专业方向与特色本专业设置计算数学、软件设计和经济金融三个专业方向;要求学生具有厚实的数学基础,注重培养学生灵活地应用数学方法和计算机软件解决实际问题的能力。
四、培养年限:四年五、授予学位:理学学士六、主要课程简介1、课程编号:120101101-3课程名称:数学分析(Mathematical Analysis)课程性质:专业必修课主要内容:实数集与函数,极限与连续性,导数与微分(包括微分中值定理、L'Hospital 法则、函数极值判定、Taylor公式等),积分(包括广义积分),级数(包括幂级数、Fourier 级数),多元函数微分学,重积分,含参变量积分,曲线积分与曲面积分。
教材:数学分析(第三版),华东师范大学数学系编。
参考书目:数学分析学习指导书,吴良森等编;数学分析,刘玉连等编。
2、课程编号:120101102-2课程名称:高等代数(Advanced Algebra)课程性质:专业必修课主要内容:本课程主要包括多项式理论与线性代数两个部分。
高等教育出版社样书目录(数学类)
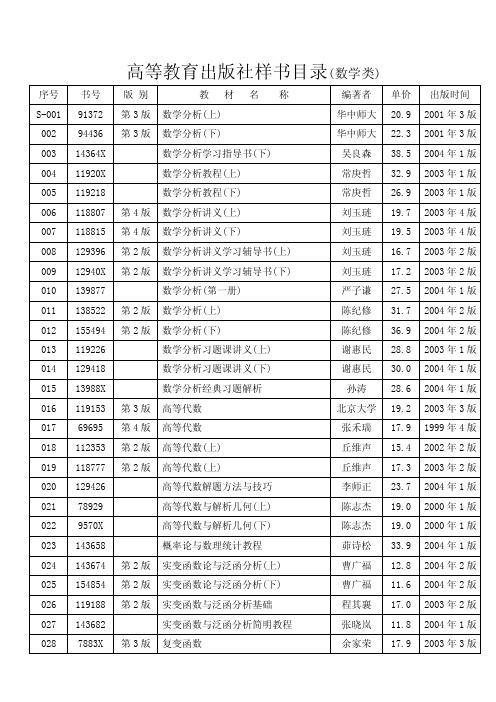
同济大学 10.1 2001 年 2 版
重温微积分
齐民生 39.6 2004 年 1 版
第 2 版 微积分(上)
同济大学 24.9 2003 年 2 版
第 2 版 微积分(下)
同济大学 23.1 2003 年 2 版
微积分学习辅导与习题选解
同济大学 28.4 2004 年 1 版
第 2 版 微积分学简明教程(上)
余家荣 17.9
出版时间 2001 年 3 版 2001 年 3 版 2004 年 1 版 2003 年 1 版 2003 年 1 版 2003 年 4 版 2003 年 4 版 2003 年 2 版 2003 年 2 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 1 版 2004 年 1 版 2004 年 1 版 2003 年 3 版 1999 年 4 版 2002 年 2 版 2003 年 2 版 2004 年 1 版 2000 年 1 版 2000 年 1 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 2 版 2004 年 1 版 2003 年 3 版
高等教育出版社样书目录(数学类)
版别
教材名 称
编著者 单价 出版时间
第4版 第3版
概率论与数理统计教程 概率论与数理统计教程学习辅导与习题 选解
概率论与数理统计
沈恒范 沈恒范 盛骤
20.6 2003 年 4 版 17.6 2003 年 1 版 19.3 2001 年 3 版
概率论与数理统计习题全解指南
第 2 版 数学史概论
李文林 21.0 2002 年 2 版
大学文科高等数学(第一册)
姚孟臣 11.9 1997 年 1 版
《信息论基础》课程教学大纲

《信息论基础》课程教学大纲一、《信息论基础》课程说明(一)课程代码:14131054(二)课程英文名称:Information Theory(三)开课对象:信息管理与信息系统专业(四)课程性质:信息论是20世纪40年代后期从长期通讯实践中总结出来的一门学科,是研究信息的有效处理和可靠传输的一般规律的科学。
本课程是信息管理与信息系统本科的专业课。
它应用近代数理统计方法研究信息传输、存贮和处理,并在长期通信工程实践中不断发展。
因而它是一门新兴科学,亦称为通信的数学理论。
建立在通信理论的数学知识基础之上的信息论在数据压缩、调制解调器、广播、电视、卫星通信,计算机存储,因特网通讯,密码学等方面有着广泛的用途。
要使学生领会信息论的基本思想,具备解决实际问题的能力。
从而学习信息论基础,是将信息论渗透到并应用于更广泛的各种科学技术领域的必经之路,也有助于进一步发展和深化信息概念与信息理论。
先修课程为概率论与数理统计(五)教学目的:本课程是信息管理与信息系统本科生的专业课,采用概率论与随机过程等数学方法研究信息的测度、信道容量以及信源与信道编码等理论问题;主要目的是让学生了解Shannon信息论的基本内容,掌握其中的基本公式和基本运算,培养利用信息论的基本原理分析和解决实际问题的能力,为进一步学习通信和信息以及其他相关领域的高深技术奠定良好的理论基础。
(六)教学内容:掌握熵与互信息的概念,性质与计算;掌握离散信源熵的计算;掌握离散信源编码定理与Huffman编码方法;掌握特殊离散无记忆信道与高斯信道容量的计算;掌握信道编码定理;理解R(d)函数与有失真的信源编码定理.(七)学时数、学分数及学时数具体分配学时数: 36分数: 2(八)教学方式:采用多媒体教学方式(九)考核方式和成绩记载说明考试方式将结合平时作业、平时考核(40%)、期末考试(60%)的各个环节。
使学生能够注重平时学习的过程,改变学生从应试型到能力型。
信息论基础简介

我们可以看到此时传输这23个字只需要: (4+3+3)×1+(5×2)×2+3×3=39
个字符。这样就利用信息出现的频率减小了文字的冗 余度,使得传输更有效。
A ·— B — ··· C — ·— · D — ·· E· F ··— · G ——· H ···· I ··
J ·— — — K — ·— L ·— ·· M —— N —· O ——— P ·— — · Q — — ·— R ·— ·
美国则是由一批数学修养很高的工程技术人员 致力于信息有效处理和可靠传输的可实现性
我国数学家和信息科学专家在20世纪 50年代将信息论引进中国。如胡国定、王 寿仁、万哲先、江泽培、蔡长年、章照止、 沈世镒等,为信息论的发展作出了自己的 贡献。
信源 接受者
通讯基本模型
信源 编码器
信道 编码器
噪声
信道 (存储介质)
1948年发表《通信的数学理论》,奠定了信息论的基础。
IEEE在1950年成立了信息论学会,于1973年设立申农讲 座,是国际信息论届的最高荣誉。
前苏联的辛钦(Shiqin)、柯尔莫哥洛夫 (Kolmogorov)、宾斯基(Pinsker)和达布鲁新 (Dabrushin)等一批著名数学家致力于信息论的 公理化体系和更一般的数学模型
只能用低于信道容量的速率来可靠的传输信息, 否则就会出现错误。
• 利用增加的冗信息进行纠错,形成了纠错技术, 如:Hamming码、Golay码、循环码、BCH码等。
消息=
Yes 信道编码: Yes=0
Yes 或 No
No=1
0
噪声
信道
接受者
10
YNeos
信道译码: 0=Yes
信息论基础

教师:吴旭 手机:18236888638 Email:wuxu@
1
信息论与编码原理
教பைடு நூலகம்: 曹雪虹,张宗橙.信息论与编码(第二版). 9 2009 北京:清华大学出版社,200
2
参考书:
1.叶中行.信息论基础.北京:高等教育出版社, 2.孙丽华,陈荣伶 .信息论与编码.江西:科学技 术出版社,2002 3.田丽华.编码理论.西安:西安电子科技大学 出版社,2003 4.张鸣瑞,邹世开.编码理论.北京:北京航天航空 出版社,1990 5. 姜丹.信息论与编码.北京:中国科学技术大学 出版社, 2004 6. 曹雪虹,张宗橙.信息论与编码.北京:北京邮 电大学出版社, 2001 7. 傅祖芸.信息理论与编码学习辅导及精选题 解.北京:电子工业出版社,2004
1.2 通信系统的模型
�
�
通信系统的模型是什么?各部件的功能 作用是什么? 通信系统的性能指标有哪些?
28
信息论基础的重要性
�
�
�
信息论是信息科学和技术的基本理论,信息科 学大厦的地基; 没有信息论的基础,从事通信与信息领域的研 究和创新是不可能的事情; 总之,信息论是高层次信息技术人才必不可少 的基础知识。
� 信息的基本概念在于它的不确定性,任 何已经确定的事物都不含有信息。 例.如果你问你的同学“明天是星期几”,则 答案中含有多少信息量? 情况一.你不知道今天是星期几 情况二.你知道今天是星期一 � 通信过程是一种消除不确定性的过程, 不确定性的消除,就获得了信息。 例.同学对你说”你编码原理考试通过了”, 你得到了消息,获得了信息吗?
�
信息:是指各个事物运动的状态及状态变化的方式。 人们从来自对周围世界的观察得到的数据中获得信 息。信息是抽象的意识或知识,它是看不见、摸不 到的。人脑的思维活动产生的一种想法,当它仍储 存在脑子中的时候就是一种信息。信息是信号与消 息的更高表达层次。三个层次中,信号最具体,信 息最抽象。它们三者之间的关系是哲学上的内涵与 外延的关系。
《信息论基础》课程教学大纲

《信息论基础》课程教学大纲一、《信息论基础》课程说明(一)课程代码:14131054(二)课程英文名称:informationtheory(三)开学对象:信息管理与信息系统专业(四)课程性质:信息论是20世纪40年代后期从长期通讯实践中总结出来的一门学科,是研究信息的有效处理和可靠传输的一般规律的科学。
本课程是信息管理与信息系统本科的专业课。
它应用近代数理统计方法研究信息传输、存贮和处理,并在长期通信工程实践中不断发展。
因而它是一门新兴科学,亦称为通信的数学理论。
建立在通信理论的数学知识基础之上的信息论在数据压缩、调制解调器、广播、电视、卫星通信,计算机存储,因特网通讯,密码学等方面有着广泛的用途。
要使学生领会信息论的基本思想,具备解决实际问题的能力。
从而学习信息论基础,是将信息论渗透到并应用于更广泛的各种科学技术领域的必经之路,也有助于进一步发展和深化信息概念与信息理论。
先修课程为概率论与数理统计(五)教学目的:本课程就是信息管理与信息系统本科生的专业课,使用概率论与随机过程等数学方法研究信息的测度、信道容量以及信源与信道编码等理论问题;主要目的就是使学生介绍shannon信息论的基本内容,掌控其中的基本公式和基本运算,培育利用信息论的基本原理分析和化解实际问题的能力,为进一步自学通信和信息以及其他有关领域的高深技术打下较好的理论基础。
(六)教学内容:掌握熵与互信息的概念,性质与计算;掌握离散信源熵的计算;掌握离散信源编码定理与huffman编码方法;掌握特殊离散无记忆信道与高斯信道容量的计算;掌握信道编码定理;理解r(d)函数与有失真的信源编码定理.(七)学时数、学分数及学时数具体分配学时数:36分数:2学时数具体内容分配:教学内容第一章绪论第二章信源和信息熵第三章信道与信道容量第四章率为杂讯函数第五章编码定理合计210481236合计210481236讲授实验/课堂教学(八)教学方式:使用多媒体教学方式(九)考核方式和成绩记载说明考试方式将融合平时作业、平时考核(40%)、期末考试(60%)的各个环节。
《信息论基础》课程的教学探讨

《信息论基础》课程的教学探讨作者:胡爱花来源:《教育教学论坛》 2017年第8期摘要:根据《信息论基础》的教学内容,灵活采用多种教学方法,结合多媒体技术,应用相关计算软件,有助于提高对课堂教学内容的理解。
进一步探索信息论与其他学科的关联,加强实践环节,增强学生学习的趣味性与主观能动性。
最后,丰富课程的考核方式,使学生加深对相关知识的掌握,拓宽课堂学习内容。
关键词:信息论基础;信息;教学方法;Matlab中图分类号:G642.41 文献标志码:A 文章编号:1674-9324(2017)08-0161-02一、引言我们人类生活在信息的海洋之中,如古代的“烽火告警”。
可以说,我们一时一刻都离不开接受信息、传递信息与利用信息。
信息论围绕信息这一基本概念展开,是由通信技术与概率论、随机过程和数理统计相结合而逐步发展起来的一门学科。
目前,信息论在通信、计算机、自动控制、生物学、语言学、统计学、社会学、物理等众多领域取得广泛的应用。
《信息论基础》是高等院校数学类信息与计算科学专业、通信类专业的核心课程,以香农(Shannon)经典信息论为主要学习对象,内容丰富、理论性强。
课程开设的目的在于使学生掌握信息理论的相关概念与计算方法,了解信息论的研究目的与实际应用。
通过本课程的学习,培养学生的创新思维,分析并解决相关问题。
虽然信息科学涉及到众多学科,实用性比较强,但学生普遍反映不好学,学了也不知道如何用,学习过程比较被动,学习效果也不明显。
因此,教师很有必要对《信息论基础》课程的教学方法进行思考、研究与探讨,以期提高教学质量,增强学生学习的主观能动性,掌握相关知识,达到学以致用。
二、教学改革方案首先,根据《信息论基础》的教学内容,灵活采用多种教学方法。
《信息论基础》理论性强,如果完全围绕课本,以板书为主要手段展开教学,会使得课堂氛围比较呆板,很难有效激发学生地学习兴趣。
因此,课堂内容应该结合多媒体技术,应用相关计算软件进行教学。
信息论基础-高等教育出版社-叶中行

定义1.3.3 设随机变量X,Y,Z的联合分布为 p( x, y, z ),则给定Z 条件下X 和Y的条件互信息为
(x, y | z) p I(X ; Y | Z )= p( z ) (x, y | z)log p (x | z)(y | z) p p zZ x y
易验证以下关系式成立 I(X ; Y | Z )=H(X | Z )-H(X | Y , Z ) =H(Y | Z )-H(Y | X , Z ) =H(X | Z )+H(Y | Z )-H(X , Y | Z ) =I(Y ; X | Z )
信源
信源编码器 等效信源 等效信宿
信道编码器
等效干扰 信道
信 道
信道译码器
干 扰 源
信宿
信源译码器
信息传输系统模型
1.信源 产生消息的源。 2. 编码器 将消息变成适合于信道传送 的信号的设备。 信源编码器,提高传输效率 编码器 信道编码器,提高传输可靠性 3. 信道 信息传输和存储的媒介 4. 译码器 译码是编码的逆变换,分为 信道译码和信源译码。 5. 信宿 消息的接收者。
自信息:信源发出的某个信号所含的信息 量,记为 I ( x) 自信息与信号发生概率之间关系
(1) x 的概率越大,其发生的可能性越大,
不确定性越小,I ( x)应当越小
(2) 信源连续独立发出两个信号x,y,它们的 联合分布 p(x,y)=p(x)p(y),则x,y的自信息 是它们各自信息量之和,即I(x,y)=I(x)+I(y)
y
P {Y = y | X = x}, x , y
r
表示条件概率分布,则给定X = x条件下的熵
而给定随机变量X 条件下Y的熵记为H Y | X),它 ( 是H Y | X x)关于X 的平均值, (
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
定义1.1.1 设x 有概率p( x),则x的自信息定义为 1 I(x)=log p( x)
自信息满足的公理
(1) 非负性:I(x) 0
(2) 若p(x)=0,则I(x)
(3) 若p(x)=1,则I(x)=0
(4) 严格单调性:如果p(x)>p(y),则I(x)<I(y)
(5) 如果p(x,y)=p(x)p(y),则I(x,y)=I(x)+I(y)
定理1.1.1 若自信息I(x)满足上述5个条件,则 1 I(x)=clog p(x) 其中c为常数
定理1.3.10 (数据处理不等式) 如果U X Y V 构成马氏链,则 I(U ;V ) I(X ; Y )
§1.41.4.1 称定义于区间(a,b)上的一个函数 信息量的一些基本性质 定义
(x)为凸函数,如果对任意x1,x2 a,b)和 f ( 0 1,有 ( x1 +(1-)x2) (x1)(1-)(x2) f f f
第1章 随机变量的信息度量
§1.1 自信息 §1.2 熵、联合熵、条件熵 §1.3 相对熵和互信息 §1.4 信息量的一些基本性质 §1.5 广义熵 习题课
§1.1 自信息
信息:通信领域指通信的消息;信号处理 方面指包括了数字、数据、图像、语音等 进行运算和处理所需的条件、内容和结果 信源:消息的来源。 信源的分类:离散信源和连续信源 信源的表示方法:用随机变量X表示一个 离散信源,X的可能取值,即信源可能输 出的不同符号用集合χ表示
I(X ; Y )=D((x, y)||(x)(y)) p p p (x, y) p = (x, y)log p (x)(y) p p x y =EP x , y)log ( (X , Y) p (X)(Y) p p
定理1.3.3 I(X ; Y )=H(X )+H(Y )-H(X , Y ) =H(X )-H(X | Y ) =H(Y )-H(Y | X ) =I(Y ; X )
信息论研究的主要内容
狭义信息论,即通信的数学理论,主要研究狭义 信息的度量方法,研究各种信源、信道的描述和信 源、信道的编码。
实用信息论,研究信息传输和处理问题,也就是 狭义信息论方法在调制解调、编码译码以及检测理论 等领域的应用。
广义信息论,包括信息论在自然和社会中的新的 应用,如模式识别、机器翻译、自学习自组织系统、 心理学、生物学、经济学、社会学等一切与信息问题 有关的领域。
X 输入
第一级 处理器
Z
第二级 处理器
Y
级联处理器示意图 数据处理定理:
数据处理过程中只会丢掉一些信息,绝不会 创造出新的信息,这就是所谓的信息不增性。
U
X 编码
Y 信道
译码
V
一般通信系统
I(U ;V ) I(X ;V ) I(X ;V ) I(X ;Y )
I(U ;V ) I(X ; Y )
定义1.2.2 设一对随机变量(X,Y)的联合 分布为 (x, y)= P r{ X = x,Y = y},x , y p
则定义(X,Y)的联合熵H X,Y)为 ( H X,Y)=- (x,y)log(x,y) ( p p
x y
或者写成数学期望形式: H X,Y) - E log p(X,Y) ( =
熵的单位 比特(bit)
e
10
奈特(nat)
哈特(hartley)
对数底与熵单位的对应关系
期望,即E pg ( X ) g ( x) p( x)
x
用E表示数学期望, p表示关于分布p的数学 E
1 熵可表示为随机变量log 的数学期望 p(X) 1
H(X) E plog p(X) 1 = (log ) p( x) p(x) x =- p ( x) log p ( x)
注2: 类似于H Y | X), , Z | X)=- p( x, y, z ) log p( y, z | x) (
x y z
定义如下: H Z | Y , X)=-- p( x, y, z ) log p( z | x, y ) (
定理1.3.7 I(X ; Y | Z ) 0,且符合成立的充要条件是 给定Z 条件下X 和Y 互相独立。
定理1.3.8 (互信息的链法则) I(X 1 , X 2 ... X n ; Y )=(X i ; Y | X i 1 ,X i 2 ,X 1) I
i=1 n
系1.3.9 如果X Z Y 构成马氏链,则 I(X ; Y ) I(X ; Z )及I(X ; Y ) I(Z ; Y )
x y z
链法则也可以推广到多维情形,为了简化,今后 记: X n X 1 , X 2 ...X n),x n x1 ,x2 ,...xn) ( (
定理1.2.3(熵的链法则) 设X 1 , X 2 ...X n的联合分布为(x1 ,x2 ,...xn),则 p H X 1 , X 2 ...X n)= H X i | X i-1 ...X 1) ( (
H X i | X i-1 ...X 1) H X i) ( ( H X 1 , X 2 ...X n) H X i) ( (
i=1 n
定义1.3.3 设随机变量X,Y,Z的联合分布为 p( x, y, z ),则给定Z 条件下X 和Y的条件互信息为
(x, y | z) p I(X ; Y | Z )= p( z ) (x, y | z)log p (x | z)(y | z) p p zZ x y
易验证以下关系式成立 I(X ; Y | Z )=H(X | Z )-H(X | Y , Z ) =H(Y | Z )-H(Y | X , Z ) =H(X | Z )+H(Y | Z )-H(X , Y | Z ) =I(Y ; X | Z )
定义1.3.4 设随机变量X,Y,Z的联合分布为 p( x, y, z ),称给定Z 条件下X 和Y 互相独立, 如果 p ( x, y | z ) p ( x | z ) p ( y | z ) 对于任意x ,y ,z 成立。我们把 这种条件独立性简记为X Y | Z,这时也称 X,Z , Y 构成马氏链,记为X Z Y。
信息论基础
绪论 第1章 第2章 第3章 第4章 第5章 第6章
随机变量的信息度量 随机过程的信息度量和渐近等分性 数据压缩和信源编码 数据可靠传输和信道编码 限失真信源编码和率失真函数 连续信源和信道编码理论
绪论
信息论是应用近代概率统计方法研究信息 传输、交换、存储和处理的一门学科,也 是源于通信实践发展起来的一门新兴应用 科学 研究信息的基本性质及度量方法,研究信 息的获取、传输、存储和处理的一般规律 的科学 研究可能性和存在性问题,为具体实现提 供理论依据
信源
信源编码器 等效信源 等效信宿
信道编码器
等效干扰 信道
信 道
信道译码器
干 扰 源
信宿
信源译码器
信息传输系统模型
1.信源 产生消息的源。 2. 编码器 将消息变成适合于信道传送 的信号的设备。 信源编码器,提高传输效率 编码器 信道编码器,提高传输可靠性 3. 信道 信息传输和存储的媒介 4. 译码器 译码是编码的逆变换,分为 信道译码和信源译码。 5. 信宿 消息的接收者。
i=1 n
§1.3 相对熵和互信息
定义1.3.1 定义在同一字母集合 上的两个概率 分布p(x)和q(x)的相对熵定义为: (x) p D(p|q)= (x) p log q(x) x
在上述定义中,一般规定: 0 p 0 log 0 p log q 0 注意!一般的说,D(p||q) D(q||p)
§1.2 熵、联合熵、条件熵
熵:对整个信源来说,每个信号的平均信 息量的多少 定义1.2.1 离散随机变量X的熵定义为
H ( X ) p( x) log p( x)
x
也可记为H(p),也称为概率分布p的熵
注意!熵只是概率分布p的函数,与X 取什么值并无关系
对数函数底 2 H(X)
自信息:信源发出的某个信号所含的信息 量,记为 I ( x) 自信息与信号发生概率之间关系
(1) x 的概率越大,其发生的可能性越大,
不确定性越小,I ( x)应当越小
(2) 信源连续独立发出两个信号x,y,它们的 联合分布 p(x,y)=p(x)p(y),则x,y的自信息 是它们各自信息量之和,即I(x,y)=I(x)+I(y)
x11 x 2
...
2
xn
(x1 ,x2 ,...xn) (x1 ,x2 ,...xn) p log p
n
定义1.2.4 设随机变量对(X,Y)有联合分布(x, y),用 p p ( y | x )= 定义为
H Y | X x)=- p( y | x) log p( y | x) (
定理1.3.1
D(p||q) 0,且等号成立的充要条件是,
(x)=q(x)对所有的x 成立。 p
系1.3.2 (熵最大定理)H(X ) log ,其中等号成立的 充要条件是X 服从均匀分布(x)= p 母集中所包含元素的个数。 1
,其中 表示字
定义 1.3.2 设两个随机变量(X,Y )的联合分布为(x, y), p 边际分布分别为(x),(y),互信息I(X ; Y )是(x, y)与 p p p 乘积分布(x)(y)的相对熵,即 p p
y
P {Y = y | X = x}, x , y
