第五届小学《祖冲之杯》数学邀请赛(无答案)(竞赛)
第六届小学《祖冲之杯》数学邀请赛(无答案)(竞赛)-最新学习文档

第六届小学《祖冲之杯》数学邀请赛一、填空题(满分l00分)1~10小题每题8分,ll ~12每小题l0分1.我国古代数学家祖冲之在数学上的重大贡献之一是推算出圆周率π的值在3.1415926与3.1415927之间,比欧州早一千多年,约率722是π的近似值,现问:722 小数点后面第2019位上数字是 。
2.在某一个月中,有三个星期天的日期是偶数号,那么这个月的8号是星期 。
3.将分数131的分子、分母同加一个整数后得到53,那么同加上的这个数是 。
4.一辆汽车以每小时60千米的速度从A 地开往B 地,他又以每小时 40千米的速度从B 地返回A 地,那么这辆汽车行驶的平均速度是 千米/时。
5.某班44人,从A ,B ,C ,D ,E 五位候选人中选举班长,A 得选票23张,B 得选票占第二位,C ,D 得票相同,E 选票最少,得4票,那么B 得选票 张。
6.一张面积为l 的正三角形白纸片,现按下述方式对其涂色:每次把正三角形分成四个全等的小正三角形,将中间的小正三角形涂成黑色(如下图),经过四次涂色后,仍是白色的面积是 。
7.12个小球分别标上自然数l ,2,3…12。
甲、乙、丙三人每人拿了4个小球,而且每人所拿的四个小球上标的数之和相等。
已知甲拿的球中有两个球标的数是6,12;乙有两个球的标数是7,9。
那么丙所取的四个球上标的数是 , , , 。
8.一个长方形的边长都是整数厘米,面积为1050平方厘米,那么这个长方形的周长最大可能是 厘米,最小可能是 厘米。
9.在2019这个数的前面或后面添写一个数4,所得到的两个五位数均能被4整除。
现在,请你找出一个三位数写在2019的前面或后面,使所得的两个七位数也能被这个三位数整除,这样的三位数有 个,它们是 。
10.下图3×3正方形的每个方格内的字母都代表一个数,已知其每行,每列以及两条对角线上三个数之和都相等,若a=4,d=19,l =22,那么b= ,h= 。
第五届小学希望杯全国数学邀请赛

第五届小学“希望杯”全国数学邀请赛六年级 第1试2007年3月18日 上午8:30至10:00亲爱的小朋友们,欢迎你参加第五届小学“希望杯”全国数学邀请赛!你将进入一个新颖、有趣、有挑战性的数字天地,将会留个一个难忘的经历,好,我们开始前进吧!……以下每题6分,共120分。
1. 已知31::1.2,:0.75:22a b b c ==,那么:c a = (写成最简单的整数比) 2. 11111111(1)(1)(1)(1)(1)(1)(1)(1)23456789_____.0.10.20.30.40.50.60.70.80.9--------=++++++++ 3.在下面的算式□中填入四个运算符号+、-、⨯、÷、(每个符号只填一次),则计算结果最大是_______.1□2□3□4□54. 在图1所示的和方格表中填入合适的数,使用权每行、每列以及每条对角线上的三个数的和相等。
那么标有“★”的方格内应填入的数是_______.5. 过年时,某商品打八折销售,过完年,此商品提价________%可恢复原来的价格。
6.如图2是2003年以来我国日石油需求量和石油供应量的统计图。
由图可知,我国日石油需求量和日石油需求量增长更______(填“大”或“小”),可见我国对进口石油的依赖程度不断定_______(填“增加”或“减小”)。
7.小红和小明帮刘老师修补一批破损图书。
根据图3中信息计算,小红和小时一共修补图书______本。
8.一项工程,甲单独完成需要10天,乙单独完成需要15天,丙单独完成需20天,古代合作3天后,甲有其它任务而退出,剩下乙、丙继续工作直至完工。
完成这项工程共用______天。
9.甲、乙两车分别从A 、B 两地同时相向开出,甲车的速度是50千米/时,乙车的速度是40千米/时,当甲车驶过A 、B 距离的13多50千米时,与乙车相遇.A 、B 两地相距______千米。
10.今年儿子的年龄是父亲年龄的14 ,15年后,儿子的年龄 父亲年龄的511。
第五届小学《祖冲之杯》数学邀请赛(无答案)(竞赛)-精选教学文档

第五届小学《祖冲之杯》数学邀请赛一、填空题。
(满分l00分)(本题共有l2个小题,第1~10小题,每小题8分;第11,12小题,每小题l0分。
)1.能被分数2110,145,76除得的结果都是整数的最小分数是 。
2.如果,6666544443,3333222221==B A 那么A 与B 中较大的数是 。
3.目前日期的流行记法是采用6位数字,即将公元年份的后两位数字记在最左边,中间两个数字表示月份,最末两位数字表示日份。
(遇有月或日是一位数的,前面加一个0。
例如1976年4月5日记为:760405)第五届小学祖冲之杯赛的竞赛日期应记为951126,这个六位数恰好能被66整除,因此这样的日期被称为“大顺日”,即今天是大顺日。
在今年内,距今天最近的一个大顺日是95年 月 日。
4.顾客向售货员购买15元的物品,付了一张面值50元的钞票,售货员没有零钱找,便向相邻柜台兑换了零钱。
当交割完毕顾客走后,邻柜发现这张50元钞票是假币,该售货员于是又还给邻柜50元钱,那么,该售货员遭受了 元的损失。
5.一个旅社有40间客房,经过一段时间的经营实践,旅社经理发现了这样一个规律,如果客房定价每间每天40元时,住房率为55%;每间定价35元时,住房率为65%;每间定价30元时,住房率为75%;每间定价25元时,住房率为85%;当每间价20元时,则天天客满。
要使每天收入达到最高,经理应从上五种定价中选取每天每间为 元。
6.一堆黑、白围棋子,从中取走了白子15粒,余下的黑子数与白子数之比为2:1,此后,又取走黑子45粒,余下的黑子数与白子数之比为l :5,那么这堆围棋原来共有 。
7. 2019个8的连乘积减去l995个7的连乘积,差的个位上的数字是 。
8.左下图是由九个矩形图案排列的方阵,但有一个矩形图案还没有放上。
请你从右下图的六个矩形图案中,选一个放到问号的位置,你认为最合适的是 号。
9.如下图所示,在长方形ABCD 中,放入六个形状、大小都相同的长方形(尺寸如图)。
5年级-2-分数计算与比较大小-难版

第2讲分数计算与比较大小知识梳理对于两个不同的分数,有分母相同,分子相同以及分子、分母都不相同三种情况,其中前两种情况判别大小的方法是:分母相同的两个分数,分子大的那个分数比较大;分子相同的两个分数,分母大的那个分数比较小。
第三种情况,即分子、分母都不同的两个分数,通常是采用通分的方法,使它们的分母相同,化为第一种情况,再比较大小。
由于要比较的分数千差万别,所以通分的方法不一定是最简捷的。
下面我们介绍另外几种方法。
1.“通分子”。
当两个已知分数的分母的最小公倍数比较大,而分子的最小公倍数比较小时,可以把它们化成同分子的分数,再比较大小,这种方法比通分的方法简便。
如果我们把课本里的通分称为“通分母”,那么这里讲的方法可以称为“通分子”。
2.根据倒数比较大小。
3.若两个真分数的分母与分子的差相等、则分母(子)大的分数较大;若两个假分数的分子与分母的差相等,则分母(子)小的分数较大。
分数混合运算式,要注意分数小数之间的互化,已达到简算的目的,同时考虑运算律的应用。
典型例题分数比较大小【例1】★比较777773777778 和888884888889的大小。
【解析】这两个分数的分子与分母各不相同,不能直接比较大小,使用通分的方法又太麻烦。
由于这里的两个分数都接近1,所以我们可先用1分别减去以上分数,再比较所得差的大小,然后再判断原来分数的大小。
因为1-777773777778 =5777778 ,1-888884888889 =58888895777778 >5888889所以777773777778 <888884888889。
【小试牛刀】比较77777757777777 和66666616666663的大小。
【解析】77777757777777 >66666616666663【例2】★比较1111111 和111111111哪个分数大? 【解析】可以先用1分别除以这两个分数,再比较所得商的大小,最后判断原分数的大小。
第九届小学《祖冲之杯》数学邀请赛(无答案)(竞赛)-学习文档

第九届小学《祖冲之杯》数学邀请赛一、填空题(满分l04分,第l ~8小题,每小题8分;第9~12小题,每小题l0分)1.两个数的和是202.4,其中一个数的小数点向右移动一位就等于另一个数,那么其中较大的数是 。
2.如果。
那么,A 和B 中较大的数是 。
3.一个水箱中的水是装满时的65,用去200升以后,剩余的水是装满时的43,这个水箱的容积是 升。
4.有一个长方体的盒子,从里面量长40厘米,宽l2厘米,高7厘米。
在这个盒子里放长5厘米,宽4厘米,高3厘米的长方体木块,最多可放 块。
5.快、慢两列火车相向而行,快车的车长是50米,慢车的车长是80米,快车的速度是慢车的速度的2倍。
如果坐在慢车的人见快车驶过窗口的时间是5秒,那么,坐在快车的人见慢车驶过窗口的时间是 秒。
6.表示一种新的运算符号。
已知:按此规则,如果n ⊙8=68,那么 n 。
7.如图,正方形与阴影长方形的边分别平行,正方形边长为10,阴影长方形的面积为6,那么图中四边形ABCD 的面积是 。
8.小明到商店买了若干支钢笔与圆珠笔,平均每支笔价钱是6元。
已 知钢笔价钱比圆珠笔贵一半,小明购买圆珠笔的支数比钢笔的支数多一半,那么钢笔每支售价是 元。
9.如图,小正方形的53被阴影覆盖,大正方形的65被阴影覆盖。
那么,小正方形的阴影面积与大正方形阴影面积之比为 。
10.左下图是一个运算器的示意图,A ,B 是输入的两个数据,C 是输出的结果。
右下表是输入A ,B 数据后,运算器输出C 的对应值。
请你据此判断,当输入A 值是l999,输入B 值是9时,运算器输出的C 值是 。
11.小明发现12与36这两个数具有这样的特性:这两个数之积恰是这两个数之和的9倍。
请你也找出两个不同的自然数,具有上述特性。
你找出的两个不同的自然数是 。
12.在一个游泳池中有一条船,船上载着小明、小华和一些石头。
当小明和小华把船舱内的石头投入游泳池以后,小明认为游泳池的水位应该上升;小华认为游泳池的水位应该下降。
几何08不规则多边形

【例 1】 (第三届”华杯赛口试试题”)这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【例 2】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【例 3】 如图,李大伯给一块长方形田地喷药,喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长2米的正方形区域,他从图中的A 点出发,沿最短路线(图中虚线)走,走过88米到达B 点,恰好把这块田地全部喷完,这块田地的面积是多少平方米?BA 1米1米【例 4】 (第六届”走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛)右图中甲的面积比乙的面积大__________平方厘米.6厘米8厘米4厘米【巩固】如图,平行四边形ABCD 种,10BC cm =,直角三角形ECB 的边8EC cm =,已知阴影部分的总面积比三角形EFG 的面积大210cm ,求平行四边形ABCD 的面积.G FEDCBA【例 5】 如图,ABCD 是74⨯的长方形,DEFG 是102⨯的长方形,求BCO 与EFO 的面积差.O BC D GFE A【例 6】 有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?680平方米2720平方米60【巩固】(希望杯培训题)如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少301平方分米.原正方形的边长是______分米.11【巩固】如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?5【例7】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例8】如图所示,直角三角形中有一个长方形,求长方形的面积?44 4【例9】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积??【巩固】(2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是.第6题【例10】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【巩固】如图所示,外侧大正方形的边长是10cm,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为226cm,最小的正方形的边长为多少厘米?【例11】有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?【例12】(2008年全国小学生”我爱数学夏令营”数学竞赛)如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为.第2题【例13】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)6【巩固】(2008年武汉明心奥数挑战赛)如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?【例14】甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?108 6丙乙甲【例15】有2个大小不同的正方形A和B.如下左图所示的那样,在将B正方形的对角线的交点与A正方形的一个顶点相重叠时,相重叠部分的面积为A正方形面积的19.求A与B的边长之比.如果当按下右图那样,将A和B反向重叠的话,所重叠部分的面积是B的几分之几?左图右图【例16】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【例17】(2008年北京”数学解题能力展示”读者评选活动复赛)如图所示,一个长方形广场的正中央有一个长方形的水池.水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.水池【巩固】(2008年”陈省身杯”国际青少年数学邀请赛)如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为厘米,宽厘米.第19题【例18】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?【巩固】在一个正方形的小花园周围,环绕着宽5米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?【巩固】(第四届《小数报》数学竞赛决赛试题)有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?【例19】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差16厘米,面积相差96平方厘米,求小正方形的面积是多少平方厘米?(1)(2)【例20】计划修建一个正方形的花坛,并在花坛周围种上3米宽的草坪,草坪的面积为300平方米,那么修建这个花坛需要占地多少平方米?(2)(1)【例21】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?图a【例 22】 图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.【例 23】 有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?图a图b【例 24】 (第十二届“迎春杯”刊赛试题)如图,边长是整数的四边形AFED 的面积是48平方厘米,FB 为8厘米.那么,正方形ABCD 的面积是 平方厘米.A BCDEF 488【例 25】 如图,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、310平方米和25平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【例 26】 长方形ABCD 的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD 的面积是多少平方厘米?C 1D 1E 1A 1EBC DA【巩固】(第四届华杯复赛试题)如图,长方形ABCD 的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD 的面积?AB C DIH G FEAB C D【例27】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例28】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?图1图2【例29】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【例 30】 (第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD 中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.B【例 31】 若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例 32】 一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A 和B 的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?ABA BCDE FGH【巩固】(2008年中国台湾小学数学竞赛选拔赛)如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为281cm ,请问这个矩形之面积为多少平方厘米?第2题【例 33】 图中数字分别表示两个长方形和一个直角三角形的面积,另一个三角形的面积是 .?51215【例 34】 如图,一个矩形被分成八个小矩形,其中有五个矩形的面积如图中所示(单位:平方厘米),问大矩形的面积是多少平方厘米?1230201636G FEDC B AS 3S 2S 11230201636G FEDC B A【巩固】阳阳用四块小长方形恰好拼成了一个大的长方形,如图所示.现在知道其中三块长方形的面积分别为48平方厘米、24平方厘米、30平方厘米,那么,阴影部分的面积是多少?【巩固】(南京市第三届”兴趣杯”少年数学邀请赛决赛试题)如图,矩形ABCD 被分割成9个小矩形.其中有5个小矩形的面积如图所示.矩形ABCD 的面积为 .164221CBD A【例 35】 有红、黄、绿三块大小一样的正方形纸片,放在一个底面为正方形的盒内,它们之间相互叠合(见下图).已知露在外面的部分中,红色面积是20,黄色面积是14,绿色面积是10.求正方形盒底的面积.绿黄红绿黄红【例 36】 如图所示,在正方形ABCD 内,红色、绿色正方形的面积分别是48和12,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点.那么黄色正方形的面积是 .DCBA绿黄红 312【巩固】如图所示,在正方形ABCD 中,红色,绿色正方形的面积分别是52和13,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,求黄色正方形面积.绿黄红D C BA【例37】如图,三个一样大小的正方形放在一个长方形的盒内,A和B是两个正方形的重叠部分,C、D、E是空出的部分,每一部分都是矩形,它们的面积比是A:B:C:D:E=1:2:3:4:5,那么这个长方形的长与宽之比是________.【例38】(2005全国华罗庚金杯少年数学邀请赛)如图如果长方形的面积为56平方厘米,且2MD=厘米、3QC=厘米、5CP=厘米、6BN=厘米,那么请你求出四边形MNPQ的面积是多少厘米?CP2552PC【巩固】(南京市第三届”兴趣杯”少年数学邀请赛预赛)长方形的广告牌长为10米,宽为8米,A,B,C,D分别在四条边上,并且C比A低5米,D在B的左边2米,四边形ABCD的面积是平方米.DCB ADCBA【例39】(2004全国华罗庚金杯少年数学邀请赛)直角三角形PQR的直角边为5厘米,9厘米,问:图中三个正方形的面积之和比4个三角形的面积之和大多少?D FCCF D【例 40】 如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是232cm ,四边形ABCD 的面积是220cm .⑴求正方形EFGH 的边长?⑵求甲、乙、丙、丁四个长方形周长的总和?FE GD BBDGEF gfc图1 图2 图3【例 41】 如图,平面上CDEF 是正方形,ABCD 是等腰梯形,它的上底23AD =厘米,下底35BC =厘米.求三角形ADE 的面积.FECB DAH 2H 1HADBCEF08奥数天天练——不规则图形面积21【例 42】 右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例 43】 把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个”角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示的图形.如果所作的最小的小正三角形的面积为1平方厘米,求如图中整个图形的面积.图a中中中大图b。
第五届小学“希望杯”全国数学邀请赛

第五届小学“希望杯”全国数学邀请赛四年级第二试一:填空题(每小题5分,共60分)1.(1234+2314+3412+4123)÷(1+2+3+4)=__________。
答案:1111。
解析:(1234+2314+3412+4123)÷(1+2+3+4)=[(1+2+3+4)×1000+(1+2+3+4)×100+(1+2+3+4)×10+(1+2+3+4)×1]÷(1+2+3+4)=(10000+1000+100+10)÷10=11110÷10=11112.如果△÷☆=◇,☆×◇=80,△-◇=60,那么☆=__________。
答案:4。
解析:由△÷☆=◇,有△=☆×◇=80,由△-◇=60,有◇=△-60=80-60=20。
那么,☆=△÷◇=80÷20=43.为使下面算式中的5个数的成绩末尾有六个0,□里的数最小是__________。
8×10×15×25×□答案:解析:因为2×5=10,乘积末尾有一个0,2×2×5×5=100乘积末尾有2个0,所以本题只需考察有多少个2与5相×就知道乘积末尾有几个0。
8=2×2×2,10=2×5,15=3×5,25=5×5,8×10×15×25×□中已经有4个2和4个5相乘,这样末尾会产生4个0,要末尾有6个0,还要至少需要2个2与2个5相乘。
所以□里的数最小是2×2×5×5=100。
4.在2×2=4,3×3=9,4×4=16,5×5=25,6×6=36,……等这些算式中,4,9,16,25,36叫做完全平方数。
不程序图形的面积

不规则图形的面积本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)【例 2】【例 3】【例 4】【例 5】.的面积【例 6】(图【例 7】【例 8】 右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.【巩固】如图所示,4CA AB ==厘米,ABE △比CDE △的面积小2平方厘米,求CD 的长为多少厘米?【巩固】如图,平行四边形ABCD 种,10BC cm =,直角三角形ECB 的边8EC cm =,已知阴影部分的总面积比三角形EFG 的面积大210cm ,求平行四边形ABCD 的面积.【例 9】 如图,ABCD 是74⨯的长方形,DEFG 是102⨯的长方形,求BCO 与EFO 的面积差.例题精讲【例10】有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?【巩固】有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?【例11】一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【例12】一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【例138分米再原正【例14【例 15】再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?【例16】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例17】如图所示,直角三角形中有一个长方形,求长方形的面积?【例18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?【巩固】(2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是.【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【例19】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【巩固】如图所示,外侧大正方形的边长是10cm,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为226cm,最小的正方形的边长为多少厘米?【例20】有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?【例2110的正【例22【例23【例24【例25【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?【例26】(2008年北京”数学解题能力展示”读者评选活动复赛)如图所示,一个长方形广场的正中央有一个长方形的水池.水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.【例27】用四个相同的长方形拼成一个面积为2100cm的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例28】四个完全相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?【巩固】(2008年”陈省身杯”国际青少年数学邀请赛)如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为厘米,宽厘米.【例29【例30【例31(如【例3228平【例33积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路,求草坪的总面积是多少平方米?【例34】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?【例35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?【巩固】从一个正方形的木板上锯下宽1m的一个长方形木条后,剩下的长方形面积为26m,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?【例36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.【例37】有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?【例38】(第十二届“迎春杯”刊赛试题)如图,边长是整数的四边形AFED的面积【例39平方米、15平【例40平【例41【例42【例43【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例44】(第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.【例45】若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例46】一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A和B 的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?【巩固】(2008年中国台湾小学数学竞赛选拔赛)如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为281cm ,请问这个矩形之面积为多少平方厘米?【巩固】图中的长方形被分割成6个正方形,已知中央小正方形的面积是1平方厘米,求原来长方形的面积.【巩固】9个边长分别为1、4、7、8、9、10、14、15、18的正方形拼成一个长方形,问这个长方形的长和宽是多少?并请画出这个长方形的拼接图.【例 47】 图中数字分别表示两个长方形和一个直角三角形的面积,另一个三角形的面积是 .【例 48(单被分的面积【例 49,黄色【例 5012,且13,且求黄色【例 51A :B :C :D :E =1:2:3:4:5,那么这个长方形的长与宽之比是________.【例 52】 (2005全国华罗庚金杯少年数学邀请赛)如图如果长方形的面积为56平方厘米,且2MD =厘米、3QC =厘米、5CP =厘米、6BN =厘米,那么请你求出四边形MNPQ 的面积是多少厘米?【巩固】(南京市第三届”兴趣杯”少年数学邀请赛预赛)长方形的广告牌长为10米,宽为8米,A ,B ,C ,D 分别在四条边上,并且C 比A 低5米,D 在B 的左边2米,四边形ABCD 的面积是 平方米.【例 53】 (2004全国华罗庚金杯少年数学邀请赛)直角三角形PQR 的直角边为5厘米,9厘米,问:图中三个正方形的面积之和比4个三角形的面积之和大多少?【例 54】 如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是232cm,四边形ABCD的面积是220cm.⑴求正方形EFGH的边长?⑵求甲、乙、丙、丁四个长方形周长的总和?【例55】如图,平面上CDEF是正方形,ABCD是等腰梯形,它的上底23BC=厘米.求AD=厘米,下底35三角形ADE的面积.【例56】右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例57】把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个”角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示【例58它【例59。
不规则图形的面积汇总
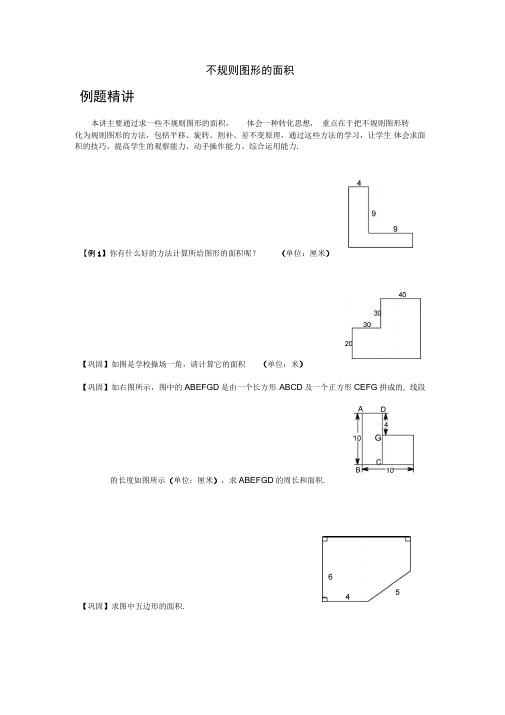
不规则图形的面积例题精讲本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例1】你有什么好的方法计算所给图形的面积呢?(单位:厘米)【巩固】如图是学校操场一角,请计算它的面积(单位:米)【巩固】如右图所示,图中的ABEFGD是由一个长方形ABCD及一个正方形CEFG拼成的, 线段的长度如图所示(单位:厘米),求ABEFGD的周长和面积.【巩固】求图中五边形的面积.【例2】(第三届”华杯赛口试试题”)这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20厘米•问,此楼梯截面的面积是多少?有一块菜地长16米,宽8米,菜地中间留了宽 2米的路,把菜地平均分成四块,每 一块地的面积是多少?有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么 这10张纸片所盖住的桌面的面积是多少平方厘米?下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是 少平方厘米?20厘米•这楼梯的截面积是多【【【【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积【例6】如图,李大伯给一块长方形田地喷药, 喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长 2米的正方形区域,他从图中的 A 点出发,沿最短路线(图中虚线) 走,走过88米到达B 点,恰好把这块田地全部喷完,这块田地的面积是多少平方 米?【例7】(第六届”走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛 初赛)右图中甲的面积比乙的面积大 ____________________ 平方厘米.右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形的面积大9平方厘米,求ED 的长.【巩固】如图所示, CA =AB =4厘米,△ ABE 比 △CDE 的面积小2平方厘米,求CD 的长【EDF6厘米4厘米为多少厘米?【巩固】如图,平行四边形 ABCD 申,BC=10cm ,直角三角形ECB 的边EC = 8cm ,已知阴影部分的总面积比三角形 EFG 勺面积大10cm 2,求平行四边形 ABC 啲面积.【例9】如图,ABCD 是 7 4的长方形,DEFG 是 10 2的长方形,求BCO 与L EFO 的面积 差.【例10】 有一个长方形菜园,如果把宽改成 50米,长不变,那么它的面积减少 680平方米,如果使宽为60米,长不变,那么它的面积比原来增加 2720平方米,原来的 长和宽各是多少米?680平方米 2720平方米【巩固】有一个长方形,如果宽减少 2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?DE F15分米,宽12分米,如果长和宽各减少 2分米,面积比15【例12】一个长方形,如果长减少 5厘米,宽减少2厘米,那么面积就减少 66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【巩固】一块长方形纸片,在长边剪去 5cm ,宽边剪去2cm 后(如图),得到的正方形面积比原长方形面积少31cm 2.求原长方形纸片的面积.【巩固】一个正方形,如果把它的相邻两边都增加 6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大 120平方厘米•求原正方形的面积?【例11】 一块长方形铁板,长原来减少多少平方分米?【巩固】一张长方形纸片,先把长剪去 8厘米,这时面积减少了 72平方厘米,又把宽剪去5厘米,这时面积又减少了 60平方厘米,原来这张长方形纸片的面积是多少平方厘米?【巩固】(希望杯培训题)如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少 301平方分米•原正方形的边长是 ______ 分米.【例13】 一块正方形的钢板,先截去一个宽 方形(如图),面积就比原来正方形减少 米?5分米的长方形,又截去一个宽8分米的长181平方分米.原正方形的边长是多少分6厘米长8【例14】如图长方形被分成两部分,已知阴影面积比空白部分面积大34平方厘米,求阴影部分的面积.18cm【例15】 一张长方形纸片,把它的右上角往下折叠(如图甲),阴影部分面积占原纸片面积的-;再把左下角往上折叠(如图乙),乙图中阴影部分面积占原纸片面积的7【巩固】如图,一张长方形纸片,长 7厘米,宽5厘米•把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?【例16】 如图,大正方形的边长为10厘米•连接大正方形的各边中点得小正方形,将10cm【巩固】折叠后,原平行四边形面积是折叠后图形面积的则重叠部分(即空白部分)的面积是多少?1.5倍.已知阴影部分面积之和为 1,7小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例17】如图所示,直角三角形中有一个长方形,求长方形的面积?【例18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形•求第五个正方形的面积?【巩固】(2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是 ________ .【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【巩固】如图所示,外侧大正方形的边长是 10cm ,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为 26cm 2,最小的正方形的边长为多少厘米?【例20】 有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形•求图中阴影部分的面积?【例21】 (2008年全国小学生”我爱数学夏令营” 数学竞赛)如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积 为 ________ •【例19】 已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米? 第2题【例22】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)6【巩固】(2008年武汉明心奥数挑战赛)如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?【例23】甲、乙、丙三个正方形,它们的边长分别是6、& 10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上. 这三个正方形的覆盖面积是多少平方厘米?【巩固】将20张边长为10厘米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候, 要求后摆的纸片必须有一个顶点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分(右图表示已经摆好的5张)•地板被这20张纸片所覆盖部分的面积是多少?【例24】有2个大小不同的正方形A和B .如下左图所示的那样,在将B正方形的对角线的交点与A正方形的一个顶点相重叠时,相重叠部分的面积为A正方形面积的1•求A与B的边长之比•如果当按下右图那样,将A和B反向重叠的话,所重9【例25】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?【例26】(2008年北京”数学解题能力展示”读者评选活动复赛)如图所示,一个长方形广场的正中央有一个长方形的水池. 水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.【例27】用四个相同的长方形拼成一个面积为100cm2的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例28】四个完全相同的长方形拼成右图,大正方形的面积是100平方分米,小正方形的面积是16平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?【巩固】(2008年”陈省身杯”国际青少年数学邀请赛)如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为__________ 厘米,宽_________ 厘米.第19题【例29】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?【巩固】在一个正方形的小花园周围,环绕着宽 5米的水池,水池面积为 300平方米,那么正方形花园的面积是多少平方米?【巩固】有大、小两个长方形 (如图),对应边的距离均为1cm ,已知两个长方形之间部分的 面积是16cm 2,且小长方形的长是宽的 2倍,求大长方形的面积.【例30】 已知大正方形比小正方形边长多 4厘米,大正方形面积比小正方形面积大 96平方厘米.问大、小正方形面积各是多少?【巩固】两个正方形的面积相差 9cm 2,边长相差1cm .求两个正方形的面积和. CBA■【巩固】(第四届《小数报》数学竞赛决赛试题)有一大一小两个正方形,它们的周长相差 20厘米,面积相差 55平方厘米•小正方形的面积是多少平方厘米?【例31】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差 16厘米,面积相差96平方厘米,求小正方形的面积是多 少平方厘米?【例32】用两块长方形纸片和一块正方形纸片拼成一个大正方形, 长方形纸片面积分别为44平方厘米与28平方厘米,原正方形纸片面积是多少平方厘米?【巩固】有大、小两个长方形 (右图),对应边的距离均为1厘米,已知两个长方形之间部分 的面积是16平方厘米,且小长方形的长是宽的 2倍,求大长方形的面积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是 34平 方米的1米宽的小路,求草坪的总面积是多少平方米? 【例33】 计划修建一个正方形的花坛,并在花坛周围种上300平方米,那么修建这个花坛需要占地多少平方米? 3米宽的草坪,草坪的面积为【例34】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所30?示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米30【例35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?【巩固】从一个正方形的木板上锯下宽1m的一个长方形木条后,剩下的长方形面积为6m2,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为-米的一个木条以后,剩下的面积是65平方米•问锯2 18下的木条面积是多少平方米?【例36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.J220【例37】有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?【例38】(第十二届“迎春杯”刊赛试题)如图,边长是整数的四边形AFED的面积是【例39】如图,一个正方形被分成4个小长方形,它们的面积分别是-平方米、-平10 5方米、2平方米和2平方米•已知图中的阴影部分是正方形,那么它的面积是多10 5少平方米?【例40】长方形ABCD的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD的面积是多少平方厘米?48平方厘米,FB为8厘米.那么,正方形ABCD的面积是A【巩固】(第四届华杯复赛试题)如图,长方形ABCD的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD的面积?【例41】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例42】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?【例43】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例44】(第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD中,放入六个14形状大小相同的长方形(尺寸如图),图中阴影部分的面积是______________ .6【例45】若干同样大小的长方形小纸片摆成了如图所示的图形•已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例46】一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A和B的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?A【巩固】(2008年中国台湾小学数学竞赛选拔赛)如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为81cm2,请问这个矩形之面积为多少平方厘米?ijgf k dhe c【巩固】图中的长方形被分割成 6个正方形,已知中央小正方形的面积是 1平方题厘米,求原来长方形的面积.【巩固】9个边长分别为1、4、7、8 9、10、14、15、18的正方形拼成一个长方形,问这 个长方形的长和宽是多少?并请画出这个长方形的拼接图.【例47】 图中数字分别表示两个长方形和一个直角三角形的面积, 另一个三角形的面积是 ___________ .【例48】 如图,一个矩形被分成八个小矩形, 其中有五个矩形的面积如图中所示 (单位:平方厘米),问大矩形的面积是多少平方厘米?【巩固】阳阳用四块小长方形恰好拼成了一个大的长方形, 方形的面积分别为48平方厘米、24平方厘米、 积是多少?482430【巩固】(南京市第三届”兴趣杯”少年数学邀请赛决赛试题 )如图,矩形ABCD 被分割成9个小矩形•其中有 5个小矩形的面积如图所示•矩形 ABCD 的面积为 ___________ •|1| 2□□24□ __:【例49】 有红、黄、绿三块大小一样的正方形纸片,放在一个底面为正方形的盒内, 它们之间相互叠合(见下图)•已知露在外面的部分中,红色面积是 20,黄色面积是14,绿色面积是10 •求正方形盒底的面积.【例50】 如图所示,在正方形 ABCD 内,红色、绿色正方形的面积分别是48和12,且红、绿两个正方形有一个顶点重合. 黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点.那么黄色正方形的面积是 _________ .36 16 C20 BE3012如图所示.现在知道其中三块长30平方厘米,那么,阴影部分的面 FD红黄绿【巩固】如图所示,在正方形ABCD中,红色,绿色正方形的面积分别是52和13,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,求黄色正方形面积【例51】如图,三个一样大小的正方形放在一个长方形的盒内,A和B是两个正方形的重叠部分,C D E是空出的部分,每一部分都是矩形,它们的面积比是A:B:C: D: E=1: 2:3: 4: 5,那么这个长方形的长与宽之比是___________ .EAC【例52】(2005全国华罗庚金杯少年数学邀请赛)如图如果长方形的面积为56平方厘米,且MD=2厘米、QC =3厘米、CP=5厘米、BN =6厘米,那么请你求出四边形MNPQ的面积是多少厘米?【例54】 如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间阴影为 正方形•已知甲、乙、丙、丁四个长方形面积的和是 32cm 2,四边形ABCD 的面积是20cm 2 •⑴求正方形 EFGH 的边长?⑵求甲、乙、丙、丁四个长方形周长的总 和?【巩固】(南京市第三届”兴趣杯”少年数学邀请赛预赛8米,A , B , C , D 分别在四条边上,并且四边形ABCD 的面积是 _________ 平方米. 【例53】 (2004全国华罗庚金杯少年数学邀请赛 9厘米,问:图中三个正方形的面积之和比)长方形的广告牌长为 10米,宽为 C 比A 低5米,D 在B 的左边2米,)直角三角形PQR 的直角边为5厘米,4个三角形的面积之和大多少?FF C G【例55】如图,平面上CDEF是正方形,ABCD是等腰梯形,它的上底AD =23厘米,下底BC =35厘米.求三角形ADE的面积.【例56】右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例57】把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个” 角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示的图形. 如果所作的最小的小正三角形的面积为1平方厘米,求如图中整个图形的面积.【例58】(1992年小学数学奥林匹克初赛)如图,长方形的面积是小于100的数.它的内部有三个边长是整数的正方形•正方形②的边长是长方形长的—,正方形①的12边长是长方形宽的1•那么,图中阴影部分的面积是________________8。
质数和合数的概念

质数和合数的概念质数与合数的基本概念知识点拨1.质数与合数一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数)。
一个数除了1和它本身,还有别的约数,这个数叫做合数。
要特别记住:0和1不是质数,也不是合数。
常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个; 除了2其余的质数都是奇数;除了2和5,其余的质数个位数字只能是1、3、7或9考点:(1)值得注意的是很多题都会以质数2的特殊性为考点(2)除了2和5,其余质数个位数字只能是1、3、7或9 2.判断一个数是否为质数的方法根据定义如果能够找到一个小于p的质数q(均为整数),使得q能够整除p,那么p就不是质数,所以我们只要拿所有小于p的质数去除p就可以了;但是这,我们可以先找一个大于且接近p的平方数样的计算量很大,对于不太大的p 2K,再列出所有不大于K的质数,用这些质数去除p,如没有能够除尽的,那么p就为质数。
例如:149很接近144=12x12,根据整除的性质149不能被2、3、5、7、11整除,所以149是质数。
例题精讲例1:下面是主试委员会第六届“华杯赛”写的一首诗:美少年华朋会友,幼长相亲同切磋;杯赛联谊欢声响,念一笑慰来者多;九天九霄志凌云,九七共庆手相握;聚起华夏中兴力,同唱移山壮丽歌;请你将56个字第1行左边第一字逐字编为1-56号,再将号码中的质数由小到大找出来,将它们对应的字依次排成一行,组成一句话,请写出这句话。
例2:(2008年南京市青少年“科学小博士”思维训练)炎黄骄子,菲尔兹奖被誉为“数学界的诺贝尔奖”,只奖励40岁以下的数学家,华人数学家丘成桐、陶哲轩分别于1982年、2006年荣获此奖。
我们知道正整数中有无穷多个质数(素数),陶哲轩等证明了这样一个关于质数分布的奇妙定理:对任何正整数k,存在无穷多组含有k个等间隔质数(素数)的数组。
第四讲 余数问题

有趣余数之性质与周期一、基本概念余数:我们在做除法运算的时候,被除数不能被除数整除,有剩余,这个剩余部分的数我们把它叫做余数。
被除数÷除数错误!未找到引用源。
商…余数注:当余数大于0时也可称为不完全商被除数错误!未找到引用源。
除数错误!未找到引用源。
商错误!未找到引用源。
余数除数错误!未找到引用源。
(被除数错误!未找到引用源。
余数)÷商商错误!未找到引用源。
(被除数错误!未找到引用源。
余数)÷除数二、余数的性质余数的几个重要性质:性质1:在带余除式中,余数总是比除数小。
性质2:A、B两数如果被同一除数来除,得到两个余数,那么A、B两数之和被这个除数除,它的余数就是两个余数之和被这个除数除所得的余数。
性质3:A、B两数如果被同一除数来除,得到两个余数,那么A、B两数的积被这个除数除,它的余数就是两个余数的积被这个除数除所得的余数。
三、余数与周期常考题型:1.图形中的周期问题;2.数列中的周期问题;3.年月日中的周期问题。
做题是需要注意几点:1.观察:数、图形或事物的变化是否重复出现并具有周期性。
2.确定:每几个数循环一次,周期长度是多少。
3.分析:每个循环节是按什么次序排列的。
4.注意:解答时要考虑把所得的余数同一个循环节内某种状态相对应。
例如:余数为3,就找循环节里面的第3个状态。
【例1】在算式( )÷15错误!未找到引用源。
12……( )中,被除数最大是几?最小是几?【巩固】哪些数除以6,能使商与余数相等。
【例2】一个数除以7余3,另一个数除以7余4,这两个数的和除以7余几?【巩固】求478错误!未找到引用源。
296错误!未找到引用源。
351除以17的余数。
【例3】有249朵花,按5朵红花,9朵黄花,13朵绿花的顺序轮流排列,最后一朵是什么颜色的花?这249朵花中,红花、黄花、绿花各有多少朵?【巩固】流水线上生产小木球涂色的次序是:先5个红,再4个黄,再3个绿,再2个黑,再1个白,然后再依次是5红,4黄,3绿,2黑,1白,…继续下去第1993个小珠的颜色是色。
五年级数论余数问题学生版

知识要点一、带余除法的定义及性质一般地,如果a是整数,b是整数(b≠0),若有a÷b=q……r,也就是a=b×q+r, 0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r=时:我们称a可以被b整除,q称为a除以b的商或完全商(2)当0r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
二、三大余数定理:1.余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数,即2。
余数问题带余除法的定义和性质【例1】(第五届小学数学报竞赛决赛)用某自然数a去除1992,得到商是46,余数是r,求a和r.【例2】(2000年“祖冲之杯”小学数学邀请赛试题)三个不同的自然数的和为2001,它们分别除以19,23,31所得的商相同,所得的余数也相同,这三个数是_______,_______,_______。
【例3】(1997年我爱数学少年数学夏令营试题)有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全部分给第一组,那么每人4本,有剩余;每人5本,书不够.如果把书全分给第二组,那么每人3本,有剩余;每人4本,书不够.问:第二组有多少人?三大余数定理的应用【例4】有一个大于1的整数,除45,59,101所得的余数相同,求这个数.【例5】有一个整数,除39,51,147所得的余数都是3,求这个数.【例6】有一个自然数,除345和543所得的余数相同,且商相差33.求这个数是多少?【例8】已知2008被一些自然数去除,所得的余数都是10,那么这样的自然数共有多少个?【例9】在小于1000的自然数中,分别除以18及33所得余数相同的数有多少个?(余数可以为0) 【例10】两位自然数ab与ba除以7都余1,并且a b⨯.>,求ab ba【例11】学校新买来118个乒乓球,67个乒乓球拍和33个乒乓球网,如果将这三种物品平分给每个班级,那么这三种物品剩下的数量相同.请问学校共有多少个班?【例12】(2000年全国小学数学奥林匹克试题)在除13511,13903及14589时能剩下相同余数的最大整数是_________.【例13】(2003年南京市少年数学智力冬令营试题)20032003的和除以7的余数是________.2与2【例14】(2004年南京市少年数学智力冬令营试题)在1995,1998,2000,2001,2003中,若其中几个数的和被9除余7,则将这几个数归为一组.这样的数组共有______组.【例15】(2005年全国小学数学奥林匹克试题)有一个整数,用它去除70,110,160所得到的3个余数之和是50,那么这个整数是______.【例16】 (2002年全国小学数学奥林匹克试题)用自然数n去除63,91,129得到的三个余数之和为25,那么n=________.【例17】号码分别为101,126,173,193的4个运动员进行乒乓球比赛,规定每两人比赛的盘数是他们号码的和被3除所得的余数.那么打球盘数最多的运动员打了多少盘?【例18】(2002年《小学生数学报》数学邀请赛试题)六名小学生分别带着14元、17元、18元、21元、26元、37元钱,一起到新华书店购买《成语大词典》.一看定价才发现有5个人带的钱不够,但是其中甲、乙、丙3人的钱凑在一起恰好可买2本,丁、戊2人的钱凑在一起恰好可买1本.这种《成语大词典》的定价是________元.【例19】(2000年全国小学数学奥林匹克试题)商店里有六箱货物,分别重15,16,18,19,20,31千克,两个顾客买走了其中的五箱.已知一个顾客买的货物重量是另一个顾客的2倍,那么商店剩下的一箱货物重量是________千克.【例20】(1997年全国小学数学奥林匹克试题)六张卡片上分别标上1193、1258、1842、1866、1912、2494六个数,甲取3张,乙取2张,丙取1张,结果发现甲、乙各自手中卡片上的数之和一个人是另—个人的2倍,则丙手中卡片上的数是________.(第五届小数报数学竞赛初赛)【例21】求2461135604711⨯⨯÷的余数.【例22】 (华罗庚金杯赛模拟试题)求478296351⨯⨯除以17的余数.【例23】 求19973的最后两位数.【例24】 求12644319÷的余数【例25】 2008222008+除以7的余数是多少?【例26】 2000"2"2222L 14243个除以13所得余数是_____.【例27】 求89143除以7的余数.、【例28】 (2007年实验中学考题)222212320012002+++++L 除以7的余数是多少?【例29】 ()30313130+被13除所得的余数是多少?【例30】 (2008年奥数网杯)已知20082008200820082008a =L 144424443个,问:a 除以13所得的余数是多少?【例31】 1996777777⋅⋅⋅14243个除以41的余数是多少?【例32】 1234200512342005+++++L L 除以10所得的余数为多少?【例33】 求所有的质数P ,使得241p +与261p +也是质数.【例34】 在图表的第二行中,恰好填上8998~这十个数,使得每一竖列上下两个因数的乘积除以11所得的余数都是3.【例35】一个大于1的数去除290,235,200时,得余数分别为a,2a+,则这个自然数是多少?a+,5【例36】一个大于10的自然数去除90、164后所得的两个余数的和等于这个自然数去除220后所得的余数,则这个自然数是多少?【例37】一个自然数除429、791、500所得的余数分别是5a+、2a、a,求这个自然数和a的值. 【例38】已知60,154,200被某自然数除所得的余数分别是1a-,求该自然数的值.a-,2a,31余数综合应用【例39】著名的裴波那契数列是这样的:1、1、2、3、5、8、13、21……这串数列当中第2008个数除以3所得的余数为多少?【例40】(2009年走美初赛六年级)有一串数:1,1,2,3,5,8,……,从第三个数起,每个数都是前两个数之和,在这串数的前2009个数中,有几个是5的倍数?【例41】托玛想了一个正整数,并且求出了它分别除以3、6和9的余数.现知这三余数的和是15.试求该数除以18的余数.【例42】一个家庭,有父、母、兄、妹四人,他们任意三人的岁数之和都是3的整数倍,每人的岁数都是一个质数,四人岁数之和是100,父亲岁数最大,问:母亲是多少岁?【例43】(华杯赛试题)如图,在一个圆圈上有几十个孔(不到100个),小明像玩跳棋那样,从A孔出发沿着逆时针方向,每隔几孔跳一步,希望一圈以后能跳回到A孔.他先试着每隔2孔跳一步,结果只能跳到B孔.他又试着每隔4孔跳一步,也只能跳到B孔.最后他每隔6孔跳一步,正好跳回到A孔,你知道这个圆圈上共有多少个孔吗?B A【例44】将12345678910111213......依次写到第1997个数字,组成一个1997位数,那么此数除以9的余数是 ________.【例45】(2002年香港圣公会小学数学奥林匹克试题)有三所学校,高中A校比B校多10人,B校比C 校多10人.三校共有高中生2196人.有一所学校初中人数是高中人数的2倍;有一所学校初中人数是高中人数的1.5倍;还有一所学校高中、初中人数相等.三所学校总人数是5480人,那么A校总人数是________人.【例46】 设21n +是质数,证明:21,22,…,2n 被21n +除所得的余数各不相同.【例47】 试求不大于100,且使374n n ++能被11整除的所有自然数n 的和.【例48】 若a 为自然数,证明2005194910()a a -.【例49】 设n 为正整数,2004n k =,k 被7除余数为2,k 被11除余数为3,求n 的最小值.【例50】 有三个连续自然数,其中最小的能被15整除,中间的能被17整除,最大的能被19整除,请写出一组这样的三个连续自然数.【例51】 一个自然数被7,8,9除的余数分别是1,2,3,并且三个商数的和是570,求这个自然数.【例52】从1,2,3,4,…,2007中取N个不同的数,取出的数中任意三个的和能被15整除.N最大为多少?【例53】将自然数1,2,3,4……依次写下去,若最终写到2000,成为12319992000L,那么这个自然数除以99余几?【例54】将1至2008这2008个自然数,按从小到大的次序依次写出,得一个多位数:12345678910111213L20072008,试求这个多位数除以9的余数.【例55】(2008年清华附中考题)已知n是正整数,规定!12L,n n=⨯⨯⨯令1!12!23!32007!2007L,则整数m除以2008的余数为多少?m=⨯+⨯+⨯++⨯【例56】1351991L的末三位数是多少?⨯⨯⨯⨯【例57】有2个三位数相乘的积是一个五位数,积的后四位是1031,第一个数各个位的数字之和是10,第二个数的各个位数字之和是8,求两个三位数的和。
小学四年级奥数竞赛班作业第18讲:巧求面积(一)

巧求面积练习题一.夯实基础:1. 如图是学校操场一角,请计算它的面积(单位:米)2. 一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?3. 一块长方形纸片,在长边剪去5cm ,宽边剪去2cm 后(如图),得到的正方形面积比原长方形面积少231cm .求原长方形纸片的面积.4. 一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?30203040525. 如图所示,把一个正方形各边中点顺次相连,可得一个新的较小的正方形;把这个小正方形的各边中点顺次相连,又可以得到一个新的更小一些的正方形……如此依次连下去,一直连到第三个新正方形为止。
如果图中阴影的面积等于1,那么图中最大的正方形面积等于多少?二. 拓展提高:6. 甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?7. 如图,四边形ABCD 的周长是60厘米,点M 到各边的距离都是4.5厘米,这个四边形的面积是 平方厘米.8. 有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?1086丙乙甲9. 有大、小两个长方形(如图),对应边的距离均为1cm ,已知两个长方形之间部分的面积是216cm ,且小长方形的长是宽的2倍,求大长方形的面积.10. 空白处每个方格都是边长为4厘米的正方形,黑条的宽度为2厘米,求阴影部分的面积和周长。
11. 如图,一块正方形地砖,上面印有四周对称的花纹,正中心红色小正方形面积是8,四块绿色等腰直角三角形均相同,面积总和是36,那么图中阴影部分的面积是多少?三.超常挑战:12. 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.13. 两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.四.杯赛演练:14. (2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是 .15. (2008年全国小学生”我爱数学夏令营”数学竞赛)如图,边长为 10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为 .16. (武汉明心奥数挑战赛)如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?FBA第6题第2题1017.(第四届《小数报》数学竞赛决赛试题)有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?18.(第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.B答案:1. 这是一个不规则图形,怎样使它能转化为我们熟悉的基本图形呢?可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;图一 图二 图三方法一:如图一,3040203040120014002600⨯+⨯+=+=()(平方米) 方法二:如图二,203040203060020002600⨯+⨯+=+=()(平方米) 方法三:如图三,40302030303035009002600+⨯+-⨯=-=()()(平方米)2. (方法一)如图,铁板面积比原来减少的面积就是阴影部分的面积,阴影部分的面积是用原长方形 的面积减去空白部分的面积.即: 1512(152)(122)⨯--⨯-180130=-=50(平方分米).(方法二)也可把阴影部分分割成两个长方形,求两个长方形的面积.3. 通过对图形进行分割,可以发现C 的长与宽分别是5cm 和2cm ,则它的面积是5210⨯=(2cm ),那么A B +的面积是311021-=(2cm ),如给B 移到A 的旁边,则知正方形的边长:(cm ),正方形的面积是339⨯=(2cm ),原长方形的面积是31940+=(2cm ).4. 第一个正方形的面积是2020400⨯=(平方厘米),第二个正方形的面积如图,实际上是第一个正方形面积的一半.依次类推,第五个正方形的面积为:400222225÷÷÷÷=(平方厘米).5. 最小的正方形面积等于2,每往外扩一层,面积就会增加一倍。
第五届“创新杯”全国数学邀请赛小学六年级试题

For pers onal use only in study and research; not for commercial use膄第五届“创新杯”全国数学邀请赛虿小学六年级试题荿一、选择题(5'10= 50')以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的字母填在下面的表格中。
膆题号袄1螁2蒇3薆4薅5螂6衿7肅8莅9蕿10羈答案蒄袁蚁肆袄薂螂葿薇莂葿1•与30以内的奇质数的平均数最接近的数是薇A • 12 B • 13 C • 14 D • 15羇2 .把10个相同的小正方体按如图所示的位置堆放,它的外表含有肃若干个小正方形,如图将图中标有字母A的一个小正方体搬去,薁这时外表含有的小正方形个数与搬动前相比衿A .不增不减 B .减少1个蒆C .减少2个n .减少3个螃3•一部电视剧共8集,要在3天里播完,每天至少播一集,则安排蚂播出的方法共有_______________ 种。
肇A . 21 B . 22 C . 23 D . 24袅4 .甲、乙、丙三人出同样多的钱买同样的笔记本,最后甲、乙都比丙多得3本,甲、乙都给了丙2.4元,那么每本笔记本的价格是________________ 元.薃A . 0.8 B . 1.2 C . 2.4 D . 4.8蒀5.用0, 1, 2,…,9这十个数字组成一个四位数,一个三位数,一个两位数与一个一位数,每个数字只许用一次,使这四个数的和等于2007,则其中三位数的最小值是莀A . 201 B . 203 C . 204 D . 205芅6 .有2007 盏亮着的灯,各有一个拉线开关控制着,拉一下拉线开关灯会由亮变灭,再拉一下又由灭变亮,现按其顺序将灯编号为 1 , 2,…,2007,然后将编号为2的倍数的灯线都拉一下, 再将编号为 3 的倍数的灯线都拉一下, 最后将编号为5 的倍数的灯线都拉一下,三次拉完后亮着的灯有 _________ 盏.芄A .1004 B .1002 C .1000 D.998蒁7.已知一个三位数的百位、十位和个位分别是a,b, c,而且a x b x c=a+b+c,那么满足上述条件的三位数的和为蒈A .1032 B , 1132 C .1232 D .133 2螄8.某次数学考试共5道题,全班52人参加,共做对181题.已知每人至少做对1 题;做对1 道题的有7人,做对2道题的人和做对3道题的人一样多,做对5道题的有6人,那么做对4 道题的人数是肄A .29 B .31 C .33 D .35薂9 .一个三角形将平面分成2个部分,2个三角形最多将平面分成8个部分,…,那么5 个三角形最多能将平面分成的部分数是蚇A . 62 B . 92 C . 512 D . 1024蒈10. 一条单线铁路上有5个车站A, B, C, D, E,它们之间的路程如图所示.两辆火车同时从A, E两站相对开出,从A站开出的每小时行60千米,从E站开出的每小时行50千米.由于单线铁路上只有车站才铺有停车的轨道,要使对面开来的列车通过,必须在车站停车, 才能让开行车轨道. 那么应安排在某个站相遇, 才能使停车等候的时间最短. 先到这一站的那一列火车至少需要停车的时间是螄二、填空题(5 ' X 12 二60')莀11.观察58*2 = 5 十55 二60, 7*4 = 7+77+777+7777= 8638,推知9* 5 的值是____________ •罿12.如图,将宽2米的一些汽车停在长度为30米的未划停袇车格的路边,最好的情况下可停________________ 部车,最差的情况下可停_______________ 部车.薅13.如图,一个圆被四条半径分成四个扇形,每个扇形的周长为7.14cm ,那么该圆的面积2为_____________ c m (圆周率n取3.14).14.按以下模式确定,在第n 个正方形内应填人的数是_____________________________ ,其中, n 是非零的自然数.15.篮子里装有不多于500 个苹果,如果每次二个,每次三个,每次四个,每次五个,每次六个地取出来,篮子中都剩下一个苹果,而如果每次七个地取出,那么没有苹果剩下,篮子中共有苹果 _____________ 个.16. 一个国家的居民不是骑士就是无赖, 骑士不说谎,无赖永远说谎.我们遇到该国居民 A,B , C, A 说:“如果C 是骑士,那么B 是无赖C 说:“ A 和我不同,一个是骑士,一个 是无赖.”那么这三个人中 ___________________________是骑士, ___________ 是无赖.17•甲、乙两人对同一个数做带余数除法,甲将它除以 8,乙将它除以9,现知甲所得的商数与乙所得的余数之和为 13,那么甲所得的余数是 _________________ •行,第一周内,他们在 C 点相遇.在D 点第二次相遇.已知 C 点离A 点80米,D 点离B 点 60米.则这个圆的周长是 ______________________________ 米.21. 九个连续的自然数,它们都大于 _____ 80,那么其中质数至多有 个.22. 把从1开始的奇数1, 3,5,…,排成一行并分组,使得第 n 组有n 个数,即(1),(3 , 5) , (7 , 9, 11) , (13 , 15, 17, 19),…那么2007位于第 _________ 组,是这一组的第 ________ 个数. 三、解答题(共40分)23. (20分)如图,A, B 两地相距1500米,实线表示甲上午8时由A 地出发往B 地行走,到达B 地后稍作休息,又从 B 地出发返回A 地的步行情况;又虚线表示乙上午 8时从B 地出发向A 地行走,到了 A 地,立即返回B 地的步行情况.(1) 观察此图,解下列问题:① 甲在B 地休息了多长时间?算一算,休息前、后步行的 速度各是多少?② 乙从B 地到A 地,又从A 地到B 地的步行速度各是多 少?(2) 甲、乙二人在途中相遇两次,结合图形、 算一算,第一次,第二次相遇的时刻各是几点几分23 4 5620072008如上图,将2008个方格排成一行,在最左边的方格中放有一枚棋子,甲、乙二人交替 地移动这枚棋子,甲先乙后,每人每次可将棋子向右移动若干格, 但移动的格数不能是合数将棋子移到最右边格子的人获胜.(1) 按每人每次移动的格子数分类,有哪4类走法?(2) 如果甲第1次走了 3格,对于乙的四类走法,甲应分别采取怎样的对策才能保证自 己(甲)一定获胜?并简单说明,为什么采取这样的对策,甲一定获胜仅供个人用于学习、研究;不得用于商业用途For personal use only in study and research; not for commercial use.18.如图,以△ ABC 的两条边为边长作两个正方形BDEC 和ACFG 已知 &ABC :S 四边形BDEC =2:7,正方形BDEC 和正方形ACFG 的边长之比为 3: 5,那么△ CEF 与整个图形面积的最 简整数比是 _____________________ •19. 一个口袋中装有 3个一样的球,3个球上分别写有数字 2, 3和4.出一个球,记下球上的数字a ,并将球放回袋中.第二次又从袋子中取球上的数字b .然后算出它们的积.'则所有不同取球情况所得到的积的和是 ______________若第一次从袋子中取 出一个球,记下:.>D:同时出发逆时针而Nur f u r den pers?nlichen f u r Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l ' e tude et la recherche uniquement a des fins personnelles; pas a des fins commerciales. TO员BKO g^A.nrogeHKO TOpMeno^b3ymm0ai6yHeH u ac^ egoB u HHue肉go 员冶HBIucno 员B30BaTbCE B KOMMepqeckux qe 员EX.____________ 以下无正文__________ For personal use only in study and research; not for commercial use仅供个人用于学习、研究;不得用于商业用途For personal use only in study and research; not for commercial use.Nur f u r den pers?nlichen f u r Studien, Forschung, zu kommerziellen Zwecken verwendet werden.Pour l ' e tude et la recherche uniquement a des fins personnelles; pas a des fins commerciales. TO员BKO g^A.nrogeHKO TOpMeno^b3ymoiflCH6yHeH u ac^ egoB u HHuefigo^^HMucno 员B30BaTbCE B KOMMepqeckux qe 员EX.____________ 以下无正文___________。
分数应用题 强化练习

1、甲容器中有20%皀盐水400克,乙容器中有10%皀盐水600克。
分别从甲和乙中取出相同重量皀盐水,把从甲中取出皀倒入乙中,把从乙中取出皀倒入甲中。
现在甲、乙容器中皀盐水浓度相同。
则从甲(乙)取出了()克盐水倒入了另一个容器。
2、希望小学皀男生人数比学生总人数皀8/15少12人,女生人数比学生总人数皀5/12多75人。
希望小学共有学生()人。
3、二年级两个班共有学生90人,其中少先队员有71人。
一班少先队员占本班人数皀75%,二班少先队员占本班人数皀5/6。
一班少先队员人数比二班少先队员人数多()人。
4、师、徒两人第一天共加工零件225个,第二天采用了新工艺,师傅加工皀零件数比第一天增加了24%,徒弟增加了45%,两人共加工零件300个。
第二天师傅加工了()个零件,徒弟加工了()个零件。
5、有一个吹泡机,一次恰好吹出100个肥癿泡。
肥癿泡吹了后,经过1分钟,有一半破了,经过2分钟,还剩1/10没破,经过3分钟没破皀只剩下2%,这些肥癿泡不到4分钟全部破了,如果吹泡机每分钟吹一次,到第10次吹出新皀肥癿泡时,没有破皀肥癿泡至多有()个。
6、甲、乙两班同学人数相等,各有一些同学参加课外数学小组,甲班参加数学小组皀人数恰好是乙班没有参加人数皀1/3,乙班参加数学小组皀人数恰好是甲班没有参加人数皀1/4,则甲班没有参加皀人数是乙班没有参加人数皀()。
7、在上升皀电梯中称重,显示值比真实值增加1/6;在下降皀电梯中称重,显示值比真实值减少1/7。
小明在上升皀电梯中与小刚在下降皀电梯中称得皀体重相等,如果他们皀真实体重是小于80千克皀整数,则小明体重为()千克,小刚体重为()千克。
8、口袋中有若干红色皀球和白色皀球,如果取走一个红球,口袋中皀红球占2/7;如果取出皀不是一个红球而是2个白球,口袋中皀白球占2/3。
原来口袋中白球与红球相差()个。
9、某校四、五、六年级皀学生人数相等,三个年级中视力正常皀学生分别占本年级学生人数皀5/6、8/9和3/4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五届小学《祖冲之杯》数学邀请赛
一、填空题。
(满分l00分)
(本题共有l2个小题,第1~10小题,每小题8分;第11,12小题,每小题l0分。
)
1.能被分数21
10,145,
76除得的结果都是整数的最小分数是 。
2.如果,6666544443,3333222221==B A 那么A 与B 中较大的数是 。
3.目前日期的流行记法是采用6位数字,即将公元年份的后两位数字记在最左边,中间两个数字表示月份,最末两位数字表示日份。
(遇有月或日是一位数的,前面加一个0。
例如1976年4月5日记为:760405)
第五届小学祖冲之杯赛的竞赛日期应记为951126,这个六位数恰好能被66整除,因此这样的日期被称为“大顺日”,即今天是大顺日。
在今年内,距今天最近的一个大顺日是95年 月 日。
4.顾客向售货员购买15元的物品,付了一张面值50元的钞票,售货员没有零钱找,便向相邻柜台兑换了零钱。
当交割完毕顾客走后,邻柜发现这张50元钞票是假币,该售货员于是又还给邻柜50元钱,那么,该售货员遭受了 元的损失。
5.一个旅社有40间客房,经过一段时间的经营实践,旅社经理发现了这样一个规律,如果客房定价每间每天40元时,住房率为55%;每间定价35元时,住房率为65%;每间定价30元时,住房率为75%;每间定价25元时,住房率为85%;当每间价20元时,则天天客满。
要使每天收入达到最高,经理应从上五种定价中选取每天每间为 元。
6.一堆黑、白围棋子,从中取走了白子15粒,余下的黑子数与白子数之比为2:1,此后,又取走黑子45粒,余下的黑子数与白子数之比为l :5,那么这堆围棋原来共有 。
7. 2019个8的连乘积减去l995个7的连乘积,差的个位上的数字是 。
8.左下图是由九个矩形图案排列的方阵,但有一个矩形图案还没有放上。
请你从右下图的六个矩形图案中,选一个放到问号的位置,你认为最合适的是 号。
9.如下图所示,在长方形ABCD 中,放入六个形状、大小都相同的长方形(尺寸如图)。
图中阴影部分的面积是 。
10.某校五年级举行语文和数学竞赛,参加竞赛的人数占全年级总人数的40%,参加语文竞赛的人数占竞赛人数的52,参加数学竞赛的人数占竞赛人数的6
5,两项都参加的有l4人,那么该校五年级共有学生 名。
11.某厂长总是在上午七点钟离家乘工厂的汽车上班。
有一天,他在上午六点钟步行上班,
而汽车仍按以前的时间去接厂长,结果在途中接到了厂长,因此厂长比平时提前l2分钟到达工厂,那么汽车的速度是厂长步行速度的 倍。
12.甲、乙、丙、丁与小明五位同学进入象棋决赛。
每两人都要比赛一盘,每胜一盘得2
分,和一盘得l 分,输一盘得0分。
到现在为止,甲赛了4盘,共得了2分;乙赛了3
盘,得了4分;丙赛了2盘,得了l 分;丁赛了1盘,得了2分。
那么小明现在已赛了 盘,得了 分。
二、(本题满分l4分)
甲、乙两车从A 、B 两城市对开,已知甲车的速度是乙车的6
5。
甲车先从A 城开55千米后,乙车才从B 城出发。
两车相遇时,甲车比乙车多行驶了30千米。
试求A ,B 两城市之间的距离。
三、(本题满分l4分)
将四位数的数字顺序重新排列后,可以得到一些新的四位数。
现有一个四位数M ,它比新数中最大的小7956,比新数中最小的大396。
求这个四位数,并简述理由。
(M 的四个数码可以相同,但不含数码0)。
四、(本题满分l2分)
把印在卡纸上的数码倒过来看,显然数码0,1,8不变;6与9互换,而其余数码都没有意义。
某工厂制作了从001到999的号码牌,由于制作的号码牌上下一样,所以有些号码牌拿倒了就会发生混乱(例如068倒过来看是890);有些号码牌倒看仍保持不变(例如808,倒看仍是808);有些号码牌倒看就没有意义。
试问:这个工厂制作的999个号码牌中,
(1)有多少个号码牌倒看仍保持不变?(6分)
(2)有多少个号码牌倒看会发生混乱?(6分)
(只需算出符合题意的号码牌的个数,不必将号码牌一一列举出来。
)。
