圆的错题精练
(易错题精选)初中数学圆的易错题汇编附答案(1)

(易错题精选)初中数学圆的易错题汇编附答案(1)一、选择题1.如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过的图形面积为()A.32πB.83πC.6πD.以上答案都不对【答案】D【解析】【分析】从图中可以看出,线段AB扫过的图形面积为一个环形,环形中的大圆半径是AC,小圆半径是BC,圆心角是60度,所以阴影面积=大扇形面积-小扇形面积.【详解】阴影面积=() 603616103603π⨯-=π.故选D.【点睛】本题的关键是理解出,线段AB扫过的图形面积为一个环形.2.如图,在平面直角坐标系中,点P是以C(﹣2,7)为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是()A.6 B.8 C.10 D.12【答案】C【解析】【分析】设点P(x,y),表示出PA2+PB2的值,从而转化为求OP的最值,画出图形后可直观得出OP的最值,代入求解即可.【详解】设P (x ,y ),∵PA 2=(x +1)2+y 2,PB 2=(x ﹣1)2+y 2,∴PA 2+PB 2=2x 2+2y 2+2=2(x 2+y 2)+2,∵OP 2=x 2+y 2,∴PA 2+PB 2=2OP 2+2,当点P 处于OC 与圆的交点上时,OP 取得最值,∴OP 的最小值为CO ﹣CP =3﹣1=2,∴PA 2+PB 2最小值为2×22+2=10.故选:C .【点睛】本题考查了圆的综合,解答本题的关键是设出点P 坐标,将所求代数式的值转化为求解OP 的最小值,难度较大.3.下列命题中,是假命题的是( )A .任意多边形的外角和为360oB .在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C VC .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析.【详解】解:A. 任意多边形的外角和为360o ,是真命题;B. 在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C V ,根据HL ,是真命题;C. 在一个三角形中,任意两边之差小于第三边,是真命题;D. 同弧所对的圆周角等于圆心角的一半,本选项是假命题.故选D .【点睛】本题考核知识点:判断命题的真假. 解题关键点:熟记相关性质或定义.4.如图,ABC ∆是O e 的内接三角形,45A ∠=︒,1BC =,把ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆,点A 的对应点为点D ,则点A ,D 之间的距离是()A .1B .2 C .3 D .2【答案】A【解析】【分析】 连接AD ,构造△ADB ,由同弧所对应的圆周角相等和旋转的性质,证△ADB 和△DBE 全等,从而得到AD=BE=BC=1.【详解】如图,连接AD ,AO ,DO∵ABC ∆绕圆心O 按逆时针方向旋转90︒得到DEB ∆,∴AB=DE ,90AOD ∠=︒,45CAB BDE ∠=∠=︒∴1452ABD AOD ∠=∠=︒(同弧所对应的圆周角等于圆心角的一半), 即45ABD EDB ∠=∠=︒,又∵DB=BD ,∴DAB BED ∠=∠(同弧所对应的圆周角相等),在△ADB 和△DBE 中 ABD EDB AB EDDAB BED ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ADB ≌△EBD (ASA ),∴AD=EB=BC=1.故答案为A.【点睛】本题主要考查圆周角、圆中的计算问题以及勾股定理的运用;顶点在圆上,两边都与圆相交的角角圆周角;掌握三角形全等的判定是解题的关键.5.如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为()A.50°B.60°C.80°D.90°【答案】C【解析】【分析】根据圆内接四边形的性质得:∠GBC=∠ADC=50°,由垂径定理得:··=,则∠CM DMDBC=2∠EAD=80°.【详解】如图,∵四边形ABCD为⊙O的内接四边形,∴∠GBC=∠ADC=50°.∵AE⊥CD,∴∠AED=90°,∴∠EAD=90°﹣50°=40°,延长AE交⊙O于点M.∵AO⊥CD,∴··=,∴∠DBC=2∠EAD=80°.CM DM故选C.【点睛】本题考查了圆内接四边形的性质:圆内接四边形的任意一个外角等于它的内对角,还考查了垂径定理的应用,属于基础题.6.如图,AB是⊙O的直径,点C是⊙O上一点,点D在BA的延长线上,CD与⊙O交于另一点E,DE=OB=2,∠D=20°,则弧BC的长度为()A.23πB.13πC.43πD.49π【答案】A【解析】【分析】连接OE、OC,如图,根据等腰三角形的性质得到∠D=∠EOD=20°,根据外角的性质得到∠CEO=∠D+∠EOD=40°,根据等腰三角形的性质得到∠C=∠CEO=40°,根据外角的性质得到∠BOC=∠C+∠D=60°,根据求弧长的公式得到结论.【详解】解:连接OE、OC,如图,∵DE=OB=OE,∴∠D=∠EOD=20°,∴∠CEO=∠D+∠EOD=40°,∵OE=OC,∴∠C=∠CEO=40°,∴∠BOC=∠C+∠D=60°,∴»BC的长度=260?2360π⨯=23π,故选A.【点睛】本题考查了弧长公式:l=••180n Rπ(弧长为l,圆心角度数为n,圆的半径为R),还考查了圆的认识及等腰三角形的性质及三角形外角的性质,熟练掌握等腰三角形的性质和三角形外角性质是关键.7.如图,点A,B,C,D都在半径为2的⊙O上,若OA⊥BC,∠CDA=30°,则弦BC的长为()A.4 B.22C.3D.23【答案】B【解析】【分析】根据垂径定理得到CH=BH,»»=,根据圆周角定理求出∠AOB,根据正弦的定义求出AC BCBH,计算即可.【详解】如图BC与OA相交于H∵OA⊥BC,∴CH=BH,»»=,AC AB∴∠AOB=2∠CDA=60°,∴BH=OB⋅sin∠3,∴3故选D.【点睛】本题考查的是垂径定理、圆周角定理,熟练掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.8.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为()A.5B.5C.5或5cm D.3或3【答案】C【解析】连接AC,AO,∵O的直径CD=10cm,AB⊥CD,AB=8cm,∴AM=12AB=12×8=4cm,OD=OC=5cm,当C点位置如图1所示时,∵OA=5cm,AM=4cm,CD⊥AB,∴OM=222254OA AM-=-=3cm,∴CM=OC+OM=5+3=8cm,∴AC=22224845AM CM+=+=cm;当C点位置如图2所示时,同理可得OM=3cm,∵OC=5cm,∴MC=5−3=2cm,在Rt△AMC中,AC=22224225AM CM+=+=cm.故选C.9.将直尺、有60°角的直角三角板和光盘如图摆放,A为60°角与直尺的交点,B为光盘与直尺的交点,AB=4,则光盘表示的圆的直径是()A.4 B.3C.6 D.43【答案】B【解析】【分析】设三角板与圆的切点为C,连接OA、OB,根据切线长定理可得AB=AC=3,∠OAB=60°,然后根据三角函数,即可得出答案.【详解】设三角板与圆的切点为C,连接OA、OB,由切线长定理知,AB=AC=3,AO平分∠BAC,∴∠OAB=60°,在Rt△ABO中,OB=AB tan∠OAB=43,∴光盘的直径为83.故选:B.【点睛】本题主要考查了切线的性质,解题的关键是熟练应用切线长定理和锐角三角函数.10.中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.下列说法中错误的是( )A.勒洛三角形是轴对称图形B.图1中,点A到¶BC上任意一点的距离都相等C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心1O的距离都相等D.图2中,勒洛三角形的周长与圆的周长相等【答案】C【解析】【分析】根据轴对称形的定义,可以找到一条直线是的图像左右对着完全重合,则为轴对称图形.鲁列斯曲边三角形有三条对称轴. 鲁列斯曲边三角形可以看成是3个圆心角为60°,半径为DE 的扇形的重叠,根据其特点可以进行判断选项的正误.【详解】鲁列斯曲边三角形有三条对称轴,就是等边三角形的各边中线所在的直线,故正确;点A到¶BC上任意一点的距离都是DE,故正确;勒洛三角形上任意一点到等边三角形DEF 的中心1O 的距离都不相等,1O 到顶点的距离是到边的中点的距离的2倍,故错误;鲁列斯曲边三角形的周长=3×60180DE DE ππ⨯=⨯ ,圆的周长=22DE DE ππ⨯=⨯ ,故说法正确.故选C.【点睛】主要考察轴对称图形,弧长的求法即对于新概念的理解.11.如图,四边形ABCD 是⊙O 的内接正方形,点P 是劣弧弧AB 上任意一点(与点B 不重合),则∠BPC 的度数为( )A .30°B .45°C .60°D .90°【答案】B【解析】 分析:接OB ,OC ,根据四边形ABCD 是正方形可知∠BOC=90°,再由圆周角定理即可得出结论.详解:连接OB ,OC ,∵四边形ABCD 是正方形,∴∠BOC=90°,∴∠BPC=12∠BOC=45°. 故选B .点睛:本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.12.如图,在矩形ABCD 中,6AB =,对角线10AC =,O e 内切于ABC ∆,则图中阴影部分的面积是( )A .24π-B .242π-C .243π-D .244π-【答案】D【解析】【分析】 先根据勾股定理求出BC ,连接OA 、OB 、OC 、过点O 作OH ⊥AB ,OE ⊥BC ,OF ⊥AC ,设O e 的半径为r ,利用面积法求出r=2,再利用三角形ABC 的面积减去圆O 的面积得到阴影的面积.【详解】∵四边形ABCD 是矩形,∴∠B=90°,∵6AB =,10AC =,∴BC=8,连接OA 、OB 、OC 、过点O 作OH ⊥AB ,OE ⊥BC ,OF ⊥AC ,设O e 的半径为r ,∵O e 内切于ABC ∆,∴OH=OE=OF=r , ∵11()22ABC S AB BC AB AC BC r =⋅=++⋅V , ∴1168(6108)22r ⨯⨯=++⋅, 解得r=2,∴O e 的半径为2,∴2168-2224-4ABC O S S S ππ=-=⨯⨯⨯=V e 阴影, 故选:D .【点睛】此题考查矩形的性质,勾股定理,三角形内切圆的定义,阴影面积的求法,添加合适的辅助线是解题的关键.13.如图,抛物线y =ax 2﹣6ax+5a (a >0)与x 轴交于A 、B 两点,顶点为C 点.以C 点为圆心,半径为2画圆,点P 在⊙C 上,连接OP ,若OP 的最小值为3,则C 点坐标是( )A .5252B .(4,﹣5)C .(3,﹣5)D .(3,﹣4)【答案】D【解析】【分析】首先根据二次函数的解析式求出点A 、B 、C 三点的坐标,再由当点O 、P 、C 三点共线时,OP 取最小值为3,列出关于a 的方程,即可求解.【详解】∵2650y ax ax a a +-=(>) 与x 轴交于A 、B 两点, ∴A (1,0)、B (5,0),∵226534y ax ax a a x a =+=---() , ∴顶点34C a (,-), 当点O 、P 、C 三点共线时,OP 取最小值为3,∴OC =OP+2=5, 29165(0)a a +=> ,∴1a = ,∴C (3,﹣4),故选:D .【点睛】本题考查了二次函数的图象和性质,解题的关键是明确圆外一点到圆上的最短距离即该点与圆心的距离减去半径长.14.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,OC 交⊙O 于点D ,若∠ABD =24°,则∠C 的度数是( )A.48°B.42°C.34°D.24°【答案】B【解析】【分析】根据切线的性质求出∠OAC,结合∠C=42°求出∠AOC,根据等腰三角形性质求出∠B=∠BDO,根据三角形外角性质求出即可.【详解】解:∵∠ABD=24°,∴∠AOC=48°,∵AC是⊙O的切线,∴∠OAC=90°,∴∠AOC+∠C=90°,∴∠C=90°﹣48°=42°,故选:B.【点睛】考查了切线的性质,圆周角定理,三角形内角和定理,解此题的关键是求出∠AOC的度数,题目比较好,难度适中.15.如图,点I是Rt△ABC的内心,∠C=90°,AC=3,BC=4,将∠ACB平移使其顶点C与I重合,两边分别交AB于D、E,则△IDE的周长为()A.3 B.4 C.5 D.7【答案】C【解析】【分析】连接AI、BI,根据三角形的内心的性质可得∠CAI=∠BAI,再根据平移的性质得到∠CAI=∠AID,AD=DI,同理得到BE=EI,即可解答.【详解】连接AI、BI,∵∠C=90°,AC=3,BC=4,∴AB225AC BC∵点I为△ABC的内心,∴AI平分∠CAB,∴∠CAI=∠BAI,由平移得:AC∥DI,∴∠CAI=∠AID,∴∠BAI=∠AID,∴AD=DI,同理可得:BE=EI,∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=5故选C.【点睛】此题考查了平移的性质和三角形内心的性质,解题关键在于作出辅助线16.下列命题中正确的个数是()①过三点可以确定一个圆②直角三角形的两条直角边长分别是5和12,那么它的外接圆半径为6.5③如果两个半径为2厘米和3厘米的圆相切,那么圆心距为5厘米④三角形的重心到三角形三边的距离相等.A.1个B.2个C.3个D.4个【答案】A【解析】【分析】①根据圆的作法即可判断;②先利用勾股定理求出斜边的长度,然后根据外接圆半径等于斜边的一半即可判断;③根据圆与圆的位置关系即可得出答案;④根据重心的概念即可得出答案.【详解】①过不在同一条直线上的三点可以确定一个圆,故错误;②∵直角三角形的两条直角边长分别是5和12,∴斜边为2251213+= , ∴它的外接圆半径为.113652⨯=,故正确; ③如果两个半径为2厘米和3厘米的圆相切,那么圆心距为5厘米或1厘米,故错误; ④三角形的内心到三角形三边的距离相等,故错误;所以正确的只有1个,故选:A .【点睛】本题主要考查直角三角形外接圆半径,圆与圆的位置关系,三角形内心,重心的概念,掌握直角三角形外接圆半径的求法,圆与圆的位置关系,三角形内心,重心的概念是解题的关键.17.如图,已知某圆锥轴截面等腰三角形的底边和高线长均为10cm ,则这个圆锥的侧面积为( )A .50cm 2B .50πcm 2C .255cm 2D .255πcm 2【答案】D【解析】【分析】 根据勾股定理求出圆锥的母线长,求出底面圆周长,根据扇形面积公式计算即可.【详解】解:如图所示,∵等腰三角形的底边和高线长均为10cm ,∴等腰三角形的斜边长=22105+=55,即圆锥的母线长为55cm ,圆锥底面圆半径为5,∴这个圆锥的底面圆周长=2×π×5=10π,即为侧面展开扇形的弧长,圆锥的侧面积=12×10π×55=255πcm 2, 故选:D .【点睛】本题考查了圆锥的计算,解题的关键是弄清楚圆锥的侧面积的计算方法,特别是圆锥的轴截面是等腰三角形,勾股定理的应用,以及圆锥的底面周长等于圆锥的侧面扇形的弧长.18.如图,若干全等正五边形排成环状.图中所示的是前3个正五边形,则要完成这一圆环还需..()个这样的正五边形A.6 B.7 C.8 D.9【答案】B【解析】【分析】【详解】如图,∵多边形是正五边形,∴内角是15×(5-2)×180°=108°,∴∠O=180°-(180°-108°)-(180°-108°)=36°,36°度圆心角所对的弧长为圆周长的1 10,即10个正五边形能围城这一个圆环,所以要完成这一圆环还需7个正五边形.故选B.19.如图,四边形ABCD是⊙O的内接四边形,若∠BOD=86°,则∠BCD的度数是()A.86°B.94°C.107°D.137°【答案】D【解析】【分析】【详解】解:∵∠BOD=86°,∴∠BAD=86°÷2=43°,∵∠BAD+∠BCD=180°,∴∠BCD=180°-43°=137°,即∠BCD的度数是137°.故选D.【点睛】本题考查圆内接四边形的对角互补.②圆内接四边形的任意一个外角等于它的内对角(就是和它相邻的内角的对角).20.已知圆锥的三视图如图所示,则这个圆锥的侧面展开图的面积为()A.60πcm2B.65πcm2C.120πcm2D.130πcm2【答案】B【解析】【分析】先利用三视图得到底面圆的半径为5cm,圆锥的高为12cm,再根据勾股定理计算出母线长为13cm,然后根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式计算.【详解】根据三视图得到圆锥的底面圆的直径为10cm,即底面圆的半径为5cm,圆锥的高为12cm,所以圆锥的母线长225+12=13,所以这个圆锥的侧面积=12×2π×5×13=65π(cm2).故选B.【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了三视图.。
六年级数学上册第五单元圆黄金易错20题专项训练——填空题

六年级数学上册第五单元圆黄金易错20题专项训练——填空题一.填空题1.秋游时同学们围成一个圆圈做游戏,这个圆圈的周长是15.7米,老师站在中心点上,每个同学与老师间的距离是米,围成的圆圈的面积是平方米。
2.圆的大小与有关系,圆的位置与有关系。
3.把一个半径8厘米的圆形纸片对折两次,可以得到一个扇形。
这个扇形的面积是圆的,是平方厘米。
4.一个半径是2cm的圆,按3:1的半径比放大,得到的圆的周长是cm,面积是cm²。
5.在一个直径6米的圆形花池一周建一条2米宽的小路,这条小路面积是平方米。
6.在一个直径是3.9米的圆形餐桌的正中间放了一个直径是2.7米的圆形玻璃转盘,餐桌边缘和转盘边缘的最短距离是米。
7.在一个圆内画一个最大的正方形,这个正方形的对角线是12厘米,那么这个圆的周长是厘米,面积是平方厘米。
8.一块半径是rcm的半圆形木块,它的周长是。
9.把一个圆分成若干(偶数)等份,剪开后用这些小扇形拼成一个近似的长方形。
分成的份数越多拼成的图形就越接近于一个长方形;这个长方形的长相当于圆的,长方形的宽相当于圆的。
如果拼成的长方形的周长和圆的周长相比增加了4cm,则这个圆的面积是,周长是。
10.李叔叔用卷尺量得圆桌面的周长是6.28m,这个圆桌面的直径是m。
11.用圆规画一个周长为12.56厘米的圆,圆规两脚间的距离应取厘米,所画圆的直径是厘米,面积是平方厘米。
12.陈林用圆规画一个圆,如果圆规两脚间的距离是2厘米,则圆的直径是cm,周长是cm.13.一个圆片的周长是6.28厘米,这个圆片的直径是厘米,面积是平方厘米,这个圆片做成两个半圆,其中一个半圆的周长是。
14.一根铁丝刚好围成一个直径3cm的圆,如果现在用这根铁丝围成一个最大正方形,这个正方形的周长是cm。
15.将一个圆平均分成若干个完全相同的小扇形,拼成的近似长方形的周长比圆的周长多20厘米,这个圆的面积是平方分米.16.一个周长是25.12米的圆形花坛,它的面积是平方米.17.一个圆的周长是31.4米,半径增加1米后,面积增加了平方米.18.一个圆的半径扩大到原来的n倍,那么它的周长就扩大到原来的倍,面积扩大到原来的倍.19.剪一个面积15.7cm2的圆形纸片,至少需要面积是cm2的正方形纸片.20.一个圆形花坛的底面周长是6.28m,这个花坛的占地面积是平方米.六年级数学上册第五单元圆黄金易错20题专项训练——填空题参考答案一.填空题1.解:15.7÷3.14÷2=2.5(米)3.14×2.52=3.14×6.25=19.625(平方米)答:每个同学与老师间的距离是2.5米,围成的圆圈的面积是19.625平方米。
苏教版五年级下册数学《圆的认识》错题集

圆的周长 练习题
3.用一根30米的长的绳子绕一棵大树的树干3周, 绳子还剩下1.74米,这棵大树树干的直径是多少 米?
4.一辆自行车的车轮半径是40厘米,车轮每分钟 转100圈,要通过2512米的桥,大约需要几分钟?
圆的周长 《补充习题》P69
9.用一根长7米的绳子绕一棵树的树干3圈, 还剩0.7米。树干绕绳处的直径大约是多少 米?(得数保留两位小数)
圆的周长 《补充习题》P69
10.把下图圆的半径增加2厘米,它的周长 增加多少厘米?
r=3cm
圆的周长 练习题
1.小华和小军沿着一个半径是500米的圆形湖 边同时从同一点相背而行。小华每分钟行81米, 小军每分钟行76米。两人经过多少分钟相遇?
圆的周长 《练习与测试》P86
7.下图这样的半圆形的周长是多少厘米?
d=6cm
圆的周长 《练习与测试》P86
8.张军绕一个圆形花坛走一圈,一共走了314步。 已知张军的平均步长是0.5米,这个花坛的半径 大约是多少米?
圆的周长 《补充习题》P69
8.一个挂钟,钟面上的时针长5厘米。 这根时针的尖端一昼夜划过的路线, 一共有多少厘米?
6.用一根铁丝正好围成一个边长9.42厘 米的正方形。如果把这个铁丝改围成一 个圆,圆的面积是多少平方厘米?
圆的面积 《练习与测试》P90
6.用一根铁丝正好围成一个边长9.42厘 米的正方形。如果把这个铁丝改围成一 个圆,圆的面积是多少平方厘米?
圆的面积 《练习与测试》P91
2.张大伯每次喂鱼时,总是站在岸边一个固定位置抛 撒饲料,他最远能把饲料抛出6米。如果把经常撒有 饲料的地方称为“食场”,那么这个食场的面积大约 是多少平方米?
关于圆的易错题(超经典)

中考冲刺——关于圆的易错题(讲解用)例1 ⊙O1与⊙O2相交于A、B两点,⊙O1的半径为10,⊙O2的半径为17,公共弦AB=16,求两圆的圆心距。
思路提示:对两圆相交问题,一些考生往往只考虑两圆的圆心在公共弦两侧的情况,即图4(1)的情况,很容易遗漏图4(2)的情况,所以正确答案是O O12=21或O O12=9。
图4例2、⊙O的半径为1cm,弦AB cm=3,AC cm=2,则∠BAC=________。
思路提示:由于弦AB和CD可能在圆心的同侧,也可能在圆心的异侧,有如图5两种可能。
根据垂径定理及解直角三角形知识可求出∠CAO=45°和∠BAO=30°,从而可知∠BAC=15°或∠BAC=75°。
图5圆与圆的位置不确定例3、两圆相切,圆心距是10cm,其中一圆的半径为4cm,则另一圆的半径是_____。
思路提示:两圆相切有内切和外切两种情况,所以另一圆的半径为6cm或14cm。
例4、⊙O1的半径为2cm,⊙O2的半径为5cm,两圆没有公共点,则两圆的圆心距d的取值范围为___________。
思路提示:两圆没有公共点,则⊙O1与⊙O2有外离或内含两种情况,外离时,d>7cm;内含时,0cm≤d<3cm。
点在弧上的位置不确定例5、 PA,PC分别切⊙O于A,C两点,B为⊙O上与A,C不重合的点,若∠P=50°,则∠ABC=_________度。
思路提示:由于点B可能在优弧ABC上,也可能在劣弧AC上,有如图6两种可能,所以∠ABC=65°或∠ABC=115°。
图6例6、在⊙O中,AB为直径,CD为弦,AB⊥CD,P为圆周上与C,D 不重合的任意一点,判断∠COB与∠CPD的数量关系,并证明你的结论。
思路提示:由于点P可能在优弧CPD上,也可能在劣弧CD上,有如图7两种可能。
当P在优弧CPD上时,∠COB=∠CPD;当P在劣弧CD上时,∠COB=180 CPD。
数学 圆的综合的专项 培优易错试卷练习题及详细答案

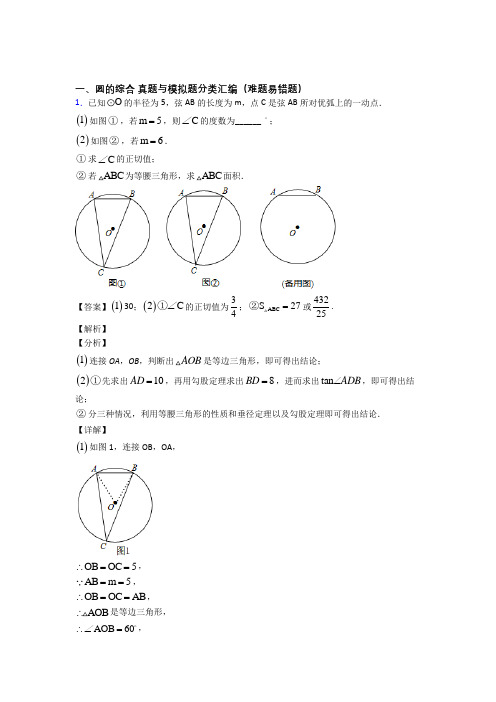
一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)若DF=2,且AF=4,求BD和DE的长.【答案】(1)证明见解析(2)23【解析】【分析】(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DF•DA,据此解答即可.【详解】(1)如图所示,连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴BD CD=,∴OD⊥BC.又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为⊙O半径,∴直线DM是⊙O的切线.(2)连接BE.∵E为内心,∴∠ABE=∠CBE.∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴DF DBDB DA=,即DB2=DF•DA.∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DF•DA=12,∴DB=DE=23.【点睛】本题主要考查了三角形的内心与外心,圆周角定理以及垂径定理的综合应用,解题时注意:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.2.如图,点A、B、C分别是⊙O上的点, CD是⊙O的直径,P是CD延长线上的一点,AP=AC.(1)若∠B=60°,求证:AP是⊙O的切线;(2)若点B是弧CD的中点,AB交CD于点E,CD=4,求BE·AB的值.【答案】(1)证明见解析;(2)8.【解析】(1)求出∠ADC的度数,求出∠P、∠ACO、∠OAC度数,求出∠OAP=90°,根据切线判定推出即可;(2)求出BD长,求出△DBE和△ABD相似,得出比例式,代入即可求出答案.试题解析:连接AD,OA,∵∠ADC=∠B,∠B=60°,∴∠ADC=60°,∵CD是直径,∴∠DAC=90°,∴∠ACO=180°-90°-60°=30°,∵AP=AC,OA=OC,∴∠OAC=∠ACD=30°,∠P=∠ACD=30°,∴∠OAP=180°-30°-30°-30°=90°,即OA⊥AP,∵OA为半径,∴AP是⊙O切线.(2)连接AD,BD,∵CD是直径,∴∠DBC=90°,∵CD=4,B为弧CD中点,∴BD=BC=,∴∠BDC=∠BCD=45°,∴∠DAB=∠DCB=45°,即∠BDE=∠DAB,∵∠DBE=∠DBA,∴△DBE∽△ABD,∴,∴BE•AB=BD•BD=.考点:1.切线的判定;2.相似三角形的判定与性质.3.如图,AB,BC分别是⊙O的直径和弦,点D为BC上一点,弦DE交⊙O于点E,交AB于点F,交BC于点G,过点C的切线交ED的延长线于H,且HC=HG,连接BH,交⊙O 于点M,连接MD,ME.求证:(1)DE⊥AB;(2)∠HMD=∠MHE+∠MEH.【答案】(1)证明见解析;(2)证明见解析.【解析】分析:(1)连接OC,根据等边对等角和切线的性质,证明∠BFG=∠OCH=90°即可;(2)连接BE,根据垂径定理和圆内接四边形的性质,得出∠HMD=∠BME,再根据三角形的外角的性质证明∠HMD=∠DEB=∠EMB即可.详解:证明:(1)连接OC,∵HC=HG,∴∠HCG=∠HGC;∵HC切⊙O于C点,∴∠OCB+∠HCG=90°;∵OB=OC,∴∠OCB=∠OBC,∵∠HGC=∠BGF,∴∠OBC+∠BGF=90°,∴∠BFG=90°,即DE⊥AB;(2)连接BE,由(1)知DE⊥AB,∵AB是⊙O的直径,∴,∴∠BED=∠BME;∵四边形BMDE内接于⊙O,∴∠HMD=∠BED,∴∠HMD=∠BME;∵∠BME是△HEM的外角,∴∠BME=∠MHE+∠MEH,∴∠HMD=∠MHE+∠MEH.点睛:此题综合性较强,主要考查了切线的性质、三角形的内角和外角的性质、等腰三角形的性质、内接四边形的性质.4.(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.(1)如图①,求证:ED为⊙O的切线;(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.【答案】(1)见解析;(2)12【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO 的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度试题解析:解:(1)连接OD,∵ED=EF,∴∠EDF=∠EFD,∵∠EFD=∠CFO,∴∠EDF=∠CFO.∵OD=OC,∴∠ODF=∠OCF.∵OC⊥AB,∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,∴ED为⊙O的切线;(2)连接OD,过点D作DM⊥BA于点M,由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,解得,a=8,即ED=8,EO=10.∵sin∠EOD=45EDEO=,cos∠EOD=35ODOE=,∴DM=OD•sin∠EOD=6×45=245,MO=OD•cos∠EOD=6×35=185,∴EM=EO﹣MO=10﹣18 5=325,EA=EO+OA=10+6=16.∵GA切⊙O于点A,∴GA⊥EA,∴DM∥GA,∴△EDM∽△EGA,∴DM EMGA EA=,即24325516GA=,解得GA=12.点睛:本题考查的是切线的判定、垂径定理和勾股定理的应用、等腰三角形的性质、角的三角函数值、相似三角形的判定及性质,解题的关键是:(1)通过等腰三角形的性质找出∠EDO=90°;(2)通过相似三角形的性质找出相似比.5.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧OB上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.【答案】(1)详见解析;(2)D 3,34a),E33a,34a),F3,0),P 3,2a);S△DEF33a2.【解析】试题分析:(1)连接PB,OP,利用AB切⊙O1于B求证△PBE∽△POD,得出PB PEOP PD=,同理,△OPF∽△BPD,得出PB PDOP PF=,然后利用等量代换即可.(2)连接O1B,O1P,得出△O1BP和△O1PO为等边三角形,根据直角三角形的性质即可解得D、E、F、P四个点的坐标.再利用三角形的面积公式可直接求出三角形DEF的面积.试题解析:(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a, a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,过E作EM⊥x轴于M,∵AO切⊙O1于O,∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a, a),∵E(﹣a, a),D(﹣a, a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为: a,∴S△DEF=×a×a=a2.故答案为:D(﹣a, a),E(﹣a, a),F(﹣a,0),P(﹣a,);S△DEF=a2.6.已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.(1)请你添加一个适当的条件,使得四边形ABCD是平行四边形,并证明你的结论;(2)作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);(3)在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF=45,求⊙O的半径.【答案】(1)当AD=BC时,四边形ABCD是平行四边形,理由见解析;(2)作出相应的图形见解析;(3)圆O的半径为2.5.【解析】分析:(1)添加条件AD=BC,利用一组对边平行且相等的四边形为平行四边形验证即可;(2)作出相应的图形,如图所示;(3)由平行四边形的对边平行得到AD与BC平行,可得同旁内角互补,再由AE与BE为角平分线,可得出AE与BE垂直,利用直径所对的圆周角为直角,得到AF与FB垂直,可得出两锐角互余,根据角平分线性质及等量代换得到∠AGF=∠AEB,根据sin∠AGF的值,确定出sin∠AEB的值,求出AB的长,即可确定出圆的半径.详解:(1)当AD=BC时,四边形ABCD是平行四边形,理由为:证明:∵AD∥BC,AD=BC,∴四边形ABCD为平行四边形;故答案为:AD=BC;(2)作出相应的图形,如图所示;(3)∵AD∥BC,∴∠DAB+∠CBA=180°,∵AE与BE分别为∠DAB与∠CBA的平分线,∴∠EAB+∠EBA=90°,∴∠AEB=90°,∵AB为圆O的直径,点F在圆O上,∴∠AFB=90°,∴∠FAG+∠FGA=90°,∵AE平分∠DAB,∴∠FAG=∠EAB,∴∠AGF=∠ABE,∴sin∠ABE=sin∠AGF=45AE AB =,∵AE=4,∴AB=5,则圆O的半径为2.5.点睛:此题属于圆综合题,涉及的知识有:圆周角定理,平行四边形的判定与性质,角平分线性质,以及锐角三角函数定义,熟练掌握各自的性质及定理是解本题的关键.7.如图,线段BC所在的直线是以AB为直径的圆的切线,点D为圆上一点,满足BD=BC,且点C、D位于直径AB的两侧,连接CD交圆于点E. 点F是BD上一点,连接EF,分别交AB、BD于点G、H,且EF=BD.(1)求证:EF∥BC;(2)若EH=4,HF=2,求BE的长.【答案】(1)见解析;(2) 233π【解析】【分析】(1)根据EF=BD可得EF=BD,进而得到BE DF,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”即可得出角相等进而可证.(2)连接DF,根据切线的性质及垂径定理求出GF、GE的长,根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”及平行线求出相等的角,利用锐角三角函数求出∠BHG,进而求出∠BDE的度数,确定BE所对的圆心角的度数,根据∠DFH=90°确定DE为直径,代入弧长公式即可求解.【详解】(1)∵EF=BD,∴EF=BD∴BE DF∴∠D=∠DEF又BD=BC,∴∠D=∠C,∴∠DEF=∠CEF∥BC(2)∵AB是直径,BC为切线,∴AB⊥BC又EF∥BC,∴AB⊥EF,弧BF=弧BE,GF=GE=12(HF+EH)=3,HG=1DB平分∠EDF,又BF∥CD,∴∠FBD=∠FDB=∠BDE=∠BFH ∴HB=HF=2∴cos∠BHG=HGHB =12,∠BHG=60°.∴∠FDB=∠BDE=30°∴∠DFH=90°,DE为直径,DE=43,且弧BE所对圆心角=60°.∴弧BE=16×43π=233π【点睛】本题是圆的综合题,主要考查圆周角、切线、垂径定理、弧长公式等相关知识,掌握圆周角的有关定理,切线的性质,垂径定理及弧长公式是解题关键.8.在平面直角坐标系XOY中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,若P、Q为某等边三角形的两个顶点,且有一边与x轴平行(含重合),则称P、Q 互为“向善点”.如图1为点P、Q互为“向善点”的示意图.已知点A的坐标为(1,3),点B的坐标为(m,0)(1)在点M(﹣1,0)、S(2,0)、T(3,3A点互为“向善点”的是_____;(2)若A、B互为“向善点”,求直线AB的解析式;(3)⊙B3⊙B上有三个点与点A互为“向善点”,请直接写出m的取值范围.【答案】(1)S ,T .(2)直线AB 的解析式为y =3x 或y =﹣3x +23;(3)当﹣2<m <0或2<m <4时,⊙B 上有三个点与点A 互为“向善点”.【解析】【分析】(1)根据等边三角形的性质结合“向善点”的定义,可得出点S ,T 与A 点互为“向善点”; (2)根据等边三角形的性质结合“向善点”的定义,可得出关于m 的分式方程,解之经检验后可得出点B 的坐标,根据点A ,B 的坐标,利用待定系数法即可求出直线AB 的解析式;(3)分⊙B 与直线y=3x 相切及⊙B 与直线y=-3x+23相切两种情况求出m 的值,再利用数形结合即可得出结论.【详解】(1)∵30330,3tan 60︒--===,3333tan 60︒-==, ∴点S ,T 与A 点互为“向善点”.故答案为S ,T .(2)根据题意得:303-=, 解得:m 1=0,m 2=2,经检验,m 1=0,m 2=2均为所列分式方程的解,且符合题意,∴点B 的坐标为(0,0)或(2,0).设直线AB 的解析式为y =kx +b (k ≠0),将A (1,),B (0,0)或(2,0)代入y =kx +b ,得:30k b b ⎧+=⎪⎨=⎪⎩320k b k b ⎧+=⎪⎨+=⎪⎩ 解得:30k b ⎧=⎪⎨=⎪⎩323k b ⎧=⎪⎨=⎪⎩, ∴直线AB 的解析式为y 3或y 33.(3)当⊙B 与直线y 3相切时,过点B 作BE ⊥直线y 3于点E ,如图2所示.∵∠BOE =60°,∴sin60°=32BE OB , ∴OB =2,∴m =﹣2或m =2;当⊙B 与直线y =﹣3x +23相切时,过点B 作BF ⊥直线y =﹣3x +23于点F ,如图3所示.同理,可求出m =0或m =4.综上所述:当﹣2<m <0或2<m <4时,⊙B 上有三个点与点A 互为“向善点”.【点睛】本题考查了等边三角形的性质、特殊角的三角函数值、待定系数法求一次函数解析式、解分式方程以及解直角三角形,解题的关键是:(1)根据等边三角形的性质结合“向善点”的定义,确定给定的点是否与A 点互为“向善点”;(2)根据点的坐标,利用待定系数法求出一次函数解析式;(3)分⊙B 与直线y=3x 相切及⊙B 与直线y=-3x+23相切两种情况考虑.9.如图,已知等边△ABC ,AB=16,以AB 为直径的半圆与BC 边交于点D ,过点D 作DF ⊥AC ,垂足为F ,过点F 作FG ⊥AB ,垂足为G ,连结GD .(1)求证:DF 是⊙O 的切线;(2)求FG 的长;(3)求tan∠FGD的值.【答案】(1)证明见解析;(2)6;(3).【解析】试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.试题解析:(1)如图①,连结OD,∵△ABC为等边三角形,∴∠C=∠A=∠B=60°,而OD=OB,∴△ODB是等边三角形,∠ODB=60°,∴∠ODB=∠C,∴OD∥AC,∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,∴tan∠FGD=tan∠GDH=考点:(1)圆的基本性质;(2)三角函数.10.如图,OA,OD是⊙O半径.过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B.(1)求证:直线CD是⊙O的切线;(2)如果D点是BC的中点,⊙O的半径为 3cm,求DE的长度.(结果保留π)【答案】(1)证明见解析;(2)DE的长度为π.【解析】(1)证明:∵AC是⊙O切线,∴OA⊥AC,∴∠OAC=90°,∵CO平分∠AOD,∴∠AOC=∠COD,在△AOC和△DOC中,∴△AOC≌△DOC,∴∠ODC=∠OAC=90°,∴OD⊥CD,∴直线CD是⊙O的切线.(2)∵OD⊥BC,DC=DB,∴OC=OB,∴∠OCD=∠B=∠ACO,∵∠B+∠ACB=90°,∴∠B=30°,∠DOE=60°,∴的长度==π.[来源:]。
数学 圆的综合的专项 培优易错试卷练习题附答案解析

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙A过▱OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).(1)若∠BOH=30°,求点H的坐标;(2)求证:直线PC是⊙A的切线;(3)若OD=10,求⊙A的半径.【答案】(1)(132)详见解析;(3)5 3 .【解析】【分析】(1)先判断出OH=OB=2,利用三角函数求出MH,OM,即可得出结论;(2)先判断出∠PCD=∠DAE,进而判断出∠PCD=∠CAE,即可得出结论;(3)先求出OE═3,进而用勾股定理建立方程,r2-(3-r)2=1,即可得出结论.【详解】(1)解:如图,过点H作HM⊥y轴,垂足为M.∵四边形OBCD是平行四边形,∴∠B=∠ODC∵四边形OHCD是圆内接四边形∴∠OHB=∠ODC∴∠OHB=∠B∴OH=OB=2∴在Rt△OMH中,∵∠BOH=30°,∴MH=12OH=1,33∴点H的坐标为(13(2)连接AC.∵OA=AD,∴∠DOF=∠ADO∴∠DAE=2∠DOF∵∠PCD=2∠DOF,∴∠PCD=∠DAE∵OB与⊙O相切于点A∴OB⊥OF∵OB∥CD∴CD⊥AF∴∠DAE=∠CAE∴∠PCD=∠CAE∴∠PCA=∠PCD+∠ACE=∠CAE+∠ACE=90°∴直线PC是⊙A的切线;(3)解:⊙O的半径为r.在Rt△OED中,DE=12CD=12OB=1,OD=10,∴OE═3∵OA=AD=r,AE=3﹣r.在Rt△DEA中,根据勾股定理得,r2﹣(3﹣r)2=1解得r=53.【点睛】此题是圆的综合题,主要考查了平行四边形的性质,圆内接四边形的性质,勾股定理,切线的性质和判定,构造直角三角形是解本题的关键.2.如图,AB是半圆O的直径,C是的中点,D是的中点,AC与BD相交于点E.(1)求证:BD平分∠ABC;(2)求证:BE=2AD;(3)求DEBE的值.【答案】(1)答案见解析(2)BE=AF=2AD(3)21 2 -【解析】试题分析:(1)根据中点弧的性质,可得弦AD=CD,然后根据弦、弧、圆周角、圆心角的性质求解即可;(2)延长BC与AD相交于点F, 证明△BCE≌△ACF, 根据全等三角形的性质可得BE=AF=2AD;(3)连接OD,交AC于H.简要思路如下:设OH为1,则BC为2,OB=OD=2,DH=21-, 然后根据相似三角形的性质可求解.试题解析:(1)∵D是的中点∴AD=DC∴∠CBD=∠ABD∴BD平分∠ABC(2)提示:延长BC与AD相交于点F,证明△BCE≌△ACF,BE=AF=2AD(3)连接OD,交AC于H.简要思路如下:设OH为1,则BC为2,OB=OD=2,DH=21-, DEBE=DHBCDE BE =21-3.四边形ABCD 的对角线交于点E,且AE=EC,BE=ED,以AD 为直径的半圆过点E,圆心为O.(1)如图①,求证:四边形ABCD 为菱形;(2)如图②,若BC 的延长线与半圆相切于点F,且直径AD=6,求弧AE 的长.【答案】(1)见解析;(2)π2 【解析】 试题分析:(1)先判断出四边形ABCD 是平行四边形,再判断出AC ⊥BD 即可得出结论; (2)先判断出AD =DC 且DE ⊥AC ,∠ADE =∠CDE ,进而得出∠CDA =30°,最后用弧长公式即可得出结论.试题解析:证明:(1)∵四边形ABCD 的对角线交于点E ,且AE =EC ,BE =ED ,∴四边形ABCD 是平行四边形.∵以AD 为直径的半圆过点E ,∴∠AED =90°,即有AC ⊥BD ,∴四边形ABCD 是菱形;(2)由(1)知,四边形ABCD 是菱形,∴△ADC 为等腰三角形,∴AD =DC 且DE ⊥AC ,∠ADE =∠CDE .如图2,过点C 作CG ⊥AD ,垂足为G ,连接FO .∵BF 切圆O 于点F ,∴OF ⊥AD ,且132OF AD ==,易知,四边形CGOF 为矩形,∴CG =OF =3. 在Rt △CDG 中,CD =AD =6,sin ∠ADC =CG CD =12,∴∠CDA =30°,∴∠ADE =15°. 连接OE ,则∠AOE =2×∠ADE =30°,∴3031802AE ππ⋅⨯==.点睛:本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.4.已知,如图:O 1为x 轴上一点,以O 1为圆心作⊙O 1交x 轴于C 、D 两点,交y 轴于M 、N 两点,∠CMD 的外角平分线交⊙O 1于点E ,AB 是弦,且AB ∥CD ,直线DM 的解析式为y=3x+3.(1)如图1,求⊙O 1半径及点E 的坐标.(2)如图2,过E 作EF ⊥BC 于F ,若A 、B 为弧CND 上两动点且弦AB ∥CD ,试问:BF+CF 与AC 之间是否存在某种等量关系?请写出你的结论,并证明.(3)在(2)的条件下,EF 交⊙O 1于点G ,问弦BG 的长度是否变化?若不变直接写出BG 的长(不写过程),若变化自画图说明理由.【答案】(1)r=5 E(4,5)(2)BF+CF=AC (3)弦BG的长度不变,等于2【解析】分析:(1)连接ED、EC、EO1、MO1,如图1,可以证到∠ECD=∠SME=∠EMC=∠EDC,从而可以证到∠EO1D=∠EO1C=90°.由直线DM的解析式为y=3x+3可得OD=1,OM=3.设⊙O1的半径为r.在Rt△MOO1中利用勾股定理就可解决问题.(2)过点O1作O1P⊥EG于P,过点O1作O1Q⊥BC于Q,连接EO1、DB,如图2.由AB∥DC可证到BD=AC,易证四边形O1PFQ是矩形,从而有O1P=FQ,∠PO1Q=90°,进而有∠EO1P=∠CO1Q,从而可以证到△EPO1≌△CQO1,则有PO1=QO1.根据三角形中位线定理可得FQ=12BD.从而可以得到BF+CF=2FQ=AC.(3)连接EO1,ED,EB,BG,如图3.易证EF∥BD,则有∠GEB=∠EBD,从而有BG=ED,也就有BG=DE.在Rt△EO1D中运用勾股定理求出ED,就可解决问题.详解:(1)连接ED、EC、EO1、MO1,如图1.∵ME平分∠SMC,∴∠SME=∠EMC.∵∠SME=∠ECD,∠EMC=∠EDC,∴∠ECD=∠EDC,∴∠EO1D=∠EO1C.∵∠EO1D+∠EO1C=180°,∴∠EO1D=∠EO1C=90°.∵直线DM的解析式为y=3x+3,∴点M的坐标为(0,3),点D的坐标为(﹣1,0),∴OD=1,OM=3.设⊙O1的半径为r,则MO1=DO1=r.在Rt△MOO1中,(r﹣1)2+32=r2.解得:r=5,∴OO1=4,EO1=5,∴⊙O1半径为5,点E的坐标为(4,5).(2)BF+CF=AC.理由如下:过点O1作O1P⊥EG于P,过点O1作O1Q⊥BC于Q,连接EO1、DB,如图2.∵AB∥DC,∴∠DCA=∠BAC,∴AD=BC BD∴,=AC,∴BD=AC.∵O1P⊥EG,O1Q⊥BC,EF⊥BF,∴∠O1PF=∠PFQ=∠O1QF=90°,∴四边形O1PFQ是矩形,∴O1P=FQ,∠PO1Q=90°,∴∠EO1P=90°﹣∠PO1C=∠CO1Q.在△EPO1和△CQO1中,111111EO P CO QEPO CQOO E O C∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EPO1≌△CQO1,∴PO1=QO1,∴FQ=QO1.∵QO1⊥BC,∴BQ=CQ.∵CO 1=DO 1,∴O 1Q =12BD ,∴FQ =12BD . ∵BF +CF =FQ +BQ +CF =FQ +CQ +CF =2FQ ,∴BF +CF =BD =AC .(3)连接EO 1,ED ,EB ,BG ,如图3.∵DC 是⊙O 1的直径,∴∠DBC =90°,∴∠DBC +∠EFB =180°,∴EF ∥BD ,∴∠GEB =∠EBD ,∴BG =ED ,∴BG =DE .∵DO 1=EO 1=5,EO 1⊥DO 1,∴DE =52,∴BG =52,∴弦BG 的长度不变,等于52.点睛:本题考查了圆周角定理、圆内接四边形的性质、弧与弦的关系、垂径定理、全等三角形的判定与性质、矩形的判定与性质、三角形中位线定理、平行线的判定与性质、勾股定理等知识,综合性比较强,有一定的难度.而由AB ∥DC 证到AC =BD 是解决第(2)小题的关键,由EG ∥DB 证到BG =DE 是解决第(3)小题的关键.5.如图,一条公路的转弯处是一段圆弧().AB ()1用直尺和圆规作出AB 所在圆的圆心O ;(要求保留作图痕迹,不写作法)()2若AB 的中点C 到弦AB 的距离为2080m AB m =,,求AB 所在圆的半径.【答案】(1)见解析;(2)50m【解析】分析:()1连结AC 、BC ,分别作AC 和BC 的垂直平分线,两垂直平分线的交点为点O ,如图1;()2连接OA OC OC ,,交AB 于D ,如图2,根据垂径定理的推论,由C 为AB 的中点得到1OC AB AD BD AB 402⊥===,,则CD 20=,设O 的半径为r ,在Rt OAD 中利用勾股定理得到222r (r 20)40=-+,然后解方程即可.详解:()1如图1,点O 为所求;()2连接OA OC OC ,,交AB 于D ,如图2,C 为AB 的中点,OC AB ∴⊥,1402AD BD AB ∴===, 设O 的半径为r ,则20OA r OD OD CD r ==-=-,,在Rt OAD 中,222OA OD AD =+,222(20)40r r ∴=-+,解得50r =,即AB 所在圆的半径是50m .点睛:本题考查了垂径定理及勾股定理的应用,在利用数学知识解决实际问题时,要善于把实际问题与数学中的理论知识联系起来,能将生活中的问题抽象为数学问题.6.已知:AB 是⊙0直径,C 是⊙0外一点,连接BC 交⊙0于点D ,BD=CD,连接AD 、AC .(1)如图1,求证:∠BAD=∠CAD(2)如图2,过点C 作CF ⊥AB 于点F,交⊙0于点E,延长CF 交⊙0于点G.过点作EH ⊥AG 于点H ,交AB 于点K,求证AK=2OF ;(3)如图3,在(2)的条件下,EH 交AD 于点L,若0K=1,AC=CG,求线段AL 的长.图1 图2 图3【答案】(1)见解析(2)见解析(3)12105 【解析】试题分析:(1)由直径所对的圆周角等于90°,得到∠ADB =90°,再证明△ABD ≌△ACD 即可得到结论;(2)连接BE .由同弧所对的圆周角相等,得到∠GAB =∠BEG .再证△KFE ≌△BFE ,得到BF =KF =BK .由OF =OB -BF ,AK =AB -BK ,即可得到结论. (3)连接CO 并延长交AG 于点M ,连接BG .设∠GAB =α.先证CM 垂直平分AG ,得到AM =GM ,∠AGC +∠GCM =90°.再证∠GAF =∠GCM =α.通过证明△AGB ≌△CMG ,得到BG =GM =12AG .再证明∠BGC =∠MCG =α.设BF =KF =a , 可得GF =2a ,AF =4a . 由OK =1,得到OF =a +1,AK =2(a +1),AF = 3a +2,得到3a +2=4a ,解出a 的值,得到AF ,AB ,GF ,FC 的值.由tanα=tan ∠HAK =12HK AH =, AK =6,可以求出 AH 的长.再由1tan tan 3BAD BCF ∠=∠= ,利用公式tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠,得到∠GAD =45°,则AL =2AH ,即可得到结论.试题解析:解:(1)∵AB 为⊙O 的直径,∴∠ADB =90°,∴∠ADC =90°.∵BD =CD ,∠BDA =∠CDA ,AD =AD ,∴△ABD ≌△ACD ,∴∠BAD =∠CAD .(2)连接BE .∵BG =BG ,∴∠GAB =∠BEG .∵CF ⊥AB ,∴∠KFE =90°.∵EH ⊥AG ,∴∠AHE =∠KFE =90°,∠AKH =∠EKF ,∴∠HAK =∠KEF =∠BEF .∵FE =FE ,∠KFE =∠BFE =90°,∴△KFE ≌△BFE ,∴BF =KF =BK .∵ OF =OB -BF ,AK =AB -BK ,∴AK =2OF .(3)连接CO 并延长交AG 于点M ,连接BG .设∠GAB =α.∵AC =CG , ∴点C 在AG 的垂直平分线上.∵ OA =OG ,∴点O 在AG 的垂直平分线上, ∴CM 垂直平分AG ,∴AM =GM ,∠AGC +∠GCM =90°.∵AF ⊥CG ,∴∠AGC +∠GAF =90°,∴∠GAF =∠GCM =α.∵AB 为⊙O 的直径,∴∠AGB = 90°,∴∠AGB =∠CMG =90°.∵AB =AC =CG ,∴△AGB ≌△CMG ,∴BG =GM =12AG . 在Rt △AGB 中, 1tan tan 2GB GAB AG α∠=== . ∵∠AMC =∠AGB = 90°,∴BG ∥CM , ∴∠BGC =∠MCG =α.设BF =KF =a , 1tan tan 2BF BGF GF α∠===,∴GF =2a ,1tan tan 2GF GAF AF α∠=== ,AF =4a .∵OK =1,∴OF =a +1,AK =2OF =2(a +1),∴AF =AK +KF =a +2(a +1)=3a +2,∴3a +2=4a ,∴a =2, AK =6,∴AF =4a =8,AB =AC =CG =10,GF =2a =4,FC =CG -GF =6. ∵tanα=tan ∠HAK =12HK AH =,设KH =m ,则AH =2m ,∴AK 22(2)m m +=6,解得:m =655,∴AH =2m 125.在Rt △BFC 中,1tan 3BF BCF FC ∠== .∵∠BAD +∠ABD =90°, ∠FBC +∠BCF =90°,∴∠BCF =∠BAD ,1tan tan 3BAD BCF ∠=∠= ,∴tan ∠GAD =tan tan 1tan tan GAF BAD GAF BAD ∠+∠-∠⋅∠=1123111123+=-⨯,∴∠GAD =45°,∴HL=AH ,AL 2AH 12107.如图,AB是圆O的直径,射线AM⊥AB,点D在AM上,连接OD交圆O于点E,过点D作DC=DA交圆O于点C(A、C不重合),连接O C、BC、CE.(1)求证:CD是⊙O的切线;(2)若圆O的直径等于2,填空:①当AD=时,四边形OADC是正方形;②当AD=时,四边形OECB是菱形.【答案】(1)见解析;(2)①1;②3.【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;(2)①依据正方形的四条边都相等可知AD=OA;②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.试题解析:解:∵AM⊥AB,∴∠OAD=90°.∵OA=OC,OD=OD,AD=DC,∴△OAD≌△OCD,∴∠OCD=∠OAD=90°.∴OC⊥CD,∴CD是⊙O的切线.(2)①∵当四边形OADC是正方形,∴AO=AD=1.故答案为:1.②∵四边形OECB是菱形,∴OE=CE.又∵OC=OE,∴OC=OE=CE.∴∠CEO=60°.∵CE ∥AB ,∴∠AOD=60°.在Rt △OAD 中,∠AOD=60°,AO=1,∴AD=. 故答案为:.点睛:本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定,特殊锐角三角函数值的应用,熟练掌握相关知识是解题的关键.8.如图1,在Rt △ABC 中,∠ABC=90°,BA=BC ,直线MN 是过点A 的直线CD ⊥MN 于点D ,连接BD .(1)观察猜想张老师在课堂上提出问题:线段DC ,AD ,BD 之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B 作BE ⊥BD ,交MN 于点E ,进而得出:DC+AD= BD .(2)探究证明将直线MN 绕点A 顺时针旋转到图2的位置写出此时线段DC ,AD ,BD 之间的数量关系,并证明(3)拓展延伸在直线MN 绕点A 旋转的过程中,当△ABD 面积取得最大值时,若CD 长为1,请直接写BD 的长.【答案】(12;(2)AD ﹣2BD ;(3)2+1.【解析】【分析】(1)根据全等三角形的性质求出DC ,AD ,BD 之间的数量关系(2)过点B 作BE ⊥BD ,交MN 于点E .AD 交BC 于O ,证明CDB AEB ∆∆≌,得到CD AE =,EB BD =,根据BED ∆为等腰直角三角形,得到2DE BD =,再根据DE AD AE AD CD =-=-,即可解出答案.(3)根据A 、B 、C 、D 四点共圆,得到当点D 在线段AB 的垂直平分线上且在AB 的右侧时,△ABD 的面积最大.在DA 上截取一点H ,使得CD=DH=1,则易证2CH AH ==,由BD AD =即可得出答案.【详解】解:(1)如图1中,由题意:BAE BCD ∆∆≌,∴AE=CD ,BE=BD ,∴CD+AD=AD+AE=DE ,∵BDE ∆是等腰直角三角形,∴DE=2BD ,∴DC+AD=2BD ,故答案为2.(2)2AD DC BD -=.证明:如图,过点B 作BE ⊥BD ,交MN 于点E .AD 交BC 于O .∵90ABC DBE ∠=∠=︒,∴ABE EBC CBD EBC ∠+∠=∠+∠,∴ABE CBD ∠=∠.∵90BAE AOB ∠+∠=︒,90BCD COD ∠+∠=︒,AOB COD ∠=∠,∴BAE BCD ∠=∠,∴ABE DBC ∠=∠.又∵AB CB =,∴CDB AEB ∆∆≌,∴CD AE =,EB BD =,∴BD ∆为等腰直角三角形,2DE BD =.∵DE AD AE AD CD=-=-,∴2AD DC BD-=.(3)如图3中,易知A、B、C、D四点共圆,当点D在线段AB的垂直平分线上且在AB 的右侧时,△ABD的面积最大.此时DG⊥AB,DB=DA,在DA上截取一点H,使得CD=DH=1,则易证2CH AH==,∴21BD AD==+.【点睛】本题主要考查全等三角形的性质,等腰直角三角形的性质以及图形的应用,正确作辅助线和熟悉图形特性是解题的关键.9.如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.(1)求证:直线EF是⊙O的切线;(2)若CF=3,cosA=25,求出⊙O的半径和BE的长;(3)连接CG,在(2)的条件下,求CGEF的值.【答案】(1)见解析;(2)2,65(3)CG:EF=4:7【解析】试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD==,设⊙O的半径为R,解方程=,求出R=,那么AB=2OD=,解Rt△AEF,根据余弦函数的定义得到cosA==,求出AE=,然后由BE=AB﹣AE即可求解.试题解析:(1)证明:如图,连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD,∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线;(2)解:∵OD∥AB,∴∠COD=∠A.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD==,设⊙O的半径为R,则=,解得R=,∴AB=2OD=.在Rt△AEF中,∵∠AEF=90°,∴cosA===,∴AE=,∴BE=AB﹣AE=﹣=2.【点睛】本题考查了切线的判定,解直角三角形,三角形中位线的性质知识点.要证某线是圆的切线,已知此线过圆上某点,连结圆心与这点(即为半径),再证垂直即可.10.如图,已知等边△ABC,AB=16,以AB为直径的半圆与BC边交于点D,过点D作DF⊥AC,垂足为F,过点F作FG⊥AB,垂足为G,连结GD.(1)求证:DF是⊙O的切线;(2)求FG的长;(3)求tan∠FGD的值.【答案】(1)证明见解析;(2)6;(3).【解析】试题分析:(1)连接OD,根据等边三角形得出∠A=∠B=∠C=60°,根据OD=OB得到∠ODB=60°,得到OD∥AC,根据垂直得出切线;(2)根据中位线得出BD=CD=6,根据Rt△CDF的三角函数得出CF的长度,从而得到AF的长度,最后根据Rt△AFG的三角函数求出FG的长度;(3)过点D作DH⊥AB,根据垂直得出FG∥DH,根据Rt△BDH求出BH、DH的长度,然后得出∠GDH的正切值,从而得到∠FGD的正切值.试题解析:(1)如图①,连结OD,∵△ABC为等边三角形,∴∠C=∠A=∠B=60°,而OD=OB,∴△ODB是等边三角形,∠ODB=60°,∴∠ODB=∠C,∴OD∥AC,∵DF⊥AC,∴OD⊥DF,∴DF是⊙O的切线(2)∵OD∥AC,点O为AB的中点,∴OD为△ABC的中位线,∴BD=CD=6.在Rt△CDF中,∠C=60°,∴∠CDF=30°,∴CF=CD=3,∴AF=AC-CF=12-3=9 在Rt△AFG中,∵∠A=60°,∴FG=AF·sinA=9×=(3)如图②,过D作DH⊥AB于H.∵FG⊥AB,DH⊥AB,∴FG∥DH,∴∠FGD=∠GDH.在Rt△BDH中,∠B=60°,∴∠BDH=30°,∴BH=BD=3,DH=BH=3.∴tan∠GDH===,∴tan∠FGD=tan∠GDH=考点:(1)圆的基本性质;(2)三角函数.。
圆的有关概念练习(判断正误)有答案

圆的有关概念练习(判断正误)学校:________ 班级:________ 姓名:________ 学号:________一、单选题(共15小题)1.(2006秋•永川区校级期中)下列说法正确的有()①圆内接梯形一定是等腰梯形②圆外切四边形一定是正方形③相等的圆周角所对的弧相等④相等的圆心角所对弧相等⑤同圆中的两弦不等,则小弦所对弦心距较大⑥平分弦的直线就平分弦所对的弧.A.2个B.3个C.4个D.5个2.(2012秋•岱岳区校级期末)下列说法正确的有()①在同圆或等圆中能够完全重合的弧叫等弧;②在同一平面内,圆是到定点距离等于定长的点的集合;③度数相等的弧叫做等弧;④优弧大于劣弧;⑤直角三角形的外心是其斜边中点.A.①②③④⑤B.①②⑤C.①②③⑤D.②④⑤3.(2017秋•化德县校级月考)下列说法中,正确的有()①圆的半径垂直于弦;②直径是弦;③圆的内接平行四边形是矩形;④圆内接四边形的对角互补;⑤长度相等的两条弧是等弧;⑥相等的圆心角所对的弧相等.A.2个B.3个C.4个D.5个4.下列说法中,正确的有()①在同圆或等圆中,相等的弦所对的弧相等;③在同圆或等圆中,相等的弦所对的圆周角相等④在同圆或等圆中,相等的弦所对的圆心角相等.A.1个B.2个C.3个D.4个5.(2017春•莱州市期末)下列说法正确的是()A.顶点在圆内的角叫做圆心角B.圆上任意两点间的部分叫做圆弧C.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做扇形D.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的6.(2015秋•厦门校级期中)下列说法正确的是()A.等边三角形是中心对称图形B.三点可以确定一个圆C.矩形的四个顶点一定共圆D.三角形三条角平分线的交点为三角形的外心7.(2016秋•道里区校级期中)下列说法正确的个数是()①平分弦的直径垂直于弦;②三点确定一个圆;③在同圆中,相等的弦所对的圆周角相等;④直径为圆中最长的弦.A.1个B.2个C.3个D.4个8.(2015秋•石河子校级月考)下列说法正确的是()A.相等的弧所对的弦相等B.平分弦的直径垂直于弦,并且平分弦所对的两条弧C.经过圆心的角是圆心角D.经过三个点一定可以做一个圆9.(2015秋•咸丰县月考)下列说法正确的有()①半径相等的两个圆是等圆;②半径相等的两个半圆是等弧;③过圆心的线段是直径;④分别在两个等圆上的两条弧是等弧.A.1个B.2个C.3个D.4个10.(2017秋•慈溪市月考)下列说法正确的是()A.平分弦的直径垂直于弦B.垂直平分弦的直线必经过圆心C.相等的圆周角所对的弧相等D.三点确定一个圆11.(2015秋•端州区期末)下列说法正确的是()A.三点确定一个圆B.平分弦的直径垂直于弦,并且平分弦所对的两条弧C.与直径垂直的直线是圆的切线D.能够互相重合的弧是等弧12.(2017秋•江都区校级月考)下列说法正确的是()A.三角形的外心到三角形三个顶点的距离相等B.经过三个点一定可以作圆C.任意一个圆一定有内接三角形,并且只有一个内接三角形D.优弧一定大于劣弧13.(2014秋•江阴市期中)下列说法正确的有几个()①经过三个点一定可以作圆;②任意一个圆一定有内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个外接圆并且只有一个外接圆;④垂直于弦的直径必平分弦;⑤经过不在同一直线上的四个点一定可以作圆.A.3 B.2 C.1 D.014.(2018秋•盐都区期中)下列说法正确的是()A.等弧所对的圆心角相等B.相等的圆心角所对的弧相等C.经过三点可以作一个圆D.三角形的内心到这个三角形的各顶点距离相等15.下列说法正确的是()A.顶点在圆上的角是圆周角B.两边都和圆相交的角是圆周角C.圆心角是圆周角的2倍D.在同圆中,同弧所对的圆周角等于它所对的圆心角度教的一半二、填空题(共1小题)16.下列说法:①相等的弦所对的圆心角相等②相等的弧所对的弦相等③平分弦的直径必垂直于弦,并且平分弦所对的两条弧④弦是所对的两条弧的中点连线必垂直平分这条弦⑤经过不在同一直线上的四个点一定可以作圆,其中说法正确的是.圆的有关概念练习(判断正误)参考答案一、单选题(共15小题)1.【解答】解:①正确,因为平行弦间的弧相等,符合等腰梯形的判断;(2)不正确,因为正方形的四个角相等,不符合圆内接四边形的性质;(3)不正确,一定是在同圆或等圆中;(4)不正确,一定是在同圆或等圆中;(5)正确,符合同圆或等圆中的,弦越长弦心距越短;(6)不正确,平分不是直径的弦的直径就平分弦所对的弧.故选:A.2.【解答】解:①在同圆或等圆中能够完全重合的弧叫等弧正确;②在同一平面内,圆是到定点距离等于定长的点的集合,正确;③度数相等的弧叫做等弧,错误;④同圆中优弧大于劣弧,故原命题错误;⑤直角三角形的外心是其斜边中点,正确.故选:B.3.【解答】解:①圆的半径垂直于弦,错误;②直径是弦,正确;③圆的内接平行四边形是矩形,正确;④圆内接四边形的对角互补,正确;⑤长度相等的两条弧是等弧,错误;⑥相等的圆心角所对的弧相等,错误,正确的有3个,故选:B.4.【解答】解:①在同圆或等圆中,相等的弦所对的弧相等,符合圆心角、弧、弦的关系,故本小题正确;②在同圆或等圆中,相等的弦所对的弦心距不一定相等,故本小题错误;③在同圆或等圆中,相等的弦所对的圆周角相等,符合圆心角、弧、弦的关系,故本小题正确;④在同圆或等圆中,相等的弦所对的圆心角相等,符合圆心角、弧、弦的关系,故本小题正确.故选:C.5.【解答】解:A、错误.顶点在圆心的角叫做圆心角;B、正确;C、错误.由一条弧和经过这条弧的两个端点的两条线段组成的图形叫做弓形;D、错误.在一个圆中,圆心角为1°的扇形的面积等于圆的面积的;、故选:B.6.【解答】解:A、等边三角形不是中心对称图形,故错误;B、不在同一直线上的三点确定一个圆,故错误;C、矩形的四个顶点一定共圆,故正确;D、三角形的三条角平分线的交点为三角形的内心,故错误;故选:C.7.【解答】解:平分弦(非直径)的直径垂直于弦,所以①错误;不共线的三点确定一个圆,所以②错误;在圆中,任何一条弦都对应着两条弧,而这两条弧一般是不相等的,只有弦是直径时,所对的两条弧才相等,故③错误;直径为圆中最长的弦,故④正确;故选:A.8.【解答】解:A、相等的弧所对的弦相等,正确;B、平分弦的直径垂直于弦,并且平分弦所对的两条弧,说法错误,应为平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,故此选项错误;C、经过圆心的角是圆心角,说法错误,应为顶点在圆心,两条半径的夹角是圆心角,故此选项错误;D、经过三个点一定可以做一个圆,说法错误,应为不在同一直线上的三点确定一个圆,故此选项错误;故选:A.9.【解答】解:①半径相等的两个圆是等圆,正确;②半径相等的两个半圆是等弧,正确;③过圆心的线段是直径,错误;④分别在两个等圆上的两条弧是等弧,错误.故选:B.10.【解答】解:A、若两条弦为两条不互相垂直的直径,则不成立,故本选项错误;B、垂直平分弦的直线必经过圆心,正确;C、在同圆或等圆中,相等的圆心角所对的弧相等,错误;D、不在同一直线上的三点确定一个圆,错误.故选:B.11.【解答】解:A、不共线的三点确定一个圆,所以A选项错误;B、平分弦(非直径)的直径垂直于弦,并且平分弦所对的两条弧,所以B选项错误;C、过直径的端点且与直径垂直的直线是圆的切线,所以C选项错误;D、能够互相重合的弧为等弧,所以D选项正确.故选:D.B、不共线的三个点确定一个圆,故此结论错误;C、任意一个圆一定有内接三角形,有无数个内接三角形,故此结论错误;D、在同圆或等圆中,同一条弦所对的两条弧优弧一定大于劣弧,错误;故选:A.13.【解答】解:①经过不在同一条直线上的三点确定一个圆,故①错误;②任意一个圆一定有内接三角形,一个圆有无数个内接三角形,故②错误;③任意一个三角形一定有一个外接圆并且只有一个外接圆,故③正确;④垂直于弦(不过圆心的弦)的直径必平分弦,故④错误;⑤经过不在同一条直线上的三点确定一个圆,故⑤错误;故选:C.14.【解答】解:A、等弧所对的圆心角相等,则A正确;B、在同心圆中,相等的圆心角所对的弧不相等,则B错误;C、经过不共线三点可以作一个圆,则C错误;D、三角形的内心到这个三角形的三边距离相等,则D错误;故选:A.15.【解答】解:A、顶点在圆上,并且两边都与圆相交的角叫做圆周角,原说法错误,故本选项错误;B、没有强调顶点在圆上,原说法错误,故本选项错误;C、同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半,原说法错误,故本选项错误;D、在同圆中,同弧所对的圆周角等于它所对的圆心角度教的一半,说法正确,故本选项正确.故选:D.二、填空题(共1小题)16.【解答】解:①在同圆或等圆中,相等的弦所对的圆心角相等,错误;②在同圆或等圆中,相等的弧所对的弦相等,错误;③平分弦(非直径)的直径必垂直于弦,并且平分弦所对的两条弧,错误;④弦是所对的两条弧的中点连线必垂直平分这条弦,正确;⑤经过不在同一直线上的四个点不一定可以作圆,错误;故答案为:④。
数学 圆的综合的专项 培优易错试卷练习题及答案
一、圆的综合 真题与模拟题分类汇编(难题易错题)1.已知O 的半径为5,弦AB 的长度为m ,点C 是弦AB 所对优弧上的一动点. ()1如图①,若m 5=,则C ∠的度数为______;()2如图②,若m 6=.①求C ∠的正切值;②若ABC 为等腰三角形,求ABC 面积.【答案】()130;()2C ∠①的正切值为34;ABC S 27=②或43225. 【解析】【分析】 ()1连接OA ,OB ,判断出AOB 是等边三角形,即可得出结论;()2①先求出10AD =,再用勾股定理求出8BD =,进而求出tan ADB ∠,即可得出结论;②分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.【详解】()1如图1,连接OB ,OA ,OB OC 5∴==,AB m 5==,OB OC AB ∴==,AOB ∴是等边三角形,AOB 60∠∴=,1ACB AOB 302∠∠∴==, 故答案为30;()2①如图2,连接AO 并延长交O 于D ,连接BD ,AD 为O 的直径,AD 10∴=,ABD 90∠=,在Rt ABD 中,AB m 6==,根据勾股定理得,BD 8=, AB 3tan ADB BD 4∠∴==, C ADB ∠∠=,C ∠∴的正切值为34; ②Ⅰ、当AC BC =时,如图3,连接CO 并延长交AB 于E ,AC BC =,AO BO =,CE ∴为AB 的垂直平分线,AE BE 3∴==,在Rt AEO 中,OA 5=,根据勾股定理得,OE 4=,CE OE OC 9∴=+=,ABC 11S AB CE 692722∴=⨯=⨯⨯=; Ⅱ、当AC AB 6==时,如图4,连接OA 交BC 于F ,AC AB =,OC OB =,AO ∴是BC 的垂直平分线,过点O 作OG AB ⊥于G , 1AOG AOB 2∠∠∴=,1AG AB 32==, AOB 2ACB ∠∠=,ACF AOG ∠∠∴=,在Rt AOG 中,AG 3sin AOG AC 5∠==, 3sin ACF 5∠∴=, 在Rt ACF 中,3sin ACF 5∠=, 318AF AC 55∴==, 24CF 5∴=, ABC 111824432S AF BC 225525∴=⨯=⨯⨯=; Ⅲ、当BA BC 6==时,如图5,由对称性知,ABC 432S 25=.【点睛】圆的综合题,主要圆的性质,圆周角定理,垂径定理,等腰三角形的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.2.如图,在⊙O 中,直径AB ⊥弦CD 于点E ,连接AC ,BC ,点F 是BA 延长线上的一点,且∠FCA =∠B .(1)求证:CF 是⊙O 的切线; (2)若AE =4,tan ∠ACD = 12,求AB 和FC 的长.【答案】(1)见解析;(2) ⑵AB=20 , 403CF =【解析】 分析:(1)连接OC ,根据圆周角定理证明OC ⊥CF 即可;(2)通过正切值和圆周角定理,以及∠FCA =∠B 求出CE 、BE 的长,即可得到AB 长,然后根据直径和半径的关系求出OE 的长,再根据两角对应相等的两三角形相似(或射影定理)证明△OCE ∽△CFE ,即可根据相似三角形的对应线段成比例求解.详解:⑴证明:连结OC∵AB 是⊙O 的直径∴∠ACB=90°∴∠B+∠BAC=90°∵OA=OC∴∠BAC=∠OCA∵∠B=∠FCA∴∠FCA+∠OCA=90°即∠OCF=90°∵C 在⊙O 上∴CF 是⊙O 的切线⑵∵AE=4,tan ∠ACD12AE EC = ∴CE=8 ∵直径AB ⊥弦CD 于点E∴AD AC =∵∠FCA =∠B∴∠B=∠ACD=∠FCA∴∠EOC=∠ECA∴tan ∠B=tan ∠ACD=1=2CE BE ∴BE=16∴AB=20∴OE=AB÷2-AE=6 ∵CE ⊥AB∴∠CEO=∠FCE=90°∴△OCE ∽△CFE ∴OC OE CF CE = 即106=8CF ∴40CF 3= 点睛:此题主要考查了圆的综合知识,关键是熟知圆周角定理和切线的判定与性质,结合相似三角形的判定与性质和解直角三角形的知识求解,利用数形结合和方程思想是解题的突破点,有一定的难度,是一道综合性的题目.3.等腰Rt △ABC 和⊙O 如图放置,已知AB=BC=1,∠ABC=90°,⊙O 的半径为1,圆心O 与直线AB 的距离为5.(1)若△ABC 以每秒2个单位的速度向右移动,⊙O 不动,则经过多少时间△ABC 的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC 的速度为每秒2个单位,⊙O 的速度为每秒1个单位,则经过多少时间△ABC 的边与圆第一次相切?(3)若两个图形同时向右移动,△ABC 的速度为每秒2个单位,⊙O 的速度为每秒1个单位,同时△ABC 的边长AB 、BC 都以每秒0.5个单位沿BA 、BC 方向增大.△ABC 的边与圆第一次相切时,点B 运动了多少距离?【答案】(152-;(2) 52;(32042- 【解析】 分析:(1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC 移至△A′B′C′处,A′C′与⊙O 切于点E ,连OE 并延长,交B′C′于F .由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;(2)设运动的时间为t 秒,根据题意得:CC′=2t ,DD′=t ,则C′D′=CD+DD′-CC′=4+t -2t=4-t ,由第(1)的结论列式得出结果;(3)求出相切的时间,进而得出B 点移动的距离.详解:(1)假设第一次相切时,△ABC 移至△A′B′C′处,如图1,A′C′与⊙O 切于点E ,连接OE 并延长,交B′C′于F ,设⊙O 与直线l 切于点D ,连接OD ,则OE ⊥A′C′,OD ⊥直线l ,由切线长定理可知C′E=C′D ,设C′D=x ,则C′E=x ,∵△ABC 是等腰直角三角形,∴∠A=∠ACB=45°,∴∠A′C′B′=∠ACB=45°,∴△EFC′是等腰直角三角形,∴C′F=2x ,∠OFD=45°, ∴△OFD 也是等腰直角三角形,∴OD=DF ,∴2x+x=1,则x=2-1,∴CC′=BD -BC-C′D=5-1-(2-1)=5-2,∴点C 运动的时间为522-; 则经过522-秒,△ABC 的边与圆第一次相切; (2)如图2,设经过t 秒△ABC 的边与圆第一次相切,△ABC 移至△A′B′C′处,⊙O 与BC 所在直线的切点D 移至D′处,A′C′与⊙O 切于点E ,连OE 并延长,交B′C′于F ,∵CC′=2t ,DD′=t ,∴C′D′=CD+DD′-CC′=4+t -2t=4-t ,由切线长定理得C′E=C′D′=4-t ,由(1)得:4-t=2-1, 解得:t=5-2,答:经过5-2秒△ABC 的边与圆第一次相切;(3)由(2)得CC′=(2+0.5)t=2.5t ,DD′=t ,则C′D′=CD+DD′-CC′=4+t -2.5t=4-1.5t ,由切线长定理得C′E=C′D′=4-1.5t ,由(1)得:4-1.5t=2-1,解得:t=1022-, ∴点B 运动的距离为2×1022-=2042-.点睛:本题要求学生熟练掌握圆与直线的位置关系,并结合动点问题进行综合分析,比较复杂,难度较大,考查了学生数形结合的分析能力.4.如图所示,以Rt △ABC 的直角边AB 为直径作圆O ,与斜边交于点D ,E 为BC 边上的中点,连接DE .(1)求证:DE 是⊙O 的切线;(2)连接OE ,AE ,当∠CAB 为何值时,四边形AOED 是平行四边形?并在此条件下求sin ∠CAE 的值.【答案】(1)见解析;(2)10. 【解析】 分析:(1)要证DE 是⊙O 的切线,必须证ED ⊥OD ,即∠EDB+∠ODB=90°(2)要证AOED 是平行四边形,则DE ∥AB ,D 为AC 中点,又BD ⊥AC ,所以△ABC 为等腰直角三角形,所以∠CAB=45°,再由正弦的概念求解即可.详解:(1)证明:连接O 、D 与B 、D 两点,∵△BDC 是Rt △,且E 为BC 中点,∴∠EDB=∠EBD .(2分)又∵OD=OB 且∠EBD+∠DBO=90°,∴∠EDB+∠ODB=90°.∴DE 是⊙O 的切线.(2)解:∵∠EDO=∠B=90°,若要四边形AOED 是平行四边形,则DE ∥AB ,D 为AC 中点,又∵BD ⊥AC ,∴△ABC 为等腰直角三角形.∴∠C AB=45°.过E 作EH ⊥AC 于H ,设BC=2k ,则EH=22k ,AE=5k , ∴sin ∠CAE=1010EH AE .点睛:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.5.如图,AB 是圆O 的直径,射线AM ⊥AB ,点D 在AM 上,连接OD 交圆O 于点E ,过点D 作DC=DA 交圆O 于点C (A 、C 不重合),连接O C 、BC 、CE .(1)求证:CD 是⊙O 的切线;(2)若圆O 的直径等于2,填空:①当AD= 时,四边形OADC 是正方形;②当AD= 时,四边形OECB 是菱形.【答案】(1)见解析;(2)①1;②3.【解析】试题分析:(1)依据SSS证明△OAD≌△OCD,从而得到∠OCD=∠OAD=90°;(2)①依据正方形的四条边都相等可知AD=OA;②依据菱形的性质得到OE=CE,则△EOC为等边三角形,则∠CEO=60°,依据平行线的性质可知∠DOA=60°,利用特殊锐角三角函数可求得AD的长.试题解析:解:∵AM⊥AB,∴∠OAD=90°.∵OA=OC,OD=OD,AD=DC,∴△OAD≌△OCD,∴∠OCD=∠OAD=90°.∴OC⊥CD,∴CD是⊙O的切线.(2)①∵当四边形OADC是正方形,∴AO=AD=1.故答案为:1.②∵四边形OECB是菱形,∴OE=CE.又∵OC=OE,∴OC=OE=CE.∴∠CEO=60°.∵CE∥AB,∴∠AOD=60°.在Rt△OAD中,∠AOD=60°,AO=1,∴AD=.故答案为:.点睛:本题主要考查的是切线的性质和判定、全等三角形的性质和判定、菱形的性质、等边三角形的性质和判定,特殊锐角三角函数值的应用,熟练掌握相关知识是解题的关键.6.如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.(1) 试判断BE与FH的数量关系,并说明理由;(2) 求证:∠ACF=90°;(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求的长.图1 图2【答案】(1)BE="FH" ;理由见解析(2)证明见解析(3)=2π【解析】试题分析:(1)由△ABE≌△EHF(SAS)即可得到BE=FH(2)由(1)可知AB=EH,而BC=AB,FH=EB,从而可知△FHC是等腰直角三角形,∠FCH 为45°,而∠ACB也为45°,从而可证明(3)由已知可知∠EAC=30°,AF是直径,设圆心为O,连接EO,过点E作EN⊥AC于点N,则可得△ECN为等腰直角三角形,从而可得EN的长,进而可得AE的长,得到半径,得到所对圆心角的度数,从而求得弧长试题解析:(1)BE=FH.理由如下:∵四边形ABCD是正方形∴∠B=90°,∵FH⊥BC ∴∠FHE=90°又∵∠AEF=90°∴∠AEB+∠HEF="90°" 且∠BAE+∠AEB=90°∴∠HEF=∠BAE ∴∠AEB=∠EFH 又∵AE=EF∴△ABE≌△EHF(SAS)∴BE=FH(2)∵△ABE≌△EHF∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE="CH"∴CH=FH∴∠FCH=45°,∴∠FCM=45°∵AC是正方形对角线,∴∠ACD=45°∴∠ACF=∠FCM +∠ACD =90°(3)∵AE=EF,∴△AEF是等腰直角三角形△AEF外接圆的圆心在斜边AF的中点上.设该中点为O.连结EO得∠AOE=90°过E作EN⊥AC于点NRt△ENC中,EC=4,∠ECA=45°,∴EN=NC=Rt△ENA中,EN =又∵∠EAF=45°∠CAF=∠CEF=15°(等弧对等角)∴∠EAC=30°∴AE=Rt△AFE中,AE== EF,∴AF=8AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°=2π·4·(90°÷360°)=2π考点:1、正方形;2、等腰直角三角形;3、圆周角定理;4、三角函数7.如图,点B在数轴上对应的数是﹣2,以原点O为原心、OB的长为半径作优弧AB,使点A在原点的左上方,且tan∠AOB=3,点C为OB的中点,点D在数轴上对应的数为4.(1)S扇形AOB=(大于半圆的扇形);(2)点P是优弧AB上任意一点,则∠PDB的最大值为°(3)在(2)的条件下,当∠PDB最大,且∠AOP<180°时,固定△OPD的形状和大小,以原点O为旋转中心,将△OPD顺时针旋转α(0°≤α≤360°)①连接CP,AD.在旋转过程中,CP与AD有何数量关系,并说明理由;②当PD∥AO时,求AD2的值;③直接写出在旋转过程中,点C到PD所在直线的距离d的取值范围.【答案】(1)103(2)30(3)①AD=2PC②20+83或20+83③1≤d≤3【解析】【分析】(1)利用扇形的面积公式计算即可.(2)如图1中,当PD与⊙O相切时,∠PDB的值最大.解直角三角形即可解决问题.(3)①结论:AD=2PC.如图2中,连接AB,AC.证明△COP∽△AOD,即可解决问题.②分两种情形:如图3中,当PD∥OA时,设OD交⊙O于K,连接PK交OC于H.求出PC即可.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得.③判断出PC的取值范围即可解决问题.【详解】(1)∵tan∠AOB3,∴∠AOB=60°,∴S 扇形AOB =23002103603ππ⋅⋅= (大于半圆的扇形), (2)如图1中,当PD 与⊙O 相切时,∠PDB 的值最大.∵PD 是⊙O 的切线,∴OP ⊥PD ,∴∠OPD =90°, ∵21sin 42OP PDO OD ∠=== ∴∠PDB =30°, 同法当DP ′与⊙O 相切时,∠BDP ′=30°,∴∠PDB 的最大值为30°.故答案为30.(3)①结论:AD =2PC .理由:如图2中,连接AB ,AC .∵OA =OB ,∠AOB =60°,∴△AOB 是等边三角形,∵BC =OC ,∴AC ⊥OB ,∵∠AOC =∠DOP =60°,∴∠COP =∠AOD ,∵2AO OD OC OP==, ∴△COP ∽△AOD , ∴2AD AO PC OC==,∴AD=2PC.②如图3中,当PD∥OA时,设OD交⊙O于K,连接PK交OC于H.∵OP=OK,∠POK=60°,∴△OPK是等边三角形,∵PD∥OA,∴∠AOP=∠OPD=90°,∴∠POH+∠AOC=90°,∵∠AOC=60°,∴∠POH=30°,∴PH=1OP=1,OH=3PH=3,2∴PC=2222+=++=+,PH CH1(13)523∵AD=2PC,∴AD2=4(5+23)=20+83.如图④中,当PA∥OA时,作PK⊥OB于K,同法可得:PC2=12+(3﹣1)2=5﹣23,AD2=4PC2=20﹣83.③由题意1≤PC≤3,∴在旋转过程中,点C到PD所在直线的距离d的取值范围为1≤d≤3.【点睛】本题属于圆综合题,考查了切线的性质,相似三角形的判定和性质,旋转变换,勾股定理,等边三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题.8.如图,已知AB是⊙O的直径,BC是弦,弦BD平分∠ABC交AC于F,弦DE⊥AB于H,交AC于G.①求证:AG=GD;②当∠ABC满足什么条件时,△DFG是等边三角形?③若AB=10,sin∠ABD=35,求BC的长.【答案】(1)证明见解析;(2)当∠ABC=60°时,△DFG是等边三角形.理由见解析;(3)BC的长为145.【解析】【分析】(1)首先连接AD,由DE⊥AB,AB是O的直径,根据垂径定理,即可得到AD AE=,然后根据在同圆或等圆中,同弧或等弧所对的圆周角相等,证得∠ADE=∠ABD,又由弦BD平分∠ABC,可得∠DBC=∠ABD,根据等角对等边的性质,即可证得AG=GD;(2)当∠ABC=60°时,△DFG是等边三角形,根据半圆(或直径)所对的圆周角是直角与三角形的外角的性质,易求得∠DGF=∠DFG=60°,即可证得结论;(3)利用三角函数先求出tan∠ABD34=,cos∠ABD=45,再求出DF、BF,然后即可求出BC.【详解】(1)证明:连接AD,∵DE⊥AB,AB是⊙O的直径,∴AD AE=,∴∠ADE=∠ABD,∵弦BD平分∠ABC,∴∠DBC=∠ABD,∵∠DBC=∠DAC,∴∠ADE=∠DAC,∴AG=GD;(2)解:当∠ABC=60°时,△DFG是等边三角形.理由:∵弦BD平分∠ABC,∴∠DBC=∠ABD=30°,∵AB是⊙O的直径,∴∠ACB=90°,∴∠CAB =90°﹣∠ABC =30°,∴∠DFG =∠FAB+∠DBA =60°,∵DE ⊥AB ,∴∠DGF =∠AGH =90°﹣∠CAB =60°,∴△DGF 是等边三角形;(3)解:∵AB 是⊙O 的直径,∴∠ADB =∠ACB =90°,∵∠DAC =∠DBC =∠ABD ,∵AB =10,sin ∠ABD =35, ∴在Rt △ABD 中,AD =AB•sin ∠ABD =6,∴BD =22AB BD -=8,∴tan ∠ABD =34AD BD =,cos ∠ABD =4=5BD AB , 在Rt △ADF 中,DF =AD•tan ∠DAF =AD•tan ∠ABD =6×34=92, ∴BF =BD ﹣DF =8﹣92=72, ∴在Rt △BCF 中,BC =BF•cos ∠DBC =BF•cos ∠ABD =72×45=145. ∴BC 的长为:145.【点睛】此题考查了圆周角定理、垂径定理、直角三角形的性质、三角函数的性质以及勾股定理等知识.此题综合性较强,难度较大,解题的关键是掌握数形结合思想与转化思想的应用,注意辅助线的作法.9.如图,AB 是O 的直径,DF 切O 于点D ,BF DF ⊥于F ,过点A 作AC //BF 交BD 的延长线于点C .(1)求证:ABC C ∠∠=;(2)设CA 的延长线交O 于E BF ,交O 于G ,若DG 的度数等于60,试简要说明点D 和点E 关于直线AB 对称的理由.【答案】(1)见解析;(2)见解析.【解析】【分析】(1)作辅助线,连接OD,由DF为⊙O的切线,可得OD⊥DF,又BF⊥DF,AC∥BF,所以OD∥AC,∠ODB=∠C,由OB=OD得∠ABD=∠ODB,从而可证∠ABC=∠C;(2)连接OG,OD,AD,由BF∥OD,GD=60°,可求证BG=GD AD==60°,由平行线的性质及三角形的内角和定理可求出∠OHD=90°,由垂径定理便可得出结论.【详解】(1)连接OD,∵DF为⊙O的切线,∴OD⊥DF.∵BF⊥DF,AC∥BF,∴OD∥AC∥BF.∴∠ODB=∠C.∵OB=OD,∴∠ABD=∠ODB.∴∠ABC=∠C.(2)连接OG,OD,AD,DE,DE交AB于H,∵BF∥OD,∴∠OBG=∠AOD,∠OGB=∠DOG,∴GD AD==BG.∵GD=60°,∴BG=GD AD==60°,∴∠ABC=∠C=∠E=30°,∵OD//CE∴∠ODE=∠E=30°.在△ODH中,∠ODE=30°,∠AOD=60°,∴∠OHD=90°,∴AB⊥DE.∴点D和点E关于直线AB对称.【点睛】本题考查的是切线的性质、圆周角定理及垂径定理,解答此题的关键是作出辅助线,利用数形结合解答.10.设C为线段AB的中点,四边形BCDE是以BC为一边的正方形,以B为圆心,BD长为半径的⊙B与AB相交于F点,延长EB交⊙B于G点,连接DG交于AB于Q点,连接AD.求证:(1)AD是⊙B的切线;(2)AD=AQ;(3)BC2=CF×EG.【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.【解析】【分析】()1连接BD,由DC AB⊥,C为AB的中点,由线段垂直平分线的性质,可得=,再根据正方形的性质,可得90AD BD∠=;ADB()2由BD BGCD BE,利用等边对等角与平行线的性质,即可求得=与//122.52G CDG BDG BCD ∠=∠=∠=∠=,继而求得67.5ADQ AQD ∠=∠=,由等角对等边,可证得AD AQ =; ()3易求得67.5GDE GDB BDE DFE ∠=∠+∠==∠,90DCF E ∠=∠=,即可证得Rt DCF ∽Rt GED ,根据相似三角形的对应边成比例,即可证得结论.【详解】证明:()1连接BD ,四边形BCDE 是正方形,45DBA ∴∠=,90DCB ∠=,即DC AB ⊥,C 为AB 的中点,CD ∴是线段AB 的垂直平分线,AD BD ∴=, 45DAB DBA ∴∠=∠=,90ADB ∴∠=,即BD AD ⊥,BD 为半径,AD ∴是B 的切线;()2BD BG =,BDG G ∴∠=∠,//CD BE ,CDG G ∴∠=∠,122.52G CDG BDG BCD ∴∠=∠=∠=∠=, 9067.5ADQ BDG ∴∠=-∠=,9067.5AQB BQG G ∠=∠=-∠=, ADQ AQD ∴∠=∠,AD AQ ∴=;()3连接DF ,在BDF 中,BD BF =,BFD BDF ∴∠=∠,又45DBF ∠=,67.5BFD BDF ∴∠=∠=,22.5GDB ∠=,在Rt DEF 与Rt GCD 中,67.5GDE GDB BDE DFE ∠=∠+∠==∠,90DCF E ∠=∠=,Rt DCF ∴∽Rt GED ,CF CD ED EG∴=, 又CD DE BC ==,2BC CF EG ∴=⋅.【点睛】本题考查了相似三角形的判定与性质、切线的判定与性质、正方形的性质以及等腰三角形的判定与性质.解题的关键是注意掌握数形结合思想的应用,注意辅助线的作法.。
部编数学九年级上册专题07圆易错题(解析版)含答案
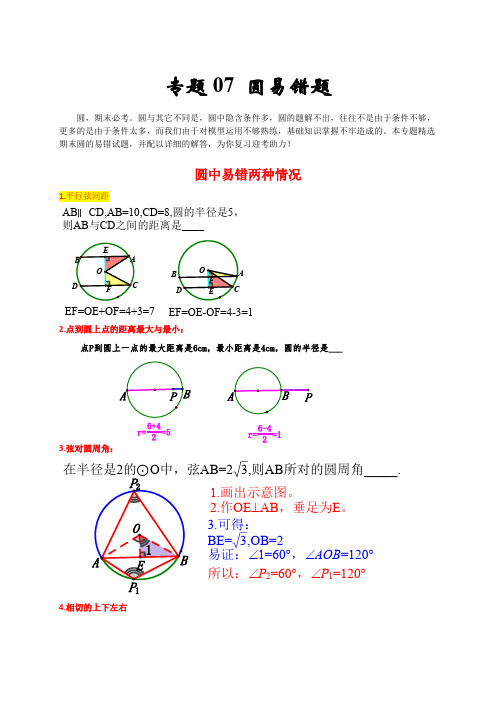
r=6-42=1r=6+42=5点P 到圆上一点的最大距离是6cm ,最小距离是4cm ,圆的半径是___专题07 圆易错题圆,期末必考。
圆与其它不同是,圆中隐含条件多,圆的题解不出,往往不是由于条件不够,更多的是由于条件太多,而我们由于对模型运用不够熟练,基础知识掌握不牢造成的。
本专题精选期末圆的易错试题,并配以详细的解答,为你复习迎考助力!圆中易错两种情况1.平行弦间距2.点到圆上点的距离最大与最小:3.弦对圆周角:4.相切的上下左右EF=OE-OF=4-3=1EF=OE+OF=4+3=7AB ∥CD,AB=10,CD=8,圆的半径是5,则AB 与CD 之间的距离是____所以:∠P 2=60°,∠P 1=120°3.可得:BE=3,OB=2易证:∠1=60°,∠AOB =120°1.画出示意图。
2.作OE ⊥AB ,垂足为E 。
在半径是2的⊙O 中,弦AB=23,则AB 所对的圆周角_____.1一.选择题1.如图,△ABC 与△ACD 中,AD =AC =DC =BAC :∠B :∠ACB =1:2:3,则△ABC 的外心与△ACD 的内心之间的距离为( )A .2BC .D .3试题分析:如图,过点D 作DG ⊥AC 于点G ,并延长交AB 于点F ,得△ABC 的外心,过点A 作AE 平分∠DAC 交DG 于点E ,则点E 为△ACD 的内心,证明△ACD 和△AEF 是等边三角形,从而可以解答.答案详解:解:如图,过点D 作DG ⊥AC 于点G ,并延长交AB 于点F ,△ACD 中,AD =AC =DC =∴△ACD 是等边三角形,点G 为AC 中点,过点A 作AE 平分∠DAC 交DG 于点E ,则点E 为△ACD 的内心,∠EAC =30°,∵△ABC 中,∠BAC :∠B :∠ACB =1:2:3,∴∠BAC =30°,∠B =60°,∠ACB =90°,∴BC ∥EF ,∠EAF =∠EAC +∠BAC =60°,简记:上切下切左切右切线段直线分类讨论实战训练∴∠AFE=∠B=60°,∵AG=CG,∴点F为AB中点,即点F为△ABC的外心,∴△AEF是等边三角形,∵AC=∴在Rt△ABC中,AB=4,∴EF=AF=2.则△ABC的外心与△ACD的内心之间的距离为2.所以选:A.2.如图,Rt△ABC中,AB⊥BC,AB=4,BC=3,P是平面上的一个点,连换AP,BP,已知∠P 始终为直角,则线段CP长的最大值为( )A.6B C+2D.5试题分析:首先证明点P在以AB为直径的⊙O上,连接OC,并延长CO与交⊙O于点P,此时PC最大,利用勾股定理求出OC即可解决问题.答案详解:解:∵∠APB=90°,∴点P在以AB为直径的⊙O上,连接OC,并延长CO与交⊙O于点P,此时PC最大,在Rt△BCO中,∵∠OBC=90°,BC=3,OB=2,∴OC=∴PC=OC+OP=+2,∴PC+2.所以选:C.3.给出下列结论:①有一个角是100°的两个等腰三角形相似.②三角形的内切圆和外接圆是同心圆.③圆心到直线上一点的距离恰好等于圆的半径,则该直线是圆的切线.④等腰梯形既是轴对称图形,又是中心对称图形.⑤平分弦的直径垂直于弦,并且平分弦所对的两弧.⑥过直线外一点有且只有一条直线平行于已知直线.其中正确命题有( )个.A.2个B.3个C.4个D.5个试题分析:根据圆相关知识点进行判断即可.答案详解:解:①、因为100°是钝角,所以只能是等腰三角形的顶角,则根据三角形的内角和定理,知它们的底角也对应相等,根据两角对应相等的两个三角形是相似三角形,则两个等腰三角形相似,故正确;②、三角形的内切圆的圆心是三条角平分线的交点,外接圆的圆心是三条垂直平分线的交点,只有等边三角形的内心和外心才重合,故错误;③、应当是圆心到直线的距离而不是圆心到直线上一点的距离恰好等于圆的半径,注意两者的说法区别:前者是点到直线的距离,后者是两个点之间的距离,故错误;④、等腰梯形不是中心对称图形,故错误;⑤、平分弦中的弦不能是直径,因为任意的两条直径都是互相平分,故错误;⑥、本题是平行公理,故正确.因此正确的结论是①⑥.所以选:A.4.如图,△ABC和△AMN都是等边三角形,点M是△ABC的外心,那么MN:BC的值为( )A.23B.3C.14D.49试题分析:延长AM交BC于点D,连接BM,根据△ABC是等边三角形可知AD⊥BC,设MD=x,则BM=AM=2x,利用锐角三角函数的定义用x表示出AB的长,再根据相似三角形的性质即可得出结论.答案详解:解:如图,延长AM交BC于点D,连接BM,∵△ABC是等边三角形,点M是△ABC的外心,∴AD⊥BC,∠ABM=∠BAM=30°,AM=BM,设MD=x,则BM=AM=2x,∴AD=3x,BD,∴AB=2BD=,∵△ABC和△AMN都是等边三角形,∴AB=BC=,AM=MN=2x,∴MN:BC=2x:=所以选:B.5.如图,在平面直角坐标系中,以M(2,3)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,则AC的长为( )A.4B.C.D.6试题分析:设⊙M与x轴相切于点D,连接MD,过点M作ME⊥AC,垂足为E,根据垂径定理可得AC=2AE,再利用切线的性质可得∠MDO=90°,然后根据点M的坐标可得ME=2,MA=MD=3,最后在Rt△AEM中,利用勾股定理进行计算即可解答.答案详解:解:设⊙M与x轴相切于点D,连接MD,过点M作ME⊥AC,垂足为E,∴AC =2AE ,∵⊙M 与x 轴相切于点D ,∴∠MDO =90°,∵M (2,3),∴ME =2,MD =3,∴MA =MD =3,在Rt △AEM 中,AE ==∴AC =2AE =所以选:B .6.如图,AB 是⊙O 的弦,PO ⊥OA 交AB 于点P ,过点B 的切线交OP 的延长线于点C ,若⊙O 的OP =1,则BC 的长为( )A .2BC .52D 试题分析:根据切线的性质可得∠OBC =90°,从而可得∠OBA +∠ABC =90°,再根据垂直定义可得∠POA =90°,从而可得∠A +∠APO =90°,然后利用等腰三角形的性质,以及等角的余角相等,对顶角相等可得∠ABC =∠BPC ,从而可得BC =CP ,最后在Rt △OBC 中,利用勾股定理进行计算即可解答.答案详解:解:∵BC 与⊙O 相切于点B ,∴∠OBC =90°,∴∠OBA +∠ABC =90°,∵PO⊥OA,∴∠POA=90°,∴∠A+∠APO=90°,∵OA=OB,∴∠A=∠OBA,∴∠ABC=∠APO,∵∠APO=∠BPC,∴∠ABC=∠BPC,∴BC=CP,设BC=CP=x,在Rt△OBC中,OB2+BC2=OC2,2+x2=(x+1)2,∴BC=2,所以选:A.7.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC、AD.若∠BAC=28°,则∠D的度数是( )A.56°B.58°C.60°D.62°试题分析:连接BC,根据直径所对的圆周角是直角可得∠ACB=90°,从而利用直角三角形的两个锐角互余可得∠B=62°,然后利用同弧所对的圆周角相等即可解答.答案详解:解:连接BC,∵AB是⊙O的直径,∴∠ACB=90°,∵∠BAC=28°,∴∠B=90°﹣∠BAC=62°,∴∠B=∠D=62°,所以选:D.8.如图,AB是⊙O的直径,CD是⊙O的弦,连接BD、BC,若∠ABD=56°,则∠BCD的度数为( )A.34°B.56°C.68°D.102°试题分析:连接AD,根据AB是直径可知∠ADB=90°=∠DAB+∠ABD,即可求出∠DAB,根据圆周角定的推论可得∠DAB=∠BCD,则问题得解.答案详解:解:连接AD,如图:∵AB是⊙O的直径,∴∠ADB=90°=∠DAB+∠ABD,又∵∠DAB=∠BCD,∠ABD=56°,∴∠DAB=90°﹣∠ABD=90°﹣56°=34°,∴∠BCD=34°.所以选:A.9.如图,线段AB是⊙O的直径,点C在圆上,∠AOC=60°,点P是线段AB延长线上的一点,连结PC,则∠APC的度数不可能是( )A.30°B.25°C.10°D.5°试题分析:连接CB,根据一条弧所对的圆周角等于它所对的圆心角的一半,求出∠ABC的度数,再利用三角形的外角即可解答.答案详解:解:连接CB,∵∠AOC=60°,∴∠ABC=12∠AOC=30°,∵∠ABC是△PBC的一个外角,∴∠ABC>∠APC,∴∠APC的度数不可能是30°,所以选:A.10.下列语句:①长度相等的弧是等弧;②过平面内三点可以作一个圆;③平分弦的直径垂直于弦;④90°的圆周角所对的弦是直径;⑤等弦对等弧.其中正确的个数是( )A.1个B.2个C.3个D.4个试题分析:根据等弧的概念、确定圆的条件、垂径定理的推论、圆周角定理判断即可.答案详解:解:①长度相等的弧不一定是等弧,本小题说法错误;②过平面内不在同一直线上的三点可以作一个圆,本小题说法错误;③平分弦(不是直径)的直径垂直于弦,本小题说法错误;④90°的圆周角所对的弦是直径,本小题说法正确;⑤在同圆或等圆中,等弦所对的劣等弧,所对的优弧是等弧,本小题说法错误;所以选:A.11.如图,点A,B,C,D都在圆上,线段AC与BD交于点M,MB=MD,当点B,D,M保持不变,点A在圆上自点B向点D运动的过程中(点A不与点B,点D重合),那么线段MA与MC 的乘积( )A.不变B.先变大,后变小C.变大D.先变小,后变大试题分析:根据相交弦定理直接解答即可.答案详解:解:∵点A,B,C,D都在圆上,∴MB•MD=AM•MC,∵MB=MD,当点B,D,M保持不变,∴MB•MD为定值,∴AM•MC为定值.所以选:A.二.填空题(共28小题)12.如图,半圆O的直径DE=12cm,在Rt△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm.半圆O以2cm/s的速度从左向右运动,当圆心O运动到点B时停止,点D、E始终在直线BC上.设运动时间为t(s),运动开始时,半圆O在△ABC的左侧,OC=8cm.当t= 1s,4s,7s,16s 时,Rt△ABC的一边所在直线与半圆O所在的圆相切.试题分析:分4种情况讨论:①当圆心O运动到点E与点C重合是时;②当圆心O运动到AC 右侧与AC相切时;③过C点作CF⊥AB,交AB于F点,当半圆O与△ABC的边AB相切时,圆心O到AB的距离等于6cm,且圆心O又在直线BC上,即当O点运动到C点时,半圆O与△ABC的边AB相切,此时点O运动了8cm,所求运动时间为t=4.答案详解:解:①当圆心O运动到点E与点C重合是时,∵AC⊥OE,OC=OE=6cm,此时AC与半圆O所在的圆相切,点O运动了2cm,所求运动时间为t=2÷2=1(s);②当圆心O运动到AC右侧与AC相切时,此时OC=6cm,点O运动的距离为8+6=14(cm),所求运动时间为t=14÷2=7(s);③如图1,过C点作CF⊥AB,交AB于F点;∵∠ABC=30°,BC=12cm,∴FO=6cm;当半圆O与△ABC的边AB相切时,∵圆心O到AB的距离等于6cm,且圆心O又在直线BC上,∴O与C重合,即当O点运动到C点时,半圆O与△ABC的边AB相切;此时点O运动了8cm,所求运动时间为t=8÷2=4(s),当点O运动到B点的右侧,且OB=12cm时,如图2,过点O作OQ⊥直线AB,垂足为Q.在Rt△QOB中,∠OBQ=30°,则OQ=6cm,即OQ与半圆O所在的圆相切.此时点O运动了32cm.所求运动时间为:t=32÷2=16s,综上可知当t的值为1s或4s或7秒或16s时,Rt△ABC的一边所在直线与半圆O所在的圆相切.所以答案是:1s,4s,7s,16s.13.已知点M (2.0),⊙M 的半径为1,OA 切⊙M 于点A ,点P 为⊙M 上的动点,当P 的坐标为 (1,0),(3,0)(32,2) 时,△POA 是等腰三角形.试题分析:根据题意画出图形分三种情况讨论:当点P 在x 轴上,PA =PO =1,OA =OP ″=3,当点P 是切点时,AO =AP = 答案详解:解:如图,当P 的坐标为(1,0),(3,0),(32,2)时,△POA 是等腰三角形.理由如下:连接AM ,∵M (2.0),⊙M 的半径为1,∴OM =2,AM =PM =1,∴OP =1,∵OA 切⊙M 于点A ,∴∠MAO =90°,∴∠AOM =30°,∴∠AMO =60°,∴PA =AM =PM =1,∴OP =PA =1,∴P (1,0);当OA =OP ′时,连接AP ′交x 轴于点H ,∵OA 切⊙M 于点A ,∴OP ′切⊙M 于点P ′,∴∠P ′OM =∠AOM =30°,∴∠AOP ′=60°,∴△AOP ′是等边三角形,∴AP ′=OA ==∴OH ==32,P ′H =12AP ′∴P ′(32,2);∵MA =MP ″,∠AMO =60°,∴∠MAP ″=∠MP ″A =30°,∴∠AOP ″=∠MP ″A =30°,∴OA =OP ″,∴P ″(3,0).综上所述:当P 的坐标为(1,0),(3,0),(32,2)时,△POA 是等腰三角形.所以答案是:(1,0),(3,0),(32,2).14.已知三角形ABC 是锐角三角形,其中∠A =30°,BC =4,设BC 边上的高为h ,则h 的取值范围是 试题分析:做出三角形的外接圆,根据h ≤AO +OP 求解即可.答案详解:解:如图1,作△ABC 的外接圆⊙O ,连接OA ,OB ,OC ,过O 作OP ⊥BC ,∵∠BAC=30°,∴∠BOC=60°,∵OB=OC,∴△OBC是等边三角形,∵BC=4,∴OA=BC=4,PO=∴h≤AO+OP=如图2,A1B⊥BC,A2C⊥BC,则A1B=∵三角形ABC是锐角三角形,∴点A在A1A2之间,∴h的取值范围是:h≤所以答案是:h≤15.如图,已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是边AB上的动点,Q是边BC上的动点,且∠CPQ=90°,则线段CQ的取值范围是 203≤CQ≤12 .试题分析:根据直径所对的圆周角是直角,则分析以CQ为直径的圆和斜边AB的公共点的情况:一是半圆和AB相切;二是半圆和AB相交.首先求得相切时CQ的值,即可进一步求得相交时CQ的范围.答案详解:解:∵Rt△ABC中,AC=5,BC=12,∠ACB=90°,∴AB=13,①当半圆O与AB相切时,如图,连接OP,则OP⊥AB,且AC=AP=5,∴PB=AB﹣AP=13﹣5=8;设CO=x,则OP=x,OB=12﹣x;在Rt△OPB中,OB2=OP2+OB2,即(12﹣x)2=x2+82,解之得x=10 3,∴CQ=2x=20 3;即当CQ=203且点P运动到切点的位置时,△CPQ为直角三角形.②当203<CQ≤12时,半圆O与直线AB有两个交点,当点P运动到这两个交点的位置时,△CPQ为直角三角形③当0<CQ<203时,半圆O与直线AB相离,即点P在AB边上运动时,均在半圆O外,∠CPQ<90°,此时△CPQ不可能为直角三角形.∴当203≤CQ≤12时,△CPQ可能为直角三角形.所以答案是:203≤CQ ≤12.16.如图,点O 为△ABC 的外接圆圆心,点E 为圆上一点,BC 、OE 互相平分,CF ⊥AE 于F ,连接DF .若OE =DF =1,则△ABC试题分析:由BC 、OE 互相平分可证明四边形BECO 为平行四边形,由OC =OB 可得BECO 为菱形,可得∠BOD =60°,∠BAE =∠EAC =30°,CF ⊥AE 于F ,可证△AGC 为等边三角形,F 为中点,则由中位线性质可得BG =2DF .在Rt △BHC 中利用勾股定理可求GH ,进而得到AB 、AC ,得到△ABC 的周长.答案详解:解:延长CF 交AB 于点G ,过C 作CH ⊥AB 于H ,连BO .∵BC 、OE 互相平分,∴四边形BECO 为平行四边形,∵OB =OC ,∴四边形BECO 为菱形,∴BE =EC ,∵OE =∴Rt △BOD 中,tan ∠OBD =OD BD =∴∠OBD =30°,∴∠BOD =60°,∴∠BAE =∠EAC =30°,∵CF ⊥AE ,∴F为GC中点,△AGC为等边三角形,∴BG=2DF=2,在Rt△BCH中,BH2+HC2=BC2,∴(2+GH)2+)2=62,解得GH GH∴AG=AC=﹣1∴△ABC的周长为所以答案是:17.如图,D为△ABC的内心,点E在AC上,且AD⊥DE,若DE=2,AD=CE=3,则AB的长43 .试题分析:延长ED交AB于点F,连接BD,将线段AB分为AF和BF两部分,分别计算:先证明△ADE≌△ADF,利用勾股定理得AE的长度,即为AF的长度,再证明△BFD∽△DEC,利用相似,列比例式求得BF,两者相加即可.答案详解:解:如图,延长ED交AB于点F,连接BD,∵AD⊥DE∴∠ADE=∠ADF=90°∵D为△ABC的内心∴∠DAE=∠DAF∵AD=AD∴△ADE≌△ADF(ASA)∵AE=AF,DE=DF=2∴AE∴AF∵∠ABC+∠ACB+∠BAC=180°∴∠ADC=180°﹣(∠DAC+∠DCA)=180°−12(∠BAC+∠ACB)=180°−12(180°﹣∠ABC)=90°+12∠ABC=90°+∠ABD=90°+∠CBD=90°+∠CDE∴∠ABD=∠CBD=∠CDE ∵△ADE≌△ADF∠AFD=∠AED∴∠BFD=∠DEC∴△BFD∽△DEC∴BFDE=DFCE∴BF2=23∴BF=4 3∴AB=AF+BF 4 34318.如图,在△ABC中,∠BAC=30°,∠ACB=60°,BC=1,点P从点A出发沿AB方向运动,到达点B时停止运动,连结CP,点A关于直线CP的对称点为A',连结A'C,A'P.点P到达点B 时,线段A'P扫过的面积为 43π−试题分析:依据轴对称的性质,即可得到AC =A 'C ,进而得出点A '的运动轨迹为以C 为圆心,AC 长为半径的一段圆弧;再根据扇形面积的计算公式,即可得到线段A 'P 扫过的面积.答案详解:解:∵△ABC 中,∠BAC =30°,∠ACB =60°,BC =1,∴∠ABC =90°,AC =2BC =2,AB =如图①所示,点A 关于直线CP 的对称点为A ',∴AC =A 'C ,∴点A '的运动轨迹为以C 为圆心,AC 长为半径的一段圆弧,当点P 与点B 重合时,线段A 'P 扫过的区域为弓形,如图②,∠APA '=180°,∠ACA '=120°,∴线段A 'P 扫过的面积为120π×22360−12××1=43π−所以答案是:43π−19.点M 是半径为5的⊙O 内一点,且OM =4,在过M 所有⊙O 的弦中,弦长为整数的弦的条数为 8 .试题分析:先求出过M 所有⊙O 的弦的取值范围,再取整数解.答案详解:解:过点M 作AB ⊥OM 于M ,连接OA ,因为OM =4,半径为5,所以AM =3,所以AB =3×2=6,所以过点M 的最长弦为5×2=10,最短弦为6,在6和10之间的整数有7,8,9,由于左右对称,弦的条数有6条,加上AB 和OM ,共8条.20.AB=AC=AD,∠CAB=100°,则∠BDC= 50°或130° .试题分析:分两种情况,当点D在优弧BDC上时,当点D′在劣弧BC上时,然后利用圆周角定理进行计算即可解答.答案详解:解:如图:∵AB=AC=AD,∴点B、C、D在以点A为圆心,以AB长为半径的圆上,当点D在优弧BDC上时,∵∠CAB=100°,∴∠BDC=12∠BAC=50°,当点D′在劣弧BC上时,∵四边形BDCD′是圆内接四边形,∴∠BD′C=180°﹣∠BDC=130°,综上所述:∠BDC=50°或130°,所以答案是:50°或130°.21.如图,AB是⊙O的弦,AB=P是优弧APB上的动点,∠P=45°,连接PA,PB,AC是△ABP的中线.(1)若∠CAB=∠P,则AC= 2 ;(2)AC试题分析:(1)作BH⊥AC,根据△BAC∽△BPA,求出BC=2,再证明H和C重合即可得到答案;(2)确定点C的运动轨迹,轨迹点圆关系找到AC的最大值就是AC'长,再计算求解.答案详解:解:如图1,过点B作BH⊥AC于点H,∵∠B=∠B,∠CAB=∠P,∴△BAC∽△BPA,∴BABP=BCBA,∴BA2=BC•BP,∵AC是△ABP的中线,∴BP=2BC,∴(2=BC•2BC,∴BC=2,在Rt△ABH中,∠CAB=∠P=45°,AB=∴BH=AH=2,又∵BC=2,∴点H和点C重合,∴AC=AH=2.所以答案是:2;(2)如图2,∵点P的运动轨迹是圆,∴点C的运动轨迹是OB为直径的圆,∴当AC'经过圆心O'时最大.∵∠P=45°,∴∠AOB=90°,又∵AB=∴AO=BO=2,OO'=1,∴AO'=∵O'C'=1,∴AC'=1+∴AC的最大值为1+所以答案是:1+22.如图,已知点A(3,0)、B(﹣1,0)点Q是y轴上一点,当∠AQB=135°时点Q的坐标是 试题分析:分两种情况:①如图,当Q在y轴的负半轴上时,作辅助线,构建全等三角形和等腰直角三角形,证明△QEC≌△CFB,设CE=a,根据三角函数列方程可解答;②同理Q在y轴的正半轴上时,根据对称得出点Q的坐标.答案详解:解:分两种情况:①如图,当Q在y轴的负半轴上时,过点B作BC⊥AQ,交AQ的延长线于C,过点C作EF⊥y 轴于E,过点B作BF⊥EF于F,∵∠AQB=135°,∴∠CQB=45°,∵∠BCQ=90°,∴△BCQ是等腰直角三角形,∴CQ=CB,∵∠BCF+∠ECQ=∠ECQ+∠CQE=90°,∴∠BCF=∠CQE,∵∠F=∠CEQ=90°,∴△QEC≌△CFB(AAS),∴EQ=CF,CE=BF,设CE=a,则CF=EQ=3﹣a,BF=CE=a,∴OQ=a﹣(3﹣a)=2a﹣3,∵∠AQO=∠CQE,∴tan∠AQO=tan∠CQE,即AOOQ =CE EQ,∴12a−3=a3−a,解得:a1a2=,当a=OQ=2a﹣32,∴Q(0,2;②当Q在y轴的正半轴上时,同理可得Q(02).综上,点Q的坐标为(0,202).所以答案是:(0,202).23.已知等腰△ABC的外心是O,AB=AC,∠BOC=100°,则∠ABC= 25°或65° .试题分析:画出相应图形,分△ABC为锐角三角形和钝角三角形2种情况解答即可.答案详解:解:(1)圆心O在△ABC外部,在优弧BC上任选一点D,连接BD,CD.∴∠BDC=12∠BOC=50°,∴∠BAC=180°﹣∠BDC=130°;∵AB=AC,∴∠ABC=(180°﹣∠BAC)÷2=25°;(2)圆心O在△ABC内部.∠BAC=12∠BOC=50°,∵AB=AC,∴∠ABC=(180°﹣∠BAC)÷2=65°;所以答案是25°或65°.24.已知⊙O中,两弦AB和CD相交于点P,若AP:PB=2:3,CP=2cm,DP=12cm,则弦AB 的长为 10 cm.试题分析:根据相交弦定理“圆内两弦相交于圆内一点,各弦被这点所分得的两线段的长的乘积相等”进行计算.答案详解:解:设AP=2x,由AP:PB=2:3得PB=3x,由相交弦定理得:PA•PB=PC•PD,∴2x•3x=2×12,x=2(舍去负值),∴AB=AP+PB=5x=10cm.25.在△ABC中,AB=6,AC=8,高AD=4.8,设能完全覆盖△ABC的圆的半径为r,则r的最小值为 5或4 .试题分析:分类讨论:当AD在△ABC内部,利用勾股定理求法可得三角形第3边长,可得三角形的形状为直角三角形,完全覆盖△ABC的圆的最小半径为直角三角形斜边的一半;当AD在△ABC外部,即△ABC是钝角三角,以AC为直径的圆是能完全覆盖△ABC的最小圆.答案详解:解:(1)当AD在△ABC内部,如图:∵AB=6,AC=8,高AD=4.8,∴BD=3.6,CD=6.4,∴BC=10,∵62+82=102.∴△ABC是以BC为斜边的直角三角形,∴完全覆盖△ABC的圆的最小半径为10×12=5;(2)当AD在△ABC外部,即△ABC是钝角三角,∵以AC为直径的圆是能完全覆盖△ABC的最小圆,∴能完全覆盖△ABC的圆的半径R的最小值为8×12=4,所以答案是:5或4.26.已知△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣1,﹣3),C(3,﹣3)则△ABC外接试题分析:三角形的外心是三边中垂线的交点,设△ABC的外心为M;由A、B、C的坐标知:AB、BC的垂直平分线正好经过(1,0),由此可得到M(1,0),由勾股定理即可求得⊙M的半径长.答案详解:解:设△ABC的外心为M,如图:∵A(﹣1,3),B(﹣1,﹣3),C(3,﹣3),∴AB、BC的垂直平分线过(1,0),故M(1,0);MA就是⊙M的半径长,由勾股定理得:MA即△ABC27.如图,AB是⊙O的直径,AD、BC是⊙O的切线,P是⊙O上一动点,若AD=3,AB=4,BC=6,则△PDC的面积的最小值是 4 .试题分析:由CD是固定的,所以当P到CD的距离最小时△PCD的面积最小,过P作EF∥CD,交AD于点E,交BC于点F,当EF与⊙O相切时,P到CD的距离最短,连接OP并延长交CD于点Q,过O作OH∥BC,交EF于点G,交CD于点H,则可知OH为梯形ABCD的中位线,OG为梯形ABFE的中位线,可求得OH,过D作DM⊥BC于点M,可求得CD=EF=5,由切线长定理可知AE=EP,BF=PF,可得AE+BF=EF=5,可求得OG=2.5,可求得GH=2,又OP=2,且OPPQ=OGGH,可求得PQ=1.6,可求得△PCD的面积,可得出答案.答案详解:解:由CD是固定的,所以当P到CD的距离最小时△PCD的面积最小,如图,过P作EF∥CD,交AD于点E,交BC于点F,当EF与⊙O相切时,P到CD的距离最短,连接OP并延长交CD于点Q,过O作OH∥BC,交EF于点G,交CD于点H,则可知OH为梯形ABCD的中位线,OG为梯形ABFE的中位线,∴OH=12(AD+BC)=4.5,过D作DM⊥BC于点M,则DM=AB=4,MC=BC﹣AD=3,∴CD=EF=5,由切线长定理可知AE=EP,BF=PF,∴AE+BF=EF=5,∴OG=12(AE+BF)=2.5,∴GH=OH﹣OG=4.5﹣2.5=2,又∵OP=2,且OPPQ=OGGH,∴2PQ=2.52,∴PQ=1.6,∴S△PCD =12PQ•CD=12×1.6×5=4,所以答案是:4.28.如图,⊙O既是正△ABC的外接圆,又是正△DEF的内切圆,则内外两个正三角形的相似比是 12 .试题分析:过O作OM⊥AC于M,ON⊥EF于N,连接OC、OF,设OC=ON=R,根据等边三角形性质推出∠MCO =∠OFN =30°,求出OM 、OF 的值,根据勾股定理求出CM 、FN ,根据垂径定理求出AC 、EF 值,即可求出答案.答案详解:解:过O 作OM ⊥AC 于M ,ON ⊥EF 于N ,连接OC 、OF ,设OC =ON =R ,∵⊙O 既是正△ABC 的外接圆,又是正△DEF 的内切圆,∴∠MCO =∠OFN =30°,∵∠CMO =∠FNO =90°,∴OM =12R ,OF =2R ,由勾股定理得:CM ==2R ,由垂径定理得:AC =2CM =,同理EF =2NF =,即内外两个正三角形的相似比是AC :EF =1:2=12,所以答案是:12.29.如图,点C 在以O 为圆心的半圆内一点,直径AB =4,∠BCO =90°,∠OBC =30°,将△BOC 绕圆心逆时针旋转到使点C 的对应点C ′在半径OA 上,则边BC 扫过区域(图中阴影部分)面积为 π .(结果保留π)试题分析:根据直角三角形的性质求出OC 、BC ,根据扇形面积公式计算即可.答案详解:解:∵∠BCO =90°,∠OBC =30°,∴OC =12OB =1,BC则边BC 扫过区域的面积为:120π×22360+12××1−120π×12360−12××1=43π−13π−=π.所以答案是:π.30.如图,C 、D 是⊙O 上两点,位于直径AB 的两侧,设∠ABC =24°,则∠BDC = 66 °.试题分析:根据直径所对的圆周角是直角可得∠ACB =90°,然后利用直角三角形的两个锐角互余可得∠A =66°,从而利用同弧所对的圆周角相等即可解答.答案详解:解:∵AB 是⊙O 的直径,∴∠ACB =90°,∵∠ABC =24°,∴∠A =90°﹣∠ABC =66°,∴∠BDC =∠A =66°,所以答案是:66.31.某园林单位要在一个绿化带内开挖一个△ABC 的工作面,使得∠ACB =60°,CD 是AB 边上的高,且CD =6,则△ABC 的面积最小值是试题分析:作△ABC 的外接圆⊙O ,连接OA 、OB 、OC ,作OE ⊥AB 于E ,设OA =OC =2x .根据圆周角和等腰三角形的性质得OE =12OA =x ,AE =,再由线段的不等关系可得最小值,最后根据三角形面积公式答案.答案详解:解:作△ABC 的外接圆⊙O ,连接OA 、OB 、OC ,作OE ⊥AB 于E ,设OA =OC =2x .∵∠AOB =2∠ACB ,∠ACB =60°,∴∠AOB =120°,∠ACB =60°,OA =OB =R ,OE ⊥AB ,∴AE =EB ,∠AOE =∠BOE =60°,∴OE =12OA =x ,AE =,∵OC +OE ≥CD ,CD =6,∴3x ≥6,∴x ≥2,∴x 的最小值为2.∵E 为AB 中点,∴AB =AE +BE =2AE =,∵AB 的最小值为∴S △ABC 的最小值=12CD ⋅AB =12×6×=所以答案是:32.如图,正方形ABCD 的边长为4,E 是AD 的中点,点P 是边AB 上的一个动点,连接PE ,以P为圆心,PE 的长为半径作⊙P .当⊙P 与正方形ABCD 的边相切时,则AP 的长为 32或试题分析:分⊙P 与BC 相切、⊙P 与DC 相切两种情况,根据切线的性质、勾股定理计算即可.答案详解:解:当⊙P 与BC 相切时,PE =PB =4﹣AP ,在Rt △PAE 中,AP 2+AE 2=PE 2,即AP 2+22=(4﹣AP )2,解得:AP =32,当⊙P 与DC 相切时,PE =4,则AP ==综上所述,当⊙P 与正方形ABCD 的边相切时,则AP 的长为32或所以答案是:32或33.如图,在扇形AOB 中,OA =2,点P 为AB 上一动点,过点P 作PC ⊥OA 于点C ,PD ⊥OB 于点D ,连接CD ,当CD 取得最大值时,扇形OAB 的周长为 4+π .试题分析:∠AOB =90°时,CD 最大,由求出扇形的周长即可.答案详解:解:由PC ⊥OA ,PD ⊥OB 可知,∠OCP +∠ODP =180°,∴O 、C 、P 、D 四点共圆,CD 为此圆直径时,CD 最大,∴当∠AOB =90°时,CD 最大,如图:此时扇形周长为2+2+90⋅π⋅2180=4+π.所以答案是:4+π.34.如图,圆内一条弦CD 与直径AB 相交成30°角,且分直径成1cm 和5cm 两部分,则这条弦的弦心距是 1cm .试题分析:首先过点O 作OF ⊥CD 于点F ,设弦CD 与直径AB 相交于点E ,由分直径成1cm 和5cm两部分,可求得直径,半径的长,继而求得OE的长,又由圆内一条弦CD与直径AB相交成30°角,即可求得这条弦的弦心距.答案详解:解:过点O作OF⊥CD于点F,设弦CD与直径AB相交于点E,∵分直径成1cm和5cm两部分,∴AB=6cm,∴OA=12AB=3cm,∴OE=OA﹣AE=2cm,∵∠OEF=30°,∴OF=12OE=1(cm).所以答案是:1cm.35.已知圆的两条平行弦分别长6dm和8dm,若这圆的半径是5dm,则两条平行弦之间的距离为 7dm 或1dm .试题分析:如图,AB∥CD,AB=6dm,CD=8dm,过O点作OE⊥AB于E,交CD于F点,连OA、OC,根据垂径定理得AE=BE=12AB=3,由于AB∥CD,EF⊥AB,则EF⊥CD,根据垂径定理得CF=FD=12CD=4,然后利用勾股定理可计算出OE=4,OF=3,再进行讨论:当圆心O在AB与CD之间时,AB与CD的距离=OE+OF;当圆心O不在AB与CD之间时,AB与CD 的距离=OE﹣OF.答案详解:解:如图,AB∥CD,AB=6dm,CD=8dm,过O点作OE⊥AB于E,交CD于F点,连OA、OC,∴AE=BE=12AB=3,∵AB∥CD,EF⊥AB,∴EF⊥CD,∴CF=FD=12CD=4,在Rt△OAE中,OA=5dmOE4,同理可得OF=3,当圆心O在AB与CD之间时,AB与CD的距离=OE+OF=4+3=7(dm);当圆心O不在AB与CD之间时,AB与CD的距离=OE﹣OF=4﹣3=1(dm).所以答案是7dm或1dm.36.如图,P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,若x、y都是整数,则这样的点共有 12 个.试题分析:因为P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,根据题意,x2+y2=25,若x、y都是整数,其实质就是求方程的整数解.答案详解:解:∵P(x,y)是以坐标原点为圆心、5为半径的圆周上的点,即圆周上的任意一点到原点的距离为5,=5,即x2+y2=25,又∵x、y都是整数,∴方程的整数解分别是:x=0,y=5;x=3,y=4;x=4,y=3;x=5,y=0;x=﹣3,y=4;x=﹣4,y=3;x=﹣5,y=0;x=﹣3,y=﹣4;x=﹣4,y=﹣3;x=0,y=﹣5;x=3,y=﹣4;x=4,y=﹣3.共12对,所以点的坐标有12个.分别是:(0,5);(3,4);(4,3);(5,0);(﹣3,4);(﹣4,3);(﹣5,0);(﹣3,﹣4);(﹣4,﹣3);(0,﹣5);(3,﹣4);(4,﹣3).37.在⊙O中,若弦BC垂直平分半径OA,则弦BC所对的圆周角等于 60或120 °.试题分析:根据弦BC垂直平分半径OA,可得OD:OB=1:2,得∠BOC=120°,根据同弧所对圆周角等于圆心角的一半即可得弦BC所对的圆周角度数.答案详解:解:如图,∵弦BC垂直平分半径OA,∴OD:OB=1:2,∴∠BOD=60°,∴∠BOC=120°,∴弦BC所对的圆周角等于60°或120°.所以答案是:60或120.38.圆中一条弦所对的圆心角为60°,那么它所对的圆周角度数为 30或150 度.试题分析:由圆周角定理知,弦所对的优弧上的圆周角是30°;由圆内接四边形的对角互补可知,弦所对劣弧上的圆周角=180°﹣30°=150°.因此弦所对的圆周角度数有两个.答案详解:解:如图,∠AOB=60°;则∠C=12∠AOB=30°;∵四边形ADBC是⊙O的内接四边形,∴∠D=180°﹣∠C=150°;因此弦AB所对的圆周角度数为30°或150°.39.一圆中两弦相交,一弦长为2a且被交点平分,另一弦被交点分成1:4两部分,则另一弦长为 5a2 .试题分析:设另一条弦被分成的两段长分别是x,4x,根据相交弦定理求解.圆内两条相交弦,被交点分成的线段的乘积相等.答案详解:解:设另一条弦被分成的两段长分别是x,4x.根据相交弦定理,得x•4x=a2,x=a 2.所以5x=52 a.三.解答题40.如图,CD为⊙O的直径,CD⊥AB,垂足为F,AO⊥BC,垂足为E,连接AC.(1)求∠B的度数;(2)若CE=O的半径.试题分析:(1)根据垂径定理求出BE=CE,根据线段垂直平分线性质求出AB=AC,同理得AC =BC,则△ABC是等边三角形,从而得结论;(2)求出∠BCD=30°和OE=4,根据直角三角形中含30°角的性质求出圆O的半径即可.答案详解:解:(1)如图,∵AO⊥BC,AO过O,∴CE=BE,∴AB=AC,同理得:AC=BC,∴AB=AC=BC∴△ABC是等边三角形∴∠B=60°;(2)∵△ABC是等边三角形,∴∠ACB=60°,∵AC=BC,CD⊥AB,∴∠BCD=30°,∵CE=在Rt△CEO中,OE=4,∴OC=2OE=8,即圆O的半径为8.41.如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.(1)求证:点D为AC的中点;(2)若DF=4,AC=16,求⊙O的直径.试题分析:(1)根据直径所对的圆周角是直角可得∠C=90°,从而利用平行线的性质可得∠OFA =∠C=90°,从而可得OF⊥AC,然后利用垂径定理即可解答;(2)利用垂径定理可得AF=12AC=8,然后在Rt△AFO中,利用勾股定理进行计算即可解答.答案详解:(1)证明:∵AB是⊙O的直径,∴∠C=90°,∵OD∥BC,∴∠OFA=∠C=90°,∴OF⊥AC,∴AD=CD,∴点D为AC的中点;(2)解:∵OF⊥AC,∴AF=12AC=8,在Rt△AFO中,AO2=AF2+OF2,∴OA2=64+(OD﹣DF)2,∴OA2=64+(OA﹣4)2,∴OA=10,∴⊙O的直径为20.42.如图,AB是⊙O的直径,弦CD交AB于点E,连接AC、AD.若∠BAC=35°,(1)求∠D的度数;(2)若∠ACD=65°,求∠CEB的度数.试题分析:(1)连接CB,根据直径所对的圆周角是直角可得∠ACB=90°,从而利用直角三角形的两个锐角互余可得∠ABC=55°,然后利用同弧所对的圆周角相等即可解答;(2)利用三角形的外角性质,进行计算即可解答.答案详解:解:(1)连接CB,∵AB是⊙O的直径,∴∠ACB=90°,∵∠BAC=35°,∴∠ABC=90°﹣∠BAC=55°,∴∠ABC=∠D=55°,∴∠D的度数为55°;(2)∵∠CEB是△ACE的一个外角,∴∠CEB=∠BAC+∠ACD=100°,∴∠CEB的度数为100°.43.如图,AB是⊙O的直径,点C为⊙O上一点,D为弧BC的中点,过D作DF⊥AB于点E,交⊙O于点F,交弦BC于点G,连接CD,BF.(1)求证:BC=DF.(2)若BC=8,BE=2,求⊙O的半径.试题分析:(1)根据AAS证明△CDB≌△DBF,可得结论;(2)先根据垂径定理可得DE=4,设⊙O的半径为r,利用勾股定理求解即可.答案详解:(1)证明:∵D是BC的中点,∴BD=CD,∵AB为⊙O的直径,DF⊥AB,∴BD=BF,∴BD=BF=CD,∴BF=CD=BD,∠DCB=∠BDF=∠CBD=∠F,∴△CDB≌△DBF(AAS),∴BC=DF;(2)解:如图,连接OD交BC于点M,∵AB为⊙O的直径,DF⊥AB,∴DE=EF,。
圆的易错题六年级

圆的易错题六年级一、填空题。
1. 一个圆的半径是3厘米,它的直径是()厘米,周长是()厘米,面积是()平方厘米。
- 解析:在圆中,直径d = 2r(r是半径),所以直径d=2×3 = 6厘米;圆的周长公式C = 2π r,π取3.14时,C=2×3.14×3 = 18.84厘米;圆的面积公式S=π r^2,S = 3.14×3^2=3.14×9 = 28.26平方厘米。
2. 一个圆的周长是18.84分米,这个圆的半径是()分米,面积是()平方分米。
- 解析:根据圆的周长公式C = 2π r,可得r=(C)/(2π),C = 18.84分米,π = 3.14,则r=(18.84)/(2×3.14)=3分米;再根据面积公式S=π r^2,S = 3.14×3^2=28.26平方分米。
3. 在一个边长为8厘米的正方形内画一个最大的圆,这个圆的半径是()厘米,面积是()平方厘米。
- 解析:在正方形内画最大的圆,圆的直径等于正方形的边长,所以圆的半径r = 8÷2=4厘米;面积S=π r^2=3.14×4^2=3.14×16 = 50.24平方厘米。
4. 一个圆的面积是28.26平方米,它的半径是()米。
- 解析:根据圆的面积公式S=π r^2,28.26=π r^2,π = 3.14,则r^2=(28.26)/(3.14) = 9,r = 3米。
5. 把一个圆平均分成若干份,拼成一个近似的长方形,这个长方形的长相当于圆的(),宽相当于圆的()。
- 解析:把圆平均分成若干份拼成近似长方形,这个长方形的长相当于圆周长的一半,宽相当于圆的半径。
二、判断题。
6. 圆的半径扩大3倍,它的面积也扩大3倍。
(×)- 解析:圆的面积公式S=π r^2,半径扩大3倍变为3r,则面积S'=π(3r)^2=9π r^2,面积扩大了9倍,而不是3倍。
人教版小学数学六年级上册第五单元《圆》错例分析

人教版小学数学六年级上册第五单元《圆》错例分析---------------------------------------------------------------最新资料推荐------------------------------------------------------ 人教版小学数学六年级上册第五单元《圆》错例分析人教版小学数学六年级上册第五单元《圆》错例一【错例来源】人教版六年级上册课堂作业第 42 页第 4 题的第 2 小题。
【错题再现】请分别以下面的线段为直径和半径画圆。
学生的作业中出现的情况如下:(1)(2)(3) 【题意解读】这一作业是《圆的认识》教学后相应的作业练习,这是《圆》单元教学的第一课时,即圆的认识。
知识与技能的目标是通过让学生画圆、剪圆、折圆等活动,使学生认识圆,了解圆的各部分名称,掌握圆的特征以及半径、直径的关系,理解圆心、半径、直径的作用。
而这一题的练习设计正是这一知识与技能目标的全面深入地诠释。
以下面的线段为直径和半径画圆,第一,考查的是学生对直径、半径概念的理解,如果只是让学生去选择哪条是圆的半径,哪条是直径?那只是考查学生对圆各部分名称,直径、半径的了解。
而这题让学生通过以这条线段为直径、半径来画圆,便是对圆的各部分名称的理解和掌握,以及对知识的应用,那才是这课知识的内化与提升。
第二,学生在理解半径和直径作图时,需要考虑圆规尖脚的位置,即圆心位置的确定,让学生在画图的过程中,体验思维的开放性。
1 / 11同时,也很好的理解了圆心、半径、直径的作用。
第三,这题除了在考查学生的知识与技能的掌握情况外,还注重学生审题能力和思维能力的考查和培养。
如题目中分别直径和半径画圆,需要学生有全面思考问题的能力和细致分析解决问题的能力。
【情况说明】经过调查发现,一个班级中有30%的学生画对,有25%的学生以这条线段为直径画一个圆,30%的学生以这条线段为半径画一个圆,10%的学生以这条线段为直径、半径,但圆心在线段中间画两个圆,还有 5%的学生没有画。
【数学】数学圆的综合的专项培优 易错 难题练习题(含答案)及详细答案

一、圆的综合 真题与模拟题分类汇编(难题易错题)1.如图,AB 为⊙O 的直径,点E 在⊙O 上,过点E 的切线与AB 的延长线交于点D ,连接BE ,过点O 作BE 的平行线,交⊙O 于点F ,交切线于点C ,连接AC(1)求证:AC 是⊙O 的切线;(2)连接EF ,当∠D= °时,四边形FOBE 是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.2.如图,在⊙O 中,直径AB ⊥弦CD 于点E ,连接AC ,BC ,点F 是BA 延长线上的一点,且∠FCA =∠B .(1)求证:CF 是⊙O 的切线; (2)若AE =4,tan ∠ACD = 12,求AB 和FC 的长.【答案】(1)见解析;(2) ⑵AB=20 , 403CF =【解析】 分析:(1)连接OC ,根据圆周角定理证明OC ⊥CF 即可;(2)通过正切值和圆周角定理,以及∠FCA =∠B 求出CE 、BE 的长,即可得到AB 长,然后根据直径和半径的关系求出OE 的长,再根据两角对应相等的两三角形相似(或射影定理)证明△OCE ∽△CFE ,即可根据相似三角形的对应线段成比例求解.详解:⑴证明:连结OC∵AB 是⊙O 的直径∴∠ACB=90°∴∠B+∠BAC=90°∵OA=OC∴∠BAC=∠OCA∵∠B=∠FCA∴∠FCA+∠OCA=90°即∠OCF=90°∵C 在⊙O 上∴CF 是⊙O 的切线⑵∵AE=4,tan ∠ACD12AE EC = ∴CE=8 ∵直径AB ⊥弦CD 于点E∴AD AC =∵∠FCA =∠B∴∠B=∠ACD=∠FCA∴∠EOC=∠ECA∴tan ∠B=tan ∠ACD=1=2CE BE ∴BE=16∴AB=20∴OE=AB÷2-AE=6∵CE ⊥AB∴∠CEO=∠FCE=90°∴△OCE ∽△CFE ∴OC OE CF CE= 即106=8CF ∴40CF 3= 点睛:此题主要考查了圆的综合知识,关键是熟知圆周角定理和切线的判定与性质,结合相似三角形的判定与性质和解直角三角形的知识求解,利用数形结合和方程思想是解题的突破点,有一定的难度,是一道综合性的题目.3.已知,如图:O 1为x 轴上一点,以O 1为圆心作⊙O 1交x 轴于C 、D 两点,交y 轴于M 、N 两点,∠CMD 的外角平分线交⊙O 1于点E ,AB 是弦,且AB ∥CD ,直线DM 的解析式为y=3x+3.(1)如图1,求⊙O 1半径及点E 的坐标.(2)如图2,过E 作EF ⊥BC 于F ,若A 、B 为弧CND 上两动点且弦AB ∥CD ,试问:BF+CF 与AC 之间是否存在某种等量关系?请写出你的结论,并证明.(3)在(2)的条件下,EF 交⊙O 1于点G ,问弦BG 的长度是否变化?若不变直接写出BG的长(不写过程),若变化自画图说明理由.【答案】(1)r=5 E(4,5)(2)BF+CF=AC (3)弦BG的长度不变,等于2【解析】分析:(1)连接ED、EC、EO1、MO1,如图1,可以证到∠ECD=∠SME=∠EMC=∠EDC,从而可以证到∠EO1D=∠EO1C=90°.由直线DM的解析式为y=3x+3可得OD=1,OM=3.设⊙O1的半径为r.在Rt△MOO1中利用勾股定理就可解决问题.(2)过点O1作O1P⊥EG于P,过点O1作O1Q⊥BC于Q,连接EO1、DB,如图2.由AB∥DC可证到BD=AC,易证四边形O1PFQ是矩形,从而有O1P=FQ,∠PO1Q=90°,进而有∠EO1P=∠CO1Q,从而可以证到△EPO1≌△CQO1,则有PO1=QO1.根据三角形中位线定理可得FQ=12BD.从而可以得到BF+CF=2FQ=AC.(3)连接EO1,ED,EB,BG,如图3.易证EF∥BD,则有∠GEB=∠EBD,从而有BG=ED,也就有BG=DE.在Rt△EO1D中运用勾股定理求出ED,就可解决问题.详解:(1)连接ED、EC、EO1、MO1,如图1.∵ME平分∠SMC,∴∠SME=∠EMC.∵∠SME=∠ECD,∠EMC=∠EDC,∴∠ECD=∠EDC,∴∠EO1D=∠EO1C.∵∠EO1D+∠EO1C=180°,∴∠EO1D=∠EO1C=90°.∵直线DM的解析式为y=3x+3,∴点M的坐标为(0,3),点D的坐标为(﹣1,0),∴OD=1,OM=3.设⊙O1的半径为r,则MO1=DO1=r.在Rt△MOO1中,(r﹣1)2+32=r2.解得:r=5,∴OO1=4,EO1=5,∴⊙O1半径为5,点E的坐标为(4,5).(2)BF+CF=AC.理由如下:过点O1作O1P⊥EG于P,过点O1作O1Q⊥BC于Q,连接EO1、DB,如图2.∵AB∥DC,∴∠DCA=∠BAC,∴AD=BC BD∴,=AC,∴BD=AC.∵O1P⊥EG,O1Q⊥BC,EF⊥BF,∴∠O1PF=∠PFQ=∠O1QF=90°,∴四边形O1PFQ是矩形,∴O1P=FQ,∠PO1Q=90°,∴∠EO1P=90°﹣∠PO1C=∠CO1Q.在△EPO1和△CQO1中,111111EO P CO QEPO CQOO E O C∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△EPO1≌△CQO1,∴PO1=QO1,∴FQ=QO1.∵QO1⊥BC,∴BQ=CQ.∵CO1=DO1,∴O1Q=12BD,∴FQ=12BD.∵BF+CF=FQ+BQ+CF=FQ+CQ+CF=2FQ,∴BF+CF=BD=AC.(3)连接EO1,ED,EB,BG,如图3.∵DC是⊙O1的直径,∴∠DBC=90°,∴∠DBC+∠EFB=180°,∴EF∥BD,∴∠GEB=∠EBD,∴BG=ED,∴BG=DE.∵DO1=EO1=5,EO1⊥DO1,∴DE=52,∴BG=52,∴弦BG的长度不变,等于52.点睛:本题考查了圆周角定理、圆内接四边形的性质、弧与弦的关系、垂径定理、全等三角形的判定与性质、矩形的判定与性质、三角形中位线定理、平行线的判定与性质、勾股定理等知识,综合性比较强,有一定的难度.而由AB∥DC证到AC=BD是解决第(2)小题的关键,由EG∥DB证到BG=DE是解决第(3)小题的关键.4.如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,交BC的延长线于点E,使得∠DAC=∠B.(1)求证:DA是⊙O切线;(2)求证:△CED∽△ACD;(3)若OA=1,sinD=13,求AE的长.【答案】(1)证明见解析;(22【解析】分析:(1)由圆周角定理和已知条件求出AD⊥AB即可证明DA是⊙O切线;(2)由∠DAC=∠DCE,∠D=∠D可知△DEC∽△DCA;(3)由题意可知AO=1,OD=3,DC=2,由勾股定理可知AD=2,故此可得到DC2=DE•AD,故此可求得DE的长,于是可求得AE的长.详解:(1)∵AB为⊙O的直径,∴∠ACB=90°,∴∠CAB+∠B=90°.∵∠DAC=∠B,∴∠CAB+∠DAC=90°,∴AD⊥AB.∵OA是⊙O半径,∴DA为⊙O的切线;(2)∵OB=OC,∴∠OCB=∠B.∵∠DCE=∠OCB,∴∠DCE=∠B.∵∠DAC=∠B,∴∠DAC=∠DCE.∵∠D=∠D,∴△CED∽△ACD;(3)在Rt△AOD中,OA=1,sin D=13,∴OD=OAsinD=3,∴CD=OD﹣OC=2.∵AD=22OD OA-=22.又∵△CED∽△ACD,∴AD CDCD DE=,∴DE=2CDAD=2,∴AE=AD﹣DE=22﹣2=2.点睛:本题主要考查的是切线的性质、圆周角定理、勾股定理的应用、相似三角形的性质和判定,证得△DEC∽△DCA是解题的关键.5.如图所示,以Rt△ABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.(1)求证:DE是⊙O的切线;(2)连接OE,AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求sin∠CAE的值.【答案】(1)见解析;(2)10 10.【解析】分析:(1)要证DE是⊙O的切线,必须证ED⊥OD,即∠EDB+∠ODB=90°(2)要证AOED是平行四边形,则DE∥AB,D为AC中点,又BD⊥AC,所以△ABC为等腰直角三角形,所以∠CAB=45°,再由正弦的概念求解即可.详解:(1)证明:连接O、D与B、D两点,∵△BDC是Rt△,且E为BC中点,∴∠EDB=∠EBD.(2分)又∵OD=OB 且∠EBD+∠DBO=90°,∴∠EDB+∠ODB=90°.∴DE 是⊙O 的切线.(2)解:∵∠EDO=∠B=90°,若要四边形AOED 是平行四边形,则DE ∥AB ,D 为AC 中点,又∵BD ⊥AC ,∴△ABC 为等腰直角三角形.∴∠C AB=45°.过E 作EH ⊥AC 于H ,设BC=2k ,则EH=22k ,AE=5k , ∴sin ∠CAE=10EH AE .点睛:本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.6.如图,△ABC 中,∠A=45°,D 是AC 边上一点,⊙O 经过D 、A 、B 三点,OD ∥BC . (1)求证:BC 与⊙O 相切;(2)若OD=15,AE=7,求BE 的长.【答案】(1)见解析;(2)18.【解析】分析:(1)连接OB ,求出∠DOB 度数,根据平行线性质求出∠CBO=90°,根据切线判定得出即可;(2)延长BO 交⊙O 于点F ,连接AF ,求出∠ABF ,解直角三角形求出BE .详解:(1)证明:连接OB .∵∠A=45°,∴∠DOB=90°.∵OD∥BC,∴∠DOB+∠CBO=180°.∴∠CBO=90°.∴直线BC是⊙O的切线.(2)解:连接BD.则△ODB是等腰直角三角形,∴∠ODB=45°,BD=OD=15,∵∠ODB=∠A,∠DBE=∠DBA,∴△DBE∽△ABD,∴BD2=BE•BA,∴(15)2=(7+BE)BE,∴BE=18或﹣25(舍弃),∴BE=18.点睛:本题考查了切线的判定,圆周角定理,解直角三角形等知识点,能综合运用定理进行推理和计算是解此题的关键,题目综合性比较强,难度偏大.7.(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.(1)如图①,求证:ED为⊙O的切线;(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.【答案】(1)见解析;(2)12【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO 的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度试题解析:解:(1)连接OD,∵ED=EF,∴∠EDF=∠EFD,∵∠EFD=∠CFO,∴∠EDF=∠CFO.∵OD=OC,∴∠ODF=∠OCF.∵OC⊥AB,∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,∴ED为⊙O的切线;(2)连接OD,过点D作DM⊥BA于点M,由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+2,由勾股定理得,EO2=ED2+DO2,即(a+2)2=a2+62,解得,a=8,即ED=8,EO=10.∵sin∠EOD=45EDEO=,cos∠EOD=35ODOE=,∴DM=OD•sin∠EOD=6×45=245,MO=OD•cos∠EOD=6×35=185,∴EM=EO﹣MO=10﹣18 5=325,EA=EO+OA=10+6=16.∵GA切⊙O于点A,∴GA⊥EA,∴DM∥GA,∴△EDM∽△EGA,∴DM EMGA EA=,即24325516GA=,解得GA=12.点睛:本题考查的是切线的判定、垂径定理和勾股定理的应用、等腰三角形的性质、角的三角函数值、相似三角形的判定及性质,解题的关键是:(1)通过等腰三角形的性质找出∠EDO=90°;(2)通过相似三角形的性质找出相似比.8.如图,OB是以(O,a)为圆心,a为半径的⊙O1的弦,过B点作⊙O1的切线,P为劣弧OB上的任一点,且过P作OB、AB、OA的垂线,垂足分别是D、E、F.(1)求证:PD2=PE•PF;(2)当∠BOP=30°,P点为OB的中点时,求D、E、F、P四个点的坐标及S△DEF.【答案】(1)详见解析;(2)D(﹣34a,34a),E(﹣334a,34a),F(﹣32a,0),P(﹣3a,2a);S△DEF=33a2.【解析】试题分析:(1)连接PB,OP,利用AB切⊙O1于B求证△PBE∽△POD,得出PB PEOP PD=,同理,△OPF∽△BPD,得出PB PDOP PF=,然后利用等量代换即可.(2)连接O1B,O1P,得出△O1BP和△O1PO为等边三角形,根据直角三角形的性质即可解得D、E、F、P四个点的坐标.再利用三角形的面积公式可直接求出三角形DEF的面积.试题解析:(1)证明:连接PB,OP,∵PE⊥AB,PD⊥OB,∴∠BEP=∠PDO=90°,∵AB切⊙O1于B,∠ABP=∠BOP,∴△PBE∽△POD,∴=,同理,△OPF∽△BPD∴=,∴=,∴PD2=PE•PF;(2)连接O1B,O1P,∵AB切⊙O1于B,∠POB=30°,∴∠ABP=30°,∴∠O1BP=90°﹣30°=60°,∵O1B=O1P,∴△O1BP为等边三角形,∴O1B=BP,∵P为弧BO的中点,∴BP=OP,即△O1PO为等边三角形,∴O1P=OP=a,∴∠O1OP=60°,又∵P为弧BO的中点,∴O1P⊥OB,在△O1DO中,∵∠O1OP=60°O1O=a,∴O1D=a,OD=a,过D作DM⊥OO1于M,∴DM=OD=a,OM=DM=a,∴D(﹣a, a),∵∠O1OF=90°,∠O1OP=60°∴∠POF=30°,∵PE⊥OA,∴PF=OP=a,OF=a,∴P(﹣a,),F(﹣a,0),∵AB切⊙O1于B,∠POB=30°,∴∠ABP=∠BOP=30°,∵PE⊥AB,PB=a,∴∠EPB=60°∴PE=a,BE=a,∵P为弧BO的中点,∴BP=PO,∴∠PBO=∠BOP=30°,∴∠BPO=120°,∴∠BPE+∠BPO=120°+60°=180°,即OPE三点共线,∵OE=a+a=a,过E作EM⊥x轴于M,∵AO切⊙O1于O,∴∠EOA=30°,∴EM=OE=a,OM=a,∴E(﹣a, a),∵E(﹣a, a),D(﹣a, a),∴DE=﹣a﹣(﹣a)=a,DE边上的高为: a,∴S△DEF=×a×a=a2.故答案为:D(﹣a, a),E(﹣a, a),F(﹣a,0),P(﹣a,);S△DEF=a2.9.(1)问题背景如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证:2PA=PB+PC.小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);第二步:证明Q,B,P三点共线,进而原题得证.请你根据小明同学的思考过程完成证明过程.(2)类比迁移如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.(3)拓展延伸如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=43AC,AB⊥AC,垂足为A,则OC的最小值为.【答案】(1)证明见解析;(2)OC最小值是2﹣3;(3)32.【解析】试题分析:(1)将△PAC绕着点A顺时针旋转90°至△QAB(如图①),只要证明△APQ 是等腰直角三角形即可解决问题;(2)如图②中,连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,在△BOQ中,利用三边关系定理即可解决问题;(3)如图③构造相似三角形即可解决问题.作AQ⊥OA,使得AQ=43OA,连接OQ,BQ,OB.由△QAB∽OAC,推出BQ=43OC,当BQ最小时,OC最小;试题解析:(1)将△PAC绕着点A顺时针旋转90°至△QAB(如图①);∵BC是直径,∴∠BAC=90°,∵AB=AC,∴∠ACB=∠ABC=45°,由旋转可得∠QBA=∠PCA,∠ACB=∠APB=45°,PC=QB,∵∠PCA+∠PBA=180°,∴∠QBA+∠PBA=180°,∴Q,B,P三点共线,∴∠QAB+∠BAP=∠BAP+∠PAC=90°,∴QP2=AP2+AQ2=2AP2,∴QP=2AP=QB+BP=PC+PB,∴2AP=PC+PB.(2)如图②中,连接OA,将△OAC绕点A顺时针旋转90°至△QAB,连接OB,OQ,∵AB⊥AC,∴∠BAC=90°,由旋转可得QB=OC,AQ=OA,∠QAB=∠OAC,∴∠QAB+∠BAO=∠BAO+∠OAC=90°,∴在Rt△OAQ中,OQ=32,AO=3 ,∴在△OQB中,BQ≥OQ﹣OB=32﹣3 ,即OC最小值是32﹣3;(3)如图③中,作AQ⊥OA,使得AQ=43OA,连接OQ,BQ,OB.∵∠QAO=∠BAC=90°,∠QAB=∠OAC ,∵QA AB OA AC =43, ∴△QAB ∽OAC ,∴BQ=43OC , 当BQ 最小时,OC 最小,易知OA=3,AQ=4,OQ=5,BQ≥OQ ﹣OB ,∴OQ≥2,] ∴BQ 的最小值为2,∴OC 的最小值为34×2=32, 故答案为32. 【点睛】本题主要考查的圆、旋转、相似等知识,能根据题意正确的添加辅助线是解题的关键.10.如图,已知AB 为⊙O 的直径,AB=8,点C 和点D 是⊙O 上关于直线AB 对称的两个点,连接OC 、AC ,且∠BOC <90°,直线BC 和直线AD 相交于点E ,过点C 作直线CG 与线段AB 的延长线相交于点F ,与直线AD 相交于点G ,且∠GAF =∠GCE(1)求证:直线CG 为⊙O 的切线;(2)若点H 为线段OB 上一点,连接CH ,满足CB =CH ,①△CBH ∽△OBC②求OH +HC 的最大值【答案】(1)证明见解析;(2)①证明见解析;②5.【解析】分析:(1)由题意可知:∠CAB=∠GAF ,由圆的性质可知:∠CAB=∠OCA ,所以∠OCA=∠GCE ,从而可证明直线CG 是⊙O 的切线;(2)①由于CB=CH ,所以∠CBH=∠CHB ,易证∠CBH=∠OCB ,从而可证明△CBH ∽△OBC ;②由△CBH ∽△OBC 可知:BC HB OC BC =,所以HB=24BC ,由于BC=HC ,所以OH+HC=4−24BC +BC ,利用二次函数的性质即可求出OH+HC 的最大值. 详解:(1)由题意可知:∠CAB=∠GAF ,∵AB 是⊙O 的直径,∴∠ACB=90°∵OA=OC ,∴∠CAB=∠OCA ,∴∠OCA+∠OCB=90°,∵∠GAF=∠GCE ,∴∠GCE+∠OCB=∠OCA+∠OCB=90°,∵OC 是⊙O 的半径,∴直线CG 是⊙O 的切线;(2)①∵CB=CH ,∴∠CBH=∠CHB ,∵OB=OC ,∴∠CBH=∠OCB ,∴△CBH ∽△OBC②由△CBH ∽△OBC 可知:BC HB OC BC= ∵AB=8,∴BC 2=HB•OC=4HB , ∴HB=24BC , ∴OH=OB-HB=4-24BC ∵CB=CH ,∴OH+HC=4−24BC +BC , 当∠BOC=90°,此时∵∠BOC <90°,∴0<BC <,令BC=x 则CH=x ,BH=24x ()221142544OH HC x x x ∴+=-++=--+ 当x=2时,∴OH+HC 可取得最大值,最大值为5点睛:本题考查圆的综合问题,涉及二次函数的性质,相似三角形的性质与判定,切线的判定等知识,综合程度较高,需要学生灵活运用所知识.。
圆的易错题汇编及答案解析

MN BC MN67 BM7,贝U BM=7-- MND ,6同理可得5CN=5-严,圆的易错题汇编及答案解析一、选择题1.如图,点E为ABC的内心,过点E作MN P BC交AB于点M,交AC于点N,若AB 7 , AC 5 , BC 6,则MN 的长为(【答案】B【解析】【分析】连接EB EC,如图,利用三角形内心的性质得到/ 所以/仁/3,则BM=ME,同理可得MN 7 BM 7—— -------- ,贝y BM=7--MND6 7 6方程,然后解方程即可.【详解】连接EB EC,如图,•••点E为AABC的内心,••• EB 平分/ ABC, EC平分/ ACB,•••/ 2=/ 3,•••/ 仁/3,••• BM=ME,同理可得NC=NE•/ MN // BC,•••△ AMNsA ABC,C. D. 5. 5仁/2,禾用平行线的性质得/ 2=/ 3, NC=NE接着证明AAMN sA ABC,所以5,同理可得CN=5-— MN②,把两式相加得到MN的6B. 4Q 圆锥形纸帽的底面圆的半径为BH 60,母线长为12,13形纸帽的表面丄2 色 2 1312720(cm 2). 13① +② 得 MN=12-2MN ,••• MN=4 .故选:B . 【点睛】此题考查三角形的内切圆与内心,相似三角形的判定与性质,解题关键在于掌握与三角形 各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角 形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.2.用一个直径为10cm 的玻璃球和一个圆锥形的牛皮纸纸帽制作一个不倒翁玩具,不倒翁 轴截面如图所示,圆锥的母线AB 与eO 相切于点B ,不倒翁的顶点 A 到桌面L 的最大距离是18cm .若将圆锥形纸帽表面全涂上颜色,则涂色部分的面积为(AB 12,利用面积法求得 BH,然后利用圆锥的侧面展开图为扇形和扇形的面积公13式计算圆锥形纸帽的表面. 【详解】解:连接OB ,作BH OA 于H ,如图, Q 圆锥的母线 AB 与eO 相切于点B ,OB AB ,在 Rt AOB 中,OA 18 5 13, OB 5,AB J 132 5212,1 1 Q -OAgBH ^OBgAB ,B . 600 cm 213720C.——13cm 2D . 72 cm 2【答案】 【解【分析】连接OB ,如图,利用切线的性质得 OBAB ,在 Rt AOB 中利用勾股定理得C本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆锥的计算.直尺紧靠在一起平放在桌面上.已知铁片的圆心为10cm处,铁片与直尺的唯一公共点A落在直尺的B,下列说法错误的是()A.圆形铁片的半径是4cmC.弧AB的长度为4 n cm【答案】CB.四边形AOBC为正方形D.扇形OAB的面积是4 n crfi【解析】【分析】【详解】解:由题意得:BC, AC分别是O•••0A丄CA, 0B丄BC,又•••/ C=90, OA=OB,四边形AOBC是正方形,.•.OA=AC=4,故A, B 正确;O的切线, B, A为切点,• AB的长度为:90=2 n,故C错误;180_ 90 42S扇形OAB= -------- =4 n,故D正确.360故选C.【点睛】本题考查切线的性质;正方形的判定与性质;弧长的计算;扇形面积的计算.4.如图,在矩形ABCD中,AB 6, BC 4,以A为圆心,AD长为半径画弧交点E,以C为圆心,CD长为半径画弧交CB的延长线于点F,则图中阴影部分的面积是()AB于3.如图,圆形铁片与直角三角尺、三角尺的直角顶点C落在直尺的处,铁片与三角尺的唯一公共点为O,14cm本题考查扇形面积的计算,根据阴影面积=扇形FCD 的面积-(矩形 ABCD 的面积-扇形EAD 的面积)是解答本题的关键.2sin Bn 2,则线段AC 的长为()5D . 5【解析】 【分析】首先连接CO 并延长交O 0于点D ,连接AD ,由O 0的半径是5, sinB=-,即可求得答案.5【详解】JE A . 13 【答案】C 【解析】 B . 13 24 C. 13 24 D . 5 24【分析】 先分别求出扇形 FCD 和扇形EAD 的面积以及矩形 ABCD 的面积,再根据阴影面积=扇形FCD 的面积-(矩形 ABCD 的面积-扇形 EAD 的面积) 【详解】 即可得解. 2 290 62 90 42 解:••• S 扇形 FCD --------------- 9, S 扇形 EAD ---------------- 360 360 4 , S 矩形 ABCD 6 424, 二S 阴影=S 扇形FCD —( S 矩形ABCD- S 扇形EAD ) =9 n-( 24- 4 n) =9 n — 24+4 n =13 n — 24故选:C. 【点睛】 C. CD 是O O 的直径,可得/ CAD=90,又由【答案】C0,半径 A0=5,解:连接CO并延长交O O于点D,连接AD,由CD是O O的直径,可得/ CAD=90 , •••/ B和/ D所对的弧都为弧AC,•••/ B=/D,即sinB=sinDn?,5•••半径A0=5, ••• CD=10,AC •- sin D ——CD ••• AC=4, AC 10【点睛】本题考查了同弧所对的圆周角相等,以及三角函数的内容,注意到直径所对的圆周角是直角是解题的关键.6 .如图,AC BC , AC BC 8,以BC为直径作半圆,圆心为点0 ;以点C为圆心,BC为半径作AB,过点0作AC的平行线交两弧于点D、E,则图中阴影部分的面积是()Ao20匚A.——8j33 B.空8433D. 473 空3【分析】如图,连接CE 4, BC= CE= 8, 图中S阴影=S扇形BCE-S扇形BOD-S AOCE根据已知条件易求得OB= OC= OD= / ECB= 60 ° OE= 4J3,所以由扇形面积公式、三角形面积公式进行解答即可.【详解:如图,连接CE••• AC丄BC, AC= BC= 8,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB, .•./ ACB= 90° OB= OC= OD= 4, BC= CE= 8.又••• OE// AC, •••/ ACB=/ COE= 90°•••在RtAOEC中,OC= 4, CE= 8,•••/ CEO= 30° / ECB= 60° OE= 4 羽,二S阴影=S扇形BCE- S扇形BOD- S AO CE=咪4 42-2 4 4V3=竺-8733故选:A.【点睛】本题考查了扇形面积的计算.不规则图形的面积一定要注意分割成规则图形的面积进行计算.7.如图,AB是eO的直径,C是eO上一点(A、B除外),AOD 132,贝U C 的度数是()BB. 48C. 34D. 24【答案】D【解析】【分析】根据平角得出BOD的度数,进而利用圆周角定理得出C的度数即可.【详解】解:Q AOD 132 ,BOD 48, C 24,故选:D . 【点睛】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于 这条弧所对的圆心角的度数的一半是解答此题的关键.&在平面直角坐标系内,以原点0为圆心,1为半径作圆,点P 在直线y J 3x 2j 3上运动,过点P 作该圆的一条切线,切点为 A ,贝y PA 的最小值为( )【答案】D 【解析】【分析】 先根据题意,画出图形,令直线 y= 73x+ 2J 3与x 轴交于点C ,与y 轴交于点D ,作0H 丄CD 于H , 作 0H 丄CD 于H ;然后根据坐标轴上点的坐标特点,由一次函数解析式,求得 C 、D 两点的坐标值;再在RtAPOC 中,利用勾股定理可计算出CD 的长,并利用面积法可计算出 0H 的值;最后连接0A ,利用切线的性质得 0A 丄PA 在RtAP0H 中,利用勾股定理,得到PA Jop 2 [,并利用垂线段最短求得 PA 的最小值即可.【详解】如图,令直线y=J 3x+2j 3与x 轴交于点C,与y 轴交于点D ,作0H 丄CD 于H , 当 x=0 时,y=273,贝y D (0,2^3),当 y=o 时,J 3x+2爲=0,解得 x=-2,则 C (-2,0),•- CD J 22(2轴21 1••• 2OH?CD=I OC?OD,A . 3B . 2c. 73D. J2... OH=2M &4连接OA ,如图,••• PA 为O O 的切线, •••OA 丄 PA•- PA JOP2OA 2 JOP 2 1,当OP 的值最小时,PA 的值最小, 而OP 的最小值为OH 的长,•- PA的最小值为 yj^/y)21^72 .故选D.【点睛】 本题考查了切线的性质,解题关键是熟记切线的性质:圆的切线垂直于经过切点的半 径•若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.9 .如图,已知AB 是O O 是直径,弦CD 丄AB , AC=2j 2 , BD=1,贝sin /ABD 的值是()D . 3【答案】C 【解析】 【分析】先根据垂径定理, 利用勾股定理求得 AB 的长,得到sin / ABC 的大小,最终得到 sin / ABD 【详解】可得 BC 的长,再利用直径对应圆周角为90°得到△ABC 是直角三角形,解:•••弦CD丄AB, AB过O, ••• AB 平分CD••• BC=BD,•••/ ABO/ ABD,•/ BD=1,••• BC=1,••• AB 为O O 的直径, •••/ ACB=90°,由勾股定理得:AB =J AC••• sin / ABD=sin / ABOJ ACAB故选:C. 【点睛】本题考查了垂径定理、直径对应圆周角为90°勾股定理和三角函数,解题关键是找出图形中的直角三角形,然后按照三角函数的定义求解10•如图, ABC 是一块绿化带,将阴影部分修建为花圃.已知AB 15, AC 9,BC 12,阴影部分是 ABC 的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上, 则小鸟落在花圃上的概率为().C.—8【答案】B 【解析】 【分析】由AB=5, BC=4, AC=3,得至U AB 2=B C ?+AC 2,根据勾股定理的逆定理得到 △ABC 为直角三角形,于是得到△ABC 的内切圆半径=4+3-5 =1,求得直角三角形的面积和圆的面积,即可得2到结论. 【详解】解:••• AB=5, BC=4, AC=3,••• AB 2=BC 2+AC 2,:.△ ABC 为直角三角形, •••△ ABC 的内切圆半径=4+3-5 =1,2••• S ^ABC =1AC?BC=1X 4 X 3=62 2A . 6B . 6 D. 5S 圆=n,•••小鸟落在花圃上的概率=-6故选B.【点睛】本题考查几何概率,直角三角形内切圆的半径等于两直角边的和与斜边差的一半及勾股定理的逆定理,解题关键是熟练掌握公式.11.如图,O O的直径C» 10cm , AB是O O的弦,AB丄CD,垂足为M , OM : OC= 3:【解析】【分析】OM = 3, OC= 5,连接OA,根据勾股定理和垂径定理可求得【详解】解:如图所示,连接OA.O O 的直径CD= 10cm, 则O O的半径为5cm,即OA= OC= 5,又••• OM : OC= 3: 5,所以OM = 3,••• AB丄CD,垂足为M , OC过圆心AM = BM ,在RtMOM 中,AM=J5令=4,C. 6cm D. 4cm由于O O的直径CD= 10cm,则O O的半径为5cm,又已知OM : OC= 3: 5,则可以求出AB.8cm ••• AB= 2AM = 2X4=【点睛】本题考查了垂径定理和勾股定理的应用,构造以半径、弦心距和弦长的一半为三边的直角 三角形,是解题的关键.12•如图,点A,B,S 在圆上,若弦AB 的长度等于圆半径的42倍,则 ASB 的度数是本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧 所对的圆心角的一半.13.如图,VABC 是eO 的内接三角形,且 AB AC , ABC 56 , eO 的直径CD 交AB 于点E ,贝y AED 的度数为()【答案】 【解【分析】 设圆心为90 B . 30连接OA OB ,如图,先证明C. 45 ° D . 60VOAB 为等腰直角三角形得到 AOB 【详解】 解:设圆心为,然后根据圆周角定理确定ASB 的度数.O ,连接OA •••弦AB 的长度等于圆半径的OB ,如图,近倍,即 AB 72O A ,二 OA2OB 2AB 2,••• VOAB 为等腰直角三角形,AOB 90ASB - AOB 45 °2C100C. 101° D .102本题考查了圆周角定理,等腰三角形的性质,外角的性质,解题的关键是作出辅助线 得到/ BOC 的度数.14.如图,已知圆 O 的半径为10, AB 丄CD ,垂足为P,且AB = CD = 16,贝U OP 的长为 ()连接OB ,根据等腰三角形的性质得到/A ,从而根据圆周角定理得出/ BOC,再根据OB=OC 得出/ OBC,即可得到/ OBE,再结合外角性质和对顶角即可得到/【详解】 解:连接OB ,AED 的度数..•AB=AC,•• / ABC=/ ACB=56 ,•• / A=180°-56。
圆的易错题汇编附解析

算出阴影部分的面积及大正方形的面积,这个比值就是所求的概率.
【详解】
解:设小正方形的边长为1,则其面积为1.
圆的直径正好是大正方形边长,
根据勾股定理,其小正方形对角线为 ,即圆的直径为 ,
大正方形的边长为 ,
则大正方形的面积为 ,则小球停在小正方形内部(阴影)区域的概率为 .
故选: .
【点睛】
A.1个B.2个C.3个D.4个
【答案】A
【解析】
【分析】
先对原命题进行判断,再判断出逆命题的真假即可.
【详解】
解:①若a>b,则ac>bc是假命题,逆命题是假命题;
②若a=1,则 =a是真命题,逆命题是假命题;
③内错角相等是假命题,逆命题是假命题;
④90°的圆周角所对的弦是直径是真命题,逆命题是真命题;
【答案】B
【解析】
【分析】
根据垂径定理得到CH=BH, ,根据圆周角定理求出∠AOB,根据正弦的定义求出BH,计算即可.
【详解】
如图BC与OA相交于H
∵OA⊥BC,
∴CH=BH, ,
∴∠AOB=2∠CDA=60°,
∴BH=OB⋅sin∠AOB= ,
∴BC=2BH=2 ,
故选D.
【点睛】
本题考查的是垂径定理、圆周角定理,熟练掌握垂直于弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
故选C.
考点:1.旋转的性质2.含30度角的直角三角形.
13.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC=4,BD为⊙O的直径,则BD等于( )
A.4B.6C.8D.12
【答案】C
【解析】
【分析】
根据三角形内角和定理求得∠C=∠ABC=30°,再根据圆周角定理及直角三角形的性质即可求得BD的长.
数学 圆的综合的专项 培优易错试卷练习题含详细答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,AB是⊙O的直径,PA是⊙O的切线,点C在⊙O上,CB∥PO.(1)判断PC与⊙O的位置关系,并说明理由;(2)若AB=6,CB=4,求PC的长.【答案】(1)PC是⊙O的切线,理由见解析;(2)35 2【解析】试题分析:(1)要证PC是⊙O的切线,只要连接OC,再证∠PCO=90°即可.(2)可以连接AC,根据已知先证明△ACB∽△PCO,再根据勾股定理和相似三角形的性质求出PC的长.试题解析:(1)结论:PC是⊙O的切线.证明:连接OC∵CB∥PO∴∠POA=∠B,∠POC=∠OCB∵OC=OB∴∠OCB=∠B∴∠POA=∠POC又∵OA=OC,OP=OP∴△APO≌△CPO∴∠OAP=∠OCP∵PA是⊙O的切线∴∠OAP=90°∴∠OCP=90°∴PC是⊙O的切线.(2)连接AC∵AB是⊙O的直径∴∠ACB=90°(6分)由(1)知∠PCO=90°,∠B=∠OCB=∠POC∵∠ACB=∠PCO∴△ACB∽△PCO∴∴.点睛:本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.同时考查了勾股定理和相似三角形的性质.2.在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.(1)已知点A(2,0),B(0,23),则以AB为边的“坐标菱形”的最小内角为;(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;(3)⊙O的半径为2,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.【答案】(1)60°;(2)y=x+1或y=﹣x+3;(3)1≤m≤5或﹣5≤m≤﹣1【解析】分析:(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;(2)先确定直线CD与直线y=5的夹角是45°,得D(4,5)或(﹣2,5),易得直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4,同理可得结论.详解:(1)∵点A(2,0),B(0,23),∴OA=2,OB=23.在Rt△AOB中,由勾股定理得:AB=22()=4,∴∠ABO=30°.223∵四边形ABCD是菱形,∴∠ABC=2∠ABO=60°.∵AB∥CD,∴∠DCB=180°﹣60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°.故答案为:60°;(2)如图2.∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.过点C作CE⊥DE于E,∴D(4,5)或(﹣2,5),∴直线CD的表达式为:y=x+1或y=﹣x+3;(3)分两种情况:①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3.∵⊙O的半径为2,且△OQ'D是等腰直角三角形,∴OD=2OQ'=2,∴P'D=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4.∵⊙O的半径为2,且△OQ'D是等腰直角三角形,∴OD=2OQ'=2,∴BD=3﹣2=1.∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,﹣1),同理可得:OA=2,∴AB=3+2=5.∵△ABP是等腰直角三角形,∴PB=5,∴P(0,﹣5),∴当﹣5≤m≤﹣1时,以QP为边的“坐标菱形”为正方形;综上所述:m的取值范围是1≤m≤5或﹣5≤m≤﹣1.点睛:本题是一次函数和圆的综合题,考查了菱形的性质、正方形的性质、点P,Q的“坐标菱形”的定义等知识,解题的关键是理解题意,学会利用图象解决问题,学会用分类讨论的思想思考问题,注意一题多解,属于中考创新题目.3.如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB、AC于E、F,已知EF∥BC.(1)求证:BC是⊙O的切线;(2)若已知AE=9,CF=4,求DE长;(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.【答案】(1)证明见解析(2)DE=6(318367-【解析】试题分析:(1)连接OD,由角平分线的定义得到∠1=∠2,得到DE DF=,根据垂径定理得到OD⊥EF,根据平行线的性质得到OD⊥BC,于是得到结论;(2)连接DE,由DE DF=,得到DE=DF,根据平行线的性质得到∠3=∠4,等量代换得到∠1=∠4,根据相似三角形的性质即可得到结论;(3)过F作FH⊥BC于H,由已知条件得到∠1=∠2=∠3=∠4=30°,解直角三角形得到FH=12DF=12×6=3,3227CF HF-=,根据三角函数的定义得到tan∠AFE=tan∠C=37HFCH=;根据相似三角形到现在即可得到结论.试题解析:(1)连接OD,∵AD是△ABC的角平分线,∴∠1=∠2,∴DE DF =,∴OD ⊥EF ,∵EF ∥BC ,∴OD ⊥BC ,∴BC 是⊙O 的切线;(2)连接DE ,∵DE DF =,∴DE=DF ,∵EF ∥BC ,∴∠3=∠4,∵∠1=∠3,∴∠1=∠4,∵∠DFC=∠AED ,∴△AED ∽△DFC , ∴AE DE DF CF =,即94DE DE =, ∴DE 2=36,∴DE=6;(3)过F 作FH ⊥BC 于H ,∵∠BAC=60°,∴∠1=∠2=∠3=∠4=30°, ∴FH=12DF=162⨯=3,∴=,∵EF ∥BC ,∴∠C=∠AFE ,∴tan ∠AFE=tan ∠C=HF CH =; ∵∠4=∠2.∠C=∠C ,∴△ADC ∽△DFC , ∴AD CD DF CF=, ∵∠5=∠5,∠3=∠2,∴△ADF ∽△FDG , ∴AD DF DF DG=,∴CD DF CF DG =,即33764DG+=, ∴DG=18367-.点睛:本题考查了切线的判定、圆周角定理、相似三角形的判定与性质、解直角三角形、平行线的性质,正确作出辅助线是解题的关键.4.在平面直角坐标系中,已知点A (2,0),点B (0,),点O (0,0).△AOB 绕着O 顺时针旋转,得△A'OB',点A 、B 旋转后的对应点为A',B',记旋转角为α.(Ⅰ)如图1,A'B'恰好经过点A 时,求此时旋转角α的度数,并求出点B'的坐标; (Ⅱ)如图2,若0°<α<90°,设直线AA'和直线BB'交于点P ,求证:AA'⊥BB'; (Ⅲ)若0°<α<360°,求(Ⅱ)中的点P 纵坐标的最小值(直接写出结果即可).【答案】(Ⅰ)α=60°,B'(3,);(Ⅱ)见解析;(Ⅲ)点P 纵坐标的最小值为﹣2.【解析】【分析】(Ⅰ)作辅助线,先根据点A (2,0),点B (0,),确定∠ABO =30°,证明△AOA'是等边三角形,得旋转角α=60°,证明△COB'是30°的直角三角形,可得B'的坐标;(Ⅱ)依据旋转的性质可得∠BOB'=∠AOA'=α,OB =OB',OA =OA',即可得出∠OBB'=∠OA'A =(180°﹣α),再根据∠BOA'=90°+α,四边形OBPA'的内角和为360°,即可得到∠BPA'=90°,即AA'⊥BB';(Ⅲ)作AB 的中点M (1,),连接MP ,依据点P 的轨迹为以点M 为圆心,以MP =AB =2为半径的圆,即可得到当PM ∥y 轴时,点P 纵坐标的最小值为﹣2.【详解】解:(Ⅰ)如图1,过B'作B'C⊥x轴于C,∵OA=2,OB=2,∠AOB=90°,∴∠ABO=30°,∠BAO=60°,由旋转得:OA=OA',∠A'=∠BAO=60°,∴△OAA'是等边三角形,∴α=∠AOA'=60°,∵OB=OB'=2,∠COB'=90°﹣60°=30°,∴B'C=OB’=,∴OC=3,∴B'(3,),(Ⅱ)证明:如图2,∵∠BOB'=∠AOA'=α,OB=OB',OA=OA',∴∠OBB'=∠OA'A=(180°﹣α),∵∠BOA'=90°+α,四边形OBPA'的内角和为360°,∴∠BPA'=360°﹣(180°﹣α)﹣(90°+α)=90°,即AA'⊥BB';(Ⅲ)点P纵坐标的最小值为-2.理由是:如图,作AB的中点M(1,),连接MP,∵∠APB =90°,∴点P 的轨迹为以点M 为圆心,以MP =AB =2为半径的圆,除去点(2,2),∴当PM ⊥x 轴时,点P 纵坐标的最小值为﹣2. 【点睛】本题属于几何变换综合题,主要考查了旋转的性质,含30°角的直角三角形的性质,四边形内角和以及圆周角定理的综合运用,解决问题的关键是判断点P 的轨迹为以点M 为圆心,以MP 为半径的圆.5.如图①,抛物线y =ax 2+bx+c 经过点A (﹣2,0)、B (4,0)、C (0,3)三点.(1)试求抛物线的解析式;(2)点P 是y 轴上的一个动点,连接PA ,试求5PA+4PC 的最小值;(3)如图②,若直线l 经过点T (﹣4,0),Q 为直线l 上的动点,当以A 、B 、Q 为顶点所作的直角三角形有且仅有三个时,试求直线l 的解析式.【答案】(1)233384y x x =-++;(2)5PA+4PC 的最小值为18;(3)直线l 的解析式为334y x =+或334y x =--. 【解析】【分析】(1)设出交点式,代入C 点计算即可 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D ,易证△CDP ∽△COB ,得到比例式PC PD BC OB =,得到PD=45PC ,所以5PA+4PC =5(PA+45PC )=5(PA+PD ),当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小,利用等面积法求出AE=185,即最小值为18 (3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆, 当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,所以只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90°,即∠AQB =90°时,只有一个满足条件的点Q ,∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个;此时,连接FQ ,过点Q 作QG ⊥x 轴于点G ,利用cos ∠QFT 求出QG ,分出情况Q 在x 轴上方和x 轴下方时,分别代入直接l 得到解析式即可【详解】解:(1)∵抛物线与x 轴交点为A (﹣2,0)、B (4,0)∴y =a (x+2)(x ﹣4)把点C (0,3)代入得:﹣8a =3∴a =﹣38∴抛物线解析式为y =﹣38(x+2)(x ﹣4)=﹣38x 2+34x+3 (2)连接AC 、BC ,过点A 作AE ⊥BC 于点E ,过点P 作PD ⊥BC 于点D∴∠CDP =∠COB =90°∵∠DCP =∠OCB∴△CDP ∽△COB ∴PC PD BC OB= ∵B (4,0),C (0,3)∴OB =4,OC =3,BC∴PD =45PC ∴5PA+4PC =5(PA+45PC )=5(PA+PD ) ∴当点A 、P 、D 在同一直线上时,5PA+4PC =5(PA+PD )=5AE 最小∵A (﹣2,0),OC ⊥AB ,AE ⊥BC∴S △ABC =12AB•OC =12BC•AE ∴AE =631855AB OC BC ⨯==∴5AE =18∴5PA+4PC 的最小值为18.(3)取AB 中点F ,以F 为圆心、FA 的长为半径画圆当∠BAQ =90°或∠ABQ =90°时,即AQ 或BQ 垂直x 轴,∴只要直线l 不垂直x 轴则一定找到两个满足的点Q 使∠BAQ =90°或∠ABQ =90° ∴∠AQB =90°时,只有一个满足条件的点Q∵当Q 在⊙F 上运动时(不与A 、B 重合),∠AQB =90°∴直线l 与⊙F 相切于点Q 时,满足∠AQB =90°的点Q 只有一个 此时,连接FQ ,过点Q 作QG ⊥x 轴于点G∴∠FQT =90°∵F 为A (﹣2,0)、B (4,0)的中点∴F (1,0),FQ =FA =3∵T (﹣4,0)∴TF =5,cos ∠QFT =35FQ TF = ∵Rt △FGQ 中,cos ∠QFT =35FG FQ = ∴FG =35FQ =95∴x Q =1﹣9455=-,QG =2222912FQ 355FG ⎛⎫-=-= ⎪⎝⎭①若点Q 在x 轴上方,则Q (41255-,)设直线l 解析式为:y =kx+b ∴4041255k b k b -+=⎧⎪⎨-+=⎪⎩ 解得:343k b ⎧=⎪⎨⎪=⎩ ∴直线l :334y x =+ ②若点Q 在x 轴下方,则Q (41255--,) ∴直线l :334y x =-- 综上所述,直线l 的解析式为334y x =+或334y x =--【点睛】本题是二次函数与圆的综合题,同时涉及到三角函数、勾股定理等知识点,综合度比较高,需要很强的综合能力,第三问能够找到满足条件的Q点是关键,同时不要忘记需要分情况讨论6.如图,点A,B,C,D,E在⊙O上,AB⊥CB于点B,tanD=3,BC=2,H为CE延长线上一点,且AH=10,CH52=.(1)求证:AH是⊙O的切线;(2)若点D是弧CE的中点,且AD交CE于点F,求证:HF=HA;(3)在(2)的条件下,求EF的长.【答案】(1)证明见解析(2)证明见解析(3102【解析】【分析】(1)连接AC,由AB⊥CB可知AC是⊙O的直径,由圆周角定理可得∠C=∠D,于是得到tanC=3,故此可知AB=6,在Rt△ABC中,由勾股定理得:AC2= 40,从而可得AC2+AH2=CH2,根据勾股定理的逆定理可得AC⊥AH,问题得证;(2)连接DE、BE,由弦切角定理可知∠ABD=∠HAD,由D是CE的中点,可得∠CED=∠EBD,再由圆周角定理可得∠ABE=∠ADE,结合三角形的外角即可证明∠HAF=∠AFH,从而可证得AH=HF;(3)由切割线定理可得EH=2,由(2)可知AF=FH=10,从而可得EF=FH﹣EH=10-2.【详解】(1)如图1所示:连接AC.∵AB⊥CB,∴AC是⊙O的直径,∵∠C=∠D,∴tanC=3,∴AB=3BC=3×2=6,在Rt△ABC中,由勾股定理得:AC2=AB2+BC2=40,又∵AH2=10,CH2=50,∴AC2+AH2=CH2,∴△ACH为直角三角形,∴AC⊥AH,∴AH是圆O的切线;(2)如图2所示:连接DE、BE,∵AH是圆O的切线,∴∠ABD=∠HAD,∵D是CE的中点,∴CD ED,∴∠CED=∠EBD,又∵∠ABE=∠ADE,∴∠ABE+∠EBD=∠ADE+∠CED,∴∠ABD=∠AFE,∴∠HAF=∠AFH,∴AH=HF ;(3)由切割线定理可知:AH 2=EH•CH ,即(10)2=52EH ,解得:EH=2,∵由(2)可知AF=FH=10,∴EF=FH ﹣EH=10-2. 【点睛】本题主要考查圆的综合应用,解答主要应用了切线的判定定理、弦切角定理、切割线定理、圆周角定理、勾股定理、勾股定理的逆定理、三角形的外角的性质等,正确添加辅助线是解题的关键.7.如图,AB 为⊙O 的直径,BC 为⊙O 的弦,过O 点作OD ⊥BC ,交⊙O 的切线CD 于点D ,交⊙O 于点E ,连接AC 、AE ,且AE 与BC 交于点F .(1)连接BD ,求证:BD 是⊙O 的切线;(2)若AF :EF=2:1,求tan ∠CAF 的值.【答案】(1)证明见解析;(23. 【解析】【分析】 (1)根据全等三角形的性质得到∠OBD=∠OCD=90°,根据切线的判定定理即可得到结论; (2)根据已知条件得到AC ∥DE ,设OD 与BC 交于G ,根据平行线分线段成比例定理得到AC :EG=2:1,EG=12AC ,根据三角形的中位线的性质得到OG=12AC 于是得到AC=OE ,求得∠ABC=30°,即可得到结论.【详解】证明:(1)∵OC=OB ,OD ⊥BC ,∴∠COD=∠BOD ,在△COD 与△BOD 中, OC OB COD BOD OD OD ===⎧⎪∠∠⎨⎪⎩,∴△COD ≌△BOD ,∴∠OBD=∠OCD=90°,∴BD是⊙O的切线;(2)解:∵AB为⊙O的直径,AC⊥BC,∵OD⊥CB,∴AC∥DE,设OD与BC交于G,∵OE∥AC,AF:EF=2:1,∴AC:EG=2:1,即EG=12AC,∵OG∥AC,OA=OB,∴OG=12AC,∵OG+GE=12AC+12AC=AC,∴AC=OE,∴AC=12AB,∴∠ABC=30°,∴∠CAB=60°,∵CE BE,∴∠CAF=∠EAB=12∠CAB=30°,∴tan∠CAF=tan30°3【点睛】本题考查了切线的判定和性质,垂径定理,全等三角形的判定与性质,三角形的中位线的性质,三角函数的定义,正确的识别图形是解题的关键.8.如图,在△ABC中,以AC为直径作⊙O交BC于点D,交AB于点G,且D是BC中点,DE⊥AB,垂足为E,交AC的延长线于点F.(1)求证:直线EF是⊙O的切线;(2)若CF=3,cosA=25,求出⊙O的半径和BE的长;(3)连接CG,在(2)的条件下,求CGEF的值.【答案】(1)见解析;(2)2,65(3)CG:EF=4:7【解析】试题分析:(1)连结OD.先证明OD是△ABC的中位线,根据中位线的性质得到OD∥AB,再由DE⊥AB,得出OD⊥EF,根据切线的判定即可得出直线EF是⊙O的切线;(2)先由OD∥AB,得出∠COD=∠A,再解Rt△DOF,根据余弦函数的定义得到cos∠FOD==,设⊙O的半径为R,解方程=,求出R=,那么AB=2OD=,解Rt△AEF,根据余弦函数的定义得到cosA==,求出AE=,然后由BE=AB﹣AE即可求解.试题解析:(1)证明:如图,连结OD.∵CD=DB,CO=OA,∴OD是△ABC的中位线,∴OD∥AB,AB=2OD,∵DE⊥AB,∴DE⊥OD,即OD⊥EF,∴直线EF是⊙O的切线;(2)解:∵OD∥AB,∴∠COD=∠A.在Rt△DOF中,∵∠ODF=90°,∴cos∠FOD==,设⊙O的半径为R,则=,解得R=,∴AB=2OD=.在Rt △AEF 中,∵∠AEF=90°,∴cosA===, ∴AE=,∴BE=AB ﹣AE=﹣=2.【点睛】本题考查了切线的判定,解直角三角形,三角形中位线的性质知识点.要证某线是圆的切线,已知此线过圆上某点,连结圆心与这点(即为半径),再证垂直即可.9.对于平面内的⊙C 和⊙C 外一点Q ,给出如下定义:若过点Q 的直线与⊙C 存在公共点,记为点A ,B ,设AQ BQ k CQ+=,则称点A (或点B )是⊙C 的“K 相关依附点”,特别地,当点A 和点B 重合时,规定AQ=BQ ,2AQ k CQ =(或2BQ CQ ). 已知在平面直角坐标系xoy 中,Q(-1,0),C(1,0),⊙C 的半径为r .(1)如图1,当2r =①若A 1(0,1)是⊙C 的“k 相关依附点”,求k 的值.②A 22,0)是否为⊙C 的“2相关依附点”.(2)若⊙C 上存在“k 相关依附点”点M ,①当r=1,直线QM 与⊙C 相切时,求k 的值.②当3k =r 的取值范围.(3)若存在r 的值使得直线3y x b =+与⊙C 有公共点,且公共点时⊙C 的3相关依附点”,直接写出b 的取值范围.【答案】(1)2.②是;(2)①3k =②r 的取值范围是12r <≤;(3)333b -<. 【解析】【分析】(1)①如图1中,连接AC 、1QA .首先证明1QA 是切线,根据2AQ k CQ =计算即可解决问题;②根据定义求出k 的值即可判断;(2)①如图,当1r =时,不妨设直线QM 与C 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥,根据定义计算即可; ②如图3中,若直线QM 与C 不相切,设直线QM 与C 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,可得()222MQ NQ MN NQ NQ ND NQ DQ +=++=+=,2CQ ,推出2MQ NQ DQ k DQ CQ CQ +===,可得当3k =3DQ =221CD CQ DQ -=,假设C 经过点Q ,此时2r ,因为点Q 早C 外,推出r 的取值范围是12r <; (3)如图4中,由(2)可知:当3k =12r <.当2r 时,C 经过点(1,0)Q -或(3,0)E ,当直线3y x b =-+经过点Q 时,3b =3y x b =-+经过点E 时,33b =,即可推出满足条件的b 的取值范围为333b -<<.【详解】(1)①如图1中,连接AC 、1QA .由题意:1OC OQ OA ==,∴△1QA C 是直角三角形,190CA Q ∴∠=︒,即11CA QA ⊥,1QA ∴是C 的切线,122222QA k QC ∴===. ②2(12,0)A +在C 上,2212122k -+++∴==,2A ∴是C 的“2相关依附点”.故答案为:2,是;(2)①如图2,当1r =时,不妨设直线QM 与C 相切的切点M 在x 轴上方(切点M 在x 轴下方时同理),连接CM ,则QM CM ⊥.(1,0)Q -,(1,0)C ,1r =,2CQ ∴=,1CM =,∴3MQ =,此时23MQ k CQ==; ②如图3中,若直线QM 与C 不相切,设直线QM 与C 的另一个交点为N (不妨设QN QM <,点N ,M 在x 轴下方时同理),作CD QM ⊥于点D ,则MD ND =,()222MQ NQ MN NQ NQ ND NQ DQ ∴+=++=+=,2CQ =,∴2MQ NQ DQ k DQ CQ CQ +===,∴当3k =时,3DQ =,此时221CD CQ DQ =-=,假设C 经过点Q ,此时2r ,点Q 早C 外,r ∴的取值范围是12r <.(3)如图4中,由(2)可知:当3k =12r <.当2r 时,C 经过点(1,0)Q -或(3,0)E ,当直线3y x b =-+经过点Q 时,3b =-,当直线3y x b =-+经过点E 时,33b =,∴满足条件的b 的取值范围为333b -<<.【点睛】本题考查了一次函数综合题、圆的有关知识、勾股定理、切线的判定和性质、点A (或点)B 是C 的“k 相关依附点”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会考虑特殊位置解决问题,属于中考压轴题.10.如图,已知四边形ABCD 内接于⊙O ,点E 在CB 的延长线上,连结AC 、AE ,∠ACB =∠BAE =45°.(1)求证:AE 是⊙O 的切线;(2)若AB=AD ,AC =32,tan ∠ADC=3,求BE 的长.【答案】(1)证明见解析;(2)52BE = 【解析】试题分析:(1)连接OA 、OB ,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)过点A 作AF ⊥CD 于点F,由AB=AD ,得到∠ACD =∠ACB =45°,在Rt △AFC 中可求得AF =3,在Rt △AFD 中求得DF =1,所以AB =AD =10 ,CD = CF +DF =4,再证明△ABE ∽△CDA ,得出BE AB DA CD=,即可求出BE 的长度; 试题解析:(1)证明:连结OA ,OB ,∵∠ACB =45°,∴∠AOB =2∠ACB = 90°,∵OA=OB ,∴∠OAB =∠OBA =45°,∵∠BAE =45°,∴∠OAE =∠OAB +∠BAE =90°,∴OA ⊥AE .∵点A 在⊙O 上,∴AE 是⊙O 的切线.(2)解:过点A 作AF ⊥CD 于点F ,则∠AFC =∠AFD =90°. ∵AB=AD ,∴AB =AD∴∠ACD =∠ACB =45°,在Rt △AFC 中,∵AC =∠ACF =45°,∴AF=CF=AC ·sin ∠ACF =3,∵在Rt △AFD 中, tan ∠ADC=3AF DF =, ∴DF =1,∴AB AD ==且CD = CF +DF =4,∵四边形ABCD 内接于⊙O ,∴∠ABE =∠CDA ,∵∠BAE =∠DCA ,∴△ABE ∽△CDA , ∴BE AB DA CD =,∴= ∴52BE =.。
数学 圆的综合的专项 培优易错试卷练习题附答案

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图1,直角梯形OABC中,BC∥OA,OA=6,BC=2,∠BAO=45°.(1)OC的长为;(2)D是OA上一点,以BD为直径作⊙M,⊙M交AB于点Q.当⊙M与y轴相切时,sin∠BOQ=;(3)如图2,动点P以每秒1个单位长度的速度,从点O沿线段OA向点A运动;同时动点D以相同的速度,从点B沿折线B﹣C﹣O向点O运动.当点P到达点A时,两点同时停止运动.过点P作直线PE∥OC,与折线O﹣B﹣A交于点E.设点P运动的时间为t (秒).求当以B、D、E为顶点的三角形是直角三角形时点E的坐标.【答案】(1)4;(2)35;(3)点E的坐标为(1,2)、(53,103)、(4,2).【解析】分析:(1)过点B作BH⊥OA于H,如图1(1),易证四边形OCBH是矩形,从而有OC=BH,只需在△AHB中运用三角函数求出BH即可.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2),则有OH=2,BH=4,MN⊥OC.设圆的半径为r,则MN=MB=MD=r.在Rt△BHD中运用勾股定理可求出r=2,从而得到点D与点H重合.易证△AFG∽△ADB,从而可求出AF、GF、OF、OG、OB、AB、BG.设OR=x,利用BR2=OB2﹣OR2=BG2﹣RG2可求出x,进而可求出BR.在Rt△ORB中运用三角函数就可解决问题.(3)由于△BDE的直角不确定,故需分情况讨论,可分三种情况(①∠BDE=90°,②∠BED=90°,③∠DBE=90°)讨论,然后运用相似三角形的性质及三角函数等知识建立关于t的方程就可解决问题.详解:(1)过点B作BH⊥OA于H,如图1(1),则有∠BHA=90°=∠COA,∴OC∥BH.∵BC∥OA,∴四边形OCBH是矩形,∴OC=BH,BC=OH.∵OA=6,BC=2,∴AH=0A﹣OH=OA﹣BC=6﹣2=4.∵∠BHA=90°,∠BAO=45°,∴tan∠BAH=BHHA=1,∴BH=HA=4,∴OC=BH=4.故答案为4.(2)过点B作BH⊥OA于H,过点G作GF⊥OA于F,过点B作BR⊥OG于R,连接MN、DG,如图1(2).由(1)得:OH =2,BH =4.∵OC 与⊙M 相切于N ,∴MN ⊥OC .设圆的半径为r ,则MN =MB =MD =r .∵BC ⊥OC ,OA ⊥OC ,∴BC ∥MN ∥OA .∵BM =DM ,∴CN =ON ,∴MN =12(BC +OD ),∴OD =2r ﹣2,∴DH =OD OH -=24r -.在Rt △BHD 中,∵∠BHD =90°,∴BD 2=BH 2+DH 2,∴(2r )2=42+(2r ﹣4)2.解得:r =2,∴DH =0,即点D 与点H 重合,∴BD ⊥0A ,BD =AD .∵BD 是⊙M 的直径,∴∠BGD =90°,即DG ⊥AB ,∴BG =AG .∵GF ⊥OA ,BD ⊥OA ,∴GF ∥BD ,∴△AFG ∽△ADB , ∴AF AD =GF BD =AG AB =12,∴AF =12AD =2,GF =12BD =2,∴OF =4,∴OG同理可得:OB AB ,∴BG =12AB .设OR =x ,则RG x .∵BR ⊥OG ,∴∠BRO =∠BRG =90°,∴BR 2=OB 2﹣OR 2=BG 2﹣RG 2,∴(2﹣x 2=()2﹣(x )2.解得:x =5,∴BR 2=OB 2﹣OR 2=(2﹣(5)2=365,∴BR =5.在Rt △ORB 中,sin ∠BOR =BR OB35. 故答案为35. (3)①当∠BDE =90°时,点D 在直线PE 上,如图2.此时DP =OC =4,BD +OP =BD +CD =BC =2,BD =t ,OP =t . 则有2t =2.解得:t =1.则OP =CD =DB =1.∵DE ∥OC ,∴△BDE ∽△BCO ,∴DE OC =BD BC =12,∴DE =2,∴EP =2, ∴点E 的坐标为(1,2).②当∠BED =90°时,如图3.∵∠DBE =OBC ,∠DEB =∠BCO =90°,∴△DBE ∽△OBC ,∴BEBC =2DB BE OB ∴,∴BE =5t . ∵PE ∥OC ,∴∠OEP =∠BOC .∵∠OPE =∠BCO =90°,∴△OPE ∽△BCO ,∴OEOB =25OPBC∴,=2t,∴OE=5t.∵OE+BE=OB=255,∴t+5t=25.解得:t=53,∴OP=53,OE=55,∴PE=22OE OP-=103,∴点E的坐标为(51033,).③当∠DBE=90°时,如图4.此时PE=PA=6﹣t,OD=OC+BC﹣t=6﹣t.则有OD=PE,EA=22PE PA+=2(6﹣t)=62﹣2?t,∴BE=BA﹣EA=42﹣(62﹣2t)=2t﹣22.∵PE∥OD,OD=PE,∠DOP=90°,∴四边形ODEP是矩形,∴DE=OP=t,DE∥OP,∴∠BED=∠BAO=45°.在Rt△DBE中,cos∠BED=BEDE=2,∴DE=2BE,∴t=22(t﹣22)=2t﹣4.解得:t=4,∴OP=4,PE=6﹣4=2,∴点E的坐标为(4,2).综上所述:当以B、D、E为顶点的三角形是直角三角形时点E的坐标为(1,2)、(51033,)、(4,2).点睛:本题考查了圆周角定理、切线的性质、相似三角形的判定与性质、三角函数的定义、平行线分线段成比例、矩形的判定与性质、勾股定理等知识,还考查了分类讨论的数学思想,有一定的综合性.2.如图1,已知扇形MON 的半径为2,∠MON=90°,点B 在弧MN 上移动,联结BM ,作OD ⊥BM ,垂足为点D ,C 为线段OD 上一点,且OC=BM ,联结BC 并延长交半径OM 于点A ,设OA=x ,∠COM 的正切值为y.(1)如图2,当AB ⊥OM 时,求证:AM=AC ;(2)求y 关于x 的函数关系式,并写出定义域;(3)当△OAC 为等腰三角形时,求x 的值.【答案】 (1)证明见解析;(2) 2=+y x 02<≤x 1422=x . 【解析】 分析:(1)先判断出∠ABM =∠DOM ,进而判断出△OAC ≌△BAM ,即可得出结论; (2)先判断出BD =DM ,进而得出DM ME BD AE =,进而得出AE =122x (),再判断出2OA OC DM OE OD OD==,即可得出结论; (3)分三种情况利用勾股定理或判断出不存在,即可得出结论.详解:(1)∵OD ⊥BM ,AB ⊥OM ,∴∠ODM =∠BAM =90°.∵∠ABM +∠M =∠DOM +∠M ,∴∠ABM =∠DOM .∵∠OAC =∠BAM ,OC =BM ,∴△OAC ≌△BAM , ∴AC =AM .(2)如图2,过点D 作DE ∥AB ,交OM 于点E . ∵OB =OM ,OD ⊥BM ,∴BD =DM . ∵DE ∥AB ,∴DM ME BD AE =,∴AE =EM .∵OM 2,∴AE =122x (). ∵DE ∥AB ,∴2OA OC DM OE OD OD ==, ∴22DM OA y OD OE x =∴=+,02x ≤<(3)(i)当OA=OC时.∵111222DM BM OC x===.在Rt△ODM中,222124OD OM DM x=-=-.∵2121224xDM xyOD xx=∴=+-,.解得1422x-=,或1422x--=(舍).(ii)当AO=AC时,则∠AOC=∠ACO.∵∠ACO>∠COB,∠COB=∠AOC,∴∠ACO>∠AOC,∴此种情况不存在.(ⅲ)当CO=CA时,则∠COA=∠CAO=α.∵∠CAO>∠M,∠M=90°﹣α,∴α>90°﹣α,∴α>45°,∴∠BOA=2α>90°.∵∠BOA≤90°,∴此种情况不存在.即:当△OAC为等腰三角形时,x的值为1422-.点睛:本题是圆的综合题,主要考查了相似三角形的判定和性质,圆的有关性质,勾股定理,等腰三角形的性质,建立y关于x的函数关系式是解答本题的关键.3.如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,交BC于D,过O作OE∥BC,交OD于E,连接AD、AE、CE.(1)求证:∠ACE=∠DCE;(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;(3)若AC=4,23CDFCOESS∆∆=,求CF的长.【答案】(1)证明见解析,(2)60°;(343【解析】【分析】(1)易证∠OEC=∠OCE,∠OEC=∠ECD,从而可知∠OCE=∠ECD,即∠ACE=∠DCE;(2)延长AE交BC于点G,易证∠AGC=∠B+∠BAG=60°,由于OE∥BC,所以∠AEO=∠AGC=60°,所以∠EAO=∠AEO=60°;(3)易证12COECAESS=,由于23CDFCOESS=,所以CDFCAESS=13,由圆周角定理可知∠AEC=∠FDC=90°,从而可证明△CDF∽△CEA,利用三角形相似的性质即可求出答案.【详解】(1)∵OC=OE,∴∠OEC=∠OCE.∵OE∥BC,∴∠OEC=∠ECD,∴∠OCE=∠ECD,即∠ACE=∠DCE;(2)延长AE交BC于点G.∵∠AGC是△ABG的外角,∴∠AGC=∠B+∠BAG=60°.∵OE∥BC,∴∠AEO=∠AGC=60°.∵OA=OE,∴∠EAO=∠AEO=60°.(3)∵O是AC中点,∴12COECAESS=.23CDFCOESS=,∴CDFCAESS=13.∵AC是直径,∴∠AEC=∠FDC=90°.∵∠ACE=∠FCD,∴△CDF∽△CEA,∴CFCA=3,∴CF=3CA=43.【点睛】本题考查了圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.4.如图,已知△ABC中,AB=AC,∠A=30°,AB=16,以AB为直径的⊙O与BC边相交于点D,与AC交于点F,过点D作DE⊥AC于点E.(1)求证:DE是⊙O的切线;(2)求CE的长;(3)过点B作BG∥DF,交⊙O于点G,求弧BG的长.【答案】(1)证明见解析(2)33)4π【解析】【分析】(1)如图1,连接AD,OD,由AB为⊙O的直径,可得AD⊥BC,再根据AB=AC,可得BD=DC,再根据OA=OB,则可得OD∥AC,继而可得DE⊥OD,问题得证;(2)如图2,连接BF,根据已知可推导得出DE=12BF,CE=EF,根据∠A=30°,AB=16,可得BF=8,继而得DE=4,由DE为⊙O的切线,可得ED2=EF•AE,即42=CE•(16﹣CE),继而可求得CE长;(3)如图3,连接OG,连接AD,由BG∥DF,可得∠CBG=∠CDF=30°,再根据AB=AC,可推导得出∠OBG=45°,由OG=OB,可得∠OGB=45°,从而可得∠BOG=90°,根据弧长公式即可求得BG的长度.【详解】(1)如图1,连接AD,OD;∵AB为⊙O的直径,∴∠ADB=90°,即AD⊥BC,∵AB=AC,∴BD=DC,∵OA=OB,∴OD∥AC,∵DE⊥AC,∴DE⊥OD,∴∠ODE=∠DEA=90°,∴DE为⊙O的切线;(2)如图2,连接BF,∵AB为⊙O的直径,∴∠AFB=90°,∴BF∥DE,∵CD=BD,∴DE=12BF,CE=EF,∵∠A=30°,AB=16,∴BF=8,∴DE=4,∵DE 为⊙O 的切线,∴ED 2=EF•AE ,∴42=CE•(16﹣CE ),∴CE=8﹣43,CE=8+43(不合题意舍去);(3)如图3,连接OG ,连接AD ,∵BG ∥DF ,∴∠CBG=∠CDF=30°,∵AB=AC ,∴∠ABC=∠C=75°,∴∠OBG=75°﹣30°=45°,∵OG=OB ,∴∠OGB=∠OBG=45°,∴∠BOG=90°,∴BG 的长度=908180π⨯⨯=4π.【点睛】本题考查了圆的综合题,涉及了切线的判定、三角形中位线定理、圆周角定理、弧长公式等,正确添加辅助线、熟练掌握相关的性质与定理是解题的关键.5.如图,AB 为O 的直径,弦//CD AB ,E 是AB 延长线上一点,CDB ADE ∠=∠. ()1DE 是O 的切线吗?请说明理由;()2求证:2AC CD BE =⋅.【答案】(1)结论:DE 是O 的切线,理由见解析;(2)证明见解析.【解析】【分析】 (1)连接OD ,只要证明OD DE ⊥即可;(2)只要证明:AC BD =,CDB DBE ∽即可解决问题.【详解】()1解:结论:DE是O的切线.理由:连接OD.∠=∠,CDB ADE∴∠=∠,ADC EDBCD AB,//∴∠=∠,CDA DAB=,OA OD∴∠=∠,OAD ODA∴∠=∠,ADO EDBAB是直径,∴∠=,90ADB∴∠=∠=,ADB ODE90∴⊥,DE OD∴是O的切线.DE()2//CD AB,∠=∠,ADC DAB∴∠=∠,CDB DBE∴=,AC BDAC BD∴=,∠=∠,EDB DABDCB DAB∠=∠,∴∠=∠,EDB DCB∴∽DBE,CDBCD DB∴=,BD BE2∴=⋅,BD CD BE2∴=⋅.AC CD BE【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,准确寻找相似三角形解决问题,属于中考常考题型.6.如图,PA、PB是⊙O的切线,A,B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC、BC.(Ⅰ)求∠ACB的大小;(Ⅱ)若⊙O半径为1,求四边形ACBP的面积.33【答案】(Ⅰ)60°;(Ⅱ)【解析】分析:(Ⅰ)连接AO,根据切线的性质和切线长定理,得到OA⊥AP,OP平分∠APB,然后根据角平分线的性质和三角形的外角的性质,30°角的直角三角形的性质,得到∠ACB的度数;(Ⅱ)根据30°角的直角三角形的性质和等腰三角形的性质,结合等底同高的性质求三角形的面积即可.详解:(Ⅰ)连接OA,如图,∵PA、PB是⊙O的切线,∴OA⊥AP,OP平分∠APB,∠APB=30°,∴∠APO=12∴∠AOP=60°,∵OA=OC,∴∠OAC=∠OCA,∴∠ACO=1AOP=30°,2同理可得∠BCP=30°,∴∠ACB=60°;(Ⅱ)在Rt△OPA中,∵∠APO=30°,∴33,OP=2OA=2,∴OP=2OC,而S△OPA=12×1×3,∴S△AOC=12S△PAO=34,∴S△ACP=334,∴四边形ACBP的面积=2S△ACP=33.点睛:本题考查了切线的性质,解直角三角形,等腰三角形的判定,熟练掌握切线的性质是解题的关键.7.已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.【答案】(1)证明见解析;(2)PA=PB+PC.理由见解析;(3)若∠BAC=120°时,(2)3 PA=PB+PC.【解析】试题分析:(1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.试题解析:(1)如图①,连接PC.∵△ACQ是由△ABP绕点A逆时针旋转得到的,∴∠ABP=∠ACQ.由图①知,点A、B、P、C四点共圆,∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),∴∠ACP+∠ACQ=180°(等量代换);(2)PA=PB+PC.理由如下:如图②,连接BC,延长BP至E,使PE=PC,连接CE.∵弦AB=弦AC,∠BAC=60°,∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).∵A、B、P、C四点共圆,∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),∵∠BPC+∠EPC=180°,∴∠BAC=∠CPE=60°,∵PE=PC,∴△PCE是等边三角形,∴CE=PC,∠E=∠ECP=∠EPC=60°;又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,∴∠BCE=∠ACP(等量代换),在△BEC和△APC中,CE PCBCE ACPAC BC=⎧⎪∠=∠⎨⎪=⎩,∴△BEC≌△APC(SAS),∴BE=PA,∴PA=BE=PB+PC;(3)若∠BAC=120°时,(2)中的结论不成立,3 PA=PB+PC.理由如下:如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.∵∠BAC=120°,∠BAC+∠BPC=180°,∴∠BPC=60°.∵弦AB=弦AC,∴∠APB=∠APQ=30°.在△ABP和△AQP中,PB PQAPB APQAP AP=⎧⎪∠=∠⎨⎪=⎩,∴△ABP≌△AQP(SAS),∴AB=AQ,PB=PQ(全等三角形的对应边相等),∴AQ=AC(等量代换).在等腰△AQC中,QG=CG.在Rt△APG中,∠APG=30°,则AP=2AG,PG=3AG,∴PB+PC=PG﹣QG+PG+CG=PG﹣QG+PG+QG=2PG=23AG,∴3PA=23AG,即3PA=PB+PC.【点睛】本题考查了圆的综合题,解题的关键要能掌握和灵活运用圆心角、弧、弦间的关系,全等三角形的判定与性质,圆内接四边形的性质等.8.AB是⊙O直径,在AB的异侧分别有定点C和动点P,如图所示,点P在半圆弧AB上运动(不与A 、B 重合),过C 作CP 的垂线CD ,交PB 的延长线于D ,已知5AB =,BC ∶CA =4∶3.(1)求证:AC ·CD =PC ·BC ;(2)当点P 运动到AB 弧的中点时,求CD 的长;(3)当点P 运动到什么位置时,PCD ∆的面积最大?请直接写出这个最大面积.【答案】(1)证明见解析;(2)CD =1423;(3)当PC 为⊙O 直径时,△PCD 的最大面积=503. 【解析】【分析】(1)由圆周角定理可得∠PCD=∠ACB=90°,可证△ABC ∽△PCD ,可得AC BC CP CD =,即可得证.(2)由题意可求BC=4,AC=3,由勾股定理可求CE 的长,由锐角三角函数可求PE 的长,即可得PC 的长,由AC•CD=PC•BC 可求CD 的值;(3)当点P 在AB 上运动时,12PCD S PC CD =⨯⨯,由(1)可得:43CD PC =,可得2142233PCD SPC PC PC =⨯⨯=,当PC 最大时,△PCD 的面积最大,而PC 为直径时最大,故可求解.【详解】证明:(1)∵AB 为直径,∴∠ACB =90°∵PC ⊥CD ,∴∠PCD =90°∴∠PCD =∠ACB ,且∠CAB =∠CPB∴△ABC ∽△PCD ∴AC BC CP CD= ∴AC •CD =PC •BC(2)∵AB =5,BC :CA =4:3,∠ACB =90°∴BC =4,AC =3,当点P 运动到AB 的中点时,过点B 作BE ⊥PC 于点E∵点P 是AB 的中点, ∴∠PCB =45°,且BC =4∴CE =BE =22BC 2 ∵∠CAB =∠CPB∴tan ∠CAB =43=BC AC =tan ∠CAB =BE PE ∴PE =322∴PC =PE +CE =3222=22 ∵AC •CD =PC •BC ∴3×CD 72×4 ∴CD =23(3)当点P 在AB 上运动时,S △PCD =12×PC ×CD , 由(1)可得:CD =43PC ∴S △PCD =1423PC PC ⨯⨯=23PC 2, ∴当PC 最大时,△PCD 的面积最大,∴当PC 为⊙O 直径时,△PCD 的最大面积=23×52=503【点睛】本题是圆的综合题,考查了相似三角形的判定和性质,圆的有关知识,锐角三角函数,求出PC 的长是本题的关键.9.如图,AB 为⊙O 的直径,BC 为⊙O 的弦,过O 点作OD ⊥BC ,交⊙O 的切线CD 于点D ,交⊙O 于点E ,连接AC 、AE ,且AE 与BC 交于点F .(1)连接BD ,求证:BD 是⊙O 的切线;(2)若AF :EF=2:1,求tan ∠CAF 的值.【答案】(1)证明见解析;(23. 【解析】【分析】 (1)根据全等三角形的性质得到∠OBD=∠OCD=90°,根据切线的判定定理即可得到结论; (2)根据已知条件得到AC ∥DE ,设OD 与BC 交于G ,根据平行线分线段成比例定理得到AC :EG=2:1,EG=12AC ,根据三角形的中位线的性质得到OG=12AC 于是得到AC=OE ,求得∠ABC=30°,即可得到结论.【详解】证明:(1)∵OC=OB ,OD ⊥BC ,∴∠COD=∠BOD ,在△COD 与△BOD 中, OC OB COD BOD OD OD ===⎧⎪∠∠⎨⎪⎩,∴△COD ≌△BOD ,∴∠OBD=∠OCD=90°,∴BD 是⊙O 的切线;(2)解:∵AB为⊙O的直径,AC⊥BC,∵OD⊥CB,∴AC∥DE,设OD与BC交于G,∵OE∥AC,AF:EF=2:1,∴AC:EG=2:1,即EG=12AC,∵OG∥AC,OA=OB,∴OG=12AC,∵OG+GE=12AC+12AC=AC,∴AC=OE,∴AC=12AB,∴∠ABC=30°,∴∠CAB=60°,∵CE BE=,∴∠CAF=∠EAB=12∠CAB=30°,∴tan∠CAF=tan30°=33.【点睛】本题考查了切线的判定和性质,垂径定理,全等三角形的判定与性质,三角形的中位线的性质,三角函数的定义,正确的识别图形是解题的关键.10.如图,直角坐标系中,直线y kx b=+分别交x,y轴于点A(-8,0),B(0,6),C(m,0)是射线AO上一动点,⊙P过B,O,C三点,交直线AB于点D(B,D不重合).(1)求直线AB的函数表达式.(2)若点D在第一象限,且tan∠ODC=53,求点D的坐标.【答案】(1)364y x=+;(2)D(8825,21625).【解析】【分析】(1)把A、B两点坐标代入y=kx+b求出k、b的值即可;(2)连结BC,作DE⊥OC于点E,根据圆周角定理可得∠OBC=∠ODC,由tan∠ODC=53可求出OC的长,进而可得AC的长,利用∠DAC的三角函数值可求出DE的长,即可得D点纵坐标,代入直线AB解析式求出D点横坐标即可得答案.【详解】(1)∵A(-8,0)、B(0,6)在y=kx+b上,∴086k bb=-+⎧⎨=⎩,解得346kb⎧=⎪⎨⎪=⎩,∴直线AB的函数表达式为y=34x+6.(2)连结BC,作DE⊥OC于点E,∵∠BOC=90°,∴BC为⊙P的直径,∴∠ADC=90°,∵∠OBC=∠ODC,tan∠ODC=53,∴OC5OB3=,∵OB=6,OA=8,∴OC=10,AC=18,AB=10,∵cos∠DAC=OAAB =45,sin∠DAC=OBAB=35,472AD AC cos DAC 1855∠=⋅=⨯=, 723216DE AD sin DAC 5525∠=⋅=⨯=, ∵D 点在直线AB 上, ∴2163x 6254=+, 解得:88x 25=, ∴D (8825,21625)【点睛】本题考查待定系数法求一次函数解析式、圆周角定理及锐角三角函数的定义,熟练掌握直径所对的圆周角等于90°及正切、正弦、余弦等三角函数的定义是解题关键.。
(易错题精选)初中数学圆的经典测试题附解析

(易错题精选)初中数学圆的经典测试题附解析一、选择题1.已知线段AB 如图,(1)以线段AB 为直径作半圆弧»AB ,点O 为圆心;(2)过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、,交»AB 于点E F 、;(3)连接,OE OF .根据以上作图过程及所作图形,下列结论中错误的是( )A .CE DF =B .»»AE BF =C .60EOF ∠=︒D . =2CE CO【答案】D【解析】【分析】 根据作图可知AC CO OD DB ===,据此对每个选项逐一判断即可.【详解】根据HL 可判定ECO FDO ≅V V ,得CE DF =,A 正确;∵过半径OA OB 、的中点C D 、分别作CE AB DF AB ⊥⊥、,连接AE ,CE 为OA 的中垂线,AE OE =在半圆中,OA OE =∴OA OE AE ==,AEO △为等边三角形,60EOF =o ∠AOE=∠FOD=∠, C 正确;∴圆心角相等,所对应的弧长度也相等,»»AE BF=,B 正确 ∵60,90EOC =o o ∠AOE=∠, ∴=3CE CO ,D 错误【点睛】本题考查了全等三角形的判定和性质,勾股定理等知识点,解题的关键在于证明60o ∠AOE=.2.如图,已知AB 是⊙O 的直径,CD 是弦,且CD ⊥AB ,BC=3,AC=4,则sin ∠ABD 的值是( )A.43B.34C.35D.45【答案】D【解析】【分析】由垂径定理和圆周角定理可证∠ABD=∠ABC,再根据勾股定理求得AB=5,即可求sin∠ABD 的值.【详解】∵AB是⊙O的直径,CD⊥AB,∴弧AC=弧AD,∴∠ABD=∠ABC.根据勾股定理求得AB=5,∴sin∠ABD=sin∠ABC=45.故选D.【点睛】此题综合考查了垂径定理以及圆周角定理的推论,熟悉锐角三角函数的概念.3.如图,已知AB是⊙O是直径,弦CD⊥AB,AC=22,BD=1,则sin∠ABD的值是()A.2B.13C.23D.3【答案】C【解析】【分析】先根据垂径定理,可得BC的长,再利用直径对应圆周角为90°得到△ABC是直角三角形,利用勾股定理求得AB的长,得到sin∠ABC的大小,最终得到sin∠ABD【详解】解:∵弦CD ⊥AB ,AB 过O ,∴AB 平分CD ,∴BC =BD ,∴∠ABC =∠ABD ,∵BD =1,∴BC =1,∵AB 为⊙O 的直径,∴∠ACB =90°,由勾股定理得:AB 3==,∴sin ∠ABD =sin ∠ABC =3AC AB = 故选:C .【点睛】本题考查了垂径定理、直径对应圆周角为90°、勾股定理和三角函数,解题关键是找出图形中的直角三角形,然后按照三角函数的定义求解4.下列命题中,是假命题的是( )A .任意多边形的外角和为360oB .在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C VC .在一个三角形中,任意两边之差小于第三边D .同弧所对的圆周角和圆心角相等【答案】D【解析】【分析】根据相关的知识点逐个分析.【详解】解:A. 任意多边形的外角和为360o ,是真命题;B. 在ABC V 和'''A B C V 中,若''AB A B =,''BC B C =,'90C C ∠=∠=o ,则ABC V ≌'''A B C V ,根据HL ,是真命题;C. 在一个三角形中,任意两边之差小于第三边,是真命题;D. 同弧所对的圆周角等于圆心角的一半,本选项是假命题.故选D .【点睛】本题考核知识点:判断命题的真假. 解题关键点:熟记相关性质或定义.5.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是()A.20°B.35°C.40°D.55°【答案】B【解析】【分析】连接FB,由邻补角定义可得∠FOB=140°,由圆周角定理求得∠FEB=70°,根据等腰三角形的性质分别求出∠OFB、∠EFB的度数,继而根据∠EFO=∠EBF-∠OFB即可求得答案.【详解】连接FB,则∠FOB=180°-∠AOF=180°-40°=140°,∴∠FEB=12∠FOB=70°,∵FO=BO,∴∠OFB=∠OBF=(180°-∠FOB)÷2=20°,∵EF=EB,∴∠EFB=∠EBF=(180°-∠FEB)÷2=55°,∴∠EFO=∠EBF-∠OFB=55°-20°=35°,故选B.【点睛】本题考查了圆周角定理、等腰三角形的性质等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.6.如图,△ABC的外接圆是⊙O,半径AO=5,sinB=25,则线段AC的长为()A.1 B.2 C.4 D.5【答案】C【解析】【分析】首先连接CO并延长交⊙O于点D,连接AD,由CD是⊙O的直径,可得∠CAD=90°,又由⊙O的半径是5,sinB=25,即可求得答案.【详解】解:连接CO并延长交⊙O于点D,连接AD,由CD是⊙O的直径,可得∠CAD=90°,∵∠B和∠D所对的弧都为弧AC,∴∠B=∠D,即sinB=sinD=25,∵半径AO=5,∴CD=10,∴2 sin105AC ACDCD===,∴AC=4,故选:C.【点睛】本题考查了同弧所对的圆周角相等,以及三角函数的内容,注意到直径所对的圆周角是直角是解题的关键.7.下列命题是假命题的是()A.三角形两边的和大于第三边B.正六边形的每个中心角都等于60oC.半径为R2RD.只有正方形的外角和等于360︒【答案】D【解析】【分析】根据三角形三边关系、中心角的概念、正方形与圆的关系、多边形的外角和对各选项逐一进行分析判断即可.【详解】A 、三角形两边的和大于第三边,A 是真命题,不符合题意;B 、正六边形6条边对应6个中心角,每个中心角都等于360606︒︒=,B 是真命题,不符合题意;C 、半径为R 的圆内接正方形中,对角线长为圆的直径2R ,设边长等于x ,则:222(2)x x R +=,解得边长为2x R :=,C 是真命题,不符合题意;D 、任何凸3n n ≥()边形的外角和都为360︒,D 是假命题,符合题意, 故选D.【点睛】本题考查了真假命题,熟练掌握正多边形与圆、中心角、多边形的外角和等知识是解本题的关键.8.如图,AB 是⊙O 的直径,点C 是⊙O 上一点,点D 在BA 的延长线上,CD 与⊙O 交于另一点E ,DE=OB=2,∠D=20°,则弧BC 的长度为( )A .23πB .13πC .43πD .49π 【答案】A【解析】【分析】连接OE 、OC ,如图,根据等腰三角形的性质得到∠D=∠EOD=20°,根据外角的性质得到∠CEO=∠D+∠EOD=40°,根据等腰三角形的性质得到∠C=∠CEO=40°,根据外角的性质得到∠BOC=∠C+∠D=60°,根据求弧长的公式得到结论.【详解】解:连接OE 、OC ,如图,∵DE=OB=OE,∴∠D=∠EOD=20°,∴∠CEO=∠D+∠EOD=40°,∵OE=OC,∴∠C=∠CEO=40°,∴∠BOC=∠C+∠D=60°,∴»BC的长度=260?2360π⨯=23π,故选A.【点睛】本题考查了弧长公式:l=••180n Rπ(弧长为l,圆心角度数为n,圆的半径为R),还考查了圆的认识及等腰三角形的性质及三角形外角的性质,熟练掌握等腰三角形的性质和三角形外角性质是关键.9.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC,若∠A=60°,∠ADC=85°,则∠C的度数是()A.25°B.27.5°C.30°D.35°【答案】D【解析】分析:直接利用三角形外角的性质以及邻补角的关系得出∠B以及∠ODC度数,再利用圆周角定理以及三角形内角和定理得出答案.详解:∵∠A=60°,∠ADC=85°,∴∠B=85°-60°=25°,∠CDO=95°,∴∠AOC=2∠B=50°,∴∠C=180°-95°-50°=35°故选D.点睛:此题主要考查了圆周角定理以及三角形内角和定理等知识,正确得出∠AOC度数是解题关键.10.如图,将△ABC绕点C旋转60°得到△A′B′C′,已知AC=6,BC=4,则线段AB扫过的图形面积为()A.32πB.83πC.6πD.以上答案都不对【答案】D【解析】【分析】从图中可以看出,线段AB扫过的图形面积为一个环形,环形中的大圆半径是AC,小圆半径是BC,圆心角是60度,所以阴影面积=大扇形面积-小扇形面积.【详解】阴影面积=() 603616103603π⨯-=π.故选D.【点睛】本题的关键是理解出,线段AB扫过的图形面积为一个环形.11.如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8 cm,MB=2 cm,则直径AB的长为()A.9 cm B.10 cm C.11 cm D.12 cm【答案】B【解析】【分析】由CD⊥AB,可得DM=4.设半径OD=Rcm,则可求得OM的长,连接OD,在直角三角形DMO中,由勾股定理可求得OD的长,继而求得答案.【详解】解:连接OD,设⊙O半径OD为R,∵AB是⊙O的直径,弦CD⊥AB于点M,∴DM=12CD=4cm,OM=R-2,在RT△OMD中,OD²=DM²+OM²即R²=4²+(R-2)²,解得:R=5,∴直径AB的长为:2×5=10cm.故选B.【点睛】本题考查了垂径定理以及勾股定理.注意掌握辅助线的作法及数形结合思想的应用.12.如图,将边长为2cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动8次后,正方形的中心O经过的路线长是()cm.A.2B.8 C.3πD.4π【答案】D【解析】【分析】由题意可得翻转一次中心O经过的路线长就是1个半径为1,圆心角是90°的弧长,然后进行计算即可解答.【详解】解:∵正方形ABCD2cm,∴对角线的一半=1cm,则连续翻动8次后,正方形的中心O经过的路线长=8×901180π⨯=4π.故选:D.【点睛】本题考查了弧长的计算,审清题意、确定点O的路线和长度是解答本题的关键.13.如图,抛物线y=ax2﹣6ax+5a(a>0)与x轴交于A、B两点,顶点为C点.以C点为圆心,半径为2画圆,点P 在⊙C 上,连接OP ,若OP 的最小值为3,则C 点坐标是( )A .522(,22-B .(4,﹣5)C .(3,﹣5)D .(3,﹣4)【答案】D【解析】【分析】首先根据二次函数的解析式求出点A 、B 、C 三点的坐标,再由当点O 、P 、C 三点共线时,OP 取最小值为3,列出关于a 的方程,即可求解.【详解】∵2650y ax ax a a +-=(>) 与x 轴交于A 、B 两点, ∴A (1,0)、B (5,0),∵226534y ax ax a a x a =+=---() , ∴顶点34C a (,-), 当点O 、P 、C 三点共线时,OP 取最小值为3,∴OC =OP+2=5, 29165(0)a a +=> ,∴1a = ,∴C (3,﹣4),故选:D .【点睛】本题考查了二次函数的图象和性质,解题的关键是明确圆外一点到圆上的最短距离即该点与圆心的距离减去半径长.14.如图,3个正方形在⊙O 直径的同侧,顶点B 、C 、G 、H 都在⊙O 的直径上,正方形ABCD 的顶点A 在⊙O 上,顶点D 在PC 上,正方形EFGH 的顶点E 在⊙O 上、顶点F 在QG 上,正方形PCGQ 的顶点P 也在⊙O 上.若BC =1,GH =2,则CG 的长为( )A.125B.6C.21+D.22【答案】B【解析】【分析】【详解】解:连接AO、PO、EO,设⊙O的半径为r,OC=x,OG=y,由勾股定理可知:22222222211{22r xr x x yr y=++=++=++()①()②()③,②﹣③得到:x2+(x+y)2﹣(y+2)2﹣22=0,∴(x+y)2﹣22=(y+2)2﹣x2,∴(x+y+2)(x+y﹣2)=(y+2+x)(y+2﹣x).∵x+y+2≠0,∴x+y﹣2=y+2﹣x,∴x=2,代入①得到r2=10,代入②得到:10=4+(x+y)2,∴(x+y)2=6.∵x+y>0,∴x+y=6,∴CG=x+y=6.故选B.点睛:本题考查了正方形的性质、圆、勾股定理等知识,解题的关键是设未知数列方程组解决问题,难点是解方程组,利用因式分解法巧妙求出x的值,学会把问题转化为方程组,用方程组的思想去思考问题.15.如图,在边长为8的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A.183π-B.183πC.32316πD.1839π-【答案】C【解析】【分析】由菱形的性质得出AD=AB=8,∠ADC=120°,由三角函数求出菱形的高DF ,图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积,根据面积公式计算即可.【详解】解:∵四边形ABCD 是菱形,∠DAB=60°,∴AD=AB=8,∠ADC=180°-60°=120°,∵DF 是菱形的高,∴DF ⊥AB ,∴DF=AD •sin60°=3843⨯=, ∴图中阴影部分的面积=菱形ABCD 的面积-扇形DEFG 的面积 =2120(43)84332316ππ⨯⨯-=-. 故选:C.【点睛】本题考查了菱形的性质、三角函数、菱形和扇形面积的计算;由三角函数求出菱形的高是解决问题的关键.16.如图,AB 是⊙O 的直径,弦CD ⊥AB 于E 点,若AD =CD = 23.则»BC的长为( )A .3πB .23πC .33πD .33π 【答案】B【解析】【分析】根据垂径定理得到3CE DE ==»»BCBD = ,∠A=30°,再利用三角函数求出OD=2,即可利用弧长公式计算解答.【详解】如图:连接OD ,∵AB 是⊙O 的直径,弦CD ⊥AB 于E 点,AD =CD = 23∴3CE DE ==,»»BC BD = ,∠A=30°, ∴∠DOE=60°,∴OD=2sin 60DE =o, ∴»BC的长=»BD 的长=60221803ππ⨯=, 故选:B.【点睛】此题考查垂径定理,三角函数,弧长公式,圆周角定理,是一道圆的综合题.17.如图,已知某圆锥轴截面等腰三角形的底边和高线长均为10cm ,则这个圆锥的侧面积为( )A .50cm 2B .50πcm 2C .52D .5cm 2【答案】D【解析】【分析】 根据勾股定理求出圆锥的母线长,求出底面圆周长,根据扇形面积公式计算即可.【详解】解:如图所示,∵等腰三角形的底边和高线长均为10cm ,22105+=55,圆锥底面圆半径为5,∴这个圆锥的底面圆周长=2×π×5=10π,即为侧面展开扇形的弧长,圆锥的侧面积=1255cm 2, 故选:D .【点睛】本题考查了圆锥的计算,解题的关键是弄清楚圆锥的侧面积的计算方法,特别是圆锥的轴截面是等腰三角形,勾股定理的应用,以及圆锥的底面周长等于圆锥的侧面扇形的弧长.18.如图,已知圆O的半径为10,AB⊥CD,垂足为P,且AB=CD=16,则OP的长为()A.6 B.6C.8 D.8【答案】B【解析】【分析】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,首先利用勾股定理求得OM的长,然后判定四边形OMPN是正方形,求得正方形的对角线的长即可求得OP的长.【详解】作OM⊥AB于M,ON⊥CD于N,连接OP,OB,OD,∵AB=CD=16,∴BM=DN=8,∴OM=ON==6,∵AB⊥CD,∴∠DPB=90°,∵OM⊥AB于M,ON⊥CD于N,∴∠OMP=∠ONP=90°∴四边形MONP是矩形,∵OM=ON,∴四边形MONP是正方形,∴OP=.故选B.【点睛】本题考查的是垂径定理,正方形的判定与性质及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.19.如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C 作OA的平行线分别交两弧点D、E,则阴影部分的面积为()A.53π﹣3B.533C.3πD353π【答案】A【解析】【分析】连接OE.可得S阴影=S扇形BOE-S扇形BCD-S△OCE.根据已知条件易求得BC=OC=CD=2,BO=OE=4.∠BOE=60o,CE=23所以由扇形面积公式、三角形面积公式进行解答即可.【详解】解:连接OE,可得S阴影=S扇形BOE-S扇形BCD-S△OCE,由已知条件可得,BC=OC=CD=2,又,BO=OE=4,∴∠BOE=o60,可得CE=23S扇形BOE=2604360π⋅⋅8=3π,S扇形BCD2902==360ππ⋅⋅,S△OCE=1=223=23 2⨯⨯∴S阴影=S扇形BOE-S扇形BCD-S△OCE=8--233ππ=533π故选A.【点睛】本题主要考查扇形面积公式、三角形面积公式,牢记公式并灵活运用可求得答案.20.如图,在Rt△ABC中,∠ABC=90°,AB=23,BC=2,以AB的中点为圆心,OA的长为半径作半圆交AC于点D,则图中阴影部分的面积为( )A.532π-B.532π+C.23π-D.432π-【答案】A【解析】【分析】连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,利用∠A的正切值求出∠A=30°,继而可求得OH、AH长,根据圆周角定理可求得∠BOC =60°,然后根据S阴影=S△ABC-S△AOD-S扇形BOD进行计算即可.【详解】连接OD,过点O作OH⊥AC,垂足为 H,则有AD=2AH,∠AHO=90°,在Rt△ABC中,∠ABC=90°,AB=23,BC=2,tan∠A=323BCAB==,∴∠A=30°,∴OH=12OA=32,AH=AO•cos∠A=3332⨯=,∠BOC=2∠A=60°,∴AD=2AH=3,∴S阴影=S△ABC-S△AOD-S扇形BOD=()26031132323222360π⨯⨯⨯-⨯⨯-=532π-,故选A.【点睛】本题考查了垂径定理,圆周角定理,扇形面积,解直角三角形等知识,正确添加辅助线,熟练掌握和灵活运用相关知识是解题的关键.。
第2章 对称图形-圆(易错必刷30题7种题型专项训练)(原卷版)

第2章对称图形-圆(易错必刷30题7种题型专项训练)一.垂径定理(共1小题)1.(2022秋•潍城区期中)如图,⊙O的直径AB与弦CD交于点E,若B为的中点,则下列说法错误的是()A.B.OE=BE C.CE=DE D.AB⊥CD二.圆心角、弧、弦的关系(共1小题)2.(2022秋•邳州市期中)如图,AB、CD是⊙O的两条弦,∠AOC=∠BOD.求证:AB=CD.三.圆周角定理(共19小题)3.(2022秋•邳州市期中)如图,在⊙O中,∠A=30°,则的度数为()A.30°B.15°C.60°D.40°4.(2022秋•海淀区校级期中)如图,点A,B,C均在⊙O上,若∠AOB=50°,则∠ACB的度数是()A.25°B.50°C.75°D.100°5.(2022秋•拱墅区校级期中)如图,点A在⊙O上,∠OBC=25°,则∠BAC的度数为()A.55°B.65°C.75°D.130°6.(2022秋•郾城区期中)如图,⊙O中,OA⊥弦BC,点E为垂足,点D在优弧上,则下列语句中,错误的是()A.BE=CE B.C.∠AOB=2∠ADC D.∠BCD=∠CBO7.(2022秋•巧家县期中)如图,A、B、D为⊙O上的点,∠ADB=57°,则∠AOB为()A.100°B.124°C.104°D.114°8.(2022秋•镇江期中)如图,C、D是⊙O上两点,位于直径AB的两侧,设∠ABC=24°,则∠BDC =°.9.(2022秋•邗江区期中)如图,已知点A,B,C依次在⊙O上,∠B﹣∠A=40°,则∠AOB的度数为.10.(2022秋•仪征市期中)如图,已知点A,B,C依次在⊙O上,∠B﹣∠A=30°,则∠AOB的度数为°.11.(2022秋•梁溪区校级期中)如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,则∠ACB =°.12.(2022秋•崇川区期中)如图,圆的两条弦AB,CD相交于点E,且,∠A=36°,则且∠CEB的度数为.13.(2022秋•镇江期中)如图,AB为⊙O直径,CD为弦,AB⊥CD于E,连接CO,AD,∠BAD=26°,则∠BOC=.14.(2022秋•东台市期中)如图,AB是半圆O的直径,∠ABD=35°,点C是上的一点,则∠C=度.15.(2022秋•武昌区期中)已知⊙O的两条弦为AB、AC,连接半径OA、OB、OC,若AC=AB=OA,则∠BOC的度数为.16.(2022秋•东台市期中)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.(1)判断△BDE的形状,并证明你的结论;(2)若AB=10,BE=2,求BC的长.17.(2022秋•大丰区期中)如图,AB是⊙O的直径,弦CD交AB于点E,连接AC、AD.若∠BAC=35°,(1)求∠D的度数;(2)若∠ACD=65°,求∠CEB的度数.18.(2022秋•工业园区校级期中)如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC.垂足为点D.AE=AB,BE分别交AD、AC于点F、G.(1)判断△F AG的形状.并说明理由;(2)延长AD交⊙O于点M,连接ME,求证:ME⊥AC.19.(2022秋•梁溪区校级期中)如图,⊙O的直径AE=8,∠B=∠EAC,求AC的长.20.(2022秋•确山县期中)如图所示,⊙O的直径AB为6cm,∠ACB的平分线交⊙O于点D.(1)判断△ADB的形状,并证明;(2)求BD的长.21.(2022秋•南浔区期中)如图,已知AC是⊙O的直径,AB,CD是⊙O中的两条弦,且AB∥CD,连结AD,BC.(1)求证:四边形ABCD是矩形;(2)若∠BAC=30°,⊙O的直径为10,求矩形ABCD的面积.四.点与圆的位置关系(共1小题)22.(2022秋•新吴区期中)如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为()A.+1B.+C.2+1D.2﹣五.三角形的外接圆与外心(共2小题)23.(2022秋•溧阳市期中)如图,△ABC是⊙O的内接三角形,直径AB=4,CD平分∠ACB交⊙O于点D,交AB于点E,连接AD、BD.(1)若∠CAB=25°,求∠AED的度数;(2)求AD的长.24.(2022秋•江都区期中)如图,四边形ABCD是平行四边形,∠B=60°,经过点A,C,D的圆与BC相交于点E,连接AE.(1)求证:△ABE是等边三角形.(2)F是上一点,且F A=FC,连接EF.求证:EF=BC.六.切线的性质(共5小题)25.(2022秋•丹阳市校级期中)如图,在边长为2的菱形ABCD中,∠BAD=120°,以点C为圆心画弧,且与AB,AD边相切,则图中阴影部分的面积是()A.B.C.D.26.(2022秋•五华区校级期中)下列说法正确的是()A.平分弦的直径垂直于弦,并且平分弦所对的两条弧B.圆的切线垂直于圆的半径C.三角形的外心到三角形三边的距离相等D.同弧或等弧所对的圆周角相等27.(2022秋•兴隆台区校级期中)如图,在平面直角坐标系中,以M(2,3)为圆心,AB为直径的圆与x 轴相切,与y轴交于A,C两点,则AC的长为()A.4B.C.D.628.(2022秋•五华区校级期中)P A,PB是⊙O的切线,A,B是切点,点C是⊙O上不与A,B重合的一点,若∠APB=70°,则∠ACB的度数为.29.(2022秋•矿区期中)如图,△ABC内接于⊙O,直线EF与⊙O相切于点B,若∠C=40°,则∠ABF =.七.切线的判定与性质(共1小题)30.(2022秋•邳州市期中)如图,AB为⊙O的直径,过圆上一点D作⊙O的切线CD交BA的延长线于点C,过点O作OE∥AD交CD于点E,连接BE.(1)直线BE与⊙O相切吗?并说明理由;(2)若CA=2,CD=4,求DE的长.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的错题精练
填空题
1.把一个圆剪拼成一个和它面积相等的长方形,周长增加了8cm,原来这个圆的面积是()cm2。
2.甲轮滚动5周的距离,乙轮要滚动4周;甲轮与乙轮的直径比是(),周长比是()。
3.在一个半径为8厘米的圆内画一个最大的正方形,这个正方形的面积是()平方厘米。
4.在一个圆内,以它的半径为边长做一个正方形,已知正方形面积是8cm2,圆的面积是( ) cm2。
5.大圆半径是小圆半径的2倍,大圆面积比小圆面积多24平方厘米,小圆面积是()平方厘米。
6.圆的半径增加,圆的周长增加(),圆的面积增加()。
7.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
8.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
9.在一个面积是16平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
10.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()11.一个圆的周长扩大3倍,面积就扩大()倍。
12.如图,六个大小不同的圆的圆心都在线段AB上,AB=100厘米,则这六个圆的周长的和
是__________.
13.如图,圆环面积是小圆面积的8倍,则大圆半径是小圆的_____倍.
14.一根铁丝刚好围成一个周长为(2+π)厘米的圆,如果把这个铁丝围成一个半圆,那么这个半圆的面积为________平方厘米(保留π)
15.一个圆的周长是25.12cm,如将周长延长至37.68cm,则半径应是原来半径的_______倍。
选择题
1.把一个圆剪拼成宽等于半径的近似的长方形后()。
A.周长减少,面积不变B.周长增加,面积不变
C.周长不变,面积减少D.周长和面积都不变
2.圆的半径增加2厘米,它的周长增加()。
A.1厘米B.π厘米C.2π厘米D.4π厘米
3.一个圆的直径扩大2倍,它的面积扩大()
A.2倍B.4倍C.6倍
4.一台拖拉机,后轮直径是前轮的4倍,后轮滚动4圈,前轮滚动()圈。
A.4B.8C.16
5.一个半圆形的周长是51.4cm,它的半径是………………()
A.16.37 cm
B.8.185 cm
C.10 cm
D.15 cm。
操作题(对的打“√”,错的打“×”)
(1)通过圆心的线段,叫做圆的直径。
……………………()
(2)周长是所在圆直径的3.14倍。
…………………………()
(3)同一个圆内,半径是直径的一半。
……………………………………()
(4)任何圆的圆周率都是π。
…………………………………()
(5)半径是 2厘米的圆,它的周长和面积相等。
()
(6)两个圆的面积相等,则两个圆的半径一定相等。
()
(7)如果一个圆的直径缩小2倍,那么它的周长也缩小2倍,面积则缩小4倍()操作题
1.阴影部分面积为25平方厘米,求圆环面积。
2.长方形面积为50平方厘米,求面积。
3、求图中阴影部分的面积(单位:厘米)
4、求阴影部分的面积(厘米)
3.下面是一个圆平均分成若干份后拼成的一个近似长方形,求出该圆的面积。
(单位:厘米)
4.一个水缸,从里面量,缸口直径是 50厘米,缸壁厚 5厘米。
要制做一个缸盖,使它正好盖住缸口的外沿,这个缸盖的面积是多少平方厘米?如果在缸盖的边沿贴上一圈金属(不计接头),这个金属条长多少厘米?
5.将一根长 100米的绳子,绕一棵大树20圈少48厘米,这棵大树横截面面积是多少平方厘米?
6. 两圆半径之差为3cm,周长之和为157cm,两圆面积分别是多少?(取π=3.14)
7. 学习了圆这章后,小明、小丽和小杰对圆产生了兴趣,小丽用4条1米长的细绳围成了4个圆,小明用2条2米长的绳子围成了2个圆,小杰用1条4米长的绳子围成了一个圆,每个人都觉得自己围出的图形面积大。
你能帮助他们判断谁围出的图形面积最大,为什么?
羊 8. 如图,一头羊被6米长的绳子拴在长为6米,宽为3米的长方形池塘的一个顶点上,池塘周围是草地,问这头羊可以吃到的草地的面积。
9. 我们知道要计算圆的周长和面积,总要用到π,是不是所有的曲线的长度以及它们围起来的面积都是与π有关呢?不一定。
例如计算图(1)所示的图形的阴影部分的面积就不需要π帮忙,只要把图形中右边的半圆移到左边,这样阴影部分的面积就等于一个长方形的面积。
已知图(2)中四个圆的半径为
21,试用上面的方法求图中阴影部分的面积。
10.如图,圆的半径为4厘米,想一想,如何运用运动,巧妙地求出图中阴影部分的面积。
11.如图,半圆的直径为4,三个阴影部份的面积分别为1s 、2s 、3s ,321S S S +=,求图中长方形的宽x.
图(1)
图(2)。
