基于MATLAB小波工具箱的开发与应用
基于Matlab小波工具箱的数字图像处理及小波分析

k k ,2/)]2(t ψ1+⊃j j V V图2.2 Mallat重构示意图三、常用小波函数介绍在小波分析理论在数学和工程领域中一个很重要的问题就是小波基的选择,选择一个最优的小波基,可以使图像处理更加优化。
在小波分析理论中有很多种的小波函数,下面介绍一些常用的小波基函数:3.1 Haar小波Haar小波是Haar于1990年提出的一种正交小波,它是小波理论分析发展过程中最早用到的的小波。
Haar小波是由一组互相正交归一的函数集,即Haar函数衍生产生的,是具有紧支撑的正交小波函数,其定义如下[5]:1012()1121tt tψ≤≤⎧⎪=-≤≤⎨⎪⎩其他(3.1)Haar小波是一个最简单的时域不连续的小波,它类似一个阶梯函数,由于它的紧支撑性和正交性,使得Haar小波的应用很普遍。
图3-1所示为Haar波的函数图像。
图3-1 Haar小波函数图像由于Haar小波在时域上是不连续的,所以作为基本小波性能不是特别好。
但也有自己的优点:①计算简单;②在2ja=的多分辨率系统中Haar小波构成一组最简单的正交归一的小波族。
因为()tψ不但与(2),()j t j Zψ∈正交,而且与自己的整数位移正交。
③()tψ的傅里叶变换是:24()sin()2j e jaψΩΩ=-ΩΩ(3.2)3.2Mexican hat(墨西哥草帽)小波Mexican Hat 小波又被称Marr 小波。
Marr 小波函数就是高斯函数的二阶导数,其表达式为:222()(1)t t t e ψ-=- (3.3)222()2e ωψωπω= (3.4)因为它的形状像墨西哥帽的截面,所以也称为墨西哥帽函数。
墨西哥帽函数在时间域与频率域都有很好的局部化,并且满足0)(=⎰∞∞-dx x ψ (3.5)由于它的尺度函数不存在,所以不具有正交性。
其波形如图3-2所示。
Marr 小波的时域、频域都有很好的局部特性,但由于它的正交性尺度函数不存在,所以不具有正交性,主要用于信号处理和边缘检测。
基于MATLAB的小波分析应用(第二版)(周伟)1-4章 (2)

说明 获取在消噪或压缩过程中的默认阈值 去噪的阈值选择 获取一维或二维小波去噪阈值 使用 Birgé-Massart 算法获取一维小波变换的阈值 使用 Birgé-Massart 算法获取二维小波变换的阈值 使用小波进行一维信号的自动消噪 用小波进行消噪或压缩 产生含噪声的小波测试数据 估计一维小波系数的噪声 小波包去噪的阈值选择 用小波包变换进行信号的压缩或去噪 小波包分解系数的阈值处理 一维信号小波系数的阈值处理 二维信号小波系数的阈值处理 软阈值或硬阈值处理 阈值设置管理
说明 尺度对应频率 尺度函数 二维尺度函数 小波管理 小波滤波器组 最大小波分解尺度
第2章 MATLAB小波工具箱简介 3. 小波函数 MATLAB小波工具箱提供的小波变换函数如表2-3所示,它 们主要用于产生一些基本的小波函数及其相应的滤波器。
第2章 MATLAB小波工具箱简介
表2-3 小波变换函数
第2章 MATLAB小波工具箱简介 表2-6 二维离散小波变换函数
函数名 appcoef2 detcoef2
dwt2 dwtmode
idwt2 upcoef2
说明 提取二维小波分解的低频系数 提取二维小波分解的高频系数 单尺度二维离散小波变换 离散小波变换的延拓模式 单尺度二维离散小波逆变换 二维小波分解系数的直接重构
第2章 MATLAB小波工具箱简介
表2-15 树 管 理 函 数
函数名
说明
函数名
说明
allnodes 计算树结点
noleaves 列举非终结点
函数名 laurpoly ls2filt
lsinfo lwt lwt2
lwtcoef lwtcoef2 wave2lp wavenames
说明 构造 Laurent 多项式 将提升方案转化为滤波器组 关于提升方案的信息 一维提升小波变换 二维提升小波变换 一维提升小波变换系数的提取或重构 二维提升小波变换系数的提取或重构 将 Laurent 多项式与小波关联 能够应用于提升小波变换的小波名称
小波分析中的matlab使用
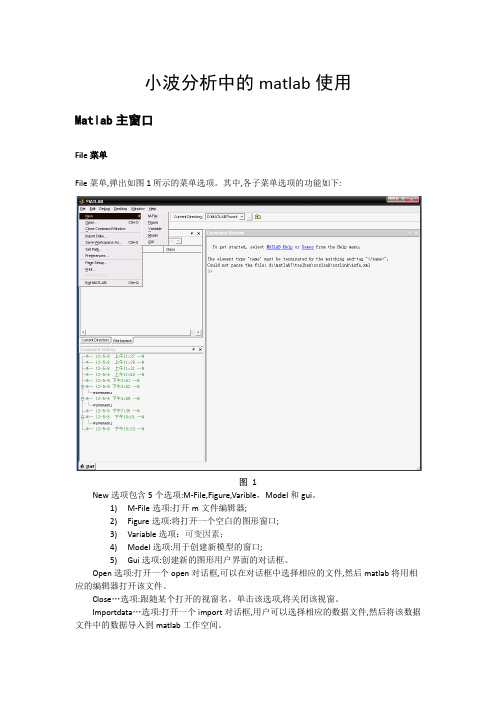
小波分析中的matlab使用Matlab主窗口File菜单File菜单,弹出如图1所示的菜单选项。
其中,各子菜单选项的功能如下:图 1New选项包含5个选项:M-File,Figure,Varible,Model和gui。
1)M-File选项:打开m文件编辑器;2)Figure选项:将打开一个空白的图形窗口;3)Variable选项:可变因素;4)Model选项:用于创建新模型的窗口;5)Gui选项:创建新的图形用户界面的对话框。
Open选项:打开一个open对话框,可以在对话框中选择相应的文件,然后matlab将用相应的编辑器打开该文件。
Close…选项:跟随某个打开的视窗名。
单击该选项,将关闭该视窗。
Importdata…选项:打开一个import对话框,用户可以选择相应的数据文件,然后将该数据文件中的数据导入到matlab工作空间。
Saveworkspaceas…选项:打开一个savetomat-File对话框,用户需要为保存的工作空间命名。
Setpath…选项:打开设置路径对话框。
通过该对话框可以更改matlab执行命令时搜索的路径。
Preferences:首选参数。
Pagesetup选项:用于设置页面布局,页面的页眉,页面所用的文字。
Print…选项:用于打印预定义好的页面内容,也可以设置一些参数。
Printselection…选项:当选中命令窗口内的一部分内容后,该选项将处于激活状态,此时单击该选项,将打印对话框中选中的内容。
Exitmatlab选项:关闭matlab。
也可以通过快捷键ctrl+O来关闭。
Edit菜单单击edit菜单,会弹出如图2所示的菜单选项。
其中,各子菜单选项的功能如下:Undo选项:取消上一次的操作。
Redo选项:重复上一次的操作。
Cut选项:剪切所选中的部分。
Copy选项:选复制被选中的部分。
Paste选项:把存放在缓冲区中的内容粘贴到光标所在的位置。
Pastespecial选项:打开导入数据向导,该向导引导用户把存放在缓冲区中的内容以特定格式存放到剪贴板变量中。
精品课件-基于MATLAB的小波分析应用-第5章

第5章 小波变换与信号处理
其中,COEFS为连续小波变换后的返回系数CWTx(a, b)矩 阵,系数以行方式存储在矩阵中。矩阵的行数为小波变换中 尺度的个数,列数为信号采样点的个数,即矩阵的第一行对 应第一个尺度变换后的系数,第二行对应第二个尺度变换后 的系数,依此类推。
第5章 小波变换与信号处理
第5章 小波变换与信号处理
2. 信号的连续小波分解实例 下面以信号noissin为例说明如何对一个信号进行连续小 波分解,信号noissin是一个含噪声的周期性信号。 程序代码如下:
%装载noissin信号 load noissin; x = noissin; figure(1); plot(x); figure(2);
第5章 小波变换与信号处理
plot(cA2); title('尺度2的低频系数'); %提取尺度1的高频系数 cD1 = detcoef(C,L,1); %提取尺度2的高频系数 cD2 = detcoef(C,L,2); figure(3); subplot(2,1,1); plot(cD1);
第5章 小波变换与信号处理
第5章 小波变换与信号处理
2) 多尺度一维离散小波变换 MATLAB中实现多尺度离散小波变换的函数为wavedec,其 调用格式有以下两种: (1) [C, L] = wavedec(X, N, 'wname') (2) [C, L] = wavedec(X, N, Lo_D, Hi_D) 其中,N为尺度,且必须为正整数,'wname'为小波名称, Lo_D和Hi_D分别为分解低通和高通滤波器。输出参数C由[cAj, cDj, cDj-1,…, cD1]组成,L由[cAj的长度,cDj的长度, cDj-1的长度,…,cD1的长度,X的长度]组成。例如,一个 三尺度的分解结构的组织形式如图5.4所示。
第六章基于MATLAB的小波分析

第六章基于MATLAB的小波分析小波分析是一种用来分析和处理信号的数学方法,其基本原理是通过将信号分解成不同频率范围的小波基函数来揭示信号的特征。
MATLAB是一种功能强大的科学计算和数据分析软件,提供了丰富的工具箱和函数,可以方便地进行小波分析。
在MATLAB中,小波分析可以通过使用Wavelet Toolbox来实现。
该工具箱提供了几种常用的小波基函数,如Daubechies、Coiflets、Symlets等,同时还包括了一系列小波分析的函数。
下面将介绍基于MATLAB的小波分析的基本步骤。
首先,需要导入待分析的信号数据。
可以使用MATLAB的数据导入和处理工具来加载信号数据,如load函数、importdata函数等。
加载数据后,可以使用plot函数将信号数据可视化,以便直观地了解信号的特点。
接下来,需要选择合适的小波基函数进行分析。
小波基函数的选择与信号的特征和分析目标相关。
可以使用waveinfo函数来查看Wavelet Toolbox提供的小波基函数的特性和参数,并选择适合的小波基函数。
然后,使用wavedec函数对信号进行小波分解。
wavedec函数可以将信号分解成多个尺度的小波系数。
分解得到的小波系数包括近似系数和细节系数,近似系数反映了信号在低频范围的特征,而细节系数则反映了信号在高频范围的细节特征。
分解后,可以使用可视化函数如plot、imshow等来展示小波系数的分布和变化情况。
通过观察小波系数的变化,可以得到信号的频率特征和局部特征。
除了观察小波系数,还可以根据需要进行小波系数的处理和分析。
例如,可以使用细节系数来提取信号中的细节特征,如边缘、尖峰等,也可以使用近似系数来提取信号的整体趋势。
最后,可以使用waverec函数将处理过的小波系数重构成原始信号。
重构得到的信号可以与原始信号进行对比,以验证分析的结果和提取的特征。
综上所述,MATLAB提供了丰富的工具和函数来实现小波分析,可以方便地进行信号的频率分析和特征提取。
matlab wsst 实现方法

matlab wsst 实现方法使用MATLAB实现WSST方法引言:小波分析是一种在时间和频率域上进行信号分析的有效工具。
小波分析可以将信号分解成不同频率的成分,使得对信号的分析更加全面和准确。
其中,WSST(Wavelet Synchrosqueezed Transform)方法是一种基于小波分析的信号处理方法,可以用于时频分析、频谱估计和信号特征提取等领域。
本文将介绍如何使用MATLAB实现WSST方法,并通过一个示例来展示其应用。
一、MATLAB中的小波分析工具MATLAB提供了丰富的小波分析工具箱,可以方便地进行小波变换、小波重构和小波分析等操作。
在实现WSST方法之前,我们首先需要了解MATLAB中的小波分析工具。
1. 小波变换小波变换是一种将信号分解成不同频率的成分的方法。
MATLAB中的小波变换函数为“wavetrans”。
通过选择不同的小波基函数和尺度参数,可以得到不同频率的小波系数。
2. 小波重构小波重构是一种将小波系数合成为原始信号的方法。
MATLAB中的小波重构函数为“iwavetrans”。
通过将不同频率的小波系数进行合成,可以得到原始信号的近似重构。
3. 小波分析工具箱MATLAB提供了丰富的小波分析工具箱,包括小波变换、小波重构、小波包分析、小波阈值去噪等功能。
通过使用这些工具,可以方便地进行小波分析和信号处理。
二、WSST方法的原理WSST方法是一种基于小波分析的信号处理方法,可以将信号在时频域上进行分析。
其原理是通过对信号进行小波变换,然后对小波系数进行重构,得到信号在时频域上的表示。
WSST方法可以提取信号的时频特征,从而实现对信号的分析和处理。
1. 小波变换我们需要对信号进行小波变换。
通过选择合适的小波基函数和尺度参数,可以将信号分解成不同频率的小波系数。
MATLAB中的小波变换函数为“wavetrans”。
2. 小波重构然后,我们需要对小波系数进行重构,得到信号在时频域上的表示。
小波分析-matlab

图像特征提取
特征提取
小波变换可以将图像分解成不同频率的子图像,从而提取出图像在 不同频率下的特征。这些特征可以用于图像分类、识别和比较等应 用。
特征描述
小波变换可以生成一组小波系数,这些系数可以用于描述图像的特 征。通过分析这些系数,可以提取出图像的纹理、边缘和结构等特 征。
应用领域
小波变换在图像特征提取方面的应用广泛,包括医学影像分析、遥感 图像处理、人脸识别和指纹比较等。
05
小波分析的未来发展与展望
小波分析与其他数学方法的结合
小波分析与傅里叶分析的结合
通过小波变换和傅里叶变换的互补性,可以更好地分析信号 的时频特性。
小波分析与分形理论的结合
利用小波分析的多尺度分析能力和分形理论对复杂信号的描 述,可以更好地揭示信号的非线性特征。
小波分析在大数据处理中的应用
高效的数据压缩
高效算法
小波变换具有快速算法,可以 高效地处理大规模数据。
小波变换的应用领域
信号处理
小波变换广泛应用于信号处理领域, 如语音、图像、雷达、地震等信号的 分析和处理。
图像处理
小波变换在图像处理中用于图像压缩、 图像去噪、图像增强等方面。
医学成像
小波变换在医学成像中用于图像重建、 图像去噪、图像分割等方面。
小波变换的压缩效果优于传统的JPEG压缩算法,特别是在处理具有大
量细节和纹理的图像时。
图像增强
图像增强
小波变换可以用于增强图像的细节和边缘信息,提高图像的视觉效果。通过调 整小波系数,可以突出或抑制特定频率的信号,实现图像的锐化、平滑或边缘 检测等效果。
增强效果
小波变换能够有效地增强图像的细节和边缘信息,提高图像的清晰度和对比度。 同时,小波变换还可以用于图像去噪,去除图像中的噪声和干扰。
小波分析的应用及其MATLAB程序的实现

小波分析的应用及其MATLAB 程序的实现 摘要:在简单介绍小波分析的发展的基础上,对傅立叶变换和小波变换比较分析,介绍了小波分析在实际生活中的应用,重点阐述了MA 的应用研究现存的几个TLAB 小波分析信号处理的方法.分析了小波分析在故障诊断中问题,并对解决这些问题和未来的发展进行了探讨。
关键词:小波分析;信号处理;MATLAB1.引言故障诊断中的首要问题就是对观测信号的故障特征提取,即对观测信号进行信号处理,从中获取反映故障信息的特征。
由于故障诊断中所遇到的信号绝大多数都是非平稳信号,而特别适用于非平稳信号处理的工具就是小波分析,所以小波分析在故障诊断中的应用越来越受到人们的青睬。
小波变换的基本思想类似于傅立叶变换,小波分析优于博立叶之处在于它能够实现时域和频域的局部分析,即通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析,从而可以聚焦到信号的任意细节。
因此,小波变换被誉为分析信号的微镜。
现在,小波分析技术在信号处理、图像处理、语音分析、模识别、量子物理、生物医学工程、计算机视觉、故障诊断及众多非线性科学领域都有广泛的应用。
2、从傅立叶变换到小波变换小波分析属于时频分析的一种,传统的信号分析是建立在傅立叶变换的基础上的,由于傅立叶分析使用的是一种全局的变换,要么完全在时域,要么完全在时域,要么完全在频域,因此无法表述信号的时频局域性质,而这种性质恰恰是非平稳信号最根本和最关键的性质。
为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并发展了一系列新的信号分析理论:短时傅立叶变换、Gabor 变换、时频分析、小波变换、分数阶傅立叶变换、线调频小波变换、循环统计量理论和调幅-调频信号分析等。
其中,短时傅立叶变换和小波变换也是应传统的傅立叶变换不能够满足信号处理的要求而产生的。
短时傅立叶变换分析的基本思想是:假定非平稳信号在分析窗函数g (t )的一个短时间间隔内是平稳(伪平稳)的,并移动分析窗函数,使)()(τ-t g t f 在不同的有限时间宽度内是平稳信号,从而计算出各个不同时刻的功率谱。
关于小波分析的matlab程序

关于小波分析的matlab程序小波分析是一种在信号处理和数据分析领域中广泛应用的方法。
它可以匡助我们更好地理解信号的时域和频域特性,并提供一种有效的信号处理工具。
在本文中,我将介绍小波分析的基本原理和如何使用MATLAB编写小波分析程序。
一、小波分析的基本原理小波分析是一种基于窗口函数的信号分析方法。
它使用一组称为小波函数的基函数,将信号分解成不同频率和不同时间尺度的成份。
与傅里叶分析相比,小波分析具有更好的时频局部化性质,可以更好地捕捉信号的瞬时特征。
小波函数是一种具有局部化特性的函数,它在时域上具有有限长度,并且在频域上具有有限带宽。
常用的小波函数有Morlet小波、Haar小波、Daubechies小波等。
这些小波函数可以通过数学运算得到,也可以通过MATLAB的小波函数库直接调用。
小波分析的基本步骤如下:1. 选择合适的小波函数作为基函数。
2. 将信号与小波函数进行卷积运算,得到小波系数。
3. 根据小波系数的大小和位置,可以分析信号的时频特性。
4. 根据需要,可以对小波系数进行阈值处理,实现信号的去噪和压缩。
二、MATLAB中的小波分析工具MATLAB提供了丰富的小波分析工具箱,可以方便地进行小波分析的计算和可视化。
下面介绍几个常用的MATLAB函数和工具箱:1. `waveinfo`函数:用于查看和了解MATLAB中可用的小波函数的信息,如小波函数的名称、支持的尺度范围等。
2. `wavedec`函数:用于对信号进行小波分解,得到小波系数。
3. `waverec`函数:用于根据小波系数重构原始信号。
4. `wdenoise`函数:用于对小波系数进行阈值处理,实现信号的去噪。
5. 小波分析工具箱(Wavelet Toolbox):提供了更多的小波分析函数和工具,如小波变换、小波包分析、小波阈值处理等。
可以通过`help wavelet`命令查看工具箱中的函数列表。
三、编写小波分析程序在MATLAB中编写小波分析程序可以按照以下步骤进行:1. 导入信号数据:首先需要导入待分析的信号数据。
《基于MATLAB的小波分析应用》课件第1章

第1章 小波分析基础
因此,如何求解Wn是下一步需要解决的问题。求解的
基本思想是:找到一个函数 (x) ,像函数 (x) 的伸缩和
平移 {2n/2(2n x k) ;k Z} 能够张成空间Vn一样,函数 (x) 的伸缩和平移 {2n / 2 (2n x k ) ;k Z} 也能张成空间Wn。同
第1章 小波分析基础
图1.5 V4中的分量
第1章 小波分析基础
图1.6 W7中的分量
第1章 小波分析基础
1.3 一维连续小波变换
定义2 设 (t) L2 (R) ,其傅里叶变换为,当满足容许
条件(完全重构条件或恒等分辨条件)
ˆ () 2
C
d
R
时,称 (t) 为一个基本小波或母小波。将母函数经伸缩和 平移后得
ˆ *() ˆ (2 j ) 2
j
由上式可以看出,稳定条件实际上是对上式分母的约束 条件,它的作用是保证对偶小波的傅里叶变换存在。
Wf (a, b)
第1章 小波分析基础
1.4 离散小波变换
在实际运用中,尤其是在计算机上实现时,连续小波
变换必须加以离散化。因此,有必要讨论连续小波 a,b (t)
时要求 (x) 和 (x) 能够建立直接的联系。
第1章 小波分析基础
定理1 设Wn是由形如 kZ ak(2n x k)( ak R)的函数所组成
的线性空间,其中ak含有限个非0项,则Wn构成Vn在Vn+1中 的正交补,并且Vn1 Vn Wn 。
定理2 能量有限空间L2(R)可以分解为如下形式之和: L2 (R) V0 W0 W1
V j {0}, V j L2 (R)
jZ
jZ
(4) 平移不变性:f (x)V0 f (x k)V0 ,k Z ;
MATLAB工具箱的应用实例与推荐

MATLAB工具箱的应用实例与推荐引言:作为一种常用的科学计算软件,MATLAB拥有广泛的工具箱(Toolbox),涵盖了多个领域的专业功能与算法。
本文将介绍几个常用的MATLAB工具箱的应用实例,并推荐一些适合特定需求的工具箱。
一、信号与图像处理工具箱(Signal Processing Toolbox)信号与图像处理工具箱是MATLAB中常用的一个工具箱,它提供了丰富的信号分析和处理函数,能够帮助用户进行信号预处理、滤波、频谱分析等操作。
以下是一个应用实例:实例:心电信号分析在医学领域,心电信号分析是一项重要的研究工作。
使用信号与图像处理工具箱,我们可以通过MATLAB对心电信号进行处理与分析。
首先,可以使用滤波函数对心电信号进行降噪处理,去除不相关的干扰。
接下来,可以利用频谱分析函数,对心电信号进行频域分析,以了解信号的频谱特性。
在结合其他相关算法与方法后,我们可以进一步对心电信号进行心律失常检测、心脏疾病预测等工作。
推荐工具箱:除了信号与图像处理工具箱,在特定的领域和任务中,不同的工具箱也能够提供专门的功能与算法支持。
接下来,将为一些常见的应用领域介绍适用的MATLAB工具箱。
二、控制系统工具箱(Control System Toolbox)控制系统工具箱是专门针对控制系统设计与分析的一个工具箱,它提供了丰富的线性与非线性控制系统函数。
以下是一个应用实例:实例:PID控制器设计在工业自动化过程中,PID(Proportional-Integral-Derivative)控制器是一种常见的控制器类型。
使用控制系统工具箱,我们可以通过MATLAB设计与调整PID 控制器的参数。
首先,可以利用系统建模函数,对被控对象进行建模与参数估计。
接下来,可以使用PID自动调参函数,对PID控制器进行参数优化。
最后,通过对控制系统进行仿真与实时实验,可以验证与评估控制器的性能。
三、优化工具箱(Optimization Toolbox)优化工具箱提供了多种优化算法与函数,用于在数学模型中寻找最优解或近似最优解。
使用MATLAB小波工具箱进行小波分析:

使用MATLAB小波工具箱进行小波分析:如上图所示的小波分解过程,可以调用wfilters 来获得指定小波的分解和综合滤波器系数,例如:% Set wavelet name.wname = 'db5';% Compute the four filters associated with wavelet name given% by the input string wname.[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(wname);subplot(221); stem(Lo_D);title('Decomposition low-pass filter');subplot(222); stem(Hi_D);title('Decomposition high-pass filter');subplot(223); stem(Lo_R);title('Reconstruction low-pass filter');subplot(224); stem(Hi_R);title('Reconstruction high-pass filter');xlabel('The four filters for db5')% Editing some graphical properties,% the following figure is generated.以上例子,得到’db5’小波的分解和综合滤波器系数,并显示出来。
下面是wfilters的具体用法:Wname 可指定为列表中的任意一种小波,直接调用[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('wname')会返回分解和综合滤波器系数。
如果只想返回其中的一些而不是全部,可以调用[F1,F2] = wfilters('wname','type')其中’type’可指定为4种类型,每种类型的具体意义详见matlab wfilters帮助。
Matlab中的小波分析工具箱2

其他的一维函数:
• 抽样: dyaddow • 补零插值:dyaup • 滤波器生成:qmf,orthfilt,wfilters • 反变换:idwt,idwtper, • 重构: upwlev,waverec,wrcoef,
2020/7/10
二维离散小波变换:
• dwt2 [cA,cH,cV,cD]=dwt2(X,’wname’) [cA,cH,cV,cD]=dwt2(X,H,G)
1 s(u) exp[ 1 (u t )2 ]exp[ j2 ( fu qu 2 )]du
t
2 T
2020/7/10
2020/7/10
课程总结:
• 均方意义下的时频局部化概念。 • Gabor变换。 • 连续小波变换。
定义,容许性条件,重构定理。 • 二进小波。
定义,稳定性条件,重构定理。 • 离散小波变换。
?waveinfo('meyr')
MEYRINFO Information on Meyer wavelet.
Meyer Wavelet
General characteristics: Infinitely regular orthogonal wavelet.
2020/7/10
Family Short name
其中:(x)=(1,2,,r )T
2020/7/10
双尺度方程:
( x) Pk (2 x k ) k
其中: Pk是 r r矩阵。 由于研究无穷矩阵序列 的困难,通常的双尺度 方程 为有限项。
M
( x) Pk (2 x k ) k 0
2020/7/10
• 多小波在理论上所表现出来的优势以及它在应用领域所具 有的潜力,使其受到高度重视。在它诞生的短短几年时间 内,从理论方面,多小波的构造、多小波变换实现中,预 滤波器的设计及信号的边界处理正迅速成为新的研究热点 ,而对它在图像处理方面的应用,人们正进行积极探索, 并在静止图像编码、图像去噪两方面取得了一定的成果。
Matlab小波工具箱的使用2

Matlab小波工具箱的使用2工具箱提供了如下函数做一维信号分析:在这一部分,可以学到l 加载信号l 执行一层小波分解l 从系数重建近似和细节l 显示近似和细节l 通过逆小波变换重建信号l 执行多层小波分解l 抽取近似系数和细节系数l 重构第三层近似l 重构第1、2、3层细节l 显示多层分解的结果l 从第三层分解重构原始信号l 从信号中去除噪声l 改善分析l 压缩信号l 显示信号的统计信息和直方图一维分析---使用命令行这个例子包含一个真实世界的信号---测量3天的电功耗。
这个信号很典型,因为它包含一个明显的测量噪声,而小波分析可以有效的移除噪声。
1. 加载信号load leleccum截取信号s = leleccum(1:3920);l_s = length(s);2. 对信号执行一层小波分解使用db1小波执行一层小波分解,执行下面的语句产生近似系数cA1、细节系数cD1 [cA1,cD1] = dwt(s,'db1');3. 从系数中构建近似和细节从系数cA1和cD1中构建一层近似A1和细节D1,执行以下代码A1 = upcoef('a',cA1,'db1',1,l_s);D1 = upcoef('d',cD1,'db1',1,l_s);或A1 = idwt(cA1,[],'db1',l_s);D1 = idwt([],cD1,'db1',l_s);4. 显示近似和细节subplot(1,2,1); plot(A1); title('Approximation A1')subplot(1,2,2); plot(D1); title('Detail D1')5. 使用逆小波变换恢复信号A0 = idwt(cA1,cD1,'db1',l_s);err = max(abs(s-A0))err =2.2737e-0136. 执行多层小波分解执行3层信号分解[C,L] = wavedec(s,3,'db1');函数返回3层分解的各组分系数C(连接在一个向量里),向量L里返回的是各组分的长度。
matlab二进小波变换 -回复

matlab二进小波变换-回复如何在MATLAB中进行二进制小波变换(Binary Wavelet Transform,BWT)。
引言:二进制小波变换(Binary Wavelet Transform,BWT)是一种图像压缩和加密的方法。
它能够将图像转化为一系列包含二进制数的小波系数,这些系数可以通过二进制编码来表示。
本文将介绍如何在MATLAB中使用小波变换工具箱实现二进制小波变换。
第一步:安装小波变换工具箱要使用小波变换工具箱进行二进制小波变换,首先需要确保已经安装了MATLAB小波变换工具箱。
如果没有安装,可以通过以下步骤在MATLAB 中安装该工具箱:1. 打开MATLAB,并点击"Home" 选项卡中的"Add-Ons" 按钮。
2. 在"Add-On Explorer" 窗口中,搜索关键字"Wavelet Toolbox"。
3. 在搜索结果中找到并点击"Wavelet Toolbox"。
4. 点击"Install" 按钮,并按照提示完成安装。
第二步:加载图像加载图像是进行二进制小波变换的第一步。
在MATLAB中,可以使用imread()函数从文件中加载图像。
例如,假设我们的图像文件名为"lena.tif",以下是加载图像的代码:matlabimg = imread('lena.tif');第三步:二进制化图像在进行二进制小波变换之前,需要将图像二进制化。
这意味着将图像的亮度值转换为二进制编码。
在MATLAB中,可以使用im2bw()函数将图像二进制化。
以下是一个示例代码:matlabbw_img = im2bw(img);第四步:选择小波基函数选择小波基函数是进行二进制小波变换的关键一步。
在MATLAB中,可以使用wfilters()函数来选择小波基函数。
Matlab中小波分析工具箱

DWT
possible but without FWT
CWT
possible
Support width
infinite
Effective support [-8 8]
Regularity
indefinitely derivable
Symmetry
yes
Reference: I. Daubechies,
Matlab中小波分析工具箱
其他的一维函数:
抽样: dyaddow 补零插值:dyaup 滤波器生成:qmf,orthfilt,wfilters 反变换:idwt,idwtper, 重构: upwlev,waverec,wrcoef,
Matlab中小波分析工具箱
二维离散小波变换:
dwt2 [cA,cH,cV,cD]=dwt2(X,’wname’) [cA,cH,cV,cD]=dwt2(X,H,G)
其中:cA :低频分量, cH:水平高频分量 cV:垂直高频分量 cD:对角高频分量 X:输入信号。 wname:小波基名称 H:低通滤波器 G:高通滤波器
Matlab中小波分析工具箱
二维信号的多层小波分解:
[A,L]=wavedec2(X,N,’wname’) [A,L]=wavedec2(X,N,H,G) 其中:A :各层分量, L:各层分量长度
Ten lectures on wavelets,
CBMS, SIAM, 61, 1994, 117-119, 137, 152.
Matlab中小波分析工具箱
计算小波滤波器系数的函数:
参数表示
morlet mexihat meyer meyeraux dbwavf dbaux symwavf coifwavf biowavf
Matlab小波工具箱的使用

Matlab小波工具箱的使用1(2011-11-10 20:12:39)转载▼标签:分类:学科知识小波分析连续小波变换尺度系数信号最近想尝试一下小波的用法,就这matlab的帮助尝试了一下它的例子,顺便翻译了一下帮助的内容,发现matlab帮助做的确实不错,浅显易懂!现把翻译的文档写出来吧,想学习的共同学习吧!小波工具箱简介小波工具箱包含了图像化的工具和命令行函数,它可以实现如下功能:l 测试、探索小波和小波包的特性l 测试信号的统计特性和信号的组分l 对一维信号执行连续小波变换l 对一维、二维信号执行离散小波分析和综合l 对一维、二维信号执行小波包分解(参见帮助Using Wavelet Packets)l 对信号或图像进行压缩、去噪另外,工具箱使用户更方便的展示数据。
用户可以做如下选择:l 显示哪个信号l 放大感兴趣的区域l 配色设计来显示小波系数细节工具箱可以方便的导入、导出信息到磁盘或matlab工作空间。
具体详见File Menu Options一维连续小波分析这一部分来测试连续小波分析的特性。
连续小波分析只需要一个小波函数cwt。
在这一部分将学到如下内容:l 加载信号l 对信号执行连续小波变换l 绘制小波系数l 绘制指定尺度的小波系数l 绘制整个尺度小波系数中的最大值l 选择显示方式l 在尺度和伪频率之间切换l 细节放大l 在普通或绝对模式下显示系数l 选择执行小波分析的尺度使用命令行执行连续小波分析这个例子是一个包含噪声的正弦波1. 加载信号load noissin可以使用whos显示信号信息Name Size Bytes Class noissin1x10008000doublec = cwt(noissin,1:48,'db4');函数cwt的参数分别为分析的信号、分析的尺度和使用的小波。
返回值c包含了在各尺度下的小波系数。
对于这里,c是一个48x1000的矩阵,每一行与一个尺度相关。
matlab小波工具箱及其应用

Matlab小波工具箱的相关应用09信息02班玺瑞孟魄 20092294前言在传统的傅里叶分析中,信号是完全在频域展开的,不包含任何时域的信息,这对于某些应用来说是恰当的,因为信号的频率信息对其是非常重要的。
但其丢弃的时域信息可能对某些应用非常重要,所以人们对傅里叶分析进行了推广,如短时傅里叶变换,但是短时傅里叶变换只能在一个分辨率上进行,所以对很多应用来说还不够精确,存在很大的缺陷。
而小波分析则克服了短时傅里叶变换在单分辨率上的缺陷,具有多分辨率分析的特点,在时域和频域都有表征信号局部信息的能力,所以小波运用广泛应用于各个时域分析领域,而matlab小波工具箱正是处理小波变换的一个有用工具。
在matlab中,小波工具箱提供了两种实现方式,命令行方式和图形方式[1]。
命令方式比较灵活,可以看到具体的处理过程,适合对于matlab比较熟悉的人。
而图形方式(GUI, Graphical User Interface)操作简便,界面友好,对于matlab初学者或是不熟悉小波分析具体过程的人来说,GUI是最佳选择。
GUI的主要问题是处理模式相对固定,不如命令行凡是灵活,而且可视化的操作模式看不到具体的操作机制。
本实验运主要进行了,一维小波变换,二维小波变换,图像压缩,图像降噪,边缘提取,图像扩展等操作。
通过本次试验,从命令行方式和GUI方式两个方面,运用到了matlab小波工具箱的部分功能,一方面熟悉了matlab小波工具箱,另一方面,通过matlab 对图像的处理方式,加深了对《数字图像处理》中“数字”的理解。
方法一维离散小波变换公式[2]对于还有其中表示近似值或尺度系数,表示细节或小波系数,,,)是离散变量的函数。
一维连续小波变换连续的平方可积函数的连续小波变换与实数值的小波的关系如下其中,和分别成为尺度和变换参数。
给定,可以通过反连续小波变换求得:其中,是的傅里叶变换。
二维小波变换在二维情况下,需要一个二维尺度函数和三个二维小波和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=6
>( G 6
!% !$.! !$.F$ !% !$.! !6 $>).F$
(, ) >(
!K.
信号的离散小波变换可以看作分别用低通与带通滤 波器将信号分解成低频部分!平滑部分.和高频部分!细节 部 分 . 。它们分 别 反 映 信 号 的 概 貌 和 细 节 , 类似的过程对每 次分解后的低频部分可再重复进行。 按照上述分解规律对 信号进行小波变换, 其结果可理解为信号通过一系列中心 频率不同的带通滤波器组和带宽不同的低通滤波器。
>( 6 ( >( 6
!
小波分析简介
定 义 9 : 设 !:7 , " !# , 则 按 如 下 方 式 生 成 的 函 数 族
; ! !, "! $ . < :
! !, "! $ .= !
>9 6
! ! $>" . !
!9.
! ! $>6 .=6 ! !6 $>). !I. ( 6 相 应 的 离 散 小 波 变 换!简 称 : 小 波 变 换.: ! (, )!$.=6
分析的尺度; ()&*# 为 选 取 的 小 波 。
分 析 结 果 如 图 , 所 示 。其检 测 结 果 与 图 < 一 致 , 但离 散小波变换更易于实际应用。
+>- 一 维 系 数 重 构 函 数 .?3@1A
!"#$%7.?3@1A+9BCD#9 , 3, 5, 9()&*#9 , 8-
相应的计算结 !"#$% 为 重 构 结 果 ; BCD# 可 选 择 & 或 : , 果为平滑部分或细节部分; 与 +,- 中相 3 和 5 为矩阵向量, 同; ()&*# 为 选 取 的 小 波 ; 8 为多分辨率分析的尺度。
>(
称 为 连 续 小 波 或 分 析 小 波 。! !$. 叫 作 小 波 函 数 或 母 小 波
@% , ! !, ":=6
>( G 6
!/,’4%( ?#$%&%’. 。其 中 ! 是 尺 度 参 数 , " 是 时 移 参 数 。改
变 ! 的值, 对 函 数 ! !, " ! $ . 具 有 伸 展 ! !:9. 和 收 缩 ! !@9. 的 作 用 。参 数 " 起 着 平 移 的 作 用 。小 波 ! ! $ . 的 选 择 并 不 是 任 意 的,也不是唯一的。它的选择应满足定义域是紧支撑的
上 式 中 % !$. 对 应 于 信 号 , 小 波 变 换 就 像用 镜 头 相 对 于 目标平行移动, ! !$. 代 表 镜 头 所 起 的 作 用 , " 相当于使镜 头相对于目标平行移动, ! 的作用相当于镜头向目标推进 或远离。当 ! 较大时, 视野宽而分析频率低, 可以做平滑 部 分!概 貌.的 观 察 ; 当 ! 较小时, 视野窄而分析频率高, 可 以 对细 节 进行观 察 。 前 面 所 述 的 连 续 小 波 变 换 由 于 计 算 量 及存 储 量 大 , 所以多 用 于 理 论 分 析 方 面 。实 际 应 用 中 需 要 对 尺 度 参 数 ! 和定位参数 " 进行离散化处理。 可以选取: != !7(! ( 是 整 数 , 选 取 " = )" 7!7(! " 7:7 , 于是有: ! 7:9. ; ) 为 整 数.,
+,- 多 分 辨 率 分 析 函 数 ./01213
43 , 567./01213+% , 8, 9()&*#9-
为 矩 阵 向 量 4!&) , … 3 为多分辨率分析结果, !:) ;< , … !:=6 ; 5 为多分辨率分析结果中矩阵向量的对应长度
4’&) , ’:);< , … … ’:=6 ; % 为被分析的信号; 8 为多分辨率
分析结果如图 < 所示。从图中可以清晰地看出突变 点 发 生 在 M== 点 处 。
分 析 结 果 如 图 > 所 示 。从 图 中 可 以 看 出 , 信号的整体 变化趋势被清晰地显示出来。
在对信号进行离散变换时, 常 常 先 将 其 利 用 (&N#:#! 进行多分辨率分析, 进而对其结果进行重构, 其实质是提 取 感 兴 趣 的 特 征 。应 用 如 下 :
基于 !"#$"% 小波工具箱的开发与应用
天 津 大 学 管 理 学 院 !"###$%&
摘
要 : !"#$"% 环 境 下 小 波 工 具 箱 的 使 用 方 法 和 技 巧 , 通过实例介绍了小波工具箱相关函 小波分析 信号
数的应用并给出了图形结果的输出方法。 关 键 词 : !"#$"% 语 言
*P7 7 7Q, 和 图 % 相 应 程 序 中 的 OHLR *GSE *E, , T UT , 就 能 达 到
目的,-’ 具 有 大 量 丰 富 的 数 值 计 算 及 图 像处 理 功 能
的函数。 实用的小波工具箱为小波的应用奠定了坚实的基 础 。它 具 有 操 作 简 单 方 便 、 性能稳定、 运行可靠等优点, 为
!
应用实例
通过上面叙述的连续小波变换函数可以方便地计算
出 相 应 的 结 果 。具 体 如 下 :
+<- 含 突 变 点 信 号 $E#FGEH 的 连 续 小 波 变 换 *#%I 图 J/K5/L 源 程 序 :
’"&: $E#FGEH ; %7$E#FGEH ; !"#$%73.K+% , <: >= , 9*"E’9- ; !"’"E*&D+4= = =6*#%I+&G%+!"#$%-- ;
/.$ 控 制 - ; > 采 样 , /.<=/.? 接 < 路 开 关 量 输 出 。
模拟 ; 数字转换采用 % *%, 模 拟 量 数 据 采 集 通 道。 种方式: +% 位 - ; > 转 换 方 式 和 满 刻 度 为 <#@A 的 实现精确定点与 8B. 转 换 方 式 。 利 用 琐 相 环 技 术 , 定时采样。 输入可复用开关量输入接口的 1 只 *$, 人机接口。 按键, 用户可自定义其功能。输出采用 6.> 液晶显示 器或者通过串入并出的数码管显示及打印机输出。 采 用 实 时 时 钟 >2+%11? *<,>2+%11? 实 时 时 钟。 芯片以 提 供 时 间 信 息 。
*收 稿 日 期 : %77+J++J++,
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
( 上接第 %7 页)
%9%9% 扩 展 功 能 接 口 *+,: ; " 端 口 扩 展。采 用 1%)) 可 编 程 芯 片 扩 展
外部 < %< 路 : ; " 接 口 。 /- 口 作 为 开 关输入量 接 口 , 路空接点开关量输入与 1 只按键混合使用。 /’ 口 输 出 为 打 印 机 数 据 总 线 接 口 。 /. 口 的 < 根 口 线 /.7=
广大工程技术人员开发小波应用程序提供了方便的工具。 参考文献
+ % $
陈 逢 时9子 波 变 换 理 论 及 其 在 信 号 处 理 中 的 应 用9北 京 : 国 防工业出版社, +CC1 赵松年, 熊 小 芸9子 波 变 换 与 子 波 分 析9北 京 : 电子工业出 版社, +CC? 李江红, 田 涛 9#GRHGS 和 8DEFGH .II 接 口 中 编 译 环 境 的 设 置9微 型 机 与 应 用 , %777 ; *<,
!A,-B#C’ DEBB,(’. , 即 在 一 个 很 小 的 区 间 之 外 , 函 数 为
零, 函数应有速降特性, 以 便 获 得 空 间 局 域 化 。另 外 , 它还 要满足平均值为零, 即小波应具有振荡性, 而且是一个迅 速衰减的短波。 定 义 6: 设 ! ! $.为 小 波 函 数 , 对 ; ! !, " ! $ .< 按 式 !9. 给 出 ,
+ >- 含 噪 声 的 正 弦 信 号 )"R%%R) 的 离 散 小 波 变 换 J/K5/L 源 程 序 :
’"&: )"R%%R) ; %7)"R%%R) ; ’%7’#)OBI+%- ; 43 , 567(&N#:#!+% , P, 9:GM9- ; /P7(E!"#$+9&9 , 3, 5, 9:GM9 , P- ; 2P7(E!"#$+9:9 , 3, 5, 9:GM9 , <- ; %QGD’"B+> , <, <- ; D’"B+&G%+%- , 9H9- ; %QGD’"B+> , <, ,- ; D’"B+&G%+/P- , 9H9- ; %QGD’"B+> , <, >- ; D’"B+&G%+2P- , 9H9- ;
/01203 是 美 国 /#’4",(5* 公 司 于 67 世 纪 87 年 代
推 出的 一 种 以 矩 阵 为 基 本 编 程 单 元 的 高 效 数 值 计 算 语 言, 它集科学计算、 信号处理、 图 像处 理 于 一 体 。本 文 旨 在 介 绍 利 用 /01203 小 波 工 具 箱 处 理 实 际 应 用 问 题 的 技 术和方法。
