自适应模糊PID控制器及其MATLAB仿真

合集下载

模糊_PID控制的MATLAB仿真分析

图４ＰＩＤ和模糊ＰＩＤ响应曲线
参考资料［１］舒进．电液比例控制多轮独立转向技术研究：［博士学位论文］．北京：北京理工大学，２００４［２］陈丽兰．模糊ＰＩＤ控制器的控制策略研究．煤矿自动化，２００１．２：１３－１４［３］周恩涛，廖生行，牟丹．电液比例阀控系统模糊－ＰＩＤ控制的研究．机床与液压，２００３．１６：２２５－２２７［４］张颖超，郭姝梅．ＭＡＴＬＡＢ及其在模糊控制系统仿真中的应用．系统仿真学报，２００１．１１：３１９－３２０，３２６［５］储岳中，陶永华．基于ＭＡＴＬＡＢ的自适应模糊ＰＩＤ控制系统计算机仿真．安徽工业大学学报，２００１．１：４９－５２［６］朱摩西．模糊ＰＩＤ控制器，工业控制计算机，１９９６．３：１９－２０
２．２成孔与清孔质量控制２．２．１孔的垂直度控制在准确放样后进行护筒埋设，在护筒上口作好桩中心标记以便钻机对中。钻机对中过程中，应注意钻机底座的水平问题。底座本身即与水平面不平行，致使钻杆夹具无法保持水平，引起钻杆的不垂直，从而影响灌注桩的垂直性，尽管此时钻头中心与护筒所标设的桩中心重合，而实际桩位已偏斜。因此在对位及钻孔过程中，均应观测调整钻机的水平和垂直度。在施工过程中，监理应随时注意观察钻杆的垂直度情况。２．２．２入岩和终孔入岩和终孔是影响钻孔灌注桩承载力的重要因素。实际操
１．３偏差变化ＥＣ的大小表明偏差变化的速率，ＥＣ越大，ＫＰ取值越小，ＫＩ取值越大，反之亦然。
１．４微分作用类似于人的预见性，它阻止偏差的变化，有助于减小超调，克服振荡，使系统趋于稳定，加快系统的动作速度，减小调整时间，改善系统的动态性能。因此，在Ｅ较大时，ＫＤ取零，实际为ＰＩ控制；在Ｅ较小时，ＫＤ取一正直，实行ＰＩＤ控制。

自适应模糊PID控制器的设计与仿真

自适应模糊PID控制器的设计与仿真自适应模糊PID控制器是一种结合了模糊控制和PID控制的自适应控制器，它能够在系统的不同工况下根据实际需求对PID参数进行自适应调整，从而使得系统具有更好的动态性能和稳定性。

本文将介绍自适应模糊PID控制器的设计思路和仿真过程。

1.设计思路1.1系统建模首先需要对待控制的系统进行建模，得到系统的数学模型。

这可以通过实验数据或者理论分析来完成。

一般情况下，系统的数学模型可以表示为：$G(s)=\frac{Y(s)}{U(s)}=\frac{K}{s(Ts+1)}$其中，K是系统的增益，T是系统的时间常数。

1.2设计模糊控制器接下来需要设计模糊控制器，包括模糊规则、模糊集和模糊运算等。

模糊控制器的输入是系统的误差和误差的变化率，输出是PID参数的调整量。

1.3设计PID控制器在模糊控制器的基础上，设计PID控制器。

PID控制器的输入是模糊控制器的输出，输出是控制信号。

1.4设计自适应机制引入自适应机制，根据系统的性能指标对PID参数进行自适应调整。

一般可以采用Lyapunov函数进行系统性能的分析和优化。

2.仿真过程在仿真中，可以使用常见的控制系统仿真软件，如MATLAB/Simulink 等。

具体的仿真过程如下：2.1设置仿真模型根据系统的数学模型，在仿真软件中设置仿真模型。

包括系统的输入、输出、误差计算、控制信号计算等。

2.2设置模糊控制器根据设计思路中的模糊控制器设计，设置模糊控制器的输入和输出，并设置模糊规则、模糊集和模糊运算等参数。

2.3设置PID控制器在模糊控制器的基础上，设置PID控制器的输入和输出，并设置PID参数的初始值。

2.4设置自适应机制设置自适应机制，根据系统的性能指标进行PID参数的自适应调整。

2.5运行仿真运行仿真，观察系统的响应特性和PID参数的变化情况。

根据仿真结果可以对设计进行调整和优化。

3.结果分析根据仿真结果，可以分析系统的稳定性、动态性能和鲁棒性等指标，并对设计进行调整和改进。

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)

模糊自适应整定PID控制matlab仿真程序(刘金锟-先进PID控制及其MATLAB仿真)2这个例子的程序百度文库里有很多版本，但我下了很多都有错误，运行不了。

以下程序我一字一字的敲出来的，已经成功运行，绝对无误。

仿真实例，被控对象为p G (s)=ss s 1047035.8752350023++ 采样时间为1ms ，采用模糊PID 控制进行阶跃响应，在第300个采样时间时控制器输出加1.0的干扰，相应的运行结果如图1~13所示。

仿真程序如下：将以下程序保存为fuzzypid.m 文件，即可得到仿真结果。

%fuzzy tunning PID controlclear all ;clear all ;a=newfis('fuzzpid');a=addvar(a,'input','e',[-3,3]); %parameter ea=addmf(a,'input',1,'NB','zmf',[-3,-1]);a=addmf(a,'input',1,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',1,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',1,'Z','trimf',[-2,0,2]);a=addmf(a,'input',1,'PS','trimf',[-1,1,3]);a=addmf(a,'input',1,'PM','trimf',[0,2,3]);a=addmf(a,'input',1,'PB','smf',[1,3]);a=addvar(a,'input','ec',[-3,3]); %parameter eca=addmf(a,'input',2,'NB','zmf',[-3,-1]);a=addmf(a,'input',2,'NM','trimf',[-3,-2,0]);a=addmf(a,'input',2,'NS','trimf',[-3,-1,1]);a=addmf(a,'input',2,'Z','trimf',[-2,0,2]);a=addmf(a,'input',2,'PS','trimf',[-1,1,3]);a=addmf(a,'input',2,'PM','trimf',[0,2,3]);a=addmf(a,'input',2,'PB','smf',[1,3]);a=addvar(a,'output','kp',[-0.3,0.3]); %parameter kpa=addmf(a,'output',1,'NB','zmf',[-0.3,-0.1]);a=addmf(a,'output',1,'NM','trimf',[-0.3,-0.2,0]);a=addmf(a,'output',1,'NS','trimf',[-0.3,-0.1,0.1]);a=addmf(a,'output',1,'Z','trimf',[-0.2,0,0.2]);a=addmf(a,'output',1,'PS','trimf',[-0.1,0.1,0.3]);a=addmf(a,'output',1,'PM','trimf',[0,0.2,0.3]);a=addmf(a,'output',1,'PB','smf',[0.1,0.3]);a=addvar(a,'output','ki',[-0.06,0.06]); %parameter ki a=addmf(a,'output',2,'NB','zmf',[-0.06,-0.02]);a=addmf(a,'output',2,'NM','trimf',[-0.06,-0.04,0]);a=addmf(a,'output',2,'NS','trimf',[-0.06,-0.02,0.02]); a=addmf(a,'output',2,'Z','trimf',[-0.04,0,0.04]);a=addmf(a,'output',2,'PS','trimf',[-0.02,0.02,0.06]);a=addmf(a,'output',2,'PM','trimf',[0,0.04,0.06]);a=addmf(a,'output',2,'PB','smf',[0.02,0.06]);a=addvar(a,'output','kd',[-3,3]); %parameter kda=addmf(a,'output',3,'NB','zmf',[-3,-1]);a=addmf(a,'output',3,'NM','trimf',[-3,-2,0]);a=addmf(a,'output',3,'NS','trimf',[-3,-1,1]);a=addmf(a,'output',3,'Z','trimf',[-2,0,2]);a=addmf(a,'output',3,'PS','trimf',[-1,1,3]);a=addmf(a,'output',3,'PM','trimf',[0,2,3]);a=addmf(a,'output',3,'PB','smf',[1,3]);rulelist=[1 1 7 1 5 1 1;1 2 7 1 3 1 1;1 3 62 1 1 1;1 4 62 1 1 1;1 5 5 3 1 1 1;1 6 4 42 1 1;1 7 4 4 5 1 1;2 1 7 1 5 1 1;2 2 7 13 1 1;2 3 6 2 1 1 1;2 4 53 2 1 1;2 5 53 2 1 1;2 6 4 43 1 1;2 734 4 1 1;3 1 6 14 1 1;3 2 6 2 3 1 1;3 3 6 3 2 1 1;3 4 5 3 2 1 1;3 54 4 3 1 1;3 6 3 5 3 1 1;3 7 3 54 1 1;4 1 6 2 4 1 1;4 2 6 2 3 1 1;4 35 3 3 1 1;4 4 4 4 3 1 1;4 5 3 5 3 1 1;4 6 2 6 3 1 1;4 7 2 6 4 1 1;35 1 5 2 4 1 1;5 2 5 3 4 1 1;5 3 4 4 4 1 1;5 4 3 5 4 1 1;5 5 3 5 4 1 1;5 6 2 6 4 1 1;5 7 2 7 4 1 1;6 1 5 47 1 1;6 2 4 4 5 1 1;6 3 3 5 5 1 1;6 4 2 5 5 1 1;6 5 2 6 5 1 1;6 6 27 5 1 1;6 7 1 7 7 1 1;7 1 4 4 7 1 1;7 2 4 4 6 1 1;7 3 2 5 6 1 1;7 4 2 6 6 1 1;7 5 2 6 5 1 1;7 6 1 7 5 1 1;7 7 1 7 7 1 1];a=addrule(a,rulelist);a=setfis(a,'DefuzzMethod','mom');writefis(a,'fuzzpid');a=readfis('fuzzpid');%PID controllerts=0.001;sys=tf(5.235e005,[1,87.35,1.047e004,0]); dsys=c2d(sys,ts,'tustin');[num,den]=tfdata(dsys,'v');u_1=0.0;u_2=0.0;u_3=0.0;y_1=0;y_2=0;y_3=0;x=[0,0,0]';4error_1=0;e_1=0.0;ec_1=0.0;kp0=0.40;kd0=1.0;ki0=0.0;for k=1:1:500time(k)=k*ts;rin(k)=1;%using fuzzy inference to tunning PIDk_pid=evalfis([e_1,ec_1],a);kp(k)=kp0+k_pid(1);ki(k)=ki0+k_pid(2);kd(k)=kd0+k_pid(3);u(k)=kp(k)*x(1)+kd(k)*x(2)+ki(k)*x(3);if k==300 %adding disturbance(1.0v at time 0.3s)u(k)=u(k)+1.0;endif u(k)>=10u(k)=10;endif u(k)<=-10u(k)=-10;endyout(k)=-den(2)*y_1-den(3)*y_2-den(4)*y_3+num(1)*u(k)+num(2)*u_1+num(3)*u_2+num(4)*u_3;error(k)=rin(k)-yout(k);%%%%%%%%%%%%%%%%%%%%%%%%%return of pid parameters%%%%%%%%%%%%%%%%%%%%%%%% u_3=u_2;u_2=u_1;u_1=u(k);y_3=y_2;y_2=y_1;y_1=yout(k);5x(1)=error(k); %calculating Px(2)=error(k)-error_1; %calculating Dx(3)=x(3)+error(k); %calculating De_1=x(1);ec_1=x(2);error_2=error_1;error_1=error(k);endshowrule(a)figure(1);plot(time,rin,'b',time,yout,'r'); xlabel('time(s)');ylabel( 'rin,yout');figure(2);plot(time,error,'r');xlabel('time(s)');ylabel( 'error ');figure(3);plot(time,u,'r');xlabel('time(s)');ylabel( 'u ');figure(4);plot(time,kp,'r');xlabel('time(s)');ylabel( 'kp ');figure(5);plot(time,ki,'r');xlabel('time(s)');ylabel( 'ki ');figure(6);plot(time,kd,'r');xlabel('time(s)');ylabel( 'kd ');figure(7);plotmf(a,'input',1);figure(8);plotmf(a,'input',2);figure(9);plotmf(a,'output',1);figure(10);plotmf(a,'output',2);figure(11);plotmf(a,'output',3);plotfis(a);fuzzy fuzzpid.fis6仿真运行结果：789。

模糊PID控制器设计及MATLAB仿真_李健

图 1 模糊 PID 控制结构图
PID 参数模糊自整定是先找出 PID 控制器的 3 个参数 Kp、 Ki 和 Kd 与偏差 e 和偏差变化率 ec 之间的模糊关系，在运行中通过不断检测 e 和 ec，根据模糊控制规则来对 3 个参量进行在
线修改，以满足不同 e 和 ec 对控制器参数的不同要求，从而使
起较大的超调。微分系数 Kd 影响系统的动态特性，Kd 越大，越
能抑制偏差变化，但过大会延长调节时间，降低抗干扰能力。
根据参数 Kp、Ki、Kd 对系统输出特性的影响情况，可归纳出系统在被控过程中对于不同的偏差和偏差变化率，参数 Kp、Ki、 Kd 的自整定原则：
摘要将模糊控制器和 PID 控制器结合在一起，构造了一个模糊 PID 控制器，利用模糊推理的方法调整 PID 控制器的参数，并利用 MATLAB 的 SUMLINK 工具箱，对系统进行仿真，仿真结果表明模糊 PID 控制器能使系统达到满意的控制效果。关键词：PID 控制器，模糊控制，MATLAB，SIMULINK，系统仿真
1．3 模糊控制算法的确立
PID 参数的整定必须考虑到在不同时刻 3 个参数的作用以
及相互之间的互联关系。模糊自整定 PID 是在 PID 算法的基础
上通过计算当前系统误差 e 和误差变化 ec，利用模糊规则进行
模糊推理，查询模糊矩阵表进行参数调整。参数修正公式：
＇
Kp ＝Kp ＋（e，ec）p
被控对象具有良好的动、静态性能。
1．2 PID 控制器的确立
通常，PID 控制器的控制算式为：

模糊pidmatlab(simulink)仿真详细步骤

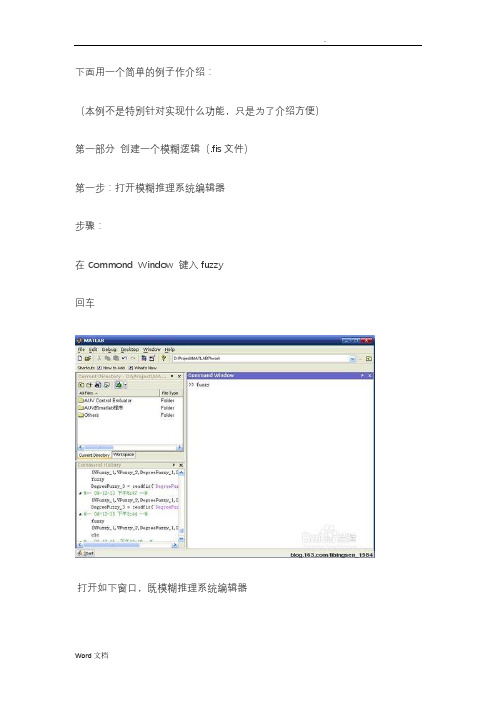
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name中键入名称，在Type 中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

模糊自适应PID控制控制的Matlab仿真设计研究

模糊自适应PID控制的Matlab仿真设计研究姓名：陈明学号：201208070103班级：湖南大学智能1201一、模糊控制思想、PID控制理论简介：在工业生产过程中，许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。

通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现．便于工程应用。

1.1模糊控制的思想：应用模糊数学的基本理论和方法, 控制规则的条件、操作用模糊集来表示、并把这些模糊控制规则以及有关信息, 诸如PID 控制参数等作为知识存入计算机知识库, 然后计算机根据控制系统的实际情况(系统的输入, 输出) , 运用模糊推理。

1.2PID算法：u (t) = Kp·e (t) + Ki·∫t0e (t) dt + Kd·de (t)dt= Kp e (t) + Ki Σei (t) + Kdec (t)其中, u (t) 为控制器输出量, e ( t ) 为误差信号, ec (t) 为误差变化率, Kp , Ki , Kd 分别为比例系数、积分系数、微分数。

然而，课本中，为了简化实验难度，只是考虑了kp，ki参数的整定。

1.3模糊PID控制器的原理图：二、基于Matlab的模糊控制逻辑模块的设计关于模糊逻辑的设计，主要有隶属函数的编辑，参数的选型，规则导入，生成三维图等2.1 模糊函数的编辑器的设定：打开matlab后，在命令窗口输入“fuzzy”，回车即可出现模糊函数编辑器，基本设置等。

基于课本的实验要求，我选的是二输入（e, e c）二输出（k p ,k i）。

需要注意的是，在命名输入输出函数的时候，下标字母需要借助下划线的编辑，即e_c 能够显示为e c。

2.2四个隶属函数的N, Z, P 函数设定：在隶属函数的设定中，N 选用的是基于trimf（三角形隶属函数） , Z是基于zmf （Z型隶属函数），P是基于smf（S型隶属函数）。

模糊PID基本原理及matlab仿真实现(新手!新手!新手!)

模糊PID基本原理及matlab仿真实现（新⼿！新⼿！新⼿！）有关模糊pid的相关知识就把⾃⼰从刚接触到仿真出结果看到的⼤部分资料总结⼀下，以及⼀些⾃⼰的ps以下未说明的都为转载内容在讲解模糊PID前，我们先要了解PID控制器的原理（本⽂主要介绍模糊PID的运⽤,对PID控制器的原理不做详细介绍）。

PID控制器（⽐例-积分-微分控制器）是⼀个在⼯业控制应⽤中常见的反馈回路部件，由⽐例单元P、积分单元I和微分单元D组成。

PID控制的基础是⽐例控制；积分控制可消除稳态误差，但可能增加超调；微分控制可加快⼤惯性系统响应速度以及减弱超调趋势。

1.1传统PID控制传统PID控制器⾃出现以来，凭借其结构简单、稳定性好、⼯作可靠、调整⽅便等优点成为⼯业控制主要技术。

当被控对象的结构和参数具有⼀定的不确定性，⽆法对其建⽴精确的模型时，采⽤PID控制技术尤为⽅便。

PID控制原理简单、易于实现，但是其参数整定异常⿇烦。

对于⼩车的速度控制系统⽽⾔，由于其为时变⾮线性系统不同时刻需要选⽤不同的PID参数，采⽤传统的PID控制器，很难使整个运⾏过程具有较好的运⾏效果。

1.2模糊PID控制模糊PID控制，即利⽤模糊逻辑并根据⼀定的模糊规则对PID的参数进⾏实时的优化，以克服传统PID参数⽆法实时调整PID参数的缺点。

模糊PID控制包括模糊化，确定模糊规则，解模糊等组成部分。

⼩车通过传感器采集赛道信息，确定当前距赛道中线的偏差E以及当前偏差和上次偏差的变化ec，根据给定的模糊规则进⾏模糊推理，最后对模糊参数进⾏解模糊，输出PID控制参数。

2.1模糊化模糊控制器主要由三个模块组成：模糊化，模糊推理，清晰化。

具体如下图所⽰。

⽽我们将⼀步步讲解如何将模糊PID算法运⽤到智能车上。

（最好⽤笔⼀步步⾃⼰写⼀遍）⾸先我们的智能车会采集到赛道的相关数据，例如摄像头车，其采集到的数据经过算法处理之后会得到与中线的偏差E，以及当前偏差和上次偏差的变化（差值）EC两个值（即此算法为2维输⼊，同理也可以是1维和3维，但2维更适合智能车）。

模糊自适应PID控制器及Simulink仿真(本科论文毕业论文)

模糊自适应PID控制器及Simulink仿真作者姓名专业电气工程及其自动化指导教师姓名专业技术职务讲师山东轻工业学院本科毕业设计（论文）原创性声明本人郑重声明：所呈交的毕业设计（论文），是本人在指导教师的指导下独立研究、撰写的成果。

设计（论文）中引用他人的文献、数据、图件、资料，均已在设计（论文）中加以说明，除此之外，本设计（论文）不含任何其他个人或集体已经发表或撰写的成果作品。

对本文研究做出重要贡献的个人和集体，均已在文中作了明确说明并表示了谢意。

本声明的法律结果由本人承担。

毕业设计（论文）作者签名：2012年6月6日山东轻工业学院关于毕业设计（论文）使用授权的说明本毕业设计（论文）作者完全了解学校有关保留、使用毕业设计（论文）的规定，即：学校有权保留、送交设计（论文）的复印件，允许设计（论文）被查阅和借阅，学校可以公布设计（论文）的全部或部分内容，可以采用影印、扫描等复制手段保存本设计（论文）。

指导教师签名：毕业设计（论文）作者签名：年月日2012年6月6日目录摘要 (1)ABSTRACT (1)第一章绪论 (1)1.1PID控制器的发展与应用 (1)1.2PID控制器参数设置中存在的问题 (2)模糊自适应PID控制器发展研究现状 (2)1.4本文的主要工作 (4)第二章 PID控制原理简介 (4)引言 (4)2.2PID控制原理 (5)2.3PID控制器系统概述 (5)2.3.1比例控制(P) (7)2.3.2 积分调节(I) (7)微分调节(D) (9)第三章 PID控制器应用技术简介 (10)数字PID控制算法原理 (11)位置式PDI控制算法 (11)3.3控制规律的选择 (12)3.4PID控制器的参数整定 (13)第四章模糊PID控制器及系统仿真 (13)模糊自适应PID控制系统 (13)4.2常规PID和模糊自适应PID控制系统的仿真比较 (14)常规PID控制系统仿真 (14)模糊自适应PID控制系统仿真 (16)二者的比较 (18)第五章总结 (20)参考文献 (23)致谢 (24)摘要随着工业生产的发展，于20世纪30年代，美国开始使用PID功调节器，它比直接作用式调节器具有更好的控制效果，因而很快得到了工业界的认可。

基于MATLAB的PID控制器参数整定及仿真

基于MATLAB的PID控制器参数整定及仿真PID控制器是一种经典的控制器，在工业自动化控制系统中广泛应用。

其主要功能是根据系统的误差信号，通过调整输出信号的比例、积分和微分部分来减小误差，并达到系统的稳定控制。

PID控制器参数整定是指确定合适的比例常数Kp、积分常数Ki和微分常数Kd的过程。

本文将介绍基于MATLAB的PID控制器参数整定及仿真的方法。

首先，在MATLAB中建立一个包含PID控制器的模型。

可以通过使用MATLAB的控制系统工具箱来实现这一过程。

在工具箱中，可以选择合适的建模方法，如直接设计模型、积分节点模型或传输函数模型。

通过这些工具，可以方便地建立控制系统的数学模型。

其次，进行PID控制器参数整定。

PID控制器参数整定的目标是通过调整比例常数Kp、积分常数Ki和微分常数Kd，使系统的响应特性达到最佳状态。

常用的PID参数整定方法有经验法、试误法、Ziegler-Nichols方法等。

1.经验法：根据系统的特性和经验，选择合适的PID参数。

这种方法常用于初步整定，但可能需要根据实际情况调整参数。

2.试误法：通过逐步试验和调整PID参数，使系统的输出响应逐渐接近期望值，从而达到最佳控制效果。

3. Ziegler-Nichols方法：该方法是一种经典的系统辨识方法，通过测试系统的临界稳定性，得到系统的传递函数参数，并据此计算出合适的PID参数。

最后，进行PID控制器参数整定的仿真。

在MATLAB中，可以通过使用PID模块进行仿真。

可以输入相应的输入信号和初始参数，观察系统的输出响应，并通过调整参数，得到最佳的控制效果。

总结起来，基于MATLAB的PID控制器参数整定及仿真的过程包括：建立控制系统模型、选择PID参数整定方法、进行PID参数整定、进行仿真实验。

PID控制器参数整定的好坏直接影响控制系统的工作性能。

通过基于MATLAB的仿真实验，可以方便地调整和优化控制系统的PID参数，提高系统的响应速度、稳定性和抗干扰性能。

自适应模糊PID控制系统及其MATLAB仿真

关键词：自适应；Ｉ制；ＴＡＰＤ控ＭＡＬＢ仿真中图分类号：Ｐ９．；ｉ７．Ｔ３１９Ｔｔ３４２
争・・・・・・・・・争夺夺夺夺夺争夺争
文献标识码：Ａ
文章编号：７－６（０１０－０４０１１８４２１）５０３－６７２
第１０卷
第５期
漯河职业技术学院学报
ＪｕａｆＬｕｈｃｔｏａｃｎｌｇｌｅｅｏｒｌｏｏｅＶｏａｉｎｌＴｅｈｏｏｙＣｏｌｇｎ
Ｖｏ．１Ｎｏ．１０５
Ｓｐ２１ｅ．０１
２１０１年９月
ｄｉ１．９９ｊｉｎ１７－８４２１．５０５ｏ：０３６／．ｓ．６１７６．００．１ｓ１
摘
要：据自适应ＰＤ控制系统的结构和原理，究ＭＴＡ根Ｉ研ＡＬＢ仿真工具箱及仿真方法，并给出仿真实例和分
析结果。将自适应技术和ＰＤ控制技术相结合，以辅助软件ＭＴＡＩ借ＡＬＢ有力地验证了这一技术的优势。
定，据专家或者操作者的手动控制经验总结出来的一即根
系列控制规则也即模糊控制规则表。模糊控制规则一般具有如下形式：
系统相结合，构建自适应模糊ＰＤ控制系统，用模糊推Ｉ运理，实现对ＰＤ参数的实时调整，了验证自适应技术对Ｉ为ＰＤ控制的改进，Ｉ文章通过ＭＴＡＡＬＢ的ＳＬＮＩＩＫ模块对ＭＵ

自适应模糊PID 控制器的设计及基于MATLAB 的计算机仿真

自适应模糊P I D控制器的设计及基于M AT LAB的计算机仿真Ξ侯北平,卢　佩,付连昆(天津轻工业学院自动化系,天津300222) 摘　要:将模糊控制器和P I D控制器结合在一起,利用模糊逻辑控制实现了P I D控制器参数在线自调整,进一步完善了P I D控制器的性能,提高了系统的控制精度。

并把M A TLAB中的Fuzzy Too lbox和S I M UL I N K有机结合起来,方便的实现了该自适应模糊P I D控制系统的计算机仿真,拓宽了Fuzzy Too lbox和S I M UL I N K的应用范围。

关键词:模糊控制;P I D控制器;M A TLAB;S I M UL I N K;系统仿真中图分类号:T P273+.4;T P391.9　文献标识码:A　文章编号:10012456X(2001)0420032204THE D ESIGN OF SEL F-ADAPT IVE FUZZ Y P I D CONTROLL ERAND ITS COM PUTER SI M ULAT I ON BASED ON M AT LABHOU Be i-p i ng,L U Pe i,FU L i an-kun(D ep artm en t of A u tom ati on Engineering T ian jin U n iversity of L igh t Indu stry,T ian jin300222,Ch ina)Abstract:T he u sing of Fuzzy logic con tro ller m akes the param eter’s self2adap ti on of P I Dcon tro ller po ssib le w hen Fuzzy logic con tro ller and P I D con tro ller are com b ined together.Italso perfects the p roperties of P I D con tro ller and i m p roves the p recisi on of con tro l system.T he o rgan ic com b inati on of Fuzzy Too lbox and S I M UL I N K realized the compu ter si m u lati onof th is self2adap tive Fuzzy P I D con tro l system conven ien tly,and also p romo tes the app licati onof M A TLAB.Keywords:Fuzzy L ogic con tro l;P I D con tro ller;M A TLAB;S I M UL I N K;System si m u lati on M A TLAB是M ath W o rk s公司1982年推出的一套高性能的数值计算和可视化软件,到目前它已发展成为国际公认最出色的数学应用软件。

模糊pid_matlab(simulink)仿真详细步骤

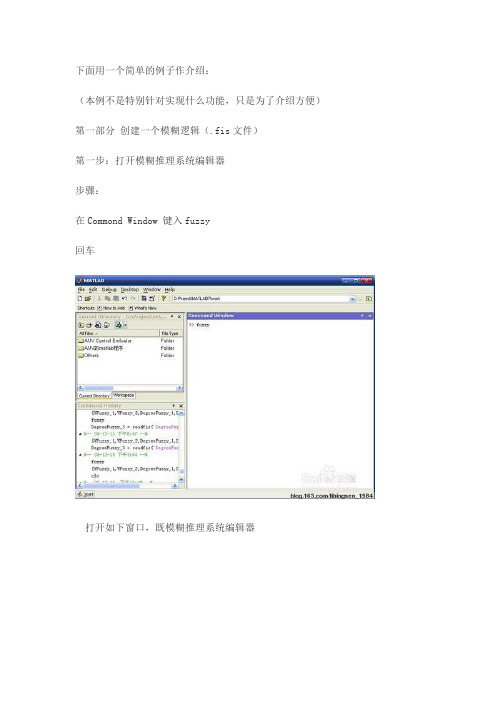
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值围，本例中In_x和In_y的取值围均为[0 10], Out_x和Out_y的取值围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type 中选择形状，在Params中键入围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

基于MATLAB的模糊PID控制器的设计

基于MATLAB的模糊PID控制器的设计模糊PID控制器是一种能够根据系统的实际输出和设定值之间的误差来决定系统的控制量的控制器。

它结合了传统的比例、积分和微分控制器的优点，并通过模糊逻辑来优化控制效果。

在MATLAB中设计模糊PID控制器，我们需要先确定控制系统的模型。

假设我们要设计一个温度控制器，温度传感器测得的温度与设定值之间的误差可以作为输入。

根据传感器的精度和系统的响应特性，我们可以确定模糊PID控制器的参数范围和输出范围。

首先，我们需要定义模糊PID控制器的输入和输出的模糊集合。

例如，温度误差可以划分为“负大”、“负中”、“负小”、“零”、“正小”、“正中”和“正大”等模糊集合。

根据经验和系统要求，可以设定每个模糊集合的范围和模糊隶属度函数。

接下来，我们需要确定模糊PID控制器的规则库。

规则库定义了根据输入的模糊集合和模糊规则来决定输出的模糊集合。

例如，如果温度误差为“负大”且误差变化率为“正中”，则输出的控制量可以设定为“增大”。

在MATLAB中，可以使用Fuzzy Logic Toolbox工具箱来设计模糊PID控制器。

首先，需要创建一个fuzzy对象，用于描述模糊逻辑系统。

然后，可以使用addInput、addOutput和addRule等函数来定义模糊逻辑系统的输入、输出和规则。

可以根据系统的要求调整模糊集合的范围和模糊隶属度函数，以及规则库的定义。

在完成模糊逻辑系统的定义后，还需要确定模糊PID控制器的输出转换函数。

输出转换函数将模糊控制量转换为实际控制量。

通常，可以使用一些常用的转换函数，如线性转换、二阶转换等。

最后，可以使用simulate函数或evalfis函数来模拟模糊PID控制器的输出。

simulate函数可以模拟模糊逻辑系统的整个过程，包括输入的模糊化、规则推理和输出的去模糊化。

evalfis函数可以直接计算模糊逻辑系统的输出。

通过以上步骤，我们可以在MATLAB中设计一个基于模糊逻辑的PID 控制器，并进行模拟和优化。

模糊PID控制及其MATLAB仿真讲解

模糊PID控制及其MATLAB实现姓名：专业班级：学号：授课教师：摘要PID（比例积分微分）控制具有结构简单、稳定性能好、可靠性高等优点,尤其适用于可建立精确数学模型的控制系统。

而对于一些多变量、非线性、时滞的系统，传统的PID控制器并不能达到预期的效果。

随着模糊数学的发展，模糊控制的思想逐渐得到控制工程师们的重视，各种模糊控制器也应运而生。

而单纯的模糊控制器有其自身的缺陷—控制效果很粗糙、控制精度无法达到预期标准。

但利用传统的PID控制器和模糊控制器结合形成的模糊自适应的PID控制器可以弥补其缺陷；它将系统对应的误差和误差变化率反馈给模糊控制器进而确定相关参数，保证系统工作在最佳状态，实现优良的控制效果。

论文介绍了参数自适应模糊PID控制器的设计方法和步骤。

并利用MATLAB 中的SIMULINK 和模糊逻辑推理系统工具箱进行了控制系统的仿真研究，并简要地分析了对应的仿真数据。

关键词: 经典PID控制; 模糊控制; 自适应模糊PID控制器; 参数整定; MATLAB仿真ABSTRACTPID(Proportion Integration Differentiation) control, with lots of advantages including simple structure, good stability and high reliability, is quite suitable to establish especially the control system which accurate mathematical model is available and needed. However, taken multivariable, nonlinear and time-lag into consideration, traditional PID controller can not reach the expected effect.Along with the development of Fuzzy Mathematics, control engineers gradually pay much attention to the idea of Fuzzy Control, thus promoting the invention of fuzzy controllers. However, simple fuzzy controller has its own defect, where control effect is quite coarse and the control precision can not reach the expected level. Therefore, the Fuzzy Adaptive PID Controller is created by taking advantage of the superiority of PID Controller and Fuzzy Controller. Taken this controller in use, the corresponding error and its differential error of the control system can be feed backed to the Fuzzy Logic Controller. Moreover, the three parameters of PID Controller is determined online through fuzzification, fuzzy reasoning and defuzzification of the fuzzy system to maintain better working condition than the traditional PID controller.Meanwhile，the design method and general steps are introduced of the Parameter self-setting Fuzzy PID Controller. Eventually, the Fuzzy Inference Systems Toolbox and SIMULINK toolbox are used to simulate Control System. The results of the simulation show that Self-organizing Fuzzy Control System can get a better effect than the Classical PID controlled evidently.Keywords: Classic PID control; Fuzzy Control; Parameters tuning; the Fuzzy Adaptive PID Controller; MATLAB simulation目录第一章绪论 (1)1.1 研究的背景及意义 (1)1.2 经典PID控制系统的分类与简介 (2)1.2.1 P控制 (2)1.2.2 PI控制 (2)1.2.3 PD控制 (2)1.2.4 比例积分微分（PID）控制 (2)1.3 模糊逻辑与模糊控制的概念 (3)1.3.1 模糊控制相关概念 (3)1.3.2 模糊控制的优点 (4)1.4 模糊控制技术的应用概况 (4)1.5 本文的研究目的和内容 (5)第二章PID控制 (6)2.1 PID的算法和参数 (6)2.1.1 位移式PID算法 (6)2.1.2 增量式PID算法 (7)2.1.3 积分分离PID算法 (7)2.1.4 不完全微分PID算法 (8)2.2 PID参数对系统控制性能的影响 (9)2.2.1 比例系数K P对系统性能的影响 (9)2.2.2 积分时间常数T i对系统性能的影响 (9)2.2.3 微分时间常数T d对系统性能的影响 (9)2.3 PID控制器的选择与PID参数整定 (10)2.3.1 PID控制器的选择 (10)2.3.2 PID控制器的参数整定 (10)第三章模糊控制器及其设计 (11)3.1 模糊控制器的基本结构与工作原理 (11)3.2 模糊控制器各部分组成 (11)3.2.1 模糊化接口 (11)3.2.2 知识库 (12)3.2.3 模糊推理机 (12)3.2.4 解模糊接口 (13)3.3模糊推理方式 (13)3.3.1 Mamdani模糊模型（迈达尼型） (13)3.3.2 Takagi-Sugeno模糊模型(高木-关野) (13)3.4模糊控制器的维数确定 (14)3.5 模糊控制器的隶属函数 (15)3.6模糊控制器的解模糊过程 (17)3.7 模糊PID控制器的工作原理 (18)第四章模糊PID控制器的设计 (19)4.1 模糊PID控制器组织结构和算法的确定 (19)4.2 模糊PID控制器模糊部分设计 (19)4.2.1 定义输入、输出模糊集并确定个数类别 (19)4.2.2 确定输入输出变量的实际论域 (20)4.2.3 定义输入、输出的隶属函数 (20)4.2.4 确定相关模糊规则并建立模糊控制规则表 (20)第五章模糊PID控制器的MATLAB仿真 (24)5.1 模糊PID控制的仿真 (24)5.1.1 FIS编辑器 (24)5.1.2 隶属函数 (25)5.1.3 模糊规则库 (25)5.2 对模糊控制器编程仿真 (27)第六章结语 (31)参考文献 (32)第一章绪论1.1 研究的背景及意义随着越来越多的新型自动控制应用于实践，其控制理论的发展也经历了经典控制理论、现代控制理论和智能控制理论三个阶段。

模糊pid控制matlab程序

模糊pid控制matlab程序
模糊PID控制是一种结合模糊控制和PID控制的方法，它可以
在控制系统中应对非线性和不确定性。

在MATLAB中，实现模糊PID
控制可以分为以下几个步骤：
1. 定义模糊系统，首先，需要使用MATLAB中的Fuzzy Logic Toolbox来定义模糊系统。

可以使用fuzzy函数来创建一个模糊系
统对象，并定义输入、输出和隶属函数等参数。

2. 设计模糊控制器，接下来，需要设计模糊控制器。

可以使用fisedit函数来打开模糊逻辑编辑器，通过编辑器来定义模糊控制
器的输入、输出和规则等。

3. 整合PID控制器，在MATLAB中，可以使用pid函数来创建
一个PID控制器对象。

然后，将模糊控制器和PID控制器整合在一起，可以通过串联、并联或级联的方式来实现模糊PID控制。

4. 闭环控制，最后，将设计好的模糊PID控制器应用于闭环控
制系统中。

可以使用sim函数来进行仿真，观察系统的响应和性能。

需要注意的是，模糊PID控制的设计涉及到模糊集合的定义、隶属函数的选择、规则的设置等，需要根据具体的控制对象和要求来进行调整和优化。

同时，对于PID控制器的参数调节也需要谨慎处理，可以使用MATLAB中的工具箱来进行参数整定和性能分析。

总的来说，实现模糊PID控制的MATLAB程序需要综合运用模糊逻辑工具箱和控制系统工具箱，通过适当的建模和调节来实现模糊PID控制器的设计和应用。

自适应模糊PID控制器的设计及基于MATLAB的计算机仿真

摘要0将模糊控制器和 123控制器结合在一起*利用模糊逻辑控制实现了 123控制器参数在线自调整*进一步完善了 123控制器的性能*提高了系统的控制精度4并把 567869中的 :;<<=7>>?@>A和 B25C82DE 有机结合起来*方便的实现了该自适应模糊 123控制系统的计算机仿真*拓宽了 :;<<=7>>?@>A和 B25C82DE 的应用范围4 关键词 0模糊控制 F123 控制器 F567869FB25C82DEF系统仿真中图分类号071.G,H IJF71,KLIK 文献标识码06 文章编号0L--LMJNOP+.--L/-JM--,.M-J
立打下了基础K
9:[ \]^控制器的确立本系统中的 _!‘控制器有 a个输入量S$H$-H2’H
24和 25D而输出即为控制量 b#c)D它的控制算法为S
h b#c)T
2’d$#c)e
ci j
f fggT
$#g)e
k
fflm$#c)i
$#ci
j)no
ci j
h T 2’$#c)e 24 $#g)e 25m$#c)i $#ci gT k
如果能实现 ’()控制器的参数在线自调整%那么就地一步完善了 ’()控制器的性能%以适应控制系统的参数变化和工作条件变化& 研究表明%模糊控制和 ’() 控制的结合是提高控制性能的有效手段 & 为提高系统的控制精度和鲁棒性%提出了一种利用模糊逻辑对 ’()控制器进行在线自调整的方法&

模糊PID控制系统设计及MATLAB仿真

相比传统的PID控制系统，基于Matlab的模糊PID控制系统具有更好的适应性和鲁棒性。在面对具有非线性、时变等特点的被控对象时，模糊PID控制系统可以更好地实现精确控制。仿真结果表明，该方法在改善系统的动态性能和稳态精度方面均具有显著的优势。
然而，基于Matlab的模糊PID控制系统仍然存在一些问题需要进一步研究和解决。例如，针对不同的被控对象，如何自适应地调整模糊PID控制器的参数仍然是一个亟待解决的问题。此外，如何进一步提高模糊PID控制系统的鲁棒性和自适应性也是未来研究的重要方向。
模糊PID控制系统设计及MATLAB仿真
01 引言
03 参考内容
目录
02
模糊PID控制系统设计
摘要：本次演示主要介绍了模糊PID控制系统的设计方法及其在MATLAB环境下的仿真过程。首先，阐述了模糊PID控制系统的基本原理和设计流程，并通过一个实际案例加以说明。接下来，介绍了MATLAB仿真的基本原理和实施步骤，并展示了仿真结果。最后，总结了本次演示的主要内容，并指出了未来的研究方向。
（4）设计控制表：根据模糊规则和控制要求，计算出各模糊变量的控制表。
（5）设计去模糊化器：去模糊化器的作用是将模糊量转换为精确量，以便输出到被控对象。
3、设计案例
以一个简单的温度控制系统为例，介绍模糊PID控制系统的设计应用。该系统的输入为温度误差和温度变化率，输出为加热器的控制信号。首先，确定输入输出变量，定义相应的模糊变量。然后，根据控制要求和系统特性制定模糊规则，并计算出各模糊变量的控制表。最后，设计去模糊化器，将模糊量转换为精确量，输出加热器的控制信号。通过这样的设计流程，可以实现对该温度控制系统的数学计算软件，它可以用于各种控制系统仿真的工具。在MATLAB中，可以使用Simulink模块进行系统建模和仿真。Simulink提供了丰富的库和工具箱，可以方便地构建各种类型的控制系统模型，并对系统进行仿真和分析。

模糊PID控制器MATLAB仿真探讨

９周林娜，张庆灵，杨春雨Ｔ－Ｓ模糊系统的鲁棒局部稳定
４总结
常规ｐＩＤ控制时通过｛胃节ＰＩＤ３个参数，就可以得到系统比较理想的响应图，控制效果的优良与参数的调整有很大的关系，也能提高快速性。但３个参数
系统工程与电子技术，２００６，２８（１２）：１８６３—１８６６
作者简介：韩启勇，在读硝士研兜±，Ｉ程师，主要从事
燃东北大学设计研究院（沈阳１１００１３）
使用方便，适应性强，可以广泛应用于各种工业过程
控制领域。但是Ｐ［Ｄ控制器也存在参数调节需要一定
过程，最优参数选取比较麻烦的缺点，对一些系统参
摘要：在借鉴传统ＰＩＤ控制应用工业现场基础上。引进模糊规则的调用方式。根据偏差绝对值和偏差变化率绝对值的改变，在线调节数会变化的过程，ＰＩＤ控制就无法有效地对系统进行
ＰＭ
ＺＯｚ０ＰＳＰＭＰＭ
ＰＢｚ０ＺＯＰＳＰＭ
糊子集的隶属度赋值表和各参数模糊控制模型，应用模糊合成推理设计ＰＩＤ参数的模糊矩阵表，查出修正参数代入下式计算：
铲．ｐ＋｛ｅｉ，ｅｑ｝ｐ
ｋｆ－ｋ．ｉ＋｛ｅｉ，∞ｉ｝ｉ
ｋｄ－－－－ｋ＇ｄ＋｛ｅｉ，ｅｃｉ｝ｄ
弛阳
ＰＢ
髓
ＰＢ
在线运行过程中，控制系统通过对模糊逻辑规则的结果处理、查表和运算，完成对ＰＩＤ参数的在线自
ｈａｓｂｅｔｔｅｒｄｙｎａｍｉｃＰＩＤｃｏｎｔｒｏｌｌｅｒ
ｃａｎ
ｐｅｒｆｏｒｍａｎｃｅ．Ｗｅ
ｂｅｕｓｅｄ
ｔｏ
ｈｏｐｅｔｈｅｆｕｚｚｙ
ｒｅｐｌａｃｅｔｈｅｔｒａｄｉｔｉｏｎａｌ
ＰＩＤｃｏｎｔｒｏｌｌｅｒｉｎｓｏｍｅｏｆｔｈｅｉｎｄｕｓｔｒｉａｌａｐｐｌｉｃａｔｉｏｎｓｔｏ

模糊自适应PID控制的Matlab仿真设计研究_陈明201208070103

模糊自适应PID控制的Matlab仿真设计研究：明学号：201208070103班级：大学智能1201一、模糊控制思想、PID控制理论简介：在工业生产过程中，许多被控对象受负荷变化或干扰因素很多基于模糊自适应控制理论, 设计了一种模糊自适应PID 控制器, 具体介绍了这种PID 控制器的控制特点及参数设计规则, 实现PID 控制器的在线自整定和自调整。

通过matlab 软件进行实例,仿真表明, , 提高控制系统实时性和抗干扰能力,易于实现．便于工程应用。

然而，课本中，为了简化实验难度，只是考虑了kp，ki参数的整定。

基于课本的实验要求，我选的是二输入（e, ）二输出（）。

需要注意的是，在命名输入输出函数的时候，下标字母需要借助下划线的编辑，即e_c 能够显示为。

2.2四个隶属函数的N, Z, P 函数设定：在隶属函数的设定中，N 选用的是基于trimf（三角形隶属函数） , Z是基于zmf（Z 型隶属函数），P是基于smf（S型隶属函数）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

自适应模糊PID控制器及其MATLAB仿真王一帆,石中锁(北京科技大学信息工程学院,北京100083)[摘要]利用模糊控制实现了PID控制器参数自整定,进一步完善了PID控制器的性能,提高了系统的控制精度。

把MATLAB中的Fuzzy Toolbox和Simulink结合起来,实现了该自适应模糊PID控制系统的仿真。

仿真结果表明该控制器是一种性能优良的控制器,而MATLAB中的工具箱和Si mulink是进行计算机仿真的有力工具。

[关键词]模糊控制;PID控制器;MATLAB;Si mulink;仿真0引言控制系统计算机仿真是应用现代科学手段对控制系统进行科学研究的十分重要的手段之一。

利用仿真工具对控制系统进行设计与仿真,可以有效地对比各种控制模型与方案,选取并优化相关控制参数,从而对整个控制系统的性能进行优化与提高,尤其是对于一些新型控制理论与算法的研究,进行系统仿真更是必不可少的。

MATLAB是MathW orks公司1982年推出的一套高性能的数值计算和可视化软件,目前已发展成为国际公认最出色的数学应用软件之一。

其强大的扩展功能为各领域的应用提供了基础。

它面向控制领域推出的建模可视化功能Simulink和模糊控制、神经网络、控制系统等工具箱为控制系统的仿真提供了有力的支持,极大地推动了仿真研究的发展。

本文将模糊控制和PID控制结合在一起,根据各自的特点构造了一个自适应模糊PID控制系统,并在MATLAB中的模糊逻辑工具箱和Simulink 基础上,对该控制系统进行了仿真研究。

1控制系统的建模及实现方案PID控制算法作为一种传统的控制方法以其计算量小、实时性好、易于实现等特点广泛应用于过程控制。

当建立起控制对象的精确数学模型时,只要正确设定参数K p、K i和K d,PID控制器便可实现其作用,但是它存在着参数修改不方便、不能进行自整定等缺点。

由于工业对象普遍存在着非线性、时变性等不确定性因素,此时PID控制效果将难以达到预期的目标。

而模糊控制不依赖于工业对象模型,它不是用数值变量而是用语言变量来描述系统特征,并依据系统的动态信息和模糊控制规则进行推理以获得合适的控制量,因而具有较强的鲁棒性,但控制精度却不太理想。

如果能实现PID控制器的参数在线自调整,那么就进一步完善了PID控制器的性能,以适应控制系统的参数变化和工作条件变化。

研究表明,模糊控制和PID控制的结合是提高控制性能的有效手段。

为提高系统的控制精度和鲁棒性,提出了一种利用模糊逻辑对PID控制器进行在线自调整的方法。

自适应模糊PID控制器以误差e和误差变化率ec作为输入,可以满足不同时刻偏差e和偏差变化率ec对PID参数自调整的要求,利用模糊控制规则对PID参数进行修改便构成了自适应模糊PID系统。

如图1所示。

图1自适应模糊PID控制系统结构在本系统中,模糊控制器的设计将是设计的核心,因为它的好坏将直接影响到K p、K i和K d的选取,从而影响到系统的控制精度。

2模糊PID控制器的设计211模糊控制器的算法设计在本设计方案中,PID参数自整定的思想就是[收稿日期]2006-03-28;[修改稿收到日期]2006-07-04[作者简介]王一帆(1982-),男,北京人,硕士,研究方向为单片机的开发与应用。

#499#先找出PID 控制器的3个参数K p 、K i 和K d 与偏差e 和偏差变化率ec 之间的模糊关系,在运行中通过不断检测e 和ec,再根据模糊控制规则来对3个参量进行在线修改,以满足不同e 和ec 对控制器参数的不同要求,从而使被控对象具有良好的动、静态性能。

(1)输入输出变量的确立基于对系统的上述分析,我们将偏差e 和偏差变化率ec 作为模糊控制器的输入,PID 控制器的3个参数K p 、K i 和K d 作为输出。

(2)输入、输出变量的模糊语言描述设定输入变量e 和ec 语言值的模糊子集为{负大,负中,负小,零,正小,正中,正大},并简记为{NB ,NM,NS ,Z O,PS,PM,PB },将偏差e 和偏差变化率ec 量化到(-3,3)的区域内。

同样,设定输出量K p 、K i 和K d 的模糊子集为{ZO,PS,PM ,PB },并将其量化到区域(0,3)内。

输入输出变量图2 输入e 、ec的隶属函数曲线图3 输出K p 、K i 和K d 的隶属函数曲线的隶属函数曲线在MATLAB 的模糊逻辑编辑器中分别如图2,图3所示。

(3)模糊控制规则的语言描述根据参数K p 、K i 和K d 对系统输出特性的影响情况,可以归纳出在不同的e 和ec 时,被控参数K p 、K i 和K d 的自整定要求,从而可得模糊控制规则,在MATLAB 的模糊逻辑编辑器中的实现如图4所示。

图4 添加规则后的规则编辑器界面212 模糊控制器的编辑在MATLAB 命令窗口运行Fuzzy 函数进入模糊逻辑编辑器,并建立一个新的FIS 文件,选择控制器类型为Mamdani 型,根据上面的分析分别输入e 、ec 、K p 、K i 和K d 的隶属函数和量化区间,并以If ,then 的形式输入模糊控制规则。

接下来设置其他参数:取与(and)的方法为min,或(or)的方法为max,推理(implication)方法为min,合成(a ggre -gation)方法为max,非模糊化(defuzzification)方法为重心平均(centroid),这样就建立了一个FIS 系统文件,取名为f 1fis 。

在MATLAB 的M 文件编辑器里建立一个名为fpid 1m 的文件,其内容为:matrix =readifs(-f 1fis .);这样就完成了模糊工具箱同Simulink 的链接,为整个控制系统的建立打下了基础。

213 PID 控制器的确立本系统中的PID 控制器有5个输入量:e 、ec 、K p 、K i 和K d ,而输出即为控制量U(n),它的控制算法为:U(n )=K p {e(n)+T T i E n -1i =0e(i)+T dT[e(n)-e(n -1)]}=#500#K p e(n)+K I E n -1i =0e(i )+K D [e(n)-e(n -1)]式中,U(n)、e(n )分别为第n 个采样时刻控制器输出(控制量)和输入(偏差信号),K p 为比例增益,T i 、T d 分别为积分、微分时间常数,T 为采样周期,K I =K P Tlink 里T i,K D =K P T d T 。

根据以上数学模型,在Simu 面很容易建立起PID 控制器模型。

3 利用S imulink 对控制系统仿真在Simulink 的菜单中,我们选择Fuzzy Logic Toolbox 中的Fuzzy logic controller 模块,并键入名字matrix 。

在这基础之上,我们加上量化因子K e 、K ec 、U p 、U i 和U d 。

这样,符合我们要求的模糊控制器便建立起来了。

模糊控制器和PID 控制器的结构分别如图5,图6所示。

图5 模糊逻辑控制器结构图图6 PID 控制器结构图显然,量化因子K e 、K ec 将e 和ec 量化为(-3,3)上的模糊量,经模糊控制规则动态处理,成为(0,3)上的模糊控制量,经量化因子U P 、U i 和U d 将其精确化,便可得到PID 控制器的控制参量K p 、K i 和K d 。

将模糊控制器和PID 控制器封装在一起便可得图7(a),图7(b)所示的自适应模糊PID控制器的两种形式。

图7 自适应模糊PID 控制器的两种形式自适应模糊PI D 控制系统如图8所示,其系统响应曲线如图9所示。

而没有使用模糊控制的PID 控制系统的响应曲线如图10所示。

对比图9和图10可以看出,模糊PID 控制系统无超调,响应时间为212s,调节时间为212s;而没有使用模糊控制的PID 控制系统的超调量为20%,响应时间为214s,调节时间为814s 。

4 结论仿真结果表明,采用Fuzzy PID 复合控制的算法,系统的响应速度快、调节精度高;稳态性能好,而且没有超调和振荡,具有较强的鲁棒性。

这是单纯的PID 控制难以实现的,它的一个显著特点#501#图8 自适应模糊PID控制系统图9 模糊PID 控制系统响应曲线就是在同样精度要求下,系统的过渡时间变短,这在实际的过程控制中将有重大的意义。

实践证明,Fuzzy Logic Toolbox 可以方便地通过编辑FIS 文件来设计模糊控制器,可以灵活地设定和修改控制器参量,从而找到最优方案。

而Simulink 可以非常直观地构造控制系统并观察其结果。

实验结果表明,MATLAB 中的工具箱和Simulink是进行计算机仿真的有力工具。

图10 PID 系统响应曲线[参考文献][1]冯冬青,谢宋和.模糊智能控制[M ].北京:化学工业出版社,1998,80-114.[2]方一鸣.基于MATLAB 的模糊控制系统仿真[J].自动化与仪器仪表,2000,(2):100-205.[3]李士勇.智能控制理论与应用[M].哈尔滨:哈尔滨工业大学出版社,1990,50-55.[4]程卫国.MATLAB5.3应用指南[M ].北京:人民邮电出版社,2000,42-77.[5]侯北平,卢佩.基于MATLAB 的BP 神经网络建模及系统仿真[J].自动化与仪表,2001(1):112-145.[6]楼顺天,胡昌华,张伟.基于MATLAB 的系统分析与设计)模糊系统[M ].西安:西安科技大学出版社,2001,58-99.[7]薛定宇.控制系统计算机辅助设计)MATLAB 语言及应用[M ].北京:清华大学出版社,1999,24-78.[8]闻新,周露,李东江,等.MATLAB 模糊逻辑工具箱的分析与应用[M ].北京:科学出版社,2001,10-83.[9]章卫国,杨向忠.模糊控制理论与应用[M ].西安:西北工业大学出版社,2000,32-89.[10]刘曙光,魏俊民,竺志超.模糊控制技术[M].北京:中国纺织出版社,2001,55-72.[编辑:张胜]#502#。