数学速算技巧二100以内平方数的记忆

合集下载

数学速算技巧大全

数学速算技巧大全一、乘法速算技巧1、平方速算法：对于任意两个数a和b，如果a的个位数是5，那么a的平方可以通过先将个位数加1，然后乘以个位数再在最后加上25得到。

例如，25的平方等于(2+1)×2+25=625、这个方法也适用于以5结尾的数字，比如45的平方等于4×5+45=20252、两位数乘一位数：首先将这两个数的个位数相乘，然后将两个数的十位数相加，最后将结果合并即可。

例如，24×3=(2×3)+(4×3)=723、两位数乘两位数：将两个数的个位数相乘，然后将两个数的十位数相乘，最后将结果相加。

例如，23×24=(2×4)+(3×4)=8+12=20+4=552二、除法速算技巧1、除以9的技巧：将这个数的各位数相加，然后将结果除以9，最后的商就是原来的数除以9的商。

例如，45÷9=(4+5)÷9=92、除以11的技巧：将数的各位数从右至左相加，并按照奇数位相加减偶数位相加的规则进行操作。

如果得到的结果是负数，则将其变为正数。

最后结果就是原来的数除以11的商。

例如，756÷11=6+(5-2)-(7+5)=6-2+7=9三、加法速算技巧1、竖式加法：两个数的位数对齐，从右往左依次相加，如果两个数的和超过10，需要进位，进位后再与下一位相加。

2、凑整法：对于近似的加法，可以借助10的倍数进行凑整，然后计算往前的差值。

例如，27+18可以看作是30+15，结果是45四、减法速算技巧1、竖式减法：两个数的位数对齐，从右往左依次相减，如果相减结果为负数，则需要借位。

2、借位法：当个位数不够减时，可以向高位借位，然后与高位相减。

五、平方根速算技巧1、巧算平方根：对于一些特定的平方数，可以通过记住其平方根的值来进行计算。

例如，10的平方根约等于3.16，20的平方根约等于4.47，30的平方根约等于5.48，50的平方根约等于7.07六、百分数计算技巧以上就是一些常用的数学速算技巧，当然还有很多其他的技巧，通过不断的学习和练习，我们可以提高我们在解题中的速度和准确性。

数学之道：十大速算窍门

数学之道：十大速算窍门1. 数字拆分法将大数字拆分成易于计算的小数字，例如将 12345 拆分为10000 + 2000 + 300 + 40 + 5，分别进行计算再相加。

2. 倍数加速法利用数字的倍数特性，快速计算结果。

例如，计算156 乘以2，可以先计算 150 乘以 2 得到 300，再加上 6 乘以 2 得到 12，最终结果为 312。

3. 数字分组法将数字进行分组，例如将 1234 分为 12 和 34，先计算 12 乘以5 得到 60，再计算 34 乘以 5 得到 170，最后将两个结果相加得到230。

4. 加减交换律在加减法运算中，可以改变数字的顺序，这样可以简化计算。

例如，计算 123 + 45，可以改为计算 123 + 54，更容易计算出结果。

5. 乘法分配律利用乘法分配律，将复杂的乘法运算简化。

例如，计算 (2 + 3) 乘以 4，可以先计算 2 乘以 4 得到 8，再计算 3 乘以 4 得到 12，最后将两个结果相加得到 20。

6. 数字定位法对于较大的数字，可以通过数字定位法快速计算出结果。

例如，计算 123456 乘以 7，可以先计算 123456 乘以 10 得到 1234560，再减去 123456 得到 1111004。

7. 平方速算法利用平方数的特性，快速计算数字的平方。

例如，计算 13 的平方，可以先计算 10 的平方得到 100，再计算 3 的平方得到 9，最后将两个结果相加得到 169。

8. 立方速算法利用立方数的特性，快速计算数字的立方。

例如，计算 5 的立方，可以先计算 4 的立方得到 64，再加上 1 的立方得到 65。

9. 递减相加法在加法运算中，可以使用递减相加法，将计算简化。

例如，计算 123 + 45，可以先从 123 中减去 40 得到 83，再加上 5 得到 88。

10. 递增相减法在减法运算中，可以使用递增相减法，将计算简化。

例如，计算 123 - 45，可以先加上 1 得到 124，再减去 40 得到 84。

1-20平方顺口溜

1-20平方顺口溜
平方根口诀：11-19的平方：原数加尾数，尾平方；逢10进位；41-49的平方：尾加15，10减尾再平方，占2位；51-59的平方：尾加二十五，尾平方占2位；91-99的平方：尾数乘2加80，10减尾数再平方，占2位。

1到20的平方根：1²=1 ，2²=4，3²=9，4²=16，5²=25，6²=36，7²=49，8²=64，9²=81，10²=100，11²=121，12²=144，13²=169，14²=196，15²=225 ，16²=256，17²=289，18²=324，19²=361，20²=400。

一个正数如果有平方根，那么必定有两个，它们互为相反数。

如果知道了这两个平方根的一个，那么就可以及时的根据相反数的概念得到它的另一个平方根。

负数在实数系内不能开平方。

只有在复数系内，负数才可以开平方。

负数的平方根为一对共轭纯虚数。

例如：-1的平方根为±i，-9的平方根为±3i，其中i为虚数单位。

第1页共1页。

小学数学速算技巧顺口溜都在这里了

小学数学速算技巧顺口溜都在这里了一二三四五六七八九
这些数记住真不累。

十一十二到十九
补零在前就变成了。

二十一二三四五六
单词背过来法不偷。

二十七八九十
倒过来再加个零。

十一乘法口诀表
二一得二二，三一得三三
四一得四四，五一得五五
六一得六六，七一得七七。

八一得八八，九一得九九。

十一乘法口诀定律
十一乘法搞不烂
个位数和十位数神奇变化
如11乘以12得132
乘法口诀法则来
纵横交错精通牢。

先竖后横再相乘
积尾和向前调。

乘法口诀记心间
竖线分开倒不难。

个位乘下一位
数写下来遇元或十。

算数口诀有所求
基本运算得加赋。

先加后减再相乘
除法加括号最优。

分数化小数，好方法
分子除以分母当选。

循环小数最终安宁
循环节除较百分之九九。

小数加减遇无尽
小数无限留三位。

对齐小数点进位进
结果有理数不偷。

平方三角不成才圆面计算效果佳。

三点一线图形间空间叠加难清洁。

平方数的记忆方法

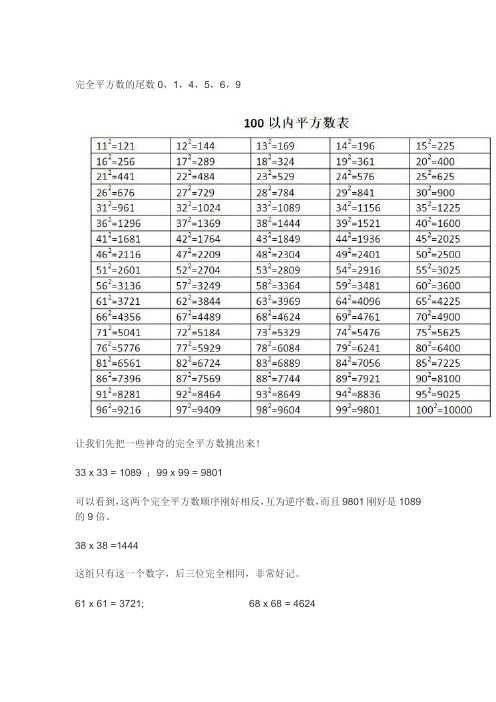
完全平方数的尾数0，1，4，5，6，9让我们先把一些神奇的完全平方数挑出来！33 x 33 = 1089 ；99 x 99 = 9801可以看到，这两个完全平方数顺序刚好相反，互为逆序数，而且9801刚好是1089的9倍。

38 x 38 =1444这组只有这一个数字，后三位完全相同，非常好记。

61 x 61 = 3721; 68 x 68 = 4624这是一组乘法口诀组成的完全平方数，三七二十一，四六二十四，怎么样，记住了吗？88 x 88 = 774412 x 12=144,21 x 21=441,13 x13 =169,31 x 31=961除了感叹一下完全平方数的神奇之外，我们还能说什么呢？其余的数字我们再来分组研究：第一组1~9和整十数1到9的平方是乘法口诀里面背过的，然后10到90的整十数的平方，就是在1到9的平方后面加两个零，那么相应的，我们在开方的时候，两个零，就可以开出一个零。

第二组11~1911到19的平方可以直接用口诀：头乘头，尾加尾，尾乘尾例：11 x 11 = 1 x 1 连1+1 连1 x 1 = 12117 x 17 = 1 x 1 连7+7 连7 x 7 = 289 (注意进位)第三组个数上是五的数个位数字是5的两位数平方，我们可以借用一下“首同尾和十”的方法（十位数字相同，个位数字的和等于10），头x (头+1）x 100 + 尾x尾。

例：15 x 15 = 1 x (1 +1 )x100+5 x 5 = 22525 x 25 = 2 x (2 + 1)x100+5 x 5 = 62535 x 35 = 3 x (3 + 1)x100+5 x 5 = 122545 x 45 = 4 x (4 + 1)x100+5 x 5 = 202555 x 55 = 5 x (5 + 1)x100+5 x 5 = 302565 x 65 = 6 x (6 + 1)x100+5 x 5 = 422575 x 75 = 7 x (7 + 1)x100+5 x 5 = 562585 x 85 = 8 x (8 + 1)x100+5 x 5 = 722595 x 95 = 9 x (9 + 1)x100+5 x 5 = 9025第四组51~59这里可以借用一下“尾同首和十”的方法（个位数字相同，十位数字的和等于10），(头1×头2＋尾)×100＋尾×尾。

100以内平方数速记

上文中主要对一些有趣的完全平方数进行了介绍，这篇是将所有的100以内完全平方数全部列举，并介绍一些速记方法。

我把它们分为20位一组，共4组，希望大家能每天记住一组，这样会记得快一些，大家加油！第一组：21～30 71～8020以内的平方如果还不熟记的话着实不应该啊！这两组呢，细心同学会发现21～30是以25为中心，71～80以75为中心，所以它们可以说是对联：22222222 30900 80640021441 84129 715041 62417922484 78428 ========222222222 725184 60847823529 72927 735329 59297724576 67626 745476 5=========22277676 25625 755625=== 末位5的平方可以用“头同尾合十”来算，观察这两副对联的每一行，末2位全部一样！所以，41、84、29、76这4个数大家一定要熟记！末2位解决掉之后，说说百位和千位。

20～30百位较小，死记不难。

71～80规律不明显，有两种记法：①规律很明显吧，不过21～29平方要特别熟记啊！② 73、74的千位为5，百位和它们本身个位一样，2765776=是符合一个数平方后末两位与它本身相同的，比较重要，应熟记；2786084=，上文提过，先把这4个记住。

其余71、72首位仍为5，百位比它们个位小1；77、79直接死记吧！第二组：41～50 51～60上一组比较难记，下面来一组比较轻松的。

先记51～60，这一组可用尾同头合十来算！22222222512601 55126 101522704 55227 204532809 55328 309542916 55429 416=⨯+===⨯+===⨯+===⨯+==22553025 55530 525=⨯+==后面的几个规律留给大家自己来找吧！22222222715041 21441 50446725184 22484 51447735329 23529 53548796241 29841 62854==-===-===-===-=对于41～50，其实和上述差不多，只不过用减法。

掌握数学：十大速算技巧解析

掌握数学：十大速算技巧解析1. 快速乘法快速乘法是一种能够快速计算两个数字相乘的技巧。

其中一个常见的方法是使用交叉相乘法。

例如，计算37乘以25，可以将37分解为30和7，将25分解为20和5，然后进行交叉相乘得到600和35，最后将结果相加得到635。

2. 近似除法近似除法是一种用来估算除法结果的技巧。

例如，计算96除以7，可以先将96近似为100，然后将7近似为10，接着进行简单的除法计算得到10，最后将结果乘以10得到近似的商为100。

3. 平方技巧平方技巧是一种用来快速计算一个数字的平方的方法。

例如，计算13的平方，可以将13分解为10和3，然后使用公式(10+3)^2= 10^2 + 2*10*3 + 3^2 = 100 + 60 + 9 = 169，得到13的平方为169。

4. 百分比转换百分比转换是一种将一个数转换为百分数的技巧。

例如，将0.75转换为百分数，可以将0.75乘以100得到75%。

5. 整数除法整数除法是一种用来计算两个整数相除得到整数商和余数的方法。

例如，计算47除以6，可以得到商为7和余数为5。

6. 近似开方近似开方是一种用来估算一个数的平方根的技巧。

例如，要估算√38，可以找到最接近38的完全平方数，即36，然后将38近似为36，接着计算√36 = 6，得到近似的平方根为6。

7. 十进制转换十进制转换是一种将一个数转换为不同进制的方法。

例如，将10转换为二进制，可以使用除以2取余数的方法，得到10的二进制表示为1010。

8. 快速乘方快速乘方是一种用来快速计算一个数的幂的方法。

例如，计算2的10次方，可以使用二进制的方法，将10表示为1010，然后按照相应的位数进行计算，得到结果为1024。

9. 等差数列求和等差数列求和是一种用来计算一个等差数列的和的方法。

例如，计算1到100的和，可以使用等差数列求和公式(首项 + 末项) * 项数 / 2，得到结果为5050。

200以内整数平方的速算方法

200以内整数平方的速算方法四川省邻水县九龙中学任贤德数学教育的目的之一是培养和提高学生的运算能力,而在数学解题中常遇到数的平方的计算, 数字平方的计算中,有一些数能够速算.为此,本文将介绍200以内整数平方的速算方法,以供参考,不妥之处,望同仁斧正.Ⅰ.1-25以内整数平方的速算1⑴1-10的平方就不用多说了.⑵11-19的平方的速算.定理1:设有11-19中某数,则此数的平方等于此数与它个位数字之和的10倍,再加上此数个位数字的平方.例1.① 172＝（17＋7）×10＋72＝240＋49＝289② 192＝（19＋9）×10＋92＝280＋81＝361⑶21-29平方的速算.定理2:设有21-29中某数,则此数的平方等于此数与它个位数字之和的2倍乘以10,再加上此数个位数字的平方.例2.①282＝（28＋8）×2×10＋82＝720＋64＝784②232＝（23＋3）×2×10＋32＝520＋9＝5291-25以内整数的平方要熟记,它们是本文后面其它数字平方计算的基础,只要熟记25以内整数的平方值，我们就能快速地计算由26-200以内的整数的平方值附11-25的平方值:112＝121 122＝144 132＝169 142＝196 152＝225 162＝256 172＝289 182＝324 192＝361 202＝400 212＝441 222＝484 232＝529 242＝576 252＝625Ⅱ.26-75以内整数平方的速算定义1.若两数之和为50，则称此二数互余，其中一数为另一数的余数。

如17＋23＝50，则27与23互余，27的余数是23（或23的余数是27）。

定理3：设有26—75的某数，则此数的平方等于此数减去25再乘以100，并将所得结果加上此数余数的平方。

证：依题意：a2＝[50－(50－a)2]＝502－2×50×(50－a)＋(50－a)2＝2500－100×(50－a)＋(50－a)2＝ (a－25)×100＋(50－a)2故命题成立。

数学十大速算技巧

数学十大速算技巧在数学中，速算技巧可以帮助我们更加高效地进行计算，节约时间和精力。

这些技巧包括不同的方法，将复杂的计算转化为简单的计算。

以下是数学中的十大速算技巧：1.乘法口诀表：乘法口诀表是最基础和常用的速算技巧之一、通过熟记乘法口诀表，我们可以快速地计算两个数的乘积。

2.快速平方：当我们需要计算一个数的平方时，我们可以使用快速平方技巧。

例如，要计算12的平方，我们可以将12分为10和2，然后计算(10+2)^2，即100+2^2+2×10=1443.快速立方：类似于快速平方，我们可以使用快速立方技巧来计算一个数的立方。

例如，要计算8的立方，我们可以将8分为5和3，然后计算(5+3)^3，即5^3+3^3+3×5×(5+3)=125+27+120=2724.数根法：数根法是一种可以帮助我们计算数的数学特性。

通过将一个数的各个位数相加，直到得到一个个位数，这个个位数就是数的数根。

例如，数根法可以用来快速判断一个数是否能被3整除。

5.快速除法：在进行除法计算时，我们可以使用快速除法技巧。

例如，当我们需要计算289除以17时，我们可以近似地计算280除以17，然后减去余数：16、即我们得到16和1/176.快速乘法：在进行大数乘法时，我们可以使用快速乘法技巧，将乘积分解为更小的乘法。

例如，要计算65乘以48，我们可以计算(60+5)乘以48，然后将结果分为两部分：60乘以48和5乘以48，然后将两个结果相加。

7.颠倒法：颠倒法是一种可以帮助我们进行简化运算的技巧。

例如，当我们需要计算1除以148时，我们可以先颠倒148，得到1/8418.中间积法：在进行两个大数相乘时，我们可以使用中间积法，不需要将两个数完全展开。

例如，要计算263的平方，我们可以计算(250+13)^2，然后将结果分为两部分：250的平方和2×(250×13)+13的平方。

9.快速开方：在进行开方计算时，我们可以使用快速开方技巧。

100以内平方数速记

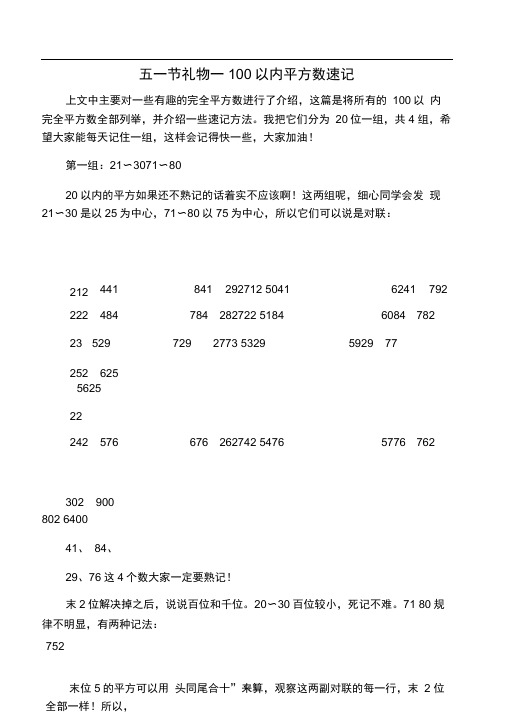
五一节礼物一100以内平方数速记上文中主要对一些有趣的完全平方数进行了介绍，这篇是将所有的100以内完全平方数全部列举，并介绍一些速记方法。

我把它们分为20位一组，共4 组，希望大家能每天记住一组，这样会记得快一些，大家加油！第一组：21〜3071〜8020以内的平方如果还不熟记的话着实不应该啊！这两组呢，细心同学会发现21〜30是以25为中心，71〜80以75为中心，所以它们可以说是对联：212 441 841 292712 5041 6241 792 222 484 784 282722 5184 6084 78223 529 729 2773 5329 5929 77252 625562522242 576 676 262742 5476 5776 762302 900802 640041、84、29、76这4个数大家一定要熟记！末2位解决掉之后，说说百位和千位。

20〜30百位较小，死记不难。

71 80规律不明显，有两种记法：752① 712 5041 212 441 50 4 46722 5184 222 484 51 4 47 732 5329 232 529 53 5 48 792 6241 292 841 62 8 54规律很明显吧，不过21〜29平方要特别熟记啊！②73、74的千位为5,百位和它们本身个位一样，762 5776是符合一个数平方后末两位与它本身相同的，比较重要，应熟记；782 6084,上文提过，先把这4个记住。

其余71、72首位仍为5,百位比它们个位小1；77、79直接死记吧！第二组：41〜5051〜60上一组比较难记，下面来一组比较轻松的。

先记51〜60,这一组可用尾同头合十来算！512 2601 5 5 1 26 12 01522 2704 5 5 2 27 22 04532 2809 5 5 3 28 32 09542 2916 5 5 4 29 42 16552 3025 5 5 5 30 52 25后面的几个规律留给大家自己来找吧！对于41〜50,其实和上述差不多，只不过用减法492 2401 5 5 1 24 12 01 482 2304 5 5 2 23 22 04472 2209 5 5 3 22 32 09452 20255 5 5 20还是一样，后面的规律留给大家自己啦！第三组：31〜4061〜70这两组平方数规律不明显，但都极易出题，推荐记牢！ 312 961322 1024 （这个是210啊！不难记） 332 1089 （与992 9801联合，不难记） 342 1156 （死记的） 5 5 25）352 1225 （头同尾合十，3 4 12,362 1296 372 1369382 1444 （末三位均是4,好记吧！此数极常考） 392 1521 （死记的） 402 1600612 3721 （三七二^一，四六二十四，这两个都是622 3844 （这个容易错，千万别顺口记成 3824 了） 632 3969 （上文提过，全是 3日倍数！） 642 4096 （这个就是传说中212啊！） 652 4225 （头同尾合十）462 2116 5 5 4 21 42 16 52 2560多的平方）662 4356 （我新发现的，由4个连续自然数组成的完全平方数）672 4489 （至今没找到好方法，只好死记）682 4624 （不多说了吧，四六二十四与全偶）692 4761 （目前只有死记）702 4900第四组：81〜9091〜100这两组数离100比较近，所有可以用完全平方公式来解：（100 k）2 100 200k k2992 9801k 1100 200 1 9801982 9604k 2 100 400 4 9604972 9409k 3 100 600 9 9409962 9216k 4100 800 16 9216952 9025k 5 100 1000 25 9025还是-一样，90〜94留给大家了！对于81 〜89,k为10几，所以对于111〜19 一定要熟记!892 7921k 11 1011 200 112 7921882 7744k 12 100 12 00 122 7744 872 7569k 13 100 13 00 132 7569 862 7396k 14 100 14 00 142 7396852 7225k 15 1015 200 152 7225842 7056k 16 1016 200 162 7056832 6889k 17 100 17 200 172 6889822 6724k 18 100 18 200 182 6724812 6561k 19 100 19 200 192 6561最后，介绍一个大家普遍知道的方法，即加法计算。

数学速算技巧二100以内平方数的记忆

让我们先把一些神奇的完全平方数挑出来！33 x 33 = 1089 ；99 x 99 = 9801可以看到，这两个完全平方数顺序刚好相反，互为逆序数，而且9801刚好是1089的9倍。

38 x 38 =1444这组只有这一个数字，后三位完全相同，非常好记。

61 x 61 = 3721; 68 x 68 = 4624这是一组乘法口诀组成的完全平方数，三七二十一，四六二十四，怎么样，记住了吗？88 x 88 = 7744除了感叹一下完全平方数的神奇之外，我们还能说什么呢？12 x 12=144,21 x 21=441,13 x13 =169,31 x 31=961其余的数字我们再来分组研究：第一组1~9和整十数1到9的平方是乘法口诀里面背过的，然后10到90的整十数的平方，就是在1到9的平方后面加两个零，那么相应的，我们在开方的时候，两个零，就可以开出一个零。

第二组11~1911到19的平方可以直接用口诀：头乘头，尾加尾，尾乘尾例：11 x 11 = 1 x 1 连1+1 连 1 x 1 = 12117 x 17 = 1 x 1 连7+7 连7 x 7 = 289 (注意进位)第三组个数上是五的数个位数字是5的两位数平方，我们可以借用一下“首同尾和十”的方法（十位数字相同，个位数字的和等于10），头x (头+1）x 100 + 尾x尾。

数学学习秘籍：十大速算技巧

数学学习秘籍：十大速算技巧
数学是一门重要而又普遍的学科，对于学生来说，掌握好数学是非常关键的。

然而，有些学生可能会觉得数学很难，速算更是一门高难度的技巧。

为了帮助你更好地掌握数学和速算，以下是十大速算技巧的秘籍：
1. 快速的九九乘法表
九九乘法表是数学研究的基础，熟练掌握九九乘法表可以帮助你在计算中更快速地得出结果。

2. 逢五进一法则
在进行加减法计算时，遇到以5结尾的数字可以使用逢五进一的法则，将其舍入为最接近的整数。

3. 快速的平方计算
熟练掌握平方数的计算方法可以帮助你在速算中更快地得出结果。

4. 除法的简化
在进行除法计算时，可以通过简化被除数和除数来简化计算过程，使得计算更加迅速。

5. 百分数的转化
熟练掌握百分数的转化方法可以帮助你在计算中更快速地得出结果。

6. 近似计算
在进行大数相加或相乘的计算时，可以通过近似计算来简化计算过程，减少出错的概率。

7. 快速的立方计算
熟练掌握立方数的计算方法可以帮助你在速算中更快地得出结果。

8. 分数的化简
在进行分数计算时，可以通过化简分数来简化计算过程，使得计算更加迅速。

9. 快速的开方计算
熟练掌握开方数的计算方法可以帮助你在速算中更快地得出结果。

10. 快速的单位换算
熟练掌握常见单位的换算方法可以帮助你在计算中更快速地得出结果。

以上是十大速算技巧的秘籍，希望能对你的数学研究有所帮助。

记住，只有通过不断的练和实践，才能真正掌握这些技巧，并在数
学研究中取得更好的成绩。

加油！。

平方数速记技巧

平方数速记技巧Mastering the technique of quickly recognizing square numbers can greatly enhance a person's mental calculation speed and efficiency.熟练掌握平方数速记技巧能大大提高一个人的心算速度和效率。

When confronted with a math problem or a situation that requires quick calculations, being able to instantly identify square numbers can give someone a significant advantage. 当面对数学问题或需要快速计算的情况时，能够立即识别平方数将使一个人具备显著的优势。

Square numbers are the result of multiplying a number by itself, such as 1x1=1, 2x2=4, 3x3=9, and so on. 平方数是将一个数字与自身相乘的结果，例如1x1=1，2x2=4，3x3=9等等。

By memorizing the square numbers up to a certain point, individuals can quickly recall these values when needed without having to perform calculations each time. 通过记忆一定范围内的平方数，个人在需要时可以快速地回想起这些值，而无需每次都进行计算。

One effective way to memorize square numbers is by creating a mental image or association for each number. 记忆平方数的有效方法之一是为每个数字创建一个心理形象或联想。

速算数的平方

速算数的平方
速算数的平方是指在短时间内快速计算出某个数的平方值。

通常使用的方法是利用数学运算规律和简化计算的技巧，避免繁琐的手算。

以下是一些常用的速算方法：
1、差平法：将要计算的数与离其最近的整十数之差记为a，再
用a×a+2a作为平方值。

例如，计算63的平方，离其最近的整十数
是60，63-60=3，那么63的平方就等于3×3+2×3×60=3969。

2、平方差：将要计算的数分解成两个数的差的形式，然后再运
用(a+b)(a-b)=a-b的公式计算平方值。

例如，计算98的平方，可以将其分解为100-2，那么98的平方就等于100×100-2×2=9604。

3、倍增法：将要计算的数化为2的幂次方的形式，然后运用(a
×2)=a×2的公式计算平方值。

例如，计算24的平方，可以将其化
为2×3，那么24的平方就等于2×3=576×9=5184。

以上是几种常用的速算方法，掌握了这些方法可以在日常生活、工作中更快地进行计算，提高工作效率。

- 1 -。

平方数速算技巧

平方数速算技巧《平方数速算技巧：数学也可以很好玩！》嘿，朋友们！今天咱来聊聊这个超级实用又有点神奇的“平方数速算技巧”。

你们可别小瞧了它，它能让那些看着头疼的数字们瞬间变得乖乖听话嘞！想当年啊，我还是个学生的时候，一遇到要算平方数就头大。

那一串串数字跟麻花似的，绕得我晕头转向。

但后来啊，我发现了一些神奇的小技巧，一下子就感觉打开了新世界的大门！比如说，咱先拿个简单的两位数来说。

要算35 的平方，嘿嘿，这时候技巧就派上用场啦！先把35 拆分成30 和5。

然后呢，用30 的平方（也就是900）加上两个30 乘以5（也就是300），再加上5 的平方（也就是25）。

咋样，神奇不？这答案不就呼之欲出了嘛，900+300+25=1225，35 的平方就是1225 啦！我当时就感觉，哇塞，这数学也太好玩了吧！还有更绝的呢！要是碰到个位是5 的数，那就更简单啦。

就拿75 来说，直接用十位上的数字7 乘以它后面那个数8，得56，再在后面加上25，哇，75 的平方就出来啦，5625！是不是特别神奇？感觉自己像个数学小魔法师一样。

而且啊，这些技巧可不仅仅是为了好玩，在实际生活中也超有用的嘞！比如说计算房间的面积、计算材料的用量啥的，都能让咱快速又准确地得出答案，不再被那些数字折磨得死去活来。

不过呢，要掌握这些技巧可不只是听听就行啦，还得自己多多练习。

就像学骑车一样，光看别人骑得溜可不行，自己得上去蹬几圈才能真正学会。

一开始可能会有点手忙脚乱，算得也不一定对，但别灰心呀，多练几次，慢慢就熟练啦。

总之呢，平方数速算技巧就像是一把开启数学大门的神奇钥匙，让我们能轻松愉快地在数字的世界里畅游。

大家可别再害怕那些平方数啦，掌握了这些技巧，让数学变得好玩又简单！快去试试吧，你会发现一个不一样的数学天地哦！。

平方数速算

平方数速算平方数速算，也叫「平方法」，是一种数学算术方法，可以快速计算指定数字的平方根。

它是一种广泛应用的解决方案，可以帮助解开复杂的数学问题。

平方数速算源于印度古典数学及古代日本运筹学家的思想和研究。

加瓦钦格尼、穆哈、阿里比爱特和日本的冈村俊平等人都有关于平方数速算的著作。

他们把此方法应用在建筑、建筑结构设计、建设规划等方面，帮助建筑师准确算出建筑物尺寸和壁面高度，以及其他情况。

此外，有了平方数速算，数学家们可以更轻松地计算终端点到指定位置的距离，也可以更快捷的计算三角形的面积。

一般而言，平方数速算的计算方法有两种：一种是欧氏平方根，另一种是牛顿迭代法，它用于计算非完全的数的平方根。

欧氏平方根是一种简单而快速的方法，它是从概念上考虑最基本的方法。

它的步骤如下：1. 识别想要计算的数字。

2. 用一个较小的数字来临时表示：先用“1”来表示想要求值的数。

3. 乘以“1”可以得出它的平方，一般情况下会得到一个比想要求的数更小的数。

4. 再以实际想要求的数减去上一步得到的结果，再加上“1”，得到的结果乘以“1 2”刚好等于想要求的数，这就是它的平方根。

牛顿迭代法是一种最常见的求平方根的方法，它根据联立函数求得结果，其步骤如下：1. 选取一个初始值（此方法用了一个”1”代替），计算要求的平方根。

2. 根据“1”和结果，根据0.5（0.5是测试值），乘以倒数得出比要求的数再小的值（新值）。

3. 乘以0.5，再乘以于新值，加上”1”，求出带被求根定的新值，以此循环，直到求到的结果与想要求的根值相近为止，这时结果就是目标值的平方根。

因此，平方数速算可以节省大量的时间和精力，用来求解许多复杂而又重要的数学问题，是被建筑师、数学家们都广泛应用的一种方法。

巧记常用平方立方数的数学知识记忆方法

巧记常用平方立方数的数学知识记忆方法巧记常用平方立方数的数学知识记忆方法数字1-10的平方，相信难不到任何人。

但是10以上的，又会经常用到的，就比较让人头痛了。

立方数呢?数字5以上的立方，就已经让人感觉摸不着头脑了。

下面，店铺来为你介绍的巧记常用平方立方数。

巧记常用平方立方数的方法记数字，对任何人来说都可以很轻松，只要掌握了秘密武器：图像记忆法!众所周知，数字可以转化成编码，编码即图像，从而变得生动具体。

那么数字是如何转化成图像的呢?通过谐音、象形、组合等形式，就可以转化成图像。

比如：12-婴儿，13-医生，谐音法。

11-筷子，22-鸳鸯，象形法。

20-耳环，50-五环，组合。

利用数字编码，可以做到很多看似不可能做到的，如轻松牢记数百数千位圆周率，一分钟牢记百个随机无序数字，几分钟记住一幅扑克牌的顺序……记电话号码这些，当然更不在话下了。

近来看到很多人在为数列犯难，尤其是平方数和立方数形成的数列，要求看到数列就能反应出原始数字。

死记效率低，而且也忘得快。

因此总结了常用的有难度的平方数和立方数。

巧记常用平方立方数，用的就是数字编码加谐音联想的方法。

记忆时，一定要在大脑中想像图像，想像情景，这才是增强记忆的不二法门：11——21的平方11=121——11121(原地踏步走时，喊的口号)12=144——婴儿咬狮子13=169——医生咬牛角14=196——钥匙依旧溜15=225——鹦鹉鸳鸯舞16=256——要留二胡留17=289——遗弃恶霸脚18=324——篱笆塞耳屎19=361——泥鳅山鹿咬20=40021=441——鳄鱼撕司仪为了与平方数区分开，立方数的原数放在后面5——21的立方125=5——婴儿呜呜哭216=6——鳄鱼溜溜球343=7——绅士扇妻512=8——我要爱爸729=9——企鹅救舅1331=11——医生杀鱼用筷子1728=12——遗弃恶霸选婴儿2197=13——鳄鱼就吃医生2744=14——爱妻时时丢钥匙3375=15——蝴蝶欺负鹦鹉4096=16——司令酒楼种杨柳4913=17——四舅一生娶一妻5832=18——我把扇儿做篱笆6859=19——喇叭胡椒泡药酒8000=209261=21——球儿轮椅追鳄鱼数学知识记忆方法1.口诀记忆法中学数学中，有些方法如果能编成顺口溜或歌诀，可以帮助记忆。