第四章习题解答(P195

合集下载

第四章习题解答及参考答案

(x y ), (x , y ) 。对于准单色点光源，其强度可表为：
1, 1 2 2
I (α , β ) = I 0δ (α − a1 , β − β1 )
在近轴近似条件下。由范希特-泽尼克定理得：
∞ 2π eiϕ ∫ ∫ I 0δ (α − α1 , β − β1 ) exp −i dα dβ ( ∆xα + ∆yβ ) −∞ λz u (P 1, P 2) = ∞ ∫ ∫ I 0δ (α − α1 , β − β1 ) dα dβ −∞
∑ δ (v − v
0
+ n∆v )
其中 ∆v 是纵模间隔， v0 为中心频率；为简洁起见，假定 N 为奇数。 ⑴证明复相干度的模为： γ (τ ) = ⑵若 N=3，且 0 ≤ τ ≤ 解： ⑴ γ (τ ) =
sin ( Nπ∆vτ ) N sin (π∆vτ )
1 ，画出 γ (τ ) 和 ∆vτ 的关系曲线。 ∆v
[
]
∆v = v2 − v1
①
所以
γ (τ ) = sinc (δvτ ) cos(π∆ντ ) Lc λ = = 58930. λ δλ
⑵可见到的条纹总数为 N =
⑶在复相干度的模的表示式①中，由于 ∆v >> δv ，故其第一个因子是 τ 的慢变化非周期函数，第二个因子则是 τ 的快变化周期函数，其变化周期为 τ = 1 / ∆v ，故条纹对比度的变化
所以
γ (τ ) =
N sin ( π∆vτ )
⑵当 N=3 时
γ (τ ) =
sin ( 3π∆vτ ) 3sin (π∆vτ )
[4-4]在图 X4-1 所示的杨氏双缝干涉实验中，采用缝宽为 a 的准单色扩展缝光源，并假设此缝光源具有均匀的辐射强度 I 0 ，中心波长为 λ = 600 nm ⑴写出 Q1 , Q2 点的复空间相干度； ⑵若 a=0.1mm, z=1m, d=3mm, 求观察屏上杨氏干涉条纹的对比度； ⑶若 z 和 d 仍取上述值，要求观察屏上的条纹对比度为 0.41，问缝光源的宽度 a 应为多少？

李云飞版食品工程原理第四章课后习题答案

4.3 习题解答【4-1】用光滑小球在粘性流体中自由沉降可测定该液体的粘度。

测试时用玻璃筒盛满待测液体，将直径为6mm 的钢球在其中自由沉降，下落距离为200mm ，记录钢球的沉降时间。

现用此法测试一种密度为1300 kg/m 3的糖浆，记录的沉降时间为7.32秒，钢球的比重为7.9，试求此糖浆的粘度。

解：小球的沉降速度 s m smHu t /0273.032.72.0===τ设在斯托克斯区沉降，则由斯托克斯定律：)(74.40273.01881.9)13007900()006.0(18)(2s Pa u gd tp p ⋅=⨯-=-=ρρμ校核：算出颗粒雷诺数 Re p =1045.074.413000273.0006.0<=⨯⨯=μρt p u d属斯托克斯沉降。

上述计算有效。

∴糖浆的粘度为4.74Pa.s【4-2】某谷物的颗粒粒径为4mm ，密度为1400 kg/m 3。

求在常温水中的沉降速度。

又若此谷物的淀粉粒在同样的水中的沉降速度为0.1mm/s ，试求其粒径。

解：（1）已知：d p =4mm ，ρp =1400kg/m 3，μ=0.001Pa ·s假设谷物颗粒在滞流区沉降则())/(49.3001.01881.9)10001400()104(18232s m g d u p pt =⨯⨯-⨯=-=-μρρ但11040.1001.0100049.3104Re 43>⨯=⨯⨯⨯==-μρt p p u d∴假设不成立又假设颗粒在湍流区沉降则())/(218.0100081.9)10001400(10474.174.13s m g d u p p t=⨯-⨯=-=-ρρρ此时500872001.01000218.0104Re 3>=⨯⨯⨯==-μρt p p u d∴假设成立，颗粒沉降速度为0.218 m/s (2) u t ’=0.1mm/s ，假设沉降发生在滞流区则 )(1014.281.9)10001400(001.0101.018)(1853''m g u d p t p --⨯=⨯-⨯⨯⨯=-=ρρμ校核：100214.0001.01000101.01014.2Re 35''<=⨯⨯⨯⨯==--μρt p p u d∴ 假设成立，此谷物的淀粉粒直径为2.14×10-5m【4-3】气体中含有大小不等的尘粒，最小的粒子直径为10μm 。

钢结构基础第四章课后习题答案

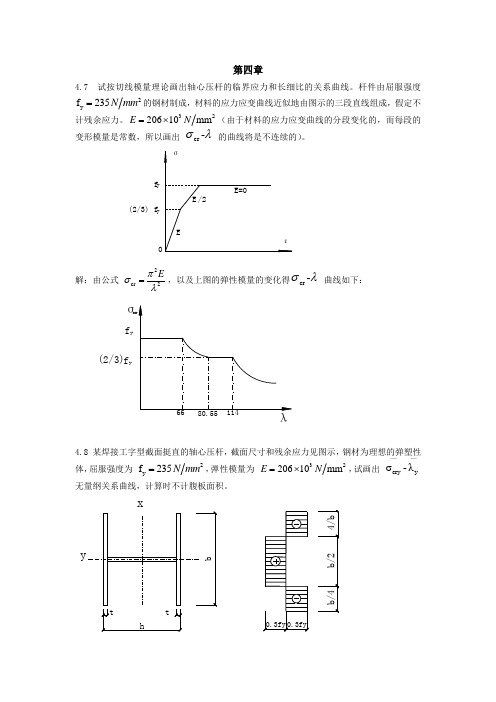
第四章4.7 试按切线模量理论画出轴心压杆的临界应力和长细比的关系曲线。

杆件由屈服强度2y f 235N mm =的钢材制成，材料的应力应变曲线近似地由图示的三段直线组成，假定不计残余应力。

320610mm E N =⨯2（由于材料的应力应变曲线的分段变化的，而每段的变形模量是常数，所以画出 cr -σλ 的曲线将是不连续的）。

解：由公式 2cr 2Eπσλ=，以及上图的弹性模量的变化得cr -σλ 曲线如下：4.8 某焊接工字型截面挺直的轴心压杆，截面尺寸和残余应力见图示，钢材为理想的弹塑性体，屈服强度为 2y f 235N mm =，弹性模量为 320610mm E N =⨯2，试画出 cryy σ-λ——无量纲关系曲线，计算时不计腹板面积。

f yyf (2/3)f y(2/3)f yx解：当 cr 0.30.7y y y f f f σ≤-=, 构件在弹性状态屈曲；当 cr 0.30.7y y y f f f σ>-=时，构件在弹塑性状态屈曲。

因此，屈曲时的截面应力分布如图全截面对y 轴的惯性矩 3212y I tb =，弹性区面积的惯性矩 ()3212ey I t kb =()322232232212212ey cryy y y yI t kb E E E k I tb πππσλλλ=⨯=⨯= 截面的平均应力 2220.50.6(10.3)2y ycr y btf kbt kf k f btσ-⨯⨯==-二者合并得cry y σ-λ——的关系式cry cry342cry σ(0.0273)σ3σ10y λ+-+-= 画图如下4.10 验算图示焊接工字型截面轴心受压构件的稳定性。

钢材为Q235钢，翼缘为火焰切割边，沿两个主轴平面的支撑条件及截面尺寸如图所示。

已知构件承受的轴心压力为N=1500KN 。

0.6f yfyλσ0.20.40.60.81.0cry解：已知 N=1500KN ，由支撑体系知对截面强轴弯曲的计算长度 ox =1200cm l ，对弱轴的计算长度 oy =400cm l 。

概率论与数理统计第四章课后习题及参考答案

概率论与数理统计第四章课后习题及参考答案1．在下列句子中随机地取一个单词，以X 表示取到的单词包含的字母的个数，试写出X 的分布律，并求)(X E ．Have a good time解：本题的随机试验属于古典概型．所给句子共4个单词，其中有一个单词含一个字母，有3个单词含4个字母，则X 的所有可能取值为1，4，有41)1(==X P ，43)4(==X P ，从而413434411)(=⋅+⋅=X E ．2．在上述句子的13个字母中随机地取一个字母，以Y 表示取到的字母所在的单词所含的字母数，写出Y 的分布律，并求)(Y E ．解：本题的随机试验属于古典概型．Y 的所有可能取值为1，4，样本空间Ω由13个字母组成，即共有13个样本点，则131)1(==Y P ，1312)4(==Y P ，从而1349131241311)(=⋅+⋅=Y E ．3．一批产品有一、二、三等品及废品4种，所占比例分别为60%，20%，10%和10%，各级产品的出厂价分别为6元、8.4元、4元和2元，求产品的平均出厂价．解：设产品的出厂价为X (元)，则X 的所有可能取值为6，8.4，4，2，由题设可知X 的分布律为X 68.442P6.02.01.01.0则16.51.021.042.08.46.06)(=⨯+⨯+⨯+⨯=X E (元)．4．设随机变量X 具有分布：51)(==k X P ，5,4,3,2,1=k ，求)(X E ，)(2X E 及2)2(+X E ．解：3)54321(51)(=++++=X E ，11)54321(51)(222222=++++=X E ，274)(4)()44()2(222=++=++=+X E X E X X E X E ．5．设离散型随机变量X 的分布列为k k kk X P 21)!2)1((=-=， ,2,1=k ，问X 是否有数学期望．解：因为∑∑∞=∞==⋅-111212)1(k k k k kkk 发散，所以X 的数学期望不存在．6．设随机变量X 具有密度函数⎪⎩⎪⎨⎧≤≤-=其他．,0,22,cos 2)(2πππx x x f 求)(X E 及)(X D ．解：因为x x 2cos 在]2,2[ππ-上为奇函数，所以0d cos 2d )()(222=⋅==⎰⎰-∞+∞-πππx x x x x f x X E ，2112d cos 2d )()(2222222-=⋅==⎰⎰-∞+∞-ππππx x x x x f x X E ，故2112)]([)()(222-=-=πX E X E X D ．7．设随机变量X 具有密度函数⎪⎩⎪⎨⎧<<-≤<=其他．,0,21,2,10,)(x x x x x f 求)(X E 及)(X D ．解：1d )2(d d )()(2112=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ，67d )2(d d )()(2121322=-+==⎰⎰⎰∞+∞-x x x x x x x f x X E ，61)]([)()(22=-=X E X E X D ．8．设随机变量X 在)21,21(-上服从均匀分布，求)sin(X Y π=的数学期望与方差．解：由题可知X 的密度函数为⎪⎩⎪⎨⎧<<-=其他．,0,2121,1)(x x f 则0d 1sin d )(sin )][sin()(2121=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ，21d 1sin d )(sin )]([sin )(21212222=⋅===⎰⎰-∞+∞-x x x x f x X E Y E πππ，21)]([)()(22=-=Y E Y E Y D ．9．某正方形场地，按照航空测量的数据，它的边长的数学期望为350m ，又知航空测量的误差随机变量X 的分布列为X (m)30-20-10-0102030P05.008.016.042.016.008.005.0而场地边长随机变量Y 等于边长的数学期望与测量误差之和，即X Y +=350，求场地面积的数学期望．解：设场地面积为S ，则2Y S =，16.01042.0016.0)10(08.0)20(05.030)(⨯+⨯+⨯-+⨯-+⨯-=X E 005.03008.020=⨯+⨯+，16.01042.0016.0)10(08.0)20(05.0)30()(222222⨯+⨯+⨯-+⨯-+⨯-=X E 18605.03008.02022=⨯+⨯+，故)350700(])350[()()(2222++=+==X X E X E Y E S E 122686350)(700)(22=++=X E X E ．10．A ，B 两台机床同时加工零件，每生产一批较大的产品时，出次品的概率如下表所示：A 机床次品数X 0123概率P7.02.006.004.0B 机床次品数X 0123概率P8.006.004.010.0问哪一台机床加工质量较好．解：44.004.0306.022.017.00)(=⨯+⨯+⨯+⨯=X E ，8.004.0306.022.017.00)(22222=⨯+⨯+⨯+⨯=X E ，6064.0)]([)()(22=-=X E X E X D ，44.010.0304.0206.018.00)(=⨯+⨯+⨯+⨯=Y E ，12.110.0304.0206.018.00)(22222=⨯+⨯+⨯+⨯=Y E ，9264.0)]([)()(22=-=Y E Y E Y D ，)()(Y E X E =，但)()(Y D X D <，故A 机床加工质量较好．11．设随机变量X 与Y 相互独立，且方差存在，试证：22)]()[()()]([)()()(Y E X D Y D X E Y D X D XY D ++=，由此得出)()()(Y D X D XY D ≥．证：22)]([])[()(XY E XY E XY D -=222)]()([)(Y E X E Y X E -=2222)]([)]([)()(Y E X E Y E X E -=2222)]([)]([})]([)(}{)]([)({Y E X E Y E Y D X E X D -++=22)]()[()()]([)()(Y E X D Y D X E Y D X D ++=．因为)(X D ，)(Y D ，2)]([X E ，2)]([Y E 非负，所以)()()(Y D X D XY D ≥．12．已知随机变量X 的密度函数为⎩⎨⎧≤≤++=其他．,010,)(2x c bx x a x f又已知5.0)(=X E ，15.0)(=X D ，求a ，b ，c ．解：c b a x c bx x a x x f ++=++==⎰⎰∞+∞-2131d )(d )(1102，c b a x c bx x a x x x f x X E 213141d )(d )()(5.0102++=++===⎰⎰∞+∞-，⎰⎰++-=-==∞+∞-1222d )()5.0(d )()]([)(15.0xc bx x a x x x f X E x X D 41314151-++=c b a ，解之得12=a ，12-=b ，3=c ．13．设),(Y X 的分布律为(1)求)(X E 及)(Y E ；(2)设XYZ =，求)(Z E ；(3)设2)(Y X Z -=，求)(Z E ．解：(1)2)13.00(3)1.001.0(2)1.01.02.0(1)(=++⨯+++⨯+++⨯=X E ，0)1.01.01.0(1)3.001.0(0)01.02.0()1()(=++⨯+++⨯+++⨯-=Y E ，(2)1.01)3.001.0(00)31(1.021(2.01)(⨯+++⨯+⨯-+⨯-+⨯-=Z E 1511.0311.021-=⨯+⨯+，(3)1.0)01(0)]1(3[1.0)]1(2[2.0)]1(1[)(2222⨯-+⨯--+⨯--+⨯--=Z E 51.0)13(1.0)12(1.0)11(3.0)03(0)02(22222=⨯-+⨯-+⨯-+⨯-+⨯-+．14．设随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤+=其他．,0,10,20,3),(y x yx y x f求)(X E ，)(Y E ，)(Y X E +及)(22Y X E +．解：⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(911d d 31020=+⋅=⎰⎰y x y x x ，⎰⎰∞+∞-∞+∞-=y x y x yf Y E d d ),()(95d d 31020=+⋅=⎰⎰y x y x y ，⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(916d d 3)(1020=+⋅+=⎰⎰y x y x y x ，⎰⎰∞+∞-∞+∞-+=+y x y x f y x Y X E d d ),()()(2222613d d 3)(102022=+⋅+=⎰⎰y x y x y x ．15．),(Y X 在区域}1,0,0|),{(≤+≥≥=y x y x y x D 上服从均匀分布，求)(X E ，)23(Y X E -及)(XY E ．解：由题可知),(Y X 的联合密度函数为⎩⎨⎧≤≤-≤≤=其他．,0,10,10,2),(y y x y x f ⎰⎰∞+∞-∞+∞-=y x y x f x X E d d ),()(31d d 21010==⎰⎰-yy x x ，⎰⎰∞+∞-∞+∞--=-y x y x f y x Y X E d d ),()23()23(31d d )23(21010=-=⎰⎰-yy x y x ，⎰⎰∞+∞-∞+∞-=y x y x xyf XY E d d ),()(121d d 21010==⎰⎰-y y x xy ．16．设二维随机变量),(Y X 的概率密度函数为⎪⎩⎪⎨⎧>+≤+=．1,0,1,1),(2222y x y x y x f π证明：随机变量X 与Y 不相关，也不相互独立．证：⎰⎰⎰⎰⋅=⋅=∞+∞-∞+∞-πθθππ201d d cos 1d d 1)(r r r y x x X E ，同理，0)(=Y E ，⎰⎰⎰⎰⋅⋅=⋅=∞+∞-∞+∞-πθθθππ201d d sin cos 1d d 1)(r r r r y x xy XY E ，0)()()(),cov(=-=Y E X E XY E Y X ，故随机变量X 与Y 不相关．当11≤≤-x 时，ππ21112d 1d ),()(22x y y y x f x f x x X -===⎰⎰---∞+∞-，其他，0)(=x f X ，故⎪⎩⎪⎨⎧≤≤--=其他．,0,11,12)(2x x x f X π同理，⎪⎩⎪⎨⎧≤≤--=其他．,0,11,12)(2y y y f Y π易得)()(),(y f x f y x f Y X ≠，故随机变量X 与Y 不相互独立．17．设随机变量1X ，2X 的概率密度分别为⎩⎨⎧≤>=-．0,0,0,e 2)(21x x x f x ，⎩⎨⎧≤>=-．0,0,0,e 4)(42y y y f y 试用数学期望的性质求：(1))(21X X E +及)32(221X X E -；(2)又设1X ，2X 相互独立，求)(21X X E ．解：由题可知1X ～)2(E ，2X ～)4(E ，则21)(1=X E ，41)(2=X E ，161)(2=X D ，81)]([)()(22222=+=X E X D X E ．(1)43)()()(2121=+=+X E X E X X E ，85)(3)(2)32(221221=-=-X E X E X X E ．(2)81)()()(2121==X E X E X X E ．18．(1)设1X ，2X ，3X 及4X 独立同在)1,0(上服从均匀分布，求)51(41∑=k k kX D ；(2)已知随机变量X ，Y 的方差分别为25和36，相关系数为4.0，求Y X U 23+=的方差．解：(1)由题易得121)(=i X D ，)51(41∑=k k kX D )(5141∑==k kkX D )](4)(3)(2)([514321X D X D X D X D +++=21)4321(121512222=+++⋅=．(2)由已知25)(=X D ，36)(=Y D ，4.0)()(),cov(==Y D X D Y X XY ρ，得12),cov(=Y X ，)2,3cov(2)2()3()23()(Y X Y D X D Y X D U D ++=+=513),cov(232)(2)(322=⋅⋅++=Y X Y D X D ．19．一民航送客车载有20位旅客自机场开出，旅客有10个车站可以下车，如果到达一个车站没有旅客下车就不停车，以X 表示停车的次数，求)(X E (设每位旅客在各个车站下车是等可能的，并设各旅客是否下车相互独立)．解：引入随机变量⎩⎨⎧=站无人下车．，在第站有人下车；，在第i i X i 01，10,,2,1 =i ．易知1021X X X X +++= ．按题意，任一旅客在第i 站不下车的概率为9.0，因此20位旅客都不在第i 站下车的概率为209.0，在第i 站有人下车的概率为209.01-，也就是209.0)0(==i X P ，209.01)1(-==i X P ，10,,2,1 =i ．由此209.01)(-=i X E ，10,,2,1 =i ．进而)()()()()(10211021X E X E X E X X X E X E +++=+++= 784.8)9.01(1020=-=(次)．20．将n 只球(1～n 号)随机地放进n 只盒子(1～n 号)中去，一只盒子装一只球．若一只球装入与球同号的盒子中，称为一个配对，记X 为总的配对数，求)(X E ．解：引入随机变量⎩⎨⎧=号盒子．号球未放入第第号盒子号球放入第第i i i i X i ,0,,1，n i ,,2,1 =，则n X X X X +++= 21，显然n X P i 1)1(==，则nX P i 11)0(-==，n i ,,2,1 =，从而nX E i 1)(=，n i ,,2,1 =，于是1)()()()()(2121=+++=+++=n n X E X E X E X X X E X E ．21．设随机变量),(Y X 的分布律为试验证X 和Y 是不相关的，但X 和Y 不是相互独立的．证：0)25.00(2)025.0(1)025.0()1()25.00(2)(=+⨯++⨯++⨯-++⨯-=X E ，5)25.00025.0(4)025.025.00(1)(=+++⨯++++⨯=Y E ，0)4(25.0)8(0225.0125.0)1(02)(⨯-+⨯-+⨯+⨯+⨯-+⨯-=XY E 025.0804=⨯+⨯+，所以0)()()(),cov(=-=Y E X E XY E Y X ，故X 与Y 不相关．易知25.025.00)2(=+=-=X P ，5.0025.025.00)1(=+++==Y P ，0)1,2(==-=Y X P ，有)1()2()1,2(=-=≠=-=Y P X P Y X P ，故X 与Y 不相互独立．22．设二维随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤+=其他．,0,10,10,),(y x y x y x f 求)(X E ，)(Y E ，)(X D ，)(Y D ，)(XY E ，),cov(Y X 及XY ρ．解：127d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ，125d d )(d d ),()(1010222=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ，14411)]([)()(22=-=X E X E X D ，由轮换对称性，得127)(=Y E ，14411)(=Y D ，31d d )(d d ),()(1010=+==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ，1441)()()(),cov(-=-=Y E X E XY E Y X ，111)()(),cov(-==Y D X D Y X XY ρ．23．设X ～),(2σμN ，Y ～),(2σμN ，且X ，Y 相互独立．求Y X Z βα+=1和Y X Z βα-=2的相关系数(α，β是不为0的常数)．解：由题可知μ==)()(Y E X E ，2)()(σ==Y D X D ，则2222)]([)()(σμ+=+=X E X D X E ，2222)]([)()(σμ+=+=Y E Y D Y E ，μβαβα)()()(1+=+=Y X E Z E ，μβαβα)()()(2-=-=Y X E Z E ，222221)()()()()(σβαβαβα+=+=+=Y D X D Y X D Z D ，222222)()()()()(σβαβαβα+=+=-=Y D X D Y X D Z D ，)()])([()(222221Y X E Y X Y X E Z Z E βαβαβα-=-+=))(()()(22222222σμβαβα+-=-=Y E X E ，222212121)()()()(),cov(σβα-=-=Z E Z E Z Z E Z Z ，22222121)()(),cov(21βαβαρ+-==Z D Z D Z Z Z Z ．24．设),(Y X 的联合概率密度为⎩⎨⎧≤≤≤≤--=.,0,10,10,2),(其他y x y x y x f (1)求),cov(Y X ，XY ρ和)32(Y X D -；11(2)X 与Y 是否独立？解：(1)125d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ，41d d )2(d d ),()(1010222=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x x y x y x f x X E ，61d d )2(d d ),()(1010=--==⎰⎰⎰⎰∞+∞-∞+∞-y x y x xy y x y x xyf XY E ，14411)]([)()(22=-=X E X E X D ，由轮换对称性，125)(=Y E ，14411)(=Y D ，1441)()()(),cov(-=-=Y E X E XY E Y X ，111)()(),cov(-==Y D X D Y X XY ρ，)3,2cov(2)3()2()32(Y X Y D X D Y X D -+-+=-144155),cov(12)(3)(222=-+=Y X Y D X D ．(2)当10≤≤x 时，x y y x y y x f x f X -=--==⎰⎰∞+∞-23d )2(d ),()(10，其他，0)(=x f X ，故⎪⎩⎪⎨⎧≤≤-=其他．,0,10,23)(x x x f X 同理，⎪⎩⎪⎨⎧≤≤-=其他．,0,10,23)(y y y f Y 因为)()(),(y f x f y x f Y X ≠，故X 与Y 不相互独立．。

材料力学第四章习题选及其解答

4-1. 试求图示各梁中截面1、2、3上的剪力和弯矩，这些截面无限接近于截面C或D 。

设p 、q 、a 均为已知。

解：（c ）（1）截开1截面，取右段，加内力（22112322qaa qa a P M qaqa P Q -=⨯-⨯-==+=（3）截开2截面，取右段，加内力（4）求内力2222122qaM a qa a P M qaqa P Q -=+⨯-⨯-==+=（d ）（1）求约束反力N R N R D A 300 100==（2）截开1截面，取左段，加内力(d)B(f)B(c)M=qa 2M M M=qa 2B（3）求1截面内力NmR M N R Q A A 202.010011-=⨯-=-=-=（4）截开2截面，取左段，加内力（5）求2截面内力NmR M N R Q A A 404.010022-=⨯-=-=-=（6）截开3截面，取右段，加内力（7）求3截面内力NmP M N P Q 402.020023-=⨯-===（f ）（1）求约束反力qa R qa R D C 25 21==（2）截开1截面，取左段，加内力Q 1M 12BMB（3）求1截面内力2112121 qa a qa M qa Q -=⨯-=-=（4）截开2截面，取右段，加内力（5）求2截面内力222223qa M a P M qaR P Q D -=-⨯=-=-= 4-3. 已知图示各梁的载荷P 、q 、M0和尺寸a 。

(1)列出梁的剪力方程和弯矩方程；(2)作剪力图和弯矩图；(3)确定∣Q ∣max 和∣M ∣max 。

q(c)M 0=qa 2 (d)(f)(e) (g)q(h)1BM (a)(b) Bq解：（a ）（1）求约束反力Pa M P R A A == 2（2）列剪力方程和弯矩方程⎪⎩⎪⎨⎧∈=-⨯-+⨯=∈-=+⨯=⎩⎨⎧∈=-=∈==),0[ )(2)(],0( 2)(]2,( 02)(),0( 2)(2222211111222111a x Pa a x P M x R x M a x Pa Px M x R x M a a x P R x Q a x P R x Q A A A A A A （3）画Q 图和M 图（4）最大剪力和最大弯矩值(i)q(j)BP=20kN(l)q(k)qM xxPa M P Q ==max max 2（b ）（1）求约束反力223 qa M qa R B B ==（2）列剪力方程和弯矩方程⎪⎪⎩⎪⎪⎨⎧∈-⨯-=∈-=⎩⎨⎧∈-=∈-=)2,[ )2()(],0[ 21)()2,[ )(],0[ )(2222121112221111a a x a x qa x M a x qx x M a a x qa x Q a x qx x Q （3）画Q 图和M 图（4）最大剪力和最大弯矩值2maxmax 23 qa M qa Q == （c ）（1）求约束反力qBxxqM 0=qa 2M2 2qa M qa R A A ==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值2max max 2qa M qa Q ==（d ）（1）求约束反力P R R B A == 0（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值Pa M P Q ==max maxxxxx（e ）（1）求约束反力P R P R B A 35 43==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值Pa M P Q 35 35max max ==（f ）（1）求约束反力aM R a M R B A 0023 23== （2）直接画Q 图和M 图xx5P/3x（3）最大剪力和最大弯矩值0max 0max23 23M M a M Q == （g ）（1）求约束反力qa R q R B A 81 a 83==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值2max max1289 a 83qa M q Q == （h ）（1）求约束反力M xqxxP R P R B C 25 29==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值Pa M P Q 25 27max max ==（i ）（1）求约束反力qa R q R B C 83a 89==（2）直接画Q 图和M 图qBxxxx（3）最大剪力和最大弯矩值2max max1289 a 85qa M q Q == （j ）（1）求约束反力kN R R B C 40 40kN ==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值kNm M kN Q 15 30max max ==（k ）（1）求约束反力2 0 qa M R B B ==（2）直接画Q 图和M 图BP=20kNqBxx（3）最大剪力和最大弯矩值2max max qa M qa Q ==（l ）（1）求约束反力qa R qa R B A 21 21 ==（2）直接画Q 图和M 图（3）最大剪力和最大弯矩值2max max 81 21qa M qa Q ==4-9. 作图示刚架的剪力图和弯矩图。

80x86微机原理参考答案

80x86微机原理参考答案第一章计算机基础（P32）1-1电子管，晶体管，中小规模集成电路、大规模、超大规模集成电路。

1-2把CPU和一组称为寄存器（Registers）的特殊存储器集成在一片大规模集成电路或超大规模集成电路封装之中，这个器件才被称为微处理器。

以微处理器为核心，配上由大规模集成电路制作的只读存储器（ROM）、读写存储器（RAM）、输入／输出、接口电路及系统总线等所组成的计算机，称为微型计算机。

微型计算机系统是微型计算机配置相应的系统软件,应用软件及外部设备等.1-3写出下列机器数的真值：（1）01101110 （2）10001101（3）01011001 （4）11001110答案：（1）+110 （2）-13(原码) -114（反码）-115（补码）（3）+89 （4）-78（原码）-49（反码）-50（补码）1-4写出下列二进制数的原码、反码和补码（设字长为8位）：（1）+010111 （2）+101011（3）-101000 （4）-111111答案：（1）[x]原=00010111 [x]反= 00010111 [x]补= 00010111（2）[x]原=00101011 [x]反= 00101011 [x]补= 00101011（3）[x]原=10101000 [x]反= 11010111 [x]补= 11011000（4）[x]原=10111111 [x]反= 11000000 [x]补=110000011-5 当下列各二进制数分别代表原码，反码，和补码时，其等效的十进制数值为多少？（1）00001110 表示原码14，反码14，表示补码为14（2）11111111 表示原码－127，反码－0，表示补码为－1（3）10000000 表示原码-0，反码-127，表示补码为－128（4）10000001 表示原码－1，反码－126，表示补码为－1271-6 已知x1=+0010100，y1=+0100001，x2=-0010100，y2=-0100001，试计算下列各式。

材料力学第四章习题选及其解答.docx

4-1. 试求图示各梁中截面1、2、3上的剪力和弯矩，这些截面无限接近于截面C或D 。

设p 、q 、a 均为已知。

(1)列出梁的剪力方程和弯矩方程；(2)作剪力图和弯矩图；(3)确定∣Q ∣max 和∣M ∣max 。

数字通信练习题答案

数字通信练习题答案练习一一、名词解释： 1.数字信号数字信号：信号的变化在时间和数值上是离散的，这种信号称数字信号。

2.数字通信信源发出的信息经变换和处理后，送往信道上传输的信号是数字信号的通信系统称为数字通信系统。

3.信息传输速率（传信率）每秒中内所传输的信息量I 。

Rb=信息量(I)/时间(t) 4.符号传输速率（数码率）每秒钟内传输的码元数。

5.误码率传输过程中发生的误码个数n 和传输的总码元数N 之比。

二、简答题1. 模拟信号和数字信号的主要区别是什么？模拟信号和数字信号的主要区别是在于幅度的取值是离散还是连续的。

2. 通信网由哪三要素组成？通信网由终端、交换系统、传输系统三要素组成。

3．数字通信系统中主要性能指标是什么？数字通信系统中主要性能指标是指有效性、可靠性。

4．M 进制符号系统信息传输速率和符号传输速率转换公式是什么？M 进制符号系统中信息传输速率和符号传输速率转换公式为（Rb=N B ·log 2M ）。

三．计算题1.在125微秒内传输256个二进制码元，其信息传输速率是多少？若该信号在2秒内有3个码元产生误码，则其误码率是多少？（见自学指导书P6）2.在125微秒内传输256个四进制码元，则其符号传输速率和信息传输速率分别是多少？若该信号在2秒内有3个误码，则误码率是多少？（见自学指导书P6）3.某数字信号的符号传输速率是1200波特，3秒中产生5个误码，问误码率是多少？ Pe=5/(1200×3)=0.0014。

,,p N np e N e lim系统噪声等因素决定信道质量由传输系统特性总码元数误码个数∞→=4.某数字信号的符号传输速率是9600波特，采用四进制数字信号传送，则其信息传输速率是多少？Rb=9600×2=19200（bit）5.在100.38s 内传送848个二进制码元，求信息的传输速率。

Rb=848/100.38=8.448(Mbit)6.八进制系统中，码元速率是1600波特，求该系统的信息传输速率。

金属工艺学_课后习题参考答案

⾦属⼯艺学_课后习题参考答案第⼀章（p11）1、什么就是应⼒？什么就是应变？答：应⼒就是试样单位横截⾯得拉⼒；应变就是试样在应⼒作⽤下单位长度得伸长量2．缩颈现象在拉伸实验中当载荷超过拉断前所承受得最⼤载荷时,试样上有部分开始变细，出现了“缩颈".缩颈发⽣在拉伸曲线上bk段。

不就是，塑性变形在产⽣缩颈现象前就已经发⽣,如果没有出现缩颈现象也不表⽰没有出现塑性变形。

4、布⽒硬度法与洛⽒硬度法各有什么优缺点?下列材料或零件通常采⽤哪种⽅法检查其硬度?库存钢材硬质合⾦⼑头锻件台虎钳钳⼝洛⽒硬度法测试简便,缺点就是测量费时,且压痕较⼤,不适于成品检验。

布⽒硬度法测试值较稳定,准确度较洛⽒法⾼。

;迅速，因压痕⼩，不损伤零件,可⽤于成品检验.其缺点就是测得得硬度值重复性较差,需在不同部位测量数次. 硬质合⾦⼑头,台虎钳钳⼝⽤洛⽒硬度法检验。

库存钢材与锻件⽤布⽒硬度法检验。

5、下列符号所表⽰得⼒学性能指标名称与含义就是什么？抗拉强度它就是指⾦属材料在拉断前所能承受得最⼤应⼒、屈服点它就是指拉伸试样产⽣屈服时得应⼒。

规定残余拉伸强度疲劳强度它就是指⾦属材料在应⼒可经受⽆数次应⼒循环不发⽣疲劳断裂,此应⼒称为材料得疲劳强度. 应⼒它指试样单位横截⾯得拉⼒。

冲击韧度它就是指⾦属材料断裂前吸收得变形能量得能⼒韧性。

ＨRC 洛⽒硬度它就是指将⾦刚⽯圆锥体施以１0０Ｎ得初始压⼒，使得压头与试样始终保持紧密接触,然后，向压头施加主载荷，保持数秒后卸除主载荷。

以残余压痕深度计算其硬度值. HBS布⽒硬度它就是指⽤钢球直径为10ｍｍ,载荷为300０Ｎ为压头测试出得⾦属得布⽒硬度。

HＢW 布⽒硬度它就是指以硬质合⾦球为压头得新型布⽒度计。

第⼆章(p23)(1)什么就是“过冷现象"?过冷度指什么?答:实际结晶温度低于理论结晶温度（平衡结晶温度),这种线性称为“过冷”。

理论结晶温度与实际结晶温度之差，称为过冷度.(2)⾦属得晶粒粗细对其⼒学性能有什么影响?细化晶粒得途径有哪些？答：⾦属得晶粒粗细对其⼒学性能有很⼤影响。

运筹学第四章习题答案

解:对偶问题为:min=4y1+6y2
y1+y2≥﹣2
y1+ky2=﹣2
s.t
﹣y1－y2≤1
y1无符号约束 y2≥0
精选2021版课件
5
将原问题的最优解代入原问题目标函数得原问题的最优值为:
﹣2×5－2×(﹣1)+0=﹣8
由此可知其对偶问题的最优值也为﹣8.
即:4y1+6y2=﹣8 ①
又由于原问题的最优解X1*＞0,X2*＜0是松约束,故对偶问题的约束必为紧约束,即对偶问题的前两个约束必为等式:
y1+2y2+3y3≤1
s.t 2y1+y2+2y3≤1
3y1－y2+4y3≤2
y1≥0 y2、y3≤0
精选2021版课件
1
（2）max z=4x1－2x2+3x3－x4
X1+x2+2x3+x4≤7
s、t
2x1－x2+2x3－x4=﹣2
X1－2x2+x4≥﹣3
X1、x3≥0 x2、x4无符号约束
解：其对偶问题为：
3
求得:第一,第二约束为松约束,第三,第四约束是紧约束.因此, 由互补松弛条件,原问题最优解中,x1*=0,x2*=0
∵y1*≥0,y2*≥0是松约束,故原问题的约束必为紧约束,即原问题约束必为等式:
X1+2x2+2x3+3x4=20
2x1+x2+3x3+2x4=20
即:
2x3+3x4=20
3x3+2x4=20
解之得:
x3*=4 x4*=4 x*=(0,0,4,4)

汽车理论第三版第四章习题答案

1)计算并绘制利用附着系数曲线与制动效率曲线。 2)求行驶车速30km/h，在 =0.80路面上车轮不抱死的制动距离。计算时取制动系反应时间，制动减速度上升时间。 3)求制功系前部管路损坏时汽车的制功距离，制功系后部管路损坏时汽车的制功距离。
青岛理工大学邹旭东 zxd@
1）汽车超载后，需要通过制动器以及车轮与地面消耗的摩擦功增大，因此持续制动的时间增长，制动距离增大，降低了制动效能。 2）下长坡多次制动要控制车速时制动器产生的热量增多，热衰退加剧，可能使制动失效。
青岛理工大学邹旭东 zxd@
2 ua0 3.6 ' τ2 + = (s ) 2 1 ua0 25.92abmax
' τ 2'
因。
青岛理工大学邹旭东 zxd@
4.3题
一中型货车装有前、后制动器分开的双管路制功系，其有关参数如下：
载荷空载满载总质量 ma/kg 4080 9290 质心高轴距质心至前制动力分 hg/m L/m 轴距离a/m 配系数β 0.845 3.95 2.10 0.38 1.170 3.95 2.95 0.38
4.3题 1)
利用附着系数与制动强度关系 1 0.9 0.8 利用附着系数 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 制动强度
青岛理工大学邹旭东 zxd@
空载前轴空载后轴满载前轴满载后轴制动强度
Fu G′ = P
Fu1 βF G= = = 0.65G′ P P
F 1 F 2 F = 0.5G′ G= u + u = 2P 2P 2P

概率论第四章课后习题答案

习题四1.设)2,5(~2N X ，求下列概率（1）)52(≤≤X P ;(2))2(≤X P ;(3))3(>X P ;(4))93(≤≤-X P .解：（1）)0255.1()25525252()52(≤-≤-=-≤-≤-=≤≤X P X P X P 4332.019332.05.01)5.1()0()5.1()0(=-+=-Φ+Φ=-Φ-Φ=（2）)25225252()22()2(-≤-≤--=≤≤-=≤X P X P X P )5.3()5.1()5.1255.3(-Φ--Φ=-≤-≤-=X P 0666.09332.099977.0)5.1()5.3(=-=Φ-Φ=（3）8413.0)1()1(1)125()25325()3(=Φ=-Φ-=->-=->-=>X P X P X P （4）)2254()25925253()93(≤-≤-=-≤-≤--=≤≤-X P X P X P 9772.01999968.09772.01)4()2()4()2(=-+=-Φ+Φ=-Φ-Φ=2．已知某次测试的成绩),73(~2σN X ，95分以上的同学占2.28%.求（1）介于80分与90分之间的同学的比例；（2）小于60分的同学的比例.解：因0228.0%28.2)7395(1)739573()95(==-Φ-=->-=>σσσX P X P即9772.0)22(=Φσ，查表得222=σ，则11=σ，故).11,73(~2N X（1）)11171173117()1173901173117380()9080(<-<=-<-<-=<<X P X P X P 2005.07389.09394.0)64.0()55.1(=-=Φ-Φ=（2）)18.1()11131173()1173601173()60(-Φ=-<-=-<-=<X P X P X P 119.0881.01)18.1(1=-=Φ-=3．已知随机变量),2(~2σN X ，且44.0)13(=≤-X P ，求)22(≥-X P .解：因)24222()42()13(σσσ-≤-≤-=≤≤=≤-X P X P X P44.0)0()2(=Φ-Φ=σ即94.0)0(44.0)2(=Φ+=Φσ，则12.094.022)2(22)22()22(=⨯-=Φ-=≥-=≥-σσσX P X P4. 已知随机变量),(~2σμN X ，且)1()3()1(-Φ=≥=-<X P X P 求σμ,.解：依题有)1()1()1()1(-Φ=--Φ=--<-=-<σμσμσμX P X P)1()3()3(1)3()3(-Φ=--Φ=-Φ-=-≥-=≥σμσμσμσμX P X P由此可得，⎪⎩⎪⎨⎧=-=+1311σμσμ，解得.2,1==σμ6.设随机变量)1,0(~N X ，求)(2X E .解：因1)(,0)(==X D X E ，则.1)]([)()(22=+=X E X D X E 11．一加法器同时收到48个噪声电压(1,2,,48)i X i =，设它们是相互独立的随机变量，且都在区间[0,10]上服从均匀分布，记481i i X X ==∑，求(180)P X >.解：依题可知，32512)010()(,52100)(22=-===+==i i X D X E σμ，由独立同分布中心极限定理得48481(180)(180)ii i Xn P X P X P μ=->=>=>∑∑11(3)(3)0.99865=-Φ=-Φ-=Φ=12. 一部件包括100个部分，每部分的长度是一个随机变量，它们相互独立，且服从同一分布，其数学期望为2mm ，均方差为0.05mm.规定总长度200mm 误差在1mm 内算合格品，试求产品合格的概率.解：设随机变量i X 表示“第i 个部分的长度”，1,2,,100.i =则12100,,,X X X 相互独立，05.0)(,2)(====i i X D X E σμ且1001ii X X ==∑表示“该部件的总长度”，由独立同分布中心极限定理得(0.1)21P X n P μ-<=<=Φ- 2(2)120.977210.9554=Φ-=⨯-=13. 掷硬币900次，试求：（1）至少出现正面480次的概率；（2）出现正面在420次到480次之间的概率.解：设随机变量X 表示“掷900次硬币中出现正面的次数”，则15)1(,450),21,900(~=-=p np np B X ，由棣莫弗—拉普拉斯中心极限定理得（1）0228.09772.01)2(1)1545048015450()480(=-=Φ-≈-≥-=≥X P X P （2）9544.019772.021)2(2)153015450()480420(=-⨯=-Φ≈<-=<<X P X P 14. 一船舶在某海区航行，已知每遭受一次波浪的冲击，纵摇角大于 3的概率31=p ，若船舶遭受了90000次波浪冲击，问其中有30500~29500次纵摇角度大于 3的概率是多少？解：设随机变量X 表示“在90000次波浪冲击中纵摇角大于 3的次数”，则2100)1(,30000),31,90000(~=-=p np np B X ，由棣莫弗—拉普拉斯中心极限定理得1)54.3(2)2100500210030000()3050029500(-Φ≈<-=<<X P X P9996.019998.02=-⨯=16.设有30个电子器件3021,,,D D D ，它们的使用情况如下：1D 损坏，2D 接着使用；2D 损坏，3D 接着使用等等.设器件i D 的使用寿命服从参数1.0=λ（单位：1-h ）的指数分布.令T 为30个器件使用的总时数，问T 超过350h 的概率是多少？解：设随机变量i T 表示“第i 个电子器件的使用寿命”，.30,,2,1 =i 依题可知，3021,,,T T T 相互独立，1001)(,101)(),1.0(~22======λσλμi i i T D T E e T ，且∑==301i i T T ，由独立同分布中心极限定理得)30101030350(1)350()350()350(301301⨯-Φ-≈->-=>=>∑∑==σμσμn n n n TP T P T P i ii i。

阶段测验三(第四章-第五章)【随机】--马克思主义基本原理概论(过程考核)3

马克思主义基本原理概论（过程考核）阶段测验记录> 阶段测验三（第四章-第五章）【随机】阶段测验三（第四章-第五章）【随机】一、单项选择题1、商品的最本质因素是（）。

A、使用价值B、价值C、交换价值D、流通价值【正确答案】：B【您的答案】：A【答案解析】：有使用价值但没有价值的物品，也不是商品，价值是商品的最本质因素。

参见教材P170。

2、货币退出流通领域，作为社会财富的一般代表而被保存起来，这被称作货币的（）。

A、贮藏手段B、世界货币手段C、支付手段D、流通手段【正确答案】：A【您的答案】：D【答案解析】：货币的贮藏手段职能，是指货币退出流通领域，作为社会财富的一般代表而被保存起来。

参见教材P174。

3、商品的使用价值反映的是（）。

A、人与人的关系B、人与自然的关系C、生产关系D、交换关系【正确答案】：B【您的答案】：B 【答案正确】【答案解析】：使用价值是商品的自然属性，它反映的是人与自然的关系，并存在于人类的一切社会活动之中，是个永恒的范畴。

参见教材P169。

4、早期的商业起着小商品生产者之间交换商品的（）作用。

A、支撑B、中介C、流通D、主导【正确答案】：B【您的答案】：C【答案解析】：早期的商业起着小商品生产者之间交换商品的中介作用。

参见教材P177。

5、在资本主义社会，决定劳动力价值的因素中一般不包括（）。

A、生存资料的价值B、生产资料的价值C、延续和养育后代所需的费用D、必要的教育培训费用【正确答案】：B【您的答案】：B 【答案正确】【答案解析】：劳动力商品的价值包括以下三部分生活资料的价值：一是维持劳动者自身生存所必需的生活资料的价值，用以再生产他的劳动力；二是劳动者繁育后代所必需的生活资料的价值，用以延续劳动力的供给；三是劳动者接受教育和训练所支出的费用，用以培训适合资本主义再生产所需要的劳动力。

参见教材P180。

6、资本有机构成可以用符号表示为（）。

A、 c：vB、 m：vC、 c+vD、 m／（c+v）【正确答案】：A【您的答案】：A 【答案正确】【答案解析】：由资本技术构成所决定，并且反映资本技术构成变化的资本价值构成，叫做资本有机构成，可用公式c：v来表示。

第195篇通风安全考试要点课后习题答案第4章通风动力2021

第195篇通风安全考试要点课后习题答案第4章通风动力4.1自然风压是怎样产生的？进、排风井井口标高相同的井巷系统内是否会产生自然风压。

在一个有高差的闭合回路中，水平底平面承受的空气高度是一样的，两侧有高差巷道中空气的温度或密度不等，则该回路就会产生自然风压。

进、排风井井口标高相同，如果空气密度相同，则不会产生自然风压，如果空气密度不相同，则会产生自然风压。

4.2影响自然风压大小和方向的主要因素是什么？是否用人为的方法产生或增加自然风压。

影响自然风压的决定因素是两侧空气柱的密度差。

而密度又受到温度T、大气压力P、气体常数R和相对湿度等因素影响。

矿井的开拓方式、采深、地形和地理位置的不同影响自然风压的大小。

空气成分和湿度影响密度，但影响较小。

矿井回路中最高点与最低点间的高差与自然风压成正比。

主要通风机工作对自然风压的大小和方向也有一定影响。

4.3如图4-1-1所示井巷系统，当井巷中空气流动时，2、3两点的绝对静压力之差是否等于自然风压。

为什么。

4-4如图（4-4）所示的井巷系统，各点空气的物理参数如下表，求该系统的自然风压。

风流流动用能量方程分析Ht2=ht3Ht2=hv2+F2+密度g2Ht3=hv3+f3+密度g2+200所以两点的绝对静压力不同。

4-5主要通风机附属装置各有什么作用。

设计和施工时应符合哪些要求。

1.风硐：是连接风机和井筒的一段巷道。

要求：1.断面适当增大。

2.转弯平缓，成圆弧形。

3.风井与风硐的连接处应精心设计，风硐的长度尽量缩短，减少局部阻力。

4.风硐直线部分要有一定坡度，以利流水T。

5.风硐应安装测定风流压力的测压管。

6.施工时应使其壁面光滑，风门要严密，使漏风量小。

2.扩散器：风机出口外接一定长度、断面逐渐扩大的构筑物。

作用：降低出口速压以提高风机静压。

要求：1.小型离心式通风机的扩散器由金属板焊接而成。

扩散器扩散角不宜扩大，阻止脱。

2.出口处断面与入口处断面之比约为3-4.3.扩散器四面张角大小应视风流从叶片出口的绝对速度方向而定。

武工大生化作业解答

P77~78习题参考答案3 Fischer式 Haworth式构象式β-D-脱氧核糖CCH2CCCH2OHHOH OHHOHO OHHCH2OHHHHOHHOHCH2OHOHHHHHOα-D-半乳糖CCCCCCH2OHOHHOH OHHHOHHOHOCH2OHHHOHHHHOHHOOCH2OHHOHHHHOHOHHβ-L-山梨糖CCCCCH2OHOHHOH2COHO HOHHHOOHHOH2CHHOOHHCH2OHHO OHHHHHOH2CCH2OHOHFischer式 Haworth式构象式β-D-N-乙酰神经氨酸（唾液酸）CH3-HOH2CH32OHCOO-CCH2CCCCCOHOHOHOHHAcNHOCH2OHOHHHH20三糖β-半乳糖苷酶半乳糖+D-葡萄糖其中的糖苷键均为β型糖之间的连接为半乳糖-半乳糖-葡萄糖CH2OAcHCCHCHHC2OCH3OCH3CH3OCH3OOAc2，3，4，6-四甲基-1，5-二乙酰基-半乳糖醇CH2OAcHCCHCHHC2OAcOCH3CH3OCH3OOAc2，3，4-三甲基-1，5，6-三乙酰基-半乳糖醇CH2OCH3CHCHHCCH2OCH3CH3OCH3OOCH3AcO1，2，3，5，6-五甲基-4-乙酰基-三梨醇NaBH4还原再乙酰化3CH2OCH3CHCHHCCH2OCH3CH3OCH3OOCH3HO3332OCH32OHP121习题解答10：疏水部分亲水部分COOCH2R1R2COOCHCH2O POO-O CH2CH2NH3+a疏水部分亲水部分bCNH CHCH2CH OHCH2O PO-O XOCH3（CH2）12CHR1O疏水部分亲水部分cCNH CHCH2CH OHCH2CH3（CH2）12CHO GalOR疏水部分亲水部分d寡糖链（含唾液酸）CNH CHCH2CH OHCH2CH3（CH2）12CHOORHO疏水部分亲水部分eDAG +PC鞘磷脂磷脂酶C×磷酸胆碱（油溶）（水溶）15：P155作业订正H 3N +（CH 2）4CHCOOH3+2N （CH 2）4CHCOO -23N +（CH 2）4CHCOO -3+3N +（CH 2）4CHCOO NH2pK COOHpK α-NH 3+pK ε-NH 3+000.80.2平衡时R -R 0R +R 2+pH=pK ε-NH 3+ + lgR -R0=10.53+lg0.2/0.8=9.92pK COOH平衡时R 0R +Me 2CHCH 2CHCOOHNH 3+Me 2CHCH 2CHCOO -NH 3++ H +0.3-xxxx 20.3-x=10-2.36xpH=- lg[H +]=-lgx=1.464a：4b ：平衡时R -R 0Me 2CHCH 2CHCOO-3+Me 2CHCH 2CHCOO -NH20.3-xxx+ H +x 20.3-x = 10-9.6xpH=- lg[H +]=-lgx=11.5H 3N +CH 2COO -H 3N +CH 2COOHH ++初始 0 1 0平衡 0.3 0.7 ？pH=pKa 1+lg =2.34+lg =2.71（加0.3MHCl ）R 0R +0.70.3H ++H 3N +CH 2COO -H 2NCH 2COO -初始 1 0 0平衡 0.7 0.3 ？pH=pKa 2+lg = 9.6+ lg =9.23（加0.3MNaOH ）R 0R -0.70.36His 2++-pK 1=1.82pK R =6.0pK 2=9.178pH=pK 1+lg[His +]/[His 2+] 即 6.4=1.82+lg[His +]/[His 2+]pH=pK R +lg[His]/[His +] 即 6.4=6.0+lg[His]/[His +]pH=pK 2+lg[His -]/[His]即 6.4=9.17+lg[His -]/[His][His 2+]+[His +]+[His]=0.25Asp Gly Thr Leu LyspI 2.98 5.97 6.53 5.98 9.74pI-pH 0 2.97 3.53 2.98 6.74pH3.0带电荷0 + ++ + +++淋洗顺序: Asp ＞Thr ＞Gly ＞Leu ＞Lys(Thr 含侧链-OH,Leu 含大的疏水残基)15补充1：指出用电泳技术分离下列物质，pH 是多少最适合，并说明理由？（6分）。

《概率论与随机过程》第4章习题解答

4.6 已知平稳过程)(t X 的自相关函数为||)(τατ-=e R X ，求)(t X 的功率谱密度)(ωX G ，并作图。

解：()()0()()022()eee 11e e ()()11()()()2()()j X j j j j G e d d d j j j j j j j j ατωτωατωατωατωατωτττωαωαωαωαωαωααωαωαωα∞---∞∞---+-∞∞---+-∞==+=---+=-+-+--+==-++⎰⎰⎰4.7 已知平稳过程)(t X 的自相关函数为τωττα0||cos )(-=e R X ，求)(t X 的功率谱密度)(ωX G ，并作图。

解：00000000000()()00[()][()][()][()]0[()]0()ecos 11e (e e )(e e )e 2211e e )(e e )22111e 2()(j X j j j j j j j j j j j G e d d d d d j j ατωτωτωτωτωτωατωατωωατωωατωωατωωατωωατωωττττττωωα∞---∞∞-----+-∞∞----+---+-++-∞---==+++=+++=----⎰⎰⎰⎰⎰0000[()]0[()][()]000000022220020e )111e e 2()()1112()()1112()()1222()()()j j j j j j j j j ωωατωωατωωατωωαωωαωωαωωαωωαωωαωωαααωωαωωααωω-+--∞∞--+-++⎧⎫⎨⎬+-⎩⎭⎧⎫+--⎨⎬-+++⎩⎭⎧⎫=--⎨⎬--+-⎩⎭⎧⎫++⎨⎬-+++⎩⎭⎧⎫⎪⎪=+⎨⎬-+++⎪⎪⎩⎭=-+2220()ααωωα+++4.9已知平稳过程X(t)，求Y(t)=A+B X(t)的功率谱密度，A ，B 为常数解：()(){})(R B 2A )(R B )]E[ABX(t E[ABX(t)]A )BX(t A BX(t)A E )(R X 2X 2X 22Y τττττ++=++++=+++=ABm ()22X X 22X ()A2B R ()2A 2()()j Y X G ABm e d ABm B G ωτωττπδωω∞--∞⎡⎤=++⎣⎦=++⎰4.11 已知平稳过程)(t X 的功率谱密度为⎩⎨⎧<=其它，，01)(0ωωωX G ，求)(t X 的自相关函数）（τX R ，并作图。

线性代数居余马版第四章详细课后题答案

1、由过渡矩阵的定义，设从基1234,,,εεεε到基1234,,,γγγγ的过渡矩阵为A ，则()()12341234,,,,,,A A γγγγεεεε==，初等行变换求得1111111111111141111A -⎛⎫ ⎪--⎪= ⎪-- ⎪--⎝⎭，所以11111151111211111111144111111A γβ-⎛⎫⎛⎫⎛⎫⎪⎪ ⎪-- ⎪⎪ ⎪=== ⎪⎪ ⎪--- ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭2(1)、记γ在基123,,ααα下为*γ. 设从基123,,εεε到基123,,ααα的过渡矩阵为A ，则()()123123,,,,A A αααεεε==，初等行变换求得11875521311A --⎛⎫⎪=-- ⎪ ⎪--⎝⎭，所以 1187532*5216131121A γγ---⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪==--= ⎪⎪ ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎝⎭2(2)、设从基123,,ααα到基123,,βββ的过渡矩阵为C ，记()123,,B βββ=，则()()123123,,,,C βββααα=，即AC B =，所以1187535127714152112192093114164128C A B -----⎛⎫⎛⎫⎛⎫⎪⎪ ⎪==--= ⎪⎪ ⎪ ⎪⎪ ⎪---⎝⎭⎝⎭⎝⎭2(3)、记γ在基123,,βββ下为**γ，所以11***C B A γγγ--==，经初等变换得11811319452761811261913365212644284099997104B A -⎛⎫ ⎪⎛⎫ ⎪- ⎪⎪=--=--- ⎪ ⎪⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭，所以 115276181225311***3652126110644284099183C B A γγγ---⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪===---=- ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭3(1)、记()1234,,,A αααα=，()1234,,,B ββββ=，记γ在基1234,,,ββββ下为*γ.设从基1234,,,αααα到基1234,,,ββββ的过渡矩阵为P ，所以由过渡矩阵的定义有B AP =，则1P A B -=，经初等变换可得11001110101110010P A B -⎛⎫ ⎪ ⎪== ⎪⎪⎝⎭，10111110000011111P --⎛⎫⎪-⎪= ⎪ ⎪--⎝⎭所以，()1*0101P γγ-==-.3(2)、设ξ在基1234,,,αααα下的记为*ξ，从基1234,,,ββββ到基1234,,,αααα的过渡矩阵为Q ，所以由过渡矩阵的定义有A BQ =，则1111()Q B A A B P ----===，所以()1*1311TQ P ξξξ-===-3(3)、记α在基1234,,,ββββ下为*α，所以()1*3102P αα-==.4、记()1234,,,E εεεε=，()1234,,,B ββββ=. 设从基1234,,,εεεε到基1234,,,ββββ的过渡矩阵为P ，由过渡矩阵的定义知()()12341234,,,,,,P ββββεεεε=，即P B =. 设()Ta b c d γ=，又γ在基1234,,,ββββ下的坐标不变，所以P P γγγγ=⇒=，即20561********013a a b b c c d d ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪= ⎪⎪ ⎪- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭25633623a c d a a b c d b a b c d c a c d d ++=⎧⎪+++=⎪⇒⎨-+++=⎪⎪++=⎩5602360020a c d abcd a b c d a c d ++=⎧⎪+++=⎪⇒⎨-+++=⎪⎪++=⎩，其系数矩阵10561001123601011111001110120000A ⎛⎫⎛⎫ ⎪⎪⎪⎪= ⎪⎪- ⎪⎪⎝⎭⎝⎭初等变换，所以0a db d P Acd d dγγγ=-⎧⎪=-⎪=⇒=⇒⎨=-⎪⎪=-⎩，所以γ的通解为()1111,Tk k R γ=-∈.5(1)、略5(2)、设与向量,,αβγ都正交的向量为()1234,,,Tx x x x ξ=，则()()(),0,0,0αξβξγξ=⎧⎪=⎨⎪=⎩⇒12341234123420230220x x x x x x x x x x x x +-+=⎧⎪++-=⎨⎪---+=⎩，其系数矩阵121110552311013311220000--⎛⎫⎛⎫⎪ ⎪-- ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭初等变换得基础解系为()5310T -，()5301T-所以与向量,,αβγ都正交的向量为()()1253105301TTk k ξ=-+-6、设向量()1234,,,Tx x x x ξ=与所给向量均正交，所以12341234123400230x x x x x x x x x x x x +-+=⎧⎪--+=⎨⎪+++=⎩，其系数矩阵41001111311110100211310013⎛⎫ ⎪-⎛⎫ ⎪ ⎪-- ⎪ ⎪⎪ ⎪⎝⎭ ⎪⎝⎭初等变换，基础解系为410133T⎛⎫-- ⎪⎝⎭，所以可取()4013T ξ=--，)4013T--.7、证：已知()()()12,,,0m βαβαβα====，记i i k αγ=∑，其中i k 为任意常数，则γ为12,,,m ααα的任一线性组合。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

⑷ X *（Y MOD 2）=0
⑸ X GE Y =0
⑹ Y AND Z =0
10、设有一个有符号数组，共M 个字，试编写一程序求其中最大的数，若需求绝对值最大的数，程序
应如何修改？又若数组元素为无符号数，求最大数的程序应如何修改？
解：⑴在有符号数组中找出最大数的程序
data segment
mov cx,m
l1: lodsw
cmp ax,max
jng lab
mov max,ax
lab: loop l1
mov ah,4ch
int 21h
main endp
code ends
end start
⑵在有符号数组中找出绝对值最大数的程序
在LODSW 指令后插入：
And ax,ax
DATA ENDS
请写出数据段中MAX，VAL1，VAL2，LEND 符号所对应的值。
答：上述程序的数据段中
MAX=03F9H，VAL1=03F9H MOD 0AH=7，VAL2=VAL1*2=7*2=0EH，LEND=BUF2-BUFF=0006-0000=0006H
标号段内偏移地址数据备注
⑴MOV WORD1 [BX+2][DI]，AX ；√
⑵MOV AX，WORD1[，WORD2 ；×，内存储器单元之间不能直接传送。
⑷MOV SWORD，DS ；√
⑸MOV SP，DWORD[BX][SI] ；×，DWORD 是保留字
解：根据题意编写程序：
data segment
str1 db 'aSdas'
str2 db 'asdas'
data ends
code segment
assume cs:code,ds:data
start : mov ax,data
mov ds,ax
mov es,ax
lea si,str1
X EQU 60
Y EQU 70
Z EQU 8
试求下列表达式的值：
⑴X * Y-Z
⑵X/8+Y
⑶X MOD （Y/Z）
⑷X *（Y MOD 2）
⑸X GE Y
⑹Y AND Z
解： ⑴ X * Y-Z = 60*70-8=4192=1060H
⑵ X/8+Y =77.5=4DH
⑶ X MOD （Y/Z）=4
第四章习题解答（P195）
2、有下列数据段：
DATA SEGMENT
MAX EQU 03F9H
VAL1 EQU MAX MOD 0AH
VAL2 EQU VAL1*2
BUFF DB 4，5，‘1234’
BUF2 DB ？
LEND EQU BUF2-BUFF
m equ 10
dat dw m dup(?)
max dw ?
data ends
code segment
assume cs:code,ds:data
main proc far
start:mov ax,data
mov ds,ax
mov ax,dat
mov max,ax
cld
lea si,dat
⑹MOV [BX][SI]，CX ；√
⑺MOV AX，WORD1+WORD2 ；×，两个变量不能直接相加
⑻MOV AX，WORD2+0FH ；√
⑼MOV BX，0FFSET WORD1 ；√
⑽MOV SI，OFFSET WORD2[BX] ；×，OFFSET 后应跟变量或标号
9、巳知X，Y，Z 被赋值如下：
BUFF 0000 04
0001 05
0002 31 ‘1’
0003 32 ‘2’
0004 33 ‘3’
0005 34 ‘4’
BUF2 0006 00
……
3、设下列指令语句中的标识符均为字变量，请指出哪些指令是非法的，并指出其错误之处。
Jns lab1
Neg ax
lab1: cmp ax,max
初始化时，（MAX）=0（最小的绝对值）
⑶在无符号数组中找出最大数的程序
把条件判断指令：
Jng lab
改为：jbe lab
12、设有两个等字长、字节型字符串，试编写一汇编子程序，比较它们是否完全相同；若相同则将字
符Y 送入AL 中，否则将字符N 送入AL 中。
lea di,str2
mov cx,5
repz cmpsb
jnz labne
mov al,'Y'
jmp exit
labne:mov al,'N'
exit:mov ah,4ch
int 21h
code ends
end start