第四章 习题解答
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
原子物理学第四章习题解答

第四章习题解答4-1 一束电子进入1.2T 的均匀磁场时,试问电子的自旋平行于和反平行于磁场的电子的能量差为多大?解:∵磁矩为μu r 的磁矩,在磁场B u r中的能量为:U = -μu r ·B u r= -sz μ B电子自旋磁矩 sz μ=±B μ∴电子自旋平行于和反平行于磁场的能量差u =B μ B – (-B μB) =2B μ B ∴u = 2B μ B =2 ×0.5788×410-eV ·1T -× 1.2 T = 1.39 ×410- eV4-2 试计算原子处于23/2D 状态的磁矩μ及投影μz 的可能值. 解:由23/2D 可知 S=12 J=32L=2 ∴j g =32+12(1)(1)(1)S S L L J J +-++=32+121323223522⨯-⨯⨯=45又j μ=j g Bμ45B μ =1.55 B μ∴μ=1.55 B μ又,j z j j B m g μμ= 又3113,,,2222j m =--∴,142×255j z B B μμμ=±=±或,346×255j z B B μμμ=±=±即,6226(,,,)5555j z B μμ=--4-3 试证实:原子在63/2G 状态的磁矩等于零,并根据原子矢量模型对这一事实作出解释.解:由63/2G 可知:S =52 J = 32L = 4∴5745 31(1)(1)3122··03522(1)22×22JS S L LgJ J⨯-⨯+-+=+=+=+∴(1)0J j Bj j gμμ=+=即原子在63/2G状态的磁矩等于零。
解释:∵原子的总角动量为J L S=+u r u r u r,而处于63/2G态原子各角动量为:(1)4(41)20 4.47L L L=+=+==h h h h5535(1)(1) 2.9622S S S=+=+==h h h h3315(1)(1) 1.94222J J J=+=+==h h h h则它们的矢量关系如图示:Lu r和Su r同时绕Ju r旋进,相对取项保持不变由三角形余弦定理可知:22222211()[(1)(1)(1)]22L J L J S L L J J S S⋅=+-+++-+u r u rh h h=22355715[45]222222=⨯+⨯-⨯=hh而222221573515()(45)2222224S J S J L⋅=+-=⨯+⨯-⨯=-u r u r hh∴相应的磁矩2B BS Sg S Sμμμ=-=-u r u r u rh hB B Lg L L μμμ∆=-=-u ru r u r hhS L μμμ=+u r u ru r由于磁矩μu r 随着角动量绕J u r 旋进,因而对外发生效果的是μu r在J u r 方向上的分量。
功和能习题解答

第四章 功和能一 选择题1. 一辆汽车从静止出发,在平直公路上加速前进时,若发动机功率恒定,则正确的结论为:( )A. 加速度不变B. 加速度随时间减小C. 加速度与速度成正比D. 速度与路径成正比 解:答案是B 。
简要提示:在平直公路上,汽车所受阻力恒定,设为F f 。
发动机功率恒定,则P =F v ,其中F 为牵引力。
由牛顿运动定律得a m F F =-f ,即:f F P/m -v a =。
所以,汽车从静止开始加速,速度增加,加速度减小。
2. 下列叙述中正确的是: ( ) A. 物体的动量不变,动能也不变. B. 物体的动能不变,动量也不变. C. 物体的动量变化,动能也一定变化. D. 物体的动能变化,动量却不一定变化. 解:答案是A 。
3. 一颗卫星沿椭圆轨道绕地球旋转,若卫星在远地点A 和近地点B 的角动量与动能分别为L A 、E k A 和L B 、E k B ,则有:( )A. L B > L A , E k B > E k AB. L B > L A , E k B = E k AC. L B = L A , E k B > E k A地球BA选择题3图D. L B = L A , E k B = E k A 解:答案是C 。
简要提示:由角动量守恒,得v B > v A ,故E k B > E k A 。
4. 对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加. (2) 质点运动经一闭合路径,保守力对质点作的功为零.(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零. 在上述说法中: ( )A. (1)、(2)是正确的;B. (2)、(3)是正确的;C. 只有(2)是正确的;D. 只有(3)是正确的. 解:答案是C 。
5. 如图所示,足够长的木条A 置于光滑水平面上,另一木块B 在A 的粗糙平面上滑动,则A 、B 组成的系统的总动能:( )A. 不变B. 增加到一定值C. 减少到零D. 减小到一定值后不变 解:答案是D 。
量子力学周世勋习题解答第四章

第四章习题解答4.1.求在动量表象中角动量x L 的矩阵元和2x L 的矩阵元。
解:⎰⋅⋅'-'-=τπd e p z p y e L r p i y z rp i p p x)ˆˆ()21()(3 ⎰⋅⋅'--=τπd e zp yp e r p i y z rp i)()21(3 ⎰⋅⋅'-∂∂-∂∂-=τπd e p p p p i e rp i zy y z r p i))(()21(3⎰⋅'-∂∂-∂∂-=τπd e p p p p i r p p i z y y z)(3)21)()(()()(p p p p p p i y z z y'-∂∂-∂∂= δ ⎰''=τψψd L x L p x p p p x 2*2)()( ⎰⋅⋅'--=τπd e p z p y e r p i y z r p i23)ˆˆ()21( ⎰⋅⋅'---=τπd e p z p y p z p y e r p i y z y z rp i)ˆˆ)(ˆˆ()21(3 ⎰''-∂∂-∂∂-=τπd e p p p p i p z p y e rp i yz z y y z r p i))()(ˆˆ()21(3 ⎰⋅⋅'--∂∂-∂∂=τπd e p z p y e p p p p i r p i y z rp i y z z y)ˆˆ()21)()((3 ⎰⋅'-∂∂-∂∂-=τπd e p p p p r p p i y z z y)(322)21()()()(22p p p p p p yz z y'-∂∂-∂∂-= δ #4.2 求能量表象中,一维无限深势阱的坐标与动量的矩阵元。
解:基矢:x a n a x u n πsin 2)(=能量:22222a n E n μπ =对角元:2sin 202a xdx a m x a x a mm ==⎰π 当时,n m ≠ ⎰⋅⋅=a mn dx ax x a m a x 0)(sin )(sin 2π[][]1)1()(4)(1)(11)1(])(sin )()(cos )([])(sin )()(cos )([1)(cos )(cos 12222222022202220---=⎥⎦⎤⎢⎣⎡+----=⎥⎥⎦⎤+++++-⎢⎢⎣⎡--+--=⎥⎦⎤⎢⎣⎡+--=--⎰n m n m a aa n m mnan m n m a x a n m n m ax x a n m n m a x a n m n m ax x a n m n m a a dx x a n m x a n m x a ππππππππππππ[][]a n m mn i n m n m a a n i x a n m n m a x a n m n m a a n i dxx a n m x a n m a n i xdxa n x a m an i xdxan dx d x a m a i dx x u p x u p n m nm aa a a n m mn )(21)1(]1)1()(1)(1 )(cos)()(cos )()(sin )(sin cos sin 2sin sin 2)(ˆ)(2220202020*---=--⎥⎦⎤⎢⎣⎡-++=⎥⎦⎤⎢⎣⎡--+++=⎥⎦⎤⎢⎣⎡-++-=⋅-=⋅-==--⎰⎰⎰⎰πππππππππππππππ#4.3 求在动量表象中线性谐振子的能量本征函数。
弹性力学(徐芝纶)第四章习题答案

第四章 习题解答4-14-2、解:本题为轴对称应力问题,相应的径向位移为: ()()()()()θ+θ+⎥⎦⎤⎢⎣⎡υ-+υ-+-υ-+υ+-=sin cos ln K I Cr 12Br 311r Br 12r A 1E 1u r (1) 轴对称应力通式为()()02ln 232ln 2122=+++-=+++=θθτσσr r C r B rAC r B r A由应力边界条件()()()()0,00,===-=====b r r b r r a r r a r r q θθτστσ并结合位移单值条件可知B=0,求得:22222222ab qa C a b qb a A -=--= 因半径的改变与刚体位移I ,K 无关,且为平面应变问题,将A 、B 、C 代入(1)式,并将υυυυ-→-→1,12EE 得:内半径的改变:()()()⎪⎪⎭⎫⎝⎛-+-+-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυυυ11*111112222222222222a b a b Eqa a a b qa a a b q b a E u ar r外半径的改变:()()()2222222222221*11111a b ab E qa b a b qa b a b q b a Eu br r --=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυ 圆筒厚度的改变:()()()⎪⎪⎭⎫⎝⎛-++---=∆-∆=∆==υυυ112a b a b E qa u u R ar r b r r4-2另解:半径为r 的圆筒周长为r π2,受载后周长则为 ()θθεπεππ+=+1222r r r , 于是半径为 ()θε+1r ,半径的改变量则为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--=⎪⎭⎫⎝⎛---=C r A C rA r E E r r r 212111*2222υυυσυυσυεθθ将对应的A 、C 及r=a,b 分别代入,可求出内外半径的改变及圆筒厚度的改变。
(解答)《随机过程》第四章习题

第四章 二阶矩过程、平稳过程和随机分析 习题解答1、 设∑=-=Nk k k kn U n X 1)cos(2ασ,其中k σ和k α为正常数,)2,0(~πU U k ,且相互独立,N k ,,2,1 =,试计算},1,0,{ ±=n X n 的均值函数和相关函数,并说明其是否是平稳过程。
解:计算均值函数和相关函数如下0)}{cos(2)cos(2}{)(11=-=⎭⎬⎫⎩⎨⎧-==∑∑==Nk k k k N k k k k n X U n E U n E X E n ασασμ∑∑∑∑∑∑======-=--=--=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡-⋅⎥⎦⎤⎢⎣⎡-=Ni i i N i i i i i i Ni Nj j j i i j i N j j j j N i i i i X m n U m U n E U m U n E U m U n E m n R 12121111)](cos[)}cos(){cos(2)}cos(){cos(2)cos(2)cos(2),(ασαασαασσασασ因此可知,},1,0,{ ±=n X n 是平稳随机过程。
2、 设有随机过程))(cos()(t t A t X πηω+=,其中0>ω为常数,}0),({≥t t η是泊松过程,A 是与)(t η独立的随机变量,且2/1}1{}1{===-=A P A P 。
(1) 试画出此过程的样本函数,并问样本函数是否连续? (2) 试求此过程的相关函数,并问该过程是否均方连续? 解:(1)样本函数不连续。
(2)令:012≥>t t ,下面求相关函数:)(221)(212210)(1212211212121211212212122112221122121121212cos cos )]}(cos[)]({cos[21!)]([)]}(cos[)]({cos[)1(21))]}()(()(cos[))]()(()(2)({cos[21))]}()(()(cos[))]()(()({cos[21))}(cos())({cos(}{))}(cos())(cos({)}()({),(t t t t k t t k kX e t t e t t t t e k t t t t t t t t t t t t t t t E t t t t t t t t E t t t t E A E t t t t A E t X t X E t t R ----∞=--⋅=⋅-++=⋅-⋅-++-=-+-+-+++=-+-++++=++⋅=++==∑λλλωωωωλωωηηπωηηππηωηηπωηηπωπηωπηωπηωπηω因为:t t t R ωξ2cos ),(=因此该过程是均方连续的随机过程。
第4章 习题解答
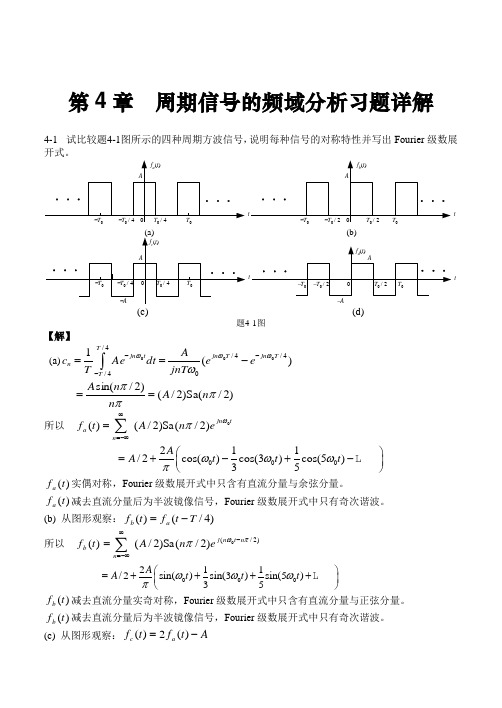
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
大学电路习题第4章
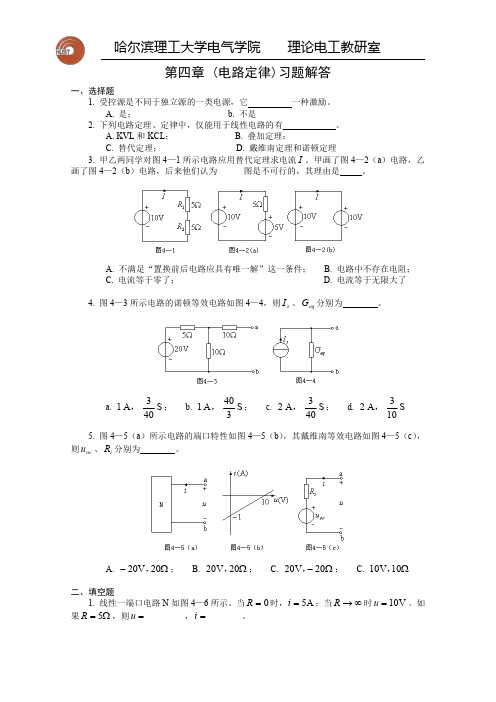
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源,它一种激励。
A.是; b.不是2.下列电路定理、定律中,仅能用于线性电路的有。
A.KVL 和KCL ; B.叠加定理;C.替代定理; D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。
甲画了图4—2(a )电路,乙画了图4—2(b )电路,后来他们认为图是不可行的,其理由是。
A.不满足“置换前后电路应具有唯一解”这一条件;B.电路中不存在电阻;C.电流等于零了;D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4,则s I 、eq G 分别为。
a.S 403A 1,;b.S 340A 1,;c.S 403A 2,;d.S 103A 2,5.图4—5(a )所示电路的端口特性如图4—5(b ),其戴维南等效电路如图4—5(c ),则oc u 、i R 分别为。
A.Ω-20V 20,;B.Ω20V 20,;C.Ω-20V 20,; C.Ω10V 10,二、填空题1.线性一端口电路N 如图4—6所示。
当0=R 时,A 5=i ;当∞→R 时V 10=u 。
如果Ω=5R ,则=u ,=i 。
2.图4—7所示电路中,N 为线性电路,且Ω=10R 。
当0=s u ,0=s i 时,V 5=u ;当A 2=s i ,0=s u 时,V 8=u ;当0=s i ,V 10=s u 时,V 6=u 。
那么,当A 6=s i ,V 4=s u 时,=i 。
3.图4—8(a )所示电路的戴维南等效电路如图4—8(b ),那么=s U ,=eq R 。
4.图4—9(a )所示电路的戴维南等效电路如图4—9(b ),则=s U ,=eq R 。
5.在图4—10(a )所示的电路中,i u 1024-=(i 的单位用安培时,u 的单位为伏特),其戴维南等效电路如图4—10(b ),则=s u ,=0R 。
三、计算题1.用叠加定理计算图4—11所示电路中的u 。
计算机系统结构 第四章(习题解答)
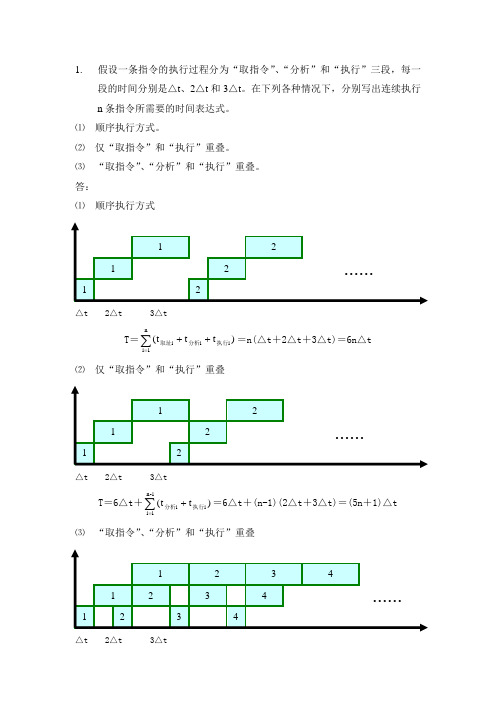
1. 假设一条指令的执行过程分为“取指令”、“分析”和“执行”三段,每一段的时间分别是△t 、2△t 和3△t 。
在下列各种情况下,分别写出连续执行n 条指令所需要的时间表达式。
⑴ 顺序执行方式。
⑵ 仅“取指令”和“执行”重叠。
⑶ “取指令”、“分析”和“执行”重叠。
答:⑴ 顺序执行方式12 ......1 2 12T =∑=++n1i i i i )t t t (执行分析取址=n(△t +2△t +3△t)=6n △t⑵ 仅“取指令”和“执行”重叠12 ......1 212T =6△t +∑=+1-n 1i i i )t t (执行分析=6△t +(n-1)(2△t +3△t)=(5n +1)△t⑶ “取指令”、“分析”和“执行”重叠12 34 ......1 2 3 41234△t2△t3△t△t2△t3△t△t2△t3△tT =6△t +∑=1-n 1i i )t (执行=6△t +(n-1)(3△t)=(3n +3)△t2. 一条线性流水线有4个功能段组成,每个功能段的延迟时间都相等,都为△t 。
开始5个任务,每间隔一个△t 向流水线输入一个任务,然后停顿2个△t ,如此重复。
求流水线的实际吞吐率、加速比和效率。
答:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...1 2 3 4 5 6 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 56 7 8 9 10 11 12 13 14 151 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23我们可以看出,在(7n+1)Δt 的时间内,可以输出5n 个结果,如果指令的序列足够长(n →∞),并且指令间不存在相关,那么,吞吐率可以认为满足:)n (t75t )n /17(5t )1n 7(n 5TP ∞→∆=∆+=∆+=加速比为:)n (720n /17201n 7n 20t )1n 7(t 4n 5S ∞→=+=+=∆+∆⨯=从上面的时空图很容易看出,效率为:)n (75n /1751n 7n 5t )1n 7(4t 4n 5E ∞→=+=+=∆+⨯∆⨯=3. 用一条5个功能段的浮点加法器流水线计算∑==101i i A F 。
概率论与数理统计统计课后习题答案-总主编-邹庭荣-主编-程述汉-舒兴明-第四章

概率论与数理统计统计课后习题答案-总主编-邹庭荣-主编- 程述汉-舒兴明-第四章第四章习题解答11 •设随机变量X〜B (30,-),则E (X)=( D ).6A.-;D.5.1E (X) = np = 30 562 •已知随机变量X和Y相互独立,且它们分别在区间[-1 , 3]和[2, 4]上服从均匀分布,则E(XY)=( A ).A. 3;B. 6;C. 10;D. 12.E(X) =1 E(Y) =3因为随机变量X和Y相互独立所以E(XY) = E(X)E(Y) = 33.设X表示10次独立重复射击命中目标的次数,每次射中目标的概率为0.4,贝U X2的数学期望E(X 2) = 1&4 .X LI B(10,0.4) E(X) =4 D(X) =2.42 2E(X ) =(E(X)) D(X) =18.44.某射手有3发子弹,射一次命中的概率为-,如果命中了就停止射击,3否则一直射到子弹用尽.设表示X耗用的子弹数.求E (X).解:X123P2/32/91/92 2 1 13E(X)=—十—:2 +3 9 9 95 .设X的概率密度函数为x, 0ExE1f (x) - x, 1 :: x 乞2[0, 其它求 E(X) , E(X2).解: E(X) = J xf(x)dx = J x2dx + J x(2-x)dx =1,0 ' 11 32 27f (x)dx x dx 亠 i x (2「x)dx .- -bo -E(X 2)「;x 2求 E(X) , E(Y),E(XY).解:X-12P 0.650.35E(X)二「0.65 0.35 2 =0.05 .Y-112P0.40.250.35E(Y) = -0.4 0.25 1 0.35 2 =0.55E(XY)=(-1) (-1) 0.25 (-1) 1 0.1 (-1) 2 0.32 (-1) 0.15 2 1 0.15 2 2 0.05 =-0.257 •设二维随机向量(X, Y)的联合概率密度为求(1)E(X Y); (2) E(XY).E(XY) = _;.;(xy)f(x,y)dxdy=讥(广(xy)「dy)dx = 38.设随机变量X与Y相互独立,且D(X)=1, D(Y)=2 , J则D(X-Y)= 3 .D(X _Y) = D(X) D(Y) =39.设正方形的边长在区间]0, 2]服从均匀分布,则正方形面积A=X2的f(x,y)二e0,1°,0 :x y其它解: y) dxdy( x x y )e y d y dx 3方差为64/45 _________ .4 1E(X)=1, D(X) ,12 3X的密度函数f(x)= 102,0乞x乞26 •设随机向量(X, Y)的联合分布律为:E(X Y)=二y)求 D(X ),D(Y ),D(X-Y ).解:由本章习题5知E(X)=1 , E(X 2)=7,于是有62 21D(X)二 E(X )-(E(X)).6221 4E (XTE (X)「D (X)n 〒.4"be 42E(X )= x f(x)dx = 01 4 16x dx =2 5D(X 2) =E(X 4)—[E(X 2)]210•设随机变量X 的分布律为X -1 0 1 2P1/5 1/2 1/5 1/10求 D(X).解:D(X) = E(X 2) -(E(X))2, E(X2 21 2 1 2E(X ) =(-1) -01- 2 551 19 224D(X)=E (X 2)-(E(X))2=5 25 2511•设随机变量X 的概率密度函数为f(x)亠1,求 D(X ).::1I解:E(X) xf (x) dxxe*dx=0, 2E(X 2)x 2f(x)dx=2 x 2e^dx = 2 ,0 212•设随机变量X , Y 相互独立,其概率密度函数分别为x,f x (x)二 2 -x,0 _x _1 1 :: x _ 2y_ 0其它16 564 45由Y LI E(1)知 E(X) =D(X) =1.由于随机变量X , Y 相互独立,所以D(X -Y)二 D(X) D(Y) =7.613•设 D(X)=1,D(Y)=4,相关系数 P XY =0.5,则 cov(X,Y)=_1 __________ covX,Y)= » D(X)D(Y) =114•设二维随机变量(X, Y )的联合密度函数为求 cov(X,Y ), ?XY •DJI nI 22。
模电第四章答案

第四章习题解答4-1如题4-1图所示MOSFE转移特性曲线,说明各属于何种沟道?若是增强型,开启电压等于多少?若是耗尽型,夹断电压等于多少?答:(a)P-EMOSFET,开启电压V GSM2V(b)P-DMOSFET,夹断电压V Gsoff (或统称为开启电压V GS Q 2V(c)P-EMOSFET,开启电压V Gsth 4V(d)N-DMOSFET,夹断电压V GS Off (或也称为开启电压V GS Q4V4-2 4个FET的转移特性分别如题4-2图(a)、(b)、(c)、(d)所示。
设漏极电流i D的实际方向为正,试问它们各属于哪些类型的FET?分别指出i D的实际方向是流进还是流出?答:(a)P-JFET,i D的实际方向为从漏极流出。
(b)N-DMOSFET,i°的实际方向为从漏极流进。
(c)P-DMOSFET,i D的实际方向为从漏极流出。
(d)N-EMOSFET, i D的实际方向为从漏极流进。
4-3 已知N 沟道EMOSFET 的卩n C ox=100y A/V2,V GS(th)=0.8V, W/L=10,求下列情况下的漏极电流:(a)V GS=5V,V DS=1V ; (b)V GS=2V,V DS=1.2V ;(c)V GS=5V,V DS=0.2V; (d)V GS=V DS=5V。
解:已知N-EMOSFET 的n C ox 100 A/V2, V GSth 0.8V W L 10(a)当V GS 5V,V DS 1V 时,MOSFET 处于非饱和状态V°s V GS V GS thI D /2V GS V Gsth V DS V2DS今0.1mA V2 102 5 0.8 1 12 3.7mA(b)当V GS2V,V DS 1.2V 时,J S V GS th 1-2V V DS,MOSFET 处于临界饱和I D i n C ox ¥V GS V GS th 弓0.1叫 2 10 2 0.8 20.72mA(c)当V GS5V,V DS0.2V 时,% V GS th 4.2V V DS,MOSFET 处于I D ; nC oxWL 2V GSV GS th J SV DS4 0.1mA V 2 1025 0.80.2 0.220.82mA(d )当 V GSV DS5V 时,V DSV GSV GS th,MOSFET 处于饱和状态1nC oxWV GS V GS th20.1mA v 2 105 0.8 2 8.82mA4-4 N 沟道 EMOSFET 的 V GS(th)=1V ,卩 n C ox (W/L ) =0.05mA/V 2,V GS =3V 。
第04章_JavaScript和jQuery习题解答

第4章JavaScript 和jQuery 第四章习题解答1.JavaScript 的特点是什么?JavaScript 与jQuery 是什么关系?【解答】JavaScript 是一种广泛用于网页客户端开发的脚本语言。
通过JavaScript ,可以动态选择、添加、删除、修改HTML 元素和CSS 。
jQuery 是一种免费的开源JavaScript 库,这些库函数也是用JavaScript 来编写的,但是语法更加简洁、直观。
另外,jQuery 还自动处理了各种浏览器的兼容性问题,让开发人员编写的客户端代码在各种操作系统平台下、各种浏览器以及同一种浏览器的不同版本中呈现完全相同的效果。
2.使用DOM 访问指定节点的方法主要有哪几种?【解答】使用DOM 访问指定节点的方法主要有三种,分别为:1)getElementById(id):返回文档中具有指定id 属性的element 节点2)getElementByName(name):返回文档中具有指定name 属性的element 节点3)getElementsByTagName(tagName):返回文档中具有指定标记名的所有element 节点3.如何使用jQuery 获取和设置元素的某个CSS 属性的值?【解答】jQuery 提供获取或设置元素的CSS 属性的方法主要有以下几种方式1)css(propertyName) 该方法只有一个参数,用于获取匹配元素的CSS 属性值,参数propertyName 指定要获取的属性。
2)css(propertyName,value) 该方法有两个参数,用于设置匹配元素的CSS 属性。
3)css(propertyName, function(index, value)) 该方法也是为所有匹配的元素设置CSS 属性。
4)css({properties}) 该方法为匹配的每个元素设置一个或多个CSS 属性4.jQuery 获取和设置HTML 页面元素的值的方法有哪些?【解答】jQuery 提供获取或设置HTML 页面元素的值的方法主要有以下几种方式1)html([value])、html(function(index, html)) html([value]):不带参数时,获取第一个匹配元素的html 内容。
高分子科学部分习题解答

第四章习题解答7.用等摩尔己二胺与已二酸制备尼龙66,应加多少乙酸才能在反应程度达99.7%时,得到分子量为16000的聚合物?解法一:酰胺的01141121132M +== 对于分子量为16000的聚酰胺6.14111316000==n X 已知p=0.997。
根据p 与非等摩尔投料比共同控制n X 时有112n rX r rp +=+-求得r =0.992。
''22A BB B B BN N r N N N N ==++设己二酸和己二胺加料均为1mol 时,乙酸为N mol则'120.992122Br N ⨯==⨯+,得'0.0081B N =, 即乙酸和己二酸加料摩尔比为0.0081:1。
解法二:设己二酸和己二胺加料均为1mol 时,乙酸为N mol2214112f N N ⨯⨯==+++22160004113220.9972n X p f N===--⨯+N=0.0082mol第五章习题解答4.从乙酸乙烯酯出发制取聚乙烯醇缩甲醛:1) 写出各步反应式并注明各步主产物的名称及用途。
2) 纤维用和悬浮聚合分散剂用的聚乙烯醇有何差别?3) 实验测得一聚乙酸乙烯酯样品的数均聚合度为200,将其进行湿法水解得聚乙烯醇,发现其数均聚合度降为180,试结合第三章所学知识,解释这一现象。
4) 下列合成路线是否可行?请说明理由。
乙酸乙烯酯乙烯醇聚乙烯醇产物水解缩醛化解:1)自由基聚合反应:nCH2=CHOCOCH3AIBN*CH2CHOCOCH3*n产物为聚醋酸乙烯酯。
醇解反应:CH2CHOCOCH3**n CH3OH*CH2CH*OHn产物为聚乙烯醇,可做分散剂。
缩醛化反应:CH2CHOH 2CHOHHCHO-H2OCH2CHCH2O CH OCH2产物为聚乙烯醇缩甲醛.可制维尼纶.2)纤维用和悬浮聚合分散剂用的聚乙烯醇的差别在于醇解度不同.前者要求醇解度高,以便缩醛化.后者要求醇解度中等,以使水溶性好.3)因为醇解所用溶剂为甲醇,而甲醇的链转移常数很大,所以醇解时发生链转移.聚合度变小.4)不可行.因为乙烯醇与乙醛为互变异构体,两者同时存在.不能用其直接聚合得聚乙烯醇.8.将PMMA、PAN、PE、PVC四种聚物进行热降解反应,分别得到何种产物。
《运筹学》 第四章习题及 答案

《运筹学》第四章习题一、思考题1.运输问题的数学模型具有什么特征?为什么其约束方程的系数矩阵的秩最多等于1-+n m ?2. 用左上角法确定运输问题的初始基本可行解的基本步骤是什么?3. 最小元素法的基本思想是什么?为什么在一般情况下不可能用它直接得到 运输问题的最优方案?4. 沃格尔法(V ogel 法)的基本思想是什么?它和最小元素法相比给出的运输问题的初始基本可行解哪一个更接近于最优解?为什么?5. 试述用闭回路法检验给定的调运方案是否最优的原理,其检验数的经济意义是什么?6. 用闭回路法检验给定的调运方案时,如何从任意空格出发去寻找一条闭回路?这闭回路是否是唯一的?7. 试述用位势法求检验数的原理、步骤和方法。
8. 试给出运输问题的对偶问题(对产销平衡问题)。
9. 如何把一个产销不平衡的运输问题(产大于销或销大于产)转化为产销平衡的运输问题。
10.一般线性规划问题应具备什么特征才可以转化为运输问题的数学模型? 11.试述在表上作业法中出现退化解的涵义及处理退化解的方法。
二、判断下列说法是否正确1.运输问题模型是一种特殊的线性规划模型,所以运输问题也可以用单纯形方法求解。
2.因为运输问题是一种特殊的线性规划模型,因而求其解也可能出现下列四种情况:有唯一最优解;有无穷多个最优解;无界解;无可行解。
3.在运输问题中,只要给出一组(1-+n m )个非零的{}j i x ,且满足∑==nj i j i a x 1,∑==mi j j i b x 1,就可以作为一个基本可行解。
4.表上作业法实质上就是求解运输问题的单纯形法。
5.按最小元素法或元素差额法给出的初始基本可行解,从每一空格出发都可以找到一闭回路,且此闭回路是唯一的。
6.如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数k ,最优调运方案将不会发生变化。
7.如果运输问题单位运价表的某一行(或某一列)元素分别乘上一个常数k ,最优调运方案将不会发生变化。
组合数学第四章习题解答

4.23 凸多面体中与一个顶点相关的各角之和与2 的差称为该顶点的欠角,证明凸多面体各顶点欠 角之和为4
证:设V,S,E分别为顶点集,面集,边(棱)集。 由欧拉定理 |V|+|S|-|E|=2. 设aij为与顶点vi, 面Sj为相关的面角,ej为Sj的的边数, 给定Sj则∑aij=(ej-2)π 欠角和为∑(2π-∑aij)=∑2π-∑ ∑aij =2|V|π-∑ ∑aij=2|V|π-∑(ej-2)π =2|V|π-∑ejπ+2|S|π =2|V|π+2|S|π-2|E|π=4π
G×G’的单位元素是(e,e’),试证G×G’是群 (1)封闭性显然 (2)结合律显然 (3)逆元素显然
(4)单位元显然
4.27 一个项链由7颗珠子装饰成的,其中两颗珠 子是红的,3颗是蓝的,其余两颗是绿的,问有多少 种装饰方案,试列举之。
G (1)(2)(3)(4)(5)(6)(7) (1234567),(1357246), (1473625),(1526374), (1642753),(1765432)
4.24 足球由正五边形与正六边形相嵌而成 (a)一个足球由多少正五边形与正六边形组成 (b)把一个足球所有的正六边形都着以黑色,正五 边形则着以其它各色,每个正五边形着色各不相 同,有多少种方案?
4.25 若G和G是两个群
G G ' {( g ,g ')g G ,g ' G ' }, ( g ,g ')( g ,g ') ( g g ,g 'g '), 1 1 2 2 1 2 1 2
4.21 在正四面体的每个面上都引一条高,有多少 种方案?
解:除了绕顶点-对面的中心轴旋转均不会 产生不变的图象外, 绕其他轴的旋转相当于正 4面体的面3着色。参照讲义4.6例3可得不同的 方案数为 M=[34+3·32]/12=9
运筹学习题答案(第四章)(课堂PPT)

Ⅰ
1500
6
Ⅱ
2000
4.5
Ⅲ
1000
3
page 9 28 April 2020
School of Management
运筹学教程
第四章习题解答
表4-14
商标
兑制要求
售价(元/kg)
红
Ⅲ少于10% Ⅰ多于50%
5.5
黄
Ⅲ少于70% Ⅰ多于20%
5.0
蓝
Ⅲ少于50% Ⅰ多于10%
4.8
解:x11 1125, x12 300, x13 75, x21 1125,
x2
d1
d
2
d3
d1
d
2
d3
150 40 40
x1
,
x2
,
d
i
,
d
i
0, i
1,2,3
解:x1
55, x2
40,
d
2
15
满足P1,不满足P2
page 3 28 April 2020
School of Management
运筹学教程
第四章习题解答
min
P1
(d
3
d
4
第四章习题解答
解:目标规划模型如下:
min
P1d1
,
P2
(d
2
d
3
d
4
),
P3d
5
,
P4
d
6
x1 x2 x3 1000
x1
d1
d1
300,
x2
d
3
d
3
350,
x1
第4章习题解答

第4章 习题讲解 章
为变址寄存器, R1为基址寄存器 PC为程序计数器 为基址寄存器, 【题4-6 】 R为变址寄存器, R1为基址寄存器,PC为程序计数器 OP I
寻址 方式 (1) ) (2) ) (3) ) (4) ) (5) ) (6) ) I 0 0 0 0 1 1 X 00 01 10 11 00 11
【题4-5】指令格式结构如下所示,试分析指令格式及 】指令格式结构如下所示, 寻址方式的特点 的特点。 寻址方式的特点。
15 12 11 9 8 6 5 3 2 0
OP
寻址方式
寄存器
寻址方式
寄存器
答: ① 所示指令是单字长二地址指令。 所示指令是单字长二地址指令 单字长二地址指令。
操作码字段OP有 可以指定2 16条指令 ② 操作码字段 有4位,可以指定24=16条指令。 可以是RR RS或SS型指令 RR、 型指令。 寻址方式有2 ③ 寻址方式有23=8种,可以是RR、RS或SS型指令。
第4章 典型例题 章
为操作码字段, 【例4.2】指令格式如下所示,OP为操作码字段,试分 】 指令格式如下所示, 为操作码字段 析指令格式特点。 析指令格式特点。
15 10 7 4 3 0
OP
——
源寄存器
变址寄存器
位移量 (16位) 位
答:
双字长二地址指令; ① 双字长二地址指令; 操作码字段OP OP为 可以指定2 64种操作 种操作; ② 操作码字段OP为6位,可以指定26=64种操作; 一个操作数在源寄存器( 16个 ③ 一个操作数在源寄存器(共16个)中,另一个操作数在内存储 器中(有效地址由变址寄存器和位移量决定) 所以是RS 指令。 RS型 器中 ( 有效地址由变址寄存器和位移量决定 ) , 所以是 RS 型 指令 。
matlab第四章课后作业解答

matlab第四章课后作业解答第四章习题解答1、求下列多项式的所有根,并进⾏验算。
(3)267235865x x x x-+-(4)4)32(3-+x 解:>> p=zeros(1,24);>> p(1)=5;p(17)=-6;p(18)=8;p(22)=-5;>> root=roots(p)root =0.97680.9388 + 0.2682i0.9388 - 0.2682i0.8554 + 0.5363i0.8554 - 0.5363i0.6615 + 0.8064i0.6615 - 0.8064i0.3516 + 0.9878i0.3516 - 0.9878i-0.0345 + 1.0150i-0.0345 - 1.0150i-0.4609 + 0.9458i-0.4609 - 0.9458i-0.1150 + 0.8340i-0.1150 - 0.8340i-0.7821 + 0.7376i-0.7821 - 0.7376i-0.9859 + 0.4106i-0.9859 - 0.4106i-1.0416-0.7927>> polyval(p,root)ans =1.0e-012 *-0.07120.0459 - 0.0081i0.0459 + 0.0081i-0.0419 + 0.0444i-0.0419 - 0.0444i0.0509 + 0.0929i0.0509 - 0.0929i-0.2059 + 0.0009i-0.2059 - 0.0009i-0.0340 + 0.0145i-0.0340 - 0.0145i0.1342 + 0.0910i0.1342 - 0.0910i0.0025 + 0.0027i0.0025 - 0.0027i-0.0077 + 0.4643i-0.0077 - 0.4643i-0.3548 - 0.1466i-0.3548 + 0.1466i-0.0251-0.0073(4) >> p1=[2 3];>> p=conv(conv(p1,p1),p1)-[0 0 0 4];>> root=roots(p)root =-1.8969 + 0.6874i-1.8969 - 0.6874i-0.7063>> polyval(p,root)ans =1.0e-014 *-0.7105 - 0.6217i-0.7105 + 0.6217i6、求解下列⽅程组在区域1,0<<βα内的解-=+=.sin 2.0cos 7.0,cos 2.0sin 7.0βαββαα解:以初值)5.0,5.0(),(00=βα进⾏求解>> fun=inline('[0.7*sin(x(1))+0.2*cos(x(2))-x(1),0.7*cos(x(1))-0.2*sin(x(2))-x(2)]');>> [x,f,h]=fsolve(fun,[0.5 0.5])Optimization terminated: first-order optimality is less than options.TolFun.x =0.5265 0.5079f =1.0e-007 *-0.1680 -0.2712h =1因⽽,该⽅程组的近似根为5079.0,5265.0==βα。
水力学 第四章课后题答案

4.7 水平突然扩大管路,如图所示,已知:直径 d1=5cm,直径d2=10cm,管中流量Q=20l/s,试 求:U形水银比压计中的压差读数Δh。
解:以管轴中心线为基准面,写1-1,2-2断面
的能量方程
p1
g
1v12
2g
p2
g
2v22
2g
hj
p1 p2 v22 v12 (v1 v2 )2
(2)经2分钟流入量水箱的水量为0.329m3。试 求弯管的局部水头损失系数ζ值。
解:流量 Q V 0.329 0.00274m3 / s
T 120
v Q 1.4m / s
A
hf
l d
v2 2g
0.6m
hj hw hf 0.629 0.6 0.029m
hj
v2 2g
2ghj v2
4.1 雷诺数的物理意义?为什么可以判别流态?说明由层流到湍流的物理过程。
答:在流体运动中惯性力对黏滞力比值的无量纲数。Re=UL/ν .其中U为速度特 征尺度,L为长度特征尺度,ν为运动学黏性系数.
P116.P118 4.2 层流有什么特点?如何判别? 答:P116,雷诺数判别 4.3 何谓粘性底层?它的厚度对沿程水头损失有何影响? 答:在湍流中,紧靠固体边界附近的地方,因脉动流速很小,由脉动流速产生 的附加切应力也很小,而流速梯度却很大,所以粘滞切应力起主导作用,其流态 基本上属于层流。因此湍流中不是整个液流都是湍流,在紧靠固体边界表面有一 层极薄的层流层存在,该层流层就叫粘性底层。
0
1
0.023
[2 lg(3.7 d )]2
求出的λ值与假设相符合
通过上述计算说明同一个管径的水管中流过不同 的流量Q,其管壁可以是光滑区,或过渡粗糙区, 也可以是粗糙区。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-1 如图是用频率为1 000 kHz 的载波信号同时传输两路信号的频谱图。
试写出它的电压表达式,并画出相应的实现方框图。
计算在单位负载上的平均功率P av 和频谱宽度BW AM 。
解:(1)为二次调制的普通调幅波。
第一次调制:调制信号:F = 3 kHz载频:f 1 = 10 kHz ,f 2 = 30 kHz第二次调制:两路已调信号叠加调制到主载频f c = 1000 kHz 上。
令 Ω = 2π ⨯ 3 ⨯ 103 rad/sω1 = 2π ⨯ 104 rad/s ω2= 2π ⨯ 3 ⨯ 104 rad/s ωc = 2π ⨯ 106 rad/s第一次调制:v 1(t ) = 4(1 + 0.5cos Ωt )cos ω1tv 2(t ) = 2(1 + 0.4cos Ωt )cos ω2t第二次调制:v O (t ) = 5 cos ωc t + [4(1 + 0.5cos Ωt )cos ω1t + 2(1 + 0.4cos Ωt )cos ω2t ] cos ωc t = 5[1+0.8(1 + 0.5cos Ωt )cos ω1t + 0.4(1 + 0.4cos Ωt )cos ω2t ] cos ωc t(2) 实现方框图如图所示。
(3) 根据频谱图,求功率。
○1 载频为10 kHz 的振幅调制波平均功率 V m01 = 2V ,M a1 = 0.5W 5.4)211(2W 22121a 01av1201m 01=+===M P P V P ;○2 f 2 = 30 kHz V m02 = 1V ,M a2 = 0.4W 08.1)211(2W 5.02122a 02av2202m 02=+===M P P V P ; ○3 主载频f c = 1000 kHz V m0 = 5VW 5.122120m 0==V P总平均功率P av = P 0 + P av1 + P av2 = 18.08 W ○4 BW AM 由频谱图可知F max = 33 kHz得 BW AM = 2F = 2(1033 -1000) = 66 kHz4-3 试画出下列三种已调信号的波形和频谱图。
已知ωc >>Ω (1) v (t ) = 5cos Ωt cos ωc t (V); (2) v (t ) = 5cos(ωc +Ω) t ;(3) v (t ) = (5 + 3cos Ωt ) cos ωc t 。
解:(1) 双边带调制信号(a);(2) 单边带调制信号(b);(3) 普通调幅信号(c)。
4-6 何谓过调幅?为何双边带调制信号和单边带调制信号均不会产生过调幅? 答:调制信号振幅大于载波信号振幅的情况称为过调幅。
因为双边带和单边带调制信号已经将载波信号抑制,故均不会产生过调幅。
4-8 一非线性器件的伏安特性为⎩⎨⎧≤>=00Dv v v g i式中v = V Q 十v 1+ v 2 = V Q +V 1m cos ω1t +V 2m cos ω2t 。
若V 2m 很小,满足线性时变条件,则在V Q = -V 1m /2、0、V 1m 三种情况下,画出g (v 1)波形,并求出时变增量电导g (v 1)的表示式,分析该器件在什么条件下能实现振幅调制、解调和混频等频谱搬移功能。
解:根据伏安特性画出增量电导随v 的变化特性g (v )如图所示。
(1)1m Q 21V V -=时,画出g (t ) 波形如图所示。
图中通角由,2121cos m m==V V θ求得3π=θ D 3π3πD031d 2π1g t g g ==⎰-ω )3πsin(π2d cos π1D 3π3πD n n n g t t n g g ==⎰-ωωt n n n g g t g n 11D D cos )3πsin(1π231)(ω∑∞=+= (2) V Q = 0时,画出g (v ) 的波形如图所示。
])12(cos π)12(2)1(21[)cos33π2cos π221()()(111D 11D 11D t n n g t t g t K g t g n n ωωωω---+=⋅⋅⋅+-+==∑∞=-(3) V Q = V 1m ,g (t ) = g D ,如图所示。
可见,(1)、(2)中g (t ) 含有基波分量,能实现频谱搬移功能,而(3)中g (t )仅有直流分量,故无法实现频谱搬移功能。
为实现消除一些有害无用的组合频率分量,使输出有用信号的质量提高,在实现频谱搬移功能时,应遵循有用信号较弱,参考信号较强的原则。
调制时:v 1 = V cm cos ωc t (载波),v 2 = V Ωm cos Ωt (调制信号)解调时:v 1 = V cm cos ωc t (参考信号),v 2 = V sm (1 + M a cos Ωt )cos ωc t (调幅信号) 混频时:v 1 = V Lm cos ωL t (本振信号),v 2 = V sm (1 + M a cos Ωt )cos ωc t (调幅信号)4-9 在如图所示的差分对管调制电路中,已知v c (t ) = 360cos10π ⨯ 106t (mV ),v Ω (t ) = 5cos2π ⨯ 103t (mV ),V CC =|V EE |= 10 V ,R EE =15 k Ω,晶体三极管 β 很大,V BE(on)可忽略。
试用开关函数求i C =(i C1 - i C2)值。
解:由教材(4-2-14)可知i C = i C1 - i C2 = )2(th Tc 0V vi令,TCM c V Vx =i 0 = I 0 + i Ω(t )其中mA))(10π2cos(1031)()(mA 31V 533EE EEEE 0t R t v t i R V I ΩΩ⨯⨯=≈=-≈-, mA))](10π2cos(101[31330t i ⨯+=-又1085.13mV26mV360T cm c >===V V x 则⋅⋅⋅-+-=≈t t t t K t x c c c c 2c c 5cos 5π43cos 3π4cos π4)()cos 2(th ωωωωω 所以)mA ]()10π50cos(084.0)10π30cos(14.0)10π10cos(42.0)][10π2cos(101[)()]10π2cos(101[31)cos 2(th 66633c 233c c 0C ⋅⋅⋅-⨯+⨯-⨯⨯+=⨯+≈=--t t t t t K t t x i i ωω4-11一双差分对平衡调制器如图所示,其单端输出电流kTqv R v I kT qv i i I i 2th 22th 221E 201650I +≈-+=试分析为实现下列功能(不失真),两输人端各自应加什么信号电压?输出端电流包含哪些频率分量,输出滤波器的要求是什么?(1)混频(取ωI =ωL - ωC );(2)双边带调制;(3)双边带调制波解调。
解:(1) 混频:v 1(t ) = v L (t ) =V Lm cos ωL t ,v 2(t ) = v S (t ) = V sm cos ωc t ,当V Lm > 260 mV ,V sm < 26 mV 工作在开关状态时,产生的组合频率分量有ωL ± ωc ,3ωL ± ωc ,⋅⋅⋅,(2n +1)ωL ± ωc ,输出采用中心频率为 ωI 的带通滤波器。
(2) 双边带调制:v 1(t ) = v c (t ) = V cm cos ωc t ,v 2(t ) = v Ω(t ) = V Ωm (t )cos Ωt 。
工作在开关状态时,产生的组合频率分量有ωc ± Ω,3ωc ± Ω,⋅⋅⋅,(2n +1)ωc ± Ω。
输出采用中心频率为 ωc ,BW 0.7 > 2F 的带通滤波器。
(3) 双边带调制波解调:v 1(t ) = v r (t ) = V rm cos ωc t ,v 2(t ) = v S (t ) = V m0cos Ωt cos ωc t 。
开关工作时,产生的组合频率分量有Ω,2ωc ± Ω,4ωc ± Ω,⋅⋅⋅,2n ωc ± Ω。
输出采用低通滤波器,BW 0.7 > 2F 。
4-16 采用双平衡混频组件作为振幅调制器,如图所示。
图中v c (t ) = V cm cos ωc t ,v Ω(t ) = V Ωm cos Ωt 。
各二极管正向导通电阻为R D ,且工作在受v C (t )控制的开关状态。
设R L >>R D ,试求输出电压v O (t )表达式。
解:作混频器,且v C >> v Ω,各二极管均工作在受v C 控制的开关状态。
当 v C > 0,D 1、D 2导通,D 3、D 4截止 当 v C < 0,D 3、D 4导通,D 1、D 2截止 (1) 当 v C > 0时,等效电路,i I = i 1 - i 2 回路方程为:⎩⎨⎧=-+--=-++-②①00)(C D 2L I L 21D 1C v R i R i v R i i R i v v ΩΩ ○1 - ○2 2( i 1 - i 2)R L + 2 v Ω + ( i 1 - i 2)R D = 0DL 21I 22R R v i i i Ω+-=-= 考虑v C 作为开关函数K 1(ωc t )所以 )(2)(2c 1DL I t K R R t v i Ωω+-=(2) 同理可求v C < 0时i Ⅱ)π(2)(2c 1D L 43-+-=-=t K R R t v i i Ωω(3) R L 总电流 i = i Ⅰ- i Ⅱ)(2)(2)]π()([2)(2c 2DL c 1c 1D L t K R R t v t K t K R R t v ΩΩωωω+-=--+-=(4) v O (t ) ∵ R L >> R D ∴)()()()(22)(c 2c 2DL LO t K t v t K t v R R R t v ΩΩωω-≈+-=4-23 晶体三极管混频器的输出中频频率为f I = 200 kHz ,本振频率为f L = 500 kHz ,输人信号频率为f c = 300 kHz 。
晶体三极管的静态转移特性在静态偏置电压上的幂级数展开式为i C = I 0+av be +2be bv +3be cv 。
设还有一干扰信号v M =V Mm cos (2π×3.5×105t ),作用于混频器的输人端。
