第二章 RE到NFA的转换
编译原理课后习题答案+清华大学出版社第二版

用以引用非局部(包围它的过程)变量时,寻找该变量的地址。 DL: 动态链,指向调用该过程前正在运行过程的数据段基地址,用以过程执行结束释放
数据空间时,恢复调用该过程前运行栈的状态。 RA: 返回地址,记录调用该过程时目标程序的断点,即调用过程指令的下一条指令的地
编译程序大致有哪几种开发技术?
答案:
(1)自编译:用某一高级语言书写其本身的编译程序。 (2)交叉编译:A 机器上的编译程序能产生 B 机器上的目标代码。 (3)自展:首先确定一个非常简单的核心语言 L0,用机器语言或汇编语言书写出它的编
译程序 T0,再把语言 L0 扩充到 L1,此时 L0⊂ L1 ,并用 L0 编写 L1 的编译程序 T1,再把语 言 L1 扩充为 L2,有 L1 ⊂ L2 ,并用 L1 编写 L2 的编译程序 T2,……,如此逐步扩展下 去, 好似滚雪球一样,直到我们所要求的编译程序。 (4)移植:将 A 机器上的某高级语言的编译程序搬到 B 机器上运行。
(main).
答案: 程序执行到赋值语句 b∶=10 时运行栈的布局示意图为:
1
《编译原理》课后习题答案第二章
第 3题 写出题 2 中当程序编译到 r 的过程体时的名字表 table 的内 容。
name
kind
level/val
adr
size
答案:
题 2 中当程序编译到 r 的过程体时的名字表 table 的内容为:
盛威网()专业的计算机学习网站
2
《编译原理》课后习题答案第一章
合实现方案,即先把源程序翻译成较容易解释执行的某种中间代码程序,然后集中解释执行 中间代码程序,最后得到运行结果。
编译原理实验NFA确定化为DFA

编译原理实验NFA确定化为DFA编译原理中的NFA(Non-deterministic Finite Automaton,非确定性有限自动机)是一种能够识别正则语言的形式化模型。
它的设计简单,但效率较低。
为了提高识别效率,需要将NFA转化为DFA(Deterministic Finite Automaton,确定性有限自动机)。
本文将介绍NFA确定化为DFA的一般方法,并以一个具体例子来说明该过程。
首先,我们来了解一下NFA和DFA的差异。
NFA可以有多个转移路径,每个输入符号可以对应多个状态转移,而DFA每个输入符号只能对应唯一的状态转移。
这使得NFA在识别过程中具有非确定性,无法确定下一个状态。
而DFA则能够准确地根据当前状态和输入符号确定下一个状态。
NFA确定化为DFA的一般方法如下:1.创建DFA的初始状态。
该状态对应NFA的起始状态以及从起始状态经过ε(空)转移可以到达的所有状态。
2.对DFA的每个状态进行如下处理:a)对当前状态的每个输入符号进行处理。
b)根据当前状态和输入符号,确定下一个状态。
如果有多个状态,需要将它们合并为一个DFA状态。
c)重复上述步骤,直到处理完所有输入符号。
3.对于合并的DFA状态,需要重复执行第2步的处理过程,直到没有新的合并状态产生为止。
4.最终得到的DFA包含的状态即为NFA确定化的结果。
下面以一个具体的例子来说明NFA确定化为DFA的过程。
考虑以下NFA:(状态)(输入符号)(转移状态)1a,ε1,22a33b44a5首先,创建DFA的初始状态,根据NFA的起始状态和通过ε转移可以到达的状态。
在该例子中,起始状态为1,通过ε转移可以到达状态1和2、因此,初始状态为{1,2}。
接下来,对初始状态{1,2}进行处理。
对于输入符号a,根据NFA的状态转移表可以得到DFA的下一个状态为{1,2,3},因为NFA的状态1通过a和ε可以到达状态3、对于输入符号b,当前状态没有转移。
编译原理教程课后习题答案第二章
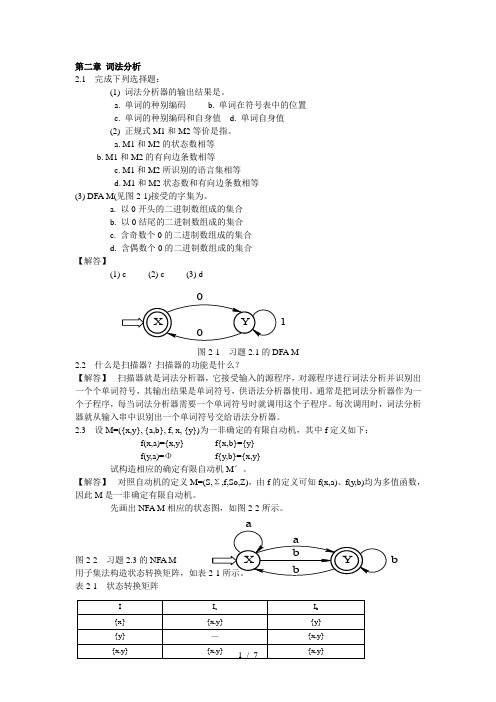
第二章 词法分析2.1 完成下列选择题:(1) 词法分析器的输出结果是。
a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。
a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器?扫描器的功能是什么?【解答】 扫描器就是词法分析器,它接受输入的源程序,对源程序进行词法分析并识别出一个个单词符号,其输出结果是单词符号,供语法分析器使用。
通常是把词法分析器作为一个子程序,每当词法分析器需要一个单词符号时就调用这个子程序。
每次调用时,词法分析器就从输入串中识别出一个单词符号交给语法分析器。
2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机,其中f 定义如下:f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。
【解答】 对照自动机的定义M=(S,Σ,f,So,Z),由f 的定义可知f(x,a)、f(y,b)均为多值函数,因此M 是一非确定有限自动机。
先画出NFA M 相应的状态图,如图2-2所示。
图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵,如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名,形成表2-2所示的状态转换矩阵,即得到 M ′=({0,1,2},{a,b},f,0,{1,2}),其状态转换图如图2-3所示。
表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。
编译原理课后习题答案+清华大学出版社第二版

注意:如果问编译程序有哪些主要构成成分,只要回答六部分就可以。如果搞不清楚, 就回答八部分。
第 2题
若 PL/0 编译程序运行时的存储分配策略采用栈式动态分配,并用动态链和静态链的方
式分别解决递归调用和非局部变量的引用问题,试写出下列程序执行到赋值语句 b∶=10
时运行栈的布局示意图。 var x,y; procedure p; var a; procedure q; var b;
begin (q)
答案:
PL/0 编译程序所产生的目标代码中有 3 条非常重要的特殊指令,这 3 条指令在 code 中的位置和功能以及所完成的操作说明如下:
INT 0 A 在过程目标程序的入口处,开辟 A 个单元的数据段。A 为局部变量的个数+3。 OPR 0 0
3
《编译原理》课后习题答案第二章
在过程目标程序的出口处,释放数据段(退栈),恢复调用该过程前正在运行的过程的数 据段基址寄存器 B 和栈顶寄存器 T 的值,并将返回地址送到指令地址寄存器 P 中,以使调 用前的程序从断点开始继续执行。
3
《编译原理》课后习题答案第一章
第6题
计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?
答案:计算机执行用高级语言编写的程序主要途径有两种,即解释与编译。 像 Basic 之类的语言,属于解释型的高级语言。它们的特点是计算机并不事先对高级语
言进行全盘翻译,将其变为机器代码,而是每读入一条高级语句,就用解释器将其翻译为一 条机器代码,予以执行,然后再读入下一条高级语句,翻译为机器代码,再执行,如此反 复。
《编译原理》课后习题答案第二章

4、试为文法G[P]:
P∷=begin S end S∷=A|C
A∷=V:=E C∷=if E then S
E∷=V E∷=E+V V∷=i
采用某种程序设计语言构造递归下降识别程序。
解:由于文法存在左递归,进行文法等价变换,得到等价文法G′[P]:
步骤三检查可得f的值与原有的优先矩阵一致所以上表函数即为所求优先函数bell有向图法形式化步骤一构造布尔矩阵b步骤二使用warshall算法构造布尔矩阵b1521步骤三则优先函数为
第二章
习题1
6.答:省略表示法:{1.3,1.33,1.333…};描述表示法:{1.3i|i=1,2,3…}
7.答:x+={0,12,123,1234…};
最小化:
(2)由e构造转换系统:
去ε弧及无用状态和死状态:
因为现在只有一个状态,所以无需再最小化,此时就是最小化.
13.解:建立方程组如下:
W=Ua+Vb ①
U=Va+c ②
V=Ub+c ③
把③代入②得,U=(Ub+c)a+c
=Uba+ca+c
把它改写成U=(ca+c){ba},因此U=(ca|c){ba} ④
follow(E)={#,)}
follow(E′)={#,)}
follow(T)={#,),+,-}
follow(T′)={#,),+,-}
follow(F)={*,/,#,),+,-}
识别输入符号串i*i-(i+i)/i,则识别过程
步骤 栈 输入 输出
0 #E i*i-(i+i)/i# E∷=TE′
RG、FA、RE等相互之间的转换

NFA确定化过程:
(初态、其它状态、终态)
0,1
S0 A ε B ε
C1
Z
0
S ABC BC BCZ
ABC BC BC BC
① δ(S,ε)=;
② δ(S, 0)=A;
③ δ(A, 0)=; δ(B, 0)=B; δ(C, 0)=;
1
state
DFA state
S
S,ABC
S,ABC
S,ABC
BCZ ABC,BC,BCZ S,ABC,BC,BCZ
❖ DFA的终态(为所有含有NFA的终态的状态)
S ABC BC BCZ
0
ABC BC BC BC
1
state
S
S,ABC
BCZ ABC,BC,BCZ
BCZ BC,BCZ
BCZ BCZ
DFA state S,ABC S,ABC S,ABC,BC,BCZ S,ABC,BC,BCZ S,ABC,BC,BCZ 26
1 ε4 b 5 ε
6
令r4= r*3 ,则有:
ε
0ε
ε 1
a
3
ε
ε4 b 5 ε
ε
6ε7
令r5=a, 令r6=b 令r7=b 令r8= r5 r6 令r9= r8 r7
则有
7 a 8 b 9 b 10
令r10= r4 r9 则最终得到NFA M:
ε
ε 0ε 1
2
a
3
ε
ε4 b 5 ε
6 ε 7 a 8 b 9 b 10
S∈I
—— J是从状态子集I中的每个状态出发,经过标记为a的弧 而达到的状态集合.
—— Ia是状态子集,其元素为J中的状态,加上从J中每一个 状态出发通过ε弧到达的状态
临床实验室管理试题及答案

临床实验室管理试题及答案第一章临床实验室管理概论1.什么叫做临床实验室?临床实验室是指以诊断、预防,或者治疗人类任何疾病和损伤,或者评价人类健康为目的,而对人体的标本进行生物学、微生物学、血清学、化学、血液免疫学、生物物理学、细胞学、病理学检查或其他检查的机构。
(这些检查也包括确定、测量,或者用其他方法来叙述机体中是否存在不同物质或者有机体。
仅仅收集和/或准备标本,或者提供邮递服务,但不进行检验的机构不能认为是临床实验室。
)2.临床实验室的作用和工作准则有哪些?作用——利用必要的实验室技术对疾病的诊断、筛查、监测疾病的发展过程和观察患者对治疗的反应等方面提供信息。
工作准则——安全、准确、及时、有效、经济、便民、保护患者隐私。
3.什么叫做临床实验室管理?其主要内容包括哪些?临床实验室管理就是对实验室的人力、财力、物力投入进行有效的整合以达到尽可能满足医疗服务要求的创造性活动。
主要内容有:人力资源管理、质量管理、仪器设备管理、环境安全管理、财务管理、信息管理(LIS系统)、市场管理4.目前国际上普遍认同的临床实验室质量管理要求是什么?实验室期望达到的目的或目标;实验室负责人具有指导团队达到目标的权利;实现目标必须的人力、设备、资金等资源;各类人员为达到实验室目标需承担的责任;完善的管理体系和要求5. 我国负责临床实验室管理的专业机构是什么?我国卫生部临床检验中心第二章临床检验质量管理技术1.临床实验室的质量目标是什么?使检验结果最好地符合病人实际情况;及时地发出检验报告;并依据检验结果结合病人临床状况,主动为临床诊断提供咨询。
这即是当今国际标准化(ISO)对质量广义定义“满足需求和期望”在实验室中的体现。
2.什么叫做临床实验室质量管理体系?是指挥和控制实验室建立质量方针和质量目标并实现质量目标的相互关联或相互作用的一组要素。
3.临床实验室质量管理体系的建立大致分为哪四个过程?质量体系的策划与准备、质量体系文件的编制、质量体系的试运行、质量体系的评价和完善。
全国软考真题(中级) 网络工程师 2019年上半年上午 考试真题及答案解析(选择题)

全国软考真题(中级)网络工程师2019年上半年上午考试真题及答案解析(选择题)一、单项选择题(共75分,每题1分。
每题备选项中,只有1个最符合题意)●1.计算机执行指令的过程中,需要由( )产生每条指令的操作信号,并将信号送往相应的部件进行处理,以完成指定的操作。
A.CPU的控制器B.CPU 的运算器C.DMA 控制器D.Cache控制器【参考答案】A【答案解析】运算器和控制器组成中央处理器(CPU)。
控制器负责依次访问程序指令,进行指令译码,并协调其他设备,通常由程序计数器(PC)、指令寄存器、指令译码器状态/31c牛寄存器、时序发生器、微操作信号发生器组成。
运算器负责完成算术、逻辑运算功能,通常由ALU (算术逻辑单元)、寄存器、多路转换器、数据总线组成。
●2.DMA控制方式是在( )之间直接建立数据通路,进行数据的交换处理。
A.CPU与主存B.CPU与外设C.主存与外设D.外设与外设【参考答案】C【答案解析】DMA控制器是一种在系统内部转移数据的独特外设,可以将其视为一种能够通过一组专用总线将内部和外部存储器与每个具有DMA能力的外设连接起来的控制器。
●3.在( )校验方法中,采用模2运算来构造校验位。
A.水平奇偶B.垂直奇偶C.海明码D.循环冗余【参考答案】D【答案解析】冷门●4.以下关于RISC (精简指令系统计算机)技术的叙述中,错误的是( )。
A.指令长度固定、指令种类尽量少B.指令功能强大、寻址方式复杂多样C.增加寄存器数目以减少访存次数D.用硬布线电路实现指令解码,快速完成指令译码【参考答案】B【答案解析】RISC与CISC:为提高操作系统的效率,人们最初选择向指令系统中添加更多、更复杂的指令来实现,导致指令集越来越大。
这种类型的计算机称为复杂指令集计算机(cisq。
对指令数目和寻址方式做精简,指令的指令周期相同,采用流水线技术,指令并行执研雖更好,这就是精简指令集计算机 (RISC)●5、6.甲公司购买了一个工具软件,并使用该工具软件开发了新的名为“恒友”的软件,甲公司在销售新软件的同时,向客户提供工具软件的复制品,则该行为( )。
(完整版)哈工大编译原理习题及答案

1.1何谓源程序、目标程序、翻译程序、编译程序和解释程序?它们之间可能有何种关系?1.2一个典型的编译系统通常由哪些部分组成?各部分的主要功能是什么?1.3选择一种你所熟悉的程序设计语言,试列出此语言中的全部关键字,并通过上机使用该语言以判明这些关键字是否为保留字。
1.4选取一种你所熟悉的语言,试对它进行分析,以找出此语言中的括号、关键字END以及逗号有多少种不同的用途。
1.5试用你常用的一种高级语言编写一短小的程序,上机进行编译和运行,记录下操作步骤和输出信息,如果可能,请卸出中间代码和目标代码。
第一章习题解答1.解:源程序是指以某种程序设计语言所编写的程序。
目标程序是指编译程序(或解释程序)将源程序处理加工而得的另一种语言(目标语言)的程序。
翻译程序是将某种语言翻译成另一种语言的程序的统称。
编译程序与解释程序均为翻译程序,但二者工作方法不同。
解释程序的特点是并不先将高级语言程序全部翻译成机器代码,而是每读入一条高级语言程序语句,就用解释程序将其翻译成一段机器指令并执行之,然后再读入下一条语句继续进行解释、执行,如此反复。
即边解释边执行,翻译所得的指令序列并不保存。
编译程序的特点是先将高级语言程序翻译成机器语言程序,将其保存到指定的空间中,在用户需要时再执行之。
即先翻译、后执行。
2.解:一般说来,编译程序主要由词法分析程序、语法分析程序、语义分析程序、中间代码生成程序、代码优化程序、目标代码生成程序、信息表管理程序、错误检查处理程序组成。
3.解:C语言的关键字有:auto break case char const continue default do double else enum externfloat for goto if int long register return short signed sizeof static struct switch typedef union unsigned void volatile while。
NFA转化为DFA编译原理实验报告

NFA转化为DFA编译原理实验报告一、引言正则表达式是一种用于描述字符串模式的符号语言,可以通过正则表达式来进行字符串匹配、替换和等操作。
而有限状态自动机(NFA)是一种可以识别正则表达式的数学模型,是实现正则表达式的基础。
二、实验内容本实验使用Python语言编写,主要实现了以下功能:1.输入正则表达式,构建对应的NFA。
2.将NFA转化为DFA。
3.输出DFA的状态转移表。
三、实验过程1.构建NFA首先,通过用户输入正则表达式,使用Thompson算法构建对应的NFA。
Thompson算法使用了三种基本构建块:连接、选择和闭包。
通过多个基本构建块的组合,可以构建出更加复杂的正则表达式的NFA。
其中,连接操作通过在两个状态之间添加一个空转移实现,选择操作通过添加两个新的开始和接受状态,并将其与原始状态进行连接。
闭包操作通过添加两个新的开始和接受状态,并分别连接到原始状态和自身。
2.NFA转DFANFA转DFA的主要思路是从NFA的初始状态开始,通过遍历所有可能的输入字符,计算对应的闭包和移动集合。
闭包集合表示从当前状态出发通过空转移可以到达的所有状态,移动集合表示从当前状态出发经过一次输入字符转移的所有可能状态。
通过计算闭包和移动集合,可以得到DFA的所有状态和状态转移关系。
在转换过程中,需要考虑ε-closure运算和move运算的效率和正确性。
3.输出DFA状态转移表最后,将计算得到的DFA的状态转移关系输出为状态转移表的形式,方便后续的分析和使用。
四、实验结果本实验通过输入不同的正则表达式,得到了对应的NFA,并成功将NFA转化为DFA,并输出了DFA的状态转移表。
通过实验结果可以发现,无论正则表达式的复杂度如何,DFA都可以给出准确的匹配结果,实现了对正则表达式的准确识别。
五、实验总结通过本实验,我进一步理解了正则表达式、NFA和DFA之间的关系。
正则表达式作为一种表示字符串模式的符号语言,可以通过NFA来进行匹配和等操作。
重力热管换热器课程设计

重力热管换热器课程设计目录第一章概述1.1课题的背景1.2国内外热管的应用1.3本课题主要研究内容第二章重力热管换热器的理论基础2.1重力热管的工作原理2.2重力热管的组成2.3重力热管的基本特性第三章环肋管、直肋管、光管的传热计算 3.1烟气及空气参数的确定3.1.1翅片管的应用计算3.1.2纵肋管的应用计算3.2计算结果汇总3.2.1换热器外形结构图3.2.2热管热力计算设计程序3.3经济效益比较第四章结论参考文献附:NFA :管束最小流通面积 n:热管数m:换热器纵深排数 E :迎风面宽度 B :管排数α:蒸发换热系数f η:肋片效率1β:肋化比fl :翅片长度f η:翅片效率fd:翅片外径f δ:翅片厚度1ε:管外污垢系数fe h :管外有效换热系数c fS:空气侧翅片间距cf δ:空气侧翅片节距hQ:烟气放出热量hft :烟气定性温度h fS:烟气侧翅片间距h f δ:烟气侧翅片节距fh :流体换热系数1ψ:气液阻断系数H A :每米长热管管外总表面积fA :每米长热管的翅片表面积S :横向管子中心距HU:总传热系数 mt ∆:对数平均温差c R :外部对流换热热阻o δ:壁厚hHA :加热侧总传热面积ct 2:冷空气出口温度 od :光管外径第一章 概述在众多的传热元件中,热管是人们所知的最有效的传热元件之一。
它可将大量的热量通过其很小的截面积远距离的传输而无需外加动力。
近年来热管技术飞快发展,特别是热管换热器在余热回收方面取得了良好的效果。
1.1 课题的背景能源工业是国民经济的基础产业,是实现现代化的物质基础,世界各国都把建立可靠、安全、稳定的能源供应保障体系作为国民经济的战略问题之一。
随着经济的高速增长和人民生活水平的不断提高,世界各国对能源的需求量急剧增长。
1997年全世界一次能源消费量(不包括生物能)己超过130亿吨标煤,其中石油占39.1%,天然气占23%,煤炭占27.6%,核电占7.45%。
编译原理第2章习题课

1.构造正规式的DFA。
(1)1(0|1)*101状态转换表:化简后得:(2)(a|b)*(aa|bb)(a|b)*NFA化为DFA:化简后得;2.将下图确定化和最小化。
aa⇒a,b解: 首先取A=ε-CLOSURE({0})={0},NFA确定化后的状态矩阵为:NFA确定化后的DFA为:aa⇒abb将A,B 合并得:ab⇒a3.构造一个DFA ,它接受∑={0,1}上所有满足如下条件的字符串,每个1都有0直接跟在后边。
解:按题意相应的正规表达式是0*(0 | 10)*0*构造相应的DFA ,首先构造NFA 为DFA 为44.给出NFA等价的正规式R。
方法一:首先将状态图转化为得0,1NFA等价的正规式为(0|1)*11方法二:NFA→右线性文法→正规式A→0A|1A|1BB→1CC→εA=0A+1A+1BB=1A=0A+1A+11A=(0+1)*11→(0|1)*115.试证明正规式(a|b )*与正规式(a *|b *)*是等价的。
证明: (1)正规式(a|b)*的NFA 为=>ba其最简DFA 为=>b(2)正规式(a*|b*)*的 NFA 为: aa εεεεbbDFA 的状态转换表:由于这两个正规式的最小DFA 相同,所以正规式(a|b)*等价于正规式(a*|b*)*。
6.设字母表∑={a,b},给出∑上的正规式R=b*ab(b|ab)*。
(1)试构造状态最小化的DFA M,使得L(M)=L(R)。
(2)求右线性文法G,使L(G)=L(M)。
解:(1)构造NFA:(2)将其化为DFA,转换矩阵为:再将其最小化得:(2)对应的右线性文法G=({X,W,Y},{a,b},P,X)P: X→aW|bXW→b Y|b y→a W|bY|b3.8文法G[〈单词〉]为:〈单词〉-〉〈标识符〉|〈整数〉〈标识符〉-〉〈标识符〉〈字母〉|〈标识符〉〈数字〉|〈字母〉〈整数〉-〉〈数字〉|〈整数〉〈数字〉〈字母〉-〉A|B|C〈数字〉|->1|2|3(1)改写文法G为G’,使L(G’)=L(G)。
正规式、NFA、DFA、MFA的转换

计算机专业软件类课程实验报告课程名称:编译原理实验题目:正规式、NFA、DFA、MFA的转换实验小组成员:实验小组组长:任课教师:专业名称:计算机科学与技术班级名称:计科1班实验起止时间:2014-5-19~2014-5-29一、实验目的1、理解什么是正规式2、理解NFA、DFA、MFA的概念;3、掌握正规式和NFA之间的等价变换;4、掌握NFA和DFA之间的等价变换;5、掌握DFA和MFA之间的等价变换;6、了解程序设计语言Java的语言机制。
二、实验内容程序的流程图如下所示:1、根据用户输入的表达式,验证是否为合法的正规式2、根据正规式,将其转换为NFA3、根据NFA,将其转换为DFA4、根据DFA,将其转换为MFA三、实验需求1、正规式验证对输入的表达式能够做出正确的判断,如果是合法的正规式,则激活正规式转为NFA的功能;如果不是合法的正规式,则会弹出消息框进行提示2、正规式转为NFA对经过验证的正规式,根据算法,将其转换为NFA,得出开始符号集、终结符号集以及符号集,并激活NFA 转为DFA的功能;也可以点击打开按钮,选择一个格式符合规范的NFA文件,同时激活NFA转为DFA的功能;也可以对得到的NFA进行保存3、NFA转为DFA对第一个文本框中的NFA,根据算法,将其转换为DFA,得出开始符号集、终结符号集以及符号集,并激活DFA 转为MFA的功能;也可以点击打开按钮,选择一个格式符合规范的DFA文件,同时激活DFA转为MFA的功能;也可以对得到的DFA进行保存4、DFA转为MFA对第二个文本框中的DFA,根据算法,将其转换为MFA,得出开始符号集、终结符号集以及符号集;也可以点击打开按钮,选择一个格式符合规范MFA文件;也可以对得到的MFA进行保存四、主要数据结构介绍1、自定义一个JavaBean,这个类里只有三个属性,节点的开始符号,接受符号,终结符号,并有他们的get()、set()方法,将类名定义为Node2、整个程序涉及到的NFA、DFA、MFA都存放在ArrayList<Node>中,每次通过迭代器Iterator<Node>进行迭代3、在正规式转为NFA时,将创建一个开始符号栈和一个终结符号栈,分别用来存储开始符号和终结符号4、在NFA转换为DFA时,创建一个对象数组Object[][2],每个数组单元第一列为ArrayList<String>,存放的是节点号,第二列是一个Boolean,标记该状态T是否被访问过5、在DFA转换为MFA时,创建一个对象数组Object[],每个数组单元为ArrayList<String>,存放的是每次划分的节点信息五、主要模块算法介绍1、正规式验证将输入的正规式使用toCharArray()转换成一个一个字符,然后对字符进行处理,主要是验证左右括号是否匹配正确,以及”|”,”.”,”*”等符号位置是否合法,输入的表达式中是否含有非法字符2、正规式转为NFA对经过验证的正规式进行一个字符一个字符的判断,其中”*”的优先级最高,其次是”.”,最后是”|”。
NFA如何转换成等价的DFA

NFA如何转换成等价的DFANFA(Non-deterministic Finite Automaton)和DFA (Deterministic Finite Automaton)都是有限自动机,它们在计算理论中起着重要的作用。
NFA允许在一个状态下有多个转移选项,而DFA则要求在给定输入下只有一个确定的转移选项。
本文将从NFA转换为DFA的角度进行讨论。
首先,让我们回顾一下NFA的定义。
NFA由以下五个元素组成:1.一个有限的状态集合Q。
2.一个有限的输入字母表Σ。
3.一个状态转移函数δ:QxΣ->P(Q),其中P(Q)表示Q的幂集,即所有可能子集的集合。
4.一个初始状态q0∈Q。
5.一个接受状态集合F⊆Q。
NFA接受一个输入字符串的条件是,通过状态转移函数从初始状态q0开始,能够读取字符串中的每个符号并转移到一个接受状态。
要将NFA转换为DFA,我们可以使用子集构造法。
该方法的核心思想是,DFA的每个状态对应于NFA的一个状态集合。
转换函数用于计算DFA 中的其中一状态通过一些输入符号转移到的状态。
接受状态集合由NFA中的状态集合中有至少一个接受状态的状态组成。
下面是将NFA转换为DFA的具体步骤:1.创建一个新DFA,其中初始状态是NFA的初始状态集合。
将其添加到DFA状态集合中。
2.对于每个DFA状态集合,对每个输入符号执行以下步骤:-使用NFA状态集合中的状态和输入符号计算出新的状态集合。
这可以通过查找NFA状态集合中每个状态在给定输入下能够到达的状态来完成。
-如果新的状态集合不在DFA状态集合中,将其添加到DFA状态集合中。
-添加一个转移函数,使得在给定输入下从当前DFA状态集合转移到新的状态集合。
3.标记任何DFA状态集合,其包含来自NFA接受状态集合的状态作为接受状态。
通过执行上述步骤,可以将NFA转换为等价的DFA。
这个DFA可以接受与原来的NFA相同的输入字符串。
NFA到DFA的转换可以进一步帮助我们理解自动机的功能,并且可以扩展到其他计算理论中的问题。
正规式、NFA、DFA、MFA的转换

计算机专业软件类课程实验报告课程名称:编译原理实验题目:正规式、NFA、DFA、MFA的转换实验小组成员:实验小组组长:任课教师:专业名称:计算机科学与技术班级名称:计科1班实验起止时间:2014-5-19~2014-5-29一、实验目的1、理解什么是正规式2、理解NFA、DFA、MFA的概念;3、掌握正规式和NFA之间的等价变换;4、掌握NFA和DFA之间的等价变换;5、掌握DFA和MFA之间的等价变换;6、了解程序设计语言Java的语言机制。
二、实验内容程序的流程图如下所示:1、根据用户输入的表达式,验证是否为合法的正规式2、根据正规式,将其转换为NFA3、根据NFA,将其转换为DFA4、根据DFA,将其转换为MFA三、实验需求1、正规式验证对输入的表达式能够做出正确的判断,如果是合法的正规式,则激活正规式转为NFA的功能;如果不是合法的正规式,则会弹出消息框进行提示2、正规式转为NFA对经过验证的正规式,根据算法,将其转换为NFA,得出开始符号集、终结符号集以及符号集,并激活NFA 转为DFA的功能;也可以点击打开按钮,选择一个格式符合规范的NFA文件,同时激活NFA转为DFA的功能;也可以对得到的NFA进行保存3、NFA转为DFA对第一个文本框中的NFA,根据算法,将其转换为DFA,得出开始符号集、终结符号集以及符号集,并激活DFA 转为MFA的功能;也可以点击打开按钮,选择一个格式符合规范的DFA文件,同时激活DFA转为MFA的功能;也可以对得到的DFA进行保存4、DFA转为MFA对第二个文本框中的DFA,根据算法,将其转换为MFA,得出开始符号集、终结符号集以及符号集;也可以点击打开按钮,选择一个格式符合规范MFA文件;也可以对得到的MFA进行保存四、主要数据结构介绍1、自定义一个JavaBean,这个类里只有三个属性,节点的开始符号,接受符号,终结符号,并有他们的get()、set()方法,将类名定义为Node2、整个程序涉及到的NFA、DFA、MFA都存放在ArrayList<Node>中,每次通过迭代器Iterator<Node>进行迭代3、在正规式转为NFA时,将创建一个开始符号栈和一个终结符号栈,分别用来存储开始符号和终结符号4、在NFA转换为DFA时,创建一个对象数组Object[][2],每个数组单元第一列为ArrayList<String>,存放的是节点号,第二列是一个Boolean,标记该状态T是否被访问过5、在DFA转换为MFA时,创建一个对象数组Object[],每个数组单元为ArrayList<String>,存放的是每次划分的节点信息五、主要模块算法介绍1、正规式验证将输入的正规式使用toCharArray()转换成一个一个字符,然后对字符进行处理,主要是验证左右括号是否匹配正确,以及”|”,”.”,”*”等符号位置是否合法,输入的表达式中是否含有非法字符2、正规式转为NFA对经过验证的正规式进行一个字符一个字符的判断,其中”*”的优先级最高,其次是”.”,最后是”|”。
正规式-NFA-最小化DFA说明

正规式->最小化DFA说明整体的步骤是三步:一,先把正规式转换为NFA(非确定有穷自动机),二,在把NFA通过“子集构造法”转化为DFA,三,在把DFA通过“分割法”进行最小化。
一步很简单,就是反复运用下图的规则,图1这样就能转换到NFA了。
给出一个例题,来自Google book。
本文主要根据这个例题来讲,图2二.子集构造法。
同样的例题,把转换好的NFA确定化,图3这个表是从NFA到DFA的时候必须要用到的。
第一列第一行I的意思是从NFA的起始节点经过任意个ε所能到达的结点集合。
Ia表示从该集合开始经过一个a所能到达的集合,经过一个a的意思是可以略过前后的ε。
同样Ib也就是经过一个b,可以略过前后任意个ε。
至于第二行以及后面的I是怎么确定的。
我参考了一些题目才明白,原来就是看上面的Ia和Ib哪个还没出现在I列,就拿下来进行运算,该列对应的Ia和Ib就是前面我说的那样推导。
如果还不太明白,看图就是了。
你会发现I中的几个项目都在Ia和Ib中出现了。
而且是完全出现这步做完以后,为了画出最后的DFA,那么肯定得标出一些号来,比如1.2.3.。
或者A。
B。
c,我一般标的方法是先把I列全部标上1.2.3.递增。
然后看1表示的集合和Ia和Ib中的哪个集合一样,就把那个集合也表示为1.继续向下做。
最后会得到这样一个表格。
图4至此,就可以表示出DFA了。
就对照上面那个表,从0节点开始经过a到1.经过b到2,就这样画就行了。
最后的DFA如下图,图5双圈的表示终态,这个是怎么来的呢。
去看看图4,会发现有些项之前有双圈标志,这个是因为在NFA 图2中,9为终态,所以所有包含9的集合都被认为是终态集,改成1.2.3.。
方便画节点后就需要把这些点作为终态了。
三.最小化,分割法。
FA的最小化就是寻求最小状态DFA最小状态DFA的含义:1.没有多余状态(死状态)除多余状态什么是多余状态?从这个状态没有通路到达终态;S1从开始状态出发,任何输入串也不能到达的那个状态。
词法分析核心算法(1)正规式》NFA

正规式转换为不确定的有穷自动机的算法1. 目的与要求:通过设计、编写和调试将正规式转换为不确定的有穷自动机的程序,掌握转换过程中的相关概念和方法,NFA的表现形式可以是图标或者图形。
2. 问题描述:任意给定一个正规式r(包括链接、或、闭包运算),根据如下算法,设计一个程序,生成与该正规式等价的NFA N.算法:首先,分析给定的正规式r,将其分解成最基本的子表达式,使用下面的规则(1)和规则(2)为r中的每个基本符号(ε或字母表中的符号)构造NFA。
如果符号a在r中出现多次,则要为它的每次出现构造一个NFA。
然后,使用规则(3)逐步地组合前面构造的NFA,直到获得整个正规式的NFA为止。
基本规则如下:(1)对于ε,构造如下图所示的NFA,它识别{ε};(2)对于Σ中的每个符号a,构造如下图所示的NFA,它识别{a};(3)如果N(s)和N(t)分别是正规式s和t的NFA,则:[1]对正规式s∣t,构造合成的NFA N(s∣t),结果如下图所示:加入x和y节点,从x引ε弧到N(s)和N(t)的开始状态,从N(s)和N(t)的接受状态引ε弧到y节点;[2]对正规式st,构造合成的NFA N(st),结果如下图所示:N(s)的开始状态成为合成后的NFA的开始状态,N(t)的接受状态成为合成后的NFA的接受状态,N(s)的接受状态和N(t)的开始状态合并;[3]对于正规式s*,构造合成的NFA N(s*),如下图所示:[4]对于括号括起来的正规式(s),使用N(s)本身作为他的NFA.3. 基本要求:(1)输入一个正规式r;(2)输出与正规式r等价的NFA(可以是表格形式或图形形式)。
测试数据:输入正规式:r=(a∣b)*(aa∣bb)(a∣b)*4. 实现提示:(1)NFA的表示可以是图形或者表格形式,状态之间的变换也可以直接表示为每两个状态一组,表示为“起始状态——输入字符——>到达状态”,如“①——a——>②”表示在①状态下读入输入字符a,变换到②状态。
nfa状态转换矩阵

nfa状态转换矩阵NFA状态转换矩阵概述:有限状态自动机(Finite State Automaton,简称FSA)是一种描述有限状态、输入和输出的计算模型,常用于正则表达式匹配、编译器设计和自然语言处理等领域。
在FSA中,状态转换矩阵(Transition Matrix)是描述状态之间转换关系的核心工具。
本文将就NFA状态转换矩阵展开讨论。
什么是NFA状态转换矩阵?NFA(Non-Deterministic Finite Automaton)是一种拥有多个可能的下一状态的有限状态自动机。
NFA状态转换矩阵是描述NFA中状态之间转换关系的二维矩阵。
矩阵的行表示当前状态,列表示输入字符,矩阵元素表示从当前状态经过输入字符转移到下一状态的可能性。
NFA状态转换矩阵的构成:NFA状态转换矩阵由以下几个要素构成:1. 状态集合:NFA中所有可能的状态组成的集合,用Q表示。
2. 输入字母表:NFA接受的输入字符的集合,用Σ表示。
3. 状态转换函数:描述状态之间转换关系的函数,用δ表示。
对于NFA而言,函数的返回值是一个状态集合,表示从当前状态经过输入字符可能转移到的下一状态集合。
4. 初始状态:NFA的起始状态,用q0表示。
5. 接受状态集合:NFA中接受状态的集合,用F表示。
如何构建NFA状态转换矩阵?构建NFA状态转换矩阵的步骤如下:1. 确定状态集合Q:根据问题的具体要求,确定NFA中可能存在的所有状态。
2. 确定输入字母表Σ:根据问题的具体要求,确定NFA能够接受的输入字符集合。
3. 构建状态转换函数δ:根据问题的具体要求,确定状态之间转换的规则。
可以使用状态转换图或状态转换表的方式来表示。
4. 确定初始状态q0:确定NFA的起始状态。
5. 确定接受状态集合F:确定NFA中的接受状态。
举例说明:假设有一个NFA,其状态集合为{q0, q1, q2},输入字母表为{0, 1},状态转换函数δ的定义如下:δ(q0, 0) = {q0, q1}δ(q0, 1) = {q0}δ(q1, 0) = {q2}该NFA的初始状态为q0,接受状态集合为{q2}。
(09)第二章 第二讲 DFA与NFA的等价性

输入 状态
a
{q0,q}
b
{q} {q0,q}
q0 q
ø
a
a,b
b
q0
b
q
二、实例
构造DFA MD如下: QD={[q0],[q],[q0,q],ø},q0D=[q0] ,FD={[q],[q0,q]},
δD的定义如下: 由于 δ(q0,a)={q0,q},所以有:δD([q0],a)=[q0,q]; 由于 δ(q0,b)={q}, 所以有:δD([q0],b)=[q]; 由于 δ(q,a)=ø, 所以有:δD([q],a)=ø; 由于 δ(q,b)={q0,q}, 所以有:δD([q],b)=[q0,q];
二、实例
例2:设 NFA M=({q0,q1,q2},{a,b},δ,q0 ,{q2}), 其 中δ定义如下: a
δ(q0,a)={q1}, δ(q0,b)=ø , δ(q1,a)={q1,q2}, δ(q0,b)=ø, q δ(q2,a)=ø , δ(q2,b)={q1};
a q0 b
1
a
构造DFA MD=(QD,T,δD,q0D , FD)如下:
输入 状态(共有23个)
[q0,q2]
[q0,q1,q2] a
a,b
b
δD定义如下:
[q0] [q1] [q2] [q0,q1] [q0,q2] [q1,q2] [q0,q1,q2]
a
a [q1] b
[q1,q2]
a
a
[q1] [q1,q2] ø [q2] [q1,q2] [q1] [q1,q2] [q1,q2]
第二章 有限自动机和右线性文法 第二讲 DFA与NFA的等价性
一、定理及其证明
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NFA(A) ε
特别声明
• 上述规则只对具有一个开始状态和一个终止状态的NFA 上述规则只对具有一个开始状态和一个终止状态的NFA 有效; 有效; • 任何NFA都可以经过变换符合上述要求; 任何NFA都可以经过变换符合上述要求; NFA都可以经过变换符合上述要求
ε …… ε NFA ……
= L(A)
NFA(A)
RE到NFA转换
• A | B,L( A | B )=L(A)∪L(B) B, )=L(A)∪
ε ε
NFA(A)
ε
NFA(B)
ε
RE到NFA转换
• A B, L( A B )= L(A)L(B) B,
NFA(A)
ε
NFA(B)
RE到NFA转换
• A* ,L( A*) = L(A)*
DFA构造词法分析程序 根据 DFA构造词法分析程序
ID: ReadNext(); case CurrentChar of “0..9”, “a..z”,“A..Z”:str[len++] = CurrentChar; : goto ID; other: if IsKeyword(str) {tk.type = IsKeyword(str) } else {tk.type = IDE, strcpy(tk.val, str) }; if CurrentChar <> EOF goto Done; else exit(1); //标识符的标号 标识符的标号
ε ε
RE到NFA的转换 RE到NFA的转换
• 例1:将正则表达式 (a | b)* a b b (a | b)转化成等价的NFA b)转化成等价的NFA. 转化成等价的NFA
ε ε a b ε ε a b
b a b
RE到NFA的转换 RE到NFA的转换
• 例2:将正则表达式a((a|b)*ab*a)b 转化成等价的NFA.
a a 0 1 b a
b a 2 3 b 4
RE到NFA的转换 RE到NFA的转换
• 例3:将正则表达式 (0 | 1)*00转化成等价的NFA.
第2章 outline
à à å å å å
• •
一、词法分析概述 1,词法分析程序的功能 2,词法分析相关的一些问题 二、正则表达式 三、有限自动机 确定有限自动机DFA 1,确定有限自动机DFA 非确定有限自动机NFA NFA到DFA的转换 NFA, 2,非确定有限自动机NFA,NFA到DFA的转换 DFA的化简 3,DFA的化简 正则表达式到NFA NFA的转换 4,正则表达式到NFA的转换 四、词法分析程序构造
//关键字 关键字
DFA构造词法分析程序 根据 DFA构造词法分析程序
全局变量: 全局变量 - char str[50]; - int len = 0; - Token tk; - int total = 0; 数 ----- 存储已经读入的串 存储已经读入的串; ----- str的长度 str数组下标 的长度, 数组下标 的长度 ----- 当前 当前token ----- 识别出的 识别出的token的个 的个
ReadOne ‘ ‘, \n, \t
‘ ‘, \n, \t
other3
ToyL的有限自动机
Digit NZNZ-Digit other1 Done Num Start Digit |Letter other2
Letter Id +,+,-,[,(,{ ……
ReadNext ‘ ‘, \n, \t
DFA构造词法分析程序 根据 DFA构造词法分析程序
Num: ReadNext(); case CurrentChar of “0..9”: str[len++] = CurrentChar; goto Num ; other: tk.type = NUM; //other1:数字以外的字符 数字以外的字符 ; strcpy(tk.val, str); if CurrentChar <> EOF goto Done; //已经读入下一字符 已经读入下一字符 else exit(1); //数字状态的标号 数字状态的标号
4、正则表达式到NFA的转换
• 正则表达式和有限自动机都是形式语言,都可以描 正则表达式和有限自动机都是形式语言, 形式语言 述程序设计语言的单词结构 单词结构。 述程序设计语言的单词结构。 • 正则表达式便于描述和理解 • 有限自动机便于实现 • 二者的描述能力是等价的,都描述正则语言,可相 二者的描述能力是等价的,都描述正则语言, 互转换。 互转换。 • 一般地,设计词法分析程序的步骤是:先用RE定义 一般地,设计词法分析程序的步骤是:先用RE定义 RE 单词结构,然后将RE转化成NFA NFA再转化成 RE转化成NFA, 再转化成DF 单词结构,然后将RE转化成NFA,NFA再转化成DF DFA化简并实现得到词法分析程序 化简并实现得到词法分析程序。 A,DFA化简并实现得到词法分析程序。
RE到NFA转换-Thompson算法
• • 转换基于语言等价原则 转换基于语言等价原则 语言等价 ∅ 是RE,L(∅)={ } RE,L(∅
S0 S0
• ε是RE, L(ε)={ ε } L( • 任何 c ∈Σ, c 是RE, ∈Σ, L(c)={c}
S0
c
S
• ( A ), L( (A) )
DFA构造词法分析程序 根据 DFA构造词法分析程序
if (!ReadNext()) exit(1); /*读入一个字符到 读入一个字符到CurrentChar中,若到输入串结束 读入一个字符到 中 (CurrentChar = EOF),则结束分析 否则继续分析。*/ 否则继续分析。 ,则结束分析;否则继续分析 start: //开始状态的标号 开始状态的标号 case CurrentChar of “1..9”: str[len++] = CurrentChar; goto Num ; “a..z”, “A..Z”: str[len++] = CurrentChar; goto ID; “+”, “-”, “>”,”(”,…: tk.type =PLUS; ReadNext(); goto Done; “\t”,”\n”,” ”: goto WS; other: error(); //出现字母表以外的字符 出现字母表以外的字符
//单词类别 //单词类别 //语义信息 //语义信息
DFA构造词法分析程序 根据 DFA构造词法分析程序
单词类别: 单词类别 typedef enum { IDE, NUM, //标识符,整数 标识符, 标识符 PLUS, MINUS, MUL, // +, -, *, , , DIV, GT, LT, EQ, // /, >, <, = SEMI, LPAREN, RPAREN // ;, (. ) LG, RG, // {, } ELSE, INT ,WHILE, READ, WRITE , IF } TkType
if (CurrentChar == EOF) exit(1); goto start; //开始扫描新的 开始扫描新的token 开始扫描新的
开发词法分析程序应注意的一些问题
• 去掉注释、空格、制表符等格式控制符号 去掉注释、空格、
• • • •
{… x = 0; /*变量初始化*/ /*变量初始化* 变量初始化 x = y * z ; //计算x //计算x 计算 …}
四、词法分析程序构造
• 手工构造词法分析程序 • 利用自动生成工具LEX-生成词法分析程序 利用自动生成工具LEXLEX
手工构造词法分析程序
转换
用正则表达式 定义词法规则
NFA 转换 DFA 化简
开发 词法分析程序
实现
最简 DFA
用DFA实现词法分析 DFA实现词法分析
• DFA
• DFA的输出就是接受还拒绝,只能检查串是否被DFA接受; DFA的输出就是接受还拒绝,只能检查串是否被DFA接受; 的输出就是接受还拒绝 检查串是否被DFA接受
• 词法分析程序
• 识别出可接受的单词,并建立它的内部表示 识别出可接受的单词,
• <token-type, attribute-value> <tokenattribute-
ToyL词法规则的正则定义 ToyL词法规则的正则定义
• • • • • • • • • • a|…|z|A| |z|A|…|Z letter = a| |z|A| |Z 0|…|9 digit = 0| |9 NZ-digit = 1|…|9 NZ1| |9 Keywords ords: Keywords: Keyword = var| if | then | else| while| read| write| int Identifiers: Identifiers: identifier = letter (digit|letter)* Constant: Constant: integer: NZinteger: int = NZ-digit digit* | 0 symbols: +|Other symbols: syms = +|-| *|/ | > | < | = | : | ; | ( | ) | { | } Whitespace: ws = (‘ ‘ | \n | \t)+ Lexical structure: lex = Reserved | identifier | int | syms | ws
开发词法分析程序应注意的一些问题
• 进行宏替换
• #define LEN 100
• 包含文件的拷贝
• #include “stdio.h”
