2012年广东中考数学压轴题及答案
2012年中考数学压轴题精选附答案
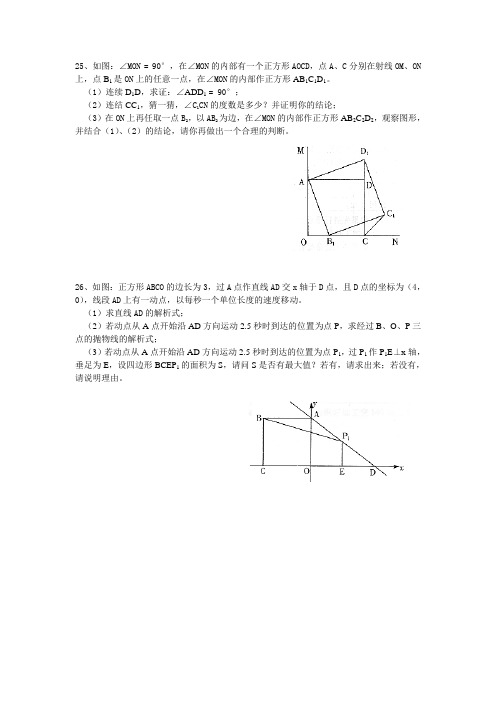
25、如图:∠MON = 90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON 上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1= 90°;(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
26、如图:正方形ABCO的边长为3,过A点作直线AD交x轴于D点,且D点的坐标为(4,0),线段AD上有一动点,以每秒一个单位长度的速度移动。
(1)求直线AD的解析式;(2)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P,求经过B、O、P三点的抛物线的解析式;(3)若动点从A点开始沿AD方向运动2.5秒时到达的位置为点P1,过P1作P1E⊥x轴,垂足为E,设四边形BCEP1的面积为S,请问S是否有最大值?若有,请求出来;若没有,请说明理由。
24.如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分∠ABC交AC于点M,AD⊥3,AD=12.BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=5⑴求证:△ANM≌△ENM;⑵求证:FB是⊙O的切线;⑶证明四边形AMEN是菱形,并求该菱形的面积S.7),且顶点C的横坐标为4,该图象在x 轴上截25.如图,二次函数的图象经过点D(0,39得的线段AB的长为6.⑴求二次函数的解析式;⑵在该抛物线的对称轴上找一点P,使PA+PD最小,求出点P的坐标;⑶在抛物线上是否存在点Q,使△QAB与△ABC相似?如果存在,求出点Q的坐标;如果不存在,请说明理由.七、(本大题8分)20.如图8,半圆的直径10AB =,点C 在半圆上,6BC =. (1)求弦AC 的长;(2)若P 为AB 的中点,PE AB ⊥交AC 于点E ,求PE 的长.21.如图9,已知正比例函数和反比例函数的图象都经过点(33)A ,. (1)求正比例函数和反比例函数的解析式;(2)把直线O A 向下平移后与反比例函数的图象交于点(6)B m ,,求m 的值和这个一次函数的解析式;(3)第(2)问中的一次函数的图象与x 轴、y 轴分别交于C 、D ,求过A 、B 、D 三点的二次函数的解析式;(4)在第(3)问的条件下,二次函数的图象上是否存在点E ,使四边形O ECD 的面积1S 与四边形O ABD 的面积S 满足:123S S =?若存在,求点E 的坐标;若不存在,请说明理由.P BC EA (图8)23.(本小题9分)如图,AB 是⊙O 的直径,C 是AB 延长线上一点,CD 与⊙O 相切于点E ,AD ⊥CD (1)求证:AE 平分∠DAC ; (2)若AB=3,∠ABE=60°,①求AD 的长;②求出图中阴影部分的面积。
2012全国各地中考数学压轴题精选(21-30)解析版

2012年各地中考数学压轴题精选21~30_解析版【21.2012上海】24.如图,在平面直角坐标系中,二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),与y轴交于点C,点D在线段OC上,OD=t,点E在第二象限,∠ADE=90°,tan∠DAE=,EF⊥OD,垂足为F.(1)求这个二次函数的解析式;(2)求线段EF、OF的长(用含t的代数式表示);(3)当∠ECA=∠OAC时,求t的值.考点:相似三角形的判定与性质;待定系数法求二次函数解析式;全等三角形的判定与性质;勾股定理。
解答:解:(1)二次函数y=ax2+6x+c的图象经过点A(4,0)、B(﹣1,0),∴,解得,∴这个二次函数的解析式为:y=﹣2x2+6x+8;(2)∵∠EFD=∠EDA=90°∴∠DEF+∠EDF=90°,∠EDF+∠ODA=90°,∴∠DEF=∠ODA∴△EDF∽△DAO∴.∵,∴=,∴,∴EF=t.同理,∴DF=2,∴OF=t﹣2.(3)∵抛物线的解析式为:y=﹣2x2+6x+8,∴C(0,8),OC=8.如图,连接EC、AC,过A作EC的垂线交CE于G点.∵∠ECA=∠OAC,∴∠OAC=∠GCA(等角的余角相等);在△CAG与△OCA中,,∴△CAG≌△OCA,∴CG=4,AG=OC=8.如图,过E点作EM⊥x轴于点M,则在Rt△AEM中,∴EM=OF=t﹣2,AM=OA+AM=OA+EF=4+t,由勾股定理得:∵AE2=AM2+EM2=;在Rt△AEG中,由勾股定理得:∴EG===∵在Rt△ECF中,EF=t,CF=OC﹣OF=10﹣t,CE=CG+EG=+4由勾股定理得:EF2+CF2=CE2,即,解得t1=10(不合题意,舍去),t2=6,∴t=6.【22. 2012广东】22.如图,抛物线y=x2﹣x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.(1)求AB和OC的长;(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).考点:二次函数综合题。
2012中考数学压轴题及答案40例(6)

2012中考数学压轴题及答案40例(6)21.如图,在平面直角坐标系中,已知矩形ABCD的三个顶点B(4,0)、C(8,0)、D(8,8).抛物线y=ax2+bx过A、C两点.(1)直接写出点A的坐标,并求出抛物线的解析式;(2)动点P从点A出发,沿线段AB向终点B运动,同时点Q从点C出发,沿线段CD向终点D运动,速度均为每秒1个单位长度,运动时间为t秒.过点P作PEAB交AC于点E.①过点E作EFAD于点F,交抛物线于点G.当t为何值时,线段EG最长?②连接EQ,在点P、Q运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形?请直接写出相应的t值.解:(1)点A的坐标为(4,8).1分将A(4,8)、C(8,0)两点坐标分别代入y=ax2+bx,得解得a=-,b=4.抛物线的解析式为y=-x2+4x.3分(2)①在Rt△APE和Rt△ABC中,tanPAE==,即==.PE=AP=t,PB=8-t.点E的坐标为(4+t,8-t).2点G的纵坐标为-(4+t)2+4(4+t)=-t2+8.5分EG=-t2+8-(8-t)=-t2+t∵-0,当=4时,线段EG最长为2.7分②共有三个时刻.8分t1=,t2=,t3=40-.11分22.如图,抛物线y=-x2+2x+3与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A、B、C三点的坐标和抛物线的对称轴;(2)连结BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点,过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形?②设△BCF的面积为S,求S与m的函数关系式.解:(1)A(-1,0),B(3,0),C(0,3).2分抛物线的对称轴是:x=1.3分(2)①设直线BC的解析式为:y=kx+b.将B(3,0),C(0,3)分别代入得:解得直线BC的解析式为y=-x+3.当x=1时,y=-1+3=2,E(1,2).当x=m时,y=-m+3,P(m,-m+3).4分将x=1代入y=-x2+2x+3,得y=4,D(1,4).将x=m代入y=-x2+2x+3,得y=-m2+2m+3.F(m,-m2+2m+3).5分线段DE=4-2=2,线段PF=-m2+2m+3-(-m+3)=-m2+3m6分∵PF∥DE,当PF=DE时,四边形PEDF为平行四边形.由-m2+3m=2,解得:m1=2,m2=1(不合题意,舍去).当m=2时,四边形PEDF为平行四边形.7分②设直线PF与x轴交于点M.由B(3,0),O(0,0),可得:OB=OM+MB=3.则S=S△BPF+S△CPF8分=PFBM+PFOM=PFOB=(-m2+3m)3=-m2+m(03)即S与m的函数关系式为:S=-m2+m(03).9分23.如图,在矩形OABC中,已知A、C两点的坐标分别为A(4,0)、C(0,2),D为OA的中点.设点P是AOC平分线上的一个动点(不与点O重合).(1)试证明:无论点P运动到何处,PC总与PD相等;(2)当点P运动到与点B的距离最小时,试确定过O、P、D三点的抛物线的解析式;(3)设点E是(2)中所确定抛物线的顶点,当点P运动到何处时,△PDE的周长最小?求出此时点P的坐标和△PDE的周长;(4)设点N是矩形OABC的对称中心,是否存在点P,使CPN=90?若存在,请直接写出点P的坐标.解:(1)∵点D是OA的中点,OD=2,OD=OC.又∵OP是COD的角平分线,POC=POD=45.△POC≌POD,PC=PD;3分(2)如图,过点B作AOC的平分线的垂线,垂足为P,点P即为所求.易知点F的坐标为(2,2),故BF=2,作PMBF.∵△PBF是等腰直角三角形,PM=BF=1.点P的坐标为(3,3).∵抛物线经过原点可设抛物线的解析式为y=ax2+bx.又∵抛物线经过点P(3,3)和点D(2,0)解得过O、P、D三点的抛物线的解析式为y=x2-2x;7分(3)由等腰直角三角形的对称性知D点关于AOC的平分线的对称点即为C点.连接EC,它与AOC的平分线的交点即为所求的P点(因为PE+PD=EC,而两点之间线段最短),此时△PED的周长最小.∵抛物线y=x2-2x的顶点E的坐标(1,-1),C点的坐标(0,2) 设CE所在直线的解析式为y=kx+b则解得CE所在直线的解析式为y=-3x+2.联立,解得,故点P的坐标为(,).△PED的周长即是CE+DE=;11分(4)存在点P,使CPN=90,其坐标为(,)或(2,2).14分24.如图1,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.(1)求该抛物线所对应的函数关系式;(2)将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A 出发向B匀速移动,设它们运动的时间为t秒(03),直线AB与该抛物线的交点为N(如图2所示).①当t=时,判断点P是否在直线ME上,并说明理由;②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.解:(1)∵因所求抛物线的顶点M的坐标为(2,4)可设其对应的函数关系式为y=a(x-2)2+4.1分又抛物线经过坐标原点O(0,0),a(0-2)2+4=0.2分解得a=-1.3分所求函数关系式为y=-(x-2)2+4,即y=-x2+4x.4分(2)①点P不在直线ME上,理由如下:5分根据抛物线的对称性可知E点的坐标为(4,0).设直线ME的解析式为y=kx+b,将M(2,4),E(4,0)代入,得解得.直线ME的解析式为y=-2x+8.6分当t=时,OA=AP=,P(,).7分∵点P的坐标不满足直线ME的解析式y=-2x+8当t=时,点P不在直线ME上.8分②S存在最大值,理由如下:9分∵点A在x轴的非负半轴上,且N在抛物线上,OA=AP=t.P(t,t),N(t,-t2+4t),AN=-t2+4t(03)PN=AN-AP=-t2+4t-t=-t2+3t=t(3-t)010分(ⅰ)当PN=0,即t=0或t=3时,以点P,N,C,D为顶点的多边形是三角形,此三角形的高为AD.S=DCAD=32=3.11分(ⅱ)当PN0时,以点P,N,C,D为顶点的多边形是四边形.∵PN∥CD,ADCD.S=(CD+PN)AD=(3-t2+3t)2=-t2+3t+3=-(t-)2+(0当t=时,S最大=.12分综上所述,当t=时,以点P,N,C,D为顶点的多边形面积S 有最大值,最大值为.13分说明:(ⅱ)中的关系式,当t=0和t=3时也适合.25.如图1,已知抛物线y=ax2-2ax-3与x轴交于A、B两点,其顶点为C,过点A的直线交抛物线于另一点D(2,-3),且tanBAD=1.(1)求抛物线的解析式;(2)连结CD,求证:AD(3)如图2,P是线段AD上的动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值;(4)点Q是抛物线上的动点,在x轴上是否存在点F,使以A,D,F,Q为顶点的四边形是平行四边形?若存在,直接写出点F的坐标;若不存在,请说明理由.解:(1)如图1,过点D作DHx轴于H,则OH=2,DH=3.∵tanBAD=1,AH=DH=3,AO=3-2=1.1分A(-1,0).2分把A(-1,0)代入y=ax2-2ax-3,得a+2a-3=0.a=1.3分抛物线的解析式为y=x2-2x-3.4分(2)∵y=x2-2x-3=(x-1)2-4C(1,-4).5分连结AC,则AD2=32+32=18,CD2=(2-1)2+(-3+4)2=2,AC2=(1+1)2+42=20.AD2+CD2=AC2,△ACD是直角三角形,且ADC=90.7分ADCD.8分(3)设直线AD的解析式为y=kx+b,把A(-1,0),D(2,-3)代入求得直线BC的解析式为y=-x-1.9分设点P的横坐标为x,则P(x,-x-1),E(x,x2-2x-3).∵点P在点E的上方EP=(-x-1)-(x2-2x-3)=-x2+x+2=-(x-)2+10分当x=时,线段PE长度的最大值=.12分(4)存在,点F的坐标分别为F1(-3,0),F2(1,0),F3(,0),F4(,0).16分关于点F坐标的求解过程(原题不作要求,本人添加,仅供参考) 如图3①若四边形ADQ1F1为平行四边形,则AF1=DQ1,DQ1∥AF1.点Q1的纵坐标为-3,代入y=x2-2x-3,得x2-2x-3=-3,x1=0,x2=2.∵D(2,-3),Q1(0,-3),DQ1=2,AF1=2.F1(-3,0).②若四边形AF2DQ2为平行四边形,同理可得F2(1,0).③若四边形AQ3F3D为平行四边形,则AQ3=DF3.点Q3的纵坐标为3,代入y=x2-2x-3,得x2-2x-3=3,x3=,x4=.-1-()=,OF3=2-()=.F3(,0).④若四边形AQ4F4D为平行四边形,则OF4=()-()+()=F4(,0).26.已知二次函数y=ax2+bx+c(a0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m2)与x轴交于点D.(1)求二次函数的解析式;(2)在直线x=m(m2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示);(3)在(2)成立的条件下,抛物线上是否存在一点F,使得四边形ABEF为平行四边形?若存在,请求出m的值及四边形ABEF的面积;若不存在,请说明理由.解:(1)∵二次函数y=ax2+bx+c的图象经过点A(1,0),B(2,0),C(0,-2)解得二次函数的解析式y=-x2+3x-2.2分(2)当△EDB∽△AOC时,有=或=∵AO=1,CO=2,BD=m-2.当=时,得=,ED=.∵点E在第四象限,E1(m,).4分当=时,得=,ED=2m-4.∵点E在第四象限,E2(m,4-2m).6分(3)假设抛物线上存在一点F,使得四边形ABEF为平行四边形,则EF=AB=1,点F的横坐标为m-1.当点E1的坐标为(m,)时,点F1的坐标为(m-1,).∵点F1在抛物线的图象上,=-(m-1)2+3(m-1)-2.2m2-11m+14=0,解得m1=,m2=2(不合题意,舍去).F1(,-).S□ABEF=1=.9分当点E2的坐标为(m,4-2m)时,点F2的坐标为(m-1,4-2m).∵点F2在抛物线的图象上,4-2m=-(m-1)2+3(m-1)-2.m2-7m+10=0,解得m1=5,m2=2(不合题意,舍去).F2(4,-6).S□ABEF=16=6.12分注:其它解法可参照评分标准给分.27.已知:t1,t2是方程t2+2t-24=0,的两个实数根,且t1(1)求这个抛物线的解析式;(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求□OPAQ的面积S与之间的函数关系式,并写出自变量的取值范围;(3)在(2)的条件下,当□OPAQ的面积为24时,是否存在这样的点P,使□OPAQ为正方形?若存在,求出P点的坐标;若不存在,说明理由.解:(1)由t2+2t-24=0,解得t1=-6,t2=4.1分∵t1∵抛物线y=x2+bx+c的图象经过点A,B两点解得这个抛物线的解析式为y=x2+x+4.4分(2)∵点P(x,y)在抛物线上,且位于第三象限,y0,即-y0.又∵S=2S△APO=2|O A||y|=|OA||y|=6|y|S=-6y.6分=-6(x2+x+4)=-4(x2+7x+6)=-4(x+)2+25.7分令y=0,则x2+x+4=0,解得x1=-6,x2=-1.抛物线与x轴的交点坐标为(-6,0)、(-1,0)x的取值范围为-6(3)当S=24时,得-4(x+)2+25=24,解得:x1=-4,x2=-3.9分代入抛物线的解析式得:y1=y2=-4.点P的坐标为(-3,-4)、(-4,-4).当点P为(-3,-4)时,满足PO=PA,此时,□OPAQ是菱形.当点P为(-4,-4)时,不满足PO=PA,此时,□OPAQ不是菱形.10分要使□OPAQ为正方形,那么,一定有OAPQ,OA=PQ,此时,点的坐标为(-3,-3),而(-3,-3)不在抛物线y=x2+x+4上,故不存在这样的点P,使□OPAQ为正方形.12分精心整理,仅供学习参考。
2012年中考数学压轴题1(含答案)

1、如图,已知抛物线2(1)y a x =-+a ≠0)经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式;(2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形? (3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长. 1、解:(1)抛物线2(1)0)y a x a =-+≠经过点(20)A -,09a a ∴=+= ∴二次函数的解析式为:2y x x =++ (2)D为抛物线的顶点(1D ∴过D 作DN OB ⊥于N,则DN =,3660AN AD DAO =∴==∴∠=,°OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形66(s)OP t ∴=∴=②当DP OM ⊥时,四边形DAOP 是直角梯形过O 作OH AD ⊥于H ,2AO =,则1AH = (如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求AH 55(s)OP DH t ∴===③当PD OA =时,四边形DAOP 是等腰梯形26244(s)OP AD AH t ∴=-=-=∴=综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形. · 7分 (3)由(2)及已知,60COB OC OB OCB ∠==°,,△是等边三角形则6262(03)OB OC AD OP t BQ t OQ t t =====∴=-<<,,,过P 作PE OQ ⊥于E ,则3PE =113633(62)222BCPQS t t ∴=⨯⨯⨯-⨯23363328t ⎫-⎪⎝⎭当32t =时,BCPQ S 6338∴此时3339333324444OQ OP OE QE PE ==∴=-==,=, 22223393344PQ PE QE ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭2、如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax 2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD 向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值2、解.(1)点A 的坐标为(4,8) 将A (4,8)、C (8,0)两点坐标分别代入y=ax2+bx 8=16a+4b得0=64a+8b得a=-12,b=4解∴抛物线的解析式为:y=-12x2+4x …………………3分 (2)①在Rt △APE 和Rt △ABC 中,tan ∠PAE=PE AP =BC AB ,即PE AP =48 ∴PE=12AP=12t .PB=8-t .(第4题)∴点E的坐标为(4+12t ,8-t ).∴点G 的纵坐标为:-12(4+12t )2+4(4+12t )=-18t2+8. ∴EG=-18t2+8-(8-t) =-18t2+t.∵-18<0,∴当t=4时,线段EG 最长为2.②共有三个时刻.t1=163, t2=4013,t3= .3、如图,已知直线128:33l y x =+与直线2:216l y x =-+相交于点C l l 12,、分别交x 轴于A B 、两点.矩形DEFG 的顶点D E 、分别在直线12l l 、上,顶点F G 、都在x 轴上,且点G 与点B 重合.(1)求ABC △的面积;(2)求矩形DEFG 的边DE 与EF 的长;(3)若矩形DEFG 从原点出发,沿x 轴的反方向以每秒1个单位长度的速度平移, 设移动时间为(012)t t ≤≤秒,矩形DEFG 与ABC △重叠部分的面积为S ,求S 关t 的函数关系式,并写出相应的t 的取值范围.3、(1)解:由28033x +=,得4x A =-∴.点坐标为()40-,.由2160x -+=,得8x B =∴.点坐标为()80,.∴()8412AB =--=由2833216y x y x ⎧=+⎪⎨⎪=-+⎩,.解得56x y =⎧⎨=⎩,.∴C 点的坐标为()56,. ∴111263622ABC C S AB y ==⨯⨯=△·.(2)解:∵点D 在1l 上且2888833D B D x x y ==∴=⨯+=,.∴D 点坐标为()88,.又∵点E 在2l上且821684E D E E y y x x ==∴-+=∴=,..∴E 点坐标为()48,.∴8448OE EF =-==,.(3)①当03t <≤时,如图1,矩形DEFG 与ABC △重叠部分为五边形CHFGR (0t =时,为四边形CHFG ).过C 作CM AB ⊥于M ,则Rt Rt RGB CMB △∽△.∴BG RG BM CM =,即36t RG=,∴2RG t =.Rt Rt AFH AMC △∽△, ∴()()11236288223ABC BRG AFH S S S S t t t t =--=-⨯⨯--⨯-△△△.即241644333S t t =-++.4、如图13,二次函数)0(2<++=p q px x y 的图象与x 轴交于A 、B 两点,与y 轴交于点C (0,-1),ΔABC 的面积为45。
广东省2012年中考数学试题分类解析汇编 专题12 押轴题

某某2012年中考数学试题分类解析汇编专题12:押轴题一、选择题1.(2012某某省3分)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【】A. 5 B.6 C.11 D.16【答案】C。
【考点】三角形三边关系。
【分析】设此三角形第三边的长为x,则根据三角形两边之和大于第三边,两边之差小于第三边的构成条件,得10﹣4<x<10+4,即6<x<14,四个选项中只有11符合条件。
故选C。
2. (2012某某某某3分)如图,把一个斜边长为2且含有300角的直角三角板ABC绕直角顶点C顺时针旋转900到△A1B1C,则在旋转过程中这个三角板扫过的图形的面积是【】A3 C.334πD.11312π【答案】D。
【考点】旋转的性质,勾股定理,等边三角形的性质,扇形面积。
【分析】因为旋转过程中这个三角板扫过的图形的面积分为三部分扇形ACA1、 BCD和△ACD 计算即可:在△ABC中,∠ACB=90°,∠BAC=30°,AB=2,∴BC=12AB=1,∠B=90°-∠BAC=60°。
∴22AC AB BC3-∴ABC 13S BC AC 22∆=⨯⨯=。
设点B 扫过的路线与AB 的交点为D ,连接CD ,∵BC=DC ,∴△BCD 是等边三角形。
∴BD=CD=1。
∴点D 是AB 的中点。
∴ACD ABC 1133S S 2224∆∆==⨯=S 。
∴1ACD ACA BCD ABC S S S ∆∆=++扇形扇形的面扫过积22903 601333113 3603604464124πππππ⨯⨯⨯⨯=++=++=+() 故选D 。
3. (2012某某某某3分)如图,正比例函数y 1=k 1x 和反比例函数22k y =x的图象交于A (﹣1,2)、B (1,﹣2)两点,若y 1<y 2,则x 的取值X 围是【 】A .x <﹣1或x >1B .x <﹣1或0<x <1C .﹣1<x <0或0<x <1D .﹣1<x <0或x >1【答案】D 。
2012年中考数学压轴题及解析分类汇编

中考数学压轴题:函数相似三角形问题(一)例1直线113y x =-+分别交x 轴、y 轴于A 、B 两点,△AOB 绕点O 按逆时针方向旋转90°后得到△COD ,抛物线y =ax 2+bx +c 经过A 、C 、D 三点.(1) 写出点A 、B 、C 、D 的坐标;(2) 求经过A 、C 、D 三点的抛物线表达式,并求抛物线顶点G 的坐标;(3) 在直线BG 上是否存在点Q ,使得以点A 、B 、Q 为顶点的三角形与△COD 相似?若存在,请求出点Q 的坐标;若不存在,请说明理由.例2 Rt △ABC 在直角坐标系内的位置如图1所示,反比例函数(0)ky k x=≠在第一象限内的图像与BC 边交于点D (4,m ),与AB 边交于点E (2,n ),△BDE 的面积为2.(1)求m 与n 的数量关系; (2)当tan ∠A =12时,求反比例函数的解析式和直线AB 的表达式; (3)设直线AB 与y 轴交于点F ,点P 在射线FD 上,在(2)的条件下,如果△AEO 与△EFP 相似,求点P 的坐标.图12012中考数学压轴题函数相似三角形问题(二)例3 如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3).(1)直接写出抛物线的对称轴、解析式及顶点M的坐标;(2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、B1的坐标分别为(x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标;(3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1 图2例4 如图1,已知点A (-2,4) 和点B (1,0)都在抛物线22=++上.y mx mx n (1)求m、n;(2)向右平移上述抛物线,记平移后点A的对应点为A′,点B的对应点为B′,若四边形A A′B′B为菱形,求平移后抛物线的表达式;(3)记平移后抛物线的对称轴与直线AB′的交点为C,试在x轴上找一个点D,使得以点B′、C、D为顶点的三角形与△ABC相似.图12012中考数学压轴题函数相似三角形问题(三) 例5 如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点.(1)求此抛物线的解析式;(2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;(3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.,图1例6 如图1,△ABC 中,AB =5,AC =3,cos A =310.D 为射线BA 上的点(点D 不与点B 重合),作DE //BC 交射线CA 于点E ..(1) 若CE =x ,BD =y ,求y 与x 的函数关系式,并写出函数的定义域; (2) 当分别以线段BD ,CE 为直径的两圆相切时,求DE 的长度;(3) 当点D 在AB 边上时,BC 边上是否存在点F ,使△ABC 与△DEF 相似?若存在,请求出线段BF 的长;若不存在,请说明理由.图1 备用图 备用图例 7 如图1,在直角坐标系xOy 中,设点A (0,t ),点Q (t ,b ).平移二次函数2tx y -=的图象,得到的抛物线F 满足两个条件:①顶点为Q ;②与x 轴相交于B 、C 两点(∣OB ∣<∣OC ∣),连结A ,B .(1)是否存在这样的抛物线F ,使得OC OB OA ⋅=2?请你作出判断,并说明理由;(2)如果AQ ∥BC ,且tan ∠ABO =23,求抛物线F 对应的二次函数的解析式.图12012中考数学压轴题函数等腰三角形问题(一)例1 如图1,已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P (0,m )是线段OC 上一动点(C 点除外),直线PM 交AB 的延长线于点D .(1)求点D 的坐标(用含m 的代数式表示); (2)当△APD 是等腰三角形时,求m 的值;(3)设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H (如图2).当点P 从O 向C 运动时,点H 也随之运动.请直接写出点H 所经过的路长(不必写解答过程).图1 图2例2 如图1,已知一次函数y =-x +7与正比例函数43y x 的图象交于点A ,且与x 轴交于点B .(1)求点A 和点B 的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.图12012中考数学压轴题函数等腰三角形问题(二)例3 如图1,在直角坐标平面内有点A(6, 0),B(0, 8),C(-4, 0),点M、N 分别为线段AC和射线AB上的动点,点M以2个单位长度/秒的速度自C向A方向作匀速运动,点N以5个单位长度/秒的速度自A向B方向作匀速运动,MN交OB于点P.(1)求证:MN∶NP为定值;(2)若△BNP与△MNA相似,求CM的长;(3)若△BNP是等腰三角形,求CM的长.图1例4 如图1,在矩形ABCD 中,AB =m (m 是大于0的常数),BC =8,E 为线段BC 上的动点(不与B 、C 重合).连结DE ,作EF ⊥DE ,EF 与射线BA 交于点F ,设CE =x ,BF =y .(1)求y 关于x 的函数关系式;(2)若m =8,求x 为何值时,y 的值最大,最大值是多少? (3)若12y m,要使△DEF 为等腰三角形,m 的值应为多少?图12012中考数学压轴题函数相似三角形问题(三)例5 已知:如图1,在平面直角坐标系xOy 中,矩形OABC 的边OA 在y 轴的正半轴上,OC 在x 轴的正半轴上,OA =2,OC =3,过原点O 作∠AOC 的平分线交AB 于点D ,连接DC ,过点D 作DE ⊥DC ,交OA 于点E .(1)求过点E 、D 、C 的抛物线的解析式;(2)将∠EDC 绕点D 按顺时针方向旋转后,角的一边与y 轴的正半轴交于点F ,另一边与线段OC 交于点G .如果DF 与(1)中的抛物线交于另一点M ,点M 的横坐标为56,那么EF =2GO 是否成立?若成立,请给予证明;若不成立,请说明理由; (3)对于(2)中的点G ,在位于第一象限内的该抛物线上是否存在点Q ,使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形?若存在,请求出点Q 的坐标;若不存在成立,请说明理由.图1例6 在平面直角坐标系内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM//x轴(如图1所示).点B与点A关于原点对称,直线y=x+b(b为常数)经过点B,且与直线CM相交于点D,联结OD.(1)求b的值和点D的坐标;(2)设点P在x轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的圆与圆O外切,求圆O的半径.图12012中考数学压轴题函数直角三角形问题(一)例1 如图1,已知抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B 左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段34PQ AB =时,求tan ∠CED 的值;②当以C 、D 、E 为顶点的三角形是直角三角形时,请直接写出点P 的坐标. 温馨提示:考生可以根据第(3)问的题意,在图中补出图形,以便作答.图1例2 设直线l 1:y =k 1x +b 1与l 2:y =k 2x +b 2,若l 1⊥l 2,垂足为H ,则称直线l 1与l 2是点H 的直角线.(1)已知直线①122y x =-+;②2y x =+;③22y x =+;④24y x =+和点C (0,2),则直线_______和_______是点C 的直角线(填序号即可);(2)如图,在平面直角坐标系中,直角梯形OABC 的顶点A (3,0)、B (2,7)、C (0,7),P 为线段OC 上一点,设过B 、P 两点的直线为l 1,过A 、P 两点的直线为l 2,若l 1与l 2是点P 的直角线,求直线l 1与l 2的解析式.图12012中考数学压轴题函数直角三角形问题(三)例 5 如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S .① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1例6 已知Rt △ABC 中,︒=∠90ACB ,CB CA =,有一个圆心角为︒45,半径的长等于CA 的扇形CEF 绕点C 旋转,且直线CE ,CF 分别与直线AB 交于点M ,N .(1)当扇形CEF 绕点C 在ACB ∠的内部旋转时,如图1,求证:222BN AM MN +=;思路点拨:考虑222BN AM MN +=符合勾股定理的形式,需转化为在直角三角形中解决.可将△ACM 沿直线CE 对折,得△DCM ,连DN ,只需证BN DN =,︒=∠90MDN 就可以了.请你完成证明过程.(2)当扇形CEF 绕点C 旋转至图2的位置时,关系式222BN AM MN +=是否仍然成立?若成立,请证明;若不成立,请说明理由.图1 图2图5 图6 图72012中考数学压轴题函数平行四边形问题(一)例 1 已知平面直角坐标系xOy (如图1),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长;(2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.图1例2将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图1所示.(1)请直接写出抛物线c 2的表达式;(2)现将抛物线c1向左平移m个单位长度,平移后得到新抛物线的顶点为M,与x轴的交点从左到右依次为A、B;将抛物线c2向右也平移m个单位长度,平移后得到新抛物线的顶点为N,与x轴的交点从左到右依次为D、E.①当B、D是线段AE的三等分点时,求m的值;②在平移过程中,是否存在以点A、N、E、M为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(二)例3 如图1,在平面直角坐标系中,已知抛物线经过A(-4,0)、B(0,-4)、C(2,0)三点.(1)求抛物线的解析式;(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△MAB的面积为S,求S关于m的函数关系式,并求出S的最大值;(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.图1 图2例4在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图22012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ 的面积(用含x的代数式表示);(3)当(2)中的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB上是否存在点E,使得以点E、D、O、A为顶点的四边形是平行四边形?如果存在,直接写出BECD的值;如果不存在,请说明理由.图12012中考数学压轴题函数梯形问题(一)例1 已知平面直角坐标系xOy中,抛物线y=ax2-(a+1)x与直线y=kx的一个公共点为A(4,8).(1)求此抛物线和直线的解析式;(2)若点P在线段OA上,过点P作y轴的平行线交(1)中抛物线于点Q,求线段PQ长度的最大值;(3)记(1)中抛物线的顶点为M,点N在此抛物线上,若四边形AOMN恰好是梯形,求点N的坐标及梯形AOMN的面积.备用图图1 图2例 2 已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4,设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y =2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D 的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN //x 轴,交PB 于点N . 将△PMN 沿直线MN 对折,得到△P 1MN . 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒,求S 关于t 的函数关系式.图1 图22012中考数学压轴题函数梯形问题(二)例3 如图1,在平面直角坐标系xOy 中,抛物线的解析式是y =2114x ,点C 的坐标为(–4,0),平行四边形OABC 的顶点A ,B 在抛物线上,AB 与y 轴交于点M ,已知点Q (x ,y )在抛物线上,点P (t ,0)在x 轴上.(1) 写出点M 的坐标;(2) 当四边形CMQP 是以MQ ,PC 为腰的梯形时.① 求t 关于x 的函数解析式和自变量x 的取值范围;② 当梯形CMQP 的两底的长度之比为1∶2时,求t 的值.图1例 4 已知,矩形OABC 在平面直角坐标系中位置如图1所示,点A 的坐标为(4,0),点C 的坐标为)20(-,,直线x y 32-=与边BC 相交于点D . (1)求点D 的坐标;(2)抛物线c bx ax y ++=2经过点A 、D 、O ,求此抛物线的表达式;(3)在这个抛物线上是否存在点M ,使O 、D 、A 、M 为顶点的四边形是梯形?若存在,请求出所有符合条件的点M 的坐标;若不存在,请说明理由.图12012中考数学压轴题函数平行四边形问题(三)例 5 如图1,等边△ABC 的边长为4,E 是边BC 上的动点,EH ⊥AC 于H ,过E 作EF ∥AC ,交线段AB 于点F ,在线段AC 上取点P ,使PE =EB .设EC =x (0<x ≤2).(1)请直接写出图中与线段EF 相等的两条线段(不再另外添加辅助线);(2)Q 是线段AC 上的动点,当四边形EFPQ 是平行四边形时,求平行四边形EFPQ 的面积(用含x 的代数式表示);(3)当(2)中 的平行四边形EFPQ 面积最大值时,以E 为圆心,r 为半径作圆,根据⊙E 与此时平行四边形EFPQ 四条边交点的总个数,求相应的r 的取值范围.图1例6 如图1,抛物线322++-=x x y 与x 轴相交于A 、B 两点(点A 在点B 的左侧),与y 轴相交于点C ,顶点为D .(1)直接写出A 、B 、C 三点的坐标和抛物线的对称轴;(2)连结BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF //DE 交抛物线于点F ,设点P 的横坐标为m .①用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?②设△BCF 的面积为S ,求S 与m 的函数关系.图1例 7 如图,在平面直角坐标系xOy 中,直线1y x =+与334y x =-+交于点A ,分别交x 轴于点B 和点C ,点D 是直线AC 上的一个动点.(1)求点A 、B 、C 的坐标.(2)当△CBD 为等腰三角形时,求点D 的坐标.(3)在直线AB 上是否存在点E ,使得以点E 、D 、O 、A 为顶点的四边形是平行四边形?如果存在,直接写出BE CD的值;如果不存在,请说明理由.图12012中考数学压轴题函数面积问题(一)例 1 如图1,直线l 经过点A (1,0),且与双曲线m y x=(x >0)交于点B (2,1).过点(,1)P p p -(p >1)作x 轴的平行线分别交曲线m y x =(x >0)和m y x=-(x <0)于M 、N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB ∽△PNA ;(3)是否存在实数p ,使得S △AMN =4S △AMP ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.图1例2 如图1,在平面直角坐标系xOy 中,直角梯形OABC 的顶点O 为坐标原点,顶点A 、C 分别在x 轴、y 轴的正半轴上,CB ∥OA ,OC =4,BC =3,OA =5,点D 在边OC 上,CD =3,过点D 作DB 的垂线DE ,交x 轴于点E .(1)求点E的坐标;(2)二次函数y=-x2+bx+c的图像经过点B和点E.①求二次函数的解析式和它的对称轴;②如果点M在它的对称轴上且位于x轴上方,满足S△CEM=2S△ABM,求点M的坐标.图12012中考数学压轴题函数面积问题(二)例3 如图1,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1).点D是线段BC上的动点(与端点B、C不重合),过点D作直线12y x b=-+交折线OAB于点E.(1)记△ODE的面积为S,求S与b的函数关系式;(2)当点E在线段OA上时,若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,试探究四边形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由.例 4 如图1,在△ABC中,∠C=90°,A C=3,BC=4,CD是斜边AB上的高,点E在斜边AB上,过点E作直线与△ABC的直角边相交于点F,设AE=x,△AEF的面积为y.(1)求线段AD的长;(2)若EF⊥AB,当点E在斜边AB上移动时,①求y与x的函数关系式(写出自变量x的取值范围);②当x取何值时,y有最大值?并求出最大值.(3)若点F在直角边AC上(点F与A、C不重合),点E在斜边AB上移动,试问,是否存在直线EF将△ABC的周长和面积同时平分?若存在直线EF,求出x的值;若不存在直线EF,请说明理由.图1 备用图2012中考数学压轴题函数面积问题(三)例5 如图1,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP 与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.图1 图2例6 在直角坐标系中,抛物线c=2经过点(0,10)和点(4,2).+y+xbx(1)求这条抛物线的解析式.(2)如图1,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线=2滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,y++cbxxAB落在x轴上.①求边BC的长.②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.。
2012中考数学压轴题及答案40例(2)

2012中考数学压轴题及答案40例(2)5.如图,在直角坐标系xOy 中,点P 为函数214y x =在第一象限内的图象上的任一点,点A 的坐标为(01),,直线l 过(01)B -,且与x 轴平行,过P 作y 轴的平行线分别交x 轴,l 于C Q ,,连结AQ 交x 轴于H ,直线PH 交y 轴于R .(1)求证:H 点为线段AQ 的中点; (2)求证:①四边形APQR 为平行四边形;②平行四边形APQR 为菱形;(3)除P 点外,直线PH 与抛物线214y x =有无其它公共点?并说明理由. (08江苏镇江28题解析)(1)法一:由题可知1AO CQ ==.90AOH QCH ∠=∠=,AHO QHC ∠=∠,AOH QCH ∴△≌△. ····················································································· (1分)OH CH ∴=,即H 为AQ 的中点. ································································· (2分) 法二:(01)A ,,(01)B -,,OA OB ∴=. ······················································ (1分)又BQ x ∥轴,HA HQ ∴=. ·········································································· (2分) (2)①由(1)可知AH QH =,AHR QHP ∠=∠,AR PQ ∥,RAH PQH ∴∠=∠,RAH PQH ∴△≌△. ····················································································· (3分) AR PQ ∴=,又AR PQ ∥,∴四边形APQR 为平行四边形. ··············································· (4分)②设214P m m ⎛⎫ ⎪⎝⎭,,PQ y ∥轴,则(1)Q m -,,则2114PQ m =+.过P 作PG y ⊥轴,垂足为G ,在Rt APG △中,22222222111111444AP AG PG m m m m PQ ⎛⎫⎛⎫=+=-+=+=+= ⎪ ⎪⎝⎭⎝⎭.∴平行四边形APQR 为菱形. ·········································································· (6分)(3)设直线PR 为y kx b =+,由OH CH =,得22m H ⎛⎫⎪⎝⎭,,214P m m ⎛⎫ ⎪⎝⎭,代入得: 2021.4m k b km b m ⎧+=⎪⎪⎨⎪+=⎪⎩, 221.4m k b m ⎧=⎪⎪∴⎨⎪=-⎪⎩,∴直线PR 为2124m y x m =-. ······················ (7分) 设直线PR 与抛物线的公共点为214x x ⎛⎫ ⎪⎝⎭,,代入直线PR 关系式得:22110424m x x m -+=,21()04x m -=,解得x m =.得公共点为214m m ⎛⎫ ⎪⎝⎭,. 所以直线PH 与抛物线214y x =只有一个公共点P . ········································ (8分) 6.如图13,已知抛物线经过原点O 和x 轴上另一点A ,它的对称轴x =2 与x 轴交于点C ,直线y =-2x -1经过抛物线上一点B (-2,m ),且与y 轴、直线x =2分别交于点D 、E . (1)求m 的值及该抛物线对应的函数关系式; (2)求证:① CB =CE ;② D 是BE 的中点;(3)若P (x ,y )是该抛物线上的一个动点,是否存在这样的点P ,使得PB =PE ,若存在,试求出所有符合条件的点P 的坐标;若不存在,请说明理由.(1)∵ 点B (-2,m )在直线y =-2x -1上,∴ m =-2×(-2)-1=3. ………………………………(2分) ∴ B (-2,3)∵ 抛物线经过原点O 和点A ,对称轴为x =2, ∴ 点A 的坐标为(4,0) .设所求的抛物线对应函数关系式为y =a (x -0)(x -4). ……………………(3分) 将点B (-2,3)代入上式,得3=a (-2-0)(-2-4),∴ 41=a . ∴ 所求的抛物线对应的函数关系式为)4(41-=x x y ,即x x y -=241. (6分)(2)①直线y =-2x -1与y 轴、直线x =2的交点坐标分别为D (0,-1) E (2,-5). 过点B 作BG ∥x 轴,与y 轴交于F 、直线x =2交于G , 则BG ⊥直线x =2,BG =4.在Rt △BGC 中,BC =522=+BG CG .∵ CE =5,∴ CB =CE =5. ……………………(9分) ②过点E 作EH ∥x 轴,交y 轴于H , 则点H 的坐标为H (0,-5).又点F 、D 的坐标为F (0,3)、D (0,-1), ∴ FD =DH =4,BF =EH =2,∠BFD =∠EHD =90°.∴ △DFB ≌△DHE (SAS ),∴ BD =DE .即D 是BE 的中点. ………………………………(11分)(3) 存在. ………………………………(12分) 由于PB =PE ,∴ 点P 在直线CD 上,∴ 符合条件的点P 是直线CD 与该抛物线的交点.设直线CD 对应的函数关系式为y =kx +b .将D (0,-1) C (2,0)代入,得⎩⎨⎧=+-=021b k b . 解得 1,21-==b k . A BCODExy x =2 G FH∴ 直线CD 对应的函数关系式为y =21x -1.∵ 动点P 的坐标为(x ,x x -241),∴21x -1=x x -241. ………………………………(13分) 解得 531+=x ,532-=x . ∴ 2511+=y ,2511-=y . ∴ 符合条件的点P 的坐标为(53+,251+)或(53-,251-).…(14分) (注:用其它方法求解参照以上标准给分.)7.如图,在平面直角坐标系中,抛物线y =-32x 2+b x +c 经过A (0,-4)、B (x 1,0)、 C (x 2,0)三点,且x 2-x 1=5. (1)求b 、c 的值;(4分)(2)在抛物线上求一点D ,使得四边形BDCE 是以BC 为对 角线的菱形;(3分)(3)在抛物线上是否存在一点P ,使得四边形B P O H 是以OB 为对角线的菱形?若存在,求出点P 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.(3分)解: (解析)解:(1)解法一: ∵抛物线y =-32x 2+b x +c 经过点A (0,-4),∴c =-4 ……1分又由题意可知,x 1、x 2是方程-32x 2+b x +c =0的两个根, ∴x 1+x 2=23b , x 1x 2=-23c =6 ······························································· 2分 由已知得(x 2-x 1)2=25 又(x 2-x 1)2=(x 2+x 1)2-4x 1x 2=49b 2-24 ∴49b 2-24=25 解得b =±314 ····································································································· 3分 当b =314时,抛物线与x 轴的交点在x 轴的正半轴上,不合题意,舍去. ∴b =-314. ···································································································· 4分解法二:∵x 1、x 2是方程-32x 2+b x +c=0的两个根, 即方程2x 2-3b x +12=0的两个根. ∴x =4969b 32-±b , ······································································· 2分∴x 2-x 1=2969b 2-=5,解得 b =±314 ·························································································· 3分 (以下与解法一相同.)(2)∵四边形BDCE 是以BC 为对角线的菱形,根据菱形的性质,点D 必在抛物线的对称轴上, ························································································· 5分 又∵y =-32x 2-314x -4=-32(x +27)2+625····························· 6分∴抛物线的顶点(-27,625)即为所求的点D . ································· 7分 (3)∵四边形BPOH 是以OB 为对角线的菱形,点B 的坐标为(-6,0),根据菱形的性质,点P 必是直线x =-3与 抛物线y =-32x 2-314x -4的交点, ······················································· 8分∴当x =-3时,y =-32×(-3)2-314×(-3)-4=4, ∴在抛物线上存在一点P (-3,4),使得四边形BPOH 为菱形. ·········· 9分 四边形BPOH 不能成为正方形,因为如果四边形BPOH 为正方形,点P 的坐标只能是(-3,3),但这一点不在抛物线上. ········································· 10分8.已知:如图14,抛物线2334y x =-+与x 轴交于点A ,点B ,与直线34y x b =-+相交于点B ,点C ,直线34y x b =-+与y 轴交于点E . (1)写出直线BC 的解析式. (2)求ABC △的面积.(3)若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动(不与A B ,重合),同时,点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动.设运动时间为t 秒,请写出MNB △的面积S 与t 的函数关系式,并求出点M 运动多少时间时,MNB △的面积最大,最大面积是多少?(解析)解:(1)在2334y x =-+中,令0y = 23304x ∴-+=12x ∴=,22x =-(20)A ∴-,,(20)B ,············································· 1分又点B 在34y x b =-+上 302b ∴=-+32b =BC ∴的解析式为3342y x =-+ ·········································································· 2分 (2)由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩,得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩················································· 4分 914C ⎛⎫∴- ⎪⎝⎭,,(20)B ,4AB ∴=,94CD =·························································································· 5分 1994242ABC S ∴=⨯⨯=△ ····················································································· 6分 (3)过点N 作NP MB ⊥于点PEO MB ⊥ NP EO ∴∥BNP BEO ∴△∽△ ··························································································· 7分 BN NP BE EO∴=····································································································· 8分 由直线3342y x =-+可得:302E ⎛⎫ ⎪⎝⎭, ∴在BEO △中,2BO =,32EO =,则52BE = 25322t NP∴=,65NP t ∴= ··················································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ················································································ 10分2312(2)55S t =--+ ························································································· 11分 此抛物线开口向下,∴当2t =时,125S =最大 ∴当点M 运动2秒时,MNB △的面积达到最大,最大为125. ······················ 12分。
2012中考数学压轴题及答案40例(7)

∴yB=a()2= 5分 设抛物线F2的对称轴与x轴交于点P,如图1. ∵a>0,∴BP=. ∵顶点N(,-),∴NP=|-|=. ∴BP=NP. 6分 ∵抛物线是轴对称图形,∴OP=AP. ∴四边形ABMN是平行四边形. 7分 ∵BN是抛物线F2的对称轴,∴BN⊥OA. ∴四边形ABMN是菱形. 8分 ∵BN=BP+NP,∴BN=. ∵四边形ABMN的面积为×OA·BN=×|m|× ∴当m>0时,四边形ABMN的面积为×m×=. 9分 当m<0时,四边形ABMN的面积为×(-m)×=-. 10 分 (3)点C的坐标为(0,+c)(参考图2).
=(yD-yP)(xB-xA) =[(x+)-(x 2+x)](1+2) =-x 2-x+ =-(x+)2+ ∴当x=-时,△PAB的面积有最大值,最大值为. 8分 此时yP=×(-)2+×(-)=-. ∴此时P点的坐标为(-,-). 9分
∴直线ON的解析式为y=-x.
由x=-x 2+x,得x1=0,x2=6. ∴N(6,-3). 过点N作NC⊥x轴于C. 在Rt△BCN中,BC=6-4=2,NC=3 ∴NB==. ∵OB=4,∴NB≠OB,∴∠BON≠∠BNO,∴△OBN与 △OAB不相似. 同理,在对称轴左边的抛物线上也不存在符合条件的 点. ∴在x轴下方的抛物线上不存在点N,使△OBN与△OAB相 似. 10分 31.如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段 OA绕原点O顺时针旋转120°,得到线段OB. (1)求点B的坐标; (2)求经过A、O、B三点的抛物线的解析式; (3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长 最小?若存在,求出点C的坐标;若不存在,请说明理由. (4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么
2012中考数学压轴题及答案40例(1)

2012中考数学压轴题及答案40例(1)1.如图:抛物线经过A (-3,0)、B (0,4)、C (4,0)三点.(1) 求抛物线的解析式.(2)已知AD = AB (D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动;同时另一个动点Q 以某一速度从点B 沿线段BC 移动,经过t 秒的移动,线段PQ 被BD 垂直平分,求t 的值;(3)在(2)的情况下,抛物线的对称轴上是否存在一点M ,使MQ+MC 的值最小?若存在,请求出点M 的坐标;若不存在,请说明理由。
(注:抛物线2y ax bx c =++的对称轴为2b x a=-)解:设抛物线的解析式为2(0)y ax bx c a =++≠,依题意得:c=4且934016440a b a b -+=⎧⎨++=⎩ 解得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩所以 所求的抛物线的解析式为211433y x x =-++(2)连接DQ ,在Rt △AOB 中,2222345AB AO BO=+=+=所以AD=AB= 5,AC=AD+CD=3 + 4 = 7,CD = AC - AD = 7 – 5 = 2 因为BD 垂直平分PQ ,所以PD=QD ,PQ ⊥BD ,所以∠PDB=∠QDB 因为AD=AB ,所以∠ABD=∠ADB ,∠ABD=∠QDB ,所以DQ ∥AB 所以∠CQD=∠CBA 。
∠CDQ=∠CAB ,所以△CDQ ∽ △CABD Q C D A BC A= 即210,577D Q D Q ==所以AP=AD – DP = AD – DQ=5 –107=257,2525177t =÷=所以t 的值是257(3)答对称轴上存在一点M ,使MQ+MC 的值最小 理由:因为抛物线的对称轴为122b x a=-=所以A (- 3,0),C (4,0)两点关于直线12x =对称连接AQ交直线12x =于点M ,则MQ+MC 的值最小过点Q 作QE ⊥x 轴,于E ,所以∠QED=∠BOA=90 DQ ∥AB ,∠ BAO=∠QDE , △DQE ∽△ABO Q E D QD E B OA B A O== 即107453Q E D E ==所以QE=87,DE=67,所以OE = OD + DE=2+67=207,所以Q (207,87)设直线AQ 的解析式为(0)y kx m k =+≠则2087730k m k m ⎧+=⎪⎨⎪-+=⎩由此得8412441k m ⎧=⎪⎪⎨⎪=⎪⎩所以直线AQ 的解析式为8244141y x =+联立128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 由此得128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 所以M 128(,)241则:在对称轴上存在点M 128(,)241,使MQ+MC 的值最小。
2012年广东各地区中考压轴题

2012年广东省各地市数学中考压轴题1. (2012广东省9分)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF 交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.(1)求证:△ABG≌△C′DG;(2)求tan∠ABG的值;(3)求EF的长.2. (2012广东省9分)如图,抛物线213y=x x 922--与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC 、AC . (1)求AB 和OC 的长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合),过点E 作直线l 平行BC ,交AC 于点D .设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围;(3)在(2)的条件下,连接CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π).3. (2012广东佛山10分)规律是数学研究的重要内容之一.初中数学中研究的规律主要有一些特定的规则、符号(数)及其运算规律、图形的数值特征和位置关系特征等方面.请你解决以下与数的表示和运算相关的问题:(1)写出奇数a用整数n表示的式子;(2)写出有理数b用整数m和整数n表示的式子;(3)函数的研究中,应关注y随x变化而变化的数值规律(课本里研究函数图象的特征实际上也是为了说明函数的数值规律).下面对函数y=x2的某种数值变化规律进行初步研究:由表看出,当x的取值从0开始每增加1个单位时,y的值依次增加1,3,5...请回答:当x的取值从0开始每增加12个单位时,y的值变化规律是什么?当x的取值从0开始每增加1n个单位时,y的值变化规律是什么?4. (2012广东佛山11分)(1)按语句作图并回答:作线段AC(AC=4),以A为圆心a为半径作圆,再以C为圆心b为半径作圆(a<4,b<4,圆A与圆C交于B、D两点),连接AB、BC、CD、DA.若能作出满足要求的四边形ABCD,则a、b应满足什么条件?(2)若a=2,b=3,求四边形ABCD的面积.5. (2012广东广州14分)如图,抛物线233y=x x+384--与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C . (1)求点A 、B 的坐标;(2)设D 为已知抛物线的对称轴上的任意一点,当△ACD 的面积等于△ACB 的面积时,求点D 的坐标;(3)若直线l 过点E (4,0),M 为直线l 上的动点,当以A 、B 、M 为顶点所作的直角三角形有且只有三个时,求直线l 的解析式.6、(2012广东广州14分)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长;(2)当60°<α<90°时,①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.②连接CF,当CE2﹣CF2取最大值时,求tan∠DCF的值.7、(2012广东梅州10分)(1)已知一元二次方程x2+px+q=0(p2﹣4q≥0)的两根为x1、x2;求证:x1+x2=﹣p,x1•x2=q.(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(﹣1,﹣1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.8. (2012广东梅州11分)如图,矩形OABC中,A(6,0)、C(0,2)、D(0,3),射线l过点D且与x轴平行,点P、Q分别是l和x轴正半轴上动点,满足∠PQO=60°.(1)①点B的坐标是;②∠CAO=度;③当点Q与点A重合时,点P的坐标为;(直接写出答案)(2)设OA的中心为N,PQ与线段AC相交于点M,是否存在点P,使△AMN为等腰三角形?若存在,请直接写出点P的横坐标为m;若不存在,请说明理由.(3)设点P的横坐标为x,△OPQ与矩形OABC的重叠部分的面积为S,试求S与x的函数关系式和相应的自变量x的取值范围.9. (2012广东汕头12分)有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).(1)用树状图或列表法表示(x,y)所有可能出现的结果;(2)求使分式222x3xy y+x yx y---有意义的(x,y)出现的概率;(3)化简分式222x3xy y+x yx y---,并求使分式的值为整数的(x,y)出现的概率.10. (2012广东深圳9分)如图,已知△ABC的三个顶点坐标分别为A(-4,0)、B(1,0)、C(-2,6).(1)求经过A、B、C三点的抛物线解析式;(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F,为顶点的三角形与△ABC相似吗?请说明理由.11. (2012广东深圳9分)如图,在平面直角坐标系中,直线l:y=-2x+b (b≥0)的位置随b的不同取值而变化.(1)已知⊙M的圆心坐标为(4,2),半径为2.当b=时,直线l:y=-2x+b (b≥0)经过圆心M:当b=时,直线l:y=-2x+b(b≥0)与OM相切:(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式,12、(2012广东湛江12分)如图,在平面直角坐标系中,直角三角形AOB的顶点A、B分别落在坐标轴上.O为原点,点A的坐标为(6,0),点B的坐标为(0,8).动点M从点O出发.沿OA向终点A以每秒1个单位的速度运动,同时动点N从点A出发,沿AB向终点B以每秒个单位的速度运动.当一个动点到达终点时,另一个动点也随之停止运动,设动点M、N运动的时间为t秒(t>0).(1)当t=3秒时.直接写出点N的坐标,并求出经过O、A、N三点的抛物线的解析式;(2)在此运动的过程中,△MNA的面积是否存在最大值?若存在,请求出最大值;若不存在,请说明理由;(3)当t为何值时,△MNA是一个等腰三角形?(2012广东肇庆10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC于点E,交BC于点D,连结BE、AD交于点P. 求证:(1)D是BC的中点;(2)△BEC ∽△ADC;(3)AB⋅CE=2DP⋅AD.14、(2012广东肇庆10分)已知二次函数2y mx nx p =++图象的顶点横坐标是2,与x 轴交于A (x 1,0)、B (x 2,0),x 1﹤0﹤x 2,与y 轴交于点C ,O 为坐标原点,tan tan CA BO 1O C ∠-∠=.(1)求证: n 4m 0+=;(2)求m 、n 的值;(3)当p ﹥0且二次函数图象与直线y x 3=+仅有一个交点时,求二次函数的最大值.15 (2012广东珠海9分)已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.16(2012广东珠海9分)如图,在等腰梯形ABCD中,ABDC,,AC、BD交于H,平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移,分别交等腰梯形ABCD的边于M、N和R、Q,分别交对角线AC于F、G;当直线RQ到达点C时,两直线同时停止移动.记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2,若直线MN平移的速度为1单位/秒,直线RQ平移的速度为2单位/秒,设两直线移动的时间为x秒.(1)填空:∠AHB=;AC=;(2)若S2=3S1,求x;(3)设S2=mS1,求m的变化范围.。
2012年广东省中考数学试卷及详细参考答案

2012年广东省中考数学试卷参考答案与试题解析一、选择题(本大题共5小题,每小题3分,共15分)在每个小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1.(2011•河南)﹣5的绝对值是()A.5B.﹣5 C.D.﹣考点:绝对值。
分析:根据绝对值的性质求解.解答:解:根据负数的绝对值等于它的相反数,得|﹣5|=5.故选A.点评:此题主要考查的是绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.2.(2012•广东)地球半径约为6400000米,用科学记数法表示为()A.0.64×107B.6.4×106C.64×105D.640×104考点:科学记数法—表示较大的数。
分析:科学记数法的形式为a×10n,其中1≤a<10,n为整数.解答:解:6400000=6.4×106.故选B.点评:此题考查用科学记数法表示较大的数,其规律为1≤|a|<10,n为比原数的整数位数小1的正整数.3.(2012•广东)数据8、8、6、5、6、1、6的众数是()A.1B.5C.6D.8考点:众数。
分析:众数指一组数据中出现次数最多的数据,根据众数的定义即可求解.解答:解:6出现的次数最多,故众数是6.故选C.点评:本题主要考查了众数的概念,注意众数是指一组数据中出现次数最多的数据,它反映了一组数据的多数水平,一组数据的众数可能不是唯一的,比较简单.4.(2012•广东)如图所示几何体的主视图是()A.B.C.D.考点:简单组合体的三视图。
分析:主视图是从立体图形的正面看所得到的图形,找到从正面看所得到的图形即可.注意所有的看到的棱都应表现在主视图中.解答:解:从正面看,此图形的主视图有3列组成,从左到右小正方形的个数是:1,3,1.故选:B.点评:本题主要考查了三视图的知识,主视图是从物体的正面看得到的视图,关键是掌握主视图所看的位置.5.(2012•广东)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是()A.5B.6C.11 D.16考点:三角形三边关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年中考数学压轴题1.(本题满分12分)今年“五一”期间,某旅游公司对某条旅游线路推出如下套餐:如果出团人数不超过25人,人均费用500元;如果出团人数超过25人,每增加1人,人均费用降低10元,但人均费用不得低于400元.(1)某单位组织一批员工到该线路参观旅游,如果人均费用想要低于500元,但不低于420元,那么参观旅游的人数在什么范围内?请通过计算说明;(2)若该单位已付旅游费用13500元,求该单位安排了多少名员工去参观旅游.2.(本题满分12分)在Rt △ABC 中,∠BAC =90°,∠B =30°,线段AD 是BC 边上的中线. (1)如图(Ⅰ),将△ADC 沿直线BC 平移,使点D 与点C 重合,得到△FCE ,连结AF . 求证:四边形ADEF 是等腰梯形;(2)如图(Ⅱ),在(1)的条件下,再将△FCE 绕点C 顺时针旋转,设旋转角为α(0°<α<90°)连结AF 、DE .①当AC ⊥CF 时,求旋转角α的度数;②当α=60°时,请判断四边形ADEF 的形状,并给予证明.第23题图(Ⅱ)ADCEFBA EF第23题图(Ⅰ)BAC第23题备用图B3.(本题满分12分)如图,Rt △ABO 的两直角边OA 、OB 分别在x 轴的负半轴和y 轴的正半轴上,O 为坐标原点,A 、B 两点的坐标分别为(-3,0)、(0,4),抛物线223y x bx c =++经过B点,且顶点在直线52x =上.(1)求抛物线对应的函数关系式;(2)若△DCE 是由△ABO 沿x 轴向右平移得到的,当四边形ABCD 是菱形时,试判断点C 和点D 是否在该抛物线上,并说明理由;(3)在(2)的条件下,连结BD ,已知在对称轴上存在一点P ,使得△PBD 的周长最小.请求出点P 的坐标.(4)在(2)、(3)的条件下,若点M 是线段OB 上的一个动点(与点O 、B 不重合),过点M 作MN ∥BD 交x 轴于点N ,连结PM 、PN ,设OM 的长为t ,△PMN 的面积为S ,求S 与t 的函数关系式,并写出自变量t 的取值范围.S 是否存在最大值?若存在,求出最大值并求此时M 点的坐标;若不存在,请说明理由.4、为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A 、B 两种型号的设备,其中每台的价格、月处理污水量如下表.经调查:购买一台A 型设备比购买一台B 型设备多2万元,购买2台A 型设备比购买3台B 型设备少6万元.(1)求b a ,的值;第24题图(2)由于受资金限制,运河综合治理指挥部决定购买污水处理设备的资金不超过110万元,问每月最多能处理污水多少吨?5、矩形纸片ABCD 中,12A D cm =,现将这张纸片按下列图示方式折叠,AE 是折痕.(1)如图1,P ,Q 分别为AD ,BC 的中点,点D 的对应点F 在PQ 上,求PF 和AE 的长; (2)如图2,BCCQ AD DP 31,31==,点D 的对应点F 在PQ 上,求AE 的长; (3)如图3,BCn CQ AD nDP 1,1==,点D 的对应点F 在PQ 上.①直接写出AE 的长(用含n 的代数式表示); ②当n 越来越大时,AE 的长越来越接近于 .ABCDP Q EF(第23题图1) A B C D PQ EF(第23题图2) A BCD PQEF(第23题图3)6、如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边的中点,点P从点A开始沿AC方向以每秒的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.(1)当点P在线段AO上运动时.①请用含x的代数式表示OP的长度;②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围);(2)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.1.解:(1)设参观旅游的人数为x 人,依题意得:⎩⎨⎧≥-->420)25(1050025x x ------------------------------------------------------------------------2分 解得:3325≤<x ,---------------------------------------------------------------------------------4分 答:该单位参观旅游的人数应在多于25人但不超过33人的范围内.-----------------5分 (2)∵500×25=12500元<13500元, 故多于25人. ---------------------------------------- 6分 设参观旅游的人数为x 人,则每人费用为10)25(500⨯--x ,-------------------------- 7分 依题意得:13500]10)25(500[=⨯--x x ----------------------------------------------------8分 整理得,01350752=+-x x ,-------------------------------------------------------------------9分 解得:1245,30x x ==------------------------------------------------------------------------------10分 当45=x 时,40030010)25(500<=⨯--x (不合题意,舍去)当30=x 时,40045010)25(500>=⨯--x ---------------------------------------------------11分 答:该单位安排了30名员工参观旅游.--------------------------------------------------------12分 2.(1)证明:∵△ADC 沿直线BC 平移得到△FCE , ∴AD ∥FC ,且AD =FC ,∴四边形ADCF 是平行四边形,∴AF ∥DC ,即AF ∥DE ,------------------------------------------------1分 ∵∠BAC =90°,∠B =30°,∴∠ACD =60°,∵AD 是BC 边上的中线,∴AD=DC ,-------------------------------2分 ∴△ADC 是等边三角形,------------------------------------------------3分 ∵△ADC ≌△FCE ,∴△FCE 是等边三角形,∴AD=FE ,------------------------------------------------------------------4分 ∵AF ≠DE ,∴四边形ADEF 是等腰梯形.--------------------------5分第23题图(Ⅱ)ADCEB12A D CF第23题图(Ⅰ)B(2)①解:由(1)可知∠1=60°,-----------------------------------6分 当AC ⊥CF 时,∠2=90°-60°=30°,∴旋转角α的度数为30°,----------------------------------------------7分 ②四边形ADEF 为矩形,------------------------------------------------8分 由(1)可知△ADC 和△FCE 是全等正三角形,∴CA =CE =CD =CF ,------------------------------------------------------9分 当α=60°时,如图(Ⅲ),∠ACF =60°+60°=120°,∴∠ACE =120°+60°=180° ,∴A 、C 、E 三点共线,同理:D 、C 、F 三点共线,--------10分 ∴AE =DF ,-----------------------------------------------------------------------------11分 ∴四边形ADEF 为矩形.-----------------------------------------------------------12分 3.解:(1)∵抛物线223y x bx c =++经过B (0,4),∴4=c ,------1分 ∵顶点在直线52x =上,∴=-ab 22534=-b ,310=b , ∴所求函数关系式为:4310322+-=x x y --------------------------------------2分(2)在Rt △ABO 中,OA =3,OB =4,∴5AB ==, ∵四边形ABCD 是菱形,∴BC =CD =DA =AB =5,∴C 、D 两点的坐标分别是(5,4)、(2,0).---------------------------------3分 当5x =时,2210554433y =⨯-⨯+=,-----------------------------------------4分 当2x =时,2210224033y =⨯-⨯+=,∴点C 和点D 在所求抛物线上.(3)设CD 与对称轴交于点P ,则P 为所求的点,设直线CD 对应的函数关系式为y kx b =+,则5420k b k b +=⎧⎨+=⎩,解得:48,33k b ==-,∴4833y x =-,第24题图ADC第23题图(Ⅲ)B当52x =时,32382534=-⨯=y ,∴P (25,32),-----------------------------8分(4)∵MN ∥BD ,∴△OMN ∽△OBD ,∴ODON OBOM =,24ON t =,t ON 21=,--------------------------------------------9分设对称轴交x 轴于点F ,则654525)3221)(21+=⨯+=⋅+=t t OF OM PF S PFOM (梯形, ∵241212121t t t ON OM S MON =⋅=⋅=∆,656132)2125(2121+-=⨯-=⋅=∆t t PF NF S PNF ,∴-+=6545t S 241t)6561(+--t tt 1217412+-=()40<<t --------------------------------------------------10分 由S 144289)617(4112174122+--=+-=t t t ,∴当617=t 时,S 取得最大值为144289,-------------------------------------------------------------------------11分此时点M 的坐标为(0,617).----------------------------------------------------------------------------------12分4、(1)根据题意,得⎩⎨⎧=-=-6232a b b a ,解得⎩⎨⎧==1012b a (3分)(2)设购买A 型设备x 台,则B 型设备)10(x -台,能处理污水y 吨 110)10(1012≤-+x x 50≤≤∴x (2分)180040)10(180220+=-+=x x x y ,y ∴而x 的增大而增大 (5分)当20001800540,5=+⨯==y x 时(吨) 所以最多能处理污水2000吨 (7分) 5.(1)PQ 是矩形ABCD 中BC AD ,的中点,︒=∠==∴90,2121APF AF AD AP ,CDE︒=∠∴30AFP , 363=⨯=∴AP PF ︒=∠∴60FAD ,︒=∠=∠∴3021FAD DAE ,cmAD AE 3830cos =︒=∴(2)431==AD DP ,832==∴AD AP5481222=-=∴FP作CD FG ⊥于点G ,︒=∠90AFE , EFG AFP ∠=∠∴, AFP ∆∴∽EFG ∆EFGF AFPF =∴, 4==DP GF5512==∴EF DE ,5301222=+=∴DE ADAE(3)nAD nDP 121== ,nn AP )1(12-=∴nn PF AF FP 121222-=-=∴ 同理AFP ∆∽EFG ∆ EFGF AFPF =∴1212-==∴n EF DE 1221222-=+=∴n n DEAD AE当n 越来越大时,AE 越来越接近于12. 6、ABCD PQE FGA BCD PQE FG。
