不同雷诺数下的圆柱绕流数值模拟研究
不同雷诺数下的圆柱绕流数值模拟研究
２ ０１ ５在
中
国
水
运
ＶｏＩ ．１ ５ Ｊｕｌ Ｙ
Ｎｏ． ７
７月
Ｃｈ ｉ ｎ ａ Ｗａ ｔｅｒ Ｔｒ ａ ｎｓ ｐ ｏｒ ｔ
２ ０１ ５
不 同雷诺数下 的圆柱绕流数值模拟研究
陈 禹，李 强 ，郭廷 凯
（ 浙江海洋 学院 船舶与海洋Ｉ － 程系 ，浙江 舟 山 ３ １ ６ ０ ２ ２ ） 摘 要：通过 ａ ｂ ａ ｑ ｕ ｓ的 ＣＦ Ｄ 模 块 ，在水动力作用下 ，对刚性 圆柱 展开了绕流三维仿真计算 ，同时也对 圆柱绕 流
的水动力特性进行了研究 。通过仿真计算得到了漩涡脱落形态、升力系数、 阻力系数 曲线 以及斯特劳哈尔数 ，经过 分析 比较可以看出 ，不同雷诺数情况下圆柱绕流在性质上存在着 比较大 的差异 。结果表 明，随着雷诺数 的增大 ，层 流变为紊 流 ，升力以及阻力系数 的变化 幅度出现 了不稳 定性 ，漩 涡的脱落 形态 也变得 不规则。 关键 词：圆柱 绕流 ；数值模 拟 ；升力 系数 ；阻力系数 ；漩涡 脱落 中图分类号：Ｔ Ｈ ３ １ １ 文献标识码 ：Ａ 文章编号：１ ０ ０ ８ － ７ ９ ７ ３（ ２ ０ １ ５ ）０ ７ — ０ ０ ８ ８ — ０ ３
王亚玲等为得到较高雷诺数 时圆柱绕流 的三维特性 ， 采
用有限体积 法 ， 选取 了 Ｒｅ ＝ １ ０ 。 和 Ｒｅ ＝１ ０ ， 对黏性 不可 压缩 流场条件下 的圆柱绕流展开 了了三维仿真 试验『 ６ 】 。苏铭德和 康 钦军 选取 Ｒｅ ＝ １ ０ 和 ２Ｘ １ ０ ，使 用大涡模拟 的方法 ，对 圆
收稿 日期 ：２ ０ １ ５ — ０ ５ — ０ ３ 作者简介 ：陈
ａ
不同雷诺数下倾斜圆柱绕流三维数值模拟研究
不同雷诺数下倾斜圆柱绕流三维数值模拟研究近年来，研究倾斜圆柱绕流特性引起了学界的广泛关注。
圆柱绕流可分为水平和垂直两类，其中倾斜圆柱绕流为一种特殊的二维绕流状态，它在一定雷诺数范围内具有更复杂的流场结构特性，并且受水文物理过程的影响更为显著，研究其特性更为重要。
本研究使用时间和空间设置，以带边界流作为边界条件，利用基于六边形网格的数值模拟方法研究不同雷诺数下的倾斜圆柱绕流特性。
实验参数包括：倾斜角度α=20°，Re=1000 ~ 10000，向心轴比例范围为0.5 ~ 2.0，圆柱入口处外提升速度Um=0.3 ~ 0.8，及空气密度ρ=1。
有鉴于此，本研究根据不同雷诺数和向心轴比例，计算出倾斜圆柱绕流特性。
首先，主要考察不同雷诺数Re下倾斜圆柱绕流的流态特性，包括在不同位置的压力梯度，流场动量，温度梯度，流态结构以及涡度等信息。
其次，重点考察不同向心轴比例和轴向外提升速度下倾斜圆柱绕流的流态特性，包括压降，动量，温度梯度，以及不同方向的涡度分布。
结果表明，不同的雷诺数和向心轴比例会对倾斜圆柱绕流的流动特性产生明显不同的影响。
随着雷诺数的增大，压力梯度增大，动量梯度减小，温度梯度增大，涡度明显减少，圆柱内部的流场会变得更加复杂，气泡变小，而且其会从一种混合流场演变为一种逆流的流场结构。
另外，随着向心轴比例的增加，轴向外提升速度的变化会出现显著影响，但随着向心轴比例的增加，压力梯度会逐渐减小，动量梯度增大，温度梯度变化不大，涡度分布也会有较大变化。
研究结果表明，在不同雷诺数和向心轴比例范围内，倾斜圆柱绕流的流动特性会发生明显的变化。
本研究对于进一步理解流动特性和确定流动行为有重要的理论意义，同时也为实际工程的设计提供了参考。
总的来说，本研究通过应用数值模拟方法研究不同雷诺数下倾斜圆柱绕流特性，得出上述结论。
未来可以将此模拟实验方法应用于建立更复杂物理系统的研究，以更深入地理解绕流特性和其流动性质。
不同雷诺数下方柱绕流的数值模拟
2
计算结果与讨论
分别对雷诺数为 100, 1 103 , 1 104 和 2 2
3 4
计算得到了方柱上的阻力系数和升力系数. 阻力系数 C D 与升力系数 C L 的定义分别为: CD = FD , 1 L 2 U2 2 CL = FL 1 L 2 U2 2 ( 12)
104 时的情况进行了计算 . 当 Re = 100 时, 直接采 用 N S 方程进行计算 ; 当 Re = 1 10 , 1 10 和 2 2 10 4 时 , 则引入 k 湍流模型进行计算. 下面 给出不同雷诺数下的计算结果 . 图 2 给出了计算得到的涡线图 . 在 4 个不同 的雷诺数下, 都会在柱体的尾部出现规则的旋涡 脱落 , 尾涡交替的甩在方柱上下两侧的壁面上 , 这 就是著名的卡门涡街 . 同时我们可以发现, 方柱后 尾涡的形态会随雷诺 数的变化而产 生一定的变 化. 当雷诺数较低时 ( Re = 100) , 尾涡会拖得比较
[ 6]
图1
计算模型
各边界条件分别为: 入口 : 给定无量纲速度, u = 1, v = 0 . 出口 : 给定无量纲压力 p = 0 , 速度采用 u / x = 0, v / x = 0 . 固壁 : 采用无滑移边界条件, 即 u = 0, v = 0 . 上下边界 : u = 1, v = 0. 不可压缩牛顿流体运动的控制方程 N S 方 程可表示为: ui = 0 xi u i + uj t 式( 2 ) 中 ui = - 1 xj p + xi ui xj xj
[ 4]
得到了绕流的速度场以及柱体上的受力参数. 总 结了方柱后的涡脱落形式和流场的动力学参数随 雷诺数的变化规律 , 并将计算结果与前人的实验 和计算结果进行了对比.
不同雷诺数下倾斜圆柱绕流三维数值模拟研究
８７
向流影响ꎬ其尾流形态特征、受力特性及旋涡脱落频率与竖直圆柱相比存在明显差异ꎮ 近年来ꎬ针对倾斜圆
柱绕流的研究受到海洋工程界和学术界的广泛关注ꎮ
第 ３８ 卷第 １ 期
２０２０ 年 １ 月
ቤተ መጻሕፍቲ ባይዱ
海
洋
工
程
ＴＨＥ ＯＣＥＡＮ ＥＮＧＩＮＥＥＲＩＮＧ
Ｖｏｌ. ３８ Ｎｏ. １
Ｊａｎ. ２０２０
文章编号:１００５￣９８６５(２０２０)０１￣００８６￣１５
不同雷诺数下倾斜圆柱绕流三维数值模拟研究
高洋洋１ ꎬ张演明１ ꎬ刘 彩１ ꎬ王 滨２
(１. 浙江大学 海洋学院ꎬ浙江 舟山 ３１６０２１ꎻ ２. 中国电建集团华东勘测设计研究院有限公司ꎬ浙江 杭州
在海洋工程中ꎬ钢悬链线立管因其结构简单、经济可靠及对上部平台运动更好的适应性越来越多的被应
用于深水油气资源开发中ꎮ 钢悬链线立管近触底区由于倾斜角度变化大ꎬ在流体绕流倾斜立管的过程中ꎬ尾
涡相互干扰机制更加复杂ꎬ更易导致立管发生疲劳破坏ꎮ 然而目前基于竖直圆柱的尾涡特性研究因忽略轴
收稿日期:２０１９￣０５￣０６
ｃｙｌｉｎｄｅｒ ａｔ ｄｉｆｆｅｒｅｎｔ Ｒｅｙｎｏｌｄｓ ｎｕｍｂｅｒｓ
ＧＡＯ Ｙａｎｇｙａｎｇ １ ꎬ ＺＨＡＮＧ Ｙａｎｍｉｎｇ １ ꎬ ＬＩＵ Ｃａｉ １ ꎬ ＷＡＮＧ Ｂｉｎ ２
(１. Ｏｃｅａｎ Ｃｏｌｌｅｇｅꎬ Ｚｈｅｊｉａｎｇ Ｕｎｉｖｅｒｓｉｔｙꎬ Ｚｈｏｕｓｈａｎ ３１６０２１ꎬ Ｃｈｉｎａꎻ ２. Ｐｏｗｅｒ Ｃｈｉｎａ Ｈｕａｄｏｎｇ Ｅｎｇｉｎｅｅｒｉｎｇ Ｃｏｒｐｏｒａｔｉｏｎ Ｌｉｍｉｔｅｄꎬ
Ｒｅｙｎｏｌｄｓ ｎｕｍｂｅｒｓ ( Ｒｅ ＝ １００ꎬ １ ５００ ａｎｄ ３ ９００) ａｎｄ ｉｎｃｌｉｎｅｄ ａｎｇｌｅｓ ( ￣６０° ≤ α ≤ ６０°) ｂａｓｅｄ ｏｎ ｔｈｅ ｃｏｍｐｕｔａｔｉｏｎａｌ ｆｌｕｉｄ ｄｙｎａｍｉｃｓ
FLUENT仿真计算不同雷诺数下的圆柱绕流
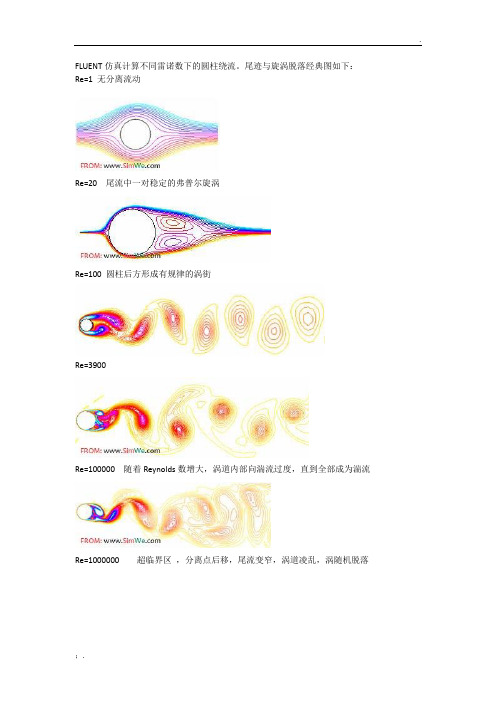
FLUENT仿真计算不同雷诺数下的圆柱绕流。
尾迹与旋涡脱落经典图如下：Re=1 无分离流动Re=20 尾流中一对稳定的弗普尔旋涡Re=100 圆柱后方形成有规律的涡街Re=3900Re=100000 随着Reynolds数增大，涡道内部向湍流过度，直到全部成为湍流Re=1000000 超临界区，分离点后移，尾流变窄，涡道凌乱，涡随机脱落Re=10000000 极超临界区，分离点继续后移，尾流变窄，湍流涡道重新建立。
图3 Cd随Re的变化曲线图3中实曲线是由Wieselsberger,A.Roshko以及G.W.Jones和J.J.Walker测量数据绘制得到，图中圆点部分是FLUENT计算值在Re=106（超临界区），从经典数据和我们的计算结果都可以看到，圆柱体的平均阻力系数急剧下降。
这是因为在Re=3×105附近，边界层流动由层流状态转变为湍流状态，虽然湍流边界层流动的摩擦阻力较层流边界层大，但它从物面的分离较晚，所以形成较小的尾流区。
由于钝体绕流的阻力主要是压差阻力，所以此时物体的总阻力有了一个明显的下降。
入口VELOCITY_INLET,出口OUTFLOW，上下WALL.Re=1,20,100,二维层流模型。
Re=3900后，三维大涡模型计算不准与网格划分与一些参数设置有关。
1。
圆柱中心离上下边界（wall)的距离大于10D(D为圆柱直径），影响较小。
2。
湍流模型采用大涡模型（LES)。
是目前最复杂，最完善的一种湍流模型。
试验曲线来自，《Boundary-Layer Theory》, Dr.HERMANN SCHLICHTING, Translated by Dr.J.KESTIN,Seventh Edition，用MATLB绘制4.阻力系数的求法请参考此论坛我发的教程FLUENT三分立系数的求法。
不同雷诺数下圆柱绕流多重分形研究
不同雷诺数下圆柱绕流多重分形研究圆柱绕流是一种常见的流体力学问题，其中水流绕过一个圆柱体时会产生涡流。
雷诺数是衡量流体动态特征的重要参数，它可以用来表示流体的粘性、压力和流速之间的相对关系。
在不同雷诺数下，圆柱绕流的形态可能会有所不同。
在低雷诺数（Re < 40）的情况下，流体的粘性较大，因此圆柱绕流的形态会呈现出较为平滑的涡旋结构。
随着雷诺数的增加，流体的粘性会逐渐减小，圆柱绕流的形态也会逐渐变得复杂。
在雷诺数较高的情况下（Re > 40），圆柱绕流的形态会呈现出多重分形的特征，即流体中出现了多个涡旋结构，这种现象被称为“多重涡旋”。
在研究圆柱绕流多重分形的过程中，通常会使用数值模拟的方法来研究圆柱绕流的动态特征。
常用的数值模拟方法包括有限差分法、有限元法和有限体积法等。
这些方法可以用来求解流体动力学方程，从而研究不同雷诺数下圆柱绕流的形态变化。
在研究圆柱绕流多重分形的过程中，还可以使用实验方法来研究圆柱绕流的形态变化。
例如，可以使用流动可视化的方法来观察圆柱绕流的形态，或者使用绕流量测量仪器来测量绕流的强度。
除了使用数值模拟和实验方法研究圆柱绕流的多重分形之外，还可以使用理论分析的方法来研究这一现象。
例如，
可以使用流体力学的理论模型来分析圆柱绕流的形态变化，或者使用分形理论来研究圆柱绕流的多重分形现象。
总的来说，圆柱绕流多重分形是一个比较复杂的研究课题，需要综合运用数值模拟、实验和理论分析的方法才能全面地研究这一现象。
圆柱绕流的数值模拟解析
圆柱绕流的数值模拟张玉静 20070360204 过控（2）班化工与能源学院摘要:使用计算流体力学软件FLUENT,模拟均匀来流绕固定圆柱的流动,模拟雷诺数为5，20,40,100时的绕流流动,得到流场的流函数等值线图和速度矢量图。
计算结果表明:当雷诺数增加时,流动表现出一系列不同的构造。
当Re=5时，流动不发生分离,其后未形成旋涡，当Re=20,40,100时，流体发生分离，其后形成旋涡，且旋涡随着Re的增大而增大。
利用计算流体力学软件FLUENT可以成功地模拟圆柱绕流问题,反映出流动特性。
关键词:圆柱绕流；FLUENT；雷诺数Abstract:Uniform flow around a mounting cylinder is simulated with the application of FLUENT software while Reynolds number is 5,20,40,100. Stream function and velocity vector distributions are indicated. The results show that a series of construction appears as Reynolds number increases. When Re is 5, Flow separation does not occur, and it does not form vortex . When Re is 20,40,100, Flow separation occurs, and it forms vortex. V ortex increases with the increase of Re. Using computational fluid dynamics software FLUENT can successfully simulate flow around cylindrical, reflect the flow characteristic.Key words：Flow around a circular cylinder；FLUENT；Reynolds number1 圆柱绕流理论分析研究的状况一个世纪以来,圆柱绕流一直是众多理论分析、实验研究及数值模拟对象。
亚临界雷诺数下圆柱和方柱绕流数值模拟
亚临界雷诺数下圆柱和方柱绕流数值模拟最近，随着大规模流体动力学（LFD）和其他非结构性的方法的发展，数值模拟的重要性和应用也变得越来越广泛。
在绕流过程中，绕流模拟对于准确预测流体动力学行为至关重要。
近年来，圆柱和方柱绕流一直是重要的研究热点，其真实性受到广泛关注。
圆柱和方柱绕流数值模拟，是以相对低的雷诺数Re以及它们相对的相变过程的重要工具。
Re意味着流体动力学的影响，基于Re的亚临界状态共存精确研究流体动力学。
鉴于影响数值模拟精度的数值误差的存在，理论精度和实际应用的完整性和有效性是一个重要的问题。
亚临界状态下的圆柱和方柱绕流模拟，使用分布式交错网格（DMGs），以及完全控制差分过程（FDC），已被广泛应用于当前的数值模拟研究。
在这个过程中，FDC和DMG网格可以用来准确预测流体运动，这些预测可以用来更准确地预测流体动力学参数。
在这项研究中，我们提出了一种圆柱和方柱绕流模拟方法，以及用于仿真过程的FDC/DMG技术。
我们的方法基于亚临界雷诺数（Re），以及针对Re的相变过程。
通过引入非定常非均匀网格（CNG）来改进算法的准确性和实用性。
将计算结果与实验数据进行了比较和分析，以验证该模拟方法的有效性。
本研究的主要结论如下：（1）使用亚临界雷诺数可以准确预测圆柱和方柱绕流的流体动力学参数；（2）带有CNG的FDC/DMG可以更加准确地预测绕流过程中的数值模拟；（3）使用FDC/DMG可以更准确的描述实际流体动力学参数；（4）本研究的方法可以更加准确地预测不同Re下的流体动力学行为。
总的来说，本研究为亚临界雷诺数下圆柱和方柱绕流的模拟提供了一个可行的解决方案，它可以准确预测不同Re下的流体动力学行为。
本研究还提出了一种改进的算法，可以用来更加准确地模拟绕流，提高模拟的真实性和有效性。
通过本研究，我们有望更好地理解数值仿真，并将其用于实际的工程和科学应用中，为后续的更深入的研究提供更多的可能性。
经过本次研究，我们可以得出一个结论：亚临界雷诺数下的圆柱和方柱绕流数值模拟，使用FDC/DMG技术，可以更加准确地预测绕流的流体动力学参数，提高真实性和有效性。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
不同雷诺数下的圆柱绕流数值模拟研究
引言：
圆柱绕流是流体力学领域中一个经典的、被广泛研究的问题。
在众多
的工业应用中，圆柱绕流的研究对于风力发电机组的设计优化、管道内部
液体运动的控制等方面具有重要实际意义。
雷诺数是描述流体流动的一个
无量纲参数，它与流体的流速、流体的粘性有关。
本文将对不同雷诺数下
的圆柱绕流进行数值模拟研究。
方法：
数值模拟是一种有效的研究流体力学问题的方法，它能够通过计算机
模拟得到流体的速度场、压力场等关键参数，从而进一步分析流体的特性。
在本文中，我们将使用计算流体力学方法进行圆柱绕流的数值模拟研究。
结果与讨论：
我们选取了不同雷诺数的圆柱绕流作为研究对象，分别为200、400、600、800和1000，通过数值模拟得到了不同雷诺数下的圆柱绕流的速度
场和压力场等关键参数。
首先，我们分析了速度场的分布。
通过数值模拟可以得到圆柱绕流过
程中流体速度的分布情况。
随着雷诺数的增加，流体速度场呈现出不同的
特征。
在雷诺数较低的情况下，流体绕圆柱流动的速度场分布较为简单，
流速主要集中在圆柱前部和尾部。
随着雷诺数的增加，流体速度场呈现出
更复杂的结构，流速分布更加均匀。
其次，我们研究了压力场的分布。
通过数值模拟可以得到圆柱绕流过
程中流体压力的分布情况。
在不同雷诺数下，圆柱周围存在不同的压力区
域。
当雷诺数较低时，圆柱前后表面存在较大的压差，压力分布较为不均匀。
而当雷诺数增加时，压力分布更加均匀，圆柱表面的压力变化较小。
最后，我们研究了绕流过程中的阻力情况。
通过数值模拟得到了不同
雷诺数下圆柱绕流过程中的阻力系数。
我们发现，随着雷诺数的增加，阻
力系数逐渐增大。
这是因为当雷诺数较低时，流体绕圆柱流动的速度较低，阻力较小；而当雷诺数增加时，流体流动速度较高，阻力也逐渐增大。
结论：
本文通过数值模拟的方式研究了不同雷诺数下的圆柱绕流问题。
通过
分析速度场、压力场和阻力系数等关键参数，我们得出了以下结论：随着
雷诺数的增加，流体速度场更加复杂，流速分布更加均匀；压力场分布更
加均匀，圆柱表面的压力变化较小；阻力系数随着雷诺数的增大而增加。
在工程应用方面，本研究对于风力发电机组的设计优化、管道内部液
体运动的控制等方面具有重要意义。
通过探究圆柱绕流问题的特性，可以
为工程设计提供理论依据和实验参考。
2. Anderson J D. 计算流体力学基础[J]. 宇航出版社, 2000.。