江苏省扬州市邗江区美琪学校九年级数学上册《5.1 圆(二)》》学案(无答案) 苏科版
九年级数学上册 5.1 圆教案(2) 苏科版

课题:书法---写字基本知识课型:新授课教学目标:1、初步掌握书写的姿势,了解钢笔书写的特点。
2、了解我国书法发展的历史。
3、掌握基本笔画的书写特点。
重点:基本笔画的书写。
难点:运笔的技法。
教学过程:一、了解书法的发展史及字体的分类:1、介绍我国书法的发展的历史。
2、介绍基本书体:颜、柳、赵、欧体,分类出示范本,边欣赏边讲解。
二、讲解书写的基本知识和要求:1、书写姿势:做到“三个一”:一拳、一尺、一寸(师及时指正)2、了解钢笔的性能:笔头富有弹性;选择出水顺畅的钢笔;及时地清洗钢笔;选择易溶解的钢笔墨水,一般要固定使用,不能参合使用。
换用墨水时,要清洗干净;不能将钢笔摔到地上,以免笔头折断。
三、基本笔画书写1、基本笔画包括:横、撇、竖、捺、点等。
2、教师边书写边讲解。
3、学生练习,教师指导。
(姿势正确)4、运笔的技法:起笔按,后稍提笔,在运笔的过程中要求做到平稳、流畅,末尾处回锋收笔或轻轻提笔,一个笔画的书写要求一气呵成。
在运笔中靠指力的轻重达到笔画粗细变化的效果,以求字的美观、大气。
5、学生练习,教师指导。
(发现问题及时指正)四、作业:完成一张基本笔画的练习。
板书设计:写字基本知识、一拳、一尺、一寸我的思考:通过导入让学生了解我国悠久的历史文化,激发学生学习兴趣。
这是书写的起步,让学生了解书写工具及保养的基本常识。
基本笔画书写是整个字书写的基础,必须认真书写。
课后反思:学生书写的姿势还有待进一步提高,要加强训练,基本笔画也要加强训练。
课题:书写练习1课型:新授课教学目标:1、教会学生正确书写“杏花春雨江南”6个字。
2、使学生理解“杏花春雨江南”的意思,并用钢笔写出符合要求的的字。
重点:正确书写6个字。
难点:注意字的结构和笔画的书写。
教学过程:一、小结课堂内容,评价上次作业。
二、讲解新课:1、检查学生书写姿势和执笔动作(要求做到“三个一”)。
2、书写方法是:写一个字看一眼黑板。
(老师读,学生读,加深理解。
苏教版数学九年级上册教学设计《2-1圆(2)》

苏教版数学九年级上册教学设计《2-1圆(2)》一. 教材分析苏教版数学九年级上册《2-1圆(2)》这一节内容,是在学生已经掌握了圆的基本概念、圆的周长和面积的基础上,进一步探讨与圆有关的一些性质和定理。
本节课的内容主要包括圆的直径、半径、弧、弦等概念,以及它们之间的关系。
教材通过丰富的实例和图示,引导学生探究和发现圆的性质,培养学生的观察能力、推理能力和解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的数学基础,对圆的基本概念和性质有一定的了解。
但是,对于圆的直径、半径、弧、弦等概念和它们之间的关系,可能还不是很清晰。
因此,在教学过程中,需要通过具体的实例和图示,帮助学生理解和掌握这些概念和性质。
同时,学生已经具备了一定的观察能力和推理能力,可以引导学生通过观察、实验、推理等方式,发现和证明圆的性质。
三. 教学目标1.知识与技能目标:让学生理解和掌握圆的直径、半径、弧、弦等概念,以及它们之间的关系。
2.过程与方法目标:通过观察、实验、推理等方式,培养学生发现和解决问题的能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的观察能力、推理能力和解决问题的能力。
四. 教学重难点1.重点:圆的直径、半径、弧、弦等概念,以及它们之间的关系。
2.难点:圆的性质的证明和应用。
五. 教学方法1.引导发现法:通过具体的实例和图示,引导学生观察、实验、推理,发现和证明圆的性质。
2.合作交流法:分组讨论,引导学生相互交流、合作,共同解决问题。
3.练习法:通过适量的练习,巩固所学知识,提高解决问题的能力。
六. 教学准备1.教学课件:制作课件,包括实例、图示、练习等,以便于教学过程中的展示和操作。
2.学习材料:准备相关的学习材料,如圆的模型、直尺、圆规等,以便于学生观察和操作。
3.练习题:准备适量的练习题,以便于课堂练习和巩固所学知识。
七. 教学过程1.导入(5分钟)通过复习圆的基本概念、圆的周长和面积,引出本节课的内容:圆的直径、半径、弧、弦等概念。
九年级数学上册《5.1 圆》教案 苏科版

《5.1 圆》教案一.情境创设多媒体展示圆在生活中各领域的应用。
提出问题:体育老师上铅球课,需要在操场上画一个半径为2米的圆。
你能帮他想想办法吗? 二.实验探究1.圆的描述定义:学生尝试解决师引导:从数学的角度,我们可以把固定的一端看成一个点(点O),拉直的绳子看作线段OP,你能从数学的角度来描述这一运动过程吗?(多媒体演示运动过程)同桌互说----学生反馈------师引导----归纳得出圆的定义给出圆心、半径、及圆的符号语言。
强调:圆是一条封闭的曲线,不包括圆心,不是一个圆面问题(1)画一个以点O为圆心的圆,这样的圆你能画出几个?(2)画一个半径为2cm的圆,这样的圆你能画出几个?(3)画一个唯一确定的圆,你需要明确哪些要素?强调:圆的两要素:圆心确定位置,半径确定大小。
2.点与直线的位置关系及圆的集合定义:活动1:在你们的帮助下,体育老师已经把圆画好了,这时正好一只足球踢过来,从圆上穿过去。
如果我们把球抽象成一个点(点A),它会和圆(⊙O)产生几种不同的位置关系呢?动手画一画(同桌交流-----实物投影展示)提问:(多媒体演示点的运动过程)这一运动过程中,什么量不变?什么量发生变化?它们之间有什么联系?作一个半径为3cm的⊙O⑴作一点A,使得OA=3cm,则点A在⊙O ,这样的点你能作出几个?它们与⊙O有怎样的位置关系?引导提问:①这无数个点都满足什么数量关系?(到点O的距离等于半径即d=r)它们与圆有怎样的位置关系?(在圆上)因此由数量关系可推位置关系,引出“等价于”②画出这无数个点,构成什么图形?(圆)多媒体演示③我们把无数个满足同一条件的点称为点的集合。
因此,我们可以把⊙O看作满足什么条件的所有点的集合?④若一个半径为5cm的⊙P,从集合的角度可以怎样描述这个圆。
⑤由此,你能从集合的角度对圆进行描述吗?我们可以把圆看作满足什么条件的点的集合?-- 引出圆的集合定义.⑵作一点A,使OA<3cm, 则点A在⊙O , 这样的点你能作出几个?它们与⊙O有怎么的位置关系?⑶作一点A,使OA<3cm, 则点A在⊙O , 这样的点你能作出几个?它们与⊙O 有怎么的位置关系?(引出“等价于”,同时从集合的角度定义点在圆内,点在圆上,点在圆外)巩固练习:1、已知⊙O 的半径为5(1)若PO=5.5,则点P 在 ;(2)若PO=4,则点P 在 ;(3)若PO = ,则点P 在圆上。
江苏省扬州市邗江区美琪学校九年级数学上册《4.3 用一元二次方程解决问题》》学案2(无答案) 苏科版

《4.3 用一元二次方程解决问题》学习目标: 1、进一步体会通过建立方程解决实际问题的意义和方法2、进一步体会运用方程解决问题的关键是寻找等量关系,提高分析问题、解决问题的能力学习重点:学会用列方程的方法解决有关形积问题.学习难点:如何找出形积问题中的等量关系一、自学展示:1、一块正方形铁皮的四个角各剪去一个边长为4㎝的小正方形,做成一个无盖的盒子。
已知盒子的容积是400㎝,求原铁皮的边长。
二、合作学习1、小明有一块长方形铁皮,长是宽的2倍,现他在四角各截去一个正方形后,制成了高是5㎝,cm的无盖长方体容器。
你能求这块铁皮的长和宽吗?容积是5003分析:一般情况下,应设要求的未知量为未知数;应从题中寻找未知数所表示的未知量与已知量之间的等量关系;这个问题的等量关系是“长×宽×高=容积”与“长=宽×2”。
2、某商店6月份的利润是2500元,要使8月份的利润达到3600元,这两个月利润的月平均增长的百分率是多少?分析:如果设这两个月的利润平均月增长的百分率是x,那么7月份的利润是______________元,8月份的利润是__________________元。
根据题意列方程:3、某服装店花2000元进了批服装,按50%的利润定价,无人购买。
决定打折出售,但仍无人购买,结果又一次打折后才售完。
经结算,这批服装共盈利430元。
如果两次打折相同,每次打了几折?三.课堂整理用方程解决实际问题首先要找出相等关系,然后通过将已知数或含未知数的代数式代入,从而得到方程。
1、形体类问题要注意其中变化的量及不变的量.2、利润问题基本量之间的关系.四、当堂练习1.一块长方形菜地的面积是150m2,如果它的长减少5m,那么菜地就变成正方形.求原菜地的长和宽2、某蔬菜交易市场2月份的蔬菜交易量是5000t ,4月份达到7200t ,平均每月增长的百分率是多少?3、某种服装原价为每件80元,经两次降价,现售价为每件51.2元,求平均每次降价的百分率.4、在一幅长80cm ,宽50cm 的矩形风景画的四周镶一条金色纸边,制成一幅所图所示的矩形图.如果要使整个挂图的面积是5400cm 2,求金色纸边的宽。
江苏省扬州市邗江区美琪学校九年级数学上册《4.3 用一元二次方程解决问题》》学案1(无答案) 苏科版

《4.3 用一元二次方程解决问题》教案学习目标:1.进一步理解方程是刻画客观世界的有效模型,2.通过对实际问题的决实际问题的过程,知道解应用题的一般步骤和关键所在学习重点:认识不等式学习难点:文字语言转化为数学不等式一、自学展示:1、建造一个池底为正方形、深度为2米的长方体无盖水池,池壁的造价为100元/平方米池底的造价为200元/平方米,总造价为6400元,求正方形池底的长。
2、两个连续奇数的积是323,求这两个数。
3、已知两个数的和等于12,积等于32,则这两个数是多少?二、探究学习:1.尝试:通常用一元一次方程解决实际问题要经历怎样的过程?2.概括总结:用方程解决实际问题的一般步骤为:找相等关系;设未知数,列方程,解方程,检验,答题。
例1、我社组团去龙湾风景区旅游,收费标准为:如果人数不超过30人,人均旅游费用为800元,如果人数多于30人,那么每增加1人,人均旅游费用降低10元,但人均旅游费用不得低于今为500元。
甲公司分批组织员工到龙湾风景区旅游,现计划用28000元组织第一批员工去旅游,问这次旅游可以安排多少人参加?三、归纳总结:1、列一元二次方程解决实际问题的一般步骤.2、解的取舍情况.四、当堂练习1、某电视机厂计划用两年的时间把某种型号的电视机的成本降低36%, 若每年下降的百分数相同,则这个百分数为()A、10%B、20%C、120%D、180%2、若两个连续整数的积是56,则它们的和是 ( )A、±15B、15C、-15D、113、一种药品经过两次降价后,每盒的价格由原来的60元降至48.6元,那么平均每次降价的百分率是。
4、某地区开展“科技下乡”活动三年来,接受科技培训的人员累计达95万人次,其中第一年培训了20万人次。
设每年接受科技培训的人次的平均增长率都为x,根据题意列出的方程是___________。
5、西瓜经营户以2元/kg的价格购进一批小型西瓜,以3元/kg的价格出售,每天可售出200kg,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0、1元/kg,每天可多售出40kg,另外,每天的房租等固定成本共24元,该经营户要想每天盈利润200元,应将每千克小型西瓜的售价降低多少元?7、常州春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:这次共有多少员工去天水湾风景区旅游?。
苏科版数学九年级上册2.1 圆(第2课时)教学设计

苏科版数学九年级上册2.1 圆(第2课时)教学设计一. 教材分析苏科版数学九年级上册2.1 圆(第2课时)的教学内容主要包括圆的周长和圆的面积。
这部分内容是学生在学习了直线、射线、线段的基础上,进一步研究圆的性质,对于学生来说,这部分内容较为抽象,需要通过实例和操作活动,让学生理解和掌握圆的周长和面积的计算方法。
二. 学情分析九年级的学生已经具备了一定的几何知识,对图形有了一定的认识,但圆的知识比较抽象,需要通过实际操作来理解和掌握。
同时,学生的学习习惯和思维方式各有不同,需要教师在教学过程中注意引导和激发学生的学习兴趣。
三. 教学目标1.知识与技能:理解圆的周长和面积的计算方法,能够运用圆的周长和面积公式解决实际问题。
2.过程与方法:通过实际操作,培养学生的观察能力、思考能力和动手能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队协作能力和自主学习能力。
四. 教学重难点1.圆的周长的计算方法。
2.圆的面积的计算方法。
五. 教学方法1.采用问题驱动法,引导学生思考和探索圆的周长和面积的计算方法。
2.采用合作学习法,让学生在小组内讨论和分享学习心得,培养学生的团队协作能力。
3.采用实践操作法,让学生动手操作,加深对圆的周长和面积的理解。
六. 教学准备1.准备相关的教学材料,如教材、课件、圆的模型等。
2.准备课堂活动所需的器材,如圆规、直尺、剪刀、胶水等。
七. 教学过程1.导入(5分钟)教师通过展示生活中的圆形物体,如硬币、轮子等,引导学生观察和思考圆的性质,激发学生的学习兴趣。
2.呈现(10分钟)教师通过课件或板书,呈现圆的周长和面积的计算公式,让学生初步了解圆的周长和面积的计算方法。
3.操练(10分钟)教师分发相关的练习题,让学生独立完成,巩固对圆的周长和面积的理解。
4.巩固(10分钟)教师学生进行小组讨论,让学生分享自己的学习心得,互相提问和解答疑问,进一步巩固对圆的周长和面积的计算方法。
江苏省扬州市邗江区美琪学校九年级数学上册《第5章 复习课》学案(无答案) 苏科版

《第5章复习课》学案(无答案)学习目标:1.理解、掌握圆的有关性质、直线和圆的位置关系、圆和圆的位置关系、正多边形和圆的关系.2.探索、总结、归纳与圆有关的各种问题,进行知识梳理,构建圆的知识体系.3.渗透数形结合和分类的数学思想,并逐步学会用数学的眼光认识世界、解决问题,学会有条理的表达、推理.学习重点:与圆有关的知识的梳理.学习难点:会用圆的有关知识解决问题.教学过程点点点点二、过三点的圆及外接圆1.过一点的圆有________个.2.过两点的圆有_________个,这些圆的圆心的都在_______________上.3.过三点的圆有______________个.4.如何作过不在同一直线上的三点的圆(或三角形的外接圆、找外心、破镜重圆、到三个村庄距离相等).5.锐角三角形的外心在三角形____,直角三角形的外心在三角形____,钝角三角形的外心在三角形____.三、垂径定理(涉及半径、弦、弦心距、平行弦等)1.如图,已知AB、CD是⊙O的两条平行弦,⊙O的半径是5cm, AB=8cm,CD=6cm.求AB、CD的距离.2.如图4,⊙M与x轴相交于点A(2,0),B(8,0),与y轴相切于点C ,则圆心M 的坐标是 。
四、圆心角、弦、弧、弦心距、圆周角1.如图,⊙O 为△ABC 的外接圆, AB 为直径,AC=BC , 则∠A 的 度数为( )A.30° B.40° C.45° D.60°2. 在⊙O 中,弦AB 所对的圆心角∠AOB=100°,则弦AB 所对的圆周角为______.五、直线和圆的位置关系直圆 相相离相相六、切线的判定与性质切线的判定一般有三种方法:1.定义法:和圆有唯一的一个公共点2.距离法: d=r3.判定定理:过半径的外端且垂直于半径七、三角形的内切圆1. Rt △ ABC 三边的长为a 、b 、c ,则内切圆的半径是r=______________2.外心到___________________的距离相等,是________________________的交点; 内心到______________________的距离相等,是_______________________的交点;八、圆与圆的位置关系九、弧长及扇形的面积:1、弧长公式 ;2、扇形面积公式 . 十、圆锥的侧面积和全面积: 圆锥侧面积计算公式 .课堂练习: 1. 判断题(1) 直径是弦.( )(2) 半圆是弧,但弧不一定是半圆. ( )(3) 到点O 的距离等于2cm 的点的集合是以O 为圆心,2cm 为半径的圆. ( ) (4) 过三点可以做且只可以做一个圆. ( )(5) 三角形的外心到三角形三边的距离相等. ( )(6) 经过弦的中点的直径垂直于弦,且平分弦所对的两条弧. ( ) (7) 经过圆O 内一点的所有弦中,以与OP 垂直的弦最短. ( ) (8)在半径是4的圆中,垂直平分半径的弦长是32.( ) 2. 已知OC 是半径,AB 是弦,AB ⊥OC 于E,CE=1,AB=10,则OC=______. 3. AB 是弦,OA=20cm,∠AOB=120°,则S △AOB=______.4. 在⊙O 中,弦AB,CD 互相垂直于E,AE=2,EB=6,ED=3,EC=4,则⊙O 的直径是______.5. 在⊙O 中弦AB,CD 互相平行,AB=24cm,CD=10cm,且AB 与CD 之间的距离是17cm,则⊙O 的半径是______cm.6. 圆的半径是6cm,弦AB=6cm,则劣弧AB 的中点到弦AB 的中点的距离是______cm.7. 在⊙O 中,半径长为5cm,AB ∥CD,AB=6,CD=8,则AB,CD 之间的距离是______cm.8. 圆内接四边形ABCD 中,∠A:∠B:∠C=2:3:6,则四边形的最大角是______度.9.在直径为12cm 的圆中,两条直径AB,CD 互相垂直,弦CE 交AB 于F,若CF=8cm,则AF 的长是______cm.10.两圆半径长是方程035122=+-x x 的两根,圆心距是2,则两圆的位置关系是______. 11.正三角形的边长是6㎝,则内切圆与外接圆组成的环形面积是______C ㎡. 12.已知扇形的圆心角是120°,扇形弧长是20π,则扇形=______. 13.已知正六边形的半径是6,则该正六边形的面积是______.14.若圆的半径是2cm,一条弦长是32,则圆心到该弦的距离是______. 15.在⊙O 中,弦AB 为24,圆心到弦的距离为5,则⊙O 的半径是______cm.16.若AB 是⊙O 的直径,弦CD ⊥AB 于E,AE=9cm,BE=16cm,则CD=______cm.17.若⊙O 的半径是13cm,弦AB=24cm,弦CD=10cm,AB ∥CD,则弦AB 与CD 之间的距离是______cm. 18.⊙O 的半径是6,弦AB 的长是6,则弧AB 的中点到AB 的中点的距离是______19.已知⊙O 中,AB 是弦,CD 是直径,且CD ⊥AB 于M.⊙O 的半径是15cm,OM:OC=3:5,则AB=______. 20.已知O 到直线l 的距离O D 是72cm,l 上一点P,PD=26cm.⊙O 的直径是20,则P 在⊙O______.21.已知AB 是⊙O 的直径,AC 是弦,直线CE 切⊙O 于C ,AD ⊥CE,垂足是D,求证:AC 平分∠BAD.22.已知AB 是⊙O 的直径,P 是⊙O 外一点,PC ⊥AB 于C,交⊙O 于D,PA 交⊙O 于E ,PC 交⊙O 于D ,交BE 于F 。
江苏省扬州市邗江区美琪学校九年级数学上册《一元二次方程的解法(第3课时)》学案(无答案)苏科版

B. 2x
2-4x+4=-3+4
C.x 2-2x+1= 3 +1
D. x
2
2-2x+1=-
3
+1
2
5、用配方法解下列方程,配方错误的是(
)
A.x 2+2x-99=0 化为 (x+1) 2=100
B.t 2-7t-4=0 化为 (t- 7 ) 2= 65 24
2
2
C.x +8x+9=0 化为 (x+4) =25
2
2 2 10
D.3x -4x-2=0 化为 (x- ) =
39
6、用配方法解下列方程:
(1)2x 2+1=3x;
(2)3y
2-y-2=0 ;
7、试用配方法证明:
2x2-x+3 的值不小于
23
.
8
8 、已知 (a+b) 2=17, ab=3. 求 (a-b) 2 的值 .
2
难点:把一元二次方程转化为的 ( x+ m)2= n( n≥ 0) 形式
一、自学展示
1、用配方法解下列方程: (1)x 2-6x-16=0 ;
(2)x
2+3x-2=0 ;
2、请你思考方程 x2 - 5 x +1=0 与方程 2x2-5x+2=0 有什么关系? 2
二、探索学习 问题 1、如何解方程 2x2-5x+2=0 ?
《一元二次方程的解法 ( 第 3 课时 ) 》学案(无答案)
知识目标 1、 会用配方法二次项系数不为
1 的一元二次方程
2、 探究将一般 一元二次方程化成( x m)2 n (n 0) 形式的过程,理解
江苏省扬州市邗江区美琪学校九年级数学上册《一元二次方程的解法(第1课时)》学案(无答案)苏科版

1 《第4章元二次方程的解法(1)》学案学习目标
1、了解形如()0()2n n m x 的一元二次方程的解法
2、会用直接开平方法解形如()2=非负数形式的一元二次方程
3、在直接开平方法解一元二次方程的过程中,体会转化的思想。
重点:会用直接开平方法解一元二次方程难点:
理解直接开平方法与平方根的定义的关系
一、预习展示
1、如果a x
2那么x 叫做a 的______,记作________; 2、如果42x ,那么记作________;
3、3的平方根是
;0的平方根是;-4的平方根。
4、把下列方程化为一般形式,并说出各项及其系数。
(1)245
x x (2)235
x (3)2
2122y y y y 二、探索学习
例一、如何解方程042x 呢?又是如何解方程:022x ?(使学生注意直接开平方法的实质和操作过程)
形如方程02k x
)0(k 可变形为)0(2k k x 的形式,用直接开平方法求解。
例2、如何解方程2)1(2x 及方程(x -1)2
-4 = 0。
江苏省扬州市邗江区美琪学校九年级数学上册《一元二次方程的解法(第5课时)》学案(无答案)苏科版

《一元二次方程的解法(第5课时)》学案
学习目标:
1、用公式法解一元二次方程的过程中,进一步理解代数式b2-4ac对根的情况的判断作用
2、能用b2-4ac的值判别一元二次方程根的情况
3、在理解根的判别式的过程中,体会严密的思维过程
重点:一元二次方程根与系数的关系
难点:由一元二次方程的根的情况求方程中字母系数的取值
一、自学展示
1、一元二次方程ax2+bx+c = 0(a≠0)当240
b ac时,X1,2 =
2、解下例方程:
(1)x2 -4x+4=0 (2)2x2 -3x -4=0 (3) x2+3x+5=0
二、探索学习
1、引导学生思考:不解方程,你能判断下列方程根的情况吗?
⑴x2+2x-8 = 0 ⑵x2 = 4x-4 ⑶x2-3x = -3
2、一元二次方程根的情况与一元二次方程中二次项系数、一次项系数及常数项有关吗?
能否根据这个关系不解方程得出方程的解的情况呢?
⑴x2+x-1 = 0 ⑵x2-23x+3 = 0 ⑶ 2x2-2x+1 = 0
分析:本题三个方程的解法都是用公式法来解,由公式法解一元二次方程的过程中先
求出b2-4ac的值可以发现它的符号决定着方程的解。
3、你能得出什么结论?
由此可以发现一元二次方程ax2+bx+c = 0(a≠0)的根的情况可由b2-4ac来判定:当b2-4ac>0时,方程有
当b2-4ac = 0时,方程有
当b2-4ac <0时,方程
我们把b2-4ac叫做一元二次方程ax2+bx+c = 0(a≠0)的根的判别式。
4、若已知一个一元二次方程的根的情况,是否能得到的值的符号呢?
当一元二次方程有两个不相等的实数根时,b2-4ac
1。
江苏省扬州市邗江区美琪学校九年级数学上册《5.9 圆锥

《5.9 圆锥的侧面积和全面积》学案学习目标:1.了解圆锥的侧面积计算公式,并会应用公式解决问题.2.经历探索圆锥侧面积计算公式的过程,发展学生的实践探索能力.学习重点:1. 经历探索圆锥侧面积计算公式的过程. 2.了解圆锥的侧面积计算公式,并会应用公式解决问题.学习难点:经历探索圆锥侧面积计算公式. 教学过程 一、自学展示:复习“圆锥的侧面展开图是一个扇形”。
二、探究学习1.圆锥的基本概念:(1)连结圆锥的 S 和 的线段SA 、SA 1……叫做圆锥的母线,(2)连接 S 与 O 的线段叫做圆锥的高。
2.圆锥中的各元素与它的侧面展开图——扇形的各元素之间的关系:将圆锥的侧面沿母线l 剪开,展开成平面图形,可以得到一个扇形,设圆锥的底面半径为r,这个扇形的半径等于什么?扇形弧长等于什么?3.圆锥侧面积计算公式:圆锥的母线即为扇形的半径,而圆锥底面的周长是扇形的弧长,这样, S 圆锥侧=S 扇形=21·2πr · l = πrl 4.圆锥全面积计算公式S 圆锥全=S 圆锥侧+S 圆锥底面= πr l +πr 2=πr (l +r )5.典型例题例1:制作如图所示的圆锥形铁皮烟囱帽,其尺寸要求为:底面直径80cm,母线长50cm,求烟囱帽铁皮的面积(精确到1cm²)r h lS 1r l O例2:如图所示的扇形中,半径R=10,圆心角θ=144°用这个扇形围成一个圆锥的侧面.(1)求这个圆锥的底面半径r;(2)求这个圆锥的高(精确到0.1)6.巩固练习1.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.2.如图.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.三、课堂整理1、圆锥的侧面积公式与全面积公式;2、圆锥中的各元素与它的侧面展开图——扇形的各元素之间的关系.四、课堂练习:《补充习题》。
江苏省扬州市邗江区美琪学校九年级数学上册《5.8弧长及扇形的面积》学案(无答案)苏科版

1 《5.8 弧长及扇形的面积》学案学习目标:1.经历探索弧长计算公式及扇形面积计算公式的过程2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题学习重点:弧长与扇形的计算公式的推导与应用. 学习难点:弧长与扇形的计算公式的应用. 教学过程一、自学展示1.复习小学里学习过的圆的周长计算公式、圆面积计算工式。
2.我们知道,弧长是它所对应的圆周长的一部分,那么弧长、怎样计算呢?二、新知探究1.探索弧长计算公式因为360°的圆心角所对弧长就是圆周长C=2πR ,所以1°的圆心角所对的弧长是3602R,即180R。
这样,在半径为R 的圆中,n °的圆心角所对的弧长l 的计算公式为:l =180Rn 注:引导学生用“方程的观点”去认识弧长计算公式,它揭示了l 、n 、R 这3个量之间的一种相等关系。
如果这三个量中,任意知道两个量,就可以根据公式求出第三个量。
2.探索扇形面积计算公式(1)类比弧长的计算公式可知:圆心角为n °的扇形面积与整个圆面积的比和n °与360°的比一致,因此,扇形的面积应等于圆的面积乘以扇形的圆心角占360的几分之几,即圆心角是360°的扇形面积就是圆面积S=πR 2,所以圆心角是1°的扇形面积是。
3602R 这样,在半径为R 的圆中,圆心角为的扇形面积的计算公式为:S=360nπR 2注:类似于弧长的计算公式,扇形面积的计算公式也是表示三个量之间的相等关系,在S 、n 、R 中任意知道两个量都可以根据公式求出第三个量的值。
(2)扇形面积的另一个计算公式比较扇形面积计算公式与弧长计算公式,可以发现:可以将扇形面积的计算公式:S=360nπR 2化为S=180Rn ·21R ,从面可得扇形面积的另一计算公式: S=21lR3.典型例题例1.如图,把直角三角形ABC 的斜边AB 放在直线l 上,按顺时针方向在l 上转动两次,。
江苏省扬州市邗江区美琪学校九年级数学上册《5.5 直线与圆的位置关系(第4课时)》学案(无答案) 苏科版

《5.5 直线与圆的位置关系(第4课时)》学案(无答案) 学习目标: 1.了解切线长的概念2.经历探索切线长性质的过程,并运用这个性质解决问题.学习重点:掌握切线长的性质.学习难点:运用切线长的性质解决问题.教学过程一、自学展示1、如图,点A 在⊙O 上,如何过点A 作⊙O 的切线?2、如图,直角三角板的直角顶点A 在⊙O 上,一条直角边 经过圆心O ,`另一条直角边经过⊙O 外一点P , PA 是⊙O 的切线吗?为什么?二、探究学习1.尝试(1)P 为⊙O 外一点,如何用直角三角板经过点P 作⊙O 的切线?这样的切线 能作几条?(2)如图PA 、PB 是⊙O 的两条切线,切点分别是A 、B ,沿直线OP 将图形对折,你发现了哪些等量关系?你能通过证明验证这些关系吗?2.概括定义:在经过_____一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长 性质:从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
3.典型例题例1.如图,已知⊙O 的半径为3cm ,点P 和圆心O 的距离为 6cm ,经过点P 有⊙O 的两条切线PA 、PB ,则切线长为_____cm ,这两条切线的夹角为____,∠AOB =______.•P O A• • O A• B O A P例2.如图1,PA 、PB 是,切点分别是A 、B ,直线EF 也是⊙O 的切线,切点为P ,交PA 、PB 为E 、F 点,已知12PA cm =,70P ∠=︒,(1)求△PEF 的周长;(2)求EOF ∠的度数。
例3.数学课上,数学老师把一个乒乓球放在一个V 形架中,如图是它的平面示意图,CA 、CB 是⊙O 的切线,切点分别是A 、B ,某同学通过测量,量得AB =4cm ,∠ACB =600,如何求出乒乓球的直径?4.练习(1)如图AB 是⊙O 的直径,C 为圆上任意一点,过C 的切线分别与过A 、B 两点的切线交于P 、Q ,求证:PO ⊥OQ(2)如图AB 是⊙O 的直径,C 为圆上任意一点,过C 的切线分别与过A 、B 两点的切线交于P 、Q ,已知AP =1cm ,BQ =9cm ,求⊙O 的半径.三、归纳总结1、理解了切线长的定义、性质;2、熟悉常见的基本图形(例6图形)和常用辅助线(作过切点的半径). 四、课堂练习:《补充习题》。
江苏省扬州市邗江区美琪学校九年级数学上册《5.1 圆(

《5.1 圆(二)》学习目标:1、认识圆的弦、弧、优弧与劣弧、直径及其相关概念.2、认识圆心角、等圆、等弧的概念.3、了解“同圆或等圆的半径相等”并能用之解决问题.学习重点:了解圆的相关概念.学习难点:容易混淆圆的概念的辨析.自学要求:1、复习点与圆的位置关系2、预习圆的相关概念教学过程:一、自学展示:理解与圆有关概念1、请在图上画出弦CD,直径AB.并说明___________________________叫做弦;_________________________________叫做直径.2、弧、半圆、优弧与劣弧的概念及表示方法.弧:____________________________________.半圆:__________________________________________________.优弧:_________________________________,表示方法:________.劣弧:_________________________________,表示方法:________.3、借助图形理解圆心角、同心圆、等圆.圆心角:_____________________________________.同心圆: _____________________________________.等圆: _____________________________________.4、同圆或等圆的半径_______.等弧: ______________________________________________.二、探究学习例. 已知:如图,点A、B和点C、D分别在同心圆上.且∠AOB=∠C OD,∠C与∠D相等吗?为什么?巩固练习1.判断下列结论是否正确。
(1)直径是圆中最大的弦。
( )(2)长度相等的两条弧一定是等弧。
( )(3)半径相等的两个圆是等圆。
( )(4)面积相等的两个圆是等圆。
江苏省扬州市邗江区美琪学校九年级数学上册《5.2 圆的对称性(二)》学案(无答案) 苏科版
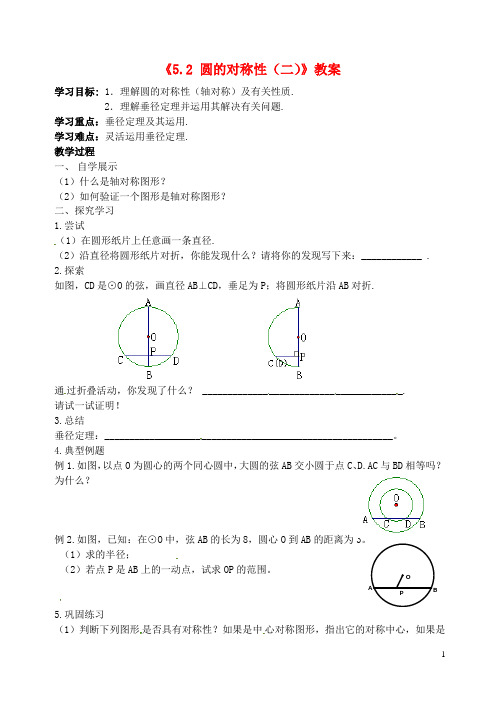
《5.2 圆的对称性(二)》教案学习目标: 1.理解圆的对称性(轴对称)及有关性质.2.理解垂径定理并运用其解决有关问题.学习重点:垂径定理及其运用.学习难点:灵活运用垂径定理.教学过程一、自学展示(1)什么是轴对称图形?(2)如何验证一个图形是轴对称图形?二、探究学习1.尝试(1)在圆形纸片上任意画一条直径.(2)沿直径将圆形纸片对折,你能发现什么?请将你的发现写下来:____________ .2.探索如图,CD是⊙O的弦,画直径AB⊥CD,垂足为P;将圆形纸片沿AB对折.通过折叠活动,你发现了什么? _______________________________________.请试一试证明!3.总结垂径定理:_________________________________________________________。
4.典型例题例1.如图,以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C、D.AC与BD相等吗?为什么?例2.如图,已知:在⊙O中,弦AB的长为8,圆心O到AB的距离为3。
(1)求的半径;(2)若点P是AB上的一动点,试求OP的范围。
5.巩固练习(1)判断下列图形是否具有对称性?如果是中心对称图形,指出它的对称中心,如果是OA BP轴对称图形,指出它的对称轴。
B①②③④⑤AO O O OCDODCA BCBADA BC(2)如图,在⊙O中,弦AB的长为8,圆心O到AB的距离是3.求⊙O的半径.(3)如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.(4)如图,OA=OB,AB交⊙O与点C、D,AC与BD是否相等?为什么?(5)在直径为650mm的圆柱形油罐内装进一些油后,其横截面如图,若油面宽AB=600mm,求油的最大深度.(6)设AB、CD是⊙O的两条弦,AB∥CD,若⊙O的半径为5,AB=8,CD=6,则AB与CD之间的距离为_____________(有两种情况).三、课堂整理1.圆的轴对称性及有关性质.2.理解垂径定理并运用其解决有关问题.四、当堂练习:《补充习题》。
江苏省扬州市邗江区美琪学校九年级数学上册《5.3 圆周

E OD CB AFEODCBAEODCBA《5.3 圆周角(二)》教案学习目标:1.经历探索圆周角的有关性质的过程2.知道圆周角定义,掌握圆周角定理,会用定理进行推证和计算。
3.体会分类、转化等数学思想.学习重点:圆周角的性质及应用.学习难点:圆周角的性质及应用.自学要求:复习学过的与圆有关的角,及它们之间的关系。
教学过程一、自学展示:我们学过哪些与圆有关的角?它们之间有什么关系?二、探究学习1.尝试、交流(1)BC是☉O的直径,它所对的圆周角是锐角、还是钝角、还是直角?为么?(2)圆周角∠BAC=900,弦BC过圆心吗?为什么?2.总结:直径所对的圆周角是角,900的圆周角所对的弦是。
3.典型例题例1.如图AB是⊙O的直径,弦CD与AB相交于点E,∠ACD=60°,∠ADC=50°,求∠CEB的度数.例2.(1)如左图,△ABC的顶点都在⊙O上,AD是△ABC的高,AE是⊙O的直径.△ABE与△ACD相似吗?为什么?变式:如右图,△ABF与△ACB相似吗?ABECDO(2)如图, A 、B 、E 、C 四点都在⊙O 上,AD 是△ABC 的高,∠CAD=∠EAB,AE 是⊙O 的直径吗?为什么?三、课堂整理:1. 探索了圆周角的有关性质2.圆周角定义、圆周角定理,会用定理进行推证和计算。
3.体会分类、转化等数学思想.四、当堂练习1.如图,AB 、CD 是⊙O 的直径,弦CE ∥AB. 弧BD 与弧BE 相等吗?为什么?2.如图,AB 是⊙O 的直径,AC 是⊙O 的弦,以OA 为直径的⊙D 与AC 相交于点E ,AC=10,求AE 的长.3.如图,点A 、B 、C 、D 在圆上,AB=8,BC=6,AC=10,CD=4.求AD 的长.4.如图,AB 是⊙O 的直径,CD ⊥AB ,P 是CD 上的任意一点(不与点C 、D 重合),∠APC 与∠APD 相等吗?为什么?EO D C第1题 C D A B第3题 A CDO E 第2题5.4确定圆的条件学习目标:1.经历不在同一直线上的三点确定一个圆的探索过程2.了解不在同一直线上的三点确定一个圆,了解三角形的外接圆、三角形的外心、圆的外接三角形的概念3.会过不在同一直线上的三点作圆.学习重点:确定圆的条件.学习难点:不在同一直线上的三点确定一个圆的探索过程.自学要求:1、复习确定一个圆需要哪两个要素?2、经过一点可以作多少条直线?经过两点可以作多少条直线?经过三点可以作多少条直线?那么几点可以确定一条直线?类似地,几点可以确定一个圆呢?教学过程一、自学展示:1、确定一个圆需要哪两个要素?2、经过一点可以作多少条直线?经过两点可以作多少条直线?经过三点可以作多少条直线?那么几点可以确定一条直线?二、探究学习1、尝试:分别讨论过一点、两点、三点分别可以作几个圆?(1)经过一点可以作多少个圆?如何确定圆心、半径?(2)经过两点可以作多少个圆?如何确定圆心、半径?(3)经过三点可以作多少个圆?如何确定圆心、半径?2、总结:(1)不在同一直线上的点确定一个圆(2)三角形的外接圆、三角形的外心、圆的外接三角形的概念3、画一画:作锐角三角形ABC的外心4.总结:三角形外心的位置(1)由“3”,锐角三角形ABC的外心在△ABC的部;(2)三角形按角分类,可以分为哪几类?(3)分别画直角三角形、钝角三角形的外心,你有什么发现?5.典型例题例1.已知锐角三角形ABC,用直尺和圆规作三角形ABC的外接圆。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《5.1 圆(二)》
学习目标:1、认识圆的弦、弧、优弧与劣弧、直径及其相关概念.
2、认识圆心角、等圆、等弧的概念.
3、了解“同圆或等圆的半径相等”并能用之解决问题.
学习重点:了解圆的相关概念.
学习难点:容易混淆圆的概念的辨析.
自学要求:1、复习点与圆的位置关系
2、预习圆的相关概念
教学过程:
一、自学展示:理解与圆有关概念
1、请在图上画出弦CD,直径AB.
并说明___________________________叫做弦;
_________________________________叫做直径.
2、弧、半圆、优弧与劣弧的概念及表示方法.
弧:____________________________________.
半圆:__________________________________________________.
优弧:_________________________________,表示方法:________.
劣弧:_________________________________,表示方法:________.
3、借助图形理解圆心角、同心圆、等圆.
圆心角:_____________________________________.
同心圆: _____________________________________.
等圆: _____________________________________.
4、同圆或等圆的半径_______.
等弧: ______________________________________________.
二、探究学习
例. 已知:如图,点A、B和点C、D分别在同心圆上.且∠AOB=∠C OD,∠C与∠D相等吗?
为什么?
巩固练习
1.判断下列结论是否正确。
(1)直径是圆中最大的弦。
( )
(2)长度相等的两条弧一定是等弧。
( )
(3)半径相等的两个圆是等圆。
( )
(4)面积相等的两个圆是等圆。
( )
(5)同一条弦所对的两条弧一定是等弧。
( )
2.如图,点A 、B 、C 、D 都在⊙O 上.在图中画出以这4点为端点的各条弦.这样的弦共有多少条?
3.(1)在图中,画出⊙O 的两条直径;
(2)依次连接这两条直径的端点,得一个四边形.判断这个四边形的形状,并说明理由.
三、课堂整理:
四、当堂练习:《补充习题》。
