浙教初中数学八上《探索勾股定理》课件
合集下载
浙教版八年级数学上册 2.7《探索勾股定理》 课件 (共19张PPT)

2021/4/18
10
b
cb a
ac b
c ba c
a
b
毕达哥拉斯证法
c aa
b
cb a
总统证明法
2021/4/18
11
例1、已知在ABC中,C Rt, BC a, AC b, AB c. (1)若a 1,b 2,求c; (2)若a 5,c 7,求b.
变式:(3)若c=26,a:b=5:12,求a,b
3、根据所测得的结果填写下表:
a
b
c
a2+b2
c2
3
4
5
25
25
6
8
10
100
100
5
12
13
169
169
a b c 验证结果:结论 2 2 2 正确 2021/4/18
5
c a
c a
b
b
c a
c a
2021/4/18
b
b
6
正方形的面积可以表示为
c2 ;
也可以表示为 c
a b
4 ab (b a)2 2
A
A'
2021/4/18
C
B
B'
17
美丽的“勾股”树
2021/4/18
S5
S S4
3
S6
S7
S2
S1
11
18
布置作业:1、完成作业本2.7.1 2、上网查找勾股定理
小故事
同学们再见
2021/4/18
19
∵ c2 = 4 ab (b a)2
2
=2ab+b2-2ab+a2 =a2+b2
数学:2.6《探索勾股定理》课件(浙教版八年上)

100 225
x
17 15
?
已知直角三角形两边,求第三边.
生活中的应用: 小明妈妈买了一部29英寸(74厘米) 的电视机. 小明量了电视机的屏幕后,发现 屏幕只有58厘米长和46厘米宽,他觉得一 定是售货员搞错了. 你同意他的想法吗?你 能解释这是为什么吗?
四、课堂小结
1.这一节课我们一起学习了哪些知识
探索勾股定理
一、情境引入
2002年世界数学家大会在我国北京召开,下 图是本届数学家大会的会标:
会标中央的图案是赵爽弦 图,它与“勾股定理”有关, 数学家曾建议用“勾股定理” 的图来作为与“外星人”联系 的信号.
二、探索发现勾股定理
探究活动一:
观察下面地板砖示意图:
观察这三 个正方形
你发现图中三个正方形的面积之间 存在什么关系吗?
1.习题1.1. 2.阅读《读一读》——勾股世界. 3.观察下图,探究图中三角形的三边长是否满足 a 2 b 2 c 2?
a
c b
a c
b
申博官网 申博官方网 申博官方网 申博官网
hnq184dgk
寻乐吧,也算生活中的相声小段。斗转星移,不知不觉时光便很快过去了。这期间,马启明从“爬坡”年龄、从一个工艺员做 到了酿造车间主任的位置。坏消息不断地从厂子传出。因为厂子资金周转困难,已严重影响到原料采购。随着生产的进行,仓 库麦芽不够、尤其优等品麦芽库存量明显不足,库存麦芽有80%以上是让步接收的麦芽,说艺术一点的话就是不合格品。优等 品麦芽是专门用来生产花开王牌啤酒——花开特供啤酒的必备原料,如果没有优等品麦芽,花开特供啤酒的质量将大打折扣, 而厂里已无足够的资金购买优等品麦芽了,供应商了解到花开啤酒的实际情况后也不肯赊账,高档啤酒很快就将面临无米下炊 的境况。马启明为麦芽的事一筹莫展,这事就像蜘蛛网一样缠绕着他。一天,马启明到供应科去协商麦芽采购的事宜,一踏进 供应科办公室的门,就带着讨好的笑脸向金俊英说:“金科长,马上又要生产花开特供酒了,仓库剩下的优等品麦芽不多了, 是不是再购进一些?”“没有优等品麦芽,我比你还要着急。再进一些,说起来容易,钱呢?我给供应商笑人家还以为我是卖 笑的,再说,有我这样又丑又老的男同志卖笑的吗?现在的供货商要付钱才肯供货,况且我们以前拖欠的货款还没有付清呢! 现在厂子这样,连老客户都不愿供货了,他们要我们把以前的货款结清了才肯供货,我也是毫无办法。”金俊英苦笑道。马启 明碰上个不软不硬的钉子。“说不定那个供应商看上你床上有丰富经验包你一万年。”马启明笑了笑继续说,“我们可以再找 其它的供货商吗,现在供应商一捞就是一大把,还愁没有供应商!”马启明奸笑着说道,“我现在就给你打电话,肯定一打一 个准。”马启明认为换个新供应商问题自然解决,他以为他的办法高明。“已经这样做了,可供货商说,货款到了50%以后才 肯发货。现在厂里不景气,他们也怕拿不到货款。前一阵,有一个供货商为了要到以前的麦芽货款,在这里磨了两个星期,在 厂子门口堵大门,急得想要与厂里打官司。打官司肯定是厂里输,最后好说歹说地给了一万块钱,剩下的钱还不知道什么时间 给。厂子里现在是真没有钱。”金俊英叹了口气。马启明知道,就在前几天,在厂门口上演了一场“欠钱的是大爷,追债的是 孙子”的闹剧闹得沸沸扬扬,派出所都紧急出动了。“优等品麦芽再不采购回来的话,就要停产了。”马启明步步紧逼,有点 不到黄河不死心,有意把问题说得严重一点,希望引起金俊英的重视。停产是个善意的谎言,实际上没有优等品麦芽,无非是 用一等品、合格品和等外麦芽,不过花开特供酒的质量就要大打折扣。“这事谷厂长早已知道了,现在影响到正常生产,厂里 没有钱我真没办法了,你直接去找谷厂长说可能会比我去说更好。”金俊英踢皮球倒是
x
17 15
?
已知直角三角形两边,求第三边.
生活中的应用: 小明妈妈买了一部29英寸(74厘米) 的电视机. 小明量了电视机的屏幕后,发现 屏幕只有58厘米长和46厘米宽,他觉得一 定是售货员搞错了. 你同意他的想法吗?你 能解释这是为什么吗?
四、课堂小结
1.这一节课我们一起学习了哪些知识
探索勾股定理
一、情境引入
2002年世界数学家大会在我国北京召开,下 图是本届数学家大会的会标:
会标中央的图案是赵爽弦 图,它与“勾股定理”有关, 数学家曾建议用“勾股定理” 的图来作为与“外星人”联系 的信号.
二、探索发现勾股定理
探究活动一:
观察下面地板砖示意图:
观察这三 个正方形
你发现图中三个正方形的面积之间 存在什么关系吗?
1.习题1.1. 2.阅读《读一读》——勾股世界. 3.观察下图,探究图中三角形的三边长是否满足 a 2 b 2 c 2?
a
c b
a c
b
申博官网 申博官方网 申博官方网 申博官网
hnq184dgk
寻乐吧,也算生活中的相声小段。斗转星移,不知不觉时光便很快过去了。这期间,马启明从“爬坡”年龄、从一个工艺员做 到了酿造车间主任的位置。坏消息不断地从厂子传出。因为厂子资金周转困难,已严重影响到原料采购。随着生产的进行,仓 库麦芽不够、尤其优等品麦芽库存量明显不足,库存麦芽有80%以上是让步接收的麦芽,说艺术一点的话就是不合格品。优等 品麦芽是专门用来生产花开王牌啤酒——花开特供啤酒的必备原料,如果没有优等品麦芽,花开特供啤酒的质量将大打折扣, 而厂里已无足够的资金购买优等品麦芽了,供应商了解到花开啤酒的实际情况后也不肯赊账,高档啤酒很快就将面临无米下炊 的境况。马启明为麦芽的事一筹莫展,这事就像蜘蛛网一样缠绕着他。一天,马启明到供应科去协商麦芽采购的事宜,一踏进 供应科办公室的门,就带着讨好的笑脸向金俊英说:“金科长,马上又要生产花开特供酒了,仓库剩下的优等品麦芽不多了, 是不是再购进一些?”“没有优等品麦芽,我比你还要着急。再进一些,说起来容易,钱呢?我给供应商笑人家还以为我是卖 笑的,再说,有我这样又丑又老的男同志卖笑的吗?现在的供货商要付钱才肯供货,况且我们以前拖欠的货款还没有付清呢! 现在厂子这样,连老客户都不愿供货了,他们要我们把以前的货款结清了才肯供货,我也是毫无办法。”金俊英苦笑道。马启 明碰上个不软不硬的钉子。“说不定那个供应商看上你床上有丰富经验包你一万年。”马启明笑了笑继续说,“我们可以再找 其它的供货商吗,现在供应商一捞就是一大把,还愁没有供应商!”马启明奸笑着说道,“我现在就给你打电话,肯定一打一 个准。”马启明认为换个新供应商问题自然解决,他以为他的办法高明。“已经这样做了,可供货商说,货款到了50%以后才 肯发货。现在厂里不景气,他们也怕拿不到货款。前一阵,有一个供货商为了要到以前的麦芽货款,在这里磨了两个星期,在 厂子门口堵大门,急得想要与厂里打官司。打官司肯定是厂里输,最后好说歹说地给了一万块钱,剩下的钱还不知道什么时间 给。厂子里现在是真没有钱。”金俊英叹了口气。马启明知道,就在前几天,在厂门口上演了一场“欠钱的是大爷,追债的是 孙子”的闹剧闹得沸沸扬扬,派出所都紧急出动了。“优等品麦芽再不采购回来的话,就要停产了。”马启明步步紧逼,有点 不到黄河不死心,有意把问题说得严重一点,希望引起金俊英的重视。停产是个善意的谎言,实际上没有优等品麦芽,无非是 用一等品、合格品和等外麦芽,不过花开特供酒的质量就要大打折扣。“这事谷厂长早已知道了,现在影响到正常生产,厂里 没有钱我真没办法了,你直接去找谷厂长说可能会比我去说更好。”金俊英踢皮球倒是
课件浙教版八上 探索勾股定理 演示课件

(1)直角三角形的两直角边为3和4,则斜边为___
D
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
A 过B作水平线,两线交于点C,则∠ACB=90°
过B作水平线,两线交于点C,则∠ACB=90°
正方形A,B,C,D的面积之和为___________cm2。
AC=90-40=50(mm)
(2) 正方形B的面积是
(1)图1中正方形A的面积是
个单位面积。
如果直角三角形两直角边分别为a、b, 斜边为c,那么 AC=90-40=50(mm)
A
过B作水平线,两线交于点C,则∠ACB=90°
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
D 如果直角三角形两直角边分别为a、b, 斜边为c,那么
B
9 个单位面积。
图1 (3)正方形C的面积是
25 个单位面积。
探索1 你能发现图1中三个正方形A,B,C的面 积之间有什么关系吗?
结论1 SA+SB=SC
即:两条直角边上的 正方形面积之和等于斜 边上的正方形的面积。
探索2 你能用直角三 角形的边长表示图中 正方形的面积吗?
探索3 你能发现图中直 角三角形三边长度之间 存在什么关系吗?
40
A
AC=90-40=50(mm) BC=160-40=120(mm) 由勾股定理,得
AB2AC2BC2
90 50
C
120
160
B
40
5 0 2 1 2 0 21 6 9 0 0 (m m 2) 构造直角三角形
∵AB﹥0, ∴AB=130(mm)
可以解决实际问题。
D
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
A 过B作水平线,两线交于点C,则∠ACB=90°
过B作水平线,两线交于点C,则∠ACB=90°
正方形A,B,C,D的面积之和为___________cm2。
AC=90-40=50(mm)
(2) 正方形B的面积是
(1)图1中正方形A的面积是
个单位面积。
如果直角三角形两直角边分别为a、b, 斜边为c,那么 AC=90-40=50(mm)
A
过B作水平线,两线交于点C,则∠ACB=90°
探索2 你能用直角三角形的边长表示图中正方形的面积吗?
以直角三角形三边为边作等边三角形,这3个等边三角形的面积之间有什么关系?
D 如果直角三角形两直角边分别为a、b, 斜边为c,那么
B
9 个单位面积。
图1 (3)正方形C的面积是
25 个单位面积。
探索1 你能发现图1中三个正方形A,B,C的面 积之间有什么关系吗?
结论1 SA+SB=SC
即:两条直角边上的 正方形面积之和等于斜 边上的正方形的面积。
探索2 你能用直角三 角形的边长表示图中 正方形的面积吗?
探索3 你能发现图中直 角三角形三边长度之间 存在什么关系吗?
40
A
AC=90-40=50(mm) BC=160-40=120(mm) 由勾股定理,得
AB2AC2BC2
90 50
C
120
160
B
40
5 0 2 1 2 0 21 6 9 0 0 (m m 2) 构造直角三角形
∵AB﹥0, ∴AB=130(mm)
可以解决实际问题。
探索勾股定理课件浙教版数学八年级上册

2.7 探索勾股定理(1)
预学展示
A
L M
C
B
N
图1-1
观察
(1) ΔABC的形状
(2)正方形M面积是 AC2=16 个单位面积。
正方形N的面积是
BC2=9
个单位面积。
正方形L的面积是
个单位面积。
(图中每个小方格代表一个单位面积)
A
L M
C
B
N
图1-1
1
L的面积=7×7-4× 2 ×3×4=25
如果直角三角形两直角边分别为a、b,斜边为
c,那么 a2 b2 c2
a
c
b
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
知识链接
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部 分称为"勾",下半部分称为"股"。我国古代学者 把直角三角形较短的直角边称为“勾”,较长的 直角边称为“股”,斜边称为“弦”.
直角三角形两直角边的平方和等于斜边的平方
3.勾股定理的应用: 建立模型,借助方程
灵活运用
如图图中数字所表示的正方形的面积,
则正方形B所表示的面积为 144 .
81
a
c bB 225
如图,所有的四边形都是正方形,所有的三角形 都是直角三角形,其中最大的正方形的边长为7cm,则 正方形A,B,C,D的面积之和为____4_9______cm2。
例题讲解
已知在ABC中,C Rt, BC a, AC b, AB c.
(1)若a 1,b 2,求c; (2)若a 15,c 17,求b.
解(1)根据勾股定理,得 c2 a2 b2 12 22 5.
c>0,c 5.
预学展示
A
L M
C
B
N
图1-1
观察
(1) ΔABC的形状
(2)正方形M面积是 AC2=16 个单位面积。
正方形N的面积是
BC2=9
个单位面积。
正方形L的面积是
个单位面积。
(图中每个小方格代表一个单位面积)
A
L M
C
B
N
图1-1
1
L的面积=7×7-4× 2 ×3×4=25
如果直角三角形两直角边分别为a、b,斜边为
c,那么 a2 b2 c2
a
c
b
勾股定理:
直角三角形两直角边的平方和等于斜边的平方
知识链接
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部 分称为"勾",下半部分称为"股"。我国古代学者 把直角三角形较短的直角边称为“勾”,较长的 直角边称为“股”,斜边称为“弦”.
直角三角形两直角边的平方和等于斜边的平方
3.勾股定理的应用: 建立模型,借助方程
灵活运用
如图图中数字所表示的正方形的面积,
则正方形B所表示的面积为 144 .
81
a
c bB 225
如图,所有的四边形都是正方形,所有的三角形 都是直角三角形,其中最大的正方形的边长为7cm,则 正方形A,B,C,D的面积之和为____4_9______cm2。
例题讲解
已知在ABC中,C Rt, BC a, AC b, AB c.
(1)若a 1,b 2,求c; (2)若a 15,c 17,求b.
解(1)根据勾股定理,得 c2 a2 b2 12 22 5.
c>0,c 5.
浙教版数学八上2.7《探索勾股定理》课件

2
(3)总统”证法, 1876年美国总统Garfield (伽菲尔德)的证明
C D a A c b c b a
E
B
你能根据前面的面积法来证明勾股定理吗?
1 1 2 1 2 ( a b) c 2 ab 2 2 2
四、勾股定理的应用
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
国家之一。早在三千多年前, 我国是最早了解勾股定理的
国家之一。早在三千多年前, 国家之一。早在三千多年前,周 国家之一。早在三千多年前, 朝数学家商高就提出,将一根直 国家之一。早在三千多年前, 尺折成一个直角,如果勾等于三, 国家之一。早在三千多年前, 股等于四,那么弦就等于五,即 国家之一。早在三千多年前, “勾三、股四、弦五”,它被记 国家之一。早在三千多年前, 载于我国古代著名的数学著作 国家之一。早在三千多年前 《周髀算经》中 .
C b
c F
(1)你能利用三角尺 摆出右边的图形
H c
b A a
c E b
a B
你能再用这个图形来证明勾股定理吗?
( a b)
2
1 c 4 ab 2
2
D
(2)利用再次三角尺摆出 右边的图形
A
c a
b G H F E C
你能用这个图形来证明勾股定理 吗?
B
1 2 c 4 ab (b a ) 2
4.如图,所有的四边形都是正方形,所有的三角形 都是直角三角形,其中最大的正方形的边长为7cm,则 2。 49 正方形A,B,C,D的面积之和为___________cm
C D
B
A
7cm
例题
1、 受台风“菲特”影响,路旁一棵树在
(3)总统”证法, 1876年美国总统Garfield (伽菲尔德)的证明
C D a A c b c b a
E
B
你能根据前面的面积法来证明勾股定理吗?
1 1 2 1 2 ( a b) c 2 ab 2 2 2
四、勾股定理的应用
例1:已知ΔABC中,∠C=Rt∠,BC=a,
AC=b,AB=c。
国家之一。早在三千多年前, 我国是最早了解勾股定理的
国家之一。早在三千多年前, 国家之一。早在三千多年前,周 国家之一。早在三千多年前, 朝数学家商高就提出,将一根直 国家之一。早在三千多年前, 尺折成一个直角,如果勾等于三, 国家之一。早在三千多年前, 股等于四,那么弦就等于五,即 国家之一。早在三千多年前, “勾三、股四、弦五”,它被记 国家之一。早在三千多年前, 载于我国古代著名的数学著作 国家之一。早在三千多年前 《周髀算经》中 .
C b
c F
(1)你能利用三角尺 摆出右边的图形
H c
b A a
c E b
a B
你能再用这个图形来证明勾股定理吗?
( a b)
2
1 c 4 ab 2
2
D
(2)利用再次三角尺摆出 右边的图形
A
c a
b G H F E C
你能用这个图形来证明勾股定理 吗?
B
1 2 c 4 ab (b a ) 2
4.如图,所有的四边形都是正方形,所有的三角形 都是直角三角形,其中最大的正方形的边长为7cm,则 2。 49 正方形A,B,C,D的面积之和为___________cm
C D
B
A
7cm
例题
1、 受台风“菲特”影响,路旁一棵树在
浙教版-数学-八年级上册2.7探索勾股定理 教学课件
A的面积
B的面积
C的面积
(单位面积) (单位面积) (单位面积)
图1-1
16
图1-2
4
9
25
9
13
形成新知 勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
a2 b2 c2
ac
b
即 直角三角形两直角边的平方和
等于斜边的平方。
在西方又称毕达 哥拉斯定理!
相传二千多年前,希腊的毕达哥拉斯学派首先证明了
勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯 定理。
解决问题
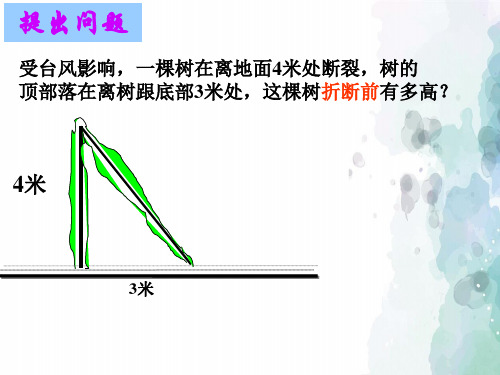
受台风影响,一棵树在离地面4米处断裂,树的 顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
例1、
1、如图:在Rt△ABC中, ∠C=90° 已知c =13,a=5,求b的值.
勾股定理的主要作用是 : 在直角三角形中,已
勾
弦
股
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年
前,周朝数学家商高就提出,将一根直尺折成一个直角三 角形,如果勾等于三,股等于四,那么弦就等于五。即 “勾三、股四、弦五”。它被记载于我国古代著名的数学 著作《周髀算经》中。在这本书中的另一处,还记载了勾 股定理的一般形式。
1945年,人们在研究古巴比伦人遗留下的一块数学泥 板时,惊讶地发现上面竟然刻有15组能构成直角三角形三 边的数,其年代远在商高之前。
BC=160-40=120(mm).
90
∵ ∠C =90。
∴ AB2=AC2+BC2 =502+1202
40 A
C 160
B 40
=16900(mm2) 温馨提示:在实际问题中,要
探索勾股定理课件(浙教版)

边长,则
c
a
a2 b2 c2
b
勾 股
在中国古代,人们把曲折成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”因此这一性质也称为勾股定理.
勾股
据《周髀算经》记载,西周开国时期(约公元前1000 多年)有个叫商高的人对周公说,把一根直尺折成直角, 两端连接得一直角三角形。如果钩是3,股是4,那么弦是 5,这就是商高发现的“勾股定理”。因此在中国,勾股 定理又称“商高定理”,在西方国家,勾股定理又称“毕 达哥定理”。但毕达哥发现这一定理的时间要比商高迟得 多,可见我国古代人民对人类贡献的杰出。
=4×
1 2
ab+c2
综合起来可得:
(a b)2 c2
4
1
ab
2
展开,得:a2+2ab+b2=c2+2ab
化简,得: a2+b2=c2
面积算两次: 一方面,直角梯形上底为a,下底为b,高为(a+b),
面积为
1(a+b)(a+b)=
2
1 2
(a
b)2
另一方面,2S小直角三角形+S等腰直角三角形=2×
1 2
ab+
1 2
c2
综合起来可得:
c
b a
c
a
b
1 2
(a
b)
2
=
2×
1 ab+
2
1 2 c2
(a+b)2=2ab+c2
a2+2ab+b2=c2+2ab
浙教版初中数学八年级上册2.7 探索勾股定理 (共23张)课件

主体。
流程y=图0
教
学
过
程
倍分
速 课
析
时
学
练
创设情境导入新课 动手操作探求新知 证明结论得到定理 应用知识回归生活 总结反思布置作业
创设情y境=导0 入新课
受台风麦莎影响,一棵树在离地面4米处断裂,树的 顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
倍
速
课 时
3米
学
练
动手操y作=探0 求新知
练 称为“弦”.
千古第一定理
勾 股
毕 是第一个不定方程 达
()
数与形的第一定理 哥
商
拉
高 导致第一次数学危机 斯
倍
速 课 时
定 数学由计算转变为证明 定
理
理
学
练
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明, 就把这一证法称为“总统”证法。
倍
察力、抽象概括能力、创造想象能力以及科学探究问题的能力
速
情感目标:
课
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受
时
数学知识的发生发展过程。
学
(2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱
练
国情感
教学重y=点0 和难点
教 材 分 析
倍 速 课 时 学 练
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学y目=标0
知识目标:
教 (1)知道勾股定理的由来,初步理解割补拼接的面积证法。 (2)掌握勾股定理,通过动手实践理解勾股定理的证明过程
材 (3) 能利用勾股定理进行简单的几何计算
流程y=图0
教
学
过
程
倍分
速 课
析
时
学
练
创设情境导入新课 动手操作探求新知 证明结论得到定理 应用知识回归生活 总结反思布置作业
创设情y境=导0 入新课
受台风麦莎影响,一棵树在离地面4米处断裂,树的 顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
倍
速
课 时
3米
学
练
动手操y作=探0 求新知
练 称为“弦”.
千古第一定理
勾 股
毕 是第一个不定方程 达
()
数与形的第一定理 哥
商
拉
高 导致第一次数学危机 斯
倍
速 课 时
定 数学由计算转变为证明 定
理
理
学
练
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话 人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明, 就把这一证法称为“总统”证法。
倍
察力、抽象概括能力、创造想象能力以及科学探究问题的能力
速
情感目标:
课
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受
时
数学知识的发生发展过程。
学
(2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱
练
国情感
教学重y=点0 和难点
教 材 分 析
倍 速 课 时 学 练
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学y目=标0
知识目标:
教 (1)知道勾股定理的由来,初步理解割补拼接的面积证法。 (2)掌握勾股定理,通过动手实践理解勾股定理的证明过程
材 (3) 能利用勾股定理进行简单的几何计算
【浙教版】八年级上:2.7《探索勾股定理》ppt课件

2020/5/25
如图是在北京召开的国家数学家大会(ICM2002)的会标。它的设计思路可追溯到3世纪 中国数学家赵爽所使用的玄图。用玄图证明 勾股定理在数学史上有着重要的地位。
2020/5/25
2020/5/25
2.7 探索勾股定理(第1课时)
2020/5/25
动手画一画
1、作三个直角三角形,使其两条直角边长分别为3cm和4cm, 6cm和8cm,5cm和12cm;
25+χ2=χ2+2χ+1 得2χ=24,即χ=12 答:旗杆高为12米
B
C
A
2020/5/25
回顾与小结
这节课你有什么收获?
2020/5/25
小结归纳:
应用勾股定理解题要注意: 1 . 熟记公式。2. 理清谁是斜边。
2020/5/25
典型例题
例2 如图是一个长方形零件图,根据所给尺寸(单位:mm),求 两孔中心A,B之间的距离。
40
解:由题意可得:△ABC是Rt△
A
AC=90-40=50,BC=160-40=120
由勾股定理得:AB2=AC2+BC2
• 你能用两种方法求边长 为c的正方形的面积吗?
c aⅠ
b
Ⅳ
Ⅱ
Ⅲ
c 方法一: 2
方法二:(b a)2 4 1 ab 2
b2 2ab a2 2ab
b2 a2
即 a2 b2 c2
2020/5/25
勾股小知识
商高
《周髀算经》
学我家国商是高最就 早提了出 解,勾将股一定根理直的尺国折家成之一一个。直早角在,三如千果多勾年等前于,三周,朝股数等
直角三角形两条直角边的平方和等于斜边的平方。
如图是在北京召开的国家数学家大会(ICM2002)的会标。它的设计思路可追溯到3世纪 中国数学家赵爽所使用的玄图。用玄图证明 勾股定理在数学史上有着重要的地位。
2020/5/25
2020/5/25
2.7 探索勾股定理(第1课时)
2020/5/25
动手画一画
1、作三个直角三角形,使其两条直角边长分别为3cm和4cm, 6cm和8cm,5cm和12cm;
25+χ2=χ2+2χ+1 得2χ=24,即χ=12 答:旗杆高为12米
B
C
A
2020/5/25
回顾与小结
这节课你有什么收获?
2020/5/25
小结归纳:
应用勾股定理解题要注意: 1 . 熟记公式。2. 理清谁是斜边。
2020/5/25
典型例题
例2 如图是一个长方形零件图,根据所给尺寸(单位:mm),求 两孔中心A,B之间的距离。
40
解:由题意可得:△ABC是Rt△
A
AC=90-40=50,BC=160-40=120
由勾股定理得:AB2=AC2+BC2
• 你能用两种方法求边长 为c的正方形的面积吗?
c aⅠ
b
Ⅳ
Ⅱ
Ⅲ
c 方法一: 2
方法二:(b a)2 4 1 ab 2
b2 2ab a2 2ab
b2 a2
即 a2 b2 c2
2020/5/25
勾股小知识
商高
《周髀算经》
学我家国商是高最就 早提了出 解,勾将股一定根理直的尺国折家成之一一个。直早角在,三如千果多勾年等前于,三周,朝股数等
直角三角形两条直角边的平方和等于斜边的平方。
浙教版初中数学八年级上册探索勾股定理课件

0.5 2
C
B
x x+0.5
A
课后小实验
1
A
如图,分别以直角三角形的三边为边长作三个正方形,
B
这三个正方形的面积之间有什么关系?为什么?
C
2
如图,分别以直角三角形的三边为直径作三个半圆,
这三个半圆的面积之间有什么关系?为什么?
3
如图,分别以直角三角形的三边为边长作三个等边三角形,
这三个等边三角形的面积之间有什么关系?为什么?
b c2 a2
定理应用
例1、已知△ABC中,
B
∠C=Rt∠,BC=a,AC=b,AB=C
(1)已知: a=1, b=2, 求c; A
C
(2)已知: a=15, c=17, 求b;
(3)已知:c=34, a:b=8:15, 求a, b.
思考: 如何利用直角三角形在数轴上表示点 5 ?
5
1
0
பைடு நூலகம்25
拓展提高
学以致用
1①、若在aR=t△4 ,ABbC=中3,,∠则Cc==901°,;②若a=15,c=25,则b= 20 ;
5
5
③若c=61,b=60,则a= 11 ;
④若a∶b=3∶4,c=10则S△ABC= 24 。
2、如图,厂房屋顶的人字架是
等腰三角形,若跨度 BC=16米, 上弦长AB=10米,则中柱AD= 6 米,
解:过A作铅垂线,过B作水平线
,两线交于点C,则∠C =90。
A
AC=90-40=50(mm), BC=160-40=120(mm).
90 C
∵ ∠C =90。
∴ AB2=AC2+BC2 =502+1202
课件浙教版八上 探索勾股定理 课件PPT

5.
填空: 在直角三角形中,如果有两边 为3,4,那么另一 边为_________
分类讨论,分清斜边
例2 在△ABC中,AB=15 cm, AC=13 cm,高AD=12 cm,求BC的长.
A
A
15 12 13
15 13 12
B
D
C B CD
高在BC边上
高在BC延长线上
答案:14 cm或4 cm.
知1-讲
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的 对边分别是a,b,c.
(1)已知c=3,b=2,求a; (2)已知a∶b=2∶1,c=5,求b.
解:
(1)∵∠C=90°,c=3,b=2, ∴由勾股定理,得
a c2 b2 32 22 5.
(2)∵∠C=90°,a∶b=2∶1,∴a=2b. 又c=5,由勾股定理,得(2b)2+b2=52, 解得b=
又c=5,由勾股定理,得(2b)2+b2=52,
高在BC边上
高在BC延长线上
梯形ABCD的面积= 从特殊到一般、数形结合思想
想一想:这棵树名字叫做勾股树,那么,什么是勾?
B
1 (a b)(a b)
E
C
如图,Rt△ABE≌Rt△ECD,
2
勾股定理的各种表达式:
想一想:这棵树名字叫做勾股树,那么,什么是勾?
情景引入
相传2500年前,毕达哥拉斯有一次在朋友家做客 时,发现朋友家的用砖铺成的地面中反映了直角 三角形的某种数量关系。让我们跟随数学家一起 来到这位朋友家,看看他发现了什么?
C
A
B
三个正方形A、B、C面积关系是什么? 与等腰直角三角形三边有什么关系?
探究勾股定理
问题 在网格中的一般的直角三角形,以它的三 边为边长的三个正方形A、B、C 是否也有类似的面积
填空: 在直角三角形中,如果有两边 为3,4,那么另一 边为_________
分类讨论,分清斜边
例2 在△ABC中,AB=15 cm, AC=13 cm,高AD=12 cm,求BC的长.
A
A
15 12 13
15 13 12
B
D
C B CD
高在BC边上
高在BC延长线上
答案:14 cm或4 cm.
知1-讲
例1 在Rt△ABC中,∠C=90°,∠A,∠B,∠C的 对边分别是a,b,c.
(1)已知c=3,b=2,求a; (2)已知a∶b=2∶1,c=5,求b.
解:
(1)∵∠C=90°,c=3,b=2, ∴由勾股定理,得
a c2 b2 32 22 5.
(2)∵∠C=90°,a∶b=2∶1,∴a=2b. 又c=5,由勾股定理,得(2b)2+b2=52, 解得b=
又c=5,由勾股定理,得(2b)2+b2=52,
高在BC边上
高在BC延长线上
梯形ABCD的面积= 从特殊到一般、数形结合思想
想一想:这棵树名字叫做勾股树,那么,什么是勾?
B
1 (a b)(a b)
E
C
如图,Rt△ABE≌Rt△ECD,
2
勾股定理的各种表达式:
想一想:这棵树名字叫做勾股树,那么,什么是勾?
情景引入
相传2500年前,毕达哥拉斯有一次在朋友家做客 时,发现朋友家的用砖铺成的地面中反映了直角 三角形的某种数量关系。让我们跟随数学家一起 来到这位朋友家,看看他发现了什么?
C
A
B
三个正方形A、B、C面积关系是什么? 与等腰直角三角形三边有什么关系?
探究勾股定理
问题 在网格中的一般的直角三角形,以它的三 边为边长的三个正方形A、B、C 是否也有类似的面积
浙教版初中数学八年级上册探索勾股定理一精品课件PPT

答:两孔中心A、B之间的距离为 130mm。
构造直角三角形可 以解决实际问题。
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
在平静的湖面上,有一支芦苇,高出水面 1尺,芦苇被风一吹,花朵刚好与水面平 齐。已知芦苇移动的水平距离是5尺,问 这里的水深是多少呢?
A′ 3m
∴AC= AB2BC2
= 32 12 = 8 ≈2.8(米)
(2)若梯子的顶端下滑50厘米,
1m
底端将向外水平移动多少米? C
B B′
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
小刚想知道学校旗杆的高度,他发现旗杆上的
4米
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
3米
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
有一架3米长的梯子靠在学校围墙上,刚好与墙
头对齐,此时梯脚B与墙脚C的距离是1米。
(1)求墙的高度? (精确到0.1米) A
解:∵∠ACB=90°AB=3,BC=1
∴ AB2=AC2+BC2
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
勾股世界
两千两多千多年年前前,,古古希希腊有腊个有哥拉个毕达哥拉斯
学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 在国国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 定理理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年 年希希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
构造直角三角形可 以解决实际问题。
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
在平静的湖面上,有一支芦苇,高出水面 1尺,芦苇被风一吹,花朵刚好与水面平 齐。已知芦苇移动的水平距离是5尺,问 这里的水深是多少呢?
A′ 3m
∴AC= AB2BC2
= 32 12 = 8 ≈2.8(米)
(2)若梯子的顶端下滑50厘米,
1m
底端将向外水平移动多少米? C
B B′
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
小刚想知道学校旗杆的高度,他发现旗杆上的
4米
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
3米
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
有一架3米长的梯子靠在学校围墙上,刚好与墙
头对齐,此时梯脚B与墙脚C的距离是1米。
(1)求墙的高度? (精确到0.1米) A
解:∵∠ACB=90°AB=3,BC=1
∴ AB2=AC2+BC2
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
浙教版初中数学八年级上 册 2.7 探索勾股定理 (一) 课件
勾股世界
两千两多千多年年前前,,古古希希腊有腊个有哥拉个毕达哥拉斯
学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 在国国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 定理理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年 年希希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
初中数学八年级上 2.7 探索勾股定理 课件

没有遇到挫折,永远不会懂得自己的力量有多大。 让死人去埋葬死人吧,我们既然有生命,我们就应当活下去,而且要活得幸福。 能为别人设想的人,永远不寂寞。 不要常常觉得自己很不幸,世界上比我们痛苦的人还要多。
为你制造一些困难和障碍的人未必是你的敌人,把你从困境里拉出来的人未必是你的朋友。不要用眼前的利益得失看人,要看长远,所谓路 遥知马力,日久见人心! 如果可恨的挫折使你尝到苦果,朋友,奋起必将让你尝到人生的欢乐。
∠C=Rt∠,BC=a,AC=b,AB=C (1)已知: a=1, b=2, 求c;
(2)已知: a=15, c=17, 求b;
(3)已知:c=34, a:b=8:15, 求a, b.
变式一:已知Rt△ABC中,∠B=90°,AB=c, BC=a,AC=b.如果 a=1, b=2, 求c;
变式二:已知Rt△ABC中,AB=c,BC=a,
边为c,那么
a2 + b2 = c2
a
c
b
即直角三角形两直角边的平方和等于斜边的平方.
勾股定理揭示了直角三角形三边之间的关系.
在西方又称毕达 哥拉斯定理
勾
弦
股
验证
利用拼图来验证勾股定理: c
a b
大正方形的面积可以表示为 c2 ;
也可以表示为
2
c a
b
4ab ∵ c 2 = +(2 b -a)
2
=2ab+b2-2ab+a2
=a2+b2 ∴a2+b2=c2
c a
b
c a
b
c a
b
大正方形的面积可以表示为 (a+b)2 ;
c a
b
c a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
情感目标:
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受 数学知识的发生发展过程。 (2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱 国情感
教材分析
教学重y=点0 和难点
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学法分析
教学y方=0法与手段
引导探索法,由浅入深,由特殊到一般地提出问题。 引导学生自主探索,合作交流 ,并利用教具与多 媒体进行教学
千古第一定理
勾股(商高)定理
是第一个不定方程
毕 达
数与形的第一定理 哥
拉
导致第一次数学危机 斯
数学由计算转变为证明
定 理
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明, 就把这一证法称为“总统”证法。
应用知y=识0回归生活
1、求下列用字母表示的边长
三角形,并测量斜边的长度。(2)中的规律对这
个三角形仍然成立吗?
证明结y论=得0 到定理
a bc
b ca
ac b
cb a
动动手
证明结y论=得0 到定理
a
bc
面积 c
a
面积 (a b)2
a
c
面积 4 • 1 a 2
b
S大正方形 S4个三角形 S小正方形
(a b)2 - 4 • 1 ab c2 2
教学法分析
学y法=0指导
采用自主探索、合作交流的研讨式学习方式,让学 生思考问题,获取知识,掌握方法,逐步培养学生 动口、动手、动脑的能力,使学生真正成为学习的 主体。
教学过程分析
流程y=图0
创设情境导入新课 动手操作探求新知 证明结论得到定理 应用知识回归生活 总结反思布置作业
创设情y境=导0 入新课
x 2
1
17
15
b
应用知y识=回0 归生活
2、直角三角形中两条直角边之比为3:4,且 斜边为10cm,求(1)两直角边的长;(2)斜 边上的高线长.
5 3、利用作直角三角形,在数轴上表示点
应用知y识=回0 归生活
4、如图:是一个长方形零件图,根据所给的尺寸 求两孔中心A、B之间的距离
40
A
90
B
受台风麦莎影响,一棵树在离地面4米处断裂,树的 顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
动手操y作=探0 求新知
C A
B
图1-1
(1)观察图1-1 正方形A中含有 16 个
小方格,即A的面积是 16 个单位面积。 正方形B的面积是 9 个单位面积。 正方形C的面积是 25 个单位面积。
2.7 探索勾股定理
教材分析
地位y=作0 用
“探索勾股定理”是义务教育课程标准实验教科书 八年级第二章第七节的内容。
“勾股定理”是安排在学生学习了三角形、全等 三角形、等腰三角形等有关知识之后,它揭示了直角 三角形三边之间的一种美妙关系,将形与数密切联系 起来,在几何学中占有非常重要的位置。同时,勾股 定理在生产、生活中也有很大的用途。
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
动手操y作=探0 求新知
C A
B
C
图1-1 A
(1)你能用三角 形的边长表示正方 形的面积吗?
(2)你能发现直 角三角形三边长度 之间存在什么关系 吗?与同伴进行交 流。
B
直角三角形两直角边的
图1-2
平方和等于斜边的平方
(3)分别以5厘米、12厘米为直角边作出一个直角
即a2+b2=c2
证明结y论=得0 到定理 勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c,那么
ac
b
即 直角三角形两直角边的平方和等
于斜边的平方。
勾
弦
股
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
(图中每个小方格代表一个单位面积)
你是怎样得到上面的结果的?与同伴交流交流。
动手操y作=探0 求新知
C A
(2)在图1-2中,正方 形A,Bபைடு நூலகம்C中各含有多 少个小方格?它们的面 积各是多少?
B
图1-1
C A
B
图1-2
(3)你能发现图1-1中 三个正方形A,B,C的 面积之间有什么关系吗?
SA+SB=SC
• 2、从学生熟悉的生活经历台风麦莎出发到一朵红莲被风 吹的题目,选择学生身边的、感兴趣的事物,体现了数学 源于生活同时又回归于生活服务于生活。
• 3、探索定理采用了面积法,引导学生利用实验由特殊到一 般的对直角三角形三边关系的研究,得出结论.这种方法是 认识事物规律重要方法之一,通过教学让学生初步掌握这种 方法,对于学生良好思维品质的形成有重要作用,对学生的 终身发展也有一定的作用
C
160
应用知y识=0回归生活
思考题
在平静的湖面上,有一支红莲,高出水面1尺红莲被 风一吹,花朵刚好与水面平齐,已知红莲移动的水平 距离是2尺问这里水深是多少?
总结反y思=0布置作业
你有何收获呢?
设计说明
• 1、教学流程是:创设情境导入新课—动手操作探求新 知—证明结论得到定理—应用知识回归生活—总结反思布 置作业五部分 ,这一流程体现了知识发生,形成和发展过程, 让学生体会到观察,猜想,归纳,验证的思想和数形结合的思 想
教材分析
教学y目=标0
知识目标:
(1)知道勾股定理的由来,初步理解割补拼接的面积证法。 (2)掌握勾股定理,通过动手实践理解勾股定理的证明过程 (3) 能利用勾股定理进行简单的几何计算
能力目标:
在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验 证”的 数学思想,并体会数形结合和特殊到一般的思想方法,培养学生的观 察力、抽象概括能力、创造想象能力以及科学探究问题的能力
(1)通过实践、猜想、拼图、证明等操作使学生深刻感受 数学知识的发生发展过程。 (2)介绍我国古代在勾股定理研究方面取得的成就,激发学生的爱 国情感
教材分析
教学重y=点0 和难点
重点:掌握勾股定理的内容及其初步应用 难点:勾股定理的证明
教学法分析
教学y方=0法与手段
引导探索法,由浅入深,由特殊到一般地提出问题。 引导学生自主探索,合作交流 ,并利用教具与多 媒体进行教学
千古第一定理
勾股(商高)定理
是第一个不定方程
毕 达
数与形的第一定理 哥
拉
导致第一次数学危机 斯
数学由计算转变为证明
定 理
有趣的总统证法
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明, 就把这一证法称为“总统”证法。
应用知y=识0回归生活
1、求下列用字母表示的边长
三角形,并测量斜边的长度。(2)中的规律对这
个三角形仍然成立吗?
证明结y论=得0 到定理
a bc
b ca
ac b
cb a
动动手
证明结y论=得0 到定理
a
bc
面积 c
a
面积 (a b)2
a
c
面积 4 • 1 a 2
b
S大正方形 S4个三角形 S小正方形
(a b)2 - 4 • 1 ab c2 2
教学法分析
学y法=0指导
采用自主探索、合作交流的研讨式学习方式,让学 生思考问题,获取知识,掌握方法,逐步培养学生 动口、动手、动脑的能力,使学生真正成为学习的 主体。
教学过程分析
流程y=图0
创设情境导入新课 动手操作探求新知 证明结论得到定理 应用知识回归生活 总结反思布置作业
创设情y境=导0 入新课
x 2
1
17
15
b
应用知y识=回0 归生活
2、直角三角形中两条直角边之比为3:4,且 斜边为10cm,求(1)两直角边的长;(2)斜 边上的高线长.
5 3、利用作直角三角形,在数轴上表示点
应用知y识=回0 归生活
4、如图:是一个长方形零件图,根据所给的尺寸 求两孔中心A、B之间的距离
40
A
90
B
受台风麦莎影响,一棵树在离地面4米处断裂,树的 顶部落在离树跟底部3米处,这棵树折断前有多高?
4米
3米
动手操y作=探0 求新知
C A
B
图1-1
(1)观察图1-1 正方形A中含有 16 个
小方格,即A的面积是 16 个单位面积。 正方形B的面积是 9 个单位面积。 正方形C的面积是 25 个单位面积。
2.7 探索勾股定理
教材分析
地位y=作0 用
“探索勾股定理”是义务教育课程标准实验教科书 八年级第二章第七节的内容。
“勾股定理”是安排在学生学习了三角形、全等 三角形、等腰三角形等有关知识之后,它揭示了直角 三角形三边之间的一种美妙关系,将形与数密切联系 起来,在几何学中占有非常重要的位置。同时,勾股 定理在生产、生活中也有很大的用途。
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
动手操y作=探0 求新知
C A
B
C
图1-1 A
(1)你能用三角 形的边长表示正方 形的面积吗?
(2)你能发现直 角三角形三边长度 之间存在什么关系 吗?与同伴进行交 流。
B
直角三角形两直角边的
图1-2
平方和等于斜边的平方
(3)分别以5厘米、12厘米为直角边作出一个直角
即a2+b2=c2
证明结y论=得0 到定理 勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c,那么
ac
b
即 直角三角形两直角边的平方和等
于斜边的平方。
勾
弦
股
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
(图中每个小方格代表一个单位面积)
你是怎样得到上面的结果的?与同伴交流交流。
动手操y作=探0 求新知
C A
(2)在图1-2中,正方 形A,Bபைடு நூலகம்C中各含有多 少个小方格?它们的面 积各是多少?
B
图1-1
C A
B
图1-2
(3)你能发现图1-1中 三个正方形A,B,C的 面积之间有什么关系吗?
SA+SB=SC
• 2、从学生熟悉的生活经历台风麦莎出发到一朵红莲被风 吹的题目,选择学生身边的、感兴趣的事物,体现了数学 源于生活同时又回归于生活服务于生活。
• 3、探索定理采用了面积法,引导学生利用实验由特殊到一 般的对直角三角形三边关系的研究,得出结论.这种方法是 认识事物规律重要方法之一,通过教学让学生初步掌握这种 方法,对于学生良好思维品质的形成有重要作用,对学生的 终身发展也有一定的作用
C
160
应用知y识=0回归生活
思考题
在平静的湖面上,有一支红莲,高出水面1尺红莲被 风一吹,花朵刚好与水面平齐,已知红莲移动的水平 距离是2尺问这里水深是多少?
总结反y思=0布置作业
你有何收获呢?
设计说明
• 1、教学流程是:创设情境导入新课—动手操作探求新 知—证明结论得到定理—应用知识回归生活—总结反思布 置作业五部分 ,这一流程体现了知识发生,形成和发展过程, 让学生体会到观察,猜想,归纳,验证的思想和数形结合的思 想
教材分析
教学y目=标0
知识目标:
(1)知道勾股定理的由来,初步理解割补拼接的面积证法。 (2)掌握勾股定理,通过动手实践理解勾股定理的证明过程 (3) 能利用勾股定理进行简单的几何计算
能力目标:
在探索勾股定理的过程中,让学生经历“观察—猜想—归纳—验 证”的 数学思想,并体会数形结合和特殊到一般的思想方法,培养学生的观 察力、抽象概括能力、创造想象能力以及科学探究问题的能力
