第一章习题解答
第一章 习题答案

第一章 习题答案1-1 根据题1-1图所示的电动机速度控制系统工作原理图(1) 将a ,b 与c ,d 用线连接成负反馈状态;(2) 画出系统方框图。
解 (1)负反馈连接方式为:d a ↔,c b ↔;(2)系统方框图如图解1-1 所示。
1-2 题1-2图是仓库大门自动控制系统原理示意图。
试说明系统自动控制大门开闭的工作原理,并画出系统方框图。
题1-2图 仓库大门自动开闭控制系统解 当合上开门开关时,电桥会测量出开门位置与大门实际位置间对应的偏差电压,偏差电解 c u 增高,偏差电压 r 。
此时,-=r e u u 使c u 过程:系统中,加热炉是被控对象,炉温是被控量,给定量是由给定电位器设定的电压r u (表征炉温的希望值)。
系统方框图见图解1-3。
1-4 题1-4图是控制导弹发射架方位的电位器式随动系统原理图。
图中电位器1P 、2P 并联后跨接到同一电源0E 的两端,其滑臂分别与输入轴和输出轴相联结,组成方位角的给定元件和测量反馈元件。
输入轴由手轮操纵;输出轴则由直流电动机经减速后带动,电动机采用电枢控制的方式工作。
试分析系统的工作原理,指出系统的被控对象、被控量和给定量,画出系统的方框图。
题1-4图 导弹发射架方位角控制系统原理图解 当导弹发射架的方位角与输入轴方位角一致时,系统处于相对静止状态。
当摇动手轮使电位器1P 的滑臂转过一个输入角i θ的瞬间,由于输出轴的转角i o θθ≠,于是出现一个误差角o i e θθθ-=,该误差角通过电位器1P 、2P 转换成偏差电压o i e u u u -=,e u 经放大后驱动电动机转动,在驱动导弹发射架转动的同时,通过输出轴带动电位器2P 的滑臂转过一定的角度o θ,直至i o θθ=时,o i u u =,偏差电压0=e u ,电动机停止转动。
这时,导弹发射架停留在相应的方位角上。
只要o i θθ≠,偏差就会产生调节作用,控制的结果是消除偏差e θ,使输出量o θ严格地跟随输入量i θ的变化而变化。
电路理论习题解答 第一章

1.5
u /V
内阻不为零
+ us
R0
I
+
u
RL
−
伏安关系曲线
−
I/A 0.15
0
1.5
u /V
注:这里的伏安关系曲线只能在第一象限,原因也是,一旦出了第一象限, u 和 I 的比值就 变为负的了,反推出的 RL 就变为负值了,与题意不符。
V
V
1.5V
1.5V
R 内阻为零时 内阻不为零时
R
1-9 附图是两种受控源和电阻 RL 组成的电路。现以 RL 上电压作为输出信号,1)求两电路的电 压增益(A,gmRL);2)试以受控源的性质,扼要地说明计算得到的结果。
1) 如果不用并联分压(在中学就掌握的东西),当然也可以用两个回路的 KVL 方程和顶部 节点的 KCL 方程,得出上面的 H(jω)的表达式,但是显然这样做是低效的。 2) 事实上,本课程的目的是希望学习者能够根据不同的题目,尽可能采用多种方法中的一 种最简单的方法去解决问题。因此, a) 只要没有要求,任意的逻辑完整的解题思路都是可取的; b) 学习者可以视自己的练习目的选择一种简单熟悉的方法、或者一种较为系统的方法、 或者多种方法来完成习题。
第一章习题答案 1-1 已知电路中某节点如图,I1=-1A,I2=4A,I4=-5A,I5=6A,用 KCL 定律建立方程并求解 I3 ( 4A )
图 1-1 解:由 KCL 定律:任一集中参数电路中的任一节点,在任一时刻,流入该节点的电流之和与 流出该节点的电流之和相同。 即: I1+I3+I4+I5=I2 =〉-1+(-5)+6+I3=4 =〉I3=4(A)
1 2
电工部分习题解答(1,2,3)

第一章 习题解答1-1 在图1-39所示的电路中,若I 1=4A ,I 2=5A ,请计算I 3、U 2的值;若I 1=4A ,I 2=3A ,请计算I 3、U 2、U 1的值,判断哪些元件是电源?哪些是负载?并验证功率是否平衡。
解:对节点a 应用KCL 得 I 1+ I 3= I 2 即4+ I 3=5, 所以 I 3=1A 在右边的回路中,应用KVL 得6⨯I 2+20⨯I 3= U 2,所以U 2=50V 同理,若I 1=4A ,I 2=3A ,利用KCL 和KVL 得I 3= -1A ,U 2= -2V 在左边的回路中,应用KVL 得20⨯I 1+6⨯I 2= U 1,所以U 1=98V 。
U 1,U 2都是电源。
电源发出的功率:P 发=- U 1 I 1- U 2 I 3=-98⨯4-2=-394W 负载吸收的功率:P 吸=2021I +622I +2023I =394W 二者相等,整个电路功率平衡。
1-2 有一直流电压源,其额定功率P N =200W ,额定电压U N =50V ,内阻R o =0.5Ω,负载电阻R L 可以调节,其电路如图1-40所示。
试求:⑴额定工作状态下的电流及负载电阻R L 的大小;⑵开路状态下的电源端电压;⑶电源短路状态下的电流。
解:⑴A U P I N N N 450200===Ω===5.12450N N L I U R ⑵ =⨯+==0R I U U U N N S OC 50+4⨯0.5 = 52V ⑶ A R U I S SC 1045.0520===图1-39 习题1-1图 图1-40 习题1-2图1-9 求图1-44所示电路中电阻的电流及其两端的电压,并求图1-44a 中电压源的电流及图1-44 b 中电流源的电压,判断两图中的电压源和电流源分别起电源作用还是负载作用。
解:图1-44a 中,A I R 2=,V U R 2=,电压源的电流A I 2=。
物理化学 答案 第一章_习题解答

-
知此气体的 Cp,m=29.10 J·K 1,求过程的ΔU、ΔH、Q 和 W 。 解: (1)等容
ΔU = n ⋅ Cv ,m (T2 − T1 ) = 1 × (29.1 − 8.314) × 75 = 1559 J ΔH = n ⋅ C p ,m (T2 − T1 ) = 1 × 29.1 × 75 = 2183 J
η = −Wr / Q1 = (T1 − T2 ) / T1 = (500 − 300) / 600 = 40%
第二个卡诺热机效率
η ′ = −Wr / Q1′ = (T1 − T2′) / T1 = (500 − 250) / 600 = 50%
∵
η =η′
∴两个热机的效率不相同
(2)第一个热机吸收的热量: Q1 =
γ =1.4,试求 Cv,m。若该气体的摩尔热容近似为常数,试求在等容条件下加热该气体至 t2=
80℃所需的热。 解:∵ γ =
C p,m Cv , m
=
Cv , m + R Cv , m
= 1.4
∴ Cv, m =
R
γ
=
8.314 = 20.79 J ⋅ K -1 ⋅ mol-1 0.4
Qv = n ⋅ Cv ,m ⋅ ΔT = =
4
3 3 ⎧ ⎧ ⎪V1 = 5dm ⎪V2 = 6dm Q (可 ) = 0 ⎯⎯⎯⎯ → ⎨ ⎨ ⎪T1 = 298.15 K ⎪T2 = 278.15 K ⎩ ⎩
由理想气体绝热可逆过程方程式可知
T2 / T1 = (V1 / V2 ) Cv ,m =
R / Cv , m
运筹学教程(第三版)习题答案(第一章)

b 3/2 1
c x1 0 1 0
d x2 1 0 0
0 x3 5/14
0 x4 -3/4
-2/14 10/35 -5/14d+2/14c 3/14d-10/14c
School of Management
运筹学教程
第一章习题解答
之间时最优解为图中的A点 当c/d在3/10到5/2之间时最优解为图中的 点 ; 当 在 到 之间时最优解为图中的 c/d大于 且c大于等于 时最优解为图中的 点;当c/d 大于5/2且 大于等于 时最优解为图中的B点 大于等于0时最优解为图中的 大于 小于3/10且 d大于 时最优解为图中的 点 ; 当 c/d大于 大于0时最优解为图中的 小于 且 大于 时最优解为图中的C点 大于 5/2且c小于等于 时或当 小于 小于等于0时或当 小于3/10且d小于 时最优解 小于0时最优解 且 小于等于 时或当c/d小于 且 小于 为图中的原点。 为图中的原点。
page 7 14 March 2012
School of Management
运筹学教程
第一章习题解答
对下述线性规划问题找出所有基解, 1.3 对下述线性规划问题找出所有基解,指出哪 些是基可行解,并确定最优解。 些是基可行解,并确定最优解。
max Z = 3 x1 + x 2 + 2 x 3 12 x1 + 3 x 2 + 6 x 3 + 3 x 4 = 9 8 x + x − 4 x + 2 x = 10 1 2 3 5 st 3 x1 − x 6 = 0 x j ≥ 0( j = 1, L , 6) ,
School of Management
《电磁场与电磁波》课后习题解答第一章

n(x2
y2
z2)
(x2 y2 z2)2 (x2 y2 z2)
(n 3)rn
【习题 1.20 解】
1
已知 r (x2 y2 z2 )2
r xex yey zez
所以
(1)
r
(ex
x
ey
y
ez
z
)
(
xex
yey
zez )
ex ey ez
xyz
Bx ex By ey Bz ez
取一线元: dl exdx eydy ezdz
则有
B dl
ex ey ez Bx By Bz 0 dx dy dz
则矢量线所满足的微分方程为
dx dy dz Bx By Bz
或写成
dx dy dz =k(常数) a2 z a3 y a3x a1z a1 y a2x
对(3)(4)分别求和
(4)
d (a1x) d (a2 y) d (a3 z) 0 xdx ydy zdz 0
d (a1x a2 y a3 z) 0 d(x2 y2 z2) 0
所以矢量线方程为
a1x a2 y a3 z k1
x2 y2 z2 k2
【习题 1.6 解】
ex ey ez A B (ex 9ey ez ) (2ex 4ey 3ez ) 1 9 1
2 4 3
31ex 5ey 14ez
【习题 1.3 解】
已知 A ex bey cez , B ex 3ey 8ez ,
(1)要使 A B ,则须散度 A B 0
所以从 A B 1 3b 8c 0 可得: 3b 8c 1
即 12ex 9ey ez • aex bey 12a 9b 0 ⑴
物理初二第一章练习题答案

物理初二第一章练习题答案1. 速度和加速度的关系根据物理学的基本概念,速度是物体运动的一个重要参量,而加速度则表示物体速度变化的快慢。
在初二的物理学习中,我们常常需要研究速度和加速度之间的关系。
以下是第一章练习题的答案:题目1:一个从静止开始的物体以恒定的加速度3 m/s²沿着一条直线运动,求它在5秒后的速度是多少?答案:根据物理学中的加速度公式v = u + at,其中v是末速度,u是初速度,a是加速度,t是时间。
给定初速度u=0,加速度a=3 m/s²,时间t=5秒。
代入公式计算可得v = 0 + 3 × 5 = 15 m/s。
题目2:一辆汽车在道路上以25 m/s的速度匀速行驶,经过10秒后它的位置是多少?答案:根据物理学中的位移公式s = ut,其中s是位移,u是速度,t 是时间。
给定速度u=25 m/s,时间t=10秒。
代入公式计算可得s = 25 ×10 = 250 m。
题目3:一个物体的速度从10 m/s增加到20 m/s,经过2秒的时间,求它的加速度是多少?答案:根据物理学中的加速度公式a = (v - u) / t,其中a是加速度,v是末速度,u是初速度,t是时间。
给定初速度u=10 m/s,末速度v=20 m/s,时间t=2秒。
代入公式计算可得a = (20 - 10) / 2 = 5 m/s²。
2. 动量守恒定律在物理学中,动量守恒定律是一个重要的原理,它指出在一个系统内,所有物体的总动量在没有外力作用的情况下保持不变。
以下是第一章练习题中涉及到动量守恒定律的答案:题目1:一辆质量为1000 kg的小轿车以20 m/s的速度向东行驶,和一辆质量为1500 kg的卡车以15 m/s的速度向东行驶发生碰撞,碰撞后两车结合在一起,求结合后的速度是多少?答案:根据动量守恒定律,碰撞前的总动量等于碰撞后的总动量。
小轿车的动量为mv1,卡车的动量为mv2,碰撞后的总动量为(m1 +m2)v。
《初等数论》各章习题参考解答

《初等数论》各章习题参考解答第一章习题参考解答1.解:因为25的最小倍数是100,9的最小倍数是,所以满足条件的最小正整数11111111100a =。
2.解:3在100!的分解式中的指数()1001001001003100!33113148392781⎡⎤⎡⎤⎡⎤⎡⎤=+++=+++=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦, 在100!的分解式中的指数()1001001001001002100!50251261942481664⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=++++=++++=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦,∴ ()9448474847100!2343123,,61k k k k =⋅⋅=⋅⋅=⋅=。
故 max 47n =,min 3M k =,(),61k =。
故 当M 最小值是3的倍数,但不是2的倍数。
3.解:112121n n n n x x ++++++等价于()()21221n n n x x x ++-+-,从而3x ³(n 就不会太大,存在反向关系)。
由()()22121n nn x x x -+-?+,得()()2212n n n x x -+?,即()()()121122nn x x -+?。
若2n ³,则()()()()251221114242nn x xx x-?+??,导致25140x x -+?,无解。
所以,只有1n =,335314x x x +-?,只能是37,14x +=,从而4,11x =。
综上所述,所求正整数对()()(),4,111,1x n =、。
4.解:按题意,2m n >>,记*,m n k k N =+?;则()222211111n n k nk n k k a a a a a a a a a a a a +++-+-?-+--++-22211111n k k n k k a a a a a a a a a ++?---+?-+-,故 存在无穷多个正整数a 满足2111n k k a a a a ++-+-。
(完整版)自动控制原理_第一章课后习题解答

第一章1.1 图1.18是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
c+-SM___ 1Q浮浮浮浮浮浮2Q浮浮浮浮浮浮浮浮浮浮浮浮fi-+解:系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控变量。
电位器用来设置期望液位高度*c(通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度*c上。
一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度*c。
系统方框图如图解1. 4.1所示。
1.2恒温箱的温度自动控制系统如图1.19所示。
(1) 画出系统的方框图;(2) 简述保持恒温箱温度恒定的工作原理;(3) 指出该控制系统的被控对象和被控变量分别是什么。
M放大器电机减速器调压器 220~热电偶电阻丝- +- +图1.19 恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增高,炉温就上升。
调压器电压由其滑动触点位置所控制,滑臂则由伺服电动机驱动.炉子的实际温度用热电偶测量,输出电压作为反馈电压与给定电压进行比较,得出的偏差电压经放大器放大后,驱动电动机经减速器调节调压器的电压。
在正常情况下,炉温等于期望温度T ,热电偶的输出电压等于给定电压。
此时偏差为零,电动机不动,调压器的滑动触点停留在某个合适的位置上。
第一章习题解答

第一章习题解答(P37)2、设机器字长为6 位,写出下列各数的原码、补码、反码和移码。
10101 11111 10000-10101 -11111 -10000解: ① [10101]原=[10101]补=[10101]反=010101B[10101]移=2n-1-1+010101=11111+10101=110100B② [-10101]原=110101B[-10101]反=101010B[-10101]补=101011B[-10101]移=11111-10101=001010B③ [11111]原=[11111]补= [11111]反=011111B[11111]移=11111+11111=111110B④ [-11111]原=111111B[-11111]反=100000B[-11111]补=100001B[-11111]移=11111-11111=000000B⑤ [10000]原=[10000]补=[10000]反=010000B[10000]移=11111+10000=101111B⑥ [-10000]原=110000B[-10000]反=101111B[-10000]补=110000B[-10000]移=11111-10000=001111B3、利用补码进行加减法运算比用原码进行运算有何优越性?答: 利用补码进行加减法运算比用原码进行运算的优越性主要表现在只用一套加法器电路就可以进行加减法运算,简化了电路,降低了运算器的成本。
5、设机器字长为8 位,最高位为符号位,试对下列各算式进行二进制补码运算。
(1) 16+6=?解:∵ [16]补=10H[6]补=06H∴ [16+6]补=[16]补+[6]补=10H+06H=16H(2) 8+18=?解:∵ [8]补=08H[18]补=12H∴ [8+18]补=[8]补+[18]补=08H+12H=1AH(3) 9+(-7)=?解:∵ [9]补=09H[-7]补=F9H∴ [9+(-7)]补=[9]补+[-7]补=09H+F9H=02H(4)-25+6=?解:∵ [-25]补=E7H[6]补=06H∴ [-25+6]补=[-25]补+[6]补=E7H+06H=EDH(5) 8-18=?解:∵ [8]补=08H[-18]补=EEH∴ [8-18]补=[8]补+[-18]补=08H+EEH=F6H(6) 9-(-7)=?解:∵ [9]补=09H[-(-7)]补=07H∴ [9-(-7)]补=[9]补+[-(-7)]补=09H+07H=10H (7) 16-6=?解:∵ [16]补=10H[-6]补=FAH∴ [16-6]补=[16]补+[-6]补=10H+FAH=0AH(8) -25-6=?解:∵ [-25]补=E7H[-6]补=FAH∴ [-25-6]补=[-25]补+[-6]补=E7H+FAH=E1H6、设机器字长为8 位,最高位为符号位,试用“双高位”法判别下述二进制运算有没有溢出产生。
基础化学习题解答(第一章)

习题解答(第一章物质结构基础)思考与习题1.填空题(1)原子核外电子运动具有波粒二象性、能量变化不连续的特征,其运动规律可用量子力学来描述。
(2)当主量子数为3时,包含有3s、3p、3d三个亚层,各亚层为分别包含1、3、5个轨道,分别能容纳2、6、10个电子。
(3)同时用n、l、m和m s四个量子数可表示原子核外某电子的运动状态;用n、l、m 三个量子数表示核外电子运动的一个轨道;而n、l两个量子数确定原子轨道的能级。
(4)改错的现象称为能级交错。
3d4S(6)原子序数为35的元素,其基态原子的核外电子分布式为1s22s22p63s23p63d104s24p5,用原子实表示为[Ar]3d104s24p5,其价电子构型为4s24p5,价电子构型的轨道表示式为;该元素位于元素周期表的第ⅦA 族,第四周期,元素符号是Br 。
(7)等价轨道处于全充满(p6、d10、f14)、半充满(p3、d5、f7)和全空(p0、d0、f0)状态时,具有较低的能量,比较稳定。
这一规律通常又称为洪德规则的特例。
(8)原子间通过共用电子对而形成的化学键,叫做共价键。
共价键的本质是原子轨道的重叠,其形成条件是两个具有自旋相反单电子的原子轨道,尽可能达到最大重叠。
(9)表征化学键性质的物理量,统称为键参数,常用的有键能、键长、键角。
(10)H2S分子的构型为V形,中心原子S采取sp3不等性杂化,键角∠HSH<109°28′(提示:填写>,=或<)。
(11)完成下表2.选择题(1)下列原子轨道中,属于等价轨道的一组是( C )。
A .2s ,3sB .2p x ,3p xC .2p x ,2p yD .3d xy ,4d xy(2)下列用一套量子数表示的电子运动状态中,能量最高的是( B )。
A .4,1,-1,-12B .4,2,0,-12C .4,0,0,+12D .3,1,1,+12(3)下列不存在的能级是( C )。
第一章习题解答及参考答案

∫
−∞
sin (ωx ) d x =1 πx x
又有
ω x ω sin π ( ω π x ) = ω sin c ω sin = π (ω π x ) π πx π π sin (ωx ) ∞ = ω →∞ πx 0 lim x=0 x≠0
∞
∞ ∞ x comb eiπx = ∑ δ ( x − m )eimπ = ∑ δ ( x − m )cos mπ 2 m = −∞ m = −∞
当 m = 奇数时, comb( x ) + comb( x )e
iπx
=0;
∞
当 m = 偶数时,令 m = 2n ,则 cos 2πx = 1 ,并且有:
1 2 1 − 2
dξ = 1 5 −x 2
3 5 ≤ x ≤ 时(见图(c)), 2 2
∫1Biblioteka 2 x−2dξ =④ 当x>
5 1 和 x < − 时,重叠面积等于零。 2 2
卷积后所得图形如附图 1-3 所示。
附图 1-3 习题[1-5](2)卷积结果的函数图形
[1-6]试用卷积定理计算下列各式。 (1) sinc ( x ) ∗ sinc ( x ) (2) F sinc ( x ) sinc ( 2 x )
∞ 1/ 2 x − ξ −1 x − ξ −1 x −1 dξ = ∫− ∞ rect(ξ ) rect dξ = ∫−1 / 2 rect 2 2 2
其中
x − ξ − 1 1 x − 2 ≤ ξ ≤ x rect = 2 其他 0 1 1 1 1 3 1 ≤ ξ ≤ ;当 ξ = − 时有 − ≤ x ≤ ,而当 ξ = 时有 2 2 2 2 2 2
《一元函数微积分》习题解答第一章

《一元函数微积分》 习题1—11.确定下列函数的定义域: (1)912-=x y ;解:要使函数有意义,则:092>-x 即 3>x 或3-<x .所以函数定义域:),3()3,(+∞⋃--∞.(2)x y a arcsin log =;解:要使函数有意义,则0arcsin >x ,即10≤<x .所以函数定义域:(0,1]. (3)2111x x y --+=; 解:01012≠+≥-x x 且,即111-≠≤≤-x x 且.所以函数定义域:(-1,1].(4))32(log 213-+-=x x y a ; 解:03202>-≠-x x 且,即232>≠x x 且.所以函数定义域:),2()2,23(+∞⋃. (5))4(log 21arccos 2x x y a -+-=; 解:0412112>-≤-≤-x x 且,则2231<<-≤≤-x x 且。
所以函数定义域:)2,1[- (6)xy πsin 1=.解:0sin ≠x π,则Z k k x ∈≠,.(其中是Z 整数集),函数定义域:_Z 或}{Z k k x x ∈≠,.2.求函数⎪⎩⎪⎨⎧=≠=000,1sin x x xy 的定义域和值域,并求⎪⎭⎫⎝⎛π2f 和)0(f . 解:定义域:),(+∞-∞. 当0≠x 时,01≠x ,故11sin 1≤≤-x. 所以值域:[-1,1]. 12sin )2(==ππf ,0)0(=f .3.下列各题中,函数)(x f 和)(x g 是否相同,为什么? (1) 2)(,)(x x g x x f ==;解: 不同 因为||)(2x x x g ==,即)(x g 的值域是全体非负实数,而)(x f 的值域是全体实数.(2) 2sin 21)(,cos )(2x x g x x f -==; 解: 相同因为)(x f 和)(x g 的定义域均为实数R ,值域为[-1,1],且)(cos 2sin21)(2x f x xx g ==-= (3)1)(,11)(2-=+-=x x g x x x f ; 解: 不同因为)1(111)(2≠-=+-=x x x x x f .两函数的定义域不同. (4)0)(,)(x x g xxx f ==. 解: 相同因为)0(1)(),0(1)(0≠==≠==x x x g x xxx f 定义域均为非零实数,在定义域内函数值恒等于1.4.设x x f sin )(=, 证明:)2cos(2sin2)()(x x x x f x x f ∆+∆=-∆+. 证明: 由三角函数知:)2cos(2sin 2sin )sin()()(xx x x x x x f x x f ∆+∆=-∆+=-∆+.5.设5)(2++=bx ax x f 且38)()1(+=-+x x f x f ,试确定a , b 的值.解: 因为 5)(2++=bx ax x f故)5()2(5)1()1()1(22+++++=++++=+b a x b a ax x b x a x f 由题设3852)()1(+=++=-+x a ax x f x f 所以有:82=a 且3=+b a 得:1,4-==b a .6.下列函数哪些是偶函数? 哪些是奇函数?哪些既非奇函数又非偶函数? (1) )1(22x x y -=; 解: 定义域:),(+∞-∞)()1(])(1[)()(2222x f x x x x x f =-=---=-所以函数是偶函数. (2)323x x y -=; 解: 定义域:),(+∞-∞32323)()(3)(x x x x x f +=---=-,)()(x f x f ≠-且)()(x f x f -≠-.所以函数既非奇函数又非偶函数.(3)2211x x y +-=;解: 定义域:),(+∞-∞)(11)(1)(1)(2222x f xx x x x f =+-=-+--=- 所以函数是偶函数. (4))1)(1(+-=x x x y 解: 定义域:),(+∞-∞x x x x x x f -=+-=3)1)(1()(,)()()()(33x f x x x x x f -=+-=---=-.所以函数是奇函数. (5)1cos sin +-=x x y ; 解: 定义域:),(+∞-∞1cos sin 1)cos()sin()(+--=+---=-x x x x x f ,则)()(x f x f ≠-且)()(x f x f -≠-所以函数既非奇函数又非偶函数.(6)2xx a a y -+=.解: 定义域:),(+∞-∞)(2)(x f a a x f xx =+=--所以函数是偶函数.7.设)(x f 为定义在),(+∞-∞上的任意函数,证明:(1))()()(1x f x f x F -+=为偶函数; (2) )()()(2x f x f x F --=为奇函数.证明: 由题设)(x f 为定义在),(+∞-∞的函数, 则)(),(21x F x F 的定义域也为),(+∞-∞ (1) )()()()()()()(111x F x f x f x F x f x f x F =+-=-⇒-+= ,. 故)(1x F 是偶函数. (2) )()()()()()()(222x F x f x f x F x f x f x F -=--=-⇒--= ,.故)(2x F 为奇函数.8. 证明: 定义在),(+∞-∞上的任意函数可以表示为一个奇函数与一个偶函数和. 证明: 设)(x f 是定义在),(+∞-∞上的任意函数.由7题知 )()()(1x f x f x F -+=为偶函数,)()()(2x f x f x F --=为奇函数. 且 )(21)(21)(21x F x F x f +=. 故命题成立.9. 设)(x f 为定义在),(L L -上的奇函数,若)(x f 在),0(L 上单增, 证明: )(x f 在)0,(L -上也单增.证明: 由题设知对于任意),(L L x -∈有:)()(x f x f -=-不妨设任意的1x ,2x 满足021<<<-x x L , 则012>-<->x x L .)(x f 在),0(L 上单增, 则)()(21x f x f ->- ,)(x f 奇函数)()(),()(2211x f x f x f x f -=--=-∴即 )()(21x f x f ->- )()(21x f x f < 所以)(x f 在)0,(L -上也单增.10. 下列各函数中哪些是周期函数? 对于周期函数,指出其周期: (1) )2cos(-=x y ;解:)2cos()22cos(-=+-x x π, 函数是周期函数且周期π2=T . (2) x y 4cos =; 解: x x x 4cos )24cos()2(4cos =+=+ππ, 函数是周期函数且周期2π=T .(3) x y πsin 1+=;解: )2(sin 1)2sin(1sin 1++=++=+x x x ππππ,函数是周期函数且周期2=T . (4) x x y cos =; 解: 非周期函数 (5) x y 2sin =; 解: )](2cos 1[21)]22cos(1[21)2cos 1(21sin 2ππ+-=+-=-=x x x x , 函数是周期函数且周期π=T . (6) x x y tan 3sin +=解: )32(3sin )23sin(3sin ππ+=+=x x x , )tan(tan π+=x x ,故原函数的周期为两函数x x tan ,3sin 的周期π32和π最小公倍数. 所以周期为π2=T .11. 下列各组函数中哪些不构成复合函数? 把能构成复合函数的写,成复合函数,并指出定义域. (1) 3x y =,t x sin =;解: 构成复合函数t y 3sin =, 定义域: ),(+∞-∞. (2) ua y =,2x u =;解: 构成复合函数2x a y =, 定义域: ),(+∞-∞. (3) u y a log =,232+=x u ;解: 构成复合函数)22(log 2+=x y a , 定义域: ),(+∞-∞. (4) u y =,2sin -=x u ;解: 不构成复合函数u y =要求0≥u , 但是2sin -=x u 的值域:]1,3[--. (5) u y =,3x u =; 解: 构成复合函数3x y =, 定义域: ),0[+∞.(6) u y a log =, 22-=x u .解: 构成复合函数)2(log 2-=x y a , 定义域: ),2()2,(+∞⋃--∞.12. 下列函数是由哪些简单函数复合而成的?(1) 321)1(++=x y ;解: 3u y =,1)1(2++=x u . (2) 2)1(ln 3+=x y ;解: u y 3=, 2v u =, 1ln +=x v .(3) )13(sin 3+=x y ;解: 3u y =, v u sin =, 13+=x v . (4) 32cos log x y a =.解: 3u y =, v u a log =, 2w v =, x w cos =.13. 求下列函数的反函数: (1) x y sin 2=;]2,2[ππ-∈x 解: 原函数的定义域:]2,2[ππ-∈x , 值域:]2,2[-. 反解: 2arcsin yx =. 得反函数: 2arcsinx y =. (2) )2(log 1++=x y a ;解: 原函数的定义域: ),2(+∞-, 值域:),(+∞-∞. 反解: 21-=-y a x .得反函数: 21-=-x ay反函数的定义域),(+∞-∞:, 值域: ),2(+∞-.(3) 122+=x xy .解: 121112112122+-=+-+=+=xx x x x y 由于112>+x, 则11210<+<x . 原函数的定义域: ),(+∞-∞, 值域:.)1,0( 反解: yy x-=12, y y x -=1log 2.得反函数: xx y -=1log 2反函数的定义域: )1,0(, 值域: ),(+∞-∞.14. 某批发商店按照下列价格表整盒在批发销售某种盒装饮料:当购货量小于或等于20盒时,每盒2.50元;当购货量小于或等于50盒时,其超过20盒的饮料每盒2.30元; 当购货量小于或等于100盒时,其超过50盒的饮料每盒2.00元; 当购货量大于100时,其超过100盒的饮料每盒1.80元;设x 是销售量, y 是总价, 试建立总价y 和销售量x 之间的函数关系式,并作出它的图形. 解: 由题知: 当200≤≤x 时, x y 5.2=;当5020≤<x 时, 43.2)20(3.2205.2+=-+⨯=x x y ;当10050≤<x 时, 192)50(2)2050(3.2205.2+=-+-⨯+⨯=x x y ; 当100>x 时, 398.1)100(8.1219+=-+=x x y⎪⎪⎩⎪⎪⎨⎧>+≤<+≤<+≤≤=100398.110050192502043.22005.2x x x x x x x xy 图形(略)15. 设某商品的市场供应函数p p S Q 480)(+-==, 其中Q 为供应量, p 为市场价格. 商品的单位生产成本是1.5元, 试建立总利润L 与市场价格p 的函数关系式. 解: 供应函数p p S Q 480)(+-==则总利润120864)480)(5.1()5.1(2+-=+--=-=p p p p Q p L .16. 用p 代表单价, 某商品的需求函数为p p D Q 500007)(-==, 当Q 超过1 000时成本函数为Q C 2500020+=, 试确定能达到损益平衡的价格 (提示: 当总收入=总成本时,便达到损益平衡).解: 当1000>Q 时 1000500007)(>-==p p D Q 则价格120<p . 达到损益平衡, 则 C pQ =即: )500007(25000202500020)500007(p Q p p -+=+=-039001652=+-p p得282.107165±=p又因为价格120<p , 故59.28=p答: 当需求量超过1000时,达到损益平衡的价格是28.59.17. 在半径为r 的球内嵌入一个内接圆柱, 试将圆柱的体积V 表示为圆柱的高h 的函数, 并求此函数的定义域.解: 设圆柱的半径为R, 则满足4)2(22222h r h r R -=-=圆柱的体积: 3222241)4(h h r h h r h R V ππππ-=-==. 定义域: )2,0(r18. 已知华氏温度F 与摄氏温度℃的线性关系, 在101325帕(一个标准大气压)下, 水的冰点温度不32F 或0℃, 水的沸点温度为212F 或100℃.(1) 写出华氏温度F 与摄氏温度℃的函数关系; (2) 画出该函数的图形;(3) 摄氏20℃相当于华氏几度?解: (1)由华氏温度F 与摄氏温度℃的线性关系, 设当摄氏温度为x ℃时, 华氏温度为y F , 则有关系式 b ax y += 其中a , b 为常数. 由题知:⎩⎨⎧==⇒⎩⎨⎧+=+⋅=328.1100212032b a b a b a 函数关系: 328.1+=x y (其中x 的度量单位是℃, y 的度量单位是F) (2) 函数图形(略)(3) 摄氏20℃时, y =1.8⨯20℃+32=68(F) 习题1-2 1.(1)0;(2)1;(3)-1;(4)发散 2.(1)证明:0>∀ε,要使ε<=-+nn 1111,即ε1>n 。
完整版高等代数习题解答(第一章)

完整版高等代数习题解答(第一章)高等代数题解答第一章多项式补充题1.当a,b,c取何值时,多项式f(x)=x-5与g(x)=a(x-2)^2+b(x+1)+c(x^2-x+2)相等?提示:比较系数得a=-1,b=-1,c=6.补充题2.设f(x),g(x),h(x)∈[x],f^2(x)=xg^2(x)+x^3h^2(x),证明:假设f(x)=g(x)=h(x)不成立。
若f(x)≠0,则∂(f^2(x))为偶数,又g^2(x),h^2(x)等于或次数为偶数,由于g^2(x),h^2(x)∈[x],首项系数(如果有的话)为正数,从而xg^2(x)+x^3h^2(x)等于或次数为奇数,矛盾。
若g(x)≠0或h(x)≠0,则∂(xg^2(x)+x^3h^2(x))为奇数,而f^2(x)为偶数,矛盾。
综上所证,f(x)≠g(x)或f(x)≠h(x)。
1.用g(x)除f(x),求商q(x)与余式r(x):1)f(x) =x^3-3x^2-x-1,g(x) =3x^2-2x+1;2)f(x) =x^4-2x+5,g(x) =x^2-x+2.1)解法一:待定系数法。
由于f(x)是首项系数为1的3次多项式,而g(x)是首项系数为3的2次多项式,所以商q(x)必是首项系数为1的1次多项式,而余式的次数小于2.于是可设q(x)=x+a,r(x)=bx+c。
根据f(x)=q(x)g(x)+r(x),即x^3-3x^2-x-1=(x+a)(3x^2-2x+1)+bx+c,右边展开,合并同类项,再比较两边同次幂的系数,得a=-1/3,b=-2/3,c=-1,故得q(x)=x-1/3,r(x)=-x-1/3.2)解法二:带余除法。
用长除法得商q(x)=x^2+x-1,余式r(x)=-5x+7.2.m,p,q适合什么条件时,有1)x^2+mx-1/x^3+px+q;2)x^2+mx+1/x^4+px^2+q.解:1)将x^3+px+q除以x^2+mx-1得商为x+m+1/(x+m-1),所以当m≠1时有解。
第一章 习题解答 物理化学

第一章习题解答1.1 物质的体膨胀系数αV与等温压缩率κT的定义如下:试导出理想气体的、与压力、温度的关系解:对于理想气体:PV=nRT , V= nRT/P求偏导:1.2 气柜储存有121.6kPa,27℃的氯乙烯(C2H3Cl)气体300m3,若以每小时90kg的流量输往使用车间,试问储存的气体能用多少小时?解:将氯乙烯(M w=62.5g/mol)看成理想气体:PV=nRT , n= PV/RT n=121600⨯300/8.314⨯300.13 (mol)=14618.6molm=14618.6⨯62.5/1000(kg)=913.66 kgt=972.138/90(hr)=10.15hr1.3 0℃,101.325kPa的条件常称为气体的标准状况,试求甲烷在标准状况下的密度?解:将甲烷(M w=16g/mol)看成理想气体:PV=nRT , PV =mRT/ M w甲烷在标准状况下的密度为=m/V= PM w/RT=101.325⨯16/8.314⨯273.15(kg/m3)=0.714 kg/m31.4 一抽成真空的球形容器,质量为25.0000g。
充以4℃水之后,总质量为125.0000g。
若改充以25℃,13.33kPa的某碳氢化合物气体,则总质量为25.0163g。
试估算该气体的摩尔质量。
水的密度按1 g.cm-3计算。
(答案来源:)解:球形容器的体积为V=(125-25)g/1 g.cm-3=100 cm3将某碳氢化合物看成理想气体:PV=nRT , PV =mRT/ M wM w= mRT/ PV=(25.0163-25.0000)⨯8.314⨯300.15/(13330⨯100⨯10-6) M w =30.51(g/mol)1.5 两个容器均为V的玻璃球之间用细管连接,泡内密封着标准状况下的空气。
若将其中一个球加热到100℃,另一个球则维持0℃,忽略连接细管中的气体体积,试求该容器内空气的压力。
理论力学作业解答
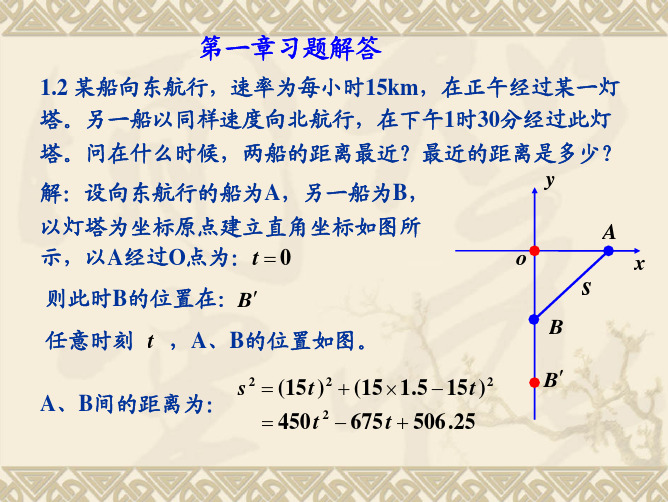
1.2 某船向东航行,速率为每小时15km,在正午经过某一灯 塔。另一船以同样速度向北航行,在下午1时30分经过此灯 塔。问在什么时候,两船的距离最近?最近的距离是多少? y 解:设向东航行的船为A,另一船为B, 以灯塔为坐标原点建立直角坐标如图所 示,以A经过O点为:t = 0 则此时B的位置在:B′ 任意时刻 t ,A、B的位置如图。 A、B间的距离为:
d ( − kv 0 cos α tg θ ) 1 dt = k ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
对上式积分可得:
1 ∫0 dt = k
t
∫α
−α
d ( − kv 0 cos α tg θ ) ( g + kv 0 cos α tg α ) − kv 0 cos α tg θ
v v0
α
v mg
θ
x
α v v
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
随着质点运动,切线方 向与 x 轴夹角减少,故有:
ρ
ds ρ =− dθ
(3)
dv m = − mkv − mg sin θ (1) dt v2 m = mg cos θ ( 2)
s 2 = (15 t ) 2 + (15 × 1 .5 − 15 t ) 2 = 450 t 2 − 675 t + 506 .25
A
o
s
B B′
x
s = 450 t − 675 t + 506 .25
2 2
y
A
当 A、B相距最近时有: d (s2 ) = 900 t − 675 = 0 dt 可得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 命题逻辑习题与解答⒈ 判断下列语句是否为命题,并讨论命题的真值。
⑴ 032=-x 。
⑵ 前进!⑶ 如果2078>+,则三角形有四条边。
⑷ 请勿吸烟!⑸ 你喜欢鲁迅的作品吗?⑹ 如果太阳从西方升起,你就可以长生不老。
⑺ 如果太阳从东方升起,你就可以长生不老。
解 ⑶,⑹,⑺表达命题,其中⑶,⑹表达真命题,⑺表达假命题。
⒉ 将下列命题符号化: ⑴ 逻辑不是枯燥无味的。
⑵ 我看见的既不是小张也不是老李。
⑶ 他生于1963年或1964年。
⑷ 只有不怕困难,才能战胜困难。
⑸ 只要上街,我就去书店。
⑹ 如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐。
⑺ 如果林芳在家里,那么他不是在做作业就是在看电视。
⑻ 三角形三条边相等是三个角相等的充分条件。
⑼ 我进城的必要条件是我有时间。
⑽ 他唱歌的充分必要条件是心情愉快。
⑾ 小王总是在图书馆看书,除非他病了或者图书馆不开门。
解 ⑴ p :逻辑是枯燥无味的。
“逻辑不是枯燥无味的”符号化为p ⌝。
⑵ p :我看见的是小张。
q :我看见的是老李。
“我看见的既不是小张也不是老李”符号化为q p ⌝∧⌝。
⑶ p :他生于1963年。
q :他生于1964年。
“他生于1963年或1964年”符号化为q p ⊕。
⑷ p :害怕困难。
q :战胜困难。
“只有不怕困难,才能战胜困难”符号化为p q ⌝→。
⑸ p :我上街。
q :我去书店。
“只要上街,我就去书店”符号化为q p →。
⑹ p :小杨晚上做完了作业。
q :小杨晚上没有其它事情。
r :小杨晚上看电视。
s :小杨晚上听音乐。
“如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐”符号化为s r q p ∨→∧。
⑺ p :林芳在家里。
q :林芳做作业。
r :林芳看电视。
“如果林芳在家里,那么他不是在做作业就是在看电视”符号化为r q p ∨→。
⑻ p :三角形三条边相等。
q :三角形三个角相等。
“三角形三条边相等是三个角相等的充分条件”符号化为q p →。
⑼ p :我进城。
q :我有时间。
“我进城的必要条件是我有时间”符号化为q p →。
⑽ p :他唱歌。
q :他心情愉快。
“他唱歌的充分必要条件是心情愉快” 符号化为q p ↔。
⑾ p :小王在图书馆看书。
q :小王病了。
r :图书馆开门。
“小王总是在图书馆看书,除非他病了或者图书馆不开门”符号化为p r q →⌝∨⌝)(。
⒊ 列出除∧,∨,⊕,→,↔之外的所有二元联结词的真值表。
解 共有16个二元联结词,记除∧,∨,⊕,→,↔之外的二元联结词为1121,,,∆∆∆ 。
⒋ 求下列公式在真值赋值)0/,0/,1/,1/(4321p p p p 下的值: ⑴ )(321p p p ∧∨⑵ ))()(()(4321321p p p p p p p ∨∧∨⌝∨∧∧ ⑶ )))((()(4321321p p p p p p p ⌝∧⌝∨∧⌝∨⌝∨∧⌝ ⑷ 4312)(p p p p ∨⌝→⌝↔ ⑸ )()(4231p p p p →⌝∧↔⑹ 421321)(p p p p p p ⌝∨↔⌝∧→∨ ⑺ )()(4231p p p p ⊕⌝∧↔解 记真值赋值)0/,0/,1/,1/(4321p p p p 为v 。
⑴ 1)01(1))((321=∧∨=∧∨p p p v 。
⑵ 1))00()11(()011()))()(()((4321321=∨∧∨⌝∨∧∧=∨∧∨⌝∨∧∧p p p p p p p v ⑶ ))))((()((4321321p p p p p p p v ⌝∧⌝∨∧⌝∨⌝∨∧⌝1)0)0)11(((0)11(=⌝∧⌝∨∧⌝∨⌝∨∧⌝=。
⑷ 100)11())((4312=∨⌝→⌝↔=∨⌝→⌝↔p p p p v 。
⑸ 0)01()01())()((4231=→⌝∧↔=→⌝∧↔p p p p v 。
⑹ 101)101(1))((421321=⌝∨↔⌝∧→∨=⌝∨↔⌝∧→∨p p p p p p v 。
⑺ 0)01()01())()((4231=⊕⌝∧↔=⊕⌝∧↔p p p p v 。
5. 用真值表判断以下公式是不是永真式、永假式、可满足式。
(1) ))()(()(r q p r q r p →∨→→→→ (2) p p p ⌝→⌝→)((3) ))(()(p q p q p →⌝→→→(4) ))()(())((r p q p r q p →→→→→→ (5) r r q r p q p →→∧→∧∧)()()( (6) )(q p p →⌝∧⌝(7) ))(()(p q p q p ⌝→⌝→→→解 (1), (2), (4), (5), (7)是永真式,(6)是永假式,(3)是非永真的可满足式。
6. 指出满足下列公式的所有真值赋值。
(1) )()(r p q p ∨⌝∨∧ (2) ))((q p r q p ∨∧⌝∧∨ (3) )()(r q r p r p ∨∧∨⌝→∨ (4) )(r q p ↔⊕解 (1) )0/,0/,0/(r q p ,)1/,0/,0/(r q p ,)0/,1/,0/(r q p ,)1/,1/,0/(r q p ,)1/,0/,1/(r q p ,)0/,1/,1/(r q p ,)1/,1/,1/(r q p 。
(2) )0/,1/,0/(r q p ,)0/,0/,1/(r q p ,)1/,0/,1/(r q p ,)0/,1/,1/(r q p ,)1/,1/,1/(r q p 。
(3) )0/,0/,0/(r q p ,)0/,1/,0/(r q p 。
(4) )0/,0/,0/(r q p ,)1/,1/,0/(r q p ,)1/,0/,1/(r q p ,)0/,1/,1/(r q p 。
7. 若公式A 既不是永真式,也不是永假式,则A 的每个替换实例一定既不是永真式,也不是永假式。
对吗?解 不对。
若A 是非永真的可满足式,则它的替换实例中既有永真式,也有永假式,也有非永真的可满足式。
8.用真值表证明以下等值式。
(1) (2) (3) (4)9.用等值演算证明以下等值式。
(1) )()(r p q r q p →→⇔→→ (2) r q p r p q p ∧→⇔→∧→)()( (3) q r p q r q p →∧⇔→∨→)()( (4) )()(q p p p q p →→⌝⇔→→ (5) q r p q r q p →∨⇔→∧→)()( (6) q p q p ⌝↔⇔↔⌝)(解 (1) )()()()(r p q r p q r q p r q p →→⇔∨⌝∨⌝⇔∨⌝∨⌝⇔→→ (2) r q p r q p r p q p r p q p ∧→⇔∧∨⌝⇔∨⌝∧∨⌝⇔→∧→)()()()()( (3) q r p q r p q r q p q r q p →∧⇔→∧⌝⇔∨⌝∨∨⌝⇔→∨→)()()( (4) )(1)(q p p q p p p q p p q p →→⌝⇔∨⌝∨⌝⌝⇔⇔∨⌝∨⌝⇔→→ (5) q r p q r q p q r q p ∨⌝∧⌝⇔∨⌝∧∨⌝⇔→∧→)()()()()(q r p q r p →∨⇔∨∨⌝⇔)((6) q p q p q p q p q p ⌝↔⇔⌝⊕⌝⇔⊕⊕⊕⇔⊕⇔↔⌝)(1))1(()( 10.用等值演算证明以下公式是永真式。
(1) p q p p q ↔→⌝∧→)()((2) )()()(s q r p s r q p ∧→∧→→∧→(3) )()()()(s r q p s p r p q p ∨∨→→→∨→∨→ (4) )()()(r q r p r q p →∨→→→∨解 (1) p q p p q ↔→⌝∧→)()(1)()(⇔↔⇔↔⌝∨∧∨⌝⇔p p p q p p q (2) )()()(s q r p s r q p ∧→∧→→∧→ s q r p s r q p ∧→∧∧∨⌝∧∨⌝⇔)()( s q r s r p q p ∧→∧∨⌝∧∧∨⌝⇔)()(1⇔∧→∧∧∧⇔s q r s p q(3) )()()()(s r q p s p r p q p ∨∨→→→∨→∨→ )(s r q p s p r p q p ∨∨→→∨⌝∨∨⌝∨∨⌝⇔1⇔∨∨∨⌝→∨∨∨⌝⇔s r q p s r q p(4) )()()(r q r p r q p →∨→→→∨ r q r p r q p ∨⌝∨∨⌝∨∨∨⌝⌝⇔))(( r q p r q p ∨⌝∨⌝∨⌝∧∨⇔))((111)()(⇔∧⇔∨⌝∨⌝∨⌝∧∨⌝∨⌝∨∨⇔r q p r r q p q p11.用等值演算证明以下公式是永假式。
(1) p q p p q ⌝↔→⌝∧→)()( (2) )()()(r p r q q p →⌝∧→∧→解 (1) p q p p q ⌝↔→⌝∧→)()(0)()(⇔⌝↔⇔⌝↔⌝∨∧∨⌝⇔p p p q p p q (2) )()()(r p r q q p →⌝∧→∧→)()()(r p r q q p ∨⌝⌝∧∨⌝∧∨⌝⇔ r p r q q p ⌝∧∧∨⌝∧∨⌝⇔)()())(())((r r q p q p ⌝∧∨⌝∧∧∨⌝⇔0⇔⌝∧⌝∧∧⇔r q q p12.找出与下列公式等值的尽可能简单的由},{∧⌝生成的公式。
13.找出与下列公式等值的尽可能简单的由},{∨⌝生成的公式。
(1) )(p r q p →⌝∧⌝∧⌝(2) q p r q p ∧⌝∧⌝∨→)( (3) p q p ⌝∧∧解 (1) )(p r q p →⌝∧⌝∧⌝)(p r q p ∨⌝⌝∧⌝∧⌝⇔ )()(p q p r q p ∧⌝∧⌝∨⌝⌝∧⌝∧⌝⇔r q p ⌝⌝∧⌝∧⌝⇔)(r q p ⌝∨∨⌝⇔(2) ))(()()(q p r q p q p r q p q p r q p ⌝∨∨⌝∨∨⌝⌝⌝⇔∧⌝∧⌝∨∨⌝⇔∧⌝∧⌝∨→ (3) )(p q p p q p ∨⌝∨⌝⌝⇔⌝∧∧14.设A 是由}{↔生成的公式。
证明:A 是永真式当且仅当每个命题变元在A 中出现偶数次。
证明 首先证明:若A 是由}{↔生成的仅出现一个命题变元p 的公式,则⎩⎨⎧⇔中出现奇数次在若中出现偶数次在若A p pA p A 1对p 在A 中的出现次数进行归纳。
① 若p 在A 中出现1次,即A 为p ,显然p A ⇔。
② 若p 在A 中出现2次,即A 为p p ↔,显然1⇔A 。
③ 设p 在A 中的出现n 次,A 为C B ↔,p 在B ,C 中的出现次数分别为k 和l ,则l k n +=,n k <且n l <。
