安徽六校教育研究会2020届高三第二次素质测试理科数学答案及评分标准
1.安徽六校教育研究会2020届高三第二次素质测试数学试题(理)含答案
数学(理科)
注意事项: 1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑。如需
改动,用橡皮擦干净后,再填涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本 试卷上无效。
2
2
(1)求角 C 的大小;
(2)若 c 4 , | CA CB | 38 ,求△ABC 的周长.
18.(12 分)
如图,四棱锥 P ABCD 中,侧面 PAB 为等腰直角三角形, BC 平面 PAB , PA PB ,
AB BC 2 , AD BD 5 .
P
(1)求证: PA 平面 PBC ;
1 解得 cosC ,所以 C 60 .
2
(2)由余弦定理, c2 a2 b2 ab 16 ,再由 | CA CB |2 a2 b2 ab 38 ,
(6 分)
解得 a2 b2 27 , ab 11 ,所以 (a b)2 49 , a b 7 ,
故 △ABC 的周长为11 .
1
6
从而离心率 e 1 (0, ) .
a2
3
三、解答题:共 70 分。
(一)必考题:共 60 分。
17.(12 分)
【解析】(1)由题, 2sin2 A B 2cos2 A B 2cos Acos B
2
2
1 cos(A B) 1 cos( A B) 2cos Acos B 2 2cos( A B) 2 2cosC 1 ,
2
2
角形, MF MN ,故 2PM 2MN 2(PM MN ) (2 EM MF) 2AA1 2 .
安徽六校教育研究会2020届高三第二次素质测试 理科数学(含答案)

安徽六校教育研究会2020届高三第二次素质测试数学(理科)一、选择题:本大题共12小题,每题5分.满分60分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1.己知集合A={x ∈R|x 1>-1},集合B={ x ∈R||x|>1},则A ∩B= A .(1,+ ∞) B .(0,+ ∞) C .(-∞,-1) ∪ (0,+ ∞) D .(-∞,-1) ∪ (1,+ ∞) 2.已知复数z 满足:zi=3+4i (i 为虚数单位),则z =A. 4+3iB.4- 3iC.-4+3iD. -4-3i3.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在2015年以前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为70%.2015年开始全面实施“精准扶贫”政策后,扶贫效果明显提高,其中2019年度实施的扶贫项目,各项目参加户数占比(参加该项目户数占2019年贫困户总数的比)及该项目的脱贫率见下表:那么2019年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的A .2837 倍B .3547倍 C. 3548倍 D .57倍 4.函数y=sin|x|+x 在x ∈[-2,2 ]上的大致图象是5.已知双曲线C: 2222b y a x -=l (a>0,b>0)的右焦点为F ,O 为坐标原点,以OF 为直径的圆与双曲线C 的一条渐近线交于点O 及点A )23,23(,则双曲线C 的方程为 A .1322=-y x B . 16222=-y x C .1322=-y x D. 12622=-y x 6.已知实数x,y 满足不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+04404201y x y x y x ,则|3x+4y|的最小值为A. 2B. 3C. 4D. 57.已知某几何体的三视图如图所示,则该几何体外接球的表面积为A. 24πB. 28πC. 32πD. 36π8.《易经>包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深, 对今天的几何学和其它学科仍有深刻的影响,下图就是《易经》中记载的几何图形一一八卦田,图中正八边形代表八卦,中间的圆代表阴阳太极图,图中八块面积相等的曲边梯形代表八卦田.已知正八边形的边长为l0m ,代表阴阳太极图的圆的半径为4m ,则每块八卦田的面积约为A .47.79m 2 B. 54.07m 2 C .57.21m 2 D .114.43 m 29.已知数列{a n }中,a 1=l ,a 2 =2,且当n 为奇数时,a n+2-a n =2;当n 为偶数时,a n+2+l= 3(a n +1).则此数列的前20项的和为A .23311-+90B .23311-+100C .23312- +90D .23312-+100 10.函数)20,0,0)(sin()(πϕωϕω<<>>+=A x A x f 的部分图象如图所示,己知 3)65()0(==πg g ,函数y=f (x )的图象可由y= g(x)图象向右平移3π个单位长度而得到,则函数f(x)的解析式为A. x x f 2sin 2)(=B. )32sin(2)(π+=x x f C. x x f 2sin 2)(-= D. )32sin(2)(π+-=x x f 11.已知函数f(x)=(lnax-1)(x 2+ax-4).若x>0时,f(x)≥0恒成立,则实数a 的值为A .2eB .4eC .e e-4 D .2-e e12.如图所示,棱长为l 的正方体ABCD - A 1B 1C 1D 1中,P 为线段AB 1的中点,M ,N 分别 为线段AC 1和棱B 1C 1,上任意一点,则MN PM 22+的最小值为A. 22 B .2 C .3 D .2 二、填空题:本题共4小题,每题5分,共20分。
安徽六校教育研究会2020届高三第二次素质测试理科综合试卷

后,这种软体动物体内便存在叶绿体并可以进行光合作用。在光学显微镜下观察绿叶海
蜗牛的细胞,可以分辨的结构有
A.叶绿体和核糖体
B.叶绿体和细胞壁
C.叶绿体和细胞核
D.细胞核和细胞壁
2. PTEN 是一种抑癌基因,表达的 PTEN 蛋白可以提高生物体的抗癌能力,但泛素连接酶
可导致 PTEN 蛋白被降解。西兰花经消化生成的 3-吲哚甲醇能与泛素连接酶结合,调
安徽六校教育研究会 2020 届高三第二次素质测试
理科综合能力测试
注意事项: 1.答题前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。 写在本试卷上无效。
种类
叶片形态
叶片厚度 叶片面积
/ mm
/ mm2
叶片被毛
渗透压 气孔开放度日均值 / kPa (/ mmol H2O·m-2·s-1)
A种 B种 C种
平展或微瓦状 瓦状 卷筒状
0.208 0.235 0.323
95.10 14.88 11.90
少许绿色柔毛 密灰色柔毛
密直立或伏贴绢毛
1 276 1 807 2 286
3.考试结束后,将本试卷和答题卡一并交回。 可能用到的相对原子质量:H-1,C-12,O-16,Na-23,S-32,Ca-40
一、选择题:本题共 13 小题,每小题 6 分,共 78 分。在每小题给出的四个选项中,只有一
项是符合题目要求的。
1. 绿叶海蜗牛能从它的藻类食物中“偷”来叶绿体,并吸收入自己的细胞内。首次捕食绿藻
10.下列对实验现象的解释正确的是
安徽六校教育研究会2020届高三第二次素质测试理综化学试题

安徽六校教育研究会2020届高三第二次素质测试理科综合能力测试注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H-1,C-12,O-16,Na-23,S-32,Ca-40一、选择题:本题共7小题,每小题6分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
7.北宋《本草图经》中载有:“绿矾形似朴消(Na2SO4·10H2O)而绿色,取此一物置于铁板上,聚炭,封之囊袋,吹令火炽,其矾即沸,流出色赤如融金汁者,是真也。
”下列对此段话的理解正确的是A.朴消是黑火药的成分之一 B.上述过程发生的是置换反应C.此记载描述的是鉴别绿矾的方法 D.“色赤”物质可能是单质铜8. 有机物X的结构简式如右图所示,下列有关说法错误的是A.X的分子式为C13H10O5 B.X分子中有五种官能团C.X能使溴的四氯化碳溶液褪色 D.X分子中所有碳原子可能共平面9.N A代表阿伏加德罗常数的值。
下列叙述正确的是A.46g乙醇中存在的共价键总数为7N AB.34g硫化氢在足量的氧气中燃烧转移电子总数为8N AC.标准状况下,22.4LHF含有的原子数为2N AD.64gCaC2晶体中阴离子和阳离子总数为2N A10.下列对实验现象的解释正确的是11.X、Y、Z为原子序数依次增大的短周期主族元素。
元素W分别与元素X、Y、Z结合形成质子数相同的甲、乙、丙三种分子。
反应②是工业制硝酸的重要反应,乙与丙的混合物不能用玻璃瓶盛装。
上述物质有如图所示的转化关系:下列说法错误的是A.甲是易液化气体,常用作致冷剂 B.可以用甲在一定条件下消除丁对环境的污染C.甲、丙分子可以直接化合生成离子化合物D.丁是一种红棕色气体,是大气主要污染物之一12.常温下,将1molCaC2O4粉末置于盛有500mL蒸馏水的烧杯中,然后向烧杯中加入Na2CO3固体(忽视溶液体积的变化)并充分搅拌,加入Na2CO3固体的过程中,溶液中Ca2+和CO32-的浓度变化曲线如图所示,下列说法中不正确的是A.a=5.6B.常温下,Ksp(CaC2O4)>Ksp(CaCO3)C.b点对应的溶液中,离子浓度关系为D.若使1molCaC2O4全部转化为CaCO3,至少要加入2.12molNa2CO313.苯甲酸在水中的溶解度为:0.18g(4℃)、0.34g(25℃)、6.8g(95℃)。
安徽六校教育研究会2020届高三第二次素质测试理综试题 word含答案.doc

安徽六校教育研究会2020届高三第二次素质测试理科综合能力测试注意事项:1.答题前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上。
2.回答选择题时,选出每小题参考答案后,用铅笔把答题卡上对应题目的参考答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他参考答案标号。
回答非选择题时,将参考答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
可能用到的相对原子质量:H-1,C-12,O-16,Na-23,S-32,Ca-40一、选择题:本题共13小题,每小题6分,共78分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.绿叶海蜗牛能从它的藻类食物中“偷”来叶绿体,并吸收入自己的细胞内。
首次捕食绿藻后,这种软体动物体内便存在叶绿体并可以进行光合作用。
在光学显微镜下观察绿叶海蜗牛的细胞,可以分辨的结构有A.叶绿体和核糖体B.叶绿体和细胞壁C.叶绿体和细胞核D.细胞核和细胞壁2.PTEN是一种抑癌基因,表达的PTEN蛋白可以提高生物体的抗癌能力,但泛素连接酶可导致PTEN蛋白被降解。
西兰花经消化生成的3-吲哚甲醇能与泛素连接酶结合,调节其效用,抑制肿瘤生长。
下列叙述正确的是A.PTEN基因突变细胞就会癌变B.PTEN蛋白能控制细胞正常生长和分裂的进程C.3-吲哚甲醇对泛素连接酶的效用起促进作用D.3-吲哚甲醇可能改变了泛素连接酶的空间结构3.光合作用的发现是众多科学家不断努力的结果。
1937年,英国科学家希尔首次获得了离体叶绿体悬浮液,将此悬浮液(含水,不含CO2)与黄色的高铁(Fe3+)盐混合,照光后发现叶绿体有气泡放出、溶液由黄色变为浅绿色(Fe2+)。
在遮光下,则没有气泡产生,也没有颜色变化。
下列叙述错误的是A.实验过程中可以检测到糖的生成B.实验表明氧气是叶绿体在光照的条件下产生的C.溶液颜色变化的原因是叶绿体在光照条件下生成的还原剂将Fe3+还原为Fe2+D.与恩格尔曼的水绵实验相比,希尔的实验排除了细胞内其他结构的影响4.下表是对某单基因遗传病进行调查后整理出的数据。
【理科数学】安徽六校教育研究会2020届高三第二次素质测试卷含答案
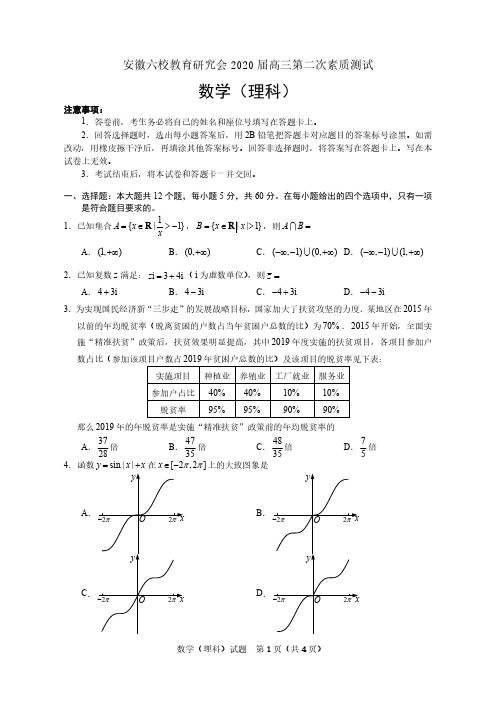
直径,过点 B 作小圆 O 的切线交大圆于另一点 C ,切点为 M ,点
A
P 为劣弧 BC 上的任一点(不包括 B,C 两点),则 AM (BP CP)
C P
M
O
B
的最大值是
.
16.已知两动点 A, B 在椭圆 C : x2 y2 1(a 1) 上,动点 P 在直线 3x 4 y 10 0 上,若 APB a2
2
2
(1)求角 C 的大小;
(2)若 c 4 , | CA CB | 38 ,求△ABC 的周长.
3(an 1) .则此数列的前 20 项的和为
311 3
A.
90
2
311 3
B.
100
2
312 3
C.
90
2
312 3
D.
100
2
5 10.函数 g(x) Asin( x )( A 0, 0,0 2 ) 的部分图象如图所示,已知 g(0) g( )
6
3 ,函数 y f (x) 的图象可由 y g(x) 图象向右平移 个单位长度而得到,则函数 f (x) 的
施“精准扶贫”政策后,扶贫效果明显提高,其中 2019 年度实施的扶贫项目,各项目参加户
数占比(参加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 种植业 养殖业 工厂就业 服务业
参加户占比 40% 40% 10% 10%
脱贫率 95% 95% 90% 90%
那么 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的
安徽六校教育研究会 2020 届高三第二次素质测试
数学(理科)
注意事项: 1.答卷前,考生务必将自己的姓名和座位号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用 2B 铅笔把答题卡对应题目的答案标号涂黑。如需
安徽六校教育研究会2020届高三第二次素质测试理科数学试卷含答案

3(an 1) .则此数列的前 20 项的和为
311 3
A.
90
2
311 3
B.
100
2
312 3
C.
90
2
312 3
D.
100
2
5 10.函数 g(x) Asin( x )( A 0, 0,0 2 ) 的部分图象如图所示,已知 g(0) g( ) 3 ,
6
函数 y f (x) 的图象可由 y g(x) 图象向右平移 个单位长度而得到,则函数 f (x) 的解析式为
2.已知复数 z 满足: zi 3 4i ( i 为虚数单位),则 z
A. 4 3i
B. 4 3i
C. 4 3i
D. 4 3i
3.为实现国民经济新“三步走”的发展战略目标,国家加大了扶贫攻坚的力度.某地区在 2015 年以
前的年均脱贫率(脱离贫困的户数占当年贫困户总数的比)为 70% .2015 年开始,全面实施“精
准扶贫”政策后,扶贫效果明显提高,其中 2019 年度实施的扶贫项目,各项目参加户数占比(参
加该项目户数占 2019 年贫困户总数的比)及该项目的脱贫率见下表:
实施项目 种植业 养殖业 工厂就业 服务业
参加户占比 40% 40% 10% 10%
脱贫率 95% 95% 90% 90%
那么 2019 年的年脱贫率是实施“精准扶贫”政策前的年均脱贫率的
4x y 4 0
A. 2
B. 3
C. 4
D. 5
7.已知某几何体的三视图如图所示,则该几何体外接球的表面积为
A. 24
4
B. 28
C. 32 D. 36
3
3
正视图
安徽六校教育研究会2020届高三第二次素质测试理科综合参考答案及评分标准

理科综合(生物)解析及评分标准
1. 答案:C 解析:绿叶海蜗牛是软体动物,无细胞壁,捕食藻类后,细胞内存在叶绿体。在光学显微镜 下无法分辨核糖体,可以分辨的结构是叶绿体和细胞核,C 正确
2. 答案:D
解析:癌细胞的产生不是单一基因突变的结果,至少在一个细胞中发生 5~6 个相关的基因 突变才会导致细胞癌变,A 错误。控制细胞正常生长和分裂的进程是原癌基因的作用,抑癌 基因主要作用是阻止细胞不正常增殖,B 错误。3-吲哚甲醇与泛素连接酶结合后抑制肿瘤生 长,而泛素连接酶会导致抑制细胞癌变的 PTEN 蛋白的降解,故 3-吲哚甲醇应抑制泛素连 接酶的功能,C 错误。3-吲哚甲醇与泛素连接酶结合,可调节该蛋白质的功能,而蛋白质的 结构与功能相适应,所以推测 3-吲哚甲醇可能改变了泛素连接酶的空间结构,D 正确。
符合题目要求,第19~21题有多项符合题目要求。全部选对的得6分,选对但不全的得3分,
有选错的得0分。
题号
14
15
16
17
18
19
20
21
答案
D
C
B
D
B
AD
AB
BD
14. 选 D
解析: 设用光子能量为 5.0 eV 的光照射时,光电子的最大初动能为 Ekm,当反向电压 达到 U=1.60V 以后,电流表读数为零说明具有最大初动能的光电子也达不到阳极,因此
CO32-
H2CO3 或 CO2
(2 分)
0
V(HCl)/mL
27.(14 分)
(1)坩埚(1 分) O=N-Cl (1 分)
(2)Fe(OH)3 为胶状沉淀,对[Pd(NH3)2]2+具有很强的吸附作用,若不进行此操作,[Pd(NH3)2]2+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设 M (t,3) ,则 P(2t, 6) ,代入抛物线 C 的方程解得 2t 9 ,
3 13
1
9 13
于是 MO MA MP 2 ,所以 S△OPA 2 MA yP 2 .
(12 分)
20.(12 分)
【解析】(1) f '(x) 2e2x ex (sin x cos x) , f '(0) 2 , f (0) ,
所以直线 l 方程为 y (2 )x ,
即 y (2 )(x 1) 2 ,恒过点 (1, 2) .
(5 分)
(2)将 (1, 6) 代入直线 l 方程,得 2 .考虑方程 f (x) 0 ,
即 e2x 2cos xex 1 0 ,等价于 ex ex 2cos x 0 ,
z
因为 PA PB , AD BD ,所以 PO AB , DO AB ,
P
因为 BC 平面 PAB ,所以 PAB 平面 ABCD ,
所以 PO 平面 ABCD , PO OD ,
如图,以 O 为坐标原点, OD,OB,OP 分别为 x, y, z 正半轴建立 A
O
B y
空间直角坐标系 O xyz ,
k
k
因为 g(1) 1.1, g(2) 0.69, g(3) 0.604, g(4) 0.594, g(5) 0.61 ,所以 k 4 时平均检验次数最
少,约为1000 0.594 594 次.
(12 分)
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的第一题计分。
(5 分) (10 分)
23.[选修 4−5:不等式选讲](10 分) 【解析】(1) a3 b3 (2a2b 2ab2 ) (a b)(a2 ab b2 ) 2ab(a b)
(a b)(a2 ab b2 ) (a b)[(a b)2 3 b2 ] 24
∵ a b ,∴ a b 0 ,又 (a b )2 3 b2 0 ,∴ a3 b3 2a2b 2ab2 . 24
2
2
角形, MF MN ,故 2PM 2MN 2(PM MN ) (2 EM MF) 2AA1 2 .
2
2
二、填空题:本题共 4 小题,每小题 5 分,共 20 分。
3 13. .
212
14. 160 .
15. 4 10 8 .
6 16. (0, )
3
16.提示:不难知,圆 x2 y2 a2 1 上任意一点向椭圆 C 所引的两条切线互相垂直,因此当直线 3x 4 y 10 0 与圆 x2 y2 a2 1 相离时, APB 恒为锐角,故 a2 1 d 2 4 ,1 a2 3 ,
(12 分)
18.(12 分) 【解析】(1)因为 BC 平面 PAB , PA 平面 PAB ,所以 BC PA ,
由 △PAB 为等腰直角三角形,所以 PA PB , 又 PB BC B ,故 PA 平面 PBC .
(5 分)
理科数学答案 第 1 页(共 3 页)
(2)取 AB 的中点 O ,连接 OP,OD ,
安徽六校教育研究会 2020 届高三第二次素质测试
理科数学参考答案
一、选择题:本大题共 12 个题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符 合题目要求的。
1
2
3
4
5
6
7
8
9
10
11
12
D
A
B
D
C
B
C
B
A
A
C
D
11.提示:考虑函数 y ln ax 1(x 0) 与 y x2 ax 4(x 0) 的图象,不难知它们有公共的零点 t 时,
1
6
从而离心率 e 1 (0, ) .
a2
3
三、解答题:共 70 分。
(一)必考题:共 60 分。
17.(12 分)
【解析】(1)由题, 2sin2 A B 2cos2 A B 2cos Acos B
2
2
1 cos(A B) 1 cos( A B) 2cos Acos B 2 2cos( A B) 2 2cosC 1 ,
b a 11
b3 a3 b a
b2 ab a2
(2) ( ) ,即
,即
(*)
a2 b2
ab
a2b2
ab
a2b2
ab
b2 ab a2 b a
① 当 ab 0 时,(*)即
1 恒成立,
ab
ab
(5 分)
b a ba ∵ 2 2 (当且仅当 a b 时取等号),故 3
f (x) 0 恒成立.于是, at 4 t2 e ,解得 a e . 4e
12.提示:取 AC 中点 E ,过 M 作 MF 面 A1B1C1D1 ,则 △APM≌△AEM ,故 PM EM ,而对固 定的点 M ,当 MN B1C1 时, MN 最小.此时由 MF 面 A1B1C1D1 ,可知 △MFN 为等腰直角三
记 g(x) ex ex 2 cos x ,则 g'(x) ex ex 2sin x 2 ex ex 2sin x 2 2sin x 0 ,
于是函数 g(x) 在 R 上单调递增,又 g( ) e 2 e 2 0 , g(0) 2 0 ,
2
所以函数 g(x) 在区间 ( ,0) 上存在唯一零点,即函数 f (x) 存在唯一零点.
则 AO BO PO 1 , DO AD2 AO2 2 ,
D
C
又 BC AB , DO PA ,所以 OD // BC 且 OD BC ,于是
x
Hale Waihona Puke P(0,0,1) , A(0, 1,0) , D(2,0,0) , C(2,1,0) , PC (2,1, 1) , AP (0,1,1) , AD (2,1,0) ,
a b ab
b2 ab a2 b a
② 当 ab 0 时,(*)即
1 恒成立,
ab
ab
ba
ba
ba
∵ [( ) ( )] 2 ( ) ( ) 2 (当且仅当 a b 时取等号),故 1
ab
ab
ab
综上, [1,3] .
(10 分)
理科数学答案 第 3 页(共 3 页)
22.[选修 4−4:坐标系与参数方程](10 分)
【解析】(1)曲线 C2 的方程化成直角坐标方程为 x2 y2 8y 即 x2 ( y 4)2 16 , 圆心 C2 (0, 4) ,半径 r 4 ,曲线 C1 为过定点 P(2, 2) 的直线, 易知 P(2, 2) 在圆 C2 内,当 PC2 AB 时, 线段 AB 长最小为 2 r2 | PC2 |2 2 16 [(2 0)2 (2 4)2 ] 4 2 . (2)当点 M 与点 P 不重合时,设 M (x, y) ,∵ C2M PM , ∴ C2M PM x(x 2) ( y 4)( y 4) 0 ,化简得: (x 1)2 ( y 3)2 2 , 当点 M 与点 P 重合时,也满足上式, 故点 M 的轨迹方程为 (x 1)2 ( y 3)2 2 .
9 若线段 AF 与抛物线 C 有公共点,即 a 时,
4 则 A, P, F 三点共线时, | PA | | PF | 的最小值为 | PF | (a 1)2 32 5 ,此时 a 3 .
综上,实数 a 的值为 3 或 4 .
(6 分)
(2)因为 MOA MAO AOF ,所以 MA∥x 轴且 MO MA MP ,
1 解得 cosC ,所以 C 60 .
2
(2)由余弦定理, c2 a2 b2 ab 16 ,再由 | CA CB |2 a2 b2 ab 38 ,
(6 分)
解得 a2 b2 27 , ab 11 ,所以 (a b)2 49 , a b 7 ,
故 △ABC 的周长为11 .
.
| PC | | n | 6 3 9
(12 分)
19.(12 分) 9
【解析】(1)由题, F (1,0) ,若线段 AF 与抛物线 C 没有公共点,即 a 时, 4
设点 P 在抛物线准线 x 1 上的射影为 D ,则 D, P, A 三点共线时,
| PA | | PF | 的最小值为| AD | a (1) 5 ,此时 a 4 ;
2
(12 分)
理科数学答案 第 2 页(共 3 页)
21.(12 分)
1 1 k 【解析】(1)由题, X 的可能取值为 和 ,
kk
P( X
1 )
(1
p)k
, P(X
1
k )
1
(1
p)k
,故
X
的分布列为
k
k
1
1 k
X
k
k
P (1 p)k 1 (1 p)k
E(X )
1
(1
p)k
1
k
[1 (1
p)k ] 1 (1
p)k
1
.
k
k
k
(5 分)
(2)(ⅰ)由(1),记
f ( p) 1 (1
p)k
1 ,因为 k
0 ,所以
f ( p) 在
p (0,1) 上单调递增
,
k
故 p 越小, f ( p) 越小,即所需平均检验次数越少,该方案越合理.
(8 分)
(ⅱ)记 g(k) 1 (1 p)k 1 1 0.9k 1 ,当 g(k) 1且取最小值时,该方案最合理,
设平面 PAD 的法向量为 n (x, y, z) ,则
n AP y z 0
,令 x 1 得平面 PAD 的一个法向量 n (1, 2, 2) ,
