2008年福建省南平市中考数学试题及答案(扫描版)
南平市初中毕业、升学考试数学试题及参考答案

南平市初中毕业、升学考试数学试题及参考答案20XX年福建省南平市初中毕业、升学考试数学试题(满分:150分;考试时间:120分钟)★友情提示:① 所有答案都必须填在答题卡相应的位置上,答在本试卷上一律无效;② 可以携带使用科学计算器,并注意运用计算器进行估算和探究;③ 未注明精确度、保留有效数字等的计算问题不得采取近似计算.★参考公式:b4ac b2 b,抛物线y ax bx c(a≠0)的对称轴是x 顶点坐标是4a 2a 2a2一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂)...1.-3的相反数是A.13B.1 3C.3 D.-32.计算:2=A.B.5C.2D.23.若要对一射击运动员最近5次训练成绩进行统计分析,判断他的训练成绩是否稳定,则需要知道他这5次训练成绩的A.中位数B.平均数C.众数D.方差4.正多边形的一个外角等于30°,则这个多边形的边数为A.6 B.9 C.12 D.15 5.下列计算正确的是..325A. a a a44B. a a aC. a a a54D.(ab) ab2366.为验证“掷一个质地均匀的骰子,向上的一面点数为偶数的概率是0.5”,下列模拟实验中,不科学的是...A.袋中装有1个红球1个绿球,它们除颜色外都相同,计算随机摸出红球的频率B.用计算器随机地取不大于10的正整数,计算取得奇数的频率C.随机掷一枚质地均匀的硬币,计算正面朝上的频率D.如图,将一个可以自由转动的转盘分成甲、乙、丙3个相同的扇形,转动转盘任其自由停止,计算指针指向甲的频率数学试题第1页(共4页)7.一个三角形的周长是36,则以这个三角形各边中点为顶点的三角形的周长是..A.6B.12C.18D.368.已知反比例函数y1的图象上有两点A(1,m)、B(2,n),x则m与n的大小关系为A.m>n B.m<n C.m=n D.不能确定9.如图所示,水平放置的长方体的底面是长为4和宽为2的矩形,它的主视图的面积为12,则长方体的体积等于..A.16 B.24 C.32 D.4810.如图,正方形纸片ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1,则EF的长为A.(第9题图)D F3 29 C.4B.5 2B E(第10题图)D.3二、填空题(本大题共8小题,每小题3分,共24分.请将答案填入答题卡的...相应位置)11.计算:=.12.样本数据2,8,3,5,6的极差是.13.分解因式:2x 4x 214.如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,点D 在⊙O 上,∠ADC=68°,则∠BAC=°.15.将直线y 2x向上平移1个单位长度后得到的直线是.16.如图,在山坡AB上种树,已知∠C=90°,∠A=28°,AC=6米,则相邻两树的坡面距离AB≈ 米.(精确到0.1米)17.某校举行A、B两项趣味比赛,甲、乙两名学生各自随机选择参加其中的一项,则他们恰好参加同一项比赛的概率是.18.设x 表示大于..x的最小整数,如 3 =4, 1.2 =-1,则下列结论中正确的是.(填写所有正确结论的序号)..) ① 0 0;f x ② [x) x的最小值是0;2B(第14题图)BA(第16题图)Cfx③) x) [x) x=0.5成立.[x) x的最大值是1;④ 存在实数fx,使数学试题第2页(共4页)三、解答题(本大题共8小题,共86分.请在答题卡的相应位置作答)...1 19.(1)(7分)计算:(3)π 4 20XX年0.37,① 2x 1<(2)(7分)解不等式组:3x<2x 8.②216x x20.20.(8分)解分式方程:x 3x 321.(8分)如图,已知四边形ABCD是平行四边形,若点E、F分别在边BC、AD上,连接AE、CF.请再从下列三个备选条件中,选择添加一个恰...........当的条件,使四边形AECF是平行四边形,并予以证明..备选条件:AE=CF,BE=DF,∠AEB=∠CFD.我选择添加的条件是:.(注意:请根据所选择的条件在答题卡相应试题的图BCD(第21题图)中,画出符合要求的示意图,并加以证明)22.(10分)“六一”前夕,质检部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品.以下是根据抽查结果绘制出的不完整的统计表和扇形图:类别儿童玩具90童车童装抽查件数%童车25%童装%(第22题图)请根据上述统计表和扇形图提供的信息,完成下列问题:(1)分别补全上述统计表和扇形图;(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,请估计能买到合格品的概率是多少?23.(10分)如图,直线l与⊙O 交于C、D两点,且与半径OA垂直,垂足为H,已知OD=2,∠O=60°.(1)求CD的长;(2)在OD的延长线上取一点B,连接AB、AD,若AD=BD,求证:AB是⊙O的切线.A(第23题图)数学试题第3页(共4页)24.(10分)某乡镇决定对小学和初中学生按照每生每天3元的标准进行营养补助,其中家庭困难寄宿生的补助标准为:小学生每生每天4元,初中生每生每天5元.已知该乡镇现有小学和初中学生共1 000人,且小学、初中均有2%的学生为家庭困难寄宿生.设该乡镇现有小学生x人.(1)用含x的代数式表示:该乡镇小学生每天共需营养补助费是元;该乡镇初中生每天共需营养补助费是元;(2)设该乡镇小学和初中学生每天共需营养补助费为y元,求y与x之间的函数关系式;(3)若该乡镇小学和初中学生每天共需营养补助费为3029元,问小学生、初中生分别有多少人?25.(12分)在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(m,1)(m>0).将此矩形绕点O逆时针旋转90°,得到矩形OA B C .(1)写出点A、A 、C 的坐标;(2)设过点A、A 、C 的抛物线解析式为y ax2 bx c,求此抛物线的解析式;(a、b、c可用含m的式子表示)(3)试探究:当m的值改变时,点B关于点O的对称点D 是否可能落在(2)中的抛物线上?若能,请求出此时m的值.26.(14分)如图,在△ABC中,点D、E分别在边BC、AC上,连接AD、DE,且∠1=∠B=∠C.(1)由题设条件,请写出三个正确结论;(要求:不再....添加其它字母和辅助线,找结论过程中添加的字母或辅助线不能出现在结论中,不必证明)答:结论一:;结论二:;结论三:.(2)若∠B=45°,BC=2,当点D在BC 上运动时(点D不与点B、C重合),① 求CE的最大值;② 若△ADE是等腰三角形,求此时BD的长.(注意:在第(2)小题求解过程中,若有运用(1)。
2008年福建南平市中考数学试题及参考答案

找家教、下试题,上易学网 打造华南地区最好的家教、试题平台2008年福建省南平市初中毕业、升学考试数学试题(满分:150分;考试时间:120分钟)★友情提示:①所有答案都必须填在答题卡相应的位置上,答在本试卷上一律无效; ②可以携带使用科学计算器,并注意运用计算器进行估算和探究;③未注明精确度、保留有效数字等的计算问题不得采取近似计算. 一、选择题(本大题共9小题,每小题4分,共36分.每小题只有一个正确的选项,请在答题卡...的相应位置填涂) 1.计算:3-=( ) A .3B .3-C .13D .13- 2.计算:53x x ÷=( )A .2xB .53x C .8x D .13.有一个质地均匀且六个面上分别刻有1到6的点数的正方体骰子,掷一次骰子,向上的一面的点数为2的概率是( )A .0B .12C .16D .14.下列图形中,既是轴对称图形,又是中心对称图形的是( )A .等腰梯形B .平行四边形C .正三角形D .矩形5.小丽家下个月的开支预算如图所示.如果用于教育的支出是150元,则她家下个月的总支出为( )A .625元B .652元C .750元D .800元6.如图1所示的几何体的主视图...是( )7.已知ABC DEF △∽△,相似比为3,且ABC △的周长为18,则D E F △的周长为( )A .2B .3C .6D .548.有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中平均一个人传染的人数为( )A .8人B .9人C .10人D .11人9.如图,正比例函数(0)y kx k =>与反比例函数4y x=的图 象相交于A C ,两点,过点A 作x 轴的垂线交x 轴于点B ,连接BC ,则ABC △的面积等于( ) A .2 B .4 C .6 D .8找家教、下试题,上易学网 打造华南地区最好的家教、试题平台二、填空题(本大题共9小题,每小题3分,共27分.请将答案填入答题卡...的相应位置) 10= .11.当x = 时,分式12x -没有意义. 12.如图,奥运五环标志里,包含了圆与圆的位置关系中的 外离..和 . 13.为了解一批节能灯的使用寿命,宜采用 的方式进行调查.(填:“全面调查”或“抽样调查”) 14.“明天会下雨”是 事件.(填“必然”或“不可能”或“可能”)15.如图,菱形ABCD 中,O 是对角线AC BD ,的交点,5cm AB =,4cm AO =,则BD = cm .16.因式分解:322a a a ++= .17.如图,ABC △中,AB AC >,D E ,两点分别在边AC AB ,上,且DE 与BC 不平行.请填上一个..你认为合适的条件: , 使ADE ABC △∽△.(不再添加其他的字母和线段;只填一个条件,多填不给分!)18.定义:a 是不为1的有理数,我们把11a-称为a 的差倒数.... 如:2的差倒数是1112=--,1-的差倒数是111(1)2=--.已知113a =-,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数,……,依此类推,则2009a = .三、解答题(本大题共8小题,共87分.请在答题卡...的相应位置作答) 19.(8分)先化简,再求值:()()(2)a b a b b b +-+-,其中1a =-,1b =.20.(8分)解不等式组:23432x x x x +<+⎧⎪⎨->⎪⎩①②找家教、下试题,上易学网 打造华南地区最好的家教、试题平台21.(9分)如图,线段AB 经过圆心O ,交O 于点A C ,,点D 在O 上,连接AD BD ,,30A B ∠=∠= .BD 是O 的切线吗?请说明理由.22.(10分)某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)25 26 21 17 28 26 20 25 26 3020 21 20 26 30 25 21 19 28 26(1)请根据以上信息完成下表:(2上述数据中,众数是 万元,中位数是 万元,平均数是 万元;(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.23.(12分)“母亲节”到了,九年级(1)班班委发起慰问烈属王大妈的活动,决定在“母亲节”期间全班同学利用课余时间去卖鲜花筹集慰问金.已知同学们从花店按每支1.2元买进鲜花,并按每支3元卖出.(1)求同学们卖出鲜花的销售额y (元)与销售量x (支)之间的函数关系式;(2)若从花店购买鲜花的同时,还总共用去40元购买包装材料,求所筹集的慰问金w (元)与销售量x (支)之间的函数关系式;若要筹集不少于500元的慰问金,则至少要卖出鲜花多少支?(慰问金=销售额-成本)找家教、下试题,上易学网 打造华南地区最好的家教、试题平台24.(12分)2008年初,我国南方部分省区发生了雪灾,造成通讯受阴.如图,现有某处山坡上一座发射塔被冰雪从C 处压折,塔尖恰好落在坡面上的点B 处,在B 处测得点C 的仰角为38 ,塔基A 的俯角为21,又测得斜坡上点A 到点B 的坡面距离AB 为15米,求折.断前..发射塔的高.(精确到0.1米)25.(14分)如图,平面直角坐标系中有一矩形纸片OABC ,O 为原点,点A C ,分别在x轴,y 轴上,点B 坐标为((其中0m >),在BC 边上选取适当的点E 和点F ,将OCE △沿OE 翻折,得到OGE △;再将ABF △沿AF 翻折,恰好使点B 与点G 重合,得到AGF △,且90OGA ∠=.(1)求m 的值;(2)求过点O G A ,,的抛物线的解析式和对称轴;(3)在抛物线的对称轴...上是否存在点P ,使得OPG △是等腰三角形?若不存在,请说明理由;若存在,直接答出....所有满足条件的点P 的坐标(不要求写出求解过程). 【提示:抛物线2(0)y ax bx c a =++≠的对称轴是2b x a =-,顶点坐标是2424b ac b a a ⎛⎫-- ⎪⎝⎭,】找家教、下试题,上易学网 打造华南地区最好的家教、试题平台26.(14分)(1)如图1,图2,图3,在ABC △中,分别以AB AC ,为边,向ABC △外作正三角形,正四边形,正五边形,BE CD ,相交于点O .①如图1,求证:ABE ADC △≌△;②探究:如图1,BOC ∠= ;如图2,BOC ∠= ;如图3,BOC ∠= .(2)如图4,已知:AB AD ,是以AB 为边向ABC △外所作正n 边形的一组邻边;AC AE ,是以AC 为边向ABC △外所作正n 边形的一组邻边.BE CD ,的延长相交于点O .①猜想:如图4,BOC ∠= (用含n 的式子表示);②根据图4证明你的猜想.找家教、下试题,上易学网 打造华南地区最好的家教、试题平台2008年福建省南平市初中毕业、升学考试数学试题参考答案及评分说明说明:(1)解答右端所注分数,表示考生正确作完该步应得的累计分数,全卷满分150分.(2)对于解答题,评卷时要坚持每题评阅到底,勿因考生解答中出现错误而中断本题的评阅.当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的考试要求,可酌情给分,但原则上不超过后面应得分数的一半,如果有较严重的错误,就不给分.(3)如果考生的解法与本参考答案不同,可参照本参考答案的评分标准相应评分.(4)评分只给整数分.一、选择题(本大题共9小题,每小题4分,共36分)1.A ; 2.A ; 3.C ; 4.D ; 5.C ; 6.B ; 7.C ; 8.B ; 9.B .二、填空题(本大题共9小题,每小题3分,共27分)10.4; 11.2; 12.相交; 13.抽样调查; 14.可能; 15.6;16.2(1)a a +; 17.1B ∠=∠或2C ∠=∠或AE AD AC AB =; 18.34. 三、解答题(本大题共8小题,共87分)19.解:原式2222a b b b =-+- ························································································· 4分 22a b =- ································································································································ 6分 当1a =-,1b =时,原式2(1)21=--=- ········································································ 8分20.解:由①得,243x x -<- ··························································································· 1分 1x < ········································································································································ 3分 由②得,32x x -> ················································································································ 4分 3x -> ····································································································································· 5分 3x <- ····································································································································· 6分∴不等式组的解集为3x <- ·································································································· 8分 21.答:BD 是O 的切线. ······························································································· 2分 理由1:连接OD ,OA OD = ,30ADO A ∴∠=∠=·················································· 4分 30A B ∠=∠= ,180()120BDA A B ∴∠=-∠+∠= ················································ 7分 90BDO BDA ADO ∴∠=∠-∠= 即OD BD ⊥BD ∴是O 的切线. ····························································· 9分理由2:连接OD ,OA OD = ,30ADO A ∴∠=∠= ······························································ 4分60BOD ADO A ∴∠=∠+∠= ·············································· 7分30B ∠= ,找家教、下试题,上易学网 打造华南地区最好的家教、试题平台 180()90BDO BOD B ∴∠=-∠+∠= ,即OD BD ⊥BD ∴是O 的切线. ··········································································································· 9分 理由3:连接OD ,OA OD = ,30ADO A ∴∠=∠=·················································· 4分 在BD 的延长线上取一点E ,30A B ∠=∠= 60ADE A B ∴∠=∠+∠= ·································································································· 7分 90EDO ADO ADE ∴∠=∠+∠= ,即OD BD ⊥BD ∴是O 的切线. ··········································································································· 9分 理由4:连接OD ,OA OD = ,30ADO A ∴∠=∠=·················································· 4分 连接CD ,则90ADC ∠= ··································································································· 5分 60ODC ADC ADO ∴∠=∠-∠= ····················································································· 6分 OD OC = ,60OCD ∴∠=30B ∠= ,30BDC OCD B ∴∠=∠-∠= ··································································· 7分 90ODB ODC BDC ∴∠=∠+∠= ,即OD BD ⊥BD ∴是O 的切线. ··········································································································· 9分22.解:(1)3,5,2,2(每空1分) ················································································ 4分(2)26,25,24(每空1分) ······························································································ 7分(3)不能 ································································································································ 8分 因为此时众数26万元>中位数25万元 ·············································································· 10分 (或:因为从统计表中可知20名营业员中,只有9名达到或超过目标,不到半数)23.解:(1)3y x = ·············································································································· 4分(2)3 1.240w x x =--········································································································ 7分 1.840x =- ····························································································································· 8分 ∴所筹集的慰问金w (元)与销售量x (支)之间的函数关系式为 1.840w x =-解法一:当500w ≥时,1.840500x -≥ ········································································ 10分 解得300x ≥∴若要筹集不少于500元的慰问金,至少要售出鲜花300支 ············································ 12分 解法二:由1.840500x -=,解得300x = ······································································ 11分 1.840w x =- 中1.80>w ∴随x 的增大而增大,∴若要筹集不少于500元的慰问金,至少要售出鲜花300支 ············································ 12分 24.解:作BD AC ⊥于D ,由已知得:38CBD ∠= ,21ABD ∠= ,15AB =米找家教、下试题,上易学网 打造华南地区最好的家教、试题平台 在Rt ADB △中,sin AD ABD AB∠= ,sin 15sin 21 5.38AD AB ABD ∴=∠=⨯ ≈ ······················· 3分cos BD ABD AB∠= , cos 15cos 2114.00BD AB ABD ∴=∠=⨯ ≈ ···················· 5分在Rt BDC △中,tan CD CBD BD∠= tan 14.00tan3810.94CD BD CBD ∴=∠⨯ ≈≈ ··························································· 8分 cos BD CBD BC ∠= ,14.0017.77cos cos38BD BC CBD ∴=∠≈≈ ····································· 10分 5.3810.9417.7734.09AD CD BC ∴++++=≈ ··························································· 11分 34.1≈答:折断前发射塔的高约为34.1米. ················································································· 12分 注意:按以下方法进行近似计算视为正确,请相应评分.①若到最后再进行近似计算结果为:15cos2115sin 2115cos 21tan 3834.1cos38AD CD BC ++=⨯+⨯+≈; ②若解题过程中所有三角函数值均先精确到0.01,则近似计算的结果为:5.4010.8817.6633.9433.9AD CD BC ++++=≈≈.25.(1)解法一:(B ,由题意可知AG AB =OG OC ==OA m = ················································ 2分 90OGA ∠= ,222OG AG OA ∴+= ·············································································· 3分 222m ∴+=.又0m > ,2m ∴= ·················································································· 4分解法二:(B ,由题意可知AG AB =OG OC ==OA m = ················································ 2分 90OGA ∠= ,45GOA GAO ∴∠=∠= ········································································ 3分2cos cos 45OG m OA GOA ∴====∠ ················································································ 4分 (2)解法一:过G 作直线GH x ⊥轴于H ,则1OH =,1HG =,故(11)G ,. ······················································································ 5分。
2008年福建省各市中考数学试题

1 ,试求每张乒乓球门票的价格. 8
22. (12 分)如图,在平面直角坐标系中,将四边形 ABCD 称为“基本图形”,且各点的坐标 分别为 A(4,4) ,B(1,3) ,C(3,3) ,D(3,1). (1)画出“基本图形”关于原点 O 对称的四边形 A1B1C1D1,并求出 A1,B1,C1,D1 的坐标.
17.已知 α 为锐角,则 m=sinα +cosα 的值( ) A.m>1 B.m=1 C.m<1 D.m≥1 三、解答题(本大题共 8 小题,共 92 分) 18. (8 分)计算:2008 +|-1|- 3 cos30°+ (
0
1 3 ). 2
19.(10 分)化简求值:(
a2 b2 a2 b2 1 +2)÷ ,其中 a 2 , b . ab ab 2
数学试题第 3 页(共 78 页)
A1(
,
),B1(
,
),C1(
,
),D1(
,
) ;
(2)画出“基本图形”关于 x 轴的对称图形 A2B2C2D2 ; (3)画出四边形 A3B3C3D3,使之与前面三个图形组成的图形既是中心对称图形又是轴对称图形.
23. (13 分)汶川地震发生后,全国人民抗震救灾,众志成城. 某地政府急灾民之所需, 立即组织 12 辆汽车,将 A、B、C 三种救灾物资共 82 吨一次性运往灾区,假设甲、乙、 丙三种车型分别运载 A、B、C 三种物资. 根据下表提供的信息解答下列问题: 车 型 甲 5 乙 8 丙 10
5 x 19 及题意知 y>0, x>0且x 必须是 2 的整数倍, 2
x y
2 14 4 9 6 4 8 -1 „ „ 10 分
2008年福建省南平市初中毕业升学考试

2008年福建省南平市初中毕业、升学考试语文样卷(满分:150分;考试时间:120分钟)一、语言积累与运用(30分)1. 阅读下面文字,请根据拼音在括号内填写相应的汉字。
(4分)武夷山景色宜人,妩mèi ( )多姿,有“人间仙境在武夷”之美誉。
一带曲水wǎn( )如锦缎,如飘如拂,别有一种清瘦俊逸的神韵。
其名山胜迹,点缀于窈tiǎo( )曲折的碧水两岸,yǎn()然一幅次第展开的国画长卷。
2. 默写(10分)①李杜诗篇万口传,至今已觉不新鲜。
,。
(赵翼《论诗》)②_______________________,________________________。
晴空一鹤排云上,便引诗情到碧霄。
(刘禹锡《秋词》)③文天祥《过零丁洋》一诗中与孟子“舍生取义”的精神一脉相承的名句是:“?。
”④龚自珍在《己亥杂诗》中用“,”两句诗形象地表达了自己虽然辞官,但仍关心国家命运的思想感情。
⑤每当你登上山巅,极目远眺,往往会感悟到王安石在《登飞来峰》中表达的“,”的人生哲理。
3. 2008年奥运会在北京召开,请为组委会拟一条标语,欢迎国外来宾。
(15字以内)(2分)4. 我国文化名人灿若群星:曹操、王湾、白居易(乐天)、苏轼、陆游、陶渊明(陶潜)、范仲淹(文正)……小华同学就此想拟写一副对联,上联他已经写出来了,请你帮他写出下联。
(3分)上联:曹操沧海边上抒豪情壮志下联:5. 请完成下面的名著阅读题。
(6分)①阅读下面名著选段,完成文后问题:“……武松先把两个拳头去蒋门神脸上虚影一影,忽地转身便走。
蒋门神大怒,抢将来。
被武松一飞脚踢起,踢中蒋门神小腹上。
双手按了,便蹲下去。
武松一踅,踅将过来,那只右脚早踢起,直飞在蒋门神额角上,踢着正中,望后便倒。
武松追入一步,踏住胸脯,提起这醋钵儿大小拳头,望蒋门神脸上便打。
原来说过的,打蒋门神扑手:先把拳头虚影一影,便转身,却先飞起左脚,踢中了,便转过身来,再飞起右脚。
2008年福建省南平市初中毕业升学考试

2008年福建省南平市初中毕业、升学考试物理试题(样卷)(满分:100分;考试时间:90分钟)考生须知:1、全卷五大题,35小题,试卷共6页,及答题卡。
2、答案一律写在答题卡上,否则以0分计算,交卷时只交答题卡,本卷由考场处理,考生不得擅自带走。
3、作图题可以先用铅笔画,待确定后再用签字笔描清楚。
一、选择题(以下每小题只有一个正确答案,每小题2分,共24分)1.下列说法中符合实际的是A.一支新铅笔的长度约为18cm B.一个中学生的质量约为6kgC.闽北的年平均气温约为50℃D.一节干电池的电压约为36V2.电子琴是人们运用电子技术和计算机技术制成的电子合成乐器,它能模仿各种乐器发出的声音,关键是因为它能模仿各种乐器发出声音的A.音调B.音色C.响度D.频率3.下列自然现象中,属于熔化的是A.春天,冰雪消融B.夏天的早晨,花草上附着露水C.深秋的早晨,大雾弥漫D.冬天的早晨,霜打枝头4.小明同学在做作业时,发现电灯亮度突然变暗了,原因可能是电灯的A.额定功率变小了B.额定功率变大了C.实际功率变小了D.实际功率变大了5.下列学习用品中,在通常情况下属于导体的是A.塑料刻度尺B.金属小刀片C.绘画橡皮擦D.物理课本6.下列现象中,能用惯性知识来解释的是A.用力拉弹簧,弹簧会伸长B.刀用久了,要把刀刃磨得锋利一些C.为了防止“追尾”事故发生,交警友情提示:请保持车距D.飞机的机翼通常都做成上面凸起,下面平直的形状7.张明家住在多年前修建的老房子里,家中的电路设计不适应大功率用电器的使用。
有一天,他妈妈在同时使用电饭煲和电炒锅时,张明突然发现厨房里的电线冒烟了,他应该首先采取的措施是A.立即启动排气扇,将烟雾排出B.立即给外地的爸爸打电话C.立即向冒烟电线泼水D.立即叫妈妈切断自家电源图3 图4 图18.下列家用电器的额定功率最接近40W 的是A .电饭煲B .电热水器C .微波炉D .台灯9.下列关于热机和环境保护的说法,正确的是A .热机的大量使用会造成环境污染B .所有的热机都是使用汽油做燃料C .热机排出的废气都是无害气体D .热机产生的噪声,可以被消声器完全消除10.如图1所示,电源电压保持不变,闭合开关S ,当滑动变阻器滑片P 向右移动时,关于电压表、电流表的示数变化情况,下列说法正确的是A .电压表示数变大B .电压表示数变小C .电流表示数变大D .电流表示数变小11.加油站常标有“严禁用塑料桶装运汽油”的警示语,这是因为A .塑料桶受碰撞容易破裂B .塑料桶会与汽油发生化学反应C .塑料桶容易变形D .桶内汽油会不断与桶壁摩擦,使塑料桶带了电,容易造成火灾隐患12.有些物理量的大小不易直接观测,但它变化时引起其它量的变化却容易直接观测。
福建省南平市初中升学考试中考数学试卷试题

福建省南平市初中升学考试中考数学试卷试题2011年福建省南平市初中毕业、升学考试中考试题数学(满分:150分;考试时间:120分钟)一、选择题(本大题共10小题,每小题4分,共40分。
每小题只有一个正确的选项,请在答.题卡..的相应位置填涂) 1.(2010福建南平,1,4分)2的相反数等于A . -2B .2C .-21D .21 【答案】A2.(2010福建南平,2,4分)方程组⎩⎨⎧=-=+326y x y x 的解是A .⎩⎨⎧-==39y xB .⎩⎨⎧-==17y xC .⎩⎨⎧==15y xD .⎩⎨⎧==33y x 【答案】C3.(2010福建南平,3,4分)下列调查中,适宜采用全面调查方式的是A .了解南平市的空气质量情况B .了解闽江流域的水污染情况C .了解南平市居民的环保意识D .了解全班同学每周体育锻炼的时间【答案】D4.(2010福建南平,4,4分)下列运算中,正确..的是A .1553a a a =⋅B .253a a a =÷C .632)(a a -=-D .623)(ab ab =【答案】C5.(2010福建南平,5,4分)下列说法错误..的是 A .必然事件发生的概率是1 B .不确定事件发生的概率是0.5C .不可能事件发生的概率是0D .随机事件发生的概率介于0和1之间【答案】B6.(2010福建南平,6,4分)边长为4的正三角形的高为A .2B .4C .3D .32【答案】D7(2010福建南平,7,4分).已知⊙O 1、⊙O 2的半径分别是2、4,若O 1O 2=6,则⊙O 1与⊙O 2的位置关系是A .内切B .相交C .外切D .外离【答案】C8.(2010福建南平,8,4分)有一等腰梯形纸片ABCD,(如图),AD∥BC,AD=1,BC=3,沿梯形的高DE剪下。
由△DEC与四边形ABED不一定...能.拼接成的图形是DACA.直角三角形B.矩形C.平行四边形D.正方形【答案】D9.(2010福建南平,9,4分)某商店销售一种玩具,每件售价92元,可获利15%,求这种玩具的成本价。
2008年中考数学试题及答案解析
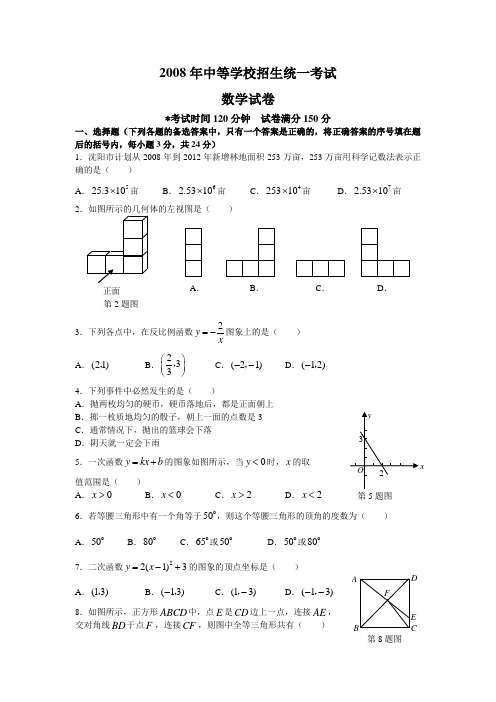
2008年中等学校招生统一考试数学试卷*考试时间120分钟 试卷满分150分一、选择题(下列各题的备选答案中,只有一个答案是正确的,将正确答案的序号填在题后的括号内,每小题3分,共24分)1.沈阳市计划从2008年到2012年新增林地面积253万亩,253万亩用科学记数法表示正确的是( ) A .525.310⨯亩B .62.5310⨯亩C .425310⨯亩D .72.5310⨯亩2)3.下列各点中,在反比例函数2y x=-图象上的是()A .(21),B .233⎛⎫⎪⎝⎭,C .(21)--,D .(12)-,4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨5.一次函数y kx b =+的图象如图所示,当0y <时,x 的取 值范围是( ) A .0x > B .0x <C .2x >D .2x <6.若等腰三角形中有一个角等于50,则这个等腰三角形的顶角的度数为( ) A .50B .80C .65或50D .50或807.二次函数22(1)3y x =-+的图象的顶点坐标是( )A .(13),B .(13)-,C .(13)-,D .(13)--, 8.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE , 交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )正面第2题图A .B .C .D .第5题图xADCEFB第8题图A .1对B .2对C .3对D .4对二、填空题(每小题3分,共24分)9.已知A ∠与B ∠互余,若70A ∠=,则B ∠的度数为 . 10.分解因式:328m m -= .11.已知ABC △中,60A ∠=,ABC ∠,ACB ∠的平分线交于点O ,则BOC ∠的度数为 .12.如图所示,菱形ABCD 中,对角线AC BD ,相交于点O ,若再补 充一个条件能使菱形ABCD 成为正方形,则这个条件是 (只填一个条件即可). 13.不等式26x x -<-的解集为 .14.如图所示,某河堤的横断面是梯形ABCD ,BC AD ∥,迎水坡AB 长13米,且12tan 5BAE ∠=,则河堤的高BE 为 米.15.观察下列图形的构成规律,根据此规律,第8第15题图16.在平面直角坐标系中,点A 的坐标为(11),,点B 的坐标为(111),,点C 到直线AB 的距离为4,且ABC △是直角三角形,则满足条件的点C 有 个.三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.计算:101(1)52-⎛⎫π-+-+- ⎪⎝⎭18.解分式方程:1233xx x=+--.19.先化简,再求值:222()()2y x y x y x y ++---,其中13x =-,3y =.第1个 ……第2个 第3个 第4个ADC BO 第12题图 B C DA 第14题图20.如图所示,在66⨯的方格纸中,每个小方格都是边长为1的正方形,我们称每个小正方形的顶点为格点,以格点为顶点的图形称为格点图形,如图①中的三角形是格点三角形. (1)请你在图①中画一条直线将格点三角形分割成两部分,将这两部分重新拼成两个不同的格点四边形,并将这两个格点四边形分别画在图②,图③中; (2)直接写出这两个格点四边形的周长.四、(每小题10分,共20分)21.如图所示,AB 是O 的一条弦,OD AB ⊥,垂足为C ,交O 于点D ,点E 在O 上.(1)若52AOD ∠=,求DEB ∠的度数;(2)若3OC =,5OA =,求AB 的长.22.小刚和小明两位同学玩一种游戏.游戏规则为:两人各执“象、虎、鼠”三张牌,同时各出一张牌定胜负,其中象胜虎、虎胜鼠、鼠胜象,若两人所出牌相同,则为平局.例如,小刚出象牌,小明出虎牌,则小刚胜;又如,两人同时出象牌,则两人平局. (1)一次出牌小刚出“象”牌的概率是多少?(2)如果用A B C ,,分别表示小刚的象、虎、鼠三张牌,用1A ,1B ,1C 分别表示小明的象、虎、鼠三张牌,那么一次出牌小刚胜小明的概率是多少?用列表法或画树状图(树形图)法加以说明.图① 第20题图图②图③第21题图 小刚 小明A 1B 1C 1A B C 第22题图23.在学校组织的“喜迎奥运,知荣明耻,文明出行”的知识竞赛中,每班参加比赛的人数相同,成绩分为A B C D ,,,四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:请你根据以上提供的信息解答下列问题:(1)此次竞赛中二班成绩在C 级以上(包括C 级)的人数为 ; (2)请你将表格补充完整:(3)请从下列不同角度对这次竞赛成绩的结果进行分析:①从平均数和中位数的角度来比较一班和二班的成绩; ②从平均数和众数的角度来比较一班和二班的成绩;③从B 级以上(包括B 级)的人数的角度来比较一班和二班的成绩. 六、(本题12分)24.一辆经营长途运输的货车在高速公路的A 处加满油后,以每小时80千米的速度匀速行驶,前往与A 处相距636千米的B 地,下表记录的是货车一次加满油后油箱内余油量y (升)与行驶时间x (1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y 与x 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)(2)按照(1)中的变化规律,货车从A 处出发行驶4.2小时到达C 处,求此时油箱内余油多少升?(3)在(2)的前提下,C 处前方18千米的D 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B 地.(货车在D 处加油过程中的时间和路程忽略不计)第23题图 一班竞赛成绩统计图 二班竞赛成绩统计图25.已知:如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD ,的中点. (1)求证:①BE CD =;②AMN △是等腰三角形.(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立; (3)在(2)的条件下,请你在图②中延长ED 交线段BC 于点P .求证:PBD AMN △∽△.八、(本题14分) 26.如图所示,在平面直角坐标系中,矩形ABOC 的边BO 在x 轴的负半轴上,边OC 在y 轴的正半轴上,且1AB =,OB =ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD .点A 的对应点为点E ,点B 的对应点为点F ,点C 的对应点为点D ,抛物线2y ax bx c =++过点A E D ,,. (1)判断点E 是否在y 轴上,并说明理由; (2)求抛物线的函数表达式;(3)在x 轴的上方是否存在点P ,点Q ,使以点O B P Q ,,,为顶点的平行四边形的面积是矩形ABOC 面积的2倍,且点P 在抛物线上,若存在,请求出点P ,点Q 的坐标;若不存在,请说明理由.2008年沈阳市中等学校招生统一考试C E ND A BM图① C A EM B D N图② 第25题图第26题图数学试题参考答案及评分标准一、选择题(每小题3分,共24分) 1.B 2.A 3.D 4.C 5.C 6.D7.A8.C二、填空题(每小题3分,共24分) 9.2010.2(2)(2)m m m +-11.12012.90BAD ∠=(或AD AB ⊥,AC BD =等)13.4x >14.1215.65 16.8 三、(第17小题6分,第18,19小题各8分,第20小题10分,共32分)17.解:原式1(2)5=+-+- ···························································· 4分125=-+- ··················································································· 5分6= ······································································································ 6分18.解:12(3)x x =-- ·················································································· 2分126x x =--7x = ··········································································································· 5分 检验:将7x =代入原方程,左边14==右边 ························································ 7分所以7x =是原方程的根 ·················································································· 8分 (将7x =代入最简公分母检验同样给分)19.解:原式2222222xy y x xy y x y =++-+-- ················································ 4分 xy =- ········································································································· 6分 当13x =-,3y =时,原式1313⎛⎫=--⨯= ⎪⎝⎭······················································································ 8分 20.解:(1)答案不唯一,如分割线为三角形的三条中位线中任意一条所在的直线等.································· 2分拼接的图形不唯一,例如下面给出的三种情况:图① 图② 图③ 图④图①~图④,图⑤~图⑦,图⑧~图⑨,画出其中一组图中的两个图形. ······················ 6分 (2)对应(1)中所给图①~图④的周长分别为4+8,4+4+ 图⑤~图⑦的周长分别为10,8+8+图⑧~图⑨的周长分别为2+4+ ···································· 10分 四、(每小题10分,共20分) 21.解:(1)OD AB ⊥,AD DB ∴= ··························································· 3分 11522622DEB AOD ∴∠=∠=⨯= ································································· 5分 (2)OD AB ⊥,AC BC ∴=,AOC △为直角三角形, 3OC =,5OA =,由勾股定理可得4AC == ·············································· 8分 28AB AC ∴== ························································································· 10分 22.解:(1)1()3P =一次出牌小刚出象牌“” ··················································· 4分(2)树状图(树形图):·············································································· 8分图⑤ 图⑥图⑦图⑧ 图⑨A 1B 1C 1 AA 1B 1C 1 BA 1B 1C 1C开始小刚 小明或列表···························································· 8分 由树状图(树形图)或列表可知,可能出现的结果有9种,而且每种结果出现的可能性相同,其中小刚胜小明的结果有3种. ········································································ 9分1()3P ∴=一次出牌小刚胜小明. ····································································· 10分 五、(本题12分) 23.解:(1)21······························································································ 2分 (2)一班众数为90,二班中位数为80 ······························································· 6分 (3)①从平均数的角度看两班成绩一样,从中位数的角度看一班比二班的成绩好,所以一班成绩好; ···································································································· 8分 ②从平均数的角度看两班成绩一样,从众数的角度看二班比一班的成绩好,所以二班成绩好; ················································································································· 10分 ③从B 级以上(包括B 级)的人数的角度看,一班人数是18人,二班人数是12人,所以一班成绩好. ······························································································· 12分 六、(本题12分) 24.解:(1)设y 与x 之间的关系为一次函数,其函数表达式为y kx b =+ ················ 1分将(0100),,(180),代入上式得, 10080b k b =⎧⎨+=⎩ 解得20100k b =-⎧⎨=⎩20100y x ∴=-+ ·························································································· 4分验证:当2x =时,20210060y =-⨯+=,符合一次函数; 当 2.5x =时,20 2.510050y =-⨯+=,也符合一次函数.∴可用一次函数20100y x =-+表示其变化规律,而不用反比例函数、二次函数表示其变化规律. ··················································· 5分 y ∴与x 之间的关系是一次函数,其函数表达式为20100y x =-+ ··························· 6分 (2)当 4.2x =时,由20100y x =-+可得16y =即货车行驶到C 处时油箱内余油16升. ····························································· 8分 (3)方法不唯一,如:方法一:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 设在D 处至少加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯+=+, ··················································· 11分 解得,69a =(升) ····················································································· 12分方法二:由(1)得,货车行驶中每小时耗油20升, ············································· 9分 汽车行驶18千米的耗油量:1820 4.580⨯=(升) D B ,之间路程为:63680 4.218282-⨯-=(千米)汽车行驶282千米的耗油量:2822070.580⨯=(升) ················································································· 11分 70.510(16 4.5)69+--=(升) ···································································· 12分 方法三:由(1)得,货车行驶中每小时耗油20升, ············································· 9分设在D 处加油a 升,货车才能到达B 地.依题意得,63680 4.220101680a -⨯⨯++≤,解得,69a ≥ ····························································································· 11分 ∴在D 处至少加油69升,货车才能到达B 地. ················································· 12分七、(本题12分) 25.证明:(1)①BAC DAE ∠=∠ BAE CAD ∴∠=∠AB AC =,AD AE = ABE ACD ∴△≌△BE CD ∴= ·································································································· 3分 ②由ABE ACD △≌△得ABE ACD ∠=∠,BE CD =M N ,分别是BE CD ,的中点,BM CN ∴= ················································· 4分 又AB AC = ABM ACN ∴△≌△AM AN ∴=,即AMN △为等腰三角形 ···························································· 6分 (2)(1)中的两个结论仍然成立. ···································································· 8分 (3)在图②中正确画出线段PD由(1)同理可证ABM ACN △≌△ CAN BAM ∴∠=∠ BAC MAN ∴∠=∠ 又BAC DAE ∠=∠MAN DAE BAC ∴∠=∠=∠AMN ∴△,ADE △和ABC △都是顶角相等的等腰三角形 ································· 10分 PBD AMN ∴∠=∠,PDB ADE ANM ∠=∠=∠PBD AMN ∴△∽△ ···················································································· 12分 八、(本题14分)26.解:(1)点E 在y 轴上 ·············································································· 1分 理由如下:连接AO ,如图所示,在Rt ABO △中,1AB =,BO =2AO ∴=1sin 2AOB ∴∠=,30AOB ∴∠= 由题意可知:60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上,∴点E 在y 轴上. ································································· 3分 (2)过点D 作DM x ⊥轴于点M1OD =,30DOM ∠=∴在Rt DOM △中,12DM =,2OM =点D 在第一象限,∴点D 的坐标为12⎫⎪⎪⎝⎭, ················································································ 5分 由(1)知2EO AO ==,点E 在y 轴的正半轴上∴点E 的坐标为(02),∴点A的坐标为( ·················································································· 6分抛物线2y ax bx c =++经过点E ,2c ∴=由题意,将(A ,12D ⎫⎪⎪⎝⎭,代入22y ax bx =++中得32131242a a ⎧+=⎪⎨+=⎪⎩解得89a b ⎧=-⎪⎪⎨⎪=⎪⎩∴所求抛物线表达式为:2829y x x =--+ ·················································· 9分(3)存在符合条件的点P ,点Q . ································································· 10分。
福建省南平市中考数学试题及答案

福建省南平市中考数学试卷一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂)1.(4分)﹣的倒数是()A.﹣2 B.2C.﹣D.2.(4分)如图是由六个棱长为1的正方体组成的一个几何体,其主视图的面积是()A.3B.4C.5D.63.(4分)下列图形中,不是中心对称图形的是()A.平行四边形B.矩形C.菱形D.等边三角形4.(4分)如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,则下列结论中不正确的是()A.∠B=48°B.∠AED=66°C.∠A=84°D.∠B+∠C=96°5.(4分)以下事件中,必然发生的是()A.打开电视机,正在播放体育节目B.正五边形的外角和为180°C.通常情况下,水加热到100℃沸腾D.掷一次骰子,向上一面是5点6.(4分)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是()A.A D=AB B.∠BOC=2∠D C.∠D+∠BOC=90°D.∠D=∠B7.(4分)今年6月某日南平市各区县的最高气温(℃)如下表:区县延平建瓯建阳武夷山浦城松溪政和顺昌邵武光泽气温(℃)33 32 32 30 30 29 29 31 30 28则这10个区县该日最高气温的众数和中位数分别是()A.32,32 B.32,30 C.30,30 D.30,328.(4分)关于x的一元二次方程x2﹣2x+2+m2=0的根的情况是()A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定9.(4分)给定一列按规律排列的数:,则这列数的第6个数是()A.B.C.D.10.(4分)如图,Rt△ABC的顶点B在反比例函数的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是()A.12 B.C.D.二、填空题(本大题共8小题,每小题3分,共24分.请将答案填入答题卡的相应位置)11.(3分)计算:=3.12.(3分)甲、乙、丙、丁四位同学在5次数学测验中,他们成绩的平均数相同,方差分别为,,,,则成绩最稳定的同学是丁.13.(3分)写出一个第二象限内的点的坐标:(﹣1,1).14.(3分)分解因式:3a2+6a+3=3(a+1)2.15.(3分)计算:(a2b)3=a6b3.16.(3分)长度分别为3cm,4cm,5cm,9cm的四条线段,任取其中三条能组成三角形的概率是(或0.25).17.(3分)分式方程的解是x=9.18.(3分)设点P是△ABC内任意一点.现给出如下结论:①过点P至少存在一条直线将△ABC分成周长相等的两部分;②过点P至少存在一条直线将△ABC分成面积相等的两部分;③过点P至多存在一条直线将△ABC分成面积相等的两部分;④△ABC内存在点Q,过点Q有两条直线将其平分成面积相等的四个部分.其中结论正确的是①②④.(写出所有正确结论的序号)三、解答题(本大题共8小题,共86分.请在答题卡的相应位置作答)19.(14分)(1)计算:.(2)化简:.20.(8分)解不等式组:.21.(8分)如图,在▱ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.22.(10分)初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:请根据上述统计图提供的信息,完成下列问题:(1)这次抽查的样本容量是160;(2)请补全上述条形统计图和扇形统计图;(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?23.(10分)某校为了实施“大课间”活动,计划购买篮球、排球共60个,跳绳120根.已知一个篮球70元,一个排球50元,一根跳绳10元.设购买篮球x个,购买篮球、排球和跳绳的总费用为y元.(1)求y与x之间的函数关系式;(2)若购买上述体育用品的总费用为4 700元,问篮球、排球各买多少个?24.(10分)6月11日,“神舟”十号载人航天飞船发射成功!如图,飞船完成变轨后,就在离地球(⊙O)表面约350km的圆形轨道上运行.当飞船运行到某地(P点)的正上方(F点)时,从飞船上能看到地球表面最远的点Q(FQ是⊙O的切线).已知地球的半径约为6 400km.求:(1)∠QFO的度数;(结果精确到0.01°)(2)地面上P,Q两点间的距离(PQ的长).(π取3.142,结果保留整数)25.(12分)在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB.设=k.(1)证明:△BGF是等腰三角形;(2)当k为何值时,△BGF是等边三角形?(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.26.(14分)如图,已知点A(0,4),B(2,0).(1)求直线AB的函数解析式;(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x ﹣m)2+n与线段OA交于点C.①求线段AC的长;(用含m的式子表示)②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.福建省南平市中考数学试卷一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂)1.A2.B3.D4.B5.C6.B7.C8.C9.A10.D二、填空题(本大题共8小题,每小题3分,共24分.请将答案填入答题卡的相应位置)11.3.12.丁.13.(﹣1,1).14.3(a+1)2.15.a6b3.16.(或0.25).17.x=9.18.①②④.三、解答题(本大题共8小题,共86分.请在答题卡的相应位置作答)19.解:(1)原式=4×5+(π﹣1)﹣3=20+π﹣1﹣3=16+π;(2)原式=+﹣===.20.解:∵由①得:2x<5,,由②得:,,x>﹣3,∴不等式组的解集为.21.证明:在□ABCD中,AD=BC且AD∥BC∵BE=FD,∴AF=CE∴四边形AECF是平行四边形22.解:(1)100÷62.5%=160.即这次抽查的样本容量是160.故答案为160;(2)不常用计算器的人数为:160﹣100﹣20=40;不常用计算器的百分比为:40÷160=25%,不用计算器的百分比为:20÷160=12.5%.条形统计图和扇形统计图补全如下:(3)∵“不常用”计算器的学生数为40,抽查的学生人数为160,∴从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是:.答:从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”的概率是.23.解:(1)依题意,得y=70x+50(60﹣x)+10×120=20x+4200;(2)当 y=4700时,4700=20x+4200(7分)解得:x=25∴排球购买:60﹣25=35(个)答:篮球购买25个、排球购买35个.24.解:(1)∵FQ是⊙O的切线,∴OQ⊥FQ,∴∠OQF=90°,∴在Rt△OQF中,OQ=6400,OF=OP+PF=6400+350=6750,∴sin∠QFO=\frac{OQ}{FQ}=≈0.9481,∴∠QFO≈71.46°;答:∠QFO的度数约为71.46°;(2)∵∠QFO=71.46°,∴∠FOQ=90°﹣71.46°=18.14°,∴\widehat{PQ}的长=≈2071,答:地面上PP、Q两点间的距离约为2 071 km.25.解:(1)证明:∵EF⊥AC于点F,∴∠AFE=90°∵在Rt△AEF中,G为斜边AE的中点,∴,在Rt△ABE中,同理可得,∴GF=GB,∴△BGF为等腰三角形;(2)当△BGF为等边三角形时,∠BGF=60°∵GF=GB=AG,∴∠BGE=2∠BAE,∠FGE=2∠CAE∴∠BGF=2∠BAC,∴∠BAC=30°,∴∠ACB=60°,∴,∴当k=时,△BGF为等边三角形;(3)由(1)得△BGF为等腰三角形,由(2)得∠BAC=∠BGF,∴当△BGF为锐角三角形时,∠BGF<90°,∴∠BAC<45°,∴AB>BC,∴k=>1;当△BGF为直角三角形时,∠BGF=90°,∴∠BAC=45°∴AB=BC,∴k==1;当△BGF为钝角三角形时,∠BGF>90°,∴∠BAC>45°∴AB<BC,∴k=<1;∴0<k<1.26.解:(1)设直线AB的函数解析式为:y=kx+b.∵点A坐标为(0,4),点B坐标为(2,0),∴,解得:,即直线AB的函数解析式为y=﹣2x+4;(2)①∵以M为顶点的抛物线为y=(x﹣m)2+n,∴抛物线顶点M的坐标为(m,n).∵点M在线段AB上,∴n=﹣2m+4,∴y=(x﹣m)2﹣2m+4.把x=0代入y=(x﹣m)2﹣2m+4,得y=m2﹣2m+4,即C点坐标为(0,m2﹣2m+4),∴AC=OA﹣OC=4﹣(m2﹣2m+4)=﹣m2+2m;②存在某一时刻,能够使得△ACM与△AMO相似.理由如下:过点M作MD⊥y轴于点D,则D点坐标为(0,﹣2m+4),∴AD=OA﹣OD=4﹣(﹣2m+4)=2m.∵M不与点A、B重合,∴0<m<2,又∵MD=m,∴AM==m.∵在△ACM与△AMO中,∠CAM=∠MAO,∠MCA>∠AOM,∴当△ACM与△AMO相似时,假设△ACM∽△AMO,∴,即,整理,得 9m2﹣8m=0,解得m=或m=0(舍去),∴存在一时刻使得△ACM与△AMO相似,且此时m=.。
南平中考数学试题及答案
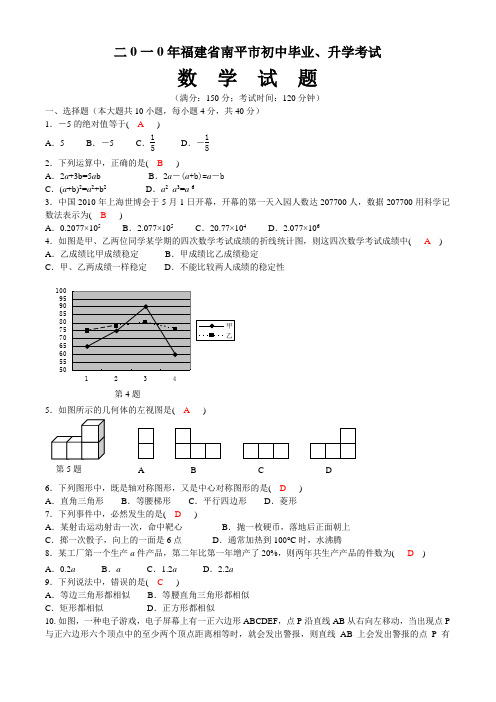
二0一0年福建省南平市初中毕业、升学考试数 学 试 题(满分:150分;考试时间:120分钟)一、选择题(本大题共10小题,每小题4分,共40分) 1.-5的绝对值等于( A )A .5B .-5C .15D .-152.下列运算中,正确的是( B )A .2a +3b=5a bB .2a -(a +b)=a -bC .(a +b)2=a 2+b 2D .a 2 ·a 3=a 63.中国2010年上海世博会于5月1日开幕,开幕的第一天入园人数达207700人,数据207700用科学记数法表示为( B ) A .0.2077×105 B .2.077×105 C .20.77×104 D .2.077×1064.如图是甲、乙两位同学某学期的四次数学考试成绩的折线统计图,则这四次数学考试成绩中( A ) A .乙成绩比甲成绩稳定 B .甲成绩比乙成绩稳定C .甲、乙两成绩一样稳定D .不能比较两人成绩的稳定性5.如图所示的几何体的左视图是( A )6.下列图形中,既是轴对称图形,又是中心对称图形的是( D ) A .直角三角形 B .等腰梯形 C .平行四边形 D .菱形 7.下列事件中,必然发生的是( D )A .某射击运动射击一次,命中靶心B .抛一枚硬币,落地后正面朝上C .掷一次骰子,向上的一面是6点D .通常加热到100°C 时,水沸腾 8.某工厂第一个生产a 件产品,第二年比第一年增产了20%,则两年共...生产产品的件数为( D ) A .0.2a B .a C .1.2a D .2.2a 9.下列说法中,错误的是( C )A .等边三角形都相似B .等腰直角三角形都相似C .矩形都相似D .正方形都相似10.如图,一种电子游戏,电子屏幕上有一正六边形ABCDEF ,点P 沿直线AB 从右向左移动,当出现点P 与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线AB 上会发出警报的点P有第5题 A B C D( C )A .3个B .4个C .5个D .6个二、填空题:本大题共8小题,每小题3分,共24分. 11.计算:20=_______. 答案:112.分解因式:a 3-2a 2+a=_______________. 答案: a ( a -1)213.写出一个有实数根的一元二次方程___________________. 答案不唯一,例如: x 2-2x+1 =014.如图,△ABC 是⊙O 的内接等边三角形,则∠BOC=_______°.答案:12015.一口袋中装着除颜色不同外其他完全相同的10只球,其中有红球3只,白球7只,现从口袋中随机摸出一只球,则摸到红球的概率是__________.答案:31016.某地在一周内每天的最高气温(°C )分别是:24、20、22、23、25、23、21,则这组数据的极差是___________. 答案:5°C17.如图,在△ABC 中,D 、E 分别是AB 、AC 上的点,DE ∥BC ,且AD=13AB ,则△ADE 的周长与△ABC的周长的比为__________.答案: 1318.函数y= 4x 和y=1x 在第一象限内的图像如图,点P 是y= 4x 的图像上一动点,PC ⊥x 轴于点C ,交y=1x第17题A BCDE第14题A BCO·第10题A B P的图像于点B.给出如下结论:①△ODB 与△OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积大小不会发生变化;④CA= 13AP.其中所有正确结论的序号是______________.答案:①③④解析:因点A 和B 都在反比例函数y=1x 的图像上,根据反比例函数K 的几何意义可知, △ODB 与△OCA 的面积都等于12 ,所以①是正确的;因△ODB 与△OCA 的面积都等于12 ,它们面积之和始终等于1,而矩形OCPD 面积始终等于4,所以四边形PAOB 的面积始终等于3,即大小不会发生变化,所以③是正确的;连接OP,△OPC 面积始终等于2, △OCA 的面积都等于12 ,因它们同底(OC 作底),所以它们面积的比等于高AC 与PC 的比,即AC:PC=1:4,所以CA= 13AP,因此④也是正确的;由图的直观性可知,P 点至上而下运动时,PB 在逐渐增大,而PA在逐渐减小,所以②是错误的.三、解答题(本大题共8小题,共86分)19.(8分)解不等式组:⎩⎪⎨⎪⎧x +4<6 ①3x -12>x ②解:由①得x <2由②得x >1∴原不等式组的解集是1<x <220.(8分)解方程:x x +1 + 2x -1=1解:方程两边同时乘以(x+1)(x -1)得 x (x -1)+2(x +1)=x 2 解得x =-3经检验: x =-3是原方程的根. ∴原方程的根是x =-3 21.(10分)如图,⊙O 的直径AB 长为6,弦AC 长为2,∠ACB 的平分线交⊙O 于点D ,求四边形ADBC 的面积.第18题解:∵AB 是直径, ∴∠ACB=∠ADB=90°,在Rt △ABC 中,AB=6, AC= 2,∴BC=AB 2-AC 2 =62-22 = 4 2 ∵∠ACB 的平分线交⊙O 于点D ,∴∠DAC=∠BCD ∴AD ⌒=DB ⌒, ∴AD=BD ∴在Rt △ABD 中,AD=BD=22AB=3 2 ∴四边形ADBC 的面积=S △ABC+S △ABD=12 AC ·BC+12AD ·BD=12 ×2×4 2 +12×(3 2 )2 =9+4 2 22.(10分)今年端午节,某乡镇成立一支龙舟队,共30名队员,他们的身高情况如下表:身高(cm ) 165 166 169 170 172 174 人数 3 2 6 7 8 4 根据表中的信息回答以下问题:(1)龙舟队员身高的众数是______,中位数是______.(2)这30名队员平均身高是多少cm ?身高大于平均身高的队员占全队的百分之几?解:(1)172cm ,170cm ;(2)x -=165×3+166×2+169×6+170×7+172×8+174×430 =170.1,由表可知,身高大于平均身高的队员共有12人,占全队的百分比为 1230=40%.23.(10分)我国西南五省市的部分地区发生严重旱灾,为鼓励节约用水,某市自来水公司采取分段收费标准,右图反映的是每月收取水费y (元)与用水量x (吨)之间的函数关系. (1)小明家五月份用水8吨,应交水费______元;(2)按上述分段收费标准,小明家三、四月份分别交水费26元和18元,问四月份比三月份节约用水多少吨?解:(1)16; (2)解法一:·第21题ABCO D 第23题由图可得 用水10吨内每吨2元,10吨以上每吨 50-2020-10 =3元三月份交水费26元>20元。
2008年福州初中毕业升学统一考试、数学试卷含答案

2008年福州市初中毕业会考 高级中等学校招生考试(全卷共4页,三大题,共22小题;满分150分;考试时间120分钟) 友情提示:所有答案都必须填涂在答题卡上,答在本试卷上无效.毕业学校 姓名 考生号一、选择题(共10小题,每小题4分,满分40分;每小题只有一个正确的选项,请在答题卡的相应位置填涂)1.5-的相反数是( )A A .5B .5-C .15D .15-2.如图所示的物体是一个几何体,其主视图是( )C3.2008北京奥运会主会场“鸟巢”的座席数是91000个,这个数用科学记数法表示为( )BA .50.9110⨯B .49.110⨯C .39110⨯D .39.110⨯4.实数a b ,在数轴上的位置如图所示,下列各式正确的是( )DA .0a >B .bC .D .5.下列计算正确的是( )C A .246x x x +=B .235x y xy +=C .326()x x =D .632x x x ÷=6.下列调查中,适合用全面调查方式的是( )A A .了解某班学生“50米跑”的成绩 B .了解一批灯泡的使用寿命 C .了解一批炮弹的杀伤半径 D .了解一批袋装食品是否含有防腐剂7.已知三角形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作为第三边的是( ) B A .13cm B .6cm C .5cm D .4cm 8.一次21y x =-的图象大致是( )B9.如图,已知直线AB CD ,相交于点O ,OA 平分EOC ∠,100EOC ∠=,则BOD ∠的度数是( )CA .20B .40C .50D .8010.已知抛物线21y x x =--与x 轴的一个交点为(0)m ,, 则代数式22008m m -+的值为( )DA .2006B .2007C .2008D .2009二、填空题(共5小题,每小题4分,满分20分.请将答案填入答题卡的相应位置) 11.因式分解:244x x ++= .(x+2)212.如图,在ABC △中,D E ,分别是AB AC ,的中点,若5DE =,则BC 的长是 .1013.在一个袋子中装有除颜色外其它均相同的2个红球和3个白球,从中任意摸出一个球,则摸到红球的概率是 .2/514.如图,AB 是⊙的弦,OC AB ⊥于点C ,若8cm AB =,3cm OC =,则⊙O 的半径为 cm .515.如图,在反比例函数2y x=(0x >)的图象上,有点1234P P P P ,,,,它们的横坐标依次为1,2,3,4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为123S S S ,,,则123S S S ++= .3/2(第12题)A BC ED (第14题)AE DO CB(第9题)三、解答题(满分90分.请将解答过程填入答题卡的相应位置.作图或添辅助线用铅笔画完,需用水笔再描黑) 16.(每小题7分,满分14分) (1)计算:01(π4)sin 302---; 解:原式=2211321-=-+-(2)化简:aa a a a 21)242(22+⋅---. 解:原式=aa a a a a a a a a 1)2(12)2)(2(212422=+⋅--+=+⋅--17.(每小题7分,满分14分)(1)如图,在等腰梯形ABCD 中,AD BC ∥,M 是AD 的中点,求证:MB MC =.证明:因为四边形ABCD 是等腰梯形,所以AB=D C ,∠A=∠D .因为M 为AD 的中点,所以AM=DM .在△ABM 和△DCM 中,⎪⎩⎪⎨⎧=∠=∠=DM AM D A DC AB ,所以△ABM ≌△DCM(SAS),所以AM=MC .(2)如图,在Rt OAB △中,90OAB ∠=,且点B 的坐标为(4,2). ①画出OAB △向下平移3个单位后的111O A B △;2y x=xyOP 1P 2P 3P 4 12 34(第15题)②画出OAB △绕点O 逆时针旋转90后的22OA B △,并求点A 旋转到点2A 所经过的路线长(结果保留π).解:(1)图略;(2)图略.点A 旋转到点A 2所经过的路线长=ππ2418090=⨯ 18.(本题满分12分)某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A B C D ,,,四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A 级:90分~100分;B 级:75分~89分;C 级:60分~74分;D 级:60分以下) (1)求出D 级学生的人数占全班总人数的百分比; (2)求出扇形统计图中C 级所在的扇形圆心角的度数; (3)该班学生体育测试成绩的中位数落在哪个等级内;(4)若该校九年级学生共有500人,请你估计这次考试中A 级和B 级的学生共有多少人? 解:(1)4%;(2)72;(3)B(4)依题意,知:A 级和B 级学生的人数和占全班总人数的76%,所以500×76%=380,所以估计这次考试中A 级和B 级的学会上共有380人.19.(本题满分11分)如图,AB 是⊙O 的直径,AD 是弦,22.5DAB ∠=,延长AB 到点C ,使得45ACD ∠=. (1)求证:CD 是⊙O 的切线;(2)若AB =BC 的长.(1)证法一:连接O D ,因为∠DAB=22.50,∠DOC=2∠DAB ,所以∠DOC=450,又因为∠ACD=450,所以∠ODC=1800-∠ACD -∠DOC=900,即OD ⊥CD,所以CD 为⊙O 的切线;证法二:连接O D ,因为∠DAB=22.50,∠ACD=450,所以∠ADC=1800-∠DAB -∠ACD=112.50,又OA=OD ,所以∠ADO=∠DAB=22.50,所以∠ODC=∠ADC -∠ADO=900,即OD ⊥CD,所以CD 为⊙O 的切线;(2)由(1)可得△ODC 是等腰直角三角形,因为AB=22,AB 是直径,所以OD=OB=2,所以OC=2OD=2,所以BC=O C -OB=2-2.20.(本题满分12分)今年5月12日,四川汶川发生了里氏8.0级大地震,给当地人民造成了巨大的损失.“一方有难,八方支援”,我市锦华中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:吴老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:信息一:这三个班的捐款总金额是7700元; 信息二:(2)班的捐款金额比(3)班的捐款金额多300元; 信息三:(1)班学生平均每人捐款的金额大于..48元,小于..51元. 请根据以上信息,帮助吴老师解决下列问题:(1)求出(2)班与(3)班的捐款金额各是多少元; (2)求出(1)班的学生人数.解:(1)设(2)班的捐款金额为x 元,(3)班的捐款金额为y 元,则有⎩⎨⎧=--=+30020007700y x y x ,解之,得⎩⎨⎧==27003000y x .答:略;(2)设(1)班的学生人数为x 人,则根据题意,得⎩⎨⎧〉〈200051200048x x ,所以3241511139〈〈x ,因为x 是正整数,所以x=40或41.答:略..(本题满分13分)如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm/s ,点Q 运动的速度是2cm/s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题: (1)当t =2时,判断△BPQ 的形状,并说明理由; (2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;(3)作QR //BA 交AC 于点R ,连结PR ,当t 为何值时,△APR ∽△PRQ ?解:(1)△BPQ 是等边三角形,当t=2时,AP=2×1=2,BQ=2×2=4,所以BP=AB-AP=6-2=4,所以BQ=BP.又因为∠B=600,所以△BPQ 是等边三角形.(2)过Q 作QE ⊥AB,垂足为E,由QB=2y,得QE=2t ·sin600=3t,由AP=t,得PB=6-t,所以S △BPQ=21×BP ×QE=21(6-t)×3t=-23t 2+33t ;(3)因为Q R ∥BA,所以∠QRC=∠A=600,∠RQC=∠B=600,又因为∠C=600,所以△QRC 是等边三角形,所以QR=RC=QC=6-2t.因为BE=BQ ·cos600=21×2t=t,所以EP=AB-AP-BE=6-t-t=6-2t,所以EP ∥QR,EP=QR,所以四边形EPRQ 是平行四边形,所以PR=EQ=3t,又因为∠PEQ=900,所以∠APR=∠PRQ=900.因为△APR ~△PRQ,所以∠QPR=∠A=600,所以tan600=PRQR,即3326=-tt,所以t=56,所以当t=56时, △APR ~△PRQ22.(本题满分14分)如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x 轴,OC 所在的直线为y 轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标;(2)设顶点为F 的抛物线交y 轴正半轴...于点P ,且以点E 、F 、P 为顶点的三角形是等腰三角形,求该抛物线的解析式;(3)在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.解:(1)E(3,1);F(1,2);(2)在R t △EBF 中,∠B=900,所以EF=5212222=+=+BF EB .设点P 的坐标为(0,n),(第21题)(第22题)其中n >0,因为顶点F(1,2),所以设抛物线的解析式为y=a(x-1)2+2(a ≠0) .①如图1,当EF=PF 时,EF 2=PF 2,所以12+(n-2)2=5,解得n 1=0(舍去),n 2=4,所以P(0,4),所以4=a(0-1)2+2,解得a=2,所以抛物线的解析式为y=2(x-1)2+2. ②如图2,当EP=FP 时,EP 2=FP 2,所以(2-n)2+1=(1-n)2+9,解得n =-25(舍去) . ③当EF=EP 时,EP=5<3,这种情况不存在.综上所述,符合条件的抛物线为y=2(x-1)2+2. (3)存在点M 、N,使得四边形MNFE 的周长最小.如图3,作点E 关于x 轴的对称点E /,作点F 关于y 轴的对称点F /,连接E /F /,分别与x 轴、y 轴交于点M 、N,则点M 、N 就是所求.所以E /(3,-1)、F /(-1,2),NF=NF /,ME=ME /,所以BF /=4,BE /=3,所以FN+NM+ME=F /N+NM+ME /=F /E /=2243 =5.又因为EF=5,所以FN+MN+ME+EF=5+5,此。
南平市中考数学样卷

1 / 3A .B .C .D .2008年初中毕业、升学考试数 学 试 题(样卷)(满分:150分;考试时间:120分钟)考生注意:① 解答的内容一律写在答题卡上,否则以0分计算.交卷时只交答题卡,本卷由考场处理,考生不得擅自带走;② 可以携带使用科学计算器,并注意运用计算器进行估算和探究; ③ 未注明精确度、保留有效数字等的计算问题不得采取近似计算.一、选择题(本大题共9小题,每小题4分,共36分.每小题都有四个备选答案,请把你认为正确的一个答案的代号写在题后的括号内.)1. 点P 在第四象限,且点P 到x 轴距离为3,到 y 轴距离为2,则P 点坐标为………( ) A . (-3,2 ) B . (3,-2) C . (2,3 ) D . (2,-3)2. 下列计算中,正确..的是……………………………………………………( )A .39±=B .2)2(2-=-C . 3)3(33=-D . ππ=-3. 掷一颗质地均匀的骰子2 400次,向上一面的点数为3点的次数大约是…………( ) A . 400次 B . 600次 C . 1 200次 D . 2 400次4.如果反比例函数xky =的图象经过点P (-2,3),那么k 的值是……………………()A . 6-B . 23-C . 32-D . 65. 如图,甲顺着大半圆从A 地到B 地,乙顺着两个小半圆从A 地到B 地,设甲、乙走过的路程 分别为a 、b ,则…………………………………( ) A . a >b B . a <bC . a =b D. 不能确定 6. 某次体育活动中,统计甲、乙两班学生每分钟跳绳的成绩(单位:次)情况如下表: ① 甲班学生的平均成绩高于乙班学生的平均成绩;② 甲班学生成绩的波动比乙班学生成绩的波动大;③ 甲班学生成绩优秀人数比乙班学生成绩优秀人数少.(跳绳次数≥140次为优秀) 其中正确..命题的个数是……………………………………( ) A . 0个 B . 1个 C . 2个 D . 3个7.使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,如图所示的四种情况中合格的是……………………………………………………………( )8. 用两个全等的非等腰的直角三角形拼下列图形,一定可以拼出的图形为………( )①平行四边形 ②矩形 ③菱形 ④正方形 ⑤等腰三角形 A .①④⑤ B .②③④ C .①②⑤ D .①②③ 9. 如图,把边长为3的正三角形绕着它的中心旋转180°后, 重叠部分的面积为 .......................... ( )A .349B . 323C . 343D . 23二、填空题(本大题共9小题,每小题3分,共27分)10. 若a 有意义,则a ___________0.(填“≥”或“≤”) 11. 因式分解:a a 422+=________________. 12. 样本数据52,50,49,51,48的方.差.是_________. 13. 如图,分别自由转动三个转盘(转盘被等分成6个扇形),指针指向白色..区域的概率按从小到大的顺序是_____<_____<_____.(只须填写相应的序号)14. 已知1=x 是方程022=-+x ax 的一个根,则a =______________.15. 如图,是由几个相同的小正方体搭成的几何体的三视图,则搭成这个几何体的小正方体的个数是______________个.俯视图左视图 主视图(第15题)①② ③(第13题)B甲 乙 (第5题)2 / 316. 请从① AB ∥CD ;②BC =AD ;③ BC ∥AD ;④AB =CD这四个条件中选取两个..,使四边形ABCD 成为平行四边形: ______________.(只需填写所选取的两个条件的序号即可)17. 如图,△ABC 中,AB =9,AC =6,点E 在AB 上且AE =3,点F 在AC 上,连接EF ,若△AEF 与△ABC 相似,则 AF =_________________. 18. 如图,直线434+=x y 与x 轴,y 轴分别交于A ,B 两点,点C 在OB 上,若将△ABC 沿AC 折叠,使点B 恰好落在 x 轴上的点D 处,则点C 的坐标是_________________.三、解答题(本大题共8小题,共87分)19.(8分)解不等式组:⎪⎩⎪⎨⎧-<+>+2321132x x x x20.(8分)解分式方程:11112=---xx x21.(9分)如图,在等腰△ABC 中,AC =AB ,以AB为直径的⊙O 交BC 于点E ,过点E 作⊙O 的切线交AC 于点D ,交AB 的延长线于点P .问:PD 与AC 是否互相垂直?请说明理由.22.(10分)为贯彻实施新修订的《义务教育法》,某市2006-2007学年对全市六个乡镇农村学生实行免除学杂费,由政府财政补助,总额达2 016万元,如图是根据该市农村学生人数情况制成的条形统计图.(1)该市农村学生平均每人免除学杂费多少元? (2)该市农村学生人数约占全市学生人数的70%.若下学年该市学生总数 及城乡学生人数比例不变,要将此惠民政策在全市实施,估计政府财 政补助共需多少万元?(注:本题城市和农村学生均指义务教育阶段学生)23.(12分)某煤气公司规定,每户居民每月使用的煤气费由基本月租费、保险费和超额费组成.当煤气使用量不超过a m 3时,当月需缴纳保险费3元和基本月租费b 元;当煤气使用量超过a m 3时,超出的部分还要..按3.2元/m 3计费.如果小红家3月、4月煤气使用量与缴费情况如右表,其中仅.3.月份煤气使用量未超过..........a m 3. (1)请求出a ,b 的值;(2)如果小红家5月份缴交煤气费42元, 那么她家这个月煤气使用量为多少m 3?24.(12分)如图,在路边O 处安装路灯,路面宽ED 为16米,灯柱OB 与路边的距离OE 为2米,且灯柱OB 与灯杆AB 成120°角.路灯A 采用锥形灯罩,灯罩轴线AC 与灯杆AB 垂直,并与路面ED 交于点C ,AE 恰好与OD 垂直.当路灯A 到路面的距离AE 为多少米时,点C 正好是路面ED 的中点?并求此时灯柱OB 的高.(精确到0.1米)CDO BPE① ② EA (第17题)ABOCDEABOCDE120°义务教育阶段农村学生人数情况0.70.61.01.11.40.80.20.40.60.811.21.41.6ABC DEF乡 镇人数(万人)xOAB C yD(第18题)25.(14分)武夷山市某茶厂生产某品牌茶叶,它的成本价是每千克180元,售价是每千克230元,年销售量为10000千克.随着产量增加,为了扩大销售量,增加效益,公司决定拿出一定量的资金做广告.根据市场调查,若每年投入广告费为x(万元)时,产品的年销售量将是原销售量的y 倍,且y与x之间的关系如图所示,可近似看作是抛物线的一部分.(1)根据图象提供的信息,求y与x之间的函数关系式;(2)求年利润S(万元)与广告费x(万元)之间的函数关系式;(年利润S=年销售总额-成本费-广告费)(3)问广告费x(万元)在什么范围内,公司获得的年利润S(万元)随广告费的增大而增多?26.(14分)如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.(1)求∠PCQ的度数;(2)当AB=4,AP∶PC=1∶3时,求PQ的大小;(3)当点P在线段AC上运动时(P不与A重合),请写出一个反映P A2,PC2,PB2之间关系的等式,并加以证明.ABPCQOx(万12.7(倍)4.23 / 3。
XXXX福建省南平市中考数学试卷及答案(Word解析版)

XXXX福建省南平市中考数学试卷及答案(Word解析版)福建省南平市XXXX高中数学试卷多项选择题(10项,每项4分,每项40分。
每个项目只有一个正确的选择,请填写答案表上的相应位置)1.(4分)(XXXX南平市6月31日各区县最高气温(℃)如下表所示:武夷山市、简阳县、延平县、建瓯县、顺昌县松溪镇和邵武广泽32 32 30 29 31 30 28的气温(℃)为33。
10个区县当日最高气温的模式和中位数分别为()A32、32B.32、30C.30、30D.30和32。
中位数分析:首先,将10个数字按降序排列为28、29、29、30、30、31、32、32、33,然后根据众数和中位数的定义求解。
答案:解决方案:将10个数字按降序排列为出现次数最多的28、29、29、30、30、30、31、32、32、33、30,因此当天10个区县的最高气温模式为30;第五个数字和第六个数字分别是30和30,所以中位数是= 30。
8.(4分)(6月11日,XXXX,“神舟”10号载人飞船成功发射!如图所示,在完成变轨后,宇宙飞船将运行在离地球约350公里的圆形轨道上(⊚ o)。
当航天器直接在某个地方(点p)(点f)上方运行时,可以从航天器上看到地球表面上最远的点Q(FQ是≧0的切线)。
地球的半径已知约为6400公里。
发现:(1)∠qfo的程度;(结果精确到0.01) (2)地面上P点和Q点之间的距离(PQ长度)。
(π取3.142,结果保留整数)测试地点:切线的性质;弧长的计算;求解直角三角形的应用。
专题:计算。
分析:(1)如果根据切线的性质得到OQ⊥FQ,则在Rt△OQF中,根据正弦的定义得到sin≈qfo = \ \ frac { OQ } { FQ } =≈0.9481,然后得到≈qfo;(2)首先计算∠FOQ,然后根据弧长公式计算弧长PQ。
解决方案:解决方案:(1)FQ与⊙O相切,∴OQ⊥FQ,∴OQF = 90,∴在Rt中△OQF,OQ=6400,OF=OP+PF=6400+350=6750,∴sin∠QFO = \ \ frac { OQ } { FQ } =∫答案:∠qfo的度数约为71.46。
