(完整版)插值计算器
插值法的最简单计算公式

插值法的最简单计算公式全文共四篇示例,供读者参考第一篇示例:插值法是一种常用的数值计算方法,用于通过已知数据点推断出未知数据点的值。
在实际问题中,往往会遇到数据点不连续或者缺失的情况,这时就需要通过插值法来填补这些数据点,以便更准确地进行计算和分析。
插值法的最简单计算公式是线性插值法。
线性插值法假设数据点之间的变化是线性的,通过已知的两个数据点来推断出中间的未知数据点的值。
其计算公式为:设已知数据点为(x0, y0)和(x1, y1),需要插值的点为x,其在(x0, x1)之间,且x0 < x < x1,插值公式为:y = y0 + (y1 - y0) * (x - x0) / (x1 - x0)y为插值点x对应的值,y0和y1分别为已知数据点x0和x1对应的值。
通过这个线性插值公式,可以方便地计算出中间未知点的值。
举一个简单的例子来说明线性插值法的应用。
假设有一组数据点为(1, 2)和(3, 6),现在需要插值得到x=2时的值。
根据线性插值公式,我们可以计算出:y = 2 + (6 - 2) * (2 - 1) / (3 - 1) = 2 + 4 * 1 / 2 = 2 + 2 = 4当x=2时,线性插值法得到的值为4。
通过这个简单的例子,可以看出线性插值法的计算公式的简单易懂,适用于很多实际问题中的插值计算。
除了线性插值法,还有其他更复杂的插值方法,如多项式插值、样条插值等,它们能够更精确地拟合数据并减小误差。
在一些简单的情况下,线性插值法已经足够满足需求,并且计算起来更加直观和方便。
在实际应用中,插值法经常用于图像处理、信号处理、数据分析等领域。
通过插值法,可以将不连续的数据点连接起来,填补缺失的数据,使得数据更加完整和连续,方便后续的处理和分析。
插值法是一种简单而有效的数值计算方法,其中线性插值法是最简单的计算公式之一。
通过这个简单的公式,可以方便地推断出未知数据点的值,并在实际应用中发挥重要作用。
炉内传热计算器
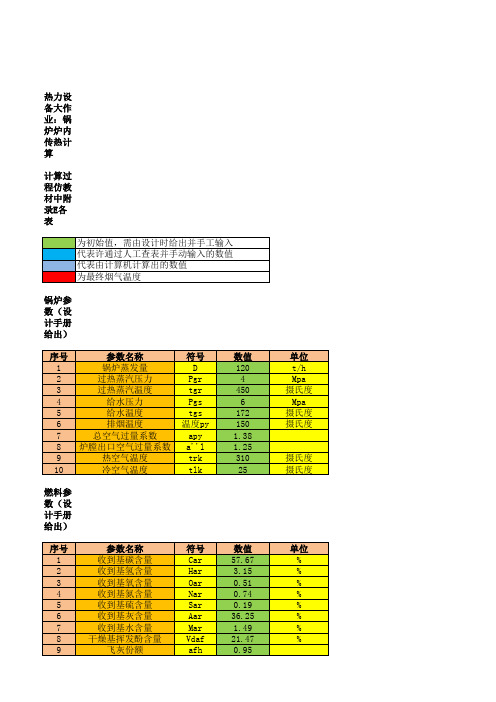
由结果 值与假 设值进 行校 核,并 不断试 算,直 至满足 要求
结果分 析
对烟气 出口温 度影响 较大的 有煤种 的含碳 量,计 算发现 烟气出 口温度 较低, 然后检 查了一 次,发 现没问 题,于 是认为 煤种含 碳量影 响很 大,从 燃烧理 论中亦 可得到 类似的 结论 然后影 响较大 的还有 炉膛的 体积及 面积, 这直接 影响了 有效辐 射层厚 度
折算灰份
符号 V0
V0N2 V0H20 V0RO2 V0g afa Gfa Aar,c
数值 5.9510 4.7072 0.4639 1.0775 6.2486 0.9500 0.3444 17.3023
烟气特 性表 (此表 无需输 入任何 数值)
序号 1 2 3 4 5 6 7 8
参数名称
符号
烟道进口过量空气系数 alfa'
VC
16
水蒸气容积份额
rH2O
17 三原子气体容积份额
rn
18 烟气密度(标准状态) 密度g
19
炉膛压力
p
20
三元子气体分压力
pn
21
pn与s乘积
pns
22
烟气辐射减弱系数
kg
23
飞灰减弱系数
kfa
um kj/kgK
kg/m3 Mpa mMpa m*Mpa m*Mpa-1 m*Mpa-1
24 焦炭粒子辐射减弱系数 kco
序号
参数名称
1 燃料带入热量
2 排烟温度
3 排烟焓
4 冷空气温度
5 理论冷空气焓
符号 Qin 温度ex Iex tca Ica
数值 20951 150.00
1670.80 25.00 278.66
插值法的计算公式

插值法的计算公式
插值法是一种常用的数值计算方法,可以用来估计一个函数在某些未知点的函数值。
在插值法中,我们需要知道函数在一些已知点上的值,然后根据这些值来求解函数在其他点上的值。
以下是插值法的计算公式:
1. 拉格朗日插值法
对于给定的函数f(x),已知n个插值点(x1,y1),(x2,y2),...,(xn,yn),可以通过拉格朗日插值法来求解f(x)在任意点x处的函数值。
拉格朗日插值公式:
f(x) = Σ(i=1 to n) yi*li(x)
其中,li(x)表示拉格朗日插值基函数,计算公式为:
li(x) = Π(j=1 to n, j≠i) (x-xj)/(xi-xj)
2. 牛顿插值法
牛顿插值法是一种递推算法,可以通过已知的插值点(x0,y0),(x1,y1),...,(xn,yn)来求解f(x)在任意点x处的函数值。
牛顿插值公式:
f(x) = y0 + Σ(i=1 to n) [Π(j=0 to i-1) (x-xj)/(xi-xj)] * Δi
其中,Δi表示牛顿前向差商,计算公式为:
Δ0y0 = y0
Δi yi = (Δi-1 yi+1 - Δi-1 yi) / (xi+i - xi)
以上是插值法的计算公式,可以根据具体的问题选择合适的插值方法来进行求解。
插值法的最简单计算公式

插值法的最简单计算公式全文共四篇示例,供读者参考第一篇示例:插值法是数值分析领域中常用的一种方法,它可以用来估计未知函数在给定点处的值。
插值法的基本思想是基于已知数据点,构建一个多项式函数来逼近未知函数的值。
在实际应用中,插值法常常被用来对离散数据进行平滑处理,或是用来预测未来的数据。
最简单的插值方法之一是线性插值法。
线性插值法假设未知函数在两个已知数据点之间是线性变化的,即可以通过这两个点之间的直线来估计未知函数在中间点处的值。
线性插值的计算公式如下:设已知数据点为(x0, y0)和(x1, y1),要估计中间点x处的函数值y,则线性插值公式为:\[y = y0 + \frac{x - x0}{x1 - x0} * (y1 - y0)\]这个公式的推导比较简单,可以通过代入已知数据点计算出来。
如果已知数据点为(0, 1)和(2, 3),要估计在x=1处的函数值,根据线性插值公式,计算如下:在x=1处的函数值为2。
线性插值法的优点是简单易懂,计算速度快,并且可以比较精确地估计函数值。
但是线性插值法的精度受限于已知数据点之间的线性关系,如果函数在两个数据点之间发生了急剧变化,线性插值法可能无法准确估计函数值。
除了线性插值法,还有许多其他更复杂的插值方法,如拉格朗日插值、牛顿插值、三次样条插值等。
这些方法在不同的情况下可以提供更精确的函数估计值,但也需要更复杂的计算步骤。
插值法是一种常用的数值分析方法,可以帮助我们更好地处理数据和预测未知函数的值。
在实际应用中,可以根据具体情况选取合适的插值方法来进行计算。
第二篇示例:插值法是一种用于估算未知数值的方法,它基于已知数据点之间的关系进行推断。
在实际应用中,插值法经常用于数据处理、图像处理、数学建模和预测等领域。
插值法的计算公式通常比较复杂,但是我们可以通过简化的方式来理解和计算插值结果。
最简单的插值方法之一是线性插值法。
在线性插值法中,我们假设已知数据点之间的关系是线性的,然后通过线性方程来估算未知点的数值。
插法计算公式

插法计算公式插法计算公式,这可真是个让不少同学头疼的家伙,但其实它也没那么可怕啦!咱们先来说说啥是插法计算公式。
简单来讲,就是在已知一些数据点的情况下,通过一定的方法找到中间某个未知点的值。
比如说,咱们知道了几个温度测量的数据,像早上 8 点是 15 度,中午 12 点是 25 度,那如果想知道 10 点大概是多少度,这时候插法计算公式就派上用场啦。
我记得有一次给学生们讲这个知识点的时候,有个小同学瞪着大眼睛,一脸迷茫地问我:“老师,这到底是啥呀,感觉好复杂!”我笑着告诉他:“别着急,咱们一步一步来。
”插法计算公式有线性插值和非线性插值。
线性插值呢,就像是在两点之间拉一条直直的线,然后根据比例去找到中间点的值。
比如说,从 A 点到 B 点,已知 A 点的值是 10,B 点的值是 20,我们要找距离A 点三分之一位置的那个点的值,那就是 10 + (20 - 10)× 1/3 。
非线性插值就稍微复杂一点啦,比如说抛物线插值、三次样条插值等等。
这就好比不是走直线,而是走一条弯弯的曲线去找到那个值。
咱们再拿个具体的例子来说吧。
假设一个商店在一周内每天的销售额分别是:周一 500 元,周二 800 元,周三 1000 元,周四 1200 元,周五 1500 元,周六 2000 元,周日 1800 元。
现在想知道周二到周三中间,也就是周二下午 6 点左右的销售额大概是多少。
这时候咱们就可以用线性插值来算一算。
首先算出周二到周三销售额的变化量:1000 - 800 = 200 元。
然后计算周二下午 6 点距离周二开始的时间比例,假设一天按 24 小时算,下午 6 点就是 18 点,那时间比例就是(18 - 8)/ 24 = 5/12 。
最后用周二的销售额加上变化量乘以这个比例:800 + 200 × 5/12 ≈ 917 元。
这样就大概算出了周二下午 6 点的销售额啦。
在实际生活中,插法计算公式用处可多啦。
插值法计算公式范文

插值法计算公式范文插值法是一种数值计算方法,用于在已知数据点之间进行估计或预测。
它基于假设函数在相邻数据点之间是连续的,并利用这种连续性来进行估计。
插值法的计算公式可以根据不同的方法和情况而有所不同。
下面将介绍两种常用的插值方法及其计算公式。
1.线性插值法线性插值法假设假设函数在相邻数据点之间是线性的,即通过两个数据点的直线来进行估计。
设已知数据点为(x0,y0)和(x1,y1),要在这两个数据点之间的任意位置x进行估计,计算公式如下:y=y0+(x-x0)*(y1-y0)/(x1-x0)这个公式表示了一个斜率为(y1-y0)/(x1-x0)的直线,通过(x0,y0)点,并与x轴交于x点。
通过该公式,我们可以根据已知数据点在特定位置进行线性插值估计。
2.拉格朗日插值法拉格朗日插值法是一种基于拉格朗日多项式的插值方法。
假设已知n+1个数据点(x0, y0),(x1, y1),...(xn, yn),要在这些数据点之间的任意位置x进行估计,计算公式如下:y = L0(x) * y0 + L1(x) * y1 + ... + Ln(x) * yn其中Li(x)表示拉格朗日插值多项式的第i个基函数Li(x) = (x - x0) * (x - x1) * ... * (x - xi-1) * (x - xi+1)* ... * (x - xn) / ((xi - x0) * (xi - x1) * ... * (xi - xi-1) * (xi - xi+1) * ... * (xi - xn))这个公式表示了一个以数据点(xi, yi)为中心的拉格朗日插值多项式的基函数,通过已知数据点进行插值估计。
总结:插值法是一种根据已知数据点之间的连续性进行估计的数值计算方法。
线性插值法和拉格朗日插值法是两种常用的插值方法。
线性插值法假设函数在相邻数据点之间是线性的,通过两个数据点的直线进行估计。
拉格朗日插值法基于拉格朗日多项式,通过已知数据点进行插值估计。
插值法计算方法举例

插值法计算方法举例插值法是一种数值逼近方法,用于在给定的一些数据点之间进行数值求解。
插值法的基本思想是通过已知数据点的函数值来构建一个插值函数,并利用该插值函数来估计未知数据点的函数值。
以下是一些常见的插值方法。
1.线性插值:线性插值是最简单的插值方法之一、假设我们有两个已知数据点 (x1, y1) 和 (x2, y2),我们想要在这两个数据点之间估计一个新的点的函数值。
线性插值方法假设这两个点之间的函数关系是线性的,即 y = f(x)= mx + c,其中 m 是斜率,c 是截距。
通过求解这两个点的斜率和截距,我们可以得到插值函数的表达式,从而计算出新点的函数值。
2.拉格朗日插值:拉格朗日插值是一种经典的插值方法,它利用一个多项式函数来逼近已知数据点之间的关系。
对于一组已知数据点 (x1, y1), (x2, y2), ..., (xn, yn),拉格朗日插值方法构建一个函数 L(x) 来逼近真实的函数f(x)。
L(x) 的表达式为 L(x) = y1 * L1(x) + y2 * L2(x) + ... + yn* Ln(x),其中 Li(x) 是拉格朗日插值基函数,定义为Li(x) = Π(j=1to n, j≠i) (x - xj) / (xi - xj)。
通过求解 L(x) 的表达式,我们可以计算出任意新点的函数值。
3.牛顿插值:牛顿插值是另一种常用的插值方法,它是通过一个递推的过程来构建插值函数。
对于一组已知数据点 (x1, y1), (x2, y2), ..., (xn, yn),牛顿插值方法定义一个差商表,然后根据该表构建一个递推的多项式函数来逼近真实的函数 f(x)。
差商表的计算使用了递归的方式,其中第 i 阶差商定义为 f[xi, xi+1, ..., xi+j] = (f[xi+1, xi+2, ..., xi+j] - f[xi, xi+1, ..., xi+j-1]) / (xi+j - xi)。
插值法的简便计算

插值法的简便计算插值法是一种常见的数值分析方法,用于在给定的数据点之间估计未知函数的值。
在实际应用中,插值法的计算可能会比较复杂,但是有一些简便的计算方法可以帮助我们更快地完成插值计算。
一、拉格朗日插值法拉格朗日插值法是一种常用的插值方法,它可以通过已知的数据点来估计未知函数的值。
其基本思想是:假设已知n个数据点(x1,y1),(x2,y2),...,(xn,yn),并且这些点两两不同,那么可以构造一个n次多项式P(x),使得P(xi)=yi(i=1,2,...,n)。
然后,通过这个多项式来估计未知函数在某个点x0处的值f(x0)。
拉格朗日插值法的计算比较繁琐,但是可以通过一些简便的计算来减少计算量。
具体来说,可以使用以下公式来计算多项式P(x):P(x)=Σ(yi*li(x))其中,li(x)是拉格朗日基函数,定义为:li(x)=Π((x-xj)/(xi-xj))(i≠j)这个公式中,Π表示连乘积,xi和xj是已知的数据点,i≠j。
通过这个公式,我们可以快速计算出多项式P(x)的值。
二、牛顿插值法牛顿插值法是另一种常用的插值方法,它也可以通过已知的数据点来估计未知函数的值。
其基本思想是:假设已知n个数据点(x1,y1),(x2,y2),...,(xn,yn),并且这些点两两不同,那么可以构造一个n次插值多项式N(x),使得N(xi)=yi(i=1,2,...,n)。
然后,通过这个多项式来估计未知函数在某个点x0处的值f(x0)。
牛顿插值法的计算也比较繁琐,但是可以通过一些简便的计算来减少计算量。
具体来说,可以使用以下公式来计算插值多项式N(x):N(x)=b0+b1(x-x1)+b2(x-x1)(x-x2)+...+bn(x-x1)(x-x2)...(x-xn)其中,bi是牛顿插值系数,可以通过以下公式来计算:bi=Δyi/Δxi(i=1,2,...,n)其中,Δyi和Δxi分别表示相邻数据点的函数值和自变量之差。
设计费插值法计算公式(二)

设计费插值法计算公式(二)设计费插值法计算公式资深创作者们常常使用设计费插值法来计算项目的设计费用。
这种方法可以根据项目的复杂程度、工作量和时间等因素,合理确定设计费用。
下面将列举一些相关的计算公式,并提供相应的例子来说明。
1. 基本设计费基本设计费计算公式:基本设计费 = 设计单价× 设计量这里的设计单价是指每个设计单元的费用,设计量是指项目中需要设计的总量。
例如,一个网站的设计费用计算如下:基本设计费 = 100元/页面× 10个页面 = 1000元2. 复杂程度系数复杂程度系数是根据项目的难度和专业要求而定,用于调整基本设计费的计算结果。
计算公式如下:复杂程度系数 = 1 + 难度系数例如,某平面设计项目的复杂程度系数为,基本设计费为1000元,则经过调整后的设计费用为:调整后的设计费用 = 1000元× (1 + ) = 1200元3. 工作量系数工作量系数是根据项目的工作量和时间要求而定,用于调整设计费用的计算结果。
计算公式如下:工作量系数 = 1 + 工作量比例例如,某建筑设计项目的工作量比例为,基本设计费为20000元,则经过调整后的设计费用为:调整后的设计费用 = 20000元× (1 + ) = 30000元4. 外部影响因素系数外部影响因素系数是用于调整设计费用的计算结果,考虑到项目可能受到的外部因素影响,比如市场需求、竞争程度等。
计算公式如下:外部影响因素系数 = 1 + 外部影响系数例如,某市场推广设计项目的外部影响系数为,基本设计费为5000元,则经过调整后的设计费用为:调整后的设计费用 = 5000元× (1 + ) = 6500元5. 综合计算公式综合计算公式可以根据项目的具体情况,综合考虑上述因素,得出最终的设计费用。
计算公式如下:设计费用 = 基本设计费× 复杂程度系数× 工作量系数× 外部影响因素系数例如,某品牌形象设计项目的基本设计费为20000元,复杂程度系数为,工作量系数为,外部影响因素系数为,则最终的设计费用为:设计费用 = 20000元× × × = 39600元以上是设计费插值法的相关计算公式和例子,通过合理使用这些公式,能够帮助资深创作者们更准确地计算设计费用,确保项目的可行性和盈利性。
插值法计算方法举例

插值法计算方法举例插值法是一种用来通过已知数据点的近似值来推测未知数据点的方法。
它通常用于数据的平滑和预测,尤其在缺少数据或数据不完整的情况下。
以下是一些插值法的具体计算方法举例:1. 线性插值法(Linear Interpolation):线性插值法是最简单的插值方法之一、假设我们有两个已知数据点(x1, y1)和(x2, y2),要推测处于两个数据点之间的未知点(x, y)。
线性插值法通过使用已知点之间的线性关系来计算未知点的值。
具体公式为:y=y1+(x-x1)*((y2-y1)/(x2-x1))2. 多项式插值法(Polynomial Interpolation):多项式插值法通过使用一个低次数的多项式函数来逼近已知数据点,并预测未知数据点。
常见的多项式插值方法包括拉格朗日插值和牛顿插值。
其中,拉格朗日插值使用一个n次多项式来逼近n个已知点,而牛顿插值使用差商(divided differences)和差商表来逼近已知点。
具体公式为:P(x) = a0 + a1 * (x - x1) + a2 * (x - x1) * (x - x2) + ... + an * (x - x1) * (x - x2) * ... * (x - xn-1)3. 样条插值法(Spline Interpolation):样条插值法是一种更复杂的插值方法,它通过拟合已知数据点之间的线段和曲线,来推测未知数据点。
常见的样条插值方法包括线性样条插值、二次样条插值和三次样条插值。
样条插值法具有良好的平滑性和曲线性质,通常在连续数据的插值和平滑方面效果更好。
具体公式为:S(x) = Si(x),其中x属于[xi, xi+1],Si(x)是第i段(i = 1, 2, ..., n-1)中的插值函数。
4. 逆距离加权插值法(Inverse Distance Weighting, IDW):逆距离加权插值法是一种基于距离的插值方法,通过使用已知数据点的权重来推测未知数据点。
几何增长率插值

几何增长率插值
第一种方法:用函数计算器开高次方减1其计算公式是:a(1+x)^n=c,其中a是基期数额,n为年限,c是期末数额,x为平均增长率。
那么,如果需要计算x的话,数学公式为:x=(c/a)^(1/n)—1,其意思是用期末数额除以基期数额开年限次方减1,而开年限次方就是乘年限倒数次方。
第二种方法:在EXCEL中计算平均增长率在EXCEL中计算平均增长率的公式有两种写法。
一种写法是使用EXCEL函数计算平均增长率这种方法还有两种写法,其一是用EXCEL计算两年的平均增长率由于用EXCEL计算两年平均增长率只要开平方就可以了,所以公式可以写为:=SQRT(c/a)—1,SQRT是EXCEL 的开方函数,因此在EXCEL中计算两年平均增长率可以用这个公式。
把公式x=(c/a)^(1/n)—1直接写入需要计算平均增长率的EXCEL单元格中,因为EXCEL是支持数学公式的,因此可以在EXCEL单元格中直接写数学公式而计算平均增长率的。
设计费插值法计算公式(一)

设计费插值法计算公式(一)设计费插值法计算公式1. 什么是设计费插值法设计费插值法是一种用于计算设计费用的方法,通过根据项目的不同特点,结合相关参数,利用数学计算公式得出设计费用的估算值。
该方法可以较为准确地预测设计项目的费用,并为设计师和客户提供一个参考依据。
2. 计算公式设计费插值法的计算公式可以根据具体的项目需求和参数进行调整,以下是一些常见的设计费插值法计算公式:单位比例法该方法通过定义设计师的工作量和设计项目的规模之间的比例关系来计算设计费用。
具体的计算公式如下:设计费用 = 设计师工作量 × 单位费用其中,设计师工作量指的是完成设计项目所需的工作时间或工作量,单位为小时或人日;单位费用是指设计师每小时或每人日的费用。
例子:假设设计师工作量为100小时,单位费用为500元/小时,则设计费用 = 100小时× 500元/小时 = 50000元。
项目复杂度法该方法通过考虑设计项目的复杂度来计算设计费用,复杂度可以根据项目的难度、创新性等因素来确定。
具体的计算公式如下:设计费用 = 基础费用 × 复杂度系数其中,基础费用指的是设计项目的基本费用,可以根据项目的常规要求来确定;复杂度系数是一个根据设计项目的具体复杂程度而调整的系数。
例子:假设基础费用为10000元,复杂度系数为,则设计费用 = 10000元× = 15000元。
面积插值法该方法适用于建筑设计等需要根据实际面积来计算费用的项目。
具体的计算公式如下:设计费用 = 单位面积费用 × 设计项目面积其中,单位面积费用指的是每平方米的设计费用,可以根据市场行情或协商来确定;设计项目面积为实际需要设计的项目面积。
例子:假设单位面积费用为100元/平方米,设计项目面积为200平方米,则设计费用 = 100元/平方米× 200平方米 = 20000元。
3. 结论设计费插值法是一种常用的计算设计费用的方法,通过合理选择适用的计算公式,可以较为准确地估算设计项目的费用。
