A REVIEW OF IMAGE DENOISING ALGORITHMS, WITH A NEW
211018240_基于深度可分离选择性残差网络的真实图像增强算法

现代电子技术Modern Electronics Technique2023年4月1日第46卷第7期Apr.2023Vol.46No.70引言图像去噪作为具有挑战性的计算机视觉低级任务,在高级视觉任务的预处理阶段起着重要作用,如三维块匹配滤波(BM3D )[1]、非局部均值滤波(NLM )[2]等传统基于模型的去噪方法都是基于图像先验信息从而进行去噪工作,尽管其大多数去噪任务可达到可接受的性能,但复杂的计算量、工作耗时和手动调参等关键问题在一定程度上阻碍了基于模型的方法的效率[3]。
近年来,基于学习的方法[4]在去噪任务耗时时间及去噪性能上明显优于传统方法。
例如残差学习[5]、密集连接[6]、残差密集块[7]、注意力机制[8]、通道注意块[9]和分层架构[10]等精巧的模块在提取图像特征过程中发挥着重要作用。
基于深度学习的经典方法,例如文献[4]利用残差学习结合批量归一化的方式实现图像去噪的卷积神经网络(DnCNN )。
文献[11]在文献[12]提出的生成对抗网络(Generative Adversarial Net⁃Works ,GAN )的基础上将GAN 生成的噪声图片混合干净的图像构成数据集,通过训练神经网络来完成去噪的工作。
然而这些复杂的架构在图像去噪的过程中仍然浪费了很多计算,并且性能的提升却只有较小幅度。
本文目的在于模型的准确性及计算效率之间取得平衡,提出了融合深度可分离卷积和残差密集块的网络架构,融合模块称之为可分离选择性残差块。
此外,在基于M⁃Net [13]的网络架构中,使用像素混洗采样[14]和双线性采样的方式进行多尺度特征融合来提取空间特征信息,最基于深度可分离选择性残差网络的真实图像增强算法温剑,邵剑飞,邵建龙(昆明理工大学信息工程与自动化学院,云南昆明650500)摘要:图像去噪作为低级视觉任务,在图像处理领域常被重点研究。
针对图像去噪网络训练周期长和图像纹理细节模糊的问题,为提升图像去噪效果,减少训练参数量,缩短训练周期,提出了一种改进M⁃Net 网络融合深度可分离卷积及选择性残差网络的图像盲去噪方法。
A Fast and Accurate Plane Detection Algorithm for Large Noisy Point Clouds Using Filtered Normals

A Fast and Accurate Plane Detection Algorithm for Large Noisy Point CloudsUsing Filtered Normals and Voxel GrowingJean-Emmanuel DeschaudFranc¸ois GouletteMines ParisTech,CAOR-Centre de Robotique,Math´e matiques et Syst`e mes60Boulevard Saint-Michel75272Paris Cedex06jean-emmanuel.deschaud@mines-paristech.fr francois.goulette@mines-paristech.frAbstractWith the improvement of3D scanners,we produce point clouds with more and more points often exceeding millions of points.Then we need a fast and accurate plane detection algorithm to reduce data size.In this article,we present a fast and accurate algorithm to detect planes in unorganized point clouds usingfiltered normals and voxel growing.Our work is based on afirst step in estimating better normals at the data points,even in the presence of noise.In a second step,we compute a score of local plane in each point.Then, we select the best local seed plane and in a third step start a fast and robust region growing by voxels we call voxel growing.We have evaluated and tested our algorithm on different kinds of point cloud and compared its performance to other algorithms.1.IntroductionWith the growing availability of3D scanners,we are now able to produce large datasets with millions of points.It is necessary to reduce data size,to decrease the noise and at same time to increase the quality of the model.It is in-teresting to model planar regions of these point clouds by planes.In fact,plane detection is generally afirst step of segmentation but it can be used for many applications.It is useful in computer graphics to model the environnement with basic geometry.It is used for example in modeling to detect building facades before classification.Robots do Si-multaneous Localization and Mapping(SLAM)by detect-ing planes of the environment.In our laboratory,we wanted to detect small and large building planes in point clouds of urban environments with millions of points for modeling. As mentioned in[6],the accuracy of the plane detection is important for after-steps of the modeling pipeline.We also want to be fast to be able to process point clouds with mil-lions of points.We present a novel algorithm based on re-gion growing with improvements in normal estimation and growing process.For our method,we are generic to work on different kinds of data like point clouds fromfixed scan-ner or from Mobile Mapping Systems(MMS).We also aim at detecting building facades in urban point clouds or little planes like doors,even in very large data sets.Our input is an unorganized noisy point cloud and with only three”in-tuitive”parameters,we generate a set of connected compo-nents of planar regions.We evaluate our method as well as explain and analyse the significance of each parameter. 2.Previous WorksAlthough there are many methods of segmentation in range images like in[10]or in[3],three have been thor-oughly studied for3D point clouds:region-growing, hough-transform from[14]and Random Sample Consen-sus(RANSAC)from[9].The application of recognising structures in urban laser point clouds is frequent in literature.Bauer in[4]and Boulaassal in[5]detect facades in dense3D point cloud by a RANSAC algorithm.V osselman in[23]reviews sur-face growing and3D hough transform techniques to de-tect geometric shapes.Tarsh-Kurdi in[22]detect roof planes in3D building point cloud by comparing results on hough-transform and RANSAC algorithm.They found that RANSAC is more efficient than thefirst one.Chao Chen in[6]and Yu in[25]present algorithms of segmentation in range images for the same application of detecting planar regions in an urban scene.The method in[6]is based on a region growing algorithm in range images and merges re-sults in one labelled3D point cloud.[25]uses a method different from the three we have cited:they extract a hi-erarchical subdivision of the input image built like a graph where leaf nodes represent planar regions.There are also other methods like bayesian techniques. In[16]and[8],they obtain smoothed surface from noisy point clouds with objects modeled by probability distribu-tions and it seems possible to extend this idea to point cloud segmentation.But techniques based on bayesian statistics need to optimize global statistical model and then it is diffi-cult to process points cloud larger than one million points.We present below an analysis of the two main methods used in literature:RANSAC and region-growing.Hough-transform algorithm is too time consuming for our applica-tion.To compare the complexity of the algorithm,we take a point cloud of size N with only one plane P of size n.We suppose that we want to detect this plane P and we define n min the minimum size of the plane we want to detect.The size of a plane is the area of the plane.If the data density is uniform in the point cloud then the size of a plane can be specified by its number of points.2.1.RANSACRANSAC is an algorithm initially developped by Fis-chler and Bolles in[9]that allows thefitting of models with-out trying all possibilities.RANSAC is based on the prob-ability to detect a model using the minimal set required to estimate the model.To detect a plane with RANSAC,we choose3random points(enough to estimate a plane).We compute the plane parameters with these3points.Then a score function is used to determine how the model is good for the remaining ually,the score is the number of points belonging to the plane.With noise,a point belongs to a plane if the distance from the point to the plane is less than a parameter γ.In the end,we keep the plane with the best score.Theprobability of getting the plane in thefirst trial is p=(nN )3.Therefore the probability to get it in T trials is p=1−(1−(nN )3)ing equation1and supposing n minN1,we know the number T min of minimal trials to have a probability p t to get planes of size at least n min:T min=log(1−p t)log(1−(n minN))≈log(11−p t)(Nn min)3.(1)For each trial,we test all data points to compute the score of a plane.The RANSAC algorithm complexity lies inO(N(Nn min )3)when n minN1and T min→0whenn min→N.Then RANSAC is very efficient in detecting large planes in noisy point clouds i.e.when the ratio n minN is 1but very slow to detect small planes in large pointclouds i.e.when n minN 1.After selecting the best model,another step is to extract the largest connected component of each plane.Connnected components mean that the min-imum distance between each point of the plane and others points is smaller(for distance)than afixed parameter.Schnabel et al.[20]bring two optimizations to RANSAC:the points selection is done locally and the score function has been improved.An octree isfirst created from point cloud.Points used to estimate plane parameters are chosen locally at a random depth of the octree.The score function is also different from RANSAC:instead of testing all points for one model,they test only a random subset and find the score by interpolation.The algorithm complexity lies in O(Nr4Ndn min)where r is the number of random subsets for the score function and d is the maximum octree depth. Their algorithm improves the planes detection speed but its complexity lies in O(N2)and it becomes slow on large data sets.And again we have to extract the largest connected component of each plane.2.2.Region GrowingRegion Growing algorithms work well in range images like in[18].The principle of region growing is to start with a seed region and to grow it by neighborhood when the neighbors satisfy some conditions.In range images,we have the neighbors of each point with pixel coordinates.In case of unorganized3D data,there is no information about the neighborhood in the data structure.The most common method to compute neighbors in3D is to compute a Kd-tree to search k nearest neighbors.The creation of a Kd-tree lies in O(NlogN)and the search of k nearest neighbors of one point lies in O(logN).The advantage of these region growing methods is that they are fast when there are many planes to extract,robust to noise and extract the largest con-nected component immediately.But they only use the dis-tance from point to plane to extract planes and like we will see later,it is not accurate enough to detect correct planar regions.Rabbani et al.[19]developped a method of smooth area detection that can be used for plane detection.Theyfirst estimate the normal of each point like in[13].The point with the minimum residual starts the region growing.They test k nearest neighbors of the last point added:if the an-gle between the normal of the point and the current normal of the plane is smaller than a parameterαthen they add this point to the smooth region.With Kd-tree for k nearest neighbors,the algorithm complexity is in O(N+nlogN). The complexity seems to be low but in worst case,when nN1,example for facade detection in point clouds,the complexity becomes O(NlogN).3.Voxel Growing3.1.OverviewIn this article,we present a new algorithm adapted to large data sets of unorganized3D points and optimized to be accurate and fast.Our plane detection method works in three steps.In thefirst part,we compute a better esti-mation of the normal in each point by afiltered weighted planefitting.In a second step,we compute the score of lo-cal planarity in each point.We select the best seed point that represents a good seed plane and in the third part,we grow this seed plane by adding all points close to the plane.Thegrowing step is based on a voxel growing algorithm.The filtered normals,the score function and the voxel growing are innovative contributions of our method.As an input,we need dense point clouds related to the level of detail we want to detect.As an output,we produce connected components of planes in the point cloud.This notion of connected components is linked to the data den-sity.With our method,the connected components of planes detected are linked to the parameter d of the voxel grid.Our method has 3”intuitive”parameters :d ,area min and γ.”intuitive”because there are linked to physical mea-surements.d is the voxel size used in voxel growing and also represents the connectivity of points in detected planes.γis the maximum distance between the point of a plane and the plane model,represents the plane thickness and is linked to the point cloud noise.area min represents the minimum area of planes we want to keep.3.2.Details3.2.1Local Density of Point CloudsIn a first step,we compute the local density of point clouds like in [17].For that,we find the radius r i of the sphere containing the k nearest neighbors of point i .Then we cal-culate ρi =kπr 2i.In our experiments,we find that k =50is a good number of neighbors.It is important to know the lo-cal density because many laser point clouds are made with a fixed resolution angle scanner and are therefore not evenly distributed.We use the local density in section 3.2.3for the score calculation.3.2.2Filtered Normal EstimationNormal estimation is an important part of our algorithm.The paper [7]presents and compares three normal estima-tion methods.They conclude that the weighted plane fit-ting or WPF is the fastest and the most accurate for large point clouds.WPF is an idea of Pauly and al.in [17]that the fitting plane of a point p must take into consider-ation the nearby points more than other distant ones.The normal least square is explained in [21]and is the mini-mum of ki =1(n p ·p i +d )2.The WPF is the minimum of ki =1ωi (n p ·p i +d )2where ωi =θ( p i −p )and θ(r )=e −2r 2r2i .For solving n p ,we compute the eigenvec-tor corresponding to the smallest eigenvalue of the weightedcovariance matrix C w = ki =1ωi t (p i −b w )(p i −b w )where b w is the weighted barycenter.For the three methods ex-plained in [7],we get a good approximation of normals in smooth area but we have errors in sharp corners.In fig-ure 1,we have tested the weighted normal estimation on two planes with uniform noise and forming an angle of 90˚.We can see that the normal is not correct on the corners of the planes and in the red circle.To improve the normal calculation,that improves the plane detection especially on borders of planes,we propose a filtering process in two phases.In a first step,we com-pute the weighted normals (WPF)of each point like we de-scribed it above by minimizing ki =1ωi (n p ·p i +d )2.In a second step,we compute the filtered normal by us-ing an adaptive local neighborhood.We compute the new weighted normal with the same sum minimization but keep-ing only points of the neighborhood whose normals from the first step satisfy |n p ·n i |>cos (α).With this filtering step,we have the same results in smooth areas and better results in sharp corners.We called our normal estimation filtered weighted plane fitting(FWPF).Figure 1.Weighted normal estimation of two planes with uniform noise and with 90˚angle between them.We have tested our normal estimation by computing nor-mals on synthetic data with two planes and different angles between them and with different values of the parameter α.We can see in figure 2the mean error on normal estimation for WPF and FWPF with α=20˚,30˚,40˚and 90˚.Us-ing α=90˚is the same as not doing the filtering step.We see on Figure 2that α=20˚gives smaller error in normal estimation when angles between planes is smaller than 60˚and α=30˚gives best results when angle between planes is greater than 60˚.We have considered the value α=30˚as the best results because it gives the smaller mean error in normal estimation when angle between planes vary from 20˚to 90˚.Figure 3shows the normals of the planes with 90˚angle and better results in the red circle (normals are 90˚with the plane).3.2.3The score of local planarityIn many region growing algorithms,the criteria used for the score of the local fitting plane is the residual,like in [18]or [19],i.e.the sum of the square of distance from points to the plane.We have a different score function to estimate local planarity.For that,we first compute the neighbors N i of a point p with points i whose normals n i are close toFigure parison of mean error in normal estimation of two planes with α=20˚,30˚,40˚and 90˚(=Nofiltering).Figure 3.Filtered Weighted normal estimation of two planes with uniform noise and with 90˚angle between them (α=30˚).the normal n p .More precisely,we compute N i ={p in k neighbors of i/|n i ·n p |>cos (α)}.It is a way to keep only the points which are probably on the local plane before the least square fitting.Then,we compute the local plane fitting of point p with N i neighbors by least squares like in [21].The set N i is a subset of N i of points belonging to the plane,i.e.the points for which the distance to the local plane is smaller than the parameter γ(to consider the noise).The score s of the local plane is the area of the local plane,i.e.the number of points ”in”the plane divided by the localdensity ρi (seen in section 3.2.1):the score s =card (N i)ρi.We take into consideration the area of the local plane as the score function and not the number of points or the residual in order to be more robust to the sampling distribution.3.2.4Voxel decompositionWe use a data structure that is the core of our region growing method.It is a voxel grid that speeds up the plane detection process.V oxels are small cubes of length d that partition the point cloud space.Every point of data belongs to a voxel and a voxel contains a list of points.We use the Octree Class Template in [2]to compute an Octree of the point cloud.The leaf nodes of the graph built are voxels of size d .Once the voxel grid has been computed,we start the plane detection algorithm.3.2.5Voxel GrowingWith the estimator of local planarity,we take the point p with the best score,i.e.the point with the maximum area of local plane.We have the model parameters of this best seed plane and we start with an empty set E of points belonging to the plane.The initial point p is in a voxel v 0.All the points in the initial voxel v 0for which the distance from the seed plane is less than γare added to the set E .Then,we compute new plane parameters by least square refitting with set E .Instead of growing with k nearest neighbors,we grow with voxels.Hence we test points in 26voxel neigh-bors.This is a way to search the neighborhood in con-stant time instead of O (logN )for each neighbor like with Kd-tree.In a neighbor voxel,we add to E the points for which the distance to the current plane is smaller than γand the angle between the normal computed in each point and the normal of the plane is smaller than a parameter α:|cos (n p ,n P )|>cos (α)where n p is the normal of the point p and n P is the normal of the plane P .We have tested different values of αand we empirically found that 30˚is a good value for all point clouds.If we added at least one point in E for this voxel,we compute new plane parameters from E by least square fitting and we test its 26voxel neigh-bors.It is important to perform plane least square fitting in each voxel adding because the seed plane model is not good enough with noise to be used in all voxel growing,but only in surrounding voxels.This growing process is faster than classical region growing because we do not compute least square for each point added but only for each voxel added.The least square fitting step must be computed very fast.We use the same method as explained in [18]with incre-mental update of the barycenter b and covariance matrix C like equation 2.We know with [21]that the barycen-ter b belongs to the least square plane and that the normal of the least square plane n P is the eigenvector of the smallest eigenvalue of C .b0=03x1C0=03x3.b n+1=1n+1(nb n+p n+1).C n+1=C n+nn+1t(pn+1−b n)(p n+1−b n).(2)where C n is the covariance matrix of a set of n points,b n is the barycenter vector of a set of n points and p n+1is the (n+1)point vector added to the set.This voxel growing method leads to a connected com-ponent set E because the points have been added by con-nected voxels.In our case,the minimum distance between one point and E is less than parameter d of our voxel grid. That is why the parameter d also represents the connectivity of points in detected planes.3.2.6Plane DetectionTo get all planes with an area of at least area min in the point cloud,we repeat these steps(best local seed plane choice and voxel growing)with all points by descending order of their score.Once we have a set E,whose area is bigger than area min,we keep it and classify all points in E.4.Results and Discussion4.1.Benchmark analysisTo test the improvements of our method,we have em-ployed the comparative framework of[12]based on range images.For that,we have converted all images into3D point clouds.All Point Clouds created have260k points. After our segmentation,we project labelled points on a seg-mented image and compare with the ground truth image. We have chosen our three parameters d,area min andγby optimizing the result of the10perceptron training image segmentation(the perceptron is portable scanner that pro-duces a range image of its environment).Bests results have been obtained with area min=200,γ=5and d=8 (units are not provided in the benchmark).We show the re-sults of the30perceptron images segmentation in table1. GT Regions are the mean number of ground truth planes over the30ground truth range images.Correct detection, over-segmentation,under-segmentation,missed and noise are the mean number of correct,over,under,missed and noised planes detected by methods.The tolerance80%is the minimum percentage of points we must have detected comparing to the ground truth to have a correct detection. More details are in[12].UE is a method from[12],UFPR is a method from[10]. It is important to notice that UE and UFPR are range image methods and our method is not well suited for range images but3D Point Cloud.Nevertheless,it is a good benchmark for comparison and we see in table1that the accuracy of our method is very close to the state of the art in range image segmentation.To evaluate the different improvements of our algorithm, we have tested different variants of our method.We have tested our method without normals(only with distance from points to plane),without voxel growing(with a classical region growing by k neighbors),without our FWPF nor-mal estimation(with WPF normal estimation),without our score function(with residual score function).The compari-son is visible on table2.We can see the difference of time computing between region growing and voxel growing.We have tested our algorithm with and without normals and we found that the accuracy cannot be achieved whithout normal computation.There is also a big difference in the correct de-tection between WPF and our FWPF normal estimation as we can see in thefigure4.Our FWPF normal brings a real improvement in border estimation of planes.Black points in thefigure are non classifiedpoints.Figure5.Correct Detection of our segmentation algorithm when the voxel size d changes.We would like to discuss the influence of parameters on our algorithm.We have three parameters:area min,which represents the minimum area of the plane we want to keep,γ,which represents the thickness of the plane(it is gener-aly closely tied to the noise in the point cloud and espe-cially the standard deviationσof the noise)and d,which is the minimum distance from a point to the rest of the plane. These three parameters depend on the point cloud features and the desired segmentation.For example,if we have a lot of noise,we must choose a highγvalue.If we want to detect only large planes,we set a large area min value.We also focus our analysis on the robustess of the voxel size d in our algorithm,i.e.the ratio of points vs voxels.We can see infigure5the variation of the correct detection when we change the value of d.The method seems to be robust when d is between4and10but the quality decreases when d is over10.It is due to the fact that for a large voxel size d,some planes from different objects are merged into one plane.GT Regions Correct Over-Under-Missed Noise Duration(in s)detection segmentation segmentationUE14.610.00.20.3 3.8 2.1-UFPR14.611.00.30.1 3.0 2.5-Our method14.610.90.20.1 3.30.7308Table1.Average results of different segmenters at80%compare tolerance.GT Regions Correct Over-Under-Missed Noise Duration(in s) Our method detection segmentation segmentationwithout normals14.6 5.670.10.19.4 6.570 without voxel growing14.610.70.20.1 3.40.8605 without FWPF14.69.30.20.1 5.0 1.9195 without our score function14.610.30.20.1 3.9 1.2308 with all improvements14.610.90.20.1 3.30.7308 Table2.Average results of variants of our segmenter at80%compare tolerance.4.1.1Large scale dataWe have tested our method on different kinds of data.We have segmented urban data infigure6from our Mobile Mapping System(MMS)described in[11].The mobile sys-tem generates10k pts/s with a density of50pts/m2and very noisy data(σ=0.3m).For this point cloud,we want to de-tect building facades.We have chosen area min=10m2, d=1m to have large connected components andγ=0.3m to cope with the noise.We have tested our method on point cloud from the Trim-ble VX scanner infigure7.It is a point cloud of size40k points with only20pts/m2with less noise because it is a fixed scanner(σ=0.2m).In that case,we also wanted to detect building facades and keep the same parameters ex-ceptγ=0.2m because we had less noise.We see infig-ure7that we have detected two facades.By setting a larger voxel size d value like d=10m,we detect only one plane. We choose d like area min andγaccording to the desired segmentation and to the level of detail we want to extract from the point cloud.We also tested our algorithm on the point cloud from the LEICA Cyrax scanner infigure8.This point cloud has been taken from AIM@SHAPE repository[1].It is a very dense point cloud from multiplefixed position of scanner with about400pts/m2and very little noise(σ=0.02m). In this case,we wanted to detect all the little planes to model the church in planar regions.That is why we have chosen d=0.2m,area min=1m2andγ=0.02m.Infigures6,7and8,we have,on the left,input point cloud and on the right,we only keep points detected in a plane(planes are in random colors).The red points in thesefigures are seed plane points.We can see in thesefig-ures that planes are very well detected even with high noise. Table3show the information on point clouds,results with number of planes detected and duration of the algorithm.The time includes the computation of the FWPF normalsof the point cloud.We can see in table3that our algo-rithm performs linearly in time with respect to the numberof points.The choice of parameters will have little influence on time computing.The computation time is about one mil-lisecond per point whatever the size of the point cloud(we used a PC with QuadCore Q9300and2Go of RAM).The algorithm has been implented using only one thread andin-core processing.Our goal is to compare the improve-ment of plane detection between classical region growing and our region growing with better normals for more ac-curate planes and voxel growing for faster detection.Our method seems to be compatible with out-of-core implemen-tation like described in[24]or in[15].MMS Street VX Street Church Size(points)398k42k7.6MMean Density50pts/m220pts/m2400pts/m2 Number of Planes202142Total Duration452s33s6900sTime/point 1ms 1ms 1msTable3.Results on different data.5.ConclusionIn this article,we have proposed a new method of plane detection that is fast and accurate even in presence of noise. We demonstrate its efficiency with different kinds of data and its speed in large data sets with millions of points.Our voxel growing method has a complexity of O(N)and it is able to detect large and small planes in very large data sets and can extract them directly in connected components.Figure 4.Ground truth,Our Segmentation without and with filterednormals.Figure 6.Planes detection in street point cloud generated by MMS (d =1m,area min =10m 2,γ=0.3m ).References[1]Aim@shape repository /.6[2]Octree class template /code/octree.html.4[3] A.Bab-Hadiashar and N.Gheissari.Range image segmen-tation using surface selection criterion.2006.IEEE Trans-actions on Image Processing.1[4]J.Bauer,K.Karner,K.Schindler,A.Klaus,and C.Zach.Segmentation of building models from dense 3d point-clouds.2003.Workshop of the Austrian Association for Pattern Recognition.1[5]H.Boulaassal,ndes,P.Grussenmeyer,and F.Tarsha-Kurdi.Automatic segmentation of building facades using terrestrial laser data.2007.ISPRS Workshop on Laser Scan-ning.1[6] C.C.Chen and I.Stamos.Range image segmentationfor modeling and object detection in urban scenes.2007.3DIM2007.1[7]T.K.Dey,G.Li,and J.Sun.Normal estimation for pointclouds:A comparison study for a voronoi based method.2005.Eurographics on Symposium on Point-Based Graph-ics.3[8]J.R.Diebel,S.Thrun,and M.Brunig.A bayesian methodfor probable surface reconstruction and decimation.2006.ACM Transactions on Graphics (TOG).1[9]M.A.Fischler and R.C.Bolles.Random sample consen-sus:A paradigm for model fitting with applications to image analysis and automated munications of the ACM.1,2[10]P.F.U.Gotardo,O.R.P.Bellon,and L.Silva.Range imagesegmentation by surface extraction using an improved robust estimator.2003.Proceedings of Computer Vision and Pat-tern Recognition.1,5[11] F.Goulette,F.Nashashibi,I.Abuhadrous,S.Ammoun,andurgeau.An integrated on-board laser range sensing sys-tem for on-the-way city and road modelling.2007.Interna-tional Archives of the Photogrammetry,Remote Sensing and Spacial Information Sciences.6[12] A.Hoover,G.Jean-Baptiste,and al.An experimental com-parison of range image segmentation algorithms.1996.IEEE Transactions on Pattern Analysis and Machine Intelligence.5[13]H.Hoppe,T.DeRose,T.Duchamp,J.McDonald,andW.Stuetzle.Surface reconstruction from unorganized points.1992.International Conference on Computer Graphics and Interactive Techniques.2[14]P.Hough.Method and means for recognizing complex pat-terns.1962.In US Patent.1[15]M.Isenburg,P.Lindstrom,S.Gumhold,and J.Snoeyink.Large mesh simplification using processing sequences.2003.。
一种基于区域自适应的非局部均值(Nonlocal Means)图像去噪方法

Region-based non-local means algorithm for noise removalW.L.Zeng and X.B.LuThe non-local means (NLM)provides a useful tool for image denoising and many variations of the NLM method have been proposed.However,few works have tried to tackle the task of adaptively choos-ing the patch size according to region characteristics.Presented is a region-based NLM method for noise removal.The proposed method first analyses and classifies the image into several region types.According to the region type,a local window is adaptively adjusted to match the local property of a region.Experimental results show the effectiveness of the proposed method and demonstrate its superior-ity to the state-of-the-art methods.Introduction:The use of the non-local means (NLM)filter for noise removal has been extensively studied in the past few years.The NLM filter was first addressed in [1].The discrete version of the NLM is as follows:u (k ,l )=(i ,j )[N (k ,l )w (k ,l ,i ,j )v (i ,j )(1)where u is the restored value at pixel (k,l )and N (k,l )stands for theneighbourhood of the pixel (k,l ).The weight function w (k,l,i,j )is defined asw (k ,l ,i ,j )=1exp −||T k ,l v −T i ,j v ||22,a(2)where T k,l and T i,j denote two operators that extract two patches of sizeq ×q centred at pixel (k,l )and (i,j ),respectively;h is the decay para-meter of the weights; . 2,a is the weighted Euclidean norm using a Gaussian kernel with standard deviation a ,and Z (k,l )is the normalised constantZ (k ,l )= (i ,j )exp −||T k ,l v −T i ,j v ||22,ah 2(3)The core idea of the NLM filter exploits spatial correlation in the entireimage for noise removal and can produce promising results.This method is time consuming and not able to suppress any noise for non-repetitive neighbourhoods.Numerous methods were proposed to accel-erate the NLM method [2–4].Also,variations of the NLM method have been proposed to improve the denoising performance [5–7].In smooth areas,a large matching window size could be used to reduce the influ-ence of misinterpreting noise as local structure.Conversely,a small matching window size could be used for the edge /texture region,which means not only the local structure existing within a neighbour-hood can be effectively used but can also speed up the matching process.To the best of our knowledge,few works have tried to tackle the task of adaptively choosing the patch size according to region characteristics.To overcome the disadvantage of the NLM method and its variances,in this Letter we present an adaptive NLM (ANLM)method for noise removal.The proposed method first analyses and classifies the image into several region types based on local structure information of a pixel.According to the region type,a local window is adaptively adjusted to match the local property of a region.Experimental results show the effectiveness of the proposed method.Proposed NLM algorithm:The adaptive patches based non-local means algorithm is conducted according to the region classification results,owing to the fact that the structure tensor can obtain more local structure information [8].Therefore,we use it to classify the region.For each pixel (i,j )of the region,the structure tensor matrix is defined asT s =t 11t 12t 12t 22 =G s ∗(g x (i ,j ))2G s ∗g x (i ,j )g y (i ,j )G s ∗g y (i ,j )g x (i ,j )G s ∗(g y (i ,j ))2where g x and g y stand for gradient information in the x and y directions,G s denotes a Gaussian kernel with a standard deviation s .Theeigenvalues l 1and l 2of T s are given byl 1=12t 11+t 22+ (t 11−t 22)2+4t 212 and l 2=1t 11+t 22− (t 11−t 22)2+4t 212 For a pixel in the smooth region,there is a small eigenvalue difference;for a pixel in an edge /texture region,there is a large eigenvalue differ-ence.Therefore,region classification can be achieved by examining the eigenvalue difference of each pixel.Let l (i ,j )=|l 1(i ,j )−l 2(i ,j )|.We propose the following classifi-cation scheme to partition the whole image region into n classes {c 1,···,c n }:(i ,j )[c 1,if l (i ,j )≤l min +(l max −l min )n c 2,if l (i ,j )≤l min +2(l max −l min )n ...c n ,if l (i ,j )≤l min +n (l max −l min )n ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎩where l min and l max are the minimum and maximum of {l (i ,j ):(i ,j )[V },respectively.To exploit the local structure information and reduce noise in different regions,we adaptively choose the matching window based on the region classification result.The scheme for selecting the matching window is asfollows:if (k ,l )[c r ,T k ,l :=T r k ,l ,where T rk ,l denotes an operator of the r-type region that extracts one patch of size q r ×q r .To reduce the influ-ence of misinterpreting noise as local structure,a larger patch size is adopted for a smooth region.In contrast,a small patch size is employed for the edge /texture region.Intuitively,the number of the class n should be as big as possible.In practice,the gain is insignificant for n greater than 4.Therefore,we choose n ¼4in our experiments.Table 1:PSNR performance comparison of ‘Lena’,‘Barbara’,‘Peppers’imagesFig.1Comparison of results with additive Gaussian noise of s ¼35a Original image b Noisy image c NLM d WUNLM e ANLMExperimental results:In this Section,we compare our proposed ANLM method with the NLM method [2]and the weight update NLM (WUNLM)method [3].We test the proposed method on ‘Lena’,‘Barbara’,and ‘Peppers’,which were taken from the USC-SIPI Image Database (/database/base).The performance of the method was evaluated by measuring the peak signal-to-noise ratio (PSNR).In general h corresponds to the noise level and is usuallyELECTRONICS LETTERS 29th September 2011Vol.47No.20,1125-1127fixed to the standard deviation of the noise.The size of the search window is21×21.Table1shows results obtained with three methods across four noise levels.Figs.1a and b,show the‘Barbara’image and the corresponding noisy image generated by adding Gaussian white noise with variance s¼35,respectively.Figs.1c–e show denoised images by using the NLM,WUNLM,and ANLM methods,respectively.From the standpoint of perceptual view and PSNR values,the proposed ANLM method produced the best quality. Conclusions:An adaptive NLM(ANLM)method for noise removal is presented.In the method,an image isfirst analysed and classified into several region types.According to the region type,a local window is adaptively adjusted to match the local property of a region. Experimental results show the effectiveness of the proposed method and demonstrate its superiority to the state-of-the-art methods. Acknowledgments:This work was supported by the National Natural Science Foundation of China under grant60972001,the National Key Technologies R&D Program of China under grant2009BAG13A06 and the Scientific Innovation Research of College Graduate in Jiangsu Province under grant CXZZ_0163.#The Institution of Engineering and Technology20115August2011doi:10.1049/el.2011.2456W.L.Zeng(School of Transportation,Southeast University,Nanjing 210096,People’s Republic of China)X.B.Lu(School of Automation,Southeast University,Nanjing210096, People’s Republic of China)E-mail:xblu2008@References1Budades,A.,Coll,B.,and Morel,J.M.:‘A review of image denoising algorithms,with a new one’,Multiscale Model Simul.,2005,4,(2), pp.490–5302Mahmoudi,M.,and Sapiro,G.:‘Fast image and video denoising via nonlocal means of similar neighborhoods’,IEEE Signal Process.Lett., 2005,12,(12),pp.839–8423Vignesh,R.,Oh,B.T.,and Kuo,C.-C.J.:‘Fast non-local means(NLM) computation with probabilistic early termination’,IEEE Signal Process.Lett.,2010,17,(3),pp.277–2804Brox,T.,Kleinschmidt,O.,and Cremers,D.:‘Efficient nonlocal means for denoising of textural patterns’,IEEE Trans.Image Process.,2008, 17,(7),pp.1083–10925Kervrann,C.,and Boulanger,J.:‘Optimal spatial adaptation for patch-based image denoising’,IEEE Trans.Image Process.,2006,15,(10), pp.2866–28786Ville,D.V.D.,and Kocher,M.:‘SURE-based non-local means’,IEEE Signal Process.Lett.,2009,16,(11),pp.973–9767Park,S.W.,and Kang,M.G.:‘NLM algorithm with weight update’, Electron.Lett.,2010,16,(15),pp.1061–10638Brox,T.,Weickert,J.,Burgeth,B.,and Mrazek,P.:‘Nonlinear structure tensors’,Image put.,2006,24,pp.41–55ELECTRONICS LETTERS29th September2011Vol.47No.20。
Signal and Image Processing

Signal and Image Processing Signal and image processing are essential fields in today's digital world, playing a crucial role in various applications such as medical imaging, telecommunications, and computer vision. These technologies involve the manipulation and analysis of signals and images to extract meaningful information and enhance the quality of data. Signal processing focuses on analyzing and modifying signals, such as audio, video, and sensor data, while image processing deals with the manipulation of digital images to improve their quality or extract useful information. One of the key challenges in signal and image processing is noise reduction. Noise can degrade the quality of signals and images, making it difficult to extract meaningful information. Various techniques, such as filtering and denoising algorithms, are used to remove noise and improve the quality of the data. These techniques play a crucial role in applications such as medical imaging, where accurate image reconstruction is essential for diagnosis and treatment. Another important aspect of signal and image processing is feature extraction. Feature extraction involves identifying and extracting relevant information from signals and images to facilitate further analysis or classification. In image processing, features such as edges, textures, and shapes can be extracted to characterize and classify objects in the image. In signal processing, featuressuch as frequency components or time-domain characteristics can be extracted to analyze and classify signals. Classification and recognition are also key tasksin signal and image processing. Classification involves categorizing signals or images into different classes based on their features, while recognition involves identifying specific objects or patterns within signals or images. Machinelearning algorithms, such as neural networks and support vector machines, are commonly used for classification and recognition tasks in signal and image processing. These algorithms can learn from labeled data to classify signals or images with high accuracy. In addition to noise reduction, feature extraction,and classification, signal and image processing also play a crucial role in image enhancement and restoration. Image enhancement techniques are used to improve the visual quality of images by adjusting contrast, brightness, and color balance. Image restoration techniques, on the other hand, aim to recover the original imagefrom degraded or distorted versions. These techniques are essential inapplications such as surveillance, remote sensing, and medical imaging, where image quality is critical for analysis and interpretation. Overall, signal and image processing are interdisciplinary fields that combine elements of mathematics, physics, computer science, and engineering to analyze and manipulate signals and images. These technologies have a wide range of applications in various industries, including healthcare, telecommunications, and entertainment. By developing advanced algorithms and techniques for noise reduction, feature extraction, classification, and image enhancement, researchers and engineers continue to push the boundaries of signal and image processing, enabling new and innovative applications in the digital age.。
Fast-NLM

Accelerating non-local means algorithm with random projectioni and Y.T.YangThe non-local means (NLM)algorithm suppresses noise via replacing the noisy pixel by the weighted average of all the pixels with similar neighbourhood vectors.However,the weights calculation is computa-tionally expensive,as a result of which the NLM algorithm is quite slow for practical applications.A random projection approach is intro-duced to reduce the dimension of neighbourhood vectors used in the NLM filtering process,which yields a faster and more accurate denois-ing effect.Experimental results illustrate the effectiveness of the pro-posed method.Introduction:Image denoising,although it has been studied over a long time,is still an unsolved problem that remains a wide-open field of research in image processing.Recently,Buades et al.[1]established a new non-local means (NLM)denoising framework based on the idea that averaging repeated structures contained in an image will reduce the noise.In this framework,each pixel is estimated as the weighted average of all the pixels in the image,and the weights are determined by the similarity between the neighbourhood vectors surrounding the pixels.Although the NLM denoising method suppresses noise and preserves details in an image well,its implementation is computationally expens-ive owing to the tedious weights calculation process in denoising.The above-mentioned problem can be solved in the following ways.First,reducing the number of candidate neighbourhoods for weights calcu-lation,which has been realised in [2]by limiting the weight calculation to a sub-image surrounding the pixel being processed,moreover,[3]and [4]report further efforts to eliminate unrelated neighbourhoods in the search window.Secondly,reducing the complexity of weight calcu-lation,which is addressed in [5]by using the fast Fourier transform (FFT)combined with the summed squares image (SSI)and in [6]by introducing a multi-resolution pyramid architecture.Motivated by the above-mentioned ideas,we introduce a random projection approach to project neighbourhood vectors onto lower-dimensional subspaces,which promotes both the accuracy and the computational performance of the NLM algorithm considerably.Non-local means algorithm:Consider a discrete noisy imagey i ,j =x i ,j +n i ,j ,(i ,j )[I(1)where y i ,j ,x i ,j ,n i ,j denote the observed value,the ‘true’value and the noise perturbation at the pixel (i ,j ),respectively.The NL-means filter is written asˆxi ,j =1Z k ,l(i ,j )[ˆN d ×d (k ,l )w k ,l ,i ,j y i ,j (2)where the normalising termZ k ,l =(i ,j )[ˆNd ×d (k ,l )w k ,l ,i ,j(3)and the weight for each pair of neighbourhood vectors isw k ,l ,i ,j =exp −ˆN d ×d (k ,l )−ˆN d ×d (i ,j ) 22,ah 2(4)where ˆNd ×d (m ,n )represents the square neighbourhood vector of size d ×d centred at location (m ,n ), · 22,a denotes the Gaussian-weighted-semi-norm,and h is a global smoothing parameter used to control the amount of blurring introduced in the denoising process.Proposed method:To accelerate the non-local means filtering,we propose an alternative strategy that employs the random projection approach introduced in [7]to perform dimensional reduction for each neighbourhood vector.In detail,we recalculate the Euclidean distanceˆN d ×d (k ,l )−ˆN d ×d (i ,j ) 22,ain (4)by replacing the vectors ˆN d ×d (i ,j )and ˆNd ×d (k ,l )with lower-dimensional ones f RP [i ,j ]and f RP [k ,l ]deter-mined by random projection,respectively.In random projection,the original d -dimensional data is projected to a k -dimensional subspace via using a random k ×d matrix R ,which can be mathematicallyrepresented asf RP [·]=R k ×d ·ˆNd ×d (·)(5)In order to guarantee the random matrix R k ×d is orthogonal,whichyields a projection with no significant distortion,the elements of R k ×d are often Gaussian distributed.Thereafter,the weight for each pair of vectors can be defined asw RP k ,l ,i ,j =exp − f RP [k ,l ]−f RP[i ,j ] 22,ah 2(6)Finally,the non-local means filtering can be performed by replacingw k ,l ,i ,j in (2)with w RP k ,l ,i ,j .The computational complexity of the search window limited non-local means algorithm [2]is of O(N 2M 2d 2),where N 2,M 2and d 2are the number of pixels in the image,in the search window and in the neighbourhood,respectively.In comparison,the complexity when using a k -dimensional subspace is O(N 2M 2kd ).The additional cost in performing random projection is O(N 2kd 2).Therefore,the total com-plexity for the proposed method is O(N 2kd (M 2+d )).In the case of d ..k ,the saving of computational cost is very significant.Experimental results:We performed two sets of experiments to gauge the advantage of using the proposed method rather than the search window limited NLM algorithm:one set to test execution time,and the other set to test denoising quality.In the experiments,three types of images (Lena,Fingerprint,and Texture)with different sizes were used to implement the performance assessment in MATLAB.Moreover,the execution times were run on an IBM T61p 2.2GHz laptop,and the denoising performance is quantitatively evaluated by the criterions of PSNR and SSIM [8].For the following simulation,the search window size is set to be M ¼21,and each neighbourhood vector is projected to a k -dimensional subspace (k ¼1).In the experiments of execution time test,the neighbourhood size d took on the value of 5,7and 9,respectively.Table 1shows the speed acceleration afforded by the proposed method,from which we can see the acceleration is more obvious with the increase of neighbourhood size.In the following experiments of denoising quality assessment,the neighbourhood size d is fixed to be 7,and the variation value of Gaussian additional noise is 0.03.The results in Table 2show that our proposed method achieves higher PSNR and SSIM,which indicates that the accuracy of the proposed method is superior to the search window limited NLM algorithm.Table 1:Comparison of computational performance under differentneighbourhood sizes (the values listed in the Table are the execution times,units seconds)Table 2:Comparison of denoising quality with quantitativecriterionsConclusions:In this Letter,we recalled the non-local means filtering algorithm for image denoising;we then accelerated the NLM by intro-ducing a random projection based dimensional reduction approach toproject the neighbourhood vectors ˆNd ×d (·)onto a lower-dimensional subspace,which results in considerable savings in the cost of weight calculation.Experimental results validate that the accuracy and compu-tational cost of the NLM image denoising algorithm can be improved by computing weight after a random projection.Acknowledgments:This work is partly supported by the National Natural Science Fund of China (nos 60902080and 60725415)and the Fundamental Research Funds for Central Universities (no.72104909).ELECTRONICS LETTERS 3rd February 2011Vol.47No.3#The Institution of Engineering and Technology201116September2010doi:10.1049/el.2010.2618i and Y.T.Yang(Department of Microelectronics,Xidian University,Xi’an,People’s Republic of China)E-mail:rlai@References1Buades,A.,Coll,B.,and Morel,J.M.:‘A review of image denoising algorithms,with a new one’,Multiscale Model.Simul.SIAM Interdiscip.J.,2005,4,(2),pp.490–5302Buades,A.,Coll,B.,and Morel,J.M.:‘Denoising image sequences does not require motion estimation’.Proc.IEEE2005Int.Conf.Advanced Video and Signal Based Surveillance,Teatro Sociale,Italy,pp.70–74 3Mahmoudi,M.,and Sapiro,G.:‘Fast image and video denoising via nonlocal means of similar neighborhoods’,IEEE Signal Process.Lett., 2005,12,(12),pp.839–8424Orchard,J.,Ebrahimi,M.,and Wong,A.:‘Efficient non-local means denoising using the SVD’.Proc.2008IEEE Int.Conf.Image Processing,San Diego,CA,USA,pp.1732–17355Wang,J.,Guo,Y.W.,Ying,Y.T.,Liu,Y.L.,and Peng,Q.S.:‘Fast non-local algorithm for image denoising’.Proc.2006IEEE Int.Conf.Image Processing,Atlanta,GA USA,pp.1429–14326Karnati,V.,Uliyar,M.,and Dey,S.:‘Fast non-local algorithm for image denoising’.Proc.2008IEEE Int.Conf.Image Processing,San Diego, CA,USA,pp.3873–38767Bingham,E.,and Mannila,H.:‘Random projection in dimensional reduction:applications to image and text data’.Proc.2001ACM Int.Conf.Knowledge Discovery and Data Mining,San Francisco,CA, USA,pp.245–2508Wang,Z.,Bovik,A.C.,Sheikh,H.R.,and Simoncelli,E.P.:‘Image quality assessment:from error visibility to structural similarity’,IEEE Trans.Image Process.,2004,13,(4),pp.600–612ELECTRONICS LETTERS3rd February2011Vol.47No.3。
英文概述

Digital image denoising technology researchDescribedIn the information society, the image in the information transmission is used more and more widely. Therefore, ensuring the minimum of the noise and pollution in the process of image collection and transmission became an important part of the field.This paper mainly analysis and discuss the neighborhood average method, median filtering method, wiener filtering method and the fuzzy wavelet transform method of image denoising algorithm. Firstly introduce the common image processing functions and its applications. Secondly elaborate the principles and characteristics of the four denoising algorithm. Finally using Matlab software to a noise images (including gaussian noise or salt & pepper noise), and getting some conclusions from the simulation denoising analysis: average filtering is typical of linear filter, which is better used for gaussian noise. The median filter is a common nonlinear filtering method, especially effective to salt & pepper noise. Through wiener filtering, the gaussian noise is inhibited obviously. Wavelet coefficients threshold processing in wavelet domain can remove noise and the the signal which is not expect.1.1 research backgroundIn the 21st century, mankind has entered the information age, the computer plays an important role in dealing with all kinds of information. Accordingto statistics, from the human nature in the information and visual information accounted for 75% ~ 75%. As the saying goes, "seeing is believing", some situations or things, no matter how much ink is difficult to express clearly, however, if use an image description, can be clear at a glance. Visible, in the modern highly information-based society, graphics and image in the information dissemination, the role of more and more big, in the field of image processing, digital image processing has been rapid development.Image is an important source of the information society, people get information. Through image sensor will be useful in the real world image signal sampling, quantization, coding, transmission, in the process of recovery, there are many factors that affect image quality. So the imagebefore the use, usually have to pass strict pretreatment such as denoising, quantitative, compression coding, etc. Noise pollution directly affects the image edge detection, feature extraction, image segmentation, pattern recognition, such as processing, make people from various angles to explore in order to improve the quality of image. So use the appropriate method to eliminate noise in image processing is an important preprocessing step. Image processing technology in the 20th century first applied in the remote transmission of the image, and improve the image quality of the application of jet propulsion laboratory in 1964, the U.S. use a computer to "wandering" seven spacecraft sent back picture of the moon, and a huge success. Now the image processing technology has deep into the science research, military technology, industrial and agricultural production, medicine, meteorology and astronomy and other fields. Scientists use can obtain the earth resources satellite photos, weather condition; Doctors can be by X-ray or CT images of human body each parts of the fault are analyzed. But in many cases the image information is influenced by various noise, seriously will affect the image of the useful information, so the noise of the image processing is very important.1.2 the current research status of image denoisingImage processing, the input is low quality images, the output is to improve the quality of image. Commonly used image processing methods such as image enhancement and restoration, coding, compression. Optical coherence tomography is developing rapidly in recent years a tomographic imaging technology. Because its no radiation damage and biological tissue with micron level, high detection sensitivity and resolution of the advantages of faster scanning rate, the medical diagnosis of the lesion, especially has an attractive application prospect of biological organisms live detection. Due to the presence of noise, these physiological signal distortion. Even beyond recognition, it brought difficult to image information. Therefore, we must to deal with images with noise, improve the image quality. Maximum extent, show the characteristics of the signal itself.In the processing of the image, most has the very high correlation between adjacent pixel gray level, that is to say, most of an image pixel gray level difference is small. Because of the existence of this kind of gray correlation, the general image of energy mainly concentrated in the low frequency area, only the detail of the image part of the energy in high frequency region. Because there is noise in the image and digital transmission, and this part of the interference information mainly concentrated in the high frequency region, so eliminate noise is the general method of attenuation of highfrequency components or low pass filtering, but also bring with it negative impact is the detail of the image also has certain attenuation, will look from visual effect of fuzzy image than before. One of the better denoising method should be to get rid of noise influence to image details and image blur.In order to improve image quality, effective information extracted from image, must be the noise of image preprocessing. According to the noise frequency spectrum distribution of the law and statistical characteristic and the characteristic of the image, appeared a variety of denoising method. Classic denoising method: spatial domain synthesis, frequency synthesis, and the optimal linear synthesis, etc. Adapted to the emergence of the many applications: such as mean filter, median filter, low-pass filter, wiener filter and minimal distortion method, etc.. These methods are widely used, promote the great development of the digital signal processing. Improve the image quality significantly. In recent years, wavelet transform has been widely used to remove noise. Compared with traditional denoising method. It is using the nonlinear domain values, at the same time in the time domain and frequency domain has good localization property, and the time window and frequency window width can be adjusted. For high frequency components using fine temporal or spatial sampling step gradually, thus can be focused to any details of an object. Thus can improve the high scattering characteristics of the noise of the speckle contrast, good to eliminate the speckle noise . Wavelet transform to remove the noise in constant development, the denoising method are many, such as the nonlinear wavelet threshold denoising method, wavelet transform modulus maxima de-noising, and based on the scale of the wavelet transform domain correlation denoising method, etc.1.3 main work in this paperImage in the process of acquisition and transmission, often by the interference of noise, and noise reduction as far as possible keep the original signal is the purpose of the main features of the at the same time, remove the noise in the signal. The image denoising method can filter out high frequency component of image although can reach the effect of noise reduction, but also destroyed the image detail. The details of the image edge feature is most useful information, in this paper, the neighborhood averaging method, median filtering, wiener filtering method and fuzzy wavelet transform method of image denoising algorithms are analyzed and discussed.1.4General situation of MatlabMatlab (Matrix Laboratory) for the first time for the Mathworks company in 1983 launched a set of numerical analysis and calculation of the high performance software, its function constantly expanding, version upgrades unceasingly, at present the latest version of the 7.1 version. Matlab to matrix operations, numerical analysis, graphics, programming techniques together, provides users with a strong scientific and engineering problems of analysis and calculation and programming tools, it also provides a professional level of symbolic computation, word processing, visual modeling, simulation and real-time control, and other functions, is to have all the language features and characteristics of a new generation of software development platform. Matlab has become suitable for a multitude of disciplines, a variety of work platform, powerful large software. In countries such as Europe and the United States colleges and universities, has become a Matlab linear algebra, automatic control theory, mathematical statistics, digital signal processing, time series analysis, advanced course of basic teaching tools such as dynamic system simulation. As the degree of bachelor's, master's and doctoral students must master basic skills. In design research institutes and industrial development, Matlab has been widely applied to research and solve specific problems. In China, has increasingly taken seriously, Matlab will become popular in a short period of time, because no matter which subject or engineering fields can find the right function in Matlab.Today's information society, the image is on one of the most important source of information. With the rapid development of computer technology, image fusion technology and computer technology constantly, produce a series of image processing software, such as VC and Matlab, the software is widely used for the development of image technology provides a powerful support. Matlab has become internationally recognized as one of the most excellent technology applications, with simple programming, data visualization function is strong, strong operability, etc, and is equipped with a powerful, professional function rich image processing toolbox, work on image processing is the necessary software tools.1.5 the Matlab developing processName by the MATrix and Matlab LABoratory first three letters of two words. That is in the late seventy s of the 20th century: the computer science at the university of new Mexico's then the Cleve Moler professor for motivation, to reduce the financial burden of student programming for students to design a set of call LINPACK and EISPACK library application of the popular and easy to use interface, which is written in FORTRAN, the bud of Matlab.After a few years of school, is fuelled by a Little by Little, Moler, Steve Bangert cooperation, established the MathWorks company in 1984, and the MATLAB officially into the market. From that moment forth, Matlab kernel are written using C language, and in addition to the existing numerical calculation ability, also added a data graph visual function.Matlab is only just a few short years, with its good openness and reliability of operation, make the original sealed package in the field of control. In time into the ninety s of the 20th century, the Matlab control has become an international industry accepted standard calculation software.MathWorks company launched in 1993 Matlab4.0 versions, say goodbye to the DOS version from now on. 4. X version in inheriting and developing the existing numerical calculation and graphic visual ability at the same time, appeared the following a few important changes:(1) the launch of the SIMULINK. It is an interactive operation of dynamic systems modeling, simulation, analysis, integration environment. It makes it possible to consider many simplifying assumptions had to do before the nonlinear factors and random factors, thus greatly improving the people's cognitive ability to nonlinear, stochastic dynamic systems.(2) is developed with an external direct data exchange component, real-time data analysis, processing, and through the Matlab hardware development path.(3) launched a symbolic computation toolkit. MathWorks company in 1993 from the university of Waterloo in Canada bought the right to use the Maple, Maple as the "engine" has developed -- Symbolic Math Toolbox 1.0.(4) structure for the Notebook. MathWorks company aiming at the most widely application scope of Word, using DDE, OLE, realize the seamless connection of MATLAB and Word, so that professional scientific and technical workers in scientific computing, graphics, video, text processing in a body's high standards of environment.Matlab5.0 air, 1997 edition, Matlab has a rich data types and structures, more friendly, more rapid sophisticated object-oriented graphic visual, more resources, more extensive mathematics and data analysis application development tools. Indeed, by the end of 1999, Mathematica has up to version 4.0, it is especially reinforced previous lack of mass data processing ability.In the international academia, Matlab has been identified as accurate and reliable scientific computing standard software. In many international academic journals, (information science journals in particular), you can see the application of Matlab. In design research institutes and industrial sector, regarded as the first choice of the research, development, efficiently Matlabsoftware tool.1.6characteristics of Matlab languageMatlab language has the following features:(1) programming efficiencyIt is a high-level language for scientific and engineering computing, allows using mathematical form of the language program, and than Basic, Fortran and C language is more close to our writing, such as thinking mode, the formula of Matlab program is listed on the formula and solving problems in the calculus of paper. Therefore, Matlab language can also colloquially known as calculus paper type science algorithm because it language to write simple, so the programming efficiency is high, easy to understand.(2) the user easy to useMatlab is an interpreted language implementation language (in) has not been specialized tools before they are compiled, it is flexible, convenient, the debugger means rich, the debugging speed and needs less learning time. Compared with other language, Matlab language better solve the above problem, connect edit, compile, and execute. It can on the same picture for flexible operation quickly ruled out input program of writing errors, grammar errors and semantic errors, thus speeding up the speed of users write, modify, and debug program, can say it is in the process of programming and debugging a is more simple than the VB language.(3) the ability to expandHigh version of the Matlab language has the rich library functions, when making complex mathematical operations can be called directly, and the library functions of Matlab as well as user files on the form, so the user files also can be used as a library of Matlab function to call. Thus, the user can according to your need convenient to establish and expand the new library function, in order to improve the efficiency of using Matlab and extend its capabilities.(4) the statement is simple, connotation is richMat1ab language function, is the most basic one of the most important components in different number of input variables (including no input variable) and different number of output variables, representing different meaning (a bit like of object-oriented polymorphism). This not only make the library functions of Matlab function more rich, and greatly reduces the need of disk space, makes Matlab M file is simple, short and efficient. (5) matrix and array operation efficient and convenientMatlab language policy in the matrix arithmetic operators, relational operators, logical operators, conditional operators, and the assignmentoperator, and most of these operators can be copied without any change to the array between operations, some, such as arithmetic operators just increase ", "between array can be used in the calculations. It does not need to define the dimensions of the array, special matrix and matrix function is given, a special library function, so in solving such as signal processing, modeling, system identification, control, optimization, etc, is very simple, efficient and convenient.(6) convenient drawing functionMatlab graphics is very convenient, it has a series of drawing functions, such as linear coordinate, logarithm coordinate, semilogarithmic coordinates and polar coordinates, are just call different drawing functions, question mark figure, XY annotation on the diagram, drawing grid (grid) also simply call the corresponding command, simple and feasible. In addition, the adjustment when drawing function called the independent variable can be painted the same color of the dot, line, double line, or multiple lines. This for the sake of scientific research of the design is not as good as the general purpose programming language.Anyhow, Matlab language design ideas can be said to represent the development direction of current computer high-level language. Believe will find its great potential in continuous use.。
遥感图像去云雾噪声的实现

遥感图像去云雾噪声的实现石文轩;吴敏渊;邓德祥【摘要】为了去除相机拍摄的遥感图像中的云雾,提出了一种新的非局域均值算法来处理遥感图像序列中的云雾噪声.首先,根据遥感图像在云雾阴影下的梯度值的性质,得出了在云雾阴影下图像灰度值偏低而梯度值却变化不大的结论,从而在权重值的计算中耦合了梯度值信息.然后,利用序列图像的帧间冗余信息来计算新的权重值.最后,用新的权重值对图像进行恢复.用UltraCamD相机对在我国新疆地区和山西地区上空拍摄的两组遥感图像序列进行的实验表明:与传统的图像恢复算法相比,用提出的方法恢复图像可获得更好的图像质量;与原始图像相比,恢复后图像的峰值信噪比提高了9 dB以上.实验结果表明,该算法可以在不知道云层运动方向和相机运动方向以及噪声模型的情况下有效地对薄云雾覆盖的遥感图像进行恢复.【期刊名称】《光学精密工程》【年(卷),期】2010(018)001【总页数】7页(P266-272)【关键词】非局域均值;梯度特征;图像序列;图像去噪;云雾【作者】石文轩;吴敏渊;邓德祥【作者单位】武汉大学,电子信息学院,湖北,武汉,430079;武汉大学,电子信息学院,湖北,武汉,430079;武汉大学,电子信息学院,湖北,武汉,430079【正文语种】中文【中图分类】TP7511 引言遥感卫星获得的大地影像数据大部分是光学影像。
光学影像极易受到气候因素的影响,而云雾遮挡就是其中影响之一。
图像中云雾噪声直接影响了图像信息的判读、分析和使用,使得图像数据的有效利用率降低。
运用图像处理技术,研究如何有效去除云雾噪声、提高遥感图像数据利用率具有重要意义。
作为一种去噪问题,很多算法都是近年来的研究热点,比如:利用各向异性的热传导偏微分方程去噪[1],基于TV全变分模型的去噪[2-3],自适应正则化模型去噪[4]等,这些算法将热传导偏微分方程理论应用于图像去噪中,利用热传导的性质对图像进行各向同性或各向异性的扩散处理,并且用待处理的图像作为偏微分方程的边界条件,加入正则化模型进行图像去噪。
基于双目视觉的待涂装焊缝的识别
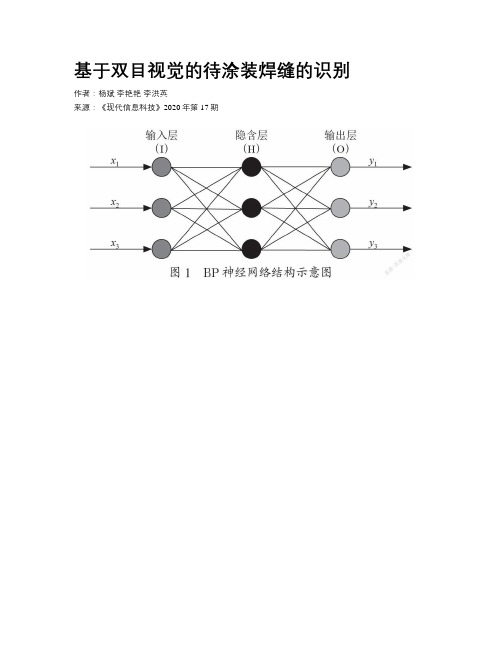
基于双目视觉的待涂装焊缝的识别作者:杨斌李艳艳李洪英来源:《现代信息科技》2020年第17期摘要:在工件涂装的过程中会遇到焊缝差异不易区分和识别的问题,基于此问题文章提出一种基于LeNet-5的待涂装焊缝识别系统。
该系统先将数据增强后的图像进行图像去噪预处理,对LeNet-5卷积神经网络进行模型训练;然后將双目系统实时拍摄的焊缝图像运用训练好的模型实现焊缝类型快速识别;最后根据得出的分类信息引导焊缝涂装机器人进行精准的焊缝喷涂。
实验结果表明,该系统可以快速提取焊缝图像更全面的特征,大大提高了焊缝识别准确率。
关键词:焊缝识别;图像去噪;深度学习;LeNet-5中图分类号:TP242 文献标识码:A 文章编号:2096-4706(2020)17-0149-04Abstract:In the process of the workpiece coating,the welding seam difference is difficult to be distinguished and identified. Based on this problem,this paper proposes a LeNet-5-based welding seam identification system to be coated. The system first carries out image denoising preprocessing after data enhancement,conducts model training for LeNet-5 convolutional neural network,and then applies the trained model to realize rapid recognition of weld types for weld images taken in real time by the binocular system. Finally,according to the obtained classification information,the welding seam coating robot is guided to carry out accurate welding seam spraying. The experimental results show that the system can quickly extract more comprehensive features of weld images and greatly improve the accuracy of weld recognition.Keywords:welding seam identification;image denoising;deep learning;LeNet-50 引言我国是制造大国,在零器件加工和制造行业中焊缝涂装是其零部件生产或者组装过程中不可缺少的重要流程之一。
【denoise】图像降噪专题

【denoise】图像降噪专题⼀⽂道尽传统图像降噪⽅法《Image Denoising with Deep Convolutional Neural Networks》《Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising》《Noise2Noise: Learning Image Restoration without Clean Data》《Semantic Image Inpainting with Deep Generative Models》《Image De-raining Using a Conditional Generative Adversarial Network》《DeblurGAN: Blind Motion Deblurring Using Conditional Adversarial Networks》课题:如何解决基于⽣成对抗⽹络的去噪任务的领域失配问题?⼀、整体思路1.1 提出问题:如何针对真实的图像噪声,设计出有效的图像去噪⽹络(包含⽹络框架、损失函数及训练策略)来解决领域失配问题,是真实图像去噪领域另⼀关键问题。
1.2 解决办法:1. 通过对图像上存在的复杂噪声进⾏建模,可以准确刻画并模拟⽣成真实图像噪声,从⽽为后续去噪⽹络提供⼤规模可靠的训练数据对。
2. 针对传统图像去噪⽹络存在的领域失配问题,设计并实现适应于真实图像去噪任务的⽹络框架以及相应的损失函数和训练策略,从⽽实现具有较强泛化能⼒的⾼性能真实图像去噪。
⼆、研究内容2.1 图像去噪⽹络架构的研究2.2 图像去噪⽹络的训练策略研究2.3 图像去噪⽹络中的损失函数设计研究三、数据集:本课题拟采取三种类型的数据对来增强真实图像去噪的泛化能⼒。
这三种类型的数据对分别为:3.1 真实的含噪图像与其对应的⼲净图像3.2 基于条件⽣成对抗⽹络⽣成的含噪图像以及⼲净图像3.3 原始噪声图像以及基于条件⽣成对抗⽹络⽣成的含噪图像,需要指出的是,这⾥输⼊ 与输出 + 是⼲净图像 的不同含噪图像。
基于先验信息的全变分图像复原算法

基于先验信息的全变分图像复原算法张俊峰;罗立民;舒华忠;伍家松【摘要】In order to improve the performance of image restoration of the total variation (TV)mod-el,an improved TV image restoration algorithm based on prior information is proposed.First,the nonlocal means(NLM)filtering algorithm,which can effectively protect the structural information of the filtered image,is employed to reduce the noise withinthe image to restore.Thus,the filtered prior image information is obtained.Then,an improved total variation restoration model based on the obtained prior information is established.The proposed model can notonly maintain the TV model' advantage of protecting the boundary information of restorated image,but also maintain the NLM model' advantage of protecting the structure information.Finally,the proposed model is opti-mized by the split Bregman alternating direction multiplier iteration algorithm and the restored image is obtained.The experimental results show that compared with other algorithms,the proposed algo-rithm achieves better restoration effect in terms of the subjective visual effect and the objective quan-titative indices such as peak signal to noise ratio (PSNR)and structural similarity (SSIM).%为了提高全变分模型的图像复原效果,提出一种基于先验信息的全变分图像复原算法。
天基光学遥感图像的信噪比提升技术综述

航天返回与遥感第 45 卷 第 2 期102SPACECRAFT RECOVERY & REMOTE SENSING2024 年 4 月天基光学遥感图像的信噪比提升技术综述王智 1,2 魏久哲 1,2 王芸 1,2 李强 1,2(1 北京空间机电研究所,北京 100094)(2 先进光学遥感技术北京市重点实验室,北京 100094)摘 要 随着遥感技术的不断发展,天基光学遥感向全时域、智能化方向发展。
微光遥感因需要在夜间和晨昏时段等低照度条件下对地物进行探测,成像具有低对比度、低亮度、低信噪比的特性。
针对低信噪比特性会导致大量复杂物理噪声将图像景物特征淹没,严重影响地面目标识别与判读的情况,文章基于遥感成像的全链路物理模型,总结天基光学遥感图像信噪比提升的技术途径,分别对基于传统滤波的方式、基于物理模型的方式、基于深度学习的方式的研究现状进行分析,对比并总结各类方式中主要代表算法之间的特点及差异,对未来天基光学遥感图像信噪比提升的技术发展方向进行展望。
关键词 去噪算法 全链路模型 信噪比 遥感图像 天基遥感中图分类号:TP751 文献标志码:A 文章编号:1009-8518(2024)02-0102-12DOI:10.3969/j.issn.1009-8518.2024.02.010A Review of SNR Enhancement Techniques forSpace-Based Remote Sensing ImagesWANG Zhi1,2 WEI Jiuzhe1,2 WANG Yun1,2 LI Qiang1,2( 1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China )( 2 Key Laboratory of Advanced Optical Remote Sensing Technology of Beijing, Beijing 100094, China )Abstract With the continuous development of the field of remote sensing, space-based remote sensing is developing in the direction of all-sky and intelligent. Since low-light remote sensing is used to detect ground objects under low illumination conditions such as night and morning and night periods, it results in the characteristics of low contrast, low brightness and low signal-to-noise ratio of remote sensing images, among which, low signal-to-noise ratio leads to a large number of complex physical noises drowning the image features, seriously affecting the recognition and interpretation of ground objects. This paper summarizes the actual full-link physical model based on optical remote sensing imaging and the technical approaches to improve the signal-to-noise ratio of remote sensing images, and summarizes the methods based on traditional filtering, physical model and deep learning respectively. By comparing the differences among the main representative algorithms of various methods, the paper summarizes their respective characteristics. The future development direction of the improvement of the signal-to-noise ratio of space-based remote sensing images is forecasted.Keywords denoising algorithm; full link model; SNR; remote sensing image; space-based remote sensing收稿日期:2023-11-03基金项目:国家自然科学基金重点项目(62331006)引用格式:王智, 魏久哲, 王芸, 等. 天基光学遥感图像的信噪比提升技术综述[J]. 航天返回与遥感, 2024, 45(2): 102-113.WANG Zhi, WEI Jiuzhe, WANG Yun, et al. A Review of SNR Enhancement Techniques for Space-Based Remote Sensing Images[J]. Spacecraft Recovery & Remote Sensing, 2024, 45(2): 102-113. (in Chinese)第 2 期王智 等: 天基光学遥感图像的信噪比提升技术综述103 0 引言随着航天技术的迅猛发展,航天遥感技术成为人类认识地球,寻找、利用、开发地球资源,了解全球变化以及气象观测的有效手段。
图像去噪的基本原理、典型方法和最新方法 电子技术专业毕业设计 毕业论

摘要数字图像在其形成、传输和记录的过程中,由于成像系统、传输介质和记录设备的不完善往往使得获取的图像受到多种噪声的污染。
因此在模式识别、计算机视觉、图像分析和视频编码等领域,噪声图像的前期处理极其重要,其处理效果的好坏将直接影响到后续工作的质量和结果。
本文主要介绍图像去噪的基本原理、典型方法和最新方法。
考虑到图像去噪技术的飞速发展,本文在论述其基本理论的同时还着重介绍近年来国内有关的最新研究成果和最新方法。
本文被分成四个部分。
第一部分是绪论,论述图像去噪发展趋势及研究图像去噪的理由与意义。
第二部分论述中值滤波法和自适应平滑滤波法的基本原理,完成基于matlab中值滤波的代码实现,并对其结果进行分析。
本文提出两种新的算法,即中值滤波的改进算法即自适应加权算法,和自适应平滑滤波的改进算法。
并且也得出这两种算法的仿真结果,并且对结果进行分析。
第三部分首先论述基于频域的图像去噪方法的基本原理,然后本文对巴特沃斯低通滤波和巴特沃斯高通滤波的基本原理作了论述,并且分别完成基于matlab的巴特沃斯低通滤波和高通滤波的代码实现,对结果进行分析。
同时对程序中的重要语句分别作注释。
第四部分是本文最重要的一章,重点阐述基于小波域的两种图像去噪方法和算法,即小波阈值去噪法与小波维纳滤波去噪法。
在小波阈值去噪法中,本文重点论述小波阈值去噪的三个步骤,并介绍传统经典的阈值化方法即软阈值法、硬阈值法以及四种确定阈值的方法。
其中包括统一阈值法、基于零均值正态分布的置信区间阈值、最小最大阈值法和理想阈值估计法,并且完成小波阈值去噪法的代码实现,将小波阈值去噪法的去噪结果和中值滤波法的去噪结果进行比较分析,得出结论。
在小波维纳滤波去噪法中本文着重论述小波维纳滤波去噪法的基本原理,得到小波维纳滤波去噪法的仿真结果,并且将波维纳滤波去噪法的结果与维纳滤波去噪法的结果进行对比分析。
关键词:图像去噪,维纳滤波,中值滤波,小波变换,阈值AbstractIn its formation, transmission and recording of the process of digital images, because imaging system , transmission media and recording equipment are often imperfect, the obtained images are polluted by a variety of noises. In pattern recognition, computer vision, image analysis and video coding and other fields,noise image pre-processing is extremely important and whether its effect is good or bad will have a direct impact on the following quality and results. This paper introduces the basic principle, the typical method and the latest methods of image denoising.Taking the rapid development of technology of image denoising into account, the paper discusses the basic theory and at the same time also the latest research results and the latest methods in recent years.This paper is divided into four parts.introduction The first part is the introduction and discusses development trend of image denoising and the reasons and significance of studying image denoising. The second part, deals with the basic principles of median filter and adaptive smoothing filter, achieves the completion of median filtering code based on Matlab, and analyzes the results. This paper presents two new algorithm, which is the improved algorithms of the filtering called adaptive weighted algorithm, and the improved algorithm of adaptive smoothing. And the paper has reached this algorithm simulation results, and analyzed the results. The third part firstly discusses the basic principles of image denoising based on frequency domain . Then this paper discusses the basic principles of Butterworth low-pass filter and Butterworth high-pass filtering, and completes the code achieved based on Matlab Butterworth low-pass filter and high-pass filtering and analyzes the results. Meanwhile important statements of the procedures are explained. The fourth part of this article is the most important chapter and focuses on the two methods and algorithms of image denoising based on wavelet domain, which are the wavelet domain thresholding method and wavelet wiener filter method. In wavelet thresholding method, the paper focuses on the three steps of wavelet thresholding and discusses the traditional classical threshold methods,which are soft, and the threshold hard threshold law, and introduces four ways of determining the threshold.The four ways include a single threshold value, intervalthreshold based on the zero mean normal confidence, the largest minimum threshold value and ideal threshold estimates.The paper completes achieving code of wavelet thresholding method and comparatively analyzes the results of wavelet thresholding method and the results of denoising filter method. In wavelet wiener filter ,the paper method focuses on the basic principle of wavelet wiener filter, achieves simulation results of wavelet wiener filter method, and compares the results of wavelet wiener filter method with the results of the wiener filter method.Keywords : image denoising, Wiener filter, filtering, wavelet transform, threshold第1章绪论1.1 图像去噪的发展趋势图像信号处理中最困难的问题之一是:怎样滤出图像中的噪声而又不模糊图像的特征及边缘。
去噪点的方法

去噪点的方法Noise reduction is a common challenge in various fields, including photography, audio recording, and signal processing. There are several methods to address this issue, each with its own advantages and disadvantages.去噪是摄影、音频录制和信号处理等各个领域普遍面临的问题。
要解决这个问题,有几种方法可供选择,每种方法都有其优缺点。
One approach to noise reduction is filtering, which involves using algorithms to remove unwanted frequencies or signals from the data. This method is effective in certain scenarios, but it may also result in the loss of important information or introduce unwanted artifacts.一种去噪的方法是滤波,即利用算法从数据中去除不需要的频率或信号。
这种方法在某些情况下很有效,但也可能导致重要信息的丢失或引入不需要的伪影。
Another common method is spectral subtraction, which involves estimating the noise spectrum and subtracting it from the originalsignal. While this approach can be effective in certain situations, it also relies on accurate noise estimation, which can be challenging in real-world scenarios.另一种常见的方法是频谱减法,即估计噪声频谱并从原始信号中减去。
基于局部和非局部正则化的图像压缩感知

基于局部和非局部正则化的图像压缩感知朱俊;陈长伟;苏守宝;常子楠【摘要】Nonlocal low‐rank regularization based approach (NLR) shows the state‐of‐the‐art performance in compressive sensing (CS) recovery which exploits both structured sparsity of similar patches .Howev‐er ,it cannot efficiently preserve the edges because it only exploits the nonlocal regularization and ignores the relationship betweenpixels .Meanwhile ,Logdet function that is used in NLR cannot well approxi‐mate the rank ,because it is a fixed function and the optimi zation results obtained by this function essen‐tially deviate from the real solution .A local and nonlocal regularization based CS approach is proposed to‐ward exploiting the local sparse‐gradient property of image and low‐rank property of similar patches . Schatten‐p norm is used as a better non‐convex surrogate for the rank function .In addition ,the alterna‐ting direction method of multipliers method (ADMM ) is utilized to solve the resulting nonconvex optimi‐zation problem .Experimental results demonstr ate that the proposed method outperforms existing state‐of‐the‐art CS algorithms for image recovery .%基于低秩正则化的非局部低秩约束(Nonlocal low‐rank regularization ,NLR)算法利用相似块的结构稀疏性,获得了目前最好的重构结果。
基于双边滤波与离散余弦变换的NLM去噪算法

基于双边滤波与离散余弦变换的NLM去噪算法张业宏;陈恩平;么跃轩;刘宝华【摘要】针对非局部均值去噪算法(NLM)易造成图像边缘模糊问题,提出了一种基于双边滤波和离散余弦变换的改进算法.该算法将双边滤波中的像素空间邻近函数与NLM算法的权值函数相结合,提出新的权值计算公式进而保护图像细节;利用离散余弦变换能量集中特性来计算像素相似性权值进而提高运算速度.首先将图像分割成子块,对子块进行离散余弦变换,然后在得到的离散余弦变换系数矩阵中筛选数据,最后用新权值计算公式在经筛选的离散余弦变换系数矩阵中度量像素的相似性.实验结果表明,与原NLM相比,该算法更好地保护了图像边缘细节特征和结构信息,峰值信噪比最大提高了1.4 dB,证明本文的算法去噪效果更佳.【期刊名称】《燕山大学学报》【年(卷),期】2018(042)003【总页数】6页(P259-264)【关键词】图像去噪;双边滤波;空间邻近函数;离散余弦变换;非局部均值【作者】张业宏;陈恩平;么跃轩;刘宝华【作者单位】燕山大学河北省并联机器人与机电系统实验室,河北秦皇岛066004;燕山大学机械工程学院,河北秦皇岛066004;燕山大学河北省并联机器人与机电系统实验室,河北秦皇岛066004;燕山大学机械工程学院,河北秦皇岛066004;燕山大学机械工程学院,河北秦皇岛066004【正文语种】中文【中图分类】TP391.410 引言图像是人们获取信息的重要媒介,不过数字图像在获取和传输的过程中难免会引入噪声从而降低了图像的质量,利用去噪方法可以有效去除图像噪声[1],因此图像去噪成为图像研究领域非常重要的研究方向之一。
近几十年,学者们己经提出了多种去噪方法,大致基于偏微分方程理论[2]、小波理论[3]和统计模型理论[4]。
基于偏微分方程理论算法利用梯度进行各向异性扩散迭代去噪,但会产生“阶梯”效应以及边缘噪声得不到有效抑制;基于小波理论算法能够有效地去除噪声,可以较好地保留纹理细节信息,但通常会在结果图像中引入较多伪影;基于统计模型理论算法关注像素点灰度变化特征,然而没有考虑到图像的结构信息。
多线程非局部均值三维MRI去噪方法及其实现

多线程非局部均值三维MRI去噪方法及其实现陈耿;吴亚锋;张培;Pew-Thian Yap【摘要】非局部均值滤波算法已经在多种图像去噪场合得到了验证,并且显示出了优异的性能.在核磁共振图像去噪中,该算法存在计算量大的问题.针对该问题,将多线程技术引入到算法实现中,提高了非局部均值滤波算法的计算效率.仿真数据和真实数据的实验结果表明:在保证图像去噪效果不变的情况下,四核处理器主机内,多线程算法较之于单线程算法的运行速度提高了2.53倍.【期刊名称】《科学技术与工程》【年(卷),期】2014(014)015【总页数】4页(P185-188)【关键词】非局部均值滤波;核磁共振图像去噪;ITK;多线程编程【作者】陈耿;吴亚锋;张培;Pew-Thian Yap【作者单位】西北工业大学数据处理中心,西安710072;UNC MIND Lab,Chapel Hill USA;西北工业大学数据处理中心,西安710072;UNC MIND Lab,Chapel Hill USA;UNC MIND Lab,Chapel Hill USA【正文语种】中文【中图分类】TN911.73去噪预处理是核磁共振图像(magnetic resonance image,MRI)处理的基础。
由成像设备直接获取到的MR图像存在着大量的干扰噪声(如噪声伪影,运动伪影,算法伪影等),这些噪声会影响后续分析处理的准确性。
譬如在配准和分割算法中,首先要对采集得到的MR图像进行去噪以增强算法的鲁棒性。
MR图像去噪中一个很重要的问题是如何在去除噪声的前提下,有效地保留图像中的有用信息,特别是其中的边缘信息,因为这些信息有着重要的医学诊断价值。
Buades等人[1]于2005年提出了非局部均值滤波算法(non-local means,NLM)。
该算法依据自然图像中存在着许多重复结构的特点,利用这种冗余信息可以有效地去除图像中的噪声。
同时,该算法将参与运算的像素由像素邻域扩展到了整个图像范围,运算中利用到了图像中的所有像素,而不仅仅局限于像素邻域之中。
lanczos插值 matlab代码

《深度探究:Lanczos插值在Matlab中的应用》在计算机图形学和数字图像处理领域,图像的放大和缩小是一项常见的任务。
而在这个过程中,插值算法则扮演着至关重要的角色。
本文将对Lanczos插值方法在Matlab中的应用进行深入探讨,旨在帮助读者更加深刻和全面地理解这一主题。
1. Lanczos插值简介Lanczos插值是一种用于信号处理和图像处理的插值算法。
它是由Cornelius Lanczos在20世纪初提出的,旨在解决插值过程中产生的模糊和失真问题。
Lanczos插值通过计算与窗函数相关的加权和来实现对目标像素的插值估计,能够有效地保持图像的边缘和细节信息,因此被广泛应用于数字图像处理中。
2. Lanczos插值算法原理在Matlab中,Lanczos插值算法可以通过内置函数实现。
其原理主要包括两个关键步骤:构建Lanczos核函数和应用核函数进行插值计算。
通过计算Lanczos核函数的系数和权重,可以得到一个离散的Lanczos核函数。
根据目标像素的位置和邻近像素的数值,将Lanczos核函数应用于图像,从而实现对目标像素的插值估计。
3. Lanczos插值在Matlab中的实现在Matlab中,可以使用内置的imresize函数来实现Lanczos插值。
通过设置插值方法参数为'lanczos3'或'lanczos8',可以选择使用3阶或8阶的Lanczos插值方法。
还可以根据具体需求调整滤波器的窗口大小和权重系数,以获得不同程度的插值效果。
4. 个人观点和理解作为一种高质量的插值算法,Lanczos插值在数字图像处理中具有广泛的应用前景。
在实际使用中,我们不仅可以根据图像的特点选择合适的Lanczos插值阶数和参数,还可以结合其他图像处理技术,如去噪和锐化,进一步提高图像的质量和清晰度。
我认为深入了解和掌握Lanczos插值算法在Matlab中的应用对于提升图像处理效果具有重要意义。
图像处理中不适定问题

图像处理中不适定问题作者:肖亮博士发布时间:09-10-25 阅读:600所属分类:默认栏目图像处理中不适定问题(ill posed problem)或称为反问题(inverse Problem)的研究从20世纪末成为国际上的热点问题,成为现代数学家、计算机视觉和图像处理学者广为关注的研究领域。
数学和物理上的反问题的研究由来已久,法国数学家阿达马早在19世纪就提出了不适定问题的概念:称一个数学物理定解问题的解存在、唯一并且稳定的则称该问题是适定的(Well Posed).如果不满足适定性概念中的上述判据中的一条或几条,称该问题是不适定的。
典型的图像处理不适定问题包括:图像去噪(Image De-nosing),图像恢复(Image Restorsion),图像放大(Image Zooming),图像修补(Image Inpainting),图像去马赛克(image Demosaicing),图像超分辨(Image super-resolution )等。
迄今为止,人们已经提出许多方法来解决图像处理中的不适定性。
但是如何进一步刻画图像的边缘、纹理和角形等图像中重要视觉几何结构,提高该类方法在噪声抑制基础上有效保持结构和纹理能力是有待深入研究的问题。
1 不适定图像处理问题的国内外研究现状评述由于图像处理中的反问题往往是不适定的。
解决不适定性的有效途径是在图像处理中引入关于图像的先验信息。
因此图像的先验模型对于图像反问题和其它计算机视觉还是图像处理问题至关重要。
对于图像的先验模型的研究,研究者们从多个角度进行研究,其代表主要有“统计方法”和“正则化几何建模方法”,“稀疏表示方法”三种主流方法,而最近兴起的图像形态分量分析(MCA)方法吸引了大批国内外研究者的广泛关注。
1.1 正则化几何模型日新月异关于自然图像建模的“正则化几何方法”是最近几年热点讨论的主题。
其中一类方法是利用偏微分方程理论建立图像处理模型,目前的发展趋势是从有选择性非线性扩散的角度设计各类低阶、高阶或者低阶与高阶综合的偏微分方程, 或者从实扩散向复扩散推广, 从空域向空频域相结合以及不同奇异性结构的综合处理[1]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M ULTISCALE M ODEL.S IMUL.c 2005Society for Industrial and Applied Mathematics Vol.4,No.2,pp.490–530A REVIEW OF IMAGE DENOISING ALGORITHMS,WITH A NEWONE∗A.BUADES†,B.COLL†,AND J.M.MOREL‡Abstract.The search for efficient image denoising methods is still a valid challenge at the crossing of functional analysis and statistics.In spite of the sophistication of the recently proposed methods,most algorithms have not yet attained a desirable level of applicability.All show an out-standing performance when the image model corresponds to the algorithm assumptions but fail in general and create artifacts or remove imagefine structures.The main focus of this paper is,first, to define a general mathematical and experimental methodology to compare and classify classical image denoising algorithms and,second,to propose a nonlocal means(NL-means)algorithm ad-dressing the preservation of structure in a digital image.The mathematical analysis is based on the analysis of the“method noise,”defined as the difference between a digital image and its denoised version.The NL-means algorithm is proven to be asymptotically optimal under a generic statistical image model.The denoising performance of all considered methods are compared in four ways; mathematical:asymptotic order of magnitude of the method noise under regularity assumptions; perceptual-mathematical:the algorithms artifacts and their explanation as a violation of the image model;quantitative experimental:by tables of L2distances of the denoised version to the original image.The most powerful evaluation method seems,however,to be the visualization of the method noise on natural images.The more this method noise looks like a real white noise,the better the method.Key words.image restoration,nonparametric estimation,PDE smoothingfilters,adaptive filters,frequency domainfiltersAMS subject classification.62H35DOI.10.1137/0406160241.Introduction.1.1.Digital images and noise.The need for efficient image restoration meth-ods has grown with the massive production of digital images and movies of all kinds, often taken in poor conditions.No matter how good cameras are,an image improve-ment is always desirable to extend their range of action.A digital image is generally encoded as a matrix of grey-level or color values.In the case of a movie,this matrix has three dimensions,the third one corresponding to time.Each pair(i,u(i)),where u(i)is the value at i,is called a pixel,short for“picture element.”In the case of grey-level images,i is a point on a two-dimensional(2D)grid and u(i)is a real value.In the case of classical color images,u(i)is a triplet of values for the red,green,and blue components.All of what we shall say applies identically to movies,three-dimensional(3D)images,and color or multispectral images.For the sake of simplicity in notation and display of experiments,we shall here be content with rectangular2D grey-level images.∗Received by the editors September30,2004;accepted for publication(in revised form)Janu-ary10,2005;published electronically July18,2005./journals/mms/4-2/61602.html†Universitat de les Illes Balears,Anselm Turmeda,Ctra.Valldemossa Km.7.5,07122Palma de Mallorca,Spain(vdmiabc4@uib.es,tomeu.coll@uib.es).These authors were supported by the Ministerio de Ciencia y Tecnologia under grant TIC2002-02172.During this work,thefirst author had a fellowship of the Govern de les Illes Balears for the realization of his Ph.D.thesis.‡Centre de Math´e matiques et Leurs Applications,ENS Cachan61,Av du Pr´e sident Wilson94235 Cachan,France(morel@cmla.ens-cachan.fr).This author was supported by the Centre National d’Etudes Spatiales(CNES),the Office of Naval Research under grant N00014-97-1-0839,the Direction G´e n´e rale des Armements(DGA),and the Minist`e re de la Recherche et de la Technologie.490ON IMAGE DENOISING ALGORITHMS 491The two main limitations in image accuracy are categorized as blur and noise.Blur is intrinsic to image acquisition systems,as digital images have a finite number of samples and must satisfy the Shannon–Nyquist sampling conditions [31].The second main image perturbation is noise.Each one of the pixel values u (i )is the result of a light intensity measurement,usually made by a charge coupled device (CCD)matrix coupled with a light focusing system.Each captor of the CCD is roughly a square in which the number of incoming photons is being counted for a fixed period corresponding to the obturation time.When the light source is constant,the number of photons received by each pixel fluctuates around its average in accordance with the central limit theorem.In other terms,one can expect fluctuations of order √n for n incoming photons.In addition,each captor,if not adequately cooled,receives heat spurious photons.The resulting perturbation is usually called “obscurity noise.”In a first rough approximation one can writev (i )=u (i )+n (i ),where i ∈I ,v (i )is the observed value,u (i )would be the “true”value at pixel i ,namely the one which would be observed by averaging the photon counting on a long period of time,and n (i )is the noise perturbation.As indicated,the amount of noise is signal-dependent;that is,n (i )is larger when u (i )is larger.In noise models,the normalized values of n (i )and n (j )at different pixels are assumed to be independent random variables,and one talks about “white noise.”1.2.Signal and noise ratios.A good quality photograph (for visual inspec-tion)has about 256grey-level values,where 0represents black and 255represents white.Measuring the amount of noise by its standard deviation,σ(n ),one can define the signal noise ratio (SNR)asSNR =σ(u )σ(n ),where σ(u )denotes the empirical standard deviation of u ,σ(u )= 1|I | i ∈I(u (i )−u )212,and u =1|I | i ∈I u (i )is the average grey-level value.The standard deviation of the noise can also be obtained as an empirical measurement or formally computed whenthe noise model and parameters are known.A good quality image has a standard deviation of about 60.The best way to test the effect of noise on a standard digital image is to add a Gaussian white noise,in which case n (i )are independently and identically distributed (i.i.d.)Gaussian real variables.When σ(n )=3,no visible alteration is usually ob-served.Thus,a 603 20SNR is nearly invisible.Surprisingly enough,one can add white noise up to a 21ratio and still see everything in a picture!This fact is il-lustrated in Figure 1and constitutes a major enigma of human vision.It justifies the many attempts to define convincing denoising algorithms.As we shall see,the results have been rather deceptive.Denoising algorithms see no difference between small details and noise,and therefore they remove them.In many cases,they create new distortions,and the researchers are so used to them that they have created a492 A.BUADES,B.COLL,AND J.M.MORELFig.1.A digital image with standard deviation55,the same with noise added(standard deviation3),the SNR therefore being equal to18,and the same with SNR slightly larger than2. In this second image,no alteration is visible.In the third,a conspicuous noise with standard deviation25has been added,but,surprisingly enough,all details of the original image still are visible.taxonomy of denoising artifacts:“ringing,”“blur,”“staircase effect,”“checkerboard effect,”“wavelet outliers,”etc.This fact is not quite a surprise.Indeed,to the best of our knowledge,all denoising algorithms are based on•a noise model;•a generic image smoothness model,local or global.In experimental settings,the noise model is perfectly precise.So the weak point of the algorithms is the inadequacy of the image model.All of the methods assume that the noise is oscillatory and that the image is smooth or piecewise smooth.So they try to separate the smooth or patchy part(the image)from the oscillatory one.Actually, manyfine structures in images are as oscillatory as noise is;conversely,white noise has low frequencies and therefore smooth components.Thus a separation method based on smoothness arguments only is hazardous.1.3.The“method noise.”All denoising methods depend on afiltering pa-rameter h.This parameter measures the degree offiltering applied to the image.For most methods,the parameter h depends on an estimation of the noise varianceσ2. One can define the result of a denoising method D h as a decomposition of any image v as(1.1)v=D h v+n(D h,v),where1.D h v is more smooth than v,2.n(D h,v)is the noise guessed by the method.Now it is not enough to smooth v to ensure that n(D h,v)will look like a noise. The more recent methods are actually not content with a smoothing but try to recover lost information in n(D h,v)[19,25].So the focus is on n(D h,v).Definition 1.1(method noise).Let u be a(not necessarily noisy)image and D h a denoising operator depending on h.Then we define the method noise of u as the image difference(1.2)n(D h,u)=u−D h(u).This method noise should be as similar to a white noise as possible.In addition, since we would like the original image u not to be altered by denoising methods,theON IMAGE DENOISING ALGORITHMS 493method noise should be as small as possible for the functions with the right regularity.According to the preceding discussion,four criteria can and will be taken into account in the comparison of denoising methods:•A display of typical artifacts in denoised images.•A formal computation of the method noise on smooth images,evaluating how small it is in accordance with image local smoothness.•A comparative display of the method noise of each method on real images with σ=2.5.We mentioned that a noise standard deviation smaller than 3is subliminal,and it is expected that most digitization methods allow themselves this kind of noise.•A classical comparison receipt based on noise simulation:it consists of taking a good quality image,adding Gaussian white noise with known σ,and then computing the best image recovered from the noisy one by each method.A table of L 2distances from the restored to the original can be established.The L 2distance does not provide a good quality assessment.However,it reflects well the relative performances of algorithms.On top of this,in two cases,a proof of asymptotic recovery of the image can be obtained by statistical arguments.1.4.Which methods to compare.We had to make a selection of the denoising methods we wished to compare.Here a difficulty arises,as most original methods have caused an abundant literature proposing many improvements.So we tried to get the best available version,while keeping the simple and genuine character of the original method:no hybrid method.So we shall analyze the following:1.the Gaussian smoothing model (Gabor quoted in Lindenbaum,Fischer,andBruckstein [17]),where the smoothness of u is measured by the Dirichlet integral |Du |2;2.the anisotropic filtering model (Perona and Malik [27],Alvarez,Lions,andMorel [1]);3.the Rudin–Osher–Fatemi total variation model [30]and two recently proposediterated total variation refinements [35,25];4.the Yaroslavsky neighborhood filters [41,40]and an elegant variant,theSUSAN filter (Smith and Brady [33]);5.the Wiener local empirical filter as implemented by Yaroslavsky [40];6.the translation invariant wavelet thresholding [8],a simple and performingvariant of the wavelet thresholding [10];7.DUDE,the discrete universal denoiser [24],and the UINTA,unsupervisedinformation-theoretic,adaptive filtering [3],two very recent new approaches;8.the nonlocal means (NL-means)algorithm,which we introduce here.This last algorithm is given by a simple closed formula.Let u be defined in a bounded domain Ω⊂R 2;thenNL (u )(x )=1C (x )e −(G a ∗|u (x +.)−u (y +.)|2)(0)2u (y )d y ,where x ∈Ω,G a is a Gaussian kernel of standard deviation a ,h acts as a filtering parameter,and C (x )= e −(G a ∗|u (x +.)−u (z +.)|2)(0)h 2d z is the normalizing factor.In orderto make clear the previous definition,we recall that(G a ∗|u (x +.)−u (y +.)|2)(0)= R 2G a (t )|u (x +t )−u (y +t )|2d t .494 A.BUADES,B.COLL,AND J.M.MORELThis amounts to saying that NL(u)(x),the denoised value at x,is a mean of the values of all pixels whose Gaussian neighborhood looks like the neighborhood of x.1.5.What is left.We do not draw into comparison the hybrid methods,in particular the total variation+wavelets[7,12,18].Such methods are significant improvements of the simple methods but are impossible to draw into a benchmark: their efficiency depends a lot upon the choice of wavelet dictionaries and the kind of image.Second,we do not draw into the comparison the method introduced recently by Meyer[22],whose aim it is to decompose the image into a BV part and a texture part(the so called u+v methods),and even into three terms,namely u+v+w, where u is the BV part,v is the“texture”part belonging to the dual space of BV, denoted by G,and w belongs to the Besov space˙B∞−1,∞,a space characterized by the fact that the wavelet coefficients have a uniform bound.G is proposed by Meyer as the right space to model oscillatory patterns such as textures.The main focus of this method is not yet denoising.Because of the different and more ambitious scopes of the Meyer method[2,36,26],which makes it parameter-and implementation-dependent, we could not draw it into the st but not least,let us mention the bandlet[15]and curvelet[34]transforms for image analysis.These methods also are separation methods between the geometric part and the oscillatory part of the image and intend tofind an accurate and compressed version of the geometric part. Incidentally,they may be considered as denoising methods in geometric images,as the oscillatory part then contains part of the noise.Those methods are closely related to the total variation method and to the wavelet thresholding,and we shall be content with those simpler representatives.1.6.Plan of the paper.Section2computes formally the method noise for the best elementary local smoothing methods,namely Gaussian smoothing,anisotropic smoothing(mean curvature motion),total variation minimization,and the neighbor-hoodfilters.For all of them we prove or recall the asymptotic expansion of thefilter at smooth points of the image and therefore obtain a formal expression of the method noise.This expression permits us to characterize places where thefilter performs well and where it fails.In section3,we treat the Wiener-like methods,which proceed by a soft or hard threshold on frequency or space-frequency coefficients.We examine in turn the Wiener–Fourierfilter,the Yaroslavsky local adaptive discrete cosine trans-form(DCT)-basedfilters,and the wavelet threshold method.Of course,the Gaussian smoothing belongs to both classes offilters.We also describe the universal denoiser DUDE,but we cannot draw it into the comparison,as its direct application to grey-level images is unpractical so far.(We discuss its feasibility.)Finally,we examine the UINTA algorithms whose principles stand close to the NL-means algorithm.In section5,we introduce the NL-meansfilter.This method is not easily classified in the preceding terminology,since it can work adaptively in a local or nonlocal way.We first give a proof that this algorithm is asymptotically consistent(it gives back the conditional expectation of each pixel value given an observed neighborhood)under the assumption that the image is a fairly general stationary random process.The works of Efros and Leung[13]and Levina[16]have shown that this assumption is sound for images having enough samples in each texture patch.In section6,we com-pare all algorithms from several points of view,do a performance classification,and explain why the NL-means algorithm shares the consistency properties of most of the aforementioned algorithms.ON IMAGE DENOISING ALGORITHMS4952.Local smoothingfilters.The original image u is defined in a bounded domainΩ⊂R2and denoted by u(x)for x=(x,y)∈R2.This continuous image is usually interpreted as the Shannon interpolation of a discrete grid of samples[31]and is therefore analytic.The distance between two consecutive samples will be denoted byε.The noise itself is a discrete phenomenon on the sampling grid.According to the usual screen and printing visualization practice,we do not interpolate the noise samples n i as a band limited function but rather as a piecewise constant function, constant on each pixel i and equal to n i.We write|x|=(x2+y2)12and x1.x2=x1x2+y1y2as the norm and scalar productand denote the derivatives of u by u x=∂u∂x ,u y=∂u∂y,and u xy=∂2u∂x∂y.The gradientof u is written as Du=(u x,u y)and the Laplacian of u asΔu=u xx+u yy.2.1.Gaussian smoothing.By Riesz’s theorem,image isotropic linearfiltering boils down to a convolution of the image by a linear radial kernel.The smoothing requirement is usually expressed by the positivity of the kernel.The paradigm of suchkernels is,of course,the Gaussian x→G h(x)=1(4πh2)e−|x|24h2.In that case,G h hasstandard deviation h,and the following theorem is easily seen.Theorem2.1(Gabor1960).The image method noise of the convolution with a Gaussian kernel G h isu−G h∗u=−h2Δu+o(h2).A similar result is actually valid for any positive radial kernel with bounded variance,so one can keep the Gaussian example without loss of generality.The preceding estimate is valid if h is small enough.On the other hand,the noise reduction properties depend upon the fact that the neighborhood involved in the smoothing is large enough,so that the noise gets reduced by averaging.So in the following we assume that h=kε,where k stands for the number of samples of the function u and noise n in an interval of length h.The spatial ratio k must be much larger than1to ensure a noise reduction.The effect of a Gaussian smoothing on the noise can be evaluated at a referencepixel i=0.At this pixel,G h∗n(0)=i∈IP iG h(x)n(x)d x=i∈Iε2G h(i)n i,where we recall that n(x)is being interpolated as a piecewise constant function,the P i square pixels centered in i have sizeε2,and G h(i)denotes the mean value of the function G h on the pixel i.Denoting by V ar(X)the variance of a random variable X,the additivity of variances of independent centered random variables yieldsV ar(G h∗n(0))=i ε4G h(i)2σ2 σ2ε2G h(x)2d x=ε2σ28πh2.So we have proved the following theorem.Theorem2.2.Let n(x)be a piecewise constant white noise,with n(x)=n i on each square pixel i.Assume that the n i are i.i.d.with zero mean and varianceσ2. Then the“noise residue”after a Gaussian convolution of n by G h satisfiesV ar(G h∗n(0)) ε2σ2 8πh2.496 A.BUADES,B.COLL,AND J.M.MORELIn other terms,the standard deviation of the noise,which can be interpreted as thenoise amplitude,is multiplied by εh √8π.Theorems 2.1and 2.2traduce the delicate equilibrium between noise reductionand image destruction by any linear smoothing.Denoising does not alter the image at points where it is smooth at a scale h much larger than the sampling scale ε.The first theorem tells us that the method noise of the Gaussian denoising method is zero in harmonic parts of the image.A Gaussian convolution is optimal on harmonic functions and performs instead poorly on singular parts of u ,namely edges or texture,where the Laplacian of the image is large.See Figure 3.2.2.Anisotropic filters and curvature motion.The anisotropic filter (AF)attempts to avoid the blurring effect of the Gaussian by convolving the image u at x only in the direction orthogonal to Du (x ).The idea of such a filter goes back to Perona and Malik [27]and actually again to Gabor (quoted in Lindenbaum,Fischer,and Bruckstein [17]).SetA F h u (x )=G h (t )u x +t Du (x )⊥|Du (x )|dt for x such that Du (x )=0and where (x,y )⊥=(−y,x )and G h (t )=1√2πh e −t 22h 2is theone-dimensional (1D)Gauss function with variance h 2.At points where Du (x )=0an isotropic Gaussian mean is usually applied,and the result of Theorem 2.1holds at those points.If one assumes that the original image u is twice continuously dif-ferentiable (C 2)at x ,the following theorem is easily shown by a second-order Taylor expansion.Theorem 2.3.The image method noise of an anisotropic filter A F h isu (x )−A F h u (x ) −12h 2D 2u Du ⊥|Du |,Du ⊥|Du | =−12h 2|Du |curv (u )(x ),where the relation holds when Du (x )=0.By curv (u )(x ),we denote the curvature,i.e.,the signed inverse of the radius of curvature of the level line passing by x .When Du (x )=0,this means thatcurv (u )=u xx u 2y −2u xy u x u y +u yy u 2x(u 2x +u 2y )32.This method noise is zero wherever u behaves locally like a one-variable function,u (x,y )=f (ax +by +c ).In such a case,the level line of u is locally the straight line with equation ax +by +c =0,and the gradient of f may instead be very large.In other terms,with anisotropic filtering,an edge can be maintained.On the other hand,we have to evaluate the Gaussian noise reduction.This is easily done by a 1D adaptation of Theorem 2.2.Notice that the noise on a grid is not isotropic;so the Gaussian average when Du is parallel to one coordinate axis is made roughly on √2more samples than the Gaussian average in the diagonal direction.Theorem 2.4.By anisotropic Gaussian smoothing,when εis small enough with respect to h ,the noise residue satisfiesVar (A F h (n ))≤ε√2πhσ2.ON IMAGE DENOISING ALGORITHMS 497In other terms,the standard deviation of the noise n is multiplied by a factor at mostequal to (ε√2πh)1/2,this maximal value being attained in the diagonals.Proof .Let L be the line x +t Du⊥(x )|Du (x )|passing by x ,parameterized by t ∈R ,and denote by P i ,i ∈I ,the pixels which meet L ,n (i )the noise value,constant on pixel P i ,and εi the length of the intersection of L ∩P i .Denote by g (i )the averageof G h (x +t Du⊥(x )|Du (x )|)on L ∩P i .Then one has A F h n (x )i εi n (i )g (i ).The n (i )are i.i.d.with standard variation σ,and thereforeV ar (A F h (n ))= i ε2iσ2g (i )2≤σ2max(εi ) iεi g (i )2.This yieldsVar (A F h (n ))≤√2εσ2 G h (t )2dt =ε√2πhσ2.There are many versions of A F h ,all yielding an asymptotic estimate equivalent to the one in Theorem 2.3:the famous median filter [14],an inf-sup filter on segments centered at x [5],and the clever numerical implementation of the mean curvature equation in [21].So all of those filters have in common the good preservation of edges,but they perform poorly on flat regions and are worse there than a Gaussian blur.This fact derives from the comparison of the noise reduction estimates of Theorems2.1and 2.4and is experimentally patent in Figure3.2.3.Total variation.The total variation minimization was introduced by Ru-din and Osher [29]and Rudin,Osher,and Fatemi [30].The original image u is supposed to have a simple geometric description,namely a set of connected sets,the objects,along with their smooth contours,or edges.The image is smooth inside the objects but with jumps across the boundaries.The functional space modeling these properties is BV (Ω),the space of integrable functions with finite total variation T V Ω(u )= |Du |,where Du is assumed to be a Radon measure.Given a noisy image v (x ),the above-mentioned authors proposed to recover the original image u (x )as the solution of the constrained minimization problemarg min uT V Ω(u ),(2.1)subject to the noise constraintsΩ(u (x )−v (x ))d x =0and Ω|u (x )−v (x )|2d x =σ2.The solution u must be as regular as possible in the sense of the total variation,while the difference v (x )−u (x )is treated as an error,with a prescribed energy.The constraints prescribe the right mean and variance to u −v but do not ensure that it is similar to a noise (see a thorough discussion in [22]).The preceding problem is naturally linked to the unconstrained problem arg min u T V Ω(u )+λΩ|v (x )−u (x )|2d x (2.2)498 A.BUADES,B.COLL,AND J.M.MORELfor a given Lagrange multiplierλ.The above functional is strictly convex and lower semicontinuous with respect to the weak-star topology of BV.Therefore the minimum exists,is unique,and is computable(see,e.g.,[6]).The parameterλcontrols the tradeoffbetween the regularity andfidelity terms.Asλgets smaller the weight of the regularity term increases.Thereforeλis related to the degree offiltering of the solution of the minimization problem.Let us denote by TVFλ(v)the solution of problem(2.2)for a given value ofλ.The Euler–Lagrange equation associated with the minimization problem is given by(u(x)−v(x))−12λcurv(u)(x)=0(see[29]).Thus,we have the following theorem.Theorem2.5.The image method noise of the total variation minimization(2.2) isu(x)−TVFλ(u)(x)=−12λcurv(TVFλ(u))(x).As in the anisotropic case,straight edges are maintained because of their small curvature.However,details and texture can be oversmoothed ifλis too small,as is shown in Figure3.2.4.Iterated total variation refinement.In the original total variation model the removed noise,v(x)−u(x),is treated as an error and is no longer studied.In practice,some structures and texture are present in this error.Several recent works have tried to avoid this effect[35,25].2.4.1.The Tadmor–Nezzar–Vese approach.In[35],the authors have pro-posed to use the Rudin–Osher–Fatemi model iteratively.They decompose the noisy image,v=u0+n0,by the total variation model.So taking u0to contain only ge-ometric information,they decompose by the very same model n0=u1+n1,where u1is assumed to be again a geometric part and n1contains less geometric informa-tion than n0.Iterating this process,one obtains u=u0+u1+u2+···+u k as a refined geometric part and n k as the noise residue.This strategy is in some sense close to the matching pursuit methods[20].Of course,the weight parameter in the Rudin–Osher–Fatemi model has to grow at each iteration,and the authors propose a geometric seriesλ,2λ,...,2kλ.In that way,the extraction of the geometric part n k becomes twice more taxing at each step.Then the new algorithm is as follows:1.Starting with an initial scaleλ=λ0,v=u0+n0,[u0,n0]=arg minv=u+n|Du|+λ0|v(x)−u(x)|2d x.2.Proceed with successive applications of the dyadic refinement n j=u j+1+n j+1,[u j+1,n j+1]=arg minn j=u+n|Du|+λ02j+1|n j(x)−u(x)|2d x.3.After k steps,we get the following hierarchical decomposition of v:v=u0+n0=u0+u1+n1=.....=u0+u1+···+u k+n k.ON IMAGE DENOISING ALGORITHMS 499The denoised image is given by the partial sum k j =0u j ,and n k is the noise residue.This is a multilayered decomposition of v which lies in an intermediate scale of spaces,in between BV and L 2.Some theoretical results on the convergence of this expansion are presented in [35].2.4.2.The Osher et al.approach.The second algorithm due to Osher et al.[25]also consists of an iteration of the original model.The new algorithm is as follows:1.First,solve the original total variation model u 1=arg min u ∈BV|∇u (x )|d x +λ(v (x )−u (x ))2d x to obtain the decomposition v =u 1+n 1.2.Perform a correction step to obtain u 2=arg min u ∈BV|∇u (x )|d x +λ(v (x )+n 1(x )−u (x ))2d x ,where n 1is the noise estimated by the first step.The correction step adds this first estimate of the noise to the original image and raises the decomposition v +n 1=u 2+n 2.3.Iterate:compute u k +1as a minimizer of the modified total variation mini-mization,u k +1=arg min u ∈BV|∇u (x )|d x +λ (v (x )+n k (x )−u (x ))2d x ,wherev +n k =u k +1+n k +1.Some results are presented in [25]which clarify the nature of the above sequence:•{u k }k converges monotonically in L 2to v ,the noisy image,as k →∞.•{u k }k approaches the noise-free image monotonically in the Bregman distanceassociated with the BV seminorm,at least until u ¯k −u ≤σ2,where u isthe original image and σis the standard deviation of the added noise.These two results indicate how to stop the sequence and choose u ¯k .It is enoughto proceed iteratively until the result gets noisier or the distance u ¯k −u 2gets smallerthan σ2.The new solution has more details preserved,as Figure 3shows.The above iterated denoising strategy being quite general,one can make the computations for a linear denoising operator T as well.In that case,this strategyT (v +n 1)=T (v )+T (n 1)amounts to saying that the first estimated noise n 1is filtered again and its smooth components are added back to the original,which is in fact the Tadmor–Nezzar–Vese strategy.2.5.Neighborhood filters.The previous filters are based on a notion of spatial neighborhood or proximity.Neighborhood filters instead take into account grey-level values to define neighboring pixels.In the simplest and more extreme case,the de-noised value at pixel i is an average of values at pixels which have a grey-level value close to u (i ).The grey-level neighborhood is thereforeB (i,h )={j ∈I |u (i )−h <u (j )<u (i )+h }.。
