97年第十届北京大学生数学竞赛
合集下载
2010全国大学生数学建模竞赛北京赛区获奖名单

北京航空航天大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京大学 北京大学 北京邮电大学 北京大学 北京邮电大学 北京大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 北京邮电大学 中国农业大学 中国地质大学(北京) 北京邮电大学 北京大学 北京邮电大学 北京邮电大学 北京大学 北京邮电大学 中国石油大学(北京) 北京大学 中国人民大学 北京大学 北京邮电大学 北京邮电大学 北京邮电大学 北京语言大学 北京师范大学 北京邮电大学 中国人民大学 中央财经大学 北京邮电大学世纪学院 中华女子学院 中国农业大学 北京理工大学 北京交通大学 北京师范大学 北京邮电大学 装甲兵工程学院 北京邮电大学
队员3 队员3
指导教师
奖项
王小雪 指导小组 全国一等奖 张国波 贺祖国 全国一等奖 史海波 数模指导组全国一等奖 于楠 彭临平 全国一等奖 范爱琳 指导小组 全国一等奖 郑梦天 郑勋烨 全国一等奖 肖牧 指导小组 全国一等奖 王占孔 贺祖国 全国一等奖 杨亚旭 韩丽涛 全国一等奖 王璟尧 袁健华 全国一等奖 刘瑞恺 指导小组 全国一等奖 龚任飞 指导小组 全国一等奖 邹贤青 彭临平 全国一等奖 全拥 孙海燕 全国一等奖 徐悟 指导小组 全国一等奖 叶子豪 孙海燕 全国一等奖 吕晓帆 冯伟 全国一等奖 周瑾 指导小组 全国一等奖 傅文君 齐紫微 全国一等奖 王情 指导小组 全国一等奖 高原 徐厚宝 全国一等奖 祝晨琪 韩丽涛 全国一等奖 欧阳涣堃 指导小组 全国一等奖 孙砚培 全国一等奖 李毅彬 房永飞 全国一等奖 黄海龙 贺祖国 全国一等奖 周霁颖 指导小组 全国一等奖 朱箫笛 指导小组 全国一等奖 王凯 邢星星 王宏宇 王存 孙靳睿 陈丹琦 于亚薇 杨博 田其龙 宋晓天 杨婷婷 陈婉芳 张欣雨 伍惠敏 陆恂 陈俊龙 叶逢铸 颜聪 李俊 王妍 指导小组 帅天平 彭临平 王兵团 指导小组 王品 许传青 全国一等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖 全国二等奖
1997年世界大学生数学竞赛初试试题及详细答案

i
i) If xj ≤ 0 then max xi ≤ xj + 1.
i
ii) If xj ≥ 0 then min xi ≥ xj − 1.
sets:
n , y = 0. We split the indices {1, 2, . . . , n} into five Consider y ∈ Z0
∞
α=
1
1+
1 nk
.
The uniquness of the infinite product will follow from the fact that on every step nk has to be determine by (1). Indeed, if for some k we have 1+ 1 ≥ θk−1 nk
k 1 (1
α +
1 ni )
1 + nk1 θk−1 1 −1 . < θk = =1+ 2 1 ≤ 1 nk − 1 1 + nk 1 + nk 3
Hence, for each k , nk+1 ≥ n2 k. Since n1 ≥ 2, nk → ∞ so that θk → 1. Hence
Problem 4. Let α be a real number, 1 < α < 2. a) Show that α has a unique representation as an infinite product α= 1+ 1 n1 1+ 1 ... n2
where each ni is a positive integer satisfying n2 i ≤ ni+1 . b) Show that α is rational if and only if its infinite product has the following property: For some m and all k ≥ m, nk+1 = n2 k. Solution. a) We construct inductively the sequence {n i } and the ratios θk = so that θk > 1 for all k. Choose nk to be the least n for which 1+ (θ0 = α) so that for each k , (1) Since θk−1 ≤ 1 + we have 1+ 1 nk+1 1+ 1 1 < θk−1 ≤ 1 + . nk nk − 1 1 nk − 1 1 < θk−1 n
i) If xj ≤ 0 then max xi ≤ xj + 1.
i
ii) If xj ≥ 0 then min xi ≥ xj − 1.
sets:
n , y = 0. We split the indices {1, 2, . . . , n} into five Consider y ∈ Z0
∞
α=
1
1+
1 nk
.
The uniquness of the infinite product will follow from the fact that on every step nk has to be determine by (1). Indeed, if for some k we have 1+ 1 ≥ θk−1 nk
k 1 (1
α +
1 ni )
1 + nk1 θk−1 1 −1 . < θk = =1+ 2 1 ≤ 1 nk − 1 1 + nk 1 + nk 3
Hence, for each k , nk+1 ≥ n2 k. Since n1 ≥ 2, nk → ∞ so that θk → 1. Hence
Problem 4. Let α be a real number, 1 < α < 2. a) Show that α has a unique representation as an infinite product α= 1+ 1 n1 1+ 1 ... n2
where each ni is a positive integer satisfying n2 i ≤ ni+1 . b) Show that α is rational if and only if its infinite product has the following property: For some m and all k ≥ m, nk+1 = n2 k. Solution. a) We construct inductively the sequence {n i } and the ratios θk = so that θk > 1 for all k. Choose nk to be the least n for which 1+ (θ0 = α) so that for each k , (1) Since θk−1 ≤ 1 + we have 1+ 1 nk+1 1+ 1 1 < θk−1 ≤ 1 + . nk nk − 1 1 nk − 1 1 < θk−1 n
中国大学生数学建模竞赛发展史
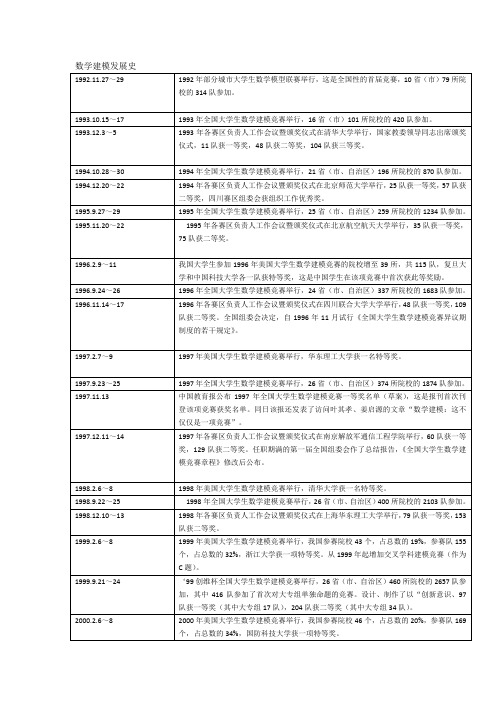
2000.9.26~29
2000网易杯全国大学生数学建模竞赛举行,27省(市、自治区)517所院校的3210队参加,其中608队参加大专组竞赛,香港城市大学有1个队首次参赛
2000.12.6~8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行,119队获一等奖(其中大专组23队),245队获二等奖(其中大专组55队)。
1998年全国大学生数学建模竞赛举行,26省(市、自治区)400所院校的2103队参加。
1998.12.10~13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行,79队获一等奖,153队获二等奖。
1999.2.6~8
1999年美国大学生数学建模竞赛举行,我国参赛院校43个,占总数的19%,参赛队155个,占总数的32%,浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛(作为C题)。
2003.2
2003年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加300队,占总数的47%,浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行,30省(市、自治区)637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行,厦门大学承办,608队获全国奖,其中本科组一等奖151队,二等奖306队,大专组一等奖48队,二等奖103队。
2004.2
2004年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加398队,占总数的54%,成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27~29
1992年部分城市大学生数学模型联赛举行,这是全国性的首届竞赛,10省(市)79所院校的314队参加。
2000网易杯全国大学生数学建模竞赛举行,27省(市、自治区)517所院校的3210队参加,其中608队参加大专组竞赛,香港城市大学有1个队首次参赛
2000.12.6~8
2000年各赛区负责人工作会议暨颁奖仪式在中山大学珠海校区举行,119队获一等奖(其中大专组23队),245队获二等奖(其中大专组55队)。
1998年全国大学生数学建模竞赛举行,26省(市、自治区)400所院校的2103队参加。
1998.12.10~13
1998年各赛区负责人工作会议暨颁奖仪式在上海华东理工大学举行,79队获一等奖,153队获二等奖。
1999.2.6~8
1999年美国大学生数学建模竞赛举行,我国参赛院校43个,占总数的19%,参赛队155个,占总数的32%,浙江大学获一项特等奖。从1999年起增加交叉学科建模竞赛(作为C题)。
2003.2
2003年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加300队,占总数的47%,浙江大学、北京大学、东南大学、东华大学各一队获特等奖。
2003.9.22~25
2003高教社杯全国大学生数学建模竞赛举行,30省(市、自治区)637所院校的5406队参加。
2003.12.6~7
2003年各赛区工作会议暨颁奖仪式在厦门举行,厦门大学承办,608队获全国奖,其中本科组一等奖151队,二等奖306队,大专组一等奖48队,二等奖103队。
2004.2
2004年美国大学生数学建模竞赛(MCM)和交叉学科竞赛(ICM)举行,我国共参加398队,占总数的54%,成都电子科技大学一队获特等奖。
数学建模发展史
1992.11.27~29
1992年部分城市大学生数学模型联赛举行,这是全国性的首届竞赛,10省(市)79所院校的314队参加。
【第十届全国大学生数学竞赛】决赛名单与获奖信息
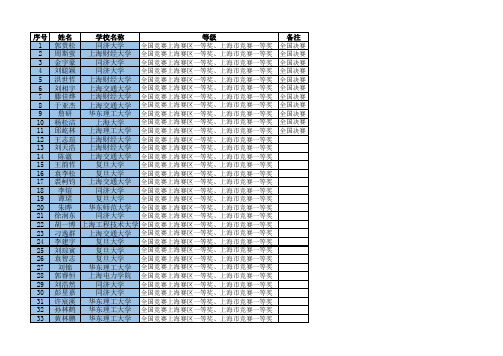
103 李乐章
复旦大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
104 汪国良 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
105 杜雨航 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
106 崔天阳 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
107 黄浩 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
98 张汇韬 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
99 王从武 上海电力学院 全国竞赛上海赛区二等奖、上海市竞赛二等奖
100 陈寅 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
101 何路 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
102 朱文凯
同济大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
93 戴佳贝 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
94 于家梁 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
95 蒋明威 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
96 张济旭 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
97 李嘉森 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
133 杨淋 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
134 李炳昭 上海财经大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
135 王昊天 上海工程技术大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
136 李抒澄 上海工程技术大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
137 赵铭华 上海交通大学 全国竞赛上海赛区二等奖、上海市竞赛二等奖
刘琮寅
第十届全国大学生数学竞赛决赛数学(低年级组)获奖名单

证书编号 编号:SD2019001 编号:SD2019002 编号:SD2019003 编号:SD2019004 编号:SD2019005 编号:SD2019006 编号:SD2019007 编号:SD2019008 编号:SD2019009 编号:SD2019010 编号:SD2019011 编号:SD2019012 编号:SD2019013 编号:SD2019014
武汉大学 付佳奇
一
清华大学 郑书恒
一
浙江大学 戴炜拓
一
浙江大学 陈龙腾
一
浙江大学 李家雨
一
清华大学 黄 畅
一
武汉大学 冯 健
二
四川大学 张霖秋
二
复旦大学 史书珣
二
东南大学 顾王韫
二
山东大学 刘 浩
二
中国科学技术大学 戎明远
二
北京师范大学 龙辰纲
二
河南科技学院 潘 岩
二
西安交通大学 李迪龙
二
编号:SD2019015 编号:SD2019016 编号:SD2019017 编号:SD2019018 编号:SD2019019 编号:SD2019020 编号:SD2019021 编号:SD2019022 编号:SD2019023 编号:SD2019024 编号:SD2019025 编号:SD2019026 编号:SD2019027 编号:SD2019028 编号:SD2019029
学校名称 姓名 武汉大学 白 杨 北京大学 邱 添 中国科学技术大学 何志强 北京大学 庄子杰 山东大学 李博文 复旦大学 刘梓辰 武汉大学 尚镇冰 浙江大学 林徐扬 中国科学技术大学 肖子达 中国科学技术大学 闫顺兴 北京大学 申武杰 南开大学 何家亮 四川大学 刘 念 北京大学 鲁一逍
第十届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类)

第十届全国大学生数学竞赛决赛试题参考答案及评分标准(非数学类,2019年3月30日)一、填空题(本题满分30分,每小题6分)1、设函数在点在处连续,则的值为答案:2、设则答案:3、设曲线L是空间区域的表面与平面的交线,则答案:4、设函数由方程确定,其中具有连续二阶偏导数,则答案:5、已知二次型,则的规范形为答案:二、设内三阶连续可导,满足,又设数列满足严格单调减少且计算【解】由于在区间(-1,1)内三阶可导,在处有Taylor公式又,所以分①由于数列严格单调且,则,且为严格单调增加趋于正无穷的数列,注意到,故由Stolz定理及①式,有分分三、设上具有连续导数,且证明:对于成立【证明】令则故函数在上严格单调增加,记的反函数为,则定义在上,且4分于是根据积分中值定理,存在使得分因此注意到则即分四、计算三重积分:,其中【解】采用“先二后一”法,并利用对称性,得其中分用极坐标计算二重积分,得交换积分次序,得分作变量代换:并利用对称性,得所以.分五、之和.【解】级数通项令分其中.因为所以满足解这个一阶线性方程,得由得,故且分六、设A是n阶幂零矩阵,即满足证明:若A的秩为r,且则存在n阶可逆矩阵P其中为r阶单位矩阵. 【证】存在n阶可逆矩阵H,Q,使得因为所以有分对QH作相应分块为则有因此分而所以显然,所以为行满秩矩阵.8分因为使得分令则有分七、设为单调递减的正实数列,收敛,证明:收敛,所以对任意给定,存在自然数,使得当时,有因为单调递减的正数列,所以分注意到当时,有令得到分下面证明:对于任意自然数n,如果满足则有事实上,即得到分利用(2),令可以得到即分又由知,存在自然数,使得分取则当时,有因此分。
第十届全国大学生数学竞赛决赛(非数学类)获奖名单
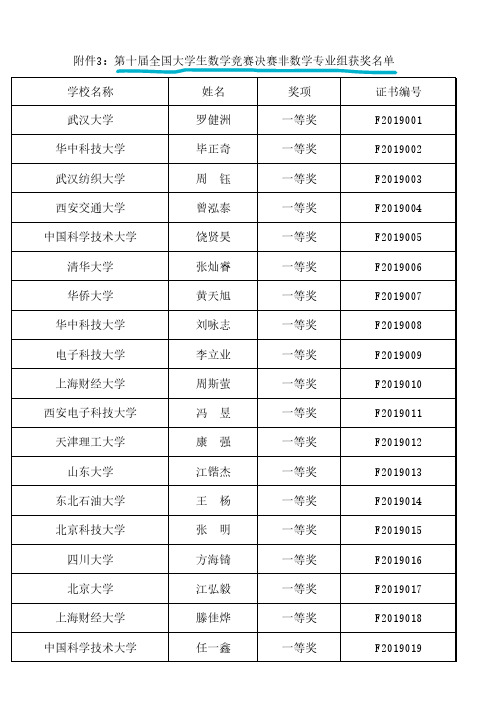
太原理工大学 北京大学 清华大学
华南理工大学 哈尔滨工业大学
丽水学院 燕山大学 电子科技大学 北京航空航天大学 厦门大学 合肥工业大学宣城校区 同济大学 华东理工大学 合肥工业大学 西安交通大学 湖北工业大学 华中科技大学 中国民航大学 陆军工程大学国防工程学院 陆军勤务学院 山东大学
王金宇 高铭齐 倪赞林 吴珍谦 李雨杭 苏文 张再哲 李诚佳 乐洋 何鸿光 陈家鑫 刘聪颖 詹研 朱基宏 潘翔宇 刘子文 阚腾 吴昊 曹晨 廖雪文 王一宁
二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖
F2019083 F2019084 F2019085 F2019086 F2019087 F2019088 F2019089 F2019090 F2019091 F2019092 F2019093 F2019094 F2019095 F2019096 F2019097 F2019098 F2019099 F2019100 F2019101 F2019102 F2019103
张庆达
河海大学
石蕴
内蒙古科技大学
覃康朔
浙江大学
任梓洋
三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖
济南大学
胡广富
贵州大学
张繁盛
江苏大学
曾宇
长安大学
周星星
空军工程大学
涂捷
北京邮电大学
韩帅杰
上海财经大学
洪世哲
中国石油大学(北京)克拉玛依校区 郭 涛
第十届全国大学生数学竞赛决赛数学(高年级组)获奖名单
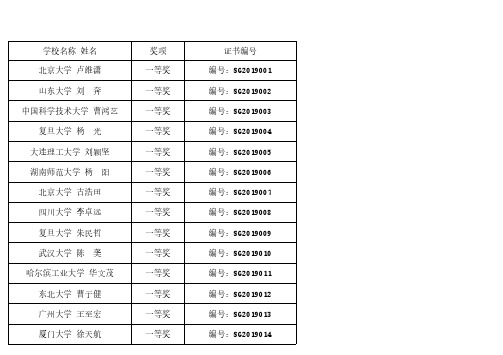
厦门大学 卓志坚 嘉应学院 邓士诚 华南理工大学 姚立鹏 合肥工业大学 徐 顺 北京大学 郑礼鑫 湖南科技大学 高艺漫 云南大学 朱屹恒 大连理工大学 李德维 河南大学 张可忻 武汉大学 胡天智 北京大学 黄峄凡 郑州师范学院 李泽坤 西北工业大学 顾子康 曲阜师范大学 周睿涵 四川大学 陶飏天择
编号:SG2019090 编号:SG2019091 编号:SG2019092 编号:SG2019093 编号:SG2019094 编号:SG2019095 编号:SG2019096 编号:SG2019097 编号:SG2019098 编号:SG2019099 编号:SG2019100 编号:SG2019101 编号:SG2019102
证书编号 编号:SG2019001 编号:SG2019002 编号:SG2019003 编号:SG2019004 编号:SG2019005 编号:SG2019006 编号:SG2019007 编号:SG2019008 编号:SG2019009 编号:SG2019010 编号:SG2019011 编号:SG2019012 编号:SG2019013 编号:SG2019014
国防科技大学 李哲民
二等奖
东南大学 沈伟皓
二等奖
广西大学 顾浩楠
三等奖
西安交通大学 周宇博
三等奖
江西师范大学 王和明
三等奖
温州大学 林 磊
三等奖
天津大学 陈 越
三等奖
ห้องสมุดไป่ตู้
新疆大学 韦春燕
三等奖
哈尔滨工业大学(威海) 王远成 三等奖
扬州大学 李子戌
三等奖
郑州大学数学与统计学院 周 硕 三等奖
石河子大学 姚鸿彬
三等奖
重庆交通大学 李 冉
