【选修2-1课件】3.3空间向量的数乘运算(2)
高中数学选修2精品课件3.1.2空间向量的数乘运算(2)

C 在平面 内且 AB a , AC b ,对于空间任意一点 O ⑶∵已知点 B 、 ∴点 P 在平面 上 是存在唯一有序实数对 ( x, y), 使 OP OA xAB yAC ③
注:①、②、③式都称为平面的向量表示式, 即平面由空间一点及两个不共线向量唯一确定.
求证: ⑴四点E、F、G、H共面; ⑵平面EG//平面AC.
14
例2 (课本例)已知
ABCD ,从平面A, OG kOC , OH kOD
求证:①四点E、F、G、H共面; ②平面AC//平面EG. 证明: ∵四边形ABCD为 ① ∴AC AB AD (﹡)
1 3
1 3
( A)1
( B)0
(C )3
1 ( D) 3
17
课外补充练习:
1.下列说明正确的是: D (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线 2.下列说法正确的是:C (A)平面内的任意两个向量都共线 (B)空间的任意三个向量都不共面 (C)空间的任意两个向量都共面 (D)空间的任意三个向量都共面
共面的充要条件是,存在唯一的一对实数 x,y,使 c c=x a+y b
B C A
O
9
思考 1:如图,平面 为经过已知点 A 且平行两不共线
的非零向量 a 、 b 的平面,如何表示平面 A 上的任一点 P P 呢? p C
b
⑴∵ AP与a 、b 共面, ∴ 唯一有序实数对 ( x, y),
复习:
1、如果向量e1和e2是一平面内的两个不平 行的向量,那么,该平面内的任一向量a与 e1, e2有什么关系?
选修2-1 3.1.23.1.2空间向量的数乘运算PPT

零向量与 任何向量平
行 (1)向量平行与直线平行的比较;
(2)关注零向量;
(3)对空间任意两个向量a与b ,如 果 a// b,那么a与b有什么相等关系?反过来 呢?
(1)当我们说a,b共线时,表示a,
b的两条有向线段所在直线既可能是同一 直线,也可能是平行线;
(2)当我们说 a // b时,也具有同样 的意义.
对于空间向量的数乘运算的运算 律的证明,方法与证明平面向量数乘 运算的运算律类似.
(1) λa与a之间是什么关系? (2) λa与a所在直线之间的关系?
பைடு நூலகம்
知识要点
3.共线向量(或平行向量)的定义
表示空间向量的有向线段所在直线互 相平行或重合,则称这些向量叫共线向量 (colliner vectors)或平行向量(parallel vectors) 记作
知非零向量a的直线,对于空间任意一
点像O,点P在直线l上的充要条件是存
在实数t,使
P
B
OP = OA + ta.
(1)
a
A
O
其中向量a叫做直线l的方向向量 (direction vector)
在l上取AB=a,则(1)式可化为
OP = (1- t)OA + t OB.
(2)
说明: (1),(2)都叫做空间直线的向量 参数表示式.由此可知,空间任意直线由 空间一点及直线的方向向量唯一确定.
知识要点
4.共线向量基本定理
对于空间任意两个向量a ,b(b≠0),a // b的充要条件是存在实数λ,使
a = λb
(1)b≠0的理解.若b=0,则a任意,λ 不唯一;
(2)若a // b,b // c,则a一定平行 于c吗?(不一定,考虑中间向量为零向 量)
人教课标版高中数学选修2-1《空间向量的数乘运算》名师课件2

例题讲解
例2. 如图,已知平行四边形ABCD,过平面AC外
一点O作射线OA,OB,OC,OD,在四条射线上
分别取点E,F,G,H,并且使
O
OE OF OG OH k, OA OB OC OD
求证: E,F,G,H四点共面. A
DC B
H
G
E
F
例题讲解
证明 :因 OE OF OG OH k, OA OB OC OD
a
对空间任意一点O,AP = OP - OA,
P
所以OP - OA = ta, 即OP = OA + ta, ①
B
A l
若在l上取AB = a,则有
OP = OA + tAB.
②
O
①和②都称为空间直线的向量表示式,空间任意 直线由空间一点及直线的方向向量惟一决定. 由此可判断空间任意三点是否共线.
新知探究
素养提炼
(4)共面向量的充要条件给出了平面的向量表示式,说明空间中 任意一个平面都可以由两个不共线的平面向量表示出来. (5)空间一点 P 位于平面 MAB 内的充分必要条件是存在有序实 数对(x,y),使M→P=xM→A+yM→B.满足这个关系式的点 P 都在平 面 MAB 内;反之,平面 MAB 内的任一点 P 都满足这个关系式.
课堂小结
1.空间向量的数乘运算; 2.共线向量的概念、定理及应用; 3.直线l的方向向量; 4.共面向量的概念、定理及应用。
作业
P89 1、2
新知探究
C
p
P
b
A aB
P与A,B,C共面 O
AP x AB y AC
OP OA x AB y AC
OP xOA yOB zOC (其中x y z 1)
人教版高中数学选修3.1.2空间向量的数乘运算 (2)ppt课件

则点 P 在直线 l 上 唯一实数 t R, 使 OP OA t AB ③ 注:①、②、③式都称为空间直线的向量表示式, 即空间直线由空间一点及直线的方向向量唯一确定 . 12
三.共面向量:
1.共面向量:平行于同一平面的向量,叫做共面向量. A 注意:空间任意两个向量是 O 共面的,但空间任意三个向 量就不一定共面的了。 a
2. 共面向量定理 : 如果两个向量 a 、 b 不共线 , 则向 量 p 与 向量 a 、 b 共面的 充要条件是存 在唯一的 有 序实数对 ( x, y ) 使 p xa yb .
1 (4) AB AD+ CC1=AM . 2
6
复习回顾 平面向量共线定理
7
复习回顾 平面向量共线定理
平面任意两个向量 ,使 a b a // b 的 充要条件是存在实数 规定 : o 与任一向量 a 是共线向量
平面向量共线定理:
a
b ( b ≠ 0 ),
即“平面向量的基本定理”就是 空间向量的共面定理
p
b
A
a
B
13
例3 (课本例)已知
ABCD ,从平面AC外一点O引向量
OE kOA, OF kOB, OG kOC , OH kOD
求证:四点E、F、G、H共面;
O
点评:根据共面向量定理,只要满足下列条件四 点共面。
EG x EH y EF
3.1.2
空间向量的数乘运算
回顾: 上一节课 ,我们把平面向量的有关概念及加减运
【选修2-1课件】3[1].2空间向量的数乘运算
![【选修2-1课件】3[1].2空间向量的数乘运算](https://img.taocdn.com/s3/m/41d49442a31614791711cc7931b765ce04087a6b.png)
做共线向量(或平行向量),记作 a // b
零向量与任意向量共线.
2.共线向量定理:,对于空间任意两个向量 a , b ( b 0 ),
a // b R , a b .
12
推论:如果 l为经过已知点A且平行已知非零
向量 a的直线,那么对任一点O,点P在直线 上l 的
2
一、数乘空间向量的运算法则
与平面向量一样,实数 与空间向量 a 的乘积
a 仍然是一个向量.
⑴当 0时, a 与向量 a 的方向相同; ⑵当 0时, a 与向量 a 的方向相反; ⑶当 0 时, a 是零向量.
例如:
2a
a
3a 3
显然,空间向量的数乘运算满足分配律 及结合律
a // b R , a b .
8
思考:如图, l 为经过已知点 A 且平行非零向量 a 的直线,
则点 P 在直线 l 上的充要条件是?
•l
A•
•
aB
P
O
注:非零向量 a 叫做 直线 l 的方向向量.
点 P 在直线 l 上 唯一实数 t R, 使 AP t a ①
点 P 在直线 l 上 唯一实数 t R, 使 OP OA t a ②
求证:点 M 在直线 OE 上. G
E
分析:ቤተ መጻሕፍቲ ባይዱ
C
F
证三点共线可 尝试用向量来分析.
B M
D
O
N
A
10
例4、已知四边形ABCD是空间四边形,E、H分别是
边AB、AD的中点,F、G分别是CB、CD上的点,
且 CF 2 CB,CG 2 CD.
3
3
求证:四边形EFGH是梯形。
高中数学选修2-1第3章3.1.2空间向量的数乘运算课件人教A版

1 2 1 2 1 2 1 2
-5-
3.1.2 空间向量的数乘运算
目标导航
知识梳理 知识梳理
重难聚焦
典例透析
2.共线向量与共面向量 (1)①共线向量:如果表示空间向量的有向线段所在的直线互相 平行或重合,则这些向量叫做共线向量或平行向量. ②对空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ,使 a=λb.
-10-
3.1.2 空间向量的数乘运算
目标导航
知识梳理
重难聚焦
典例透析
2.向量共面的充要条件及其应用 剖析:(1)空间一点 P 位于平面 MAB 内的充要条件是:存在有序 实数对(x,y),使������������ = ������������������ + ������������������ . 满足这个关系式的点P 都在平面 MAB 内;反之,平面 MAB 内的任一点 P 都满足这个关系式.这个充要 条件常用来证明四点共面. (2)共面向量的充要条件是判断三个向量是否共面的依据,也可 用来把已知共面条件转化为向量式,以便应用向量这一工具.另外,在 许多情况下,可以用“若存在有序实数组(x,y,z),使得对于空间任意一 点 O,都有������������ = ������������������ + ������������������ + ������������������ , 且x+y+z=1 成立,则 P,A,B,C 四 点共面”作为判定空间中四点共面的依据.
-6-
3.1.2 空间向量的数乘运算
目标导航
知识梳理 知识梳理
重难聚焦
典例透析
(2)①共面向量:平行于同一个平面的向量,叫做共面向量. ②如果两个向量a,b不共线,那么向量p与向量a,b共面的充要条件 是存在唯一的有序实数对(x,y),使p=xa+yb.
高二数学人教A版选修2-1课件:3.1.2 空间向量的数乘运算

即������������ =y������������ +z������������ .
∴点 P 与点 A,B,C 共面.
+
������������
=
2 3
������������
−
������������
+
1 3
������������1
=23 (������������
+
������������ )-������������
+
1 3
(������
������1
+
������1 ������1 )
=23 (������������
知识精要
典题例解
迁移应用
一 二三
知识精要
典题例解
迁移应用
1.设 M 是△ABC 的重心,记������������=a,������������=b,������������=c,则������������=(
)
答案:D
解析:∵M 是△ABC 的重心,
∴������������
=
2 3
������������
目标导航
预习导引
123
已知在空间四边形 OABC 中,M,N 分别是对边 OA,BC 的中点,
点 G 在 MN 上,且 MG=2GN.设������������=a,������������=b,������������=c,则用 a,b,c 表示向
选修2-1空间向量的数乘运算2

量,叫做共面向量.
O
a
A
a
注意:空间任意两个 向量是共面的,但空 间任意三个向量就不 一定共面的了。
2. 共面向量定理 : 如果两个向量 a 、 b 不共线 , 则向 量 p 与向量 a 、 b 共面的充要条件是存在唯一的有 序实数对 ( x, y) 使 p xa yb .
一、 数乘空间向量的运算法则
与平面向量一样 , 实数 与空间向量 a 的乘积
a 仍然是一个向量. ⑴当 0 时, a 与向量 a 的方向相同; ⑵当 0 时, a 与向量 a 的方向相反; ⑶当 0 时, a 是零向量.
例如:
a
3a
3a
4
显然,空间向量的数乘运算满足分配律 及结合律
1 (4) AB AD+ CC1=AM . 2
6
二、共线向量及其定理
定义:表示空间向量的有向线段所在直线互相平行或 重合,则称这些向量叫共线向量.(或平行向量)
思考 ⑴ : 对空间任意两个向量 a 与 b , 如果 a b , 那 么 a 与 b 有什么关系?反过来呢?
类似于平面,对于空间任意两个向量 a , b ( b 0 ),
△BCD 的重心,试用 a 、 b 、 c 表示下列向量:
⑴ DM
1 ( a b) c 2
B M
⑵ AG
A
1 ( a b c) 3
D
G C
11
A a B
9
b
C
p
P
思考 2(课本 P88 思考) B、 C, 已知空间任意一点 O 和不共线的三点 A 、 满 足 向 量 关 系 式 OP xOA yOB zOC ( 其 中 x y z 1 )的点 P 与点 A 、 B、 C 是否共面?
2019版高中数学人教版A版选修2-1课件:3.1.2 空间向量的数乘运算

解析答案
→ (4)AQ. 解 ∵CQ∶QA′=4∶1,
∴A→Q=A→C+C→Q=A→C+45(A—A—′→-A→C) =15A→C+45A—A—′→=15A→B+15A→D+45A—A—′→ =15a+15b+45c.
解析答案
题型二 向量共线问题
例2 如图,四边形ABCD和ABEF都是平行四边形,且不共面,M,N 分别是AC,BF的中点,则 C→E与M→N 是否共线?
反思与感悟
解析答案
跟踪训练 1 如图所示,在平行六面体 ABCD—A′B′C′D′中,A→B=a,
A→D=b,A—A—′→=c,P 是 CA′的中点,M 是 CD′的中点,N 是 C′D′的 中点,点 Q 在 CA′上,且 CQ∶QA′=4∶1,用 a,b,c 表示以下向量: (1)A→P; 解 ∵P是CA′的中点, ∴A→P=12(A→C+A→ A′)=12(A→B+A→D+A—A—′→) =12(a+b+c).
M,N,P 分别是 AA1,BC,C1D1 的中点,试用 a,b,c 表示以下各向量: (1)A→P;
解 ∵P是C1D1的中点, ∴A→P=A—A→1+A—1—D→1+D—1→P=a+A→D+12D—1—C→1 =a+c+12A→B=a+c+12b.
解析答案
(2)A—1→N;
解 ∵N是BC的中点,
答案
知识点二 共线向量 (1)共线向量定义 表示空间向量a,b的有向线段所在的直线 互相平行或重合 , 则 向 量 a,b叫做 共线向量 或 平行向量 ,记作a∥b. (2)两向量共线的充要条件 对空间任意两个向量a,b (b≠0),a∥b的充要条件是存在实数λ,使a =λb.
答案
(3)共线向量的推论 如果 l 为经过已知点 A 且平行于已知非零向量 a 的直线,那么对于空间任 一点 O,点 P 在直线 l 上的充要条件是存在实数 t,使O→P=O→A+ta,①. 其中向量 a 叫做直线 l 的 方向向量 .在 l 上取A→B=a,则①式可化为O→P= O→A+tA→B,②.此推论可以用来判断任意三点共线.
2020版高中人教A版数学选修2-1课件:3.1.2空间向量的数乘运算

A1C1的中心,若
uuur AE
uuur xAB
uuur yAD
uuuur zAA1,
则x+y+z=______.
【思维·引】
1.利用向量加减法的三角形法则进行表示.
2.把
uuur AE
用指定向量表示后找对应系数.
【解析】1.选B.
uuur BD
uuur BO
uuur OC
uuur CD
uuur OB
uuur uuur AB与CD
有什么关系?反
之,成立吗?
提示:AuuBur与CuuDur 共线,反之若
uuur uuur AB与CD
共线,则直线AB与直
线CD平行或重合.
(3)空间中任意两个向量是否都共面? 提示:是,向量可以自由平移,任意两个向量都可以平移 到一个平面内.
3.直线的方向向量
如图所示,l为经过已知点A且平行于已
提示:(1)×.当b=0,a≠0时,a∥b,但不存在实数λ,使 a=λb.故应限制b≠0. (2)×.根据共线向量的定义,若 AuuBur则PCuAuDurB, ∥CD或 A,B,C,D四点共线. (3)√.由于a=4e1- e522=-4 (e1 =110-e42 )b,所以a∥b.
(4)√.若k1≠0,则向量e1能用e2,e3表示,与向量e1,e2,e3是 三个不共面的向量矛盾,同理k2,k3也都是0.
1
uuur AC
1
uuur BD.
2
2
2
2
所以
uuur uur uuur AC, EF, BD
共面.
角度2 利用共线、共面求参数值
【典例】若点P在平面ABC内,O为平面ABC外的任意一点,
【人教A版】高中选修2-1数学:3.1.2-空间向量的数乘运算-教学课件

第三章 §3.1 空间向量及其运算3.1.2 空间向量的数乘运算学习目标1.掌握空间向量数乘运算的定义及数乘运算的运算律.2.了解平行(共线)向量、共面向量的意义,掌握它们的表示方法.3.理解共线向量的充要条件和共面向量的充要条件及其推论,并能应用其证明空间向量的共线、共面问题.内容索引问题导学题型探究当堂训练问题导学知识点一 空间向量的数乘运算思考实数λ和空间向量a 的乘积λa 的意义是什么?向量的数乘运算满足哪些运算律?λ>0时,λa 和a 方向相同;λ<0时,λa 和a 方向相反;λa 的长度是a 的长度的|λ|倍.空间向量的数乘运算满足分配律及结合律:①分配律:λ(a +b )=λa +λb ,②结合律:λ(μa )=(λμ)a .答案梳理 (1)实数与向量的积与平面向量一样,实数λ与空间向量a 的乘积λa 仍然是一个向量,称为向量的数乘运算,记作λa ,其长度和方向规定如下:①|λa |= .②当λ>0时,λa 与向量a 方向相同;当λ<0时,λa 与向量a 方向 ;当λ=0时,λa =0.(2)空间向量数乘运算满足以下运算律①λ(μa )= ;②λ(a +b )=;③(λ1+λ2)a = (拓展).λ1a +λ2a |λ||a |相反(λμ)a λa +λb知识点二 共线向量与共面向量思考1回顾平面向量中关于向量共线的知识,给出空间中共线向量的定义.如果表示空间向量的有向线段所在的直线互相平行或重合,那么这些向量叫做共线向量或平行向量.答案思考2空间中任何两个向量都是共面向量,这个结论是否正确?正确.根据向量相等的定义,可以把向量进行平移,空间任意两个向量都可以平移到同一平面内,成为共面向量.答案梳理 (1)平行(共线)向量定义表示空间向量的有向线段所在的直线的位置关系:互相____________充要条件对空间任意两个向量a ,b (b ≠0),存在实数λ,使______点P 在直线l 上的充要条件存在实数t 满足等式 ,在直线l 上取向量+t ___向量a 为直线l 的________平行或重合a =λb 方向向量(2)共面向量定义平行于同一个的向量三个向量共面的充要条件向量p 与不共线向量a ,b 共面的充要条件是存在 的有序实数对(x ,y ),使__________点P 位于平面ABC 内的充要条件存在有序实数对(x ,y ),使=__________对空间任一点O ,有+__________p =x a +y b 惟一平面题型探究类型一 向量共线问题求证:E,F,B三点共线.证明反思与感悟判定向量a,b(b≠0)共线,只需利用已知条件找到x,使a=x b即可.证明点共线,只需证明对应的向量共线.设AC 中点为G ,连接EG ,FG ,解答类型二 空间向量的数乘运算及应用解答解答解答引申探究解答反思与感悟利用数乘运算进行向量表示的技巧(1)数形结合:利用数乘运算解题时,要结合具体图形,利用三角形法则、平行四边形法则,将目标向量转化为已知向量.(2)明确目标:在化简过程中要有目标意识,巧妙运用中点性质.解答类型三 空间向量共面问题证明反思与感悟(1)利用四点共面求参数向量共面的充要条件的实质是共面的四点中所形成的两个不共线的向量一定可以表示其他向量,对于向量共面的充要条件,不仅会正用,也要能够逆用它求参数的值.(2)证明空间向量共面或四点共面的方法①向量表示:设法证明其中一个向量可以表示成另两个向量的线性组合,即若p=x a+y b,则向量p,a,b共面.③用平面:寻找一个平面,设法证明这些向量与该平面平行.解答证明证明证明当堂训练∵2a -b =2·a +(-1)·b ,∴2a -b 与a ,b 共面.1.对于空间的任意三个向量a ,b ,2a -b ,它们一定是A.共面向量 B.共线向量C.不共面向量D.既不共线也不共面的向量√答案解析答案解析√-8答案解析4.以下命题:①两个共线向量是指在同一直线上的两个向量;②共线的两个向量互相平行;③共面的三个向量是指在同一平面内的三个向量;④共面的三个向量是指平行于同一平面的三个向量.②④答案解析其中正确命题的序号是______.根据共面与共线向量的定义判定,易知②④正确.5.已知A,B,M三点不共线,对于平面ABM外的任意一点O,判断在下列各条件下的点P与点A,B,M是否共面.解答由共面向量定理的推论知,点P与点A,B,M共面.∵3+(-1)+(-1)=1,∴点B与点P,A,M共面,即点P与点A,B,M共面.解答∴点P与点A,B,M不共面.∵4+(-1)+(-1)=2≠1,∴点P与点A,B,M不共面.12345规律与方法。
高中数学新人教A版选修2-1精品课件3.1.2《空间向量及其运算-数乘运算》课件

注:两个空间向量的加、减法与两个平面向量 的加、减法实质是一样的.因为 …….
4
b b
a a
我们知道平面向量还有数乘运算. 类似地,同样可以定义空间向量的数乘运 算,其运算律是否也与平面向量完全相同呢?
5
定义:
例如:
6
显然,空间向量的数乘运算满足分配律 及结合律
A
D F
7
B
E
C
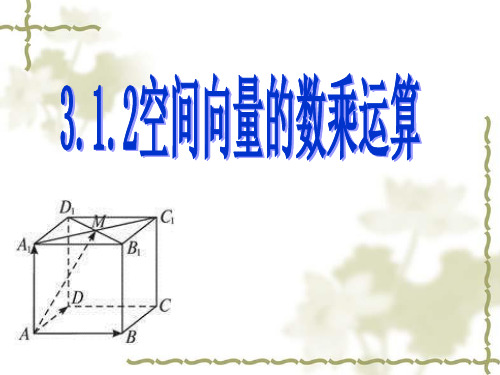
思考1:已知平行六面体ABCD-A1B1C1D1,化简下列向量 表达式,并标出化简结果的向量.(如图)
3.1.2《空间向量及其运算 -数乘运算》
1
教学目标
• 1.理解空间向量的概念,掌握空间向量的 数乘运算. • 2.用空间向量的运算意义和运算律解决立 几问题.. • 教学重点:空间向量的数乘运算及运算律. • 教学难点:用向量解决立几问题.
2
复习回顾
数乘运算
思考1
向量的平 行
3
加法:三角形法则或 平行四边形法则 减法:三角形法则 加法交换律 加法结合律
思考2:已知平行六面体ABCD-A1B1C1D1, 求满足下列各式的x的值。
D1 A1 B1 C1
D A B
C
10
例2:已知平行六面体ABCD-A1B1C1D1, 求满足下列各式的x的值。
D1 A1 B1 C1
D A B
C
11
例2:已知平行六面体ABCD-A1B1C1D1, 求满足下列各式的x的值。
D1 A1 B1 M C1
G
D A B C
8
平行六面体
思考2
D1 A1 B1
C1
a
D A B C
平行六面体:平行四边形ABCD按向量 a 平移 到A1B1C1D1的轨迹所形成的几何体. 记做ABCD-A1B1C1D1
人教版高中数学选修2-1 3.1.2空间向量的数乘运算教学课件 (共29张PPT)
平行于同一平面的向量,叫做共面向量。
结论:1)空间任意两个向量都是共面向量。
2)空涉 间中及任空意间两任个意向两量总个是向共量面问的题.,那平 三个 向量呢面?向如何量判中断有三关个结向论量仍是否适共用面它呢们?。
探究: 空间任意不共线的两个向量a,b,
如果p xa yb, 那么向量p与向量a,b有什么位置关系? 反过来,向量p与a,b有什么位置关系时, 有p xa yb?
方向关系
模的关系
λ>0
方向_相__同___
λ=0
λa=_0__,其方向是任意的
λa的模是a的模的 _|λ_|_倍
λ<0
方向_相__反___
自学
空间向量的数乘运算满足分配律及结合律
❖ 即:
(((a例1】 已知在空间四边形 OABC 中,M, N 分别是对边 OA,BC 的中点,点 G 在
【例2】
题型二 向量共线问题 设两非零向量 e1、e2 不共线,A→B=e1+e2,B→C=2e1+
8e2,C→D=3(e1-e2).试问:A、B、D 是否共线,请说明理由.
解 ∵B→D=B→C+C→D=(2e1+8e2)+3(e1-e2)=5(e1+e2), ∴B→D=5A→B,又∵B 为两向量的公共点,
问题1
不一定
c
a
b
问题2
共面
a
p
b
O1
a
O2
p b
问题3
共面
a
O2
p b
问题4
存在
必修四学过的 平面向量基本定理
空间向量共面定理
如果两个向量 a,b 不共线,那么p 与a,b 共面的充要条
件是存在惟一的有序实数对(x,y),使p xa yb
高中数学新课标人教A版选修2-1:3.1.2 空间向量的数乘运算 课件(共25张ppt)

2.在下列条件中,使 M 与 A,B,C 一定共面的 是( C ) → =3OA → -2OB → -OC → A.OM
→ +OA → +OB → +OC → =0 B.OM → → → C. MA+MB+MC= 0
1→ → 1→ → D.OM= OB-OA+ OC 4 2
3.下列说法正确的是( D )
b a
如图,l 为经过已知点 A 且平行于已知非零向量 O,点 P 在直线 l 上的充要 条件是存在实数 t,使 OP OA ta , 其中向量 a 叫做直 线 l 的方向向量.
P B A
a 的直线,对空间任意一点
a
若P为A,B中点, 则
1 OP OA OB 2
C b A a B
p
P
或对空间任一点O,有 OP = OA + xAB + yAC
C b A a B
p
③
P
O ③ 式称为空间平面ABC的向量表示式,空间中任意 平面由空间一点及两个不共线向量惟一确定.
P与A,B,C共面
AP xAB yAC
C.充要条件
例2. 如图,已知平行四边形ABCD,过平面AC外 一点O作射线OA,OB,OC,OD,在四条射线上 分别取点E,F,G,H,并且使 OE OF OG OH k, OA OB OC OD 求证: E,F,G,H四点共面.
O D B H G F
C
A
E
OE OF OG OH 证明 :因 k, OA OB OC OD 所以 OE kOA, OF kOB, OG kOC , OH kOD. 由于四形ABCD是平行四形,所以 AC AB AD . 因此 EG OG OE kOC kOA=k AC k ( AB AD) k (OB OA OD OA) OF OE OH OE EF EH 由向量共面的充要件知E , F, G, H 四共面.
高二数学人教A版选修2-1课件:3.1.2 空间向量的数乘运算(共25张)

探究点2 共面向量
共面向量:平行于同一个平面的向量,叫做共面 向量.
b
d
c
a
注意:空间任意两个向量是共面的,但空间任意 三个向量既可能共面,也可能不共面.
那么什么情况下三个向量共面呢?
由平面向量基本定理知,如果 , 是平面内的两个不共线的向量,那么 对于这一平面内的任意向量 ,有且 只有一对实数 , 使
C={x|x是实数}. 集合C是由所有属于集合A和集合B的元素组成的.
例如:
显然,空间向量的数乘运算满足分配律及结 合律
如果表示空间向量的有向线段所在直线互相平行或 重合,则 这 些向量叫做共线向量或平行向量.
若P为A,B中点, 则
P
aB Alຫໍສະໝຸດ OA lP B
O
①和②都称为空间直线的向量表示式,空间任意 直线由空间一点及直线的方向向量惟一决定. 由此可判断空间任意三点是否共线.
A.必要不充分条件 B.充分不必要条件
C.充要条件
D.既不充分也不必要条件
O
DC
A
B
H
G
E
F
证明
1.下列命题中正确的个数是( D )
①若 与 共线, 与 共线,则 与 共线;
②向量 , , 共面即它们所在的直线共面;
③若 ∥ ,则存在惟一的实数λ,使 =λ .
A.1 B.2
C.3
1.空间向量的数乘运算.(重点) 2.共线向量及共面向量的应用.(重点、难点) 3.向量的共面、共线与直线的位置关系.
观察下列各个集合,你能说出集合C与集合 A,B之间的关系吗?
(1) A={1,3,5}, B={2,4,6} ,C={1,2,3,4,5,6}. (2) A={x|x是有理数},B={x|x是无理数},
高二数学课件 空间向量的数乘运算课件人教版_选修2-1

作业:P89练习:1,2,3. 《学海》第2课时
第三章 空间向量与立体几何
3.1 空间向量及其运算 3.1.2空间向量的数乘运算
1. 空间向量的数乘运算
实数与空间向量a的乘积 a
仍然是一个向量.
(1)大小:|λa|=|λ|·|a|; (2)方向:λ>0时同向,
λ<0时反向, λ=0时λa=0.
1. 空间向量的数乘运算
(3)运算律:
分配律:(a+b)=a+b 结合律:(a)=a
OP OA ta
OP OA tAB
O
OP OA t(OB OA) OP (1 t)OA tOB
3. 共面向量
平行于同一平面的向量,叫做共面向量
空间任意两个向量是共面的,但空间 任意三个向量就不一定共面。
3. 共面向量
若向量a,b不共线,则向量p与a,b共面 的充要条件是:存在惟一的有序实数对 (x,y),使p=xa+yb.
bC
p
p
A aB
C
A
空间一点P位于平面ABC内 存在有序实数对(x,y),使
AP xAB yAC OP OA xAB yAC
P B
O
OP OA x(OB OA) y(OC OA)
对空间任一点O和不共线三点A、B、C,
若OP xOA yOB zOC,则点P在平 面ABC内的充要条件是 x+y+z=1.
(2)平面AC//平面EG. O
DC
A
B
H E
G F
小结作业
1.向量平行、共面与直线平行、共面是 不同的概念,共线向量通过平移可以移 到同一条直线上,共面向量通过平移可 以移到同一个平面上.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B’
C’
c
b
M
a
B
N
C
小结
1 .a b (b ≠ 0) ⇔ ∃ λ ∈ R , a = λ b
推论:P , A, B三点共线 ⇔ ∃λ ∈ R, AP = λ AB ⇔ OP = (1 − λ )OA + λ OB
2.若a与b不共线则c 与a,b 共面 ⇔ c = xa + yb
推论:P , A, B, C四点共面 ⇔ AP = x AB + y AC ⇔ OP = xOA + yOB + zOC ( x + y + z = 1)
B A
C
则通过平移一定可以使他们位于同一平面内, 则通过平移一定可以使他们位于同一平面内, O
由平面向量基本定理可知,一定存在唯一的实数对 , , 由平面向量基本定理可知,一定存在唯一的实数对x,y, 使c=x a+y b 则可选定一点O, (2)充分性:如果c 满足关系式c=xa+yb,则可选定一点 , )充分性: a 于是OC=OA+AC=xa+yb=c, = = = + = 作OA=xa,OB=AC=yb,于是 = 显然OA,OB,OC,都在平面 显然 , , ,都在平面OAB内,故c,a,b共面 内
共面向量定理的剖析
如果两个向量 不共线, a,b 不共线,
存在唯一的一对实数x, 存在唯一的一对实数x y ,使 c=x a+y b
★ 向量c与向量a,b共面
★ c =xa +yb
(性质) 性质) 向量c与向量a,b共面 (判定) 判定)
如图, 且平行两不共线 思考 1:如图,平面 α 为经过已知点 A 且平行两不共线 的非零向量 a 、 的平面,如何表示平面 A 上的任一点 P b 平面,如何表示平面 表示 P 呢? p C
= OF − OE = kOB − kOA
O
= k ( OB − OA ) = kAB 由①知 EG = kAC
D
C
⇒ EG // AC EF // AB
由面面平行判定定理的推论得: 由面面平行判定定理的推论得:
A
H
B
G
面 EG // 面 AC
E
F
课外补充练习: 外补充练习: 练习
A 1.对于空间任意一点 ,下列命题正确的是: 对于空间任意一点O,下列命题正确的是: 对于空间任意一点
A
H
B
G
= OF − OE + OH − OE E F = EF + EH 共面。 所以 E、F、G、H共面。 、 、 、 共面
例2 已知
ABCD ,从平面 外一点 引向量 从平面AC外一点 外一点O引向量
OE = kOA ,ຫໍສະໝຸດ OF = kOB , OG = kOC , OH = kOD
求证: 四点 、 、 、 共面 共面; 求证:①四点E、F、G、H共面; 平面EG。 ②平面AC//平面 。 平面 证明: 证明: EF ②
A a B
b
O
①点 P 在平面 α 上 ⇔ ∃ 唯一有序实数对 (x, y),使 AP = xa+ yb 唯一有序实数对 有序实数
存在唯一有序实数对 P B C ② 点 P 在平面 ABC 上 ⇔ ∃ 是存在唯一有序实数对 (x, y),使 A =xA +yA
是存在唯一有序实数对 ⇔ ∃ 是存在唯一有序实数对 (x, y),使 OP = OA + xAB + yAC
3、共面向量定理: 共面向量定理:
如果两个向量a, 不共线 则向量c与向量 不共线, 与向量a, 如果两个向量 ,b不共线,则向量 与向量 ,b 唯一的一对实数 , , 共面的充要条件是,存在唯一 共面的充要条件是,存在唯一的一对实数 x,y,使 c=x a+y b = + c
证明: 证明: (1)必要性:如果向量c与向量a,b共面, 与向量a 共面, )必要性:
2.共线向量定理:,对于空间任意两个向量 a , b ( b ≠ 0 ), 共线向量定理: 对于 共线向量定理 对于空间任意两个向量
a // b ⇔ ∃ λ ∈ R , a = λ b .
推论: 为经过已知点A 推论:如果 l 为经过已知点A且平行已知非零 的直线,那么对任一点O, O,点 向量 a的直线,那么对任一点O,点P在直线 l上
1 1 1 (1)OM = OA + OB + OC ; 3 3 3 (2)OM = 2OA − OB − OC.
课本例)如图 例2(课本例 如图,已知平行四边形 课本例 如图,已知平行四边形ABCD,从平 从平 面AC外一点 引向量 OE = k OA , OF = k OB, 外一点O引向量 外一点
16
例3:已知斜三棱柱 :已知斜三棱柱ABC-A’B’C’,设AB=a, , =
在面对角线AC’上和棱 上 上和棱BC上 AC=b,AA’=c,在面对角线 = = 上和棱 分别取点M和 , 分别取点 和N,使AM=kAC’,BN=kBC = , = (0≤k≤1)。 )。
A’
求证:MN与向量 a 和 c 共面 求证: 与向量 变式: 变式: 求证: 求证:MN∥平面 ∥平面ABB’A’
3.3空间向量的 3.3空间向量的 数乘运算( 数乘运算(2)
一、共线向量: 共线向量:
1.共线向量: 1.共线向量:如果表示空间向量的有向线 共线向量
段所在直线互相平行或重合, 段所在直线互相平行或重合,则这些向量叫 做共线向量(或平行向量), ),记作 做共线向量(或平行向量),记作 a // b 零向量与任意向量共线. 零向量与任意向量共线.
1 则 OP = OA+ OB 则A、B、P三点共线。 2
(
)
向量参数表示式
共面向量:平行于同一平面的向量 叫做共面向量 共面向量 平行于同一平面的向量,叫做共面向量 平行于同一平面的向量 叫做共面向量.
a
O A
α
a
注意: 注意:空间任意两个 向量是共面的, 向量是共面的,但空 间任意三个向量就不 一定共面的了。 一定共面的了。
其中向量 a叫做直线 若 OP = OA + t AB
的充要条件是存在实数t,满足等式 的充要条件是存在实数t,满足等式OP = OA + ta t,
l
的方向向量. 的方向向量.
P B A
a
(或 AP = t AB)
三点共线。 则A、B、P三点共线。 、 、 三点共线 A,B中点 若 = xOA 中点, O 若OP P为A,B中点, ( x + y = 1), + yOB
OG = k OC , OH = k OD ,
求证: 求证: 共面; ⑴四点E、F、G、H共面; 四点E、F、G、H共面 平面AC. ⑵平面EG//平面 平面 平面
课本例)已知 例2 (课本例 已知 课本例
ABCD ,从平面 外一点 引向量 从平面AC外一点 外一点O引向量
OE = kOA , OF = kOB , OG = kOC , OH = kOD
思考2(课本 思考) 思考 (课本P88思考) 思考
试证明:对于不共线的三点 B C 试证明 对于不共线的三点 A、 、 空间一点 P 满足 关系式 OP = xOA + yOB + zOC ,则 点 P 在平面 ABC 内 则 ⇔ x+ y+ z =1.
例1、已知 ,B,C三点不共线,对平面 三点不共线, 、已知A, , 三点不共线 对平面ABC外的 外的 任一点O,确定在下列条件下, 是否与 是否与A, , 任一点 ,确定在下列条件下,M是否与 ,B,C 三点共面: 三点共面:
复习: 复习:
1、如果向量e1和e2是一平面内的两个不平行 、如果向量 的向量,那么,该平面内的任一向量a与 的向量,那么,该平面内的任一向量 与 e1, e2 有什么关系? 有什么关系
2、平面向量基本定理 、
如果e 是一平面内的两个不平行的向量, 如果 1和e2是一平面内的两个不平行的向量, 那么,该平面内的任一向量a, 那么,该平面内的任一向量 ,存在惟一的一 对实数a 对实数 1,a2,使 a= a1 e1 +a2 e2 =
(A)若 OP = OA + t AB ,则P、A、B共线 若 、 、 共线 (B)若 3OP = OA + AB ,则P是AB的中点 若 是 的中点 (C)若 OP = OA − t AB ,则P、A、B不共线 若 、 、 不共线 (D)若 OP = − OA + AB ,则P、A、B共线 若 、 、 共线 2.已知点 在平面 已知点M在平面 已知点 在平面ABC内,并且对空间任意一点 内 O, , OM = xOA +
求证: 四点 、 、 、 共面 共面; 求证:①四点E、F、G、H共面; 平面EG. ②平面AC//平面 平面 证明: 四边形ABCD为 证明: 四边形 ∵ 为 ① ∴AC = AB + AD (﹡)
D
O
EG = OG − OE = kOC − kOA
C
= k ( OC − OA ) = kAC = k ( AB + AD ) (﹡)代入 = k ( OB − OA + OD − OA )
1 1 的值为( 的值为 OB + OC , 则x的值为 D) 3 3
( A)1
( B) 0
(C )3
1 ( D) 3
练习: 课外补充练习:
1.下列说明正确的是: D 下列说明正确的是: 下列说明正确的是 (A)在平面内共线的向量在空间不一定共线 在平面内共线的向量在空间不一定共线 (B)在空间共线的向量在平面内不一定共线 在空间共线的向量在平面内不一定共线 (C)在平面内共线的向量在空间一定不共线 在平面内共线的向量在空间一定不共线 (D)在空间共线的向量在平面内一定共线 在空间共线的向量在平面内一定共线 2.下列说法正确的是: 2.下列说法正确的是:C 下列说法正确的是 (A)平面内的任意两个向量都共线 平面内的任意两个向量都共线 (B)空间的任意三个向量都不共面 空间的任意三个向量都不共面 (C)空间的任意两个向量都共面 空间的任意两个向量都共面 (D)空间的任意三个向量都共面 空间的任意三个向量都共面
