《1.1.1集合的含义与表示(2)》同步练习2

合集下载

人教A版高中数学必修一1.1.1《集合的含义与表示》同步练习题答案和解析

人教A 版高中数学必修一1.1.1《集合的含义与表示》同步练习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合A 只含有一个元素a ，则下列各式正确的是( ) A ．0∈A B ．a ∉AC ．a∈AD ．a ＝A2．设x ∈N ，且1x∈N ，则x 的值可能是( ) A ．0 B ．1 C ．－1D ．0或13．下面四个关系式：π∈{x|x 是正实数}，0.3∈Q，0∈{0}，0∈N，其中正确的个数是( ) A ．4 B ．3 C ．2D ．14．集合{x∈N|－1<x<112}的另一种表示方法是( ) A ．{0，1，2，3，4} B ．{1，2，3，4} C ．{0，1，2，3，4，5}D ．{1，2，3，4，5}5．已知集合A ＝{x∈N *|，则必有( ) A ．－1∈A B ．0∈AC ．D ．1∈A6．集合M ＝{(x ，y)|xy<0，x∈R，y∈R}是( ) A ．第一象限内的点集 B ．第三象限内的点集 C ．第四象限内的点集D ．第二、四象限内的点集7．若集合{},,a b c 中的三个元素可构成某个三角形的三条边长，则此三角形一定不是（） A ．直角三角形B ．锐角三角形C ．钝角三角形D ．等腰三角形8．已知A ＝{x|3－3x>0}，则有( ) A ．3∈A B ．1∈A C ．0∈A D ．－1∉A二、填空题9．集合A ＝{x|x∈N 且42x-∈Z}，用列举法可表示为A ＝________. 10．一边长为6，一边长为3的等腰三角形所组成的集合中有________个元素.11．点(1,3)P 和集合},)(2{|Ax y y x =+＝之间的关系是________. 12．用列举法表示集合A ＝{(x ，y)|x ＋y ＝3，x∈N，y∈N *}为________. 13．若{}2,2,3,4A =-，{}2|,B x x t t A ==∈，用列举法表示B = .14．下列集合中：A ＝{x ＝2，y ＝1}，B ＝{2，1}，C ＝{(x ，y)| 31x y x y +=⎧⎨-=⎩}，D ＝{(x ，y)|x ＝2且y ＝1}，与集合{(2，1)}相等的共有________个.三、解答题15．“今有三女，长女五日一归，中女四日一归，小女三日一归，问三女何时相会”.(选自《孙子算经》)，请将三女前三次相会的天数用集合表示出来.16．设A 是由满足不等式x <6的自然数组成的集合，若a ∈A 且3a ∈A ，求a 的值． 17．已知集合A 含有两个元素a 和a 2，若1∈A，求实数a 的值.18．已知集合A ＝{0，2，5，10}，集合B 中的元素x 满足x ＝ab ，a∈A，b∈A 且a≠b，写出集合B ．19．已知集合S 满足条件：若a S ∈，则1(0,1)1aS a a a+∈≠≠±-．若3S ∈，试把集合S 中的所有元素都求出来． 20．集合A ＝{x|2y x y x=⎧⎨=⎩ }可化简为___以下是两位同学的答案，你认为哪一个正确？试说明理由. 学生甲：由2y xy x=⎧⎨=⎩得x ＝0或x ＝1，故A ＝{0，1}；学生乙：问题转化为求直线y ＝x 与抛物线y ＝x 2的交点，得到A ＝{(0，0)，(1，1)}.参考答案1．C 【解析】分析：根据集合A 的表示，判断出a 是A 的元素，根据元素与集合的关系，是属于与不属于，从而得到答案. 详解：集合{}A a =，a A ∴∈.故选C.点睛：在解决元素与集合的关系时，注意它们的关系只有“属于”与“不属于”两种. 2．B 【解析】首先x≠0，排除A ，D ；又x∈N，排除C ，故选B. 3．A 【解析】本题考查元素与集合之间的关系，由数集的分类可知四个关系式均正确.选A. 4．C 【解析】 ∵x∈N，且－1<x<112，∴集合中含有元素0，1，2，3，4，5，故选C. 点睛：集合的表示方法：列举法、描述法、图示法．其中描述法要注意代表元素，是点集还是数集．列举法应用于有限集，特别为单元素集合. 5．D 【解析】∵x∈N *1，2，即A ＝{1，2}，∴1∈A.选D. 6．D 【解析】根据描述法表示集合的特点，可知集合表示的是横、纵坐标异号的点的集合，这些点在第二、四象限内.选D.点睛：集合的表示方法：列举法、描述法、图示法．其中描述法要注意代表元素，是点集还是数集7．D 【分析】根据集合中元素的互异性可知，D 正确；给,,a b c 取特值可知，,,A B C 不正确. 【详解】根据集合中元素的互异性可知，a b c ≠≠，所以此三角形一定不是等腰三角形，故D 正确；当3,4,5a b c ===时，三角形为直角三角形，故A 不正确；当 6.8.9a b c ===时，三角形为锐角三角形，故B 不正确；当6,8,11a b c ===时，三角形为钝角三角形，故C 不正确；故选：D. 【点睛】本题考查了集合中元素的互异性，属于基础题. 8．C 【解析】因为A ＝{x|3－3x>0}＝{x|x<1}，所以0∈A.选C. 9．{0，1，3，4，6} 【解析】注意到42x-∈Z，因此，2－x ＝±2，±4，±1，解得x ＝－2，0，1，3，4，6，又∵x∈N，∴x＝0，1，3，4，6. 10．1 【解析】这样的三角形只有1个，是两腰长为6，底边长为3的等腰三角形. 11．P A ∈ 【详解】在2y x =+中，当1x =时，3y =，因此点P 是集合A 的元素，故P A ∈. 故答案为：P A ∈.12．{(0，3)，(1，2)，(2，1)} 【解析】集合A 是由方程x ＋y ＝3的部分整数解组成的集合，由条件可知，当x ＝0时，y ＝3；当x ＝1时，y ＝2；当x ＝2时，y ＝1.故A ＝{(0，3)，(1，2)，(2，1)}. 13．{}4,9,16 【分析】解决该试题的关键是对于t 令值，分别得到x 的值，然后列举法表示. 【详解】因为集合{}2,2,3,4A =-，而集合B 中的元素是将集合A 中的元素一一代入，通过平方得到的集合，即{}2|,B x x t t A ==∈，2,4t x ∴=±=；3,9t x ==；4,16t x ==,{}4,9,16B ∴=，那么用列举法表示B ={}4,9,16.本试题主要是考查了集合的描述法与列举法的准确运用，属于基础题. 14．2 【解析】因为集合{(2，1)}的元素表示的是有序实数对，由已知集合的代表元素知，元素为有序实数对的是C ，D ，而A 表示含有两个元素x ＝2，y ＝1的集合，B 表示含有2个元素的集合. 15．{60，120，180}. 【解析】试题分析：先判断三女相会的日数必为5，4，3的公倍数，再求最小的三个整数，并用集合形式表示试题解析：三女相会的日数，即为5，4，3的公倍数，它们的最小公倍数为60，因此三女前三次相会的天数用集合表示为{60，120，180}. 16．a ＝0或1. 【解析】试题分析：试题解析：∵a∈A 且3a∈A，∴a<6且3a<6，∴a<2. 又∵a 是自然数∴a ＝0或1. 17．a ＝－1.【解析】试题分析：本题中已知集合A 中有两个元素且1∈A，据集合中元素的特点需分a ＝1和a 2＝1两种情况，最后注意集合中元素的互异性，进行验证. 试题解析：若1∈A，则a ＝1或a 2＝1，即a ＝±1. 当a ＝1时，集合A 有重复元素，∴a≠1；当a ＝－1时，集合A 含有两个元素1，－1，符合互异性. ∴a=-1.点睛：利用元素的性质求参数的方法，已知一个元素属于集合，求集合中所含的参数值．具体解法：(1)确定性的运用：利用集合中元素的确定性解出参数的所有可能值．(2)互异性的运用：根据集合中元素的互异性对集合中元素进行检验． 18．B ＝{0，10，20，50}. 【解析】试题分析：先按是否取零进行讨论，再根据乘积结果，利用集合元素互异性进行取舍试题解析：解析当或时，x ＝0；当或时，x ＝10；当或时，x ＝20；当或时，x ＝50.所以B ＝{0，10，20，50}.点睛：常利用集合元素的互异性确定集合中的元素，根据题目一一列举可能取值(应用列举法和分类讨论思想)，然后根据集合元素的互异性进行检验，相同元素重复出现只算作一个元素，判断出该集合的所有元素，即得该集合元素的个数． 19．113,2,,32-- 【分析】由条件“若a S ∈，则11aS a+∈-”可进行一步步推导，根据所得值循环出现可得答案．【详解】∵3S ∈，∴13213S +=-∈-，从而1(2)11(2)3S +-=-∈--，则11131213S ⎛⎫+- ⎪⎝⎭=∈⎛⎫-- ⎪⎝⎭， ∴1123112S +=∈-，出现循环，根据集合中元素的互异性可得集合S 中的所有元素为113,2,,32--．【点睛】本题考查了集合中元素的互异性，属于基础题. 20．甲正确【解析】试题分析：先解方程组得解集，再根据集合代表元素得应为数集，不是点集，因此选甲试题解析：同学甲正确，同学乙错误.由于集合A 的代表元素为x ，因此满足条件的元素只能为x ＝0，1；而不是实数对故同学甲正确.。

湘教版高中数学必修1同步练习 1.1.1集合的含义和表示第2课时含答案

1．已知集合A＝{x∈N|x≤≤，则有()．A．－1∈A B．0∈AC A D．2∈A2．集合M＝{x|x2－6x＋9＝0}的所有元素之和等于()．A．3 B．6 C．9 D．03．方程组3,1x yx y+=⎧⎨-=-⎩的解集不可表示为()．A．3, (,)1x yx yx y⎧⎫+=⎧⎪⎪⎨⎨⎬-=-⎩⎪⎪⎩⎭B．1, (,)2xx yy⎧⎫=⎧⎪⎪⎨⎨⎬=⎩⎪⎪⎩⎭C．{1,2}D．{(1,2)}4．下列集合中为∅的是()．A．{0} B．{x|x2－1＝0}C．{x|x＜0} D．{x|x2＋1＝0}5．设A＝{a|a使方程ax2＋2x＋1＝0有唯一实数解}，则A用列举法可表示为()．A．A＝{1} B．A＝{0}C．A＝{0,1} D．A＝{0}或{1}6．集合{x|－3≤x≤3，x∈N}，用列举法表示为________．7．若集合A＝{x|2x－5＜x－1}，B＝)，用适当的符号填空：①4________A；B；③－2________A；④1________B．8．用描述法表示集合1111,,,234⎧⎫⎨⎬⎩⎭为__________．9．用适当的方法表示下列集合，并且说明它们是有限集还是无限集．(1)方程x2－9＝0的解集；(2)大于0且小于10的奇数构成的集合；(3)不等式x－3＞2的解集；(4)抛物线y＝x2上的点集；(5)方程x2＋x＋1＝0的解集．10．已知集合A＝{x|x2＋2x＋m＝0}．(1)若2∈A，求实数m的值；(2)若集合A中有两个元素，求m的取值范围；(3)若集合A是空集，求m的取值范围．参考答案1.答案：B解析：A＝{x∈N|x≤＝{0,1}，因此0∈A．2.答案：A解析：M＝{x|x2－6x＋9＝0}＝{x|(x－3)2＝0}＝{x|x＝3}＝{3}，即M中仅有一个元素3.3.答案：C解析：方程组只有一个解，解的形式是数对，而C选项中的集合中含有两个元素，且元素是实数，不是数对，故不可能是方程组的解集．4.答案：D解析：选项D中的集合表示方程x2＋1＝0的解集，该方程没有实数解，故该集合为∅.5.答案：C解析：当a＝0时，方程2x＋1＝0有唯一解12x=-；当a≠0，且Δ＝22－4a＝0，即a＝1时，方程x2＋2x＋1＝0有唯一解x＝－1.6.答案：{0,1,2,3}解析：集合{x|－3≤x≤3，x∈N}表示不小于－3且不大于3的自然数，因此只有0,1,2,3四个元素．7.答案：①∉②∈③∈④∉8.答案：1,4 x x n nn+⎧⎫=∈≤⎨⎬⎩⎭N且解析：观察元素1，12，13，14的特征可设1xn=，n∈N＋且n≤4，故用描述法表示为1,4x x n nn+⎧⎫=∈≤⎨⎬⎩⎭N且.9.解：(1)用列举法表示为{3，－3}，用描述法表示为{x|x2－9＝0}，集合中有两个元素，是有限集．(2)用列举法表示为{1,3,5,7,9}，用描述法表示为{x|x＝2k－1，k∈N＋，且1≤k≤5}，集合中有五个元素，是有限集．(3)用描述法表示为{x|x＞5}，集合中有无数个元素，是无限集．(4)用描述法表示为{(x，y)|y＝x2}，抛物线上的点有无数个，因此该集合是无限集．(5)方程x2＋x＋1＝0无实数解，故该方程的解集为，是有限集．10.解：(1)由2∈A知，2是A中的元素，即2是方程x2＋2x＋m＝0的一个根，因此22＋2×2＋m＝0，解得m＝－8；(2)集合A中有两个元素，即方程x2＋2x＋m＝0有两个不相等的实数根，因此Δ＝4－4m＞0，解得m＜1；(3)集合A是空集，即方程x2＋2x＋m＝0没有实数根，因此Δ＝4－4m＜0，解得m＞1.。

高中数学必修一全册同步练习含参考答案

高中数学必修一同步练习1.1.1 集合的含义与表示课后作业· 练习案【基础过关】1．若集合中只含一个元素1，则下列格式正确的是A.1=B.0C.1D.12．集合的另一种表示形式是A.{0,1,2,3,4}B.{1,2,3,4}C.{0,1,2,3,4,5}D.{1,2,3,4,5} 3．下列说法正确的有①集合，用列举法表示为{1,0,l}；②实数集可以表示为或;③方程组的解集为.A.3个B.2个C.1个D.0个4．直角坐标系中，坐标轴上点的集合可表示为A.B.C.D.5．若集合含有两个元素1，2，集合含有两个元素1，，且，相等，则____. 6．已知集合，，且，则为 . 7．设方程的根组成的集合为，若只含有一个元素，求的值. 8．用适当的方法表示下列集合：(1)所有被3整除的整数；(2)满足方程的所有x的值构成的集合B.【能力提升】集合，，，设，则与集合有什么关系？详细答案【基础过关】1．D【解析】元素与集合之间只存在“∈”与“∉”的关系，故1∈A正确.2．B【解析】由x－2＜3得x＜5，又，所以x＝1，2，3，4，即集合的另一种表示形式是{1，2，3，4}.3．D【解析】对于①，由于x∈N，而－1∉N，故①错误；对于②，由于“{ }”本身就具有“全部”、“所有”的意思，而且实数集不能表示为{R}，故②错误；对于③，方程组的解集是点集而非数集，故③错误.4．C【解析】坐标轴上的点分为x轴、y轴上的点，在x轴上的点纵坐标为0，在y轴上的点横坐标为0.5．【解析】由于P，Q相等，故，从而.6．(2，5)【解析】∵a∈A且a∈B，∴a是方程组的解，解方程组，得∴a为(2，5).7．A中只含有一个元素，即方程(a∈R)有且只有一个实根或两个相等的实根.(1)当a＝0时，方程的根为；(2)当a≠0时，有△＝4－4a＝0，即a＝1，此时方程的根为.∴a的值为0或1.【备注】误区警示：初学者易自然认为(a∈R)是一元二次方程，而漏掉对a 的讨论，导致漏解.举一反三：若把“若A只含有一个元素”改为“若A含有两个元素”，则结论又如何？由题意知，a≠0，且△＝4－4a＞0，解得a＜1.所以a＜1且a≠0.8．(1){x|x＝3n，n∈Z}；(2)B＝{x｜x＝|x|，x∈R}.【能力提升】∵a∈P，b∈M，c＝a＋b，设，，，，∴，又∴c∈M.1.1.2集合间的基本关系班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．设，，若，则的取值范围是A. B. C. D.2．设集合，，则A.M =NB.M⊆NC.M ND.N3．已知集合，，若，求实数的值.4．满足条件{1,2,3}M{1,2,3,4,5,6}的集合的个数是A.8B.7C.6D.55．设集合和，那么与的关系为 .6．含有三个实数的集合,既可表示成,又可表示成，则.7．设集合，，求A∩B.8．已知M={x | x2-2x-3=0},N={x | x2+ax+1=0,a∈R},且N M,求a的取值范围.【能力提升】已知，，是否存在实数，使得对于任意实数，都有?若存在,求出对应的的值；若不存在，说明理由.答案【基础过关】1．D【解析】∵，∴a≥22．D【解析】本题考查集合间的基本关系.,；而；即N.选D.3．由A＝B，可得，解得x＝1.4．C【解析】本题考查子集.由题意得M={1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,3,4,5},{1,2,3,4,6},{1,2,3,6,5}共6个.选C. 5．M＝P【解析】∵xy＞0，∴x，y同号，又x＋y＜0，∴x＜0，y＜0，即集合M表示第三象限内的点.而集合P表示第三象限内的点，故M＝P.6．-1【解析】本题考查相等集合.由题意得,所以,即；此时，所以，，且，解得.所以.7．，解得；所以.【解析】本题考查集合的基本运算.8．解：M={x | x 2-2x -3=0}={3,-1};∵N M,当N=∅时，N M 成立,N={x | x 2+ax+1=0},∴a 2-4＜0, ∴-2＜a ＜2;当N≠∅时，∵N M, ∴3∈N 或 -1∈N;当3∈N 时，32-3a+1=0即a= -310,N={3,31},不满足N M;当-1∈N 时，(-1)2-a+1=0即a=2,N={-1},满足N M;∴a 的取值范围是-2<a ≤2.【解析】本题考查集合间的基本关系. 【能力提升】不存在.要使对任意的实数b 都有，则1，2是A 中的元素，又∵A ＝{a －4，a ＋4}，∴或这两个方程组均无解，故这样的实数a 不存在.1.1.3 集合的基本运算班级:__________姓名:__________设计人__________日期__________课后作业【基础过关】1．若，，，，则满足上述条件的集合的个数为A.5B.6C.7D.82．已知全集U={1,2,3,4,5,6,7,8},A={3,4,5}, B={1,3,6},那么集合{2,7,8}是A.A∪BB.A∩BC.(∁U A)∩(∁U B)D.(∁U A)∪(∁U B)3．若集合P={x∈N|-1<x<3},Q={x|x=2a,a∈P},则P∩Q=A.⌀B.{x|-2<x<6}C.{x|-1<x<3}D.{0,2}4．设全集U=R,集合M={x|x>1或x<-1},N={x|0<x<2},则N∩(∁U M)=A.{x|-2≤x<1}B.{x|0<x≤1}C.{x|-1≤x≤1}D.{x|x<1}5．某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为.6．集合A={(x,y)|x+y=0},B={(x,y)|x-y=2},则A∩B= .7．设集合A={x|0<x-m<3},B={x|x≤0,或x≥3},分别求满足下列条件的实数m.(1)A∩B=⌀;(2)A∪B=B.8．已知集合A={x|2≤x<7},B={x|3<x<10},C={x|x<a}.(1)求A∪B,(∁R A)∩B;(2)若A∩C≠⌀,求a的取值范围.【能力提升】已知集合A={x|x2-3x+2=0},B={x|x2-ax+a-1=0},C={x|x2-x+2m=0}.(1)若A∪B=A,求a的值;(2)若A∩C=C,求m的取值范围.详细答案【基础过关】1．D2．C【解析】借助Venn图易得{2,7,8}=∁U(A∪B),即为(∁U A)∩(∁U B).3．D【解析】由已知得P={0,1,2},Q={0,2,4},所以P∩Q={0,2}.4．B【解析】∁U M={x|-1≤x≤1},结合数轴可得N∩(∁U M)={x|0<x≤1}.5．12【解析】设两项运动都喜爱的人数为x,依据题意画出Venn图,得到方程15-x+x+10-x+8=30,解得x=3,∴喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12.6．{(1,-1)}【解析】A∩B={(x,y)|}={(1,-1)}.7．因为A={x|0<x-m<3},所以A={x|m<x<m+3}.(1)当A∩B=⌀时,需,故m=0.即满足A∩B=⌀时,m的值为0.(2)当A∪B=B时,A⊆B,需m≥3,或m+3≤0,得m≥3,或m≤-3.即满足A∪B=B时,m的取值范围为{m|m≥3,或m≤-3}.8．(1)因为A={x|2≤x<7},B={x|3<x<10},所以A∪B={x|2≤x<10}.因为A={x|2≤x<7},所以∁R A={x|x<2,或x≥7},则(∁R A)∩B={x|7≤x<10}.(2)因为A={x|2≤x<7},C={x|x<a},且A∩C≠⌀,所以a>2.【能力提升】A={1,2}.(1)因为A∪B=A,所以B⊆A,故集合B中至多有两个元素1,2.而方程x2-ax+a-1=0的两根分别为1,a-1,注意到集合中元素的互异性,有①当a-1=2,即a=3时,B={1,2},满足题意;②当a-1=1,即a=2时,B={1},满足题意.综上可知,a=2或a=3.(2)因为A∩C=C,所以C⊆A.①当C=⌀时,方程x2-x+2m=0无实数解,因此其根的判别式Δ=1-8m<0,即m>.②当C={1}(或C={2})时,方程x2-x+2m=0有两个相同的实数解x=1(或x=2),因此其根的判别式Δ=1-8m=0,解得m=,代入方程x2-x+2m=0,解得x=,显然m=不符合要求.③当C={1,2}时,方程x2-x+2m=0有两个不相等的实数解x1=1,x2=2,因此x1+x2=1+2≠1,x1x2=2=2m,显然不符合要求.综上,m>.1.2.1 函数的概念班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．下列函数中,值域为(0,+∞)的是( )A.y=B.y=C.y=D.y=x2+12．下列式子中不能表示函数的是A. B. C. D.3．函数y=+的定义域是( )A.(-1,1)B.(-∞,-1)∪(1,+∞)C.(0,1)D.{-1,1}4．若满足，且，，则等于A. B. C. D.5．若为一确定区间，则的取值范围是 .6．函数的图象是曲线，其中点，，的坐标分别为(0，0)，(1，2)，(3，1)，则的值等于 .7．求下列函数的定义域.(1)；(2).8．已知.(1)求，的值；(2)求的值. 【能力提升】已知函数f(x)对任意实数a,b,都有f(ab)=f(a)+f(b)成立.(1)求f(0),f(1)的值;(2)若f(2)=p,f(3)=q(p,q为常数),求f(36)的值.答案【基础过关】1．B【解析】y=的值域为[0,+∞),y=的值域为(-∞,0)∪(0,+∞),y=x2+1的值域为[1,+∞).故选B.2．A【解析】一个x对应的y值不唯一.3．D【解析】要使函数式有意义,需满足,解得x=±1,故选D.4．B【解析】f(72)＝f(8×9)＝f(8)＋f(9)＝3f(2)＋2f(3)＝3p＋2q.5．【解析】由题意3a－1＞a，则.【备注】误区警示：本题易忽略区间概念而得出，则的错误.6．2【解析】由图可知f(3)＝1，∴f[f(3)]＝f(1)＝2.【备注】误区警示：本题在求解过程中会因不理解f[f(3)]的含义而出错.7．(1)由已知得∴函数的定义域为.(2)由已知得：∵|x＋2|－1≠0，∴|x＋2|≠1，得x≠－3，x≠－1.∴函数的定义域为(－∞，－3)∪(－3，－1)∪(―1，＋∞).8．(1)，.(2)∵，∴＝＝1＋1＋1＋＋1(共2012个1相加)＝2012.【能力提升】(1)令a=b=0,得f(0)=f(0)+f(0),解得f(0)=0;令a=1,b=0,得f(0)=f(1)+f(0),解得f(1)=0.(2)方法一令a=b=2,得f(4)=f(2)+f(2)=2p,令a=b=3,得f(9)=f(3)+f(3)=2q,令a=4,b=9,得f(36)=f(4)+f(9)=2p+2q.方法二因为36=22×32,所以f(36)=f(22×32)=f(22)+f(32)=f(2×2)+f(3×3)=f(2)+f(2)+f(3)+f(3)=2f(2)+2f(3)=2p+2q .【解析】题设只有一个函数方程,因此考虑特殊值0,1,通过解方程获解.1.2.2函数的表示法班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．已知是反比例函数，当时，，则的函数关系式为A. B. C. D.2．已知函数若,则的取值范围是A. B.C. D.3．已知函数f(x)=,则函数f(x)的图象是( )A. B. C. D.4．已知则A.2B.-2C.D.5．已知函数，且，则 .6．已知函数f(x)对于任意实数x满足条件f(x+2)=,若f(1)=-5,则f[f(5)]= .7．已知，为常数，且，，，方程有两个相等的实数根.求函数的解析式.8．如图，是边长为2的正三角形，记位于直线左侧的图形的面积为，试求函数的解析式.【能力提升】下图是一个电子元件在处理数据时的流程图:(1)试确定y与x的函数关系式;(2)求f(-3), f(1)的值;(3)若f(x)=16,求x的值.答案【基础过关】1．C【解析】根据题意可设(k≠0)，∵当x＝2时，y＝1，∴，∴k＝2.2．D【解析】若x∈[－1，1]，则有f(x)＝2∉[-1，1]，∴f(2)＝2；若x∉[－1，1]，则f(x)＝x∉[－1，1]，∴f[f(x)]＝x，此时若f[f(x)]＝2，则有x＝2.【备注】误区警示：本题易将x∉[－1，1]的情况漏掉而错选B.3．A【解析】当x=-1时,y=0,即图象过点(-1,0),D错;当x=0时,y=1,即图象过点(0,1),C错;当x=1时,y=2,即图象过点(1,2),B错.故选A.4．C【解析】∵，∴.【备注】无5．【解析】，∴，∴，解得.6．-【解析】由已知条件f(x+2)=可得f(x+4)==f(x),所以f(5)=f(1)=-5,所以f[f(5)]=f(-5)=f(-1)===-.7．∵，且方程f(x)＝x有两个相等的实数根，∴，∴b＝1，又∵f(2)＝0，∴4a＋2＝0，∴，∴.8．OB所在的直线方程为.当t∈(0，1]时，由x＝t，求得，所以；当t∈(1，2]时，；当t∈(2，＋∞)时，，所以【能力提升】(1)由题意知y=.(2)f(-3)=(-3)2+2=11, f(1)=(1+2)2=9.(3)若x≥1,则(x+2)2=16,解得x=2或x=-6(舍去);若x<1,则x2+2=16,解得x=(舍去)或x=-.综上可得,x=2或x=-.1.3.1单调性与最大（小）值班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．若函数在区间上是增函数，在区间上也是增函数，则函数在区间上A.必是增函数B.必是减函数C.先增后减D.无法确定单调性2．下列函数在(0，1)上是增函数的是A. B. C. D.3．函数,在上是A.减函数B.增函数C.先减后增D.无单调性4．下面说法错误的是A.函数的单调区间一定是函数的定义域B.函数的多个单调增区间的并集不一定是其单调增区间C.具有奇偶性的函数的定义域关于原点对称D.关于原点对称的图象一定是奇函数的图象5．已知函数在区间上为减函数,则的取值范围是_____________.6．设奇函数f(x)的定义域为[-5,5],且当x∈[0,5]时,f(x)的图象如图所示,则不等式f(x)<0的解集是.7．.已知函数,若.(l)求的值.(2)利用单调性定义证明函数在区间的单调性.8．首届世界低碳经济大会在南昌召开，大会以“节能减排，绿色生态”为主题.某单位在国家科研部门的支持下，进行技术攻关，采用了新工艺，把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨，最多为600吨，月处理成本(元)与月处理量(吨)之间的函数关系可近似地表示为，且每处理一吨二氧化碳得到可利用的化工产品价值为100元.(1)该单位每月处理量为多少吨时，才能使每吨的平均处理成本最低？(2)该单位每月能否获利？如果获利，求出最大利润；如果不获利，则国家至少需要补贴多少元才能使该单位不亏损？【能力提升】函数f(x)的图象如图所示.(1)说出f(x)的单调区间,以及在每一个单调区间上它是增函数还是减函数;(2)依据图象说明函数的最值情况.答案【基础过关】1．D【解析】因为(a，b)，(c，d)不是两个连续的区间，所以无法确定其单调性.2．B【解析】选项A中y＝1－2x为减函数，C中y＝5为常数函数，D中的定义域为[1，＋∞).3．B【解析】解答本题可先画出函数图象，由图象分析.函数f(x)的图象如图所示，由图结合单调性的定义可知，此函数在R上是增函数.4．A【解析】单调区间是定义域的子集，不一定是定义域，当多个单调区间并起来时，由单调性定义知，不再是单调区间.具有奇偶性的函数的定义域关于原点对称，是函数奇偶性判定的要求.奇函数的图象关于原点对称，反之，关于原点对称的图象一定是奇函数的图象.5．(－∞,1]6．(-2,0)∪(2,5]【解析】由图可知在区间(2,5]上f(x)<0,因为奇函数的图象关于原点对称,所以在(-2,0)上也有f(x)<0.7．(1)由2f(2)＝f(3)＋5,得,解得a＝2.(2)由(1)知.任取x1,x2∈(1,＋∞)且x1＜x2,,因为1＜x1＜x2,所以x1－1＞0,x2－1＞0,x2－x1＞0.所以f(x1)－f(x2)＞0,即f(x1)＞f(x2).所以f(x)在(1,＋∞)上是减函数.8．(1)由题意可知，二氧化碳的每吨平均处理成本为令，可以证明t(x)在(0，400)为减函数，在[400，＋∞)上是增函数，故每月处理量为400吨时，才能使每吨的平均处理成本最低，最低成本为200元.(2)设该单位每月获利为S，则.因为400≤x≤600，所以当x＝400时，S有最大值－40 000.故该单位不获利，需要国家每月至少补贴40 000元，才能不亏损.【能力提升】(1)由题图可知:函数f(x)的单调增区间为[0,];单调减区间为(-∞,0)和(,+∞).(2)观察图象可知,函数没有最大值和最小值.1.3.2奇偶性班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．设在[-2，-1]上为减函数，最小值为3，且为偶函数，则在[1，2]上A.为减函数，最大值为3B.为减函数，最小值为-3C.为增函数，最大值为-3D.为增函数，最小值为32．已知函数是偶函数，其图象与轴有四个交点，则方程的所有实根之和是A.4B.2C.1D.03．函数是奇函数，图象上有一点为，则图象必过点A. B.C. D.4．设，其中为常数，若，则的值为A.-7B.7C.17D.-175．已知定义在上的奇函数，当时，，那么时，.6．若函数为区间[-1，1]上的奇函数，则；.7．作出函数的图象，并根据函数的图象找出函数的单调区间.8．已知函数是定义在R上的偶函数，且当时，该函数的值域为，求函数的解析式.【能力提升】已知函数f(x)=-x2+x,是否存在实数m,n(m<n),使得当x∈[m,n]时,函数的值域恰为[2m,2n]?若存在,求出m,n的值;若不存在,说明理由.答案【基础过关】1．D2．D3．C【解析】奇函数f(x)满足f(－x)＝－f(x)，故有f(－a)＝－f(a).因为函数f(x)是奇函数，故点(a，f(a))关于原点的对称点(－a，－f(a))也在y＝f(x)上，故选C.4．D【解析】∵，∴27a＋3b＝－12，∴f(3)＝27a＋3b－5＝－17.5．－x2－|x|＋16．0 07．当x－2≥0，即x≥2时，；当x－2＜0，即x＜2时，＝.所以这是分段函数，每段函数图象可根据二次函数图象作出(如图)，其中，[2，＋∞)是函数的单调增区间；是函数的单调减区间.8．由f(x)为偶函数可知f(x)＝f(－x)，即，可得恒成立，所以a＝c＝0，故.当b＝0时，由题意知不合题意；当b＞0，x∈[1，2]时f(x)单调递增，又f(x)值域为[－2，1]，所以当b＜0时，同理可得所以或.【能力提升】假设存在实数m,n,使得当x∈[m,n]时,y∈[2m,2n],则在[m,n]上函数的最大值为2n.而f(x)=-x2+x=-(x-1)2+在x∈R上的最大值为,∴2n≤,∴n≤.而f(x)在(-∞,1)上是增函数,∴f(x)在[m,n]上是增函数,∴,即.结合m<n≤,解得m=-2,n=0.∴存在实数m=-2,n=0,使得当x∈[-2,0]时,f(x)的值域为[-4,0].2.1.1指数与指数幂的运算班级:__________姓名:__________设计人__________日期__________课后练习【基础过关】1．化简的结果为A. B. C.- D.2．计算的结果是A. B. C. D.3．设，则有A. B.C. D.4．下列说法中正确的个数是( )(1)49的四次方根为7; (2)=a(a≥0);(3)()5=a5; (4)=(-3.A.1B.2C.3D.45．若10m=2,10n=4,则= . 6．已知x=(2 01-2 01),n∈N*,则(x+)n的值为. 7．化简下列各式:(1)(·)÷;(2)()·(-3)÷().8．求下列各式的值:(1)2; (2)(; (3)+(-π0.【能力提升】已知+=3,求下列各式的值:(1)x+x-1;(2).答案【基础过关】1．A【解析】要使式子有意义，需，故x＜0，所以原式.2．A【解析】本题考查指数运算.注意先算中括号内的部分。

高中数学 1.1.1集合的含义与表示同步练习新人教A版必修1

1．1．1集合的含义与表示同步练习一、选择题1、给出下列表述：1）联合国常任理事国2）3）方程210x x +-=的实数根4）全国著名的高等院校。

以上能构成集合的是（）A 、1）3）B 、1）2）C 、1）3）4）D 、1）2）3）4）2、集合{21,1,2x x --}中的x 不能取得值是（） A 、2 B 、3 C 、4 D 、53、下列集合中表示同一集合的是（）A 、{(3,2)},{(2,3)}M N ==B 、{1,2},{(1,2)}M N ==C 、{(,)|1},{|1}M x y x y N y x y =+==+=D 、{3,2},{2,3}M N ==4、下列语句：（1）0与{0}表示同一个集合（2）由1,2,3组成的集合可表示为{1,2, 3}或{3,2,1}；（3）方程0)2()1(22=--x x 的所有解的集合可表示为{1，1，2}；（4）集合}54{<<x x 是有限集，正确的是（）A 、只有（1）和（4）B 、只有（2）和（3）C 、只有（2）D 、以上语句都不对5、如果3x y ==，集合{|,}M m m a a b Q ==+∈，则有（） A 、x M y M ∈∈且 B 、x M y M ∉∈且 C 、x M y M ∈∉且 D 、x M y M ∉∉且 6、集合A={x Z k k x ∈=,2} B={Z k k x x ∈+=,12} C={Z k k x x ∈+=,14}又,,B b A a ∈∈则有（）A 、（a+b ）∈ AB 、(a+b) ∈BC 、(a+b) ∈ CD 、 (a+b) ∈ A 、B 、C 任一个7、下列各式中，正确的是（）A 、-2{2}x x ∈≤ B 、{12<>x x x 且} C 、{Z k k x x ∈±=,14}},12{Z k k x x ∈+=≠ D 、{Z k k x x ∈+=,13}={Z k k x x ∈-=,23}二、填空题8、由小于10的所有质数组成的集合是。

集合知识点汇总与练习试题

1.1 集合1.1.1 集合的含义与表示一集合与元素1.集合是由元素组成的集合通常用大写字母A、B、C，…表示，元素常用小写字母a、b、c，…表示。

2.集合中元素的属性（1）确定性：一个元素要么属于这个集合，要么不属于这个集合，绝无模棱两可的情况。

（2）互异性：集合中的元素是互不相同的个体，相同的元素只能出现一次。

（3）无序性：集合中的元素在描述时没有固定的先后顺序。

3.元素与集合的关系（1）元素a是集合A中的元素，记做a∈A，读作“a属于集合A”；（2）元素a不是集合A中的元素，记做a∉A，读作“a不属于集合A”。

4.集合相等如果构成两个集合的元素一样，就称这两个集合相等，与元素的排列顺序无关。

二集合的分类1.有限集：集合中元素的个数是可数的，只含有一个元素的集合叫单元素集合；2.无限集：集合中元素的个数是不可数的；3.空集：不含有任何元素的集合，记做∅.三集合的表示方法1.常用数集（1）自然数集：又称为非负整数集，记做N；（2）正整数集：自然数集内排除0的集合，记做N+或N※；（3）整数集：全体整数的集合，记做Z（4）有理数集：全体有理数的集合，记做Q（5）实数集：全体实数的集合，记做R3.集合的表示方法（1）自然语言法：用文字叙述的形式描述集合。

如大于等于2且小于等于8的偶数构成的集合。

（2）列举法：把集合的元素一一列举出来，并用花括号“｛｝”括起来表示集合的方法，一般适用于元素个数不多的有限集，简单、明了，能够一目了然地知道集合中的元素是什么。

注意事项：①元素间用逗号隔开；②元素不能重复；③元素之间不用考虑先后顺序；④元素较多且有规律的集合的表示：｛0,1,2,3，…，100｝表示不大于100的自然数构成的集合。

（3）描述法：用集合所含元素的共同特征表示集合的方法，一般形式是｛x∈I | p(x)｝.注意事项：①写清楚该集合中元素的代号；②说明该集合中元素的性质；③不能出现未被说明的字母；④多层描述时，应当准确使用“且”、“或”；⑤所有描述的内容都要写在集合符号内；⑥语句力求简明、准确。

人教A版数学必修一《1.1.1集合的含义与表示～1.1.2集合间的基本关系》同步测试题.docx

《1.1.1集合的含义与表示～1.1.2集合间的基本关系》同步测试题一、选择题1.下列对象能构成集合的是( ).①不超过的正整数；②必修一课本中的所有难题；③中国的大城市；④平方后等于自身的数；⑤平面上到点O的距离等于1的所有点.A.①②③B.③④⑤C.①④⑤D.①②④考查目的：考查集合的意义.答案：C.解析：①④⑤中对象的性质明确，能够构成集合；②中的“难题”没有具体的标准，难以确定；③中的“大城市”也没有具体的标准，不能构成集合.本题答案选C.2.若以集合A的四个元素为边长构成一个四边形，那么这个四边形可能是( ).A.梯形B.平行四边形C.菱形D.矩形考查目的：考查集合元素具有互异性这一特征.答案：A.解析：由于集合A中的四个元素互不相等，故它们组成的四边形的四条边互不相等，因此本题选A.3.方程组的解集是( ).A. B. C. D.考查目的：考查集合的表示法.答案：C.解析：解方程组得，用描述法表示为，用列举法表示为，因此本题选C.二、填空题4.已知集合，若，则实数的值为 .考查目的：考查元素与集合的属于关系.答案：，或.解析：依题意得，即，解得，或.5.已知集合，，则B中所含元素的个数为 .考查目的：本题是信息迁移题，主要考查集合与元素的关系，以及对信息的理解和处理能力.答案：10.解析：依题意，在集合B中，当时，1，2，3，4；当时，1，2，3；当时，1，2；当时，1，故B中所含元素共10个.6.将集合用列举法表示为 .考查目的：考查二元一次方程自然数解的意义，以及集合表示法之间的相互转化.答案：.解析：∵，∴是偶数，且，∴当时，；当时，；当时，，故原集合用列举法表示为.三、解答题7.已知含有三个元素的集合，求的值.考查目的：考查集合相等及集合元素的互异性.答案：-1.解析：由题意知且，由两个集合相等得或，解得或.经检验不合题意，∴，∴=.8.已知集合，，若，求实数的所有可能取值的集合.考查目的：考查集合之间的关系，空集的意义及其相关性质.答案：.解析：当时，，符合要求．当时，，或，解得或，∴实数的所有可能取值的集合为.。

人教A版数学第一册第一单元《1.1.1 集合的含义与表示》同步检测(含答案)

《1.1.1 集合的含义与表示》同步检测一、基础达标1.下列各组对象不能构成一个集合的是( )A.不超过20的非负实数B.方程x 2-9=0在实数范围内的解C.√3的近似值的全体D.某校身高超过170厘米的同学的全体2.下列各组中集合P 与Q 表示同一个集合的是( )A.P 是由元素1,√3,π构成的集合,Q 是由元素π,1,|-√3|构成的集合B.P 是由π构成的集合,Q 是由3.141 59构成的集合C.P 是由2,3构成的集合,Q 是由有序数对(2,3)构成的集合D.P 是满足不等式-1≤x≤1的自然数构成的集合,Q 是方程x 2=1的解集3.集合M 是由大于-2且小于1的实数构成的,则下列关系式正确的是( )A.√5∈MB.0∉MC.1∈MD.-π2∈M4.已知集合Ω中的三个元素l,m,n 分别是△ABC 的三边边长,则△ABC 一定不是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形5.(多选)下面几个命题中正确的命题有( )A.集合N *中最小的数是1B.若-a ∉N *,则a∈N *C.若a∈N *,b∈N *,则a+b 的最小值是2D.x 2+4=4x 的解集中有2个元素6.已知a,b 是非零实数,代数式|a |a +|b |b +|ab |ab 的值组成的集合是M,则下列判断正确的是( )A.0∈MB.-1∈MC.3∉MD.1∈M7.已知集合A是由全体偶数组成的,集合B是由全体奇数组成的,若a∈A,b∈B,则a+b A,ab A(填“∈”或“∉”).8.若集合A中有两个元素-1和2,集合B中有两个元素x,a2,若A与B相等,则x= ,a= .9.设集合A是由1,k2为元素构成的集合,则实数k的取值范围是.10.已知-3是由x-2,2x2+5x,12三个元素构成的集合中的元素,求x的值.二、能力提升11.已知集合M是方程x2-x+m=0的解组成的集合,若2∈M,则下列判断正确的是( )A.1∈MB.0∈MC.-1∈MD.-2∈M所以方程为x2-x-2=0,解得x1=-1,x2=2.故方程的另一个解为-1.选C.12.由实数x,-x,|x|,√x2,-√x33所组成的集合,其元素的个数最多为( )A.2B.3C.4D.513.已知关于x的不等式x-a≥0的解组成的集合为A,若3∉A,则实数a的取值范围是.14.已知集合A含有三个实数,分别为a2,ba,a,若0∈A且1∈A,则a2 020+b2020= .15.集合A中共有3个元素-4,2a-1,a2,集合B中也共有3个元素9,a-5,1-a,已知9∈A,且集合B中再没有其他元素属于A,根据上述条件求出实数a的值.三、素养综合16.已知集合M中有两个元素x,2-x,若-1∉M,则下列说法一定错误的是.(填序号)①2∈M;②1∈M;③x≠3.参考答案一、基础达标1.答案 CA项,不超过20的非负实数,元素具有确定性、互异性、无序性,能构成一个集合.B项,方程x2-9=0在实数范围内的解,元素具有确定性、互异性、无序性,能构成一个集合.C项,√3的近似值的全体,元素不具有确定性,不能构成一个集合.D项,某校身高超过170厘米的同学,元素具有确定性、互异性、无序性,能构成一个集合.故选C.2.答案 A3.答案 D√5>1,故A错;-2<0<1,故B错;1不小于1,故C错;-2<-π<1,故D正确.24.答案 D因为集合中的元素是互异的,所以l,m,n互不相等,即△ABC不可能是等腰三角形,故选D.5.答案ACN*是正整数集,最小的正整数是1,故A正确;当a=0时,-a∉N*,且a∉N*,故B错误;若a∈N*,则a的最小值是1,又b∈N*,b的最小值也是1,当a和b都取最小值时,a+b取最小值2,故C正确;x2+4=4x的解集为{2},故D错误.故AC正确.6.答案 B当a,b全为正数时,代数式的值是3;当a,b全是负数时,代数式的值是-1;当a,b 是一正一负时,代数式的值是-1.综上可知B正确.7.答案∉;∈解析∵a是偶数,b是奇数,∴a+b是奇数,ab是偶数,故a+b∉A,ab∈A.8.答案-1;±√2解析由集合相等的概念可知x=-1,a2=2,即a=±√2.9.答案k≠1且k≠-1解析∵1∈A,k2∈A,结合集合中元素的互异性可知k2≠1,解得k≠1且k≠-1.10.解析由题意知x-2=-3或2x2+5x=-3.当x-2=-3,即x=-1时,集合中的三个元素为-3,-3,12,不满足集合中元素的互异性,所以x=-1舍去.当2x2+5x=-3,即x=-32或x=-1(舍去)时,集合中的三个元素为-72,-3,12,满足集合中元素的互异性.综上可知x=-32.二、能力提升11.答案 C由2∈M可知,2为方程x2-x+m=0的一个解,所以22-2+m=0,解得m=-2.所以方程为x2-x-2=0,解得x1=-1,x2=2.故方程的另一个解为-1.选C.12.答案 A当x>0时,x=|x|=√x2,-√x33=-x,此时集合中共有2个元素;当x=0时,x=|x|=√x2=-√x33=-x,此时集合中共有1个元素;当x<0时,√x2=|x|=-√x33=-x,此时集合中共有2个元素.综上,此集合中最多有2个元素,故选A.13.答案a>3解析因为3∉A,所以3是不等式x-a<0的解,所以3-a<0,解得a>3.14.答案 1解析由0∈A,“0不能做分母”可知a≠0,故a2≠0,所以ba=0,即b=0.由1∈A,可知a2=1或a=1.当a=1时,得a2=1,由集合中元素的互异性,知a=1不符合题意; 当a2=1时,解得a=-1或a=1(舍去).故a=-1,b=0,所以a2 020+b2 020的值为1.15.解析∵9∈A,∴2a-1=9或a2=9,①若2a-1=9,则a=5,此时A中的元素为-4,9,25,B中的元素为9,0,-4,显然-4∈A且-4∈B,与已知矛盾,故舍去.②若a2=9,则a=±3.当a=3时,A中的元素为-4,5,9,B中的元素为9,-2,-2,B中有两个-2,与集合中元素的互异性矛盾,故舍去;当a=-3时,A中的元素为-4,-7,9,B中的元素为9,-8,4,符合题意.综上所述,a=-3.三、素养综合16.答案②解析依题意得{x≠-1,2-x≠-1,x≠2-x,解得x≠-1,x≠1且x≠3,当x=2或2-x=2,即x=2或x=0时,集合M中的元素为0,2,故①正确;当x=1或2-x=1,即x=1时,集合M中的元素为1,1,不满足集合中元素的互异性,故②不正确;③显然正确.。

人教A版必修1同步精练：1.1.1集合的含义与表示(含答案)

1.1.1集合的含义与表示1．用适当的方法表示下列集合：（1）由方程2(1)(2)(3)0x x x -+-=的所有实数根组成的集合；（2）大于2且小于7的整数；（3）一次函数3y x =+与26y x =-+的图象的交点组成的集合；（4）所有正偶数组成的集合；（5）直角坐标系中第三象限的点组成的集合；（6）以A 为圆心，r 为半径的圆上的所有点组成的集合；（7）所有正方形组成的集合．2．（2012（新课标）理）已知集合{1,2,3,4,5}A =,{(,),,}B x y x A y A x y A =∈∈-∈，则B 中所含元素的个数为A ．3B ．6C ．8D ．103．（1）设a b ∈R ，，集合},,0{},,1{b ab a b a =+，则b a -= ；（2）若2{2,,}{2,2,}a b a b =，求实数,a b 的值．（3）设{,,}A x xy x y =-，{0,||,}B x y =，且A B =，求,x y 的值。

4.（1）已知2{2,25,12}A a a a =-+，且3A -∈，求a 的值。

（2）已知2{0,1,}x x ∈，求实数x 的值。

5.（1）若1{}20x x ax b ∈++=，3{}20x x bx a ∈++=，则______,a =______b =.（2）由代数式,x x -,最多含有多少个元素?6.已知集合A={}2320,x ax x a R -+=∈,(1)若A 是空集，求a 的取值范围;(2)若A 是单元素集，求a 的值;(3)若A 中至多只有一个元素，求a 的取值范围.7．已知集合4{|}3A x N Z x =∈∈-，试用列举法表示集合A .。

2021-2022学年度人教版高一数学必修一各章节同步练习(含答案)

2021-2022学年度人教版高一数学必修一各章节同步练习（含答案）第一章 1.1 1.1.1集合的含义与表示基础巩固一、选择题1．在“①高一数学中的难题；②所有的正三角形；③方程x 2－2＝0的实数解”中，能够构成集合的是( )A ．②B ．③C ．②③D ．①②③[答案] C[解析] 高一数学中的难题的标准不确定，因而构不成集合，而正三角形标准明确，能构成集合，方程x 2－2＝0的解也是确定的，能构成集合，故选C.2．已知集合A ＝{x |x ≤10}，a ＝2＋3，则a 与集合A 的关系是( ) A ．a ∈A B ．a ∉A C ．a ＝A D ．{a }∈A[答案] A[解析] 由于2＋3＜10，所以a ∈A .3．(2015·山东临沂检测)集合{x ∈N *|x －2＜3}的另一种表示形式是( ) A ．{0,1,2,3,4} B ．{1,2,3,4} C ．{0,1,2,3,4,5} D ．{1,2,3,4,5}[答案] B[解析] 由x －2＜3，得x ＜5，又x ∈N *，所以x ＝1,2,3,4，即集合的另一种表示形式是{1,2,3,4}．4．方程组⎩⎪⎨⎪⎧3x ＋y ＝22x －3y ＝27的解集是( )A.⎩⎪⎨⎪⎧x ＝3y ＝－7B ．{x ，y |x ＝3且y ＝－7}C ．{3，－7}D ．{(x ，y )|x ＝3且y ＝－7} [答案] D[解析] 解方程组⎩⎪⎨⎪⎧3x ＋y ＝22x －3y ＝27得⎩⎪⎨⎪⎧x ＝3y ＝－7，用描述法表示为{(x ，y )|x ＝3且y ＝－7}，用列举法表示为{(3，－7)}，故选D. 5．已知集合S ＝{a ，b ，c }中的三个元素是△ABC 的三边长，那么△ABC 一定不是( ) A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰三角形[答案] D[解析] 由集合中元素的互异性知a ，b ，c 互不相等，故选D.6．已知集合A 是由0，m ，m 2－3m ＋2三个元素组成的集合，且2∈A ，则实数m 的值为( )A ．2B ．3C ．0或3D ．0或2或3[答案] B[解析] 因为2∈A ，所以m ＝2或m 2－3m ＋2＝2，解得m ＝0或m ＝2或m ＝3.又集合中的元素要满足互异性，对m 的所有取值进行一一检验可得m ＝3，故选B.二、填空题7．用符号∈与∉填空：(1)0________N *；3________Z ； 0________N ；(－1)0________N *； 3＋2________Q ；43________Q .(2)3________{2,3}；3________{(2,3)}； (2,3)________{(2,3)}；(3,2)________{(2,3)}． (3)若a 2＝3，则a ________R ，若a 2＝－1，则a ________R . [答案] (1)∉ ∉ ∈ ∈ ∉ ∈ (2)∈ ∉ ∈ ∉ (3)∈ ∉[解析] (1)只要熟记常用数集的记号所对应的含义就很容易辨别．(2)中3是集合{2,3}的元素；但整数3不是点集{(2,3)}的元素；同样(2,3)是集合{(2,3)}的元素；因为坐标顺序不同，(3,2)不是集合{(2,3)}的元素．(3)平方等于3的数是±3，当然是实数，而平方等于－1的实数是不存在的．8．设a ，b ∈R ，集合{1，a ＋b ，a }＝⎩⎨⎧⎭⎬⎫0，ba，b ，则b －a ＝________.[答案] 2[解析] 显然a ≠0，则a ＋b ＝0，a ＝－b ，b a＝－1，所以a ＝－1，b ＝1，b －a ＝2. 三、解答题9．已知集合A 含有a －2,2a 2＋5a,12三个元素，且－3∈A ，求a 的值． [解析] ∵－3∈A ，则－3＝a －2或－3＝2a 2＋5a ， ∴a ＝－1或a ＝－32.当a ＝－1时，a －2＝－3,2a 2＋5a ＝－3，不满足集合中元素的互异性，∴a ＝－1舍去．当a ＝－32时，经检验，符合题意．故a ＝－32.[注意] (1)分类讨论意识的建立．解答含有字母的元素与集合之间关系的问题时，要有分类讨论的意识，如本例按照元素－3与a －2,2a 2＋5a,12的关系分类，即可做到不重不漏．(2)注意集合中元素的互异性．求解与集合有关的字母参数时，需利用集合元素的互异性来检验所求参数是否符合要求，如本例在求出a 的值后，需代入验证是否满足集合中元素的互异性．10．已知集合A ＝{x |ax 2－3x ＋2＝0}． (1)若A 是单元素集合，求集合A ；(2)若A 中至少有一个元素，求a 的取值范围．[分析] 将求集合中元素问题转化为方程根问题．(1)集合A 为单元素集合，说明方程有唯一根或两个相等的实数根．要注意方程ax 2－3x ＋2＝0可能不是一元二次方程．(2)至少有一个元素，说明方程有一根或两根．[解析] (1)因为集合A 是方程ax 2－3x ＋2＝0的解集，则当a ＝0时，A ＝{23}，符合题意；当a ≠0时，方程ax 2－3x ＋2＝0应有两个相等的实数根，则Δ＝9－8a ＝0，解得a ＝98，此时A ＝{43}，符合题意．综上所述，当a ＝0时，A ＝{23}，当a ＝98时，A ＝{43}．(2)由(1)可知，当a ＝0时，A ＝{23}符合题意；当a ≠0时，要使方程ax 2－3x ＋2＝0有实数根，则Δ＝9－8a ≥0，解得a ≤98且a ≠0.综上所述，若集合A 中至少有一个元素，则a ≤98.[点评] “a ＝0”这种情况容易被忽视，如“方程ax 2＋2x ＋1＝0”有两种情况：一是“a ＝0”，即它是一元一次方程；二是“a ≠0”，即它是一元二次方程，只有在这种情况下，才能用判别式“Δ”来解决．能力提升一、选择题1．(2015·河北衡水中学期末)下列集合中，不同于另外三个集合的是( ) A ．{x |x ＝1} B ．{x |x 2＝1} C ．{1} D ．{y |(y －1)2＝0}[答案] B[解析] {x |x 2＝1}＝{－1,1}，另外三个集合都是{1}，选B.2．下列六种表示法：①{x ＝－1，y ＝2}；②{(x ，y )|x ＝－1，y ＝2}；③{－1,2}；④(－1,2)；⑤{(－1,2)}；⑥{(x ，y )|x ＝－1或y ＝2}．能表示方程组⎩⎪⎨⎪⎧2x ＋y ＝0，x －y ＋3＝0的解集的是( )A ．①②③④⑤⑥B ．②③④⑤C ．②⑤D ．②⑤⑥[答案] C[解析] 方程组⎩⎪⎨⎪⎧2x ＋y ＝0，x －y ＋3＝0的解是⎩⎪⎨⎪⎧x ＝－1，y ＝2.故选C.3．已知x ，y ，z 为非零实数，代数式x |x |＋y |y |＋z |z |＋|xyz |xyz的值所组成的集合是M ，则下列判断正确的是( )A ．0∉MB ．2∈MC ．－4∉MD ．4∈M[答案] D[解析] 当x ＞0，y ＞0，z ＞0时，代数式的值为4，所以4∈M ，故选D.4．设A ，B 为两个实数集，定义集合A ＋B ＝{x |x 1＋x 2，x 1∈A ，x 2∈B }，若A ＝{1,2,3}，B ＝{2,3}，则集合A ＋B 中元素的个数为( )A ．3B ．4C ．5D ．6[答案] B[解析] 当x 1＝1时，x 1＋x 2＝1＋2＝3或x 1＋x 2＝1＋3＝4；当x 1＝2时，x 1＋x 2＝2＋2＝4或x 1＋x 2＝2＋3＝5；当x 1＝3时，x 1＋x 2＝3＋2＝5或x 1＋x 2＝3＋3＝6.∴A ＋B ＝{3,4,5,6}，共4个元素．二、填空题5．已知P ＝{x |2＜x ＜k ，x ∈N ，k ∈R }，若集合P 中恰有3个元素，则实数k 的取值范围是________．[答案] {k |5＜k ≤6}[解析] x 只能取3,4,5，故5＜k ≤6.6．(2015·湖南郴州模拟)用列举法写出集合{33－x ∈Z |x ∈Z }＝________.[答案] {－3，－1,1,3} [解析] ∵33－x∈Z ，x ∈Z ， ∴3－x 为3的因数． ∴3－x ＝±1，或3－x ＝±3. ∴33－x ＝±3，或33－x＝±1. ∴－3，－1,1,3满足题意．三、解答题7．数集A 满足条件：若a ∈A ，则1＋a 1－a ∈A (a ≠1)．若13∈A ，求集合中的其他元素．[分析] 已知a ∈A ，1＋a 1－a ∈A ，将a ＝13代入1＋a1－a 即可求得集合中的另一个元素，依次，可得集合中的其他元素．[解析] ∵13∈A ，∴1＋131－13＝2∈A ，∴1＋21－2＝－3∈A ，∴1－31＋3＝－12∈A ，∴1－121＋12＝13∈A . 故当13∈A 时，集合中的其他元素为2，－3，－12.8．若一数集的任一元素的倒数仍在该集合中，则称该数集为“可倒数集”． (1)判断集合A ＝{－1,1,2}是否为可倒数集； (2)试写出一个含3个元素的可倒数集．[解析] (1)由于2的倒数为12不在集合A 中，故集合A 不是可倒数集．(2)若a ∈A ，则必有1a ∈A ，现已知集合A 中含有3个元素，故必有一个元素有a ＝1a，即a ＝±1，故可以取集合A ＝{1,2，12}或{－1,2，12}或{1,3，13}等．第一章 1.1 1.1.2集合间的基本关系基础巩固一、选择题1．对于集合A ，B ，“A ⊆B ”不成立的含义是( ) A ．B 是A 的子集B ．A 中的元素都不是B 的元素C ．A 中至少有一个元素不属于BD ．B 中至少有一个元素不属于A [答案] C[解析] “A ⊆B ”成立的含义是集合A 中的任何一个元素都是B 的元素．不成立的含义是A 中至少有一个元素不属于B ，故选C.2．下列命题中，正确的有( ) ①空集是任何集合的真子集；②若A B ，BC ，则A C ；③任何一个集合必有两个或两个以上的真子集；④如果不属于B 的元素也不属于A ，则A ⊆B .A ．①②B ．②③C ．②④D ．③④[答案] C[解析] ①空集只是空集的子集而非真子集，故①错；②真子集具有传递性；故②正确；③若一个集合是空集，则没有真子集，故③错；④由韦恩(Venn)图易知④正确，故选C.3．已知集合A ＝{x |x 是三角形}，B ＝{x |x 是等腰三角形}，C ＝{x |x 是等腰直角三角形}，D ＝{x |x 是等边三角形}，则( )A ．A ⊆B B ．C ⊆B C ．D ⊆C D ．A ⊆D[答案] B[解析] ∵正方形必为矩形，∴C ⊆B . 4．下列四个集合中，是空集的是( ) A ．{0}B ．{x |x ＞8，且x ＜5}C ．{x ∈N |x 2－1＝0} D ．{x |x ＞4}[答案] B[解析] 选项A 、C 、D 都含有元素．而选项B 无元素，故选B.5．若集合A ⊆{1,2,3}，且A 中至少含有一个奇数，则这样的集合A 有( )A．3个B．4个C．5个D．6个[答案] D[解析] 集合{1,2,3}的子集共有8个，其中至少含有一个奇数的有{1}，{3}，{1,2}，{1,3}，{2,3}，{1,2,3}，共6个．6．设集合A＝{x|1<x<2}，B＝{x|x<a}，若A B，则实数a的取值范围为( )A．a≥2B．a≤1C．a≥1D．a≤2[答案] A[解析] 在数轴上表示出两个集合(图略)，因为A B，所以a≥2.二、填空题7．用适当的符号填空：(1){x|x是菱形}________{x|x是平行四边形}；{x|x是三角形}________{x|x是斜三角形}．(2)Z________{x∈R|x2＋2＝0}；0________{0}；Ø________{0}；N________{0}．[答案] (1)(2)∈[解析] (1)判断两个集合之间的关系，可以根据子集的定义来加以判断，特别要注意判断出包含关系后，还要进一步判断是否具有真包含关系．(2)集合{x∈R|x2＋2＝0}中，由于实数范围内该方程无解，因此{x∈R|x2＋2＝0}＝Ø；0是集合{0}中的元素，它们之间是属于关系；{0}是含有一个元素0的集合；Ø是不含任何元素的集合，故Ø{0}；自然数集N 中含有元素0，但不止0这一个元素．8．(2012·大纲全国改编)已知集合A＝{1,2，m3}，B＝{1，m}，B⊆A，则m＝________.[答案] 0或2或－1[解析] 由B⊆A得m∈A，所以m＝m3或m＝2，所以m＝2或m＝－1或m＝1或m＝0，又由集合中元素的互异性知m≠1.所以m＝0或2或－1.三、解答题9．判断下列集合间的关系：(1)A＝{x|x－3＞2}，B＝{x|2x－5≥0}；(2)A＝{x∈Z|－1≤x<3}，B＝{x|x＝|y|，y∈A}．[解析] (1)∵A＝{x|x－3＞2}＝{x|x＞5}，B ＝{x |2x －5≥0}＝{x |x ≥52}，∴利用数轴判断A 、B 的关系．如图所示，AB .(2)∵A ＝{x ∈Z |－1≤x <3}＝{－1,0,1,2}，B ＝{x |x ＝|y |，y ∈A ，∴B ＝{0,1,2}，∴BA .10．已知集合M ＝{x |x ＝m ＋16，m ∈Z }，N ＝{x |x ＝n 2－13，n ∈Z }，P ＝{x |x ＝p 2＋16，p ∈Z }，试确定M ，N ，P 之间的关系．[解析] 解法一：集合M ＝{x |x ＝m ＋16，m ∈Z }，对于集合N ，当n 是偶数时，设n ＝2t (t ∈Z )，则N ＝{x |x ＝t －13，t ∈Z }；当n 是奇数时，设n ＝2t ＋1(t ∈Z )，则N ＝{x |x ＝2t ＋12－13，t ∈Z }＝{x |x ＝t ＋16，t ∈Z }．观察集合M ，N 可知M N .对于集合P ，当p 是偶数时，设p ＝2s (s ∈Z )，则P ＝{x |x ＝s ＋16，s ∈Z }，当p 是奇数时，设p ＝2s －1(s ∈Z )，则P ＝{x |x ＝2s －12＋16，s ∈Z } ＝{x |x ＝s －13，s ∈Z }．观察集合N ，P 知N ＝P . 综上可得：MN ＝P .解法二：∵M ＝{x |x ＝m ＋16，m ∈Z }＝{x |x ＝6m ＋16，m ∈Z }＝{x |x ＝3×2m ＋16，m ∈Z }，N ＝{x |x ＝n 2－13，n ∈Z }＝{x |x ＝3n －26，n ∈Z }＝{x |x ＝3n －1＋16，n －1∈Z }，P ＝{x |x ＝p 2＋16，p ∈Z }＝{x |x ＝3p ＋16，p ∈Z }，比较3×2m ＋1,3(n －1)＋1与3p ＋1可知，3(n －1)＋1与3p ＋1表示的数完全相同， ∴N ＝P,3×2m ＋1只相当于3p ＋1中当p 为偶数时的情形， ∴MP ＝N .综上可知M P ＝N .能力提升一、选择题1．(2015·瓮安一中高一期末试题)设集合M ＝{x |x ＝k 2＋14，k ∈Z }，N ＝{x |x ＝k 4＋12，k∈Z }，则( )A ．M ＝NB ．M NC ．M ND ．M 与N 的关系不确定[答案] B[解析] 解法1：用列举法，令k ＝－2，－1,0,1,2…可得M ＝{…－34，－14，14，34，54…}， N ＝{…0，14，12，34，1…}，∴MN ，故选B.解法2：集合M 的元素为：x ＝k 2＋14＝2k ＋14(k ∈Z )，集合N 的元素为：x ＝k 4＋12＝k ＋24(k ∈Z )，而2k ＋1为奇数，k ＋2为整数，∴M N ，故选B.[点评] 本题解法从分式的结构出发，运用整数的性质方便地获解．注意若k 是任意整数，则k ＋m (m 是一个整数)也是任意整数，而2k ＋1,2k －1均为任意奇数，2k 为任意偶数．2．(2015·湖北孝感期中)集合A ＝{(x ，y )|y ＝x }和B ＝⎩⎨⎧⎭⎬⎫x ，y |⎩⎪⎨⎪⎧2x －y ＝1x ＋4y ＝5，则下列结论中正确的是( )A ．1∈AB ．B ⊆AC ．(1,1)⊆BD ．Ø∈A[答案] B[解析] B ＝⎩⎨⎧⎭⎬⎫x ，y |⎩⎪⎨⎪⎧2x －y ＝1x ＋4y ＝5＝{(1,1)}，故选B. 3．已知集合A ＝{1,2}，B ＝{x |ax －2＝0}，若B ⊆A ，则a 的值不可能是( ) A ．0B ．1C ．2D ．3[答案] D[解析] 由题意知，a ＝0时，B ＝Ø，满足题意；a ≠0时，由2a∈A ⇒a ＝1,2，所以a 的值不可能是3.4．集合P ＝{3,4,5}，Q ＝{6,7}，定义P *Q ＝{(a ，b )|a ∈P ，b ∈Q }，则P *Q 的子集个数为( )A ．7B ．12C ．32D ．64[答案] D[解析] 集合P *Q 的元素为(3,6)，(3,7)，(4,6)，(4,7)，(5,6)，(5,7)，共6个，故P *Q 的子集个数为26＝64.二、填空题5．已知集合M ＝{x |2m ＜x ＜m ＋1}，且M ＝Ø，则实数m 的取值范围是________． [答案] m ≥1[解析] ∵M ＝Ø，∴2m ≥m ＋1，∴m ≥1.6．集合⎩⎨⎧x ，y ⎪⎪⎪⎪ ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫y ＝－x ＋2，y ＝12x ＋2⊆{(x ，y )|y ＝3x ＋b }，则b ＝________.[答案] 2[解析] 解方程组⎩⎪⎨⎪⎧y ＝－x ＋2y ＝12x ＋2得⎩⎪⎨⎪⎧x ＝0y ＝2，代入y ＝3x ＋b 得b ＝2. 三、解答题7．设集合A ＝{－1,1}，集合B ＝{x |x 2－2ax ＋b ＝0}，若B ≠Ø且B ⊆A ，求实数a 、b 的值．[解析] ∵B 中元素是关于x 的方程x 2－2ax ＋b ＝0的根，且B ⊆{－1,1}，∴关于x 的方程x 2－2ax ＋b ＝0的根只能是－1或1，但要注意方程有两个相等根的条件是Δ＝0.∵B ＝{x |x 2－2ax ＋b ＝0}⊆A ＝{－1,1}，且B ≠Ø， ∴B ＝{－1}或B ＝{1}或B ＝{－1,1}．当B ＝{－1}时，Δ＝4a 2－4b ＝0且1＋2a ＋b ＝0，解得a ＝－1，b ＝1. 当B ＝{1}时，Δ＝4a 2－4b ＝0且1－2a ＋b ＝0，解得a ＝b ＝1. 当B ＝{－1,1}时，有(－1)＋1＝2a ，(－1)×1＝b ，解得a ＝0，b ＝－1.8．设集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}． (1)若B ⊆A ，求实数m 的取值范围； (2)当x ∈Z 时，求A 的非空真子集个数；(3)当x ∈R 时，不存在元素x 使x ∈A 与x ∈B 同时成立，求实数m 的取值范围． [解析] (1)当m ＋1>2m －1，即m <2时，B ＝Ø，满足B ⊆A . 当m ＋1≤2m －1，即m ≥2时，要使B ⊆A 成立，只需⎩⎪⎨⎪⎧m ＋1≥－2，2m －1≤5，即2≤m ≤3.综上，当B ⊆A 时，m 的取值范围是{m |m ≤3}． (2)当x ∈Z 时，A ＝{－2，－1,0,1,2,3,4,5}， ∴集合A 的非空真子集个数为28－2＝254. (3)∵x ∈R ，且A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}，又不存在元素x 使x ∈A 与x ∈B 同时成立， ∴当B ＝Ø，即m ＋1>2m －1，得m <2时，符合题意；当B ≠Q ，即m ＋1≤2m －1，得m ≥2时，⎩⎪⎨⎪⎧m ≥2，m ＋1>5，或⎩⎪⎨⎪⎧m ≥2，2m －1<－2，解得m >4.综上，所求m 的取值范围是{m |m <2或m >4}．第一章 1.1 1.1.3 第一课时并集和交集基础巩固一、选择题1．下面四个结论：①若a ∈(A ∪B )，则a ∈A ；②若a ∈(A ∩B )，则a ∈(A ∪B )；③若a ∈A ，且a ∈B ，则a ∈(A ∩B )；④若A ∪B ＝A ，则A ∩B ＝B .其中正确的个数为( )A ．1B ．2C．3 D．4[答案] C[解析] ①不正确，②③④正确，故选C.2．已知集合M＝{x|－3<x≤5}，N＝{x|x>3}，则M∪N＝( )A．{x|x>－3} B．{x|－3<x≤5}C．{x|3<x≤5}D．{x|x≤5}[答案] A[解析] 在数轴上表示集合M，N，如图所示，则M∪N＝{x|x>－3}．3．(2015·全国高考卷Ⅰ文科，1题)已知集合A＝{x|x＝3n＋2，n∈N}，B＝{6,8,12,14}，则集合A∩B中元素的个数为( )A．5 B．4C．3 D．2[答案] D[解析] A∩B＝{8,14}，故选D.4．(2015·浙江省期中试题)集合A＝{1,2}，B＝{1,2,3}，C＝{2,3,4}，则(A∩B)∪C＝( )A．{1,2,3} B．{1,2,4}C．{2,3,4} D．{1,2,3,4}[答案] D[解析] A∩B＝{1,2}，(A∩B)∪C＝{1,2,3,4}，故选D.5．若A∪B＝Ø，则( )A．A＝Ø，B≠ØB．A≠Ø，B＝ØC．A＝Ø，B＝ØD．A≠Ø，B≠Ø[答案] C6．设集合A＝{x|－1≤x≤2}，集合B＝{x|x≤a}，若A∩B＝Ø，则实数a的取值集合为( )A．{a|a<2} B．{a|a≥－1}C．{a|a<－1} D．{a|－1≤a≤2}[答案] C[解析] 如图．要使A ∩B ＝Ø，应有a <－1. 二、填空题7．若集合A ＝{2,4，x }，B ＝{2，x 2}，且A ∪B ＝{2,4，x }，则x ＝________. [答案] 0,1或－2[解析] 由已知得B ⊆A ，∴x 2＝4或x 2＝x ，∴x ＝0,1，±2，由元素的互异性知x ≠2，∴x ＝0,1或－2.8．已知集合A ＝{x |x ≥5}，集合B ＝{x |x ≤m }，且A ∩B ＝{x |5≤x ≤6}，则实数m ＝________.[答案] 6[解析] 用数轴表示集合A 、B 如图所示．由于A ∩B ＝{x |5≤x ≤6}，得m ＝6.三、解答题9．设集合A ＝{a 2，a ＋1，－3}，B ＝{a －3,2a －1，a 2＋1}，A ∩B ＝{－3}，求实数a 的值．[解析] ∵A ∩B ＝{－3}，∴－3∈B . ∵a 2＋1≠－3，∴①若a －3＝－3，则a ＝0，此时A ＝{0,1，－3}，B ＝{－3，－1,1}，但由于A ∩B ＝{1，－3}与已知A ∩B ＝{－3}矛盾， ∴a ≠0.②若2a －1＝－3，则a ＝－1，此时A ＝{1,0，－3}，B ＝{－4，－3,2}，A ∩B ＝{－3}．综上可知a ＝－1.10．已知集合A ＝{x |－1≤x ＜3}，B ＝{x |2x －4≥x －2}． (1)求A ∩B ；(2)若集合C ＝{x |2x ＋a ＞0}，满足B ∪C ＝C ，求实数a 的取值范围． [解析] (1)∵B ＝{x |x ≥2}，A ＝{x |－1≤x ＜3}， ∴A ∩B ＝{x |2≤x ＜3}．(2)∵C ＝{x |x ＞－a2}，B ∪C ＝C ⇔B ⊆C ，∴－a2<2，∴a ＞－4.能力提升一、选择题1．已知集合M ＝{－1,0,1}，N ＝{x |x ＝ab ，a ，b ∈M 且a ≠b }，则M ∪N ＝( ) A ．{0,1} B ．{－1,0} C ．{－1,0,1} D ．{－1,1}[答案] C[解析] 由题意可知，集合N ＝{－1,0}，所以M ∪N ＝M .2．若集合M ＝{(x ，y )|x ＋y ＝0}，P ＝{(x ，y )|x －y ＝2}，则M ∩P 等于( ) A ．(1，－1) B ．{x ＝1或y ＝－1} C ．{1，－1} D ．{(1，－1)}[答案] D[解析] M ∩P 的元素是方程组⎩⎪⎨⎪⎧x ＋y ＝0x －y ＝2的解∴M ∩P ＝{(1，－1)}．3．(2015·衡水高一检测)若集合A ，B ，C 满足A ∩B ＝A ，B ∪C ＝C ，则A 与C 之间的关系为( )A ．C AB ．AC C ．C ⊆AD ．A ⊆C[答案] D[解析] ∵A ∩B ＝A ，∴A ⊆B ，又B ∪C ＝C ，∴B ⊆C ，∴A ⊆C ，故选D.4．当x ∈A 时，若x －1∉A ，且x ＋1∉A ，则称x 为A 的一个“孤立元素”，由A 的所有孤立元素组成的集合称为A 的“孤星集”，若集合M ＝{0,1,3}的孤星集为M ′，集合N ＝{0,3,4}的孤星集为N ′，则M ′∪N ′＝( )A ．{0,1,3,4}B ．{1,4}C ．{1,3}D ．{0,3}[答案] D[解析] 由条件及孤星集的定义知，M ′＝{3}，N ′＝{0}，则M ′∪N ′＝{0,3}．二、填空题5．以下四个推理：①a ∈(A ∪B )⇒a ∈A ；②a ∈(A ∩B )⇒a ∈(A ∪B )；③A ⊆A ⇒A ∪B ＝B ；④A ∪B ＝A ⇒A ∩B ＝B .其中正确的为________．[答案] ②③④[解析] ①是错误的，a ∈(A ∪B )时可推出a ∈A 或a ∈B ，不一定推出a ∈A .6．已知集合A ＝{x |x 2＋px ＋q ＝0}，B ＝{x |x 2－px －2q ＝0}，且A ∩B ＝{－1}，则A ∪B ＝________.[答案] {－2，－1,4}[解析] 因为A ∩B ＝{－1}，所以－1∈A ，－1∈B ，即－1是方程x 2＋px ＋q ＝0和x 2－px －2q ＝0的解，所以⎩⎪⎨⎪⎧－12－p ＋q ＝0，－12＋p －2q ＝0，解得⎩⎪⎨⎪⎧p ＝3，q ＝2，所以A ＝{－1，－2}，B ＝{－1,4}，所以A ∪B ＝{－2，－1,4}．三、解答题7．已知A ＝{x |2a ＜x ≤a ＋8}，B ＝{x |x ＜－1或x ＞5}，A ∪B ＝R ，求a 的取值范围． [解析] ∵B ＝{x |x ＜－1或x ＞5}，A ∪B ＝R ，∴⎩⎪⎨⎪⎧2a ＜－1，a ＋8≥5，解得－3≤a ＜－12.8．设A ＝{x |x 2＋8x ＝0}，B ＝{x |x 2＋2(a ＋2)x ＋a 2－4＝0}，其中a ∈R .如果A ∩B ＝B ，求实数a 的取值范围．[解析] ∵A ＝{x }x 2＋8x ＝0}＝{0，－8}，A ∩B ＝B ，∴B ⊆A . 当B ＝Ø时，方程x 2＋2(a ＋2)x ＋a 2－4＝0无解，即Δ＝4(a ＋2)2－4(a 2－4)＜0，得a ＜－2. 当B ＝{0}或{－8}时，这时方程的判别式Δ＝4(a ＋2)2－4(a 2－4)＝0，得a ＝－2.将a ＝－2代入方程，解得x ＝0，∴B ＝{0}满足．当B ＝{0，－8}时，⎩⎪⎨⎪⎧Δ＞0，－2a ＋2＝－8，a 2－4＝0，可得a ＝2.综上可得a ＝2或a ≤－2.[点评] (1)当集合B ⊆A 时，如果集合A 是一个确定的集合，而集合B 不确定，运算时，要考虑B ＝Ø的情形，切不可漏掉．(2)利用集合运算性质化简集合，有利于准确了解集合之间的关系．第一章 1.1 1.1.3 第二课时补集基础巩固一、选择题1．(2015·重庆三峡名校联盟)设全集I＝{1,2,3,4,5}，集合A＝{2,3,5}，集合B＝{1,2}，则(∁I B)∩A为( )A．{2} B．{3,5}C．{1,3,4,5} D．{3,4,5}[答案] B[解析] 因为全集I＝{1,2,3,4,5}，集合B＝{1,2}，则∁I B＝{3,4,5}．所以(∁I B)∩A为{3,5}．故选B.[易错警示] 本小题的关键是先求出集合B的补集，再求交集．集合的运算是集合关系的基础知识，要理解清楚，可能渗透在一个大题中，不熟练会导致整体看不懂或理解错误．2．设全集U＝{1,2,3,4,5}，A＝{1,3,5}，则∁U A的所有非空子集的个数为( )A．4 B．3C．2 D．1[答案] B[解析] ∵∁U A＝{2,4}，∴非空子集有22－1＝3个，故选B.3．若P＝{x|x＜1}，Q＝{x|x＞－1}，则( )A．P⊆Q B．Q⊆PC．(∁R P)⊆Q D．Q⊆∁R P[答案] C[解析] ∵P＝{x|x＜1}，∴∁R P＝{x|x≥1}．又Q＝{x|x＞－1}，∴(∁R P)⊆Q，故选C.4．若全集U＝{1,2,3,4,5,6}，M＝{2,3}，N＝{1,4}，则集合{5,6}等于( )A．M∪N B．M∩NC．(∁U M)∪(∁U M) D．(∁U M)∩(∁U N)[答案] D[解析] ∵M∪N＝{1,2,3,4}，∴(∁U M)∩(∁U N)＝∁U(M∪N)＝{5,6}，故选D.5．已知全集U＝R，集合A＝{x|－2≤x≤3}，B＝{x|x＜－1或x＞4}，那么集合A∪(∁U B)等于( )A．{x|－2≤x≤4}B．{x|x≤3，或x≥4}C．{x|－2≤x＜－1}D．{x|－1≤x≤3}[答案] A[解析] 由题意可得∁U B＝{x|－1≤x≤4}，A＝{x|－2≤x≤3}，所以A∪(∁U B)＝{x|－2≤x≤4}，故选A.6．已知集合A＝{x|x＜a}，B＝{x|x＜2}，且A∪(∁R B)＝R，则a满足( )A ．a ≥2B ．a ＞2C ．a ＜2D ．a ≤2[答案] A[解析] ∁R B ＝{x |x ≥2}，则由A ∪(∁R B )＝R 得a ≥2，故选A. 二、填空题7．已知集合A ＝{3,4，m }，集合B ＝{3,4}，若∁A B ＝{5}，则实数m ＝________. [答案] 58．U ＝R ，A ＝{x |－2<x ≤1或x >3}，B ＝{x |x ≥4}，则∁U A ＝________，∁A B ＝________. [答案] {x |x ≤－2或1<x ≤3} {x |－2<x ≤1或3<x <4} 三、解答题9．已知全集U ＝{2,3，a 2－2a －3}，A ＝{2，|a －7|}，∁U A ＝{5}，求a 的值． [解析] 解法1：由|a －7|＝3，得a ＝4或a ＝10.当a ＝4时，a 2－2a －3＝5，当a ＝10时，a 2－2a －3＝77∉U ，∴a ＝4.解法2：由A ∪∁U A ＝U 知⎩⎪⎨⎪⎧|a －7|＝3a 2－2a －3＝5，∴a ＝4.10．(2015·唐山一中月考试题)已知全集U ＝{x |x ≤4}，集合A ＝{x |－2<x <3}，B ＝{x |－3≤x ≤2}，求A ∩B ，(∁U A )∪B ，A ∩(∁U B )．[分析] 利用数轴，分别表示出全集U 及集合A ，B ，先求出∁U A 及∁U B ，然后求解． [解析] 如图所示，∵A ＝{x |－2<x <3}，B ＝{x |－3≤x ≤2}， ∴∁U A ＝{x |x ≤－2或3≤x ≤4}， ∁U B ＝{x |x <－3或2<x ≤4}． ∴A ∩B ＝{x |－2<x ≤2}， (∁U A )∪B ＝{x |x ≤2或3≤x ≤4}，A ∩(∁UB )＝{x |2<x <3}．[点评] (1)数轴与Venn 图有同样的直观功效，在数轴上可以直观地表示数集，所以进行数集的交、并、补运算时，经常借助数轴求解．(2)不等式中的等号在补集中能否取到要引起重视，还要注意补集是全集的子集．能力提升一、选择题1．如图，阴影部分用集合A 、B 、U 表示为( )A．(∁U A)∩B B．(∁U A)∪(∁U B)C．A∩(∁U B) D．A∪(∁U B)[答案] C[解析] 阴影部分在A中，不在B中，故既在A中也在∁U B中，因此是A与∁U B的公共部分．2．设S为全集，则下列说法中，错误的个数是( )①若A∩B＝Ø，则(∁S A)∪(∁S B)＝S；②若A∪B＝S，则(∁S A)∩(∁S B)＝Ø；③若A∪B＝Ø，则A＝B.A．0 B．1C．2 D．3[答案] A[解析] 借助文氏图可知，①②正确，对于③于由A∪B＝Ø，∴A＝Ø，B＝Ø，∴A＝B，故选A.3．设全集U＝{1,2,3,4,5}，集合S与T都是U的子集，满足S∩T＝{2}，(∁U S)∩T＝{4}，(∁U S)∩(∁U T)＝{1,5}则有( )A．3∈S,3∈T B．3∈S,3∈∁U TC．3∈∁U S,3∈T D．3∈∁U S,3∈∁U T[答案] B[解析] 若3∈S,3∈T，则3∈S∩T，排除A；若3∈∁U S，3∈T，则3∈(∁U S)∩T，排除C；若3∈∁U S,3∈∁U T，则3∈(∁U S)∩(∁U T)，排除D，∴选B，也可画图表示．4．(2008·北京)已知全集U＝R，集合A＝{x|－2≤x≤3}，B＝{x|x<－1或x>4}，那么集合A∩(∁U B)等于( )A．{x|－2≤x<4} B．{x|x≤3或x≥4}C．{x|－2≤x<－1} D．{x|－1≤x≤3}[答案] D[解析] ∁U B＝{x|－1≤x≤4}，A∩∁U B＝{x|－1≤x≤3}，故选D.二、填空题5．已知全集为R ，集合M ＝{x ∈R |－2＜x ＜2}，P ＝{x |x ≥a }，并且M ⊆∁R P ，则a 的取值范围是________．[答案] a ≥2[解析] M ＝{x |－2＜x ＜2}，∁R P ＝{x |x ＜a }． ∵M ⊆∁R P ，∴由数轴知a ≥2.6．已知U ＝R ，A ＝{x |a ≤x ≤b }，∁U A ＝{x |x ＜3或x ＞4}，则ab ＝________. [答案] 12[解析] ∵A ∪(∁U A )＝R ，∴a ＝3，b ＝4，∴ab ＝12. 三、解答题7．已知集合A ＝{x |x 2＋ax ＋12b ＝0}和B ＝{x |x 2－ax ＋b ＝0}，满足(∁U A )∩B ＝{2}，A ∩(∁UB )＝{4}，U ＝R ，求实数a ，b 的值．[提示] 由2∈B,4∈A ，列方程组求解．[解析] ∵(∁U A )∩B ＝{2}，∴2∈B ，∴4－2a ＋b ＝0.① 又∵A ∩(∁U B )＝{4}，∴4∈A ，∴16＋4a ＋12b ＝0.②联立①②，得⎩⎪⎨⎪⎧4－2a ＋b ＝0，16＋4a ＋12b ＝0，解得⎩⎪⎨⎪⎧a ＝87，b ＝－127.经检验，符合题意：∴a ＝87，b ＝－127.[点评] 由题目中所给的集合之间的关系，通过分析得出元素与集合之间的关系，是解决此类问题的关键．8．已知全集U ＝R ，集合A ＝{x |x <－1}，B ＝{x |2a <x <a ＋3}，且B ⊆∁R A ，求a 的取值范围．[分析] 本题从条件B ⊆∁R A 分析可先求出∁R A ，再结合B ⊆∁R A 列出关于a 的不等式组求a 的取值范围．[解析] 由题意得∁R A ＝{x |x ≥－1}．(1)若B ＝Ø，则a ＋3≤2a ，即a ≥3，满足B ⊆∁R A . (2)若B ≠Ø，则由B ⊆∁R A ，得2a ≥－1且2a <a ＋3，即－12≤a <3.综上可得a ≥－12.第一章 1.1 1.1.3第三课时习题课基础巩固一、选择题1．(2015·全国高考卷Ⅱ文科，1题)已知集合A＝{x|－1<x<2}，B＝{x|0<x<3}，则A∩B ＝( )A．{x|－1<x<3} B．{x|－1<x<0}C．{x|0<x<2} D．{x|2<x<3}[答案] A[解析] A∪B＝{x|－1<x<3}，故选A.2．设U＝R，A＝{x|x＞0}，B＝{x|x＞1}，则A∩(∁U B)等于( )A．{x|0≤x＜1} B．{x|0＜x≤1}C．{x|x＜0} D．{x|x＞1}[答案] B[解析] 画出数轴，如图所示，∁U B＝{x|x≤1}，则A∩∁U B＝{x|0＜x≤1}，故选B.3．图中阴影部分所表示的集合是( )A．B∩(∁U(A∪C))B．(A∪B)∪(B∪C)C．(A∪C)∩(∁U B)D．[∁U(A∩C)]∪B[答案] A[解析] 阴影部分位于集合B内，且位于集合A、C的外部，故可表示为B∩(∁U(A∪C))，故选A.4．已知全集U＝R，集合A＝{x|－2≤x≤3}，B＝{x|x＜－2或x＞4}，那么集合(∁U A)∩(∁U B)等于( )A．{x|3＜x≤4}B．{x|x≤3或x≥4}C．{x|3≤x＜4} D．{x|－1≤x≤3}[答案] A[解析] 方法1：∁U A＝{x|x＜－2或x＞3}，∁U B＝{x|－2≤x≤4}∴(∁U A )∩(∁U B )＝{x |3＜x ≤4}，故选C.方法2：A ∪B ＝{x |x ≤3或x ＞4}，(∁U A )∩(∁U B )＝∁U (A ∪B )＝{x |3＜x ≤4}．故选A. 5．已知集合A ＝{x |－1≤x ≤1}，B ＝{x |－1≤x ≤a }，且(A ∪B )⊆(A ∩B )，则实数a ＝( )A ．0B ．1C ．2D ．3[答案] B[解析] ∵(A ∪B )⊆(A ∩B )，∴(A ∪B )＝(A ∩B )， ∴A ＝B ，∴a ＝1.6．设U 为全集，对集合X ，Y 定义运算“*”，X *Y ＝∁U (X ∩Y )，对于任意集合X ，Y ，Z ，则(X *Y )*Z ＝( )A ．(X ∪Y )∩∁U ZB ．(X ∩Y )∪∁U ZC ．(∁U X ∪∁U Y )∩ZD ．(∁U X ∩∁U Y )∪Z [答案] B[解析] X *Y ＝∁U (X ∩Y )(X *Y )*Z ＝∁U [∁U (X ∩Y )∩Z ]＝∁U (∁U (X ∩Y ))∪∁U Z ＝(X ∩Y )∪∁U Z ，故选B. 二、填空题7．(河北孟村回民中学2014～2015学年高一九月份月考试题)U ＝{1,2}，A ＝{x |x 2＋px ＋q ＝0}，∁U A ＝{1}，则p ＋q ＝________.[答案] 0[解析] 由∁U A ＝{1}，知A ＝{2}即方程x 2＋px ＋q ＝0有两个相等根2，∴p ＝－4，q ＝4，∴p ＋q ＝0.8．已知集合A ＝{(x ，y )|y ＝2x －1}，B ＝{(x ，y )|y ＝x ＋3}，若m ∈A ，m ∈B ，则m 为________．[答案] (4,7)[解析] 由m ∈A ，m ∈B 知m ∈(A ∩B )，由⎩⎪⎨⎪⎧y ＝2x －1y ＝x ＋3，得⎩⎪⎨⎪⎧x ＝4y ＝7，∴A ∩B ＝{(4,7)}．三、解答题9．已知全集U ＝R ，A ＝{x |2≤x <5}，B ＝{x |3≤x <7}，求： (1)(∁R A )∩(∁R B ) (2)∁R (A ∪B )(3)(∁R A )∪(∁R B ) (4)∁R (A ∩B )[分析] 在进行集合运算时，充分利用数轴工具是十分有效的手段，此例题可先在数轴上画出集合A 、B ，然后求出A ∩B ，A ∪B ，∁R A ，∁R B ，最后可逐一写出各小题的结果．[解析] 如图所示，可得A ∩B ＝{x |3≤x <5}，A ∪B ＝{x |2≤x <7}．∁R A ＝{x |x <2或x ≥5}， ∁R B ＝{x |x <3或x ≥7}．由此求得(1)(∁R A )∩(∁R B )＝{x |x <2或x ≥7}． (2)∁R (A ∪B )＝{x |x <2或x ≥7}．(3)(∁R A )∪(∁R B )＝{x |x <2或x ≥5}∪{x <3或x ≥7}＝{x |x <3或x ≥5}． (4)∁R (A ∩B )＝{x |x <3或x ≥5}．[点评] 求解集合的运算，利用数轴是有效的方法，也是数形结合思想的体现． 10．已知U ＝R ，A ＝{x |x 2＋px ＋12＝0}，B ＝{x |x 2－5x ＋q ＝0}，若(∁U A )∩B ＝{2}，(∁UB )∩A ＝{4}，求A ∪B .[分析] 先确定p 和q 的值，再明确A 与B 中的元素，最后求得A ∪B . [解析] ∵(∁U A )∩B ＝{2}，∴2∈B 且2∉A . ∵A ∩(∁U B )＝{4}，∴4∈A 且4∉B .∴⎩⎪⎨⎪⎧42＋4p ＋12＝0，22－5×2＋q ＝0.解得p ＝－7，q ＝6，∴A ＝{3,4}，B ＝{2,3}，∴A ∪B ＝{2,3,4}．能力提升一、选择题1．设A 、B 、C 为三个集合，(A ∪B )＝(B ∩C )，则一定有( ) A ．A ⊆C B ．C ⊆A C ．A ≠C D ．A ＝Ø[答案] A[解析] ∵A ∪B ＝(B ∩C )⊆B ，又B ⊆(A ∪B )，∴A ∪B ＝B ，∴A ⊆B ，又B ⊆(A ∪B )＝B ∩C ，且(B ∩C )⊆B ， ∴(B ∩C )＝B ，∴B ⊆C ，∴A ⊆C .2．设P ＝{3,4}，Q ＝{5,6,7}，集合S ＝{(a ，b )|a ∈P ，b ∈Q }，则S 中元素的个数为( )A．3 B．4C．5 D．6[答案] D[解析] S＝{(3,5)，(3,6)，(3,7)，(4,5)，(4,6)，(4,7)}共6个元素，故选D.3．(2015·陕西模拟)已知全集U＝{1,2,3,4,5}，集合A＝{x|x2－3x＋2＝0}，B＝{x|x ＝2a，a∈A}，则集合∁U(A∪B)中元素的个数为( )A．1 B．2C．3 D．4[答案] B[解析] 因为集合A＝{1,2}，B＝{2,4}，所以A∪B＝{1,2,4}，所以∁U(A∪B)＝{3,5}．4．设全集U＝R，集合A＝{x|x≤1或x≥3}，集合B＝{x|k＜x＜k＋1，k＜2}，且B∩(∁U A)≠Ø，则( )A．k＜0 B．k＜2C．0＜k＜2 D．－1＜k＜2[答案] C[解析] ∵U＝R，A＝{x|x≤1或x≥3}，∴∁U A＝{x|1＜x＜3}．∵B＝{x|k＜x＜k＋1，k＜2}，∴当B∩(∁U A)＝Ø时，有k＋1≤1或k≥3(不合题意，舍去)，如图所示，∴k≤0，∴当B∩(∁U A)≠Ø时，0＜k＜2，故选C.二、填空题5．(2014·福建，理)若集合{a，b，c，d}＝{1,2,3,4}，且下列四个关系：①a＝1；②b≠1；③c＝2，④d≠4有且只有一个是正确的，则符合条件的有序数组(a，b，c，d)的个数是________．[答案] 6[解析] 根据题意可分四种情况：(1)若①正确，则a＝1，b＝1，c≠2，d＝4，符合条件的有序数组有0个；(2)若②正确，则a≠1，b≠1，c≠2，d＝4，符合条件的有序数组为(2,3,1,4)和(3,2,1,4)；(3)若③正确，则a≠1，b＝1，c＝2，d＝4，符合条件的有序数组为(3,1,2,4)；(4)若④正确，则a≠1，b＝1，c≠2，d≠4，符合条件的有序数组为(2,1,4,3)，(4,1,3,2)，(3,1,4,2)．所以共有6个．故答案为6.6．设数集M ＝{x |m ≤x ≤m ＋34}，N ＝{x |n －13≤x ≤n }，且M ，N 都是集合{x |0≤x ≤1}的子集，如果把b －a 叫做集合{x |a ≤x ≤b }的“长度”，那么集合M ∩N 的“长度”的最小值是________．[答案]112[解析] 如图，设AB 是一长度为1的线段，a 是长度为34的线段，b 是长度为13的线段，a ，b 可在线段AB 上自由滑动，a ，b 重叠部分的长度即为M ∩N 的“长度”，显然，当a ，b各自靠近线段AB 两端时，重叠部分最短，其值为34＋13－1＝112.三、解答题7．已知集合A ＝{x |x 2－ax ＋a 2－19＝0}，B ＝{x |x 2－5x ＋6＝0}，C ＝{x |x 2＋2x －8＝0}，试探求a 取何实数时，(A ∩B )Ø与A ∩C ＝Ø同时成立．[解析] B ＝{x |x 2－5x ＋6＝0}＝{2,3}，C ＝{x |x 2＋2x －8＝0}＝{2，－4}，由A ∩BØ与A ∩C ＝Ø同时成立可知，3是方程x 2－ax ＋a 2－19＝0的解，将3代入方程得a 2－3a －10＝0，解得a ＝5或a ＝－2.当a ＝5时，A ＝{x |x 2－5x ＋6＝0}＝{2,3}，此时A ∩C ＝{2}，与此题设A ∩C ＝Ø矛盾，故不适合．当a ＝－2时，A ＝{x |x 2＋2x －15＝0}＝{3，－5}，此时(A ∩B )Ø与A ∩C ＝Ø同时成立，则满足条件的实数a ＝－2.8．设A ，B 是两个非空集合，定义A 与B 的差集A －B ＝{x |x ∈A ，且x ∉B }． (1)试举出两个数集，求它们的差集；(2)差集A －B 与B －A 是否一定相等？说明理由；(3)已知A ＝{x |x >4}，B ＝{x |－6<x <6}，求A －(A －B )和B －(B －A )． [解析] (1)如A ＝{1,2,3}，B ＝{2,3,4}，则A －B ＝{1}． (2)不一定相等，由(1)B －A ＝{4}，而A －B ＝{1}，故A －B ≠B －A .又如，A ＝B ＝{1,2,3}时，A －B ＝Ø，B －A ＝Ø，此时A －B ＝B －A ，故A －B 与B －A 不一定相等． (3)因为A －B ＝{x |x ≥6}，B －A ＝{x |－6<x ≤4}， A －(A －B )＝{x |4<x <6}， B －(B －A )＝{x |4<x <6}．第一章 1.2 1.2.1函数的概念基础巩固一、选择题1．下列四种说法中，不正确的是( )A ．在函数值域中的每一个数，在定义域中都至少有一个数与之对应B ．函数的定义域和值域一定是无限集合C ．定义域和对应关系确定后，函数的值域也就确定了D ．若函数的定义域中只含有一个元素，则值域也只含有一个元素 [答案] B2．f (x )＝1＋x ＋x1－x 的定义域是( )A ．[－1，＋∞)B ．(－∞，－1]C ．RD ．[－1,1)∪(1，＋∞)[答案] D[解析] ⎩⎪⎨⎪⎧1＋x ≥01－x ≠0，解得⎩⎪⎨⎪⎧x ≥－1，x ≠1，故定义域为[－1,1)∪(1，＋∞)，选D.3．各个图形中，不可能是函数y ＝f (x )的图象的是( )[答案] A[解析] 因为垂直x 轴的直线与函数y ＝f (x )的图象至多有一个交点，故选A. 4．(2015·曲阜二中月考试题)集合A ＝{x |0≤x ≤4}，B ＝{y |0≤y ≤2}，下列不表示从A 到B 的函数是( )A ．f x →y ＝12xB ．f x →y ＝13xC ．f x →y ＝23xD ．f x →y ＝x[答案] C[解析] 对于选项C ，当x ＝4时，y ＝83＞2不合题意．故选C.5．下列各组函数相同的是( )A ．f (x )＝x 2－1x －1与g (x )＝x ＋1B ．f (x )＝－2x 3与g (x )＝x ·－2x C ．f (x )＝2x ＋1与g (x )＝2x 2＋xxD ．f (x )＝|x 2－1|与g (t )＝t 2－12[答案] D[解析] 对于A.f (x )的定义域是(－∞，1)∪(1，＋∞)，g (x )的定义域是R ，定义域不同，故不是相同函数；对于B.f (x )＝|x |·－2x ，g (x )＝x ·－2x 的对应法则不同；对于C ，f (x )的定义域为R 与g (x )的定义域是{x |x ≠0}，定义域不同，故不是相同函数；对于D.f (x )＝|x 2－1|，g (t )＝|t 2－1|，定义域与对应关系都相同，故是相同函数，故选D.6．函数y ＝f (x )的图象与直线x ＝a 的交点个数有( ) A ．必有一个 B ．一个或两个 C ．至多一个 D ．可能两个以上[答案] C[解析] 当a 在f (x )定义域内时，有一个交点，否则无交点．二、填空题 7．已知函数f (x )＝11＋x，又知f (t )＝6，则t ＝________. [答案] －56[解析] f (t )＝1t ＋1＝6.∴t ＝－568．用区间表示下列数集： (1){x |x ≥1}＝________； (2){x |2＜x ≤4}＝________； (3){x |x ＞－1且x ≠2}＝________.[答案] (1)[1，＋∞) (2)(2,4] (3)(－1,2)∪(2，＋∞)三、解答题9．求下列函数的定义域，并用区间表示：(1)y ＝x ＋12x ＋1－1－x ；(2)y ＝5－x|x |－3.[分析] 列出满足条件的不等式组⇒解不等式组⇒求得定义域[解析] (1)要使函数有意义，自变量x 的取值必须满足⎩⎪⎨⎪⎧x ＋1≠01－x ≥0，解得x ≤1且x ≠－1，即函数定义域为{x |x ≤1且x ≠－1}＝(－∞，－1)∪(－1,1]．(2)要使函数有意义，自变量x 的取值必须满足⎩⎪⎨⎪⎧5－x ≥0|x |－3≠0，解得x ≤5，且x ≠±3，即函数定义域为{x |x ≤5，且x ≠±3}＝(－∞，－3)∪(－3,3)∪(3,5]． [规律总结] 定义域的求法：(1)如果f (x )是整式，那么函数的定义域是实数集R ；(2)如果f (x )是分式，那么函数的定义域是使分母不为0的实数的集合；(3)如果f (x )为偶次根式，那么函数的定义域是使根号内的式子大于或等于0的实数的集合；(4)如果f (x )是由几个部分的数学式子构成的，那么函数的定义域是使各部分式子都有意义的实数的集合．(5)如果函数有实际背景，那么除符合上述要求外，还要符合实际情况．函数定义域要用集合或区间形式表示，这一点初学者易忽视． 10．已知函数f (x )＝x ＋3＋1x ＋2. (1)求函数的定义域； (2)求f (－3)，f (23)的值；(3)当a ＞0时，求f (a )，f (a －1)的值．[解析] (1)使根式x ＋3有意义的实数x 的集合是{x |x ≥－3}，使分式1x ＋2有意义的实数x 的集合是{x |x ≠－2}，所以这个函数的定义域是{x |x ≥－3}∩{x |x ≠－2}＝{x |x ≥－3，且x ≠－2}．(2)f (－3)＝－3＋3＋1－3＋2＝－1； f (23)＝23＋3＋123＋2＝113＋38＝38＋333. (3)因为a ＞0，故f (a )，f (a －1)有意义．f (a )＝a ＋3＋1a ＋2；f (a －1)＝a －1＋3＋1a －1＋2＝a ＋2＋1a ＋1.能力提升一、选择题1．给出下列从A 到B 的对应：①A ＝N ，B ＝{0,1}，对应关系是：A 中的元素除以2所得的余数 ②A ＝{0,1,2}，B ＝{4,1,0}，对应关系是f ：x →y ＝x 2③A ＝{0,1,2}，B ＝{0,1，12}，对应关系是f ：x →y ＝1x其中表示从集合A 到集合B 的函数有( )个．( ) A ．1 B ．2 C ．3 D ．0[答案] B[解析] 由于③中，0这个元素在B 中无对应元素，故不是函数，因此选B. 2．(2012·高考安徽卷)下列函数中，不满足：f (2x )＝2f (x )的是( ) A ．f (x )＝|x | B ．f (x )＝x －|x | C ．f (x )＝x ＋1 D ．f (x )＝－x [答案] C[解析] f (x )＝kx 与f (x )＝k |x |均满足：f (2x )＝2f (x )得：A ，B ，D 满足条件． 3．(2014～2015惠安中学月考试题)A ＝{x |0≤x ≤2}，B ＝{y |1≤y ≤2}，下列图形中能表示以A 为定义域，B 为值域的函数的是( )[答案] B[解析] A 、C 、D 的值域都不是[1,2]，故选B. 4．(2015·盘锦高一检测)函数f (x )＝11－2x 的定义域为M ，g (x )＝x ＋1的定义域为N ，则M ∩N ＝( )A ．[－1，＋∞)B ．[－1，12)C ．(－1，12)D ．(－∞，12)[答案] B 二、填空题5．若函数f (x )的定义域为[2a －1，a ＋1]，值域为[a ＋3,4a ]，则a 的取值范围是________． [答案] (1,2)[解析] 由区间的定义知⎩⎪⎨⎪⎧2a －1＜a ＋1，a ＋3＜4a ⇒1＜a ＜2.6．函数y ＝f (x )的图象如图所示，那么f (x )的定义域是________；其中只与x 的一个值对应的y 值的范围是________．[答案] [－3,0]∪[2,3] [1,2)∪(4,5] [解析] 观察函数图象可知f (x )的定义域是[－3,0]∪[2,3]；只与x 的一个值对应的y 值的范围是[1,2)∪(4,5]．三、解答题7．求下列函数的定义域： (1)y ＝31－1－x；(2)y ＝x ＋10|x |－x；(3)y ＝2x ＋3－12－x ＋1x.[解析] (1)要使函数有意义，需⎩⎨⎧1－x ≥0，1－1－x ≠0⇔⎩⎪⎨⎪⎧x ≤1，x ≠0⇔x ≤1且x ≠0，所以函数y ＝31－1－x的定义域为(－∞，0)∪(0,1]．(2)由⎩⎪⎨⎪⎧x ＋1≠0，|x |－x ≠0得⎩⎪⎨⎪⎧x ≠－1，|x |≠x ，∴x ＜0且x ≠－1，∴原函数的定义域为{x |x ＜0且x ≠－1}． (3)要使函数有意义，需⎩⎪⎨⎪⎧2x ＋3≥0，2－x ＞0，x ≠0.解得－32≤x ＜2且x ≠0，所以函数y ＝2x ＋3－12－x ＋1x 的定义域为[－32，0)∪(0,2)．[点评] 求给出解析式的函数的定义域的步骤为：(1)列出使函数有意义的x 所适合的式子(往往是一个不等式组)；(2)解这个不等式组；(3)把不等式组的解表示成集合(或者区间)作为函数的定义域．8．已知函数f (x )＝1＋x 21－x 2，(1)求f (x )的定义域． (2)若f (a )＝2，求a 的值．(3)求证：f ⎝ ⎛⎭⎪⎫1x＝－f (x )． [解析] (1)要使函数f (x )＝1＋x 21－x 2有意义，只需1－x 2≠0，解得x ≠±1，所以函数的定义域为{x |x ≠±1}． (2)因为f (x )＝1＋x21－x2，且f (a )＝2，所以f (a )＝1＋a 21－a 2＝2，即a 2＝13，解得a ＝±33.(3)由已知得f ⎝ ⎛⎭⎪⎫1x ＝1＋⎝ ⎛⎭⎪⎫1x 21－⎝ ⎛⎭⎪⎫1x 2＝x 2＋1x 2－1，－f (x )＝－1＋x 21－x 2＝x 2＋1x 2－1， ∴f ⎝ ⎛⎭⎪⎫1x ＝－f (x )．第一章 1.2 1.2.2 第一课时函数的表示方法基础巩固一、选择题1．已知y 与x 成反比，且当x ＝2时，y ＝1，则y 关于x 的函数关系式为( ) A ．y ＝1xB ．y ＝－1xC ．y ＝2xD ．y ＝－2x[答案] C[解析] 设y ＝k x ，由1＝k 2得，k ＝2，因此，y 关于x 的函数关系式为y ＝2x.2．一等腰三角形的周长是20，底边长y 是关于腰长x 的函数，则它的解析式为( ) A ．y ＝20－2xB ．y ＝20－2x (0＜x ＜10)C ．y ＝20－2x (5≤x ≤10)D ．y ＝20－2x (5＜x ＜10)[答案] D[解析] 由题意得y ＋2x ＝20，∴y ＝20－2x .又∵2x ＞y ，∴2x ＞20－2x ，即x ＞5.由y ＞0，即20－2x ＞0得x ＜10，∴5＜x ＜10.故选D.3．设函数f (x )＝2x ＋3，g (x ＋2)＝f (x )，则g (x )的解析式是( ) A ．g (x )＝2x ＋1 B ．g (x )＝2x －1 C ．g (x )＝2x －3 D ．g (x )＝2x ＋7 [答案] B[解析] ∵g (x ＋2)＝f (x )＝2x ＋3，∴令x ＋2＝t ，则x ＝t －2，g (t )＝2(t －2)＋3＝2t －1.∴g (x )＝2x －1.4．(2015·安丘一中月考)某同学在一学期的5次大型考试中的数学成绩(总分120分)如下表所示：考试次数x12345。

数学人教版A必修1同步训练：1.1.1集合的含义与表示(附答案)

第一章集合与函数概念1. 1集合1. 1.1集合的含义与表示谋ffii常习二.........1. 下列说法正确的是()A . 2008年北京奥运会的比赛项目组成一个集合B. 某个班年龄较小的学生组成一个集合C. 集合{1,2,3}与{3,1,2}表示不同的集合3 1D. 1,0.5, 3，㊁组成的集合有四个元素2. 已知集合M具有性质：若a€ M,则2a€ M,现已知—1€M ,则下列元素一定是M中的元素的是…()A. 1B. 0C.—2D. 23. 用符号€或？填空.(1) 3.14 ____ Q, 0 ________ N, V2 ________ Z ,(—1)0 _______ N; _ _ _ _(2) 2V3 ______ {x|xv Vii},3 V2 _________ {x|x > 4}, V2 + 75 _______ {x|x w 2+ 3};(3) 3 ______ {x|x = n2+ 1, n € N},5 _______ {x|x = n2+ 1,n€ N};(4) ( —1,1) ____ {y|y = x2} , —1,1) ______ {(x , y)|y = x2}.4. 试选择适当的方法表示下列集合：(1) 直角坐标系中纵坐标与横坐标相等的点的集合；(2) 一年之中的四个季节组成的集合；(3) 方程x2+ x —1 = 0的实数解组成的集合；(4) 满足不等式1V 1 + 2x V 19的素数组成的集合.课堂巩固1若方程X2—5x + 6= 0和方程x2—x—2= 0的所有解构成的集合为M ，则M 中元素的个数为( )A．4 B．3 C．2 D．12. 已知集合S={a , b, c}中的三个元素可构成△ ABC的三条边长，那么△ ABC 一定不是()A .锐角三角形B .直角三角形C.钝角三角形 D .等腰三角形3. 设集合A = {1,2,3} , B = {1,3,5} , x € A，且x?B，贝U x 等于( )A．1 B．2 C．3 D．54．已知集合M={x|x=3n，n€ Z}，N={x|x=3n＋1，n€ Z}，P= {x|x = 3n—1, n€ Z}，且a€ M , b € N, c€ P,设d= a—b+ c,则()A．d€ M B．d€ NC．d€ P D．d€ M 且d€ N5. ____________________________________________ 设直线y = 2x+ 3上的点集为P,贝U P= _____________________ ；点(2,7)与点集P的关系为(2,7) __________ P.6．已知集合P={4,5,6} , Q={1,2,3} ．定义P?Q={x|x=p —q, p€ P, q€ Q}，贝陳合P?Q的所有元素之和为 __________________ .7．下面三个集合：①{x|y = x2+ 1}:②{y|y = x2+ 1}:③{(x , y)|y = x2+ 1}.(1) 它们是不是相同的集合？(2) 它们各自的含义是什么？8. 设S= {x|x = m+ n 2, m、n € Z}.(1) 若a€ Z,则a是否是集合S中的元素？⑵对S中的任意两个X I、X2,则X i+ X2、X i X2是否属于S?Cr课后检叭.1. 已知集合A = {X€ N3W X w 3}，则必有( )A . —1€ A B. 0 € AC. ,3€ AD. 2 € A2. 已知集合M = {X€ N|(8—X)€ N}，则M中元素的个数是()A . 10B . 9C. 8D.无数个3. (2008江西高考，2)定义集合运算：A*B = {z|z = xy ,x € A, y € B}.设A = {1,2} , B = {0,2}，则集合A*B的所有元素之和为()A. 0B. 2C. 3D. 6b4 .设a, b€ R，集合{1 , a+ b, a} = {0 , a，b}，贝U b —a 等于()A . 1B . —1C . 2 D. —25 .集合{3, i，3,4,…}可表示为()2n+1 一*A . {x|x = , n € N }6. 填空题： (1) 用列举法表示集合｛x € R |(x - 1)2 3 4(x + 1) = 0｝为11. 已知 f(x) = X 2 — ax + b(a 、b € R ), A = {x € R |f(x) -x = 0}, B = {x € R |f(x) — ax = 0}，若A = {1 , — 3}，试用列举法表示集合 B. 2 用列举法表示集合｛x € N 反土 € N ｝为 _______ ；3 用描述法表示集合｛2,4,6,8｝为 __________ ;一 1114 用描述法表示集合｛1, 2，3 4｝为 ____________ .7 .已知 x € ｛1,2 , x 2｝，贝U x = ______ .a b ab8. 设a , b 是非零实数，则y =商+血+ 的所有值组成的集合为 ________ .9. 已知集合 A = ｛x|ax 2 + 2x + 1 = 0, a € R ｝，若 A 中只有一个元素，求a 的值，并求出这个元素.1 + a10. 数集M 满足条件，若a € M,则一€ M(a 工±1且a ^ 0),1 — a已知3€ M ,试把由此确定的集合 M 的元素全部求出来.B.C.{x|x{x|x n {x|x n 2n + 1 n €N答案与解析第一章集合与函数概念1. 1集合1. 1.1集合的含义与表示课前预习1. A v A中各比赛项目是确定的且各不相同，二A正确; B中元素是不确定的；C中两集合是相等的；D中有3个元素.2. C •/ —1€ M ,二2X (—1)€ M，即—2€ M.3. (1) € € ? € (2)? € € ⑶？€⑷？€(1) 略.(2) 2 3 = 12> 11, 3 2 = 18> 16 = 4,2+ .5 = ■'( 2+ ；5)2= 7+ 2 ：10<「7+ 2 J2=(2+ 3)2= 2+. 3.(3) 令n2+ 1 = 3, n = 土2, n?N.令n2+ 1 = 5, n=±2,取n = 2,贝U n€ N.(4) {y|y = x2}中元素是数，而(—1,1)代表一个点.4. 解：(1){(x , y)|y = x} ；(2){春季，夏季，秋季，冬季};1 45 1 V!(3){ —2- "2，—2+R ；(4){2,3,5,7}.课堂巩固1. B I x2—5x + 6 = 0,二x = 2 或x = 3.又T x2—x — 2 = 0,二x = 2 或x=— 1.由集合中元素的互异性，知M = { —1,2,3}.2. D 由集合元素的互异性，知 ab、c各不相同.3. B 由已知，易知x可能等于1、2、3,且不能等于1、3、5,所以只能等于2.4. B 三个集合都是整数集的子集，集合M中的整数都能被3整除，集合N中的整数被3整除余数是1,集合P中的整数被3整除余数是2•三个集合中的整数n也可用其他字母来表示.于是，d = 3n—3l —1 + 3s —1 = 3(n —l + s)—2= 3(n —l + s—1) + 1 € N.5. {(x , y)|y = 2x + 3} € 点集P= {(x , y)|y = 2x + 3}.当x = 2 时，y = 2X 2+ 3= 7,二(2,7) € P.6. 15 当p = 4, q= 1,2,3 时，p —q= 3,2,1;当p= 5, q= 1,2,3 时，p —q = 4,3,2;当p= 6, q= 1,2,3 时，p —q = 5,4,3.所以P?Q = {1,2,3,4,5}，其所有元素之和为 1 + 2+ 3+ 4+ 57. 解：(1)不是相同的集合.(2)集合①是函数y = x2+ 1的自变量x所允许取到的值组成的集合，因为x可以取任意实数，所以{x|y = x2+ 1} = R;集合②是函数y = x2+ 1的所有函数值y所允许取到的值组成的集合，由二次函数图象，知y > 1，所以{y|y = x2+ 1} = {y|y > 1}；集合③是函数y= x2+ 1图象上的所有点的坐标组成的集合.如图所示：8. 解：(1)a是集合S的元素，因为a= a+ O X ,2€ S.(2)不妨设X1= m+ n 2, X2= p + q 2, m、n、p、q € Z.则x〔+ X2= (m+ n 2)+ (p+ q 2)= (m + p) + (n + q) .2, m、n、p、q € Z .二X1 + X2 € S; X1 x2= (m+ n 2) (p+ q 2) = (mp + 2nq) + (mq + np) 2, m、n、p、q€ Z.二x1 x2€ S综上,x1+ x2、x1 x2都属于S.课后检测1. B化简集合A = {0,1}，显然0€ A.2. B v x € N，且(8 - x) € N ,二x = 0,1,2,3,4,5,6,7,8,共9 个数.3. B v z= x y, x € A, y € B,••• z 的取值有：1X 0= 0,1 X 2 = 2,2X 0= 0,2X 2 = 4,故A*B = {0,2,4}.•••集合A*B 的所有元素之和为0 + 2 + 4 = 6.4. C由题意得，a z 0, b z 0,所以 a + b = 0, a = — b.于是，显然，键要分清起始数并限定范围.6. (1){ — 1,1} (2){0,3,4,5}(3) {x|(x — 2)(x — 4)(x — 6)(x — 8)= 0}或{大于 1 小于 9 的偶数}1 *(4){x|x = n ，n W 4 且 n €N }7. 0或2 当x = 1时，矛盾，故x z 1；当x = 2时，或x = 1(舍去).综上可知x = 0或2. {1,0， a} = {0，— 1，— a}. a =— 1，b = 1， b — a = 2.丄 5 7 9“ 357 由3, ^，3，4可得，5. D9W 2，3，4从中发现规律，关x 2= 1,这与集合中元素的互异性相 x 2 = 4符合题意；当x = x 2时x = 0素一1和3,用列举法表示为{ — 1,3}.9. 解：集合A 为单元素集，即方程ax 2 + 2x + 1 = 0有唯一解或两个相等的实数解.由于此方程二次项的系数不确定，所以要对a 分类讨论. a b aby = |a|+ |b| + |ab|=- 1 ；当 ab>0 时，则 a>0, b>0 或 a<0, b<0,"亠 a b ab b>o ,则有 y = G|+ jb|+面=3；b <°,则有 y = |t|+ jb|+琵=-1. 侖+备+聶的所有值组成的集合元素共有两个元8. { - 1,3}当 ab<0 时，若a>0, 若a<0, 所以y =1① a = 0 时，x = — 2；② a z 0 时，△= 4 一4a = 0, 所以a = 1,此时x =— 1.1+a 1+310.解：T a = 3€ M ,二 ==—2€ M. 1—a 1—311 —2 1 ….1一3 1 …=—三 € M. - - =3 € M.1 +23 1 +1 21 + 31 1 +2 =3 € M.1 — 2再把3代入将重复上面的运算过程，由集合中元素的互异性1 1可知 M = {3 , — 2, — 3,㊁}.点评：集合中的元素是互异的，即同一集合中的元素是互不相同的.它通常被用作检验所求未知数的值是否符合题意. 只要构成两个集合的元素是一样的，这两个集合就是相等的，与两个集合中元素的排列顺序无关.11. 解：f(x) — x = 0,即卩 x 2— (a + 1)x + b = 0.•-A = {1 , — 3},'+ (— 3) = a + 1, 二由韦达定理，得11X (— 3) = b.2f(x) — ax = 0,亦即 x + 6x — 3= 0.a = — 3,b = — 3.…f(x) = x + 3x — 3.••• B = {x|x2+ 6x —3= 0} = { —3—2 3, —3 + 2 3}.点评：列举法和描述法是表示集合的两种常用方法. 用列举法时要注意：元素间用逗号隔开；元素不重复；可不考虑元素间的顺序；若元素的个数较多需要省略时，必须把元素间的规律显示清楚后方可使用省略号. 用描述法时要注意：写清元素的一般符号及取值范围；明确集合中元素的特征；不能出现未被说明的字母；准确使用“且”与“或”等.。

2019高考数学总复习第一章1.1.1集合的含义与表示(第二课时)同步练习新人教A版必修1

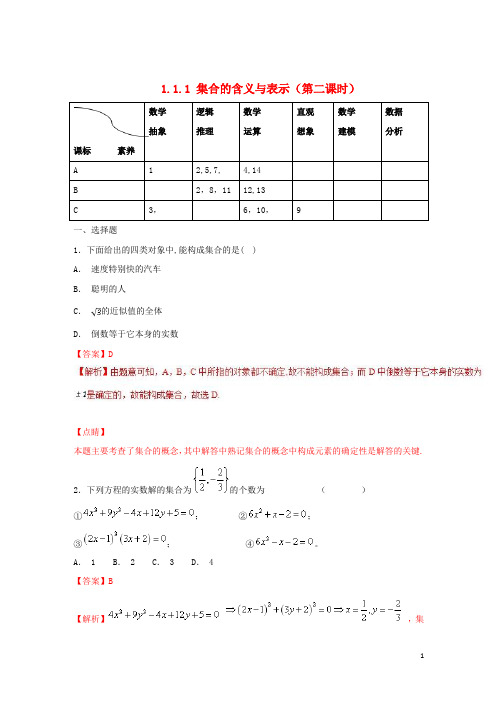
1.1.1 集合的含义与表示（第二课时）一、选择题1．下面给出的四类对象中,能构成集合的是( ) A ．速度特别快的汽车 B ．聪明的人 C ．的近似值的全体D ．倒数等于它本身的实数【答案】D【点睛】本题主要考查了集合的概念，其中解答中熟记集合的概念中构成元素的确定性是解答的关键.2．下列方程的实数解的集合为的个数为（）①； ②； ③； ④。

A ． 1B ． 2C ． 3D ． 4 【答案】B【解析】，集合为；，集合为；，集合为；，集合为；集合为的个数为2，选B.3．设A，B为两个实数集，定义集合A＋B＝{x|x1＋x2，x1∈A，x2∈B}，若A＝{1,2,3}，B＝{2,3}，则集合A＋B中元素的个数为 ( )A． 3 B． 4 C． 5 D． 6【答案】B【解析】当x1＝1时，x1＋x2＝1＋2＝3或x1＋x2＝1＋3＝4；当x1＝2时，x1＋x2＝2＋2＝4或x1＋x2＝2＋3＝5；当x1＝3时，x1＋x2＝3＋2＝5或x1＋x2＝3＋3＝6.∴A＋B＝{3,4,5,6}，共4个元素．故选B.4．已知x，y，z为非零实数，代数式的值所组成的集合是M，则下列判断正确的是( )A． 0∉M B． 2∈MC．－4∉M D． 4∈M【答案】D5．下列集合中，不同于另外三个集合的是 ( )A． {x|x＝1} B． {x|x2＝1}C． {1} D． {y|(y－1)2＝0}【答案】B【解析】 {x|x2＝1}＝{－1,1}，另外三个集合都是{1}，选B.6．方程组的解集是 ( )A． B． {x，y|x＝3且y＝－7}C． {3，－7} D． {(x，y)|x＝3且y＝－7}【答案】D【解析】解方程组得，用描述法表示为{(x，y)|x＝3且y＝－7}，用列举法表示为{(3，－7)}，故选D 7．(2015·山东临沂检测)集合{x∈N*|x－2＜3}的另一种表示形式是( )A． {0,1,2,3,4} B． {1,2,3,4}C． {0,1,2,3,4,5} D． {1,2,3,4,5}【答案】B【解析】由x－2＜3，得x＜5，又x∈N*，所以x＝1,2,3,4，即集合的另一种表示形式是{1,2,3,4}．故选B.8．已知集合A＝{x|x≤10}，a＝，则a与集合A的关系是( )A． a∈A B． a∉A C． a＝A D．{a}∈A【答案】A【解析】由于＋＜10，所以a∈A. 故选A.9．下列各组两个集合A和B表示同一集合的是A．B．C．D．【答案】C考点：集合的元素二、填空题10．已知集合A含有三个元素1,0，x，若x2∈A，则实数x＝________.【答案】-1【解析】当时，解得，与集合元素的互异性矛盾，故不成立；当时，解得，结合互异性可得；当时，解得或，不满足元素的互异性，舍去。

1.1.1集合的含义与表示同步练习及答案解析.doc

1.1.1 集合的含义与表示建议用时实际用时满分实际得分 45分钟 100分一、选择题(本大题共6小题，每小题6分，共36分)1．下列几组对象可以构成集合的是( )A ．充分接近π的实数的全体B ．善良的人C ．某校高一所有聪明的同学D ．某单位所有身高在1.7 m 以上的人2．下列四个说法中正确的个数是( )①集合N 中最小的数为1；②若a ∈N ，则－a N ；③若a ∈N ，b ∈N ，a b ，则a ＋b 的最小值为2；④所有小的正数组成一个集合．A ．0B ．1C ．2D ．33．集合A ＝{y |y ＝x 2＋1}，集合B ＝{(x ，y )|y ＝x 2＋1}(A ，B 中x ∈R ，y ∈R )，选项中元素与集合的关系都正确的是( )A ．2∈A ，且2∈BB ．(1,2)∈A ，且(1,2)∈BC ．2∈A ，且(3,10)∈BD ．(3,10)∈A ，且2∈B4．已知集合S 的三个元素a ，b ，c 是△ABC 的三边长，那么△ABC 一定不是( )A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等腰三角形5．已知x 、y 、z 为非零实数，代数式x |x |＋y |y |＋z |z |＋|xyz |xyz的值所组成的集合是M ，则下列判断正确的是( )A ．0MB ．2∈MC ．－4MD ．4∈M6. 若集合}044|{2=++=x kx x A 中有且仅有一个元素，则实数k 的值为（）A.{0}k ∈B.{1}k ∈C.{1,0}k ∈D.{1,1}k ∈-二、填空题（本大题共3小题，每小题6分，共18分）7．用“∈”或“”填空.(1)－3 ______N ； (2)3.14 ______Q ；(3)13 ______Z ； (4)－12______R ； (5)1 ______N *； (6)0 _______N .8．定义集合运算A *B ＝{M |M ＝xy ，x ∈A ，y ∈B }．设A ＝{1,2}，B ＝{0,2}，则集合A *B 的所有元素之和为________．9．由下列对象组成的集体属于集合的是________(填序号)．①不超过3的正整数；②高一数学课本中所有的难题；③中国的大城市；④平方后等于自身的数；⑤某校高一(2)班中考数学成绩在90分以上的学生．三、解答题（本大题共3小题，共46分）10．（14分）已知集合M＝{－2,3x2＋3x－4，x2＋x－4}，若2∈M，求x11．（15分）下面三个集合：A＝{x|y＝x2＋1}；B＝{y|y＝x2＋1}；C＝{(x，y)|y＝x2＋1}．问：(1)它们是不是相同的集合？(2)它们各自的含义是什么？12．（17分）设A 为实数集，且满足条件：若a ∈A ，则a11∈A (a ≠1)．求证：(1)若2∈A ，则A 中必还有另外两个元素；(2)集合A 不可能是单元素集一、选择题1. D 解析：A 、B 、C 都不满足元素的确定性，故不能构成集合.2. A 解析：N 是自然数集，最小的自然数是0，故①错；当为0时，也为0，是自然数，故②错；③中最小值应为1，故③错；“所有小的正数”范围不明确，不满足集合元素的确定性，故不能构成集合，故④错.故选A.3.C 解析：集合A 中元素y 是实数，不是点，故选项B ，D 不对．集合B 的元素(x ，y )是点而不是实数，2∈B 不正确，所以A 错．4. D 解析：由元素的互异性知a ，b ，c 均不相等,故一定不是等腰三角形.5. D 解析当x 、y 、z 中三个为正、两个为正、一个为正、全为负时，代数式的值分别为：4,0,0，－4，∴4∈M 正确，故选D.6.C 解析：（1）若0=k，则{1}A =-；（2）若0≠k ，16160k ∆=-=，1k =，∴{1,0}.k ∈ 二、填空题7. (1) (2)∈ (3) (4)∈ (5)∈ (6)∈解析：理解各符号的意义是关键.N 是自然数集，N *是正整数集，Q 是有理数集，Z 是整数集，R 是实数集.8. 6 解析: ∵A *B ＝{0,2,4}，所以集合A *B 的所有元素之和为6.9.①④⑤ 解析：②中“难题”标准不明确，不满足确定性；③中“大城市”标准不明确，不满足确定性.三、解答题10.解：当3x 2＋3x －4＝2时，3x 2＋3x －6＝0，x 2＋x －2＝0，x ＝－2或x ＝1.经检验，x ＝－2，x ＝1均不合题意．当x 2＋x －4＝2时，x 2＋x －6＝0，x ＝－3或2.经检验，x ＝－3或x ＝2均合题意． ∴x ＝－3或x ＝2.11.解：(1)在、、三个集合中，虽然代表元素满足的表达式一致，但代表元素互不相同，所以它们是互不相同的集合．(2)集合的代表元素是x ，满足＝2＋1，故＝{|＝2＋1}＝.集合的代表元素是，满足＝2＋1的≥1，故＝{|＝2＋1}＝{|≥1}.集合的代表元素是(，)，满足条件＝2＋1，即表示满足＝2＋1的实数对(，)；也可认为满足条件＝2＋1的坐标平面上的点．12.证明：(1)若a ∈A ，则a-11∈A （≠1）.又∵2∈A ，∴11－2＝－1∈A . ∵－1∈A ，∴11－(－1)＝12∈A .∵12∈A ，∴11－12＝2∈A . ∴A 中必还有另外两个元素，为－1，12. (2)若A 为单元素集，则a ＝a -11，即a 2－a ＋1＝0，方程无解． ∴a ≠a-11，∴A 不可能为单元素集。

必修一第一章集合与函数概念同步练习(含答案)

第一章集合与函数概念同步练习1.1.1 集合的含义与表示一. 选择题：1.下列对象不能组成集合的是（）A.小于100的自然数B.大熊猫自然保护区C.立方体内若干点的全体D.抛物线2x y =上所有的点 2.下列关系正确的是（）A.N 与+Z 里的元素都一样B.},,{},,{c a b c b a 与为两个不同的集合C.由方程0)1(2=-x x 的根构成的集合为}1,1,0{D.数集Q 为无限集 3.下列说法不正确的是（）A.*0N ∈B.Z ∉1.0C.N ∈0D.Q ∈24.方程⎩⎨⎧-=-=+3212y x y x 的解集是（）A.}1,1{-B.)1,1(-C.)}1,1{(-D.1,1-二.填空题：5.不大于6的自然数组成的集合用列举法表示______________.6.试用适当的方式表示被3除余2的自然数的集合____________.7.已知集合}7,3,2,0{=M ，由M 中任取两个元素相乘得到的积组成的集合为 ________. 8.已知集合}012{2=++∈=x ax R x M 只含有一个元素，则实数=a ______,若M 为空集,可a 的取值范围为_________.三.解答题：9.代数式}{)8(2x x x ∈-- ，求实数x 的值。

10.设集合A=},,2),{(N y x x y y x ∈+-=，试用列举法表示该集合。

11.已知}33,2{12+++∈x x x 试求实数x 的值。

1.1.2 集合的含义与表示一. 选择题：1.集合Φ与}0{的关系，下列表达正确的是（） A.φ=}0{ B.φ⊆}0{ C.}0{∈φ D.φ}0{⊇2.已知集合A=}3,2,1{，则下列可以作为A 的子集的是（）A.}4,1{B.}3,2{C.}4,2{D.}4,3,1{ 3.集合},,{c b a 的非空真子集个数是（）A.5B.6C.7D.8 4.已知集合M={正方形}，N={菱形}，则（）A.N M =B.N M ∈C.M ≠⊂ND.N ≠⊂M二.填空题5.用适当的符号填空①},2_____{0Z n n x x ∈=②}_____{1质数③},,_____{}{c b a a ④}0))((_____{},{=--b x a x x b a ⑤},12______{},14{++∈+=∈+=N k k x x N k k x x 6.写出集合}1{2=x x 的所有子集_______________________7.设集合}{},63{a x x B x x A <=≤<-=，且满足A ≠⊂,B 则实数a 的取值范围是_________三.解答题8.已知集合B 满足}2,1{≠⊂B ⊆}5,4,3,2,1{，试写出所有这样的集合 9.已知}5{>=x x A ，}3{x x B <=，试判断A 与B 的关系 10.已知A=}3,4,1{},2,1{a B a =+，且B A ⊆，求a 的值1.1.3集合的基本运算（一）一.选择题1.已知集合A=}4,3,2,1{，}6,4,1{=B ，则=B A I （） A.}4,2,1{ B.}6,4,3,2,1{ C.}4,1{ D.}4,3,1{2.设A=}2{->x x ，}21{<<-=x x B ，则=B A Y （） A.R B.}2{<x x C.}1{->x x D.}2{->x x3.设{=A 等腰三角形} ，B={等边三角形}，C={直角三角形}，=C B A I Y )(（） A.{等腰三角形} B.{直角三角形} C.φ D.{等腰直角三角形}4.已知集合}90{<<∈=x Z x M ，},2{+∈==N n n x x N ，则=N M I （）A.{}6,4,2B.{}8,6,4,2C.{}7,6,5,4,3,2D.{}8,7,6,5,4,3,2,1 二.填空题5.{偶数}I {奇数}=__________.6.已知集合}31{<≤-=x x A ，}13{≤<-=x x B ，则=B A I __________.7.若集合A B A =I ，则=B A Y ___________.8.已知集合}33{<≤-=x x A ，}2{≤=x x B ，则=B A Y ___________.三.解答题9.集合},,523),{(R y x y x y x A ∈=-=},,132),{(R y x y x y x B ∈-=+=，求 B A I 10.已知集合},3,1{a A =，}1,1{2+-=a a B ，且A B A =Y ，求a 的值 11.已知集合},02{2=+-∈=b ax x R x A }05)2(6{2=++++∈=b x a x R x B且}21{=B A I ，求B A Y1.1.3集合的基本运算（二）一.选择题1.已知全集R U =，集合}1{<=x x M ，则M C u 为（） A.}1{≥x x B.}1{>x x C.}1{<x x D.}1{≤x x2.设全集}4,3,2{=U ，}2,3{-=a A ，}3{=A C u ，则a 的值是（） A.7 B.1- C.17-或 D.71-或3.已知全集R U =，集合}32{<≤-=x x A ，则A C u =（）A.}32{≥-≤x x x 或B.}32{>-≤x x x 或C.}32{>-<x x x 或D.}32{≥-<x x x 或 4.已知全集}8,7,6,5,4,3,2,1{=U ，集合}5,4,3{=A ，}6,3,1{=B ，那么集合 C={2，7，8}可以表示为（）A.B C uB.B A IC.B C A C u u ID.B C A C u u Y二.填空题5.设全集R U =，}62{<≤=x x A ，}4{≤=x x B ，则B A I =__，__=B C A u I ,__=B A C u I .6.全集=U {三角形}，=A {直角三角形}，则A C u =____________.7.设全集}4,3,2,1,0{=U }3,2,1,0{=A ，}4,3,2{=B ，则=B A C u I ____8.已知全集},2,1,0{=U 且}2{=A C u ，则A 的真子集共有___个.三.解答题9.设全集R U =，集合},43{R x x x M ∈<≤-=，},51{R x x x N ∈≤<-=,求①N M Y ②N C M C u u I10.设全集=U {1，2，3，4，5，6，7，8，9}，集合}2{=B A I ，}9,1{=B C A C u u I ，}8,6,4{=B A C u I ，求B A ,11.已知}1,4,2{2+-=x x U ，}1,2{+=x B ，}7{=B C u ，求x 的值1.2.1函数的概念（一）一.选择题1.函数13)(+=x x f 的定义域为（）A.)31,(--∞B.),31(+∞- C.),31[+∞- D.]31,(--∞2.已知函数q px x x f ++=2)(满足0)2()1(==f f ，则)1(-f 的值为（） A.5 B.5- C.6 D.6-3.下列函数中)()(x g x f 与表示同一函数的是（）A.1)()(0==x g x x f 与 B.xx x g x x f 2)()(==与C.22)1()()(+==x x g x x f 与D.33)()(x x g x x f ==与 4.下列各图象中，哪一个不可能为)(x f y =的图象（）二.填空题5.已知x x x f 2)(2-=，则=)2(f ______________.6.已知12)1(2+=+x x f ,则=)(x f ______________.7.已知)(x f 的定义域为],4,2[则)23(-x f 的定义域为_______________. 8.函数11)(22---=x x x f 的定义域为______________.三.解答题9.设⎩⎨⎧≥+<-=)0(22)0(12)(2x x x x x f ，求)2(-f 和)3(f10.求下列函数的定义域（1）321)(+=x x f （2）x x x g -++=1)10()(011.已知)(x f 为一次函数，且34)]([+=x x f f ，求)(x fx(D)(B)(C) (A)x1.2.1函数的概念（二）一、选择题1.函数x x y 22-=的定义域为}3,2,1,0{，其值域为（） A.}3,0,1{- B.}3,2,1,0{ C.}31{≤≤-y y D.}30{≤≤y y2.函数)(11)(2R x xx f ∈+=的值域是（） A.)1,0( B.]1,0( C.)1,0[ D.]1,0[ 3.下列命题正确的有（） ①函数是从其定义域到值域的映射②x x x f -+-=23)(是函数③函数)(2N x x y ∈=的图象是一条直线④x x g xx x f ==)()(2与是同一函数 A.1个 B.2个 C.3个 D.4个 4.函数xx x y -+=)32(的定义域为（）A.⎭⎬⎫⎩⎨⎧-≠<230x x x 且B.{}0<x xC.{}0>x xD.⎭⎬⎫⎩⎨⎧-≠≠∈230x x R x 且二.填空题5.已知函数⎪⎩⎪⎨⎧≥<<--≤+=2,221,1,2)(2x x x x x x x f ，若3)(=x f ，则x 的值为__________.6.设函数33)(2+-=x x x f ，则)()(a f a f --等于____________.7.设函数x x x f --=1)(，则=)]1([f f ____________.8.函数[]3,1,322∈+-=x x x y 的值域是________________.三.解答题9.求函数242x x y --=的值域10.已知函数1122---=x x y ，求20072008y x +的值 11.已知函数bax xx f +=)(（a .0≠a ，b 且为常数）满足1)2(=f ，x x f =)(有唯一解，求函数)(x f y =的解析式和)]3([-f f 的值.1.2.2 函数表示法（一）一、选择题1.设集合{}c b a A ,,=，集合B=R ，以下对应关系中，一定能成建立A 到B 的映射的是（）A.对A 中的数开B.对A 中的数取倒数C.对A 中的数取算术平方D.对A 中的数开立方2.某人从甲村去乙村，一开始沿公路乘车，后来沿小路步行，图中横轴表示走的时间，纵轴表示某人与乙村的距离，则较符合该人走法的图是（）3.已知函数23)12(+=+x x f ，且2)(=a f ，则a 的值等于（）A.8B.1C.5D.1-4.若x xx f -=1)1(，则当10≠≠x x 且时，)(x f 等于（）A.x 1B.11-xC.x -11D.11-x二.填空题5.若[]36)(+=x x g f ，且12)(+=x x g ，则=)(x f ______________.6.二次函数的图象如图所示，则此函数的解析式为___________.ttt ABDC7.已知函数⎩⎨⎧<≥=0,0,)(2x x x x x f 则=-)2(f ________,)4(f =_______8.集合}5,3,1{-=B ，12)(-=x x f 是A 到B 的函数，则集合 A 可以表示为____________________三.解答题9.已知函数)(x f 是一次函数，且14)]([-=x x f f ，求)(x f 的解析式10.等腰三角形的周长为24，试写出底边长y 关于腰长x 的函数关系式，并画出它的图象 11.作出函数31--+=x x y 的图象，并求出相应的函数值域1.2.2 函数表示法（二）一、选择题1.已知集合{}{}20,40≤≤=≤≤=y y B x x A ，按对应关系f ，不能成为从A 至B 的映射的一个是（） A.x y x f 21:=→ B.2:-=→x y x f C.x y x f =→: D.2:-=→x y x f2.如图，函数1+=x y 的图象是（）y3.设}8,6,2,1,0,21{},4,2,1,0{==B A ，下列对应关系能构成A 到B 的映射的是（）A.1:3-→x x fB.2)1(:-→x x fC.12:-→x x fD.x x f 2:→4.已知函数⎩⎨⎧>+-≤+=1,31,1)(x x x x x f ，则⎥⎦⎤⎢⎣⎡)25(f f =（） A.21 B.23 C.25 D.29 二.填空题5.设函数⎪⎪⎩⎪⎪⎨⎧≥<≤-<≤-+=2,320,2101,22)(x x x x x x f ，则)43(-f 的值为______, )(x f 的定义域为_____.6.)(x f 的图象如图，则)(x f =____________.7.对于任意R x ∈都有)(2)1(x f x f =+，当10≤≤x 时，)5.1-的值是____________.8.23)1(+=+x x f ，且2)(=a f ，则a 的值等于____________.三.解答题9.作出下列函数的图象（1）x y -=1,)2(≤∈x Z x 且（2）3422--=x x y ,)30(<≤xA B CD10.已知函数⎩⎨⎧<+≥-=4),3(4,4)(x x f x x x f ，求)1(-f 的值11.求下列函数的解析式（1）已知)(x f 是二次函数，且1)()1(,2)0(-=-+=x x f x f f ，求)(x f （2）已知x x f x f 5)()(3=-+，求)(x f1.3.1 函数单调性与最大（小）值（一）一.选择题1.若),(b a 是函数)(x f y =的单调递增区间，()b a x x ,,21∈，且21x x <，（） A.)()(21x f x f < B.)()(21x f x f = C.)()(21x f x f > D.以上都不正确2.下列结论正确的是（）A.函数x y -=在R 上是增函数B.函数2x y =在R 上是增函数C.x y =在定义域内为减函数D.xy 1=在)0,(-∞上为减函数 3.函数111--=x y （） A.在),1(+∞-内单调递增 B.在),1(+∞-内单调递减 C.在),1(+∞内单调递增 D.在),1(+∞内单调递减 4.下列函数在区间),0(+∞上为单调增函数的是（） A.x y 21-= B.x x y 22+= C.2x y -= D.xy 2=二.填空题5.已知函数)(x f 在),0(+∞上为减函数，那么)1(2+-a a f 与)43(f 的大小关系是________.6.函数)(x f y =7.已知13)(22-+-=a ax ax x f )0(<a ，则3(f ______.8.函数342+--=x x y 的单调递增区间为_______,当=x _______时,y 有最______值为____.三.解答题9.已知)(x f y =在定义域)1,1(-上为减函数，且)1()1(2-<-a f a f 求a 的取值范围。