ncode 资料customer_correlation

合集下载

一套完整的疲劳分析设计试验管理系统nSoft

中国机械工程 CHINA MECHANICAL ENGINEERING 1998年11月第9卷第11期科技期刊一套完整的疲劳分析设计试验管理系统nSoft林晓斌摘要介绍了nCode 国际有限公司发展的一套完整的疲劳分析系统nSoft 。

该系统专门为解决工程系统的疲劳问题而设计，主要由数据分析、数据显示、疲劳分析软件以及其它一些专门软件组成。

可用在数据采集、疲劳设计分析以及实验室疲劳模拟等部门。

关键词疲劳分析动态数据处理工程设计实验室模拟中国图书资料分类法分类号 TP202nSoft 是一个“由工程师为工程师设计”的工程疲劳分析系统，它的功能覆盖了工程抗疲劳设计分析3个主要领域，即数据采集、疲劳分析以及实验室模拟，并将它们紧密地结合在一起，见图1。

nSoft 集现代疲劳理论、数据信号分析处理和最新的计算机技术于一体，为工程界提供了全套功能强大的抗疲劳设计工具。

图1 工程抗疲劳设计分析中的几个主要步骤1 nSoft 系统简介nSoft 是由许多独立模块组成的一个开放系统。

每一模块可在计算机操作环境下独立启动，模块之间的传递主要通过数据文件实现。

可处理的数据文件长度没有限制。

nSoft 也有一个独特的管理界面，它可以帮助用户设置操作环境，记录所执行的命令，启动各个模块，查阅在线操作手册，阅读疲劳背景知识电子文件等，nSoft 配有功能强大的、nCode 自己发展的命令语言nCL ，使用nCL 可以使得繁琐重复的工作自动化，并允许用户进行二次开发，发展出自己所需要的模块。

nSoft 配置的报告编辑工具，可让用户获得满意的报告格式，并且也能很方便地将nSoft 产生的图形及结果记录文件复制到一般的图文编辑软件里去。

nSoft 当前能在多种操作平台上工作，如DOS 、微软视窗95/NT 、UNIX(SGI 、SPARC 、HP 、IBM)、X 和MOTIF 。

另外，为了帮助用户进行疲劳分析，nSoft 还配有丰富的材料性能、应力强度因子和应力集中因子数据库。

快消品从业人员必懂的英文销售术语

快消品从业人员必懂的英文销售术语常见的150余条英文销售术语整理如下:DA（Distribution & Assortment）分销Location：位置Display：陈列Pricing：价格Inventory：库存Merchandising：助销Promotion：促销KA（Key Account）：重点客户GKA（Global Key Account）：全球性重点客户NKA（National Key Account）：全国性重点客户LKA（Local Key Account）：地方性重点客户RKA（Retail Key Account ）：零售重点客户SM（ShoppingMall）：大型购物消费中心简称销品茂HYM（Hypermarket）：巨型超级市场，简称大卖场SPM（Supermarket）：超级市场，简称超市S-SPM（Small-Supermarket）：小型超市M-SPM（Middle-Supermarket）：中型超市L-SPM（Large-Supermarket）：大型超市C&C（Cash & Carry）：仓储式会员店CVS（Convenience Store）：便利店GS（Gas Station）：加油站便利店DS（Discount Store）：折扣店MT（Modern Trade ）：现代渠道TT（Tradiditional Trade）：传统渠道OT（Organized Trade）：现代特殊渠道OP（On Premise ）：餐饮渠道HBR（Hotel,Bar,Restaurant）：旅馆、酒吧、餐馆等封闭性通路WHS（Wholesaler）：批发商2nd tier Ws：二级批发商DT（Distributor）：经销商，分销商2ndDT：二级分销商DIST（Distributor System）：专营分销商MW（Managed Wholesalers）：管制批发商PW（Passive Wholesalers）：传统批发商DSD（Direct Store Delivery）：店铺直接配送CSTD（Company Sells Third Party Delivers）：我销他送DC（Distribution Center）：配送中心TPL（Third Party Logistics）：第三方物流CRP（Contiuous Replenishment）：持续补货CAO（Computer Assisted Ordering）：计算机辅助订货PUR（Purchase）：进货OOS（Out of Stock）：缺货Inventory day：库存天数SKU（Stock Keeping Uint）：最小库存计量单位UPC：通用产品编码Bar Code：条形码Slim（Slim）：纤细,苗条(包装)TC：铁罐包装AC：铝罐包装TP（TETRA PAK）：利乐无菌包装(俗称纸包装)PET：宝特瓶(俗称胶瓶)POSM（Point of Sale Materials）：陈列品GE（Gondola End）：端架MIT（Marketing Inpact Team）：卖场整合性陈列；堆箱TG（Type Genus ）：堆头Island Display：堆头式陈列Floor Display：落地割箱陈列Pallet Display：卡板陈列Strip Display：挂条陈列Sidekick Display：侧挂陈列Checkout Display：收银台陈列Cooler Display：冰柜陈列Secondary Display：二次陈列Cross Display：交叉陈列PG（Promotion Girl）：促销员P-T（Part-timer）：临时工，特指临促POP（Point Of Purchase）：门店广告Price discount：特价On-Pack：绑赠Sampling：试吃Road Show：路演，大型户外促销活动DM（Direct Mail ）：商场快讯商品广告；邮报PR（Public Relation）：公共关系NP（News Paper）：报纸杂志AD（Advertisement）：广告GRP（Gross Rating Point）：毛评点;总收视点（媒介用语）Loyalty：忠诚度Penetration：渗透率Value Share：市场份额AVE（Average）：平均数WTD（Weighted）：加权NUM（Numeric）：数值PP（Previous Period）：上期YA（Year Ago）：去年同期VOL（Volume）：销售量VAL（Value）：销售额VAL-PP（Value PP）：上期销售额VAL-YA（Value YA）：去年同期销售额YTD（Year To Date ）：截至当期的本年累计MTD（Means Month to Date）：本月到今天为止SPPD（Sales Per Point of Distribution）：每点销售额BTL（Below The Line）：线下费用ATL（Above The Line）：线上费用ABC（Activity based costing）：成本动因核算法（又称：巴雷托分析法）U&A（Usage and Attitude）：消费态度和行为(市场调查)FGD（Focus Group Discuss）：座谈会(市调一种)Store Check：终端调查，铺市率调查CR：销售代表CR-OP：销售代表-餐饮渠道CR-OT：销售代表-现代特殊渠道CR-MT：销售代表-现代渠道CR-TT：销售代表-传统渠道OTCR：现代渠道销售代表WDR：批发拓展代表ADR：客户拓展代表DCR：分销商合约代表DSR：分销商销售代表KSR：大客户销售主任KAM：重点客户经理CDM：渠道拓展经理MDR：市场拓展代表MDE：市场拓展主任MDM：市场拓展经理TMM：通路行销市场经理TDS：区域拓展主任TDM：区域拓展经理LTDM：高级区域拓展经理UM：业务单位经理（大区经理）GM（General Manager）：总经理GMDR（General Manager Direct Reports ）：总经理直接下属VP（Vice President）：副总裁FVP（First Vice President）：第一副总裁AVP（Assistant Vice President）：副总裁助理CEO（Chief Executive Officer）：首席执行官COO（Chief Operations Officer）：首席运营官CFO（Chief Financial Officer）：首席财务官CIO（Chief Information Officer）：首席信息官Director：总监HRD（Human Resource Director）：人力资源总监OD（Operations Director）：运营总监MD（Marketing Director）：市场总监OM（Operations Manager）：运营经理PM （Product Manager）：产品经理BM（Brand Manager）：品牌经理4P（Product、Price、Place、Promotion）：4P营销理论(产品、价格、渠道、促销)4C（Customer、Cost、Convenience、Communication）：4C营销理论(顾客、成本、便利、沟通)4V（Variation、Versatility、Value、Vibration）：4V营销理论(差异化、功能化、附加价值、共鸣)SWOT（Strengths、Weaknesses、Opportunities、Threats）：SWOT分析法(优势、劣势、机遇、威胁)FABE（Feature、Advantage、Benefit、Evidence）：FABE法则(特性、优点、利益、证据)USP（Unique Selling Propostion）：独特销售主张3A（Avalible、Able、Adsire）：买得到、买得起、乐得买PDCA（Plan、Do、Check、Action）：PDCA循环管理(计划、执行、检查、行动)OEM（Original Equipment Manufacturer）：原始设备制造商,俗称“贴牌”ODM（Original Design Manufacturer）：原装设计制造商OBM（Own Brand Manufacturer）：自有品牌制造商IPO（Initial Public Offering）：首次公开募股LOGO：商标Slogan：广告语FMCG（Fast Moving Consumer Goods）：快速消费品DCG（Durable Consumer Goods）：耐用消费品。

ncode分析流程

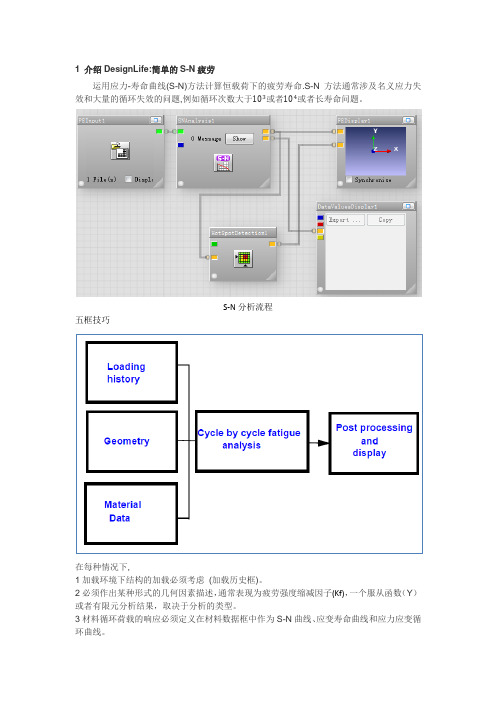
1 介绍DesignLife:简单的S-N疲劳运用应力-寿命曲线(S-N)方法计算恒载荷下的疲劳寿命.S-N方法通常涉及名义应力失效和大量的循环失效的问题,例如循环次数大于103或者104或者长寿命问题。

S-N分析流程五框技巧在每种情况下,1加载环境下结构的加载必须考虑(加载历史框)。

2必须作出某种形式的几何因素描述，通常表现为疲劳强度缩减因子(Kf)，一个服从函数（Y）或者有限元分析结果，取决于分析的类型。

3材料循环荷载的响应必须定义在材料数据框中作为S-N曲线、应变寿命曲线和应力应变循环曲线。

这里有三个输入合并在一个cycle-by-cycle fatigue analysis中，和一个后处理结果显示。

最初的结果应该是被最先考虑的，因为每个输入都遭受不同的变化和处理，由于模型或大或小的改变输入，初始疲劳分析结果影响后期处理灵敏度的结果。

放大：shift+中键框选，或者shift+左键拖动或者shift+右键自由图画旋转：ctrl+左键平移：ctrl+右键1、设置求解器属性2、设置材料属性(Edit Material Map) 本例恒载荷选PeakValley无影响3、赋材料参数4、编辑载荷（恒幅）即：最大3倍重力。

5、Run 完成2 介绍DesignLife:简单E-N疲劳E-N方法通常涉及到的一些循环载荷相对较大,大的塑性变形和与他们他们有关的,相对较短的寿命。

典型的是指低周疲劳和应变疲劳，即使对高周疲劳也很有效。

低周疲劳转化为高周疲劳通常发生104到105次循环。

不像S-N方法，通过提供时间历程文件作为载荷文件的输入，E-N方法更加量化了结构区域发生破坏的循环次数。

E-N分析流程因为E-N方法既可以用于高周疲劳也可以用于低周疲劳，它非常灵活。

也有可能用高周疲劳或者低周疲劳产生同样的结果。

1、编辑E-N分析属性PeakVally减少了时间历程点数目，Limit用于粗糙计算疲劳2、编辑材料属性3、指定分析载荷即默认配置。

canonical_correlation_analysis_stata_概述及解释说明

canonical correlation analysis stata 概述及解释说明1. 引言1.1 概述在统计分析和数据挖掘领域，Canonical Correlation Analysis（CCA）是一种常用的多变量分析技术，用于探索两组或多组变量之间的关联性。

该方法能够帮助我们理解不同变量集合之间的相关结构，以及它们对总体方差贡献的程度。

本文将结合使用Stata软件来介绍CCA的基本原理、数据准备、模型建立与推断等关键步骤，并通过实际应用案例进行详细解读和讨论。

1.2 文章结构全文共分为五个主要部分。

首先，引言部分提供了文章的背景、目标和整体架构。

接下来，第二部分介绍了CCA的理论基础，包括相关概念和数学模型。

第三部分详细说明了如何在Stata软件中进行CCA分析，包括数据导入与处理、模型拟合与结果解释以及结果可视化和评估等方面。

第四部分通过一个具体的应用案例展示了CCA在实践中的应用，并进行结果分析和讨论。

最后，在第五部分中对整篇文章进行总结，并展望未来可能的研究方向。

1.3 目的本文的主要目的是向读者介绍CCA方法在统计分析中的应用，并提供一个使用Stata软件进行CCA分析的实际操作指南。

通过深入了解CCA方法和技巧，读者可以更好地理解多变量数据集之间的关系，并将该方法应用于自己感兴趣的研究领域中。

接下来，将详细介绍CCA的理论基础、数据准备和模型建立与推断等方面内容。

2. Canonical Correlation Analysis (CCA):2.1 理论基础:Canonical Correlation Analysis (CCA)是一种统计分析方法，用于探索和量化两个多元变量集之间的关系。

它能够帮助我们理解这两组变量中的成对观测之间的相关性，并找到最大化这两组变量之间相关性的线性组合。

CCA通过计算两组变量的投影向量来实现这一目标，从而将其转化为线性无关性问题。

2.2 数据准备:在执行CCA之前，需要确保数据的准备工作已经完成。

ncode标记数值

ncode标记数值1. 什么是ncode标记数值？ncode是一种标记数值的方法，用于将特定的数值进行标记和编码，以便在数据处理和分析中使用。

ncode标记数值是一种常用的数据处理技术，它能够将数值转换为具有特定含义的代码，方便数据的管理和分析。

2. ncode标记数值的应用领域ncode标记数值广泛应用于各个领域，包括科学研究、统计学、金融分析、市场调研等。

以下是一些具体的应用领域：2.1 科学研究在科学研究中，研究人员常常需要处理大量的数据。

通过使用ncode标记数值，可以对数据进行分类、排序和筛选，从而更好地理解和分析数据。

例如，在生物学研究中，可以使用ncode标记数值对基因进行编码，以便对不同基因进行比较和分析。

2.2 统计学统计学是ncode标记数值的主要应用领域之一。

通过将数值进行标记，可以更好地进行统计分析和数据建模。

例如，在社会调查中，可以使用ncode标记数值对不同的调查问题进行编码，以便对数据进行统计分析和结果展示。

2.3 金融分析在金融领域，ncode标记数值被广泛应用于股票市场和投资分析。

通过将股票价格和交易量进行编码，可以更好地进行趋势分析和模型建立。

这对于投资者来说是非常重要的，因为它可以帮助他们做出更明智的投资决策。

2.4 市场调研在市场调研中，ncode标记数值可以用于对消费者行为和市场趋势进行编码和分析。

通过将市场数据进行标记，可以更好地了解消费者的需求和喜好，从而为企业的市场战略提供有力的支持。

3. ncode标记数值的具体操作方法ncode标记数值的具体操作方法可以分为以下几个步骤：3.1 确定数值的含义首先，需要确定数值的含义和要标记的内容。

这可以根据具体的应用场景和需求来确定。

例如，在股票市场中，可以将不同的股票价格范围进行编码，如将价格在0-10之间的股票标记为A类，10-20之间的股票标记为B类，以此类推。

3.2 设计编码规则根据数值的含义，设计编码规则。

Ncode案例doc资料

虚拟疲劳分析软件DesignLife应用案例传统的汽车整车和零部件开发通常都通过产品在试验室中的台架耐久性试验，或试车场道路试验，以验证产品是否满足其设计目标，这一过程周期很长，成本很高，发现问题较晚。

在当今的产品开发中，汽车企业越来越多地应用虚拟模拟分析技术，在实物样机出来之前就对其进行疲劳耐久性预测，在设计的早期消除不合格的设计，并通过设计比较，挑选出好的设计。

实践证明，进行虚拟寿命分析，能大大加快产品的开发，减少试验的工作量，节省成本。

新一代CAE疲劳分析软件ICE-flow DesignLife是nCode公司的旗舰产品之一。

它不仅继承了已经在工程上得到广泛应用的FE-Fatigue的功能特点，而且在软件的使用方便性方面也有了极大的改进。

本文首先介绍虚拟寿命分析的一般步骤，然后将重点介绍在汽车零部件疲劳分析中应用DesignLife的几个案例，以帮助读者深入了解并把握虚拟疲劳分析中的一些要点和难点。

典型步骤疲劳分析是一项较为复杂的工作，通常需要分析者对所分析的问题，以及需要从分析中获得什么样的结果有一个深刻的理解。

通常所说的虚拟疲劳分析，指的是基于有限元分析结果的疲劳分析，就是将有限元分析结果，通常是应力应变结果，作为疲劳分析的一个主要输入。

通过一个疲劳分析模型，计算出零部件或结构表面的疲劳寿命分布，以帮助判断设计寿命是否达到，或进行寿命优化设计。

步骤如下：1. 选择一个合适的疲劳分析模型汽车疲劳分析中常用的分析模型有局部应力法、局部应变法、焊点疲劳分析法和焊缝疲劳分析法，另外还有较为复杂的Dang Van多轴安全因子法、振动疲劳分析和高温疲劳分析等。

不同的分析方法需要不同的有限元分析结果和材料性能输入。

2. 准备有限元分析结果一旦疲劳分析模型已经选择，那么需要什么有限元分析结果也将明确。

比如，局部应力或应变法通常需要应力结果，而焊点分析法则需要焊点单元的力和力矩。

有限元分析通常对每一个作用在零部件或结构中的力和力矩做单位静力线性计算，应力输出结果可以是未平均的，或已平均的节点值，或者单元值。

物流学 key terms

Channel intermediaries 渠道中介Cost trade-offs 成本权衡Economic utility 经济效用FOB destination pricingsystems 目的港船上交货定价FOB origin pricing systems装运港船上交货定价Form utility 形式效用Freight absorption 费用吸收Inbound logistics 内向物流Landed costs 抵岸成本Logistics 物流Mass logistics 大规模物流Materials management 物料管理 Phantom freight 虚假运费Place utility 空间效用Possession utility 拥有效用Power retailer 强势零售商postponement 延迟 Reverse logistics 逆向物流Stock-keeping units (SKUs) 最小存货单位Stockouts 缺货Systems approach 系统方法Tailored logistics 剪裁式物流Time utility 时间效用Total cost approach 总成本方法Benchmarking 标杆管理 Cause-and-effect (associative)forecasting 因果预测Collaborative planning, forecasting and replenishment (CPFR) 协作计划、预测和补货Customer satisfaction 顾客满意Customer service 顾客服务Demand management 需求管理Judgmental forecasting 主观判断预测Make-to-order 按订单生产Make-to-stock 备货型生产Order cycle 订货周期Order delivery 订单交付Order fill rate 订单满足率Order management 订单管理Order picking and assembly拣货与组合Order processing 订单处理Order transmittal 订单传递Order triage 订单类选Pick-to-light technology 按灯拣选技术Service recovery 服务补救Time series forecasting 时间序列预测Transit time 运送时间Building-blocks concept 组块概念Closed-loop systems 闭环系统Container 集装箱Cube out 容量满载Ergonomics 人类工效学（人因工程学）Materials handling 物料搬运Package testing 包装测试Packaging 包装Pallets (skid) 托盘（平台）Part-to-picker system 储位至拣货者系统Picker-to-part system 拣货者至储位系统Shrink-wrap 伸缩包装Package testing 包装测试Packaging 包装Pallets (skid) 托盘（平台）Part-to-picker system 储位至拣货者系统Picker-to-part system 拣货者至储位系统Shrink-wrap 伸缩包装Slip sheet 滑板Unitization 单元化Unit loads 单位装载Unit load devices 单位装载设备Weighing out 重量满载Accessorial service 补充服务Barge 驳船Broker 经纪人Common carrier 公共承运人Consignee 收货人Contract carrier 契约承运人Department of transportation交通部Dimensional (dim) weight体积计重Excess capacity 剩余能力Exempt carrier 豁免承运人Freight forwarder 货运代理人Intermodal transportation 联合运输Line-haul 长途运输Parcel carriers 包裹承运人Piggyback transportation驮背式运输Private carrier 自有车辆承运人Rail gauge 轨间距Shippers’ associations 托运人协会 Slurry systems 泥浆系统Surface transportation board 地面运输委员会TEU 国际标准箱单位Terminal 集散中心Ton miles 吨英里Transportation 运输Amodal shipper 非模式托运人Bill of lading 提单Class rate system 等级费率系统Commodity rate 商品费率Demurrage 滞期费（逾期费）Density 密度Detention 滞留费Diversion 转港Documentation 单证Expediting 加急运输Freight bill 运费清单Freight claims 货物索赔Hazardous material 危险品Reconsignment 再交付Routing 运输路线选择Routing guide 路径指南Stowability 易装载性Tracing 货物追踪Transportation management运输管理Weight break 分界重量 ABC analysis ABC分类法Complementary products 互补产品 Cycle (base) stock 周转（基本）库存Dead inventory 呆滞库存Economic order quantity (EOQ) 经济订货量Fixed order interval system 固定订货期系统Inventory 库存Fixed order quantity system 固定订货量系统Inventory carrying (holding) costs 库存持有成本Inventory flow diagram 库存流图Inventory shrinkage 库存缩减Inventory turnover 库存周转Just-in-time (JIT) approach 准时制方法Nodes 节点Pipeline (in-transit) stock 管道（在途）库存Reorder (trigger) point (ROP) 再订货点Safety (buffer) stock 安全（缓冲）库存Speculative stock 投机性库存Stockout costs 缺货成本Substitute products 替代产品Vendor-managed inventory (VMI) 供方管理库存Bribes 贿赂Electronic procurement 电子采购Excess (surplus) materials 多余的（过剩的）物料Global procurement (sourcing) 全球采购Investment recovery 投资回收ISO 9000 质量管理体系标准Kickbacks 回扣Maverick spending 开销独行其是者 Obsolete materials 过时的物料Procurement 采购Procurement card (p-card) 采购卡（p卡）Purchasing 购买Quality 质量Reverse auctions 逆向拍卖Scrap materials 残余的物料Six Sigma 六西格玛Socially responsible procurement 社会责任采购Supplier development (reversemarketing) 供应商开发（逆向营销） Supply management 供应管理Waste materials 废弃的物料Activity-based costing 作业成本法Batch number 批号Container Security Initiative 集装箱安全倡议Control 控制C-TPAT 海关贸易合作反恐条例Graphical information systems (GIS)图形信息系统Pilferage 内盗Product recall 产品召回Productivity 生产率Short-interval scheduling 短期排程 System security 系统安全Theft (stealing) 偷盗Transponders 收发机TWIC 运输员工识别卡“C-level” position C级职位Centralized logistics organization 集权型物流组织Comprehensive systems analysis 综合系统分析Customer profitability analysis 顾客收益率分析Decentralized logistics organization分权型物流组织Disintermediation 非中介化Flexibility 柔性Fragmented logistics structure 分立的物流架构Industry systems analysis 行业系统分析Information (channel) strategy 信息（渠道）战略Market strategy 市场战略Partial systems analysis 部分系统分析Process strategy 过程战略Relevancy 关联性Responsiveness 响应性Systems analysis 系统分析Systems constraints 系统约束Unified logistics structure 统一的物流架构。

correlation 标准流程

correlation 标准流程下载温馨提示:该文档是我店铺精心编制而成，希望大家下载以后，能够帮助大家解决实际的问题。

文档下载后可定制随意修改，请根据实际需要进行相应的调整和使用，谢谢!并且，本店铺为大家提供各种各样类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，如想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!理解与执行Correlation分析的标准流程Correlation分析是一种统计方法，用于衡量两个或多个变量之间的关系强度和方向。

货代常用词汇中英文对照

货代常用词汇中英文对照第一篇：货代常用词汇中英文对照SHIPPER---发货人...CONSIGNEE--收货人...货代常用英文（一）船代Shipping agent 船舶代理Handling Agent 操作代理Booking Agent 订舱代理Cargo Canvassing 揽货FFF： Freight Forwarding Fee 货代佣金Brokerage / Commission 佣金（二）订舱Booking 订舱Booking Note 订舱单Booking Number 订舱号Dock Receipt 场站收据M/F(Manifest)：a manifest that lists only cargo, without freight and charges 舱单Cable/T elex Release 电放A Circular Letter 通告信/通知书PIC： Person in Charge 具体负责操作人员The said party 所涉及的一方On Board B/L：On Board提单A B/L in which a carrier acknowledges that goods have been placed on board a certain vessel。

Used to satisfy the requirements of a L/CCancellation 退关箱（三）港口BP Base Port 基本港Prompt release 即时放行Transit time 航程时间 / 中转时间Cargo availability at destination in 货物运抵目的地Second Carrier（第）二程船In transit 中转Transportation hub 中转港（四）拖车Tractor 牵引车/拖头Low-bed 低平板车Trailer 拖车Transporter 拖车Trucking Company 车队（汽车运输公司）Axle load 轴负荷Tire-load 轮胎负荷Toll Gate 收费口（五）保税Bonded Area 保税区Bonded Goods(Goods in Bond)保税货物Bonded Warehouse 保税库Caged stored at bonded warehouse 进入海关监管Fork Lift 叉车Loading Platform 装卸平台（六）船期A Friday（Tuesday / Thursday）sailing 周五班A fortnight sailing 双周班A bi-weekly sailing 周双班A monthly sailing 每月班On-schedule arrival / departure 准班抵离ETA ：Estimated(Expected)Time of Arrival 预计到达时间ETB： Estimated（Expected）Time of Berthing 预计靠泊时间ETD Estimated(Expected)Time of Departure 预计离泊时间The sailing Schedule/Vessels are subject to change without prior notice。

统计学中的专业术语

Canonical correlation, 典型相关Caption, 纵标目Case-control study, 病例对照研究Categorical variable, 分类变量Catenary, 悬链线Cauchy distribution, 柯西分布Cause-and-effect relationship, 因果关系Cell, 单元Censoring, 终检Center of symmetry, 对称中心Centering and scaling, 中心化和定标Central tendency, 集中趋势Central value, 中心值CHAID -χ2 Automatic Interaction Detector, 卡方自动交互检测Chance, 机遇Chance error, 随机误差Chance variable, 随机变量Characteristic equation, 特征方程Characteristic root, 特征根Characteristic vector, 特征向量Chebshev criterion of fit, 拟合的切比雪夫准则Chernoff faces, 切尔诺夫脸谱图Chi-square test, 卡方检验/χ2检验Choleskey decomposition, 乔洛斯基分解Circle chart, 圆图Class interval, 组距Class mid-value, 组中值Class upper limit, 组上限Classified variable, 分类变量Cluster analysis, 聚类分析Cluster sampling, 整群抽样Code, 代码Coded data, 编码数据Coding, 编码Coefficient of contingency, 列联系数Coefficient of determination, 决定系数Coefficient of multiple correlation, 多重相关系数Coefficient of partial correlation, 偏相关系数Coefficient of production-moment correlation, 积差相关系数Coefficient of rank correlation, 等级相关系数Coefficient of regression, 回归系数Coefficient of skewness, 偏度系数Coefficient of variation, 变异系数Cohort study, 队列研究Column, 列Column effect, 列效应Column factor, 列因素Combination pool, 合并Combinative table, 组合表Common factor, 共性因子Common regression coefficient, 公共回归系数Common value, 共同值Common variance, 公共方差Common variation, 公共变异Communality variance, 共性方差Comparability, 可比性Comparison of bathes, 批比较Comparison value, 比较值Compartment model, 分部模型Compassion, 伸缩Complement of an event, 补事件Complete association, 完全正相关Complete dissociation, 完全不相关Complete statistics, 完备统计量Completely randomized design, 完全随机化设计Composite event, 联合事件Composite events, 复合事件Concavity, 凹性Conditional expectation, 条件期望Conditional likelihood, 条件似然Conditional probability, 条件概率Conditionally linear, 依条件线性Confidence interval, 置信区间Confidence limit, 置信限Confidence lower limit, 置信下限Confidence upper limit, 置信上限Confirmatory Factor Analysis , 验证性因子分析Confirmatory research, 证实性实验研究Confounding factor, 混杂因素Conjoint, 联合分析Consistency, 相合性Consistency check, 一致性检验Consistent asymptotically normal estimate, 相合渐近正态估计Consistent estimate, 相合估计Constrained nonlinear regression, 受约束非线性回归Constraint, 约束Contaminated distribution, 污染分布Contaminated Gausssian, 污染高斯分布Contaminated normal distribution, 污染正态分布Contamination, 污染Contamination model, 污染模型Contingency table, 列联表Contour, 边界线Contribution rate, 贡献率Control, 对照Controlled experiments, 对照实验Conventional depth, 常规深度Convolution, 卷积Corrected factor, 校正因子Corrected mean, 校正均值Correction coefficient, 校正系数Correctness, 正确性Correlation coefficient, 相关系数Correlation index, 相关指数Correspondence, 对应Counting, 计数Counts, 计数/频数Covariance, 协方差Covariant, 共变Cox Regression, Cox回归Criteria for fitting, 拟合准则Criteria of least squares, 最小二乘准则Critical ratio, 临界比Critical region, 拒绝域Critical value, 临界值Cross-over design, 交叉设计Cross-section analysis, 横断面分析Cross-section survey, 横断面调查Crosstabs , 交叉表Cross-tabulation table, 复合表Cube root, 立方根Cumulative distribution function, 分布函数Cumulative probability, 累计概率Curvature, 曲率/弯曲Curvature, 曲率Curve fit , 曲线拟和Curve fitting, 曲线拟合Curvilinear regression, 曲线回归Curvilinear relation, 曲线关系Cut-and-try method, 尝试法Cycle, 周期Cyclist, 周期性。

A客户英文缩写词

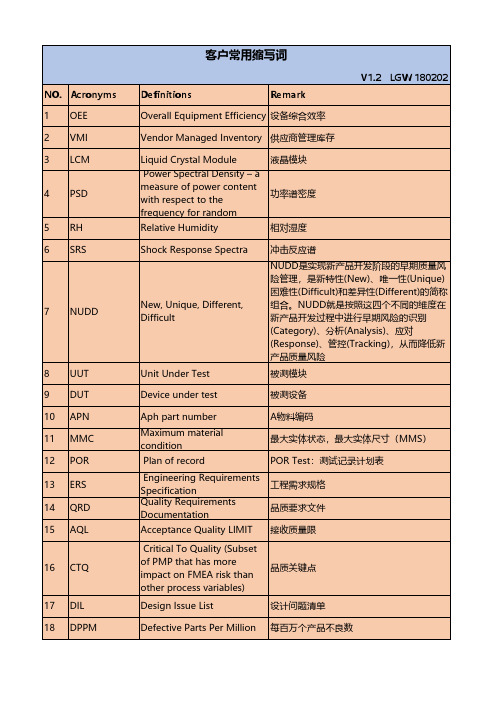
Automated Test Engineering 自动测试工程师
Direct Respoቤተ መጻሕፍቲ ባይዱsible Individual
Engineering planing special
直接责任人
项目专员：负责试产前备料&产后的产品分发（Ship to File）
75 DST-0
76 DMT-1
77 Strife Test 78 FAI 79 ORT 80 SPC 81 IQC 82 IPQC 83 OQC 84 FQC 85 OBA 86 RMA 87 FAT 88 SAT 89 MSA 90 MED 91 MBO 92 PDCA
Test Code Module
设备在现场安装好后，进行的验收测量系统分析测量/计量设备开发设备验收产品数据汇总分析
93 ORT 94 RRT 95 Proto 96 EVT 97 DVT 98 PVT 99 RZ
100 RF
101 BTR 102 EPM 103 TPM 104 SQE 105 ATE 106 DRI 107 EPS 108 PQM 109 EE 110 PD 111 CQA 112 PM 113 PE 114 GSM
设计问题清单
Defective Parts Per Million 每百万个产品不良数
19 PCD 20 CLCA
21 CM/OEM
22 AVL
23 CQR 24 CQP 25 SOP 26 ECO 27 ECN 28 EOL 29 MIL 30 PMP 31 DEV 32 GRR 33 MRD 34 ESD 35 FA/CA 36 CTB 37 HTHH 38 MRB 39 NPO 40 CMM 41 OMM 42 DOE 43 MCO

correlation函数

correlation函数一、引言在数据分析和机器学习中，我们经常需要探索变量之间的关系。

其中，相关性是一个重要的统计指标，用于衡量两个变量之间的线性关系。

为了计算相关性，我们可以使用correlation函数。

二、什么是correlation函数？correlation函数是用于计算两个变量之间的相关性的函数。

它返回一个值，该值介于-1和1之间。

如果两个变量呈现完全正相关，则correlation函数返回1；如果两个变量呈现完全负相关，则返回-1；如果两个变量之间没有任何线性关系，则返回0。

三、如何使用correlation函数？在Python中，我们可以使用NumPy库中的corrcoef函数来计算两个变量之间的相关系数。

以下是该函数的语法：np.corrcoef(x, y=None, rowvar=True)其中：x：一个数组或矩阵，表示第一个变量。

y：（可选）一个数组或矩阵，表示第二个变量。

默认值为None。

rowvar：（可选）布尔值，表示每行是否代表一个观测值。

默认值为True。

该函数将返回一个矩阵，其中包含x和y之间的相关系数。

如果只传递了x，则将返回x本身内部各列之间的相关系数矩阵。

以下是一些示例代码：import numpy as np# 生成随机数据x = np.random.rand(100)y = np.random.rand(100)# 计算相关系数r = np.corrcoef(x, y)[0, 1]print("Correlation coefficient:", r)四、如何解释correlation函数的结果？当correlation函数返回一个值时，我们需要对其进行解释。

以下是一些常见的解释：1. 如果correlation函数返回1，则表示两个变量呈现完全正相关。

这意味着当一个变量增加时，另一个变量也会增加。

2. 如果correlation函数返回-1，则表示两个变量呈现完全负相关。

ncode 资料customer_correlation

GlyphWorks在关联试车方案制定中的应用
• 校验及处理道路载荷数据 (1)
– Data manipulation (GW Signal) • Data channel splitting and merging, • Data re-sampling, • Data extraction or concatenation • Unit conversion, • Data manipulation between tests • Data transformation for load forces and moments • Computed channels from existing channels
© 2007 Slide 19nC源自de InternationalSlide 19
Conclusions
• Customer correlation can be achieved by using the nCode GlyphWorks!
© 2007 Slide 20nCode International
Slide 8
Use ‘Rainflow’ to prepare rainflow matrix from time history for correlation
Time History
3D Matrix
2D Range
© 2007 Slide 9 nCode International
Slide 9
© 2007 Slide 13nCode International
Slide 13
GlyphWorks在关联试车方案制定中的应用
• 创建用户目标雨流矩阵 (GW ScheduleCreate & Signal)

correlation coefficient 相关系数

Pearson product-moment correlation coefficient In statistics, the Pearson product-moment correlation coefficient (sometimes referred to as the PMCC , and typically denoted by r ) is a measure of the correlation (linear dependence) between two variables X and Y , giving a value between +1 and −1 inclusive. It is widely used in the sciences as a measure of the strength of linear dependence between two variables. It was developed by Karl Pearson from a similar but slightly different idea introduced by Francis Galton in the 1880s.[1] [2] The correlation coefficient is sometimes called "Pearson's r."Several sets of (x , y ) points, with the correlation coefficient of x and y for each set. Notethat the correlation reflects the noisiness and direction of a linear relationship (top row),but not the slope of that relationship (middle), nor many aspects of nonlinear relationships(bottom). N.B.: the figure in the center has a slope of 0 but in that case the correlationcoefficient is undefined because the variance of Yis zero.DefinitionPearson's correlation coefficientbetween two variables is defined as thecovariance of the two variables dividedby the product of their standarddeviations:The above formula defines the population correlation coefficient, commonly represented by the Greek letter ρ (rho).Substituting estimates of the covariances and variances based on a sample gives the sample correlation coefficient ,commonly denoted r:An equivalent expression gives the correlation coefficient as the mean of the products of the standard scores. Based on a sample of paired data (X i , Y i), the sample Pearson correlation coefficient iswhere , and are the standard score, sample mean, and sample standard deviation respectively.Mathematical propertiesThe absolute value of both the sample and population Pearson correlation coefficients are less than or equal to 1.Correlations equal to 1 or -1 correspond to data points lying exactly on a line (in the case of the sample correlation),or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr (X ,Y ) = corr (Y ,X ).A key mathematical property of the Pearson correlation coefficient is that it is invariant to separate changes in location and scale in the two variables. That is, we may transform X to a + bX and transform Y to c + dY , where a , b ,c , and d are constants, without changing the correlation coefficient (this fact holds for both the population and sample Pearson correlation coefficients). Note that more general linear transformations do change the correlation:see a later section for an application of this.The Pearson correlation can be expressed in terms of uncentered moments. Since μX = E(X ), σX 2 = E[(X − E(X ))2]= E(X 2) − E 2(X ) and likewise for Y , and sincethe correlation can also be written asAlternative formulae for the sample Pearson correlation coefficient are also available:The above formula conveniently suggests a single-pass algorithm for calculating sample correlations, but, depending on the numbers involved, it can sometimes be numerically unstable.InterpretationThe correlation coefficient ranges from −1 to 1. A value of 1 implies that a linear equation describes the relationship between X and Y perfectly, with all data points lying on a line for which Y increases as X increases. A value of −1implies that all data points lie on a line for which Y decreases as X increases. A value of 0 implies that there is no linear correlation between the variables.More generally, note that (X i − X )(Y i − Y ) is positive if and only if X i and Y i lie on the same side of their respective means. Thus the correlation coefficient is positive if X i and Y i tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative if X i and Y i tend to lie on opposite sides of their respective means.Geometric interpretationRegression lines for y=g x (x) [red] and x=g y(y) [blue ]For uncentered data, the correlation coefficientcorresponds with the the cosine of the anglebetween both possible regression lines y=g x (x) andx=g y(y).For centered data (i.e., data which have beenshifted by the sample mean so as to have anaverage of zero), the correlation coefficient canalso be viewed as the cosine of the anglebetween the two vectors of samples drawn fromthe two random variables (see below).Some practitioners prefer an uncentered(non-Pearson-compliant) correlation coefficient.See the example below for a comparison.As an example, suppose five countries are found tohave gross national products of 1, 2, 3, 5, and 8billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%,13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: x = (1, 2, 3,5, 8) and y = (0.11, 0.12, 0.13, 0.15, 0.18).By the usual procedure for finding the angle between two vectors (see dot product), the uncentered correlationcoefficient is:Note that the above data were deliberately chosen to be perfectly correlated: y = 0.10 + 0.01 x . The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by E(x ) = 3.8 and y by E(y ) =0.138) yields x = (−2.8, −1.8, −0.8, 1.2, 4.2) and y = (−0.028, −0.018, −0.008, 0.012, 0.042), from whichas expected.Interpretation of the size of a correlation CorrelationNegative Positive None−0.09 to 0.00.0 to 0.09Small−0.3 to −0.10.1 to 0.3Medium−0.5 to −0.30.3 to 0.5Large −1.0 to −0.50.5 to 1.0Several authors [3] have offered guidelines for the interpretation of a correlation coefficient. Cohen (1988),[3] has observed, however, that all such criteria are in some ways arbitrary and should not be observed too strictly. The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.9 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences where there may be a greater contribution from complicating factors.InferenceA graph showing the minimum value of Pearson's correlation coefficient that issignificantly different from zero at the 0.05 level, for a given sample size.Statistical inference based on Pearson'scorrelation coefficient often focuses on oneof the following two aims. One aim is to testthe null hypothesis that the true correlationcoefficient is ρ, based on the value of thesample correlation coefficient r . The otheraim is to construct a confidence intervalaround r that has a given probability ofcontaining ρ.Randomization approachesPermutation tests provide a direct approachto performing hypothesis tests andconstructing confidence intervals. Apermutation test for Pearson's correlationcoefficient involves the following two steps:(i) using the original paired data (x i , y i ),randomly redefine the pairs to create a newdata set (x i , y i ′), where the i ′ are a permutation of the set {1,...,n }. The permutation i ′ is selected randomly, with equal probabilities placed on all n ! possible permutations. This is equivalent to drawing the i ′ randomly "without replacement" from the set {1,..., n }. A closely-related and equally-justified (bootstrapping) approach is to separately draw the i and the i ′ "with replacement" from {1,..., n }; (ii) Construct a correlation coefficient r from the randomized data. To perform the permutation test, repeat (i) and (ii) a large number of times. The p-value for the permutation test is one minus the proportion of the r values generated in step (ii) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here "larger" can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.The bootstrap can be used to construct confidence intervals for Pearson's correlation coefficient. In the "non-parametric" bootstrap, n pairs (x i , y i ) are resampled "with replacement" from the observed set of n pairs, and the correlation coefficient r is calculated based on the resampled data. This process is repeated a large number of times,and the empirical distribution of the resampled r values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ρ can be defined as the interval spanning from the 2.5th to the 97.5th percentile of the resampled r values.Approaches based on mathematical approximationsFor approximately Gaussian data, the sampling distribution of Pearson's correlation coefficient approximately follows Student's t-distribution with degrees of freedom N − 2. Specifically, if the underlying variables have abivariate normal distribution, the variablehas a Student's t-distribution in the null case (zero correlation).[4] This also holds approximately even if the observed values are non-normal, provided sample sizes are not very small.[5] For constructing confidence intervals and performing power analyses, the inverse of this transformation is also needed:Alternatively, large sample approaches can be used.Early work on the distribution of the sample correlation coefficient was carried out by R. A. Fisher[6][7] and A. K. Gayen.[8] Another early paper[9] provides graphs and tables for general values of ρ, for small sample sizes, and discusses computational approaches.Fisher TransformationIn practice, confidence intervals and hypothesis tests relating to ρ are usually carried out using the Fisher transformation:If F(r) is the Fisher transformation of r, and n is the sample size, then F(r) approximately follows a normal distribution withand standard errorThus, a z-score isunder the null hypothesis of that , given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-value can be obtained from a normal probability table. For example, if z = 2.2 is observed and a two-sided p-value is desired to test the null hypothesis that , the p-value is 2·Φ(−2.2) = 0.028, where Φ is the standard normal cumulative distribution function.Confidence IntervalsTo obtain a confidence interval for ρ, we first compute a confidence interval for F( ):The inverse Fisher transformation bring the interval back to the correlation scale.For example, suppose we observe r = 0.3 with a sample size of n=50, and we wish to obtain a 95% confidence interval for ρ. The transformed value is artanh(r) = 0.30952, so the confidence interval on the transformed scale is 0.30952 ± 1.96/√47, or (0.023624, 0.595415). Converting back to the correlation scale yields (0.024, 0.534).Pearson's correlation and least squares regression analysisThe square of the sample correlation coefficient, which is also known as the coefficient of determination, estimates the fraction of the variance in Y that is explained by X in a linear regression analysis. As a starting point, the total variation in the Yaround their average value can be decomposed as followsiwhere the are the fitted values from the regression analysis. This can be rearranged to giveThe two summands above are the fraction of variance in Y that is explained by X (right) and that is unexplained by X (left).Next, we apply a property of least square regression analysis, that the sample covariance between andis zero. Thus, the sample correlation coefficient between the observed and fitted response values in the regression can be writtenThusis the proportion of variance in Y explained by a linear function of X.Sensitivity to the data distributionExistenceThe population Pearson correlation coefficient is defined in terms of moments, and therefore exists for any bivariate probability distribution for which the population covariance is defined and the marginal population variances are defined and are non-zero. Some probability distributions such as the Cauchy distribution have undefined variance and hence ρ is not defined if X or Y follows such a distribution. In some practical applications, such as those involving data suspected to follow a heavy-tailed distribution, this is an important consideration. However, the existence of the correlation coefficient is usually not a concern; for instance, if the range of the distribution is bounded, ρ is always defined.Large sample propertiesIn the case of the bivariate normal distribution the population Pearson correlation coefficient characterizes the joint distribution as long as the marginal means and variances are known. For most other bivariate distributions this is not true. Nevertheless, the correlation coefficient is highly informative about the degree of linear dependence between two random quantities regardless of whether their joint distribution is normal[1] . The sample correlation coefficient is the maximum likelihood estimate of the population correlation coefficient for bivariate normal data, and is asymptotically unbiased and efficient, which roughly means that it is impossible to construct a more accurate estimate than the sample correlation coefficient if the data are normal and the sample size is moderate or large. For non-normal populations, the sample correlation coefficient remains approximately unbiased, but may not be efficient. The sample correlation coefficient is a consistent estimator of the population correlation coefficient as long as the sample means, variances, and covariance are consistent (which is guaranteed when the law of large numbers can be applied).RobustnessLike many commonly-used statistics, the sample statistic r is not robust[10] , so its value can be misleading if outliers are present[11][12] . Specifically, the PMCC is neither distributionally robust, nor outlier resistant[10] (see Robust statistics#Definition). Inspection of the scatterplot between X and Y will typically reveal a situation where lack of robustness might be an issue, and in such cases it may be advisable to use a robust measure of association. Note however that while most robust estimators of association measure statistical dependence in some way, they are generally not interpretable on the same scale as the Pearson correlation coefficient.Statistical inference for Pearson's correlation coefficient is sensitive to the data distribution. Exact tests, and asymptotic tests based on the Fisher transformation can be applied if the data are approximately normally distributed, but may be misleading otherwise. In some situations, the bootstrap can be applied to construct confidence intervals, and permutation tests can be applied to carry out hypothesis tests. These non-parametric approaches may give more meaningful results in some situations where bivariate normality does not hold. However the standard versions of these approaches rely on exchangeability of the data, meaning that there is no ordering or grouping of the data pairs being analyzed that might affect the behavior of the correlation estimate.A stratified analysis is one way to either accommodate a lack of bivariate normality, or to isolate the correlation resulting from one factor while controlling for another. If W represents cluster membership or another factor that it is desirable to control, we can stratify the data based on the value of W, then calculate a correlation coefficient within each stratum. The stratum-level estimates can then be combined to estimate the overall correlation while controlling for W.[13]Calculating a weighted correlationSuppose observations to be correlated have differing degrees of importance that can be expressed with a weight vector w. To calculate the correlation between vectors x and y with the weight vector w (all of length n),[14][15]•Weighted mean:•Weighted covariance•Weighted correlationRemoving correlationIt is always possible to remove the correlation between random variables with a linear transformation, even if the relationship between the variables is nonlinear. A presentation of this result for population distributions is given by Cox & Hinkley.[16]A corresponding result exists for sample correlations, in which the sample correlation is reduced to zero. Suppose a vector of n random variables is sampled m times. Let X be a matrix where is the j th variable of sample i. Letbe an m by m square matrix with every element 1. Then D is the data transformed so every random variable has zero mean, and T is the data transformed so all variables have zero mean and zero correlation with all other variables - the moment matrix of T will be the identity matrix. This has to be further divided by the standard deviation to get unit variance. The transformed variables will be uncorrelated, even though they may not be independent.where an exponent of -1/2 represents the matrix square root of the inverse of a matrix. The covariance matrix of T will be the identity matrix. If a new data sample x is a row vector of n elements, then the same transform can be applied to x to get the transformed vectors d and t:This decorrelation is related to Principal Components Analysis for multivariate data.Reflective correlationThe reflective correlation is a variant of Pearson's correlation in which the data are not centered around their mean values. The population reflective correlation isThe reflective correlation is symmetric, but it is not invariant under translation:The sample reflective correlation isThe weighted version of the sample reflective correlation isReferences[1]J. L. Rodgers and W. A. Nicewander. Thirteen ways to look at the correlation coefficient (/stable/2685263). TheAmerican Statistician, 42(1):59–66, February 1988.[2]Stigler, Stephen M. (1989). "Francis Galton's Account of the Invention of Correlation" (/stable/2245329). StatisticalScience4 (2): 73–79. doi:10.1214/ss/1177012580. .[3]Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.)[4]N.A Rahman, A Course in Theoretical Statistics; Charles Griffin and Company, 1968[5]Kendall, M.G., Stuart, A. (1973)The Advanced Theory of Statistics, Volume 2: Inference and Relationship, Griffin. ISBN 0852642156(Section 31.19)[6]Fisher, R.A. (1915). "Frequency distribution of the values of the correlation coefficient in samples from an indefinitely large population".Biometrika10 (4): 507–521. doi:10.1093/biomet/10.4.507.[7]Fisher, R.A. (1921). "On the probable error of a coefficient of correlation deduced from a small sample" (/2440/15169) (PDF). Metron1 (4): 3–32. . Retrieved 2009-03-25.[8]Gayen, A.K. (1951). "The frequency distribution of the product moment correlation coefficient in random samples of any size draw fromnon-normal universes". Biometrika38: 219–247. doi:10.1093/biomet/38.1-2.219.[9]Soper, H.E., Young, A.W., Cave, B.M., Lee, A., Pearson, K. (1917). "On the distribution of the correlation coefficient in small samples.Appendix II to the papers of "Student" and R. A. Fisher. A co-operative study", Biometrika, 11, 328-413. doi:10.1093/biomet/11.4.328[10]Wilcox, Rand R. (2005). Introduction to robust estimation and hypothesis testing. Academic Press.[11]Devlin, Susan J; Gnanadesikan, R; Kettenring J.R. (1975). "Robust Estimation and Outlier Detection with Correlation Coefficients" (http:///stable/2335508). Biometrika62 (3): 531–545. doi:10.1093/biomet/62.3.531. .[12]Huber, Peter. J. (2004). Robust Statistics. Wiley.[13]Multivariable Analysis- A Practical Guide for Clinicians. 2nd Edition. (/uk/catalogue/catalogue.asp?isbn=052154985X&ss=exc) Mitchell H. Katz. University of California, San Francisco. ISBN 9780521549851. ISBN 052154985X DOI:10.2277/052154985X[14]/Archive/sci.stat.math/2006-02/msg00171.html[15] A MATLAB Toolbox for computing Weighted Correlation Coefficients (/matlabcentral/fileexchange/20846)[16]Cox, D.R., Hinkley, D.V. (1974) Theoretical Statistics, Chapman & Hall (Appendix 3) ISBN 0412124203Article Sources and Contributors10 Article Sources and ContributorsPearson product-moment correlation coefficient Source: /w/index.php?oldid=406110938 Contributors: AgarwalSumeet, Albmont, Amillar, Arbitrary username,Arcadian, AxelBoldt, Baccyak4H, Beno1000, Bobo192, Bramschoenmakers, Can't sleep, clown will eat me, Chris53516, Cometstyles, Countchoc, Damian Yerrick, Deditos, Delirium, Denfjättrade ankan, DerHexer, Dfarrar, Discospinster, Dpryan, Dr.enh, Drbreznjev, Dysprosia, FrancisTyers, G-J, G716, Garion96, Giftlite, Gringotumadre, Ichbin-dcw, Ignoramibus,Irregulargalaxies, JamesBWatson, JeremyA, Jfitzg, Jmath666, JohnEBredehoft, JorisvS, Jtneill, Juancitomiguelito, Karada, Karl Dickman, Karol Langner, Kinneyboy90, Kku, Kyawtun,Landroni, Ldm, MER-C, Mahahahaneapneap, Male1979, Mc4932, Mcld, Melcombe, Michael Hardy, Mild Bill Hiccup, Mmmready, MrOllie, MrYdobon, NeonMerlin, Notheruser, O18, Parodi, Pearle, Qniemiec, Qwfp, Rajah, Ramkgupta1, RedCoat10, Rgclegg, Rich Farmbrough, Rifleman 82, Rjwilmsi, Skbkekas, Stewartadcock, Sykko, Talgalili, Tdslk, Tellyaddict, Tesi1700, Tomharrison, Trontonian, Versus22, Vinhtantran, Vrenator, WikHead, Wikifriend pt001, Wootini, Xenoglossophobe, Yamiken, Yerpo, 170 anonymous editsImage Sources, Licenses and ContributorsImage:Correlation examples.png Source: /w/index.php?title=File:Correlation_examples.png License: Public Domain Contributors: Original uploader was Imagecreator at en.wikipediaFile:Regression lines.png Source: /w/index.php?title=File:Regression_lines.png License: Creative Commons Attribution-Sharealike 3.0 Contributors: User:Qniemiec Image:correlation significance.svg Source: /w/index.php?title=File:Correlation_significance.svg License: Creative Commons Attribution 3.0 Contributors:User:SkbkekasLicenseCreative Commons Attribution-Share Alike 3.0 Unported/licenses/by-sa/3.0/。

ncode拟合曲线

ncode拟合曲线【原创版】目录1.Ncode 拟合曲线简介2.Ncode 拟合曲线的原理3.Ncode 拟合曲线的步骤4.Ncode 拟合曲线的应用实例5.Ncode 拟合曲线的优缺点正文1.Ncode 拟合曲线简介code 拟合曲线是一种在计算机科学和数据分析领域中广泛应用的算法，它可以通过一系列数据点来生成一条光滑的曲线，以达到对数据进行更精确描述和预测的目的。

Ncode 拟合曲线在许多领域中都有重要作用，例如，在生物学中可以用于绘制蛋白质结构，金融领域中可以用于预测股票价格等。

2.Ncode 拟合曲线的原理code 拟合曲线的原理是基于最小二乘法，即通过最小化误差的平方和来寻找最佳拟合曲线。

具体来说，它通过计算每个数据点到拟合曲线的垂直距离的平方和，来确定最佳拟合曲线。

这个过程可以用迭代法或者直接解方程组来完成。

3.Ncode 拟合曲线的步骤code 拟合曲线的具体步骤如下：（1）确定拟合曲线的类型，如线性拟合、多项式拟合、指数拟合等。

（2）根据拟合曲线的类型，选择相应的函数形式，如线性拟合用y=ax+b，多项式拟合用 y=ax^n+bx^(n-1)+...+k。

（3）利用最小二乘法，求解出拟合曲线的参数，如 a、b、n 等。

（4）将求解出的参数代入函数形式，得到最终的拟合曲线。

4.Ncode 拟合曲线的应用实例code 拟合曲线在许多领域中都有广泛应用，例如，在生物学中可以用于绘制蛋白质结构，从而帮助科学家理解蛋白质的功能和作用机制；在金融领域中，可以用于预测股票价格，帮助投资者做出更明智的决策。

5.Ncode 拟合曲线的优缺点code 拟合曲线的优点在于，它可以通过一系列数据点来生成一条光滑的曲线，使得数据更加易于理解和分析。

同时，它也可以用于预测未来的趋势和变化。

然而，Ncode 拟合曲线也存在一些缺点，例如，如果数据中存在噪声或者异常值，可能会影响拟合曲线的准确性。

Correlations

Amount Relatives and the Meaning of ChainsKai von Fintel (MIT)Goalsempirical:amount relatives (ARs)semantics:compositional derivation of two readings of ARs architecture:one item – two contributions (movement? co-binding?) speculation: a completely different way of looking at itCarlson’s Discovery (Carlson 1977)(1)The booksthat∅*whichthere are on the table are useless.Puzzle: Why no Definiteness Effect (DE) in (1)?(2)*Few people admitted that there had been them at the party.(3)*No perfect relationship is such that there is it.(examples from Heim 1987)CorrelationsApparent relativization of the there-associatePossibility of Antecedent-Contained DeletionNo wh-relative pronoun allowedLimited class of determiners (the, every, all (the), FC-any)Carlson’s Idea: Amount Relatives (degree-denoting relative clauses)The relative clause specifies the amount/number of books referred to.It functions as a cardinality modifier.It denotes the number of books on the table.The noun books moves from the RC-internal position into the external head position. We will see that it is semantically active in both positions!the books there are on the table ⇒theAmount Relative Clausemaxλnthere arebooks on the tablemanybooksCircumvention of the DE(4) a.* There was that horse in the pasture.b.* There were those horses in the pasture.c.There were that many horses in the pasture.Some Degree Semantics (e.g. Cresswell 1976)(5)There are more books on the table than there are on the shelf.The maximal n such that there are n-many books on the tableis larger thanthe maximal n such that there are n-many books on the shelfThe Composition of Amount Relatives(6)there were n-many books on the table∃x:books x&on the table x&many n,xmany (n,x) ⇒ x has n atomic individuals as partsFor perspicuity’s sake, let’s write x=n for many n,xThere is a plurality x of books on the table which has n atomicindividuals as parts.There is a plurality of n books on the table.(7)The amount variable wh-moves. We get a predicate of amounts:λn.∃x:books x&on the table x&x=nThe set of numbers n such that there is a plurality of n books on thetable.(8)Maximalization:maxλn.∃x:books x&on the table x&x=nmax is a function that applies to a set and returns the maximal elementin that set. Here it will give us the number n such that there are exactlyn books on the table.(9)(that there were n-many books on the table)-many booksλx.books x&x=maxλn.∃y:books y&on the table y&y=nλx.books x&x=books on the tableThe set of pluralities of books that have the same number ofindividuals as there are books on the table(10)≈ as many books as there were books on the tableIt remains quite unclear what the determiner the would be doing.Books in Two PlacesNote that for this account to work, the nominal (books) has to make a contribution in two places: inside the relative clause and in its surface position. According to Carlson’s analysis, the nominal originates inside the amount relative and raises to its surface position. He does not comment on the fact that it needs to be interpreted in both positions.(11)No subdeletion in amount relatives:a.I saw more bulbs than Jeb saw flowers.b.* I saw the bulbs that Jeb saw flowers.Real Life Amount Readings (“Identity of Quantity”)(12)It will takes us the rest of our lives to drink the champagne that theyspilled that evening. (Heim 1987: (40)).(13)There isn’t the water in the sink that there is in the bathtub.(Lisa Selkirk, pc. to Irene Heim)Further Evidence for Amount Abstraction ⇒ Negative Islands(14)Please give me the books that aren’t on the table.(15)*Please give me the books that there aren’t on the table.(16)*There are more books on the table than there aren’t on the shelf. Amount Idioms(17)The headway that Mel made was satisfactory. (Carlson)(18)The many books that Mary has to read for the course are a problem.(Heim, Vienna lectures)Possible analysis: covert clausal complementation of some sort(19)It was satisfactory that Mel made the headway he made.(20)It is a problem that Mary has to read (so) many books for the course. Alternative: satisfactory, be a problem as predicates of amounts (of headway made, of books Mary has to read for the course).(21) a.Mel made a satisfactory amount of headway.b.Mel made satisfactory headway.The “identity of quantity” reading isn’t the only reading these sentences have. In fact, normally we only get an “identity of objects” reading.(22)I took with me the books that there were on the table.“cannot mean that I took with me from the library as many books asthere were books on the table in the kitchen; it only means that I tookthose actual books in the kitchen.” (G&L, p. 133)(23)How many books did you take from the library?a.I took as many books as there are on this table.b.I took (all) the books that there are on this table.Hope for Carlson/Heim?(24)“Identity of objects” entails “identity of quantity”So, perhaps, we always just have identity of quantity but it issometimes pragmatically strengthened into identity of objects(25)How many books did you take?a.I took as many books as there were on the table.b.I took however many books there were on the table.Amount relatives have genuine identity of objects readings(26)A:You will get an F because you didn’t read the books that there areon the reading list.B:What do you mean? There are ten books on the reading list and I did read ten books.Degrees are not simple numbers but triples of a number, a property and a plurality.Degrees are used to store information about the object measured other than its dimensions.They also store a sortal the object falls under and in fact the object itself.This semantic storage mechanism allows G&L to interpret the nominal only in its internal source position (its syntactic movement is said to be semantically inert).The “identity of objects’ readings is achieved by retrieving the object from the degree triple.Similar to other semantic storage systems as alternatives to syntactic movement.(27)n,books,xmeasure value, measure domain/sortal, object measured(28)DEGREE,x iff x=y and P=R and P x and x=nA triple <n,R,y> is the degree (relative to sortal P) of x iff(i)y is x (the object measured)(ii)R is P (the measure sortal)(iii)P is true of x (the object falls under the measure sortal)(iv)n is the amount of x(29)three=λP.λx.P x&DEGREE,x(30)three books==λx.books x&DEGREE,x=λx.books x&x=3the set of pluralities containing exactly three books(31)d many=λPλx.P x&DEGREE P d,x(32)λd. that there were (d many books) on the tableλd.∃x books x&DEGREE books d,x&on the table xλn,P,y.∃x books x&DEGREE,x&on the table xλn,P,y.∃x books x&P=books&x=y&x=n&on the table xλn,books,y.books y&y=n&on the table ythe set of all measure triples, of which the object measured is a sum of books on thetableNote: even though the there-construction quantifies away the variable introduced by books, a second individual variable is introduced to be manipulated higher up in the structure. This variable is introduced as one of the three components of G&L-degrees. A kind of Existential Disclosure.(33)λx. there is someone who is x in the garden(34)There is someone who is Bill Clinton in the garden.vs. There is Bill Clinton in the garden.(35)Maximalization (basically as before)(36)SUBSTANCE maxλn,books,y.books y&y=n&on the table y= the maximal sum of books on the table⇒ identity of objectsThe identity of quantity readings (true amount readings) are obtained by working with the amount and sortal parts of the degree triple.CriticismNon-standard assumptions about degrees designed to pass on information up the tree. Essentially mimics movement.Danger of overgeneration. Why don’t as many as-sentences have identity of objects readings?An Alternative?First a slight variation on the Carlson/Heim analysis. Give up on the assumption that there effects existential quantification. The only quantifier inside the relative clause is the cardinal quantifier d many.(37)n many books on the tablen many=λPλQ.P∩Q≥n(38)the books (that there are n many books on the table)-manydelete link, interpret both copies of bookstheλx.books x&x=maxλn.n many books on the tablethe noun phrase n many books inside the relative clause is a weakquantifier (OK in there-context)the resulting degree/amount description is predicated of the plurality ofbooks the whole DP refers to⇒ this again is the identity of quantity readingOne More Movementtheλxmaxλnthere aren many books⇓xon tablemanybooks⇓xbooksThe head nominal moves out of the relative clause. It moves one more step. It binds two variables.(39)the books books (that there are n many books on the table)-manyinterpret link, treat both tails as bound plurality variablesthe books λx. x (that there are n many of x on the table)-manytheλx.books x&λy.y=maxλn.n many of x on the table x=theλx.books x&x=maxλn.n many of x on the table(40)of x⇒ the set of individuals in the plurality x(41)Identity of Quantityλx.books x&x=books∩on the tableIdentity of Objectsλx.books x&x=x∩on the table(42)so far:predicate that is true of any plurality of books s.t. all of them are on the table(43)the books that there are on the tabledefinite plural determiner picks out the maximal element from a setwidespread assumption(44)the books that there are on the table= the maximally inclusive plurality x of books such that the number ofindividual parts of x is the same as the number of individual parts of xthat are on the table= all the books on the tableWhat about the Definiteness Effect?(45)Partitives are OK in there sentencesWhere are my horses?There are six of them in the pasture.(46)Problem: partitives are only OK in there-sentences with a codaa.* There were two of my brothers.b.There were two of my brothers on that flight.(Heim, class handout 1986)(47)Amount relatives are OK without a codaI have read all the good books that there are.(48)Could (47) be an identity of quantity case?Yes. In fact, identity of quantity reading will coincide with any putativeidentity of objects reading!A plurality of books that contains just as many members as the pluralityof all the books that exist simply must contain all the books that exist.Interim SummaryWe have a compositional derivation for the two readings of ARs. It works without semantic storage and without non-standard assumptions about what degrees are. It comes with a price: we have movement of an item that is then interpreted both in its source position and in its target position.Movement without Chain Formation?Apparently a respectable possibility in recent minimalist syntax.Hornstein (1999) analyzes Control structures as involving NP-movement.Lechner (1999) uses the possibility in the analysis of comparatives.Alternative? Pronominals with particular binding requirements?Imagine that the amount relative contains a silent pronominal. This item comes with the requirement of having to be bound quite locally.The head nominal is generated external to the AR. It moves slightly to establish a binding relation with the silent pronominal inside the AR.The two readings for ARs come about by choosing two different types for the binding chain (type e for identity of objects; type <et> for identity of quantity).ConsiderationsLocality conditions? Something like Control Theory?A Third Way? (cf. Shimoyama on Japanese IHRCs)(49)The books that there are on the table are useless.⇒ There are books on the table. The books are useless.(50)Interpret AR (after reconstruction of head nominal) as separateassertion.Matrix sentence contains an E-type pronoun (disguised definitedescription), whose content is recovered from AR.(51)Crucial kind of example for Japanese IHRCs:Taro-wa [[Yoko-ga reezooko-ni kukkii-o hotondoTaro-TOPIC Yoko-NOM refrigerator-LOC cookie-ACC mostirete-oita ]–no ] –o paatii-ni motte ittaput-AUX-NM-ACC party-to brought‘Yoko put most cookies in the refrigerator and Taro brought them (= thecookies Yoko had put in the refrigerator) to the party.’Clearly, we would not have much hope for an analysis that has somerelative clause operator binding a variable introduced by most cookies,a strong quantifier.(52)Similar puzzles in English ARs:a.I want to talk to every witness that there may be.= There may be witnesses. I want to talk to every witness.b.Any beer that there may be in that cooler is mine.= There may be beer in that cooler. Any of it is mine.Let’s look at one of these examples in more detail:(53)I want to talk to every witness that there may be.does not mean:I want to talk to everyone who may be a witness.also does not mean:I want to talk to every x such that x is a witness and x possibly exists.(54)Step 1Reconstruct head nominal into its source position.[We also mess around with plurality.]I want to talk to every [there may be witnesses]Step 2Interpret “relative clause” as separate assertion.Interpret the remaining NP as containing an E-type pronoun.There may be witnesses.I want to talk to every one of them (= the witnesses).Step 3While the universal quantifier (every one of the witnesses) triggers anexistence presupposition, the entire construction explicitly does notcarry such a presupposition. This would in fact clash with the asserted(mere) possibility of there being witnesses.The presupposition conflict is resolved by locally accommodating thepresupposition into the restriction of want , which is a modal quantifierover worlds.There may be witnesses.If there are witnesses, I want to talk to every one of the witnesses.ReferencesCarlson, Greg (1977). “Amount Relatives”. Language 58, 520-542.Cresswell, Max (1976) “The Semantics of Degree”. In Barbara Partee (ed.) Montague Grammar. New York: Academic Press.Heim, Irene (1987). “Where Does the Definiteness Restriction Apply? Evidence from the Definiteness of Variables”. In Eric Reuland and Alice terMeulen (eds.), The Representation of (In)Definiteness, Cambridge,MA: MIT Press. 21-42.Hornstein, Norbert (1999) “Movement and Control”, Linguistic Inquiry 30(1), 69-96.Lechner, Winfried (1999) Comparatives and DP-Structure, PhD Dissertation, University of Massachusetts at Amherst.Shimoyama, Junko (1999) "Internally Headed Relative Clauses in Japanese and E-Type Anaphora" Journal of East Asian Linguistics 8, 147-182.Contact Kai von FintelRoom E39-245Department of Linguistics and PhilosophyMassachusetts Institute of TechnologyCambridge, MA 02139U.S.A.fintel@/linguistics/www/fintel.home.htmlAppendix 1: Overt Numerals(55)the threemanyfewbooks that there are on the tableNote: the numeral cannot originate inside the relative clause, since by assumption the wh-element moved to Comp in the relative clause corresponds to the amount modifier in there.(56)Grosu & Landman:the numeral combines with (the singleton set of) a plurality (the maximal sum ofbooks on the table)the numeral specifies the cardinality of the pluralitythree=λP:P=3.Pif the cardinality of P is 3 then the numeral will return P, otherwise the function isundefineda “test”(57)The Alternative:the numeral combines with a predicate true of any plurality of books on the tablethree intersectively picks out the three-membered pluralitiesthe definite plural determiner will want to pick out the maximal three-memberedpluralityif there are only three books on the table there will be one maximal three-memberedplurality of books on the table fineif there are more than three books on the table there will be more than one three-membered plurality of books on the table the will not be able to return a resultAppendix 2: Determiner Restrictions?Carlson: those determiners that can co-occur with a cardinal expression under them Grosu & Landman: those determiners that “preserve maximality”E-type:those determiners that can head an E-type expression (essentially only the)。

Oracle Financial Services Retail Customer Analytic

Intended Audience ..............................................................................................................................................................xv Documentation Accessibility .............................................................................................................................................xv Access to Oracle Support...................................................................................................................................................xv Structure ................................................................................................................................................................................xv Related Information Sources ............................................................................................................................................xvi

co_ext_order_entry的用法 -回复

co_ext_order_entry的用法-回复标题：深入理解与应用co_ext_order_entry在现代企业中，订单管理系统是业务运营的重要组成部分。

其中，co_ext_order_entry是一个关键的概念，它涉及到订单的创建、修改和管理等过程。

本文将详细解析co_ext_order_entry的用法，帮助读者更好地理解和应用这一重要功能。

一、理解co_ext_order_entryco_ext_order_entry，全称为"cross-organization external order entry"，即跨组织外部订单录入。

这个概念主要应用于大型企业或者有多元化业务线的公司，其核心目标是实现不同部门、不同组织之间的订单信息共享和协同处理。

在这样的系统中，co_ext_order_entry主要用于以下几种场景：1. 外部客户或供应商直接在系统中下订单。

2. 公司内部的不同部门或团队之间进行订单协作。

3. 跨组织的订单处理，例如集团下属的多个子公司之间的订单流转。

二、co_ext_order_entry的流程使用co_ext_order_entry的过程主要包括以下几个步骤：1. 订单创建：外部客户或供应商通过特定的接口或者平台，输入订单的基本信息，如产品名称、数量、价格、交货日期等。

2. 订单审核：订单信息被提交后，系统会根据预设的规则进行审核。

这可能包括库存检查、价格验证、信用评估等环节。

3. 订单确认：审核通过后，订单会被确认并进入处理阶段。

此时，相关的信息会被同步到公司的各个部门或者组织，以便于后续的操作。

4. 订单执行：各部门或组织根据订单信息进行生产和配送等操作。

在这个过程中，co_ext_order_entry系统会实时更新订单的状态，以便于所有相关人员了解订单的最新进展。

5. 订单完成：当订单的所有环节都完成后，系统会自动更新订单状态为已完成，并生成相关的报表和发票。

ncode 资料customer_correlation

一套完整的疲劳分析设计试验管理系统nSoft

快消品从业人员必懂的英文销售术语

相关性分析(相关系数)-范本模板

ncode分析流程

canonical_correlation_analysis_stata_概述及解释说明

ncode标记数值

Ncode案例doc资料

物流学 key terms

correlation 标准流程

最新供应链管理专有名词资料

货代常用词汇中英文对照

统计学中的专业术语

A客户英文缩写词

correlation函数

ncode 资料customer_correlation

correlation coefficient 相关系数

ncode拟合曲线

Correlations

Oracle Financial Services Retail Customer Analytic

co_ext_order_entry的用法 -回复