向量与三角形四心

合集下载

向量与三角形的四心

向量与三角形内心、外心、重心、垂心知识的交汇一、四心的概念介绍（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、四心与向量的结合（1）⇔=++0OC OB OA O 是ABC ∆的重心.证法1：设),(),,(),,(),,(332211y x C y x B y x A y x O⇔=++⎩⎨⎧=-+-+-=-+-+-0)()()(0)()()(321321y y y y y y x x x x x x ⎪⎪⎩⎪⎪⎨⎧++=++=⇔33321321yy y y x x x x⇔O 是ABC ∆的重心.证法2：如图 OC OB OA ++2=+= ∴2= ∴D O A 、、三点共线，且O 分AD为2：1 ∴O 是ABC ∆的重心（2）⇔⋅=⋅=⋅O 为ABC ∆的垂心.证明：如图所示O 是三角形ABC 的垂心，BE 垂直AC ，AD 垂直BC ， D 、E 是垂足. 0)(=⋅=-⇔⋅=⋅ ⊥⇔ 同理⊥，⊥⇔O 为ABC ∆的垂心（3）设a ,b ,c 是三角形的三条边长，O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心. 证明：b c 、分别为AC AB 、方向上的单位向量， ∴b ACc AB+平分BAC ∠,(λ=∴AO b c +)，令c b a bc++=λ ∴c b a bc ++=（b ACc AB+) 化简得0)(=++++AC c AB b OA c b a∴0=++OC c OB b OA aB CDB CD（4==⇔O 为ABC ∆的外心。

典型例题：例1：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心中点. 分析：如图所示ABC ∆，E D 、分别为边AC BC 、的2=+ ∴λ2+=+=AD AP λ2=∴ AP ∴//AD∴点P 的轨迹一定通过ABC ∆的重心，即选C .例2：（03全国理4）O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P满足++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（ B ）A ．外心B ．内心C ．重心D ．垂心分析：分别为方向上的单位向量，+平分BAC ∠,∴点P 的轨迹一定通过ABC ∆的内心，即选B .例3：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心分析：如图所示AD 垂直BC ，BE 垂直AC ， D 、E 是垂足. +⋅+B CDC+=-=0∴点P 的轨迹一定通过ABC ∆的垂心，即选D .练习：1．已知ABC ∆三个顶点C B A 、、及平面内一点P ，满足0=++PC PB PA ，若实数λ满足：λ=+，则λ的值为（）A ．2B ．23 C ．3 D ．6 2．若ABC ∆的外接圆的圆心为O ，半径为1，=++，则=⋅( )A ．21B ．0C ．1D ．21- 3．点O 在ABC ∆内部且满足022=++OC OB OA ，则ABC ∆面积与凹四边形ABOC 面积之比是（）A ．0B ．23C ．45D ．34 4．ABC ∆的外接圆的圆心为O ，若OC OB OA OH ++=，则H 是ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心5．O 是平面上一定点，C B A 、、是平面上不共线的三个点，若222OB BC OA =+ 222+=+，则O 是ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心6．ABC ∆的外接圆的圆心为O ，两条边上的高的交点为H ，)(m ++=，则实数m =7．（06陕西）已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC→| =12 , 则△ABC 为( ) A ．三边均不相等的三角形 B ．直角三角形C ．等腰非等边三角形D ．等边三角形8．已知ABC ∆三个顶点C B A 、、，若CA BC CB AB AC AB AB ⋅+⋅+⋅=2，则ABC ∆为（）A ．等腰三角形B ．等腰直角三角形C ．直角三角形D ．既非等腰又非直角三角形练习答案：C 、D 、C 、D 、D 、1、D 、C。

向量有关的三角形四心问题

向量有关的三角形四心问题《向量有关的三角形四心问题》一、引言三角形是地理学，几何学，数学和计算机科学等领域中非常重要的概念。

在三角形的各种应用中，三角形四心问题是一个重要的概念。

三角形四心问题是指：给定一个三角形，在三角形内找出四个点，使得它们构成一个方形。

本文将讨论这个问题，分析其解法，并用向量来解答它。

二、方法1、三角形四心问题的基本思想三角形四心问题的基本思想是求解一个特定的三角形，使得该三角形的顶点能够构成一个方形或一个正方形。

该思想的基本步骤如下：(1)确定三角形的三个角：首先需要确定三角形的三个角，即A，B，C三个角的角度（以度数表示）。

(2)确定三角形的边长：一旦确定了三角形的角度，就可以确定三角形的边长，即a，b，c三个边的长度。

(3)确定三角形的三个顶点：三角形的三个顶点可以通过已知的三角形的三个角（A，B，C）和三边长（a，b，c）进行求解。

(4)求解方法：有了三角形的三个顶点之后，就可以求解三角形四心问题，即求解四个点，使得它们构成一个方形。

2、三角形四心问题的向量解法三角形四心问题的向量解法就是利用向量的性质来求解三角形四心问题，基本思想是：（1）引入三个向量首先，定义三个向量：OAB，OBC和OAC，分别表示三角形A，B，C三个顶点之间的向量，即OA，OB，OC三个向量。

（2）求解OA，OB，OC的和通过OA + OB + OC的和可以求得三角形四心问题的答案，其中OA，OB，OC的和就是求解三角形四心问题的关键步骤。

（3）求解四个点最后，根据OA + OB + OC的和求解出答案，即求出四个点，使得它们构成一个方形。

三、结论本文通过分析三角形四心问题提出了基于向量的解法，即利用向量的性质来求解三角形四心问题。

该解法可以有效地求解出三角形四心问题的解。

向量与三角形内心外心重心垂心

向量与三角形的重心、垂心、内心、外心的关系一、四心的概念介绍、（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、四线与向量的结合121212,PA =1=,=.ABOA OB PB AB λλλλλλ=++u u r u u u r u u u r1.定理：如图，设OP 则，且(记忆:交叉分配系数)=()OA OBAP BPλ+u u u r u u u r2.若M 是OP 上的任意一点，则OM (记忆:分母对应分配系数)应用1:（1）中线: （2）高线:（3）角平分线: （4）中垂线:应用2.四线上的动点表示:(1)中线上的动点: ()AB AC λ+u u u r u u u r 或()||sin ||sin ABAC AB B AC Cλ+u u u ru u u r u u ur u u u r(2)高线上的动点:()cos cos AB ACAB B AC Cλ+u u u r u u u r u u u r u u u r, (3)角平分线上的动点:()AB ACAB AC λ+u u u r u u u r u u u r u u u r(4)中垂线上的动点: ()2||cos ||cos OB OC AB ACOP AB B AC Cλ+=++u u u r u u u r u u u r u u u r u u u r u u u r u u u r ,三、四心与向量的结合 1.BOC AOC AOB O ABC S OA S OB S OC ∆∆∆∆++=u u u r u u u r u u u r r 定理：设是内任意一点，则（记忆：拉力平衡原则）应用:（1）O 是ABC ∆的重心. ⇔b a S S S AOB AOC BOC ：：：：=∆∆∆=1:1:1⇔ 0OA OB OC ++=u u u r u u u r u u u r r（2）O 为ABC ∆的垂心. ⇔ C tan B tan A tan S S S AOB AOC BOC ：：：：=∆∆∆ ⇔0OC C tan OB B tan OA A tan =++（3）O 为ABC ∆的内心.⇔c b a S S S AOB AOC BOC ：：：：=∆∆∆=sin :sin :sin A B C⇔0OC C sin OB B sin OA A sin 0OC c OB b OA a =++=++或⇔0aOA bOB cOC ++=u u u r u u u r u u u r r （4）O 为ABC ∆的外心⇔ ⇔ 0OC C 2sin OB B 2sin OA A 2sin =++2.四心的向量表示：（1）O 是ABC ∆的重心. ⇔ 1()3PO PA PB PC =++u u u ru u u ru u u ru u u r（2）O 为ABC ∆的垂心. ⇔OA OB OB OC OC OA ⋅=⋅=⋅u u u r u u u r u u u r u u u r u u u r u u u r（3）O 为ABC ∆的内心.⇔()()()0AB AC BC BA CA CBOA OB OC AB AC BC BA CA CB•-=•-=•-=u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r （4）O 为ABC ∆的外心 ⇔OC OB OA ==四．典型例题：一、与三角形“四心”相关的向量问题题1：已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足||||AB AC OP OA AB AC λ⎛⎫=++ ⎪⎝⎭u u u r u u u ru u u r u u u r u u u r u u u r , [0,)λ∈+∞. 则P 点的轨迹一定通过△ABC 的 A. 外心 B. 内心 C. 重心 D. 垂心题2：已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()OP OA AB AC λ=++u u u r u u u r u u u r u u u r, [0,)λ∈+∞. 则P 点的轨迹一定通过△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题3：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()||sin ||sin AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u u r u u u r ,[0,)λ∈+∞, 则动点P 的轨迹一定通过△ABC 的 C 2sin :B 2sin :A 2sin AOB sin AOC sin BOC sin S S S AOB AOC BOC =∠∠∠=∆∆∆：：：：A. 重心B. 垂心C. 外心D. 内心题4：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()||cos ||cos AB ACOP OA AB B AC Cλ=++u u u r u u u ru u u r u u u r u u u r u u u r ,[0,)λ∈+∞, 则动点P 的轨迹一定通过△ABC 的( )A. 重心B. 垂心C. 外心D. 内心题5：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()2||cos ||cos OB OC AB ACOP AB B AC Cλ+=++u u u r u u u r u u u r u u u r u u u r u u u r u u u r , [0,)λ∈+∞, 则动点P 的轨迹一定通过△ABC 的( )A. 重心B. 垂心C. 外心D. 内心题6：三个不共线的向量,,OA OB OC u u u r u u u r u u u r 满足()||||AB CA OA AB CA ⋅+u u u r u u u r u u u r u u u r u u u r =(||BA OB BA ⋅u u u r u u u r u u u r+||CB CB u u u r u u u r ) =()||||BC CA OC BC CA ⋅+u u u r u u u r u u u r u u u r u u u r = 0，则O 点是△ABC 的( )A. 垂心B. 重心C. 内心D. 外心题7：已知O 是△ABC 所在平面上的一点，若OA OB OC ++u u u r u u u r u u u r= 0, 则O 点是△ABC的( )A. 外心B. 内心C. 重心D. 垂心题8：已知O 是△ABC 所在平面上的一点，若1()3PO PA PB PC =++u u u r u u u r u u u r u u u r(其中P 为平面上任意一点), 则O 点是△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题9：已知O 是△ABC 所在平面上的一点，若OA OB OB OC OC OA ⋅=⋅=⋅u u u r u u u r u u u r u u u r u u u r u u u r，则O点是△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题10：已知O 为△ABC 所在平面内一点，满足2222||||||||OA BC OB CA +=+u u u r u u u r u u u r u u u r=22||||OC AB +u u u r u u u r ，则O 点是△ABC 的( )A. 垂心B. 重心C. 内心D. 外心题11：已知O 是△ABC 所在平面上的一点，若()OA OB AB +⋅u u u r u u u r u u u r =()OB OC BC +⋅u u u r u u u r u u u r= ()OC OA CA +⋅u u u r u u u r u u u r= 0，则O 点是△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题12：已知O 是△ABC 所在平面上的一点，若aOA bOB cOC ++u u u r u u u r u u u r= 0，则O 点是△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题13：已知O 是△ABC 所在平面上的一点，若aPA bPB cPCPO a b c++=++u u u r u u u r u u u ru u u r (其中P 是△ABC 所在平面内任意一点)，则O 点是△ABC 的( )A. 外心B. 内心C. 重心D. 垂心题14：△ABC 的外接圆的圆心为O ，两边上的高的交点为H ，OH u u u r =()m OA OB OC ++u u u r u u u r u u u r，则实数m =____________.二、与三角形形状相关的向量问题题15：已知非零向量ABu u u r 与AC uuu r 满足()||||AB AC BC AB AC +⋅u u u r u u u ru u ur u u u r u u u r = 0且12||||AB AC AB AC ⋅=u u u r u u u ru u u r u u u r ，则△ABC 为( ) A. 三边均不相等的三角形 B. 直角三角形 C. 等腰非等边三角形 D. 等边三角形题16：已知O 为△ABC 所在平面内一点，满足|||2|OB OC OB OC OA -=+-u u u r u u u r u u u r u u u r u u u r，则△ABC 一定是( )A. 等腰直角三角形B. 直角三角形C. 等腰三角形D. 等边三角形题17：已知△ABC ，若对任意t R ∈，||BA tBC -u u u r u u u r ≥||AC u u u r，则△ABC( )A. 必为锐角三角形B. 必为钝角三角形C. 必为直角三角形D. 答案不确定题18：已知a , b, c 分别为△ABC 中∠A, ∠B, ∠C 的对边，G 为△ABC 的重心，且a GA b GB c GC ⋅+⋅+⋅u u u r u u u r u u u r= 0, 则△ABC 为( )A. 等腰直角三角形B. 直角三角形C. 等腰三角形D. 等边三角形三、与三角形面积相关的向量问题题19：已知点O 是△ABC 内一点，23OA OB OC ++u u u r u u u r u u u r= 0, 则：(1) △AOB 与△AOC 的面积之比为___________________； (2) △ABC 与△AOC 的面积之比为___________________； (3) △ABC 与四边形ABOC 的面积之比为_____________. 四、向量的基本关系(共线)题20：如图，已知点G 是△ABC 的重心，若PQ uuu r过△ABC 的重心，记CA u u u r = a ,CB u u u r = b , CP u u u r = m a , CQ uuu r = n b , 则11m n+=_____.练习．O 为ABC ∆平面上一定点，该平面上一动点p 满足{|(sin ABM P OP OA C ABλ==++u u u ru u u r u u u r u u u r sin )0}AC B ACλ>u u u r u u u r ，，则ABC ∆的（）一定属于集合M .（A ）重心（B ）垂心（C ）外心（D ）内心GABCMP Q。

向量与三角形的四心、奔驰定理latex版

觅宁参考出品【知识清单】1向量与重心(1)重心定义:三角形三条中线的交点叫做三角形的,一般记为G.(2)G是△ABC的重心⇐⇒G的坐标为;(3)G是△ABC的重心⇐⇒# »GA+# »GB+# »GC=;(4)若# »AP=λ(# »AB+# »AC),λ∈R,则P在BC边的上;(5)若G是△ABC的重心,P是△ABC所在平面内一点则# »P G=(# »P A+# »P B+# »P C);(6)若G是△ABC的重心,则当P在G处时,|P A|2+|P B|2+|P C|2取得最值;(7)若G是△ABC的重心,则S△GAB:S△GBC:S△GAC:S△ABC=. 2向量与垂心(1)垂心定义:三角形三条高线的交点叫做三角形的;(2)若# »AP=λ(# »ABc cos B+# »ACb cos C),λ∈R,则P在BC边的上;(3)在△ABC中,# »HA·# »BC=# »HB·# »AC=# »HC·# »AB⇐⇒H是三角形ABC的;(4)在△ABC中,# »HA·# »HB=# »HB·# »HC=# »HC·# »HA⇐⇒H是三角形ABC的;(5)在△ABC中,|# »HA|2+|# »BC|2=|# »HB|2+|# »CA|2=|# »HC|2+|# »AB|2⇐⇒H是三角形ABC的.3向量与外心(1)三角形三条边的中垂线（垂直平分线）的交点叫做三角形的,即三角形的圆心.(2)外心到三角形的三个的距离相等;第1页共2页(3)锐角三角形的外心在三角形；直角三角形的外心在；钝角三角形的外心三角形;(4)在△ABC中,|# »OA|=|# »OB|=|# »OC|⇐⇒O是三角形ABC的;(5)在△ABC中,(# »OA+# »OB)·# »AB=(# »OB+# »OC)·# »BC=(# »OA+# »OC)·# »AC=0⇐⇒O是三角形ABC的;(6)在圆O中，AB为弦，则# »AO·# »AB=.4向量与内心(1)三角形三条角平分线的交点叫做,内心即三角形的圆心，内心到三角形距离相等.(2)若# »AP=λ(# »AB|# »AB|+# »AC|# »AC|),λ∈R,则P在.(3)在△ABC中,a # »OA+b# »OB+c# »OC=#»0⇐⇒O是△ABC的.5奔驰定理(1)奔驰定理:若O为△ABC内一点,满足m # »OA+n# »OB+k# »OC=#»0,则S△AOB:S△BOC:S△AOC:S△ABC=.(2)已知P为△ABC内一点,则有S△P BC·# »P A+S△P AC·# »P B+S△P AB·# »P C=(3)在△ABC中,若sin2A·# »OA+sin2B·# »OB+sin2C·# »OC=#»0,则O为△ABC的;(4)在△ABC中,sin A·# »OA+sin B·# »OB+sin C·# »OC=#»0,则O为△ABC的;(5)在△ABC中,tan A·# »OA+tan B·# »OB+tan C·# »OC=#»0,则O为△ABC的.第2页共2页觅宁参考出品一、向量与三角形的重心1.在△ABC 中,已知O 为△ABC 所在平面内一点,若# »OA +# »OB +# »OC =0,则点O 是△ABC 的()A.内心B.垂心C.外心D.重心【答案】D2.已知O 是△ABC 所在平面上一定点,动点P 满足# »OP =# »OA +λ(# »AB |# »AB |sin B+# »AC |# »AC |sin C ),λ∈[0,+∞),则动点P 的轨迹一定通过△ABC 的()A.外心 B.内心C.重心D.垂心【答案】C3.已知A,B,C 是坐标平面内的不共线的三点,O 是坐标原点，动点P 满足# »OP =13[(1−λ)# »OA +(1−λ)# »OB +(1+2λ)# »OC ],λ∈R ,则点P 的轨迹一定经过△ABC 的()A.内心B.垂心C.外心D.重心第1页共5页【答案】D二、向量与三角形的垂心4.已知O 是△ABC 所在平面上一定点,动点P 满足,# »OP =# »OA +λ(# »AB |# »AB |cos B +# »AC |# »AC |cos C ),λ∈[0,+∞),则动点P 的轨迹一定通过△ABC 的()A.外心 B.内心C.重心D.垂心【答案】D5.在△ABC 中,若# »OA ·# »OB =# »OB ·# »OC =# »OC ·# »OA ,则点O 是△ABC 的()A.内心B.垂心C.外心D.重心【答案】B6.已知O 是△ABC 所在平面上一点,且|# »OA |2+|# »BC |2=|# »OB |2+|# »CA |2,则点O()A.在过点C 且与AB 垂直的直线上B.在∠A 的平分线所在直线上C.在边AB 的中线所在直线上D.以上都不对【答案】A第2页共5页三、向量与三角形的外心7.已知O是△ABC所在平面上一定点,动点P满足# »OP=# »OB+# »OC2+λ(# »AB|# »AB|cos B+# »AC|# »AC|cos C),λ∈[0,+∞),则动点P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心【答案】A8.在△ABC中,已知O为△ABC所在平面内一点,若(# »OA+# »OB)·# »AB=(# »OB+# »OC)·# »BC=(# »OC+# »OA)·# »CA=0,则点O是△ABC的()A.内心B.垂心C.外心D.重心【答案】C四、向量与三角形的内心9.已知O是△ABC所在平面上一定点,动点P满足# »OP=# »OA+λ(# »AB|# »AB|+# »AC|# »AC|),λ∈[0,+∞),则动点P的轨迹一定通过△ABC的() A.外心 B.内心 C.重心 D.垂心【答案】B10.在△ABC中,已知O为△ABC所在平面内一点，若a # »OA+b # »OB+c# »OC=0,其中a,b,c分别为△ABC的内角A,B,C的对边长,则点O是△ABC的() A.内心 B.垂心 C.外心 D.重心第3页共5页【答案】A11.在△ABC中,已知O为△ABC所在平面内一点，若# »P O=a# »P A+b# »P B+c# »P Ca+b+c,其中a,b,c分别为△ABC的内角A,B,C的对边长,P为△ABC所在平面内的任意一点,则点O是△ABC的()A.内心B.垂心C.外心D.重心【答案】A五、奔驰定理与向量的四心12.已知O是△ABC内部一点,满足# »OA+2# »OB+m# »OC=0,且S△AOBS△ABC=47,则实数m等于() A.2 B.3 C.4 D.5【答案】C13.若△ABC内接于以O为圆心,以1为半径的圆,且3# »OA+4# »OB+5# »OC=0.则△ABC的面积为()A.712B.65C.85D.125【答案】B 第4页共5页14.在△ABC 中,AB =2,AC =3,BC =4,O 为△ABC 的内心,若# »AO =λ# »AB +µ# »BC ,则3λ+6µ的值为()A.1B.2C.3D.4【答案】C15.已知H 是△ABC 的垂心,若# »HA +2# »HB +3# »HC =0,则A =()A.π6B.π4C.π3D.π2【答案】B16.设点P 在△ABC 内且为△ABC 的外心,∠BAC =30◦,如图.若△P BC ,△P CA ,△P AB 的面积分别为12,x ,y ,则x +y 的最大值是()BCAPA.√22 B.√32C.√23D.√33【答案】D第5页共5页。

与三角形四心相关的向量结论.doc

与三角形四心相关的向量结论.doc一、定义1. 三角形的三条中线分别连接三角形的对边中点，它们的交点称为三角形的重心。

既然我们要讨论与三角形的四个特殊点有关的向量结论，就先给出这四个特殊点的定义。

二、引理引理 1：两向量 $\vec{a}$，$\vec{b}$ 之间的角度 $\theta = \arccos(\cos\theta) = \arccos\frac{\vec{a}\cdot\vec{b}}{|\vec{a}||\vec{b}|}$。

三、重心重心是三角形的三条中线的交点，记为 $G$。

设三角形三个顶点为 $A$，$B$，$C$，则重心 $G$ 满足 $\vec{OG} = \frac{1}{3}(\vec{OA}+\vec{OB}+\vec{OC})$，其中$O$ 为原点。

$$\vec{OG}=\frac{\vec{OA}+\vec{GA}+\vec{OB}+\vec{OC}}{3}$$将 $\vec{GA}=\frac{2}{3}\vec{MA}$，其中 $M$ 为对边 $BC$ 的中点，代入得四、内心证明：设 $\angle B = \alpha$，$\angle C = \beta$，$\angle A = \gamma$，$\angle DFE=\gamma_1$，$\angle EFD=\alpha_1$，$\angle FDE=\beta_1$，则有$$\begin{aligned}a&=\frac{BC}{EF}=\frac{2BC}{2EF}=\frac{2AC\sin\gamma}{2AF\sin\gamma_1}=\frac{AC}{AF}\cdot\frac{\sin\gamma}{\sin\gamma_1}\\b&=\frac{CA}{FD}=\frac{2CA}{2FD}=\frac{2AB\sin\beta}{2BD\sin\beta_1}=\frac{AB}{BD}\cdot\frac{\sin\beta}{\sin\beta_1}\\c&=\frac{AB}{DE}=\frac{2AB}{2DE}=\frac{2BC\sin\alpha}{2 CE\sin\alpha_1}=\frac{BC}{CE}\cdot\frac{\sin\alpha}{\sin\alpha_1}\end{aligned} $$根据正弦定理可得代入 $\vec{OI}$ 的式子得到这是一个加权平均的形式，其中 $AF:BC$，$BD:CA$，$CE:AB$ 分别表示三个小三角形的面积比。

三角形“四心”向量形式的结论及证明

三角形“四心”向量形式的结论及证明三角形的“四心”是指三角形的重心、外心、内心和垂心。

它们的位置可以用向量的形式来描述。

本文将分别介绍三角形“四心”的向量形式以及其证明。

1.重心:重心是指三角形三个顶点的中线交点所在的点，用G表示。

假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则重心G的坐标可以通过以下公式得到：G=(A+B+C)/3其向量形式为：OG=(OA+OB+OC)/3其中O为坐标原点。

证明：由定义可知，重心是三角形三个顶点的中线交点所在的点。

而中线的坐标可以通过两个顶点的坐标的平均值得到。

因此，重心的坐标是三个顶点坐标的平均值。

根据向量加法的性质，可以得到上述结论。

2.外心:外心是指可以通过三角形的三个顶点作为圆心，找到一个圆使得三条边都是这个圆的切线。

用O表示外心。

假设三角形的三个顶点分别为A(x1,y1)、B(x2,y2)和C(x3,y3)，则外心O的坐标可以通过以下公式得到：O=(a^2*A+b^2*B+c^2*C)/(a^2+b^2+c^2)其中a、b、c分别表示三角形的边长BC、AC和AB的长度。

其向量形式为：OO=(a^2*OA+b^2*OB+c^2*OC)/(a^2+b^2+c^2)其中O为坐标原点。

证明：设外心为O，连接OA、OB、OC，并设AO的长度为R，BO的长度为R'，CO的长度为R''。

根据定义可知，OA，OB，OC都是截圆半径，可以得到以下关系：OA⊥BC，OB⊥AC，OC⊥AB由于OA、OB、OC是向量，因此上述关系可以写为：OA·BC=0，OB·AC=0，OC·AB=0其中“·”表示点乘。

根据向量的点乘性质可知：OA·(B-C)=0，OB·(C-A)=0，OC·(A-B)=0将向量差展开得：OA·B-OA·C=0，OB·C-OB·A=0，OC·A-OC·B=0进一步展开可得：R^2-R'^2=0，R'^2-R''^2=0，R''^2-R^2=0整理得：R^2-R'^2=R''^2-R^2移项得：2R^2=R'^2+R''^2根据圆的定义可知，外心到三角形的每个顶点的距离都相等，因此R=R'=R''。

向量与三角形内心、外心、重心、垂心

二、四线与向量的结合121212,PA =1=,=.ABOA OB PB AB l l l l l l =++1.1.定理：如图，设定理：如图，设定理：如图，设OP OP 则则，且 (记忆:交叉分配系数) =()OA OBAP BP l +2.2.若若M 是OP OP上的任意一点，则上的任意一点，则上的任意一点，则OM OM (记忆:分母对应分配系数) 应用1: （1）中线: （2）高线: （3）角平分线: （4）中垂线: 应用2.四线上的动点表示: (1)中线上的动点: ()AB AC l +或()||sin ||sin AB AC AB B AC Cl +(2)高线上的动点:()cos cos AB AC AB BAC C l +, (3)角平分线上的动点:()AB ACABACl +(4)中垂线上的动点: ()2||cos ||cos OB OCAB AC OP AB B AC Cl +=++,O ABC OA S OB S OC D 定理：设是内任意一点，b a SAOBAOC：：：=D =1:1:1Û0OA OB OC ++=B tan A tan S AOB AOC ：：：=D 0OC OB OA 0aOA bOB cOC 1()3PO PA PB PC =++OA OB OB OC OC OA ×=×=× )))AB AC BC BA CA OC OB OA 已知O 是平面上一定点，||||AB AC AB AC l æö=++ç÷, l 题2：已知O 是平面上一定点，()OP OA AB AC l =++, l ÎO 是平面上的一定点，A ()||sin ||sin AB AC OP OA AB B AC Cl =++是平面上的一定点，A 、B ()||cos ||cos AB AC AB B AC Cl +题5：已知O 是平面上的一定点，A 、B 、C 是平面上不共线的三个点，动点()OB OCABAC++D. 内心,,OA OB OC 满足()||||AB CA OA AB CA ×+=(||BA OB BA ×+||CB CB ) ()||||BC CAOC BC CA ×+= 0内心 D. 外心OA OB OC ++= 0, 1()PO PA PB PC D. 垂心OA OB OB OC OC OA ×=×=×，则 D. 垂心 2222|||||||OA BC OB CA +=+=22|||OC AB +，则 D. 外心题11：已知O 是△ABC )OA OB AB +×()OB OC BC +×()OC OA CA +×= 0，则 D. 垂心aOA bOB cOC ++= = 00，则D. 垂心aPA bPB cPC =题14：△ABC 的外OH =()m OA OB OC ++，则实数二、与三角形形状相关的向量问题题15：已知||||ABACAB AC 12||||AB AC AB AC ×=，则△等边三角形|||2|OB OC OB OC OA -=+-，则等边三角形||BA tBC -≥||AC ，则△题18：已知a , b, c 分别为△GA b GB c GC ×+×+×= = 00, 则△内一点，23OA OB OC ++= 0, 则：题20：如图，已知点是△ABC 的重心，若PQ 过△ABC 的重心，记CA = a ,则11m n +=_____.|(sin AB OP OA C ABl =++sin )AC B ACG C P Q 。

高中数学：向量中的三角形“四心”

高中数学：向量中的三角形“四心”
向量的加减法离不开三角形，三角形的重心、垂心、内心、外心是三角形性质的重要组成部分，你知道它们的向量表示吗？
结论1：若点O为△ABC所在的平面内一点，满足
，则点O为△ABC的垂心。

证明：由，得，即，所以。

同理可证。

故O为
△ABC的垂心。

结论2：若点O为△ABC所在的平面内一点，满足
，则点O为△ABC的垂心。

证明：由，得
，所以。

同理可证。

容易得到由结论1知O为△ABC的垂心。

结论3：若点G为△ABC所在的平面内一点，满足
，则点G为△ABC的重心。

证明：由，得。

设BC边中点为M，则，所以，即点G在中线AM 上。

设AB边中点为N，同理可证G在中线CN上，故点G为△ABC的重心。

结论4：若点G为△ABC所在的平面内一点，满足
，则点G为△ABC的重心。

证明：由，得
，得。

由结论3知点G为△ABC的重心。

结论5：若点P为△ABC所在的平面内一点，并且满足
，则点P为
△ABC的内心。

证明：由于，可得。

设与同方向的单位向量为，与同方向的单位向量为，则。

因为为单位向量，所以向量在∠A的平分线上。

由，知点P在∠A的平分线上。

同理可证点P在∠B的平分线上。

故点G为△ABC的内心。

结论6：若点O为△ABC所在的平面内一点，满足
，则点O为△ABC的外心。

证明：因为，所以
同理得由题意得，所以
，得。

故点O为△ABC的外心。

三角形中的四心与向量

三角形中的四“心”与向量平面几何中的三角形四“心”，即三角形的内心（内角平分线的交点，内切圆的圆心）、重心（中线的交点）、垂心（高线的交点）、外心（各边垂直平分线的交点，三角形外接圆的圆心）。

在引入向量这个工具后，我们可以通过向量来表示三角形的四“心”，这样使我们对向量形式的多样性和向量运算的灵活性有更清楚的认识。

一、重心：例1、已知O 是ABC V 所在平面上的一点，若0OA OB OC ++=u u u r u u u r u u u r r ,则O 是ABC V的A.外心B.内心C.重心D.垂心【解析】若0OA OB OC ++=u u u r u u u r u u u r r ，则=OA OB OC +-u u u r u u u r u u u r ，以,OA OB u u u r u u u r 为邻边作平行四边形'OAC B ，设OC 与AB 交于点D ，则D 为AB 中点，有'=OA OB OC +u u u u r u u u r u u u r ，得'=OC OC -u u u u r u u u r ，即',,,C O D C 四点共线，故CD 为ABC V 的中线，同理,AE BF亦为ABC V 的中线，所以O 是ABC V 的重心。

例2、已知O 是平面上一定点，,,A B C 是平面上不共线的三点，动点P 满足(),(0,)OP OA AB AC λλ=++∈+∞u u u r u u u r u u u r u u u r ，则动点P 的轨迹一定通过ABC V 的A.外心B.内心C.重心D.垂心【解析】上式可化为()AP AB AC λ=+u u u r u u u r u u u r ，当(0,)λ∈+∞时，由于()AB AC λ+u u u r u u u r 表示BC 边上的中线所在直线的方向向量，故动点P 的轨迹一定通过ABC V 的重心。

高中数学平面向量与三角形的“四心”

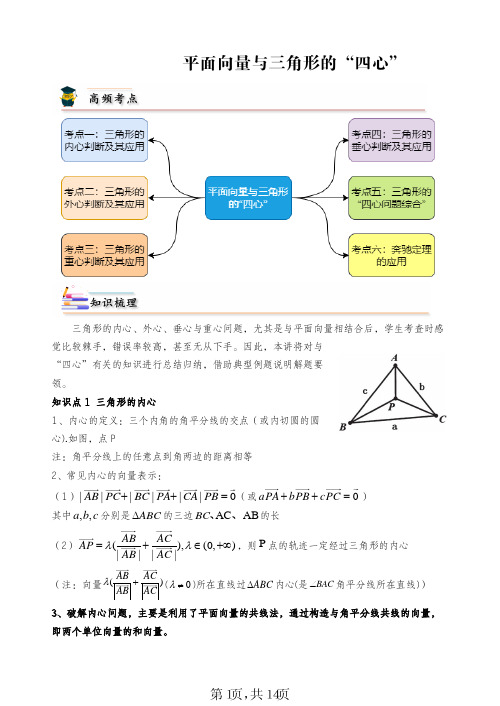
培优专题1 平面向量与三角形的“四心”三角形的内心、外心、垂心与重心问题，尤其是与平面向量相结合后，学生考查时感觉比较棘手，错误率较高，甚至无从下手。

因此，本讲将对与“四心”有关的知识进行总结归纳，借助典型例题说明解题要领。

知识点1 三角形的内心1、内心的定义：三个内角的角平分线的交点（或内切圆的圆心).如图，点P注：角平分线上的任意点到角两边的距离相等 2、常见内心的向量表示：（1）||||||0AB PC BC PA CA PB ++=（或0aPA bPB cPC ++=）其中,,a b c 分别是ABC ∆的三边AC AB BC 、、的长（2）(),(0,)||||AB ACAP AB AC λλ=+∈+∞，则P 点的轨迹一定经过三角形的内心（注：向量()AB AC ABACλ+(0λ≠)所在直线过ABC ∆内心(是BAC ∠角平分线所在直线)）3、破解内心问题，主要是利用了平面向量的共线法，通过构造与角平分线共线的向量，即两个单位向量的和向量。

拓展：是平面上一定点，，，是平面上不共线的三个点，动点满足，证明的轨迹一定通过的内心．【解析】证明：、分别表示与、方向相同的单位向量，的方向与的角平分线方向一致；又，；的方向与的角平分线方向一致，点的轨迹一定通过的内心．知识点2 三角形的外心1、外心的定义：三角形三边的垂直平分线的交点（或外接圆的圆心）注：外心到三角形各顶点的距离相等. 2、常用外心的向量表示：（1）222||||||OA OB OC OA OB OC ==⇔==（2）()()()0OA OB AB OB OC BC OA OC AC +⋅=+⋅=+⋅= 变形：P 为平面ABC 内一动点，若()()()()()()0OA OB PB PA OB OC PC PB OA OC PC PA +⋅−=+⋅−=+⋅−=，则O 为三角形的外心3、破解外心问题，关键是运用平面向量的加减法和数量积的运算，结合数量积的运算律从而得到三角形的外心。

高中数学-三角形内心、外心、重心、垂心与向量关系

高中数学-三角形内心、外心、重心、垂心与向量关系（附向量知识点）一、三角形四心知识点（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

二、向量知识点☆零向量：长度为0的向量，记为0 ，其方向是任意的，0与任意向量平行☆单位向量：模为1个单位长度的向量向量0a 为单位向量⇔｜0a｜＝1☆平行向量（共线向量）：方向相同或相反的非零向量平行向量也称为共线向量☆向量加法AB BC +=AC向量加法有“三角形法则”与“平行四边形法则”：AB BC CD PQ QR AR +++++=，但这时必须“首尾相连”．☆实数与向量的积：①实数λ与向量a的积是一个向量，记作λa，它的长度与方向规定如下：（Ⅰ）a a⋅=λλ；（Ⅱ）当0>λ时，λa 的方向与a 的方向相同；当0<λ时，λa 的方向与a的方向相反；当0=λ时，0 =a λ，方向是任意的☆两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ，使得b =a λ☆平面向量的基本定理：如果21,e e 是一个平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数21,λλ使：2211e e a λλ+=，其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底☆平面向量的坐标运算：(1) 若()()1122,,,a x y b x y ==，则()1212,a b x x y y ±=±±，1212a b x x y y ⋅=⋅+⋅(2) 若()()2211,,,y x B y x A ，则()2121,AB x x y y =--(3) 若a =(x,y)，则λa =(λx, λy)(4) 若()()1122,,,a x y b x y ==，则1221//0a b x y x y ⇔-= (5) 若()()1122,,,a x y b x y ==，则a b ⊥，02121=⋅+⋅y y x x☆向量的运算向量的加减法，数与向量的乘积，向量的数量（内积）及其各运算的坐标表示和性质☆两个向量的数量积：已知两个非零向量a 与b ，它们的夹角为θ，则a ·b =︱a ︱·︱b ︱cos θ 叫做a 与b 的数量积（或内积）规定00a ⋅=☆向量的投影：︱b ︱cos θ=||a ba ⋅∈R ，称为向量b 在a 方向上的投影投影的绝对值称为射影 ☆数量积的几何意义： a ·b 等于a 的长度与b 在a 方向上的投影的乘积☆向量的模与平方的关系：22||a a a a ⋅==☆乘法公式成立： ()()2222a b a b a b a b +⋅-=-=-；()2222a ba ab b ±=±⋅+222a a b b =±⋅+☆向量的夹角：已知两个非零向量a 与b ，作OA =a , OB =b ,则∠AOB=θ （01800≤≤θ）叫做向量a 与b 的夹角cos θ=cos ,a b a ba b•<>=•=222221212121y x y x +⋅+当且仅当两个非零向量a 与b 同方向时，θ=00，当且仅当a 与b 反方向时θ=1800，同时0与其它任何非零向量之间不谈夹角这一问题补充：线段的定比分点()()()设，，，，分点，，设、是直线上两点，点在P x y P x y P x y P P P 11122212ll 上且不同于、，若存在一实数，使，则叫做分有向线段P P P P PP P 1212λλλ→=→P P P P P P P P 12121200→><所成的比（，在线段内，，在外），且λλx x x y y y P P P x x x y y y =++=++⎧⎨⎪⎪⎩⎪⎪=+=+⎧⎨⎪⎪⎩⎪⎪12121212121122λλλλ，为中点时，()()()如：，，，，，，∆ABC A x y B x y C x y 112233则重心的坐标是，∆ABC G x x x y y y 12312333++++⎛⎝ ⎫⎭⎪三、三角形四心与向量关系典型例题：例1：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足)(AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心分析：如图所示ABC ∆，E D 、分别为边AC BC 、的中点.AD AC AB 2=+ ∴AD OA OP λ2+= AP OA OP += AD AP λ2=∴AP ∴//AD ∴点P 的轨迹一定通过ABC ∆的重心，即选C .例2：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（ B ）A ．外心B ．内心C ．重心D ．垂心分析：ACAB分别为AC AB 、方向上的单位向量，∴AC AB +平分BAC ∠,∴点P 的轨迹一定通过ABC ∆的内心，即选B .例3：O 是平面上一定点，C B A 、、是平面上不共线的三个点，动点P 满足AC AB OA OP ++=λ，[)+∞∈,0λ ，则点P 的轨迹一定通过ABC ∆的（）A ．外心B ．内心C ．重心D ．垂心分析：如图所示AD 垂直BC ，BE 垂直AC ， D 、E 是垂足.AC AB +BC ⋅=BC AC BC AB ⋅+=+-=0∴点P 的轨迹一定通过ABC ∆的垂心，即选D .三、四心与向量的结合（1）⇔=++0OC OB OA O 是ABC ∆的重心.证法1：设),(),,(),,(),,(332211y x C y x B y x A y x O⇔=++0OC OB OA ⎩⎨⎧=-+-+-=-+-+-0)()()(0)()()(321321y y y y y y x x x x x x ⎪⎪⎩⎪⎪⎨⎧++=++=⇔33321321y y y y x x x x ⇔O 是ABC ∆的重心. 证法2：如图OC OB OA ++02=+=OD OA ∴OD AO 2=∴D O A 、、三点共线，且O 分AD 为2：1 ∴O 是ABC ∆的重心（2）⇔⋅=⋅=⋅OA OC OC OB OB OA O 为ABC ∆的垂心.证明：如图所示O 是三角形ABC 的垂心，BE 垂直AC ，AD 垂直BC ， D 、E 是垂足.0)(=⋅=-⇔⋅=⋅CA OB OC OA OB OC OB OB OA AC OB ⊥⇔同理BC OA ⊥，ABOC ⊥⇔O 为ABC ∆的垂心B CDB CD（3）设a ,b ,c 是三角形的三条边长，O 是∆ABC 的内心O OC c OB b OA a ⇔=++0为ABC ∆的内心.证明：bACc AB 、分别为AC AB 、方向上的单位向量， ∴bACc AB +平分BAC ∠, (λ=∴AO bACc AB +)，令c b a bc ++=λ ∴c b a bc AO ++=（bACc AB +) 化简得0)(=++++AC c AB b OA c b a∴0=++OC c OB b OA a（4==⇔O 为ABC ∆的外心。

微专题8 平面向量与三角形的“四心”

+

| |
或＝＋
⁠
若△ABC及内一点O满足关系式：S△OBC·＋S△OAC·＋S△OAB·＝0，即为经
典的“奔驰定理”.若△ABC的三边为a，b，c，有a·＋b·＋c·＝0，则O
为△ABC的（
）
A.外心
B.内心
C.重心
D.垂心
解析：B
∵＝＋，＝＋，∴a·＋b·＋c·＝a·
＝·，则点G可能通过△ABC的
（填：重心、内心、垂心或外
⁠
心）.
解析：由·＝·⇔·－·＝0⇔·（－）＝0，
【例4】在△ABC中，设 2 － 2 ＝2·，那么动点M形成的图形必经过
△ABC的
A.垂心
（
）
B.内心
C.外心
D.重心
解析如图所示，设线段BC的中点为D，则＋＝2，
∵ 2 － 2 ＝2·
，∴（＋）·
（－）＝
2·
，∴·
（＋－2）＝0，∴·
【例1】已知点O为△ABC所在平面内一点，若动点P满足＝＋λ（＋
）（λ≥0），则动点P的轨迹一定经过△ABC的（
A.外心
B.内心
C.垂心
D.重心
）
解析因为动点P满足＝＋λ（＋）（λ≥0），所以＝λ（＋
），取BC中点D（图略），则＝2λ，则动点P的轨迹一定过△ABC的重
＋b（＋）＋c（＋）＝（a＋b＋c）·＋b·＋c·＝0，

∴＝
++
+

，∵ ，分别是，方向上的单位向量，∴向

量＋平分∠BAC，即AO平分∠BAC，同理BO平分∠ABC，∴O为

用向量解决三角形“四心”问题

用向量解决三角形“四心”问题外心，内心，重心，垂心是三角形的四个重要几何特征，这里简称为“四心”，而向量是一个具有代数和几何双重身份的数学工具。

因此，掌握有关结论，对于处理有关“心”的问题非常有益。

性质设O 为ABC ∆所在平面内一点，,BC a CA b AB c ===，则（1）O 为ABC ∆的外心OA OB OC ⇔==；（2）O 为ABC ∆的内心aOA bOB cOC O ⇔++=；（3）O 为ABC ∆的重心OA OB OC O ⇔++=（4）O 为ABC ∆的垂心0OA BC OB CA OC AB ⇔⋅=⋅=⋅=这一组性质的应用在历年高考与竞赛中屡见不鲜，现例举如下： 1．内心例题1（2003年全国卷）O 是平面上一定点，,,A B C 是平面上不共线的三点，且满足(),[0,)AB AC OP OA AB ACλλ=++∈+∞.则P 点的轨迹一定通过ABC ∆的（）.(A) 内心 (B) 外心 (C) 重心 (D) 垂心解析：由已知，(),AB AC AP OP OA AB AC λ=-=+ 而向量,AB ACAB AC λλ构成了菱形的两条邻边，点P 一定在和向量上，即BAC ∠的角平分线上，故选（A ）.2. 重心例题2.（2004年全国高中数学联赛试题）如图1，设O 为ABC ∆内一点，且满足230OA OB OC ++=，则ABC ∆的面积与AOC ∆的面积之比为（）.(A) 2 (B)32 (C) 3 (D) 53解析：如图2，延长OB 至1B ，使12OB OB =；延长OC 至1C ，使13OC OC =.则11230OA OB OC OA OB OC ++=++=，故O 为11AB C ∆的重心.11111111111139112611618AOC AOC AB C AOB AOB AB C BOC B OC AB C S S S S S S S S S ======三式相加，得1113ABCAB C S S = .故应选 (C). 3.垂心例题3.（2003年山东省高中数学竞赛试题）设P 为ABC ∆内任一点，求证：AB 1B1CB CO 图2A BCO 图10AP BC BP CA CP AB ⋅+⋅+⋅=.解析：由欲证结论的特点，不难联想到三角形垂心的向量特征。

三角形四心的向量公式及证明

三角形四心的向量公式及证明在我们的数学世界里，三角形可是个相当重要的角色。

而三角形的“四心”——重心、外心、内心和垂心，更是藏着许多有趣的秘密，特别是它们与向量公式之间的奇妙关系。

先来说说重心。

重心是三角形三条中线的交点。

假设三角形的三个顶点分别是 A(x₁,y₁) 、B(x₂,y₂) 、C(x₃,y₃) ，那么重心 G 的坐标就是 ((x₁ + x₂ + x₃) / 3, (y₁ + y₂ + y₃) / 3) 。

这背后的向量公式是这样的：若有向量 $\overrightarrow{GA} + \overrightarrow{GB} +\overrightarrow{GC} = \overrightarrow{0}$ ，则点 G 就是重心。

给大家举个小例子吧，我曾经在课堂上给学生们讲这个知识点的时候，有个学生就特别好奇地问我：“老师，这重心在生活中有啥用啊？”我笑着回答他：“你想想看啊，假如我们要做一个三角形的风筝，要让它飞得稳，重心的位置就得找好，不然它可就歪歪扭扭飞不起来啦！”这一下，同学们都恍然大悟，对重心的理解也更深刻了。

再聊聊外心。

外心是三角形三边中垂线的交点，也就是三角形外接圆的圆心。

若点 O 是外心，那么 $|\overrightarrow{OA}| =|\overrightarrow{OB}| = |\overrightarrow{OC}|$ 。

说到外心，我想起有一次带学生们在操场上做数学实践活动。

我们用绳子和标杆模拟画出三角形，然后一起找它的外心。

同学们兴致勃勃，七嘴八舌地讨论着，那场面别提多热闹了。

接着是内心。

内心是三角形三条内角平分线的交点，也就是内切圆的圆心。

若点 I 是内心，$\overrightarrow{a}\overrightarrow{IA} +\overrightarrow{b}\overrightarrow{IB} +\overrightarrow{c}\overrightarrow{IC} = \overrightarrow{0}$ （其中 a、b、c 是三角形三边的长度）。

高考数学二级结论快速解题：专题09 三角形”四心“向量形式的充要条件(解析版)

专题09三角形”四心“向量形式的充要条件一、结论1、三角形“四心”：重心，垂心，内心，外心（1）重心——中线的交点：重心将中线长度分成2：1；（2）垂心——高线的交点：高线与对应边垂直；（3）内心——角平分线的交点（内切圆的圆心）：角平分线上的任意点到角两边的距离相等；（4）外心——中垂线的交点（外接圆的圆心）：外心到三角形各顶点的距离相等。

2、设O 为ABC 所在平面上一点,内角A ,B ,C 所对的边分别为a ,b ,c ,则（1）O 为ABC 的外心 ||||||2sin aOA OB OC A.（2）O 为ABC 的重心 0OA OB OC.（3）O 为ABC 的垂心 OA OB OB OC OC OA.（4）O 为ABC 的内心 0aOA bOB cOC.3、奔驰定理奔驰定理：设O 是ABC 内一点，BOC ,AOC ,AOB 的面积分别记作A S ,B S ,C S 则0A B C S OA S OB S OC.说明：本定理图形酷似奔驰的车标而得名.奔驰定理在三角形四心中的具体形式：①O 是ABC 的重心 ::1:1:1A B C S S S 0OA OB OC.②O 是ABC 的内心 ::::A B C S S S a b c 0aOA bOB cOC.③O 是ABC 的外心::sin 2:sin 2:sin 2A B C S S S A B C sin 2sin 2sin 20A OA B OB C OC.OAB CASCS BS④O 是ABC 的垂心::tan :tan :tan A B C S S S A B C tan tan tan 0A OA B OB C OC.奔驰定理是三角形四心向量式的完美统一.二、典型例题1．（2022·四川西昌·高二期末（理））在平面上有ABC 及内一点O 满足关系式：0OBC OAC OAB S OA S OB S OC△△△即称为经典的“奔驰定理”，若ABC 的三边为a ，b ，c ，现有0a OA b OB c OC则O 为ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】B 【解析】记点O 到AB 、BC 、C A 的距离分别为123h h h ，，，212OBC S a h ，312OAC S b h ，112OAB S c h ，因为0OBC OAC OAB S OA S OB S OC △△△，则233111=0222a h OAb h OBc h OC ，即2310a h OA b h OB c h OC ，又因为0a OA b OB c OC，所以123h h h ，所以点P 是△ABC 的内心.故选：B【反思】设O 为ABC 所在平面上一点,内角A ,B ,C 所对的边分别为a ,b ,c ,则O 为ABC 的内心 0aOA bOB cOC .利用结论可直接得到O 为ABC 的内心.2．（2021·全国·高一课时练习）已知O 是△ABC 所在平面上的一点，若OA OB OC 0，则点O 是△ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】C 【解析】作BD ∥OC ，CD ∥OB ，连接OD ，OD 与BC 相交于点G ，则BG=CG (平行四边形对角线互相平分)，∴OB OC OD ，又OA OB OC 0，可得OB OC =-OA ，∴OD =-OA ，∴A ，O ，G 在一条直线上，可得AG 是BC 边上的中线，同理，BO ，CO 也在△ABC 的中线上.∴点O 为三角形ABC 的重心.故选：C.【反思】设O 为ABC 所在平面上一点,内角A ,B ,C 所对的边分别为a ,b ,c ,则O 为ABC 的重心 0OA OB OC.利用结论可直接得到O 为ABC 的重心.3．（多选）（2022·全国·高三专题练习）在ABC 所在平面内有三点O ，N ，P ，则下列说法正确的是（）A．满足||||||OA OB OC，则点O 是ABC 的外心B ．满足0NA NB NC，则点N 是ABC 的重心C ．满足PA PB PB PC PC PA，则点P 是ABC 的垂心D ．满足(0||||AB AC BC AB AC，且12||||AB AC AB AC ，则ABC 为等边三角形【答案】ABCD 【解析】解：对于A ，因为||||||OA OB OC，所以点O 到ABC 的三个顶点的距离相等，所以O 为ABC 的外心，故A 正确；对于B ，如图所示，D 为BC 的中点，由0NA NB NC 得：2ND NA，所以||:||2:1AN ND ，所以N 是ABC 的重心，故B 正确；对于C ，由PA PB PB PC 得：()0PA PC PB ，即0AC PB，所以AC PB ；同理可得：AB PC ，所以点P 是ABC 的垂心，故C 正确；对于D ，由()0||||AB AC BC AB AC得：角A 的平分线垂直于BC ，所以AB AC ；由12||||AB AC AB AC得：1cos 2A ，所以3A ，所以ABC 为等边三角形，故D 正确．故选：ABCD ．【反思】设O 为ABC 所在平面上一点,内角A ,B ,C 所对的边分别为a ,b ,c ,则（1）O 为ABC 的外心 ||||||2sin aOA OB OC A.（2）O 为ABC 的重心 0OA OB OC.（3）O 为ABC 的垂心 OA OB OB OC OC OA.4.已知G 是ABC 的重心，且满足56sin 40sin 35sin 0A GA B GB C GC，则B =.【答案】3【分析】要牢记,,OA OB OC前面的系数之比为1:1:1，求得三内角的正弦比，再利用正、余弦定理求得.【解析】∵G 是ABC 的重心，∴0GA GB GC∴56sin :40sin :35sin 1:1:1A B C ∴sin :sin :sin 5:7:8A B C 由正弦定理，::sin :sin :sin 5:7:8a b c A B C 由余弦定理，2222225871cos 22582a cb B ac∵(0,)B ，∴3B.【反思】利用奔驰定理在三角形四心中的具体形式：O 是ABC 的重心::1:1:1A B C S S S 0OA OB OC，可得到56sin :40sin :35sin 1:1:1A B C ，通过进一步利用三角形的正余弦定理，求出角B .三、针对训练举一反三一、单选题1．（2021·宁夏·银川一中高三阶段练习（理））ABC 中，a ､b ､c 分别是BC ､AC ､AB 的长度，若a OA b OB c OC O，则O 是ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】B【详解】,OB OA AB OC OA AC 0aOA bOB cOCOA AB aOA b c OA ACa b c OA b AB c AC||||bAB cAC bc AB AC OA a b c a b cAB ACOA 在BAC 的角平分线上，同理OB在ABC 的角平分线上，点O 为三角形ABC 的角平分线的交点故点O 是三角形的内心.故选：B.2．（2021·山东枣庄·高一期中）已知点G 是三角形ABC 所在平面内一点，满足0GA GB GC，则G 点是三角形ABC 的（）A ．垂心B ．内心C ．外心D ．重心【答案】D【详解】因为0GA GB GC，所以GA GB GC CG ，以GA ､GB 为邻边作平行四边形GADB ，连接GD ，交AB 于点O，如图所示：则CG GD，所以13GO CO ，点O 是AB 边的中点，所以CG 所在的直线CO 是AB 边上的中线，同理可证AG 所在的直线是BC 边上的中线，BG 所在的直线是AC 边上的中线，所以G 点是三角形ABC 的重心.故选：D .3．（2021·福建·厦门市湖滨中学高二开学考试）若O 是平面上的定点，A ，B ，C 是平面上不共线的三点，且满足OP OC CB CA（R ），则P 点的轨迹一定过ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】C【详解】因为OP OC CB CA（R ），所以CP CB CA ，所以CB CA在ABC 的边AB 上的中线所在直线上，则CB CA在ABC 的中线所在直线上，所以P 点的轨迹一定过ABC 的重心，故选：C4．（2021·全国·高一课时练习）若O 是平面内一定点，A ，B ，C 是平面内不共线的三点，若点P 满足2OB OC OP +λAP(λ∈(0，+∞))，则点P 的轨迹一定通过△ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】C 【详解】设线段BC 的中点为D ，则有1(2OD OB OC)，因此由已知得OP OD +λAP ，即OP OD =λAP ，于是DP =λAP，则//DP AP ，因此P 点在直线AD 上，又AD 是△ABC 的BC 边上的中线，因此点P 的轨迹一定经过三角形ABC 的重心．故选：C5．（2022·全国·高三专题练习）设O 是平面上一定点，A ､B ､C 是平面上不共线的三点，动点P 满足()AB AC OP OA AB AC， 0, ，则动点P 的轨迹一定通过△ABC 的（）A ．外心B ．内心C ．重心D ．垂心【答案】B 【详解】因为()AB ACOP OA AB AC，所以()AB ACAP AB AC，如图，设,AB ACAE AF ABAC都是单位向量，则由向量的加法法则可得四边形AETF 是菱形，所以AP AT，AT 平分BAC ，所以动点P 的轨迹一定通过△ABC 的内心，故选：B6．（2022·全国·高三专题练习）在ABC 中，CB a =，CA b=，且sin sin a b OP OC m a B b A=+，m R ，则点P 的轨迹一定通过ABC 的（）A ．重心B ．内心C ．外心D ．垂心【答案】A 【详解】过C 作CH AB ，交AB 于H ，取AB 中点D ，连接CD，如图所示：根据三角函数定义可得sin sin a B b A CH，因为sin sin a b OP OC m a B b A=+，所以=+m OP OC a b CH，即2m CP CD CH，即点P 的轨迹在中线CD 上，而三角形三边中线的交点为该三角形的重心，所以点P 的轨迹一定通过ABC 的重心.故选：A 二、多选题7．（2021·广东广州·高一期末）已知O ，N ，P ，I 在ABC 所在的平面内，则下列说法正确的是（）A ．若||||||OA OB OC ，则O 是外心B ．若PA PB PB PC PC PA u u u r u u u r u u u r u u u r u u u r u u u r，则P 是垂心C ．若0NA NB NC，则N 是重心D ．若0CB IA AC IB BA IC，则I 是内心【答案】ABC 【详解】根据外心的定义，易知A 正确；对B ，0PB PA PC PB CA PB CA，同理可得：,PA CB PC AB ，所以P 是垂心，故B 正确；对C ，记AB 、BC 、CA 的中点为D 、E 、F ，由题意2NA NB ND NC，则||2||NC ND ，同理可得：||2||,||2||NA NE NB NF ，则N 是重心，故C 正确；对D ，由题意，,,CB IA AC IB BA IC ，则I 是垂心，故D 错误.故选：ABC.8．（2021·重庆实验外国语学校高一期中）对于给定的ABC ，其外心为O ，重心为G ，垂心为H ，内心为Q ，则下列结论正确的是（）A ．212AO AB ABB ．GA GB GA GC GB GCC ．0HA HB HC D ．若A P Q 、、三点共线，则存在实数使||||AB AC AP AB AC【答案】AD 【详解】解：对于A ：给定的ABC ，其外心为O ，所以2211()22AO AB AD DO AB AB DO AB AB，故A 正确；对于B ：由于点G 为给定的ABC 的重心，故0GA GB GA GC GA CB，故B 错误；对于C ：点H 为给定的ABC 的垂心，所以()0AH HB HC AB HC，因为重心为G ，则有 11,33AG AB AC BG BA BC ，13CG CA CB ，所以0GA GB GC，若0HA HB HC，则点H 为重心，与题意矛盾，因为故C 错误；对于D ：由于点P 在A 的平分线上，所以AB AC AB AC 和为单位向量，所以||||AB AC AB AC 在A 的平分线上，所以存在实数使()||||AB ACAP AB AC，故D 正确．故选：AD ．9．（2021·广东·东莞市光明中学高一阶段练习）点O 在ABC 所在的平面内，则以下说法正确的有（）A ．若0OA OB OC ，则点O 是ABC 的重心．B ．若0||||||||AC AB BC BA OA OB AC AB BC BA，则点O 是ABC 的内心．C．若()()0OA OB AB OB OC BC ，则点O 是ABC 的外心．D ．若OA OB OB OC OC OA，则点O 是ABC 的垂心．【答案】ABCD 【详解】对A ，设D 为BC 中点，由于()2OA OB OC OD，所以O 为BC 边上中线的三等分点（靠近点D ），所以点O 是ABC 的重心，故A 正确；对B ，向量,||||AC ABAC AB分别表示在边AC 和AB 上的单位向量AC 和 AB ，记它们的差为向量B C ，则当0||||AC AB OA AC AB时，即OA B C 时，点O 在BAC 的平分线上，同理由0||||BC BA OB BC BA可得点O 在ABC 的平分线上，所以点O 是ABC 的内心，故B 正确；对C ，OA OB 是以OA OB ，为邻边的平行四边形的一条对角线，而AB是另一条对角线，则由()0OA OB AB 可得该平行四边形为菱形，即||||OA OB，同理由()0OB OC BC 可得||OC OB ∣∣，所以点O 是ABC 的外心，故C 正确；对D ，由OA OB OB OC 得0OA OB OB OC，则0OB CA ，所以OB CA ，同理可得,OA BC OC AB ，所以点O 是ABC 的垂心，故D 正确.故选：ABCD.三、填空题10．（2020·四川·遂宁中学高一阶段练习）已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足2cos cos OB OC AB AC OP AB B AC C， 0, ，则动点P 的轨迹一定通过ABC 的________(填序号）．①内心②垂心③重心④外心【答案】④设BC 的中点为D ，∵2cos cosOB AB A O OC AB C A B C P C ，∴cos cos AB AC O C OD B P AB A C ，即cos cosAB AC DP AB C A B C ，两端同时点乘BC ，∵ BC DP =cos cos B AB AC A C B AC BC BC = cos cos cos cos AB BC B AC BC C AB B AC C =BC BC =0，所以DP BC ，所以点P 在BC 的垂直平分线上，即P 经过△ABC 的外心故答案为：④.四、解答题11．（2021·全国·高一课时练习）已知三角形的三条中线交于一点G （也称为三角形的重心），且点G 将每条中线分为2:1的两段（如图，:2:1AG GM ）．设ABC 三个顶点分别为 11,A x y ， 22,B x y ， 33,C x y ，求证：(1)点G 的坐标为123123,33x x x y y y；(2)0GA GB GC ．【答案】(1)证明见解析(2)证明见解析【解析】(1)设 ,G x y ， 22,B x y ∵， 33,C x y 且M 为BC 中点，2323,22x x y y M又 11,A x y ∵ 11=,GA x x y y ，2323,22x x y y GM x y:2:1AG GM ∵=2GA GM 232311,2,22x x y y x x y y x y2312312222x x x x x y y y y y12312333x x x x y y y y G 的坐标为123123,33x x x y y y (2)M ∵为BC 中点，+=2GB GC GM =2GA GM ∵0GA GB GC。

专题08 三角形”四心“向量形式的充要条件(教师版)-2024年高考二级结论速解技巧

一、单选题 1．（2022·全国·高三专题练习）平面上有 ABC 及其内一点 O，构成如图所示图形，若将OAB ，△OBC ，
OCA 的面积分别记作 Sc ， Sa ， Sb ，则有关系式 Sa ⋅OA + Sb ⋅OB + Sc ⋅OC = 0 ．因图形和奔驰车的 logo 很相
似，常把上述结论称为“奔驰定理”．已知 ABC 的内角 A，B，C 的对边分别为 a，b，c，若满足
1 2
a
⋅
h2
，
S
OA=C
1 2
b
⋅
h3
，
S
OA=B
1 2
c
⋅
h1
，
因为
S△OBC
⋅
OA
+
S△OAC
⋅
OB
+
S△OAB
⋅
OC
= 0 ，则
1 2
a
⋅
h2
⋅
OA
+
1 2
b
⋅
h3
⋅
OB
+
1 2
c
⋅
h3
⋅
OC =0
，即
a ⋅ h2 ⋅ OA + b ⋅ h3 ⋅ OB + c ⋅ h1 ⋅ OC =0 ，又因为 a ⋅ OA + b ⋅ OB + c ⋅ OC =0 ，所以 h=1 h=2 h3 ，所以点 P 是△ABC 的内
内的一点，∠BAC，∠ABC，∠ACB 分别是的△ABC 三个内角，以下命题正确的有（）
A．若 OA + 2OB + 3OC = 0 ，则 SA : SB : SC = 1: 2 : 3
B．若 O=A

第4讲向量与四心

第4讲向量与四心四心的概念：外心:三角形的外心是三角形三条垂直平分线的交点(或三角形外接圆的圆心)内心：三角形的内心是三角形三条内角平分线的交点(或内切圆的圆心)。

垂心：三角形的垂心是三角形三边上的高的交点(通常用H 表示)。

重心：三角形的重心是三角形三条中线的交点。

与三角形的“四心”有关的一些常见的重要的向量关系式有1设()+∞∈,0λ，则向量AC ABλ必平分∠BAC，该向量必通过△ABC 的内心;2设()+∞∈,0λ，则向量AC AB λ必平分∠BAC 的邻补角3设()+∞∈,0λ，则向量AC AB λ必垂直于边BC，该向量必通过△ABC 的垂心4△ABC 中+一定过BC的中点，通过△ABC 的重心5点O 是△ABC 的外心222OC OB OA ==⇔6点O 是△ABC 的重心0=++⇔OC OB OA 7点O 是△ABC 的垂心⇔OA OC OC OB OB OA ⋅=⋅=⋅（移项证明）8点O 是△ABC 的内心=⋅+⋅+⋅⇔c b a (其中a、b、c 为△ABC 三边)9△ABC 的外心O 、重心G 、垂心H 共线，即∥10设O 为△ABC 所在平面内任意一点，G 为△ABC 的重心，，I 为△ABC 的内心，则有)(31OC OB OA OG++=cb a OCc OB b OA a OI ++++=并且重心G（X A +X B +X C 3，Y A +Y B +Y C3）内心I（aX A +bX B +cX C a+b+c ，ay A +by B +cy Ca+b+c）推论（结合奔驰定理）ABC 内有一点O ，0xO A yO B zO C ++=1.如果点O 是ABC 的重心：::1:1:1x y z =2.如果点O 是ABC 的内心：::sin :sin :sin x y z A B C =3.如果点O 是ABC 的外心：::sin 2:sin 2:sin 2x y z A B C =4.如果点O 是ABC 的垂心：::tanA :tanB :tanCx y z =典型例题1．已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()[0||sin ||sin AB ACOP OA AB B AC C λλ=++∈，)+∞，则点P 的轨迹一定通过ABC ∆的()A ．外心B ．内心C ．重心D ．垂心【解答】解： ||sin ||sin AB B AC C =设它们等于t ，∴1()OP OA AB AC tλ=++而2AB AC AD+= 1()AB AC tλ+表示与AD 共线的向量AP 而点D 是BC 的中点，所以即P 的轨迹一定通过三角形的重心．故选：C ．2．已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足()2||cos ||cos OB OC AB ACOP AB B AC Cλ+=++ ，[0λ∈，)+∞，则动点P 的轨迹一定通过ABC ∆的()A ．内心B ．垂心C ．重心D ．外心【解答】解：设BC 的中点为D ，(2||cos ||cos OB OC AB ACOP AB B AC Cλ+=++，∴()||cos ||cos AB ACOP OD AB B AC C λ=++，即(||cos ||cos AB ACDP AB B AC Cλ=+，两端同时点乘BC ， ||||cos()||||cos (()(||||)0||cos ||cos ||cos ||cos AB BC AC BC AB BC B AC BC CDP BC BC BC AB B AC C AB B AC Cπλλλ-=+=+=-+=，DP BC ∴⊥，∴点P 在BC 的垂直平分线上，即P 经过ABC ∆的外心故选：D ．3．O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足(||||AB ACOP OA AB AC λ=++，(0,)λ∈+∞，则点P 的轨迹一定通过ABC ∆的()A ．外心B ．内心C ．重心D ．垂心【解答】解：||AB AB 、||ACAC分别表示向量AB 、AC 方向上的单位向量，||||AB ACAB AC ∴+的方向与BAC ∠的角平分线重合，又()||||AB AC OP OA AB AC λ=++可得到()||||AB ACOP OA AP AB AC λ-==+∴向量AP的方向与BAC ∠的角平分线重合，∴一定通过ABC ∆的内心故选：B ．模拟自测1．O 是平面上一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足()OP OA AB AC λ=++，[0λ∈，)+∞，则P 的轨迹一定通过ABC ∆的()A ．外心B ．垂心C ．内心D ．重心2．P 是ABC ∆所在平面上一点，若PA PB PB PC PC PA ==，则P 是ABC ∆的()A ．外心B ．内心C ．重心D ．垂心3．已知O 是ABC ∆所在平面上的一点，若aPA bPB cPCPO a b c++=++（其中P 是ABC 所在平面内任意一点），则O 点是ABC ∆的()A ．外心B ．内心C ．重心D ．垂心4．已知ABC ∆的三内角A ，B ，C 所对边的长依次为a ，b ，c ，M 为该三角形所在平面内的一点，若0aMA bMB cMC ++=，则M 是ABC ∆的()A ．内心B ．重心C ．垂心D ．外心5．已知O 是平面内一点，且222OA OB OC ==，则O 是ABC ∆的()A ．垂心B ．外心C ．重心D ．内心6．已知O 为ABC ∆所在平面内一点，且满足222222OA BC OB CA OC AB +=+=+ ，则O 点的轨迹一定通过ABC ∆的()A ．外心B ．内心C ．重心D ．垂心7已知点O 、N 、P 在ABC ∆所在平面内，且OA OB OC == ，0NA NB NC ++=，PA PB PB PC PC PA ==，则点O 、N 、P 依次为ABC ∆的()A ．重心、外心、垂心B ．重心、外心、内心C ．外心、重心、垂心D ．外心、重心、内心8．已知点P 是ABC ∆的内心（三个内角平分线交点）、外心（三条边的中垂线交点）、重心（三条中线交点）、垂心（三个高的交点）之一，且满足222AP BC AC AB =- ，则点P 一定是ABC ∆的()A ．内心B ．外心C ．重心D ．垂心9．已知非零向量AB ，AC 满足()0||||AB AC BC AB AC += ，且1||||2AB AC AB AC =，则ABC∆的形状是()A ．三边均不相等的三角形B ．直角三角形C ．等腰（非等边）三角形D ．等边三角形10．已知点C 为线段AB 上一点，P 为直线AB 外一点，PC 是APB ∠角的平分线，I为PC 上一点，满足(0)||||AC APBI BA AC AP λλ=++>，||||4PA PB -= ，||10PA PB -= ，则||BI BABA的值为()A ．2B ．3C ．4D ．5参考答案1）解：令D 为BC 的中点，则()2OP OA AB AC OA AD λλ=++=+ ，于是有2AP AD λ= ，∴点A 、D 、P 共线，即点P 的轨迹通过三角形ABC 的重心．故选：D ．2）解：PA PB PB PC PC PA ==，则由PA PB PB PC =得：()0,0PB PC PA PB AC ⋅-=⋅=即，PB AC∴⊥同理PA BC ⊥，PC AB ⊥，即P 是垂心故选：D ．3）解：由aPA bPB cPCPO a b c ++=++得aPO bPO cPO aPA bPB cPC ++=++ ，即()()()0a PA PO b PA PO c PC PO -+-+-=．即0aOA bOB cOC ++= ．即()()0aOA b OA AB c OA AC ++++=．再设1e 为AB 的单位向量，2e 为AC 的单位向量，所以12()()a b c OA bc e e ++=-+ ，所以12()bcOA e e a b c=-+++ ．则说明O 在A ∠的角平分线上，同理可得O 也在B ∠，C ∠的平分线上，故O 为ABC ∆的内心．故选：B ．4）解：M 是三角形ABC 的内心．理由如下：已知0aMA bMB cMC ++=，延长CM 交AB 于D ，根据向量加法得：MA MD DA =+ ，MB MD DB =+ ，代入已知得：()()0a MD DA b MD DB cMC ++++=，因为MD 与MC共线，所以可设MD kMC = ，上式可化为()(ka kb c MC +++ )0aDA bDB +=，由于DA 与DB 共线，MC 与DA 、DB不共线，所以只能有：0ka kb c ++=，0aDA bDB +=，由0aDA bDB += 可知：DA 与DB 的长度之比为b a，所以由内角平分线定理的逆定理可得CD 为ACB ∠的平分线，同理可证AM ，BM 的延长线也是角平分线．故M 为内心．故选：A ．5）解：O 是平面内一点，且222OA OB OC == ，可得：||||||OA OB OC ==，所以O 是ABC ∆的外心．故选：B ．6）解：BC OC OB =- ，CA OA OC =- 、AB OB OA =-，∴由222222OA BC OB CA OC AB +=+=+ ，得222222()()()OA OC OB OB OA OC OC OB OA +-=+-=+- ，OB OC OA OC OA OB ∴== ，即()()()OC OB OA OA OC OB OB OC OA -=-=- ，OC AB OA BC OB AC ∴== ，则OC AB ⊥，OA BC ⊥，OB AC ⊥．O ∴是ABC ∆的垂心．故选：D ．7）证明： OA OB OC ==，O ∴到三角形三个顶点的距离相等，O ∴是三角形的外心，根据所给的四个选项，第一个判断为外心的只有C ，D 两个选项，∴只要判断第三个条件可以得到三角形的什么心就可以，PA PB PB PC PC PA == ，∴()0PB PA PC -=，∴0PB CA =，∴PB CA ⊥ ，同理得到另外两个向量都与相对应的边垂直，得到P 是三角形的垂心，故选：C ．8）解：设D 为BC 的中点，可得2AC AB AD +=22()()AC AB AC AB AC AB -=+- ，∴点P 满足2222()AP BC AC AB AD AC AB =-=-，向量BC AC AB =- ，∴22AP BC AD BC = ，移项得2()0BC AD AP -=即0BC PD = ，得BC PD ⊥．结合D 为BC 的中点，可得P 在BC 的垂直平分线上又点P 是ABC ∆的内心、外心、重心和垂心之一∴结合三角形外接圆的性质，得点P 是ABC ∆的外心故选：B ．9）解：()0||||AB AC BC AB AC += ，||AB AB ，||ACAC分别为单位向量，A ∴∠的角平分线与BC 垂直，AB AC ∴=，1cos ||||2AB AC A AB AC == ，3A π∴∠=，3B C A π∴∠=∠=∠=，∴三角形为等边三角形．故选：D ．10）解： ||||10PA PB AB -==，PC 是APB ∠角的平分线，又满足(0)||||AC AP BI BA AC AP λλ=++>，即(||||AC APAI AC AP λ=+，所以I 在BAP ∠的角平分线上，由此得I 是ABP ∆的内心，过I 作IH AB ⊥于H ，I 为圆心，IH 为半径，作PAB ∆的内切圆，如图，分别切PA ，PB 于E 、F ，||||4PA PB -= ，||10PA PB -=，11||||(||||||)[||(||||)]322BH BF PB AB PA AB PA PB ==+-=--=，在直角三角形BIH 中，||cos ||BH IBH BI ∠= ，所以||cos ||3||BI BA BI IBH BH BA =∠==．故选：B ．。

平面向量与三角形的四心

专题9：平面向量与三角形的四心三角形的四心：1. 外心:2. 内心:3. 垂心:4. 重心：例1. O 是ABC ∆所在平面上一点，且OA OB OC ==，则O 是ABC ∆的( ）A. 内心B. 外心 C 。

垂心 D. 重心例2. O 是平面上一定点,A ，B,C 是平面上不共线的三个点，动点P 满足 (),0ABACOP OA AB AC λλ=++>,则点P 的轨迹一定通过ABC ∆的（）A. 内心 B 。

外心 C 。

垂心 D. 重心例3. 点P 是ABC ∆所在平面上一点，若PA PB ⋅=PC PB ⋅=PA PC ⋅，则点P 是ABC ∆的（）A. 内心B. 外心C. 垂心 D 。

重心例4。

证明：点P 是ABC ∆所在平面上一点，有G 是ABC ∆的重心⇔1()3PG PA PB PC =++针对训练：1. O ，P 两点在ABC ∆所在平面内，且(OP OA)(AB AC)0-⋅-=，则点P 的轨迹一定通过ABC ∆的（）A 。

内心B 。

外心 C. 垂心 D. 重心2. 已知A ，B ，C 是平面上不共线的三点,O 是ABC ∆的重心，动点P 满足111(OA OB 2OC)322OP =++，则点P 一定为ABC ∆的（） A 。

AB 边中线的中点 B. AB 边中线的三等分点（非重心）C. 重心D. AB 边的中点3. 在同一个平面上有ABC ∆及一点O 满足关系式：222222OA BC OB CA OC AB +=+=+,则点O 一定为ABC ∆的（） A. 内心 B. 外心 C 。

垂心 D 。

重心4.已知O 是平面上的一定点，A,B,C 是平面上不共线的三点，动点P 满足： ()OP OA AB AC λ=++，则P 的轨迹一定通过ABC ∆的（）A 。

内心B 。

外心C 。

垂心 D. 重心5. 在ABC ∆所在平面上的一动点M 满足222AM BC AC AB ⋅=-，则动点M 的轨迹必过ABC ∆的________________(内心,垂心,外心,重心)。

向量与三角形四心的一些结论

【一些结论】：以下皆是向量1 若P是△ABC的重心 PA+PB+PC=02 若P是△ABC的垂心PA•PB=PB•PC=PA•PC(内积）3 若P是△ABC的心坎 aPA+bPB+cPC=0(abc是三边）4 若P是△ABC的外心|PA|²=|PB|²=|PC|²（AP就暗示AP向量|AP|就是它的模）5 AP=λ（AB/|AB|+AC/|AC|),λ∈[0,+∞) 则直线AP经由△ABC 心坎6 AP=λ（AB/|AB|cosB+AC/|AC|cosC),λ∈[0,+∞) 经由垂心7 AP=λ（AB/|AB|sinB+AC/|AC|sinC),λ∈[0,+∞）或AP=λ(AB+AC),λ∈[0,+ ∞) 经由重心8.若aOA=bOB+cOC,则0为∠A的旁心,∠A及∠B,C的外角等分线的交点【以下是一些结论的有关证实】1.O是三角形心坎的充要前提是aOA向量+bOB向量+cOC向量=0向量充分性：已知aOA向量+bOB向量+cOC向量=0向量,延伸CO交AB于D,依据向量加法得：OA=OD+DA,OB=OD+DB,代入已知得：a(OD+DA)+b(OD+DB) +cOC=0,因为OD与OC共线,所以可设OD=kOC,上式可化为(ka+kb+c) OC+( aDA+bDB)=0向量,向量DA与DB共线,向量OC与向量DA.DB不共线,所以只能有：ka+kb+c=0,aDA+bDB=0向量,由aDA+bDB=0向量可知：DA与DB的长度之比为b/a,所以CD为∠ACB的等分线,同理可证其它的两条也是角等分线.须要性：已知O是三角形心坎,设BO与AC订交于E,CO与AB订交于F,∵O是心坎∴b/a=AF/BF,c/a=AE/CE过A作CO的平行线,与BO 的延伸线订交于N,过A作BO的平行线,与CO的延伸线订交于M,所以四边形OMAN是平行四边形依据平行四边形轨则,得向量OA=向量OM+向量ON=(OM/CO)*向量CO+(ON/BO)*向量BO=(AE/CE)*向量CO+(AF/BF)*向量BO=(c/a)*向量CO+(b/a)*向量BO∴a*向量OA=b*向量BO+c*向量CO∴a*向量OA+b*向量OB+c*向量OC=向量02.已知△ABC 为斜三角形,且O是△ABC地点平面上的一个定点,动点P知足向量OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},求P点轨迹过三角形的垂心OP=OA+入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},OP-OA=入{(AB/|AB|＾2*sin2B)+AC/(|AC|＾2*sin2C)},AP=入{(AB /|AB|＾2*sin2B)+AC /(|AC|＾2*sin2C)},AP•BC=入{(AB•BC /|AB|＾2*sin2B)+AC•BC /(|AC|＾2*sin2C)},AP•BC=入{|AB|•|BC|cos(180° -B) / (|AB|＾2*sin2B) +|AC|•|B C| cosC/(|AC|＾2*sin2C)},AP•BC=入{-|AB|•|BC| cos B/ (|AB|＾2*2sinB cos B) +|AC|•|BC| cosC/(|AC|＾2*2sinC cosC)},AP•BC=入{-|BC|/ (|AB|*2sinB ) +|BC|/(|AC|*2sinC )},依据正弦定理得：|AB|/sinC=|AC|/ sinB,所以|AB|*sinB=|AC|*sinC∴-|BC|/ (|AB|*2sinB ) +|BC|/(|AC|*2sinC )=0,即AP•BC=0,P点轨迹过三角形的垂心3.OP=OA+λ(AB/(|AB|sinB)+AC/(|AC|sinC)) OP-OA=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP=λ(AB/(|AB|sinB)+AC/(|AC|sinC))AP与AB/|AB|sinB+AC/|AC|sinC共线依据正弦定理：|AB|/sinC=|AC|/sinB,所以|AB|sinB=|AC|sinC,所以AP与AB+AC共线AB+AC过BC中点D,所以P点的轨迹也过中点D,∴点P 过三角形重心.4.OP=OA+λ(ABcosC/|AB|+ACcosB/|AC|)OP=OA+λ(ABcosC/|AB |+ACcosB/|AC|)AP=λ(ABcosC/|AB|+ACcosB/|AC|)AP•BC=λ(AB•B C cosC/|AB|+AC•BC cosB/|AC|)=λ([|AB|•|BC|cos(180° -B)cosC/|AB|+|AC|•|BC| cosC cosB/|AC|]=λ[-|BC|cosBcosC+|BC| cosC cosB]=0,所以向量AP与向量BC垂直,P 点的轨迹过垂心.5.OP=OA+λ(AB/|AB|+AC/|AC|) OP=OA+λ(AB/|AB|+AC/|AC|) OP-OA =λ(AB/|AB|+AC/|AC|)AP=λ(AB/|AB|+AC/|AC|)AB/|AB|.AC/|AC|各为AB.AC偏向上的单位长度向量,向量AB与AC的单位向量的和向量,因为是单位向量,模长都相等,组成菱形,向量AB与AC的单位向量的和向量为菱形对角线,易知是角等分线,所以P点的轨迹经由心坎。

向量与三角形四心

向量与三角形的四心

向量有关的三角形四心问题

向量与三角形内心外心重心垂心

向量与三角形的四心、奔驰定理latex版

与三角形四心相关的向量结论.doc

三角形“四心”向量形式的结论及证明

向量与三角形内心、外心、重心、垂心

高中数学：向量中的三角形“四心”

三角形中的四心与向量

高中数学平面向量与三角形的“四心”

高中数学-三角形内心、外心、重心、垂心与向量关系

微专题8 平面向量与三角形的“四心”

用向量解决三角形“四心”问题

三角形四心的向量公式及证明

高考数学二级结论快速解题：专题09 三角形”四心“向量形式的充要条件(解析版)

专题08 三角形”四心“向量形式的充要条件(教师版)-2024年高考二级结论速解技巧

第4讲 向量与四心

平面向量与三角形的四心

向量与三角形四心的一些结论

第4讲向量与四心