(人教版)高中数学必修二(全册)单元测试卷汇总
高中数学必修二测试题及答案人教版

第一章 空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个( ).主视图 左视图 俯视图 (第1题) A .棱台 B .棱锥 C .棱柱 D .正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A .2+2B .221+C .22+2 D .2+13.棱长都是1的三棱锥的表面积为( ).A .3B .23C .33D .434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A .25πB .50πC .125πD .都不对 5.正方体的棱长和外接球的半径之比为( ). A .3∶1 B .3∶2 C .2∶3 D .3∶36.在△ABC 中,AB =2,BC =1.5,∠ABC =120°,若使△ABC 绕直线BC 旋转一周,则所形成的几何体的体积是( ).A .29πB .27πC .25πD .23π7.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是( ).A .130B .140C .150D .1608.如图,在多面体ABCDEF 中,已知平面ABCD 是边长为3的正方形,EF ∥AB ,EF =23,且EF 与平面ABCD 的距离为2,则该多面体的体积为( ).A .29 B .5 C .6 D .2159.下列关于用斜二测画法画直观图的说法中,错误..的是( ). A .用斜二测画法画出的直观图是在平行投影下画出的空间图形B .几何体的直观图的长、宽、高与其几何体的长、宽、高的比例相同C .水平放置的矩形的直观图是平行四边形D .水平放置的圆的直观图是椭圆10.如图是一个物体的三视图,则此物体的直观图是( ).(第8题)(第10题)二、填空题11.一个棱柱至少有______个面,面数最少的一个棱锥有________个顶点,顶点最少的一个棱台有________条侧棱.12.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.13.正方体ABCD-A1B1C1D1 中,O是上底面ABCD的中心,若正方体的棱长为a,则三棱锥O-AB1D1的体积为_____________.14.如图,E,F分别为正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是___________.(第14题)15.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.16.一个直径为32厘米的圆柱形水桶中放入一个铁球,球全部没入水中后,水面升高9厘米则此球的半径为_________厘米.三、解答题17.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm 和40 cm,求它的深度.18 *.已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.[提示:过正方体的对角面作截面]19.如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=22,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.(第19题)20.养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m,高4 m,养路处拟建一个更大的圆锥形仓库,以存放更多食盐,现有两种方案:一是新建的仓库的底面直径比原来大4 m(高不变);二是高度增加4 m(底面直径不变).(1)分别计算按这两种方案所建的仓库的体积;(2)分别计算按这两种方案所建的仓库的表面积;(3)哪个方案更经济些?第一章 空间几何体参考答案A 组一、选择题 1.A解析:从俯视图来看,上、下底面都是正方形,但是大小不一样,可以判断可能是棱台.2.A解析:原图形为一直角梯形,其面积S =21(1+2+1)×2=2+2.3.A解析:因为四个面是全等的正三角形,则S 表面=4×43=3. 4.B解析:长方体的对角线是球的直径, l =2225+4+3=52,2R =52,R =225,S =4πR 2=50π. 5.C解析:正方体的对角线是外接球的直径. 6.D解析:V =V 大-V 小=31πr 2(1+1.5-1)=23π.7.D解析:设底面边长是a ,底面的两条对角线分别为l 1,l 2,而21l =152-52,22l =92-52,而21l +22l =4a 2,即152-52+92-52=4a 2,a =8,S 侧面=4×8×5=160. 8.D解析:过点E ,F 作底面的垂面,得两个体积相等的四棱锥和一个三棱柱,V =2×31×43×3×2+21×3×2×23=215.9.B解析:斜二测画法的规则中,已知图形中平行于 x 轴的线段,在直观图中保持原长度不变;平行于 y 轴的线段,长度为原来的一半.平行于 z 轴的线段的平行性和长度都不变.10.D解析:从三视图看底面为圆,且为组合体,所以选D. 二、填空题11.参考答案:5,4,3.解析:符合条件的几何体分别是:三棱柱,三棱锥,三棱台.12.参考答案:1∶22∶33.r 1∶r 2∶r 3=1∶2∶3,31r ∶32r ∶33r =13∶(2)3∶(3)3=1∶22∶33.13.参考答案:361a .解析:画出正方体,平面AB 1D 1与对角线A 1C 的交点是对角线的三等分点, 三棱锥O -AB 1D 1的高h =33a ,V =31Sh =31×43×2a 2×33a =61a 3. 另法:三棱锥O -AB 1D 1也可以看成三棱锥A -OB 1D 1,它的高为AO ,等腰三角形OB 1D 1为底面.14.参考答案:平行四边形或线段.15.参考答案:6,6.解析:设ab =2,bc =3,ac =6,则V = abc =6,c =3,a =2,b =1, l =1+2+3=6. 16.参考答案:12.解析:V =Sh =πr 2h =34πR 3,R =32764×=12. 三、解答题 17.参考答案:V =31(S +S S ′+S )h ,h =S S S S V ′+′+3=6001+4002+60030001903×=75.18.参考答案:如图是过正方体对角面作的截面.设半球的半径为R ,正方体的棱长为a ,则CC'=a ,OC =22a ,OC'=R .(第18题)在Rt △C'CO 中,由勾股定理,得CC' 2+OC 2=OC' 2,即 a 2+(22a )2=R 2. ∴R =26a ,∴V 半球=26πa 3,V 正方体=a 3. ∴V 半球 ∶V 正方体=6π∶2. 19.参考答案:S 表面=S 下底面+S 台侧面+S 锥侧面=π×52+π×(2+5)×5+π×2×22 =(60+42)π. V =V 台-V 锥 =31π(21r +r 1r 2+22r )h -31πr 2h 1 =3148π.20.解:(1) 参考答案:如果按方案一,仓库的底面直径变成16 m ,则仓库的体积V 1=31Sh =31×π×(216)2×4=3256π(m 3).如果按方案二,仓库的高变成8 m ,则仓库的体积COAV 2=31Sh =31×π×(212)2×8=3288π(m 3).(2) 参考答案:如果按方案一,仓库的底面直径变成16 m ,半径为8 m . 棱锥的母线长为l =224+8=45, 仓库的表面积S 1=π×8×45=325π(m 2). 如果按方案二,仓库的高变成8 m .棱锥的母线长为l =226+8=10,仓库的表面积S 2=π×6×10=60π(m 2).(3) 参考答案:∵V 2>V 1,S 2<S 1,∴方案二比方案一更加经济些.。
人教版高中数学选择性必修第二册 全册模块综合检测2(含解析)
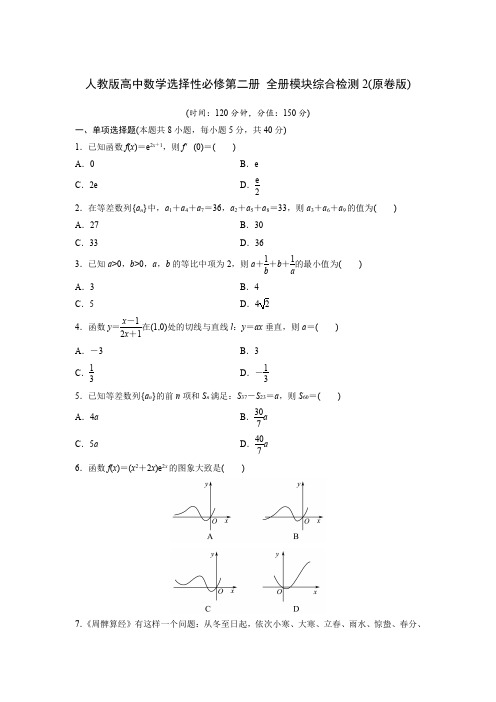
人教版高中数学选择性必修第二册全册模块综合检测2(原卷版)(时间:120分钟,分值:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.已知函数f(x)=e2x+1,则f′(0)=()A.0B.eC.2e D.e22.在等差数列{a n}中,a1+a4+a7=36,a2+a5+a8=33,则a3+a6+a9的值为() A.27B.30C.33D.363.已知a>0,b>0,a,b的等比中项为2,则a+1b+b+1a的最小值为()A.3B.4 C.5D.424.函数y=x-12x+1在(1,0)处的切线与直线l:y=ax垂直,则a=() A.-3B.3C.13D.-135.已知等差数列{a n}的前n项和S n满足:S37-S23=a,则S60=()A.4a B.307aC.5a D.407a6.函数f(x)=(x2+2x)e2x的图象大致是()7.《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,则芒种日影长为()A.一尺五寸B.二尺五寸C.三尺五寸D.四尺五寸8.已知函数f(x)=x3-x和点P(1,-1),则过点P与该函数图象相切的直线条数为() A.1B.2C.3D.4二、多项选择题(本题共4小题,每小题5分,共20分)9.已知数列{a n}的前n项和为S n,S n=2a n-2,若存在两项a m,a n,使得a m a n=64,则() A.数列{a n}为等差数列B.数列{a n}为等比数列C.a21+a22+…+a2n=4n-13D.m+n为定值10.若函数e x f(x)(e=2.7182…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数为()A.f(x)=2-x B.f(x)=3-xC.f(x)=x3D.f(x)=x2+211.设等比数列{a n}的公比为q,其前n项和为S n,前n项积为T n,并且满足条件a1>1,a6a7>1,a6-1<0,则下列结论正确的是()a7-1A.0<q<1B.a6a8>1C.S n的最大值为S7D.T n的最大值为T612.设f′(x)为函数f(x)的导函数,已知x2f′(x)+xf(x)=ln x,f(1)=12,则下列结论正确的是()A.xf(x)在(1,+∞)单调递增B.xf(x)在(0,1)单调递减C.xf(x)在(0,+∞)上有极大值12D.xf(x)在(0,+∞)上有极小值12三、填空题(本题共4小题,每小题5分,共20分)13.已知等差数列{a n}中,a4=8,a8=4,则其通项公式a n=________.a1a9,则a n=________,数列14.已知正项等比数列{a n}满足a1=1,a2a6a7=116{log2a n}的前n项和为________.15.函数f(x)=12x2-ln x的单调递减区间是________.16.已知函数f(x)=ln x+mx,若函数f(x)的极小值不小于0,则实数m的取值范围为________.四、解答题(本题共6小题,共70分)17.(10分)等比数列{a n}中,已知a1=2,a4=16.(1)求数列{a n}的通项公式a n;(2)若a3,a5分别是等差数列{b n}的第4项和第16项,求数列{b n}的通项公式及前n项和S n.18.(12分)已知函数f(x)=12x2-3ln x.(1)求f(x)在(1,f(1))处的切线方程;(2)试判断f(x)在区间(1,e)上有没有零点.若有,判断零点的个数.19.(12分)设数列{a n}是等差数列,其前n项和为S n,且a3=2,S9=54.(1)求数列{a n}的通项公式;(2)证明:1a1+3+1a2+3+1a3+3+…+1a100+3>13.20.(12分)设函数f(x)=e x-ax-1(a∈R).(1)若a=2,求函数f(x)在区间[0,2]上的最大值和最小值;(2)当x≥0时,f(x)≥0,求a的取值范围.21.(12分)等差数列{a n}中,S3=21,S6=24,(1)求数列{a n}的前n项和公式S n;(2)求数列{|a n|}的前n项和T n.22.(12分)已知a,b∈R,设函数f(x)=e x-ax-b x2+1.(1)若b=0,求f(x)的单调区间;(2)当x∈[0,+∞)时,f(x)的最小值为0,求a+5b的最大值.注:e=2.71828…为自然对数的底数.人教版高中数学选择性必修第二册全册模块综合检测2(解析版)(时间:120分钟,分值:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.已知函数f (x )=e 2x +1,则f ′(0)=()A .0B .e C .2e D .e 2C解析:∵f (x )=e 2x +1,∴f ′(x )=2e 2x +1,∴f ′(0)=2e.故选C .2.在等差数列{a n }中,a 1+a 4+a 7=36,a 2+a 5+a 8=33,则a 3+a 6+a 9的值为()A .27B .30C .33D .36B解析:因为a 1+a 4+a 7=3a 4=36,所以a 4=12.因为a 2+a 5+a 8=33,所以a 5=11.所以d=a 5-a 4=-1,所以a 3+a 6+a 9=3a 6=3(a 5+d )=30.故选B .3.已知a >0,b >0,a ,b 的等比中项为2,则a +1b +b +1a 的最小值为()A .3B .4C .5D .42C解析:∵a +1b +b +1a =(a +b )+a +b ab=(a +b =54(a +b )≥54·2ab =5,等号成立当且仅当a =b =2,原式的最小值为5.4.函数y =x -12x +1在(1,0)处的切线与直线l :y =ax 垂直,则a =()A .-3B .3C .13D .-13A解析:∵y ′=3(2x +1)2,∴y ′|x =1=13,∴函数在(1,0)处的切线的斜率是13,所以,与此切线垂直的直线的斜率是-3,∴a =-3.故选A .5.已知等差数列{a n }的前n 项和S n 满足:S 37-S 23=a ,则S 60=()A .4aB .307a C .5aD .407aB 解析:因为S 37-S 23=a 24+a 25+…+a 37=a 24+a 372×14=7(a 24+a 37)=a .所以S 60=a 1+a 602×60=30(a 24+a 37)=307a .故选B .6.函数f (x )=(x 2+2x )e 2x 的图象大致是()A 解析:由于f ′(x )=2(x 2+3x +1)·e 2x ,而y =x 2+3x +1的判别式Δ=9-4=5>0,所以y=x 2+3x +1开口向上且有两个根x 1,x 2.不妨设x 1<x 2,所以f (x )在(-∞,x 1),(x 2,+∞)上递增,在(x 1,x 2)上递减.所以C ,D 选项不正确.当x <-2时,f (x )>0,所以B 选项不正确.由此得出A 选项正确.故选A .7.《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,冬至、立春、春分日影之和为三丈一尺五寸,前九个节气日影之和为八丈五尺五寸,则芒种日影长为()A .一尺五寸B .二尺五寸C .三尺五寸D .四尺五寸B解析:由题知各节气日影长依次成等差数列,设为{a n },S n 是其前n 项和,则S 9=9(a 1+a 9)2=9a 5=85.5,所以a 5=9.5,由题知a 1+a 4+a 7=3a 4=31.5,所以a 4=10.5,所以公差d =a 5-a 4=-1.所以a 12=a 5+7d =2.5尺.故选B .8.已知函数f (x )=x 3-x 和点P (1,-1),则过点P 与该函数图象相切的直线条数为()A .1B .2C .3D .4B解析:因为f (1)=13-1=0,所以点P (1,-1)没有在函数的图象上.设切点坐标为(x 0,y 0),则y 0=x 30-x 0,则f ′(x )=3x 2-1.由导数的几何意义可知,过切点的斜率为k =3x 20-1,过P (1,-1)和切点的斜率表示为k =y 0+1x 0-1,-x0,3x20-1,化简可得x20(2x0-3)=0,所以x0=0或x0=32.所以切点有两个,因而有两条切线方程.故选B.二、多项选择题(本题共4小题,每小题5分,共20分)9.已知数列{a n}的前n项和为S n,S n=2a n-2,若存在两项a m,a n,使得a m a n=64,则() A.数列{a n}为等差数列B.数列{a n}为等比数列C.a21+a22+…+a2n=4n-13D.m+n为定值BD解析:由题意,当n=1时,S1=2a1-2,解得a1=2,当n≥2时,S n-1=2a n-1-2,所以S n-S n-1=a n=2a n-2-(2a n-1-2)=2a n-2a n-1,所以a na n-1=2,数列{a n}是以a1=2为首项,q=2为公比的等比数列,a n=2n,故选项A错误,选项B正确;数列{a2n}是以a21=4为首项,q1=4为公比的等比数列,所以a21+a22+…+a2n=a21(1-q n1)1-q1=4×(1-4n)1-4=4n+1-43,故选项C 错误;a m a n=2m2n=2m+n=64=26,所以m+n=6为定值,故选项D正确.故选BD.10.若函数e x f(x)(e=2.7182…是自然对数的底数)在f(x)的定义域上单调递增,则称函数f(x)具有M性质.下列函数中所有具有M性质的函数为()A.f(x)=2-x B.f(x)=3-xC.f(x)=x3D.f(x)=x2+2AD解析:对于选项A,f(x)=2-x,则g(x)=e x f(x)=e x·2-x为实数集上的增函数;对于选项B,f(x)=3-x,则g(x)=e x f(x)=e x·3-x为实数集上的减函数;对于选项C,f(x)=x3,则g(x)=e x f(x)=e x·x3,g′(x)=e x·x3+3e x·x2=e x(x3+3x2)=e x·x2(x+3),当x<-3时,g′(x)<0,∴g(x)=e x f(x)在定义域R上先减后增;对于选项D,f(x)=x2+2,则g(x)=e x f(x)=e x(x2+2),g′(x)=e x(x2+2)+2x e x=e x(x2+2x+2)>0在实数集R上恒成立,∴g(x)=e x f(x)在定义域R上是增函数.故选AD.11.设等比数列{a n}的公比为q,其前n项和为S n,前n项积为T n,并且满足条件a1>1,a6a7>1,a6-1a7-1<0,则下列结论正确的是()A.0<q<1B.a6a8>1C.S n的最大值为S7D.T n的最大值为T6AD 解析:易知q >0,若q >1,则a 6>1,a 7>1,与a 6-1a 7-1>0矛盾,故0<q <1.所以0<a 7<1.所以a 6a 8=a 27<1.因为a 7>0,a 8>0,所以S n 的最大值一定不为S 7.因为0<a 7<1,a 6>1,所以T n 的最大值为T 6,故选AD .12.设f ′(x )为函数f (x )的导函数,已知x 2f ′(x )+xf (x )=ln x ,f (1)=12,则下列结论正确的是()A .xf (x )在(1,+∞)单调递增B .xf (x )在(0,1)单调递减C .xf (x )在(0,+∞)上有极大值12D .xf (x )在(0,+∞)上有极小值12ABD解析:由x 2f ′(x )+xf (x )=ln x 得x >0,则xf ′(x )+f (x )=ln x x ,由[xf (x )]′=ln xx .设g (x )=xf (x ),即g ′(x )=ln xx>0得x >1.由g ′(x )<0得0<x <1,即xf (x )在(1,+∞)单调递增,在(0,1)单调递减,即当x =1时,函数g (x )=xf (x )取得极小值g (1)=f (1)=12.故选ABD .三、填空题(本题共4小题,每小题5分,共20分)13.已知等差数列{a n }中,a 4=8,a 8=4,则其通项公式a n =________.12-n 解析:∵等差数列{a n }中,a 4=8,a 8=4,4=a 1+3d =8,8=a 1+7d =4,解得a 1=11,d =-1,∴a n =11+(n -1)×(-1)=12-n .14.已知正项等比数列{a n }满足a 1=1,a 2a 6a 7=116a 1a 9,则a n =________,数列{log 2a n }的前n 项和为________.2-n +1-n (n -1)2解析:由a 1=1,a 2a 6a 7=1161a 9得a 5=a 1q 4=116,q =12,a n -1=2-n+1.而log 2a n =-n +1,所以{log 2a n }的前n 项和为-n (n -1)2.15.函数f (x )=12x 2-ln x 的单调递减区间是________.(0,1]解析:f (x )=12x 2-ln x ,则f ′(x )=x -1x =x 2-1x =(x +1)(x -1)x≤0,故0<x ≤1.16.已知函数f (x )=ln x +mx,若函数f (x )的极小值不小于0,则实数m 的取值范围为________.1e,+∞解析:由f (x )=ln x +m x 得f ′(x )=1x -m x 2=x -mx2,定义域为(0,+∞).当m ≤0时,f ′(x )>0,函数y =f (x )单调递增,函数无极值;当m >0时,令f ′(x )=0⇒x =m ,当x ∈(0,m )时,f ′(x )<0,函数y =f (x )单调递减;当x ∈(m ,+∞)时,f ′(x )>0,函数y =f (x )单调递增.所以当x =m 时,函数y =f (x )取极小值,且为f (m )=ln m +1.依题意有ln m +1≥0⇒m ≥1e ,因此,实数m 的取值范围是1e ,+∞四、解答题(本题共6小题,共70分)17.(10分)等比数列{a n }中,已知a 1=2,a 4=16.(1)求数列{a n }的通项公式a n ;(2)若a 3,a 5分别是等差数列{b n }的第4项和第16项,求数列{b n }的通项公式及前n 项和S n .解:(1)设{a n }的公比为q ,由已知得16=2q 3,解得q =2,所以a n =2n .(2)由(1)得a 3=8,a 5=32,则b 4=8,b 16=32.设{b n }的公差为d b 1+3d =8,b 1+15d =32,b 1=2,d =2.从而b n =2+2(n -1)=2n .所以数列{b n }的前n 项和S n =(2+2n )n2=n 2+n .18.(12分)已知函数f (x )=12x 2-3ln x .(1)求f (x )在(1,f (1))处的切线方程;(2)试判断f (x )在区间(1,e)上有没有零点.若有,判断零点的个数.解:(1)由已知得f ′(x )=x -3x ,有f ′(1)=-2,f (1)=12,∴在(1,f (1))处的切线方程为y -12=-2(x -1),化简得4x +2y -5=0.(2)由(1)知f ′(x )=(x -3)(x +3)x ,因为x >0,令f ′(x )=0,得x = 3.所以当x ∈(0,3)时,有f ′(x )<0,则(0,3)是函数f (x )的单调递减区间;当x ∈(3,+∞)时,有f ′(x )>0,则(3,+∞)是函数f (x )的单调递增区间;当x ∈(1,e)时,函数f (x )在(1,3)上单调递减,在(3,e)上单调递增.又因为f (1)=12,f (e)=12e 2-3>0,f (3)=32(1-ln 3)<0,所以f (x )在区间(1,e)上有两个零点.19.(12分)设数列{a n }是等差数列,其前n 项和为S n ,且a 3=2,S 9=54.(1)求数列{a n }的通项公式;(2)证明:1a 1+3+1a 2+3+1a 3+3+…+1a 100+3>13.(1)解:设数列{a n }的公差为d ,∵S 9=9a 5=54,∴a 5=6,∴d =a 5-a 35-3=2,∴a n =a 3+(n -3)d =2n -4.(2)证明:∵1a n +3=12n -1>22n -1+2n +1=2n +1-2n -1,∴1a 1+3+1a 2+3+1a 3+3+…+1a 100+3>(3-1)+(5-3)+…+(201-199)=201-1>14-1=13,∴1a 1+3+1a 2+3+1a 3+3+…+1a 100+3>13.20.(12分)设函数f (x )=e x -ax -1(a ∈R ).(1)若a =2,求函数f (x )在区间[0,2]上的最大值和最小值;(2)当x ≥0时,f (x )≥0,求a 的取值范围.解:(1)f (x )=e x -2x -1,取f ′(x )=e x -2=0,即x =ln 2,函数在[0,ln 2]上单调递减,在(ln 2,2]上单调递增,且f (0)=0,f (2)=e 2-5,f (ln 2)=1-2ln 2,故函数的最大值为f (2)=e 2-5,最小值为f (ln 2)=1-2ln 2.(2)f (x )=e x -ax -1,f ′(x )=e x -a ,f (0)=0.当a ≤0时,f ′(x )=e x -a >0,函数单调递增,故f (x )≥f (0)=0,成立;当a >0时,f ′(x )=e x -a =0,即x =ln a ,故函数在(0,ln a )上单调递减,在(ln a ,+∞)上单调递增,故f (ln a )<f (0)=0,不成立.综上所述,a 的取值范围为(-∞,0].21.(12分)等差数列{a n }中,S 3=21,S 6=24,(1)求数列{a n }的前n 项和公式S n ;(2)求数列{|a n |}的前n 项和T n .解:(1)设{a n }首项为a 1,公差为d ,由S 3=21,S 6=24,a 1+3×22d =21,a 1+6×52d =24,1=9,=-2.∴S n =n ×9+n (n -1)2×(-2)=-n 2+10n .(2)由(1)知,a n =9+(n -1)×(-2)=-2n +11,由a n ≥0得-2n +11≥0,即n ≤112.当n ≤5时,T n =|a 1|+|a 2|+…+|a n |=a 1+a 2+…+a n =S n =-n 2+10n ;当n ≥6时,T n =|a 1|+…+|a 5|+|a 6|+…+|a n |=(a 1+a 2+…+a 5)-(a 6+…+a n )=S 5-(S n -S 5)=n 2-10n +50.综上,T nn 2+10n (n ≤5),2-10n +50(n ≥6).22.(12分)已知a ,b ∈R ,设函数f (x )=e x -ax -b x 2+1.(1)若b =0,求f (x )的单调区间;(2)当x ∈[0,+∞)时,f (x )的最小值为0,求a +5b 的最大值.注:e =2.71828…为自然对数的底数.解:(1)f (x )=e x -ax ,f ′(x )=e x -a ,当a ≤0时,f ′(x )=e x -a ≥0恒成立,函数单调递增;当a >0时,f ′(x )=e x -a =0,x =ln a ,当x ∈(-∞,ln a )时,f ′(x )<0,函数单调递减;当x ∈(ln a ,+∞)时,f ′(x )>0,函数单调递增.综上所述,a ≤0时,f (x )在R 上单调递增;a >0时,f (x )在(-∞,ln a )上单调递减,在(ln a ,+∞)上单调递增.(2)f (x )=e x-ax -bx 2+1≥0在x ∈[0,+∞)上恒成立,=e -12a -52b ≥0,故a +5b ≤2e ,现在证明存在a ,b ,a +5b =2e ,使f (x )的最小值为0.取a =3e 4,b =5e 4(此时可使f 0),f ′(x )=e x -a -bx x 2+1,f ″(x )=e x -b (x 2+1)x 2+1,b =5e 4<1,故当x ∈[0,+∞)时,(x 2+1)x 2+1≥1,e x ≥1,故f ″(x )≥0,f ′(x )在[0,+∞)上单调递增,f 0,故f (x )在0f (x )min =0.综上所述,a +5b 的最大值为2 e.。
人教版高中数学必修第二册 第九章 统计 单元测试卷 (含答案)

人教版高中数学必修第二册第九章统计单元测试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷60分,第Ⅱ卷90分,共150分,考试时间120分钟.第Ⅰ卷(选择题共60分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.从某地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是()A.抽签法B.按性别分层随机抽样C.按学段分层随机抽样D.随机数法2.从某小学随机抽取100名学生,将他们的身高(单位:厘米)分布情况汇总如下表:身高[100,110)[110,120)[120,130)[130,140)[140,150]频数535302010由此表估计这100名学生身高的中位数为(结果保留4位有效数字)()A.119.3B.119.7C.123.3D.126.73.高二(1)班某宿舍有7人,他们的身高(单位:cm)分别为170,168,172,172,175,176,180,则这7个数据的第60百分位数为()A.168B.175C.172D.1764.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中的一组.已知该组的频率为m,该组上的频率分布直方图的高为h,则|a-b|等于()A.mhB.C.D.m+h5.2020年2月8日,在韩国首尔举行的四大洲花样滑冰锦标赛双人自由滑比赛中,中国组合隋文静、韩聪以总分217.51分拿下四大洲赛冠军,这也是他们第六次获得四大洲冠军.中国另一对组合彭程、金杨以213.29分摘得银牌.花样滑冰锦标赛有9位评委进行评分,首先这9位评委给出某对选手的原始分数,评定该对选手的成绩时从9个原始成绩中去掉一个最高分、一个最低分,得到7个有效评分,7个有效评分与9个原始评分相比,不变的数字特征是()A.中位数B.平均数C.方差D.极差6.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到如图C4-1所示的频率分布直方图,由于不慎将部分数据丢失,但知道后5组频数之和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为()图C4-1A.64B.54C.48D.277.某商场一年中各月份的收入、支出情况的统计如图C4-2所示,则下列说法中正确的是()图C4-2A.支出最高值与支出最低值的比是8∶1B.4至6月份收入的平均数为50万元C.利润最高的月份是2月份D.2至3月份的收入的变化率与11至12月份的收入的变化率相同8.为了研究一种新药的疗效,选100名患者随机分成两组,每组50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成图C4-3,其中“*”表示服药者,“+”表示未服药者.则下列说法中,错误的是()图C4-3A.服药组的指标x的平均数和方差比未服药组的都小B.未服药组的指标y的平均数和方差比服药组的都大C.以统计的频率作为概率,估计患者服药一段时间后指标x低于100的概率为0.94D.这种疾病的患者的生理指标y基本都大于1.5二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,至少有两项是符合题目要求的)9.“悦跑圈”是一款基于社交型的跑步应用,用户通过该平台可查看自己某时间段的运动情况.某人根据2019年1月至2019年11月期间每月跑步的里程(单位:十公里)的数据绘制了如图C4-4所示的折线图,根据该折线图,下列结论正确的是()图C4-4A.月跑步里程逐月增加B.月跑步里程的最大值出现在9月C.月跑步里程的中位数为8月份对应的里程D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳10.某学校为了调查学生在一周生活方面的支出(单位:元)情况,抽取了一个容量为n的样本,将样本数据按[20,30),[30,40),[40,50),[50,60]分组后所得频率分布直方图如图C4-5所示,其中支出在[50,60]内的学生有60人,则下列说法正确的是()图C4-5A.样本中支出在[50,60]内的频率为0.03B.样本中支出不少于40元的人数有132C.n的值为200D.若该校有2000名学生,则一定有600人支出在[50,60]内11.统计某校n名学生某次数学同步练习的成绩(单位:分,满分150分),根据成绩依次分成六组[90,100),[100,110),[110,120),[120,130),[130,140),[140,150],得到频率分布直方图如图C4-6所示,若不低于140分的人数为110,则下列说法正确的是()图C4-6A.m=0.031B.n=800C.100分以下的人数为60D.成绩在区间[120,140)内的人数超过50%12.某市12月17日至21日期间空气质量呈现重度及以上污染水平,经市政府批准,该市启动了空气重污染红色预警,期间实行机动车“单双号”限行等措施.某社会调查中心联合问卷网,对2400人进行问卷调查,并根据调查结果得到如图C4-7所示的扇形图,则下列结论正确的是()图C4-7A.“不支持”部分所占的比例是10%B.“一般”部分对应的人数是800C.扇形图中如果圆的半径为2,则“非常支持”部分对应扇形的面积是65πD.“支持”部分对应的人数是1080请将选择题答案填入下表:题号12345678总分答案题号9101112答案第Ⅱ卷(非选择题共90分)三、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.一组数据按从小到大的顺序排列为10,12,13,x,17,19,21,24,其中位数为16,则x=.14.某校为了了解学生收看“空中课堂”的方式,对该校500名学生进行了调查,并把结果绘制成如图C4-8所示的扇形图,那么该校通过手机收看“空中课堂”的学生人数是.图C4-815.国家禁毒办于2019年11月5日至12月15日在全国青少年毒品预防教育数字化网络平台上开展2019年全国青少年禁毒知识答题活动,活动期间进入答题专区,点击“开始答题”按钮后,系统自动生成20道题.已知某校高二年级有甲、乙、丙、丁、戊五位同学在这次活动中答对的题数分别是17,20,16,18,19,则这五位同学答对题数的方差是.16.从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图C4-9所示).由图中数据可知a=.若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用比例分配的分层随机抽样的方法选取18人参加一项活动,则从身高在[140,150]内的学生中选取的人数应为.图C4-9四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)将一组数据按从小到大的顺序排列,得到-1,0,4,x,7,14,已知这组数据的中位数为5,求这组数据的平均数与方差.18.(12分)某车站在春运期间为了了解旅客的购票情况,随机调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时,单位为min).下面是对所得数据进行统计分析后得到的频率分布表和频率分布直方图.频率分组频数[5,10)100.10[10,15)10②[15,20)①0.50[20,25]300.30合计1001.00解答下列问题:(1)在表中填写出缺失的数据并补全频率分布直方图(如图C4-10所示);(2)估计旅客购票用时的平均数.图C4-1019.(12分)某班主任利用周末时间对该班2019年最后一次月考的语文作文分数进行了统计,发现分数都位于20~55之间,现将分数情况按[20,25),[25,30),[30,35),[35,40),[40,45),[45,50),[50,55]分成七组后,作出频率分布直方图如图C4-11所示,已知m=2n.(1)求频率分布直方图中m,n的值;(2)求该班这次月考语文作文分数的平均数和中位数.(每组数据用该组区间的中点值作为代表)图C4-1120.(12分)已知甲、乙两人在相同条件下各射靶10次,每次射击的命中环数如图C4-12所示.(1)求甲、乙两人射击命中环数的平均数和方差;(2)请根据甲、乙两人射击命中环数的平均数和方差,分析谁的射击水平高.图C4-1221.(12分)某地区100位居民的人均月用水量(单位:t)的分组及各组的频数分别为[0,0.5],4;(0.5,1],8;(1,1.5],15;(1.5,2],22;(2,2.5],25;(2.5,3],14;(3,3.5],6;(3.5,4],4;( 4,4.5],2.(1)列出样本的频率分布表.(2)画出频率分布直方图,并根据直方图估计这组数据的平均数、中位数、众数.(3)当地政府制定了人均月用水量不超过3t的标准,若超过3t则加倍收费,当地政府说,85%以上的居民不超过这个标准,这个解释对吗?为什么?22.(12分)我国是世界上严重缺水的国家之一,某市为了制定合理的节水方案,对家庭用水情况进行了调查,通过抽样,获得了某年100户家庭的月均用水量(单位:t),将数据按照[0,2),[2,4),[4,6),[6,8),[8,10]分成5组,制成了如图C4-13所示的频率分布直方图.(1)假设同组中的每个数据都用该组区间的中点值代替,求全市家庭月均用水量平均数的估计值(精确到0.01);(2)求全市家庭月均用水量的25%分位数的估计值(精确到0.01).图C4-13参考答案与解析1.C[解析]由题意得,最合理的抽样方法是按学段分层随机抽样,故选C.2.C[解析]设中位数为t,则有5100+35100+30100× -12010=0.5,解得t≈123.3.故选C.3.B[解析]将这7人的身高从小到大排序,可得168,170,172,172,175,176,180.∵7×60%=4.2,∴第5个数据为所求的第60百分位数,即这7个数据的第60百分位数为175.故选B.,所以h= | - |,则|a-b|= ,故选C.4.C[解析]在频率分布直方图中小长方形的高等于频率组距5.A[解析]根据题意可知,不变的数字特征是中位数.故选A.6.B[解析]前两组的频数为100×(0.05+0.11)=16.因为后五组的频数之和为62,所以前三组的频数之和为38,所以第三组的频数为38-16=22.又最大频率为0.32,故第四组的频数为0.32×100=32.所以a=22+32=54.故选B.7.D[解析]由图可知,支出最高值为60万元,支出最低值为10万元,其比是6∶1,故A错误;4至6月份的平均收入为13×(50+30+40)=40(万元),故B错误;利润最高的月份为3月份和10月份,故C 错误;由图可知2至3月份的收入的变化率与11至12月份的收入的变化率相同,故D正确.故选D.8.B[解析]服药组的指标x的取值相对集中,方差较小,且服药组的指标x的平均数小于未服药组的指标x的平均数,故选项A中说法正确;未服药组的指标y的取值相对集中,方差较小,故选项B 中说法错误;服药组的指标x值有3个大于100,所以估计患者服药一段时间后指标x低于100的概率为0.94,故选项C中说法正确;未服药组的指标y值只有1个数据比1.5小,则这种疾病的患者的生理指标y基本都大于1.5,故选项D中说法正确.故选B.9.BCD[解析]2月跑步里程比1月的小,故A错误;月跑步里程9月最大,故B正确;月跑步里程从小到大对应的月份依次为2月、7月、3月、4月、1月、8月、5月、6月、11月、10月、9月,故月跑步里程的中位数为8月份对应的里程,故C正确;1月至5月的月跑步里程相对于6月至11月,波动性更小,变化比较平稳,故D正确.故选BCD.10.BC[解析]由频率分布直方图得,样本中支出在[50,60]内的频率为1-(0.01+0.024+0.036)×10=0.3,故A错误;样本中支出不少于40元的人数为0.0360.3×60+60=132,故B正确;n=600.3=200,故C正确;在D中,若该校有2000名学生,则大约有600人支出在[50,60]内,故D错误.故选BC.11.AC[解析]由图可知10×(m+0.020+0.016+0.016+0.011+0.006)=1,解得m=0.031,故A正确;因为不低于140分的频率为0.011×10=0.11,所以n=1100.11=1000,故B错误;因为100分以下的频率为0.006×10=0.06,所以100分以下的人数为1000×0.06=60,故C正确;对选项D,成绩在区间[120,140)内的频率为0.031×10+0.016×10=0.47<0.5,人数不超过50%,故D错误.故选AC.12.ACD[解析]“不支持”部分所占的比例是1-45%-30%-15%=10%,A正确;“一般”部分对应的人数是2400×15%=360,B不正确;“非常支持”部分对应扇形的面积是π×22×30%=65π,C正确;“支持”部分对应的人数为2400×45%=1080,D正确.故选ACD.13.15[解析]由中位数的定义知 +172=16,∴x=15.14.25[解析]∵该校通过手机收看“空中课堂”的学生人数所占的百分比为1-(25%+70%)=5%,∴该校通过手机收看“空中课堂”的学生人数是500×5%=25.15.2[解析]这五位同学答对题数的平均数 =17+20+16+18+195=18,则方差s2=15×[(17-18)2+(20-18)2+(16-18)2+(18-18)2+(19-18)2]=2.16.0.0303[解析]因为10×(0.035+0.020+0.010+0.005+a)=1,所以a=0.030.身高在[120,130),[130,140),[140,150]三组内的学生人数为100×(0.030+0.020+0.010)×10=60,其中身高在[140,150]内的学生中人数为100×0.010×10=10,所以从身高在[140,150]内的学生中选取的人数应为1060×18=3.17.解:因为数据-1,0,4,x,7,14的中位数为5,所以4+ 2=5,解得x=6.设这组数据的平均数为 ,方差为s2,则 =16×(-1+0+4+6+7+14)=5,s2=16×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=743.18.解:(1)表中缺失的数据分别为①50,②0.10.补全后的频率分布直方图如图所示.(2)估计旅客购票用时的平均数为7.5×0.10+12.5×0.10+17.5×0.50+22.5×0.30=17.5(min).19.解:(1)由频率分布直方图,得=2 ,(0.01+0.03+0.06+ +0.03+ +0.01)×5=1,解得 =0.04, =0.02.(2)该班这次月考语文作文分数的平均数为22.5×0.05+27.5×0.15+32.5×0.3+37.5×0.2+42.5×0.15+47.5×0.1+52.5×0.05=36.25.因为(0.01+0.03+0.06)×5=0.5,所以该班这次月考语文作文分数的中位数为35.20.解:(1)由折线图可知甲射击10次命中的环数分别为9,5,7,8,7,6,8,6,7,7.乙射击10次命中的环数分别为2,4,6,8,7,7,8,9,9,10.则x 甲=110×(9+5+7+8+7+6+8+6+7+7)=7(环).x 乙=110×(2+4+6+8+7+7+8+9+9+10)=7(环),甲2=110×[(9-7)2+(5-7)2+(7-7)2×4+(6-7)2×2+(8-7)2×2]=1.2,乙2=110×[(2-7)2+(4-7)2+(6-7)2+(7-7)2×2+(8-7)2×2+(9-7)2×2+(10-7)2]=5.4.(2)因为x 甲=x 乙, 甲2< 乙2,所以甲的射击稳定性比乙好,故甲的射击水平高.21.解:(1)作出频数分布表,如下.分组频数频率[0,0.5]40.04(0.5,1]80.08(1,1.5]150.15(1.5,2]220.22(2,2.5]250.25(2.5,3]140.14(3,3.5]60.06(3.5,4]40.04(4,4.5]20.02合计1001.00(2)由频率分布表画出频率分布直方图,如图所示.由频率分布直方图得这组数据的平均数=0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02.∵人均月用水量在[0,2]内的频率为0.04+0.08+0.15+0.22=0.49,在(2,2.5]内的频率为0.25,∴中位数为2+0.5−0.490.25×0.5=2.02.众数为2+2.52=2.25.(3)月用水量在3t以上的居民的比例为6%+4%+2%=12%,即大约有12%的居民月用水量在3t以上,88%的居民月用水量不超过3t,因此政府的解释是正确的.22.解:(1)因为0.06×2×1+0.11×2×3+0.18×2×5+0.09×2×7+0.06×2×9=4.92.因此全市家庭月均用水量平均数的估计值为4.92t.(2)频率分布直方图中,用水量低于2t的频率为0.06×2=0.12.用水量低于4t的频率为0.06×2+0.11×2=0.34.故全市家庭月均用水量的25%分位数的估计值为2+0.25−0.120.11≈3.18(t).。
人教版必修2高中数学全册单元检测卷及答案

【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
】2019-2020学年必修第二册第八章单元训练金卷立体几何初步(一)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.以下命题中正确的是( )A .以直角三角形的一直角边为轴旋转所得的旋转体是圆锥B .以直角梯形的一腰为轴旋转所得的旋转体是圆台C .有一个面是多边形,其余各面都是三角形的几何体叫做棱锥D .圆锥的侧面展开图为扇形,这个扇形的半径为圆锥底面圆的半径 2.下列说法正确的是( )只装订不密封准考证号 考场号 座位号A .过三个点有且仅有一个平面B .空间中的两条直线不平行则相交C .圆锥过轴的截面一定是一个等腰三角形D .直角梯形绕它的一条边旋转一周形成的曲面围成的几何体是圆台3.如图,球面上有A 、B 、C 三点,90ABC ∠=︒,3BA BC ==,球心O 到平面ABC 322) A .72πB .36πC .18πD .8π4.已知三棱锥P ABC -的四个顶点都在球O 的球面上,ABC △是边长为3PA ⊥平面ABC ,若三棱锥P ABC -的体积为3球O 的表面积为( ) A .18πB .20πC .24πD .203π5.三棱柱111ABC A B C -底面为正三角形,侧棱与底面垂直,若2AB =,11AA =,则点A 到平面1A BC 的距离为( )A 3B 3C 33D 36.在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,15AA =,则V 的最大值是( ) A .4πB .92π C .1256πD .323π7.设直三棱柱111ABC A B C -的体积为V ,点P 、Q 分别在侧棱1AA 、1CC 上,且1PA QC =,则三棱锥1B BPQ -的体积为( )A .16VB .14VC .13VD .12V8.如图,一圆锥形物体的母线长为4,其侧面积为4π,则这个圆锥的体积为( )A .153B .833C .153π D .833π 9.如图,在正四棱柱1111ABCD A B C D -中,1AB =,13AA =E 为AB 上的动点,则1D E CE +的最小值为( )A .22B .10C .51+D .22+10.如图,1111ABCD A B C D -为正方体,下面结论:①BD P 平面11CB D ;②1AC BD ⊥;③1AC ⊥平面11CB D ,其中正确结论的个数是( )A .0B .1C .2D .311.如图,棱长为1的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点,则下列结论错误的是( )A .11DC D P ⊥B .平面11D A P ⊥平面1A APC .1APD ∠的最大值为90︒D .1AP PD +的最小值为22+12.如图,三棱锥S ABC -中,2SA AB AC ===,30ASB BSC CSA ∠=∠=∠=︒,M ,N 分别为SB ,SC 上的点,则AMN △周长的最小值为( )A .4B .3C .3D .22第Ⅱ卷二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.棱长为2的正方体1111ABCD A B C D -中,M 是棱1AA 的中点,过C ,M ,1D 作正方体的截面,则截面的面积是 . 14.已知三棱锥P ABC -,PA ⊥平面ABC ,AC BC ⊥,3BC PA ==,1AC =,则三棱锥P ABC -的侧面积 .15.如图,六面体ABCDEF 中,AB CD P ,AB CD ⊥,且112AB AD CD ===,ADEF 是正方形,平面ADEF ⊥平面ABCD ,则点D 到平面BEC 的距离为 .16.如图,四边形ABCD 中,1AB AD CD ===,2BD =,BD CD ⊥,将四边形ABCD 沿对角线BD 折成四面体A BCD '-,则四面体A BCD'-体积的最大值为 .三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(10分)如图,在直三棱柱111ABC A B C -中,90ACB ∠=︒,点D 是AB 的中点. (1)求证:1AC BC ⊥; (2)求证:1AC P 平面1CDB .18.(12分)如图,在三棱锥V ABC -中,平面VAB ⊥平面ABC ,VAB △为等边三角形,AC BC ⊥且2AC BC ==,O ,M 分别为AB ,VA 的中点.(1)求证:VB P 平面MOC ; (2)求证:平面MOC ⊥平面VAB ; (3)求三棱锥V ABC -的体积.19.(12分)如图,边长为2的正方形ABCD与等边三角形ABE所在的平面互相垂直,M,N分别是DE,AB的中点.(1)证明:MN P平面BCE;的体积.(2)求三棱锥B EMN20.(12分)如图(1),ABC △中,90ABC ∠=︒,22AB BC ==M 为AC 中点,现将ABM △沿着BM 边折起,如图(2)所示.(1)求证:平面BCM ⊥平面ACM ;(2)若平面ABM ⊥平面BCM ,求证AM BC ⊥,并求三棱锥B ACM -外接球的直径.21.(12分)如图,三棱柱111ABC A B C -,1AA ⊥底面ABC ,且ABC △为正三角形,16AA AB ==,D 为AC 中点. (1)求三棱锥1C BCD -的体积; (2)求证:平面1BC D ⊥平面11ACC A ; (3)求证:直线1AB P 平面1BC D .22.(12分)如图所示,在正三棱柱111ABC A B C -中,12AB AA ==,由顶点B 沿棱柱侧面(经过侧棱1AA )到达顶点1C ,与1AA 的交点记为M . (1)三棱柱侧面展开图的对角线长;(2)从B 经过M 到1C 的最短路线长及此时1A MAM的值.2019-2020学年必修第二册第八章单元训练金卷立体几何初步(一)答 案一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】A对于A ,由圆锥的定义可知A 正确;对于B ,若旋转轴不是直角梯形的直腰,则旋转体不是圆台,故B 错误; 对于C ,若其余各面三角形没有公共顶点,则几何体不是棱锥,故C 错误; 对于D ,圆锥的侧面展开图的半径是圆锥的母线,故D 错误. 2.【答案】C对于A ,当三点共线时,过这三点有无数个平面,故A 不正确;对于B ,空间中的两条直线的位置关系有平行、相交、异面,故B 不正确; 对于C ,由圆锥的结构特征知:圆锥过轴的截面一定是一个等腰三角形,故C 正确; 对于D ,直角梯形绕它垂直于底边的腰旋转一周形成的曲面围成的几何体是圆台,故D 不正确. 3.【答案】B∵AC 是小圆的直径,所以过球心O 作小圆的垂线,垂足O '是AC 的中点.2232323()22OC =-=,32AC =,223='O O , ∴223OC OO O C ''=+=,即球半径为3,所以球体的体积是343363⨯π⨯=π.4.【答案】B∵三棱锥P ABC -的体积为23213(23)2334PA ⨯⨯⨯=, ∴2PA =,将三棱锥补成三棱柱,可得球心在三棱柱的中心,球心到底面的距离d 等于三棱柱的高PA 的一半,∵ABC △是边长为3ABC △外接圆的半径2r =, 5O 的表面积为4520π⋅=π. 5.【答案】B在三棱柱111ABC A B C -中,连接1A B ,1A C ,则11A B AC =, 取BC 的中点D ,连接AD ,1A D ,则有AD BC ⊥,1A D BC ⊥,AD 与1A D 交于D ,且AD 与1A D 都在平面1A AD 中,所以BC ⊥平面1A AD ,过A 作1AO A D ⊥,则AO ⊥面1A BC ,因为2AB =,11AA =,111ABC A B C -底面为正三角形, 所以3AD =,12A D =,11A A BC A ABC V V --=,111133A BC ABC h S AA S ⋅⋅=⋅⋅△△,1111221233232h ⋅⋅⋅⋅=⋅⋅⋅32h =,所以A 到平面1A BC 的距离为32.6.【答案】D如图,由题知,球的体积要尽可能大时,球需与三棱柱内切,先保证截面圆与ABC△内切,记圆O的半径为r,则由等面积法得1111682222ABCS AC r AB r BC r=⋅+⋅+⋅=⨯⨯△,所以()68AC AB BC r++=⨯,又6AB=,8BC=,所以10AC=,所以2r=,由于三棱柱高为5,此时可以保证球在三棱柱内部,若r增大,则无法保证球在三棱柱内,故球的最大半径为2,所以323Vπ=.7.【答案】C设A到BC的距离为h,∵直三棱柱111ABC A B C-的体积为V,点P、Q分别在侧棱1AA、1CC上,且1PA QC=,∴112V BC h AA=⨯⨯⨯,三棱锥1B BPQ-的体积为111111323B BPQ P BB QV V h BC AA V--==⨯⨯⨯=.8.【答案】C一个圆锥的母线长为4,它的侧面积为4π,设圆锥的底面半径是r,母线长为l,则得到4rlπ=π,解得1r=,这个圆锥的底面半径是1,∴圆锥的高为224115-=,所以圆锥的体积为21153r hπ=π.9.【答案】B画出几何体的图形,连接1D A延长至G,使得AG AD=,连接1C B延长至F,使得BF BC=,连接EF,则ABFG为正方形,连接1D F,则1D F为1D E CE+的最小值2222111310D F GF D G=+=+=.10.【答案】D由正方体的性质得,11BD B DP,所以结合线面平行的判定定理可得:BD P平面11CB D,所以①正确;连接AC、11AC,由正方体的性质得AC BD⊥,1AA BD⊥,又1AC AA A=I,所以BD⊥平面11AAC C,因为1AC⊂平面11AAC C,所以1AC BD⊥,所以②正确;由正方体的性质得11BD B DP,由②可得1AC BD⊥,所以111AC B D⊥,同理可得11AC CB⊥,进而结合线面垂直的判定定理得到1AC⊥平面11CB D,所以③正确.11.【答案】C∵111A D DC⊥,11A B DC⊥,∴1DC⊥面11A BCD,1D P⊂面11A BCD,11DC D P⊥,∴A正确;∵平面11D A P即为平面11D A BC,平面1A AP即为平面11A ABB,切11D A⊥平面11A ABB,∴平面11D A BC⊥平面11A ABB,∴平面11D A P⊥平面1A AP,∴B正确;当122A P<<时,1APD∠为钝角,∴C错误;将面1AA B与面11A BCD沿展成平面图形,线段1AD即为1AP PD+的最小值,在11D A A△中,11135D A A∠=︒,利用余弦定理解三角形得122AD=+,即122AP PD+≥+,∴D正确.12.【答案】D将三棱锥的侧面沿SA剪开展成如图所示的平面图形,可知当A,M,N,共线时,AMN△的周长最小,且AA'的长度即为所求的最小值,在SAA'△中,2SA SA'==,30A SB BSC ASC'∠=∠=∠=︒,故90ASA'∠=︒,所以2222AA SA A S''=+=.二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)13.【答案】92如图所示,由面面平行的性质知截面与平面11AA B的交线MN是1AA B△的中位线,所以截面是梯形1CD MN,其中2MN=,122CD=,15CN D M==,梯形1CD MN的高为22232(5)()2h=-=,所以1329(222)222S=+⨯=.14.【答案】532如图所示,三棱锥P ABC -中,PA ⊥平面ABC ,∴PA AB ⊥,PA AC ⊥,PA BC ⊥,又AC BC ⊥,PA AC A =I ,∴BC ⊥平面PAC ,∴BC PC ⊥, ∴三棱锥P ABC -的各个面都是直角三角形, 又3BC PA ==,1AC =,∴三棱锥P ABC-的侧面积为PAB PAC PBCS S S S =++△△△2222111533(3)1313(3)12222=⨯⨯++⨯⨯+⨯⨯+=.15.【答案】6易证BC ⊥平面BDE ,∴BC BE ⊥,易求得6BEC S ∆=, 而1BCD S =△,设点D 到平面BEC 的距离是h , 由E BCD D BCE V V --=可得1133BCD BCE S DE S h ⋅=⋅△△, 解得66BCD BCE S DE h S ⋅===△△. 16.【答案】16要使四面体A BCD '-体积的最大,则平面A BD '平面BCD ,由BD CD ⊥,平面A BD '⊥平面BCD ,得CD ⊥平面A BD ',∴CD BD ⊥, ∵四边形ABCD 中,1AB AD CD ===,2BD =,∴A '到底面BCD 的距离为22, ∴四面体A BCD '-体积的最大值为1121213226V =⨯⨯⨯⨯=.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.【答案】(1)证明见解析;(2)证明见解析. (1)证明:∵90ACB ∠=︒,所以AC CB ⊥,又在直三棱柱111ABC A B C -中,有1AC BB ⊥, ∴AC ⊥平面11BB C C ,所以1AC BC ⊥.(2)设1BC 与1B C 交于点P ,连DP ,易知P 是1BC 的中点, 又D 是AB 中点,∴1AC DP P ,∵DP ⊂平面1CDB ,1AC 不在平面1CDB 上,∴1AC P 平面1CDB .18.【答案】(1)证明见解析;(2)证明见解析;(3)3. (1)证明:∵O ,M 分别为AB ,VA 的中点,∴OM VB P , ∵VB ⊄平面MOC ,OM ⊂平面MOC ,∴VB P 平面MOC . (2)∵AC BC =,O 为AB 的中点,∴OC AB ⊥,∵平面VAB ⊥平面ABC ,OC ⊂平面ABC ,∴OC ⊥平面VAB , ∵OC ⊂平面MOC ,∴平面MOC ⊥平面VAB . (3)在等腰直角三角形ACB 中,2AC BC ==,∴2AB =,1OC =,∴3VAB S =△,∵OC ⊥平面VAB ,∴133C VAB VAB V OC S -=⋅=△, ∴3V ABC C VAB V V --==. 19.【答案】(1)证明见解析;(2)3. (1)证明:取AE 中点P ,连接MP ,NP ,由题意可得MP AD BC P P ,∵MP ⊄平面BCE ,BC ⊂平面BCE ,∴MP P 平面BCE , 同理可证NP P 平面BCE ,∵MP NP P =I ,∴平面MNP P 平面BCE , 又MN ⊂平面MNP ,∴MN P 平面BCE .(2)由(1)可得MP DA P ,且12MP DA =, ∵平面ABCD ⊥平面ABE ,平面ABCD I 平面ABE AB =,且DA AB ⊥,∴DA ⊥平面ABE ,∴M 到平面ENB 的距离为112MP DA ==, ∵N 为AB 的中点,∴12EBN ABE S S =△△, ∴111113322132322B EMN M EBN ABE V MP V S --⨯==⨯=⨯⨯⨯⨯=△. 20.【答案】(1)证明见解析;(2)23(1)证明:由图(1)知,BM AM ⊥,BM MC ⊥,AM MC M =I ,所以BM ⊥平面AMC ,又因为BM ⊂平面BMC ,所以平面BCM ⊥平面ACM .(2)因为平面ABM ⊥平面BCM ,平面ABM I 平面BCM BM =,BM AM ⊥,AM ⊂平面ABM ,所以AM ⊥平面BMC ,所以AM MC ⊥,即AM 、MC 、BM 两两垂直,而易知2AM BM MC ===, 所以该三棱锥外接球与以MA 、MB 、MC 为相邻棱组成的长方体的外接球为同一个球,所以三棱锥B ACM -外接球的直径为22222223++=. 21.【答案】(1)93;(2)证明见解析;(3)证明见解析. (1)∵ABC △为正三角形,D 为AC 中点,∴BD AC ⊥, 由6AB =可知,3CD =,33BD =,∴19322BCD S CD BD =⋅⋅=△, 又∵1AA ⊥底面ABC ,且16AA AB ==, ∴1C C ⊥底面ABC ,且16C C =, ∴111933C BCDBCD V S C C -=⋅⋅=△.(2)∵1AA ⊥底面ABC ,BD ⊂平面ABC ,∴1AA BD ⊥, 又BD AC ⊥,1AA AC A =I ,1AA ,AC ⊂平面11ACC A , ∴BD ⊥平面11ACC A ,又BD ⊂平面1BC D ,∴平面1BC D ⊥平面11ACC A . (3)连接1B C 交1BC 于O ,连接OD ,又1AB ⊄平面1BC D ,OD ⊂平面1BC D ,∴1AB P 平面1BC D . 22.【答案】(1)210;(2)25,11A MAM=. 沿侧棱1BB 将正三棱柱的侧面展开,得到一个矩形11BB B B ''(如图所示).(1)矩形11BB B B ''的长326BB '=⨯=,宽12BB =, 所以三棱柱侧面展开图的对角线长为22162210BB '=+=. (2)由侧面展开图可知:当B ,M ,1C 三点共线时, 由B 经M 到点1C 的路线最短, 所以最短路线长为2214225BC =+=显然11ABM AC M ≅Rt Rt △△,所以1A M AM =,即11A MAM=.【若缺失公式、图片现象属于系统读取不成功,文档内容齐全完整,请放心下载。
人教版高中数学必修第二册第九章 统计 单元检测(含答案)

人教版高中数学必修第二册第九章统计单元检测说明:本试卷满分100分,分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
考试时间45分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列抽样方法是简单随机抽样的是A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方法确定号码的后四位是2709的为三等奖B.某车间包装一种产品,在自动包装传送带上,每隔30分钟抽一包产品,称其重量是否合格C.从8台电脑中逐个不放回地随机抽取2台,进行质量检验,假设8台电脑已编好号,对编号随机抽取D.从20个零件中一次性抽出3个进行质量检查2.对于考试成绩的统计,如果你的成绩处在第95的百分位数上,以下说法正确的是A.你得了95分B.你答对了95%的试题C.95%的参加考试者得到了和你一样的考分或还要低的分数D.你排名在第95名3.演讲比赛共有9位评委分别给出某选手的原始评分,评定该选手的成绩时,从9个原始评分中去掉1个最高分、1个最低分,得到7个有效评分.7个有效评分与9个原始评分相比,不变的数字特征是A.中位数B.平均数C.方差D.极差4.某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用比例分配的分层随机抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n=A.9B.10C.12D.135.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为A.0.5B.0.6C.0.7D.0.86.设样本数据x1,x2,…,x2020的方差为4,若y i=2x i+4(i=1,2,…,2020),则y1,y2,…,y2020的方差为A.13B.14C.15D.167.已知一组数据:125,121,123,125,127,129,125,128,130,129,126,124,125,127,126.则这组数据的第25百分位数和第80百分位数分别是A.125128B.124128C.125129D.125128.58.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是A.月接待游客量逐月增加B.年接待游客量逐年增加C.各年的月接待游客量高峰期大致在7,8月D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳二、多项选择题:本题共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分.9.为了了解参加运动会的2000名运动员的年龄情况,从中抽取20名运动员的年龄进行统计分析.就这个问题,下列说法中正确的有________.①2000名运动员是总体;②每个运动员是个体;③所抽取的20名运动员是一个样本;④样本容量为20;⑤这个抽样方法可采用随机数法抽样;A.④B.①②C.②③D.⑤10.某地区经过一年的新农村建设,农村的经济收入增加了一倍.实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例.得到如下饼图:则下面结论中正确的是A.新农村建设后,种植收入减少B.新农村建设后,其他收入增加了一倍以上C.新农村建设后,养殖收入增加了一倍D.新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半三、填空题:本题共4小题,每小题5分,共20分.11.某次体检,6位同学的身高(单位:米)分别为1.72,1.78,1.75,1.80,1.69,1.77则这组数据的第50%位数_________(米).12.某学校高一年级1802人,高二年级1600人,高三年级1499人,先采用分层抽样的方法从中抽取98名学生参加全国中学生禁毒知识竞赛,则在高一、高二、高三三个年级中抽取的人数分别为_________13.若40个数据的平方和是56,平均数是22,则这组数据的标准差是________14.在高一年级学生身高的调查中,采用分层随机抽样,如果不知道样本数据,只知道抽取男生23人,其平均数和方差分别为170.6和12.59,女生27人,其平均数和方差分别为160.6和38.62.用这些数据对高一年级全体学生的身高平均值为_______,方差________四、解答题:本题共3小题,每小题10分,共30分.解答应写出文字说明、证明过程或演算步骤.15.对甲、乙两名同学的学习成绩进行抽样分析,各抽5门功课,得到的观测值如下:(1)甲、乙的平均成绩谁最好.(2)谁的各门功课发展较平衡16.有1个容量为100的样本,数据的分组及各组的频数如下:[12.5,15.5),6;[15.5,18.5),16;[18.5,21.5),18;[21.5,24.5),22;[24.5,27.5),20;[27.5,30.5),10;[30.5,33.5],8.(1)列出样本的频率分布表(含累计频率).(2)画出频率分布直方图.(3)根据频率分布表的累计频率估计样本的90%分位数.甲6080709070乙806070807517.我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:t),制作了频率分布直方图.(1)由于某种原因频率分布直方图部分数据丢失,请在图中将其补充完整;(2)用样本估计总体,如果希望80%的居民每月的用水量不超过标准,则月均用水量的最低标准定为多少吨?并说明理由;(3)从频率分布直方图中估计该100位居民月均用水量的平均数.(同一组中的数据用该区间的中点值代表)人教版高中数学必修第二册第九章统计单元检测答案解析说明:本试卷满分100分,分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
【人教A版】高中数学必修二:全册作业与测评 综合质量评估(附答案)

综合质量评估(第一至第四章)(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知圆的方程是(x-2)2+(y-3)2=4,则点P(3,2)满足( )A.是圆心B.在圆上C.在圆内D.在圆外【解析】选C.因为(3-2)2+(2-3)2=2<4,故点P(3,2)在圆内.2.直线x-y-4=0与圆x2+y2-2x-2y-2=0的位置关系是( )A.相交B.相切C.相交且过圆心D.相离【解析】选D.圆的方程为(x-1)2+(y-1)2=4,则圆心到直线的距离d=错误!未找到引用源。
=2错误!未找到引用源。
>2,所以直线与圆相离.【补偿训练】(2015·郑州高一检测)对任意实数k,圆C:(x-3)2+(y-4)2=13与直线l:kx-y-4k+3=0的位置关系是( )A.相交B.相切C.相离D.与k取值有关【解析】选 A.对任意实数k,直线l:kx-y-4k+3=0恒过定点(4,3),而(4-3)2+(3-4)2<13,故定点(4,3)在圆C内部,所以直线与圆相交.3.(2015·乌海高一检测)已知空间两点P1(-1,3,5),P2(2,4,-3),则|P1P2|等于( ) A.错误!未找到引用源。
B.3错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
【解析】选A.错误!未找到引用源。
=错误!未找到引用源。
=错误!未找到引用源。
.4.已知两圆的方程是x2+y2=1和x2+y2-6x-8y+9=0,那么这两个圆的位置关系是( ) A.外离 B.相交 C.外切 D.内切【解析】选C.将圆x2+y2-6x-8y+9=0,化为标准方程得(x-3)2+(y-4)2=16.所以两圆的圆心距为错误!未找到引用源。
=5,又r1+r2=5,所以两圆外切.5.设l,m,n表示三条直线,α,β,γ表示三个平面,给出下列四个结论:①若l⊥α,m⊥α,则l∥m;②若m⊂β,n是l在β内的射影,m⊥l,则m⊥n;③若m⊂α,m∥n,则n∥α;④若α⊥γ,β⊥γ,则α⊥β.其中正确的为( )A.①②B.①②③C.①②③④D.③④【解析】选A.①正确,②可用线面垂直证明,正确,③中,n可能在α内;④中,可能有α,β相交或平行,故选A.6.(2015·临汾高一检测)垂直于直线y=x+1且与圆x2+y2=1相切于第一象限的直线方程是( )A.x+y-错误!未找到引用源。
(人教版)高中数学必修二(全册)同步练习+单元检测卷汇总

(人教版)高中数学必修二(全册)同步练习+单元检测卷汇总课后提升作业一棱柱、棱锥、棱台的结构特征(45分钟70分)一、选择题(每小题5分,共40分)1.下列说法中正确的是( )A.棱柱的面中,至少有两个面互相平行B.棱柱中两个互相平行的平面一定是棱柱的底面C.棱柱中一条侧棱的长就是棱柱的高D.棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形【解析】选A.棱柱的两底面互相平行,故A正确;棱柱的侧面也可能有平行的面(如正方体),故B错;立在一起的一摞书可以看成一个四棱柱,当把这摞书推倾斜时,它的侧棱就不是棱柱的高,故C错;由棱柱的定义知,棱柱的侧面一定是平行四边形,但它的底面可以是平行四边形,也可以是其他多边形,故D错.2.四棱柱有几条侧棱,几个顶点( )A.四条侧棱、四个顶点B.八条侧棱、四个顶点C.四条侧棱、八个顶点D.六条侧棱、八个顶点【解析】选C.结合正方体可知,四棱柱有四条侧棱,八个顶点.3.下列说法错误的是( )A.多面体至少有四个面B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形C.长方体、正方体都是棱柱D.三棱柱的侧面为三角形【解析】选D.三棱柱的侧面是平行四边形,故D错误.4.如图,将装有水的长方体水槽固定底面一边后倾斜一个小角度,则倾斜后水槽中的水形成的几何体是( )A.棱柱B.棱台C.由一个棱柱与一个棱锥构成D.不能确定【解析】选 A.根据棱柱的结构特征,当倾斜后水槽中的水形成了以左右(或前后)两个侧面为底面的四棱柱.5.(2016·郑州高一检测)如图都是正方体的表面展开图,还原成正方体后,其中两个完全一样的是( )A.(1)(2)B.(2)(3)C.(3)(4)D.(1)(4)【解题指南】让其中一个正方形不动,其余各面沿这个正方形的各边折起,进行想象后判断.【解析】选B.在图(2)(3)中,⑤不动,把图形折起,则②⑤为对面,①④为对面,③⑥为对面,故图(2)(3)完全一样,而(1)(4)则不同. 【补偿训练】下列图形经过折叠可以围成一个棱柱的是( )【解析】选D.A,B,C中底面多边形的边数与侧面数不相等.6.若棱台上、下底面的对应边之比为1∶2,则上、下底面的面积之比是( )A.1∶2B.1∶4C.2∶1D.4∶1【解析】选 B.由棱台的概念知,上、下两底面是相似的多边形,故它们的面积之比等于对应边长之比的平方,故为1∶4.7.(2016·温州高一检测)在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线的条数共有( )A.20条B.15条C.12条D.10条【解析】选 D.因为棱柱的侧棱都是平行的,所以过任意不相邻的两条侧棱的截面为一个平行四边形,共可得5个截面,每个平行四边形可得到五棱柱的两条对角线,故共有10条对角线.8.(2015·广东高考)若空间中n个不同的点两两距离都相等,则正整数n的取值( )A.大于5B.等于5C.至多等于4D.至多等于3【解析】选 C.正四面体的四个顶点是两两距离相等的,即空间中n 个不同的点两两距离都相等,则正整数n的取值至多等于4.二、填空题(每小题5分,共10分)9.在正方体上任意选择4个顶点,它们可能是如下各种几何体的4个顶点,这些几何体是________.(写出所有正确结论的编号)①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体.【解析】如图:①正确,如图四边形A1D1CB为矩形;②错误,任意选择4个顶点,若组成一个平面图形,则必为矩形或正方形,如四边形ABCD为正方形,四边形A1BCD1为矩形;③正确,如四面体A1ABD;④正确,如四面体A1C1BD;⑤正确,如四面体B1ABD;则正确的说法是①③④⑤.答案:①③④⑤10.(2016·天津高一检测)一个棱柱有10个顶点,所有的侧棱长的和为60cm,则每条侧棱长为________cm.【解析】因为n棱柱有2n个顶点,又此棱柱有10个顶点,所以它是五棱柱,又棱柱的侧棱都相等,五条棱长的和为60cm,可知每条侧棱长为12cm.答案:12三、解答题(每小题10分,共20分)11.根据下面对几何体结构特征的描述,说出几何体的名称.(1)由8个面围成,其中2个面是互相平行且全等的六边形,其他各面都是平行四边形.(2)由5个面围成,其中一个是正方形,其他各面都是有1个公共顶点的三角形.【解析】(1)根据棱柱的结构特征可知,该几何体为六棱柱.(2)根据棱锥的结构特征可知,该几何体为四棱锥.12.已知三棱柱ABC-A′B′C′,底面是边长为1的正三角形,侧面为全等的矩形且高为8,求一点自A点出发沿着三棱柱的侧面绕行一周后到达A′点的最短路线长.【解析】将三棱柱侧面沿侧棱AA′剪开,展成平面图形如图,则AA″即为所求的最短路线.在Rt△AA1A″中,AA1=3,A1A″=8,所以AA″==.【延伸探究】本题条件不变,求一点自A点出发沿着三棱柱的侧面绕行两周后到达A′点的最短路线长.【解析】将两个相同的题目中的三棱柱的侧面都沿AA′剪开,然后展开并拼接成如图所示,则AA″即为所求的最短路线.在Rt△AA1A″中,AA1=6,A1A″=8,所以AA″===10.【能力挑战题】如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.问:(1)折起后形成的几何体是什么几何体?(2)这个几何体共有几个面,每个面的三角形有何特点?(3)每个面的三角形面积为多少?【解析】(1)如图,折起后的几何体是三棱锥.(2)这个几何体共有4个面,其中△DEF为等腰三角形,△PEF为等腰直角三角形,△DPE和△DPF均为直角三角形.(3)S△PEF=a2,S△DPF=S△DPE=×2a×a=a2,S△DEF=S正方形ABCD-S△PEF-S△DPF-S△DPE=(2a)2-a2-a2-a2=a2.关闭Word文档返回原板块温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
(常考题)人教版高中数学必修第二册第二单元《复数》检测卷(含答案解析)(3)

一、选择题1.已知复数1z ,2z 满足()1117i z i +=-+,21z =,则21z z -的最大值为( ) A .3B .4C .5D .6 2.若复数(1a i z i i +=-是虚数单位)为纯虚数,则实数a 的值为( ) A .-2 B .-1 C .1 D .23.设i 为虚数单位,复数z 满足21i i z =-,则复数z 的共轭复数等于( ) A .1-iB .-1-iC .1+iD .-1+i 4.已知复数2a i i +-是纯虚数(i 是虚数单位),则实数a 等于 A .-2 B .2 C .12 D .-15.若复数z 满足()11z i i --⋅=+,则z =( )A B C .D .36.已知下列三个命题:①若复数z 1,z 2的模相等,则z 1,z 2是共轭复数;②z 1,z 2都是复数,若z 1+z 2是虚数,则z 1不是z 2的共轭复数;③复数z 是实数的充要条件是z z =.则其中正确命题的个数为( )A .0个B .1个C .2个D .3个7.已知(,)a bi a b R +∈是11i i +-的共轭复数,则a b +=( ) A .1- B .12- C .12 D .18.复数252i +i z =的共轭复数z 在复平面上对应的点在( )A .第一象限B .第二象限C .第三象限D .第四象限 9.已知复数1223,z i z a bi =+=+(,R,0a b b 且∈≠),其中i 为虚数单位,若12z z 为实数,则a b 的值为( ) A .32- B .23- C .23 D .3210.设复数z 满足()1i i z +=,则z =( )A .2B .12CD .2 11.在下列命题中,正确命题的个数是( )①两个复数不能比较大小;②复数1z i =-对应的点在第四象限;③若22(1)(32)x x x i -+++是纯虚数,则实数1x =±;④若221223()()0z z z z -+-=,则123z z z ==.A .0B .1C .2D .3 12.复数21i z i +=-,i 是虚数单位,则下列结论正确的是 A .5z = B .z 的共轭复数为31+22i C .z 的实部与虚部之和为1 D .z 在复平面内的对应点位于第一象限二、填空题13.已知复数1510z i =+ ,234z i =-,复数z 满足12111z z z =+,则z =_____________.14.若复数z 满足|3|1z i -+,则32z i +-(i 为虚数单位)的最小值为______. 15.若复数72ai z i+=-的实部为3,其中a 是实数,i 是虚数单位,则2z 的虚部为______. 16.复数2021111i z i +⎛⎫=-+ ⎪-⎝⎭的辐角主值为________.17.如果虚数z 满足38z =,那么3222z z z +++的值是________.18.已知复数()()()4231234a i z i i -=-+⋅-,且1z =,则实数a =_________. 19.已知复数z 满足43(z i i i+=为虚数单位),则z 的共轭复数z =____. 20.如果复数z 的模不大于1,而z 的虚部的绝对值不小于,则复平面内复数z 的对应点组成图形的面积是___.三、解答题21.(1101032213122132i i i ⎛⎫⎛⎫++-+ ⎪ ⎪ ⎪ ⎪-+⎝⎭⎝⎭; (2)若复数z 满足112z z -=,1arg 3z z π-⎛⎫= ⎪⎝⎭,求复数3(2||)32z z z --的三角形式.22.已知i 是虚数单位,复数11()z ai a R =-∈,复数2z 的共轭复数234z i =-. (1)若12z z R +∈,求实数a 的值;(2)若12z z 是纯虚数,求1z . 23.i 是虚数单位,且2(1)2(5)3i i a bi i-+++=+(,a b ∈R ). (1)求,a b 的值;(2)设复数1()z yi y R =-+∈,且满足复数()a bi z +⋅在复平面上对应的点在第一、三象限的角平分线上,求||z .24.已知复数1sin 2i z x λ=+,2()i z m m x =+(,,m x λ∈R ),且12z z =. (1)若0λ=且0πx <<,求x 的值;(2)设()f x λ=;①求()f x 的最小正周期和单调递减区间;②已知当x α=时,12λ=,试求cos(4)3πα+的值. 25.已知m ∈R ,复数z =()()22211m m m m i m +++--,当m 为何值时: (1)z ∈R ;(2)z 是虚数;(3)z 是纯虚数.26.已知复数12i z m =-,复数21i z n =-,其中i 是虚数单位,m ,n 为实数. (1)若1m =,1n =-,求12z z +的值;(2)若212z z =,求m ,n 的值.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】先求得1z ,设出2z ,然后根据几何意义求得21z z -的最大值.【详解】 由()()()()11711768341112i i i i z i i i i -+--++====+++-,令2z x yi =+,x ,y R ∈,由 222||11z x y =⇒+=,()()2134z z x y i -=-+-=2z 对应点在单位圆上,所以21z z -表示的是单位圆上的点和点()3,4的距离, ()3,4到圆心()0,05=,单位圆的半径为1, 所以21max 516z z -=+=.故选:D【点睛】 本小题主要考查复数除法运算,考查复数模的最值的计算.2.C解析:C【分析】 利用复数代数形式的除法运算化简复数1a i z i+=-,再根据实部为0且虚部不为0求解即可. 【详解】 ()()()()i 1i i 11i 1i 1i 1i 22a a a a z +++-+===+-+-为纯虚数, 1010a a +≠⎧∴⎨-=⎩,即1a =,故选C. 【点睛】本题考查复数代数形式的除法运算,考查复数的基本概念,是基础题. 复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数、复数的模这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.3.B解析:B【分析】利用复数的运算法则解得1z i =-+,结合共轭复数的概念即可得结果.【详解】∵复数z 满足21i i z=-,∴()()()2121111i i i z i i i i +===---+, ∴复数z 的共轭复数等于1i --,故选B.【点睛】本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.4.C解析:C【解析】2a i i +-21255a a i -+=+是纯虚数,所以21210,0552a a a -+=≠∴=,选C. 5.A解析:A【分析】把已知等式变形,利用复数代数形式的乘除运算化简,再由复数模的计算公式求解.【详解】由()11z i i --⋅=+,得()()21111i i i z i i i +-+--===--,则2z i =-+,∴z ==故选:A【点睛】本题主要考查了复数的除法运算,复数的模的运算,属于中档题. 6.C解析:C【分析】运用复数的模、共轭复数、虚数等知识对命题进行判断.【详解】对于①中复数1z 和2z 的模相等,例如1=1+z i ,2z ,则1z 和2z 是共轭复数是错误的;对于②1z 和2z 都是复数,若12+z z 是虚数,则其实部互为相反数,则1z 不是2z 的共轭复数,所以②是正确的;对于③复数z 是实数,令z a =,则z a =所以z z =,反之当z z =时,亦有复数z 是实数,故复数z 是实数的充要条件是z z =是正确的.综上正确命题的个数是2个.故选C【点睛】本题考查了复数的基本概念,判断命题是否正确需要熟练掌握基础知识,并能运用举例的方法进行判断,本题较为基础.7.A解析:A【解析】【分析】先利用复数的除法运算法则求出11i i+-的值,再利用共轭复数的定义求出a +bi ,从而确定a ,b 的值,求出a +b . 【详解】 ()()21(1)21112i i i i i i ++===-+-i ,∴a +bi =﹣i ,∴a =0,b =﹣1,∴a +b =﹣1,故选:A .【点睛】本题主要考查了复数代数形式的乘除运算,考查了共轭复数的概念,是基础题. 8.C解析:C【解析】【分析】根据复数的运算求得2i z =-+,得到z 2i =--,再根据复数的表示,即可求解,得到答案.【详解】由题意,根据复数的运算可得复数252i +i 2i z ==-+, 则z 2i =--,所以z 对应点(2,1)--在第三象限,故选C .【点睛】本题主要考查了复数的运算,以及复数的表示,其中解答中熟记复数的运算法则,以及复数的表示是解答的关键,着重考查了推理与运算能力,属于基础题.9.B解析:B【分析】先根据复数乘法计算,再根据复数概念求a,b 比值.【详解】因为()1223(z z i a bi =++)()23(32a b a b =-++) i , 所以320a b +=,因为0b ≠,所以23a b =-,选B. 【点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 、模为(,)a b 、共轭为.-a bi10.A解析:A【解析】由()1i z i +=,得()()()i 1i i 11i 1i 1i 1i 22z -=+++-==,z ∴=故选A . 11.A解析:A【解析】对于选项①,不能说两个复数不能比较大小,如复数3和4就可比较大小,所以该命题是错误的.对于选项②,复数1z i =-对应的点在第二象限,所以该命题是错误的.对于选项③,若()()22132x x x i -+++是纯虚数,则21x -=0且232x x ++≠0,所以x=1,所以该命题是错误的. 对于选项④,若()()2212230z z z z -+-=,可以123,0,1z i z z ===, 所以该命题是错误的. 故选A. 12.D解析:D【分析】 利用复数的四则运算,求得1322z i =+,在根据复数的模,复数与共轭复数的概念等即可得到结论.【详解】 由题意()()()()22121313111122i i i i z i i i i i ++++====+--+-,则2z ==,z 的共轭复数为1322z i =-, 复数z 的实部与虚部之和为2,z 在复平面内对应点位于第一象限,故选D .【点睛】复数代数形式的加减乘除运算的法则是进行复数运算的理论依据,加减运算类似于多项式的合并同类项,乘法法则类似于多项式乘法法则,除法运算则先将除式写成分式的形式,再将分母实数化,其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b (,)a b 、共轭为a bi -.二、填空题13.【分析】根据复数的四则运算公式求得再结合复数的模的计算公式即可求解【详解】由题意复数则所以所以故答案为:【点睛】本题主要考查了复数的四则运算以及复数模的计算其中解答中熟记复数的四则运算公式以及复数模【分析】根据复数的四则运算公式,求得552z i =-,再结合复数的模的计算公式,即可求解. 【详解】 由题意,复数1510z i =+ ,234z i =-, 则()()()()1211111510344251034510510343425i i i z z z i i i i i i -++=+=+=+=+-+--+, 所以()()()254225554242422i z i i i i ⨯-===-++-,所以z ==.故答案为:2. 【点睛】本题主要考查了复数的四则运算,以及复数模的计算,其中解答中熟记复数的四则运算公式,以及复数模的计算公式,准确运算是解答的关键,着重考查推理与运算能力. 14.【分析】设由知点在以为圆心1为半径的圆上及圆的内部表示点与点的距离数形结合即可得到答案【详解】设由可得此式表示复平面上的点在以为圆心1为半径的圆上及圆的内部此式表示点与点的距离故所以的最小值为故答案1【分析】设,,z a bi a b R =+∈,由||1z i +,知点(,)P a b在以1)A -为圆心,1为半径的圆上及圆的内部,2z i =(,)P a b与点(2)B 的距离,数形结合即可得到答案.【详解】设,,z a bi a b R =+∈,由||1z i +可得22((1)1a b -++≤,此式表示复平面上 的点(,)P a b在以1)A -为圆心,1为半径的圆上及圆的内部,2z i =(,)P a b与点(2)B 的距离,故min 11PB AB =-==1.所以2z i +-1.1【点睛】本题考查复数的几何意义,考查学生数形结合思想以及数学运算求解能力,是一道中档题. 15.6【分析】化简复数实部为3求出a 进而求出【详解】解:由题意知的虚部为6故答案为:6【点睛】本题考查复数的基础知识和含参复数的运算属于基础题解析:6【分析】化简复数,实部为3,求出a ,进而求出2z .【详解】 解:7(7)(2)2(2)(2)ai ai i z i i i +++==--+(14)(72)1472555a a i a a i -++-+==+. 由题意知1435a -=,1a ∴=-, 3z i ∴=+,286z i ∴=+,2z ∴的虚部为6.故答案为:6.【点睛】本题考查复数的基础知识和含参复数的运算,属于基础题.16.【分析】先化简再根据辐角主值的定义求解即可【详解】因为所以所以所以复数z 的辐角主值为故答案为:【点睛】本题主要考查了复数的基本运算与辐角主值的辨析属于基础题 解析:34π 【分析】 先化简2021111i z i +⎛⎫=-+ ⎪-⎝⎭再根据辐角主值的定义求解即可.【详解】 因为11i i i +=-,所以2021202111i i i i +⎛⎫== ⎪-⎝⎭所以331cos sin 44z i i ππ⎫=-+=+⎪⎭,所以复数z 的辐角主值为34π. 故答案为:34π 【点睛】 本题主要考查了复数的基本运算与辐角主值的辨析,属于基础题.17.6【分析】利用立方差公式由得再将所求式子进行等价变形为最后利用整体代入计算求值【详解】由得又z 为虚数得∴故答案为:6【点睛】本题考查立方差公式的应用复数的四则运算考查转化与化归思想考查逻辑推理能力和 解析:6【分析】利用立方差公式,由38z =,得()2(2)240z z z -++=,再将所求式子进行等价变形为()323222242z z z z z z +++=+++-,最后利用整体代入计算求值.【详解】由38z =,得()2(2)240z z z -++=.又z 为虚数,得2240z z ++=.∴()3232222428026z z z z z z +++=+++-=+-=.故答案为:6【点睛】本题考查立方差公式的应用、复数的四则运算,考查转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意整体代入法的灵活运用. 18.【分析】化简的表达式根据列方程由此求得的值【详解】依题意由于即即即即解得故填:【点睛】本小题主要考查复数的除法乘法和乘方运算考查复数模的运算考查运算求解能力属于中档题解析:2±【分析】化简z 的表达式,根据1z =列方程,由此求得a 的值.【详解】依题意,()()()433434a i z i i -=--⋅-()()()()44343434i i a i i ---⋅-=-42534a i i -⎛⎫=-⋅ ⎪-⎝⎭()()()()434253434a i i i i ⎡⎤-+=-⋅⎢⎥-+⎣⎦()434432525a a i ++-⎡⎤=-⋅⎢⎥⎣⎦,由于1z =,即()4344325125a a i ++-⎡⎤-⋅=⎢⎥⎣⎦,即()()44344334431252525a a i a a i ++-++-⎡⎤==⎢⎥⎣⎦,即()24334125255a a i -++=,即223443125255a a +-⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭,22525125a +=,24a =,解得2a =±. 故填:2±【点睛】本小题主要考查复数的除法、乘法和乘方运算,考查复数模的运算,考查运算求解能力,属于中档题. 19.【分析】利用复数的运算法则共轭复数的定义即可得出结果【详解】由可得即所以故答案是:【点睛】该题考查的是有关复数的问题涉及到的知识点有复数的运算法则以及共轭复数的概念属于简单题目解析:34i -+【分析】利用复数的运算法则、共轭复数的定义即可得出结果.【详解】 由43z i i +=可得34z i i =-,即23434z i i i =-=--, 所以34z i =-+,故答案是:34i -+.【点睛】该题考查的是有关复数的问题,涉及到的知识点有复数的运算法则以及共轭复数的概念,属于简单题目.20.【解析】分析:先根据复数的模以及复数的虚部列不等式再根据扇形面积减去三角形面积得弓形面积详解:设则如图因此复平面内复数z 的对应点组成图形为两个弓形其面积为扇形面积减去三角形面积是点睛:本题重点考查复 解析:23-3π 【解析】分析:先根据复数的模以及复数的虚部列不等式,再根据扇形面积减去三角形面积得弓形面积.详解:设(,)z x yi x y R =+∈,则2211,2x y y +≤≥ ,如图,2.3AOB π∠=因此复平面内复数z 的对应点组成图形为两个弓形,其面积为扇形面积减去三角形面积是21212232(111sin )23233πππ⨯⋅-⨯⨯⨯=- 点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 22a b +(,)a b 、共轭为.-a bi三、解答题21.(1)122-;(2)22(cos sin )233i ππ+; 【分析】(1)由(1)cos sin 244i i ππ+=+,1cos()sin()2233i i ππ-+=-+-,结合复数的三角形式的乘方运算即可求值;(2)由题意得11(cos sin )233z i z ππ-=+,进而得到z 、z 代入目标式化简后转化为三角形式即可.【详解】(11010101011(1)122222i i i i i ⎛⎫⎛⎫⎛⎫⎛++-+=-+++-+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ -⎝⎭⎝⎭⎝⎭⎝⎭,而101010101(1)(cos sin )[cos()sin()]2224433i i i i i i ππππ⎛⎫⎛-+++-+=-+++-+- ⎪ ⎪ ⎝⎭⎝⎭∴原式551010221(cossin )[cos()sin()]cos sin 2233332i i i i i i ππππππ=-+++-+-=-+++=-; (2)由题意知:11(cos sin )233z i z ππ-=+,所以(cos sin )333z i ππ=+,sin )33z i ππ=-,∴322(2||)3sin )233z z i i z ππ--+=-=+ 【点睛】本题考查了复数的三角形式,利用复数三角形式的乘方运算化简求值,并由已知复数的模、复角求目标复数的三角形式.22.(1)4;(2)54. 【分析】(1)先求出124(4)z +z =+a i -,再根据12z z R +∈,求出实数a 的值;(2)由已知得1234(34)25z a a i z --+=,再根据12z z 是纯虚数求出a 的值即得解. 【详解】 223434z i z i =-∴=+(1)由已知得12(1)(34)4(4)z +z =ai ++i =+a i --12,40z z R a +∈-=∴4a ∴=(2)由已知得121(1)(34)34(34)34(34)(34)25z ai ai i a a i z i i i -----+===++- 12z z 是纯虚数,340340a a -=⎧∴⎨+≠⎩, 解得34a =,135144z i ∴=-==. 【点睛】本题主要考查复数的计算和复数的概念,考查复数模的计算,意在考查学生对这些知识的理解掌握水平,属于基础题.23.(1)3,1a b ==-(2【解析】分析:(1)由复数的四则运算可化简复数,再由复数相等可知实部与虚部都要相等,可求得,a b .(2)由复数的乘法运算可化简复数式为标准式,再由复数在第一、三象限的角平分线上可知复数实部等于虚部,求得参数y,再由复数模公式求得复数模.详解:(1)∵()()21253i i a bi i -+++=+ 1033i i==-+ , 又∵,a b R ∈ ∴3,1a b ==-(2)()()()31a bi z i yi +⋅=--+()()331y y i =-+++由题意可知:331y y -+=+,解得2y =-∴z ==点睛:本题主要考查复数四则运算与乘方综合运算和复数相等,及复数与坐标对应关系,及复数的模.24.(1)6π,23π;(2)①周期T π=,单调减区间511[,]1212k k ππππ++,k ∈Z ;②78- 【分析】根据复数相等的概念列方程,求得关于,,sin 2,cos 2m x x λ的关系式.(1)将0λ=代入上述求得的关系式,由此解出x 的值.(2)由上述求得的关系式,求得()f x λ=的表达式.①利用辅助角公式和三角函数最小正周期和的单调减区间的求法,求得()f x 的最小正周期和单调递减区间.②利用二倍角公式和诱导公式,求得cos(4)3πα+的值.【详解】 由于12z z =,所以sin 22x m m xλ=⎧⎪⎨=⎪⎩,故sin 22x x λ=. (1)当0λ=时,sin 220x x -=,则tan 2x =0πx <<所以022πx <<,所以π23x =或4π23x =,所以π6x =或2π3x =. (2)由于sin 22x x λ=,故()πsin 222sin 23f x x x x ⎛⎫=-=-⎪⎝⎭. ①函数()f x 的最小正周期为2ππ2T ==.由ππ3π2π22π232k x k +≤-≤+,解得5π11πππ1212k x k +≤≤+,所以函数()f x 的单调递减区间为511[,]1212k k ππππ++,k ∈Z . ②依题意π1sin 222sin 232x αα⎛⎫=-= ⎪⎝⎭,所以π1sin 234α⎛⎫-=- ⎪⎝⎭.所以ππcos 4cos 2236αα⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭22ππ2cos 212sin 2163αα⎛⎫⎛⎫=+-=-- ⎪ ⎪⎝⎭⎝⎭1721168=⨯-=-. 【点睛】本小题主要考查复数相等的概念,考查辅助角公式,考查三角函数最小正周期、单调区间的求法,考查二倍角公式和诱导公式,考查运算求解能力,属于中档题.25.(1)1m =-+1m =-2)1m ≠-+1m ≠-1m ≠;(3)0m =或2m =-.【分析】(1)解221m m +-=0,1m ≠,即可得解;(2)虚部不为0,则该复数为虚数,则2210m m +-≠,1m ≠即可得解;(3)复数是纯虚数,则实部为0,虚部不为0,根据()20m m +=,2210m m +-≠,1m ≠即可得解.【详解】(1)z ∈R ,所以221m m +-=0,1m ≠,212m -±==-所以,当1m =-+1m =--z ∈R ;(2)z 是虚数,则2210m m +-≠,1m ≠,当1m ≠-+1m ≠--1m ≠时,z 是虚数;(3)z 是纯虚数,()20m m +=,2210m m +-≠,1m ≠,所以0m =或2m =-时,z 是纯虚数.【点睛】此题考查复数的概念,根据复数的分类求解参数的取值,需要熟练掌握复数的概念,准确求解.26.(1(2)0,1.m n =⎧⎨=⎩ 【分析】(1)根据题意求出()()121212i z i z i +=-++=-,即可得到模长;(2)根据212z z =,化简得()2212m i n ni -=--,列方程组即可求解. 【详解】(1)当1m =,1n =-时112z i =-,21z i =+,所以()()121212i z i z i +=-++=-,所以12z z +==. (2)若212z z =,则()221m i ni -=-,所以()2212m i n ni -=--,所以2122m n n ⎧=-⎨-=-⎩解得0,1.m n =⎧⎨=⎩ 【点睛】此题考查复数模长的计算和乘法运算,根据两个复数相等,求参数的取值范围.。
新课标高中数学(必修2)单元测试卷12套(附详解答案)

新课标高中数学(必修2)单元测试卷目录第一章空间几何体[基础训练A组] (1)第一章空间几何体[综合训练B组] (3)第一章空间几何体[提高训练C组] (5)第二章点、直线、平面之间的位置关系[基础训练A组] ........................................... 错误!未定义书签。
第二章点、直线、平面之间的位置关系[综合训练B组] ........................................... 错误!未定义书签。
第二章点、直线、平面之间的位置关系[提高训练C组] ........................................... 错误!未定义书签。
第三章直线与方程[基础训练A组] .............................................................................. 错误!未定义书签。
第三章直线与方程[综合训练B组] ............................................................................... 错误!未定义书签。
第三章直线与方程[提高训练C组] ............................................................................... 错误!未定义书签。
第四章圆与方程[基础训练A组] .................................................................................. 错误!未定义书签。
第四章圆与方程[综合训练B组] ................................................................................... 错误!未定义书签。
(人教版A版)高中数学必修第二册 第六章综合测试试卷02及答案

第六章综合测试一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.在ABC △中,内角,A B C ,的对边分别为,,a b c ,若a =,2A B =,则cos B 等于( )2.已知两个单位向量a 和b 的夹角为60°,则向量-a b 在向量a 上的投影向量为()A.12a B.aC.12-aD.-a3.已知点(2,1),(4,2)A B -,点P 在x 轴上,当PA PB u u r u u rg 取最小值时,P 点的坐标是( )A.(2,0)B.(4,0)C.10,03æöç÷èøD.(3,0)4.已知,,A B C 为圆O 上的三点,若有OA OC OB +=u u r u u u r u u u r ,圆O 的半径为2,则OB CB =u u u r u u rg ( )A.1-B.2-C.1D.25.已知点(4,3)A 和点(1,2)B ,点O 为坐标原点,则||()OA tOB t +ÎR u u r u u u r的最小值为( )A.B.5C.36.已知锐角三角形的三边长分别为1,3,a ,那么a 的取值范围为( )A.(8,10)B.C.D.7.已知圆的半径为4,,,a b c 为该圆的内接三角形的三边,若abc =,则三角形的面积为( )A.B.8.已知向量,a b 满足(2)(54)0+×-=a b a b ,且1==a b ,则a 与b 的夹角q 为( )A.34p B.4pC.3pD.23p 9.已知sin 1sin cos 2a a a =+,且向量(tan ,1)AB a =u u u r ,(tan ,2)BC a =u u u r ,则AC u u u r 等于( )A.(2,3)-B.(1,2)C.(4,3)D.(2,3)10.在ABC △中,E F ,分别为,AB AC 的中点,P 为EF 上的任意一点,实数,x y 满足PA xPB yPC ++=0u u r u u r u u u r,设,,,ABC PBC PCA PAB △△△△的面积分别为123,,,S S S S ,记(1,2,3)ii S i Sl ==,则23l l ×取到最大值时,2x y +的值为( )A.1-B.1C.32-D.32二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)11.已知ABC △中,角,,A B C 的对边分别为,,a b c ,且满足,3B a c p=+=,则ac=( )A.2B.3C.12D.1312.点P 是ABC △所在平面内一点,满足20PB PC PB PC PA --+-=u u r u u u r u u r u u u r u u r,则ABC △的形状不可能是( )A.钝角三角形B.直角三角形C.等腰三角形D.等边三角形三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)13.已知,12e e 是平面内的单位向量,且12×=12e e .若向量b 满足1×=×=12b e b e ,则=b ________.14.已知向量,a b 满足5,1==a b ,且4-≤a b ,则×a b 的最小值为________.15.如图,在直角梯形ABCD 中,AB DC ∥,AD DC ^,2DC A A B D ==,E 为AD 的中点,若CA CE DB l m =+u u r u u u r u u u r,则l =________,m =________.(本题第一空2分,第二空3分)16.如图所示,某海岛上一观察哨A 上午11时测得一轮船在海岛北偏东60°的C 处,12时20分测得轮船在海岛北偏西60°的B 处,12时40分轮船到达位于海岛正西方且距海岛5km 的E 港口,如果轮船始终匀速直线前进,则船速的大小为________.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)如图所示,以向量,OA OB ==u u r u u u r a b 为邻边作OADB Y ,11,33BM BC CN CD ==u u u r u u u r u u u r u u u r,用,a b 表现,,OM ON MN u u u r u u u r u u u r.18.(本小题满分12分)已知ABC △的内角,,A B C 所对的边分别为,,a b c ,且2a =,3cos 5B =.(1)若4b =,求sin A 的值;(2)若4ABC SD =,求,b c 的值.19.(本小题满分12分)在ABC △中,角,,A B C 所对的边分别为,,a b c ,已知sin cos 1sin 2C C C +=-,(1)求sin C 的值;(2)若ABC △的外接圆面积为(4p +,试求AC BC u u u r u u u rg 的取值范围.20.(本小题满分12分)某观测站在城A 南偏西20°方向的C 处,由城A 出发的一条公路,走向是南偏东40°,距C 处31千米的B 处有一人正沿公路向城A 走去,走了20千米后到达D 处,此时,C D 间的距离为21千米,问这人还要走多少千米可到达城A ?21.(本小题满分12分)已知正方形ABCD ,E F 、分别是CD AD 、的中点,BE CF 、交于点P ,连接AP .用向量法证明:(1)BE CF ^;(2)AP AB =.22.(本小题满分12分)已知向量(sin ,cos )x x =a ,sin ,sin 6x x p æöæö=-ç÷ç÷èøèøb ,函数()2f x =×a b ,()4g x f x pæö=ç÷èø.(1)求()f x 在,2p p éùêúëû上的最值,并求出相应的x 的值;(2)计算(1)(2)(3)(2014)g g g g ++++L 的值;(3)已知t ÎR ,讨论()g x 在[,2]t t +上零点的个数.第六章综合测试答案解析一、1.【答案】B【解析】由正弦定理得sin sin a Ab B=,a \=可化为sin sin A B =又sin 22sin cos 2,sin sin B B B A B B B =\==,cos B \=.2.【答案】A【解析】由已知可得111122×=´´=a b ,211()122-×=-×=-=a b a a a b ,则向量-a b 在向量a 上的投影向量为()12-××=a b a a a a .3.【答案】D【解析】Q 点P 在x 轴上,\设P 上的坐标是(,0),(2,1),(4,2)x PA x PB x \=--=-u u r u u r,22(2)(4)266(3)3PA PB x x x x x \×=---=-+=--u u r u u r ,\当3x =时,PA PB ×u u r u u r 取最小值.P \点的坐标是(3,0).4.【答案】D【解析】OA OC OB +=u u r u u u r u u u rQ ,OA OC =u u r u u u r ,\四边形OABC 是菱形,且120AOC Ð=°,又圆O 的半径为2,22cos602OB CB \×=´´°=u u u r u u r.5.【答案】D【解析】点(4,3),(1,2)A B ,O 为坐标原点,则(4,32)OA tOB t t +=++u u r u u u r,22222()(4)(32)520255(2)55OA tOB t t t t t \+=+++=++=++u u r u u u r ≥,\当2t =-时,等号成立,此时OA tOB +u u r u u u r取得最小值6.【答案】B【解析】设1,3,a 所对的角分别为,,C B A ÐÐÐ,由余弦定理的推论知2222222213cos 0,21313cos 0,2131cos 0,23a A a B a a C a ì+-=ï´´ïï+-=í´´ïï+-=ï´´î>即()()222100,280,680,a a a a a ì-ïï-íï+ïî>>>解得a ,故选B .7.【答案】C【解析】设圆的半径为R ,内接三角形的三边,,a b c 所对的角分别为,,A B C .28sin sin sin a b cR A B C====Q,sin 8cC \=,1sin 216ABC abc S ab C D \====.8.【答案】C【解析】22(2)(54)5680+×-=+×=-Q a b a b a a b b ,又11,63,cos 2q ==\×=\=a b a b ,又[0,],3pq p q Î\=,故选C .9.【答案】D【解析】sin 1sin cos 2a a a =+Q ,cos sin a a \=,tan 1a \=,(2tan ,3)(2,3)AC AB BC a \=+==u u u r u u u r u u u r .故选D .10.【答案】D【解析】由题意可得,EF 是ABC △的中位线,P \到BC 的距离等于ABC △的边BC 上的高的一半,可得12323121,2S S S S l l ++===.由此可得223231216l l l l +æö×=ç÷èø≤,当且仅当23S S =,即P 为EF 的中点时,等号成立.0PE PF \+=u u r u u u r .由向量加法的四边形法则可得,2PA PB PE +=u u r u u r u u r ,2PA PC PF +=u u r u u u r u u u r ,两式相加,得20PA PB PC ++=u u r u u r u u u r.0PA xPB yPC ++=u u r u u r u u u r Q ,\根据平面向量基本定理,得12x y ==,从而得到322x y +=.二、11.【答案】AC 【解析】3B p=Q,a c +=,2222()23a c a c ac b \+=++=,①由余弦定理可得,2222cos3a c acb p+-=,②联立①②,可得222520a ac c -+=,即22520a a c c æöæö-+=ç÷ç÷èøèø,解得2a c =或12a c =.故选AC .12.【答案】ACD【解析】P Q 是ABC △所在平面内一点,且|||2|0PB PC PB PC PA --+-=u u r u u u r u u r u u u r u u r,|||()()|0CB PB PA PC PA \--+-=u u r u u r u u r u u u r u u r,即||||CB AC AB =+u u r u u u r u u u r ,||||AB AC AC AB \-=+u u u r u u u r u u u r u u u r ,两边平方并化简得0MC AB ×=u u u r u u u r ,AC AB \^u u u r u u u r,90A °\Ð=,则ABC △一定是直角三角形.故选ACD .三、13.【解析】解析令1e 与2e 的夹角为q .1cos cos 2q q \×=×==1212e e e e ,又0q °°≤≤180,60q \=°.()0×-=Q 12b e e ,\b 与,12e e 的夹角均为30°,从而1||cos30°=b .14.【答案】52【解析】|4|-==a b ,52×≥a b ,即×a b 的最小值为52.15.【答案】65 25【解析】以D 为原点,DC 边所在直线为x 轴,DA 边所在直线为y 轴建立平面直角坐标系.不妨设1AB =,则(0,0),(2,0),(0,2),(1,2),(0,1)D C A B E .(2,2),(2,1),(1,2)CA CE DB =-=-=u u r u u u r u u u r,,(2,2)(2,1)(1,2)CA CE DB l m l m =+\-=-+u u r u u u r u u u rQ ,22,22,l m l m -+=-ì\í+=î解得6,52.5l m ì=ïïíï=ïî16.km /h【解析】轮船从C 到B 用时80分钟,从B 到E 用时20分钟,而船始终匀速前进,由此可见,4BC EB =.设EB x =,则4BC x =,由已知得30BAE Ð=°,150EAC Ð=°.在AEC △中,由正弦定理的sin sin EC AEEAC C=Ð,sin 5sin1501sin 52AE EAC C EC x x°Ð\===g .在ABC △中,由正弦定理得sin120sin BC ABC=°,sin sin120BC C AB \===°g 在ABE △中,由余弦定理得22216312cos30252533BE AB AE AB AE °=+-=+-=g g,故BE =.\船速的大小为/h)BEt==.四、17.【答案】解:BA OA OB =-=-u u r u u r u u u rQ a b ,11153666OM OB BM OB BC OB BA \=+=+=+=+u u u r u u u r u u u r u u u r u u u r u u u r u u r a b .又OD =+u u u r a b ,222333ON OC CN OD \=+==+u u u r u u u r u u u r u u u r a b ,221511336626MN ON OM \=-=+--=-u u u r u u u r u u u r a b a b a b .18.【答案】解:3cos 05B =Q ,且0B p <<,4sin 5B \==.由正弦定理得sin sin a bA B=,42sin 25sin 45a BA b´\===.(2)1sin 42ABC S ac B D ==Q ,142425c \´´´=,5c \=.由余弦定理得2222232cos 25225175b a c ac B =+-=+-´´´=,b \=.19.【答案】(1)解:ABC △中,由sin cos 1sin 2C C C +=-,得22sin cos 2sin sin 2222C C C C=-,sin 02C Q >,1cos sin 222C C \-=-,两边平方得11sin 4C -=,解得3sin 4C =.(2)设ABC △的外接圆的半径为R ,由(1)知sin cos 22C C >,24C p\>,2C p\>,cos C \==.易得2sin c R C =,22294sin (44c R C \==,由余弦定理得,2229(42214c a b ab ab ææ=+=+-+ççççèè≥g g ,902ab \<≤,cos AC BC ab C éö\=Î÷ê÷ëøu u u r u u u r g g ,即AC BC u u u r u u u r g的取值范围是éö÷ê÷ëø.20.【答案】解:如图所示,设ACD a Ð=,CDB b Ð=.在CBD △中,由余弦定理的推论得2222222021311cos 2220217BD CD CB BD CD b +-+-===-´´g,sin b \==()11sin sin 60sin cos60sin 60cos 27a b b b °°°æö\=-=-=--=ç÷èøg在CBD △中,由正弦定理得21sin 60sin AD a=°,21sin 15sin 60AD a \==°(千米).\这人还要再走15千米可到达城A .21.【答案】证明:如图,建立平面直角坐标系xOy ,其中A 为原点,不妨设2AB =,则(0,0),(2,0),(2,2),(1,2),(0,1)A B C E F .(1)(1,2)(2,0)(1,2)BE OE OB =-=-=-u u r u u u r u u u r Q ,(0,1)(2,2)(2,1)CF OF OC =-=-=--u u u r u u u r u u u r ,(1)(2)2(1)0BE CF \×=-´-+´-=u u r u u u r ,BE CF \^u u r u u u r ,即BE CF ^.(2)设(,)P x y ,则(,1)FP x y =-u u r ,(2,)BP x y =-u u r ,由(1)知(2,1)CF =--u u u r ,(1,2)BE =-u u r ,FP CF u u r u u u r Q ∥,2(1)x y \-=--,即24y x =-+.同理,由BP BE u u r u u r ∥,即24y x =-+.22,24,x y y x =-ì\í=-+î解得6,58,5x y ì=ïïíï=ïî即68,55P æöç÷èø.222268455AP AB æöæö\=+==ç÷ç÷èøèøu u u r u u u r ,||||AP AB \=u u u r u u u r ,即AP AB =.22.【答案】(1)解:21()22sin sin(2sin cos sin 262f x x x x x x x p ö=×=-+=+=÷øab 1sin 22sin 223x x x p æö-+=-+ç÷èø,2x p p éùÎêúëûQ,252333x p p p \-≤,1sin 23x p æö\--ç÷èø≤,\当3232x p p -=,即1112x p =时,()f x 取得最小值1,当2233x p p -=,即2x p =时,()f x .(2)由(1)得()sin 23f x x p æö=-+ç÷èø()sin 423g x f x x p p p æöæö\==-ç÷ç÷èøèø4T \=(1)(2)(3)(4)(5)(6)(7)(8)(2009)(2010)(2011)(2012)g g g g g g g g g g g g \+++=+++==+++L .又(1)(2)(3)(4)g g g g +++=,(1)(2)(3)(2014)503(1)(2)g g g g g g \++++=´++=L=.(3)()g x 在[,2]t t +上零点的个数等价于sin 23x y p p æö-çè=÷ø与y =.在同一平面直角坐标系内作出这两个函数的图象(图略).当4443k t k +<<,k ÎZ 时,由图象可知,sin 23x y p p æö-çè=÷ø与y =()g x 无零点;当44243k t k ++≤<或10444,3k t k k ++ÎZ <≤时,sin 23x y p p æö-çè=÷ø与y =1个交点,即()g x 有1个零点;当10244,3k t k k ++ÎZ ≤≤时,sin 23x y p p æö-çè=÷ø与y =2个交点,即()g x 有2个零点.。
(人教版)高中数学必修二(全册)单元测试卷汇总

(人教版)高中数学必修二(全册)单元测试卷汇总、阶段通关训练(一)(60分钟 100分)一、选择题(每小题5分,共3。
分)1・已知某几何体的三视图如图所示,那么这个几何体是□ □便視囲A. 长方体 C.匹棱锥【解析】选A.该几何体是长方体,如图所示» 入城商中目字必零二01 :酚俭1王训停 爺人椒版為中教学宕偌2!; &馈通关训号 信,奴薮版快9E 必偌二好:阶段遑关训澤 司:人馭艇苣中数猝偌二桂測:跻蜀■美训遂 琼人板版毫中gtl 修二窗I ;樓埃蜃量怦估 S 人会版毎中數⑴ C 2) Word 版言眾忻 Word 版合解忻 W 。
招版含解忻 (AS ) Word 板合樹ff (B 卷)WordB.圆性 D.四棱台正視图悟视图2.以钝角三角形旳较小边所在的直线为轴,其他两边旋转一周所得到的几何体是()A .两个圆锥拼桜而成的组合体B.一个圖台C.一个圆锥D . 一个圆锥挖去一个同底的小圆维【解析】选D.如图以AB为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.3.已知AAB攏边长为2a的正三角形,那么△ABCE勺平面直观图△ A'B‘ C'的面积为()D.\Ga~【鮮析】选C.直观图面积S与原图面积S具有关系:S' Mfs.因为S 好芸12a)所以S …c 三•X\/3a'=^a .4- 4 4【补偿训练】某三角形的直观图是斜边长为2的等腰直角三角形,如图所示,则原三信形的面积是【解析】根据宜观图和原图形的关系可知原图形的面积为X 2vl X 2二2卮 答案:2^24. 某三梭锥的三视图如图所示,则该三検锥的体积是【解析】选B .由三视图可判断该三棱锥底面为等腰直角三角形,三 棱锥旳高为 2. RI V=x x 1 x 1 x 2=.^【补偿洲练】已知正三棱镣V-ABC 的正视图、侧视图和帽视图如图所 示,则该正三枝锥侧视图的面积是A.B. C. D.1A.v39B.6\,r 3D.6俯视C.即3【解析】选D .如图,根据三视图间的关系可得BCM3,所以侧视图 中VA 二\|铲一任X ? X 2妁七整,所以三橙锥侧视图面积S- 海=x 2V 3X 2\顶二6,故选 D.5.(2016 •蚌瑋高二检测)若一个回锥的侧面展开图是面积为 2工的半圆面,则该圆锥的体积为B.V3 X C .拓x【解析】选A.设园锥的母线长为I,底面半径为r,由题意|7苗2 = 211,vnl = 2TTT ,解得'所以圆锥的高为 h=\F —尸=寸3 , V= * r 2h= r x 12x r = L . 6.(2016 •雅安高二检测)设正方体的全面积为 24,邪么其内切球的体积是A .扼KB.兀32 D.—【解析】 选B.正方体的全面积为24,所以,设正方体的棱长为a.6 宀 24, a 二2,正方体的内切球的直径就是正方体的校长,所以球的半径为1,内切球旳体积:V = 7t . ID RC乙 第*已回刮寻詠回王曲>=s '哥USS 甲'里蛔国皿【果到】&&価91实逐刘t ¥豈我到国丑屬T 風濕&一天喔宰邕€好日-6肝里N 二縛:毒虽•*+£,W=M*£Axl X >t=S rft凰峯4 Z^A^Ax^ x=A '風刘"坦 NN 八一醇E3HI 诳乙 弟学段皿期一旧耳闻1/峯'皓也乎书屋絶三零净【爆蜴】醇車回1/溟【四'(国⑰)国隴三阳财回廿必日(脈玛二堆※困• 9L0S1-8LL :孝晶U=x 韧 N 刮’壽」三三)阜尚‘X 興覃毋号密祺[菓到】 麹*辛矣廚留丄壬至藏乌去廖犯讪目丄竺羽诲同争宙【睾里區墙】^实些阳号屛醇斟濯施*09实邊回回淮即回通士互士 .乙屿%邊国基’9L 实雙団驚勢N(G&详‘&9鲤W 辱)谴乏帯 '二=M 媛苴'務nD所以AQ=\吃,A O=R^/6.所以S丼二4兀F<=24T.答案:24 x10•圖台的底面半径分别为1和2,母线长为3,则此圖台的体积为【解析】圆台的高h= 732 - (2 - I)2 =2 <1 ,所以体积71 2 aV=y(R+Rr4-r )h=^^i(. 答案:學三、解答题(共4小题,共50分)11.(12分)如區几何体上半部分是母线长为5,底面圆半径为3的圆锥,下半部分是下底面圆半径为2,母线长为2的圆台,计算该几何体的表面枳和体枳【韻析】圖锥侧面积为S = X rl=15r ,圖台的侧面积为缶冗(r+r ' )1二10冗,圖台的底面宜积为订’』牝,所以表面积为:S=S+S+S s=15i +10兀+4H=29X;圆锥的体积V-xr2hi=12x ,圆台的体积V:= r h2(r :+rr , +「’ 2)=^y^r ,所以体积为:V=V+U=12i------ X .312.(12分)如图是一个几何体的正视图和俯视图(1)试判断该几何体是什么几何体?(2)画出其侧视图,并求该平面图形的面积.(3)求出该几何体的体积.【解析】(1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥.(2)该几何体的側视图如图.其中AB=AC AD^BC,且BC的长是俯视图正六边形对边的距离,即BC=v3a, AD是正六棱锥的高,即AD十3a,所以该平面图形的面积(3)没这个正六棱锥的底面积是S,体积为V,则S=6< —a=—a\4 2所以V=x三歯x JJa=a°.13.(13分)如图所示,在四边形ABC畔,Z DAB=90 , ZADCF35 ,AB二5 CD二不臣,AD二2求四边形ABC说AD旋转一周所成几何体的表面积及体积.【鮮析】S 表面二S SOFB +S Bo ma +S 四部面=it x 5~+ i x (2+5) x 5+ r X 2X 2V2=(4 克+60) x .V=V H&-V B*=z (4-r if z+Fj )h- x h148=I (25+10+4) X 4- Jt X 4X 2. x .14.(13分)(2016 ,湖北实验中学高一检测 )如图,△ ABC中,ZACB=90 , Z ABC=30* , BC%3 在三角形内挖去一个半圆(圆心。
(人教版A版)高中数学必修第二册 第九章综合测试试卷03及答案

第九章综合测试一、选择题(本题共12小题,每小题5分,共60分)1.下面抽样方法是简单随机抽样的是()A .从平面直角坐标系中抽取5个点作为样本B .从仓库中的1 000箱饮料中一次性抽取20箱进行质量检查C .从某连队200名战士中,挑选出50名最优秀的战士去参加抢险救灾活动D .从l0个手机中逐个不放回地随机抽取2个进行质量检验(假设10个手机已编好号,对编号随机抽取)2.对某校1 200名学生的耐力进行调查,抽取其中120名学生,测试他们1 500 m 跑步的成绩,得出相应的数值,在这项调查中,样本是指( )A .l20名学生B .1200名学生C .120名学生的成绩D .1200名学生的成绩3.简单随机抽样和分层随机抽样之间的共同点是( )A .都是从总体中逐个抽取的B .将总体分成几部分,按事先确定的规则在各部分抽取C .抽样过程中每个个体被抽到的机会相等D .将总体分成几层,然后各层按照比例抽取4.某市有大型、中型与小型商店共1 500家,它们的数量之比为l:5:9,用分层随机抽样的方法抽取其中的30家进行调查,则中型商店应抽取( )A .10家B .18家C .2家D .20家5.抽样统计甲射击运动员10次的训练成绩分别为86,85,88,86,90,89,88,87,85,92,则这10次成绩的80%分位数为( )A .88.5B .89C .91D .89.56.甲、乙两名同学6次考试的成绩统计如图9-4-1,甲、乙两名同学成绩的平均数分别为x 甲,x 乙,标准差分别为s 甲,s 乙,则()A .x x 乙甲<,s s 乙甲<B .x x 乙甲<,s s 乙甲>C .x x 乙甲>,s s 乙甲<D .x x 乙甲>,s s 乙甲>7.某校高中三个年级的人数扇形统计图如图9-4-2所示,按年级用分层随机抽样的方法抽取一个样本,已知样本中高一年级学生有8人,则样本量为()A .24B .30C .32D .358.总体由编号为00,01,02,…,48,49的50个个体组成,利用下面的随机数表选取8个个体,选取方法是从随机数表第6行的第9列和第10列数字开始从左到右依次选取两个数字,则选出的第4个个体的编号为()附:第6行至第9行的随机数表2635790033709160162038827757495032114919730649167677873399746732274861987164414870862888851916207477011l 163024042979799196835125A .3B .16C .38D .499.对以下两组数据进行分析,下列说法不正确的是( )甲:8121327243722202526乙:9141311181920212123A .甲的极差是29B .甲的中位数是25C .乙的众数是21D .甲的平均数比乙的大10.某中学有高中生3 000人,初中生2 000人,高中生中男生、女生人数之比为3:7,初中生中男生、女生人数之比为6:4,为了解学生的学习状况,用分层随机抽样的方法从该校学生中抽取一个容量为n 的样本,已知从初中生中抽取男生12人,则从高中生中抽取女生的人数是( )A .12B .15C .20D .2111.如果一组数据1x ,2x ,…,n x 的平均数是x ,方差是2s 1+2,…n + )A ,2s B +,2sC +,23s D +212.在去年某地区的足球比赛上,一队每场比赛平均失球数是1.5,全年比赛失球个数的标准差是1.1;二队每场比赛平均失球数是2.1,全年比赛失球个数的标准差是0.4.下列说法:①平均来说一队比二队防守技术好;②二队比一队防守技术水平更稳定;③一队防守有时表现很差,有时表现又非常好;④二队很少不失球,其中正确的有()A.l个B.2个C.3个D.4个二、填空题(本题共4小题,每小题5分,共20分)13.某种福利彩票的中奖号码是从1~36个号码中,选出7个号码来按规则确定中奖情况,从36个号码中选出7个号码,适宜的抽样方法是________.14.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为________.15.气象意义上从春季进入夏季的标志为“连续5天的日平均温度均不低于22 ℃”、现有甲、乙、丙三地连续5天的日平均温度的相关记录数据(记录数据都是正整数,单位:℃):①甲地:5个数据的中位数为24,众数为22;②乙地:5个数据的中位数为27,总体均值为24;③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.2这三地肯定进入夏季的地区有________个.16.某校为了解本校中、老年教师的身体状况,采用分层随机抽样的方法,从中年教师中抽取20人,从老年教师中抽取10人参加体检,经医院反馈信息知某项体检指标:中年教师均值为90,方差为4,老年教师均值为96,方差为6.据此估计该校中、老年教师该项指标的方差为________.三、解答题(本题共6小题,共70分)17.(10分)某电视台举行颁奖典礼,邀请来自三个地区的20名演员演出,其中从30名A地区演员中随机挑选10人,从18名B地区演员中随机挑选6人,从10名C地区演员中随机挑选4人.试用抽签法确定选中的演员,并确定他们的表演顺序.18.(12分)某市组织了一次普法知识竞赛,从甲、乙两单位中各随机抽取了5名职工的成绩,统计如下:甲单位职工的成绩(分)8788919193甲单位职工的成绩(分)8589919293根据表中的数据,分别求出样本中甲、乙两单位职工成绩的平均数和方差,并判断哪个单位的职工对法律知识的掌握更为稳定.19.(12分)某大学共有“机器人”兴趣团队1 000个,大一、大二、大三、大四分别有100个、200个、300个、400个.为挑选优秀团队,现用分层随机抽样的方法,从以上团队中抽取20个.(1)应从大三中抽取多少个团队?(2)将20个团队分为甲、乙两组,每组10个团队,进行理论和实践操作考试(共150分),甲、乙两组的成绩如下:甲:125,141,140,137,122,114,119,139,121,142乙:127,116,144,127,144,116,140,140,116,140从甲、乙两组中选一组强化训练,备战机器人大赛.从统计学数据看,若选择甲组,理由是什么?若选择乙组,理由是什么?20.(12分)某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护仍是百姓最为关心的问题,参与调查者中关注此问题的约占80%现从参与关注生态文明建设的人群中随机选出200人,并将这200人按年龄分组:第1组[)15,25,第2组[)25,35,第3组[)35,45,第4组[)45,55,第5组[]55,56,得到的频率分布直方图如图9-4-3所示。
新教材人教A版高中数学必修第二册全册各章综合测验汇总(共五套,附解析)

高中数学必修第二册全册各章测验汇总章末质量检测(一) 平面向量及其应用 ............................................................................... 1 章末质量检测(二) 复数 ....................................................................................................... 8 章末质量检测(三) 立体几何初步 ..................................................................................... 14 章末质量检测(四) 统计 ..................................................................................................... 23 章末质量检测(五)概率 (32)章末质量检测(一) 平面向量及其应用一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在⊙O 中,向量OB →,OC →,AO →是( ) A .有相同起点的向量 B .共线向量 C .模相等的向量 D .相等的向量解析:由图可知OB →,OC →,AO →是模相等的向量,其模均等于圆的半径,故选C. 答案:C2.若A (2,-1),B (4,2),C (1,5),则AB →+2BC →等于( ) A .5 B .(-1,5) C .(6,1) D .(-4,9)解析:AB →=(2,3),BC →=(-3,3),∴AB →+2BC →=(2,3)+2(-3,3)=(-4,9). 答案:D3.设向量a ,b 均为单位向量,且|a +b |=1,则a 与b 的夹角θ为( ) A.π3 B.π2 C.2π3 D.3π4解析:因为|a +b |=1,所以|a |2+2a ·b +|b |2=1,所以cos θ=-12.又θ∈[0,π],所以θ=2π3.答案:C4.若A (x ,-1),B (1,3),C (2,5)三点共线,则x 的值为( ) A .-3 B .-1 C .1 D .3解析:AB →∥BC →,(1-x,4)∥(1,2),2(1-x )=4,x =-1,故选B. 答案:B5.已知向量a ,b 满足a +b =(1,3),a -b =(3,-3),则a ,b 的坐标分别为( ) A .(4,0),(-2,6) B .(-2,6),(4,0) C .(2,0),(-1,3) D .(-1,3),(2,0)解析:由题意知,⎩⎪⎨⎪⎧a +b =1,3,a -b =3,-3,解得⎩⎪⎨⎪⎧a =2,0,b =-1,3.答案:C6.若a =(5,x ),|a |=13,则x =( ) A .±5 B.±10 C .±12 D.±13解析:由题意得|a |=52+x 2=13, 所以52+x 2=132,解得x =±12. 答案:C7.如图,设A 、B 两点在河的两岸,一测量者在A 的同侧,选定一点C ,测出AC的距离为50 m ,∠ACB =45°,∠CAB =105°,则A ,B 两点的距离为( ) A .50 2 m B .50 3 m C .25 2 m D.2522m解析:由正弦定理得AB =AC ·sin∠ACB sin B=50×2212=502(m).答案:A8.已知平面内四边形ABCD 和点O ,若OA →=a ,OB →=b ,OC →=c ,OD →=d ,且a +c =b+d ,则四边形ABCD 为( )A .菱形B .梯形C .矩形D .平行四边形 解析:由题意知a -b =d -c , ∴BA →=CD →,∴四边形ABCD 为平行四边形,故选D. 答案:D9.某人在无风条件下骑自行车的速度为v 1,风速为v 2(|v 1|>|v 2|),则逆风行驶的速度的大小为( )A .v 1-v 2B .v 1+v 2C .|v 1|-|v 2| D.v 1v 2解析:题目要求的是速度的大小,即向量的大小,而不是求速度,速度是向量,速度的大小是实数,故逆风行驶的速度大小为|v 1|-|v 2|.答案:C10.已知O 为坐标原点,点A 的坐标为(2,1),向量AB →=(-1,1),则(OA →+OB →)·(OA→-OB →)等于( )A .-4B .-2C .0D .2解析:因为O 为坐标原点,点A 的坐标为(2,1), 向量AB →=(-1,1), 所以OB →=OA →+AB →=(2,1)+(-1,1)=(1,2), 所以(OA →+OB →)·(OA →-OB →)=OA →2-OB →2=(22+12)-(12+22) =5-5=0.故选C. 答案:C11.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若sin A sin B =ac,(b +c +a )(b+c -a )=3bc ,则△ABC 的形状为( )A .直角三角形B .等腰非等边三角形C .等边三角形D .钝角三角形 解析:∵sin A sin B =a c ,∴a b =ac,∴b =c .又(b +c +a )(b +c -a )=3bc ,∴b 2+c 2-a 2=bc ,∴cos A =b 2+c 2-a 22bc =bc 2bc =12.∵A ∈(0,π),∴A =π3,∴△ABC 是等边三角形.答案:C12.在△ABC 中,若|AB →|=1,|AC →|=3,|AB →+AC →|=|BC →|,则AB →·BC→|BC →|=( )A .-32 B .-12C.12D.32解析:由向量的平行四边形法则,知当|AB →+AC →|=|BC →|时,∠A =90°.又|AB →|=1,|AC →|=3,故∠B =60°,∠C =30°,|BC →|=2,所以AB →·BC →|BC →|=|AB →||BC →|cos 120°|BC →|=-12.答案:B二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.已知A ,B ,C 是不共线的三点,向量m 与向量AB →是平行向量,与BC 是共线向量,则m =________.解析:∵A ,B ,C 不共线,∴AB →与BC →不共线.又m 与AB →,BC →都共线,∴m =0. 答案:014.若向量OA →=(1,-3),|OA →|=|OB →|,OA →·OB →=0,则|AB →|=________. 解析:方法一:设OB →=(x ,y ),由|OA →|=|OB →|知x 2+y 2=10,又OA →·OB →=x -3y=0,所以x =3,y =1或x =-3,y =-1.当x =3,y =1时,|AB →|=25;当x =-3,y =-1时,|AB →|=2 5.故|AB →|=2 5.方法二:由几何意义知,|AB →|就是以OA →,OB →为邻边的正方形的对角线长,又|OA →|=10,所以|AB →|=10×2=2 5.答案:2 515.给出以下命题:①若a ≠0,则对任一非零向量b 都有a·b ≠0; ②若a ·b =0,则a 与b 中至少有一个为0; ③a 与b 是两个单位向量,则a 2=b 2. 其中正确命题的序号是________.解析:上述三个命题中只有③正确,因为|a |=|b |=1,所以a 2=|a |2=1,b 2=|b |2=1,故a 2=b 2.当非零向量a ,b 垂直时,有a·b =0,显然①②错误.答案:③16.用两条成120°角的等长绳子悬挂一个灯具,已知灯具重量为10 N ,则每根绳子的拉力大小为________N.解析:如图,由题意得,∠AOC =∠COB =60°,|OC →|=10,则|OA →|=|OB →|=10,即每根绳子的拉力大小为10 N.答案:10三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)如图所示,已知OA →=a ,OB →=b ,OC →=c ,OD →=d ,OE →=e ,OF →=f ,试用a ,b ,c ,d ,e ,f 表示:(1)AD →-AB →; (2)AB →+CF →; (3)EF →-CF →.解析:(1)因为OB →=b ,OD →=d , 所以AD →-AB →=BD →=OD →-OB →=d -b . (2)因为OA →=a ,OB →=b ,OC →=c ,OF →=f , 所以AB →+CF →=(OB →-OA →)+(OF →-OC →)=b +f -a -c . (3)EF →-CF →=EF →+FC →=EC →=OC →-OE →=c -e .18.(12分)已知|a |=2,|b |=3,a 与b 的夹角为60°,c =5a +3b ,d =3a +k b ,当实数k 为何值时,(1)c ∥d ;(2)c ⊥d .解析:由题意得a ·b =|a ||b |cos 60°=2×3×12=3.(1)当c ∥d ,c =λd ,则5a +3b =λ(3a +k b ). ∴3λ=5,且kλ=3,∴k =95.(2)当c ⊥d 时,c ·d =0,则(5a +3b )·(3a +k b )=0. ∴15a 2+3k b 2+(9+5k )a ·b =0, ∴k =-2914.19.(12分)已知向量a =(1,3),b =(m,2),c =(3,4),且(a -3b )⊥c . (1)求实数m 的值; (2)求向量a 与b 的夹角θ.解析:(1)因为a =(1,3),b =(m,2),c =(3,4), 所以a -3b =(1,3)-(3m,6)=(1-3m ,-3).因为(a -3b )⊥c ,所以(a -3b )·c =(1-3m ,-3)·(3,4) =3(1-3m )+(-3)×4 =-9m -9=0, 解得m =-1.(2)由(1)知a =(1,3),b =(-1,2), 所以a ·b =5,所以cos θ=a ·b |a ||b |=510×5=22.因为θ∈[0,π],所以θ=π4.20.(12分)已知向量a =(1,3),b =(2,-2). (1)设c =2a +b ,求(b -a )·c ; (2)求向量a 在b 方向上的投影.解析:(1)由a =(1,3),b =(2,-2),可得c =(2,6)+(2,-2)=(4,4),b -a=(1,-5),则(b -a )·c =4-20=-16.(2)向量a 在b 方向上的投影为a ·b |b |=-422=- 2. 21.(12分)已知O ,A ,B 是平面上不共线的三点,直线AB 上有一点C ,满足2AC→+CB →=0,(1)用OA →,OB →表示OC →;(2)若点D 是OB 的中点,证明四边形OCAD 是梯形. 解析:(1)因为2AC →+CB →=0, 所以2(OC →-OA →)+(OB →-OC →)=0, 2OC →-2OA →+OB →-OC →=0, 所以OC →=2OA →-OB →.(2)证明:如图, DA →=DO →+OA →=-12OB →+OA →=12(2OA →-OB →).故DA →=12OC →.故四边形OCAD 为梯形.22.(12分)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,已知(a -3b )·cos C=c (3cos B -cos A ).(1)求sin B sin A的值;(2)若c =7a ,求角C 的大小.解析:(1)由正弦定理得,(sin A -3sin B )cos C =sin C (3cos B -cos A ), ∴sin A cos C +cos A sin C =3sin C cos B +3cos C sin B , 即sin(A +C )=3sin(C +B ),即sin B =3sin A ,∴sin Bsin A=3.(2)由(1)知b =3a ,∵c =7a ,∴cos C =a 2+b 2-c 22ab =a 2+9a 2-7a 22×a ×3a =3a 26a 2=12,∵C ∈(0,π),∴C =π3.章末质量检测(二) 复数一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数i -i 2的实部为( ) A .0 B .1 C .i D .-2 解析:i -i 2=1+i. 答案:B2.用C ,R 和I 分别表示复数集、实数集和虚数集,那么有( ) A .C =R ∩I B .R ∩I ={0}C .R =C ∩ID .R ∩I =∅解析:由复数的概念可知R ⊂C ,I ⊂C ,R ∩I =∅. 答案:D3.下列说法正确的是( )A .如果两个复数的实部的差和虚部的差都等于0,那么这两个复数相等B .a i 是纯虚数(a ∈R )C .如果复数x +y i(x ,y ∈R )是实数,那么x =0,y =0D .复数a +b i(a ,b ∈R )不是实数解析:两个复数的实部的差和虚部的差都等于0,则它们的实部、虚部分别相等,所以A 正确;B 中,当a =0时,a i =0是实数,所以B 不正确;要使复数x +y i(x ,y ∈R )是实数,则只需y =0,所以C 不正确;D 中,当b =0时,复数a +b i 是实数,所以D 不正确.答案:A4.复数z =-1-2i(i 为虚数单位)在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限解析:由题意得复数z 的实部为-1,虚部为-2,因此在复平面内对应的点为(-1,-2),位于第三象限.答案:C5.设z 1=3-4i ,z 2=-2+3i ,则z 1-z 2在复平面内对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 解析:z 1-z 2=5-7i. 答案:D6.复数1-7i 1+i 的虚部为( )A .0 B. 2 C .4 D .-4 解析:∵1-7i1+i=1-7i 1-i 1+i1-i =-6-8i2=-3-4i ,∴复数1-7i1+i 的虚部为-4,选D.答案:D7.复数z =(a 2-2a -3)+(a +1)i 为纯虚数,实数a 的值是( ) A .-1 B .3C .1D .-1或3解析:由题意知⎩⎪⎨⎪⎧a 2-2a -3=0,a +1≠0,解得a =3.故选B.答案:B8.已知z-1+i =2+i ,则复数z =( )A .-1+3iB .1-3iC .3+iD .3-i解析:由题意知z -=(1+i)(2+i)=2-1+3i =1+3i ,从而z =1-3i ,选B. 答案:B9.已知z =(m +3)+(m -1)i 在复平面内对应的点在第四象限,则实数m 的取值范围是( )A .(-3,1)B .(-1,3)C .(1,+∞) D.(-∞,-3)解析:由已知可得复数z 在复平面内对应的点的坐标为(m +3,m -1),且该点在第四象限,所以⎩⎪⎨⎪⎧m +3>0,m -1<0,解得-3<m <1.答案:A10.已知复数z 1=-1+2i ,z 2=1-i ,z 3=3-4i ,它们在复平面上所对应的点分别为A ,B ,C ,若OC →=λOA →+μOB →(λ,μ∈R ),则λ+μ的值是( )A .1B .2C .3D .4解析:依题意3-4i =λ(-1+2i)+μ(1-i)=μ-λ+(2λ-μ)i ,∴⎩⎪⎨⎪⎧μ-λ=32λ-μ=-4,∴⎩⎪⎨⎪⎧λ=-1μ=2,∴λ+μ=1.答案:A11.复数z =x +y i(x ,y ∈R )满足条件|z -4i|=|z +2|,则|2x+4y|的最小值为( )A .2B .4C .4 2D .16解析:由|z -4i|=|z +2|得x +2y =3. 则2x+4y≥22x +2y=2·23=4 2.12.已知f (n )=i n -i -n (i 2=-1,n ∈N ),集合{f (n )}的元素个数是( ) A .2个 B .3个 C .4个 D .无数个 解析:f (0)=i 0-i 0=0,f (1)=i -i -1=i -1i=2i ,f (2)=i 2-i -2=0, f (3)=i 3-i -3=-2i.∴{f (n )}={0,-2i,2i}. 答案:B二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.若复数z =(m -1)+(m +2)i 对应的点在直线y =2x 上,则实数m 的值是________.解析:由已知得2(m -1)-(m +2)=0,∴m =4. 答案:414.设复数z 满足i(z +1)=-3+2i(i 是虚数单位),则z 的实部是________. 解析:设z =a +b i(a ,b ∈R ),则i(z +1)=i(a +1+b i)=-b +(a +1)i =-3+2i , 所以a =1,b =3,复数z 的实部是1. 答案:115.在复平面内,复数1+i 与-1+3i 分别对应向量OA →和OB →,其中O 为坐标原点,则|AB →|=________.解析:∵AB →=(-1+3i)-(1+i)=-2+2i , ∴|AB →|=2 2. 答案:2 216.设i 是虚数单位,若复数a -103-i(a ∈R )是纯虚数,则a 的值为________. 解析:先利用复数的运算法则将复数化为x +y i(x ,y ∈R )的形式,再由纯虚数的定义求a .因为a -103-i =a -103+i 3-i 3+i=a -103+i10=(a -3)-i ,由纯虚数的定义,知a -3=0,所以a =3.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)实数m 为何值时,复数z =m +6m -1+(m 2+5m -6)i 是实数? 解析:复数z 为实数,则虚部为0,由于实部是分式,因此要求分式有意义,则⎩⎪⎨⎪⎧m 2+5m -6=0,m ≠1,解得m =-6.所以当m =-6时,复数z 是实数. 18.(12分)计算⎣⎢⎡⎦⎥⎤1+2i ·i 100+⎝ ⎛⎭⎪⎫1-i 1+i 52-⎝ ⎛⎭⎪⎫1+i 220.解析:⎣⎢⎡⎦⎥⎤1+2i ·i 100+⎝ ⎛⎭⎪⎫1-i 1+i 52-⎝ ⎛⎭⎪⎫1+i 220=[(1+2i)·1+(-i)5]2-i 10=(1+i)2-i 10=1+2i.19.(12分)复数z =(a 2+1)+a i(a ∈R )对应的点在第几象限?复数z 对应的点的轨迹方程是什么?解析:因为a 2+1≥1>0,复数z =(a 2+1)+a i 对应的点为(a 2+1,a ),所以z 对应的点在第一、四象限或实轴的正半轴上.设z =x +y i(x ,y ∈R ),则⎩⎪⎨⎪⎧x =a 2+1,y =a ,消去a 可得x =y 2+1,所以复数z 对应的点的轨迹方程是y 2=x -1.20.(12分)设复数z 1=(a 2-4sin 2θ)+(1+2cos θ)i ,a ∈R ,θ∈(0,π),z 2在复平面内对应的点在第一象限,且z 22=-3+4i.(1)求z 2及|z 2|;(2)若z 1=z 2,求θ与a 的值.解析:(1)设z 2=m +n i(m ,n ∈R ),则z 22=(m +n i)2=m 2-n 2+2mn i =-3+4i ,即⎩⎪⎨⎪⎧m 2-n 2=-3,2mn =4,解得⎩⎪⎨⎪⎧m =1,n =2,或⎩⎪⎨⎪⎧m =-1,n =-2,所以z 2=1+2i 或z 2=-1-2i.又因为z 2在复平面内对应的点在第一象限,所以z 2=-1-2i 应舍去, 故z 2=1+2i ,|z 2|= 5.(2)由(1)知(a 2-4sin 2θ)+(1+2cos θ)i =1+2i ,即⎩⎪⎨⎪⎧a 2-4sin 2θ=1,1+2cos θ=2,解得cos θ=12,因为θ∈(0,π),所以θ=π3,所以a 2=1+4sin 2θ=1+4×34=4,a =±2.综上,θ=π3,a =±2.21.(12分)虚数z 满足|z |=1,z 2+2z +1z<0,求z .解析:设z =x +y i(x ,y ∈R ,y ≠0),∴x 2+y 2=1.则z 2+2z +1z =(x +y i)2+2(x +y i)+1x +y i =(x 2-y 2+3x )+y (2x +1)i.∵y ≠0,z 2+2z +1z<0,∴⎩⎪⎨⎪⎧ 2x +1=0,x 2-y 2+3x <0,①②又x 2+y 2=1.③ 由①②③得⎩⎪⎨⎪⎧x =-12,y =±32.∴z =-12±32i.22.(12分)已知复数z 1=i(1-i)3. (1)求|z 1|;(2)若|z |=1,求|z -z 1|的最大值.解析:(1)|z 1|=|i(1-i)3|=|2-2i|=22+-22=2 2.(2)如图所示,由|z |=1可知,z 在复平面内对应的点的轨迹是半径为1,圆心为O (0,0)的圆,而z 1对应着坐标系中的点Z 1(2,-2).所以|z-z1|的最大值可以看成是点Z1(2,-2)到圆上的点的距离的最大值.由图知|z-z1|max=|z1|+r(r为圆的半径)=22+1.章末质量检测(三) 立体几何初步一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列结论正确的是( )A.各个面都是三角形的几何体是三棱锥B.以三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫圆锥C.棱锥的侧棱长与底面多边形的边长相等,则此棱锥可能是六棱锥D.圆锥的顶点与底面圆周上的任意一点的连线都是母线解析:A错误.如图1所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥.B错误.如图2,若△ABC不是直角三角形或是直角三角形,但旋转轴不是直角边所在直线,所得的几何体都不是圆锥.C错误.若六棱锥的所有棱长都相等,则底面多边形是正六边形.由几何图形知,若以正六边形为底面,侧棱长必然要大于底面边长.D正确.答案:D2.关于直观图画法的说法中,不正确的是( )A.原图形中平行于x轴的线段,其对应线段仍平行于x′轴,其长度不变B.原图形中平行于y轴的线段,其对应线段仍平行于y′轴,其长度不变C.画与坐标系xOy对应的坐标系x′O′y′时,∠x′O′y′可画成135°D.作直观图时,由于选轴不同,所画直观图可能不同解析:根据斜二测画法的规则可知B不正确.答案:B3.若圆柱的轴截面是一个正方形,其面积为4S,则它的一个底面面积是( )A .4SB .4πSC .πSD .2πS解析:由题意知圆柱的母线长为底面圆的直径2R , 则2R ·2R =4S ,得R 2=S .所以底面面积为πR 2=πS . 答案:C4.如果一个正四面体(各个面都是正三角形)的体积为9 cm 3,则其表面积为( ) A .18 3 cm 2B .18 cm 2C .12 3 cm 2D .12 cm 2解析:设正四面体的棱长为a cm ,则底面积为34a 2 cm 2,易求得高为63a cm ,则体积为13×34a 2×63a =212a 3=9,解得a =32,所以其表面积为4×34a 2=183(cm 2).答案:A5.一个四面体共一个顶点的三条棱两两互相垂直,其长分别为1,6,3,其四面体的四个顶点在一个球面上,则这个球的表面积为( )A .16π B.32π C .36π D.64π解析:将四面体可补形为长方体,此长方体的对角线即为球的直径,而长方体的对角线长为12+62+32=4,即球的半径为2,故这个球的表面积为4πr 2=16π.答案:A6.若平面α∥平面β,直线a ∥平面α,点B 在平面β内,则在平面β内且过点B 的所有直线中( )A .不一定存在与a 平行的直线B .只有两条与a 平行的直线C .存在无数条与a 平行的直线D .存在唯一与a 平行的直线解析:当直线a ⊂平面β,且点B 在直线a 上时,在平面β内且过点B 的所有直线中不存在与a 平行的直线.故选A.答案:A7.若α∥β,A ∈α,C ∈α,B ∈β,D ∈β,且AB +CD =28,AB 、CD 在β内的射影长分别为9和5,则AB 、CD 的长分别为( )A .16和12B .15和13C .17和11D .18和10解析:如图,作AM ⊥β,CN ⊥β,垂足分别为M 、N ,设AB =x ,则CD =28-x ,BM =9,ND =5,∴x 2-81=(28-x )2-25, ∴x =15,28-x =13. 答案:B 8.如图,在棱长为4的正方体ABCD -A 1B 1C 1D 1中,P 是A 1B 1上一点,且PB 1=14A 1B 1,则多面体P -BCC 1B 1的体积为( )A.83B.163 C .4 D .5解析:V 多面体P -BCC 1B 1=13S 正方形BCC 1B 1·PB 1=13×42×1=163.答案:B9.如图,在直三棱柱ABC -A 1B 1C 1中,D 为A 1B 1的中点,AB =BC =BB 1=2,AC =25,则异面直线BD 与AC 所成的角为( )A .30° B.45° C .60° D.90°解析:如图,取B1C1的中点E,连接BE,DE,则AC∥A1C1∥DE,则∠BDE即为异面直线BD与AC所成的角(或其补角).由条件可知BD=DE=EB=5,所以∠BDE=60°,故选C.答案:C10.如图,在三棱锥P-ABC中,不能证明AP⊥BC的条件是( )A.AP⊥PB,AP⊥PCB.AP⊥PB,BC⊥PBC.平面BCP⊥平面PAC,BC⊥PCD.AP⊥平面PBC解析:A中,因为AP⊥PB,AP⊥PC,PB∩PC=P,所以AP⊥平面PBC,又BC⊂平面PBC,所以AP⊥BC,故A正确;C中,因为平面BCP⊥平面PAC,BC⊥PC,所以BC⊥平面APC,AP⊂平面APC,所以AP⊥BC,故C正确;D中,由A知D正确;B中条件不能判断出AP⊥BC,故选B.答案:B11.在等腰Rt△ABC中,AB=BC=1,M为AC的中点,沿BM把它折成二面角,折后A与C的距离为1,则二面角C-BM-A的大小为( )A.30° B.60°C.90° D.120°解析:如图所示,由AB=BC=1,∠A′BC=90°,得A′C= 2.∵M为A′C的中点,∴MC=AM=22,且CM⊥BM,AM⊥BM,∴∠CMA为二面角C-BM-A的平面角.∵AC =1,MC =AM =22,∴∠CMA =90°. 答案:C12.在矩形ABCD 中,若AB =3,BC =4,PA ⊥平面AC ,且PA =1,则点P 到对角线BD 的距离为( )A.292 B.135C.175D.1195 解析:如图,过点A 作AE ⊥BD 于E ,连接PE . ∵PA ⊥平面ABCD ,BD ⊂平面ABCD , ∴PA ⊥BD ,∴BD ⊥平面PAE ,∴BD ⊥PE . ∵AE =AB ·AD BD =125,PA =1, ∴PE =1+⎝ ⎛⎭⎪⎫1252=135.答案:B二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.正方形ABCD 绕对角线AC 所在直线旋转一周所得组合体的结构特征是________. 解析:由圆锥的定义知是两个同底的圆锥形成的组合体. 答案:两个同底的圆锥组合体14.若某空间几何体的直观图如图所示,则该几何体的表面积是________. 解析:根据直观图可知该几何体是横着放的直三棱柱,所以S 侧=(1+2+3)×2=2+2+6, S 底=12×1×2=22, 故S 表=2+2+6+2×22=2+22+ 6.答案:2+22+ 615.如图,正方体ABCD -A 1B 1C 1D 1中,AB =2,点E 为AD 的中点,点F 在CD 上.若EF ∥平面AB 1C ,则线段EF 的长度等于________.解析:∵EF ∥平面AB 1C ,EF ⊂平面ABCD ,平面ABCD ∩平面AB 1C =AC ,∴EF ∥AC ,∴F 为DC 中点.故EF =12AC = 2.答案: 216.矩形ABCD 中,AB =1,BC =2,PA ⊥平面ABCD ,PA =1,则PC 与平面ABCD所成的角是________.解析:tan∠PCA =PA AC=13=33,∴∠PCA =30°. 答案:30°三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)如图是由正方形ABCE 和正三角形CDE 所组成的平面图形,试画出其水平放置的直观图.解析:(1)以AB 所在的直线为x 轴,AB 的中垂线为y 轴建立直角坐标系,如图(1),再建立坐标系x ′O ′y ′,使两轴的夹角为45°,如图(2).(2)以O ′为中点,在x ′轴上截取A ′B ′=AB ,分别过A ′,B ′作y ′轴的平行线,截取A ′E ′=12AE ,B ′C ′=12BC .在y ′轴上截取O ′D ′=12OD .(3)连接E ′D ′,E ′C ′,C ′D ′,并擦去作为辅助线的坐标轴,就得到所求的直观图,如图(3).18.(12分)如图,正方体ABCD -A ′B ′C ′D ′的棱长为a ,连接A ′C ′,A ′D ,A ′B ,BD ,BC ′,C ′D ,得到一个三棱锥.求:(1)三棱锥A ′-BC ′D 的表面积与正方体表面积的比值; (2)三棱锥A ′-BC ′D 的体积.解析:(1)∵ABCD -A ′B ′C ′D ′是正方体, ∴A ′B =A ′C ′=A ′D =BC ′=BD =C ′D =2a ,∴三棱锥A ′-BC ′D 的表面积为4×12×2a ×32×2a =23a 2.而正方体的表面积为6a 2,故三棱锥A ′-BC ′D 的表面积与正方体表面积的比值为23a 26a 2=33. (2)三棱锥A ′-ABD ,C ′-BCD ,D -A ′D ′C ′,B -A ′B ′C ′是完全一样的. 故V 三棱锥A ′-BC ′D =V 正方体-4V 三棱锥A ′-ABD =a 3-4×13×12a 2×a =a33.19.(12分)如图,四边形ABCD 与四边形ADEF 都为平行四边形,M ,N ,G 分别是AB ,AD ,EF 的中点.求证:(1)BE ∥平面DMF ; (2)平面BDE ∥平面MNG .证明:(1)设DF 与GN 交于点O ,连接AE ,则AE 必过点O ,且O 为AE 的中点,连接MO ,则MO 为△ABE 的中位线,所以BE ∥MO .因为BE⊄平面DMF,MO⊂平面DMF,所以BE∥平面DMF.(2)因为N,G分别为AD,EF的中点,四边形ADEF为平行四边形,所以DE∥GN.因为DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG.因为M为AB的中点,N为AD的中点,所以MN为△ABD的中位线,所以BD∥MN.因为BD⊄平面MNG,MN⊂平面MNG,所以BD∥平面MNG.因为DE∩BD=D,BD,DE⊂平面BDE,所以平面BDE∥平面MNG.20.(12分)S是Rt△ABC所在平面外一点,且SA=SB=SC,D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.证明:(1)如图所示,取AB的中点E,连接SE,DE,在Rt△ABC中,D、E分别为AC、AB的中点,∴DE∥BC,∴DE⊥AB,∵SA=SB,∴△SAB为等腰三角形,∴SE⊥AB.又SE∩DE=E,∴AB⊥平面SDE.又SD⊂平面SDE,∴AB⊥SD.在△SAC中,SA=SC,D为AC的中点,∴SD⊥AC.又AC∩AB=A,∴SD⊥平面ABC.(2)由于AB=BC,则BD⊥AC,由(1)可知,SD⊥平面ABC,BD⊂平面ABC,∴SD⊥BD,又SD∩AC=D,∴BD⊥平面SAC.21.(12分)如图,在斜三棱柱ABC-A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,点E是AB的中点.(1)求证:OE∥平面BCC1B1;(2)若AC1⊥A1B,求证:AC1⊥BC.证明:(1)连接BC1,因为侧面AA1C1C是菱形,AC1与A1C交于点O,所以O为AC1的中点,又因为E是AB的中点,所以OE∥BC1,因为OE⊄平面BCC1B1,BC1⊂平面BCC1B1,所以OE∥平面BCC1B1.(2)因为侧面AA1C1C是菱形,所以AC1⊥A1C,因为AC1⊥A1B,A1C∩A1B=A1,A1C⊂平面A1BC,A1B⊂平面A1BC,所以AC1⊥平面A1BC,因为BC⊂平面A1BC,所以AC1⊥BC.22.(12分)如图所示,在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连接ED,EC,EB和DB.(1)求证:平面EDB⊥平面EBC;(2)求二面角E-DB-C的正切值.解析:(1)证明:在长方体ABCD-A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点.所以△DD1E为等腰直角三角形,∠D1ED=45°.同理∠C1EC=45°.所以∠DEC=90°,即DE⊥EC.在长方体ABCD-A1B1C1D1中,BC⊥平面D1DCC1,又DE⊂平面D1DCC1,所以BC⊥DE.又EC∩BC=C,所以DE⊥平面EBC.因为DE⊂平面DEB,所以平面DEB⊥平面EBC.(2)如图所示,过E在平面D1DCC1中作EO⊥DC于O.在长方体ABCD-A1B1C1D1中,因为平面ABCD⊥平面D1DCC1,且交线为DC,所以EO⊥面ABCD.过O在平面DBC中作OF⊥DB于F,连接EF,所以EF⊥BD.∠EFO为二面角E-DB-C的平面角.利用平面几何知识可得OF=15,又OE=1,所以tan∠EFO= 5.章末质量检测(四) 统计一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.从某年级500名学生中抽取60名学生进行体重的统计分析,下列说法正确的是( )A.500名学生是总体B.每个被抽查的学生是样本C.抽取的60名学生的体重是一个样本D.抽取的60名学生是样本容量解析:A×总体应为500名学生的体重B×样本应为每个被抽查的学生的体重C√抽取的60名学生的体重构成了总体的一个样本D×样本容量为60,不能带有单位2.某班对八校联考成绩进行分析,利用随机数表法抽取样本时,先将70个同学按01,02,03,…,70进行编号,然后从随机数表第9行第9列的数开始向右读,则选出的第7个个体是( )(注:如表为随机数表的第8行和第9行)63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54A .07B .44C .15D .51解析:找到第9行第9列数开始向右读,符合条件的是29,64,56,07,52,42,44,故选出的第7个个体是44.答案:B3.对于数据3,3,2,3,6,3,10,3,6,3,2,有以下结论: ①这组数据的众数是3.②这组数据的众数与中位数的数值不等. ③这组数据的中位数与平均数的数值相等. ④这组数据的平均数与众数的数值相等. 其中正确的结论有( ) A .1个 B .2个 C .3个 D .4个解析:由题意知,众数与中位数都是3,平均数为4.只有①正确,故选A. 答案:A4.某学校高一、高二、高三三个年级共有学生3 500人,其中高三学生数是高一学生数的两倍,高二学生数比高一学生数多300人,现在按1100的抽样比用分层抽样的方法抽取样本,则应抽取高一学生数为( )A .8B .11C .16D .10解析:若设高三学生数为x ,则高一学生数为x 2,高二学生数为x2+300,所以有x+x 2+x 2+300=3 500,解得x =1 600.故高一学生数为800,因此应抽取的高一学生数为800100=8.答案:A5.在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个长方形的面积和的25,且样本容量为140,则中间一组的频数为( )A .28B .40C .56D .60解析:设中间一组的频数为x ,则其他8组的频数和为52x ,所以x +52x =140,解得x =40.答案:B6.某校共有学生2 000名,各年级男、女生人数如表所示:一年级二年级三年级女生373380y男生377370z现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )A.24 B.18C.16 D.12解析:一年级的学生人数为373+377=750,二年级的学生人数为380+370=750,于是三年级的学生人数为2 000-750-750=500,那么三年级应抽取的人数为500×642 000=16.故选C.答案:C7.某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下图,则下面结论中错误的一个是( )A.甲的极差是29 B.乙的众数是21C.甲罚球命中率比乙高 D.甲的中位数是24解析:甲的极差是37-8=29;乙的众数显然是21;甲的平均数显然高于乙,即C成立;甲的中位数应该是23.答案:D8.为研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组.如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )A .1B .8C .12D .18解析:由图知,样本总数为N =200.16+0.24=50.设第三组中有疗效的人数为x ,则6+x 50=0.36,解得x =12. 答案:C9.一组数据的方差为s 2,平均数为x ,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平均数为( )A.12s 2,12x B .2s 2,2x C .4s 2,2x D .s 2,x解析:将一组数据的每一个数都乘以a ,则新数据组的方差为原来数据组方差的a 2倍,平均数为原来数据组的a 倍.故答案选C.答案:C10.某超市连锁店统计了城市甲、乙的各16台自动售货机在12:00至13:00间的销售金额,并用茎叶图表示如图,则可估计有( )A .甲城市销售额多,乙城市销售额不够稳定B .甲城市销售额多,乙城市销售额稳定C .乙城市销售额多,甲城市销售额稳定D .乙城市销售额多,甲城市销售额不够稳定解析:十位数字是3,4,5时乙城市的销售额明显多于甲,估计乙城市销售额多,甲的数字过于分散,不够稳定,故选D.答案:D11.在某次测量中得到的A 样本数据如下:82,84,84,86,86,86,88,88,88,88.若B 样本数据恰好是A 样本数据都加上2所得数据,则A ,B 两样本的下列数字特征对应相同的是( )A .众数B .平均数C .中位数D .标准差解析:设A 样本数据为x i ,根据题意可知B 样本数据为x i +2,则依据统计知识可知A ,B 两样本中的众数、平均数和中位数都相差2,只有方差相同,即标准差相同.答案:D12.将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91.现场作的9个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以x 表示:则7个剩余分数的方差为( ) A.1169 B.367 C .36 D.677解析:由题图可知去掉的两个数是87,99,所以87+90×2+91×2+94+90+x=91×7,解得x =4.故s 2=17[(87-91)2+(90-91)2×2+(91-91)2×2+(94-91)2×2]=367.故选B. 答案:B二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在题中横线上) 13.将一个容量为m 的样本分成3组,已知第一组频数为8,第二、三组的频率为0.15和0.45,则m =________.解析:由题意知第一组的频率为 1-(0.15+0.45)=0.4, 所以8m=0.4,所以m =20.答案:2014.某单位有职工100人,不到35岁的有45人,35岁到49岁的有25人,剩下的为50岁以上(包括50岁)的人,用分层抽样的方法从中抽20人,各年龄段分别抽取的人数为________.解析:由于样本容量与总体个体数之比为20100=15,故各年龄段抽取的人数依次为45×15=9(人),25×15=5(人),20-9-5=6(人).答案:9,5,615.某市高三数学抽样考试中,对90分以上(含90分)的成绩进行统计,其频率分布图如图所示,若130~140分数段的人数为90人,则90~100分数段的人数为________.解析:由频率分布图知,设90~100分数段的人数为x ,则0.40x =0.0590,所以x=720.答案:72016.设样本数据x 1,x 2,…,x 2017的方差是4,若y i =2x i -1(i =1,2,…,2 017),则y 1,y 2,…,y 2017的方差为________.解析:本题考查数据的方差.由题意得D (y i )=D (2x i -1)=D (2x i )=4D (x i )=4×4=16.答案:16三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)某总体共有60个个体,并且编号为00,01,…,59.现需从中抽取一个容量为8的样本,请从随机数表的倒数第5行(下表为随机数表的最后5行)第11列的1开始.依次向下读数,到最后一行后向右,直到取足样本为止(大于59及与前面重复的数字跳过),求抽取样本的号码.95 33 95 22 00 18 74 72 00 18 38 79 58 69 32 81 76 80 26 92 82 80 84 25 39 90 84 60 79 80 24 36 59 87 38 82 07 53 89 35 56 35 23 79 18 05 98 90 07 35 46 40 62 98 80 54 97 20 56 95 15 74 80 08 32 16 46 70 50 80 67 72 16 42 79 20 31 89 03 43 38 46 82 68 72 32 14 82 99 70 80 60 47 18 97 63 49 30 21 30 71 59 73 05 50 08 22 23 71 77 91 01 93 20 49 82 96 59 26 94 66 39 67 98 60解析:由随机数表法可得依次的读数为:18,24,54,38,08,22,23,0118.(12分)某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组.在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%.登山组的职工占参加活动总人数的14,且该组中,青年人占50%,中年人占40%,老年人占10%,为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本.试确定:(1)游泳组中,青年人、中年人、老年人分别所占的比例; (2)游泳组中,青年人、中年人、老年人分别应抽取的人数.解析:(1)设登山组人数为x ,游泳组中,青年人、中年人、老年人各占比例分别为a ,b ,c ,则有x ·40%+3xb 4x =47.5%,x ·10%+3xc4x=10%.解得b =50%,c =10%. 故a =1-50%-10%=40%.即游泳组中,青年人、中年人、老年人各占比例分别为40%,50%,10%.(2)游泳组中,抽取的青年人数为200×34×40%=60;抽取的中年人数为200×34×50%=75;抽取的老年人数为200×34×10%=15.19.(12分)已知一组数据按从小到大的顺序排列为-1,0,4,x,7,14,中位数为5,求这组数据的平均数与方差.解析:由于数据-1,0,4,x,7,14的中位数为5,所以4+x2=5,x =6.设这组数据的平均数为x -,方差为s 2,由题意得 x -=16×(-1+0+4+6+7+14)=5,s 2=16×[(-1-5)2+(0-5)2+(4-5)2+(6-5)2+(7-5)2+(14-5)2]=743. 20.(12分)为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将取得数据整理后,画出频率分布直方图(如图).已知图中从左到右前三个小组频率分别为0.1,0.3,0.4,第一小组的频数为5.(1)求第四小组的频率;(2)参加这次测试的学生有多少人;(3)若次数在75次以上(含75次)为达标,试估计该年级学生跳绳测试的达标率是多少.解析:(1)由累积频率为1知,第四小组的频率为1-0.1-0.3-0.4=0.2. (2)设参加这次测试的学生有x 人,则0.1x =5, 所以x =50.即参加这次测试的学生有50人. (3)达标率为0.3+0.4+0.2=90%,所以估计该年级学生跳绳测试的达标率为90%.21.(12分)市体校准备挑选一名跳高运动员参加全市中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩(单位:m)如下:甲:1.70 1.65 1.68 1.69 1.72 1.73 1.68 1.67乙:1.60 1.73 1.72 1.61 1.62 1.71 1.70 1.75(1)甲、乙两名运动员的跳高平均成绩分别是多少?(2)哪位运动员的成绩更为稳定?(3)若预测跳过1.65 m就很可能获得冠军,该校为了获得冠军,可能选哪名运动员参赛?若预测跳过1.70 m才能得冠军呢?解析:(1)甲的平均成绩为:(1.70+1.65+1.68+1.69+1.72+1.73+1.68+1.67)÷8=1.69 m,乙的平均成绩为:(1.60+1.73+1.72+1.61+1.62+1.71+1.70+1.75)÷8=1.68 m;(2)根据方差公式可得:甲的方差为0.0006,乙的方差为0.00315∵0.0006<0.00315∴甲的成绩更为稳定;(3)若跳过1.65 m就很可能获得冠军,甲成绩均过1.65米,乙3次未过1.65米,因此选甲;若预测跳过1.70 m才能得冠军,甲成绩过1.70米3次,乙过1.70米5次,因此选乙.22.(12分)某中学高一女生共有450人,为了了解高一女生的身高(单位:cm)情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:(1)(2)画出频率分布直方图;(3)估计该校高一女生身高在[149.5,165.5]范围内的有多少人?解析:(1)由题意得M=80.16=50,落在区间[165.5,169.5]内的数据频数m=50-(8+6+14+10+8)=4,。
人教版高中数学选择性必修第二册 全册模块综合检测1(含解析)

人教版高中数学选择性必修第二册全册模块综合检测1(原卷版)(时间:120分钟,分值:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.数列{a n}满足a n+1=3a n+1,a1=1,则此数列的第3项是()A.13B.10C.7D.42.{a n}为等差数列,且a7-2a4=-1,a3=0,则公差d=()A.-2B.-12D.2C.123.已知函数f(x)=3x2+2,则f′(5)=()A.15B.30C.32D.774.设等比数列{a n}满足a1+a2=-1,a1-a3=-3,则S6=()A.-63B.-21C.21D.635.函数f(x)=xx2+1的单调递增区间是()A.(-∞,-1)B.(-1,1)C.(1,+∞)D.(-∞,-1)和(1,+∞)6.数列{a n}满足a1=1,log2a n+1=log2a n+1(n∈N*),它的前n项和为S n,则满足S n>1025的最小n值是()A.9B.10C.11D.127.函数f(x)=ln xx+1的图象大致是()8.函数f (x )=ln x +ax 有小于1的极值点,则实数a 的取值范围是()A .(0,1)B .(-∞,-1)C .(-1,0)D .(-∞,-1)∪(0,+∞)二、多项选择题(本题共4小题,每小题5分,共20分)9.过点P (2,-6)作曲线f (x )=x 3-3x 的切线,则切线方程可能是()A .3x +y =0B .24x -y -54=0C .9x -y -24=0D .12x -y -24=010.记S n 为等差数列{a n }的前n 项和.若a 1+3a 5=S 7,则以下结论一定正确的是()A .a 4=0B .S n 的最大值为S 3C .S 1=S 6D .|a 3|<|a 5|11.在数列{a n }中,若a 2n -a 2n -1=p (n ≥2,n ∈N *,p 为常数),则{a n }称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为()A .若{a n }是等方差数列,则{a 2n }是等差数列B .若{a n }是等方差数列,则{a 2n }是等方差数列C .{(-1)n }是等方差数列D .若{a n }是等方差数列,则{a kn }(k ∈N *,k 为常数)也是等方差数列12.设f (x )=x a ·cos x ,x ∈π6,π3的最大值为M ,则()A .当a =-1时,M <3B .当a =2时,M <33C .当a =1时,M >32D .当a =3时,M <12三、填空题(本题共4小题,每小题5分,共20分)13.已知等差数列{a n }的前n 项和为S n ,a 1=9,S 99-S 55=-4,则a n =________.14.设函数f (x )=x 3+ax 2,若曲线y =f (x )在点P (1,f (1))处的切线方程为x +y =0,则实数a =________.15.已知等差数列{a n }的前n 项和为S n =pn 2-2n +q (p ,q ∈R ,n ∈N *),则q =______;若a 1与a 5的等差中项为8,则p +q =________.16.设a ,b ∈R ,若x ≥0时恒有0≤x 4-x 3+ax +b ≤(x 2-1)2,则ab 等于________.四、解答题(本题共6小题,共70分)17.(10分)在等差数列{a n}中,已知a1+a2+a3=21,a1a2a3=231.(1)求该数列中a2的值;(2)求该数列的通项公式a n.18.(12分)(1)求曲线y=1x在点(-1,-1)处的切线方程;(2)求经过点(4,0)且与曲线y=1x相切的直线方程.19.(12分)设f(x)=a ln x+12x-32x+1,曲线y=f(x)在点(1,f(1))处取得极值.(1)求a的值;(2)求函数f(x)的单调区间和极值.20.(12分)设数列{a n}满足:a1=1,且2a n=a n+1+a n-1(n≥2),a3+a4=12.(1)求{a n}的通项公式;(2)n项和.21.(12分)已知数列{a n}的前n项和为S n,a1=1,a2=13,a na n+1=2a n+1(n∈N*且n≥2).(1)(2)n项和T n.22.(12分)已知a∈R,函数f(x)=(-x2+ax)e x(x∈R).(1)当a=2时,求函数f(x)的单调区间;(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.人教版高中数学选择性必修第二册全册模块综合检测1(解析版)(时间:120分钟,分值:150分)一、单项选择题(本题共8小题,每小题5分,共40分)1.数列{a n }满足a n +1=3a n +1,a 1=1,则此数列的第3项是()A .13B .10C .7D .4A解析:因为a n +1=3a n +1,a 1=1,所以a 2=3a 1+1=3×1+1=4,所以a 3=3a 2+1=3×4+1=13.故选A .2.{a n }为等差数列,且a 7-2a 4=-1,a 3=0,则公差d =()A .-2B .-12C .12D .2B解析:∵a 7-2a 4=-1,∴a 3+4d -2(a 3+d )=-1,∴4d -2d =-1,∴d =-12.3.已知函数f (x )=3x 2+2,则f ′(5)=()A .15B .30C .32D .77B解析:依题意f ′(x )=6x ,所以f ′(5)=30.故选B .4.设等比数列{a n }满足a 1+a 2=-1,a 1-a 3=-3,则S 6=()A .-63B .-21C .21D .63B解析:设数列{a n }的公比为q ,∵a 1+a 2=-1,a 1-a 3=-3,1+a 1q =-1,1-a 1q 2=-3,1=1,=-2,∴S 6=a 1(1-q 6)1-q =1-643=-21.故选B .5.函数f (x )=xx 2+1的单调递增区间是()A .(-∞,-1)B .(-1,1)C .(1,+∞)D .(-∞,-1)和(1,+∞)B解析:f (x )的定义域为R ,且f ′(x )=x 2+1-2x ·x (x 2+1)2=1-x 2(x 2+1)2=(1+x )(1-x )(x 2+1)2,所以当-1<x <1时,f ′(x )>0,f (x )单调递增,所以f (x )的单调递增区间为(-1,1).故选B .6.数列{a n }满足a 1=1,log 2a n +1=log 2a n +1(n ∈N *),它的前n 项和为S n ,则满足S n >1025的最小n 值是()A .9B .10C .11D .12C 解析:数列{log 2a n }是以0为首项,公差为1的等差数列,log 2a n =0+(n -1)×1=n -1,a n=2n -1,Sn=1+2+22+23+…+2n -1=1-2n1-2=2n -1>1025,2n >1026.因为210=1024,211=2048,所以,最小n 值是11.选C .7.函数f (x )=ln xx +1的图象大致是()C解析:由f (x )=ln xx +1,得f ′(x )=1+1x -ln x(x +1)2(x >0).令g (x )=1+1x-ln x ,则g ′(x )=-1x 2-1x =-1+x x 2<0,所以g (x )在(0,+∞)上单调递减.又g (e)=1e >0,g (e 2)=1+1e 2-ln e 2=1e 2-1<0,所以存在x 0∈(e ,e 2),使得g (x 0)=0,所以当x ∈(0,x 0)时,g (x )>0,f ′(x )>0;当x ∈(x 0,+∞)时,g (x )<0,f ′(x )<0.所以f (x )在(0,x 0)上单调递增,在(x 0,+∞)上单调递减.故选C .8.函数f (x )=ln x +ax 有小于1的极值点,则实数a 的取值范围是()A .(0,1)B .(-∞,-1)C .(-1,0)D .(-∞,-1)∪(0,+∞)B解析:因为f(x)=ln x+ax,所以函数定义域为{x|x>0}.由f′(x)=1x+a=0,得a≠0,x=-1a.又函数f(x)=ln x+ax有小于1的极值点,所以-1a<1且a<0,所以a<-1.故选B.二、多项选择题(本题共4小题,每小题5分,共20分)9.过点P(2,-6)作曲线f(x)=x3-3x的切线,则切线方程可能是()A.3x+y=0B.24x-y-54=0C.9x-y-24=0D.12x-y-24=0AB解析:∵y′=3x2-3.设曲线的切点为(x0,y0),则k=3x20-3,y0=x30-3x0.∴切线方程为y-(x30-3x0)=(3x20-3)(x-x0).又切线经过点P(2,-6),则-6-(x30-3x0)=(3x20-3)(2-x0),解得x0=0或x0=3,∴切点为(0,0)时,切线方程为3x+y=0;切点为(3,18)时,切线方程为24x-y-54=0.10.记S n为等差数列{a n}的前n项和.若a1+3a5=S7,则以下结论一定正确的是() A.a4=0B.S n的最大值为S3C.S1=S6D.|a3|<|a5|AC解析:设等差数列{a n}的公差为d,则a1+3(a1+4d)=7a1+21d,解得a1=-3d,所以a n=a1+(n-1)d=(n-4)d,所以a4=0,故A正确;因为S6-S1=5a4=0,所以S1=S6,故C正确;由于无法确定d的正负,故S3可能为最大值,也可能为最小值,故B不正确;因为a3+a5=2a4=0,所以a3=-a5,即|a3|=|a5|,故D不正确.故选AC.11.在数列{a n}中,若a2n-a2n-1=p(n≥2,n∈N*,p为常数),则{a n}称为“等方差数列”.下列对“等方差数列”的判断,其中正确的为()A.若{a n}是等方差数列,则{a2n}是等差数列B.若{a n}是等方差数列,则{a2n}是等方差数列C.{(-1)n}是等方差数列D.若{a n}是等方差数列,则{a kn}(k∈N*,k为常数)也是等方差数列ACD解析:对于A,{a n}是等方差数列,可得a2n-a2n-1=p(n≥2,n∈N*,p为常数),即有{a2n}是首项为a21,公差为d的等差数列,故正确;对于B,例如:数列{n}是等方差数列,但是数列{n}不是等方差数列,所以B不正确;对于C,数列{(-1)n}中,a2n-a2n-1=[(-1)n]2-[(-1)n-1]2=0(n≥2,n∈N),所以数列{(-1)n}是等方差数列,故C正确;对于D,数列{a n}中的项列举出来是:a1,a2,…,a k…,a2k,…,数列{a kn}中的项列举出来是:a k,a2k,a3k,….∵a2kn+k-a2kn+k-1=a2kn+k-1-a2kn+k-2=…=a2kn+1-a2kn=p,∴a2kn+k-a2kn=(a2kn+k-a2kn+k-1)+(a2kn+k-1-a2kn+k-2)+…+(a2kn+1-a2kn)=kp,∴a2k(n+1)-a2kn=kp,所以,数列{a kn}是等方差数列,故D 正确.故选ACD.12.设f(x)=x a·cos x,x∈π6,π3的最大值为M,则()A.当a=-1时,M<3B.当a=2时,M<33C.当a=1时,M>32D.当a=3时,M<12AB解析:对于选项A,当a=-1时,f(x)=cos xx在区间π6,π3上递减,所以M=cosπ6π6=33π<3,故选项A正确.对于选项B,当a=2时,f(x)=x2·cos x,则f′(x)=x cos x(2-xtanx)>0,∴f(x)在区间π6,π3上递增,即M=π218<33,故选项B正确.对于选项C,当a=1时,x<tan x恒成立,所以f(x)=x cos x<tan x cos x=sin x≤32,所以M<32,故选项C 错误.对于选项D,当a=3时,f(x)=x3·cos x,则f′(x)=x2cos x(3-xtan x)>0,∴f(x)在区间π6,π3上递增,∴M=12·>12,故选项D错误.故选AB.三、填空题(本题共4小题,每小题5分,共20分)13.已知等差数列{a n}的前n项和为S n,a1=9,S99-S55=-4,则a n=________.-2n+11解析:设公差为d,因为S99-S55=-4,所以4d-2d=-4,即d=-2.所以a n=a1+(n-1)d=9-2(n-1)=-2n+11.14.设函数f(x)=x3+ax2,若曲线y=f(x)在点P(1,f(1))处的切线方程为x+y=0,则实数a=________.-2解析:因为点P(1,f(1))在该切线上,所以f(1)=-1,则f(1)=1+a=-1,解得a=-2.15.已知等差数列{a n}的前n项和为S n=pn2-2n+q(p,q∈R,n∈N*),则q=______;若a1与a5的等差中项为8,则p+q=________.02解析:由等差数列的性质可得q=0.又a1与a5的等差中项为8,所以a1+a5=16,即S5=(a1+a5)×52=40,所以25p-10=40,解得p=2,即p+q=2+0=2.16.设a ,b ∈R ,若x ≥0时恒有0≤x 4-x 3+ax +b ≤(x 2-1)2,则ab 等于________.-1解析:验证发现,当x =1时,将1代入不等式有0≤a +b ≤0,所以a +b =0,当x =0时,可得0≤b ≤1,结合a +b =0可得-1≤a ≤0.令f (x )=x 4-x 3+ax +b ,即f (1)=a +b =0.又f ′(x )=4x 3-3x 2+a ,f ′′(x )=12x 2-6x ,令f ′′(x )>0,可得x >12,则f ′(x )=4x 3-3x 2+a 在0,12上递减,在12,+∞上递增.又-1≤a ≤0,所以f ′(0)=a <0,f ′(1)=1+a ≥0.又x ≥0时恒有0≤x 4-x 3+ax +b ,结合f (1)=a +b =0知,1必为函数f (x )=x 4-x 3+ax +b 的极小值点,也是最小值点.故有f ′(1)=1+a =0,由此得a =-1,b =1.所以ab =-1.四、解答题(本题共6小题,共70分)17.(10分)在等差数列{a n }中,已知a 1+a 2+a 3=21,a 1a 2a 3=231.(1)求该数列中a 2的值;(2)求该数列的通项公式a n .解:(1)由等差数列性质得a 1+a 2+a 3=3a 2=21,∴a 2=7.(2)设等差数列公差为d ,∴a 1a 2a 3=(a 2-d )a 2·(a 2+d )=7(7-d )(7+d )=7(49-d 2)=231.解得d =±4,∴a n =a 2+(n -2)d ,即a n =4n -1或a n =-4n +15.18.(12分)(1)求曲线y =1x在点(-1,-1)处的切线方程;(2)求经过点(4,0)且与曲线y =1x 相切的直线方程.解:∵y =1x ,∴y ′=-1x2.(1)当x =-1时,得在点(-1,-1)处的切线的斜率为-1,∴切线方程为y +1=-(x +1),即x +y +2=0.(2)设切点为x 0,1x 0,则切线的斜率为-1x 20,∴切线方程为y -1x 0=-1x 20(x -x 0),∵切线过点(4,0),∴-1x 0=-1x 20(4-x 0),解得x 0=2,∴所求切线方程为y -12=-14(x -2),即x +4y -4=0.19.(12分)设f (x )=a ln x +12x -32x +1,曲线y =f (x )在点(1,f (1))处取得极值.(1)求a 的值;(2)求函数f (x )的单调区间和极值.解:(1)因为f (x )=a ln x +12x -32x +1,所以f ′(x )=a x -12x 2-32.由f ′(1)=0,可得a -2=0,解得a =2.(2)由(1)可知,f (x )=2ln x +12x -32x +1,f ′(x )=-(3x -1)(x -1)2x 2.令f ′(x )=0,解得x 1=13,x 2=1,又因为函数f (x )定义域为(0,+∞),所以f (x )(1,+∞)故f (x )的极大值为f (1)=0,f (x )的极小值为2-2ln 3.20.(12分)设数列{a n }满足:a 1=1,且2a n =a n +1+a n -1(n ≥2),a 3+a 4=12.(1)求{a n }的通项公式;(2)n 项和.解:(1)由2a n =a n +1+a n -1(n ≥2)可知数列{a n }是等差数列,设公差为d ,因为a 1=1,所以a 3+a 4=a 1+2d +a 1+3d =12,解得d =2,所以{a n }的通项公式为a n =2n -1(n ∈N *).(2)由(1)知1a n a n +2=1(2n -1)(2n +3)=n 项和S n …++13-12n +1-=13-n +1(2n +1)(2n +3).21.(12分)已知数列{a n }的前n 项和为S n ,a 1=1,a 2=13,a na n +1=2a n +1(n ∈N *且n ≥2).(1)(2)n 项和T n .(1)证明:因为a na n +1=2a n +1,所以a n =a n +1+2a n a n +1,即a n -a n +1=2a n a n +1,等式两边同时除以a n a n +1,得1a n +1-1a n=2(n ≥2),且1a 2-1a 1=2,1,公差为2的等差数列.(2)解:由(1)得1a n =2n -1,3na n =(2n -1)3n ,则T n =1×3+3×32+…+(2n -1)3n ①,3T n =1×32+…+(2n -3)3n +(2n -1)3n +1②,①-②得-2T n =3+2(32+…+3n )-(2n -1)3n +1=3+2×9×(1-3n -1)1-3-(2n -1)3n +1=2(1-n )3n +1-6,故T n =(n -1)3n +1+3.22.(12分)已知a ∈R ,函数f (x )=(-x 2+ax )e x (x ∈R ).(1)当a =2时,求函数f (x )的单调区间;(2)若函数f (x )在(-1,1)上单调递增,求a 的取值范围.解:(1)a =2时,f (x )=(-x 2+2x )·e x 的导数为f ′(x )=e x (2-x 2).由f′(x)>0,解得-2<x<2,由f′(x)<0,解得x<-2或x> 2.即有函数f(x)的单调递减区间为(-∞,-2),(2,+∞),单调递增区间为(-2,2).(2)函数f(x)=(-x2+ax)·e x的导数为f′(x)=e x[a-x2+(a-2)x].由函数f(x)在(-1,1)上单调递增,则有f′(x)≥0在(-1,1)上恒成立,即为a-x2+(a-2)x≥0,即有x2-(a-2)x-a≤0,则有1+(a-2)-a≤0且1-(a-2)-a≤0,解得a≥3 2,则a的取值范围为3 2,+。
新教材 人教A高中数学必修第二册全册各章测验及模块综合测验 精选最新配套习题含解析

人教A 必修第二册各章综合测验1、平面向量及其应用............................................................................................................ - 1 -2、复数 ................................................................................................................................. - 11 -3、立体几何初步 ................................................................................................................. - 17 -4、统计 ................................................................................................................................. - 30 -5、概率 ................................................................................................................................. - 41 - 模块综合测验 ....................................................................................................................... - 52 -1、平面向量及其应用(时间:120分钟,满分:150分)一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.向量a =(2,-1),b =(-1,2),则(2a +b )·a =( ) A .6 B .5 C .1D .-6A [由向量数量积公式知,(2a +b )·a =(3,0)·(2,-1)=6.]2.设非零向量a ,b ,c 满足|a|=|b|=|c|,a +b =c ,则向量a ,b 的夹角为( ) A .150° B .120° C .60°D .30°B [设向量a ,b 夹角为θ, |c|2=|a +b|2=|a|2+|b|2+2|a||b|cos θ,则cos θ=-12,又θ∈[0°,180°],∴θ=120°.故选B .]3.已知向量a =(1,k ),b =(2,2),且a +b 与a 共线,则a ·b 的值为( ) A .1 B .2 C .3D .4 A [a +b =(3,k +2),∵a +b 与a 共线, ∴3k -(k +2)=0,解得k =1.]4.在△ABC 中,角A ,B ,C 所对边的长分别为a ,b ,c .若b 2+c 2-a 2=65bc ,则sin(B +C )的值为( )A .-45B .45C .-35D .35B [由b 2+c 2-a 2=65bc ,得cos A =b 2+c 2-a 22bc =35,则sin(B +C )=sin A =45.]5.已知点A ,B ,C 满足|AB →|=3,|BC →|=4,|CA →|=5,则AB →·BC →+BC →·CA →+CA →·AB →的值是( )A .-25B .25C .-24D .24A [因为|AB →|2+|BC →|2=9+16=25=|CA →|2, 所以∠ABC =90°,所以原式=AB →·BC →+CA →(BC →+AB →)=0+CA →·AC → =-AC →2=-25.]6.已知A (7,1),B (1,4),直线y =12ax 与线段AB 交于点C ,且AC →=2CB →,则实数a 等于( )A .2B .1C .45D .53A [设C (x ,y ),则AC →=(x -7,y -1),CB →=(1-x,4-y ), ∵AC →=2CB →,∴⎩⎨⎧ x -7=2(1-x ),y -1=2(4-y ),解得⎩⎨⎧x =3,y =3,∴C (3,3),又∵C 在直线y =12ax 上,所以3=12a ×3, ∴a =2.]7.如图,在△ABC 中,AD →=23AC →,BP →=13BD →,若AP →=λAB →+μAC →,则λ+μ的值为( )A .49B .89C .23D .43 B [∵BP →=13BD →, ∴AP →-AB →=13(AD →-AB →), ∴AP →=23AB →+13AD →,又AD →=23AC →, ∴AP →=23AB →+29AC →=λAB →+μAC →, ∴λ=23,μ=29,∴λ+μ=89.]8.已知点M 是边长为2的正方形ABCD 的内切圆内(含边界)一动点,则MA →·MB →的取值范围是( )A .[-1,0]B .[-1,2]C .[-1,3]D .[-1,4]C [建立如图所示坐标系,设M (x ,y ),其中A (-1,-1),B (1,-1),易知x 2+y 2≤1,而MA →·MB →=(-1-x ,-1-y )·(1-x ,-1-y )=x 2+(y +1)2-1,若设E (0,-1),则MA →·MB →=|ME →|2-1,由于0≤|ME →|≤2,所以MA →·MB →=|ME →|2-1的取值范围是[-1,3],故选C .] 二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9.对任意向量a ,b ,下列关系式中恒成立的是( ) A .|a ·b |≤|a ||b | B .|a -b |≤||a |-|b || C .(a +b )2=|a +b |2D .(a +b )·(a -b )=a 2-b 2ACD [|a ·b |=|a |·|b |·|cos 〈a ,b 〉|≤|a |·|b |,故A 正确;由向量的运算法则知C ,D 正确;当b =-a ≠0时,|a -b |>||a |-|b ||,故B 错误.故选ACD .]10.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,若A =π6,a =2,c =23,则角C 的大小是( )A .π6B .π3C .5π6D .2π3BD [由正弦定理可得a sin A =c sin C ,所以sin C =c a sin A =32,而a <c ,所以A <C ,所以π6<C <56π,故C =π3或23π.]11.已知△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且满足B =π3,a +c =3b ,则ac =( )A .2B .3C .12D .13AC [∵B =π3,a +c =3b , ∴(a +c )2=a 2+c 2+2ac =3b 2,①由余弦定理可得,a 2+c 2-2ac cos π3=b 2,② 联立①②,可得2a 2-5ac +2c 2=0, 即2⎝ ⎛⎭⎪⎫a c 2-5⎝ ⎛⎭⎪⎫a c +2=0,解得a c =2或a c =12.故选AC .]12.点P 是△ABC 所在平面内一点,满足|PB →-PC →|-|PB →+PC →-2P A →|=0,则△ABC 的形状不可能是( )A .钝角三角形B .直角三角形C .锐角三角形D .等边三角形ACD [∵P 是△ABC 所在平面内一点,且 |PB →-PC →|-|PB →+PC →-2P A →|=0, ∴|CB →|-|(PB →-P A →)+(PC →-P A →)|=0, 即|CB →|=|AC →+AB →|, ∴|AB →-AC →|=|AC →+AB →|,两边平方并化简得AC →·AB →=0,∴AC →⊥AB →,∴∠A =90°,则△ABC 一定是直角三角形.故选ACD .]三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.与向量a =(1,2)平行,且模等于5的向量为________.(1,2)或(-1,-2) [因为所求向量与向量a =(1,2)平行,所以可设所求向量为(x,2x ),又因为其模为5,所以x 2+(2x )2=5,解得x =±1.因此所求向量为(1,2)或(-1,-2).]14.已知向量a =(m,2),b =(-1,n )(n >0),且a ·b =0,点P (m ,n )在圆x 2+y 2=5上,则m +n =________,|2a +b |=________.(本题第一空2分,第二空3分)334 [因为向量a =(m,2),b =(-1,n )(n >0),且a ·b =0,P (m ,n )在圆x 2+y 2=5上,∴⎩⎨⎧-m +2n =0,m 2+n 2=5,解得m =2,n =1,即m +n =2+1=3. ∴2a +b =(3,5),∴|2a +b |=34.]15.在△ABC 中,S △ABC =14(a 2+b 2-c 2),b =1,a =2,则c =________.1 [∵S △ABC =12ab sin C , ∴12ab sin C =14(a 2+b 2-c 2), ∴a 2+b 2-c 2=2ab sin C .由余弦定理得,2ab cos C =2ab sin C ,∴tan C =1,∴C =45°,∴c =a 2+b 2-2ab cos C =3-2=1.]16.如图所示,半圆的直径AB =2,O 为圆心,C 是半圆上不同于A ,B 的任意一点,若P 为半径OC 上的动点,则(P A →+PB →)·PC →的最小值是________.-12 [因为点O 是AB 的中点, 所以P A →+PB →=2PO →,设|PC →|=x ,则|PO →|=1-x (0≤x ≤1), 所以(P A →+PB →)·PC →=2PO →·PC →=-2x (1-x ) =2⎝ ⎛⎭⎪⎫x -122-12. 所以当x =12时,(P A →+PB →)·PC →取到最小值-12.]四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61. (1)求|a +b |;(2)求向量a 在向量a +b 方向上的投影. [解] (1)因为(2a -3b )·(2a +b )=61, 所以4|a |2-4a·b -3|b |2=61.因为|a |=4,|b |=3,所以a·b =-6, 所以|a +b |=|a |2+|b |2+2a·b =42+32+2×(-6)=13.(2)因为a ·(a +b )=|a |2+a·b =42-6=10,所以向量a 在向量a +b 方向上的投影为a ·(a +b )|a +b |=1013=101313.18.(本小题满分12分)如图所示,在平面直角坐标系中,|OA →|=2|AB →|=2,∠OAB=2π3,BC →=(-1,3).(1)求点B ,C 的坐标;(2)求证:四边形OABC 为等腰梯形.[解] (1)连接OB (图略),设B (x B ,y B ),则x B =|OA →|+|AB →|·cos(π-∠OAB )=52, y B =|AB →|·sin(π-∠OAB )=32,∴OC →=OB →+BC →=⎝ ⎛⎭⎪⎫52,32+(-1,3)=⎝ ⎛⎭⎪⎫32,332, ∴B ⎝ ⎛⎭⎪⎫52,32,C ⎝ ⎛⎭⎪⎫32,332. (2)证明:∵OC →=⎝ ⎛⎭⎪⎫32,332, AB →=⎝ ⎛⎭⎪⎫12,32,∴OC →=3AB →,∴OC →∥AB →. 又易知OA 与BC 不平行, |OA →|=|BC →|=2,∴四边形OABC 为等腰梯形.19.(本小题满分12分)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,c =3a sin C -c cos A .(1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c . [解] (1)由c =3a sin C -c cos A ,及正弦定理得 3sin A sin C -cos A sin C -sin C =0. 由于sin C ≠0,所以sin ⎝ ⎛⎭⎪⎫A -π6=12.又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4. 而a 2=b 2+c 2-2bc cos A , 故b 2+c 2=8. 解得b =c =2.20.(本小题满分12分)已知a =(cos α,sin α),b =(cos β,sin β),0<β<α<π. (1)若|a -b |=2,求证:a ⊥b ;(2)设c =(0,1),若a +b =c ,求α,β的值. [解] (1)证明:由题意得|a -b |2=2, 即(a -b )2=a 2-2a ·b +b 2=2. 又因为a 2=b 2=|a |2=|b |2=1, 所以2-2a ·b =2,即a ·b =0,故a ⊥b .(2)因为a +b =(cos α+cos β,sin α+sin β)=(0,1), 所以⎩⎨⎧cos α+cos β=0, ①sin α+sin β=1, ②由①得,cos α=cos(π-β), 由0<β<π,得0<π-β<π. 又0<α<π,故α=π-β. 代入sin α+sin β=1, 得sin α=sin β=12, 而α>β,所以α=5π6,β=π6.21.(本小题满分12分)如图,在△OAB 中,已知P 为线段AB 上的一点,OP →=x ·OA →+y ·OB →.(1)若BP →=P A →,求x ,y 的值;(2)若BP →=3P A →,|OA →|=4,|OB →|=2,且OA →与OB →的夹角为60°时,求OP →·AB →的值. [解] (1)∵BP →=P A →, ∴BO →+OP →=PO →+OA →, 即2OP →=OB →+OA →,∴OP →=12OA →+12OB →,即x =12,y =12. (2)∵BP →=3P A →,∴BO →+OP →=3PO →+3OA →, 即4OP →=OB →+3OA →,∴OP →=34O A →+14OB →.∴x =34,y =14. OP →·AB →=⎝ ⎛⎭⎪⎫34OA →+14OB →·(OB →-OA →)=14OB →·OB →-34OA →·OA →+12OA →·OB →=14×22-34×42+12×4×2×12=-9.22.(本小题满分12分)如图,我国南海某处的一个圆形海域上有四个小岛,小岛B 与小岛A 、小岛C 相距都为5 n mile ,与小岛D 相距为3 5 n mile.小岛A 对小岛B 与D 的视角为钝角,且sin A =35.(1)求小岛A 与小岛D 之间的距离和四个小岛所形成的四边形的面积; (2)记小岛D 对小岛B 与C 的视角为α,小岛B 对小岛C 与D 的视角为β,求sin(2α+β)的值.[解] (1)∵sin A =35,且角A 为钝角, ∴cos A =-1-⎝ ⎛⎭⎪⎫352=-45. 在△ABD 中,由余弦定理得:AD 2+AB 2-2AD ·AB ·cos A =BD 2. ∴AD 2+52-2AD ·5·⎝ ⎛⎭⎪⎫-45=(35)2⇒AD 2+8AD -20=0. 解得AD =2或AD =-10(舍).∴小岛A 与小岛D 之间的距离为2 n mile. ∵A ,B ,C ,D 四点共圆, ∴角A 与角C 互补.∴sin C =35,cos C =cos(180°-A )=-cos A =45. 在△BDC 中,由余弦定理得: CD 2+CB 2-2CD ·CB ·cos C =BD 2, ∴CD 2+52-2CD ·5·45=(35)2⇒CD 2-8CD -20=0, 解得CD =-2(舍)或CD =10. ∴S 四边形ABCD =S △ABD +S △BCD=12AB ·AD ·sin A +12CB ·CD ·sin C =12×5×2×35+12×5×10×35=3+15=18. ∴四个小岛所形成的四边形的面积为18平方n mile.(2)在△BDC 中,由正弦定理得:BC sin α=BD sin C ⇒5sin α=3535⇒sin α=55.∵DC 2+DB 2>BC 2, ∴α为锐角,∴cos α=255.又∵sin(α+β)=sin(180°-C )=sin C =35, cos(α+β)=cos(180°-C )=-cos C =-45. ∴sin(2α+β)=sin[α+(α+β)]=sin αcos(α+β)+cos αsin(α+β)=55×⎝⎛⎭⎪⎫-45+255×35=2525.2、复数(时间:120分钟,满分:150分)一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知z=11-20i,则1-2i-z等于()A.z-1B.z+1C.-10+18i D.10-18iC[1-2i-z=1-2i-(11-20i)=-10+18i.]2.3+i1+i=()A.1+2i B.1-2i C.2+i D.2-iD[3+i1+i=(3+i)(1-i)(1+i)(1-i)=3-3i+i+12=2-i.故选D.]3.若复数z满足z1-i=i,其中i为虚数单位,则z=()A.1-i B.1+iC.-1-i D.-1+iA[由已知得z=i(1-i)=i+1,则z=1-i,故选A.]4.若复数z满足i z=2+4i,则在复平面内,z对应的点的坐标是() A.(2,4) B.(2,-4)C .(4,-2)D .(4,2)C [z =2+4ii =4-2i 对应的点的坐标是(4,-2),故选C .] 5.若a 为实数,且(2+a i)(a -2i)=-4i ,则a =( ) A .-1 B .0 C .1D .2B [∵(2+a i)(a -2i)=-4i ,∴4a +(a 2-4)i =-4i. ∴⎩⎨⎧4a =0,a 2-4=-4.解得a =0.故选B .] 6.若复数2-b i1+2i(b ∈R )的实部与虚部互为相反数,则b =( ) A . 2 B .23 C .-23 D .2C [因为2-b i 1+2i =(2-b i )(1-2i )5=2-2b 5-4+b 5i ,又复数2-b i1+2i(b ∈R )的实部与虚部互为相反数,所以2-2b 5=4+b 5,即b =-23.]7.设z ∈C ,若z 2为纯虚数,则z 在复平面上的对应点落在( ) A .实轴上B .虚轴上C .直线y =±x (x ≠0)上D .以上都不对C [设z =x +y i(x ,y ∈R ),则z 2=(x +y i)2=x 2-y 2+2xy i.∵z 2为纯虚数,∴⎩⎨⎧x 2-y 2=0,xy ≠0.∴y =±x (x ≠0).] 8.已知0<a <2,复数z 的实部为a ,虚部为1,则|z |的取值范围是( ) A .(1,5) B .(1,3) C .(1,5)D .(1,3)C [由已知,得|z |=a 2+1. 由0<a <2,得0<a 2<4, ∴1<a 2+1<5.∴|z |=a 2+1∈(1,5).故选C .]二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对得5分,部分选对得3分,有选错的得0分)9.给出下列复平面内的点,这些点中对应的复数为虚数的为()A.(3,1) B.(-2,0)C.(0,4) D.(-1,-5)ACD[易知选项A、B、C、D中的点对应的复数分别为3+i、-2、4i、-1-5i,因此A、C、D中的点对应的复数为虚数.]10.已知复数z=a+b i(a,b∈R,i为虚数单位),且a+b=1,下列命题正确的是()A.z不可能为纯虚数B.若z的共轭复数为z,且z=z,则z是实数C.若z=|z|,则z是实数D.|z|可以等于1 2BC[当a=0时,b=1,此时z=i为纯虚数,A错误;若z的共轭复数为z,且z=z,则a+b i=a-b i,因此b=0,B正确;由|z|是实数,且z=|z|知,z是实数,C正确;由|z|=12得a2+b2=14,又a+b=1,因此8a2-8a+3=0,Δ=64-4×8×3=-32<0,无解,即|z|不可以等于12,D错误.故选BC.]11.已知复数z0=1+2i(i为虚数单位)在复平面内对应的点为P0,复数z满足|z-1|=|z-i|,下列结论正确的是()A.P0点的坐标为(1,2)B.复数z0的共轭复数对应的点与点P0关于虚轴对称C.复数z对应的点Z在一条直线上D.P0与z对应的点Z间的距离的最小值为2 2ACD[复数z0=1+2i在复平面内对应的点为P0(1,2),A正确;复数z0的共轭复数对应的点与点P0关于实轴对称,B错误;设z=x+y i(x,y∈R),代入|z-1|=|z-i|,得|(x-1)+y i|=|x+(y-1)i|,即(x-1)2+y2=x2+(y-1)2,整理得,y=x ,即Z 点在直线y =x 上,C 正确;易知点P 0到直线y =x 的垂线段的长度即为P 0、Z 之间距离的最小值,结合平面几何知识知D 正确.故选ACD .]12.对任意z 1,z 2,z ∈C ,下列结论成立的是( ) A .当m ,n ∈N *时,有z m z n =z m +nB .当z 1,z 2∈C 时,若z 21+z 22=0,则z 1=0且z 2=0C .互为共轭复数的两个复数的模相等,且|z |2=|z |2=z ·zD .z 1=z 2的充要条件是|z 1|=|z 2| AC [由复数乘法的运算律知A 正确;取z 1=1,z 2=i ,满足z 21+z 22=0,但z 1=0且z 2=0不成立,B 错误;由复数的模及共轭复数的概念知结论成立,C 正确; 由z 1=z 2能推出|z 1|=|z 2|, 但|z 1|=|z 2|推不出z 1=z 2,因此z 1=z 2的必要不充分条件是|z 1|=|z 2|,D 错误.]三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中的横线上)13.已知复数z =(5+2i)2(i 为虚数单位),则z 的实部为________. 21 [复数z =(5+2i)2=21+20i ,其实部是21.]14.a 为正实数,i 为虚数单位,⎪⎪⎪⎪⎪⎪a +i i =2,则a =________. 3 [a +i i =(a +i )·(-i )i·(-i )=1-a i ,则⎪⎪⎪⎪⎪⎪a +i i =|1-a i|=a 2+1=2, 所以a 2=3.又a 为正实数,所以a = 3.] 15.设a ,b ∈R ,a +b i =11-7i1-2i(i 为虚数单位),则a +b 的值为________. 8 [a +b i =11-7i 1-2i =(11-7i )(1+2i )(1-2i )(1+2i )=25+15i5=5+3i ,依据复数相等的充要条件可得a =5,b =3.从而a +b =8.]16.设z 的共轭复数是z ,若z +z =4,z ·z =8,则|z |=________,z-z =________(本题第一空2分,第二空3分).22 ±i [设z =x +y i(x ,y ∈R ),则z =x -y i ,由z +z =4,z ·z =8得, ⎩⎨⎧ x +y i +x -y i =4,(x +y i )(x -y i )=8,⇒⎩⎨⎧ x =2,x 2+y 2=8,⇒⎩⎨⎧x =2,y =±2.∴|z |=2 2.所以zz =x -y i x +y i =x 2-y 2-2xy ix 2+y 2=±i.]四、简答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)设复数z =lg(m 2-2m -2)+(m 2+3m +2)i ,当m 为何值时,(1)z 是实数? (2)z 是纯虚数? [解] (1)要使复数z 为实数, 需满足⎩⎨⎧ m 2-2m -2>0,m 2+3m +2=0,解得m =-2或-1.即当m =-2或-1时,z 是实数. (2)要使复数z 为纯虚数, 需满足⎩⎨⎧m 2-2m -2=1,m 2+3m +2≠0,解得m =3.即当m =3时,z 是纯虚数.18.(本小题满分12分)已知复数z 1=1-i ,z 1·z 2+z 1=2+2i ,求复数z 2. [解] 因为z 1=1-i ,所以z 1=1+i , 所以z 1·z 2=2+2i -z 1=2+2i -(1+i)=1+i. 设z 2=a +b i(a ,b ∈R ),由z 1·z 2=1+i , 得(1-i)(a +b i)=1+i , 所以(a +b )+(b -a )i =1+i ,所以⎩⎨⎧a +b =1,b -a =1,解得a =0,b =1,所以z 2=i.19.(本小题满分12分)已知复数z 满足|z |=1,且(3+4i)z 是纯虚数,求z 的共轭复数z .[解] 设z =a +b i(a ,b ∈R ),则z =a -b i 且|z |=a 2+b 2=1,即a 2+b 2=1.① 因为(3+4i)z =(3+4i)(a +b i)=(3a -4b )+(3b +4a )i ,而(3+4i)z 是纯虚数, 所以3a -4b =0,且3b +4a ≠0.② 由①②联立, 解得⎩⎪⎨⎪⎧a =45,b =35,或⎩⎪⎨⎪⎧a =-45,b =-35.所以z =45-35i ,或z =-45+35i.20.(本小题满分12分)复数z =(1+i )2+3(1-i )2+i ,若z 2+az <0,求纯虚数a .[解] 由z 2+a z <0可知z 2+az 是实数且为负数. z =(1+i )2+3(1-i )2+i =2i +3-3i 2+i =3-i 2+i =1-i.因为a 为纯虚数,所以设a =m i(m ∈R ,且m ≠0),则z 2+a z =(1-i)2+m i 1-i =-2i +m i -m 2=-m 2+⎝ ⎛⎭⎪⎫m 2-2i <0,故⎩⎪⎨⎪⎧-m2<0,m2-2=0,所以m =4,即a =4i.21.(本小题满分12分)已知等腰梯形OABC 的顶点A ,B 在复平面上对应的复数分别为1+2i ,-2+6i ,OA ∥BC .求顶点C 所对应的复数z .[解] 设z =x +y i(x ,y ∈R ),C (x ,y ), 因为OA ∥BC ,|OC |=|BA |, 所以k OA =k BC ,|z C |=|z B -z A |,即⎩⎨⎧21=y -6x +2,x 2+y 2=32+42,解得⎩⎨⎧ x 1=-5,y 1=0或⎩⎨⎧x 2=-3,y 2=4.因为|OA |≠|BC |,所以x 2=-3,y 2=4(舍去), 故z =-5.22.(本小题满分12分)已知复数z 满足(1+2i)z =4+3i. (1)求复数z ;(2)若复数(z +a i)2在复平面内对应的点在第一象限,求实数a 的取值范围. [解] (1)∵(1+2i)z =4+3i , ∴z =4+3i 1+2i =(4+3i )(1-2i )(1+2i )(1-2i )=10-5i5=2-i , ∴z =2+i.(2)由(1)知z =2+i ,则(z +a i)2=(2+i +a i)2=[2+(a +1)i]2=4-(a +1)2+4(a +1)i , ∵复数(z +a i)2在复平面内对应的点在第一象限, ∴⎩⎨⎧4-(a +1)2>0,4(a +1)>0, 解得-1<a <1,即实数a 的取值范围为(-1,1).3、立体几何初步(时间:120分钟,满分:150分)一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下面给出了四个条件:①空间三个点;②一条直线和一个点;③和直线a都相交的两条直线;④两两相交的三条直线.其中,能确定一个平面的条件有()A.3个B.2个C.1个D.0个D[①当空间三点共线时不能确定一个平面;②点在直线上时不能确定一个平面;③两直线若不平行也不相交时不能确定一个平面;④三条直线交于一点且不共面时不能确定一个平面. 故以上4个条件都不能确定一个平面.] 2.在长方体ABCD-A1B1C1D1中,异面直线AB,A1D1所成的角等于() A.30°B.45°C.60°D.90°D[由于AD∥A1D1,则∠BAD是异面直线AB,A1D1所成的角,很明显∠BAD =90°.]3.已知a,b,c是直线,则下面四个命题:①若直线a,b异面,b,c异面,则a,c异面;②若直线a,b相交,b,c相交,则a,c相交;③若a∥b,则a,b与c所成的角相等.其中真命题的个数为()A.0 B.3C.2 D.1D[异面、相交关系在空间中不能传递,故①②错;根据等角定理,可知③正确.]4.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6 cm,4 cm,则该棱柱的侧面积为()A.24 cm2B.36 cm2C.72 cm2D.84 cm2C[棱柱的侧面积S侧=3×6×4=72(cm2).]5.在正方体ABCD-A1B1C1D1中,动点E在棱BB1上,动点F在线段A1C1上,O为底面ABCD的中心,若BE=x,A1F=y,则四面体O-AEF的体积()A.与x,y都有关B.与x,y都无关C.与x有关,与y无关D.与y有关,与x无关B[因为V O-AEF=V E-OAF,考察△AOF的面积和点E到平面AOF的距离的值,因为BB1∥平面ACC1A1,所以点E到平面AOF的距离为定值,又AO∥A1C1,所以OA为定值,点F到直线AO的距离也为定值,即△AOF的面积是定值,所以四面体O-AEF的体积与x,y都无关,故选B.]6.如图,点S在平面ABC外,SB⊥AC,SB=AC=2,E,F分别是SC和AB 的中点,则EF的长是()A.1 B. 2C.22D.12B[取CB的中点D,连接ED,DF,则∠EDF(或其补角)为异面直线SB与AC所成的角,即∠EDF=90°.在△EDF中,ED=12SB=1,DF=12AC=1,所以EF=ED2+DF2= 2.]7.在四面体ABCD中,已知棱AC的长为2,其余各棱长都为1,则二面角A-CD-B的余弦值为()A .12B .13C .33D .23C [取AC 的中点E ,CD 的中点F ,连接BE ,EF ,BF ,则EF =12,BE =22,BF =32,因为EF 2+BE 2=BF 2,所以△BEF 为直角三角形,cos θ=EF BF =33.]8.已知三棱柱ABC -A 1B 1C 1的侧棱与底面垂直,体积为94,底面是边长为3的正三角形.若P 为底面A 1B 1C 1的中心,则P A 与平面ABC 所成角的大小为( )A .5π12B .π3C .π4D .π6B [如图所示,P 为正三角形A 1B 1C 1的中心,设O 为△ABC 的中心,由题意知:PO ⊥平面ABC ,连接OA ,则∠P AO 即为P A 与平面ABC 所成的角.在正三角形ABC 中,AB =BC =AC =3,则S =34×(3)2=334,VABC -A 1B 1C 1=S ×PO =94, ∴PO = 3. 又AO =33×3=1, ∴tan ∠P AO =PO AO =3,∴∠P AO =π3.]二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9.下列命题为真命题的是( )A .若两个平面有无数个公共点,则这两个平面重合B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直C.垂直于同一条直线的两条直线相互平行D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直BD[A错,两个平面相交时,也有无数个公共点;C错,比如a⊥α,b⊂α,c⊂α,显然有a⊥b,a⊥c,但b与c也可能相交.故选BD.]10.如图,圆柱的轴截面是四边形ABCD,E是底面圆周上异于A,B的一点,则下列结论中正确的是()A.AE⊥CEB.BE⊥DEC.DE⊥平面CEBD.平面ADE⊥平面BCEABD[由AB是底面圆的直径,得∠AEB=90°,即AE⊥EB.∵圆柱的轴截面是四边形ABCD,∴AD⊥底面AEB,BC⊥底面AEB.∴BE⊥AD.又AD∩AE=A,AD,AE⊂平面ADE,∴BE⊥平面ADE,∴BE⊥DE.同理可得,AE⊥CE,易得平面BCE⊥平面ADE.可得A,B,D正确.∵AD∥BC,∴∠ADE(或其补角)为DE与CB所成的角,显然∠ADE≠90°,∴DE⊥平面CEB不正确,即C错误.故选ABD.]11.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,侧面P AD 为正三角形,且平面P AD⊥平面ABCD,则下列说法正确的是()A.在棱AD上存在点M,使AD⊥平面PMBB.异面直线AD与PB所成的角为90°C.二面角P-BC-A的大小为45°D.BD⊥平面P ACABC[如图,对于A,取AD的中点M,连接PM,BM,∵侧面P AD为正三角形,∴PM⊥AD,又底面ABCD是菱形,∠DAB=60°,∴△ABD是等边三角形,∴AD⊥BM,又PM∩BM=M,PM,BM⊂平面PMB,∴AD⊥平面PBM,故A正确.对于B,∵AD⊥平面PBM,∴AD⊥PB,即异面直线AD与PB所成的角为90°,故B正确.对于C,∵平面PBC∩平面ABCD=BC,BC∥AD,∴BC⊥平面PBM,∴BC⊥PB,BC⊥BM,∴∠PBM是二面角P-BC-A的平面角,设AB=1,则BM=32,PM=32,在Rt△PBM中,tan∠PBM=PMBM=1,即∠PBM=45°,故二面角P-BC-A的大小为45°,故C正确.对于D,因为BD与P A不垂直,所以BD与平面P AC不垂直,故D错误.故选ABC.]12.如图所示,在四个正方体中,l是正方体的一条体对角线,点M、N、P 分别为其所在棱的中点,能得出l⊥平面MNP的图形为()AD[如图所示,正方体ABCD-A′B′C′D′.连接AC,BD.∵M、P分别为其所在棱的中点,∴MP∥AC.∵四边形ABCD为正方形,∴AC⊥BD,∵BB′⊥平面ABCD,AC⊂平面ABCD,∴BB′⊥AC,∵AC⊥BD,BD∩BB′=B,∴AC⊥平面DBB′,∵DB′⊂平面DBB′,∴AC⊥DB′.∵MP∥AC,∴DB′⊥MP,同理,可证DB′⊥MN,DB′⊥NP,∵MP∩NP=P,MP⊂平面MNP,NP⊂平面MNP,∴DB′⊥平面MNP,即l垂直平面MNP,故A正确.故D中,由A中证明同理可证l⊥MP,l⊥MN,又∵MP∩MN=M,∴l⊥平面MNP.故D正确.故选AD.]三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)13.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的表面积为________,体积为________.(本题第一空2分,第二空3分)3π33π[设圆锥的底面半径为r,根据题意,得2πr=2π,解得r=1,根据勾股定理,得圆锥的高为22-12=3,所以圆锥的表面积S=12×π×22+π×12=3π,体积V=13×π×12×3=33π.]14.已知正四棱锥的侧棱长为23,侧棱与底面所成的角为60°,则该四棱锥的高为________.3[如图,过点S作SO⊥平面ABCD,连接OC,则∠SCO=60°,∴SO=sin 60°·SC=32×23=3.]15.如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=________.1∶24[因为D,E分别是AB,AC的中点,所以S△ADE ∶S△ABC=1∶4. 又F是AA1的中点,所以A1到底面的距离H为F到底面距离h的2倍,即三棱柱A1B1C1-ABC的高是三棱锥F-ADE高的2倍,所以V1∶V2=13S△ADE·hS△ABC·H=124=1∶24.]16.已知三棱锥S-ABC的所有顶点都在球O的球面上,SC是球O的直径.若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S-ABC的体积为9,则球O的表面积为________.36π[如图,连接OA,OB.由SA=AC,SB=BC,SC为球O的直径,知OA⊥SC,OB⊥SC.由平面SCA⊥平面SCB,平面SCA∩平面SCB=SC,OA⊥SC,知OA⊥平面SCB.设球O的半径为r,则OA=OB=r,SC=2r,∴三棱锥S-ABC的体积V=13×⎝⎛⎭⎪⎫12SC·OB·OA=r33,即r33=9,∴r=3,∴S球表=4πr2=36π.]四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1∶4,母线长为10 cm,求圆锥的母线长.[解]如图,设圆锥的母线长为l,圆台上、下底面的半径分别为r、R.因为l-10l=rR,所以l-10l=14,所以l=403cm.即圆锥的母线长为403cm.18.(本小题满分12分)如图,三棱柱ABC-A1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.(1)求证:AC⊥B1C;(2)求证:AC1∥平面CDB1.[证明](1)∵C1C⊥平面ABC,∴C1C⊥AC.∵AC=9,BC=12,AB=15,∴AC2+BC2=AB2,∴AC⊥BC.又BC∩C1C=C,∴AC⊥平面BCC1B1,而B1C⊂平面BCC1B1,∴AC⊥B1C.(2)连接BC1交B1C于点O,连接OD.如图,∵O,D分别为BC1,AB的中点,∴OD∥AC1.又OD⊂平面CDB1,AC1⊄平面CDB1.∴AC1∥平面CDB1.19.(本小题满分12分)如图,已知三棱锥P-ABC,P A⊥平面ABC,∠ACB=90°,∠BAC=60°,P A=AC,M为PB的中点.(1)求证:PC⊥BC;(2)求二面角M-AC-B的大小.[解](1)证明:由P A⊥平面ABC,所以P A⊥BC,又因为∠ACB=90°,即BC⊥AC,P A∩AC=A,所以BC⊥平面P AC,所以PC⊥BC.(2)取AB中点O,连接MO,过O作HO⊥AC于H,连接MH,因为M是BP的中点,所以MO∥P A,又因为P A⊥平面ABC,所以MO⊥平面ABC,所以∠MHO为二面角M-AC-B的平面角,设AC=2,则BC=23,MO=1,OH=3,在Rt△MHO中,tan∠MHO=MOHO=33,所以二面角M-AC-B的大小为30°.20.(本小题满分12分)已知一个圆锥的底面半径为R,高为H, 在其中有一个高为x的内接圆柱.(1)求圆柱的侧面积;(2)x为何值时,圆柱的侧面积最大?[解](1)设圆柱的底面半径为r, 则它的侧面积为S=2πrx, rR=H-xH,解得r=R-RH x,所以S圆柱侧=2πRx-2πRH x2.(2)由(1)知S圆柱侧=2πRx-2πRH x2,在此表达式中,S圆柱侧为x的二次函数,因此,当x=H2时,圆柱的侧面积最大.21.(本小题满分12分)如图,在四棱锥P-ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(1)求异面直线AP与BC所成角的余弦值;(2)求证:PD⊥平面PBC;(3)求直线AB与平面PBC所成角的正弦值.[解](1)如图,由已知AD∥BC,故∠DAP或其补角为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得AP=AD2+PD2=5,所以cos∠DAP=ADAP=55.所以异面直线AP与BC所成角的余弦值为5 5.(2)因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又BC∥AD,所以PD⊥BC,又PD⊥PB,PB∩BC=B,所以PD⊥平面PBC.(3)过点D作AB的平行线交BC于点F,连接PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF与平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC-BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得DF=CD2+CF2=25,在Rt△DPF中,可得sin∠DFP=PDDF=55.所以直线AB与平面PBC所成角的正弦值为5 5.22.(本小题满分12分)如图①,在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图②.①②(1)求证:DE∥平面A1CB;(2)求证:A1F⊥BE;(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ?说明理由.[解](1)证明:∵D,E分别为AC,AB的中点,∴DE∥BC.又∵DE⊄平面A1CB,BC⊂平面A1CB,∴DE∥平面A1CB.(2)证明:由已知得AC⊥BC且DE∥BC,∴DE⊥AC.∵DE⊥A1D,DE⊥CD,A1D∩CD=D,∴DE⊥平面A1DC.而A1F⊂平面A1DC,∴DE⊥A1F.又∵A1F⊥CD,DE∩CD=D,∴A1F⊥平面BCDE,∵BE⊂平面BCDE,∴A1F⊥BE.(3)线段A1B上存在点Q,使A1C⊥平面DEQ.理由如下:如图,分别取A1C,A1B的中点P,Q,则PQ∥BC.又∵DE∥BC,∴DE∥PQ.∴平面DEQ即为平面DEP.由(2)知,DE⊥平面A1DC,A1C⊂平面A1DC,∴DE⊥A1C.又∵P是等腰三角形DA1C底边A1C的中点,∴A1C⊥DP,DE∩DP=D,∴A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q(中点),使得A1C⊥平面DEQ.4、统计(时间:120分钟,满分:150分)一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.对一个容量为N 的总体抽取容量为n 的样本,当选取抽签法抽样、随机数法抽样和分层随机抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为p 1,p 2,p 3,则( )A .p 1=p 2<p 3B .p 2=p 3<p 1C .p 1=p 3<p 2D .p 1=p 2=p 3D [在抽签法抽样、随机数法抽样和分层随机抽样中,每个个体被抽中的概率均为nN ,所以p 1=p 2=p 3,故选D .]2.某公司从代理的A ,B ,C ,D 四种产品中,按分层随机抽样的方法抽取容量为110的样本,已知A ,B ,C ,D 四种产品的数量比是2∶3∶2∶4,则该样本中D 类产品的数量为( )A .22B .33C .40D .55C [根据分层随机抽样,总体中产品数量比与抽取的样本中产品数量比相等,∴样本中D 类产品的数量为110×42+3+2+4=40.]3.在抽查产品尺寸的过程中,将其尺寸分成若干组,[a ,b ]是其中的一组.已知该组的频率为m ,该组上的频率分布直方图的高为h ,则|a -b |等于( )A .mhB .h mC .m hD .m +hC [在频率分布直方图中小长方形的高等于频率组距,所以h =m |a -b |,|a -b |=mh ,故选C .]4.我市对上、下班交通情况作抽样调查,上、下班时间各抽取12辆机动车测其行驶速度(单位:km/h)如下表:上班时间182021262728303233353640下班时间161719222527283030323637A.28与28.5 B.29与28.5C.28与27.5 D.29与27.5D[上班时间行驶速度的中位数是28+302=29,下班时间行驶速度的中位数是27+282=27.5.]5.为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m e,众数为m o,平均值为x,则()A.m e=m o=x B.m e=m o<xC.m e<m o<x D.m o<m e<xD[由条形图可知,中位数为m e=5.5,众数为m o=5,平均值为x≈5.97,所以m o<m e<x.]6.某校为了对初三学生的体重进行摸底调查,随机抽取了50名学生的体重(kg),将所得数据整理后,画出了频率分布直方图,如图所示,体重在[45,50)内适合跑步训练,体重在[50,55)内适合跳远训练,体重在[55,60]内适合投掷相关方面训练,估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为()A.4∶3∶1 B.5∶3∶1C.5∶3∶2 D.3∶2∶1B[体重在[45,50)内的频率为0.1×5=0.5,体重在[50,55)内的频率为0.06×5=0.3,体重在[55,60]内的频率为0.02×5=0.1,∵0.5∶0.3∶0.1=5∶3∶1,∴可估计该校初三学生适合参加跑步、跳远、投掷三项训练的集训人数之比为5∶3∶1,故选B.]7.为了了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如图所示,由于不慎将部分数据丢失,但知道后5组频数和为62,设视力在4.6到4.8之间的学生数为a,最大频率为0.32,则a的值为()A.64 B.54C.48 D.27B[前两组中的频数为100×(0.05+0.11)=16.因为后五组频数和为62,所以前三组频数和为38.所以第三组频数为38-16=22.又最大频率为0.32,故第四组频数为0.32×100=32.所以a=22+32=54.故选B.]8.某学习小组在一次数学测验中,得100分的有1人,得95分的有1人,得90分的有2人,得85分的有4人,得80分和75分的各有1人,则该小组数学成绩的平均数、众数、中位数分别是()A.85,85,85 B.87,85,86C.87,85,85 D.87,85,90C[∵得85分的人数最多为4人,∴众数为85,中位数为85,平均数为110(100+95+90×2+85×4+80+75)=87.]二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)9.某地区经过一年的建设,农村的经济收入增加了一倍,实现翻番.为更好地了解该地区农村的经济收入变化情况,统计了该地区建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中正确的是()A.建设后,种植收入减少B.建设后,其他收入增加了一倍以上C.建设后,养殖收入增加了一倍D.建设后,养殖收入与第三产业收入的总和超过了经济收入的一半BCD[设建设前经济收入为a,则建设后经济收入为2a,由题图可知:种植收入第三产业收入养殖收入其他收入建设前经济收入0.6a 0.06a 0.3a 0.04a建设后经济收入0.74a 0.56a 0.6a 0.1a10.在某次高中学科竞赛中,4 000名考生的参赛成绩统计如图所示,60分以下视为不及格,若同一组中的数据用该组区间中点值为代表,则下列说法中正确的是()A .成绩在[70,80)分的考生人数最多B .不及格的考生人数为1 000C .考生竞赛成绩的平均分约为70.5分D .考生竞赛成绩的中位数为75分ABC [由频率分布直方图可得,成绩在[70,80)内的频率最高,因此考生人数最多,故A 正确;由频率分布直方图可得,成绩在[40,60)的频率为0.25,因此,不及格的人数为4 000×0.25=1 000,故B 正确;由频率分布直方图可得,平均分为45×0.1+55×0.15+65×0.2+75×0.3+85×0.15+95×0.1=70.5,故C 正确;因为成绩在[40,70)内的频率为0.45,[70,80)的频率为0.3,所以中位数为70+10×0.050.3≈71.67,故D 错误.故选ABC .]11.甲、乙两班举行电脑汉字录入比赛,参赛学生每分钟录入汉字的个数经统计计算后填入下表:班级 参加人数中位数 方差 平均数 甲 55 149 191 135 乙55151110135A .甲、乙两班学生成绩的平均数相同B .甲班的成绩波动比乙班的成绩波动大C .乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀)D .甲班成绩的众数小于乙班成绩的众数ABC [甲、乙两班学生成绩的平均数都是135,故两班成绩的平均数相同,∴A 正确;s 2甲=191>110=s 2乙,∴甲班成绩不如乙班稳定,即甲班的成绩波动较大,∴B 正确;甲、乙两班人数相同,但甲班的中位数为149,乙班的中位数为151,从而易知乙班不少于150个的人数要多于甲班,∴C 正确;由题表看不出两班学生成绩的众数,∴D错误.]12.在某地区某高传染性病毒流行期间,为了建立指标来显示疫情已受控制,以便向该地区居民显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病例数计算,下列各选项中,一定符合上述指标的是()A.平均数x≤3B.平均数x≤3且标准差s≤2C.平均数x≤3且极差小于或等于2D.众数等于1且极差小于或等于4CD[A错,举反例:0,0,0,0,2,6,6,其平均数x=2≤3,不符合指标.B错,举反例:0,3,3,3,3,3,6,其平均数x=3,且标准差s=187≤2,不符合指标.C对,若极差等于0或1,在x≤3的条件下,显然符合指标;若极差等于2且x≤3,则每天新增感染人数的最小值与最大值有下列可能:(1)0,2,(2)1,3,(3)2,4,符合指标.D对,若众数等于1且极差小于或等于4,则最大值不超过5,符合指标.故选CD.]三、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中的横线上)13.下列数据的70%分位数为________.20,14,26,18,28,30,24,26,33,12,35,22.28[把所给的数据按照从小到大的顺序排列可得:12,14,18,20,22,24,26,26,28,30,33,35,因为有12个数据,所以12×70%=8.4,不是整数,所以数据的70%分位数为第9个数28.]14.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球的时间x(单位:小时)与当天投篮命中率y之间的关系:。
(常考题)人教版高中数学必修第二册第二单元《复数》检测卷(有答案解析)

一、选择题1.在复平面内与复数21i z i =+所对应的点关于虚轴对称的点为A ,则A 对应的复数为( )A .1i --B .1i -C .1i +D .1i -+ 2.已知复数()()31z m m i m Z =-+-∈在复平面内对应的点在第二象限,则1z =( )A B .2 C D .123.设复数z 满足()13i z i +=+,则z =( )A B .2 C .D 4.已知复数z 满足33z -=,则4z i -(i 为虚数单位)的取值范围为( )A .[]28,B .3⎤⎦C .[]1,9D .[]3,8 5.已知i 是虚数单位,复数z 满足()341z i i +=+,则z 的共轭复数在复平面内表示的点在( )A .第一象限B .第二象限C .第三象限D .第四象限6.复数51i i-的虚部是( ) A .12 B .2i C .12- D .2i - 7.已知复数1223,z i z a bi =+=+(,R,0a b b 且∈≠),其中i 为虚数单位,若12z z 为实数,则a b 的值为( ) A .32- B .23- C .23D .32 8.复数z 满足(12)3z i i +=+,则z =( )A .15i +B .1i -C .15i -D .1i +9.已知复数z 满足()15i z i -+=,则z =( )A .23i +B .23i -C .32i +D .32i - 10.在复平面内,复数201812z i i =++对应的点位于( ) A .第一象限B .第二象限C .第三象限D .第四象限 11.若11i ai++是纯虚数(其中i 为虚数单位),则实数a 等于( )A .1B .1-C .2D .2- 12.若32a i i -+为纯虚数,则实数a 的值为( ) A .32- B .23- C .23 D .32二、填空题13.已知1i z z -=-+,则复数z =______.14.已知1cos z isin αα=+,2cos z isin ββ=-,α,β为实数,i 为虚数单位,且125121313z z i -=+,则cos()αβ+的值为_______. 15.复数3(2) i (,)z x y x y =++-∈R ,且||2z =,则点(,)x y 的轨迹是_____________.16.若复数z 满足||1z =,则()()z i z i +-的最大值是________.17.已知i 为虚数单位,则(1)(23i)(32i)-+-+=________________;(2)(4i)(23i)+--+=________________;(3)已知复数13i z b =-,22i z a =-+,其中a ,b R ∈,若复数12z z z =+,且复数z 对应的点在第三象限,则+a b 的取值范围为________________;(4)在复平面内,复数1z 对应的点为(2,2)-,复数2z 对应的点为(1,1)-,若复数21z z z =-,则复数z 对应的点在第________________象限.18.已知复数z =a +3i 在复平面内对应的点位于第二象限,且|z|=2,则复数z 等于________.19.若复数 z =21i i-,则3z i + =__________ 20.如果复数z 的模不大于1,而z 的虚部的绝对值不小于,则复平面内复数z 的对应点组成图形的面积是___.三、解答题21.实数m 取什么值时,复数22(56)(215)z m m m m i =+++--(1)与复数212i -相等(2) 与复数1216i +互为共轭复数(3)对应的点在x 轴上方.22.化简下列复数(1)()()6532i i -++(2)()()()56234i i i -+---+23.已知关于x 的方程()2250x px p R -+=∈的两根为1x 、2x . (1)若134x i =+,求p 的值;(2)若121x x -=,求实数p 的值.24.如图,在复平面内,已知复数z 1,z 2,z 3对应的向量分别是OA OB OC ,,,i 是虚数单位,若复数123z z z z ⋅=,求11i 2z +.25.复数z 满足||1z =,且2120z z z++<.求z . 26.已知复数z 满足|z|2,2z 的虚部为2,z 所对应的点在第一象限,(1)求z ;(2)若z ,z 2,z-z 2在复平面上对应的点分别为A ,B ,C ,求cos ∠ABC .【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据复数的运算法则求出1z i =+,即可得到其对应点关于虚轴对称点的坐标,写出复数.【详解】由题()()()2122211112i i i i z i i i i -+====+++-,在复平面对应的点为(1,1), 关于虚轴对称点为(-1,1),所以其对应的复数为1i -+.故选:D【点睛】此题考查复数的几何意义,关键在于根据复数的乘法除法运算准确求解,熟练掌握复数的几何意义.2.C解析:C【解析】分析:由题意得到关于m 的不等式组,求解不等式组确定m 的范围,然后结合题意即可求得最终结果.详解:由题意可得:3010x m m Z -<⎧⎪->⎨⎪∈⎩,即13m <<且m Z ∈,故2m =,则:1z i =-+,由复数的性质112z z ===. 本题选择C 选项.点睛:本题主要考查复数的运算法则,复数的综合运算等知识,意在考查学生的转化能力和计算求解能力. 3.D解析:D【解析】分析:先根据复数除法得z ,再根据复数的模求结果.详解:因为()13i z i +=+,所以31(3)(1)212i z i i i i +==+-=-+,因此z =选D.点睛:首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b(,)a b 、共轭为.-a bi4.A解析:A【分析】 利用复数模长的三角不等式可求得4z i -的取值范围.【详解】()()4334z i z i -=-+-, 由复数模长的三角不等式可得()()334334334z i z i z i ---≤-+-≤-+-, 即35435z i -≤-≤+,即248z i ≤-≤,因此,4z i -的取值范围是[]28,.故选:A.【点睛】本题考查复数模长的取值范围的计算,考查三角不等式的应用,考查计算能力,属于中等题.5.A解析:A【分析】利用复数的运算法则、共轭复数的定义、几何意义即可得出.【详解】复数z 满足()341z i i +=+,∴()()()()3434134z i i i i +-=+-,∴257z i =-,∴712525z i =-. ∴712525z i =+. 则复平面内表示z 的共轭复数的点71,2525⎛⎫⎪⎝⎭在第一象限. 故选:A .【点睛】此题考查复数的运算和几何意义,涉及共轭复数概念辨析,关键在于熟练掌握运算法则,根据几何意义确定点的位置.6.A解析:A【解析】【分析】由题意首先化简所给的复数,然后确定其虚部即可.【详解】 由复数的运算法则可知:51i i-()()()1111122i i i i i +==-+-+, 则复数51i i-的虚部是12. 本题选择A 选项.【点睛】本题主要考查复数的运算法则,虚部的定义等知识,意在考查学生的转化能力和计算求解能力.7.B解析:B【分析】先根据复数乘法计算,再根据复数概念求a,b 比值.【详解】因为()1223(z z i a bi =++)()23(32a b a b =-++) i ,所以320a b +=,因为0b ≠,所以23a b =-,选B. 【点睛】本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b 、模为(,)a b 、共轭为.-a bi8.D解析:D【分析】把已知等式变形,利用复数代数形式的乘除运算化简求得1i z =-,利用共轭复数的定义可得结论.【详解】()12i 3i z +=+,()()()()3i 12i 3i 55i 1i 12i 12i 12i 5z +-+-∴====-++-, 所以1z i =+,故选D.【点睛】复数是高考中的必考知识,主要考查复数的概念及复数的运算.要注意对实部、虚部的理解,掌握纯虚数、共轭复数这些重要概念,复数的运算主要考查除法运算,通过分母实数化转化为复数的乘法,运算时特别要注意多项式相乘后的化简,防止简单问题出错,造成不必要的失分.9.B解析:B【解析】【分析】根据复数的运算法则计算即可.【详解】()15i z i -+=,()()()()51523111i i i z i i i i +-+∴===+++-, 2 3.z i ∴=-故选B.【点睛】本题考查了复数的运算法则和共轭复数的概念,属于基础题10.C解析:C【解析】 因为201812z i i =++()()22231122555i i i i i i --=+=-=--+- ,复数201812z i i=++对应的点的坐标为31,55⎛⎫-- ⎪⎝⎭ ,故复数201812z i i=++对应的点位于第三象限,故选C. 11.B解析:B【分析】 设11i bi ai+=+,化简后利用复数相等列方程求解即可. 【详解】 设()1,,1i bi a b R ai+=∈+, 所以()11i bi ai ab bi +=⋅+=-+,所以11ab b -=⎧⎨=⎩, 解得11a b =-⎧⎨=⎩, 故选:B .【点睛】本题主要考查复数的乘法运算,考查复数相等的性质,属于基础题.12.C解析:C【分析】先化简复数,再利用纯虚数的定义求解.【详解】 由题得()(32)(32)(23)32(32)(32)13a i a i i a a i i i i -----+==++-, 因为32a i i-+为纯虚数, 则320(23)0a a -=⎧⎨-+≠⎩,所以23a =. 故选:C【点睛】结论点睛:复数(,)z a bi a b R =+∈则0a =且0b ≠,不要漏掉了0b ≠.二、填空题13.【分析】设根据得到再利用复数相等的条件列出方程组求得的值即可求解【详解】设则因为所以即根据复数相等的条件得解得所以所以故答案为:【点睛】本题主要考查了复数相等的条件以及复数的模的计算公式的应用其中解 解析:i -【分析】设()i ,z x y x y =+∈R ,根据1i z z -=-+,得到(i 1i x y +=-+,再利用复数相等的条件列出方程组,求得,x y 的值,即可求解.【详解】设()i ,z x y x y =+∈R,则z = 因为1i z z -=-+,所以i 1i x y +=-+,即(i 1i x y +=-+,根据复数相等的条件得11x y ⎧⎪-=-⎨=⎪⎩,解得01x y =⎧⎨=⎩,所以i z =,所以i z =-. 故答案为:i -【点睛】本题主要考查了复数相等的条件,以及复数的模的计算公式的应用,其中解答中熟记复数模的计算公式和复数相等的条件,列出方程组求解是解答的关键,着重考查了推理与计算能力,属于基础题.14.【分析】根据复数减法和复数相等的条件列方程组结合两角和的余弦公式化简求得的值【详解】得即故答案为:【点睛】本小题主要考查复数减法和复数相等的条件考查两角和的余弦公式考查化归与转化的数学思想方法属于基 解析:12【分析】根据复数减法和复数相等的条件列方程组,结合两角和的余弦公式,化简求得cos()αβ+的值.【详解】1cos sin z i αα=+,2cos sin z i ββ=-,12512(cos cos )(sin sin )1313z z i i αβαβ∴-=-++=+,5cos cos ,1312sin sin ,13αβαβ⎧-=⎪⎪∴⎨⎪+=⎪⎩①② 22+①②,得22cos()1αβ-+=,即1cos()2αβ+=.故答案为:12【点睛】 本小题主要考查复数减法和复数相等的条件,考查两角和的余弦公式,考查化归与转化的数学思想方法,属于基础题.15.以为圆心2为半径的圆【分析】根据复数模的定义确定复数对应点满足条件化简即得轨迹【详解】解:∵∴即点的轨迹是以为圆心2为半径的圆故答案为:以为圆心2为半径的圆【点睛】本题考查复数模的定义以及圆的方程含 解析:以(3,2)-为圆心,2为半径的圆【分析】根据复数模的定义确定复数对应点满足条件,化简即得轨迹.【详解】解:∵||2z =,∴22(3)(2)4x y ++-=,即点(,)x y 的轨迹是以(3,2)-为圆心,2为半径的圆.故答案为:以(3,2)-为圆心,2为半径的圆【点睛】本题考查复数模的定义以及圆的方程含义,考查基本分析求解能力,属基础题. 16.【分析】设求出后再求其模利用可求模的最大值【详解】设则故其中当时故答案为:2【点睛】本题考查复数的乘法共轭复数以及复数的模处理复数的模的问题有两个思路:(1)利用复数的几何意义求解;(2)复数问题实 解析:2【分析】设,,z a bi a b R =+∈,求出()()z i z i +-后再求其模,利用221a b +=可求模的最大值.【详解】设,,z a bi a b R =+∈,则()()()22()()111z i z i a b i a b i a b +-=+-+-=+-⎡⎤⎡⎤⎣⎦⎣⎦,故()()z i z i +-==[]1,1b ∈-. 当1b =-时,max ()()2z i z i +-=,故答案为:2.【点睛】本题考查复数的乘法、共轭复数以及复数的模,处理复数的模的问题有两个思路:(1)利用复数的几何意义求解;(2)复数问题实数化即把复数的模的问题归结实部和虚部的问题(即实数范围内的问题),本题属于中档题.17.四【分析】(1)利用复数的加法法则计算即可;(2)利用复数的减法法则计算即可;(3)由题意可得则且据此可得的取值范围(4)由题意可得结合可得据此确定其所在的象限即可【详解】(1)(2)(3)因为所以解析:1i --62i -(,5)-∞四【分析】(1)利用复数的加法法则计算()()2332i i -+-+即可;(2)利用复数的减法法则计算()()423i i +--+即可;(3)由题意可得12(2)(3)i z z b a z =+=-+-,则2b <且3a <,据此可得+a b 的取值范围.(4)由题意可得122i z =-+,21z i =-,结合21z z z =-可得33z i =-,据此确定其所在的象限即可.【详解】(1)()()(23)(32)23321i i i i i -+-+=-+-+=--.(2)()()(4)(23)42362i i i i i +--+=++-=-.(3)因为13i z b =-,22i z a =-+,所以12(2)(3)i z z b a z =+=-+-,又复数z 对应的点在第三象限,所以2030b a -<⎧⎨-<⎩,所以2b <且3a <, 所以5a b +<,故+a b 的取值范围为(,5)-∞.(4)因为复数1z 对应的点为(2,2)-,复数2z 对应的点为(1,1)-,所以122i z =-+,21z i =-,又复数21z z z =-,所以1i (22i)33i z =---+=-,所以复数z 对应的点为(3,3)-,在第四象限【点睛】本题主要考查复数的加法、减法运算,复数所在象限的判定等知识,意在考查学生的转化能力和计算求解能力.18.【分析】由题意可得a <0由|z|=2可得a 的方程解出即得【详解】∵z=a+i 在复平面内对应的点位于第二象限∴a <0由|z|=2得=2解得a=﹣1或1(舍去)∴z=﹣1+i 故答案为﹣1+i 【点睛】该题解析:【分析】由题意可得a <0,由|z|=2,可得a 的方程,解出即得.【详解】∵i 在复平面内对应的点位于第二象限,∴a <0,由|z|=2,解得a=﹣1或1(舍去),∴z=﹣.故答案为﹣【点睛】该题考查复数的模、复数代数形式的表示及其几何意义,属基础题.19.【解析】分析:先化简复数z 再求再求 的值详解:由题得所以故答案为:点睛:(1)本题主要考查复数的运算共轭复数和复数的模的计算意在考查学生对这些知识的掌握水平和基本的运算能力(2)复数的共轭复数 解析:5 【解析】 分析:先化简复数z,再求3z i +,再求3z i + 的值. 详解:由题得2i 2i(1i)22i 1i 1i (1i)(1i)2z +-+====-+--+, 所以2231312,3(1)2 5.z i i i i z i +=--+=-+∴+=-+=故答案为:5.点睛:(1)本题主要考查复数的运算、共轭复数和复数的模的计算,意在考查学生对这些知识的掌握水平和基本的运算能力.(2) 复数(,)z a bi a b R =+∈的共轭复数,z a bi =-22||z a b =+.20.【解析】分析:先根据复数的模以及复数的虚部列不等式再根据扇形面积减去三角形面积得弓形面积详解:设则如图因此复平面内复数z 的对应点组成图形为两个弓形其面积为扇形面积减去三角形面积是点睛:本题重点考查复 解析:23-32π 【解析】分析:先根据复数的模以及复数的虚部列不等式,再根据扇形面积减去三角形面积得弓形面积.详解:设(,)z x yi x y R =+∈,则2211,2x y y +≤≥ ,如图,2.3AOB π∠=因此复平面内复数z 的对应点组成图形为两个弓形,其面积为扇形面积减去三角形面积是21212232(111sin )23233πππ⨯⋅-⨯⨯⨯=-点睛:本题重点考查复数的基本运算和复数的概念,属于基本题.首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b (,)a b 、共轭为.-a bi三、解答题21.(1)m =-1(2)m =1(3)m<-3或m>5.【解析】解:(1)根据复数相等的充要条件得22562{21512m m m m ++=--=-解得m =-1. (2)根据共轭复数的定义得225612{21516m m m m ++=--=-解得m =1. (3)根据复数z 的对应点在x 轴的上方可得m 2-2m -15>0,解得m<-3或m>5. 22.(1)93i -;(2)11i -.【分析】利用复数的加减运算法则求解.【详解】(1)()()6532i i -++,()()6325i =++-,93i =-.(2)()()()56234i i i -+---+,()()523614i =--+---,11i =-.【点睛】本题主要考查复数的加减,相等,还考查了运算求解的能力,属于中档题.23.(1)6;(2)p =或p =±【分析】(1)将134x i =+代入方程,将复数化为一般形式,利用复数相等可求得实数p 的值; (2)列出韦达定理,由121x x -=可得出关于p 的等式,由此可解得实数p 的值.【详解】(1)已知关于x 的方程()2250x px p R -+=∈的一根为134x i =+,所以,()()()()23434251832440i p i p p i +-++=-+-=,所以,1832440p p -=-=,解得6p ;(2)2100p ∆=-,由题意得121225x x p x x +=⎧⎨=⎩. 若0∆≥,即2100p ≥,则121x x -===,解得p =;若∆<0,即100p <,由2250x px -+=,可得22210024p p x ⎫-⎛⎫⎪-== ⎪⎪⎝⎭⎝⎭,解得12p x =+,22p x =,则121x x i -===,解得p =±.综上所述,p=或p =±【点睛】关键点点睛:解本题的关键在于以下两点:(1)在解第一问时,可利用实系数的二次方程的两个虚根互为共轭复数来求解; (2)在解第二问时,应对二次方程是否有实根进行分类讨论,并结合韦达定理求解. 24.3【分析】由题图可知,z 1=3+i ,z 2=1-2i ,z 3=-2+2i ,再求出复数z,再求i 2z +. 【详解】解:由题图可知,z 1=3+i ,z 2=1-2i ,z 3=-2+2i ,则123(3)(12)5222z z i i z z i ⋅+-===--+,∴532222z z +=-++==. 【点睛】本题主要考查复数的几何意义,考查复数的计算和模的求法,意在考查学生对这些知识的理解掌握水平,属于基础题.25.1z =-或122z =-± 【分析】由题意可知设复数cos sin z i αα=+,计算出2z ,2z ,1z ,代入2120z z z++<中可得cos 23cos 02sin cos sin 0ααααα+<⎧⎨+=⎩可求得复数z . 【详解】由题意可知:cos sin z i αα=+,则222cos sin 2sin cos z i αααα=-+,22cos 2sin z i αα=+,1cos sin i zαα=-, ∴212(cos23cos )(2sin cos sin )0z z i zααααα++=+++<, ∴cos 23cos 02sin cos sin 0ααααα+<⎧⎨+=⎩,即()cos 23cos 0sin 2cos 10αααα+<⎧⎨+=⎩, 若sin 0α=,则cos21α=,由cos23cos 0αα+<得cos 1α=-,所以1z =-,若1cos 2α=-,则1cos 2cos 23cos 02ααα=-+<,,得12z =-±,∴1z =-或12z =-±. 【点睛】本题考查复数的计算,关键在于设出复数z 的三角形式进行运算,理解复数小于零的含义,属于中档题.26.(1) z=1+i .(2) 【解析】分析:(1)设z=x+yi(x,y ∈R),根据题意得到x,y 的方程组,即得z.(2)先求z ,z 2,z-z 2在复平面上对应的点,再利用向量的夹角公式求cos ∠ABC.详解:(1)设z=x+yi(x,y ∈R).∵|z|=∴x 2+y 2=2. ①又z 2=(x+yi)2=x 2-y 2+2xyi,∴2xy=2,∴xy=1. ②由①②可1,-1,1-1.x x y y ==⎧⎧⎨⎨==⎩⎩解得或 ∴z=1+i 或z=-1-i.又x>0,y>0,∴z=1+i.(2)z 2=(1+i)2=2i,z-z 2=1+i-2i=1-i.如图所示,∴A(1,1),B(0,2),C(1,-1),()()BA 1,1,BC 1,3,∴=-=-∴cos ∠ABC BA?BC 255|BA||BC|21025====⨯ 点睛:(1)本题主要考查复数的求法和复数的几何意义,考查向量的夹角,意在考查学生对这些知识的掌握水平. (2) 设a =11(,)x y ,b =22(,)x y ,θ为向量a 与b 的夹角,则121222221122cos x y x y θ=+⋅+.。
(人教版A版)高中数学必修第二册 第七章综合测试试卷02及答案

第七章综合测试一、单项选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设1234i,23i z z =-+=-其中i 为虚数单位,则12z z +在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限2.已知i 为虚数单位,复数122i,2i z a z =+=-,且21z z =,则实数a 的值为( )A .1B .1-C .1或1-D .1±或03.复数:满足31i z z +=-(i 为虚数单位),则复数z 对应的点的轨迹是( )A .直线B .正方形C .圆D .射线4.已知复数(12i)(23i)z =++(i 是虚数单位),则z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限5.若复数z 满足(12i)5z +=,i 为虚数单位,则z 的虚部为( )A 2i-B .2C .2-D .2i6.定义运算a b ad bc c d =-,则符合条件1142i iz z -=+(i 是虚数单位)的复数z 在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限7.已知复数2349i+i +i +i ++i 1+iz =L (i 是虚数单位),则复数z 在复平面内对应的点为( )A .11,22æöç÷èøB .(1,1)C .11,22æö-ç÷èøD .(1,1)-8.设z 是纯虚数,i 是虚数单位,若21iz +-是实数,则z =( )A .2i -B .1i 2-C .1i 2D .2i9.对于复数,,,a b c d ,若集合{,,,}S a b c d =具有性质“对任意,x y S Î,必有xy S Δ,则当,,,a b c d 同时满足①1a =:②21b =;③2c b =时,b c d ++=( )A .1B .1-C .0D .i10.已知i 是虚数单位,给出下列命题,其中正确的是( )A .满足i i z z -=+的复数z 对应的点的轨迹是圆B .若2,i 1m Î=-Z ,则123i i i i 0m m m m ++++++=C .复数i z a b =+(其中,a b ÎR )的虚部为iD .在复平面内,实轴上的点都表示实数,虚轴上的点都表示虚数二、多项选择题(本大题共2小题,每小题5分,共10分.在每小题给出的四个选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)11.已知复数z ,下列结论正确的是( )A .“0z z +=”是“z 为纯虚数”的充分不必要条件B .“0z z +=”是“z 为纯虚数”的必要不充分条件C .“z z =”是“z 为实数”的充要条件D .“z z ÎR g ”是“z 为实数”的充分不必要条件12.设()()2225322i,z t t t t t =+-+++ÎR ,i 为虚数单位,则以下结论正确的是( )A .z 对应的点在第一象限B .z 一定不为纯虚数C .z 一定不为实数D .z 对应的点在实轴的下方三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题中横线上)13.已知i 为虚数单位,若复数24(2)i()z a a a =-+-ÎR 是纯虚数,则1z +=________;z z =g ________.(本题第一空2分,第二空3分)14.如图所示,网格中的小正方形的边长是1,复平面内的点Z 对应复数z ,则复数12z i-(i 为虚数单位)的共轭复数的虚部是________.15.若34i z =-(i 为虚数单位),则z z=________.16.复数12,z z 分别对应复平面内的点12M M 、,且1212z z z z +=-,线段12M M 的中点M 对应的复数为43i +(i 为虚数单位),则2212z z +=________.四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(本小题满分10分)已知复数z 满足13z i z =+-,i 是虚数单位,化简22(1i)(34i)2z++.18.(本小题满分12分)(1)已知m ÎR ,i 是虚数单位,复数()()2245215i z m m m m =--+--是纯虚数,求m 的值;(2)已知复数z 满足方程(2)i 0z z +-=,i 是虚数单位,求z 及|2i |z +的值.19.(本小题满分12分)(1)已知2i 1-(i 是虚数单位)是关于x 的方程10mx n +-=的根,,m n ÎR ,求+m n 的值;(2)已知2i 1-(i 是虚数单位)是关于x 的方程210x mx n ++-=的一个根,,m n ÎR ,求+m n 的值.20.(本小题满分12分)已知复数()21223(25)i,10i 15z a z a a a =+-=+--+,其中a 为实数,i 为虚数单位.(1)若复数1z 在复平面内对应的点在第三象限,求a 的取值范围;(2)若12z z +是实数(2z 是2z 的共轭复数),求1z 的值.21.(本小题满分12分)欧拉公式cos sin ix e x i x =+(e 为自然对数的底数,i 为虚数单位,x ÎR )是由瑞士著名数学家欧拉提出的,它将指数函数的定义域扩大到复数,阐述了三角函数和指数函数的关系,它在复变函数论里占有非常重要的地位,被誉为“数学中的天桥”,根据欧拉公式:(1)判断复数2i e 在复平面内对应的点位于第几象限,并说明理由;(2)若0ix e <,求cos x 的值.22.(本小题满分12分)若,42i,sin icos z z z w q q Î+=+=-C (q 为实数),i 为虚数单位.(1)求复数z ;(2)求z w -的取值范围.第七章综合测试答案解析一、1.【答案】B【解析】1234i,23i z z =-+=-Q ,1234i 23i 1i z z \+=-++-=-+,12z z \+在复平面内对应的点坐标为(1,1)-,位于第二象限,故选B .2.【答案】C【解析】因为复数12i z a =+,22i z =-,且12z z =,所以2441a +=+,解得1a =±,故选C .3.【答案】C【解析】设i(,)z x y x y =+ÎR ,则33i 1i i x y x y ++=+-,所以2222(31)9(1)x y x y ++=+-,即224430x y x y +++=.所以复数z 对应的点的轨迹为圆.故选C .4.【答案】B【解析】(12i)(23i)47i z =++=-+Q ,z \在复平面内对应的点的坐标为(4,7)-,位于第二象限,故选B .5.【答案】C 【解析】依题意得,512i 12iz ==-+,所以z 的虚部为2-,故选C .6.【答案】D【解析】依题意得,i 42i z z +=+,42i 3i 1iz +\==-+,对应的点的坐标为(3,1)-,位于第四象限,故选D .7.【答案】A 【解析】2349i i i i i i 1i 1i ==1i 1iz +++++--+++=++L L i (1i)i 11i 1i (1i)(1i)22-==+++-,所以复数z 在复平面呢对应的点的坐标为11,22æöç÷èø.8.【答案】A【解析】z Q 为纯虚数,\设i z b =(b ÎR 且0b ¹),则2i 2(i 2)(1i)21(2)i 1i 1i (1i)(1i)22z b b b b ++++-+===++---+,又21i z +-Q 为实数,1(2)02b \+=,即2b =-,2i z \=-.9.【答案】B【解析】由题意知1,i b c =-=±.当i c =时,满足性质“对任意,x y S Î,必有xy S Δ的d 为i -;同理,当i c =-时,i d =.综上可知,0c d +=,1b c d \++=-.10.【答案】B【解析】对于A ,满足i i z z -=+的复数:对应的点的轨迹是实轴,不是圆,A 错误;对于B ,若2,i 1m Î=-Z ,则123i i i i i (1i 1i)0m m m m n ++++++=+--=,B 正确;对于C ,复数i z a b =+(其中,a b ÎR )的虚部为b ,i 是虚数单位,C 错误;对于D ,在复平面内,实轴上的点都表示实数,虚轴上的点除原点外都表示虚数,D 错误.故选B .二、11.【答案】BC【解析】对于复数z ,若0z z +=,z 不一定为纯虚数,可以为0,反之,若z 为纯虚数,则0z z +=,\“0z z +=”是“z 为纯虚数”的必要不充分条件,A 错误,B 正确;“z z =”是“z 为实数”的充要条件,C 正确;若z z ×ÎR ,z 不一定为实数,也可以为虚数,反之,若z ÎR ,则z z ×ÎR .\“z z ×ÎR ”是“z 为实数”的必要不充分条件,D 错误.故选BC .12.【答案】CD【解析】对于A ,22549492532488t t t æö+-=+--ç÷èø>,2222(1)10t t t ++=++>,所以复数z 对应的点可能在第一象限,也可能在第二象限,故A 错误;对于B ,当222530,220,t t t t ì+-=ïí++¹ïî即3t =-或12t =时,z 为纯虚数,故B 错误;对于C ,因为2220t t ++>恒成立,所以z 一定不为实数,故C 正确;对于D ,由选项A 的分析知,z 对应的点在实轴的上方,所以z 对应的点在实轴的下方,故D 正确.故选CD .三、13.16【解析】Q 复数24(2)i()z a a a =-+-ÎR 是纯虚数,240,20,a a ì-=ï\í-¹ïî解得2a =-,4i z \=-,4i z =,114i z \+=-=,z z ×.14.【答案】1-【解析】由题图可知,点Z 的坐标为(2,1),2i z \=+,2i (2i)(12i)i 12i 12i (12i)(12i)z +++\===---+,其共轭复数为i -,\其共轭复数的虚数是1-.15.【答案】34i 55+【解析】依题意得,34i 55z z ==+.16.【答案】100【解析】设O 为坐标原点,由1212z z z z +=-知,以线段12,OM OM 为邻边的平行四边形是矩形,即12M OM Ð为直角,又M 是斜边12M M 的中点,5OM ==u u u r ,所以1210M M =u u u u u u r ,所以22222121212100z z OM OM M M +=+==u u u r u u u r u u u u u u r .四、17.【答案】解:设i(,)z a b a b =+ÎR ,则由13i z z =+-13i i 0a b -++=,10,30,a b +-=\-=ïî解得4,3,a b =-ìí=î43iz \=-+22(1i)(34i)2i(724i)247i (247i)(43i)34i 22(43i)43i (43i)(43i)z ++-++++\====+-+--+.18.【答案】(1)解:由复数z 是纯虚数,可得22450,2150,m m m m ì--=ïí--¹ïî即251,53,m k m m m ì==-ïí¹¹-ïî或且解得1m =-.(2)解:由题意可得,2i 2i(1i)1+i 1i (1i)(1i)z -===++-,从而1i z =-,所以2i (1i)z +=-+.19.【答案】(1)解:由已知得(2i 1)10m n -+-=,(1)2i 0n m m \--+=,10,20,n m m --=ì\í=î解得1,0,n m =ìí=î1m n \+=.(2)解:解法一:由已知得2(2i 1)(2i 1)10m n -+-+-=,(4)(24)i 0n m m \--+-=,40,240,n m m --=ì\í-=î解得6,2,n m =ìí=î8m n \+=.解法二:2i 1-Q 是实系数方程21=0x mx n ++-的根,\12i --也是此方程的根,因此,(12)(12),(12)(12)1,i i m i i n -++--=-ìí-+--=-î解得6,2,n m =ìí=î8m n \+=.20.【答案】(1)复数1z 在复平面内对应的点在第三象限,则20,1250.a a ìï-íï-î<解得1,5,2a a ìïíïî><即52a 1<<,故实数a 的取值范围是51,2æöç÷èø.(2)解:()22310i 5z a a =+-+Q ()22310i 5z a a \=--+()()22122332(25)i 10i (25)10i 1551z z a a a a a a a a éù\+=+-+--=++---ëû-++-.12z z +Q 是实数,()225100(15)a a a a \---=¹¹且.由()225100a a ---=得22150a a +-=,解得3a =或5a =-(舍).12(25)i 1i 1z a a \=+-=-+-,1z \=.21.【答案】(1)解:位于第二象限.理由如下:2i cos 2isin 2e =+在复平面内对应的点的坐标为(cos 2,sin 2),由于22pp <,因此cos2<0,sin 20>,\点(cos 2,sin 2)在第二象限,故复数2i e 在复平面内对应的点位于第二象限。
人教版高中数学必修二(全)教材配套章末检测题 附答案解析

人教版高一数学必修二教材配套检测题目录第一章空间几何体教材配套检测题 (2)第一章空间几何体章末检测题参考答案 (5)第二章点、直线、平面之间的位置关系教材配套检测题 (6)第二章点、直线、平面之间的位置关系章末检测题参考答案 (9)第三章直线与方程教材配套检测题 (11)第三章直线与方程检章末测题参考答案 (13)第四章圆与方程教材配套检测题 (16)第四章圆与方程章末检测题参考答案 (18)人教版高一数学必修二第一章 空间几何体 教材配套检测题一、选择题1. 下列命题中正确的是.A 有两个面平行,其余各面都是四边形的几何体叫棱柱 .B 有两个面平行,其余各面都是平行四边形的几何体叫棱柱.C 有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体叫棱柱.D 用一个平面去截棱锥,底面与截面之间的部分组成的几何体叫棱台2. 如下图所示,最左边的几何体由一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得,现用一个竖直的平面去截这个几何体,则所截得的截面图形可能是.A (1)(2) .B (1)(3) .C (1)(4) .D (1)(5) 3. 如图,一个空间几何体的正视图、侧视图、俯视图为全等 的等腰直角三角形,如果直角三角形的直角边的长为1,那么 这个几何体的体积为1.6A .B 12.C 13.D 14. 球的表面积与它的内接正方体的表面积之比为.A 3π .B 4π .C 2π .D π 5. 如下图所示的正方体中,M 、N 分别是1AA 、1CC 的中点,作四边形1D MBN ,则四边形1D MBN 在正方体各个面上的正投影图形中,不可能出现的是AC MN 1A (1)(2)(3)(5)AB CD6. 如图,在长方体1111ABCD A B C D -中,6AB =,4AD =,13AA =,分别过BC 、11A D 的两个平 行截面将长方体分成三部分,其体积分别记为111AEA DFD V V -=,11112EBE A FCF D V V -=,11113B E B C F C V V -=. 若123::1:4:1V V V =,则截面11A EFD 的面积为 .A .B .C .D 二、填空题7. 从长方体的一个顶点出发的三条棱上各取一点E 、F 、G ,过此三点作长方体的截面,那么截 去的几何体是 。
人教版高中数学必修二第二章《点、直线、平面之间的位置关系》单元试卷(1)

第二章过关检测(90 分 ,分 100 分)知点散布表知点号分点、、面的地点关系1,3,1212平行的判断及性2,4,5,6,7,10,16(1),17 、35垂直的判断及性5,7,8,13,15,16(2),18(1)31距离9,118角度14,16(3),18(2)14一、 (本大共10 小 ,每小 4 分,共 40 分)1.以下推理不正确的选项是()A.A ∈ b,A ∈ β,B∈ b, B bB.M∈ α,M∈ β,N∈ α,N∈βα∩β=直 MNC.直 m 不在α内 , A m AD.A、B、 C∈ α,A、B、 C∈ β,且 A、 B、C 不共α与β重合2.空两条直拥有以下条件之一,两直必定平行的是()A.同垂直于一条直B.同垂直于一个平面C.同平行于一个平面D.同在一个平面内3.异面直a、 b 分在平面α、β内,若α∩β=l,直l⋯()A. 分与 a、 b 订交B.与 a、b 都不订交C.起码与 a、 b 中之一订交D.至多与 a、 b 中之一订交4.下边四个命:①分在两个平面内的两直平行;②若两个平面平行,此中一个平面内的任何一条直必平行于另一个平面;③假如一个平面内的两条直线平行于另一个平面,则这两个平面平行;④假如一个平面内的任何一条直线都平行于另一个平面,则这两个平面平行.此中正确的命题是()A. ①②B. ②④C.①③D. ②③5.一个正方体纸盒睁开后如图,在原正方体纸盒中有以下结论:①AB ⊥EF;②AB 与 CM 成 60°角;③EF 与 MN 是异面直线 ;④MN∥CD.此中正确的选项是 ()A. ①②B. ③④C.②③D. ①③6.已知 a、b 是不重合的两条直线,α、β,γ是三个两两不重合的平面,给出以下四个命题:①若 a⊥ α,a⊥ β,则α∥ β;②若α⊥ γ,β⊥ γ,则α∥ β;③若α∥ β,a,b,则 a∥ b;④若α∥ β,α∩γ= a,β∩γ= b,则 a∥ b.此中正确的选项是 ()A. ①②B. ①③C.③④D. ①④7.(2009 苍山诚信中学·文科 )已知直线 l⊥平面α,直线m平面β,给出以下命题 :①α∥β l⊥ n;② α⊥ βl ∥ M;③l ∥ m α⊥β;④l ⊥ m α∥β.此中正确的命题是 ()A. ①②③B. ②③④C.②④D. ①③8.以下命题中 ,正确的选项是 ()A. 平面α⊥β,直线m∥ α,则m⊥ βB.l ⊥平面α,平面β∥直线l,则α⊥βC.直线l 是平面α的一条斜线,且l,则α与β必不垂直D.一个平面内的两条直线与另一平面内的两条直线分别平行,则这两个平面平行9.点 P 是等腰三角形ABC 所在平面外一点,PA⊥平面 ABC ,PA= 8,在△ ABC 中 ,底边=5,则 P 到 BC 的距离为 ()BC=6,ABA.45B.3C.33D.2310.如图 ,在三棱柱 ABCA′ B′C中,点 E、 F 、 H、 K 分别为 AC′、 CB′、 A′B、 B′ C的′中点 ,G 为△ ABC 的重心 ,从 K、 H 、G、B′中取一点作为 P,使得该棱柱恰有 2 条棱与平面 PEF 平行 ,则P为()A. KB.HC.GD.B′二、填空题 (本大题共 4 小题 ,每题 4 分,共 16分 )-1⊥ l 于 A11⊥ l 于 B11=A1B 1= 1,B1B=11.若二面角αlβ是直二面角 ,A∈ α,B∈β,AA,BB,且 AA2,M 是直线 l 上的一个动点 ,则 AM + BM 的最小值等于 _________.12.已知△ ABC 中 ,∠BAC= 90°,P 为平面 ABC 外一点 ,且 PA= PB=PC,则平面 PBC 与平面 ABC的地点关系是 __________.13.以以下图 ,在直四棱柱 A1B1C1 D1-DABC 中 ,当底面四边形ABCD 知足条件 ______________时,有 A1 B⊥ B1D 1注:填上你以为正确的一种条件即可,不用考虑全部可能的情况)14.以以下图 ,平面 ABC⊥平面 ABD ,∠ ACB= 90°,CA= CB,△ ABD 是正三角形 ,则二面角 G-BD -A 的平面角的正切值为 _________.三、解答题 (本大题共 4 小题 ,共 44 分 )15.(10 分 )如图 ,已知斜三棱柱ABC-A1B1C1的底面△ ABC 为直角三角形 ,∠ C= 90°,侧棱与底面成 60°角 ,点 B1在底面的射影D为BC的中点.求证 :AC⊥平面 BCC1B1 .16.(10 分 )以下图 ,在四棱锥 P-ABCD 中 ,底面 ABCD 是正方形 ,侧棱 PD ⊥底面 ABCD ,PD =DC,E 是 PC 的中点 .求证 :PA∥平面 EDB .17.(12 分 )已知正方体ABCD -A1B1C1D1.(1)求证 :平面 A1BD∥平面 B1D 1C;(2)若 E、 F 分别是 AA1、 CC1的中点 ,求证 :平面 EB1D1∥平面 FBD .18.(12 分 )△ ABC 是正三角形 ,线段 EA 和 DC 都垂直于平面ABC.设 EA= AB= 2a,DC = a,且 F 为 BE 的中点 ,如图 .(1)求证 :DF ∥平面 ABC;(2)求证 :AF⊥ BD;(3)求平面 BDF 与平面 ABC 所成二面角的大小 .参照答案1 分析:由空间中点、线、面的地点关系可知.答案: C2分析:垂直于同一平面的两直线平行 .答案: B3分析:若 l 与 a,b 都不订交 ,则 a∥ l,b∥l,知 a∥ b,与 a,b 是异面直线矛盾 .答案: C4分析:①明显不对 ;②是两平面平行的性质 ;③只有在这两条直线订交的前提下才正确;④是两平面平行的意义.答案: B5 分析:把纸盒睁开图复原成正方体即可.答案: D6 分析:①垂直于同向来线的两个平面平行,正确 ;②错误 ,用正方体考证;③ a 与 b 也可能异面 ,错误 ;④正确 .答案: D7 分析:①中,α∥β,l⊥α知l⊥ β,又∵ m,∴l ⊥m,故①正确 ;②中 ,∵ l⊥ α,α⊥ β,∴l ∥ β或l.∴l 与 m 订交 ,异面或平行 ,故②不确立 ;③中 ,∵ l∥ m,l ⊥α,∴m⊥ α.又m,∴ α⊥ β,故③正确 ;④中 ,举反例 : α⊥ β,α∩β= m,则知足前提 ,此时α与β不平行 ;故④错误 .答案: D8 分析:用正方体考证知,B 正确 .答案: B9 分析:作AD⊥BC于点D,连接PD ,易证PD⊥BC,故PD的长即为P 到 BC 的距离 .答案: A10 分析:若P为K点,则棱柱中A′B、AA′、BB′、CC′等均与平面PEF 平行 ,不合题意 .若 P 为 H 点 ,则棱柱中 B′C、′A′B、 A′C、 AB、 BC、 AC 均与平面 PEF 平行 ,也不合题意 .若 P 为 B′点,则棱柱中无棱与平面 PEF 平行 ,只有当 P 为 G 点时 ,棱柱中恰有 2 条棱 AB 、A′B′与平面 PEF 平行 .答案: C11 分析:绕二面角的棱l 旋转半平面α,使之与半平面β恰巧组成一个平面,此时 ,A、B 两点在直线 l 的异侧 ,连接 AB 与 l 的交点即为使AM + MB 为最小值的动点 M 在直线 l 上的地点 ,求得线段 AB 的长为10 .答案:1012分析:∵ PA=PB= PC,∴P 在△ ABC 所在平面上的射影必落在△ABC 的外心上 .又外心在 BC 上,设为 O,则 PO⊥平面 ABC.又 PO 平面PBC,∴平面 PBC⊥平面 ABC.答案:垂直13 分析:由条件知BC1⊥面 A1B1C1D1,∴BC 1⊥B1D 1.若 B1D 1⊥A1C1,则 B1D1⊥面 A1C1B.∴B1D1⊥ A1B.答案:对角线相互垂直14 分析:过C点作CO⊥AB,垂足为O,作OH⊥BD,垂足为H,连接CH .∵平面 ABC⊥平面 ABD,交线为 AB,∴CO⊥平面 ABD .∴CO⊥BD .又∵ OH⊥ BD ,OH∩OC=O,∴BD ⊥平面 COH .∴BD⊥CH.∴∠ CHO 为二面角C-BD-A 的平面角 .设 AC= CB= a,则 AB=BD = AD= 2a,CO 2 a . 2∴ OH132a 6 a .224CO 2 a2 3 2 3∴ tan CHO2OH6.∴应填. 33a 4答案:23315 证明 :∵ B1D⊥面 ABC,∴B1D⊥AC .又∵∠ C= 90°,BC⊥ AC,而 B1D∩BC= D,B1D 、BC平面BCC1B1,∴AC ⊥平面 BCC1B 1.16 证明 :连接 AC,AC 交 BD 于 O,连接 EO.由于底面 ABCD 是正方形 ,因此点 O是 AC 在△ PAC 中 ,EO 因此 PA∥ EO.的中点 . 是中位线,而 EO平面EDB,且PA平面EDB ,因此PA∥平面EDB .17 证明 :(1) 由 B1B∥DD 1,且 B 1B= DD 1,得 B1D 1∥ BD .由于 BD平面B1D1C,而 B1 D1平面B1D1C,因此 BD∥平面 B1D 1C.同理 A1D∥平面 B1D1C.又 A1D∩BD = D,因此平面 A1BD ∥平面 B1D1 C. (2) 由 BD ∥B1D 1,得 BD ∥平面 EB1D 1.取 BB1中点 G,连接 AG、GF,则 AE∥B1G 且 AE= B 1G,因此 B1E∥ AG.由 GF∥ BC 且 GF= BC,BC∥AD ,得 GF∥ AD 且 GF=AD ,因此 AG∥ DF 且 AG= DF .因此 B1E∥ DF .因此 DF ∥平面 EB 1D1.因此平面 EB 1D1∥平面 FBD .18(1) 证明 :以下图 ,取 AB 中点 G,连接 CG、FG .∵E F =FB,AG=GB,∴FG1 EA.又DC 21DC . 2∴四边形 CDFG 为平行四边形 ,故 DF∥CG.∵ DF平面ABC,CG平面ABC,∴D F ∥平面 ABC.(2) 证明 :∵ EA⊥平面 ABC,∴EA ⊥CG.又△ ABC 是正三角形,∴CG⊥ AB.∴CG⊥平面 AEB.∴CG⊥AF.又∵ DF∥CG,∴DF ⊥AF.又 AE=AB ,F 为 BE 中点 ,∴A F ⊥BE.又 BE∩DF = F,∴A F ⊥平面 BDE .∴A F ⊥BD.(3)解 :延伸 ED 交 AC 延伸线于 G′,连接 BG ′.由 CD1 AE ,CD∥AE知D为EG′中点,2∴F D ∥ BG′.由 CG⊥平面 ABE,FD ∥ CG,∴BG′⊥平面 ABE.∴∠ EBA 为所求二面角的平面角.在等腰直角三角形AEB 中 ,易求∠ ABE= 45°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(人教版)高中数学必修二(全册)单元测试卷汇总阶段通关训练(一)(60分钟100分)一、选择题(每小题5分,共30分)1.已知某几何体的三视图如图所示,那么这个几何体是( )A.长方体B.圆柱C.四棱锥D.四棱台【解析】选A.该几何体是长方体,如图所示.2.以钝角三角形的较小边所在的直线为轴,其他两边旋转一周所得到的几何体是( )A.两个圆锥拼接而成的组合体B.一个圆台C.一个圆锥D.一个圆锥挖去一个同底的小圆锥【解析】选D.如图以AB为轴所得的几何体是一个大圆锥挖去一个同底的小圆锥.3.已知△ABC是边长为2a的正三角形,那么△ABC的平面直观图△A′B′C′的面积为( )A. a2B.a2C.a2D.a2【解析】选C.直观图面积S′与原图面积S具有关系:S′=S.因为S△ABC=(2a)2=a2,所以S△A′B′C′=×a2=a2.【补偿训练】某三角形的直观图是斜边长为2的等腰直角三角形,如图所示,则原三角形的面积是________.【解析】根据直观图和原图形的关系可知原图形的面积为×2×2=2.答案:24.某三棱锥的三视图如图所示,则该三棱锥的体积是( )A. B. C. D.1【解析】选 B.由三视图可判断该三棱锥底面为等腰直角三角形,三棱锥的高为2,则V=××1×1×2=.【补偿训练】已知正三棱锥V-ABC的正视图、侧视图和俯视图如图所示,则该正三棱锥侧视图的面积是( )A. B.6 C.8 D.6【解析】选D.如图,根据三视图间的关系可得BC=2,所以侧视图中VA′==2,所以三棱锥侧视图面积S△×2×2=6,故选D.VBC=5.(2016·蚌埠高二检测)若一个圆锥的侧面展开图是面积为2π的半圆面,则该圆锥的体积为( )A.πB.πC.πD.【解析】选A.设圆锥的母线长为l,底面半径为r,由题意解得所以圆锥的高为h==,V=πr2h=π×12×=π.6.(2016·雅安高二检测)设正方体的全面积为24,那么其内切球的体积是( ) A.π B.π C.π D.π【解析】选B.正方体的全面积为24,所以,设正方体的棱长为a,6a2=24, a=2,正方体的内切球的直径就是正方体的棱长,所以球的半径为1,内切球的体积:V=π.二、填空题(每小题5分,共20分)7.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为________.【解题指南】根据面积比等于相似比的平方建立关于高的等式求解. 【解析】设棱台的高为x,则有=,解之,得x=11.答案:118.(2016·绍兴高二检测)已知几何体的三视图(如图),则该几何体的体积为________,表面积为________.【解析】根据三视图分析可知,该几何体为一底面边长为2的正四棱锥,其高h==,所以体积V=×22×=,表面积S=4××2×+22=4+4.答案:4+49.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是________.【解析】如图所示,由V=Sh得,S=4,即正四棱柱底面边长为2.所以A1O1=,A1O=R=.所以S球=4πR2=24π.答案:24π10.圆台的底面半径分别为1和2,母线长为3,则此圆台的体积为________.【解析】圆台的高h==2,所以体积V=(R2+Rr+r2)h=π.答案:π三、解答题(共4小题,共50分)11.(12分)如图几何体上半部分是母线长为5,底面圆半径为3的圆锥,下半部分是下底面圆半径为2,母线长为2的圆台,计算该几何体的表面积和体积.【解析】圆锥侧面积为S1=πr l=15π,圆台的侧面积为S2=π(r+r′)l=10π,圆台的底面面积为S底=πr′2=4π,所以表面积为:S=S1+S2+S底=15π+10π+4π=29π;圆锥的体积V1=πr2h1=12π,圆台的体积V2=πh2(r2+rr′+r′2)=π,所以体积为:V=V1+V2=12π+π.12.(12分)如图是一个几何体的正视图和俯视图.(1)试判断该几何体是什么几何体?(2)画出其侧视图,并求该平面图形的面积.(3)求出该几何体的体积.【解析】 (1)由该几何体的正视图和俯视图可知该几何体是一个正六棱锥.(2)该几何体的侧视图如图.其中AB=AC,AD⊥BC,且BC的长是俯视图正六边形对边的距离,即BC=a,AD是正六棱锥的高,即AD=a,所以该平面图形的面积为·a·a=a2.(3)设这个正六棱锥的底面积是S,体积为V,则S=6×a2=a2,所以V=×a2×a=a3.13.(13分)如图所示,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.【解析】S表面=S圆台底面+S圆台侧面+S圆锥侧面=π×52+π×(2+5)×5+π×2×2=(4+60)π.V=V圆台-V圆锥=π(+r1r2+)h-πh′=π(25+10+4)×4-π×4×2=π.14.(13分)(2016·湖北实验中学高一检测)如图,△ABC中,∠ACB=90°,∠ABC=30°,BC=,在三角形内挖去一个半圆(圆心O在边BC上,半圆与AC,AB分别相切于点C,M,与BC交于点N),将△ABC绕直线BC旋转一周得到一个旋转体.(1)求该几何体中间一个空心球的表面积的大小.(2)求图中阴影部分绕直线BC旋转一周所得旋转体的体积.【解析】(1)连接OM,则OM⊥AB,设OM=r,则OB=-r,在△BMO中,sin∠ABC===,所以r=,所以S=4πr2=π.(2)因为△ABC中,∠ACB=90°,∠ABC=30°,BC=,所以AC=1,所以V=V圆锥-V球=π×AC2×BC-πr3=π×12×-π=. 【能力挑战题】(2016·葫芦岛高一检测)如图,一个圆锥的底面半径为2cm,高为6cm,其中有一个高为xcm的内接圆柱.(1)试用x表示圆柱的侧面积.(2)当x为何值时,圆柱的侧面积最大.【解题指南】(1)由题意作出几何体的轴截面,根据轴截面和比例关系列出方程,求出圆柱的底面半径,再表示出圆柱的侧面积. (2)由(1)求出的圆柱侧面面积的表达式,根据二次函数的性质求出圆柱侧面面积的最大值.【解析】(1)设所求的圆柱的底面半径为r,它的轴截面如图:由图得,=,即r=2-,所以S圆柱侧=2πrx=2πx=4πx-x2.(2)由(1)知当x=-=3时,这个二次函数有最大值为6π,所以当圆柱的高为3cm时,它的侧面积最大为6πcm2.关闭Word文档返回原板块温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
阶段通关训练(二)(60分钟100分)一、选择题(每小题5分,共30分)1.(2016·吉安高二检测)下列说法中正确的是( )A.三点确定一个平面B.两条直线确定一个平面C.两两相交的三条直线一定在同一平面内D.过同一点的三条直线不一定在同一平面内【解析】选D.选项A中,缺条件“不共线”;选项B中,须指明这两条直线的位置关系,比如两条异面直线就不能确定一个平面;选项C 中,两两相交的三条直线当相交于同一点时,它们可以不在同一平面内,比如正方体中同一顶点的三条棱.2.如图,已知△ABC为直角三角形,其中∠ACB=90°,M为AB的中点,PM垂直于△ABC所在平面,那么( )A.PA=PB>PCB.PA=PB<PCC.PA=PB=PCD.PA≠PB≠PC【解析】选 C.因为M为AB的中点,△ACB为直角三角形,所以BM=AM=CM,又PM⊥平面ABC,所以Rt△PMB≌Rt△PMA≌Rt△PMC,故PA=PB=PC.3.(2016·成都高二检测)如图,已知三条长度相等的线段AB,BC,CD,若AB⊥BC,BC⊥CD,且直线AB与CD所成角大小为60°,则直线AD与BC所成角大小为( )A.90°B.60°C.45°D.30°【解析】选C.如图,过B作BE CD,连接DE,AE,则四边形BCDE 为正方形,∠ABE为直线AB与CD所成角,∠ADE为直线AD与BC所成角.因为AB=BC=CD=BE,∠ABE=60°,所以AB=BE=AE.因为AB⊥BC,所以AB⊥DE,又BE⊥DE,AB∩BE=B,所以DE⊥平面ABE,所以DE⊥AE,所以△AED为等腰直角三角形,所以∠ADE=45°.【拓展延伸】求异面直线所成角的方法求异面直线所成角主要是如何通过平移作出其平面角,主要途径有:利用三角形的中位线、构造平行四边形、利用梯形两底平行、平行线分线段成比例的性质等,如本题通过利用条件中的垂直关系构造正方形,达到平移的目的.【补偿训练】(2016·台州高二检测)如图,在正方体ABCD-A1B1C1D1中,异面直线A1D与D1C所成的角为( )A.30°B.45°C.60°D.90°【解析】选C.由题可知,在正方体ABCD-A1B1C1D1中,A1B∥D1C,所以异面直线A1D与D1C所成的角与直线A1D与A1B所成的角相等,连接A1B,BD,∠BA1D为所求角,设正方体的棱长为1,在△A1DB中,三条边长均为,故∠BA1D=60°.4.(2016·北京高二检测)已知直线m和平面α,β,则下列四个命题中正确的是( )A.若α⊥β,m⊂β,则m⊥αB.若α∥β,m⊥α,则m ⊥βC.若α∥β,m∥α,则m∥βD.若m∥α,m∥β,则α∥β【解析】选B.若α⊥β,m⊂β,则直线m与平面α相交,或直线m 在平面α内,或直线m与平面α平行,所以选项A不正确;若α∥β,m∥α,则直线m与平面β平行,或直线m在平面β内,所以选项C 不正确.若m∥α,m∥β,则α∥β或α与β相交,所以选项D不正确.5.(2016·辽宁师大附中高一检测)如图,六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,则下列结论不正确的是( )A.CF⊥平面PADB.DF⊥平面PAFC.CF∥平面PABD.CD∥平面PAF【解析】选A.因为六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC.则AF∥CD,由线面平行的判定定理,可得CD∥平面PAF,故D正确;DF⊥AF,DF⊥PA,由线面垂直的判定定理可得DF⊥平面PAF,故B正确;CF∥AB,由线面平行的判定定理,可得CF∥平面PAB,故C正确;CF与AD不垂直,故A中,CF⊥平面PAD不正确.6.已知矩形ABCD,AB=1,BC=,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中( )A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直【解析】选B.A错误.理由如下:过A作AE⊥BD,垂足为E,连接CE,若直线AC与直线BD垂直,则可得BD⊥平面ACE,于是BD⊥CE,而由矩形ABCD边长的关系可知BD与CE并不垂直.所以直线AC与直线BD不垂直.B正确.理由:翻折到点A在平面BCD内的射影恰好在直线BC上时,平面ABC⊥平面BCD,此时由CD⊥BC可证CD⊥平面ABC,于是有AB ⊥CD.故B正确.C错误.理由如下:若直线AD与直线BC垂直,则由BC⊥CD可知BC ⊥平面ACD,于是BC⊥AC,但是AB<BC,在△ABC中∠ACB不可能是直角.故直线AD与直线BC不垂直.由以上分析显然D错误.二、填空题(每小题5分,共20分)7.下列说法:①若a∥b,a∥α,则b∥α;②若a∥α,b⊂α,则a∥b;③若a∥α,则a平行于α内所有的直线;④若a∥α,a∥b,b⊄α,则b∥α.其中正确说法的序号是________.【解析】①中b可能在α内;②a与b还可能异面或者垂直;③a还可能与α内的直线异面或垂直.答案:④8.如图,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA上一点,当点E满足条件:________时,SC∥平面EBD.【解析】当点E是SA的中点时,连接AC.设AC与BD的交点为O,连接EO.因为四边形ABCD是平行四边形,所以点O是AC的中点.又E是SA的中点,所以OE是△SAC的中位线.所以OE∥SC.因为SC⊄平面EB D,OE⊂平面EBD,所以SC∥平面EBD.答案:点E是SA的中点9.已知四棱锥P-ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E,F 分别是棱PC,PD的中点,则①棱AB与PD所在直线垂直;②平面PBC与平面ABCD垂直;③△PCD的面积大于△PAB的面积;④直线AE与直线BF是异面直线.以上结论正确的是________.(写出所有正确结论的编号)【解析】由条件可得AB⊥平面PAD,所以AB⊥PD,故①正确;若平面PBC⊥平面ABCD,由PB⊥BC,得PB⊥平面ABCD,从而PA∥PB,这是不可能的,故②错;S△PCD=CD·PD,S△PAB=AB·PA,由AB=CD,PD>PA知③正确;由E,F分别是棱PC,PD的中点,可得EF∥CD,又AB∥CD,所以EF∥AB,故AE与BF共面,④错.答案:①③10.(2016·西宁高二检测)在四面体ABCD中,AB⊥AD,AB=AD=BC=CD=1,且平面ABD⊥平面BCD,M为AB中点,则CM与平面ABD所成角的正弦值为________.【解析】如图所示,取BD中点O,连接CO,MO,由已知条件BC=CD=1,所以BD⊥CO,由平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,所以CO⊥平面ABD,则∠CMO即为直线CM与平面ABD所成的角,由AB ⊥AD,所以BD=,则得到BC⊥CD,所以CO=BD=,MO=AD=,所以在Rt△COM中,CM==,所以sin∠CMO===.答案:三、解答题(共4小题,共50分)11.(12分)(2016·台州高二检测)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,点M,N分别是AB,PC的中点,PA=AD=a.(1)求证:MN∥平面PAD.(2)求证:平面PMC⊥平面PCD.【证明】(1)设PD的中点为点E,连接AE,NE,由点N为PC的中点知EN DC,又ABCD是矩形,所以DC AB,所以EN AB,又点M是AB的中点,所以EN AM,所以AMNE是平行四边形,所以MN∥AE,而AE⊂平面PAD,NM⊄平面PAD,所以MN∥平面PAD.(2)因为PA=AD,所以AE⊥PD,又因为PA⊥平面ABCD,CD⊂平面ABCD,所以CD⊥PA,而CD⊥AD,所以CD⊥平面PAD,所以CD⊥AE,因为PD ∩CD=D,所以AE⊥平面PCD,因为MN∥AE,所以MN⊥平面PCD,又MN⊂平面PMC,所以平面PMC⊥平面PCD.【补偿训练】(2016·济南高一检测)如图所示,平面四边形PACB中,∠PAB为直角,△ABC为等边三角形,现把△PAB沿着AB折起,使得△APB与△ABC垂直,且点M为AB的中点.(1)求证:平面PAB⊥平面PCM.(2)若2PA=AB,求直线BC与平面PMC所成角的正弦值.【解析】(1)因为平面APB⊥平面ABC且交线为AB,又因为∠PAB为直角,所以AP⊥平面ABC,故AP⊥CM,又因为△ABC为等边三角形,点M为AB的中点,所以CM⊥AB,又因为PA∩AB=A,所以CM⊥平面PAB,又CM⊂平面PCM,所以平面PAB⊥平面PCM.(2)假设PA=a,则AB=2a,再设B到平面PMC的距离为h B.则V P-MBC=V B-PMC =PA·S△MBC=h B·S PMC,在直角三角形PAM中,由PA=AM=a,得PM=a,在等边三角形ABC中,AB边上的高CM=a,而三角形PMC为直角三角形,故面积为S△PMC=CM·PM=·a·a=a2.又S△MBC=S△ABC=a2.所以a·a2=h B·a2.故h B= a.所以直线BC与平面PMC所成角的正弦值sinθ===.12.(12分)如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,点D,E分别在棱PB,PC上,且DE∥BC.(1)求证:BC⊥平面PAC.(2)是否存在点E使得二面角A-DE-P为直二面角?并说明理由. 【解析】(1)因为PA⊥底面ABC,所以PA⊥BC.又∠BCA=90°,所以AC⊥BC.又因为AC∩PA=A,所以BC⊥平面PAC.(2)因为DE∥BC,又由(1)知,BC⊥平面PAC,所以DE⊥平面PAC.又因为AE⊂平面PAC,PE⊂平面PAC,所以DE⊥AE,DE⊥PE.所以∠AEP为二面角A-DE-P的平面角.因为PA⊥底面ABC,所以PA⊥AC,所以∠PAC=90°.所以在棱PC上存在一点E,使得AE⊥PC.这时∠AEP=90°,故存在点E,使得二面角A-DE-P为直二面角.13.(13分)(2016·杭州高二检测)已知直角梯形ABCD和矩形CDEF所在的平面相互垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,DC=8,(1)证明:BD⊥平面BCF.(2)设二面角E-BC-D的平面角为α,求sinα.(3)M为AD的中点,在DE上是否存在一点P,使得MP∥平面BCE?若存在,求出DP的长;若不存在,请说明理由.【解析】(1)因为平面ABCD⊥平面CDEF,且矩形CDEF中FC⊥DC,所以FC⊥面ABCD,FC⊥DB,在直角梯形ABCD中易得DB⊥BC,又FC∩BC=C,所以BD⊥平面BCF.(2)因为FC⊥平面ABCD,ED∥FC,所以ED⊥平面ABCD,又DB⊥BC,所以EB⊥BC,所以∠EBD为二面角E-BC-D的平面角α,所以sinα=sin∠EBD===.(3)猜想DP=1.取ED,EC的四等分点P,Q,使得ED=4PD,EC=4QC,则PQ∥CD,PQ=CD=6,取BC中点N,连接MN,NQ,则MN∥CD,MN=(CD+AB)=6,所以PQ MN,所以四边形PQNM为平行四边形,所以MP∥QN,又因为MP⊄平面BCE,QN⊂平面BCE,所以MP∥平面BCE.14.(13分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:平面ABE⊥平面B1BCC1.(2)求证:C1F∥平面ABE.(3)求三棱锥E-ABC的体积.【解析】(1)在三棱柱ABC-A1B1C1中,BB1⊥底面ABC,所以BB1⊥AB.又因为AB⊥BC,BB1∩BC=B,所以AB⊥平面B1BCC1,又AB⊂平面ABE,所以平面ABE⊥平面B1BCC1.(2)取AB的中点G,连接EG,FG. 因为E,F分别是A1C1,BC的中点,所以FG∥AC,且FG=AC.因为AC∥A1C1,且AC=A1C1,所以FG∥EC1,且FG=EC1,所以四边形FGEC1为平行四边形.所以C1F∥EG.又因为EG⊂平面ABE,C1F⊄平面ABE,所以C1F∥平面ABE.(3)因为AA1=AC=2,BC=1,AB⊥BC,所以AB==.所以三棱锥E-ABC的体积V=S△ABC·AA1=×××1×2=.【能力挑战题】(2016·桂林高二检测)如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC的中点.(1)求证:AB⊥PE.(2)求二面角A-PB-E的大小.【解题指南】(1)连结PD,根据等边三角形三线合一可证得PD⊥AB,由中位线可得DE∥BC,即可得DE⊥AB,根据线面垂直的判定定理可证得AB⊥平面PDE,从而可证得AB⊥PE.(2)由面面垂直的性质定理可证得PD⊥平面ABC,从而可证DE⊥PD,根据线面垂直的判定定理可证得DE⊥平面PAB,过D作DF垂直PB于F,连接EF,则EF⊥PB.根据二面角的定义可知∠DFE即为所求,在△DEF中求∠DFE即可. 【解析】(1)连结PD,因为PA=PB,D为AB的中点,所以PD⊥AB.因为D,E分别为AB,AC的中点,所以DE∥BC,又因为BC⊥AB,所以DE⊥AB.又PD∩DE=D,所以AB⊥平面PDE,因为PE⊂平面PDE,所以AB⊥PE.(2)因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,所以PD⊥平面ABC,所以DE⊥PD.又ED⊥AB,PD∩AB=D,所以DE⊥平面PAB,过D作DF垂直PB于F,连接EF,则EF⊥PB,所以∠DFE为所求二面角的平面角,则:DE=,DF=,则tan∠DFE==,故二面角A-PB-E的大小为60°.关闭Word文档返回原板块温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
