MATLAB软件设计上机指南
Matlab 上机操作指南和要求2

Matlab 上机操作指南和要求-2
1.本次课重点要实践的内容
第二讲数值及计算方法课程实践练习:
a)Matlab 数值计算功能;向量、矩阵、数组、多项式的各类
运算。
b)Matlab符号运算,关系运算符。
c)数学问题的求解和应用实例。
2. 上机方法
1)开机:选择winxp- 1 进入系统。
2)登录到ftp://10.101.4.8 /下,登录:用户名:zhanghongdown;密码:zhanghongdown,进入到“zhanghongdown“目录下,打开“上机课程-2”目录下“Matlab上机操作指南和要求 2.doc”以及“上机作业-1.doc”。
3.本次课任务
参考第二讲课件内容,完成上机作业-1中的题目。
作业格式:
将作业程序内容和结果按照题号拷贝到word文件中,文件命名为:某某上机作业 1.doc,可参考“上机课程-2”下的例子。
4.交作业方式:
登录到ftp://10.101.4.8 /下,登录:用户名:zhanghongup;密码:zhanghongup,进入到“zhanghongup“目录下,将自己的作
业拷贝到自己的目录下,文件名称命名如下:
某某上机作业 1.doc
如以后某次作业有补充或修改,进入该目录下将补充或修改内容的文件放在该目录下。
以后的每次作业在本地机上完成后,都上传到ftp自己目录下。
如无法提交,可将作业发到邮箱sunwithmoon@中或zhanghong@中。
matlab上机实验指导书

MATLAB应用基础实验指导书第一章 MATLAB及其工作环境介绍 (1)1.1 MATLAB简介 (1)1.2 MATLAB的工作环境介绍 (1)1.3 MATLAB的基本管理命令 (4)第二章 MATLAB的数值计算功能 (5)2.1 变量与赋值语句 (5)2.2 MATLAB矩阵 (5)2.3 MATLAB表达式 (10)2.4 MATLAB常用数学函数 (11)2.5 矩阵的基本运算 (12)2.6 数组运算 (16)2.7 多项式及其运算 (17)第三章 MATLAB程序设计入门 (19)3.1 M文件 (19)3.2 数据的输入输出 (21)3.3 全局变量和局部变量 (23)3.4 程序流程控制 (23)第四章 MATLAB的符号运算功能 (28)4.1 建立符号对象 (28)4.2 符号算术运算 (29)4.3 符号微积分运算 (32)4.4 符号函数的可视化 (34)第五章 MATLAB的可视化功能 (37)5.1 二维图形 (37)5.2绘制三维图形 (42)5.3 特殊坐标图形 (44)5.4 图形句柄 (45)第一章 MATLAB及其工作环境介绍1.1 MATLAB简介MATLAB是matrix和laboratory前三个字母的缩写,意思是实验室矩阵。
MATLAB 语言是一种广泛应用于工程计算及数值分析领域的新型高级语言,自1984年由美国MathWorks公司推向市场以来,经过十多年的发展与完善,MATLAB已发展成为由MATLAB语言、MATLAB工作环境、MATLAB图象处理系统、MATLAB数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的体系。
MATLAB由“主包”和三十多个扩展功能和应用学科性的工具箱组成。
MATLAB具有以下基本功能:●数值计算功能●符号计算功能●图形处理及可视化功能●可视化建模及动态仿真功能MATLAB语言是以矩阵计算为基础的程序设计语言,语法规则简单易学。
MATLAB上机实习指导书

MATLAB上机实习指导书目录实习内容一MATLAB基本操作-----------------------------------2 实习内容二数值数组及其运算---------------------------------8 实习内容三MATLAB图形绘制基础-------------------------------15 实习内容四SIMULINK仿真基础---------------------------------22 附录1 流程控制------------------------------------------------24 附录2 SIMULINK的库模块-------------------------------------- 25附录3 转义符号------------------------------------------------27实习内容一MATLAB基本操作一、实习目的掌握MATLAB的启动和退出;熟悉MATLAB的命令窗口;熟悉其它常用窗口和工具栏。
二、实习内容与步骤1、进入MATLAB的开发环境。
方法一:点击桌面上的快捷方式或matlab\文件夹下的快捷方式图标。
方法二:开始→所有程序→MA TLAB6.5→MATLAB6.5.EXE。
方法三:点击matlab\bin\win32文件夹下的matlab.exe。
这三种方法的当前目录不同。
优先选用方法一。
可见到如下交互界面(见图1-1):图1-1 Matlab默认桌名平台2、退出MATLAB的开发环境。
退出Matlab的方式很多:(1)在Matlab命令窗口的“File”菜单下选择“Exit Matlab”;(2)快捷键“Ctrl+q”;(3)在命令窗口输入“quit”命令;(4)在命令窗口输入“exit”命令;(5)用鼠标单击命令窗口右上角的“X”按钮;(6)用鼠标双击命令窗口左上角的图标“”。
Matlab第一教学与上机讲述免费全文阅读

3)文件名:无空格、无中文的文件夹作为程序的安 装文件夹。
第一章 MATLAB操作基础
二、 MATLAB 安装
具体安装:
第一章 MATLAB操作基础
三、MATLAB的开发环境
1、MATLAB系统的组成 ① MATLAB开发环境 ② MATLAB数学函数库 ③ MATLAB语言 ④ 图形功能 ⑤ 应用程序接口 五个部分。
(5)隐藏窗口
命令输入: edit---文本程序编辑窗口 figure---图像窗口 guide---guide窗口 也可在菜单栏中选择对应窗口
选择窗口的显示形式: Desktop—Desktop Layout
四、MATLAB的启动与退出
1、MATLAB系统的启动 (1)在桌面上双击MATLAB快捷方式图标。 (2)在开始菜单中单击MATLAB项。 (3)在MATLAB安装目录中双击MATLAB快捷方式
MATLAB的帮助系统(续)
④>>lookfor image %查找有关图像的函数和命令。 2、在线帮助浏览器
MATLAB设计了全新的在线帮助浏览器, 当在View菜单中选择了Help选项,或在Help菜 单中选择了MATLAB Help选项时,都可以打 开帮助浏览器。 3、演示帮助
选择Help菜单中的Demos选项,可以打开 演示窗口,观看要查询项的动画演示。
函数的主要用法。
实验一 MATLAB熟悉与操作 基础
三、实验内容(续) (1) 已知a=73,求a的平方根;
(2)已知x的值域区间为1π-4π,求其正
玄值,余玄值。
实验一 MATLAB熟悉与操作基础
四、完成上机实验报告;并在下节课之 前上交。
matlab上机实验指导书

《MATLAB软件与程序设计》学生上机实验任务书姓名:高云鹏学号:13530104班级:13级工程力学指导教师:郭秀婷兰州理工大学理学院实验一 MATLAB 运算基础一、实验目的1.熟悉启动和退出MATLAB 的方法;2.熟悉MATLAB 集成环境的组成;3.掌握MATLAB 各种表达式、变量的书写规则以及常用函数的使用。
4.掌握建立矩阵及矩阵拆分的方法;5,.掌握MA TLAB 运算二、实验内容1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1))1ln(212x x z ++=,其中⎥⎦⎤⎢⎣⎡-+=545.0212i x ; (2)0.3,9.2,8.2,,8.2,9.2,0.3,23.0ln )3.0sin(23.03.0 ---=+++-=-a aa e e z a a 2.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=723302131,76538773443412B A ,求下列表达式的值: ⑴I B A B A +-+和*6(其中I 为单位矩阵);⑵B A B A *.*和; ⑶3.^3^A A 和; ⑷B A B A \/和;⑸]2^:);],3,1([[],[B A B A 和.3.已知: ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=14.35454.9632053256545410778.01023A ,完成下列操作: (1)输出A 在[10,25]范围内的全部元素。
(2)取出A 前3行构成的矩阵B ,前两列构成矩阵C ,右下角23⨯子矩阵构成矩阵D ,B 与C 的乘积构成矩阵E 。
(3)分别求表达式E<D 、E&D 、E|D 和~E|~D 的值。
三、实验步骤 1、编写程序。
2、调试程序。
3、写出程序运行结果。
实验报告1.先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1))1ln(212x x z ,其中+=545.0212i x ;程序:x=[2,1+2i;-0.45,5]; z=0.5*log(x+sqrt(1+x^2)) 结果:z =0.7114 - 0.0253i 0.8968 + 0.3658i 0.2139 + 0.9343i 1.1541 - 0.0044i(2)0.3,9.2,8.2,,8.2,9.2,0.3,23.0ln )3.0sin(23.03.0 ---=+++-=-a aa e e z a a 程序:a=[-3.0:0.1:3.0];z=0.5*(exp(0.3*a)-exp(-0.3*a)).*sin(a+0.3)+log((0.3+a)/2) 结果: z =Columns 1 through 60.7388 + 3.1416i 0.7696 + 3.1416i 0.7871 + 3.1416i 0.7913 + 3.1416i 0.7822 + 3.1416i 0.7602 + 3.1416iColumns 7 through 120.7254 + 3.1416i 0.6784 + 3.1416i 0.6196 + 3.1416i 0.5496 + 3.1416i 0.4688 + 3.1416i 0.3780 + 3.1416iColumns 13 through 180.2775 + 3.1416i 0.1680 + 3.1416i 0.0497 + 3.1416i -0.0771 + 3.1416i -0.2124 + 3.1416i -0.3566 + 3.1416iColumns 19 through 24-0.5104 + 3.1416i -0.6752 + 3.1416i -0.8536 + 3.1416i -1.0497 +3.1416i -1.2701 + 3.1416i -1.5271 + 3.1416iColumns 25 through 30-1.8436 + 3.1416i -2.2727 + 3.1416i -2.9837 + 3.1416i -37.0245 -3.0017 -2.3085Columns 31 through 36-1.8971 -1.5978 -1.3575 -1.1531 -0.9723 -0.8083Columns 37 through 42-0.6567 -0.5151 -0.3819 -0.2561 -0.1374 -0.0255Columns 43 through 480.0792 0.1766 0.2663 0.3478 0.4206 0.4841Columns 49 through 540.5379 0.5815 0.6145 0.6366 0.6474 0.6470Columns 55 through 600.6351 0.6119 0.5777 0.5327 0.4774 0.4126Column 610.33882.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=723302131,76538773443412B A ,求下列表达式的值:⑴ I B A B A +-+和*6(其中I 为单位矩阵);程序:A=[12,34,-4;34,7,87;3,65,7]; B=[1,3,-1;2,0,3;3,-2,7]; A+6*B 结果: ans =18 52 -10 46 7 105 21 53 49 程序: I=eye(3); A-B+I 结果: ans =12 31 -3 32 8 84 0 67 1⑵B A B A *.*和 程序:A*B 结果:ans =68 44 62 309 -72 596 154 -5 241 程序:A.*B 结果:ans =12 102 4 68 0 261 9 -130 49⑶3.^3^A A 和;程序:A^3 结果:ans =37226 233824 48604 247370 149188 600766 78688 454142 118820 程序:A.^3 结果:ans =1728 39304 -64 39304 343 658503 27 274625 343⑷B A B A \/和; 程序:A/B 结果:ans =16.4000 -13.6000 7.6000 35.8000 -76.2000 50.2000 67.0000 -134.0000 68.0000 程序:A\B 结果:ans =-0.0313 0.3029 -0.3324 0.0442 -0.0323 0.1063 0.0317 -0.1158 0.1558 ⑸]2^:);],3,1([[],[B A B A 和.程序:[A,B] 结果:ans =12 34 -4 1 3 -1 34 7 87 2 0 3 3 65 7 3 -2 7 程序:[A([1,3],:);B^2] 结果:ans =12 34 -4 3 65 7 4 5 1 11 0 19 20 -5 403.已知: ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---=14.35454.9632053256545410778.01023A ,完成下列操作:(1)输出A在[10,25]范围内的全部元素。
2023修正版matlab程序设计入门

matlab程序设计入门1. 引言Matlab是一种较为常用的科学计算软件,广泛应用于工程、科学、金融等领域。
本文档将介绍Matlab程序设计的基本知识,帮助读者快速入门并掌握基本的编程技巧。
2. Matlab概述Matlab是由MathWorks公司开发的一种解释型高级编程语言和环境。
它的优势在于强大的计算和图形功能,使得它成为了数据可视化、矩阵运算和算法开发的首选工具。
Matlab支持使用脚本文件(以.m为扩展名)编写程序,也可以通过交互式命令行进行实时计算和调试。
它还提供了丰富的函数库和工具箱,方便用户进行各种数学分析和绘图操作。
3. 安装和配置Matlab在开始使用Matlab之前,我们首先需要和安装Matlab软件。
我们可以在MathWorks官方网站上购买和Matlab,在安装过程中按照提示完成安装。
在安装完成后,我们可能需要配置Matlab的环境变量,以便在命令行中使用Matlab命令。
具体的配置方法可以参考Matlab官方文档或者相关的教程。
4. Matlab基本语法Matlab的语法类似于其他编程语言,但也具有一些特殊的特性。
下面是一些Matlab编程的基本要点:4.1 变量和数据类型在Matlab中,我们可以使用变量来存储和操作数据。
变量名是区分大小写的,并且可以包含字母、数字和下划线,但不能以数字开头。
Matlab支持多种数据类型,包括数值型(如整数、浮点数)、字符串和逻辑型(true或false)。
变量可以通过赋值语句进行初始化和更新。
4.2 数组和矩阵Matlab的一个重要特性是对数组和矩阵的支持。
我们可以使用一维或多维数组来存储和处理数据。
矩阵则是一种特殊的二维数组,通常用于表示线性代数中的向量和矩阵。
Matlab提供了丰富的函数和运算符来对数组和矩阵进行操作,如索引、切片、运算等。
4.3 控制流语句Matlab支持常见的控制流语句,如条件语句(if-else)、循环语句(for、while)和函数定义等。
MATLAB基础与应用_上机(1)

• 实验二:程序设计 要求:学会使用M文件,编写简单的MATLAB程 序。学会建立M函数。编写简单的较通用的 MATLAB函数。 内容: 1)写出计算 5 32 全部方根的M文件。 2)编写适应向量、矩阵数据的标准差计算M函 数。(提示:根据nargin、length、size等确定输 入数据的维度信息)。
Matlab基础及其应用
上机实验(I)
Байду номын сангаас
1
• 实验一:熟悉MATLAB软件。 要求:启动MATLAB软件,熟悉软件的界面和菜 单。会使用帮助文件。 内容: 1)熟悉Matlab的布局和各个菜单的内容,包括 修改工作目录设置、工作变量查看、历史命令查 看、指令窗口管理、启动M文件编辑器等。 2)会使用Help命令以及帮助文档,查找函数的 语法规则。 3)在闭区间 [0,2 ] 上产生100个等间距的一维 数组,用两种不同指令实现。
• 实验三:绘图(上) 要求:用MATLAB绘制二维、三维函数图形。 内容: 0.5t y 1 e cos2t 1)在时间区间[0,10]中,绘制 曲线,并对坐标轴、标题等进行标注。 1.5t y 1 e cos t 2)在1)的图形窗口中,绘制 曲线,并添加图例和网格线。 3)对向量t进行计算构成:x=sin(t),y=cos(t),z=t。 利用绿色带圆圈的实现绘制该三维曲线。
matlab上机实验指导书3

《MA TLAB软件与程序设计》学生上机实验任务书姓名:学号:班级:指导教师:兰州理工大学理学院实验二 MATLAB 程序设计一、实验目的1.掌握MA TLAB M 文件的基本操作;2.掌握MA TLAB 程序控制结构(for 语句、if 语句、 switch 语句, while 语句);3.掌握MA TLAB 函数文件调用方法。
4.熟悉MA TLAB 函数调试的基本方法。
二、实验内容1. 输入一个百分制成绩,要求输出等级A 、B 、C 、D 、E 。
其中90~100分为A ,80~89分为B,70分~79分为C,60分~69分为D,60分以下为E 。
要求:(1)分别用if 语句和switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
2.输入20个数,求其中最大数和最小数。
要求分别用循环结构和调用matlab 的max 函数、min 函数来实现。
3. 23.0ln )3.0sin(23.03.0aa e e y a a +++−=−,当a 取-3.0、-2.9、-2.8、-2.8、···、2.8、2.9、3.0时,求各点的函数值。
要求分别用顺序结构和循环结构实现。
4.已知 )20()30()40(f f f y +=(1)当f(n)=n+10ln(n 2+5)时,y 的值是多少。
(2)当f(n)=1*2+2*3+3*4+···+n*(n+1)时,y 的值是多少。
(把f(n)写成函数文件的形式,求y 的值分别用调用函数文件的方法实现)三、实验步骤 1、编写程序。
2、调试程序。
3、写出程序运行结果。
实验报告。
MATLAB基础使用教程

MATLAB基础使用教程一、什么是MATLAB?MATLAB是一款强大的数学计算软件,广泛应用于科学研究、工程设计和数据分析等领域。
它以其简单易用的编程语言和丰富的功能,成为了许多科研工作者和工程师的首选工具。
在本篇文章中,将介绍MATLAB的基础使用方法,帮助初学者快速入门。
二、MATLAB的安装与入门1. 下载和安装MATLAB软件在MathWorks官方网站上下载适用于您的操作系统版本的MATLAB,然后按照安装向导的提示进行安装。
2. MATLAB的界面介绍在打开MATLAB后,您将看到一个包含命令窗口、编辑器和变量编辑器等组件的界面。
命令窗口是最常用的组件,您可以在其中输入MATLAB的命令并执行。
3. 基本操作在命令窗口中,可以输入简单的算术运算,如加减乘除,以及一些内置函数。
例如,输入"2+3"并按下Enter,MATLAB将返回结果5。
三、MATLAB的变量与数据类型1. 变量的定义与赋值在MATLAB中,可以使用一个变量来存储一个数值或一个数据矩阵。
要定义一个变量并赋值,只需输入变量名和等号,然后再输入数值或矩阵。
例如,输入"A=5",即可定义一个名为A的变量,并将其赋值为5。
2. 数据类型MATLAB支持多种数据类型,包括整数、浮点数、字符串和逻辑类型。
您可以使用"whos"命令查看当前可用的变量及其数据类型。
3. 矩阵与数组操作在MATLAB中,矩阵和数组是最常用的数据结构之一。
您可以使用方括号来创建矩阵或数组,并使用索引来访问其中的元素。
例如,输入"A=[1 2 3; 4 5 6]",即可创建一个2行3列的矩阵。
四、MATLAB的数学运算与函数1. 基本数学运算MATLAB支持各种基本的数学运算,包括加、减、乘、除、幂运算等。
您可以直接在命令窗口中输入相应的表达式,并按下Enter键进行计算。
matlab上机指导书

matlab上机指导书⽬录实习1. MATLAB软件环境实习2. 矩阵的建⽴和运算实习3. 编程操作练习实习4. 图形操作练习实习5. 符号运算练习实习6. 数值运算练习实习7. GUI设计⼊门实习8. SIMULINK建模练习实验1 矩阵的建⽴与运算1.上机⽬的1.1掌握MATLAB 软件的安装与运⾏1.2通过上机启动MATLAB 软件,熟悉软件的界⾯和菜单 1.3掌握变量名的命名规则及常⽤熟悉函数 1.4熟练数据操作2.上机内容例1:数学函数 A=cos(3.14); B=log(2.71928); C=exp(3.14); D=fix(3.14); E=ceil(3.14);例2:数据操作A=input('what's your name?\n','s') Emily %通过键盘输⼊ ans=Emily例3:数据处理求解⽅程02=++c bx ax 的根,其中,a=1,b=2,c=3。
a=1;b=2;c=3;d=sqrt(b^2-4*a*c); x1=(-b+d)/(2*a); x2=(-b-d)/(2*a); disp(x1) disp(x2)3.上机练习题3.1 使⽤gcd 函数求15和35的最⼤公约数。
(提⽰:先⽤help 命令查看函数⽤法);3.2 已知a=4.96,b=8.11,计算)ln(b a e ba +-的值;3.3 定义三个变量a=1,b=2,c=3,全部存⼊⼀个⽂件中,再把a ,b 存⼊另⼀个⽂件中,清空⼯作空间后,检查⼯作空间,再调⼊变量a ,再检查⼯作空间。
实验2 矩阵的建⽴与运算1.上机⽬的1.1熟练矩阵的建⽴1.2掌握矩阵的关系运算和掌握常⽤的矩阵运算指令1.3熟悉⽂件的操作2.上机内容例1:矩阵输⼊Time = [11 12 1 2 3 4 5 6 7 8 9 10]X_Data = [2.32 3.43;4.37 5.98]例2:矩阵运算g = [1 2 3 4];h = [4 3 2 1];s1 = g + h, s2 = g.*h, s3 = g.^h, s4 = g.^2, s5 = 2.^h例3:矩阵运算A=[2 0 –1;1 3 2]; B=[1 7 –1;4 2 3;2 0 1];M = A*B % 矩阵A与B按矩阵运算相乘X = A/B % A/B = A*B-1,即XB=A,求XY = B\A % B\A = B-1*A,即BY=A,求Y3.上机练习题3.1 输⼊A=[7 1 5;2 5 6;3 1 5],B=[1 1 1; 2 2 2; 3 3 3],在命令窗⼝中执⾏下列表达式,掌握其含义:A(2, 3) A(:,2) A(3,:) A(:,1:2:3) A(:,3).*B(:,2) A(:,3)*B(2,:) A*B A.*B A^2 A.^2 B/A B./A;3.2 查找已创建变量的信息,删除⽆⽤的变量;3.3 利⽤函数产⽣3X4阶单位矩阵和全部元素都是4.5的4X4阶常数矩阵;3.4 利⽤画图软件画⼀副画,存盘后,读⼊MATLAB⼯具空间,将它改名字改格式另存。
MATLAB程序设计基础教程

MATLAB程序设计基础教程MATLAB程序设计是一门广泛应用于科学和工程领域的高级编程语言。
它具有强大的数值计算和数据可视化功能,被广泛用于数据分析、模拟建模、信号处理等领域。
本文将介绍MATLAB程序设计的基础知识和常用技巧,帮助读者快速上手并掌握该编程语言。
一、MATLAB环境搭建在开始MATLAB编程之前,首先需要正确搭建MATLAB运行环境。
你可以从MathWorks官网下载和安装最新版本的MATLAB软件,根据安装向导进行配置。
安装完成后,你就可以打开MATLAB并开始编写代码了。
二、MATLAB基本语法1. 变量和数据类型在MATLAB中,可以使用变量来存储数据。
变量的命名需要满足一定规则,比如变量名只能包含字母、数字和下划线,不能以数字开头等。
MATLAB支持不同的数据类型,包括数字、字符串、逻辑值等。
2. 数组和矩阵MATLAB中的核心数据结构是数组和矩阵。
你可以使用一维或多维数组来存储和处理数据。
MATLAB提供了丰富的数组操作函数和运算符,可以进行元素访问、切片、矩阵运算等。
3. 控制流程MATLAB支持常用的控制流程语句,如条件语句(if-else)、循环语句(for、while)等。
这些语句可以帮助你根据不同的条件执行不同的代码块,或者重复执行一段代码。
三、MATLAB函数和脚本1. 函数MATLAB中可以编写自定义函数,以方便地实现特定功能。
函数是由输入参数和输出参数组成的可重复使用的代码块。
你可以在函数中进行各种操作,如计算、输出、图形绘制等。
2. 脚本除了函数,你还可以编写脚本文件来执行一系列MATLAB命令。
脚本文件通常用于较短的代码片段,不需要提供输入和输出参数。
你可以通过运行脚本文件一次性执行其中的命令。
四、MATLAB图形界面MATLAB提供了强大的图形界面(GUI)工具,用于可视化数据和交互式操作。
你可以通过GUI工具箱创建和定制各种图形,如散点图、曲线图、柱状图等。
MATLAB总结与上机指南

MATLAB总结与上机指南MATLAB总结与上机指南MATLAB是一种常用的科学计算和数据分析软件,广泛应用于工程、数学、计算机科学以及其他领域。
本篇文章将对MATLAB进行总结,并提供一些上机指南,帮助初学者更好地使用该软件。
一、MATLAB总结1. 功能丰富:MATLAB提供了许多功能强大的工具箱,包括信号处理、图像处理、智能算法、统计分析等。
可以通过调用这些工具箱来完成各种复杂的科学计算任务。
2. 编程与交互式环境:MATLAB不仅可以作为一个计算软件,还可以通过编写脚本和函数来进行程序设计和开发。
此外,MATLAB还提供了一个交互式环境,用户可以直接在命令行中输入命令进行计算与数据分析。
3. 强大的绘图功能:MATLAB提供了丰富的绘图功能,可以绘制各种类型的图形,如曲线图、散点图、三维图、等高线图等。
这些图形可以直观地展示数据的特征和趋势。
4. 并行计算和分布式计算:MATLAB支持并行计算和分布式计算,可以利用电脑集群或云计算来加速计算任务。
这对于处理大规模数据和复杂模型是非常有帮助的。
5. 丰富的文档和社区支持:MATLAB有详细的官方文档和教程,可以帮助用户快速上手。
同时,MATLAB拥有庞大的使用者社区,可以在网上寻找解决方案和技巧。
二、上机指南1. 学习基本语法:在开始使用MATLAB之前,建议先学习基本的MATLAB语法,包括变量赋值、运算符、控制流语句等。
这些基本语法是编写MATLAB脚本和函数的核心。
2. 学习基本函数:MATLAB自带了许多基本函数,如求解方程、矩阵运算、数据统计等。
了解这些函数的用法对于解决常见的科学计算问题非常有帮助。
3. 使用帮助文档:MATLAB提供了非常详细的帮助文档,可以在命令行输入"help function"或者"doc function"来查看具体函数的用法和示例。
同时,还可以在MathWorks官方网站上查找相关文档和教程。
2024版新手简明入门级matlab使用教程

数组创建和操作技巧
MATLAB中的数组可以是 行向量、列向量或矩阵。
创建数组可以使用方括号 ([])将元素括起来。例如, `A = [1, 2, 3];`将创建一个 包含元素1、2和3的行向量 A。
可以通过索引访问数组中 的元素。例如,`B = A(2);` 将创建一个新变量B,并将 其值设置为数组A中的第二 个元素2。
拓展学习资源推荐
MATLAB官方文档
提供详细的函数说明、示例代码和使用教程。
在线教程和视频
各大在线教育平台提供的MATLAB入门到精通的系列课程。
书籍推荐
《MATLAB从入门到精通》、《MATLAB编程与工程应用》等。
论坛和社区
MATLAB中文论坛、CSDN博客等,可与其他MATLAB爱好者交流学习心得。
பைடு நூலகம்
二维图形绘制方法
plot函数
subplot函数
用于绘制二维线性图形,可以自定义线型、 颜色和标记等。
用于在同一窗口中创建多个子图,方便比较 不同图形。
hold on/off命令
用于在同一坐标系中叠加绘制多个图形。
legend函数
用于添加图例,区分不同数据系列的标识。
三维图形绘制技巧
plot3函数
安装步骤
1. 访问MathWorks官网下载MATLAB安 装包。
界面布局及功能区域介绍
• MATLAB界面主要包括菜单栏、工具栏、命令窗口、工作 空间、当前文件夹窗口等部分。
界面布局及功能区域介绍
菜单栏
提供文件操作、编辑、视图等多种功 能选项。
工具栏
提供常用命令的快捷方式,如保存、运 行、调试等。
掌握MATLAB与其他编程语言的接口
MATLAB上机(基础知识)

曲线的颜色和线型
MATLAB
一维矩阵或向量的两种表示: A=[ 1 4 7 10 13] A=1:3:13 (若增量是1可以省去)
起始数据
增量
限制范围
MATLAB
练习: 绘制函数 y = e-ax.sin(bx)
在区间 [-6,6] 上的图形,
其中取a = 0.1,b = 2
MATLAB
参考答案: x=-6:0.2:6; a=0.1;b=2; y=exp(-a .* x) .* sin(b .* x); plot(x,y)
MATLAB
练习:生成如下矩阵 A=[0 0 0 0 0 0 0 0 0 5 1000000000 0300000000 0010100000 0000000000 0000000200 0 0 0 0 0 0 0 0 0 0]
MATLAB
答案:
A=zeros(7,10); A(1,10)=5; A(2,1)=1; A(3,2)=3; A(4,3)=1; A(4,5)=1;A(6,8)=2;
3; 4 5 6; 7 8 3; 4, 5, 6; 7, 8, 3 A=[1, 2, 6 4, 5, 9]; 7, 8,
9]; 9]; 3 6 9];
MATLAB
3 、算术运算符
矩阵运算符:按线性代数中矩阵运算的规则进行 (matrix operator)
+ -
*
^
\
/
数组运算符:按对应元素逐个进行 (array operator)
4 (0.1) (0.0001100 110011 ) (1.1001100 11 2 )2 10 2
MATLAB
IEEE 754关于浮点数的定义
MATLAB上机指导书

MATLAB上机指导书2019年10月目录前言实验一MATLAB基础知识 1 实验二矩阵与数组 6 实验三基本操作命令9 实验四高级操作命令11 实验五MATLAB的M函数编程14实验六MATLAB绘图15前言MATLAB的名称源自Matrix Laboratory,是一门计算语言,它专门以矩阵的形式处理数据.MATLAB将计算与可视化集成到一个灵活的计算机环境中,并提供了大内置函数,可以在广泛的工程问题中直接利用这些函数获得数值解.此外,用MATLAB 编写程序,犹如在一张草稿纸上排列公式和求解问题一样效率高,因此被称为“演算纸式的”科学工程算法语言.在我们高等数学的学习过程中,可以结合MATLAB 软件,做一些简单的编程应用,在一定程度上弥补我们常规教学的不足,同时,这也是我们探索高职高专数学课程改革迈出的一步.实验一 MATLAB 基础知识一、实验目的1、MATLAB 的使用初步练习2、MATLAB 的窗口组成 二、实验内容1、掌握表达式的输入方法2、MATLAB 的常量及其表示方法3、分号、百分比号、逗号及省略号的用法4、向量和矩阵的处理方式;常用的数学函数;搜索路径的概念;MATLAB 的帮助功能。
三、实验仪器、设备和材料1、微型计算机,能正常运行Matlab 6.0或以上版本2、Matlab6.0或以上版本 四、实验原理略(参考教材的相关部分) 五、实验步骤1、MATLAB 文件的编辑、存储和执行MATLAB 提供了两种运行方式,即命令行和M 文件方式. A .命令行方式直接在命令窗口输入命令来实现计算或作图功能. 例如,若要求表达式的值,我们可在MATLAB 命令窗口中键入下面的命令:>> 1.369^2+sin(7/10*pi)*sqrt(26.48)/2.9 (回车) 观测运行结果并解释原因也可将计算的结果赋给某一个变量,例如输入 :>> a=1.369^2+sin(7/10*pi)*sqrt(26.48)/2.9 (回车) 观测运行结果并解释原因 B .M 文件的运行方式1)文件编辑 在MATLAB 窗口中单击File 菜单依次选择NewM-File,打开M 文件输入运行界面,如下图所示。
Matlab上机学习指导1
MATLAB使用入门计算机技术的迅速发展,产生了许多功能强大的数学软件,为应用数学和工程技术的发展提供了威力无比的武器和工具,本章介绍由美国MathWorks 公司开发的集数值计算、符号计算和图形可视化三大基本功能于一体的,功能强大、简单易学的软件MA TLAB。
它是国际公认的优秀数学应用软件之一。
从20世纪80年代产生到现在,MA TLAB已经发展成为适合多学科的大型软件,在世界各高校,MA TLAB已经成为线性代数、数值分析、数理统计、优化方法、自动控制、数字信号处理、动态系统仿真等高级课程的基本教学工具。
特别是最近几年,MA TLAB在我国大学生数学建模竞赛中的应用,为参赛者在有限的时间内准确、有效的解决问题提供了有力的保证。
本章以MA TLAB6.5.1版本为例,主要通过举例介绍MA TLAB的初步应用。
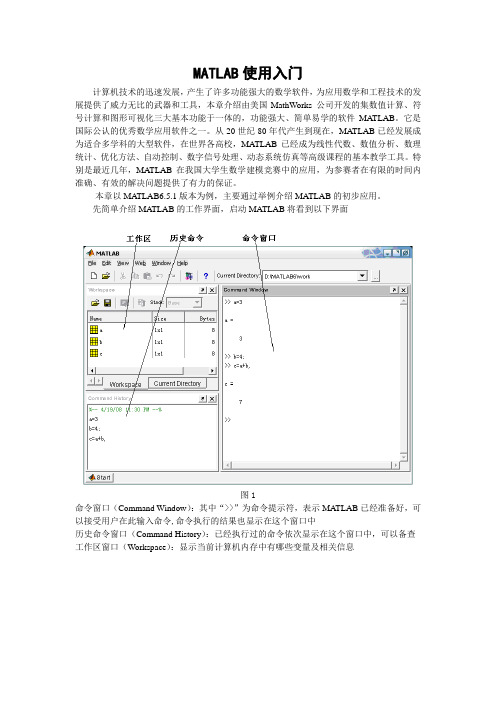
先简单介绍MA TLAB的工作界面,启动MA TLAB将看到以下界面图1命令窗口(Command Window):其中“>>”为命令提示符,表示MA TLAB已经准备好,可以接受用户在此输入命令,命令执行的结果也显示在这个窗口中历史命令窗口(Command History):已经执行过的命令依次显示在这个窗口中,可以备查工作区窗口(Workspace):显示当前计算机内存中有哪些变量及相关信息一 基本命令与运算例1:如图1所示,我们已经输入了3条命令 第一条: >> a=3 运行(点击Enter 键),结果为:a =3这表示我们定义了一个变量a ,并且给a 赋值为3,同时在工作区窗口中就会出现一个小方格,意思是现在我们占据了计算机内存中一块存储空间,空间命名为a ,空间里面现在就存放着数字3,用鼠标双击这个小方格,就会看到这个3 第二条: >> b=4;表示又定义了一个变量b ,赋值为4,运行后没有显示结果,这是因为我们在命令后面加了分号,这只是表示不把结果在命令窗口中显示出来(因为有时候我们为了解决某个问题只需显示最后结果,而不需要显示中间结果),实际上命令已经执行过了,这在工作区窗口中就能看出来第三条: >> c=a+b, 运行结果: c =7又定义了一个变量c ,同时把变量a 里面的数与变量b 里面的数加起来将结果放到c 里面 这时我们已经定义了三个变量,也就是在计算机内存中我们占据了三块存储空间,假如我们问题解决完了,不需要这几个变量了,我们就用下面的命令清除它们>> clear运行后工作区窗口中的三个小方格就会消失,表示三个变量已经清除,内存中所占据的存储空间已经释放,这样就不会影响我们后面解决其它问题了 例2:计算23)]47(212[÷-⨯+ >>(12+2*(7-4))/3^2 运行结果: ans = 2例3:计算圆面积Area 2r π=,半径rad=2,则可输入 >>rad=2; %定义变量名为rad >>area=pi*rad^2; %定义变量名为area >>area说明1:前两行命令加了分号,表示不把这两行命令的结果显示出来,但是我们需要知道面积是多少,所以第三行命令表示把变量area 的值显示出来 说明2:pi 是Matlab 里边已经有的常数(即圆周率),直接应用,不需要定义说明3:%后面为注释,用来解释前面命令的功能或作用,计算机并不执行,练习时可以不用输入,但在解决复杂问题时,恰当的注释是很有用的表1: 常用函数表2: 常用运算符例4:1)计算20.34sin 10y e-⨯=⨯>>y=sin(10)*exp(-0.3*4^2)结果 y =-0.0045系统默认4位有效数字,若想提高精度可用命令:>>vpa(y,10) %即取10位有效数字结果为 -.4477156132e-2,即210447715613.0-⨯- 2)>> x=sqrt(2)/2 %sqrt 为开方,见表1x =0.7071>> y=asin(x) %x 的反正弦 y =0.7854 (此处y 为弧度,系统默认)>> y_deg=y*180/pi %将弧度转化为角度,y_deg 为变量名 y_deg =45.0000例5: Inf 、-Inf 表示正负无穷大,例如 >> 2/0ans =Inf >> log(0)Warning: Log of zero. ans =-Inf >> exp(3000)ans =Inf (超过计算机能表示的最大的数,故显示为无穷大) NaN 表示无意义,Not a Nunber 的缩写,例如 >> 0/0ans = NaN二 向量与矩阵例1:求向量{1,1,2}a =-、{2,1,3}b = 的数量积与向量积>> a=[1,-1,2]; %生成向量a >> b=[2,1,3]; %生成向量b >> c=dot(a,b) %数量积 >> d=cross(a,b) %向量积 c = 7 d =-5 1 3例2:求矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=587256341A 的行列式 >>A = [1,4,3; 6,5,-2; 7,8,5] %生成矩阵A>>t=det(A) %求A 的行列式 运行结果: A =1 4 3 6 5 -2 7 8 5 t = -96 常用指令det(a) 求矩阵a 的行列式eig(a) 求矩阵a 的特征值 inv(a)或a^(-1) 求矩阵a 的逆矩阵 rank(a) 求矩阵a 的秩trace(a) 求矩阵a 的迹(对角线元素之和)例3:MATLAB 中有一些函数可用来直接生成特殊矩阵,如 >> u=zeros(2,3) %生成2×3全零矩阵 u =0 0 0 0 0 0>> v=ones(3) %生成3×3全1矩阵 v =1 1 1 1 1 1 1 1 1>> w=eye(3) %生成3×3对角线为1的单位阵 w =1 0 0 0 1 0 0 0 1>> x=(1:2:121); % 起始值为1,每次增加2,终止值为121的向量,去掉分号可在屏幕上显示结果>> x=(1:121); % 起始值为1,系统默认每次增加1,终止值为121的向量 >> x=linspace(0,1,101); % 利用linspace ,生成以0为起始值,1为终止值,元素数目为101的向量例4:对矩阵中的元素可以进行访问>> A = [1,4,3; 6,5,-2; 7,8,5] % 先生成矩阵A>> s=A(2,3) % s 为A 第二行第三列的元素 s =-2>> s1=A(3,:) % s1为A 的第三行 s1 =7 8 5>> s2=A(:,2) % s2为A的第二列s2 =458>> s3=A(1:2,2:3) % s3取A的一、二行,二、三列s3 =4 35 9注:A输入后一直保存在内存工作区(工作空间,Workspace)中,同时会显示矩阵的大小(几行几列),工作区内的的变量可以随时调用,除非被清除(用命令clear清除)矩阵中的元素可以修改,如>> A(2,3)=9A =1 4 36 5 97 8 5例5:矩阵的拼接>> a=1:7,b=11:2:23 % 先生成矩阵a及ba =1 2 3 4 5 6 7b =11 13 15 17 19 21 23>> c=[b a] % 利用阵列 a 及b ,组成新矩阵cc =11 13 15 17 19 21 23 1 2 3 4 5 6 7>> d=[b; a] % 利用a及b,组成新矩阵dd =11 13 15 17 19 21 231 2 3 4 5 6 7>> f=[b',a'] % b'表示b的转置,将行变成列f =11 113 215 317 419 521 623 7>> g=[f(:,1),zeros(7,1),ones(7,2)]g =11 0 1 113 0 1 115 0 1 117 0 1 119 0 1 121 0 1 123 0 1 1例6: 输入矩阵x=[4,8,12,10,23;6,3,15,13,19;9,1,2,18,14;11,7,5,21,17]运行以下命令,观察结果m=max(x) % x每列的最大值,如果x只是一行(或一列),则m就是这一行(或一列)向量的最大值n=min(x) % 每列的最小值(问:如何得到整个矩阵的最小值与最大值?)[m,n]=size(x) % 给出x的大小,即行数和列数l=length(x) % 给出x的列数,如果x是一行或一列向量,则给出这个向量的元素的个数,即长度y=x’ % 矩阵x的转置,即行与列互换d=x(1:3,3:5) % x的第1到3行,第3到5列送给d,产生一个新矩阵y(2,3)=y(2,3)/2 % y的第二行第三列的元素除以2,再替换原来的数y(2, :)=y(2, :)/2 %第二行的元素全部除以二y( :,4)=y( :,4)+y( :,2) %第四列加第二列替换原来的第四列例7:下面介绍点运算,这是matlab特有的运算,在后面画函数图象时会用到>>x=1:8x =1 2 3 4 5 6 7 8>>y=x.^2 %如果x是一个数,它平方就用x^2,但现在x是向量,后面加点表示x的每一个元素平方,y =1 4 9 16 25 36 49 64>>z=x./y %x的每一个元素除以y相应的每一个元素z =1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.14290.1250三函数作图例1:画函数sin在区间[0,10]上的图像y x>>x=0:0.1:10; %自变量x从0到10生成101个点(每隔0.1生成一个点)>>y=sin(x); %生成函数值y的101个点>>plot(x,y); %以x为自变量,y为函数值画函数图像运行结果:图3从此例可以看出,matlab 画图的原理就是描点连线,因此如果点取的不密集,画出来就成了折线图,但也不能太密,否则就超出matlab 的计算范围,适当即可例2:在同一窗口中绘正弦曲线sin y x =及抛物线2y x =,绘图区间[2,2]ππ-, 并设置相关属性如果仍然像上面那样在命令窗口中输入一句执行一句是很麻烦的,我们现在建立 M 文档来解决此问题,步骤如下:(1)新建一个M 文档,即点击主窗口工具栏中的图标,见下图:图4弹出如下窗口:图5(2)输入如下程序代码:x=-2*pi:pi/20:2*pi; % 从-2π到2π每隔π/20生成一个点,共81个点y1=sin(x); % 生成函数值y1,也是81个点plot(x,y1,'r'); % 画函数y1=sin(x)的图像,r表示红色hold on % 为了在同一窗口中继续画图,此命令保持前面已经作的图形不动y2=x.^2; % 生成函数值y2的81个点plot(x,y2,'b*'); % 画函数y2=x^2的图像, b*表示蓝色‘*’型线xlabel('x轴'); % x轴加标注ylabel('y轴'); % y轴加标注title('正弦曲线及抛物线'); % 加标题grid on; % 显示网格线axis([-4,4,-2,5]) % 调整图像显示范围,横坐标从-4到4,纵坐标从-2到5(3)输入完成后,点击图标保存、然后命名,比如命名为pic.m(其中.m是系统自动加上的,表示这是一个m文件,即matlab文件)(4)运行程序,有两种方法:第一种,点击图5中的图标即可;第二种,在命令窗口中输入文件名>> pic运行即可,两种方法都会弹出如下图形:图6说明1:程序代码中第五行命令y2=x.^2,自变量x平方时后面加了一点,这是因为x此时不是一个数,而是一系列点(81个点),即一个向量,因此x^2是没有意义的,我们要的是给x里的每一个数平方,这时我们就给x后加一个点,这种运算叫点运算(见前面向量与矩阵部分例5),再如我们要画函数1yx的图像时,就应该用命令y=1./x说明2:第三步中保存m文件,系统会自动将其保存在路径为D:\MATLAB6\work的work文件夹里,当我们需要查看我们以前所保存的文件时,就在这个文件夹里找,或者点击图标,这个叫Current Directory (见图4),意思是matlab 当前指向这个文件夹,只有这个文件夹里的程序,matlab 才会运行,当我们想运行其他文件夹里的程序时,就要将这个当前路径改成我们想要的那个文件夹 例3:画椭圆1232222=+y x建立m 文档如下: t=[0:pi/50:2*pi];%角度t 从0到2π,每隔π/50一个点X=cos(t)*3; %参数方程 Y=sin(t)*2; plot(X,Y);xlabel('x'), ylabel('y'); title('椭圆') 运行结果:略例4: 在同一个窗口中画出衰减振荡曲线13sin 3y e t -=与它的包络线304t y eπ-=及304t y eπ--=-,其中[0,4]t π∈建立m 文档如下: t=0:pi/50:4*pi; y0=exp(-t/3);y=exp(-t/3).*sin(3*t); % 注意点运算plot(t,y,'-r',t,y0,':b',t,-y0,':b') % -r 表示红色实线,:b 表示蓝色点线 grid运行结果:略例5:在同一个画面上建立几个坐标系, 用subplot(m,n,p)命令;把一个画面分成m×n个图形区域, p 代表当前的区域号,在每个区域中分别画一个图,下面在一个画面里同时画四个图像,注意哪个图像在哪个区域 x=linspace(0,2*pi,30);y=sin(x);z=cos(x);u=2*sin(x).*cos(x); v=sin(x)./cos(x); subplot(2,2,1),plot(x,y),axis([0 2*pi -1 1]), title('sin(x)') subplot(2,2,2),plot(x,z),axis([0 2*pi -1 1]), title('cos(x)') subplot(2,2,3),plot(x,u),axis([0 2*pi -1 1]), title('2sin(x)cos(x)') subplot(2,2,4),plot(x,v),axis([0 2*pi -20 20]),title('sin(x)/cos(x)') 下面举例介绍画空间图像例6:画三维螺旋线:cossin x t y t z t=⎧⎪=⎨⎪=⎩建立m文档如下:t=0:pi/50:6*pi;x=cos(t);y=sin(t);z=t;plot3(x,y,z) %plot3指画三维图像grid %添加网格线运行结果:图7也可以用下面的命令:t=linspace(0,6*pi,301); %从0到6π生成301个点plot3(cos(t), sin(t), t);grid例7:画空间中的曲面要用mesh命令画出由函数形成的立体网状图:a=linspace(-2, 2, 30); % 在x轴上从-2到2生成30个点b=linspace(-2, 2, 30); % 同上在y轴上取30点[x,y]=meshgrid(a, b);z=x.*exp(-x.^2-y.^2);mesh(x, y, z); % 画出立体网状图最后一句命令也可用下面的命令代替surf(x, y, z); % 画出立体曲面图运行结果:图8同样我们可以设置图像的颜色、光照等属性,这里不再叙述练习:画出马鞍面22z x y=-图像四符号计算所谓符号计算,是指分解因式、求导数等等给出解析表达式而不是给出数值结果的运算,下面举一些常用的例子。
MATLAB 操作上机一

MATLAB 上机操作一1、运行MATLAB ,(1)记录PC 机上显示的MATLAB 默认浏览路径(2)记录MATLAB 操作界面显示的窗口2、设a=3.52,以命令形式分别以short 、long 格式设置a 的显示格式;设b=2;c=2.2;以命令设置屏幕显示格式分别为不留空行显示、留空行显示,比较显示结果。
以命令形式恢复MA TLAB 的默认数据显示格式和屏幕显示格式。
3、以命令形式查询当前工作空间中的变量名,并查询变量c 的详细信息以记录4、以命令保存变量b 至myvariable 文件中,记录myvariable 文件的存储路径以及文件类型。
5、以命令删除变量a ,清除命令窗口显示内容。
6、设a=5.8,以MA TLAB 命令完成以下计算并记录结果(1)π⨯a (2)0a (3)00(4)∞⨯0(5)eps a ⨯(6)最小浮点数+1(7)最大浮点数-17、以冒号法生成自1.2增大至7.9的向量b ,步长为0.5.8、将1至98的数据线性等分为100个数据,保存至向量c 中9、计算(1)b+3;(2)3b ;(3)b+c10、计算矢量k j i A 43++=和k j i B 452-+-=点乘与叉乘11、生成4阶的魔方矩阵mag ,对mag 进行以下操作,记录结果(1)mag (5,2)=9;(2)mag (4:7)=[-1,0,0,1](3)mag (16)=pi(4)删除mag 第2行数据(5)删除mag 最后一列数据12、(1)列出2×2阶的单位矩阵I ,4×4阶的魔方矩阵M 和4×2阶的全1矩阵A ,全零矩阵B 。
(2)将这些矩阵拼接为6×6阶的矩阵C :⎥⎦⎤⎢⎣⎡=M B A I C ' (3)取出C 的第2,4,6行,组成3×6阶的矩阵1C ,取出第2,4,6列,组成6×3阶的矩阵2C13、产生4×6阶的均匀分布随机数矩阵R ,要求其元素在1到16之间取整数值14、沿着行方向拼接矩阵C 和R 构成矩阵S ;沿列方向复制矩阵R 两次生成矩阵T.15、重塑矩阵T 构成8×6阶的矩阵16、设A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------81272956313841 B=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----793183262345 求B A C B A C AB C *,','321∙===并求它们的逆阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
MATLAB软件设计应用技术学院2008-6第一章 MATLAB程序设计一、M文件用户如想灵活应用matlab去解决实际问题,充分调用matlab的科学技术资源,就需要编辑m文件包含matlab语言代码的文件称为m文件,其扩展名为m。
编辑m文件可使用各种文本编辑器。
m文件的类型是普通的文本文件,我们可以使用系统认可的文本文件编辑器来建立m文件。
如dos下的edit,windows的记事本和word等。
具体的创建方法:1.在matlab命令窗口点击file 菜单new → m-file2.. m文件m文件的语法类似于c语言,但又有其自身特点。
它只是一个简单的ASCII码文本文件,执行程序时逐行解释运行程序,matlab是解释性的编程语言。
m文件有两类 独立的m文件—称命令文件、可调用m文件—称函数文件(1). 命令文件—简单的m文件命令文件实际上是一串指令的集合,与在命令窗口逐行执行文件中的所有指令,其结果是一样的。
没有输入输出参数命令文件包括两部分:注释文件和程序文件%RANK Number of linearly independent rows or columns.% K = RANK(X) is the number of singular values of X% that are larger than MAX(SIZE(X)) * NORM(X) * EPS.% K = RANK(X,tol) is the number of singular values of X that% are larger than tol.% Copyright (c) 1984-94 by The MathWorks, Inc.s = svd(x);if (nargin == 1)tol = max(size(x)) * max(s) * eps;endr = sum(s > tol);(2).matlab内置函数文件matlab自定义的函数文件称内置函数文件调用内置函数的方法:使用函数名并给出相应的入口、出口参数即可。
例如:sin.m函数——用type sin查不到。
调用格式:y=sin(2*x)实际应用中:x=0:2*pi/180:2*pi;y=sin(2*x)function <因变量>=<函数名>(<自变量>)2.m文件的文件名必须是<函数名> .m。
3.程序中的变量均为局部变量,不保存在工作空间中。
其变量只在函数运行期间有效二、微分方程一般微分方程式描述系统内部变量的变化率如何受系统内部变量和外部激励,如输入,的影响。
当常微分方程式能够解析求解时,可用MATLAB的符号工具箱中的功能找到精确解。
在本书的后面将介绍该工具箱的一些特点。
在微分方程难以获得解析解的情况下,可以方便地在数值上求解。
为了说明起见,考虑描述振荡器的经典的范得波(Var der Pol)微分方程。
d x dt x dx dt x 22210--+=μ()与所有的数值求解微分方程组的方法一样,高阶微分方程式必须等价地变换成一阶微分方程组。
对于上述微分方程,通过重新定义两个新的变量,来实现这种变换。
令y1=x 且 y2=dy/dx 则 dy1/dt=y2dy dt y y 2211/()=--μ根据这个微分方程组,可用MATLAB 的函数ode23和ode45求出系统随时间变化的运动情况。
调用这些函数时,需要编写一个函数M 文件,给定当前时间及y1和y2的当前值,该函数返回上述导数值。
MATLAB 中,这些导数由一个列向量给出。
在本例中,这个列向量为yprime 。
同样,y1和y2合并写成列向量y 。
所得函数M 文件是:function yprime=vdpol(t , y);% VDPOL(t , y) returns derivatives of the Van der Pol equation: %% x ‘‘-mu *(1-x ^2)*x ‘+x=0 (‘ = d/dx , ‘‘ = d^2/dx^2) %% let y(1)=x and y(2)=x‘ %% then y(1) ‘ = y(2)% y(2) ‘ = MU*(1-y(1)^2)*y(2)-y(1)global MU % choose 0<MU<10 in Command workspaceyprime=[y(2) MU*(1-y(1)^2)*y(2)-y(1)]; % output must be a column给定这个完整地描述微分方程的函数,计算结果如下:>>global MU % define MU as a global variable in the Command Workspace >>MU=2; % set global parameter to desired value>>[t , y]=ode23(‘ vdpol ‘ , 0 , 30 , [1 ; 0]); % to=0 , tf=30 , yo=[1 ; 0] >>y1=y( : , 1); % first column is y(1) versus time points in t >>y2=y( : , 2); % second column is y(2) >>plot(t , y1 , t , y2 , ‘ -- ‘)>>xlabel(‘ Time , Second ‘) , ylabel(‘ Y(1) and Y(2) ‘) >>title(‘ Van der Pol Solution for mu=2 ‘)当mu=2时的范得波方程的运动曲线第二章流程控制与绘图一、流程控制1. For循环For循环允许一组命令以固定的和预定的次数重复。
For循环的一般形式是:for x = array{commands}end在for和end语句之间的{commands}按数组中的每一列执行一次。
在每一次迭代中,x被指定为数组的下一列,即在第n次循环中,x=array(:, n)。
例如,» for n=1:10x(n)=sin(n*pi/10);end» xx =Columns 1 through 70.3090 0.5878 0.8090 0.9511 1.0000 0.9511 0.8090Columns 8 through 100.5878 0.3090 0.0000换句话,第一语句是说:对n等于1到10,求所有语句的值,直至下一个end 语句。
第一次通过For循环n=1,第二次,n=2,如此继续,直至n=10。
在n=10以后,For循环结束,然后求end语句后面的任何命令值,在这种情况下显示所计算的x的元素。
For循环的其它重要方面是:1. For循环不能用For循环内重新赋值循环变量n来终止。
» for n=1:10x(n)=sin(n*pi/10);n=10;end» xx =Columns 1 through 70.3090 0.5878 0.8090 0.9511 1.0000 0.9511 0.8090Columns 8 through 100.5878 0.3090 0.00002.语句1 :10 是一个标准的MATLAB数组创建语句。
在For循环内接受任何有效的MATLAB数组。
» data=[3 9 45 6; 7 16 -1 5]data =3 9 45 67 16 -1 5for n=datax=n(1)-n(2)endx =-4x =-7x =46x =13. For循环可按需要嵌套。
for n=1:5for m=5:-1:1A(n,m)=n^2+m^2;enddisp(n)end12345» AA =2 5 10 17 265 8 13 20 2910 13 18 25 3417 20 25 32 4126 29 34 41 504.当有一个等效的数组方法来解给定的问题时,应避免用For循环。
例如,上面的第一个例子可被重写为» n=1:10;» x=sin(n*pi/10)x =Columns 1 through 70.3090 0.5878 0.8090 0.9511 1.0000 0.9511 0.8090Columns 8 through 100.5878 0.3090 0.0000两种方法得出同样的结果,而后者执行更快,更直观,要求较少的输入。
5.为了得到最大的速度,在For循环(While循环)被执行之前,应预先分配数组。
例如,前面所考虑的第一种情况,在For循环内每执行一次命令,变量x的大小增加1。
迫使MATLAB每通过一次循环要花费时间对x分配更多的内存。
为了消去这个步骤,For循环的例子应重写为»x=zeros(1,10); % preallocated memory for x» for n=1:10x(n)=sin(n*pi/10);end现在,只有x(n)的值需要改变。
2. While 循环与For循环以固定次数求一组命令的值相反,While 循环以不定的次数求一组语句的值。
While循环的一般形式是:while expression{commands}end只要在表达式里的所有元素为真,就执行while和end 语句之间的{commands}。
通常,表达式的求值给出一个标量值,但数组值也同样有效。
在数组情况下,所得到数组的所有元素必须都为真。
考虑下列例子:» num=0;EPS=1;» while (1+EPS)>1EPS=EPS/2;num=num+1;end» numnum =53» EPS=2*EPSEPS =2.2204e-016这个例子表明了计算特殊MATLAB值eps的一种方法,它是一个可加到1,而使结果以有限精度大于1的最小数值。
这里我们用大写EPS,因此MATLAB的eps的值不会被覆盖掉。
在这个例子里,EPS以1开始。
只要(1+EPS)>1为真(非零),就一直求While循环内的命令值。
由于EPS不断地被2除,EPS逐渐变小以致于EPS+1不大于1。
(记住,发生这种情况是因为计算机使用固定数的数值来表示数。
MATLAB用16位,因此,我们只能期望EPS接近10-16。
) 在这一点上,(1+EPS)>1是假(零),于是While循环结束。
