电容器 电场能量.ppt51 PPT资料共28页
合集下载
电容器 电场能量

R2
2 o l q C U 12 ln( R2 R1 )
• 圆柱越长,电容越大; 两圆柱之间的间隙越小, 24 电容越大。
例1 :平行板电容器两极板面积为 S ,极板间有两 层电介质, 介电常数分别为 1 ,2 ,厚为 d1 , d2 。电容 器极板上自由电荷面密度 。 求: ① 各介质内的 D,E; ② 电容器的电容 。 解: ① 由高斯定理 D dS D1 S D2 S 0
11、电容器的定义
-
C
D
电容器两个极板所带的电量为+Q、-Q,它们的电势 分别为UA、UB,定义电容器的电容为:
Q Q C U AB U A U B
16
电容器的比喻——水容器
图中三个水容器,如果要同样升高单位的高度,所 需要的水量是不同的,这反映了水容器本身的性质,与 是否灌水以及灌水多少是没有关系的。 同样的道理,对于不同的电容器来说,要使两极板 电势差升高单位大小,所需要的电量不同,这反映的是 电容器本身的性质,与其是否带电以及带电多少无关。
三、电容器的并联和串联
11、电容器的并联
C1
特点: 每个电容器两端的电势差相等 总电量:
Q Q1 Q2 C1U C 2U C1 C 2 U
C2
U
等效
等效电容:
结论: •当几个电容器并联时,其等效电容等于几个电容器 电容之和; •各个电容器的电压相等; 28 •并联使总电容增大。
各向同性电介质
q0 , q' 分布具有某些对称性
D 0 E P 0 E 0 E 0 (1 ) E
令 得
P 0 E
χ 为常数
1 r 介质的相对电容率 D 0 r E E 式中, 0 : 真空电容率 D 0 r : 介质电容率 D E
2 o l q C U 12 ln( R2 R1 )
• 圆柱越长,电容越大; 两圆柱之间的间隙越小, 24 电容越大。
例1 :平行板电容器两极板面积为 S ,极板间有两 层电介质, 介电常数分别为 1 ,2 ,厚为 d1 , d2 。电容 器极板上自由电荷面密度 。 求: ① 各介质内的 D,E; ② 电容器的电容 。 解: ① 由高斯定理 D dS D1 S D2 S 0
11、电容器的定义
-
C
D
电容器两个极板所带的电量为+Q、-Q,它们的电势 分别为UA、UB,定义电容器的电容为:
Q Q C U AB U A U B
16
电容器的比喻——水容器
图中三个水容器,如果要同样升高单位的高度,所 需要的水量是不同的,这反映了水容器本身的性质,与 是否灌水以及灌水多少是没有关系的。 同样的道理,对于不同的电容器来说,要使两极板 电势差升高单位大小,所需要的电量不同,这反映的是 电容器本身的性质,与其是否带电以及带电多少无关。
三、电容器的并联和串联
11、电容器的并联
C1
特点: 每个电容器两端的电势差相等 总电量:
Q Q1 Q2 C1U C 2U C1 C 2 U
C2
U
等效
等效电容:
结论: •当几个电容器并联时,其等效电容等于几个电容器 电容之和; •各个电容器的电压相等; 28 •并联使总电容增大。
各向同性电介质
q0 , q' 分布具有某些对称性
D 0 E P 0 E 0 E 0 (1 ) E
令 得
P 0 E
χ 为常数
1 r 介质的相对电容率 D 0 r E E 式中, 0 : 真空电容率 D 0 r : 介质电容率 D E
第四节 电容器中的电场能量

第四节电容器中的电场能量
1、电容器和电阻器都是电路中的基本元件,但它们在电路中的作用是不同的。
从能量上来看,电容器是一种元件,而电阻器是元件。
2、电容器中储存的电场能与电容器的成正比与电容器两极板间的成正比。
3、电容为0.2μF的电容器给它充电到电压为100V,这时电容器中的电荷量是,电容器储存的电场能是;继续给它充电到电压为200V,这时电容器中的电荷量是,电容器储存的电场能是,电容器中的电场能增加了。
4、两只容量相等的电容器,串联后的等效电容为C1,并联后的等效电容为C2,将C1和C2串联入电路U中,则C1和C2两端的电压U1:U2= ,电场能W1:W2= 。
5、两只容量相等的电容器,串联后的等效电容为C1,并联后的等效电容为C2,将C1和C2并联入电路U中,则C1和C2中的电荷量Q1:Q2= ,电场能W1:W2= 。
6、在图1所示的电路中,电容器A的电容C A=30μF,电容器B的电容C B= 10μF。
在开关S1、S2都断开的情况下,分别给电容器A、B充电。
充电后,M点的电位比N点高5V,O点的电位比P点低5V。
然后把S1、S2都接通,接通后U MN= V。
图1 图2
7、电路如图2所示,R1=40Ω,R2=60Ω,C=0.5μF,E=10V,电路稳定后,IC= ,Uc= ,电容器储存的能量Wc= 。
8、已知C1=0.2μF,耐压100V,已知C2=0.3μF,耐压120V。
(1)求它们串联时的等效电容和耐压。
(2)求它们并联时的等效电容和耐压。
9、图3所示电路中,已知E=6V,r=1Ω,C1=1μF,C2=2μF,C2=3μF,则abcd 各点的电位分别是多少?。
第二章2电容电容器静电能.ppt.ppt

q q q 1 2 q n C U U
C C . . . C 1 2 n
2.电容器的串联:带电量相同,分电压
U
A
C1
C2
C3
C
n
UB
令U UU 2 . . . U U U 1 n A B
q q q C C , . . . , C 1 , 2 n U U U 1 2 n
会生活。
2.清朝黄遵宪曾作诗曰:“钟声一及时,顷刻不少留。虽
有万钧柁,动如绕指柔。”这是在描写 A.电话 C.电报 B.汽车 D.火车 ( )
解析:从“万钧柁”“动如绕指柔”可推断为火车。 答案:D
[典题例析工具前往参观。然而在19世纪七十年代,江苏沿江 居民到上海,最有可能乘坐的交通工具是 A.江南制造总局的汽车 B.洋人发明的火车 ( )
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A.打破了外商对中国航运业的垄断 B.阻止了外国对中国的经济侵略 C.标志着中国近代化的起步 ( )
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵
[典题例析] [例2] (2010· 福建高考)上海是近代中国茶叶的一个外销
中心。1884年,福建茶叶市场出现了茶叶收购价格与上海
出口价格同步变动的现象。与这一现象直接相关的近代事 业是 A.电报业 C.铁路交通业 ( )
B.大众报业 D.轮船航运业
[解析]
[答案]
2019大学物理课件-电容和电容器及电场能量.ppt

E
;
3)通过场强,计算两极板间的电势差 U A U B ;
Q 4)由电容器电容的定义式 C 求出 C。 U A UB
1、平板电容器 (1)设两导体板分别带电 Q (2)两带电平板间的电场强度
d
A
B
σ Q E ε0 ε0 S
(3)两带电平板间的电势差
S
S
Q
dQ
Qd U Ed ε0 S
l RB
-+ - + RA -+ R B -+
λ , ( RA r RB ) (2)E 2 π ε0 r R λdr Q RB ( 3) U ln R 2πε r 2 π ε0 l RA 0
B A
l
Q RB (4)电容 C 2 π ε0 l ln U RA
3、球形电容器的电容 球形电容器是由半径分 别为 R1和 R2的两同心金属球壳所组成。
(4)平板电容器的电容
Q S C ε0 U d
(4)平板电容器的电容
Q S C ε0 U d
(5)如果在两极板间充满相 对电容率为 εr 的电介质时, 则其电容为:
d
S
εr
S S C ε r C 0 ε0 ε r ε d d
ε ε0εr
称为电容率。
例1
平行平板电容器的极板是边长为 l 的正方
取一体积元, dV 4πr 2 dr
2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2
Q 1 1 1 Q We ( ) 8 π ε R1 R2 2 4πε R2 R1 R2 R1 讨论
ppt7-电容器中的电场能.

第 2 页
2、电容器的放电 放电过程中,随着电容器极板上电量的减少,电容器两端 电压逐渐减小,放电电流也逐渐减小直至为零,此时放电过程 结束。 3、电容器的充放电电流
q 路中有电流产生。其电流大小为 i t
由 q CuC
充放电过程中,电容器极板上储存的电荷发生了变化,电
uC q C 所以: i t t
,可得 q CuC
需要说明的是,电路中的电流是由于电容器充、放电形 成的,并非电荷直接通过了介质。
第 3 页
电容充放电-注意事项
(1)若电容两端加直流,
u C iC C 0 t
,电容器相当于开路,所以电容器具有隔直流的作用。
(2)若将交变电压加在电容两端,则电路中有交 变的电流通过,即电容具有通交流作用。
第
二、电容器中的电场能
1、能量来源
电容器在充电过程中,两极板上有电荷积累,极板间形成 电场。电场具有能量,此能量是从电源吸取过来储存在电容器 中的。 从能量转化角度看,电容器的充放电过程,实质上是电容 器与外部能量的交换过程。在此过程中,电容器本身不消耗能 量,所以说电容器是一种储能元件。 2U 2
第 1 页
一、电容器的充电和放电
电容在充电过程中,电容器储存了电荷,也储存了能量; 在放电过程中,电容器将正、负电荷中和,也随之放出了能 量。 1、电容器的充电 充电过程中,随着电容器两极板上所带的电荷量的增加, 电容器两端电压逐渐增大,充电电流逐渐减小,当充电结束时,
电流为零,电容器两端电压。
UC = E
7.大学物理-电容和电场能(共29张)

C q U
q1 q2 qi
U1 U2
Ui
C1 C2 Ci
第9页,共29页。
三、电容器的串联(chuànlián)和并联
2.串联电容器的电容:
1 1
C i Ci
U A C1
C2
C3 Ci U B 等效 U A C U B
q q1 q2 qi
U U1 U2 Ui UA UB
1 U U1 U2 Ui 1 1 1
C q q1 q2
qi C1 C2
Ci
第10页,共29页。
例:平行板电容器极板面积为S,相距为d. 充填
一半的电介质,其相对介电常数为 r .
求:两种电容(diànróng)器的电容(diànróng)
1'
r
Ud
'
r
td/2
td
第11页,共29页。
方法: q U
典型电容:
C q U
0 0
1.平行板电容器: S d 2
E E0 q / S
r 0 r U Ed qd
0 r S
C 0 r S
d
C rC0
q 0S
真空:
r 1
C C0
第5页,共29页。
2. 球形电容器:
E
q0
4 0 r r 2
rˆ
R1 r R2
R2
qo
1) 不断开电源
两板电势差 = 电源端电压 = V 保持(bǎochí)不变
电容器储能变化:
W
1 2
C0V
2
1 CV 2
2
V2 2
(1r
)C0
0
极板电量变化
Q C0V CV (1 r )C0V 0
5.电容 电场能量
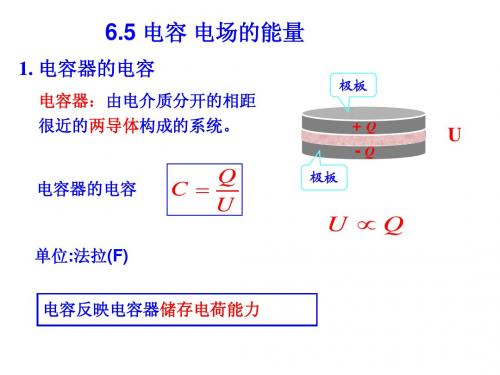
6.5 电容 电场的能量
1. 电容器的电容
极板
电容器: 电容器:由电介质分开的相距 很近的两导体构成的系统。 两导体构成的系统 很近的两导体构成的系统。
+Q
-Q
电容器的电容
U
Q C= U
极板
U ∝Q
单位:法拉 单位 法拉(F) 法拉
电容反映电容器储存电荷能力 电容反映电容器储存电荷能力
C决定于两极板 、B的形状、大小,A、 决定于两极板A、 的形状 大小, 、 的形状、 决定于两极板 B的相对位置以及 、B间的电介质,与电 的相对位置以及A、 间的电介质 间的电介质, 的相对位置以及 容器带电荷无关。 容器带电荷无关。
v E
U
Q C= U
Q E = 4πε r 2
(2) 球形电容器
uv v Q 2 Eds = 4πr E = ε ∫∫ s
r r Q 1 1 U = ∫ E ⋅ dl = ( − ) 4πε R1 R2 a
b
b
a
R2 R1
-Q
Q 4πε R1R2 C= = U R2 − R1
+Q
高斯面s
(3) 柱形电容器
uv v λl Ql Eds = E2πrl = ε = ε L ∫∫ s
Q E= 2πε 0rL (R1 < r < R2 )
(R1 < r < R2 )
v v R2 R2 u U = ∫ E r = ∫ d
R1 R1
R2 Q Q ln dr = 2πε L R1 2πε Lr
R2
l
R1
L
λ
R1
λ E= 2πε r
1 2 λ2 we = ε E = 2 2 2 8π ε r
1. 电容器的电容
极板
电容器: 电容器:由电介质分开的相距 很近的两导体构成的系统。 两导体构成的系统 很近的两导体构成的系统。
+Q
-Q
电容器的电容
U
Q C= U
极板
U ∝Q
单位:法拉 单位 法拉(F) 法拉
电容反映电容器储存电荷能力 电容反映电容器储存电荷能力
C决定于两极板 、B的形状、大小,A、 决定于两极板A、 的形状 大小, 、 的形状、 决定于两极板 B的相对位置以及 、B间的电介质,与电 的相对位置以及A、 间的电介质 间的电介质, 的相对位置以及 容器带电荷无关。 容器带电荷无关。
v E
U
Q C= U
Q E = 4πε r 2
(2) 球形电容器
uv v Q 2 Eds = 4πr E = ε ∫∫ s
r r Q 1 1 U = ∫ E ⋅ dl = ( − ) 4πε R1 R2 a
b
b
a
R2 R1
-Q
Q 4πε R1R2 C= = U R2 − R1
+Q
高斯面s
(3) 柱形电容器
uv v λl Ql Eds = E2πrl = ε = ε L ∫∫ s
Q E= 2πε 0rL (R1 < r < R2 )
(R1 < r < R2 )
v v R2 R2 u U = ∫ E r = ∫ d
R1 R1
R2 Q Q ln dr = 2πε L R1 2πε Lr
R2
l
R1
L
λ
R1
λ E= 2πε r
1 2 λ2 we = ε E = 2 2 2 8π ε r
大学物理-电容--电容器和电场能量

1.圆柱形电容器. 如图所示,圆柱形
电容器是由半径分别为 R A 和 R B 的两 同轴圆柱面 A 和 B 所构成,且圆柱体
的长度 l 远大于半径之差. 两导体之间
充满介电常数为 的电介质. 求此圆
柱形电容器的电容.
l RB RA
l
-
+ +A
RA B
-+ -+
RB
3
解: (1)设两导体圆柱面单位长度上
1
t
C0 (1
0 )
C0
0S
d
d
由于电介质插入,电容增大了
9
§5.6 电场的能量
一 带电系统的能量
把一个带电体带电Q的过程设想为不断地把dq从无穷远处搬移 到带电体上的过程
把一试探电荷q0从电场中a点移动到b点
U
dq
电场力所做功为: q0 Ua Ub
Q
把一电荷元dq从电场中无穷远移动到q导体上电场力所做功为:
-
dq
+Q + + + + + + + +
电容器贮存的电能 (任何结构电容器)
W 1 CU 2 1 UQ
2
2
11
二 电场能量
考虑一个理想平行板电容器,它的极板面积为S,极板间 电场占空间体积V=Sd,极板自由电荷为Q,板间电压为U
W 1 QU Q D U Ed
2
S
W 1 QU 1 DSEd = 1 DESd 1 DEV
§5.5 电容 电容器
一 孤立导体的电容
q U
q C C为孤立导体的电容. U
单位 1F 1C/V 1μF 106 F
电容器是由半径分别为 R A 和 R B 的两 同轴圆柱面 A 和 B 所构成,且圆柱体
的长度 l 远大于半径之差. 两导体之间
充满介电常数为 的电介质. 求此圆
柱形电容器的电容.
l RB RA
l
-
+ +A
RA B
-+ -+
RB
3
解: (1)设两导体圆柱面单位长度上
1
t
C0 (1
0 )
C0
0S
d
d
由于电介质插入,电容增大了
9
§5.6 电场的能量
一 带电系统的能量
把一个带电体带电Q的过程设想为不断地把dq从无穷远处搬移 到带电体上的过程
把一试探电荷q0从电场中a点移动到b点
U
dq
电场力所做功为: q0 Ua Ub
Q
把一电荷元dq从电场中无穷远移动到q导体上电场力所做功为:
-
dq
+Q + + + + + + + +
电容器贮存的电能 (任何结构电容器)
W 1 CU 2 1 UQ
2
2
11
二 电场能量
考虑一个理想平行板电容器,它的极板面积为S,极板间 电场占空间体积V=Sd,极板自由电荷为Q,板间电压为U
W 1 QU Q D U Ed
2
S
W 1 QU 1 DSEd = 1 DESd 1 DEV
§5.5 电容 电容器
一 孤立导体的电容
q U
q C C为孤立导体的电容. U
单位 1F 1C/V 1μF 106 F
