上海交通大学无机化学课件第二章热力学教材
合集下载
化学热力学初步(无机化学) ppt课件
5
2. 局限性:
不知道反应的机理、速率和物质的微观性质,只
讲可能性,不讲现实性。
ppt课件
5
3.2 热力学基本概念
一、体系和环境
体系:被研究的直接对象 环境: 体系外与其密切相关的部分
ppt课件
6
体系类型:根据体系与环境的关系
敞开体系:与环境有物质交换也有能量交换 封闭体系:与环境有能量交换无物质交换
转动能,平动能,电子动能及核能,电子与电子间的势
能,电子与核间的势能等。
特点:“热力学内能”是状态函数。
现还无法求出体系热力学内能的绝对值;但能测定到
ppt课件
20
2. 热力学第一定律内容
一个封闭体系,处于一种特定的内能状态U1。若这 个体系吸收一定的热量Q, 同时环境对体系做功W, 这 个体系则达到一个新的内能状态U2
量传递的方向,是由体系的观点 体
Q﹤
系
出发的;
ppt课件
w﹥
w﹤
功 18
3.3 热力学第一定律及反应热
一、研究基础
1. 热功当量 即: 1 cal = 4.1840 J
为能量守恒原理提供了科学的实验证明。
2. 能量守恒定律
1850年,科学界公认能量守恒定律是自然界的普遍规 律之一。能量守恒与转化定律可表述为:
375 K,506.5 kPa
终态
实际过程与完成过程的不同途径
ppt课件
14
五、热和功: 体系状态变化过程中的能量表现形式
热:体系与环境之间因温度不同而交换或传递的能量 称为热(Q)。
Q>0, 体系吸收热量 , Q<0, 体系释放热量 功: 除热之外,体系与环境之间以其它形式交换或传递 的能量称为功(W)。
无机化学课件第二章4_5热力学第二定律节

真空
2个分子在左边球内的概率为1/4
3个分子在左边球内的概率为1/8
理想气体的自由膨胀
统计解释: 2个分子在左边球内的概率为1/4 3个分子在左边球内的概率为1/8 n个分子在左边球内的概率为1/2n 1mol个分子在左边球内的概率1/26.022×1023 概率如此小,可见是一种不可能的状态。 所以气体的自由膨胀是必然的。
利用附录中298.15K的标准摩尔熵,可以计算
298.15K时反应的标准摩尔熵变。
△ rSm (298.15K) = ∑νB Sm (B,相态,298.15K) △ rSm >0,有利于反应正向自发进行。
rSm iSm (生成物) iSቤተ መጻሕፍቲ ባይዱ (反应物)
例:计算25℃及标准状态下,下述反应的熵变。 CaCO3(s) = CaO(s) + CO2(g)
一个过程如果导致系统的能量减小,这个过程 将是自发的。但是,放热不是判断自发性的唯一标准。
事实证明:不能用是放热还是吸热来判断化学反应 的自发方向 热力学表明,自发性由两个因素决定: 1.体系趋向于最低能量; 2.体系趋向于最大混乱度。
自发变化的特点
1. 自发变化的逆过程是非自发的。即自发变化具有单向性或 在给定条件下具有不可逆性。
• 物质的熵值随温度升高而增大,气态物质 的熵值随压力增高而减小。 CS2(1161K)< CS2(1298K) O2 (g,100kPa)> O2 (g,600kPa)
标准摩尔熵的一些规律
2.4.4 化学反应熵变和热力学第二定律
1.化学反应熵变的计算 对于化学反应:
0=ΣνBB B
△ rSm (T,K)
§2.4 热力学第二定律
2.4.1 化学反应的自发性 2.4.2 混乱度和熵 2.4.3 热力学第三定律和标准熵 2.4.4 化学反应熵变和热力学第二 定律
2个分子在左边球内的概率为1/4
3个分子在左边球内的概率为1/8
理想气体的自由膨胀
统计解释: 2个分子在左边球内的概率为1/4 3个分子在左边球内的概率为1/8 n个分子在左边球内的概率为1/2n 1mol个分子在左边球内的概率1/26.022×1023 概率如此小,可见是一种不可能的状态。 所以气体的自由膨胀是必然的。
利用附录中298.15K的标准摩尔熵,可以计算
298.15K时反应的标准摩尔熵变。
△ rSm (298.15K) = ∑νB Sm (B,相态,298.15K) △ rSm >0,有利于反应正向自发进行。
rSm iSm (生成物) iSቤተ መጻሕፍቲ ባይዱ (反应物)
例:计算25℃及标准状态下,下述反应的熵变。 CaCO3(s) = CaO(s) + CO2(g)
一个过程如果导致系统的能量减小,这个过程 将是自发的。但是,放热不是判断自发性的唯一标准。
事实证明:不能用是放热还是吸热来判断化学反应 的自发方向 热力学表明,自发性由两个因素决定: 1.体系趋向于最低能量; 2.体系趋向于最大混乱度。
自发变化的特点
1. 自发变化的逆过程是非自发的。即自发变化具有单向性或 在给定条件下具有不可逆性。
• 物质的熵值随温度升高而增大,气态物质 的熵值随压力增高而减小。 CS2(1161K)< CS2(1298K) O2 (g,100kPa)> O2 (g,600kPa)
标准摩尔熵的一些规律
2.4.4 化学反应熵变和热力学第二定律
1.化学反应熵变的计算 对于化学反应:
0=ΣνBB B
△ rSm (T,K)
§2.4 热力学第二定律
2.4.1 化学反应的自发性 2.4.2 混乱度和熵 2.4.3 热力学第三定律和标准熵 2.4.4 化学反应熵变和热力学第二 定律
上海交大工程热力学(第四版)课件 第2章 热力学第一定律

q u w t p 2 v 2 p1v1
wt w p 2 v 2 p1v1
(D )
δ wt δ w d pv
可逆过程
δ wt p d v d pv v d p
17
3)第一定律第二解析式
q h2 h1 1 2
2 2
w t ws
1 2
c f 1 gz1 p1v1
2
内增: 0
c f 2 gz 2 p 2 v 2
2
1 2 p u c f gz 0 2
23
例A4312661 例A4322661 例A4332771 例A4333771
24
归纳: 1)开口系问题也可用闭口系方法求解。 2)注意闭口系边界面上热、功交换;尤其是边界面 变形时需考虑功的交换。 3)例A4333771中若有无摩擦及充分导热的活塞,结果如何? ——解法三即可认为是这种情况,故无影响。 4)若A4333771活塞为绝热材料制造, 若活塞下有弹簧, 若· · · · · ·
第二章 热力学第一定律
First law of thermodynamics
2–1 热力学第一定律的实质 2-2 热力学能(内能)和总能 2–3 热力学第一定律基本表达式 2–4 闭口系基本能量方程式 2–5 开口系能量方程
1
2–1 热力学第一定律的实质
一、第一定律的实质
能量守恒与转换定律在热现象中的应用。
二、第一定律的表述
热是能的一种,机械能变热能,或热能变机械能的 时候,他们之间的比值是一定的。 或: 热可以变为功,功也可以变为热;一定量的热消失 时必定产生相应量的功;消耗一定量的功时,必出现 与之相应量的热。
上海交通大学大学物理A类热力学第一定律热力学第二定律概要PPT课件
R
第12页/共92页
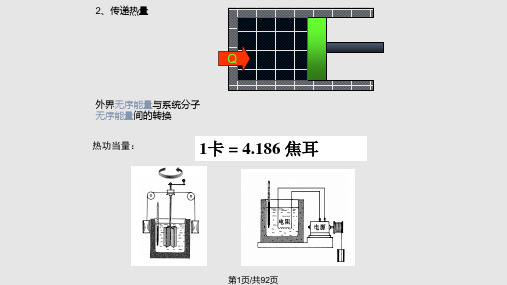
定压mol热容量 :
CP,m
dQm dT
P
C P ,m
(dQm )P dT
dE PdV dT
dE dT
P dV dT
PV RT P 恒量 PdV RdT
CP,m CV ,m R
迈耶公式
热容比
CP,m 1 R
CV ,m
CV ,m
CV ,m
i 2
R
C P ,m
1824年,法国 28 岁工程师卡诺 采用科学抽象的方法建立了理 想化的模型,即卡诺热机。用 卡诺循环来研究问题。
第39页/共92页
卡诺循环(Carnot cycle) 高温热源 A
低温热源
P
a
Q1
b
Q2
d
c
O
V
第40页/共92页
吸收热量 放出热量
P
a
Q1
b
Q2
d
c
O
V
A Q1 Q2 R lnV2 V1(T1 T2)
u 故准静态过程可以用P-V图(或P-T图,V-T图)中一
条曲线表示,反之亦如此。
功是过程量 热力学第一定律:
o
V
P-V图
内能是状态量
Q是过程量
第6页/共92页
问题: 孤立系统 理想气体 开始压强 移去挡板稳定后
真空
非准静态过程
第7页/共92页
容器体积为2V0,用绝热板分隔为 两部分。A内储有1mol单原子理想
• 摩尔热容量 C , 单位:J/mol·K • 比热容 c , 单位:J/kg·K
d Q 为过程量
C为过程量
定容mol热容量 :
理想气体准静态等容过程:
上海交通大学物理化学课件热力学第一定律下

摩尔生成焓,用下述符号表示:
f H (物质,相态,温度)
$ m
在生成焓的定义中没有规定温度,一般298.15 K时
的数据有表可查。生成焓仅是相对于稳定单质的焓值,
稳定单质的生成焓等于零。
例如:在298.15 K时
1 1 $ H 2 ( g , p ) Cl2 ( g , p $ ) HCl ( g , p $ ) 2 2
$ $ $ $ $ r H m f Hm (C) 3 f Hm (D) 2 f Hm ( A) f Hm (B)
$ B f H m ( B)
B 为计量方程中的系数,对反应物取负值,生成物取
正值。
当化合物不能直接由单质直接合成时?
C、H2和O2不能直接合成CH3COOH(l),如何求得 其标准摩尔生成焓?
如体系内各组分不是理想气体,H 3 虽不一定等于零, 但其数值与化学反应的 r H 项比较,一般来说微不足 道,可以略去不计。因此可得
r H rU ( pV )
Qp QV ( pV )
热化学方程式
表示化学反应与热效应关系的方程式称为热化学
方程式。因为U、H 的数值与体系的状态有关,所 以方程式中应该注明物态、温度、压力、组成等。
1 O (g) 2 2
r H m,1
r H m,2
CO(g)
r H m,3
r H m,3 r H m,1 r H m,2
几种热效应
1、化合物的生成焓 2、键焓* 3、离子生成焓 4、燃烧焓 5、溶解热* 6、稀释热*
标准摩尔生成焓
在标准压力下、某反应温度时,由最稳定的单质合 成标准状态下一摩尔物质的焓变,称为该物质的标准
无机化学第二章

(1) N 2 (g) + 3H 2 (g)
2NH 3 (g)
∆n(N 2 ) ∆n(H 2 ) ∆n(NH 3 ) ∆ξ1 = = = v1 (N 2 ) v1 (H 2 ) v1 (NH 3 ) −2 mol −6 mol 4 mol = = = = 2 mol −1 −3 2 1 3 NH 3 (g) (2) N 2 (g) + H 2 (g) 2 2 ∆n(N 2 ) ∆n(H 2 ) ∆n(NH 3 ) ∆ξ 2 = = = v2 (N 2 ) v2 (H 2 ) v2 (NH 3 ) −2 mol −6 mol 4 mol = = = =4 mol −1/2 −3/2 1
第二章 化学热力学基础
第一节 第二节 第三节 第四节 第五节 热力学第一定律 热化学 热化学第二定律 化学反应的摩尔吉布斯自由能变 热力学在生物化学中的应用
热力学是研究热与其他形式的能量之间转化 规律的一门科学。热力学的基础是热力学第一定 律和热力学第二定律。 利用热力学定律、原理和方法研究化学反应 以及伴随这些化学反应而发生的物理变化过程就 形成了化学热力学。 化学热力学主要研究和解决的问题有: (1)化学反应及与化学反应密切相关的物理 过程中的能量变化; (2)判断化学反应进行的方向和限度。
引入反应进度的优点是,用任一种反应物或 产物表示反应进行的程度,所得值都是相同的。 应用反应进度时,必须指明化学反应方程式。
例题
例 2-1 10 mol N2 和 20 mol H2 在合成塔混合后, 经多次循环反应生成了 4 mol NH3。试分别以如下两 个反应方程式为基础,计算反应进度变。 (1) N 2 (g) + 3H 2 (g) 2NH 3 (g)
根据系统与环境之间物质和能量的交换情况 的不同,把系统分为三类: (1)敞开系统:系统与环境之间既有能量交 换,又有物质交换。 (2)封闭系统:系统与环境之间只有能量交 换,没有物质交换。 (3)隔离系统:系统与环境之间既没有能量 交换,也没有物质交换。
无机化学一 化学热力学(共65张PPT)

第二十六页,共65页。
3.本卷须知 〔1〕 对同一(tóngyī)化学反响,K 表达式
与化学反响方程式写法和温度有关,固给出 K 时,必须指明对应的化学方程式和温度。 〔2〕对于有纯固体、纯液体参加的反响,其 K 只包含气体的分压和溶液的相对浓度。 〔3〕稀溶液进行的反响,如果反响有水参加, 可视为常数,不写在平衡常数中
TΔrSθm(298k) 转变温度:如果温度对反响(fǎnxiǎng)方向有影响,即温
度的上下决定的正负时,必然有一温度T值与 (T)=0相 对应,那么此温度称为转变温度 ΔrGθm〔298k〕= ΔrH θm〔298k〕 – TΔrSθm(298k)=0 所以T转= ΔrH θm〔298k〕 /ΔrSθm(298k〕
无机化学(wújīhuàxué)一 化学热力学
第一页,共65页。
• 状态函数:指一系列确定体系状态的物理 量
• 特征如下: • 定值性:体系处于一定状态时,它的每个
状态函数都有确定的数值 • 状态函数的变化只决定于体系的始态和终
态,与变化的途径无关(wúguān) • 假设为循环过程,状态函数的改变量为0
减少生成物的浓度,平衡(pínghéng)向正向 移动 2、增大压力,向气体分数少的方向移动 等温定压条件下,充入惰性气体,相当于减 小总压力 等温定容条件下,向系统充入惰性气体,总 压力增大,平衡(pínghéng)不移动。〔体系 压力没有变化〕
第三十三页,共65页。
3、温度(wēndù)
第三十四页,共65页。
第五页,共65页。
三、焓 体积功〔W体〕:体系对抗外压体积变
化时所做的功 非体积功〔W非〕:除体积功以外(yǐwài)的
功〔电功等〕 〔一〕等容过程 假设体系在变化过程中,体积始终保持不变
3.本卷须知 〔1〕 对同一(tóngyī)化学反响,K 表达式
与化学反响方程式写法和温度有关,固给出 K 时,必须指明对应的化学方程式和温度。 〔2〕对于有纯固体、纯液体参加的反响,其 K 只包含气体的分压和溶液的相对浓度。 〔3〕稀溶液进行的反响,如果反响有水参加, 可视为常数,不写在平衡常数中
TΔrSθm(298k) 转变温度:如果温度对反响(fǎnxiǎng)方向有影响,即温
度的上下决定的正负时,必然有一温度T值与 (T)=0相 对应,那么此温度称为转变温度 ΔrGθm〔298k〕= ΔrH θm〔298k〕 – TΔrSθm(298k)=0 所以T转= ΔrH θm〔298k〕 /ΔrSθm(298k〕
无机化学(wújīhuàxué)一 化学热力学
第一页,共65页。
• 状态函数:指一系列确定体系状态的物理 量
• 特征如下: • 定值性:体系处于一定状态时,它的每个
状态函数都有确定的数值 • 状态函数的变化只决定于体系的始态和终
态,与变化的途径无关(wúguān) • 假设为循环过程,状态函数的改变量为0
减少生成物的浓度,平衡(pínghéng)向正向 移动 2、增大压力,向气体分数少的方向移动 等温定压条件下,充入惰性气体,相当于减 小总压力 等温定容条件下,向系统充入惰性气体,总 压力增大,平衡(pínghéng)不移动。〔体系 压力没有变化〕
第三十三页,共65页。
3、温度(wēndù)
第三十四页,共65页。
第五页,共65页。
三、焓 体积功〔W体〕:体系对抗外压体积变
化时所做的功 非体积功〔W非〕:除体积功以外(yǐwài)的
功〔电功等〕 〔一〕等容过程 假设体系在变化过程中,体积始终保持不变
上海交通大学物理化学课件热力学第一定律1

1、状态函数决定于系统的状态,而过程量取决于 具体的途径。所以状态函数用来描述系统状态,而 过程量用于描述过程。
31
2、当系统中发生变化时,状态函数的变化只取决于 系统的始末状态,而与变化的具体途径无关。
在计算状态函数变化时,若给定途径不能或不易求 得,可通过设计途径进行计算。与此相反,过程量则 不能通过设计途径进行计算,因为对于不同途径,它 们的值可能不同。
We',2p''(V'' V2)
p'(V' V'')
p1(V1V')
48
外压比内压大一个无穷小的值
水
p2
始
态
V2
pe pi dp
p
p1
p 1V 1
p1
终
V1
态
阴影面积代表We',3
p2
p 2V 2
V1
V2 V
49
如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓 慢增加,恢复到原状,所作的功为:
W' e,3
V1 V2
pidV
nRT ln V2 V1
50
功与过程小结
从以上过程看出,始终态相同,但途径不同, 所作的功也大不相同。显然,可逆膨胀,体系对环 境作最大功;可逆压缩,环境对体系作最小功。
51
准静态过程
在过程进行的每一瞬间,体系都接近于平衡状 态,以致在任意选取的短时间dt内,状态参量在整 个系统的各部分都有确定的值,整个过程可以看成 是由一系列极接近平衡的状态所构成,这种过程称 为准静态过程。
体积功
体积功的计算
Wp外dV
若系统发生明显体积变化且 p 外 是连续函数,则
31
2、当系统中发生变化时,状态函数的变化只取决于 系统的始末状态,而与变化的具体途径无关。
在计算状态函数变化时,若给定途径不能或不易求 得,可通过设计途径进行计算。与此相反,过程量则 不能通过设计途径进行计算,因为对于不同途径,它 们的值可能不同。
We',2p''(V'' V2)
p'(V' V'')
p1(V1V')
48
外压比内压大一个无穷小的值
水
p2
始
态
V2
pe pi dp
p
p1
p 1V 1
p1
终
V1
态
阴影面积代表We',3
p2
p 2V 2
V1
V2 V
49
如果将蒸发掉的水气慢慢在杯中凝聚,使压力缓 慢增加,恢复到原状,所作的功为:
W' e,3
V1 V2
pidV
nRT ln V2 V1
50
功与过程小结
从以上过程看出,始终态相同,但途径不同, 所作的功也大不相同。显然,可逆膨胀,体系对环 境作最大功;可逆压缩,环境对体系作最小功。
51
准静态过程
在过程进行的每一瞬间,体系都接近于平衡状 态,以致在任意选取的短时间dt内,状态参量在整 个系统的各部分都有确定的值,整个过程可以看成 是由一系列极接近平衡的状态所构成,这种过程称 为准静态过程。
体积功
体积功的计算
Wp外dV
若系统发生明显体积变化且 p 外 是连续函数,则
上海交通大学物理化学热力学第一定律中PPT学习教案

J-T
= 0 经节流膨胀后,气体温度不变。
dp 0
第33页/共40页
转化温度
在常温下,一般气体的 均为正值。例如,空气的
,即压力下降
气体温度下降
。
J-T
J-T 0.4 K /101.325 kPa 0.4 K
101.325 kPa
但氢气、氦等气体在常温下
,经节流过程,温度反而升高。若 降低温 度可使
移项
U2 p2V2 U1 p1V1
或
H2 H1
H 0
节流过程是个等焓过程。
第页/共40页
焦–汤系数
J-T
T ( p )H
焦-汤系数 表示经节流过程后气体温度随压力的变 化率, 它是体 系的强 度性质 。
考虑到节流过程中
,故
> 0 经节流膨胀后,气体温度降低。
J-T
J-T
< 0 经节流膨胀后,气体温度升高。
。
当
时的温度称为转化温度,这时气体经 节流实 验,温 度不变 。每一 种气体 都有自 己的转 化温度 。
J-T
0
0
J-T
J-T 0
第34页/共40页
绘制等焓线
第35页/共40页
等焓线上任意一点的
切线斜率
( T p
)H
,就是
该温度压力下的J-T 值。
第36页/共40页
选择不同的起始状态,作若干条等焓 线。将 各条等 焓线的 极大值 相连, 就得到 一条虚 线,将 T-p图 分成两 个区域 。
例如氮气的转化曲线温度高,能液 化的范 围大; 而氢气 、氦则 很难液 化。
第38页/共40页
实际气体
理想气体的焦-汤系数为零,因此 理想气 体经过 节流过 程后温 度不变 。但实 际气体 的实验 结果显 示节流 前后两 边的温 度不等 。出现 这种情 况的原 因在于 理想气 体的内 能仅与 温度有 关,而 实际气 体的内 能不仅 与温度 有关, 还与体 积或压 力有关 !
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)功和热 1.热力学中把体系与环境之间因温差而变化 的或传递的能量形式称热,以Q表示。 2. 除热以外的能量交换形式都称为功,以w 表示。 3.热力学中功的分类: • 体系反抗外压所做的膨胀功或称体积功; • 除“膨胀功”以外的“其它功”或称之为 有用功、非体积功。 *在我们的课程中(除氧化还原章节外)只 研究体积功。
一、基本概念:
(1)体系(系统)和环境
体系的分类:
敞开体系; 封闭体系; 孤立体系。 我们一般主要讨论封闭体系。
问题:我们为什么一般讨论封闭体系?
直观的例子?
敞开体系
封闭体系
孤立体系
(2)状态和状态函数 1.状态是体系所有性质的综合表现 ; 2.体系的热力学性质称为状态函数 ; 3. 状态函数有三个相互联系的特征:
• 热力学中,对于热、功的符号的规定:
体系吸热:+ 体系放热:- 体系接受功: - 体系做出功: +
*均以体系为参考。 • 注意:上述两者都是状态变化过程中能量传
递的形式,其数值与状态变化的途径有关, 故热、功为非状态函数。
C6H5N2+Cl-+H2O => C6H5OH+H++Cl-+N2
讨论此例得到的结论!
讨论: 1.从()(2)可以看到: 作为量度性质
的热力学能,对宇宙来说其改变量当然是零。 ΔU体系 + ΔU环境=0 或 U体系 + U环境=常数 ――――能量守恒的实 质。
2.对于体系的始态UI和终态(UI+20):
虽然变化途径不同(Q、W不同),但ΔU却 相同。说明Q、W是非状态函数,它们与途径 有关,而热力学能是状态函数与途径无关。
引入的第一个热力学状态函数!
二、热力学第一定律
1.数学表达式:ΔU=Q-W
* 注意:另外的表达方式,第一定律的表达式与
功和热符号的规定;
2.研究内容:变化过程中热力学能、功、 热的转换方式。 3.实质:能量守恒。 *注意:这里既有过程量又有状态函数以及之
间的关系;
例题:
某过程中,体系从环境吸收热量50kJ,对 环境做功30kJ。求:
某气体
300K 300K 300K 300K 350K 360K 280K 460K
350K 350K 350K
300K
Δ T=50K Δ T=50K Δ T=50K Δ T= 0K
始态 水 298K 298K 始态
终态 272K 398K 348K 348K 终态
改变量
ΔT=50K ΔT=50K
切记:同样的过程,可以有不同的途径!
• 自发过程:一定条件下,不需要给定能量就能 够自动进行的过程。
一种特殊的过程
• 可逆过程(途径)*: 它是一种在无限接近于平衡,并且没有摩擦 力条件下进行的理想过程(如理想气体可 逆膨胀或压缩)。 • 我们主要讨论等温可逆过程
• 我们为什么要讨论等温可逆过程(途径)?
第二章 化学热力学初步
关于化学热力学
1.何为热力学?解决什么问题?——属于什么范畴? 2.何为化学热力学?解决什么问题?——非常重要的 结论! 3.化学热力学学习要求掌握的内容: • 化学反应的可能性; • 化学反应进行的方向; • 化学反应的程度。
*本章学习要注意的地方——注重概念以及使用 的条件!
(1)过程中体系热力学能的改变量ΔU和环境热 力学能的改变量ΔU‘。
解:(1) 由热力学第一定律的数学表达式可知 Q=+50kJ W =+30kJ ∴ ΔU体系 =Q - W =50 -30=20(kJ)
( 2 )如果开始时,体系先放热 40kJ ,环境对体 系做功 60kJ ,求体系的热力学能的改变量ΔU 以及终态的热力学能U 。 ( 解 ) 若 将 环 境 当 做 体 系 来 考 虑 , 则 有 Q′= 50kJ,W′= 30kJ, 故环境热力学能改变量ΔU′=Q′- W′ ∴ ΔU′环境 = 50-(30)= 20(kJ) (2) Q=-40kJ W= -60kJ ΔU体系=Q - W =20kJ ∴ UII=UI+20(kJ)
(5)热力学能(内能)
• 体系内部一切能量的总和称为体系的热力学能U。 • U的内涵和性质: a.体系内部各种形式能量的总和。 b.它的绝对值无法测量或计算。只能计算ΔU。 c.U是体系的具有加合性质的状态函数。体系的状 态一定,则有一个确定的热力学能值。 d.理想气体的热力学能只是温度的函数,所以其恒 温过程的△U=0 (?)
• 体系状态一定,状态函数有一定的值; • 体系状态变化时,状态函数的变化只决定于体系 的始态和终态,而与变化的途径无关; • 体系恢复到始态,状态函数恢复原值。
问题:满足上述几个条件可以认为是状态函数?
* 状态一定值一定; 殊途同归变化等; 周而复始变为零。
4.状态函数的类型:
• 容量性质的状态函数--------具有加和性 (如V、m); • 强度性质的状态函数 ------没有加和性(如 T、P)(与物质的量无关)。
• 可逆过程:
要求变化的过程在一连串的平衡状态下可逆地 进行。
即体系和环境都回到原始状态,不给环境 留下任何痕迹。
Q、W不是状态函数,它随途径不同而 改变。 *对于理想气体来说,热力学能U只是 温度的函数,
理想气体的恒温可逆膨胀或压缩,体系吸 收或放出的热量以及对外或接收的体积功 的数值大小相等!
*注意:要区别可逆反应与可逆过程。 • 可逆反应:
指反应物按正向反应得到产物,而产物也可按 逆向反应变成反应物。
改变量
殊途同归,增量相同
(3)过程和途径 • 体系的状态发生变化时 ,状态变化的经过 ――过程。 • 完成这个过程的具体步骤则称为途径。 方式——途径。 过程 ——状态。
问题:如何区分过程与途径?举例?
热力学中常见的过程: • 等温过程:体系的始态温度与终态温度相同,并 等于环境的温度; (T1=T2=T环) • 等压过程:始态、终态的压力与环境相同( p1 = p2=p环) • 等容过程:体系的体积不发生变化(V1=V2) • 绝热过程:体系与环境之间无热量交换(Q=0) • 循环过程:过程进行后,系统重新回到初始状态。
