三视图选择题

合集下载

三视图练习题

29.2 三视图一、选择题（共15小题；共75分）1. 下列物体的主视图、俯视图和左视图不全是圆的是 ( )A. 橄榄球B. 兵乓球C. 篮球D. 排球2. 如图，几何体的俯视图是A. B.C. D.3. 长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是A. 12 cm2B. 8 cm2C. 6 cm2D. 4 cm24. 如图所示，几何体的俯视图是A. B.C. D.5. 如图是有几个相同的小正方体组成的一个几何体．它的左视图是A. B.C. D.6. 如图是由八个相同小正方体组成的几何体，则其主视图是A. B.C. D.7. 桌面上放着1个长方体和1个圆柱体，按下图所示的方式摆放在一起，其左视图是A. B. 与原题图不一样C. D.8. 下列几何体中，有一个几何体的俯视图的形状与其它三个不一样，这个几何体是 ( )A. B.C. D.9. 图中三视图所对应的直观图是A. B.C. D.10. 如图是常用的一种圆顶螺杆，它的俯视图正确的是A. B.C. D.11. 如图的几何体的三视图是A. B.C. D.12. 如图是由一些相同的小正方体搭成的几何体的三视图，则构成这个几何体的小正方体的个数为A. 4个B. 5个C. 6个D. 7个13. 一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是A. B.C. D.14. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为．A. 6B. 8C. 12D. 2415. 如图所示是某几何体的三视图，根据图中数据，求得该几何体的体积为A. 60πB. 70πC. 90πD. 160π二、填空题（共6小题；共30分）16. 一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是．17. 如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小正方体，王亮所搭几何体表面积为．18. 如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是．19. 由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数可能是．20. 用八个同样大小的小立方体粘成一个大立方体如图 1，得到的几何体的三视图如图 2 所示，若小明从八个小立方体中取走若干个，剩余小立方体保持原位置不动，并使得到的新几何体的三视图仍是图 2，则他取出的小立方体最多可以是个．21. 在桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，设组成这个几何体的小正方体的个数为n，则n的最小值为．三、解答题（共2小题；共26分）22. 如图所示的几何体是由12块棱长为1 cm的正方体堆积而成的．请求出它的表面积．23. 如图，四边形ABCD，将其绕CD所在直线旋转一周得到一个几何体，请画出这个几何体的从正面、左面、上面看到的形状图．答案第一部分1. A2. D3. A4. C5. B6. C7. C8. A9. C 10. B11. C 12. A 13. D 14. B 15. B第二部分16. 球体17. 19；4818. 619. 4或5或6或720. 421. 5第三部分22. (1) 由题意，得S=8×12×2+5×12×2+7×12×2=40．所以它的表面积为40 cm2．23. (1) 如图所示．。

高三专项训练：三视图练习题(一)

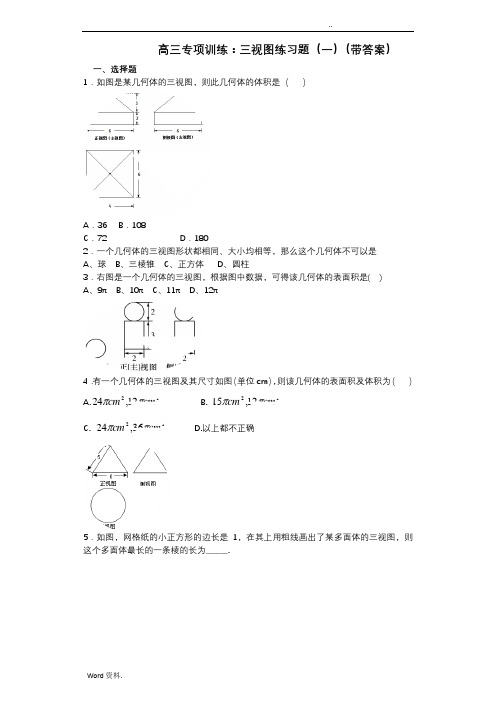
高三专项训练：三视图练习题（一）（带答案）一、选择题1．如图是某几何体的三视图，则此几何体的体积是（）A ．36B ．108C ．72D ．1802．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4．有一个几何体的三视图及其尺寸如图（单位cm ），则该几何体的表面积及体积为（）A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.A． B． CD ．36．一空间几何体的三视图如图所示，则该几何体的体积为.A. B. C D. [7．若某空间几何体的三视图如图所示，则该几何体的体积是A ．13 B ．23C ．1D ．28．右图是某几何体的三视图，则该几何体的体积为（）A ．Ｂ．Ｃ．Ｄ．1362942π+3618π+9122π+9182π+正视图俯视图9．已知一个几何体的三视图如图所示，则该几何体外接球的表面积为（）A ．43π B ． 163π C ．1912π D ． 193π 10．某几何体的正视图如图所示，则该几何体的俯视图不可能的是11．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )cm 3.A ．π+8B ．328π+C ．π+12D ．3212π+侧视图主视俯视第8题图俯视图侧视图正视图12．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）（A ）243cm （B ）223cm （C ）28cm （D ）24cm13．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．6πB ．7πC ．8πD ．9π14．如右图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（）A ．π3B ．π2C ．π23 D ．π4 15．如图是一个几何体的三视图，若它的体积是33，则图中正视图所标a=（）A ．1B 3C 3D ．316．已知某几何体的三视图如图所示（单位：cm ），其中正视图、侧视图都是等腰直角三角形，则这个几何体的体积是（）A ．338cmB ．3316cm C ．33216cm D ． 3332cm17．一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．B ．C ．D ．18．若某空间几何体的三视图如图所示，则该几何体的体积是（）A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119．某物体是空心的几何体，其三视图均为右图，则其体积为（）A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图侧视图俯视图正视第9题22 4 2侧视图 22俯视20．如图，水平放置的三棱柱ABC-A 1B 1C 1中，侧棱AA 1⊥平面A 1B 1C 1，其正视图是边长为a 的正方形．俯视图是边长为a 的正三角形，则该三棱柱的侧视图的面积为A ．a 2B ．a 2C a 2D 221．右图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（）A ．20＋3π B ．24＋3π C ．20＋4π D ．24＋4π22．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．12πB ．π34C ．3πD ．π312．23.如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为（）12正视图侧视图俯视图 AC A 11正视图侧视图俯视图24．图１是设某几何体的三视图，则该几何体的体积为（）A．942π+Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+、25．已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm）可得该几何体的体积是（）A．313cm B．323cmC．343cm D．383cm26．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27．一个几何体的三视图如图所示，则这个几何体的体积为（）正视图侧视图俯视图332正视图俯视图图1AB ．12C ．32 D1+28．一个空间几何体的三视图如图（1）所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为（）A 、64，48+B 、32，48+ C 、643，32+D 、332，48+29．若某多面体的三视图（单位: cm ）如图所示,则此多面体的体积是（） A ．21cm 3 B ．32cm 3 C ．65cm 3 D ．87cm 3正视图俯视图图（1）侧（左）视图 1111130．一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯视图是直径为2的圆(如右图），则这个几何体的表面积为A ．12π+B ．7πC ． π8D ．π2031．（一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32．已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为（） A ．6π B ．5π C．4π D．3π2π+4π+2π4π+正视侧视俯视俯视..A ．2，23B ．22，2D ．2，434．如图，有一个几何体的正视图与侧视图都是底为6cm ，腰为5cm 的等腰三角形，俯视图是直径为6cm 的圆，则该几何体的体积为 ( )A ．12πcm 3B ．24πcm 3C ．36πcm 3D ．48πcm 335 （A ）348cm （B ）324cm （C ）332cm （D ）328cm36．如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A ．4B ．3C ．32D ．237．某四面体的三视图如下图所示，则该四面体的四个面中，直角三角形的面积和是_______.二、填空题正视图左视图俯视图正视图侧视图俯视图第6题 ·38．一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________．39．如图所示是一个几何体的三视图（单位：cm ），主视图和左视图是底边长为4cm ，腰长为22的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是-__________40．某几何体的三视图如图所示，则该几何体的体积的最大值为 .41．一正多面体其三视图如图所示，该正多面体的体积为___________.主视图左视图俯视图3主视图俯视图侧视图42．若某几何体的三视图（单位：cm ）如右图所示，则该几何体的体积为 cm 2．43．已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为；44．某四面体的三视图如上图所示，该四面体四个面的面积中最大的是1正视图俯视图左视图45．一个几何体的三视图如右图所示（单位：），则该几何体的体积为__________46．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．47．如图，一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形，则其体积是_________.48．某几何体的三视图如图所示，则它的体积是___________俯视图m 3m 249．设某几何体的三视图如图所示，则该几何体表面积是50．一个几何体的三视图如右图所示，正视图是一个边长为2的正三角形，侧视图是一个等腰直角三角形，则该几何体的体积为．三视图练习题（一）参考答案1．B【解析】此几何体是一个组合体，下面是一个正四棱柱上面是一个四棱锥．其体积为166********V =⨯⨯+⨯⨯⨯=．2．D【解析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆。

《三视图》选择题

《三视图》选择题
1.图中几何体的主视图、左视图、俯视图依次是（）
A.②④③
B.①⑤③
C.②③⑤
D.②⑤③
2.两个物体的主视图都是圆，则这两个物体可能是（）
A.圆柱体、圆锥体
B.圆柱体、正方体
C.圆柱体、球
D.圆锥体、球
3.如图，小明从正面观察一个圆柱体邮筒和一个正方体箱子，看到的是（）
4.图中几何体的两种视图正确的一组是（）
5.“圆柱与球的组合体”如图所示，则它的三视图是（）
6.下列图形，不能经过折叠围成正方体的是（）
答案：
1.A 解析：根据实物的特征可以得出结果.
2.C 解析：圆柱体可以横放，那么主视图也是圆.
3.C 解析：画出主视图做出判断.
4.B 解析：注意中心的圆柱.
5.A 解析：由视图、左视图相同，俯视图是两个同心圆.
6.B 解析：可通过画图折叠.。

小学三视图练习题

小学三视图练习题### 小学三视图练习题一、选择题1. 下列哪个选项是正确的主视图？A. 从物体的左侧观察得到的视图B. 从物体的右侧观察得到的视图C. 从物体的正面观察得到的视图D. 从物体的背面观察得到的视图2. 侧视图是从哪个方向观察物体得到的？A. 正面B. 背面C. 左侧D. 右侧3. 俯视图是从哪个方向观察物体得到的？A. 从物体的上方B. 从物体的下方C. 从物体的侧面D. 从物体的正面二、填空题4. 观察一个长方体的三视图，主视图显示的是长方体的______面和______面。

5. 当物体被放置在水平面上时，其______视图通常显示物体的底部。

三、判断题6. 三视图包括主视图、侧视图和俯视图。

（）7. 所有物体的主视图都是从物体的正面观察得到的。

（）四、简答题8. 请简述什么是三视图，并说明它们各自的特点。

五、绘图题9. 根据题目提供的长方体的三视图，绘制出该长方体的立体图。

六、应用题10. 假设你有一个正方体的盒子，其边长为10厘米。

请根据正方体的三视图，计算出正方体的体积。

七、实践题11. 请用纸板制作一个简单的立方体，并从三个不同的方向观察它，记录下你观察到的三视图。

八、分析题12. 观察一个圆柱体的三视图，分析并描述主视图、侧视图和俯视图所展示的圆柱体的特征。

九、综合题13. 假设你面前有一个由多个几何体组成的复杂物体，请尝试从三个不同的方向观察它，并绘制出相应的三视图。

十、创新题14. 设计一个简单的几何体，并为其绘制三视图。

在设计时，考虑如何通过三视图来最有效地传达该几何体的形状和尺寸。

请根据上述题目进行作答，注意审题并合理运用三视图的相关知识。

祝你练习愉快！。

中考三视图练习题

中考三视图练习题一、选择题1. 下列哪个选项是正确的主视图？A. 左视图B. 俯视图C. 右视图D. 仰视图2. 三视图包括哪三个视图？A. 俯视图、左视图、右视图B. 主视图、俯视图、左视图C. 仰视图、俯视图、左视图D. 仰视图、右视图、左视图3. 观察一个物体时，哪个视图可以提供物体的宽度信息？A. 主视图B. 俯视图C. 左视图D. 仰视图4. 下列哪个选项是正确的俯视图？A. 显示物体的顶面形状B. 显示物体的侧面形状C. 显示物体的正面形状D. 显示物体的底面形状5. 当物体的主视图和左视图都相同，且都是矩形时，该物体可能是：A. 立方体B. 圆柱体C. 长方体D. 球体二、填空题6. 在三视图中，______视图显示物体的正面形状。

7. 当物体的主视图和俯视图都是圆形时，该物体可能是______。

8. 一个物体的三视图可以提供物体的______、______和______三个方向的信息。

9. 俯视图通常显示物体的______面形状。

10. 如果一个物体的主视图和左视图都是正方形，那么该物体可能是______。

三、判断题11. 一个物体的主视图和左视图可能完全不同。

（）12. 三视图中的任何一个视图都不能单独表示物体的全部信息。

（）13. 俯视图可以提供物体的高度信息。

（）14. 物体的三视图是相互独立的，没有联系。

（）15. 一个物体的三视图可以完全相同的情况是不存在的。

（）四、简答题16. 请简述三视图在工程制图中的应用意义。

17. 描述如何通过三视图来确定一个物体的形状。

五、绘图题18. 根据以下描述，绘制一个物体的三视图：- 主视图：一个矩形，长为10cm，宽为5cm。

- 俯视图：一个矩形，长为8cm，宽为6cm。

- 左视图：一个矩形，长为10cm，宽为8cm。

19. 假设你面前有一个立方体，其边长为4cm，请绘制其三视图。

六、综合应用题20. 你是一名工程师，需要根据客户提供的三视图来制作一个零件。

三视图习题加解析

三视图典型例题加解析一、选择题1如图，在下列四个几何体中，其三视图(正视图、侧视图、俯视图)中有且仅有两个相同的是( )A ．②③④B ．①②③C ．①③④D ．①②④解析：①的三个视图都是边长为1的正方形；②的俯视图是圆，正视图、侧视图都是边长为1的正方形；③的俯视图是一个圆及其圆心，正视图、侧视图是相同的等腰三角形；④的俯视图是边长为1的正方形，正视图、侧视图是相同的矩形．A2、平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为( )A.6π B ．43π C ．46πD ．63π解析：利用截面圆的性质先求得球的半径长．如图，设截面圆的圆心为O ′，M 为截面圆上任一点，则OO ′＝2，O ′M ＝1，∴OM ＝（2）2＋1＝3，即球的半径为3， ∴V ＝43π(3)3＝43π.3．若一个几何体的三视图如图所示，则此几何体的体积为( )A.112 B ．5 C.92D ．4解析：三视图还原为实物图，利用六棱柱体积公式求解．由三视图可知，此几何体为直六棱柱，且底面的面积为4，高为1，则体积V ＝Sh ＝4.D4．一个几何体的三视图如图所示，则这个几何体的表面积为( )A ．6＋ 5B ．6＋2 5C ．8＋ 5D ．8＋2 5解析：由三视图知，该几何体是一个底面为直角三角形的直棱柱，其表面积等于2×(12×1×2)＋(2×12＋22＋1×2＋2×2)＝8＋25，选D.5．如图，正方体ABCD -A ′B ′C ′D ′的棱长为4，动点E 、F 在棱AB 上，且EF ＝2，动点Q 在棱D ′C ′上，则三棱锥A ′EFQ 的体积( )A ．与点E 、F 位置有关B ．与点Q 位置有关C ．与点E 、F 、Q 位置都有关D ．与点E 、F 、Q 位置均无关，是定值解析：因为V A ′－EFQ ＝V Q －A ′EF ＝13×(12×2×4)×4＝163，故三棱锥A ′-EFQ 的体积与点E 、F 、Q 的位置均无关，是定值．6．一个几何体的三视图如图所示，则该几何体的表面积为________．解析：将三视图还原为直观图后求解．根据三视图可知几何体是一个长方体挖去一个圆柱，所以S ＝2×(4＋3＋12)＋2π－2π＝38.7．某商店门口标识墩的直观图以及正视图和俯视图如图所示，墩的上半部分是正四棱锥P -EFGH ，下半部分是长方体ABCD -EFGH .(1)请画出该标识墩的侧视图； (2)求该标识墩的体积．解析：(1)由于墩的上半部分是正四棱锥P -EFGH ，下半部分是长方形ABCD -EFGH ，故其侧视图与正视图全等．该标识墩的侧视图如图所示．(2)由三视图易得，长方体与正四棱锥的底面均是边长为40 cm 的正方形，长方体的高为20 cm ，正四棱锥的高为60 cm.故该标识墩的体积V ＝V P －EFGH ＋V ABCD -EFGH ＝13×40×40×60＋40×40×20＝64 000(cm 3)．8．已知某几何体的直观图和三视图如图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．(1)若M 为CB 的中点，证明：MA ∥平面CNB 1； (2)求这个几何体的体积．解析：(1)证明：取CB 1的中点P ，连接MP ，NP .因为M 为CB 的中点，所以MP ∥BB 1，且MP ＝12BB 1.由三视图可知，四边形ABB 1N 为直角梯形，AN ∥BB 1且AN ＝12BB 1，则MP ∥AN 且MP ＝AN ，所以四边形ANPM 为平行四边形，所以AM ∥NP .又因为AM ⊄平面 CNB 1，NP ⊂平面CNB 1，所以AM ∥平面CNB 1. (2)因为该几何体的正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形，所以BC ⊥BA ，BC ⊥B 1B .又BB 1与BA 相交于点B ，连接BN ，所以BC ⊥平面ABB 1N ，所以BC 为三棱锥C -ABN 的高．取BB 1的中点Q ，连接QN ，因为四边形ABB 1N 是直角梯形且AN ＝12BB 1＝4，所以四边形ABQN 为正方形，所以NQ ⊥BB 1，又BC ⊥平面ABB 1N ，NQ ⊂平面ABB 1N ，所以BC ⊥NQ ，又BC 与BB 1相交于点B ，所以NQ ⊥平面C 1B 1BC ，所以NQ 为四棱锥N -CBB 1C 1的高．所以该几何体的体积V ＝V C -ABN ＋VN －CBB 1C 1 ＝13CB ·S △ABN ＋13NQ ·S 四边形BCC 1B 1 ＝13×4×12×4×4＋13×4×4×8＝1603.9．给出如下四个命题：①棱柱的侧面都是平行四边形；②棱锥的侧面为三角形，且所有侧面都有一个共同的公共点；③多面体至少有四个面；④棱台的侧棱所在直线均相交于同一点.其中正确的命题个数有（） A ．1个 B ．2个 C ．3个 D ．4个【解】D ．10．圆锥底面半径为１cm，其中有一个内接正方体，求这个内接正方体的棱长．【解】分析：画出轴截面图，设正方体的棱长为x ，利用相似列关系求解. 过圆锥的顶点S 和正方体底面的一条对角线CD 作圆锥的截面，得圆锥的轴截面SEF ，正方体对角面CDD 1C 1，如图所示. 设正方体棱长为x ，则CC 1=x ，C 1D1=. 作SO ⊥EF 于O ，则SO =OE =1，1~ECC EOS ∆∆， ∴11CC EC SO EO ==.11∴ x =， cm 11．如图，正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上，点P 在球面上，如果163P ABCD V -=，则球O 的表面积是A. 4πB. 8πC. 12π D. 16π【解】如图，正四棱锥P ABCD -底面的四个顶点,,,A B C D在球O 的同一个大圆上，点P在球面上，PO 与平面ABCD 垂直，是棱锥的高，PO =R ，22ABCD S R =，163P ABCD V -=，所以2116233R R ⋅⋅=，解得R =2，则球O 的表面积是16π，选D. 12求球的表面积和体积．【解】分析：作出轴截面，利用勾股定理求解.作轴截面如图所示，CC '=AC == 设球半径为R ，则222R OC CC '=+229=+= ∴3R =，∴2436S R ππ==球，34363V R ππ==球．。

高三专项训练：三视图练习题

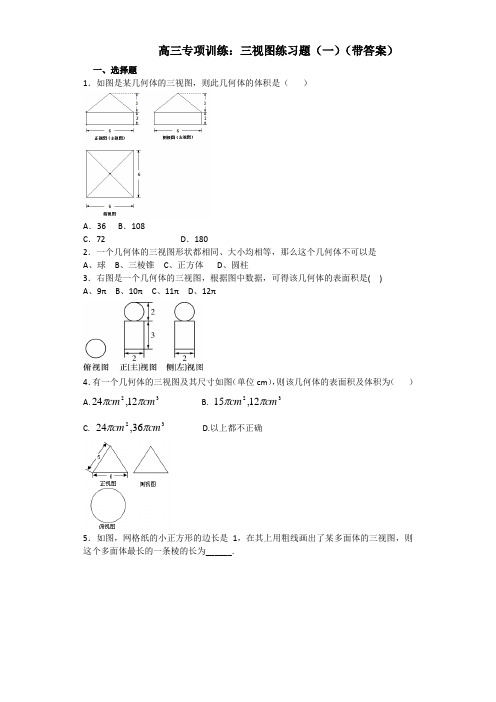
高三专项训练：三视图练习题（一）（带答案）一、选择题1．如图是某几何体的三视图，则此几何体的体积是（）A ．36B ．108C ．72D ．1802．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4．有一个几何体的三视图及其尺寸如图（单位cm ），则该几何体的表面积及体积为（）A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.A ．23B ．22C ．5D ．36．一空间几何体的三视图如图所示，则该几何体的体积为.A. 1B. 3 C 6 D. 2[7．若某空间几何体的三视图如图所示，则该几何体的体积是A ．13 B ．23C ．1D ．28．右图是某几何体的三视图，则该几何体的体积为（）A ．942π+ Ｂ．3618π+Ｃ．9122π+ Ｄ．9182π+9．已知一个几何体的三视图如图所示，则该几何体外接球的表面积为（）332正视图俯视图A ．43πB ． 163πC ．1912πD ． 193π 10．某几何体的正视图如图所示，则该几何体的俯视图不可能的是11．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )cm 3.A ．π+8B ．328π+C ．π+12D ．3212π+12．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则侧视图主视俯视22 312第8题图2俯视图 332 1侧视图正视图1 1 1其左视图的面积是（）（A ）243cm （B ）223cm （C ）28cm （D ）24cm13．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．6πB ．7πC ．8πD ．9π14．如右图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（）A ．π3B ．π2C ．π23 D ．π4 15．如图是一个几何体的三视图，若它的体积是33，则图中正视图所标a=（）A ．1B 3C 3D ．316．已知某几何体的三视图如图所示（单位：cm ），其中正视图、侧视图都是等腰直角三角形，则这个几何体的体积是（）A ．338cmB ．3316cm C ．33216cm D ． 3332cm17．一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．π12B ．π34C ．π3D ．π31218．若某空间几何体的三视图如图所示，则该几何体的体积是（）A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119．某物体是空心的几何体，其三视图均为右图，则其体积为（）A 、8B 、43π C 、483π+ D 、483π-正视图侧视图俯视图正视第9题22 4 2侧视图 22俯视20．如图，水平放置的三棱柱ABC-A 1B 1C 1中，侧棱AA 1⊥平面A 1B 1C 1，其正视图是边长为a 的正方形．俯视图是边长为a 的正三角形，则该三棱柱的侧视图的面积为A ．a 2B ．12a 2C ．32a 2 D ．3a 221．右图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（）A ．20＋3πB ．24＋3πC ．20＋4πD ．24＋4π22．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．12πB ．π34C ．3πD ．π312． 23.如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为（）A. 6+3B. 24+3C. 24+23D. 32正视图侧视图俯视图 AC A 11正视图侧视图俯视图24．图１是设某几何体的三视图，则该几何体的体积为（）A ．942π+ Ｂ．3618π+ Ｃ．9122π+ Ｄ．9182π+ 、25．已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm ）可得该几何体的体积是（）A ．313cmB ．323cm C ．343cm D ．383cm26．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是A. 长方形B. 圆柱C. 立方体D. 圆锥27．一个几何体的三视图如图所示，则这个几何体的体积为（）A 32B ．12C ．32D 312+ 正视图侧视图俯视图 332正视图俯视图图128．一个空间几何体的三视图如图（1）所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为（）A 、64，48+B 、32，48+C 、643，32+ D 、332，48+29．若某多面体的三视图（单位: cm ）如图所示,则此多面体的体积是（）A ．21cm 3B ．32cm 3C ．65cm 3 D ．87cm 3 30．一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯视图是直径为2的圆(如右图），则这个几何体的表面积为正视侧视俯视正视图俯视图图（1）侧（左）视图 11111A ．12π+B ．7πC ． π8D ．π2031．（一空间几何体的三视图如图所示,则该几何体的体积为( ). A.223π+ B. 423π+C. 2323π+D. 2343π+ 32．已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为（）A ．6πB ．5πC ．4πD ．3π33．若一个正三棱柱的三视图如下图所示，则这个正三棱柱的高和底面边长分别为（）A ．2，23B ．22，2 D ．2，434．如图，有一个几何体的正视图与侧视图都是底为6cm ，腰为5cm 的等腰三角形，俯视图是直径为6cm 的圆，则该几何体的体积为 ( )A ．12πcm 3B ．24πc m 3C ．36πcm 3D ．48πcm 3正视图 2 32 左视图俯视图正视图侧视图俯视35．一个多面体的三视图分别是正方形、等腰三角形和矩形，其尺寸如图，则该多面体的体积为（A ）348cm （B ）324cm（C ）332cm （D ）328cm36．如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A ．4B ．3C ．32D ．237．某四面体的三视图如下图所示，则该四面体的四个面中，直角三角形的面积和是_______.38．一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________．二、填空题3主视图俯视图侧视图39．如图所示是一个几何体的三视图（单位：cm ），主视图和左视图是底边长为4cm ，腰长为22的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是-__________40．某几何体的三视图如图所示，则该几何体的体积的最大值为 .41．一正多面体其三视图如图所示，该正多面体的体积为___________.42．若某几何体的三视图（单位：cm ）如右图所示，则该几何体的体积为 cm 2．31正视图俯视图左视图主视图左视图俯视图43．已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD是直角梯形,则此几何体的体积为；44．某四面体的三视图如上图所示，该四面体四个面的面积中最大的是45．一个几何体的三视图如右图所示（单位：m），则该几何体的体积为__________3m 46．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．47．如图，一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形，则其体积是_________.主视图左视图俯视图48．某几何体的三视图如图所示，则它的体积是___________49．设某几何体的三视图如图所示，则该几何体表面积是50．一个几何体的三视图如右图所示，正视图是一个边长为2的正三角形，侧视图是一个等腰直角三角形，则该几何体的体积为．三视图练习题（一）参考答案1．B【解析】此几何体是一个组合体，下面是一个正四棱柱上面是一个四棱锥．其体积为166********V =⨯⨯+⨯⨯⨯=．2．D【解析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆。

组合体三视图练习题

组合体三视图练习题一、选择题（每题2分，共20分）1. 组合体三视图包括主视图、左视图和哪个视图？A. 俯视图B. 仰视图C. 侧视图D. 底视图2. 在组合体三视图中，主视图通常表示物体的哪个面？A. 正面B. 侧面C. 顶面D. 底面3. 以下哪个不是三视图的画法规则？A. 长对正B. 高平齐C. 宽相等D. 角度一致4. 组合体三视图中，如果一个视图上的线条与另一个视图上的线条不相交，这些线条表示的是？A. 同一条线B. 不同的线C. 相互平行的线D. 相互垂直的线5. 在组合体三视图中，如果一个物体的俯视图和左视图的尺寸相同，那么这个物体可能是？A. 立方体B. 圆柱体C. 圆锥体D. 球体6. 组合体三视图中，若主视图和俯视图的尺寸不同，但左视图与主视图尺寸相同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体7. 在组合体三视图中，若主视图和左视图的尺寸相同，但俯视图的尺寸不同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体8. 组合体三视图中，若主视图和左视图的尺寸不同，但俯视图与主视图尺寸相同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体9. 在组合体三视图中，若俯视图和左视图的尺寸相同，但主视图的尺寸不同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体10. 组合体三视图中，若俯视图是一个圆形，左视图和主视图是两个相同的矩形，该物体可能是？A. 长方体B. 圆柱体C. 圆锥体D. 球体二、填空题（每题2分，共20分）11. 组合体三视图中，______视图通常用来表示物体的顶面或底面。

12. 在组合体三视图中，______视图通常用来表示物体的侧面。

13. 组合体三视图中，______视图通常用来表示物体的正面。

14. 组合体三视图的画法规则包括______、______和______。

15. 如果一个物体的三视图都是圆形，那么这个物体可能是______。

三视图习题50道(含答案)

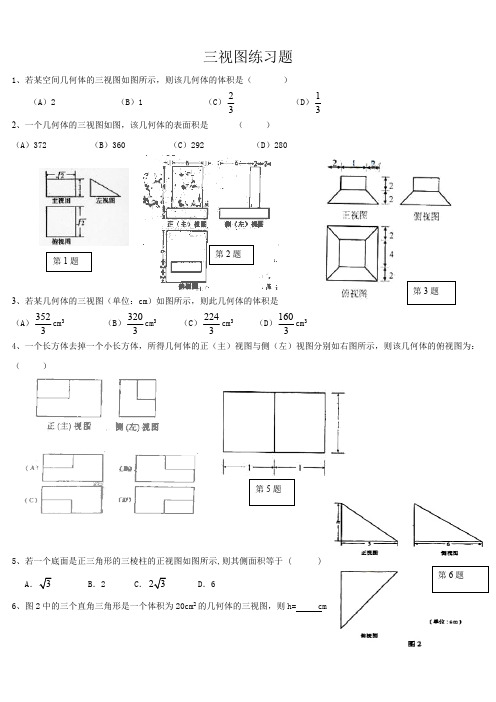
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

高中三视图试题及答案

高中三视图试题及答案一、选择题（每题2分，共10分）1. 在三视图中，主视图、左视图和俯视图分别表示物体的哪个面？A. 正面、侧面、上面B. 侧面、正面、上面C. 正面、上面、侧面D. 上面、侧面、正面2. 以下哪个选项不是三视图的组成部分？A. 主视图B. 左视图C. 右视图D. 俯视图3. 根据三视图的规则，物体的长、宽、高分别在哪个视图中表示？A. 主视图、俯视图、左视图B. 俯视图、主视图、左视图C. 左视图、主视图、俯视图D. 主视图、左视图、俯视图4. 如果一个物体的主视图和俯视图都是圆形，那么这个物体可能是：A. 圆柱体B. 圆锥体C. 球体D. 立方体5. 在绘制三视图时，如果一个物体的左视图和主视图相同，那么这个物体可能是：A. 正方体B. 长方体C. 圆柱体D. 圆锥体二、填空题（每空1分，共10分）6. 三视图包括______、______和______。

7. 物体的三视图应该按照______、______、______的顺序排列。

8. 在三视图中，______视图可以反映物体的高度和长度。

9. 如果一个物体的主视图是一个矩形，左视图是一个圆形，那么这个物体可能是______。

10. 在绘制三视图时，需要考虑物体的______、______和______。

三、简答题（每题5分，共10分）11. 简述三视图的定义及其重要性。

12. 描述如何根据一个物体的主视图和俯视图推断其形状。

四、绘图题（每题5分，共10分）13. 根据以下描述绘制一个物体的三视图：- 主视图：一个正方形- 左视图：一个矩形，宽度为正方形的边长的一半- 俯视图：一个圆形，直径等于正方形的边长14. 根据以下三视图，描述物体的形状：- 主视图：一个圆形- 左视图：一个矩形- 俯视图：一个圆形答案：一、选择题1. A2. C3. D4. C5. A二、填空题6. 主视图、左视图、俯视图7. 主视图、左视图、俯视图8. 左视图9. 圆柱体10. 长度、宽度、高度三、简答题11. 三视图是工程图学中用来描述物体形状的三个基本视图，包括主视图、左视图和俯视图。

人教版九年级下册数学第二十九章第2节《三视图》训练题 (19)(含答案解析)

（1）请画出这个几何体的三视图．
（2）如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加______个小正方体．
27．如图是由几个棱长为的小立方块搭成的几何体从上往下看的平面图形，小立方块中的数字表示该位置上小立方块的个数，求出这个几何体的体积．
28．如图，正三棱柱的底面周长为18，截去一个底面周长为6的正三棱柱，求所得几何体的俯视图的周长．
A． B． C． D．
13．一个几何体是由一些大小相同的小正方体摆成其主视图和左视图如图所示则组成这个几何体的小正方体最少有个，最多有个，（）
A．3B．4C．5D．6
14．如图所示物体的俯视图是（）
正面
A． B． C． D．
15．下列四个几何体中，主视图与左视图不相同的几何体有（）
A．1个B．2个C．3个D．0个
九年级下册数学第二十九章第2节《三视图》训练题 (19)
一、单选题
1．若某几何体的三视图如图所示，则这个几何体是（）
A． B． C． D．
2．下列几何体中，俯视图与主视图完全相同的几何体是（）
A．圆锥B．球C．圆柱D．长方体
3．如图，是由一些完全相同的小正方体搭成的几何体的主视图和俯视图，则这个几何体最多由（）个小正方体搭成．
18．23
【解析】
由主视图和左视图可得：这个几何体有3层，3列，3行，最底层有1+2+3＝6个正方体，第二层最多有5个，最少有2个，第三层最多有3个，最少有1个，求出最大值与最小值，再求和即可．
解：综合主视图和俯视图，
底面有3＋2＋1＝6个，第二层最多有5个，最少有2个，第三层最多有3个，最少有1个，
故选：B．

大学三视图考试题及答案

大学三视图考试题及答案一、选择题（每题2分，共20分）1. 三视图是指物体在三个不同方向上的投影图，这三个方向通常是（）。

A. 正面、侧面、上面B. 左面、右面、下面C. 前面、后面、侧面D. 顶面、底面、侧面答案：A2. 在三视图中，正视图通常表示物体的（）。

A. 俯视图B. 侧视图C. 正视图D. 底视图答案：C3. 俯视图是从物体的（）方向观察所得的视图。

A. 顶部B. 底部C. 前方D. 后方答案：A4. 如果一个物体的正视图和俯视图都是圆形，那么这个物体可能是（）。

A. 圆锥B. 圆柱C. 球体D. 立方体答案：C5. 在三视图中，侧视图通常指的是（）。

A. 左视图或右视图B. 前视图或后视图C. 俯视图D. 正视图答案：A6. 三视图的表达方法不包括（）。

A. 线框图B. 轴测图C. 透视图D. 阴影图答案：D7. 在三视图中，相同的线（）。

A. 粗细相同B. 长度相同C. 位置相同D. 数量相同答案：A8. 对于一个物体的三视图，以下哪项不是必须满足的条件（）。

A. 长对正B. 高平齐C. 宽相等D. 比例一致答案：C9. 在三视图中，虚线通常用来表示物体的（）。

A. 可见线B. 不可见线C. 中心线D. 轴线答案：B10. 在绘制三视图时，如果一个视图能够反映出其他两个视图中没有的信息，那么这个视图被称为（）。

A. 主视图B. 俯视图C. 侧视图D. 辅助视图答案：A二、填空题（每空2分，共20分）11. 在三视图中，______视图是最基本的视图，通常用来确定物体的正面形状。

答案：正视图12. 当物体的一个面平行于H面时，在V面和W面上的投影是______的。

答案：相同的13. 在三视图中，W面是指______面。

答案：侧面14. 如果物体的一个边平行于V面，则在W面上的投影会______。

答案：变短15. 在三视图中，如果一个圆的投影是椭圆，则这个圆相对于投影面是______的。

三视图选择题

1．如图，是由一些相同的小立方块搭成的几何体的三视图，则该几何体有_ _ __块小立方体组成．．2，．3，2 D．2，3A．3，4．如图是由几个相同的小正方体搭成的一个几何体，它的俯视图是（）5．下列几何体中，主视图相同的是（）． B．． D．9．用五块大小相同的小正方体搭成如下图所示的几何体，这个几． B． C．．A．7个 B．8个 C．9个 D．10个12．下面四个立体图形中，主视图是三角形的是（）13．如图，李师傅做了一个零件，请你告诉他这个零件的主视图．．．．D15．在下面四个几何体中，俯视图是三角形的是①②③④①②③④①②③④①②③④ A ．① B ．② C ．③ D ． ④16．右图是某几何体的三视图，该几何体是A. 三棱柱B. 三棱锥C. 长方体D.正方体19．如图是由6个大小相同的小正方体组成的几何体，它的左视图是． B． C． D．22．如图所示几何体的主视图是（）23．下面四个几何体中，左视图是四边形的几何体共有（）A．1个 B．2个 C．3个 D．4个24．如图的立体图形的左视图可能是（）．27．下列四个立体图形中，主视图为圆的是（）A． B． C． D．28．下列几何体的主视图是三角形的是（）． B． C． D．31．如图是几个小正方体组成的一个几何体，这个几何体的俯视图是（）32．如图所示茶杯，其正视图、左视图及俯视图依次为（）A．．．34．下列四个几何体中，主视图与左视图相同的几何体有（）．A．4个 B．3个 C．2个 D．1个35．分别由五个大小相同的正方形组成的甲﹑乙两个几何体如图所示，它们的三视图中完全一致的是（）A．主视图 B．左视图 C．俯视图 D．三视图A．①② B．①③ C．①④ D．②④38．在下面的四个几何体中，它们的左视图是中心对称图形的共有（）A．1个 B．2个 C．3个 D．4个39．如图，是一个圆柱和一个长方体组成的几何体，圆柱的下底．． C． D．42．下列物体的主视图是圆的是（）45．如图，几何体上半部为正三梭柱，下半部为圆柱，其俯视图是（）．（A ）（B ）（C ）． B ．．．图是（）C B A49．下列三视图所对应的直观图是（）A．圆锥 B．三棱柱 C．圆柱 D．三棱锥52．下图中，不是如图所示物体视图的是（）53．如图，是由四个相同小正方体组合而成的几何体，它的主视56．图中几何体的俯图是（）57．如图，它是一个圆锥体的三视图，则这个圆锥的侧面积为（）.59．如图所示几何体的俯视图是（）正60．一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为（）A．6个 B．8个 C．12个 D．17个61．如图，下列选项中不是正六棱柱三视图的是63．如图，这是一个正三棱柱，则它的俯视图为（）64．如图，它们是一个物体的三视图，该物体的形状是（）A.圆柱B.正方体C.圆锥D.长方体65．下图是由几个相同的小正方体搭成的一个几何体，从左边看A． B． C． D．67．如图所示的几何体，从正面看所得到的图形是（）68．如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的主69．图中的正五棱柱的左视图应为（）70．由若干个同样大小的正方体堆积成一个实物，从不同侧面观察到如图所示的投影图，则构成该实物的小正方体个数为( ).A．6个 B．7个 C．8个 D．9个71．如图所示的三视图对应的几何体是（）A．三棱柱B．圆柱C．长方体D．圆锥72．如图所示的直角三角形ABC绕直角边AC旋转一周得到一个立体图形，从正面看这个立体图形，得到的平面图形是（）.A．4 B．5 C．6 D．775．用3个相同的立方块搭成的几何体如图所示，则它的主视图是（）A． B． C． D．76．用四个相同的小立方体搭几何体，要求每个几何体的主视图、78．如图所示，该几何体的俯视图是的立体图形，它的主视图是（）A. B. C. D.．沿圆柱体上面直径截去一部分的物体如图所示，它的俯视图82．如图是一个几何体的三视图,则这个几何体的侧面积是（）主视左视俯视A ．212cm πB ．28cm πC ．26cm πD ．23cm π83．如图是某几何体的三视图，该几何体是86．如图，水平放置的圆柱形物体，中间有一细棒，则此几何体的左视图是（）87．如图是一个几何体的三视图，则这个几何体的侧面积是__________ cm2俯视图是( )91．如图所示的几何体，它的主视图是（）图是（）A． B． C． D．95．如图是由七个相同的小正方体摆成的几何体，则这个几何体的俯视图是（）． B．． D．98．如图所示几何体的俯视图是（）A ．B ．C ．D ．99．如图，该物体的俯视图是（）第II卷（非选择题）请点击修改第II卷的文字说明二、填空题（题型注释）参考答案1．10．【解析】试题分析：从主视图和左视图，在俯视图的每个小正方体内标出该位置竖直方向上共有的小正方体个数，试题分析：设底面边长为x，则222+=，解得x=2，即底面边x x长为2，根据图形，这个长方体的高是3，根据求出的底面边长是2，只能选C，故选C．考点：1．由三视图判断几何体；2．简单几何体的三视图．4．D【解析】试题分析：因为几何体的俯视图是从上面看到的视图，所以俯视图是，故选：D．考点：几何体的俯视图．5．B考点：三视图8．C【解析】试题分析：如图因为圆台的主视图、左视图是梯形,俯视图是圆环;故A错．棱柱的主视图、左视图是长方形,俯视图是三角形;故B错．球的主视图、左视图、俯视图都是圆;故C对．圆锥的主视图、左视图是三角形,俯视图是圆;故D错．故选C．考点：三视图．9．D【解析】考点：三视图.12．C【解析】试题分析：找到立体图形从正面看所得到的图形为三角形即可．试题解析：A、主视图为长方形，不符合题意；B、主视图为中间有一条竖线的长方形，不符合题意；C、主视图为三角形，符合题意；D、主视图为长方形，不符合题意；故选C．考点：简单几何体的三视图．俯视图是三角形；④长方体的俯视图是四边形，故选：C．考点：几何体的俯视图.16．A【解析】试题分析：根据几何体的三视图可得该几何体是三棱柱，故选：A.考点：几何体的三视图.17．B【解析】试题分析：主视图即正面所见的图形，上面一个，下面三个，故选B考点：三视图，，故选：C．考点：几何体的左视图．20．C【解析】试题分析：几何体的主视图是从正面看所得到的视图，该几何体从物体正面看，左边1列、右边1列上下各一个正方形，且左右正方形中间是虚线，故选：C．考点：几何体的主视图．故选：B考点：主视图23．B【解析】试题分析：左视图是四边形的几何体有圆柱，正方体，共有2个故选：B考点：三视图24．A【解析】试题分析：根据三视图的法则可得左视图为直角三角形．考点：简单组合体的三视图．27．B．【解析】试题分析：A．主视图是正方形，故此选项错误；B．主视图是圆，故此选项正确；C．主视图是三角形，故此选项错误；D．主视图是长方形，故此选项错误；故选B．考点：简单几何体的三视图．28．B考点：三视图．31．C．【解析】试题分析：这个几何体的俯视图从左到右小正方形的个数是：1，1，1，故选C．考点：简单组合体的三视图．32．C【解析】试题分析：茶杯的形状可以知道：它的正视图是一个长方形及小耳朵形弧线，俯视图是一个圆及一小线段，及左视图是长方形，我们可以③圆锥主视图与左视图都是三角形；④球的主视图与左视图都是圆；故选A．试题解析：考点：简单几何体的三视图．【解析】试题分析：主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．试题解析：从正面可看到甲从左往右三列小正方形的个数为：3，1，37．B．【解析】试题分析：主视图是从物体上面看，所得到的图形．试题解析：圆柱的主视图是长方形，圆锥的主视图是三角形，长方体的主视图是长方形，球的主视图是圆，考点：简单几何体的三视图．38．C【解析】试题分析：A．圆锥的左视图是等腰三角形，不是中心对称图形；试题分析：从上往下看，选项C是正确的.故选C.考点：简单几何体的三视图.41．A【解析】试题分析：一只茶壶从上面看到的形状图即俯视图，所以选：A.考点：俯视图.42．C【解析】试题分析：物体的主视图是从正面得到的视图，所以圆柱的主视图是45．C．【解析】试题分析：俯视图是从物体上面看到的图形，应把所看到的所有棱都表示在所得图形中，从上面看，正三棱柱的俯视图是正三角形，圆柱的俯视图是圆，且正三角形在圆内．故选：C．考点：几何体的三视图．46．C.【解析】试题分析：根据几何体的三视图可知，①的俯视图是圆，②的俯视图试题分析：因为将Rt ABC绕直角边AB旋转一周，所得的几何体是圆锥，所以它的主视图是等腰三角形，故选：D.考点：几何体的主视图.49．C【解析】试题分析：通过主视图可以排除A和B，通过俯视图可以排除D．考点：三视图50．D【解析】试题分析：本题根据题意可以发现这个图形的俯视图为一个矩形.【解析】试题分析：根据几何体的三视图的定义，可知这个图形的主视图是由上下两层小正方形组成，下层自左到右有三块，上层靠右边有一块，据此可知是C图．故选：C．考点：几何体的三视图．54．B．【解析】试题分析：圆柱的主视图是长方形，圆锥的主视图是三角形，长方体的主视图是长方形，球的主视图是圆，所以圆柱和长方体的主视图相考点：简单组合体的三视图．57．B．【解析】试题分析：易得圆锥的底面直径为6cm，高为4cm，根据勾股定理可得圆锥的底母线长，根据圆锥的侧面积=π×底面半径×母线长，把相应数值代入即可求解．试题解析：易得此几何体为圆锥，底面直径为6cm，高为4cm，则圆锥的底面半径为6÷2=3cm，=cm，5故这个几何体的侧面积为π×3×5=15π（cm2）．60．C．【解析】试题分析：从俯视图可知该桌子共摆放着三列盆子．主视图可知左侧盆子有5个，右侧有3个；而左视图可知左侧有4个，右侧与主视图的左侧盆子相同，共计12个，考点：由三视图判断几何体．61．A【解析】试题分析：根据三视图的定义可得：正六棱柱得主视图是D，左视图考点：简单几何体的三视图．64．C【解析】试题分析：选项中俯视图是圆只有圆柱和圆锥，而圆柱的正视图是矩形，所以该物体是圆锥.考点：三视图.65．A【解析】对于三视图，关键是要善于从不同的角度观察并转化为平面图形，本题中的立体图形从左边看得到的平面图形是“L”字形，故68．C【解析】试题分析：根据小正方形的数量可知，主视图的左边有2个正方形，中间有2个正方形，右边有1个正方形.考点：三视图【解析】试题分析：根据从左边看得到的图形进行选择即可.试题解析：正五棱柱的左视图选项A符合题意，故选A.∴此几何体为柱体，∵俯视图是一个三角形，∴此几何体为三棱柱，故选：A．考点：由三视图判断几何体．【解析】试题分析：Rt△ABC绕直角边AC旋转一周得到一个立体图形是圆锥，圆锥从正面看到的平面图形是等腰三角形.故选：B.BD74．A【解析】试题分析：如下图：将左视图,主视图都画在俯视图中，可以数出共4个小正方形,故选A.考点: 正方体表面展开图.75．A【解析】D故D选项符合题意，故选：D．考点：简单组合体的三视图．77．A．【解析】试题分析：从正面几何体，是一个大正方形的右上角是一个小正方形，故选A．考点：简单几何体的三视图．78．A．【解析】【解析】试题分析：由主视图和左视图确定是柱体，锥体还是球体，再由俯视图确定具体形状．解：根据主视图和左视图为三角形判断出是锥体，根据俯视图是圆形可判断出这个几何体应该是圆锥，。

高中高考数学三视图选择题综合训练2.docx

1.在一个儿何体的三视图中，正视图与俯视图如左图所示，则相应的侧视图可以为（）【答案】D【解析】试题分析：由止视图、俯视图，还原几何体为半个闘锥和冇一个侧面垂直于地面的三棱锥组成的简单组合体，故侧视图为D.考点：三视图.2.如图，网格纸上正方形小格的边长为1,图中粗线価出的是某儿何体的三视图，贝IJ儿何体的体积为（）1114A.- C. D.6323【答案】D【解析】试题分析：由题意，原几何体为三棱锥，如图所示:1 1 4r=-x-x2x2x2=-.故D」E确.3 2 3考点：三视图.【方法点睛】本题主要考查的是三视图和空间儿何体的体积，属于容易题.本题先根据三视图判断儿何体的结构特征，再计算出儿何体的体积即可.3. 若某圆柱体的上部挖掉一个半球，下部挖掉一个圆锥后所得的几何体的三视图中的正视图和俯视图如图所示，则此儿何体的表面积是（）正视图侧视图A. 24兀B. 24兀+&返兀C. 24兀+4返兀D. 32兀【答案】c—【解析】试题分析：几何体的表面积是闘柱的侧面积与半个求的表面积、関锥的侧面积的和.解：圆柱的侧而积为Si=2n X2X4=16 JT ,半球的表面积为$2二2兀X22二8兀, 圆锥的侧面积为S 台丄X2兀X2X 2逅二4逅兀, ° 2所以儿何体的表面积为s 二S1 + S 2+ s 3=247T+4V2兀；故选C.考点：由三视图求面积、体积.4. 某一简单几何体的三视图如所示，该几何体的外接球的表面积是（）A. 13nB. 16nC. 25nD. 27n【答案】C【解析】试题分析：几何体为底面为正方形的长方体，底面对角线为4,高为3.则长方体的对角线为外接球的直径.解：几何体为底面为正方形的长方体，底面对角线为4,高为3,・••长方体底面边长为 2V2. 则长方体外接球半径为「则2珂（切）2+（2西）2+3纭5・・・・r-|.・••长方体外接球的表面积s 二4 K 宀25 JT .故选C.考点：山三视图求面积、体积.5. 某四而体的三视图如图所示，则该四而体的所有棱中最长的是（）k 4 ----------------- ■— 3 —♦A. 5^2B. V41C. 4V|D. 5【答案］B —~【解析】试题分析：本题只要画出原儿何体，理清位置及数量关系，山勾股定理可得答案. 解：由三视图可知原几何体为三棱锥，其屮底WAABC为俯视图屮的玄角三角形，ZBAC为肓角，其中AC=3, AB二4, BC=5, PB丄底面ABC,且PB=4,由以上条件可知，ZPBC为直角，最长的棱为PC,在直角三角形PBC中，山勾股定理得，PC二Jp/7齐二姮，6•点M、N分别是正方体ABCD- A.BiCiD.的棱AB、AJ）冲点,用过A、M、N和D、N、C）的两个截面截去正方体的两个角后得到的几何体如图h则该几何体的正视图、侧视图（左视图）、俯视图依次为图2 中的（）S 1 图2A.①、②、③B.②、③、④C.①、③、④D.②、④、③【答案】B【解析】试题分析：肓接利用三视图的定义，正视图是光线从几何体的前而向示面正投影得到的投影图，据此可以判断出其正视图.左视图是光线从儿何体的左侧向右侧正投影得到的投影图，据此可以判断出其左视图.类似判断俯视图即可.解：由正视图的定义可知:点A、B、在后面的投影点分别是点D、C、Ci,线段AN在后面的投影面上的投影是以D 为端点几与线段CG 平行几相等的线段，即止视图为匸方形，另外线段AM 在麻面的投影线要呦成实线，被遮挡的线段DG 耍働成虚线，止视图为 ②，左视图为③，俯视图为④；故选B.考点：简单空间图形的三视图.7.如图是一个儿何体的三视图，根据图中数据，可得该儿何体的表面积为（）【答案】C【解析】试题分析：由题意可知，几何体是由一个球和一个闘柱组合而成的，分别求表面积即可• 解：从三视图可以看出该儿何体是由一•个球和一个圆柱纽合而成的，球的半径为1，圆柱的高为3,底面半径为1.所以球的表面积为4 n X 12=4 n .圆柱的侧面积为2n X3=6n,圆柱的两个底面积为 2 兀 X 12=2n ,D. 71 + y/i 【答案】A【解析】试题分析：由三视图知该儿何体是锥D-ABC^AC 是圆柱底而血径，3在底面圆周上，DO 丄平面ABC, O 是圆心, 尺寸见三视图，则 C. 12 n D. 13 n—xFxl + '»lx2xR •故选A.•个组合体，下血是圆柱, 上血是三棱锥，如图三棱侧视图)C. 2TT + V3所以该几何体的表面积为4n+2n+6n=12n. 故选C.考点：山三视图求而积、体积.考点：三视图，组合体的体积.9. 某儿何体的三视图如图所示，则它的表而积为（）.A. 6龙B. 571C. 4兀D. 3龙【答案】B【解析】试题分析：由三视图可知儿何体为圆锥和半球的组合体•半球的半径为1,圆锥的高为为2近，故圆锥的母线长为&2近$ + ]2 = 3 ,故儿何体的表血积1 9 5 = —x4>rxP+^xlx3 = 5^. 2考点：1.三视图还原主观图；2.圆锥的表面积；3.球的表面积.10. 某几何体的三视图如右图所示，则该几何体的体积是正视图匸I俯視图,・一B. 63 【答案】C 【解析】试题分析：将三视图还原成几何体。

三视图经典题

一、选择题：1、下面右边的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )2、右图中几何体的正视图是( )3、某工艺品由一个长方体和球组成(右图)，则其俯视图是( )A． B． C． D．4、某几何体的三视图如左图所示，则此几何体是( )A．正三棱柱B．圆柱C．长方体D．圆锥5、图所示的物体，从左面看得到的图是（）6、小明从正面观察下图所示的物体，看到的是( )7、某同学把下图所示的几何体的三种视图画出如下(不考虑尺寸)；在这三种视图中，其正确的是：( )A、①②,B、①③，C、②③，D、②8、由若干个同样大小的正方体堆积成一个实物，不同侧面观察到如图8所示的投影图，则构成该实物的小正方体个数为( )A. 6B. ７C. 8D. 9A. B.Ｃ．Ｄ．正面A．B．C．D．A B C D9、某超市货架上摆放着“康师傅”红烧肉面，如图1是它们的三视图，则货架上的“康师傅”红烧肉面至少有( )Ａ．8桶Ｂ．9桶Ｃ．10桶Ｄ．11桶10、图2中几何体的正视图是( )11、由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数( )A、6个B、7个C、8个D、9个主视图左视图俯视图(第12题)12、如图是一些相同的小正方体构成的几何体的正视图和左视图，在这个几何体中，小正方体的个数不可能是( )A、7B、8C、9D、1013、如图是正方体的展开图，则原正方体相对两个面上的数字和最小的是( ).A. 4B. 6C. 7D.814、右图所示是一个三棱柱纸盒，在下面四个图中，只有一个是这个纸盒的展开图，那么这个展开图是( )15、如图所示，右面水杯的俯视图是( )16、下列几何体，正(主)视图是三角形的是 ( )A．B．C．D．17、有一实物如图所示，它的主视图是( )A B C D142536第13题图主视图左视图俯视图图1A B C D18、骰子是一种特别的数字立方体，它符合规则：相对两面的点数之和总是7.下面四幅图中可以折成符合规则的骰子的是19、一个画家有14个边长为1m 的正方体，他在地面上把它们摆成如图所示的形式，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积为（）A. 19m 2B. 21m 2C. 33m 2D. 34m 2 20、如图，以Rt △ABC 为直角边AC 所在直线为轴，将△ABC 旋转一周所形成的几何体的俯视图是( )21、下面的图形是由8个棱长为1个单位的小立方体组成的立体图形，这个立体图形的左视图是( )DCBA22、有6个大小相同的正方体搭成的几何体如图所示，则关于它的视图说法正确的是( )A 主视图的面积最大B 左视图的面积最大C 俯视图的面积最大D 三个视图的面积一样大23、想一想：将左边的图形折成一个立方体，右边的四个立方体哪一个是由左边的图形折成的（）24、如图所示的立方体，如果把它展开，可以是下列图形中的（） 25、下列四个图形中，每个小正方形都标上了颜色. 若要求一个正方体两个相对面上的颜色都一样，那么不可能是这一个正方体的展开图的是（）黄红黄绿绿红红绿黄绿红红绿黄绿黄红黄绿主视图左视图26、下列展开图中，不是正方体是A 、B 、C 、D 、- 27、一个由若干个相同的正方体搭成的物体的主视图与左视图都是右边的图形，这个物体有( )种不同的搭建办法.A 、2B 、3C 、4D 、5二、填空题：1. 如图是一个几何体的三视图，根据图中提供的数据 (单位：cm)可求得这个几何体的体积为．2、如图所示，用字母M 表示与A 相对的面，请在下面的正方体展开图中填写相应的字母．3、如图是一个由若干个正方体搭建而成的几何体的主视图与左视图，那么下列图形中可以作为该几何体的俯视图的序号是:4、如图，是由若干个相同正方体组成的几何体的主视图和左视图，则组成这个几何体最少的正方体的个数是 -个.5、桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由个这样的正方体组成。

组合体三视图练习题

组合体三视图练习题一、选择题（每题5分，共20分）1. 下列哪一项不是组合体三视图的基本视图？A. 正视图B. 侧视图C. 俯视图D. 斜视图2. 在组合体三视图中，以下哪个视图可以提供物体的宽度信息？A. 正视图B. 侧视图C. 俯视图D. 斜视图3. 组合体三视图的绘制顺序通常是：A. 俯视图、侧视图、正视图B. 正视图、侧视图、俯视图C. 侧视图、俯视图、正视图D. 任意顺序4. 如果一个组合体的正视图和侧视图都是矩形，那么该组合体可能是：A. 圆柱B. 长方体C. 圆锥D. 球体二、填空题（每空5分，共30分）5. 组合体三视图包括______、______和______。

6. 当组合体中包含对称面时，绘制______视图即可。

7. 在组合体三视图中，______视图通常用来表示物体的高度。

8. 如果组合体的______视图和______视图相同，说明该物体具有对称性。

9. 组合体三视图的绘制原则是______、______和______。

10. 组合体三视图中，______视图可以提供物体的厚度信息。

三、简答题（每题20分，共40分）11. 简述组合体三视图的作用及其重要性。

12. 描述在绘制组合体三视图时，如何确定视图的尺寸比例。

四、绘图题（每题10分，共10分）13. 根据所给的组合体三视图，绘制其立体图。

[注：本题需要根据实际的组合体三视图来绘制立体图，此处无法提供具体图形，需要考生根据实际题目情况作答。

]五、综合分析题（每题10分，共10分）14. 假设你是一名机械设计师，需要根据客户提供的组合体三视图来设计一个机械部件。

请分析在设计过程中，三视图提供了哪些关键信息，以及这些信息如何帮助你完成设计。

[注：本题需要考生结合实际情况和专业知识进行分析，此处无法提供具体答案。

]请注意，以上题目仅为示例，实际试卷练习题应根据具体教学大纲和课程要求来设计。

手绘三视图考试题及答案

手绘三视图考试题及答案一、选择题1. 手绘三视图包括哪三个视图？A. 俯视图、侧视图、正视图B. 左视图、右视图、仰视图C. 顶视图、底视图、侧视图D. 正视图、侧视图、仰视图答案：A2. 下列哪个选项是正确的三视图表示方法？A. 正视图在左侧，侧视图在右侧，俯视图在下方B. 正视图在右侧，侧视图在左侧，俯视图在上方C. 正视图在上方，侧视图在下方，俯视图在左侧D. 正视图在下方，侧视图在上方，俯视图在右侧答案：A二、填空题1. 手绘三视图的目的是_________。

答案：表达物体的三维形状2. 在手绘三视图中，_________视图通常用来表示物体的高度和宽度。

答案：正视图三、简答题1. 请简述手绘三视图的绘制步骤。

答案：首先确定物体的正视图，然后根据正视图确定侧视图的位置和形状，最后根据正视图和侧视图确定俯视图的位置和形状。

2. 手绘三视图在工程制图中的应用是什么？答案：手绘三视图在工程制图中用于准确表达物体的三维形状，便于设计、制造和检验。

四、绘图题1. 根据所给物体的正视图和侧视图，绘制其俯视图。

[此处应附上正视图和侧视图的示意图]答案：[此处应附上根据给定视图绘制的俯视图]2. 请手绘一个简单的立方体的三视图。

答案：[此处应附上立方体的正视图、侧视图和俯视图]五、论述题1. 论述三视图在机械设计中的重要性。

答案：三视图在机械设计中至关重要，因为它能够准确无误地表达出设计的三维形状和尺寸，确保设计意图的准确传达。

三视图是机械设计沟通的基础，对于后续的制造、检验和装配都有着不可替代的作用。

通过三视图，设计师可以避免设计中的误解和误差，提高设计的效率和质量。

2. 分析手绘三视图与计算机辅助设计（CAD）三视图的区别。

答案：手绘三视图是一种传统的绘图方式，依赖于绘图者的手工绘制技能和对物体形状的理解。

而计算机辅助设计（CAD）三视图则利用计算机软件进行绘制，具有更高的精度和效率。

CAD软件可以快速生成三视图，并且方便修改和更新。

钳工高级三视图试题及答案

钳工高级三视图试题及答案一、选择题1. 三视图包括主视图、左视图和______。

A. 俯视图B. 右视图C. 仰视图D. 后视图答案：A2. 一个物体的三视图不能缺少的是______。

A. 主视图B. 左视图C. 俯视图D. 所有视图答案：D3. 在三视图中，表示物体高度的视图是______。

A. 主视图B. 左视图C. 俯视图D. 右视图答案：C二、填空题1. 在三视图中，______视图用来表示物体的长和宽。

答案：主2. 左视图用来表示物体的______和高。

答案：宽3. 俯视图用来表示物体的长和______。

答案：高三、判断题1. 三视图可以完全表达一个物体的形状和尺寸。

（）答案：正确2. 俯视图和主视图是同一个视图。

（）答案：错误3. 左视图和右视图可以互换。

（）答案：错误四、简答题1. 描述三视图的基本作用。

答案：三视图的基本作用是提供物体的长、宽、高三个方向的尺寸和形状信息，以便准确表达和理解物体的结构。

2. 解释为什么三视图中不能缺少任何一个视图。

答案：缺少任何一个视图都可能导致无法准确表达物体的尺寸和形状，从而影响对物体的理解和制造。

五、绘图题1. 根据给定的主视图和左视图，绘制对应的俯视图。

答案：（此处应有绘图，但无法提供）2. 给出一个圆柱体的三视图。

答案：（此处应有绘图，但无法提供）六、计算题1. 如果一个长方体的主视图尺寸为100mm x 200mm，左视图尺寸为50mm x 200mm，计算其俯视图的尺寸。

答案：100mm x 50mm2. 已知一个圆柱体的直径为100mm，高度为200mm，求其三视图的尺寸。

答案：主视图和左视图尺寸为100mm x 200mm，俯视图尺寸为直径100mm的圆。